 (1)
(1)
摘要 最大转矩电流比(MTPA)控制可充分利用磁阻转矩,提高永磁同步电机的运行效率,但无论是公式法还是高频信号注入法,均需要安装至少两个相电流传感器以获得电机的电流信息。为提高永磁同步电机驱动系统在电流传感器故障条件下的容错控制能力,同时降低系统制造成本,该文提出了一种无需电流传感器的MTPA控制策略。该策略仅使用一个速度控制器,通过公式法计算电机的dq轴控制电压指令。为提高运行效率,降低逆变器非线性影响,采用平均值补偿法对电压源型逆变器(VSI)进行非线性补偿,提高了MTPA控制精度和控制性能。实验结果表明,所提方法的控制性能与有电流传感器的MTPA方法接近,稳态时工作电流矢量幅值误差不超过1%,而未考虑VSI非线性补偿的传统方法最大误差超过30%,平均误差大于15%。实验验证了该文所提方法的动态性能,并对电机参数变化具备一定的鲁棒性。
关键词:内置式永磁同步电机 最大转矩电流比 无电流传感器 非线性补偿
内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)具有高运行可靠性、高功率密度、宽调速范围等优点,在航空航天、轨道交通和工业驱动等领域广泛应用[1-3]。由于内置式永磁同步电机将永磁体置于电机转子内部,d轴电感与q轴电感不相等,电机运行时存在磁阻转矩,而最大转矩电流比(Maximum Torque Per Ampere, MTPA)控制能够充分利用磁阻转矩,在单位定子电流下输出最大转矩,进而提高系统运行效率,受到国内外学者的广泛关注[4-5]。
目前,实现MTPA控制的方法[6-8]主要有以下几种:公式法、查表法、搜索法、高频信号注入法[9]等。其中,公式法基于电机模型通过理论推导和数学运算得到MTPA工作点,但受到电机温度、磁路饱和等因素的影响,电机参数将发生变化,导致公式计算得到的定子电流矢量角并不准确。于是一些学者结合参数辨识策略计算MTPA工作点,文献[10]提出了一种在线识别定子交轴电感、转子磁链的模型参考自适应系统(Model Reference Adaptive System, MRAS)参数辨识方法,在线计算和跟踪MTPA轨迹。查表法[11]可以避免复杂的公式运算和参数变化的影响,但需要大量的离线测试实验或有限元仿真,实际运行效果易受实际工况的影响。在线搜索法可以避免参数变化和离线测试,但是该方法存在动稳态性能不兼容的问题。文献[12]利用二阶Newton-Raphson自动搜索算法,将复杂的最大转矩电流比非线性公式转化为微控制器易实现的迭代运算,提高了电流分配精度。高频信号注入法虽然对参数变化具有较好的鲁棒性,但是带来了额外的损耗和转矩脉动,并且计算复杂。由于上述方法均需使用电流传感器以获取电机电流信息,一旦电流传感器发生故障,将导致闭环控制失败,造成损失。
针对电流传感器的故障容错控制问题,文献[13]利用二阶广义积分器和锁频环重构故障电流信息,并基于滑模观测器进行速度估计,实现了感应电机无速度传感器控制系统的电流传感器故障容错控制。文献[14]基于扩展卡尔曼滤波提出一种无电流传感器控制算法,利用永磁同步电机定子电压、转子位置和转速信息重构电机定子电流。文献[15]采用扩张状态观测器重构系统电流,以实现无电流传感器模型预测转矩控制策略。为实现无电流传感器的MTPA控制,文献[16]对传统的公式法进行了改进,利用一个速度PI控制器和公式计算获得控制电压指令,但是未考虑逆变器非线性因素的影响,导致控制性能较差。逆变器非线性因素,即电压源型逆变器(Voltage Source Inverter, VSI)由于死区、功率器件的压降以及开通关断延时,导致输出电压产生非线性畸变[17-19]。逆变器非线性因素将引起输出电流中含有较大低频谐波,产生转矩脉动,恶化控制性能,因此,需对控制电压指令进行补偿。文献[20]提出了一种在线调整自适应超扭曲算法的滑模观测器,对VSI非线性因素引起的电压失真进行了在线补偿,可以在较宽的速度范围内降低位置估计误差。文献[21]提出一种基于迭代线性插值的误差电压精确计算方法,得到相误差电压与相电流幅值的准确映射关系,进行逆变器非线性补偿。
为避免上述问题,提高内置式永磁同步电机驱动系统在电流传感器故障条件下的容错控制能力,本文提出一种加入VSI非线性补偿的无电流传感器MTPA控制策略。首先,该方法根据电机基波模型和实现MTPA控制所需满足的条件,求解出最优电压控制矢量的幅值和角度;其次,考虑了VSI非线性因素的影响,利用平均值补偿法对电压控制指令进行在线补偿,提高了算法的准确性;然后,量化分析了电机参数不匹配对所提方法控制性能的影响;最后,搭建了IPMSM实验平台,验证了该方法的可行性和有效性。
若忽略不计IPMSM的铁心磁饱和、铁损和涡流损耗,在旋转坐标系下,IPMSM的电压方程可表示为
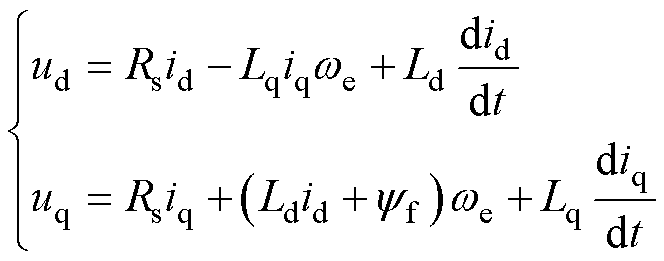 (1)
(1)
电磁转矩方程为
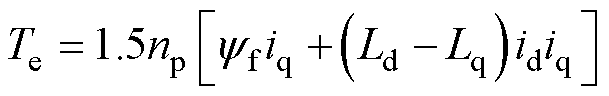 (2)
(2)
式中,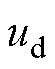 、
、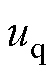 分别为d、q轴电压;
分别为d、q轴电压;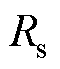 为定子绕组电阻;
为定子绕组电阻;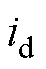 、
、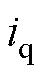 分别为d、q轴电流;
分别为d、q轴电流;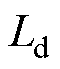 、
、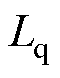 分别为d、q轴电感;
分别为d、q轴电感;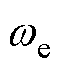 为电机的电角速度;
为电机的电角速度;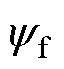 为永磁体磁链;
为永磁体磁链;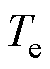 为电磁转矩;
为电磁转矩;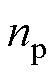 为电机极对数。
为电机极对数。
将定子电流矢量在旋转坐标系中分解,表示为
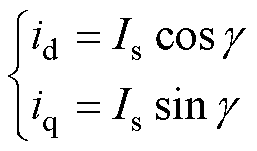 (3)
(3)
式中,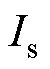 为电流矢量幅值;
为电流矢量幅值;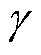 为电流矢量角。
为电流矢量角。
IPMSM的电磁转矩方程可改写为
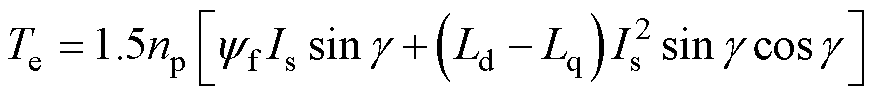 (4)
(4)
根据式(4)可知,定子矢量幅值一定时,电磁转矩与定子矢量角有关,存在一个最佳电流矢量角使得电磁转矩最大。对式(4)求导,有
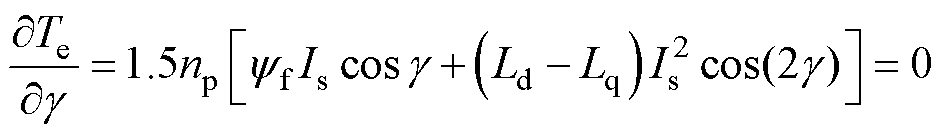 (5)
(5)
解得
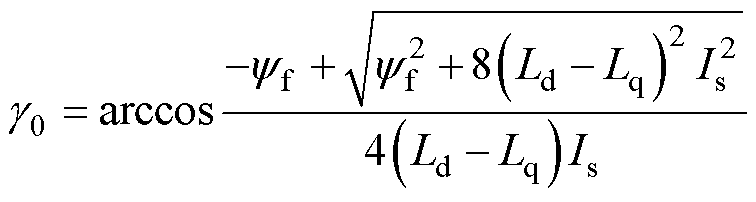 (6)
(6)
即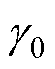 为满足最大转矩电流比的电流矢量角。
为满足最大转矩电流比的电流矢量角。
传统的MTPA控制方法,无论是公式法还是虚拟信号注入法,均需要已知电机的电流信息来求解MTPA工作点,当电流传感器发生故障后系统将无法运行。针对此问题,本文提出了一种无电流传感器MTPA控制方法,根据电机位置信息和PMSM基波模型直接求解最优电压控制指令,无需使用电流信息,控制结构简单,易于工程实现。
由式(1)可得,稳态时的永磁同步电机dq轴电压与电流的关系为
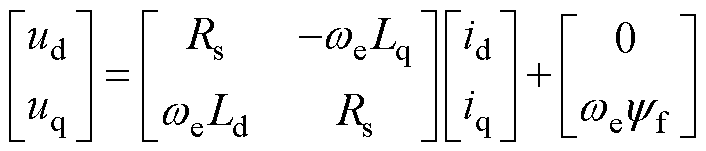 (7)
(7)
dq轴电流与电压的关系为
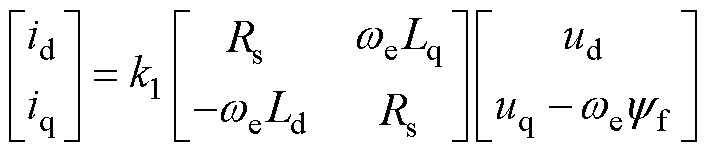 (8)
(8)
其中
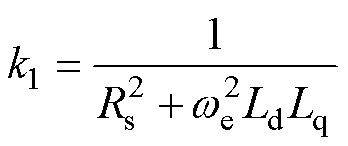
令控制电压幅值为V,电压矢量角为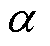 ,则有
,则有
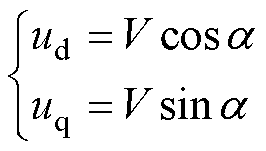 (9)
(9)
将式(9)代入式(8)可得
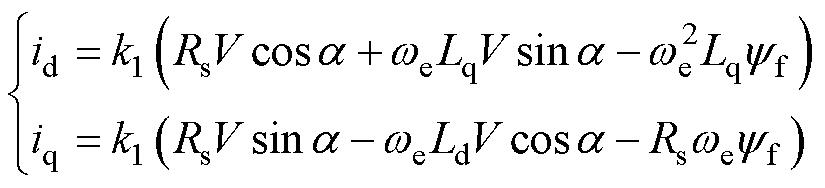 (10)
(10)
由式(6)可得
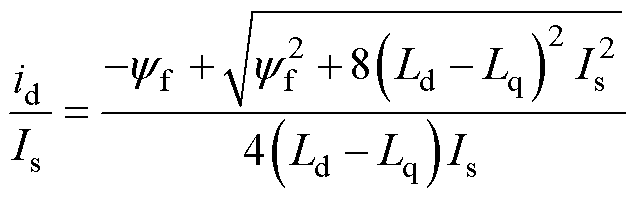 (11)
(11)
化简可得
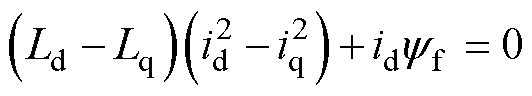 (12)
(12)
将式(10)代入式(12),并化简可得
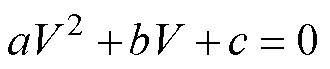 (13)
(13)
其中
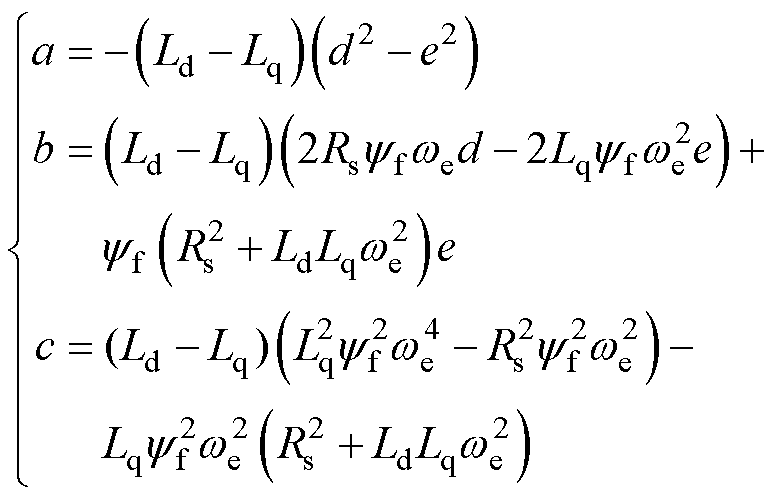 (14)
(14)
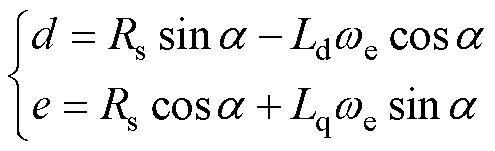 (15)
(15)
通过求解一元二次方程式(13),并舍去不合理的根,可以得到最优电压值为
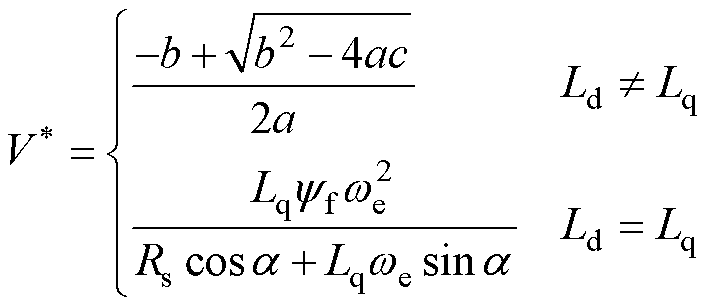 (16)
(16)
在实际应用中,受逆变器非线性(驱动信号死区、功率器件的压降以及开通关断延迟等)的影响,逆变器输出电压通常会偏离指令电压,并且会使得输出电流中含有较大低频谐波,产生转矩脉动,恶化控制性能,因此必须对指令电压进行补偿。VSI非线性因素扰动电压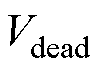 在稳态时可认为是常数[21],表述为
在稳态时可认为是常数[21],表述为
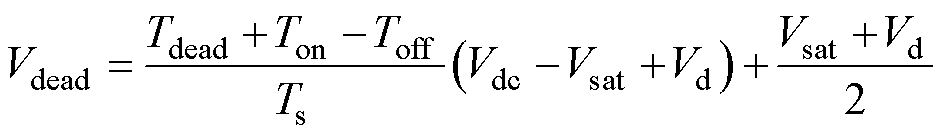 (17)
(17)
式中,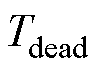 为死区时间;
为死区时间;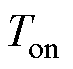 、
、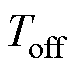 分别为功率器件开通和关断延迟时间;
分别为功率器件开通和关断延迟时间;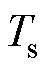 为开关周期;
为开关周期;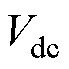 为直流母线电压;
为直流母线电压;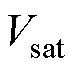 、
、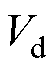 分别为功率器件和续流二极管的导通压降。
分别为功率器件和续流二极管的导通压降。
导致的三相输出电压误差为
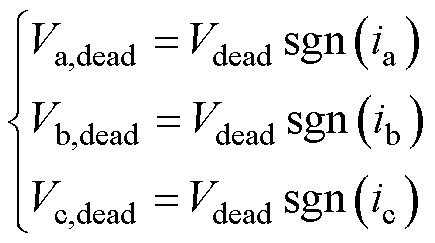 (18)
(18)
式中,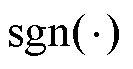 为符号函数;
为符号函数;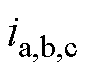 为三相电流。
为三相电流。
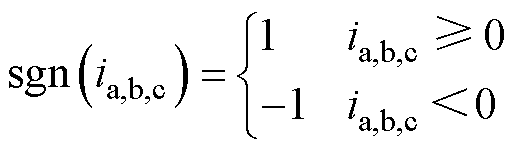 (19)
(19)
由于系统未使用电流传感器,无法实时直接得到实际三相电流的正负方向,可根据式(10)计算出dq轴的电流值,坐标变换得三相电流的观测值,以此确定三相电流正负值。
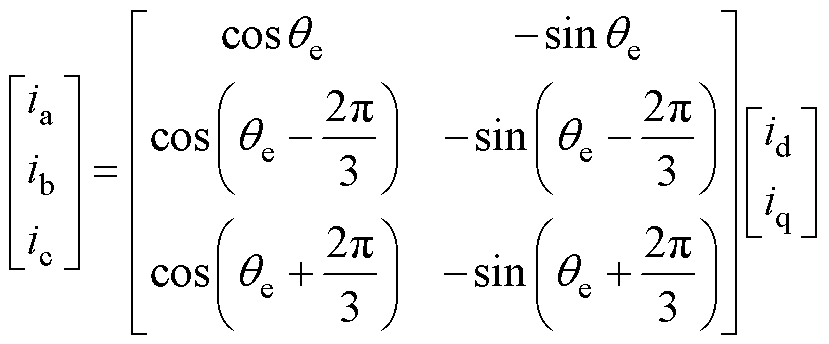 (20)
(20)
式中,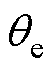 为电角度。
为电角度。
根据式(18),将三相静止坐标系变换到两相旋转坐标系,则VSI非线性因素扰动电压Vdead的dq轴分量为
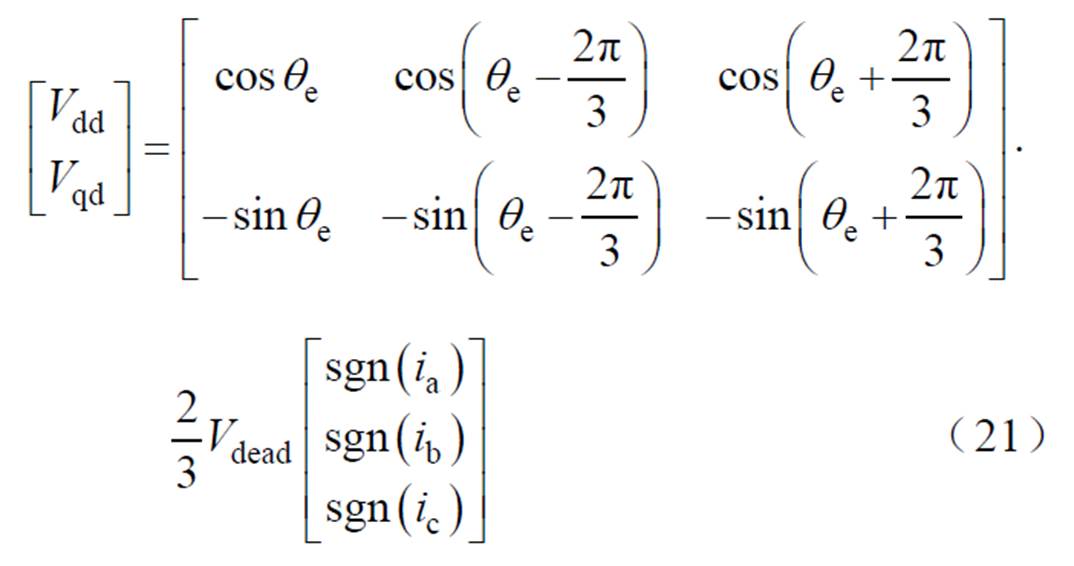
但是,受系统延时以及参数摄动的影响,式(20)计算得到的三相电流与实际电流必然存在相位差,在某些时刻两者符号相反,ia符号函数误差如图1所示。
由于观测的三相电流存在相位差,则由式(21)计算扰动电压时,将导致实时计算的电压补偿值错误,不同计算方式下的扰动电压如图2所示,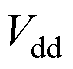 、
、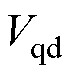 为扰动电压实际值,
为扰动电压实际值,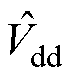 、
、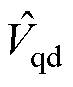 为由观测电流计算的扰动电压值,可见两者存在较大误差。
为由观测电流计算的扰动电压值,可见两者存在较大误差。
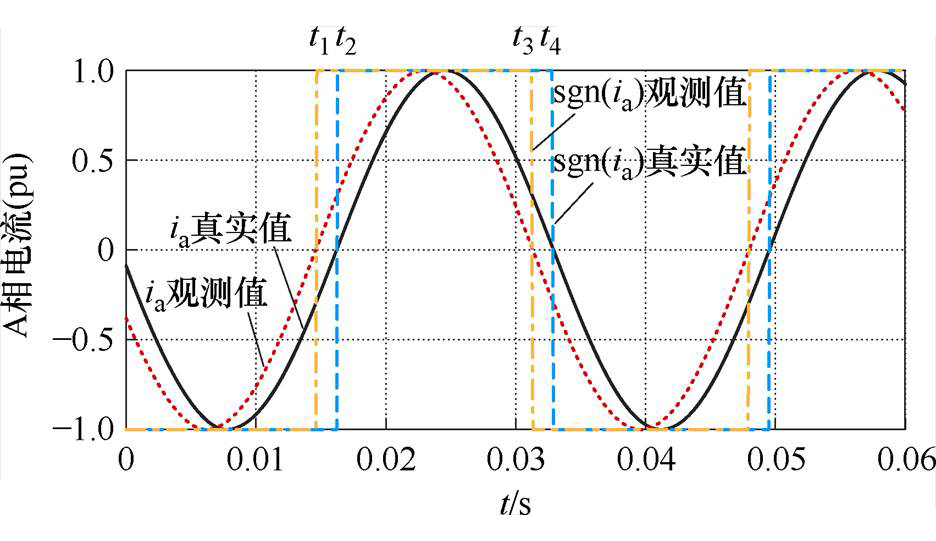
图1 ia符号函数误差
Fig.1 The sign function errors of ia
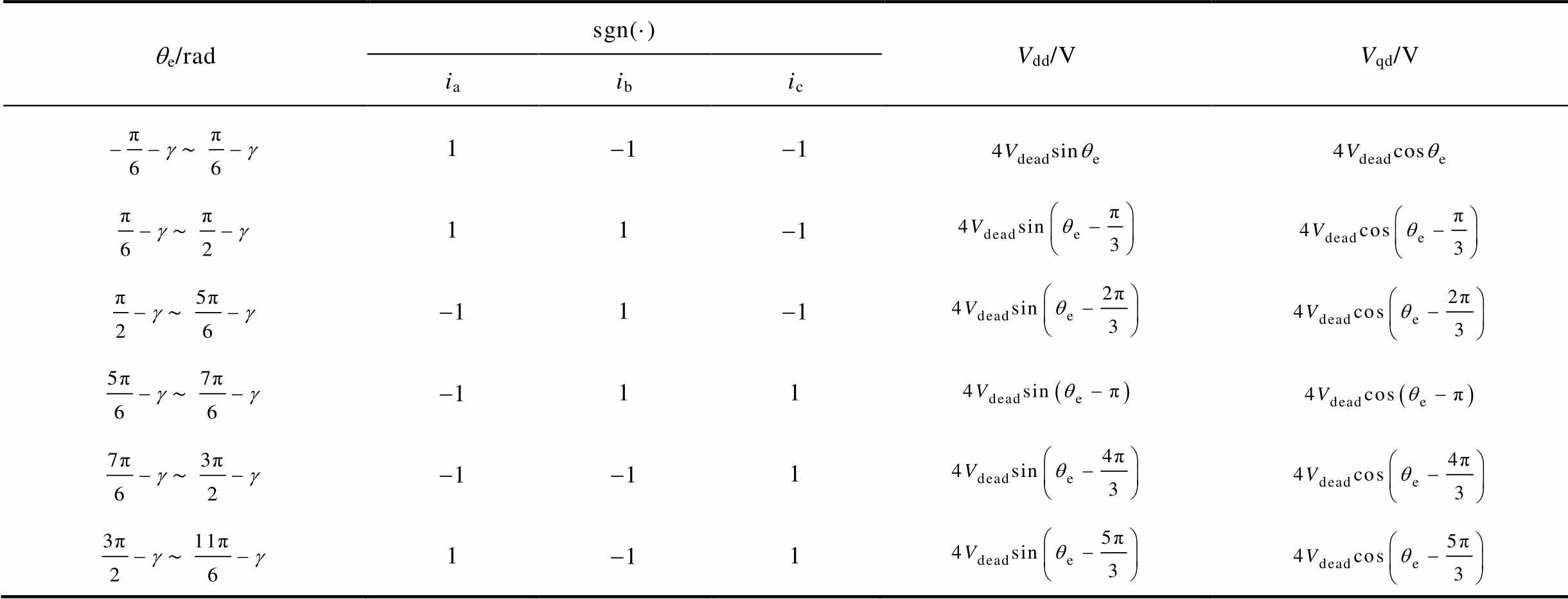
因此,本文提出一种平均值补偿法,根据式(10)计算所得dq轴最优电流和电流矢量角,得出此时VSI非线性因素扰动电压的平均值。由式(21),扰动电压与电流极性、电角度相关,不同电流极性下的扰动电压见表1。
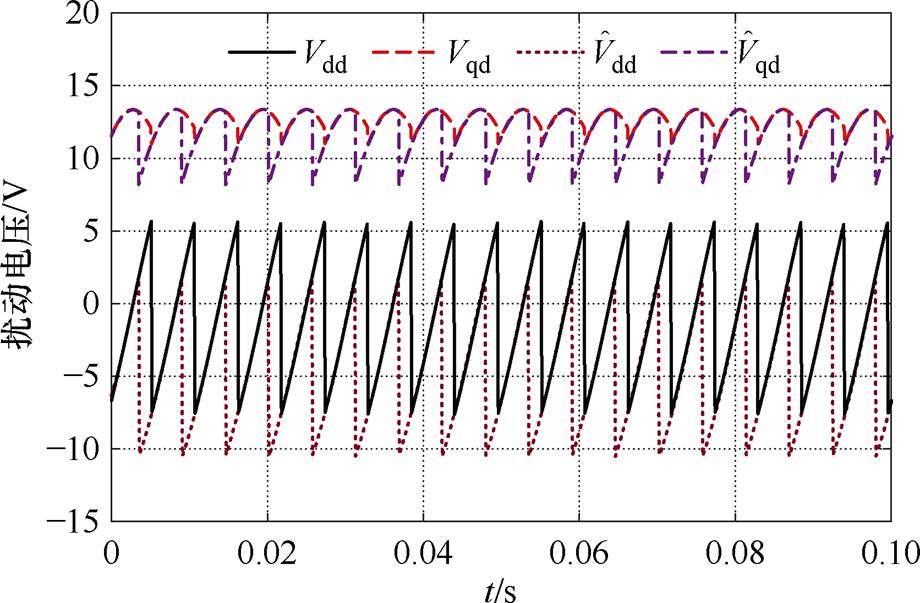
图2 不同计算方式下的扰动电压
Fig.2 Disturbance voltage with different calculation methods
表1 不同电流极性下的扰动电压
Tab.1 The disturbance voltage under different current polarities
qe/radsgn(·)Vdd/VVqd/V iaibic 1-1-1 11-1 -11-1 -111 -1-11 1-11
由表1,计算一个基波周期T内VSI非线性因素扰动电压的dq轴分量的平均值为
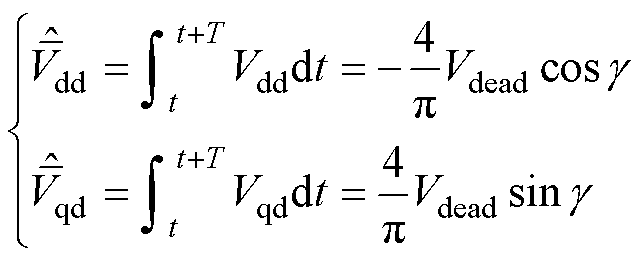 (22)
(22)
则考虑逆变器非线性因素,补偿后的电压指令值应修正为
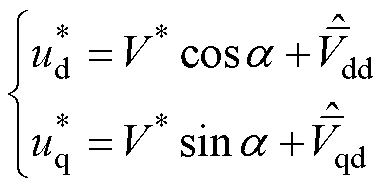 (23)
(23)
图3为本文无电流传感器MTPA控制框图[16]。系统只含有一个PI控制器,用于生成电压矢量角a,由电机转速结合电机模型计算最优电压矢量幅值,经过非线性补偿后得到最终的脉冲宽度调制(Pulse Width Modulation, PWM)控制电压指令,利用空间矢量调制方法生成相应的PWM脉冲信号控制电机转动。
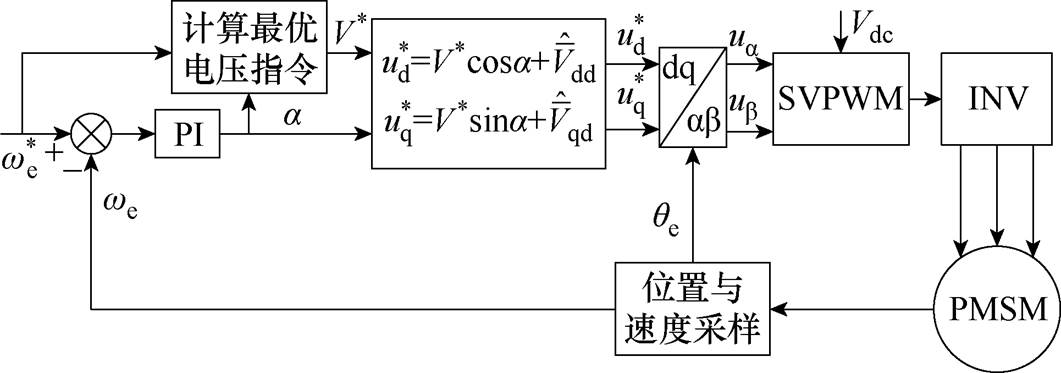
图3 无电流传感器MTPA控制框图
Fig.3 Block diagram of MTPA without current sensors
由于系统无电流传感器,须采用式(10)所得电流估计值来计算补偿电压平均值,该值可能与实际需补偿电压值之间存在误差,为探究该误差的影响,对其进行理论分析。首先,令
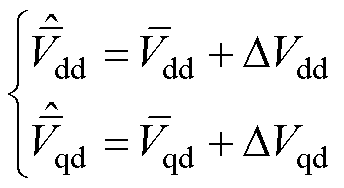 (24)
(24)
式中,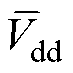 、
、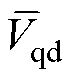 分别为VSI非线性因素引起的实际的d、q轴扰动电压平均值;
分别为VSI非线性因素引起的实际的d、q轴扰动电压平均值;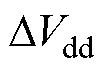 、
、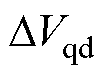 为相应的计算误差。则实际响应电流为
为相应的计算误差。则实际响应电流为
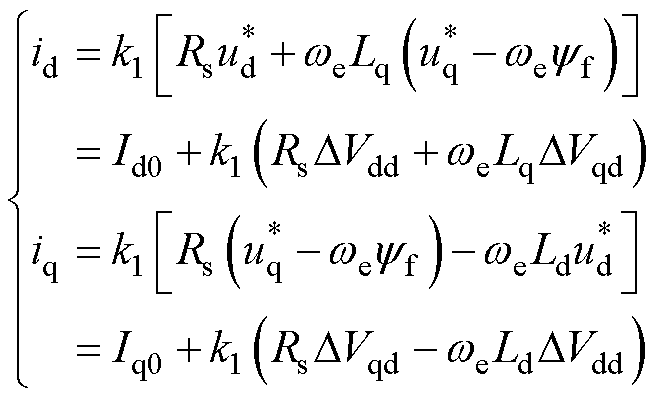 (25)
(25)
式中,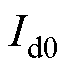 、
、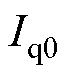 分别为估计的d、q轴电流。令
分别为估计的d、q轴电流。令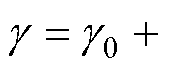
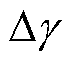 ,其中,
,其中,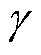 为实际电流矢量角,
为实际电流矢量角,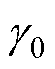 为估计电流矢量角,
为估计电流矢量角,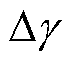 为误差。由式(22),则实际与估计的扰动电压平均值误差为
为误差。由式(22),则实际与估计的扰动电压平均值误差为
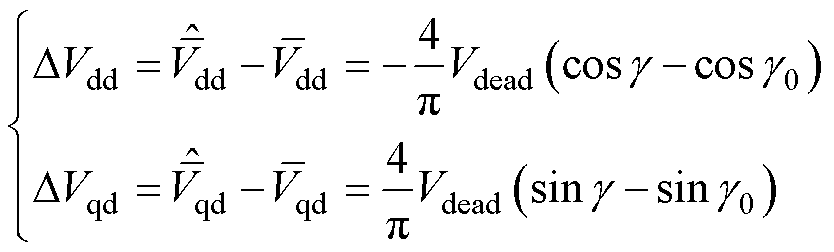 (26)
(26)
则
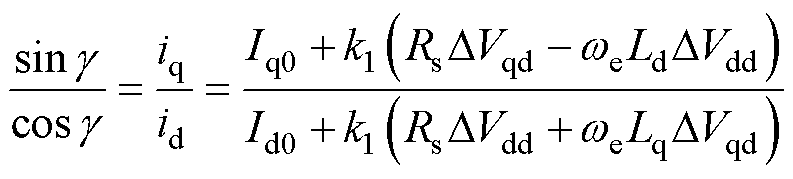 (27)
(27)
将式(26)代入式(27)并化简可得
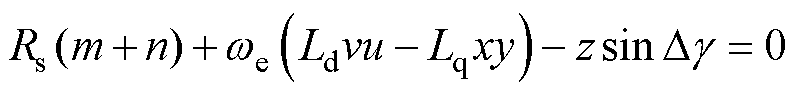 (28)
(28)
其中
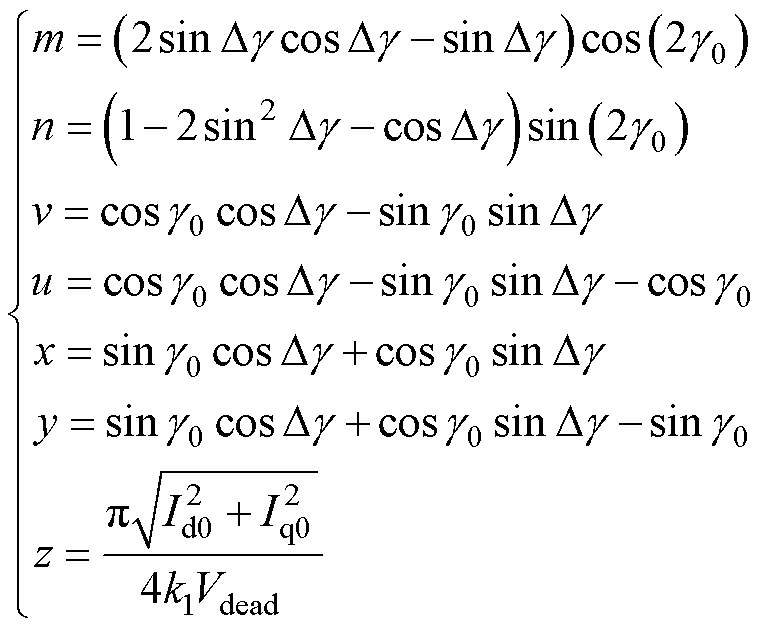 (29)
(29)
由式(28)可见,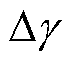 仅与
仅与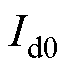 、
、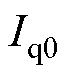 、
、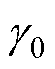 和电机参数相关。虽然式(28)形式复杂,但仍可利用Matlab解得
和电机参数相关。虽然式(28)形式复杂,但仍可利用Matlab解得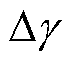 在任意MTPA工作点存在两个共轭复数解以及唯一实数解0。由于复数解无意义,因此稳态时有
在任意MTPA工作点存在两个共轭复数解以及唯一实数解0。由于复数解无意义,因此稳态时有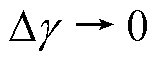 。结合式(26)以及
。结合式(26)以及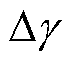 的定义,可得
的定义,可得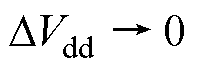 、
、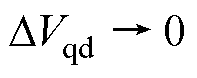 ,这意味着即使电流估计误差存在,根据所估计电流求解的电压补偿值的平均误差仍为0。
,这意味着即使电流估计误差存在,根据所估计电流求解的电压补偿值的平均误差仍为0。
永磁同步电机在运行过程中参数会受磁场及温升的影响而发生改变。由于本文方法是基于基波模型的方法,需已知电机各项参数对最优电压矢量进行公式求解,当电机参数摄动时必然会影响其求解精度。令
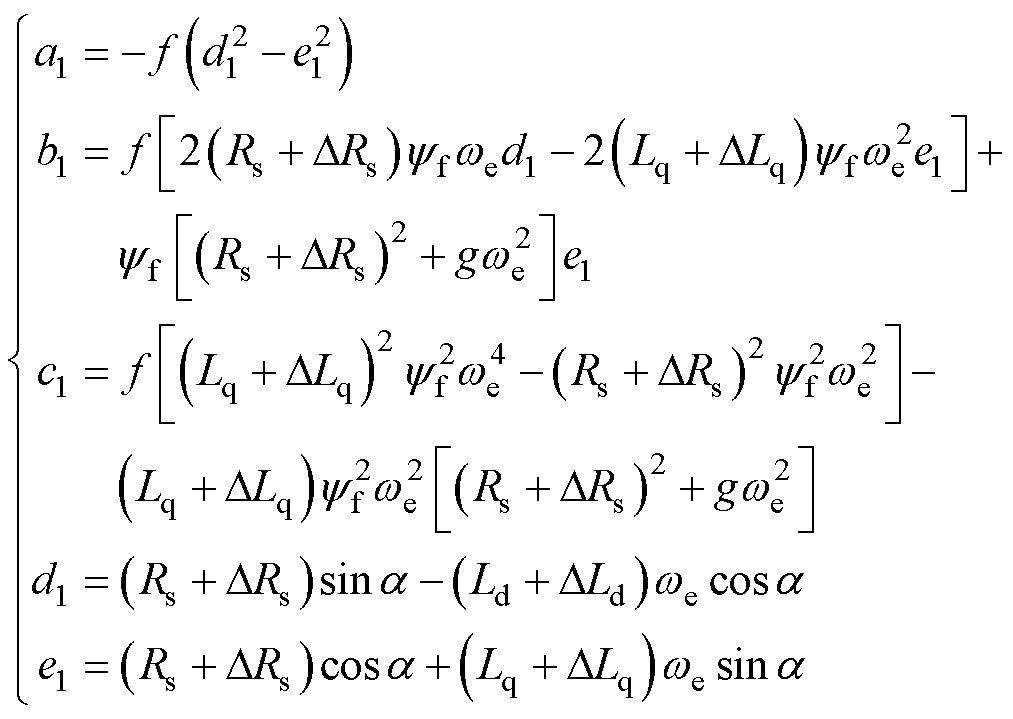 (30)
(30)
其中
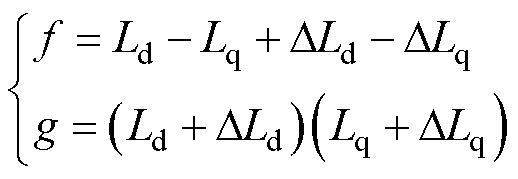 (31)
(31)
则当电机参数摄动时,求解的最优电压矢量幅值为
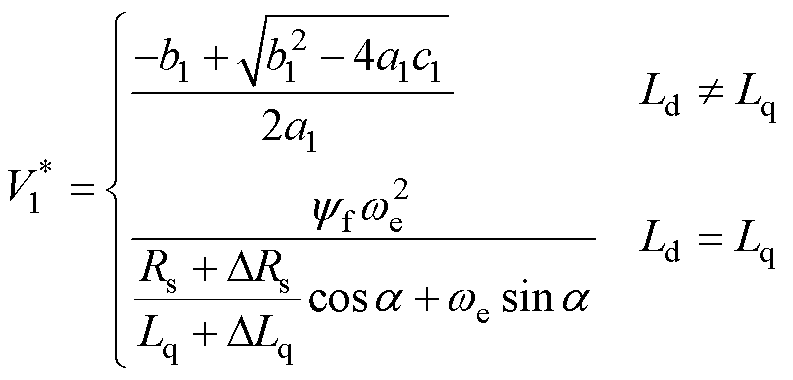 (32)
(32)
电压矢量幅值计算误差可表示为
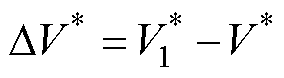 (33)
(33)
若求解的最优电压矢量存在误差,将影响系统的电流响应。根据电压方程式(1),可得稳态时电压矢量幅值误差与电流误差关系式为
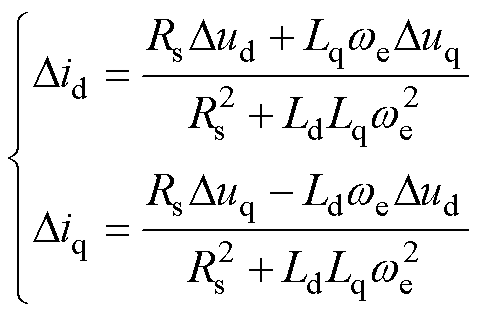 (34)
(34)
可见,dq轴电流误差与电压矢量幅值误差成正比,且比例系数大于1。进一步分析,实际系统中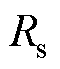 、
、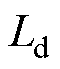 、
、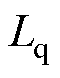 的参数值均很小,若电机转速为零低速,则系数
的参数值均很小,若电机转速为零低速,则系数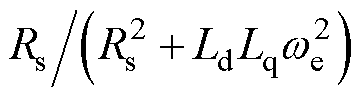 和
和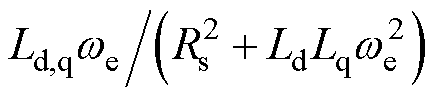 均较大,较小的电压误差
均较大,较小的电压误差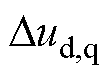 也将使得电流误差
也将使得电流误差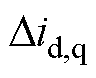 较大。若电机转速较高,则
较大。若电机转速较高,则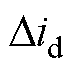 主要受
主要受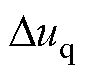 影响,
影响,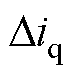 主要受
主要受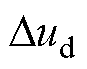 影响。
影响。
图4给出了dq轴电感变化时求解最优电压矢量幅值的误差曲线和相应的响应电流幅值误差曲线,其中,电机转速分别为5%、20%、50%额定转速,电压矢量角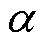 =1.65 rad。
=1.65 rad。
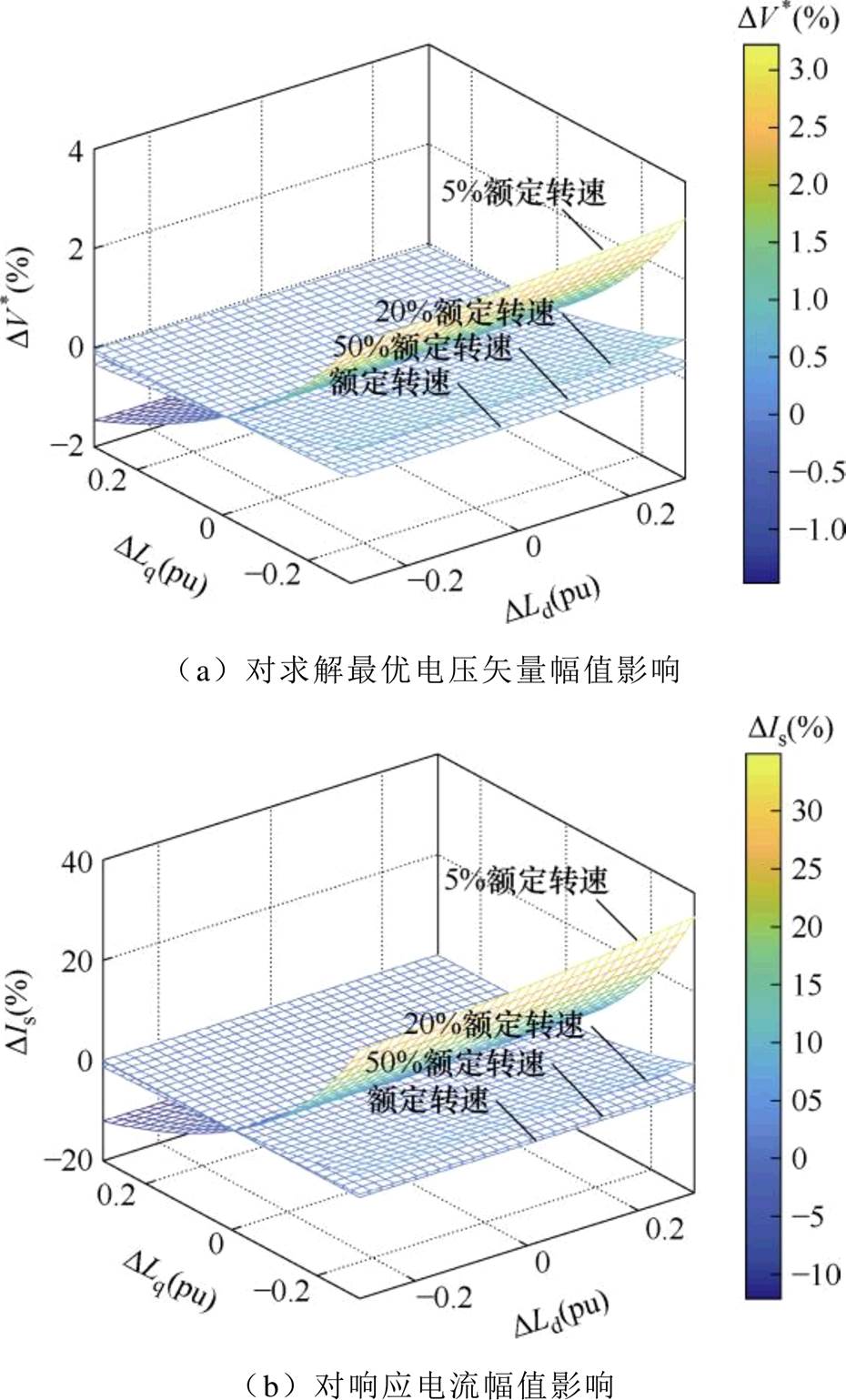
图4 参数不匹配影响
Fig.4 Impact of parameter mismatch
由图4可见,当转速为5%额定转速时,dq轴电感变化对求解最优电压矢量幅值及响应电流幅值影响比较大,这是因为本文方法是基于电机基波模型进行推导计算的,主要适用于中高速工况,在低速工况表现不佳是符合预期的。另外,当转速高于20%额定转速时,dq轴电感在±30%变化范围内,求解最优电压矢量幅值的误差在-0.5%~1%范围内,响应电流幅值的误差在-2%~6%范围内,且转速越高,误差越小。
本节通过一系列实验来验证所提考虑VSI非线性影响的无电流传感器MTPA控制策略。如图5所示为内置式永磁同步电机驱动系统实验平台,包括逆变器、永磁同步电动机、发电机、上位机和负载。其中逆变器核心控制芯片为TI公司的TMS320F28335 DSP和Cyclone Ⅳ E系列FPGA。发电机由永磁同步电动机驱动,发电机的输出连接到电阻负载,通过调节电阻值可调整负载转矩。上位机通过CAN卡连接控制板,实现上位机控制。电机参数设置见表2。
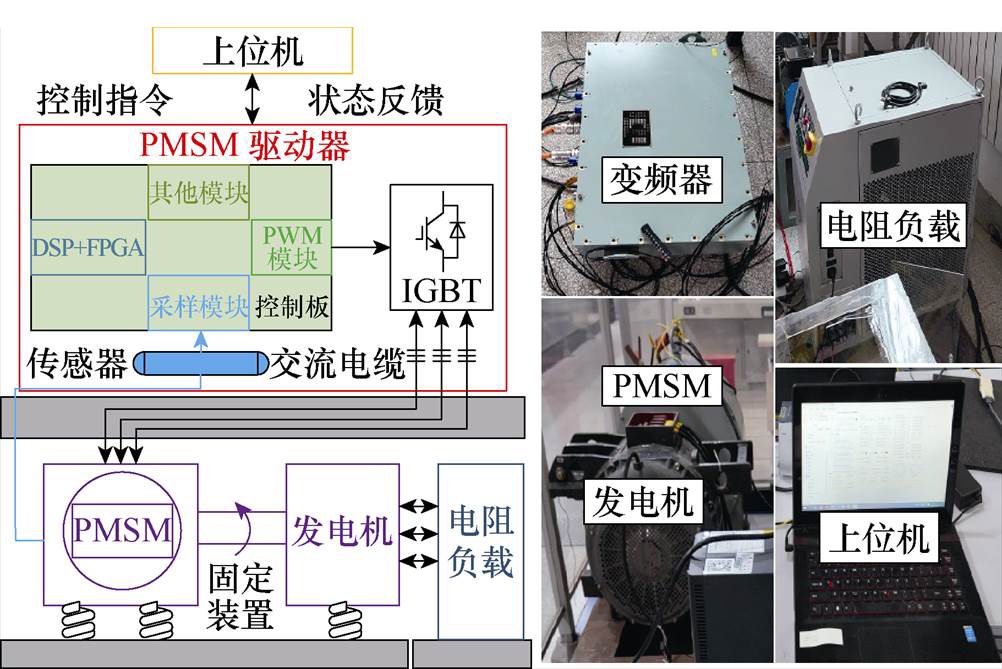
图5 实验平台
Fig.5 The experimental platform
表2 参数设置
Tab.2 Parameter design
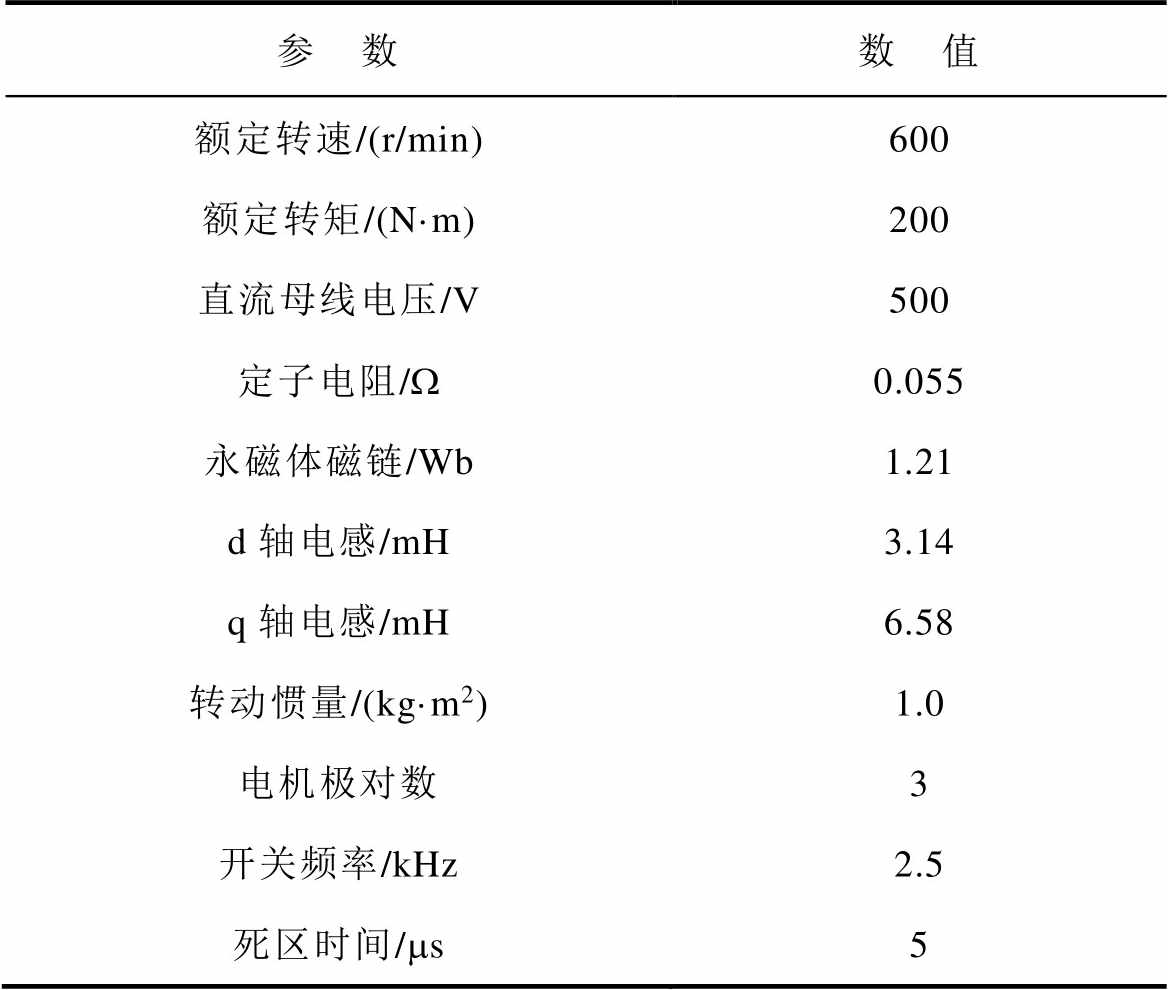
参 数数 值 额定转速/(r/min)600 额定转矩/(N·m)200 直流母线电压/V500 定子电阻/W0.055 永磁体磁链/Wb1.21 d轴电感/mH3.14 q轴电感/mH6.58 转动惯量/(kg·m2)1.0 电机极对数3 开关频率/kHz2.5 死区时间/ms5
为验证本文提出的考虑VSI非线性影响的无电流传感器MTPA控制策略,与有电流传感器的矢量控制MTPA方案和文献[16]中的传统无电流传感器MTPA控制方案进行了对比实验。其中,有电流传感器矢量控制MTPA方案亦考虑了VSI非线性因素,加入了平均值补偿;本文方案对比传统方案的最大区别是:本文方案考虑了VSI非线性影响,加入了电压补偿环节。电机转速为500 r/min,负载转矩为200 N∙m时的稳态实验结果如图6所示。
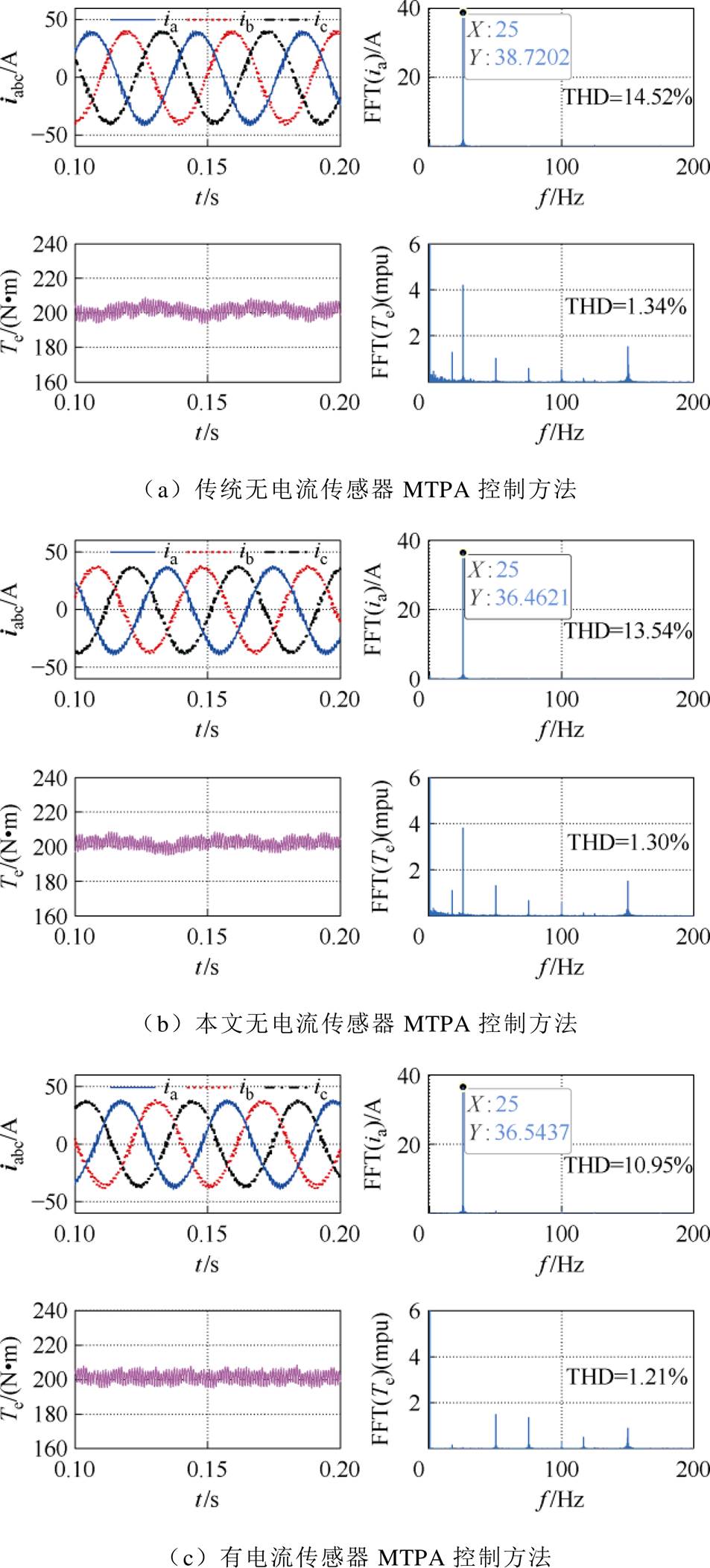
图6 电机转速500 r/min时稳态实验波形
Fig.6 Experimental curves when the motor speed is 500 r/min
由图6可见,本文方案与有电流传感器MTPA控制方案的相电流基波幅值相当,A相电流的基波幅值分别为36.46 A、36.54 A,而传统方法的A相电流基波幅值为38.72 A。这表明本文方法比传统方法更接近于MTPA工作点。由图6中对A相电流与电磁转矩的快速傅里叶变换(Fast Fourier Transform, FFT)分析可见,本文方法对比传统方法具备更好的电流质量和转矩性能。
图7为电机负载转矩为100 N∙m时,本文方法和传统方法在不同转速时的电流矢量幅值及误差。图7中,电流数据进行了标幺化处理,基准值为有电流传感器进行MTPA控制时的工作电流幅值。由图7可见,在200~600 r/min速度范围内,本文方法进行MTPA控制的电流矢量幅值误差较小,最大误差不超过0.5%,而传统方法的电流矢量幅值误差在14%~30%范围内,且转速越低,误差越大。对该现象进行分析,由式(17)可知,VSI非线性因素扰动电压在稳态下可认为是常数,由于低速时VSI输出电压较小,高速时VSI输出电压增大,则该扰动电压在低速工况时对输出电压的影响更大,使得未进行非线性补偿的传统方法偏离MTPA工作点越多。结果表明,本文方法进行非线性补偿后,系统在各工况下均能够准确运行在MTPA理论工作点。
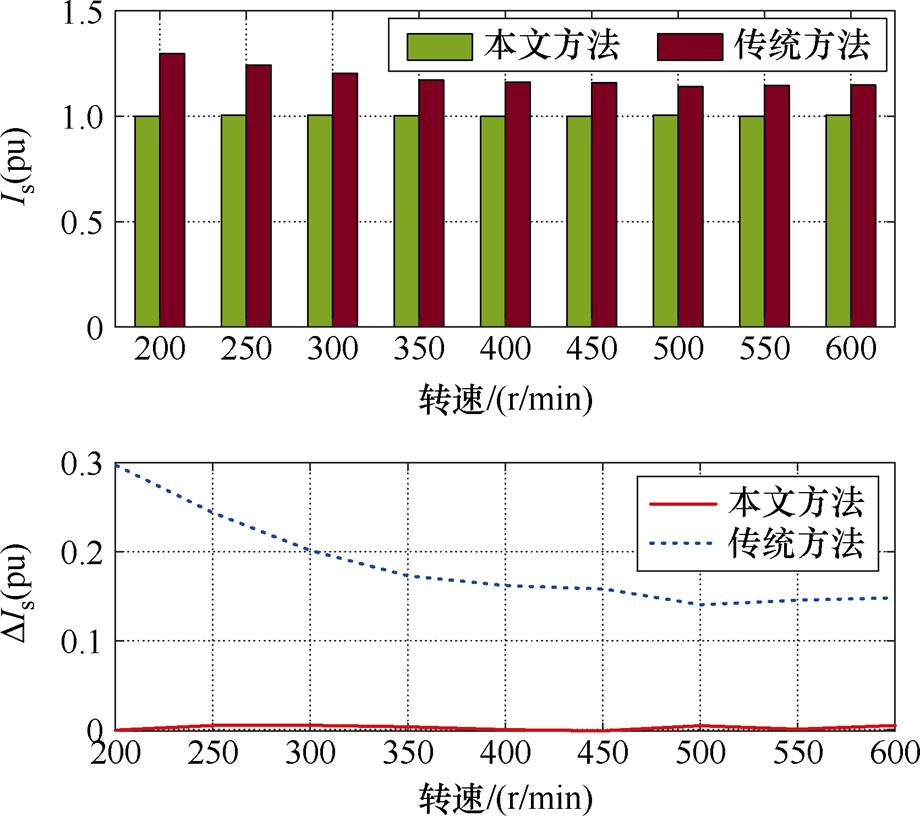
图7 电机负载转矩100 N∙m,不同转速时的电流矢量幅值
Fig.7 Current vector amplitude at different speeds when the motor load torque is 100 N∙m
图8为电机转速500 r/min时,本文方法和传统方法在不同负载转矩时的电流矢量幅值及误差。由图8可见,在50~250 N∙m负载转矩范围内,本文方法进行MTPA控制的电流矢量幅值误差较小,最大误差不超过1%,而传统方法的电流矢量幅值误差在2%~37%范围内,且负载转矩越大,误差越小。这是因为VSI非线性因素扰动电压在大负载转矩工况时对输出电压的影响更小,使得传统方法偏离MTPA工作点越小。由实验结果可见,本文方法与传统方法相比,电机运行所需的电流矢量幅值更小,与MTPA理论工作点几乎相等,表明本文方法具备良好的稳态性能。
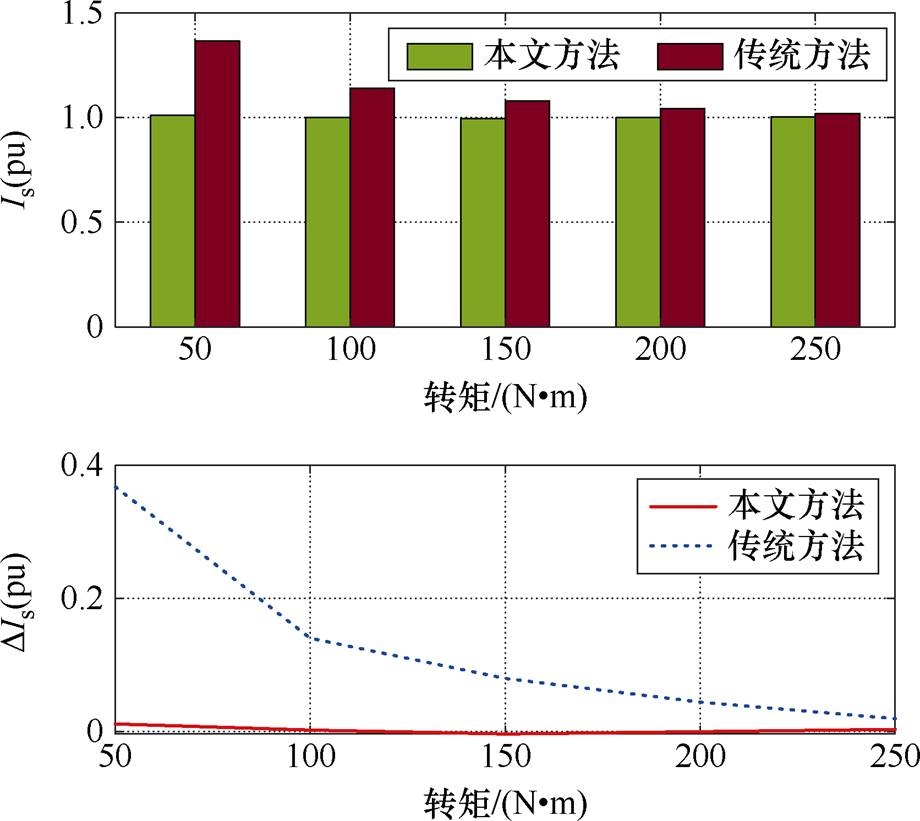
图8 电机转速500 r/min,不同转矩时的电流矢量幅值
Fig.8 Current vector amplitude at different load torque when the motor speed is 500 r/min
图9为本文方法与传统方法在电机突加、突降负载时的实验结果。为验证参数不匹配对所提控制策略的影响,图9c加入了参数摄动DLd=+30%Ld、DLq=+30%Lq。电机转速为500 r/min,负载转矩先由0 N∙m增加到200 N∙m再降为0 N∙m。
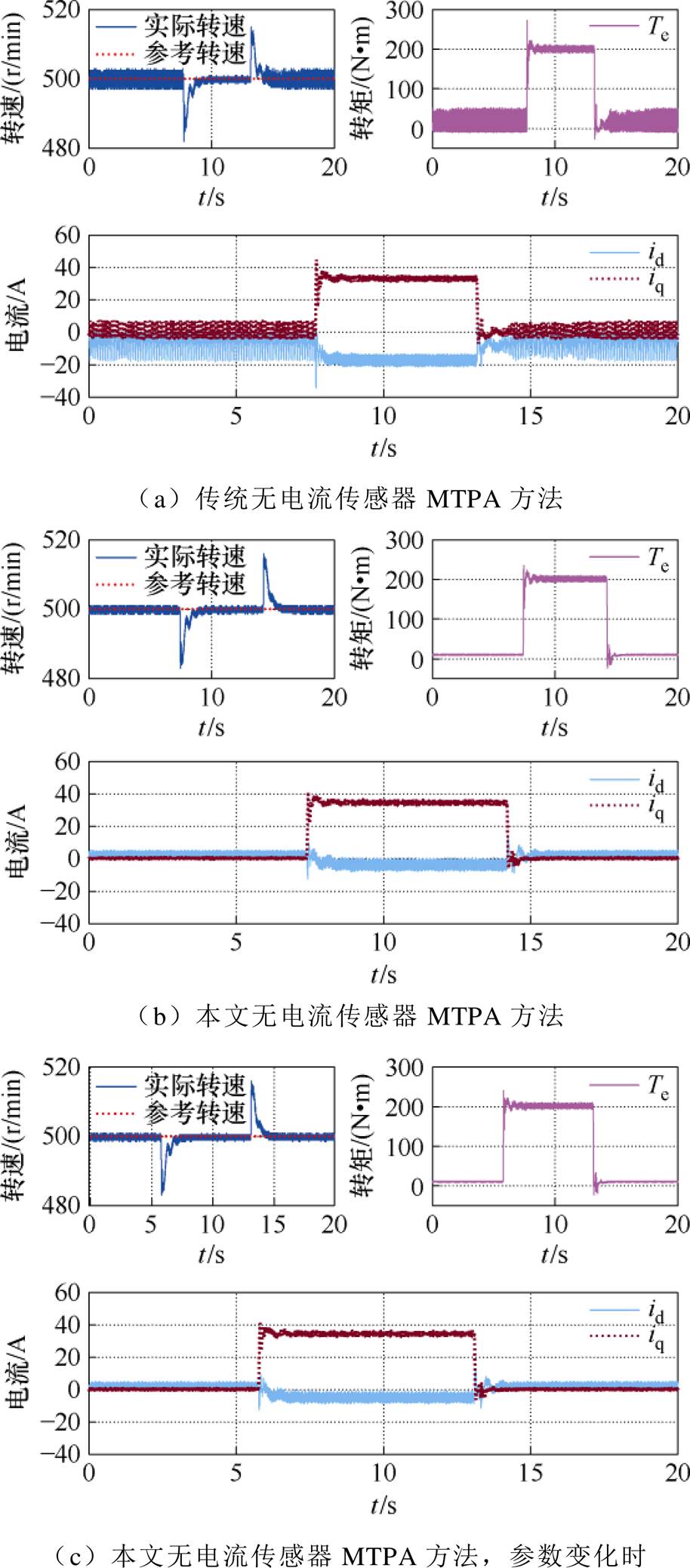
图9 转矩动态实验结果
Fig.9 Torque dynamic experimental results
由图9可见,本文方法对比传统方法在突加负载转矩的动态过程中,电流与电磁转矩的超调量更小。同时可见,电机稳定运行时,本文方法的电流纹波及转矩纹波更小。当电机参数变化时,仍然能够保持较好的控制性能。
图10为本文方法与传统方法在电机转速突变时的实验结果。为验证参数不匹配对所提控制策略的影响,图10c加入了参数摄动DLd=-30%Ld、DLq= -30%Lq。实验中电机空载,转速先由0增加到600 r/min再降为0,转速斜坡为200 r/min/s。由图10可见,本文方法对比传统方法在突加负载转矩的动态过程中,电磁转矩波形更加平滑,d轴电流明显降低。当电机参数变化时,仍然能够保持较好的控制性能。
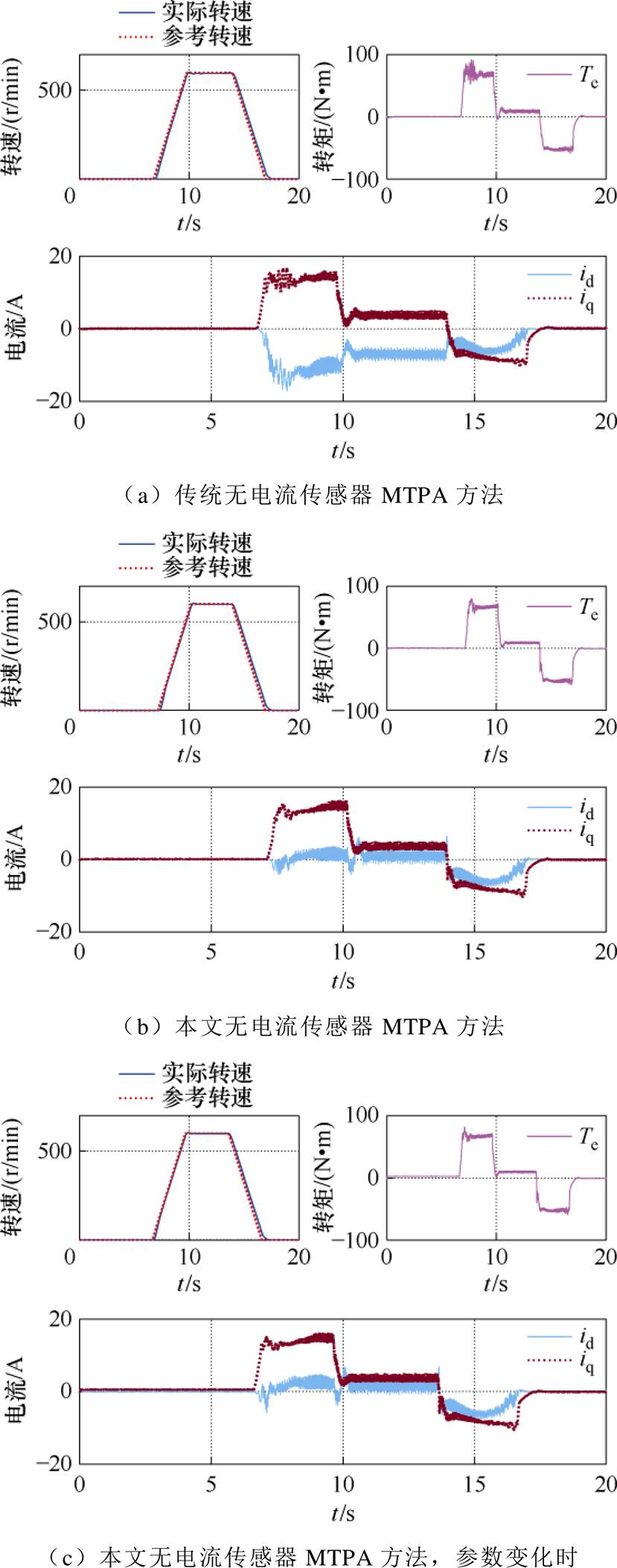
图10 转速动态实验结果
Fig.10 Experimental results for sudden changes in rotational speed
图11给出了带载起动的实验结果。实验中,控制电机先是运行在0 r/min,负载转矩给定100 N∙m,随后加速至50 r/min,图中给出了本文方法与有电流传感器方法的实验波形。传统方法无法实现该工况运行,实验时报输出电流过限故障。由图11可见,本文方法在零速及到达50 r/min稳态后的控制性能均较好,在转速加速动态过程中的转矩冲击较小,性能良好。
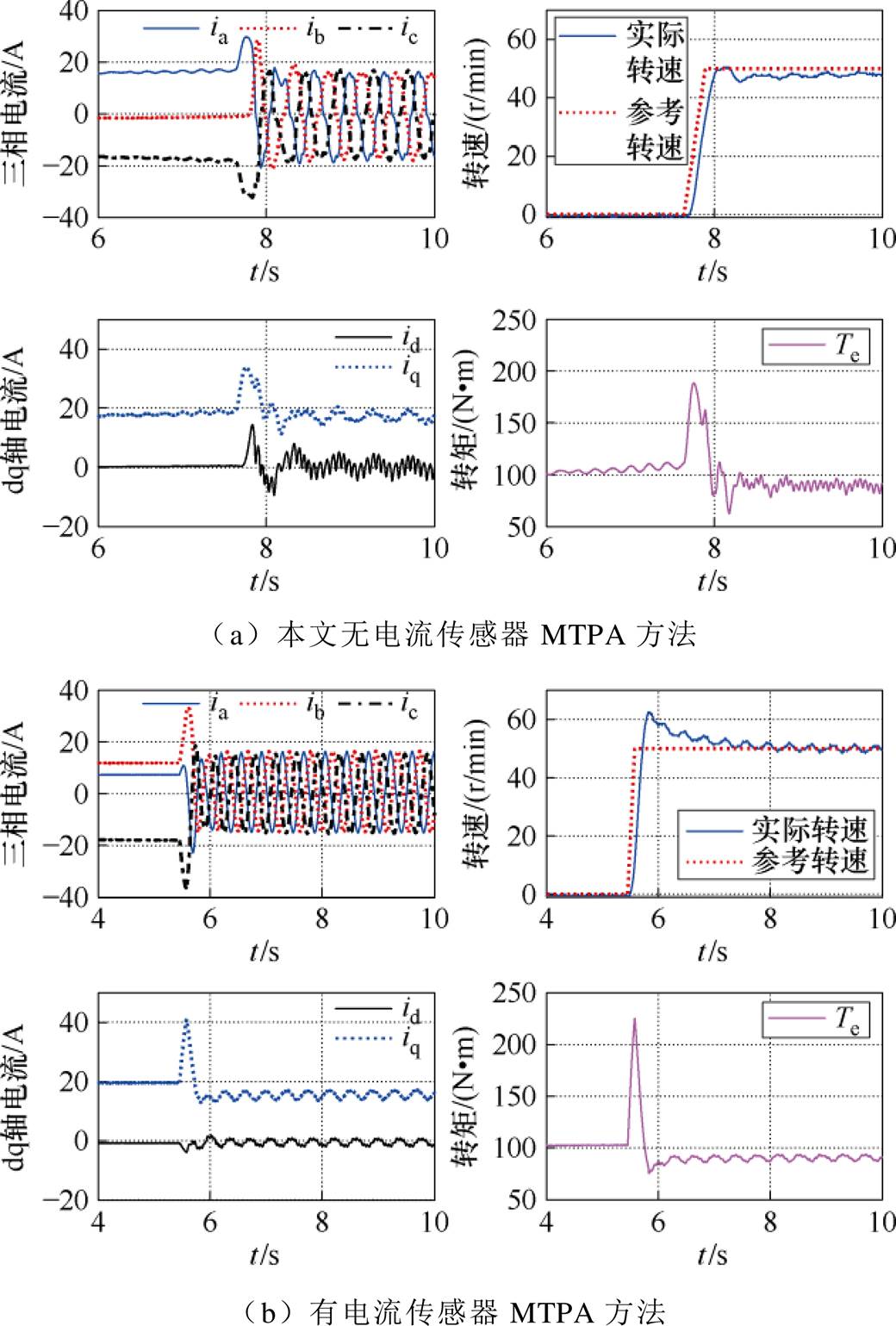
图11 带载起动实验结果
Fig.11 Experimental results of startup with load
为提高系统在电流传感器故障条件下的容错控制能力,同时降低系统制造成本,本文提出了一种无需电流传感器的MTPA控制策略。为提高系统的运行效率,考虑了VSI非线性因素的影响,对其进行平均值补偿。实验结果表明,本文方法与传统方法相比,可以更加准确地实现MTPA控制,与有电流传感器的MTPA控制方法的控制性能接近,稳态时工作电流矢量幅值误差不超过1%,而未考虑死区补偿的传统方法最大误差超过30%,平均误差大于15%。实验同时表明,本文方法对比传统方法在应对转矩突变和转速突变时具备更好的动态性能,且对电感参数变化具备一定的鲁棒性。
参考文献
[1] 肖飞, 许观达, 连传强, 等. 永磁同步电机单电流传感器系统的三相电流重构策略[J]. 电工技术学报, 2022, 37(7): 1609-1617.
Xiao Fei, Xu Guanda, Lian Chuanqiang, et al. Three- phase current reconstruction strategy of permanent magnet synchronous machine drives using a single current sensor[J]. Transactions of China Electro- technical Society, 2022, 37(7): 1609-1617.
[2] 王柄东, 王道涵, 王晓姬, 等. 交流调磁型永磁同步电机磁通协同调控最大转矩铜耗比控制[J]. 电工技术学报, 2024, 39(12): 3630-3645.
Wang Bingdong, Wang Daohan, Wang Xiaoji, et al. A maximum torque per copper loss control for AC flux-regulation permanent magnet synchronous motor with magnetic flux co-regulation[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3630- 3645.
[3] Shakib S M S I, Xiao Dan, Dutta R, et al. An optimal maximum torque per active flux and field weakening operation for deadbeat direct torque control based IPMSM drive[J]. IEEE Transactions on Industry Applications, 2024, 60(2): 3210-3220.
[4] Naganathan P, Srinivas S. MTPA associated DTC methodologies for enhanced performance and energy savings in electric vehicle mobility with induction motor drive[J]. IEEE Transactions on Transportation Electrification, 2022, 8(2): 1853-1862.
[5] 许水清, 许晓凡, 何怡刚, 等. 基于自适应滑模观测器的中点钳位型三电平并网逆变器开关管和电流传感器故障诊断[J]. 电工技术学报, 2024, 39(13): 4066-4078.
Xu Shuiqing, Xu Xiaofan, He Yigang, et al. A diagnosis method for power switch and current sensor faults in grid-connected three-level neutral-point clamped inverters based on adaptive sliding mode observer[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4066-4078.
[6] 孙元统, 巩建英, 张震, 等. 基于转矩反馈补偿的永磁同步电机MTPA控制[J]. 微电机, 2023, 56(1): 35-40.
Sun Yuantong, Gong Jianying, Zhang Zhen, et al. MTPA control of permanent magnet synchronous motor based on torque feedback compensation[J]. Micromotors, 2023, 56(1): 35-40.
[7] Yoo J, Kim H S, Sul S K. MTPA tracking control of sensorless IPMSM based on square-wave voltage signal injection[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12525-12537.
[8] An Xingke, Liu Guohai, Chen Qian, et al. Adjustable model predictive control for IPMSM drives based on online stator inductance identification[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3368-3381.
[9] 陈前, 顾理成, 赵文祥, 等. 采用VSIC-MTPA的五相内嵌式永磁容错电机短路容错控制[J]. 中国电机工程学报, 2020, 40(21): 7087-7094.
Chen Qian, Gu Licheng, Zhao Wenxiang, et al. A short-circuit fault-tolerant control for five-phase IPMFTM by adopting virtual-signal-injection-based MTPA[J]. Proceedings of the CSEE, 2020, 40(21): 7087-7094.
[10] 金宁治, 周凯, Herbert Ho-Ching Iu. 带有自适应参数辨识的IPMSM MTPA控制[J]. 电机与控制学报, 2020, 24(7): 90-101.
Jin Ningzhi, Zhou Kai, Iu H H C. Model reference adaptive identification based MTPA control method for interior PM synchronous motor[J]. Electric Machines and Control, 2020, 24(7): 90-101.
[11] 李峰, 夏超英. 考虑磁路饱和的IPMSM电感辨识算法及变参数MTPA控制策略[J]. 电工技术学报, 2017, 32(11): 136-144.
Li Feng, Xia Chaoying. Inductance identification algorithm and variable-parameters MTPA control strategy for IPMSM considering magnetic circuit saturation[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 136-144.
[12] 付兴贺, 陈锐, 殷凯轩, 等. 基于直接判据提取方式的直轴电流补偿型IPMSM最大转矩电流比控制算法[J]. 电工技术学报, 2023, 38(19): 5194-5206.
Fu Xinghe, Chen Rui, Yin Kaixuan, et al. Direct axis current compensated MTPA control algorithm of IPMSM based on direct criterion calculation[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5194-5206.
[13] 陈玥轩, 葛兴来, 左运, 等. 一种感应电机无速度传感器系统的电流传感器容错控制策略[J]. 中国电机工程学报, 2022, 42(6): 2346-2356.
Chen Yuexuan, Ge Xinglai, Zuo Yun, et al. A current sensor fault-tolerant control strategy for speed- sensorless induction motor system[J]. Proceedings of the CSEE, 2022, 42(6): 2346-2356.
[14] Carpaneto M, Fazio P, Marchesoni M, et al. Dynamic performance evaluation of sensorless permanent- magnet synchronous motor drives with reduced current sensors[J]. IEEE Transactions on Industrial Electronics, 2012, 59(12): 4579-4589.
[15] 滕青芳, 崔宏伟, 朱建国, 等. 基于无电流传感器的永磁同步电机系统模型预测控制[J]. 电机与控制学报, 2019, 23(5): 119-128.
Teng Qingfang, Cui Hongwei, Zhu Jianguo, et al. Current sensorless-based model predictive control for PMSM drive system[J]. Electric Machines and Control, 2019, 23(5): 119-128.
[16] Khayamy M, Chaoui H. Current sensorless MTPA operation of interior PMSM drives for vehicular applications[J]. IEEE Transactions on Vehicular Technology, 2018, 67(8): 6872-6881.
[17] Li Ze, Feng Guodong, Lai Chunyan, et al. Current injection-based multi-parameter estimation for dual three-phase IPMSM considering VSI nonlinearity[J]. IEEE Transactions on Transportation Electrification, 2019, 5(2): 405-415.
[18] 康薇, 肖飞, 任强, 等. 双有源桥DC-DC变换器三移相调制及其死区效应分析和补偿[J]. 电工技术学报, 2024, 39(6): 1907-1922.
Kang Wei, Xiao Fei, Ren Qiang, et al. Three-phase- shift modulation and its dead band effect analysis and compensation of dual-active-bridge DC-DC conver- ter[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1907-1922.
[19] 李国华, 苑朝鸣. 低开关频率下五电平逆变器双波段特定谐波消除方法[J]. 电气工程学报, 2023, 18(4): 171-178.
Li Guohua, Yuan Zhaoming. Double-band selective harmonic elimination method for five-level inverter with low switching frequency[J]. Journal of Electrical Engineering, 2023, 18(4): 171-178.
[20] Liang Donglai, Li Jian, Qu Ronghai, et al. Adaptive second-order sliding-mode observer for PMSM sensorless control considering VSI nonlinearity[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8994-9004.
[21] 龙江, 杨明, 陈扬洋, 等. 基于误差电压精确计算的表贴式永磁同步电机逆变器非线性补偿方法[J]. 中国电机工程学报, 2022, 42(17): 6425-6436.
Long Jiang, Yang Ming, Chen Yangyang, et al. Inverter nonlinearity compensation method for SPMSM drives based on accurate voltage error calculation[J]. Proceedings of the CSEE, 2022, 42(17): 6425-6436.
Abstract The maximum torque per ampere (MTPA) control strategy can fully use the reluctance torque to output the maximum torque per unit stator current and improve the operating efficiency of interior permanent magnet synchronous motors (IPMSMs). Still, the traditional formula method or the high-frequency signal injection method requires the installation of at least two phase-current sensors to obtain the current information of the motor. Once the current sensor fails, the closed-loop control of the system will fail and cause unpredictable damage. The paper proposes an MTPA control strategy for IPMSM without current sensors. The strategy can accurately realize the MTPA control of the permanent magnet synchronous motor by calculating the optimal voltage control instruction only from the rotational speed information and the mathematical model of the system.
Firstly, the relationship between the control voltage command and the rotational speed is calculated using the formula method according to the mathematical model of the IPMSM and the conditions of the MTPA control. Secondly, inverter nonlinearity can cause the inverter output voltage to deviate from the commanded voltage, resulting in the motor deviating from the MTPA operating point. Therefore, the mean value compensation method is proposed to compensate the command voltage for the nonlinearity. Thirdly, the effect of current estimation error on the calculated voltage compensation value is analyzed. The analysis shows that even if the current estimation error exists, the average error of the voltage compensation value based on the estimated current is still 0. Finally, the effect of parameter deviation on the control strategy is analyzed, and the influence of parameter deviation on the optimal voltage command amplitude and the response current is given.
The experimental results for steady-state conditions show that the A-phase current fundamental wave amplitude of the motor with the proposed strategy is smaller than that with the traditional strategy. The effectiveness of the proposed method is verified. The experimental results at the same load torque under different speeds show that the current vector amplitude error of the MTPA control with the proposed method is small. Its maximum error does not exceeding 0.5%, while the traditional method is 14%~30%. The experimental results at the same speed with different load torques show that the current vector magnitude error of MTPA control with the proposed method is small, with the maximum error not exceeding 1%. In contrast, the traditional method’s maximum error is in the range of 2%~37%. The experimental results of dynamic operation and loaded starting conditions show that the proposed control strategy is robust to parameter deviations and has good dynamic performance.
The following conclusions can be drawn. (1) The proposed method can realize MTPA control of IPMSM without current sensors, which is of great significance to the fault-tolerant control capability of current sensor failures in the IPMSM drive system. (2) The proposed method has good dynamic performance and is robust in the variation of motor parameters. (3) The proposed MTPA control strategy considers the effect of VSI nonlinearity, and the control voltages are compensated, effectively improving the running accuracy in MTPA.
keywords:Interior permanent magnet synchronous motor (IPMSM), maximum torque per ampere (MTPA), current sensorless, nonlinearity compensation
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.240700
国家自然科学基金资助项目(52177202)。
收稿日期2024-05-06
改稿日期2024-05-30
许观达 男,1998年生,博士研究生,研究方向为电力电子及电气传动等。
E-mail: 1985556356@qq.com
连传强 男,1986年生,博士,副研究员,研究方向为电机系统及其控制、人工智能。
E-mail: wzdslcq@163.com(通信作者)
(编辑 崔文静)