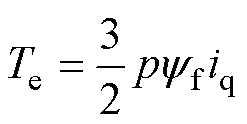（1）
摘要 在机械臂关节伺服系统中，电机通常需要带载直接起动而不能进行初始位置校准。基于开关型霍尔位置传感器的表贴式永磁同步伺服电动机能够读取电机电角度所在扇区来实现直接起动，但在起动时存在位置不准确的问题，无法获得最大的起动转矩。对此，该文提出一种基于霍尔位置传感器的表贴式永磁同步电机最速起动方法，无需额外的信号注入以及初始位置校准程序，在电机起动的首个扇区内使用所提出的角度曲线进行磁场定向控制算法中的转子位置估计，同时结合最大转矩电流比控制，能够在统计学意义上提高起动转矩，有效缩短扇区内全初始角度的起动时间期望，优化霍尔位置传感器定位不准确时的起动过程。此外，该文给出了该角度最速起动曲线的设计方法及数值解，并给出该方法在起动时间期望上的最小值证明。在实际伺服电动机参数下的仿真与实验表明：所提方法能够有效实施在现有的关节伺服系统中，与现有的方波起动方法及扇区中值起动方法相比，有效减小了全扇区角度起动时间的平均值，实现了统计学意义上电机的最速起动。
关键词：关节伺服系统 霍尔位置传感器 表贴式永磁同步电机 起动方法
近年来，工业制造发展越来越迅速，以机械臂为劳动力的先进制造技术逐渐成为制造业的主流，并使生产制造水平不断升级，生产效率得到提升[1]。伺服电动机系统作为机械臂中的核心技术之一也得到了越来越多的关注和发展。在先进制造中，产品生产及制造对机械臂提出了高性能化、小型化和集成化、全数字化等的要求，因此也使得机械臂中的伺服电动机系统朝着高速、高精度、高功率密度的方向不断发展[2]。
作为机械臂系统的动力源输出，关节内的伺服电动机系统一般使用表贴式永磁同步电机以提高功率密度，获得稳定的转矩输出[3-4]，进而实现关节速度与位置的精准控制。虽然在部分机械臂关节伺服系统中，关节输出端会安装能够直接定位的绝对式编码器，但由于减速机及传动装置的存在，仅由输出端的位置无法准确计算出电机端的机械角度及电角度，因此伺服电动机起动时的位置获取方案还是只能依赖电机端的位置传感器[5]。此外，由于受到机械臂应用场景的限制，关节内的伺服电机通常需要带载起动，且不允许进行给定指令外的旋转。因此，传统的增量式编码器由于需要通过转动一周获取零位置信号脉冲后才能实现准确的电机角度定位，并未得到广泛的使用。在该场景下应用较多的位置获取方法为霍尔位置传感器与增量式编码器结合的方案[6]，该方案使用霍尔传感器来校准电机的绝对角度，使用高线数的增量式编码器获取电机转速并提高电机角度的分辨率[7]。在电机起动时，通过霍尔位置传感器获取电机转子所在的扇区信息，无需通过额外的旋转获取初始定位，同时通过检测扇区状态的切换实现电机转子角度的校准。
但该位置获取方案由于在电机起动时仅有转子所在的扇区信息，尚未通过扇区切换校准电机角度，因此无法实现准确角度下的坐标变换，获取最大的起动转矩实现电机的最速起动[8]。针对该问题，学界及工业界通常使用两类控制方法：一类为方波起动或扇区中值角度起动的固定角度控制方法。此类方法使用扇区对应的方波电压驱动电机，或根据当前所在扇区的中间角度值进行坐标变换实现磁场定向控制，进而在起动扇区的全部角度范围内获取较大的输出转矩[9-10]。此类方法简单实用，但基于固定角度进行电机驱动控制会在初始角度较大、较小或起动中后期的情况下存在较大的角度偏差值，起动速度与起动时的转矩脉动存在可优化的空间[11]。
另一类方法为无位置传感器起动方法，利用电机绕组在不同频率信号下的数学模型，通过高频信号的注入及提取，实现静止状态下转子位置的检测[12-16]。但该类方法较为依赖电机的凸极特性，且信号注入在某种程度上会导致噪声、转矩波动与效率降低[17-19]，因此在该场景下尚未得到广泛应用。
除上两类方法外，还有一些学者提出了多种霍尔信号高分辨率位置与速度估算方法，有些通过插值法或同步坐标系滤波器法，根据电机运行的加减速规律，对不同时刻下转子位置进行估计和计算，得到较为平滑的角度信息从而提高控制精度[20-22]。或者增设观测器，根据霍尔传感器的离散信号与电压电流等电机状态，对电机角度与速度进行闭环估计，有效提高了电机的位置精度[23]。但这两类位置估算方法大多应用于中高速场合，在电机起动的初始阶段，由于尚未建立稳定的运动状态，难以使用插值或观测器法进行位置估计。
本文从表贴式永磁同步电机转矩产生机制出发，对电机起动时随机初始角度的不同加速曲线进行回归分析，根据分析结果设计电机首个扇区内的最速起动方法，并基于该方法进行了不同初始角度下的仿真实验。结果表明，该方法能够实现全扇区初始角度的最小的加速时间期望，与传统方法相比，缩短了整个扇区内不同初始角度的平均起动时间，且无需对原有控制结构进行调整或改变。
对于表贴式永磁同步电机，其输出转矩在dq轴坐标系下的数学表达式为
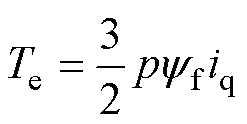（1）
式中，Te为电机电磁转矩；p为电机极对数；yf为永磁体磁链；iq为dq轴坐标系下定子q轴电流。
为了使电机能够在最短时间内起动，受制于电机驱动器能够提供的最大电流，使用磁场定向控制（Field Oriented Control, FOC）算法并基于最大转矩电流比（Maximum Torque Per Ampere, MTPA）控制能够获取最大的电磁转矩，以实现电机的最速起动目标。
在机械臂关节等伺服系统中，负载的惯量通常较大，因此伺服系统的机械时间常数tm远大于电气时间常数te，在电机起动过程中，定子电流的建立时间可以忽略。
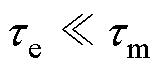（2）
依照表贴式永磁同步电机的最大转矩电流比控制，令电机中的d、q轴电流分别为
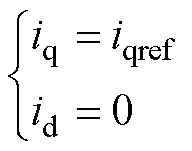（3）
式中，iqref为电机q轴电流的最大限幅指令；id为dq轴坐标系下定子d轴电流。
可以得到最大的起动转矩为
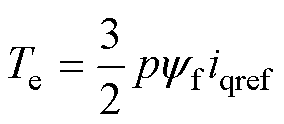（4）
根据电机动力学方程
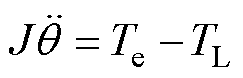（5）
式中，J为转动惯量；TL为负载转矩；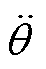
为对电机角度q 对于时间t的二阶导数。
可得其起动过程的角度轨迹为
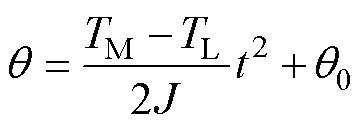（6）
其中
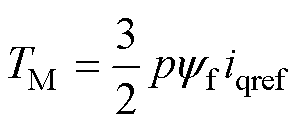
式中，TM为起动转矩系数；q0为电机初始角度。
对于基于霍尔位置传感器的电机而言，由于在驶出首个扇区的边界时便能获取电机角度的准确值，为了与其他方法比较，设电机驶出首个扇区的时间为起动时间tst，仅考虑该扇区内的起动过程，则上述理想起动方法的起动时间为
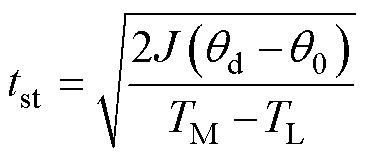（7）
式中，qd为首个扇区驶出方向的边界角度。
由上述推导可以得出，受制于驱动器的最大驱动电流，为实现电机的最速起动，理想的起动过程即为最大限幅电流指令下的匀加速起动。但该方法中持续的最大起动转矩输出需要起动过程中精确的电机角度来实现坐标的变换和准确的磁场定向，但对于基于霍尔位置传感器的表贴式永磁同步电机控制系统，电机在驶出首个扇区前仅能获取目前所在的扇区，角度分辨率为60°。因此如何设置起动过程的参考角度轨迹将影响电机起动转矩的大小，进而影响电机的起动速度。
在传统的基于霍尔位置传感器的表贴式永磁同步电机起动方法中，由于缺少电机的精确角度，常见的起动方法为基于霍尔位置传感器的扇区信息，沿用直流无刷电机的方波起动方法，输出固定的电压矢量，或者以磁场定向控制算法为基础，使用所在扇区的中值角度作为坐标变换参考角度，从而在首个扇区范围内获得较大的起动转矩。
方波起动方法较多使用在反电动势为梯形的无刷直流电机中，但在实际应用中，很多中小功率的无刷直流电机其反电动势波形平顶宽度较小，类似永磁同步电机，且霍尔传感器的扇区切换特性与方波换相特性相似，因此方波起动方法在基于霍尔位置传感器的永磁同步电机的起动及低速运行中也有较多应用。
以120°方波起动方法为例，假设电机为一对极电机，三相霍尔传感器按照常规120°间隔方式安装，正向旋转时不同扇区的霍尔信号及导通相位如图1所示。
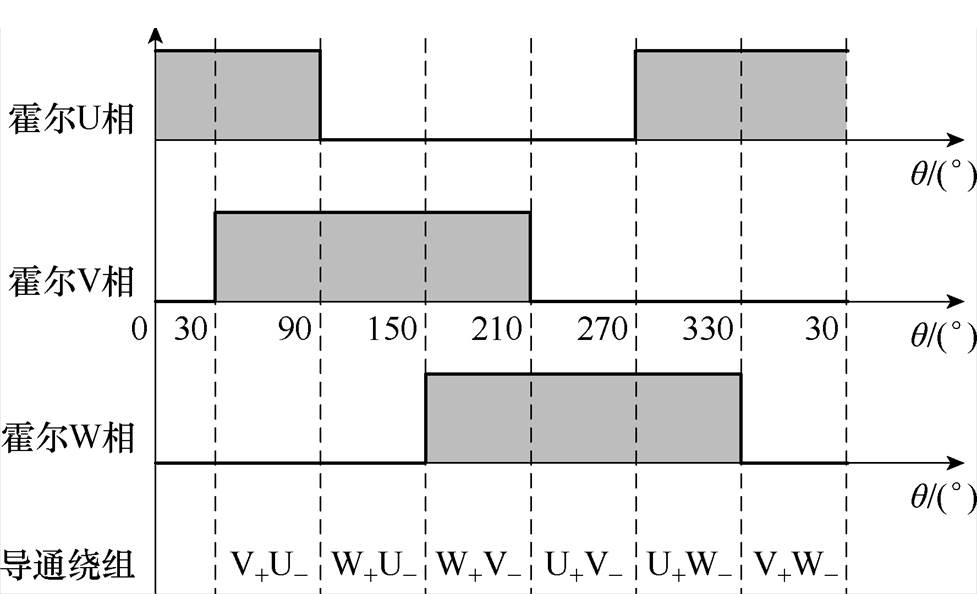
图1 方波起动方法霍尔信号及导通相位示意图
Fig.1 The Hall signal and corresponding conduction phase diagram of the square wave start-up method
可以看出，在采用120°方波导通方式起动时，每一扇区内有两个功率管导通，由于在起动时三相电流均尚未建立，因此在首个扇区内电机电流仅存在于其中两相绕组之中。如图1所示，以-30°（或330°）～30°内的第Ⅳ扇区为例，若在该扇区内起动，则电机V相上管与W相下管导通，电机的三相电流分别为
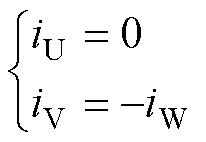（8）
忽略电机电流建立的暂态过程，同时控制电流为电机允许的最大限幅值，有
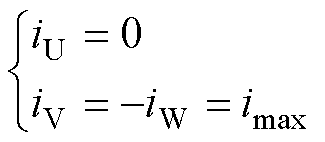（9）
式中，imax为相电流最大限幅值。则所产生的起动转矩为
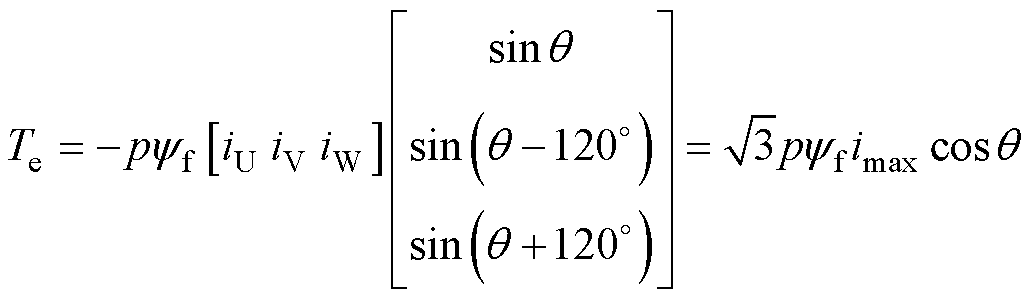（10）
可以发现，在静止ab 坐标系中电流为
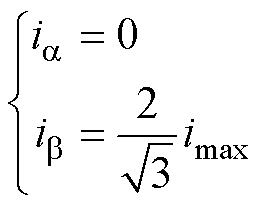（11）
恰好为转子在0°时的q轴方向。同理，对其他扇区的起动电流进行分析，可以得到不同扇区内起动电流的矢量角度分布如图2所示。
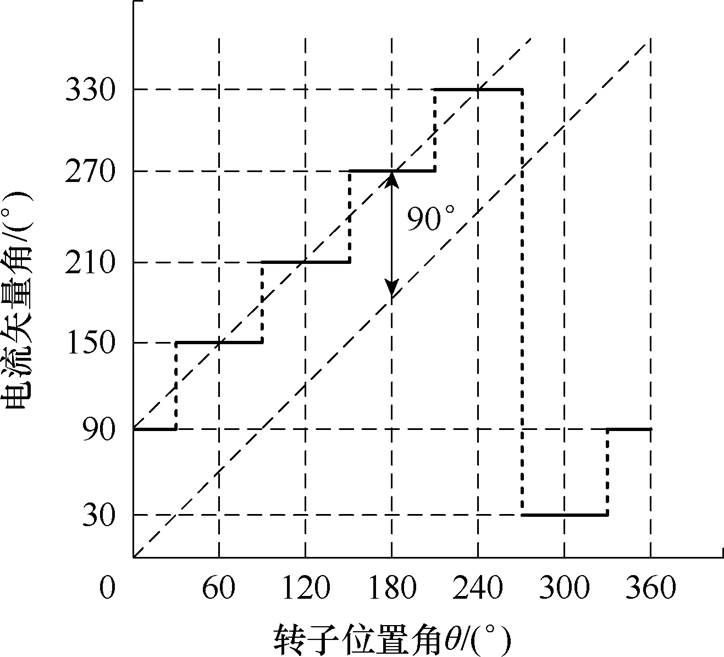
图2 方波起动方法电流矢量角与转子位置角
Fig.2 The current vector angle and rotor position angle diagram of the square wave start-up method
由图2中可以得出，在任意扇区内使用方波起动方法，其起动电流矢量与转子位于扇区中值角度时的q轴同向，因此忽略电流建立的暂态过程以及电流滞环与PI控制方式的微小差异，方波起动方法与扇区中值角度起动方法具有相同的效果。
扇区中值角度起动方法以传统的磁场定向控制为基础，使用最大转矩电流比方法进行起动。为了在扇区内获得较大的电磁转矩，设置扇区的中值角度为参考角度，进行磁场定向控制算法中的坐标 变换。
当磁场定向控制算法中坐标变换所使用的电机角度与实际角度不同时，算法中的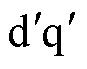
轴就会与真实的dq轴坐标系产生偏移，如图3所示。
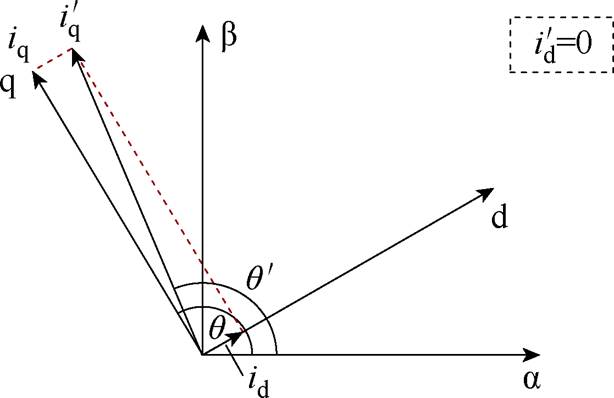
图3 角度误差带来的dq轴坐标系偏移
Fig.3 The coordinate system offset caused by the position error
在该情况下，磁场定向控制算法中的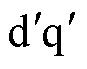轴电流与实际角度下的dq轴电流的关系为
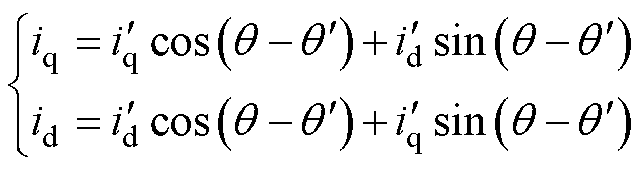（12）
式中，id与iq分别为电机真实d、q轴坐标系下的定子电流；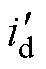
与
分别为磁场定向控制算法中估算角度对应d、q轴下的定子电流；q 、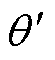
分别为电机真实角度与磁场定向控制算法中的估算角度。
与式（3）相同，在表贴式永磁同步电机的最大转矩电流比控制下，磁场定向控制算法中的电流指令分别为
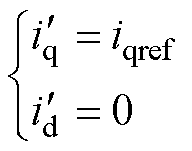（13）
将式（12）与式（13）代入式（1），可得理想电流跟踪情况下电机的实际输出转矩为
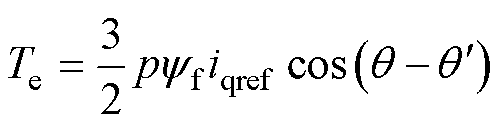（14）
由式（14）可以看出，磁场定向控制算法中所使用角度与电机实际角度的偏差会导致起动转矩的减小，且偏差量越大，转矩衰减也越大。
同样考虑霍尔传感器常规120°间隔安装方式的一对极永磁同步电机，对于扇区中值角度起动方法，假设电机在-30°（或330°）～30°内的第Ⅳ扇区逆时针旋转起动，则在起动过程中该扇区内坐标变换所使用的估算角度为
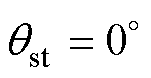（15）
此时扇区分布及起动时的坐标变换角度曲线如图4所示。
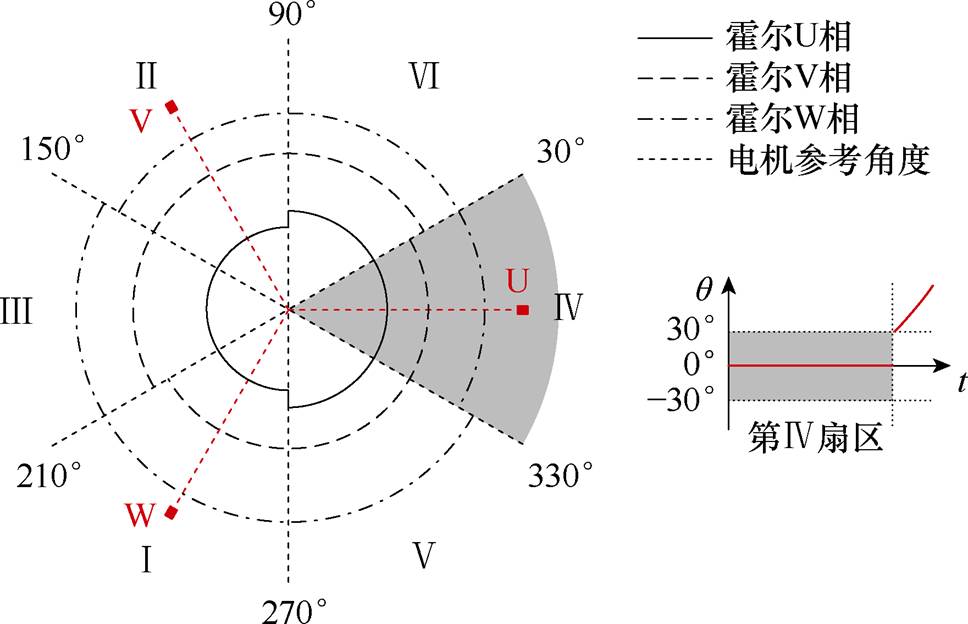
图4 以第Ⅳ扇区为例的扇区中值角度起动方法角度估算曲线
Fig.4 The assumed rotor position curve of the Hall sector median angle start-up method in the Sector Ⅳ
在此情况下，电机的实际转矩为
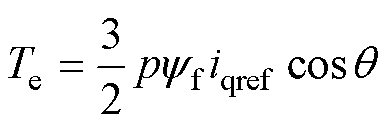（16）
将式（16）代入电机动力学方程式（5），并对时间积分可得电机在该扇区内的角度轨迹为
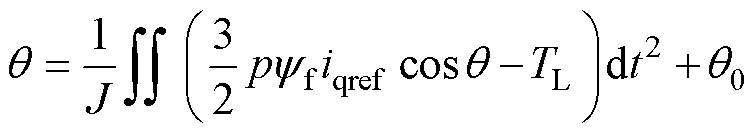（17）
为了实现最速起动，假设电机电流指令保持为最大限幅值不变，且该扇区内负载转矩近似不变，则电机角度随时间变化的曲线为
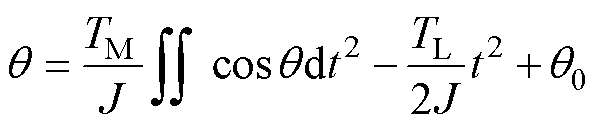（18）
由于电机初始角度q0在首个扇区内随机分布，因此该情况下电机的起动时间为方程式（19）的解。
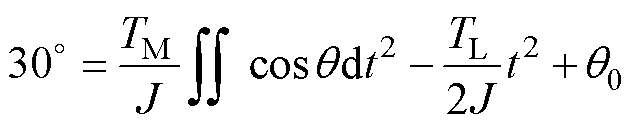（19）
与式（6）相比可得，传统起动方法由于存在无法避免的角度偏差，转矩无法一直保持在最大。因此优化坐标变换所用角度，使全扇区内的起动转矩维持在最大值附近便能有效缩短起动时间。
本节主要描述了所提出的新的最速起动方法。该方法结合表贴式永磁同步电机最大转矩电流比磁场定向控制，提出并计算了最速起动曲线。以此曲线作为首个扇区内坐标变换角度能够达到不同初始角度条件下最小的起动时间期望。其算法框图如图5所示。
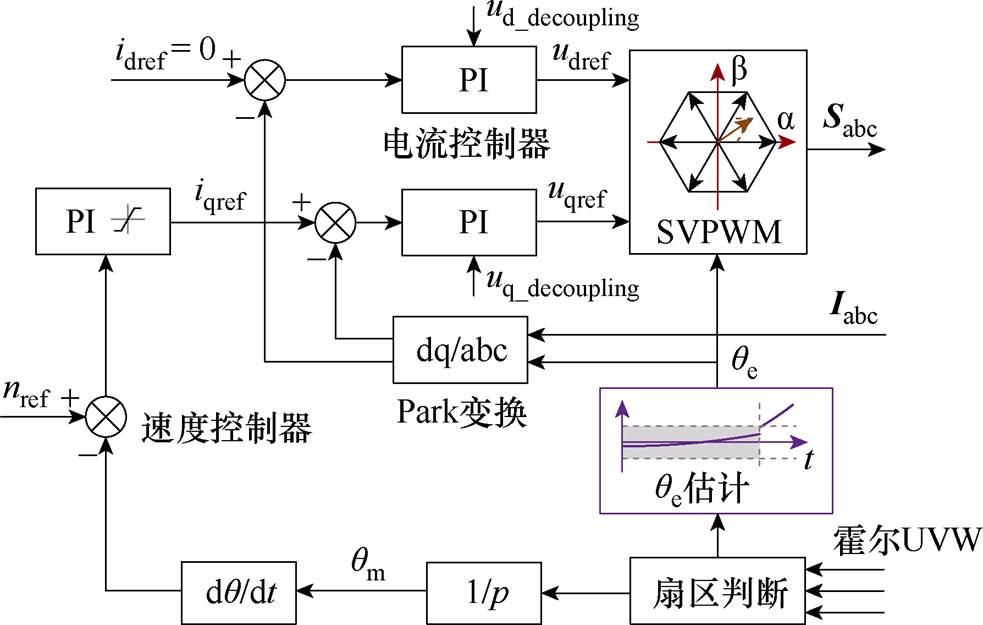
图5 所提出的最速起动方法框图
Fig.5 Block diagram of the proposed method
所提出方法保持基本控制框架不变，将磁场定向控制算法中坐标系变换角度在首个扇区内使用所提出的最速起动曲线，在驶出首个扇区后使用霍尔传感器校准＋编码器测量结合的模式获取准确 位置。
同样以此前提出的假设为例，考虑电机在第Ⅳ扇区内逆时针旋转起动的情况，计算算法中的最速起动曲线qst。为了简化计算，由于扇区内实际角度与估算角度偏差较小，电机可近似为匀加速起动，设最速起动曲线为
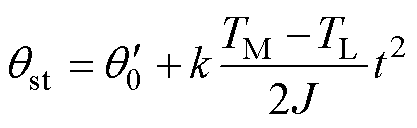（20）
式中，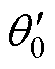
、k为所求参数。
对于起动时间tst，有
（21）
其中
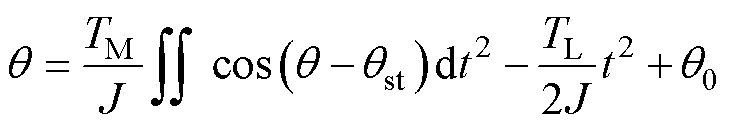
由方程式（21）可知，其解为电机初始角度q0及起动曲线qst的函数，有
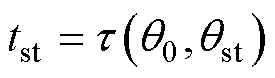（22）
所有可能初始角度下起动时间的期望值为
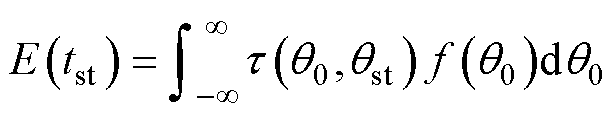（23）
式中，f(q0)为电机初始角度概率密度。由于电机初始角度在该扇区内为均匀分布的连续随机变量，则
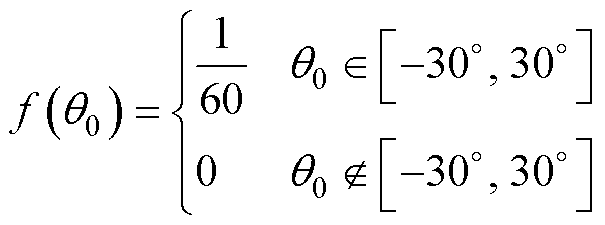（24）
因此起动时间的期望值为
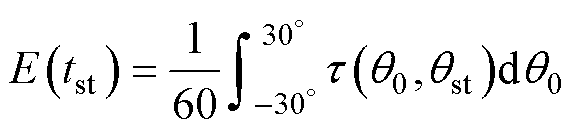（25）
为使起动时间期望值关于起动曲线取最小，有
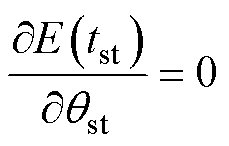（26）
将式（25）代入式（26）可得
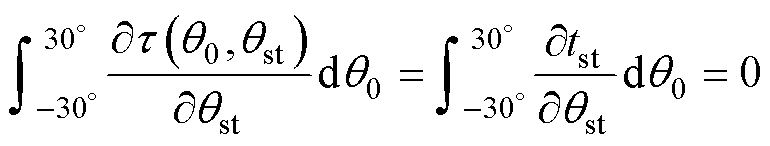（27）
对式（21）两侧关于qst求导，可得
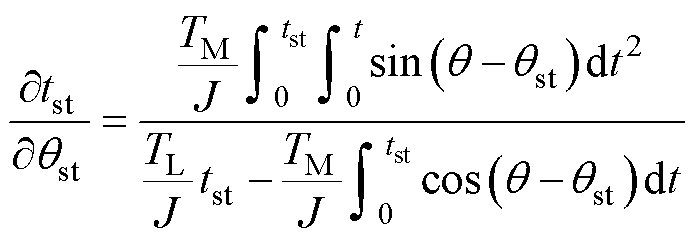（28）
将式（27）代入式（28）并化简可得
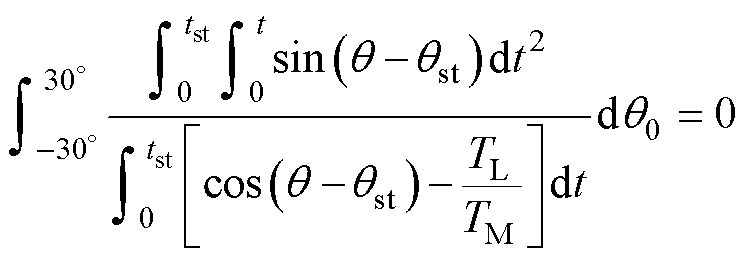（29）
在t趋近于0时，将电机初始角度q0与最速起动曲线参数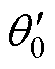代入式（29），得
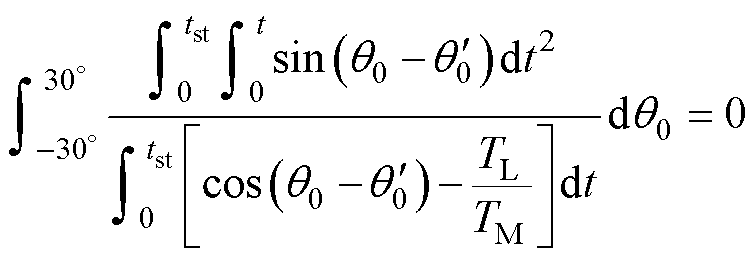（30）
由于电机近似为匀加速起动，有
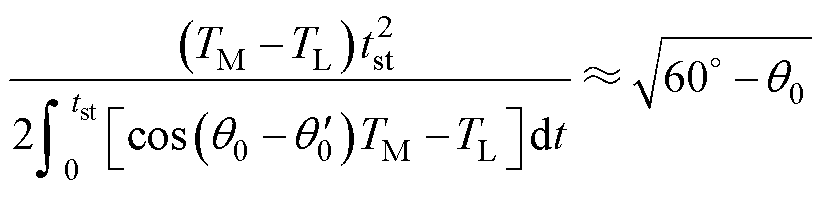（31）
将式（31）代入式（30）并化简可得
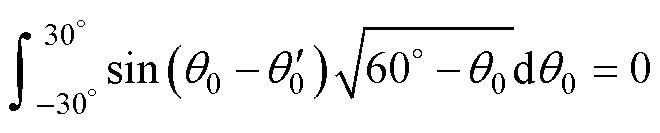（32）
进而求得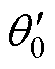的数值解为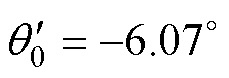
。
这意味着在初始时刻使用偏小的角度能够在起动前期获得更大的转矩，从而缩短起动时间期望。
由式（29）可得，在qst=30°时，最速起动曲线应与最小初始角度时的电机角度轨迹相交，也即
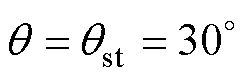（33）
其中
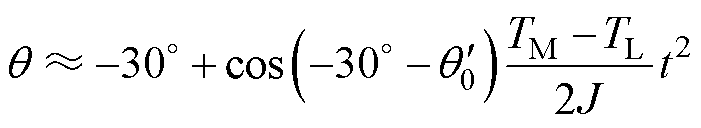
则将式（33）代入式（29）可解得参数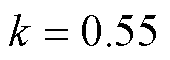
。
综上可得，该情况下此扇区的最速起动曲线为
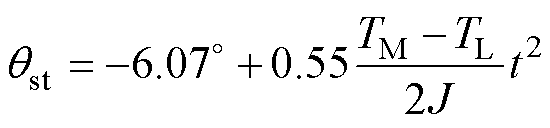（34）
以第Ⅳ扇区为例，所提出起动方法的角度估算曲线如图6所示。
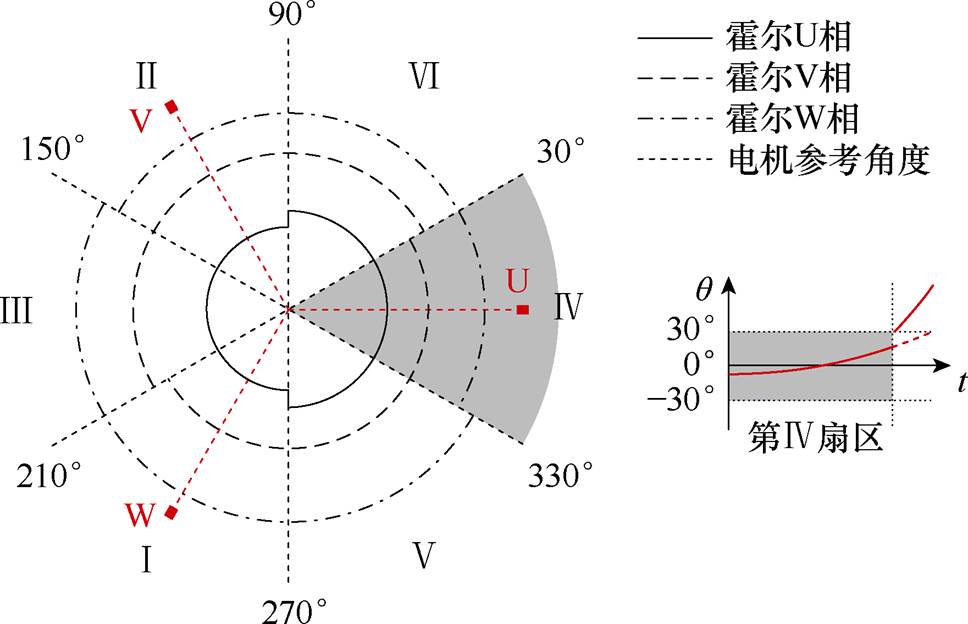
图6 以第Ⅳ扇区为例所提出起动方法的角度估算曲线
Fig.6 The assumed rotor position curve ofthe proposed quick start-up method in the Sector Ⅳ
此时任意初始角度下首个扇区的起动时间期望值对该曲线的偏导约为0，有
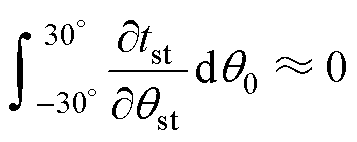（35）
而其二阶偏导大于0，有
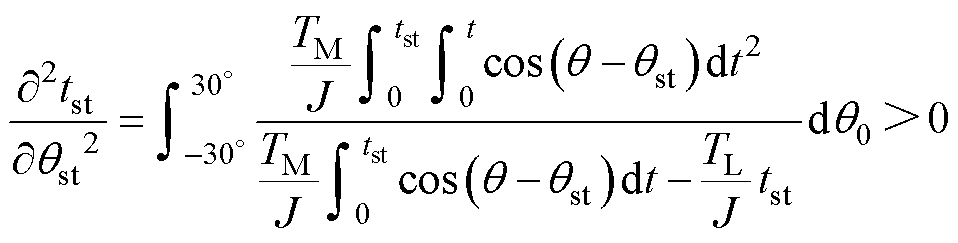（36）
因此，式（34）即为该扇区内起动时间期望极小值所对应的函数曲线。将式（34）推广至任意扇区，则有各扇区内的最速起动曲线为
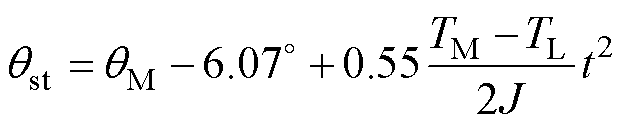（37）
式中，qM为各扇区角度中值。
重新计算该曲线对应的电机起动时间并推广至电机可能的全部初始角度，仍以逆时针起动为例，该方法与传统的扇区中值角度起动方法的起动时间对比变化分布以极坐标形式表示在图7中。图中，极角对应电机的电角度qe，极径对应所提出方法起动时间的变化值，中间圆环处为两方法起动时间相等的零刻度位置，Dt＞0表示起动时间减小，Dt＜0表示起动时间增加，则浅（黄）色阴影表示该方法较传统扇区中值法起动时间减小值的数学期望，深（蓝）色阴影表示该方法较传统扇区中值法起动时间增加值的数学期望。可以看出，所提出方法各扇区内临近小角度侧的初始角度起动时间减小最多，而接近扇区中值处两种方法起动时间相当，临近扇区较大角度侧起动时间增加。从整体分布情况来看，对于随机的初始角度，起动时间减小的期望大于增加的期望，因此所提出方法在统计学意义上具有更短的起动时间。
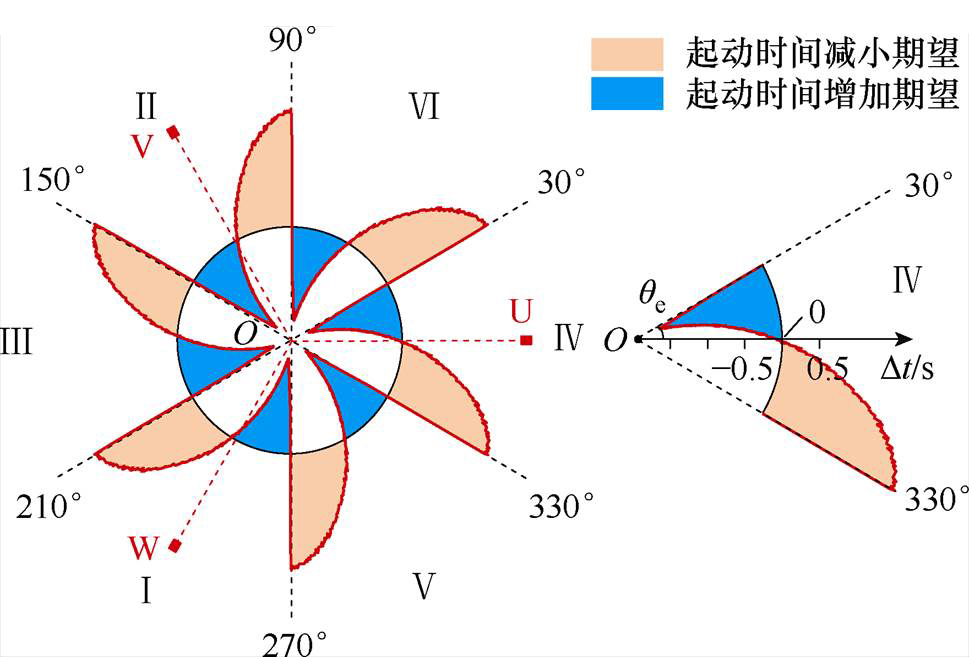
图7 所提出方法起动时间变化分布
Fig.7 The start-up time variation of the proposed method
因此，将该曲线作为磁场定向控制算法在起动时的首个扇区内的角度估算值能够实现扇区内全初始角度起动时间期望最小，且该方法易于移植在不同的电机驱动算法中。
为了验证所提出的最速起动方法，依据如图5所示的基于表贴式永磁同步电机最大转矩电流比磁场定向控制算法框图搭建仿真与实验算法。仿真与实验中所使用的三相永磁同步电机参数见表1。驱动器开关频率与电流环控制频率设为20 kHz，直流母线电压为60 V。负载转矩为额定转矩半载6.5 N·m，并使电流指令为最大限幅值9 A。
仿真基于Matlab/Simulink进行搭建。为了模拟所提出的方法在不同初始角度下的起动条件，仍以在-30°～30°的第Ⅳ扇区内起动为例进行仿真。以5°为间隔设置不同初始角度，分别采用传统的方波起动法及扇区中值角度起动法与所提出方法进行电机的起动仿真。为了更明显地测量与表征电机在首个扇区内的起动时间，使用电流环中断周期（为50 ms）数来计算时间，对比结果见表2。
表1 表贴式永磁同步电机参数
Tab.1 SPMSM Parameters
参 数数 值 极对数5 d轴电感/mH4.11 q轴电感/mH4.11 电机转动惯量/(kg·m2)0.026 5 最大限幅电流指令/A9 负载转矩/(N·m)6.5
表2 所提出最速起动方法的起动时间对比仿真结果
Tab.2 Performance comparison between traditional method and proposed quick start-up method in simulations
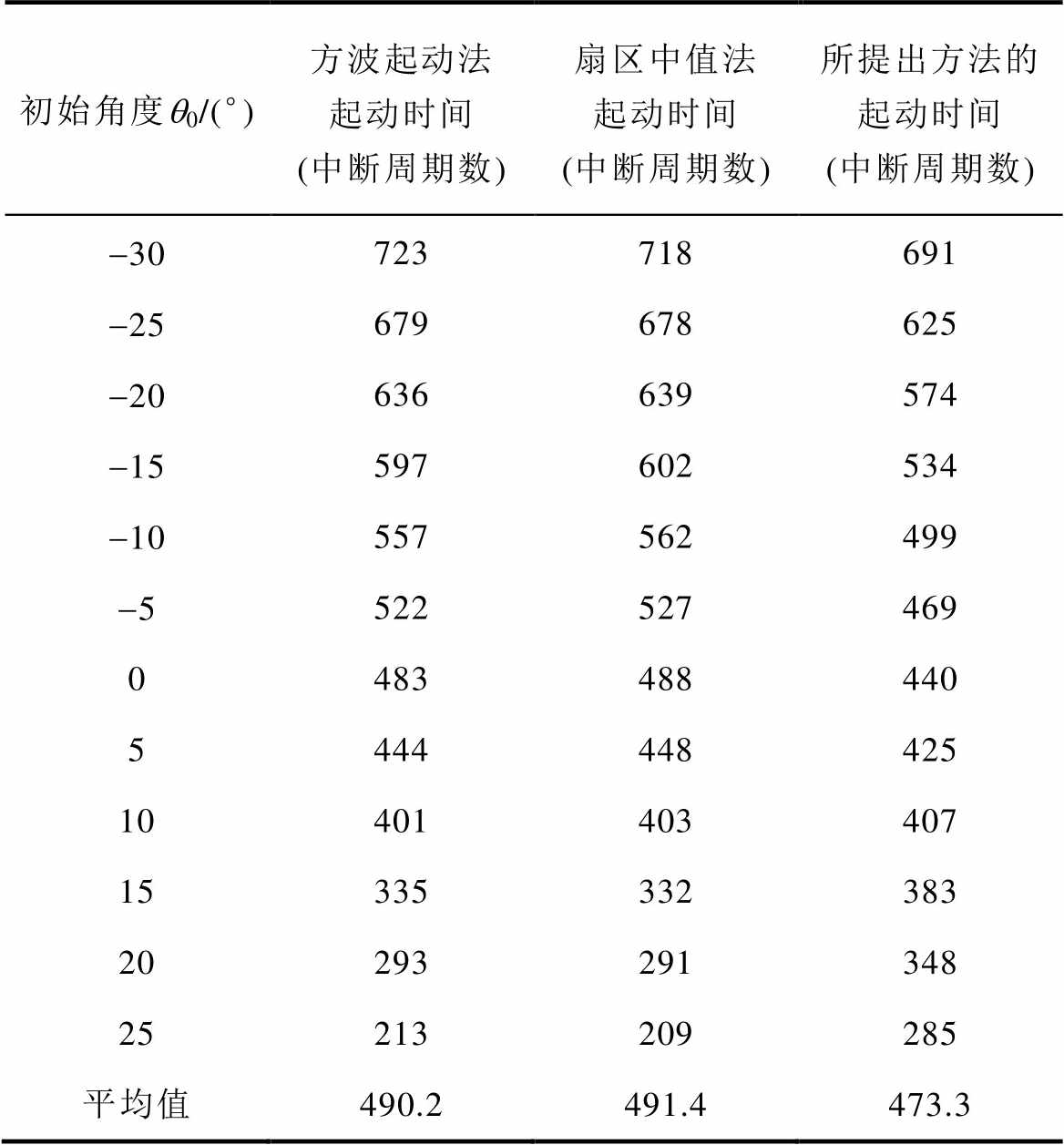
初始角度q0/(°)方波起动法起动时间(中断周期数)扇区中值法起动时间(中断周期数)所提出方法的起动时间(中断周期数) -30723718691 -25679678625 -20636639574 -15597602534 -10557562499 -5522527469 0483488440 5444448425 10401403407 15335332383 20293291348 25213209285 平均值490.2491.4473.3
如表2所述，传统的方波起动法与扇区中值法起动时间接近。在电机的初始角度位于扇区前部时，由于起动过程较长，所提出最速起动方法的起动时间较传统方法有较大提升；当电机的初始角度逐渐增大时，所提出方法的起动时间与传统方法逐渐接近；当初始角度位于将要驶出扇区的较大角度时，所提出方法的起动时间略有滞后，但由于起动过程较短，因此仅有微小的时间差距。综合上述仿真结果，对比扇区内对应全部角度的起动时间平均值，所提出方法能够有效缩短平均起动时间约3%。
为了进一步验证所提出方法的有效性，在同一参数的表贴式永磁同步电机实验台架下进行实验验证。实验平台如图8所示。
图8 实验平台
Fig.8 Experimental platform
控制算法基于DSP TMSF28388D的控制板实现；电机相电流由电流传感器LEM LH 25-HP进行测量并连接至控制板，同时由Yokogawa 701932电流探头进行测量并连接至DLM3024示波器用以记录波形。
为统一仿真与实验条件，实验中电机初始角度间隔6°在-30°～30°的第Ⅳ扇区内均匀设置。同样使用传统方波起动法及扇区中值角度起动法与所提出最速起动方法进行对比，使用电流环中断周期数来计算时间。对比实验结果见表3。
表3 所提出最速起动方法的起动时间对比实验结果
Tab.3 Performance comparison between traditional method and proposed quick start-up method in experiments
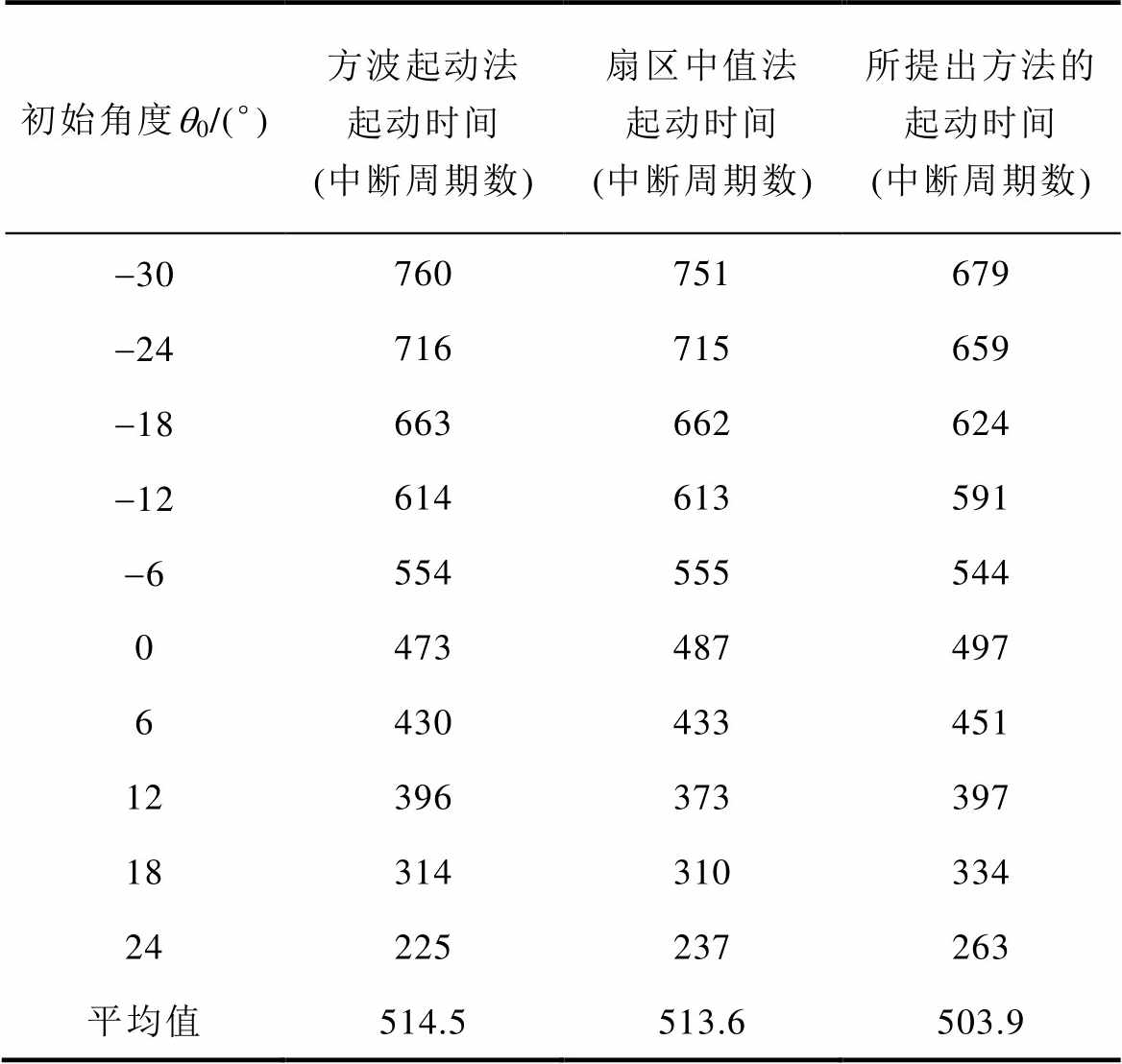
初始角度q0/(°)方波起动法起动时间(中断周期数)扇区中值法起动时间(中断周期数)所提出方法的起动时间(中断周期数) -30760751679 -24716715659 -18663662624 -12614613591 -6554555544 0473487497 6430433451 12396373397 18314310334 24225237263 平均值514.5513.6503.9
如表3所述，实验结果与仿真结果具有一致性，可以得出所提出方法能够有效缩短扇区内的平均起动时间。同时，较小初始角度时的时间缩短与较大初始角度时时间的略微延长与理论分析一致，受非理想因素与测量误差的影响，扇区内全初始角度的起动时间平均值缩短了约2%，证明了所提出方法的有效性。
实验中电机起动过程的转速v、机械角度qm及A、B相电流iA、iB波形如图9所示。
图9 起动过程的PMSM转速、角度及电流波形
Fig.9 PMSM speed, angle, and currents waveforms during the start-up process
如图9所示，电机使用三种方法起动，电机电流便很快建立稳态，其电流相位与磁场定向控制算法中的估算角度有关，估算角度的突然变化会带来电流相位的对应变化，以此可以标志出首个扇区的起动时间。图9a与图9b为传统方波起动法对应的电机转速、角度及电流波形，图9c与图9d为扇区中值角度起动法起动对应的波形，图9e与图9f为所提出最速起动方法对应的波形。可以看出，电机实际机械角度与转速的变化均近似为匀加速起动，验证了式（20）所作出的近似假设是合理的；此外转子初始角度的不同对起动时间影响较大，同时电流波形所测得的时间与所测中断周期数计算所得时间近似相等验证了表3中实验结果的准确性。
为了进一步验证所提出方法的参数鲁棒性，设置不同的带载起动实验，所提方法虑及参数失配的起动时间对比实验结果见表4，电机转速、角度及电流波形如图10所示。
表4 所提方法虑及参数失配的起动时间对比实验结果
Tab.4 Performance comparison of startup times when parameters mismatch in the proposed method
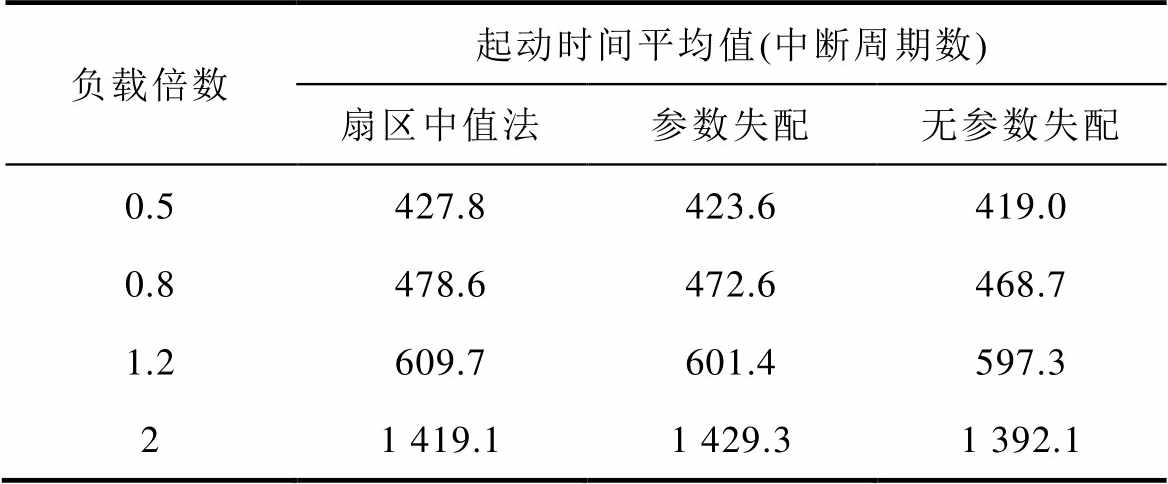
负载倍数起动时间平均值(中断周期数) 扇区中值法参数失配无参数失配 0.5427.8423.6419.0 0.8478.6472.6468.7 1.2609.7601.4597.3 21 419.11 429.31 392.1
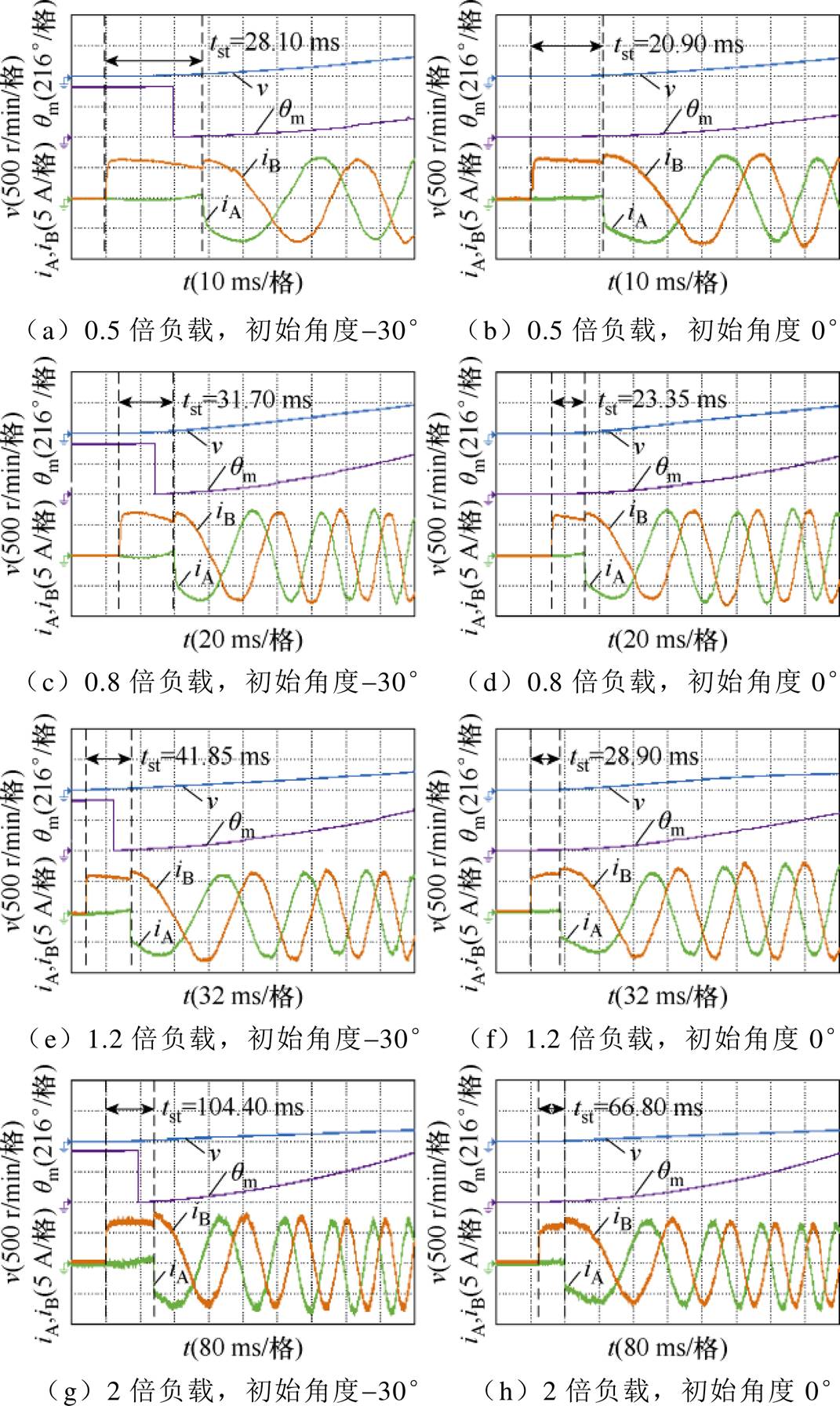
图10 参数失配时所提出方法起动过程的PMSM转速、角度及电流波形
Fig.10 PMSM speed, angle, and currents waveforms during the start-up process of the proposed method for parameters mismatch
如图10所示，对于不同的起动负载，无论是否发生参数失配，电机均能正常起动。当负载小于参数设定值时，0.5倍以内的参数失配对应的平均起动时间较无参数失配时略有增加，但仍小于传统扇区中值方法；当负载大于参数设定值时，较小的参数失配同样将增加平均起动时间，但仍优于传统扇区中值方法，当参数失配较大时，平均起动时间将继续增加。因此，所提出方法在设定参数时应尽量使用准确参数，以获得最优的起动效果。
本文提出了一种基于霍尔传感器的表贴式永磁同步电机最速起动方法。在常规控制方法中，由于算法所用角度固定，无法实现首个扇区内全初始角度平均起动时间最小。为了优化该起动时间期望值，本文设计了一种新的最速起动曲线。该曲线能够有效提升各扇区内小初始角度的起动时间，并同时兼顾其他角度时的起动过程，在统计学意义上缩短了首个扇区全初始角度的起动时间期望，有效优化霍尔传感器首个扇区定位不准确时的起动时间问题，同时该算法易于移植，能够很方便地应用于现有的各类伺服控制算法中。
参考文献
[1] 王田苗, 陶永. 我国工业机器人技术现状与产业化发展战略[J]. 机械工程学报, 2014, 50(9): 1-13.
Wang Tianmiao, Tao Yong. Research status and industrialization development strategy of Chinese industrial robot[J]. Journal of Mechanical Engin- eering, 2014, 50(9): 1-13.
[2] 孟明辉, 周传德, 陈礼彬, 等. 工业机器人的研发及应用综述[J]. 上海交通大学学报, 2016, 50(增刊1): 98-101.
Meng Minghui, Zhou Chuande, Chen Libin, et al. A review of the research and development of industrial robots[J]. Journal of Shanghai Jiao Tong University, 2016, 50(S1): 98-101.
[3] Pillay P, Krishnan R. Application characteristics of permanent magnet synchronous and brushless DC motors for servo drives[J]. IEEE Transactions on Industry Applications, 1991, 27(5): 986-996.
[4] 王海兵, 赵荣祥, 汤胜清, 等. 永磁同步电机位置检测偏差对驱动系统性能的影响研究[J]. 电工技术学报, 2018, 33(4): 910-918.
Wang Haibing, Zhao Rongxiang, Tang Shengqing, et al. Research on the influence of the position detection error to the PMSM drive system[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 910-918.
[5] 周楠, 张波. 六自由度协作型机器人的结构设计与运动规划[J]. 机械制造, 2018, 56(9): 40-44, 49.
Zhou Nan, Zhang Bo. Structural design and motion planning of 6-DOF collaborative robot[J]. Machinery, 2018, 56(9): 40-44, 49.
[6] 莫会成, 闵琳. 现代高性能永磁交流伺服系统综述: 传感装置与技术篇[J]. 电工技术学报, 2015, 30(6): 10-21.
Mo Huicheng, Min Lin. Summary of modern high performance permanent magnet AC servo system: sensor device and technology[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 10-21.
[7] 李垣江, 苗奎星, 魏海峰, 等. 基于带通频率跟踪滤波器的永磁同步电机转子位置与速度估算[J]. 电工技术学报, 2022, 37(21): 5402-5413.
Li Yuanjiang, Miao Kuixing, Wei Haifeng, el. Permanent magnet synchronous motor rotor position and speed estimation methodology based on band- pass frequency tracking filter[J]. Transaction of China Electrotechnical Society, 2022, 37(21): 5402-5413.
[8] Kim S Y, Choi C, Lee K, et al. An improved rotor position estimation with vector-tracking observer in PMSM drives with low-resolution Hall-effect sensors[J]. IEEE Transactions on Industrial Elec- tronics, 2011, 58(9): 4078-4086.
[9] 倪启南, 杨明, 徐殿国, 等. 低分辨率位置传感器永磁同步电机精确位置估计方法综述[J]. 电工技术学报, 2017, 32(22): 70-81.
Ni Qinan, Yang Ming, Xu Dianguo, et al. Review of precise position estimation method of PMSM with low-resolution position sensor[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 70-81.
[10] 钟逸飞, 孔武斌, 易磊, 等. 基于霍尔位置传感器的永磁同步电机方波启动问题研究[J]. 船电技术, 2018, 38(1): 26-29, 32.
Zhong Yifei, Kong Wubin, Yi Lei, et al. Square wave start-up control of permanent magnet synchronous motor with Hall-effect sensors[J]. Marine Electric & Electronic Engineering, 2018, 38(1): 26-29, 32.
[11] 易磊, 曲荣海, 李新华, 等. 霍尔位置检测的电动汽车永磁电机矢量控制[J]. 微特电机, 2018, 46(9): 63-67.
Yi Lei, Qu Ronghai, Li Xinhua, et al. Vector control of permanent magnet motor using hall sensors for electric vehicles[J]. Small & Special Electrical Machines, 2018, 46(9): 63-67.
[12] 朱良红, 张国强, 李宇欣, 等. 基于级联扩张观测器的永磁电机无传感器自抗扰控制策略[J]. 电工技术学报, 2022, 37(18): 4614-4624.
Zhu Lianghong, Zhang Guoqiang, Li Yuxin, et al. Active disturbance rejection control for position sensorless permanent magnet synchronous motor drives based on cascade extended state observer[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4614-4624.
[13] 王菁, 颜建虎, 季国东, 等. 一种基于双位置观测器的永磁同步电机低速无位置传感器控制方法[J]. 电工技术学报, 2023, 38(2): 375-386.
Wang Jing, Yan Jianhu, Ji Guodong, et al. A sensorless control method for permanent magnet synchronous machine based on dual position observers at low speed[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 375-386.
[14] De Donato G, Scelba G, Pulvirenti M, et al. Low-cost, high-resolution, fault-robust position and speed estimation for PMSM drives operating in safety- critical systems[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 550-564.
[15] 于安博, 刘利, 阚志忠, 等. 高频脉振信号注入永磁同步电机无滤波器初始位置辨识方法[J]. 电工技术学报, 2021, 36(4): 801-809.
Yu Anbo, Liu Li, Kan Zhizhong, et al. Initial position identification of PMSM with filterless high frequency pulse signal injection method[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 801-809.
[16] 曹春堂, 兰志勇, 沈凡享. 永磁同步电机无位置传感器控制系统中初始位置角检测综述[J]. 电气技术, 2020, 21(6): 1-6.
Cao Chuntang, Lan Zhiyong, Shen Fanxiang. Review of initial position angle detection in sensorless control system of permanent magnet synchronous motor[J]. Electrical Engineering, 2020, 21(6): 1-6.
[17] 付康壮, 刘计龙, 麦志勤, 等. 改进型IF控制结合有效磁链法的永磁同步电机全速域无位置传感器控制策略[J]. 电工技术学报, 2022, 37(22): 5704- 5716.
Fu Kangzhuang, Liu Jilong, Mai Zhiqin, et al. A full-speed domain sensorless control strategy for permanent magnet synchronous motor based on improved IF control and effective flux method[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5704-5716.
[18] Jeong Y S, Lorenz R D, Jahns T M, et al. Initial rotor position estimation of an interior permanent-magnet synchronous machine using carrier-frequency injection methods[J]. IEEE Transactions on Industry Appli- cations, 2005, 41(1): 38-45.
[19] 孙明阳, 和阳, 邱先群, 等. 随机频率三角波注入永磁同步电机无位置传感器降噪控制[J]. 电工技术学报, 2023, 38(6): 1460-1471.
Sun Mingyang, He Yang, Qiu Xianqun, et al. Random-frequency triangular wave injection based sensorless control of PMSM drives for audible noise reduction[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1460-1471.
[20] 赵远洋, 韩邦成, 陈宝栋. 基于霍尔矢量相位跟踪的永磁同步电机转子位置与速度估算方法[J]. 电工技术学报, 2019, 34(15): 3147-3157.
Zhao Yuanyang, Han Bangcheng, Chen Baodong. Speed and rotor position estimation for PMSM based on hall vector phase-tracking[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3147-3157.
[21] 张冰鑫, 刘侃, 李跃, 等. 基于累积误差补偿的永磁同步电机低速插值控制策略[J]. 电气工程学报, 2023, 18(3): 145-153.
Zhang Bingxin, Liu Kan, Li Yue, et al. Low speed interpolation control strategy of permanent magnet synchronous motor based on accumulative error compensation[J]. Journal of Electrical Engineering, 2023, 18(3): 145-153.
[22] 张懿, 张明明, 魏海峰, 等. 基于霍尔传感器的永磁同步电机高精度转子位置观测[J]. 电工技术学报, 2019, 34(22): 4642-4650.
Zhang Yi, Zhang Mingming, Wei Haifeng, et al. High precision rotor position observation of permanent magnet synchronous motor based on hall sensors[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4642-4650.
[23] 张春雷, 张辉, 叶佩青. 高霍尔位置检测精度的圆筒型永磁同步直线电机设计[J]. 电工技术学报, 2022, 37(10): 2481-2490.
Zhang Chunlei, Zhang Hui, Ye Peiqing. Design of tubular permanent magnet synchronouslinear motor by reliability-based robust design optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2481-2490.
Abstract As the power source of the robotic manipulators, the motors inside the joint servo systems generally start with a load directly and cannot execute position calibration due to the operating conditions. Therefore, the commonly used position acquisition scheme is the Hall position sensor during motor start-up. However, this scheme cannot start the motor with the maximum starting torque, as the Hall position sensor only provides the present sector of the motor rather than the precise angle. The traditional processing method utilizes a square-wave voltage to start up or take the middle value of the Hall sector as the angle input to the motor drive algorithm, thereby obtaining a large torque across the entire angle range of the Hall sector. These methods are simple but lose some torque in the event of a significant deviation in the position estimation.
This paper proposes a quick-startup method for surface-mounted permanent magnet synchronous motors (SPMSMs) based on a Hall position sensor. Firstly, the start-up process of different curves of random initial angles is analyzed. The deviation between the actual rotor position and the imprecise estimated position decreases the starting torque, as the Hall sector spans an angle range of 60°. Under these conditions, combined with the field-oriented control (FOC) algorithm and the maximum torque per ampere (MTPA) strategy, the quick start-up method is proposed, and the critical start-up curve parameters are numerically calculated. Although the initial and precise anglesduring the start-up process are not available, the proposed curve can be close to the average locus to a great extent.
The simulation and an experiment are conducted using an actual servo motor under different initial angles. The results show that when the initial rotor position is close to the minimum angle of the Hall sector, the proposed method exhibits a pronounced acceleration effect. Due to the short stroke, although the position tracking of the proposed method is slightly behind the traditional method, the time difference is negligible when the initial position approaches the maximum angle. Combined with the average start-up time of the entire initial angle in the Hall sector, the proposed method can effectively reduce the average start-up time.
A quick start-up method for SPMSM based on a Hall position sensor is proposed. In the conventional control method, the maximum starting torque and the minimum statistical value of the start-up time cannot be achieved over the entire range of initial angles. Therefore, the novel position curve is designed to improve the start-up time for small initial angles in each Hall sector while considering the start-up process at other angles. Statistical analysis has demonstrated a significant reduction in the start-up time expectation of the entire initial rotor positions. The method optimizes the torque reduction problem during the start-up process, which is caused by imprecise positioning in the first Hall sector. Moreover, the ease of transplantation allows the method to be applied to various motor drive algorithms.
keywords：Joint servo system, Hall position sensor, surface-mounted permanent magnet synchronous motor, start-up method
中图分类号：TM341
DOI: 10.19595/j.cnki.1000-6753.tces.231687
浙江省“尖兵”“领雁”研发攻关计划项目（2023C01178）和国家自然科学基金重点项目（52237003）资助。
收稿日期 2023-10-12
改稿日期2024-03-22
高慧达 男，1996年生，博士研究生，研究方向为电机系统及其控制。
E-mail: gaohuida@zju.edu.cn
史婷娜 女，1969年生，教授，博士生导师，研究方向为电机系统及其控制。
E-mail: tnshi@zju.edu.cn（通信作者）
（编辑 崔文静）