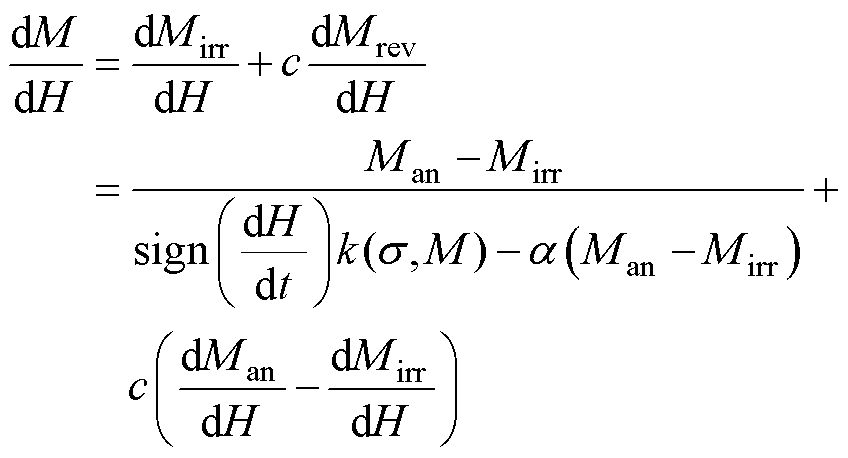（1）
摘要 在无损检测（NDT）领域，对于模拟工具能够预测磁性特征、增进理解并避免苛刻和不确定的实验预期的需求日益增长。由于高灵敏度和无损的特点，磁巴克豪森噪声（MBN）的测量与模拟已成为无损检测中的重要手段。现有的机械应力下的MBN模型虽然可以模拟MBN信号以及MBN特征值，但它们都无法全面而精确地模拟不同软磁材料在应力下的MBN信号。为此，该文首先基于改进的S-J-A磁滞模型，考虑磁各向异性、模型参数与应力之间的关系，模拟了软磁材料的不可逆磁滞回线；其次，将软磁材料的不可逆磁滞回线与MBN包络线相联系，得到磁巴克豪森噪声（MBN）的包络曲线的数学模型；然后，用包络曲线调制1～50 kHz的白噪声，模拟得到MBN信号；最后，以取向电工钢片（30QG120）、无取向硅钢（35WW230）和非晶合金（1K101）三种不同的软磁材料为研究对象，利用提出的MBN模型在不同的机械应力条件下进行MBN的模拟。通过将实验数据和现有模型进行对比，验证了所提出模型的精确性和可靠性。
关键词：无损检测（NDT） 软磁材料 磁巴克豪森信号（MBN） 磁滞模型 机械应力 应力下MBN模型
由于取向硅钢、无取向硅钢和非晶合金这三种软磁材料具有优异的磁化与损耗特性，因而被广泛用于制造电力变压器的铁心。在电力变压器的制造和运行中，由于机械加工和软磁材料的磁致伸缩效应，变压器铁心可能残余或产生机械应力，这些机械应力会对软磁材料的磁性能产生影响，从而导致设备性能下降或损坏。磁巴克豪森噪声（Magnetic Barkhausen Noise, MBN）信号可以反映这些软磁材料的残余应力状态、微观结构变化、疲劳和蠕变信息，从而便于快速评估变压器铁心的工作状态。提出一种软磁材料在机械应力下的MBN信号的数学模型对于预测软磁材料的磁化特性、深化对MBN形成机理的理解、评估软磁材料的残余应力以及设计电力变压器铁心具有重要意义[1-4]。
目前，主要有两种磁巴克豪森噪声信号的数学模拟方法：一种是基于Jiles-Atherton（J-A）磁滞模型的随机过程综合模型；另一种则是基于Ising模型的MBN模型[5]。这两种模型都基于物理假设，第一种方法具有随机性，难以通过实验验证；而第二种方法则需要大量的计算时间。
文献[6]发现在准静态磁场下磁滞回线和传统MBN能量之间存在一定的线性关系，利用这一特点对准静态磁场下的MBN噪声进行了模拟，得到了压应力下的巴克豪森噪声包络，从而得到了材料绝对量化的内部残余应力。文献[7-8]提出了一种用磁滞模型和MBN能量值（其定义为巴克豪森噪声电压VB的平方与符号函数sign(dH/dt)的乘积的时间积分）相结合来模拟MBN信号的方法。其将J-A模型和“无旋转”的多尺度模型相结合得到仅涉及磁畴壁运动的磁滞回线，之后将其与传统MBN能量值相联系，得到了MBN包络。最后，利用MBN包络调制1～50 kHz白噪声的方法，实现了MBN信号的模拟。但是，他们并没有给出MBN信号的确切的数学模型，只是通过对比发现仅涉及畴壁运动的磁滞模型和MBN能量之间存在一定的线性关系。另外，上述文献的假设前提是MBN由畴壁的运动产生。事实上，软磁材料磁畴壁的运动包括可逆和不可逆两个部分，而MBN的产生只与畴壁运动中的不可逆部分相关[9]。因此，这种MBN模拟方法并不准确。
针对上述模型存在的问题，本文基于改进的S-J-A磁滞模型[10]，给出了应力下MBN信号的确切数学模型。这个MBN模型用软磁材料的不可逆磁畴壁运动描述，从而使模拟的MBN信号更加准确。
在磁化频率为10 Hz时，MBN信号检测效果较佳[11]，因而本文分别在不同应力条件下测量和模拟了软磁材料在10 Hz磁化频率下的MBN信号，以验证模型的准确性。
原始的S-J-A磁滞模型适用于各向同性材料，而有些软磁材料则表现出显著的各向异性，且这种各向异性与外界应力密切相关。因此，传统的S-J-A模型不适用于受应力影响的各向异性软磁材料。为了提高MBN模型的适用性，本文用改进的S-J-A磁滞模型模拟应力下软磁材料的磁滞回线，其数学表达式[10]为
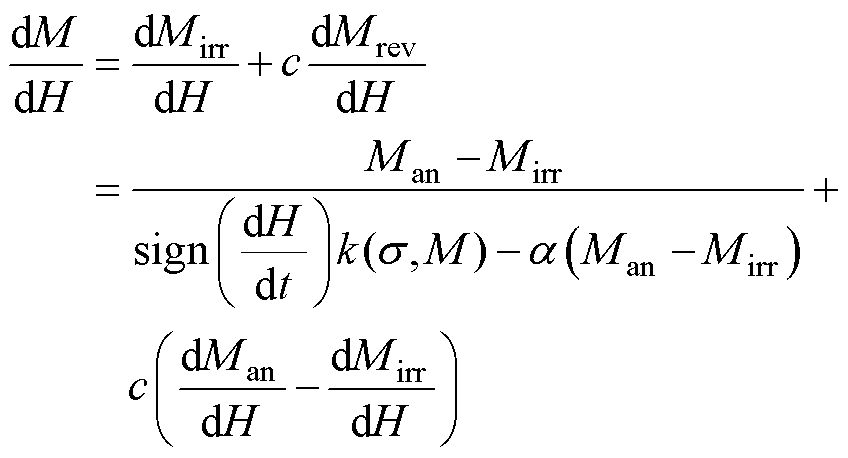（1）
式中，H为外施磁场强度；M为磁化强度；Mirr为不可逆磁化强度；Mrev为可逆磁化强度；Man为无滞回磁化强度；k(s, M)为随应力变化的钉扎点系数；s 为应力；sign( · )为符号函数；a 为磁畴内部耦合平均参数；c为可逆参数。
通过将各向异性能量作为附加项引入无滞回磁化强度表达式，来考虑软磁材料的各向异性。
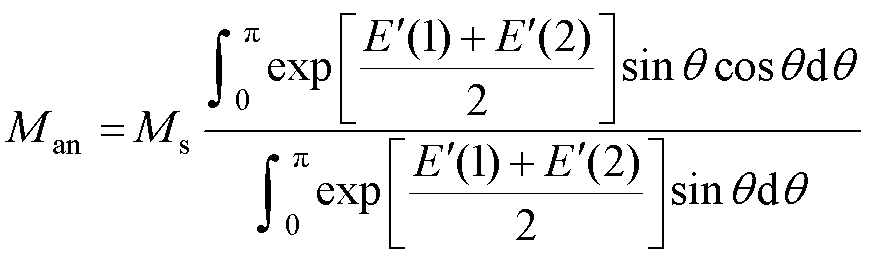（2）
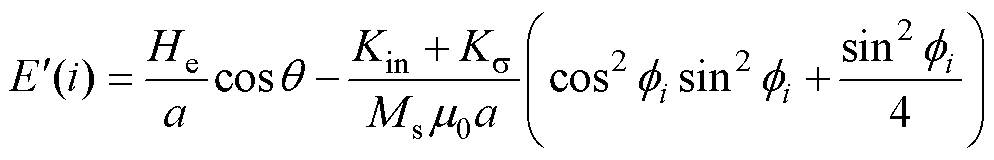（3）
式中，Ms为饱和磁化强度；q 为磁矩和外加磁场的夹角；f 为轧制方向与外加磁场的夹角；Kin为材料本身的平均各向异性能密度；He为有效磁场；Ks为机械应力引起的平均各向异性能密度；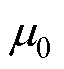
为真空磁导率。
用磁化强度与应力的乘积表示磁致伸缩量为
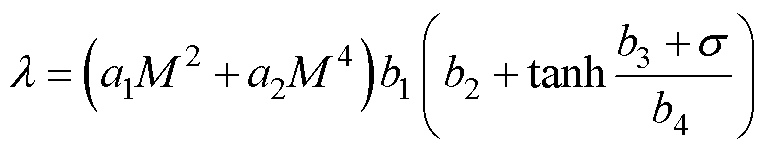（4）
式中，a1、a2、b1、b2、b3、b4由实验测得的磁滞伸缩数据拟合得到。
考虑应力对模型中钉扎系数k和磁畴密度因数a的影响，可得
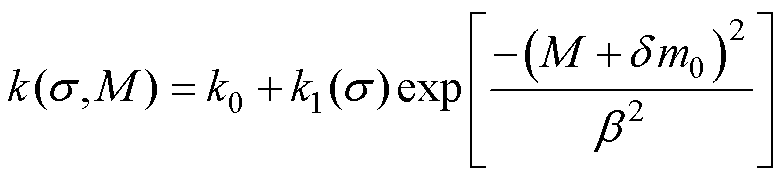（5）
式中，m0和b 为常数；k1(s)为应力对钉扎点参数的影响；k0为应力为零时的钉扎点系数。
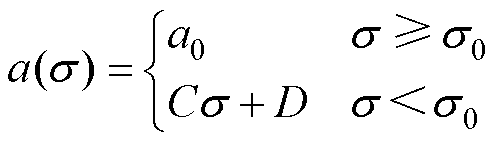（6）
式中，C、D为常数；a0为应力为零时的无滞回磁化形状参数；s0为一个常数。关于改进S-J-A模型的更多信息可以参见文献[10]。
在MBN信号检测中，MBN检测线圈的感应电压VB与畴壁的速度成正比[12-13]，即
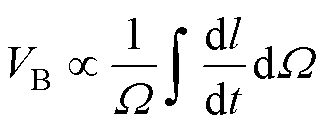（7）
式中，W 为样品磁化部分的体积；dl/dt为磁畴壁移动速度。
根据J-A磁滞模型，磁畴壁在运动过程中受到均匀分布的钉扎位点的阻碍，而畴壁运动克服钉扎位点的能量损失与磁化强度的不可逆变化成正比。因此单位体积的能量损失可以表示为
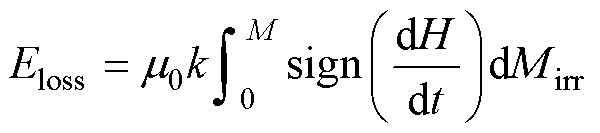（8）
式中，符号函数sign(dH/dt)确保钉扎点始终阻碍磁畴壁运动。
当磁畴壁移动时，它们会受到钉扎位点的“摩擦型”力的影响，该力总是与磁畴壁运动方向相反，阻碍畴壁的运动。假设钉扎点的阻力是恒定的，单位体积的能量损失Eloss也可以表示为
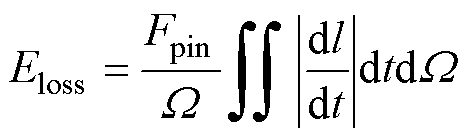（9）
式中，Fpin为钉扎点对单位体积的阻力。
由式（7）～式（9）可以得到
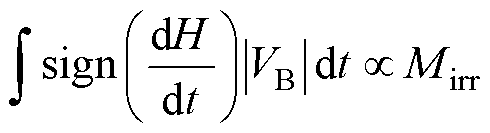（10）
由于MBN信号是一个高频信号，并且具有上下对称的特点，因此可以利用MBN信号的上半部分包络线Menvelope来代替|VB|进行时间积分，即
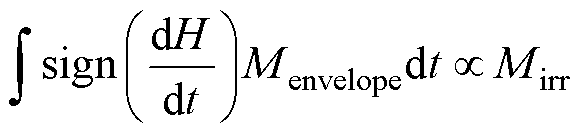（11）
式（11）两边对时间求微分并引入一个常数v0，可以得到
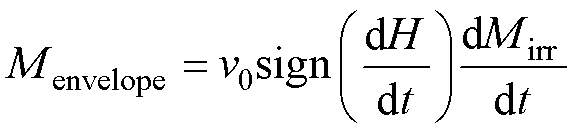（12）
根据式（1），可以将改进的S-J-A滞后模型的可逆参数c设为0，从而得到不可逆磁化曲线Mirr(t)为
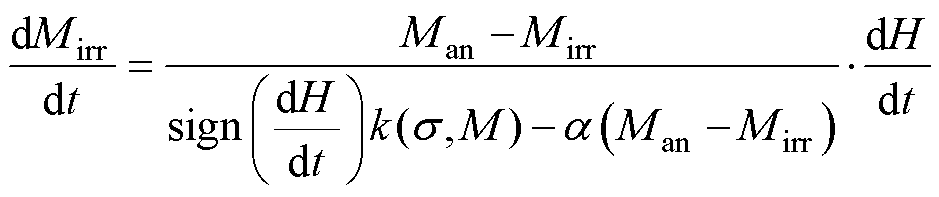（13）
将式（12）代入式（13）可以对MBN信号的上半部分包络线进行模拟，得
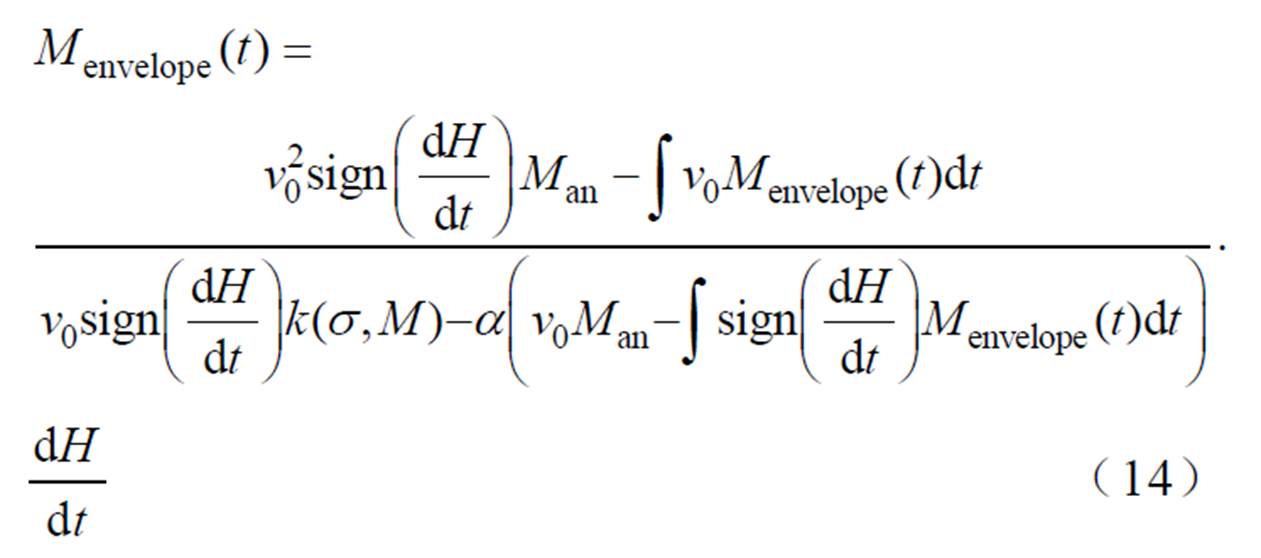
MBN产生的电动势频率范围在1～50 kHz之间。因此在Matlab中生成1～50 kHz的白噪声信号，首先使用randn函数生成高斯白噪声，并通过设计一个带通滤波器，如六阶巴特沃斯滤波器，来限制噪声的频率范围，仅保留1～50 kHz的频率成分。最后，通过该滤波器filter函数，得到指定频率范围内的带限白噪声信号，如图1所示。
本文利用幅值调制技术来实现MBN信号的模拟，具体流程如下：将白噪声信号乘以仿真得到的包络线，这样白噪声的幅值就会按照包络线的幅值变化。最终得到MBN信号[7]。
本文MBN测量平台如图2所示，该平台由五个模块组成：应力施加模块、励磁模块、信号检测模块、信号处理模块和反馈控制回路模块。应力施加模块对软磁材料单片施加机械应力。励磁模块和反馈控制模块产生特定的波形并施加到材料上。信号检测模块使用放置在样品表面的MBN检测线圈得到感应电压VB，然后经过放大和滤波处理后在PC上位机上显示高质量的MBN信号。使用缠绕在样品上的二次线圈检测磁感应强度信号，使用电流互感器检测磁场强度信号。通过这个实验平台可以获得材料的B(H)曲线以及MBN信号。硅钢片中的磁场强度H和磁感应强度B分别为
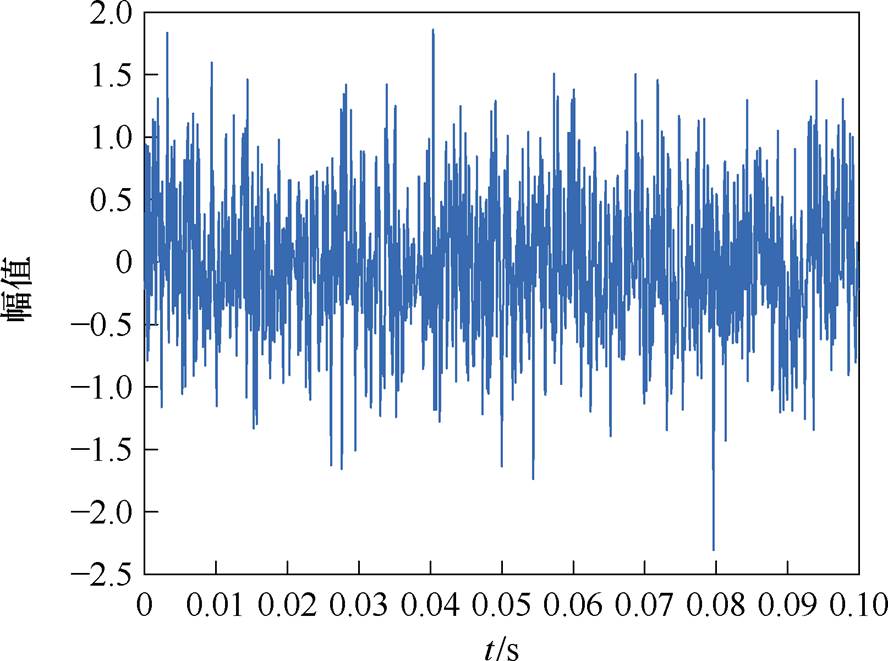
图1 频率范围在1～50 kHz之间的白噪声
Fig.1 White noise in the frequency range of 1 to 50 kHz
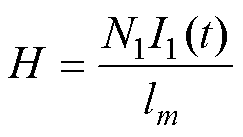（15）
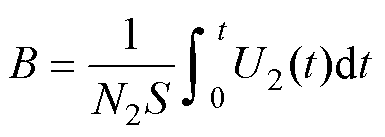（16）
式中，N1和N2为一次侧励磁线圈和二次侧感应线圈匝数；I1和U2分别为一次电流和二次电压；lm为磁通路径长度；S为测量样品有效截面积。
图2 MBN测量平台
Fig.2 MBN measurement platform
本文研究对象为取向电工钢片（30QG120）、无取向硅钢（35WW230）和非晶合金（1K101）。实验样品的参数见表1。外施一个频率为10 Hz的正弦波激励电压，使软磁材料达到饱和磁通密度，取向硅钢、无取硅钢和非晶合金的饱和磁通密度分为1.8、1.6和1.5 T。并且测量处于饱和磁通密度的软磁材料在的不同应力条件下的MBN信号以及磁滞回线B(H)。另外，由于非晶合金材料的厚度较薄，因此只对其施加拉应力进行研究。
表1 实验样品参数
Tab.1 Experimental sample parameters
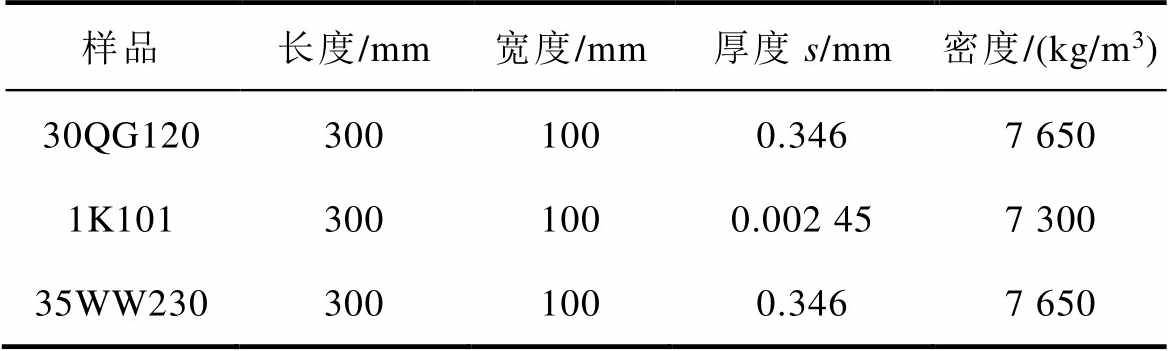
样品长度/mm宽度/mm厚度s/mm密度/(kg/m3) 30QG1203001000.3467 650 1K1013001000.002 457 300 35WW2303001000.3467 650
本文通过粒子群算法可以得到改进MBN模型的各种参数。关于参数识别在文献[10]中有详细说明。
常见的特征值包括峰-峰值、方均根值、偏度、冲击因数、能量值等，这些特征值从不同的角度展示信号的内在特性，本文选取了方均根值（Root Mean Square, RMS）峰-峰值，分析其变化规律。方均根值为
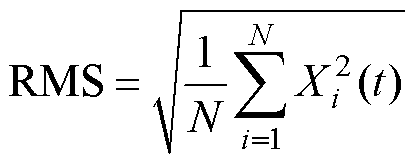（17）
式中，Ｘi(t)为第i个采样点；N为采样点数量。
本文通过计算MBN特征值的测量值和仿真值的相对误差来验证模型的准确性。
（18）
晶粒取向硅钢片通过取向处理，在轧制方向上具有优异的磁导率和导磁性能，并且表现出明显的各向异性。在宏观上可知，应力可以通过对各向异性能量的改变引起硅钢片的磁性能改变，如式（2）和式（3）所示。在微观上，由于电工钢片的各向异性以及厚度很小，造成非轧制方向的磁畴具有较高的退磁系数，进而提高了其退磁能力。为了降低能量，这种材料会形成板状结构畴。同时，由于生产和加工过程中会导致内部残留杂质和内应力，晶体排列不规则，形成了柳叶刀畴（即附加畴），这些附加畴由内部横向磁畴和表面封闭域构成，可以降低总能量[14]。无应力下取向硅钢MBN信号如图3所示。在没有拉应力的情况下，当主磁畴壁消失时，会留下表面的附加畴，导致在此情况下MBN信号由主磁畴壁的移动产生，因此只会出现一个峰值。然而，在施加拉应力下，拉伸应力会抑制附加畴的生成，随着磁场强度的增加，附加畴会重新出现。施加拉应力2、5、10 MPa下取向硅钢MBN信号如图4～图6所示。附加畴的生成伴随着畴壁的移动，因此会形成双峰结构的MBN信号，如图4a、图5a和图6a所示。
随着拉应力的增大，磁畴壁间距缩小导致磁畴壁运动损耗减小，即提高了磁畴壁的迁移率。并且随着拉应力的增大，更多的附加畴被抑制，这导致随着拉应力的增大，峰-峰值1和峰-峰值2均呈现增大的趋势，并且峰值2的增大幅度大于峰值1，拉应力下取向硅钢MBN信号峰-峰值如图7所示。由图3～图6可知，用本文MBN模型可以准确地模拟拉应力条件取向硅钢片的MBN信号和包络线。图7为测量和模拟的取向硅钢MBN信号峰-峰值随着拉应力的变化趋势。
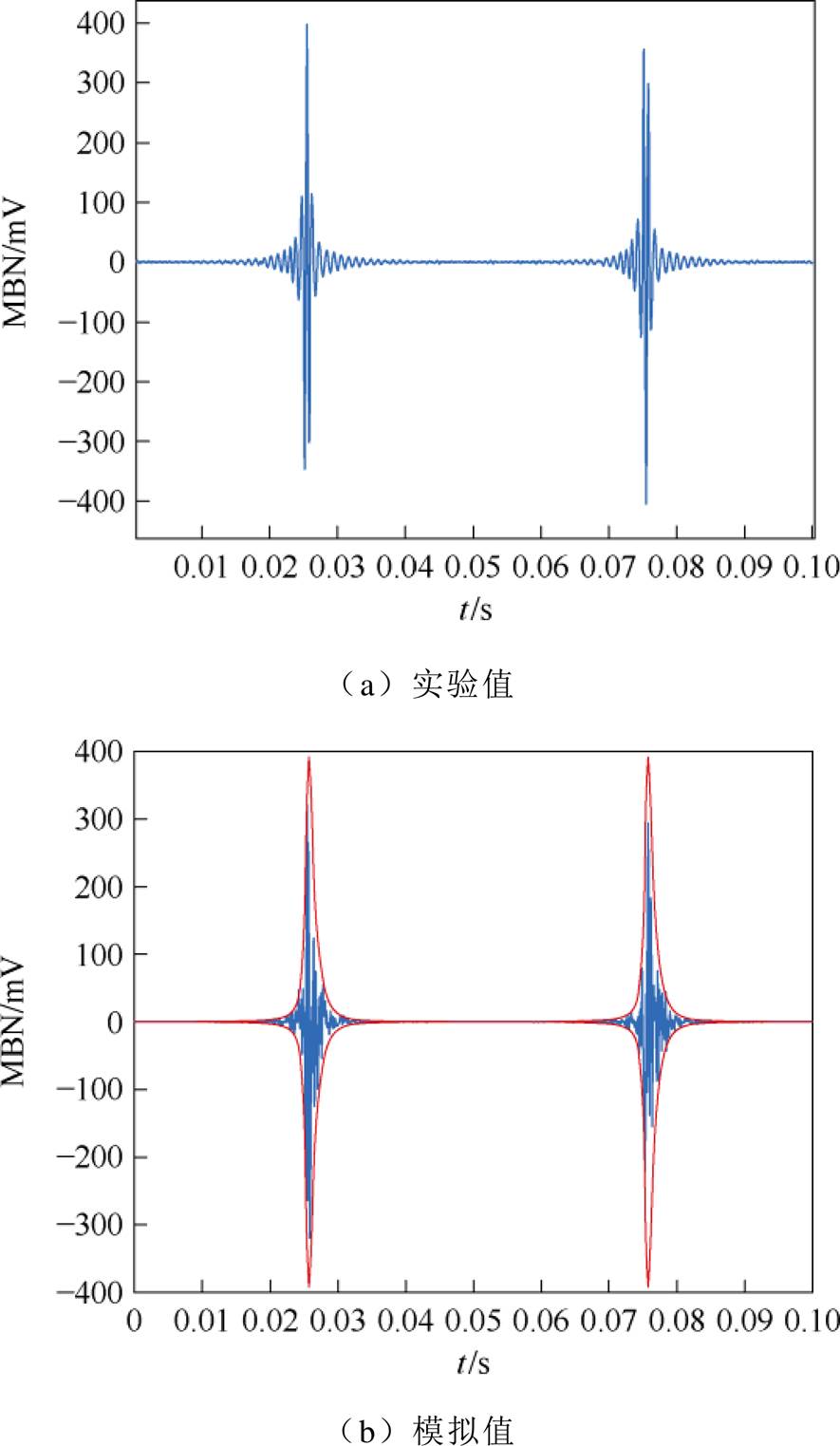
图3 无应力下取向硅钢MBN信号
Fig.3 MBN signal of oriented silicon steel without stress
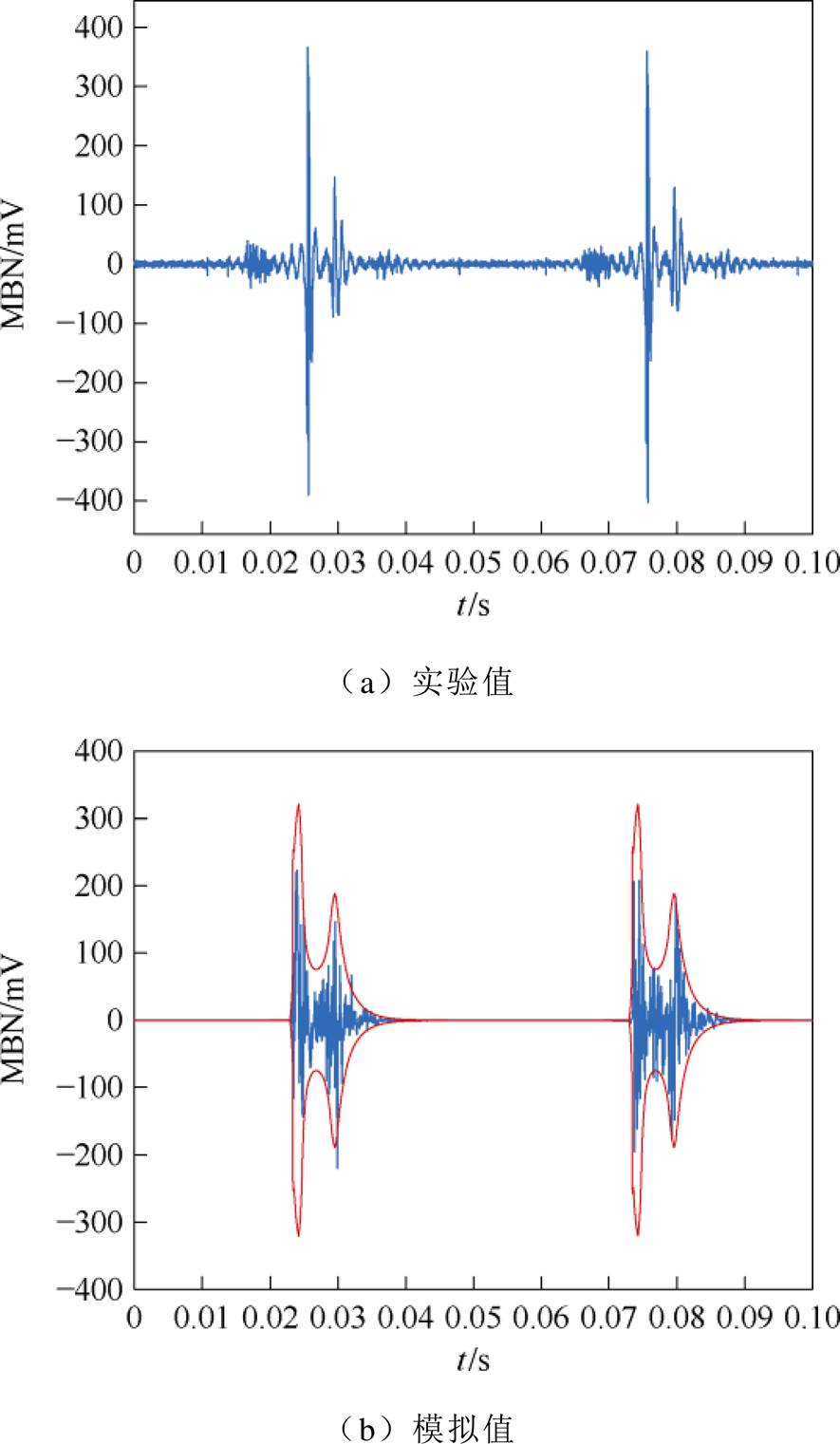
图4 2 MPa拉应力下取向硅钢MBN信号
Fig.4 MBN signal of oriented silicon steel under 2 MPa tensile stress
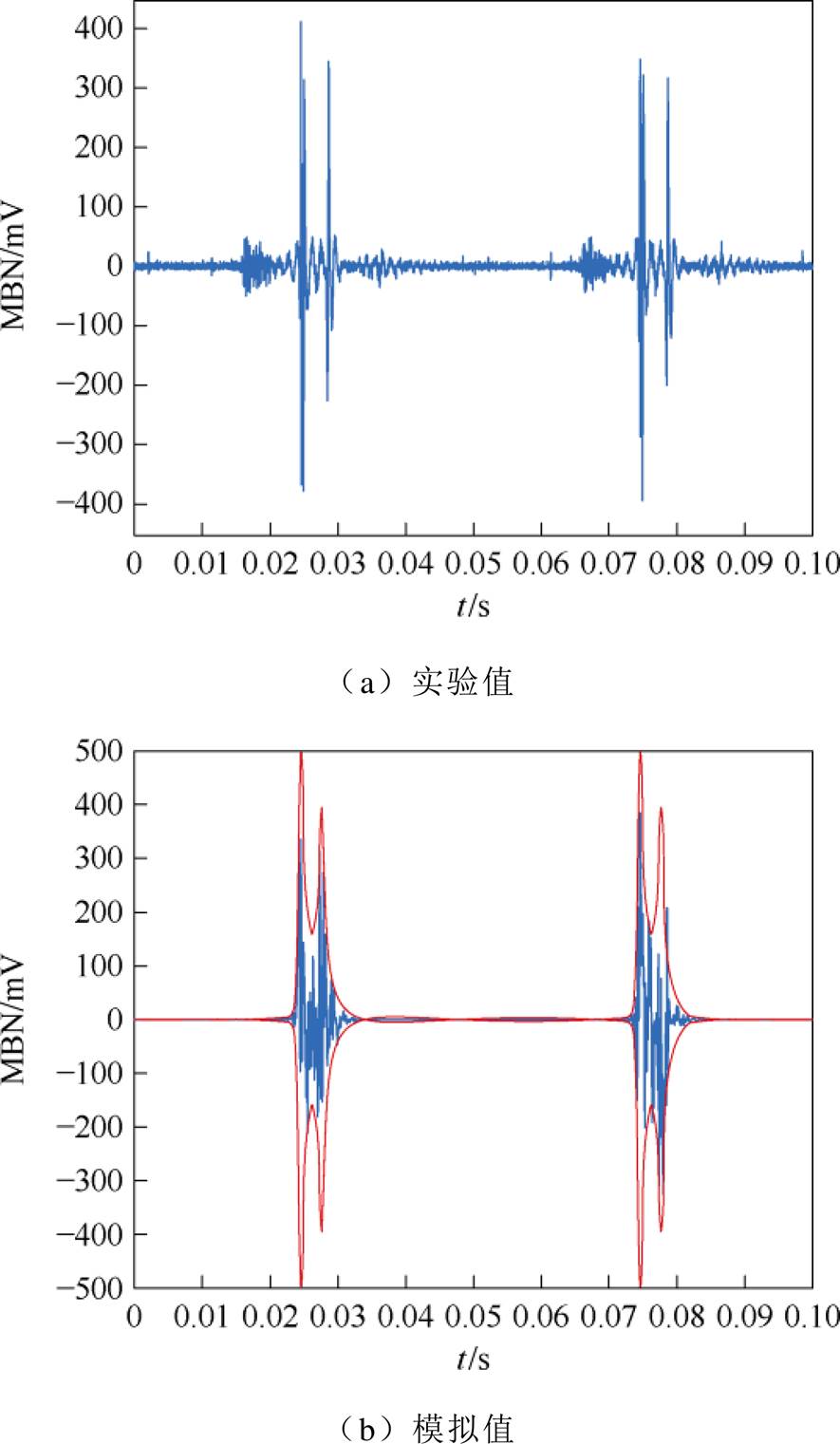
图5 5 MPa拉应力下取向硅钢MBN信号
Fig.5 MBN signal of oriented silicon steel under 5 MPa tensile stress
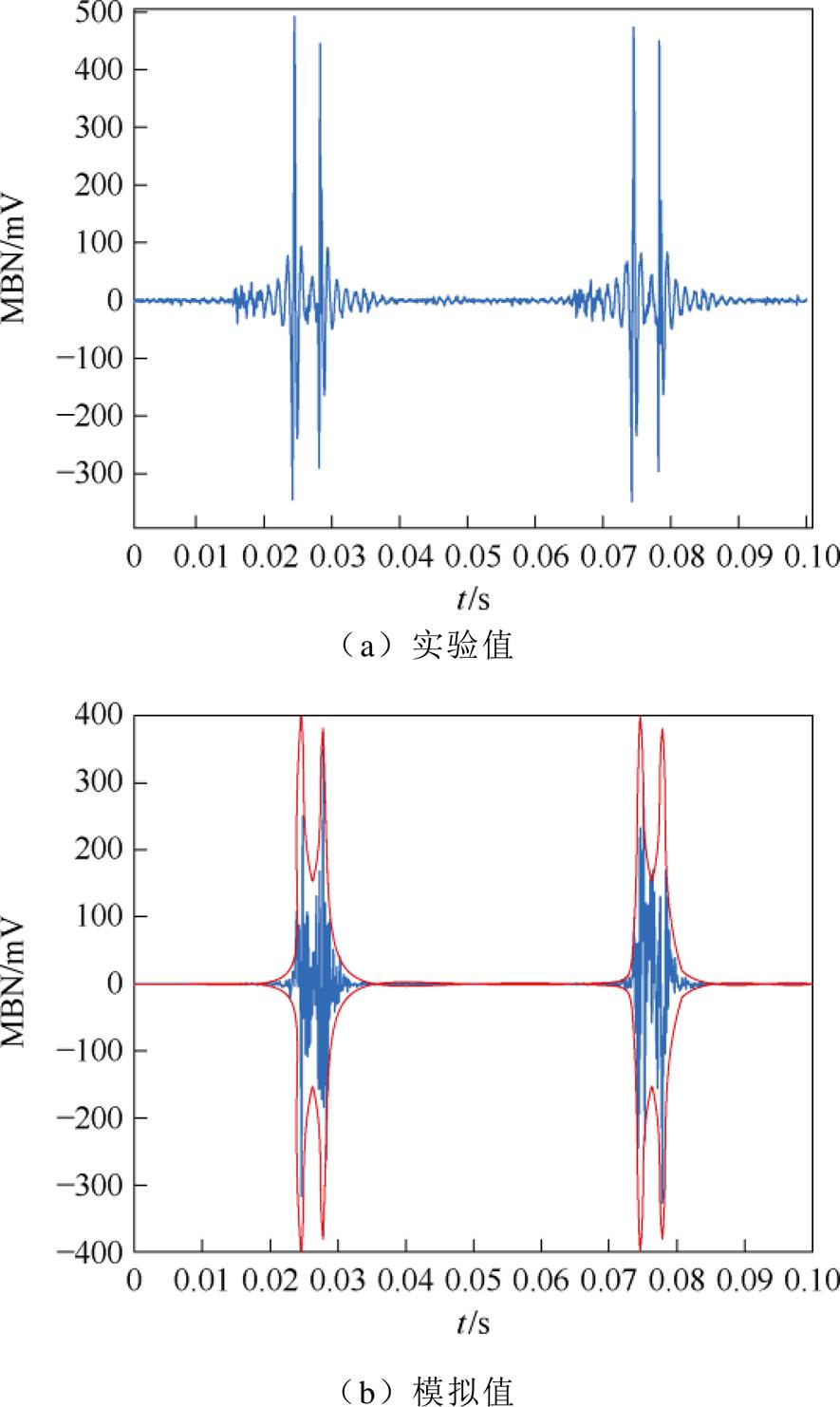
图6 10 MPa拉应力下取向硅钢MBN信号
Fig.6 MBN signal of oriented silicon steel under 10 MPa tensile stress
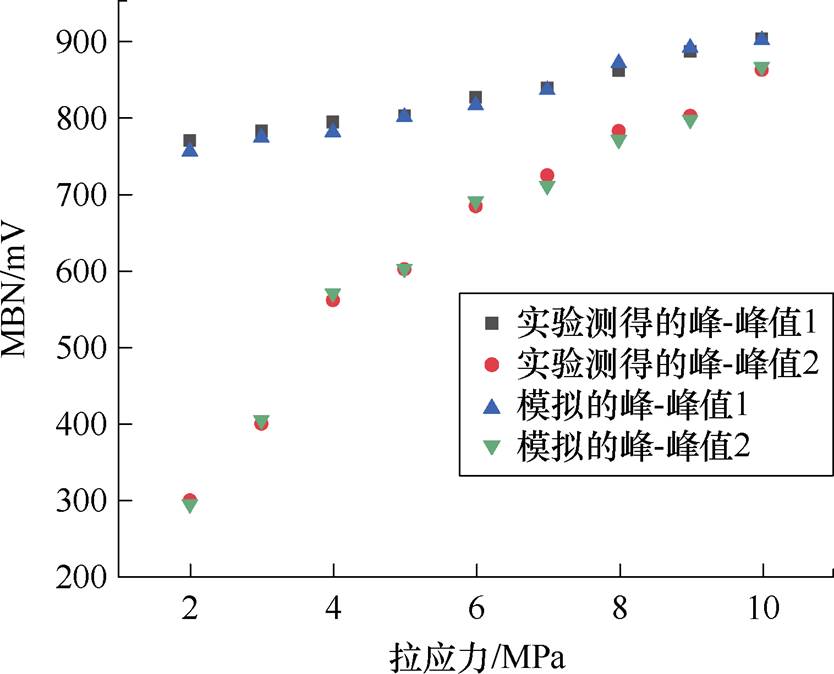
图7 拉应力下取向硅钢MBN信号峰-峰值
Fig.7 Peak-to-peak value of MBN signal in oriented silicon steel under tensile stress
对比图3、图8～图10可知，取向硅钢片MBN信号随着压应力的增大而减弱。这是由于当沿着轧制方向施加磁场和压应力时，取向电工钢片的磁畴结构发生了改变，磁畴结构会从板状的“零应力模式”转变为“应力模式Ⅰ”类型[15-17]，这种模式会增加90°畴壁面积，阻碍了磁化过程。另一方面施加压应力增加了磁畴壁能量，从而降低了磁畴壁的迁移率，导致MBN信号减弱。由图8～图10可知，本文MBN模型可以准确地模拟压应力条件下取向硅钢片的MBN信号和包络线。图11为测量和模拟的取向硅钢MBN信号峰-峰值随着压应力的变化趋势。表2为取向硅钢MBN信号实验与模拟的特征值（峰-峰值和方均根）的相对误差，体现了模型的准确性。
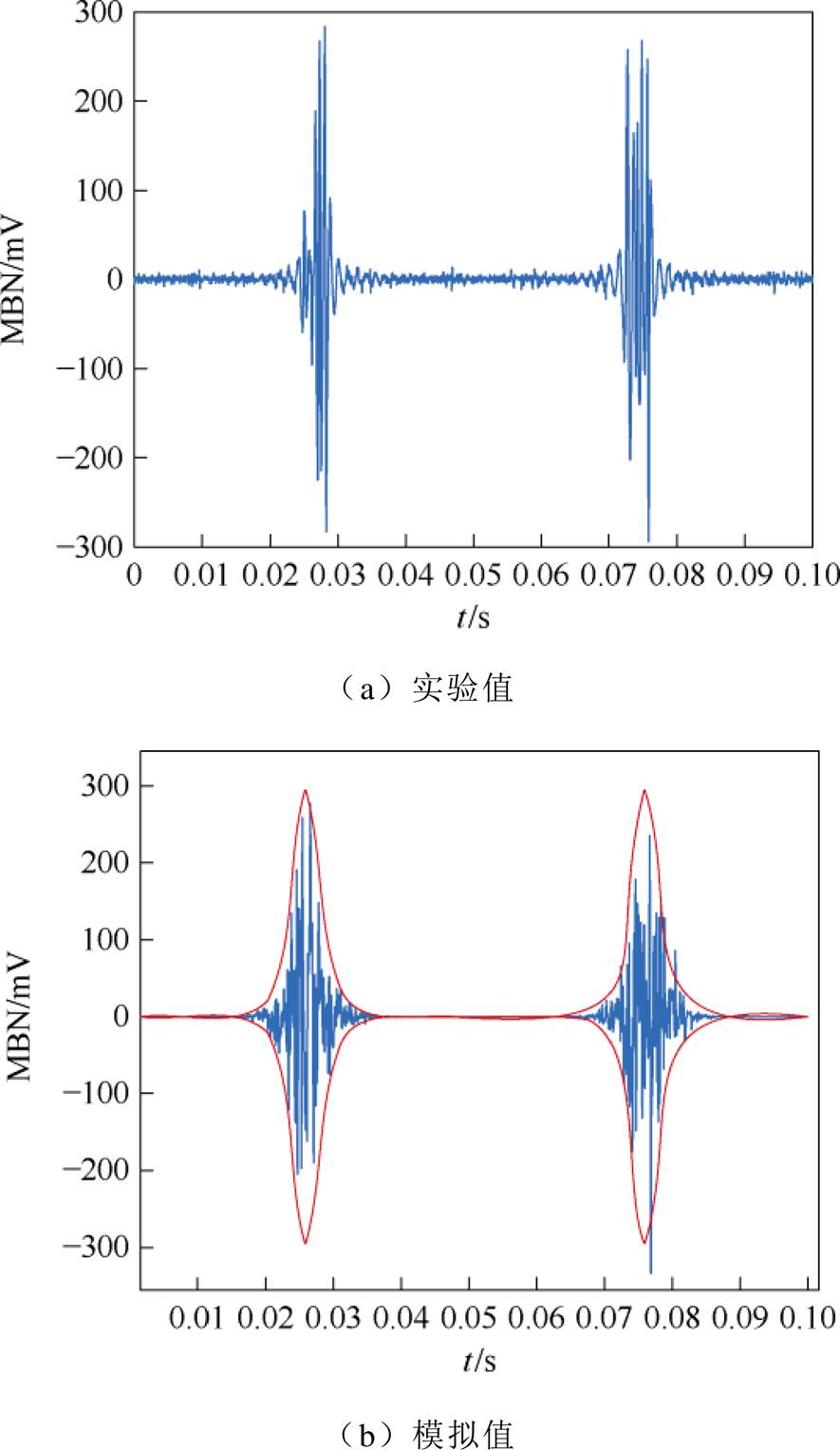
图8 2 MPa压应力下取向硅钢MBN信号
Fig.8 MBN signal of oriented silicon steel under 2 MPa compressive stress
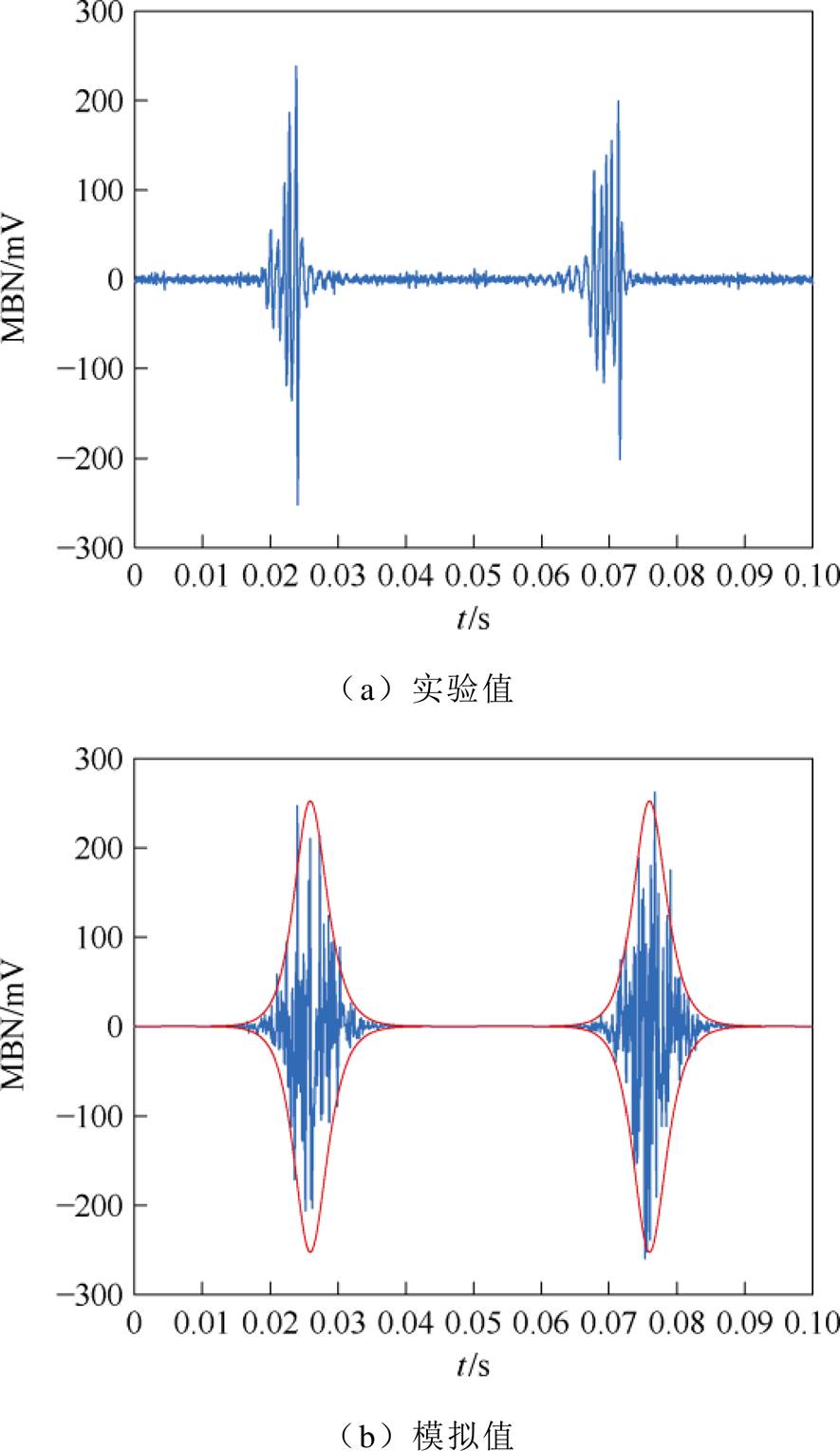
图9 3 MPa压应力下取向硅钢MBN信号
Fig.9 MBN signal of oriented silicon steel under 3 MPa compressive stress
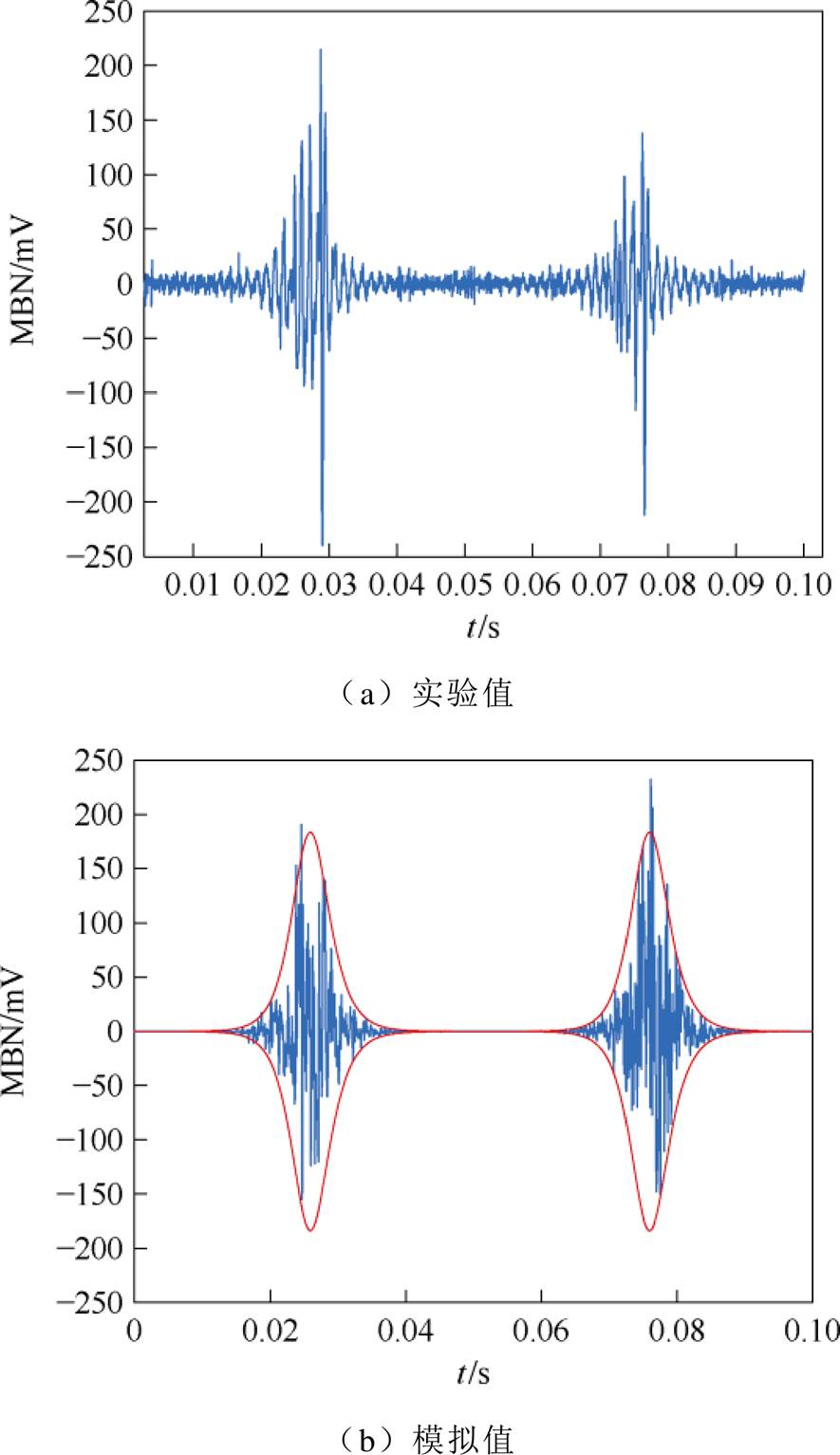
图10 5 MPa压应力下取向硅钢MBN信号
Fig.10 MBN signal of oriented silicon steel under 5 MPa compressive stress
无取向硅钢则因晶粒排列无序而磁导率相对较低，并且呈现磁性各向同性的特点。无应力以及施加拉应力2、5、10 MPa下无取向硅钢MBN信号如图12～图15所示。通常无取向硅钢的MBN信号比取向硅钢小得多，并且应力不能通过改变各向异性能而改变硅钢片的磁性能，这导致无取向硅钢在拉应力情况下呈现单峰结构。如图13a、图14a和图15a所示。
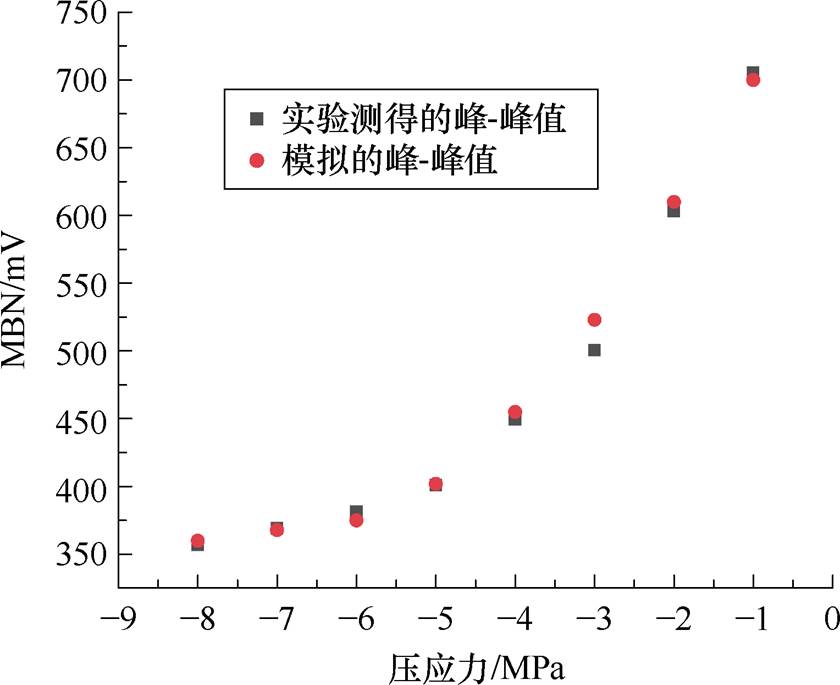
图11 压应力下取向硅钢MBN信号峰-峰值
Fig.11 Peak-to-peak value of MBN signal in oriented silicon steel under compressive stress
表2 机械应力下取向硅钢MBN信号的特征值模拟值与实验值的相对误差
Tab.2 Relative error between simulated and experimental characteristic values of MBN signal of oriented silicon steel under mechanical stress
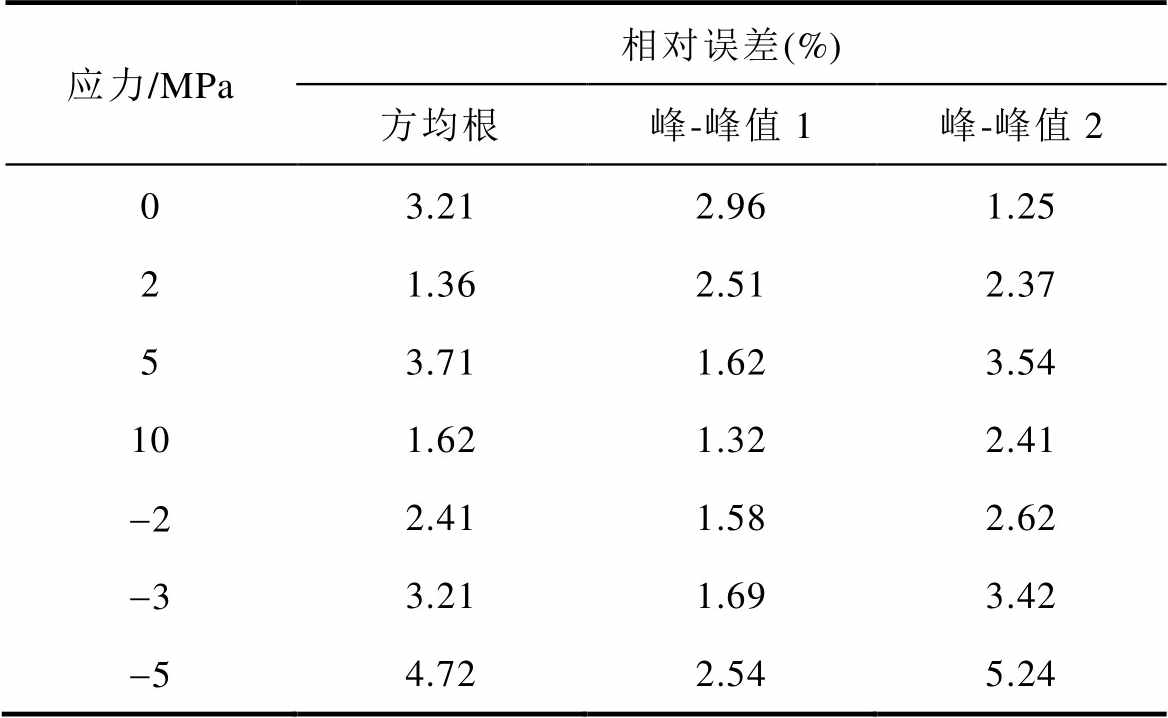
应力/MPa相对误差(%) 方均根峰-峰值1峰-峰值2 03.212.961.25 21.362.512.37 53.711.623.54 101.621.322.41 -22.411.582.62 -33.211.693.42 -54.722.545.24
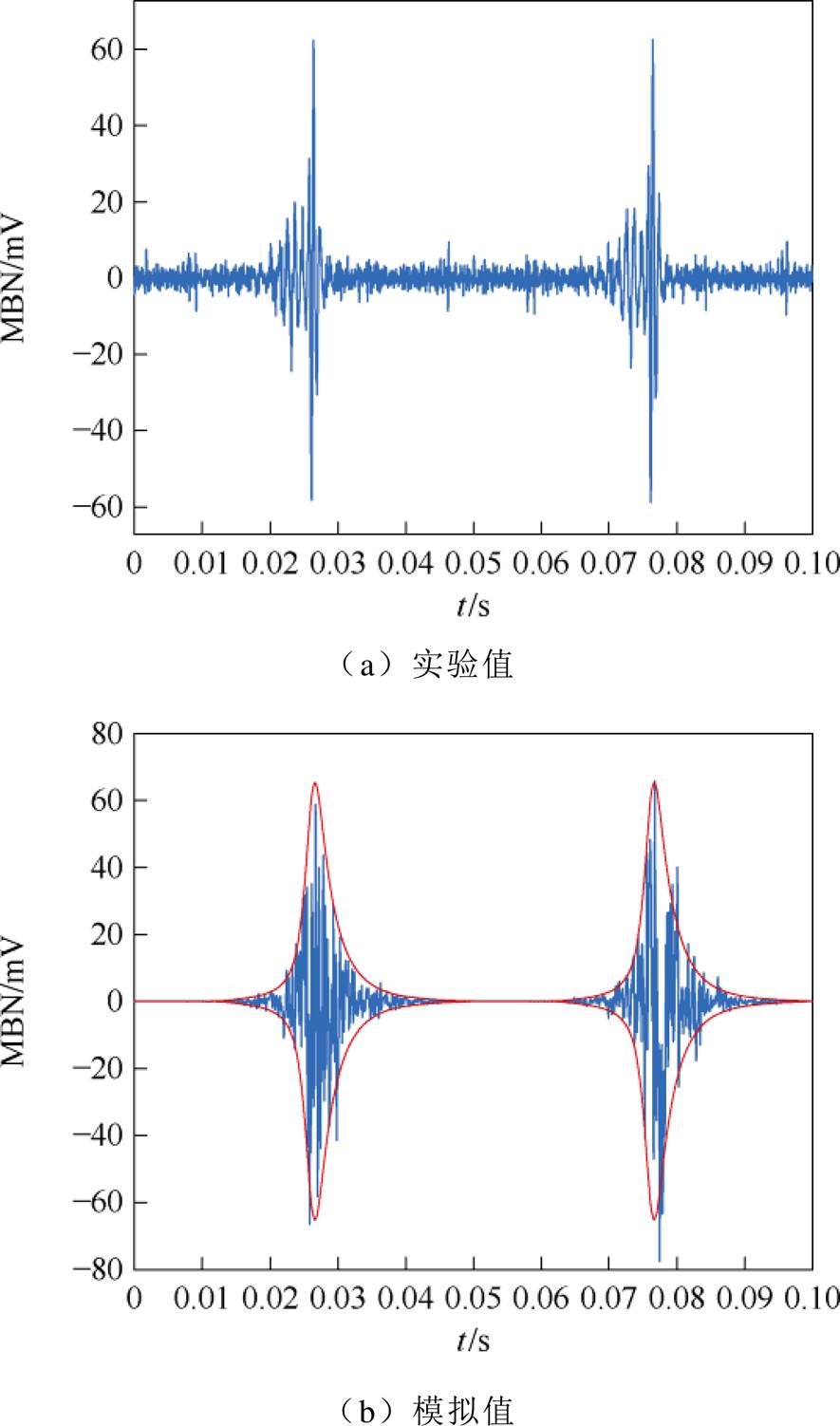
图12 无应力下无取向硅钢MBN信号
Fig.12 MBN signal of oriented non-silicon steel without tensile stress
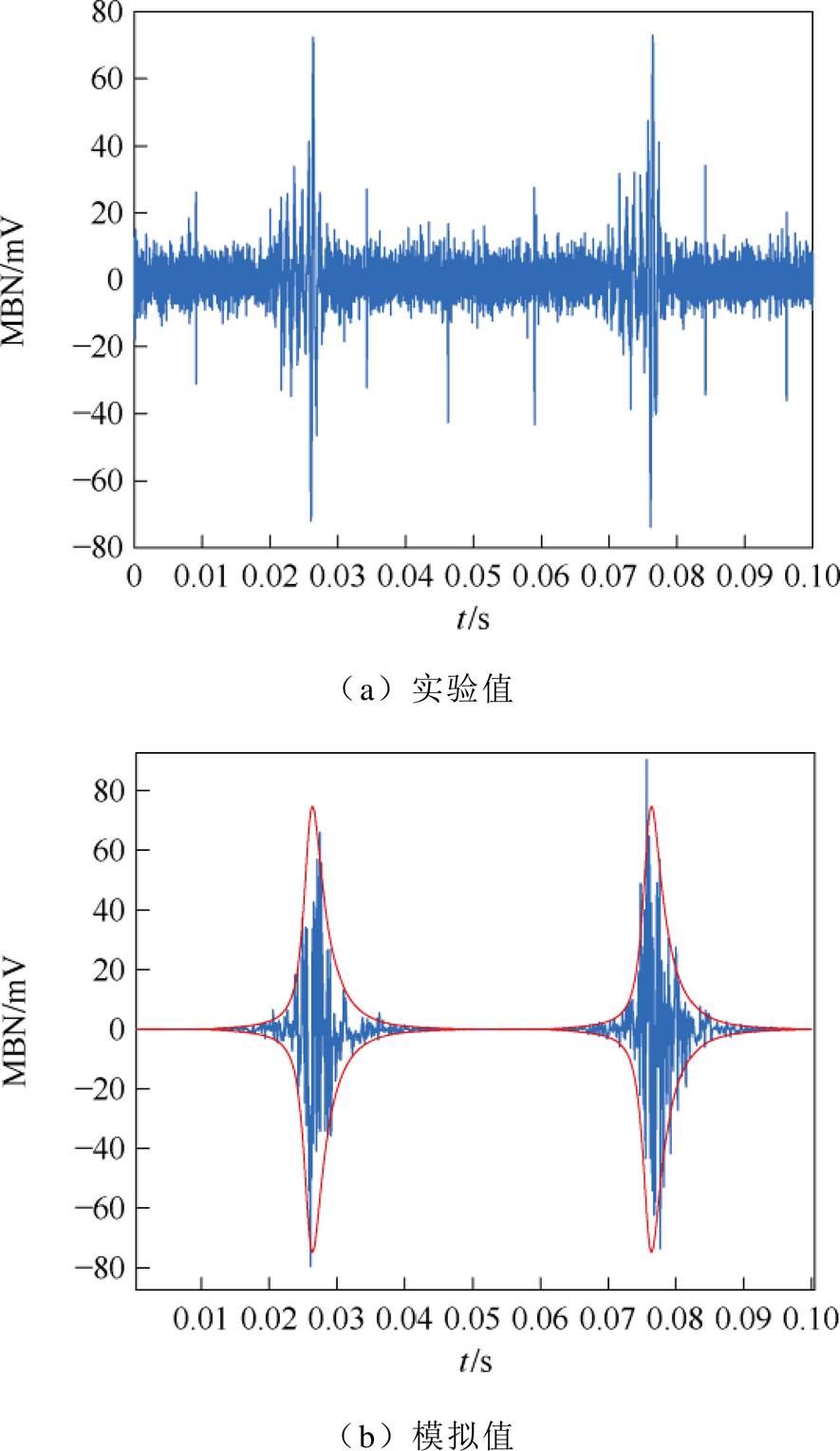
图13 2 MPa拉应力下无取向硅钢MBN信号
Fig.13 MBN signal of non-oriented silicon steel under 2 MPa tensile stress
随着拉应力的增大，无取向硅钢磁畴壁间距缩小导致磁畴壁运动损耗减小，即提高了磁畴壁的迁移率，从而使得MBN信号增强。由图13～图15可知，本文MBN模型准确地模拟了应力下无取向硅钢的MBN信号和包络线。图16为测量和模拟的无取向硅钢MBN信号峰-峰值随着拉应力的变化趋势。
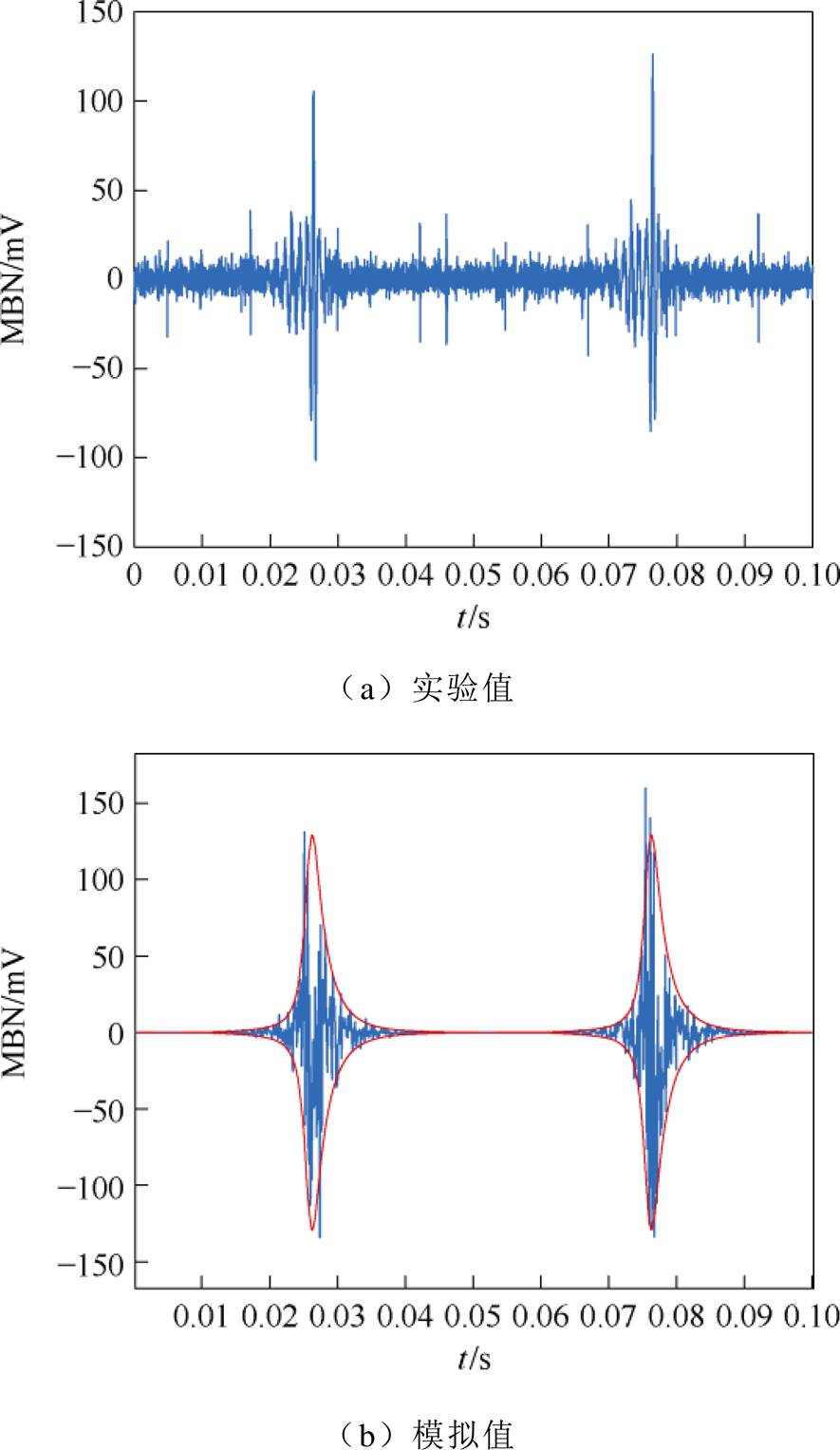
图14 5 MPa拉应力下无取向硅钢MBN信号
Fig.14 MBN signal of non-oriented silicon steel under 5 MPa tensile stress
施加2、3、5 MPa压应力下无向硅钢MBN信号如图17～图19所示。对比图12、图17～图19可知，无取向硅钢的MBN随着压应力的增大而减弱。这是由于施加压应力增加了磁畴壁的能量，畴壁移动的难度增加，导致MBN信号减弱。由图17～图19可知，本文MBN模型准确地模拟了应力下无取向硅钢的MBN信号。图20为测量和模拟的无取向硅钢MBN信号峰-峰值随着压应力的变化趋势。表3为无取向硅钢MBN信号实验与模拟的特征值（峰-峰值和方均根）的相对误差，相对误差较小，体现了模型的准确性。
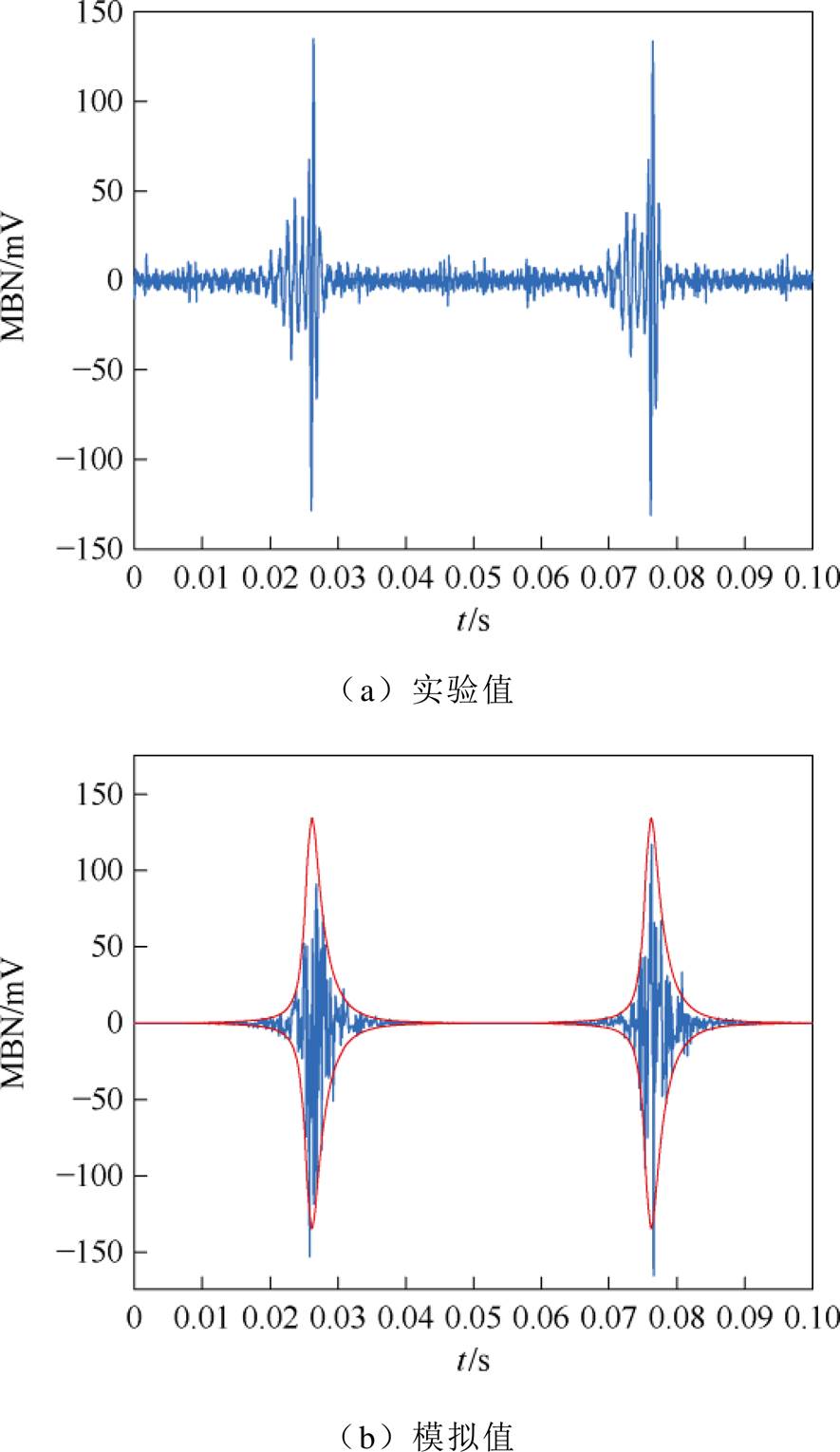
图15 10 MPa拉应力下无取向硅钢MBN信号
Fig.15 MBN signal of non-oriented silicon steel under 10 MPa tensile stress
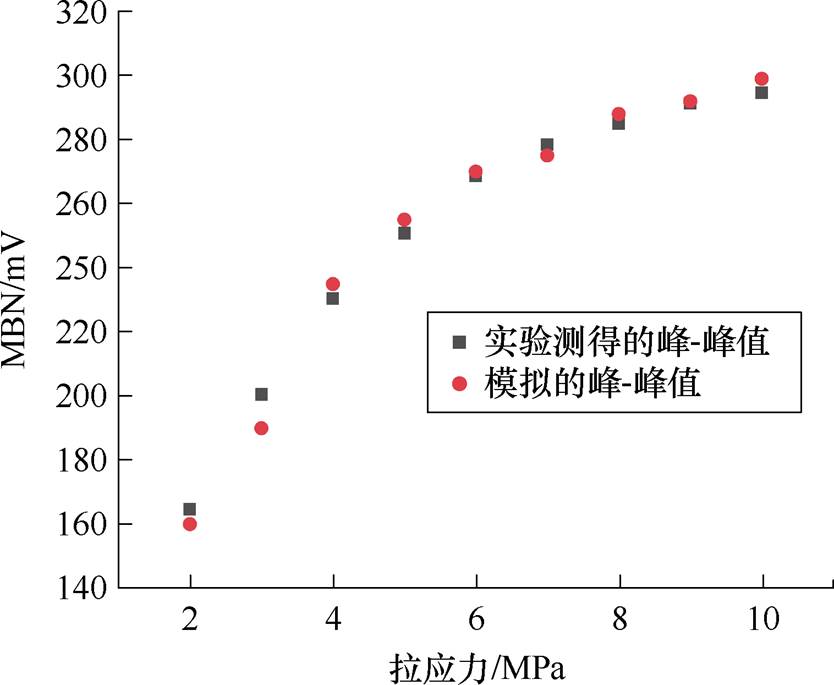
图16 拉应力下无向硅钢MBN信号峰-峰值
Fig.16 Peak-to-peak value of MBN signal in non-oriented silicon steel under tensile stress
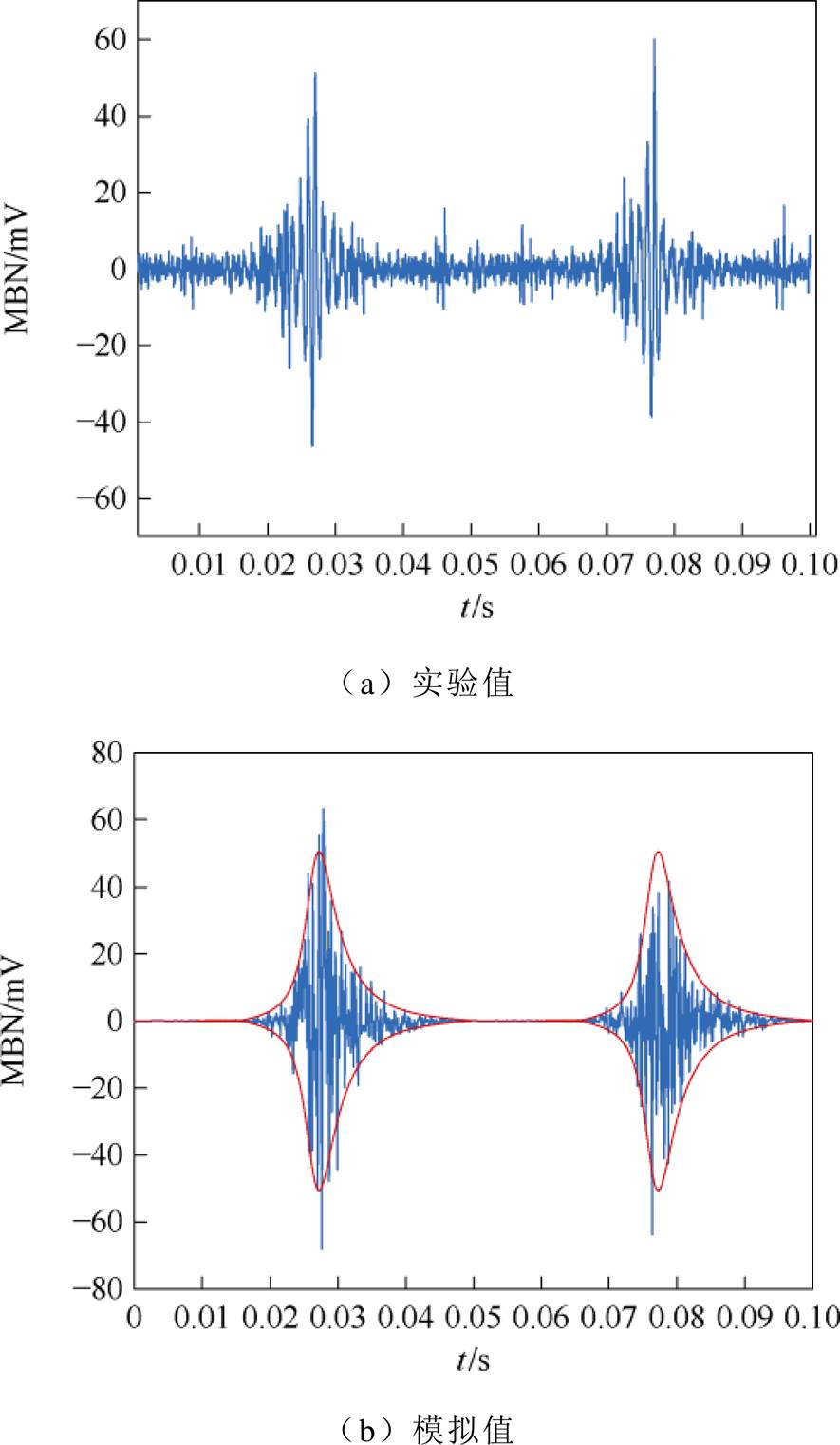
图17 2 MPa压应力下无向硅钢MBN信号
Fig.17 MBN signal of non-oriented silicon steel under 2 MPa compressive stress
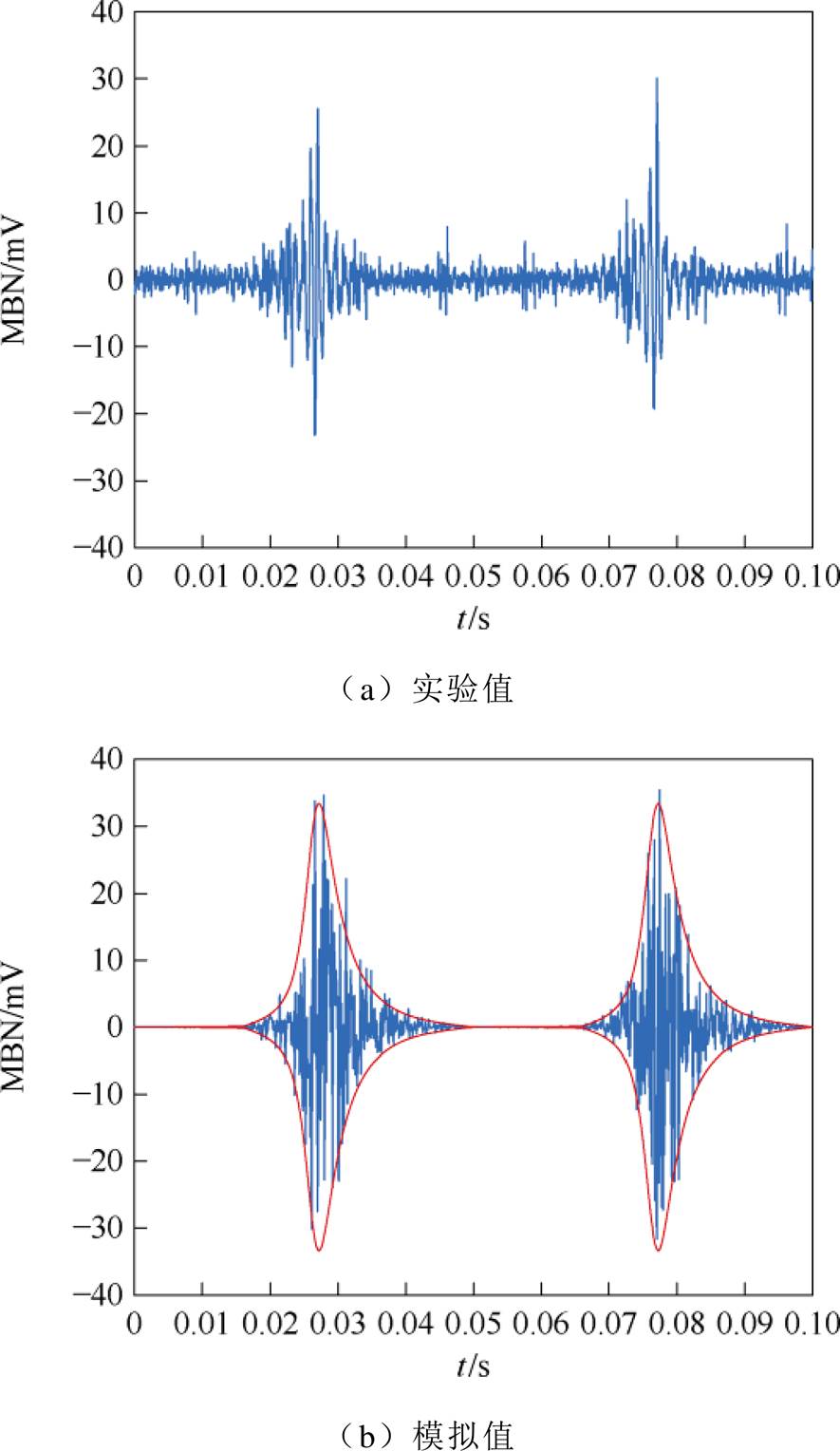
图18 3 MPa压应力下无取向硅钢MBN信号
Fig.18 MBN signal of non-oriented silicon steel under 3 MPa compressive stress
无应力下非晶合金MBN信号如图21所示。非晶合金因为没有明显的晶体结构，具有优异的磁导率和磁性能，而且其表现出各向同性。这导致非晶合金的MBN信号和取向硅钢相当，并且对非晶合金施加拉应力后，MBN信号呈现单峰结构如图22a、图23a和图24a所示。
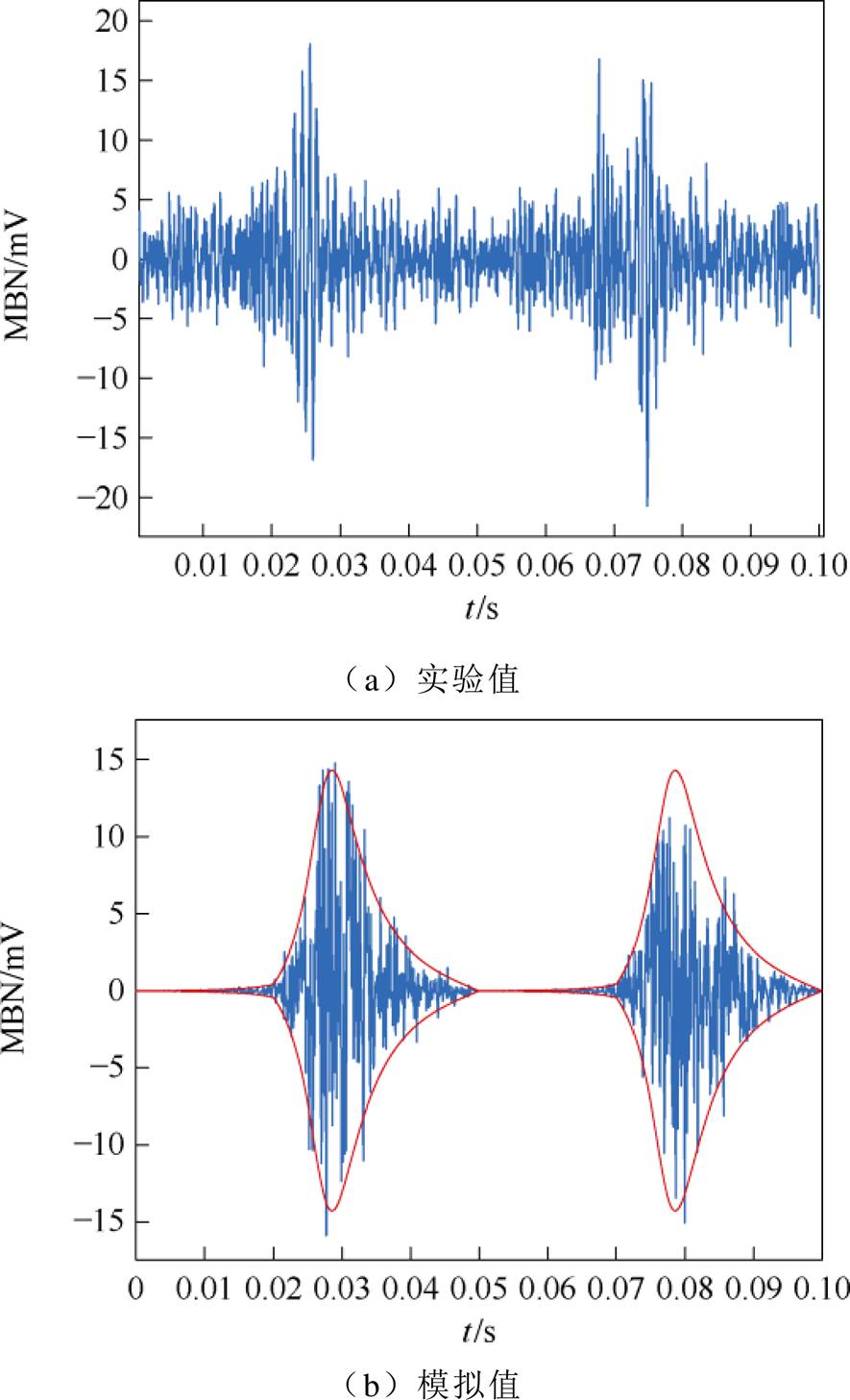
图19 5 MPa压应力下无取向硅钢MBN信号
Fig.19 MBN signal of non-oriented silicon steel under 5 MPa compressive stress
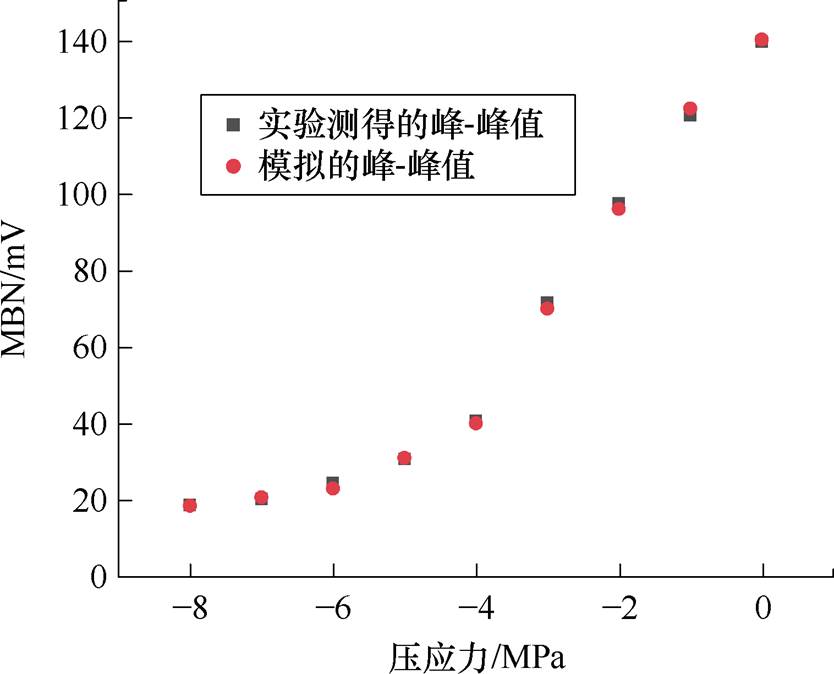
图20 压应力下无向硅钢MBN信号峰-峰值
Fig.20 Peak-to-peak value of MBN signal in non-oriented silicon steel under compressive stress
随着拉应力的增大，MBN信号峰值呈现增大的趋势。这是由于拉应力减少了磁畴壁能量，从而提高了磁畴壁的迁移率，导致MBN信号增强，如图25所示。由图22～图24可知，本文MBN模型可以准确地模拟拉应力下非晶合金的MBN信号。图25为测量与模拟的非晶合金的MBN信号的峰-峰值随着拉应力变化的趋势。表4为非晶合金MBN信号实验与模拟的特征值（峰-峰值和方均根）的相对误差，体现了模型的准确性。
表3 机械应力下无取向硅钢MBN信号的特征值模拟值与实验值的相对误差
Tab.3 Relative error between simulated and experimental characteristic values of MBN signal of non-oriented silicon steel under mechanical stress
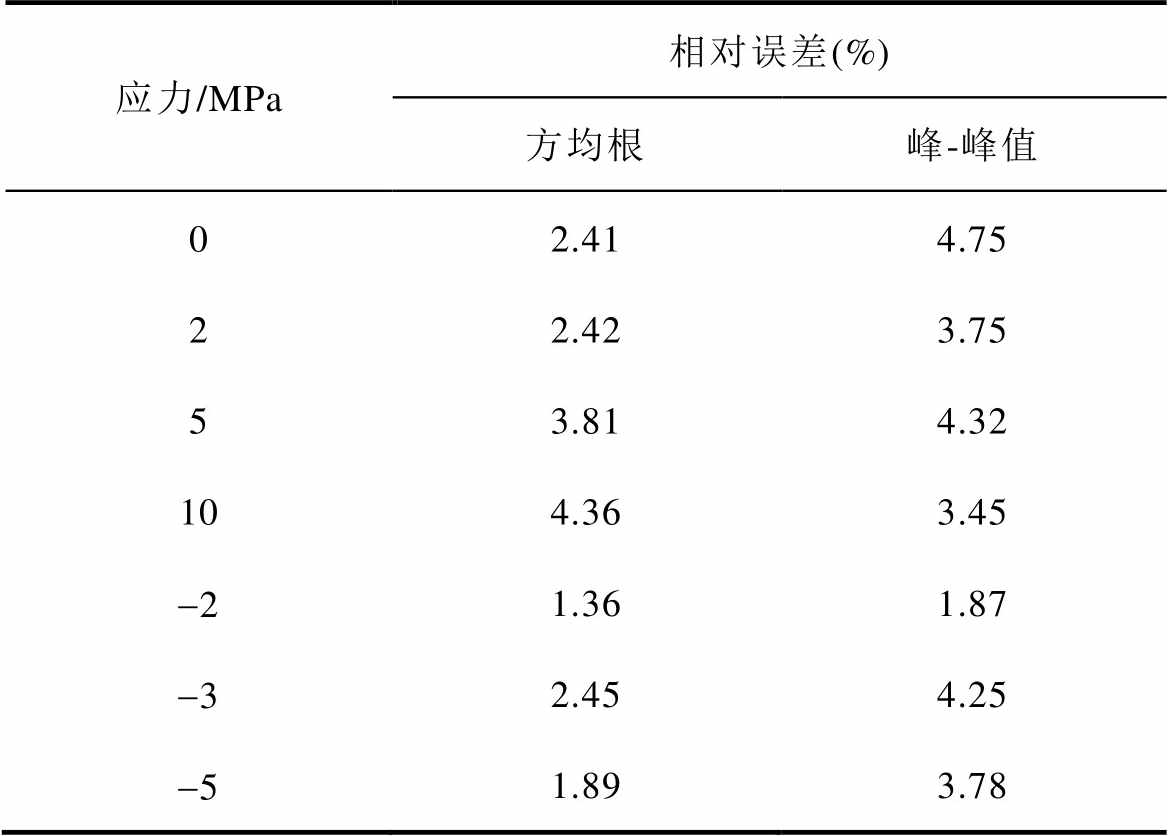
应力/MPa相对误差(%) 方均根峰-峰值 02.414.75 22.423.75 53.814.32 104.363.45 -21.361.87 -32.454.25 -51.893.78
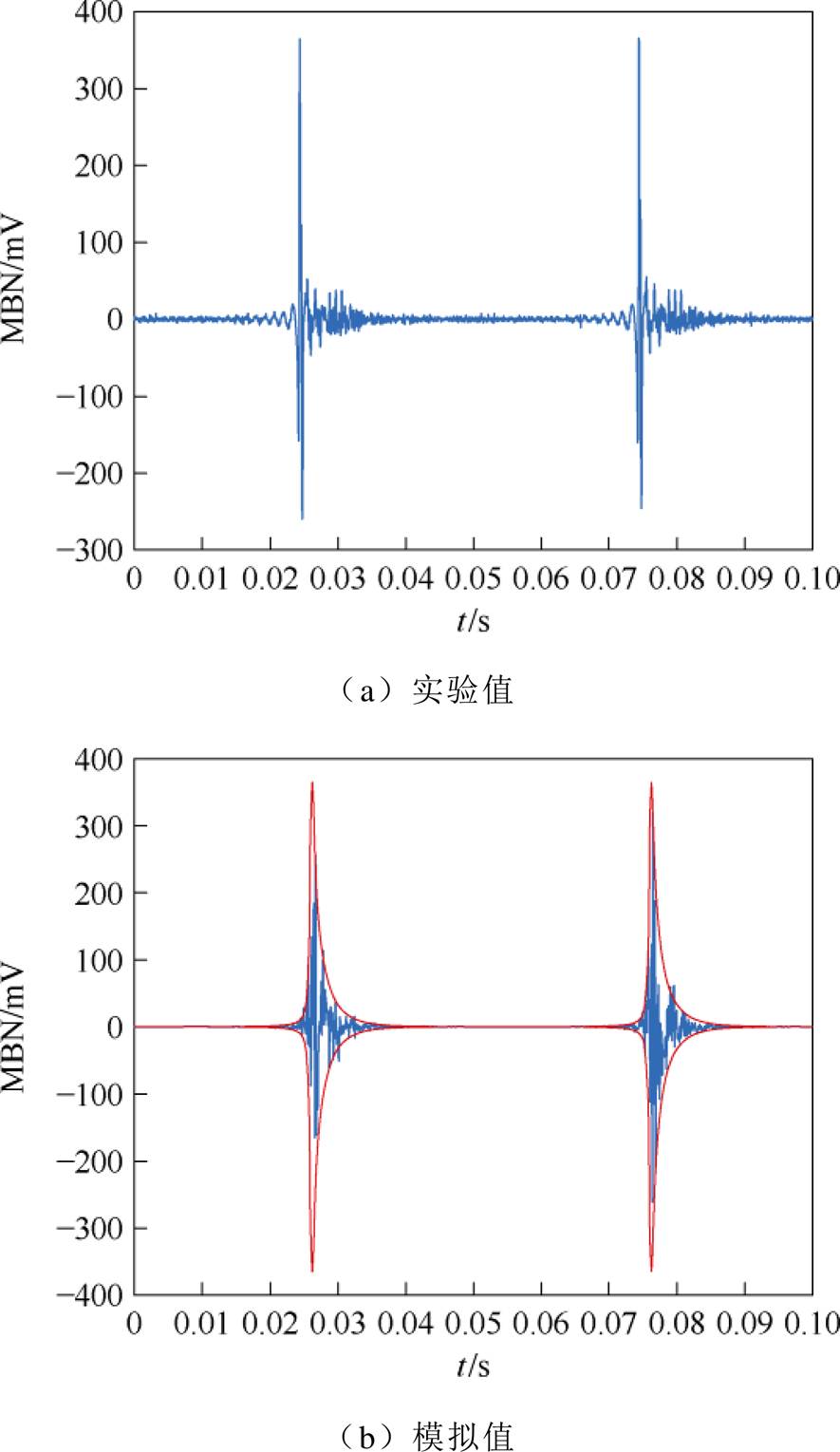
图21 无应力下非晶合金MBN信号
Fig.21 MBN signal of amorphous alloy without stress
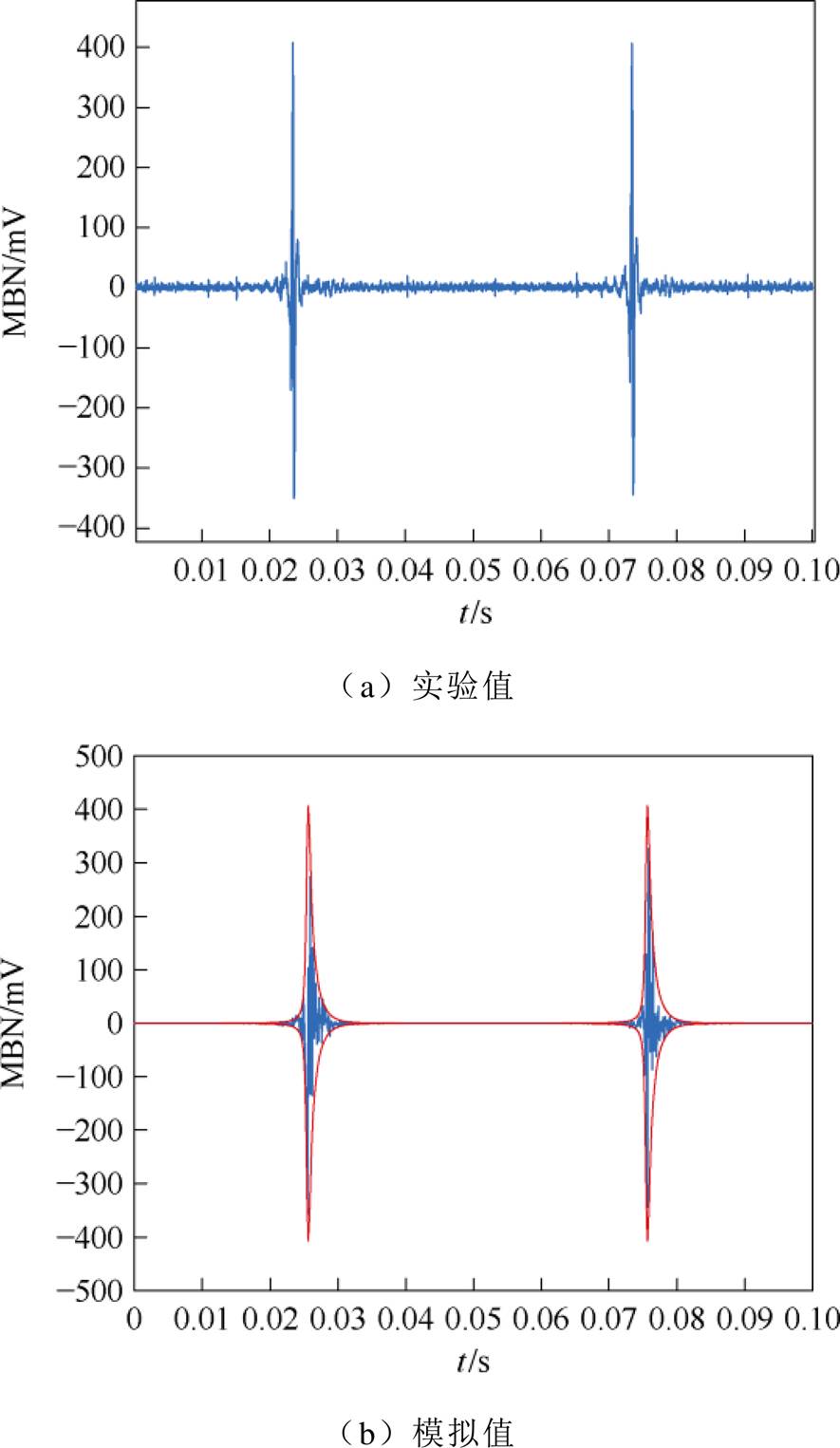
图22 10 MPa拉应力下非晶合金MBN信号
Fig.22 MBN signal of amorphous alloy under 10 MPa tensile stress
基于S-J-A磁滞模型的机械应力下的MBN模型准确地模拟了取向电工钢片（30QG120）、无取向硅钢（35WW230）和非晶合金（1K101）应力下的MBN信号，以及MBN信号的峰-峰值随应力变化的趋势。
进行了取向硅钢、无取向硅钢和非晶合金的MBN信号之间的对比，发现取向硅钢在受拉应力作用下呈现的双峰结构与其各向异性有关。对此进行了微观层面的分析，从而更深入地了解了应力对软磁材料磁性的影响以及MBN产生机理。
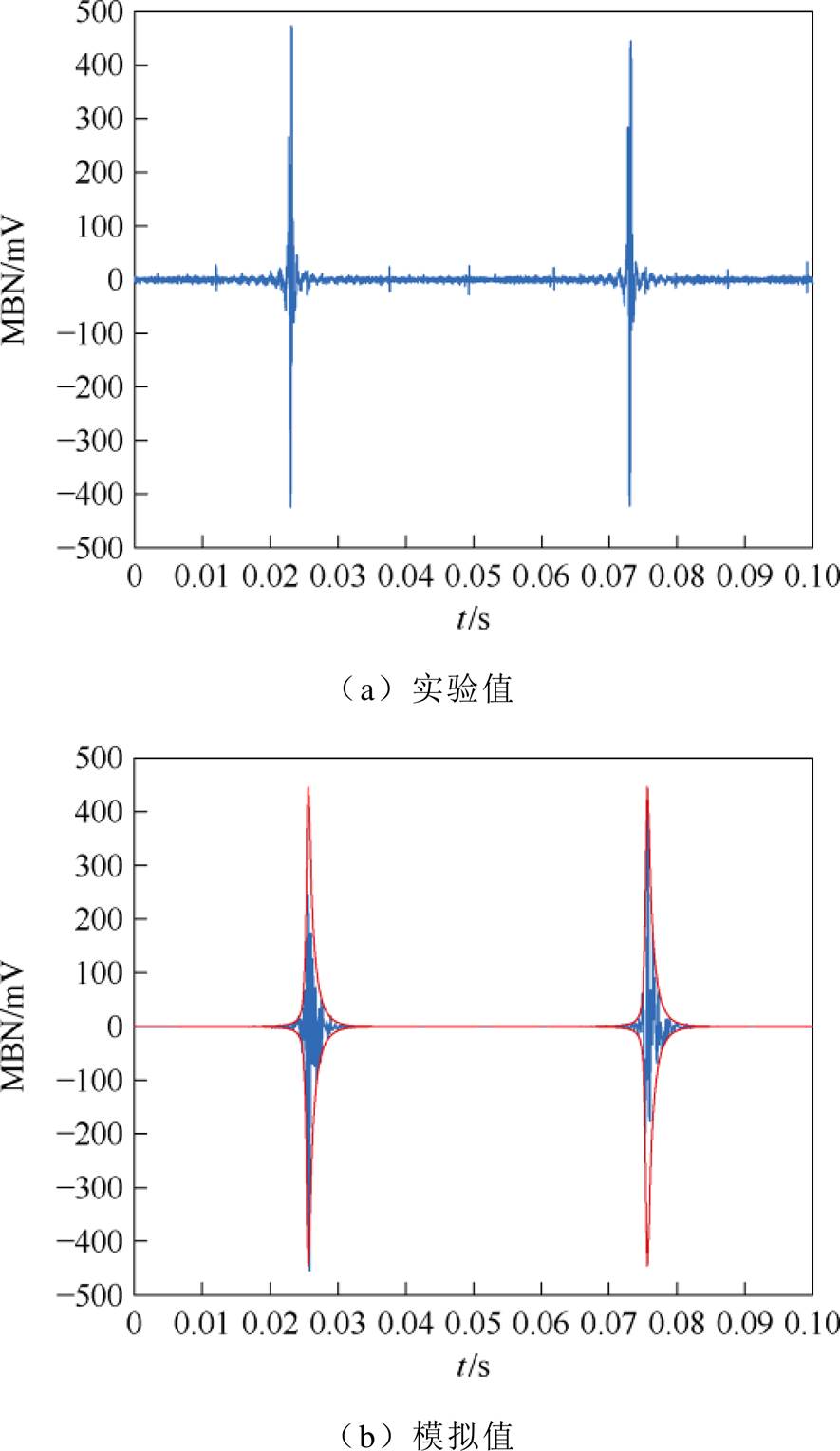
图23 30 MPa拉应力下非晶合金MBN信号
Fig.23 MBN signal of amorphous alloy under 30 MPa tensile stress
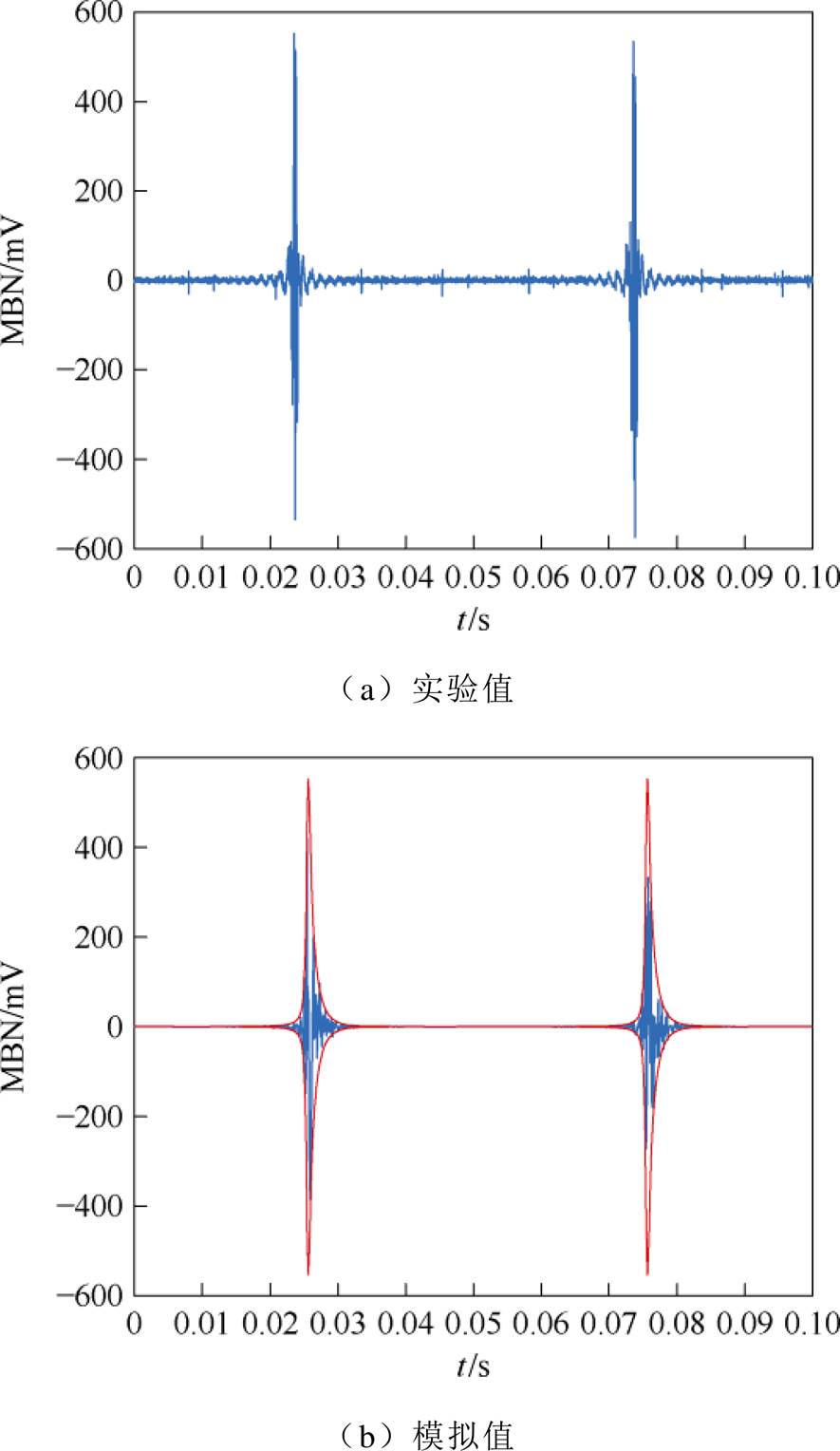
图24 60 MPa拉应力下非晶合金MBN信号
Fig.24 MBN signal of amorphous alloy under 60 MPa tensile stress
本文提出的机械应力下的MBN模型为MBN在材料表征和无损检测中的应用提供了一个可靠的工具，也为MBN的进一步工程应用奠定了基础。
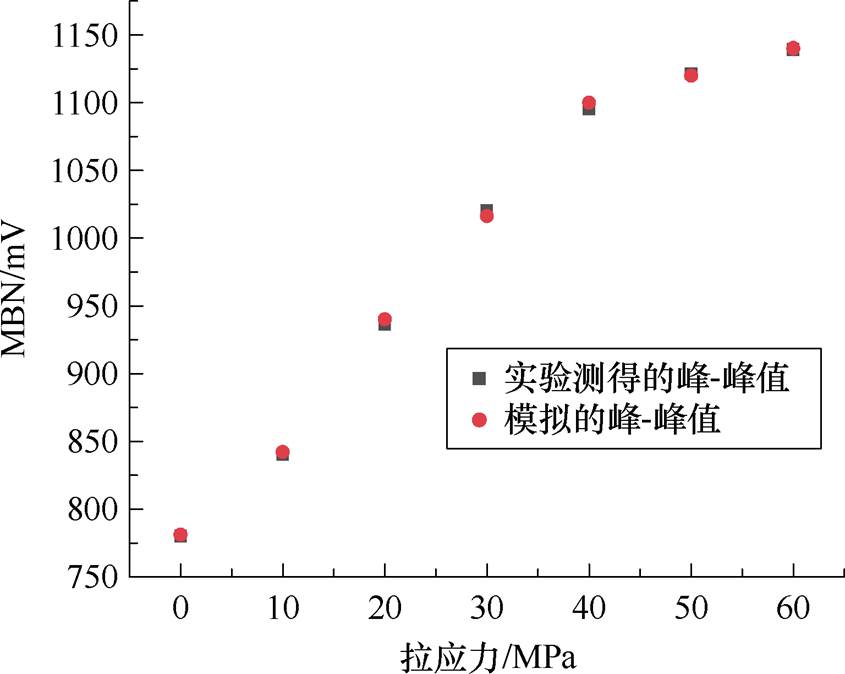
图25 拉应力下非晶合金MBN信号峰-峰值
Fig.25 Peak-to-peak value of MBN signal in amorphous alloy under compressive stress
表4 机械应力下非晶合金MBN信号的特征值模拟值与实验值的相对误差
Tab.4 Relative error between simulated and experimental characteristic values of MBN signal of o amorphous alloy under mechanical stress
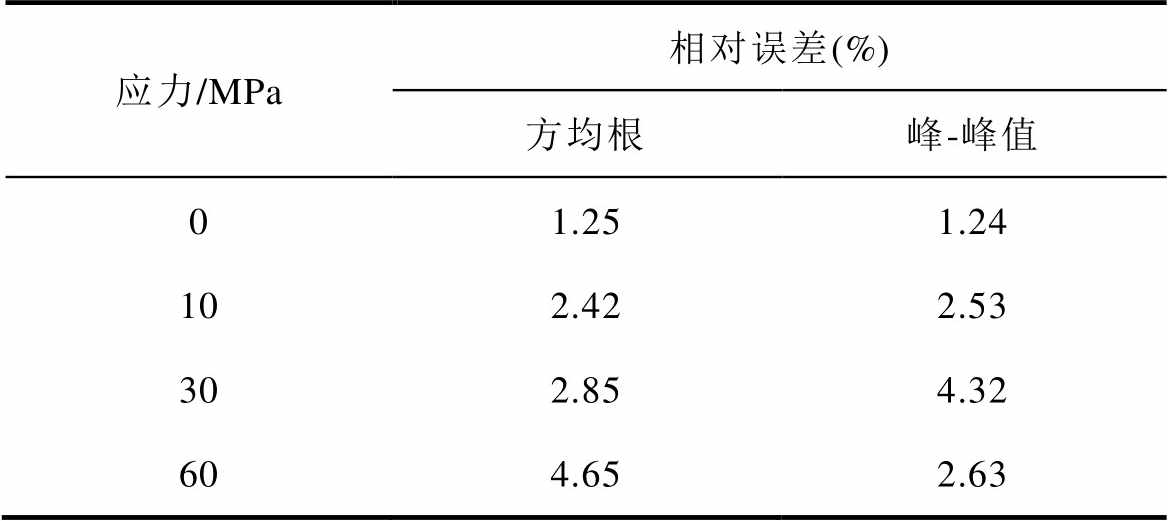
应力/MPa相对误差(%) 方均根峰-峰值 01.251.24 102.422.53 302.854.32 604.652.63
参考文献
[1] 杨庆新, 李永建. 先进电工磁性材料特性与应用发展研究综述[J]. 电工技术学报, 2016, 31(20): 1-29.
Yang Qingxin, Li Yongjian. Characteristics and developments of advanced magnetic materials in electrical engineering: a review[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 1-29.
[2] Dias M B S, Landgraf F J G. Compressive stress effects on magnetic properties of uncoated grain oriented electrical steel[J]. Journal of Magnetism and Magnetic Materials, 2020, 504: 166566.
[3] Pérez-Benitez J A, Capó-Sánchez J, Anglada-Rivera J, et al. A model for the influence of microstructural defects on magnetic Barkhausen noise in plain steels[J]. Journal of Magnetism and Magnetic Materials, 2005, 288: 433-442.
[4] 王荣山, 任爱, 钱王洁, 等. 巴克豪森噪声在电站用铁磁材料疲劳寿命评估领域的研究现状[J]. 压力容器, 2012, 29(12): 52-56, 31.
Wang Rongshan, Ren Ai, Qian Wangjie, et al. Research status of magnetic barkhausen noise in the field of fatigue life assessment of ferromagnetic material used in power plants[J]. Pressure Vessel Technology, 2012, 29(12): 52-56, 31.
[5] Li Liang, Luo Xiaoyu. Monte Carlo simulation for relationship between magnetic Barkhausen noise and elastic stress of steel[J]. Advances in Mechanical Engin-eering, 2016, 8(7): 1-6.
[6] Ducharne B, Gupta B, Hebrard Y, et al. Pheno- menological model of barkhausen noise under mechanical and magnetic excitations[J]. IEEE Transac- tions on Magnetics, 2018, 54(11): 6202606.
[7] Fagan P, Ducharne B, Daniel L, et al. Magnetic Barkhausen noise: a simulation tool[J]. AIP Advances, 2021, 11(2): 025322.
[8] Fagan P, Ducharne B, Daniel L, et al. Multiscale modelling of the magnetic Barkhausen noise energy cycles[J]. Journal of Magnetism and Magnetic Materials, 2021, 517: 167395.
[9] Jiles D C. Review of magnetic methods for non- destructive evaluation[J]. NDT International, 1988, 21(5): 311-319.
[10] 朱育莹, 李琳. 考虑各向异性和模型参数应力依赖关系的改进Sablik-Jiles-Atherton磁滞模型[J]. 电工技术学报, 2023, 38(17): 4586-4596.
Zhu Yuying, Li Lin. An improved Sablik-Jiles- Atherton hysteresis model considering anisotropy and stress dependence of model parameters[J]. Transac- tions of China Electrotechnical Society, 2023, 38(17): 4586-4596.
[11] 侯艳钊, 李琳. 软磁材料磁巴克豪森噪声测量系统与影响因素研究[J]. 华北电力大学学报(自然科学), 2024, 51(3): 65-73.
Hou Yanzhao, Li Lin. Study on measuring system for magnetic barkhausen noise of soft magnetic materials and influence factors[J]. Journal of North China Electric Power University (Natural Science Edition), 2024, 51(3): 65-73.
[12] Meng Xiaoge, Li Lin, Hou Yanzhao. Construction of energy loops using magnetic barkhausen noise[J]. IEEE Magnetics Letters, 2022, 13: 2504505.
[13] 孟肖戈, 李琳. 一种利用矫顽点微分磁化率定量评估取向电工钢片机械应力的新方法[J]. 电工技术学报, 2023, 38(7): 1705-1712.
Meng Xiaoge, Li Lin. A new method for quantitative evaluation of mechanical stress of oriented electrical steel sheets using the differential susceptibility at the coercive point[J]. Transactions of China Electro- technical Society, 2023, 38(7): 1705-1712.
[14] Corner W D, Mason J J. The effect of stress on the domain structure of Goss textured silicon-iron[J]. British Journal of Applied Physics, 1964, 15(6): 709- 718.
[15] Perevertov O, Schäfer R. Magnetic properties and magnetic domain structure of grain-oriented Fe-3%Si steel under compression[J]. Materials Research Express, 2016, 3(9): 096103.
[16] 朱育莹. 机械应力作用下取向电工钢片磁滞特性的实验研究与仿真[D]. 北京: 华北电力大学, 2023.
Zhu Yuying. Simulation and experimental research of hysteresis characteristics of grain oriented electrical steel under mechanical stress[D]. Beijing: North China Electric Power University, 2023.
[17] 孟肖戈. 基于磁巴克豪森噪声能量环的取向电工钢片应力定量评估[D]. 北京: 华北电力大学, 2023.
Meng Xiaoge. Quantitative evaluation of stress of oriented electrical steel sheet based on magnetic Backhausen noise energy loop[D]. Beijing: North China Electric Power University, 2023.
Abstract In non-destructive testing (NDT), there is a growing demand for simulation tools that can predict magnetic characteristics, enhance understanding, and avoid harsh and uncertain experimental expectations. Due to the high sensitivity and non-destructive nature, the measurement and simulation of magnetic barkhausen noise (MBN) have become important in NDT.
This paper measured the MBN signals of soft magnetic materials under different stress conditions at a magnetic frequency of 10 Hz. The experimental results revealed the significant impact of tensile and compressive stresses on the MBN signals. Specifically, as tensile stress increases, the spacing between magnetic domain walls decreases, reducing energy loss in the movement of domain walls. The migration rate of the domain walls is accordingly increased, which in turn causes the MBN signals to rise. At the same time, due to the presence of additional domains in oriented silicon steel, the MBN signals exhibit a double-peak structure. As tensile stress increases, these additional domains are suppressed. Hence, peak-to-peak values one and two increase, and the increase in peak value two is significant. When a magnetic field and compressive stress are applied along the rolling direction, the compressive stress increases the energy of the magnetic domain walls, reducing their migration rate and weakening the MBN signals. Ithelpsto better understand the changes in the magnetic properties of soft magnetic materials under different stress conditions.
Existing MBN models can not accurately simulate the MBN signals of different soft magnetic materials under stress. This paper proposes a mathematical model based on the improved S-J-A hysteresis model. This model simulates MBN signals by considering the irreversible motion of magnetic domain walls in soft magnetic materials, thereby increasing the accuracy of the simulation. Specifically, the improved S-J-A hysteresis modelsimulates the irreversible hysteresis loops of soft magnetic materials, considering the relationship between magnetic anisotropy, model parameters, and stress. Then, these irreversible hysteresis loops are linked with the MBN envelope line to establish a mathematical model for the MBN envelope curve. Next, the MBN signals are simulated by modulating white noise in the 1～50 kHz range with this envelope curve. Finally, three different soft magnetic materials are selected: oriented electrical steel sheet (30QG120), non-oriented silicon steel (35WW230), and amorphous alloy (1K101). The proposed MBN model simulates MBN signals under different mechanical stress conditions.
The proposed MBN model accurately simulates the MBN signals of the oriented electrical steel sheet (30QG120), non-oriented silicon steel (35WW230), and amorphous alloy (1K101) under stress. A comparison of MBN signals between oriented silicon steel, non-oriented silicon steel, and amorphous alloy is conducted, revealing that the double-peak structure exhibited by oriented silicon steel under tensile stress is related to its anisotropy. Microscopic analysis gains a deep understanding of the stress effects on the magnetism of soft magnetic materials and the generation mechanism of MBN. The proposed MBN model provides a reliable tool in material characterization and non-destructive testing (NDT) applications, laying the foundation for further engineering applications.
keywords：Non-destructive testing (NDT)，soft magnetic materials，magnetic Barkhausen noise (MBN), hysteresis model, mechanical stress, the MBN model under stress
中图分类号：TM275
DOI: 10.19595/j.cnki.1000-6753.tces.240705
国家自然科学基金资助项目（52177005）。
收稿日期 2024-04-30
改稿日期2024-09-13
张正辉 男，1999年生，硕士研究生，研究方向为软磁材料的MBN噪声。
E-mail: zzh1328299789@163.com（通信作者）
李 琳 男，1983年生，教授，博士生导师，研究方向为先进输电技术，电磁场理论及应用。
E-mail: lilin@ncepu.edu.cn
（编辑 郭丽军）