
图1 磁致伸缩测量系统
Fig.1 Magnetostriction measurement system
摘要 传统的损耗分离模型未考虑机械应力对损耗特性的影响,当取向硅钢片受到沿轧制方向的拉应力或压应力时,传统损耗分离模型存在较大误差。该文对机械应力下取向硅钢片的损耗特性进行了实验研究,获得了工频正弦激励及低频激励下不同拉、压应力对取向硅钢片损耗构成的影响规律,并从磁化机理进行了分析。基于传统的损耗分离模型、应力下取向硅钢片的损耗特性,根据取向硅钢片的剩余损耗参数、磁滞能量损耗的应力相关性,给出一种考虑应力作用下剩余损耗和磁滞能量损耗的修正方法,得到计及机械应力作用下改进的取向硅钢片的损耗分离模型。应用该文改进后的损耗分离模型对不同激励、不同型号的取向硅钢片的损耗构成进行了计算分析和实验验证,结果表明,改进后损耗分离模型的计算结果与实验结果吻合,验证了所提方法的有效性和计算精度。
关键词:损耗分离模型 机械应力 取向硅钢片 剩余损耗 磁滞损耗
大力发展绿色低碳经济,积极稳妥推进“碳达峰、碳中和”已成为电力行业关注的焦点[1-2]。电力变压器作为电力系统中关键装备之一,在电能的转换和传输过程中起到关键作用[3-5]。研究变压器铁心材料——取向硅钢片在不同工况下的损耗特性,可为变压器的优化设计、节能降损提供理论基础[6-9]。
变压器结构中的夹件、螺栓等紧固件在运行时使得取向硅钢片受到拉应力、压应力[10-12]。近年来,国内外学者对机械应力下取向硅钢片的磁化特性做了大量的研究[13-15]。赵小军等[16]基于综合磁性能测量平台,研究了高频激励、机械应力对硅钢片损耗的影响,但未对低频激励下取向硅钢片的损耗模型进行研究。随着海上柔性直流输电技术的广泛应用,变压器铁心会工作在16.67、20和25 Hz,系统研究低频变压器的损耗特性,即取向硅钢片在50 Hz以下频率的损耗特性同样重要[17-18]。
目前国内外研究集中于工频或高次谐波激励下取向硅钢片的损耗模型,对低频激励和机械应力下取向硅钢片的损耗模型研究甚少。刘刚等[19]对正弦及高次谐波激励下取向硅钢片损耗的计算方法进行了改进,基于Bertotti提出的损耗分离公式,在磁滞损耗中引入高阶项,提高了磁滞损耗的计算精度,但是未考虑实际工程中机械应力对取向硅钢片损耗的影响。本文对机械应力下取向硅钢片的损耗特性进行了实验研究,提出了一种考虑应力作用下的取向硅钢片剩余损耗和磁滞能量损耗的修正方法,得到了计及机械应力作用下取向硅钢片改进的损耗分离模型。采用不同低频激励、不同型号的取向硅钢片对改进后的损耗分离模型进行了计算分析和实验验证,结果表明改进后的损耗分离模型提高了损耗计算的准确性,本文研究成果可为工频电力变压器和柔性低频输电变压器的设计提供了理论依据。
本文采用BROCKHAUS磁致伸缩测量系统,对取向硅钢片在未施加应力和施加不同应力下的损耗进行了测量,测量系统如图1所示。

图1 磁致伸缩测量系统
Fig.1 Magnetostriction measurement system
磁致伸缩测量系统由电源、主机、单片磁测量装置、激光干涉仪、气动预应力系统等构成。单片磁测量装置及激光干涉仪置于气动隔振平台上,使其不受外界因素干扰。单片磁测量装置由线圈、磁轭、夹具等构成,样片所受的预应力由预应力控制器调节和显示,单片磁测量装置示意图如图2所示。
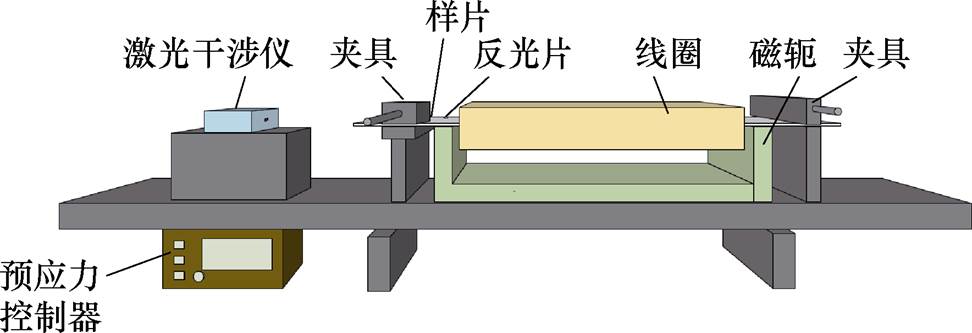
图2 单片磁测量装置示意图
Fig.2 Schematic diagram of a single sheet tester for magnetic property
取向硅钢片的比总损耗(以下简称铁损)Ps,是衡量变压器损耗的一个重要参数,用单位质量的硅钢片消耗的总功率表示,单位为W/kg。取向硅钢片的铁损小,有利于降低发热量、提高设备的可靠运行。
本文以B20R065取向硅钢片为样本,公称厚度为0.20 mm,样本尺寸为600 mm×100 mm。对样片施加沿轧制方向的拉、压应力,得到不同应力下的铁损随磁感应强度峰值Bm的变化曲线如图3所示,其中拉应力用正值表示,压应力用负值表示。
从图3可知,拉应力使损耗略微降低,压应力使损耗显著增大。根据铁磁学的磁化机理可知,施加拉应力时,为抗拒拉应力,取向硅钢片的表面闭合畴减小、静磁能增大,使180°主磁畴细化并消除90°闭合畴,沿轧制方向损耗降低;施加压应力时,外施应力产生的磁弹性能远小于静磁能和磁晶各向异性能,当其达到1%时,静态磁畴变为应力磁畴。由于内部磁畴的磁化矢量必须转动90°,因此沿轧制方向更难磁化,导致铁损显著增加[20]。
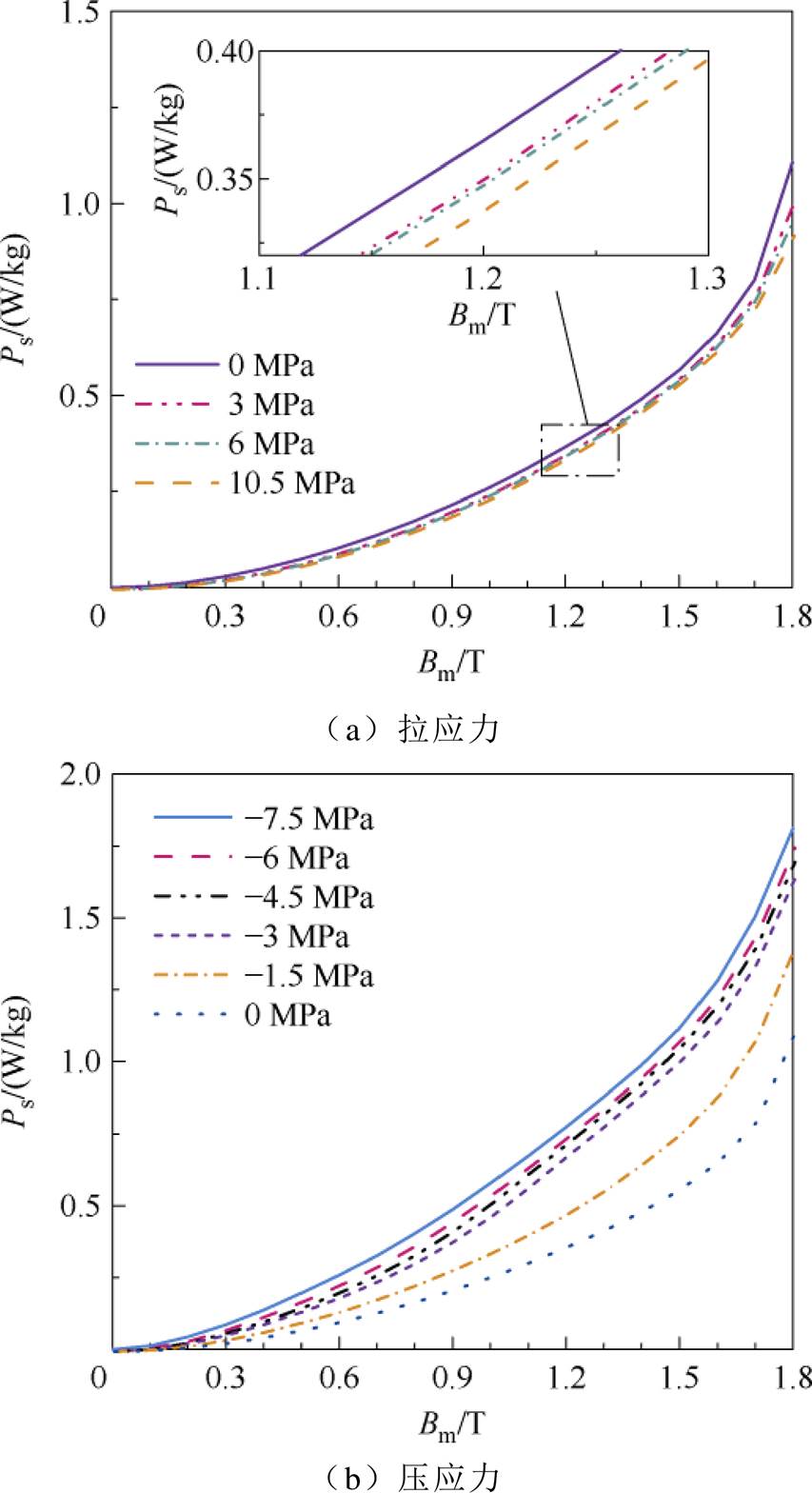
图3 不同应力下的比总损耗
Fig.3 Total loss ratios under different stresses
铁磁材料中的铁损Ps分为磁滞损耗Ph、涡流损耗Pc和剩余损耗Pe,即
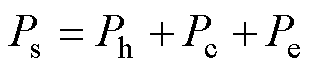 (1)
(1)
根据Bertotii提出的传统损耗分离模型[21],正弦激励下的磁滞损耗、涡流损耗和剩余损耗分别为
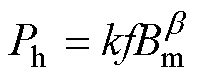 (2)
(2)
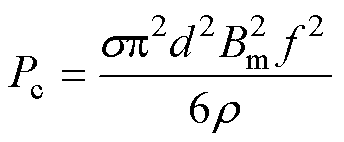 (3)
(3)
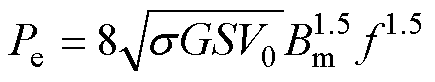 (4)
(4)
式中,f为激励电压频率(Hz);Bm为磁感应强度峰值(T);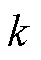 、
、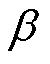 为磁滞损耗系数;
为磁滞损耗系数; 为取向硅钢片的电导率(S/m);d为样片的厚度(m);
为取向硅钢片的电导率(S/m);d为样片的厚度(m);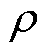 为密度(kg/m3);S为样片的截面积(m2);G为常数0.135 6;V0为剩余损耗参数,其值取决于材料自身特性。
为密度(kg/m3);S为样片的截面积(m2);G为常数0.135 6;V0为剩余损耗参数,其值取决于材料自身特性。
涡流损耗与取向硅钢片的电导率、厚度有关。当取向硅钢片受到应力作用时会产生形变,在塑性形变较大时,电导率降低,涡流损耗略微下降[22]。由于本文实验中施加的应力在弹性形变范围内,不改变取向硅钢片的电导率和厚度,可认为涡流损耗与应力无关,涡流损耗由式(3)计算得出。
在极低频率下,磁滞损耗占比远高于涡流损耗和剩余损耗,因此磁滞损耗由极低频率下的二频率法测量得到[23-24]。将涡流损耗、磁滞损耗代入式(1),得到剩余损耗。
应用传统损耗分离模型,得到B20R065取向硅钢片在应力作用下的磁滞损耗、剩余损耗计算值。图4分别为磁感应强度峰值为1.7 T时,磁滞损耗、剩余损耗的测量值和计算值随应力的变化曲线。
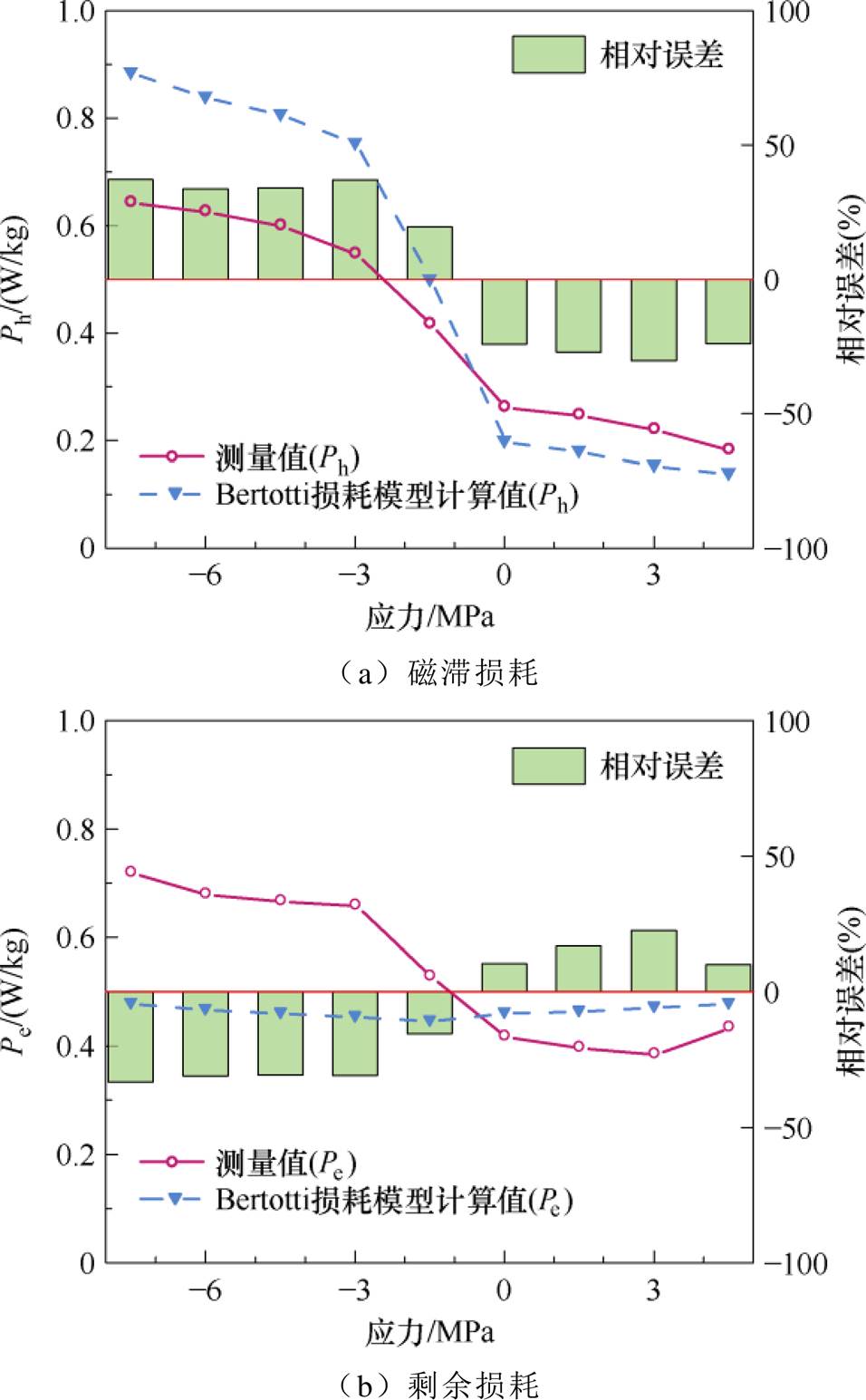
图4 磁滞损耗和剩余损耗随应力的变化曲线
Fig.4 Variation curves of hysteresis loss and excess loss with respect to stress
从图4可知,由于传统损耗分离模型中的磁滞损耗未体现应力的作用,当取向硅钢片受到机械应力作用时,应力对磁滞损耗的影响仅通过磁滞损耗系数反映,导致传统损耗分离模型在计算应力下的磁滞损耗存在较大误差;尽管剩余损耗参数V0可体现应力作用,但是目前采用一个常系数表示,无法从机理上给出施加的机械应力对不同磁感应强度下损耗的影响,因此传统损耗分离模型存在较大的计算误差。
第2节中,以B20R065型号取向硅钢片为例,研究了传统损耗分离模型对应力作用下的取向硅钢片的损耗分离结果。由于传统的损耗分离模型未能描述不同应力对磁滞损耗和剩余损耗造成的影响,从而引起一定的计算误差。上述现象在多种型号的取向硅钢片的损耗分离中同样存在,限于篇幅不再赘述。本节在传统损耗分离模型的基础上,对磁滞能量损耗和剩余损耗构成的分量进行修正,以表征应力对取向硅钢片损耗的影响。
为研究机械应力对剩余损耗的影响,根据式(4)计算得到取向硅钢片在不同磁感应强度峰值下剩余损耗参数V0。图5为磁感应强度峰值为1.0 T和1.7 T时剩余损耗参数V0随应力的变化曲线,拉应力用正值表示,压应力用负值表示。
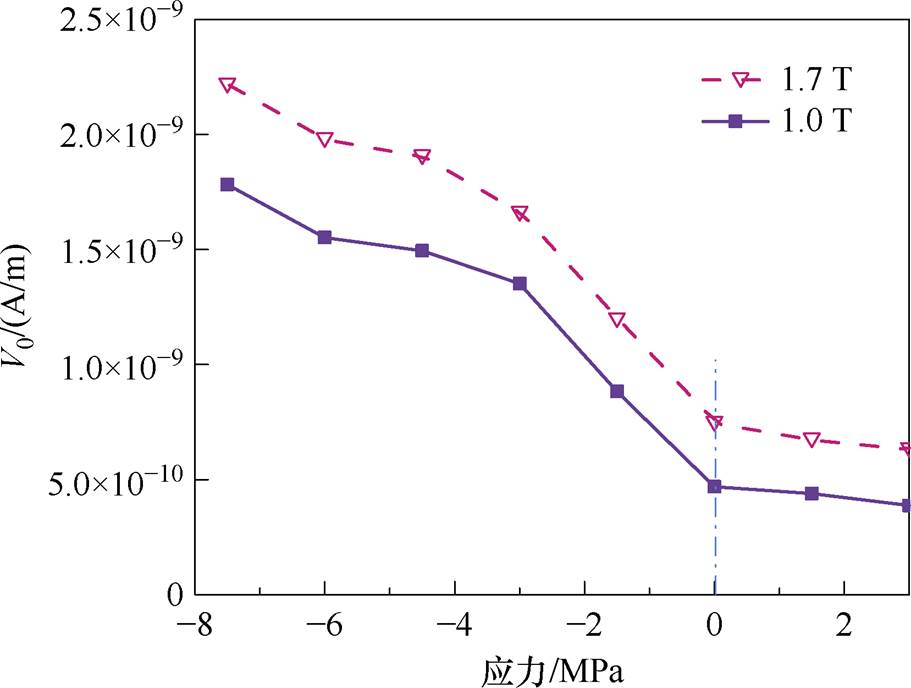
图5 剩余损耗参数V0随应力的变化曲线
Fig.5 Variation curves of excess loss parameter V0 with respect to stress
从图5可知,剩余损耗参数V0随压应力的增大而增大,随着拉应力的增大而略微减小,该规律与1.2节中的实验结果吻合。根据文献[21]可知,剩余损耗参数V0用于描述铁磁材料中各种微观结构特征,如晶粒尺寸、晶粒织构、残余应力等对损耗的影响,单位为A/m。基于实验结果和铁磁学理论,本文将剩余损耗中的参数V0设为应力及磁感应强度峰值相关的函数[25],即
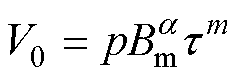 (5)
(5)
式中,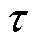 为施加机械应力大小(MPa);
为施加机械应力大小(MPa);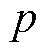 为系数;
为系数;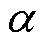 、
、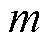 分别与磁感应强度峰值、应力相关,表示为
分别与磁感应强度峰值、应力相关,表示为
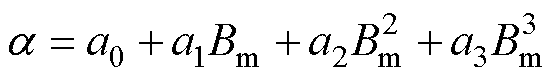 (6)
(6)
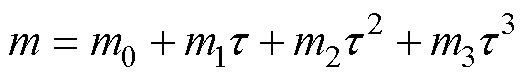 (7)
(7)
将磁滞损耗、剩余损耗代入式(1)整理可得
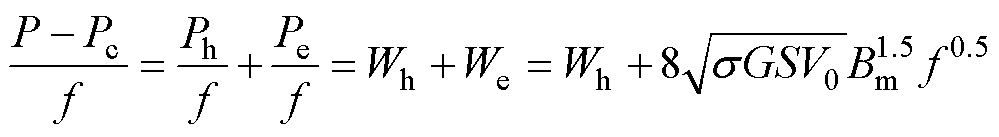 (8)
(8)
式中,Wh、We分别为一个周期内的磁滞损耗和剩余损耗,用磁滞能量损耗和剩余能量损耗表示,单位为J/kg。图6为磁滞能量损耗和剩余能量损耗随应力的变化曲线。
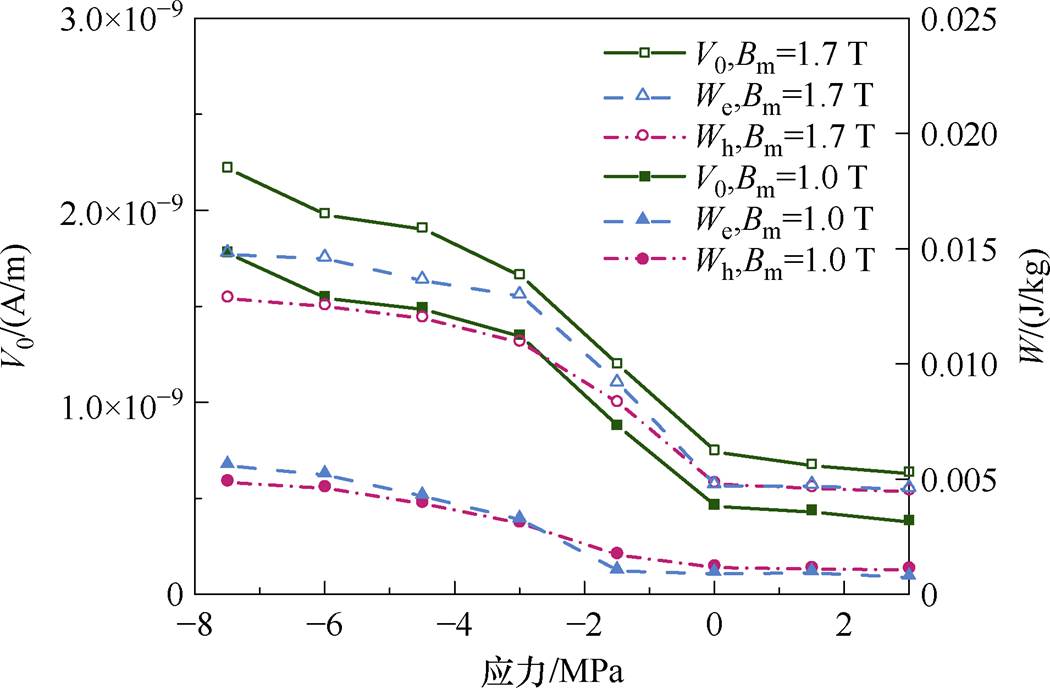
图6 Wh及We随应力的变化曲线
Fig.6 Curves of Wh and We varying with stress
从图6可知,磁滞能量损耗和剩余能量损耗在不同磁感应强度峰值下变化规律一致,都随压应力的增大而增大,随拉应力的增大而略微降低。在磁感应强度峰值一定时,磁滞能量损耗、剩余能量损耗和剩余损耗参数V0随应力的变化趋势一致,表明磁滞能量损耗和剩余损耗参数V0具有相同的应力相关性,可用于描述外加机械应力对取向硅钢片组织和磁性能的影响[26]。
将磁滞能量损耗设为应力及磁感应强度峰值相关的函数,即
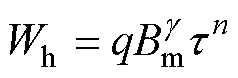 (9)
(9)
式中,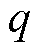 为系数;
为系数;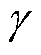 、
、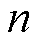 分别为与磁感应强度峰值、应力相关的系数:
分别为与磁感应强度峰值、应力相关的系数:
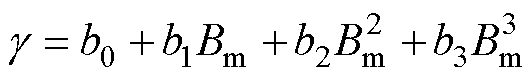 (10)
(10)
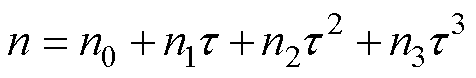 (11)
(11)
采用麦夸特法并结合全局优化算法[27-28]对剩余损耗参数V0和磁滞能量损耗进行修正,该算法的优势在于降低了对初值的要求,提高了修正的自适应性,从而提高了非线性计算结果的准确性。
将改进后的剩余损耗参数V0和磁滞能量损耗代入式(8),得到机械应力作用下的改进损耗分离模型。应用本文提出的改进损耗分离模型计算得到参数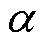 、
、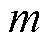 、
、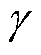 、
、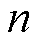 分别为
分别为
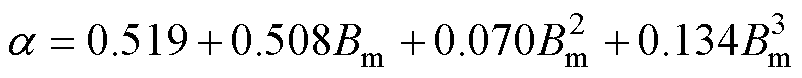 (12)
(12)
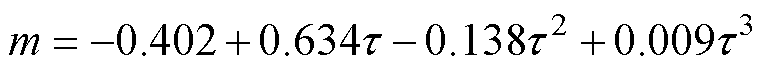 (13)
(13)
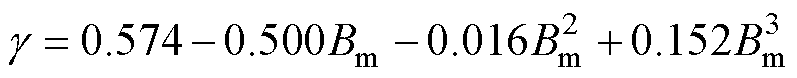 (14)
(14)
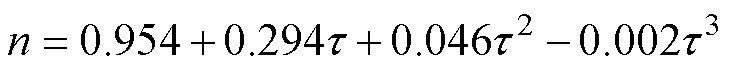 (15)
(15)
为验证第3节中改进损耗分离模型的准确性,将剩余损耗参数V0、磁滞能量损耗按式(5)、式(9)进行计算,整理得到不同应力下磁滞损耗、剩余损耗的计算值和测量值如图7所示。
从图7可知,应用本文提出的改进损耗分离模型,磁滞损耗和剩余损耗在不同应力下的计算值与测量值吻合,表明采用本文提出的改进损耗分离模型可以对不同应力、不同磁感应强度峰值下取向硅钢片的损耗进行准确分离,并且可以推广到其他频率下的取向硅钢片的损耗计算。
柔性低频交流输电技术在远距离大容量、海上风电送出等场景下更具经济优势,是一种新型高效的交流输电技术。柔性低频交流输电需要用到16.67、20、25 Hz等低频变压器[29-31],应用改进的损耗分离模型对上述频率下的损耗进行分离,可以得到不同应力下损耗的计算值。以施加-4.5 MPa应力为例,图8为不同频率下磁滞损耗、剩余损耗的测量值和计算值;表1、表2分别为磁感应强度峰值为1.7 T时,不同频率下磁滞损耗和剩余损耗的计算值及误差。
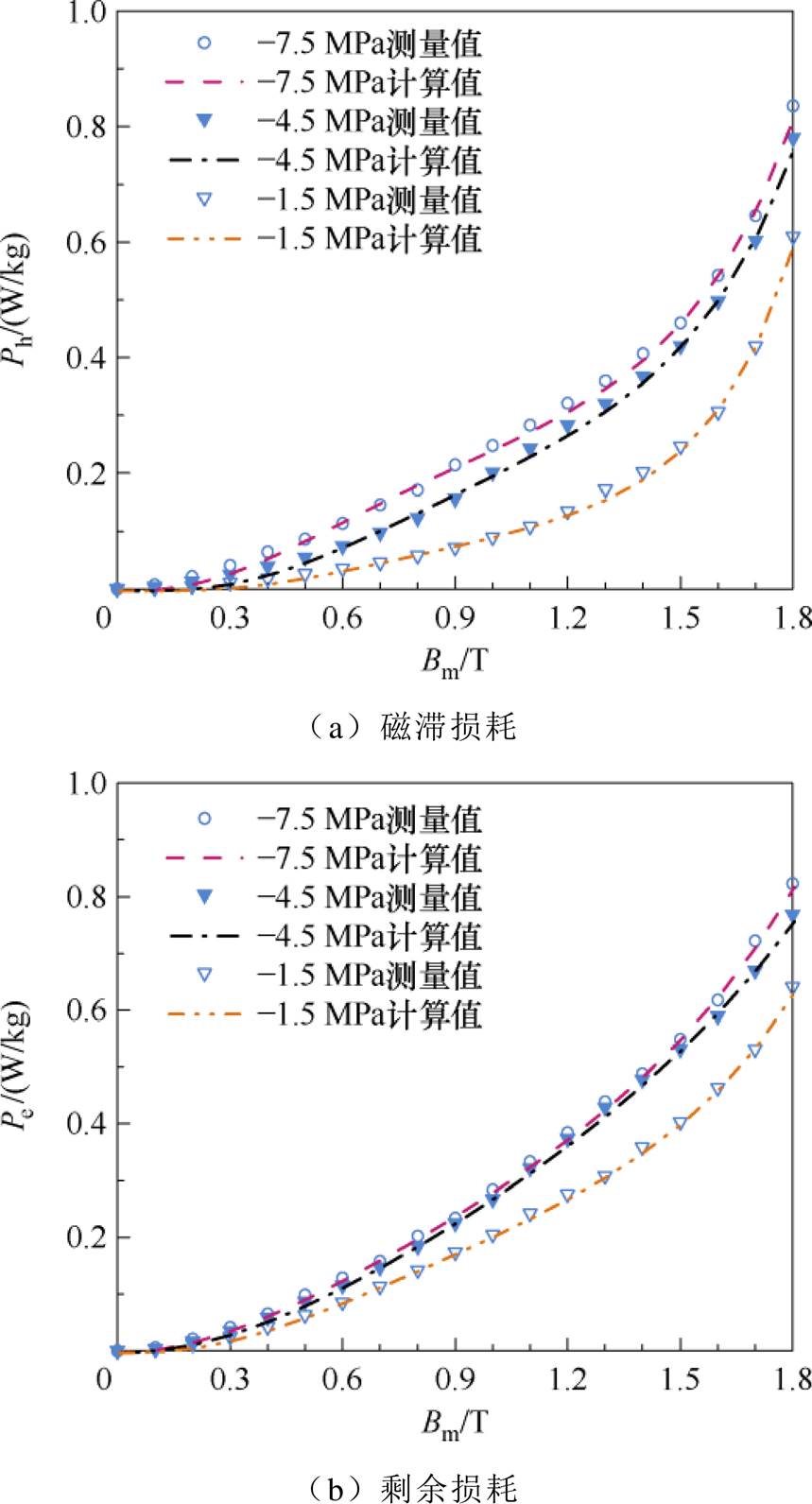
图7 磁滞损耗及剩余损耗的分离结果
Fig.7 Seperation results of excess loss and hysteresis loss
表1 不同频率下磁滞损耗的计算值及误差
Tab.1 Calculation values and errors of hysteresis loss at different frequencies
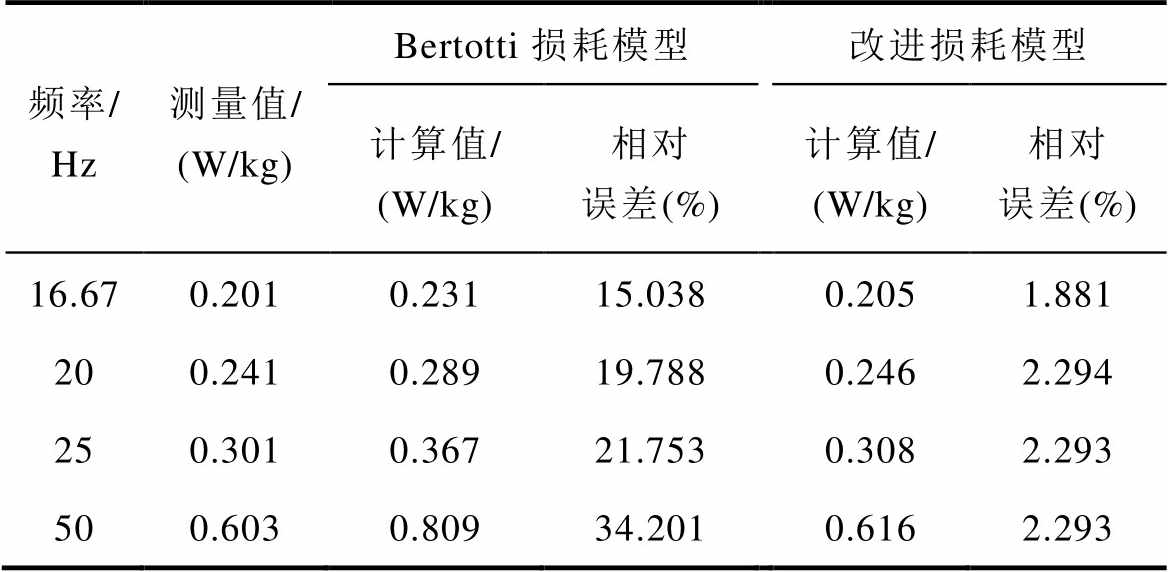
频率/Hz测量值/(W/kg)Bertotti损耗模型改进损耗模型 计算值/(W/kg)相对误差(%)计算值/(W/kg)相对误差(%) 16.670.2010.23115.0380.2051.881 200.2410.28919.7880.2462.294 250.3010.36721.7530.3082.293 500.6030.80934.2010.6162.293
表2 不同频率下剩余损耗的计算值及误差
Tab.2 Calculation values and errors of excess loss at different frequencies
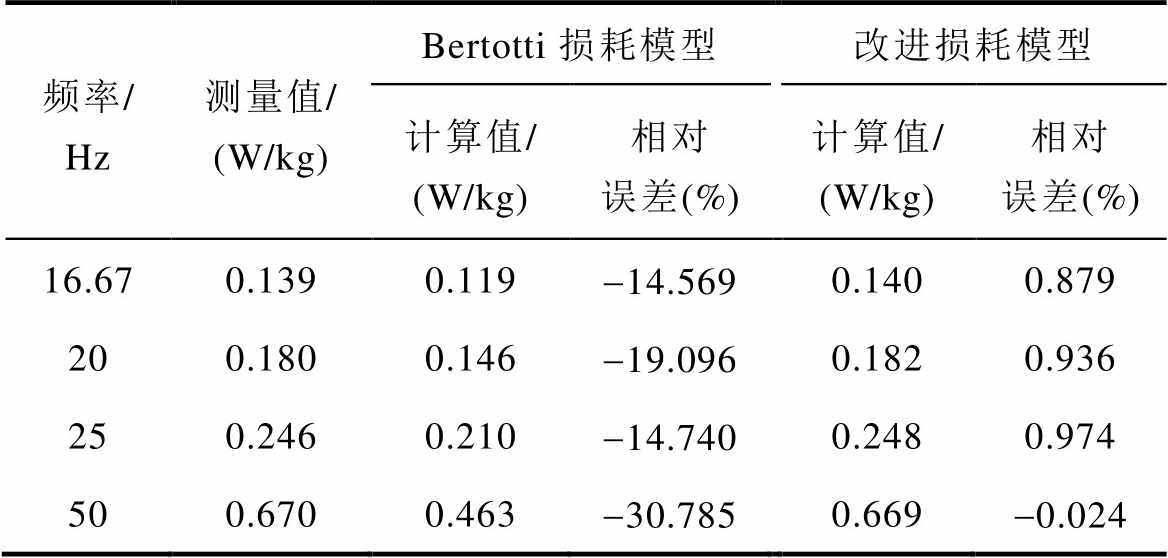
频率/Hz测量值/(W/kg)Bertotti损耗模型改进损耗模型 计算值/(W/kg)相对误差(%)计算值/(W/kg)相对误差(%) 16.670.1390.119-14.5690.1400.879 200.1800.146-19.0960.1820.936 250.2460.210-14.7400.2480.974 500.6700.463-30.7850.669-0.024
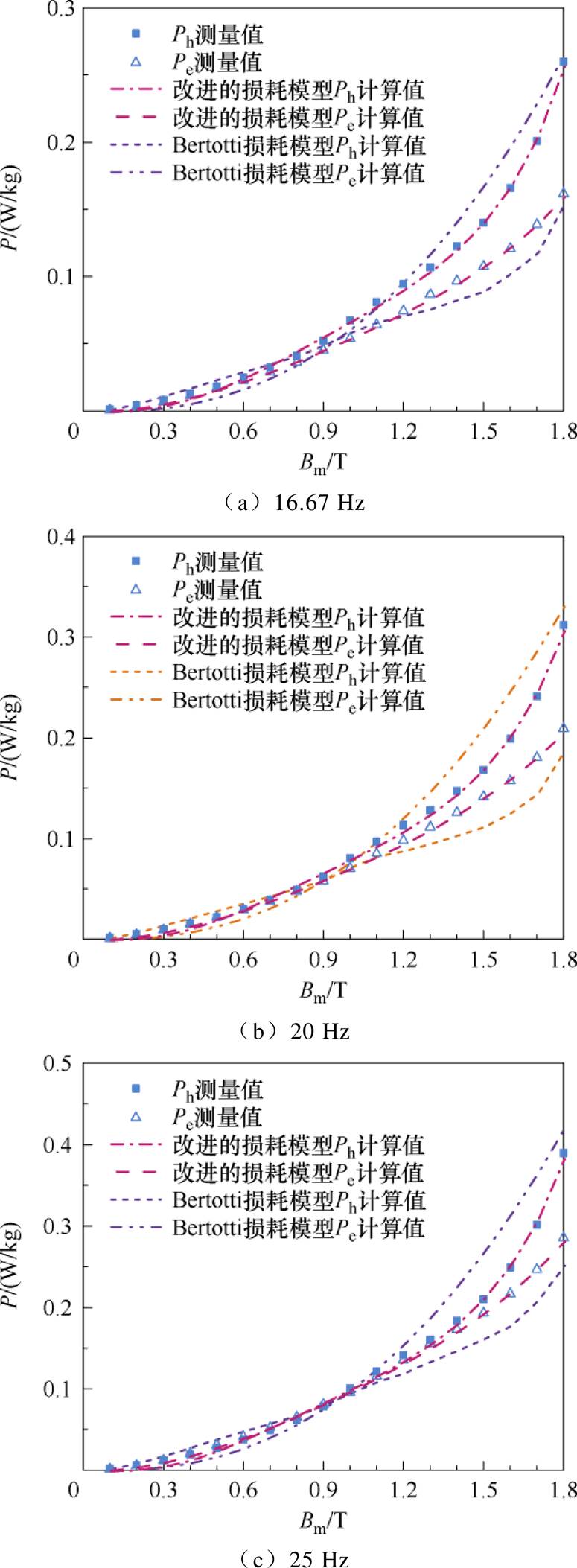
图8 不同频率下损耗测量值与计算值
Fig.8 Results of measured and calculated losses at different frequencies
根据图8中磁滞损耗和剩余损耗的计算结果及表1、表2中的计算误差可知,施加频率为16.67、20、25 Hz时,应用本文改进后的损耗分离模型在各磁感应强度峰值下磁滞损耗和剩余损耗的计算值与测量值吻合。当磁感应强度峰值为1.7 T时,改进后的损耗分离模型较传统损耗分离模型中磁滞损耗和剩余损耗的误差减小,表明施加低频激励时,改进的损耗分离模型同样具有较高的计算精度。
为验证本文模型的适用性,选取多种型号的取向硅钢片对其在工频正弦激励下的铁损进行验证计算,得到不同应力下取向硅钢片的损耗分离结果,限于篇幅不再赘述。图9给出27Q120、B23P085、18QGD065型号取向硅钢片(厚度依次为0.27、0.23、0.18 mm)在-3 MPa应力下铁损的测量值和计算值,表3为磁感应强度峰值为1.7 T时,上述型号取向硅钢片的铁损计算值及误差。
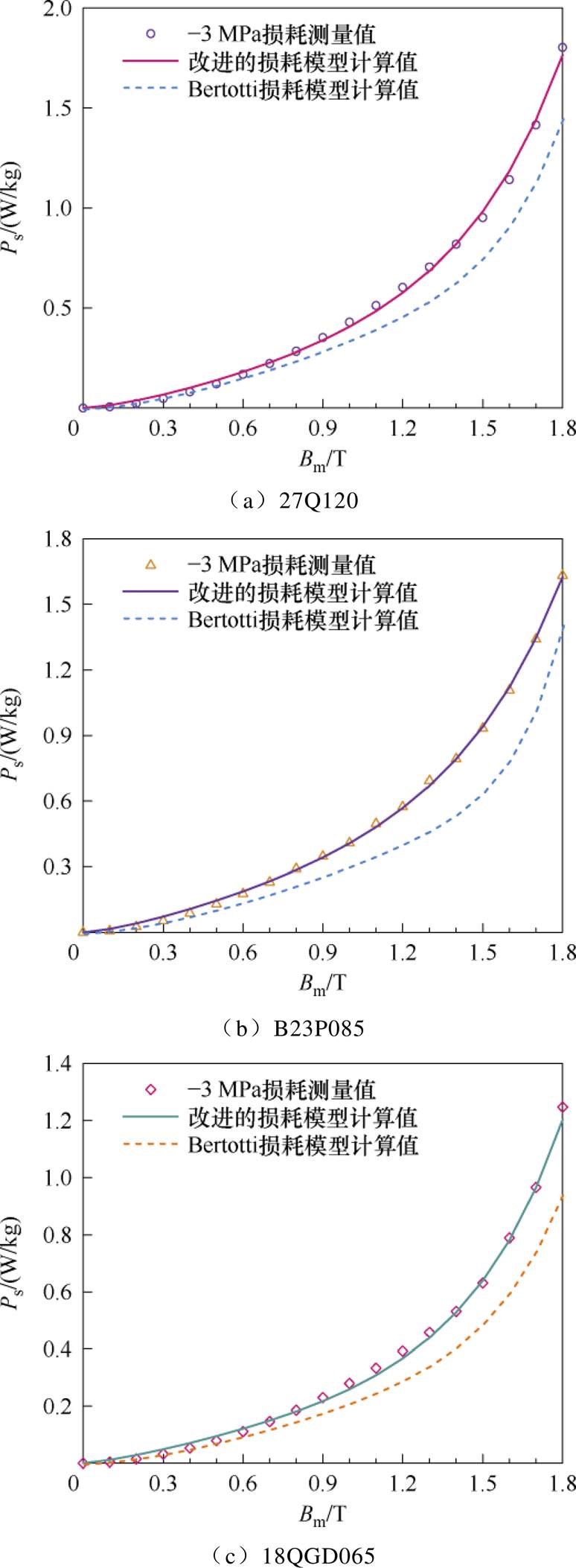
图9 不同型号取向硅钢片的损耗测量值与计算值
Fig.9 Measurements and calculation results of losses for different types of silicon steel sheets
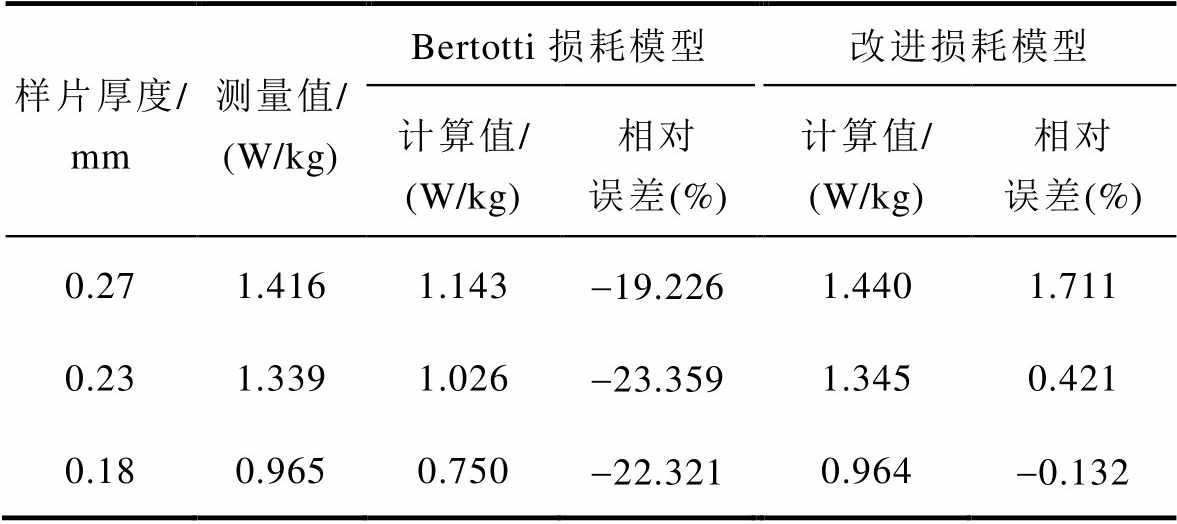
表3 不同型号取向硅钢片的损耗计算值及误差
Tab.3 Calculation error of losses for different types of silicon steel sheets
样片厚度/mm测量值/(W/kg)Bertotti损耗模型改进损耗模型 计算值/(W/kg)相对误差(%)计算值/(W/kg)相对误差(%) 0.271.4161.143-19.2261.4401.711 0.231.3391.026-23.3591.3450.421 0.180.9650.750-22.3210.964-0.132
从图9可知,不同型号的取向硅钢片由于厚度不同,使得铁损随取向硅钢片厚度的减小而降低。其原因在于,取向硅钢片的厚度增加,其表面静磁能和180°畴壁能增大,畴壁移动阻力增大,导致损耗增高。结合表3中铁损的计算值和计算误差可知,应用本文改进后的损耗分离模型,不同型号的取向硅钢片在应力下的损耗计算值与测量值吻合,表明改进后的损耗分离模型适用于不同型号、不同厚度的取向硅钢片。
本文对机械应力下取向硅钢片的损耗特性进行了实验研究,基于Bertotti损耗分离模型,提出一种计及应力作用的改进损耗分离模型。改进后的损耗分离模型考虑应力影响,在取向硅钢片受到拉应力、压应力作用时,损耗的计算值与测量值吻合,减小了传统损耗分离模型中由于未考虑应力影响导致的损耗计算误差,可得出以下结论:
1)基于铁磁学的磁化机理,通过实验对应力下取向硅钢片的损耗构成进行了研究,结果表明,剩余损耗参数V0与应力具有相关性,在剩余损耗参数中考虑应力作用,可以减小传统损耗分离模型中由于应力导致的剩余损耗计算误差。
2)在传统损耗分离模型的基础上,给出了一种改进的损耗分离模型。改进后的损耗分离模型将剩余损耗参数V0、磁滞能量损耗展开为应力和磁感应强度峰值的函数,实现了对不同应力下的损耗的准确分离。
3)为了验证改进后的损耗分离模型的有效性和计算精度,采用不同频率激励、不同型号取向硅钢片进行了实验测量和损耗分离计算。结果表明,改进后的损耗分离模型的计算结果与实验结果吻合,可以对不同应力下的取向硅钢片的损耗进行分离。
本文对应力下取向硅钢片的损耗模型进行改进,减小了传统损耗模型中的计算误差,在工程上为铁磁材料的损耗计算提供了理论基础。
参考文献
[1] 张智刚, 康重庆. 碳中和目标下构建新型电力系统的挑战与展望[J]. 中国电机工程学报, 2022, 42(8): 2806-2819.
Zhang Zhigang, Kang Chongqing. Challenges and prospects for constructing the new-type power system towards a carbon neutrality future[J]. Proceedings of the CSEE, 2022, 42(8): 2806-2819.
[2] 舒印彪, 张丽英, 张运洲, 等. 我国电力碳达峰、碳中和路径研究[J]. 中国工程科学, 2021, 23(6): 1-14.
Shu Yinbiao, Zhang Liying, Zhang Yunzhou, et al. Carbon peak and carbon neutrality path for China’s power industry[J]. Strategic Study of CAE, 2021, 23(6): 1-14.
[3] 郭莹霏, 池源, 王强钢, 等. 面向多元负荷和优质供电的虚拟增容配电变压器: 概念、应用与展望[J].电工技术学报, 2024, 39(21): 6666-6686, 6803.
Guo Yingfei, Chi Yuan, Wang Qianggang, et al. Virtual capacity-enhanced distribution transformer for diverse loads and quality power supply: concepts, applications, and prospects[J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6666-6686, 6803.
[4] 陈彬, 王川源, 刘洋, 等. 基于磁导-电容类比法和解析Preisach模型的铁心动态磁滞建模方法[J]. 电工技术学报, 2024, 39(18): 5576-5587.
Chen Bin, Wang Chuanyuan, Liu Yang, et al. Dynamic hysteresis modeling method for iron core based on permeance-capacitance analogy and analytic Preisach model[J]. Transactions of China Electro- technical Society, 2024, 39(18): 5576-5587.
[5] 潘超, 安景革, 刘闯, 等. 变压器偏磁效应噪声特性的多场耦合分析与抑制[J]. 电工技术学报, 2023, 38(18): 5077-5088.
Pan Chao, An Jingge, Liu Chuang, et al. Multi-field coupling analysis and suppression for biased magnetic noise in transformer[J]. Transactions of China Elec- trotechnical Society, 2023, 38(18): 5077-5088.
[6] 迟青光, 张艳丽, 陈吉超, 等. 非晶合金铁心损耗与磁致伸缩特性测量与模拟[J]. 电工技术学报, 2021, 36(18): 3876-3883.
Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of lossand magneto- strictive properties for the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.
[7] 孙鹤, 李永建, 刘欢, 等. 非正弦激励下纳米晶铁心损耗的计算方法与实验验证[J]. 电工技术学报, 2022, 37(4): 827-836.
Sun He, Li Yongjian, Liu Huan, et al. The calculation method of nanocrystalline core loss under non- sinusoidal excitation and experimental verification[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 827-836.
[8] 赵志刚, 贾慧杰, 刘朝阳, 等. 考虑PWM波形特征的纳米晶磁心损耗模型的研究及验证[J]. 电工技术学报, 2024, 39(6): 1602-1612.
Zhao Zhigang, Jia Huijie, Liu Zhaoyang, et al. Research and verification of nanocrystalline core loss model considering PWM waveform characteristics[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1602-1612.
[9] 康丽, 张艳丽, 唐伟, 等. 基于变系数Steinmetz公式的直流偏磁下铁心损耗计算[J]. 电工技术学报, 2019, 34(增刊1): 1-6.
Kang Li, Zhang Yanli, Tang Wei, et al. Calculation of core loss under dc bias based on the variable coefficient Steinmetz formula[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 1-6.
[10] 彭清贵, 陈学平, 来至. 压应力对小型铁氧体磁心性能的影响及测试夹具设计[J]. 磁性材料及器件, 2024, 55(2): 61-66.
Peng Qinggui, Chen Xueping, Lai Zhi. Influence of compressive stress on the performance of small ferrite core and design of test fixture[J]. Journal of Magnetic Materials and Devices, 2024, 55(2): 61-66.
[11] 李梦星, 张艳丽, 姜伟, 等. 机械应力下电工钢片磁滞与磁致伸缩回环滞后特性模拟[J]. 电工技术学报, 2022, 37(11): 2698-2706.
Li Mengxing, Zhang Yanli, Jiang Wei, et al. Simulation of hysteresis and magnetostrictive loop hysteretic characteristics of electrical steel sheets under mechanical stress[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2698-2706.
[12] 王振, 张艳丽, 龚园, 等. 机械应力下无取向电工钢片磁致伸缩特性研究[J]. 电工技术学报, 2023, 38(21): 5682-5690.
Wang Zhen, Zhang Yanli, Gong Yuan, et al. Study on magnetostrictive properties of non-oriented electrical steel sheet under mechanical stress[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5682- 5690.
[13] 李永建, 李宗明, 利雅婷, 等. 考虑磁-力耦合效应的混合磁滞模型研究[J]. 电工技术学报, 2024, 39(22): 6941-6951.
Li Yongjian, Li Zongming, Li Yating, et al. Study of hybrid hysteresis model considering magnetic-force coupling effect[J]. Transactions of China Electro- technical Society, 2024, 39(22): 6941-6951.
[14] Wang Hanghang, Chen Junquan, Jiang Yapeng. Effect of cutting stress on magnetic properties of non- oriented electrical steel[C]//2023 IEEE International Conference on Applied Superconductivity and Elec- tromagnetic Devices (ASEMD), Tianjin, China, 2023: 1-2.
[15] Li Yongjian, Fu Yu, Dou Yu, et al. Magnetic properties measurement and analysis of electrical steel sheet under cutting influence[J]. 2021, 11(2): 025115.
[16] 赵小军, 张凌云, 刘洋, 等. 机械应力对取向硅钢片综合磁性能影响的实验研究[J]. 电工技术学报, 2022, 37(22): 5776-5787.
Zhao Xiaojun, Zhang Lingyun, Liu Yang, et al. Experimental study on the effect of mechanical stress on the comprehensive magnetic properties of the grain-oriented silicon steel[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5776-5787.
[17] 刘士利, 罗英楠, 刘宗烨, 等. 基于电磁-热耦合原理的三芯铠装电缆在低频输电方式下的损耗特性研究[J]. 电工技术学报, 2021, 36(22): 4829-4836.
Liu Shili, Luo Yingnan, Liu Zongye, et al. Study on loss characteristics of three core armored cable under low-frequency transmission mode based on electro- magnetic, thermal coupling principle[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4829-4836.
[18] 李海锋, 许永治, 刘沈全, 等. 柔性低频输电系统的故障分量特征及保护适用性分析[J]. 高电压技术, 2024, 50(5): 1987-1996.
Li Haifeng, Xu Yongzhi, Liu Shenquan, et al. Analysis of fault component characteristics and protection applicability on flexible low frequency transmission system[J]. High Voltage Engineering, 2024, 50(5): 1987-1996.
[19] 刘刚, 孙立鹏, 王雪刚, 等. 正弦及谐波激励下的铁心损耗计算方法改进及仿真应用[J]. 电工技术学报, 2018, 33(21): 4909-4918.
Liu Gang, Sun Lipeng, Wang Xuegang, et al. Improvement of core loss calculation method and simulation application under sinusoidal and harmonic excitations[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4909-4918.
[20] 何忠治. 电工钢[M]. 北京: 冶金工业出版社, 1997.
[21] Bertotti G. General properties of power losses in soft ferromagnetic materials[J]. IEEE Transactions on Magnetics, 1988, 24(1): 621-630.
[22] Permiakov V, Dupré L, Pulnikov A, et al. Loss separation and parameters for hysteresis modelling under compressive and tensile stresses[J]. Journal of Magnetism and Magnetic Materials, 2004, 272: E553- E554.
[23] 赵志刚, 徐曼, 胡鑫剑. 基于改进损耗分离模型的铁磁材料损耗特性研究[J]. 电工技术学报, 2021, 36(13): 2782-2790.
Zhao Zhigang, Xu Man, Hu Xinjian. Research on magnetic losses characteristics of ferromagnetic materials based on improvement loss separation model[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2782-2790.
[24] Olivares-Galván J C, Escarela-Pérez R, Georgilakis P S, et al. Separation of no-load losses for distribution transformers using experimental methods: two frequ- encies and two temperatures[C]//7th Mediterranean Conference and Exhibition on Power Generation, Transmission, Distribution and Energy Conversion (MedPower 2010), Agia Napa, 2010: 1-5.
[25] 金秋. 间谐波激励下的电工钢损耗分析与磁化特性研究[D]. 北京: 华北电力大学, 2022.
Jin Qiu. Loss analysis and magnetization characteri- stics of electrical steel under interharmonic exci- tation[D]. Beijing: North China Electric Power University, 2022.
[26] Bertotti G. Hysteresis in Magnetism[M]. San Diego: Academic Press, 1998.
[27] Martin R V, Perigo E A. A static measurement system for soft magnetic materials[J]. IEEE Transactions on Magnetics, 2014, 50(4): 1-4.
[28] Garcia J A, Rivas M. A quasi-static magnetic hysteresis loop measurement system with drift correction[J]. IEEE Transactions on Magnetics, 2006, 42(1): 15-17.
[29] 程灵, 马光, 韩钰, 等. 薄规格取向硅钢电磁特性及在中低频率电力装备中的应用[J]. 电工钢, 2022, 4(4): 1-8.
Cheng Ling, Ma Guang, Han Yu, et al. Electro- magnetic characteristics of thin-gauge grain-oriented silicon steel and its application in medium and low frequency power equipments[J]. Electrical Steel, 2022, 4(4): 1-8.
[30] 段子越, 孟永庆, 宁联辉, 等. 柔性分频输电系统的构建规划及关键设备技术综述[J]. 电力系统自动化, 2023, 47(10): 205-215.
Duan Ziyue, Meng Yongqing, Ning Lianhui, et al. Review on construction planning and key equipment technology of flexible fractional frequency trans- mission system[J]. Automation of Electric Power Systems, 2023, 47(10): 205-215.
[31] 赵国亮, 陈维江, 邓占锋, 等. 柔性低频交流输电关键技术及应用[J]. 电力系统自动化, 2022, 46(15): 1-10.
Zhao Guoliang, Chen Weijiang, Deng Zhanfeng, et al. Key technologies and application of flexible low- frequency AC transmission[J]. Automation of Electric Power Systems, 2022, 46(15): 1-10.
Abstract The magnetic properties and loss characteristics of oriented silicon steel sheets exhibit significant deviation under stress. The traditional loss separation model generally overlooks the impact of mechanical stress on the loss characteristics, resulting in calculation errors. In recent years, most studies on the loss characteristics of oriented silicon steel sheets under mechanical stress have focused on qualitative analysis, with only a few studies making quantitative improvements to the loss separation model. This paper develops an improved loss separation model based on the traditional loss separation model by introducing stress terms into the hysteresis loss and excess loss.
Firstly, measurements from a single sheet tester with unidirectional stressing are utilized to analyze the stress dependency of the loss characteristics of the oriented silicon steel sheets. The experimental results demonstrate a significant enhancement in loss under compressive stress while exhibiting a slight decreasing trend under tensile stress. The magnetization mechanism in ferromagnetism explains the variation of the loss characteristics under mechanical stress. Secondly, the hysteresis loss and excess loss under stress are calculated based on the Bertotti traditional loss separation model. Since the stress component is not introduced into the hysteresis loss in the traditional loss separation model, the effect of stress on the hysteresis loss is only reflected by the hysteresis loss coefficient, leading to a significant error in the calculation of the hysteresis loss under stress. Although the excess loss parameter 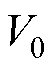 , currently expressed by a constant coefficient, embodies the effect of stress, it fails to capture the effect of the applied mechanical stress on the losses of each magnetic induction intensity. Consequently, computational inaccuracies arise when employing the Bertotti traditional loss separation model.
, currently expressed by a constant coefficient, embodies the effect of stress, it fails to capture the effect of the applied mechanical stress on the losses of each magnetic induction intensity. Consequently, computational inaccuracies arise when employing the Bertotti traditional loss separation model.
Based on the correlation between parameters 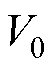 in excess loss, hysteresis loss, and stress, the traditional separation formula for losses is improved by introducing stress components into the excess loss parameters
in excess loss, hysteresis loss, and stress, the traditional separation formula for losses is improved by introducing stress components into the excess loss parameters 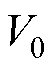 and hysteresis loss. An improved loss separation model is established and verified by varying the frequency of excitation and the type of oriented silicon steel sheet. The results indicate that the improved loss separation model can accurately separate and calculate the losses of oriented silicon steel sheets under different stresses while maintaining a remarkable precision level.
and hysteresis loss. An improved loss separation model is established and verified by varying the frequency of excitation and the type of oriented silicon steel sheet. The results indicate that the improved loss separation model can accurately separate and calculate the losses of oriented silicon steel sheets under different stresses while maintaining a remarkable precision level.
Experimental measurement and calculation analysis are performed, and the conclusions are as follows. (1) The excess loss parameter 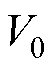 is correlated with stress, and incorporating the stress component into the excess loss parameter can effectively mitigate the calculation error caused by stress in the traditional loss separation model. (2) An improved loss separation model is proposed based on the traditional mode by incorporating the excess loss and hysteresis loss into stress-related functions. (3) The improved loss separation model is confirmed through testing with different frequency excitations and oriented silicon steel sheets, demonstrating its ability to accurately separate losses under different stresses.
is correlated with stress, and incorporating the stress component into the excess loss parameter can effectively mitigate the calculation error caused by stress in the traditional loss separation model. (2) An improved loss separation model is proposed based on the traditional mode by incorporating the excess loss and hysteresis loss into stress-related functions. (3) The improved loss separation model is confirmed through testing with different frequency excitations and oriented silicon steel sheets, demonstrating its ability to accurately separate losses under different stresses.
keywords:Loss separation model, mechanical stress, oriented silicon steel sheets, excess loss, hysteresis loss
中图分类号:TM275
DOI: 10.19595/j.cnki.1000-6753.tces.240808
国家自然科学基金资助项目(51577066)。
收稿日期 2024-05-15
改稿日期2024-06-26
李慧奇 男,1970年生,博士,教授,研究方向为电工理论与新技术。
E-mail: huiqili@263.net
廖峪茹 女,1999年生,硕士研究生,研究方向为先进输变电技术。
E-mail: liaoyuru@ncepu.edu.cn(通信作者)
(编辑 郭丽军)