基于坡印廷定理的无线电能传输系统电磁能流与耦合特性研究
王奉献1 周依桐1 张 献1 杨庆新1,2 厉光耀1
(1. 智能配用电装备与系统全国重点实验室(河北工业大学) 天津 300401 2. 天津理工大学电气工程与自动化学院 天津 300384)
摘要 无线电能传输是以电磁理论为核心的多学科强交叉的新兴研究领域,为描述无线电能传输系统耦合空间内电磁能量变换过程,并针对目前电磁能流研究由于采用复杂高阶数学手段导致其难以通过实验验证、缺乏合理的模型和分析手段描述空间能流分布特性问题,该文通过分析基础电气元件电磁能流的共性特点,基于坡印廷定理搭建了正弦激励下无线电能传输电磁能流模型,采用降阶数学模型定性探索无线电能传输空间能量耦合本质,从能量流动机理的角度划清了与其他电磁变换技术的界限。讨论了无线电能传输系统中电感耦合与电容耦合的共存现象,表明增强近区电磁场耦合是提升系统整体性能的关键,通过电磁能流的观点统一表述了电磁近场区域内无线电能传输的工作模式。最终搭建实验平台对其电感耦合方式与电容耦合方式进行了原理验证。
关键词:无线电能传输 电磁能流 电磁近区 感性耦合 容性耦合
0 引言
为满足日益增长的人类社会生产与生活所需的能量,电能作为一种具有代表性的二次能源,被广泛应用于各类社会活动中。同时,电能科技的不断进步极大地丰富了各类用电场景,推动了人类社会的进步。电工装备作为电能与其他形式能量相互转换的重要组成,广泛存在于电能产生、传输、分配以及利用的各个环节。无线电能传输装置作为电工装备的一种,满足了灵活便捷的电能传输需求,受到越来越多学者的关注,在信息化、现代化、智能化的电工技术应用演进过程中占有重要地位[1]。
1887年,赫兹依据麦克斯韦理论关于电场与磁场的关系,通过观察由开口环形铜线设计的电磁波接收器在电扰动作用下产生微弱电火花,一方面证明了电磁波的存在[2],同时也实现了间隔一定距离下电能的转移,是无线电能传输的首次科学实验,其相关成果为无线通信的实现提供了可能。美籍塞尔维亚科学家特斯拉于1893年在美国圣路易斯首次公开展示无线电通信,并在纽约长岛修建高57 m的沃登克里弗塔[3],计划通过无线方式传输电能实现全球电能供应,是无线电能传输的首次工程化尝试。
此后信息无线传输与电能无线传输成为现代社会发展的两大重要技术突破,其中无线通信技术的发展驱动人类进入了移动信息时代。相较于信息无线传输技术的井喷式发展,电能无线传输并未因特斯拉实验的搁浅而停滞不前,国内外专家学者在该领域持续不断探索并取得众多突破,2013年该技术入选世界十大科技前沿研究热点,无线电能传输有可能为人类社会的进步书写新的篇章[4-5]。
无线电能传输技术以交变电磁场作为能量传送介质,通过电场能量与磁场能量的相互转换,实现能量的无接触传递[6-7]。现有的无线电能传输技术依据传输原理可划分为磁场感应耦合式无线电能传输技术[8-11]、电场感应耦合式无线电能传输技术[12-14]、磁场谐振耦合式无线电能传输技术[15-19]、电磁辐射式无线电能传输技术[20-22]以及激光式无线电能传输技术[23],典型无线电能传输技术对比见表1。
表1 典型无线电能传输技术对比
Tab.1 Comparison of typical wireless power transfer
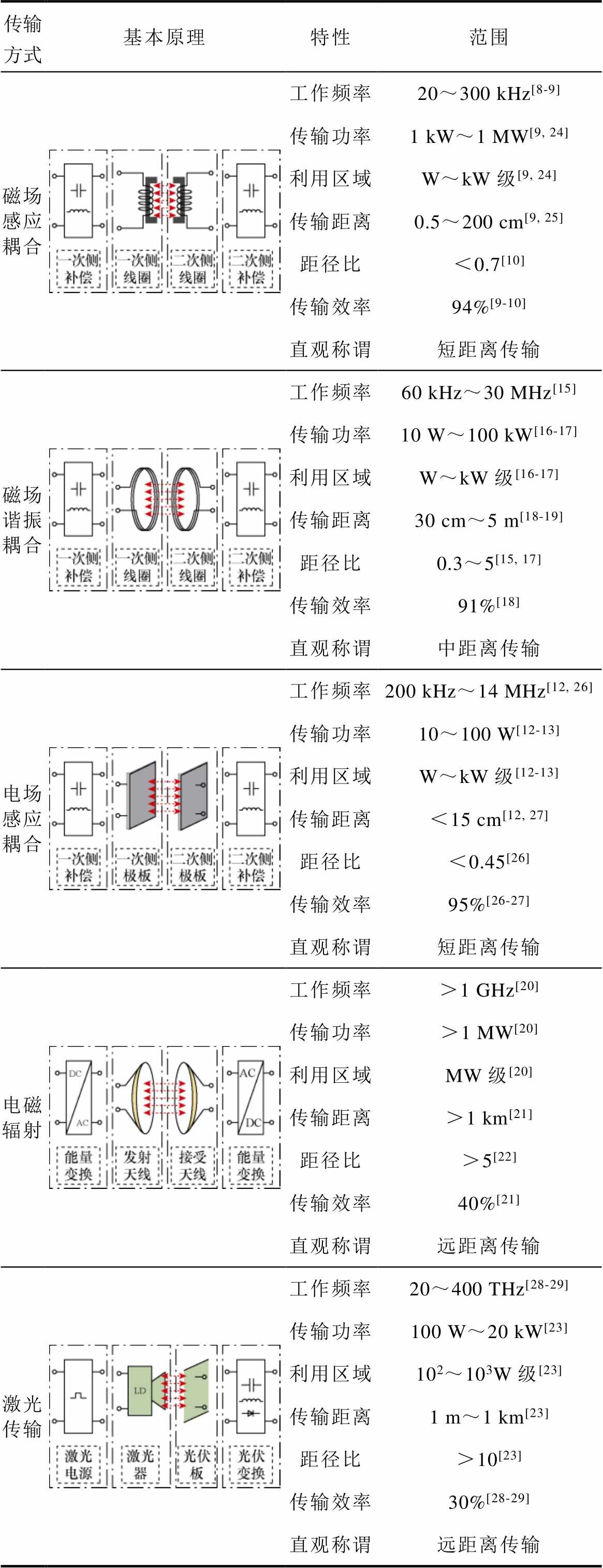
传输方式基本原理特性范围 磁场感应耦合工作频率20~300 kHz[8-9] 传输功率1 kW~1 MW[9, 24] 利用区域W~kW级[9, 24] 传输距离0.5~200 cm[9, 25] 距径比<0.7[10] 传输效率94%[9-10] 直观称谓短距离传输 磁场谐振耦合工作频率60 kHz~30 MHz[15] 传输功率10 W~100 kW[16-17] 利用区域W~kW级[16-17] 传输距离30 cm~5 m[18-19] 距径比0.3~5[15, 17] 传输效率91%[18] 直观称谓中距离传输 电场感应耦合工作频率200 kHz~14 MHz[12, 26] 传输功率10~100 W[12-13] 利用区域W~kW级[12-13] 传输距离<15 cm[12, 27] 距径比<0.45[26] 传输效率95%[26-27] 直观称谓短距离传输 电磁辐射工作频率>1 GHz[20] 传输功率>1 MW[20] 利用区域MW级[20] 传输距离>1 km[21] 距径比>5[22] 传输效率40%[21] 直观称谓远距离传输 激光传输工作频率20~400 THz[28-29] 传输功率100 W~20 kW[23] 利用区域102~103W级[23] 传输距离1 m~1 km[23] 距径比>10[23] 传输效率30%[28-29] 直观称谓远距离传输
为直观地描述无线电能传输系统耦合空间内电磁能量的分布,国内外研究团队开展了关于无线电能传输系统电磁能量流动机理的研究。里斯本科技大学研究团队提出了一种基于麦克斯韦方程组的数学模型来评估无线电能传输系统中的坡印廷矢量,通过短偶极子理论分析无线电能传输系统发射侧的电磁能值,但未考虑接收侧对空间电磁能的贡献,该理论工作需进一步完善[30]。奥克兰大学研究团队针对具有双线圈的磁感应耦合式无线电能传输系统的坡印廷矢量进行分析,并对不同负载下空间内电磁能量分布变化情况进行了探讨,同时通过坡印廷矢量的表面积分获得两个线圈之间的功率流,并与初级线圈的输入功率和次级线圈的输出功率进行比较,结果表明,对于无损系统三类功率相等[31-32]。重庆大学研究团队基于毕-撒定律分析了不同种类的负载特性下磁耦合谐振式无线电能传输系统的电磁能量传输情况,并得到初步结论:当且仅当负载为电阻性时,耦合空间内的坡印廷矢量具有实部,系统可以传递电磁能量[33]。
本文为明确基于近区电磁场的无线电能传输技术的研究边界,基于坡印廷矢量对常见电气元件的电磁能流特性和无线电能传输系统的电磁能流特性进行分析,讨论了无线电能传输系统中电感耦合作用与电容耦合作用的共存现象。利用坡印廷定理描述无线电能传输系统耦合空间内的电磁能量交换过程,临近空间内的电磁场耦合是电磁能量交换的关键。利用电感耦合与电容耦合作用的共存现象,扩宽无线电能传输系统能量传输通道的容量,实现两类耦合能量的协同传输具有潜在价值。本文工作为基于近区电磁场的无线电能传输技术的理论研究提供重要参考,同时为后续高功率密度电磁耦合机构设计提供思路。
1 电路典型元件的电磁能流分析
1.1 导线电磁能流特性分析
无线电能传输系统可视为多个RLC谐振电路的相互连接,掌握电路常用元件的电磁能流特性对于分析复杂无线电能传输的电磁能量流动过程具有重要意义。单导线电磁能流特性分析如图1所示。可将外半径b趋于无穷大的同轴电缆等效为长直单导线,并以直流源作为外接激励,则其周围(rR处)电场强度可表示为
式中,UR为线缆电压激励;a为同轴电缆内半径;b为同轴电缆外半径;rR为观察点到导线中轴线的距离。依据安培环路定律,同轴电缆内表面附近区域的磁场强度可表示为
式中,IR为线缆电流激励。
选取同轴电缆内外表面间的横截面作为积分面,则坡印廷矢量及其面积分可表示为
式中,f 为圆柱坐标系下的角度。
式(3)表明,对于由外半径b趋于无穷大的同轴电缆等效的长直单导线的临近空间,存在沿着导线电流方向的电磁功率流动。
对于等效后的单导线内部,即同轴电缆内导体内部,由欧姆定律可得其电场强度为
式中, 为单导线的电导率。
为单导线的电导率。
对于导线内部,其电场强度方向沿导线内电流方向,以单导线外表面作为积分面,可得
式中,R为单导线电阻,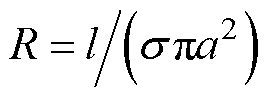 ,l为单导线的长度。进入单导线内部的功率等于该单导线损耗的焦耳功率,坡印廷矢量方向为由单导线表面指向中心。
,l为单导线的长度。进入单导线内部的功率等于该单导线损耗的焦耳功率,坡印廷矢量方向为由单导线表面指向中心。
由式(5)可知,单导线传输的功率是通过临近空间的电磁场传播的,导体仅对电磁功率的传播方向提供指引作用。当单导线为非理想导体时,进入导体内的功率以焦耳损耗的形式被单导线吸收。电磁能量传播并不依赖导体,这也为电磁能量的无接触传递提供了理论支撑。
1.2 典型NL匝螺线管系统电磁能流特性分析
对于采用导线绕制线圈并在正弦交变电流的激励下产生交变磁场及电磁能流情况,首先讨论NL匝长直密绕螺线管其中一段的电磁功率特性,依据安培环路定律以及法拉第电磁感应定律可得。螺线管内电磁场表示为
式中,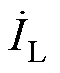 为螺线管电流激励;
为螺线管电流激励;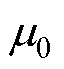 为真空磁导率;rL为观察点到螺线管中轴线的距离;dL、rL分别为NL匝螺线管高度与半径;w 为系统工作频率。则NL匝螺线管的复坡印廷矢量及复功率可表示为
为真空磁导率;rL为观察点到螺线管中轴线的距离;dL、rL分别为NL匝螺线管高度与半径;w 为系统工作频率。则NL匝螺线管的复坡印廷矢量及复功率可表示为
式中,L为螺线管的等效电感;* 表示共轭。
根据式(7)可知,NL匝螺线管消耗的无功功率由外侧指向中心,电磁功率在螺线管内部和周围空间周期性地流动,其对外不交换电磁功率。
对由一对NL匝螺线管构成的变压器的能流特性进行分析,假定系统处于理想工作状态,忽略空间漏磁及电磁场边缘效应,假定空间中电场分布均匀。图2所示为空间中电场与磁场的近似结果,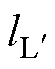 为磁心内部空间高度。
为磁心内部空间高度。
假定磁心中的磁导率无穷大,且不存在铁损,此时磁心内不存在电磁功率。实际上磁心磁导率为限定值。忽略漏磁,磁心内的磁场强度与主磁通方向一致,表示为
式中,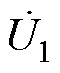 为一次电压激励;AM为磁心横截面积;
为一次电压激励;AM为磁心横截面积;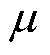 为磁心的磁导率;
为磁心的磁导率;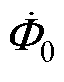 为磁心内的主磁通量;
为磁心内的主磁通量;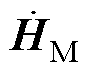 为磁心内磁场强度。特别地,本文所有涉及时谐场分析的电磁参数(如磁场强度
为磁心内磁场强度。特别地,本文所有涉及时谐场分析的电磁参数(如磁场强度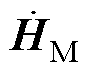 ,
,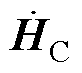 )均以复数相量的模值形式表征。以
)均以复数相量的模值形式表征。以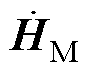 为例,
为例,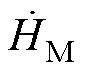 为磁心内磁场强度复数相量
为磁心内磁场强度复数相量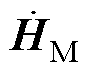 的模值。
的模值。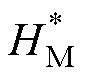 为磁心内磁场强度复数相量
为磁心内磁场强度复数相量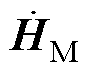 共轭的模值。
共轭的模值。
磁心内复坡印廷矢量及其消耗的复功率为
式中,BM为磁心内磁感应强度的模值;HM为磁心内磁场强度的模值。
式(9)表明磁心中的复坡印廷矢量是一个纯虚数,表示磁心并不传递有功功率,主要起电磁功率的导向作用。若磁心是完全线性、无损的,式(9)表示的功率是系统无功功率的一部分。若磁心磁导率趋于无穷大,磁心上存储的无功功率趋于零。
依据法拉第电磁感应定律及安培环路定理,磁心临近区域(下标用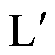 表示该区域)电场强度与磁场强度可表示为
表示该区域)电场强度与磁场强度可表示为
式中,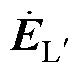 为磁心临近区域电场强度;
为磁心临近区域电场强度;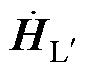 为磁心临近区域磁场强度;
为磁心临近区域磁场强度;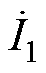 为变压器一次电流;
为变压器一次电流;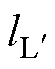 为磁心内部空间高度。
为磁心内部空间高度。
在深度方向上取单位长度,以变压器内部横截面作为积分面可以得到由一次侧到二次侧的复功率为
通过本节讨论可知,对于典型NL匝螺线管构成的变压器系统,电磁能流特性与单导线系统具有对偶性,电磁能量通过磁心临近空间电磁场传输,磁心为电磁能量流动提供指引作用[34]。
1.3 典型平面电容器系统电磁能流特性分析
对于采用电容极板在交变电流的激励下产生交变电场并实现电场耦合的情况,首先讨论单个平面电容器。忽略电容器极板之间的感应电场与边缘效应,依据全电流定律得电容极板间的电磁场可表示为
式中,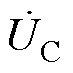 为电容板两端的电势差;dC为电容板间距;e0为真空介电常数;rC为平面电容板半径;rC为观察点到电容板中轴线的距离。则平面电容器的复坡印廷矢量及其所存储的功率可表示为
为电容板两端的电势差;dC为电容板间距;e0为真空介电常数;rC为平面电容板半径;rC为观察点到电容板中轴线的距离。则平面电容器的复坡印廷矢量及其所存储的功率可表示为
式中,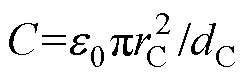 为电容器电容。
为电容器电容。
对比式(7)与式(13)可知,与螺线管情况一致,平行板电容器消耗的无功功率由外侧指向中心,电磁功率只是在电容器内部和周围空间周期性流动,其与外部空间不交换电磁功率。
对由两个平行板电容器串联构成回路的能流特性进行分析,电容耦合电路的电磁能流特性分析图3所示。假定电容器极板间的介电常数无穷大,此时电容器极板之间不存在电磁功率。实际上极板间的介电常数为限定值。忽略电磁场的边缘效应,极板间的电场强度与电流方向一致(用下标D表示与极板相关的物理量),表示为
式中,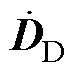 为复数形式的电位移矢量;AD为极板横截面积;
为复数形式的电位移矢量;AD为极板横截面积;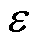 为板间介质的介电常数;
为板间介质的介电常数;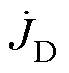 为回路电流密度。电容器内复坡印廷矢量及其消耗的复功率为
为回路电流密度。电容器内复坡印廷矢量及其消耗的复功率为
式(15)表明平面电容器内的复坡印廷矢量是一个纯虚数,表示极板间的介质并不传递有功功率,主要起电磁功率的导向作用,式(15)表示的功率是系统无功功率的一部分。若极板间介质的介电常数趋于无穷大时,极板间存储的无功功率趋于零。依据位移电流假设,极板临近区域(用下标 表示该区域的物理量)的电磁场满足
表示该区域的物理量)的电磁场满足
在深度方向上取极板直径,以电容器之间的横截面作为积分面可得由电源到负载的复功率为
因此,对平面电容器系统的电磁能流特性,与单导线、变压器具有对偶性,电容器内部不传输电磁能量,能量通过电容器边缘处电磁场实现传输。
通过本节讨论可知,对于RLC电路元件,其本身并不传输电磁能量,均是借助元件邻近空间电磁场实现电磁功率的传递。在简单直流电路中,导线仅对电磁功率具有导向作用,不参与电磁功率的传输,电磁能量以导线周围空间中的电磁场作为通道传递。在变压器电路模型中,磁心中的主磁通并不直接参与电磁功率的传输,而磁心内部空间中的漏磁与感应电场相互作用,实现电磁功率的传输。在电容器电路模型中,极板间的库仑电场不直接参与电磁功率的传输,极板边缘的外溢电场与感应磁场相互作用,实现电磁功率的传输。
2 无线电能传输系统电磁能流特性分析
无线电能传输系统可视为多个RLC独立电路的组合,电磁功率除了存储于独立电路中的电感与电容之外,根据前节讨论可知,RLC电路元件相互间存在电磁功率流动。对于单个RLC电路,以正弦电压作为激励源时,根据坡印廷定理可得
式(18)表明,对于单个RLC串联电路,假定其处于某一闭合曲面内,穿过闭合曲面的电磁功率符合能量守恒定律。其中电感与电容仅作为无源无功元件,无功功率在电感与电容之间相互交换。忽略电路对外辐射,系统的有功功率耗散在电阻上,整体上无电磁功率的外溢。对具有n个RLC串联电路系统的电磁能流特性进行分析,忽略系统的非线性影响,根据坡印廷定理可得式(19)。
式(19)表示,对于n个RLC振荡系统,电磁功率一部分存储于自身回路的电磁场中,即为自有能;另一部分存储于回路之间的电磁场中,即为互有能。一般性无线电能传输系统能量如图4所示。由于系统整体遵循能量守恒,互有能部分等于零且具有对称性。
为简化问题,对n=2时RLC串联回路系统的电磁能流进行分析,此时系统电磁场由两部分单元电路共同贡献,即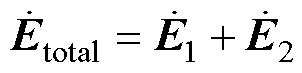 ,
,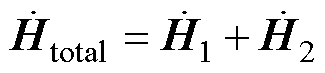 。
。
系统的自有能部分可表述为
系统的互有能部分可表述为
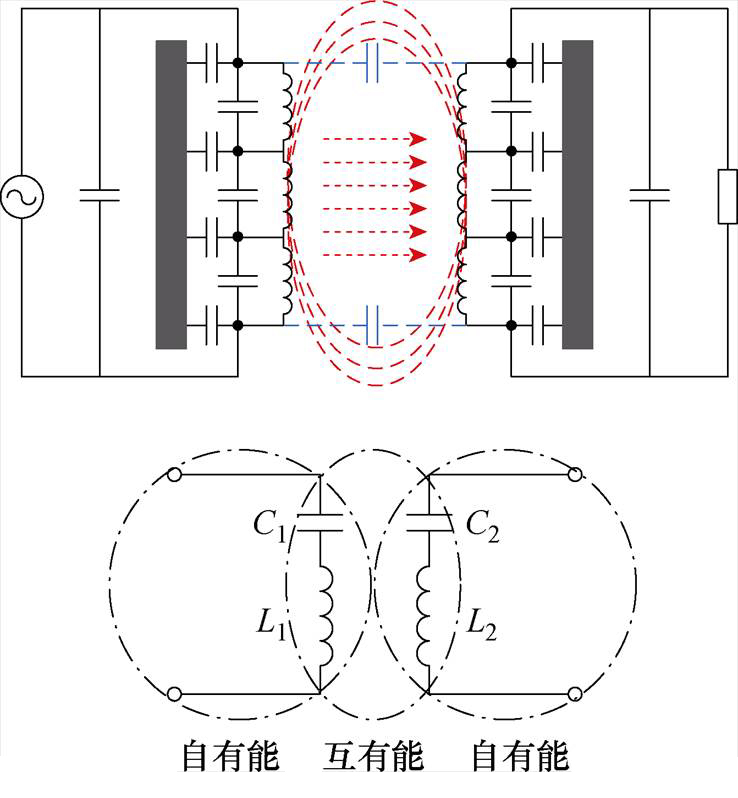
对于n=2的RLC串联电路系统,其可视为简化的串联型无线电能传输系统。由此可知,无线电能传输系统依靠原边与副边的相互耦合实现电磁功率的无接触传递。实现单元之间有功功率与无功功率的传输主要依靠临近空间互有能的相互耦合。需注意到,不同耦合机构的结构会对空间中的磁场与电场分布产生影响,但上述分析是以单侧电路整体作为分析对象,并不会影响最终结论。以基于线圈为传能载体的无线电能传输系统的能流特性为分析对象,讨论具有一般意义的空间电磁能流流动特性。
一般性无线电能传输电磁能流特性分析如图5所示。图5中,下标n和t分别表示法向和径向。
由图5可知,空间被划分为7个区域:1和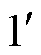 为磁屏蔽区域;2和
为磁屏蔽区域;2和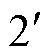 为磁屏蔽与线圈之间的空隙区域;3和
为磁屏蔽与线圈之间的空隙区域;3和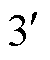 为线圈区域;4为线圈之间的空隙区域。对各区域的电磁场分析如下:
为线圈区域;4为线圈之间的空隙区域。对各区域的电磁场分析如下:
(1)磁屏蔽区域1和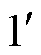 。该区域的磁感应强度不为零,由于其相对磁导率远大于真空磁导率,
。该区域的磁感应强度不为零,由于其相对磁导率远大于真空磁导率,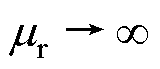 ,该区域的磁场强度为零,因此坡印廷矢量为零,此区域不存在电磁功率交换。
,该区域的磁场强度为零,因此坡印廷矢量为零,此区域不存在电磁功率交换。
(2)磁屏蔽与线圈之间的空隙区域2和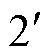 。依据磁场强度的连续性,该区域磁场强度为零,因此坡印廷矢量为零,此区域不存在电磁功率交换。
。依据磁场强度的连续性,该区域磁场强度为零,因此坡印廷矢量为零,此区域不存在电磁功率交换。
(3)线圈区域3和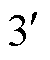 。考虑线圈内部损耗,此时坡印廷矢量由线圈表面指向线圈轴心,该部分电磁功率不参与两侧线圈之间的功率交换,以焦耳热的形式损耗。对于互有能部分,两侧线圈激发的电场与对方电流产生直接耦合,传输系统的有功功率和一部分无功功率,该区域直接决定了无线电能传输的功率等级和效率水平。
。考虑线圈内部损耗,此时坡印廷矢量由线圈表面指向线圈轴心,该部分电磁功率不参与两侧线圈之间的功率交换,以焦耳热的形式损耗。对于互有能部分,两侧线圈激发的电场与对方电流产生直接耦合,传输系统的有功功率和一部分无功功率,该区域直接决定了无线电能传输的功率等级和效率水平。
(4)线圈之间的空隙区域4,该区域磁场强度不为零,并满足右手定则。同时由磁通产生的电场强度如图5所示。该区域同时存在磁场强度与电场强度,此时坡印廷矢量由发射侧指向接收侧,电磁功率沿着水平切向传输。这一区域体现了耦合过程中的无功功率通道效应,间接决定了电磁功率传输的比例。
通过上述分析可知,理想条件下( ),电磁功率仅在线圈之间的空隙区域内传输,在其他空隙以及磁屏蔽内部磁场强度趋近于零,可认为理想条件下不存在电磁功率的传递。非理想条件下
),电磁功率仅在线圈之间的空隙区域内传输,在其他空隙以及磁屏蔽内部磁场强度趋近于零,可认为理想条件下不存在电磁功率的传递。非理想条件下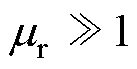 ,但
,但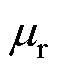 为限定值。可证得:在磁屏蔽区域1和
为限定值。可证得:在磁屏蔽区域1和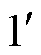 及其与线圈之间的空隙区域2和
及其与线圈之间的空隙区域2和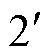 ,电场相位与磁场相位相差
,电场相位与磁场相位相差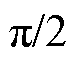 ,该区域内复坡印廷矢量仅有虚部,仅有无功功率交换。线圈之间的空隙区域4内复坡印廷矢量既有实部也有虚部,是无线电能传输的关键区域。即近区电磁场耦合是无线电能传输的关键因素,是无线电能传输能够实现高效能量传输的基础。同时无线电能传输系统无法像变压器或电容器那样通过高性能的导磁材料或介电材料引导电磁场。
,该区域内复坡印廷矢量仅有虚部,仅有无功功率交换。线圈之间的空隙区域4内复坡印廷矢量既有实部也有虚部,是无线电能传输的关键区域。即近区电磁场耦合是无线电能传输的关键因素,是无线电能传输能够实现高效能量传输的基础。同时无线电能传输系统无法像变压器或电容器那样通过高性能的导磁材料或介电材料引导电磁场。
3 典型磁耦合谐振式无线电能传输系统讨论
以理想磁屏蔽外加无限长直导线为基础模型,依据电磁场唯一性定理及镜像法可知,磁屏蔽对耦合空间内场强分布影响可等效为磁导率为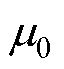 空间的镜像电流源
空间的镜像电流源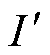 与相对磁导率为
与相对磁导率为 空间的镜像电流源
空间的镜像电流源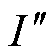 的共同作用,如图6所示,镜像电流可表示为
的共同作用,如图6所示,镜像电流可表示为
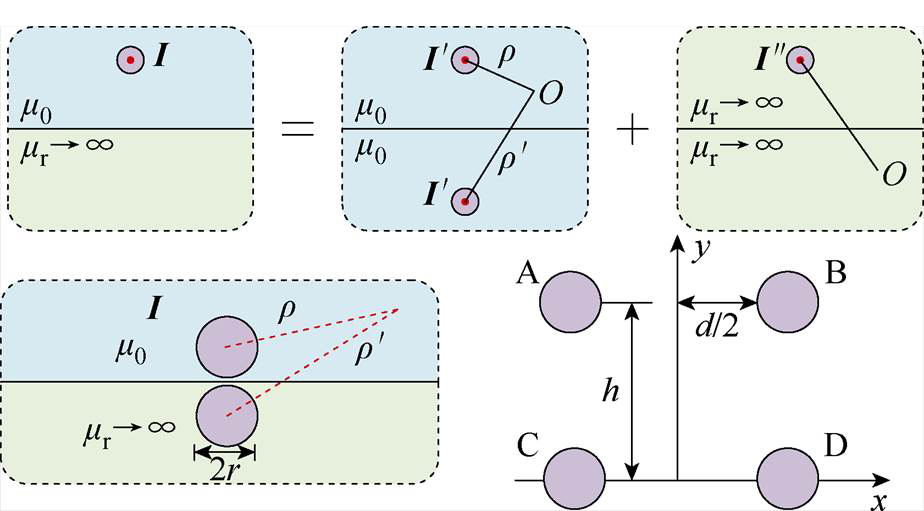
由于无线电能传输系统发射线圈与接收线圈均会放置磁屏蔽装置,因此需要做两次镜像。第一次镜像以发射端磁屏蔽为镜面,第二次镜像以接收端磁屏蔽为镜面。考虑理想磁屏蔽作用下,对于流通电流I的长直导线,其外自感与内自感可表示为
式中,h和d分别为长直平行导线的垂直间距和水平间距。
考虑屏蔽情况下的长直平行导线单位长度自感为
对由两组长直导线组成的线圈之间的互感分析,两侧镜像电流产生磁链对接收端的交链情况如图7所示。导线AB与CD间交链磁链可表示为
式中,rxy(x, y=A, B, C, D)为节点x与节点y之间的距离;ymA为导线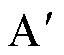 对导线C和D的磁通和;
对导线C和D的磁通和;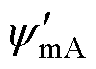 为导线
为导线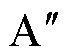 对导线C和D的磁通和;ymB为导线
对导线C和D的磁通和;ymB为导线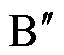 对导线C和D的磁通和;
对导线C和D的磁通和;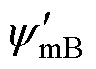 为导线
为导线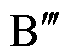 对导线C和D的磁通和。
对导线C和D的磁通和。
上方的镜像电流与下方电流的磁通交链作用相同,线圈组之间的互感可表示为
忽略长直导线自电容,水平长直导线的对地电容C0及其之间的耦合电容CM可表示为
根据前节讨论可知,耦合空间内参与功率交换的电磁功率可表示为
式中,QM为电感耦合所引起的线圈互感功率;QC为电容耦合所引起的线圈互电容功率。
式中,Iw1为导线A和B之间的电势差;Iw2为导线C和D之间的电势差;Iw1为导线A和B的工作电流;Iw2为导线C和D的工作电流。
由式(29)可知,参与功率交换的电磁功率总和除与外界激励相关外,还与线圈几何参数以及相对位置有关。对于以线圈为传能载体的无线电能传输系统,耦合作用依据来源途径不同可分为电感与电容耦合,分析不同耦合方式在传输过程中所占权重。
首先对电感耦合在能量传输过程中所占权重进行讨论,定义QIPT为次级电路广义品质因数,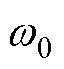 为耦合机构自然谐振频率,
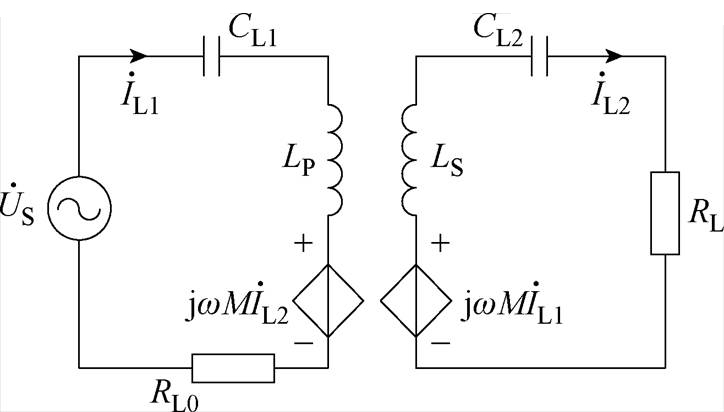
为耦合机构自然谐振频率,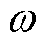 为系统工作频率,如图8所示为典型电感耦合电路。依据KVL可得回路电压方程为
为系统工作频率,如图8所示为典型电感耦合电路。依据KVL可得回路电压方程为
其中
则由电感耦合所传输的视在功率可表示为
式中,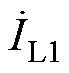 、
、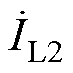 分别为一次和二次线圈电流。
分别为一次和二次线圈电流。
特别地,当满足谐振条件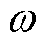 =
=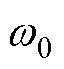 时
时
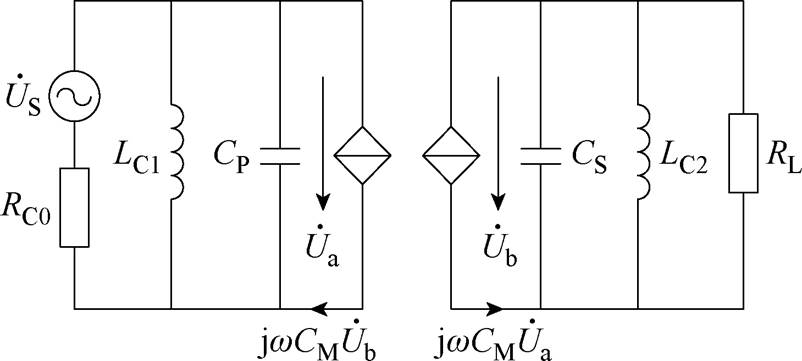
然后对电容耦合在能量传输过程中所占权重进行讨论,定义QCPT为次级电路广义品质因数。图9所示为典型电容耦合无线电能传输系统,依据KCL可得节点电流方程为
其中
式中,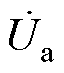 、
、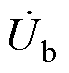 分别为对应图9中的等效受控电流源的电压。则由电容耦合所传输的视在功率可表示为
分别为对应图9中的等效受控电流源的电压。则由电容耦合所传输的视在功率可表示为
特别地,当满足谐振条件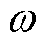 =
=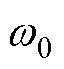 时
时
对比式(33)和式(37),磁场耦合特性与电场耦合特性之间存在数学形式上的对称。该对称性继承于电磁场的对称性,这是因为电路模型是电磁场的降阶简化模型。利用该对称特性,一方面可解释磁场感应式无线电能传输技术与电场感应式无线电能传输技术在特性上的对称性;另一方面可指导实际工程设计,通过迁移设计实现不同设计方案上功能的迁移。
本节讨论了无线电能传输系统中电感性耦合作用与电容性耦合作用的共存现象,如何利用电感性耦合与电容性耦合作用的对称特性,扩宽无线电能传输系统能量传输通道的容量,实现两类耦合能量的协同传输和近区电磁场能量的综合利用,从而提升系统电磁耦合机构的功率密度。
4 电感与电容耦合无线电能传输原理验证
本文以电磁场分析为切入点,针对典型以线圈为传能载体的无线电能传输系统,提出一种具有一般性的能量传输模型。电磁功率通过电感耦合与电容耦合两类传输途径实现无接触递送,这与传统的仅有电感耦合或电容耦合实现电磁功率传输的观点存在差异。本文观点认为两类耦合特性具有高度对称性,可由式(33)与式(37)佐证,同时对于实际工程应用的无线电能传输系统,两类耦合存在比例问题,并不能理想化地假定其中一种耦合对电磁功率传递的贡献为零。
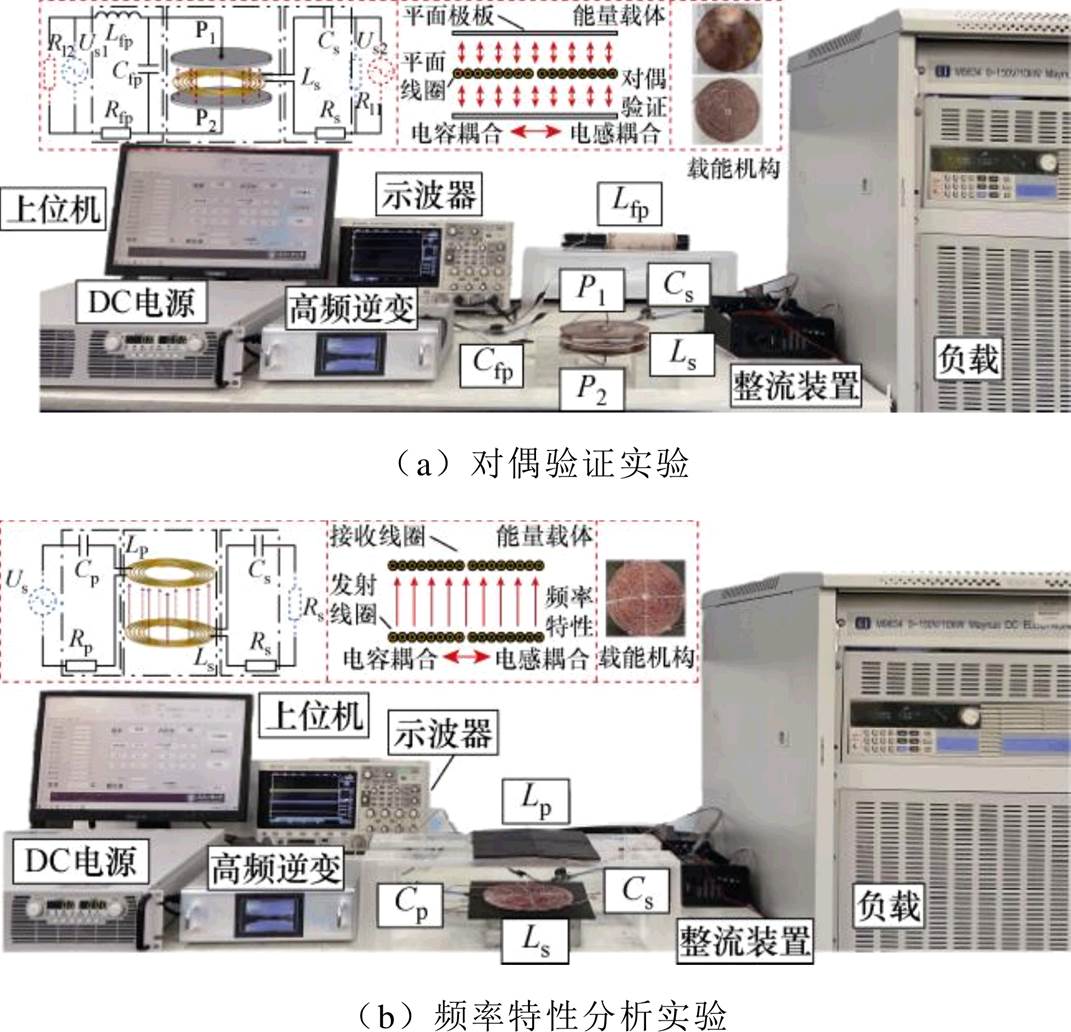
4.1 无线电能传输系统耦合特性对偶验证实验
为明确电场与磁场两类耦合机制的传输特性差异及相互作用规律,本研究通过对比实验设计:分别采用平面电容板和平面线圈为能量载体构建无线电能传输系统,开展耦合特性的对偶性验证。图10a所示为该验证实验的原理拓扑与耦合机构平面图以及实物图。其中平面极板与平面线圈直径均为15 cm,平面线圈匝数为25匝。为验证两类耦合之间的传输特性,分别以平面电容板、平面线圈为发射单元,同时将平面线圈与平面电容板分别作为对偶的能量接收单元,对系统的能量传递特性进行分析。当线圈为接收单元、平面电容板为发射单元时,系统的接收功率主要来自空间中的电感耦合功率。在实际情况下,电容耦合和电感耦合功率并存,系统的接收功率是两种耦合功率的总和。为验证两类耦合功率共存,设计对偶实验测试发射端和接收端的角色互换后系统的接收功率。若平面线圈仅承载电感耦合功率,平面电容板仅承载电容耦合功率,则在对偶实验中接收端捕获的电磁功率均为零。
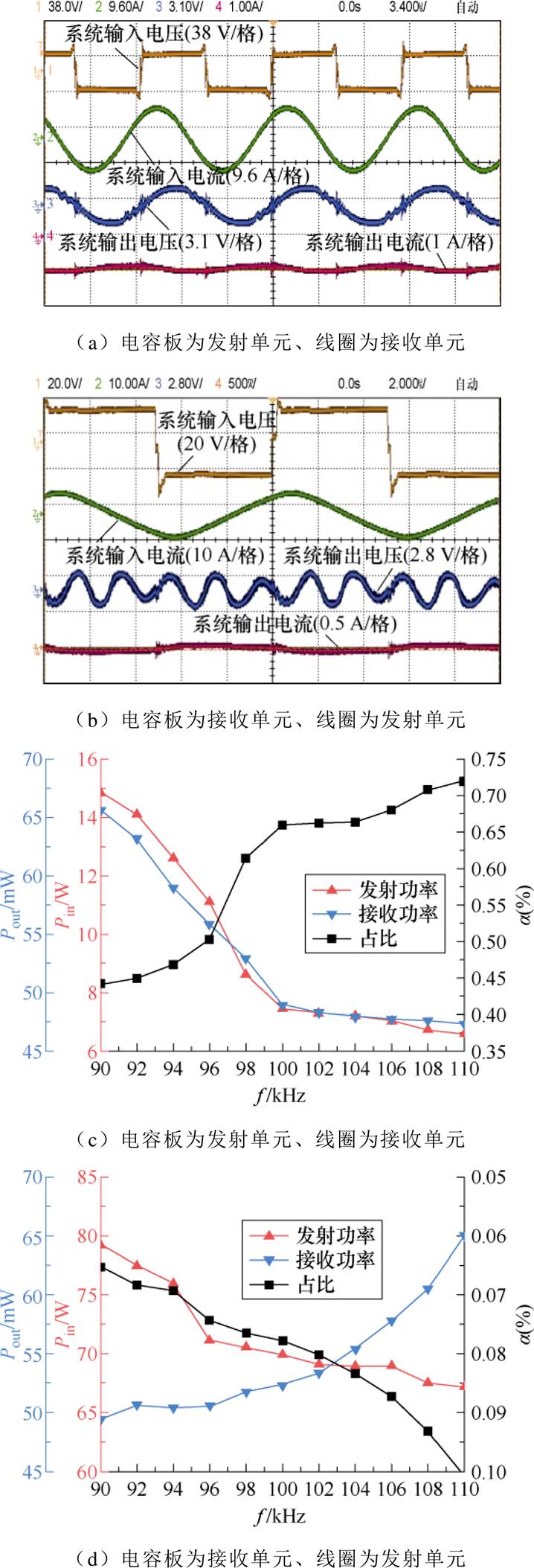
首先选取100 kHz为工作频率,此时接收线圈电感Ls=38.6 mH,补偿电容Cs=65.6 nF。发射极板容值为15 pF,为保证电路处于谐振状态,补偿电感Lfp=73.4 mH、补偿电容Cfp=34.5 nF。以平面电容板为发射单元、平面线圈为接收单元时,系统输入输出的电压电流波形如图11a所示,此时平面线圈依旧可接收空间内的电磁功率。同时为组成对偶效果,以平面电容板为接收单元、平面线圈为发射单元时,系统输入输出的电压电流波形如图11b所示,此时平面极板可捕获由平面线圈发射的电磁功率。故可证得无线电能传输系统中两类耦合具有共存特点,两类耦合作用所传递的电磁功率之间存在比例问题,这对于理解无线电能传输技术的实现具有指导意义。两类耦合所传递的电磁功率之间的比例并不固定,除了与耦合机构的结构相关外,还与系统的工作频率有关。
选取90~110 kHz作为验证频段,并保证各频率点下系统处于谐振状态。图11c所示为以平面电容板为发射单元、平面线圈为接收单元时,不同频率下平面极板的发射功率与平面线圈接收功率,同时探究工作频率与两类耦合作用对电磁功率传输贡献的比例之间的关系。随着工作频率的提升,由于高频损耗,平面极板的发射功率与平面线圈的接收功率均下降。同时随着工作频率的提升,平面线圈所接收的电磁功率与平面极板所发射的电磁功率之间的比值提升。
图11d所示为以平面电容板为接收单元、平面线圈为发射单元时,不同频率下平面极板的接收功率与平面线圈的发射功率。随着工作频率的提升,平面极板所接收的电磁功率与平面线圈所发射的电磁功率之间的比值提升。同时需注意到,根据前述分析讨论可知,两类耦合作用共存于无线电能传输系统。通过对偶验证实验可知,随着系统频率的提升电容耦合所传输的电磁能量与电感耦合所传输的电磁能量的比值提升。需要注意的是,所使用的耦合机构并非标准的线圈传能机构或极板传能机构。
4.2 两类耦合作用的频率特性分析
为验证第3节关于以线圈为能量载体的无线电能传输系统的两类耦合特性的讨论,对两类耦合作用的频率特性进行分析。图10b所示为该验证实验的原理拓扑与耦合机构平面图以及实物图。其中耦合机构均为平面线圈且尺寸参数与4.1节中平面线圈尺寸一致,见表2。频率变化范围为100~600 kHz内变化,以100 kHz为步长,系统输入功率为200 W,对系统的能量传递特性进行分析。
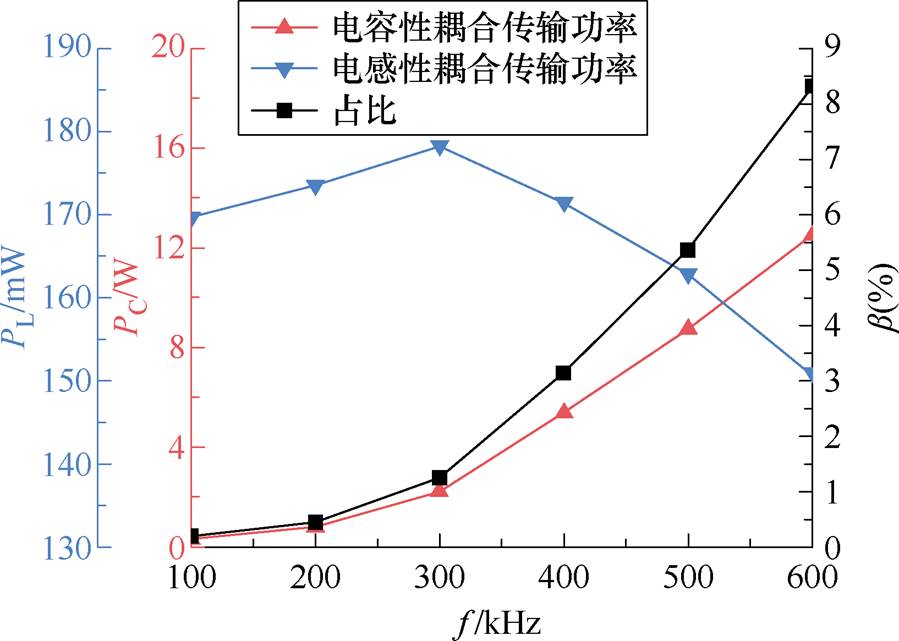
图12所示为不同频段下,系统输入输出的电压电流波形。不同频段下系统均处于谐振状态,此时电压与电流相位为零。依据式(33)和式(37)对电感耦合功率与电容耦合功率进行等效测量。将系统耦合机构的线圈电流、互感系数、负载等参数代入式(33),得到谐振状态下的磁场性耦合传输功率。同理,将系统的分布电容的耦合系数、端电压、负载等参数代入式(37),得到谐振状态下的电场性耦合传输功率。并获得两者比值随频率的变化规律。图13所示为不同频率下两类耦合功率以及比值的变化规律。随着频率的提升,电容耦合传输功率与电感耦合传输功率的变化趋势相背。尽管随着频率的增加电感耦合功率有所下降,但其对系统整体功率的影响仍小于电容耦合功率的增长。因此,即使在高频条件下增强电容耦合作用,系统整体输出功率的负面影响依然可控。且与4.1节类似,随着频率的提升,电容耦合传输通道扩宽。同时随着频率的提升,电场耦合传输功率与电感耦合传输功率之间的比值提升。
表2 无线电能传输系统实验参数
Tab.2 Experimental parameters of WPT system
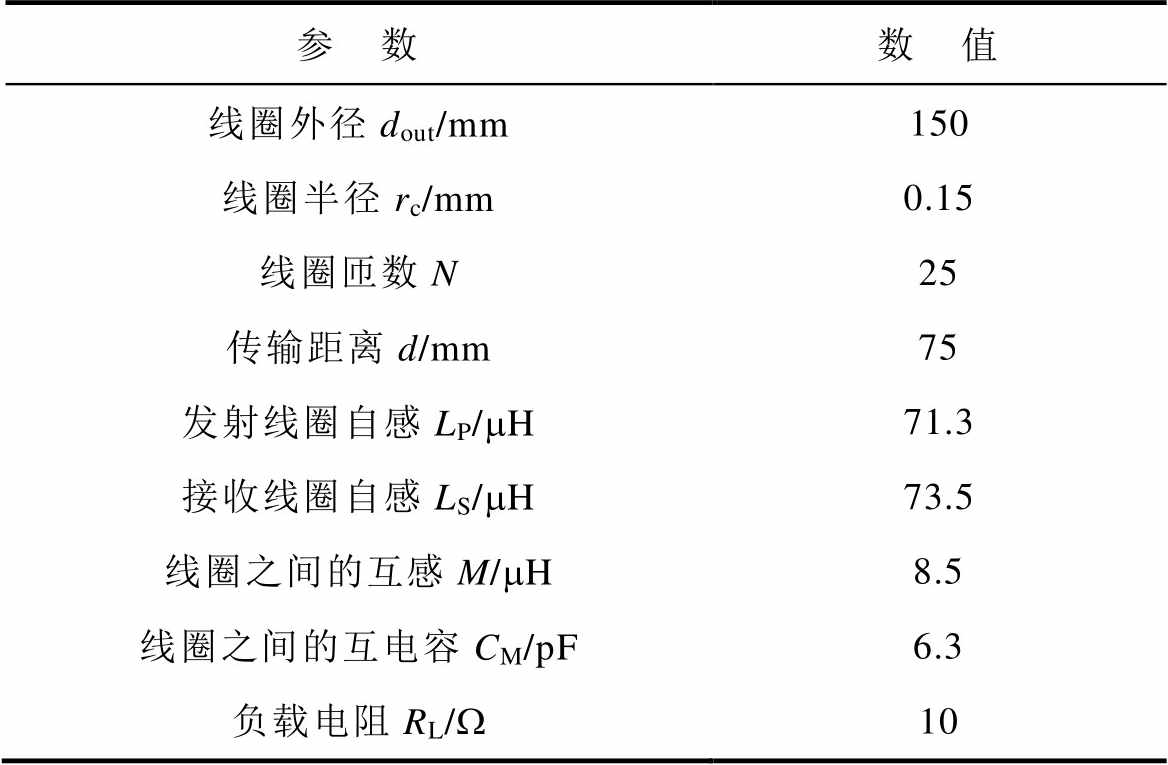
参 数数 值 线圈外径dout/mm150 线圈半径rc/mm0.15 线圈匝数N25 传输距离d/mm75 发射线圈自感LP/mH71.3 接收线圈自感LS/mH73.5 线圈之间的互感M/mH8.5 线圈之间的互电容CM/pF6.3 负载电阻RL/W10
通过对两类耦合作用的频率特性分析可知,与对偶实验结果类似,两类电磁能量的比值与系统工作频率有关。尽管从功率量级的角度考虑,两种电磁耦合的功率及其比值较低,但是根据前节讨论可知,增加耦合机构之间的耦合电容可以有效地增强电容耦合作用。因此,在某些应用场景,例如水下环境、生物医学交叉等场景中。由于介电常数的原因,可以预见耦合电容的增大是非常可观的。因此,根据不同应用领域的需求,合理地增强电容耦合作用是实现稳定、高效传输的关键。此时电容耦合作用是不可忽视的,需要考虑如何消纳这部分耦合作用,扩宽传输通道容量,实现两类耦合能量的协同传输。同时在常规工程场景中,也可以分离出增强这两种耦合作用的因素来增强电容耦合作用。
5 结论
无线电能传输系统工作过程的显著特征是非接触传导式的电磁功率流动。借助坡印廷矢量对常见电气元件的电磁能流特性和无线电能传输系统的电磁能流特性进行分析,单个电阻、电感或电容元件只有电能的存储和自身能量的消耗,对于工作于电磁近区场的无线电能传输系统,临近空间内的电磁场耦合是实现其功能的关键。其中系统能量耦合方式包括以电场为主的电容耦合和以磁场为主的电感耦合,无线电能传输系统存在电感耦合作用与电容耦合作用的共存现象。
通过电磁能流的分析,明确无线电能传输技术与其他电磁能量变换技术(变压器系统、电容器串联回路)之间的关系,可知无线电能传输技术具有鲜明的技术特征和工作模式。由于大间距气隙的存在,无线电能传输系统无法像变压器那样通过高导磁材料形成磁心引导电磁场,也无法像电容器那样通过高性能介电材料引导电磁场。为实现大间距气隙下大功率与高效率无线电能传输,需提升电感耦合与电容耦合的作用强度。
设计对偶实验验证了两类耦合作用的共存现象,并对两类耦合作用的频率特性进行分析,明确两类电磁能量与系统工作频率的关联关系。尽管两类电磁能量及其比值在量级上较低,但在某些场景中,如水下环境、生物医学交叉等场景,由于介电常数的原因,电容耦合作用将不可忽视,需考虑如何消纳电容耦合作用。同时,在常规工程场景中,也可以将增强这两种耦合作用的因素分离,以增强电容耦合作用,实现两种耦合能量的协同传输。
参考文献
[1] 杨庆新, 章鹏程, 祝丽花, 等. 无线电能传输技术的关键基础与技术瓶颈问题[J]. 电工技术学报, 2015, 30(5): 1-8.
Yang Qingxin, Zhang Pengcheng, Zhu Lihua, et al. Key fundamental problems and technical bottlenecks of the wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 1-8.
[2] Hertz H. Ueber einen Einfluss des ultravioletten Lichtes auf die electrische Entladung[J]. Annalen Der Physik, 1887, 267(8): 983-1000.
[3] Pfeiffer-Wagner K. Tapping apparatus for trans- mitting electrical energy: US10673193[P]. 2020-06-02.
[4] Ha-Van N, Liu Yining, Jayathurathnage P, et al. Cylindrical transmitting coil for two-dimensional omnidirectional wireless power transfer[J]. IEEE Transactions on Industrial Electronics, 2022, 69(10): 10045-10054.
[5] 荣灿灿, 严俐慧, 路聪慧, 等. 基于超材料与超表面的无线电能传输技术研究现状与进展综述[J]. 电工技术学报, 2023, 38(20): 5369-5384.
Rong Cancan, Yan Lihui, Lu Conghui, et al. Overview on research status and progress of wireless power transfer technology based on metamaterials and metasurfaces[J]. Transactions of China Electro- technical Society, 2023, 38(20): 5369-5384.
[6] Haus H, Melcher J. Electromagnetic fields and energy[D]. Englewood Cliffs: Prentice Hall, 1989.
[7] Bertolotti M. Waves and fields in optoelectronics[D]. Englewood Cliffs: Prentice-Hall, 2010.
[8] 陈伟华, 宋宇航, 闫孝姮, 等. 心脏起搏器无线电能传输LCC-LCC磁集成印刷螺旋线圈研究[J]. 电工技术学报, 2024, 39(17): 5289-5299.
Chen Weihua, Song Yuhang, Yan Xiaoheng, et al. Research on wireless power transmission for cardiac pacemakers using LCC-LCC magnetic integrated printed spiral coil[J]. Transactions of China Electro- technical Society, 2024, 39(17): 5289-5299.
[9] 张迪, 夏立伟, 胡洪炜, 等. 基于无线电能传输技术的无人机自主充、换电平台供电装置设计[J]. 电工技术, 2023(5): 133-136.
Zhang Di, Xia Liwei, Hu Hongwei, et al. Design of power supply device for unmanned aerial vehicle self-charging and replacing platform based on wireless power transmission technology[J]. Electric Engineering, 2023(5): 133-136.
[10] Jiang Mengjie, Chen Changsong, Jia Shuran, et al. An asymmetrical pulsewidth modulation with even harmonics for bidirectional inductive power transfer under light load conditions[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 8939-8948.
[11] 程志远, 宋晓逸, 吴晓婷, 等. 无线充电系统旋转式电磁耦合器损耗计算及热点温度研究[J]. 电工技术学报, 2024, 39(7): 1932-1942, 1956.
Cheng Zhiyuan, Song Xiaoyi, Wu Xiaoting, et al. Loss calculation and hot spot temperature research of rotary electromagnetic coupler in wireless charging system[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 1932-1942, 1956.
[12] 苏玉刚, 侯信宇, 戴欣. 磁耦合无线电能传输系统异物检测技术综述[J]. 中国电机工程学报, 2021, 41(2): 715-727.
Su Yugang, Hou Xinyu, Dai Xin. Review of foreign object detection technology in magnetic coupling wireless power transfer system[J]. Proceedings of the CSEE, 2021, 41(2): 715-727.
[13] Zang Shaoge, Zhu Qi, Zhao Lei, et al. Capacitive power transfer system with integrated wide bandwidth communication[J]. IEEE Transactions on Power Electronics, 2022, 37(8): 8805-8810.
[14] 周玮, 高侨, 陈泽林, 等. 基于同侧解耦型电场耦合机构的多发射多接收无线电能传输系统[J]. 电工技术学报, 2023, 38(18): 4811-4822.
Zhou Wei, Gao Qiao, Chen Zelin, et al. Same-sided decoupled electric-field coupler based wireless power transfer system with multi-transmitter and multi- receiver[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4811-4822.
[15] Masrur M A, Cox M. A unique military application of wireless power transfer: wireless charging through a vehicle seat with simplified design considerations[J]. IEEE Industrial Electronics Magazine, 2019, 13(4): 19-30.
[16] Li Weihan, Zhang Qianfan, Cui Chao, et al. A self-tuning S/S compensation WPT system without parameter recognition[J]. IEEE Transactions on Industrial Electronics, 2022, 69(7): 6741-6750.
[17] 李建国, 张波, 荣超. 近场磁耦合无线电能与信息同步传输技术的发展(下篇): 电路拓扑[J]. 电工技术学报, 2022, 37(16): 3989-4003.
Li Jianguo, Zhang Bo, Rong Chao. An overview of simultaneous wireless power and information transfer via near-field magnetic links (part Ⅱ): circuit topology[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 3989-4003.
[18] 段元雄, 石章海, 邱忠才, 等. 一种具有宽输出电压范围的无线电能传输电路[J]. 电工技术, 2023(15): 71-79.
Duan Yuanxiong, Shi Zhanghai, Qiu Zhongcai, et al. A wireless power transmission circuit with wide output voltage range[J]. Electric Engineering, 2023(15): 71-79.
[19] Yang Guangxiang, Liang Hua. Adaptive frequency measurement in magnetic resonance coupling based WPT system[J]. Measurement, 2018, 130: 318-326.
[20] 刘辉, 苏建徽, 张健, 等. 串联补偿无线电能传输变换器载波通信研究[J]. 电气传动, 2024, 54(9): 12-18.
Liu Hui, Su Jianhui, Zhang Jian, et al. Research on carrier communication of series compensated wireless power transfer converter[J]. Electric Drive, 2024, 54(9): 12-18.
[21] 秦庆磊, 王中训, 穆鹏华. 脉冲调制式无线电能与信息同步传输系统设计[J]. 电源学报, 2023, 21(6): 94-101.
Qin Qinglei, Wang Zhongxun, Mu Penghua. Design of synchronous transmission system of radio energy and information under pulse modulation[J]. Journal of Power Supply, 2023, 21(6): 94-101.
[22] Wang Longyang, Li Jiangui, Chen Huiying, et al. Radial-flux rotational wireless power transfer system with rotor state identification[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 6206-6216.
[23] Zhou Weiyang, Jin Ke, Zhang Ran. A fast-speed GMPPT method for PV array under Gaussian laser beam condition in wireless power transfer appli- cation[J]. IEEE Transactions on Power Electronics, 2022, 37(8): 10016-10028.
[24] Iam I W, Hoi I U, Huang Zhicong, et al. Constant- frequency and noncommunication-based inductive power transfer converter for battery charging[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(2): 2147-2162.
[25] Zaheer A, Hao Hao, Covic G A, et al. Investigation of multiple decoupled coil primary pad topologies in lumped IPT systems for interoperable electric vehicle charging[J]. IEEE Transactions on Power Electronics, 2015, 30(4): 1937-1955.
[26] 郑小瑶, 江彦伟, 疏许健, 等. 宇称-时间对称电场耦合无线电能传输系统电场分布特性研究[J]. 电源学报, 2024, 22(5): 60-66.
Zheng Xiaoyao, Jiang Yanwei, Shu Xujian, et al. Study on electric-field distribution characteristics of parity-time symmetric electric-field coupled wireless power transfer system[J]. Journal of Power Supply, 2024, 22(5): 60-66.
[27] Luo Bo, Hu A P, Munir H, et al. Compensation network design of CPT systems for achieving maximum power transfer under coupling voltage constraints[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(1): 138-148.
[28] Zhou Weiyang, Jin Ke. Efficiency evaluation of laser diode in different driving modes for wireless power transmission[J]. IEEE Transactions on Power Elec- tronics, 2015, 30(11): 6237-6244.
[29] Zhou Weiyang, Jin Ke. Optimal photovoltaic array configuration under Gaussian laser beam condition for wireless power transmission[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(5): 3662-3672.
[30] Brandão Faria J A. Poynting vector flow analysis for contactless energy transfer in magnetic systems[J]. IEEE Transactions on Power Electronics, 2012, 27(10): 4292-4300.
[31] Liu Yuan, Zhang Kehan, Hu A P. Investigation of reactive power distribution between two coils of inductive power transfer system by Poynting vector analysis[J]. International Journal of Electrical Power & Energy Systems, 2022, 136: 107621.
[32] Liu Yuan, Hu Aiguo. Study of power flow in an IPT system based on Poynting vector analysis[J]. Energies, 2018, 11(1): 165.
[33] Li Wanlu, Wang Quandi, Kang Jianwei, et al. Energy- concentrating optimization based on energy dis- tribution characteristics of MCR WPT systems with SS/PS compensation[J]. IEEE Transactions on Indu- strial Electronics, 2020, 67(12): 10410-10420.
[34] 陈德智, 刘添亦, 李冬. 变压器中的电磁能量分布与功率传输[J]. 华中科技大学学报(自然科学版), 2021, 49(4): 1-7, 19.
Chen Dezhi, Liu Tianyi, Li Dong. Electromagnetic energy distribution and power transfer in trans- former[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2021, 49(4): 1-7, 19.
Research on Electromagnetic Energy Flow and Coupling Characteristics of Wireless Power Transmission System Based on Poynting’s Theorem
Wang Fengxian1 Zhou Yitong1 Zhang Xian1 Yang Qingxin1,2 Li Guangyao1
(1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment Hebei University of Technology Tianjin 300401 China 2. School of Electrical Engineering and Automation Tianjin University of Technology Tianjin 300384 China)
Abstract This paper analyzes the electromagnetic energy flow and coupling characteristics in wireless power transmission (WPT) systems. Addressing the complexities in accurately depicting the electromagnetic energy transformation within WPT systems, the research overcomes challenges associated with the intricate mathematical methods and the absence of models capable of characterizing spatial energy flow distribution.
A model for electromagnetic energy flow in WPT under sinusoidal excitation is established based on Poynting’s theorem. A reduced-order mathematical model is developed by analyzing common electromagnetic energy flow characteristics of basic electrical components. This model qualitatively explores the energy coupling in the transmission space. The coexistence of inductive and capacitive coupling in WPT systems is discussed, emphasizing the significance of enhancing near-field electromagnetic coupling for overall system performance. The working mode of WPT in the electromagnetic near-field region is presented from the perspective of the energy flow mechanism. An experimental platform is constructed to verify the inductive and the capacitive coupling methods.
The electromagnetic energy flow characteristics of conductors, transformers, and capacitors are analyzed, facilitating power transmission through the electromagnetic fields in their vicinity rather than by themselves. The electromagnetic energy flow characteristics of WPT systems are discussed as a combination of multiple RLC circuits. It is found that electromagnetic power is partly stored in the electromagnetic fields of individual circuits (self-energy) and partly in the fields between circuits (mutual energy). The analysis is simplified by considering a system with two RLC series circuits, revealing that WPT relies on mutual coupling between the primary and secondary sides for contactless power transfer.
The paper also discusses typical magnetic resonant WPT systems using the image method to analyze the field strength distribution in the coupling space. The symmetry between inductive and capacitive coupling characteristics is revealed, offering guidance for practical engineering design. Experiments are conducted to verify the coexistence of inductive and capacitive couplings and to analyze their frequency characteristics. Results indicate that as the operating frequency increases, the ratio of capacitive coupling to inductive coupling increases, which is significant for understanding WPT technology.
In conclusion, the paper analyzes the electromagnetic energy flow and coupling characteristics in WPT systems, offering valuable insights for the theoretical research and practical application of WPT technology. It highlights the importance of understanding the coexistence of inductive and capacitive couplings and their frequency characteristics to enhance the performance of WPT systems.
keywords:Wireless power transfer, electromagnetic energy flow, electromagnetic near-field, inductive coupling, capacitive coupling
中图分类号:TM724
DOI: 10.19595/j.cnki.1000-6753.tces.L11050
国家自然科学基金(52477005)、国家留学基金委高水平公派留学生项目(CSC202406700014)、天津市自然科学基金(22JCZDJC00620)、河北省中央引导地方科技发展资金(236Z5201G)、河北省高等学校科学研究项目合作专项(CXY2024010)和河北省燕赵青年科学家项目(E2024202109)资助。
改稿日期 2024-09-01
作者简介
王奉献 男,1995年生,博士研究生,研究方向为无线电能传输技术。
E-mail: fx-wang@outlook.com
张 献 男,1983年生,教授,博士生导师,研究方向为无线电能传输技术、工程电磁场与磁技术等。
E-mail: zhangxian@hebut.edu.cn(通信作者)
(编辑 郭丽军)

 (1)
(1)
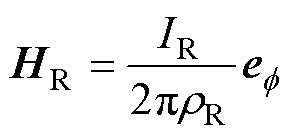 (2)
(2)

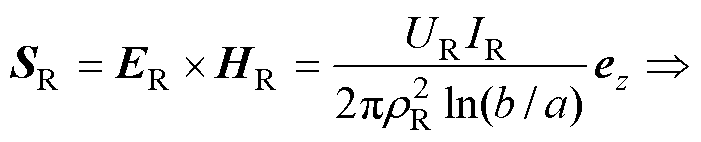
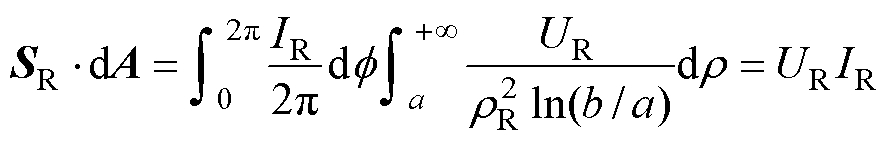 (3)
(3)
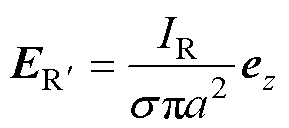 (4)
(4)
 为单导线的电导率。
为单导线的电导率。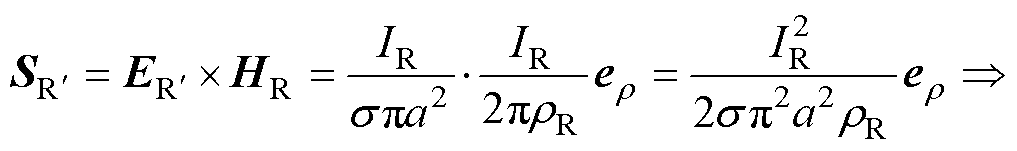
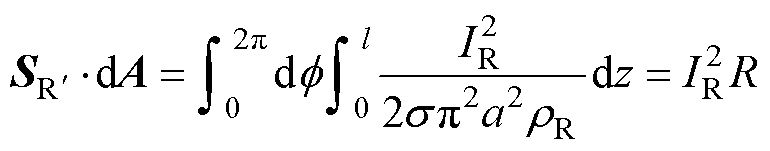 (5)
(5)
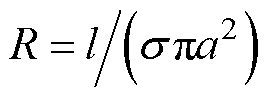 ,l为单导线的长度。进入单导线内部的功率等于该单导线损耗的焦耳功率,坡印廷矢量方向为由单导线表面指向中心。
,l为单导线的长度。进入单导线内部的功率等于该单导线损耗的焦耳功率,坡印廷矢量方向为由单导线表面指向中心。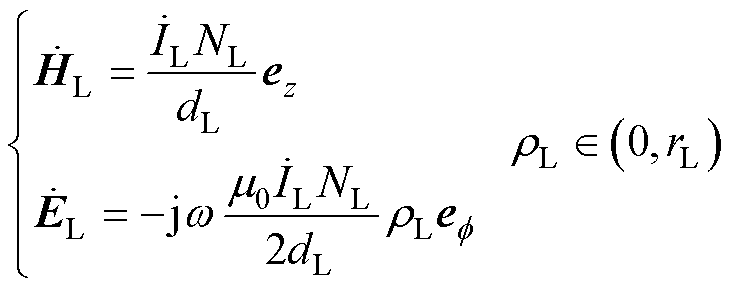 (6)
(6)
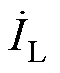 为螺线管电流激励;
为螺线管电流激励;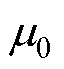 为真空磁导率;
为真空磁导率;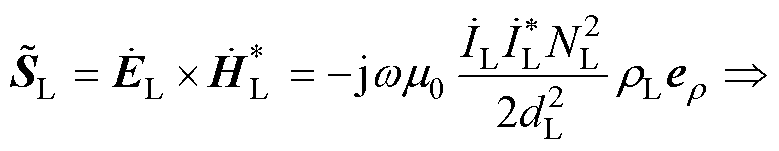
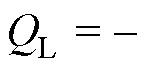
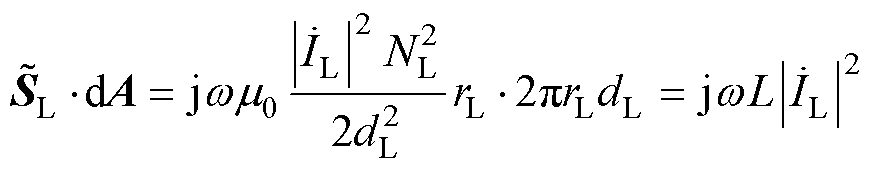 (7)
(7)
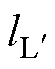 为磁心内部空间高度。
为磁心内部空间高度。
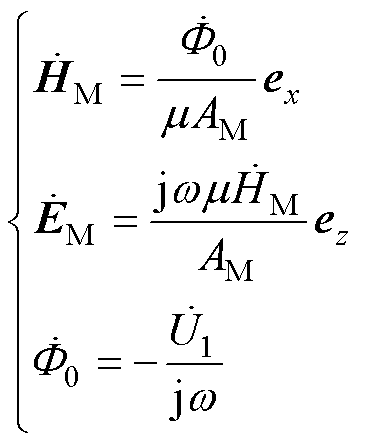 (8)
(8)
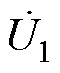 为一次电压激励;A
为一次电压激励;A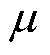 为磁心的磁导率;
为磁心的磁导率;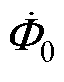 为磁心内的主磁通量;
为磁心内的主磁通量;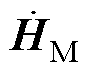 为磁心内磁场强度。特别地,本文所有涉及时谐场分析的电磁参数(如磁场强度
为磁心内磁场强度。特别地,本文所有涉及时谐场分析的电磁参数(如磁场强度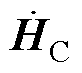 )均以复数相量的模值形式表征。以
)均以复数相量的模值形式表征。以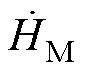 为磁心内磁场强度复数相量
为磁心内磁场强度复数相量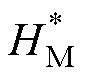 为磁心内磁场强度复数相量
为磁心内磁场强度复数相量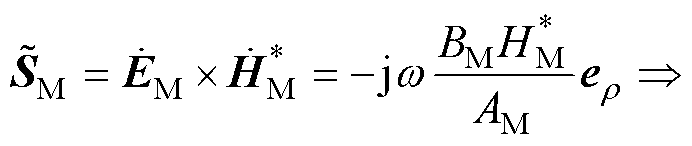
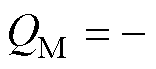
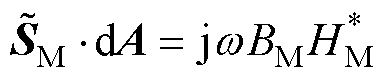 (9)
(9)
 表示该区域)电场强度与磁场强度可表示为
表示该区域)电场强度与磁场强度可表示为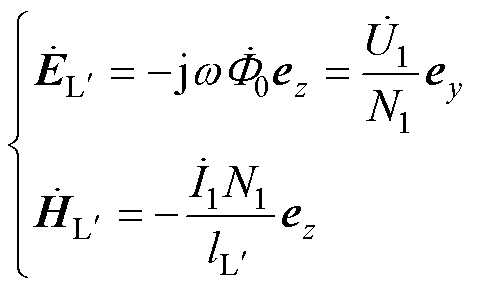 (10)
(10)
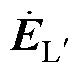 为磁心临近区域电场强度;
为磁心临近区域电场强度;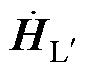 为磁心临近区域磁场强度;
为磁心临近区域磁场强度;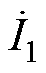 为变压器一次电流;
为变压器一次电流;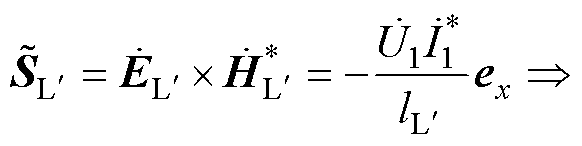
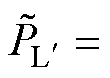
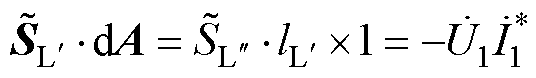 (11)
(11)
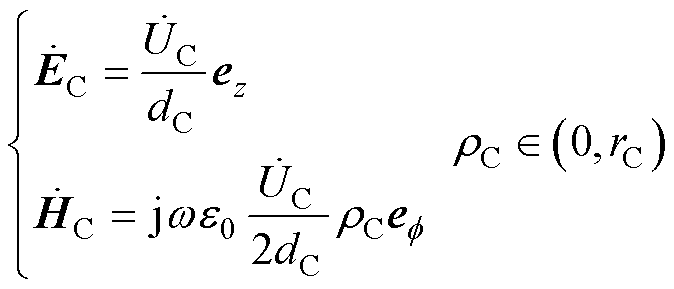 (12)
(12)
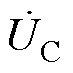 为电容板两端的电势差;d
为电容板两端的电势差;d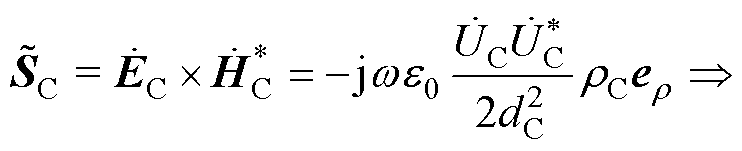
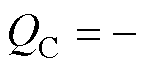
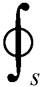
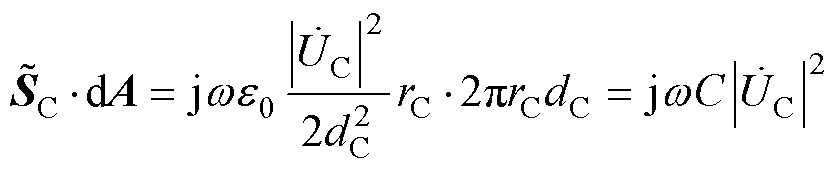 (13)
(13)
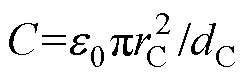 为电容器电容。
为电容器电容。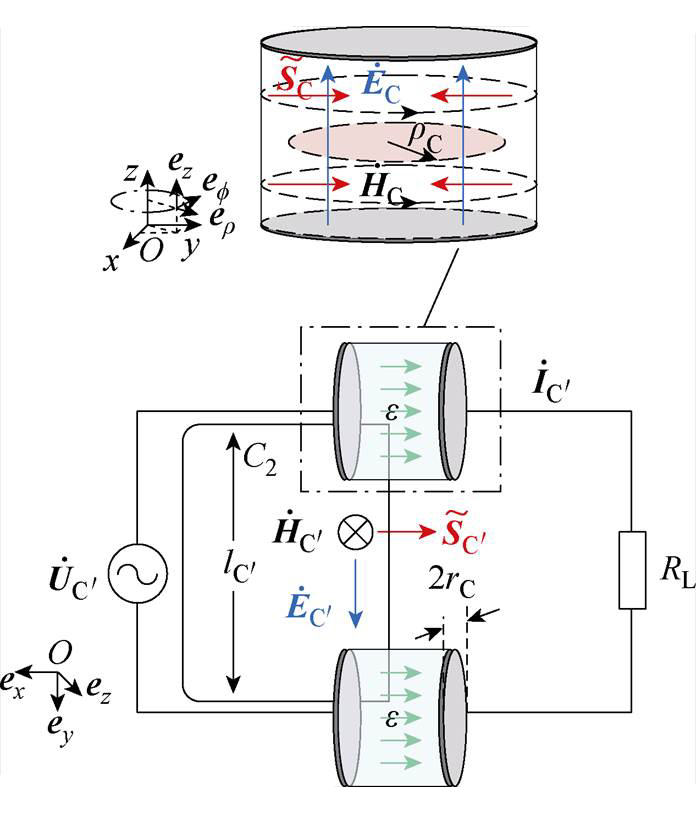
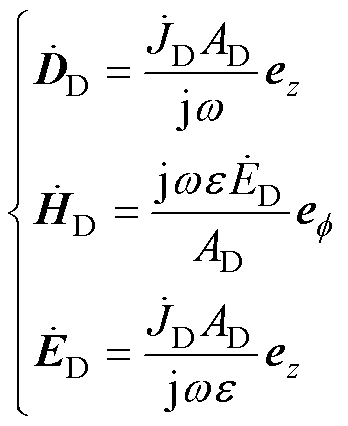 (14)
(14)
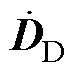 为复数形式的电位移矢量;A
为复数形式的电位移矢量;A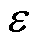 为板间介质的介电常数;
为板间介质的介电常数;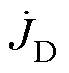 为回路电流密度。电容器内复坡印廷矢量及其消耗的复功率为
为回路电流密度。电容器内复坡印廷矢量及其消耗的复功率为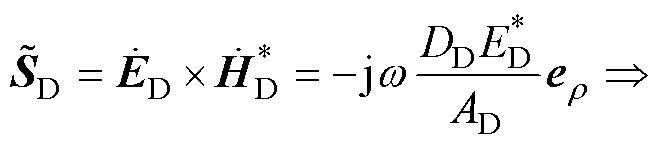
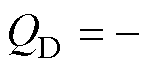
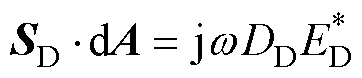 (15)
(15)
 表示该区域的物理量)的电磁场满足
表示该区域的物理量)的电磁场满足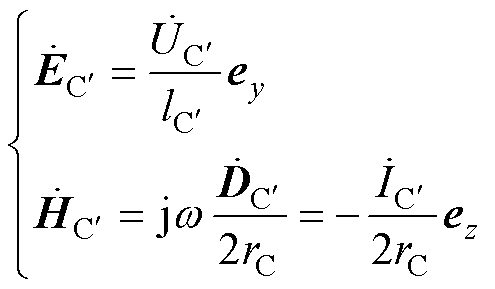 (16)
(16)
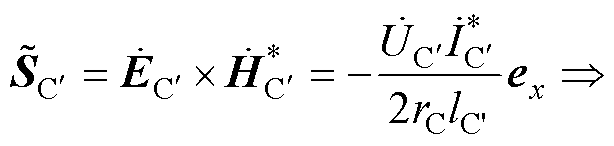
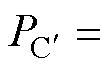
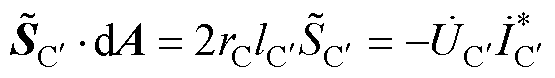 (17)
(17)
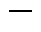
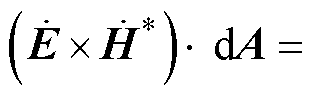
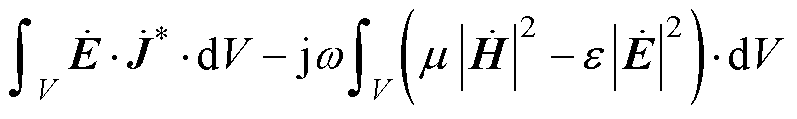 (18)
(18)
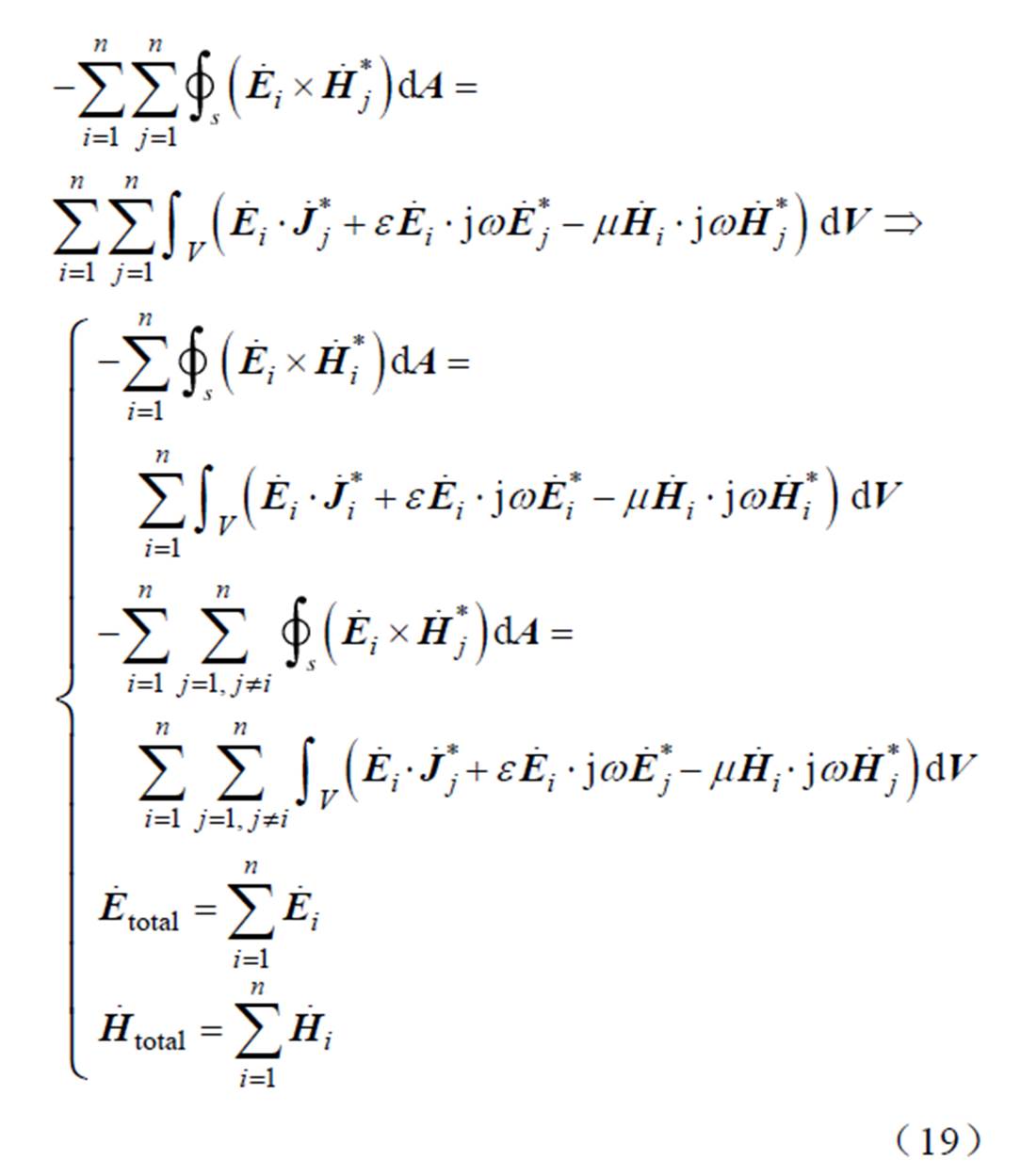
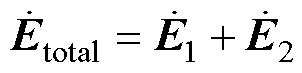 ,
,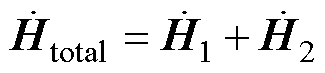 。
。
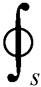
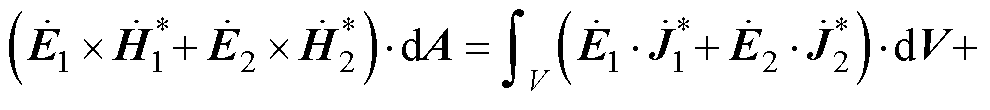
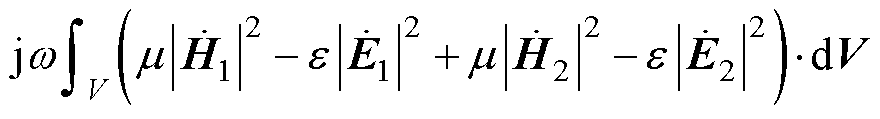 (20)
(20)
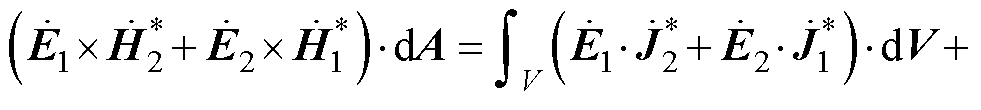
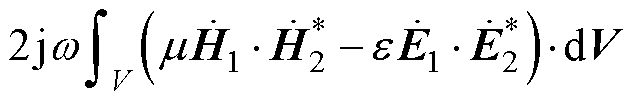 (21)
(21)
 为磁屏蔽区域;2和
为磁屏蔽区域;2和 为磁屏蔽与线圈之间的空隙区域;3和
为磁屏蔽与线圈之间的空隙区域;3和 为线圈区域;4为线圈之间的空隙区域。对各区域的电磁场分析如下:
为线圈区域;4为线圈之间的空隙区域。对各区域的电磁场分析如下: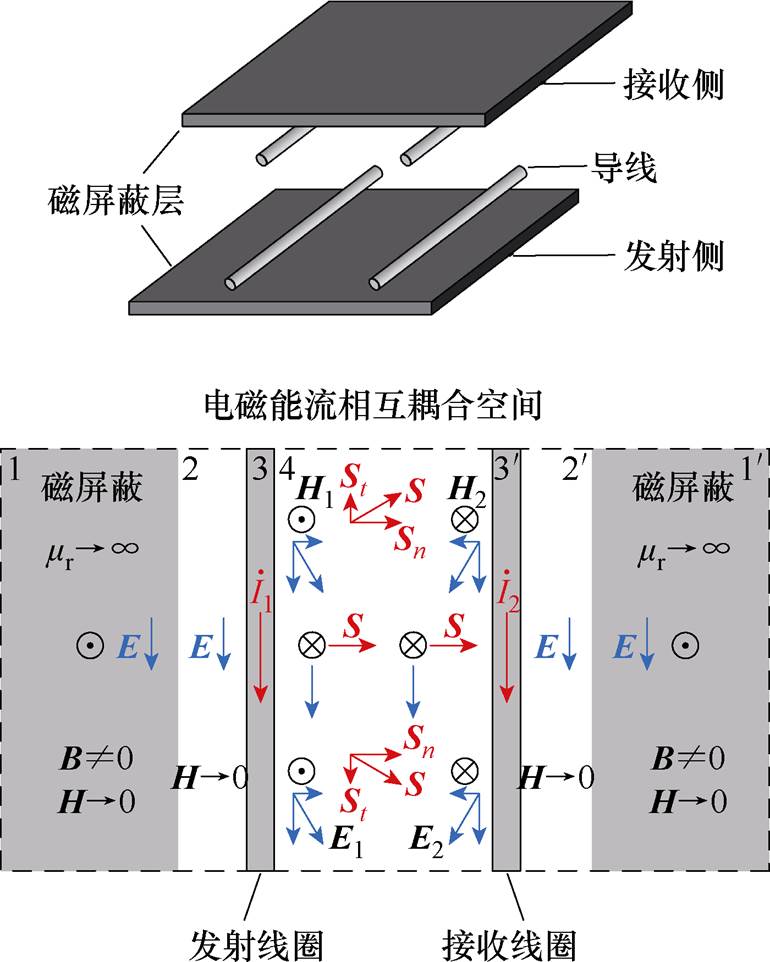
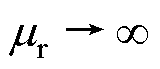 ,该区域的磁场强度为零,因此坡印廷矢量为零,此区域不存在电磁功率交换。
,该区域的磁场强度为零,因此坡印廷矢量为零,此区域不存在电磁功率交换。 ),电磁功率仅在线圈之间的空隙区域内传输,在其他空隙以及磁屏蔽内部磁场强度趋近于零,可认为理想条件下不存在电磁功率的传递。非理想条件下
),电磁功率仅在线圈之间的空隙区域内传输,在其他空隙以及磁屏蔽内部磁场强度趋近于零,可认为理想条件下不存在电磁功率的传递。非理想条件下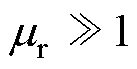 ,但
,但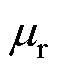 为限定值。可证得:在磁屏蔽区域1和
为限定值。可证得:在磁屏蔽区域1和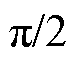 ,该区域内复坡印廷矢量仅有虚部,仅有无功功率交换。线圈之间的空隙区域4内复坡印廷矢量既有实部也有虚部,是无线电能传输的关键区域。即近区电磁场耦合是无线电能传输的关键因素,是无线电能传输能够实现高效能量传输的基础。同时无线电能传输系统无法像变压器或电容器那样通过高性能的导磁材料或介电材料引导电磁场。
,该区域内复坡印廷矢量仅有虚部,仅有无功功率交换。线圈之间的空隙区域4内复坡印廷矢量既有实部也有虚部,是无线电能传输的关键区域。即近区电磁场耦合是无线电能传输的关键因素,是无线电能传输能够实现高效能量传输的基础。同时无线电能传输系统无法像变压器或电容器那样通过高性能的导磁材料或介电材料引导电磁场。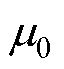 空间的镜像电流源
空间的镜像电流源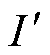 与相对磁导率为
与相对磁导率为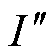 的共同作用,如图6所示,镜像电流可表示为
的共同作用,如图6所示,镜像电流可表示为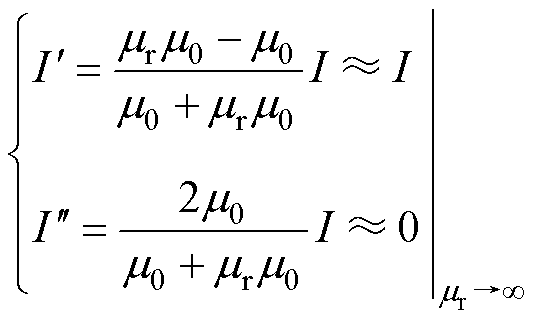 (22)
(22)
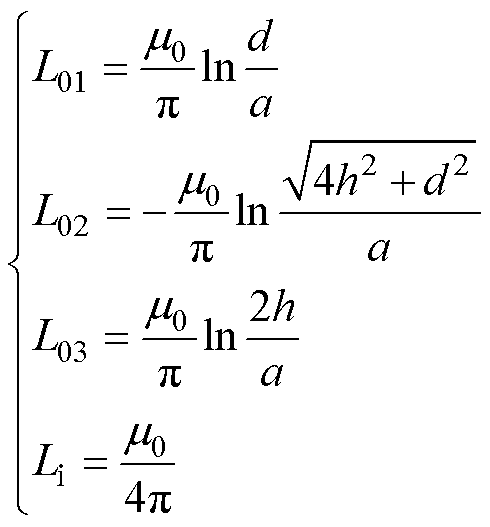 (23)
(23)
 (24)
(24)
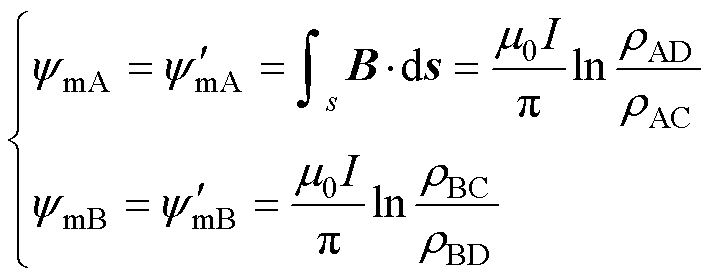 (25)
(25)
 对导线C和D的磁通和;
对导线C和D的磁通和;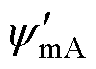 为导线
为导线 对导线C和D的磁通和;
对导线C和D的磁通和; 对导线C和D的磁通和;
对导线C和D的磁通和;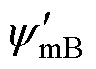 为导线
为导线 对导线C和D的磁通和。
对导线C和D的磁通和。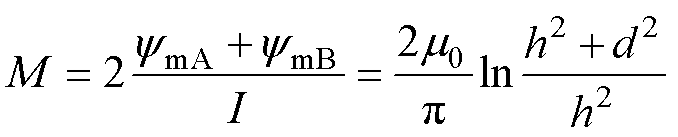 (26)
(26)
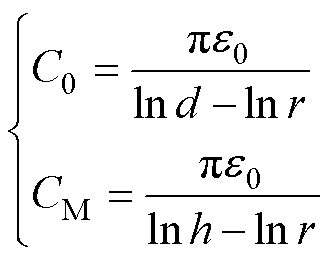 (27)
(27)
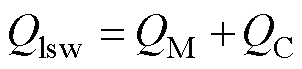 (28)
(28)
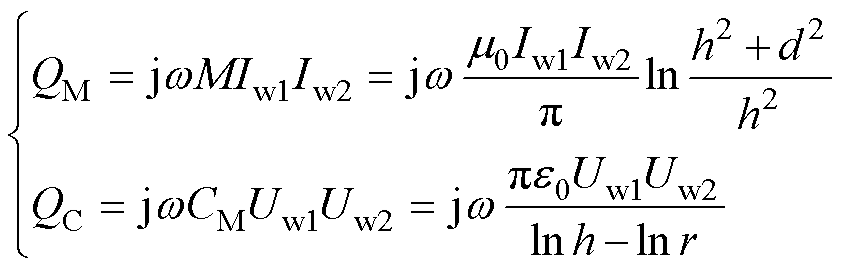 (29)
(29)
 为耦合机构自然谐振频率,
为耦合机构自然谐振频率, 为系统工作频率,如图8所示为典型电感耦合电路。依据KVL可得回路电压方程为
为系统工作频率,如图8所示为典型电感耦合电路。依据KVL可得回路电压方程为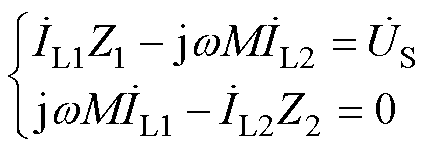 (30)
(30)
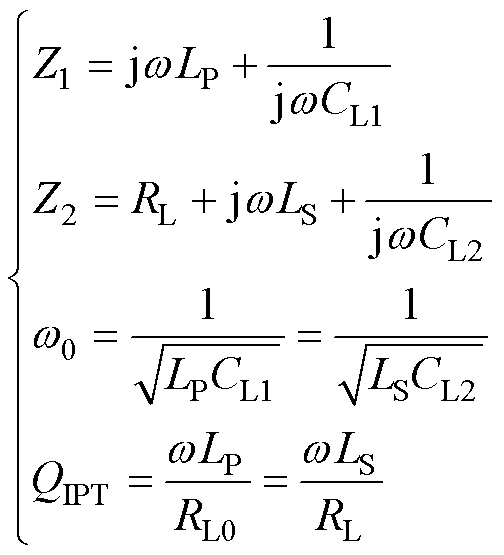 (31)
(31)
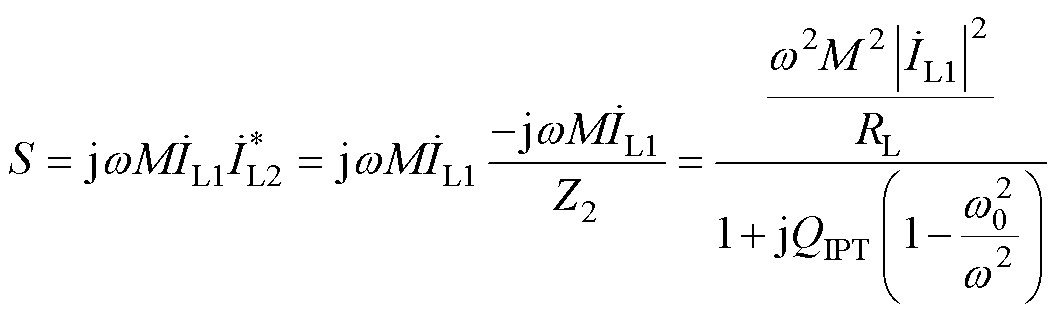 (32)
(32)
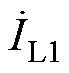 、
、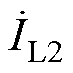 分别为一次和二次线圈电流。
分别为一次和二次线圈电流。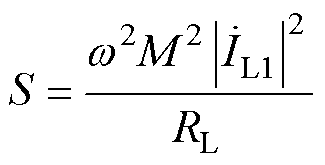 (33)
(33)
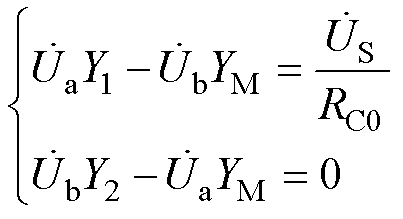 (34)
(34)
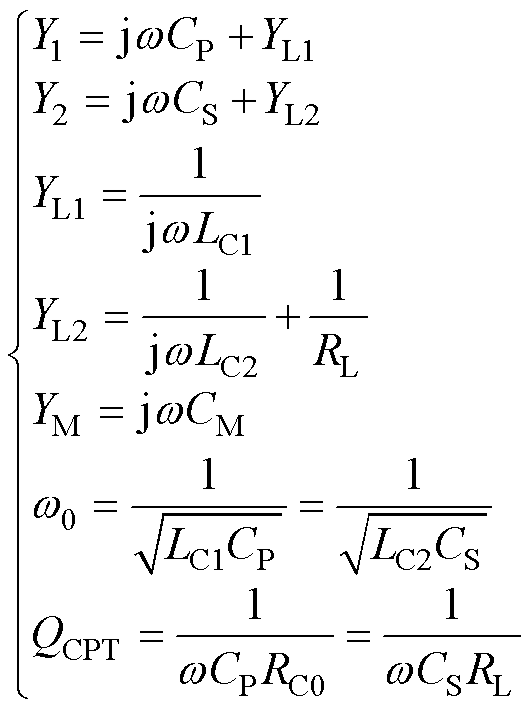 (35)
(35)
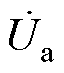 、
、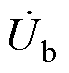 分别为对应图9中的等效受控电流源的电压。则由电容耦合所传输的视在功率可表示为
分别为对应图9中的等效受控电流源的电压。则由电容耦合所传输的视在功率可表示为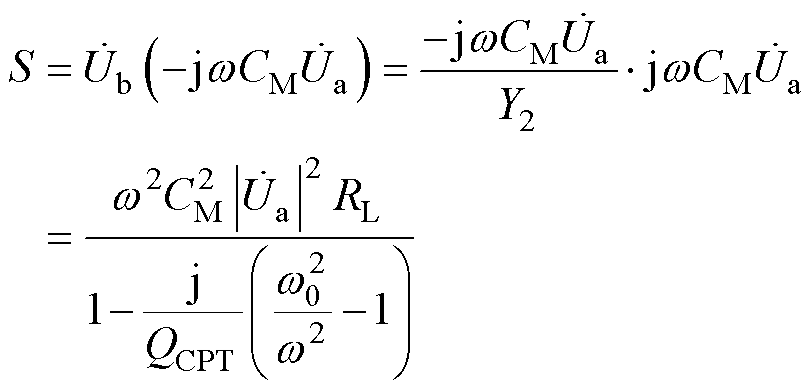 (36)
(36)
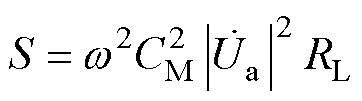 (37)
(37)