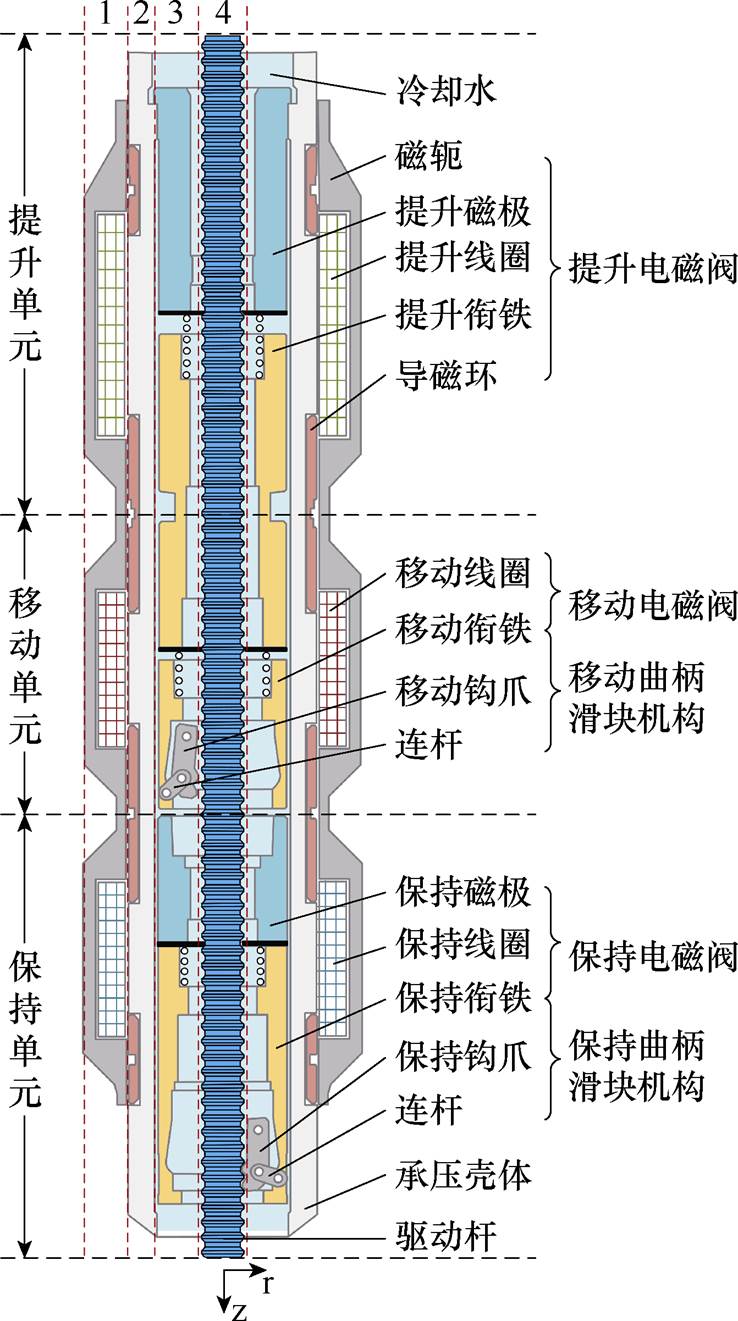
图1 CRDM截面示意图
Fig.1 CRDM cross-sectional view
摘要 磁力提升型控制棒驱动机构(CRDM)是反应堆中控制核反应速率的关键电磁执行装置。其动态过程因电流响应、磁路饱和和运动状态间的交叉耦合而复杂,预测难度较大。为实现高精度的快速多物理场耦合计算,该文提出一种动态等效磁网络(DEMN)模型。该模型的关键在于使用正交网格线对CRDM各区域进行网格划分,从而统一磁阻计算公式,实现DEMN的快速建模。动态变化时,仅需调整运动区域的网格大小或位置,避免了冗余建模,减少了网格差异导致的计算误差。结合电路模型和动力学方程,提出一种同时考虑电流瞬态变化和磁路饱和的CRDM多物理场耦合计算方法。最后将计算结果与3D有限元分析(FEA)结果、实验结果进行比较,验证了所提DEMN模型的快速性和准确性,以及多场耦合计算方法的正确性。
关键词:反应堆 控制棒驱动机构 等效磁网络 多场耦合
核能作为一种低碳、清洁、高效、经济的新兴能源,在发电、制氢、区域供热和海水淡化等领域具有广阔的发展前景[1]。然而,发展核能的前提是保证核安全,防止核泄漏[2]。在商用核电站中,控制棒驱动机构(Control Rod Drive Mechanism, CRDM)是反应堆功率调节和系统保护的关键执行机构,被归类为安全一级设备[3]。按照驱动方式不同,CRDM可分为旋转电机驱动型、磁力提升型、液压驱动型和直线电机驱动型。其中,磁力提升型CRDM以结构简单、可靠性高和提升力大等优点,被广泛应用于第三代压水堆核电站[4]。然而,磁力提升型CRDM故障将导致严重的影响,包括非计划性停堆、功率降低、经济损失,并给维修人员造成心理负担[5]。因此,深入研究磁力提升型CRDM的动态特性对提高核反应系统的安全性具有重要意义。
磁力提升型CRDM的励磁单元类似于一种特殊的电磁阀机构。它通过对线圈进行通电励磁和断电去磁,完成衔铁的吸合和释放等动作。然而,它的结构、电磁特性和动态特性与传统电磁阀机构存在不同。首先,气隙(15.875 mm)较大,其内部漏磁严重[6]。其次,长期工作在高温、高压及强辐照的环境下,为保证运行安全和可靠性,通入线圈的电流(40 A)较大,导致严重的磁饱和[7]。同时,运动部件长期浸泡在一回路冷却水中,其运动过程受电磁力、弹簧力、水阻力、摩擦力等共同作用,具有非线性、时变性等特点。因此,传统电磁阀机构的研究结论难以适用于磁力提升型CRDM。
针对上述挑战,国内外研究学者在磁力提升型CRDM的磁路模型和多物理场耦合分析方面开展了许多研究。在磁路模型方面:文献[8]基于等效磁路法介绍了CRDM的电磁参数设计原理。该方法在CRDM的早期设计中发挥了重要作用,但该方法只进行了静态计算;文献[9]基于基尔霍夫电压定律和磁共能理论,建立了CRDM的电磁模型,但忽略了漏磁和磁路饱和影响;文献[10]虽然考虑了漏磁影响,但未考虑磁路饱和,因此模型精度仍有待提高。文献[4]同时考虑漏磁和磁路饱和的影响,建立了CRDM的等效磁网络(Equivalent Magnetic Network, EMN)模型。虽然该模型在一定程度上能准确预测CRDM的电磁特性,但其建模过程依赖于磁通分布情况,缺乏通用性。同时,利用EMN模型预测电磁性能的方法被广泛应用于各类电机领域[11-13],但对于CRDM的相关研究仍然较少。
在多物理场耦合分析方面:文献[14]推导了CRDM提升过程的磁路-电路-机械运动耦合方程,并采用数值方法解算了CRDM的动态特性,然而,该方法未考虑流体阻力,它是影响CRDM动态过程的关键因素[15];文献[16]推导了CRDM的流体阻力模型,并借助软件对其提升过程进行了动态分析。但该方法对动力学分析软件的依赖限制了其应用范围;文献[17-18]提出了一种多学科协同仿真方法,利用各领域仿真软件的优势实现数据交换,从而获得高保真的动态特性;文献[19]为解决多学科软件协同仿真引起的参数不相等和维度不一致的问题,提出了一种基于时间单位微分的协同仿真方法,以提高仿真精度;文献[20]提出了一种具有自适应步长的多学科协同仿真方法和仿真平台,以平衡计算精度和计算效率之间的关系。尽管多学科协同仿真具有较高的计算精度,但同时会带来巨大的时间成本和硬件资源成本,难以适应实时性要求较高的控制系统和优化设计研究。
针对上述潜在问题,本文提出一种动态等效磁网络(Dynamic Equivalent Magnetic Network, DEMN)模型。首先,介绍磁力提升型CRDM的结构组成,并选取其提升电磁阀作为研究对象,分析其动态过程中的电-磁-机械耦合关系。然后,采用正交网格线对机构进行剖分,并将多种介质的网格单元转换为单一介质,以统一磁阻计算公式。通过改变运动区域的网格大小或位置,实现该模型的动态变化。针对固定网格单元与运动网格单元之间的错位问题,建立其连接关系和支路磁阻的计算方法,实现衔铁的连续移动。结合电路模型和动力学公式,提出一种考虑电流瞬态变化和磁路饱和的CRDM多物理场耦合计算方法。最后,利用3D有限元分析(Finite Element Analysis, FEA)和实验结果,对所提DEMN模型和多物理场耦合计算方法进行验证。
CRDM截面示意图如图1所示,磁力提升型CRDM呈柱状结构,从外到内依次包括线圈组件、耐压壳组件、钩爪组件和驱动棒组件。坐标轴“r”和“z”分别为径向和轴向。根据结构相似性,磁力提升型CRDM可分为上、中、下三个单元,分别命名为提升单元、移动单元和保持单元。每个单元均配有一个电磁阀,移动单元和保持单元中的电磁阀则与钩爪相结合,形成曲柄滑块机构。电磁阀的功能是实现衔铁与磁极之间的吸合或释放,曲柄滑块机构则将衔铁的直线运动转换为钩爪的内外摆动,以实现钩爪与驱动杆环形槽的啮合和分离。需要特别指出的是,为实现驱动杆的提升或插入堆芯等动作,这些电磁阀需按照一定次序进行通断电操作。

图1 CRDM截面示意图
Fig.1 CRDM cross-sectional view
电磁阀是CRDM中最小的驱动单元,其动态过程包括电磁动态过程和机械部件的运动过程,涉及电、磁、机械等多个物理场的相互作用[21]。作为驱动杆提升和下插动作的最终执行机构,提升电磁阀的动态过程最为重要,其电-磁-机械耦合关系如图2所示。以提升电磁阀为例,本文建立其电路模型、磁路模型和动力学模型。
1)电路方程
如图2所示,提升电磁阀的电路模型可抽象为串联连接的线圈电阻Rc和电感L。续流电阻R0和续流二极管并联在线圈两端。根据基尔霍夫电压定律(Kirchhoff’s Voltage Law, KVL),提升电磁阀的动态电压平衡方程表示为
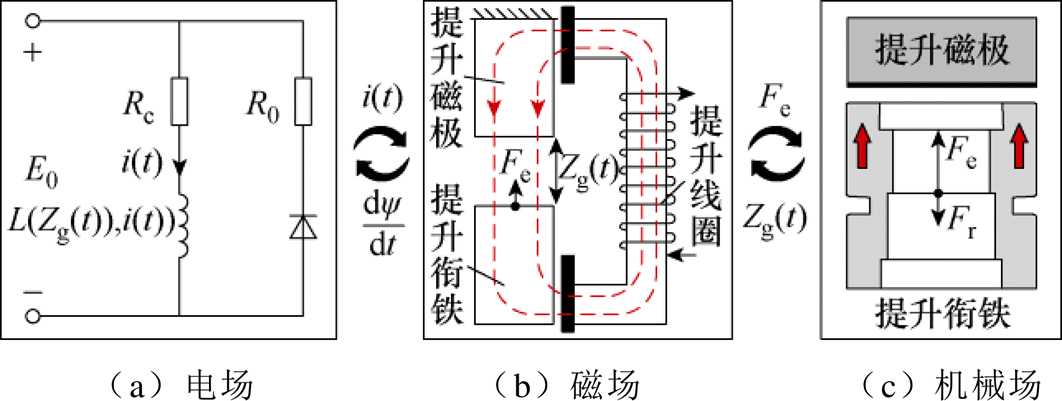
图2 提升电磁阀的电-磁-机械耦合关系
Fig.2 Electric-magnetic-mechanica coupling relationship of the lift solenoid valve
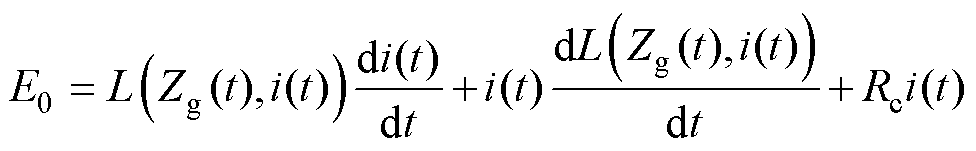 (1)
(1)
式中,E0为线圈端电压;Zg(t)为气隙长度;i(t)为流过线圈的瞬态电流;线圈电感L为气隙长度Zg(t)和电流i(t)的函数,呈现出非线性和时变性特点。由于线圈电感的存在,电压加载及衔铁在磁场作用力下的运动过程均会诱导线圈产生感应电动势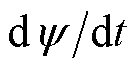 。
。
2)电磁方程
线圈通电产生磁场。提升衔铁在外加磁场作用下受到电磁力Fe,根据麦克斯韦张量法可得
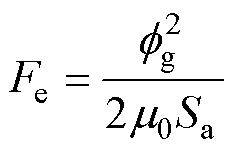 (2)
(2)
式中,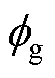 为气隙磁通;Sa为提升衔铁端面面积;
为气隙磁通;Sa为提升衔铁端面面积;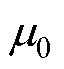 为真空磁导率。对于提升电磁阀,由于气隙磁通受
为真空磁导率。对于提升电磁阀,由于气隙磁通受
到电流大小、磁路饱和程度和气隙长度等因素的影响,利用式(2)计算电磁力往往存在较大偏差。
3)机械运动方程
当提升衔铁所受的电磁力大于其阻力时,衔铁开始运动,其动力学方程可表示为
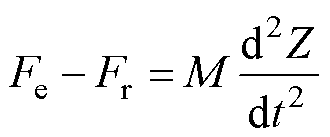 (3)
(3)
式中,Z为衔铁的位移;M为所有运动部件的质量,包括提升衔铁、驱动杆、负载;Fr为所有阻力,包括流体阻力Fw、弹簧反力Fs和摩擦力。其中,摩擦力相对较小,动态计算时一般将其忽略。
流体阻力Fw包括侧壁阻力、惯性阻力和端部阻力三部分,可表示[16]为
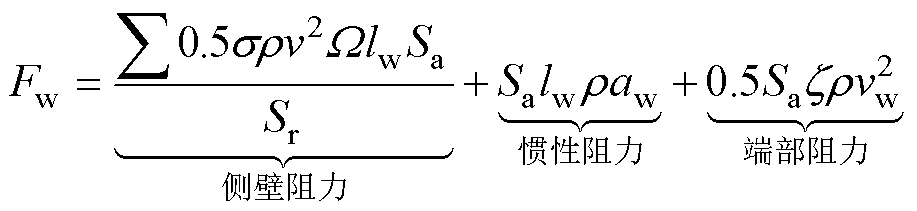 (4)
(4)
式中,v为提升衔铁的速度;∑为所有内壁和外壁的总和;Sr和lw分别为流动通道的横截面积和长度; 和
和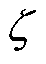 为阻力系数;
为阻力系数;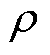 和
和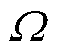 分别为液体的密度和壁的湿周长;aw为水的加速度,vw为壁相对于水的速度。值得一提的是,上述阻力中,端面阻力对衔铁的运动过程影响最大[19]。
分别为液体的密度和壁的湿周长;aw为水的加速度,vw为壁相对于水的速度。值得一提的是,上述阻力中,端面阻力对衔铁的运动过程影响最大[19]。
弹簧反力Fs定义为
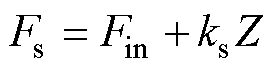 (5)
(5)
式中,Fin为弹簧预压力;ks为弹簧刚度。
从图2可以看出,磁路环节作为机-电转换的中间环节,其电磁参数的准确预测对于多物理场耦合计算尤为重要。因此,本文提出一种DEMN模型,用于计算线圈电感和电磁力。
为简化分析模型,本文做出以下合理假设:①忽略三个电磁阀机构间的磁耦合效应;②忽略因工艺引起的微小结构改变;③忽略导磁材料的磁滞效应;④将非磁性材料的磁导率视为真空磁导率。在提升电磁阀机构中,仅导磁环、磁轭、提升衔铁和提升磁极为导磁材料,其B-H曲线见文献[22]。
在二维圆柱坐标系中创建如图3所示的提升电磁阀的几何模型。通过提取各部件的顶点坐标,确定其几何形状及相对位置关系。求解区域为包含提升电磁阀的矩形区域,未定义部分默认为空气域。
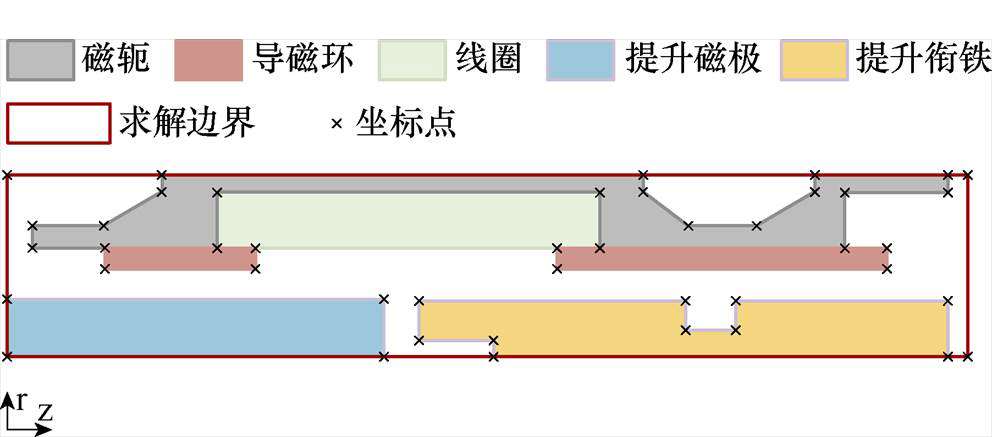
图3 提升电磁阀的几何模型
Fig.3 The geometric model of the lift solenoid valve
基于磁阻网格的EMN模型无需依赖磁通分布进行建模,具有更高的便捷性。常见的磁阻网格形状包括矩形网格[23]、钻石网格[24]、五边形网格[25]、六边形网格[26]等。然而,钻石网格、五边形网格和六边形网格在剖分过程中容易变形,导致磁阻计算公式难以统一。相比之下,矩形网格形状稳定,尺寸可自由拉伸或压缩,便于实现磁阻的统一计算和网格的自适应剖分。此外,矩形网格能够直接求得局部区域的径向和轴向电磁分量,利用张量法更易计算电磁提升力。因此,本文采用矩形网格来建立DEMN模型。
图4定义了圆柱坐标系中的矩形网格单元,其几何中心定义为一个节点。从该节点延伸至矩形单元的四个边界存在四个磁阻(两个轴向磁阻和两个径向磁阻)。各磁阻需根据其磁通流经方向进行计算,即轴向磁阻沿轴向磁通路径积分,径向磁阻沿径向磁通路径积分。
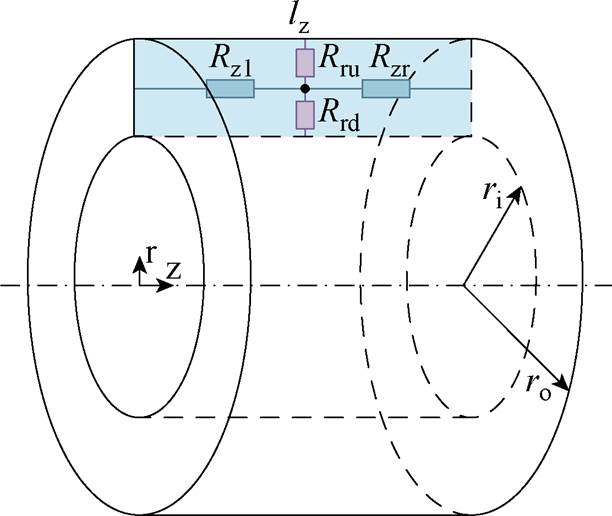
图4 矩形网格的磁阻等效示意图
Fig.4 Reluctance equivalent diagram of rectangular mesh
根据磁通管原理,图4中的磁阻计算公式为
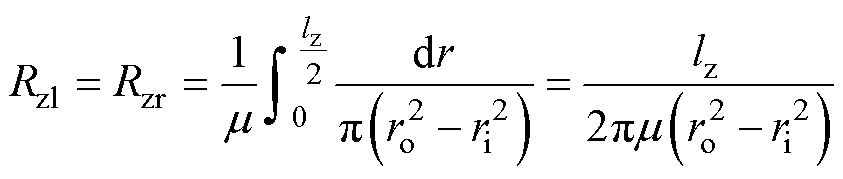 (6)
(6)
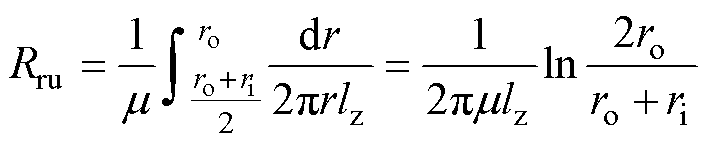 (7)
(7)
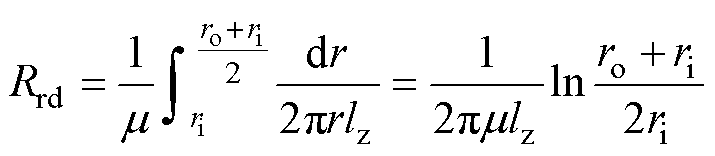 (8)
(8)
式中,Rru、Rrd、Rzl和Rzr分别为上、下、左、右磁阻;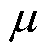 为磁导率;lz为矩形网格单元的轴向长度;ro和ri分别为矩形网格单元的外半径和内半径。值得注意的是,上磁阻和下磁阻的计算公式因其积分上下限不同而存在差异。
为磁导率;lz为矩形网格单元的轴向长度;ro和ri分别为矩形网格单元的外半径和内半径。值得注意的是,上磁阻和下磁阻的计算公式因其积分上下限不同而存在差异。
图5展示了提升电磁阀的一种剖分情况。为了生成矩形网格单元,本文采用正交网格线对提升电磁阀进行快速剖分。剖分前,将求解域分为上、下两个区域:分界线以上为固定区,分界线以下为运动区。固定区包括磁轭、导磁环和线圈;运动区包括提升磁极和提升衔铁。对固定区和运动区分别进行独立剖分,以提高剖分的灵活性。
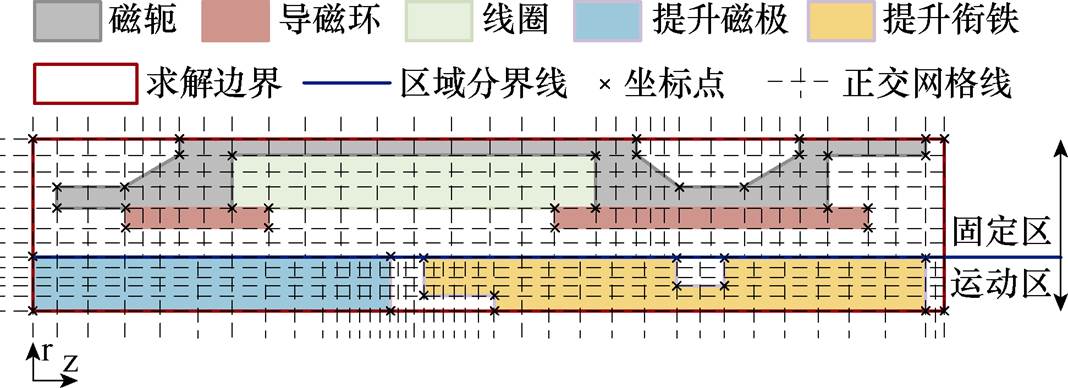
图5 提升电磁阀的网格剖分
Fig.5 Meshing of the lift solenoid valve
剖分过程分为两步:
(1)粗剖分。通过各部件的顶点坐标,同时生成竖直和水平网格线。水平网格线贯穿整个求解区域,竖直网格线在区域分界线上终止。粗剖分的目的是使网格线与材料边界对齐,确保每个矩形网格仅包含一种介质。
(2)细剖分。在粗剖分的基础上,插入更多网格线以加密网格。需要注意的是,插入网格线的数量和位置决定了DEMN模型在局部区域的网格离散化程度。通常情况下,为平衡计算时间和计算精度,气隙周围的区域剖分较密,而其他区域剖分较粗。
从图5可以看出,磁轭斜边上的矩形网格包含两种介质,增加了磁阻计算的复杂性。为解决这一问题,本文遵循介质占比较高的原则,将包含两种介质的矩形网格转化为单一介质网格。转化前后的网格单元对比如图6所示,可以看到,磁轭的斜边界被等效为阶梯边界。尽管这种处理方法可能降低斜边的建模精度,但可以通过加密斜边上的网格线来减小误差。
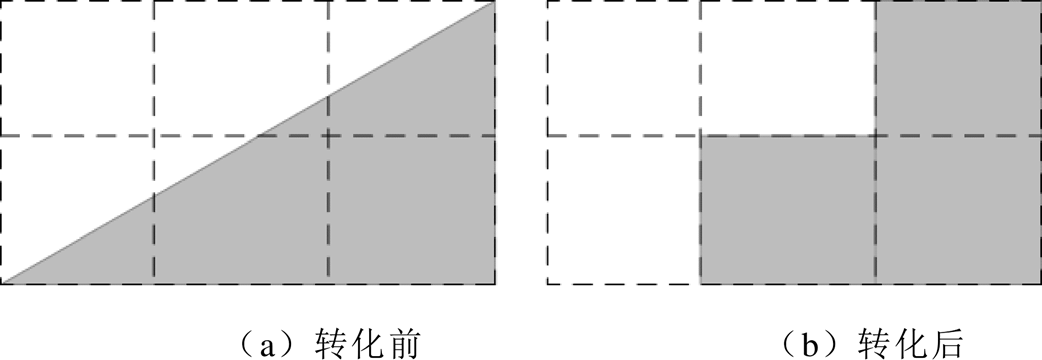
图6 混合介质矩形网格转化前后对比
Fig.6 Comparison of mixed medium rectangular mesh before and after conversion
假设将固定区和运动区分别划分为p行q列和m行n列的网格单元。用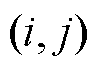 表示第i行、第j列的网格单元。以固定区为例,网格线的坐标和网格单元索引之间的关系如图7所示。其中,r和z分别为水平网格线的径向坐标值和竖直网格线的轴向坐标值,下标从0开始,共有p+1条水平网格线和q+1条竖直网格线。
表示第i行、第j列的网格单元。以固定区为例,网格线的坐标和网格单元索引之间的关系如图7所示。其中,r和z分别为水平网格线的径向坐标值和竖直网格线的轴向坐标值,下标从0开始,共有p+1条水平网格线和q+1条竖直网格线。
在获取每个单元的尺寸数据和材料属性后,可以利用式(6)~式(8)分别计算固定区和运动区中的每个磁阻,有

图7 网格单元索引
Fig.7 Grid cell index
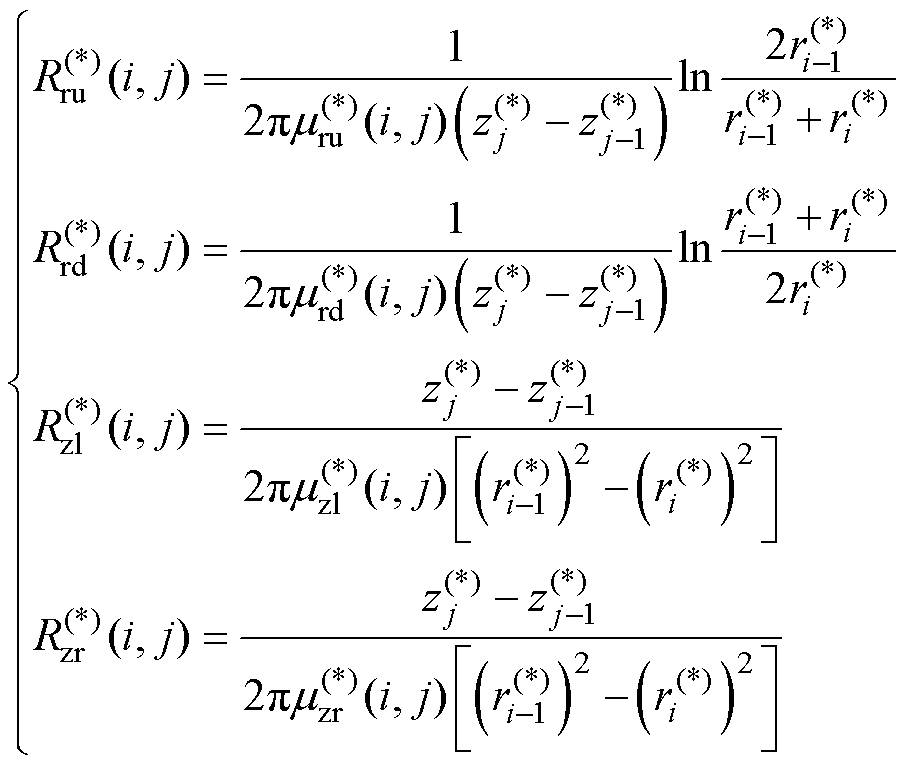 (9)
(9)
式中,(*)可选填sta或mov,以表示固定区或运动区;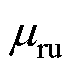 、
、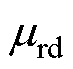 、
、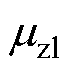 和
和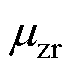 分别为上、下、左、右磁导率。由于本文统一了所有网格单元的磁阻计算公式,因此可以通过式(9)对所有网格的磁阻进行矩阵运算,从而提高计算速度。
分别为上、下、左、右磁导率。由于本文统一了所有网格单元的磁阻计算公式,因此可以通过式(9)对所有网格的磁阻进行矩阵运算,从而提高计算速度。
基于矩形网格单元的磁阻等效方法,通过连接相邻网格单元的磁阻,可以构建提升电磁阀的DEMN模型。图8展示了提升电磁阀局部区域的DEMN模型。

图8 局部区域的DEMN模型
Fig.8 DEMN model for local regions
从图8可以看到,在固定区或运动区内,两相邻节点之间的支路由两个磁阻连接而成。对任意节点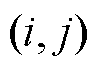 来说,其支路磁阻可表示为
来说,其支路磁阻可表示为
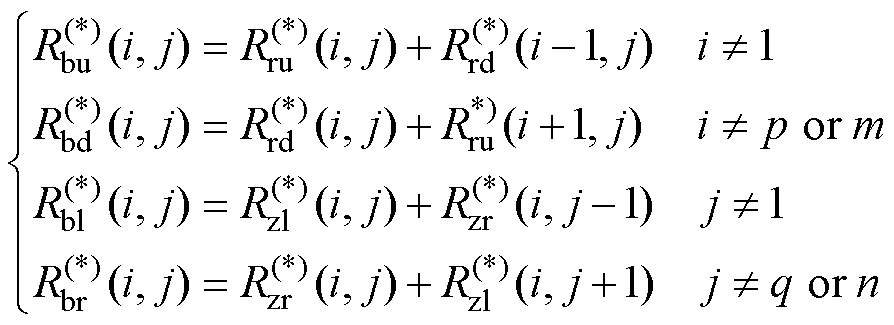 (10)
(10)
式中,Rbu、Rbd、Rbl和Rbr分别为节点的上、下、左、右支路磁阻。
由式(10)可知,通常情况下,支路磁阻是两相邻节点之间所有磁阻的代数和。然而,从图8可以看出,由于固定区和运动区的网格划分不同,区域分界线上下的网格单元无法完全对齐,使得其上下节点间的支路磁阻无法通过式(10)计算得到。
为解决上述问题,本文建立了区域边界线上下节点间的连接关系,如图9a所示。图中,运动区的节点 与固定区的节点
与固定区的节点 和
和 重叠,
重叠,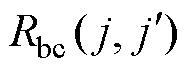 为节点
为节点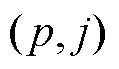 与节点
与节点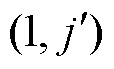 之间的支路磁阻,其他支路磁阻的编号依此类推。支路磁阻
之间的支路磁阻,其他支路磁阻的编号依此类推。支路磁阻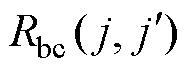 根据上下网格间重叠的占比来计算,具体公式为
根据上下网格间重叠的占比来计算,具体公式为
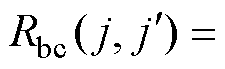
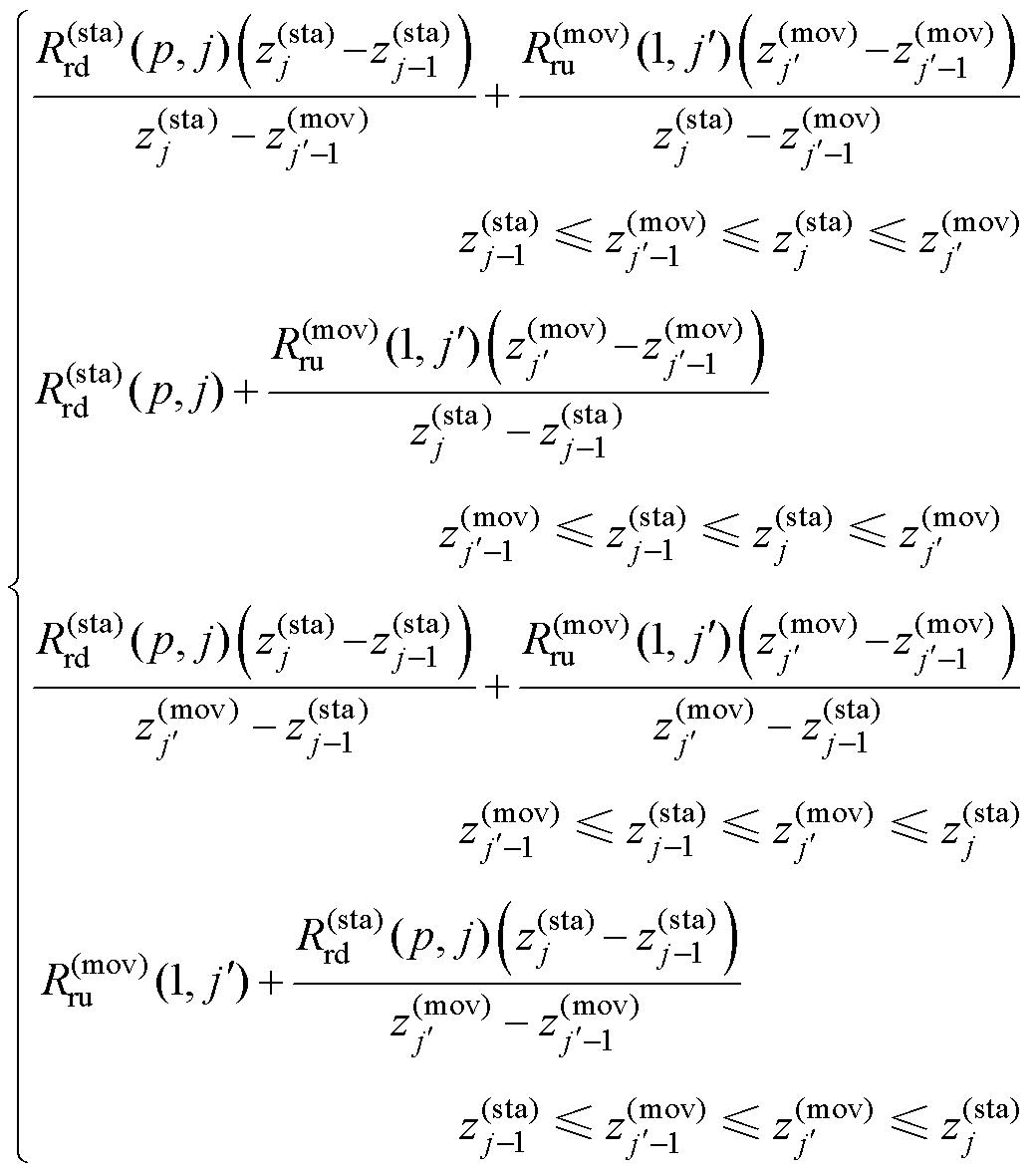 (11)
(11)
图9b展示了支路磁阻的变化关系。可以看到,支路磁阻呈现“U”形变化趋势。具体而言,运动区网格单元与固定区网格单元的重叠程度越小,支路磁阻越大;反之,重叠程度越大,支路磁阻越小。当网格单元不重叠时,支路磁阻趋于无穷大。
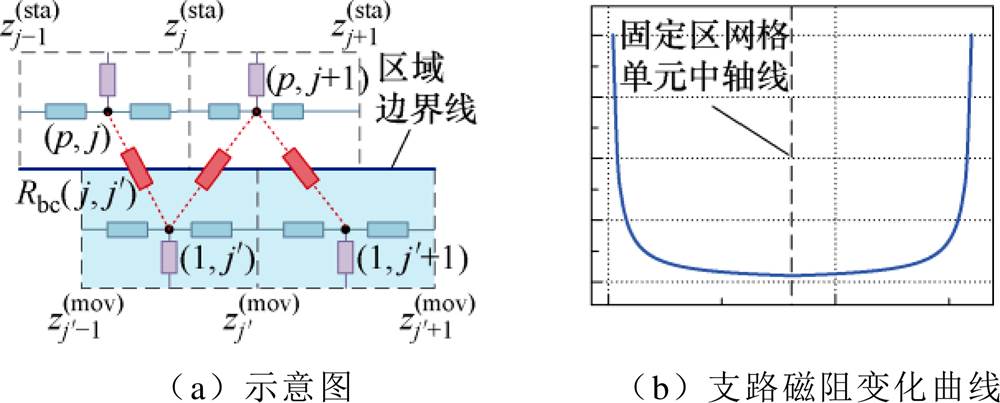
图9 区域分界线上下节点间的连接关系
Fig.9 The connection relationship between the upper and lower nodes of the regional boundary
不同衔铁位置下的网格分布如图10所示,当提升衔铁吸合时,气隙区的网格单元被压缩,端部空气区的网格单元被拉伸。为实现DEMN模型的动态变化,本文在保持网格总数不变的前提下,仅调整气隙区和端部空气区的网格大小,同时更新提升衔铁区的网格位置,以实现衔铁的连续运动。网格单元更新后,固定区和运动区的磁阻连接关系保持不变,仅需根据式(11)重新确定区域边界线上下节点间的连接关系。这种方法最大程度地避免了冗余建模,并减少了因网格剖分差异引起的计算误差。
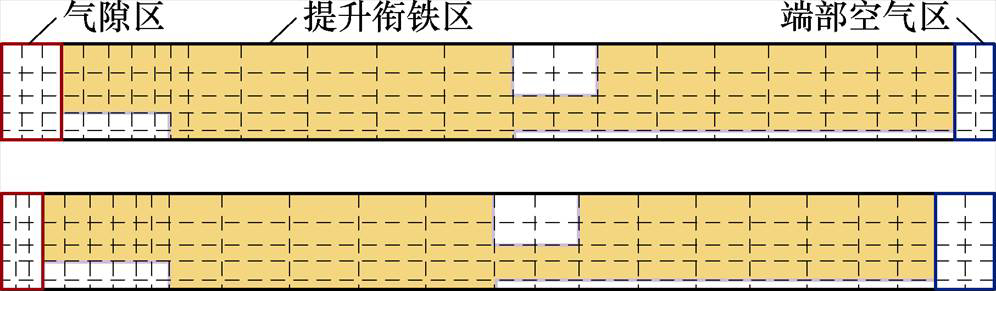
图10 不同衔铁位置下的网格分布
Fig.10 Mesh distribution under different armature positions
由安培环路定理可知,在准稳态条件下,线圈产生的磁动势(Magnetic Motive Force, MMF)可表示为
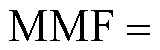
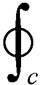
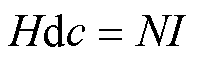 (12)
(12)
式中,H为磁场强度;c为闭环路径;N为线圈匝数;I为线圈电流。
由于提升线圈匝数较多,在轴向上分布较长,本文考虑到磁动势的空间分布效应,将线圈按轴向进行分割,并将分割后线圈产生的磁动势径向投影到磁轭上。磁动势的空间分布如图11所示,假设线圈径向的磁轭区域被划分为k个网格单元。线圈的分割线位于相邻两竖直网格线的中间,将线圈分割成k+1个子区域。
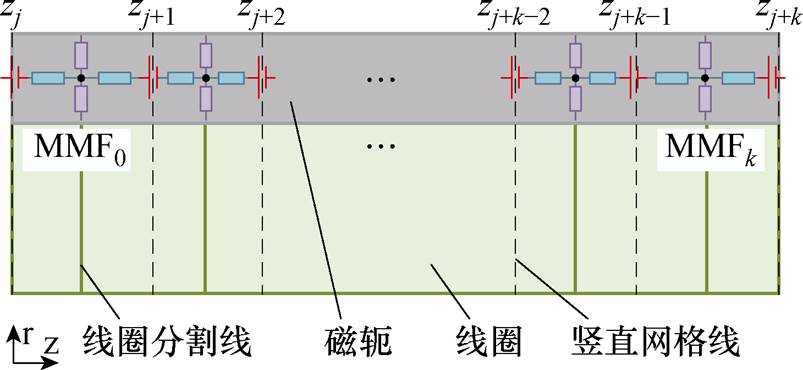
图11 磁动势的空间分布
Fig.11 Spatial distribution of magnetomotive force
MMF0~MMFk为每个子线圈产生的磁动势,有
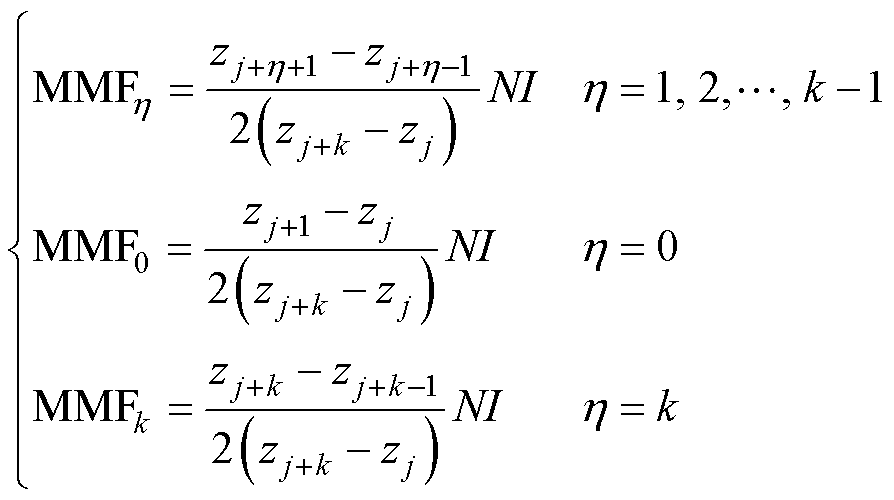 (13)
(13)
式中,下标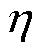 为磁动势编号。
为磁动势编号。
基于磁网络与电网络的相似性,选取任一节点作为磁动势参考点,并应用基尔霍夫电流定律(Kirchhoff’s Current Law, KCL)建立DEMN的节点方程。其矩阵形式为
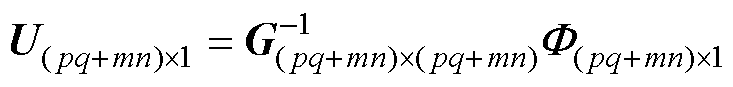 (14)
(14)
式中,U为维度为(pq+mn)×1的节点磁动势矢量,为待求的矢量;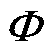 为维度为(pq+mn)×1的节点磁通源矢量;G为维度为(pq+mn)×(pq+mn)的节点磁导矩阵。节点在矢量中的排列顺序遵循:先固定区,后运动区;先行后列。因此,任意节点
为维度为(pq+mn)×1的节点磁通源矢量;G为维度为(pq+mn)×(pq+mn)的节点磁导矩阵。节点在矢量中的排列顺序遵循:先固定区,后运动区;先行后列。因此,任意节点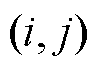 在矢量中的序号
在矢量中的序号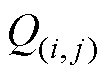 为
为
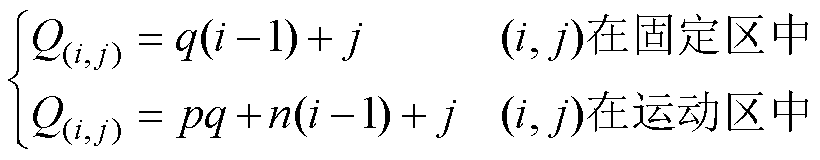 (15)
(15)
节点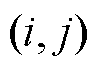 的磁通源与该节点连接的所有支路上的磁动势和磁阻相关,其计算方法为
的磁通源与该节点连接的所有支路上的磁动势和磁阻相关,其计算方法为
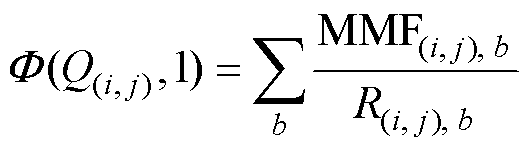 (16)
(16)
式中,b为与节点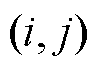 相连的节点;
相连的节点;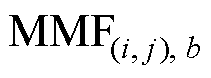 和
和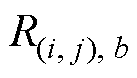 分别为节点
分别为节点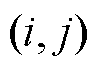 与节点b之间的磁动势和支路磁阻。根据2.4节,仅部分支路中存在磁动势,其余支路的磁动势为0。需要注意的是,磁动势和电动势一样,具有正负性。本文规定:流入节点的磁动势为正,流出节点的磁动势为负。
与节点b之间的磁动势和支路磁阻。根据2.4节,仅部分支路中存在磁动势,其余支路的磁动势为0。需要注意的是,磁动势和电动势一样,具有正负性。本文规定:流入节点的磁动势为正,流出节点的磁动势为负。
G中的元素计算方法为
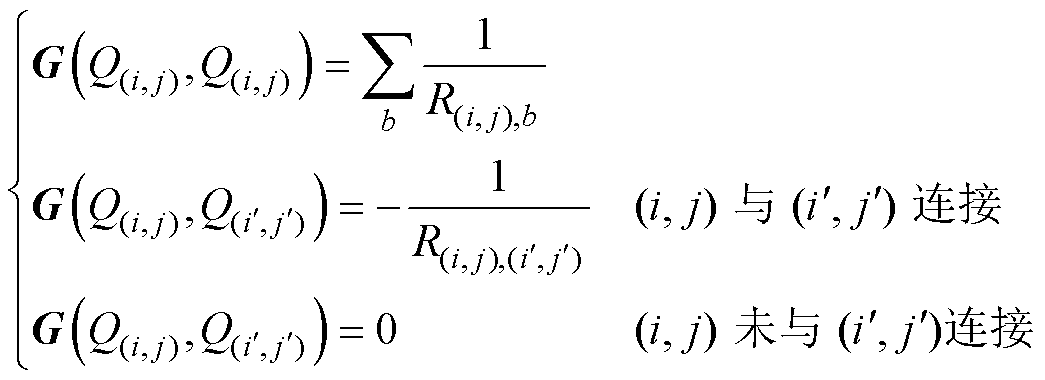 (17)
(17)
式中,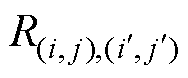 为节点
为节点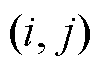 与
与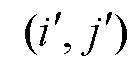 之间的支路磁阻。获得
之间的支路磁阻。获得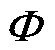 和G后,利用式(14)即可求得每个节点的磁动势。在此基础上,可进一步计算支路磁通、磁通密度、线圈电感和电磁力等电磁参数。
和G后,利用式(14)即可求得每个节点的磁动势。在此基础上,可进一步计算支路磁通、磁通密度、线圈电感和电磁力等电磁参数。
支路磁通为
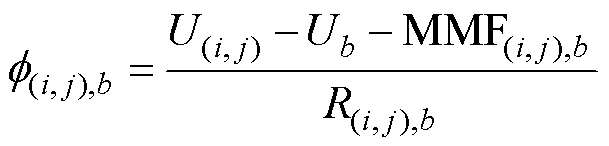 (18)
(18)
式中,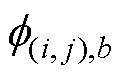 为节点
为节点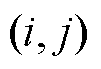 与节点b之间的支路磁通;
与节点b之间的支路磁通;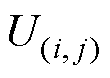 和Ub分别为节点
和Ub分别为节点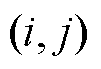 和节点b的磁动势。
和节点b的磁动势。
磁通密度为
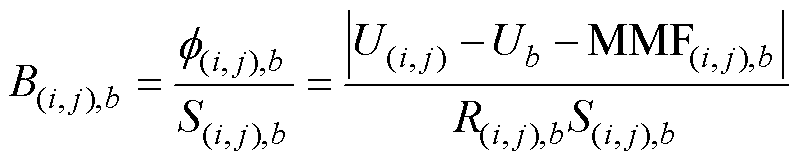 (19)
(19)
式中,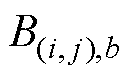 和
和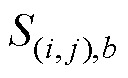 分别为节点
分别为节点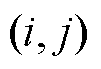 与节点b之间的磁通密度和磁通面积。值得注意的是,矩形网格单元在径向上的磁通面积是变化的,因此,在计算网格单元的径向磁通密度时,取磁通面积的平均值。
与节点b之间的磁通密度和磁通面积。值得注意的是,矩形网格单元在径向上的磁通面积是变化的,因此,在计算网格单元的径向磁通密度时,取磁通面积的平均值。
电感为
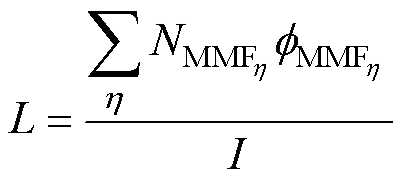 (20)
(20)
式中,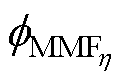 为存在磁动势的支路磁通;
为存在磁动势的支路磁通;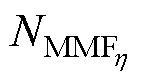 为该磁动势对应的线圈匝数。
为该磁动势对应的线圈匝数。
电磁提升力为
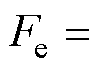
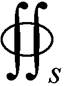
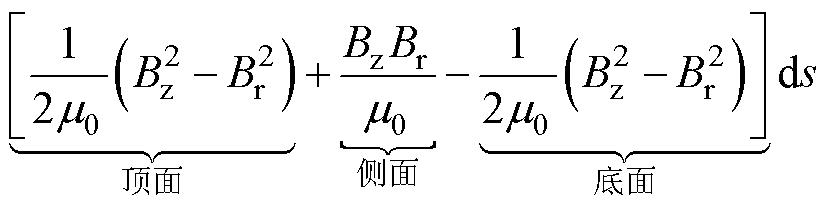 (21)
(21)
式中,Bz和Br分别为提升衔铁外表面s上的轴向和径向的磁通密度分量。
提升电磁阀的动态过程仿真必须耦合电路、磁路和机械运动方程进行求解[27]。目前,采用解析法求解提升电磁阀动态性能时,通常忽略电流的瞬态响应和磁路的饱和效应,导致电磁参数计算偏差较大,从而影响整个动态过程的计算精度。尽管多软件协同仿真可以提高计算精度,但该过程繁琐且计算时间冗长,难以满足多次迭代计算下的效率要求。
为此,本文结合DEMN模型、电路方程和机械动力学方程,提出一种同时考虑电流瞬态变化和磁路饱和效应的CRDM多物理场耦合计算方法,计算流程如图12所示。其中,DEMN模型根据当前电流I0和衔铁位移Z0计算当前时刻的动态电感和磁通密度;电路方程则根据当前时刻下的动态电感计算下一时刻的瞬态电流I1;机械动力学方程根据当前时刻下的电磁力、弹簧反力和流体阻力计算下一时刻的衔铁位移Z1。将计算出的瞬态电流I1和衔铁位移Z1再次代入DEMN模型进行计算,直至动态过程结束。该过程在Matlab/Simulink中完成电-磁-机械运动的耦合计算。
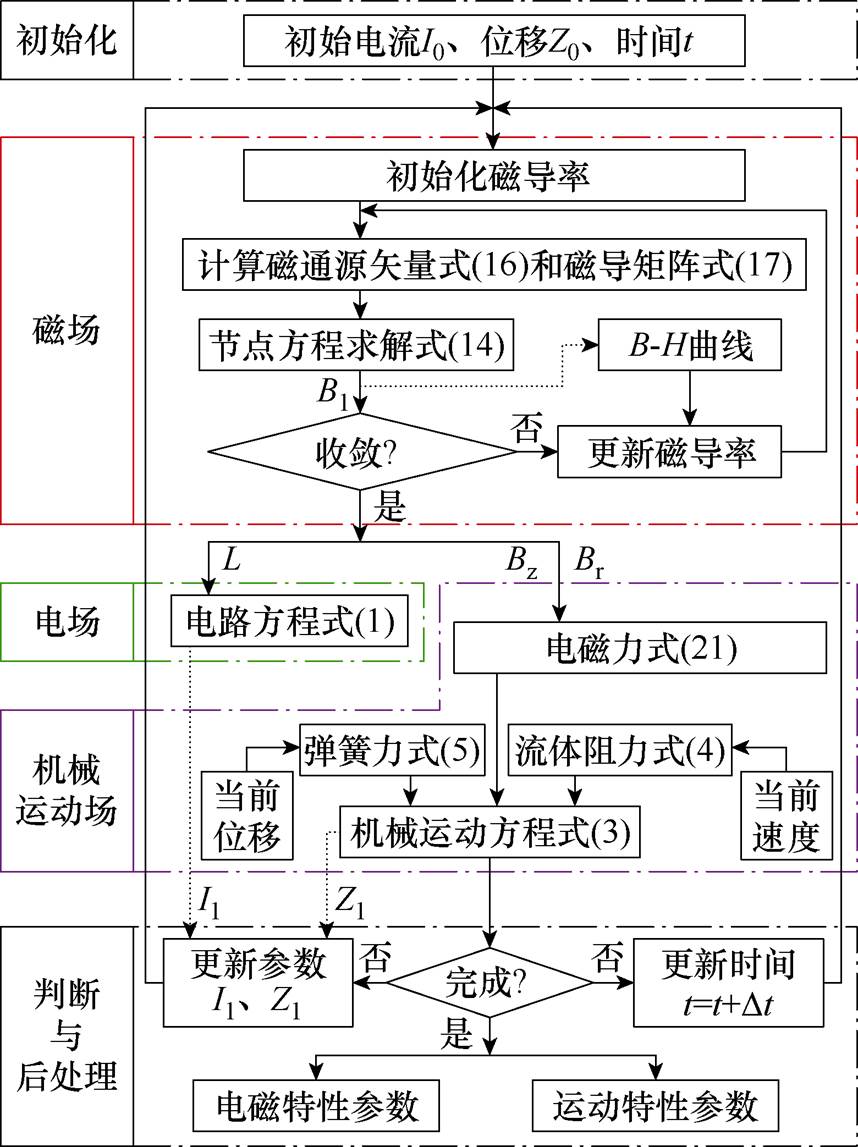
图12 电-磁-机械场耦合计算流程
Fig.12 Calculation process for electric-magnetic- mechanical coupling
需要注意的是,初始电流不能从0开始计算,在无激励条件下,DEMN模型无法计算线圈的电感和磁通密度。因此,本文设定了一个极小值。此外,DEMN模型在每次衔铁位移变化后,会更新其网格结构,以实现动态变化。
为了考虑磁路饱和效应,DEMN模型的迭代计算过程如下:
(1)根据衔铁位移,调整DEMN模型的网格。
(2)初始化各矩形网格单元的磁导率。
(3)计算每个单元的初始磁阻。使用式(14)求解节点方程,得到每个节点上的磁动势。
(4)使用式(18)和式(19)计算每个支路磁通和每个单元的新磁通密度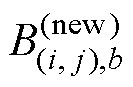 。
。
(5)根据磁性材料的B-H曲线,更新各单元的磁导率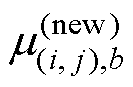 。具体来说,当新的磁通密度落在B-H曲线上相邻的两点之间时,可以采用以下插值方法得到新的磁导率。
。具体来说,当新的磁通密度落在B-H曲线上相邻的两点之间时,可以采用以下插值方法得到新的磁导率。
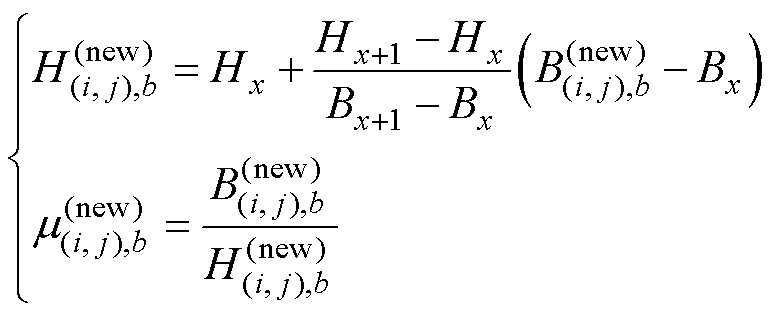 (22)
(22)
式中,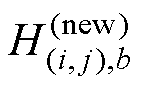 为新的磁场强度;Hx和Bx为前插值点;Hx+1和Bx+1为后插值点。
为新的磁场强度;Hx和Bx为前插值点;Hx+1和Bx+1为后插值点。
(6)迭代过程的收敛条件为
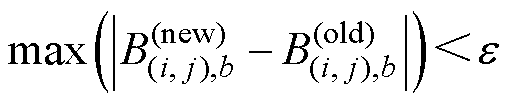 (23)
(23)
式中,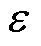 为预设的容错度;
为预设的容错度;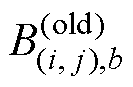 为更新前的磁通密度。判断更新前后每个单元的磁通密度差是否低
为更新前的磁通密度。判断更新前后每个单元的磁通密度差是否低
于预设误差。如果最大误差超过预设误差,则用更新后的磁导率替换上一迭代的磁导率,返回步骤(3)重新计算每个单元的磁阻。如果最大误差小于预设误差,则迭代结束。保存最后一步的支路磁通和磁通密度,并使用式(20)和式(21)计算线圈电感和电磁力。
为验证本文所提DEMN模型的有效性和准确性,将其计算结果与3D FEA结果和实验结果进行对比,包括磁通密度分布、线圈电感和电磁力等参数。此外,为验证多场耦合计算方法的正确性,将计算结果与实验结果进行对比,涵盖不同电流响应、不同负载和电流激励下的衔铁位移。
实验平台如图13所示,主要由CRDM样机、控制柜、LCR测试仪、示波器、电流钳、振动传感器、位移传感器、数据采集系统和上位机组成。其中,控制柜为线圈提供电源,LCR测试仪用于测试线圈电感,示波器用于采集线圈电流和振动信号,数据采集系统采集位移信号并传输到上位机。
根据磁路是否发生饱和,线圈电感可分为线性电感和饱和电感。线性电感使用RLC测试仪测量,饱和电感采用阶跃电压法计算[28]。为测量不同气隙下的线性电感和饱和电感,本文制造了不同厚度的导磁半环和非导磁半环,导磁半环的材料与提升衔铁一致。通过叠放非导磁半环,形成两个15.875 mm厚的半环,并从径向将其卡入气隙中,形成一个15.875 mm厚的闭合圆环。当需要改变气隙长度时,只需将气隙中最下层的非导磁半环替换为相同厚度的导磁半环即可。

图13 实验平台
Fig.13 Experiment platform
阶跃电压法测量饱和电感:在t=0时刻,给线圈两端施加恒定电压,测量流过线圈的电流。基于离散化的电路方程,可推导出任意电流下的电感表达式为
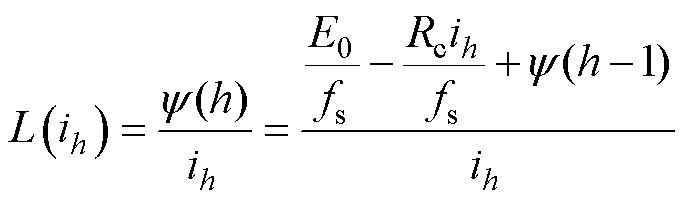 (24)
(24)
式中,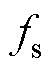 为示波器采样频率;
为示波器采样频率;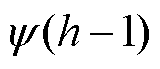 和
和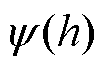 分别为第
分别为第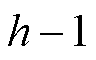 次和第h次采样时的磁链;ih为第h次采样的电流;L(ih)为电流ih下的线圈电感。
次和第h次采样时的磁链;ih为第h次采样的电流;L(ih)为电流ih下的线圈电感。
由于提升衔铁浸泡在压力壳内部的液体环境中,其运动过程无法直接测量。庆幸的是,驱动杆可伸出CRDM外部,并在运动过程中与衔铁同步提升。因此,本文将位移传感器安装在驱动杆上,通过检测驱动杆的位移间接测量提升衔铁的动态过程。同样地,在驱动杆的底端悬挂负载。
4.1.1 磁通密度分布
图14为线圈电流为40 A、气隙长度为0 mm时,提升电磁阀的磁通密度分布3D FEA结果和本文DEMN结果。经过对比发现,两者的磁通密度分布规律和大小十分接近,从而说明本文DEMN模型的有效性。磁通密度分布规律显示:磁轭的磁通密度分布相对均匀;导磁环的磁通密度主要集中在线圈槽的一端;提升磁极的磁通密度从气隙的远端到近端逐渐增加;提升衔铁的磁通密度从气隙的近端到远端先逐渐减小,再突然增大,最后再次减小。磁通密度大小显示:磁轭和导磁环的磁通密度值较小,而提升磁极和提升衔铁的局部区域出现了严重的磁饱和。因此,在研究CRDM的电磁特性时,考虑饱和效应的影响十分必要。
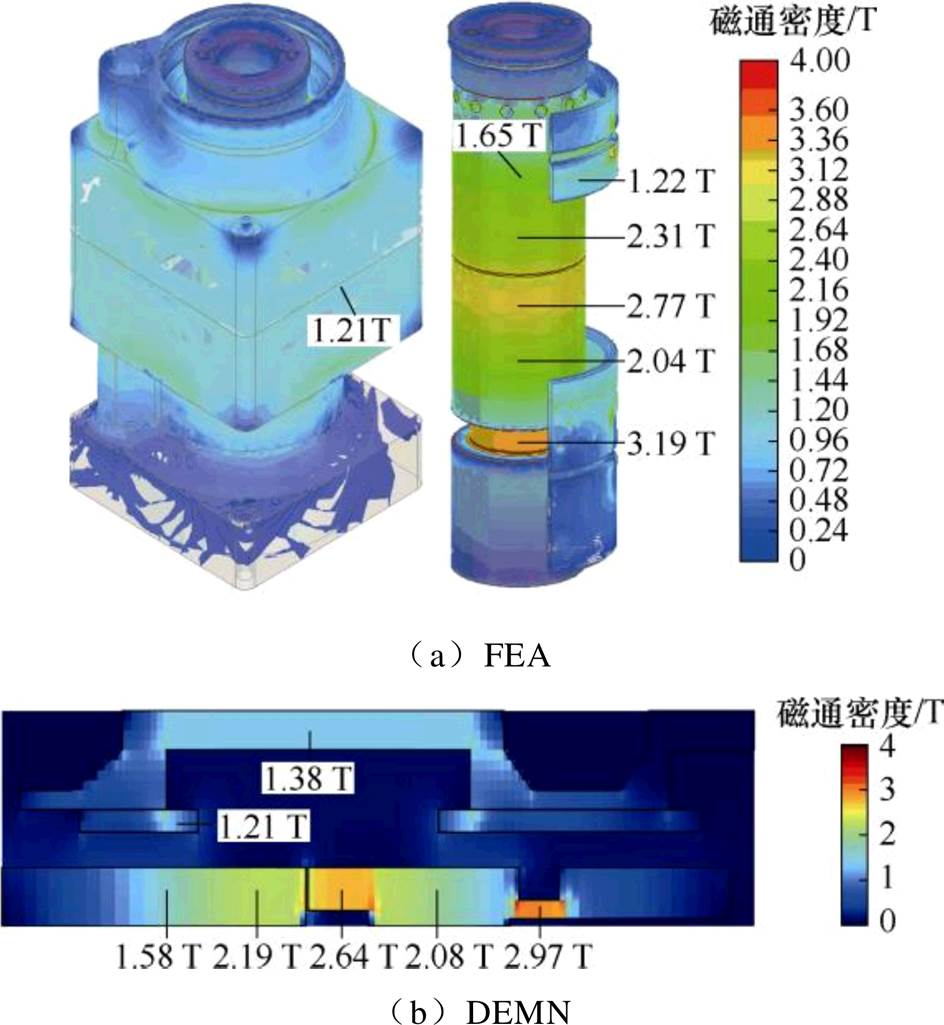
图14 磁通密度分布云图
Fig.14 Magnetic density distribution cloud map
4.1.2 电感
图15比较了不同电流和气隙长度下,由3D FEA和本文DEMN模型计算得到的线圈电感。结果显示,本文DEMN模型的计算结果在所有电流和气隙长度下均与3D FEA结果高度吻合,最大误差仅为5.7%。
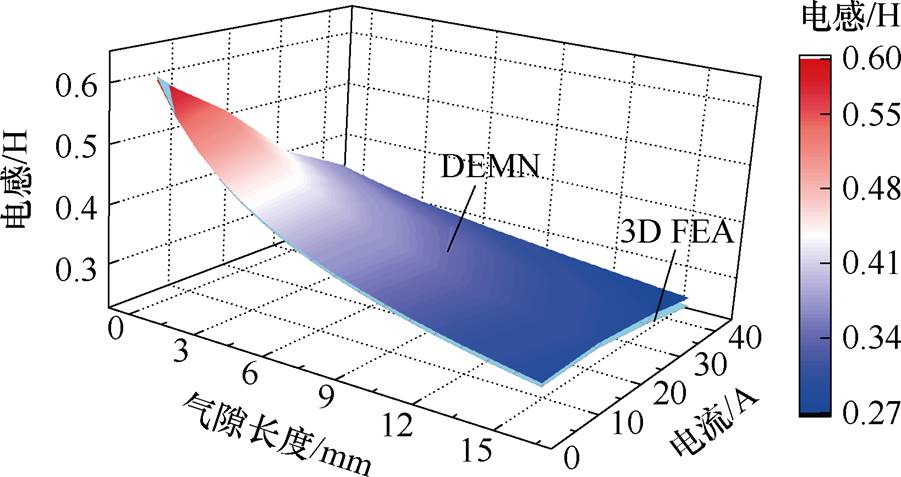
图15 线圈电感的有限元验证
Fig.15 FEA verification of coil inductance
图16对比了本文DEMN模型计算的线圈电感与实验测得的线圈电感。图16a展示了线性电感随气隙长度变化的情况。可以看到,本文的计算结果与实验结果非常接近。实验结果略小于计算结果,主要原因是实验中卡入气隙中的导磁半环之间仍存在空气间隙,导致导磁半环的磁阻较大。
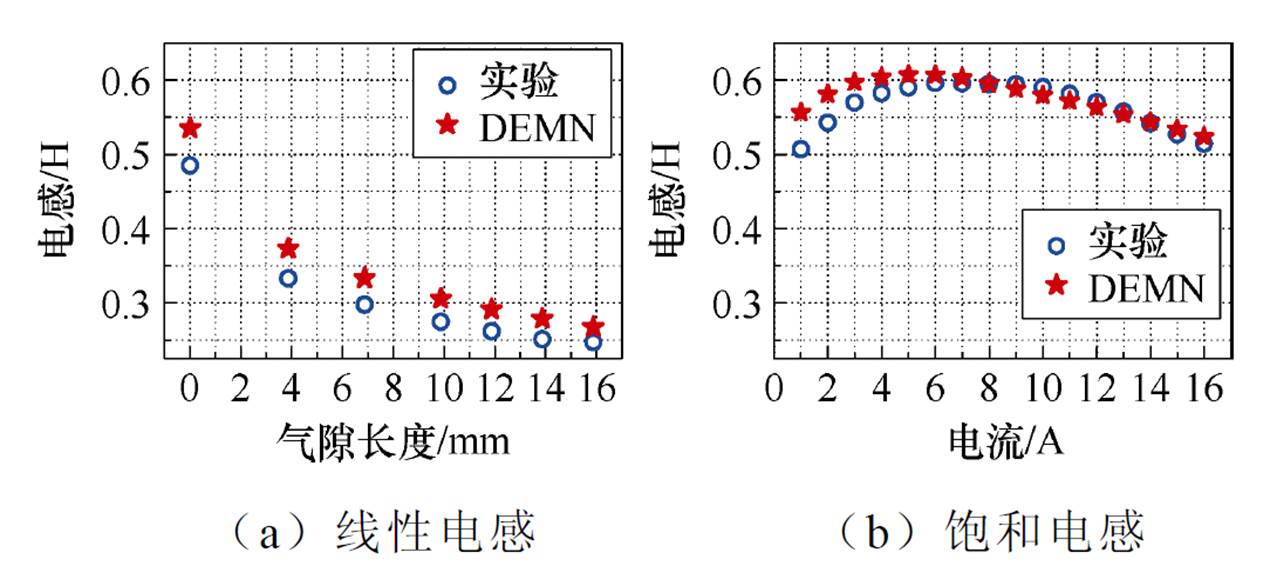
图16 线圈电感的实验验证
Fig.16 Experimental verification of coil inductance
图16b展示了气隙长度为0 mm时,不同电流下饱和电感的变化规律。可以看到,电感呈现先增加后减小的趋势。电感增加是由于在线性阶段材料的磁导率逐渐增加。当电流大于6 A后,线圈电感逐渐减小,表明磁路开始饱和并逐渐加深。从计算结果与实验结果的对比来看,二者具有较高的吻合度,验证了本文DEMN模型的准确性。
4.1.3 电磁力
图17比较了不同电流和气隙长度下的电磁力变化曲线。结果表明,本文DEMN模型的计算结果与3D FEA结果高度吻合,最大误差为0.6 kN,仅占仿真值的3.4%。这进一步说明本文DEMN模型提高了电磁参数预测的精度。
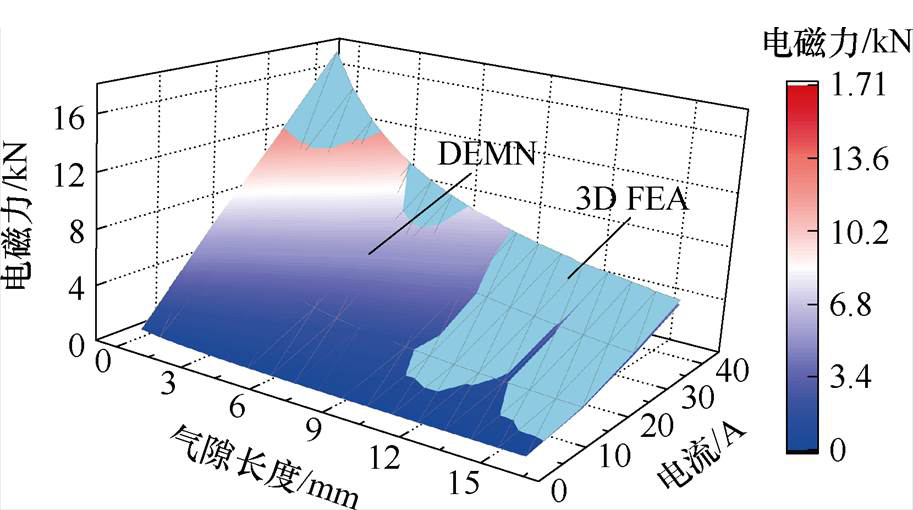
图17 不同电流和气隙条件下的电磁力分布
Fig.17 Electromagnetic force distribution under various current and air gap conditions
为进一步验证电磁力计算的准确性,本文对比了不同负载下的吸合电流和释放电流,具体数据见表1。吸合电流是指在气隙长度最大时,使提升衔铁开始吸合的临界电流;释放电流则是指在气隙长度最小时,使提升衔铁开始释放的临界电流。对比结果显示,本文DEMN计算结果的准确度在91%以上。
表1 不同负载下的吸合电流和释放电流
Tab.1 Pickup and release currents under different loads
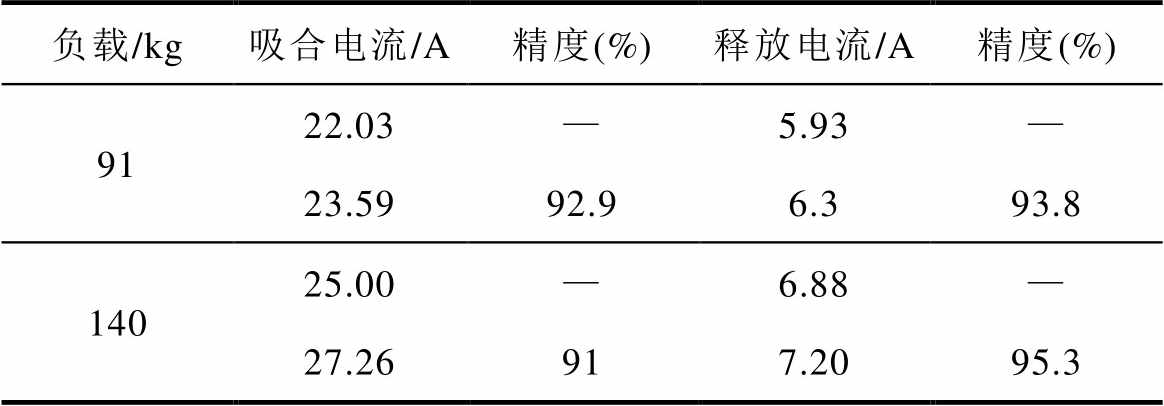
负载/kg吸合电流/A精度(%)释放电流/A精度(%) 9122.03—5.93— 23.5992.96.393.8 14025.00—6.88— 27.26917.2095.3
4.1.4 计算时间对比
FEA法和DEMN法在相同电脑配置下的计算时间和内存占比见表2。可以看到,DEMN模型将电磁阀剖分成914个单元,而3D FEA将其分解成1 383 051个单元。使用3D FEA法进行一步计算需要160 min,而DEMN法仅需27 s。显然,相较于3D FEA法,DEMN法在保持精度的同时,显著减少了计算资源和时间。即使与2D FEA相比,DEMN模型也显示出显著的优势。
表2 计算时间和资源对比
Tab.2 Comparison of calculation time and resources
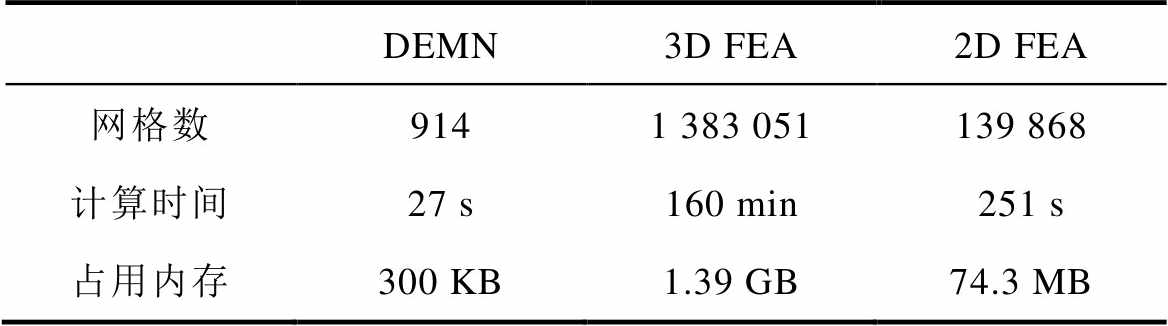
DEMN3D FEA2D FEA 网格数9141 383 051139 868 计算时间27 s160 min251 s 占用内存300 KB1.39 GB74.3 MB
4.2.1 动态电流
图18展示了负载为140 kg时,提升衔铁吸合过程中的动态电流和振动信号。可以看到,计算电流能够很好地跟随实测电流,二者的偏差主要出现在电流上升阶段。然而,由于电流上升初期衔铁尚未开始运动,因此该偏差对衔铁的运动过程影响不大。电流上升后期的偏差主要与控制策略有关,未来的研究可以将其考虑在内以减小这种误差。
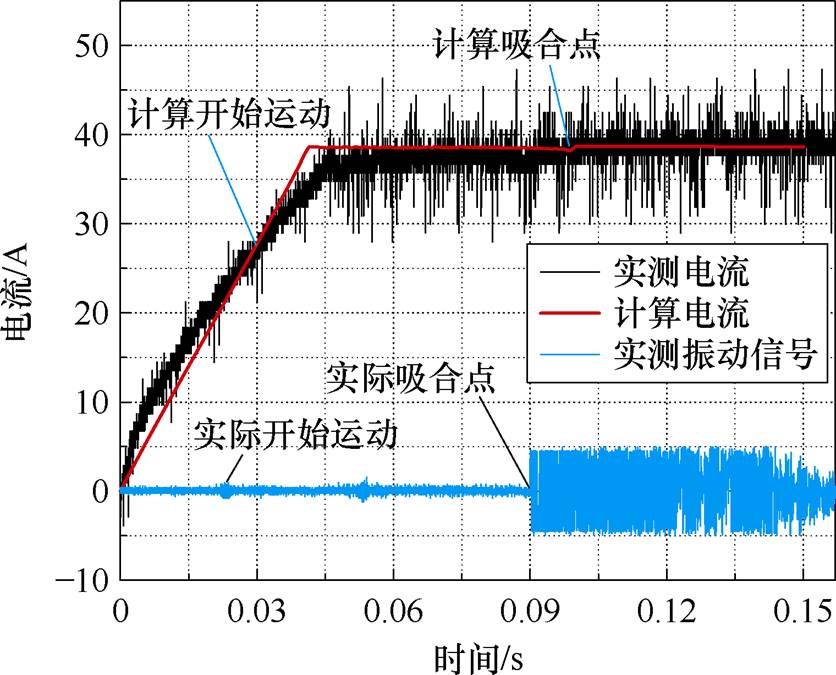
图18 动态电流和振动信号
Fig.18 Dynamic current and vibration signals
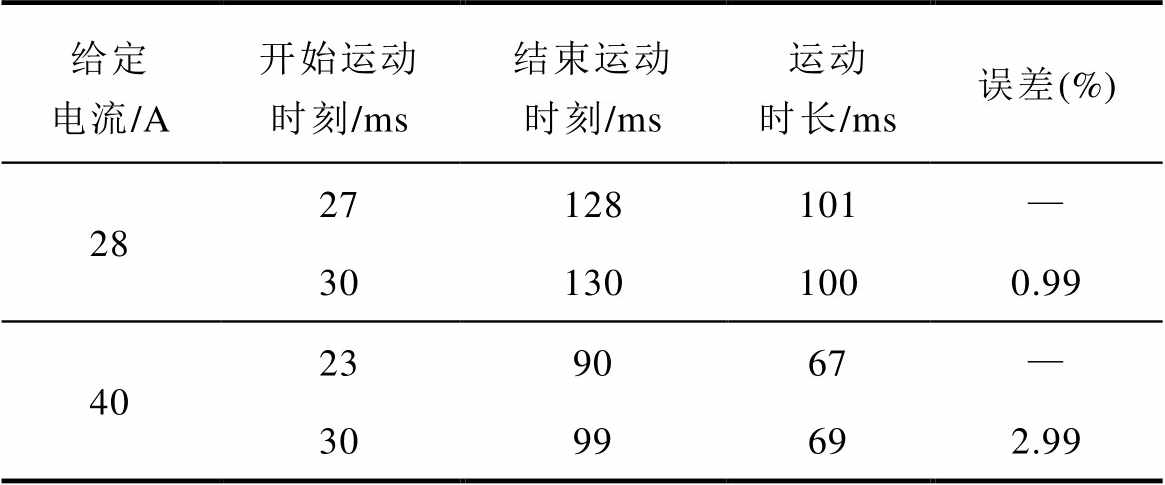
表3根据实测振动信号统计了不同电流下的衔铁运动时间。结果显示,提升衔铁开始运动的时刻略有滞后,但运动的持续时间非常接近。28 A和40 A电流下的计算误差分别为0.99%和2.99%。
表3 不同给定电流下的运动时间对比
Tab.3 Comparison of motion time under different given currents
给定电流/A开始运动时刻/ms结束运动时刻/ms运动时长/ms误差(%) 2827128101— 301301000.99 40239067— 3099692.99
4.2.2 位移
图19展示了不同负载和不同电流条件下,提升衔铁的运动位移曲线。可以看出,在所有工况下,计算结果均能很好地跟随实验结果。这表明本文方法具有较高的计算精度和稳健性。
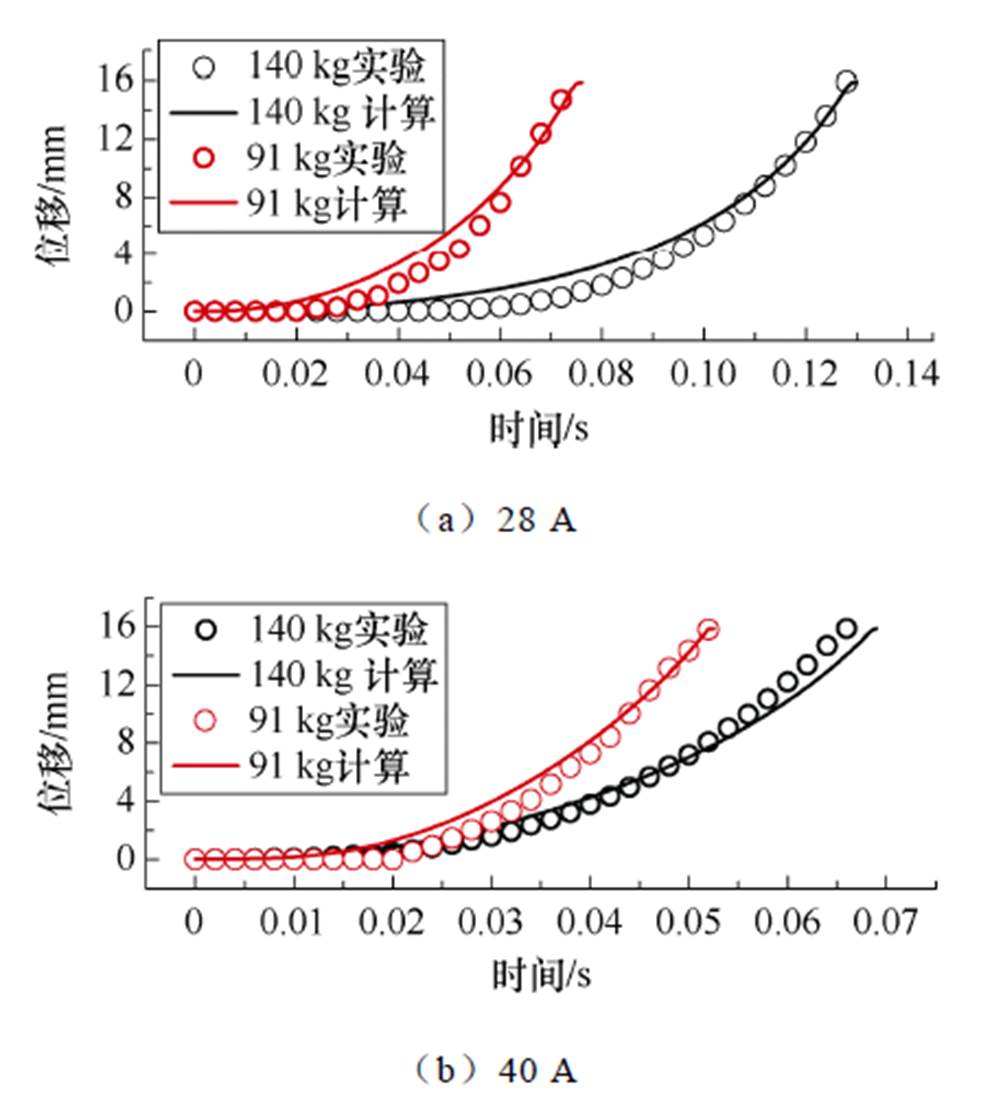
图19 运动特性曲线
Fig.19 Motion characteristic curves
本文针对反应堆磁力提升型控制棒驱动机构提出了一种DEMN模型,并基于此提出了同时考虑电流瞬态变化和磁饱和的多物理场耦合计算方法。具体结论如下:
1)采用正交网格线对机构进行矩形网格剖分,实现了等效磁阻的统一计算,加快了建模速度。
2)通过改变局部区域的网格大小或位置,实现DEMN模型的动态变化,避免了多场耦合计算过程中的重复建模问题,并降低了因网格剖分差异引起的计算误差。
3)与FEA相比,本文DEMN模型在保证计算精度的情况下,需要更少的计算资源和更短的计算时间,为FEA分析提供了一个平衡的替代方案。实验结果验证了本文所提DEMN模型和多物理场计算方法的有效性和准确性。
尽管本文以提升电磁阀为例进行了说明,但所提出的DEMN模型和多物理场耦合计算方法可扩展应用于整个CRDM的EMN模型建立、性能分析和快速优化设计。
参考文献
[1] Chen Ronghua, Su G H, Zhang Kui. Analysis on the high-quality development of nuclear energy under the goal of peaking carbon emissions and achieving carbon neutrality[J]. Carbon Neutrality, 2022, 1(1): 33.
[2] 吴宜灿, 李静云, 李研, 等. 中国核安全监管体制现状与发展建议[J]. 中国科学: 技术科学, 2020, 50(8): 1009-1018.
Wu Yican, Li Jingyun, Li Yan, et al. Investigation and proposals for China’s nuclear safety regulations[J]. Scientia Sinica (Technologica), 2020, 50(8): 1009- 1018.
[3] Yu Tianda, Wu Hao, Chen Xinan, et al. Degradation- based reliability analysis of magnetic jack type control rod drive mechanism[J]. Quality and Reliability Engineering International, 2023, 39(8): 3369-3384.
[4] Yang Yun, Xu Qiwei, Chen Yangming, et al. A fast nonlinear equivalent magnetic network model for magnetic jack type control rod drive mechanism in reactor[J]. Progress in Nuclear Energy, 2024, 169: 105058.
[5] Oluwasegun A, Jung J C. The application of machine learning for the prognostics and health management of control element drive system[J]. Nuclear Engin- eering and Technology, 2020, 52(10): 2262-2273.
[6] 许艳涛, 祖洪彪. 控制棒驱动机构步跃动作运动分析[J]. 核技术, 2013, 36(4): 347-351.
Xu Yantao, Zu Hongbiao. Stepping movement analysis of control rod drive mechanism[J]. Nuclear Techniques, 2013, 36(4): 347-351.
[7] 杨云, 于天达, 陈杨明, 等. 控制棒驱动机构磁路饱和特性分析[J]. 核动力工程, 2023, 44(3): 138- 143.
Yang Yun, Yu Tianda, Chen Yangming, et al. Analysis of magnetic saturation characteristics of control rod drive mechanism[J]. Nuclear Power Engineering, 2023, 44(3): 138-143.
[8] 朱齐荣, 朱京昌. 控制棒驱动机构的电磁设计计算[J]. 核动力工程, 1991, 12(3): 35-40.
Zhu Qirong, Zhu Jingchang. Electromagnetic design calculation of the control rod drive mechanism[J]. Nuclear Power Engineering, 1991, 12(3): 35-40.
[9] Park B J, Pham P T, Hong K S. Model reference robust adaptive control of control element drive mechanism in a nuclear power plant[J]. International Journal of Control, Automation and Systems, 2020, 18(7): 1651-1661.
[10] Yang Yun, Xu Qiwei, Chen Yangming, et al. An improved calculational model for inductance of CRDM based on equivalent magnetic circuit[J]. IEEE Transactions on Nuclear Science, 2022, 69(11): 2205-2213.
[11] 佟文明, 姚颖聪, 李世奇, 等. 考虑磁桥不均匀饱和的内置式永磁同步电机等效磁网络模型[J]. 电工技术学报, 2022, 37(12): 2961-2970.
Tong Wenming, Yao Yingcong, Li Shiqi, et al. Equivalent magnetic network model for interior permanent magnet machines considering non-uniform saturation of magnetic bridges[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2961- 2970.
[12] 佟文明, 王萍, 吴胜男, 等. 基于三维等效磁网络模型的混合励磁同步电机电磁特性分析[J]. 电工技术学报, 2023, 38(3): 692-702.
Tong Wenming, Wang Ping, Wu Shengnan, et al. Electromagnetic performance analysis of a hybrid excitation synchronous machine based on 3D equi- valent magnetic network[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 692-702.
[13] 夏云彦, 周洲, 邵远亮, 等. 基于动态磁网络法大型感应电机阻抗参数及起动特性计算[J]. 电工技术学报, 2024, 39(14): 4341-4352.
Xia Yunyan, Zhou Zhou, Shao Yuanliang, et al. Calculation of impedance parameters and starting characteristics of large induction motor based on dynamic magnetic network[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4341-4352.
[14] 沈小要. 控制棒驱动机构的分段非线性动态特性[J]. 中国工程机械学报, 2011, 9(4): 410-415.
Shen Xiaoyao. Study on segmental nonlinear dynamic properties for control rod drive mechanism[J]. Chinese Journal of Construction Machinery, 2011, 9(4): 410-415.
[15] Ling Sitong, Li Wenqiang, Li Chuanxiao, et al. Flow field fusion simulation method based on model features and its application in CRDM[J]. Nuclear Science and Techniques, 2022, 33(3): 32.
[16] 邓强, 陈西南, 刘佳, 等. 磁力提升型控制棒驱动机构提升动作过程动力学分析[J]. 机械设计与制造工程, 2017, 46(4): 106-110.
Deng Qiang, Chen Xinan, Liu Jia, et al. Dynamic analysis of the lifting process for the magnetic lifting CRDM[J]. Machine Design and Manufacturing Engineering, 2017, 46(4): 106-110.
[17] 邓强, 彭航, 谢细明, 等. 基于多学科协同仿真的控制棒驱动机构动力学分析研究[J]. 核动力工程, 2019, 40(增刊2): 78-81.
Deng Qiang, Peng Hang, Xie Ximing, et al. Dynamic analysis and study for CRDM based on multi- disciplinary cooperative simulation[J]. Nuclear Power Engineering, 2019, 40(S2): 78-81.
[18] 魏乔苑, 张飞, 吴和北, 等. 控制棒驱动机构运动过程的联合数值仿真研究[J]. 核动力工程, 2018, 39(5): 137-141.
Wei Qiaoyuan, Zhang Fei, Wu Hebei, et al. Study on united numerical simulation for stepping motion of control rod drive mechanism[J]. Nuclear Power Engineering, 2018, 39(5): 137-141.
[19] Sun Hongbiao, Li Wenqiang, Yu Tianda, et al. Research on associated motion simulation method and platform of control rod driving mechanism[J]. Advances in Mechanical Engineering, 2021, 13(9): 1-16.
[20] Sun Hongbiao, Li Wenqiang, Zheng Lanjiang, et al. Adaptive co-simulation method and platform appli- cation of drive mechanism based on fruit fly optimization algorithm[J]. Progress in Nuclear Energy, 2022, 153: 104397.
[21] 赵靖英, 李宁, 张雪辉, 等. 多簧片结构的磁保持继电器多物理场刚柔耦合仿真模型建立和实验分析[J]. 电工技术学报, 2024, 39(10): 3192-3205.
Zhao Jingying, Li Ning, Zhang Xuehui, et al. Establishment and experimental analysis of rigid flexible coupling simulation model for multiphysics of magnetic latching relay with multi-reed structure[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3192-3205.
[22] 张知竹, 刘志明, 李海博, 等. 磁力提升型控制棒驱动机构电磁场仿真分析[J]. 机械设计与制造工程, 2019, 48(12): 33-37.
Zhang Zhizhu, Liu Zhiming, Li Haibo, et al. The simulation of electromagnetic lifting control rod drive mechanism[J]. Machine Design and Manufacturing Engineering, 2019, 48(12): 33-37.
[23] 朱旭光, 刘正蒙, 刘国海, 等. 基于混合介质网格的表贴式永磁游标电机通用等效磁网络模型[J]. 中国电机工程学报, 2024, 44(5): 2009-2019.
Zhu Xuguang, Liu Zhengmeng, Liu Guohai, et al. General equivalent magnetic network model of surface permanent magnet vernier machine based on hybrid medium mesh[J]. Proceedings of the CSEE, 2024, 44(5): 2009-2019.
[24] Cao Donghui, Zhao Wenxiang, Ji Jinghua, et al. A generalized equivalent magnetic network modeling method for vehicular dual-permanent-magnet vernier machines[J]. IEEE Transactions on Energy Con- version, 2019, 34(4): 1950-1962.
[25] Ghods M, Gorginpour H, Bazrafshan M A, et al. Equivalent magnetic network modeling of dual- winding outer-rotor vernier permanent magnet machine considering pentagonal meshing in the air-gap[J]. IEEE Transactions on Industrial Elec- tronics, 2022, 69(12): 12587-12599.
[26] Liu Guohai, Jiang Shan, Zhao Wenxiang, et al. Modular reluctance network simulation of a linear permanent-magnet vernier machine using new mesh generation methods[J]. IEEE Transactions on Indu- strial Electronics, 2017, 64(7): 5323-5332.
[27] 鲍光海, 王金鹏, 王毅龙. 磁保持继电器多物理场耦合模型设计与触头弹跳影响因素分析[J]. 电工技术学报, 2023, 38(3): 828-840.
Bao Guanghai, Wang Jinpeng, Wang Yilong. Design of multi-physical field coupling model of magnetic
latching relay and analysis of influencing factors of contact bounce[J]. Transactions of China Electro- technical Society, 2023, 38(3): 828-840.
[28] Hurley W G, Wolfle W H. 应用于电力电子技术的变压器和电感: 理论、设计与应用[M]. 朱春波, 徐德鸿, 张龙龙, 译. 北京: 机械工业出版社, 2014.
Abstract The magnetic lift control rod drive mechanism (CRDM) is a critical electromagnetic actuator for regulating nuclear reaction rates. Its dynamic process is complex to predict due to the cross-coupling among current response, magnetic circuit saturation, and motion state. The latest equivalent magnetic network (EMN) model exhibits inaccuracies and relies on flux distribution during modeling, lacking generality. In multi-field coupling analysis, researchers often employ multi-software collaborative or semi-simulation methods, which incur significant time and hardware costs. This paper proposes a dynamic equivalent magnetic network (DEMN) model and a multi-physics field coupling calculation method considering transient current changes and saturation.
Firstly, the structure of the magnetic lift CRDM is introduced, and its lift solenoid valve is selected to analyze the electromagnetism-mechanics coupling during dynamic processes. Then, the mechanism is partitioned using orthogonal grid lines, and mesh units of multiple media are consolidated into a single medium to unify the reluctance calculation formula. During dynamic changes, only the grid size or position in the motion region is altered, thereby eliminating redundant modeling and reducing computational errors caused by mesh discrepancies. A connection relationship and calculation method for branch reluctance are established to address the misalignment between fixed and moving mesh units, facilitating continuous armature movement. A multi-physics field coupling calculation method is proposed by combining circuit models and kinematic formulas, which consider transient current changes and saturation. Finally, Compared with 3D finite element analysis (FEA) and experiments, the DEMN model and the proposed multi-field coupling calculation method are verified.
3D FEA results show that the magnetic density distribution, inductance, and electromagnetic force are highly consistent with the DEMN results, where the maximum error of inductance is 5.7%, and the maximum error of electromagnetic force is 3.4%. The experiments show that linear and saturated inductance variations are similar. The calculation accuracy of the release and suction currents under various loads exceeds 91%. Additionally, the dynamic results closely align with experimental results, with motion time calculation errors at 28 A and 40 A currents of 0.99% and 2.99%, respectively.
The conclusion is as follows. (1) By using orthogonal grid lines, the unified calculation of reluctance is achieved, accelerating the modeling speed. (2) By changing the grid size or position of local areas, the dynamic changes of the EMN model are achieved, avoiding the problem of repeated modeling in the multi-field coupling calculation process and reducing the calculation errors caused by differences in mesh partitioning. (3) Compared with FEA, the proposed DEMN model requires less computational resources and shorter computation time while ensuring accuracy. Compared with the experimental results, the effectiveness and accuracy of the DEMN model and multi-field coupling calculation method are verified. It can be extended to EMN modeling, performance analysis, and rapid optimization design of the entire CRDM.
keywords:Reactor, control rod drive mechanism, equivalent magnetic network, multi-field coupling
中图分类号:TL351+.1
DOI: 10.19595/j.cnki.1000-6753.tces.240710
中央高校基本科研业务费专项资金(2024CDJGF-004)、重庆市自然科学基金(CSTB2022NSCQ-MSX0430)和核反应堆系统设计技术重点实验室开放基金(KFKT-05-FWHT-WU-2023001)资助项目。
收稿日期2024-05-06
改稿日期2024-07-03
杨 云 男,1993年生,博士研究生,研究方向为核反应堆控制棒驱动机构的电磁优化设计和热分析。
E-mail: yunyang@cqu.edu.cn
徐奇伟 男,1983年生,副教授,博士生导师,研究方向为特种电机设计与控制、核反应堆控制棒驱动机构电磁优化设计。
E-mail: xuqw@cqu.edu.cn(通信作者)
(编辑 崔文静)