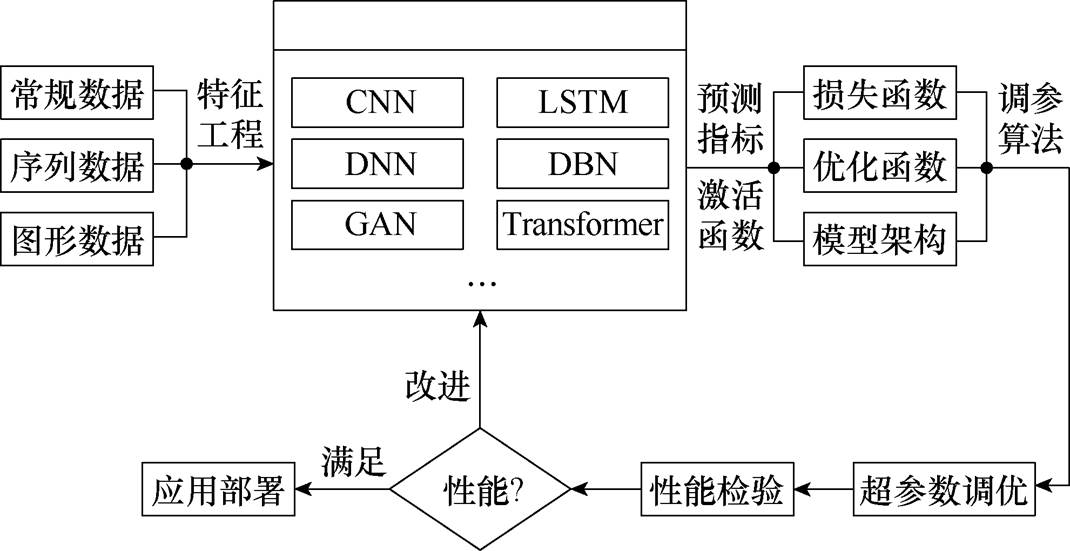
图1 数据驱动建模的通常步骤
Fig.1 Typical steps of data-driven modeling
摘要 快速发展的人工智能(AI)技术,在图像、语言、决策和诊断等领域取得了重要进展,为复杂问题的有效解决提供了一种新方法。随着电工装备智能化程度的不断增加,强弱电耦合特性使得电磁场问题呈现的多尺度、多物理场耦合和非线性问题逐渐突出,对其进行高精度数值计算建模和优化计算的难度逐渐增加。因此,该文在AI背景下,结合课题组近期研究成果,介绍深度学习对数据驱动建模、物理驱动的偏微分方程(PDE)求解、知识嵌入建模等典型交叉问题的求解方法,特别是数据和知识联合驱动的复杂电磁场综合问题智能建模现状,阐述电磁综合性能精确建模分析与优化所面临的关键问题与可能的解决方案,并给出了未来发展趋势和面临的挑战。
关键词:人工智能(AI) 电磁场 建模优化
高性能现代电工装备的高效和安全运行是支撑新基建的重要一环,也是实现碳达峰、碳中和的重要支柱。随着先进信息技术向能源领域的全面渗透和深度融合,现代电工装备多工作于强弱电和交直流混合、内部电磁干扰和外部雷击、操作和短路故障等复杂电磁场合,服役特性、电气综合性能等需进一步提高。因此,其综合性能分析成为计算难度大、多时空尺度、强耦合和非线性问题。
目前,电工装备性能分析主要通过开创于1960年代的有限差分法、有限元法、矩量法等数值模拟方法进行仿真。但随着电工装备设计变量的增多和模型结构复杂度的增加,其依然存在一些不足之处:①复杂电工装备传统数值模拟方法的仿真时间很长,可能需要数十到上百小时;②传统数值模拟方法不能通过前面的仿真结果建立预测模型,当几何结构尺寸或材料特性稍有变化,需重新进行仿真求解,不具有先验特性,也不能满足数字孪生的需要;③高速运动条件或者流体计算的对流项导致计算十分困难,甚至无法完成计算;④复杂拓扑、考虑实际工况和可靠性等因素的多样本性能分析和多目标优化困难。
事实上,人类和动物通过经验或者特征学习实现规律的掌控,提高对物理和现实世界的认知效率。因此,采用从数据中通过经验学习方法解决复杂电磁问题,是可行且具有重要价值的。随着以深度学习为代表的人工智能(Artificial Intelligence, AI)的快速发展,数据科学已成为继实验、理论和模拟三大范式的第四科学范式。深度学习与数值模拟技术的结合,近年来得到了国内外学者的关注。现阶段,以流体力学领域的研究最多,在电气工程领域同样取得了一些成果。例如,2017年,清华大学学者采用深度卷积神经网络预测二维电势分布,预测误差可以达到1%以下[1];2018年,加拿大学者利用有限元方法生成样本数据,以监督的方式训练深层卷积神经网络,学习线圈与电动机磁场分布的映射,在磁场预测中显示出了较高的准确性,能够以较低的计算成本生成新几何体的场分布[2];2020年,加拿大学者提出了一种基于序列的模块化网络和端到端网络来快速准确地预测电机驱动效率图[3]。
随着复杂高性能电工装备应用环境的日趋严苛和极限性能的不断提升,其设计参数和性能数据维度越来越高。因此,当前学者们关于人工智能和数值模拟技术的交叉研究主要集中在以下三个方面:
(1)数据驱动的计算方法。通过人工智能算法建立的代理模型能够揭示设计参数和性能数据之间的映射关系;通过学习数值模拟结果的历史特征实现数值模拟结果的预测与直接生成;以计算方程整体或部分项为目标进行学习,能完成不完备计算式、控制方程甚至电磁热力场的辅助求解。
(2)物理驱动的偏微分方程(Partial Differential Equation, PDE)求解。通过建立符合物理含义的神经网络架构实现电磁场PDE的直接求解。
(3)知识嵌入。通过显示或隐式的方法引入知识,可提高对复杂问题的求解能力,特别是能显著提升泛化能力。
深度学习在数值模拟及优化领域应用时存在一定的局限性:①一般需要足量且有效的训练样本。而对于极端工况和大型电工装备,获得足量的样本困难且代价昂贵[4];②实际工况的环境是开放、多变的,会导致结果失准、鲁棒性差。例如,装备在设计、生产及运行中存在广泛的不确定性,导致现有算法尚未在诸如电磁能装备或者实际工况下的电工装备等对准确性、鲁棒性要求高的场景中充分应用;③算法多为“黑箱模型”,在训练过程中,未将领域知识经验融入算法,存在可解释性差、数据规律挖掘不完善等问题。一般来讲,深度学习的四种基本神经网络架构分别是深度神经网络(Deep Neural Networks, DNN)、深度置信网络(Deep Belief Network, DBN)、长短期记忆网络(Long Short Term Memory, LSTM)、卷积神经网络(Convolutional Neural Networks, CNN)。近几年提出新的神经网络架构主要有残差网络[5]、Transformer[6]、注意力机制[7]、扩散模型[8]等。通过改进超参数调优方法、联合运用多种神经网络架构、引入自适应算法等可以对复杂非线性问题获得较为满意的效果。主要问题有:各种神经网络及其改进架构的适用边界尚不清晰;先进神经网络架构的引入不及时;数据质量和数量要求高;自动化调参方法的应用尚不充分。
目前,关于电气工程领域的AI综述文章以电力系统、故障诊断和储能领域为主。文献[9-11]考虑电力系统的特点和需求,梳理了数据和知识联合驱动的典型应用方式,提出了建模机制和应用方法,并在典型场景中进行了讨论和测试验证。文献[12-13]综述和讨论了数据驱动的人工智能技术在电力设备智能巡检、故障诊断、状态预测等典型业务场景中的应用研究现状。文献[14-15]综述了人工智能在电池材料研究、电池器件设计与制造、材料与器件表征、电池循环寿命与安全性评估等方面的应用,以及AI在电池研究中面临的挑战和其应用的缺点及前景。
综上所述,AI和电磁场计算的交叉研究具有现实的工程需求和理论发展的必要,而相关的综述鲜见。并且,电工装备的性能分析与优化是实现数字孪生的前提和基础。因此,本文从数据和知识联合驱动的角度出发,介绍复杂电磁场深度学习建模技术和最新进展,提出相应范式的可能建立方法,并对可行的未来研究方向和内容进行讨论和展望。
本文主要综述和讨论基于数据驱动的建模方法、物理驱动的PDE求解方法、知识嵌入的建模方法,并对未来发展方向进行展望。
数据驱动建模的通常步骤如图1所示。具体如下:①确定数据的表达形式,以及特征提取方式;②确定网络结构和超参数设置;③设计损失函数和优化函数;④优化超参数获得最佳网络;⑤设计封装形式和程序接口。

图1 数据驱动建模的通常步骤
Fig.1 Typical steps of data-driven modeling
深度学习通过构建电、磁、热、力等一维参数性能和设计参数之间的复杂非线性映射关系,可建立性能参数快速计算的代理模型。深度学习相较于传统机器学习算法能有效克服对专家经验和数据分析方法的依赖,建立更高精度的代理模型[16]。一般使用深度学习基本和改进架构。如,基于CNN的锂离子电池健康状态(State of Health, SOH)估算方法,通过卷积核提取电压、电流、温度曲线中的共有特征信息,预测精度高、网络参数少、占用内存小[17];本课题组基于深度置信网络(DBN)建立永磁同步电机齿槽转矩预测分析模型,相比反向传播(Back Propagation, BP)神经网络、径向基函数(Radial Basis Function, RBF)神经网络和支持向量机(Support Vector Machine, SVM)方法,DBN拥有最高的精度,以有限元计算的样本数据为基准,在50组样本下预测误差仅为1.24%[18]。也有深度学习和传统机器学习结合的混合算法。如,Zhao Jingying等[16]建立一种深度高斯过程回归(Deep Gaussian Process Regression, DGPR)模型来预测大型汽轮发电机转子槽内金属紧固件的涡流损耗,大幅缩短了设计周期,和SVM、岭回归、线性回归、套索回归、AdaBoost等五种机器学习模型相比误差更小。
迁移学习将挖掘得到的历史数据中隐藏的专家经验、客观物理规律迁移至相似的领域中,可降低深度学习的样本量需求[19],提高算法的泛化能力和适用范围。深度学习与迁移学习的比较如图2所示。如,本课题组建立了基于深度置信网络(DBN)的迁移模型,仅使用5%的目标域标签样本达到了传统算法的精度[20]。基于迁移学习理念,可对神经网络的训练策略进行改进,提高计算精度和训练速度[21]。
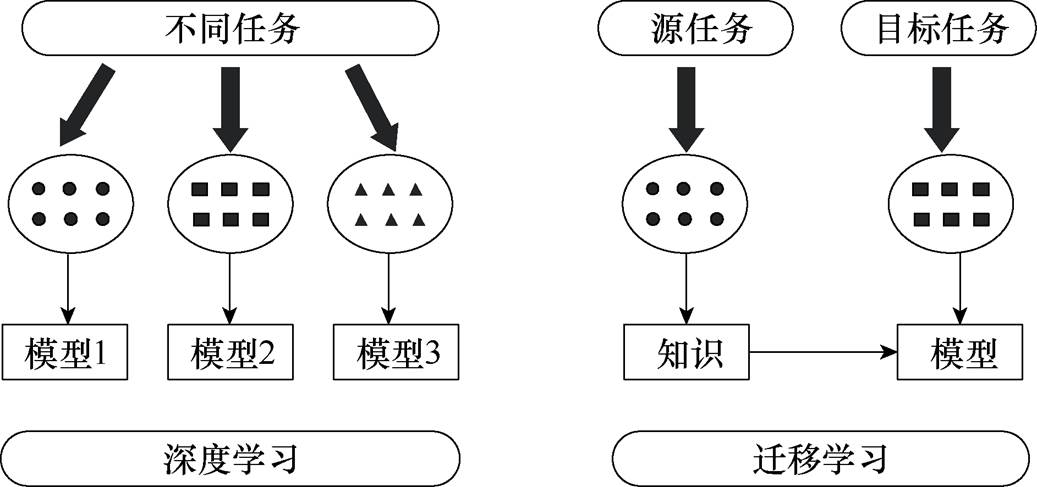
图2 深度学习与迁移学习的比较
Fig.2 Comparison between deep learning and transfer learning
总之,基于深度学习的代理模型建模方法,可引入残差网络、注意力机制等方法对神经网络结构进行调整,提高预测精度,而这对于敏感性分析、不确定性优化等是十分重要的。将从历史装备数据中学习到的知识迁移应用到目标装备性能分析中,可大幅降低样本量需求。
理论上,在隐藏层及神经元足够多、样本数量足够多和神经网络超参数设置合理的情况下,能以任意精度逼近任意预定的连续函数,但消耗计算资源往往过大,且通常难以获取足够的低成本、高精度样本。为了在有限的资源下获得较高的性能,需要具体问题具体分析,寻找特定问题的特征提取方法和合适的网络架构、训练方法,并建立一个有效的深度学习技术,这是二三维场预测的重要研究内容。
基于数据驱动的场预测深度学习技术,能够对电场、磁场和磁畴动态演变图像等二三维场图进行端到端的深度神经网络建模,展示出高精度、便捷、适用广等特点[22-25]。如何对几何外形进行编码和维度变换,是有效表征几何外形特征并降低数据维度的关键,也是场预测方法的前提和基础[2, 26]。通过引入先进算法,可进一步提高性能表现。如,起源于人类视觉认知科学的注意力机制;为解决网络层数过深而出现的性能退化现象所提出的残差网络;多头自注意力机制的Transformer[27]。
总之,应进一步发挥深度学习“一次训练、多次调用”的特性,拓展其在机理研究、优化方法、数字孪生等方面的研究。如,分析电磁能装备枢轨交界面处电磁热场的分布与推力、磨损、摩擦之间的关系,研究场时空演变对装备特性的作用机理;基于深度学习对场的快速计算,并结合优化方法,可实现场调控的优化,有望解决场局部集中的问题;通过迁移学习引入测试数据或外推至新装备、新工况,可实现电磁能装备、大型变压器和电抗器、大型电站等数值模拟困难装备或系统的性能计算,并且计算速度为s级,有望推进数字孪生的落地。
知识发现的建模方法如图3所示。其通过赋能方法和建模机制建立知识发现模型,从观测、试验或模拟的不同类型数据中挖掘和提炼定量和定性等领域知识,可构建计算式或PDE的部分项甚至全部。
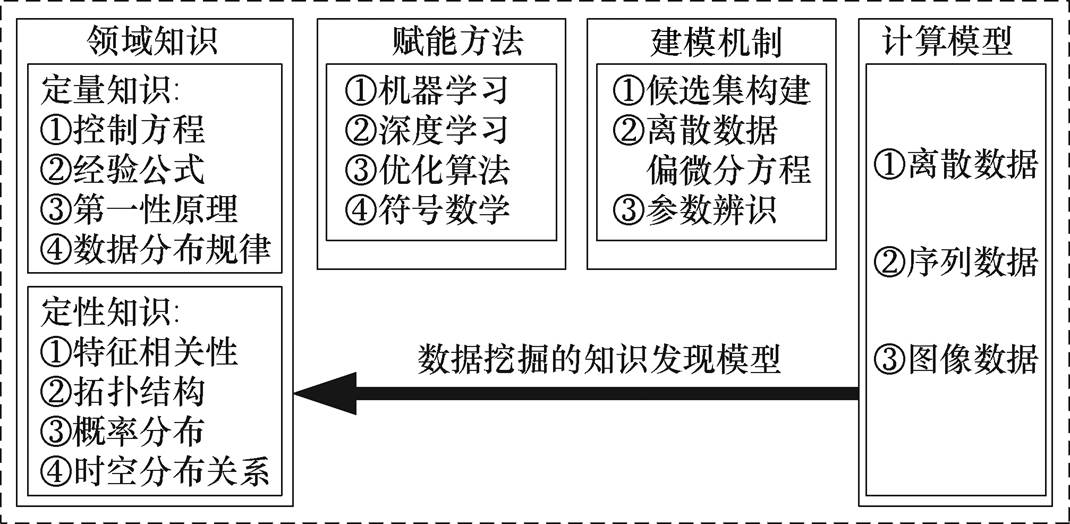
图3 知识发现的建模方法
Fig.3 Modeling method for knowledge discovery
需要特别指出的是:1998年,I. E. Lagaris等通过构建PDE强形式残差、初始时刻和边界处残差组成的神经网络损失函数,提出了时空PDE的正问题求解方法,但要求连续性的二阶微分算子,导致ReLU等常用的激活函数难以应用[28]。2019年,M. Raissi等拓展此方法实现了方程参数的反演,建立了求解正反问题的物理信息神经网络(Physics- Informed Neutral Networks, PINN)[29],如图4所示。PINN为知识发现、PDE和隐式知识建模等问题的求解提供了有效方法。如,张宇娇等提出了针对电磁场PDEs形式和神经网络架构的修改方法,实现了基于PINNs的静电场和稳恒磁场求解,计算结果准确性较好[30]。
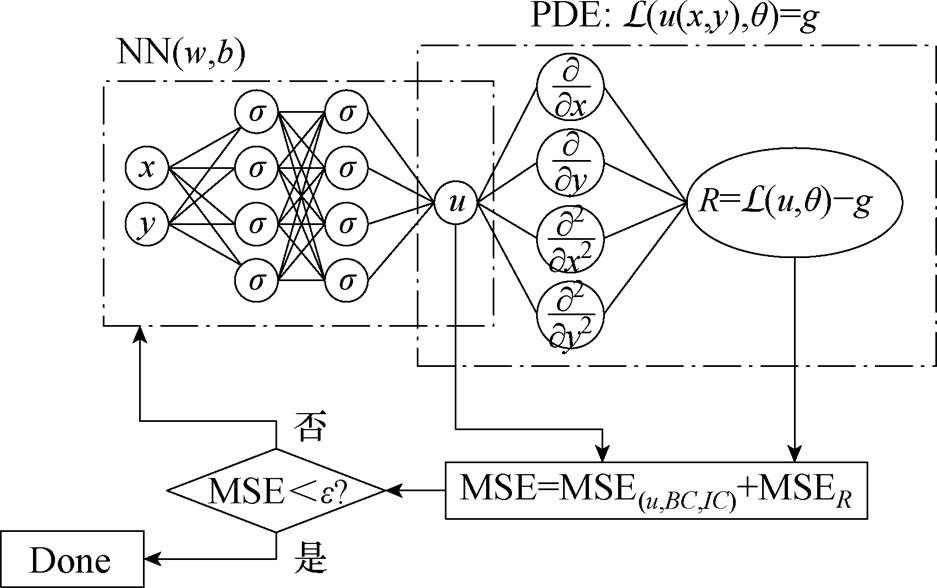
图4 物理信息神经网络
Fig.4 Physical information neural network
计算式的知识发现模型。对于简单的先验计算式,可利用先进的参数辨识算法结合少量样本数据,修订或确定计算式中的待辨识项和系数,构建高精度计算式的知识发现模型。任富强等提出了一种基于变压器绕组梯形等效网络的参数辨识方法,通过构建变压器梯形等效网络的数学模型,并根据少量可测频响数据,确定了高频梯形网络的拓扑结构,在800 kHz~2 MHz频段内得到的高频激励响应特性曲线与实测曲线具备极高的吻合度,两者误差降幅达79.54%[31]。吴春等提出了一种基于三角函数正交特性的永磁伺服系统机械参数辨识方法,高频条件下电阻和永磁体磁链的辨识误差控制在0.85%以内[32-33]。本课题组通过经验公式建立了电感计算灰箱模型,采用改进差分进化算法,使用10个样本进行参数辨识,获得了3‰左右误差的s级计算速度的简洁形式电感计算公式,并完成超高压电抗器优化[34]。
总之,计算式的知识发现模型通过参数辨识建立的高精度模型(误差可低至接近3‰[34]),辨识过程中对参数样本需求较少,能够快速迭代,具有动态、可更新和适应性强的特点,并避免了复杂的人工理论推导。尤其是对于设备的多目标优化,避免了严重阻碍构建代理模型和数值优化过程的“昂贵优化问题”。
PDE更为复杂,其知识发现的实现原理和方法也更为复杂和困难。描述数据背后潜在物理规律的PDE在部分情况下难以完全实现直接从理论推导。PDE的三种完备程度分别对应三种适用不同场景的PDE知识发现模型:
(1)欠完备PDE的知识发现模型。其简单易实现,但难以构建包含所有潜在候选项的超完备候选集,可用于发现已知PDE。2016年,S. L. Brunton等提出非线性动力学稀疏辨识算法(Sparse Identification of Nonlinear Dynamics, SINDy),根据先验知识构建一个由简单函数和导数组成的、包含冗余候选项的封闭候选集,然后使用稀疏回归算法确定方程[35]。2017年和2019年,S. H. Rudy等先后提出非线性动力学的PDE函数识别算法(PDE Functional Identification of Nonlinear Dynamics, PDE-FIND)和序列分组阈值岭回归算法(Sequential Grouped Threshold Ridge Regression, SGTR),将SINDy扩展至PDE[36]和非常系数的参数化PDE[37]。2021年,Chen Zhao等提出PINN-SR(PINN with Sparse Regression),利用自动求导得到导数的解析表达,并形成候选集,结合稀疏回归,可以在不同数据量和噪声水平下发现具有不同初始和边界条件的PDE[38]。
(2)不完备PDE的知识发现模型。其更加灵活,可用于发现较为复杂的PDE,但基本候选项的给定仍需一定的先验知识,无法发现分式结构和复合函数的PDE。2018年,龙子超等受卷积核与有限差分的近似性启发,通过构建半开放候选集,建立了从动态数据中发现PDE的卷积神经网络PDE-Net[39];2019年,结合符号网络SymNet来近似非线性响应函数,建立了PDE-Nets 2.0,可发现时间依赖的PDE[40]。2020年,Xu Hao等将神经网络和遗传算法相结合提出深度学习和遗传算法(Deep Learning and Genetic Algorithm-PDE, DLGA-PDE),通过将不同的函数项编码为基因片段,实现候选集的自动扩展[41]。
(3)未知PDE的知识发现模型。其可用于发现非常复杂的PDE,但搜索空间和计算量大。2022年,陈云天等将符号数学与遗传算法结合,提出了一种基于树结构的遗传算法(Symbolic Genetic Algorithm- PDE, SGA-PDE),通过构建开放候选集,可以直接从数据中挖掘出含分式结构和复合函数的PDE[42]。
总之,PDE的知识发现模型对比见表1。灵活程度、实现难度和PDE复杂度依次提高的封闭、半开放、开放三种候选集,需要使用手动、网络拓扑深度学习、智能算法、符号数学等方法建立。PDE知识发现模型的建模方法,通过神经网络从数据中表征PDE,可以解决不同完备程度条件下的复杂问题,并避免了复杂的人工理论推导,为复杂问题的解决提供了有效途径。如,通过对速度、电流、电压等测量数据的挖掘,建立无法准确进行理论推导的电磁能装备枢轨摩擦参数PDE,亦可用于难以准确获得的电工装备散热系数PDE的确立。
表1 PDE的知识发现模型对比
Tab.1 Comparison of knowledge discovery models for PDE
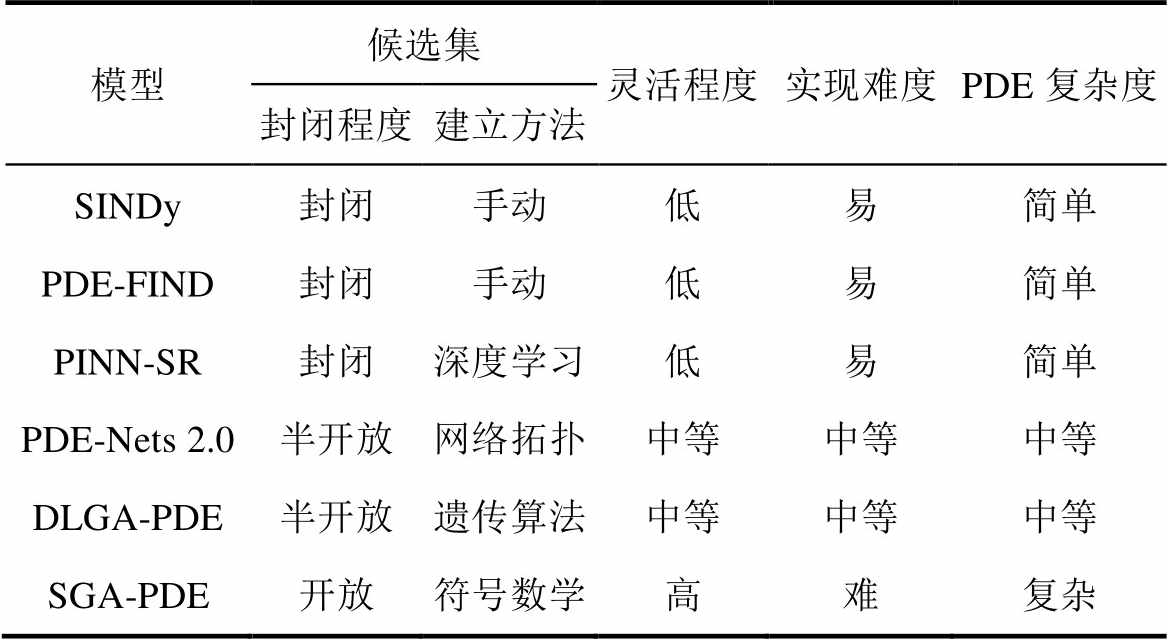
模型候选集灵活程度实现难度PDE复杂度 封闭程度建立方法 SINDy封闭手动低易简单 PDE-FIND封闭手动低易简单 PINN-SR封闭深度学习低易简单 PDE-Nets 2.0半开放网络拓扑中等中等中等 DLGA-PDE半开放遗传算法中等中等中等 SGA-PDE开放符号数学高难复杂
根据机器学习的建模过程,物理驱动的PDE求解方法可以分为知识嵌入的正则化方法和物理含义的机器学习模型结构设计方法[43-44]。PDE的直接深度学习求解方法理论含义明确,因而人们希望取得突破性进展。但其在精度、适应性、收敛速度和资源消耗等方面,目前表现仍难以实际应用。应重点研究特定条件下的建模方法。如,条件不足情况下的弱解求解;与传统数值模拟方法的结合,实现非线性和线性混合求解域的高效计算;多时空尺度问题的混合计算。
根据在神经网络中施加知识约束的强弱程度,知识嵌入的正则化方法分为“软约束”和“硬约束”两种。基于知识嵌入的正则化方法目前已在许多类型PDE求解方面应用,例如电磁场[45]、温度场[46]和流体力学中的速度场及压力场[29]等。
(1)“软约束”是指以PINN为主要代表的、将数据驱动和知识驱动两部分损失函数赋予不同权重并结合在一起的方法[47]。如,张宇娇等提出基于物理信息神经网络的电磁场计算方法[30];仲林林等通过双环优化训练机制,提出Meta-PINN,以减少基于PINN的一维电弧模拟的训练时间[48]。其他方面的研究有:2018年,J. Sirignano等使用蒙特卡罗方法替代神经网络的自动求导来近似高维变量的二阶导数,提出深度伽辽金方法(Deep Galerkin Method, DGM)求解高维PDE,解决了效率低、计算量巨大的问题[49];2018年,E. Weinan等通过变分方法构造神经网络的损失函数,提出了DeepRitz方法(DRM),由于只包含一阶导数,提高了高维PDE的求解效率,但只适合能建立变分形式的PDE[50];2020年,Zang Yaohua等提出了弱对抗网络(Weak Adversarial Network, WAN),通过推导PDE的弱形式,将求解PDE转化为Min-Max优化问题,使用两个神经网络对抗训练,分别近似弱解和试函数,得到方程的弱解[51]。上述方法通过对PDE的强形式残差、初始时刻和边界处残差加权求和构造损失函数,以确保预测结果符合知识。多个残差之间的权重依靠经验来调整,有一定的局限性。只能在平均意义上较弱地约束预测结果,无法保证每个点不违反知识,本质上是“软约束”。针对此问题,一种解决方法是引入权重自适应,通过在训练过程中动态调整权重来提高训练速度和预测精度[52-53];另一种解决方法是引入“硬约束”。
(2)“硬约束”可以保证给定的PDE在某一区域或整个域内得到严格满足。目前,对深度学习“硬约束”的研究还处于初级阶段。其中,第一种是使用“硬边界”的方式设置边界条件[44, 54-55],通过引入距离函数,将PDE强形式残差、初始时刻和边界处残差统一在同一项中,避免惩罚系数的使用,但难以用于复杂的初始条件和边界条件。第二种是硬约束神经网络输出。2021年,Chen Yuntian等提出硬约束投影(Hard Constraint Projection, HCP),构造一个投影矩阵,将神经网络预测的局部流场矩阵映射到满足物理约束的超平面上,确保预测结果严格符合物理机制。在非均质地下流动问题上,与“软约束”模型相比,HCP所需数据更少、预测精度更高、鲁棒性更强,并提高了外推预测能力[56]。
软约束方法实现原理简单,但在约束的严格性和精确性方面不如硬约束方法。硬约束方法能够提供更准确和鲁棒的结果,但在实现方法上更复杂,特别是在处理复杂的初始条件和边界条件时。在电磁场领域,这两种方法需根据具体问题的需求和特性来选择。如,使用软约束方法求解电磁能装备的电磁热场,进一步对于少数更关心的区域使用硬约束方法提高求解精度,可实现求解效率和求解精度的平衡,有望解决枢轨接触面处热场数值模拟计算困难的问题。
物理含义的机器学习模型结构设计方法通过设计特殊的神经网络结构,使得网络结构天然满足设定的物理约束。具体分为两种:根据微分与卷积之间的关系构造卷积核和根据有限元求解过程设计神经网络结构。
(1)根据微分与卷积之间的关系构造卷积核。卷积与微分之间具有深刻的数学关系,基于此构造卷积核可以实现PDE的求解[57]。2018年,龙子超等使用卷积运算替代偏微分项,并根据PDE时间离散化方法构建了dt block结构,提出了PDE-Net[39-40]。2019年,Yao Houpu等将有限元中的矩阵向量相乘转化为卷积运算,并基于雅可比求解器构建有限元分析网络(FEA-Net),通过力热耦合和多相问题验证了理论和计算优势[58]。2023年,Rao Chengping等基于物理知识设计了π-卷积模块,并将PDE、初始条件和边界条件的结构或特定项强制编码进神经网络结构,提出物理编码递归卷积神经网络(Physics- encoded Recurrent Convolutional Neural Network, PeRCNN),与PINN、ConvLSTM、PDE-Net等方法相比,模型泛化和抗噪能力明显提升,长期推理精度提升倍数大于10[59]。
(2)根据有限元求解过程设计神经网络结构。相比根据微分与卷积之间的关系构造卷积核的方法,根据有限元求解过程设计神经网络结构的方法具有更明确的物理含义。2005年,P. Ramuhalli等根据有限元中伽辽金方法的推导过程,提出了有限元神经网络(Finite Element Neural Network, FENN),神经网络权重为待求物理量,损失函数为最终有限元离散化方程组的右端向量与神经网络输出之间的误差[60]。可用于求解二维静电场[60]、三维磁场[61-62]和缺陷漏磁场[63]。由于权重数与节点数二次方成正比,网络层少而宽,当节点数变多时网络难以训练。2019年,李想等以有限元的刚度矩阵作为神经网络输入、右端向量为输出构造了一个特殊的卷积神经网络结构,利用迭代逐步更新卷积核,得到线弹性有限元方程的节点位移解[64]。但其输入数据须为常数矩阵,难以用于求解具有可变刚度阵的非线性 方程。
根据微分与卷积之间的关系构造卷积核,可以处理各种类型的PDE,灵活性更强,但整体网络可解释性不够强。根据有限元求解过程设计神经网络结构虽具有更强的可解释性,但并未明显提升求解效率,且仍面临当参数变化时需重新训练的困境。如,对于电磁能装备,可以构造卷积核实现微分运算,并通过构建具有循环结构的神经网络,实现时间序列数据动态变化的有效捕捉,有望提高对复杂物理过程计算的准确性和效率。
总之,PDE直接深度学习求解模型的对比见表2。物理含义的模型结构设计方法更像传统的数值模拟方法。而知识嵌入的正则化方法则在一定程度上放宽了对完备条件的要求,可在只有部分模型和测量数据的情况下进行建模计算。
表2 PDE直接深度学习求解模型
Tab.2 Direct deep learning solving models for PDE
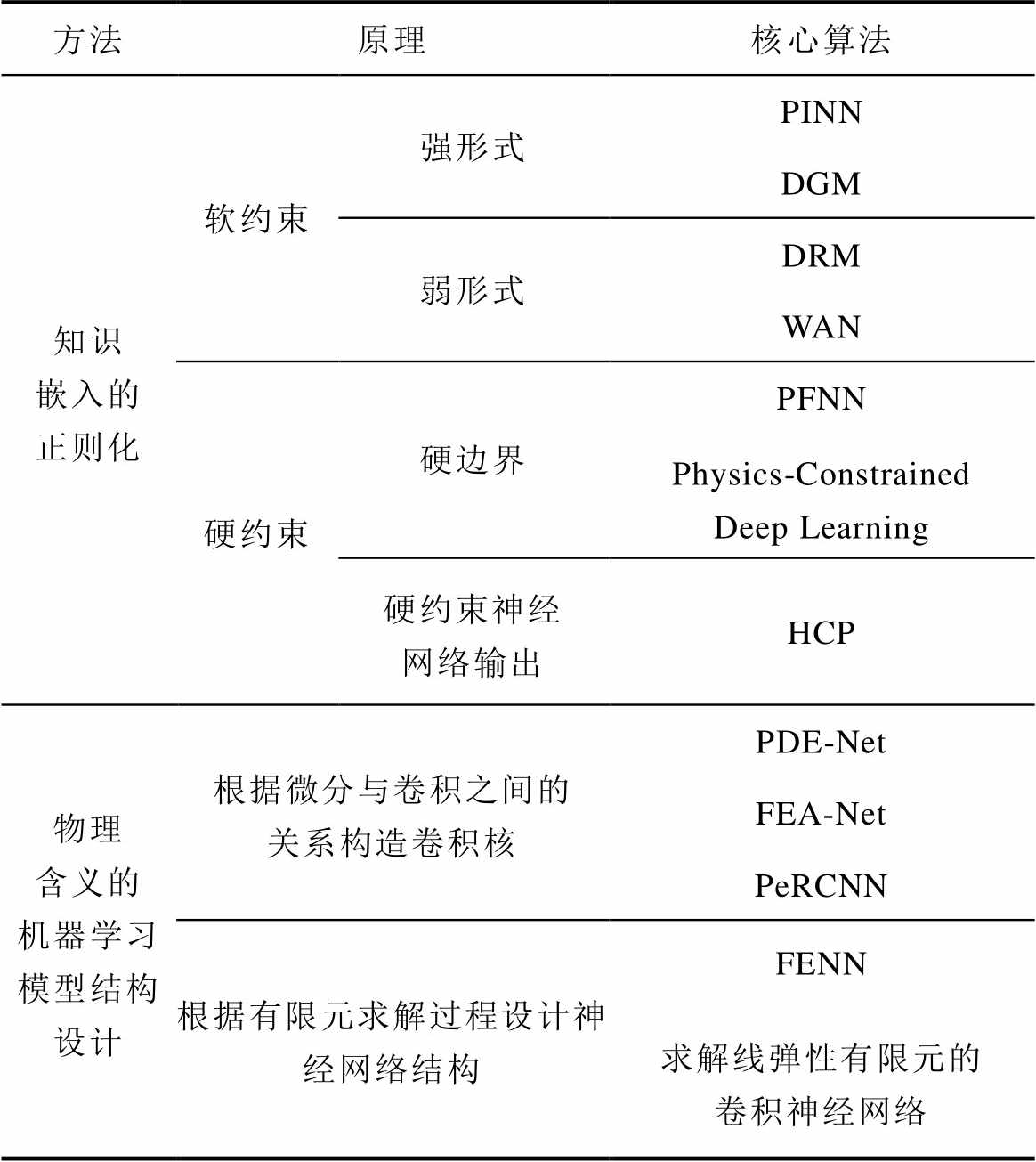
方法原理核心算法 知识嵌入的正则化软约束强形式PINN DGM 弱形式DRM WAN 硬约束硬边界PFNN Physics-Constrained Deep Learning 硬约束神经网络输出HCP 物理含义的机器学习模型结构设计根据微分与卷积之间的关系构造卷积核PDE-Net FEA-Net PeRCNN 根据有限元求解过程设计神经网络结构FENN 求解线弹性有限元的卷积神经网络
通过在数据预处理过程中显式地嵌入知识,可一定程度地提高模型的性能表现。如,2021年,Chen Yuntian等充分利用领域知识和专家经验,将时间序列数据分解为可由领域知识确定的无量纲趋势和受天气等因素影响的局部扰动,提出理论指导深度学习方法(Theory-guided Deep Learning for electrical load Forecasting, TgDLF)预测电力负荷,精度提升明显[65]。
相比于显式建模方法,AI在隐式知识建模方面受数据收集、算法实现和工程约束的限制明显减少,在工程实用性、建模和数据获取可行性等方面提升明显。
在科学和工程中,高保真模型通常是指能够获得高度精确结果数据的复杂高维系统,其成本很高。而通过降维、线性化、模型简化、部分收敛结果、等效试验或测量等方法建立低保真度模型是一种更具可获得性、更便宜的替代品,但准确性较低。近几年,将多源多保真度数据进行融合建模,降低对高保真度数据的数量依赖并提高计算精度,受到广泛关注。也可以认为这是将无法显式表达的领域知识通过高保真度数据引入模型中。这对于高保真度数据获取困难的大型现代电工装备是极为重要的。
多保真度模型主要有两种,分别是:最早研究的校正模型[66]、现在主要采用的空间映射模型[67]。校正模型通过求解高保真度和低保真度模型数据间的差异趋势实现[68]。
在2000年左右,人们开始研究基于统计或机器学习的多保真度空间映射建模方法。其通过建立不同保真度数据间的映射关系实现。基于统计的空间映射方法建模简单,但依赖先验概率假设的准确性,并且常用的蒙特卡洛方法对样本需求甚至超过了机器学习方法[69-71]。
在近十年中,随着人工智能的飞速发展,学者们开始更加重视基于机器学习的建模方法。相较于统计方法,机器学习方法可减少对严格先验假设的依赖,如数据分布的假设和模型结构的选择。为方便阐述,可以将基于机器学习的多保真度模型分为串行、并行两种主要架构。基于机器学习的多保真度模型对比见表3。
表3 多保真度模型对比
Tab.3 Comparison of multi fidelity models
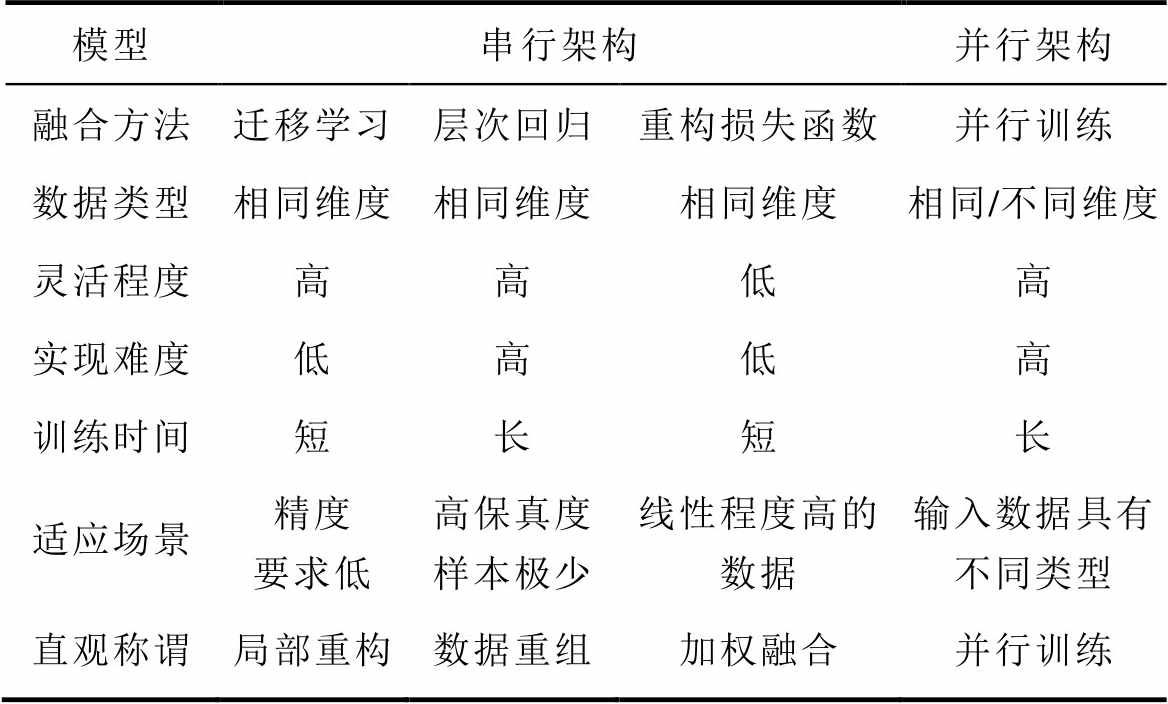
模型串行架构并行架构 融合方法迁移学习层次回归重构损失函数并行训练 数据类型相同维度相同维度相同维度相同/不同维度 灵活程度高高低高 实现难度低高低高 训练时间短长短长 适应场景精度要求低高保真度样本极少线性程度高的数据输入数据具有不同类型 直观称谓局部重构数据重组加权融合并行训练
(1)串行架构多保真度模型。其主要通过前后串行的“分步骤”训练方式利用单神经网络实现多保真度计算建模。2016年,M. Raissi等结合多保真高斯过程和深度神经网络,通过DNN学习低保真输入数据的确定性转换,扩展原始的多保真模型,提高模型对高保真数据的预测准确性,并通过一维离散基准问题进行试验证明了其有效性[72]。2021年,Li Kai等提出多保真度数据共同构建损失函数的损失函数重构方法,如图5a所示。该方法可根据高保真数据组成的测试集调整损失函数中的权重优化预测精度,并以跨声速机翼表面压力的相同维度和尺寸的数值模拟和实验多保真度数据,证明了其有效性[73]。上述两种方法建模简单、精度较高。人们进一步开展了基于迁移学习的串行架构多保真度模型研究,使用低保真度数据对神经网络进行训练后,再使用高保真度数据进行微调,实现模型局部重构,如图5b所示。2020年,S. Chakraborty使用高保真数据更新近似控制方程预训练的低保真PINN,融合了来自物理信息和数据驱动的数据,并通过一维线性和非线性相关函数逼近的例子证明了其有效性[74]。2022年,Liu Lixue等提出基于迁移学习和生成对抗网络的多保真度数据融合模型,在高保真度数据很少的情况下具有更高的稳定性[75]。对于尺寸不一致的多保真度数据,2023年,Zhang Yunyang等建立了多保真度投影头映射不同尺寸数据的迁移学习,使用两个尺寸不同的二维温度场的预测问题验证了其有效性[76]。迁移学习的引入,提高了对处理复杂多保真度问题的解决能力,但需要精心设计迁移和微调的复杂建模方法。此外,层次回归框架将输入和低保真度预测结果数据重组,并将其作为组合输入对神经网络进行训练,实现了输入数据重构,如图5c所示。该方法在多保真度建模中显示出了显著的效能和适用性。2021年,Xu Yueqi等提出基于随机森林算法的层次回归框架,在双保真度函数数据集上进行了验证[77]。2022年,Chen Shizhi等建立了基于XGBoost、MLP和SVR等方法的贝叶斯更新过程层次回归框架,通过低保真模型作为输出先验分布和多保真度模型输出低保真数据后验分布的方法,实现对每个高保真数据的似然计算,以深梁的抗剪能力证明了其准确率[78]。层次回归框架的建模过程复杂且灵活,但却依赖对机器学习算法及其组合的认知和调参水平。

图5 串行架构的多保真度典型模型
Fig.5 Typical model of multi fidelity for serial architecture
总之,串行架构多保真度模型能够先利用低保真度数据建立基础模型,然后逐渐引入高保真度数据以增加模型的复杂度和精确度,显著降低构建样本集所需的时间和计算成本。如,选取不同的网格剖分精细度,构成不同保真度的变压器仿真模型,从而得到包括结构图和磁场数值模拟结果的多保真度数据集。使用损失函数重构方法,综合考虑不同保真度数据集的总误差,实现相同精度下时间成本更低的磁场计算。在此基础上,若已知部分测量点数据,可使用输入数据重构方法进一步提高预测 精度。
(2)并行架构多保真度模型。分别使用多个神经网络模型并行处理多源多层级数据的特征和损失函数,最后将多个模型的输出进行融合,提高对于异构复杂数据的处理能力,如图6所示。2019年,Kou Jiaqing等通过加权融合定常项和非定常项数据独立训练的两个DNN模型,提高了一维离散数据的预测准确性[79];在此基础上,2021年,Wang Xu等使用更适合小样本的RBF神经网络代替DNN,提高了对机翼实验中升力和力矩的预测精度[80];2020年,Meng Xuhui等提出四个全连接神经网络组成的多保真度复合神经网络,其通过三个全连接神经网络拟合低保真数据、高低保真度数据间的线性和非线性关系,并建立物理信息残差全连接神经网络引入物理约束,使用一维函数验证了其有效性[81]。
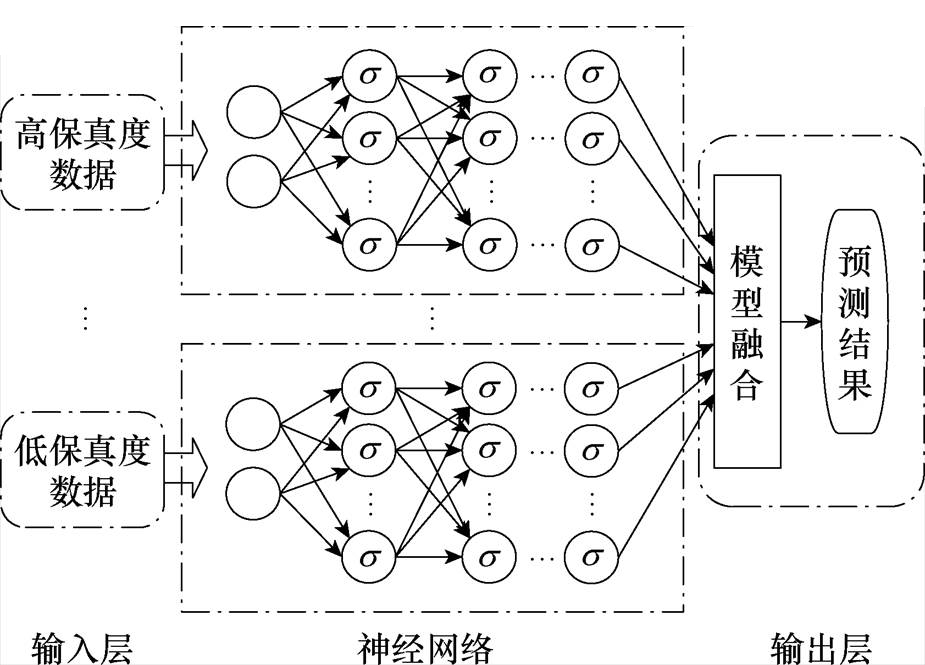
图6 并行架构的多保真度典型模型
Fig.6 Typical multi fidelity model for parallel architecture
并行数据融合架构对于处理电磁热力场计算的高效性体现在其并行处理多源异构数据的能力。通过运行多个专用模型来处理不同特征的数据流,并将独立分析后的结果汇总,提供全面解读。例如,在变压器模拟中,通过并行架构中的不同神经网络模型处理工况数据和几何结构、材料属性等设计参数,实现场量和变量的计算,支持装备的全面感知或设计优化。这种架构既能提升数据处理速度,也增强了模型的鲁棒性,适合于复杂的电磁计算任务,提高设计优化的准确性与效率。
隐式知识嵌入的算子神经网络的核心思想是使用神经网络学习算子的表示,从数据中直接学习系统的行为,而无需确定方程的具体形式,实际上是隐式地发现系统背后的物理规律。这使得模型在处理未知问题和复杂系统时更具灵活性和适用性。
2019年,Lu Lu等根据算子的普遍近似定理[82-83],构建了第一个算子神经网络-深度算子网络(Deep Operator Network, DeepONet),如图7所示。DeepONet由分支网络和主干网络组成,分别用于处理输入函数和时空坐标。完成训练之后,对于一类PDE,只需要进行神经网络的正向推理就可以获得相应的解,可用于快速实时求解一类问题[83]。为提高DeepONet在不同应用场景下的适用性,学者们进一步对其进行了扩展。2021年,Lu Lu等构建了用于科学计算的机器学习库DeepXDE,可以十分方便地构建用于求解正、反问题的PINN和DeepONet[84]。2021年,Cai Shengze等将多个可独立预测每个领域的预训练DeepONet组合,提出了DeepM&Mnet,可用于求解多物理场问题[85]。2021年,Wang Sifan等将物理信息引入DeepONet,使预测输出函数能够满足给定的PDE,提出了PI-DeepONet,即使在没有任何成对输入输出训练数据的情况下也能完成训练[86]。2022年,Jin Pengzhan等为处理多个输入函数,提出了多输入的DeepONet(Multi Input ONet, MIONet)[87]。2022年,为加速神经网络训练并提高预测精度,文献[88]提出本征正交分解的DeepONet(POD- DeepONet);为降低高保真训练数据获取成本,文献[89]提出了多保真度DeepONet。
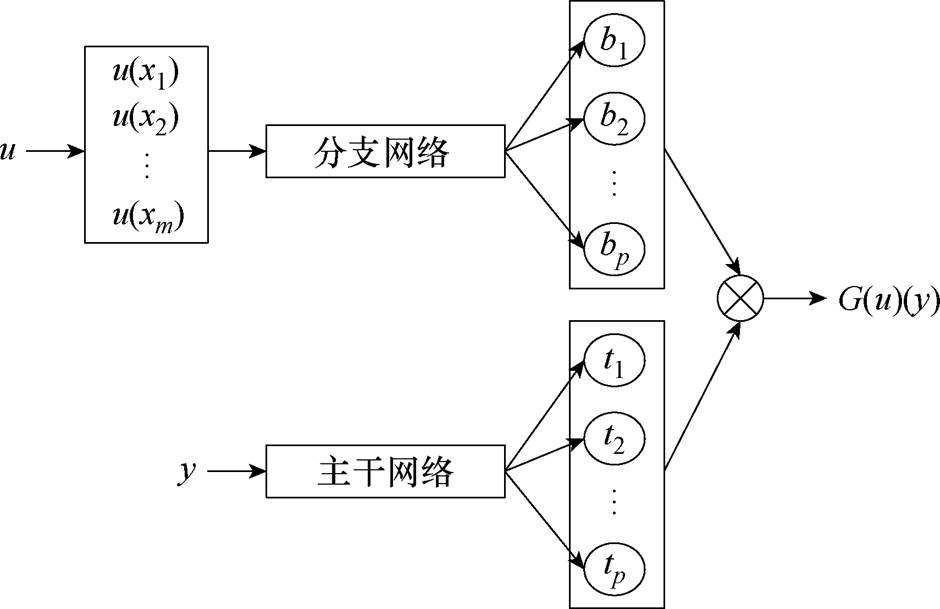
图7 DeepONet模型
Fig.7 DeepONet model
2020年,Li Zongyi等受格林函数法启发,提出了级联结构的傅里叶神经算子(Fourier Neural Operator, FNO),网络每层分成两个分支,一个分支依次对输入进行快速傅里叶变换、线性变换、傅里叶逆变换,得到低频特征;另一个分支直接进行线性变换,保留部分高频信息。由于只对低频信息做复杂运算,大大提高了计算速度[90]。基于FNO框架,学者们也开展了进一步的研究。为了解决FNO输入必须在规则的网格点上的问题,2022年,Y. Z. Ong等使用一个积分自编码器(Integral Autoencoders, IAE)学习非线性积分变化,提出离散-不变学习的积分自编码器网络(IAE-Net),训练好的神经网络可以将具有任意维度的输入转换至具有固定维度的空间中,使用任意离散格式的数据,提高了FNO的泛化能力[91]。2023年,T. Tripura等使用小波变换替代FNO的傅里叶变换,提出了小波神经算子(Wavelet Neural Operator, WNO),提升了神经网络在复杂几何和边界条件下的学习能力[92]。DeepONet与FNO两种典型的神经网络算子对比见表4。
表4 两种典型的神经网络算子
Tab.4 Two typical neural network operators

特性DeepONetFNO 输入数据任意点处规则网格点 网络结构分支结构傅立叶变换层 适用范围多维多尺度问题周期性问题
除DeepONet与FNO外,2021年,Cao Shuhao将Transformer引入PDE求解,通过对注意力机制中的Q、K、V进行不同方式组合,分别组成了Fourier类型和Galerkin类型的注意力机制,提高了模型的可解释性[93]。
算子学习具有更强的灵活性和泛化能力,适用于高度非线性、复杂求解域和复杂边界条件的问题。但需要大量标记数据进行训练,实际中当数据量不足或采集成本过高时,这些模型的泛化能力较差。因此,若能结合物理知识和数据融合,将进一步提高预测精度和可解释性。如,本文将DeepONet独特的分支结构嵌入CGAN的生成器,提出对抗算子网络(Generative Adversarial ONet, GAONet)架构,如图8所示。激励电流是影响直线推进电磁能装备电枢电磁推力的主要因素之一,建立的基于GAONet的电枢电磁推力预测方法,如图9所示。为了清晰直观地显示不同模型的预测性能,以50个数据集样本数下DBN-DNN模型的预测精度作为基准,将方均误差(Mean Square Error, MSE)和平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)分别进行归一化计算,结果如图10所示。从图中可以看出,全连接网络受数据集样本数影响最大,GAONet受数据集样本数影响最小,在样本数较少时仍能保持较高的预测精度。相比于未加入对抗训练的DeepONet,GAONet在200、100和50个样本数下MSE分别降低了14.40%、25.47%和46.29%,MAPE分别降低了6.96%、9.85%和17.23%,可见加入对抗训练的GAONet能够更加充分地学习数据的分布规律,具有更强的泛化能力,在数据量较小时具有更高的精度。
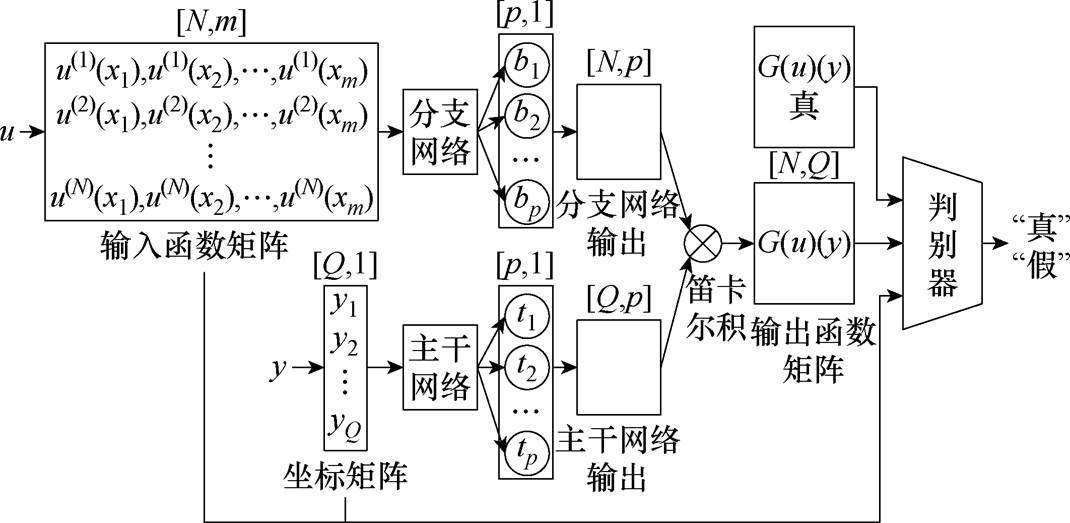
图8 对抗算子网络架构
Fig.8 Generative adversarial operator network architecture
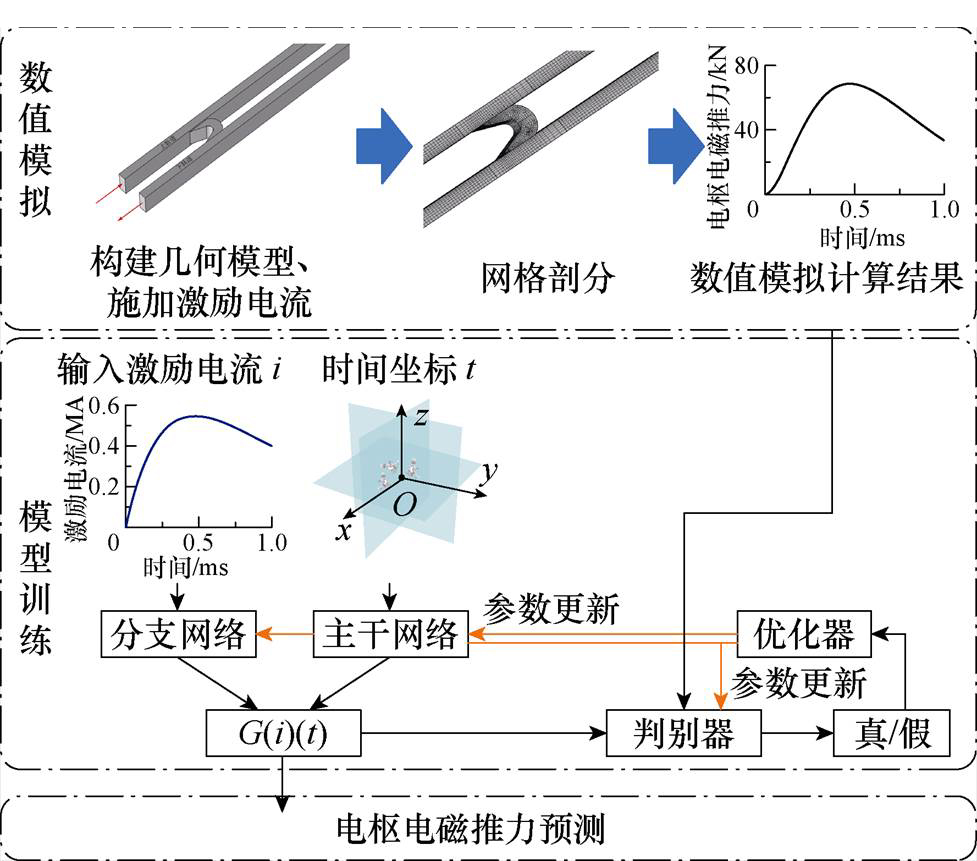
图9 基于GAONet的电枢电磁推力预测方法
Fig.9 Armature electromagnetic force prediction method based on GAONet

图10 不同模型在不同样本量下MAPE的对比
Fig.10 Comparison of MAPE between different models under different sample sizes
基于深度学习的神经网络架构种类繁多、参数众多、模型复杂,但在大数据领域的解决方案往往不适于工业领域,因此需根据具体问题建立相应的深度学习模型,这是人工智能在工业界落地的首要理念。根据作者近几年的相关研究过程和经验,认为AI背景下电磁场智能建模范式的研究以及工程落地面临的科学挑战和重要发展方向如下:
(1)先进深度学习算法。研究纯数据驱动的先进深度学习算法是AI背景下电磁场智能建模的重要基础和前提。如,引入Transformer和扩散模型,可明显提高计算精度,并降低对数据质量和数量的要求。
(2)迁移学习建模和数据挖掘。数据的产生是不依赖物理原理认知限制的。因此,在物理原理未完全明确时,应基于电磁场和性能的多维数据,研究从历史数据中挖掘隐藏的工程师经验的方法,特别是未知PDE的建立机制,有望解决物理建模难、应用受限的问题。如,通过数据挖掘,结合先验知识,建立高精度参量计算式,实现电工装备电气参数s级计算;建立具有外推能力的场计算模型,高效分析难以数值模拟的电磁能装备性能和场。
(3)可靠性问题。应考虑纯数据驱动的可解性方法,提高AI的可靠性。特别地,引入领域知识,提高数据驱动方法的可靠性和稳定性,也有望解决欠完备条件下的计算建模问题。如,结合测量数据,基于不完全准确的表面传热系数,通过PINN或者算子网络计算变压器的温度场。
(4)反问题。AI为反问题提供了强大的建模工具。如,基于正演模型反推实际工况下的场时空演变;基于少数实验,通过高精度的多维数据代理模型和优化算法,反推无法测量的参数(如,电工装备的散热系数、电磁能装备的摩擦系数)。
(5)考虑工程问题的深度融合建模。应发展复杂问题的建模机制,推动物理原理、实验数据和数值模拟的深层次融合。如,电磁能装备由于实时原位测量困难导致参数不准确,因此数值模拟难以进行。而通过AI模型,融合电磁能装备不同数值模拟方法的结果和先验物理知识,实现高精度、高适应性、高速的正反问题计算,并基于实测数据实现模型更新,有望解决这一关键科学问题。
1)数据驱动的建模方法通过数值模拟和测试数据的知识挖掘,可实现一维性能、二三维场的快速计算和方程,甚至是局部、全局性能和微观特性的实时演算。
2)物理驱动的PDE求解方法,通过构造符合物理意义的损失函数或网络结构,可完全不依赖样本实现PDE的求解,对于物理条件不完备下的问题更具有现实价值。
3)知识嵌入的建模方法,可通过隐含在高精度样本中的知识,构建高精度的正反问题模型,随着数据的积累,其精度和泛化能力进一步变强。
总之,AI与知识的融合已是大势所趋,其将促进数值模拟领域的高速发展。但是,目前AI在数值模拟领域的探索仍处于起步阶段,亟须解决自身存在的局限性。
参考文献
[1] Tang Wei, Shan Tao, Dang Xunwang, et al. Study on a Poisson’s equation solver based on deep learning technique[C]//2017 IEEE Electrical Design of Advanced Packaging and Systems Symposium (EDAPS), Haining, China, 2017: 1-3.
[2] Khan A, Ghorbanian V, Lowther D. Deep learning for magnetic field estimation[J]. IEEE Transactions on Magnetics, 2019, 55(6): 7202304.
[3] Khan A, Mohammadi M H, Ghorbanian V, et al. Efficiency map prediction of motor drives using deep learning[J]. IEEE Transactions on Magnetics, 2020, 56(3): 7511504.
[4] He Miao, He D. Deep learning based approach for bearing fault diagnosis[J]. IEEE Transactions on Industry Applications, 2017, 53(3): 3057-3065.
[5] He Kaiming, Zhang Xiangyu, Ren Shaoqing, et al. Deep residual learning for image recognition[C]// 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 2016: 770-778.
[6] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]//31st Conference on Neural Infor- mation Processing Systems, Long Beach California, USA, 2017: 1-15.
[7] Li Chen, Tan Yusong, Chen Wei, et al. ANU-Net: Attention-based nested U-Net to exploit full reso- lution features for medical image segmentation[J]. Computers & Graphics, 2020, 90: 11-20.
[8] Ho J, Jain A, Abbeel P. denoising diffusion pro- babilistic models[J/OL]. https://doi.org/10.48550/arXiv. 2006.11239.
[9] 李峰, 王琦, 胡健雄, 等. 数据与知识联合驱动方法研究进展及其在电力系统中应用展望[J]. 中国电机工程学报, 2021, 41(13): 4377-4390.
Li Feng, Wang Qi, Hu Jianxiong, et al. Combined data-driven and knowledge-driven methodology research advances and its applied prospect in power systems[J]. Proceedings of the CSEE, 2021, 41(13): 4377-4390.
[10] 韩笑, 郭剑波, 蒲天骄, 等. 电力人工智能技术理论基础与发展展望(一): 假设分析与应用范式[J]. 中国电机工程学报, 2023, 43(8): 2877-2891.
Han Xiao, Guo Jianbo, Pu Tianjiao, et al. Theoretical foundation and directions of electric power artificial intelligence (Ⅰ): hypothesis analysis and application paradigm[J]. Proceedings of the CSEE, 2023, 43(8): 2877-2891.
[11] Khodayar M, Liu Guangyi, Wang Jianhui, et al. Deep learning in power systems research: a review[J]. CSEE Journal of Power and Energy Systems, 2021, 7(2): 209-220.
[12] 唐文虎, 牛哲文, 赵柏宁, 等. 数据驱动的人工智能技术在电力设备状态分析中的研究与应用[J]. 高电压技术, 2020, 46(9): 2985-2999.
Tang Wenhu, Niu Zhewen, Zhao Boning, et al. Research and application of data-driven artificial intelligence technology for condition analysis of power equipment[J]. High Voltage Engineering, 2020, 46(9): 2985-2999.
[13] Sheng Jie, Zhang Kun, Wang Xihui, et al. Application and prospect of deep learning in new energy power system[C]//2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 2021: 461-465.
[14] 朱振威, 邱景义, 王莉, 等. 人工智能在锂离子电池研发中的应用(英文)[J]. 电化学, 2022, 28(12): 6-27.
Zhu Zhen wei, Qiu Jing yi, Wang Li, et al. application of artificial intelligence to lithium-ion battery research and development[J]. Journal of Electro- chemistry, 2022, 28(12): 6-27.
[15] Lombardo T, Duquesnoy M, El-Bouysidy H, et al. Artificial intelligence applied to battery research: hype or reality?[J]. Chemical Reviews, 2022, 122(12): 10899-10969.
[16] Zhao Jingying, Guo Hai, Wang Likun, et al. Computer modeling of the eddy current losses of metal fasteners in rotor slots of a large nuclear steam turbine generator based on finite-element method and deep Gaussian process regression[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5349-5359.
[17] 李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的锂离子电池SOH估算[J]. 电工技术学报, 2020, 35(19): 4106-4119.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to lithium-ion battery SOH estimation based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4106- 4119.
[18] 金亮, 王飞, 杨庆新, 等. 永磁同步电机性能分析的典型深度学习模型与训练方法[J]. 电工技术学报, 2018, 33(增刊1): 41-48.
Jin Liang, Wang Fei, Yang Qingxin, et al. Typical deep learning model and training method for perfor- mance analysis of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 41-48.
[19] Dong Rongzhi, Dan Yabo, Li Xiang, et al. Inverse design of composite metal oxide optical materials based on deep transfer learning and global opti- mization[J]. Computational Materials Science, 2021, 188: 110166.
[20] 金亮, 闫银刚, 杨庆新, 等. 小样本条件下永磁同步电机深度迁移学习性能预测方法[J]. 电工技术学报, 2023, 38(18): 4921-4931.
Jin Liang, Yan Yingang, Yang Qingxin, et al. Prediction method of deep transfer learning perfor- mance of permanent magnet synchronous motor under the condition of few-shot[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4921-4931.
[21] Jin Liang, Gong Dexin, Yan Yingang, et al. Armature electromagnetic force extrapolation prediction method for electromagnetic railgun at high speed[J]. Applied Sciences, 2023, 13(6): 3819.
[22] Shan Tao, Tang Wei, Dang Xunwang, et al. Study on a fast solver for Poisson’s equation based on deep learning technique[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(9): 6725-6733.
[23] 吴鑫, 张艳丽, 王振, 等. 基于深度学习的电工钢片磁畴磁化过程预测与特征量提取[J]. 电工技术学报, 2023, 38(9): 2289-2298.
Wu Xin, Zhang Yanli, Wang Zhen, et al. prediction of magnetic domains magnetization process and feature extraction of electrical steel sheet based on deep learning[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2289-2298.
[24] 黄俊杰, 朱剑琴, 程泽源. 基于卷积神经网络双层壁三维热应力预测方法[J]. 航空动力学报, 2023, 38(7): 1658-1667.
Huang Junjie, Zhu Jianqin, Cheng Zeyuan. Three- dimensional thermal stress prediction method in double-wall structure using convolutional neural networks[J]. Journal of Aerospace Power, 2023, 38(7): 1658-1667.
[25] Li Shilin, Wang Gang, Di Yuelan, et al. A physics- informed neural network framework to predict 3D temperature field without labeled data in process of laser metal deposition[J]. Engineering Applications of Artificial Intelligence, 2023, 120: 105908.
[26] Gong Ruohan, Tang Zuqi. Investigation of con- volutional neural network U-net under small datasets in transformer magneto-thermal coupled analysis[J]. COMPEL - the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2020, 39(4): 959-970.
[27] 李耀仟, 李才子, 刘瑞强, 等. 面向手术器械语义分割的半监督时空Transformer网络[J]. 软件学报, 2022, 33(4): 1501-1515.
Li Yaoqian, Li Caizi, Liu Ruiqiang, et al. Semi- supervised spatiotemporal Transformer networks for semantic segmentation of surgical instrument[J]. Journal of Software, 2022, 33(4): 1501-1515.
[28] Lagaris I E, Likas A, Fotiadis D I. Artificial neural networks for solving ordinary and partial differential equations[J]. IEEE Transactions on Neural Networks, 1998, 9(5): 987-1000.
[29] Raissi M, Perdikaris P, Karniadakis G E. Physics- informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707.
[30] 张宇娇, 孙宏达, 赵志涛, 等. 基于物理信息神经网络的电磁场计算方法[J]. 电工技术学报, 2024, 39(17): 5251-5261.
Zhang Yujiao, Sun Hongda, Zhao Zhitao, et al. Electromagnetic field calculation method based on physical informed neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5251- 5261.
[31] 任富强, 张鸿儒, 康朝阳, 等. 高频激励下变压器绕组梯形等效网络参数辨识方法研究[J]. 中国电机工程学报, 2023, 43(11): 4463-4473.
Ren Fuqiang, Zhang Hongru, Kang Zhaoyang, et al. Ladder network parameter identification of trans- former winding under high-frequency excitation[J]. Proceedings of the CSEE, 2023, 43(11): 4463-4473.
[32] 吴春, 赵宇纬, 孙明轩. 采用测量电压的永磁同步电机多参数在线辨识[J]. 中国电机工程学报, 2020, 40(13): 4329-4340.
Wu Chun, Zhao Yuwei, Sun Mingxuan. Multi- parameter online identification for permanent magnet synchronous machines using voltage measurements[J]. Proceedings of the CSEE, 2020, 40(13): 4329-4340.
[33] 吴春, 郑露华, 支恩. 基于三角函数正交特性的永磁伺服系统机械参数辨识方法[J]. 中国电机工程学报, 2022, 42(4): 1617-1625.
Wu Chun, Zheng Luhua, Zhi En. Mechanical parameter identification of permanent magnet servo systems based on orthogonality of trigonometric functions[J]. Proceedings of the CSEE, 2022, 42(4): 1617-1625.
[34] 金亮, 祝登锋, 杨庆新, 等. 超高压电抗器电感计算灰箱模型与优化[J]. 电工技术学报, 2022, 37(23): 6093-6103.
Jin Liang, Zhu Dengfeng, Yang Qingxin, et al. Grey box model and optimization for inductance calcu- lation of EHV reactors[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6093-6103.
[35] Brunton S L, Proctor J L, Kutz J N. Discovering governing equations from data by sparse identi- fication of nonlinear dynamical systems[J]. Pro- ceedings of the National Academy of Sciences of the United States of America, 2016, 113(15): 3932- 3937.
[36] Rudy S H, Brunton S L, Proctor J L, et al. Data-driven discovery of partial differential equations[J]. Science Advances, 2017, 3(4): e1602614.
[37] Rudy S, Alla A, Brunton S L, et al. Data-driven identification of parametric partial differential equations[J]. SIAM Journal on Applied Dynamical Systems, 2019, 18(2): 643-660.
[38] Chen Zhao, Liu Yang, Sun Hao. Physics-informed learning of governing equations from scarce data[J]. Nature Communications, 2021, 12(1): 6136.
[39] Long Zichao, Lu Yiping, Ma Xianzhong, et al. PDE- Net: learning PDEs from data[C]//International Conference on Machine Learning, Stockholm, Sweden, 2018: 3208-3216.
[40] Long Zichao, Lu Yiping, Dong Bin. PDE-Net 2.0: Learning PDEs from data with a numeric-symbolic hybrid deep network[J]. Journal of Computational Physics, 2019, 399: 108925.
[41] Xu Hao, Chang Haibin, Zhang Dongxiao. DLGA-PDE: Discovery of PDEs with incomplete candidate library via combination of deep learning and genetic algorithm[J]. Journal of Computational Physics, 2020, 418: 109584.
[42] Chen Yuntian, Luo Yingtao, Liu Qiang, et al. Symbolic genetic algorithm for discovering open- form partial differential equations (SGA-PDE)[J]. Physical Review Research, 2022, 4(2): 023174.
[43] Garcia Inda A J, Huang Shao ying, İmamoğlu N, et al. Physics-coupled neural network magnetic resonance electrical property tomography (MREPT) for con- ductivity reconstruction[J]. IEEE Transactions on Image Processing, 2022, 31: 3463-3478.
[44] 陆至彬, 瞿景辉, 刘桦, 等. 基于物理信息神经网络的传热过程物理场代理模型的构建[J]. 化工学报, 2021, 72(3): 1496-1503.
Lu Zhibin, Qu Jinghui, Liu Hua, et al. Surrogate modeling for physical fields of heat transfer processes based on physics-informed neural network[J]. CIESC Journal, 2021, 72(3): 1496-1503.
[45] Khan A, Lowther D A. Physics informed neural networks for electromagnetic analysis[J]. IEEE Transa- ctions on Magnetics, 2022, 58(9): 7500404.
[46] Bragone F, Morozovska K, Hilber P, et al. Physics- informed neural networks for modelling power transformer’s dynamic thermal behaviour[J]. Electric Power Systems Research, 2022, 211: 108447.
[47] Magill M, Nagel A M, de Haan H W. Neural network solutions to differential equations in nonconvex domains: solving the electric field in the slit-well microfluidic device[J]. Physical Review Research, 2020, 2(3): 033110.
[48] 仲林林, 吴冰钰, 吴奇. 基于元学习的气体放电等离子体电子Boltzmann方程数值求解[J]. 电工技术学报, 2024, 39(11): 3457-3466.
Zhong Linlin, Wu Bingyu, Wu Qi. Numerical solution of electron Boltzmann equation in gas discharge plasmas based on meta learning[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3457- 3466.
[49] Sirignano J, Spiliopoulos K. DGM: a deep learning algorithm for solving partial differential equations[J]. Journal of Computational Physics, 2018, 375: 1339- 1364.
[50] Weinan E, Yu Bing. The deep Ritz method: a deep learning-based numerical algorithm for solving variational problems[J]. Communications in Mathematics and Statistics, 2018, 6(1): 1-12.
[51] Zang Yaohua, Bao Gang, Ye Xiaojing, et al. Weak adversarial networks for high-dimensional partial differential equations[J]. Journal of Computational Physics, 2020, 411: 109409.
[52] Wang Sifan, Teng Yujun, Perdikaris P. Understanding and mitigating gradient flow pathologies in physics- informed neural networks[J]. SIAM Journal on Scientific Computing, 2021, 43(5): A3055-A3081.
[53] Wang Sifan, Yu Xinling, Perdikaris P. When and why PINNs fail to train: a neural tangent kernel perspective[J]. Journal of Computational Physics, 2022, 449: 110768.
[54] Sun Luning, Gao Han, Pan Shaowu, et al. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 361: 112732.
[55] Sheng Hailong, Yang Chao. PFNN: a penalty-free neural network method for solving a class of second-order boundary-value problems on complex geometries[J]. Journal of Computational Physics, 2021, 428: 110085.
[56] Chen Yuntian, Huang Dou, Zhang Dongxiao, et al. Theory-guided hard constraint projection (HCP): a knowledge-based data-driven scientific machine learning method[J]. Journal of Computational Physics, 2021, 445: 110624.
[57] Dong Bin, Jiang Qingtang, Shen Zuowei. Image restoration: wavelet frame shrinkage, nonlinear evolution PDEs, and beyond[J]. Multiscale Modeling & Simulation, 2017, 15(1): 606-660.
[58] Yao Houpu, Gao Yi, Liu Yongming. FEA-Net: a physics-guided data-driven model for efficient mechanical response prediction[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 363: 112892.
[59] Rao Chengping, Ren Pu, Wang Qi, et al. Encoding physics to learn reaction-diffusion processes[J]. Nature Machine Intelligence, 2023, 5: 765-779.
[60] Ramuhalli P, Udpa L, Udpa S S. Finite-element neural networks for solving differential equations[J]. IEEE Transactions on Neural Networks, 2005, 16(6): 1381- 1392.
[61] 徐超, 王长龙, 绳慧, 等. 三维磁场计算的有限元神经网络模型[J]. 电工技术学报, 2012, 27(11): 125-132.
Xu Chao, Wang Changlong, Sheng Hui, et al. FENN model for 3-D magnetic field calculation[J]. Transa- ctions of China Electrotechnical Society, 2012, 27(11): 125-132.
[62] Xu Chao, Wang Changlong, Ji Fengzhu, et al. Finite- element neural network-based solving 3-D differential equations in MFL[J]. IEEE Transactions on Mag- netics, 2012, 48(12): 4747-4756.
[63] 苑希超, 王长龙, 纪凤珠, 等. 利用有限元神经网络计算漏磁场方法研究[J]. 兵工学报, 2011, 32(11): 1395-1398.
Yuan Xichao, Wang Changlong, Ji Fengzhu, et al. A calculation method of magnetic leakage field based on finite element neural network[J]. Acta Armamentarii, 2011, 32(11): 1395-1398.
[64] 李想, 严子铭, 柳占立. 机器学习与计算力学的结合及应用初探[J]. 科学通报, 2019, 64(7): 635-648.
Li Xiang, Yan Ziming, Liu Zhanli. Combination and application of machine learning and computational mechanics[J]. Chinese Science Bulletin, 2019, 64(7): 635-648.
[65] Chen Yuntian, Zhang Dongxiao. Theory-guided deep- learning for electrical load forecasting (TgDLF) via ensemble long short-term memory[J]. Advances in Applied Energy, 2021, 1: 100004.
[66] Viana F A C, Steffen V, Butkewitsch S, et al. Optimization of aircraft structural components by using nature-inspired algorithms and multi-fidelity approximations[J]. Journal of Global Optimization, 2009, 45(3): 427-449.
[67] Fernández-Godino M G. Review of multi-fidelity models[J/OL]. arXiv.org. 10.48550.
[68] Sun Guangyong, Li Guangyao, Zhou Shiwei, et al. Multi-fidelity optimization for sheet metal forming process[J]. Structural and Multidisciplinary Optimi- zation, 2011, 44(1): 111-124.
[69] Morozova N, Trias F X, Capdevila R, et al. A CFD- based surrogate model for predicting flow parameters in a ventilated room using sensor readings[J]. Energy and Buildings, 2022, 266: 112146.
[70] Bierig C, Chernov A. Approximation of probability density functions by the Multilevel Monte Carlo Maximum Entropy method[J]. Journal of Com- putational Physics, 2016, 314: 661-681.
[71] Zheng Qiang, Zhang Jiangjiang, Xu Wenjie, et al. Adaptive multifidelity data assimilation for nonlinear subsurface flow problems[J]. Water Resources Research, 2019, 55(1): 203-217.
[72] Raissi M, Karniadakis G. Deep multi-fidelity Gaussian processes[J]. ArXiv e-Prints, 2016: arXiv: 1604.07484.
[73] Li Kai, Kou Jiaqing, Zhang Weiwei. Deep learning for multifidelity aerodynamic distribution modeling from experimental and simulation data[J]. AIAA Journal, 2022, 60(7): 4413-4427.
[74] Chakraborty S. Transfer learning based multi-fidelity physics informed deep neural network[J]. Journal of Computational Physics, 2021, 426: 109942.
[75] Liu Lixue, Song Xueguan, Zhang Chao, et al. GAN- MDF: an enabling method for multifidelity data fusion[J]. IEEE Internet of Things Journal, 2022, 9(15): 13405-13415.
[76] Zhang Yunyang, Gong Zhiqiang, Zhou Weien, et al. Multi-fidelity surrogate modeling for temperature field prediction using deep convolution neural net- work[J]. Engineering Applications of Artificial Intelligence, 2023, 123: 106354.
[77] Xu Yueqi, Song Xueguan, Zhang Chao. Hierarchical regression framework for multi-fidelity modeling[J]. Knowledge-Based Systems, 2021, 212: 106587.
[78] Chen Shizhi, Feng Decheng. Multifidelity approach for data-driven prediction models of structural behaviors with limited data[J]. Computer-Aided Civil and Infrastructure Engineering, 2022, 37(12): 1566- 1581.
[79] Kou Jiaqing, Zhang Weiwei. Multi-fidelity modeling framework for nonlinear unsteady aerodynamics of airfoils[J]. Applied Mathematical Modelling, 2019, 76: 832-855.
[80] Wang Xu, Kou Jiaqing, Zhang Weiwei. A new dynamic stall prediction framework based on symbiosis of experimental and simulation data[J]. Physics of Fluids, 2021, 33(12): 127119.
[81] Meng Xuhui, Karniadakis G E. A composite neural network that learns from multi-fidelity data: Appli- cation to function approximation and inverse PDE problems[J]. Journal of Computational Physics, 2020, 401: 109020.
[82] Chen T, Chen H. Universal approximation to non- linear operators by neural networks with arbitrary activation functions and its application to dynamical systems[J]. IEEE Transactions on Neural Networks, 1995, 6(4): 911-917.
[83] Lu Lu, Jin Pengzhan, Pang Guofei, et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators[J]. Nature Machine Intelligence, 2021, 3: 218-229.
[84] Lu Lu, Meng Xuhui, Mao Zhiping, et al. DeepXDE: a deep learning library for solving differential equations[J]. SIAM Review, 2021, 63(1): 208-228.
[85] Cai Shengze, Wang Zhicheng, Lu Lu, et al. DeepM& Mnet: Inferring the electroconvection multiphysics fields based on operator approximation by neural networks[J]. Journal of Computational Physics, 2021, 436: 110296.
[86] Wang Sifan, Wang Hanwen, Perdikaris P. Learning the solution operator of parametric partial differential equations with physics-informed DeepONets[J]. Science Advances, 2021, 7(40): eabi8605.
[87] Jin Pengzhan, Meng Shuai, Lu Lu. MIONet: learning multiple-input operators via tensor product[J]. SIAM Journal on Scientific Computing, 2022, 44(6): A3490- A3514.
[88] Lu Lu, Meng Xuhui, Cai Shengze, et al. A com- prehensive and fair comparison of two neural operators (with practical extensions) based on FAIR data[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 393: 114778.
[89] Lu Lu, Pestourie R, Johnson S G, et al. Multifidelity deep neural operators for efficient learning of partial differential equationswith application to fast inverse design of nanoscale heat transport[J]. Physical Review Research, 2022, 4(2): 023210.
[90] Li Zongyi, Kovachki N, Azizzadenesheli K, et al. Fourier neural operator for parametric partial differential equations[EB/OL]. 2020: 2010.08895. https://arxiv.org/abs/ 2010.08895v3.
[91] Ong Y Z, Shen Zuowei, Yang Haizhao. Integral autoencoder network for discretization-invariant learning[J]. Journal of Machine Learning Research, 2022, 23.
[92] Tripura T, Chakraborty S. Wavelet Neural Operator for solving parametric partial differential equations in computational mechanics problems[J]. Computer Methods in Applied Mechanics and Engineering, 2023, 404: 115783.
[93] Cao Shuhao. Choose a transformer: Fourier or Galerkin[J]. Advances in Neural Information Pro- cessing Systems, 2021, 34: 24924-24940.
Abstract The rapidly developing field of artificial intelligence (AI) has made significant advancements in areas such as image processing, language, decision-making, and diagnostics, providing new methods for solving complex problems. The increasing intelligence of electrical equipment, combined with the coupling of strong and weak electrical fields, has led to the emergence of multi-scale, multi-physical field coupling and nonlinear problems in electromagnetic fields. High-precision numerical modeling and optimization are increasingly challenging.
Therefore, this paper combines recent research outcomes from the author’s team to introduce deep learning methods for solving typical interdisciplinary problems, such as data-driven modeling, physics-driven PDE solving, and knowledge-embedding modeling. In particular, the paper discusses the current state of intelligent modeling for complex electromagnetic field problems driven by both data and knowledge. It also offers perspectives on the scientific challenges and important future directions in the research and engineering implementation of electromagnetic field intelligent modeling.
In the area of data-driven modeling, the paper explores its application in the performance analysis and optimization of electrical equipment. The discussion is divided into three parts: performance parameter calculation, electromagnetic thermal field prediction, and knowledge discovery modeling. By combining numerical simulation and experimental data, deep learning algorithms can mine potential knowledge from the data, enabling rapid computation of one-dimensional performance and two- and three-dimensional fields. This approach allows for real-time simulation of local performance, global performance, and micro characteristics.
Regarding physics-driven partial differential equation (PDE) solving, the paper discusses two main research directions: knowledge-embedding regularization methods and designing machine learning model structures based on physical meaning. Constructing loss functions or network structures that align with physical laws makesit possible to solve PDEs without relying on sample data. This method is beneficial when physical conditions are incomplete and sample data is scarce. Using AI to solve physical equations helps overcome traditional bottlenecks, improving computational efficiency and expanding application scope.
In the area of knowledge-embedding modeling, the paper discusses how to implicitly integrate domain knowledge, mainly through multi-fidelity models and neural network operator methods, to improve the precision and efficiency of computational models. By embedding the knowledge inherent in high-precision samples into the model, high-precision forward and inverse problem models can be built. As data accumulates, the model's accuracy and generalization ability will improve. This method fully utilizes the advantages of deep learning and integrates basic physical theories. As data grows, knowledge-embedding methods are expected to be crucial in solving more complex electromagnetic field problems and enhancing overall simulation outcomes.
In conclusion, the fusion of AI and knowledge has become a significant trend in the development of numerical simulation. Integrating data-driven, physics-driven, and knowledge-embedding methods has accelerated the advancement of electromagnetic field modeling and optimization. These methods have improved simulation accuracy and expanded the application range of numerical simulations for complex electromagnetic field problems. However, the exploration of AI in numerical simulation is still in its early stages, facing challenges such as insufficient model generalization, computational efficiency improvement, and physical constraint integration. Future research should focus on addressing these issues to promote the broader application and development of AI in the field of electromagnetic field numerical simulation.
keywords:Artificial intelligence (AI), electromagnetic field, modeling optimization
中图分类号:TM153
DOI: 10.19595/j.cnki.1000-6753.tces.240877
国家自然科学基金重大研究计划(92066206)、中央引导地方科技发展专项自由探索项目(226Z4503G)和河北省自然科学基金面上项目(E2024202231)资助。
收稿日期 2024-05-22
改稿日期2024-10-24
金 亮 男,1982年生,教授,博士生导师,研究方向为电磁场数值模拟与智能计算。
E-mail: jinliang_email@163.com(通信作者)
苏浩展 男,2000年生,硕士研究生,研究方向为电磁场数值模拟与智能计算。
E-mail: 2063159290@qq.com
(编辑 郭丽军)