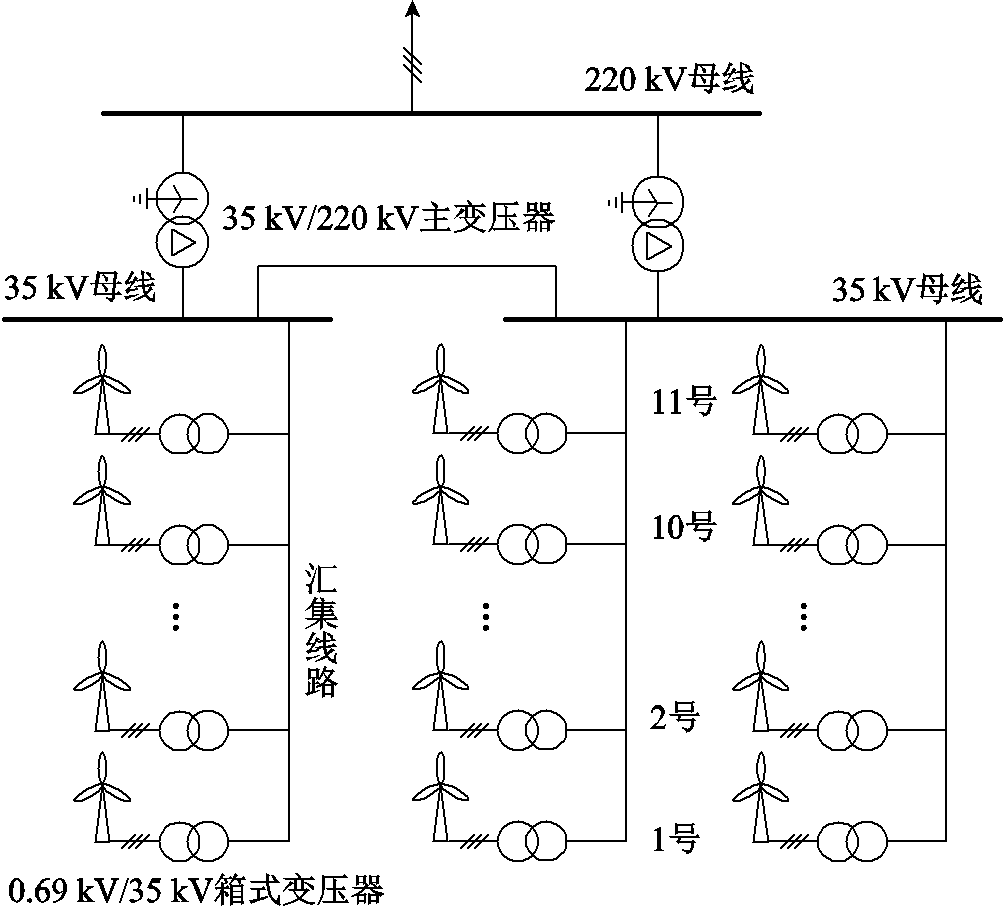
图1 永磁风场拓扑示意图
Fig.1 Topology diagram of permanent magnet wind farm
摘要 场站级的故障等值建模与分析方法是新能源集中并网地区的保护原理设计与定值计算研究的基础。传统的场站等值建模多采用单机倍乘和分群聚类算法,选取特征参数等值最终将场站模型简化,或者基于机组控制策略采用迭代算法进行求解,存在等值参数误差和计算不收敛的问题。因此,该文首先分析逆变型电源故障后电流的控制策略;然后通过两点迭代的方法求取线路电压与机组输出电流的对应曲线,进而通过遍历末端机组电压,运用前推的方式得到场站并网点电压与电流相量的对应关系,求得逆变型新能源发电场站的等值曲线;最后通过仿真计算及实际短路试验数据验证显示,对于大规模逆变型新能源场站故障稳态的等值计算,所提方法无需复杂迭代计算,计算精度高,与试验录波数据平均等值计算误差为3.28%。
关键词:逆变型电源 新能源场站 低压穿越 等值计算 短路电流计算
电力系统故障分析是进行保护原理设计和整定配置的必要前提。规模化新能源集中并网地区,逆变型新能源电源变流设备的故障特性与传统电源的区别逐渐凸显,对保护动作性能产生直接影响。然而,由于缺乏有效的新能源发电场站故障等值分析计算模型,难以量化分析保护正确动作边界并提出改进方法,亟待提出新的等值分析方法。
现阶段新能源场站故障等值分析可以分为单机倍乘法和多机等值分析法。单机倍乘法[1-4]略去了分群的步骤,关注将一整个场站折算成一台机的算法,在计算过程中模型简洁、运算量小,但存在精度相对较低的问题。
随着新能源场站规模的扩大,场站机组数量与建设面积的增加,机组间的特性差异也随之增大,此时再采用单台机等值一个场站时精度将明显下降,需要采用多机等值法。现有研究重点关注的分群指标可以分为机组正常运行参数与故障参数两个方向。对于非故障状态下的新能源机组可以借助风速[5-7]、输出功率[8-10]、等效导纳[11]、场站对系统的影响[12]等参数或者综合考虑多种运行变量[13-17]进行分群,此类分群策略所需参数获取便捷,但缺乏对故障阶段适用性的分析。对于借助机组故障状态参数的研究,文献[18]借助状态空间方程通过参数识别求取等值模型的关键参数,但依赖仿真或者实际运行数据;文献[19]利用故障后机端电压相似度作为分群依据;文献[20]基于风电机组故障后短路电流曲线轨迹挖掘影响因素,进而实现聚合等值。
然而由于机组输出参数以及机组间架空线路参数的不同,等值存在不可避免的误差[21-22]。文献[23]考虑了此处的误差,并通过等值前后的故障电流误差进行分群与等效计算;文献[24]通过分析场站内机端电压的误差计算了单机等值方法的等值误差限。可见通过传统等值的方法进行全功率逆变型场站的故障分析势必带来一定的建模误差。
对于含有新能源电源的网络故障计算也可以采用迭代法。迭代法[25-28]是指在传统的网络潮流迭代解法中考虑逆变型新能源机组的压控电流源特性,此时理论误差相比于传统等值方法将会大大减少。然而此时由于新能源场站的固有拓扑特性,迭代计算过程中不可避免地要对每一个逆变型机组进行修正,迭代计算结果收敛性差,计算耗时长。文献[29]针对配网侧采用局部迭代的方法优化全局迭代所带来的收敛性差以及收敛速度慢等问题,然而由于在场站内新能源节点分布密集,致使局部迭代优化效果不明显。
针对多机等值存在难以避免的电气参数及距离误差,同时新能源场站多节点迭代存在计算不收敛的问题,本文首先提出基于末端机组电压前推的场站等值曲线求取方法,通过两点迭代求取单台机组与线路电压的映射关系;然后通过末端机组电压向并网点方向前推计算并网点的电流与电压相量,进而可以得到场站的故障等值曲线,进一步通过分析模型固有误差所带来的影响,证明了所提方法的适用性;最后利用典型永磁风电场的仿真模型及实际人工短路试验数据验证了所提方法的可行性及准确性。
考虑到逆变型新能源场站中光伏与风电场站拓扑结构相似,本文基于实际的风电场站拓扑构建了逆变型新能源场站的详细模型。场站主要由永磁风机、架空汇集线路、35 kV与220 kV母线、箱式变压器(0.69 kV/35 kV)与主变压器(35 kV/220 kV)构成。其中永磁风机共有33台,按照每条架空汇集线路11台机组分布,汇集至35 kV母线后经主变压器接入站外220 kV系统。图1为永磁风场拓扑示意图,光伏场站与之相似。

图1 永磁风场拓扑示意图
Fig.1 Topology diagram of permanent magnet wind farm
在系统正常运行的情况下,场站内机组的换流器由电压电流双闭环控制,输出的控制参数经过调制环节最终确定换流器出口处的电压。此时逆变器输出的电流即为电压外环输出的dq轴电流参考值,根据瞬时有功功率、无功功率的计算式可以得到机组输出功率与其电压、电流的关系为
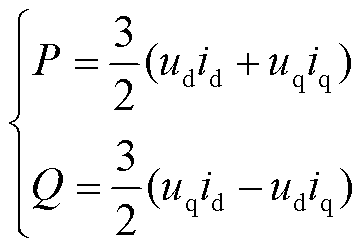 (1)
(1)
式中,P、Q分别为单台机组输出的有功功率和无功功率;ud、uq分别为逆变器端口处的d、q轴电压;id、iq分别为逆变器端口处的d、q轴电流。
风机的机械部分输出有功功率可以根据场站实际风速计算得到,即
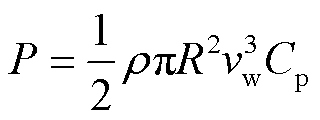 (2)
(2)
式中,ρ为空气密度;R为风轮机半径;vw为风机实际输入风速;Cp为风能利用系数。同时实际的输入风速需要考虑场站内机组间尾流效应的影响。
在计算光伏机组光电转换部分功率时,考虑到其计算公式较为复杂,影响因素多,所以常采用出力系数表征单台机组的功率输出情况。本文针对物理环节的功率输入均使用机组的出力系数代入计算。
根据逆变型电源低电压穿越控制策略的国家标准[30],机组机端电压故障后电压跌落至0.9(pu)以下时,机组换流器控制环节由功率外环控制切换至低电压穿越控制,通过控制机组输出的q轴电流,优先满足国标有关要求增发无功功率用以支撑电网电压,同时在满足换流器限幅的基础上送出有功功率。
对于机组稳态电流,在计算时可以视为与控制环节输出的电流参考值相同,进而可以分别得到逆变型新能源机组故障前后在不同控制策略下输出的d、q轴电流分别为
 (3)
(3)
 (4)
(4)
式中,α为机组出力系数,通常为实际风速与额定风速的比值;IN为机组的额定电流;Im为换流器输出电流限幅值;ud为d轴电压,对于常见的采用定d轴电压控制的系统可以将d轴电压视为机端电压,此时q轴电压为0;K为无功补偿系数,取值范围一般为1.5~3。将式(3)与式(4)代入式(1)可得
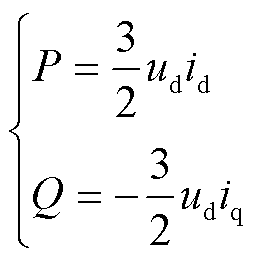 (5)
(5)
由式(5)可知,当机组按国标要求发出无功功率时,实际q轴电流应为负数,表现在dq坐标系中为q轴电流滞后d轴电压90°,故在机组进入低电压穿越控制后电压电流相量夹角呈现为电流滞后于电压。
系统发生故障后,场站内的机组换流器以锁相环输出相位即机端电压相位为参考,根据既定的控制策略输出对应的d、q轴电流。然而由于场站各机组地理位置不同,每台机组的机端电压相位存在差异,导致各机组的坐标系参考相位均不相同,因此在计算场站故障电流时需要先将各机组的电流归算至同一坐标系下[31],各机组输出dq轴电流关系如附图1所示。附图1中,di、qi分别为i号机组机端电压dq轴的方向,电压控制策略采用定d轴控制,即d轴相位为机端电压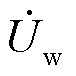 的相位,下文分析同。dref、qref为参考电压Uref的dq轴方向,考虑到本文主要分析并网点电压电流的等值关系曲线,同时后续分析时围绕并网点在故障后的电压展开的,因此将并网点电压
的相位,下文分析同。dref、qref为参考电压Uref的dq轴方向,考虑到本文主要分析并网点电压电流的等值关系曲线,同时后续分析时围绕并网点在故障后的电压展开的,因此将并网点电压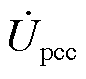 的相位作为参考电压相位。
的相位作为参考电压相位。
将场站内各机组输出电流归算至参考坐标系下,计算式为
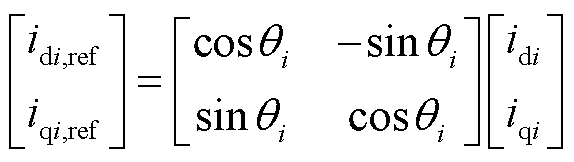 (6)
(6)
式中,idi,ref、iqi,ref分别为i号机组电流归算至参考电压相位的电流d、q轴分量;idi、iqi分别为机组按各自机端电压相位输出的电流d、q轴分量;θi为i号机组机端电压相位和参考电压相位的差值。通过电流的归算,后续计算与分析均在参考坐标系下进行,故下文分析中dq轴电流如无特殊说明均为归算后数值。
通过上文分析可知,逆变型新能源机组在故障后呈现压控电流源的特性,故障稳态电流主要影响因素为换流器控制方法、机端电压跌落程度、电压相位及风力机组出力系数即风速。考虑到同一场站内新能源机组及箱式变压器参数大致相同,各机组间故障电流产生差异的主要原因为机组所处地理位置的不同,进而使得各台机组出力系数以及相对于并网点的电气距离出现差异,致使传统等值过程中产生难以避免的误差。本文基于此提出了场站级等值曲线的方法以避免上述因素所带来的等值误差。
为降低后续前推过程中计算的复杂度,需先求取单台机组故障电流和线路电压之间的映射关系。
对于单台机组在其稳态运行和故障稳态时可以等效为压控电流源,如附图2所示。首先将机端和线路连接点视为两个节点,结合故障后单台机组的控制策略与变压器参数进行两点迭代计算,即通过线路电压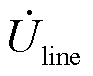 求解对应的单机输出电流
求解对应的单机输出电流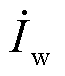 。
。
迭代过程采用式(7)进行计算。
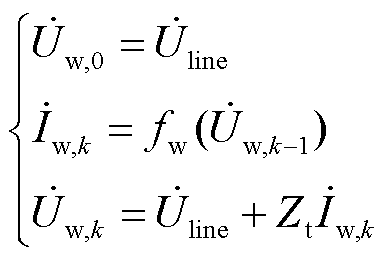 (7)
(7)
式中,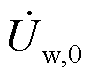 为机端电压迭代初值;fw为对应机端电压相量与输出电流相量的映射关系;
为机端电压迭代初值;fw为对应机端电压相量与输出电流相量的映射关系;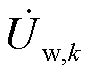 与
与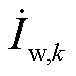 分别为第k台机组机端电压与输出电流相量,
分别为第k台机组机端电压与输出电流相量,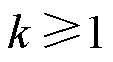 ;
;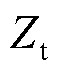 为箱式变压器阻抗。由于逆变型新能源机组在故障后需要输出无功功率,故此处q轴电流滞后于d轴电流。
为箱式变压器阻抗。由于逆变型新能源机组在故障后需要输出无功功率,故此处q轴电流滞后于d轴电流。
记录计算出对应的一组电压电流相量后,将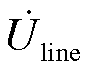 的幅值增加一个步长,考虑到接下来的前推计算中的裕度和逆变型新能源场站低电压穿越要求,永磁场站的机端电压取值范围为0.1(pu)~1.1(pu),光伏场站的取值范围为0~1.1(pu)。将每一步得到的计算结果保存至数据库,即可得到与线路电压
的幅值增加一个步长,考虑到接下来的前推计算中的裕度和逆变型新能源场站低电压穿越要求,永磁场站的机端电压取值范围为0.1(pu)~1.1(pu),光伏场站的取值范围为0~1.1(pu)。将每一步得到的计算结果保存至数据库,即可得到与线路电压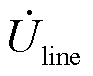 对应的单台机组输出电流的电流相量。
对应的单台机组输出电流的电流相量。
以永磁风电场站为例,运用同样的方法求取不同出力情况下的机组输出电流相量与并网点电压的映射关系,其幅值与相位如图2a、图2b所示。
当场站新能源电源参数存在差异时,按照类似的方法求取场站内不同型号的机组或者变压器的对应单机映射曲线并记录于数据库。
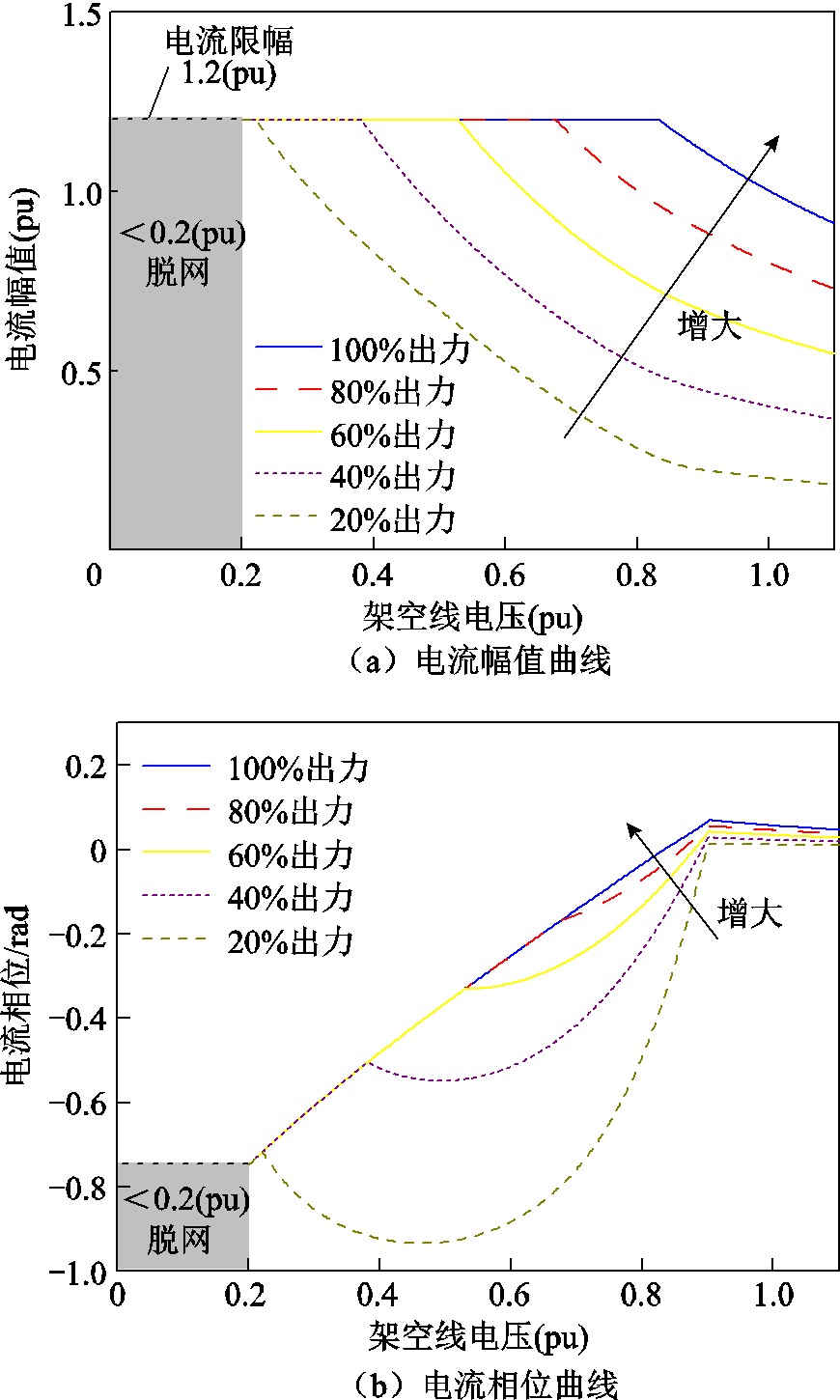
图2 单台机组映射曲线
Fig.2 Single unit mapping curves
设置末端机组电压范围为0~1.1(pu),遍历电压时步长可以根据最终曲线绘制精度需求确定。首先假设末端机组电压为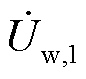 ,通常设置为0,对于汇集线路末端机组,将电压
,通常设置为0,对于汇集线路末端机组,将电压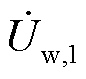 代入式(3)与式(4)分别可得机组输出的d轴与q轴电流,随后将dq轴电流代入式(8)。
代入式(3)与式(4)分别可得机组输出的d轴与q轴电流,随后将dq轴电流代入式(8)。
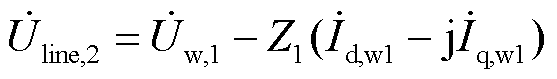 (8)
(8)
式中,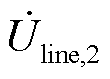 为第二台机组所连接的线路电压;
为第二台机组所连接的线路电压;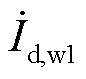 、
、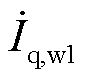 分别为末端机组输出的d轴与q轴电流。
分别为末端机组输出的d轴与q轴电流。
求得第二台机组的线路电压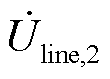 后,将电压代入2.1节中求得的单机映射曲线,即可得到对应的单机输出电流,将其与末端机组电流相加,即可得到两台机组的输出电流,依此类推,按照如图3所示的单条集电线路连接拓扑图从末端机组向并网点方向进行前推计算,直至求得
后,将电压代入2.1节中求得的单机映射曲线,即可得到对应的单机输出电流,将其与末端机组电流相加,即可得到两台机组的输出电流,依此类推,按照如图3所示的单条集电线路连接拓扑图从末端机组向并网点方向进行前推计算,直至求得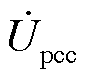 和其对应的电流相量,前推计算过程采用式(9)。
和其对应的电流相量,前推计算过程采用式(9)。
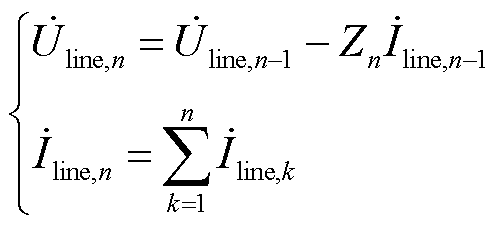 (9)
(9)
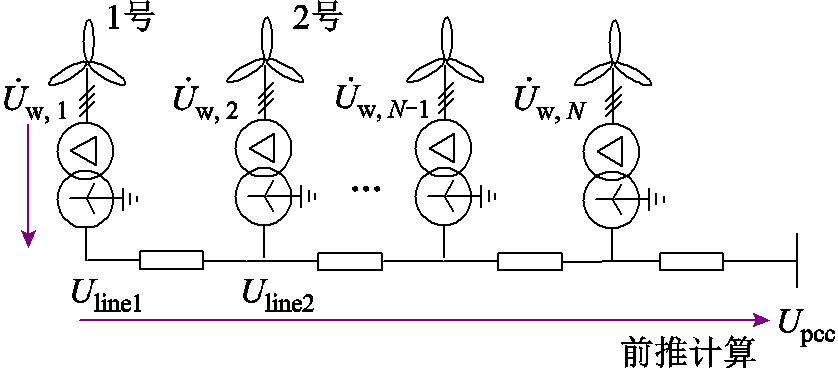
图3 单条集电线路示意图
Fig.3 Schematic diagram of single power collection line
此时记录得到的并网点电压和对应的电流相量,随后将末端机组电压幅值增加一个步长;遵循相同步骤进行计算,直至完成末端机组电压的遍历环节;最终可以得到一并网点电压与其对应的电流相量映射曲线。进一步,只需要根据实际场站拓扑将对应机组串数相叠加即可获取场站的等值曲线。
当场站不是简单链式拓扑无法直接用多串机组相加时,可以先求分支串的等值曲线。在前推过程中,分支部分即可视为普通的单台机组曲线代入计算。
本文所提方法在理论上已经大幅减小了计算的误差,然而由于单机建模无法做到与实际情况完全一致,在将单台机组等效为压控电流源模型的过程中不可避免地会引入误差。这里的误差对于单机分析时可以忽略不计,但是考虑到新能源场站中机组数量庞大,拓扑复杂,有概率产生误差叠加的情况,此时将会导致最终的计算结果与实际情况的误差超出最初的等效误差,即误差的放大。
针对计算过程中可能出现的等效模型误差对线路电压降落误差产生最大影响的场景,即误差相量与机组输出电流相量同向或反向,同时所有机组均为正误差或者负误差两种极端情况进行如下分析。
分析整串机组同种误差所引起的最终误差,首先需要分析末端机组故障电流误差对并网点电压电流关系的影响。对于单台机组而言,逆变器出口电压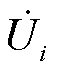 对应的电流误差与集电线路电压
对应的电流误差与集电线路电压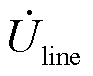 对应的电流误差趋势相同,故以下分析对于单机误差均指同一集电线路电压等效前后电流的误差。
对应的电流误差趋势相同,故以下分析对于单机误差均指同一集电线路电压等效前后电流的误差。
假设末端1号机组存在+δ的误差,有
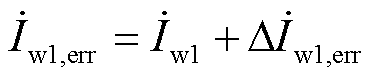 (10)
(10)
式中,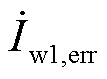 为计及误差的电流;
为计及误差的电流;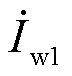 为真实电流值。由于考虑电流相量误差对线路电压降落产生最大影响的极端情况,对于计及误差的电流与真实电流的关系为
为真实电流值。由于考虑电流相量误差对线路电压降落产生最大影响的极端情况,对于计及误差的电流与真实电流的关系为
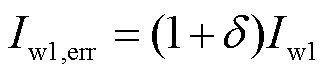 (11)
(11)
由图3可知,当仅考虑一台机组时,机组架空线联络处与并网点处电压电流关系为
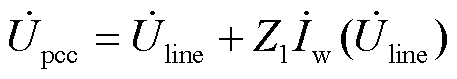 (12)
(12)
则对于计及误差的末端机组电流有
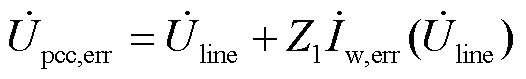 (13)
(13)
式中,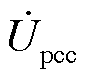 为未计及误差并网点电压;
为未计及误差并网点电压;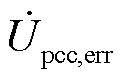 为计及误差的并网点电压;
为计及误差的并网点电压;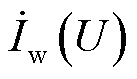 与
与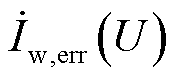 分别为对应架空线电压下未计及与计及误差的单台机组输出电流。
分别为对应架空线电压下未计及与计及误差的单台机组输出电流。
考虑到最终需要求取的是并网点处电压与电流的关系,为方便下一步分析,此时假定并网点处电压为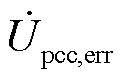 。显然对于此时的并网点电压,若考虑模型等效误差,其对应的集电线路电压为
。显然对于此时的并网点电压,若考虑模型等效误差,其对应的集电线路电压为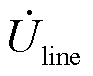 ,相量关系如图4a所示。
,相量关系如图4a所示。
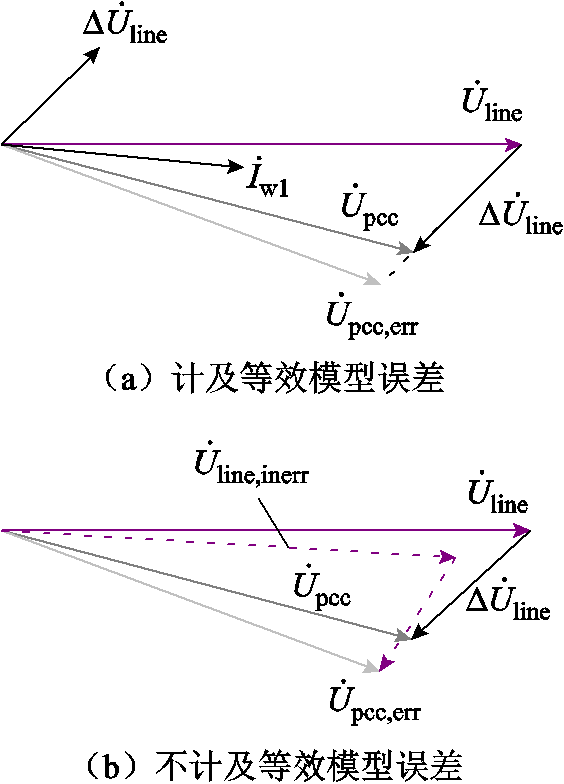
图4 单机等效模型相量图
Fig.4 Phasor diagram of single machine equivalent model
那么,对于未考虑模型等效误差的情况系统满足
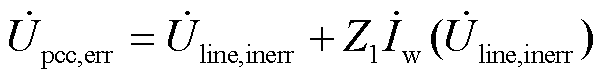 (14)
(14)
根据式(14)可得如图4b所示的相量图。由2.1节分析可知,对于任一确定的并网点电压,以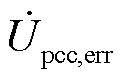 为例,在未计及误差与计及误差时的电流分别为
为例,在未计及误差与计及误差时的电流分别为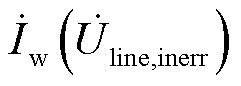 与
与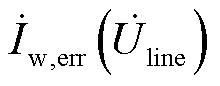 ,且满足
,且满足
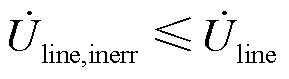 (15)
(15)
同时,由式(11)可得
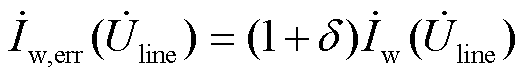 (16)
(16)
结合2.1节所求单机曲线可知,对于逆变型新能源机组有
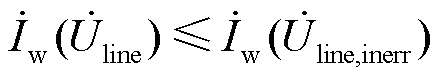 (17)
(17)
由式(16)与式(17),可得
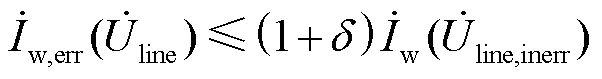 (18)
(18)
由式(18)可知,在假设单台机组等效误差为+δ时,给并网点电压电流曲线带来的误差是小于+δ的。采用类似的证明方法可得单台机组等效误差为-δ时,所带来的误差不会超过-δ。
进一步考虑两台机组的情况,此时对于2号机组在集电线路接入点电压来说,末端机组引起的电流误差不超过δ,假设此时2号机组的等效模型电流误差为δ,根据相量相加的基本定理,此时两台机组的电流误差不会超过真实值的1±δ倍。
参考单机误差的推导过程同样可以得到对于并网点电压电流曲线,两台机组等效所引起的误差不会超过δ。依次类推,对于整串机组来说,最终因为单机等效模型误差所引起的曲线最终误差将不会超过单机误差的最大值,即误差不会因为前推过程而放大。
为验证本文所提方法的可行性,以内蒙典型风场拓扑结构为例,在PSCAD中搭建了如图1所示的永磁风场详细模型,包含3(集电线路数)×11台(单条集电线路风机数)的5 MW永磁风机,机组间隔为1 km,风电场元件及换流器主要参数见附表1。同时考虑到机组出力受到风场尾流效应的影响,场站内风向及风速示意图如附图3所示,各机组风速分布情况见附表2,机组出力系数为实际风速与额定风速的比值。
以场站出口故障为例,设置对应的过渡电阻,对电压跌落至30%~90%共7种工况进行仿真结果分析。为证明所提方法的优越性,将本文方法与现有两种多机等值建模方法进行比较,模型一:考虑机组运行稳态量通过传统k-means聚类算法进行分群,元件参数等值采用加权平均电压差法[5];模型二:考虑机组运行故障分量同时采用改进的k-means聚类算法进行等值建模[23],分群数量均设置为3群。
首先根据2.1节所述方法求得不同出力情况下单台机组输出电流相量与集电线路电压的关系曲线。进一步依据2.2节所述计算过程,根据风场的拓扑结构及元件参数,依次得到各条集电线路对应的并网点电压与电流相量的等值曲线,将各组曲线按照物理连接关系对应相加后可以得到整个永磁风电场站的等值曲线,如图5所示。其中图5a为并网点电压对应的电流幅值,图5b为并网点电压对应的电流相位,并网点电压相量角度为参考角度。
本文所提方法与两种现有的多机等值方法误差的对比见附表3,可知所提等值曲线方法针对不同电压跌落情况下均有较高的计算精度,故障电流计算相对误差均未超过0.9%,可以准确地表征逆变型新能源场站故障稳态响应情况。
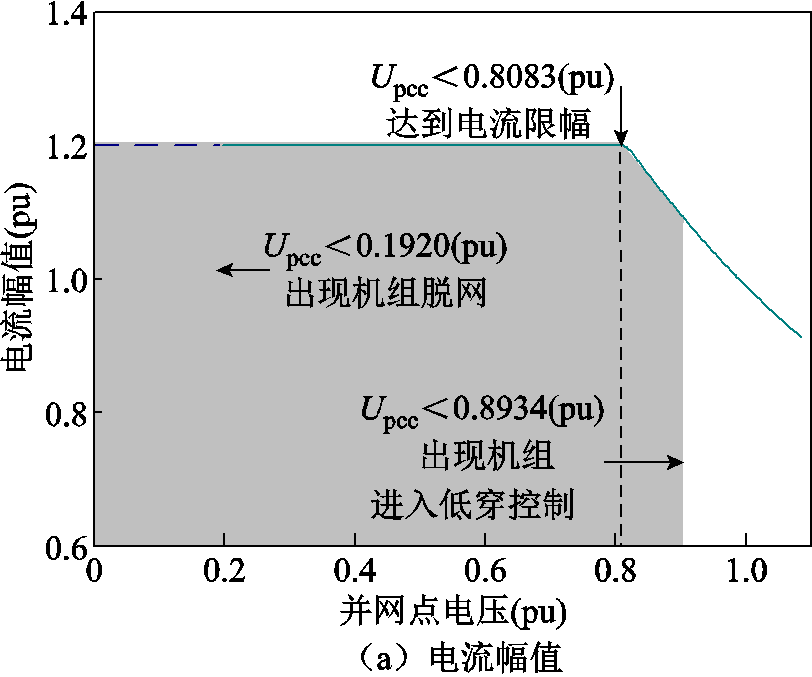
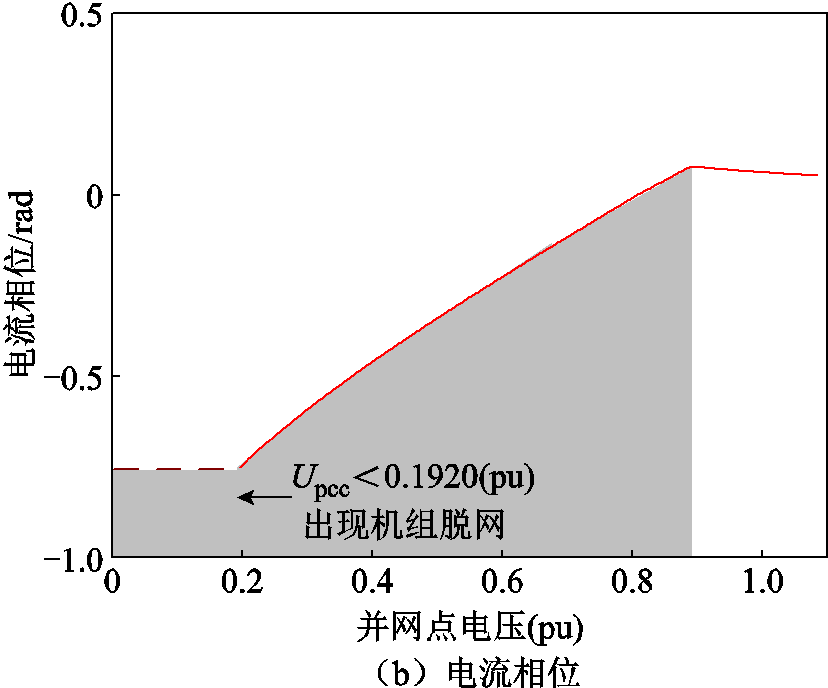
图5 永磁风电场站等值曲线
Fig.5 Equivalent curve of permanent magnet wind farm station
利用新疆疆能回庄子风电场站人工短路试验录播数据验证本文所提方法的可行性与准确性。场站内永磁同步风电机组额定功率为1.5 MW,风电场站拓扑如图6所示。故障点分别为110 kV母线与风七线35 kV处,测点为集电线路与母线连接处、最靠近35 kV母线的风电机组机端出口处。
根据单机短路试验数据,结合式(3)与式(4),参考文献[29]中所提方法,可以求得风电机组的 U-I映射曲线,其中无功补偿系数K=3,机组出力为23%,详细的电流表达式为
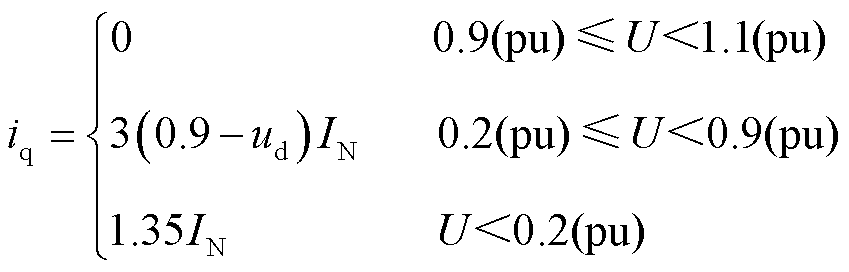 (19)
(19)
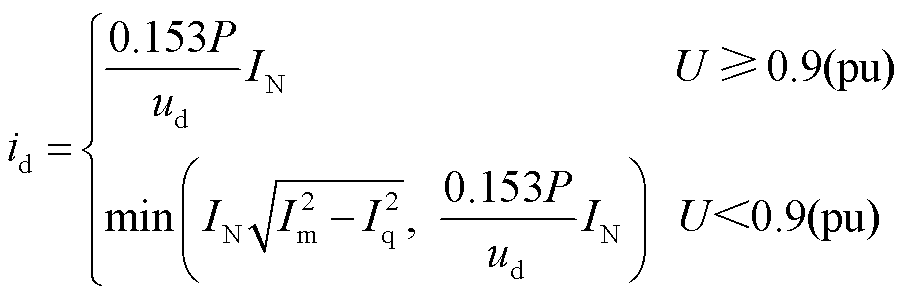 (20)
(20)
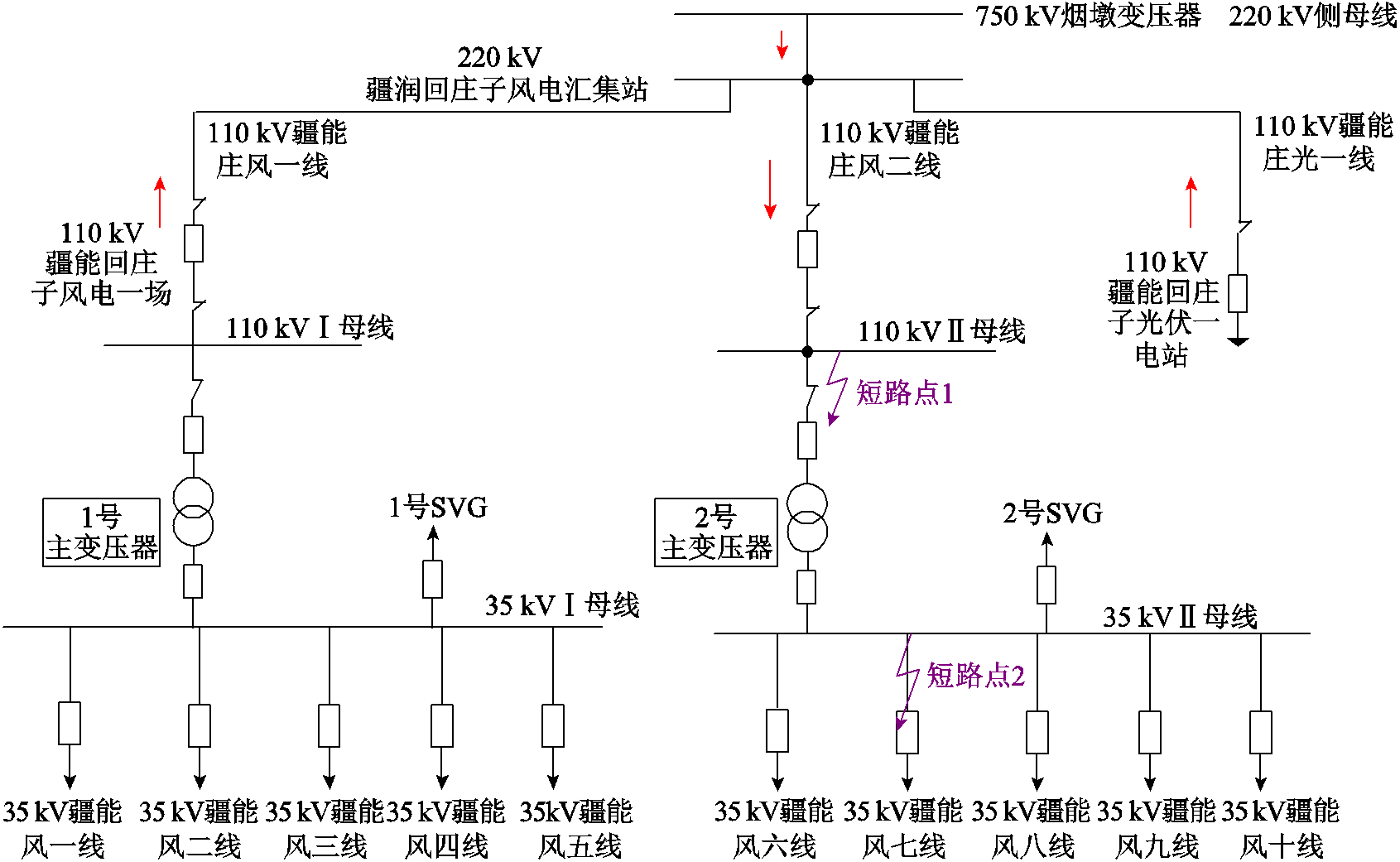
图6 短路试验场站拓扑
Fig.6 Short circuit test station topology
单台永磁风电机组的U-I理论曲线与实测值曲线如图7所示。由图7可得映射曲线与实测曲线拟合情况较好,可以用于进一步的场站等值计算。
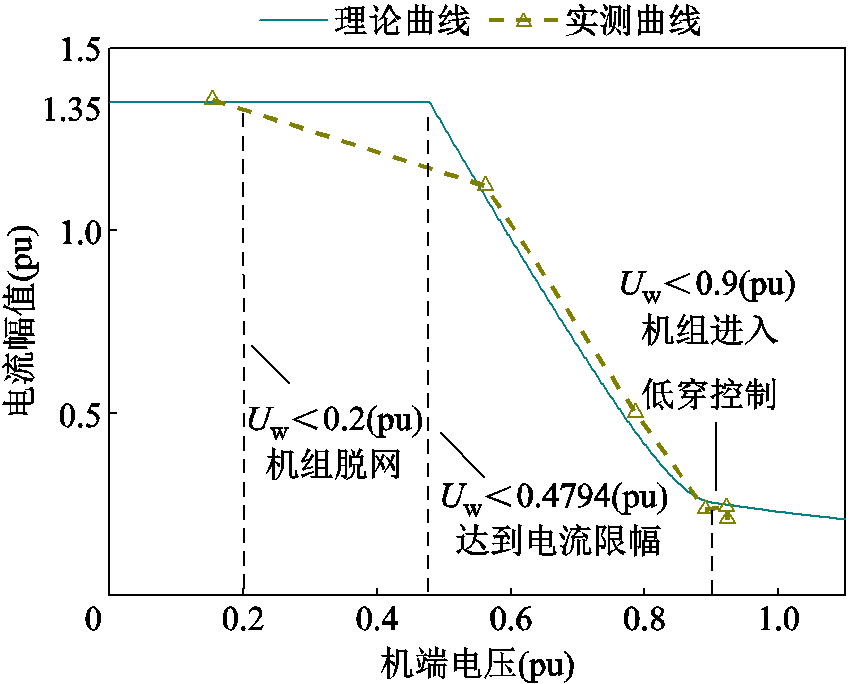
图7 单台机组的U-I曲线
Fig.7 U-I curve of a single unit
基于以上的分析结果,采用本文所提方法,可以求得汇集线路故障电流与电压的等值曲线。根据短路试验数据,分别求取机组出力为23%与38%的U-I曲线,与短路试验数据对比如图8所示。
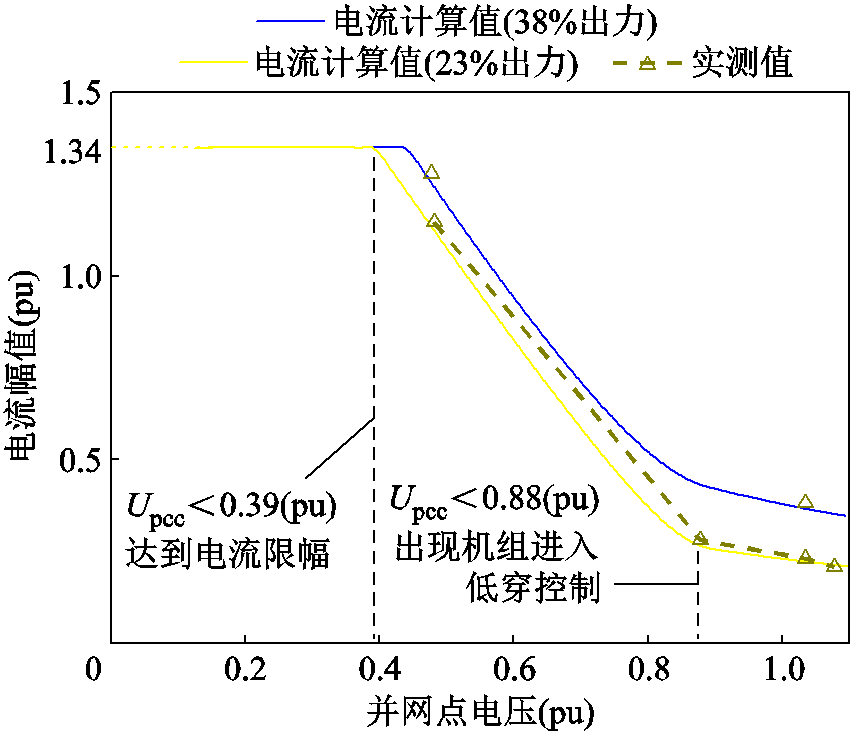
图8 单条汇集线路的U-I曲线
Fig.8 U-I curves of a single merging line
可以看出,在故障后汇集线路并网点电压跌落至48%与87%时的故障电流及故障前稳态运行时的电流,与所求理论曲线契合度较高,相对误差最大值为4.73%,平均误差为3.28%。考虑到单机映射曲线存在的拟合误差,本文所提方法具有实际应用价值。
基于2.3节对等效模型误差所产生的影响分析,为验证分析结果的正确性,本节在3.1节仿真模型的基础上设置两种误差情况进行仿真计算对比分析,情况一:每台单机模型输出电流均存在+5%误差;情况二:每台单机存在-5%~+5%随机误差。分别计算两种误差情况下并网点电压电流等值曲线,进而与未添加误差情况下的等值曲线进行比较,得出等效模型误差对场站整体等值曲线误差的影响。
对于情况一,根据附图4中误差计算结果曲线可得,在换流器进入限流之后误差略高于限流前的误差,即电压跌落超过阈值后等效误差带来的整体误差将会增大,但是场站等值曲线的绝对误差仍小于最初设置的5%单机误差。可见在此种单机误差均为正向误差的极端情况下,所提方法在计算过程中因模型等效误差带来的整体误差并不会被放大。
对于情况二,根据附图5中误差计算结果曲线可得,在每台机组等效模型存在均匀分布的随机误差时,最终相对误差的绝对值小于0.59%。实际上,由于等效建模误差均为同向最大误差是一种极端情况,在场站运行时,因单机等效模型误差所引起的场站等值曲线误差将会明显小于单机模型误差的上限。
本文基于对逆变型新能源机组故障稳态特性的研究,结合单机响应曲线,通过末端机组电压前推得到并网点电压对应的故障稳态电流,进而得到表征场站故障稳态特性的等值曲线,提高了等值精度,同时简化了计算过程,减少了迭代过程中因节点数过多导致的迭代不收敛发生的概率。仿真结果表明,所提方法相比于传统多机等值与改进的故障等值建模,短路电流平均误差降低了1.13%,在各种运行情况下的等值误差均在0.9%以内。同时利用人工短路试验数据拟合的单机曲线,通过所提方法求取的等值曲线与实际数据误差满足计算要求。
为证明所提方法的准确性与可行性,本文分析了单机等效模型的误差对最终场站等值曲线带来的影响,等值曲线计算结果误差与理论分析结果相符,证明了本文所提方法不会对单机等效模型误差产生放大影响,等值曲线的最终误差不大于单机等效模型误差。
本文工作重点在于逆变型新能源场站故障等值曲线的求取,确定场站级电压电流映射关系,对于新能源大基地多场站的故障分析计算存在参考价值。同时由于场站故障暂态响应与稳态响应间存在一定的映射关系,后续的工作重心将放在对于场站级的暂态等值建模策略的研究。
附 录
1. 多机相位归算
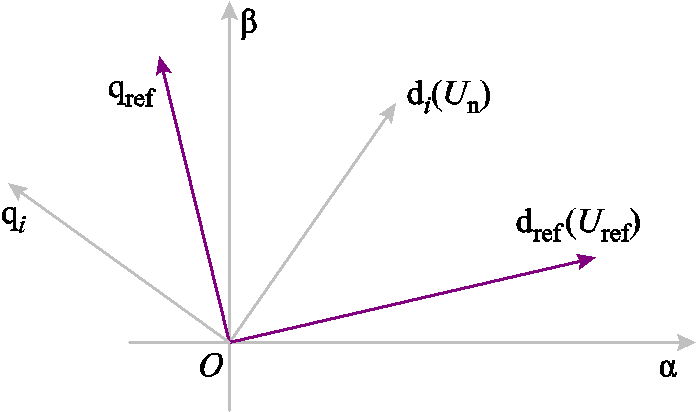
附图1 多机dq轴电流相量归算示意图
App.Fig.1 Schematic diagram of multi machine dq axis current phasor reduction
2.单机等效模型
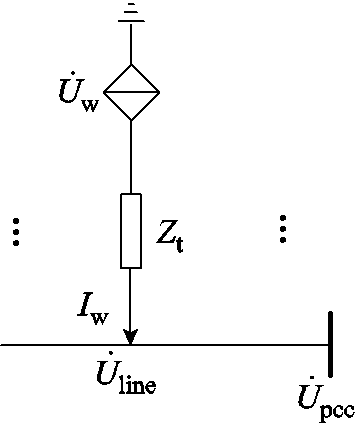
附图2 单机等效压控电流源模型
App.Fig.2 Single machine equivalent voltage controlled current source model
3. 仿真系统参数及验证结果
附表1 永磁风电场主要元件参数
App.Tab.1 Main component parameters of permanent magnet wind farm

参数数值(型号) 220kV线路型号LGJ-300 35kV线路型号LGJ-400/YJY23-26/35kV 3×70 单位电阻/(Ω/km)0.08 单位电抗/(Ω/km)0.373
(续)

参数数值(型号) 箱式变压器电压比0.69 kV/35 kV 容量/MW1.6 短路阻抗(%)6.63 主变压器电压比35 kV/220 kV 容量/MW100 阻抗(%)12.54 风机容量/MW1.5 额定风速/(m/s)8.6
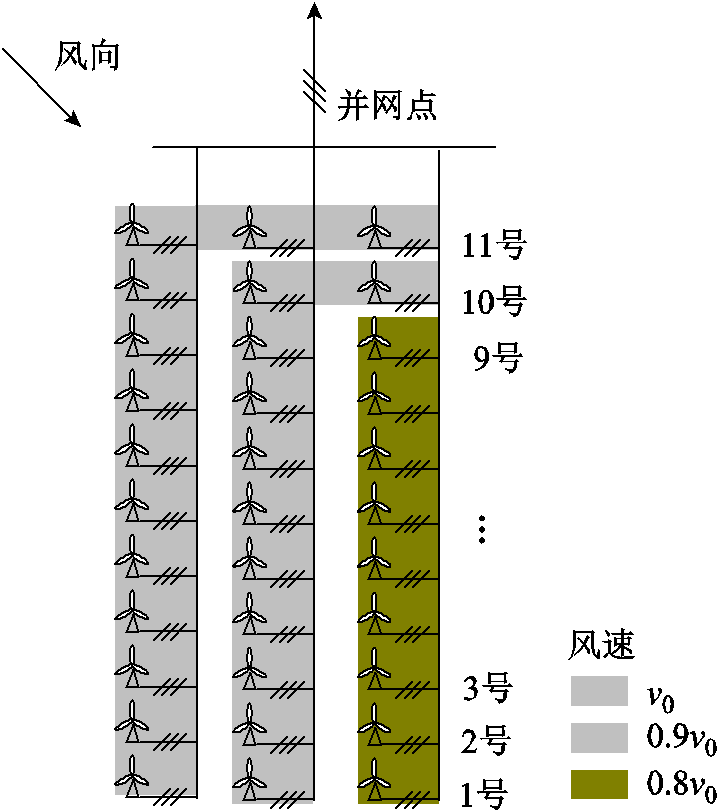
附图3 永磁风场风速分布示意图
App.Fig.3 Schematic diagram of wind speed distribution in permanent magnet wind farm
附表2 永磁风场风速分布
App.Tab.2 Wind speed distribution in permanent magnet wind farm

风机编号风速/(m/s) 1.1~1.11;2.11;3.11v0① 2.1~2.10;3.100.9v0 3.1~3.90.8v0
①v0表示额定风速。
附表3 不同电压跌落下仿真结果分析
App.Tab.3 Analysis of simulation results under different voltage drops

故障后并网点电压(%)详细模型传统算法改进算法本文方法 稳态电流(pu)稳态电流(pu)电流误差(%)稳态电流(pu)电流误差(%)稳态电流(pu)电流误差(%) 90.5281.087∠5.047°1.085∠4.182°1.5271.086∠4.297°1.3111.091∠4.333°0.640 85.8521.142∠3.517°1.154∠1.556°3.5771.158∠2.208°2.6871.142∠3.059°0.801 71.1601.198∠-5.509°1.200∠-7.138°2.8481.201∠-4.311°2.1041.200∠-5.951°0.781 56.4491.198∠-14.623°1.200∠-16.295°2.9261.201∠-14.088°0.9741.200∠-14.902°0.520 46.0651.198∠-21.608°1.200∠-20.555°1.8511.201∠-22.382°1.3841.200∠-22.150°0.402 33.3661.198∠-30.885°1.200∠-32.774°3.3071.201∠-31.897°1.7931.200∠-31.035°0.330
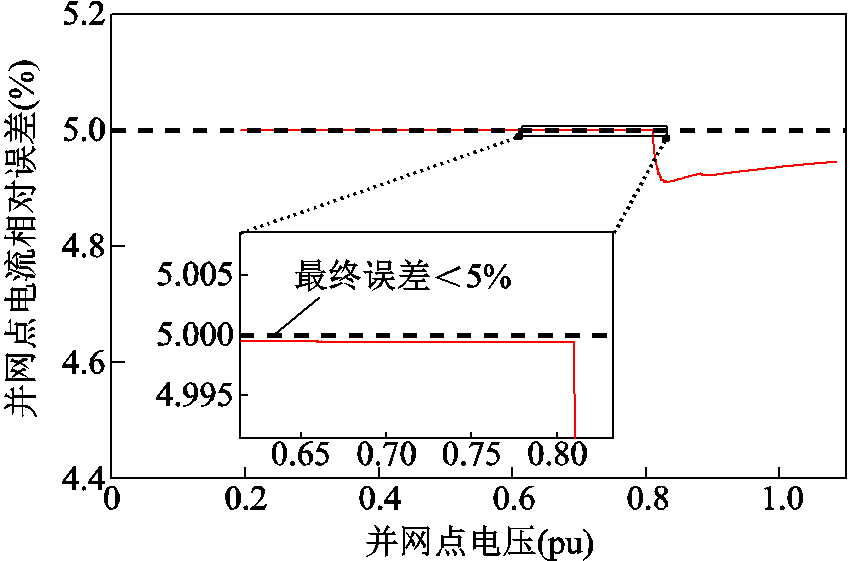
附图4 情况一场站等值曲线误差
App.Fig.4 Scenario 1 station contour curve error
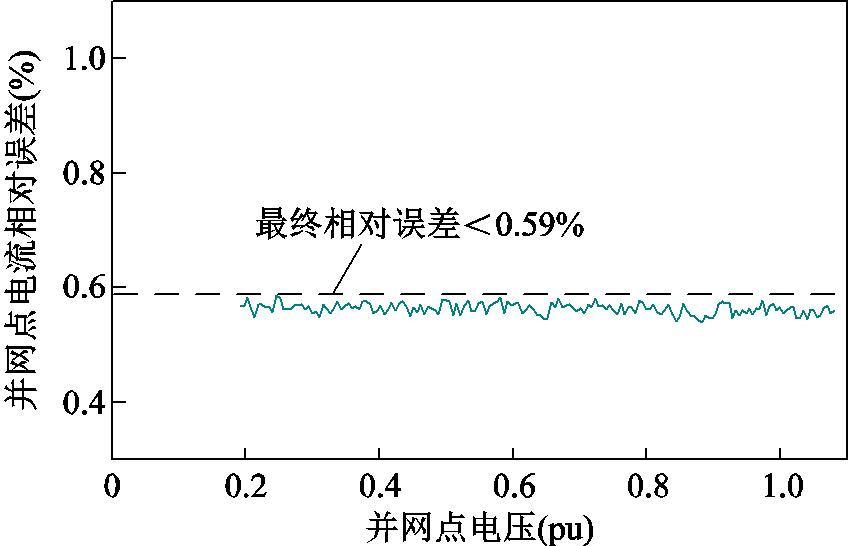
附图5 情况二场站等值曲线误差
App.Fig.5 Scenario 2 station contour curve error
参考文献
[1] 李龙源, 付瑞清, 吕晓琴, 等. 接入弱电网的同型机直驱风电场单机等值建模[J]. 电工技术学报, 2023, 38(3): 712-725.
Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 712-725.
[2] 古庭赟, 杨骐嘉, 林呈辉, 等. 基于单机等值与选择模态分析的风电场等值建模方法[J]. 电力系统保护与控制, 2020, 48(1): 102-111.
Gu Tingyun, Yang Qijia, Lin Chenghui, et al. A wind farm equivalent modeling method based on single-machine equivalent modeling and selection modal analysis[J]. Power System Protection and Control, 2020, 48(1): 102-111.
[3] 陆飞. 双馈风电模型分析及机群聚合等值技术研究[D]. 北京: 华北电力大学, 2016.
Lu Fei. Model analysis of doubly fed induction generator and research of equivalent aggregation technology for wind farm clusters[D]. Beijing: North China Electric Power University, 2016.
[4] 夏玥, 李征, 蔡旭, 等. 基于直驱式永磁同步发电机组的风电场动态建模[J]. 电网技术, 2014, 38(6): 1439-1445.
Xia Yue, Li Zheng, Cai Xu, et al. Dynamic modeling of wind farm composed of direct-driven permanent magnet synchronous generators[J]. Power System Technology, 2014, 38(6): 1439-1445.
[5] 米增强, 苏勋文, 杨奇逊, 等. 风电场动态等值模型的多机表征方法[J]. 电工技术学报, 2010, 25(5): 162-169.
Mi Zengqiang, Su Xunwen, Yang Qixun, et al. Multi-machine representation method for dynamic equivalent model of wind farms[J]. Transactions of China Electrotechnical Society, 2010, 25(5): 162-169.
[6] 曹娜, 赵海翔, 任普春, 等. 风电场动态分析中风速模型的建立及应用[J]. 中国电机工程学报, 2007, 27(36): 68-72.
Cao Na, Zhao Haixiang, Ren Puchun, et al. Establish and application of wind speed model in wind farm dynamic analysis[J]. Proceedings of the CSEE, 2007, 27(36): 68-72.
[7] Wang Peng, Zhang Zhenyuan, Huang Qi, et al. Wind farm dynamic equivalent modeling method for power system probabilistic stability assessment[C]//2019 IEEE Industry Applications Society Annual Meeting, Baltimore, MD, USA, 2019: 1-7.
[8] Jin Yuqing, Wu Daming, Ju Ping, et al. Modeling of wind speeds inside a wind farm with application to wind farm aggregate modeling considering LVRT characteristic[J]. IEEE Transactions on Energy Con-version, 2020, 35(1): 508-519.
[9] 张星, 李龙源, 胡晓波, 等. 基于风电机组输出时间序列数据分群的风电场动态等值[J]. 电网技术, 2015, 39(10): 2787-2793.
Zhang Xing, Li Longyuan, Hu Xiaobo, et al. Wind farm dynamic equivalence based on clustering by output time series data of wind turbine generators[J]. Power System Technology, 2015, 39(10): 2787-2793.
[10] 晁璞璞, 李卫星, 金小明, 等. 基于有功响应的双馈型风电场实用化等值方法[J]. 中国电机工程学报, 2018, 38(6): 1639-1646, 1900.
Chao Pupu, Li Weixing, Jin Xiaoming, et al. An active power response based practical equivalent method for DFIG wind farms[J]. Proceedings of the CSEE, 2018, 38(6): 1639-1646, 1900.
[11] 周佩朋, 李光范, 孙华东, 等. 基于频域阻抗分析的直驱风电场等值建模方法[J]. 中国电机工程学报, 2020, 40(增刊1): 84-90.
Zhou Peipeng, Li Guangfan, Sun Huadong, et al. Equivalent modeling method of PMSG wind farm based on frequency domain impedance analysis[J]. Proceedings of CSEE, 2020, 40 (S1): 84-90.
[12] Zheng Zetian, An Zhi, Shen Chen. Evaluation method for equivalent models of PMSG-based wind farms considering randomness[J]. IEEE Transactions on Sustainable Energy, 2019, 10(3): 1565-1574.
[13] Zha Xiaoming, Liao Shuhan, Huang Meng, et al. Dynamic aggregation modeling of grid-connected inverters using hamilton’s-action-based coherent equivalence[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6437-6448.
[14] 张剑, 何怡刚. 基于轨迹灵敏度分析的永磁直驱风电场等值模型参数辨识[J]. 电工技术学报, 2020, 35(15): 3303-3313.
Zhang Jian, He Yigang. Parameters identification of equivalent model of permanent magnet synchronous generator wind farm based on analysis of trajectory sensitivity[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3303-3313.
[15] Gupta A P, Mitra A, Mohapatra A, et al. A multi-machine equivalent model of a wind farm considering LVRT characteristic and wake effect[J]. IEEE Transactions on Sustainable Energy, 2022, 13(3): 1396-1407.
[16] Shabanikia N, Nia A A, Tabesh A, et al. Weighted dynamic aggregation modeling of induction machine-based wind farms[J]. IEEE Transactions on Sustainable Energy, 2021, 12(3): 1604-1614.
[17] Zhou Yuhao, Zhao Long, Hsieh T Y, et al. A multistage dynamic equivalent modeling of a wind farm for the smart grid development[J]. IEEE Transactions on Industry Applications, 2019, 55(5): 4451-4461.
[18] Kim D E, El-Sharkawi M A. Dynamic equivalent model of wind power plant using parameter identification[J]. IEEE Transactions on Energy Conversion, 2016, 31(1): 37-45.
[19] 潘学萍, 王卫康, 陈海东, 等. 计及低电压穿越影响的感应电动机动态分群[J]. 电工技术学报, 2024, 39(7): 2001-2016.
Pan Xueping, Wang Weikang, Chen Haidong, et al. Dynamic clustering of induction motors in new energy power systems considering the impact of LVRT[J] Transactions of China Electrotechnical Society, 2024, 39(7): 2001-2016.
[20] Ouyang Jinxin, Diao Yanbo, Zheng Di, et al. Dynamic equivalent model of doubly fed wind farm during electromagnetic transient process[J]. IET Renewable Power Generation, 2017, 11(1): 100-106.
[21] Ruan Jiayang, Lu Zongxiang, Qiao Ying, et al. Analysis on applicability problems of the aggregation-based representation of wind farms considering DFIGs’ LVRT behaviors[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4953-4965.
[22] 安之, 沈沉, 郑泽天, 等. 考虑风电随机性的直驱风机风电场等值模型评价方法[J]. 中国电机工程学报, 2018, 38(22): 6511-6520.
An Zhi, Shen Chen, Zheng Zetian, et al. Assessment method for equivalent models of wind farms based on direct-driven wind generators considering randomness [J]. Proceedings of the CSEE, 2018, 38(22): 6511-6520.
[23] 贾科, 孔繁哲, 张旸, 等. 基于改进K-均值算法的双馈风场故障等值建模方法[J]. 电网技术, 2023, 47(10): 4161-4169.
Jia Ke, Kong Fanzhe, Zhang Yang, et al. Fault equivalent modeling of doubly fed wind farm based on improved K-means algorithm[J]. Power System Technology, 2023, 47(10): 4161-4169.
[24] 孙华东, 李佳豪, 李文锋, 等. 大规模电力系统仿真用新能源场站模型结构及建模方法研究(二): 机电暂态模型[J]. 中国电机工程学报, 2023, 43(6): 2190-2201.
Sun Huadong, Li Jiahao, Li Wenfeng, et al. Research on model structures and modeling methods of renewable energy station for large-scale power system simulation (II): electromechanical transient model[J]. Proceedings of the CSEE, 2023, 43(6): 2190-2201.
[25] 杨杉, 同向前, 刘健, 等. 含分布式电源配电网的短路电流计算方法研究[J]. 电网技术, 2015, 39(7): 1977-1982.
Yang Shan, Tong Xiangqian, Liu Jian, et al. Short-circuit current calculation of distribution network with distributed generation[J]. Power System Technology, 2015, 39(7): 1977-1982.
[26] 匡晓云, 方煜, 关红兵, 等. 适用于含新能源逆变电源网络的全时域短路电流计算方法[J]. 电力自动化设备, 2020, 40(5): 113-122.
Kuang Xiaoyun, Fang Yu, Guan Hongbing, et al. Full-time domain short circuit current calculation method suitable for power network with inverter-interfaced renewable energy source[J]. Electric Power Auto-mation Equipment, 2020, 40(5): 113-122.
[27] 尹项根, 张哲, 肖繁, 等. 分布式电源短路计算模型及电网故障计算方法研究[J]. 电力系统保护与控制, 2015, 43(22): 1-9.
Yin Xianggen, Zhang Zhe, Xiao Fan, et al. Study on short-circuit calculation model of distributed generators and fault analysis method of power system with distributed generators[J]. Power System Protection and Control, 2015, 43(22): 1-9.
[28] Nimpitiwan N, Heydt G T, Ayyanar R, et al. Fault current contribution from synchronous machine and inverter based distributed generators[J]. IEEE Transactions on Power Delivery, 2007, 22(1): 634-641.
[29] 贾科, 侯来运, 毕天姝, 等. 基于故障区域局部迭代的工程实用化新能源短路电流计算[J]. 电力系统自动化, 2021, 45(13): 151-158.
Jia Ke, Hou Laiyun, Bi Tianshu, et al. Practical engineering calculation of short-circuit current for renewable energy based on local iteration of fault area[J]. Automation of Electric Power Systems, 2021, 45(13): 151-158.
[30] 国家市场监督管理总局, 国家标准化管理委员会. 风电场接入电力系统技术规定第1部分:陆上风电: GB/T 19963.1—2021[S]. 北京: 中国标准出版社, 2021.
[31] 贾科, 杨彬, 刘浅, 等. 基于逆变型电源暂态电流回代的系统级故障暂态解析[J]. 电力系统自动化, 2022, 46(3): 113-120.
Jia Ke, Yang Bin, Liu Qian, et al. Transient analysis of system-level fault based on transient current back-substitution of inverter interfaced generator[J]. Auto-mation of Electric Power Systems, 2022, 46(3): 113-120.
Fault Equivalent Calculation of Inverter Interfaced Renewable Energy Generator Stations Based on Extrapolation of Terminal Unit Voltage
Abstract Fault analysis in electrical power systems is a crucial prerequisite for designing protection principles and configuring settings. With the increasing integration of renewable energy sources into centralized grids, the distinctive fault characteristics of inverter-type new energy power conversion equipment are becoming more pronounced, directly influencing the performance of protection actions. However, the lack of effective fault equivalent analysis models tailored for new energy stations poses challenges in quantitatively analyzing protection operation boundaries and proposing improvement methods, necessitating the development of novel equivalent analysis methodologies.
Currently, fault equivalent analysis for new energy stations can be categorized into single-machine multiplication and multi-machine equivalent analysis methods. The single-machine multiplication method simplifies the calculation process by omitting clustering steps, resulting in reduced computational complexity. However, it often sacrifices accuracy. Conversely, multi-machine equivalent analysis considers various operational variables of units and attempts to group them accordingly. Nevertheless, due to differences in unit output parameters and overhead line parameters among units, errors unavoidably arise in the equivalent calculations. Iterative methods, although applicable for fault calculations in networks with new energy sources, struggle due to the inherent topological characteristics of such stations. During the iterative process, it is necessary to individually correct each inverter-type unit, leading to poor convergence and extended computation times.
To address the challenges of multi-machine equivalent analysis and the convergence issues encountered in iterative calculations for multi-node new energy stations, a novel methodology based on forward propagation of terminal unit voltages for deriving station equivalent curves is proposed. By iteratively establishing the mapping relationship between single units and line voltages, and subsequently propagating terminal unit voltages towards the grid connection point to calculate current and voltage phasors, the mapping curve of station grid voltage and current phasors, i.e., the station equivalent curve, is obtained. Representing an entire new energy station in the system topology with a curve enhances equivalent accuracy while simplifying the computation process, thereby reducing the likelihood of convergence issues arising from a high number of nodes during iteration.
To validate the accuracy and feasibility of the proposed method, this paper analyzes the impact of errors in single-machine equivalent models on the final station equivalent curve. Assuming the maximum amplitude error occurs in a single unit, the influence of the single-unit equivalent model on the station equivalent curve error is analyzed. Combined with the basic principle of phasor addition, it is shown that under the condition where all units have the maximum error in the same direction, the final error will not exceed the error of the single-machine equivalent model. The error of the equivalent curve calculated with model errors aligns with theoretical analysis results, demonstrating that the proposed method does not amplify errors in single-machine equivalent models during the calculation process.
Simulation results indicate that compared to traditional multi-machine equivalent and improved fault equivalent modeling, the average error of short-circuit currents is reduced by 1.13. Moreover, equivalent errors under various operating conditions remain within 0.9. Furthermore, utilizing actual artificial short-circuit test data from Xinjiang to fit single-machine curves, the average equivalent calculation error between curves obtained via the proposed method and experimental waveform data is 3.28.
Keywords:Inverter-interfaced generator, renewable energy station, low voltage ride through, equivalent calculation, short-circuit current calculation
中图分类号:TM614;TM615
DOI:10.19595/j.cnki.1000-6753.tces.232082
国家重点研发计划项目(2022YFB4202302)和优秀青年科学基金新能源电力系统保护项目(52322703)资助。
收稿日期 2023-12-13
改稿日期 2024-03-19
刘 岩 男,2000年生,硕士研究生,研究方向为沙戈荒大基地新能源场站故障等值建模与分析计算。
E-mail:814168359@qq.com
贾 科 男,1986年生,教授,博士生导师,研究方向为电力系统保护与控制、新型配电网保护与故障定位等。
E-mail:ke.jia@ncepu.edu.cn(通信作者)
(编辑 赫 蕾)