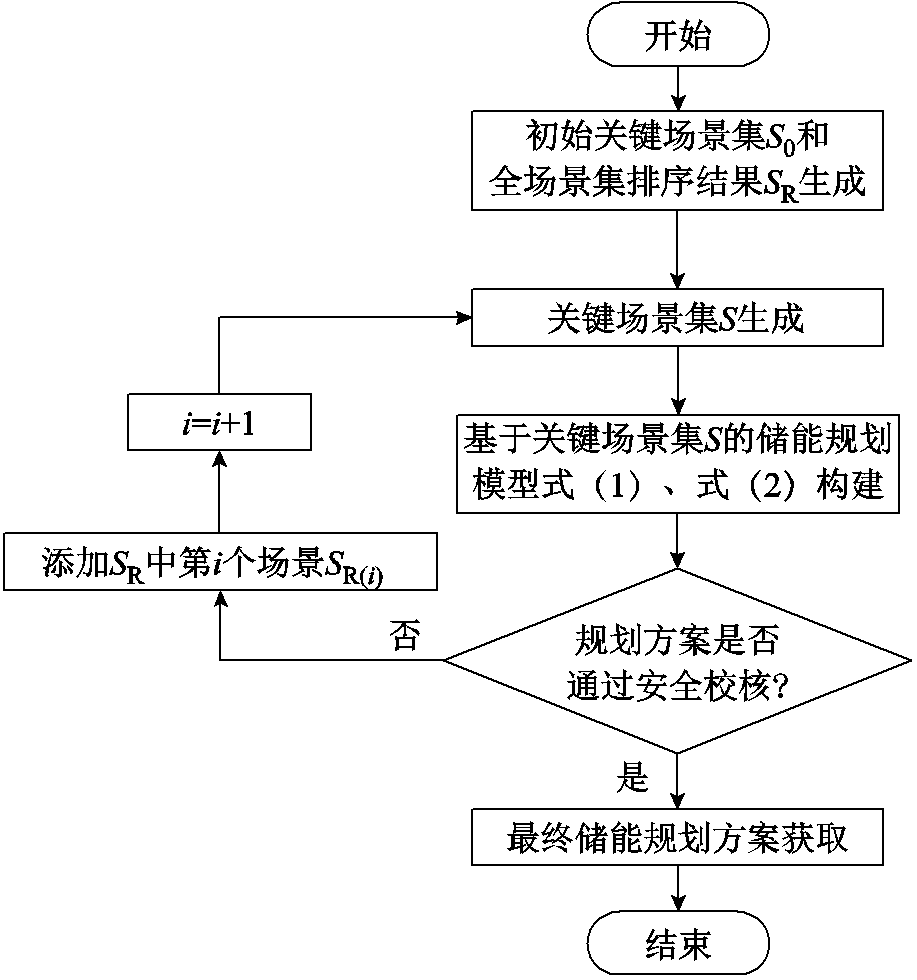
图1 基于场景集排序的闭环储能规划方法流程
Fig.1 Flow chart of the closed-loop energy storage planning method based on scenario set sorting
摘要 随着风电、光伏等新能源渗透率的不断提高,系统随机性与波动性的不断增强,科学合理地规划储能被认为是缓解新能源不确定性、提高电力系统安全性与灵活性的有效手段。然而,现有规划方法为了保证一定的计算效率,通常仅选取少量关键场景用以制定储能规划方案,无法确保其在全场景下的安全性,倘若对于全场景进行安全校核,又会因为模型规模大而导致求解时间在规划层面都难以接受。为此,该文提出一种面向全场景安全的储能投资高效规划方法。首先,针对现有规划方法存在的安全风险,提出一种面向全场景安全的闭环储能规划框架,以及基于全场景集排序结果引导的场景更新策略,可以保证规划方案在全场景下的安全性,同时兼顾一定的计算效率;其次,提出了一种基于自组织映射(SOM)神经网络及场景关键指标排序的初始关键场景集生成方法,该方法无需预先给定聚类数量,能够较准确地反映全场景的关键信息,进一步提高了计算效率;最后,基于IEEE 30节点系统以及国内某省实际341节点系统进行算例验证,结果表明所提方法可以在保障规划方案在全场景下的安全性与最优性的基础上,尽可能减少需考虑的场景数量,提高求解效率。
关键词:储能规划 多场景规划 场景筛选 安全校核 自组织映射神经网络
2021年10月26日,国务院印发《2030年前碳达峰行动方案》,明确提出要“全面推进风电、太阳能发电大规模开发和高质量发展,坚持集中式与分布式并举,加快建设风电和光伏发电基地”[1]。风、光等新能源具有很强的随机性和波动性,随着新能源渗透的不断提高,会给电力系统的灵活调节能力甚至安全稳定运行带来挑战[2-3]。电化学储能电站等储能设备被认为是缓解新能源随机性和波动性的有效手段[4-5]。然而,源荷两端的不确定性给含高比例新能源系统的储能投资决策问题带来了很大挑战。如果在储能投资规划阶段没有考虑到新能源在未来的波动情况,高估或者低估储能需求会分别带来高昂的非必要投资以及安全隐患[6]。因此,在储能规划阶段考虑系统在多场景下的运行模拟越发重要[7-8]。
为刻画新能源的短期波动、传统机组的爬坡及起停限制、储能的荷电状态耦合关系等要素,规划模型往往需要较细的时间颗粒度(例如小时级)[9-10],而储能投资规划问题往往涉及较长的时间尺度(例如未来5~10年),在整个规划时间尺度内准确地刻画系统运行状态会带来巨大的计算负担,完成求解耗时过长[11],导致规划人员难以利用规划计算工具迭代调试规划结果,实际应用难以接受。
场景削减是一种有效降低储能规划模型计算复杂度的手段,针对考虑场景削减的储能投资高效规划方法,国内外学者已开展了广泛研究,主要有两类思路:①通过场景削减方法减小规划模型规模,进而执行规划求解,此类方法通常不校验场景削减对安全性及经济性的影响,本文将其称为“开环储能规划方法”[12-13];②在储能规划问题场景筛选及削减后,求解规划模型并进行迭代校验,从而确保规划方案满足安全要求,本文称为“闭环储能规划方法”[14-15]。
开环储能规划方法作为闭环储能规划方法的基础,国内外学者主要研究如何提高场景聚合的精度[16]。部分学者通过将相似的负荷曲线[17]、新能源-负荷多维曲线[18]进行聚合,得到数量较少的典型日[19-20]、典型周[21]等典型场景,并在这些典型场景上进行储能规划[22-23];一部分学者通过对规划年全年负荷进行等级划分,得到用于规划计算的简化负荷曲线[24];也有学者引入0-1变量[25]以及状态转移矩阵[26]将负荷等级与负荷时序相耦合,以在规划模型中保留一定的时序特征;也有学者采用生成对抗神经网络[27],通过学习历史场景分布,生成海量的规划场景,进一步地,利用条件生成对抗神经网络[28-29],可以生成极端场景以及符合某些特定分布的典型场景。开环储能规划方法存在潜在假设,即认为场景聚合的效果越好,最后的规划方案与聚合前也越接近。然而,一些研究发现:场景聚合得好,规划结果未必精确[30]。由于聚合过程中极端信息的淹没[31],虽然聚类方法效果很好,但规划解精度不高甚至不可行[32]。
近年来,国内外部分学者通过优化的方法,将场景削减的效果与模型求解精度相结合,通过规划结果的精度引导关键场景的选择。针对这种闭环储能规划方法,主要研究思路是:首先通过专家经验法[33]、K-means聚类方法[34-35]等生成一组初始典型场景集,在该初始场景集下求解规划问题得到初始规划解,并分析在剩余场景下系统是否能够通过安全校核,倘若均可通过校核则认为已得到最终解;若存在未通过校核的场景,则将该场景添加至典型场景集进行下一次规划求解。然而,这种闭环储能规划方法在初始典型场景集生成、迭代添加典型场景两方面存在效率低下的问题:①在生成初始典型场景集时,专家经验法捕捉的典型场景数量往往较少,而K-means方法又需预先设定聚类数量且会淹没极端场景信息,导致这两种方法为了通过安全校核,均需较多的规划迭代次数,求解效率低下;②在迭代添加关键场景过程中,专家经验法添加所有未通过安全校核的场景,导致规划求解模型规模庞大、计算速度慢,而K-means方法通过简单增加K值来增加场景数量,其添加的场景可能并不是安全校核未通过的场景,导致此次迭代后规划方案可能仍然无法满足全场景下安全,需要进行新的迭代,求解效率低下。
对于规划场景数量的选定,目前还没有统一的方法。对于专家经验法[19],通常选择最大负荷、最小负荷、最大峰谷差、最小峰谷差四类场景,亦或是依据来水和负荷方式选择丰大、丰平、丰小、枯大、枯平、枯小六类场景;对于K-means[22]、K-medoids聚类[36]方法,聚类数量K需要预先指定,通常在可接受的计算时间里选择合适的场景数量,并在安全校核不通过时增加K值迭代计算;对于基于优化的储能规划方法[15],规划场景数量通常通过求解优化问题获得,例如判断前后两次规划解的差值是否小于阈值来确定是否增加场景数量;对于基于自组织映射(Self-Organizing Maps, SOM)神经网络的聚类方法,可根据聚类结果直接获得合适的聚类场景数量。
针对现有储能规划方法在全场景下安全性与计算效率难以兼顾的问题,本文提出了一种面向全场景安全的储能投资高效规划方法,其主要贡献如下:
1)针对现有储能规划方法将场景聚类与规划求解开环运行带来的安全风险,提出一种面向全场景安全的闭环储能规划框架,并通过构建基于起作用0-1变量固定的松弛储能规划模型,得到反映不同场景对规划解影响程度的全场景集排序结果,并基于该结果的引导实现关键场景集的高效更新,形成面向全场景安全的闭环储能规划方法。该方法可以保证规划方法的最优性,并尽可能地减少需考虑的场景数量。
2)针对现有基于K-means聚类的初始场景集生成方法需要预先给定聚类数量、易淹没极端场景、导致规划模型迭代次数多且无法保证规划方案在全场景下安全的问题,提出一种基于SOM神经网络及场景关键指标排序的初始场景集生成方法。该方法利用SOM神经网络的自组织无监督学习能力,无需预先给定聚类数量,并能在生成初始场景集时考虑到一些关键场景特征,较为准确地反映全场景关键特性,进一步提高了所提面向全场景安全的储能投资规划方法的计算效率,并在IEEE 30节点系统及国内某省实际341节点系统中验证了所提方法在安全性和计算效率上的优势。
本节针对现有储能规划方法在安全性和计算效率方面难以兼顾的不足,提出一种面向全场景安全的闭环储能规划方法,可以在保障规划方案安全性与最优性的基础上,提升一定的计算效率。并针对传统安全校核方法带来的模型规模大、计算效率低等问题,提出一种关键场景更新引导策略,该策略在安全校核未通过时仅添加少量关键场景,不仅可以保障规划结果的安全性,还可进一步减小模型规模,提高求解效率。
针对传统闭环储能规划方法在安全校核时添加所有未通过校核场景带来的效率低下问题,本节提出一种基于场景集排序的闭环储能规划方法,通过排序结果引导关键场景的添加,在保证规划解安全性的基础上,减少需添加的场景数量,提高规划模型迭代求解效率。基于场景集排序的闭环储能规划方法流程如图1所示。

图1 基于场景集排序的闭环储能规划方法流程
Fig.1 Flow chart of the closed-loop energy storage planning method based on scenario set sorting
主要步骤如下。
1)初始关键场景集S0和全场景集排序结果SR生成
通过专家经验法、K-means聚类等方法生成用于储能规划问题求解的初始关键场景集S0,并令关键场景集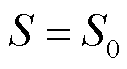 。基于场景集排序方法,获得全场景集
。基于场景集排序方法,获得全场景集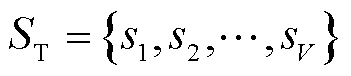 的排序结果
的排序结果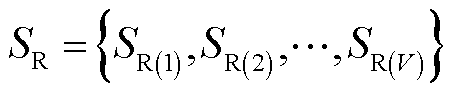 ,其中V为总场景数。场景集排序的具体方法将在1.2节详细介绍。令初始关键场景集更新迭代次数i=1。
,其中V为总场景数。场景集排序的具体方法将在1.2节详细介绍。令初始关键场景集更新迭代次数i=1。
2)基于关键场景集S的储能规划模型构建
基于关键场景集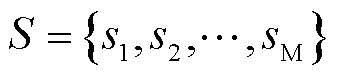 ,其中M为总关键场景数,建立基于关键场景运行约束的储能扩展规划模型式(1)、式(2),其为混合整数线性规划问题,可利用分支定界方法[37],通过构建分支定界搜索树对具有最优解可能性的可行解进行策略性穷举[38],得到储能规划方案,即储能总规划容量Ps。
,其中M为总关键场景数,建立基于关键场景运行约束的储能扩展规划模型式(1)、式(2),其为混合整数线性规划问题,可利用分支定界方法[37],通过构建分支定界搜索树对具有最优解可能性的可行解进行策略性穷举[38],得到储能规划方案,即储能总规划容量Ps。
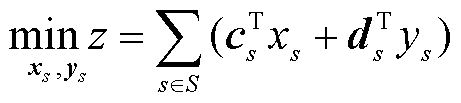 (1)
(1)
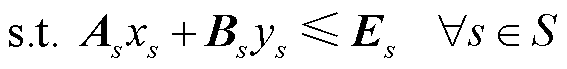 (2)
(2)
式中,s为场景编号;xs为连续变量,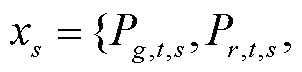
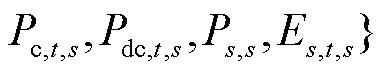 ;ys为0-1变量,
;ys为0-1变量,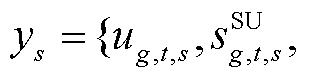
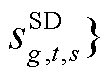 ;cs、ds、As、Bs、Es为常量矩阵。模型中各变量与约束的具体含义详见附录中式(A1)~式(A19)。式(1)为储能规划模型的目标函数,具体如式(A1)所示,包含储能投资成本式(A2)和系统运行成本式(A3);式(2)为关键场景集S下储能规划模型的约束条件,包括传统机组侧约束式(A4)~式(A8)、储能侧约束式(A9)~式(A12)、新能源侧约束式(A13)~式(A15)以及系统侧运行约束式(A16)~式(A19)。
;cs、ds、As、Bs、Es为常量矩阵。模型中各变量与约束的具体含义详见附录中式(A1)~式(A19)。式(1)为储能规划模型的目标函数,具体如式(A1)所示,包含储能投资成本式(A2)和系统运行成本式(A3);式(2)为关键场景集S下储能规划模型的约束条件,包括传统机组侧约束式(A4)~式(A8)、储能侧约束式(A9)~式(A12)、新能源侧约束式(A13)~式(A15)以及系统侧运行约束式(A16)~式(A19)。
3)储能规划方案安全校核
基于步骤2)所得储能规划方案,对所有场景进行安全校核,即判断在步骤2)配置的储能总规划容量PS下,全场景集ST下储能规划模型约束式(3)能否满足。如满足约束式(3),则所有场景均通过校核,该规划方案PS为最终规划方案;反之,则表示存在校核不通过的场景,转至步骤4)。
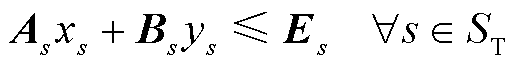 (3)
(3)
4)基于SR的关键场景集更新
基于全场景集排序结果SR,将SR中第i个场景SR(i)添加至关键场景集S,实现关键场景集的更新,即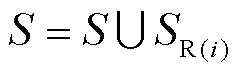 。并令i=i+1,转至步骤2)。
。并令i=i+1,转至步骤2)。
由图1可以看出,闭环储能规划方法的迭代收敛判据是全场景通过安全校核,因此可以确保规划方案的安全性。传统闭环储能规划方法缺少步骤2)中关键场景集S的生成以及步骤4)中全场景集排序结果SR的引导,随着新能源渗透率和系统不确定性的增加,为了得到在全场景下安全的储能规划方案,在步骤3)安全校核不通过时往往添加海量非关键场景,严重影响规划模型迭代求解效率。而本文所提基于场景集排序的闭环储能规划方法通过对比不同场景的关键程度,科学引导关键场景集的更新,有效提高了规划模型迭代求解的效率。
针对闭环储能规划模型在安全校核未通过时添加大量非关键场景带来的模型规模大、求解效率低的问题,本节提出一种关键场景更新引导策略,通过构建松弛储能规划模型并对不同场景约束对偶乘子进行排序,获得1.1节闭环储能规划方法步骤1)中反映全场景集ST关键程度的全场景集排序结果SR,并在安全校核未通过时基于SR的引导,顺次添加SR中的场景至关键场景集S,实现关键场景集S的高效更新。所提全场景集排序结果SR的生成方法流程如图2所示。
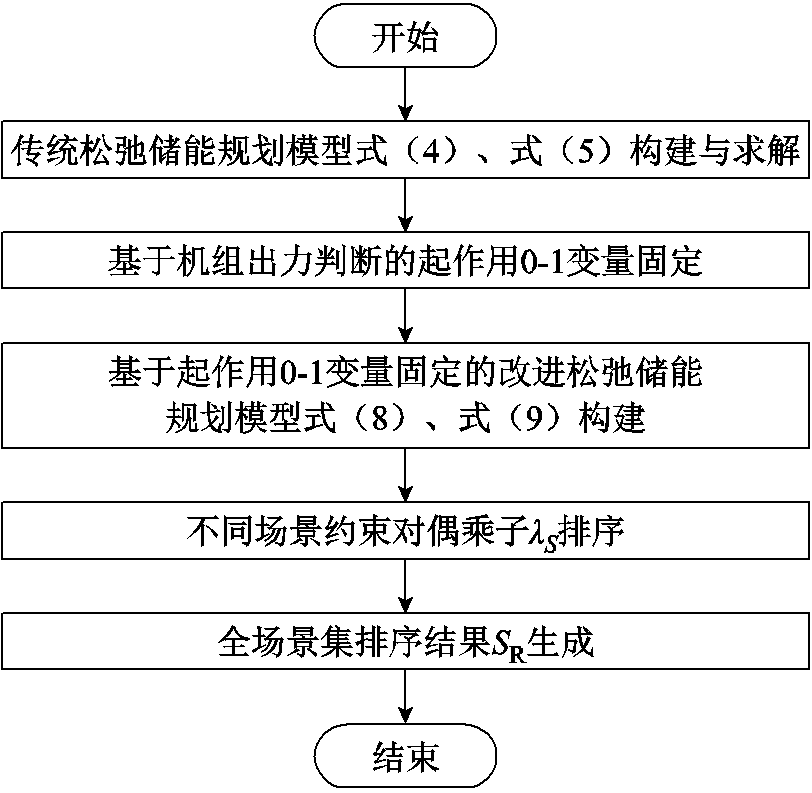
图2 全场景集排序结果SR生成方法流程
Fig.2 Flow chart of the method for generating the sorting results SR of the full scenario set
本节所提全场景集排序结果SR生成方法首先需要形成传统松弛储能规划模型。将式(1)、式(2)中的0-1变量均松弛为区间[0,1]上的连续变量,从而形成松弛储能规划模型[9]式(4)、式(5),其为线性规划问题,可采用单纯形法进行求解。
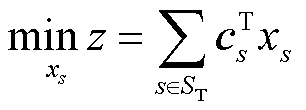 (4)
(4)
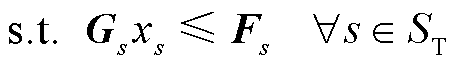 (5)
(5)
式(4)为松弛储能规划模型的目标函数;式(5)为松弛模型的约束条件,相比于式(2)松弛了含有离散变量的约束,Gs和Fs为常量矩阵。松弛模型中各变量与约束的具体含义详见附录中式(A24)。
对于松弛模型式(4)、式(5)的解,基于机组出力判断对其中起作用0-1变量进行固定,即通过式(6)、式(7)固定起作用0-1变量。若满足式(6),表明第g台火电机组在t时刻第s个场景下的出力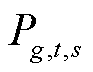 始终不小于其最小技术出力
始终不小于其最小技术出力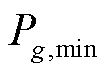 ,为常开机组,将其起停状态变量固定为1;若满足式(7),则将其起停状态变量固定为0,其中
,为常开机组,将其起停状态变量固定为1;若满足式(7),则将其起停状态变量固定为0,其中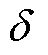 为一个预先设定的常数,通常可取0.1[39]。
为一个预先设定的常数,通常可取0.1[39]。
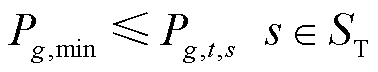 (6)
(6)
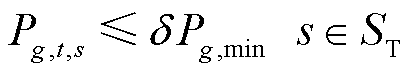 (7)
(7)
基于固定的起作用0-1变量,构建改进松弛储能规划模型。将上述方法中确定的0-1变量在式(1)、式(2)中固定,并将式(1)、式(2)中剩余的0-1变量松弛为在区间[0,1]上的连续变量,获得基于部分0-1变量预固定的改进松弛储能规划模型式(8)、式(9)。相较于传统松弛储能规划模型式(4)、式(5),式(8)、式(9)预先固定了一部分不易发生改变的0-1变量,使得待松弛变量数目减少,松弛解精度更高,从而使得本节后续获得的不同场景约束对偶乘子也更精确。
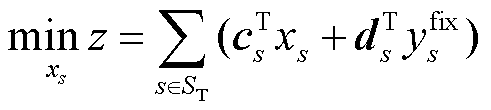 (8)
(8)
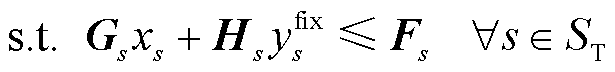 (9)
(9)
式中,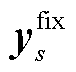 为固定的0-1变量;Hs为常量矩阵。式(8)为改进松弛储能规划模型的目标函数,式(9)为改进松弛储能规划模型的约束条件。
为固定的0-1变量;Hs为常量矩阵。式(8)为改进松弛储能规划模型的目标函数,式(9)为改进松弛储能规划模型的约束条件。
进一步地,基于最优性条件,对于不同场景下约束的对偶乘子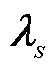 进行排序。
进行排序。
对于松弛模型式(8)、式(9),其拉格朗日函数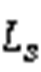 为
为
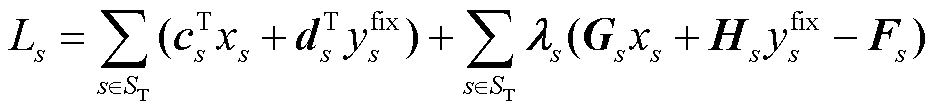 (10)
(10)
式中, ls为拉格朗日乘子组成的向量,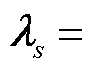
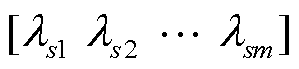 ,m为场景s中约束总数。
,m为场景s中约束总数。
当模型式(8)、式(9)取得最优解时,需要满足包括驻点条件式(11)、互补松弛条件式(12)、原可行性条件式(13)、对偶可行性条件式(14)的最优性条件[37]。
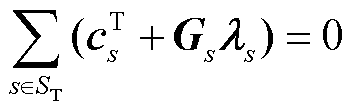 (11)
(11)
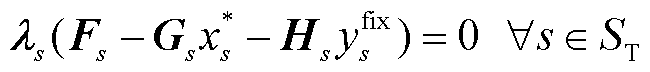 (12)
(12)
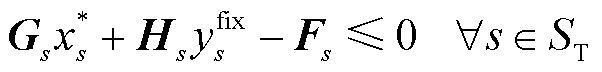 (13)
(13)
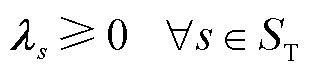 (14)
(14)
式中,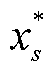 为松弛模型式(8)、式(9)的最优解。
为松弛模型式(8)、式(9)的最优解。
基于以上最优性条件,对于不同场景约束是否起作用进行判断。对于约束式(9)中第s个场景下的约束,倘若其对应的对偶乘子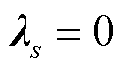 ,则互补松弛条件式(12)、对偶可行性条件式(14)恒成立,该约束不起作用,即场景s不是对于规划解产生影响的关键场景;反之,当其对应的对偶乘子
,则互补松弛条件式(12)、对偶可行性条件式(14)恒成立,该约束不起作用,即场景s不是对于规划解产生影响的关键场景;反之,当其对应的对偶乘子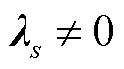 时,受互补松弛条件式(12)的限制,约束式(13)中第s个场景下的约束转换为起作用等式约束,说明场景s是对规划解产生影响的关键场景,且对偶乘子
时,受互补松弛条件式(12)的限制,约束式(13)中第s个场景下的约束转换为起作用等式约束,说明场景s是对规划解产生影响的关键场景,且对偶乘子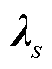 取值大小可以反映该约束对于规划解的影响程度,
取值大小可以反映该约束对于规划解的影响程度,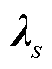 取值越大,该约束对于规划解的影响程度也越大。
取值越大,该约束对于规划解的影响程度也越大。
最后,基于上述分析,采用单纯形法求解改进松弛储能规划模型式(8)、式(9),获得不同场景约束的对偶乘子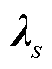 ,通过式(15)选取
,通过式(15)选取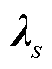 中的最大值
中的最大值 作为场景s的代表对偶乘子,并对
作为场景s的代表对偶乘子,并对 大小进行排序,根据排序结果生成全场景集排序结果SR。
大小进行排序,根据排序结果生成全场景集排序结果SR。
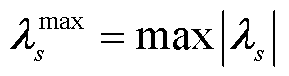 (15)
(15)
本节所提关键场景更新引导策略首先对于传统松弛储能规划模型进行改进,提高了松弛解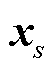 和不同场景约束对偶乘子
和不同场景约束对偶乘子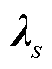 的精度,并通过最优性条件进行起作用约束判断,对于不同场景约束代表对偶乘子
的精度,并通过最优性条件进行起作用约束判断,对于不同场景约束代表对偶乘子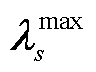 进行排序,生成全场景集排序结果SR。所提方法充分利用不同场景约束关键程度的信息,实现了关键场景集的高效更新,可有效缓解闭环储能规划模型在安全校核未通过时添加大量场景带来的模型规模大、求解效率低的问题。
进行排序,生成全场景集排序结果SR。所提方法充分利用不同场景约束关键程度的信息,实现了关键场景集的高效更新,可有效缓解闭环储能规划模型在安全校核未通过时添加大量场景带来的模型规模大、求解效率低的问题。
本节所提面向全场景安全的闭环储能投资规划方法在尽可能减少需考虑场景数量的基础上,可以保证规划方法的最优性,具体说明如下。
令所有满足约束条件式(3)的储能投资规划方案集合为可行储能方案集合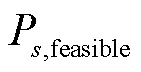 ;在全场景集ST下获得的储能投资方案为
;在全场景集ST下获得的储能投资方案为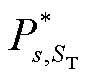 ;本文所提基于关键场景集S排序方法获得的储能投资方案为
;本文所提基于关键场景集S排序方法获得的储能投资方案为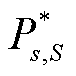 。
。
由图1可以看出,闭环储能规划方法的迭代收敛判据是规划方案通过全场景安全校核,因此可以保证安全性,即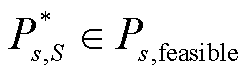 ;又因为关键场景集为全场景集的子集,即
;又因为关键场景集为全场景集的子集,即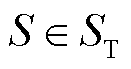 ,使得储能投资规划方案
,使得储能投资规划方案 。
。
综上所述,所提基于关键场景集排序的闭环储能规划方法可以保证结果的安全性与最优性,并提高一定的计算效率。
根据第1节提出的闭环储能规划方法,首先需要确定一组初始关键场景集S0。针对传统初始关键场景集选取方法需要预先给定聚类数量、易淹没极端场景信息、导致规划迭代次数多等问题,本节提出一种基于SOM神经网络的初始关键场景集聚类方法。并且,针对SOM神经网络无法给出聚类代表场景的问题,提出一种基于关键场景特征排序的聚类代表场景选取方法,通过选取最大负荷、最大峰谷差、最大净负荷爬坡需求等关键特征指标对每一类场景进行排序,提取每类场景中的代表场景,获得能准确反映全场景特征的初始关键场景集S0,进一步提高闭环储能规划模型的求解效率。
本节提出一种基于SOM神经网络的初始关键场景集聚类方法。该方法利用SOM神经网络的自组织能力,无需预先给定聚类数量,并能在准确反映典型场景特征的基础上充分保留极端场景信息,使得关键场景集S0能有效反映全场景关键特征,从而有效减少规划迭代次数。
SOM神经网络由芬兰学者T. Kohonen于20世纪80年代提出[40],其具有自我学习能力,可以自适应地改变神经网络的参数,即具有自组织能力,可以实现无监督学习,在模式识别、聚类等领域应用广泛。SOM神经网络由输入层和竞争层(输出层)构成,输入层为具有不同特征的高维变量,竞争层可以是一维、二维或者多维的,通常为了便于可视化展示选择一维或二维,其结构如图3所示。当一组输入向量进入SOM神经网络时,对应一个神经元被激活,即“获胜神经元”,该神经元邻域内的神经元将被更新权重以体现竞争结果,其他神经元则被抑制。

图3 含有二维竞争层的SOM神经网络结构
Fig.3 SOM neural network structure diagram with two-dimensional competition layer
采用本文所提基于SOM神经网络生成初始关键场景集S0时,首先要构建基于全场景集ST净负荷曲线的SOM神经网络,包括:①选取全场景集ST的净负荷曲线作为输入层特征向量;②构建z×z层神经网络并赋予竞争层神经元初始权重;③设定初始学习率并设置权值误差阈值及迭代次数阈值;④设置初始场景编号i=1。
完成SOM神经网络构建后,输入不同场景的净负荷曲线,获取场景si对应的获胜神经元k。对于场景si的净负荷向量Xi,通过式(16)计算得到与竞争层中每一个神经元j(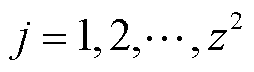 )欧式距离最小的获胜神经元k。设置初始迭代次数t=1。
)欧式距离最小的获胜神经元k。设置初始迭代次数t=1。
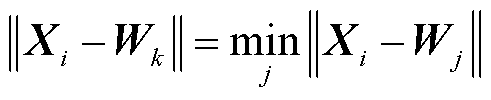 (16)
(16)
式中,Xi为第i个场景输入净负荷向量;Wk和Wj分别为竞争层中第k个和第j个神经元的权重向量; k为获胜神经元编号。
获得场景si对应的获胜神经元k后,基于邻域距离,对于竞争层神经元k进行权重更新。基于邻域函数h,通过式(17)更新场景si对应获胜神经元k邻域内第j个神经元的权重向量Wj,使其向获胜神经元k靠拢。令t=t+1,重复式(17)训练过程,当前后两次权值误差小于给定阈值,或者达到迭代次数阈值后,停止训练,完成权重更新。
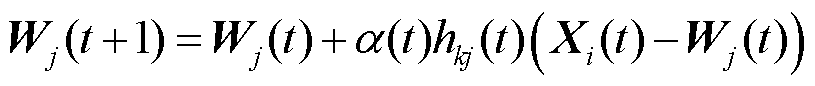 (17)
(17)
式中,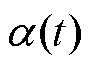 为SOM神经网络在第t次迭代时的学习率;
为SOM神经网络在第t次迭代时的学习率;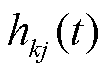 为第t次迭代获胜神经元k的邻域函数,通常选择高斯函数[41-42]。
为第t次迭代获胜神经元k的邻域函数,通常选择高斯函数[41-42]。
最后,进行迭代收敛判断。若迭代场景编号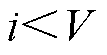 ,则令i=i+1,获取第i+1个场景对应的获胜神经元并对其邻域内神经元权重进行更新;若
,则令i=i+1,获取第i+1个场景对应的获胜神经元并对其邻域内神经元权重进行更新;若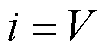 ,说明已遍历所有场景,迭代结束。通过分析竞争层神经元分布,输出场景聚类数量n和场景聚类结果
,说明已遍历所有场景,迭代结束。通过分析竞争层神经元分布,输出场景聚类数量n和场景聚类结果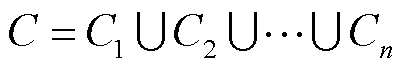 ,其中
,其中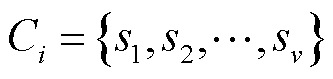 表示第i类场景
表示第i类场景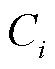 中包含v个场景。
中包含v个场景。
由于SOM神经网络只能给出场景聚类情况,无法确定每一类场景中的代表场景,本节基于三个场景特征指标,选取出第i类场景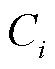 中的代表性场景
中的代表性场景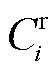 ,提出了基于场景特征排序的聚类代表场景选取方法,实现初始关键场景集S0的有效筛选。
,提出了基于场景特征排序的聚类代表场景选取方法,实现初始关键场景集S0的有效筛选。
本文所提基于场景特征排序的聚类代表场景选取方法,具体分为以下三种情况:
1)含有全场景最大负荷的代表场景选取。最大负荷可以反映电网的负荷需求,是电力系统规划时最常考虑的场景[43]。记全场景集ST下最大负荷场景为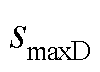 ,若
,若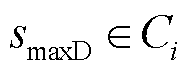 ,则选取
,则选取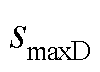 作为第i类场景
作为第i类场景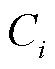 中的代表场景
中的代表场景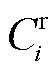 。
。
2)含有全场景最大峰谷差的代表场景选取。最大峰谷差可以反映负荷的波动情况,是储能规划时常考虑的场景[2]。记全场景集ST下最大峰谷差场景为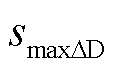 ,若
,若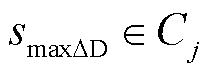 ,则选取
,则选取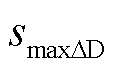 作为第j类场景
作为第j类场景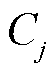 中的代表场景
中的代表场景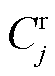 。
。
3)剩余聚类的代表场景选取。净负荷可以综合反映新能源与负荷的波动情况,最大净负荷爬坡需求式(18)可以反映电力系统在短期内的灵活性需求,是高比例新能源渗透的新型电力系统储能规划中需要重点考虑的场景特征[44]。对于第k类场景
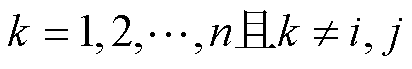 ),记其中满足式(18)的该类别场景下最大净负荷爬坡需求场景为
),记其中满足式(18)的该类别场景下最大净负荷爬坡需求场景为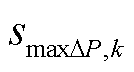 ,选取
,选取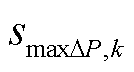 作为第k类场景中的代表场景
作为第k类场景中的代表场景
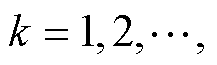
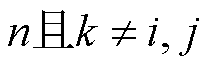 )。
)。
 (18)
(18)
式中,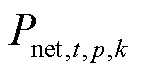 和
和 分别为系统在第k个场景类别下第p个场景中t时段和
分别为系统在第k个场景类别下第p个场景中t时段和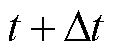 时段的净负荷需求。本节中净负荷需求指系统总负荷需求减去总新能源预测出力。
时段的净负荷需求。本节中净负荷需求指系统总负荷需求减去总新能源预测出力。
本节基于以上三种场景聚类中的代表场景,生成初始关键场景集S0,即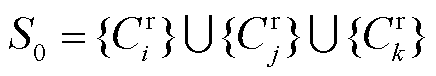 。本节所提基于SOM神经网络及关键特征排序的初始关键场景集S0筛选方法,利用SOM神经网络的无监督学习能力,无需预先给定聚类数量n,可在准确反映典型场景特征的基础上,充分保留极端场景信息,并综合考虑了最大负荷、最大峰谷差、最大净负荷爬坡需求等重要场景特征,在初始关键场景集S0筛选时能够准确反映全场景特性,有利于闭环储能规划模型计算效率的提升。
。本节所提基于SOM神经网络及关键特征排序的初始关键场景集S0筛选方法,利用SOM神经网络的无监督学习能力,无需预先给定聚类数量n,可在准确反映典型场景特征的基础上,充分保留极端场景信息,并综合考虑了最大负荷、最大峰谷差、最大净负荷爬坡需求等重要场景特征,在初始关键场景集S0筛选时能够准确反映全场景特性,有利于闭环储能规划模型计算效率的提升。
本节采用IEEE 30节点系统及国内某省实际341节点系统验证所提方法的有效性和实用性。在3.1节,对比传统储能规划方法与本文所提方法,验证所提闭环储能规划方法在安全性和高效性方面的优势;在3.2节,对比不同初始关键场景集S0选择策略及不同场景更新策略对于求解时间的影响,验证本文所提方法在计算效率上的优势;在3.3节,进一步增加全场景集ST中场景数量,验证所提方法在处理大量规划场景时的适应性。对比以下九种方法:
M0:全场景下求解储能扩展规划模型[7]。
M1:采用典型日法进行规划,典型日通过专家经验法[19]确定。
M2:采用典型日法进行规划,典型日通过K-means聚类方法[22]确定。
M3:现有典型方式规划方法,其中典型方式通过专家经验法确定,场景更新策略为添加所有未通过安全校核的场景[33]。
M4:传统K-means规划方法,其中关键场景初始集由K-means聚类方法确定,迭代过程中场景更新策略为增加K值[22]。
M5:本文所提“场景削减-规划求解-安全校核”迭代求解方法,其中场景初始集由SOM神经网络结合场景特征指标排序确定,场景更新中采用所提关键场景更新引导策略。
M6:与M5相比,初始场景集由专家经验法[14]确定。
M7:与M5相比,场景更新策略为添加所有未通过安全校核的场景[33]。
M8:与M5相比,初始场景集由K-medoids聚类方法[36]确定。
本文中所有算例均在AMD Ryzen 7 6800H CPU @3.20 GHz、16 GB RAM硬件环境下测试。储能在系统中的参数设置见表1,算例中其他参数设置情况与源代码参见文献[45]。算例中使用的SOM神经网络在Matlab环境中进行搭建,网络结构在3.1节和3.2节均设置为6×6层,在3.3节设置为20×20层,最大迭代次数设置为100。
表1 储能参数
Tab.1 Parameters of energy storage

参数数值(30/341节点系统) 储能充电效率(%)90/90 储能放电效率(%)90/90 储能持续充放电时间/h2/2 单位功率成本系数s1/(元/W)2/2 单位能量成本系数s2/[元/(W·h)]3/3 储能投资年限/年10/10 通货膨胀率(%)2/2 贴现率(%)8/8
本节采用我国某省实际负荷及新能源小时级出力数据(即每个场景中含有24个时段),在IEEE 30节点系统和包含341个节点的国内某省实际电力系统中,通过比较M0~M8的投资方案、规划结果安全性、关键场景集S场景数量及求解时间,验证所提闭环储能规划方法在安全性和高效性方面的优势,具体计算结果分别见表2和表3。其中,全场景集ST场景数目在两个系统中均为30。
表2 IEEE 30节点系统中不同方法计算结果对比
Tab.2 Comparison of calculation results of different methods in IEEE 30 bus system

方案储能规划容量/MW是否通过全场景安全校核关键场景集S场景数量求解总时间/s M055.36是30220.6 M150.38否44.1 M242.93否54.6 M355.36是1519 M460.74是1519 M555.36是54.6 M655.36是65.8 M755.36是1212.6 M855.36是99.1
表3 某省实际341节点系统中不同方法计算结果对比
Tab.3 Comparison of calculation results of different methods in actual 341-bus system in a certain province

方案储能规划容量/MW是否通过全场景安全校核关键场景集S场景数量求解总时间/s M01 588是301 169 M197否446 M21 043否573 M31 588是11169 M41 227否301 165 M51 588是673 M61 588是793 M71 588是10149 M81 588是17564
M0方法在全场景下直接求解储能规划模型,选取所有30个场景,所得方案可以确保安全性,但是耗时远远高于其他方法;M1与M2方法为开环储能规划方法,场景数量选取较少,虽然计算时间短但是无法保障安全性,无法在实际中应用;M3方法为传统专家经验法,通过安全校核可以保障规划方案的安全性,但由于其安全校核不通过时添加所有未通过场景,使得模型规模较大,求解时间较慢;M4方法基于K-means聚类方法,其会淹没极端场景信息,由表3可以看出其并不能保障规划方案在全场景下的安全性,且求解时间也不具优势;所提M5方法在保障安全性的基础上尽可能少地选取关键场景数量,减小模型规模,相较于传统闭环储能规划方法M3在计算效率上有显著优势,在两个系统上分别可以减少75.8%和56.8%的计算时间。
本节沿用3.1节计算结果,通过比较M5与M6验证所提初始关键场景集S0生成策略的有效性;通过比较M5与M7验证所提关键场景更新引导策略的有效性。IEEE 30节点系统与某省实际341节点系统全场景集净负荷曲线如图4所示。
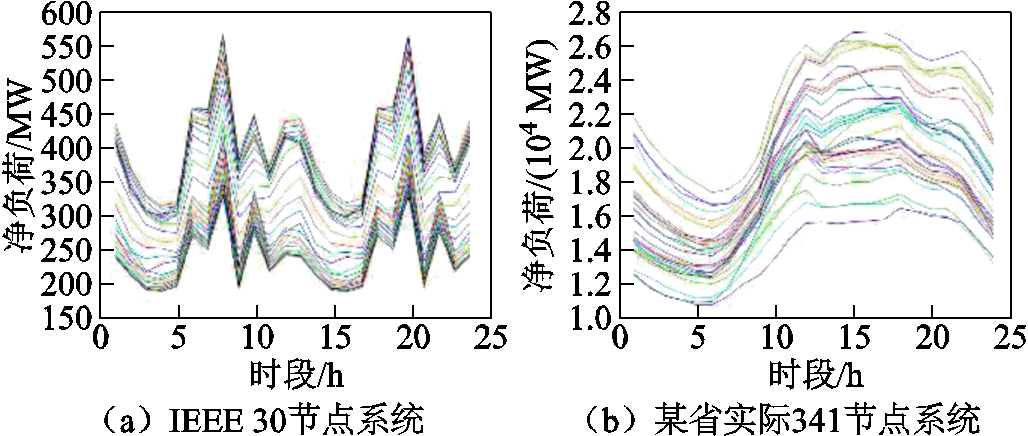
图4 IEEE 30节点系统与某省实际341节点系统全场景集净负荷曲线
Fig.4 Full scenario set load curves for IEEE 30 bus system and actual 341-bus system in a certain province
对于初始关键场景集S0的生成,在IEEE 30节点系统中,M6方法选择最大负荷日、最小负荷日、最大峰谷差日、最小峰谷差日4个典型日(对应场景编号9、15、26、27)作为初始场景集S0,具体如图5a所示,通过2次迭代添加场景实现全场景下的安全校核;M5方法通过SOM神经网络将全场景集中30组净负荷数据聚为4类,如图6所示,并基于2.2节所提特征指标排序方法确定每一类的代表场景,同样得到四个典型日(对应场景编号5、14、18、26)作为初始场景集S0,如图5b所示,仅需通过1次迭代即可通过全场景下的安全校核,所提M5方法的总计算时间相较于传统M6方法减少了20.7%。在某省实际341节点系统中,M6与M5方法的初始场景数量均为4,初始场景集分别如图7a和图7b所示,M5方法中SOM神经网络的聚类结果如图8所示,所需迭代次数分别为3和2,在总的计算时间上所提M5方法相较于M6减少了21.5%。

图5 IEEE 30节点系统初始场景集聚类结果
Fig.5 Clustering results of the initial scenario set for IEEE 30 bus system
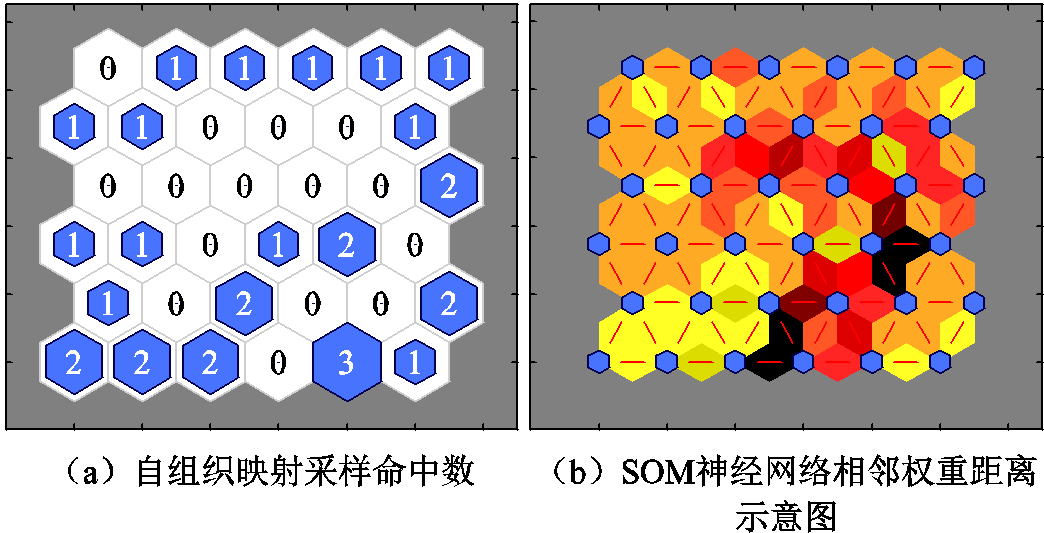
图6 IEEE 30节点系统SOM神经网络初始场景聚类结果
Fig.6 Clustering results of the initial scenario set for an IEEE 30 bus system based on SOM neural network
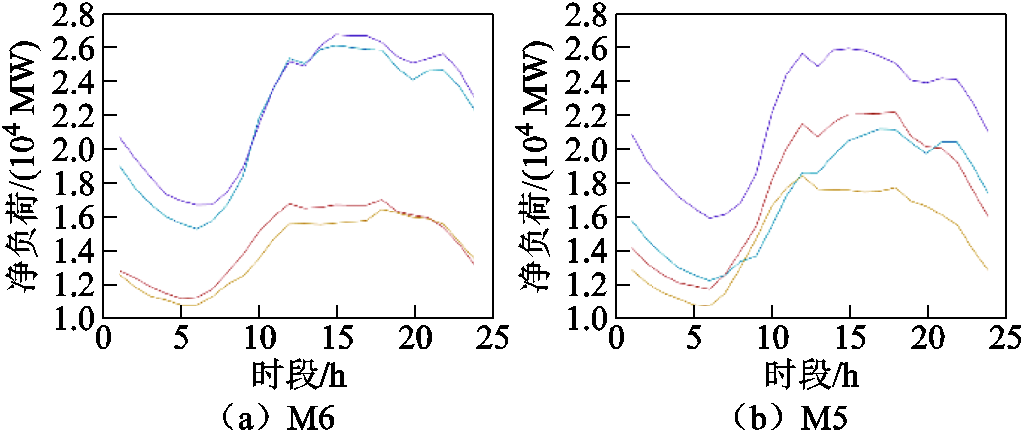
图7 某省实际341节点系统初始场景集聚类结果
Fig.7 Clustering results of the initial scenario set for actual 341-bus system in a certain province

图8 某省实际341节点系统SOM神经网络初始场景聚类结果
Fig.8 Clustering results of the initial scenario set for actual 341-bus system in a certain province based on SOM neural network
对于关键场景更新引导策略,在IEEE 30节点系统中,当安全校核不通过时,M5方法基于全场景集排序结果SR,通过1次迭代,添加1个关键场景即可得到最终规划方案;M7方法添加所有8个未通过校核的场景获得最终规划方案,M5的总计算时间较M7减少了63.5%。在某省实际341节点系统中,M5方法通过2次迭代,添加2个关键场景得到最终规划方案;M7方法添加所有6个未通过校核的场景获得最终规划方案,M5的总计算时间相较于M7减少了51%。
除了系统功率缺额导致系统灵活性不足外,线路阻塞导致系统灵活调节能力不足也是影响储能规划方案的重要因素。本节分析在不同的线路传输功率限值下,IEEE 30节点系统和某省实际341节点系统储能规划方案的变化情况。
两个系统中不同线路传输功率限值下储能规划容量分别见表4和表5。可以看出,随着线路传输功率限值的降低,系统的储能需求呈现增长趋势,这也反映了合理投资储能既可以缓解系统由于功率缺额导致的灵活爬坡能力不足的问题,也可以缓解由于线路阻塞导致的灵活性不足问题,体现了储能在延缓输电线路建设方面发挥着重要作用。
表4 IEEE 30节点系统中不同线路传输功率限值下储能规划容量
Tab.4 Energy storage planning capacity under different transmission power limits in IEEE 30 bus system

传输功率限值(%)储能规划容量/MW 10055.36 9055.36 8055.36 7077.21 60130.17
表5 某省实际341节点系统中不同线路传输功率限值下储能规划容量
Tab.5 Energy storage planning capacity under different transmission power limits in actual 341-bus system in a certain province

传输功率限值(%)储能规划容量/MW 1001 894 901 894 803 380 704 499 605 700
进一步地,在IEEE 30节点系统中,针对净负荷波动性的场景进行了算例验证,全场景集净负荷曲线如图9所示。专家经验法生成的初始关键场景集如图10a所示,基于SOM神经网络生成的初始关键场景集如图10b所示。M0~M8方法的投资方案、规划结果安全性、关键场景集场景数量及求解时间见表6。可以看出,所提方法M5在保障规划方案在全场景安全的前提下,有效减少待考虑场景数量,提高计算效率。
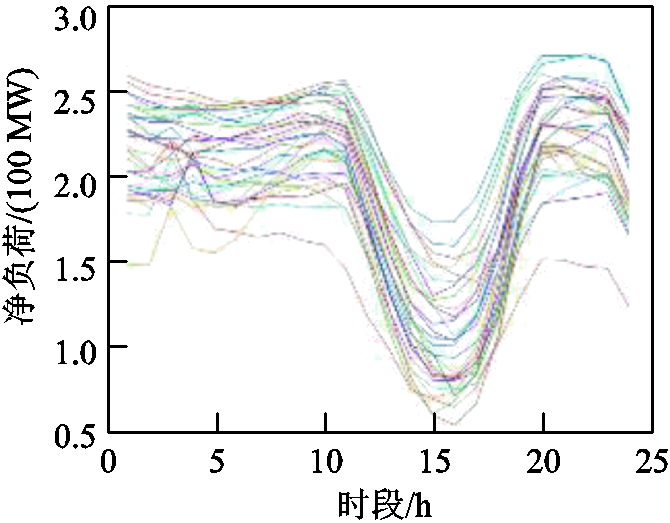
图9 具有强波动性的IEEE 30节点系统全场景集净负荷曲线
Fig.9 Full scenario set load curves for IEEE 30 bus system with high uncertainty
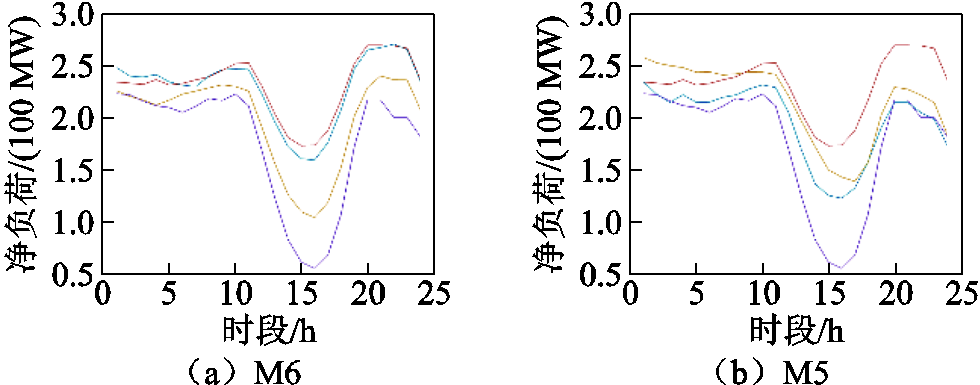
图10 具有强波动性的IEEE 30节点系统初始场景集聚类结果
Fig.10 Clustering results of the initial scenario set for IEEE 30 bus system with high uncertainty
表6 具有强波动性的IEEE 30节点系统中不同方法计算结果对比
Tab.6 Comparison of calculation results of different methods in IEEE 30 bus system with high uncertainty

方案储能规划容量/MW是否通过全场景安全校核关键场景集S场景数量求解总时间/s M0126.9是30252 M1104.5否44.2 M292.6否55.3 M3126.9是1214.5 M4126.9是1519.9 M5126.9是55.3 M6126.9是66.6 M7126.9是99.6 M8126.9是1011.2
对于在该系统上所规划的126.9 MW/253.8 MW·h储能电站,其投资成本大约为3.78亿元。在储能运行模拟中考虑表7中所示的峰谷电价[46],储能电站一年的收益约为0.744亿元,约5.08年即可收回储能投资成本。考虑到现阶段储能电站寿命周期,该规划方法具有一定的经济价值。
表7 分时电价参数
Tab.7 Parameters of time-of-use electricity price

时段电价/[元/(kW·h)] 9:00—11:00、15:00—17:000.902 031 6 8:00—9:00、13:00—15:00、17:00—22:000.747 54 11:00—13:00、22:00—次日8:000.249 18
本节在我国某省实际341节点系统上,增加全场景集ST中场景数量(即ST中场景数量增加至365),通过对比传统基于专家经验的闭环储能规划方法与所提安全高效闭环储能规划方法的储能规划方案、规划结果安全性、所考虑关键场景集S场景数量以及求解总时间,验证所提闭环储能规划方法在处理大量规划场景时的适应性。
传统闭环储能规划方法M3选择6类典型场景作为初始关键场景集S0,得到初始1 084 MW的储能规划方案,在安全校核不通过时添加所有116个未通过校核场景重新求解储能规划问题,在两周的计算时间限制(即求解时间限制为1 209 600 s)下,未能完成最终储能规划方案的求解;所提方法M5采用SOM神经网络结合场景特征指标排序确定26个场景作为初始关键场景集S0,如图11所示,并通过15次迭代添加15个场景获得最终储能规划方案,具体计算结果见表8。对比M5与M3,可以看出本文所提安全高效闭环储能规划方法在考虑大量规划场景时具有较强的适应性。

图11 某省实际多场景341节点系统初始场景集聚类结果
Fig.11 The results of the initial scenario set for actual 341-bus system in a certain province with multi scenarios
表8 某省实际341节点系统多场景储能规划方案
Tab.8 The energy storage planning scheme for actual 341-bus system in a certain province with multi scenarios

方案M3M5 储能规划容量/MW1 0841 894 是否通过全场景安全校核否是 关键场景集S场景数量12241 求解总时间/s1 209 60014 251
为克服传统闭环储能规划方法难以兼顾全场景安全性和计算效率的问题,本文提出了面向全场景安全的闭环储能投资高效规划框架,在保证规划方案安全性的前提下,兼顾一定的计算效率。并在此基础上,通过构建基于起作用0-1变量的松弛储能规划模型,提出一种关键场景更新引导策略,基于SOM神经网络及场景特征指标排序方法提出一种初始关键场景集S0筛选方法,进一步提高了规划模型的计算效率。最后,通过在IEEE 30节点系统及国内某省实际341节点系统中测试算例,验证了本文所提方法的有效性。主要内容包括:
1)为有效兼顾闭环储能规划方法的安全性和高效性,提出了基于场景集排序的闭环储能规划方法,基于最优性条件起作用判断对改进的松弛储能规划模型不同场景约束对偶乘子进行排序,获得了反映全场景集关键程度的全场景集排序结果,有效引导了关键场景的更新,在保障安全性的基础上明显提高了计算效率。为验证方法的准确性,本文在IEEE 30节点系统和某省实际341节点系统中构建了考虑少量场景的案例(全场景集中仅有30个场景),在不损失精度、保证安全性的前提下,所提方法的计算效率相较于传统典型方式规划法可分别提高3.13倍和14.9倍。在考虑完整一年365天全场景的341节点省级实际系统中,由于内嵌全场景安全约束的规划模型规模过大,传统方法在336 h(两周)的计算时间限制下未能获得最终的储能规划方法,而所提方法可在3.96 h内获得全场景安全下的储能规划方案。
2)为进一步提高闭环储能规划模型的求解效率,本文利用SOM神经网络的自组织能力,提出了基于SOM神经网络的初始关键场景集聚类方法,保留了场景的典型与极端特征。在此基础上,提出了一种基于场景特征指标排序的代表场景选取方法,提高了初始场景集对于全场景特性的反映能力,并验证了所提闭环储能规划方法在处理大量规划场景时的适应性,表明其具有实际应用价值。
本文所研究对象为安全高效的储能投资规划问题,可以提高新型电力系统的灵活调节能力,具有一定的现实意义。此外,随着新型电力系统源-网- 荷-储侧的耦合日趋增强,针对电源、电网、可调节负荷与储能侧协同规划模型的关键场景聚类与筛选方法是后续研究的重点。
附 录
1. 储能规划模型
1)目标函数
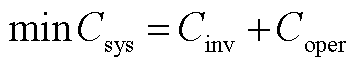 (A1)
(A1)
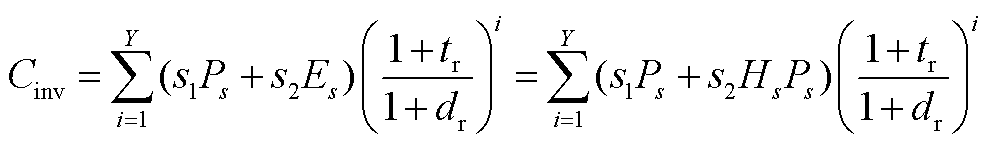 (A2)
(A2)
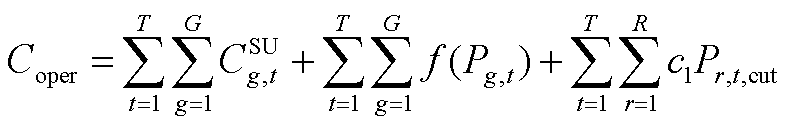 (A3)
(A3)
式中,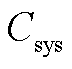 为系统总成本;
为系统总成本;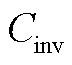 为系统投资成本;
为系统投资成本; 为系统运行成本;
为系统运行成本;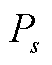 和
和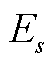 分别为储能规划的功率和容量;s1和s2分别为储能的单位功率成本系数和单位容量成本系数;
分别为储能规划的功率和容量;s1和s2分别为储能的单位功率成本系数和单位容量成本系数;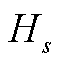 为储能的持续充放电时间,本文选取现阶段最为通用的电化学储能进行研究,
为储能的持续充放电时间,本文选取现阶段最为通用的电化学储能进行研究,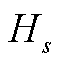 =2 h;tr为通货膨胀率;dr为贴现率;Y为储能投资年限。式(A3)中的第一项为火电机组的起停成本,第二项为火电机组的煤耗成本,第三项为弃风弃光惩罚成本;T为关键场景集中含有的总时段数;G为总火电机组数;R为总新能源机组数;
=2 h;tr为通货膨胀率;dr为贴现率;Y为储能投资年限。式(A3)中的第一项为火电机组的起停成本,第二项为火电机组的煤耗成本,第三项为弃风弃光惩罚成本;T为关键场景集中含有的总时段数;G为总火电机组数;R为总新能源机组数;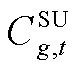 为第g台火电机组在第t个时段的起停成本;
为第g台火电机组在第t个时段的起停成本;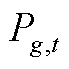 为第g台火电机组在第t个时段的出力;
为第g台火电机组在第t个时段的出力;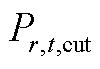 为第r台新能源机组在第t个时段的新能源削减功率;c1为新能源削减惩罚成本系数。
为第r台新能源机组在第t个时段的新能源削减功率;c1为新能源削减惩罚成本系数。
2)约束条件
(1)传统机组侧约束
出力上下限约束为
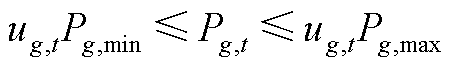 (A4)
(A4)
式中,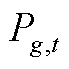 为第g台火电机组在第t个时段的出力;
为第g台火电机组在第t个时段的出力;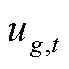 为第g台火电机组在第t个时段的起停状态,为0-1变量;
为第g台火电机组在第t个时段的起停状态,为0-1变量;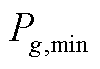 和
和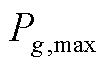 分别为第g台火电机组的最小技术出力和出力上限。
分别为第g台火电机组的最小技术出力和出力上限。
爬坡约束为
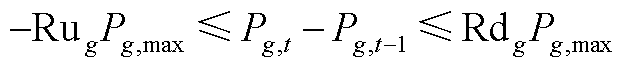 (A5)
(A5)
式中,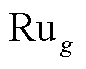 和
和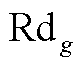 分别为第g台火电机组的上、下爬坡速率;
分别为第g台火电机组的上、下爬坡速率;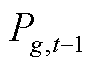 为第g台火电机组在第t-1个时段的出力。
为第g台火电机组在第t-1个时段的出力。
最小起停时间约束为
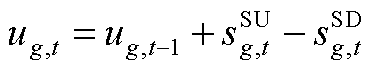 (A6)
(A6)
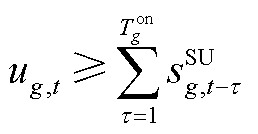 (A7)
(A7)
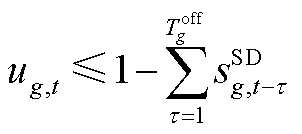 (A8)
(A8)
式中,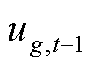 为第g台火电机组在第t-1个时段的起停状态;
为第g台火电机组在第t-1个时段的起停状态;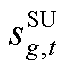 和
和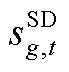 分别为第g台火电机组在第t个时段的起动/关停动作变量,为0-1变量;
分别为第g台火电机组在第t个时段的起动/关停动作变量,为0-1变量;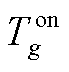 和
和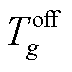 分别为第g台火电机组的最小起动、停机时间。
分别为第g台火电机组的最小起动、停机时间。
(2)储能侧约束
充放电功率下限约束为
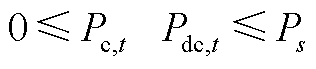 (A9)
(A9)
式中,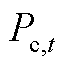 和
和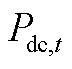 分别为储能在第t个时段的充电和放电功率;
分别为储能在第t个时段的充电和放电功率;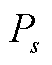 为储能的规划功率。
为储能的规划功率。
充放电逻辑约束为
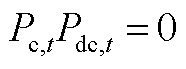 (A10)
(A10)
储能荷电状态上、下限约束为
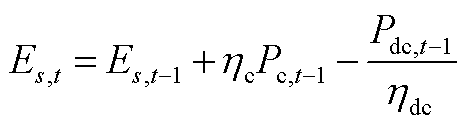 (A11)
(A11)
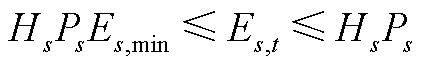 (A12)
(A12)
式中,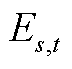 和
和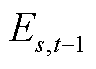 分别为储能在第t个时段和t-1个时段的荷电状态;
分别为储能在第t个时段和t-1个时段的荷电状态;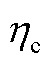 和
和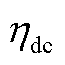 分别为储能的充、放电效率;
分别为储能的充、放电效率; 为储能荷电状态下限。
为储能荷电状态下限。
(3)新能源侧约束
新能源渗透率要求为
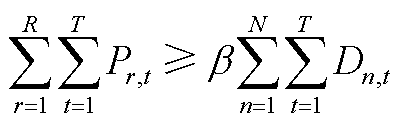 (A13)
(A13)
式中,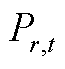 为第r台新能源机组在第t个时段的出力;
为第r台新能源机组在第t个时段的出力;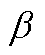 为新能源渗透率要求;
为新能源渗透率要求;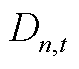 为第n个节点在第t个时段的负荷需求;N为总节点数。
为第n个节点在第t个时段的负荷需求;N为总节点数。
新能源出力上、下限约束为
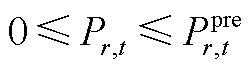 (A14)
(A14)
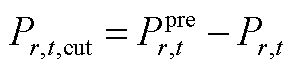 (A15)
(A15)
式中,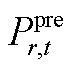 为第r台新能源机组在第t个时段的预测出力。
为第r台新能源机组在第t个时段的预测出力。
(4)系统侧运行约束
功率平衡约束为
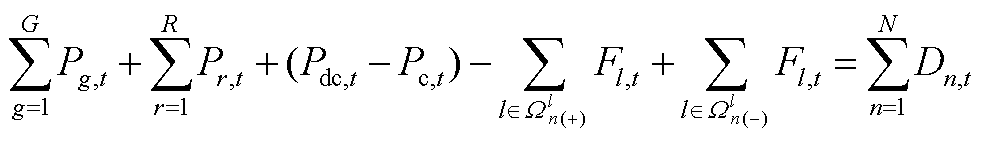 (A16)
(A16)
式中,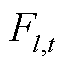 为第l条线路在第t个时段的传输功率;
为第l条线路在第t个时段的传输功率;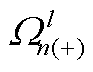 为首端点为n的线路集合;
为首端点为n的线路集合;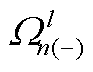 为末端点为n的线路集合。
为末端点为n的线路集合。
线路传输功率限制约束为
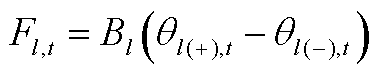 (A17)
(A17)
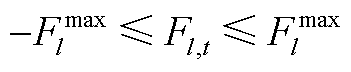 (A18)
(A18)
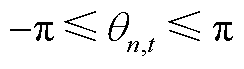 (A19)
(A19)
式中,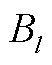 为第l条线路的电纳;
为第l条线路的电纳;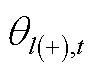 和
和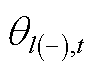 分别为线路l的首端点和末端点在第t个时段的相角;
分别为线路l的首端点和末端点在第t个时段的相角;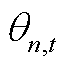 为第n个节点在第t个时段的相角;
为第n个节点在第t个时段的相角;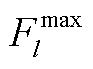 为第l条线路的传输功率限值。
为第l条线路的传输功率限值。
注意到约束式(A10)含有两项优化变量的乘积,为非线性约束,会给模型求解带来计算负担。该约束为限制储能不能同时充放电的逻辑约束,然而,考虑到储能运行中的效率损耗及运行成本,文献[47]已经证明了在所用规划模型中约束式(A10)将会自然满足。
2. 传统松弛储能规划模型
将仅含有离散变量的最小起停时间约束式(A6)~式(A8)删去,并松弛整数变量,则目标函数式(A3)转换为式(A20);火电机组出力下限被松弛,出力上下限约束式(A4)转换为约束式(A21)。
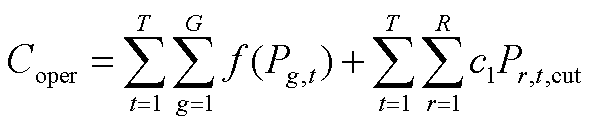 (A20)
(A20)
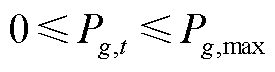 (A21)
(A21)
松弛的储能规划模型可以表示为式(A22),其为线性规划问题,可以表示为式(A23)、式(A24)所示的简化形式。
Min(式(A2)+式(A20)) (A22)
s.t. 式(A5), 式(A9)~式(A19), 式(A21)
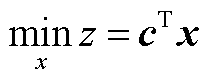 (A23)
(A23)
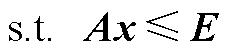 (A24)
(A24)
参考文献
[1] 中华人民共和国国务院. 国务院关于印发2030年前碳达峰行动方案的通知[J]. 中华人民共和国国务院公报, 2021(31): 48-58.
State Council of the People’s Republic of China. Circular of the state council on printing and issuing the action plan for carbon dioxide peaking before 2030[J]. Gazette of the State Council of the People’s Republic of China, 2021(31): 48-58.
[2] 鲁宗相, 李海波, 乔颖. 含高比例可再生能源电力系统灵活性规划及挑战[J]. 电力系统自动化, 2016, 40(13): 147-158.
Lu Zongxiang, Li Haibo, Qiao Ying. Power system flexibility planning and challenges considering high proportion of renewable energy[J]. Automation of Electric Power Systems, 2016, 40(13): 147-158.
[3] 陈红坤, 王雪纯, 陈磊. 考虑灵活性供给约束的区域综合能源系统节点边际能价分解分析[J]. 电工技术学报, 2023, 38(13): 3576-3589.
Chen Hongkun, Wang Xuechun, Chen Lei. Decomposition analysis on locational marginal energy prices in regional integrated energy system considering flexibility provision constraints[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3576-3589.
[4] 孙玉树, 杨敏, 师长立, 等. 储能的应用现状和发展趋势分析[J]. 高电压技术, 2020, 46(1): 80-89.
Sun Yushu, Yang Min, Shi Changli, et al. Analysis of application status and development trend of energy storage[J]. High Voltage Engineering, 2020, 46(1): 80-89.
[5] 毕皓淳, 祁琪, 刘向军, 等. 计及5G基站运行协同的分布式储能优化配置方法[J]. 电工技术学报, 2024, 39(21): 6819-6833.
Bi Haochun, Qi Qi, Liu Xiangjun, et al. An optimal configuration method for DES considering coordinated operation of 5G base station[J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6819-6833.
[6] Gabrielli P, Gazzani M, Martelli E, et al. Optimal design of multi-energy systems with seasonal storage[J]. Applied Energy, 2018, 219: 408-424.
[7] 姜海洋, 杜尔顺, 金晨, 等. 高比例清洁能源并网的跨国互联电力系统多时间尺度储能容量优化规划[J]. 中国电机工程学报, 2021, 41(6): 2101-2115.
Jiang Haiyang, Du Ershun, Jin Chen, et al. Optimal planning of multi-time scale energy storage capacity of cross-national interconnected power system with high proportion of clean energy[J]. Proceedings of the CSEE, 2021, 41(6): 2101-2115.
[8] 林雨眠, 熊厚博, 张笑演, 等. 计及新能源机会约束与虚拟储能的电-热系统分布式多目标优化调度[J].电工技术学报, 2024, 39(16): 5042-5059.
Lin Yumian, Xiong Houbo, Zhang Xiaoyan, et al. Distributed multi-objective optimal scheduling of integrated electric-heat system considering chance constraint of new energy and virtual storage[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5042-5059.
[9] Zhang Ning, Jiang Haiyang, Du Ershun, et al. An efficient power system planning model considering year-round hourly operation simulation[J]. IEEE Transactions on Power Systems, 2022, 37(6): 4925-4935.
[10] 胡俊杰, 童宇轩, 刘雪涛, 等. 计及精细化氢能利用的综合能源系统多时间尺度鲁棒优化策略[J]. 电工技术学报, 2024, 39(5): 1419-1435.
Hu Junjie, Tong Yuxuan, Liu Xuetao, et al. Multi-time-scale robust optimization strategy for integrated energy system considering the refinement of hydrogen energy use[J]. Transactions of China Electrote-chnical Society, 2024, 39(5): 1419-1435.
[11] PJM. PJM region transmission planning process[EB/OL]. (2021-12). http://www.pjm.com/-/media/documents/ manuals/m14b.ashx.
[12] 高海淑, 张玉敏, 吉兴全, 等. 基于场景聚类的主动配电网分布鲁棒综合优化[J]. 电力系统自动化, 2020, 44(21): 32-41.
Gao Haishu, Zhang Yumin, Ji Xingquan, et al. Scenario clustering based distributionally robust comprehensive optimization of active distribution network[J]. Automation of Electric Power Systems, 2020, 44(21): 32-41.
[13] Zheng Fangfang, Meng Xiaofang, Wang Lidi, et al. Operation optimization method of distribution network with wind turbine and photovoltaic considering clustering and energy storage[J]. Sustainability, 2023, 15(3): 2184.
[14] 吴俊, 薛禹胜, 舒印彪, 等. 大规模可再生能源接入下的电力系统充裕性优化 (三)多场景的备用优化[J]. 电力系统自动化, 2019, 43(11): 1-7, 76.
Wu Jun, Xue Yusheng, Shu Yinbiao, et al. Adequacy optimization for a large-scale renewable energy integrated power system part three reserve optimization in multiple scenarios[J]. Automation of Electric Power Systems, 2019, 43(11): 1-7, 76.
[15] Tso W W, Demirhan C D, Heuberger C F, et al. A hierarchical clustering decomposition algorithm for optimizing renewable power systems with storage[J]. Applied Energy, 2020, 270: 115190.
[16] 李军徽, 赵寒杰, 朱星旭, 等. 基于区域间场景等值的配电网随机潮流加速算法[J]. 电工技术学报, 2024, 39(7): 1957-1970.
Li Junhui, Zhao Hanjie, Zhu Xingxu, et al. Stochastic power flow acceleration algorithm of distribution network based on scene equivalence between regions [J]. Transactions of China Electrotechnical Society, 2024, 39(7): 1957-1970.
[17] 张斌, 庄池杰, 胡军, 等. 结合降维技术的电力负荷曲线集成聚类算法[J]. 中国电机工程学报, 2015, 35(15): 3741-3749.
Zhang Bin, Zhuang Chijie, Hu Jun, et al. Ensemble clustering algorithm combined with dimension reduction techniques for power load profiles[J]. Proceedings of the CSEE, 2015, 35(15): 3741-3749.
[18] Tejada-Arango D A, Domeshek M, Wogrin S, et al. Enhanced representative days and system states modeling for energy storage investment analysis[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6534-6544.
[19] 郭力, 杨书强, 刘一欣, 等. 风光储微电网容量规划中的典型日选取方法[J]. 中国电机工程学报, 2020, 40(8): 2468-2479.
Guo Li, Yang Shuqiang, Liu Yixin, et al. Typical day selection method for capacity planning of microgrid with wind turbine-photovoltaic and energy storage[J]. Proceedings of the CSEE, 2020, 40(8): 2468-2479.
[20] 潘超, 范宫博, 王锦鹏, 等. 灵活性资源参与的电热综合能源系统低碳优化[J]. 电工技术学报, 2023, 38(6): 1633-1647.
Pan Chao, Fan Gongbo, Wang Jinpeng, et al. Low-carbon optimization of electric and heating integrated energy system with flexible resource participation[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1633-1647.
[21] García-Cerezo Á, García-Bertrand R, Baringo L. Enhanced representative time periods for transmission expansion planning problems[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3802-3805.
[22] 黄森. 面向高比例可再生能源接入的分布式储能优化规划[D]. 北京: 华北电力大学, 2022.
Huang Sen. Optimal planning of distributed energy storage for high proportion of renewable energy[D]. Beijing : North China Electric Power University, 2022.
[23] 杜锡力, 李笑竹, 陈来军, 等. 面向多场景调节需求的集中式共享储能鲁棒优化配置[J]. 电工技术学报, 2022, 37(23): 5911-5921.
Du Xili, Li Xiaozhu, Chen Laijun, et al. Robust and optimized configuration of centralized shared energy storage for multi-scenario regulation demand[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5911-5921.
[24] Pineda S, Morales J M. Chronological time-period clustering for optimal capacity expansion planning with storage[J]. IEEE Transactions on Power Systems, 2018, 33(6): 7162-7170.
[25] Novo R, Marocco P, Giorgi G, et al. Planning the decarbonisation of energy systems: the importance of applying time series clustering to long-term models[J]. Energy Conversion and Management: X, 2022, 15: 100274.
[26] Tejada-Arango D A, Wogrin S, Centeno E. Representation of storage operations in network-constrained optimization models for medium- and long-term operation[J]. IEEE Transactions on Power Systems, 2018, 33(1): 386-396.
[27] Zhang Yufan, Ai Qian, Xiao Fei, et al. Typical wind power scenario generation for multiple wind farms using conditional improved Wasserstein generative adversarial network[J]. International Journal of Electrical Power & Energy Systems, 2020, 114: 105388.
[28] Chen Yize, Wang Yishen, Kirschen D, et al. Model-free renewable scenario generation using generative adversarial networks[J]. IEEE Transactions on Power Systems, 2018, 33(3): 3265-3275.
[29] 朱玲, 李威,王骞, 等. 基于校正条件生成对抗网络的风电场群绿氢储能系统容量配置[J]. 电工技术学报, 2024, 39(3): 714-730.
Zhu Ling, Li Wei, Wang Qian, et al. Wind farms-green hydrogen energy storage system capacity sizing method based on corrected-conditional generative adversarial network[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 714-730.
[30] Bahl B, Kümpel A, Seele H, et al. Time-series aggregation for synthesis problems by bounding error in the objective function[J]. Energy, 2017, 135: 900-912.
[31] Liu Yixian, Sioshansi R, Conejo A J. Hierarchical clustering to find representative operating periods for capacity-expansion modeling[J]. IEEE Transactions on Power Systems, 2018, 33(3): 3029-3039.
[32] García-Cerezo Á, García-Bertrand R, Baringo L. Priority chronological time-period clustering for generation and transmission expansion planning problems with long-term dynamics[J]. IEEE Transactions on Power Systems, 2022, 37(6): 4325-4339.
[33] 解蛟龙. 风/光/负荷典型场景缩减方法及在电网规划中的应用[D]. 合肥: 合肥工业大学, 2017.
Xie Jiaolong. A typical reduced-scenario analysis method for wind photoelectric, load scene and its application in power system planning[D]. Hefei: Hefei University of Technology, 2017.
[34] 赵书强, 要金铭, 李志伟. 基于改进K-means聚类和SBR算法的风电场景缩减方法研究[J]. 电网技术, 2021, 45(10): 3947-3954.
Zhao Shuqiang, Yao Jinming, Li Zhiwei. Wind power scenario reduction based on improved K-means clustering and SBR algorithm[J]. Power System Technology, 2021, 45(10): 3947-3954.
[35] 张沛, 田佳鑫, 谢桦. 计及多个风场预测误差的电力系统风险快速计算方法[J]. 电工技术学报, 2021, 36(9): 1876-1887.
Zhang Pei, Tian Jiaxin, Xie Hua. A fast risk assessment method with consideration of forecasting errors of multiple wind farms[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1876-1887.
[36] 王群, 董文略, 杨莉. 基于Wasserstein距离和改进K-medoids聚类的风电/光伏经典场景集生成算法[J]. 中国电机工程学报, 2015, 35(11): 2654-2661.
Wang Qun, Dong Wenlue, Yang Li. A wind power/photovoltaic typical scenario set generation algorithm based on Wasserstein distance metric and revised K-medoids cluster[J]. Proceedings of the CSEE, 2015, 35(11): 2654-2661.
[37] 陈宝林. 最优化理论与算法[M]. 2版. 北京: 清华大学出版社, 2005.
[38] 高倩, 杨知方, 李文沅, 等. 分支定界搜索信息深度引导的电-气互联系统调度决策加速求解方法[J]. 电工技术学报, 2023: 2024, 39(13): 3990-4002.
Gao Qian, Yang Zhifang, Li Wenyuan, et al. Dispatch acceleration of integrated electricity and gas system using branch-and-bound search information[J]. Tran-sactions of China Electrotechnical Society, 2023: 2024, 39(13): 3990-4002.
[39] 汪洋, 夏清, 康重庆. 机组组合算法中起作用整数变量的辨识方法[J]. 中国电机工程学报, 2010, 30(13): 46-52.
Wang Yang, Xia Qing, Kang Chongqing. Identi-fication of the active integer variables in security constrained unit commitment[J]. Proceedings of the CSEE, 2010, 30(13): 46-52.
[40] Kohonen T. The self-organizing map[J]. Proceedings of the IEEE, 1990, 78(9): 1464-1480.
[41] 周楠, 徐潇源, 严正, 等. 基于宽度学习系统的光伏发电功率超短期预测[J]. 电力系统自动化, 2021, 45(1): 55-64.
Zhou Nan, Xu Xiaoyuan, Yan Zheng, et al. Ultra-short-term forecasting of photovoltaic power genera-tion based on broad learning system[J]. Automation of Electric Power Systems, 2021, 45(1): 55-64.
[42] 陈宇航, 王渝红, 南璐, 等. 基于自组织映射-前馈神经网络和先知混合模型的短期负荷预测[J/OL]. 现代电力, 2023: 1-9. https://doi.org/10.19725/j.cnki. 1007- 2322.2023.0036.
Chen Yuhang, Wang Yuhong, Nan Lu. Short-Term load forecasting based on SOM-BP and prophet hybrid model[J/OL]. Modern Electric Power, 2023: 1-9. https://doi.org/10.19725/j.cnki.1007-2322.2023.0036.
[43] 康重庆, 姚良忠. 高比例可再生能源电力系统的关键科学问题与理论研究框架[J]. 电力系统自动化, 2017, 41(9): 2-11.
Kang Chongqing, Yao Liangzhong. Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(9): 2-11.
[44] 鲁宗相, 林弋莎, 乔颖, 等. 极高比例可再生能源电力系统的灵活性供需平衡[J]. 电力系统自动化, 2022, 46(16): 3-16.
Lu Zongxiang, Lin Yisha, Qiao Ying, et al. Flexibility supply-demand balance in power system with ultra-high proportion of renewable energy[J]. Automation of Electric Power Systems, 2022, 46(16): 3-16.
[45] Cheng Caoyang. Energy storage expansion planning [EB/OL]. 2023. https://github.com/cyangcheng/code-for-papers-230616.
[46] 浙江省人民政府. 浙江省发展改革委关于调整我省目录销售电价有关事项的通知[EB/OL]. 2021-10-25. https://www.zj.gov.cn/art/2021/10/25/art_1229203592_ 2370712.html.
[47] 李中浩, 余娟, 杨知方, 等. 精准计及大规模储能电池寿命的电力系统经济调度[J]. 中国电机工程学报, 2023, 43(19): 7371-7383.
Li Zhonghao, Yu Juan, Yang Zhifang, et al. Economic dispatch of power system accurately considering the life of large-scale energy storage battery[J]. Proceedings of the CSEE, 2023, 43(19): 7371-7383.
An Efficient Method for Energy Storage Planning Considering Full-Scenario Security
Abstract With the continuous increase in the penetration rate of renewable energy sources such as wind and photovoltaics, the randomness and volatility of the power system are constantly growing. Investing energy storage is considered one of the most effective ways to alleviate the uncertainty of renewable energy and enhance the security and flexibility of the power system. However, existing planning methods, to ensure the computational efficiency, usually select only a few key scenarios to formulate energy storage planning, which cannot guarantee its security under all scenarios. If security verification is performed for the planning across all scenarios, it will be difficult to accept due to the large model size leading to unacceptable solution time. Therefore, this paper proposes an efficient method for energy storage planning considering full-scenario security.
Firstly, addressing the security risks brought by open-loop scenario clustering and planning solutions in existing planning methods, a closed-loop energy storage planning framework oriented towards security under all scenarios is proposed. Secondly, by constructing a relaxed energy storage planning model based on fixed 0-1 variables to obtain a ranking result of the full scenario set reflecting the criticality of different scenarios, guiding the update of key scenarios based on this ranking result can ensure full-scenario security while balancing computational efficiency. Thirdly, this method requires a given set of initial key scenario sets. To address the issues of traditional clustering methods such as K-means, which require a predefined number of clusters, are prone to submerge extreme scenarios’ information, and can not accurately reflect the critical information of all scenarios, a method for generating an initial scenario set based on self-organizing maps (SOM) neural network and scenario critical indicator ranking is further proposed. This method does not require a predefined number of clusters and can accurately reflect critical information under all scenarios, further improving computational efficiency.
To validate the effectiveness of the proposed energy storage planning method, case studies are conducted on the IEEE 30 bus system and an actual 341-bus system in a domestic province. Scenarios are considered with full scenario set sizes of 30 and 365, and different levels of renewable energy fluctuations and line transmission capacity limits are taken into account. The results indicate that, considering the detailed system operational characteristics, existing closed-loop energy storage planning methods, due to the lack of guidance from key scenarios’ information, take an excessively long time to solve when dealing with a large number of scenarios in practical systems, exceeding two weeks in some cases. The proposed method can ensure the security and optimality of planning under all scenarios while reducing the number of scenarios to be considered and improving solution efficiency. In practical systems, the proposed method can obtain energy storage planning solutions within 4 hours.
From the numerical analysis, the following conclusions can be drawn: (1) Considering the fine temporal granularity of the power system operational characteristics in the planning year, existing energy storage planning methods are computationally expensive, even at the planning level. (2) The proposed energy storage planning method accurately considers the fine temporal granularity of the power system operational characteristics of the planning year. While ensuring the security of planning under all scenarios, it improves solution efficiency by reducing the number of scenarios to be considered and selecting more reasonable initial key scenarios. (3) In actual power system operations, the proposed energy storage planning method can consider the benefits obtained through peak-to-valley electricity price differentials and has certain economic value.
Keywords:Energy storage expansion planning, multi-scenario planning, scenario clustering, security check, self-organizing maps (SOM) neural network
中图分类号:TM715
DOI: 10.19595/j.cnki.1000-6753.tces.231501
国网总部科技项目资助(5100-202236503A-3-0-SF)。
收稿日期 2023-09-12
改稿日期 2023-12-28
程曹阳 男,1999年生,硕士研究生,研究方向为电力系统优化与规划。
E-mail:cycheng@cqu.edu.cn
余 娟 女,1980年生,教授,博士生导师,研究方向为电力与能源经济优化运行、风险评估、深度学习等。
E-mail:148454745@qq.com(通信作者)
(编辑 赫 蕾)