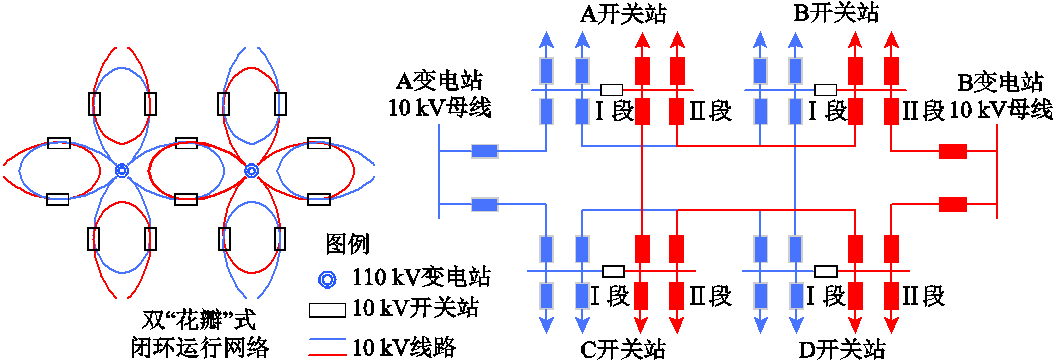
图1 双“花瓣型”配电网架结构
Fig.1 Distribution grid structure with double “petal-shaped” morphology
摘要 随着有源配电网建设的迅猛发展,“花瓣型”配电网已成为主流供电结构,为保障配电系统的安全供电,应当进一步研究适用于有源配电网的功率控制方法。电磁式旋转潮流控制器(RPFC)是有源配电网功率控制的一种可行方案。该文首先构建了基于瞬时无功理论的RPFC稳态功率解耦控制模型,然而由于旋转移相变压器转子位置角的协调控制难点,难以实现功率稳定控制;然后,通过伺服电动机两阶段转速控制和转速协调方案实现两转子角的稳定、无差控制,满足高精度、高可靠性和快速响应的功率调节需求;最后,研制了380 V/40 kV·A的RPFC样机及实验平台,并进行了功率调控和功率均衡实验。结果表明,所提控制方案能够在s级实现调控,且控制精度保持在4%以内,具有良好的动、静态性能,能够满足未来“花瓣型”配电网的柔性合环运行。
关键词:“花瓣型”配电网 旋转潮流控制器 功率控制 两阶段转速控制
“花瓣型”配电网联络线由变电站出发,经过多个开关站形成一个类似于花瓣形状的配电网,一种典型双“花瓣型”配电网架结构如图1所示。在正常运行方式下,采用多电源合环运行方式供电[1],相较于辐射型配电网明显提高了供电可靠性。但由于线路建设和负荷发展的不同步,“花瓣型”配电网表现出潮流大小、方向不可控的特点[2]。因此亟须一种有源配电网柔性交流互联装置,对合环点功率进行有效控制,保证合环的安全运行,从而大幅提升配电网的供电可靠性[3]。

图1 双“花瓣型”配电网架结构
Fig.1 Distribution grid structure with double “petal-shaped” morphology
目前具备线路潮流调控能力的装备包括智能软开关(Soft Open Point, SOP)[4]、统一潮流控制器(Unified Power Flow Controller, UPFC)[5]以及电磁式旋转潮流控制器(Rotary Power Flow Controller, RPFC)[6]。SOP的典型实现结构为背靠背电压源换流器,通过对两侧换流器施加控制策略,满足接入点输出电压幅值与相位的独立控制,实现互联线路流过有功和无功功率的双向解耦控制[7];UPFC通过控制串联电压源转换器改变串联变压器注入线路的电压,即可动态调节线路有功和无功功率[8]。然而,SOP及UPFC主要基于全控型电力电子变换装置实现,投资与运行维护成本较高(受容量不同影响,SOP成本为750~1 150元/(kV·A),UPFC成本为 1 900~2 100元/(kV·A)),短期内无法在配电网中大规模应用[9]。RPFC由两组旋转移相变压器(Rotary Phase Shift Transformer, RPST)串联组成[10],通过分别改变两组旋转移相变压器的相对角度,即可灵活控制串入线路的补偿电压,从而为电力系统的功率调控提供了新的方法。文献[11]综合对比了RPFC和UPFC技术特性,发现RPFC可以在百毫秒级的响应时间内准确控制系统的潮流,并且成本造价并不高(约为90~120元/(kV·A)),控制相对简单,具有良好的控制特性,在配电网潮流控制工况下表现出一定的应用前景。但仍处在样机开发阶段,在大规模应用之前仍有一些控制方面的技术问题有待解决和实验验证。
在配电网的稳态功率解耦控制方面,目前主要包括相角控制[12]和矢量控制[13]两种。相角控制通过改变输出电压的幅值来调节线路无功功率,通过改变相角来调节有功功率;矢量控制由功率外环和电流内环组成,首先将线路电流分解为dq轴分量,并认为有功功率仅与q轴分量相关,无功功率仅与d轴分量相关,经过计算得到交流侧电压的幅值与相位,再由锁相环提供角度,使电压从dq轴坐标变换回abc坐标系,最终得到所需串联电压。文献[14]建立了RPFC的稳态数学模型,采用相角控制的潮流调控方法,实现了输电系统受端功率的有效调节,但应用于配电网时,由于线路电阻无法忽略的原因造成了功率解耦调控的失效。文献[15]研究了基于矢量控制的UPFC功率控制策略,对比了交叉耦合控制和交叉解耦控制,交叉耦合控制结构简单,易于实现,表现出了较好的鲁棒性;交叉解耦控制具有调节潮流迅速、解耦完全的优势。因此可通过采用基于瞬时无功理论的交叉解耦控制方法实现RPFC功率环节的控制,并利用PI参数自适应规则减小超调,提高响应速度。
RPFC最外层相角控制属于其特有环节,无法再借鉴UPFC。RPFC通过伺服电动机来控制两个RPST角度,难点在于通过两台伺服电动机的转速控制实现两个RPST转子角的稳定调节。位置-速度-电流的三环嵌套式结构在伺服系统中被广泛应用[16],因此借鉴传统伺服系统控制方案,采用转子角偏差-速度-电流环的结构应用于RPFC控制系统。文献[17]指出双环定转速的RPFC控制在复杂功率控制工况下稳定性较差,通过对两RPST伺服电动机电流环节输出脉冲宽度调制(Pulse Width Modulation, PWM)的占空比进行合理调控,可以达到实现双伺服电动机协调控制。
在此基础上,本文开展基于瞬时无功理论的RPFC功率解耦控制方法研究,针对RPFC两旋转移相变压器机械特征,设计两阶段转速控制和转速协调方案提高装置运行响应速度和鲁棒性。研制了380 V/40 kV·A样机并进行功率解耦控制和功率均衡实验,结果表明RPFC均能表现出较好控制效果,验证了所提控制策略的正确性。
RPFC拓扑结构如图2所示,其转子侧作为RPST一次侧并联接入供电线路进行取能,定子侧作为RPST二次侧串联接入供电线路对线路电压进行合理补偿。RPST在静止时类似于一台变压器,通过伺服电动机和移相变压器定子铁心的物理关联,实现移相变压器的定转子角相对转动,具体相位差与定转子相对角度a1、a2相关[6]。最后将两RPST定子电压矢量叠加,实现在线路中串入一个幅值、相角可调的电压矢量。
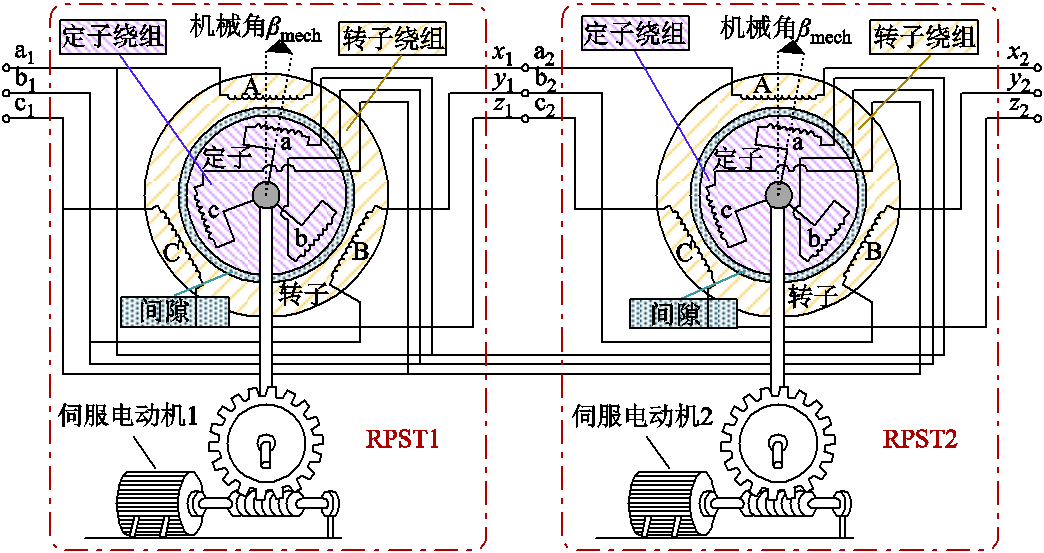
图2 RPFC拓扑结构
Fig.2 Topology structure of RPFC
RPFC单相等效电路如图3a所示。图中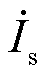 为接入RPST前系统线路电流,
为接入RPST前系统线路电流, 为系统电压,
为系统电压,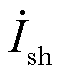 为转子总电流,
为转子总电流,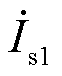 为定子侧电流,
为定子侧电流,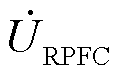 为RPFC串入线路的电压,
为RPFC串入线路的电压,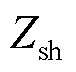 为归算到转子侧的阻抗;
为归算到转子侧的阻抗;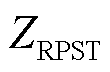 为归算到定子侧阻抗,k为RPST电压比。文献[17]对其注入电压的稳态过程进行了分析,从而可以得到RPFC稳态电压源模型如图3b所示。
为归算到定子侧阻抗,k为RPST电压比。文献[17]对其注入电压的稳态过程进行了分析,从而可以得到RPFC稳态电压源模型如图3b所示。
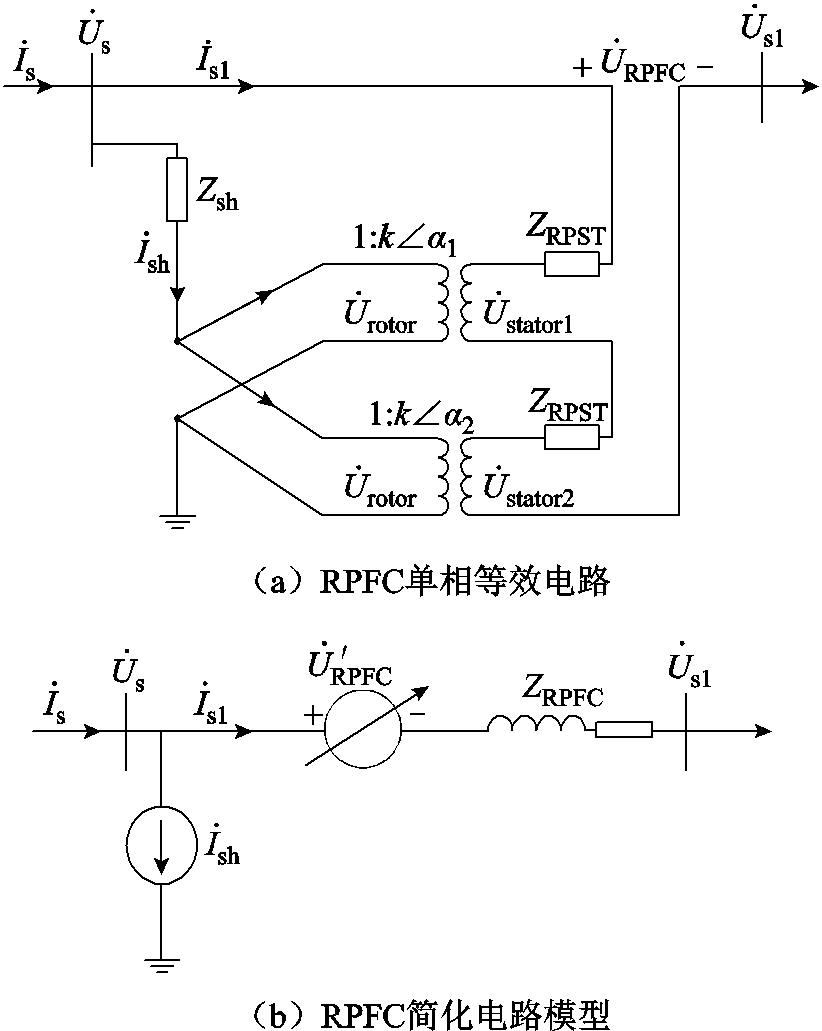
图3 RPFC工作原理
Fig.3 Working principle of RPFC
图3中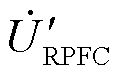 和
和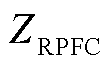 分别为
分别为
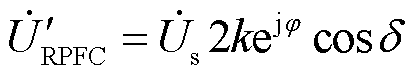 (1)
(1)
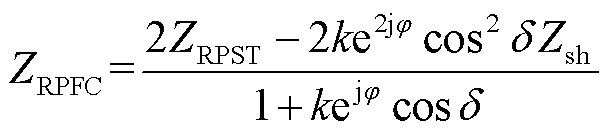 (2)
(2)
其中
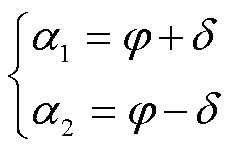 (3)
(3)
式中,j和d分别为电压幅值和相位的关键影响因素。
典型“花瓣型”配电网结构如图4所示。R1+jX1为母线1阻抗,R2+jX2为母线2阻抗,P1+jQ1为母线1负载功率,P2+jQ2为母线2负载功率,P3+jQ3为合环点流过功率,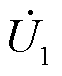 和
和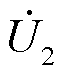 分别为开关S1两侧电压,I为闭环运行下线路l3电流。
分别为开关S1两侧电压,I为闭环运行下线路l3电流。
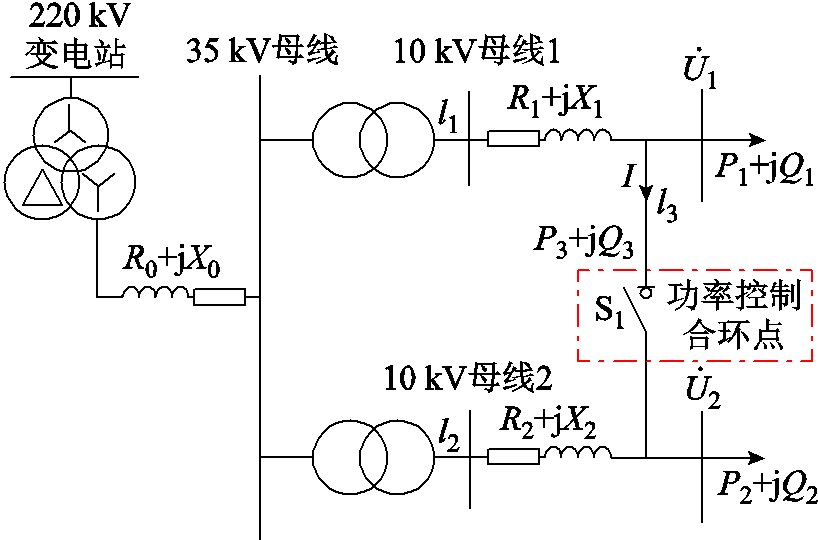
图4 “花瓣型”配电网合环运行的网架结构
Fig.4 “Petal-type” network structure of distribution networks operating in a closed loop
RPFC未投入运行时,线路l1和l2的功率按线路阻抗自然分布,令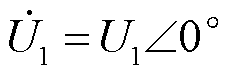 、
、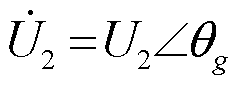 ,此时合环点流过功率满足
,此时合环点流过功率满足
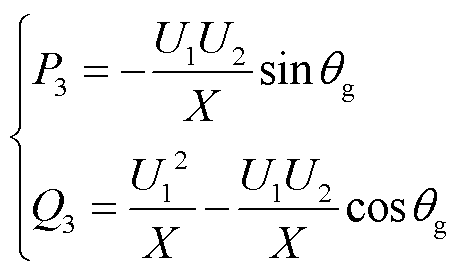 (4)
(4)
式中,X为RPFC内阻抗。RPFC投入运行后,此时l3线路阻抗受RPFC较大影响,且在RPFC中存在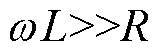 ,通过调节串入线路电压幅值和相位,可以对合环点功率进行有效控制,下面对接入RPFC的功率解耦控制模型进行分析,合环线路满足
,通过调节串入线路电压幅值和相位,可以对合环点功率进行有效控制,下面对接入RPFC的功率解耦控制模型进行分析,合环线路满足
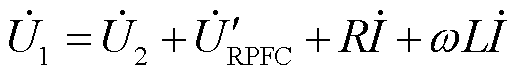 (5)
(5)
式中,R、L分别为ZRPFC的等效电阻和电感。令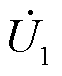 作为参考电压固定在d轴上,则有
作为参考电压固定在d轴上,则有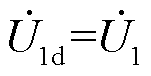 ,
,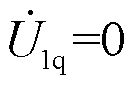 ,稳态情况下存在
,稳态情况下存在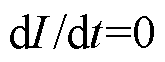 ,此时式(5)在dq坐标系下可以表示为
,此时式(5)在dq坐标系下可以表示为
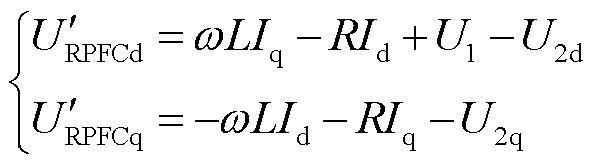 (6)
(6)
在dq旋转坐标系中,线路l1-2的传输功率P3+jQ3可表示为
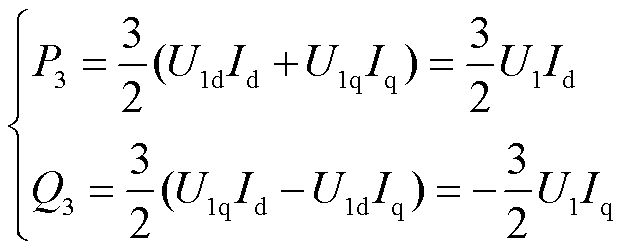 (7)
(7)
结合式(6)、式(7),在RPFC内部及输电线路同时存在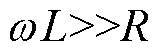 的前提下,可计算得到
的前提下,可计算得到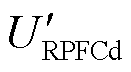 、
、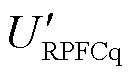 与RPFC接入点功率的关系为
与RPFC接入点功率的关系为
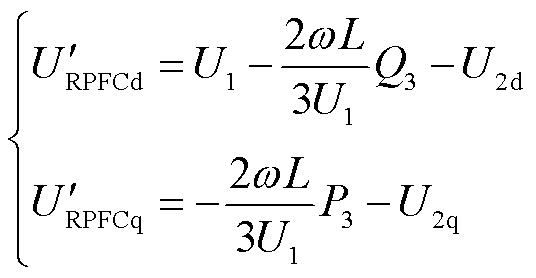 (8)
(8)
可以看到线路有功功率仅与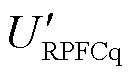 有关,而无功功率仅与
有关,而无功功率仅与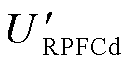 有关,此时可以得到RPFC输出电压的幅值及相位为
有关,此时可以得到RPFC输出电压的幅值及相位为
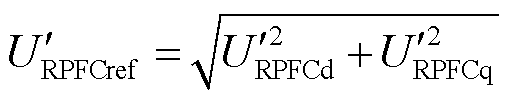 (9)
(9)
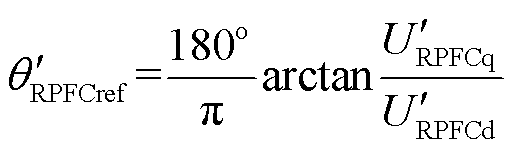 (10)
(10)
RPFC角度和输出电压相量关系如图5所示。在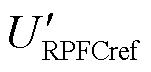 和
和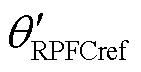 已知的情况下,可根据式(1)求出δref和φref的值,基于式(3)分别计算得到RPST旋转角a1ref和a2ref。
已知的情况下,可根据式(1)求出δref和φref的值,基于式(3)分别计算得到RPST旋转角a1ref和a2ref。
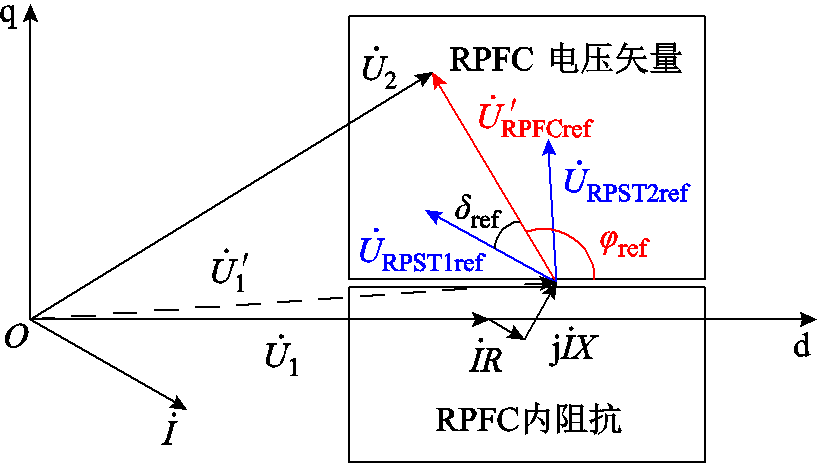
图5 RPFC角度与输出电压相量关系
Fig.5 Phase relationship between RPFC angle and output voltage
将RPST转子角a1和a2与设定值a1ref和a2ref作差后得到Da1和Da2。由图2可以看到,RPFC通过改变伺服电动机的转速和转向驱动两RPST转子角的角度偏差Da1、Da2,实现输出电压和相位满足设定要求,满足线路功率的有效控制。
因此在角度环控制中设计将TMS320F28377开发板作为数字信号处理器(Digital Signal Processing, DSP),伺服电动机作为执行机构的控制系统。在控制过程中DSP主要完成的工作包括[18]:
(1)基于Da的正负给出速度环正转或反转的指令,完成位置/速度环计算。
(2)基于位置/速度环指令,完成电流环计算,通过0~20 mA的电流产生PWM脉冲完成速度传递(例如:0 mA表示不转动,5 mA表示发出2 kHz脉冲波,伺服电动机转速为600 r/min,25 mA表示发出10 kHz脉冲波,伺服电动机转速为3 000 r/min)。
(3)获得位置/速度检测值及电流检测值并完成闭环设计。
2.2.1 快速功率响应调节(第一阶段)
在RPFC功率解耦控制中,控制环路较多,包括1.2节功率解耦控制模型中的功率环、电压环,以及1.1节RPFC工作原理中的角度环,而基于角度环的Da1、Da2输出伺服电动机转速时,固定转速的控制效果较差。这是因为低转速调节下(RPST的转速约为1 °/s)功率调控时间较长,低转速下RPFC调控效果见附录1。而高转速调节(RPST的转速约为6 °/s)可能带来转子角超调问题,此时功率环和电压环将滞后于角度环,难以稳定进入转速协调自适应阶段,使得控制系统的稳定性降低,部分情况下导致转子角出现振荡问题,见附录2。
在此基础上,设计两阶段转速控制方案以实现功率控制的快速、稳定响应。RPFC两阶段转速控制方案如图6所示。第一阶段为快速功率响应调节过程,此阶段目的为快速达到设定功率范围,减少调节时间;第二阶段为转速协调自适应控制过程,此阶段目的为减小转子角超调,避免振荡问题,提高RPFC调节稳定性。
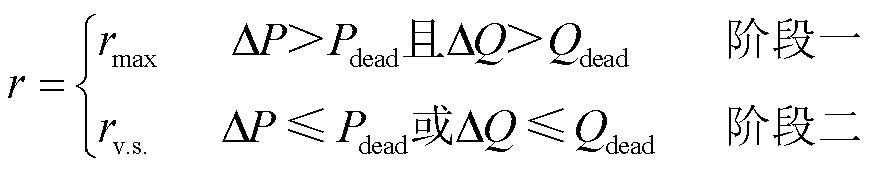 (11)
(11)
式中,r为控制器发出转速;rmax为最大转速;rv.s.为转速协调控制下的伺服电动机目标转速;DP和DQ分别为设定功率与实际功率的有功、无功偏差;Pdead和Qdead为第一阶段的功率调节死区。
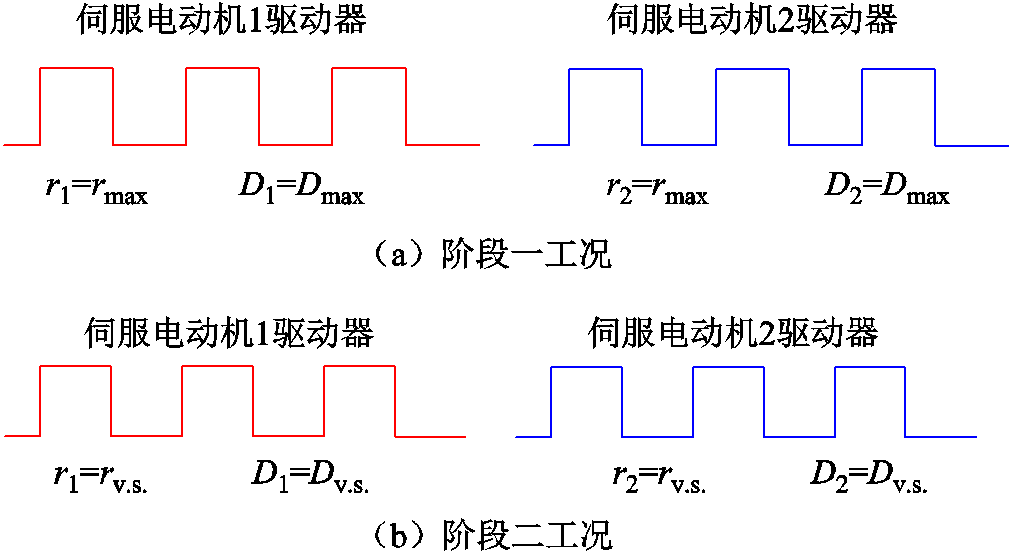
图6 RPFC两阶段转速控制方案
Fig.6 Two-stage speed control scheme of RPFC
参照图6,当功率偏差大于调节死区时,在相同脉冲下,要求伺服电动机驱动器以最大转速对RPST进行控制,而当有功或无功功率偏差小于调节死区时,进入第二阶段的无差控制过程,此时将伺服电动机最大转速进行重新规定,并且对DSP发出电流和脉冲量进行自适应设计,满足稳定功率控制要求[6]。
2.2.2 转速协调自适应调节(第二阶段)
转速自适应控制的关键点在于使a1和a2同时达到设定值。当两组旋转移相变压器的设定值与实际值的角度差Da1和Da2存在差异且均不为0时,则对两台伺服电动机的PWM波占空比大小进行量化自适应计算,如图7所示。
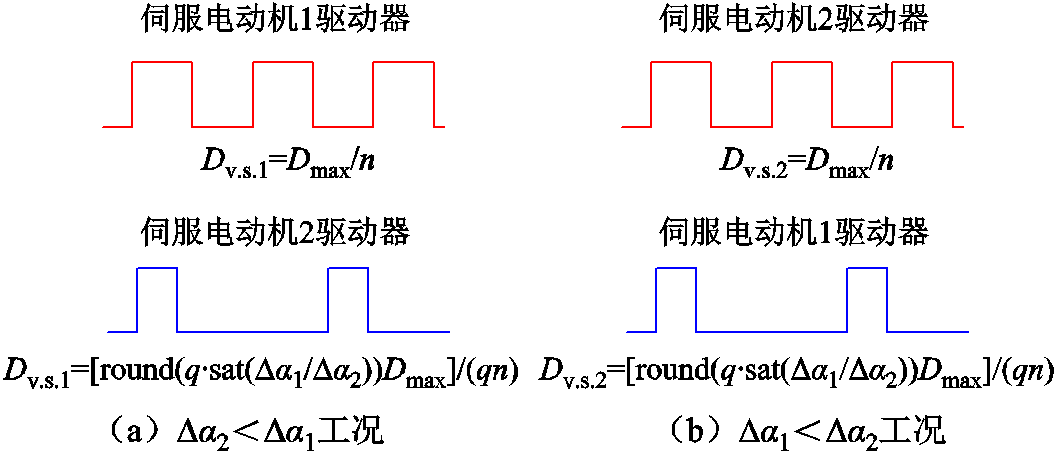
图7 RPFC转速协调自适应设计
Fig.7 Speed-coordinated adaptive design of RPFC
在Da2<Da1时存在式(12),参照图7a,此时Dv.s.1=Dmax/n,Dmax为最大脉冲量,r1保持最大转速;D2根据Da2的大小,对其占空比进行动态调整,使a1和a2同时达到设定值。
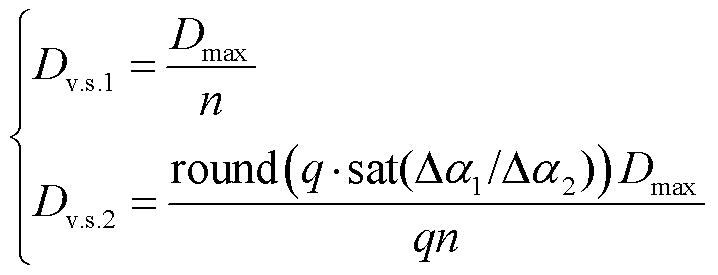 (12)
(12)
在Da1<Da2时存在
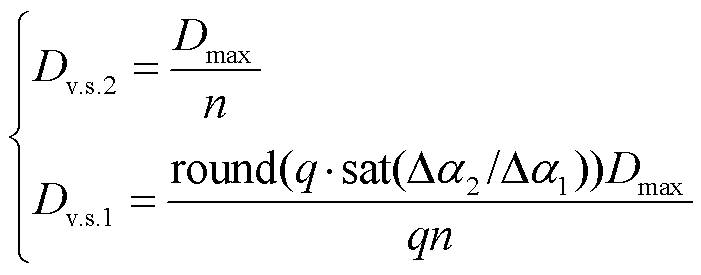 (13)
(13)
式中,Dv.s.1和Dv.s.2分别为两伺服电动机发出脉冲量;n为第二阶段转速协调自适应情况下与第一阶段快速功率响应下最大转速的比值;q为任意整数(量化单元);sat函数用于误差处理,避免分母为0导致的占空比空解或无穷大问题;round函数作为取整单元。参照图7b,此时Dv.s.2=Dmax/n,r2保持最大转速;D1根据Da1的大小,对其占空比进行动态调整,实现转速的自适应调节。
由上述分析可以看到,通过在线路中串入一定的电压矢量,即可在稳态情况下对线路功率进行有效解耦控制,而RPFC能够通过改变两转子角度,实现串入线路电压幅值和相位的连续可调。在此基础上,本文为提高响应速度和控制精度,设计了两阶段转速控制和转速协调控制方案,相比较于传统RPFC转子角控制方案[17](参照附图4),在接近目标功率时对伺服电动机转速进行自适应控制(阶段一),在进入功率调节死区前作用于转速控制;在进入功率调节死区后,阶段二对两伺服电动机驱动器脉冲信号进行自适应控制,能够显著提高系统响应速度和稳定性。RPFC电压矢量-两阶段转子角控制过程如图8所示,系统整体控制框图如图9所示。
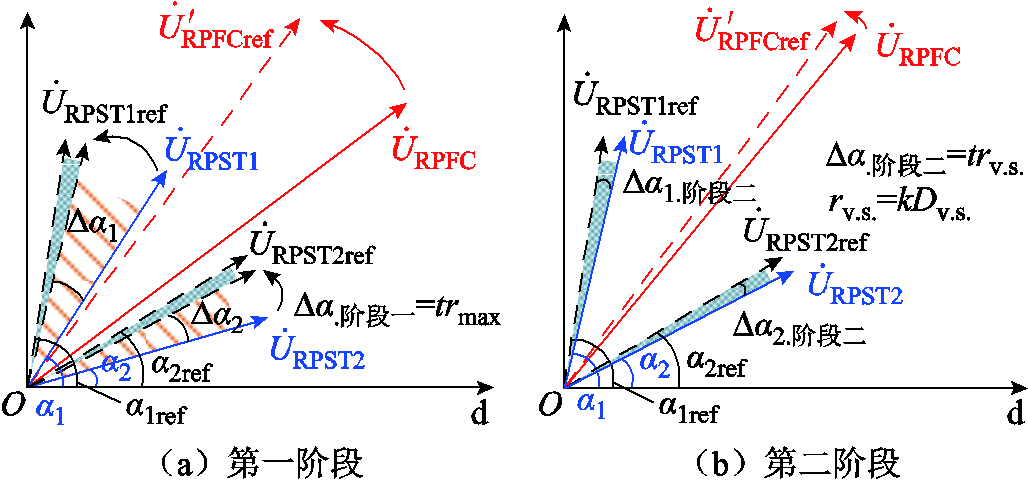
图8 RPFC电压矢量-两阶段转子角控制过程
Fig.8 Voltage vector-two-stage rotor angle control process for RPFCs
为验证所提模型及控制策略的有效性和正确性,在实验室中研制了如图10所示的380 V/40 kV·A实验样机。搭建图9中“花瓣型”配电结构以验证RPFC的功率控制功能,并采用泰克DPO2024B示波器对实验数据进行采集。详细实验接线方案如附图5所示,实验参数见表1。
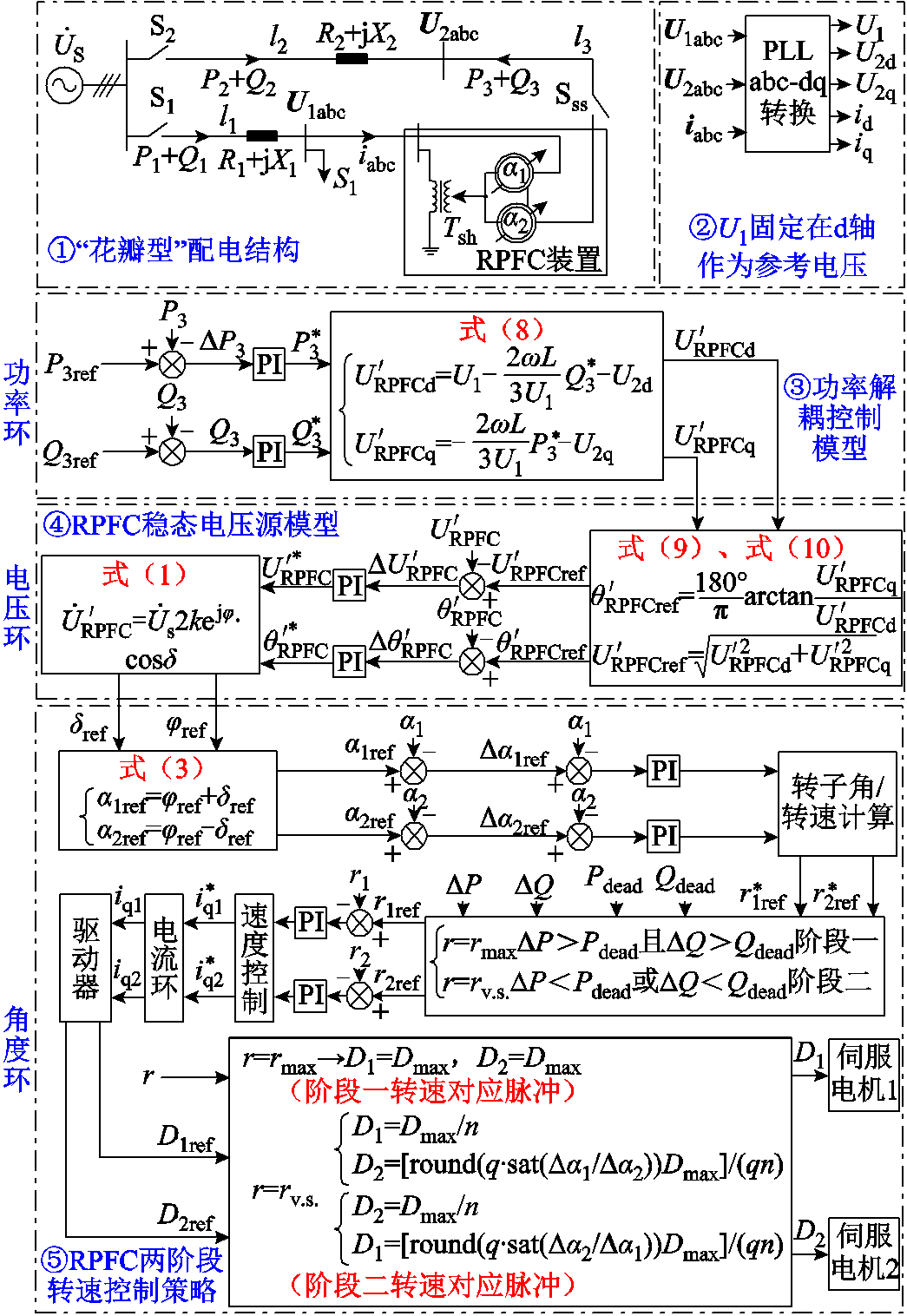
图9 RPFC功率解耦控制框图
Fig.9 Power decoupling control block diagram of RPFC

1—DSP处理器 2、3—两台RPST 4—电流采集器 5—RPST取能侧输入开关 6—Sss串联开关 7—旁路保护开关 8—RS485接口 9、10—两台伺服电动机 11—蜗轮蜗杆 12—位置继电器 13、14—负载箱 15—示波器 16—电阻、电感元件
图10 RPFC实验平台
Fig.10 Experimental platform of RPFC
表1 实验参数
Tab.1 Experimental parameters
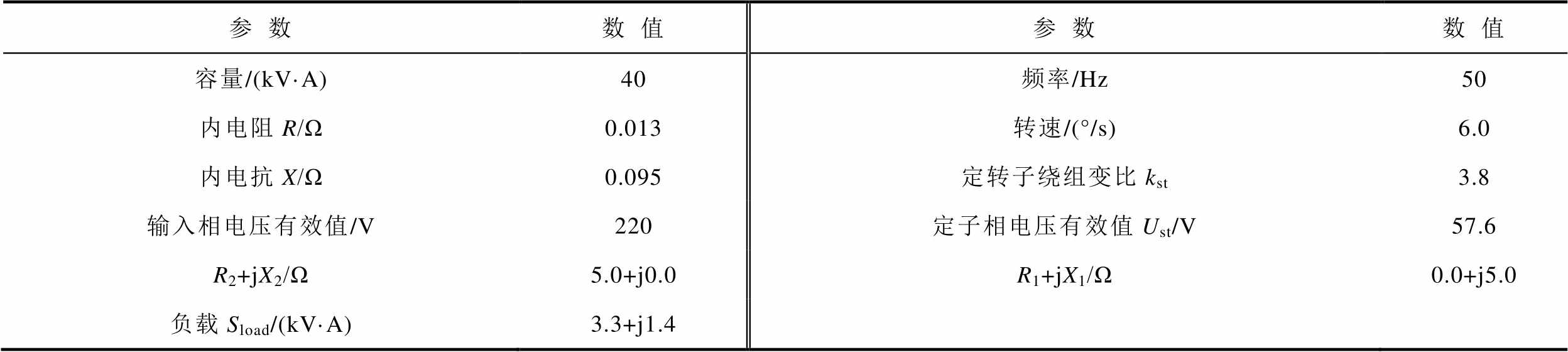
参数数值参数数值 容量/(kV·A)40频率/Hz50 内电阻R/Ω0.013转速/(°/s)6.0 内电抗X/Ω0.095定转子绕组变比kst3.8 输入相电压有效值/V220定子相电压有效值Ust/V57.6 R2+jX2/Ω5.0+j0.0R1+jX1/Ω0.0+j5.0 负载Sload/(kV·A)3.3+j1.4
3.2.1 有功功率调控实验
根据图9“花瓣型”配电结构进行功率调控实验,为验证RPFC在多种工况的有功功率控制有效性,在不影响线路无功传输功率前提下,改变合环线路有功的大小,将实验分为如下工况:
工况A1:P3ref+jQ3ref=0.0+j0.0 kV·A;
工况A2:P3ref+jQ3ref=1.0+j0.0 kV·A;
工况A3:P3ref+jQ3ref=1.6+j0.0 kV·A;
工况A4:P3ref+jQ3ref=2.2+j0.0 kV·A;
工况A5:P3ref+jQ3ref=3.5+j0.0 kV·A;
工况A6:P3ref+jQ3ref=3.3+j0.0 kV·A。
线路有功功率设定值变动时,RPFC功率调控的实验波形如图11所示,调节时间及调节精度实验结果见表2。由此可知,RPFC能够在s级时间内将线路有功功率控制在功率控制死区范围内,控制精度在4%以内,且在经过第二阶段的稳态无差控制后,能够进一步降低误差。
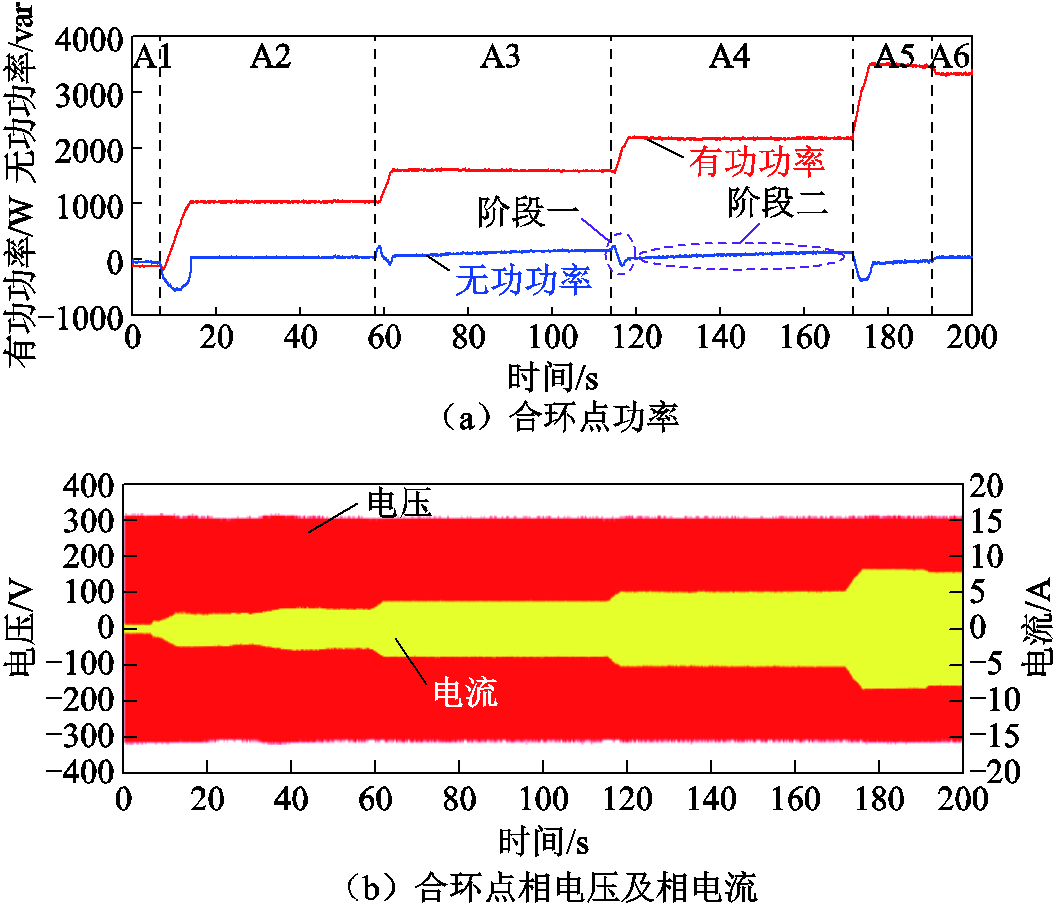
图11 有功功率调控实验
Fig.11 Experiments on active power regulation
表2 有功功率调控实验结果
Tab.2 Experimental results of active power regulation

有功功率调节工况控制目标/(kV·A)实际值/(kV·A)误差(%)调节时间/s A10.0+j0.00.0+j0.0—— A1→A21.0+j0.01.04+j0.044.07 A2→A31.6+j0.01.61+j0.10.84 A3→A42.2+j0.02.18+j0.110.73 A4→A53.5+j0.03.5-j0.050.015.5 A5→A63.3+j0.03.32+j0.040.61
3.2.2 无功功率调控实验
为验证RPFC无功功率控制有效性,在不影响线路有功传输功率前提下,改变合环线路无功功率的大小,将实验分为如下工况:
工况B1:P3ref+jQ3ref=1.5+j0.2 kV·A;
工况B2:P3ref+jQ3ref=1.5+j0.5 kV·A;
工况B3:P3ref+jQ3ref=1.5+j0.8 kV·A;
工况B4:P3ref+jQ3ref=1.5+j1.1 kV·A;
工况B5:P3ref+jQ3ref=1.5+j1.5 kV·A。
线路无功功率设定值变动时,RPFC功率调控的实验波形如图12所示,具体实验结果数据见表3。由此可知,RPFC能够在s级时间内将线路无功功率控制在功率控制死区范围内,控制精度在3.9%以内,且经过第二阶段的稳态无差控制后,能够进一步降低误差。
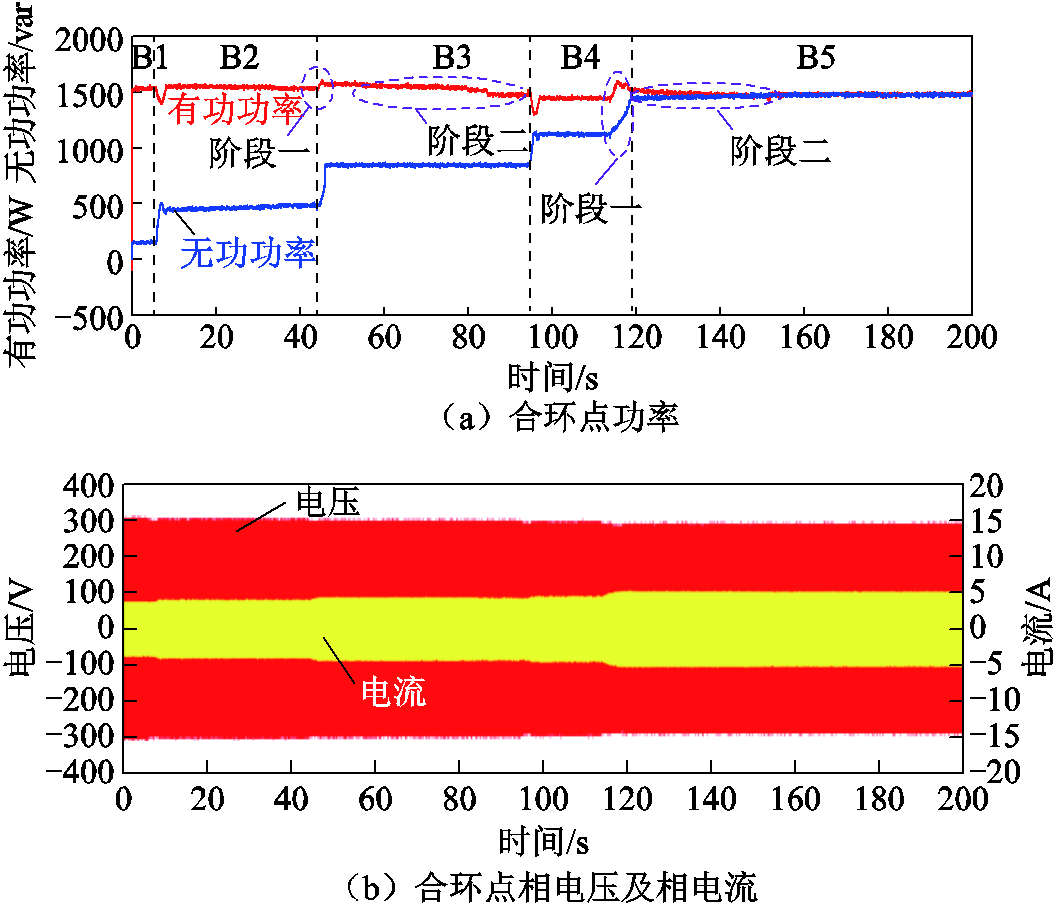
图12 无功功率调控实验
Fig.12 Experiments on reactive power regulation
3.2.3 有功/无功协同调控
为验证RPFC在有功无功同时调节情况下的有效性,将实验分为如下工况:
表3 无功功率调控实验结果
Tab.3 Experimental results of reactive power regulation

无功调节工况控制目标/(kV·A)实际值/(kV·A)误差(%)调节时间/s B11.5+j0.21.5+j0.2—— B1→B21.5+j0.51.55+j0.452.12 B2→B31.5+j0.81.55+j0.853.92.1 B3→B41.5+j1.11.45+j1.131.22.3 B4→B51.5+j1.51.48+j1.481.35.1
工况C1:P3ref+jQ3ref=0.0+j0.0 kV·A;
工况C2:P3ref+jQ3ref=1.2+j0.8 kV·A;
工况C3:P3ref+jQ3ref=1.7+j0.8 kV·A;
工况C4:P3ref+jQ3ref=2.3+j1.2 kV·A;
工况C5:P3ref+jQ3ref=2.8+j1.7 kV·A。
线路功率设定值变动时,RPFC功率调控的实验波形如图13所示,具体实验结果数据见表4。由此可知,RPFC能够在s级时间内将线路功率控制在功率控制死区范围内,控制精度在3.6%以内,且在经过第二阶段的稳态无差控制后,能够进一步降低误差。

图13 有功无功同时调控实验波形
Fig.13 Experimental waveforms of simultaneous control of active and reactive power
表4 有功功率、无功功率同时调控实验结果
Tab.4 Experimental results of simultaneous regulation of active and reactive power

有功无功同时调节工况控制目标/(kV·A)实际值/(kV·A)误差(%)调节时间/s C10.0+0.00.0+0.0—— C1→C21.2+0.81.25+0.823.69.8 C2→C31.7+0.81.77+0.752.33.2 C3→C42.3+1.22.32+1.221.02.7 C4→C52.8+1.72.83+1.751.62.8
3.3.1 功率均衡调控(有功扰动)
根据图9“花瓣型”配电结构进行功率均衡调控实验,在设定P1:P2=2:1、Q1:Q2=2:1的前提下,观察负载有功扰动时的功率控制情况,将实验分为如下工况:
工况D1:S1=3.3+j2.7 kV·A;
工况D2:S1=3.0+j2.7 kV·A;
工况D3:S1=2.7+j2.7 kV·A;
工况D4:S1=1.2+j2.7 kV·A。
负载有功功率波动时,RPFC功率均衡控制的实验结果如图14所示,具体实验结果数据结果见表5。可以看到,在功率均衡控制要求下,RPFC能够将“花瓣型”配电网的两条并行线路的功率比值控制在功率控制死区范围内,控制精度在3.6%以内,且经过第二阶段的稳态无差控制后,能够进一步降低误差。
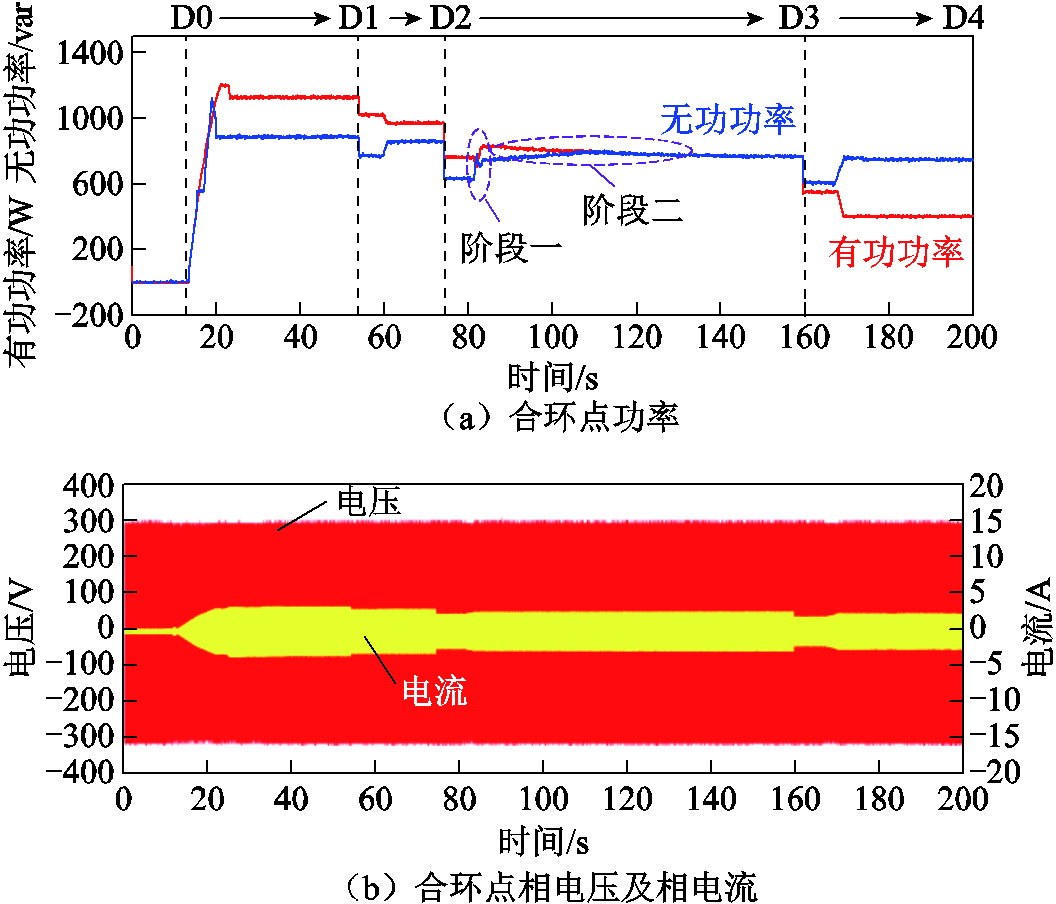
图14 有功扰动下功率均衡实验波形
Fig.14 Experimental waveforms on power equalisation under active disturbances
3.3.2 功率均衡调控(无功扰动)
在设定P1:P2=2:1、Q1:Q2=2:1的前提下,观察负载无功扰动时的功率控制情况,将实验分为如下情况:
工况E1:S1=3.3+j3.0 kV·A;
工况E2:S1=3.3+j1.8 kV·A;
工况E3:S1=3.3+j2.4 kV·A。
负载无功功率波动时,RPFC功率均衡控制的实验结果如图15所示,具体实验结果数据结果见表6。可以看到,在功率均衡控制要求下,RPFC能够将“花瓣型”配电网的两条并行线路的功率比值控制在功率控制死区范围内,控制精度在2.1%以内,且经过第二阶段的稳态无差控制后,能够进一步降低误差。
表5 有功扰动功率均衡实验结果
Tab.5 Experimental results of active disturbance power equalization (单位:kV·A)
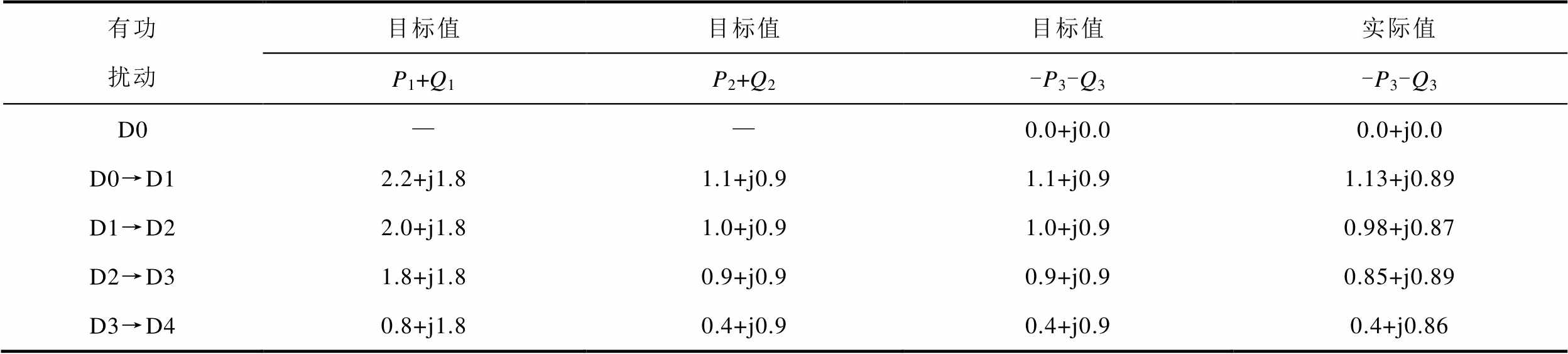
有功扰动目标值目标值目标值实际值 P1+Q1P2+Q2-P3-Q3-P3-Q3 D0——0.0+j0.00.0+j0.0 D0→D12.2+j1.81.1+j0.91.1+j0.91.13+j0.89 D1→D22.0+j1.81.0+j0.91.0+j0.90.98+j0.87 D2→D31.8+j1.80.9+j0.90.9+j0.90.85+j0.89 D3→D40.8+j1.80.4+j0.90.4+j0.90.4+j0.86
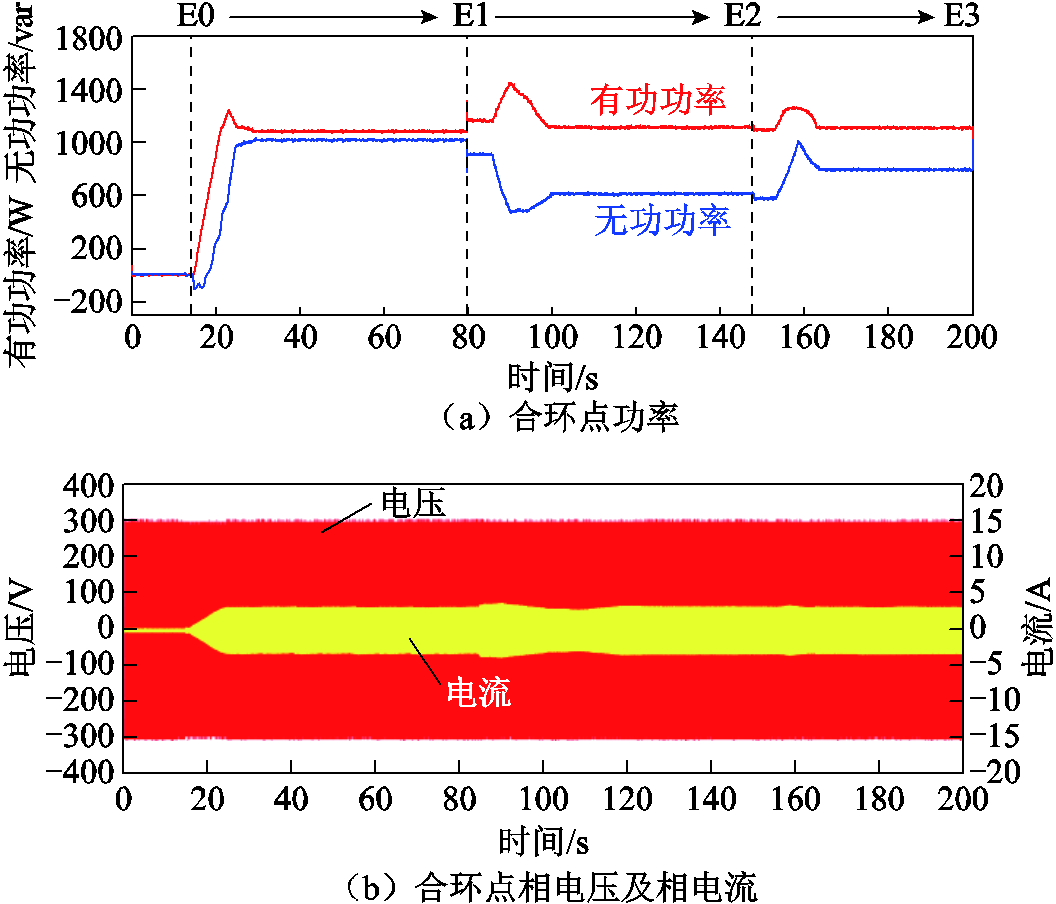
图15 无功扰动下功率均衡实验
Fig.15 Experiments on power equalisation under reactive disturbances
表6 无功扰动功率均衡实验结果
Tab.6 Experimental results of reactive disturbance power equalization (单位:kV·A)

有功扰动目标值目标值目标值实际值 P1+Q1P2+Q2-P3-Q3-P3-Q3 E0——0.0+j0.00.0+j0.0 E0→E12.2+j2.01.1+j1.01.1+j1.01.08+j1.02 E1→E22.2+j1.21.1+j0.61.1+j0.61.12+j0.62 E2→E32.2+j1.61.1+j0.81.1+j0.81.11+j0.81
3.3.3 功率均衡调控(变设定值)
在负载功率一定的情况下,通过改变l1、l2两条并行线路的输送功率变比,令S1=3.3+j2.4 kV·A,将实验分为如下工况:
工况F1:P1:P2=1:2、Q1:Q2=1:2;
工况F2:P1:P2=1:1、Q1:Q2=1:1;
工况F3:P1:P2=2:1、Q1:Q2=2:1;
工况F4:P1:P2=3:1、Q1:Q2=3:1。
两并行线路输送功率的设定变比变动时,RPFC功率均衡控制的实验结果如图16所示,具体实验结果数据见表7。可以看到,在功率均衡控制要求下,RPFC能够将“花瓣型”配电网的两条并行线路的功率比值控制在功率控制死区范围内,控制精度在3.4%以内,且经过第二阶段的稳态无差控制后,能够进一步降低误差。
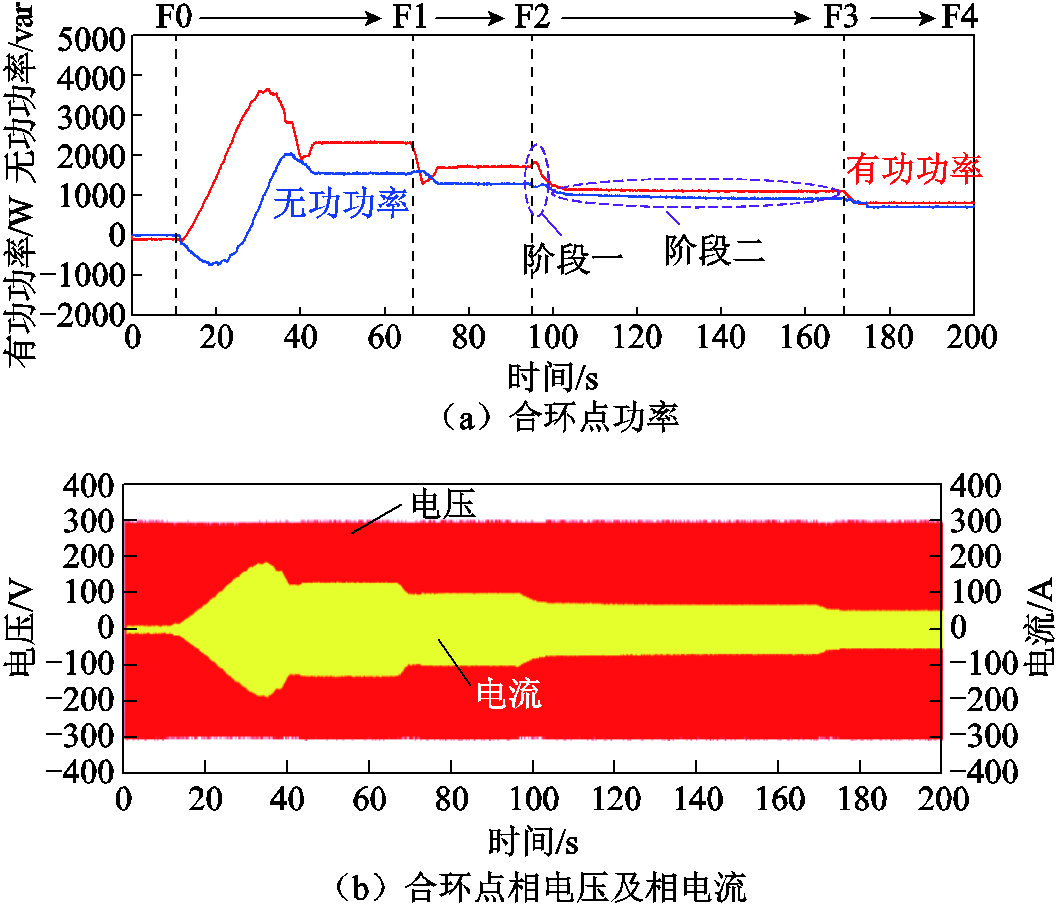
图16 多比例功率均衡实验
Fig.16 Experiments with multiple proportional power equalization
表7 多比例功率均衡实验结果
Tab.7 Experimental results of multi-scale power equalization (单位:kV·A)

有功扰动目标值目标值目标值实际值 P1+Q1P2+Q2-P3-Q3-P3-Q3 F0——0.0+j0.00.0+j0.0 F0→F11.1+j0.82.2+j1.62.2+j1.62.25+j1.58 F1→F21.65+j1.21.65+j1.21.65+j1.21.7+j1.25 F2→F32.2+j1.61.1+j0.81.1+j0.81.1+j0.85 F3→F42.5+j1.80.8+j0.60.8+j0.60.8+j0.65
为实现“花瓣型”有源配电网的安全运行,提出了在合环点接入RPFC的解决方案,能够实现对合环线路功率的稳定控制,得到结论如下:
1)所提RPFC控制系统由功率外环、电压环以及角度环组成,通过改变角度环a1、a2的大小,实现电压环中幅值和相位的连续调节,进一步实现了线路有功无功的解耦控制。
2)针对RPFC两旋转移相变压器机械特征,在角度控制环节,加入两阶段转速控制和转速协调方案,其中阶段一用于转速控制,阶段二用于驱动器脉冲信号控制,对于装置运行响应速度和鲁棒性的提高具有重要意义。
3)RPFC在绝大部分场景下,均能够在s级时间进行响应,且控制精度均保持在了4%以内,对于未来“花瓣型”配电网建设中的功率控制方法是一种有效补充。
附 录
1. 低转速下RPFC调控实验
根据图9电网结构进行变功率设定值实验,通过改变线路功率设定值Pref+jQref将实验分为五个阶段:
阶段一t0~t1:Pref+jQref=500+j500 V·A;
阶段二t1~t2:Pref+jQref=1000+j500 V·A;
阶段三t2~t3:Pref+jQref=1000+j1000 V·A;
阶段四t3~t4:Pref+jQref=2000+j1000 V·A;
阶段五t4~t5:Pref+jQref=1500+j500 V·A。
实验结果如附图1所示,可以看到当设定值发生变动后,RPFC能够对线路传输功率做出调整,响应配电网功率控制需求,但其调节时间较长,每次调节时间在15~100 s左右。
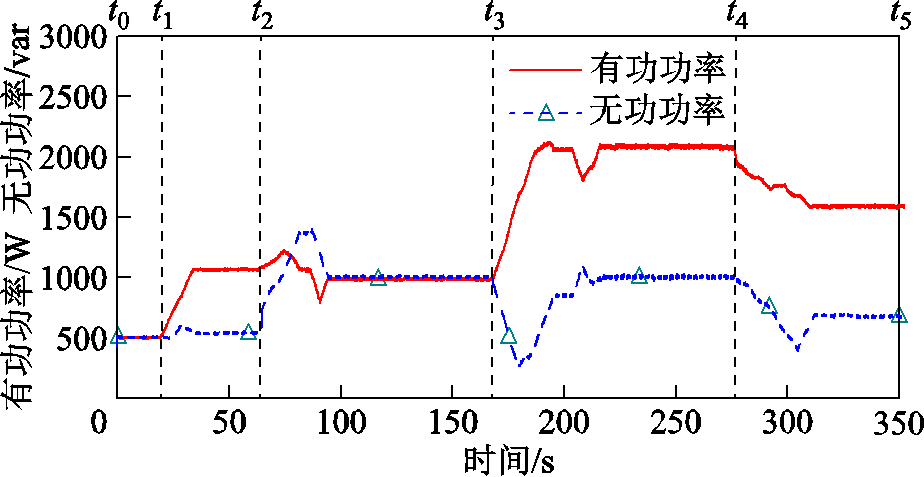
附图1 低转速下RPFC功率调控实验
App.Fig.1 Experiments of RPFC power regulation at low rotational speeds
同样根据图9进行功率扰动下调控实验,实验结果如附图2所示。将线路功率设定为Pref+jQref=2 000+j1 500 V·A,通过改变RPFC两端负荷验证其恒功率传输实验有效性,将实验分为四个阶段:
阶段一t0~t1:S1=3300+j1200 V·A、S2=2400+j500 V·A;
阶段二t1~t2:S1=3300+j1200 V·A、S2=1200+j500 V·A;
阶段三t2~t3:S1=2400+j800 V·A、S2=1200+j500 V·A;
阶段四t3~t4:S1=1200+j300 V·A、S2=1200+j500 V·A。
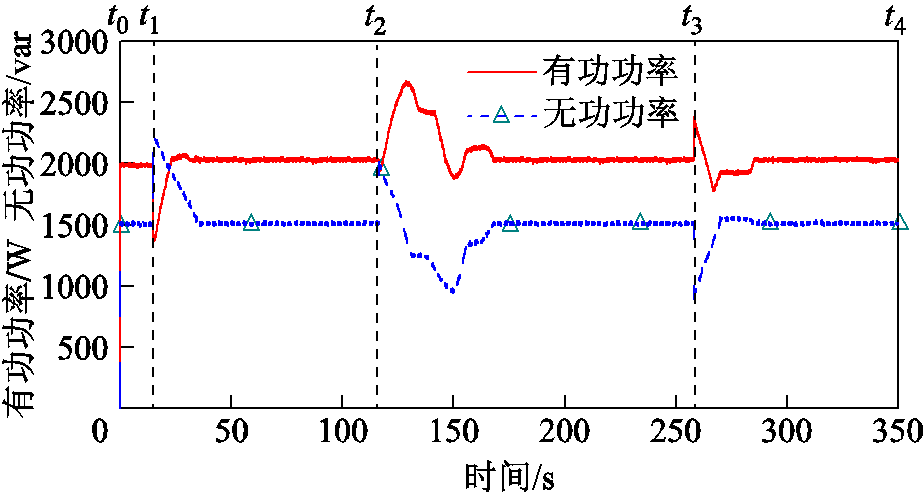
附图2 低转速下RPFC功率扰动调控实验
App.Fig.2 Experiment of RPFC power disturbance control at low speed
由附图2可以看到在功率扰动实验下,RPFC同样表现出了稳定的控制效果,但同样存在调节速度较慢的问题。
2. 高转速下RPFC调控实验
RPFC在高转速调节下由于功率环和电压环可能滞后于角度环,导致RPFC无法进入转速协调自适应阶段。此时将导致两RPST出现振荡现象,难以稳定控制线路功率。未进入转速自适应下RPFC调控实验结果如附图3所示。
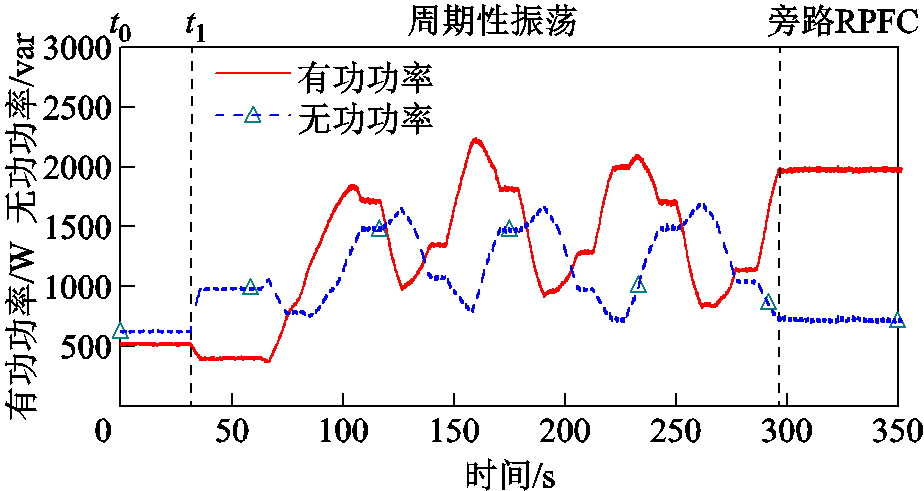
附图3 未进入转速自适应下RPFC调控实验
App.Fig.3 Experiments of RPFC regulation without access to speed adaptation
3. 传统RPFC控制方法
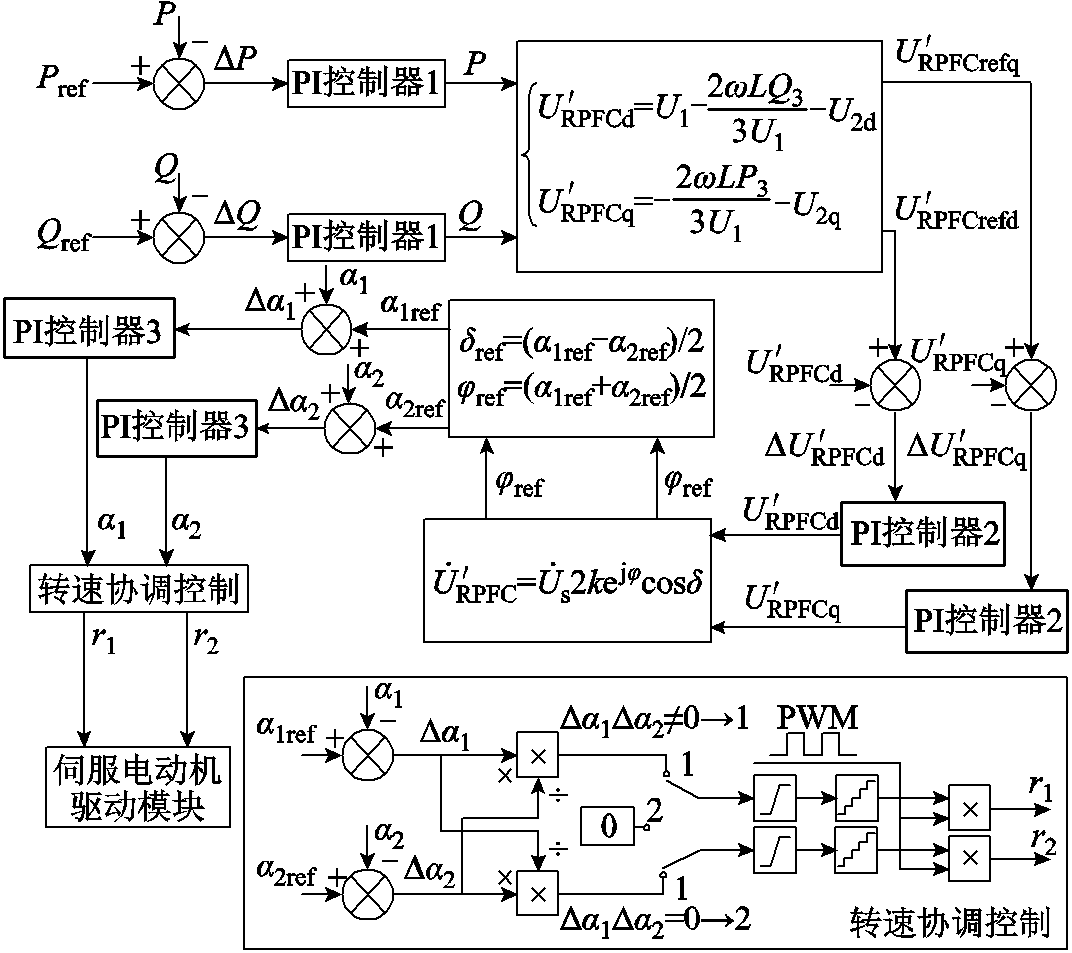
附图4 传统RPFC转子角控制方法
App.Fig.4 Traditional RPFC rotor angle control method
4. 详细RPFC接线图
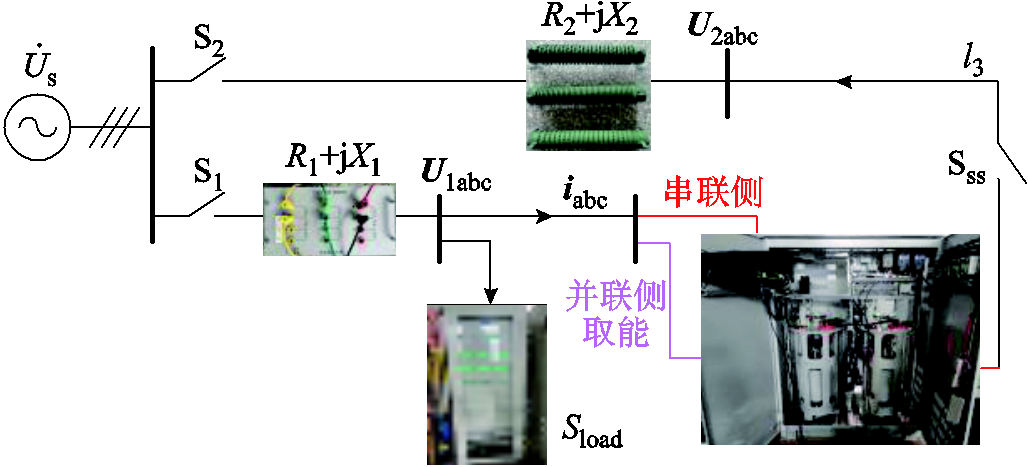
附图5 详细实验接线方案
App.Fig.5 Detailed experimental wiring scheme
参考文献
[1] 石方迪, 侯四维, 唐琪, 等. 世界一流城市配电网典型接线模式的评估及选型方法[J]. 电网技术, 2022, 46(6): 2249-2258.
Shi Fangdi, Hou Siwei, Tang Qi, et al. Evaluation and selection of typical connection modes for world-class urban distribution network[J]. Power System Technology, 2022, 46(6): 2249-2258.
[2] 刘洪, 李其哲, 徐晶, 等. 网孔型中压配电网组网形态、核心特征与研究展望[J]. 电力系统自动化, 2023, 47(16): 181-191.
Liu Hong, Li Qizhe, Xu Jing, et al. Networking morphology, key feature and research prospect of mesh-type medium-voltage distribution network[J]. Automation of Electric Power Systems, 2023, 47(16): 181-191.
[3] 徐玉韬, 冯起辉, 谈竹奎, 等. 考虑转供与重构协同的多端柔性互联配电网供电恢复策略[J]. 电工技术学报, 2024, 39(9): 2696-2709.
Xu Yutao, Feng Qihui, Tan Zhukui, et al. Power supply recovery strategy of multi-terminal flexible interconnected distribution network considering the cooperation of diversion and reconstruction[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2696-2709.
[4] 葛少云, 李俊锴, 刘洪, 等. 计及弹性响应的需求侧资源与软开关联合规划[J]. 天津大学学报(自然科学与工程技术版), 2022, 55(5): 462-470.
Ge Shaoyun, Li Junkai, Liu Hong, et al. Coordinated planning of soft open points and demand-side resources considering an elastic response[J]. Journal of Tianjin University (Science and Technology), 2022, 55(5): 462-470.
[5] 周剑桥, 张建文, 施刚, 等. 应用于配电网柔性互联的变换器拓扑[J]. 中国电机工程学报, 2019, 39(1): 277-288, 342.
Zhou Jianqiao, Zhang Jianwen, Shi Gang, et al. Exploration on power converter topologies applied in flexible interconnection of distribution system[J]. Proceedings of the CSEE, 2019, 39(1): 277-288, 342.
[6] 贾焦心, 彭维锋, 颜湘武, 等. 基于余弦定理的旋转潮流控制器功率解耦控制方法[J]. 电工技术学报, 2023, 38(13): 3425-3435.
Jia Jiaoxin, Peng Weifeng, Yan Xiangwu, et al. Research on power decoupling control method rotary power flow controller based on cosine law[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3425-3435.
[7] 胡亚静, 刘龙飞, 徐宪东. 基于软开关的互联区域能源系统功率控制[J]. 电力系统及其自动化学报, 2023, 35(3): 38-45.
Hu Yajing, Liu Longfei, Xu Xiandong. Soft opening point based power control of interconnected district energy systems[J]. Proceedings of the CSU-EPSA, 2023, 35(3): 38-45.
[8] 李群, 张宁宇, 王新宝, 等. 电力潮流灵活控制技术应用综述[J]. 电力工程技术, 2023, 42(1): 50-60.
Li Qun, Zhang Ningyu, Wang Xinbao, et al. Review on application of flexible power flow control technology[J]. Electric Power Engineering Technology, 2023, 42(1): 50-60.
[9] 颜湘武, 邵晨, 彭维锋, 等. 基于旋转式潮流控制器的有源配电网柔性合环及紧急功率控制方法[J]. 中国电机工程学报, 2023, 43(16): 6192-6205.
Yan Xiangwu, Shao Chen, Peng Weifeng, et al. Flexible loop closing and emergency power control method for active distribution network based on the rotary power flow controller[J]. Proceedings of the CSEE, 2023, 43(16): 6192-6205.
[10] 谭振龙, 张春朋, 姜齐荣, 等. 旋转潮流控制器稳态特性研究[J]. 电网技术, 2015, 39(7): 1921-1926.
Tan Zhenlong, Zhang Chunpeng, Jiang Qirong, et al. Study on steady state characteristics of rotary power flow controller[J]. Power System Technology, 2015, 39(7): 1921-1926.
[11] 谭振龙, 张春朋, 姜齐荣, 等. 旋转潮流控制器与统一潮流控制器和Sen Transformer的对比[J]. 电网技术, 2016, 40(3): 868-874.
Tan Zhenlong, Zhang Chunpeng, Jiang Qirong, et al. Comparative research on rotary power flow controller, unified power flow controller and Sen transformer[J]. Power System Technology, 2016, 40(3): 868-874.
[12] Chen Chang, Chang Changyuan, Han Xiong. Design of equivalent single-input fuzzy PI converter for buck DC-DC converters with excellent transient performance [C]//2019 IEEE 3rd International Electrical and Energy Conference (CIEEC), Beijing, China, 2019: 335-340.
[13] 刘玲玲, 徐明忻, 钟诚, 等. 电流定向旋转坐标下的统一潮流控制器串联侧变流器解耦控制研究[J]. 电测与仪表, 2019, 56(10): 27-33, 68.
Liu Lingling, Xu Mingxin, Zhong Cheng, et al. A novel power decoupling control in the current-orient rotating frame for series-side converter of unified power flow controller[J]. Electrical Measurement & Instrumentation, 2019, 56(10): 27-33, 68.
[14] Ba A O, Peng Tao, Lefebvre S. Rotary power-flow controller for dynamic performance evaluation: Part I: RPFC modeling[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1406-1416.
[15] 李海峰, 王相锋, 陈中, 等. 统一潮流控制器相角控制策略与矢量控制策略的量化比较方法[J]. 电网技术, 2016, 40(8): 2330-2337.
Li Haifeng, Wang Xiangfeng, Chen Zhong, et al. Quantitative comparison methods of a power-angle controlled and vector-current controlled UPFC[J]. Power System Technology, 2016, 40(8): 2330-2337.
[16] 王立俊, 赵吉文, 董菲, 等. 基于自适应内模观测器的永磁同步直线电机高带宽强鲁棒预测电流控制策略研究[J]. 中国电机工程学报, 2019, 39(10): 3098-3107.
Wang Lijun, Zhao Jiwen, Dong Fei, et al. High-bandwidth and strong robust predictive current control strategy research for permanent-magnet synchronous linear motor based on adaptive internal model observer[J]. Proceedings of the CSEE, 2019, 39(10): 3098-3107.
[17] 颜湘武, 邵晨, 吴鸣, 等. 基于电磁式旋转潮流控制器的有源配电网多场景控制[J]. 电工技术学报, 2023, 38(增刊1): 44-55.
Yan Xiangwu, Shao Chen, Wu Ming, et al. Multi-scene control method of active distribution network based on electromagnetic rotating power flow controller[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 44-55.
[18] 刘春强, 骆光照, 涂文聪, 等. 基于自抗扰控制的双环伺服系统[J]. 中国电机工程学报, 2017, 37(23): 7032-7039, 7095.
Liu Chunqiang, Luo Guangzhao, Tu Wencong, et al. Servo systems with double closed-loops based on active disturbance rejection controllers[J]. Proceedings of the CSEE, 2017, 37(23): 7032-7039, 7095.
Two-Stage Speed-Power Control Strategy for Rotating Power Flow Controller in “Petal-Shaped” Distribution Networks
Abstract With the rapid development of active distribution network construction, the “petal-type” distribution network has become the mainstream power supply structure, which significantly improves the reliability of power supply compared with the radiation-type distribution network, but also shows the characteristics of uncontrollable power size and direction. Therefore, an electromagnetic rotating current controller (RPFC) control device is proposed, which can effectively control the power at the closing point of the loop, ensure the safe operation of the closing loop, and thus significantly improve the power supply reliability of the distribution network.
The RPFC consists of two sets of rotary phase-shifting transformers (RPSTs), which are similar to a transformer at rest, and the relative rotation of the stator-rotor angles of the phase-shifting transformers is achieved through the physical association of servo motors and the stator cores of the phase-shifting transformers, and the specific phase-angle difference is related to the relative angles of the stator-rotor angles, a1 and a2. Finally, the two RPST stator voltage vectors are superimposed to achieve the stringing of a voltage vector with adjustable amplitude and phase angle in the line.
Firstly, the power decoupling model of distribution network based on RPFC is constructed, and after RPFC is put into operation, the power at the closing loop point can be effectively controlled by adjusting the amplitude and phase angle of the voltage strung into the line.
Then, the research of RPFC two-stage speed control method is carried out. The RPFC power decoupling model includes the power ring, voltage ring, and angle ring, while the control effect of fixed speed is poor when Da1 and Da2 output servo motor speed based on the angle ring. This is because the power regulation time is longer under low speed regulation (the RPST speed is about 1°/s). And under high speed regulation (the speed of RPST is about 6°/s) may bring the problem of rotor angle overshooting, at this time, the power ring and voltage ring will lag behind the angle ring, and it is difficult to stabilise into the speed co-ordination adaptive stage, which makes the stability of the control system reduced, and in some cases leads to the problem of rotor angle oscillation. Therefore, a two-stage speed control scheme is designed to achieve a fast and stable response of power control. The first stage is the fast power response regulation process, which aims to quickly reach the set power range and reduce the regulation time (acting on the speed of the servo motor driver); the second stage is the speed coordination and adaptive control process, which aims to reduce the overshooting of the rotor angle to avoid the oscillation problem, and to improve the stability of RPFC regulation stability (acting on the pulse wave).
Finally, a 380 V/40 kV·A RPFC prototype and experimental platform are developed, and power regulation and power balancing experiments are carried out. The results show that the proposed control scheme is capable of achieving regulation at the second level, and the control accuracy is kept within 4%, with good dynamic and static performance, and it is able to satisfy the future “petal-type” power distribution network of flexible closed-loop operation. The results show that the proposed control scheme can achieve regulation in seconds and keep the control accuracy within 4%.
Keywords:“Petal-shaped” distribution network, rotating power flow controller, power control, two-stage speed control
中图分类号:TM761
DOI: 10.19595/j.cnki.1000-6753.tces.232053
国家自然科学基金资助项目(52207102)。
收稿日期 2023-12-10
改稿日期 2024-01-24
邵 晨 男,1995年生,博士研究生,研究方向为潮流控制器理论及控制。
E-mail:shaochen@ncepu.edu.cn
颜湘武 男,1965年生,博士,研究方向为新能源电力系统分析与控制、现代电力与变换、新型储能与节能等。
E-mail:xiangwuy@ncepu.edu.cn(通信作者)
(编辑 赫 蕾)