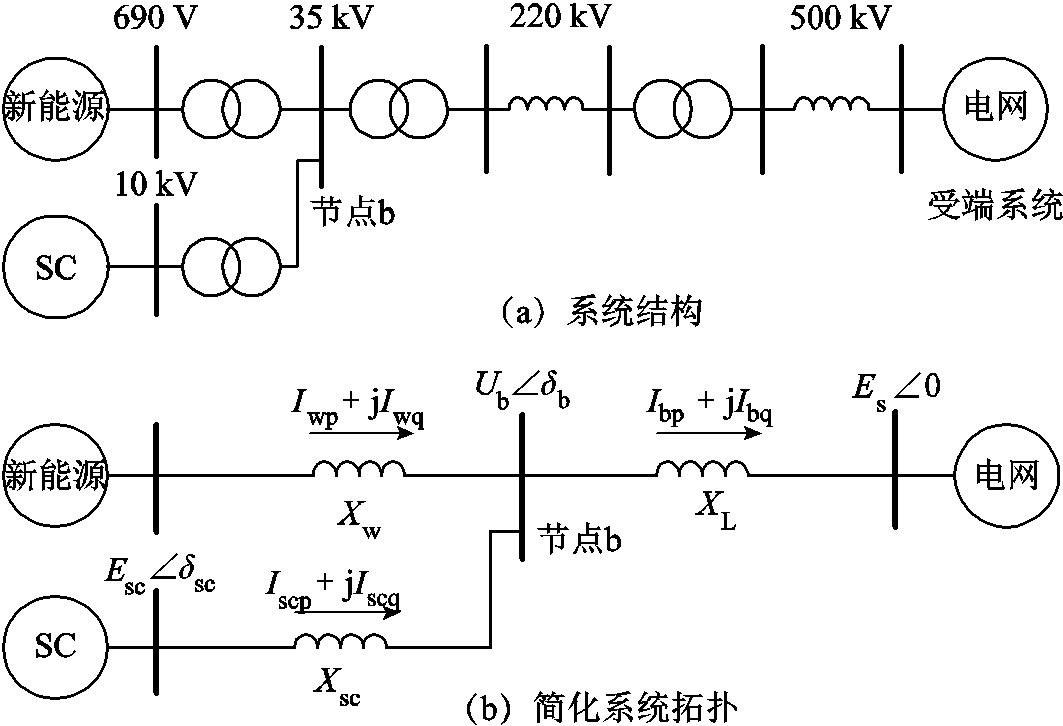
图1 含有分布式调相机的新能源送出系统模型
Fig.1 Renewable energy delivery systems with distributed condenser
摘要 当前新能源装机容量与发电量占比不断攀升,分布式调相机可有效地抑制新能源机端暂态过电压,提升新能源送出能力,然而调相机在电网故障过程中也存在暂态功角失稳风险。针对分布式调相机暂态特性与功角稳定机理,首先,建立保留新能源并网点电压特征的调相机功角时间尺度暂态分析模型,基于电气量相量关系分析了故障清除后调相机功角与新能源并网点电压的交互影响机理;其次,分析了故障暂态与故障稳态过程中新能源并网点电压相角二次跳变过程及原因,阐明了相角跳变、过渡电阻与新能源低电压穿越控制策略对调相机功角摇摆方向的影响机理;最后,基于暂态能量函数分析了新能源输出功率、调相机容量与送出距离对调相机暂态功角稳定性的影响,并在改进IEEE 39节点系统中验证了所提出机理与分析的正确性。
关键词:分布式调相机 功角稳定 暂态特性 新能源场站
随着“双碳”目标的提出,新能源装机容量与发电量占比逐年提升[1-3]。全国能源工作会议指出,将加快构建新型电力系统,预计2024年全国风电光伏新增装机容量2亿kW左右[4]。为解决新能源存在的暂态过电压问题[5-8],分布式调相机目前已应用于甘肃、青海、内蒙古等新能源富集地区,以提升新能源送出能力[9-11]。2022年1月,青海海南新能源基地21台分布式调相机成功投入运行,有效地抑制了新能源暂态过电压,将青海海南地区新能源外送能力提升350万kW[12]。然而,大规模新能源接入显著改变了系统潮流[13],使得临近新能源的分布式调相机在系统发生故障后存在功角失稳风险[14-15]。
当前分布式调相机相关研究集中于新能源经直流外送场景下调相机的控制与参数优化、调相机选址与容量配置及其小干扰稳定性。在控制与参数优化方面,可通过优化调相机次暂态电抗和提高强励能力[16-17],以提升其暂态性能,调相机控制参数也作为控制手段之一用于抑制暂态过电压[18]。在调相机选址与容量配置方面,多以提升新能源短路比与抑制暂态过电压为优化目标[19-20],并考虑经济性与配置效果[11,21]。此外,系统频率稳定与调相机的功角稳定性也可被作为调相机规划选址的参考依据[22-23]。在调相机的小干扰稳定性方面,研究多以新能源与调相机的详细控制模型为基础[24],从电网强度[25]、振荡模式与控制参数[26]等角度分析调相机对系统小干扰稳定性的影响。
由于分布式调相机具有容量小、惯量小、与新能源间电气距离短的特点,新能源对其暂态功角稳定的影响更为显著[27]。文献[14]将新能源输出功率等效为调相机与同步机节点的等效注入电流,进而分析调相机的暂态功角稳定性,使用等面积定则解释了分布式调相机功角失稳机理,并通过比较加速面积与减速面积判断调相机是否失稳。文献[15]将加装调相机系统的新能源场站与无穷大电网分别进行诺顿等值,并从新能源基地的短路比特性角度分析调相机的同步失稳机理,提出采用临界短路比判断调相机失稳风险。文献[27]基于叠加定理将新能源与分布式调相机联合系统等效为同步机组,提出基于反馈线性化的新能源低电压穿越控制策略以提升调相机暂态功角稳定性,并构建了相对应的李雅普诺夫函数。文献[28]在等面积定则的基础上分析了新能源与系统间电气距离、调相机惯量等因素对调相机暂态功角稳定的影响。现有研究多采用网络变化方法消去了新能源并网点或仅将其作为计算过程的中间量,未能考虑新能源并网点的电压动态特性,在并网点电压与调相机功角稳定交互影响方面鲜有报道。
针对上述问题,本文主要研究分布式调相机暂态特性与暂态功角稳定问题。首先,基于系统中电气量相量关系分析故障全过程中调相机的动态特性,分析了故障清除后调相机功角与新能源并网点电压的交互影响机理;其次,分析了故障暂态期间相角二次跳变的原因,揭示了故障稳态期间过渡电阻、新能源低电压穿越控制策略对调相机的功角摇摆方向的影响机理;最后,基于暂态能量函数分析了新能源输出功率、送出距离与调相机容量对调相机功角特性的影响,并在改进IEEE 39节点系统中验证了所提出机理与分析的正确性。
针对分布式调相机暂态功角稳定问题,本文建立新能源经交流线路送出系统如图1a所示,分布式调相机为同步调相机(Synchronous Condenser, SC),加装于新能源场站并网点。

图1 含有分布式调相机的新能源送出系统模型
Fig.1 Renewable energy delivery systems with distributed condenser
简化后系统拓扑如图1b所示,其中,Xsc为调相机暂态电抗 与变压器电抗XT之和,Xw为新能源升压变压器电抗,XL为输电线路以及变压器等效电抗,Es为受端电网等效同步机内电势幅值,以其转子角度δs为参考值,调相机暂态电动势角度为δsc,其幅值为Esc,新能源并网点电压幅值为Ub,与δs的相对角度为δb。
与变压器电抗XT之和,Xw为新能源升压变压器电抗,XL为输电线路以及变压器等效电抗,Es为受端电网等效同步机内电势幅值,以其转子角度δs为参考值,调相机暂态电动势角度为δsc,其幅值为Esc,新能源并网点电压幅值为Ub,与δs的相对角度为δb。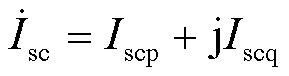 为调相机输出电流,
为调相机输出电流,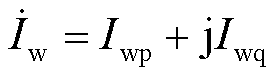 为新能源输出电流,
为新能源输出电流,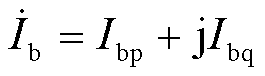 为输电线路电流。
为输电线路电流。
系统稳态运行时,可近似认为分布式调相机仅输出无功功率,与系统不存在有功交互,调相机功率因数角φsc=π/2,即δsc=δb。同时考虑新能源仅输出有功功率,即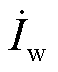 与
与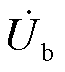 同相,在同步旋转坐标系下,可得系统中各相量关系如图2a所示。
同相,在同步旋转坐标系下,可得系统中各相量关系如图2a所示。
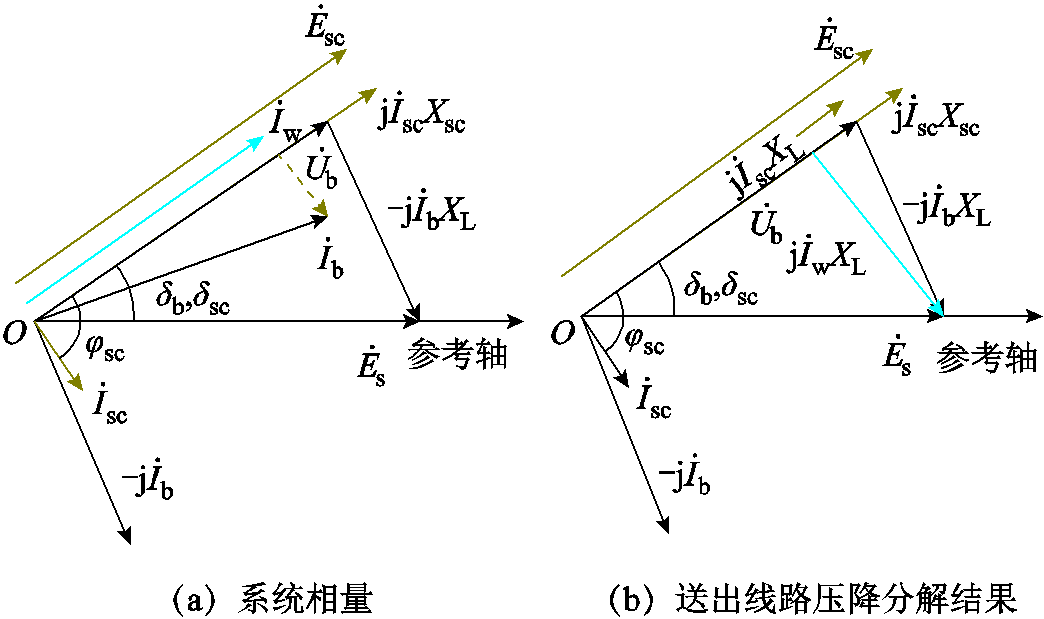
图2 系统相量关系
Fig.2 Phase relationship diagram of the system
图2中,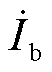 为节点b流出电流,有
为节点b流出电流,有
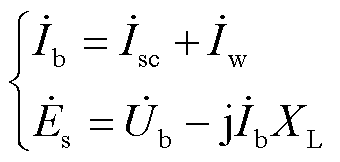 (1)
(1)
将送出线路压降分解后得到有功电流分量产生的电压降落横分量jIwXL,进而获得系统稳态运行时调相机功角表达式为
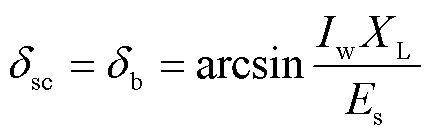 (2)
(2)
可见,随着新能源输出功率的增加,调相机功角与并网点电压相角同步增大,设调相机的原动机功率Pm=0,即等效为系统平衡点(δsc, 0)向右移动。
设对称故障发生在外送线路中某一点f,此时系统可看作原有网络在故障点处增加了注入电流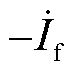 ,故障情况下原有网络与故障支路如图3所示。
,故障情况下原有网络与故障支路如图3所示。
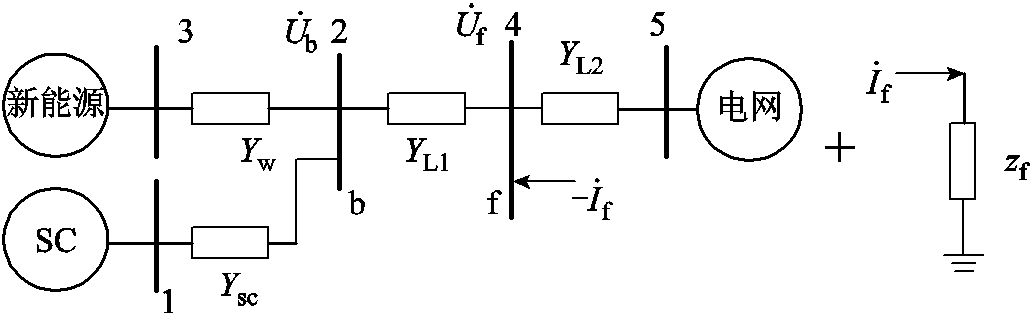
图3 故障情况下原有网络与故障支路
Fig.3 Original network and faulty branch during fault
设在节点4处发生故障,以大地为参考节点,则可得原有网络的节点导纳矩阵为
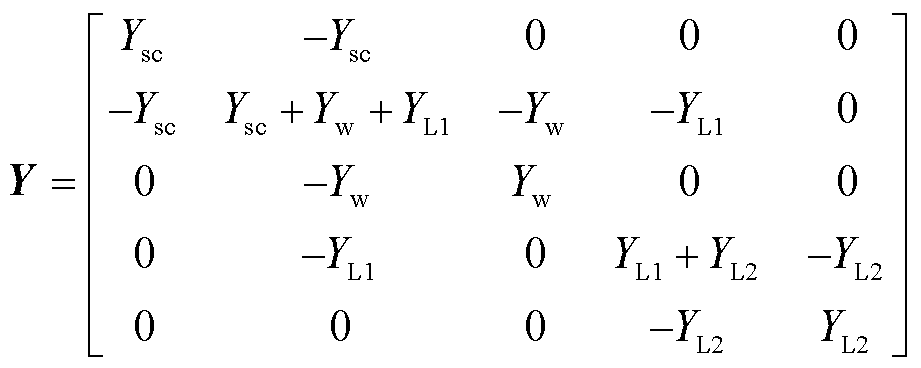 (3)
(3)
式中,Ysc=-j/Xsc;Yw=-j/Xw;YL1=-j/(kXL);YL2=-j/[(1-k)XL],k为故障与送端距离系数,k=0即故障发生在送端,k=1即故障发生在受端。
由此可得节点阻抗矩阵为Z=Y-1,根据图3分析可得,故障发生后新能源并网点节点b电压为
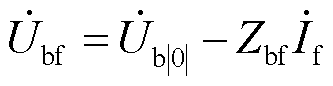 (4)
(4)
式中,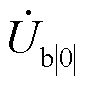 为故障发生前节点b电压;
为故障发生前节点b电压;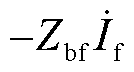 为故障电流单独作用在b节点产生的电压,即电压故障分量;Zbf为节点阻抗矩阵中b、f节点互阻抗。
为故障电流单独作用在b节点产生的电压,即电压故障分量;Zbf为节点阻抗矩阵中b、f节点互阻抗。
对于故障点f而言,除满足式(4)以外,还同时满足故障的边界条件,由此可得
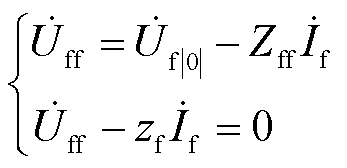 (5)
(5)
式中,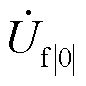 、
、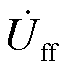 分别为故障发生前、后故障点f电压;Zff为节点阻抗矩阵中f节点自阻抗;zf为故障过渡电阻。由式(5)可得故障电流为
分别为故障发生前、后故障点f电压;Zff为节点阻抗矩阵中f节点自阻抗;zf为故障过渡电阻。由式(5)可得故障电流为
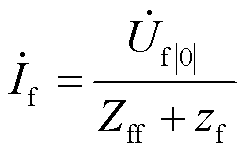 (6)
(6)
结合式(4)和式(6)可以得到故障期间节点b电压为
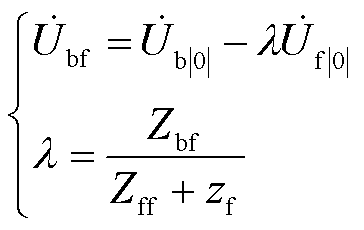 (7)
(7)
为便于分析,定义λ为故障分量系数。
由式(7)可见,故障发生后节点b处的电压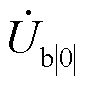 会增加故障分量,导致b点电压幅值减小,相角超前跳变,跳变角度为Dδb,如图4a所示。
会增加故障分量,导致b点电压幅值减小,相角超前跳变,跳变角度为Dδb,如图4a所示。
由故障引发的相角跳变导致并网点电压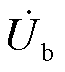 相角超前调相机内电势,φsc>90°,调相机吸收有功,增发无功。
相角超前调相机内电势,φsc>90°,调相机吸收有功,增发无功。
故障期间,调相机由于吸收有功功率,转子转速ω增加,此过程中,新能源并网点电压与调相机内电势同步以角速度ω旋转,如图4b所示,调相机内电势与并网点电压相位差δsc-δb基本维持恒定。对于复杂网络,可通过支路追加法获得网络阻抗矩阵[29],进而计算相角跳变角度。
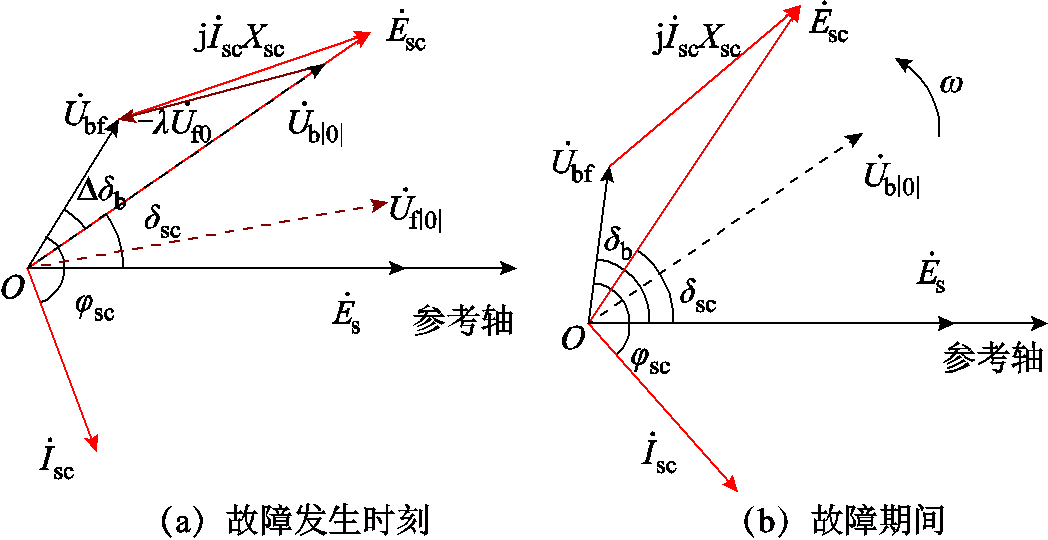
图4 故障发生时刻与故障期间系统相量图
Fig.4 Phase diagram of the system at the moment of the fault occurrence and during fault
故障清除时刻与故障清除后系统相量图如图5所示。故障清除时刻,根据1.2节分析可知,新能源并网点电压再次跳变,如图5a所示。故障清除后,新能源并网点电压相角落后于调相机内电势,此时δsc仍在持续增加,调相机输出有功功率和无功功率,如图5b所示。进一步研究此时调相机的功角特性。
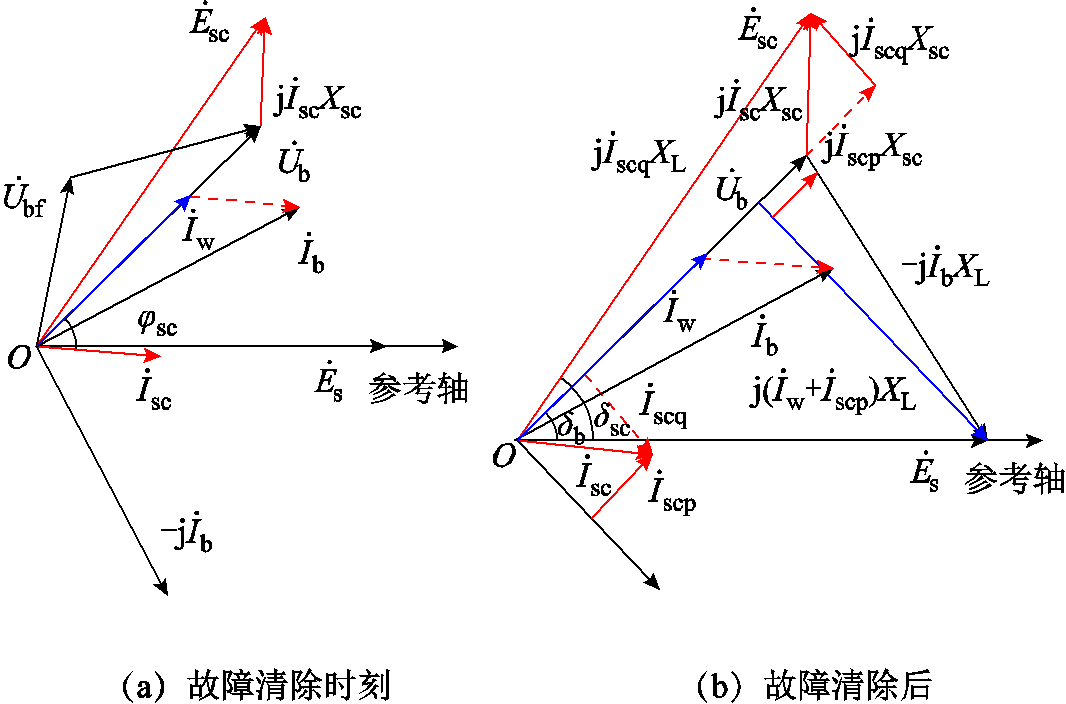
图5 故障清除时刻与故障清除后系统相量图
Fig.5 Phase diagram of the system at the end of the fault and after the fault
在系统送端部分,将调相机输出电流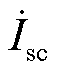 沿
沿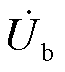 和
和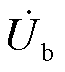 法向分解为有功电流
法向分解为有功电流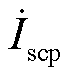 (幅值为Iscp)和无功电流
(幅值为Iscp)和无功电流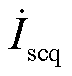 (幅值为Iscq)。设调相机输出有功电流Iscp为正方向,即当调相机吸收有功电流时,Iscp为负值。由图5b可得调相机输出有功电流为
(幅值为Iscq)。设调相机输出有功电流Iscp为正方向,即当调相机吸收有功电流时,Iscp为负值。由图5b可得调相机输出有功电流为
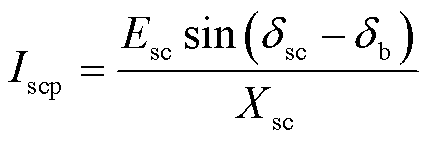 (8)
(8)
设调相机向节点b注入无功电流Iscq为正方向,即当节点b向调相机注入无功电流时,Iscq为负值,由图5b可得调相机向节点b注入无功电流为
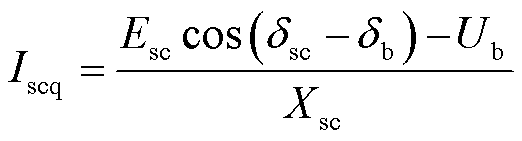 (9)
(9)
在系统受端部分,电流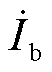 可分解为无功电流
可分解为无功电流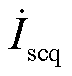 和有功电流
和有功电流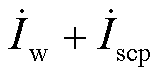 ,有功电流幅值为
,有功电流幅值为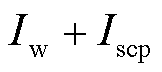 。首先考虑新能源只输出有功功率,即
。首先考虑新能源只输出有功功率,即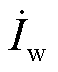 与
与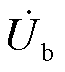 同相,则由相量图5b可得δb正弦值为
同相,则由相量图5b可得δb正弦值为
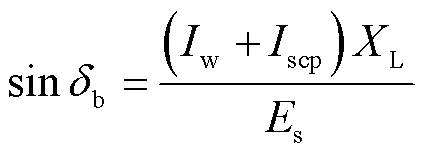 (10)
(10)
进一步由相量图5b可得b节点电压幅值Ub为
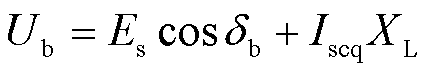 (11)
(11)
若考虑新能源同时输出无功功率,则将电流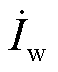 沿
沿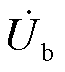 和
和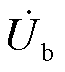 法向分解为有功电流
法向分解为有功电流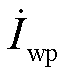 (幅值为Iwp)和无功电流
(幅值为Iwp)和无功电流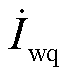 (幅值为Iwq),式(10)、式(11)可更新为
(幅值为Iwq),式(10)、式(11)可更新为
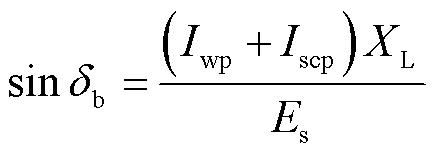 (12)
(12)
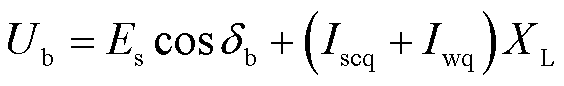 (13)
(13)
将式(8)代入式(12)可得
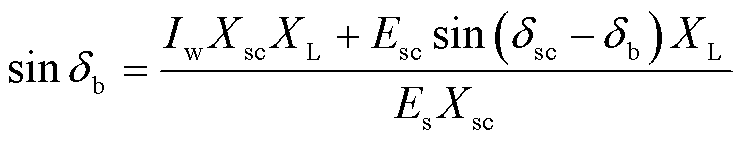 (14)
(14)
化简式(14)后可得
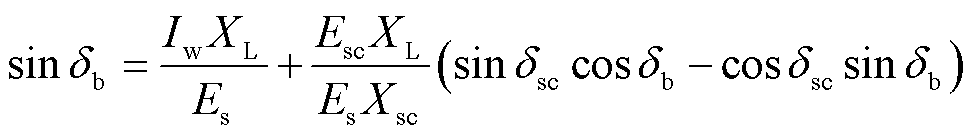 (15)
(15)
将式(9)代入式(13)可得
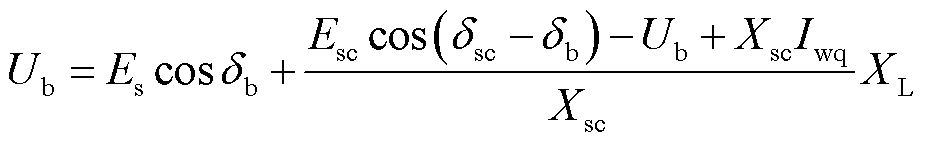 (16)
(16)
整理后可得
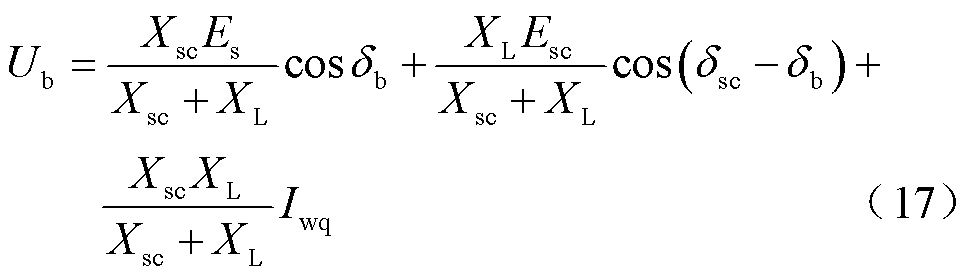
为简化表达式,令
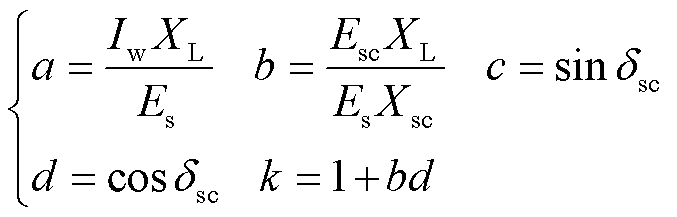 (18)
(18)
则由式(15)可得
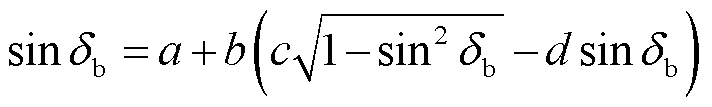 (19)
(19)
解得
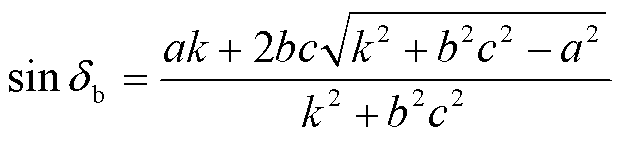 (20)
(20)
由此可进一步求解cosδb、sin(δsc-δb)、cos(δsc-δb)、Ub,具体表达式见附录式(A2)~式(A5)。
可得调相机的输出功率为
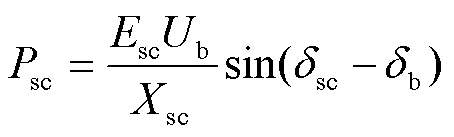 (21)
(21)
设置系统参数为:Es=1.2,Esc=1.2,Xw=0.03,Xsc=0.4,XL=0.159,均为标幺值,系统基准容量为100 MV·A。在新能源输出功率变化的情况下,调相机的功角特性曲线如图6所示。
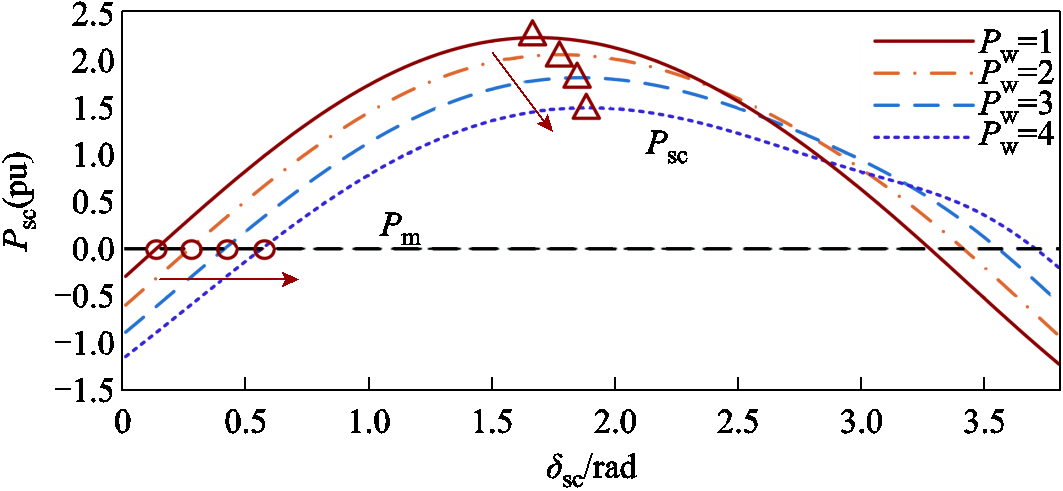
图6 不同新能源输出功率下调相机功角特性曲线
Fig.6 Power-angle characteristic curves of distributed condenser under different renewable energy outputs
由图6可见,考虑调相机输入机械功率为Pm=0,随新能源功率增加,调相机稳态运行状态下的初始功角δsc|0|增大,功角特性曲线向右下方移动,即故障结束后减速面积减小,不利于分布式调相机功角稳定。
对多机系统而言,可保留新能源并网点与调相机、同步机节点对网络进行化简。考虑三机系统含有两座新能源场站并分别加装一台调相机,系统原始网络拓扑如图7a所示。
在原始网络基础上,保留新能源并网点b1和b2,其电压幅值分别为Ub1、Ub2,相角分别为δb1、δb2,得到简化网络拓扑如图7b所示。在此系统中,研究调相机功角特性时需考虑两座新能源场站并网点间等效电抗X12上所流过的电流I12,有功电流分量为
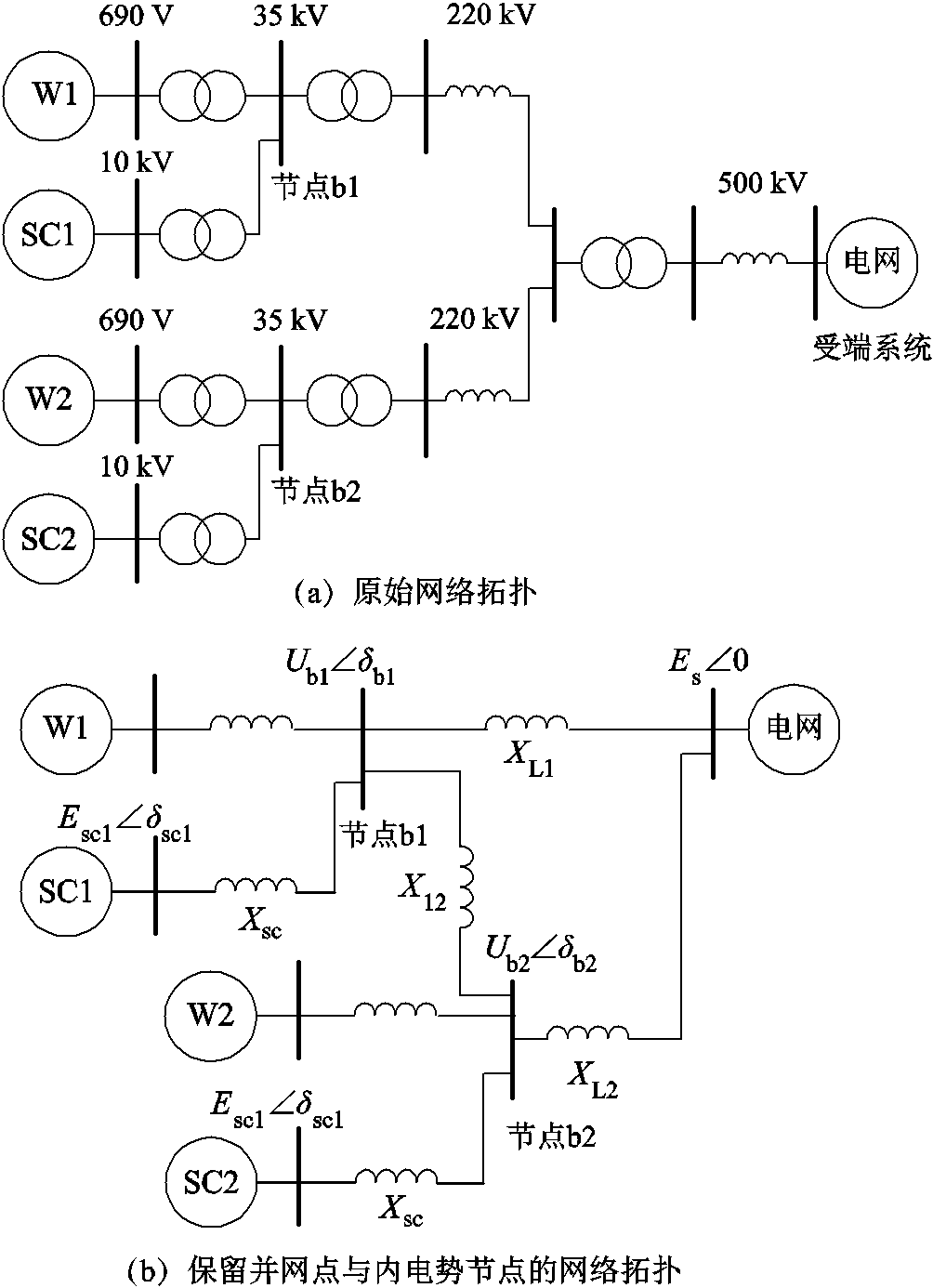
图7 三机系统拓扑结构
Fig.7 Topology diagram of three-machine system
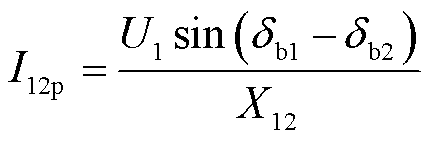 (22)
(22)
并网点b1、b2处I12无功电流分量分别为
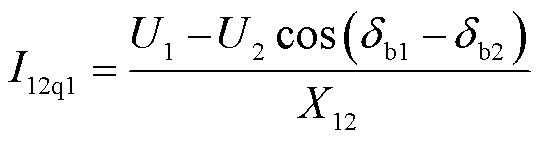 (23)
(23)
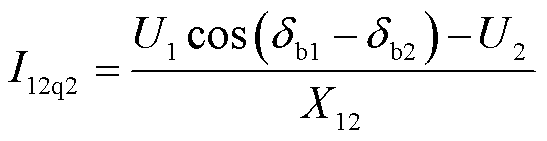 (24)
(24)
由此在式(12)、式(13)中分别考虑I12p、I12q1和I12q2,即可求解并网点电压,进而计算调相机的功角特性。设置两座新能源场站输出功率Pw相同,各自输出功率在200、300、400 MW时,两台分布式调相机功角特性如图8所示。

图8 三机系统中两台调相机功角特性
Fig.8 Power-angle characteristics of distributed condensers three-machine system
由图8可见,随着新能源输出功率的增加,三机系统中两台调相机功角特性曲面下移,而其整体变化趋势与图6中单台调相机功角特性相似,由此可进一步研究多台调相机系统的功角特性。
在调相机功角特性曲线的基础上,进一步分析故障清除后新能源并网点(Point of Common Coupling, PCC)电压的变化规律。设故障清除后系统拓扑结构与初始状态相同,此时调相机与电网的相对功角δsc仍在增加,根据式(17)、式(18)与式(20),可得故障清除后新能源机组并网点电压幅值Ub随δsc变化曲线如图9所示。
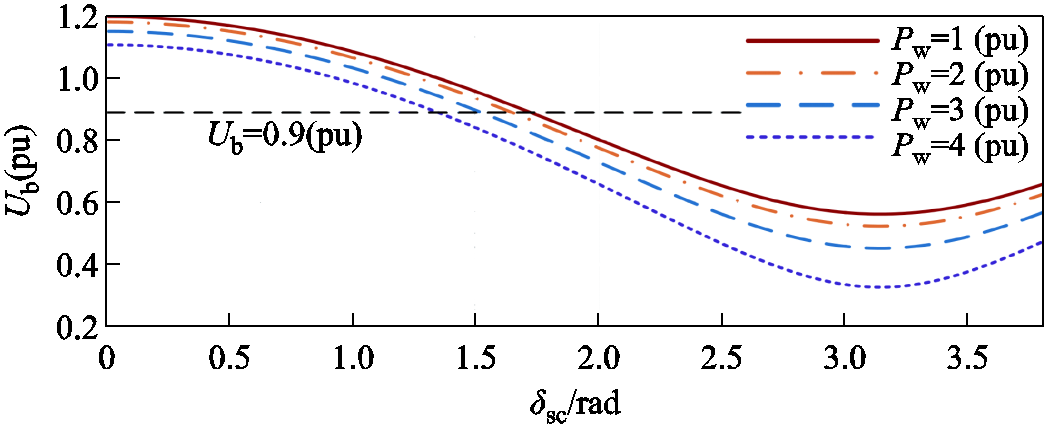
图9 不同新能源功率下并网点电压曲线
Fig.9 Voltage curves of PCC under different renewable energy outputs
由图9可见,由于故障清除后调相机与系统间相对功角继续增加,使得Ub无法快速恢复到0.9(pu)以上,致使新能源机组在故障清除后仍处于低电压穿越状态,且随新能源功率增加,持续低电压的退出阈值降低,更容易导致新能源机组在故障恢复后长时间处于低电压穿越状态。
在三机系统中,设置新能源场站输出功率均为300 MW,并网点b1与b2电压幅值变化曲面如 图10所示。可见随调相机1功角增加,新能源场站1的并网点电压呈现先下降后小幅上升的趋势,在故障清除后,功角持续增加使得并网点电压幅值Ub1低于0.9(pu),新能源仍处于低电压穿越状态。同时,调相机2的功角增加同样使得Ub1先下降后小幅上升,但其影响小于调相机1。三机系统计算与分析结果印证了单机无穷大系统所得结论。多机系统分析过程与三机系统分析过程相同,即保留新能源并网点、调相机内电势、同步机内电势节点,进而采用本文所提出方法进行分析计算。

图10 三机系统中两座新能源场站并网点电压变化曲面
Fig.10 Voltage surfaces of PCC in three-machine system
进一步进行仿真验证,设置新能源有功功率为300 MW,调相机及系统参数见附表1。工况1故障持续时间为0.2 s,故障全过程中调相机功角与新能源并网点电压波形如图11a所示。设置工况2故障持续时间为0.3 s,调相机功角与新能源并网点电压波形如图11b所示。
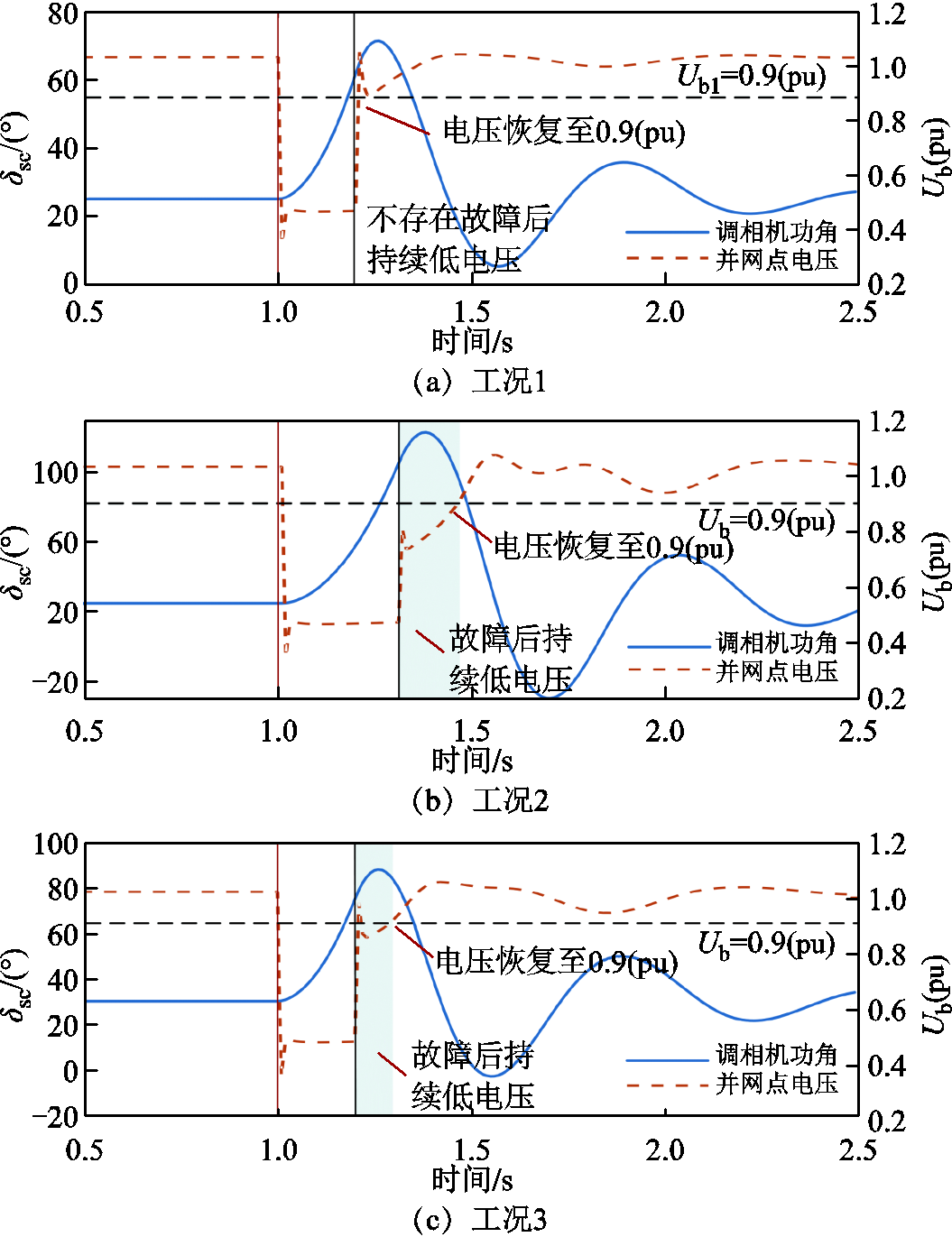
图11 不同新能源功率下并网点电压与调相机功角波形
Fig.11 Waveforms of voltage at PCC and power angle of SC under different renewable energy outputs
由图11a可见,故障持续时间较短,调相机功角摆开程度较小,未使得故障清除后并网点电压低于0.9(pu),系统不发生持续低电压,此时新能源有功电流响应情况如图12中工况1波形所示。而当系统故障未及时清除,功角持续增加导致故障切除后新能源并网点发生持续低电压(图11b色带),此时新能源有功电流响应情况如图12a工况2波形所示。
在工况1的基础上增加新能源输出功率至350 MW,设置为工况3。此时由于新能源输出功率增加,故障清除后功角曲线超过持续低电压的退出阈值,如图11c所示,进而使得新能源仍维持在低电压穿越控制,其有功电流如图12b工况3波形所示,由于新能源功率增加带来的持续低电压阶段如图12b色带区域所示。
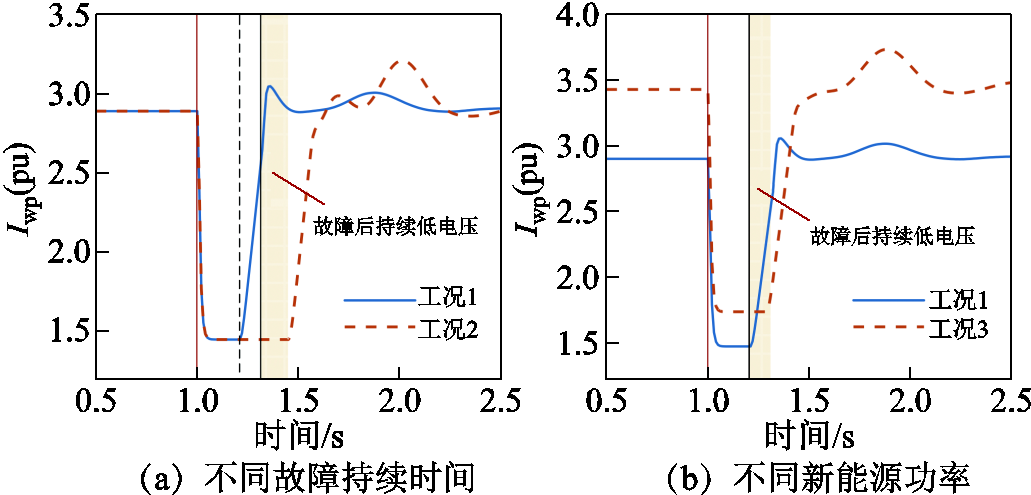
图12 不同工况下新能源有功电流波形
Fig.12 Active current waveforms of renewable energy under different conditions
故障清除后的新能源持续低电压降低新能源输出功率,使得调相机功角特性曲线上移(如图6所示),有助于分布式调相机功角恢复稳定。
基于分布式调相机故障期间动态过程进一步分析故障期间调相机功角摇摆方向及其影响因素。
通常认为故障进入稳态区间后,新能源已切换至低电压穿越控制策略[30-31],其注入系统电流Iwf∠θw,以及有功电流Iwpf、无功电流Iwqf分别为
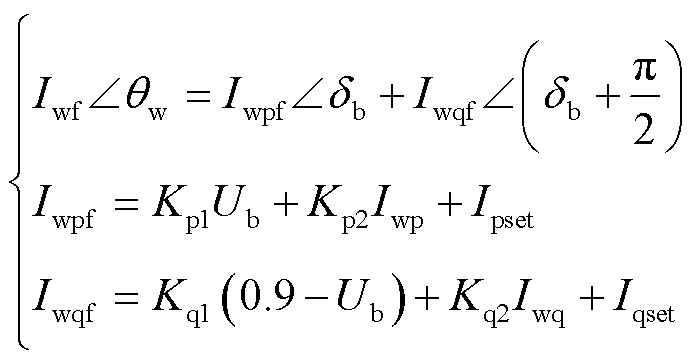 (25)
(25)
式中,Kp1、Kp2为有功电流控制系数;Ipset为低穿有功电流常数;Kq1、Kq2为无功电流控制系数;Iqset为低穿无功电流常数。
在此基础上应用叠加定理。由于此时新能源控制策略已经发生切换,导致调相机的稳态运行工况发生改变,所以需分别考虑调相机与新能源单独作用,并叠加故障分量,故障期间系统叠加定理示意图如图13所示。
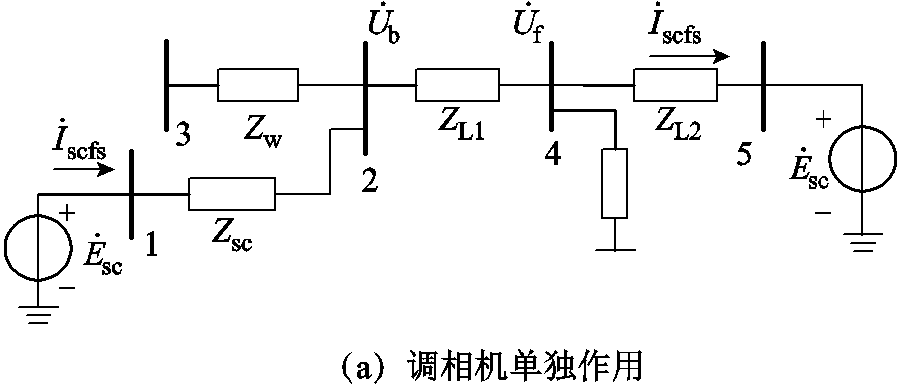
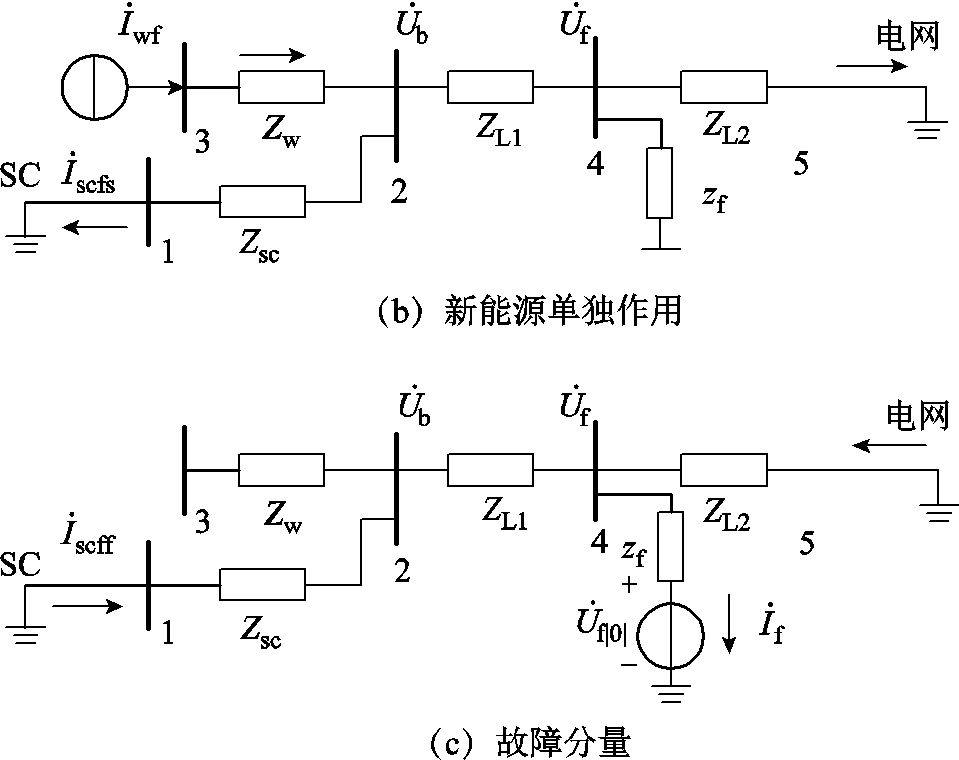
图13 故障期间叠加定理示意图
Fig.13 Schematic diagram of the superposition theorem during fault
调相机单独作用时,其输出电流幅值为Iscfs,相角为θfs,即考虑在稳态运行状态下将新能源输出电流置零。由图2可见,此时线路上没有功率流过,故Iscfs=0。考虑新能源单独作用时,新能源注入调相机的电流幅值为Iscfw,其相角为θfw,由电流分配规律可得
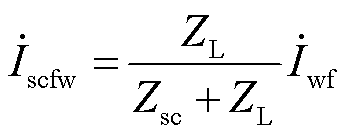 (26)
(26)
对于故障附加网络,调相机注入故障点电流为Iscff,其相角为θff。根据故障电流分布可得
 (27)
(27)
整理后可得
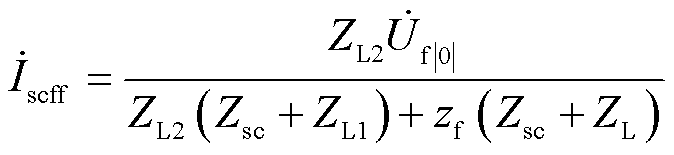 (28)
(28)
由此可得调相机故障期间的输出电流为
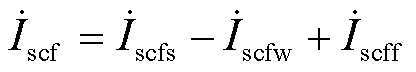 (29)
(29)
其幅值为Iscf,相角为θf。进一步可求解故障稳态期间调相机输出有功功率为
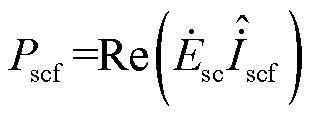 (30)
(30)
式中,上标ˆ表示共轭。
故障期间调相机转子上不平衡功率为
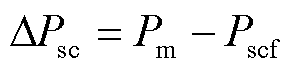 (31)
(31)
若Pscf>Pm,则调相机吸收功率,功角正向摇摆;若Pscf<Pm,则调相机输出功率,功角反向摇摆。
2.2.1 故障为金属性短路
为充分验证所提出机理,同时分析故障点经过渡阻抗接地的情况,以此作为对照。忽略系统中电阻的影响,由式(7)可见,此时λ为实数,λ随过渡阻抗xf增大而减小,且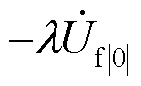 与
与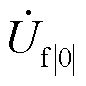 平行,即表明相角始终超前跳变,由此可得调相机在故障发生前期总会吸收有功功率,其跳变前后系统相量关系如图4所示,新能源并网点b电压相角δb向前跳变,超前于调相机功角δsc。此后,新能源控制策略已切换至低电压穿越控制,在指定电流控制模式下,新能源输出有功、无功电流进入稳态,此时δb将会发生二次跳变,以满足系统电气量的相量关系,进入故障稳态。
平行,即表明相角始终超前跳变,由此可得调相机在故障发生前期总会吸收有功功率,其跳变前后系统相量关系如图4所示,新能源并网点b电压相角δb向前跳变,超前于调相机功角δsc。此后,新能源控制策略已切换至低电压穿越控制,在指定电流控制模式下,新能源输出有功、无功电流进入稳态,此时δb将会发生二次跳变,以满足系统电气量的相量关系,进入故障稳态。
设置三相金属性短路与经过渡阻抗短路,新能源场站有功功率为400 MW,并网点电压相角、调相机功角与新能源输出有功电流如图14a、图14b所示。
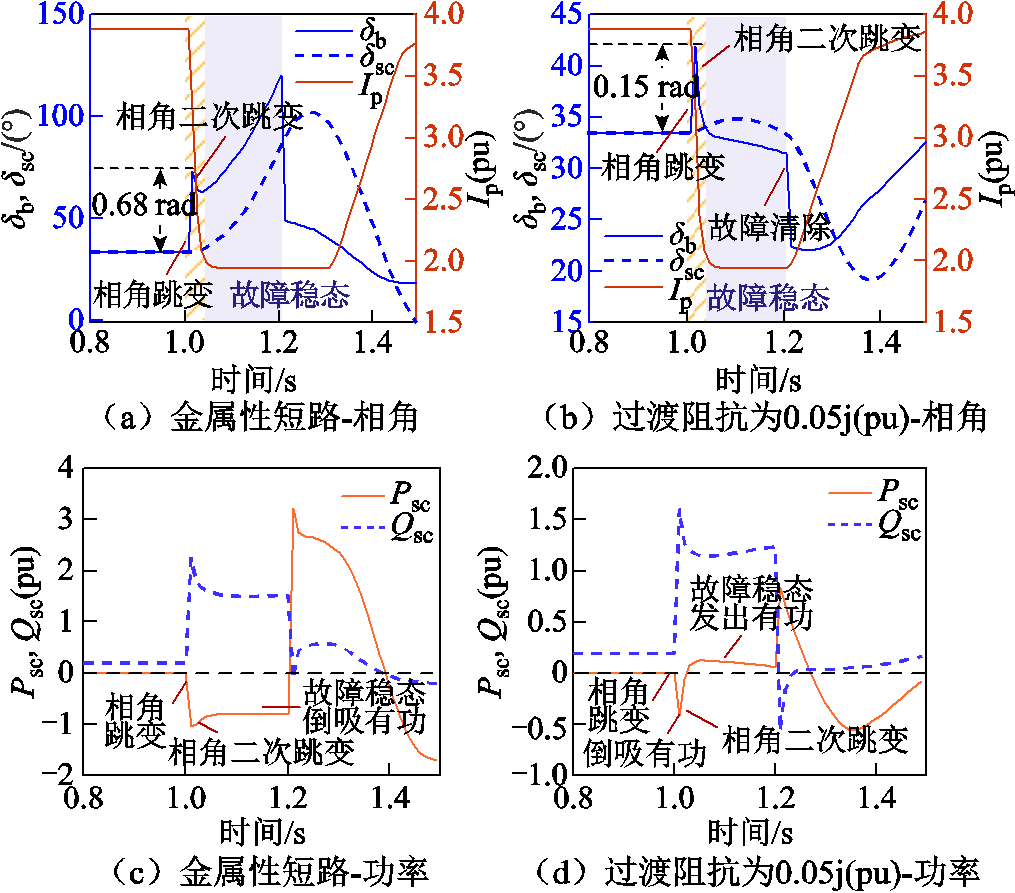
图14 不同过渡阻抗下并网点电压相角、调相机功角、有功功率、无功功率波形
Fig.14 Waveforms of PCC voltage phase and power angle, active power, reactive power of distributed condenser under different transition impedance
由图14a、图14b可见,当故障点存在过渡阻抗0.05j(pu)时,并网点电压跳变量由0.68 rad减小至0.15 rad,但不会改变相角跳变方向,在一次跳变过程中均吸收有功功率,如图14c、图14d所示。受新能源注入功率变化影响,相角发生二次跳变,此时由式(30)计算所得调相机输出有功功率,若Psc<0,转子上不平衡功率Pm-Psc>0,如图14c所示,调相机转子加速,功角正向摇摆;若Psc>0,转子上不平衡功率Pm-Psc<0,调相机转子减速,功角反向摇摆。如图14d所示。
2.2.2 故障点存在过渡电阻
当过渡阻抗为阻性时,根据式(7)可计算得到故障发生时刻调相机相角变化情况。此时λ不再为常数,即图4中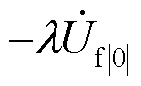 与
与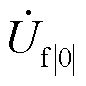 不再平行,在不同过渡电阻值下,系统相量图如图15所示。
不再平行,在不同过渡电阻值下,系统相量图如图15所示。
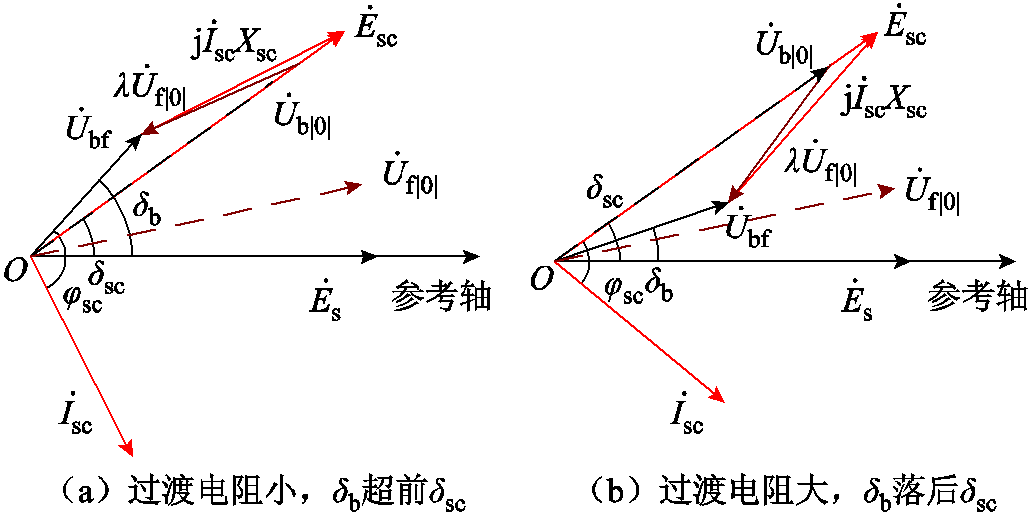
图15 不同过渡电阻下故障期间系统相量图
Fig.15 Phase diagram of the system during fault under different transition resistance
分别设置过渡电阻为0.01(pu)与0.02(pu),设置新能源场站有功功率为400 MW,并网点电压相角、调相机功角与新能源输出有功电流如图16所示。
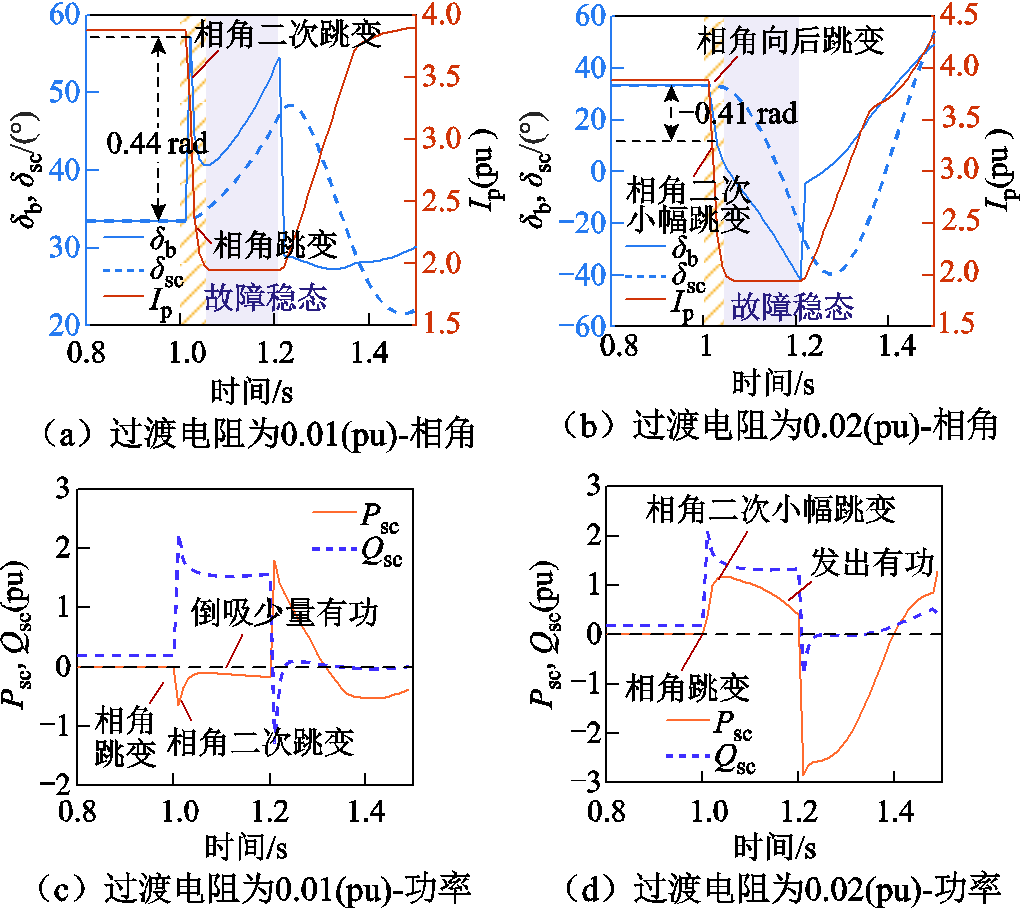
图16 不同过渡电阻下并网点电压相角、调相机功角、有功功率、无功功率波形
Fig.16 Waveforms of PCC voltage phase and power angle, active power, reactive power of distributed condenser under different transition resistance
由图16a、图16b可见,过渡电阻由0.01(pu)增加至0.02(pu),新能源并网点电压相角跳变方向改变,由超前跳变0.44 rad变为向后跳变0.41(pu),并由于新能源控制策略的切换同样存在相角二次跳变。当过渡电阻为0.01(pu)时,调相机输出功率Psc<0,如图16c所示,Pm-Psc>0,调相机转子加速,功角正向摇摆;当过渡电阻为0.02(pu)时,Psc>0,如图16d所示,Pm-Psc<0,调相机转子减速,功角反向摇摆。
根据式(21)调相机功角特性方程,可得调相机二阶转子运动方程[32]为
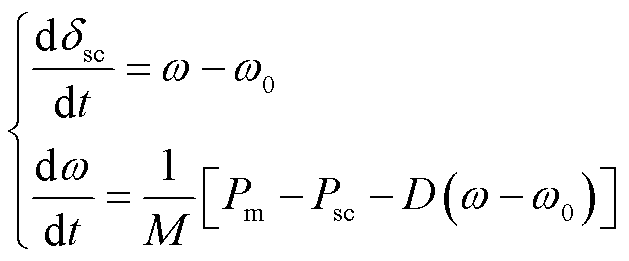 (32)
(32)
式中,ω为调相机转子电角速度,rad/s;ω0为系统额定电角速度,rad/s;M=TJ/ω0,TJ为调相机惯性时间常数,s;Pm近似为零;Psc为调相机输出有功功率标幺值;D为阻尼系数。
为量化多种影响因素对调相机暂态功角稳定的影响,构建含有分布式调相机的新能源送出系统暂态能量函数[33]。由于Psc表达式较为复杂,不考虑阻尼情况下,采用梯形法对式(32)进行首次积分可得
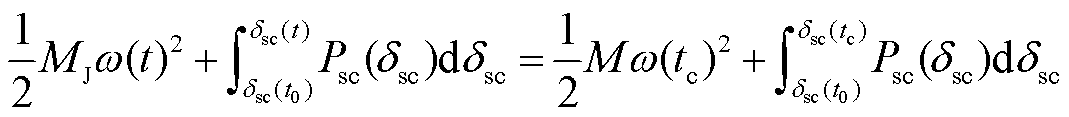 (33)
(33)
式中,δsc(tc)为故障清除时刻调相机与系统相对功角;δsc(t0)为故障清除后调相机稳定平衡点相对功角。式(33)右侧第一项为tc时刻调相机转子动能VK,第二项为tc时刻系统势能VP,左侧两项对应故障清除后t时刻调相机转子动能与系统势能,即故障清除后系统中总能量不变(考虑系统阻尼耗散能量,则系统最终恢复稳态)。若故障清除后系统吸收调相机故障期间积累的全部动能,且未达到最大势能VPmax,则系统保持稳定;否则发生功角失稳。设置系统参数与1.3节相同,不同新能源输出功率下系统势能曲线如图17所示。
由图17可见,随新能源输出功率增加,系统势能最大值VPmax下降,即系统暂态稳定裕度下降。设置新能源输出功率分别为400、100 MW,调相机及系统参数见附表1,将调相机动能与系统势能叠加获得故障清除后系统能量曲面如图18所示。
由图18可见,当新能源输出功率增加,调相机相图中稳定平衡点与鞍点均向右移动,最大势能VPmax下降,系统在鞍点处总能量降低。
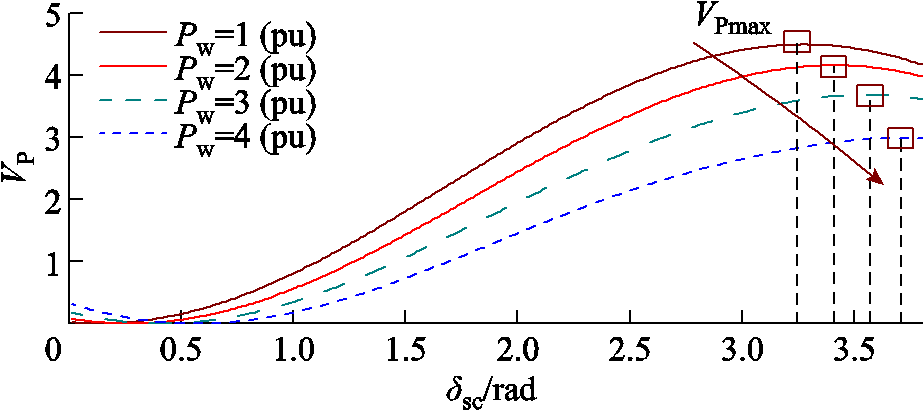
图17 不同新能源输出功率下系统势能曲线
Fig.17 Potential energy curves of the system under different renewable energy outputs

图18 暂态能量函数曲面及调相机相图
Fig.18 Energy function surfaces and phase portrait of distributed condenser
考虑调相机容量Ssc与电抗Xsc存在反比关系,与TJ存在正比关系,即SscXsc=Y,SscXsc=Z,公式设置参数与第2节相同,新能源输出功率为100 MW,设置调相机容量分别为50、100、150、200 Mvar,此时功角特性曲线与系统势能曲线如图19所示。
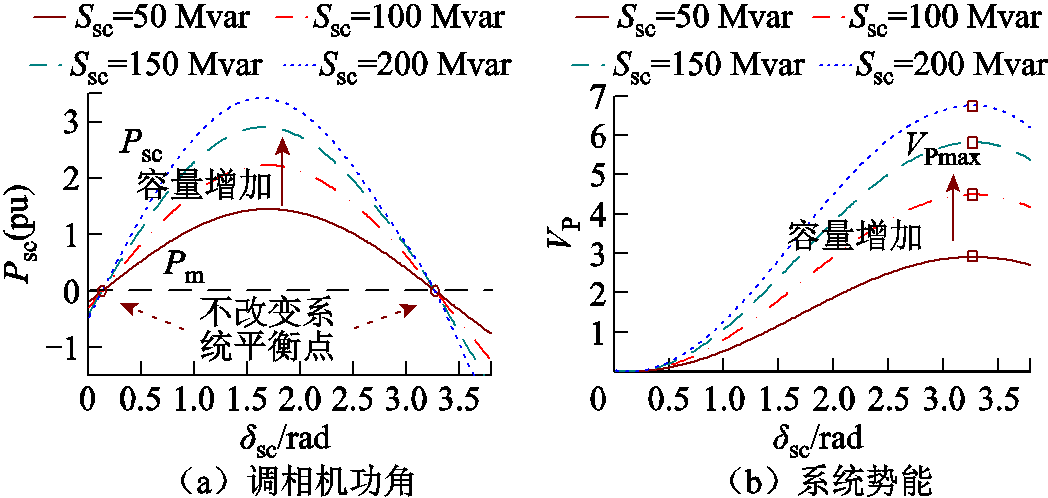
图19 不同调相机容量下功角特性曲线与系统势能曲线
Fig.19 System potential energy curve and power-angle curve under different capacity of distributed condenser
由图19可见,增大调相机容量不改变系统平衡点,调相机容量越大,功角特性曲线上移,如图19a所示,暂态稳定裕度增加,如图19b所示,越不容易发生功角失稳。此外,改变Ssc不影响系统平衡点的位置(相图验证)。此外,惯性时间常数随分布式调相机容量增加而增大,由式(32)可见,容量增加后故障期间调相机转速增幅降低,调相机与系统功角摆开幅度减小。在单机无穷大系统中设置新能源有功功率为400 MW,调相机容量分别为100、200 Mvar,1 s时送出线路发生三相短路故障,1.2 s故障清除,调相机相轨迹如图20所示。
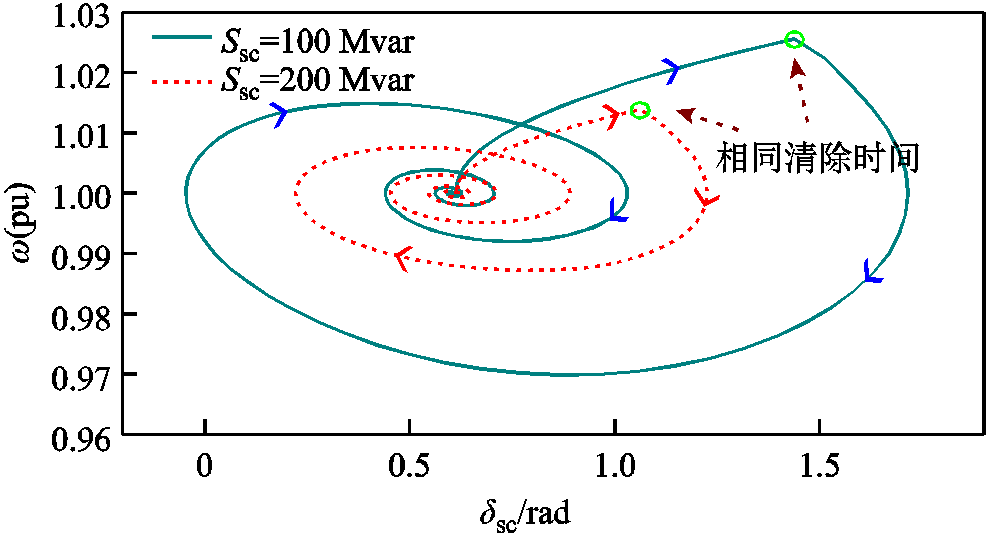
图20 不同调相机容量下的相轨迹
Fig.20 Phase trajectory diagram under different capacity of distributed condenser
由图20可见,调相机容量增加不改变系统平衡点,并使得调相机与系统间功角摇摆程度减小,功角失稳风险降低。
保持系统其他参数恒定,改变新能源输出功率,即增加Iw,功角特性曲线如图6所示,即新能源输出功率增加,功角特性曲线下移,暂态能量函数曲线如图17所示,系统最大势能VPmax下降,暂态稳定裕度下降,调相机功角失稳风险增加。对于调相机在故障期间特性,新能源低电压穿越期间控制策略为式(25),新能源功率增加,由式(29)可见,在相同故障深度下,新能源注入调相机电流增加,施加在调相机转子上的不平衡功率增加,故障期间转速增幅增加。
在单机无穷大系统中设置调相机容量为100 Mvar,新能源有功功率分别为300、400 MW,1s时送出线路发生三相短路故障,1.2 s故障清除,调相机相轨迹如图21所示。可见,新能源输出功率增加,故障期间调相机转速增幅增加,与上述理论分析结果相同。调相机与系统相对功角摆开幅度加大,功角失稳风险增加。
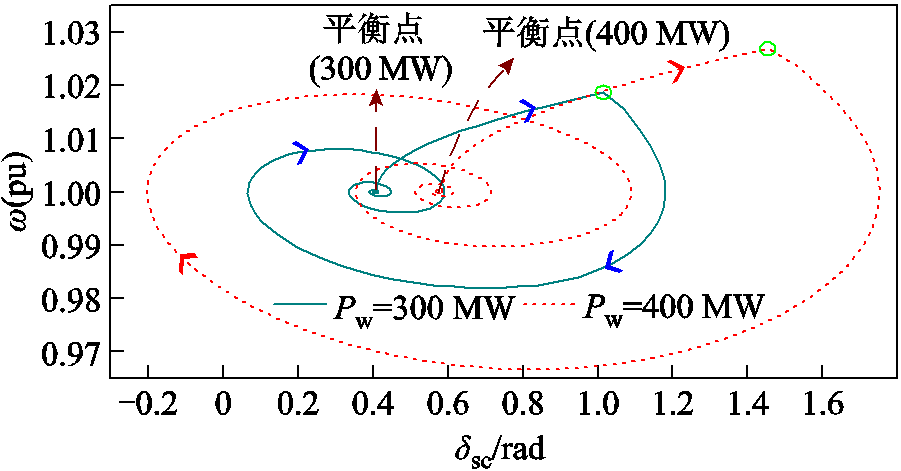
图21 不同新能源功率下的相轨迹
Fig.21 Phase trajectory diagram under different renewable energy outputs
保持系统其他参数恒定,改变送出距离,即设置500 kV线路距离分别为200、300、400、500 km,对应送出线路总电抗XL分别为0.015 9(pu)、 0.173 5(pu)、0.188、0.202 5(pu),调相机功角特性曲线与系统势能曲线如图22所示。
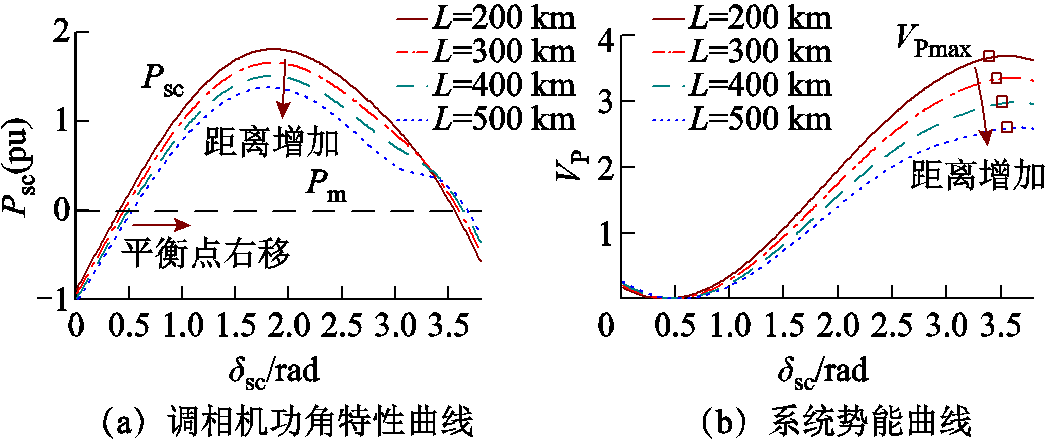
图22 不同送出距离下功角特性曲线与系统势能曲线
Fig.22 System potential energy curves and power-angle curves under different transmission distance
由图22a可见,新能源输送距离增加,调相机功角特性曲线下移,且平衡点右移,即稳态功角初始值增加。由图22b可见,随着送出线路距离增加,系统最大势能VPmax下降,暂态稳定裕度下降。在单机无穷大系统中设置新能源有功功率为400 MW,输电线路距离分别为200、500 km,1 s时送出线路发生三相短路故障,1.2 s故障清除,调相机相轨迹如图23所示。
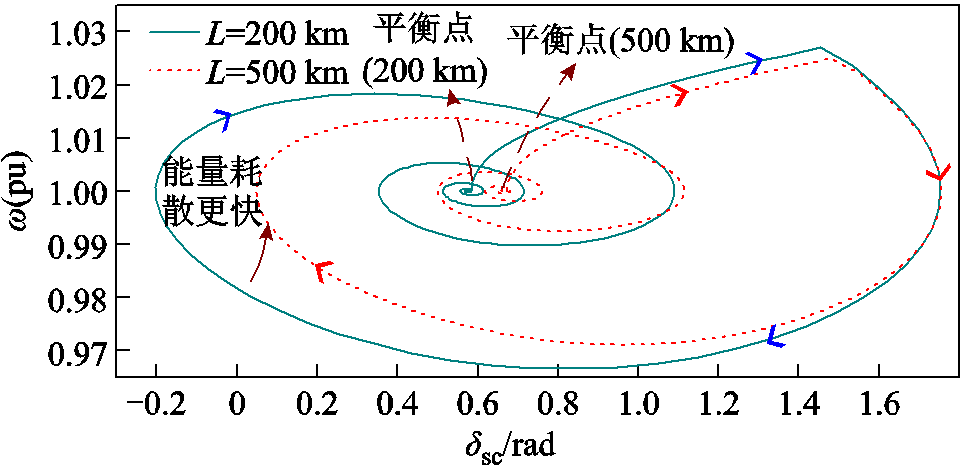
图23 不同送出距离下系统相轨迹
Fig.23 Phase trajectory diagram of the system under different transmission distances
由图23可见,线路距离增加后调相机稳态运行平衡点右移。此外,线路距离增加使得电阻增加,故障清除后系统能量耗散速度加快。
测试系统采用改进的IEEE 39节点系统,并添加母线40、41,含分布式调相机的新能源场站1接入母线37,替代原有同步机G8,其中新能源采用直驱型风电机组,分布式调相机接于母线41。线路L1为220 kV线路,对应电抗为XL1,线路L2为500 kV线路,对应电抗为XL2,分布式调相机参数与直驱风机参数设置见附表1,系统结构如图24所示。
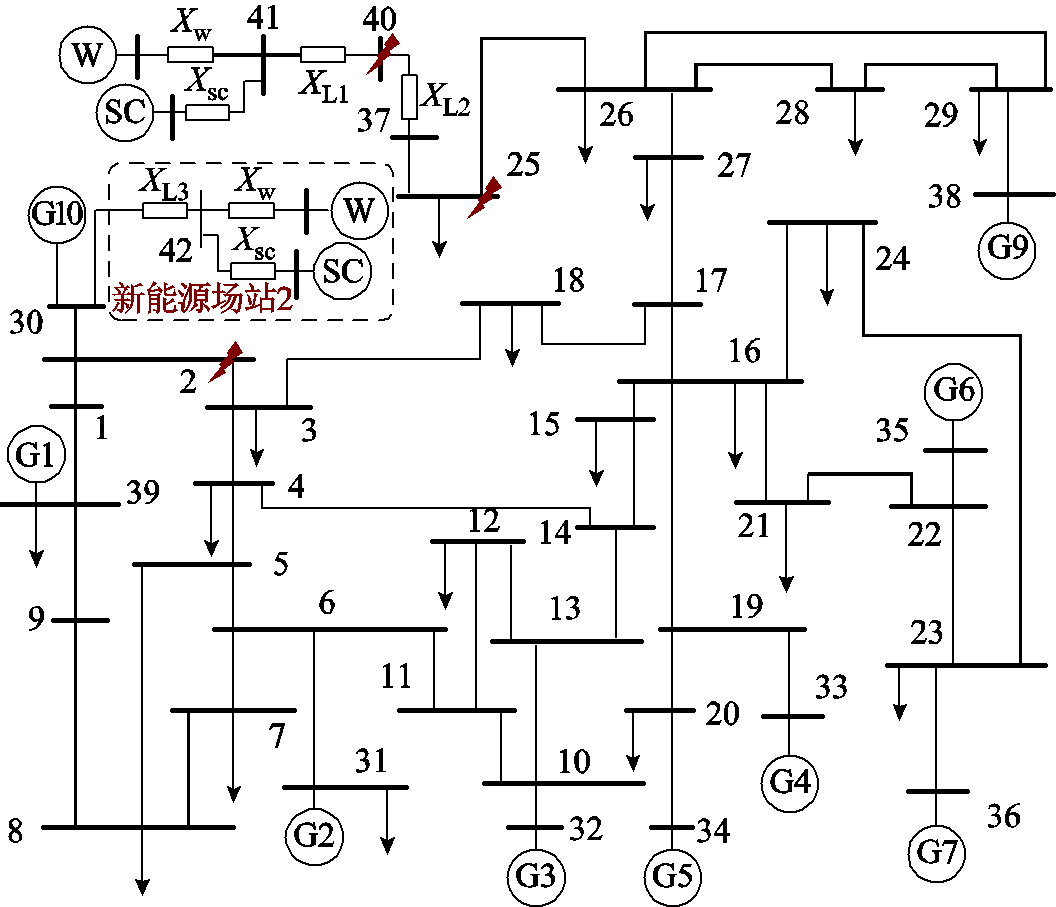
图24 测试用改进的IEEE 39节点系统结构
Fig.24 Improved IEEE 39 node system structure diagram
1)调相机功角摇摆方向
设置故障发生在母线40,当t=1 s时,系统母线40处发生三相短路故障,t=1.1 s时,故障清除。分别设置工况1、工况2,即式(25)中新能源低电压穿越控制参数Kp2为0.7、0.2,过渡电阻为0、0.01(pu),在两种工况下调相机有功功率、与G1间相对功角变化曲线如图25所示。
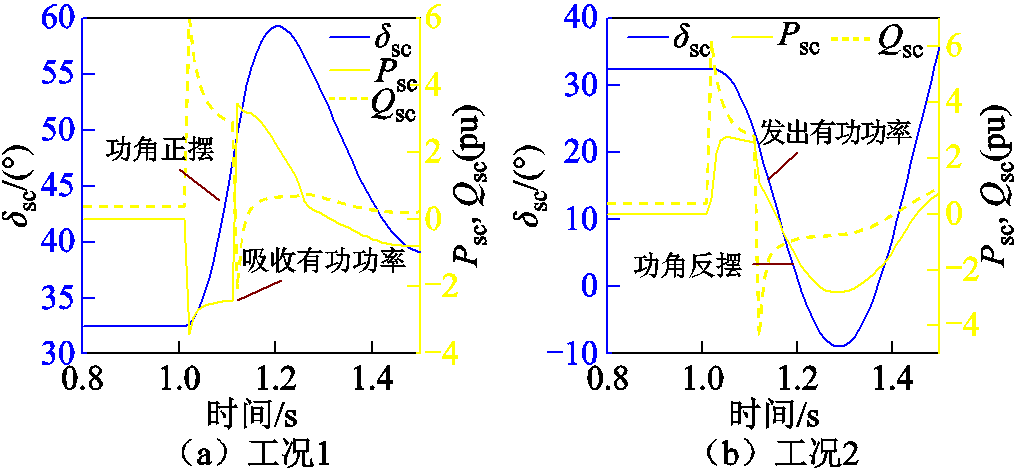
图25 不同低穿控制参数与过渡电阻下调相机相对功角、有功功率、无功功率波形
Fig.25 Power angle and output power of SC under different Kp2 and transition resistance
由图25可见,工况1中故障点不存在过渡电阻,新能源故障期间向系统注入有功电流,调相机在故障期间吸收有功功率,导致转子加速,功角正向摇摆。工况2中故障点存在过渡电阻,且新能源注入有功电流减小,调相机在故障期间发出有功功率,转子减速,功角反向摇摆。
2)并网点电压相角跳变过程
分别设置故障发生在母线25、母线40,当t=1 s时,系统母线发生三相短路故障,t=1.1 s时,故障清除,进一步设置过渡电阻为0、0.015(pu),新能源并网点电压与母线39间电压相角变化如图26所示。
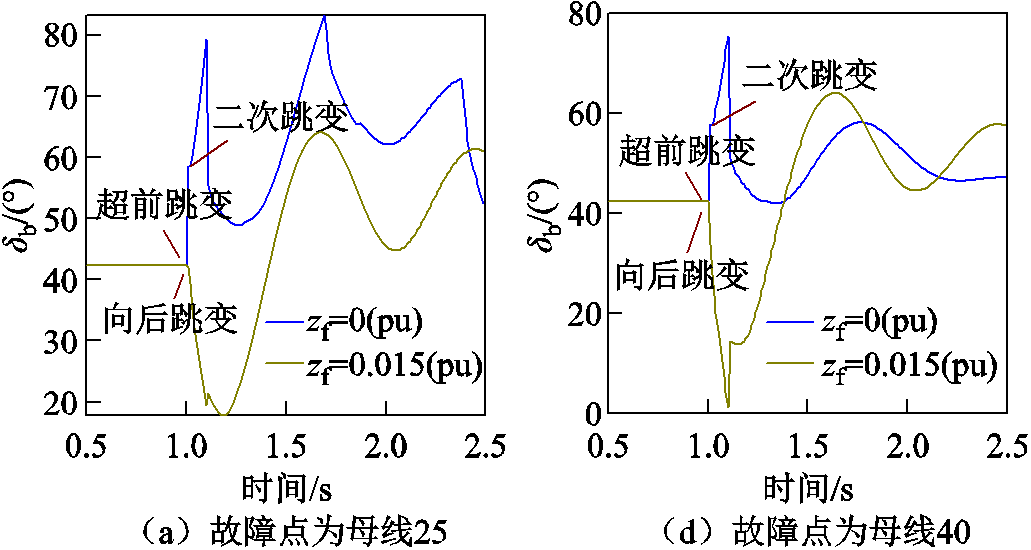
图26 不同故障位置新能源并网点电压相角变化曲线
Fig.26 Waveforms of PCC voltage phase under different fault locations
由图26可见,当故障点发生三相金属性短路时,新能源并网点电压超前跳变;当存在0.015(pu)的过渡电阻时,相角向后跳变。且在新能源切换控制策略后存在相角二次跳变,即进入故障稳态。故障清除时刻,相角再次跳变,与图5和图14分析相对应。
3)故障后并网点持续低电压
在改进系统中母线30处接入新能源场站2,替换原有同步机G10,XL3包含50 km长220 kV线路以及升压变压器,系统参数见附表1,设置两新能源场站有功功率均为600 MW,调相机容量为200 Mvar。分别在母线2、母线25处设置三相金属性短路故障,持续时间为0.1 s,COI坐标系下[34]两场站调相机功角与新能源并网点电压变化情况(母线41电压为Ub1,母线42电压为Ub2)如图27所示。
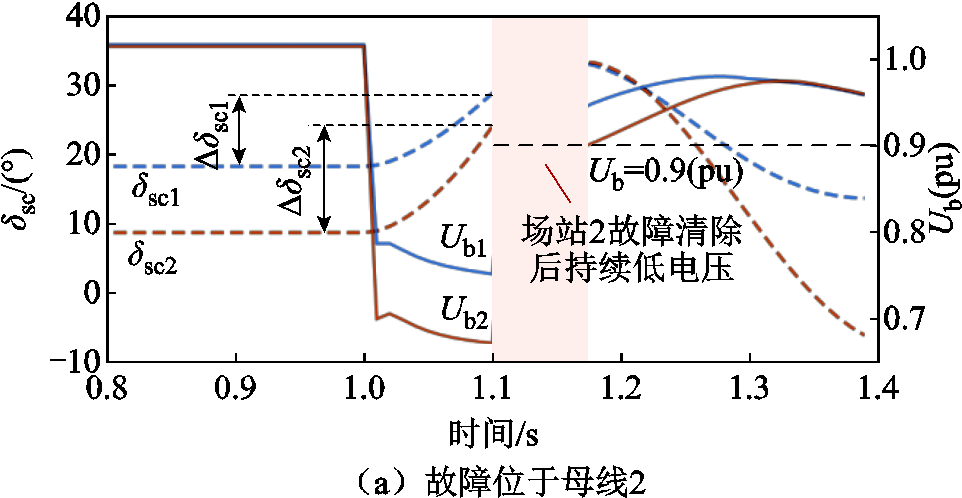
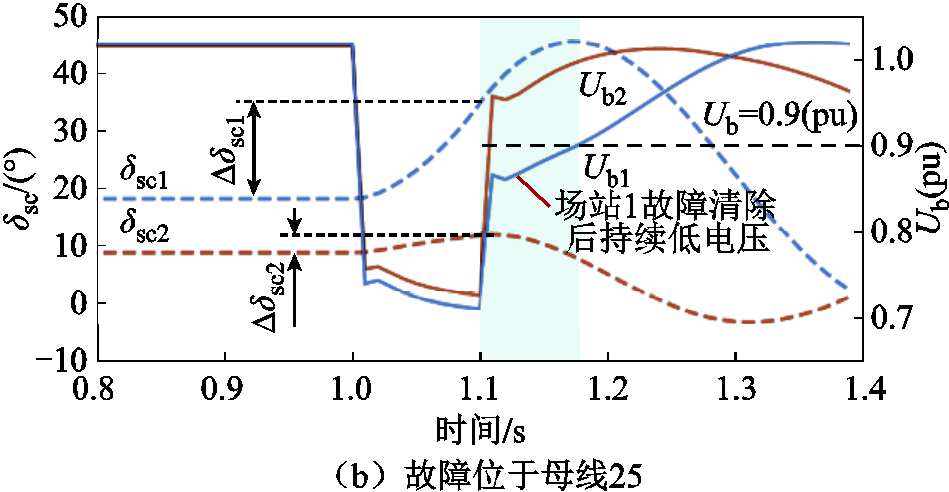
图27 不同故障位置情况下两新能源场站并网点电压与调相机功角变化曲线
Fig.27 Waveforms of PCC voltage and power angle of SC of two stations under different fault locations
采用两场站调相机故障清除时刻与稳态功角差表征调相机故障期间功角摇摆程度,分别为Dδsc1、Dδsc2。由图27a可见,当故障位于母线2处,场站2调相机功角摇摆程度大于场站1调相机,即Dδsc2>Dδsc1,母线42出现故障清除后持续低电压情况,母线41电压快速恢复至0.9(pu)以上。由图27b可见,当故障位于母线25处,场站1调相机功角摇摆程度大于场站2调相机,即Dδsc1>Dδsc2,场站1故障清除后出现持续低电压,导致新能源机组延迟退出低电压穿越状态。
通过分别改变新能源输出功率、线路L1长度(电抗XL1)与调相机容量,验证各影响因素变化对调相机功角稳定的影响。当t=1 s时,系统母线40处发生三相短路故障;t=1.2 s时,故障清除。改变新能源输出功率,新能源场站1调相机与系统其余同步机间功角变化曲线如图28所示。
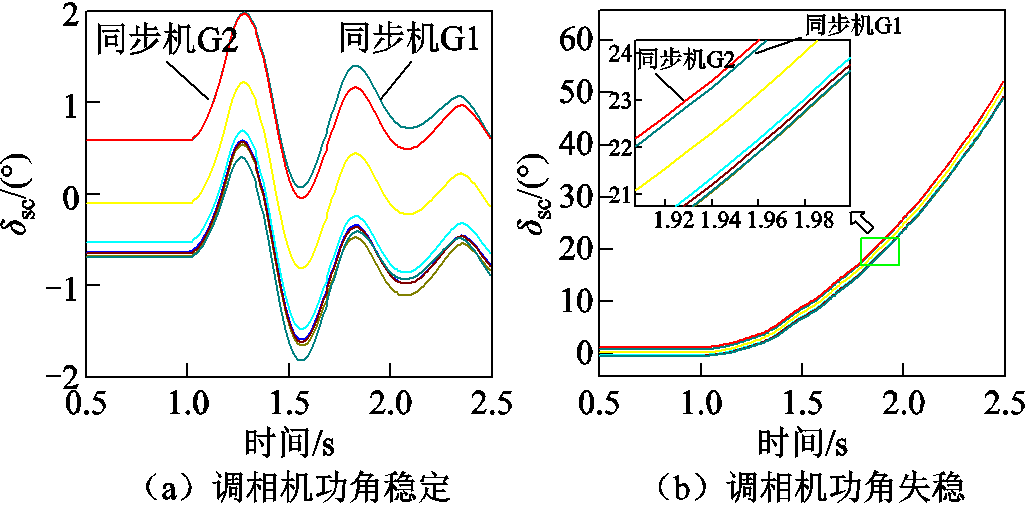
图28 调相机与系统间的功角稳定、失稳形态
Fig.28 Stabilization and destabilization pattern of power angle between distributed condenser and system
由图28可见,故障发生后系统中存在调相机与其余同步机之间的暂态功角失稳风险,采用调相机与同步机G1的相对功角表征调相机的功角稳定性。
设置调相机容量为200 Mvar,500 kV线路距离为350 km,新能源功率分别为500、700、900 MW,仿真获得调相机功角波形如图29所示。
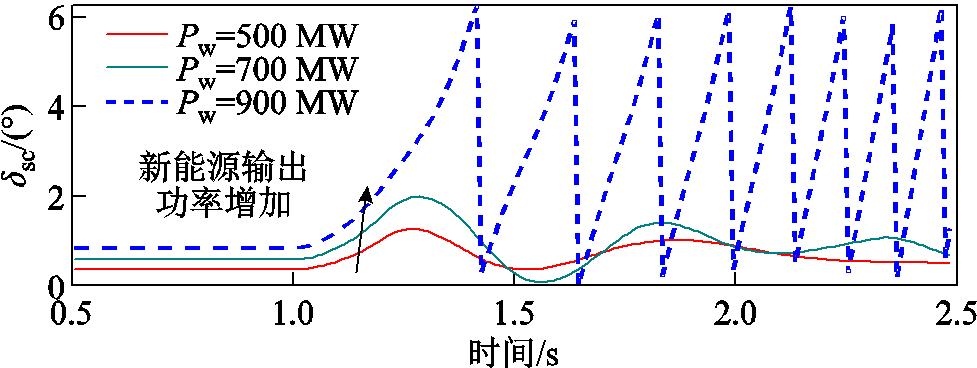
图29 不同新能源输出功率下调相机功角波形
Fig.29 Power angle waveforms of distributed condenser under different renewable energy outputs
由图29可见,随着新能源输出功率增加,调相机稳定平衡点改变,稳态功角增加,故障期间及故障清除后与其余同步机间功角摆开幅度增加,并最终功角失稳,与理论分析结果一致。设置新能源输出功率为800 MW,线路距离为460 km,调相机容量分别为200、300、400 Mvar,仿真获得调相机功角波形如图30所示。
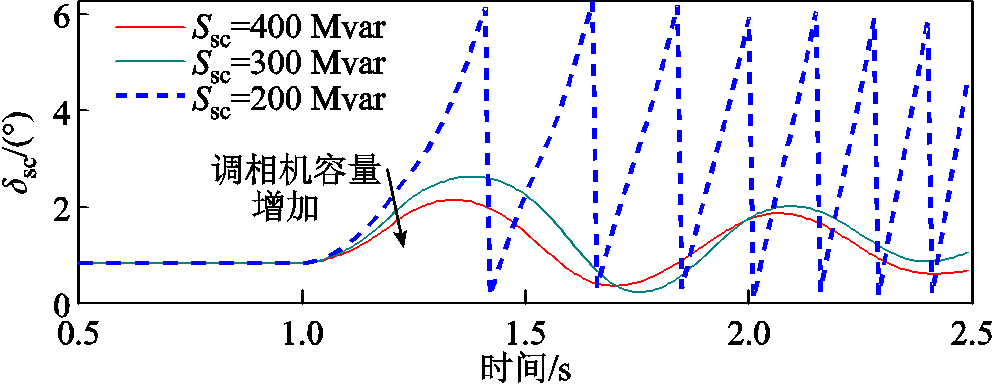
图30 不同容量下调相机功角波形
Fig.30 Power angle waveforms of distributed condenser under different capacity of distributed condenser
由图30可见,随着调相机容量增加,其平衡点不发生改变,调相机与其余同步机间功角摆开幅度减小,暂态功角稳定性提升。设置新能源输出功率为700 MW,调相机容量为200 Mvar,500 kV线路距离为200、350、500 km,仿真获得调相机功角变化波形如图31所示。
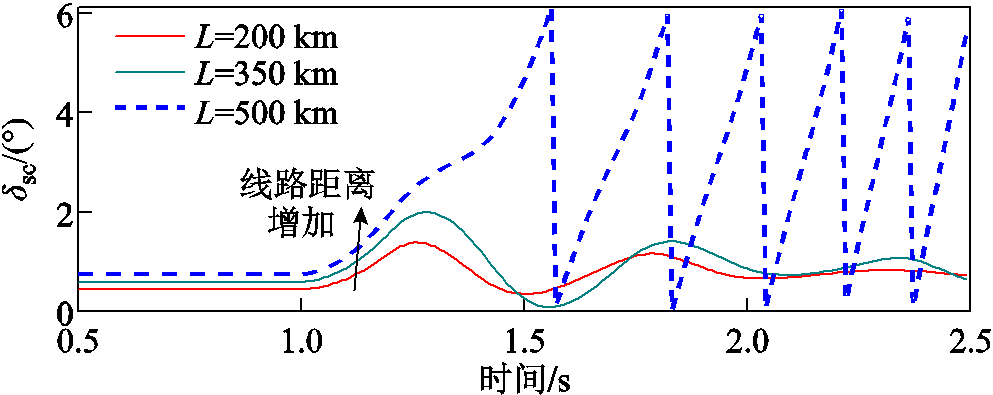
图31 不同线路距离下调相机功角变化波形
Fig.31 Power angle waveforms of distributed condenser under different transition impedance
由图31可见,随着线路距离增加,调相机稳定平衡点改变,稳态功角增加,调相机与其余同步机间功角摆开幅度增加,暂态功角稳定性下降。
通过以上分析验证可见,新能源输出功率增大与输送距离增大均会导致调相机易发生功角失稳,而增加调相机容量可降低其失稳风险。
大规模新能源接入使得场站内分布式调相机在故障期间面临功角失稳风险。本文提出了基于系统电气量相量关系的分布式调相机功角稳定分析方法,分析了故障全过程中分布式调相机的暂态特性及其功角稳定影响因素,可以得到以下结论:故障发生前,新能源功率注入使调相机稳态运行时与系统间功角差加大,并使得功角特性曲线下移,增加了功角失稳风险;故障期间,新能源控制策略切换与过渡电阻使得新能源并网点电压存在相角二次跳变,并影响故障期间调相机功角摇摆方向;故障清除后,调相机功角与新能源并网点电压存在交互作用,功角摆开使得新能源并网点电压无法恢复,导致新能源仍处于低电压穿越状态。此外,新能源输出功率、输送距离与调相机容量均会影响调相机的暂态功角稳定裕度,增加调相机容量可有效地降低其功角失稳风险,提升新能源送出能力。
附 录
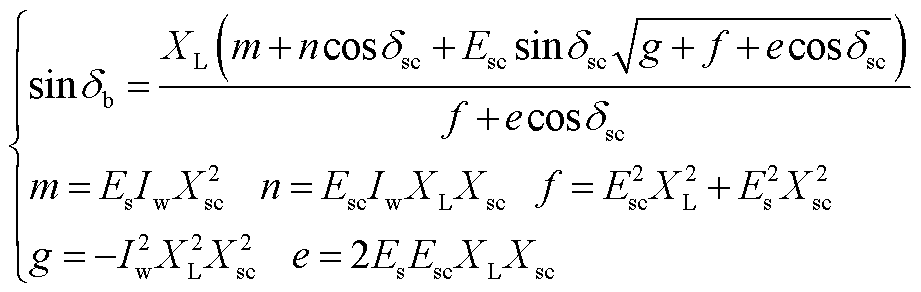 (A1)
(A1)
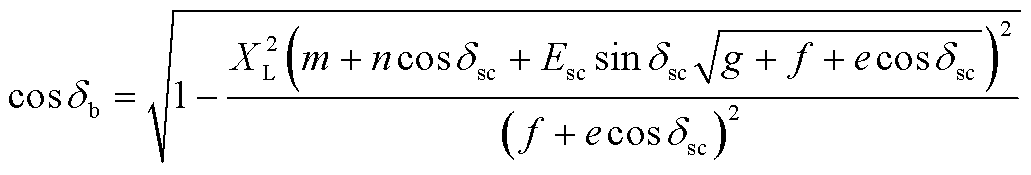 (A2)
(A2)
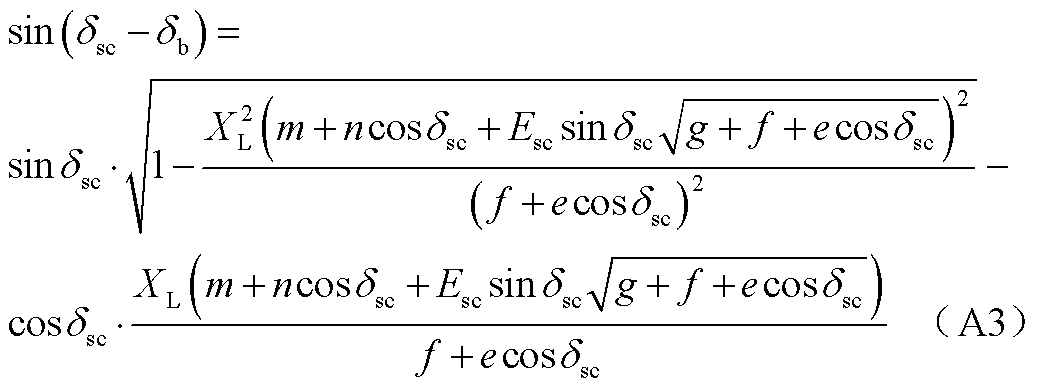
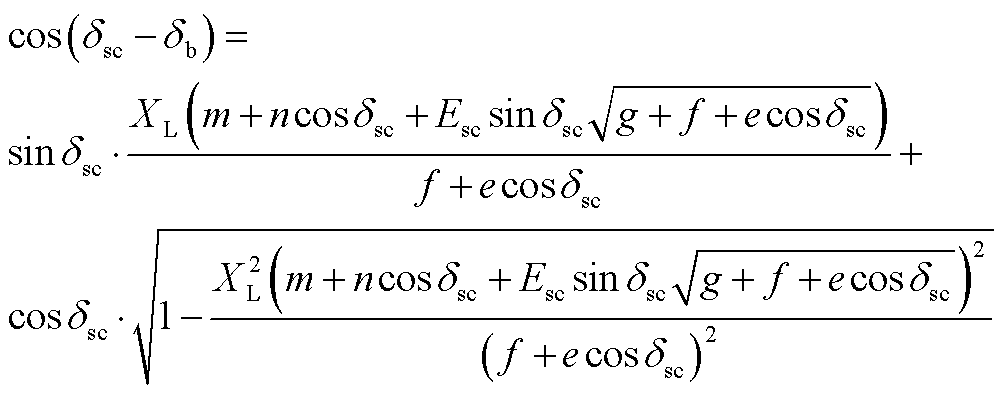 (A4)
(A4)
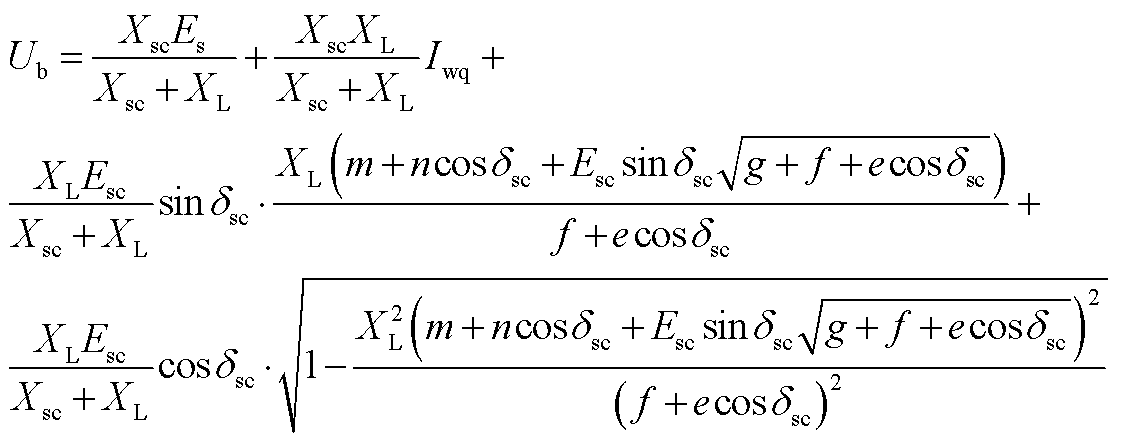 (A5)
(A5)
附表1 仿真参数设置
App.Tab.1 Parameter setting of simulation

参数数值 调相机容量Ssc/Mvar50 d轴暂态电抗0.26 阻尼系数D0 暂态电势Esc(pu)1.2 惯性时间常数TJ/s6 新能源低穿有功电流系数1Kp10 低穿有功电流系数2Kp20.5 低穿有功电流常数Ipset0 低穿无功电流系数1Kq11.5 低穿无功电流系数2Kq21 低穿无功电流常数Iqset0 系统系统基准容量Sn/(MV·A)100 新能源升压变电抗Xw(pu)0.03 调相机升压变电抗XT(pu)0.14 220 kV线路电抗X220/(Ω/km)0.308 500 kV线路电抗X500/(Ω/km)0.276 受端系统电动势Es(pu)1.2
参考文献
[1] 国家能源局. 国家能源局发布2022年全国电力工业统计数据[EB/OL]. [2023-01-18]. https://www. nea.gov.cn/2023-01/18/c_1310691509.htm.
[2] 刘飞, 陶昕, 张祥成, 等. 基于电网消纳能力的新能源发展策略研究[J]. 电气技术, 2019, 20(6): 50-55.
Liu Fei, Tao Xin, Zhang Xiangcheng, et al. Research on optimal matching scheme of renewable energy based on renewable energy consumption ability[J]. Electrical Engineering, 2019, 20(6): 50-55.
[3] 刘华志, 李永刚, 王优胤, 等. 无功电压优化对新能源消纳的影响[J]. 电工技术学报, 2019, 34(增刊2): 646-653.
Liu Huazhi, Li Yonggang, Wang Youyin, et al. Influence about reactive power voltage optimization on the dissipation of new energy[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 646-653.
[4] 国家能源局. 2024年全国能源工作会议在京召开[EB/OL]. [2023-12-21]. http://www.nea.gov.cn/2023-12/21/c_1310756596.htm.
[5] 文云峰, 杨游航, 邢鹏翔, 等. 多维因素制约下新能源消纳能力评估方法研究综述[J]. 中国电机工程学报, 2024, 44(1): 127-147.
Wen Yunfeng, Yang Youhang, Xing Pengxiang, et al. Review on the new energy accommodation capability evaluation methods considering multi-dimensional factors[J]. Proceedings of the CSEE, 2024, 44(1): 127-147.
[6] Wang Tong, Pei Lin, Wang Jiaming, et al. Overvoltage suppression under commutation failure based on improved voltage-dependent current order limiter control strategy[J]. IEEE Transactions on Industry Applications, 2022, 58(4): 4914-4922.
[7] 郭强, 李志强. 同步调相机发展综述[J]. 中国电机工程学报, 2023, 43(15): 6050-6064.
Guo Qiang, Li Zhiqiang. Summarization of synchronous condenser development[J]. Proceedings of the CSEE, 2023, 43(15): 6050-6064.
[8] 周莹坤, 孙华东, 徐式蕴, 等. 提升电网电压支撑强度的调相机优化配置方法[J]. 电网技术, 2022, 46(10): 3848-3856.
Zhou Yingkun, Sun Huadong, Xu Shiyun, et al. Synchronous condenser optimized configuration scheme for power grid voltage strength improvement[J]. Power System Technology, 2022, 46(10): 3848-3856.
[9] Nguyen H T, Yang Guangya, Nielsen A H, et al. Combination of synchronous condenser and synthetic inertia for frequency stability enhancement in low-inertia systems[J]. IEEE Transactions on Sustainable Energy, 2019, 10(3): 997-1005.
[10] 李辉, 王震, 周挺, 等. 含同步调相机的直流受端换流站全工况下多模式协调控制策略[J]. 电工技术学报, 2020, 35(17): 3678-3690.
Li Hui, Wang Zhen, Zhou Ting, et al. Multi-mode coordinated control strategy for DC receiving converter station with synchronous condenser under full operating conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3678-3690.
[11] Hadavi S, Saunderson J, Mehrizi-Sani A, et al. A planning method for synchronous condensers in weak grids using semi-definite optimization[J]. IEEE Transactions on Power Systems, 2023, 38(2): 1632-1641.
[12] 国家能源局. 世界最大规模新能源分布式调相机群在青海投运[EB/OL].[2022-1-28]. https://www.nea. gov.cn/2022-01/28/c_1310445374.htm.
[13] 林旻威, 温步瀛. 大规模风电接入对电力系统暂态稳定性影响研究综述[J]. 电气技术, 2017(4): 1-8, 38.
Lin Minwei, Wen Buying. The overview of influence of large scale wind generation on transient stability of power system[J]. Electrical Engineering, 2017(4): 1-8, 38.
[14] 杨松浩, 李秉芳, 赵天骐, 等. 新能源场站分布式同步调相机暂态功角失稳形态及机理[J]. 电力系统自动化, 2023, 47(3): 12-18.
Yang Songhao, Li Bingfang, Zhao Tianqi, et al. Transient angle instability mode and mechanism of distributed synchronous condensers in renewable energy station[J]. Automation of Electric Power Systems, 2023, 47(3): 12-18.
[15] 沈广进, 辛焕海, 刘昕宇, 等. 大型新能源基地中调相机同步失稳机理与影响因素分析[J]. 电力系统自动化, 2022, 46(20): 100-108.
Shen Guangjin, Xin Huanhai, Liu Xinyu, et al. Analysis on synchronization instability mechanism and influence factors for condenser in large-scale renewable energy base[J]. Automation of Electric Power Systems, 2022, 46(20): 100-108.
[16] 袁彬, 李辉, 向学位, 等. 考虑调相机饱和参数的分阶段励磁控制优化策略[J]. 电力系统保护与控制, 2023, 51(15): 42-54.
Yuan Bin, Li Hui, Xiang Xuewei, et al. Optimization strategy of phased excitation control considering phase modulator saturation parameters[J]. Power System Protection and Control, 2023, 51(15): 42-54.
[17] Hadavi S, Rathnayake D B, Jayasinghe G, et al. A robust exciter controller design for synchronous condensers in weak grids[J]. IEEE Transactions on Power Systems, 2022, 37(3): 1857-1867.
[18] 王蒙, 张文朝, 汪莹, 等. 高比例光伏接入的电力系统暂态过电压控制策略[J]. 太阳能学报, 2023, 44(10): 148-155.
Wang Meng, Zhang Wenchao, Wang Ying, et al. Transient overvoltage control strategy of power system considering high proportion photovoltaic access[J]. Acta Energiae Solaris Sinica, 2023, 44(10): 148-155.
[19] 杨浩, 刘虎, 丁肇豪, 等. 计及短路比提升与暂态过电压抑制的含高比例风电送端电网两阶段式调相机优化配置[J]. 电网技术, 2024, 48(2): 540-552.
Yang Hao, Liu Hu, Ding Zhaohao, et al. Two-stage optimal configuration of condenser for high-proportion wind power sending-end power grid considering short circuit ratio increase and transient overvoltage suppression[J]. Power System Technology, 2024, 48(2): 540-552.
[20] 索之闻, 刘建琴, 蒋维勇, 等. 大规模新能源直流外送系统调相机配置研究[J]. 电力自动化设备, 2019, 39(9): 124-129.
Suo Zhiwen, Liu Jianqin, Jiang Weiyong, et al. Research on synchronous condenser configuration of large-scale renewable energy DC transmission system[J]. Electric Power Automation Equipment, 2019, 39(9): 124-129.
[21] 张建坡, 孟凡, 吴林林, 等. 基于电气参数加权占比的新能源场站分布式调相机容量配置[J/OL]. 电网技术, 2023: 1-11[2023-10-18]. https://doi.org/10. 13335/j.1000-3673.pst.2023.1063.
Zhang Jianpo, Meng Fan, Wu Linlin, et al. Research on distributed condenser capacity configuration of new energy field station based on the weighted proportion of electrical parameters index[J/OL]. Power System Technology 2023: 1-11[2023-10-18]. https://doi.org/10.13335/j.1000-3673.pst.2023.1063.
[22] 沈广进. 新能源电力系统中调相机大扰动同步失稳机理和优化选址研究[D]. 杭州: 浙江大学,2023.
Shen Guangjin. Analysis of large disturbance synchronization instability and placing of synchronouscondensers for renewable-integrated power systems[D]. Hangzhou: Zhejiang University, 2023.
[23] 刘铖, 胥冬洋, 武诚, 等. 考虑频率稳定约束的分布式调相机选址定容策略[J]. 电力建设, 2023, 44(12): 106-114.
Liu Cheng, Xu Dongyang, Wu Cheng, et al. Location and sizing strategy of distributed condensers considering frequency stability constraints[J]. Electric Power Construction, 2023, 44(12): 106-114.
[24] Wang Kang, Liu Chenxi, Li Li, et al. The impact of synchronous condensers on small signal stability of a multi-infeed power electronic system based on power grid strength[C]//2021 IEEE 1st International Power Electronics and Application Symposium (PEAS), Shanghai, China, 2021: 1-6.
[25] 王康, 李子恒, 杨超然, 等. 面向大型新能源基地小干扰稳定性提升的调相机选址方法[J]. 电力系统自动化, 2022, 46(4): 66-74.
Wang Kang, Li Ziheng, Yang Chaoran, et al. Siting method of synchronous condenser for small-signal stability improvement of large-scale renewable energy base[J]. Automation of Electric Power Systems, 2022, 46(4): 66-74.
[26] Ding Lizhi, Lu Xiaonan, Tan Jin. Small-signal stability analysis of low-inertia power grids with inverter-based resources and synchronous condensers[C]// 2022 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), New Orleans, LA, USA, 2022: 1-5.
[27] Liu Xinyu, Xin Huanhai, Zheng Di, et al. Transient stability of synchronous condenser co-located with renewable power plants[J]. IEEE Transactions on Power Systems, 2024, 39(1): 2030-2041.
[28] 赵天骐, 李秉芳, 杨松浩, 等. 新能源场站分布式同步调相机暂态功角稳定性影响因素分析[J]. 电力系统自动化, 2023, 47(16): 114-122.
Zhao Tianqi, Li Bingfang, Yang Songhao, et al. Analysis of influence factors for transient rotor-angle stability of distributed synchronous condensers in renewable energy stations[J]. Automation of Electric Power Systems, 2023, 47(16): 114-122.
[29] 杨金洲, 李业成, 熊鸿韬, 等. 基于阻抗的新能源接入的受端电网暂态电压失稳高风险故障快速筛选方法[J].电工技术学报, 2024, 39(21): 6746-6758.
Yang Jinzhou, Li Yecheng, Xiong Hongtao, et al. A fast screening method for the high-risk faults with transient voltage instability in receiving-end power grids interconnected with new energy based on impedance[J]. Transactions of China Electro-technical Society, 2024, 39(21): 6746-6758.
[30] 潘学萍, 王卫康, 陈海东, 等. 计及低电压穿越影响的感应电动机动态分群[J]. 电工技术学报, 2024, 39(7): 2001-2016.
Pan Xueping, Wang Weikang, Chen Haidong, et al. Study of dynamic clustering method for induction motors in renewable energy power systems considering LVRT effects[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2001-2016.
[31] 王潇桐, 王彤, 邓俊, 等. 光伏逆变器机电暂态模型的控制模式及参数一体化辨识策略[J]. 电网技术, 2023, 47(9): 3547-3558.
Wang Xiaotong, Wang Tong, Deng Jun, et al. Control mode and parameter integration identification of photovoltaic inverter electromechanical transient model[J]. Power System Technology, 2023, 47(9): 3547-3558.
[32] Kundur P, Balu N J, Lauby M G. Power System Stability and Control[M]. New York: McGraw-Hill, 1994.
[33] Pai M A. Energy Function Analysis for Power System Stability[M]. Boston: Springer US, 1989.
[34] 杨浩, 伍柏臻, 刘铖, 等. 基于暂态关键特征逻辑推理的复杂电网响应驱动暂态稳定性判别[J].电工技术学报, 2024, 39(13): 3943-3955.
Yang Hao, Wu Baizhen, Liu Cheng, et al. Response-driven transient stability assessment for complex power grids based on logical reasoning with transient key feature[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 3943-3955.
Abstract Currently, the installed capacity and power generation of renewable energy source is climbing rapidly, but the transient overvoltage problem after renewable energy source access to the power system has become a serious challenge. Distributed condenser can effectively inhibit the transient overvoltage of renewable energy and enhance the renewable energy sending capacity. However, due to proximity to renewable energy sources, the distributed condenser also exists transient instability risk during fault, which restricts the consumption of renewable energy. Existing studies have mostly used node elimination or circuit equivalent change for network simplification, failing to consider the dynamic characteristics of point of common coupling (PCC), and there are few reports on the interaction between grid point voltage and transient stability of distributed condenser.
Aiming at transient characteristic analysis and transient stability mechanism of distributed condenser, firstly, the transient analysis model of distributed condenser with retaining the characteristics of the voltage of PCC in power angle time-scale is established. Based on the phase relationship of electrical quantities, the power-angle characteristics curve is obtained. The interaction between the power angle of the distributed condenser and the PCC voltage after fault is analyzed. Based on the derivation and analysis of the mathematical model, the expression and changing characteristics of the PCC voltage is obtained, which explains the mechanism of continuous low voltage at PCC. As a result, renewable energy source continuously under low voltage ride-through (LVRT) control. The applicability of the proposed method is further confirmed in three-machine system.
Secondly, the process and reason of phase quadratic jumping of renewable energy PCC voltage during fault transient and steady state is analyzed. The mechanism of phase jumping, transition resistance and renewable energy LVRT control strategy on the power angle swing direction of distributed condenser is revealed. For the first phase jumping, when the transition impedance is inductive, the phase of PCC voltage jumps forward, and when the transition impedance is resistive, the phase of PCC voltage jumps backward. For the second phase jumping, The injected power of distributed condenser is calculated based on the superposition theorem, which is effected by the LVRT control strategy of renewable energy.
Finally, the influence of renewable energy output power, capacity of distributed condenser and delivery distance on the transient stability of distributed condenser is analyzed based on the transient energy function. The phase trajectory diagram is used to analyze the above influencing factors. The correctness of the proposed mechanism is verified in the improved IEEE39 node system, including continuous low voltage at PCC, phase quadratic jumping, swing direction of distributed condenser, and transient stability influencing factors.
The following conclusions can be drawn from the analysis. Before the fault, the renewable energy power injection causes the power angle characteristic curve shift downward, which increases the risk of destabilization of distributed condenser. During the fault, the renewable energy control strategy and transition impedance cause the phase quadratic jumping of PCC voltage, which has a direct impact on the power angle swing direction of distributed condenser. After the fault, due to the power angle of distributed condenser swing away, the renewable energy remains in LVRT state, which is conducive to transient stability of distributed condenser. In addition, the output power of renewable energy, delivery distance, and the capacity of distributed condenser all affect the transient stabilization margin of the distributed condenser. Upgrading the capacity of distributed condenser can effectively reduce the risk of the transient instability, and improve the delivery capability of renewable energy.
Keywords:Distributed condenser, transient stability, transient characteristics, renewable energy station
中图分类号:TM721
DOI:10.19595/j.cnki.1000-6753.tces.232014
国家自然科学基金项目(52277096)和国家自然科学基金委企业创新发展联合基金集成项目(U22B6006)资助。
收稿日期 2023-12-04
改稿日期 2024-02-02
王 彤 女,1985年生,教授,博士生导师,研究方向为新能源电力系统稳定分析与控制。
E-mail:hdwangtong@126.com(通信作者)
王潇桐 男,2000年生,硕士研究生,研究方向为新能源电力系统稳定分析与控制。
E-mail:wxt8910@163.com
(编辑 赫 蕾)