
图1 54 mT超低场磁共振成像系统示意图
Fig.1 Systemic diagram of the 54 mT ULF MRI system
摘要 目前超低场磁共振成像(MRI)质量较差,为提升图像信噪比,射频线圈需尽可能贴近成像区域从而提升信噪比。该文采用间接边界元法并从逆问题角度求出线圈流函数分布,再利用线性规划寻找最优线圈结构。为验证超低场MRI诊断颅脑疾病的有效性,采用上述方法,在 54 mT下针对大鼠头-脑几何形状设计了双通道射频接收线圈,并对大鼠脑卒中及脑外伤模型进行成像试验研究。试验结果表明,54 mT MRI能够检出水肿和血肿病变,且与病理切片或临床3 T MRI图像结果相符。同时,通过脑外伤模型7天的追踪观察,54 mT图像中病变的信号演变规律与高场影像一致。针对特定成像对象和非规则布线曲面,该文利用间接边界元逆问题法设计高信噪比射频接收线圈,大鼠模型试验证明超低场磁共振成像技术具有脑卒中与脑外份早期诊断与床旁影像监护潜力与价值。
关键词:磁共振成像 超低场 射频线圈 边界元逆问题 颅脑疾病
磁共振成像(Magnetic Resonance Imaging, MRI)因其出色的软组织成像分辨率、无辐射、成像参数丰富等优势,在现代临床应用中发挥着不可替代的作用。颅脑疾病严重威胁我国人民的健康,特别是脑缺血、脑出血与脑外伤等,其发病率、死亡率与治愈致残率都很高[1]。尽快地进行磁共振影像学检查是准确诊断病因、确定诊疗方案及评估预后的关键[2-3]。背景磁感应强度低于0.1 T的超低场(Ultra-Low-Field, ULF)MRI技术,因其设备尺寸小、质量轻且无需诸如冷却、屏蔽房等设施的特点,更适用于移动成像场景,能够实现针对急诊患者的快速成像检查。超低场MRI技术需要经过临床试验验证其诊断脑卒中与脑外伤病灶的有效性,但由于患者招募困难,遂先针对动物模型进行试验验证[4]。
重庆大学超低场磁共振成像研究中心现有的54 mT超低场MRI系统工作频率约为2.322 MHz,且包含:①54 mT环形偶极结构永磁体;②双极板结构的X/Y/Z梯度线圈子系统;③方形“类螺线管”射频(Radio Frequency, RF)发射线圈;④信号处理子系统(谱仪、各路功率放大器、控制终端等)。54 mT超低场磁共振成像系统示意图如图1所示。该系统总质量约为500 kg,磁场0.5 mT边界是磁体周围直径1.2 m的圆[5]。

图1 54 mT超低场磁共振成像系统示意图
Fig.1 Systemic diagram of the 54 mT ULF MRI system
较弱的背景场导致超低场MRI图像的信噪比(Signal to Noise Ratio, SNR)较低[6-7]。射频接收线圈用于检测来自样品的MR回波信号,是信号接收与处理路径的第一步,决定了图像的质量。特别地,对于配备永磁体的超低场MRI系统,设计射频线圈时的要求首先是SNR,另外还需考虑其他特定因素,例如磁场的温度漂移、人体引起的耦合噪声、是否缺乏严格屏蔽等[8-9]。
传统线圈在设计时并未考虑要尽量地贴近被测样品,因此SNR的存在使其在超低场下无法实现高质量的成像。为了使射频线圈更贴近样品的形状,需结合布线与成像目标区域的条件和要求进行设计,即利用分布式绕线设计方法。该方法的优势在于:仅从逆问题求解出发,由目标场法倒推出产生磁场的电流密度分布,再将电流离散化得到导线绕制路径。Shen Sheng等提出了一种准螺线管射频线圈,采用有限元法(Finite Element Method, FEM)和线性规划算法在一个6.5 mT MRI扫描仪上对头部成像进行设计[10],与传统的螺旋线圈相比,其SNR和均匀性得到改善。文献[11]将文献[10]的方法运用在54 mT MRI系统上,设计出了一套正交线圈,其轴向线圈为螺线管、径向线圈为鞍型结构,但没有考虑人体贴合问题[11]。在高场MRI射频线圈设计、MRI磁体无源匀场以及其他领域的电磁场仿真中,FEM算法也有广泛的应用[12-16]。虽然FEM能够将电流微元与目标磁场分布建立映射矩阵,但是需要对布线区域进行细密的剖分,其计算量会随着布线区域的复杂程度而剧增,使其无法实现在非规则曲面上设计布线模式。
相比于FEM,边界元法(Boundary Element Method, BEM)[17]是一种更适用于求解无界区域的偏微分方程的数值方法。使用BEM可将微分方程转换为边界积分方程,只需要在边界上进行剖分,减少了方程的维数[18]。此外,在进行复杂电磁场计算时,BEM具有能够处理复杂边界、计算速度快等优势[19-23]。R. A. Lemdiasov等(2005年)和M. Poole等(2007年)两个团队先后采用BEM与流函数法设计了磁共振梯度线圈[24-25]。2014年,M. Erbe采用边界元法进行逆问题计算,结合Tikhonov正则化,设计了用于头盔型磁性颗粒头颅成像的线圈[26]。P. C. McDaniel(2020年)利用间接边界元方法设计了贴合人体头部外形的双通道RF线圈,并将其用于便携式头部成像的Halbach MRI系统,但因成像SNR低、几何畸变和成像伪影较大等缺陷降低了其临床应用的价值[27]。近来,Meng Fanqin等将BEM应用于54 mT人体颅脑磁共振成像中,设计了相应的双通道射频接收线圈[28]。这些研究成果显示了边界元法在RF线圈设计中的潜力。
本文利用间接边界元逆问题法,设计了一种在非规则曲面进行布线的超低场磁共振成像射频线圈,并以大鼠脑部为成像目标,设计了对应的双通道射频接收线圈。随后针对大鼠脑缺血、脑出血及脑外伤模型进行了成像试验,试验结果证明超低场MRI技术能够检出颅脑损伤或卒中的病灶。
本文介绍射频线圈设计分为两个部分:间接边界元方法(Indirect BEM, IBEM)逆问题求解与基于正则项的线性规划。基于IBEM逆问题求解得到在设定的布线曲面上理想的电流密度分布,从而在目标区域产生要求的磁场分布;然后利用线性规划获得尽可能接近所模拟电流分布的最优射频线圈导线布线模式。
间接边界元方法在计算过程中需引入密度函数作为中间变量。间接边界元逆问题法理论示意图如图2所示。本文设计的射频线圈的工作频率为2 MHz,那么在布线曲面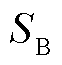 上的电流密度函数
上的电流密度函数 产生的磁场B可视为准静态磁场。因此,根据Biot-Savart定律可以确定目标区域
产生的磁场B可视为准静态磁场。因此,根据Biot-Savart定律可以确定目标区域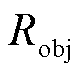 上的点
上的点 处的磁感应强度
处的磁感应强度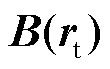 与布线表面
与布线表面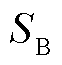 上的表面电流密度
上的表面电流密度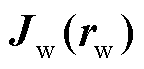 之间的关系可表示为
之间的关系可表示为
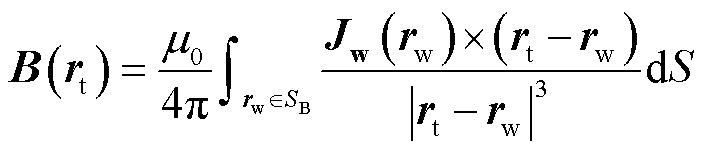 (1)
(1)
式中,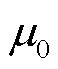 为真空磁导率。
为真空磁导率。

图2 间接边界元逆问题法示意图
Fig.2 Theoretical diagram of inverse indirect boundary method
本文将布线曲面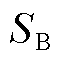 离散化为三角形微元,这是BEM的基本单元。表面电流密度的基函数由布线表面上的单元进行离散化。布线表面上的流函数可以近似表示为
离散化为三角形微元,这是BEM的基本单元。表面电流密度的基函数由布线表面上的单元进行离散化。布线表面上的流函数可以近似表示为
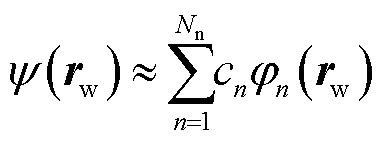 (2)
(2)
式中,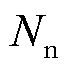 为
为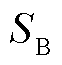 上的节点数;
上的节点数;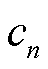 为第n个节点的流函数系数。
为第n个节点的流函数系数。
对节点n及其相关的三角形而言,节点n的流函数可进一步表示为
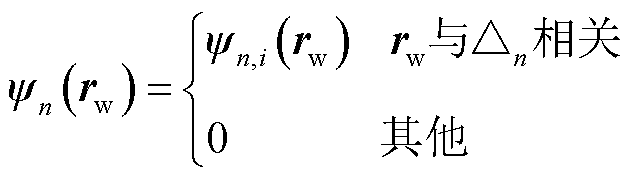 (3)
(3)
式中,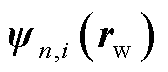 为与第i单元
为与第i单元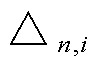 相关的流函数。
相关的流函数。
由于每个通道的射频线圈均只考虑x、y或z中某一个方向的磁场。结合式(1)~式(3),可以导出某一个方向上的“场-源”关系的离散表达形式(以x方向为例)为
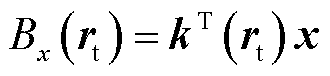 (4)
(4)
其中
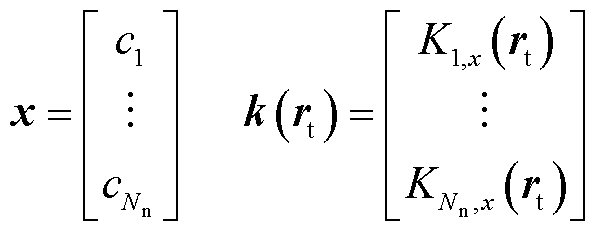 (5)
(5)
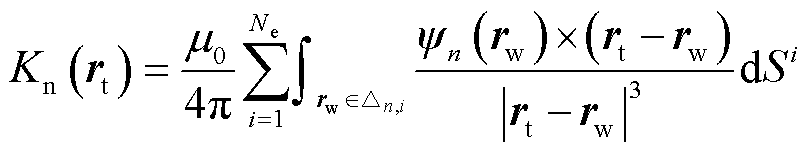 (6)
(6)
式中,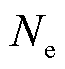 为边界元的个数;
为边界元的个数;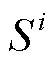 为第i个微元所对应的面积。
为第i个微元所对应的面积。
将式(4)推广到离散化后的目标区域的所有节点,则其矩阵表达式应为
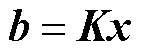 (7)
(7)
其中
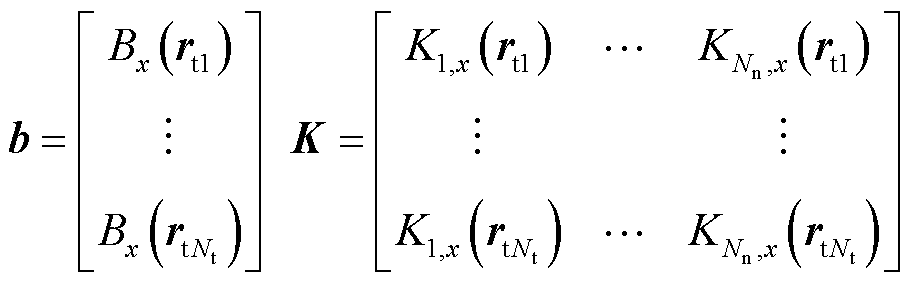 (8)
(8)
式中,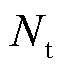 为目标场的节点个数;
为目标场的节点个数;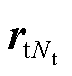 为目标场第Nt个节点的位置。
为目标场第Nt个节点的位置。
式(7)表示磁感应强度与电流流函数(或由一系列导线产生的电流分布)之间的关系,通过关联矩阵K来描述。这是BEM方法和后续寻优程序中的关键。如果将通过布线表面上的特定电流分布来求解目标区域的磁感应强度称为正问题,那么在预先确定磁场的情况下,生成一个流函数,即为“场-源”逆问题,这也是射频线圈设计的原理。
对于布线表面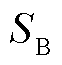 的边界
的边界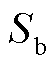 上的节点,其电流不能进入或流出边界。因此,
上的节点,其电流不能进入或流出边界。因此,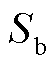 上节点的流函数值
上节点的流函数值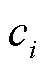 被设为相同的值,即
被设为相同的值,即
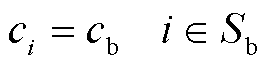 (9)
(9)
计算出流函数后,为设计出满足线圈设计要求的流函数解,需引入优化算法。根据式(7),矩阵K可能不可逆,因此该问题是一病态问题,可通过最小二乘法得到近似解,并添加Tikhonov正则项使解稳定。
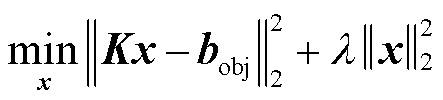 (10)
(10)
式中,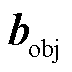 为目标区域内的磁感应强度;λ为正则化系数。这里选择单位矩阵作为Tikhonov矩阵,因此将得到一个较小的范数解。
为目标区域内的磁感应强度;λ为正则化系数。这里选择单位矩阵作为Tikhonov矩阵,因此将得到一个较小的范数解。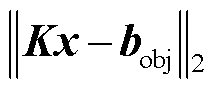 是残差项;
是残差项;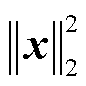 是解的范数;系数λ是通过比较残差和范数项来确定的,可以显著影响结果的平滑性和误差。然而,由于得到的理论电流布局与离散化为若干匝线圈产生的电流之间存在差异,理想解可能是不可行的。因此,本文扩大了λ的取值范围,以找到在特定匝数下的实际最优结果。在此范围内,选择生成最大目标电场强度的电流分布作为该匝数下的最佳布线模式。本文使用专门的Matlab工具箱来求解此最小化问题。
是解的范数;系数λ是通过比较残差和范数项来确定的,可以显著影响结果的平滑性和误差。然而,由于得到的理论电流布局与离散化为若干匝线圈产生的电流之间存在差异,理想解可能是不可行的。因此,本文扩大了λ的取值范围,以找到在特定匝数下的实际最优结果。在此范围内,选择生成最大目标电场强度的电流分布作为该匝数下的最佳布线模式。本文使用专门的Matlab工具箱来求解此最小化问题。
最后,任意匝数i所对应的各等值线的流函数值为
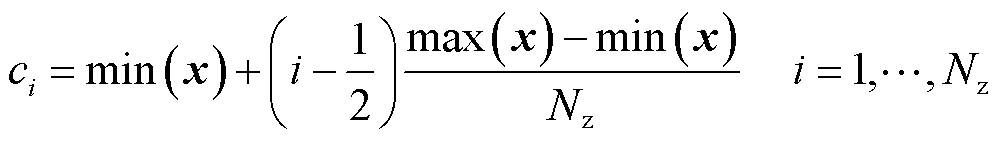 (11)
(11)
通过连接具有相同流函数值的单元,创建一条等值线,其中以三角形单元的重心位置代表该单元的连线位置,再采用插值方法对回路布线进行平滑处理。然而,考虑到布线平滑性和计算成本的折中,本文在三角形单元表面和等值线之间均匀地插入两个额外的点。最后,所有电流的回路被串联起来,形成射频线圈。
大鼠脑部整体解剖形态可近似为直径40 mm的球,即为线圈的成像目标区域[24]。为尽可能地贴近大鼠头-颈部形状,本文设计的布线曲面是由上底面直径28 mm、下底面直径80 mm、高60 mm的圆台,以及底面直径80 mm、高30 mm的圆柱组合成的曲面。目标区域与布线曲面的几何关系如图3所示。考虑到布线复杂度与可行性,在该布线曲面范围内的匝数范围设定为5~15。本文定义背景磁场B0方向为y轴,样品出入磁体的方向为z轴(即轴向),垂直于y轴与z轴的方向为x轴。下文将对x与z方向B1场设计相应的射频接收线圈。

图3 目标区域与布线曲面位置示意图
Fig. 3 Position diagram of thetarget area and wiring surface
线圈的工作频率为背景磁场对应的Lamour频率,即2.322 MHz。设计要求包括:①射频线圈SNR最大化;②线圈的带宽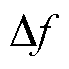 需足够大,以应对由环境影响(如温度)引起的磁体主磁场漂移,此处设置为15 kHz。在线圈的制作过程中,使用直径为1 mm的漆包铜线作为导体。
需足够大,以应对由环境影响(如温度)引起的磁体主磁场漂移,此处设置为15 kHz。在线圈的制作过程中,使用直径为1 mm的漆包铜线作为导体。
遵循2.1节中描述的设计方法与要求,本文设计并制作了包含能够产生x轴和z轴两个方向磁场的双通道射频接收线圈。采用边界元逆问题方法,得到相应流函数分布如图4所示。双通道射频接收线圈结构示意图如图5所示。图5中流函数离散化形成匝数分别为11匝与8匝的线圈结构。随后经数值仿真,得出单通道以及双通道叠加后的目标场磁场在矢状面、冠状面、横断面的分布,如图6所示。经计算,相应目标场的磁感应强度(B1)与场均匀性见表1。可见,仿真结果表明双通道叠加的磁感应强度相较于单通道线圈提升分别为19.6%与85.6%。
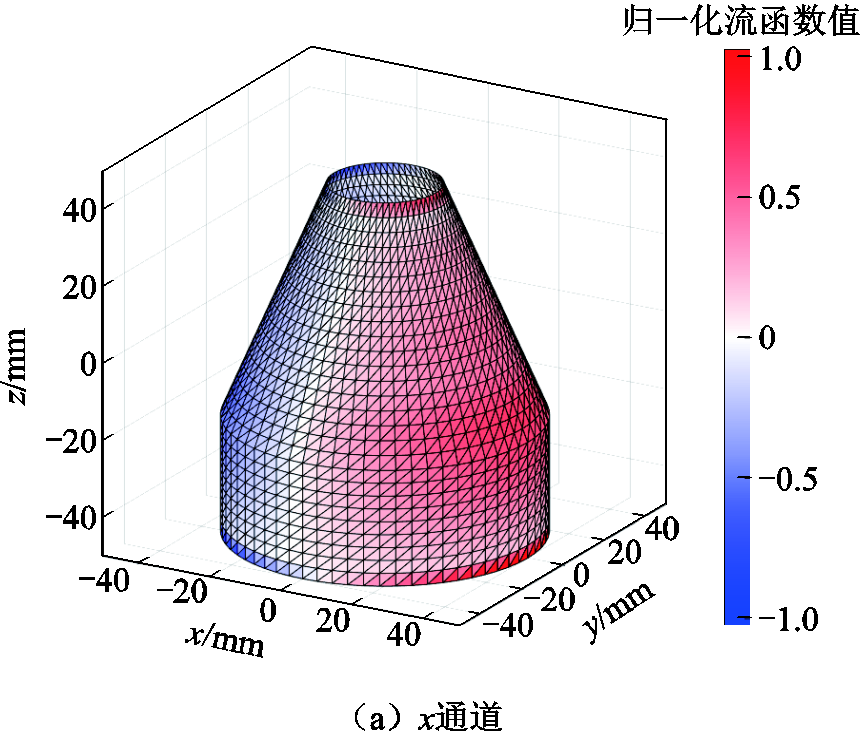
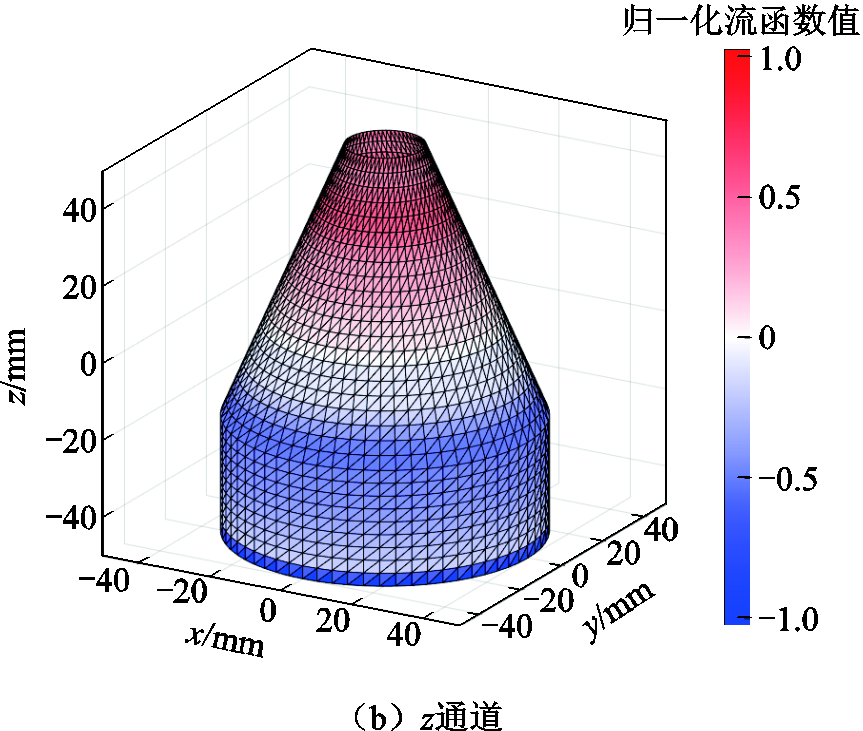
图4 射频线圈两个通道对应的布线曲面流函数分布
Fig.4 Wiring surface stream function for two channels of designed RF coils

图5 双通道射频接收线圈结构示意图
Fig.5 Dual-channel RF receive coil structure
表1 双通道射频接收线圈仿真性能对比
Tab.1 Imulated performance comparison of designed dual-channel RF receive coil

x通道z通道x+z双通道 B1/(μT/A)55.2985.80102.60 不均匀性(%)3.742.482.55
双通道射频接收线圈的两个通道分别采用 型电路匹配至工作频率(2.322 MHz),其S11、S22、S12参数分别为:-30.3 dB、-27.8 dB、-27.5 dB。由于两个子线圈S12参数低于-25 dB,可认为其耦合度极低,无需采取额外的去耦措施。后续将两个通道得到的成像数据通过最小二乘法进行叠加,得到双通道线圈叠加后的成像图像。
型电路匹配至工作频率(2.322 MHz),其S11、S22、S12参数分别为:-30.3 dB、-27.8 dB、-27.5 dB。由于两个子线圈S12参数低于-25 dB,可认为其耦合度极低,无需采取额外的去耦措施。后续将两个通道得到的成像数据通过最小二乘法进行叠加,得到双通道线圈叠加后的成像图像。

图6 射频线圈设计仿真结果:x、z通道及双通道的线圈结构及三个正交面上的目标磁场
Fig.6 Simulation results of RF coil design and optimization: coil structure of Ch. x, Ch. z and dual-channel coils, and corresponding target magnetic field distribution on sagittal, coronal, and transverse planes
在动物试验之前,设计的双通道射频接收线圈先通过样品成像试验评估其性能。本文采用1.95 mg/mL规格的CuSO4溶液制作成的样品,将其放置在接收线圈中央,同时接收线圈也处于磁体正中(如图7所示)。成像序列为T1加权(T1W)梯度回波(GRE),具体参数如下:回波时间(TE)为17 ms;重复时间(TR)为39 ms;采集次数(AVE)为1;翻转角(FA)为35°;视野(FOV)为64 mm× 64 mm;分辨率(RES)为64 × 64;层厚(THK)为3 mm;层数为1;采集时间为41 s;采集方向为横断面。两通道单独图像与正交线圈叠加结果如图8所示。成像试验共重复3次。

图7 硫酸铜溶液模型样品成像试验
Fig.7 CuSO4 solution phantom imaging experiment
计算图像SNR和场不均匀性时,在图像中选择了一个包含10×10体素的CuSO4溶液的区域作为信号区域,并且选择图像底部64×15体素作为噪声采样区域(图8图像中的方框标出)。得到的图像幅值数据经平均后,用于计算每个通道及双通道叠加图像的SNR和场不均匀性,其结果列在表2。双通道叠加图像的SNR较单通道分别提升了21.4%和15.0%,不均匀性则基本保持不变。

图8 硫酸铜溶液模型样品成像试验结果
Fig.8 ULF MRI experiments on rat animal models
表2 双通道射频接收线圈水模成像信噪比对比
Tab.2 Phantom imaging SNR comparison of designed dual-channel RF receive coil

x通道z通道x+z双通道 归一化SNR13.7514.5116.69 不均匀性(%)8.146.768.02
本文所涉及的动物试验已获得重庆大学实验动物福利伦理委员会的批准,全程受到其监督并通过了伦理审查。伦理审查号为CQU-IACUC-RE-202301-001。
3.2.1 动物模型的制备
本文使用雄性SD大鼠分别建立大鼠缺血、出血及脑外伤动物模型。造模过程中采用腹腔注射3%戊巴比妥钠(50 mg/kg)进行全身麻醉,具体方法如下:
1)大鼠脑缺血模型:即大脑动脉栓塞模型(Middle Cerebral Artery Occlusion, MCAO)。将大鼠麻醉后,采用外源性线栓法造成大鼠右侧颈内动脉闭塞。
冰冻TTC染色切片制备:待成像扫描结束后,立刻处死大鼠取出脑组织,在-20℃速冻20 min后做厚度为2 mm的连续切片,并放入2%的2,3,5氯化三苯基四氮唑(TTC)中,避光放入37℃温箱 20 min后,再用4%多聚甲醛固定。
2)大鼠脑出血模型:将大鼠麻醉后,将大鼠固定在立体定位平台上,采用高速颅骨钻在前囟后右侧旁钻一直径约为1 mm的小孔。抽取自体动脉血 50 μL,使用微量注射器缓慢注入基底节区,随后待留针10 min 后慢慢退出注射器,最后密封骨孔缝合皮肤。
3)大鼠脑外伤模型:在全身麻醉下,通过挫伤装置(TBI 0310;Precision Systems & Instrumentation,Fairfax Station,VA,USA)诱导受控皮层撞击(CCI)。在中线处制作一个长约15 mm的纵向切口,并使用便携式钻头在右顶骨进行5 mm的开颅手术。CCI参数设置如下:速度5.0 m/s,深度3.0 mm,停留时间500 ms。
3.2.2 大鼠脑部成像序列及方法
本文验证54 mT下对脑缺血、出血和外伤三种动物模型的病灶检出能力。除脑缺血模型采用标本冷冻切片染色(金标准)进行对照外,出血和外伤模型的超低场成像结果,将分别与3.0 T MRI扫描成像结果进行对比。成像过程中,均采用俯卧位横断面扫描,超低场和高场MRI成像试验如图9和图10所示。

图9 大鼠动物模型超低场MRI成像试验
Fig.9 ULF MRI experiments on rat animal models
具体成像方法介绍如下:
1)54 mT MRI成像系统结合本文设计的大鼠脑部专用射频接收线圈,成像序列如下:①GRE-T1WI: TR 39 ms, TE 17.2 ms, FOV 64 mm×64 mm, 分辨率128×128, 层厚3 mm;②GRE-T2starWI: TR 80 ms, TE 54 ms, FOV 64 mm×64 mm, 分辨率64×64, 层厚2 mm;③FSE-T2WI: TR 3 200 ms, TE 139 ms, FOV 64 mm× 64 mm, 分辨率64×64, 层厚5 mm。为防止永磁体磁场强度由于温度变化而偏移并保障试验动物的福利,成像试验在恒温25℃的电磁屏蔽室内进行。

图10 大鼠动物模型高场MRI成像试验
Fig.10 High-field MRI experiments on rat animal models.
2)西门子3.0 T(Prisma,德国)MRI扫描仪结合大鼠专用线圈(如图9b所示),成像序列如下:①GRE-T1WI序列,TR 300 ms,TE 3 ms,层厚 2 mm,横断位扫描;②FSE-T2WI序列,TR 5 590 ms,TE 127 ms,层厚5 mm,横断位扫描;③FLAIR序列,TR 9 000 ms,TE 81 ms,层厚5 mm,横断位扫描。
3.2.3 成像试验结果
在大鼠MCAO造模成功后24 h时进行54 mT MRI扫描,得到大鼠脑缺血、出血模型超低场成像试验结果,并与金标准对比验证,如图11所示。图像显示大鼠右侧大脑半球明显肿胀,病变区域T2starWI及T2WI信号增高,同时伴有脑中线结构左移,提示脑组织水肿(见图11a)。处死大鼠后取脑组织切片TCC染色示:左侧大脑半球正常组织呈红色,右侧大脑半球梗死区呈苍白色,这与54 mT MRI所示的病变形态及范围一致(见图11b)。

图11 大鼠脑缺血、出血模型超低场成像试验结果并与金标准对比验证
Fig.11 ULF imaging experimental results and comparison with golden standard for rat ischemia and hemorrhage models
大鼠脑出血造模成功之后,在24 h时先后采用54 mT和3.0 T MRI扫描仪对大鼠的脑组织进行成像。图11c揭示,两种方法都能非常清晰地显示出血灶的位置、形态、大小及信号等特征,且二者结果基本一致,均表现为:血肿位于右侧大脑半球,呈结节状T2WI低信号影,血肿周围见少许条片状高信号水肿带影,无明显占位效应。
本文对大鼠脑外伤模型进行了为期7天的追踪观察,对比了54 mT 与3.0 T的图像特点和差异,如图12所示。第1天,两种设备的T2WI图像均能非常清晰地显示相同部位的头皮肿胀;3.0 T图像对病变区水肿的显示较清楚,呈条片状T2WI高信号影,然而54 mT仅见小片状浅淡模糊影,较难做出准确判断。第3天,两种设备对头皮肿胀的显示基本同前;病变区水肿加重,54 mT及3.0 T对脑水肿的显示更加明确。第5天,头皮肿胀范围略缩小,但局部脑膨隆较前有所加重,此征象在54 mT和 3.0 T FSE-T2WI图像中均能被观察到;病变区水肿及占位效应均有所加重。第7天,脑外伤大鼠的头皮肿胀和脑内水肿情况均有减轻,之前观察到的占位效应基本消失,两种设备图像对以上的病理改变均能清楚展示。

图12 大鼠脑外伤模型成像试验54 mT与3.0 T MRI T2WI成像结果对比
Fig.12 Imaging results comparison between 54 mT and 3.0 T for rat traumatic brain injury model
急性颅脑疾病是威胁我国人民健康的重要因素之一[1]。特别是脑卒中疾病,缺血和出血性脑卒中临床症状相似,若不能在黄金抢救窗口(一般为6 h)快速判断脑卒中性质,将造成无法挽回的后果[3]。此外,脑外伤患者在急性(1~3天)、亚急性期(4~7天)病情易反复,亟须频繁的影像学检查,准确评估预后,以便形成正确的治疗方案。超低场MRI技术能将MRI成像设备移动化,满足患者快速诊断和长期随访的需求。
本文采用间接边界元逆问题法的思路设计了用于大鼠脑部成像的高SNR双通道射频接收线圈。数值仿真与水模成像试验的结果都表明,与单通道相比,双通道线圈叠加后能显著提升射频线圈性能。但是,水模成像试验中图像信噪比的叠加增强效果仅为仿真时的76.5%。这是由于54 mT超低场磁共振成像易受环境噪声干扰,而双通道叠加仅能降低共模干扰的影响,但无法消除随机噪声。这限制了双通道叠加对实际成像SNR带来的提升幅度。
双通道叠加目标场的不均匀性并没有明显改善,这是由于设计得到的双通道线圈并不是严格意义上的能够产生正圆极化的正交线圈,其产生的极化场更接近椭圆极化。这导致目标区域的某些位置的磁场会受到另一通道线圈的干扰,影响了叠加场的均匀性。
本文随后采用该射频线圈,针对三种不同的动物模型进行验证性试验。试验中,54 mT MRI能够清晰、敏感地显示包括脑缺血及脑出血的微小脑卒中病变。而进一步对TBI大鼠进行了7天的中长期影像学随访,结果提示:54 mT及3.0 T MRI均能较好地展示脑外伤急性和亚急性期的病理改变,且与既往研究报道的脑挫裂伤进展及转归周期一致[29-31];54 mT对头皮损伤的显示似乎更优于仅表现为轻度水肿的脑挫裂伤。
本文采用间接边界元逆问题法与线性规划相结合的方法,在B0为54 mT的磁场下对大鼠设计出相适应的射频接收线圈。再把两个通道的线圈所得的图像相叠加,从而实现高信噪比(SNR)的超低场磁共振图像。
针对大鼠脑部设计的超低场磁共振成像射频线圈能够发现急性期大鼠脑缺血和脑出血模型的水肿或血肿病变;同时也能针对大鼠脑外伤模型急性、亚急性期的长期观察中,发现与3.0 T MRI图像一致的病变回波信号演变规律。这证明超低场磁共振成像技术在临床上急性脑卒中诊断以及脑外伤患者具有长期影像学随访的潜力与价值。
后期工作着重于在临床试验中进一步验证超低场MRI技术的有效性,同时将该射频线圈设计方法扩展应用到诸如躯干、四肢、前列腺等场景中。
参考文献
[1] 中国疾病预防控制中心慢性非传染性疾病预防控制中心, 国家卫生健康委统计信息中心. 中国死因监测数据集2021[M]. 北京: 中国科学技术出版社, 2022.
[2] 国家卫生健康委脑卒中防治工程委员会. 中国脑卒中防治指导规范(2021年版)[A]. 2021-08-27.
[3] Campbell B C, Parsons M W. Imaging selection for acute stroke intervention[J]. International Journal of Stroke: Official Journal of the International Stroke Society, 2018, 13(6): 554-567
[4] 陈顺中, 王秋良, 孙万硕, 等. 3T动物磁共振成像传导冷却超导磁体研究[J]. 电工技术学报, 2023, 38(4): 879-888.
Chen Shunzhong, Wang Qiuliang, Sun Wanshuo, et al. The study of a 3 T conduction-cooled superconducting magnet for animal magnetic resonance imaging[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 879-888.
[5] 贺玉成. 50mT超低场磁共振成像系统研究及其在脑卒中诊断中的应用[D]. 重庆: 重庆大学, 2020.
He Yucheng. Research on 50 mT ultra-low field magnetic resonance imaging system and its application in stroke diagnosis[D]. Chongqing: Chongqing University, 2020.
[6] Sarracanie M, Salameh N. Low-field MRI: how low can we go? a fresh view on an old debate[J]. Frontiers in Physics, 2020, 8: 172.
[7] Sarracanie M, LaPierre C D, Salameh N, et al. Low-cost high-performance MRI[J]. Scientific Reports, 2015, 5: 15177.
[8] Vaughan J T, Griffiths J R. RF Coils for MRI[M]. Hoboken: John Wiley & Sons, 2012.
[9] Coffey A M, Truong M L, Chekmenev E Y. Low-field MRI can be more sensitive than high-field MRI[J]. Journal of Magnetic Resonance, 2013, 237: 169-174.
[10] Shen Sheng, Xu Zheng, Koonjoo N, et al. Optimization of a close-fitting volume RF coil for brain imaging at 6.5 mT using linear programming[J]. IEEE Transactions on Bio-Medical Engineering, 2021, 68(4): 1106-1114.
[11] Shen Sheng, Kong Xiaohan, Meng Fanqin, et al. An optimized quadrature RF receive coil for very-low-field (50.4 MT) magnetic resonance brain imaging[J]. Journal of Magnetic Resonance, 2022, 342: 107269.
[12] 万裁, 何为, 沈晟, 等. 超低场磁共振膝关节正交接收线圈设计[J]. 电工技术学报, 2024, 10(7): 1923-1931.
Wan Cai, He Wei, Shen Sheng, et al. Design of a quadrature receive coil for ultra-low-field knee magnetic resonance imaging[J]. Transactions of China Electrotechnical Society, 2024, 10(7): 1923-1931.
[13] Jasiński K, Młynarczyk A, Latta P, et al. A volume microstrip RF coil for MRI microscopy[J]. Magnetic Resonance Imaging, 2012, 30(1): 70-77.
[14] 曲洪一, 刘鑫, 王晖, 等. 磁共振成像磁体无源匀场改进策略及实验研究[J]. 电工技术学报, 2022, 37(24): 6284-6293.
Qu Hongyi, Liu Xin, Wang Hui, et al. Improved strategy and experimental research on passive shimming in magnetic resonance imaging magnet[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6284-6293.
[15] 曹龙飞, 范兴纲, 李大伟, 等. 基于快速有限元的永磁电机绕组涡流损耗半解析高效计算[J]. 电工技术学报, 2023, 38(1): 153-165.
Cao Longfei, Fan Xinggang, Li Dawei, et al. Semi analytical and efficient calculation method of eddy current loss in windings of permanent magnet machines based on fast finite element method[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 153-165.
[16] 赵镜红, 周长朵, 王涵铭, 等. 计及边端效应的直线式移相变压器等效电路分析[J]. 电工技术学报, 2024, 39(6): 1792-1805.
Zhao Jinghong, Zhou Changduo, Wang Hanming, et al. Equivalent circuit analysis of linear phase-shifting transformer considering end effect[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1792-1805.
[17] 余德浩. 自然边界积分方法及其应用[M]. 北京: 科学出版社, 2017.
[18] 张淮清, 王亚伟, 付志红. 虚边界元法在电磁场计算中的应用[J]. 电工技术学报, 2013, 28(2): 86-90.
Zhang Huaiqing, Wang Yawei, Fu Zhihong. Virtual boundary element method in computational electro-magnetics[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 86-90.
[19] 刘士利, 王泽忠, 孙静. 基于线-面模型的边界元法计算特高压交流变电站设备附近工频电场[J]. 电工技术学报, 2011, 26(3): 162-167.
Liu Shili, Wang Zezhong, Sun Jing. Calculation of power frequency electric field near equipments in UHV substations with BEM based on line-area models[J]. Transactions of China Electrotechnical Society, 2011, 26(3): 162-167.
[20] 王泽忠, 石雨鑫, 刘丽平. 应用快速多极子曲面边界元法的换流阀塔电场计算[J]. 电工技术学报, 2019, 34(2): 203-211.
Wang Zezhong, Shi Yuxin, Liu Liping. Calculating of electric field of converter valve tower by using fast multipole curved boundary element method[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 203-211.
[21] 李亚莎, 花旭, 沈星如, 等. B样条曲面边界元方法及其在特高压绝缘子串电场计算中的应用[J]. 电工技术学报, 2018, 33(2): 232-237.
Li Yasha, Hua Xu, Shen Xingru, et al. Research and application of B-spline surface boundary element method for calculating ultra-high voltage insulator strings electric fields[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 232-237.
[22] 韩杰祥, 张哲, 冉启胜, 等. 低压直流配电网主动限流控制及保护方案[J]. 电力系统自动化, 2022, 46(9): 182-190.
Han Jiexiang, Zhang Zhe, Ran Qisheng, et al. Active current-limiting control and protection scheme for low-voltage DC distribution network[J]. Automation of Electric Power Systems, 2022, 46(9): 182-190.
[23] 冀肖彤, 柳丹, 熊平, 等. 基于波形距离系数的逆变站近区交流线路保护方向元件[J]. 电力系统自动化, 2024, 48(1): 140-149.
Ji Xiaotong, Liu Dan, Xiong Ping, et al. Waveform distance coefficient based directional element for AC transmission line protection near inverter station[J]. Automation of Electric Power Systems, 2024, 48(1): 140-149.
[24] Lemdiasov R A, Ludwig R. A stream function method for gradient coil design[J]. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering, 2005, 26B(1): 67-80.
[25] Poole M, Bowtell R. Novel gradient coils designed using a boundary element method[J]. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering, 2007, 31B(3): 162-175.
[26] Erbe M. Field Free Line Magnetic Particle Imaging [M]. Wiesbaden: Springer Fachmedien Wiesbaden, 2014.
[27] McDaniel P C. Computational design and fabrication of portable MRI systems[D]. Cambridge: Massachusetts Institute of Technology, 2020.
[28] Meng Fanqin, Guo Yi, He Wei, et al. Development of a helmet-shape dual-channel RF coil for brain imaging at 54 mT using inverse boundary element method[J]. Journal of Magnetic Resonance, 2024, 360: 107636.
[29] Lindberg D M, Stence N V, Grubenhoff J A, et al. Feasibility and accuracy of fast MRI versus CT for traumatic brain injury in young children[J]. Pediatrics, 2019, 144(4): e20190419.
[30] Haghbayan H, Boutin A, Laflamme M, et al. The prognostic value of MRI in moderate and severe traumatic brain injury: a systematic review and meta-analysis[J]. Critical Care Medicine, 2017, 45(12): e1280-e1288.
[31] Hjornevik T, Leergaard T B, Darine D, et al. Three-dimensional atlas system for mouse and rat brain imaging data[J]. Frontiers in Neuroinformatics, 2007, 1: 4.
Abstract Magnetic resonance imaging (MRI) plays an irreplaceable role in modern clinical practice especially for brain diseases due to its excellent soft tissue imaging resolution, radiation-free nature, and rich imaging parameters. The ultra-low-field (ULF) MRI technology (<0.1 T) is characterized by its small size, light weightmaking it more suitable for mobile imaging scenarios and enables rapid imaging examinations for emergency patients. But the weaker background field results in a lower signal-to-noise ratio (SNR) in ULF MRI images. To enhance the signal-to-noise ratio (SNR), it is crucial for the radio frequency (RF) coil to be positioned close to the imaging area while maintaining excellent performance. To ensure that the RF coil conforms closely to the shape of the sample, an optimization algorithm is required, which should consider the conditions and requirements of wiring and the imaging target area, thus enabling the design of a distributed winding method.
In this study, the indirect boundary element method was employed to determine the coil current distribution from an inverse problem perspective. The term of indirect means that a density function needs to be introduced as an intermediate variable to bridge the gap between magnetic induction intensity of the target area and the current stream function on the wiring surface. Then, linear programming is used to obtain the optimal layout of RF coil conductors that closely resemble the simulated current distribution.
To validate the effectiveness of ULF MRI in diagnosing cranial diseases, above-mentioned method was applied to design a dual-channel RF receive coil for the head-brain geometric shape of the rat at 54 mT. The performance of proposed RF receive coil was then evaluated by CuSO4 solution phantom sample imaging tests and the signal-noise-ratio of the dual-channel coil images increased by 15.0% and 21.4% compared to the single-channel images, while the homogeneity remained unchanged.
Imaging experiments were conducted on rat models with ischemic stroke, hemorrhagic stroke, and traumatic brain injury (TBI) including T1 weighted, T2 weighted, and T2 star-weighted imaging sequences. The experiments demonstrated that 54 mT MRI can detect edema and hemorrhagic lesions, aligning with pathological slices or clinical 3.0 T MRI images. Furthermore, a 7-day medium-term follow-up study on TBI model rats was conducted. The results suggest that both 54 mT and 3.0 T MRI can effectively demonstrate the pathological changes in acute and subacute phases of TBI, consistent on the progression and outcome cycles of brain contusions. Moreover, the 54 mT MRI can show better performance in detecting scalp injuries compared to brain contusions that only manifested as mild edema.
This paper adopts a method combining indirect boundary element inverse problem technique with linear programming to design RF receive coils suitable for rats under a 54 mT B0 field. Then, the images obtained from the coils of the two channels are superimposed to achieve high signal-to-noise ratio ultra-low field magnetic resonance images. The experiments with the rat model demonstrated the potential and value of ULF MRI technology in the clinical diagnosis of acute stroke and long-term radiological follow-up of patients with traumatic brain injury.
Keywords:Magnetic resonance imaging, ultra-low field, radio frequency coil, inverse boundary element, cerebral diseases
中图分类号:TM15
DOI: 10.19595/j.cnki.1000-6753.tces.231972
国家自然科学基金(52077023)和重庆市科卫联合项目(2023MSXM016)资助。
收稿日期 2023-11-25
改稿日期 2024-01-14
孟凡钦 男,1990年生,博士研究生,研究方向为磁共振成像硬件设计与应用。
E-mail:fq.meng@cqu.edu.cn
徐 征 男,1980 年生,教授,博士生导师,研究方向为生物电磁成像技术。
E-mail:xuzheng@cqu.edu.cn(通信作者)
(编辑 郭丽军)