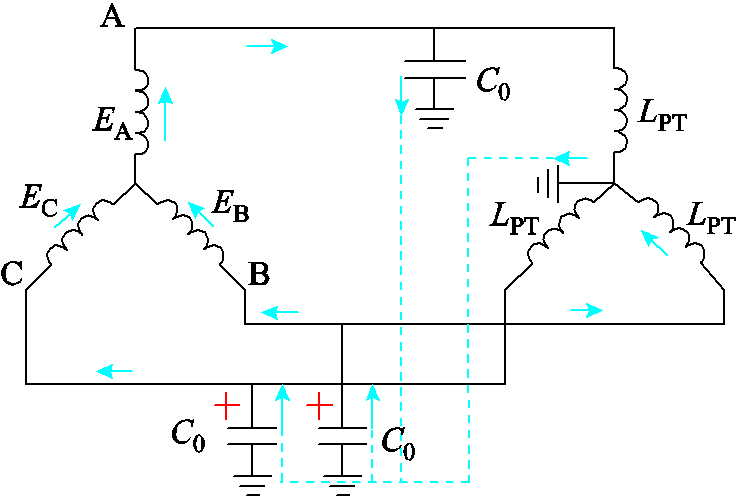
图1 3PT接法时单相接地故障消失后的电容电流分布
Fig.1 Distribution of capacitive current after single-phase ground fault recovery during 3PT connection
摘要 电磁式电压互感器(PT)高压侧保护用熔断器频繁熔断问题广泛存在于10~35 kV的中性点不接地配电网中,增加了电网的运维负担,威胁供电可靠性。为分析PT高压侧熔断器频繁熔断的深层机理,该文基于叠加原理,采用数值计算方法,分析了典型故障下的系统空载暂态电压,发现该电压呈现交直流复合的特殊形态——工频电压附加直流偏置电压,归纳总结了直流偏置电压的形成条件和机理为:故障消失时,三相杂散电容的净电荷不为零(Qn≠0),且Qn无泄放路径而形成直流偏置电压。在线路长度、PT阻抗、负载及无功补偿装置等不同因素影响下,研究了Qn泄放路径对直流偏置电压的影响规律,发现直流偏置电压作用下PT深度饱和是触发熔断器熔断的最终原因。最后,通过PSCAD/EMTDC中的10 kV配电网模型和380 V/150 V的实物动态模拟试验平台进行了仿真与试验验证。
关键词:电磁式电压互感器 配电网 熔断器 瞬时性接地故障 直流偏置电压
电磁式电压互感器(Potential Transformer, PT)是配电网中最常用的电压互感器,供计量、监测和保护使用。PT高压侧保护用熔断器频繁熔断的问题广泛存在于10~35 kV中性点不接地的配电网中。实际工程中,变电站母线PT熔断器每年熔断1~3次以上[1-3],需要运维人员频繁更换,不仅增加了运维成本,同时也严重威胁供电可靠性。
在缺少配电网实际故障全过程录波数据和PT、变压器、熔断器等配电设备详细参数及仿真模型的背景下,以往该问题的研究主要依赖理论分析和仿真计算等手段,PT熔断机理尚无明确定论。目前,主要有以下三种认识。
1)中性点不接地配电网中,单相接地故障存续期间,施加在PT上的工频电压会由相电压抬升至线电压(1.73(pu))。早期研究认为该过电压作用下的PT铁心饱和引发的励磁电流激增是导致熔断器熔断的主要原因。然而,在调研中国电科院武汉分院10 kV交流配电网真型试验基地和宁夏、天津、福建等地区的配电系统后发现,熔断器熔断发生在单相接地故障消失时的恢复送电阶段,而非单相接地故障存续期间(工频电压上升阶段)。此外,根据实际PT励磁特性曲线,1.7(pu)工频过电压作用下PT励磁电流仅为2.7(pu),该电流并不足以触发熔断器熔断。因此,工频过电压不是触发熔断器熔断的根本原因。
2)部分研究认为铁磁谐振是触发熔断器熔断的主要原因。由于PT铁心的非线性饱和特性,其等效电抗随铁心饱和状态变化。当PT等效电抗与系统杂散电容匹配时将发生铁磁谐振[4],PT电压可达2.5(pu)~3.2(pu),此时的励磁电流达百倍[5-9]。Peterson谐振分布原理[10-11]给出了典型的PT谐波振荡区域曲线,被广泛用作铁磁谐振的判据。由此开展的理论分析和实验[12-14]均表明,当系统杂散电容变大时即可远离谐振区,预防铁磁谐振。随着配电网中电缆率的不断提高,系统杂散电容显著增大,发生铁磁谐振的条件已再难具备;同时,根据铁磁谐振机理提出的消谐措施效果并不理想[15-18],实际工程中熔断器熔断问题仍十分突出。由此可见,铁磁谐振理论并不能完全解释熔断器频繁熔断事故。
3)近年来,部分研究认为瞬时性故障消失时的杂散电容放电是造成PT熔断器熔断的主要原因[19-24]。3PT接法时单相接地故障消失后的电容电流分布如图1所示,中性点不接地配电网单相接地故障下,健全相杂散电容电压由相电压抬升至线电压;当故障消失时,杂散电容上的富余电荷经PT泄放形成放电电流,直至杂散电容富余电荷泄放完毕,健全相电压恢复至相电压。杂散电容富余电荷的泄放过程可能导致PT饱和,进而触发熔断器的I2t越限而熔断。

图1 3PT接法时单相接地故障消失后的电容电流分布
Fig.1 Distribution of capacitive current after single-phase ground fault recovery during 3PT connection
基于该思路,文献[19]研究了线路杂散电容对单相接地故障恢复时PT暂态特性的影响;文献[20]采用虚拟补偿法,推导了接地故障消失后PT暂态电压和磁链的表达式,指出暂态电压和磁链为工频交流附加衰减直流的形式,由此产生的暂态励磁电流热积累是导致PT熔断器损坏的主因。文献[21-23]指出单相接地故障消失后杂散电容经PT放电会形成低频振荡,并提出在中性点安装消谐器以抑制该振荡。文献[24]结合PT励磁特性,针对间歇性弧光接地故障开展了研究,发现间歇性弧光接地期间PT铁心将进入深度饱和区而形成浪涌电流。以上研究均指出PT熔断器熔断与杂散电容充放电过程密切相关,但不同文献所推导的暂态电压形态并不一致,甚至有相互矛盾的结论;而且,以上研究多依赖仿真分析,缺乏试验录波实证。
在前人研究基础上,本文分析得出配电网典型故障下的系统空载电压为交直流复合形态——工频交流附加直流偏置电压,总结归纳了该直流偏置电压的产生条件和机理。研究了线路长度、PT阻抗、负载、无功补偿等因素对直流偏置电压的影响规律,发现不同阻抗模式下,系统暂态电压会有不同的表现形式;而暂态电压作用下的PT铁心饱和是触发熔断器熔断的最终原因。最后,通过PSCAD/EMTDC中的10 kV配电网模型和实验室380 V/150 V的实物动态模拟试验平台进行了仿真与试验验证。
中性点不接地配电网典型故障下的系统暂态电压是电源、线路杂散参数和等效负载阻抗共同作用的结果。为简化问题,本节分析空载时的系统暂态电压。第2节将着重讨论等效负载阻抗对暂态电压的影响。此外,现场事故案例表明熔断器熔断通常出现在故障消失、恢复供电的阶段。为此,本节分析故障发生、故障消失等阶段的系统空载暂态电压[25]。
单相接地故障下的系统等效电路如图2所示,其中RS、LS、CS为三相线路杂散参数,ea、eb、ec为系统三相电压源,U和ω分别为电压幅值和工频角速度,ua、ub、uc为三相线路杂散电容上的电压,ia、ib、ic为三相线路上的电流。
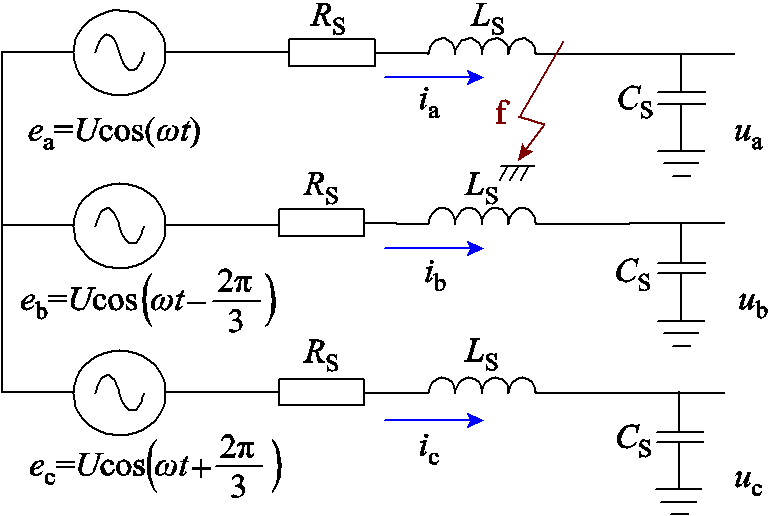
图2 单相接地故障下的系统等效电路
Fig.2 Equivalent circuit of the system under single phase grounding fault
1.1.1 故障发生
假设t=0时刻A相f点发生金属性接地故障;健全相线路杂散电容、电阻、电感经f点形成振荡回路。当金属性接地故障发生后,ua跌落至0,健全相(以B相为例)等效电路如图3a所示。
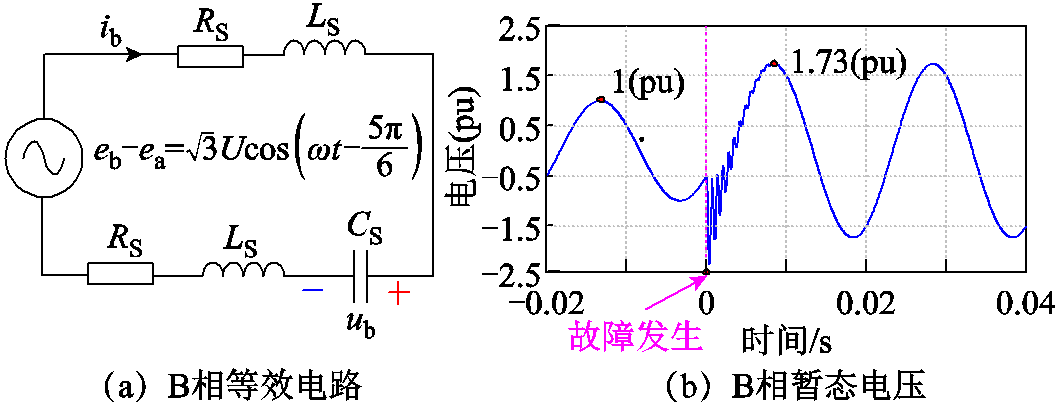
图3 等效电路和暂态电压
Fig.3 Equivalent circuit and transient voltage
根据基尔霍夫电压定律(Kirchhoff Voltage Law, KVL),ub满足状态方程式(1)。考虑实际配电线路参数通常满足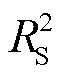 <4LS/CS,解得ub如式(2)所示。
<4LS/CS,解得ub如式(2)所示。
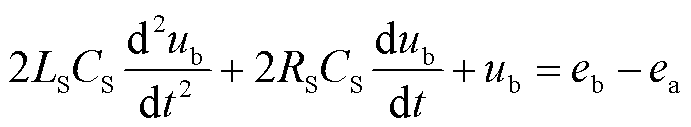 (1)
(1)
 (2)
(2)
式中,α1、β1、φ1、K3如附录中式(A1)~式(A4)所示;K1、K2由ub和ib在t=0时的初始量(ub(0)、ib(0))决定。
不失一般性地,考虑单相接地故障发生在ua峰值时刻,ub(0)、ib(0)为
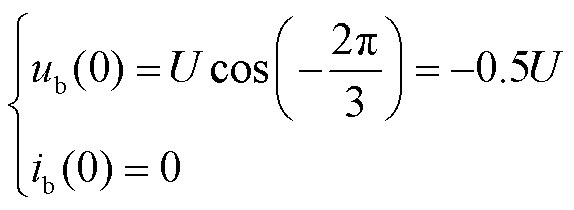 (3)
(3)
联立式(1)和式(3),解得K1和K2如附录中式(A5)、式(A6)所示。
以某10 km长配电线路为例,单位长度的线路参数为r0+jx0=0.125+j0.095 Ω/km;线路杂散电容为c0=0.298 μF/km。计算得到线路集中参数模型中的等效参数为:RS=1.25 Ω,LS=3.02 mH,CS=2.98 μF,代入式(2),健全相杂散电容电压ub如图3b所示。
由图3b可知,健全相杂散电容电压ub是高频分量和工频分量之和。高频分量由RLC回路振荡产生,并逐渐衰减为零;ub最终由工频分量决定,幅值由相电压抬升至线电压,即由1(pu)上升为1.73(pu)。
值得注意的是,为计算故障消失后的暂态电压,需提前得到ub、uc在故障消失时刻的瞬时值。ub可以由式(2)得到,而uc仅与ub存在2π/3的相位差。
1.1.2 故障消失
由于图2中空载线路无非线性元件,下面采用叠加定理分别分析零输入和零状态响应[26]。
零输入响应指将三相电压源置0后,由ub和uc的初始值决定的线路暂态电压。零输入等效电路如图4a所示,其中u1-a,u1-b,u1-c为零输入响应分量。
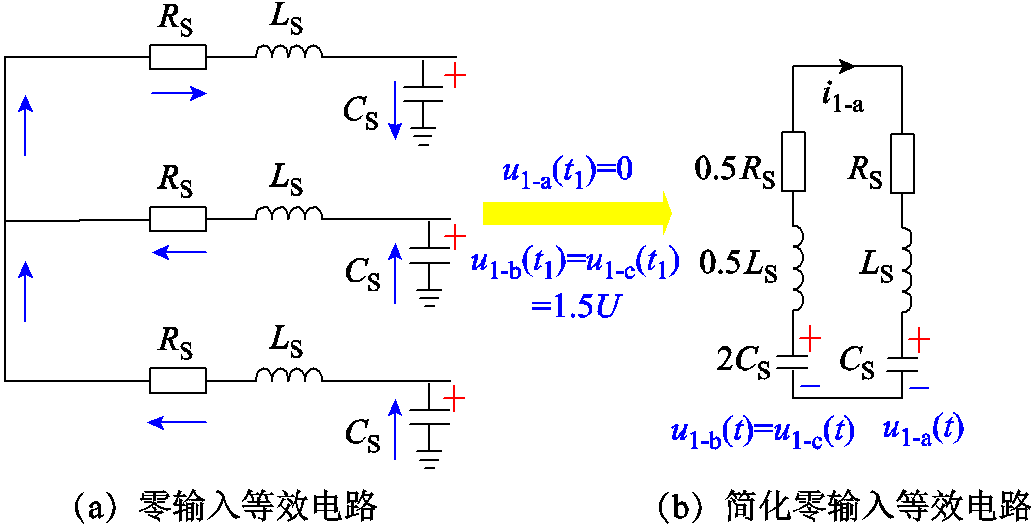
图4 故障消失后的零输入电路
Fig.4 Equivalent zero-input circuit after single-phase ground fault recovery
假设单相接地故障在t=t1时刻即故障电流首次过零时刻消失,三相杂散电容电压初始值u1-a(t1)、u1-b(t1)、u1-c(t1)分别为
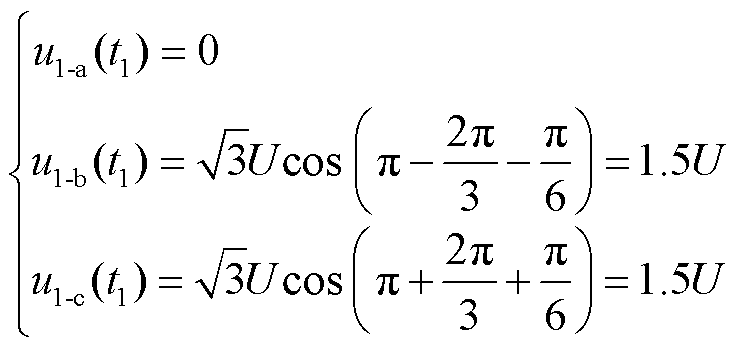 (4)
(4)
此时,零输入等效电路可简化为图4b所示,且电流i1-b满足
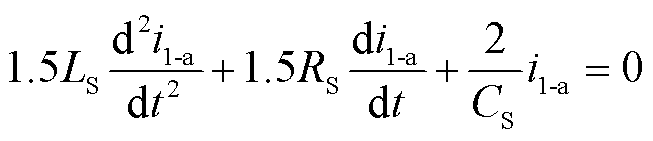 (5)
(5)
进一步解得i1-a、u1-a、u1-b、u1-c为
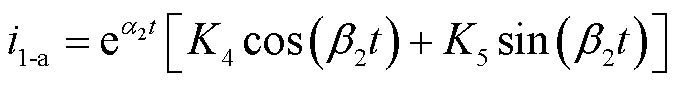 (6)
(6)
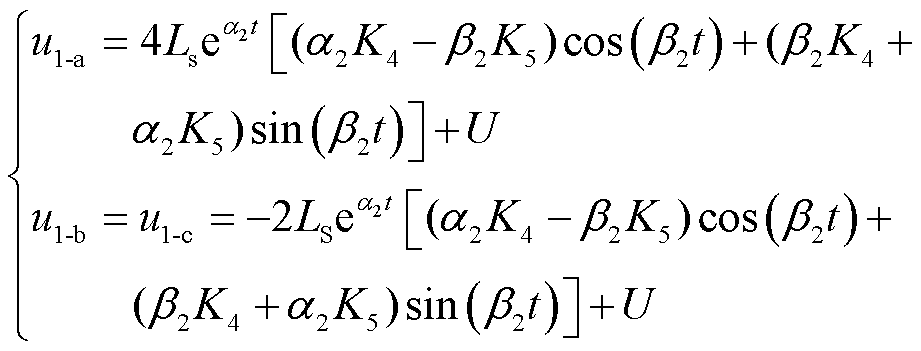 (7)
(7)
式中,α2、β2、K4、K5如附录中式(A7)~式(A10)所示。
零状态响应指将三相杂散电容上电压置0后,由三相电压源决定的线路暂态电压。此时三相线路对称,如图5所示,其中u2-a、u2-b、u2-c为零状态响应分量。因此,简化零状态等效电路如图5b所示,电压u2-a满足状态方程式(8)。
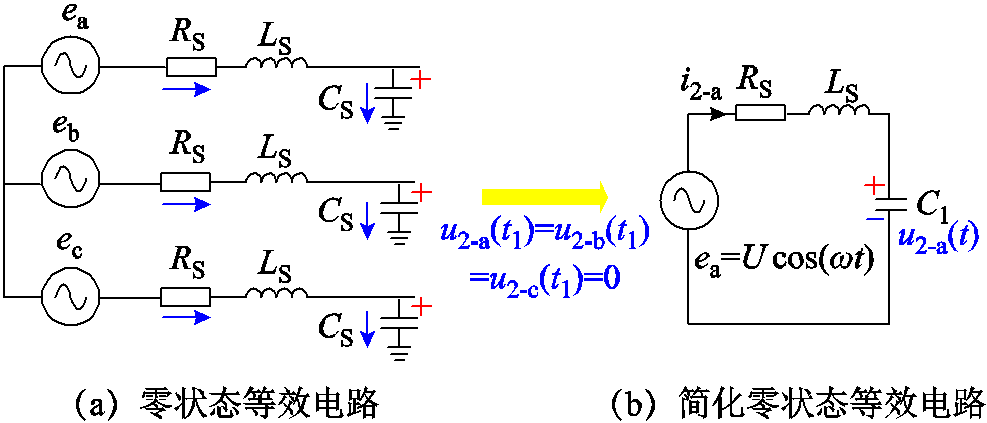
图5 故障消失后的零状态电路
Fig.5 Equivalent zero-state circuit after single-phase ground fault recovery
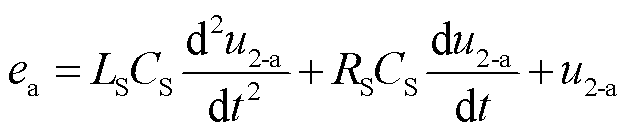 (8)
(8)
进一步解得u2-a为
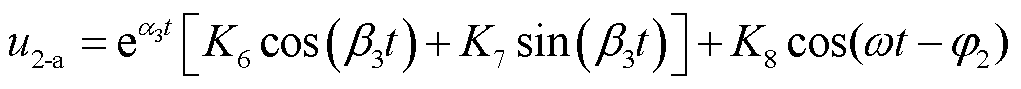 (9)
(9)
式中,α3、β3、φ2、K8如附录中式(A11)~式(A14)所示。根据零状态响应的边界条件式(10),求得K6、K7如附录中式(A15)、式(A16)所示。
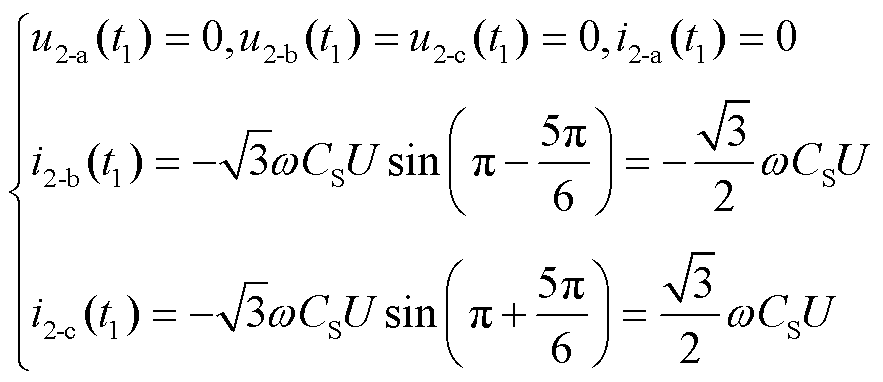 (10)
(10)
同理,故障消失后u2-b、u2-c为
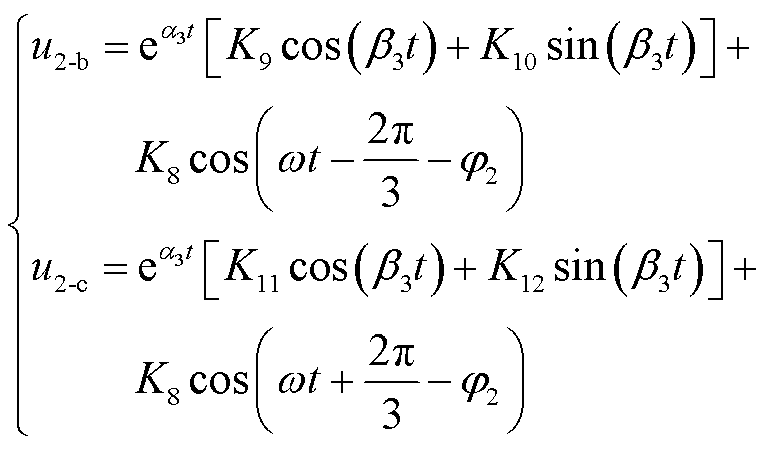 (11)
(11)
结合边界条件式(10),式(11)中常数K9、K10、K11、K12如附录中式(A17)~式(A20)所示。
将前文提及的线路参数代入式(7)、式(9)、式(11),零输入响应和零状态响应分别如图6a和图6b所示,故障消失后三相杂散电容电压总响应如图6c所示。
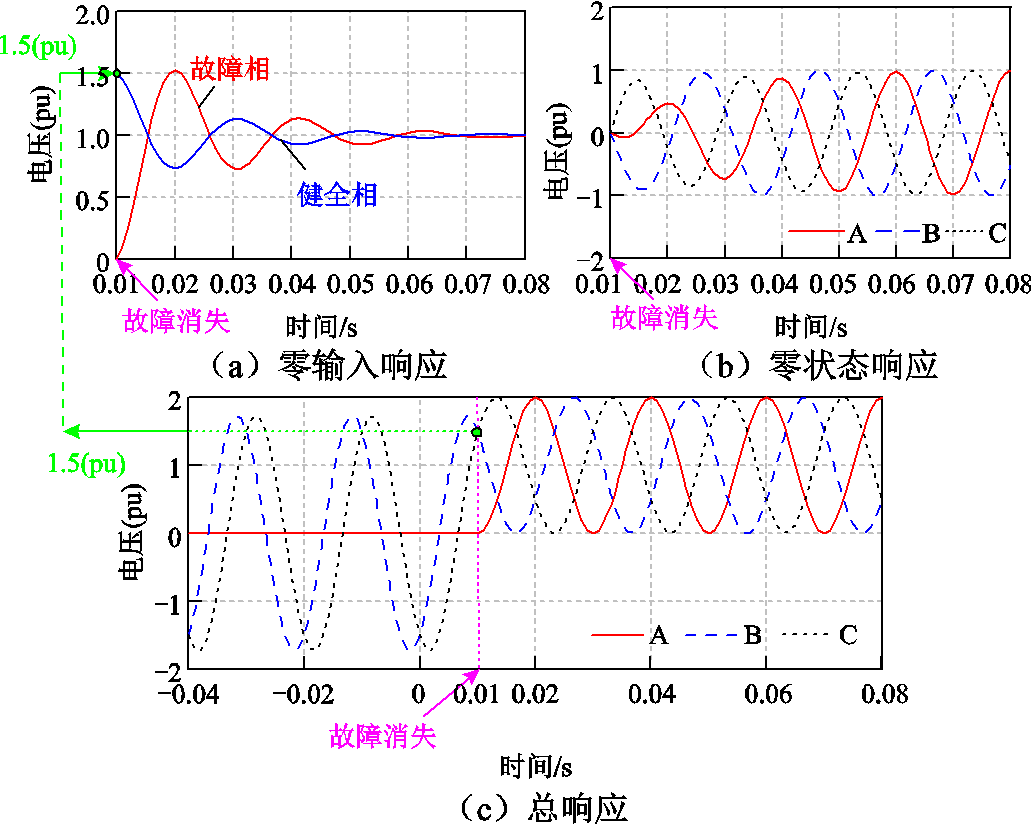
图6 空载系统暂态电压波形
Fig.6 Transient voltage waveforms of the no-load system
由图6c可知,故障消失后,各相杂散电容总电压由工频分量和直流分量构成。由图6a可知,故障消失时刻健全相杂散电容电压状态量不为零,直流分量即为零输入响应,是净电荷Qn重新分配导致的。由图6b可知,健全相工频分量由线电压降至相电压,而故障相工频分量由0上升至相电压。
综上所述,单相接地故障消失后,系统暂态电压为工频交流附加直流偏置的交直流复合形态,且该直流偏置电压由故障消失瞬间的杂散电容净电荷重新分配导致。
1.1.3 间歇性弧光接地故障
实际工程中,单相接地故障可能在短时间内连续多次发生,该工况称为间歇性弧光接地故障[27]。
假设单相接地故障t=0时刻发生、t1时刻消失,随后t2时刻A相电压达到峰值,故障电弧重燃。电弧重燃过程与首次接地故障发生过程相似。同理,可得电弧重燃后的三相电容电压u3-a、u3-b、u3-c分别为
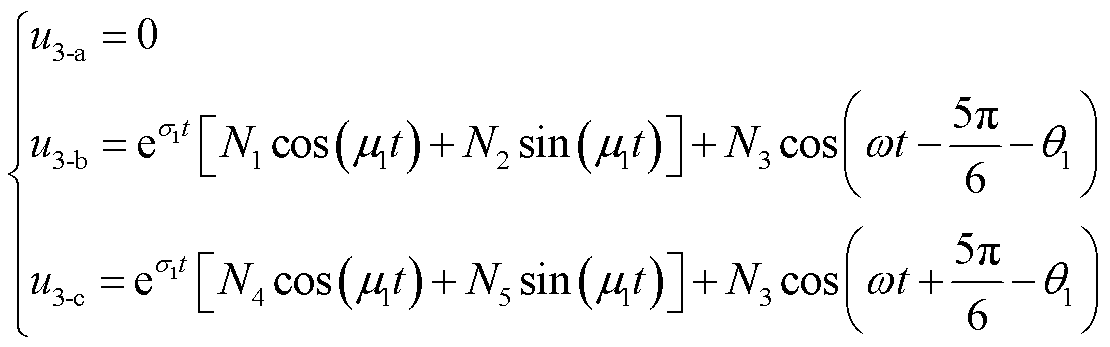 (12)
(12)
式中,系数如附录中式(A21)~式(A28)所示。
当t4时刻故障电流过零,故障电弧再次熄灭。电弧第二次熄灭时的边界条件和状态方程与第一次电弧熄灭过程相同,因此两次熄弧后的电压波形相同。
此处以连续两次故障为例,同样代入1.1.1节所述线路参数,得到三相杂散电容电压波形如图7所示。
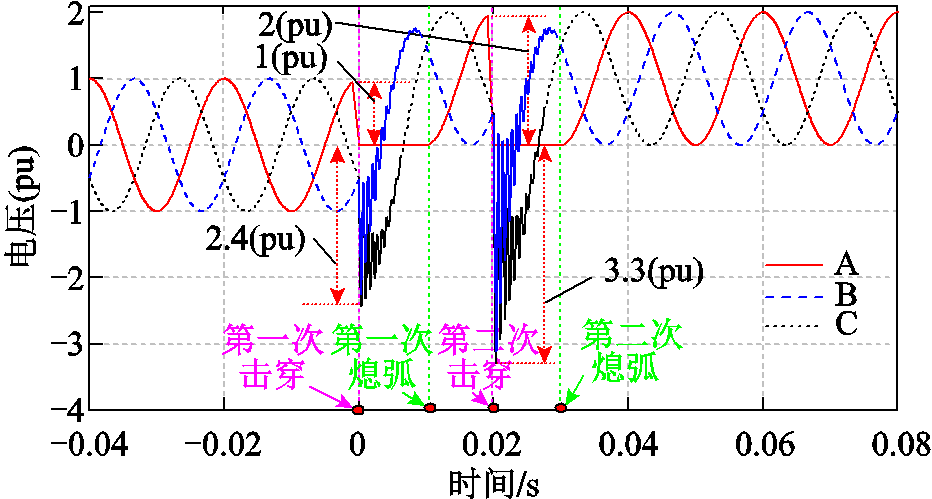
图7 弧光接地三相杂散电容电压波形
Fig.7 Waveform of arc-ground three-phase stray capacitor voltages
如图7所示,对比两次故障下的故障相电压可知,相比第一次击穿,第二次击穿时故障相电压变化量Δu由1(pu)变为2(pu),由此引发的振荡幅值更高。对比两次故障下的健全相电压可知,相比第一次击穿,第二次击穿时健全相过电压最大值由2.4(pu)变为3.3(pu),这正是由于故障相电压变化量Du增大,振荡幅值变高造成的。但无论间歇性故障发生几次,在最后一次故障消失后,系统电压总是表现为工频交流附加直流偏置的交直流复合电压形态。
1.2.1 故障发生
当t=0时刻A相电源电压达到峰值,A、B两相发生金属性接地故障。此时的等效电路和相量图如图8所示。其中,ea(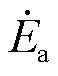 )、eb(
)、eb(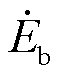 )、ec(
)、ec( )分别为额定工况的三相电压,u1(
)分别为额定工况的三相电压,u1(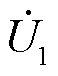 )、u2(
)、u2(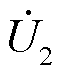 )、u3(
)、u3(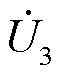 )分别为故障发生后的三相电压,u0(
)分别为故障发生后的三相电压,u0(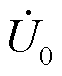 )为中性点电压。
)为中性点电压。

图8 两相接地故障下的等效电路及相量图
Fig.8 Equivalent circuit and phasor diagram under two-phase ground fault
两相接地故障发生后,故障相A、B由空载变为短路状态,两相故障电流经故障点形成闭合回路。
根据基尔霍夫电流定律(Kirchhoff Current Law, KCL),两相故障电流大小相同、方向相反。考虑故障相线路参数一致,中性点u0偏移后,两相电压同样大小相同、方向相反,因此三相电压变为
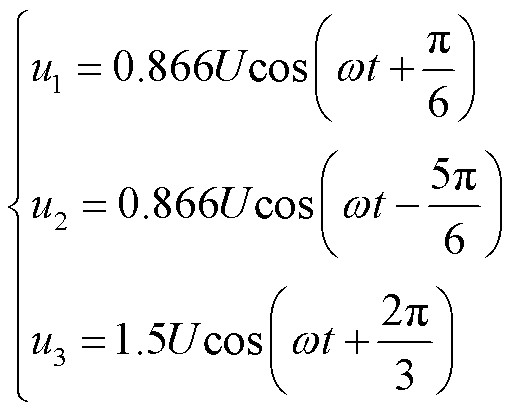 (13)
(13)
与1.1.1节相似,故障发生后,故障相杂散电容电压被钳位为0,健全相杂散电容电压为
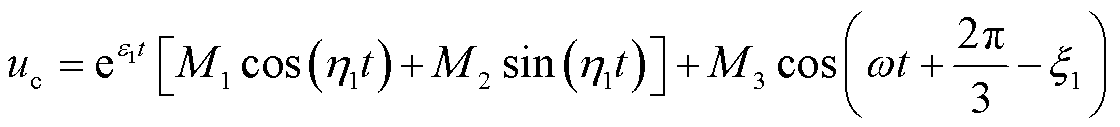 (14)
(14)
式中,系数如附录中式(A29)~式(A34)所示。
同样将1.1.1节中所述线路参数代入式(14),得到健全相杂散电容电压如图9所示。比较图3和图9可知,两相接地故障下,健全相杂散电容电压同样是由高频分量和工频分量构成的。但由于电压突变量变小,高频分量幅值明显小于单相接地故障;工频分量幅值仅由1(pu)上升至1.5(pu)。
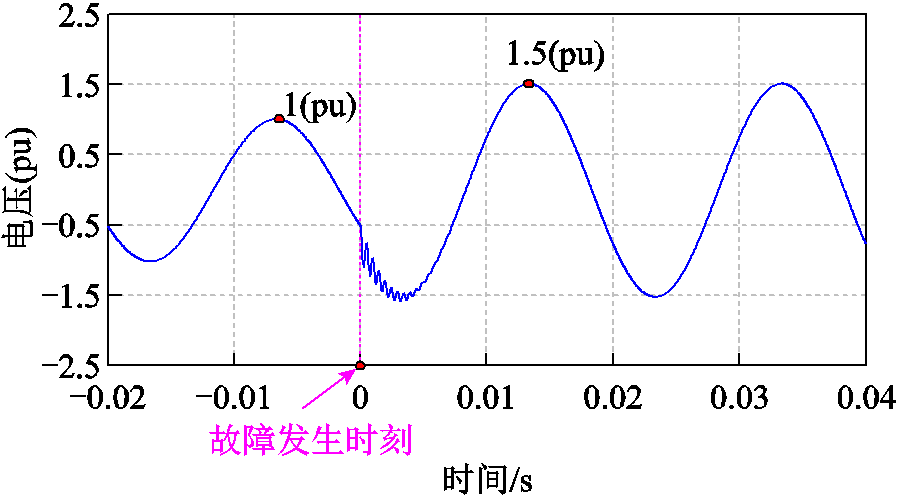
图9 故障发生后健全相电容电压
Fig.9 Waveform of C-phase capacitor voltage at breakdown time
1.2.2 故障消失
与1.1.2节相似,利用叠加定理,将t1时刻故障消失后的电路总响应分为零输入和零状态,其等效电路如图10所示。
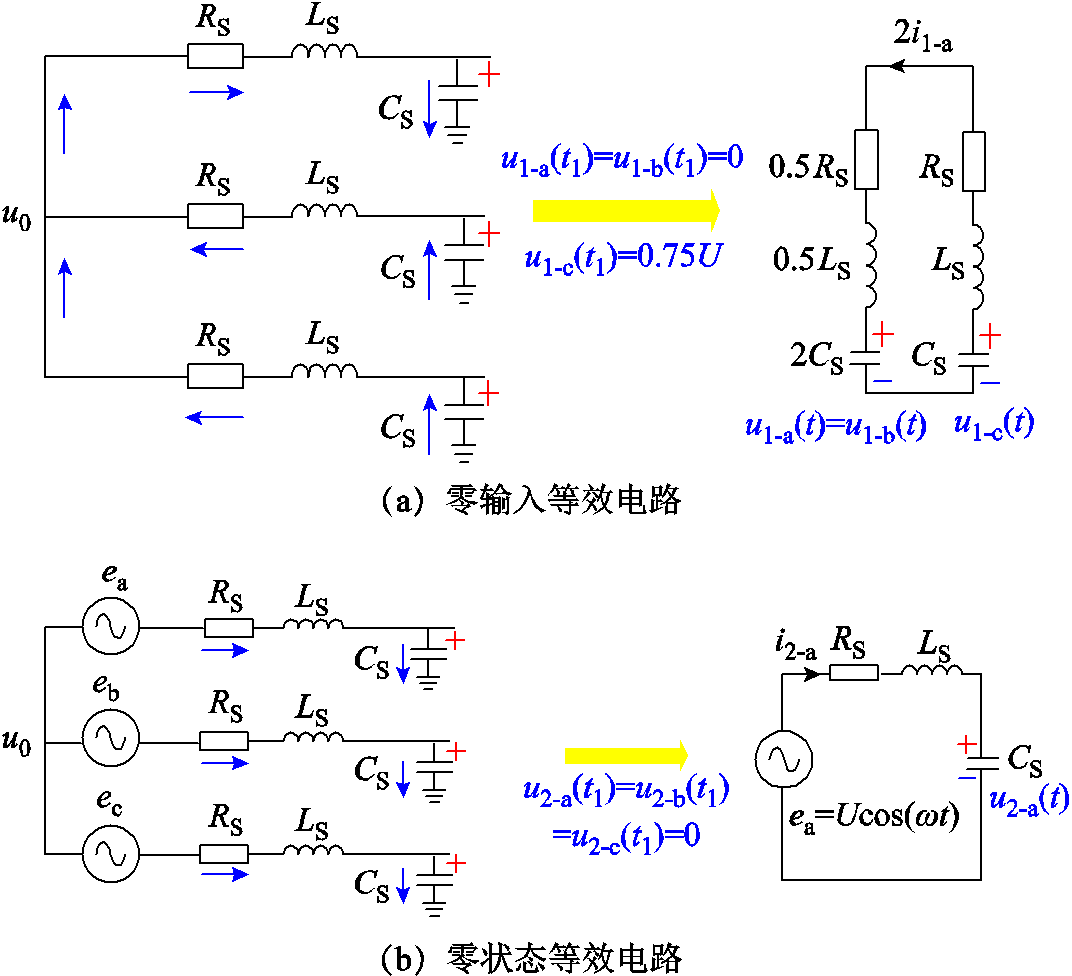
图10 两相接地故障消失前后的等效电路
Fig.10 Equivalent circuit before and after the disappearance of two-phase ground fault
图10a中故障消失时,健全相C相杂散电容电压不为零。该状态量所对应的电荷Qn将平均分配到三相杂散电容中,得到三相杂散电容电压的零输入响应如式(15)所示,其中各系数见附录中式(A35)~式(A38)。
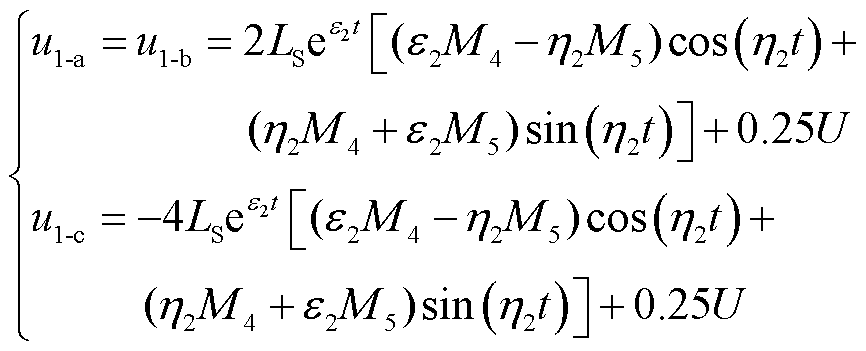 (15)
(15)
针对图10b所示故障消失后的三相对称电路,得三相杂散电容电压的零状态响应如式(16)所示,其中各系数见附录中式(A39)~式(A47)。
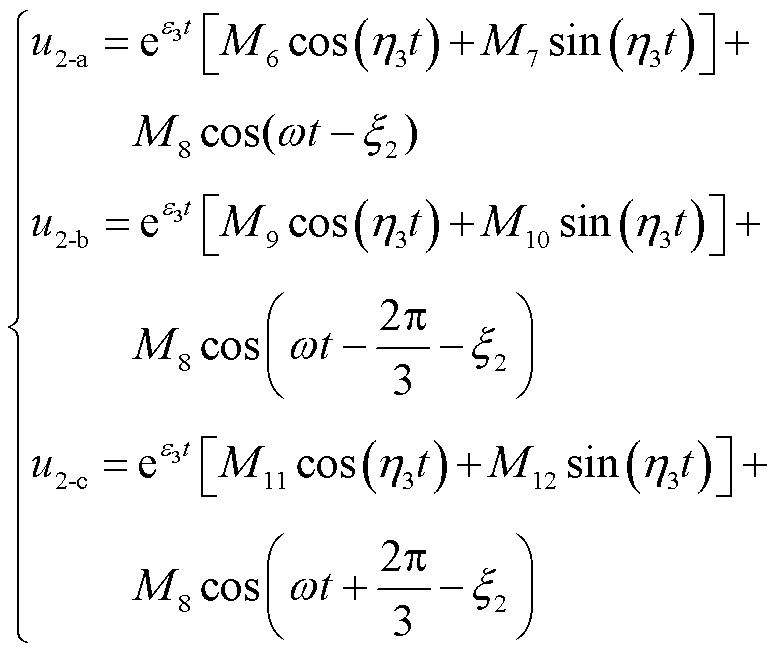 (16)
(16)
综合零状态响应和零输入响应,同样以1.1.1节所述线路参数代入式(15)、式(16),可得两相接地故障消失前后的三相杂散电容电压波形如图11所示。
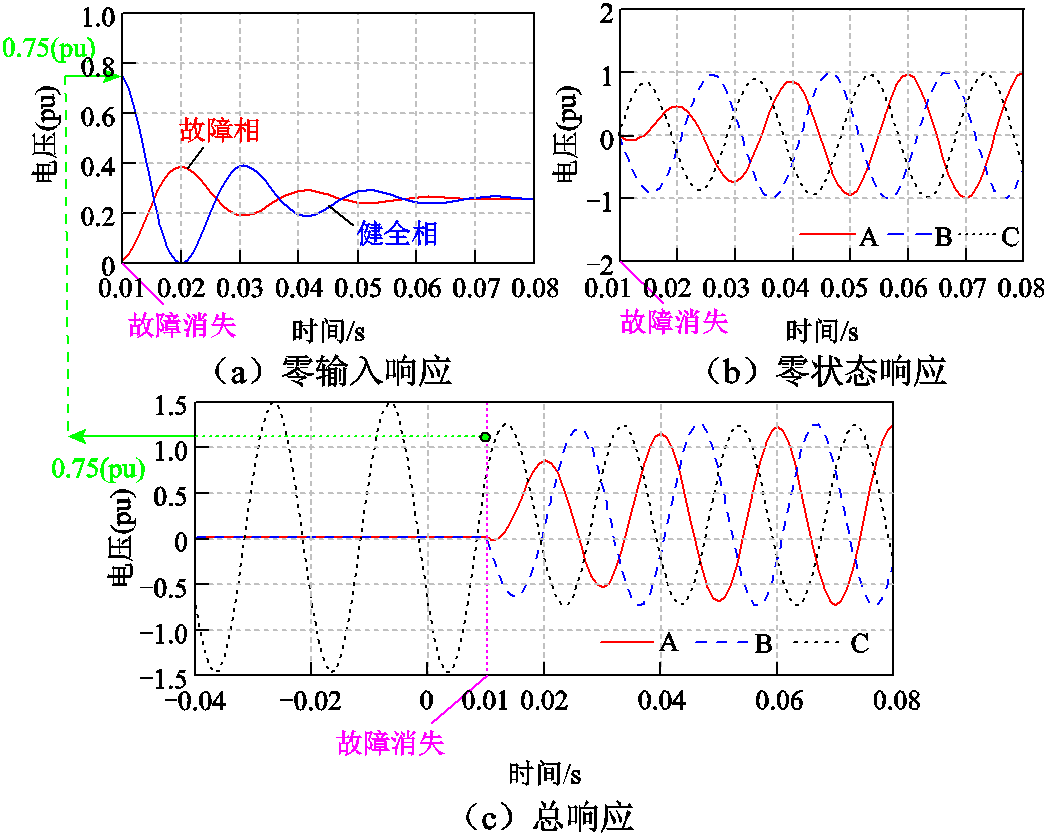
图11 两相接地故障消失前后的杂散电容电压
Fig.11 Stray capacitor voltages before and after the disappearance of two-phase ground fault
对比图6a和图11a可知,对于故障消失后的零状态响应,由于两相接地故障消失时的健全相Qn不为零,也引发了直流偏置电压。对比图6b和图11b可知,对于故障消失后的零状态响应,两相接地故障与单相接地故障相同。相比单相接地故障,两相接地故障下Qn较小,其引发的直流偏置电压也更小。
通过以上单相接地故障和两相接地故障的零输入响应分析可知,故障消失后出现的直流偏置电压与健全相杂散电容电荷Qn的重新分配密切相关。为此,本节将故障消失后的配电网络空载等效电路简化为图12,其中EA、EB、EC为三相电压源,QA、QB、QC为杂散电容上积累的电荷量。
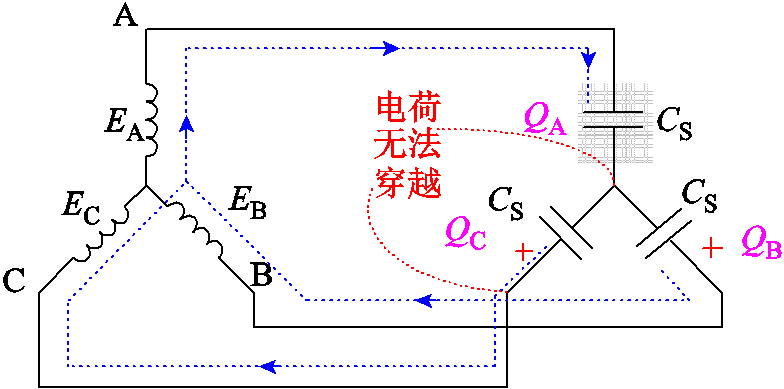
图12 直流偏置电压形成机理示意图
Fig.12 Schematic diagram of the principle of DCBV formation
任意类型的故障下,只要故障消失时杂散电容净电荷不为零,即Qn≠0,这些极化电荷没有其他路径能从杂散电容正极穿越到负极而消失,只能均匀分配到三相杂散电容中呈现出直流偏置电压。由此可得,中性点不接地系统中,Qn的重分配过程导致直流偏置电压的形成,其中Qn、三相直流偏置电压(u1-a(∞)、u1-b(∞)、u1-c(∞))为
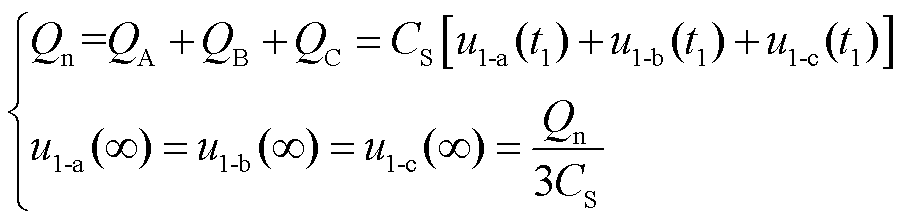 (17)
(17)
直流偏置电压峰值取决于故障消失时刻三相电容电压(u1-a(t1)、u1-b(t1)、u1-c(t1))。
单相接地故障、两相接地故障、间歇性弧光接地故障情况相似,故障消失时Qn≠0,会产生直流偏置电压。
与之不同,两相短路故障下,三相杂散电容电压仍是对称的,故障发生和消失的整个过程中Qn始终为0,不具备产生直流偏置电压的条件。三相接地故障下,虽然在故障存续期间Qn始终为0,但由于故障电流存在相位差,当某一相故障电弧熄灭后,三相接地故障演变为两相接地故障,进而产生直流偏置电压。
值得说明的是,中性点不接地系统中,单相接地故障的故障电流很小,故障电弧很有可能自动熄灭;而对于其他故障情况,故障电弧一般很难自动熄灭,需要依赖断路器分闸来消除故障。
瞬时性故障消失后的系统空载电压可能包含直流偏置电压,且该电压是由Qn引起的。实际配电系统几乎不可能完全空载,线路杂散参数、PT阻抗、负载及无功补偿等效电容等都有可能引起Qn泄放通道的改变。为此,本节以图13所示的A相电路图为例,分析直流偏置电压的影响因素,包括杂散电容(CS)、PT高压侧等效阻抗(RPT, LPT)、负载等效阻抗(Rload, Lload)、无功补偿等效电容(CSVC)等。
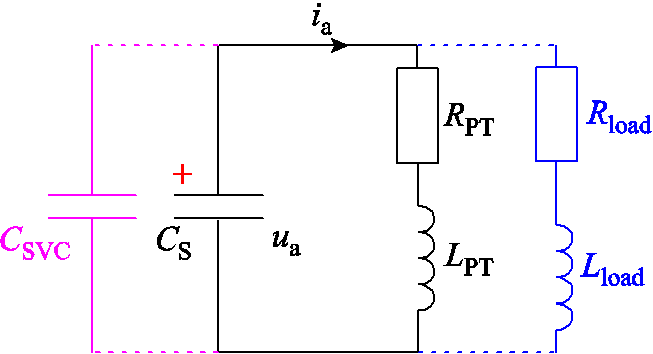
图13 Qn可能的泄放通道及影响因素
Fig.13 Possible discharge channels and influencing factors of Qn
负载等效阻抗为零时,Qn只能从CS正极经PT高压侧运动到CS负极,列写KVL方程得到
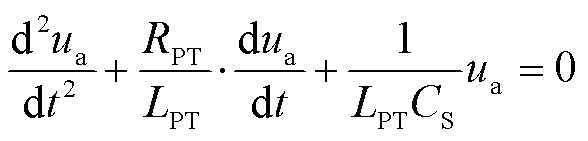 (18)
(18)
测量某工程实际用PT(JSZW12A-10NFR型)可知,RPT为2 kΩ;LPT是随铁心励磁状态变化的,铁心不饱和时该值约为50 H,当铁心处于饱和状态时,该值为百mH级别,但都满足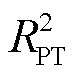 >4LPT/CS,此时,Qn放电回路处于过阻尼状态,求解得到杂散电容电压满足
>4LPT/CS,此时,Qn放电回路处于过阻尼状态,求解得到杂散电容电压满足
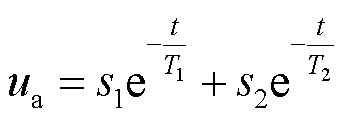 (19)
(19)
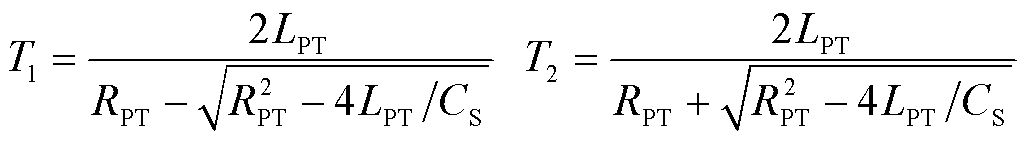 (20)
(20)
式中,s1、s2为由边界条件决定的常数。
显然T1>T2,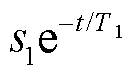 为主导分量。由此可以看出,随着CS的增大,时间常数T1增大,杂散电容电压呈现为衰减的直流偏置电压,且衰减速度与CS成反比。
为主导分量。由此可以看出,随着CS的增大,时间常数T1增大,杂散电容电压呈现为衰减的直流偏置电压,且衰减速度与CS成反比。
当PT阻抗参数设计不合理即RPT较小时,会出现满足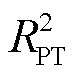 <4LPT/CS的欠阻尼情况。此时,杂散电容电压的通解形式为式(21),其中s3、s4也是由边界条件决定的常数,而其他系数如式(22)所示。
<4LPT/CS的欠阻尼情况。此时,杂散电容电压的通解形式为式(21),其中s3、s4也是由边界条件决定的常数,而其他系数如式(22)所示。
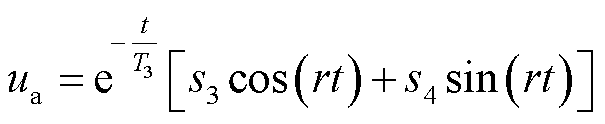 (21)
(21)
 (22)
(22)
此时,杂散电容电压零输入响应为低频振荡形式,其频率接近CS和LPT的谐振频率。
若RPT进一步小到仅为几十或几欧姆,且PT励磁特性差,铁心饱和后LPT忽略不计,虽然故障恢复后零输入响应波形仍满足式(21)形式,但直流偏置分量将按照式(22)在短时间(ms级)内衰减完毕:铁心饱和时,可将PT支路视为低阻故障;铁心退出饱和时,可将PT支路视为故障消失。
此时,单相接地故障消失后,直流偏置电压导致PT饱和,PT支路发生低阻故障;随着直流偏置电压的衰减完毕,PT退出饱和状态,低阻故障消失;在Qn的作用下又进一步产生直流偏置电压;如此周而复始,呈现近似三相铁磁谐振波形。
由此可见,当PT阻抗模式不同时,杂散电容电压的零输入响应有不同的表现形式,包括衰减的直流偏置、低频振荡、连续故障下的铁磁谐振等形式。这也是不同文献仿真所得的系统电压波形不同的根本原因。
对于小负载(大阻抗)工况,Qn依旧以PT高压侧作为主要的泄放通道;对于大负载(小阻抗)的工况,Qn将以负载等效阻抗作为主要的泄放通道,此时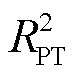 <4Lload/CS,杂散电容电压的形式满足式(21)。考虑实际系统(功率因数0.8~0.9)中,
<4Lload/CS,杂散电容电压的形式满足式(21)。考虑实际系统(功率因数0.8~0.9)中,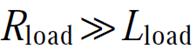 ,所以Qn将在极短的时间内衰减完毕。
,所以Qn将在极短的时间内衰减完毕。
对于安装无功补偿装置的配电系统,CSVC与CS为并联关系。由式(20)可知,杂散电容电压的衰减时间随CSVC增大而增加。
本节针对中性点不接地系统中的典型故障消失后的直流偏置电压及其影响因素进行仿真验证。
实际配电网拓扑结构非常复杂,可能包含多条进出线、带不同形式负载,但针对三相杂散电容净电荷Qn的泄放通路,复杂配电系统均可简化为图14的等效系统模型。
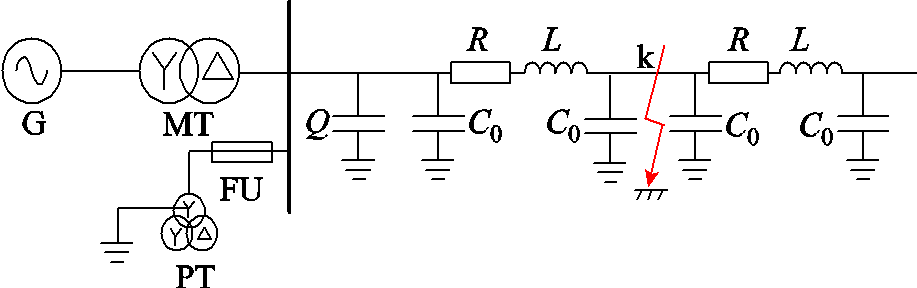
图14 PSCAD仿真模型
Fig.14 PSCAD simulation model
图14中G为110 kV电源;MT为配电网 110 kV/10 kV降压变压器;PT为10 kV电压互感器,采用3PT接法,其中单相PT型号为JDZX18-10G,仿真参数见表1;Q表示无功补偿装置等效电容,容量为1 Mvar;RLC0为配电线路集中参数模型,导线阻抗为r0+jx0=0.125+j0.095 Ω/km,导线杂散电容为C0=0.298 μF/km。
表1 PT仿真参数
Tab.1 Simulation parameters of PT
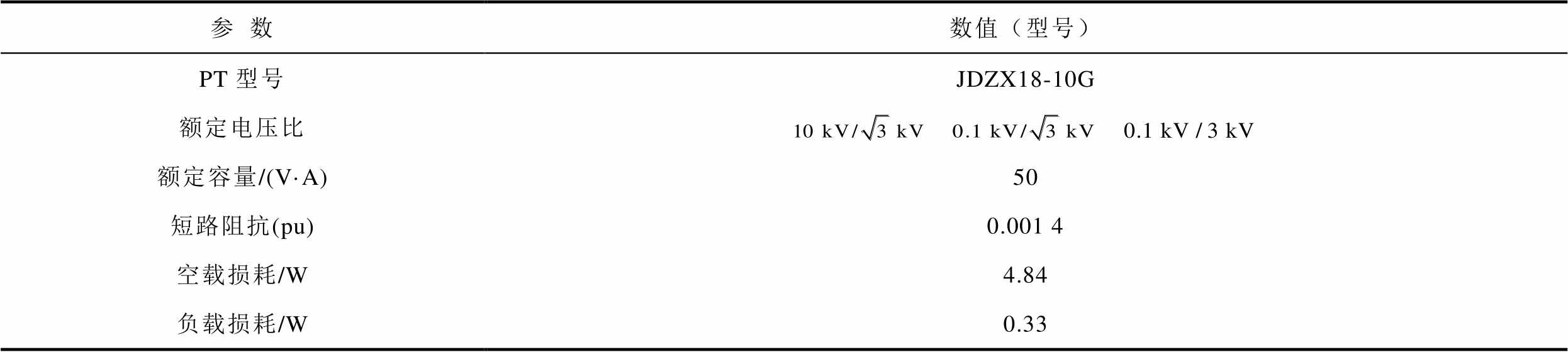
参数数值(型号) PT型号JDZX18-10G 额定电压比 额定容量/(V·A)50 短路阻抗(pu)0.001 4 空载损耗/W4.84 负载损耗/W0.33
1)算例1:直流偏置电压形成条件与机理验证
假设k点发生金属性接地故障,并在工频电流首次过零时故障消失,各种典型故障的三相杂散电容电压及三相杂散电容净电荷Qn仿真波形如图15所示。

图15 典型故障下的杂散电容电压及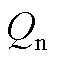 仿真波形
仿真波形
Fig.15 Stray capacitor voltage and 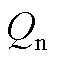 simulation waveforms under typical faults
simulation waveforms under typical faults
仿真结果表明:与第1节的理论分析一致,单相接地故障、两相接地故障下,故障消失时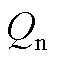 ≠0,均产生了直流偏置电压;三相接地故障的首相故障电弧熄弧后,转变为两相接地故障,进而出现直流偏置电压;两相短路故障下,
≠0,均产生了直流偏置电压;三相接地故障的首相故障电弧熄弧后,转变为两相接地故障,进而出现直流偏置电压;两相短路故障下,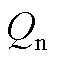 始终为零,无直流偏置电压。
始终为零,无直流偏置电压。
2)算例2:直流偏置电压的影响因素
通过在仿真模型中改变线路长度、PT阻抗模式、负载、无功补偿容量等因素,得到单相接地故障下的杂散电容电压仿真波形如图16所示。其中,红色(浅)箭头为故障发生时刻,蓝色(深)箭头为故障消失时刻。
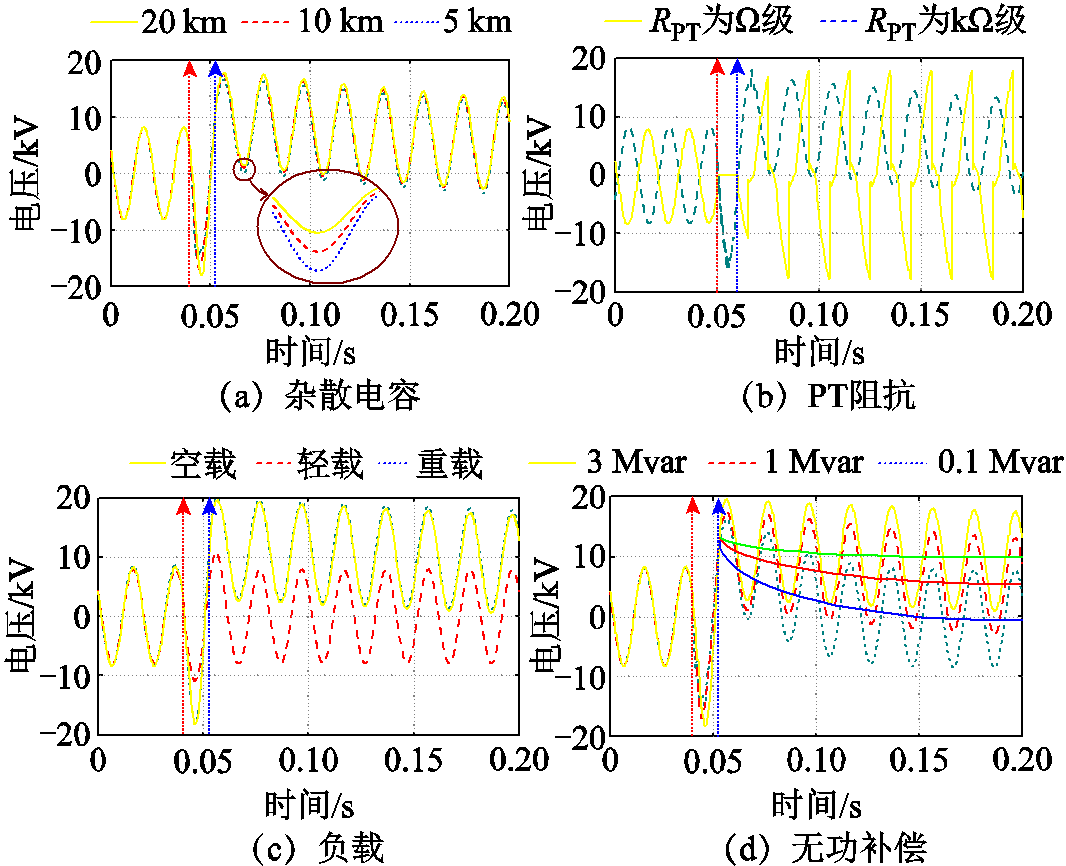
图16 直流偏置电压衰减规律及其影响因素
Fig.16 The attenuation law of DCBV and its influencing factors
仿真结果表明:与前述理论分析一致,CS随线路长度的增加而增大,直流偏置电压的衰减速度随CS的增大而增大,但变化并不明显。当RPT为kΩ级时,Qn泄放电路为过阻尼状态,直流偏置电压衰减时间常数为s级;当RPT为Ω级同时PT励磁特性较差时,直流偏置电压在极短时间内衰减完毕,随着铁心饱和状态的变化,PT支路可视为“PT支路接地故障—故障消失—PT支路接地故障”的间歇性低阻故障,呈现出类似铁磁谐振的波形。小负载时,负载等效阻抗很大,直流偏置电压衰减规律与空载时类似,大负载情况下直流偏置电压快速衰减至0。无功补偿装置容量越大,装置的等效电容越大,其影响与线路长度相同,容量越大,直流偏置电压衰减速度越慢。
为了进一步验证理论分析和仿真模型,在实验室搭建了380 V/150 V的动态模拟试验平台,其等效电路和实物如图17所示。
试验平台(150 V,50 Hz)经过调压变压器和隔离变压器与电网(380 V,50 Hz)连接。电感线圈L1、L2、L3(均为2 μH)和电容器C1、C2、C3(均为4.5 μF)模拟空载线路。电阻RC(2 Ω)和晶闸管模块VT1串联模拟故障支路。PT(JDG4-0.5)与熔断器XNRP12-0.2串联构成PT支路,其中,PT具体参数见表2;熔断器额定电流为0.2 A,且熔化热能小于1 A2·s。QF1、QF2为保护用空气开关。
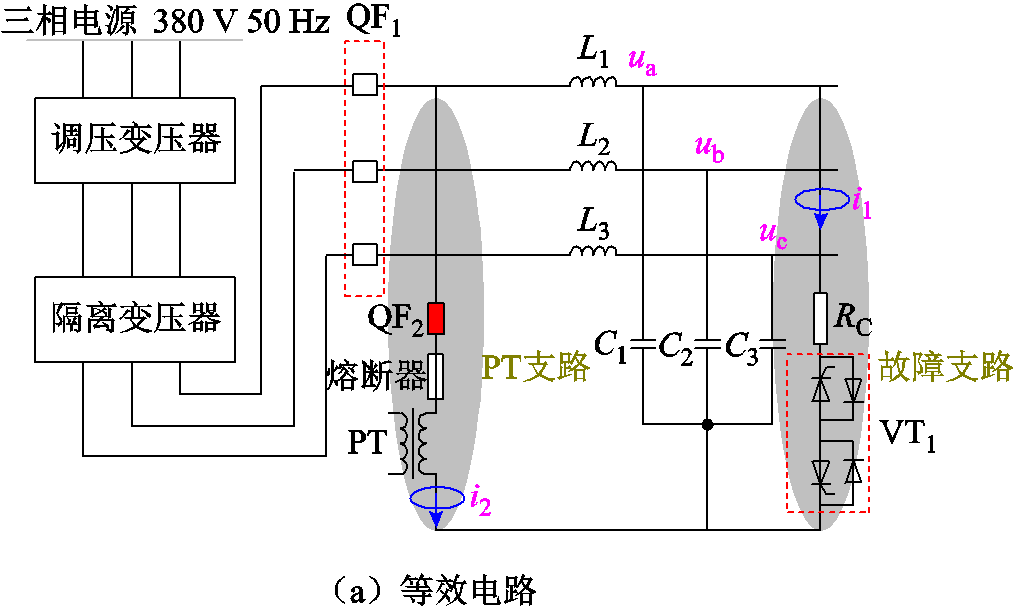

图17 动态模拟试验平台
Fig.17 Down-scaled experiment platform
表2 JDG4-0.5参数
Tab.2 Parameters of JDG4-0.5

参数数值(型号) PT型号JDG4-0.5 额定电压比380 V:100 V 额定容量/(V·A)15 一次侧直流电阻/Ω9 一次侧电感/H10 一次侧漏电感/mH9
试验中电流信号由两个电流探头(Tektronix- A622)采集;电压信号由三个高压差分探头(Sapphire-SI9010A、Pintech-PT5230)采集;所有信号由示波器(Yokogawa-DL950)记录。
如图17a所示,ua、ub、uc分别为三相电容电压,i1、i2分别为故障支路和PT支路电流。
试验中,通过触发晶闸管VT1导通来模拟单相接地故障发生;撤掉触发信号,晶闸管在电流过零点关断来模拟故障消失。试验分为空载和带PT负载两组进行:①空载试验时,保持QF1、QF2分别处于合闸、分闸状态,试验结果在4.1节中讨论;②带PT试验时,保持QF1、QF2合闸,PT支路接入系统,试验结果在4.2节中讨论。
试验过程中,导通晶闸管模块后迅速关断,试验波形如图18所示。
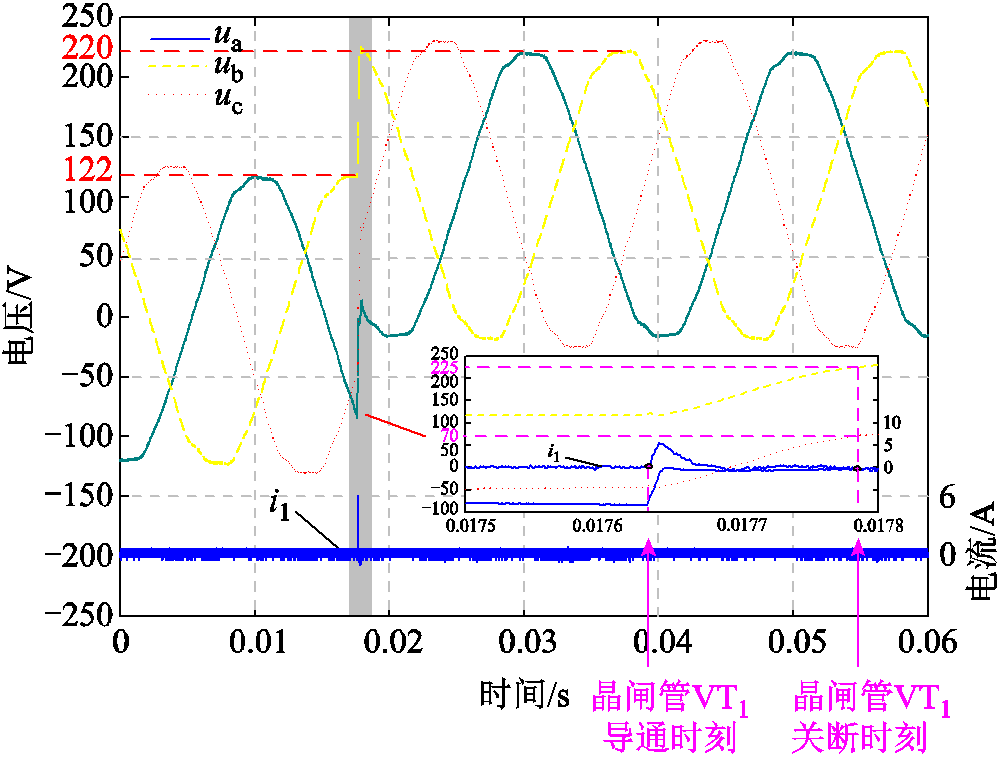
图18 空载试验波形
Fig.18 No-load test waveform
试验结果表明,正常工况下三相电容电压为122 V,随着晶闸管的导通,单相接地故障发生,极短时间内放电电流降低至0,故障自动消失。根据1.3节分析可知,健全相电容电荷将在三相电容间重新分配,产生直流偏置电压。此时三相电容电压为0、122、225 V,由式(17)计算得到直流偏置电压大小为98 V,三相电压整体呈正向偏移(峰值达220 V),与前述理论分析结果一致。
以PT阻抗特性为例,本节试验研究直流偏置电压的影响因素及危害。试验过程中,PT高压侧接入试验系统,试验波形如图19所示。
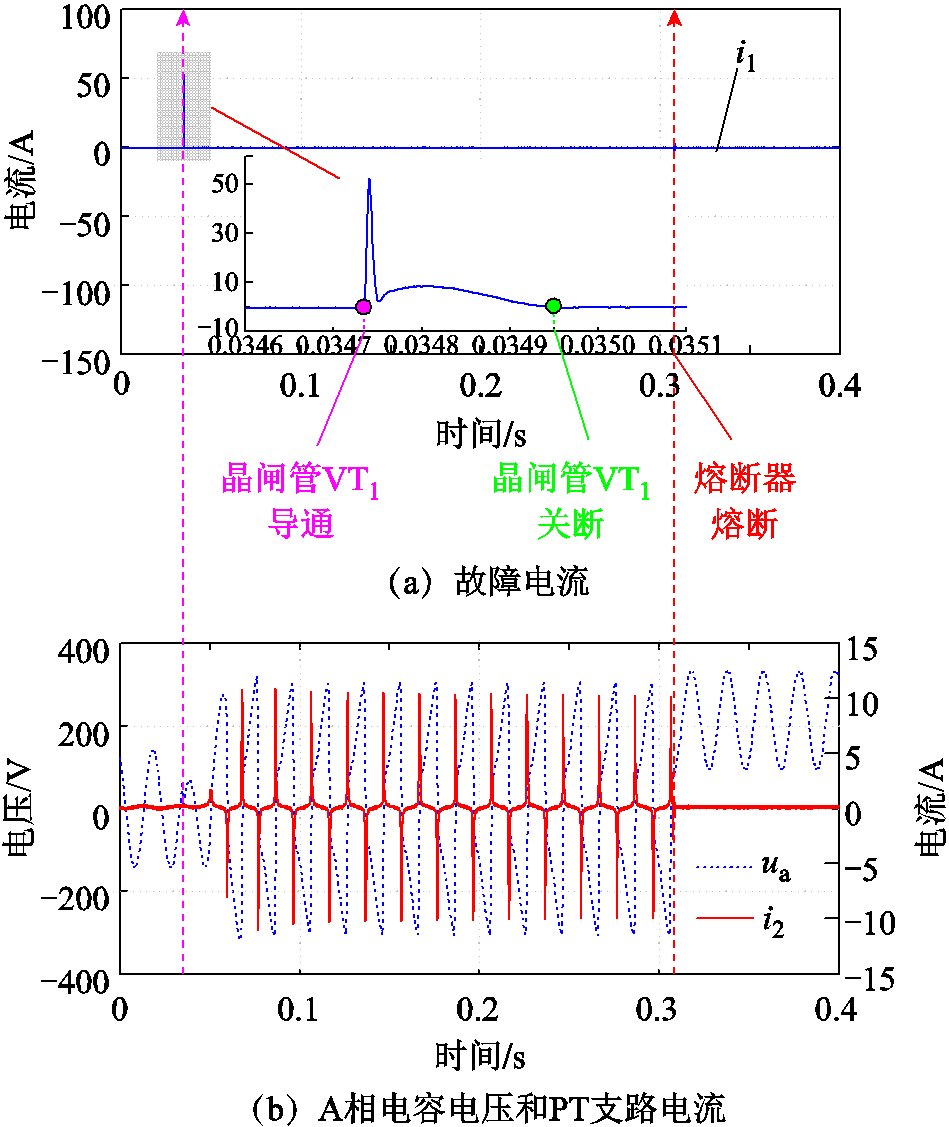
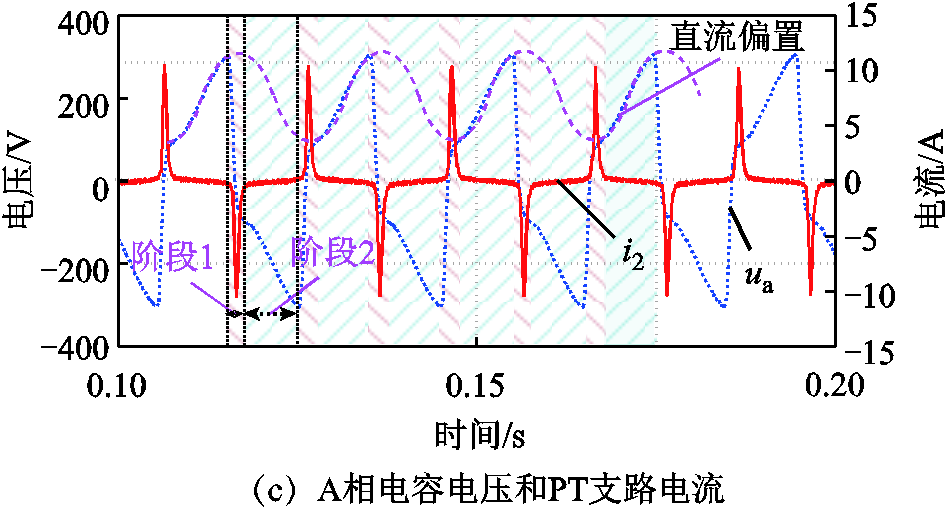
图19 直流偏置电压的危害物理验证试验
Fig.19 Physical verification test on hazards of DCBV
在图19b中,模拟单相接地故障的晶闸管VT1关断后,接PT的A相电容电压出现了近似铁磁谐振的波形,具体过程分析如下。
1)阶段1:单相低阻接地故障发生
如图19c中阶段1所示,晶闸管VT1关断后,单相接地故障消失,Qn在杂散电容上重新分配形成直流偏置电压。此时,PT作为泄放Qn的主要通道,在交直流复合电压作用下,PT铁心进入饱和,PT高压侧等效电感LPT减小至漏电感。RPT、LPT和CS满足欠阻尼条件,由式(22)可得直流偏置电压衰减时间常数为ms级,电压被快速泄放,同时PT支路电流形成尖峰脉冲。因此,铁心饱和时PT支路呈低阻抗,近似单相低阻接地故障发生。
2)阶段2:单相接地故障消失
如图19c中阶段2所示,Qn泄放后,PT铁心退出饱和,PT支路由低阻抗变为高阻抗,近似单相接地故障消失。此时,三相杂散电容上的净电荷无其他泄放途径,重新分配再次形成直流偏置电压,而进入阶段1。如此在阶段1和阶段2之间周期性循环,呈现出持续的周期性单相接地故障发生、消失过程,电容电压表现出类似铁磁谐振的波形,与图16b相符。
试验过程中,PT励磁电流呈现间歇性的脉冲,峰值可达10 A,是熔断器额定电流0.2 A的50倍。在持续的热积累作用下,最后熔断器在0.31 s时熔断,形成了空载直流偏置电压。
由此可见,与前述理论分析一致,当PT高压侧阻抗参数设计不合理时,单相接地故障消失时产生的直流偏置电压可能引发PT铁心在饱和与不饱和状态间的切换,长时间的励磁电流脉冲积累引发熔断器熔断[28]。
针对中性点不接地配电网中的PT高压侧保护用熔断器频繁熔断问题,本文基于叠加原理,采用数值计算方法,首次分析出典型故障下的系统空载暂态电压,研究了线路长度、PT阻抗、负载及无功补偿装置等因素对直流偏置电压的影响规律,并通过PSCAD/EMTDC中的10 kV配电网模型和 380 V/150 V的实物动态模拟试验平台进行了仿真与试验验证。本文主要研究结论总结如下:
1)中性点不接地系统中,故障消失后直流偏置电压的产生条件是故障消失瞬间三相电容净电荷Qn≠0,Qn无法泄放而呈现直流偏置电压。单相接地故障(间歇性弧光接地故障)、两相接地故障、三相接地故障等情况下,故障消失后均会出现直流偏置电压。
2)影响Qn泄放通道的因素包括杂散电容、PT阻抗、负载及无功补偿容量等。杂散电容和无功补偿容量越大,则直流偏置电压衰减越缓慢。小负载情况和空载情况类似,大负载情况下直流偏置电压迅速衰减。在不同PT阻抗模式下,可使电容电压表现出不同的形式。
3)当PT高压侧电阻较大,可以使电容放电回路进入过阻尼状态时,电容电压的零输入响应表现为衰减的直流分量形式;当高压侧阻抗参数较小且PT励磁特性较差时,可能引发PT支路在饱和与不饱和状态间的切换,持续的励磁电流脉冲热积累是导致熔断器熔断的最终原因。
附 录
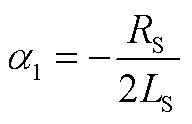 (A1)
(A1)
 (A2)
(A2)
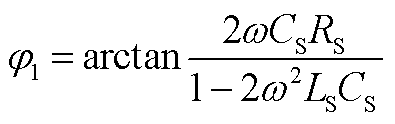 (A3)
(A3)
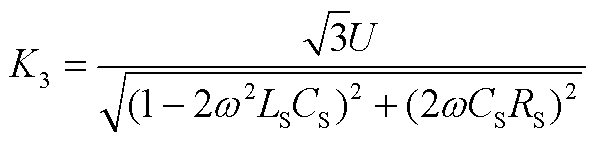 (A4)
(A4)
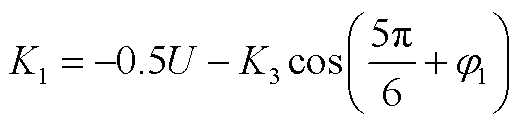 (A5)
(A5)
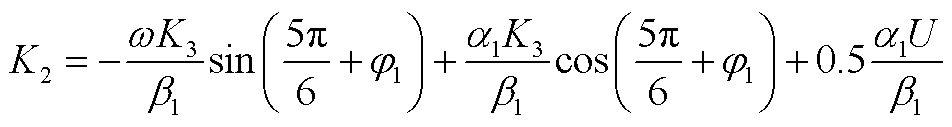 (A6)
(A6)
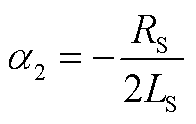 (A7)
(A7)
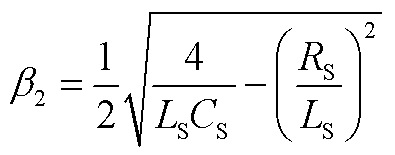 (A8)
(A8)
 (A9)
(A9)
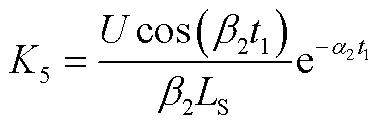 (A10)
(A10)
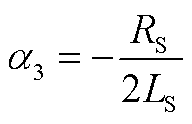 (A11)
(A11)
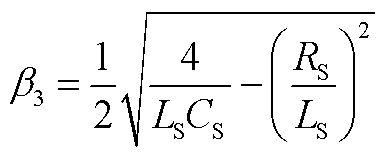 (A12)
(A12)
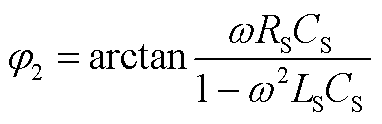 (A13)
(A13)
 (A14)
(A14)

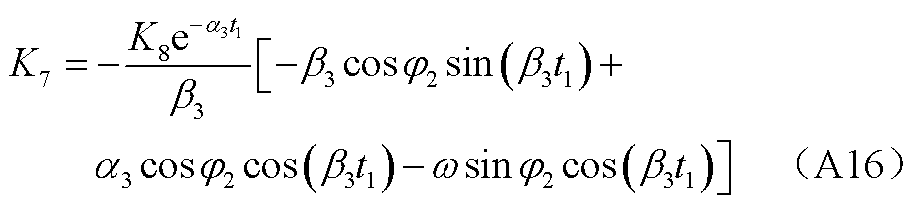


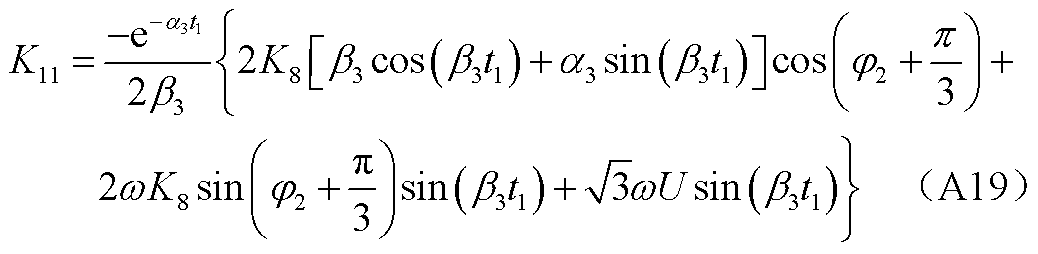
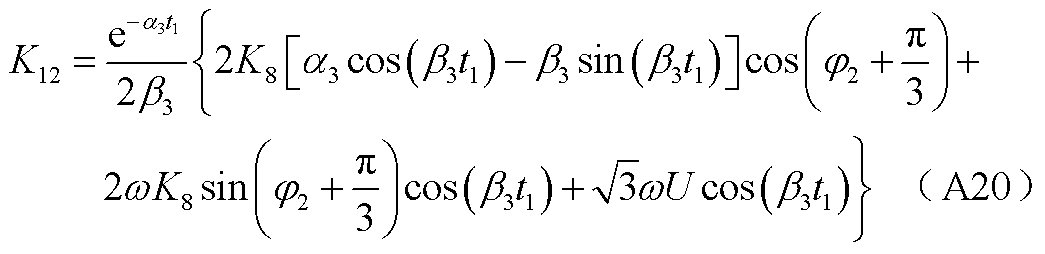
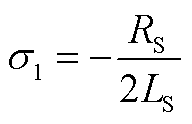 (A21)
(A21)
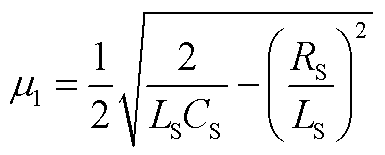 (A22)
(A22)
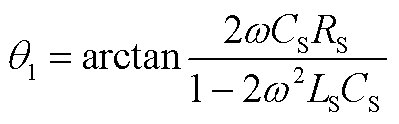 (A23)
(A23)
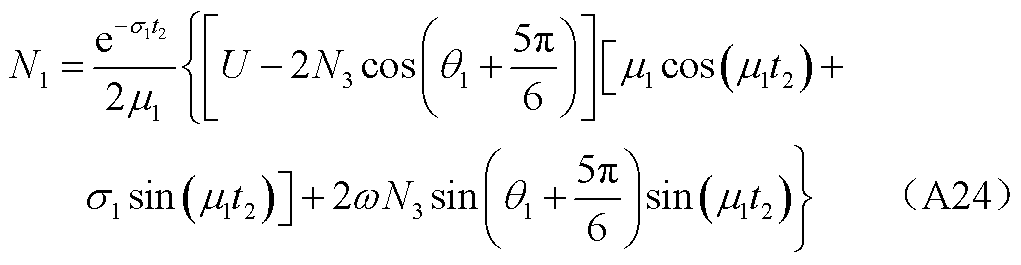
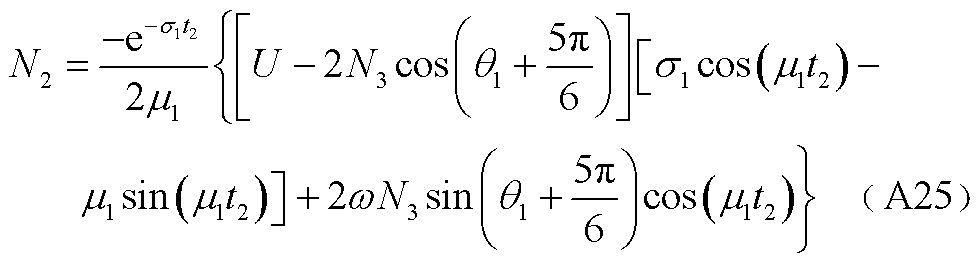
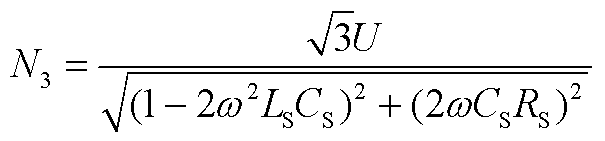 (A26)
(A26)
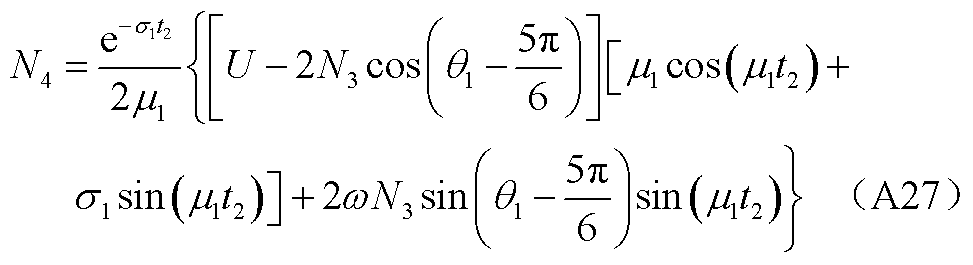
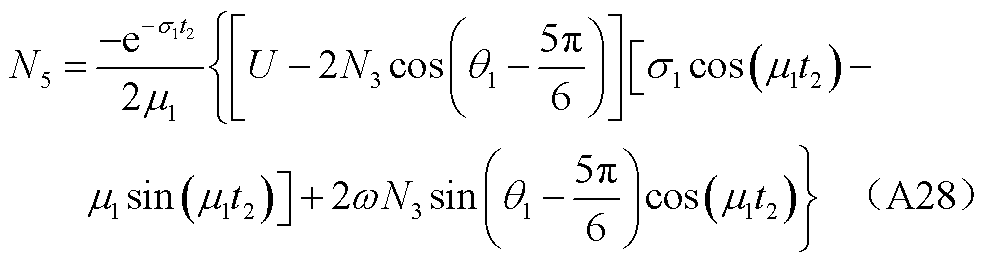
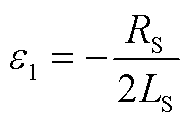 (A29)
(A29)
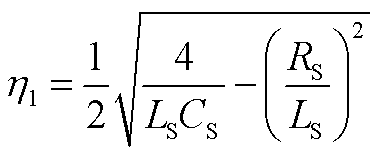 (A30)
(A30)
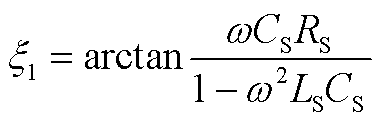 (A31)
(A31)
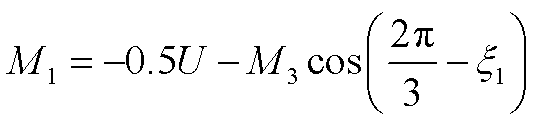 (A32)
(A32)
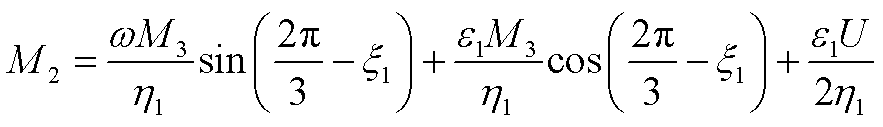 (A33)
(A33)
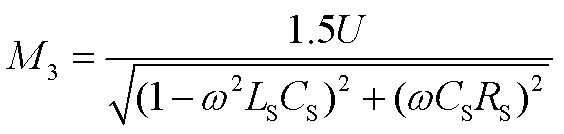 (A34)
(A34)
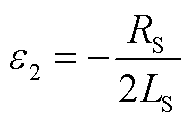 (A35)
(A35)
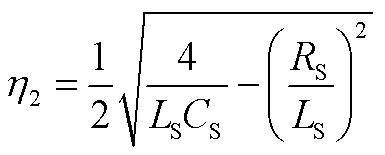 (A36)
(A36)
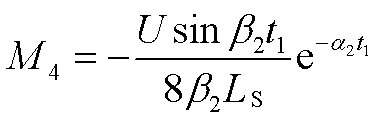 (A37)
(A37)
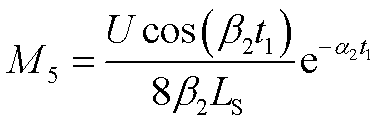 (A38)
(A38)
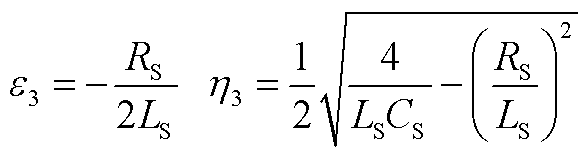 (A39)
(A39)
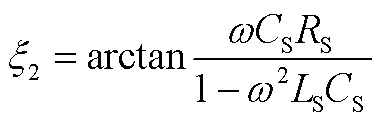 (A40)
(A40)
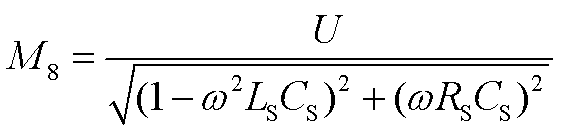 (A41)
(A41)

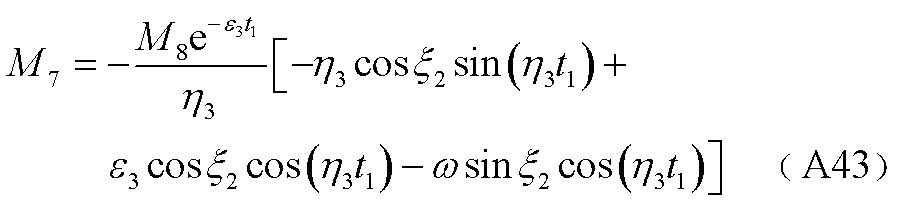
 (A44)
(A44)
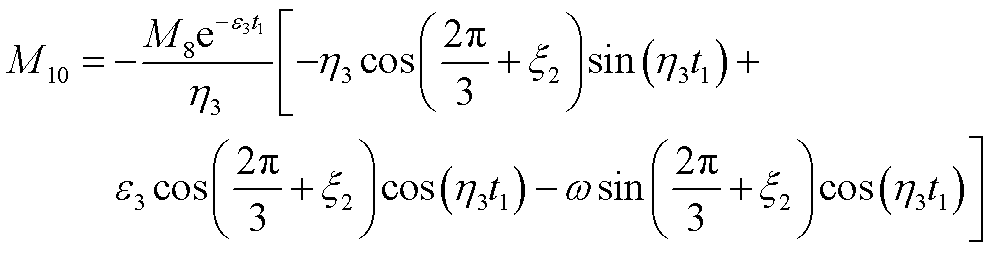 (A45)
(A45)
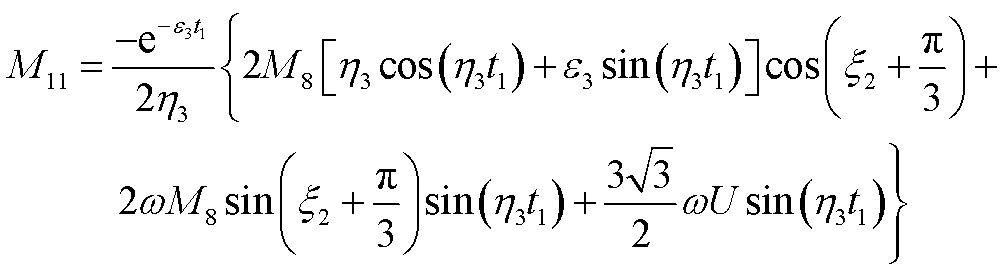 (A46)
(A46)
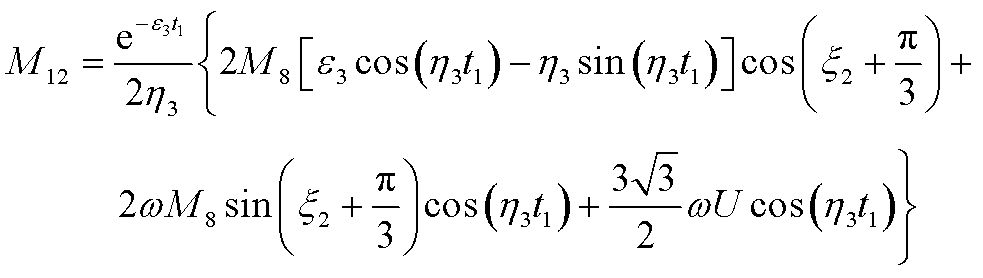 (A47)
(A47)
参考文献
[1] Ren Hongtao, Zhang Ying. Study on fault waveform library of PT high voltage side fuse in hydropower station[J]. Journal of Physics: Conference Series, 2023, 2488(1): 012018.
[2] 赵梦雅. 中压配电网电压互感器熔丝熔断防治措施的研究[D]. 北京: 华北电力大学, 2016.
Zhao Mengya. Study on the prevention measures of TV fuses blowing in medium voltage distribution network[D]. Beijing: North China Electric Power University, 2016.
[3] 张琰. 10kV电压互感器一次侧保护用熔断器轻熔断故障机理仿真研究[D]. 武汉: 华中科技大学, 2021.
Zhang Yan. Simulation research on light-blowing fault mechanism of fuse used for primary side protection of 10kV voltage transformer[D]. Wuhan: Huazhong University of Science and Technology, 2021.
[4] 王宾, 张超, 丁心志. 中性点直接接地系统单相串联铁磁谐振时域解析分析[J]. 中国电机工程学报, 2022, 42(6): 2124-2133.
Wang Bin, Zhang Chao, Ding Xinzhi. Time domain analytical analysis of single-phase series ferro-magnetic resonance in neutral point solid grounding power system[J]. Proceedings of the CSEE, 2022, 42(6): 2124-2133.
[5] Huang Weixiang, Yu Xiaoyong, Wu Lifang, et al. Simulation analysis of PT resonance for distribution network practical test platform[C]//2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, 2020: 1-5.
[6] Lin Zhen, Chen Jianbin, Xia Yuan, et al. The ferroresonance of 10kV distribution PT during live working operation[C]//The 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Online Conference, 2021: 1641-1646.
[7] Lu Pan, Wang Wen, Zhou Meina, et al. Method for actively suppressing ferromagnetic resonance of distribution network by resistive current[C]//2021 IEEE 1st International Power Electronics and Application Symposium (PEAS), Shanghai, 2021: 1-6.
[8] 林莉, 王军兵, 唐凤英, 等. 10kV电压互感器损坏的仿真计算研究[J]. 电力系统保护与控制, 2012, 40(17): 51-55.
Lin Li, Wang Junbing, Tang Fengying, et al. Simulation and computational analysis on potential transformer damage in 10kV system[J]. Power System Protection and Control, 2012, 40(17): 51-55.
[9] 杨鸣, 熊钊, 司马文霞, 等. 电磁式电压互感器“低频过电压激励-响应”逆问题求解[J]. 电工技术学报, 2021, 36(17): 3605-3613.
Yang Ming, Xiong Zhao, Sima Wenxia, et al. Solution of the inverse problem of “low-frequency overvoltage excitation to response” for electromagnetic potential transformers[J]. Transactions of China Electrote-chnical Society, 2021, 36(17): 3605-3613.
[10] Shott H S, Peterson H S. Criteria for neutral stability of wye-grounded-primary broken-delta-secondary transformer circuits[J]. Transactions of the American Institute of Electrical Engineers, 1941, 60(11): 997-1002.
[11] 耿军平. 配电网谐振过电压暂态过程的仿真计算研究[D]. 镇江: 江苏大学, 2018.
Geng Junping. Simulation and research on the transient process of distribute network resonant overvoltage[D]. Zhenjiang: Jiangsu University, 2018.
[12] 李蕾. 10kV配电网中铁磁谐振过电压及抑制措施的研究[D]. 济南: 山东大学, 2018.
Li Lei. Study on ferroresonance overvoltage and suppression measures in 10 kV distribution network[D]. Jinan: Shandong University, 2018.
[13] Peng Guixi, Yuan Shuangchen, Gao Xinhan, et al. Compound elimination method of potential transformer ferroresonance in distribution network[C]//2022 9th International Forum on Electrical Engineering and Automation (IFEEA), Zhuhai, 2022: 332-336.
[14] Yang Jinggang, Si Xinyao, Zhang Guangqing, et al. Risk assessment of ferroresonance in distribution network[C]//22nd International Symposium on High Voltage Engineering (ISH 2021), Hybrid Conference, Xi’an, China, 2021: 670-674.
[15] 王明钦, 陈维江, 李永君, 等. 油田35kV系统电压互感器高压熔断器异常熔断故障的抑制措施[J]. 电网技术, 2012, 36(12): 283-288.
Wang Mingqin, Chen Weijiang, Li Yongjun, et al. A countermeasure to deal with abnormal fusing of high voltage fuse for potential transformer in 35 kV oilfield power distribution system[J]. Power System Tech-nology, 2012, 36(12): 283-288.
[16] 梁志瑞, 赵梦雅, 牛胜锁, 等. 配电网电压互感器熔丝熔断防治措施的缺陷及新措施研究[J]. 电力自动化设备, 2016, 36(9): 17-24, 32.
Liang Zhirui, Zhao Mengya, Niu Shengsuo, et al. Defects of measures against PT fuse melting in distribution network and research of new measure[J]. Electric Power Automation Equipment, 2016, 36(9): 17-24, 32.
[17] Ren Hongtao, Wei Xianguang, Wu Haifeng. Research on fuse failure and countermeasure of potential transformer in non-effect grounding system[C]//2022 5th Asia Conference on Energy and Electrical Engineering (ACEEE), Kuala Lumpur, Malaysia, 2022: 64-68.
[18] Lu Pan, Wang Wen, Yu Qian, et al. Permanent single-line-to-ground fault removal method for ferro-resonance avoidance in neutral ungrounded distribution network[J]. IEEE Access, 2022, 10: 53724-53734.
[19] Xie Shuntian, Zhou Yuan, Tang Xiaojun, et al. Test and simulation of PT saturation characteristics during single-phase grounding fault recovery of 10 kV distribution system[C]//2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, 2020: 1-4.
[20] 韩羞草. 电压互感器高压保险熔断问题研究[D]. 北京: 华北电力大学, 2022.
Han Xiucao. Research on the fusing of voltage transformers’ high voltage fuse[D]. Beijing: North China Electric Power University, 2022.
[21] Zhao Xiaoyao, Guo Hongbing, Yang Yue. Research on suppression of fuses of potential transformer fuse[C]//Journal of Physics: Conference Series, Hangzhou, China, 2023, 2418(1): 239-246.
[22] Zhao Xiaofeng, Qiu Yingdan, Li Qian, et al. Simulation analysis and suppression method of PT low frequency oscillation in distribution network[C]//2018 International Conference on Power System Techno-logy (POWERCON), Guangzhou, China, 2018: 3151-3157.
[23] Wei Jufang, Yao Chuang, He Xiao, et al. Study of PT fuse meltdown triggered by low-frequency non-linear oscillation in distribution network[C]//Eighth Inter-national Conference on Energy Materials and Electrical Engineering (ICEMEE 2022), Guangzhou, China, 2023, 12598: 677-687.
[24] 林莉, 何月, 王军兵, 等. 中性点不接地电网单相接地时电压互感器损坏机理[J]. 高电压技术, 2013, 39(5): 1114-1120.
Lin Li, He Yue, Wang Junbing, et al. Mechanism of potential transformer damaged in ungrounded neutral power system[J]. High Voltage Engineering, 2013, 39(5): 1114-1120.
[25] 任于展, 武仕朴, 汪友华, 等. 基于暂态电流差极值的电力变压器剩磁测量方法[J]. 电工技术学报, 2022, 37(5): 1088-1097.
Ren Yuzhan, Wu Shipu, Wang Youhua, et al. Residual flux measurement method of power transformer based on extreme value of transient current difference[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1088-1097.
[26] 赖胜杰, 夏成军, 纪焕聪, 等. 计及负荷等值阻抗的配电网合环转供电分析模型[J]. 电工技术学报, 2022, 37(11): 2859-2868.
Lai Shengjie, Xia Chengjun, Ji Huancong, et al. An analysis model for power transfer from loop closing in distribution network considering load equivalent impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2859-2868.
[27] 李露露, 李永培, 周新月, 等. 10kV交联聚乙烯电缆内部多形态间歇性电弧故障建模[J]. 电工技术学报, 2022, 37(23): 6104-6115.
Li Lulu, Li Yongpei, Zhou Xinyue, et al. Modeling of internal multiform intermittent arc fault for 10kV XLPE cable[J]. Transactions of China Electro-technical Society, 2022, 37(23): 6104-6115.
[28] 黄文美, 郭萍萍, 郭万里, 等. 直流偏置对磁致伸缩材料高频动态损耗及磁特性的影响分析[J]. 电工技术学报, 2022, 37(22): 5765-5775.
Huang Wenmei, Guo Pingping, Guo Wanli, et al. Impact analysis of DC bias on high-frequency dynamic loss and magnetic characteristics for magnetostrictive materials[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5765-5775.
Analysis of DC Bias Voltage Formation and Voltage Transformer Melting Under Typical Distribution Faults
Abstract The melting of fuse installed at the high-voltage side of the electromagnetic potential transformers (PTs) occurs frequently in the ungrounded power distribution system with rated voltage of 10~35 kV, increasing the maintenance burden and endangering the reliability of power system. Focused on this problem, research on the mechanism of PT fuse melting is conducted, and the research shows that the deep saturation of the PT under the effect of the DC bias voltage (DCBV) is the ultimate cause of the fuse melting.
The paper presents theoretical derivations, simulation verifications, and experimental results regarding the generation conditions of DCBV and the mechanism of PT fuse melting. Firstly, the equivalent circuit of the power system without load during the whole fault process (single-phase ground fault, intermittent arcing ground fault, and two-phase ground fault) were derived. Subsequently, based on the principle of superposition, the equivalent circuit after the fault disappearance was decomposed into zero-input and zero-state circuits. By superimposing the zero-input response and zero-state response, the analytical expression of system voltage was obtained. According to the relationship between the DCBV and the net charge (Qn) of stray capacitors at the moment when the fault disappears, it is inferred Qn≠0 is the generation condition of DCBV.
Changing the discharge channels of Qn may affect characteristics of DCBV, showing different waveform and decay time. By taking stray capacitance, PT impedance mode, load, and reactive power compensation device into consideration, factors related with DCBV were discussed. Finally, simulation in PSCAD/EMTDC and down-scaled experiments were conducted for verification. The main findings and conclusions of this paper are listed as follows:
(1) In an ungrounded power system, if Qn≠0, and without discharge channels, Qn has to be redistributed on the stray capacitors, resulting in the DCBV. In the case of single-phase ground faults (intermittent arc ground faults), two-phase ground faults, three-phase ground faults, Qn may not be zero at the fault disappear moment, generating DCBV; In the case of a two-phase short circuit fault, Qn is always zero, hence there is no existence of DCBV.
(2) Factors including stray capacitance, PT impedance, load, and reactive power compensation capacity, are related with the characteristics of DCBV. A greater stray capacitance and reactive power compensation capacity could lead to a slower decay speed of DCBV. Under light load and no-load conditions, the DCBV persists for a longer duration, whereas under heavy load, the DCBV quickly diminishes. The use of different PT impedance modes can lead to variations in the form of the capacitor voltage.
(3) Large impedance (inductance and resistance) of high voltage winding of PT can result in the stray capacitor discharge circuit entering an overdamped state, leading to a decaying DC component in the zero-input response of the capacitor voltage. On the other hand, small impedance of high voltage winding of PT may trigger the switching of the PT branch between saturation and non-saturation states. The voltage on stray capacitors exhibits a waveform similar to ferro resonance. This continuous excitation current pulsing heat accumulation is the ultimate cause of the fuse melting.
Keywords:Electromagnetic potential transformers, distribution networks, fuses, transient grounding faults, DC bias voltage
中图分类号:TM451.3
DOI: 10.19595/j.cnki.1000-6753.tces.231914
国家电网公司总部项目(5500-202155116A-0-0-00)和国家自然科学基金项目(52277120)资助。
收稿日期 2023-11-16
改稿日期 2024-03-16
温伟杰 女,1989年生,副教授,硕士生导师,研究方向柔性直流输配电网继电保护、AC/DC换流装备、交直流开关设备、大功率电力电子开断技术。
E-mail:weijie.wen@tju.edu.cn
陈晓龙 男,1985年生,副教授,硕士生导师,研究方向为电力系统故障分析、保护与控制等 。
E-mail:xiaolong@tju.edu.cn(通信作者)
(编辑 赫 蕾)