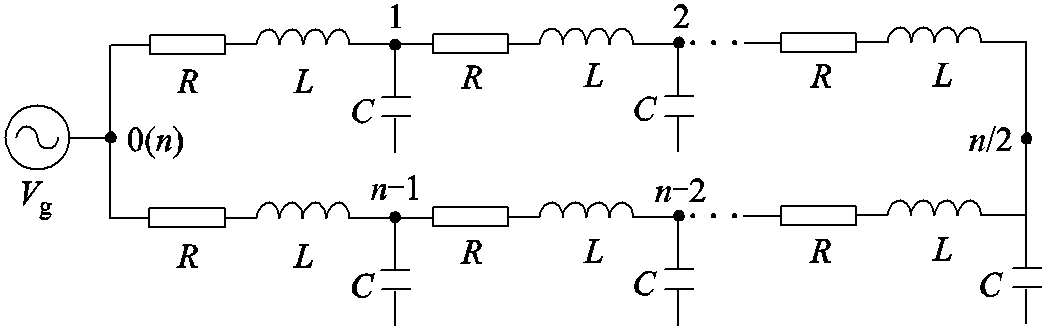
图1 环形配电馈线集总参数模型
Fig.1 Lumped-parameter model of closed-loop distribution feeders
摘要 针对环形配电网中由功率因数校正电容与馈线电感之间谐振导致的背景谐波电压放大问题,提出了一种在环形配电网中点安装驻波移相有源电力滤波器(SWPS-APF)的谐波抑制方案,其抑制原理是通过移动谐波电压驻波的相位使驻波波腹靠近或恰好落在馈线始端,从而实现背景谐波的衰减。所提方案分为驻波左移和右移两种策略,两者具有不同的适用范围,但涵盖了所有工况。相比于传统的阻性有源电力滤波器(RAPF)方案,该文所提方案抑制背景谐波的效果明显,并且所需的补偿容量也更少。最后,仿真分析和实验结果均验证了该方案的有效性。
关键词:背景谐波 有源电力滤波器 谐波抑制 驻波
配电网承担着直接向用户提供电能的责任,电能质量问题可能会影响用电设备的正常工作甚至危害用户的人身安全[1-3]。谐波畸变率是衡量电能质量的重要指标之一,所以在过去的数十年里,谐波治理一直是学术界和工业界的研究热点。对于配电网中非线性负载产生的谐波电流的补偿,无源滤波器[4]、有源滤波器(Active Power Filter, APF)[5-6]及混合滤波器方案已很好地解决了该问题。本文研究的并不是传统的谐波电流补偿问题,而是配电网中馈线电感与无功补偿电容谐振导致的背景谐波电压传播放大抑制问题[7]。
在夜间轻负荷条件下,配电系统中某些节点的电压会严重畸变,这是因为当缺少阻性负荷的阻尼时,线路电感和无功补偿电容之间可能会发生谐振,放大背景谐波电压[8]。为此,日本学者赤木泰文提出了一种安装在配电线路末端的基于电压检测的有源电力滤波器,相当于并联了一个虚拟谐波电阻,所以被称为阻性有源电力滤波器(Resistive Active Power Filter, RAPF)。但在长距离多节点配电馈线上,安装RAPF可能会导致“打鼹鼠”效应,即某些节点电压谐波含量减小,但其他节点的电压谐波含量却增加。文献[9]利用分布参数模型分析了“打鼹鼠”效应产生的原因,并指出当RAPF的虚拟电阻值等于馈线的特征阻抗时,可有效地避免该问题,获得最优的抑制效果,即理论上线路各节点相比于始端的谐波电压放大倍数均等于1。在此之后的研究均是基于RAPF的思路对抑制效果进行优化,但是这些方案要么增加APF台数,提高了成本[10],要么对APF的安装位置有很高的要求[11-12]。
上述研究均是针对射线型配电网,但随着用户对高供电可靠性的要求,环形配电网逐渐成为主流的配电网结构之一[13]。与射线型配电网一样,环形配电网同样存在背景谐波电压传播放大问题,文献[14]基于分布参数模型分析了背景谐波电压的传播规律,并指出在环形配电馈线中点安装RAPF时的抑制效果最好。文献[15]在环形配电网中点的对称位置安装两台RAPF,大大提升了抑制效果,但却增加了成本,并且安装位置与谐波波长相关。文献[16]将环形配电网并联等效为射线型配电网进行分析,并提出了在环形配电网中点安装等效无限长有源电力滤波器(Infinite Active Power Filter, IAPF)的谐波抑制方案,该方案相比于RAPF方案具有更强的适应性,但抑制效果提升不明显,却增加了控制的复杂性。文献[17]提出一种阻抗变换器方案以模拟无限长馈线,并且可以安装在环形配电网的任何节点,但至少需要两台APF协同实现。通过检测环形配电网非安装节点电压信号的双点检测方案[18]及其分频控制[19]可以提升RAPF的抑制效果,但需要远距离高速通信设备以实时传输检测信号。
为了进一步提升背景谐波电压抑制效果,本文提出基于驻波移相原理的背景谐波电压抑制方案,通过移动馈线上驻波的相位使波腹靠近或恰好落在馈线始端,从而达到抑制背景谐波电压放大的目的。本文首先分析了背景谐波电压在环形配电网中的传播规律,根据得到的规律分别提出了驻波左移和驻波右移抑制策略;然后分别讨论了两种抑制策略的适用范围和最优控制参数的选取;最后,在仿真和实验中利用APF验证了所提出方案的有效性。结果表明,与传统的RAPF方案相比,本文所提出的方案在抑制效果显著提升的同时,所需的补偿容量也更少。
环形配电馈线的集总参数模型如图1所示。对于多节点网络,其数学模型阶次较高,难以求解各节点谐波电压[20-21],所以为了便于分析,假设馈线上的电感、电阻和电容均匀分布,这样可以使用分布参数模型来分析背景谐波电压在馈线上的传播规律[16]。馈线上节点是均匀划分的,即每1 km长度设一个节点,环形馈线的始端即谐波源处被编号为节点0同时也为节点n,然后逐个编号回到始端。馈线的参数见表1 [22],本文的理论分析、仿真和实验均是基于该参数。

图1 环形配电馈线集总参数模型
Fig.1 Lumped-parameter model of closed-loop distribution feeders
表1 配电馈线参数
Tab.1 Parameters of distribution feeders

参数数 值 基波频率50 馈线电感L/(mH/km)1.98 功率因数校正电容C/(μF/km)25 馈线电阻R/(Ω/km)0.36
为了使整体抑制效果最优,背景谐波抑制装置通常安装在环形配电馈线的中点[14],即n/2节点处。此时,可将环形配电馈线中点等效为射线型配电馈线的末端,即将中点上下两条馈线并联。并联等效后的环形配电馈线集总参数模型如图2所示。
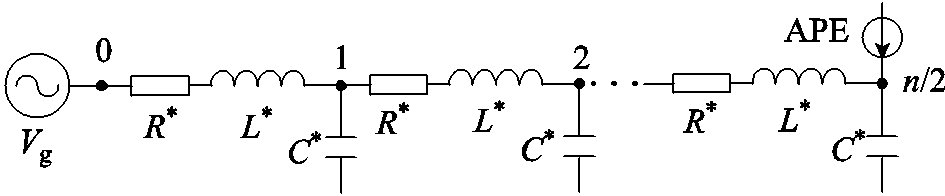
图2 环形配电馈线并联等效后的集总参数模型
Fig.2 Lumped-parameter model of equivalent closed-loop distribution feeders
并联等效处理后的环形配电馈线可当作射线型配电馈线进行分析,其长度l*为原来的一半,馈线电阻R*和馈线电感L*大小为原来的1/2,而功率因数校正电容C*大小则为原来的2倍。
对于配电馈线上背景谐波电压的传播规律,通常使用馈线的分布参数模型进行分析,该模型与集总参数模型对于较低次数谐波的响应基本相同[22]。图3所示为环形配电馈线并联等效后的分布参数模型,图中Vh为谐波电压源,V(x)为馈线上的电压驻波,安装在馈线末端的APF可等效为受控电流源,其输入导纳为1/Zv。
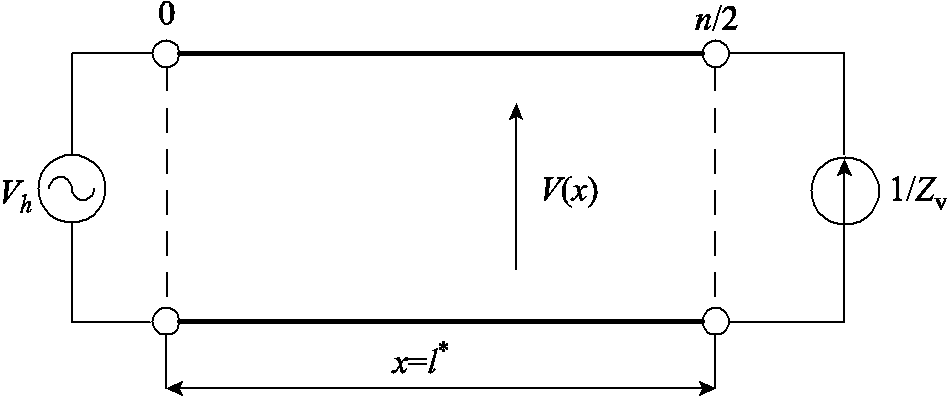
图3 环形配电馈线并联等效后的分布参数模型
Fig.3 Distributed-parameter model of equivalent closed-loop distribution feeders
假设馈线为无损传输线,即R*=0,则其特征阻抗为
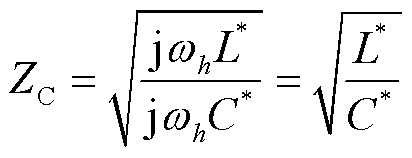 (1)
(1)
式中,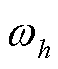 为h次谐波的角频率。
为h次谐波的角频率。
h次谐波的传播常数为
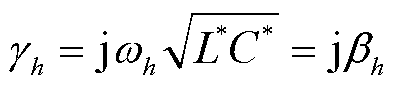 (2)
(2)
式中,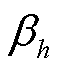 为传播常数
为传播常数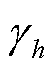 的虚部,被称为相位常数。
的虚部,被称为相位常数。
h次谐波的波长为
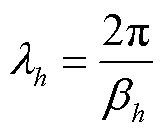 (3)
(3)
根据均匀传输线理论[23],馈线上任一点的谐波电压为
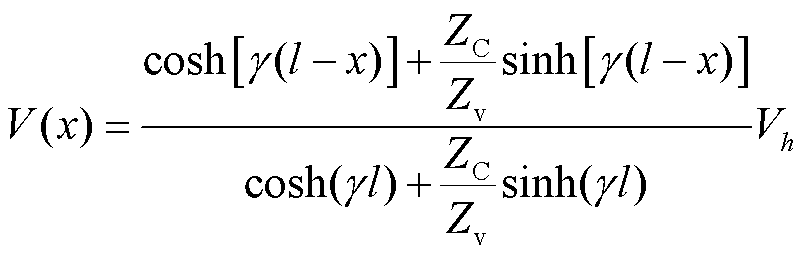 (4)
(4)
定义谐波电压幅值的放大倍数为
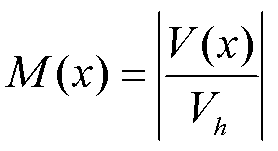 (5)
(5)
当线路末端空载时,式(5)可化简为
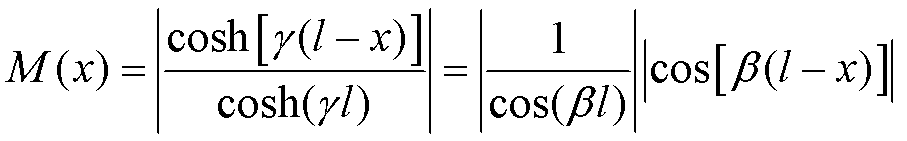 (6)
(6)
由式(6)可知,当馈线末端空载时,线路上谐波电压的幅值呈周期变化,周期为π/β,等于1/2波长。根据表1中的参数,由式(3)可以计算得到5、7、11、13次谐波的1/4波长见表2。
表2 各次谐波波长
Tab.2 Wavelengths of each harmonic

谐波次数1/4波长/km 54.49 73.21 112.04 131.73
以一段10 km长的环形配电馈线为例,根据表1中的参数绘制不同次谐波在馈线上的振荡放大情况如图4所示。图中虚线是为了直观地展示馈线上的驻波分布,并无实际意义。
这种馈线上谐波电压的分布状态被称为驻波,是由谐波电压的入射波和反射波相互叠加产生的。驻波的最高点和最低点分别被称为波腹和波节,显然当线路末端空载时,驻波的波腹总是位于末端。而线路始端位于驻波的位置由线路长度和谐波波长之间的关系确定。如果线路始端处于的位置不是驻波的波腹,那么谐波一定在馈线的某段区域被放大了。
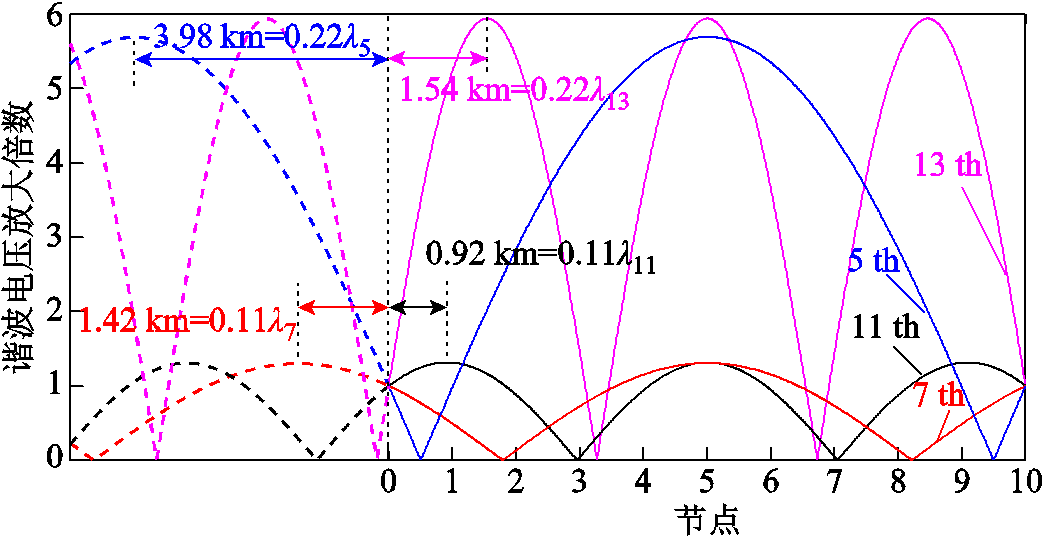
图4 10 km环形配电馈线上的谐波电压驻波
Fig.4 Harmonic voltage standing wave on 10 km closed-loop distribution feeder
换句话说,背景谐波电压在馈线上的放大程度取决于馈线始端即谐波源与离其最近波腹(包括位于谐波源左侧的波腹)之间的距离,距离越远,则背景谐波电压放大越严重。当馈线始端恰好位于驻波波节时,背景谐波电压放大最严重。相反地,当馈线始端恰好位于驻波波腹时,那么线路上就不可能有大于始端谐波电压幅值的点,即背景谐波不会被放大。
根据上述分析,本文提出一种基于谐波电压驻波相位移动的抑制方案,其原理是通过移动驻波的相位使波腹靠近或恰好落在线路始端,那么线路上就不可能有大于始端谐波电压幅值的点,即谐波不会被放大。驻波移相抑制方案可分为驻波左移和驻波右移两种情况。
驻波左移的实质是让APF模拟谐波电感特性,当馈线末端接感性负载时,式(6)可变换为
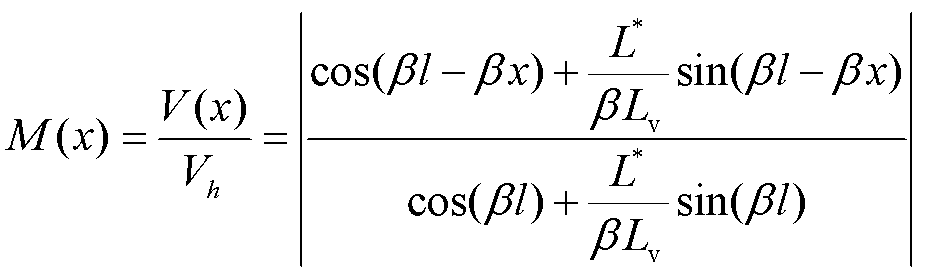 (7)
(7)
简化可得
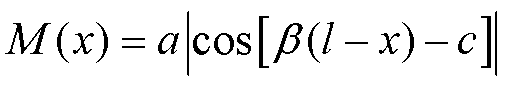 (8)
(8)
其中
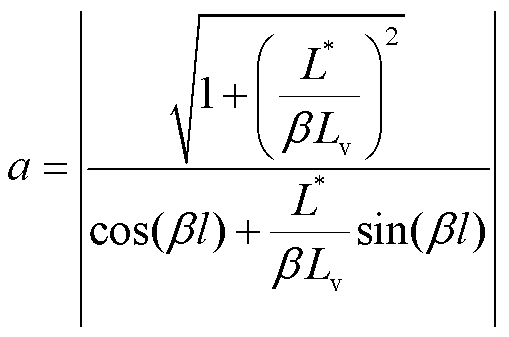 (9)
(9)
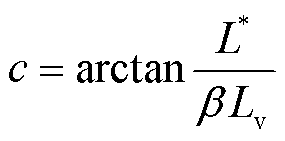 (10)
(10)
式中,Lv为末端虚拟电感值。
当Lv变化时,式(8)中的a和c也随之改变,即通过改变Lv的大小,既可以改变驻波的幅值a,也可以改变驻波的相位c。由于c的表达式为反正切函数及Lv的取值为正,c的上下限分别为0.5π和0,因此驻波左移的相位移动范围最大为半个周期,即1/4波长,并且由于反正切函数的特性,随着Lv越来越小,驻波向左移动的能力越来越弱。
以10 km环形馈线上的11次谐波电压驻波为例,驻波左移原理示意图如图5所示。由于馈线始端所处的位置并不是波腹,所以馈线上一定有谐波电压放大倍数大于1的部分。此外,馈线始端距离左波腹的距离大于1/4波长,所以驻波只能向左移动从而使右波腹靠近馈线始端达到抑制背景谐波电压放大的目的。由图5可知,当驻波波腹移动到馈线始端即节点0处时,馈线上就没有谐波电压被放大的点。需要说明的是,图中虚线是为了直观表现驻波相位移动的原理,并无实际意义。
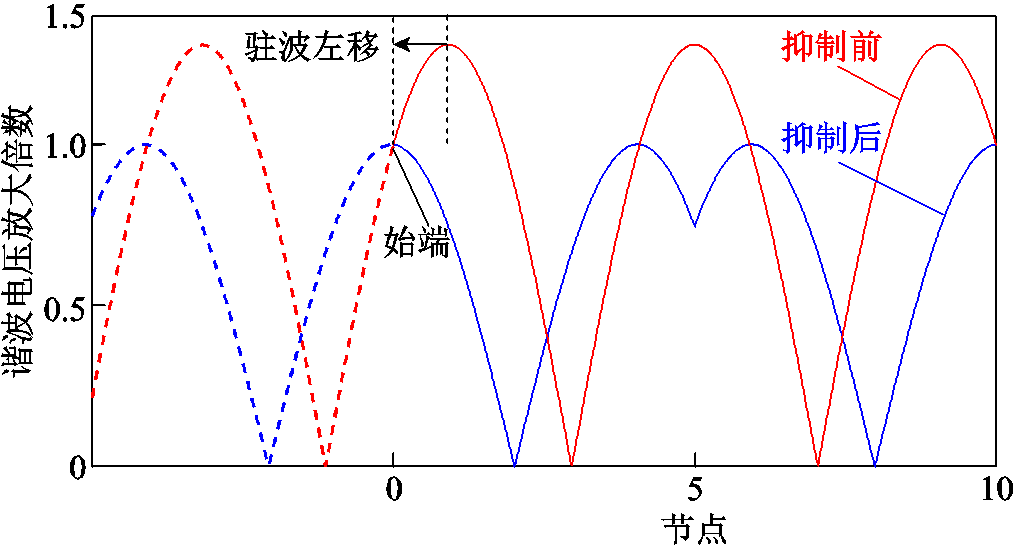
图5 驻波左移原理示意图
Fig.5 Principle schematic diagram of standing wave shifting to the left
驻波右移的实质是让APF模拟谐波电容特性,当馈线末端接容性负载时,式(6)可变换为
 (11)
(11)
简化可得
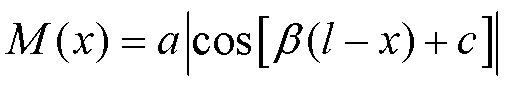 (12)
(12)
其中
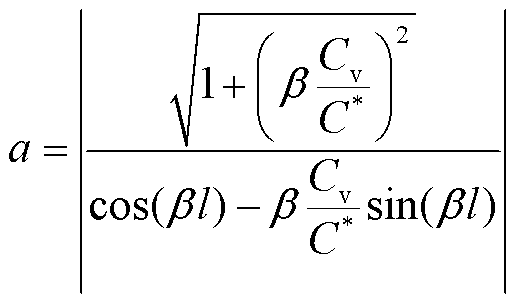 (13)
(13)
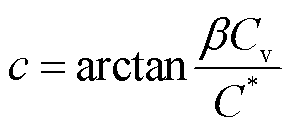 (14)
(14)
式中,Cv为末端虚拟电容值。
同驻波左移相同,通过改变Cv的大小,既可以改变驻波的幅值a,也可以改变驻波的相位c。由于c的表达式为反正切函数及Cv的取值为正,c的上下限分别为0.5π和0,因此驻波右移的相位移动范围最大为半个周期,即1/4波长,并且由于反正切函数的特性,随着Cv越来越大,驻波向右移动的能力越来越弱。
以10 km环形馈线上的5次谐波电压驻波为例,驻波右移原理示意图如图6所示。与图5中示例相反,此时馈线始端距离左波腹较近,所以应当使用驻波右移方案使左波腹靠近馈线始端从而达到抑制背景谐波电压放大的目的。
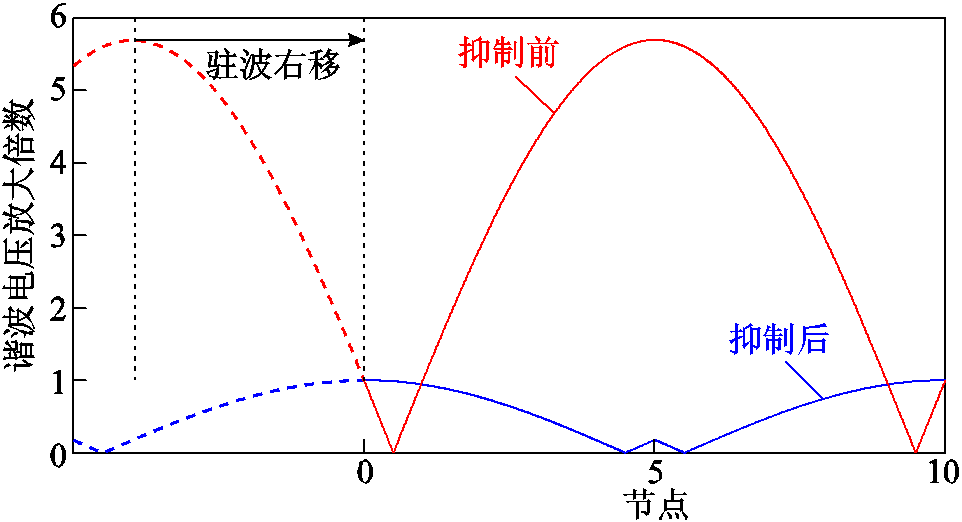
图6 驻波右移原理示意图
Fig.6 Principle schematic diagram of standing wave shifting to the right
通常来说,为了保证馈线上没有放大倍数大于1的点,需将谐波电压的驻波波腹恰好移动到馈线始端谐波源处。但是对于某些工况来说,这不是必须的,或者说不是最优的方案。本节将所有抑制工况分为三类,分别讨论其最优控制参数的选取。
本文以驻波曲线的积分量化了馈线上背景谐波电压的抑制效果(Suppression Performance, SP),具体量化公式如式(15)所示。显然,SP的值越小,表明抑制效果越好。
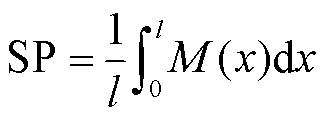 (15)
(15)
1)当环形馈线长度的一半l*小于谐波的1/4波长时,背景谐波电压从馈线始端到中点处沿线逐渐放大。此时,无论使用驻波左移还是右移策略均能有效抑制背景谐波的放大,但是驻波右移策略能够提供更优的抑制效果。以6 km环形馈线上的5次谐波电压驻波为例进行说明,具体如图7所示。
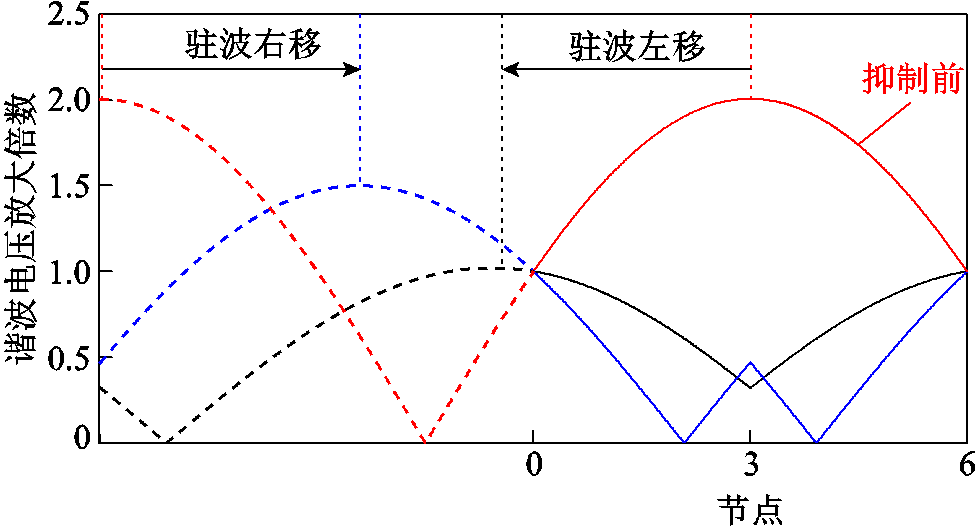
图7 驻波左移和右移后驻波曲线对比
Fig.7 Standing wave curve comparison after standing wave shifting to the left and right
由图7可知,使用驻波右移策略会使驻波波节出现在馈线上,从而使整个驻波曲线呈现“凹”的特性,所以其抑制效果比驻波左移方案更好。图8所示为量化抑制效果SP与虚拟电纳Bv之间的关系,同样验证了上述结论。
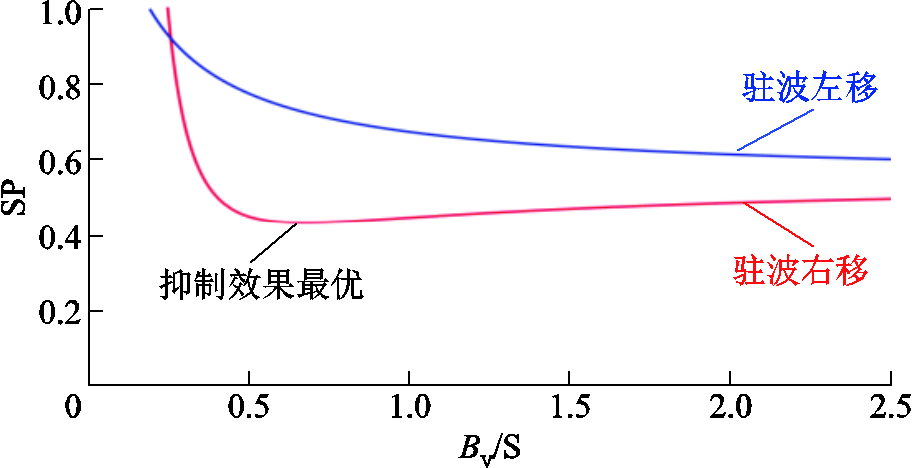
图8 驻波左移和驻波右移策略抑制效果对比
Fig.8 Suppression performance comparison of standing wave shifting to the left and right strategy
所以,对于环形馈线长度的一半l*小于谐波的1/4波长的工况,可通过方程式(16)求解最优的虚拟电容值。
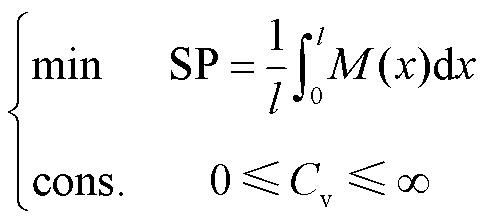 (16)
(16)
2)当环形馈线长度的一半l*介于谐波的1/4~1/2波长之间时,背景谐波电压从馈线始端到中点处沿线先减小再逐渐放大。例如,10 km环形馈线上的5次谐波电压驻波,其半波长约为9 km,驻波波腹距离馈线始端4 km,但当驻波向右移动2 km时,馈线上已没有放大倍数大于1的点,所以在该工况下,没有必要将驻波波腹移动到馈线始端,具体如图9所示。
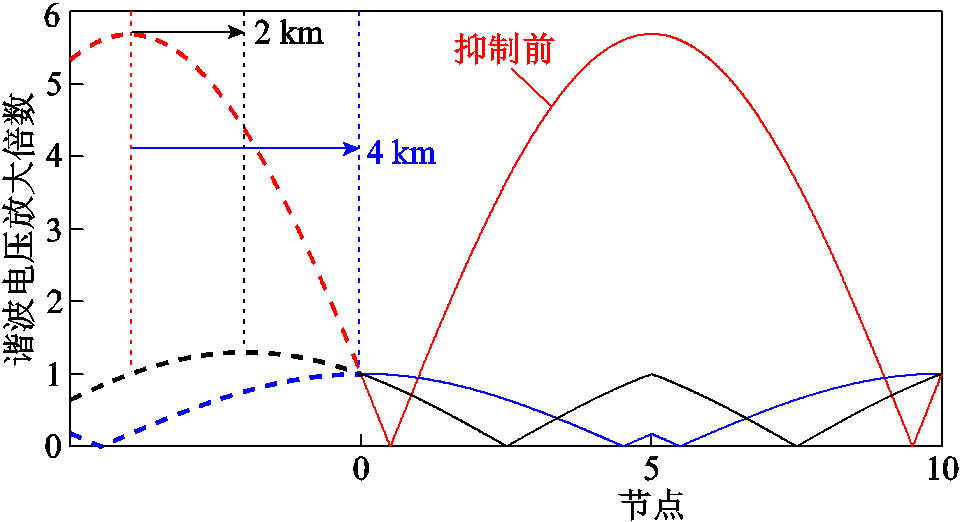
图9 不同右移距离后驻波曲线对比
Fig.9 Standing wave curve comparison after different right shift distances
根据式(11)和式(15)可以得出量化抑制效果SP与虚拟电容值Cv之间的关系曲线如图10所示,可以看到SP存在极小值。
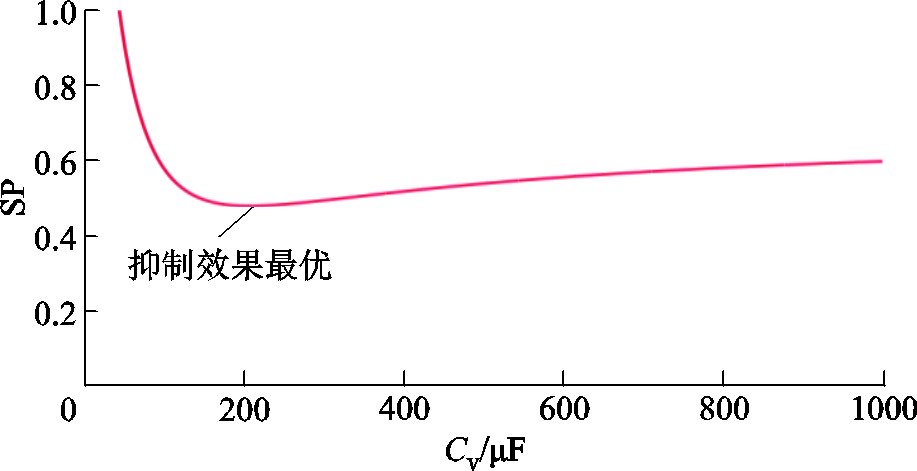
图10 抑制效果与虚拟电容值关系曲线
Fig.10 Relationship between suppression performance and virtual capacitance value
此时,同样可以利用式(16)求解最优的虚拟电虚拟电容值,求得最优值为204 μF。
3)当环形馈线长度的一半l*大于谐波的1/2波长时,必须将驻波波腹恰好移动到馈线始端,否则背景谐波电压必定在部分馈线上被放大。由式(7)和式(11)可知,驻波移相方案最多可使电压驻波移动半个周期即1/4波长,所以在不同工况中需要根据馈线始端距离左右波腹的远近来选择相应的移动方向。驻波左移和右移适用工况的范围见表3。
表3 驻波左移和右移抑制策略适用范围
Tab.3 Application range of standing wave shifting to the left and right strategy

抑制策略适用范围 驻波左移(n为偶数) 驻波右移(n为奇数)
根据式(10)和式(14),可以得到驻波移相方案中最优虚拟电感和虚拟电容的计算公式分别为
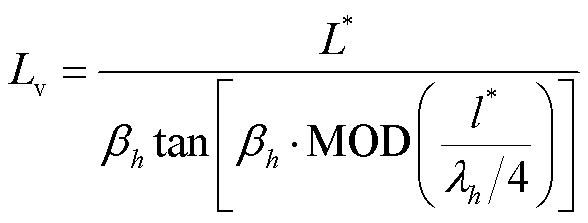 (17)
(17)
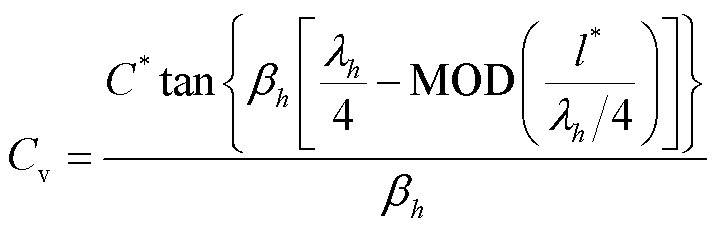 (18)
(18)
式中,MOD为求余函数。
综上所述,可以得到所有工况下,驻波移相方案移动方向和最优控制参数选取的准则,具体见表4。
表4 驻波移动方向和最优控制参数选取准则
Tab.4 Criteria of standing wave movement direction and optimal control gain selection

工况移动方向最优控制参数 驻波右移式(16) (n>0,n为偶数)驻波左移式(17) (n>1,n为奇数)驻波右移式(18)
驻波移相抑制方案由驻波移相有源电力滤波器(Standing Wave Phase Shifting based Active Power Filter, SWPS-APF)实现,其控制框图如图11所示,uabc为环形配电馈线中点的电压,Vdc为APF直流侧电压。由于各次谐波的波长不同,首先在同步旋转坐标系下利用低通滤波器提取出各次谐波电压uh,然后根据表4确定对应的抑制策略和最优控制参数,并计算出各次谐波指令电流。最后将各次谐波通道产生的指令电流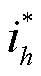 和直流电压控制部分产生的有功电流指令相加,作为APF的输出电流参考
和直流电压控制部分产生的有功电流指令相加,作为APF的输出电流参考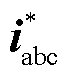 。此外,所提控制策略利用Clark变换中α和β通道的交换实现了虚拟电感和电容的模拟,避免了积分和微分环节的使用。图中,ωf为基波的角频率,LPF为一阶低通滤波器,其表达式为
。此外,所提控制策略利用Clark变换中α和β通道的交换实现了虚拟电感和电容的模拟,避免了积分和微分环节的使用。图中,ωf为基波的角频率,LPF为一阶低通滤波器,其表达式为
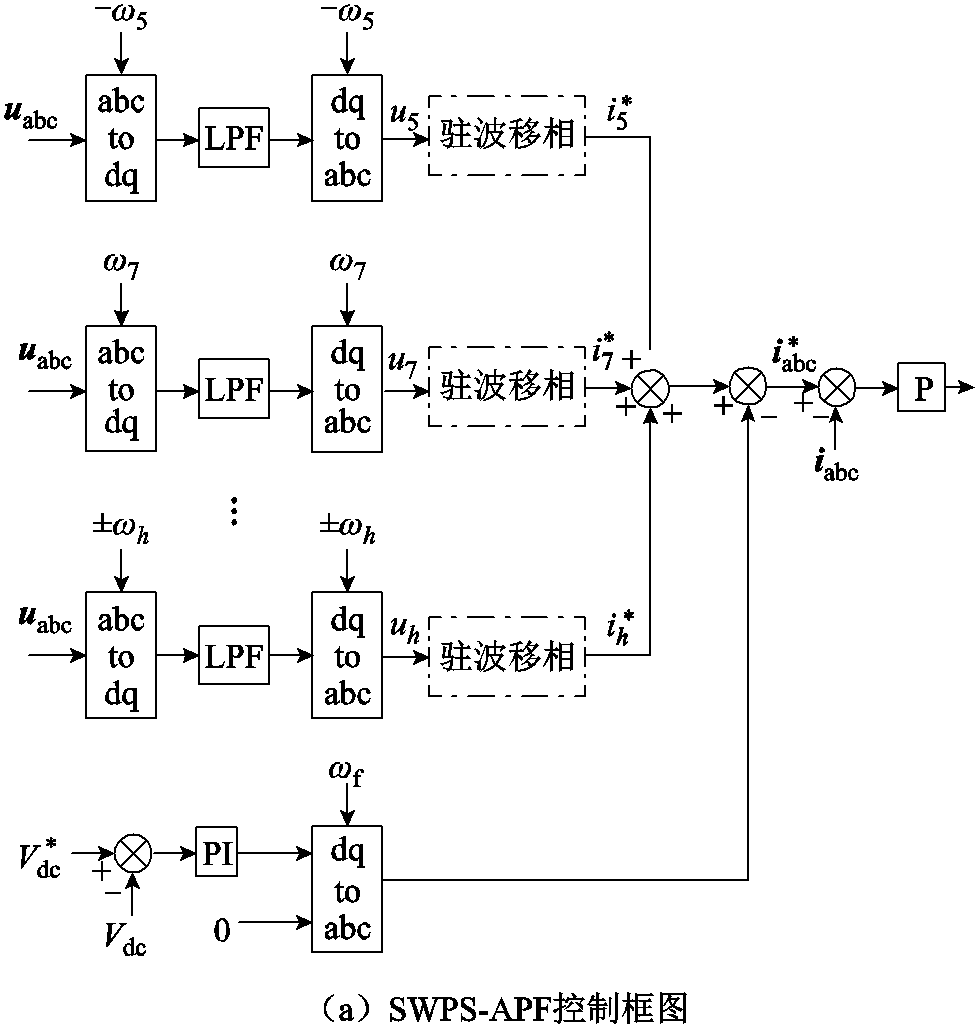
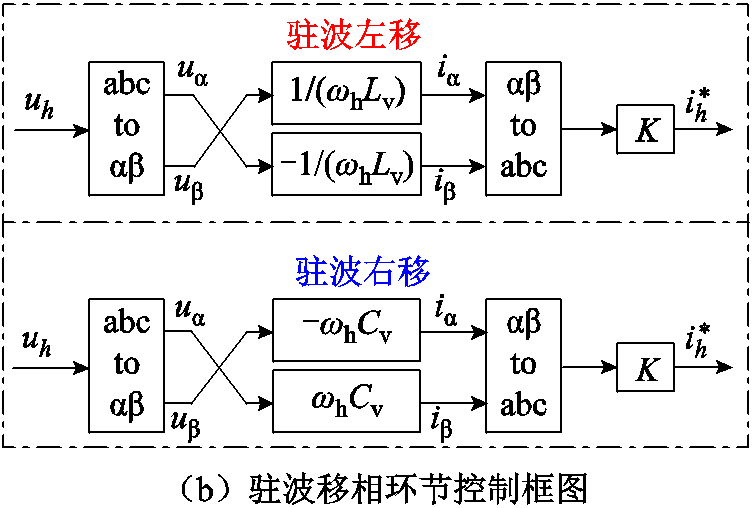
图11 驻波移相有源电力滤波器控制框图
Fig.11 Control block diagram of standing wave phase shifting based active power filter
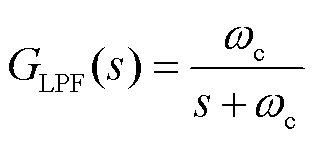 (19)
(19)
式中,ωc=2πfc, fc为低通滤波器的截止频率。当谐波呈正序时,增益K=1,谐波呈负序时,增益K=-1。
为了验证上述理论分析的正确性,在PLECS软件中搭建了10 km长的环形配电馈线仿真模型,其电压等级为10 kV(L-L,RMS),配电馈线的参数与表1中的参数一致。5、7、11、13次背景谐波电压含量分别为3%、2%、1%和0.5%。根据表3,可以计算得到各次谐波的控制参数为Cv5=204 μF,Cv7=66 μF,Lv11=1.42 mH,Lv13=0.38 mH。
首先,当没有接入SWPS-APF时,环形配电馈线上各节点相比始端节点0处的谐波电压放大倍数如图12所示。可以看到,各次谐波的点线图形状与图4中的驻波曲线基本一致,验证了基于分布参数模型的理论分析的正确性。值得注意的是,仿真结果与理论分析的放大倍数存在差异,这是因为理论分析使用的是分布参数模型,仿真和实验则为集总参数模型,但这并不会影响抑制策略的有效性[7]。
当分别接入RAPF和所提出的SWPS-APF进行抑制时,各节点的背景谐波电压放大均显著减小,各节点谐波电压放大倍数仿真结果对比如图13所示。由于RAPF是基于阻抗匹配的思想,抑制后其各节点放大倍数近似呈一条直线。而本文提出的SWPS-APF是基于驻波移相的原理,抑制后其各节点放大倍数曲线仍保留驻波的特征。
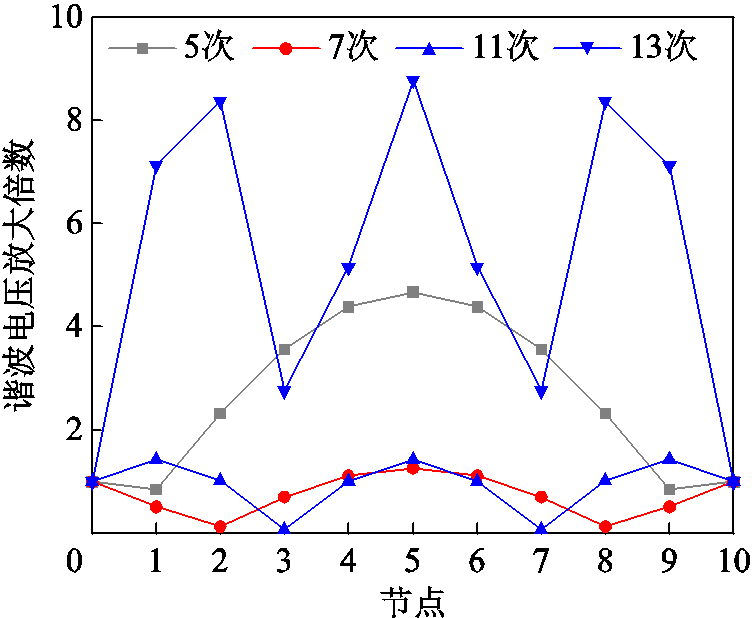
图12 无抑制时各次谐波电压放大倍数仿真结果
Fig.12 Simulation results of each harmonic voltage magnification without suppression
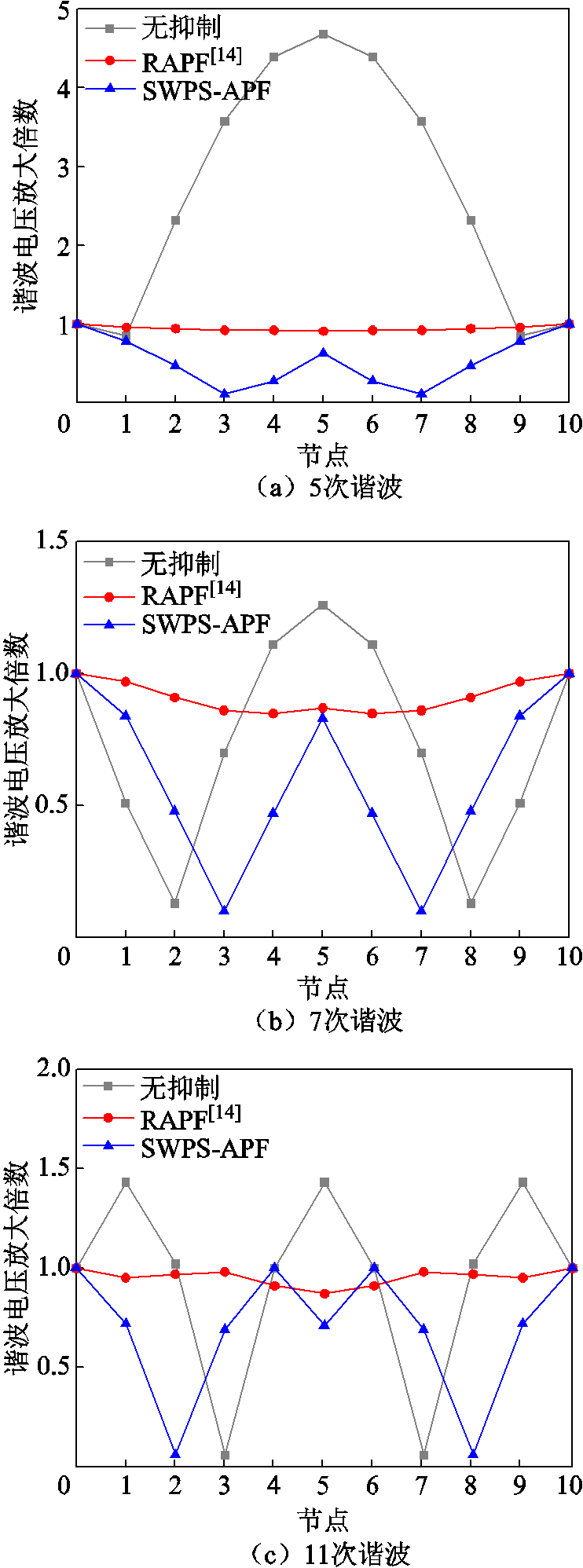
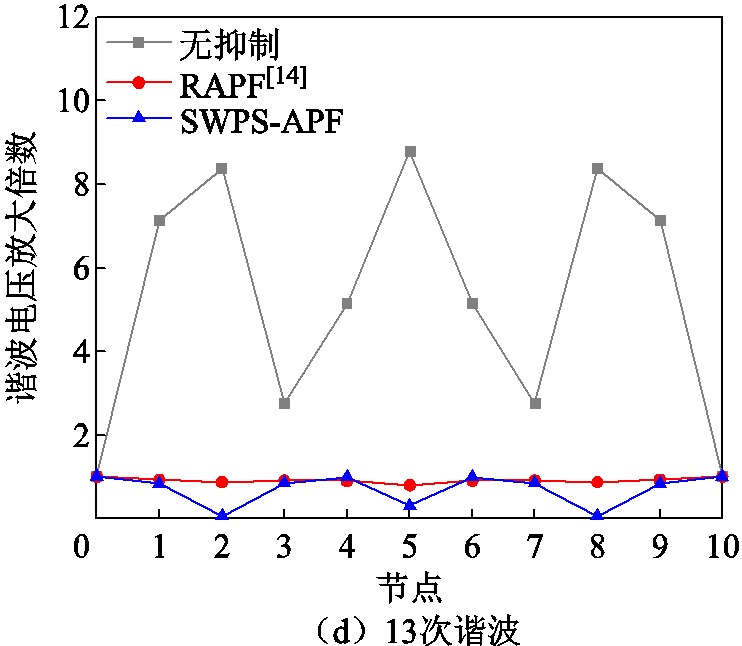
图13 各节点谐波电压放大倍数仿真结果对比
Fig.13 Simulation results comparison of harmonic voltage magnification at each node
由仿真结果可知,对于绝大多数节点谐波电压抑制效果,本文提出的驻波移相抑制方案都要优于传统的RAPF方案。此外,对RAPF和SWPS-APF的补偿容量也进行了计算,各次谐波的补偿容量和总容量的对比如图14所示。可以看到,本文提出的SWPS-APF方案在抑制效果明显优于RAPF方案的前提下,所需的补偿容量也更少。
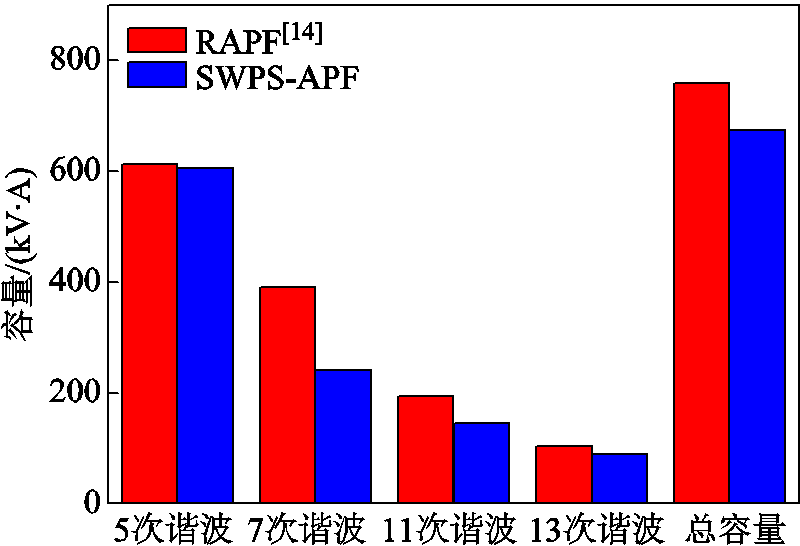
图14 SWPS-APF与RAPF补偿容量对比
Fig.14 Compensation capacity comparison of SWPS-APF and RAPF
馈线上阻性负载的存在对于背景谐波电压的谐振放大具有抑制作用,以13次谐波为例,其电压驻波随负载加重变化趋势如图15所示。由图15可知,当各节点阻性负载逐渐加重时,各节点谐波电压放大倍数逐渐减小,但是驻波的波腹和波节位置不会改变,所以本文提出的驻波移相方案仍能有效地抑制背景谐波电压放大。
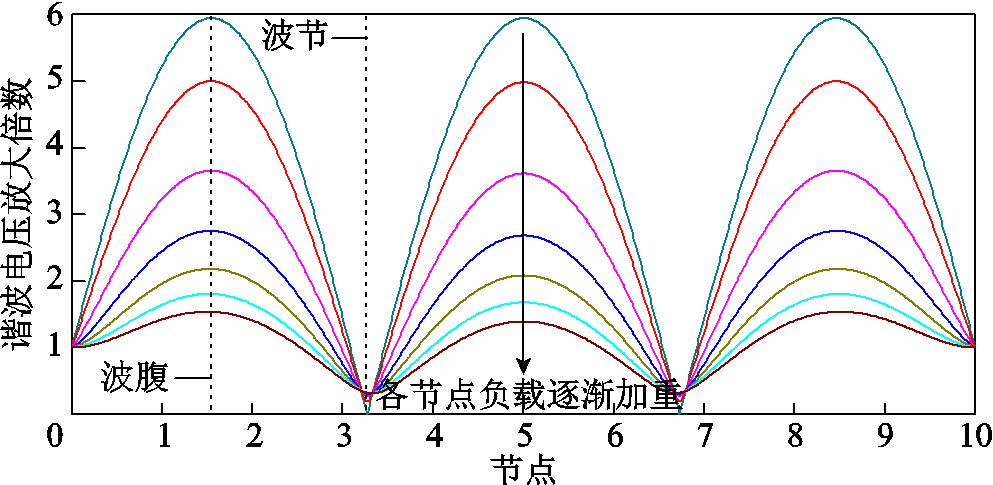
图15 13次谐波电压驻波随负载加重变化趋势
Fig.15 The trend of 13th harmonic voltage standing wave variation with increasing load
为了验证馈线上带负载时所提出方案仍然有效,在每个节点上连接了100 Ω的阻性负载,仿真结果如图16所示。由图16可知,当馈线上连接阻性负载时,所提出方案仍是有效的,并且能取得比传统RAPF抑制方案更好的抑制效果。
本文为了便于分析背景谐波电压放大规律,假设馈线上的电感、电阻和电容均匀分布,即参数一致。但在实际中,由于功率因数校正电容投切等因素不存在严格意义上均匀分布的配电馈线。因此,本节评估了馈线参数改变时的抑制效果,将节点1~9的功率因数校正电容分别设置为20、35、15、20、30、15、25、15、30 μF,仿真结果如图17所示。由图17可知,所提出驻波移相抑制方案具有较强的鲁棒性,即使在馈线参数改变时,仍能取得比传统RAPF抑制方案更好的抑制效果。
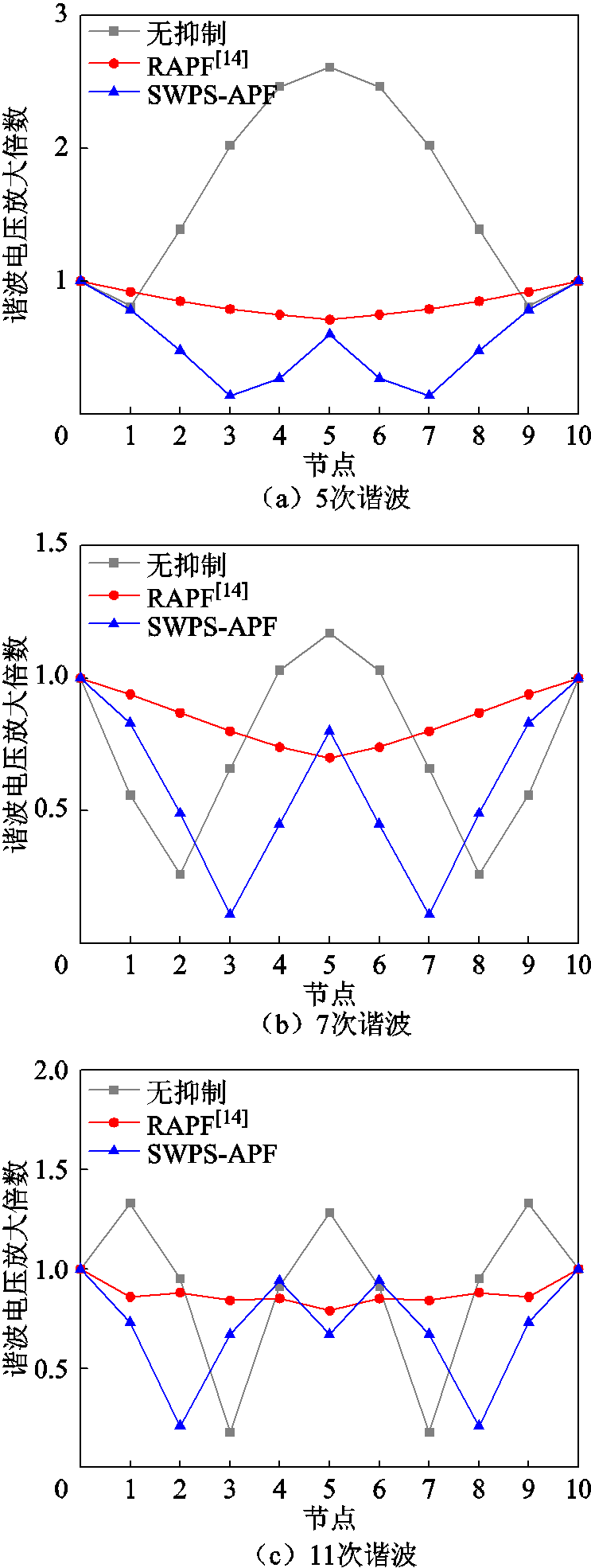
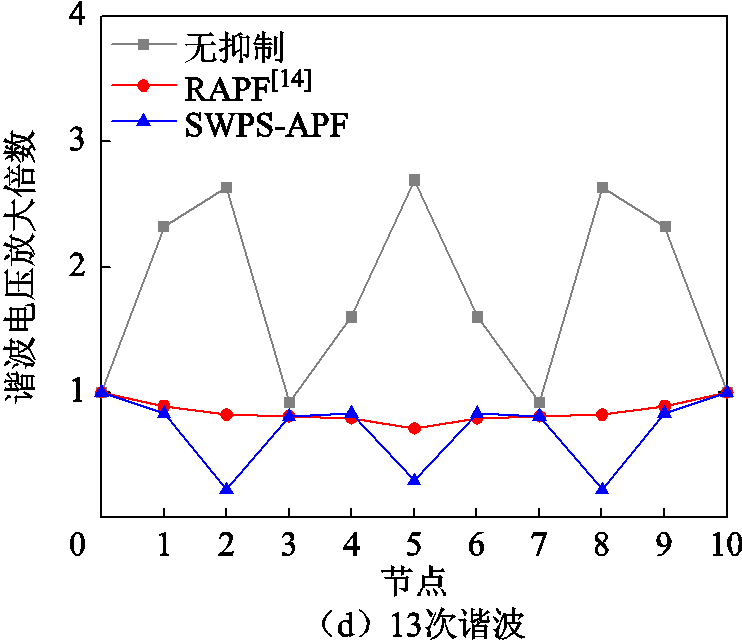
图16 有负载时各节点谐波电压放大倍数仿真结果对比
Fig.16 Simulation results comparison of harmonic voltage magnification at each node under load conditions
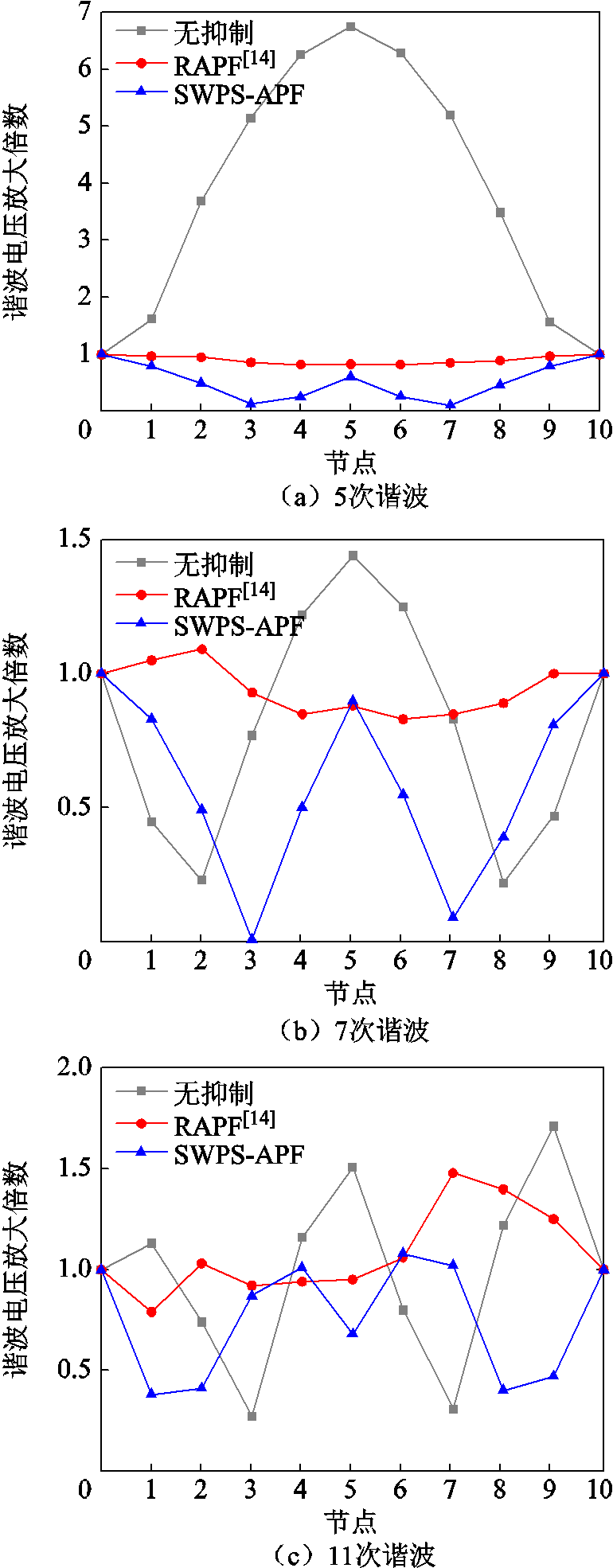
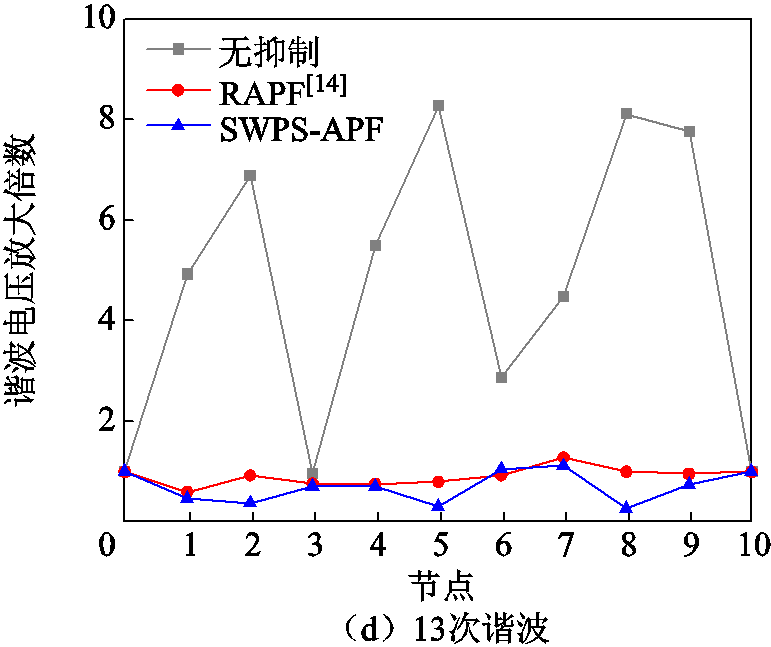
图17 馈线参数改变时各节点谐波电压放大倍数仿真结果对比
Fig.17 Simulation results comparison of harmonic voltage magnification at each node when feeder parameters change
针对环形配电网的其他背景谐波电压放大抑制方案,主要有分频调节方案[15]、IAPF方案[16]、阻抗变换器方案[17],以及双点检测方案[18]。其中分频调节方案和阻抗变换器方案需要两台APF,显著增加了成本;双点检测方案需要采集非本地安装节点的电压信号,因此需要远距离高速通信设备以实时传输检测信号;而本文所提出方案只需要一台APF,并且只需采集本地安装节点的电压信号。
为了进一步验证本文提出的驻波移相方案在抑制效果方面的优势,将其与现有的先进方案进行了对比,仿真结果如图18所示。需要说明的是,分频调节方案同时抑制5、7、11、13次谐波需要同时安装4台APF,所以本文只对比了5次和7次谐波的抑制效果。由图18可知,相比于现有的方案,所提出的SWPS-APF整体抑制效果是最优的。
然后,对现有的不同抑制方案的补偿容量也进行了计算,各次谐波的补偿容量和总容量的对比如图19所示。可以看到,所提出的SWPS-APF的补偿容量是最少的。
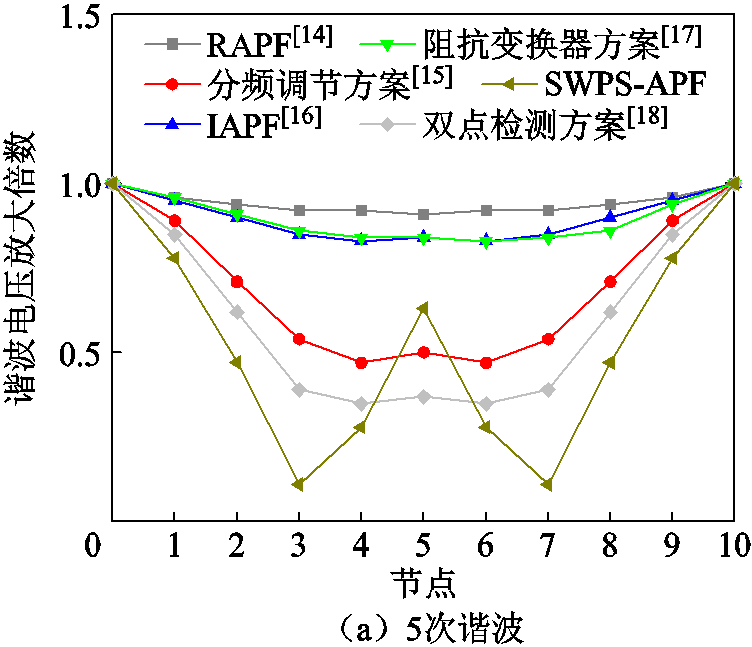
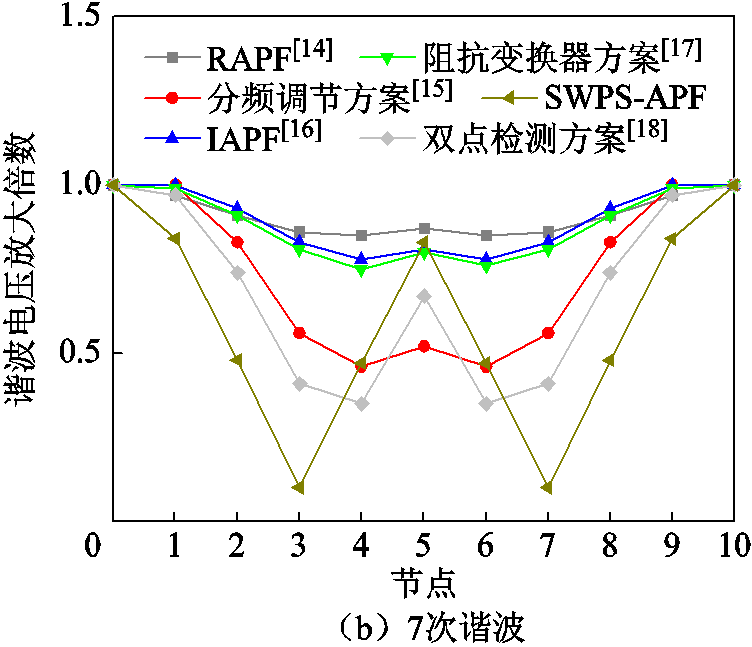
图18 不同抑制方案下各节点谐波电压放大倍数仿真结果对比
Fig.18 Simulation results comparison of harmonic voltage magnification at each node under different suppression scheme
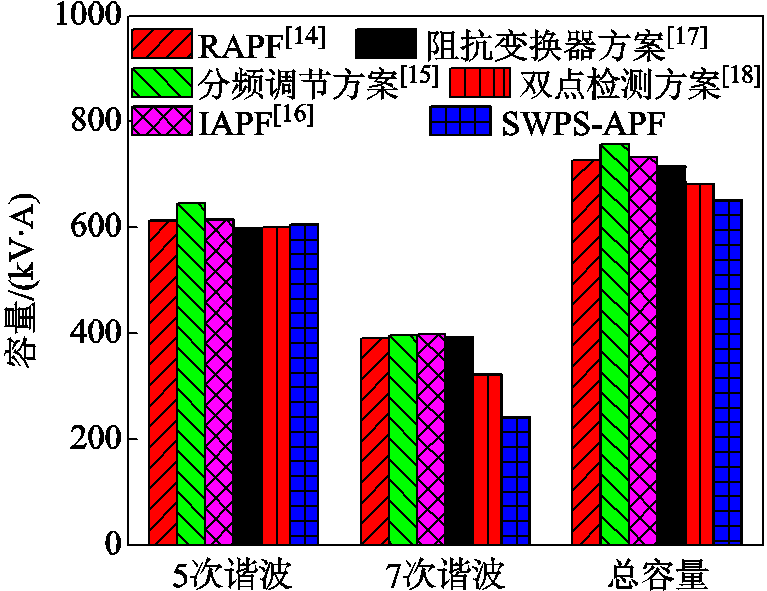
图19 各抑制方案补偿容量对比
Fig.19 Compensation capacity comparison of various suppression schemes
最后,总结得到各抑制方案的对比见表5,可以看出,本文所提出的SWPS-APF总体表现是最优的。
表5 各抑制方案对比
Tab.5 Comparison of various suppression schemes
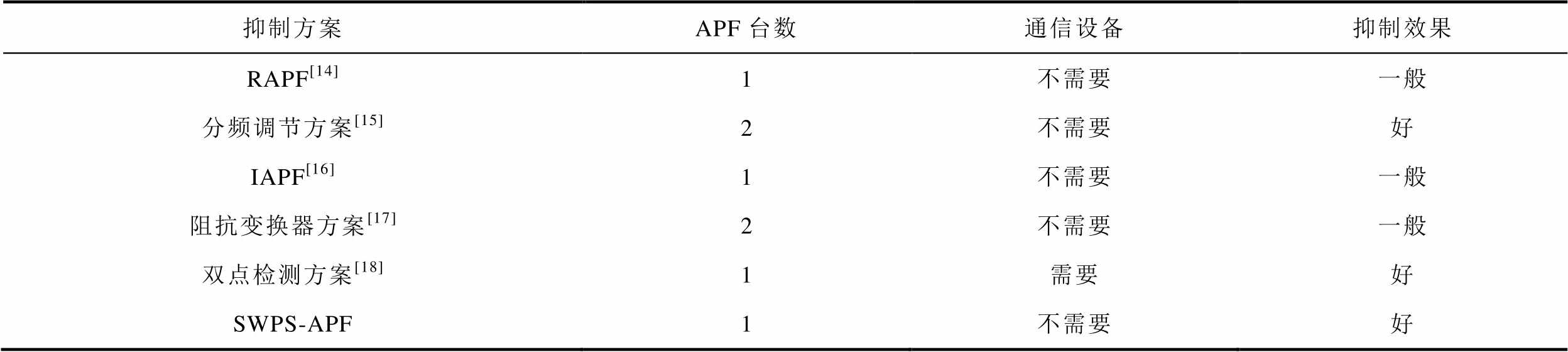
抑制方案APF台数通信设备抑制效果 RAPF[14]1不需要一般 分频调节方案[15]2不需要好 IAPF[16]1不需要一般 阻抗变换器方案[17]2不需要一般 双点检测方案[18]1需要好 SWPS-APF1不需要好
为了进一步验证所提出方案在工程实践中的有效性,搭建了10 km环形配电网系统实验平台,如图20所示。相关参数见表1和表6。需要说明的是,由于电感绕制等原因,系统中馈线电感和无功补偿电容的值并不是精确等于所标参数,所以会导致实验结果与仿真结果之间存在一定差异。

图20 实验平台
Fig.20 Experimental platform
表6 实验平台参数
Tab.6 Parameters of experimental platform

参数数值(型号) 可编程交流源Chroma 6530 IGBT开关管IKW40N120T2 DSP控制器TMS320F28335 APF直流侧电容/μF900 APF滤波电感/mH1 开关和采样频率/kHz10 馈线长度/km10 背景谐波含量(%)5th:3, 7th:2;11th:1, 13th:0.5 驻波移相控制参数Cv5=204 μF, Cv7=66 μF;Lv11=1.42 mH, Lv13=0.38 mH 低通滤波器截止频率/(rad/s)ωc=6.28 直流电压调节器kvp=0.1, kvi=5 电流调节器kip=2
首先,当环形配电馈线上没有连接APF时,由于馈线电感与无功补偿电容之间的谐振,背景谐波电压被严重放大,导致各节点电压波形畸变严重,节点0~9的电压波形如图21所示。当在环形配电网中点安装RAPF后,各节点电压谐波含量明显减小,节点0~9的电压波形如图22所示。而当在环形配电网中点安装所提出的SWPS-APF后,节点0~9的电压谐波含量进一步减小,具体波形如图23所示。


图21 无抑制时各节点电压波形
Fig.21 Voltage waveforms of each node without suppression

图22 安装RAPF时各节点电压波形
Fig.22 Voltage waveforms of each node with RAPF
节点5电压uabc,SWPS-APF指令电流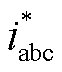 以及输出电流iabc的单相波形如图24所示。可以看到,电流闭环跟踪效果良好。
以及输出电流iabc的单相波形如图24所示。可以看到,电流闭环跟踪效果良好。

图23 安装SWPS-APF时各节点电压波形
Fig.23 Voltage waveforms of each node with SWPS-APF

图24 SWPS-APF接入时的动态波形
Fig.24 Dynamic waveforms when SWPS-APF is switched in
由安装点提取出的各次谐波电压及其相应的各次谐波指令电流波形如图25所示。根据上述分析,在10 km配电馈线中,对5次和7次谐波需使用驻波右移策略,所以相应的指令电流波形超前了电压90°。相反地,对于11次和13谐波使用了驻波左移策略,所以其指令电流波形滞后电压90°。

图25 SWPS-APF各次谐波电压和指令电流波形
Fig.25 Harmonic voltage and command current waveforms of SWPS-APF
最后,无抑制及环形配电网中点安装RAPF和SWPS-APF后各节点谐波电压放大倍数实验结果对比如图26所示。可以看到,本文提出的驻波移相抑制方案的抑制效果要显著优于传统的RAPF方案。
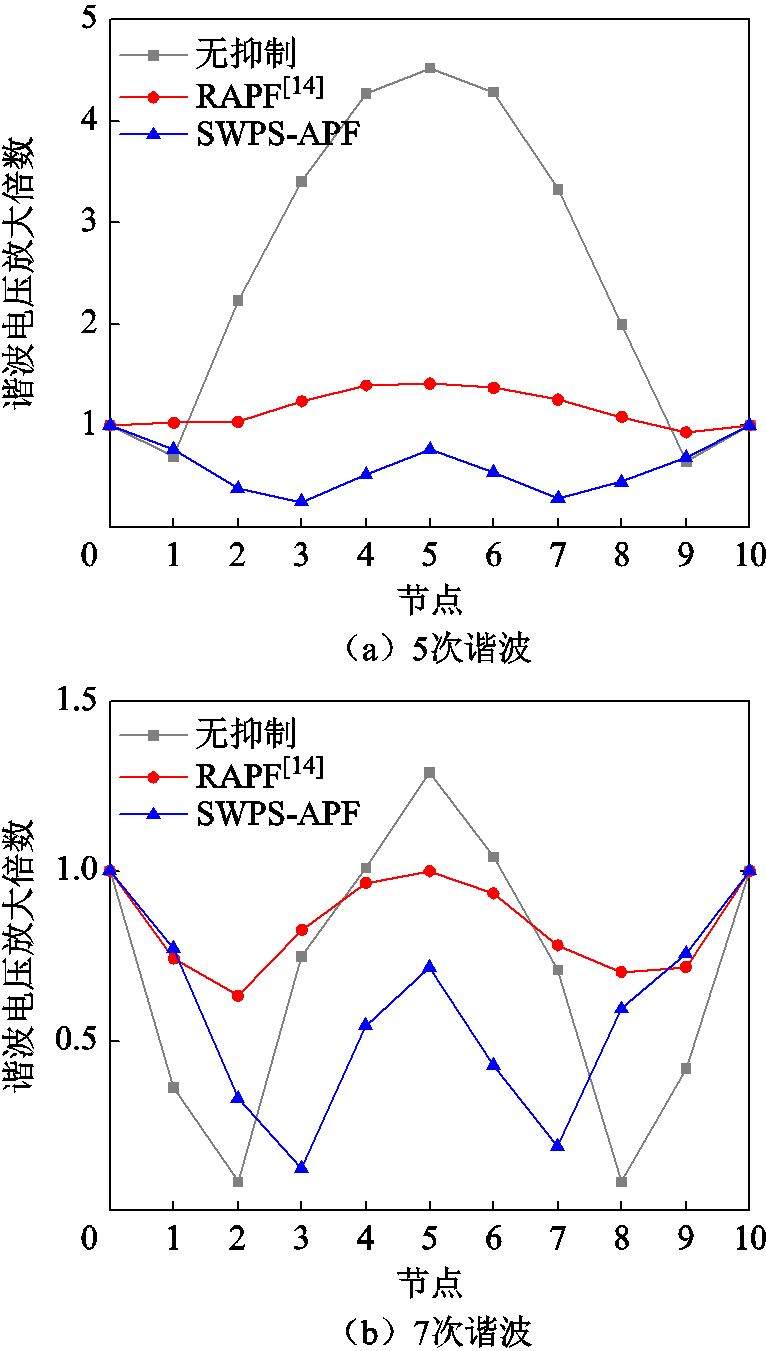
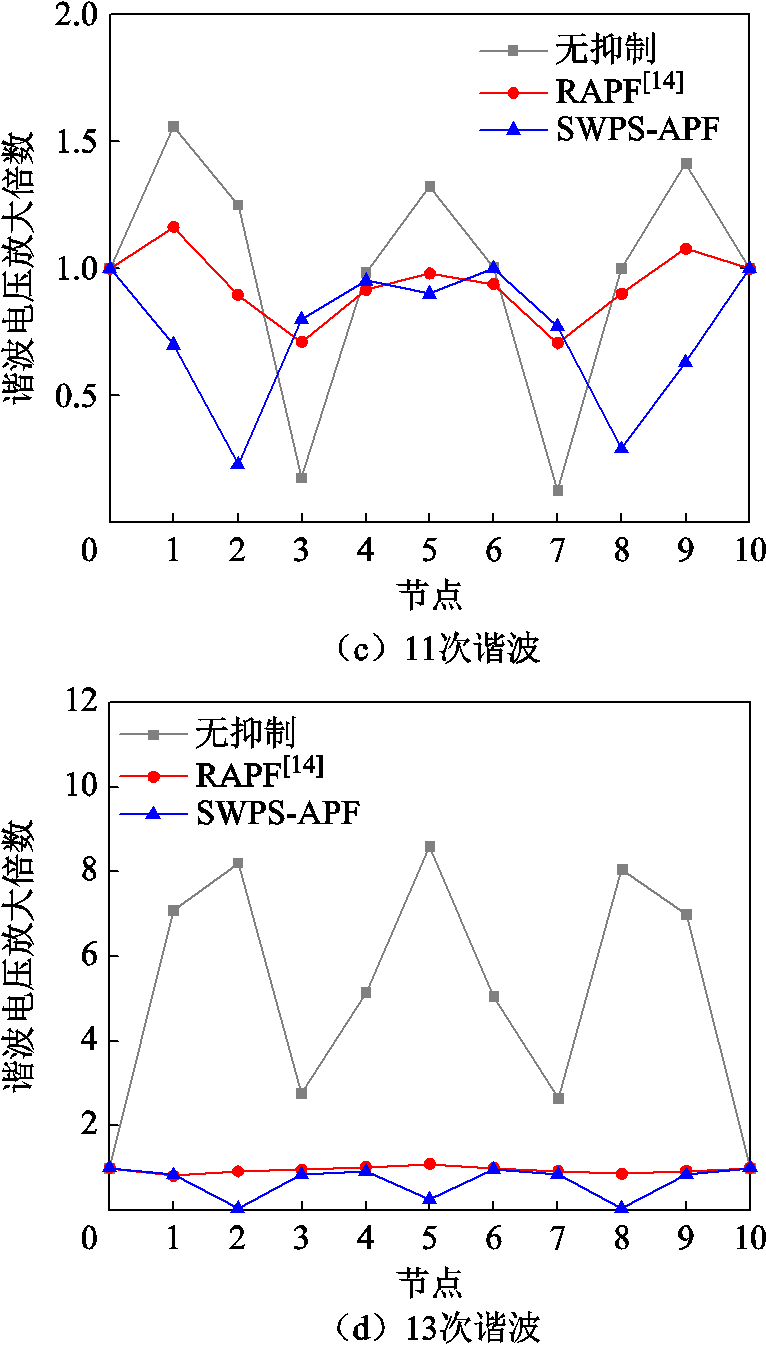
图26 各节点谐波电压放大倍数实验结果对比
Fig.26 Experimental results comparison of harmonic voltage magnification at each node
本文针对环形配电网中由功率因数校正电容与馈线电感之间谐振导致的背景谐波电压放大问题,深入分析了背景谐波电压在网络中的传播规律,并提出了一种基于驻波移相原理的背景谐波抑制方案,得到以下结论:
1)背景谐波电压在馈线上的放大程度取决于馈线始端即谐波源与离其最近波腹(包括位于谐波源左侧的波腹)之间的距离。当馈线始端恰好位于驻波波腹时,则背景谐波一定不会被放大。
2)驻波移相抑制方案可分为驻波左移和驻波右移两种抑制策略。两者具有不同的适用范围,可以通过调整其控制参数获得整体最优的抑制效果。
3)在10 km环形配电馈线中,验证了所提出SWPS-APF在抑制效果方面具有较大优势,并且发现其需要的补偿容量更少。
参考文献
[1] 郭慧珠, 孟鑫, 贺明智, 等. 无通信高电能质量的微电网平滑切换控制策略[J]. 电工技术学报, 2022, 37(10): 2611-2621.
Guo Huizhu, Meng Xin, He Mingzhi, et al. An enhanced power quality and smooth transition control strategy for a microgrid without remote pre-synchronization communication[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2611-2621.
[2] 王怡, 杨知方, 余娟, 等. 考虑可靠性需求的配电网多种设备统一优化配置[J]. 电工技术学报, 2023, 38(24): 6727-6743.
Wang Yi, Yang Zhifang, Yu Juan, et al. A unified optimal placement method for multiple types of devices in distribution networks considering reliability demand[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6727-6743.
[3] 王杨, 唐俊苗, 赵劲帅, 等. 基于自适应虚拟阻抗控制的孤岛微电网电能质量优化策略[J]. 电力系统自动化, 2023, 47(7): 63-73.
Wang Yang, Tang Junmiao, Zhao Jinshuai, et al. Power quality optimization strategy in islanded microgrid based on adaptive virtual impedance control[J]. Automation of Electric Power Systems, 2023, 47(7): 63-73.
[4] 李勇, 刘珮瑶, 胡斯佳, 等. 基于感应滤波的光伏电站谐波谐振抑制方法[J]. 电工技术学报, 2022, 37(15): 3781-3793.
Li Yong, Liu Peiyao, Hu Sijia, et al. Harmonic resonance damping method of photovoltaic power station based on inductive filtering[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3781-3793.
[5] 叶宗彬, 侯波, 张延澳, 等. 一种三相对称系统快速谐波检测算法[J]. 电工技术学报, 2023, 38(2): 510-522.
Ye Zongbin, Hou Bo, Zhang Yan’ao, et al. A fast harmonic detection algorithm for three-phase symmetric systems[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 510-522.
[6] 杨权, 梁永昌, 魏建荣, 等. 多谐波源下分布式电源并网逆变器的谐波抑制策略[J]. 电工技术学报, 2023, 38(11): 2908-2920.
Yang Quan, Liang Yongchang, Wei Jianrong, et al. Research on harmonic suppression strategy of grid connected inverter under multi-harmonic sources[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2908-2920.
[7] Akagi H. Control strategy and site selection of a shunt active filter for damping of harmonic propagation in power distribution systems[J]. IEEE Transactions on Power Delivery, 1997, 12(1): 354-363.
[8] Akagi H, Fujita H, Wada K. A shunt active filter based on voltage detection for harmonic termination of a radial power distribution line[J]. IEEE Transactions on Industry Applications, 1999, 35(3): 638-645.
[9] Wada K, Fujita H, Akagi H. Considerations of a shunt active filter based on voltage detection for installation on a long distribution feeder[J]. IEEE Transactions on Industry Applications, 2002, 38(4): 1123-1130.
[10] Cheng P T, Lee T L. Distributed active filter systems (DAFSs): a new approach to power system harmonics [J]. IEEE Transactions on Industry Applications, 2006, 42(5): 1301-1309.
[11] 孙孝峰, 曾健, 张芳, 等. 阻性有源滤波器分频控制位置的选择方案[J]. 中国电机工程学报, 2011, 31(28): 65-70.
Sun Xiaofeng, Zeng Jian, Zhang Fang, et al. Site selection strategy of discrete frequency resistive active power filter[J]. Proceedings of the CSEE, 2011, 31(28): 65-70.
[12] 孙孝峰, 王伟强, 沈虹, 等. 基于双阻性有源滤波器的背景谐波抑制策略[J]. 电工技术学报, 2016, 31(16): 145-153.
Sun Xiaofeng, Wang Weiqiang, Shen Hong, et al. Background harmonic suppression based on double resistive active power filters[J]. Transactions of China Electrotechnical Society, 2016, 31(16): 145-153.
[13] 吴振辉, 彭晓涛, 沈阳武, 等. 一种配电网环型供电模型及其合环运行方式的研究[J]. 中国电机工程学报, 2013, 33(10): 18, 57-63.
Wu Zhenhui, Peng Xiaotao, Shen Yangwu, et al. Study on a loop power supply model and its loop-close operation mode for distribution network[J]. Procee-dings of the CSEE, 2013, 33(10): 18, 57-63.
[14] Lee T L, Hu S H. Discrete frequency-tuning active filter to suppress harmonic resonances of closed-loop distribution power systems[J]. IEEE Transactions on Power Electronics, 2011, 26(1): 137-148.
[15] 王宝诚, 杨理莉, 韩瑞静, 等. 环形配电网的分频调节阻性有源电力滤波器位置策略[J]. 电工技术学报, 2017, 32(4): 241-249.
Wang Baocheng, Yang Lili, Han Ruijing, et al. Site selection strategy of discrete frequency tuned resistive active power filter for harmonic damping in loop power distribution systems[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 241-249.
[16] Sun Xiaofeng, Han Ruijing, Yang Lili, et al. Study of a novel equivalent model and a long-feeder simulator-based active power filter in a closed-loop distribution feeder[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 2702-2712.
[17] Sun Xiaofeng, Yang Lili, Wang Rui, et al. A novel impedance converter for harmonic damping in loop power distribution systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(1): 162-173.
[18] 沈虹, 李雪苗, 康佳, 等. 基于双点检测SRAPF的环形配电系统背景谐波衰减策略研究[J]. 太阳能学报, 2019, 40(2): 572-579.
Shen Hong, Li Xuemiao, Kang Jia, et al. Research on harmonic mitigating based on double point detection of single resistive active power filter in closed-loop distribution sysems[J]. Acta Energiae Solaris Sinica, 2019, 40(2): 572-579.
[19] 李雪苗. 基于双点检测SRAPF的配电网系统背景谐波衰减策略研究[D]. 秦皇岛: 燕山大学, 2017.
Li Xuemiao. Research on harmonic mitigating based on double point detection of single resistive active power filter in distribution systems[D]. Qinghuangdao: Yanshan University, 2017.
[20] Saito M, Takeshita T, Matsui N. Modeling and harmonic suppression for power distribution systems[J]. IEEE Transactions on Industrial Electronics, 2003, 50(6): 1148-1158.
[21] Santana W C, Al-Haddad K, da Silva L E B. Modeling and active damping of harmonic propagation on electric distribution systems[C]//2009 IEEE Electrical Power & Energy Conference (EPEC), Montreal, QC, Canada, 2009: 1-7.
[22] Sun Xiaofeng, Han Ruijing, Shen Hong, et al. A double-resistive active power filter system to attenuate harmonic voltages of a radial power distribution feeder[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6203-6216.
[23] 邱关源. 电路[M]. 5版. 北京: 高等教育出版社, 2006.
Applications of Standing Wave Phase Shifting Active Power Filters in Closed-Loop Distribution Power Systems
Abstract Due to the resonance between power factor correction capacitors and feeder inductors in closed-loop distribution network, the background harmonic voltage will be amplified, causing severe distortion of node voltage, which can affect the normal operation of electrical equipment and even endanger the personal safety of users. The current mainstream suppression scheme is resistive active power filter (RAPF) based on impedance matching principle, which is installed at the midpoint of closed-loop distribution network with conductance gain of Z/2 (Z is the characteristic impedance of the distribution feeder). The RAPF can effectively suppress background harmonic voltage amplification, but cannot further attenuate background harmonic voltage to achieve better suppression performance. Some improvement schemes based on RAPF can optimize suppression performance, but all come at the sacrifice of increasing costs (installing communication equipment or increasing the number of APFs).
Firstly, the propagation law of background harmonic voltage on the closed-loop distribution feeder was analyzed by the distributed parameter model. The degree of amplification of background harmonic voltage on the feeder depends on the distance between the beginning of the feeder and the nearest antinode (including the antinode located on the left side of the harmonic source). The farther the distance, the more severe the amplification of background harmonic voltage. When the beginning of the feeder is exactly at the standing wave node, the amplification of the background harmonic voltage is most severe. On the contrary, when the beginning of the feeder is exactly at the standing wave antinode, the harmonic voltage amplification factor at all positions on the feeder will not be greater than 1, that is, the background harmonic voltage will not be amplified. Based on this, the suppression scheme based on the phase shift of harmonic voltage standing wave is proposed. The principle is to move the phase of the standing wave to make the antinode close to or exactly fall on the beginning of the feeder. The propose scheme can be divided into two suppression strategies: standing wave shifting to the left and standing wave shifting to the right. The two have different applicable ranges, according to the relationship between the length of the feeder and the suppressed harmonic wavelength, the suppression conditions are divided into three types, and the selection of the direction of standing wave movement and the calculation of the optimal control parameters are discussed separately. Finally, the proposed scheme is implemented through standing wave phase shifting based active power filter (SWPS-APF) and its control block diagram is provided.
A 10 km long closed-loop distribution feeder simulation model was built in PLECS software to evaluate the suppression performance and compensation capacity of SWPS-APF under three operating conditions: no load on the feeder, 100 Ω load on the feeder, and feeder parameters changes. Experimental verification was conducted on a down-scaled experimental platform. Both simulation and experimental results indicate that the proposed scheme has significant advantages over mainstream RAPF schemes in terms of suppression performance and compensation capacity.
In conclusion, compared with various existing suppression schemes, the proposed standing wave phase shifting scheme only requires the installation of an APF at the midpoint of the closed-loop distribution feeder, without the need for communication equipment, and has lower costs. However, it can achieve better suppression performance and less compensation capacity.
Keywords:Background harmonic, active power filter, harmonic suppression, standing wave
中图分类号:TM761
DOI: 10.19595/j.cnki.1000-6753.tces.231935
河北省自然科学基金重点项目(E2021203162)、河北省科技计划项目(236Z2004G)和河北省自然科学基金项目(F2022203005)资助。
收稿日期 2023-11-21
改稿日期 2023-12-14
张 敏 男,1996年生,博士研究生,研究方向为电能质量控制。
E-mail:1309153464@qq.com
朱艳萍 女,1972年生,副教授,硕士生导师,研究方向为微电网功率运行控制、功率因数校正。
E-mail:qhdzyp@ysu.edu.cn(通信作者)
(编辑 赫 蕾)