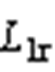 、滤波电容
、滤波电容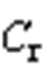 和网侧滤波电感
和网侧滤波电感 与台区1相连接。VSR经过该侧直流电容、共模电感
与台区1相连接。VSR经过该侧直流电容、共模电感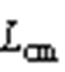 、逆变侧直流电容与电压源型逆变器(Voltage Source Inverter, VSI)相连接,逆变侧的结构与整流侧相同。其中,
、逆变侧直流电容与电压源型逆变器(Voltage Source Inverter, VSI)相连接,逆变侧的结构与整流侧相同。其中,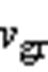 、
、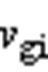 分别为两台区交流电压,
分别为两台区交流电压,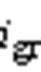 、
、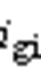 分别为两侧并网交流电流,
分别为两侧并网交流电流,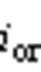 、
、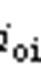 分别为两侧变流器侧输出交流电流,
分别为两侧变流器侧输出交流电流,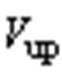 、
、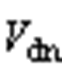 分别为直流侧上、下电容两端电压,二者之和为总直流电压
分别为直流侧上、下电容两端电压,二者之和为总直流电压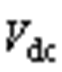 。
。摘要 非隔离型低压柔性潮流转供装置具有可主动调节配电网潮流、改善电能质量等功能,因其高效率、低成本、高功率密度等优势受到了高度关注。但多端变流器脉宽调制及动态耦合效应会产生复杂共模环流,影响系统安全稳定。为了克服这一难题,提出一种基于开关周期平均共模电压直接调制的共模环流指定谐波闭环抑制策略。首先,建立非隔离型柔性潮流转供装置的精准共模电路模型,分析阻抗和主导次共模环流特性,揭示了开关周期平均共模电压和共模环流的关联性;其次,通过双侧变流器零矢量协调分配实现了等效平均共模电压的精准调节,在不影响差模电流动态调节的基础上实现了指定次共模环流的闭环抑制调控;最后,通过实验验证了该方法的可行性和有效性。
关键词:平均共模电压 共模电流抑制 共模回路 三次谐波 零矢量
随着分布式新能源发电在中低压配电网中渗透率的不断提升,中低压配电网存在潮流无序分布、线路反向重过载、电压波动加剧等一系列难题,严重影响分布式新能源发电和配电网的稳定性和安全性[1-2]。为了克服以上问题,通过电力电子柔性互联装置对中低压配电网潮流和电压实施主动调控[3-4],近年来获得了国内外的高度关注。为了进一步提升装置的利用率和灵活性,低压柔性潮流转供装置还可应用于分布式储能直接接入[5]、主动电能质量调节[6]、电网故障情况下应急供电[7]等多个场景,从而最大限度地利用电网的供能潜力,有效提升配电网整体运行的可靠性与经济性。
传统的柔性潮流转供装置需在交流端口加装隔离变压器,因此造成转供系统重量大、成本高、效率低,严重影响了其推广和应用[8]。近年来,采用无隔离变压器的柔性潮流转供装置可显著降低系统成本和体积,成为该领域热点研究问题之一[9-10]。然而,端口变换器开关调制伴生的共模电压会对非隔离柔性潮流转供装置和配电系统产生一系列危害,如共模电压会在共模回路中产生环流,引起交流侧谐波畸变率增大,保护电路误动作,影响系统正常运行,甚至进一步导致开关器件损毁等问题[11-12]。
国内外学者对共模电压和共模环流的研究主要集中于改善电路拓扑以及优化调制策略两方面。在拓扑设计方面,在共模回路中加装共模扼流圈可增加共模阻抗,有效降低共模电流,但会使装置的成本和体积增加[13-14]。在调制策略改进方面,文献[15]提出一种无零矢量调制方法,即动态零矢量脉宽调制(Active Zero State Pulse Width Modulation, AZSPWM),该调制方法采用相邻的一对电压矢量代替零矢量,将共模电压幅值限制在直流侧电压幅值的1/6,但无零矢量的方法使并网电流畸变率增加。文献[16]采用基于调制波分解的调制策略,用合成共模电压为零的虚拟调制波代替实际调制波,实现共模电压的抑制,但此方法仅适用于奇数次电平变换器中。文献[17]采用输出脉冲电压循环对齐的方式,实现无隔离变压器背靠背两电平变换器的总共模电压为零,但是脉冲偏移会导致电流波形的严重畸变。
需要说明的是,传统的共模电压抑制方案聚焦于共模电压峰值,从而实现共模环流的间接抑制,但共模电流抑制率与共模电压峰值降低的数学关系及耦合机理尚不清晰,二者无直接对应关系,其本质上是一种开环补偿方法,造成抑制效果不理想,而且对环境和参数变化较为敏感。
为了解决上述问题,本文建立非隔离型柔性潮流转供装置的等效共模电路,对共模电流的产生机理和频谱特性开展了研究,构建了开关周期平均共模电压和共模电流的精确数学关系,提出了基于双端口变流器零矢量协同的平均共模电压直接调制方法和差模、共模电压动态解耦策略。同时,通过平均共模电压的动态调节实现了指定次共模环流的高效闭环抑制。最后,通过实验验证了本文所提出方法的可行性和有效性。
非隔离型柔性潮流转供装置拓扑结构如图1所示,该系统由两个电压源型变流器组成,电压源型整流器(Voltage Source Rectifier, VSR)经过整流侧滤波电感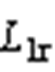 、滤波电容
、滤波电容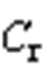 和网侧滤波电感
和网侧滤波电感 与台区1相连接。VSR经过该侧直流电容、共模电感
与台区1相连接。VSR经过该侧直流电容、共模电感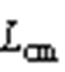 、逆变侧直流电容与电压源型逆变器(Voltage Source Inverter, VSI)相连接,逆变侧的结构与整流侧相同。其中,
、逆变侧直流电容与电压源型逆变器(Voltage Source Inverter, VSI)相连接,逆变侧的结构与整流侧相同。其中,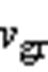 、
、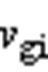 分别为两台区交流电压,
分别为两台区交流电压,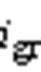 、
、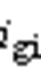 分别为两侧并网交流电流,
分别为两侧并网交流电流,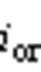 、
、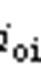 分别为两侧变流器侧输出交流电流,
分别为两侧变流器侧输出交流电流,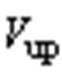 、
、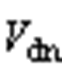 分别为直流侧上、下电容两端电压,二者之和为总直流电压
分别为直流侧上、下电容两端电压,二者之和为总直流电压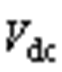 。
。
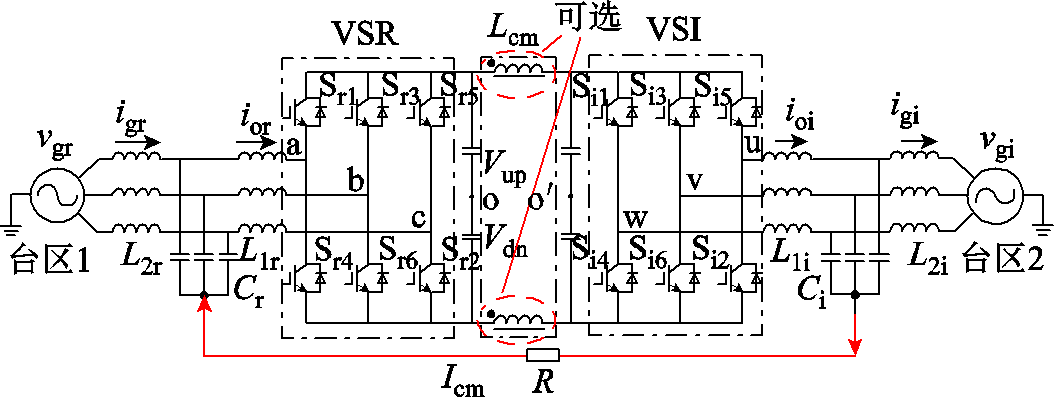
图1 柔性潮流转供装置拓扑
Fig.1 Topology of flexible power flow transfer device
为了获得更好的共模环流抑制效果,本文在直流侧加装共模电感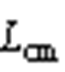 ,增大共模回路阻抗。为了提高装置的经济性,在采用本文所提方法后,共模电感可省去。
,增大共模回路阻抗。为了提高装置的经济性,在采用本文所提方法后,共模电感可省去。
在柔性潮流转供装置中,两个电网中性点之间的电压差值定义为共模电压[18],其值等于柔性潮流转供装置两个变流器模块即VSR与VSI产生的共模电压之差,即
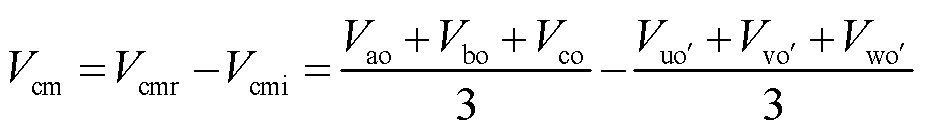 (1)
(1)
式中,Vao、Vbo、Vco为柔性潮流转供装置整流侧的三相输出电压;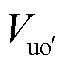 、
、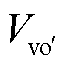 、
、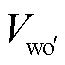 为柔性潮流转供装置逆变侧的三相输出电压;
为柔性潮流转供装置逆变侧的三相输出电压;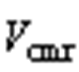 为整流侧共模电压,
为整流侧共模电压,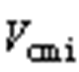 为逆变侧共模电压。
为逆变侧共模电压。
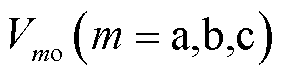 和
和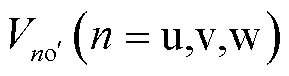 的取值为
的取值为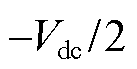 或
或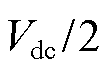 ,由开关器件的状态决定,即
,由开关器件的状态决定,即
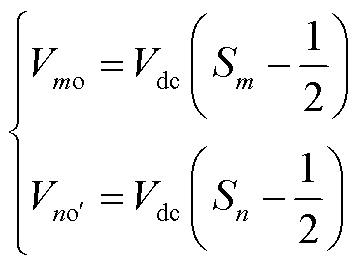 (2)
(2)
 (3)
(3)
Sd代表柔性潮流转供装置的两个变流器共六个桥臂的开关器件状态。联立式(1)~式(3)可得共模电压表达式为
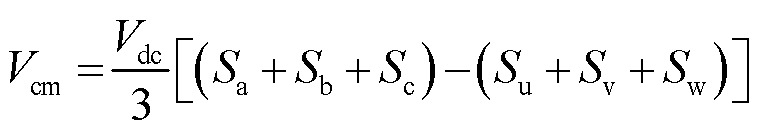 (4)
(4)
基于柔性潮流转供装置的结构及参数,进行建模分析。在本文所处场景中,柔性潮流转供装置多用于线路末端,滤波电容中性点经电阻相连接,两台区电网中性点接地点间电阻远大于共模回路中的电阻R,可等效为开路[19-20]。故系统可简化为图2。为了便于分析,两侧变流器被简化为脉冲电压源,直流侧滤波电容在共模电压作用下等效为开路,可以直接省略。两侧交流滤波器滤波电容中性点等效为:经一个电阻连接在一起形成共模回路。
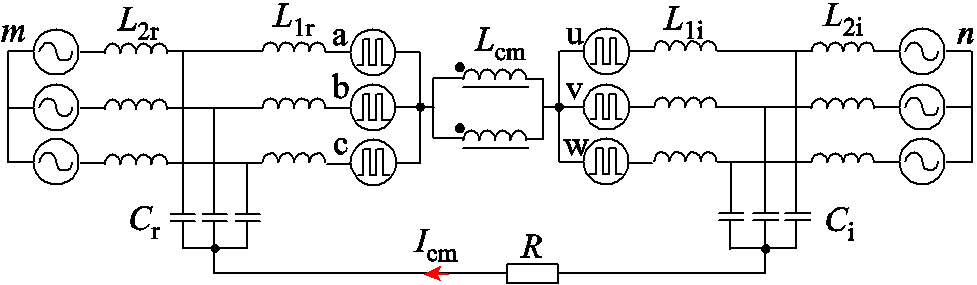
图2 系统简化模型
Fig.2 Simplified model of the system
忽略系统中低频分量的影响,仅考虑高频分量,其中ab两相共模电压与差模电压的定义[21]分别为
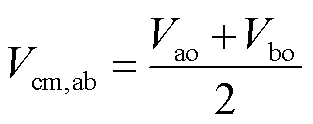 (5)
(5)
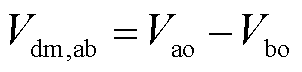 (6)
(6)
根据式(5)和式(6)可知
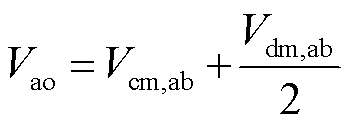 (7)
(7)
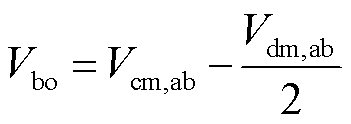 (8)
(8)
共模回路简化模型如图3所示。在图3a中对系统两相共模回路进行简化,等效差模电压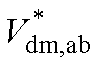 为
为
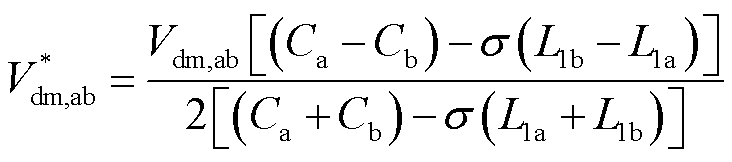 (9)
(9)
式中,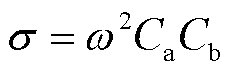 。在系统实际线路中,
。在系统实际线路中,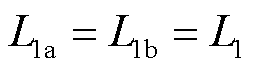 、
、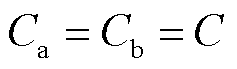 ,故差模电压
,故差模电压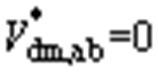 ,在共模回路中不产生有效作用。由叠加定理得到完整的三相系统的共模回路模型如图3b所示。其中,共模电感等效为差模分量减去共模分量后并联,再与共模分量串联的电感值,共模量与差模量接近,最终共模电感等效为
,在共模回路中不产生有效作用。由叠加定理得到完整的三相系统的共模回路模型如图3b所示。其中,共模电感等效为差模分量减去共模分量后并联,再与共模分量串联的电感值,共模量与差模量接近,最终共模电感等效为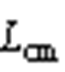 。
。

图3 共模回路简化模型
Fig.3 Simplified model of common mode loop
总共模电压为整流侧共模电压与逆变侧共模电压的差,共模阻抗为
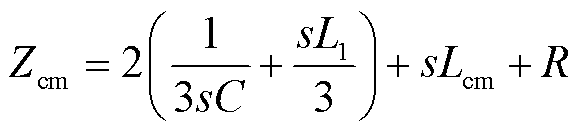 (10)
(10)
在柔性潮流转供装置的其他场景使用中,可采用与本文类似的方法对共模回路进行建模。
在共模电压与共模回路的共同作用下产生了共模电流。共模回路传递函数可根据本文柔性潮流转供装置中的器件参数计算得出,即
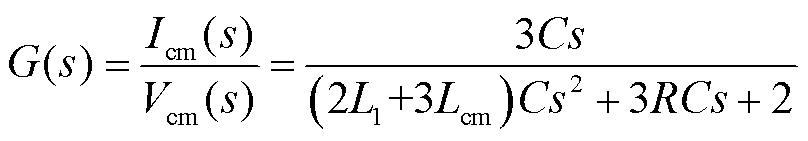 (11)
(11)
根据共模回路传递函数绘制共模回路伯德图,如图4所示。共模回路对共模电压中含量较多的3、9次谐波分量未呈现大阻抗的增益特性,在共模电压的作用下会产生较大的共模环流。对于15次以上谐波分量,共模回路增益随着频率的增加而逐渐减小,且其分量占比较少,产生的共模环流的影响可忽略。
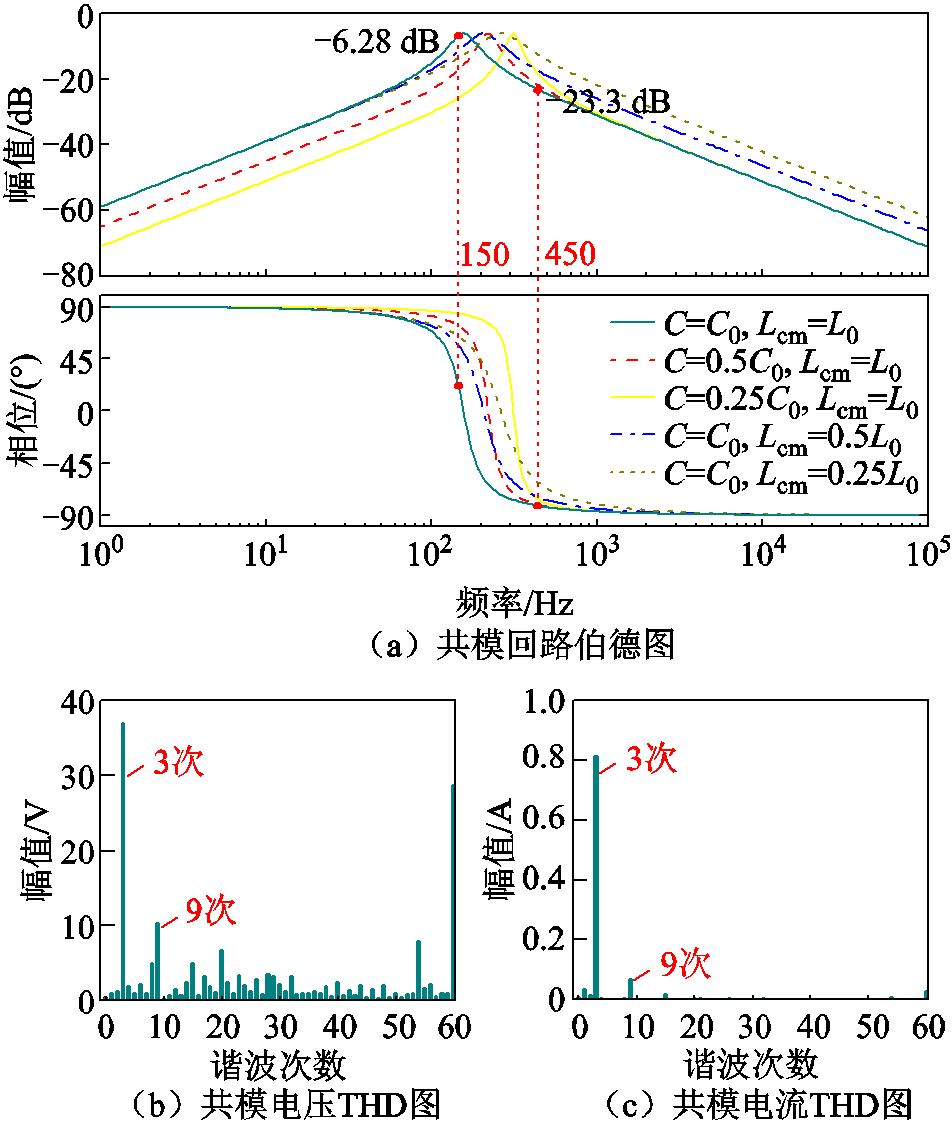
图4 共模回路伯德图及共模电压、电流THD分析
Fig.4 Common mode loop Bode diagram and THD analysis of 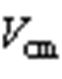 and
and 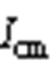
共模回路参数发生变化时(C0、L0分别为交流滤波电容、共模电感初始参数),系统谐振峰位于低频段,且低频段共模电压除了主要分量外,其余分量含量较少,外加回路阻尼的影响,谐振峰被抑制,无需考虑低频谐振对本文所提策略的影响。
由如上分析可知,在共模电压源与共模回路的共同作用下,共模电流呈现主导谐波分量为工频3次及其奇数倍次的特征,且共模回路对相应频次无明显抑制作用。通过对共模电流中的主导谐波分量即3、9次谐波分量进行有效抑制,就能实现柔性潮流转供装置的共模电流抑制。
在传统的柔性潮流转供装置中,整流器与逆变器均采用空间矢量脉宽调制(Space Vector Pulse WidthModulation, SVPWM)七段法调制[22]。假设两个变流器参考电压矢量在空间中的相对位置如图5所示。
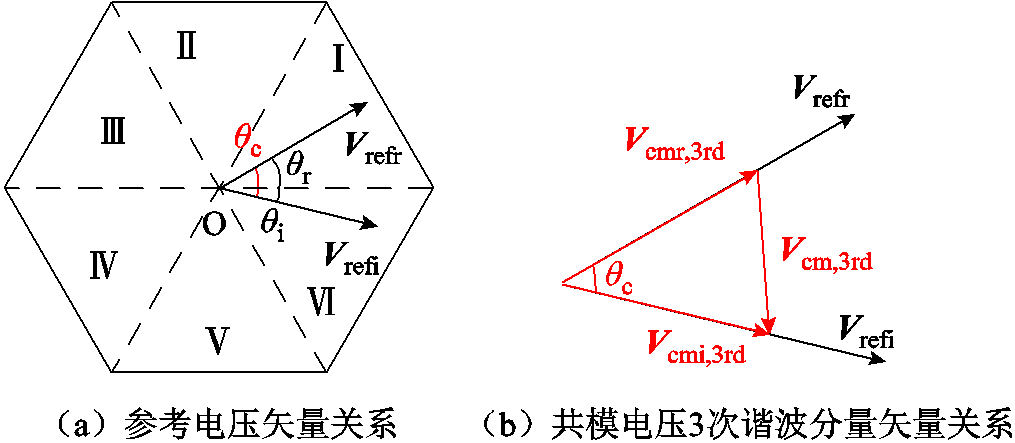
图5 静止坐标系下两端参考电压矢量示意图
Fig.5 Schematic diagram of reference voltage vectors on both sides in the stationary coordinate system
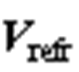 和
和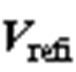 为两个变流器的参考电压矢量。
为两个变流器的参考电压矢量。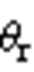 和
和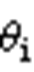 分别为
分别为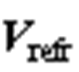 和
和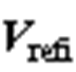 与0°轴的夹角,
与0°轴的夹角,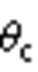 为两个参考电压矢量的相位差。两端变流器产生的共模电压3次分量
为两个参考电压矢量的相位差。两端变流器产生的共模电压3次分量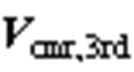 、
、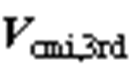 与对应电压矢量同相位,两共模电压相减得到共模电压的3次分量
与对应电压矢量同相位,两共模电压相减得到共模电压的3次分量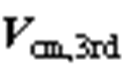 。
。
对参考电压矢量采用SVPWM七段法调制,可得其每一段所对应的共模电压幅值。以第Ⅰ扇区为例,第1、7段为零矢量V0(000),共模电压为 -Vdc/2,作用时间为T01(T0/2);第4段为零矢量V7(111),共模电压为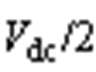 ,作用时间为T02(T0/2);第2、6段为有效矢量V1(100),其共模电压为 -Vdc/6,作用时间为
,作用时间为T02(T0/2);第2、6段为有效矢量V1(100),其共模电压为 -Vdc/6,作用时间为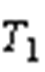 ;第3、5段为有效矢量V2(110),其共模电压为Vdc/6,作用时间为T2。其余扇区共模电压幅值变化规律与第Ⅰ扇区相同。
;第3、5段为有效矢量V2(110),其共模电压为Vdc/6,作用时间为T2。其余扇区共模电压幅值变化规律与第Ⅰ扇区相同。
为了计算每个调制周期中每一段的作用时间,需计算变流器有效电压矢量作用时间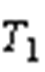 、
、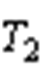 与零电压矢量作用时间T01、T02,计算如下[23]:
与零电压矢量作用时间T01、T02,计算如下[23]:
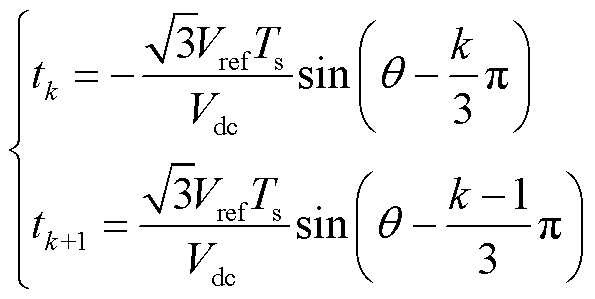 (12)
(12)
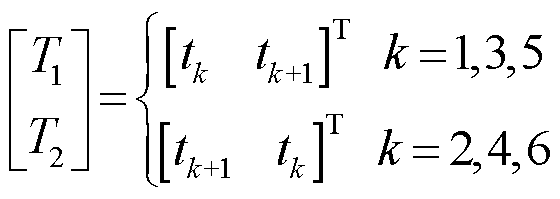 (13)
(13)
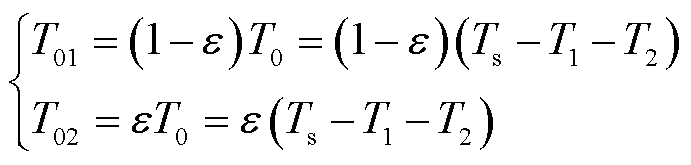 (14)
(14)
式中,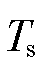 为开关周期;Vref为变流器参考电压矢量大小;
为开关周期;Vref为变流器参考电压矢量大小;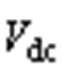 为直流电压值;k为变流器参考电压矢量所在扇区号;
为直流电压值;k为变流器参考电压矢量所在扇区号;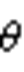 为参考电压矢量相位;零矢量分配系数
为参考电压矢量相位;零矢量分配系数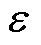 定义为中间段零矢量V7的作用时间T02占总零矢量作用时间T0的比例,传统SVPWM调制中
定义为中间段零矢量V7的作用时间T02占总零矢量作用时间T0的比例,传统SVPWM调制中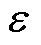
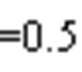 。
。
以柔性潮流转供装置中的整流器为例,定义一个调制周期中共模电压峰值与平均共模电压的关系如图6所示,通过周期平均法计算单个开关周期的平均共模电压,其值等于单个开关周期Ts内电压矢量作用时间与其共模电压值的乘积和,即图6中面积之和。图6中E表示直流母线电压的1/2,即Vdc/2。
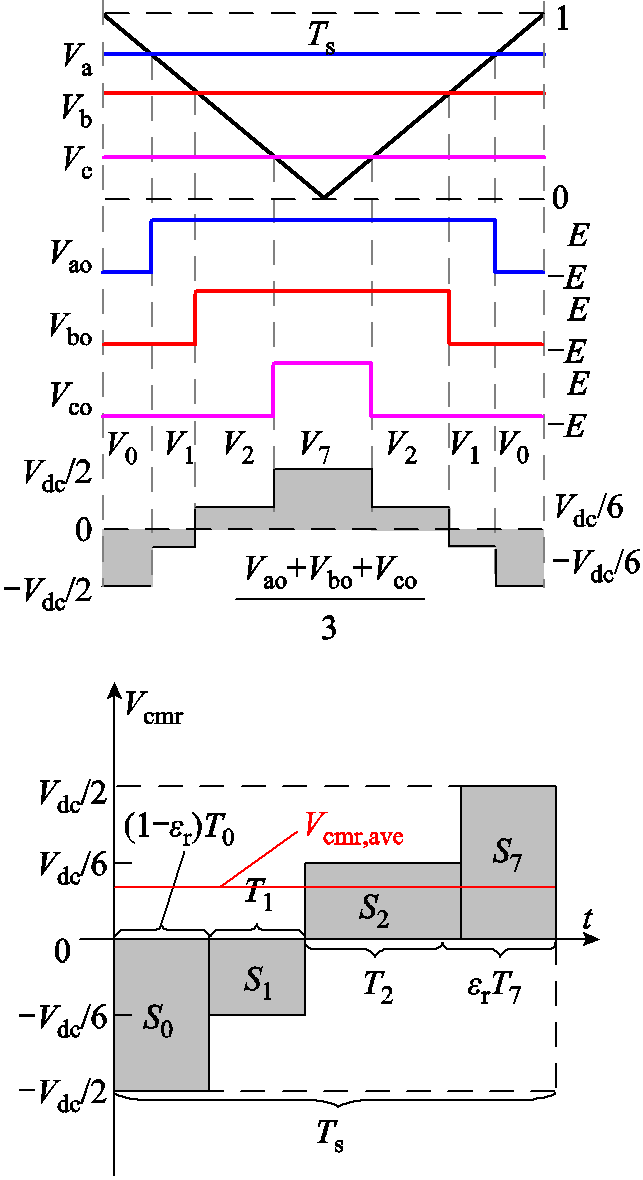
图6 平均共模电压示意图
Fig.6 Average common-mode voltage
整流器开关周期平均共模电压可定义为
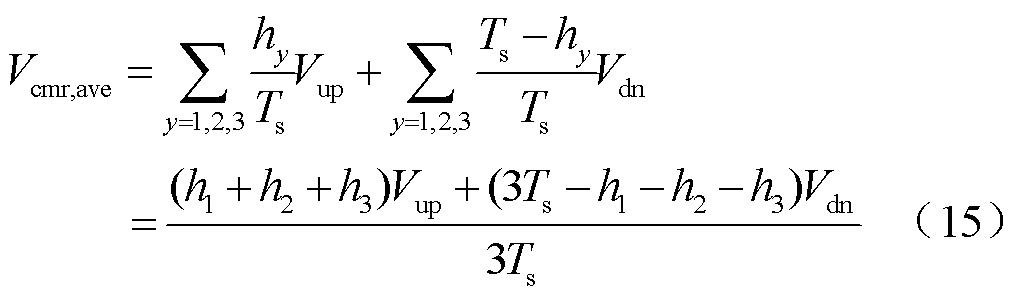
式中,hy(y=1, 2, 3)为每个开关周期内三相PWM开关器件的开通时间从小到大的值,其与零矢量、有效矢量的作用时间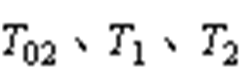 的关系为
的关系为
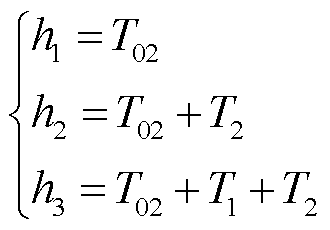 (16)
(16)
将式(14)、式(16)代入式(15)中,并化简得到
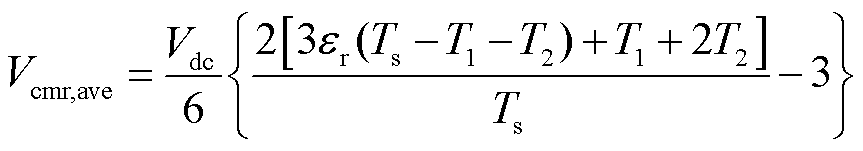 (17)
(17)
式中,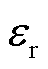 为整流侧零矢量分配系数。
为整流侧零矢量分配系数。
将式(12)、式(13)代入式(17),得到平均共模电压计算公式,如式(18)所示,其中调制度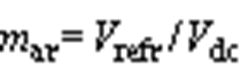 。
。
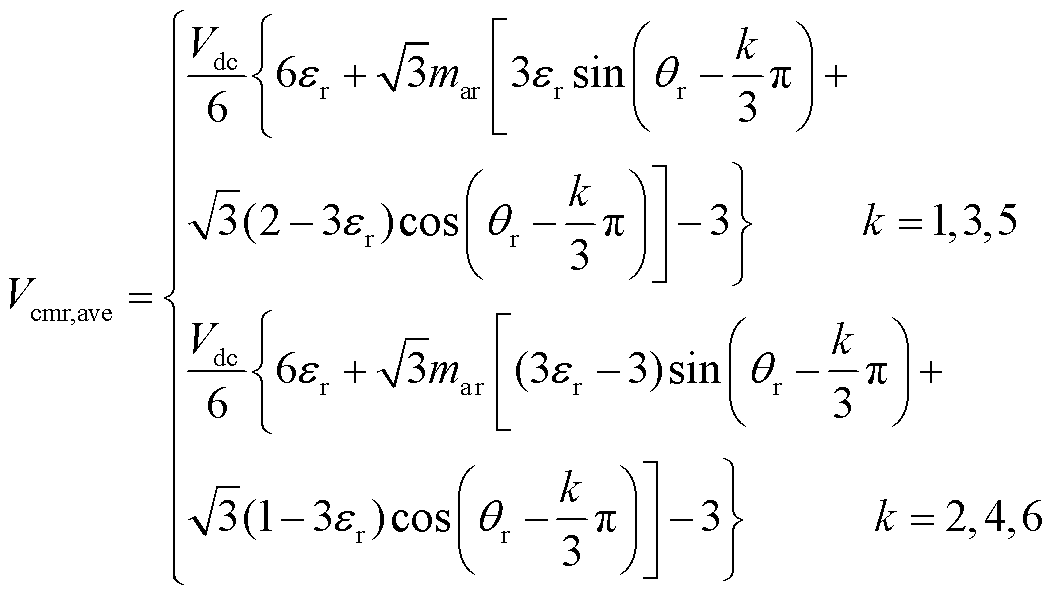 (18)
(18)
在传统SVPWM七段法调制中(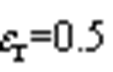 ),一个工频周期内平均共模电压数值曲线如图7a所示,可知平均共模电压主要谐波分量为3次及其奇数倍次。
),一个工频周期内平均共模电压数值曲线如图7a所示,可知平均共模电压主要谐波分量为3次及其奇数倍次。

图7 平均共模电压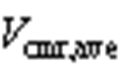 与零矢量分配系数
与零矢量分配系数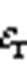 的关系
的关系
Fig.7 The changing relationship between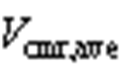 and
and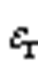
式(18)中,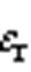 为可控变量,对其进行控制能改变平均共模电压,实现对共模电压中主要成分,即3次及9次谐波分量进行抑制,有效降低共模电压,从而抑制柔性潮流转供装置的共模电流。
为可控变量,对其进行控制能改变平均共模电压,实现对共模电压中主要成分,即3次及9次谐波分量进行抑制,有效降低共模电压,从而抑制柔性潮流转供装置的共模电流。
令式(18)中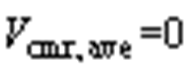 , 可得到零矢量分配系数
, 可得到零矢量分配系数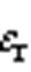 与
与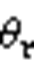 的代数关系,如式(19)所示。
的代数关系,如式(19)所示。
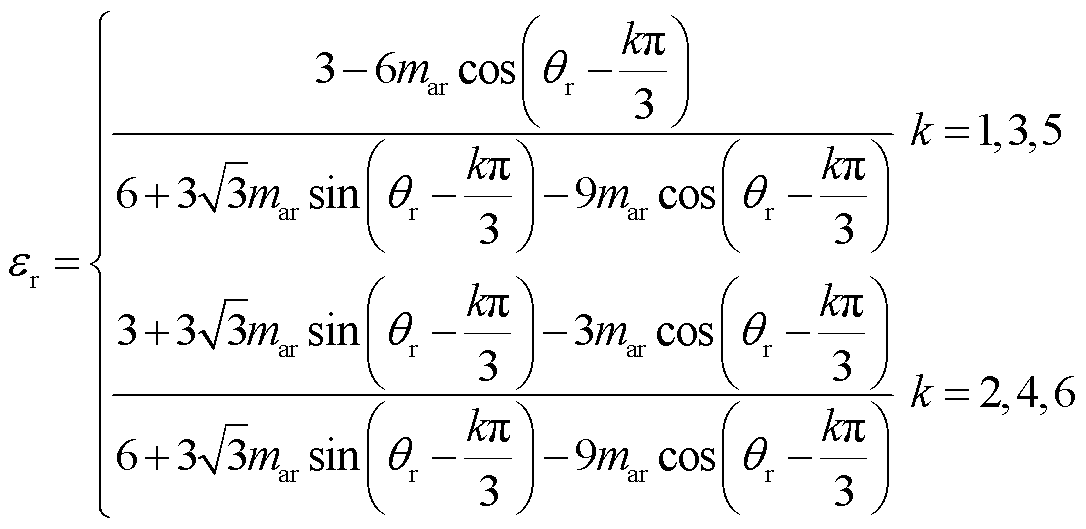 (19)
(19)
当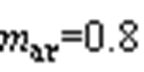 时,
时,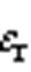 随
随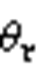 的变化如图8b所示。令平均共模电压为0,
的变化如图8b所示。令平均共模电压为0,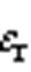 的变化趋势与平均共模电压变化趋势相反,且频率也为基波频率的3倍。图中发现
的变化趋势与平均共模电压变化趋势相反,且频率也为基波频率的3倍。图中发现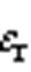 存在超出0~1的部分,为了解释这种现象,根据式(18)绘制
存在超出0~1的部分,为了解释这种现象,根据式(18)绘制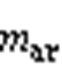 等于0.6与0.8情况下,
等于0.6与0.8情况下,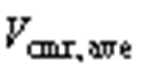 与
与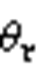 和
和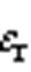 关系的三维曲面图及俯视图,如图8所示。
关系的三维曲面图及俯视图,如图8所示。


图8 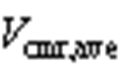 与
与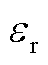 和
和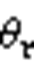 的关系
的关系
Fig.8 The relationship between 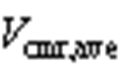 with
with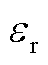 and
and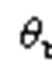
由图8可知,在一个工频周期中,只有部分平均共模电压值能够通过调节零矢量分配系数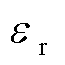 实现完全消除。当零矢量分配系数
实现完全消除。当零矢量分配系数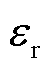 在0~1的范围内变化时,存在平均共模电压无法被完全消除的情况,需要通过两台变流器协调实现共模电流的充分抑制。
在0~1的范围内变化时,存在平均共模电压无法被完全消除的情况,需要通过两台变流器协调实现共模电流的充分抑制。
逆变侧分析与整流侧同理。为了充分抑制共模环流就需要双侧变流器的协调控制,通过合理调节两台变流器的零矢量分配系数,改变平均共模电压值,进而有效抑制共模电流。
在SVPWM调制中,仅有零矢量存在冗余度可进行自由调节,从而改变平均共模电压值。由2.1节可知,通过改变零矢量作用时间即改变零矢量分配系数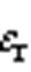 ,可改变平均共模电压值。
,可改变平均共模电压值。
根据上述分析,本文提出了基于开关周期平均共模电压3、9次谐波分量协调控制双侧变流器的零矢量分配系数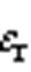 、
、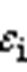 ,抑制共模电压中的主要分量,实现共模电流的抑制。因本方法直接对零矢量作用时间进行调节,对有效矢量无作用,实现了共模分量与差模分量调节之间的解耦控制,共模环流抑制不会对差模功率的控制产生影响。
,抑制共模电压中的主要分量,实现共模电流的抑制。因本方法直接对零矢量作用时间进行调节,对有效矢量无作用,实现了共模分量与差模分量调节之间的解耦控制,共模环流抑制不会对差模功率的控制产生影响。
本文所提的控制策略如图9所示。整流器采用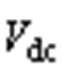 Q控制,逆变器采用定电流控制,经过闭环控制得到两侧在
Q控制,逆变器采用定电流控制,经过闭环控制得到两侧在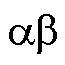 静止坐标系下的参考电压
静止坐标系下的参考电压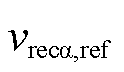 ,
,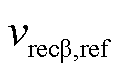 、
、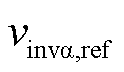 、
、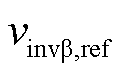 ,其中准比例谐振控制器传递函数GPRI(s)如式(20)所示。利用参考电压计算有效矢量与零矢量的作用时间。将作用时间与直流侧上下电容两端电压代入式(17)中,分别计算两侧变流器产生的平均共模电压,整流侧的平均共模电压与逆变侧的平均共模电压相减得到总平均共模电压
,其中准比例谐振控制器传递函数GPRI(s)如式(20)所示。利用参考电压计算有效矢量与零矢量的作用时间。将作用时间与直流侧上下电容两端电压代入式(17)中,分别计算两侧变流器产生的平均共模电压,整流侧的平均共模电压与逆变侧的平均共模电压相减得到总平均共模电压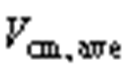 。
。

图9 系统总体控制框图
Fig.9 Control block diagram of the system
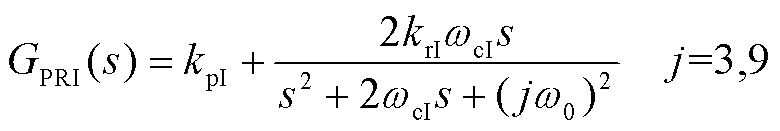 (20)
(20)
式中,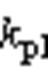 为电流环调节的PR控制器比例增益;
为电流环调节的PR控制器比例增益;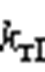 为谐振峰增益;
为谐振峰增益;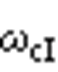 为带宽频率;
为带宽频率;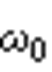 为基波角频率。
为基波角频率。
经过带通滤波器,提取平均共模电压的3次谐波分量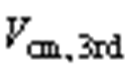 与9次分量
与9次分量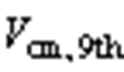 ,相加得到平均共模电压主要谐波分量
,相加得到平均共模电压主要谐波分量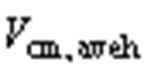 为
为
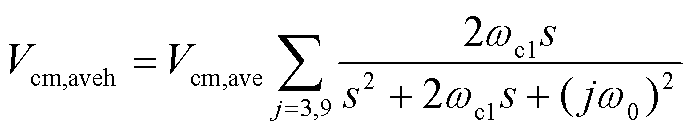 (21)
(21)
式中,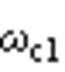 为带通滤波器的带宽频率。
为带通滤波器的带宽频率。
逆变侧变流器输出三相电流igai、igbi、igci采样后计算得到共模电流 ,与共模电流参考值比较,进行PR调节,作为平均共模电压参考值与平均共模电压的主要谐波成分进行比较,标幺化得到传统SVPWM基础上中间零矢量占空比的变化率
,与共模电流参考值比较,进行PR调节,作为平均共模电压参考值与平均共模电压的主要谐波成分进行比较,标幺化得到传统SVPWM基础上中间零矢量占空比的变化率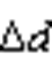 ,进而总零矢量分配系数
,进而总零矢量分配系数 表示为
表示为
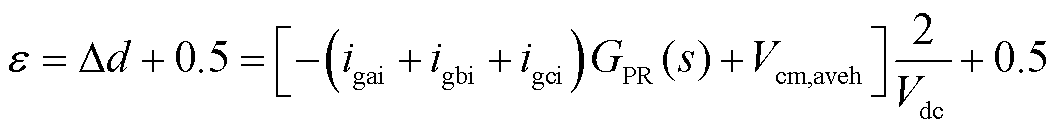 (22)
(22)
式中,GPR(s)为共模电流调节的准比例谐振控制器传递函数,即
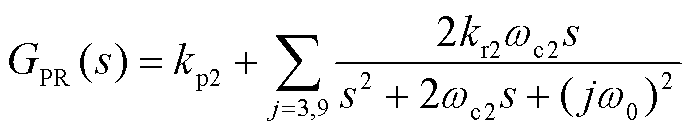 (23)
(23)
式中,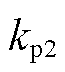 、
、 、
、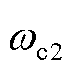 分别为共模电流调节PR控制器的比例增益、谐振峰增益和带宽频率。
分别为共模电流调节PR控制器的比例增益、谐振峰增益和带宽频率。
将整流侧平均共模电压完全抑制,通过式(19)计算整流侧零矢量分配系数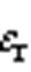 。利用其与总零矢量分配系数
。利用其与总零矢量分配系数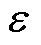 可以得到逆变侧的零矢量分配系数
可以得到逆变侧的零矢量分配系数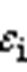 。通过零矢量分配系数
。通过零矢量分配系数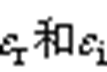 计算两变流器的两种零矢量作用时间,与原有的有效矢量作用时间合成新的调制波。
计算两变流器的两种零矢量作用时间,与原有的有效矢量作用时间合成新的调制波。
调制波与载波比较后生成驱动信号,控制潮流转供装置两变流器相应开关器件的动作,实现共模环流的直接闭环抑制。
通过本方法抑制共模电流,零矢量分配系数 (x=r,i分别代表整流侧、逆变侧)出现“越限”,会导致过调制或器件开通时间为负的错误情况。为防止这种现象出现,仅将调制波限制在0~1的范围内无法对共模环流进行充分抑制。为了解决这个问题,本文对零矢量分配系数进行协调限幅处理。
(x=r,i分别代表整流侧、逆变侧)出现“越限”,会导致过调制或器件开通时间为负的错误情况。为防止这种现象出现,仅将调制波限制在0~1的范围内无法对共模环流进行充分抑制。为了解决这个问题,本文对零矢量分配系数进行协调限幅处理。
根据式(1)中总共模电压与两侧变流器共模电压的关系,可以将一个变流器中“越限”的零矢量转移至另一变流器进行等效处理。如图10a所示,以逆变器参考电压矢量位于第Ⅰ扇区、整流器参考电压矢量位于第Ⅱ扇区为例,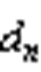 与
与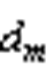 分别为逆变侧与整流侧三相驱动信号占空比,
分别为逆变侧与整流侧三相驱动信号占空比,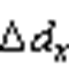 为根据零矢量分配系数计算得出的占空比变化量
为根据零矢量分配系数计算得出的占空比变化量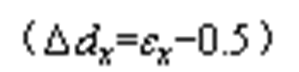 。当逆变器的零矢量分配系数
。当逆变器的零矢量分配系数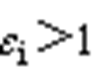 时,占空比最大相即图中u相的开关器件导通占空比
时,占空比最大相即图中u相的开关器件导通占空比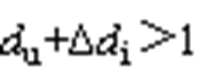 ,出现过调制。将逆变侧三相占空比同时减去其超出1的部分
,出现过调制。将逆变侧三相占空比同时减去其超出1的部分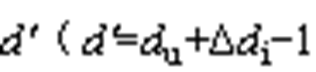 ),整流侧三相占空比也同时减
),整流侧三相占空比也同时减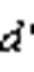 ,以保证式(1)中得到的共模电压值不变。
,以保证式(1)中得到的共模电压值不变。
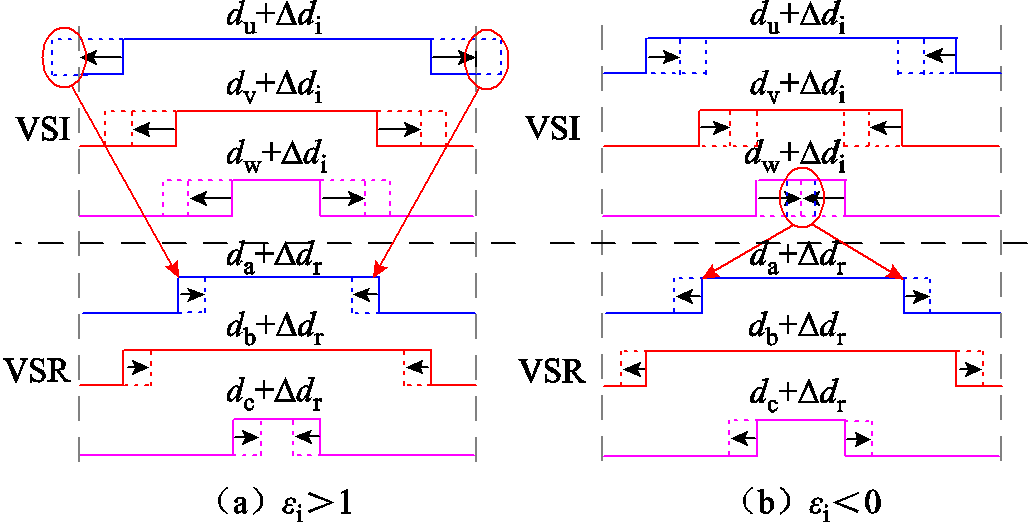
图10 协调限幅控制方案示意图
Fig.10 Schematic diagram of coordinated limiter control scheme
另一种情况如图10b所示,当逆变器的零矢量分配系数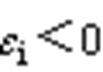 时,w相(占空比最小相)开关器件导通时间占空比
时,w相(占空比最小相)开关器件导通时间占空比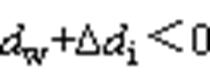 ,出现开通时间为负的错误情况。将逆变侧三相占空比同时减去小于0的部分
,出现开通时间为负的错误情况。将逆变侧三相占空比同时减去小于0的部分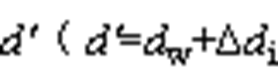 ),整流侧三相占空比也同时减
),整流侧三相占空比也同时减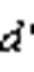 ,以保证式(1)中计算得到的共模电压值不变。
,以保证式(1)中计算得到的共模电压值不变。
整流侧在接收逆变侧“溢出”的占空比变化量后,出现类似“溢出”现象,仅进行0~1的限幅控制。协调限幅流程如图11所示,通过对零矢量分配系数进行协调,实现共模环流的充分抑制。
为了验证本文所提方案的有效性,进行了传统SVPWM、文献[15]所提方法与本文所提方法的对比实验,以及本文所提策略在差模分量动态工况下的实验,详细参数见表1,实验平台如图12所示。
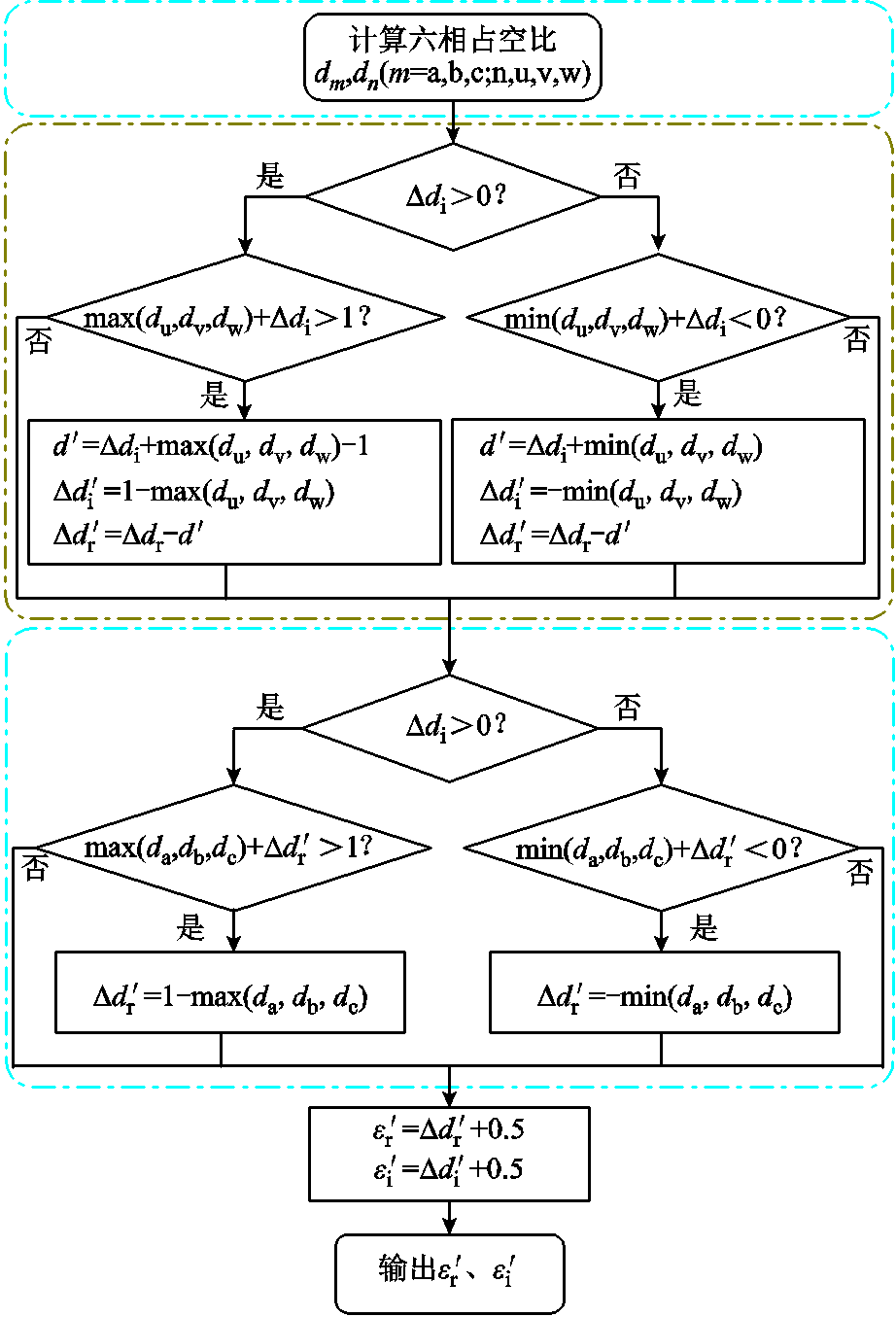
图11 零矢量分配系数限幅控制流程
Fig.11 Limiting control flow of zero vector distribution coefficient
表1 实验参数
Tab.1 The experimental parameters

主电路参数数值 系统交流侧交流电网线电压, , 400 V, 50 Hz 网侧滤波电感,/mH0.08 滤波电容,/μF150 变流器侧滤波电感, /mH0.4 滤波电容连接电阻R/Ω2 直流侧直流侧上、下电容/μF24 000 直流侧参考电压750 共模电感/mH5 变换器开关频率/Hz3 000 采样时间/ms0.1 控制参数带通滤波器带宽频率/(rad/s)10 基波角频率/(rad/s)2p×50 直流电压环PI调节器比例增益/(A/V)-20 积分增益/[A/(V∙s)]-500 电流环PR调节器比例增益/(V/A)0.25 谐振峰增益/(V/A)1 带宽频率/(rad/s)10 共模电流PR调节器比例增益/(V/A)10 谐振峰增益/(V/A)1 带宽频率/(rad/s)100

图12 实验平台
Fig.12 Experimental platform
为了使同一时间段内的共模电压峰值更加明显,本文在对比三种不同方法的共模电压峰值时将整流侧调制比固定不变,逆变侧调制比降低至0.6。图13分别为采用传统SVPWM、AZSPWM与本文所提方法的稳态共模电压瞬时值波形。由图13可知,传统SVPWM的共模电压峰值为500 V。采用AZSPWM方法时,共模电压峰值为250 V,该方法有效抑制了共模电压峰值。采用本文所提方法,共模电压峰值仍为500 V,本方法对共模电压峰值无抑制作用。
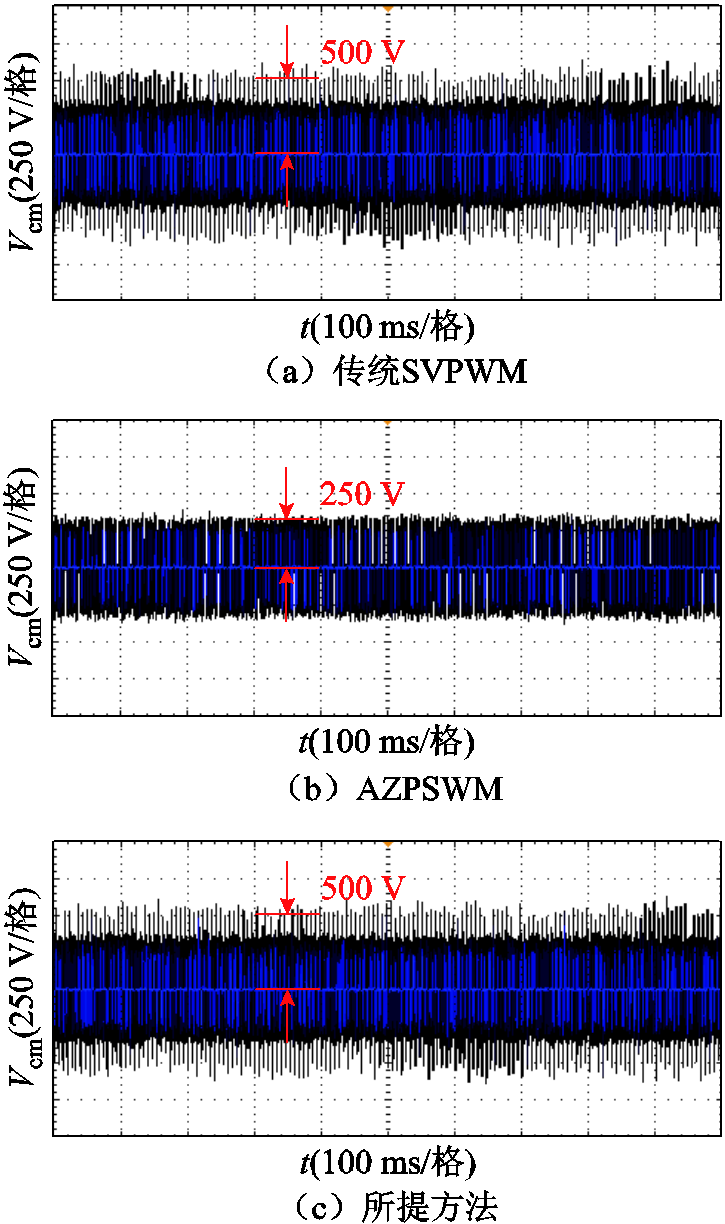
图13 不同调制方法共模电压瞬时值实验波形
Fig.13 The experimental waveform of 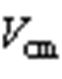 of different modulation methods
of different modulation methods
接下来在柔性潮流转供装置两端变流器调制比一致的条件下进行实验。传统SVPWM控制方法产生的波形如图14a所示,整流侧与逆变侧并网电流的总谐波畸变率(Total Harmonics Distortion, THD)分别为5.19%与4.3%,共模电流幅值为1.54 A,两侧平均共模电压均为91 V,系统总平均共模电压幅值为67.4 V。两侧零矢量分配系数均为七段法SVPWM调制时默认的数值0.5。
AZSPWM方法的波形如图14b所示,整流侧与逆变侧并网电流的THD分别增大至5.29%与4.67%,对平均共模电压、共模电流及零矢量分配系数的作用与传统SVPWM无明显差别。
本文所提方法的结果如图14c所示,采用基于平均共模电压直接调制的共模环流3、9次谐波直接闭环抑制,两侧零矢量分配系数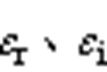 通过实时计算,并且满足协调限幅要求,实现系统总共模电流最小。平均共模电压降低至22 V,共模电流幅值降低至0.4 A。共模电流相比传统SVPWM与AZSPWM方法降低了74%。并且通过抑制系统共模电流,系统两侧的并网电流THD得到改善,分别降低至3.93%、3.37%。
通过实时计算,并且满足协调限幅要求,实现系统总共模电流最小。平均共模电压降低至22 V,共模电流幅值降低至0.4 A。共模电流相比传统SVPWM与AZSPWM方法降低了74%。并且通过抑制系统共模电流,系统两侧的并网电流THD得到改善,分别降低至3.93%、3.37%。


图14 传统SVPWM调制、AZSPWM调制与本文所提方法对比实验波形
Fig.14 The comparison of experimental waveforms between traditional methods and this method
AZSPWM方法采用动态零矢量代替零矢量,有效降低了共模电压峰值,但并未降低共模电压中的主要分量,对平均共模电压与共模电流无作用,并且由于采用相邻有效矢量代替零矢量,增加了并网电流THD。本文所提方法没有降低共模电压幅值,但是通过抑制共模电压中的主要谐波分量,抑制了平均共模电压以及共模电流值,从而降低了并网电流THD。
对传统方法与本文所提方法的共模电压和共模电流THD进行分析,如图15所示。采用本文所提调制方法,对共模电流3、9次谐波进行直接闭环抑制,共模电压中的3、9次谐波分量被抑制,共模电流中的3次谐波和9次谐波分量也随之降低。
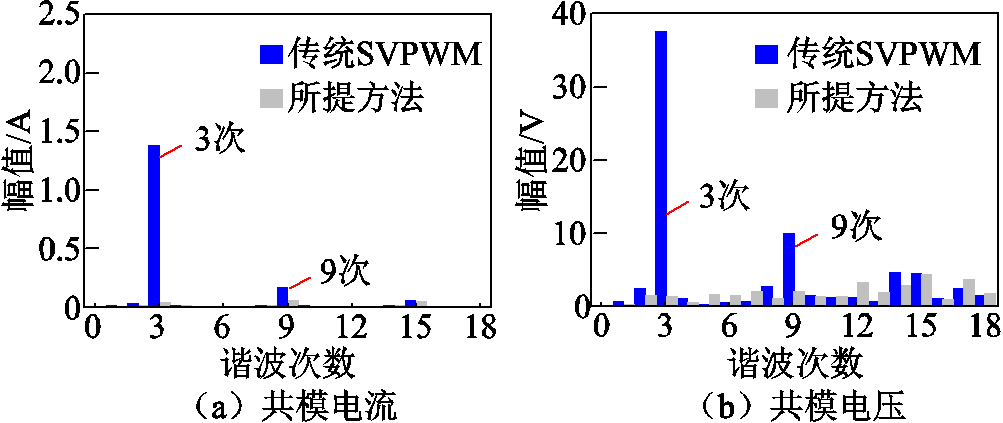
图15 共模电流、共模电压THD图对比
Fig.15 Comparison of THD of common mode current and common mode voltage
为了检验共模电流抑制策略在差模分量动态时的解耦控制性能,分别进行了逆变侧交流电压降低、转供功率降低、直流侧电压降低工况下的实验,如图16所示。

图16 系统暂态的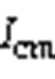 抑制效果
抑制效果
Fig.16 The diagram of 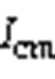 suppression effect when the state of system changes
suppression effect when the state of system changes
1)逆变侧交流电压由220 V降低至141 V,实验结果如图16a所示,由于逆变侧采用定电流控制,整流侧电流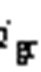 幅值降低,逆变侧电流
幅值降低,逆变侧电流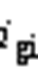 幅值经过短暂动态过程恢复到原值,共模电流幅值略有增加。实验结果表明,本文所提方法在交流电压变化时可稳定运行。
幅值经过短暂动态过程恢复到原值,共模电流幅值略有增加。实验结果表明,本文所提方法在交流电压变化时可稳定运行。
2)潮流转供装置转供的有功功率从66 kW降低至33 kW,实验结果如图16b所示。经过1~2个工频周期的动态过程,整流侧电流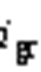 与逆变侧电流
与逆变侧电流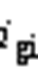 幅值均降低并达到稳定值,共模电流无明显变化。实验结果表明,转供功率变化不影响共模电流抑制效果。
幅值均降低并达到稳定值,共模电流无明显变化。实验结果表明,转供功率变化不影响共模电流抑制效果。
3)直流侧电压幅值从750 V降低至700 V,实验结果如图16c所示。当直流侧电压降低至700 V时,整流侧电流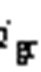 、逆变侧电流
、逆变侧电流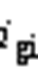 与共模电流恢复稳定值。实验结果表明,直流侧电压动态变化直至恢复稳定,共模电流抑制效果也随之恢复。
与共模电流恢复稳定值。实验结果表明,直流侧电压动态变化直至恢复稳定,共模电流抑制效果也随之恢复。
本文针对非隔离型低压柔性潮流转供装置的共模环流问题,提出了一种基于开关周期平均共模电压直接调制的指定次共模环流闭环抑制策略。通过理论分析与实验验证,得出如下结论:
1)揭示了开关周期平均共模电压与共模环流之间的联系,指出了传统共模电压峰值抑制方法对共模环流抑制的局限性。
2)明确了平均共模电压中的3、9次分量是造成共模环流的主要原因,提出了一种基于3、9次共模环流闭环调节的共模电流高效抑制策略。
3)分析和验证了所提出的共模环流抑制策略与系统中差模电流和功率调节的高度解耦特性,实现了功率和交直流电压动态调节过程中的暂态共模环流抑制。
本文所提方法不仅适用于二端口非隔离型柔性潮流转供装置,通过端口间开关周期共模电压协同,共模环流抑制策略也可应用于多端口柔性潮流转供装置中。
由于篇幅所限,本文仅考虑三相三线制柔性潮流转供系统,对于具有高灵活性和多功能的三相四线制柔性潮流转供系统,其共模环路和共模电流流通机理与本文所分析系统存在一定的差异。以滤波电容中性点与网侧中性点接中性线为例,三相四线制柔性潮流转供装置示意图如图17所示,图18为其对应的共模回路模型。作者将在今后的研究工作中对其进行进一步分析。
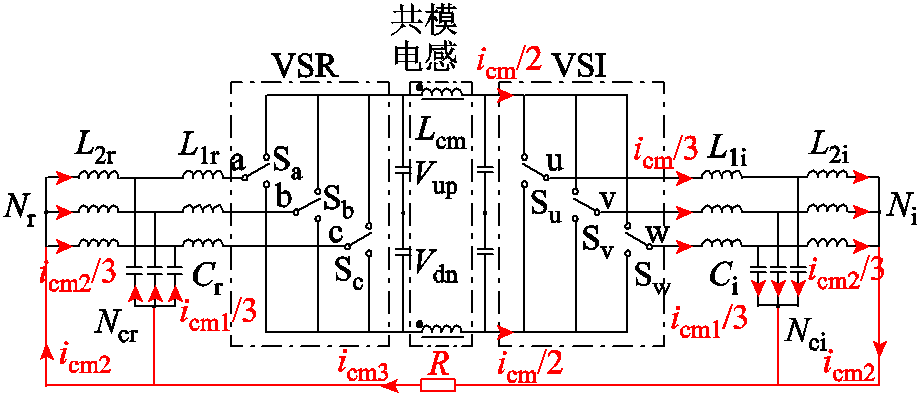
图17 三相四线制柔性潮流转供装置
Fig.17 Three-phase four-wire flexible power flow controller
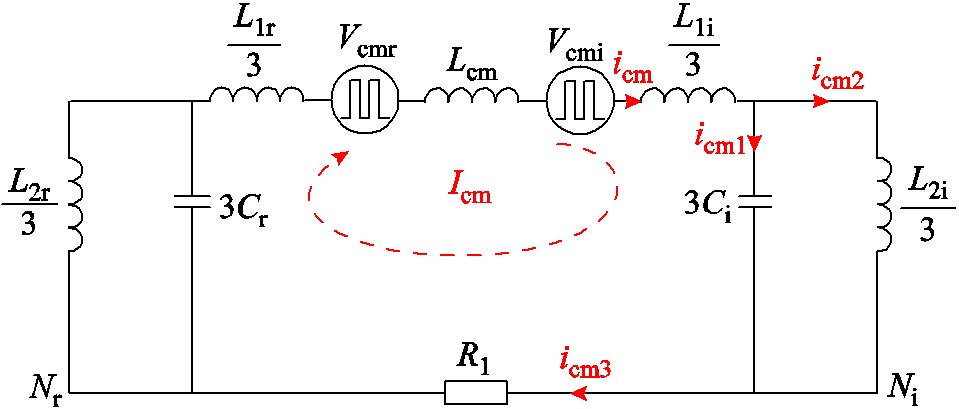
图18 三相四线制柔性潮流转供装置共模模型
Fig.18 Common-mode loop model of three-phase four-wire flexible power flow controller
参考文献
[1] 张尧翔, 刘文颖, 庞清仑, 等. 高比例风电接入系统光热发电-火电旋转备用优化方法[J]. 电工技术学报, 2022, 37(21): 5478-5489.
Zhang Yaoxiang, Liu Wenying, Pang Qinglun, et al. Optimal power spinning reserve method of concentrating solar power and thermal power for high-proportion wind power system[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5478-5489.
[2] 颜湘武, 郭燕, 彭维锋, 等. 基于旋转移相变压器的电压源型无功补偿器及其控制策略[J]. 电工技术学报, 2023, 38(16): 4448-4464.
Yan Xiangwu, Guo Yan, Peng Weifeng, et al. Voltage source var compensator based on rotary phase shifting transformer and its control strategy[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4448-4464.
[3] 王成山, 季节, 冀浩然, 等. 配电系统智能软开关技术及应用[J]. 电力系统自动化, 2022, 46(4): 1-14.
Wang Chengshan, Ji Jie, Ji Haoran, et al. Technologies and application of soft open points in distribution networks[J]. Automation of Electric Power Systems, 2022, 46(4): 1-14.
[4] 徐玉韬, 冯起辉, 谈竹奎, 等. 考虑转供与重构协同的多端柔性互联配电网供电恢复策略[J]. 电工技术学报, 2024, 39(9): 2696-2709.
Xu Yutao, Feng Qihui, Tan Zhukui, et al. Optimal power restoration strategy for multi-terminal flexible interconnected distribution networks based on flexible interconnection device and network reconfiguration [J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2696-2709.
[5] 周剑桥, 张建文, 席东民, 等. 基于SOP有功-无功协同的低压配电网末端电压越限治理[J]. 电力系统自动化, 2023, 47(6): 110-122.
Zhou Jianqiao, Zhang Jianwen, Xi Dongmin, et al. Terminal voltage overlimit mitigation for low-voltage distribution network based on coordinated active and reactive power control of soft open point[J]. Automation of Electric Power Systems, 2023, 47(6): 110-122.
[6] 沙广林, 刘斌, 邬玮晗, 等. 多端柔性互联的交直流配电系统分层控制策略[J]. 高电压技术, 2020, 46(10): 3509-3520.
Sha Guanglin, Liu Bin, Wu Weihan, et al. Hierarchical control strategy for multi-terminal flexible inter-connected AC/DC power distribution systems[J]. High Voltage Engineering, 2020, 46(10): 3509-3520.
[7] 王成山, 宋关羽, 李鹏, 等. 基于智能软开关的智能配电网柔性互联技术及展望[J]. 电力系统自动化, 2016, 40(22): 168-175.
Wang Chengshan, Song Guanyu, Li Peng, et al. Research and prospect for soft open point based flexible interconnection technology for smart distribution network[J]. Automation of Electric Power Systems, 2016, 40(22): 168-175.
[8] 杨欢, 蔡云旖, 屈子森, 等. 配电网柔性开关设备关键技术及其发展趋势[J]. 电力系统自动化, 2018, 42(7): 153-165.
Yang Huan, Cai Yunyi, Qu Zisen, et al. Key techniques and development trend of soft open point for distribution network[J]. Automation of Electric Power Systems, 2018, 42(7): 153-165.
[9] 肖华锋, 王晓标, 张兴, 等. 非隔离光伏并网逆变技术的现状与展望[J]. 中国电机工程学报, 2020, 40(4): 1038-1054.
Xiao Huafeng, Wang Xiaobiao, Zhang Xing, et al. State-of-the-art and future trend of transformerless photovoltaic grid-connected inverters[J]. Proceedings of the CSEE, 2020, 40(4): 1038-1054.
[10] Orfanoudakis G I, Koutroulis E, Sharkh S M, et al. An extended boost three-phase transformerless PV inverter for common-mode leakage current reduction[J]. IEEE Transactions on Industry Applications, 2024, 60(1): 838-850.
[11] 胡存刚, 胡军, 陈权, 等. 基于特定谐波消除PWM的三电平有源中点钳位逆变器共模电压抑制方法[J]. 电工技术学报, 2016, 31(16): 93-102.
Hu Cungang, Hu Jun, Chen Quan, et al. Suppression method of common-mode voltage for three-level active neutral-point-clamped inverter based on selective harmonics elimination PWM[J]. Transactions of China Electrotechnical Society, 2016, 31(16): 93-102.
[12] 郭磊磊, 金楠, 李琰琰, 等. 电压源逆变器虚拟矢量模型预测共模电压抑制方法[J]. 电工技术学报, 2020, 35(4): 839-849.
Guo Leilei, Jin Nan, Li Yanyan, et al. Virtual vector based model predictive common-mode voltage reductionmethod for voltage source inverters[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 839-849.
[13] Jayaraman K, Kumar M. Design of passive common-mode attenuation methods for inverter-fed induction motor drive with reduced common-mode voltage PWM technique[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 2861-2870.
[14] Son Y C, Sul S K. A new active common-mode EMI filter for PWM inverter[J]. IEEE Transactions on Power Electronics, 2003, 18(6): 1309-1314.
[15] Hava A M, Ün E. Performance analysis of reduced common-mode voltage PWM methods and comparison with standard PWM methods for three-phase voltage-source inverters[J]. IEEE Transactions on Power Electronics, 2009, 24(1): 241-252.
[16] 徐晓娜, 王奎, 李永东. 基于调制波分解的背靠背三电平变换器共模电压消除方法[J]. 中国电机工程学报, 2022, 42(8): 2957-2968.
Xu Xiaona, Wang Kui, Li Yongdong. A common-mode voltage elimination method based on modulation signal decomposition for the back-to-back three-level converter[J]. Proceedings of the CSEE, 2022, 42(8): 2957-2968.
[17] Jayaraman K, Kumar M. Design of passive common-mode attenuation methods for inverter-fed induction motor drive with reduced common-mode voltage PWM technique[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 2861-2870.
[18] 蒋栋. 电力电子变换器的先进脉宽调制技术[M]. 北京: 机械工业出版社, 2018.
[19] Lian Yujuan, Zhang Ye, Yun Wei li, et al. Common-mode resonance suppression in transformerless PWM current-source drive[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5721-5731.
[20] 薛永端, 郭丽伟, 张林利, 等. 有源配电网中性点接地方式的选择问题[J]. 电力系统自动化, 2015, 39(13): 129-136.
Xue Yongduan, Guo Liwei, Zhang Linli, et al. Selection problems of neutral grounding mode in active distribution networks[J]. Automation of Electric Power Systems, 2015, 39(13): 129-136.
[21] 郭小强, 朱铁影, 魏宝泽, 等. 飞跨电容多电平光伏逆变器共模电流抑制技术[J]. 中国电机工程学报, 2016, 36(18): 4962-4969.
Guo Xiaoqiang, Zhu Tieying, Wei Baoze, et al. Common mode current suppression technique for flying capacitor multilevel PV inverter[J]. Proceedings of the CSEE, 2016, 36(18): 4962-4969.
[22] 杨贵杰, 孙力, 崔乃政, 等. 空间矢量脉宽调制方法的研究[J]. 中国电机工程学报, 2001, 21(5): 79-83.
Yang Guijie, Sun Li, Cui Naizheng, et al. Study on method of the space vector pwm[J]. Proceedings of the CSEE, 2001, 21(5): 79-83.
[23] Bowes S R, Lai Y S. The relationship between space-vector modulation and regular-sampled PWM[J]. IEEE Transactions on Industrial Electronics, 1997, 44(5): 670-679.
Direct Common-Mode Current Closed-Loop Suppression Strategy for Non-Isolated Low-Voltage Flexible Power Flow Controller
Abstract With the continuous improvement of the penetration rate of distributed new energy power generation in distribution grids, there are a series of problems such as disordered distribution of current, reverse heavy overload of lines, and increased voltage fluctuations, which seriously affect the stability and safety of distributed new energy power generation and distribution grids. The flexible power flow controller has the excellent characteristics of two-way controllable energy and continuous current adjustment. In addition, it also has auxiliary functions such as direct access to distributed energy storage and active power quality adjustment.
Since the pulse width modulation (PWM) technology used in the converter will cause common-mode voltage (CMV). The CMVwill cause adversely affect to the system innon-isolation transformer. The common-mode current (CMC) will produce in the common-mode loop which make the harmonic distortion rate on the AC side increase and protection act incorrectly, and affect the normal operation of the system.
In order to solve this problem, a closed-loop suppression strategy for specified harmonics of CMC based on direct modulation of average common-mode voltage (AVE CMV) was proposed. An accurate common-mode circuit modelof non-isolated low-voltage flexible power flow controller was established to analyze the impedance characteristics and the dominant characteristics of CMC. The mathematical relationship between the AVE CMV and the CMC in a switching cycle was constructed and the correlation between the AVE CMV and the CMC during a switching cycle was revealed. Then, the precise adjustment of AVE CMV was realized through the coordinated distribution of the two-sided converter’s zero vector, and then an efficient decoupling method of direct regulation of the AVE CMV and space vector pulse width modulation was proposed, which realized the closed-loop suppression of the specified CMC without affecting the dynamic regulation of the differential-mode current. Finally, the feasibility and effectiveness of this method were verified through experiments.
The following conclusions can be draw from the analysis: (1) The connection between the AVE CMV of a switching cycle and the CMC is revealed, and the limitations of the traditional common-mode voltage peak suppression method on the CMC suppression are pointed out. (2) It is clarified that the third and ninth harmonic components of the AVE CMV are the main cause of CMC.ACMC efficient suppression strategy based on closed-loop regulation of the third and ninth CMC is proposed.It is pointed out that the adjustment of the AVE CMV in a switching cycle can be achieved by adjusting the action time of the zero vector, and then the suppression of the overall CMC can be achieved by coordinated control of the action time of the different zero vectors of the two converters. (3) The proposed CMC suppression strategy and the highly decoupled characteristics of differential-mode current and power regulation in the system are analyzed and verified.The transient CMC suppression in the dynamic adjustment process of power and AC and DC voltage is realized.The method proposed can be applied to not only a two-port non-isolated flexible power flow controller, but also a multi-port flexible power flowcontroller through the AVE CMV synergy of the switching cycle between the ports.
Keywords:Average common-mode voltage (AVE CMV), common mode current (CMC) suppression, common mode loop, third harmonic, zero vector
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.231988
国家自然科学基金资助项目(52077152)。
收稿日期 2023-11-27
改稿日期 2024-04-11
曹晓军 男,1999年生,硕士研究生,研究方向为配电网柔性潮流转供装置灵活控制技术。
E-mail:caoxiaojun@tju.edu.cn
何晋伟 男,1983年生,教授,博士生导师,研究方向为微电网和分布式发电、电能质量、大功率电力电子变流器技术。
E-mail:jinwei.he@tju.edu.cn(通信作者)
(编辑 郭丽军)