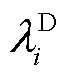 为停电事故发生前节点i上负荷功率需求,
为停电事故发生前节点i上负荷功率需求,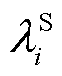 为节点i恢复供电时负荷功率需求,
为节点i恢复供电时负荷功率需求,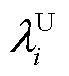 为节点i上负荷在冷负荷启动过程中的负载峰值。假设配电网在t0时刻发生停电故障,节点i上负荷失去供电。当节点i在t2时刻恢复供电,由于温控负荷同时投运,该节点上出现负荷需求量激增,并在t3时刻达到峰值功率。当第一个温控负荷在t3时刻回到预设温度时,节点i上负荷需求量开始下降,并在t4时刻回到正常运行水平。
为节点i上负荷在冷负荷启动过程中的负载峰值。假设配电网在t0时刻发生停电故障,节点i上负荷失去供电。当节点i在t2时刻恢复供电,由于温控负荷同时投运,该节点上出现负荷需求量激增,并在t3时刻达到峰值功率。当第一个温控负荷在t3时刻回到预设温度时,节点i上负荷需求量开始下降,并在t4时刻回到正常运行水平。摘要 极端灾害事件引发配电网停电后,利用分布式电源构建孤岛微电网恢复重要负荷供电,能有效提升配电网弹性。现有研究在制定配电网供电恢复策略时大都采用恒定负载模型,未考虑冷负荷启动时负载峰值引起的三相电流不平衡,无法保证孤岛微电网的安全运行。该文提出一种计及冷负荷启动时变特性的弹性配电网供电恢复方法。首先,考虑冷负荷启动特性与停电时间之间的关系,建立与时间相关的冷负荷启动模型,并通过采样法生成负荷功率需求曲线;其次,以加权负荷恢复量最大为目标,考虑微电网功率平衡、电流不平衡度等约束,建立协同区域划分、恢复路径和负荷投运时序的配电网供电恢复模型;再次,对模型进行线性化处理,将其转换为混合整数规划问题进行求解;最后,采用IEEE 37节点配电系统,对所提方法的有效性进行验证。
关键词:弹性配电网 供电恢复 微电网 电流不平衡度 冷负荷启动
全球气候变化导致自然灾害频发,对电力系统高安全、高可靠运行提出空前挑战[1]。由于配电网设计强度较低,自然灾害会导致配电网中发生大量群发性物理故障,进而引发用户停电,造成严重的经济损失和社会影响。为应对极端事件对电网安全的威胁,学术界、工业界共同提出电力系统弹性的概念[2],被普遍定义为“电网预防和适应环境变化、承受扰动及快速恢复的能力”。随着分布式能源大规模接入配电网,为实现配电网灾后弹性运行奠定了基础[3]。在未发生故障的区域,利用分布式电源构建孤岛微电网[4],对重要负荷进行供电恢复,能有效减小停电规模、缩短停电时间[5-6]。
近年来,有学者开始关注基于孤岛微电网的供电恢复方法。根据建模差异,配电网供电恢复策略主要分为两大类:两阶段供电恢复[7-8]和单阶段供电恢复[9-14]。前者对系统拓扑及操作顺序解耦进行优化,即在确定目标微电网结构后,生成可行的开关操作次序;后者将两者进行耦合,对微电网拓扑和开关动作次序同时进行决策。相比于两阶段决策方法,单阶段决策方法能实现供电恢复方案的全局最优。文献[9]提出一种考虑多源协同的供电恢复方法,以实现多个微网的并行恢复。文献[10-11]和文献[14]分别采用随机规划和鲁棒优化处理供电恢复过程中的源荷不确定性。文献[13]提出基于暂态仿真的供电恢复决策方法,以保证负荷投运时微网频率安全。文献[14]提出考虑微电网互连的供电恢复方法,在保证微电网频率安全的前提下加快恢复速率。
上述研究均假设配电网三相平衡,从而采用单相等效模型进行分析。然而,大量单相负荷会导致配电网中三相不平衡特点显著,上述假设难以成立。文献[15]对配电网中供电恢复路径及负荷的投运时序进行了优化。文献[16]提出考虑开关操作特性的三相配电网供电恢复方法。然而,文献[15-16]的不足之处在于未考虑供电恢复过程中的电流不平衡度。配电网中三相负载不平衡会导致电流不平衡,当三相同步电源的电流不平衡度达到阈值以上时,会造成分布式电源跳闸脱网[17]。为了保证微电网的安全运行,在制定供电恢复策略时需要对电流不平衡度进行限制。文献[18]-[20]基于配电网三相潮流模型,构建了分布式电源的三相电流不平衡度约束,以保证恢复过程中微电网的安全运行。
上述文献在制定配电网供电恢复方案时均采用静态负荷模型,未考虑温控负荷冷启动过程中的负荷特性。在城市配电网中,以空调为代表的温控负荷占比逐年增加。据统计,空调负荷在高峰时段占比达到30%~40%,且极端天气条件下温控负荷占比将进一步提高[21]-[22]。然而,温控负荷在投运后的短时间内会出现负荷量激增,负载峰值会影响供电恢复过程中配电网的安全性[23]。文献[24]指出,忽略温控负荷的冷启动特性会导致恢复过程中电源容量、电压、电流等运行约束越限。已有文献对考虑温控负荷冷启动的配电网供电恢复策略进行了研究。文献[25]采用延迟指数模型刻画冷负荷的启动特性,在此基础上建立配电网供电恢复多时步优化模型。但忽略停电时间对冷负荷启动特性的影响,预测误差较大的负载峰值会导致恢复方案过于保守。文献[26-27]基于采样法研究了负载峰值、峰值持续时间与负荷停电时间之间的关系。在此基础上,文献[28]提出了考虑时间效益的冷负荷启动模型,降低了恢复策略的保守性。
目前计及冷负荷启动特性的供电恢复研究主要针对三相平衡配电网,鲜有对考虑冷负荷启动的三相不平衡配电网供电恢复问题开展研究。冷负荷启动时存在较大的负载峰值,会加剧配电网中的三相电流不平衡度。考虑冷负荷启动特性受停电时长的影响,如何协同区域划分、恢复路径和负荷投运时序,在保证微电网安全运行的同时加快负荷恢复速率,是制定三相配电网供电恢复方案时的难点问题。
本文提出了一种计及冷负荷启动时变特性的弹性配电网供电恢复方法。首先,为了准确解析温控负荷投运后的功率需求,建立基于停电时长的冷负荷启动模型,通过采样法拟合冷负荷功率需求曲线;然后,考虑负载峰值对电流不平衡度的影响,建立三相配电网供电恢复模型,实现区域划分、恢复路径和负荷投运时序的协同优化,并基于多种线性化手段,将模型转换为混合整数线性规划问题;最后,基于IEEE 37节点配电网的仿真算例,论证本文所提方法在提升恢复效率和微电网安全性方面的优势。
参与供电恢复的负荷可分为固定负荷和温控负荷两类。其中,固定负荷的负荷需求在停电前后变化不大,而温控负荷由于负荷多样性的丧失,在供电恢复后会出现负荷需求量激增及波动的情况,这一过程称为冷负荷启动。冷负荷启动过程通常持续几分钟甚至数小时,并在恢复初期出现2~5倍的负载峰值[27]。在城市配电网中,冰箱、加热器等负荷是温控负荷的重要部分,本文采用此类负载代表温控负荷进行研究。
冷负荷启动过程中的功率需求曲线如图1所示。图1中,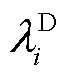 为停电事故发生前节点i上负荷功率需求,
为停电事故发生前节点i上负荷功率需求,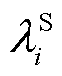 为节点i恢复供电时负荷功率需求,
为节点i恢复供电时负荷功率需求,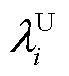 为节点i上负荷在冷负荷启动过程中的负载峰值。假设配电网在t0时刻发生停电故障,节点i上负荷失去供电。当节点i在t2时刻恢复供电,由于温控负荷同时投运,该节点上出现负荷需求量激增,并在t3时刻达到峰值功率。当第一个温控负荷在t3时刻回到预设温度时,节点i上负荷需求量开始下降,并在t4时刻回到正常运行水平。
为节点i上负荷在冷负荷启动过程中的负载峰值。假设配电网在t0时刻发生停电故障,节点i上负荷失去供电。当节点i在t2时刻恢复供电,由于温控负荷同时投运,该节点上出现负荷需求量激增,并在t3时刻达到峰值功率。当第一个温控负荷在t3时刻回到预设温度时,节点i上负荷需求量开始下降,并在t4时刻回到正常运行水平。
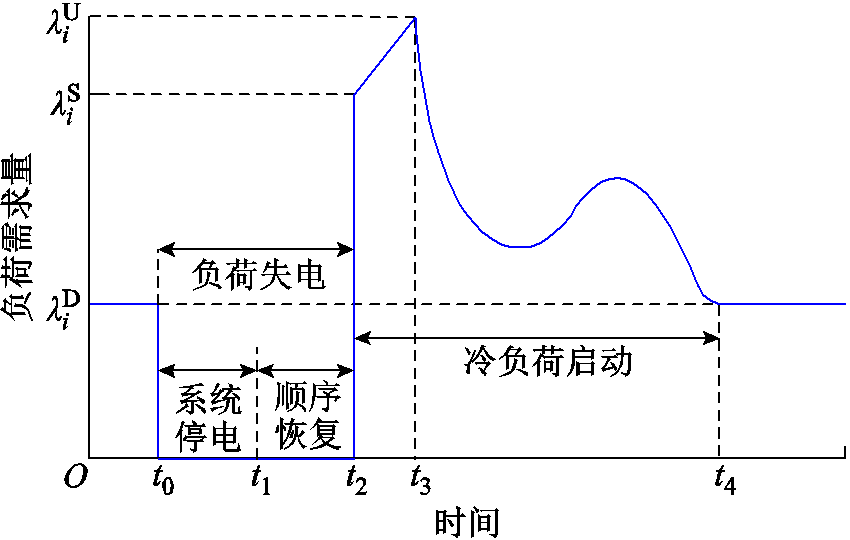
图1 冷负荷启动过程中功率需求曲线
Fig.1 Load demand curve during the CLPU process
随着停电时间的延长,节点上负荷多样性逐渐丧失。因此,冷负荷启动峰值功率和持续时间受停电时间的影响。不同停电时间下冷负荷启动的功率曲线如图2所示。相较于绿色实线,红色虚线对应的负载峰值更高,且冷负荷启动过程持续时间更长。当停电时间较长导致负荷多样性完全丧失时,冷负荷启动特性如蓝色点画线所示。因此,在制定恢复策略时,需要考虑停电时间对冷负荷启动特性建模的影响,在保证微电网安全运行的前提下,降低恢复方案的保守性。

图2 不同停电时间下的冷负荷启动功率曲线
Fig.2 CLPU profiles with different outage durations
在制定配电网供电恢复方案时,需要事先对冷负荷启动时变特性进行建模。首先,收集冷负荷启动历史数据,评估不同停电时间下的负载峰值、持续时间等参数,拟合生成冷负荷启动曲线。根据图1所示的功率需求曲线,冷负荷启动过程中的有功功率需求为
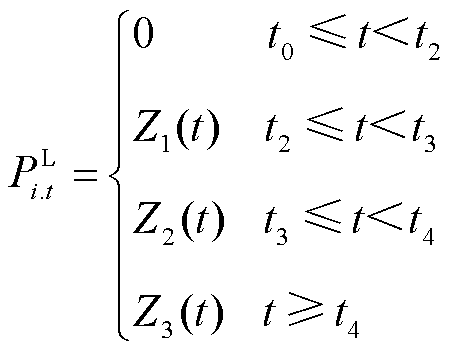 (1)
(1)
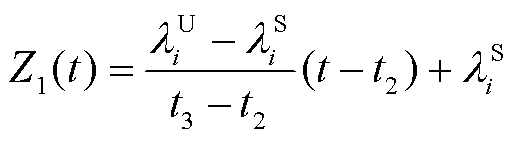 (2)
(2)
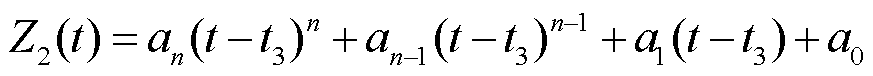 (3)
(3)
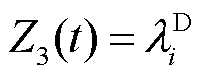 (4)
(4)
式中,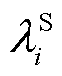 、
、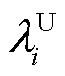 、t3和t4取决于停电时间t2,而t2取决于配电网恢复速率。
、t3和t4取决于停电时间t2,而t2取决于配电网恢复速率。
上述冷负荷启动模型为高阶非线性模型,导致模型难以求解。为此,根据采样法[24]对负荷功率需求曲线进行采样,生成各时刻负荷的功率需求。本文假设在采样间隔内负荷需求量保持不变,预测的负荷需求量可为配电网恢复决策提供参数支撑。
当配电网发生停电事故时,主要目标是尽快恢复重要负荷供电。本文以加权负荷恢复量最大为目标,建立目标函数为
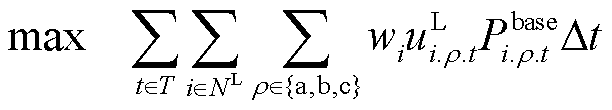 (5)
(5)
式中,NL为配电网中连有负荷的节点集合;T为恢复过程决策时步集合;wi为节点i的权重系数;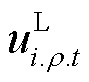 为节点i上ρ相负荷t时步的投运状态;
为节点i上ρ相负荷t时步的投运状态;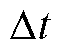 为供电恢复模型中一个时步持续时间;
为供电恢复模型中一个时步持续时间;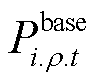 为第t时步节点i上ρ相负荷的有功需求量基准值。尽管温控负荷投运时功率需求量远大于基准值,但对供电恢复策略而言,其有效性仍通过配电网正常运行负荷需求量衡量,因此在目标函数中按照节点负荷基准值
为第t时步节点i上ρ相负荷的有功需求量基准值。尽管温控负荷投运时功率需求量远大于基准值,但对供电恢复策略而言,其有效性仍通过配电网正常运行负荷需求量衡量,因此在目标函数中按照节点负荷基准值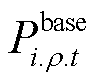 进行计算。
进行计算。
2.2.1 微网拓扑约束
参考文献[15],本文通过引入恢复路径表对供电恢复过程中的微电网拓扑进行建模。在一个含有nc个节点的配电网中(nc=|N|),恢复路径表为一个nc×nc的0-1矩阵,对角线元素xii用于表示节点i上是否连接黑启动电源;非对角线元素xij表示系统中的恢复路径,xij=1表示供电路径从节点i“离开”并“抵达”节点j。
以图3a所示的拓扑结构为例,对基于恢复路径表的微电网拓扑决策方法进行阐述。假定优化的恢复路径表如3b所示。其中x11=x77=1表示节点1和节点7上连有黑启动电源,可作为两个微电网中恢复路径的起点。以x12=1为例,表示供电路径从节点1出发抵达节点2。通过优化决策恢复路径表,可以在得到微电网中恢复路径的同时,生成优化的区域划分方案。
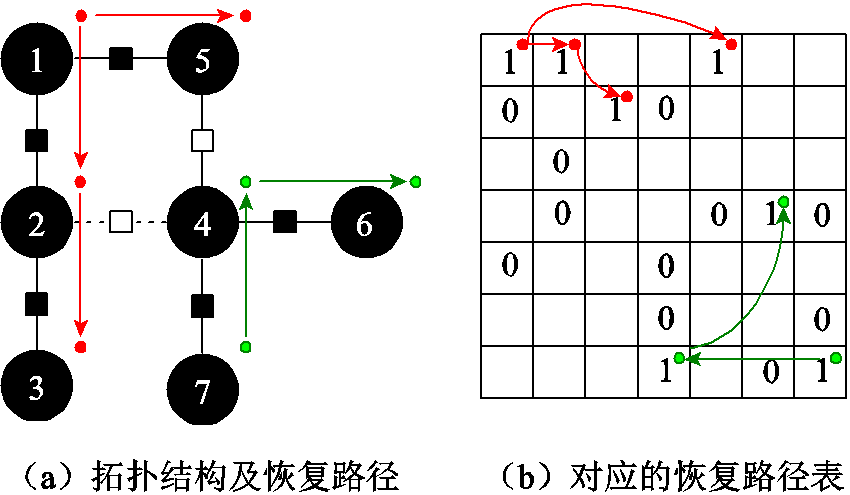
图3 恢复路径决策示意图
Fig.3 An example of restoration route table decision
为了保证恢复过程中微网的辐射状结构,在决策恢复路径时应满足
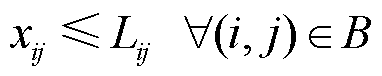 (6)
(6)
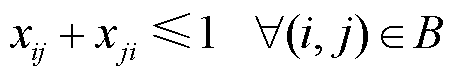 (7)
(7)
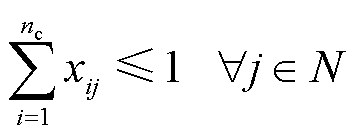 (8)
(8)
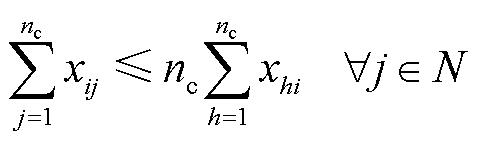 (9)
(9)
式中,N为节点集合;B为线路集合;Lij为节点i和节点j之间的线路连通情况,当节点i和节点j之间存在连通路径时,Lij=1;反之,Lij=0。式(6)表示供电路径生成的条件是两节点间存在连通路径;式(7)表示两节点间供电路径需为单向流通;式(8)表示一个节点最多可通过一条恢复路径进行恢复;式(9)表示恢复路径抵达节点i的前提是该路径可抵达其上游节点h。
2.2.2 供电状态约束
线路恢复前需要进行充电操作。首先通过引入路径时间表表示节点间线路的充电时间,并通过以下不等式计算恢复路径抵达各节点的时刻ti。
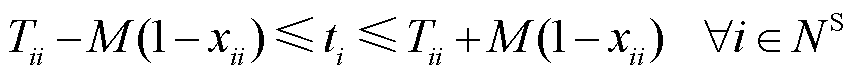 (10)
(10)
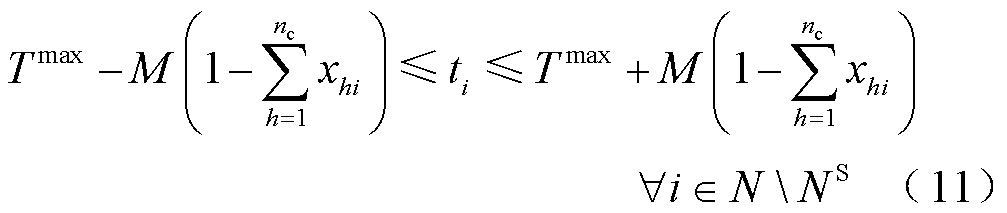
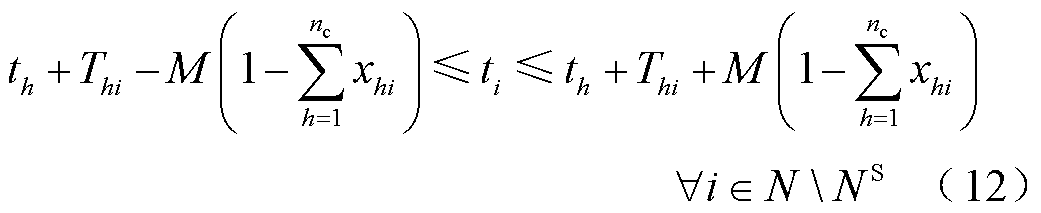
式中,NS为黑启动电源所在节点的集合;M为一个很大的常数;Tii为黑启动电源启动需要的时步数,本模型中假设黑启动电源能立刻自启动;Tmax为顺序恢复决策的时段总数;Thi为线路(h,i)完成充电需要的时步数;ti为节点i的恢复时刻。式(10)表示当节点i连有黑启动电源时,其恢复时刻ti=Tii,否则,ti不受式(10)约束;式(11)表示若无恢复路径经过节点i,则ti=Tmax,否则,ti不受式(11)约束;式(12)表示当供电路径从节点h流向节点i时,ti=th+Thi。
进一步,引入0-1决策变量si.t和bij.t分别表示节点i和线路(h,i)在第t时步的供电状态。si.t和供电路径之间的关系可表示为
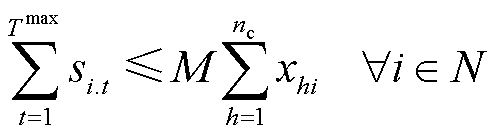 (13)
(13)
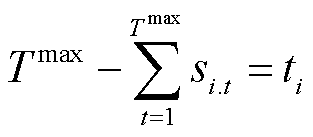 (14)
(14)
式(13)表示当存在供电路径经过节点i时,该节点才可以恢复供电;式(14)表示节点i的恢复时刻由供电路径抵达时刻ti决定。
线路恢复供电的前提是两端节点均恢复供电,可表示为
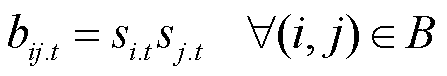 (15)
(15)
为确保节点和线路恢复供电后不再停电,可引入以下约束:
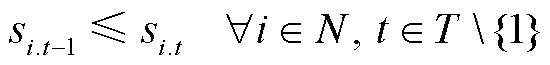 (16)
(16)
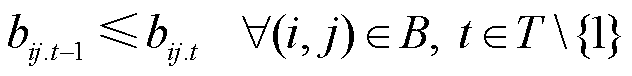 (17)
(17)
2.2.3 分布式电源操作约束
本文假设在供电恢复过程中,可用的分布式电源包括燃机和储能。其中,燃机均为三相分布式电源,在恢复过程中应满足
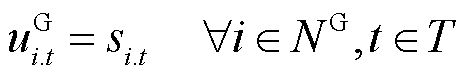 (18)
(18)
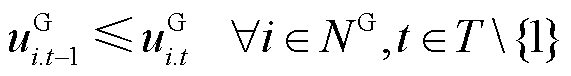 (19)
(19)
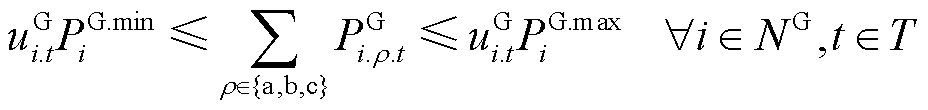 (20)
(20)
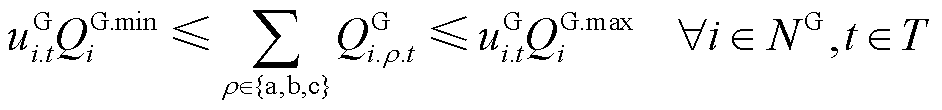 (21)
(21)
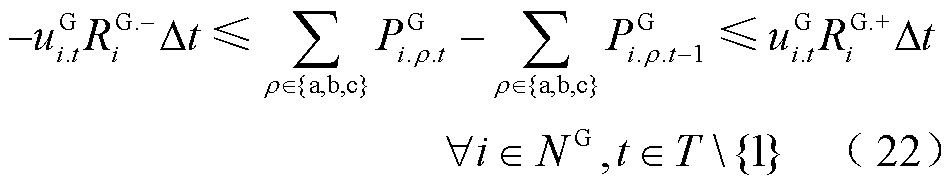
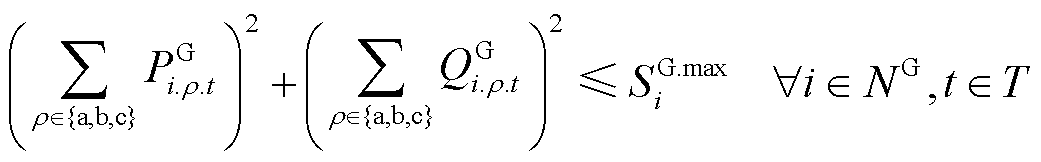 (23)
(23)
式中,NG为连有燃机的节点集合; 为节点i上燃机的起停状态;
为节点i上燃机的起停状态;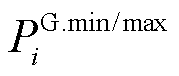 为节点i上燃机的最小/最大有功功率;
为节点i上燃机的最小/最大有功功率;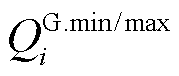 为该燃机的最小/最大无功功率;
为该燃机的最小/最大无功功率;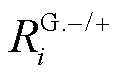 为节点i上燃机的允许下/上调功率限额;
为节点i上燃机的允许下/上调功率限额;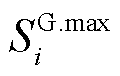 为节点i上燃机的容量;
为节点i上燃机的容量;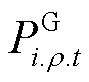 为第t时步节点i上燃机的ρ相有功功率输出;
为第t时步节点i上燃机的ρ相有功功率输出;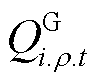 为第t时步节点i上燃机的ρ相无功功率输出。式(18)表示燃机作为黑启动电源,与其所在节点同时恢复;式(19)确保燃机启动后不再停运;式(20)和式(21)对燃机的输出功率进行了限制;式(22)限制了相邻两时步燃机的有功输出功率变化量;式(23)确保燃机输出功率小于其最大容量。
为第t时步节点i上燃机的ρ相无功功率输出。式(18)表示燃机作为黑启动电源,与其所在节点同时恢复;式(19)确保燃机启动后不再停运;式(20)和式(21)对燃机的输出功率进行了限制;式(22)限制了相邻两时步燃机的有功输出功率变化量;式(23)确保燃机输出功率小于其最大容量。
储能可通过三相或单相接入配电网。为便于建模,本文针对三相接入储能进行建模,对于单相接入的储能,其剩余两相功率输出为0。在供电恢复过程中储能应满足
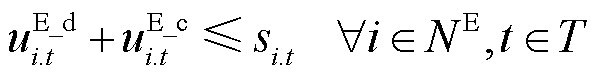 (24)
(24)
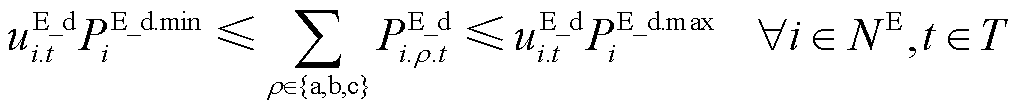 (25)
(25)
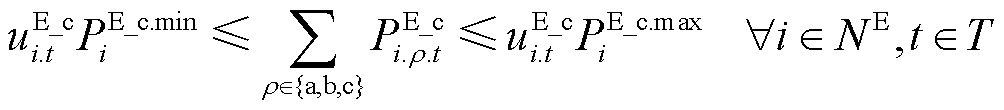 (26)
(26)
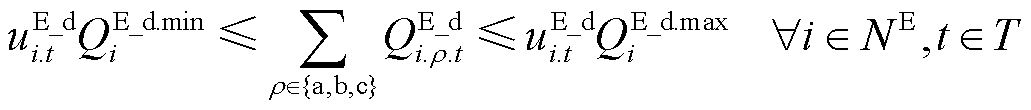 (27)
(27)
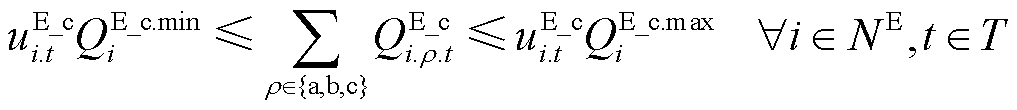 (28)
(28)
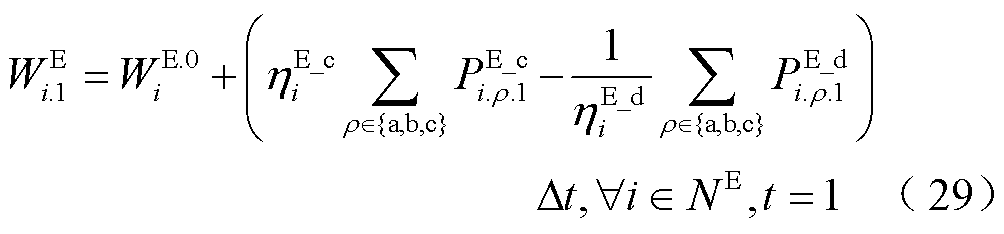
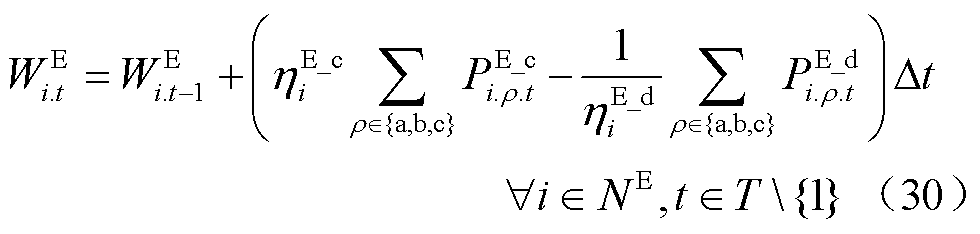
 (31)
(31)
式中,NE为连有储能的节点集合;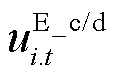 为节点i上储能的充/放电状态;
为节点i上储能的充/放电状态;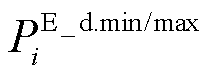 为节点i上储能的最小/最大放电有功功率;
为节点i上储能的最小/最大放电有功功率;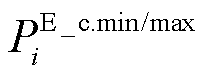 为节点i上储能的最小/最大充电有功功率;
为节点i上储能的最小/最大充电有功功率;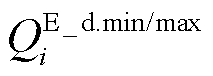 为节点i上储能的最小/最大放电无功功率;
为节点i上储能的最小/最大放电无功功率;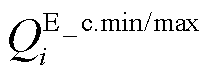 为节点i上储能的最小/最大充电无功功率;
为节点i上储能的最小/最大充电无功功率;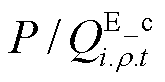 为第t时步节点i上储能的ρ相有功/无功充电功率;
为第t时步节点i上储能的ρ相有功/无功充电功率;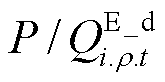 为第t时步节点i上储能的ρ相有功/无功放电功率;
为第t时步节点i上储能的ρ相有功/无功放电功率;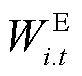 为第t时步节点i上储能剩余容量;
为第t时步节点i上储能剩余容量;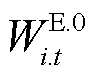 为节点i上储能的初始容量;
为节点i上储能的初始容量;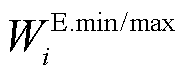 为节点i上储能剩余容量的允许下/上限,
为节点i上储能剩余容量的允许下/上限,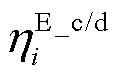 为节点i上储能的充/放电效率系数。式(24)表示一个储能仅当其所在节点恢复供电时才可以进行操作,且在一个时步只能处于一种工作状态;式(25)~式(29)对储能充放电过程中的有功和无功功率进行限制;式(29)和式(30)用于计算储能的剩余容量;式(31)对储能允许的剩余容量进行限制。
为节点i上储能的充/放电效率系数。式(24)表示一个储能仅当其所在节点恢复供电时才可以进行操作,且在一个时步只能处于一种工作状态;式(25)~式(29)对储能充放电过程中的有功和无功功率进行限制;式(29)和式(30)用于计算储能的剩余容量;式(31)对储能允许的剩余容量进行限制。
2.2.4 负荷需求量约束
在供电恢复过程中,负荷投运的前提是其所在节点恢复供电,且需要确保其在恢复供电后不再断电。本模型假设每一相负荷均通过开关接入配电网。引入0-1变量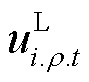 表示节点i上ρ相t时步负荷的投运状态,需要满足
表示节点i上ρ相t时步负荷的投运状态,需要满足
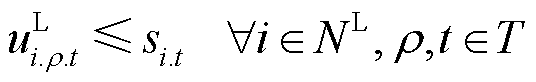 (32)
(32)
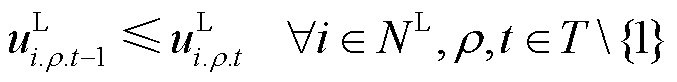 (33)
(33)
考虑到配电网中存在一定比例的三相负载,其各相负荷需同时投运。对于此类负载,引入约束条件式(34)。
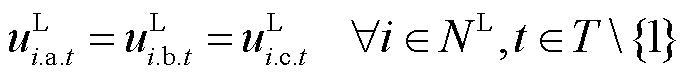 (34)
(34)
温控负荷的冷负荷启动特性取决于停电时长,且功率需求随供电时间变化而变化。顺序恢复过程持续|T|个时步,负荷有NT条冷负荷启动功率曲线(NT=|T|)。因此,引入一个1×NT维的列向量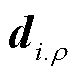 ,其中元素
,其中元素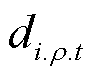 为0-1变量表示节点i上ρ相负荷是否在第t时步投运,有
为0-1变量表示节点i上ρ相负荷是否在第t时步投运,有
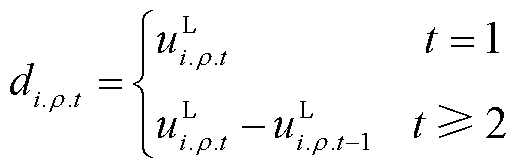 (35)
(35)
进一步,对供电恢复过程中各时步的负荷功率需求量进行建模。本文对各相负载的功率需求量分别进行建模,对于三相负载,将其功率需求简化为各相的负荷功率需求之和。
引入如式(36)所示的NT维矩阵,其中第t列元素表示节点i上ρ相温控负荷在第t时步恢复供电时各时步的有功功率需求。
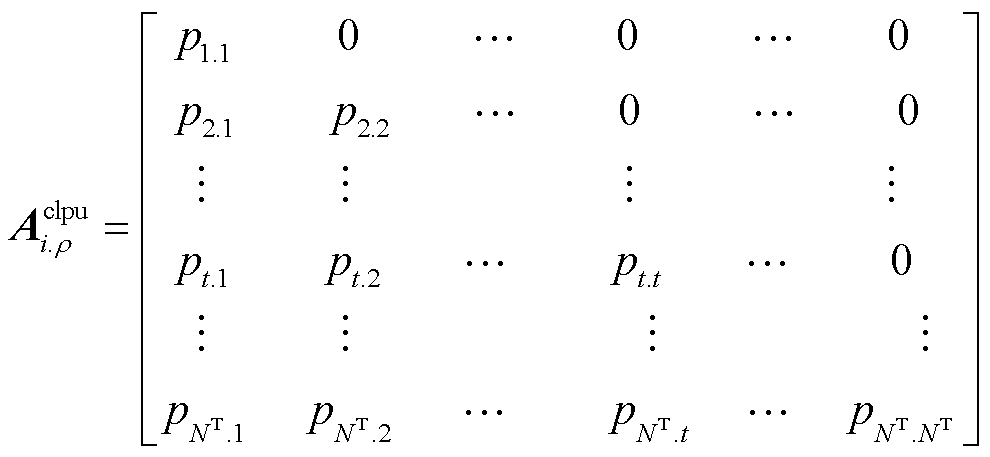 (36)
(36)
因此,当节点i上ρ相温控负荷在第t时步恢复供电时,其功率需求矩阵可通过式(37)计算得到。
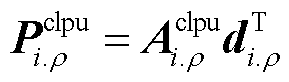 (37)
(37)
配电网供电恢复过程中,t时步节点i上ρ相负荷的有功功率需求可表示为
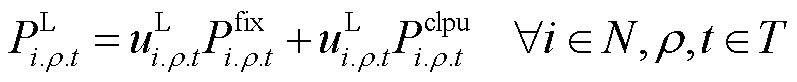 (38)
(38)
式中,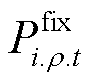 为第t时步节点i上ρ相恒定负载的有功功率需求量。
为第t时步节点i上ρ相恒定负载的有功功率需求量。
假设负荷的无功功率需求量和有功功率需求量成正比,第t时步节点i上ρ相负荷的无功功率需求可表示为
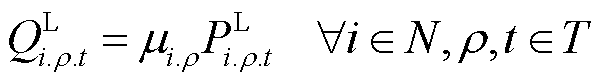 (39)
(39)
式中,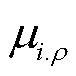 为节点i上ρ相负荷的功率因数。
为节点i上ρ相负荷的功率因数。
2.2.5 配电网潮流约束
本文采用线性的三相不平衡潮流模型[29]描述呈辐射状运行的配电网潮流约束。配电网供电恢复过程中各节点的功率平衡约束为
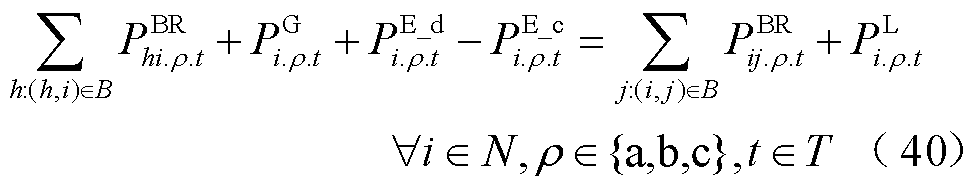
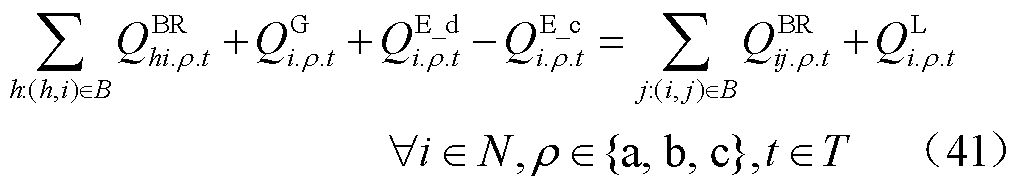
式中,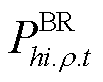 、
、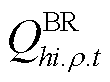 分别为第t时步ρ相线路上从节点h流向节点i的有功和无功功率。
分别为第t时步ρ相线路上从节点h流向节点i的有功和无功功率。
节点i和节点j之间的电阻和电抗可通过引入一个3×3的阻抗矩阵z来表征,有
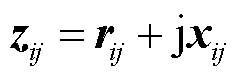 (42)
(42)
进一步,计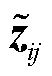 =α⊙
=α⊙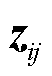 ,其中⊙表示两矩阵间对应元素相乘,常数矩阵α定义为
,其中⊙表示两矩阵间对应元素相乘,常数矩阵α定义为
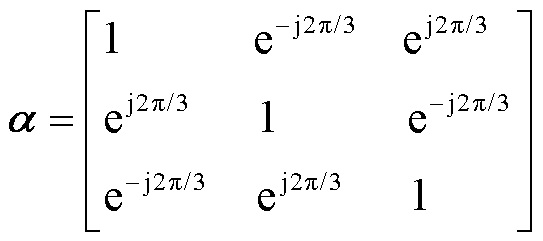 (43)
(43)
因此,相邻节点间电压关系可表示为
 (44)
(44)
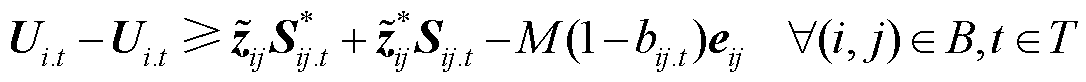 (45)
(45)
式中,矩阵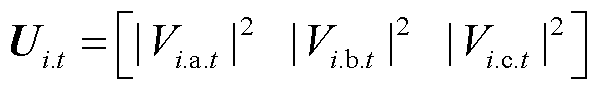 为第t时步三相电压幅值二次方构成的3×1维列向量;
为第t时步三相电压幅值二次方构成的3×1维列向量;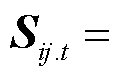
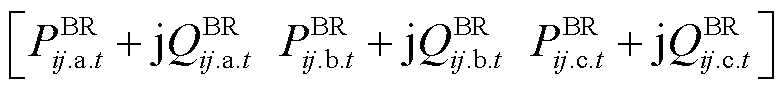 为第t时步线路(i, j)上三相功率构成的3×1维列向量;上标*表示对矩阵取共轭运算;
为第t时步线路(i, j)上三相功率构成的3×1维列向量;上标*表示对矩阵取共轭运算;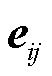 为一个表示线路所在相的3×1维二进制列向量,例如当线路(i, j)仅含b相线路时,
为一个表示线路所在相的3×1维二进制列向量,例如当线路(i, j)仅含b相线路时,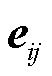 =[0 1 0]T。
=[0 1 0]T。
在配电网供电恢复过程中,已恢复的节点需满足电压安全条件,有
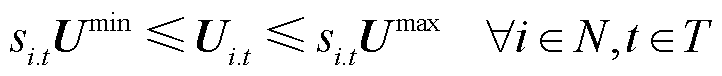 (46)
(46)
式中,矩阵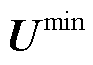 和
和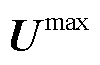 分别为允许的节点电压最小值和最大值。
分别为允许的节点电压最小值和最大值。
此外,还需要满足线路传输容量约束,即
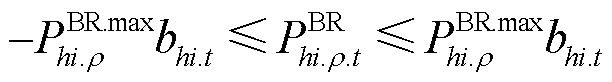 (47)
(47)
 (48)
(48)
式中,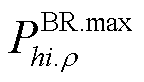 、
、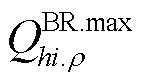 分别为ρ相线路上从节点h流向节点i的最大允许有功/无功功率。
分别为ρ相线路上从节点h流向节点i的最大允许有功/无功功率。
2.2.6 电流不平衡度约束
在配电网供电恢复过程中,需要对电流的三相不平衡度进行约束,以避免电源触发切机保护。本模型参考文献[24],定义电流不平衡度D为
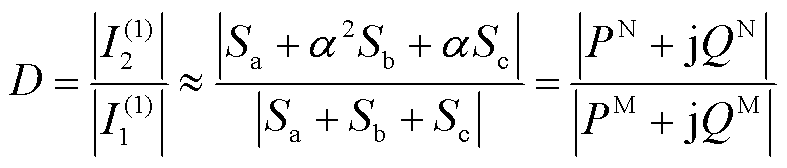 (49)
(49)
式中,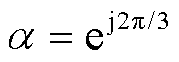 ;
;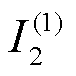 为基波负序分量;
为基波负序分量;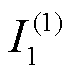 为基波正序分量;
为基波正序分量; 为三相视在功率。
为三相视在功率。
令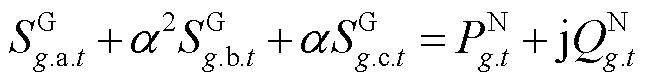 ,
,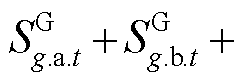
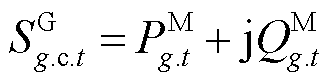 ,并基于文献[25]所提的简化方法,有
,并基于文献[25]所提的简化方法,有
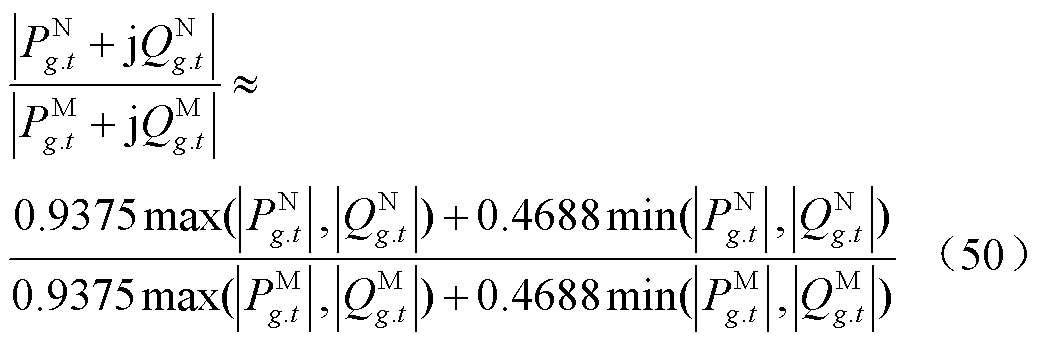
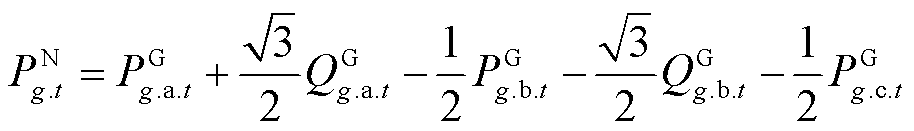 (51)
(51)
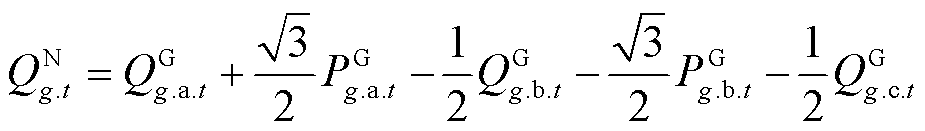 (52)
(52)
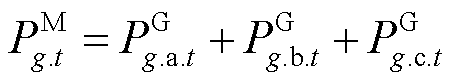 (53)
(53)
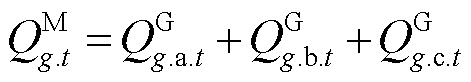 (54)
(54)
式中,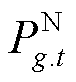 、
、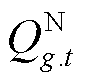 分别为第t时步分布式电源g有功/无功出力的负序分量;
分别为第t时步分布式电源g有功/无功出力的负序分量;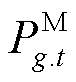 、
、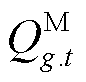 分别为第t时步分布式电源g有功/无功出力的正序分量。当电流不平衡度超过10%~20%时,三相同步机电源会进行切机操作;而储能等逆变型分布式电源能承受的电流不平衡度可达100%[25]。因此电流不平衡度约束可表示为
分别为第t时步分布式电源g有功/无功出力的正序分量。当电流不平衡度超过10%~20%时,三相同步机电源会进行切机操作;而储能等逆变型分布式电源能承受的电流不平衡度可达100%[25]。因此电流不平衡度约束可表示为
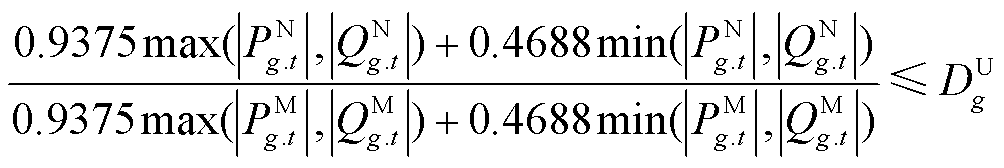 (55)
(55)
式中,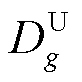 为分布式电源g允许的电流不平衡度。
为分布式电源g允许的电流不平衡度。
上述配电网供电恢复模型为混合整数非线性规划(Mixed-Integer Nonlinear Programming, MINP)模型。为便于快速求解,本节对上述模型中的非线性化进行线性化处理。
线路供电约束式(15)存在两个0-1变量相乘的情况,可用如式(56)所示的不等式组进行等效替换。
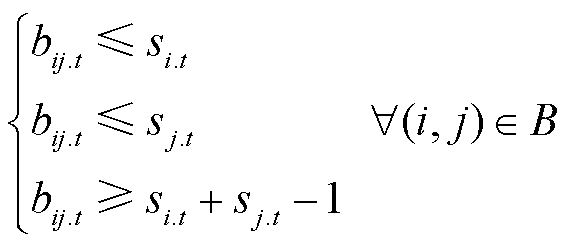 (56)
(56)
燃机输出功率约束式(23)为二次约束,其可行域为一个圆形。可采用多边形内近似法[30],将原始可行域缩小为一个内接的正多边形。多边形的每一条边与圆形区域有两个交点,其可行域可用一系列线性不等式约束表示。以点(v1,w1)和(v2,w2)为例,则该条边所对应的约束可表示为
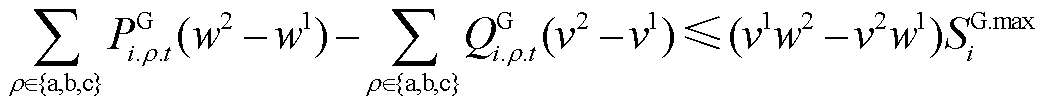 (57)
(57)
由于内近似法缩小了可行域范围,因此可以保障优化结果的可行性。该线性化方法的精度会随着多边形边数的增加而提升。
此外,电流不平衡度约束式(55)含有绝对值项及“max”“min”项,导致模型难以求解。首先引入四个连续变量和八个0-1变量对绝对值项进行线性化处理。以 为例,有
为例,有
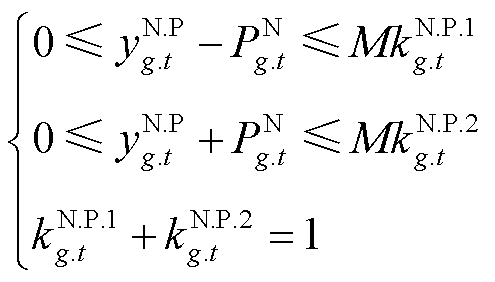 (58)
(58)
式中,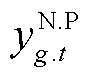 为连续变量;
为连续变量;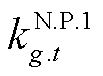 、
、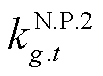 为0-1变量。
为0-1变量。
进一步,引入四个连续变量和八个0-1变量,对“max”、“min”项进行线性化处理,以max(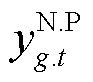 ,
,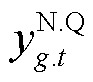 )和min(
)和min(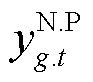 ,
,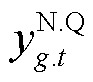 )为例,有
)为例,有
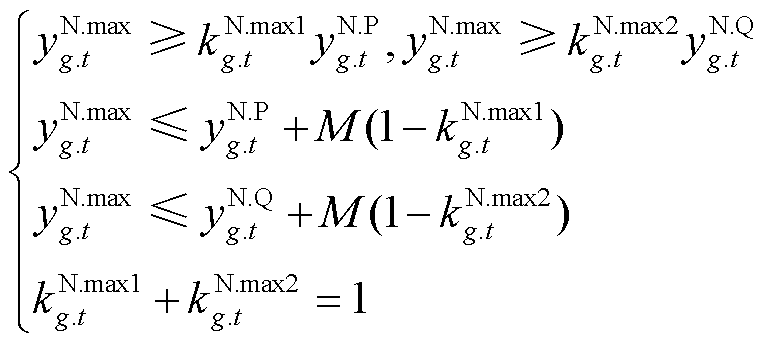 (59)
(59)
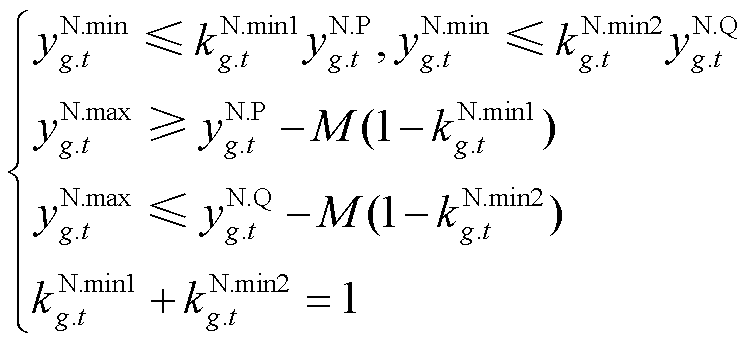 (60)
(60)
利用式(56)替代线路供电约束式(15),用式(57)对燃机出力约束进行处理,并利用式(58)~式(60)中方法处理不平衡电流约束式(55),可将MINP问题转换为混合整数线性规划(Mixed Integer Linear Program, MILP)问题,经过线性化的模型可利用CPLEX进行快速求解。
计及冷负荷启动时变特性的三相配电网供电恢复模型可表示为
 (61)
(61)
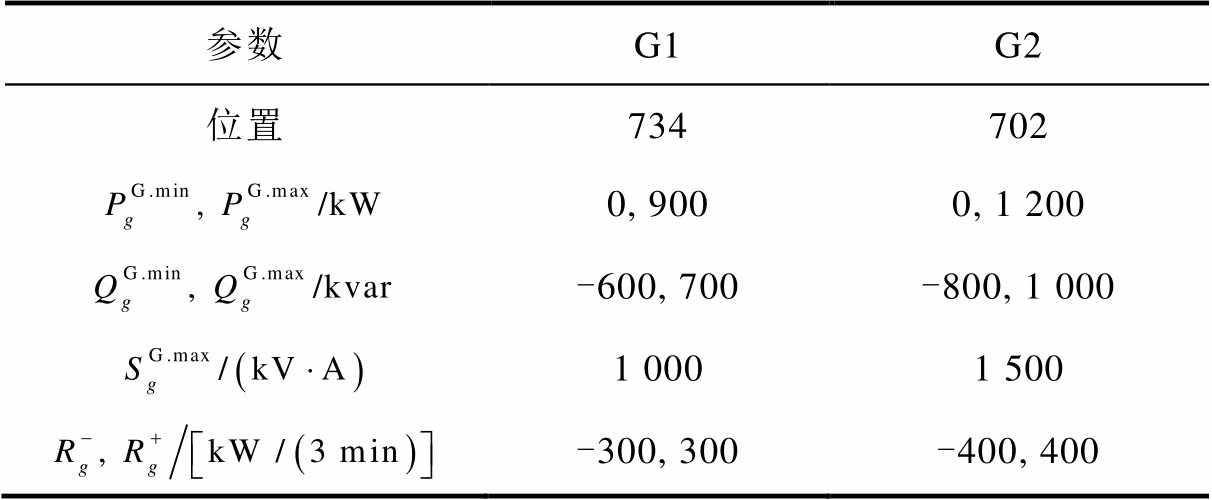
利用改进IEEE 37节点配电测试系统验证所提三相配电网供电恢复方法的有效性。假设主网由于极端自然灾害发生停电事故,配电网恢复前处于完全失电状态。改进IEEE 37节点系统拓扑结构如图4所示。配电网中配有两台具备黑启动能力的分布式电源,且三相接入配电网。此外,系统中接有三台储能设备辅助配电网进行供电恢复,其中E1单相接入配电网(a相),E2和E3三相接入配电网。燃机和储能的相关参数分别见表1和表2。

图4 改进的IEEE 37节点系统拓扑结构
Fig.4 Topology structure modified IEEE 37-node test system
表1 燃机相关参数
Tab.1 Parameters of gas turbines
参数G1G2 位置734702 0, 9000, 1 200 -600, 700-800, 1 000 1 0001 500 -300, 300-400, 400
表2 储能相关参数
Tab.2 Parameters of ESSs

参数E1E2E3 位置740708720 容量/(kV·A)6001 0001 000 0, 2000, 3000, 300 0, 2000, 3000, 300 240600600 60, 540100, 900100, 900 0.90, 0.950.90, 0.950.90, 0.95
配电网中节点负荷分为关键负荷、重要负荷和常规负荷三类,负荷权重分别设为5、2和1,各相负荷的有功、无功需求量基准值随机生成,温控负荷占比为30%。本算例中供电恢复决策时步设为 3 min,恢复过程持续10个时步。各条线路充电所需要的时步数见表3。
表3 各条线路充电所需时步数
Tab.3 Time steps for line charging in distribution system

线路时步数线路时步数线路时步数 711-7401709-7751702-7012 711-7411709-7311702-7131
(续)

线路时步数线路时步数线路时步数 711-7381709-7301713-7041 738-7371730-7033704-7142 737-7341703-7271714-7181 734-7101727-7441704-7201 710-7362744-7291720-7061 710-7352744-7281706-7253 734-7331703-7021720-7071 733-7081702-7051707-7221 708-7321705-7421707-7241 708-7091705-7121701-7992
对配电网供电恢复模型进行求解,可生成优化的供电恢复策略。由于系统中含有2台黑启动电源,因此通过操作线路开关,可并行生成两个微电网。各时步配电网中恢复的节点见表4,由于第8时步后没有节点恢复,因此仅展示前8个时步的节点恢复结果。
表4 微电网中各时刻恢复的节点
Tab.4 Restored nodes in microgrids at each time step

时步节点恢复情况 MG1MG2 1N734N702 2N737,N710, N733N703,N705,N713 3N738, N708N727,N742,N712,N701,N704 4N711,N736,N735,N732,N709N744,720 5N740,N741,N775,N730,N731N729,N728,N714,N706,N707 6—N718,N722,N724 7—— 8—N725
以分布式电源G2所构成的MG2为例,MG2中恢复路径及各时步节点恢复路径如图5所示。可以看出,在供电恢复过程中,微电网始终保持辐射状结构。
以MG1为例,分析微电网供电恢复过程中供需情况。MG1中各时步的燃机及储能的有功出力如图6所示。G1具有黑启动能力,在第1时步开始出力;E1和E2分别从第5和第3时步开始工作;在第4时步,微电网中出现功率过剩,此时储能设备E2进行充电操作;在第6时步之后,储能处于放电模式以解决燃机出力不足的情况。在供电恢复过程中,微电网内电源出力与负荷功率需求始终保持一致,以保证微电网内供需平衡。分布式电源逐渐增大功率输出以满足负荷功率需求。在温控负荷恢复供电后,其功率需求会按照冷负荷启动功率特性曲线逐渐减小,例如第4时步的有功功率需求小于第3时步。
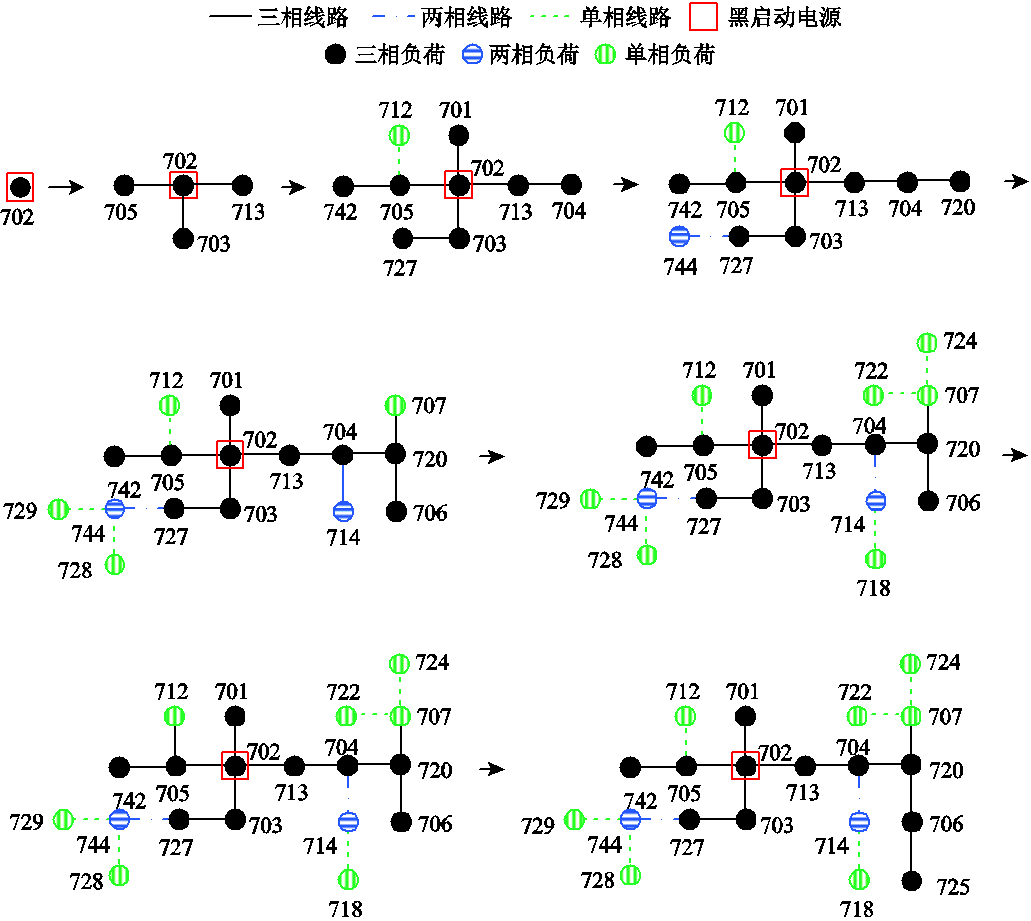
图5 MG2中恢复路径
Fig.5 Restoration paths in MG2

图6 MG1中电源有功功率
Fig.6 Active power output of sources in MG1
MG1中节点上各相负荷的投运时刻见表5。其中“F”表示该相上连有负荷但投运;“—”表示该相上不连有负荷。从表5可以看出,为了满足分布式电源的爬坡功率约束,一些负荷在节点恢复后不会立刻投运。例如,节点N711在第4时步恢复供电,但连在该节点的c相负荷在第5时步才投入运行。此外,为满足分布式电源的电流不平衡度约束,同一节点的各相负荷会在不同时步投运。例如,节点N737上c相负荷在第2时步投运,b相负荷在第3时步投运,而a相负荷在第6时步投运。
表5 MG1中节点上各相负荷恢复时刻
Tab.5 Pick-up time of loads at each node in MG1

节点三相负荷恢复时刻 A相B相C相 N711FF5 N741——5
(续)
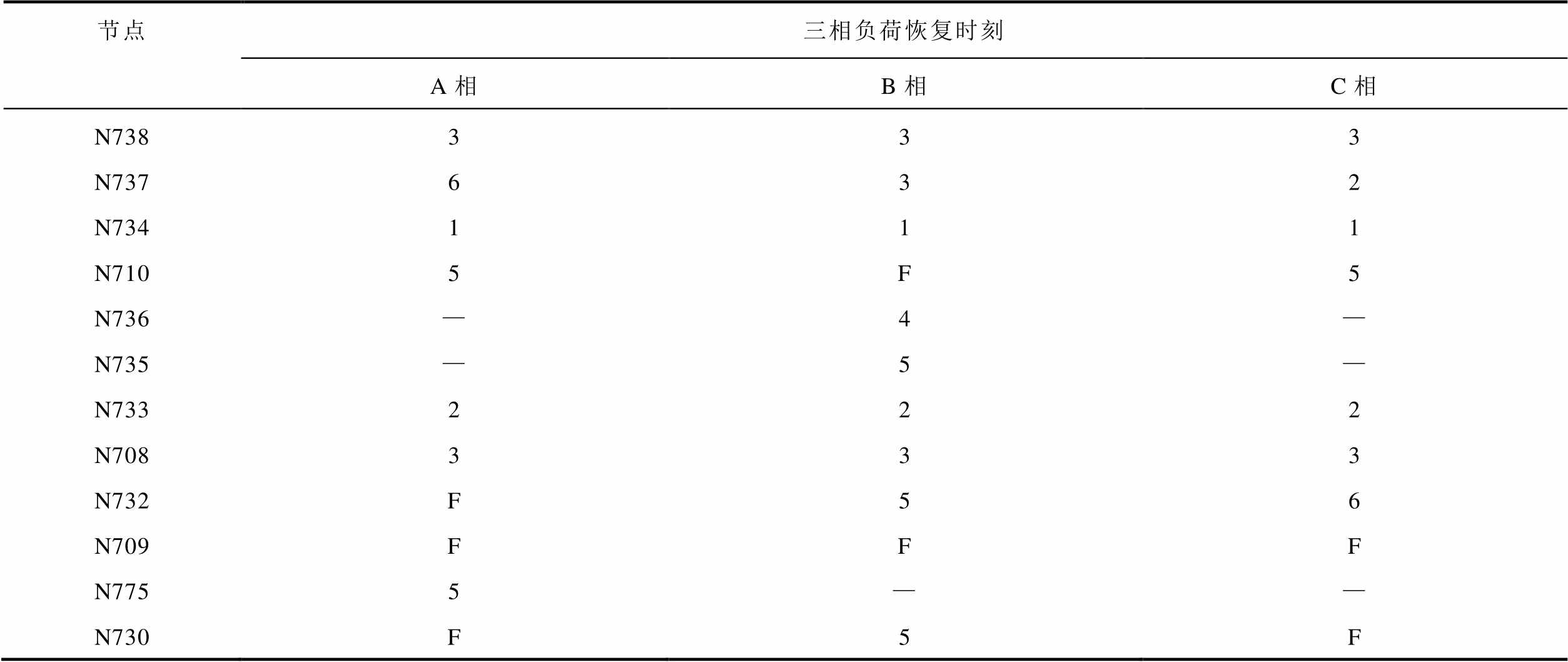
节点三相负荷恢复时刻 A相B相C相 N738333 N737632 N734111 N7105F5 N736—4— N735—5— N733222 N708333 N732F56 N709FFF N7755—— N730F5F
本节通过两种方法对比说明在三相配电网供电恢复过程中考虑冷负荷启动特性的必要性。方法1采用本文所提计及冷负荷启动特性的配电网供电恢复方法;方法2忽略温控负荷的冷负荷启动特性,负荷的功率需求即功率基准值。通过求解两个模型,生成优化的供电恢复方案。
两组对比算例中的目标函数、负荷恢复量期望值见表6。进一步,对两种方法生成的恢复方案进行可行性校验。按照生成的开关动作顺序,在相应时刻恢复节点负荷,并考虑温控负荷在投运时的冷负荷启动特性。以MG1为例,图7展示了采用两种供电恢复策略时,G1的三相电流不平衡度。
表6 目标函数及负荷恢复量期望值对比
Tab.6 Comparisons of objective values and expected load restoration amount

方法目标函数负荷恢复量/kW 136 97817 480 237 20517 661
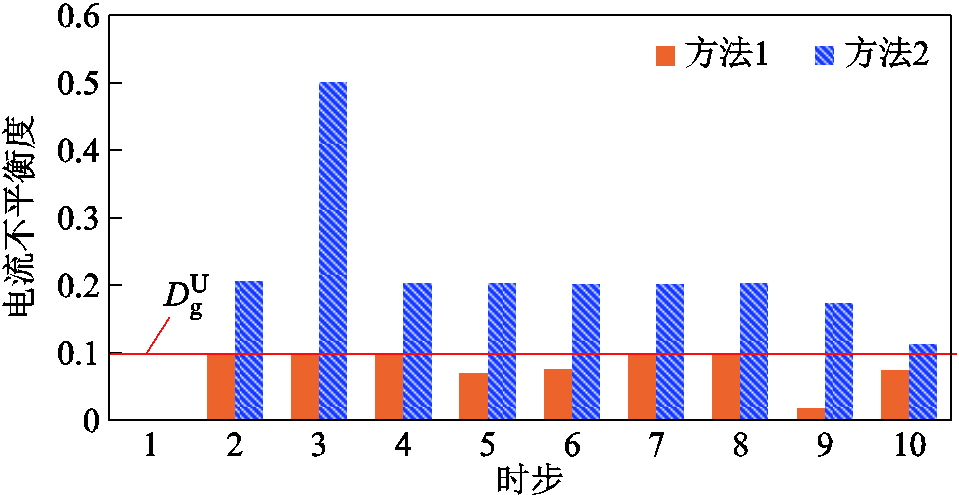
图7 两种方法下G1的电流不平衡度
Fig. 7 Current unbalance factor of G1 with two methods
从表6和图7可以看出,方法1中目标函数和负荷恢复期望值小于方法2,这是因为冷负荷启动时存在功率峰值,某些节点会延后投运以满足微网安全约束。虽然方法2中负荷恢复量期望值更高,但在实际恢复过程中,三相燃机的电流不平衡度超出安全水平,会触发电源切机保护,影响恢复策略的可行性。除了电流不平衡度约束,忽略冷负荷的启动特性还可能导致电源出力越限、爬坡功率不足等问题。当配电网中温控负荷占比较高时,上述问题将更加严重。
综上所述,在制定配电网供电恢复方案时考虑温控负荷的冷负荷启动特性,虽然会导致部分节点延后恢复,但能有效保证供电恢复策略的可靠性,从而提升配电网的弹性。
本节通过两组对比算例验证所提冷负荷启动特性模型的有效性。算例1中,考虑冷负荷启动的时变特性,通过采样法生成不同停电下的负荷功率需求;算例2中,参考文献[25],忽略停电时间对冷负荷启动特性建模的影响,采用延迟指数模型刻画冷负荷的启动特性。两组对比算例中各时步负荷恢复量对比如图8所示。
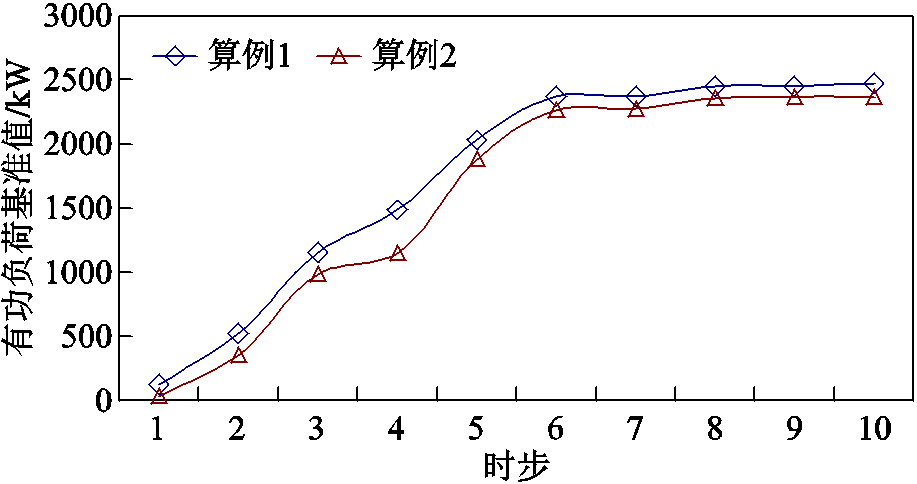
图8 算例1和算例2中负荷恢复量对比
Fig.8 Comparison of restored power in Case 1 and Case 2
从图8可以看出,相较于传统的延迟指数模型,本文考虑停电时间对冷负荷启动特性的影响,所生成的供电恢复策略可以提高近8.77%的负荷恢复量。这是因为传统冷负荷启动特性模型忽略了停电时间的影响,导致预测的负载峰值高于实际值,微网中部分负荷延迟恢复以满足微电网安全约束。而本文所提方法对冷负荷启动特性进行精准建模,在保证微电网安全运行的前提下,减小了供电恢复策略的保守性。
进一步,通过对比算例3分析微电网结构和操作顺序耦合优化在提升恢复效率方面的优势。在算例3中,事前确定微电网结构,在此基础上生成优化的开关操作次序。为了体现微电网结构的随机性,算例3中随机生成20种微电网拓扑,并选取其中的最优解与本文所提方法进行对比。两组对比算例中各微电网负荷恢复量对比如图9所示。
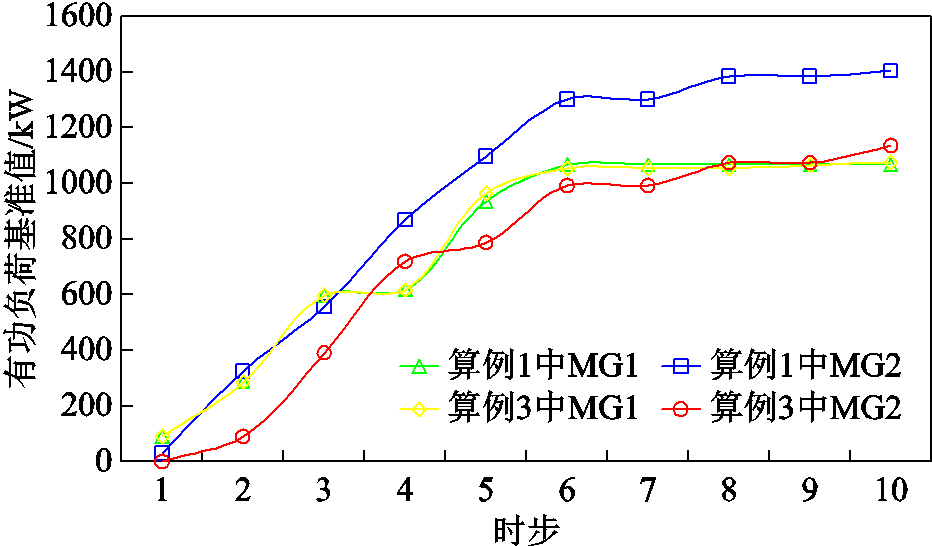
图9 算例1和算例3中各微电网内负荷恢复量对比
Fig. 9 Comparison of restored power of each MG in Case 1 and Case 3
从图9可以看出,考虑微电网结构和操作顺序的耦合优化能有效提升负荷供电量,在算例1中,第10时步两个分布式电源的利用率均为100%,在算例3中,第10时步电源G2近为85.5%。因此,考虑微电网结构和操作顺序的耦合优化能有效提升微电网中分布式电源的利用率,进而提升供电恢复过程中的负荷恢复量。
冷负荷启动时存在较大的负载峰值,会导致三相配电网中电流不平度越限。为保证配电网供电恢复过程中微电网安全运行,本文提出了一种计及冷负荷启动时变特性的弹性配电网供电恢复方法。首先考虑停电时间的影响,建立了冷负荷启动时变模型。进一步以加权负荷恢复量最大为目标,构建了三相配电网供电恢复优化模型,同时计及电流不平衡度约束以保证分布式电源运行的安全性。在模型求解过程中,采用多种线性化方法对模型中非线性项进行处理,提高了模型的求解效率。最后,采用IEEE 37节点配电测试系统验证了本文所提方法的有效性,分析了在供电恢复过程中考虑冷负荷启动特性的必要性,并对所提供电恢复策略在提升负荷恢复量方面的有效性进行了验证。
需要指出的是,本文主要针对空调等单相负载的冷负荷启动时变特性进行建模。对于三相负载,假设其功率平衡,将其负荷功率需求简化为各相的负荷功率需求之和。如何建立更为准确的三相负载冷负荷时变特性模型,将是下一步有待深入研究的工作。此外,本文主要针对供电恢复过程中的微电网稳态特性进行研究。如何在保证微电网安全运行的基础上,考虑冷负荷投运对微电网动态频率的影响,也是需要进一步深入探索的问题。
参考文献
[1] Perera A T D, Nik V M, Chen Deliang, et al. Quantifying the impacts of climate change and extreme climate events on energy systems[J]. Nature Energy, 2020, 5(2): 150-159.
[2] 别朝红, 林雁翎, 邱爱慈. 弹性电网及其恢复力的基本概念与研究展望[J]. 电力系统自动化, 2015, 39(22): 1-9.
Bie Zhaohong, Lin Yanling, Qiu Aici. Concept and research prospects of power system resilience[J]. Automation of Electric Power Systems, 2015, 39(22): 1-9.
[3] 陶然, 赵冬梅, 徐辰宇, 等. 考虑电-气-热-交通相互依存的城市能源系统韧性评估与提升方法[J]. 电工技术学报, 2023, 38(22): 6133-6149.
Tao Ran, Zhao Dongmei, Xu Chenyu. Resilience assessment and enhancement methods for urban energy system considering electricity-gas-heat-transportinterdependy[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6133-6149.
[4] 蔡胜, 谢云云, 张玉坪, 等. 考虑孤岛微电网建立过程功率冲击的弹性配电网主动预防调度[J]. 电工技术学报, 2023, 38(23): 6419-6432.
Cai Sheng, Xie Yunyun, Zhang Yuping, et al. Proactive scheduling of resilient distribution systems considering power impact during islanded microgrid formation process[J]. Transactions of China Electro-technical Society, 2023, 38(23): 6419-6432.
[5] 王晓卫, 康干坤, 梁振锋, 等. 考虑5G基站储能参与配电网供电恢复研究[J]. 电工技术学报, 2024, 39(11): 3539-3555.
Wang Xiaowei, Kang Qiankun, Liang Zhenfeng, et al. Distribution network restoration supply method considers 5G base station energy storage participa-tion[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3539-3555.
[6] 詹红霞, 肖竣文, 邓小勇, 等. 计及柔性负荷的高比例风光渗透下配电网孤岛划分策略[J]. 电力工程技术, 2022, 41(4): 108-116.
Zhan Hongxia, Xiao Junwen, Deng Xiaoyong, et al. Islanding strategy for distribution network with high proportion of wind/photovoltaic penetration considering flexible load[J]. Electric Power Engineering Technology, 2022, 41(4): 108-116.
[7] 齐郑, 张首魁, 李志, 等. 考虑时间尺度的含DG配电网故障动态恢复策略[J]. 电力系统保护与控制, 2017, 45(16): 31-38.
Qi Zheng, Zhang Shoukui, Li Zhi, et al. Dynamic service restoration strategy considering time scale for distribution network with DGs[J]. Power System Protection and Control, 2017, 45(16): 31-38.
[8] Che Liang, Shahidehpour M. Adaptive formation of microgrids with mobile emergency resources for critical service restoration in extreme conditions[J]. IEEE Transactions on Power Systems, 2019, 34(1): 742-753.
[9] Cai Sheng, Xie Yunyun, Wu Qiuwei, et al. Robust coordination of multiple power sources for sequential service restoration of distribution systems[J]. International Journal of Electrical Power & Energy Systems, 2021, 131: 107068.
[10] 梁远升, 徐真理, 李海锋, 等. 基于随机响应面法的配电网故障恢复全时段不确定性优化方法[J]. 中国电机工程学报, 2024, 44(23): 9200-9213.
Liang Yuansheng, Xu Zhenli, Li Haifeng, et al. A stochastic optimization method for fault recovery in distribution networks based on stochastic response surface method[J]. Proceeding of the CESS, 2024, 44(23): 9200-9213.
[11] 刘菲, 林超凡, 陈晨, 等. 考虑分布式新能源动态不确定性的配电网灾后时序负荷恢复方法[J]. 电力自动化设备, 2022, 42(7): 159-167.
Liu Fei, Lin Chaofan, Chen Chen, et al. Post-disaster time-series load restoration method for distribution network considering dynamic uncertainty of distributed renewable energy[J]. Electric Power Automation Equipment, 2022, 42(7): 159-167.
[12] Cai Sheng, Xie Yunyun, Wu Qiuwei, et al. Two-stage mobile emergency generator dispatch for sequential service restoration of microgrids in extreme conditions[J]. International Journal of Electrical Power & Energy Systems, 2023, 153: 109312.
[13] Zhang Qianzhi, Ma Zixiao, Zhu Yongli, et al. A two-level simulation-assisted sequential distribution system restoration model with frequency dynamics constraints[J]. IEEE Transactions on Smart Grid, 2021, 12(5): 3835-3846.
[14] Cai Sheng, Xie Yunyun, Zhang Menglin, et al. A stochastic sequential service restoration model for distribution systems considering microgrid inter-connection[J]. IEEE Transactions on Smart Grid, 2024, 15(3): 2396-2409.
[15] Chen Bo, Ye Zhigang, Chen Chen, et al. Toward a MILP modeling framework for distribution system restoration[J]. IEEE Transactions on Power Systems, 2019, 34(3): 1749-1760.
[16] Arif A, Cui Bai, Wang Zhaoyu. Switching device-cognizant sequential distribution system restoration[J]. IEEE Transactions on Power Systems, 2022, 37(1): 317-329.
[17] 杨明, 翟鹤峰, 马嘉翼, 等. 计及分布式电源发电不平衡度约束的三相不对称配电网动态重构[J]. 中国电机工程学报, 2019, 39(12): 3486-3499.
Yang Ming, Zhai Hefeng, Ma Jiayi, et al. Dynamic reconfiguration of three-phase unbalanced distribution networks considering unbalanced operation constraint of distributed generation[J]. Proceedings of the CSEE, 2019, 39(12): 3486-3499.
[18] Wang Zeyu, Wang Jianhui, Chen Chen. A three-phase microgrid restoration model considering unbalanced operation of distributed generation[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3594-3604.
[19] Bassey O, Butler-Purry K L, Chen Bo. Dynamic modeling of sequential service restoration in islanded single master microgrids[J]. IEEE Transactions on Power Systems, 2020, 35(1): 202-214.
[20] Mohy-ud-din G, Muttaqi K M, Sutanto D. A hierarchical service restoration framework for unbalanced active distribution networks based on DSO and VPP coordination[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 1756-1770.
[21] 刘志伟, 苗世洪, 杨炜晨, 等. 计及温度不确定性的配电网广义储能分层调控策略[J]. 电工技术学报, 2023, 38(21): 5794-5807.
Liu Zhiwei, Miao Shihong, Yang Weichen, et al. Generalized energy storage hierarchical regulation strategy for distribution network considering temperature uncertainty[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5794-5807.
[22] 张潼, 于鹤洋, 田江, 等. 基于非侵入式负荷辨识的聚合负荷需求响应能力在线评估[J]. 电力工程技术, 2020, 39(6): 19-25, 65.
Zhang Tong, Yu Heyang, Tian Jiang, et al. Online aggregation monitoring of low-voltage power load demand response capability based on non-intrusive load identification[J]. Electric Power Engineering Technology, 2020, 39(6): 19-25, 65.
[23] 邓荣楠, 宋梦, 高赐威, 等. 考虑用户负荷决策依赖特性的配电网灾后恢复方法对比分析[J]. 电工技术学报, 2024, 39(23): 7447-7462.
Deng Rongnan, Song Meng, Gao Ciwei, et al. Comparative analysis of distribution system load restoration considering decision-dependent behaviors of customers[J]. Transactions of China Electrotechnical Society, 2024, 39(23): 7447-7462.
[24] 丁江, 孙磊, 丁明. 计及冷负荷效应时变特性的含风储联合系统负荷恢复策略[J]. 电力自动化设备, 2023, 43(6): 108-115.
Ding Jiang, Sun Lei, Ding Ming. Load restoration strategy with wind farm-battery energy storage system considering time-variation characteristic of cold load pickup[J]. Electric Power Automation Equipment, 2023, 43(6): 108-115.
[25] Chen Bo, Chen Chen, Wang Jianhui, et al. Sequential service restoration for unbalanced distribution systems and microgrids[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1507-1520.
[26] Li Y L, Sun Wei, Yin Wenqian, et al. Restoration strategy for active distribution systems considering endogenous uncertainty in cold load pickup[J]. IEEE Transactions on Smart Grid, 2022, 13(4): 2690-2702.
[27] Xie Dunjian, Xu Yunyun, Nadarajan Sivakumar, et al. Dynamic frequency-constrained load restoration considering multi-phase cold load pickup behaviors[J]. IEEE Transactions on Power Systems, 2024, 39(1): 107-118.
[28] Wang Yifei, Su Xiaoyun, Song Meng, et al. Sequential load restoration with soft open points and time-dependent cold load pickup for resilient distribution systems[J]. IEEE Transactions on Smart Grid, 2023, 14(5): 3427-3438.
[29] Ahmadi H, Martı´ J R, von Meier A. A linear power flow formulation for three-phase distribution systems [J]. IEEE Transactions on Power Systems, 2016, 31(6): 5012-5021.
[30] Ferreira R S, Borges C L T, Pereira M V F. A flexible mixed-integer linear programming approach to the AC optimal power flow in distribution systems[J]. IEEE Transactions on Power Systems, 2014, 29(5): 2447-2459.
A Service Restoration Method for Resilient Distribution Systems Considering Time-Varying Characteristic of Cold Load Pickup
Abstract When an outage occurs in the distribution system due to extreme disaster events, the distributed generators are used to form microgrids and restore critical loads, which is essential for reducing outage duration and enhancing the resilience of distribution systems. The existing work utilizes the constant load model when designing the service restoration (SR) schemes. However, the ignorance of current unbalance caused by load peak when picking up cold loads may threaten the security of microgrids. Recently, SR approaches considering the cold load pickup (CLPU) were presented to ensure the supply-demand balance when restoring the distribution systems, but most of them simply assumed the system is three-phase balanced. This was insufficient to ensure a successful restoration because the violation of current unbalance factor may lead to the cut-off of distributed generators in microgrids. To address this issue, this paper proposed a SR method for three-phase unbalanced distribution systems considering the time-varying characteristic of CLPU. By restricting the current unbalance factor during the SR process, the security and reliability of microgrids can be improved.
First, a time-dependent CLPU model was formulated when considering the relationship between CLPU characteristic and outage duration, and the sampling method was used to generate load demand profiles. Then, considering the constraints such as power balance constraint and current unbalance factor constraint, a SR model was formulated to maximize the amount of load restoration. Next, nonlinear constraints in the original model were linearized to facilitate the solution. The main differences between the proposed SR model and those in existing literature lie in the current unbalance factor constraints, by which the load pickup sequence at each phase is optimized to reduce the current unbalance of distributed generators. In addition, zone sectionalization, restoration paths, and load pickup sequences were jointly optimized to enhance the effectiveness of the microgrid-based SR scheme.
Simulation results on the modified IEEE 37 node distribution system show that, after the event strikes, two microgrids are sequentially formed to restore the critical loads. Specifically, the black-start units are used to crank the non-black start units, and the line switches are closed orderly to extend the microgrids. The total generation of power sources in one MG is equal to the total amount of load consumption for each time step. The comparison with the SR method using constant load model shows that, the consideration of CLPU can improve the security of microgrid by restricting the current unbalance factor. The comparison with the SR method using traditional delayed exponential-based CLPU model shows that, the proposed time-dependent CLPU model can reduce the conservation of SR schemes. Comparison of different operation methods shows that, the utilization rate of the distributed generator for method with/without considering optimal microgrid topology is 100% and 85.5%, respectively.
The following conclusions can be drawn from the simulation analysis: (1) Compared with traditional distribution system SR method, considering the CLPU characteristics can reduce the current unbalance factor, thereby enhancing the security and reliability of microgrids during the SR process. (2) The proposed model considers the relationship between CLPU characteristic and outage duration. Compared with the traditional CLPU model, a less conservative scheduling strategy can be obtained. (3) The proposed model jointly optimizes the network topology and restoration sequences. Therefore, more flexible MG topology can be obtained to satisfy the supply-and-demand balance and more critical loads can be supplied.
Keywords:Resilient distribution system, service restoration, microgrid, current unbalance factor, cold load pickup (CLPU)
中图分类号:TM73
DOI: 10.19595/j.cnki.1000-6753.tces.232013
国家自然科学基金(52177090)、中央高校基本科研业务费专项资金(30923010301)和江苏高校“青蓝工程”资助项目。
收稿日期 2023-12-04
改稿日期 2024-01-09
蔡 胜 男,1994年生,博士,研究方向极端条件下电力系统运行与控制。
E-mail:cs@njust.edu.cn
谢云云 男,1985年生,副教授,研究方向为极端条件下电力系统运行与控制、新能源黑启动等。
E-mail:xyy_njust@163.com(通信作者)
(编辑 赫 蕾)