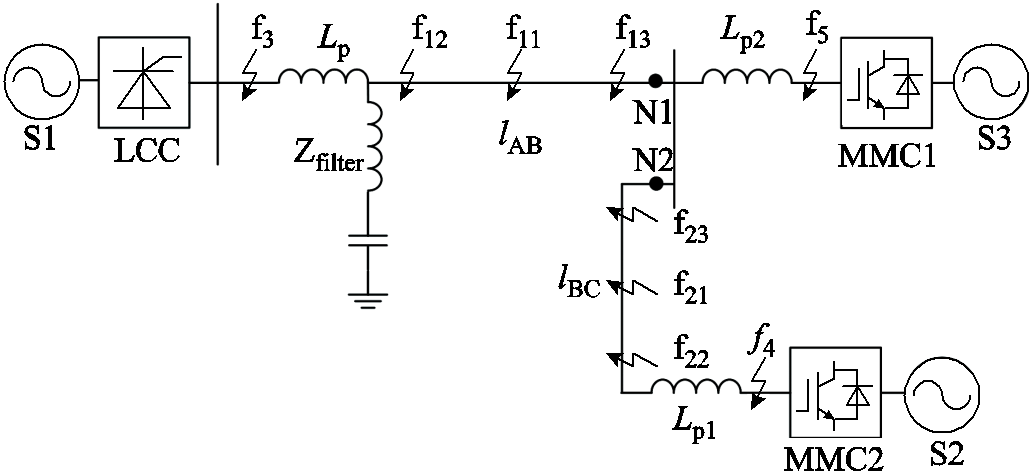
图1 三端混合直流输电系统拓扑结构
Fig.1 Topology structure of three-terminal hybrid DC transmission system
摘要 灵敏可靠的保护原理对多端混合直流输电系统的安全运行具有重要意义。现有多端混合直流输电系统线路保护原理易受过渡电阻、噪声等因素干扰，且多忽略与换流器控制环节之间的协调配合。为此，提出一种基于控制特征量的多端混合直流线路单端保护方案。首先，利用故障电流变化方向进行故障区域识别；然后，基于不同故障情况下等效阻抗回路中电感的差异，分析不同位置故障时控制信号积分值的大小差异，以此构造区内、外故障识别判据，并利用正、负极控制信号积分值比值进行故障选极；最后，通过PSCAD/EMTDC进行仿真验证，结果表明所提保护方案能够可靠、灵敏地识别各种故障，且具有较强的抗干扰和抗过渡电阻能力。
关键词：多端混合直流输电 控保协同 积分值 线路保护 拉普拉斯变换
混合高压直流输电技术（Hybird-High Voltage Direct Current transmission, Hybird-HVDC）结合了常规直流输电（Line Commutated Converter-High Voltage Direct Current, LCC-HVDC）和柔性直流输电（Modular Multilevel Converter-High Voltage Direct Current, MMC-HVDC）的优势，能有效解决换相失败、功率损耗严重等问题，逐渐成为远距离、大容量输电的发展趋势[1-3]。但混合直流输电系统通常采用架空线路，其故障发生概率较大，会在短时间内产生数倍于额定电流的故障电流。此外，混合直流输电系统运行灵活、拓扑结构复杂，对线路保护可靠、快速识别故障提出了巨大挑战。
可靠的保护原理是确保直流线路安全运行的第一道防线[4]。目前，国内外在直流线路保护方面进行了大量的研究，根据是否采用对端信息分为双端量保护和单端量保护[5]。
现有双端量保护多以纵联类为主。文献[6]利用线模前行波和后行波识别故障方向，并利用两者到达的时间差构造故障识别判据，但该方法耐受噪声干扰的能力有限。文献[7]利用故障时线模电压故障分量第一峰值时间识别区内外故障，利用线路端零模故障电压识别故障极，构造不受故障类型和故障阻抗影响的保护原理，但该方法受采样频率和系统参数影响。文献[8]根据线路边界元件两侧的电压故障分量的能量差异构建保护原理，但该方法过度依赖线路边界，不适用于混合三端直流输电系统。文献[9]将各点电压、电流变化量的平均谱半径与单环定理相结合，构造对通信通道要求低且无需时钟同步的保护原理，但该方法需要将测量结果传送到对端，速动性较差。
现有直流输电线路的单端量保护多基于行波理论。文献[10]利用初始电流行波高频相位差异构建区内外识别判据，利用低频段下线模入射电压行波相位区分短路故障和雷击干扰，但需要较高的采样频率保证保护的可靠性，对硬件要求较高。文献[11]利用换流站出口平波电抗器两侧暂态电压幅值比判断故障是否发生在直流线路上，利用反向行波幅值识别故障线路，该方法实现简单且能够兼顾快速性和灵敏性的要求，但受到线路长度的影响。文献[12]基于行波理论，通过分析区内外故障时电压行波相位特性构造保护方案。文献[13]分析行波波形特征，构造基于故障电压幅值和极值时间相配合的行波保护方法，该方法能够有效识别近端及近对端故障，但区内末端故障识别存在困难。上述单端量保护方案多用于主保护配置中，易受到过渡电阻、噪声等因素的影响[14]，且保护原理多依赖于边界特性，限制了其应用范围[15]。已有文献考虑控制策略对故障暂态特征的影响。文献[16]利用考虑换流站限流控制策略及换流站闭锁影响的暂态电流构造保护方案，但需要收集线路两端的电流量进行比较。文献[17]通过电流变化率与换流器子模块投切数量之间的关系，确定主动限流因子表达式，利用不同位置故障时主动限流因子的差异构造保护判据。上述保护方案考虑了限流控制策略对故障特性的影响，但没有考虑换流站本身控制策略与保护之间的配合。
综上所述，现有直流输电线路保护原理易受过渡电阻、噪声等因素干扰，且多忽略换流器控制环节与保护之间的交互影响及协调配合。因此，本文基于控保协同的思想，提出一种利用控制特征量的多端混合直流线路单端量保护方案。首先，基于多端混合直流系统的等值模型，对短路电流故障分量的特征进行分析，构造能够准确识别故障区域的方向判据；然后，分析区内外故障时控制特征量积分值的差异，以此构造区内外识别判据和故障选极判据；最后，进行仿真测试，验证所提保护性能。仿真结果表明，所提保护判据整定原则简单可靠，具有一定的耐过渡电阻及抗噪声干扰能力，能根据控制参数变化自适应地调整保护定值，有效改善了保护动作量下降的情况，提高了保护的可靠性与灵敏性。
三端混合直流输电系统拓扑结构如图1所示。送端为电网换相换流器（Line Commutated Converter, LCC），受端为混合型模块化多电平换流器（Modular Multilevel Converter, MMC）。lAB和lBC为直流输电线路，Lp、Lp1、Lp2为各换流站出口限流电抗器，Zfilter为直流滤波器，f11、f12、f13、f21、f22、f23表示区内故障，f3、f4、f5表示区外故障，N1、N2为保护测点。
图1 三端混合直流输电系统拓扑结构
Fig.1 Topology structure of three-terminal hybrid DC transmission system
LCC换流站由LCC换流器与线路出口处的滤波设备（包括平波电抗器和直流滤波器）[18]组成。LCC换流器的等值阻抗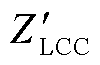
为
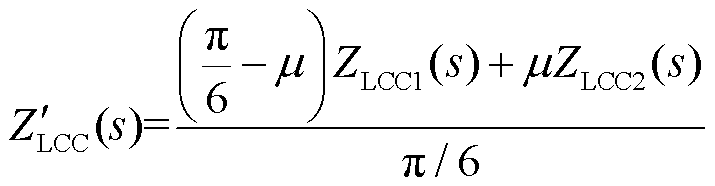（1）
式中，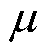
为LCC换流器的换相角；ZLCC1为非换相期LCC换流站的等值阻抗；ZLCC2为换相期LCC换流站的等值阻抗。
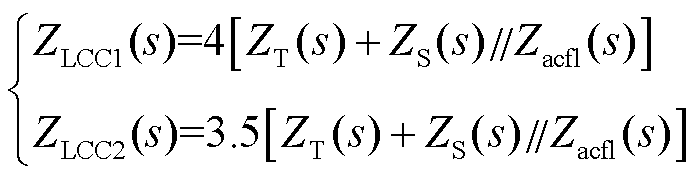（2）
式中，ZT为换流变压器的等值阻抗；ZS为送端交流系统等值阻抗；Zacfl为交流滤波器等值阻抗。
LCC换流站的等值阻抗为
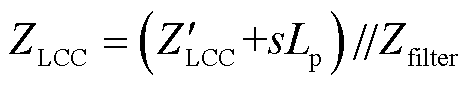（3）
式中，Lp为LCC换流站出口限流电抗器；Zfilter为直流滤波器阻抗，可表示为
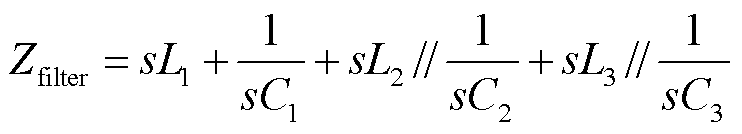（4）
式中，L1～L3、C1～C3为三调谐直流滤波器相关参数。
直流线路故障后，MMC换流站直流侧电流故障特性主要由各子模块电容放电电流决定[19]。子模块电容、桥臂、直流线路侧电感以及直流侧杂散电阻在MMC闭锁前形成放电回路[20]。由于换流器三个相单元完全相同且为并联状态[21]，因此，MMC直流侧可由电阻、电容和电感元件串联进行等效[22]，如图2所示。图中，Req、Leq和Ceq为MMC换流器等值参数，L′为换流器出口处的平波电抗器，Lg为中性线电抗器。
单相桥臂平均电容值与该时间段内的电流及调
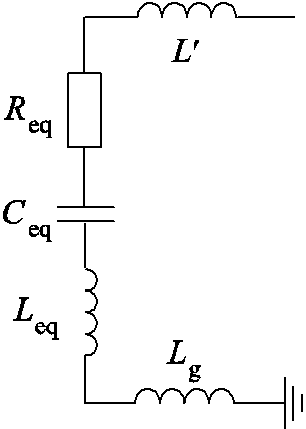
图2 MMC换流站等效电路
Fig.2 Equivalent circuit of MMC converter station
制波有关，上下桥臂投入子模块数量在不断变化。可将每个相单元中的子模块等效电容表示为
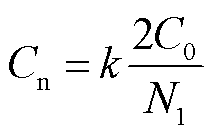（5）
式中，N1为单相投入的子模块数量；C0为子模块电容值；k为考虑上下桥臂投入子模块数量差异所取的系数，其取值为0.7～0.8[23]。
MMC换流器等值参数计算公式为
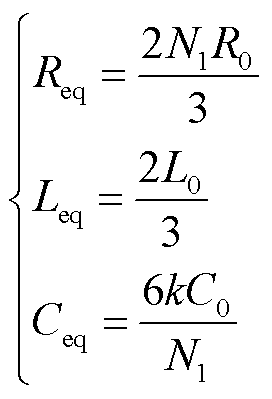（6）
式中，R0为子模块的导通电阻；L0为桥臂电抗。
因此，MMC站等值阻抗为
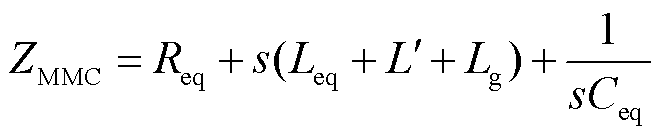（7）
与传统点对点直流输电相比，多端混合直流输电系统最大的结构特点是存在母线汇流T区。T区换流站MMC1仅装设平波电抗器，且该电抗器并联于汇流母线上[24]。直流线路发生故障时，各换流站提供的故障电流流通路径存在区别，与另外两个换流站不同，任一直流线路发生故障时，MMC1换流站提供的故障电流均经平波电抗器汇入故障点，不会经过另一条直流线路。本文利用MMC1换流站的控制特征量构建保护原理。因此本节仅对MMC1换流站控制策略进行分析。
MMC换流站采用双闭环控制策略，控制外环根据直流电压、交流功率等电气量的变化生成控制内环所需的参考电流；控制内环使直轴和交轴电流快速跟踪外环提供的参考电流。MMC1换流站外环采用功率控制，输入到内环中的直轴参考电流为
（8）
式中，kp、Tp和kvdc为控制参数；P为系统中有功功率实际值；Pref为设定的有功功率参考值；udcmin和udcmax分别为直流电压下限和上限的标幺值，取值分别为0.95(pu)和1.05(pu)；u为系统的直流电压值。
直流侧故障后的几ms内，交流侧三相分量仍保持对称，有功功率变化很小。但故障极直流电压幅值变化较大，会偏离额定电压[25]。因此故障发生后，根据式（8）可得直轴参考电流变化量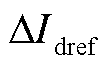
为
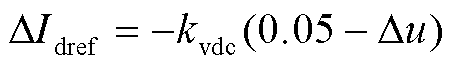（9）
式中，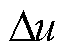
为直流电压变化量。
直流电压变化量与直轴参考电流变化量存在如式（9）所示的关系。直流故障发生时，直流电压的变化及控制参数的调节会导致直轴参考电流发生变化，在不同故障位置和故障类型下，直轴参考电流的变化程度不同，可利用这一特征构造保护原理。
三端混合直流输电系统拓扑如图3所示。多端混合直流输电系统可划分为T区左侧、T区右侧与T区三个区域，图3中I1、I2为系统稳态运行时的电流。
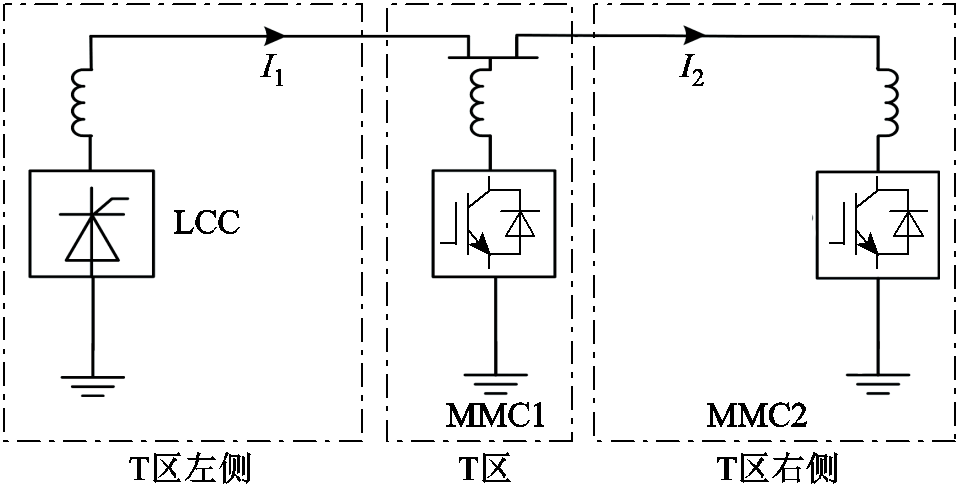
图3 三端混合直流输电系统拓扑
Fig.3 Topology diagram of three-terminal hybrid DC transmission system
由1.1节可知，三端混合直流输电系统能够等值为一个线性系统，因此可利用叠加定理对系统进行分析。直流故障发生时，系统可看作是故障前、后两个网络的叠加，因此故障电流可看作是电流故障分量与稳态分量之和[26]。以稳态电流方向为正方向，对不同区域故障时的电流故障分量进行分析。
不同区域故障下的等效电路如附图1所示，线路lAB和lBC上的电流故障分量分别为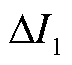
、
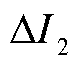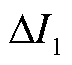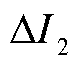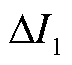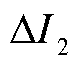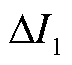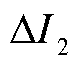。T区左侧故障时，I1、I2方向与规定正方向相反，为负，为负；T区右侧故障时，I1、I2方向与规定正方向相同，为正，为正；T区故障时，I1方向与规定正方向相同，I2方向与规定正方向相反，为正，为负。
综上所述，系统不同区域发生故障时，T区两侧直流线路上的电流故障分量方向不同，可依据其方向判断故障发生的区域。
2.2.1 电流故障分量计算
三端混合直流输电系统可等值为线性系统，在故障附加网络中求得电流的故障分量后与其对应的稳态分量叠加，即可得到故障电流的全量[27]。
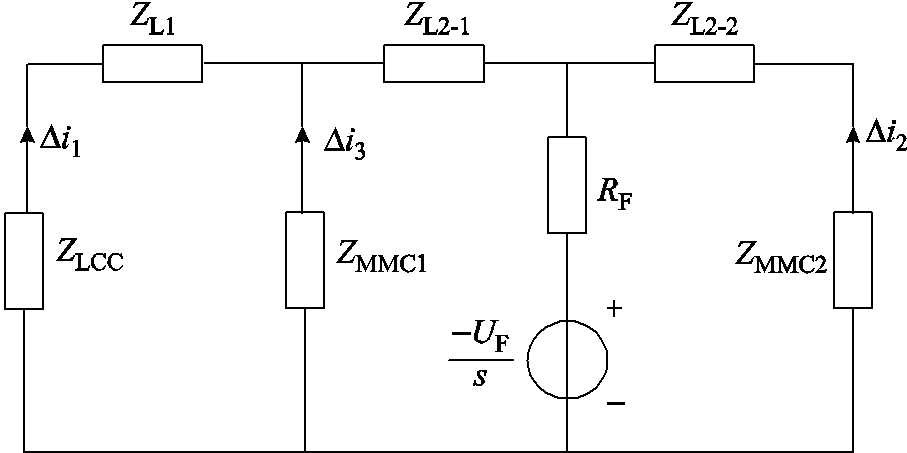
以T区左侧发生区内单极接地故障为例对短路电流故障分量进行分析。系统在复频域下的故障附加网络如图4所示。图中，UF/s为故障附加分量电源，RF为过渡电阻，ZL1-1、ZL1-2分别为直流线路lAB在故障点左侧和右侧部分的复频域等值阻抗，ZL2为直流线路lBC的复频域等值阻抗，ZLCC、ZMMC1和ZMMC2分别为三个换流站的等值阻抗，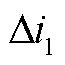
、
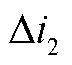及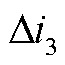
分别为故障时LCC、MMC2及MMC1换流站提供的短路电流故障分量。
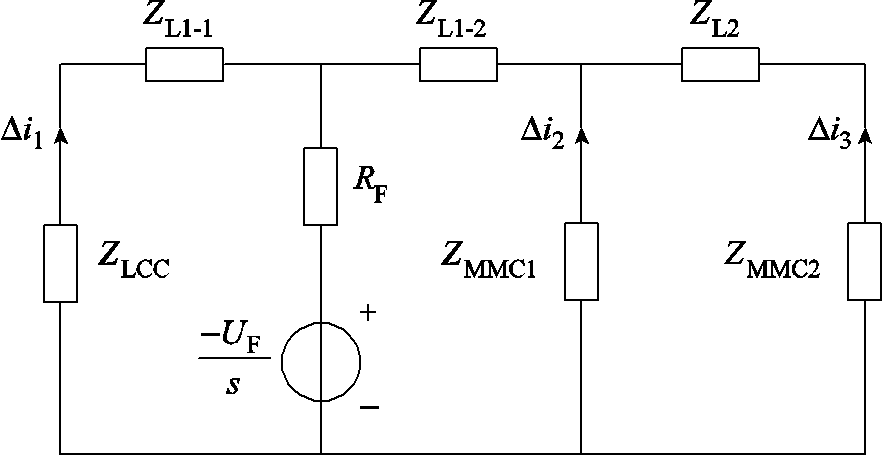
图4 T区左侧区内故障附加网络
Fig.4 The fault additional network in the left side of T area
直流线路发生单极接地故障时，直流线路单位长度电感参数可近似取为线模参数LX和地模参数LD的平均值，单位长度电阻参数可取为相应线模参数RX和地模参数RD的平均值；极间短路故障时，过渡电阻取RF/2，由于两极完全对称，仅存在线模分量，直流线路单位长度电感、电阻参数取为相应的线模参数。线模参数和地模参数数值见附表1。
MMC1换流站提供的短路电流故障分量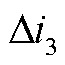为
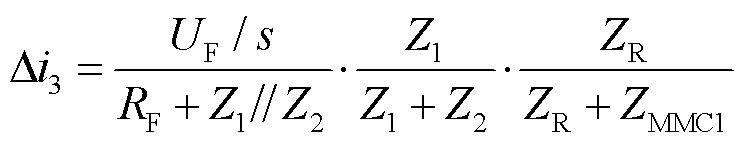（10）
式中，Z1、Z2和ZR为
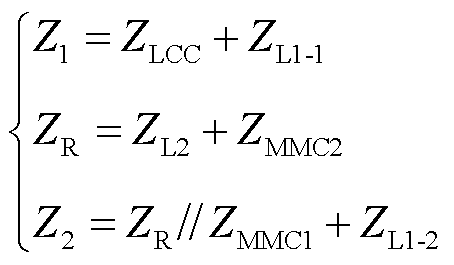（11）
在故障后的暂态时间尺度内，不同故障下短路电流的差异主要由电感引起[28]，因此忽略电容的影响，将故障等效回路中总的电感值等效为Ltotal，通过拉普拉斯反变换将式（10）改写为时域表达式，即
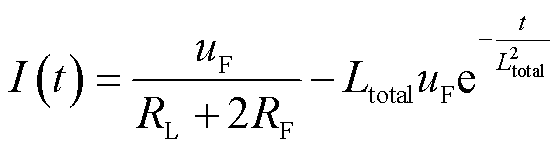（12）
式中，RL为Z2中的等效电阻；uF为故障附加分量电源的时域形式。由式（12）可知，电流故障分量与故障回路中等效电感呈负相关，因此，故障回路中的等效电感大小可反映出不同位置故障时电流故障分量的差异。
2.2.2 区内外故障识别原理
如图1所示，以T区左侧发生区内故障（f11～f13）为例进行分析。发生区内外故障时的故障放电回路如附图2所示，图中i31和i21分别为MMC1和MMC2换流站正极电流，发生单极接地故障时，流过MMC1换流站中性线上的故障电流为i31-i32，流过RL1-2和LL1-2的故障电流为i31+i21，可得T区左侧区内故障时MMC1换流站到短路点的故障等效阻抗回路如图5所示。图5中Lg1为MMC1换流站中性线接地电感，LL1-2和RL1-2分别为直流线路lAB在故障点右侧部分的电感和电阻，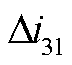
和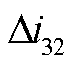
分别为MMC1换流站正、负极电流故障分量，
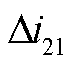为MMC2换流站正极电流故障分量。双极故障时两极对称，中性线电感上无故障电流流通，等效阻抗回路中无Lg1。
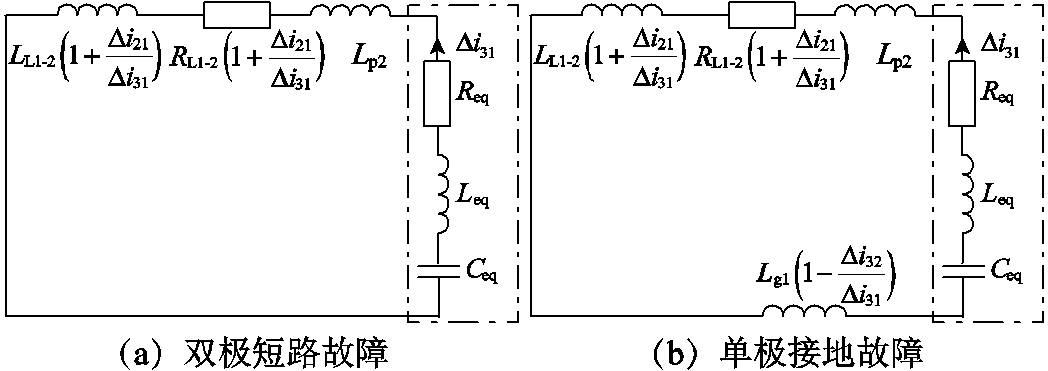
图5 T区左侧区内故障等效阻抗回路
Fig.5 Equivalent impedance circuit diagram of fault in the left side of T area
由图5a可得到故障后换流器出口电压变化量与电流变化量之间的关系为
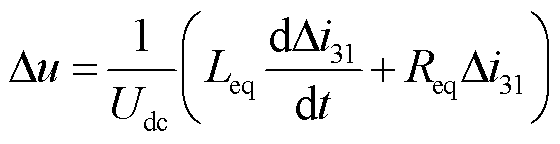（13）
式中，Udc为直流电压额定值。
1.2节中推导了电压变化量与直轴参考电流变化量的关系，将式（13）代入式（9）可得直轴参考电流变化量与电流变化量之间的关系为
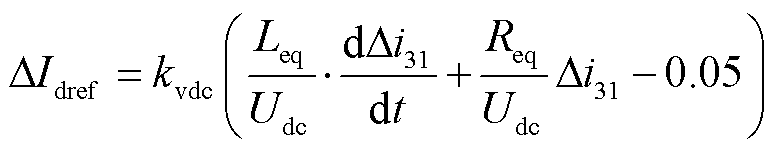（14）
为放大故障特征，对式（14）进行积分，有
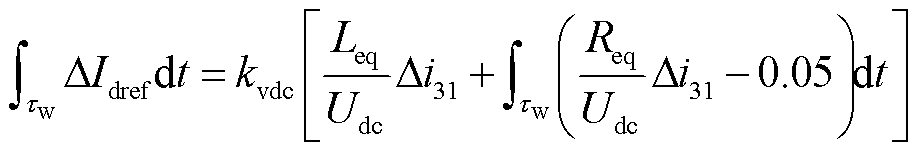（15）
式中，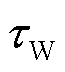
为保护的积分时间窗。
由式（15）可知，直轴参考电流变化量积分值与MMC1换流站正极电流故障分量呈正相关。结合2.2.1节的结论，可得直轴参考电流变化量积分值与故障回路中的等效电感呈负相关。因此，通过区内外故障时故障回路中等效电感的大小差异可分析出直轴参考电流变化量积分值的大小差异。
由附图2可得，T区左侧区外f3故障时，故障等效阻抗回路如图6所示，图中LL1、RL1分别为线路lAB的电感和电阻。
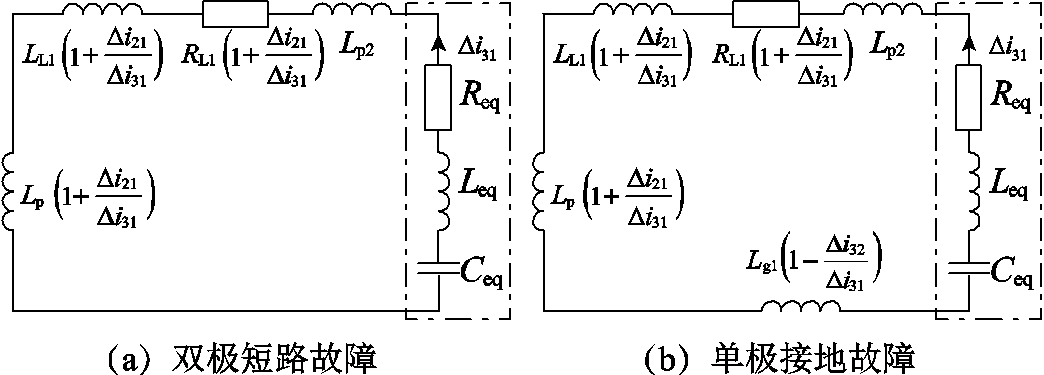
图6 T区左侧区外故障等效阻抗回路
Fig.6 Equivalent impedance circuit diagram of fault outside the left side of T area
由图5b可知，区内发生单极接地故障时等效电感值最大，有
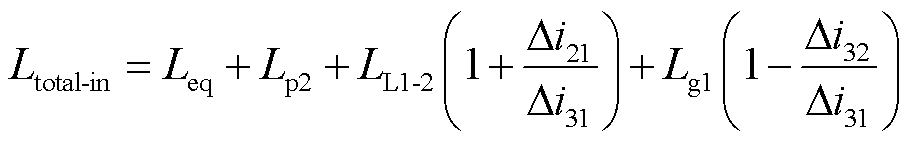（16）
由图6a可知，区外发生双极短路故障时等效电感最小，有
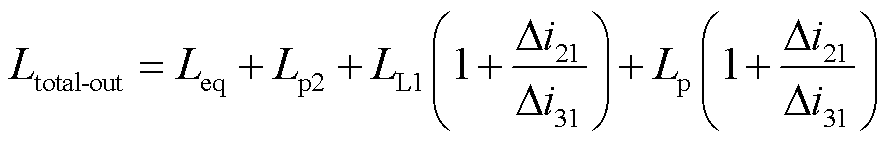（17）
根据直轴参考电流变化量积分值与等效电感之间关系，区内发生单极接地故障时，控制信号积分值为区内最小值；区外发生极间短路故障时，控制信号积分值为区内最大值。
由附表1中参数可知，Lp＞Lg1，对比式（17）和式（16）可知，区内最大等效电感值小于区外最小等效电感值。由此可得，区内故障时直轴参考电流变化量积分最小值大于区外故障时的直轴参考电流变化量积分最大值，即
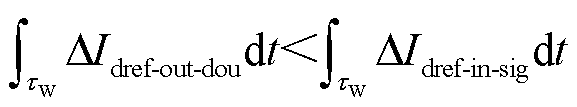（18）
式中，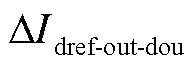
为区外发生极间短路故障时，直轴参考电流的变化量；
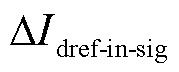为区内发生单极接地故障时，直轴参考电流的变化量。
T区右侧故障时的分析过程及结论与T区左侧故障时类似。其故障附加网络及区内外故障等效阻抗回路如附图3～附图5所示。
由2.1节可知，通过电流故障分量的方向可判别故障区域。考虑直流互感器传变特性的影响，在高压系统中，为了满足继保的要求，一般情况下使电流互感器的稳态复合误差小于5%[29]。具体判别依据为
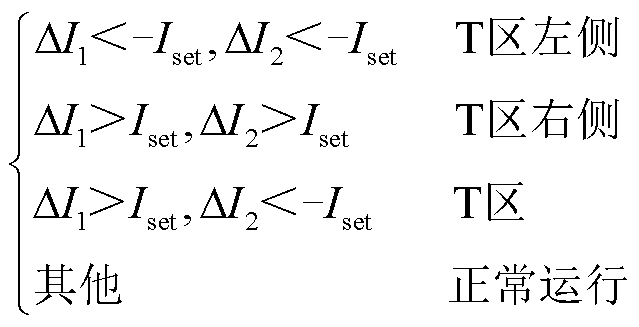（19）
式中，Iset为区域识别判据门槛值，取5%IN。为避免采样值抖动造成保护误动，当连续三个采样值满足某条区域识别判据时，可认为系统处于该条判据对应的状态。
控保协同是指在故障发生后，发挥换流器的控制潜力，利用控制信号的变化或是控制策略的切换带来的电气量的变化构造或优化保护方案。直流线路发生故障后，故障过程可分为行波初始阶段、直流控制暂态阶段及直流控制稳态阶段。目前关于高压直流线路的保护大多集中在行波初始阶段和直流控制稳态阶段。随着新型电力系统的发展，利用控保协同思想实现直流控制暂态阶段的故障保护受到关注。现有直流工程中已有利用控制测量信号构造保护原理的实例，如常规直流输电系统中基于触发角变化的保护[30]。
本文利用控制信号的变化构造区内外识别判据，将式（15）中直轴参考电流变化量积分值定义为S，有
（20）
式中，Idref(t)为故障后某时刻的控制特征信号值；Idref(0)为稳态时控制特征信号值。考虑直流保护速动性要求，积分时间窗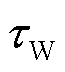=3 ms。
本文利用定积分定义计算积分值，将式（20）表示为求和形式，即
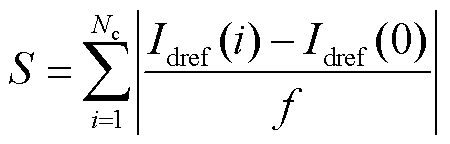（21）
式中，f为采样频率；i为当前时刻的采样点；Nc为保护积分时间窗内的采样点个数；Idref(i)为当前采样点下的控制特征信号值。
由式（18）可知，区外故障的控制信号变化量积分值总是小于区内故障的控制信号变化量积分值，据此构造区内外识别判据，如式（22）所示。
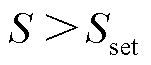（22）
式中，Sset为直轴参考电流变化量积分值整定值。Sset的整定应考虑躲过区外发生极间金属性短路故障，并保留一定的裕度，根据式（15），可表示为
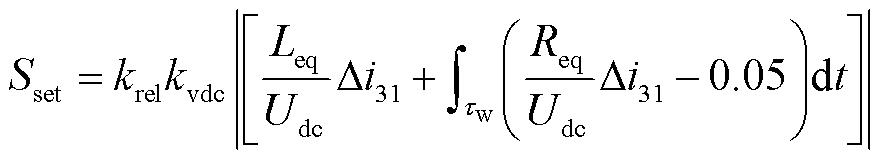（23）
式中，krel为可靠系数，为保证保护正确动作，krel=1.1。对于图1所示系统，T区左侧区外发生极间金属性短路故障时，故障等效网络如附图6所示。结合附表1中的参数，计算得MMC1换流站正极电流故障分量
为
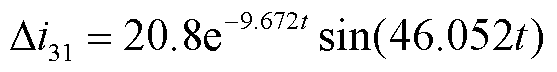（24）
求解得到的电流故障分量与仿真结果对比如附图7所示。从图中可看出，保护启动后3 ms时间窗内，电流故障分量最大值为2.48 kA，计算得到T区左侧整定值Sset=1.81×10-5。同理可得T区右侧整定值Sset=2.79×10-5。取正常运行时3 ms时间窗内的控制量进行积分计算，得到控制信号积分值为0.31×10-5。与两侧整定值相比，整定值分别为正常运行情况下的控制量积分值的6倍和9倍，这表明本文所提保护在故障时特征量变化明显，在正常运行情况下不会误动。
系统发生单极故障时，由于站内接地的原因，系统结构未发生变化，因此故障对健全极的影响较小[31]，其控制特征量的变化小于故障极；而系统发生双极故障时，故障线路之间构成了对称回路，正负极电流基本相同，两极的控制特征量变化程度基本相同[32]。可利用这一特征进行故障选极。定义正极与负极的直轴参考电流变化量积分值比值为q，即
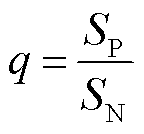（25）
式中，SP和SN分别为MMC1换流器正极和负极的直轴参考电流变化量积分值。
发生双极故障时，q值接近于1；发生正极接地故障时，q＞1；发生负极接地故障时，q＜1。保留一定的裕度，构造故障选极判据为
（26）
综上所述，本文所提基于控制特征量的多端混合直流输电线路单端量保护原理的流程如图7所示。
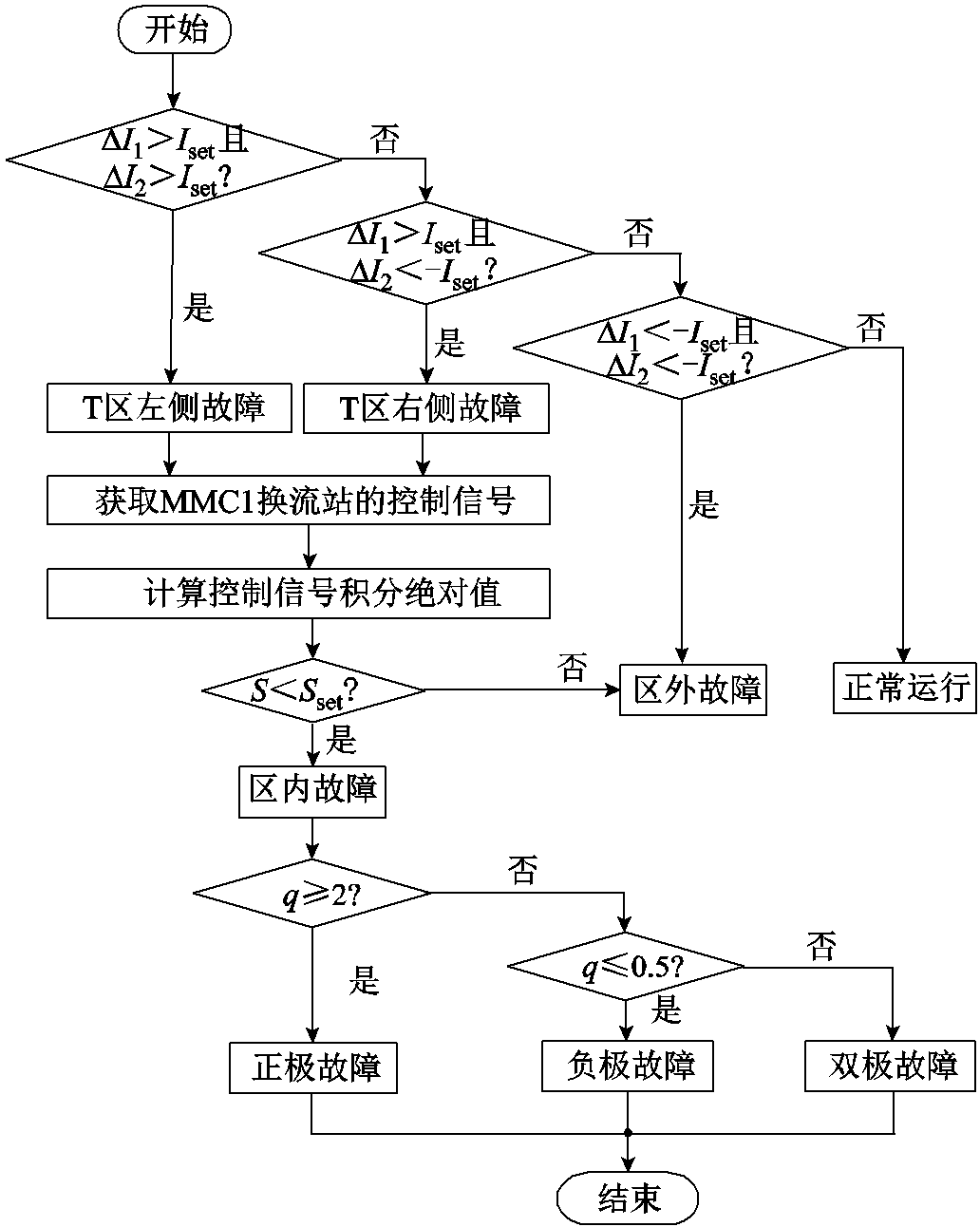
图7 保护原理流程
Fig.7 Protection principle flow chart
在该方案中，N1和N2测点的保护流程基本一致。根据式（19）判断故障发生区域，若满足T区左侧或T区右侧区域识别判据，则根据式（22）判断是否满足区内故障条件，若满足则为区内故障，若不满足则为区外故障，最后根据式（26）进行故障选极，保护动作。
为验证所提保护性能，在PSCAD/EMTDC仿真软件中搭建图1所示的三端混合直流输电系统模型。采样频率为10 kHz，采样时间窗为3 ms，保护测点N1、N2分别位于两条直流线路靠近T区一侧，均具备故障区域识别、区内外识别和故障选极功能。
不同位置、故障类型及过渡电阻会对本文所提保护的性能产生影响。为验证保护原理的有效性，在不同位置设置不同类型及过渡电阻（0、100、300 Ω）的故障进行仿真，仿真结果见表1。表1中“←”表示T区左侧故障，“→”表示T区右侧故障，“T”表示T区故障。
表1 不同故障情况下仿真测试结果
Tab.1 Simulation test results under different fault conditions
故障位置过渡电阻/Ω方向判据区内外判据/10-4选极判据判断结果 f110←1.5010.989区内极间 100←0.9590.995区内极间 300←0.5611.014区内极间 f120←0.7583.313区内正极 100←0.4833.434区内正极 300←0.2813.218区内正极 f130←1.8420.124区内负极 100←0.8820.124区内负极 300←0.4450.117区内负极 f210→1.2811.003区内极间 100→0.8801.007区内极间 300→0.5420.961区内极间 f220→0.8647.646区内正极 100→0.6057.997区内正极 300→0.3746.601区内正极 f230→1.7800.125区内负极 100→0.8610.139区内负极 300→0.4120.142区内负极 f3100←0.1280.979区外 f4100→0.2130.934区外 f5100T——区外
由表1可知，在不同位置、不同故障类型及不同过渡电阻情况下，所提保护原理能够准确识别故障，并可靠动作。
本文利用MMC1换流站的控制信号构建区内外故障识别判据及选极判据，整定值的选取也与控制参数相关，因此需要研究控制参数对保护的影响。以区内发生最不利故障的情况即f12、f22发生300 Ω正极接地故障，区外f3、f4、f5发生300 Ω极间短路故障为例进行分析。不同控制参数下的故障仿真结果见表2。
表2 不同控制参数下仿真测试结果
Tab.2 Simulation test results under different sampling frequencies
故障位置kvdc整定值/10-4方向判据区内外判据/10-4选极判据判断结果 f1210.052← 0.0542.675区内正极 150.519←0.5283.832区内正极 f2210.042←0.0623.714区内正极 150.438←0.5867.076区内正极 f310.052←0.0270.886区外 150.519←0.1801.037区外 f410.042→0.0220.758区外 150.438→0.2040.967区外 f51—T——区外 15—T——区外
由表2可以看出，控制参数发生变化时，直轴参考电流变化量积分值及整定值均发生变化，保护整定值能够随控制参数变化实现自适应调整。由分析可得，在合理调整系统控制参数使系统不会出现振荡、失稳等情况下，区内故障时直轴参考电流变化量积分值均大于保护的整定值，保护均能够准确可靠动作，且区外故障时保护不会发生误动。
采样频率会对式（21）的计算精度产生一定影响，因此设置采样频率为20、50 kHz，列出f11、f21发生极间金属性短路故障，f12、f22发生正极金属性接地故障及f3、f4、f5发生正极金属性接地故障时线路保护的仿真结果，验证采样频率对保护原理的影响。不同采样频率下仿真测试结果见表3。由表3可以看出，随着采样频率的增大，保护的整定值也会增加，但区内故障时直轴参考电流变化量积分值均大于保护的整定值，保护均能够准确可靠动作，区外故障时能够保证保护不误动。由此可见，本文所提方法对采样频率没有太高的要求，在性能相同的情况下，降低采样频率可以减少保护的运算量。
表3 不同采样频率下仿真测试结果
Tab.3 Simulation test results under different sampling frequencies
故障位置采样频率/kHz整定值/10-4方向判据区内外判据/10-4选极判据判断结果 f11200.560←5.0311.736区内极间 501.237←7.3400.990区内极间 f21200.560→2.5301.005区内极间 501.237→6.1810.991区内极间 f12200.560←1.4873.287区内正极 501.237←4.0932.935区内正极 f22200.560→1.3486.274区内正极 501.237→3.9656.680区内正极 f3200.560←0.4492.117区外 501.237←1.1612.362区外 f4200.560→0.4424.528区外 501.237→1.1063.759区外 f520—T——区外 50—T——区外
为验证所提保护的抗噪声能力，在采集到的暂态信号中分别加入信噪比为30 dB和40 dB的高斯白噪声，列出f12、f22发生极间金属性短路故障，f12、f22发生300 Ω单极接地故障，f3、f4、f5发生300 Ω极间短路故障时的仿真结果。验证噪声对所提保护的影响，测试结果见表4。
表4 不同信噪比下仿真测试结果
Tab.4 Simulation test results under different signal-to-noise ratios
故障位置信噪比/dB方向判据区内外判据/10-4选极判据判断结果 f1130←1.7990.880区内极间 40←1.3940.898区内极间 f2130→1.5461.063区内极间 40→1.3381.053区内极间 f1230←0.8332.688区内正极 40←0.4264.260区内正极 f2230→0.9473.696区内正极 40→0.3887.719区内正极 f330←0.1750.950区外 40←0.1040.676区外 f430→0.2771.338区外 40→0.1560.950区外 f530T——区外 40T——区外
由表4可知，在信噪比达到30 dB时，各保护判据仍能落入相应的动作范围内，不会发生区内故障拒动、区外故障误动，这表明所提保护原理具备一定的抗噪声干扰能力。
交流侧故障会引起直流侧功率传输减少甚至中断，三端混合直流输电系统为维持功率传输，会启动故障穿越控制策略，这会引起电流参考值的调整，因此有必要分析功率变化对保护的影响。以LCC侧功率降低500、1 000和3 000 MW运行情况为例，分析功率变化对所提保护的影响，仿真测试结果见表5。
表5 功率变化情况下仿真测试结果
Tab.5 Simulation test results under power changes
功率变化量/MW方向判据区内外判据/10-4选极判据判断结果 500—0.0371.266区外 1 000—0.0601.053区外 3 000—0.1630.909区外
表5中结果表明，在功率变化的情况下故障穿越控制策略引起的直轴参考电流的变化量的积分值未达到两侧保护的动作值，保护不会发生误动。
实际工程中，直流线路的单端量保护常采用ABB行波保护和西门子微分欠压保护构成双重保护[17]。直流线路其他单端量保护主流方案包括：利用信号分析处理方法提取暂态特征、利用智能算法识别故障及利用行波波前信息等。与上述保护相比，本文利用控制信号的暂态特征构造保护判据，无需提取行波的故障特征，且不依赖于复杂的信号分析处理方法及智能算法，实现简单。
文献[33]中介绍了ABB行波保护，其利用极模波和地模波的故障特征进行故障识别，较易受功率波动、噪声、过渡电阻及线路长度等因素的影响。从本文仿真结果可以看出，所提保护基本不受上述因素影响，且在线路长度较长时能够准确动作。
文献[34]利用经验模态分解法对线模电流进行时域分析，利用分解得到的高频本征模态函数（Intrinsic Mode Function, IMF）分量的瞬时能量构造保护原理。其原理较复杂且提取暂态特征的计算量较大。文献[35]通过频谱间差异的对比选取故障特征量，利用三个神经网络实现故障识别功能。神经网络训练工作量略大且实现起来较为复杂。所提保护原理无需复杂信号处理算法或智能算法，整定简单，更易实现。
针对现有保护方案易受过渡电阻、噪声等因素干扰，缺少与控制环节协调配合等问题，本文充分考虑三端混合直流输电系统中换流站的控制特性，在分析直流输电线路发生故障时控制信号暂态特征的基础上，提出了基于换流器直轴参考电流积分值的三端混合直流线路单端保护方案。主要结论如下：
1）直流线路发生区内故障时，MMC1换流站直轴参考电流变化量积分值大于区外故障时的数值，以此构造的保护判据，整定原则简单，保护定值能够根据控制参数的变化自适应调整，保护可靠性显著提高。
2）仿真结果表明，所提保护方案不受故障位置、故障类型影响，能够耐受300 Ω过渡电阻和30 dB高斯白噪声。
3）所提方法与传统行波保护相比，原理简单，对采样频率要求不高，数据通信量小，但是速动性弱于行波保护。
附 录
1. 故障等效电路
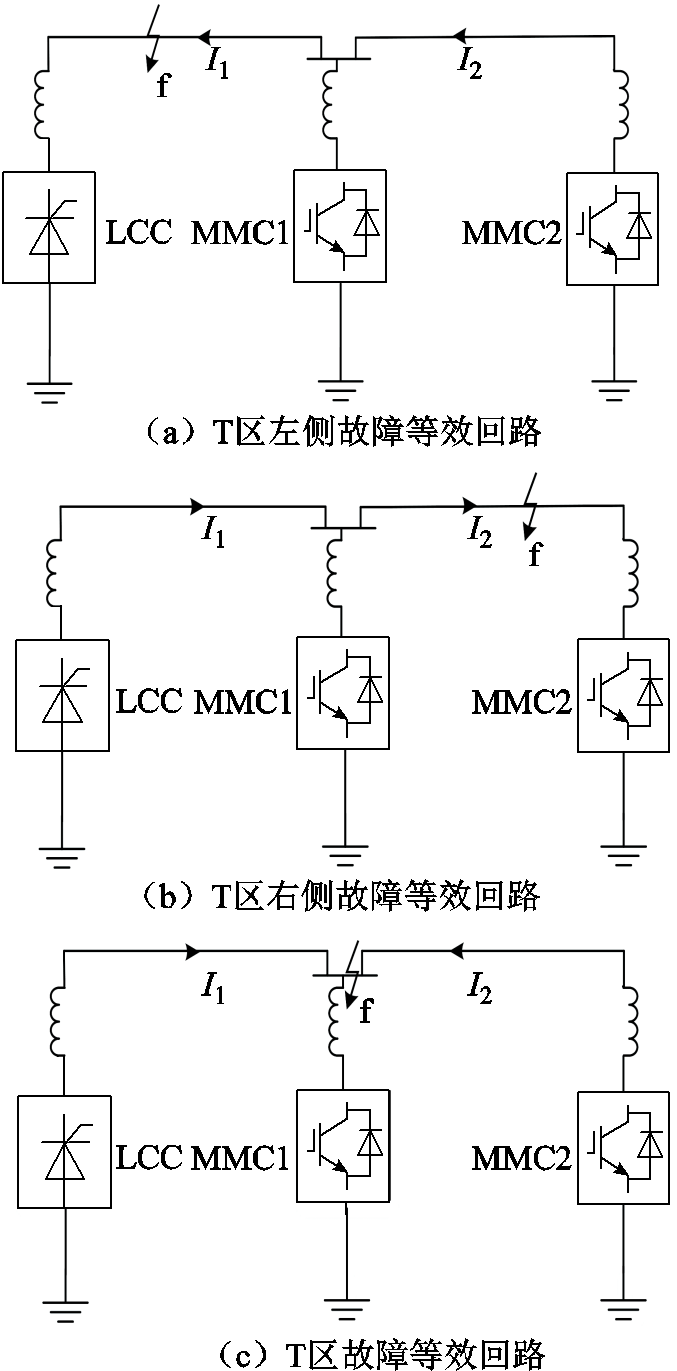
附图1 不同区域故障下的等效电路
App.Fig.1 Equivalent circuit under different regional faults
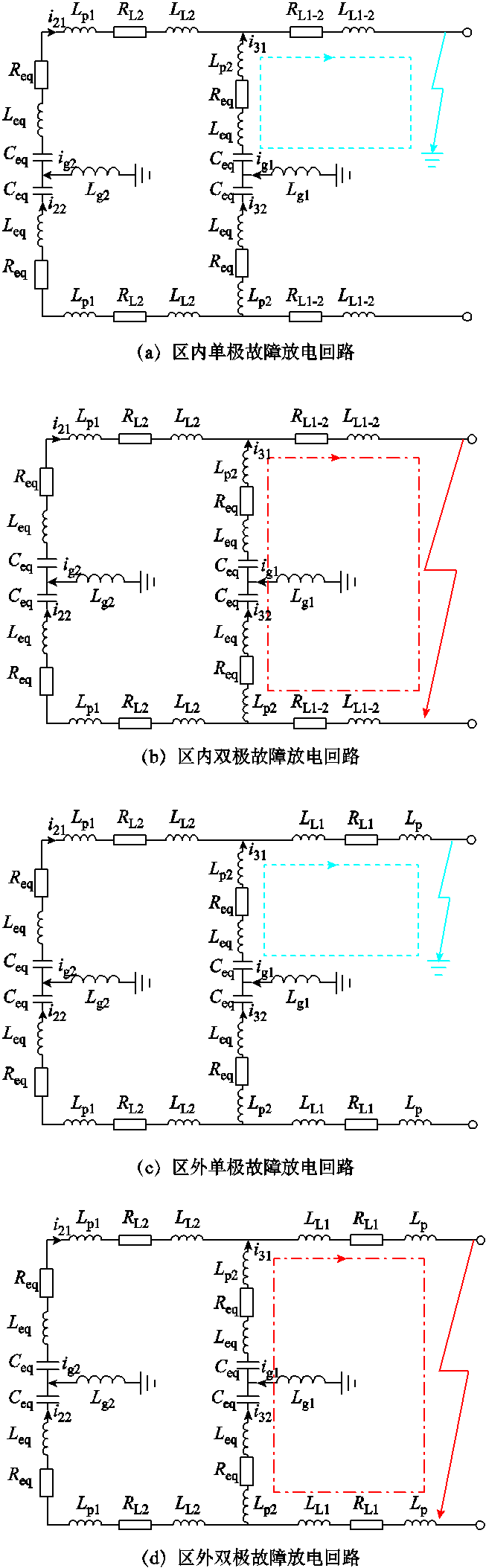
附图2 T区左侧区内外故障放电回路
App.Fig.2 Internal and external fault discharge circuit on the left side of T area
附图3 T区右侧区内故障附加网络
App.Fig.3 The fault additional network in the right side of T area
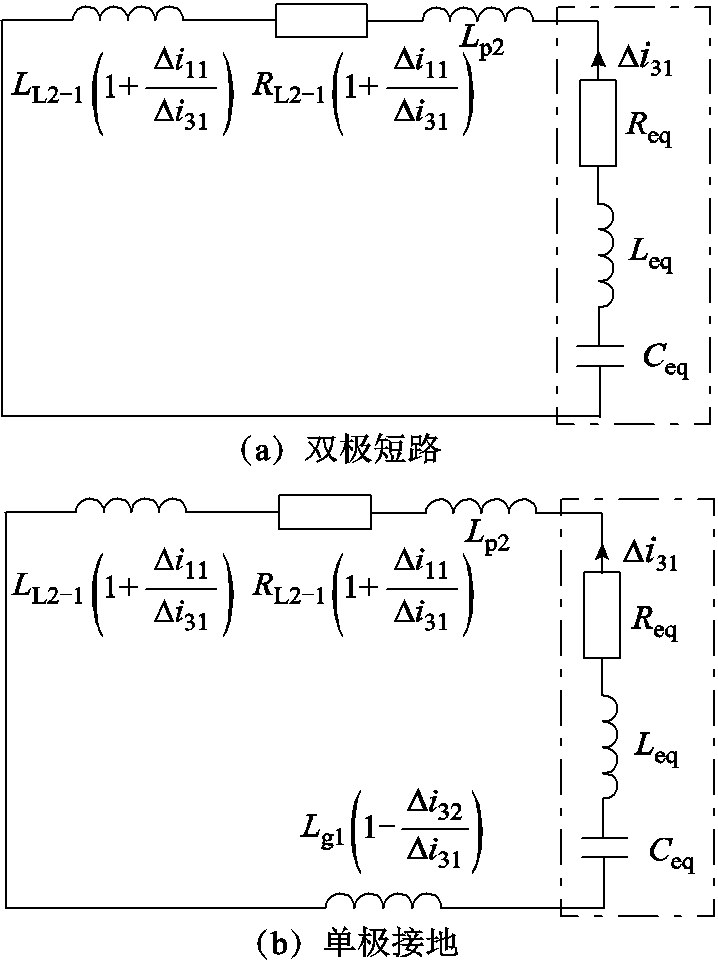
附图4 T区右侧区内故障等效阻抗回路
App.Fig.4 Equivalent impedance circuit diagram of fault in the right side of T area
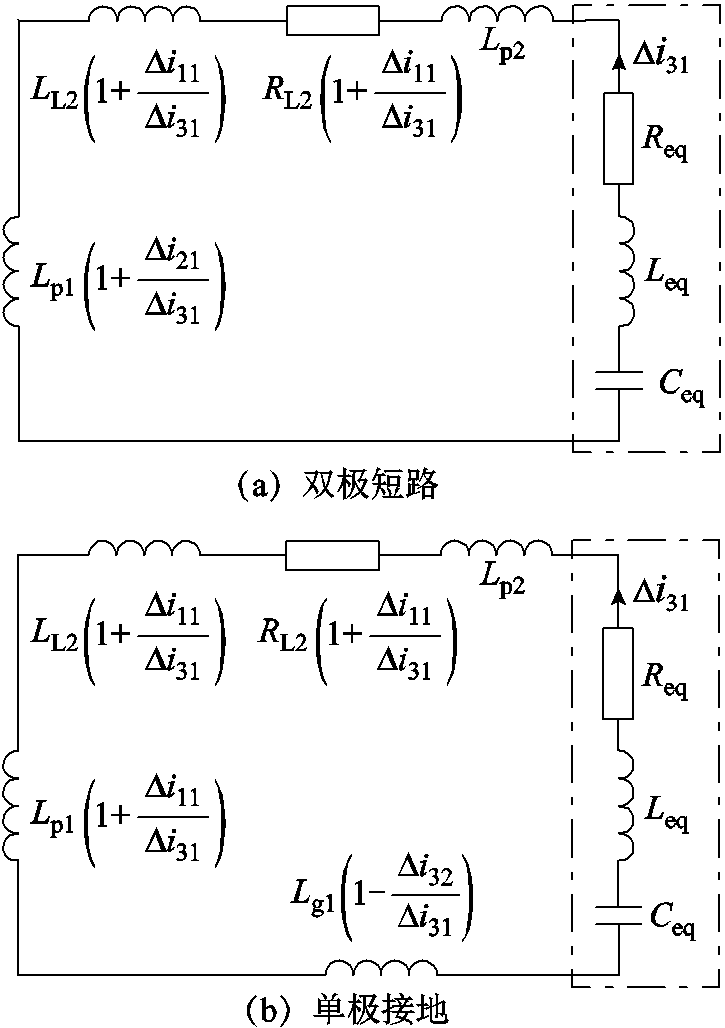
附图5 T区右侧区外故障等效阻抗回路
App.Fig.5 Equivalent impedance circuit diagram of fault outside the right side of T area
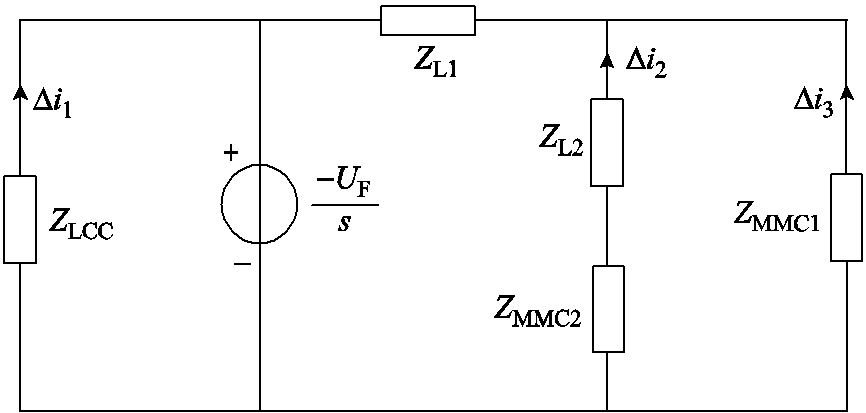
附图6 T区左侧区外故障附加网络
App.Fig.6 The fault additional network outside the right side of T area
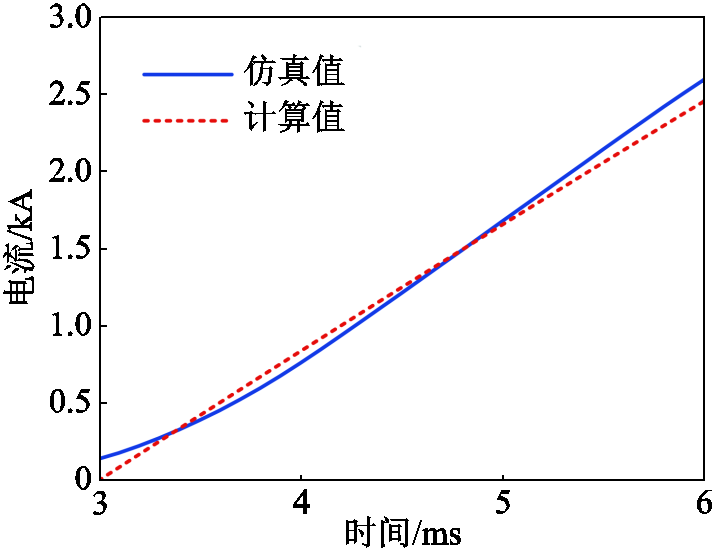
附图7 电流故障分量仿真值与计算值对比
App.Fig.7 Comparison diagram of simulation value and calculated value of current fault component
2. 系统仿真相关参数
附表1 三端混合直流输电系统参数
App.Tab.1 Three-terminal hybrid DC transmission system parameters
系统组成部分参数数值 LCC换流器L1/mH9.354 L2/mH15.919 L3/mH4.656 C1/μF1.2 C2/μF2.824 C3/μF2.647 Lp/H0.3 MMC2换流器R0/Ω0.005 L0/mH180 C0/F0.018 N1200 Lp1/H0.3 Lg2/H0.01 MMC1换流器R0/Ω0.005 L0/mH160 C0/F0.012 N1200 Lp2/mH100 kvdc8 Lg1/H0.01
（续）
系统组成部分参数数值 直流线路RD/(Ω/km)0.209 RX/(Ω/km)0.030 4 LD/(mH/km)1.78 LX/(mH/km)0.86
参考文献
[1] 王雪芹, 张大海, 李猛, 等. 基于小波能量谱和SSA-GRU的混合直流输电系统故障测距方法[J]. 电力系统保护与控制, 2023, 51(12): 14-24.
Wang Xueqin, Zhang Dahai, Li Meng, et al. Fault location method for a hybrid DC transmission system based on wavelet energy spectrum and SSA-GRU[J]. Power System Protection and Control, 2023, 51(12): 14-24.
[2] 李志川, 兰生, 魏柯. 基于MRSVD-GRU的混合三端特高压直流输电线路单极接地故障定位方法[J]. 电气技术, 2023, 24(3): 1-8, 63.
Li Zhichuan, Lan Sheng, Wei Ke. Single-pole grounding fault location method of hybrid three-terminal ultra-high voltage direct current transmission line based on MRSVD and GRU[J]. Electrical Engineering, 2023, 24(3): 1-8, 63.
[3] 李杭泽, 戴志辉, 石旭, 等. 计及控制响应的多端混合直流输电系统短路电流近似计算方法[J]. 电工技术学报, 2024, 39(9): 2810-2824.
Li Hangze, Dai Zhihui, Shi Xu, et al. Approximate calculation method of short-circuit current of multi-terminal hybrid DC transmission system considering control strategy[J]. Transactions of China Electro-technical Society, 2024, 39(9): 2810-2824.
[4] 梁远升, 黄泽杰, 李海锋, 等. 基于行波相位特性的三端混合直流线路行波保护原理[J]. 中国电机工程学报, 2021, 41(13): 4525-4543.
Liang Yuansheng, Huang Zejie, Li Haifeng, et al. Phase characteristics based travelling wave protection for transmission line of three-terminal hybrid HVDC system[J]. Proceedings of the CSEE, 2021, 41(13): 4525-4543.
[5] 杨亚宇, 邰能灵, 谢卫, 等. 利用单端边界能量的直流输电线路全线速动保护[J]. 电工技术学报, 2023, 38(9): 2403-2417.
Yang Yayu, Tai Nengling, Xie Wei, et al. A whole-line fast protection scheme for HVDC transmission line based on single-ended boundary energy[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2403-2417.
[6] Yu Xiuyong, Xiao Liye. A DC fault protection scheme for MMC-HVDC grids using new directional criterion[J]. IEEE Transactions on Power Delivery, 2021, 36(1): 441-451.
[7] Zhang Chenhao, Song Guobing, Dong Xinzhou. Non-unit ultra-high-speed DC line protection method for HVDC grids using first peak time of voltage[J]. IEEE Transactions on Power Delivery, 2021, 36(3): 1683-1693.
[8] 高淑萍, 宋晓辰, 宋国兵. 基于VMD能量熵的混合双端直流输电线路纵联保护方案[J]. 电力系统保护与控制, 2022, 50(14): 123-132.
Gao Shuping, Song Xiaochen, Song Guobing. Longitudinal protection scheme of hybrid double-terminal DC transmission lines based on VMD energy entropy[J]. Power System Protection and Control, 2022, 50(14): 123-132.
[9] 束洪春, 王广雪, 田鑫萃, 等. 基于随机矩阵理论的混合三端直流线路非单元式纵联保护[J]. 电力系统自动化, 2022, 46(19): 162-171.
Shu Hongchun, Wang Guangxue, Tian Xincui, et al. Non-unit pilot protection for hybrid three-terminal DC lines based on random matrix theory[J]. Automation of Electric Power Systems, 2022, 46(19): 162-171.
[10] 戴志辉, 牛宝仪, 邱宏逸, 等. 基于初始电流行波相位的多端混合直流线路单端保护方案[J]. 高电压技术, 2024, 50(2): 649-659.
Dai Zhihui, Niu Baoyi, Qiu Hongyi, et al. Single-ended protection scheme for multi-terminal hybrid DC lines based on initial current traveling wave phase[J]. High Voltage Engineering, 2024, 50(2): 649-659.
[11] 李晔, 李斌, 刘晓明, 等. 基于反向行波幅值比的对称单极柔性直流系统行波方向保护[J]. 电工技术学报, 2023, 38(9): 2418-2434.
Li Ye, Li Bin, Liu Xiaoming, et al. The direction protection based on the amplitude ratio of the backward traveling wave for the symmetrical monopole flexible DC system[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2418-2434.
[12] Liang Yuansheng, Jiang Liantao, Li Haifeng, et al. Fault analysis and traveling wave protection based on phase characteristics for hybrid multiterminal HVDC systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(1): 575-588.
[13] 陈淼, 贾科, 姚昆鹏, 等. 基于故障前行波极值时间的柔性直流线路单端量保护方法[J]. 中国电机工程学报, 2023, 43(10): 3742-3758.
Chen Miao, Jia Ke, Yao Kunpeng, et al. Single-ended protection method of flexible DC line based on extremum time of fault forward traveling wave[J]. Proceedings of the CSEE, 2023, 43(10): 3742-3758.
[14] Zhang Chenhao, Huang Jinhai, Song Guobing, et al. Non-unit ultra-high-speed line protection for multi-terminal hybrid LCC/MMC HVDC system and its application research[J]. IEEE Transactions on Power Delivery, 2021, 36(5): 2825-2838.
[15] 杨赛昭, 向往, 文劲宇. 架空柔性直流电网线路故障保护综述[J]. 中国电机工程学报, 2019, 39(22): 6600-6617.
Yang Saizhao, Xiang Wang, Wen Jinyu. Review of DC fault protection methods for the MMC based DC grid[J]. Proceedings of the CSEE, 2019, 39(22): 6600-6617.
[16] 李海锋, 许灿雄, 梁远升, 等. 计及换流站控制响应的多端混合直流线路后备保护设计[J]. 电力系统保护与控制, 2023, 51(3): 155-163.
Li Haifeng, Xu Canxiong, Liang Yuansheng, et al. Backup protection design for multi-terminal hybrid HVDC lines considering control response[J]. Power System Protection and Control, 2023, 51(3): 155-163.
[17] 刘思奇, 胡鹏飞, 王栋, 等. 基于MMC主动限流的VSC-HVDC双极短路故障控保协同策略[J]. 电力系统自动化, 2024: 48(10): 192-202.
Liu Siqi, Hu Pengfei, Wang Dong, et al. Collaborative control and protection strategy for bipolar short-circuit fault in VSC-HVDC based on active MMC current limiting[J]. Automation of Electric Power Systems, 2024: 48(10): 192-202.
[18] 曹虹, 周泽昕, 吕鹏飞, 等. 高压直流输电线路故障初始阶段解析方法研究[J]. 电力系统及其自动化学报, 2022, 34(7): 137-147.
Cao Hong, Zhou Zexin, Lü Pengfei, et al. Study on analysis method for HVDC transmission line faults at initial stage[J]. Proceedings of the CSU-EPSA, 2022, 34(7): 137-147.
[19] 吴丽丽, 茆美琴, 施永. 含主动限流控制的MMC-HVDC电网直流短路故障电流解析计算[J]. 电工技术学报, 2024, 39(3): 785-797.
Wu Lili, Mao Meiqin, Shi Yong. Analytical calculation of DC short-circuit fault current of modular multi-level converter-HVDC grid with active current limiting control[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 785-797.
[20] 王蕾, 孙孝峰, 王宝诚, 等. LCC-MMC混合高压直流输电系统直流线路故障保护方案研究[J]. 中国电机工程学报, 2021, 41(21): 7339-7352.
Wang Lei, Sun Xiaofeng, Wang Baocheng, et al. Research on protection scheme of DC line fault in LCC-MMC hybrid HVDC system[J]. Proceedings of the CSEE, 2021, 41(21): 7339-7352.
[21] 辛业春, 刘熠, 江守其, 等. 计及零直流电压控制的混合型MMC-HVDC输电系统短路电流计算方法[J]. 电网技术, 2023, 47(7): 2820-2828.
Xin Yechun, Liu Yi, Jiang Shouqi, et al. Short-circuit current calculation method for FHMMC-HVDC transmission systems with zero DC voltage control[J]. Power System Technology, 2023, 47(7): 2820-2828.
[22] 束洪春, 代月, 安娜, 等. 基于线性回归的柔性直流电网纵联保护方法[J]. 电工技术学报, 2022, 37(13): 3213-3226, 3288.
Shu Hongchun, Dai Yue, An Na, et al. Pilot protection method of flexible DC grid based on linear regression[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3213-3226, 3288.
[23] 黄旭, 刘轶超, 朱汉卿, 等. 基于平均电容的MMC直流故障电流计算方法研究[J]. 电气传动, 2022, 52(17): 46-51.
Huang Xu, Liu Yichao, Zhu Hanqing, et al. Research on MMC DC fault current calculation method based on average capacitance[J]. Electric Drive, 2022, 52(17): 46-51.
[24] 邢超, 蔡旺, 毕贵红, 等. 昆柳龙特高压三端混合直流输电线路边界频率特性研究[J]. 电力自动化设备, 2023, 43(2): 135-141.
Xing Chao, Cai Wang, Bi Guihong, et al. Research on boundary frequency characteristics of Kunliulong hybrid three-terminal UHVDC transmission line[J]. Electric Power Automation Equipment, 2023, 43(2): 135-141.
[25] 陈仕龙, 吴涛, 王朋林, 等. 基于深度学习的特高压三端混合直流输电线路波形特征故障区域判别方法[J]. 电力系统及其自动化学报, 2024, 36(1): 24-36.
Chen Shilong, Wu Tao, Wang Penglin, et al. Fault zone identification method for three-terminal hybrid UHVDC transmission lines based on deep learning and waveform characteristics[J]. Proceedings of the CSU-EPSA, 2024, 36(1): 24-36.
[26] 周家培, 赵成勇, 李承昱, 等. 采用电流突变量夹角余弦的直流电网线路纵联保护方法[J]. 电力系统自动化, 2018, 42(14): 165-171.
Zhou Jiapei, Zhao Chengyong, Li Chengyu, et al. Pilot protection method for DC lines based on included angle cosine of fault current component[J]. Auto-mation of Electric Power Systems, 2018, 42(14): 165-171.
[27] 汤兰西, 董新洲. MMC直流输电网线路短路故障电流的近似计算方法[J]. 中国电机工程学报, 2019, 39(2): 490-498, 646.
Tang Lanxi, Dong Xinzhou. An approximate method for the calculation of transmission line fault current in MMC-HVDC grid[J]. Proceedings of the CSEE, 2019, 39(2): 490-498, 646.
[28] 孙吉波, 王宇, 刘崇茹, 等. 基于MMC的多端直流电网双极短路故障电流计算[J]. 电力自动化设备, 2018, 38(11): 72-78.
Sun Jibo, Wang Yu, Liu Chongru, et al. Pole-to-pole short circuit current calculation of multi-terminal DC grid based on MMC[J]. Electric Power Automation Equipment, 2018, 38(11): 72-78.
[29] 黄宇. 电力系统电流互感器饱和特性及其对继电保护的影响与对策研究[D]. 成都: 西南交通大学, 2018.
Huang Yu. Research on the saturation characteristics of current transformer in power system and its influence on relay protection and countermeasures[D]. Chengdu: Southwest Jiaotong University, 2018.
[30] 祝新驰, 李海锋, 黄炟超, 等. 基于触发角变化特性的高压直流线路纵联保护[J]. 电力自动化设备, 2020, 40(6): 163-171.
Zhu Xinchi, Li Haifeng, Huang Dachao, et al. Pilot protection of HVDC power transmission lines based on variation characteristics of firing angle[J]. Electric Power Automation Equipment, 2020, 40(6): 163-171.
[31] 陈继开, 孙川, 李国庆, 等. 双极MMC-HVDC系统直流故障特性研究[J]. 电工技术学报, 2017, 32(10): 53-60, 68.
Chen Jikai, Sun Chuan, Li Guoqing, et al. Study on characteristics of DC fault in bipolar MMC-HVDC system[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 53-60, 68.
[32] 高飘, 郑晓冬, 晁晨栩, 等. 基于边界暂态能量的多端柔性直流输电线路保护[J]. 电力系统自动化, 2021, 45(17): 171-179.
Gao Piao, Zheng Xiaodong, Chao Chenxu, et al. Protection for multi-terminal flexible DC transmission lines based on boundary transient energy[J]. Auto-mation of Electric Power Systems, 2021, 45(17): 171-179.
[33] 郑伟, 张楠, 杨光源. 西门子及ABB直流线路行波保护对比和改进研究[J]. 电力系统保护与控制, 2015, 43(24): 149-154.
Zheng Wei, Zhang Nan, Yang Guangyuan. Comparative and improvement investigation on the DC transmission line traveling wave protections of Siemens and ABB[J]. Power System Protection and Control, 2015, 43(24): 149-154.
[34] 邢超, 牛元有, 王龙, 等. 特高压多端混合直流线路经验模式分解单端保护[J]. 电力系统及其自动化学报, 2024, 36(7): 122-132.
Xing Chao, Niu Yuanyou, Wang Long, et al. Single-end protection for UHV multi-terminal hybrid DC transmission line and CEEMDAN[J]. Proceedings of the CSU-EPSA, 2024, 36(7): 122-132.
[35] Yang Qingqing, Le Blond S, Aggarwal R, et al. New ANN method for multi-terminal HVDC protection relaying[J]. Electric Power Systems Research, 2017, 148: 192-201.
Abstract The hybrid DC transmission system integrates the advantages of conventional DC transmission systems and flexible DC transmission systems, gradually becoming a development trend of long-distance and large-capacity power transmission. However, its topology structure is complex and the operation mode is flexible. And it commonly employs overhead lines, the fault probability of the overhead lines is high and the fault current will be several times the rated current within a short time after the DC-side fault. Therefore, studying sensitive and reliable protection methods for DC transmission lines is of great significance. Most of the existing protection methods proposed for DC transmission lines have overlooked the coordination between control and protection. Therefore, this paper proposes a protection method for DC transmission lines utilizing control characteristic quantities.
First, the three-terminal hybrid DC transmission system is modeled. On this basis, the direction of the short-circuit current fault component after the DC-side fault is analyzed, and the fault area can be determined based on the direction change. Second, based on the superimposed network and the Laplace transformation, the time-domain expression of the DC current fault component is calculated, revealing the negative correlation with the equivalent inductance value in the fault circuit. By utilizing the relationship between the port voltage and the DC current fault component, the DC voltage variation is obtained. By substituting it into the expression of direct-axis reference current variation integral, it is found that the direct-axis reference current variation integral is also negatively correlated with the equivalent inductance value in the fault circuit. Subsequently, the difference of the equivalent inductance value in the fault circuit of internal and external faults is analyzed, and it can be seen that the maximum equivalent inductance value during internal faults is less than the minimum equivalent inductance value during external faults. Therefore, it can be deduced that the minimum integral value of the direct-axis reference current variation during internal faults is larger than that during external faults. Based on this characteristic, the protection method is constructed by using the integral value of the direct-axis reference current variation. Finally, extensive simulation analysis, taking into account various influencing factors such as fault location, fault type, sampling frequency and fault resistance, is carried out on PSCAD/EMTDC to verify the reliability and sensitivity of the proposed protection method.
The conclusions can be drawn as follows: When the three-terminal hybrid DC transmission lines have an internal fault, the integral value of the direct-axis reference current variation of the T-zone converter station is always greater than that during external fault. This paper fully makes use of the characteristics of the direct-axis reference current variation integral value of the T-zone converter station after DC-side faults to propose a protection method for DC transmission lines based on the coordination of control and protection. The proposed protection method is easy to implement and its settings value can adapt to control parameters. In addition, compared with the traveling wave protection method, the proposed protection method requires lower sampling frequency and less data communication.
Keywords：Multi-terminal hybrid DC transmission, cooperation of control and protection, integral quantity, line protection, Laplace transformation
中图分类号：TM721.1
DOI: 10.19595/j.cnki.1000-6753.tces.232070
国家自然科学基金资助项目（51877084）。
收稿日期 2023-12-13
改稿日期 2024-02-26
戴志辉 男，1980年生，教授，博士生导师，研究方向为电力系统保护与控制。
E-mail：daihuadian@163.com（通信作者）
牛宝仪 女，2000年生，硕士研究生，研究方向为直流输电系统保护与控制
E-mail：a15803265866@163.com
（编辑 赫 蕾）