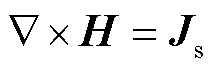 (1)
(1)
摘要 为了解决有限元法(FEM)仿真分析中三维非线性磁场计算效率低、成本高的问题,该文提出一种基于本征正交分解(POD)的三维非线性磁场问题自适应模型降阶方法。该方法基于贪婪策略,将POD与径向基函数(RBF)相结合,同时采用改进的麻雀搜索算法(ISSA)计算RBF的最优宽度参数组合,构建更适配高阶系统的降阶模型。以TEAM24标准问题——非线性时变旋转实验装置的磁场模型和一台单相牵引变压器模型为算例,验证降阶模型的高效性能。结果表明:该方法在具有较高精度的同时具有高加速比,建立的模型具有较好的可泛化性。
关键词:本征正交分解 改进的麻雀搜索算法 模型降阶 贪婪算法 三维非线性磁场
随着新工业时代的到来,数字孪生技术被认为是实现工业产品实时监控和全生命周期管理的关键技术。数字孪生的一个重要特征是要求实时地反映服役电气设备的物理特性[1-3]。有限元法(Finite Element Method, FEM)是分析低频电气设备电磁性能的常用方法,它能够对设备的运行状态进行模拟并给出准确的结果,但由于几何模型空间自由度高、时间步多以及媒质的非线性行为等原因,导致FEM分析需要大量的计算时间[4-6]。昂贵的计算成本使电气设备的优化设计以及需要实时性能分析的数字孪生技术的应用受到限制。
模型降阶技术(Model Order Reduction, MOR)是在保证模型计算精度的同时,建立高效行为模型的方法。简而言之,就是在某种情况下将一个较大系统转换为近似的较小系统的过程,以降低大型复杂系统的理论分析难度并减少数据运算量[7]。它可以有效地解决FEM计算步骤多、时间成本高的问题。常见的模型降阶方法有:平衡截断法(Balanced Truncation Method, BTM)、Krylov子空间方法、本征正交分解法(Proper Orthogonal Decomposition, POD)等[8-10]。BTM与Krylov子空间常用于线性时不变系统中,两者的区别在于,BTM较Krylov子空间法更容易获得降阶系统的误差估计,但BTM由于要求解两个Lyapunov方程,在大型系统中的计算量很大;Krylov子空间法瞬态效果良好,在一定条件下能够保持系统的稳定性,常在高阶线性电路系统中使用。
目前,POD法已经在工程领域被广泛应用,例如,流体动力学[11-13]、结构动力学[14]、热传导分析[15-16]和计算电磁学[17-18]等。它通过选择一组有效的数据样本集来构造降阶过程中所需要的变换矩阵以达到降阶的目的,即用低维数据来表示高维数据集的特征信息[19]。文献[20]将子域降阶模型与离散经验插值方法(Discrete Empirical Interpolation Method, DEIM)结合,提出一种基于POD的自适应子域模型降阶方法。文献[21]利用DEIM减小非线性项的计算复杂度,并比较了POD-DEIM和POD-BPIM方法,以更好地解决非线性静磁场问题。文献[22]比较了不同的DEIM方法和Gappy POD在同步电机中的应用,并提出在DEIM中根据转子的角位移使用不同的局部投影来提高模型的求解精度和稳定性。另外,POD模型降阶方法在电气设备复杂问题的模拟中也有较好的应用。文献[23]基于POD正交基构建了准静态电场方程的降阶模型,分析了换流变压器极性反转瞬态电场问题,结果表明POD正交基所对应的特征值越大,反映模型的物理特征越全面,降阶模型的计算精度也越高。文献[24]提出引入本征正交分解算法与DEIM对绕组稳态温升进行降阶计算,以解决计算时间成本过高的问题。
在上述文献中,因为都需要访问非线性项的组装过程,POD模型仍然依赖全阶方程组,因此更具有侵入性。同时,为了获得较高的精度,快照集的数量必须接近原始解空间,致使模型降阶的数值成本仍然很高。对此,文献[25]采用了非侵入性的方法,通过对快照奇异值分解得到向量进行插值,求解给定输入的降阶模型的解,该过程不需要访问矩阵和组装步骤。文献[26]也避免了对FEM矩阵的重复访问与组装,它利用数据驱动的思想,从快照中创建一个非线性项的简化模型。对于非线性系统的非侵入式降阶,POD通常与其他插值或拟合方法结合来完成,如Kriging模型、响应面法、径向基函数(Radial Basis Function, RBF)法等。其中,Kriging模型对于非线性模型有良好的近似能力,但插值结果易受到样本点数量和分布的影响,往往需要大量的数据;而响应面法对样本点的选取较为苛刻,且不能保证响应面通过所有的样本点,容易产生预测误差。径向基函数是一种以空间距离为变量的函数,具有形式简单、各向同性和适于数值计算的优点[27-28]。将RBF插值方法应用于模型降阶,可以获得较好的结果。为构建新型的管道内壁几何识别框架,文献[29]建立了变几何样本库的POD与RBF降阶代理模型,并讨论了不同基函数对结果的影响。需要注意的是,基函数中宽度参数的选择决定了当前样本点向周围影响衰减的快慢,所有已知样本点共同影响了未知样本点的计算结果,因此在考虑非线性的降阶计算中,样本点局部密度不同,宽度参数也不应相同,不可盲目选择。此外,不同样本采样方式得到的快照各不相同,对降阶模型的构建有很大的影响。而且在降阶模型建立过程中由快照选取带来的不确定性,也是构建POD降阶模型需要考虑的。
针对上述问题,本文提出一种适用于三维非线性磁场问题的自适应模型降阶方法。首先,基于传统FEM模型计算不同样本点对应的FEM数值解作为样本库;其次,构造基于改进麻雀搜索算法(Improved Sparrow Search Algorithm, ISSA)、考虑基函数最优宽度参数组合的ISSA-POD-RBF降阶模型;然后,通过贪婪策略进行快照矩阵与最优宽度参数组合的迭代计算,构建更加匹配原始模型的快速计算模型;最后,以TEAM24问题和一台牵引变压器为研究对象,通过对比降阶模型与FEM全阶模型的计算结果和计算时间,验证降阶模型的快速性与准确性。
通过绕组施加电流密度源的静磁场问题的控制方程表示为
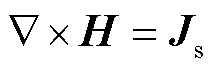 (1)
(1)
式中,H为磁场强度;Js为源电流密度。
磁通密度B用矢量磁位A可表示为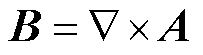 。铁磁材料中,磁导率μ与磁场呈非线性关系,本构关系可表示为
。铁磁材料中,磁导率μ与磁场呈非线性关系,本构关系可表示为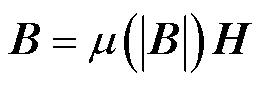 。式(1)可写为
。式(1)可写为
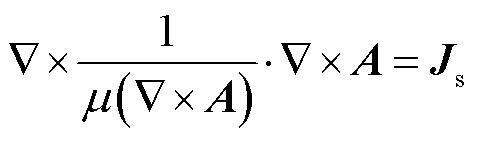 (2)
(2)
基于空间离散化的FEM,式(2)以微分方程的弱形式求解,可以写成矩阵形式
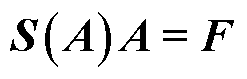 (3)
(3)
式中,S为刚度矩阵;F为源向量。刚度矩阵的元素依赖矢量磁位A,通常使用Newton-Raphson方法来处理非线性,包含∆Aj的迭代公式为
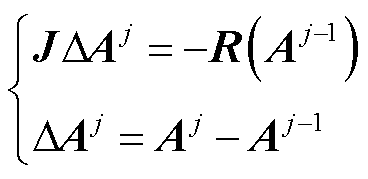 (4)
(4)
式中,R为残差向量;J为Jacobian矩阵,对应的表达式分别为
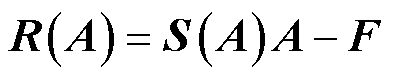 (5)
(5)
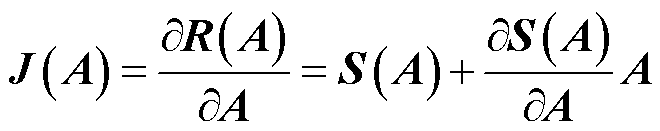 (6)
(6)
传统FEM计算非线性磁场问题时,需要一个矢量磁位A的初始值,通过给定的B-H曲线计算当前磁导率μ。使用μ计算当前刚度矩阵S,并使用上一步迭代的A计算Jacobian项与残差项。求解公式(4)获得∆A与最新解,若∆A小于设置的容差,则停止迭代;否则继续重复上述步骤。因此,FEM求解问题式(3)的计算成本通常比较昂贵,尤其是在具有大量未知量和迭代过程的大型三维非线性系统中。
POD法作为广泛使用的降阶方法,最大优点是能够有效地降低系统方程的阶数,降低计算量。本文提出的非侵入式ISSA-POD-RBF法能够在考虑材料非线性的前提下优选快照样本,有效控制全阶模型与降阶模型解之间的误差。算法整体流程如图1所示。
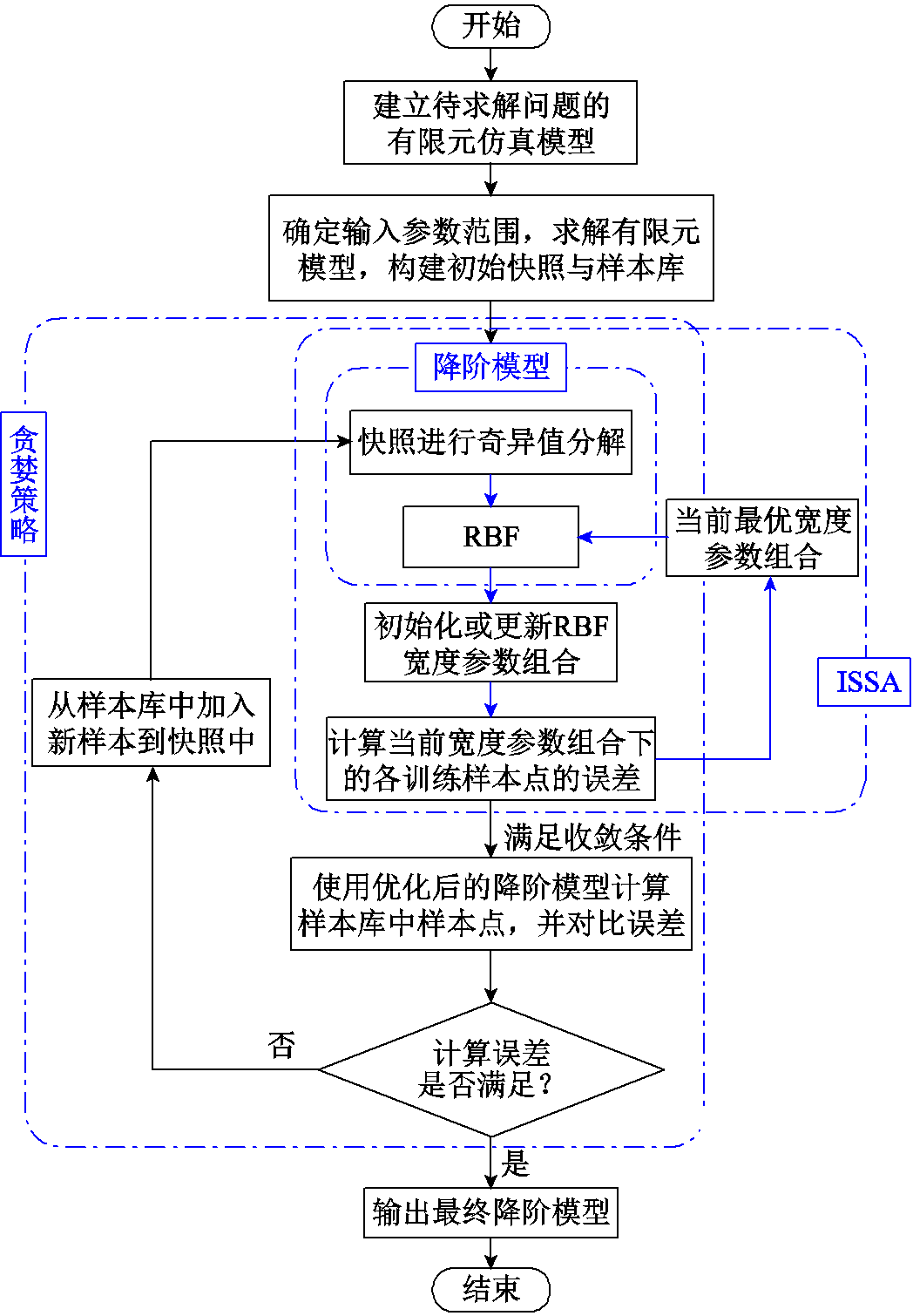
图1 整体算法流程
Fig.1 Flow chart of suggested overall algorithm
POD法的第一步是构建由数值计算数据组成的快照矩阵,本文采用贪婪策略获取最优快照矩阵。快照矩阵的每一列数据对应所研究系统在不同工作条件下或不同输入下的状态。一般而言,FEM仿真中的网格点数量远大于输入数量,因此快照矩阵的行数远大于列数。第二步是对快照矩阵进行分解与信息提取,常用的矩阵分解方法是奇异值分解(Singular Value Decomposition, SVD),分解之后的矩阵是三个子矩阵相乘的形式,其中左奇异矩阵中的每一列即为POD基向量,于是高维数据矩阵就可以表示为POD基向量的线性组合。
首先,通过求解传统FEM模型获得快照矩阵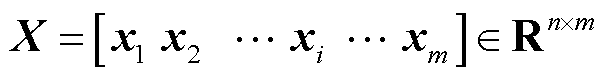 。其中,m是快照数,xi是第i组输入Ji的FEM解,即一个样本。n是每个输入下网格节点数与节点自由度数的乘积,n的数量远大于m。
。其中,m是快照数,xi是第i组输入Ji的FEM解,即一个样本。n是每个输入下网格节点数与节点自由度数的乘积,n的数量远大于m。
对快照矩阵X进行奇异值分解,即
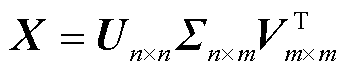 (7)
(7)
式中,U和V分别为正交左奇异矩阵和右奇异矩阵;Σ为奇异值矩阵;主对角线以外的元素都为0,主对角线上元素为奇异值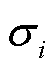 (i=1, 2,
(i=1, 2, 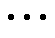 , m),且
, m),且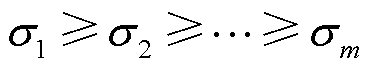 。
。
根据SVD固有属性,较大的特征值对应系统的主要特征,因此原始数据可以通过截断前几个较大的奇异值及其对应的正交基向量来近似表征。截取Σ对角线上奇异值较大的前r个元素构建表征能量保持的公式为
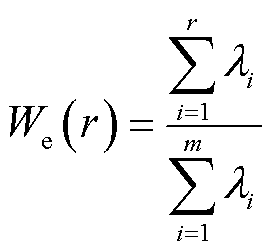 (8)
(8)
式中,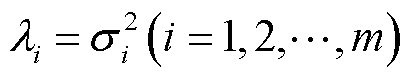 。若能量保持函数
。若能量保持函数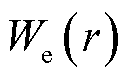 满足表征条件,则X可以近似表示为
满足表征条件,则X可以近似表示为
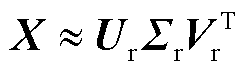 (9)
(9)
式中,Ur为n×r矩阵;Σr为r×r矩阵;VrT为r×m矩阵。SVD及截断示意图如图2所示。根据左奇异矩阵Ur构造r维POD基向量矩阵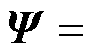
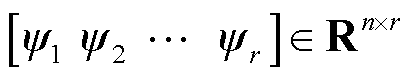 ,
,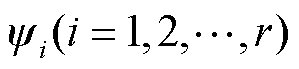 由Ur的列向量组成。则未知向量x可近似表示为
由Ur的列向量组成。则未知向量x可近似表示为
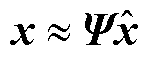 (10)
(10)
式中,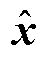 为x到Ψ所在空间上的投影。
为x到Ψ所在空间上的投影。
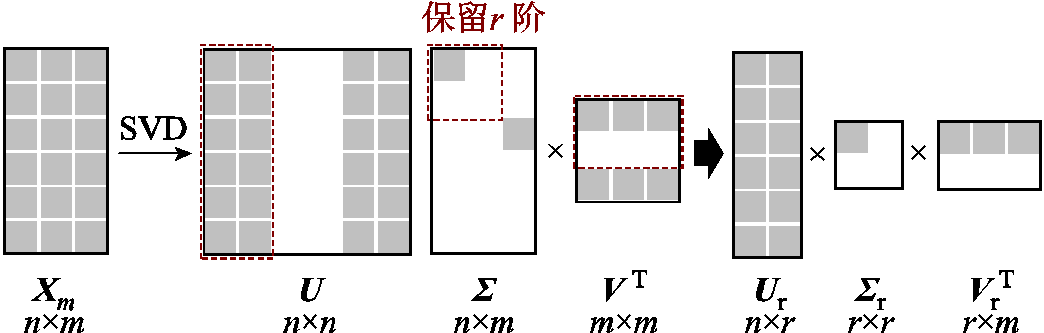
图2 SVD及截断示意图
Fig.2 Schematics of SVD and truncation
此时,若采用侵入式方法计算FEM非线性磁场问题的近似解,式(3)中A为未知向量,则降阶模型可写为
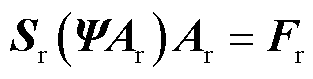 (11)
(11)
式中,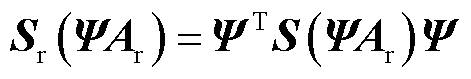 ,
,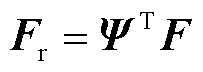 。迭代过程中残差向量和Jacobian矩阵的降阶形式为
。迭代过程中残差向量和Jacobian矩阵的降阶形式为
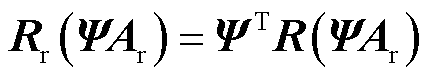 (12)
(12)
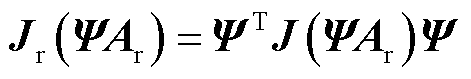 (13)
(13)
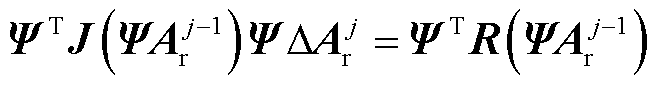 (14)
(14)
降阶模型式(11)的大小远小于全阶模型,但是简化后的Jacobian矩阵和残差向量仍然依赖系统的全阶解,计算过程仍需要组装全阶刚度矩阵,因此同样耗时。非侵入式降阶模型不依赖控制方程,因此计算速度更快。
RBF是一种常用的多元函数插值基函数,其一般形式可记为
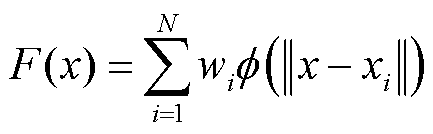 (15)
(15)
式中,x为任意点;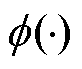 为径向基函数;
为径向基函数;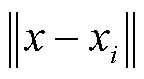 为任意点与第i个已知样本点的Euclidian距离;wi为第i个权重系数,可建立已知样本点的RBF方程求取wi;N为样本点数量。常用的径向基函数见表1,c为径向基函数的宽度参数。
为任意点与第i个已知样本点的Euclidian距离;wi为第i个权重系数,可建立已知样本点的RBF方程求取wi;N为样本点数量。常用的径向基函数见表1,c为径向基函数的宽度参数。
表1 常用径向基函数
Tab.1 Common radial basis functions

函数 高斯(Gaussian) 多二次(Multiquadric) 逆多二次(Inverse Multiquadric)
由上可知,奇异值分解的左奇异矩阵Ur对应于POD基,右奇异矩阵Vr由每组参数值投影到POD基中的FEM解构成,系统输出的预测只依赖Vr中的右奇异向量。对于新参数值Inew,近似解xap可定义为
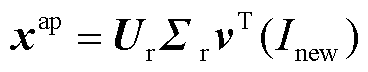 (16)
(16)
对于新参数Inew对应的ν(Inew),则通过在右奇异矩阵Vr上执行RBF插值得到。因此计算已知样本之间的径向基函数矩阵,建立RBF方程并展开,求出权重系数矩阵W。
 (17)
(17)
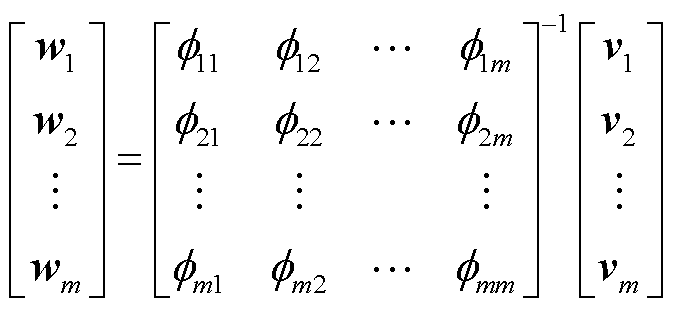 (18)
(18)
则新参数对应的右奇异向量中每个元素为
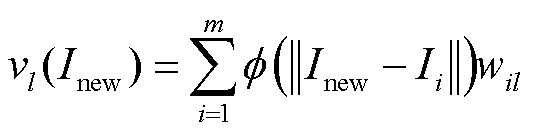 (19)
(19)
其中,l=1,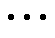 , r。
, r。
贪婪策略的基本思想是将问题的求解过程看作是一系列的选择,每次选择一个输入,每次的选择都是当前状态下的最好选择(局部最优解),从而通过每一步的最优解逐渐达到整体的最优解。
本文采用自适应的方法确定快照矩阵的样本和样本数量,具体流程如图3所示。贪婪策略每次迭代选择降阶模型与全阶模型计算结果之间的最大误差所对应的参数加入快照矩阵X,使快照矩阵包含更全面的特征信息,从而获得最佳的降阶模型。
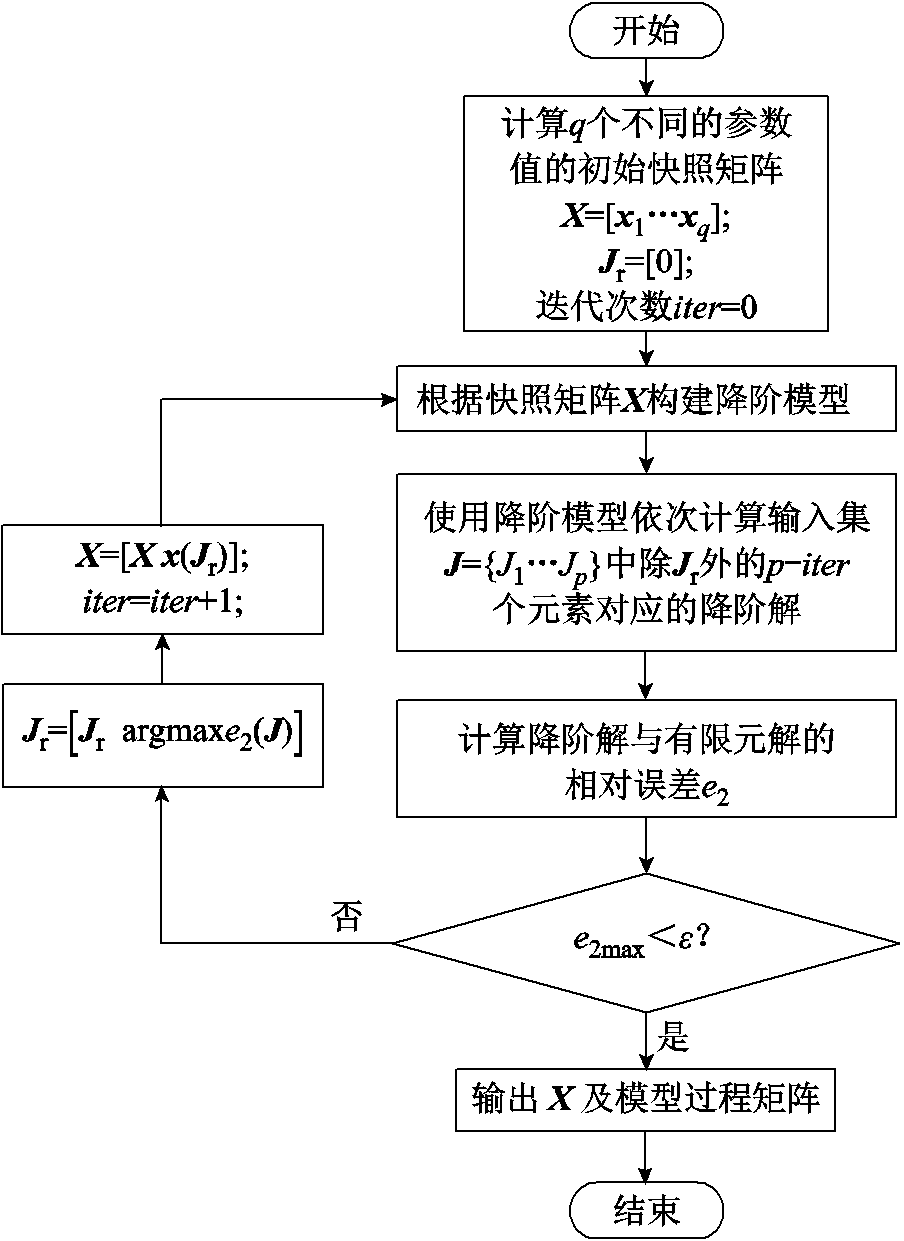
图3 贪婪策略流程
Fig.3 Flow chart of greedy strategy
(1)预先计算在合理范围内均匀分布的p个输入样本对应的FEM解作为样本库,输入样本存入输入集J。选择q个输入所对应的FEM解作为初始快照矩阵X,建立并初始化矩阵Jr,用于保存后续加入快照的对应输入。
(2)根据X构建降阶模型。使用降阶模型依次计算输入集J中元素的降阶解(不含已经选为快照样本的元素),每次选择其中降阶解和FEM解相对误差e2最大的输入所对应的FEM解加入X。
(3)重复步骤(2),直到最大相对误差满足条件e2max<ε。
本文中,降阶模型与全阶模型之间的相对误差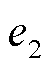 定义为
定义为
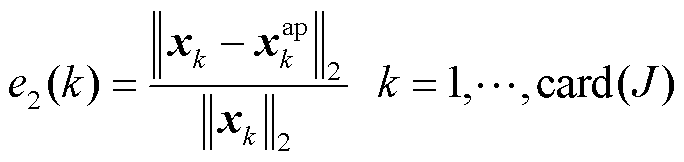 (20)
(20)
式中,xk和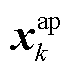 分别为第k个输入下的FEM解与降阶模型计算的近似解;
分别为第k个输入下的FEM解与降阶模型计算的近似解; 为集合J中元素的个数,也就是用来对比的样本个数。
为集合J中元素的个数,也就是用来对比的样本个数。
贪婪策略选择的快照样本点在空间内的分布往往不是均匀的。对于径向基函数而言,所有已知样本点共同影响待求解样本点的计算结果,而宽度参数c控制已知样本点在周边范围内的影响程度,分布不均匀的样本点更不应该使用同一宽度参数。文献[30]研究表明,随着宽度参数值的不断增大,模型的精度呈现先增大后减小的趋势,并且由于不同样本所表征的特性不同,没有统一的宽度参数来保证不同近似模型的精度。另一方面,对于非线性程度较高的模型,贪婪策略算法的收敛速度变慢,选择的快照样本数量增多,增加了降阶模型的计算时间,因此找到合理的宽度参数组合能够在保证精度的前提下选择最少的快照数。
因此,为了准确地获取快速、可信的近似模型,本文使用ISSA确定降阶模型的最优宽度参数组合,将宽度参数组合作为设计变量,以训练样本的最大相对误差最小为目标,可以得到最合理的宽度参数组合。
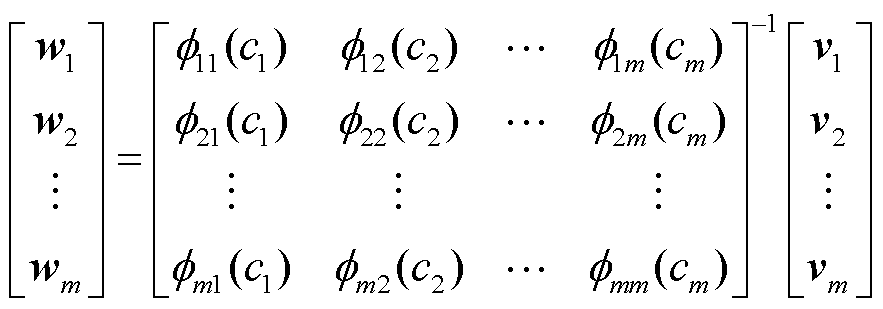 (21)
(21)
麻雀搜索算法(SSA)是模仿麻雀觅食并逃避捕食者的行为而提出的一种新颖的元启发算法[31]。本文使用改进的麻雀搜索算法对基函数的宽度参数进行合理确定。SSA将麻雀群体分为生产者、追随者和警戒者,并不断更新它们的位置,以找到目标函数的最优解。它具有收敛速度快、优化能力强等优点。但为了防止优化过程陷入局部最优,本文在麻雀搜索算法中更新追随者与警戒者的位置时引入Levy飞行策略[32]。Levy飞行随机步长公式为
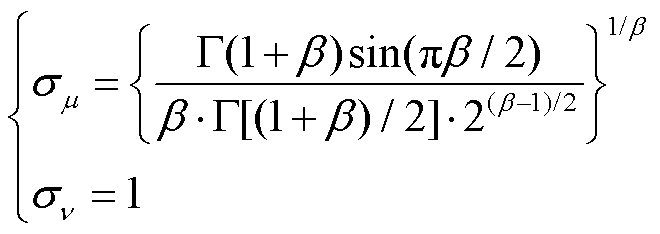 (22)
(22)
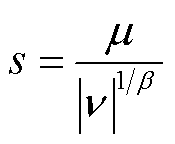 (23)
(23)
式中,μ和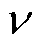 均服从正态分布,
均服从正态分布,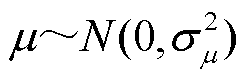 ,
,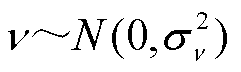 ;
;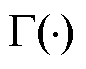 为伽马函数。追随者的位置更新方式改进部分为
为伽马函数。追随者的位置更新方式改进部分为
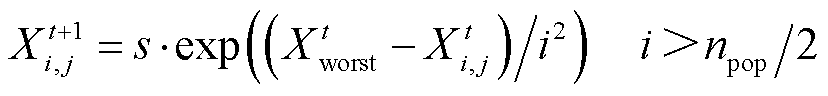 (24)
(24)
警戒者位置更新方式改进部分为
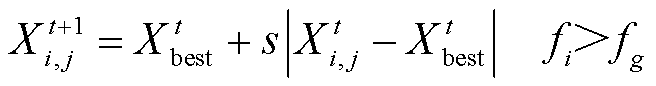 (25)
(25)
式中, 为第t代中第i个麻雀在第j维的位置,j为优化变量的维数;
为第t代中第i个麻雀在第j维的位置,j为优化变量的维数;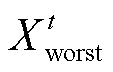 和
和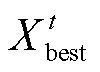 分别为第t代麻雀的全局最差位置和最优位置;
分别为第t代麻雀的全局最差位置和最优位置;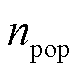 为麻雀种群数量;
为麻雀种群数量;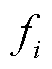 为当前麻雀个体的适应度值;fg为当前全局最优适应度值。
为当前麻雀个体的适应度值;fg为当前全局最优适应度值。
ISSA最优宽度参数组合计算流程如图4所示。
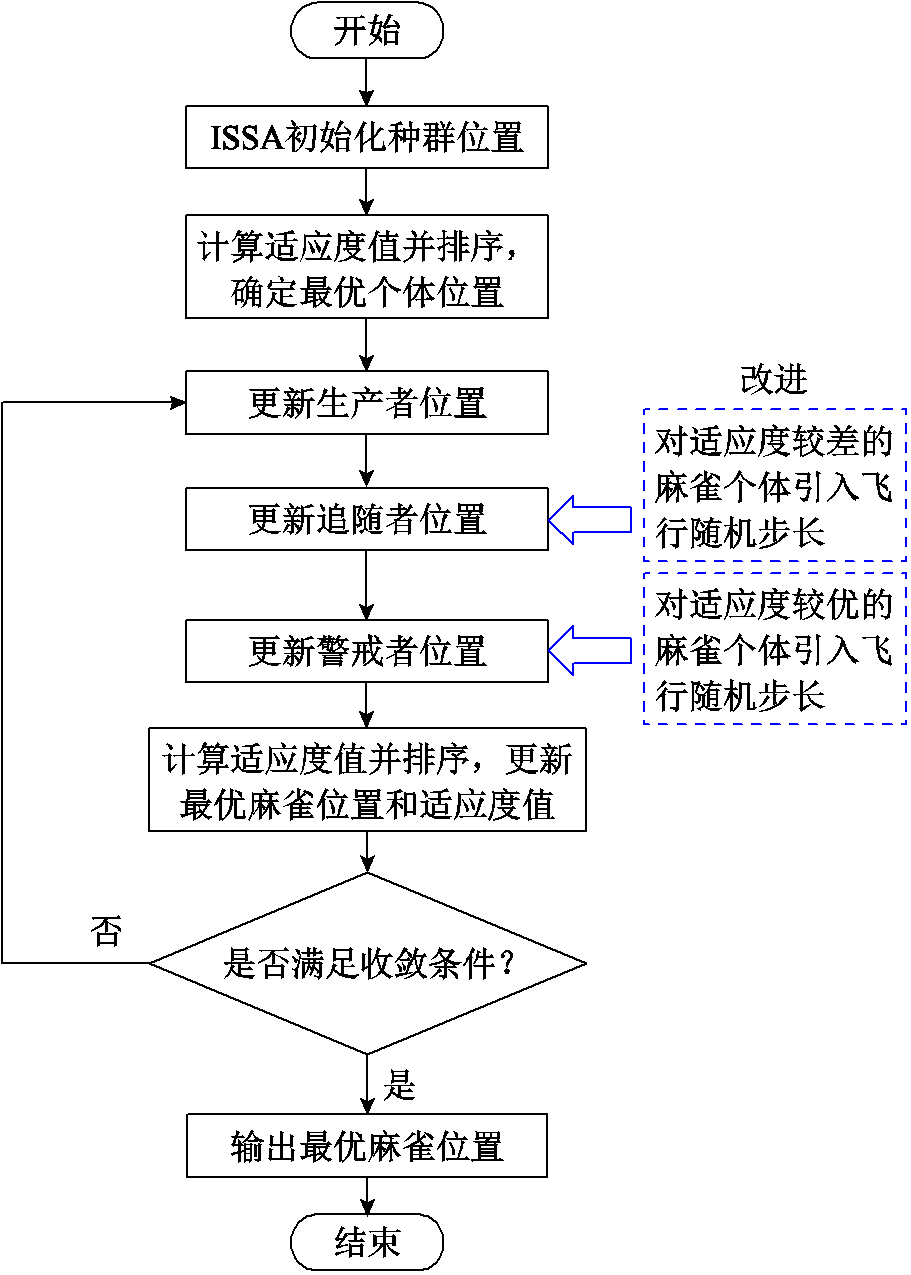
图4 ISSA最优宽度参数组合计算流程
Fig.4 Flow chart of ISSA optimal width parameter combination calculation
综上所述,基于ISSA的最优宽度参数组合计算具体步骤为:
(1)依据2.2节,使用当前快照矩阵X初步构建包含宽度参数c的POD-RBF降阶模型。并准备若干个不包含在样本库中的近似均匀分布的样本点作为训练样本。
(2)设定宽度参数c的选取区间(c>0),ISSA初始化种群。
(3)使用降阶模型逐个计算训练样本点的降阶解以及降阶解与FEM解之间的相对误差,将最大相对误差作为ISSA的适应度函数;宽度参数组合为麻雀位置,麻雀位置的维数为快照样本数目。计算初始适应度值并排序。
(4)依次更新生产者、追随者及警戒者位置。再次计算适应度值,更新当前最优麻雀位置和适应度值。
(5)判断是否满足收敛条件,若未满足,则重复步骤(4);否则输出最优麻雀位置。
(6)输出的最优麻雀位置,即最优宽度参数组合。
本文给出两个计算实例以验证所提方法的有效性。第一个是国际电磁场标准测试问题24(TEAM24),第二个是一台单相牵引变压器空载磁场计算问题。本文研究的算法基于FELAC软件采用C++语言实现。软件运行环境如下:处理器Intel core i9-12900K,主频为3.2 GHz,内存为64 GB。
TEAM24由转子和定子组成,其中,转子安装在非磁性不锈钢转轴上;定子固定在可摆动的非磁性笼内;轴向长度为25.4 mm;定子线圈匝数为350匝。三维结构模型和电流波形如图5所示。
针对TEAM24,预先准备包含100个样本点及FEM解的样本库,设置贪婪策略迭代终止条件为最大相对误差e2max<0.5%。最终确定的快照矩阵大小为(118 831×3)×13,即13个不同电流值对应的解向量,118 831×3个网格节点自由度。

图5 TEAM 24三维模型与电流波形
Fig.5 Structure of TEAM24 and waveform of current
该模型在计算时,POD基保留阶数为2阶,奇异值矩阵对应的特征值大小呈指数递减排列,其代表着各个特征值对应的特征向量中信息能量占比情况。图6为各特征值信息能量占比曲线,使用能量保持函数We(r)的常用对数作为纵坐标,图中第一阶特征向量包含原始系统的信息能量比例最大。在本模型中,2阶之后的特征向量中包含的信息能量占比均小于1´10-7,可以认为对计算结果的误差基本无影响。
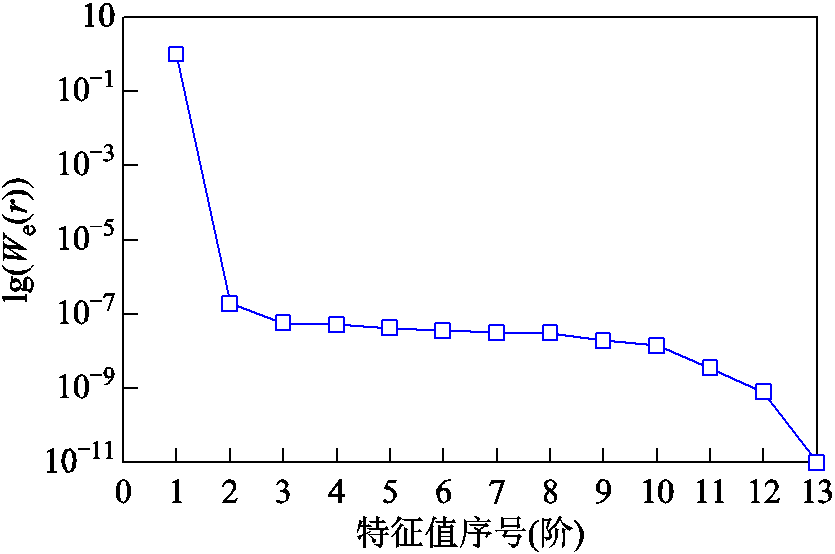
图6 各特征值信息能量占比
Fig.6 Energy share curve of different eigenvalues
为对比不同采样方式所构建降阶模型的计算效果,将经贪婪策略采样与平均采样选择出的相同数量的快照样本分别构建了降阶模型,得到不同采样方式下的相对误差计算结果如图7所示。显然,经贪婪策略选择出的快照得到的计算结果误差小得多。贪婪策略采样每次迭代都选择误差最大的样本点加入快照矩阵,这样使快照矩阵整体能包含更多、更全面的信息。
图8为最后一次贪婪迭代的ISSA的适应度值迭代曲线,同时标注了在不进行宽度参数组合迭代的情况下,所有训练样本点对应基函数的宽度参数为C =1时的误差大小。
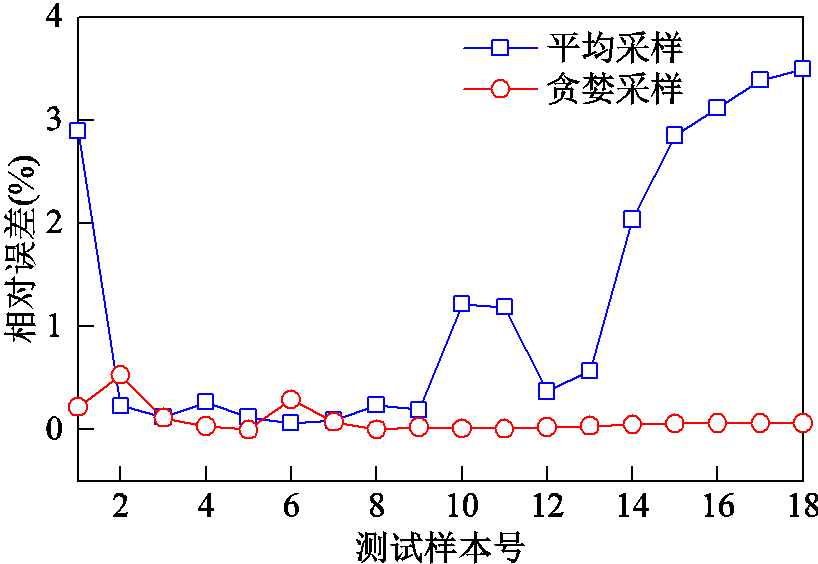
图7 不同采样方式的相对误差
Fig.7 Relative error of different sampling methods
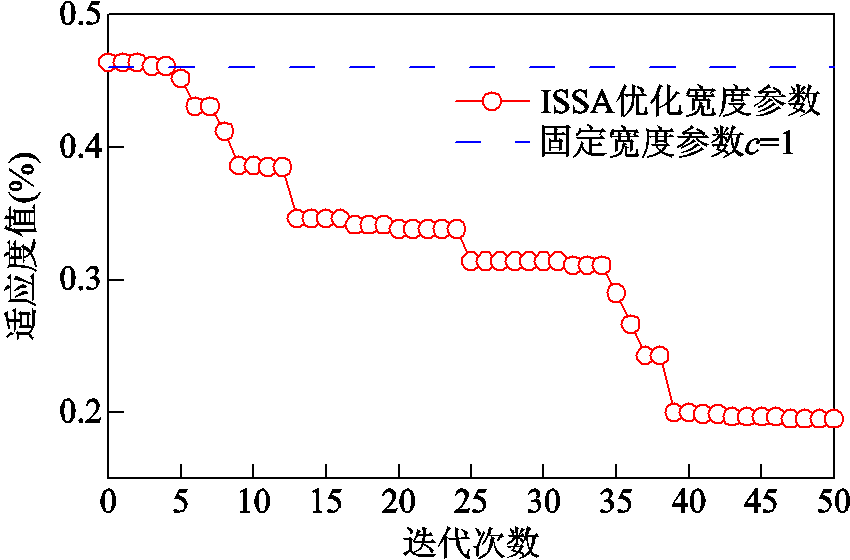
图8 ISSA适应度迭代曲线
Fig.8 Iteration curves of ISSA fitness
为验证算法性能,分别使用考虑最优宽度参数组合和单一值宽度参数的降阶模型对测试样本点进行计算(测试样本不包含在快照样本及训练样本内,两个降阶模型采用同样的快照矩阵)。图9为测试样本的相对误差值,采用式(20)计算。图9中,采用最优宽度参数组合构建的降阶模型计算的样本相对误差整体小于同一宽度参数构建的降阶模型的计算误差。对于不同输入参数的预测而言,采用最优宽度参数组合构建的降阶模型泛化性能更好。因此,选择最优的宽度参数组合,能构建更加适配快照的降阶模型,在快照样本数量有限的条件下提高整体计算精度。若采用同一宽度参数构建降阶模型想达到相同的精度需要增加快照样本的数量。
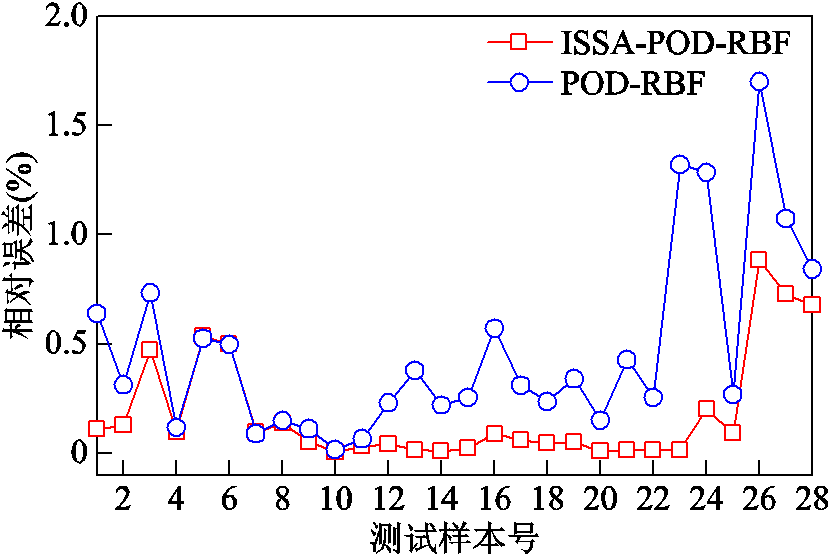
图9 不同降阶模型的测试样本点误差对比
Fig.9 Error comparison of test points for different MORs
图10和图11是使用ISSA-POD-RBF降阶模型获取的磁通密度,以及与FEM全阶模型计算的磁通密度的差值。图10输入电流值为3.82 A;图11输入电流值为7.41 A。两种情况的磁通密度误差幅度相较于总体分布来看,误差幅度非常小。磁通密度出现较大偏差的主要部分发生在定子表面的尖角处。

图10 磁通密度分布及差值分布(3.82 A)
Fig.10 Distribution of magnetic flux density and absolute error at 3.82 A
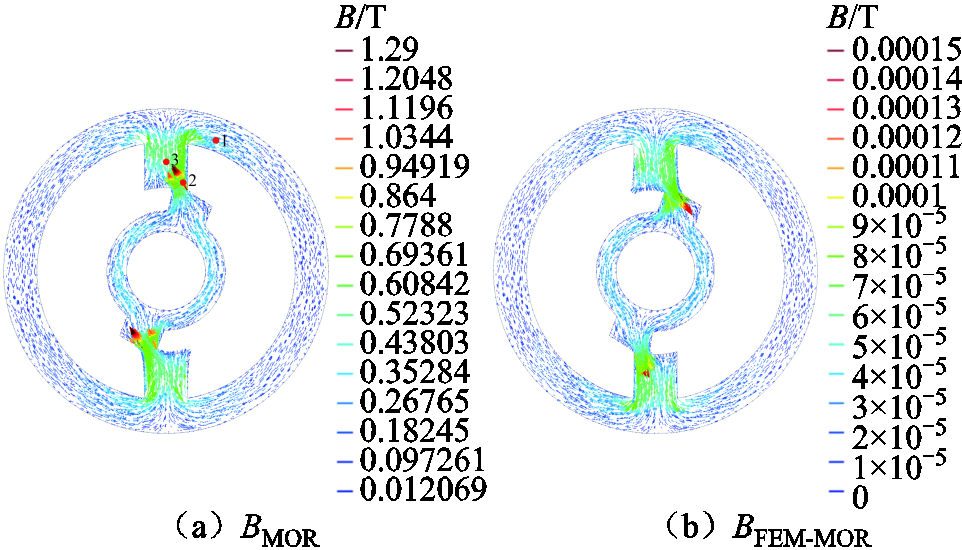
图11 磁通密度分布及差值分布(7.41 A)
Fig.11 Distribution of magnetic flux density and absolute error at 7.41 A
表2列出了输入电流为7.41 A时局部节点的磁通密度对比并标注了节点坐标,三个节点的磁通密度差值均不大于0.000 1 T,按照式(26)计算的单点误差不超过0.01%。
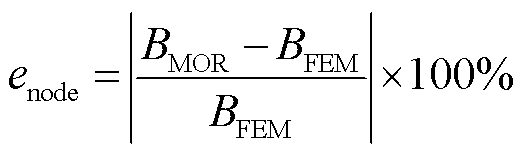 (26)
(26)
表2 7.41 A时局部节点的磁通密度对比
Tab.2 Comparison of magnetic flux density of local nodes at 7.41 A

坐标/mmBMOR/TBFEM/T误差(%) 1(31.18, 86.33, 0.0)0.309 960.309 930.009 7 2(13.10, 53.15, 0.0)0.886 940.886 860.009 0 3(0.56, 74.23, 0.0)0.507 270.507 220.009 9
降阶模型的计算效率主要与快照数量和POD基截断位置有关,而FEM全阶模型计算一个非线性问题稳态解需要多次求解高阶代数方程组。因此,降阶模型效率明显更高。
将FEM模型计算时间Tfem与降阶模型计算时间Tmor的比值定义为加速比Sp。
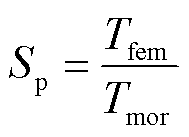 (27)
(27)
表3给出了不同模型的计算时间及对应的加速比(不包括快照准备时间)。
表3 MOR与FEM计算时间对比情况
Tab.3 Comparison of MOR and FEM calculation time

模型稳态解计算时间/s加速比Sp FEM205366.07 MOR0.56
本节采用ISSA-POD-RBF模型降阶方法对一台6 770 kV·A牵引变压器进行空载磁场分析,分析时主要考虑变压器的铁心和绕组,高压侧绕组匝数为1 384匝,铁心采用30ZH120取向硅钢片。图12为变压器铁心及绕组的模型及网格剖分情况。网格由666 160个四面体单元组成,节点数量为125 403。该变压器铁心材料B-H曲线如图13所示。

图12 变压器模型及网格剖分示意图
Fig.12 Transformer model and meshing
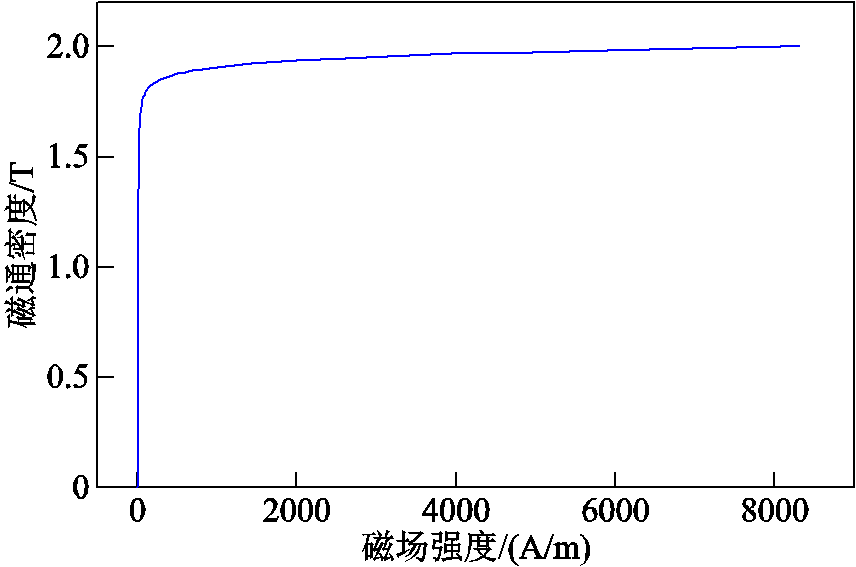
图13 铁心材料30 ZH120 B-H曲线
Fig.13 B-H curve of core material 30ZH120
使用FEM法计算100个电流值及对应FEM解作为样本库,样本点中最小的空载电流值为使变压的磁通密度未进入非线性增长部分,最大的空载电流值为使变压器的磁通密度大部分进入饱和状态。经计算,最终由40个样本点解向量构成快照矩阵,迭代终止条件为最大相对误差e2max<5%。最后一次ISSA适应度值迭代曲线如图14所示。
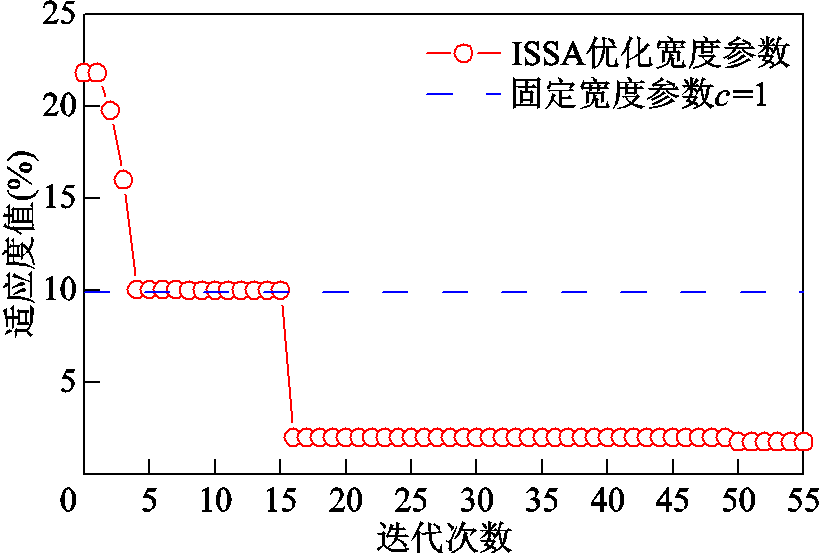
图14 ISSA适应度迭代曲线
Fig.14 Iteration curves of ISSA fitness
图15和图16是使用ISSA-POD-RBF降阶模型获取的空载变压器磁通密度,以及与FEM全阶模型计算的磁通密度的差值,输入空载电流值分别为0.005 A和0.52 A。图中两种情况误差最大的位置在变压器的内角上,铁心柱中间有较小的误差。该模型的计算误差是可以接受的,它和模拟过程中因材料特性、尺寸以及仿真操作的不确定性所带来的误差在同一数量级。
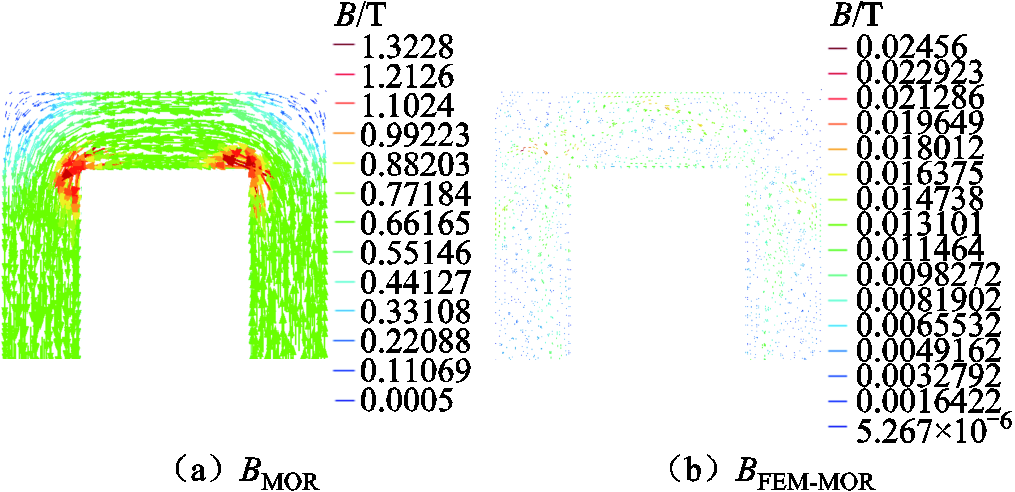
图15 磁通密度分布及差值分布(0.005 A)
Fig.15 Distribution of magnetic flux density and absolute error at 0.005 A
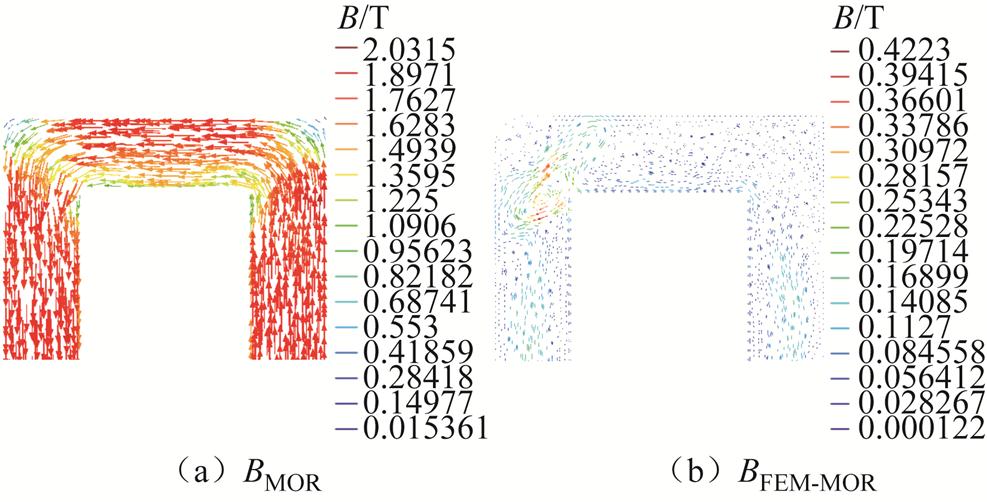
图16 磁通密度分布及差值分布(0.52 A)
Fig.16 Distribution of magnetic flux density and absolute error at 0.52 A
表4为变压器降阶模型与FEM全阶模型的计算时间对比及加速比Sp。由铁心材料的B-H曲线可知,求解变压器磁场时的材料非线性更强,FEM计算时磁导率非线性迭代求解的次数更多,这个时间成本也会随着计算模型划分的网格数增多而增大。通过对比MOR与FEM计算时间可知,降阶模型加速比为99.08,极大地缩短了计算时间。
表4 MOR与FEM计算时间对比情况
Tab.4 Computing cost comparison of MOR and FEM
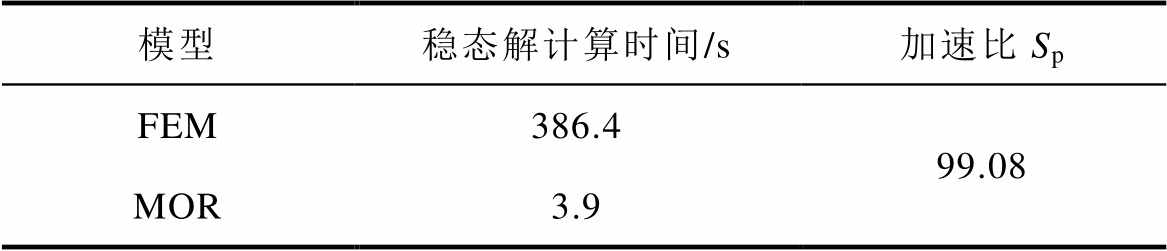
模型稳态解计算时间/s加速比Sp FEM386.499.08 MOR3.9
本文提出了一种适用于求解三维非线性磁场问题的模型降阶方法。以TEAM24问题和一台单相牵引变压器的空载磁场计算问题为例验证了所提方法的有效性。得出以下结论:
1)基于ISSA-POD-RBF的降阶模型与FEM全阶模型的计算结果相比,其误差可以接受。使用贪婪策略,可以找出FEM的计算结果中关键的样本信息,同时POD法可以储存真实模型绝大部分的非线性特征。另外,相比于FEM,RBF插值无需因非线性迭代而多次访问刚度矩阵,可以大大降低时间成本。
2)RBF中的宽度参数直接控制所选样本点的作用范围,进而影响模型的预测精度。针对不同快照样本构建的模型,选择正确合理的宽度参数组合能够大幅提升降阶模型的计算精度与可泛化性。文中基于改进的麻雀优化算法获取最合理的宽度参数组合来构建更加适配快照的降阶模型,能够在控制快照样本数量的同时提高模型计算精度。
3)对快照矩阵进行奇异值分解后,根据其特征值能量占比对截断位置进行选取。本文计算TEAM24和变压器模型中,POD基保留阶数分别为2阶和11阶,各正交基向量所对应特征值能量之和达到99.5%。另外,快照数量对奇异值分解过程的计算速度影响极大。快照数量、样本点的选择,以及POD基的保留阶数是影响降阶模型加速比的重要因素。本文两个模型算例加速比分别达到了366.07和99.08。
本文所提出的电气设备非线性磁场问题快速求解方法为电气设备电磁性能数字孪生模型的构建提供了一种实时仿真解决方案。
参考文献
[1] Ghnatios C, Masson F, Huerta A, et al. Proper Generalized Decomposition based dynamic data-driven control of thermal processes[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 213: 29-41.
[2] Chakraborty S, Adhikari S, Ganguli R. The role of surrogate models in the development of digital twins of dynamic systems[J]. Applied Mathematical Modelling, 2021, 90: 662-681.
[3] 张宁, 刘士利, 郝建, 等. 变压器油中气泡杂质相局部放电特性研究综述[J]. 电工技术学报, 2023, 38(10): 2757-2776.
Zhang Ning, Liu Shili, Hao Jian, et al. Review on partial discharge characteristics of bubble impurity phase in transformer oil[J].Transactions of China Electrotechnical Society, 2023, 38(10): 2757-2776.
[4] 张宇娇, 赵志涛, 徐斌, 等. 基于U-net卷积神经网络的电磁场快速计算方法[J]. 电工技术学报, 2024, 39(19): 2730-2742.
Zhang Yujiao, Zhao Zhitao, Xu Bin et al. Fast calculation method of electromagnetic field based on U-net convolution neural network[J].Transactions of China Electrotechnical Society, 2024, 39(19): 2730-2742.
[5] 谭皓元, 兰志勇, 罗元钧, 等. 无铁心圆筒型永磁同步直线电动机磁场分析[J]. 电气技术, 2023, 24(7): 39-46.
Tan Haoyuan, Lan Zhiyong, Luo Yuanjun, et al. Design and magnetic field analysis of ironless tubular permanent magnet synchronous linear motor[J]. Electrical Engineering, 2023, 24(7): 39-46.
[6] 曹龙飞, 范兴纲, 李大伟, 等. 基于快速有限元的永磁电机绕组涡流损耗半解析高效计算[J]. 电工技术学报, 2023, 38(1): 153-165.
Cao Longfei, Fan Xinggang, Li Dawei, et al. Semi analytical and efficient calculation method of eddy current loss in windings of permanent magnet machines based on fast finite element method[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 153-165.
[7] 谢飞. 基于POD的电磁场非线性问题快速计算方法研究[D]. 沈阳: 沈阳工业大学, 2022.
Xie Fei. Research on fast calculation method of electromagnetic field nonlinear problem based on POD[D]. Shenyang University of Technology, 2022.
[8] 王进钊, 严干贵, 刘侃. 基于交替方向隐式平衡截断法的直驱风电场次同步振荡分析的模型降阶研究[J]. 发电技术, 2023, 44(6): 850-858.
Wang Jinzhao, Yan Gangui, Liu Kan. Research on model reduction of direct drive wind farm sub-synchronous oscillation analysis based on alternating direction implicit balanced truncation method[J]. Power Generation Technology, 2023, 44(6): 850-858.
[9] 田野, 卜凯阳, 李楚杉, 等. 用于IGBT模块温度观测的3-D降阶混合型热模型[J]. 电工技术学报, 2024, 39(16): 5104-5120.
Tian Ye, Bu Kaiyang, Li Chushan, et al. A hybrid 3-D reduced-order thermal model for temperature observation of IGBT modules[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5104-5120.
[10] 刘刚, 胡万君, 刘云鹏, 等. 降阶技术与监测点数据融合驱动的油浸式变压器绕组瞬态温升快速计算方法[J]. 电工技术学报, 2024, 39(19): 6162-6174.
Liu Gang, Hu Wanjun, Liu Yunpeng, et al. A fast calculation method for transient temperature rise of oil immersed transformer windings driven by fusion of order reduction technology and monitoring point data[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6162-6174.
[11] 邱亚松, 白俊强, 华俊. 基于本征正交分解和代理模型的流场预测方法[J]. 航空学报, 2013, 34(6): 1249-1260.
Qiu Yasong, Bai Junqiang, Hua Jun. Flow field estimation method based on proper orthogonal decomposition and surrogate model[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1249-1260.
[12] 刘钊, 王沐晨, 李金玖, 等. 基于POD的尾流激励叶片气动力降阶模型[J]. 兵器装备工程学报, 2021, 42(2): 82-86, 173.
Liu Zhao, Wang Muchen, Li Jinjiu, et al. Reduced order aerodynamic model of wake excited blade based on POD[J]. Journal of Ordnance Equipment Engineering, 2021, 42(2): 82-86, 173.
[13] Xie Dan, Xu Min. A comparison of numerical and semi-analytical proper orthogonal decomposition methods for a fluttering plate[J]. Nonlinear Dynamics, 2015, 79(3): 1971-1989.
[14] 魏代同, 陈星, 陈玉刚, 等. 基于本征正交分解的叶片碰摩系统降阶方法[J]. 航空动力学报, 2022, 37(4): 711-720.
Wei Daitong, Chen Xing, Chen Yugang, et al. Reduced order method of blade rubbing system based on proper orthogonal decomposition[J]. Journal of Aerospace Power, 2022, 37(4): 711-720.
[15] 胡金秀, 高效伟. 变系数瞬态热传导问题边界元格式的特征正交分解降阶方法[J]. 物理学报, 2016, 65(1): 273-289.
Hu Jinxiu, Gao Xiaowei. Reduced order model analysis method via proper orthogonal decomposition for variable coefficient of transient heat conduction based on boundary element method[J]. Acta Physica Sinica, 2016, 65(1): 273-289.
[16] 朱强华, 杨恺, 梁钰, 等. 基于特征正交分解的一类瞬态非线性热传导问题的新型快速分析方法[J]. 力学学报, 2020, 52(1): 124-138.
Zhu Qianghua, Yang Kai, Liang Yu, et al. A novel fast algorithm based on model order reduction for one class of transient nonlinear heat conduction problem[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(1): 124-138.
[17] Pierquin A, Henneron T, Clénet S, et al. Model-order reduction of magnetoquasi-static problems based on POD and arnoldi-based Krylov methods[J]. IEEE Transactions on Magnetics, 2015, 51(3): 7206204.
[18] Farzam Far M, Martin F, Belahcen A, et al. Orthogonal interpolation method for order reduction of a synchronous machine model[J]. IEEE Transactions on Magnetics, 2018, 54(2): 8100506.
[19] 蒋耀林. 模型降阶方法[M]. 北京: 科学出版社, 2010.
Jiang Yaolin. Model reduction methods [M]. Beijing: Science Press, 2010.
[20] Sato Y, Clemens M, Igarashi H. Adaptive subdomain model order reduction with discrete empirical interpolation method for nonlinear magneto-quasi-static problems[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1100204.
[21] Henneron T, Montier L, Pierquin A, et al. Comparison of DEIM and BPIM to speed up a POD-based nonlinear magnetostatic model[J]. IEEE Transactions on Magnetics, 2017, 53(6): 7204204.
[22] Müller F, Siokos A, Kolb J, et al. Efficient estimation of electrical machine behavior by model order reduction[J]. IEEE Transactions on Magnetics, 2021, 57(6): 8105804.
[23] 谢裕清, 李琳. 基于本征正交分解的换流变压器极性反转电场降阶模型[J]. 中国电机工程学报, 2016, 36(23): 6544-6551, 6622.
Xie Yuqing, Li Lin. A reduced order model via proper orthogonal decomposition for polarity reverse electric fields in converter transformers[J]. Proceedings of the CSEE, 2016, 36(23): 6544-6551, 6622.
[24] 胡万君, 刘刚, 朱章宸, 等. 油浸式电力变压器绕组稳态温升降阶计算方法研究[J]. 中国电机工程学报, 2023, 43(16): 6505-6516.
Hu Wanjun, Liu Gang, Zhu Zhangchen, et al. Study on calculation method of steady-state temperature rise and fall order of oil-immersed power transformer winding[J]. Proceedings of the CSEE, 2023, 43(16): 6505-6516.
[25] Farzam Far M, Martin F, Belahcen A, et al. Orthogonal interpolation method for order reduction of a synchronous machine model[J]. IEEE Transactions on Magnetics, 2018, 54(2): 8100506.
[26] Pierquin A, Henneron T. Nonlinear data-driven model order reduction applied to circuit-field magnetic problem[J]. IEEE Transactions on Magnetics, 2021, 57(11): 7402509.
[27] 刘刚, 高成龙, 胡万君, 等. 基于鲸鱼优化算法超参数优化的径向基函数响应面模型的油浸式变压器绕组挡板结构优化[J]. 电工技术学报, 2024, 39(17): 5331-5343.
Liu Gang, Gao Chenglong, Hu Wanjun, et al. optimization of winding block washer structure for oil immersed transformers based on radial basis function response surface model with whale optimization algorithmhyper-parameters optimization[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5331-5343.
[28] 刘刚, 高成龙, 胡万君, 等. 基于改进的连续局部枚举采样和径向基函数响应面法的变压器静电环结构优化设计[J]. 电工技术学报, 2023, 38(23): 6266-6278.
Liu Gang, Gao Chenglong, Hu Wanjun, et al. optimized design of transformer electrostatic ring based on radial basis function response surface method with enhanced successful local enumeration sampling[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6266-6278.
[29] 余波, 陶盈盈. 基于POD-RBF方法的管道内壁几何识别[J]. 应用数学和力学, 2023, 44(4): 406-418.
Yu Bo, Tao Yingying. Identification of pipeline inner wall geometry based on the POD-RBF method[J]. Applied Mathematics and Mechanics, 2023, 44(4): 406-418.
[30] Wu Zeping, Wang Donghui, Patrick Okolo N, et al. Unified estimate of Gaussian kernel width for surrogate models[J]. Neurocomputing, 2016, 203: 41-51.
[31] 李昕燃, 靳伍银. 基于改进麻雀算法优化支持向量机的滚动轴承故障诊断研究[J]. 振动与冲击, 2023, 42(6): 106-114.
Li Xinran, Jin Wuyin. Fault diagnosis of rolling bearings based on ISSA-SVM[J]. Journal of Vibration and Shock, 2023, 42(6): 106-114.
[32] Beccar-Varela M P, Gonzalez-Huizar H, Mariani M C, et al. Lévy flights and wavelets analysis of volcano-seismic data[J]. Pure and Applied Geophysics, 2020, 177(2): 723-736.
Fast Calculation Method of 3D Nonlinear Magnetic Field Based on Adaptive Model Order Reduction
Abstract Digital twins, as a key technology to achieve real-time monitoring and full life-cycle management of industrial products, are required to reflect the physical characteristics of in-service electrical equipment in real time through simulation. The finite element method (FEM) is commonly used for analyzing electromagnetic properties of low-frequency electrical equipment. For complex three-dimensional problems, the high spatial freedom of geometric model and many time steps result in a large amount of computational time required for finite element analysis. In addition, if the nonlinear behavior of the equipment medium is considered, the stiffness matrix has to contain the parameter information of the previous calculation, and the matrix has to be reassembled for each iteration, which greatly reduces the efficiency of the finite element calculation. The expensive computational cost limits the application of digital twin technology for the optimal design of electrical equipment and for real-time performance analysis.
The greedy strategy and improved sparrow search algorithm (ISSA) are combined with the proper orthogonal decomposition (POD) method to propose an adaptive model reduction method applicable for three-dimensional nonlinear magnetic field problems. Firstly, the full-order FEM was used to model and simulate the research object, and the FEM solutions corresponding to different sample points were calculated as the sample library. Secondly, the POD was combined with radial basis function (RBF) interpolation, while the ISSA-POD-RBF reduced-order model considering optimal combination of RBF width parameters was constructed based on the ISSA; Finally, the iterative computation of snapshot matrix and optimal width parameter combination was carried out by the greedy strategy to construct a fast computational model that more closely matches the original full-order model.
To verify the effectiveness of the proposed model reduction method, the TEAM24 problem and a traction transformer are taken as the research objects.The speed and accuracy of the reduction model are investigated by comparing computational results and computation time of the reduction model with the FEM full-order model. In the TEAM24 problem, a sample library containing 100 samples corresponding to the FEM solutions is prepared in advance, and the iteration termination condition of the greedy strategy is set to the maximum relative error e2max<0.5%. The final size of the snapshot matrix is determined to be (118 831×3)×13, and the POD basis retains the order of 2nd order.The results show thatthe relative errors of the samples computed by the reduced-order model constructed with the optimal combination of width parameters were overall smaller than the computational errors of the reduced-order model constructed with the same width parameters. The single-point error of flux density comparison at local nodes does not exceed 0.01%. The computational times of the proposed reduced-order model and the FEM full-order model are 205 s and 0.56 s, respectively, and the acceleration ratio is 366.07. In the three-dimensional model, the size of the finalized snapshot matrix is (125 403×3)×40, and the POD basis retains the order of 11th order. The results show that the computational errors of the model are in the same order of magnitude as those introduced during simulation due to uncertainties in material properties, dimensions, and simulation operations. The computational times of the proposed reduced-order model and the FEM full-order model are 386.4 s and 3.9 s, respectively, with an acceleration ratio of 99.08.
The proposed fast solution method for the nonlinear magnetic field problem of electrical equipment provides a real-time simulation solution for the construction of digital twin models of electromagnetic performance of electrical equipment.
Keywords:Proper orthogonal decomposition, improved sparrow search algorithm, model order reduction, greedy algorithm, three-dimensional nonlinear magnetic fields
中图分类号:TM15
DOI: 10.19595/j.cnki.1000-6753.tces.232159
国家自然科学基金项目(51707125)和辽宁省教育厅项目(LNYJG2022060)资助。
收稿日期 2023-12-25
改稿日期 2024-01-22
刘禹彤 女,1995年生,博士研究生,研究方向为电磁场理论及数值计算模型降阶技术。
E-mail:xrdsliu@163.com
任自艳 女,1982年生,教授,博士生导师,研究方向为电工装备的优化设计算法及电磁场数值分析与计算。
E-mail:rzyhenan@163.com(通信作者)
(编辑 郭丽军)