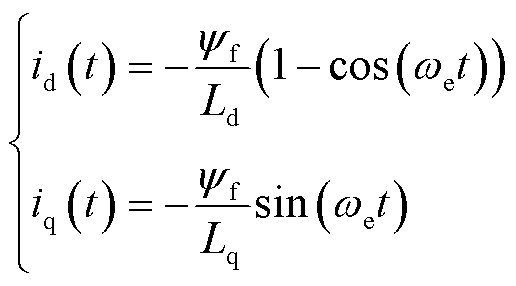（1）
摘要 针对永磁同步电机传统双脉冲和多脉冲注入带速重投方法在位置、转速估计方面存在稳态精度低、转速跟踪慢等问题，提出一种重复窄短路脉冲与高阶锁相的带速重投策略。通过提高带速重投过程的脉冲宽度调制（PWM）频率，实现更窄的短路脉冲输出，更准确地控制电流幅值。为了解决传统固定脉冲宽度带来的高速电流纹波大的问题，根据两个测试短路脉冲的电流幅值信息自适应调整短路脉冲宽度和时间间隔，保证全速范围的短路脉冲幅值小且受控。同时为了提高电流采样信噪比，采用电流过采样技术，多次采集相电流后求平均值，进一步提升位置估计精度。并设计三阶锁相环实现短路电流快速准确锁相，实现转子位置和转速的连续估计。实验结果表明，所提出策略在全速范围将电流幅值控制在额定电流的5%以内，减小电流纹波，降低母线电压泵升速率，提高位置和转速估计精度，从而实现快速、无电流冲击的带速重投。
关键词：永磁同步电机 重投策略 重复窄脉冲 电流过采样 三阶锁相环
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）具有高功率密度、高效率、强动态性能等优点，在工业控制、电动汽车、轨道交通、航空航天等领域应用越来越广泛[1-2]。在一些大转动惯量应用领域，如空调室外风机在外界风力作用下高速转动，需要控制器上电后系统能够平滑快速起动；家用电器中高速电吹风、吸尘器等在使用过程中可能会操作开关频繁起动，此时电机转子并未减速到零；高速列车牵引电机在跨相区供电、工作在惰性工况（列车减速或制动）、无电区或电力系统出现故障时，有短暂停止供电，此时驱动系统需要在未知转速下重新起动。在类似的场合下，即在电机驱动器重新投入闭环时刻，电机仍有初转速，此时需要使用带速重投方法[3]，否则会产生冲击电流，造成母线电压泵升和电机抖动，严重时还会损坏功率器件[4]。PMSM带速重投需要实时获得转子磁极位置和转速信息，从而施加特定相位和幅值的初始电压，以减小电流冲击和母线电压泵升。但是，采用位置传感器会增加系统成本，降低系统在复杂环境中的可靠性等，因此对PMSM无位置传感器控制带速重投技术的需求日益增加。PMSM无位置传感器控制起动策略常采用高频注入法估计初始位置[5]，实现无反转平滑起动。然而，对于一些电感凸极率不高的表贴式PMSM，难以实施高频注入法。因此，设计一种更通用的PMSM带速重投方法，对提高PMSM系统的可靠性至关重要。
近年来，除了高频信号注入法外，多种带速重投的方法相继被提出，主要分为三类：电压检测法、虚拟电阻法、零电压矢量（Zero-Voltage Vector, ZVV）脉冲法。电压检测法通过增加三相端电压检测电路，计算反电动势，实时估计转子位置和转速，重投效果最好[6]。但是这类方法需要增加电压检测硬件电路，特别是对于高压需要电气隔离的应用场合，增加隔离电压检测电路会显著增加系统成本。虚拟电阻法将逆变器等效成大电阻，串联到电机定子阻感回路中，从而限制切入时刻的大电流冲击。但是该方法需要根据电机定子电阻、定子电感、采样时间等参数提前计算虚拟电阻的上限值，过大的虚拟电阻会导致系统不稳定，且该方法收敛过程时间较长[7]。
在上述三类方法中，ZVV方法实现简单、通用性强，受到广泛关注。文献[8]使用了单ZVV方法实现位置和转速估计，但是该方法需要提前设定脉冲的作用时间。对于高转速电机，存在电流冲击大、易触发过电流保护、母线电压泵升高等问题。文献[9]在双ZVV方法的基础上给出一种确定短路脉冲作用时间的方法，即通过在两次短路零矢量脉冲前增加测试脉冲来确定合适的脉冲作用时间。但是，双脉冲方法仅依靠两个点的电流幅值计算电流矢量位置，再通过位置微分计算转速，位置估计精度较依赖电流采样精度。文献[10]提出三ZVV方法，并且在转子位置估计过程中考虑了电流传感器误差并加以补偿，以及量化了电感变化对位置估计的影响。但是所补偿的角度仍然是通过双脉冲计算的转速估计得来，这样计算的补偿角度可能会放大位置误差。文献[11]采用三次短路脉冲估计转子位置与转速，它的原理与问题也与双脉冲方法基本相同。文献[12]提出了一种重复ZVV脉冲方法，通过重复施加ZVV脉冲获取转速平均值，并根据平均转速与转速误差选择重复次数，但是每次估计的转速同样是根据两个脉冲电流矢量变化的频率得来。文献[13]在传统ZVV方法的基础上构造了两个反馈环来调节不同转速下ZVV脉冲的作用时间，然后设计二阶锁相环（Phase-Locked Loop, PLL）跟踪转子位置。但是并没有考虑锁相环初始时刻的位置和转速，易导致锁相环收敛转速较慢等问题。文献[14]提出单母线电流采样驱动器中施加三对有效电压矢量形成等效零矢量，并结合二阶锁相环跟踪转子位置，将ZVV方法扩展至单母线电流采样场合。文献[15]在三相六开关逆变器向三相四开关逆变器过渡重起过程中，提出了一种利用双有效电压矢量合成等效零电压矢量的方法。
针对现有方法存在的问题和不足，本文提出一种重复窄短路脉冲与高阶锁相的带速重投策略。首先，分析传统ZVV方法的原理以及存在的问题；其次，提出重复窄短路脉冲与高阶锁相带速重投方法；最后进行实验，从母线电压泵升、位置/转速跟踪动态性能和稳态性能等几个方面对比并验证所提方法的有效性。
在ZVV脉冲作用时，将d、q轴电压方程经过Laplace反变换可以解得d、q轴响应电流[16]为
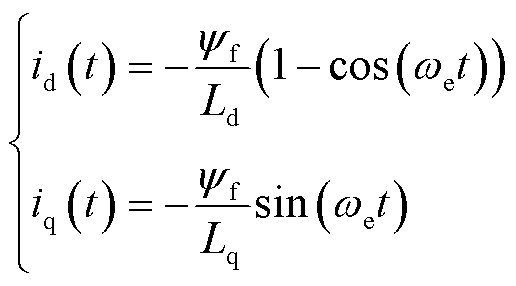（1）
式中，id、iq分别为d、q轴电流；Ld、Lq分别为d、q轴电感；we为电角转速；yf为永磁体磁链。
根据采样的相电流，计算a和b轴电流[17]为
（2）
式中，ia、ib分别为a和b轴电流；ia、ib分别为a和b相电流。
通过ab轴电流计算电流矢量角[18]为
（3）
式中，qI为电流矢量与a轴的夹角；arctan2表示(-p, p)范围内反正切函数。
图1为电流矢量在不同坐标系中与转子位置的关系。其中，施加两个短路脉冲后所对应的电流矢量分别为is1与is2。其与a轴的夹角分别为qI1与qI2。在同一时刻，电流矢量在静止参考系与旋转参考系下的位置相同。因此，在相同间隔时间内，电流矢量旋转转速与转子转速一致，所以估计的电角转速
表示为
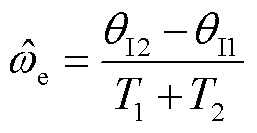（4）
式中，T1为脉冲作用时间；T2为脉冲间隔时间。
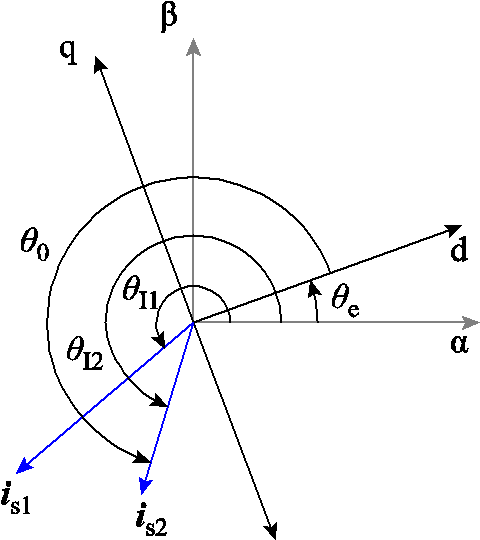
图1 电流矢量与转子位置的关系
Fig.1 Relationship between current vector and rotor position
估计的转子位置
为
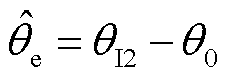（5）
式中，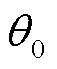
为电流矢量与d轴的夹角。
为了解重起过程母线电压泵升的具体原因、电流采样噪声对位置跟踪性能的影响及锁相环收敛转速引起的电流矢量角跟踪慢等问题，本小节将从以下三个方面展开分析。
1.2.1 母线电压泵升分析
当施加短路脉冲时，假设当前电流流动方向如图2a所示（其他电流情况同理），a、b、c三相的反电动势ea、eb、ec产生电流给电感充电。当处于脉冲间隔时间段时，所有功率开关管全部断开，电流流动方向如图2b所示，其等效Boost电路如图3所示。图3中，es为永磁体旋转产生的反电动势矢量。
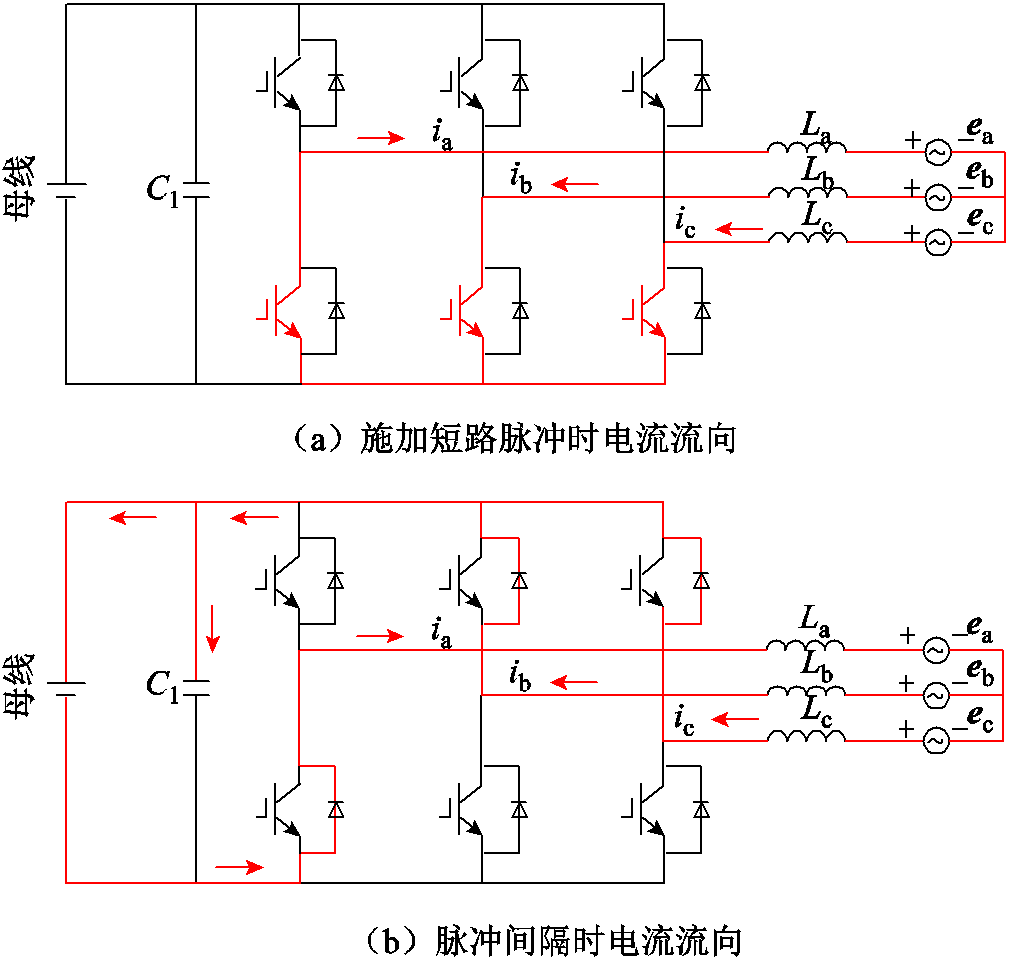
图2 施加短路脉冲与脉冲间隔时的电流流动
Fig.2 Current flowing during short-circuit pulses and pulse intervals
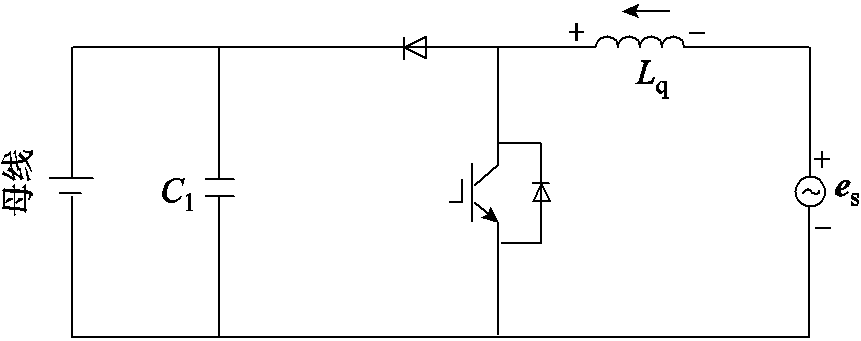
图3 经二极管续流时的等效Boost电路
Fig.3 Equivalent Boost voltage circuit in braking state
从图2与图3中可以看到，经过二极管释放的电流会流入母线电容C1和电源上，从而形成类似于Boost升压电路，给母线电容充电，造成母线电压泵升。
考虑脉冲作用时间T1，当电流矢量转过的角度较小时，将d、q轴电流公式式（1）通过泰勒级数展开并近似[19]为
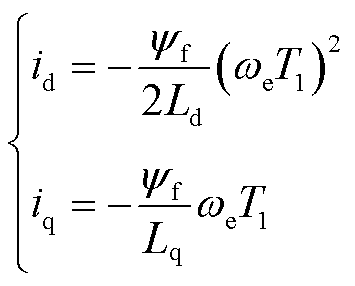（6）
则电感上的储能Es为
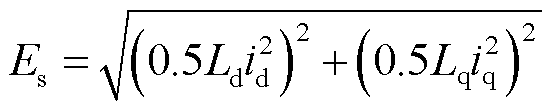（7）
由于脉冲作用时间是μs级，d轴电流很小，因此式（7）可以等效为
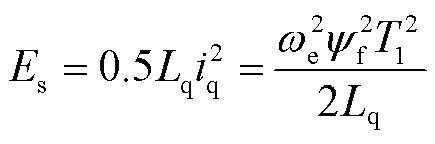（8）
根据图3等效Boost电路，假设电机电感上储存的能量全部转移到电容上，则有
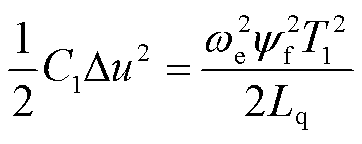（9）
则电容电压泵升∆u为
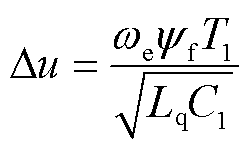（10）
经过以上分析，母线电压泵升速率与we、T1成正比，与
成反比。因此对于小电感电机，电压泵升的转速更快，同时减小T1有助于减缓电压泵升。
1.2.2 电流采样噪声引起的锁相环误差分析
传统二阶锁相环的传递函数[20]为
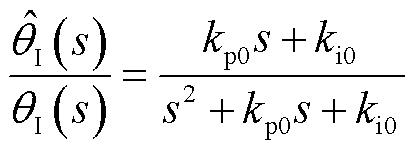（11）
式中，kp0、ki0为二阶锁相环的可调参数。
根据图1，a、b轴短路电流可以表示为
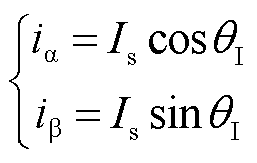（12）
式中，Is为电流矢量的幅值。
在不影响整个控制系统稳定性的前提下，引入白噪声后的ab轴电流变为
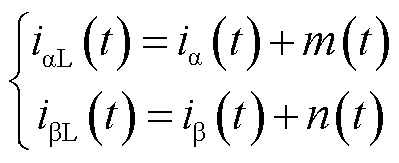（13）
式中，iaL、ibL分别为加入噪声后的a、b轴电流；m(t)和n(t)为采样白噪声。
在引入采样噪声后，利用外差法重新计算电流矢量角跟踪误差，有
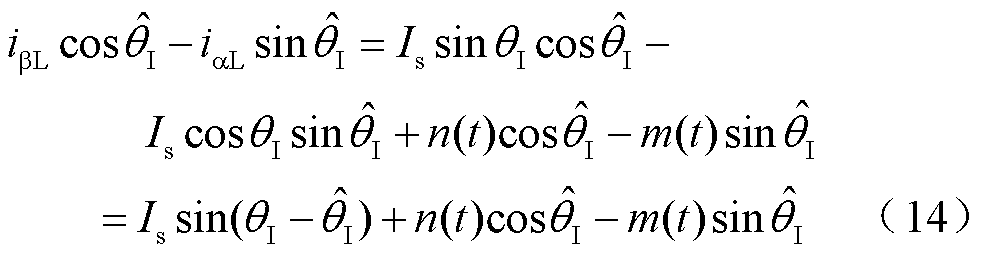
式中，
为电流矢量与a轴夹角的估计值。
将式（14）作为二阶锁相环的输入，则当锁相环达到稳态时，即式（14）=0。由式（14）可知，由于无法保证m(t)=0和n(t)=0，因此会存在与噪声数值相关的位置跟踪误差。
1.2.3 锁相环收敛转速引起的误差分析
为了分析二阶锁相环与三阶锁相环[21]的动态跟踪性能差异，图4为在仿真条件下相同的阻尼比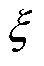
与自然角频率wn（wn=50p rad/s，x=0.707，极点的调节系数k=10）时，二阶锁相环与三阶锁相环在阶跃指令下输出响应曲线；图5为图4的位置跟踪误差曲线。
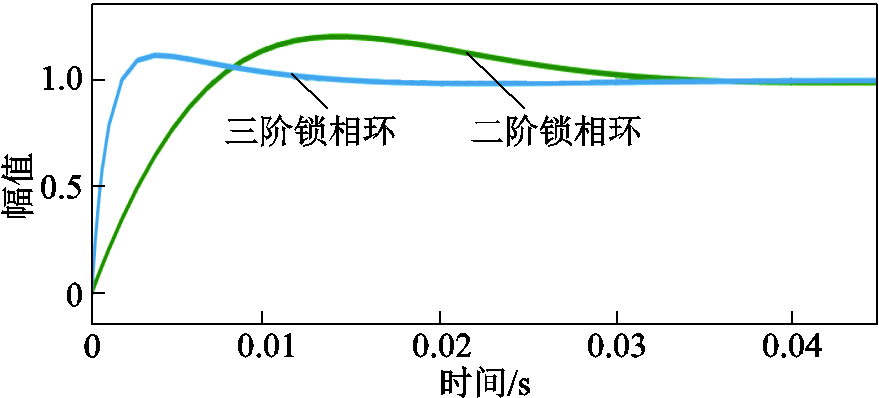
图4 二阶锁相环与三阶锁相环的阶跃响应曲线
Fig.4 Step response curves of second-order and third-order PLLs
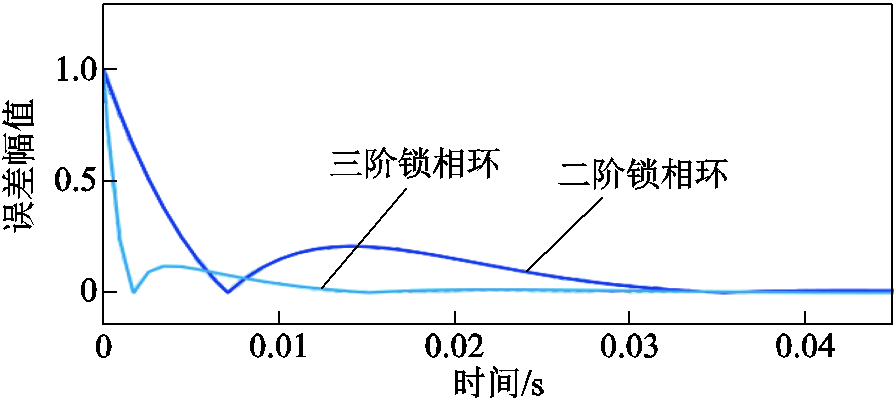
图5 二阶锁相环与三阶锁相环的位置跟踪误差曲线
Fig.5 Position tracking errors of second-order and third-order PLLs
从图4和图5可以看出，在动态跟踪过程中，三阶锁相环的动态响应转速快于二阶锁相环，且位置跟踪误差能够快速收敛到零；稳态时两者跟踪精度没有明显区别。由此可以看出，三阶锁相环在具有相似稳态跟踪精度的情况下，可以加速锁相环收敛，进而提供更好的暂态性能。
从第1节的分析可知，电流采样误差和二阶锁相环会降低位置估计精度且造成收敛转速慢等问题。相电流续流过程中，母线电压会泵升。为了提高电流采样精度、加速位置收敛过程、减缓母线电压泵升，实现切换过程的无电流冲击，提出了一种加入电流过采样技术的重复窄短路脉冲与高阶锁相的带速重投方法。通过加入电流过采样技术提高电流采样的准确性。根据1.2.1节分析，小电感电机电压泵升转速快，本文的重复窄短路脉冲可减少对短路电流幅值的需求，有效降低小电感电机下的电压泵升转速。同时，高阶锁相环可以提高相位跟踪动态响应转速，使转速与位置跟踪收敛得更快、更准，避免切换过程产生的大电流冲击。
2.1.1 窄短路脉冲意义
无论是双脉冲法还是多脉冲方法，其注入脉冲的作用时间都是固定的，这会导致不同转速下短路电流大小不同，对系统产生的电流冲击也不同。低转速下，短路电流小，对系统的电流冲击小；高转速下，短路电流大，对系统的电流冲击大。并且，大电流的续流时间更长，母线电压泵升更高。因此，为了减小电流冲击，降低电压泵升转速与幅度，同时又保证不损失位置估计精度，可以根据实时检测的电流幅值自适应限定脉冲作用时间。
为了能够更精确地控制短路电流，将带速重投过程的脉冲宽度调制（Pulse Width Modulation, PWM）频率提高，本实验中，正常控制PWM频率为10 kHz，考虑带速重投过程程序执行时间，将PWM频率提高。具体可以将PWM频率提高到多少，需要根据实际带速重投过程程序执行时间和功率开关管的开关速率来确定。即PWM的周期需要大于带速重投代码执行过程的最大时间，且施加的开关频率功率器件可以正常开通和关断。本文实验中，将PWM频率提高为40 kHz，载波与实际脉冲时间如图6所示。短路脉冲优点有：①在不损失位置估计精度的情况下短路脉冲作用时间更短；②作用时间越短，每一个PWM周期短路电流增加越小，从而实现更精确控制电流幅值的目的；③作用时间越短，根据式（10），电压泵升速率越慢。另外，本文带速重投过程脉冲群作用时间小于5 ms（见第3.6节），因此不会影响功率器件的开关损耗及其温升。而且提高载频方便，更改周期寄存器即可。
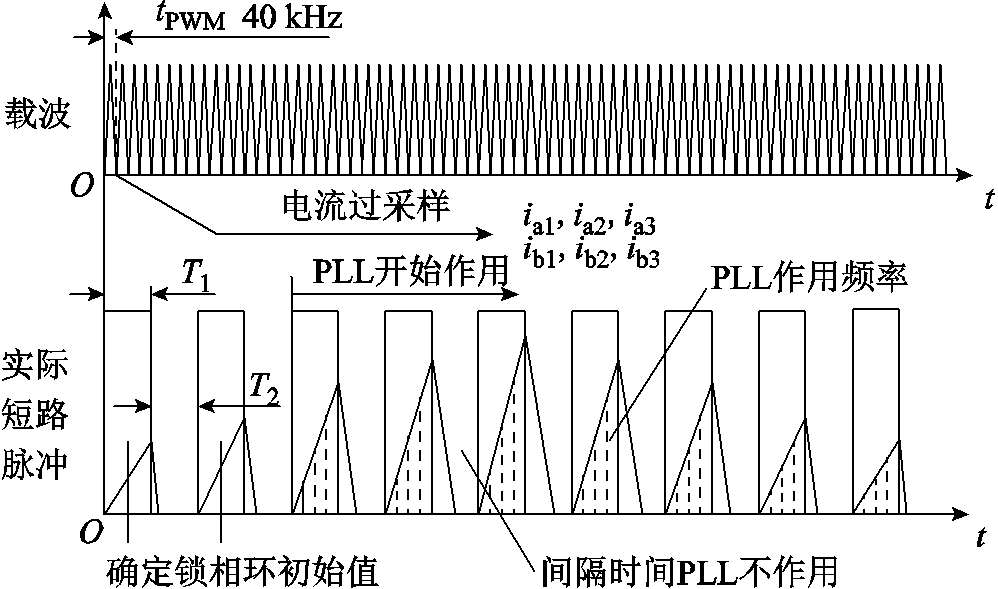
图6 载波与实际脉冲时间
Fig.6 Carrier wave and actual pulse time
2.1.2 确定脉冲作用时间T1
短路脉冲的持续作用时间会直接影响短路脉冲产生的电流幅值大小。脉冲作用时间设置太短，产生的电流太小，会造成估计的转速与位置误差较大；设置太长又会导致短路电流过大，对系统产生电流冲击。
综上所述，所提方法会在第一个脉冲根据设置电流幅值的大小自适应地调整短路脉冲的作用时间，即需要确定短路脉冲持续多少个PWM周期[22]。对于不同转速，均可以通过测试脉冲，确定合适的短路脉冲持续时间T1，如图6所示。
2.1.3 确定脉冲间隔时间T2
脉冲间隔时间会影响锁相环的跟踪性能。若间隔时间太短，短路电流可能无法完全回零，增加下一周期锁相环输入的波动；若间隔时间太长，实际转速变化较大，会增加锁相环在下一周期初始跟踪的误差，降低位置跟踪的性能。
首先根据式（6）求出电流幅值，近似为
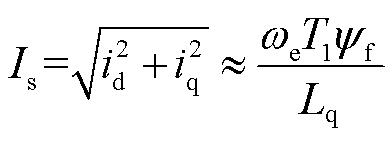（15）
将式（15）作相应变换可以估算出第一次脉冲结束的转速，即
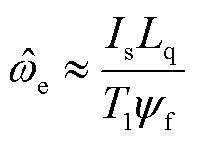（16）
脉冲的间隔时间可以根据式（4）与式（16）确定，根据式（4）可以得到
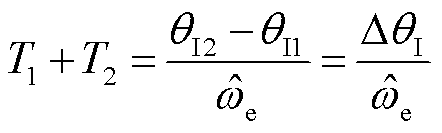（17）
式中，DqI为两次脉冲电流矢量角的变化量。
根据qI的变化量与估计出的转速误差关系，当DqI≤30°时，估计出的转速误差在可接受范围内[9]。另外，为了保证电流在间隔时间内可以衰减到零，脉冲间隔时间应该大于或等于脉冲作用时间。并且第一个脉冲结束，T1已经确定。综上所述，间隔时间应该满足
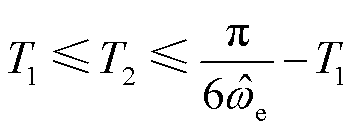（18）
在2.1节的基础上，根据前面两个测试脉冲及式（4）与式（5），分别确定初始电流矢量位置和转速，赋给三阶锁相环积分环节作为初始值，加速锁相环收敛。所设计三阶锁相环的传递函数[23]为
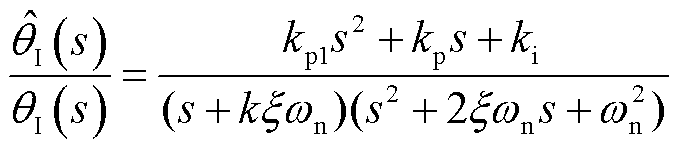（19）
式中，kp1、kp、ki为三阶锁相环的三个可调参数。其结构框图如图7所示。
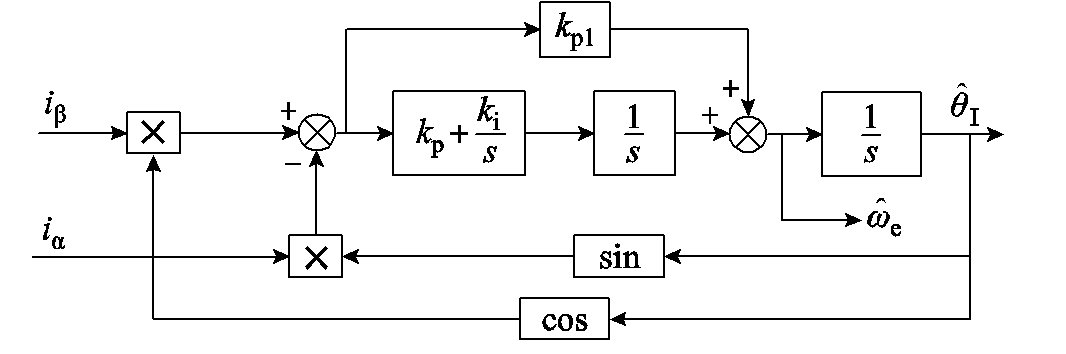
图7 三阶锁相环的结构框图
Fig.7 Block diagram of the proposed third-order PLL
图1中，电流矢量与d轴的夹角q0[10]为
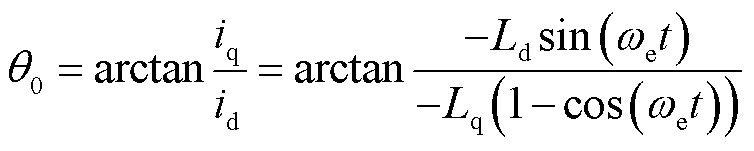（20）
以图1为参考，根据估计转子位置为
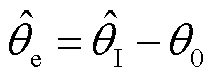（21）
由式（19）可知，三阶锁相环增加了一个系统极点，通过设置k的大小可以调节新增极点与原来二阶锁相环极点的关系，当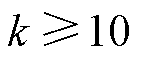
时，此时整个系统的响应可近似为具有相同主导极点的二阶系统，从而简化分析过程。本例中，根据近似的二阶系统阻尼比、自然角频率和调节系数计算三阶锁相环参数，即
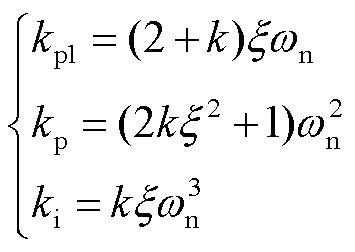（22）
为了对比三阶锁相环和二阶锁相环的性能，选择相同的阻尼系数和自然角频率确定二阶锁相环参数为
（23）
经过以上分析，本文调节系数k=10，x选择二阶最佳阻尼比0.707，以确保系统在整个参数变化范围内保持稳定[24]。另外，为保证系统的响应转速，自然角频率应结合转速环带宽进行设计，同时也不能太高，防止高频噪声。设计时根据系统的转速环带宽设置wn=50p rad/s。图8为在相同阻尼比与自然角频率下，按照式（22）与式（23）设置参数后，二阶与三阶锁相环闭环传递函数的伯德图。从图中可以看到，三阶锁相环的截止频率大于二阶，由此说明使用三阶锁相环具有更好的稳定性以及更快的响应转速，可以加快切入位置观测器后的收敛转速，避免电流冲击和母线电压泵升。另外，PLL锁相也不复杂，正常无位置传感器算法也在使用，计算量也不大，对PMSM正常无位置传感器控制算法没有影响，因为切入观测器过程，短路脉冲已经结束。
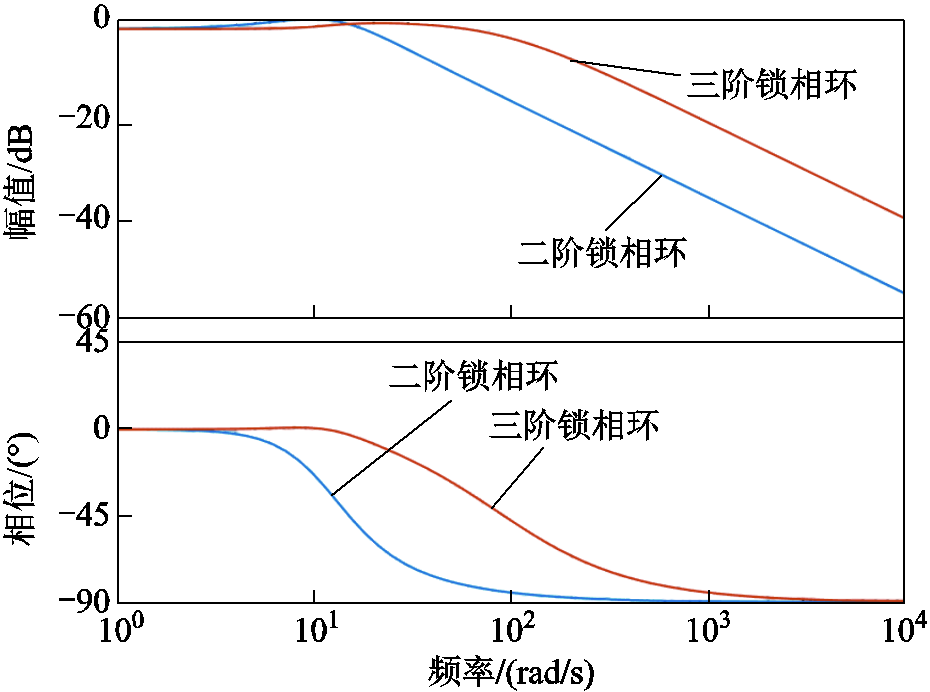
图8 二阶与三阶锁相环闭环伯德图
Fig.8 Closed-loop Bode diagrams of second-order and third-order PLLs
考虑到电流采样受噪声影响，单次电流采样会受到较大干扰，降低锁相环的跟踪精度，为此加入电流过采样技术[25]。首先通过微控制器（Microcontroller Unit, MCU）自带的高速模数转换器（Analogy-to-Digital Converter, ADC）对相电流在触发时刻进行连续过采样，若连续采样N次相电流，则有
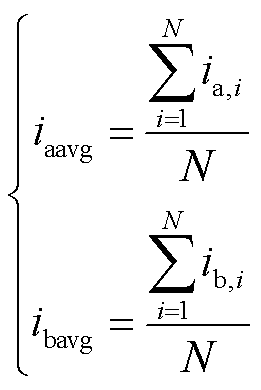（24）
式中，iaavg和ibavg分别为对a和b相电流过采样N次后的平均值；c相电流可以通过三相电流和为零进行重构。采样过程中，尽量配置a、b相电流为同时采样模式，减少彼此之间采样导致的相位差。
加入电流过采样后的载波与脉冲时间关系如图6所示，然后根据式（2）使用过采样后的平均相电流计算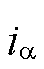
与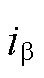
。
最后，所提策略的整个控制系统结构框图如图9所示。测试电机系统由电流环控制，系统给是否带速重投指令（N表示不给指令，Y表示给指令），当给重投指令时，重复窄短路脉冲注入后先确定短路脉冲作用时间、间隔时间与锁相环的积分初始值，再使用锁相环连续跟踪转子位置，图9中的高阶锁相环（High-order Phase Locked Loop, HPLL）为文中使用的三阶锁相环。等带速重投结束切换至电流闭环后，指令恢复为N。控制器使用龙伯格观测器估计的角度进行控制[26]，
与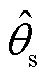
分别为观测器估计的转速与角度。
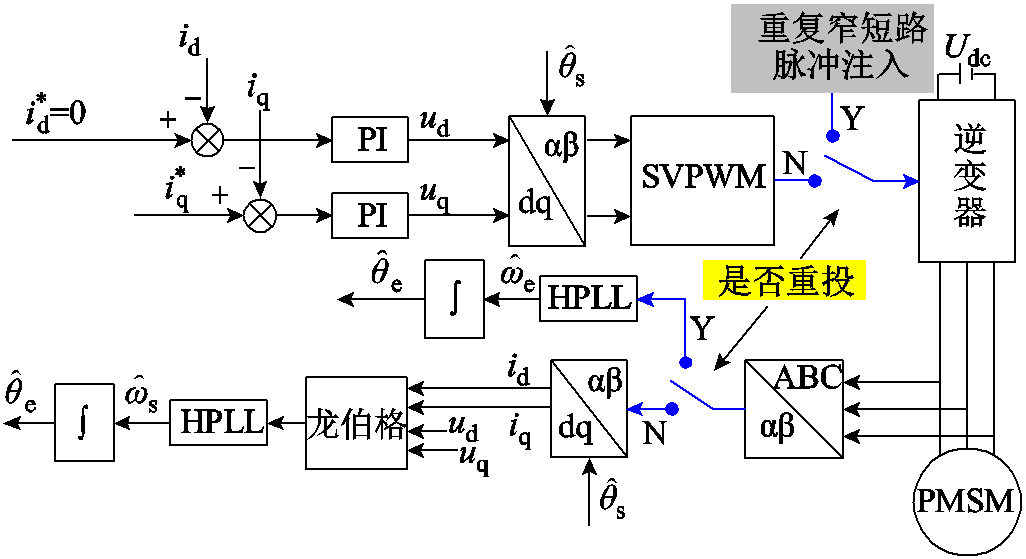
图9 重复窄短路脉冲与高阶锁相控制框图
Fig.9 Control block diagram of repetitive narrow short-circuit pulses with higher order PLL
为验证本文提出方法的有效性，本节在相同测试条件下对比了传统双脉冲（参照文献[19]设计）、多脉冲二阶锁相环（参照文献[14]设计）及提出的重复窄短路脉冲与高阶锁相三种方法的带速重投性能。
图10为永磁同步电机对拖实验平台，包括测试电机和陪试电机，以及两套电机驱动器。两台永磁同步电机的控制参数见表1。根据2.2节，为保证对比公平性，二阶锁相环和三阶锁相环的带宽和阻尼比相同，为wn=50 p rad/s，x =0.707，三阶锁相环调节参数k=10。由此计算出二阶锁相环的控制参数kp0、ki0与三阶锁相环的控制参数kp1、kp、ki。
图10 实验平台
Fig.10 Experimental platform
表1 测试电机与陪试电机参数
Tab.1 Parameters of the test and accompanying PMSMs
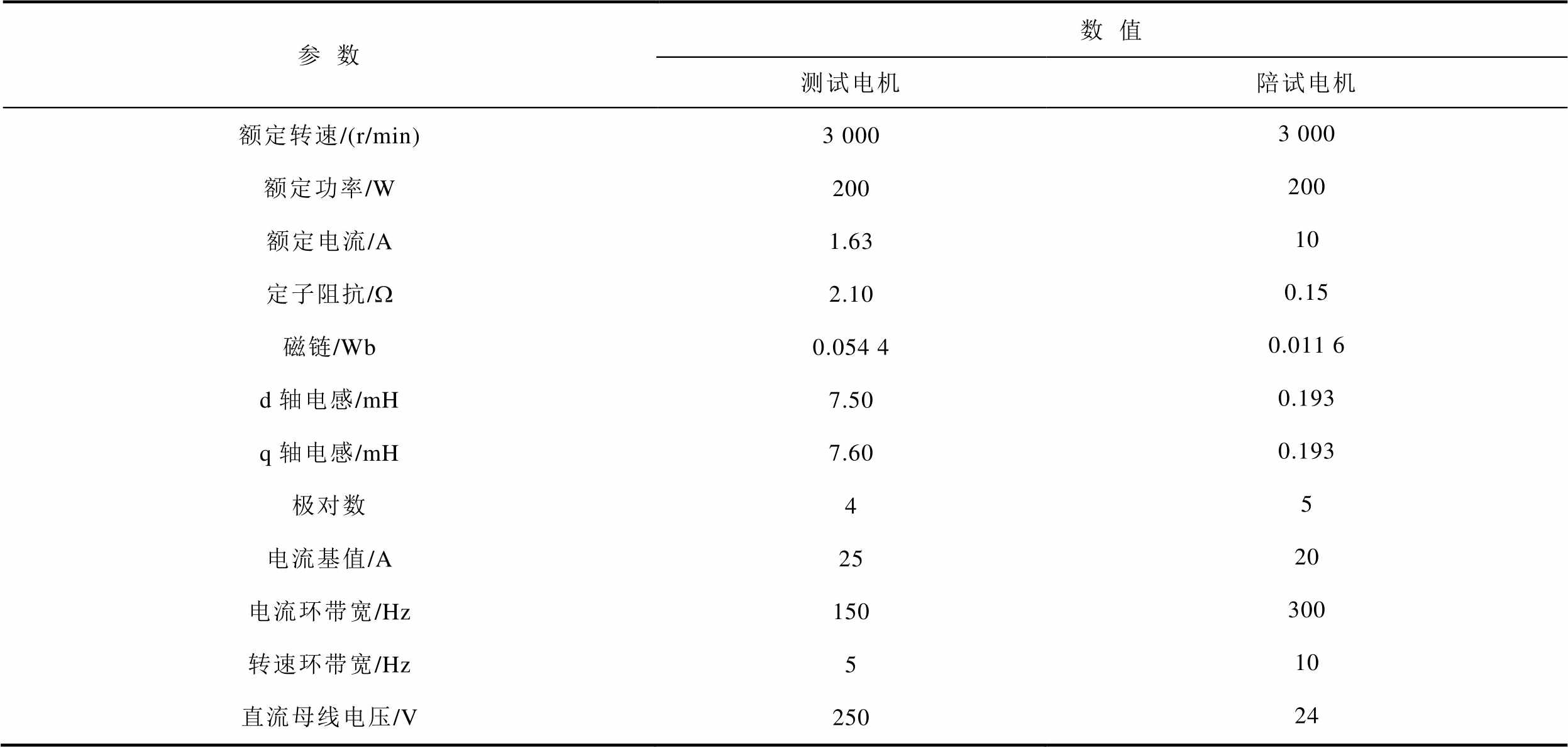
参数数值 测试电机陪试电机 额定转速/(r/min)3 0003 000 额定功率/W200200 额定电流/A1.6310 定子阻抗/W2.100.15 磁链/Wb0.054 40.011 6 d轴电感/mH7.500.193 q轴电感/mH7.600.193 极对数45 电流基值/A2520 电流环带宽/Hz150300 转速环带宽/Hz510 直流母线电压/V25024
实验中，陪试电机处于有位置传感器转速环工作模式，测试电机执行带速重投后切换至基于龙伯格观测器的电流闭环无位置传感器控制模式。
图11～图13为测试电机在900 r/min与2 400 r/min时加或者不加重复窄短路脉冲带速重投方法的实验结果。图11a～图13a为不加短路脉冲的实验结果，图11b～图13b为加短路脉冲的实验结果。图中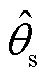，为龙伯格观测器估计的角度，qe为真实角度，
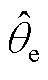为带速重投过程估计角度。从图12可以看出，不加短路脉冲直接带速重投会有大电流冲击，尤其是在高转速2 400 r/min情况下，并且会造成母线电压急剧泵升触发过电压保护，如图13a所示。而加短路脉冲带速重投基本没有电流冲击，且能有效抑制母线电压泵升的速率，如图13b所示。
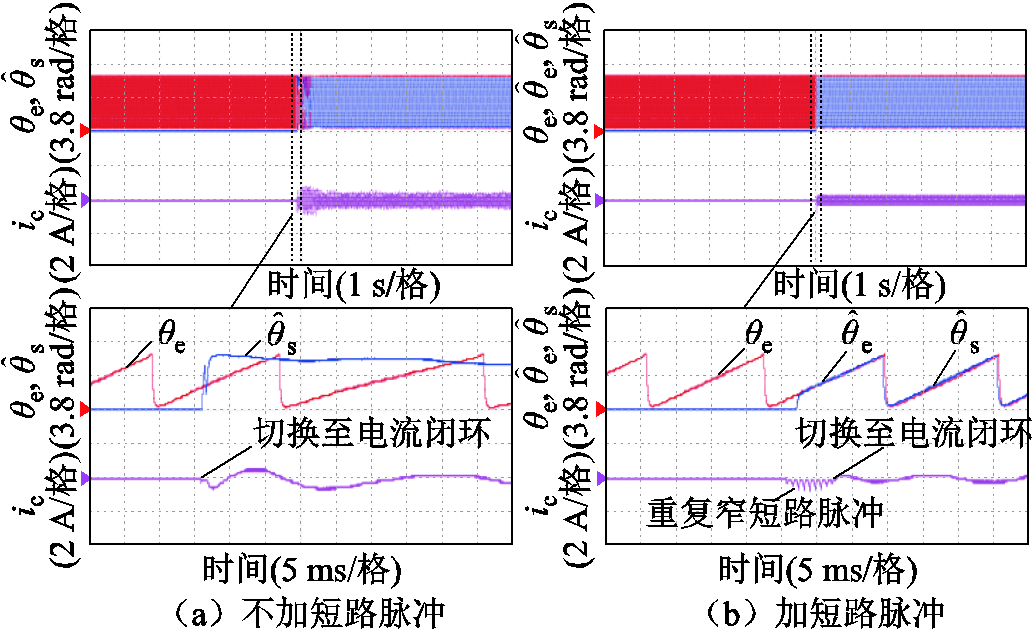
图11 900 r/min加/不加重复窄短路脉冲带速重投实验波形
Fig.11 Experimental waveforms of with or without using repeated narrow short-circuit pulses for restarting at 900 r/min
图12 2 400 r/min加/不加重复窄短路脉冲带速重投实验波形
Fig.12 Experimental waveforms of with or without using repeated narrow short-circuit pulses for restarting at 2 400 r/min
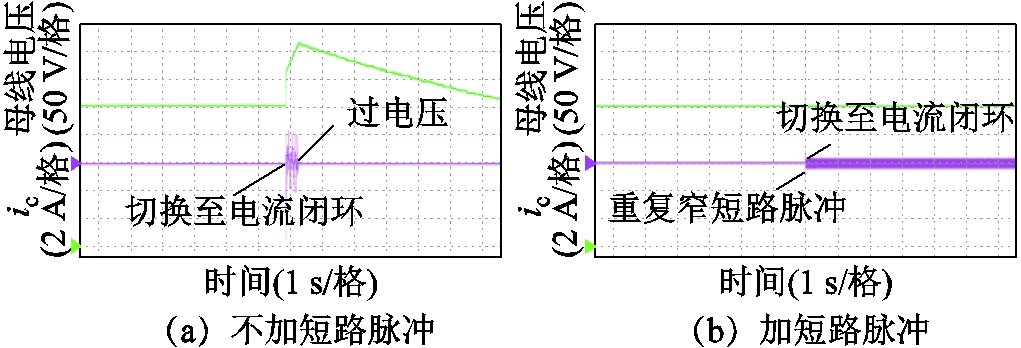
图13 2 400 r/min加/不加重复窄短路脉冲母线电压实验波形
Fig.13 Experimental waveforms of bus voltage with or without using repeated narrow short-circuit pulses at 2 400 r/min
图14a～图14c分别为电机在2 400 r/min情况下，施加传统双脉冲、传统多脉冲与所提重复窄短路脉冲时的母线电压泵升波形。测试时首先按照各种方法的原理调整控制参数，保证三种方法的位置估计精度和控制性能相似后（下同），再进行性能分析及对比。传统多脉冲与所提重复窄短路脉冲设置了相同的脉冲作用时间与间隔时间，但是所提策略可以通过设置电流幅值限制短路电流大小，从而降低电压泵升的幅度。从图14中可以看到，从第一个脉冲间隔开始的2.4 ms内传统双脉冲和多脉冲二阶锁相方法的母线电压泵升幅度分别为22 V与7 V，而所提重复窄短路脉冲方法测试的电压泵升幅度仅为1 V，是三种方法中最小的，由此说明了所提方法可以有效地减缓电压泵升转速，提高控制系统的可靠性。
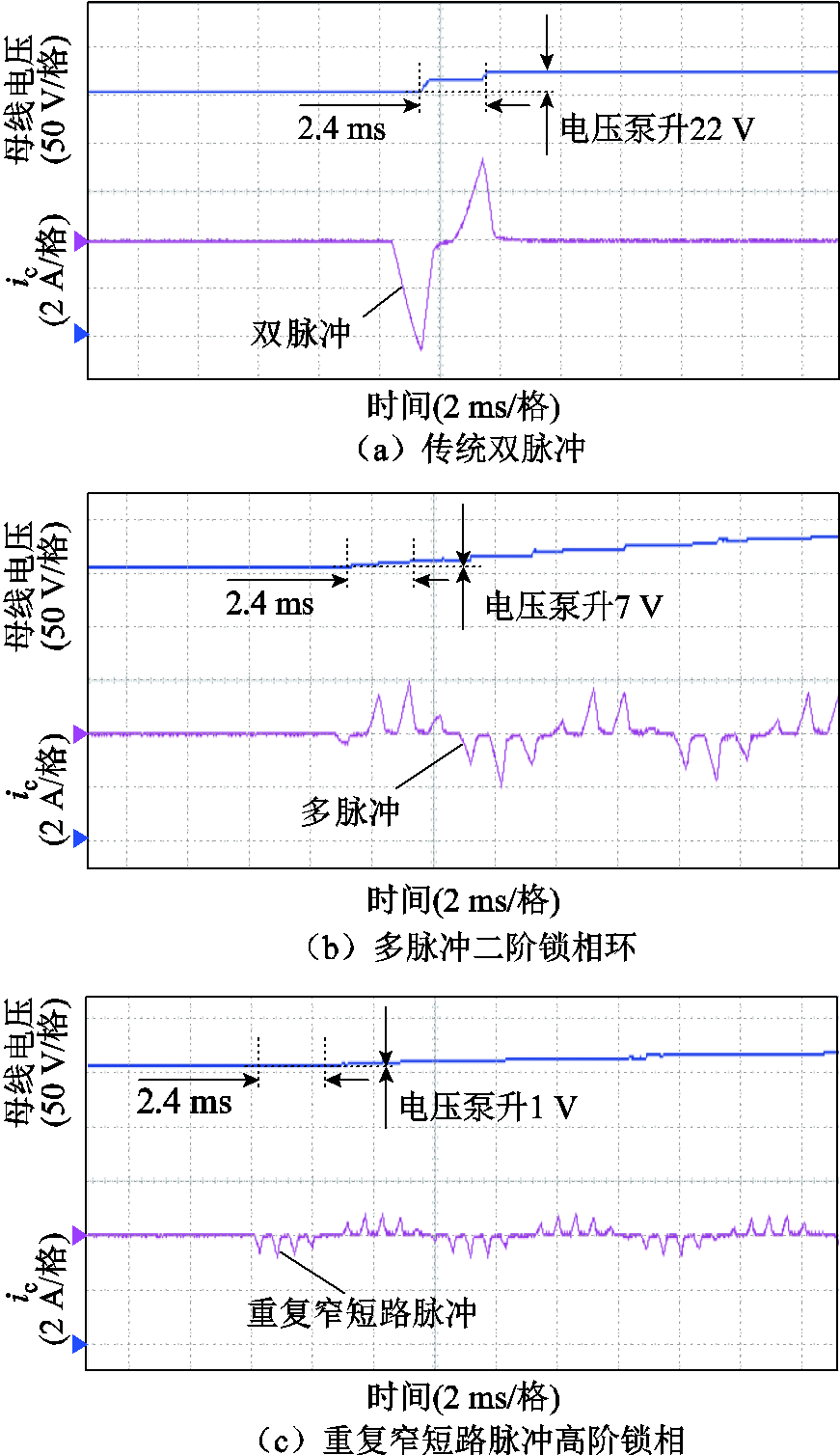
图14 三种方法母线电压泵升对比实验波形
Fig.14 Experimental waveforms of DC-bus voltage pumping up for three methods
对比传统双脉冲、多脉冲二阶锁相环与所提策略在脉冲注入阶段转速跟踪的精度与快慢，图15～图17分别为三种方法在900 r/min与2 400 r/min时的转速跟踪实验波形。图中，n为真实转速，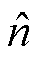
为估算转速。从实验波形中可以看到，传统双脉冲估算由于只有单次估算，转速存在稳态误差，另外短路脉冲作用时，相电流的正负与电机转子位置有关，由于短路脉冲作用时，转子位置是不断变化的，所以相电流的正负也在变化。在900 r/min与2 400 r/min时，使用多脉冲二阶锁相环跟踪转速的动态响应时间分别为860 μs与1.92 ms。而采用重复窄短路脉冲高阶锁相方法的转速跟踪时间分别为670 μs与1.46 ms，小于多脉冲二阶锁相环，从而表明所提方法的转速估计收敛转速更快。理想情况下，由于锁相环估计的连续特性，锁相环方法都不存在稳态误差。
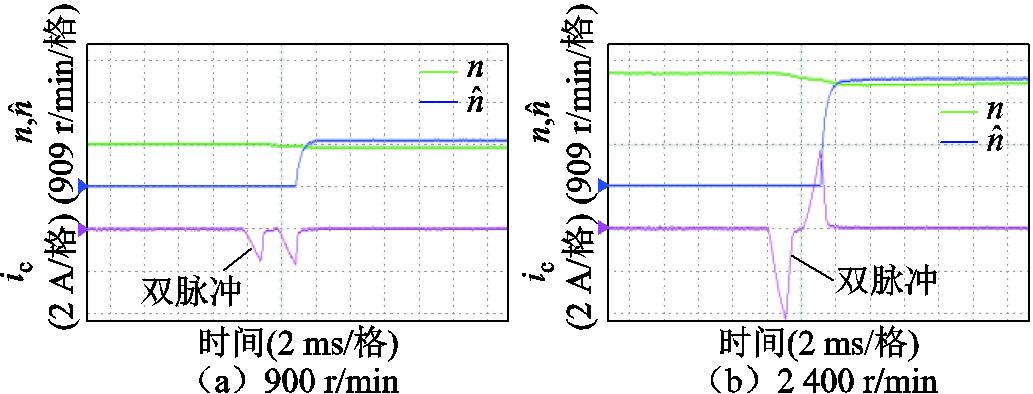
图15 传统双脉冲转速跟踪实验波形
Fig.15 Experimental waveforms of conventional double-pulse speed tracking
图16 多脉冲二阶锁相环转速跟踪实验波形
Fig.16 Experimental waveforms of multi-pulse with second-order PLL speed tracking
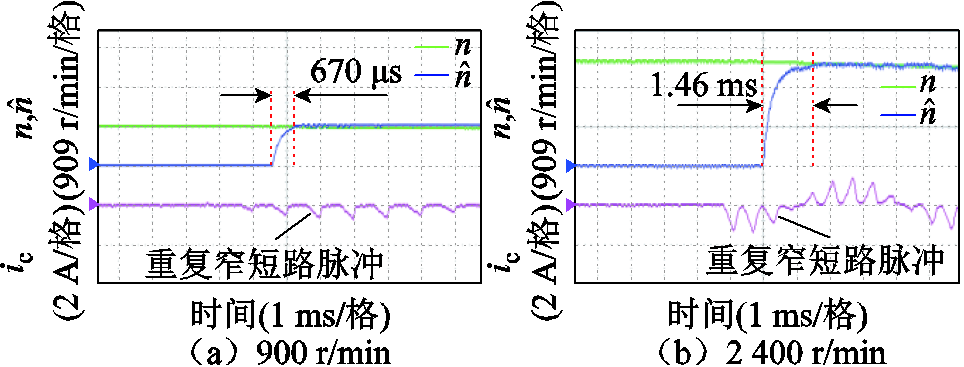
图17 重复窄短路脉冲高阶锁相转速跟踪实验波形
Fig.17 Experimental waveforms of repeated narrow short-circuit pulses with high-order PLL speed tracking
图18～图20分别为三种方法在900 r/min与 2 400 r/min时，完成转子转速与位置估计后切换至电流闭环状态的实验波形，为了对比脉冲注入阶段使用两种锁相环的位置跟踪性能，两种锁相环的脉冲注入时间较长，900 r/min时为92 ms，2 400 r/min时为28 ms。从实验波形中可以看到，图18使用传统双脉冲在两种转速下的切换过程有较大的电流冲击。图19使用多脉冲二阶锁相环与图20所提方法在900 r/min与2 400 r/min时切换稳定，基本没有电流冲击。但是多脉冲二阶锁相环角度收敛的转速明显要慢很多，如果在未收敛时刻切换将会产生电流冲击，这对于需要快速切入闭环运行状态的工况是非常不利的，但如果使用高阶锁相环就会加快收敛转速。图21为所提策略在电机反转时分别在900 r/min与2 400 r/min时带速重投实验波形，从图中可以看到所提策略在反转时位置估计依然准确，且切换过程无电流冲击。
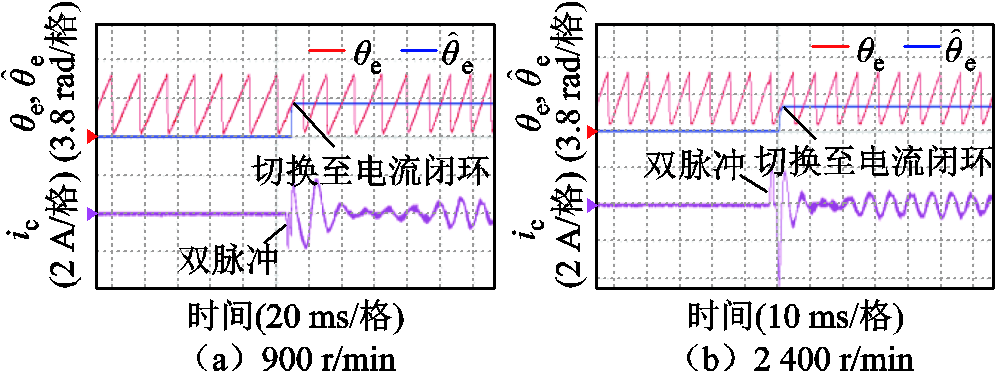
图18 传统双脉冲带速重投实验波形
Fig.18 Experimental waveforms of conventional double-pulse restarting
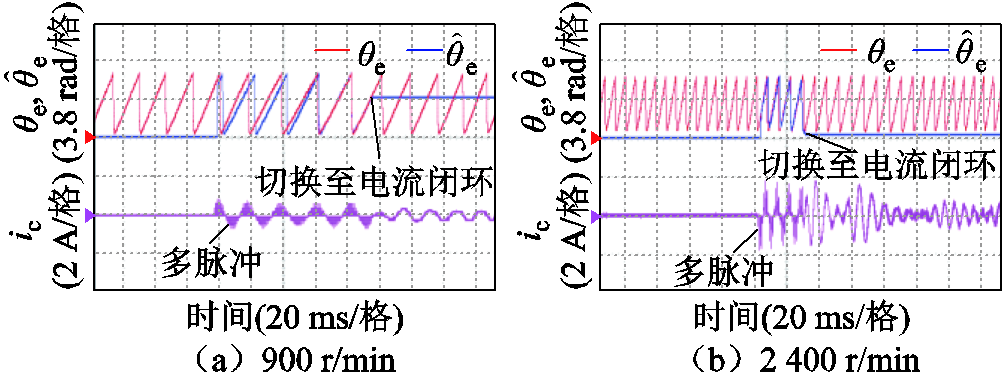
图19 多脉冲二阶锁相环带速重投实验波形
Fig.19 Experimental waveforms of multi-pulse with second-order PLL restarting
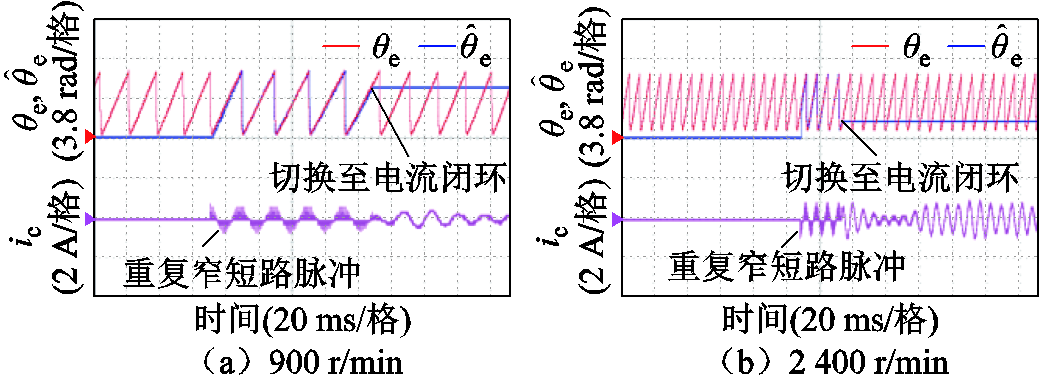
图20 重复窄短路脉冲高阶锁相正转带速重投实验波形
Fig.20 Experimental waveforms of repeated narrow short-circuit pulses with high-order PLL positive restarting
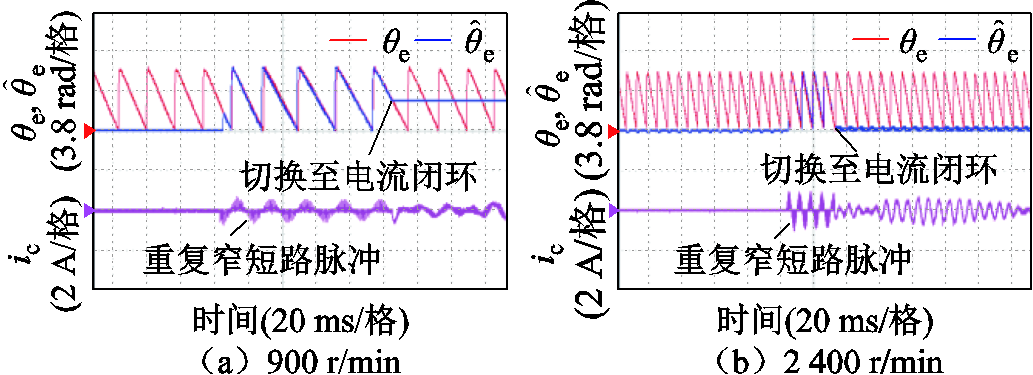
图21 重复窄短路脉冲高阶锁相反转带速重投实验波形
Fig.21 Experimental waveforms of repeated narrow short-circuit pulses with high-order PLL anti-rotational restarting
图22为三种方法在不同转速下的位置估计误差与转速估计误差分布，图中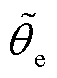
为位置估计误差，
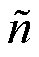为转速估计误差，整个分布结果是在每个测试转速重复10次测试得到。从图22a中可以看到，传统双脉冲的位置误差与转速误差最大，位置误差在 0.5 rad以下，转速误差大部分在100 r/min以上。从图22b中可以看到，多脉冲二阶锁相环的位置误差大部分在0.2 rad以下，转速误差大部分在50 r/min以下，但是受收敛转速影响，整体误差波动较大。从图22c中可以看到，重复窄短路脉冲高阶锁相的位置误差在0.1 rad以下居多，转速误差在20 r/min以下，而且整体误差分布均匀。
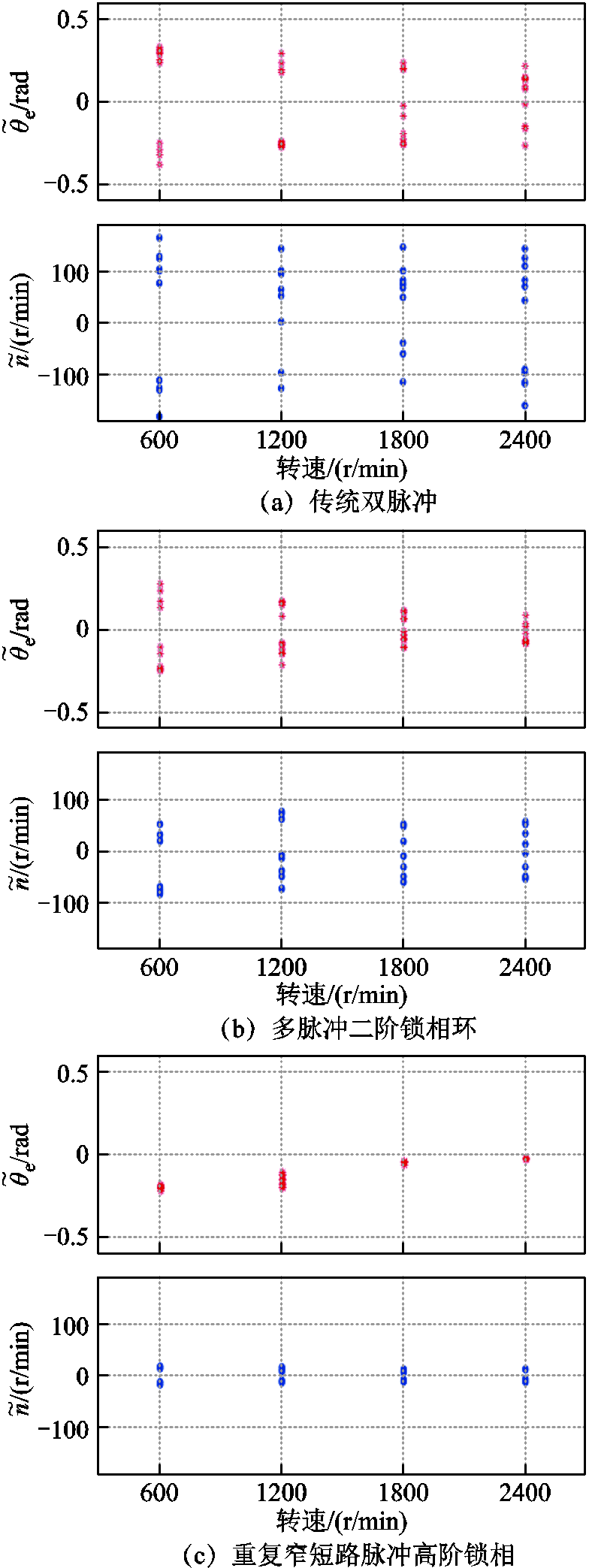
图22 三种方法不同转速下角度与转速误差分布
Fig.22 Distribution of angle and speed errors at different rotation speeds for three methods
为了对比三种方法在减速过程中的带速重投性能，图23a～图23c分别为三种方法从2 400 r/min以600 r/min/s加转速减速时，当转速小于1 500 r/min时执行带速重投的实验波形。从实验波形可以看到，在减速过程中的实验结果与恒速重投的实验结果基本相同，图23a中传统双脉冲切换会有大电流冲击，图23b中多脉冲二阶锁相环收敛转速较慢，图23c中所提策略位置估计更准确，且切换过程无电流冲击。
图23 三种方法减速过程带速重投实验波形
Fig.23 Experimental waveforms of restarting during deceleration process for three methods
实际工况中，希望带速重投过程快速，根据三阶锁相环设计的带宽参数及图17中实际转速跟踪时间，可以大大缩小脉冲注入时间，本实验中选择脉冲群持续时间为5 ms。本小节对比了所提策略在不同电流幅值下的快速带速重投实验。图24a～ 图24d为在2 400 r/min下，电流幅值分别为0.75、1、1.25、1.5 A时带速重投的实验波形。从图中可以看到，在满足位置估计精度的前提下，所提方法在5%电流基值内均能在5 ms内实现较好的位置跟踪和切换。但是电流幅值太小会增加估计误差，正如图24a中所示，0.75 A电流幅值时切换会产生电流冲击。
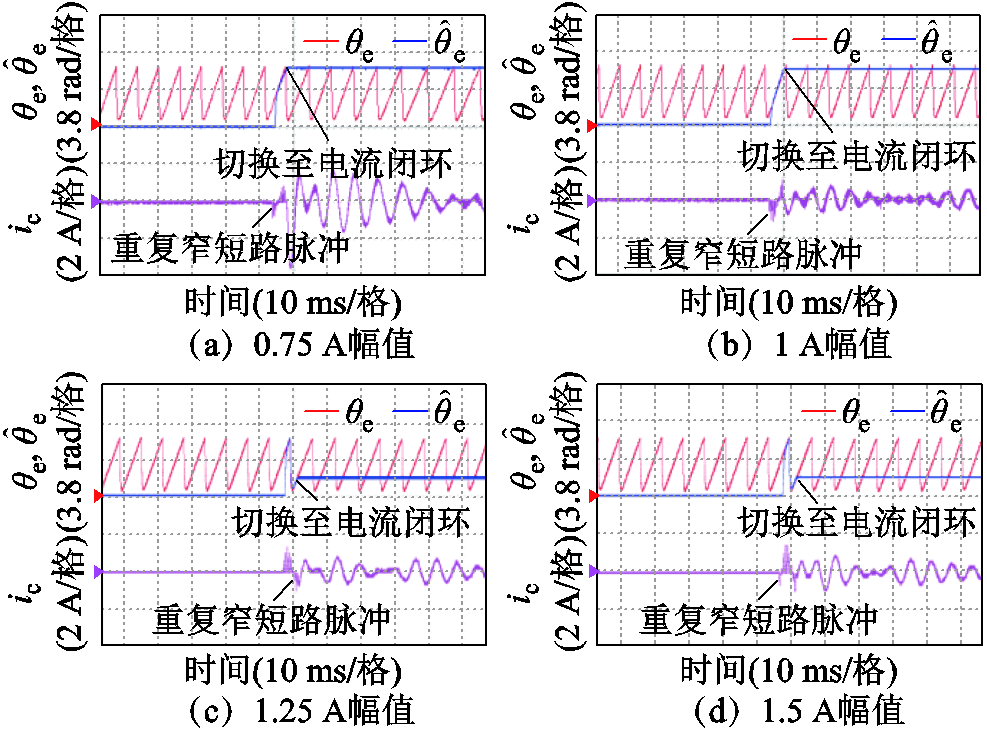
图24 2 400 r/min不同电流幅值下快速带速重投实验波形
Fig.24 Experimental waveforms of fast restarting under different current amplitudes at 2 400 r/min
针对永磁同步电机带速重投零电压矢量注入方法中传统双脉冲与多脉冲二阶锁相环方法存在的母线电压泵升、位置估算精度低及动态跟踪转速慢等问题，提出了一种加入电流过采样技术的重复窄短路脉冲与高阶锁相的永磁同步电机带速重投方法，通过实验验证了所提方法的有效性，实验结果表明：
1）所提出的带速重投方法通过增加PWM频率和自适应调整脉冲宽度和间隔，可以减小电流纹波、减缓母线电压泵升速率。
2）所提出的带速重投方法通过高阶锁相环及电流过采样处理，可以加快位置和转速的收敛速率，提高位置和转速估计精度，并减少带速重投所需时间，实现平滑的电流、位置切换。
参考文献
[1] 李思毅, 苏健勇, 杨贵杰. 基于自抗扰控制的永磁同步电机弱磁控制策略[J]. 电工技术学报, 2022, 37(23): 6135-6144.
Li Siyi, Su Jianyong, Yang Guijie. Flux weakening control strategy of permanent magnet synchronous motor based on active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6135-6144.
[2] 刘蔚, 李万铨, 王明峤, 等. 复杂工况下的永磁同步电机典型绕组故障在线诊断[J]. 电工技术学报, 2024, 39(6): 1764-1776.
Liu Wei, Li Wanquan, Wang Mingqiao, et al. Online diagnosis of typical winding faults in permanent magnet synchronous motors under complex working conditions[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1764-1776.
[3] 张伟伟, 肖飞, 刘计龙, 等. 轨道交通车辆永磁同步牵引系统断电区穿越控制策略[J]. 电工技术学报, 2021, 36(16): 3483-3492.
Zhang Weiwei, Xiao Fei, Liu Jilong, et al. Power-off area traversing control strategy of permanent magnet synchronous motor traction system in rail transit vehicle[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3483-3492.
[4] 丁荣军, 桂卫华, 尚敬. 感应电机无转速传感器控制带速重投研究[J]. 机车电传动, 2008(3): 12-14, 18.
Ding Rongjun, Gui Weihua, Shang Jing. Study on restarting at unknown speed with speed-sensorless control of induction motor[J]. Electric Drive for Locomotives, 2008(3): 12-14, 18.
[5] Wang Gaolin, Zhou Honglei, Zhao Nannan, et al. Sensorless control of IPMSM drives using a pseudo-random phase-switching fixed-frequency signal injection scheme[J]. IEEE Transactions on Industrial Electronics, 2018, 65(10): 7660-7671.
[6] 黄希. 风机用永磁同步电机全速范围无位置传感器控制技术研究[D]. 杭州: 浙江工业大学, 2020.
Huang Xi. Research on sensorless control technology of permanent magnet synchronous motor for fan in full speed range[D]. Hangzhou: Zhejiang University of Technology, 2020.
[7] Wang Chenchen, Gou Lifeng, Dong Shifan, et al. Sensorless control of IPMSM based on super-twisting sliding mode observer with CVGI considering flying start[J]. IEEE Transactions on Transportation Electrification, 2022, 8(2): 2106-2117.
[8] Du Fei, Li Jian, Li Guofeng. Restart strategy for sensorless PMSM drive with single zero voltage vector in railway application[C]//2023 IEEE International Symposium on Sensorless Control for Electrical Drives (SLED), Seoul, Korea (South), 2023: 1-7.
[9] 郭希铮, 刘帅, 宋玉美. 永磁同步电机无位置传感器带速重投研究[J]. 电工技术学报, 2016, 31(增刊2): 255-261.
Guo Xizheng, Liu Shuai, Song Yumei. Research on restart at coasting condition for rotation sensorless permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society, 2016, 31(S2): 255-261.
[10] Lee K, Ahmed S, Lukic S M. Universal restart strategy for high-inertia scalar-controlled PMSM drives[J]. IEEE Transactions on Industry Applications, 2016, 52(5): 4001-4009.
[11] 赵赫, 黄科元, 周佳新, 等. 适用于高速永磁同步电机的带速重投策略[J]. 电力电子技术, 2021, 55(6): 19-21.
Zhao He, Huang Keyuan, Zhou Jiaxin, et al. The speed sensorless restart strategy of high-speed PMSM[J]. Power Electronics, 2021, 55(6): 19-21.
[12] Seo D W, Bak Y, Lee K B. An improved rotating restart method for a sensorless permanent magnet synchronous motor drive system using repetitive zero voltage vectors[J]. IEEE Transactions on Industrial Electronics, 2020, 67(5): 3496-3504.
[13] Chen Bao, Shen Anwen, Li Peihe, et al. Restart strategy for sensorless PMSM drive system based on zero-voltage vector[J]. IET Electric Power Appli-cations, 2020, 14(12): 2362-2369.
[14] Wu Chun, Zheng Luhua, Ying Wangrui, et al. A restart method of permanent magnet synchronous machine sensorless drives with a single DC-bus current sensor[J]. IEEE Transactions on Transportation Electrification, 2024, 10(3): 5715-5724.
[15] Chen Wei, Zhu Lixiang, Wang Sai, et al. Rotating restart method for TPFS inverter-fed sensorless PMSM drive system based on dual effective voltage vectors injection[J]. IEEE Transactions on Power Electronics, 2024, 39(9): 11708-11722.
[16] Taniguchi S, Mochiduki S, Yamakawa T, et al. Starting procedure of rotational sensorless PMSM in the rotating condition[J]. IEEE Transactions on Industry Applications, 2009, 45(1): 194-202.
[17] 田里思, 宗耐龙, 刘立伟, 等. 基于单电流传感器的永磁同步电机混合脉宽调制技术研究[J]. 电工技术学报, 2024, DOI: 10.19595/j.cnki.1000-6753. tces.240519.
Tian Lisi, Zong Nailong, Liu Liwei, et al. Research on mixed pulse width modulation technology of permanent magnet synchronous motor based on single current sensor[J]. Transactions of China Electrotechnical Society, 2024, DOI: 10.19595/j.cnki.1000-6753.tces. 240519.
[18] 梅三冠, 卢闻州, 樊启高, 等. 基于滑模观测器误差补偿的永磁同步电机无位置传感器控制策略[J]. 电工技术学报, 2023, 38(2): 398-408.
Mei Sanguan, Lu Wenzhou, Fan Qigao, et al. Sensorless control strategy of permanent magnet synchronous motor based on error compensation estimated by sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 398-408.
[19] 袁倩, 杨中平, 林飞, 等. 无传感器下永磁同步牵引电机的带速重投研究[J]. 电工技术学报, 2013, 28(增刊1): 377-382.
Yuan Qian, Yang Zhongping, Lin Fei, et al. Sensorless restart method of permanent magnet synchronous traction motor[J]. Transactions of China Electro-technical Society, 2013, 28(S1): 377-382.
[20] Zhang Guoqiang, Wang Gaolin, Xu Dianguo, et al. ADALINE-network-based PLL for position sensorless interior permanent magnet synchronous motor drives[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1450-1460.
[21] 吴春, 应王瑞, 郑露华, 等. 一种旋转变压器双采样差分位置解码方法[J]. 电工技术学报, 2024, 39(15): 4896-4908.
Wu Chun, Ying Wangrui, Zheng Luhua, et al. A dual-sampling differential position decoding method for resolvers[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4896-4908.
[22] 张国强, 李润东, 黄圆明, 等. 基于自适应零电压矢量双脉冲法的永磁同步电机带速重投策略[J]. 电气传动, 2023, 53(12): 10-15.
Zhang Guoqiang, Li Rundong, Huang Yuanming, et al. Flying start of PMSM strategy based on adaptive double zero voltage vector pulse method[J]. Electric Drive, 2023, 53(12): 10-15.
[23] Auger F, Mansouri-Toudert O, Chibah A. Design of advanced resolver-to-digital converters[C]// Electrimacs, Cergy-Pontoise, France, 2011, 90(91): 115.
[24] Zhang Guoqiang, Yan Yunhao, Wang Qiwei, et al. Adaptive step-size predictive PLL based rotor position estimation method for sensorless IPMSM drives[J]. IEEE Transactions on Power Electronics, 2024, 39(5): 6136-6147.
[25] 吴春, 董士帆, 钟德刚, 等. 基于电流过采样的永磁同步电机电压脉冲注入无位置传感器控制[J]. 电工技术学报, 2018, 33(24): 5678-5687.
Wu Chun, Dong Shifan, Zhong Degang, et al. Voltage pulse injection based sensorless control for permanent magnet synchronous machine with current over-sampling method[J]. Transactions of China Electro-technical Society, 2018, 33(24): 5678-5687.
[26] 吴春, 陈子豪, 傅子俊. 永磁同步电机全速范围无位置传感器控制及FPGA实现[J]. 电机与控制学报, 2020, 24(7): 121-129.
Wu Chun, Chen Zihao, Fu Zijun. Sensorless control of permanent magnet synchronous machines in full speed range and FPGA implementation[J]. Electric Machines and Control, 2020, 24(7): 121-129.
Abstract In some applications with large moment of inertia, permanent magnet synchronous motor (PMSM) drive systems are always required to be capable of a rapid startup when the power source is shut down and then is turned on again during a short time, such as tens of milliseconds. In recent years, scholars have put forward several methods for fast restarting of PMSM drives. However, these methods have not fully considered the rapidity of the restarting process, direct current-bus (dc-bus) voltage pumping up and inrush current influences comprehensively. To address these issues, this article proposes a restart strategy based on repetitive narrow short-circuit pulses and a high-order phase-locked loop (PLL). In the restarting process, the small current magnitude can be controlled by increasing the frequency of the pulse-width modulation (PWM), which can reduce the short-circuit voltage pulse action time and decrease the pumping rate of dc-bus voltage. In addition, the high-order PLL reduces the tracking error of position and speed estimation during acceleration and deceleration processes.
First, the increase in the PWM frequency generates narrower short-circuit voltage pulses and smaller current amplitude. Second, by setting a current reference and using two test voltage pulses, the period and the interval of the short-circuit voltage pulses can be adjusted, which can solve the problem of large current ripple due to the traditional fixed voltage pulses at high speeds, and realize that the induced current ripple amplitude is small and controllable in full-speed operations. Third, the third-order PLL is designed to facilitate a rapid and accurate position tracking, as well as continuous estimation of position and speed. Fourth, a current oversampling method is adopted to average phase currents, thereby improving the signal-to-noise ratio of current sampling and the accuracy of position estimation. The experimental results demonstrate that at 2400 r/min, the pumping dc-bus voltages of the conventional double-pulse and the multi-pulse methods within 2.4 ms are 22 V and 7 V, respectively. Meanwhile, that of the proposed method is only 1 V. These results verify the effectiveness of the proposed method in suppressing the pumping voltage. On the other hand, at 900 and 2400 r/min, the traditional double-pulse method shows a steady-state error of the estimated speed, and the dynamic response time of the speed tracking with the conventional PLL are 860 μs and 1.92 ms, respectively. In comparison, the speed tracking time of the proposed method is 670 μs and 1.42 ms, respectively. These results demonstrate that the proposed method is faster in the restart process. Moreover, the proposed restart strategy controls the current amplitude below 5% of the rated current, which suppresses the inrush current and lowers the pumping voltage. Furthermore, it enhances the accuracy of the position and speed estimation, and realizes a rapid restart without inrush current.
The following conclusions can be drawn from the experimental results: (1) In comparison with the conventional double-pulse and multi-pulse methods, the proposed method has several advantages including a high PWM frequency, an adaptive adjustment of the zero-voltage width and interval, a reduction in the current ripple, and a deceleration in the pumping dc-bus voltage. (2) The proposed method achieves a narrower short-circuit pulse and a lower current amplitude while enhancing the accuracy of the position and speed estimation, reducing the time required for restarting process, and facilitating the switching process to closed-loop sensorless control without an inrush current.
Keywords：Permanent magnet synchronous motor (PMSM), restart strategy, repetitive narrow pulses, current over sampling, third-order phase-locked loop (PLL)
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.L11017
国家自然科学基金（52007169）和浙江省自然科学基金（LY23E070004）资助项目。
收稿日期 2024-07-08
改稿日期 2024-07-23
吴 春 男，1987年生，副教授，博士生导师，研究方向为永磁同步电机无位置传感器控制等。
E-mail：wuchun@zjut.edu.cn（通信作者）
康李佳 男，1998年生，硕士研究生，研究方向为永磁同步电机无位置传感器在线参数辨识及带速重投。
E-mail：kanglj23@163.com
（编辑 崔文静）