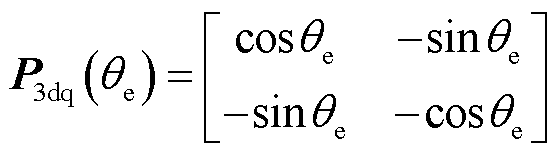 (1)
(1)
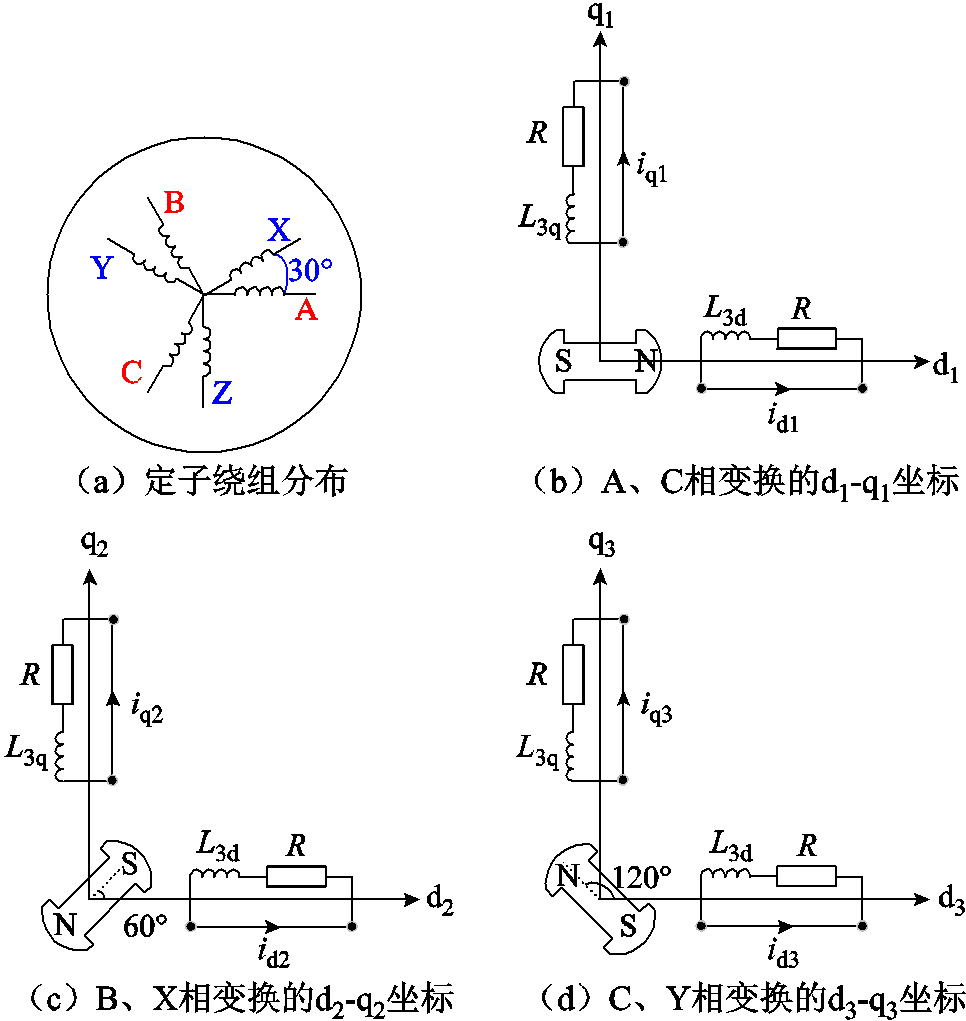
图1 三个d-q坐标解耦
Fig.1 Three d-q coordinate decoupling diagrams
摘要 该文针对双三相永磁同步电机传统建模复杂度高、绕组电流谐波抑制困难等问题,提出一种基于三重旋转坐标变换模型的模型预测电流控制方法。该建模方法物理意义清晰,通过平衡各套绕组功率,能有效抑制绕组电流谐波,无需复杂的谐波控制方法。首先,利用双三相绕组特殊的绕组结构,将六相绕组分为三组自正交对,提出一种三重旋转坐标变换,并据此建立电机模型;然后,通过与空间矢量解耦(VSD)方法的对比分析,说明所提建模方法通过三套旋转绕组间的电流平衡实现电流谐波抑制;最后,提出基于三重旋转坐标变换的模型预测电流控制方法。仿真结果表明,基于三重旋转坐标变换能够有效抑制绕组5、7次电流谐波,无需基于VSD模型预测电流控制(VSD-MPCC)中的权重系数调整,且在理想情况下谐波抑制效果优于VSD-MPCC。
关键词:双三相永磁同步电机 三重旋转坐标系 模型预测控制 谐波抑制
双三相永磁同步电机(Dual Three Phase-Permanent Magnet Synchronous Motor, DTP-PMSM)兼具永磁电机和多相电机的特点[1-4],与传统三相电机相比,除了高功率因数、高功率密度、结构简单等优点外,还具有转矩增强、高效率和低转矩脉动的特点,在高功率和安全性应用方面具有更广阔的应用前景,如应用在电动汽车、电驱动轮船、电动航天器、风力发电系统等[5]。它由两个独立的三相绕组集组成,位移相差30°[6],特殊结构决定了其控制方法的多样性。有效的控制方案是双三相永磁同步电机驱动的重要组成部分,与性能和整个应用密切相关。然而,由于两个绕组之间的耦合和不对称性,双三相永磁同步电机的控制比其他机器更具挑战性[7]。
模型预测电流控制(Model Predictive Current Control,MPCC)具有动态响应快、电流控制性能好、易于考虑系统线性约束、控制灵活等优点,将预测下一时刻的电流值经过价值函数寻优得到最优的电压矢量[8-12],在价值函数中可以直观体现对谐波抑制的部分。空间矢量解耦(Vector Space Decoupled, VSD)是应用较广泛的多相建模方法之一,将电机变量分别投影至基波子平面和谐波子平面,由于作用在谐波子平面的阻抗为电机相电阻和定子绕组漏感,很小的谐波电压就会激起较大的谐波电流。采用VSD模型的电流预测控制,需要同时在基波子平台与谐波子平台控制电流达到参考值,因此在价值函数中引入了权重系数平衡两个子平台的代价比例。由于权重系数选取过程复杂,是一个无量纲的变量,没有固定的选择方法,只能通过反复的试错过程才能确定相对较优的值,增加了控制过程的复杂性[13]。
对于传统基于VSD模型预测电流控制存在的谐波权重系数选取复杂问题[14-16],国内外学者提出一种改进的方法,单纯从控制出发,算法复杂且未达到预期效果。双d-q电流控制是这种特殊绕组类型的另一种替代方法,它能够平衡电流。然而,这种替代方法的缺点是交叉耦合会产生电流谐波,此外,还存在绕组利用率较低,不利于电机容错运行的问题[17-22]。综上所述,在平衡电流、抑制谐波电流、简单性和高绕组可用性方面,需要进一步改进并提供更好的控制解决方案。
针对以上问题,本文提出基于三重旋转坐标变换的模型预测电流控制。首先基于所提新型坐标变换方法建立电机数学模型;然后基于坐标变换式分析所提模型与双d-q坐标变换模型、空间解耦电机模型的数学联系,说明所提建模方法的优点;最后结合电流模型预测控制,通过仿真分析说明所提建模方法能够在有效抑制双三相电机谐波电流的基础上提高电机的稳态与动态性能。
三个d-q坐标解耦如图1所示。对于双三相电机,传统认为是ABC和XYZ的双三相绕组,两套绕组之间相差30°的特殊结构,其中A相和Z相差90°,B相和X相、C相和Y相同理,构成三重虚拟静止坐标系(3-α-β)对应A-Z相、B-X相、C-Y相。如图1a所示。因此,原六维系统中的变量可以映射到3-α-β坐标系中,彼此相距120°。三个固定坐标分别指定为α1-β1、α2-β2和α3-β3。每个α-β坐标系中的变量可以通过改进的Park变换直接转换为d-q坐标系的分量,得到三重d-q坐标系为
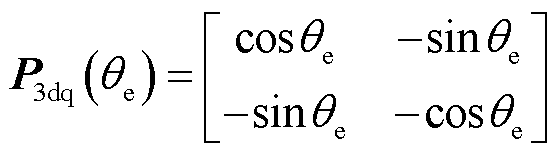 (1)
(1)

图1 三个d-q坐标解耦
Fig.1 Three d-q coordinate decoupling diagrams
因此,总的变换可以表示为
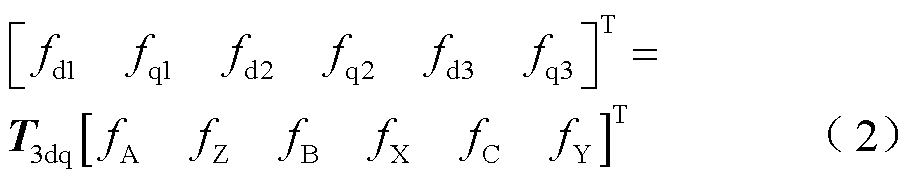
其中
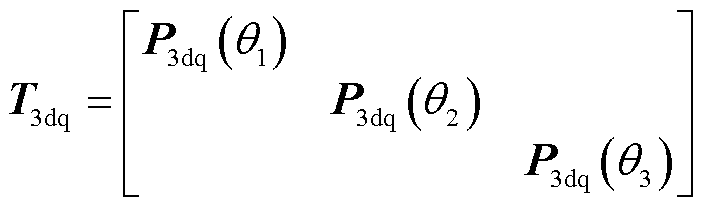 (3)
(3)
式中,θ1=θe,θ2=θe-120°,θ3=θe+120°;符号f为电机变量,可以表示电压、电流或磁链。原六维坐标系中的电压、磁链和转矩方程可以通过两边乘以T3dq将其映射到三重d-q坐标系中。通过简化和省略高次谐波电感分量,三重d-q坐标系中的电压方程可表示为
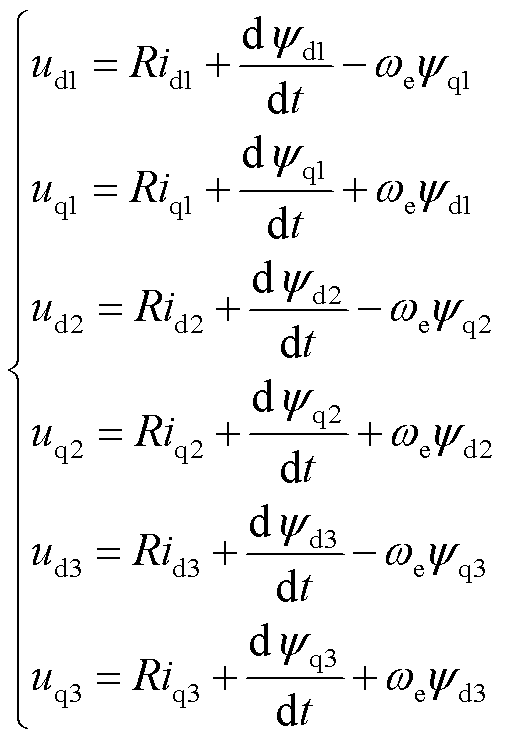 (4)
(4)
式中,udi、uqi分别为d、q轴的定子电压分量,i =1,2,3;idi、iqi分别为d、q轴的定子电流分量;ψdi、ψqi分别为d、q轴的磁链分量;R为定子电阻;ωe为电角速度。
磁链方程为
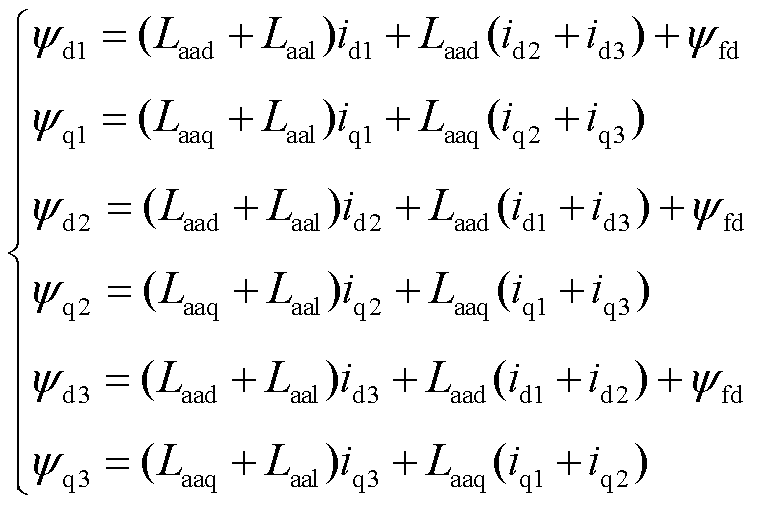 (5)
(5)
式中,Laad、Laaq分别为d、q轴主自感;Laal为漏自感;ψfd为永磁体磁链。根据机电能量转换原理,电磁转矩Te可表示为磁场量能对机械角度θm求偏导,即
 (6)
(6)
其中
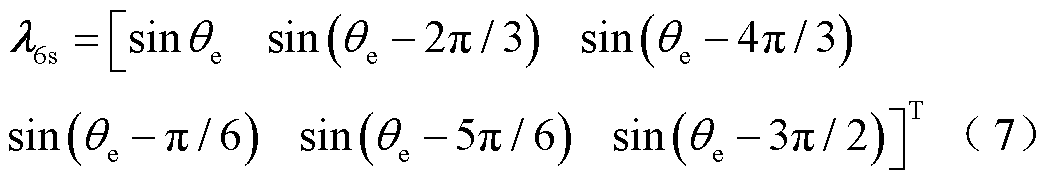
式中,i6s为定子相电流;λ6s为磁链矩阵系数;p为电机极对数。
变换到三重d-q坐标系下的电磁转矩为
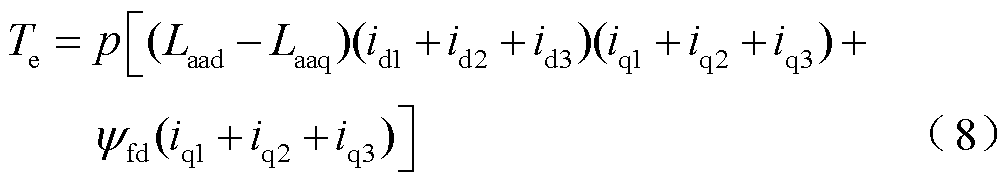
从磁链方程式(5)可以看出,此时三重d-q坐标系之间存在复杂的交叉耦合。因此,希望通过将新模型中的变量与能够进行物理解释的传统双d-q模型中的变量相关联,以彻底理解新模型中的变量。比较两个模型之间的变换矩阵,传统双d-q模型的Clarke-Park变换如下。
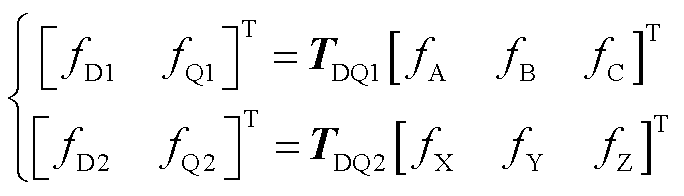 (9)
(9)
其中
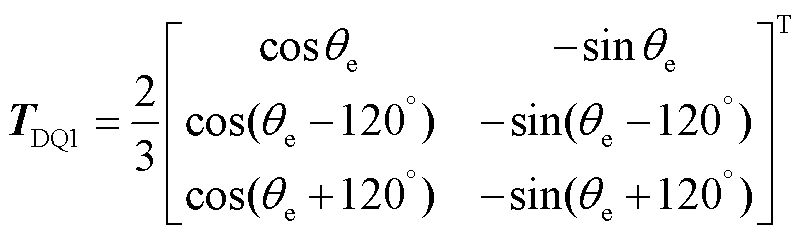 (10)
(10)
 (11)
(11)
两个模型中的变量可以与原六相变量相关联,即
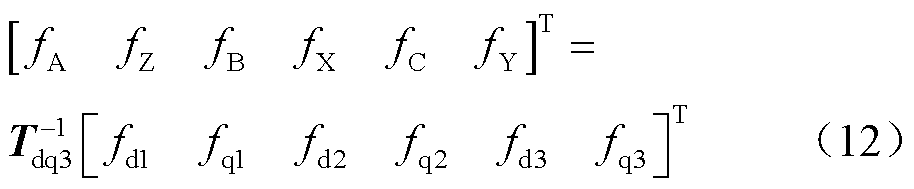
 (13)
(13)
由式(12)、式(13)可得
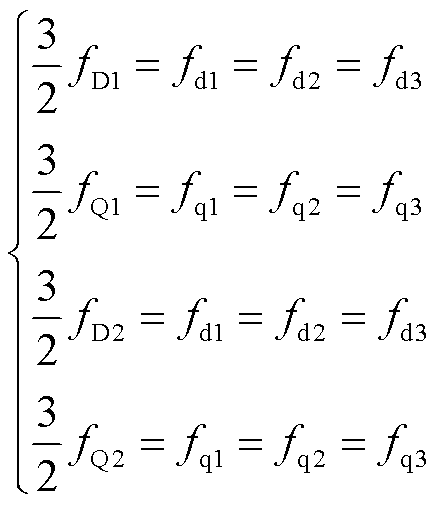 (14)
(14)
这表明,即使没有特殊调节电流分配,三重d-q坐标系中的变量也始终是平衡的。观察图1a也可以得出相同的结论。3-α-β坐标系由三套正交坐标轴组成,其中α轴分别与A、B、C绕组轴线对齐,β轴分别与X、Y、Z绕组轴线反相对齐。3-α-β坐标系通过3套相位相差120°的Park变换得到旋转3-d-q坐标系,由于采用等幅值变换,3-d-q坐标系的分量与传统双d-q坐标系分量的幅值比例关系为3/2。
由式(5)和式(14),磁链方程可以改写为
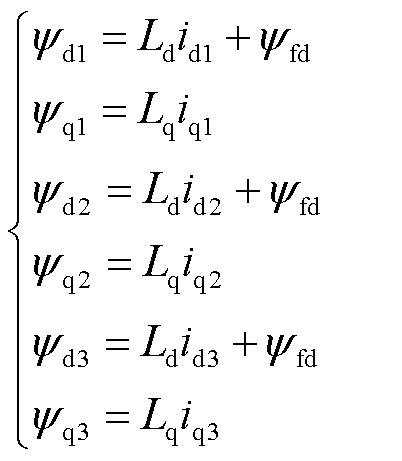 (15)
(15)
式中,Ld=3Laad+Laal;Lq=3Laaq+Laal。可以看出,三重d-q坐标系彼此完全解耦,将式(15)代入式(4)中,使得电机电压方程在三重d-q坐标系的形式为
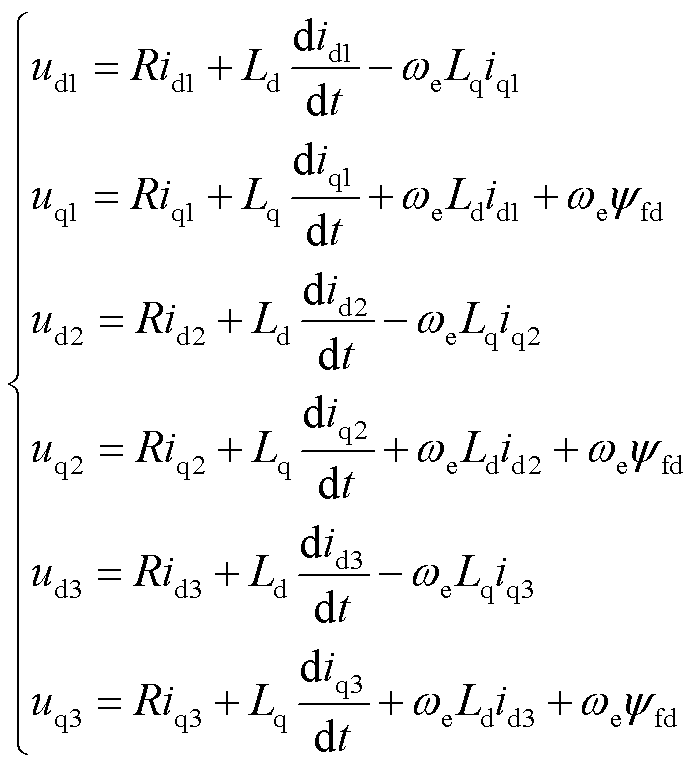 (16)
(16)
将式(15)代入式(8)中得到电磁转矩为
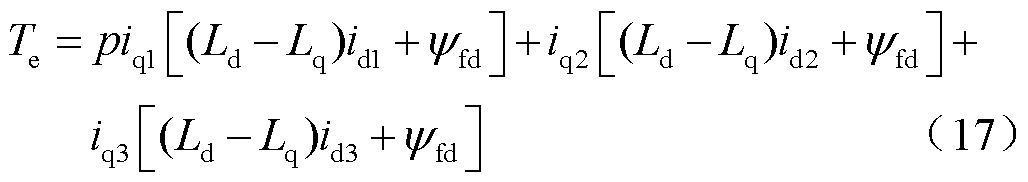
可以看出,总输出转矩是三组两个正交绕组产生的转矩之和。因此,双三相电机可以看作三组独立的正交两相绕组。双三相永磁同步电机设计为表贴式电机时,Laad ≈Laaq,则电磁转矩Te可以简化为
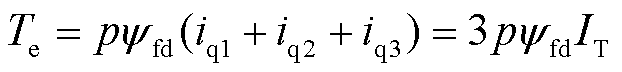 (18)
(18)
式中,IT为转矩电流。
在多相电机的早期研究中,VSD被广泛认为是最有效的电机矢量控制方法。因此,通过将所提出的方法与VSD控制模型联系起来,为该方法提供更好的理论解释。VSD电流变换矩阵表示为
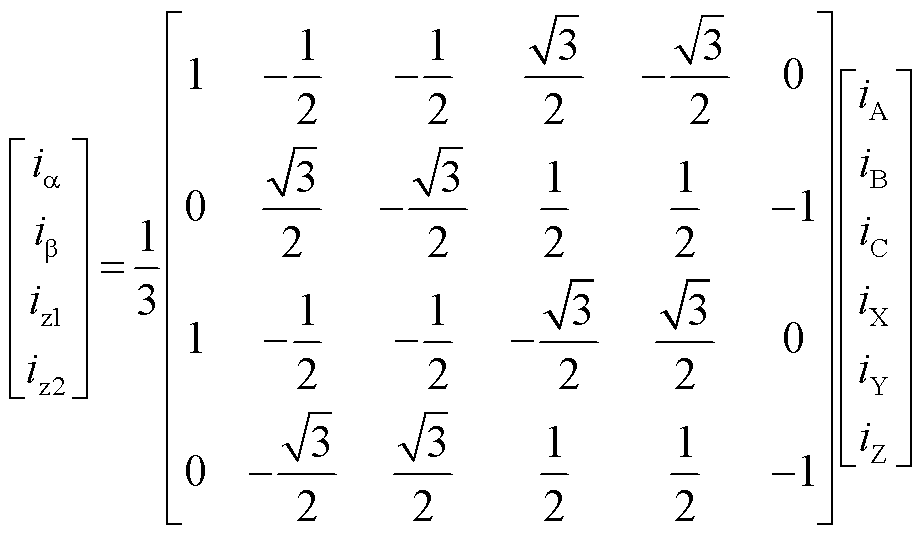 (19)
(19)
显然,iα、iβ、iz1和iz2每相电流分量涉及其余五相电流,与三重d-q变换相比,其复杂度很高。通过固定的3-α-β坐标系,即VSD变换,可映射到3-α-β坐标系为
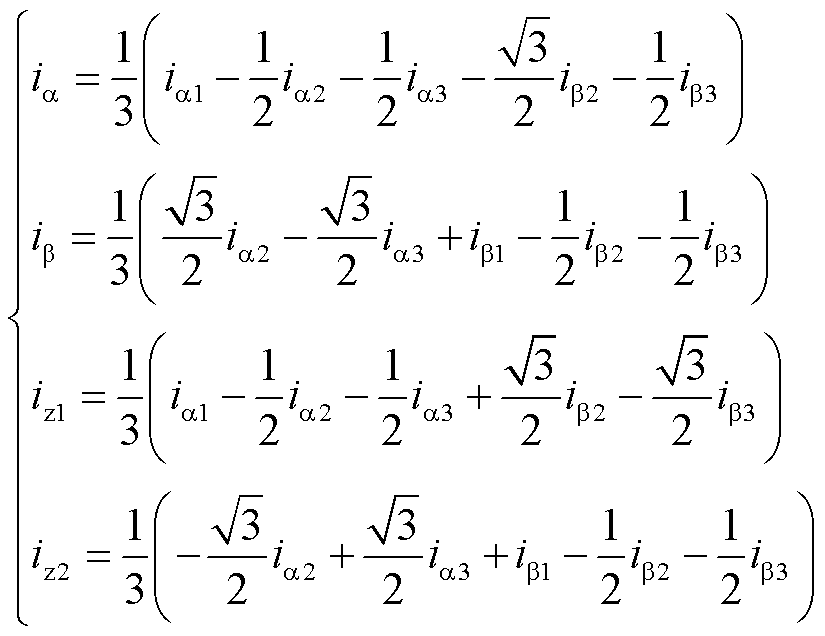 (20)
(20)
为了直观、彻底地理解这种关系,这些变量被转换为d-q坐标系,有
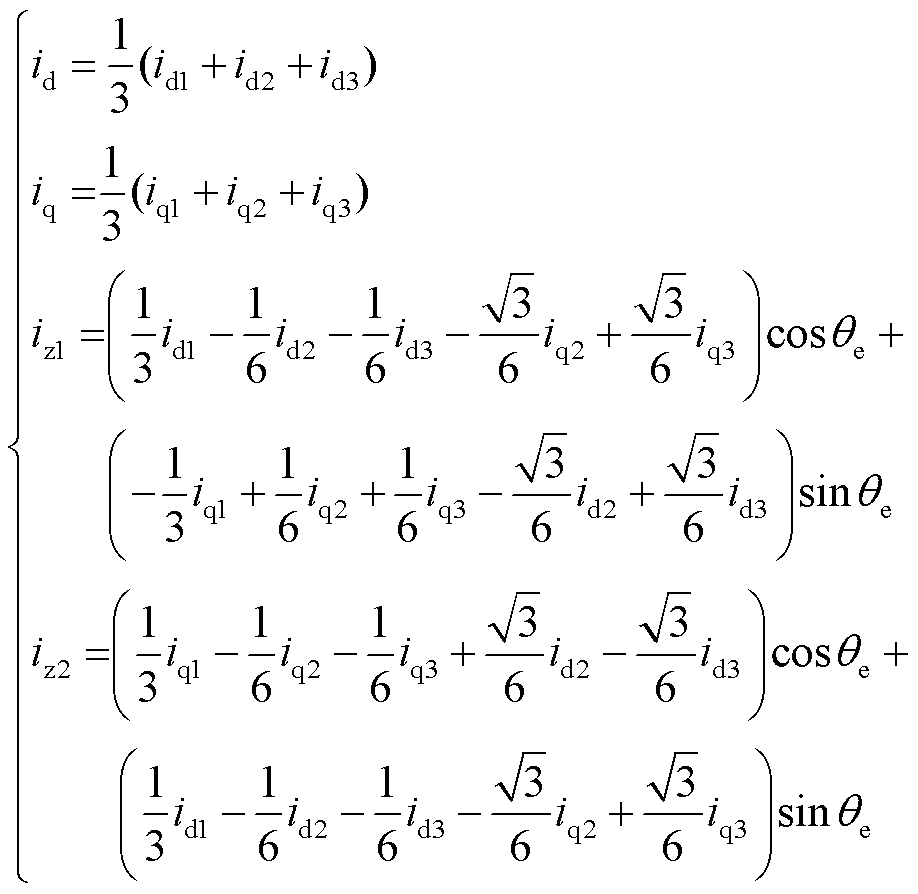 (21)
(21)
VSD中的d-q电流分量与三重d-q坐标系中的d1、d2、d3以及q1、q2和q3分量之和成比例;另一方面,z1、z2电流谐波分量不仅与三重固定变换变量相关,而且与转子位置相关。可以看出,如果d1、d2、d3和q1、q2、q3分量之和是VSD中的3倍,则三重d-q变换在控制中可以具有与VSD在控制中相同的基本控制性能,从而采取新型的模型进行控制,且三重d-q变换d-q坐标系分量实现解耦。稳定性问题:为了抑制谐波分量,iz1和iz2需为零,即
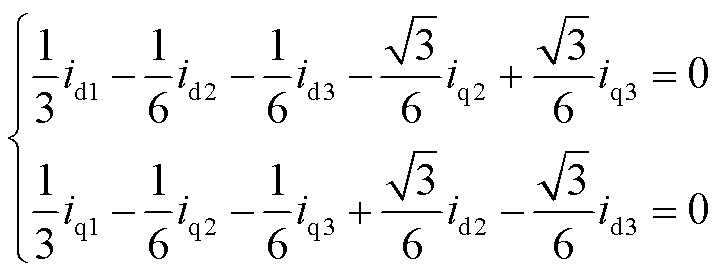 (22)
(22)
考虑到中性点电流总和为零,有
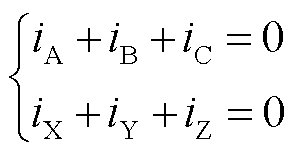 (23)
(23)
通过Park变换转换为d-q轴,中性点电流可重写为
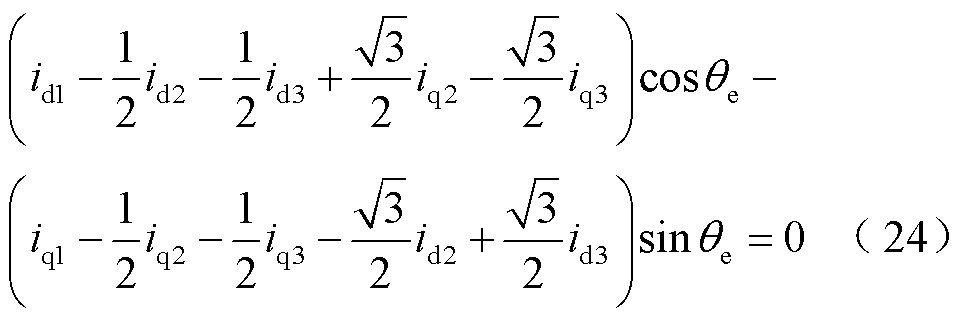
因此,d1-q1、d2-q2和d3-q3轴上的电流之间的关系可以写为
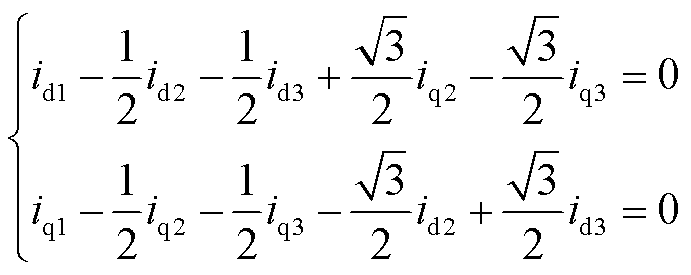 (25)
(25)
通过对比式(22)和式(25),为了抑制谐波分量,需要满足
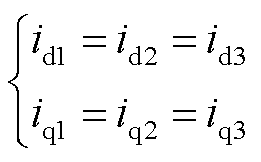 (26)
(26)
因此,可以得出结论,只要三重d-q坐标系中的分量平衡,则其控制性能与VSD相同。
六相电压源逆变器共有6个桥臂,每个桥臂对应上、下两个开关器件,两个器件的开关状态互补,因此每个桥臂对应两种开关状态,整个逆变器共有64种开关状态。在中性点隔离时,不考虑零序空间的电压矢量,由式(27)和式(28)可分别得到逆变器所有开关状态在α-β空间和z1-z2空间所对应的电压矢量。
α-β空间的电压矢量为
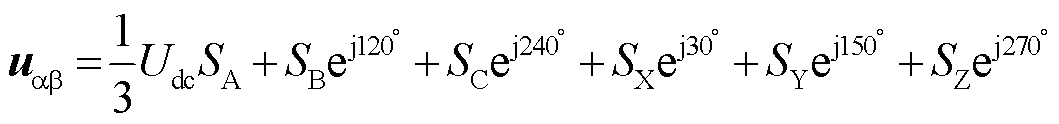 (27)
(27)
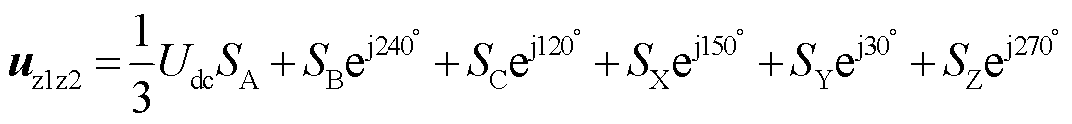 (28)
(28)
式中,Sj(j=A,B,C,X,Y,Z)代表6个桥臂的状态,Sj=1代表上桥臂开通,Sj=0代表下桥臂开通。α-β子空间和z1-z2子空间所对应的全部电压矢量集如图2所示。图中,可分为大矢量VL、中矢量VM、基本矢量VB和小矢量VS,其幅值分别为
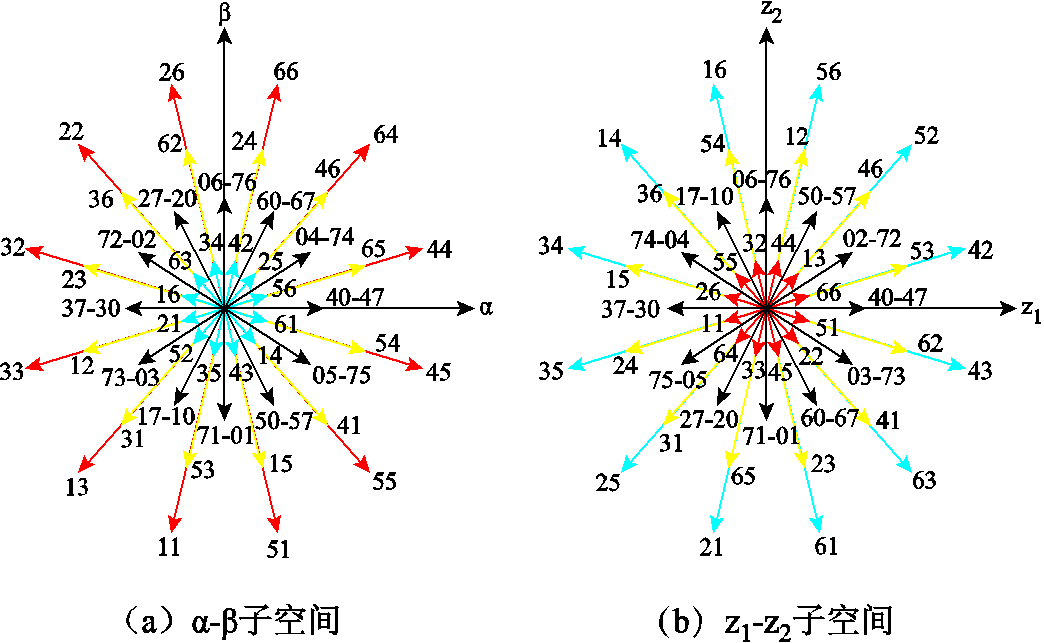
图2 电压矢量集
Fig.2 Voltage vector set
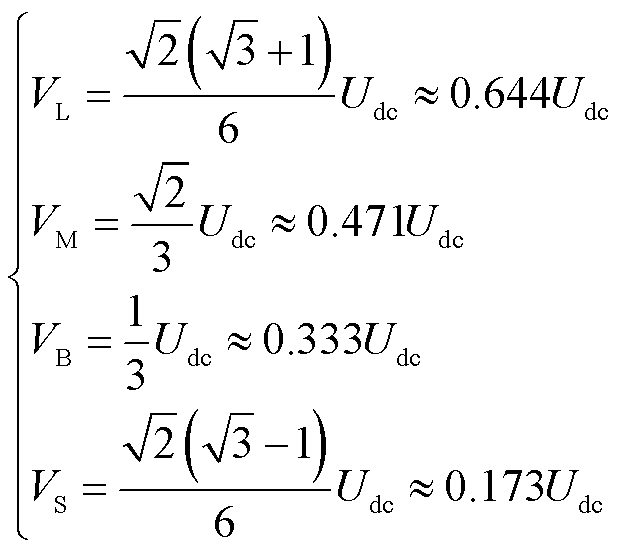 (29)
(29)
空间矢量解耦模型将电机变量变换到3个正交解耦的子空间中,命名为α-β、z1-z2、z3-z4。其中,12m±1(m=1,2,3,…)阶次电机分量映射至α-β子空间,参与电机机电能量转换;6m±1阶次电机分量映射至z1-z2子空间,不参与电机机电能量转换,但产生电流谐波和谐波损耗;零序分量映射至z3-z4子空间,因中性点隔离空间分量幅值为零,式(19)已经变换到α-β、z1-z2、z3-z4空间,为便于控制参与机电能量转换的α-β子空间,进一步变换至转子磁场定位的同步坐标系d-q中。
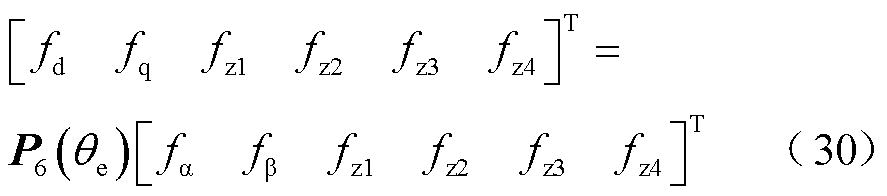
其中
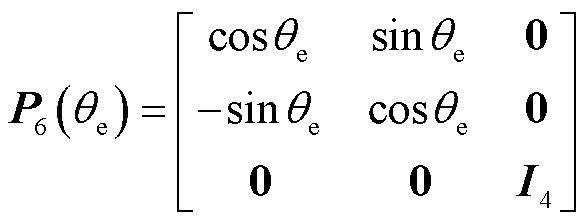 (31)
(31)
式中,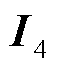 为计阶单位阵。
为计阶单位阵。
排除掉z3-z4子空间,空间矢量解耦模型的电压与磁链方程分别为
 (32)
(32)
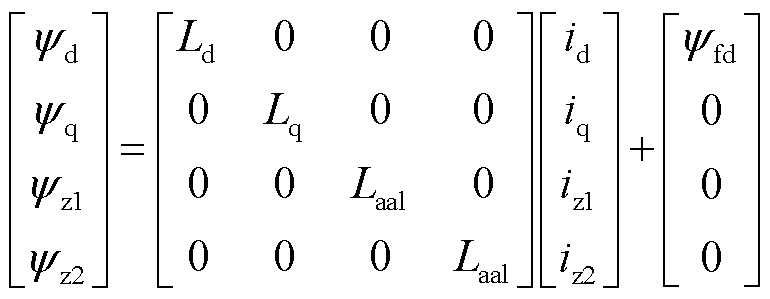 (33)
(33)
再对基于VSD建立的双三相PMSM模型进行离散化,得到离散化表达式为
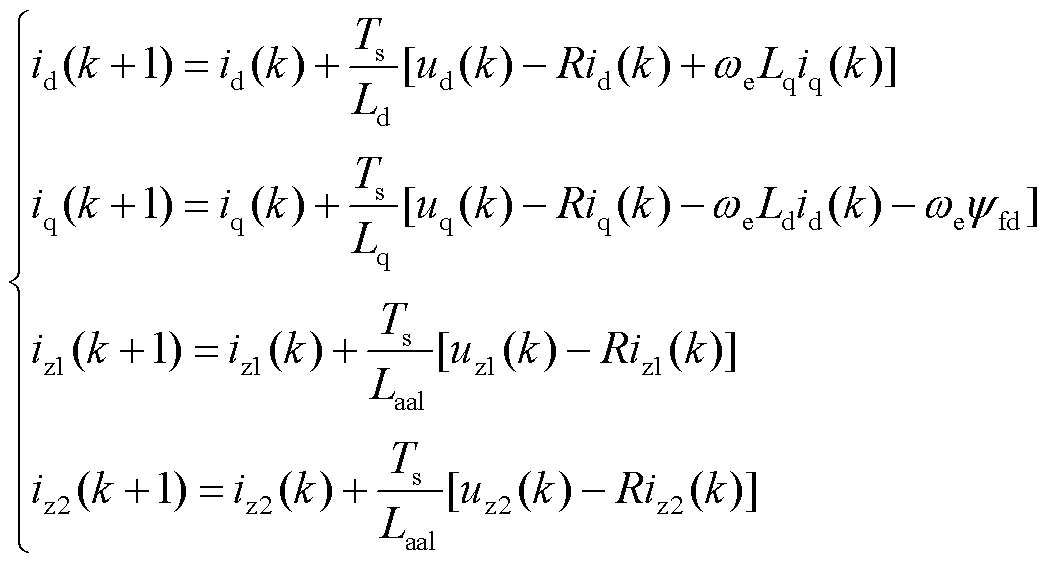 (34)
(34)
计算每个开关状态对应的电压矢量得到下一时刻的电流预测值,再经过价值函数J寻优得到最优解即最小Jmin,此时Jmin下对应的电压矢量,其开关状态输出给逆变器。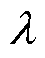 为谐波子空间的权重系数,调试过程相对繁琐,且缺乏明确的物理意义指导。Ts为采样周期,通过离散状态方程得到k+1时刻的预测值,进而得到下一时刻预测值将其代入设定的价值函数中进行寻优,价值函数为
为谐波子空间的权重系数,调试过程相对繁琐,且缺乏明确的物理意义指导。Ts为采样周期,通过离散状态方程得到k+1时刻的预测值,进而得到下一时刻预测值将其代入设定的价值函数中进行寻优,价值函数为
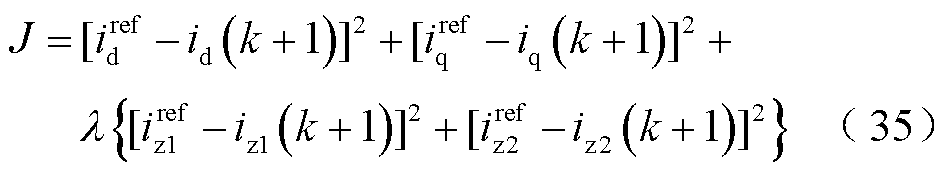
式中,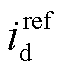 、
、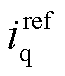 、
、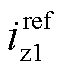 、
、 分别为d、q、z1、z2轴电流指令,其中
分别为d、q、z1、z2轴电流指令,其中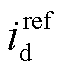 给定0,
给定0,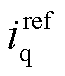 由速度外环得到,为抑制电流谐波,
由速度外环得到,为抑制电流谐波,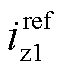 、
、 给定为0。
给定为0。
为提高直流母线电压利用率,选择最外围12个大矢量VL作为电压矢量控制集。
由第2节与VSD模型对比分析结论,保证了三重d-q坐标系中的电流分量平衡,基于三重d-q坐标系下也有良好的控制性能,三重d-q坐标系建模更加简化、控制方便,且控制时避免考虑谐波子空间的影响。控制方案要保证绕组之间的平衡均流,控制方案框图如图3所示,3个α-β静止坐标系彼此独立,通过Park变换将反馈电流转换到三重d-q坐标系得到d1、d2、d3和q1、q2、q3的直流变量。

图3 基于三重坐标系的MPCC系统框图
Fig.3 Block diagram of MPCC system based on triple coordinate system
基于三重d-q坐标变换建模,得到电压方程和磁链方程,在预测模型中将其离散化,经过数学处理得到离散化状态方程为
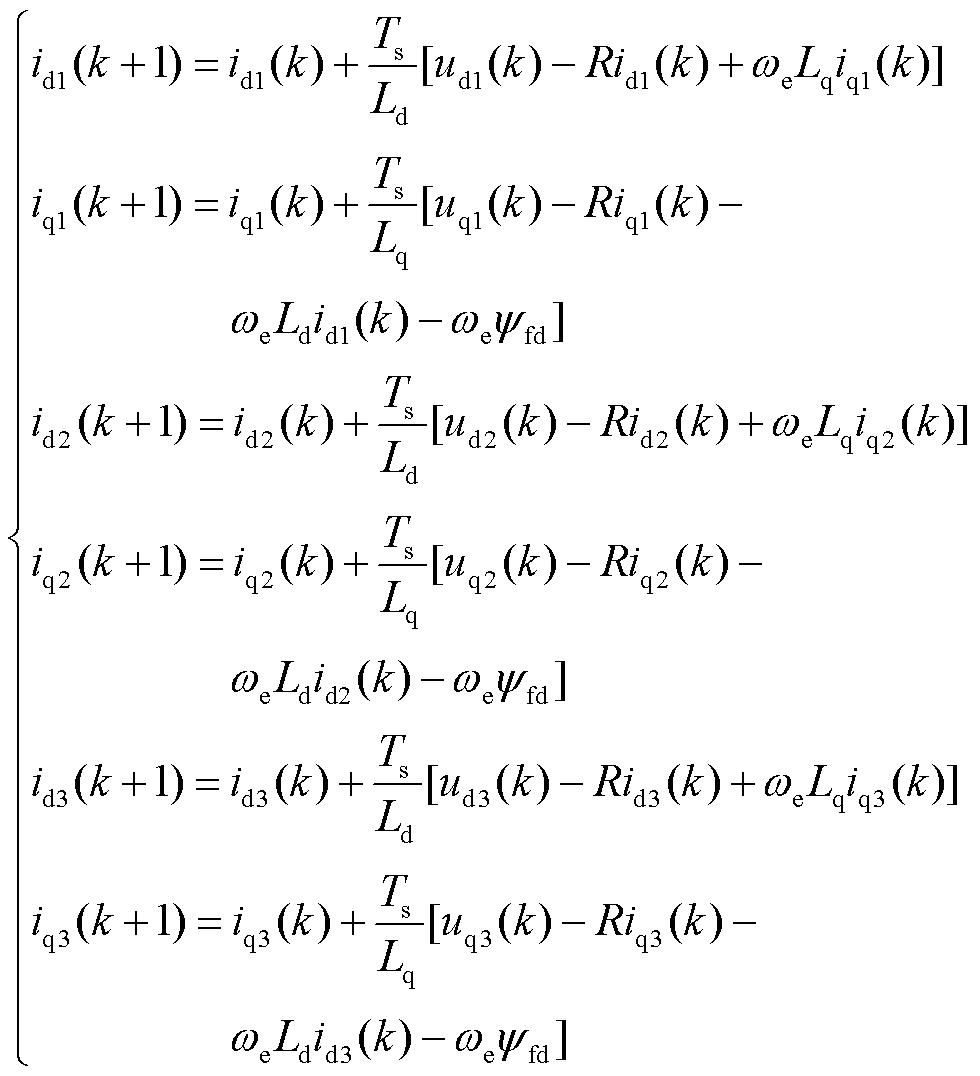 (36)
(36)
在三重坐标系下电流经过改进的Park变换得到三组id1、iq1,id2、iq2,id3、iq3电流,离散化后得到k时刻的电流值id1(k)、iq1(k),id2(k)、iq2(k),id3(k)、iq3(k),再经过预测模型通过离散状态方程得到k+1时刻的预测值id1(k+1)、iq1(k+1),id2(k+1)、iq2(k+1),id3(k+1)、iq3(k+1),得到下一时刻预测值后,将其代入设定的价值函数中进行寻优。
在三重d-q坐标系下,可以避免考虑谐波子平面的影响,所以在构造价值函数时省去了谐波的权重,每步只需计算idq,不需要再经调试选取权重系数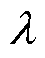 ,简化了模型预测电流控制的计算过程,构造的价值函数为
,简化了模型预测电流控制的计算过程,构造的价值函数为
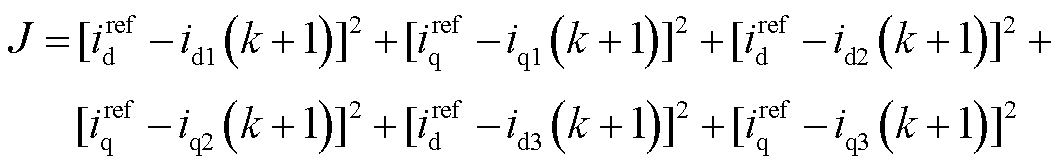 (37)
(37)
式中,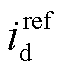 、
、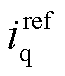 为期望值。
为期望值。
由于三重d-q坐标系中的分量平衡条件,可以在一个预测模型中实现价值函数的寻优,即将式(36)代入式(37)中经过寻优得到Jmin,最优价值函数Jmin下对应的电压矢量,将其开关状态输出给逆变器。
3dq-MPCC同样选择最外围12个大矢量VL作为电压矢量控制集。
在Matlab/Simulink中分别搭建基于VSD建模的MPCC(VSD-MPCC)策略模型和基于三重坐标系的MPCC(3dq-MPCC)策略模型并仿真对比其稳态性能和动态性能。为比较所提算法对电机5、7次电流谐波的抑制能力,在永磁磁链中引入5次磁链分量和7次磁链分量,电机相关参数见表1。
表1 电机参数
Tab.1 Motor parameters

参数数值 极对数p3 定子电阻Rs/Ω1.4 d轴电感Ld/H0.008 q轴电感Lq/H0.008 1次永磁体磁链ψf/Wb0.68 5次永磁体磁链ψf5/Wb7次永磁体磁链ψf7/Wb0.050.02 漏感Lz/H0.001 7 转动惯量/(kg·m2)0.015
给定三种不同工况:工况1低速轻载,给定转速为300 r/min、负载转矩为50 N·m;工况2高速轻载,给定转速为800 r/min、负载转矩为50 N·m;工况3高速重载,给定转速为800 r/min、负载转矩为150 N·m。仿真时在模型预测中设置的采样频率为10 kHz。
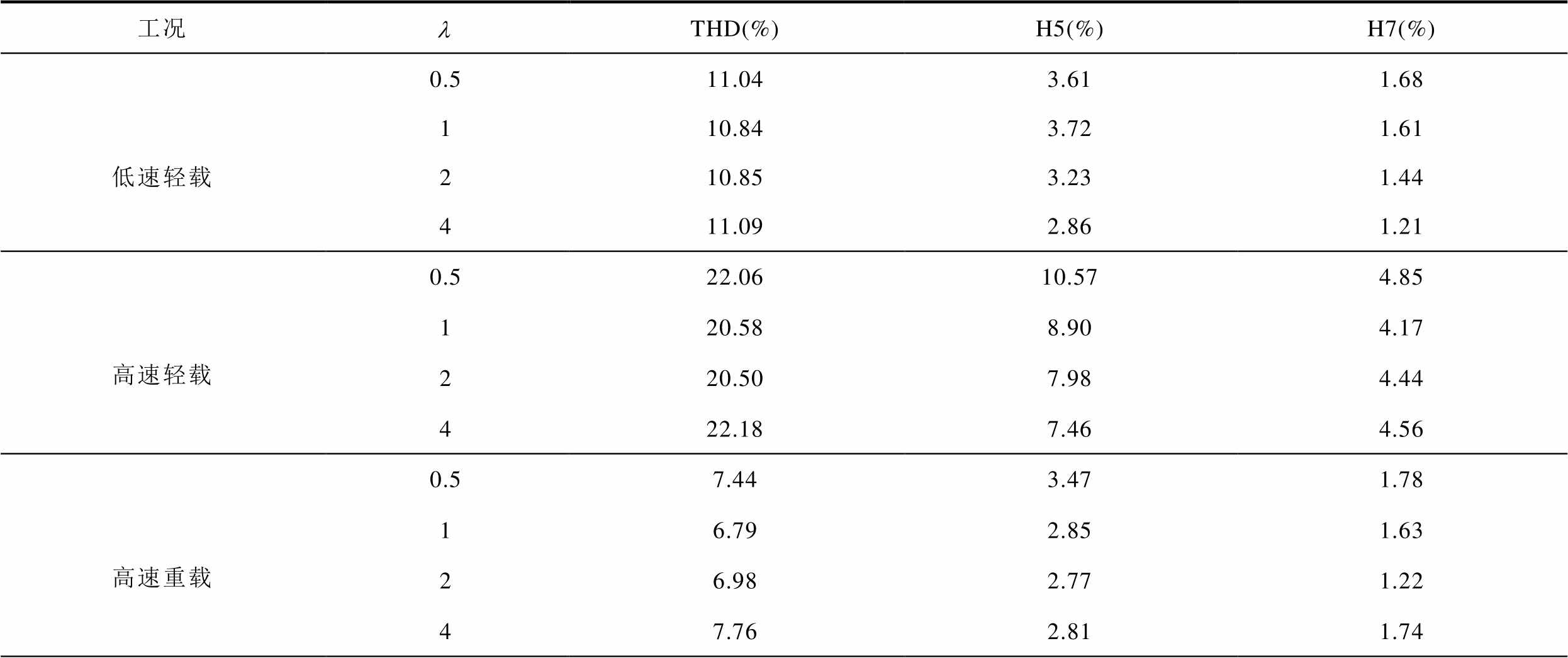
由于权重系数是一个无量纲的变量,没有固定的选择方法,只能通过反复的试错过程才能确定相对较优的值,三种不同工况下对比了不同权重系数VSD-MPCC的相电流总谐波畸变率(Total Harmonic Distortion, THD)、相电流5次谐波畸变率(H5)、相电流7次谐波畸变率(H7),结果见表2。
表2 三种工况下不同权重系数VSD-MPCC的相电流THD、H5、H7
Tab.2 Phase currents THD, H5 and H7 of VSD-MPCC with different weight coefficients under three working conditions
工况THD(%)H5(%)H7(%) 低速轻载0.511.043.611.68 110.843.721.61 210.853.231.44 411.092.861.21 高速轻载0.522.0610.574.85 120.588.904.17 220.507.984.44 422.187.464.56 高速重载0.57.443.471.78 16.792.851.63 26.982.771.22 47.762.811.74
随着权重系数的增加,VSD-MPC的电流谐波H5、H7减小,因此代价函数中谐波子空间的权重增加,可更好地抑制谐波电流,但同时考虑电机动态性能,由于基波空间的权重降低,电流跟随能力下降,因此动态性能随权重系数增加而降低。
图4为不同权重系数下VSD-MPCC相电流动态性能。代表的工况为:电机空载起动,给定转速800 r/min,负载转矩在0.1 s加入200 N·m,到0.2 s突变至100 N·m。从图4a中可以看出,VSD-MPCC在λ=2和λ=4时都能够快速响应转矩变化,但在0.1 s时的暂态有所区别,暂态过程如图4b所示,λ=2比λ=4响应速度更快且脉动的幅度更小,得出结论为动态性能随权重系数的增加而降低,最终折中考虑谐波抑制作用和动态性能选定权重系数。
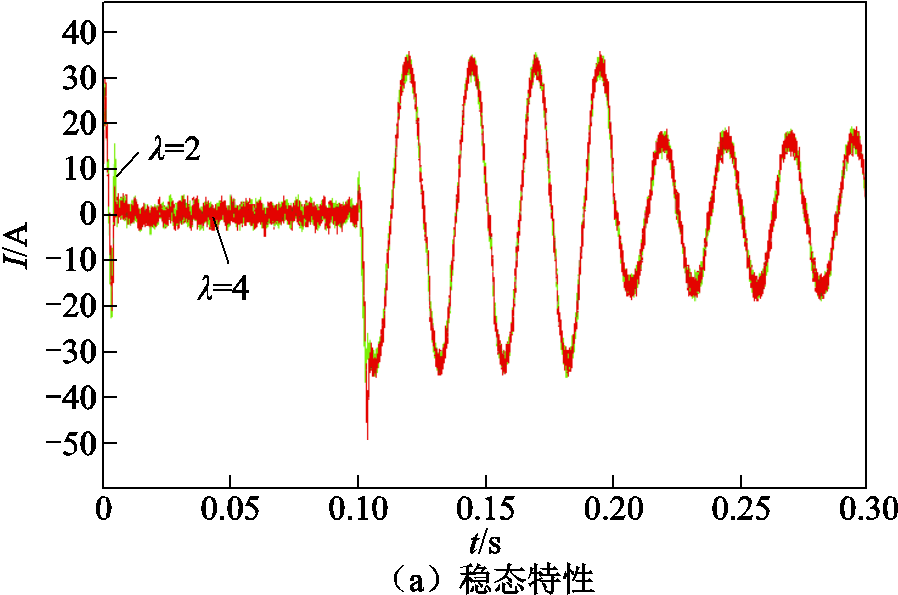
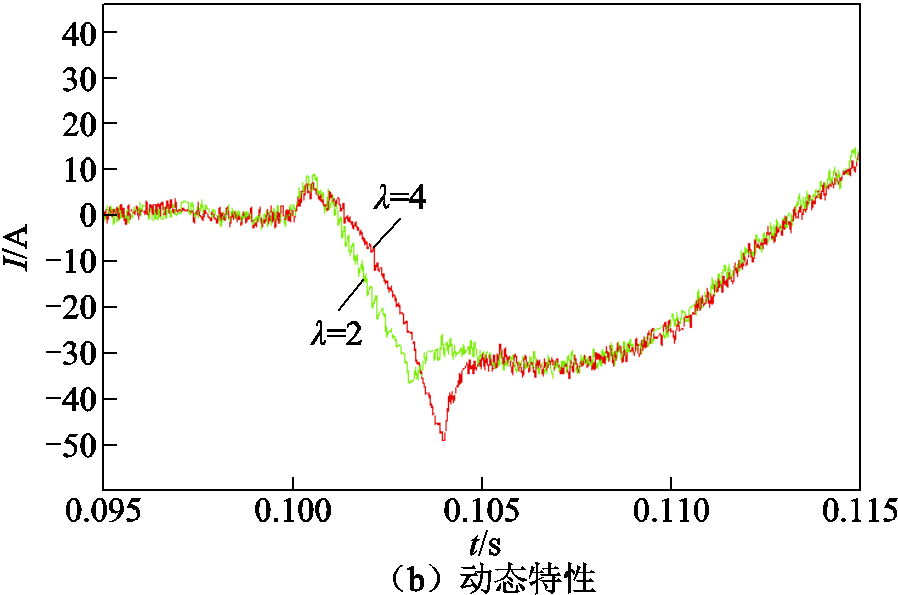
图4 不同权重系数下VSD-MPCC相电流动态性能
Fig.4 Phase current dynamic performance of VSD-MPCC with different weight coefficients
表2中,最优权重系数λ的选取随工况发生变化,这增加了VSD-MPC算法的复杂性。后续仿真中,VSD-MPC在低速轻载工况下λ=4,在高速轻载工况下λ=2,在高速重载工况下λ=2。
在三种典型的稳态工况下,对比了VSD-MPCC与3dq-MPCC两种控制方法的相电流、转速波形谐波电流分布,工况1结果如图5~图7所示,工况2结果如图8~图10所示,工况3结果如图11~图13所示。以下将结合不同工况进行综合讨论与分析。
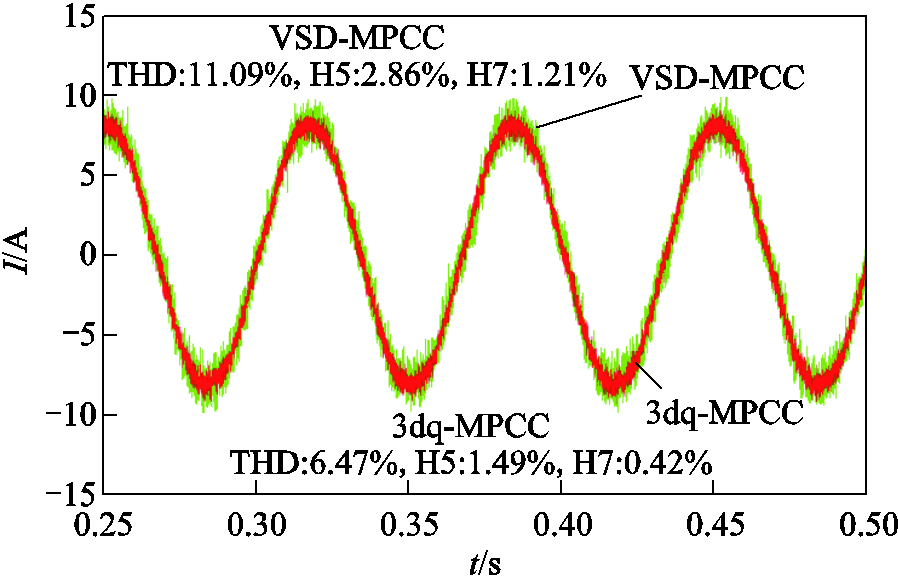
图5 工况1:相电流对比
Fig.5 Motor condition 1: phase current contrast

图6 工况1:转速对比
Fig.6 Motor condition 1: speed comparison
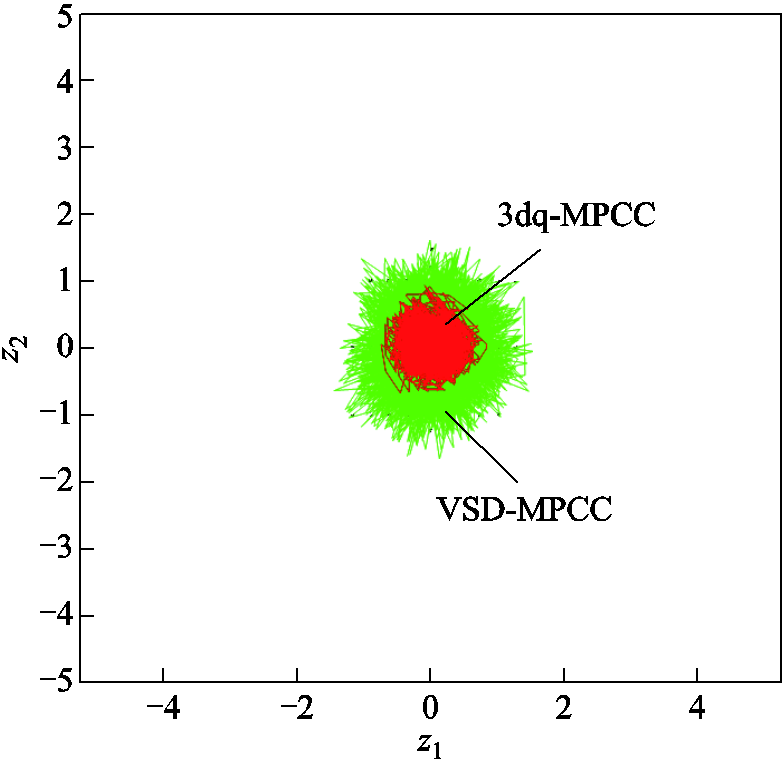
图7 工况1:谐波轨迹对比
Fig.7 Motor condition 1: harmonic trace comparison
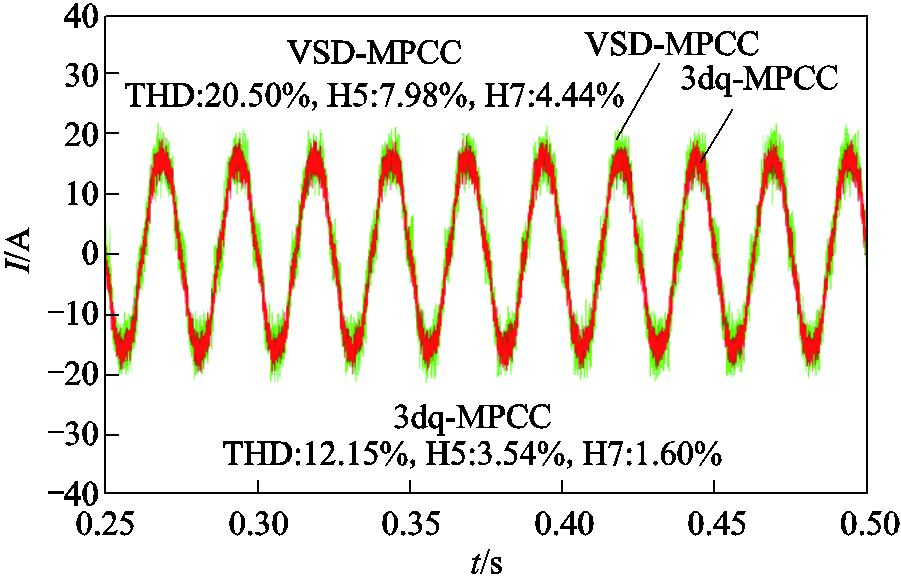
图8 工况2:相电流对比
Fig.8 Motor condition 2: phase current contrast
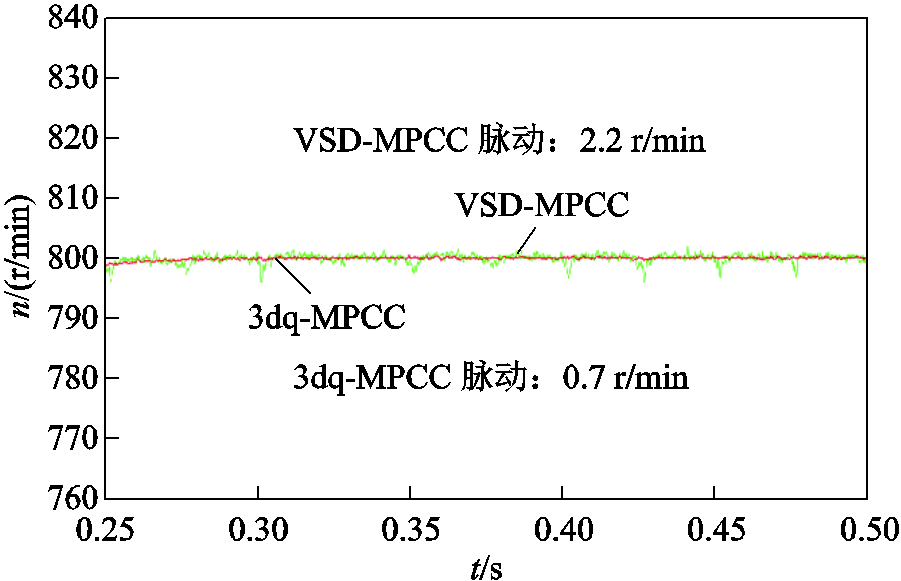
图9 工况2:转速对比
Fig.9 Motor condition 2: speed comparison
首先,在相电流方面,不论是低速轻载、高速轻载还是高速重载工况下,3dq-MPCC方法均展现出更好的正弦性,表现出较低的THD和更小的谐波分量。在低速轻载工况(见图5)下,3dq-MPCC的相电流THD为6.47%,明显低于VSD-MPCC的11.09%,其中H5和H7谐波分量分别降低了1.37%和0.79%。
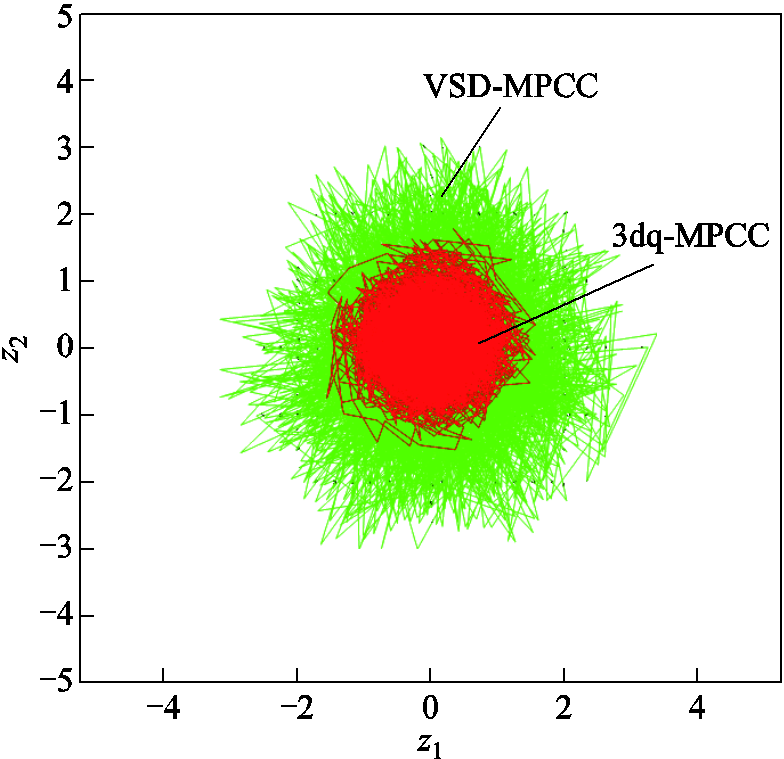
图10 工况2:谐波轨迹对比
Fig.10 Motor condition 2: Harmonic trace comparison
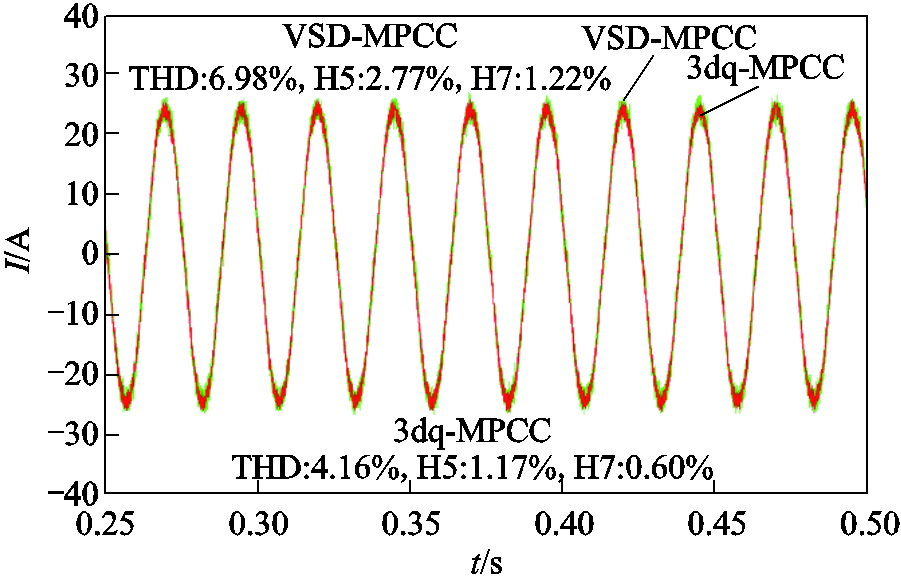
图11 工况3:相电流对比
Fig.11 Motor condition 3: Phase current contrast diagram
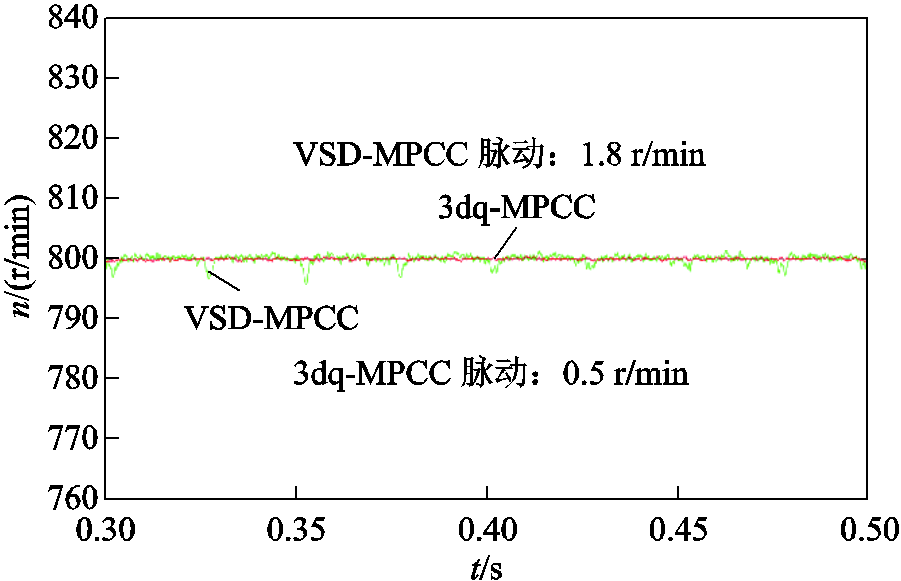
图12 工况3:转速对比
Fig.12 Motor condition 3: speed comparison
类似的趋势在高速轻载工况(见图8)和高速重载工况(见图11)中也得到了验证,3dq-MPCC的THD分别为12.15%和4.16%,显著优于VSD-MPCC的20.50%和6.98%。从整体趋势看,3dq-MPCC的相电流谐波抑制效果在不同速度下均优于VSD-MPCC。
其次,电机转速的波动特性同样表明了 3dq-MPCC的控制优势。在低速轻载300 r/min工况(见图6)下,3dq-MPCC的转速脉动范围仅为 0~0.2 r/min,远小于VSD-MPCC的1.6 r/min;在高速轻载800 r/min工况(见图9)和高速重载工况(见图12)中,3dq-MPCC的转速脉动分别为0.7 r/min和0.5 r/min,均显著优于VSD-MPCC的2.2 r/min和1.8 r/min。
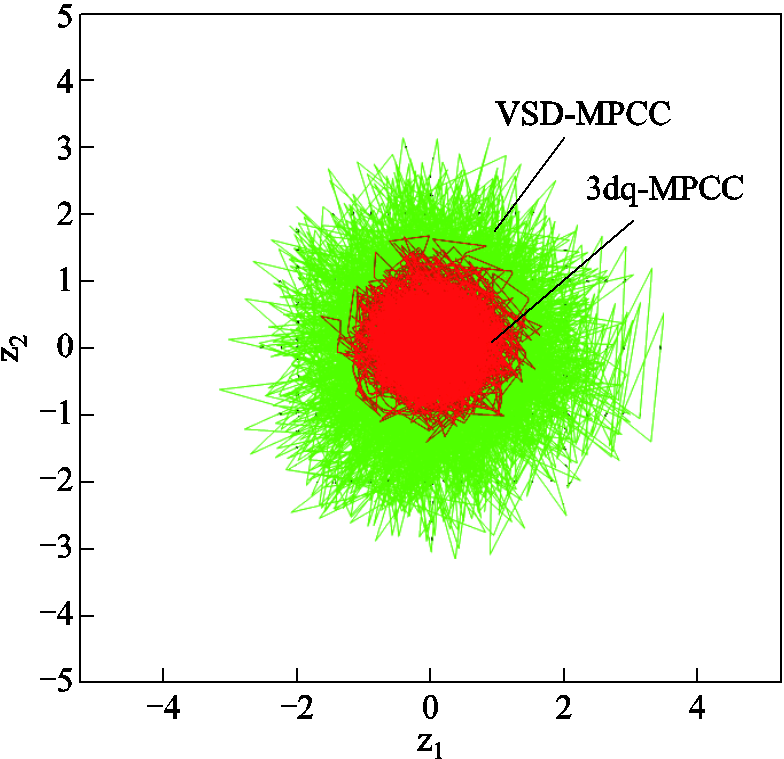
图13 工况3:谐波轨迹对比
Fig.13 Motor condition 3: harmonic trace comparison
这表明在不同速度下,3dq-MPCC具有更高的转速稳定性和更小的转速波动幅度,特别是在高速工况下,其优势更加明显。
最后,谐波空间电流轨迹进一步证实了3dq-MPCC的谐波抑制能力(见图7、图10、图13)。在所有三种工况下,VSD-MPCC的谐波电流轨迹范围明显大于3dq-MPCC,低速轻载工况下谐波最大值达1.5 A,而3dq-MPCC仅为0.6 A;高速轻载和高速重载工况下这一差异也保持一致,3dq-MPCC的谐波抑制效果显著优于VSD-MPCC,展现出其在降低谐波电流方面的强大能力。
综上所述,3dq-MPCC在各稳态工况下均展现出更优的电流谐波抑制、转速稳定性和电流波形质量,尤其是在高转速和重载条件下,控制性能相比VSD-MPCC更为突出,验证了其在复杂电机控制中的优越性;且无需通过繁琐的试错过程来调整权重系数,在简化控制算法的同时,还实现了更佳的谐波抑制效果,以及更稳定的转速性能,保持了优异的稳态性能。
图14为3dq-MPCC和VSD-MPCC的动态性能。代表的工况为:电机空载起动,给定转速 600 r/min,负载转矩在0.1 s加入200 N·m,到0.2 s突变至100 N·m。
为了更清晰地讨论3dq-MPCC和VSD-MPCC两种控制方法在不同工况下的表现,可以从相电流、q轴电流以及转速三个方面分别进行对比分析,尤其着眼于其动态响应性能。

图14 电机相电流动态性能
Fig.14 Phase current dynamic performance of motor
首先,在相电流的动态响应方面,如图14a和图14b所示,两种控制方法在转矩突变时都表现出较好的快速响应能力。然而,3dq-MPCC和VSD-MPCC在0.1 s时的暂态表现存在细微差异。具体而言,VSD-MPCC在0.1 s出现波动并在0.104 s逐渐稳定,整个暂态过程持续约0.004 s;相较之下,3dq-MPCC的暂态过程则更为短暂,其在0.1 s波动后于0.102 s左右稳定,持续时间仅约0.002 s,且波动幅度相对更小。这表明3dq-MPCC的动态响应速度和稳定性略优于VSD-MPCC。值得注意的是,在0.2 s时,二者的相电流响应性能基本一致,均展现出良好的动态性能。
其次,在q轴电流的动态响应中,3dq-MPCC与VSD-MPCC同样表现出细微的性能差异。电机q轴电流动态性能如图15所示。图15a和图15b表明,在0.1 s时,VSD-MPCC的q轴电流从0 A开始增长,并在0.104 s达到并稳定在32 A左右,暂态过程持续约0.004 s。而3dq-MPCC则从0.1 s开始波动,至0.102 s便已稳定至32 A左右,其暂态过程仅持续约0.002 s,并且波动幅度也明显小于VSD-MPCC。因此,在动态响应速度和波动控制方面,3dq-MPCC优于VSD-MPCC。与此同时,二者在0.2 s时的动态响应性能几乎一致,表明在负载突变情况下,两种控制方法均能有效应对电流变化。

图15 电机q轴电流动态性能
Fig.15 q-axis current dynamic performance of motor
最后,在转速动态响应的分析中,电机转速动态性能如图16所示,3dq-MPCC和VSD-MPCC在0.1 s时的表现也存在差异。VSD-MPCC在0.1 s时的转速从600 r/min开始波动,并在0.103 s逐步跟踪设定的转速,暂态过程大约持续0.003 s。而3dq-MPCC的暂态过程则相对较快,在0.102 5 s左右已开始跟踪给定转速,暂态过程持续约0.002 5 s,且波动幅度相对较小。然而,虽然3dq-MPCC的动态响应速度更快,但在0.102 5 s之后,VSD-MPCC在稳定性和跟踪精度方面略优于3dq-MPCC。值得一提的是,在0.2 s时,两种控制方法在转速动态响应方面的性能接近,均展现了良好的有载突变响应能力。
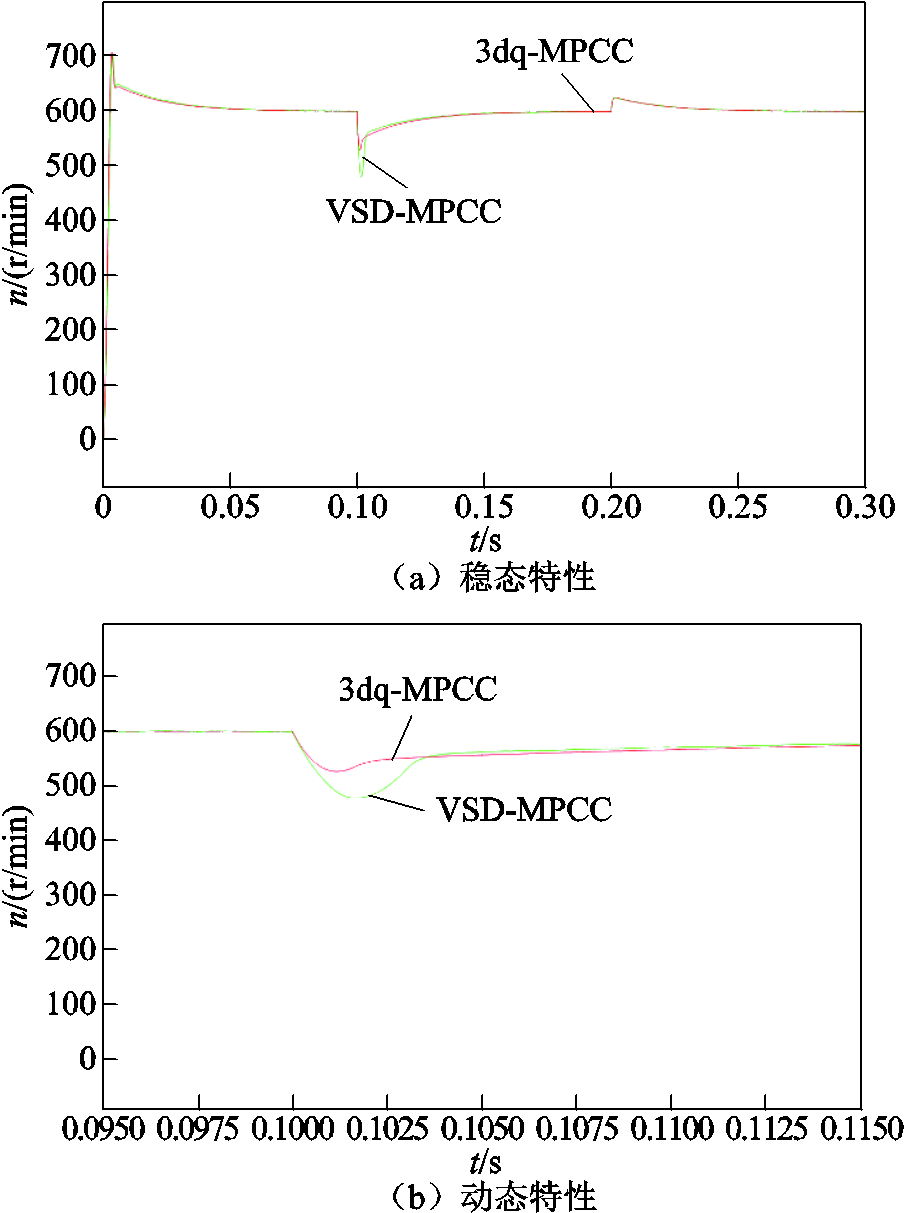
图16 电机转速动态性能
Fig.16 Motor speed dynamic performance
动态性能对比结论:证明了3dq-MPCC和VSD-MPCC同样能够有模型预测控制良好的动态响应能力,动态性能几乎一致;二者在有载突变时都有良好的动态响应能力,而由空载到有载的动态响应能力是3dq-MPCC略优于VSD-MPCC,但是在给定转速的跟踪能力是VSD-MPCC略优于3dq-MPCC。
通过仿真研究,从稳态特性和动态特性两方面对比分析了本文提出的3dq-MPCC与传统VSD-MPCC在相电流、电机转速、波空间电流轨迹和q轴电流等方面的性能。与传统VSD-MPCC相比,3dq-MPCC避免了复杂的谐波子平面权重系数取值,证明了3dq-MPCC策略的简化性以及可以提高谐波抑制效果。同时,研究结果也表明了3dq-MPCC能够获得良好的动态和稳态性能。
本文针对传统的建模复杂度高、计算量大,且存在谐波影响严重的问题,提出一种双三相永磁同步电机基于三重d-q坐标变换建模的模型预测电流控制策略。基于双三相永磁同步电机的特殊结构,提出三重d-q坐标系的电机模型,简化了双三相永磁同步电机建模方法。基于三重d-q坐标系的模型预测方法,避免了传统VSD模型所需考虑的谐波空间权重系数,在不牺牲性能的情况下简化了控制算法。仿真结果表明,所提控制策略能在有效抑制谐波电流的同时保持优异的动静态性能。此外,该方案理论上实现了双三相电机的三冗余控制。下一步将开展实验研究,进一步分析所提方法的有效性和优点。
参考文献
[1] Ye Donglin, Li Jian, Chen Junhua, et al. Study on steady-state errors for asymmetrical six-phase permanent magnet synchronous machine fault-tolerant predictive current control[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 640-651.
[2] Gao Jian, Dai Litao, Zhang Wenjuan, et al. Multi-interval efficiency design optimization for permanent magnet synchronous generators used in hybrid electric special vehicles[J]. IEEE Transactions on Industrial Electronics, 2021, 68(6): 4646-4656.
[3] 田代宗, 孙宇光, 王善铭, 等. 多相整流永磁同步发电机绕组内部相间短路的故障分析[J]. 电工技术学报, 2020, 35(6): 1262-1271.
Tian Daizong, Sun Yuguang, Wang Shanming, et al. Analysis of stator internal phase-to-phase short-circuit in the multiphase permanent magnet synchronous generator with rectifier load system[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1262-1271.
[4] Zhao Wenxiang, Tao Tao, Zhu Jihong, et al. A novel finite-control-set model predictive current control for five-phase PM motor with continued modulation[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 7261-7270.
[5] Ruan Zhihuang, Song Wenxiang, Yan Yan. Current harmonic suppression for dual three-phase permanent magnet synchronous motor drives[J]. IEEE Access, 2019, 7: 143888-143898.
[6] 陈荣, 翟凯淼, 舒胡平. 永磁同步电机双矢量固定开关频率模型预测控制研究[J]. 电工技术学报, 2023, 38(14): 3812-3823.
Chen Rong, Zhai Kaimiao, Shu Huping. Predictive control of dual vector fixed switching frequency model for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3812-3823.
[7] 李家祥, 汪凤翔, 柯栋梁, 等. 基于粒子群算法的永磁同步电机模型预测控制权重系数设计[J]. 电工技术学报, 2021, 36(1): 50-59.
Li Jiaxiang, Wang Fengxiang, Ke Dongliang, et al. Weighting factors design of model predictive control for permanent magnet synchronous machine using particle swarm optimization[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 50-59.
[8] 郑博元, 李炳均, 徐永向, 等. 考虑电压约束时双三相永磁同步电机一相开路的建模与容错控制策略[J]. 中国电机工程学报, 2023, 43(1): 294-303.
Zheng Boyuan, Li Bingjun, Xu Yongxiang, et al. Modeling and fault-tolerant control for DTP-PMSM with one phase open circuit fault considering voltage constraints[J]. Proceedings of the CSEE, 2023, 43(1): 294-303.
[9] 孙全增, 张志锋. 双三相永磁同步电机低共模电压模型预测电流控制[J]. 电工技术学报, 2023, 38(14): 3708-3722.
Sun Quanzeng, Zhang Zhifeng. Low common-mode voltage model predictive current control for dual three-phase permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3708-3722.
[10] 苗轶如, 宋鹏云, 吕铭晟, 等. 表贴式永磁同步电机预测转矩控制的无权重代价函数设计方法[J]. 电工技术学报, 2023, 38(12): 3141-3150.
Miao Yiru, Song Pengyu, Lü Mingcheng, et al. Design of cost function without weighting factor for predictive torque control of surface-mounted permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3141-3150.
[11] 魏尧, 柯栋梁, 黄东晓, 等. 基于时间序列的永磁同步电机连续控制集无模型预测电流控制[J]. 电工技术学报, 2023, 38(22): 6027-6038.
Wei Yao, Ke Dongliang, Huang Dongxiao, et al. A continuous-control-set type model-free predictive current control based on time-series for permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6027-6038.
[12] 郭磊磊, 王朋帅, 李琰琰, 等. 不同代价函数下永磁同步电机模型预测控制参数失配可视化分析[J]. 电工技术学报, 2023, 38(4): 903-914.
Guo Leilei, Wang Pengshuai, Li Yanyan, et al. Visual analysis of parameters mismatch in model predictive control for permanent magnet synchronous motor under different cost functions[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 903-914.
[13] 张建亚, 王凯, 朱姝姝, 等. 双三相永磁同步电机多谐波电流协同控制策略[J]. 中国电机工程学报, 2020, 40(2): 644-652.
Zhang Jianya, Wang Kai, Zhu Shushu, et al. Control strategies of dual three-phase permanent magnet machines with multi-harmonics[J]. Proceedings of the CSEE, 2020, 40(2): 644-652.
[14] 段卓琳, 张栋, 范涛. SiC电机驱动系统传导电磁干扰建模及预测[J]. 电工技术学报, 2020, 35(22): 4726-4738.
Duan Zhuolin, Zhang Dong, Fan Tao. Modeling and prediction of electromagnetic interference in SiC motor drive systems[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4726-4738.
[15] 黄林森, 赵文祥, 吉敬华, 等. 稳态性能改善的双三相永磁电机直接转矩控制[J]. 电工技术学报, 2022, 37(2): 355-367.
Huang Linsen, Zhao Wenxiang, Ji Jinghua, et al. Direct torque control for dual three-phase permanent-magnet machine with improved steady-state perfor-mance[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 355-367.
[16] Luo Yixiao, Liu Chunhua. Elimination of harmonic currents using a reference voltage vector based-model predictive control for a six-phase PMSM motor[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6960-6972.
[17] Xu Shuai, Sun Zhenyao, Yao Chunxing, et al. Model predictive control with constant switching frequency for three-level T-type inverter-fed PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 8839-8850.
[18] 宋战锋, 毛丰羽, 崔严谨, 等. 参考跟踪和扰动抑制解耦的双三相永磁同步电机容错控制策略[J]. 电工技术学报, 2023, 38(2): 435-450.
Song Zhanfeng, Mao Fengyu, Cui Yanjin, et al. An fault-tolerant control strategy based on decoupling between reference tracking and periodic disturbance attenuation for dual-three-phase permanent magnet synchronous machine[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 435-450.
[19] 肖海峰, 许宇豪, 李文真, 等. 五相永磁同步电机串级模型预测电流控制[J]. 电气技术, 2023, 24(8): 1-11.
Xiao Haifeng, Xu Yuhao, Li Wenzhen, et al. Model predictive current control based on series cost function for five-phase permanent magnet synchronous machines[J]. Electrical Engineering, 2023, 24(8): 1-11.
[20] 刘忠永, 范涛, 何国林, 等. 高性能永磁同步电机显式模型预测控制算法研究[J]. 电工技术学报, 2023, 38(22): 6039-6058.
Liu Zhongyong, Fan Tao, He Guolin, et al. Research on high-performance explicit model predictive control algorithm for permanent magnet synchronous motors [J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6039-6058.
[21] 刘蔚, 李万铨, 王明峤, 等. 复杂工况下的永磁同步电机典型绕组故障在线诊断[J]. 电工技术学报, 2024, 39(6): 1764-1776.
Liu Wei, Li Wanquan, Wang Mingqiao, et al. Online diagnosis of typical winding faults in permanent magnet synchronous motors under complex working conditions[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1764-1776.
[22] 周华伟, 陈铖, 向小龙, 等. 基于扰动观测器的五相永磁同步电机开路和短路容错矢量控制[J]. 电工技术学报, 2024, 39(15): 4782-4793.
Zhou Huawei, Chen Cheng, Xiang Xiaolong, et al. Disturbance-observer-based field-oriented control of five-phase PMSM under open-circuit and short-circuit faults[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4782-4793.
Model Predictive Current Control Strategy for Dual Three-Phase Permanent Magnet Synchronous Motors Based on Triple Rotating Coordinate Transformation
Abstract The traditional vector space decoupled (VSD)-based model predictive current control (MPCC) for dual three-phase permanent magnet synchronous motors (PMSM) involves complex selection of harmonic weight coefficients. Dual d-q current control provides an alternative for balancing currents, but it introduces cross-coupling-induced harmonics and limits winding utilization, which can affect fault-tolerant operation. To address these challenges, a model predictive current control strategy based on triple rotational coordinate transformation is proposed. This study develops a mathematical model using the triple coordinate transformation method and examines its relationship with the dual d-q coordinate model and the VSD motor model. The proposed model is analyzed, and its performance is assessed through simulations.
The dual three-phase windings of the PMSM are reorganized into a triple virtual stationary coordinate system (3-α-β) based on the phase alignment, which is then transformed into three sets of d-q components using the Park transform. A mathematical model of the motor is formulated within the triple d-q coordinate framework, and a comparative analysis shows that the components are decoupled. It is further demonstrated that the harmonic current components are eliminated when the currents in the triple d-q system are balanced. Simulations are conducted for both VSD-MPCC and the proposed 3dq-MPCC for validation.
The simulation results demonstrate the following: VSD-MPCC effectively suppresses harmonic currents while considering the motor's dynamic performance. However, it involves a complex process for selecting weight coefficients. (1) steady-state performance comparison. In terms of phase current, the 3dq-MPCC control method consistently exhibits superior sinusoidal characteristics, lower total harmonic distortion (THD), and reduced harmonic components under varying operating conditions, including low-speed and light-load, high-speed and light-load, and high-speed and heavy-load scenarios. Under low-speed and light-load conditions, the phase current THD of 3dq-MPCC is 6.47%, significantly lower than the 11.09% observed in VSD-MPCC. Moreover, the H5 and H7 harmonic components are reduced by 1.37% and 0.79%, respectively. Similar trends are observed under high-speed conditions. For example, at high-speed and light-load, 3dq-MPCC achieves a THD of 12.15%, compared to 20.50% for VSD-MPCC. Under high-speed and heavy-load conditions, the respective THD values are 4.16% and 6.98%. The motor speed fluctuation analysis further underscores the control advantages of 3dq-MPCC. At 300 r/min under low-speed and light-load conditions, the speed fluctuation range of 3dq-MPCC is only 0.2 r/min, much smaller than the 1.6 r/min of VSD-MPCC. At high-speed and light-load (800 r/min) and high-speed and heavy-load conditions, the speed fluctuation ranges of 3dq-MPCC are 0.7 r/min and 0.5 r/min, respectively, compared to 2.2 r/min and 1.8 r/min for VSD-MPCC. Additionally, the harmonic space current trajectory analysis confirms the superior harmonic suppression capability of 3dq-MPCC. Across all three conditions, the harmonic current trajectory range of VSD-MPCC is significantly larger than that of 3dq-MPCC. For example, under low-speed and light-load conditions, the maximum harmonic current trajectory range of VSD-MPCC reaches 1.5 A, while that of 3dq-MPCC is only 0.6 A. Similar differences are observed under high-speed conditions. (2) Dynamic Performance Comparison Under dynamic conditions (e.g., motor start at no load, a set speed of 600 r/min, load torque increased to 200 N·m at 0.1 s, then suddenly reduced to 100 N·m at 0.2 s): In terms of the phase current dynamic response, VSD-MPCC stabilizes at 0.104 s following a transient period of approximately 0.004 s after a fluctuation at 0.1 s. In contrast, 3dq-MPCC stabilizes at about 0.102 s, with a transient duration of only 0.002 s and a smaller fluctuation range. For the Q-axis current dynamic response, VSD-MPCC requires about 0.004 s to stabilize, while 3dq-MPCC stabilizes in approximately 0.002 s with significantly smaller fluctuations. In the speed dynamic response, the transient process of VSD-MPCC lasts about 0.003 s, while that of 3dq-MPCC is shorter at 0.0025 s, with a comparatively smaller fluctuation range.
The simulation results demonstrate a comparison between the proposed 3dq-MPCC and the traditional VSD-MPCC in terms of steady-state and dynamic characteristics, focusing on phase current, motor speed, harmonic current trajectory, and Q-axis current. The proposed 3dq-MPCC eliminates the complexity associated with selecting harmonic weight coefficients in VSD-MPCC, thereby simplifying the control strategy. Furthermore, the results indicate that 3dq-MPCC effectively suppresses harmonic currents and achieves favorable steady-state and dynamic performance.
Keywords:Dual three-phase permanent magnet synchronous motor, triple rotating reference frame, model predictive control, harmonic suppression
中图分类号:TM341
DOI: 10.19595/j.cnki.1000-6753.tces.L11027
国家自然科学基金项目(52107136、52207047)、国家自然基金青年项目(52207048)、国家自然科学基金青年科学基金项目(52107136)和湖北省自然科学基金一般面上项目(No.506)资助。
收稿日期 2024-07-11
改稿日期 2024-09-27
储 炜 男,2000年生,硕士研究生,研究方向为永磁电机驱动控制。
E-mail:chuwei0314@163.com
林黄达 男,1986年生,讲师,研究方向为多相永磁电机驱动系统。
E-mail:lindalena23@nue.edu.com(通信作者)
(编辑 陈 诚)