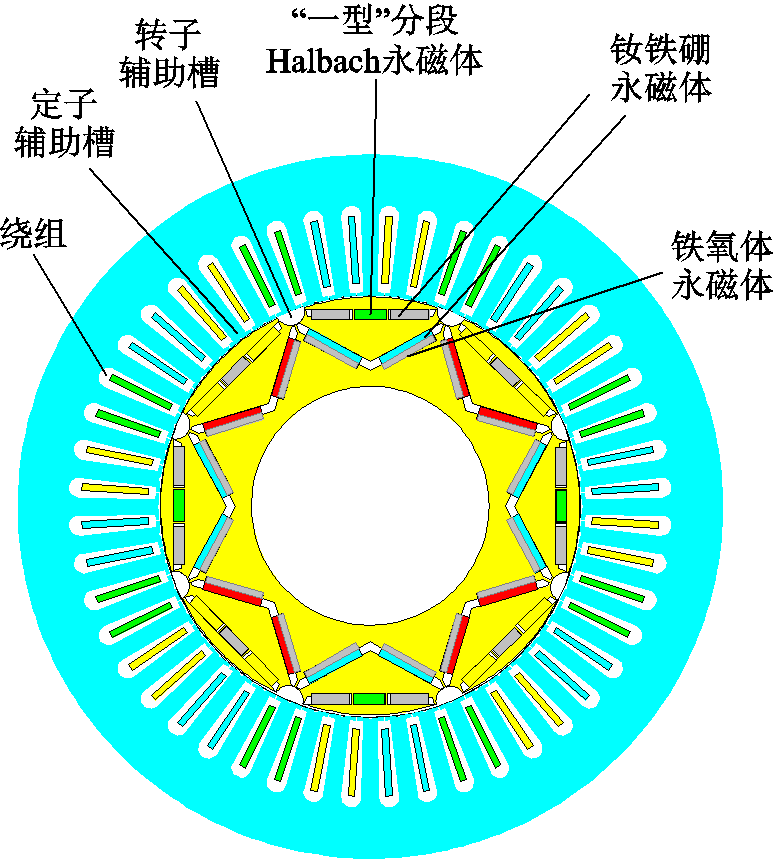
图1 电机结构
Fig.1 Motor structure drawing
摘要 针对内置式永磁同步电机电磁振动噪声大的问题，该文提出一种定转子开设辅助槽，转子采用钕铁硼和铁氧体混合永磁体，同时部分永磁体分段Halbach充磁方式的电机拓扑结构。首先，求解电机振动噪声解析表达式，并搭建电机有限元模型。其次，提出一种结合参数敏感度分析和响应面法的电机拓扑协同优化方法，考虑到拓扑参数间的耦合作用影响，根据所提方法对拓扑结构参数进行优化。然后，将优化后电机通过电磁场、机械场、声场进行多物理场耦合仿真，得到电机振动噪声特性，并将定子最大振动幅值和噪声声压级结果与V型内置式永磁电机相比较，结果表明：在保证电磁转矩不受影响的前提下，该结构抑制了转矩脉动、齿槽转矩以及径向电磁力的幅度，减小了电机振动幅值和噪声声压级。最后，在机械场中计算转子所受等效应力和总变形，验证电机结构的合理性。
关键词：内置式永磁同步电机 Halbach永磁体 径向电磁力 振动噪声
内置式永磁同步电机（Interior Permanent Magnet Synchronous Motor, IPMSM）的振动噪声主要由空气动力学、机械摩擦和电磁力造成[1-3]，径向电磁力波动引起的电磁振动噪声成为了国内外学者研究的热点[4-5]。文献[6]计算了电磁力的数学表达式，并采用磁动势与磁导的乘积来求解电机的气隙磁通密度。文献[7]基于麦克斯韦方程组，分析了径向电磁力在空间和时间阶次的构成，并总结出各阶次的分布规律。文献[8]计算了因极槽配合而产生的低阶电磁力波幅值，并提出了一种定子齿开设辅助槽的永磁电机结构优化方案。文献[9]提出定子齿顶偏移结构的内置式永磁同步电机，该结构使电机各阶次径向电磁力幅值减小，定子齿部受力显著降低。文献[10]研究了逆变器的谐波电流对内置式永磁同步电机电磁振动的影响，重点分析了0、8阶次电磁力。文献[11]对永磁同步电机的各阶次模态振型的频率和阻尼比进行了计算，通过实验测量和仿真验证对比结果的准确性。
随着电机多物理场优化目标与参数的增加，传统的优化方法往往达不到约束条件，文献[12]针对直线电机提出一种基于Kriging算法的改进型高效优化方法，并将优化结果与有限元结果对比验证了全局优化算法的准确性与高效性。文献[13]对轴向磁场永磁记忆电机进行敏感度分析，并采用改进的非支配排序遗传算法寻优，该优化方法具有优异的收敛能力与高效率。文献[14]提出一种电机整体模型-数据融合优化方法，将局部磁极的优化与电机整体关键参数相结合，并利用改进贝叶斯算法提升了电机的优化效率。文献[15]对内置式无轴承永磁电机采用响应面与多目标粒子群优化相结合的方式，并利用帕累托前沿筛选得到最优异的电机性能。文献[16-18]提出了回归机器学习算法，对非线性复杂参数建立了电机的数学模型，通过正交试验设计法与改进型非支配排序遗传算法对电机实现分期优化设计，利用序列非线性规划算法对永磁电机的强敏感度参数进行了多目标优化。上述电机优化研究方法存在优化目标与参数复杂度较低，未针对多个特定目标重点优化，同时算法迭代效率较低，优化结果缺乏全面性的问题。
本文针对IPMSM的振动噪声问题，提出一种结合参数敏感度分层和响应面法的拓扑协同优化方案。首先，对电机的振动噪声进行理论分析，并构建了电机有限元模型；其次，对拓扑结构参数采用分层协同优化方法；然后，将优化后的电机结构在多物理场中仿真分析得到振动噪声情况，并与V型IPMSM电机进行比较；最后，在机械场中验证电机结构的稳定性。
基于Maxwell软件，建立了如图1所示的电机模型，该内置式永磁同步电机采用Halbach开槽型，具体结构参数见表1。
图1 电机结构
Fig.1 Motor structure drawing
表1 电机结构参数
Tab.1 Motor structure parameters
参数数值（型号）参数数值（型号） 定子外径/mm270定子槽数48 定子内径/mm162极对数4 转子外径/mm160额定转速/(r/min)6 000 永磁体材料NdFe35 ferrite额定功率/kW80
在气隙磁场谐波作用下，电机将产生不同频率不同阶次的电磁力波，分别分析定转子磁动势和气隙磁导，得到气隙磁通密度为
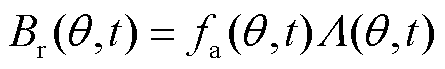（1）
式中，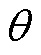
为永磁体Halbach充磁角度。根据磁动势乘以磁导的方法可知，径向气隙磁通密度
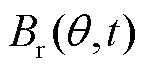可以用气隙磁通密度磁动势
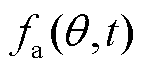和气隙比磁导函数L(q,t)的乘积来表示。
气隙磁通密度的磁动势与定子和永磁体的磁动势之间的关联为
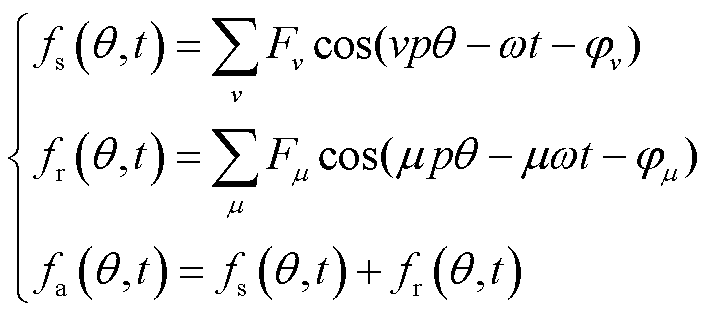（2）
式中，fs(q,t)、fr(q,t)分别为定子、永磁体磁动势；v、m分别为定子、永磁体谐波磁动势次数；jv、jm分别为定子、永磁体谐波磁动势相位；Fv、Fm分别为定子、永磁体谐波磁动势幅值；p为极对数；w为基频角速度。
电机的径向与切向电磁力幅值Fr、Ft分别为
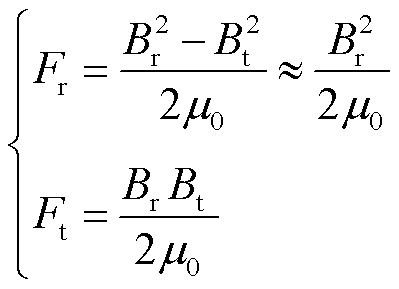（3）
式中，Br、Bt分别为定子齿的径向、切向气隙磁通密度；m0为真空磁导率。
电机径向电磁力可以分为表2中六种组合方式，其具体数学表达式为
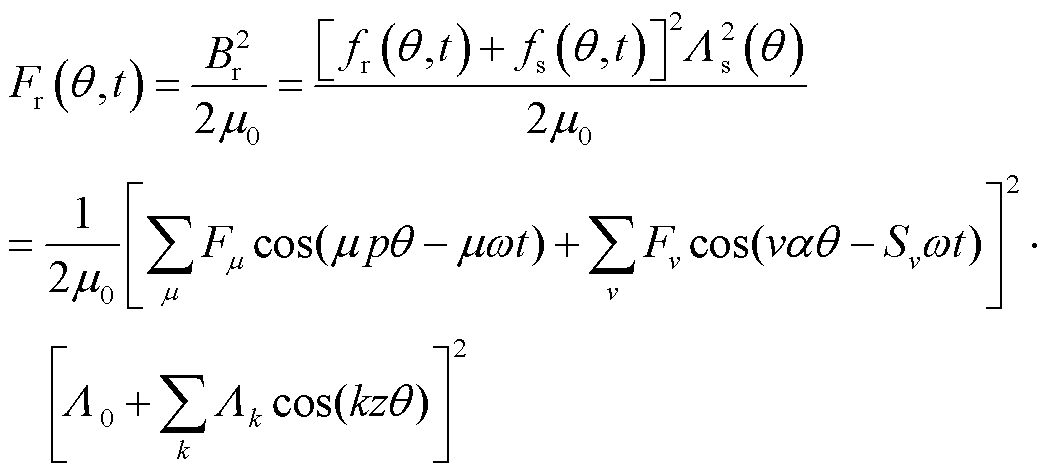
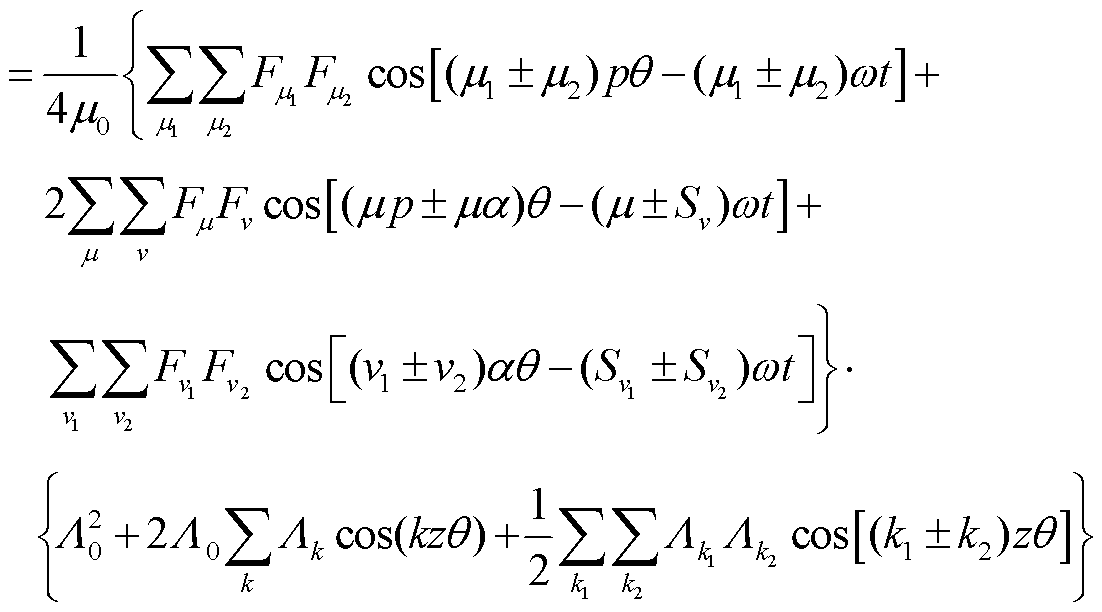（4）
式中，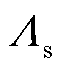
为定子气隙磁导；
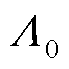为基波气隙磁导；z为定子槽数；α为电机单元数；vα为电枢磁场的磁动势谐波次数，v=6n+1（n=0,±1,±2,…）；μp为转子永磁体的磁动势谐波次数，μ=2m+1（m= 0,1,2,…）；Sv为电枢磁场v次谐波的旋转方向，“1,-1”分别代表正转和反转；Lk为第k次谐波磁导。
表2 径向电磁力分类
Tab.2 Radial electromagnetic force classification
来源空间阶次频率 永磁磁场 永磁磁场与定子开槽相互作用 永磁磁场与电枢磁场相互作用 永磁磁场、定子开槽与电枢磁场相互作用 电枢磁场 电枢磁场与定子开槽相互作用
电机在径向电磁力作用下的定子形变量可以表示为
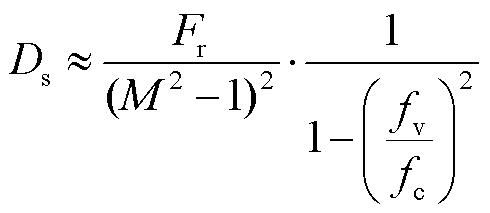（5）
式中，Ds为定子铁心形变量；M为径向电磁力阶数；fv、fc分别为电磁振动频率、电机固有频率。
根据式（5）可得，电机定子的铁心形变量与力波阶数的4次方存在反比例关系。更小的力波阶数会对电机的振动产生更大的影响，因此，选择低阶径向电磁力波作为振动优化的重点。
电机振动系统的响应可以表示为
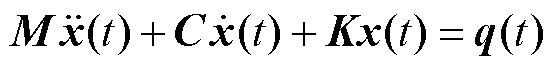（6）
式中，x、q分别为振动位移和电磁力向量；M、C、K分别为n阶的质量、阻尼与刚度的方阵；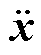
、
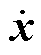分别为加速度矢量、速度矢量。
采用IPMSM单环模型对模态进行分析，将定子磁钢轭部假设成一个圆环，齿部和绕组等结构都作为附加质量，并忽略电机机壳的影响。定子铁心0阶固有频率可以表示为
（7）
式中，Dc为定子直径；e为定子杨氏模量；r为定子密度；mc、mt、mw分别为定子轭与齿部质量、绕组质量。
定子1阶模态受单边拉力，其固有频率[19]为
（8）
其中
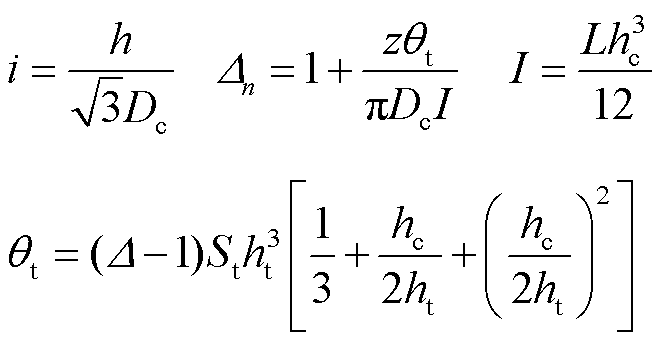
式中，h为定子轴向长度；L为定子齿截面宽度；hc为定子轴向长度；ht为定子齿高；St为定子齿截面积；i为材料的刚度因子。
当定子模态阶数大于或等于2时，受到多个方向的拉力，其n阶模态的固有频率可表示为
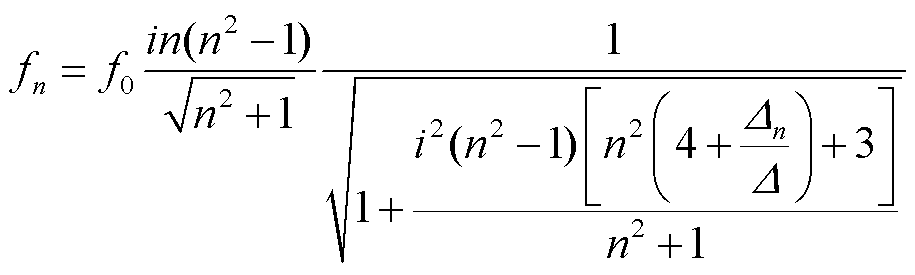（9）
电机振动产生噪声的辐射传播，可以由声压级、声功率、A计权网络等表述，人耳从接受听感到感到痛阈之间声压相差106倍，用Lp可以直观地表示噪声间的大小差异，其表达式为
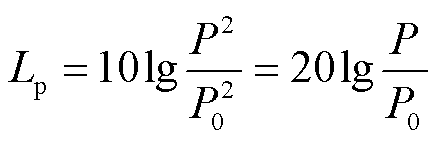（10）
式中，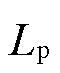
为声压级（dB）；P为声压（N/m2）；P0为基准声压，
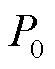=2×10-5 N/m2。
电机定转子拓扑参数复杂，传统单一的结构优化方法很难权衡多个优化目标，各参数优化间的非线性影响增大了电机优化的难度。传统的优化方案将所有的待优化参数归为一类统筹，并未判断参数优化的优先级与层次，故进行有限元电机样本点抽样后，很大概率会发生敏感度较高的参数范围被忽略的情况，该有限元数据结合算法寻优可能并不能反映最优的电机性能。因此，考虑多个参数优化中的协同耦合作用影响具有重要意义。本文提出一种参数分层分级优化方法，首先对所有待优化参数进行分层，第一层采用电机拓扑协同优化方案，第二层采用传统的扫描法寻优，具体分层方案如图2所示。
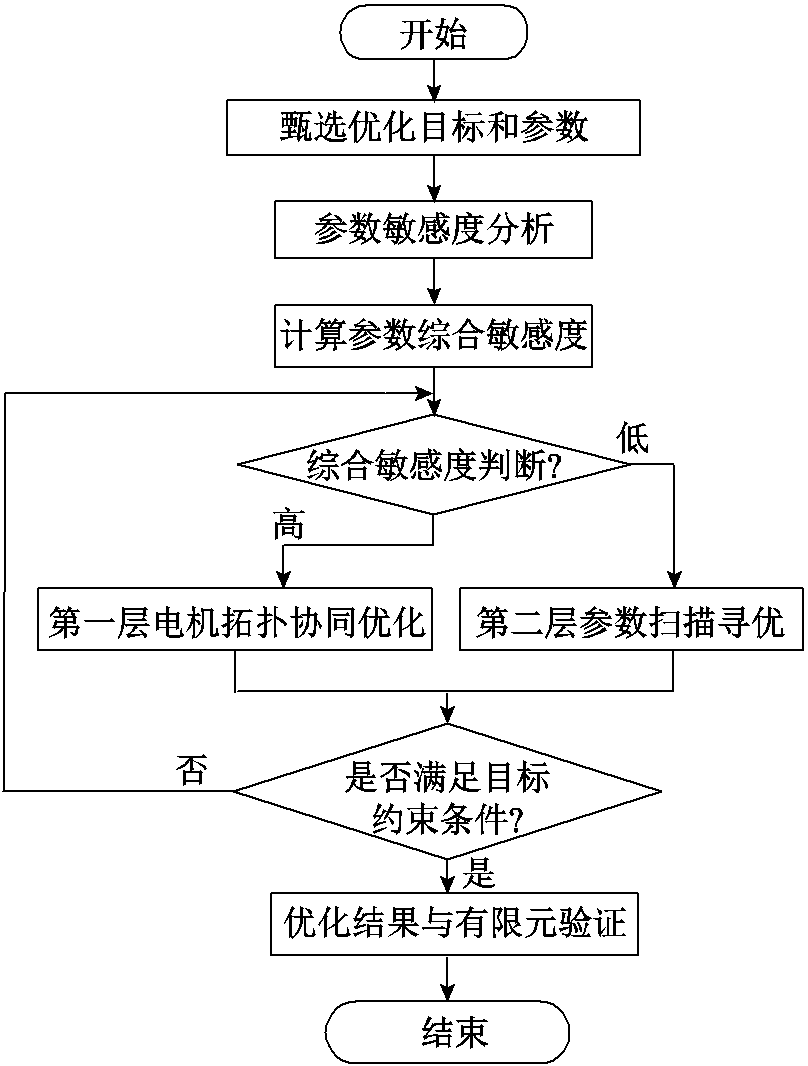
图2 电机参数分层优化方法
Fig.2 Hierarchical optimization method of motor parameters
根据所提出的电机拓扑结构，筛选出10个定转子参数见表3，图3、图4分别为第一层、第二层参数示意图，其中铁氧体永磁体宽度L2和NdFeB钕铁硼永磁体宽度L1之和为5 mm定值，与原结构单一钕铁硼永磁体宽度一致。优化目标主要针对转矩均值Te、径向电磁力幅值Fr、定子振动幅值Vs、噪声声压级平均值Lv。
表3 电机待优化参数名称
Tab.3 Parameter name of the motor to be optimized
优化参数结构名称 R1/mm定子齿部开槽半径 R2/mm转子齿部开槽半径 L2/mm铁氧体永磁体宽度 q/(°)永磁体Halbach充磁角度 H1/mm一型永磁体距转子内径高度 L3/mm一型中间永磁体磁障长度 L4/mm一型两端永磁体磁障长度 L5/mmV型永磁体端部磁障长度 W1/mmV型永磁体端部磁障宽度 q1/(°)V型永磁体开合角度
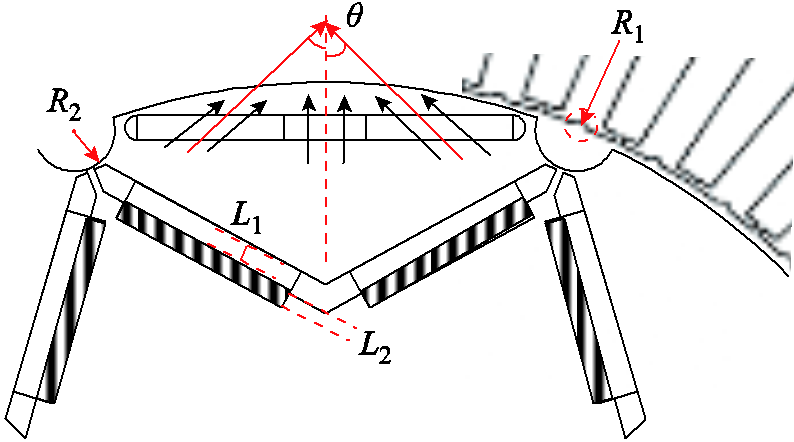
图3 第一层参数示意图
Fig.3 First layer parameter diagram
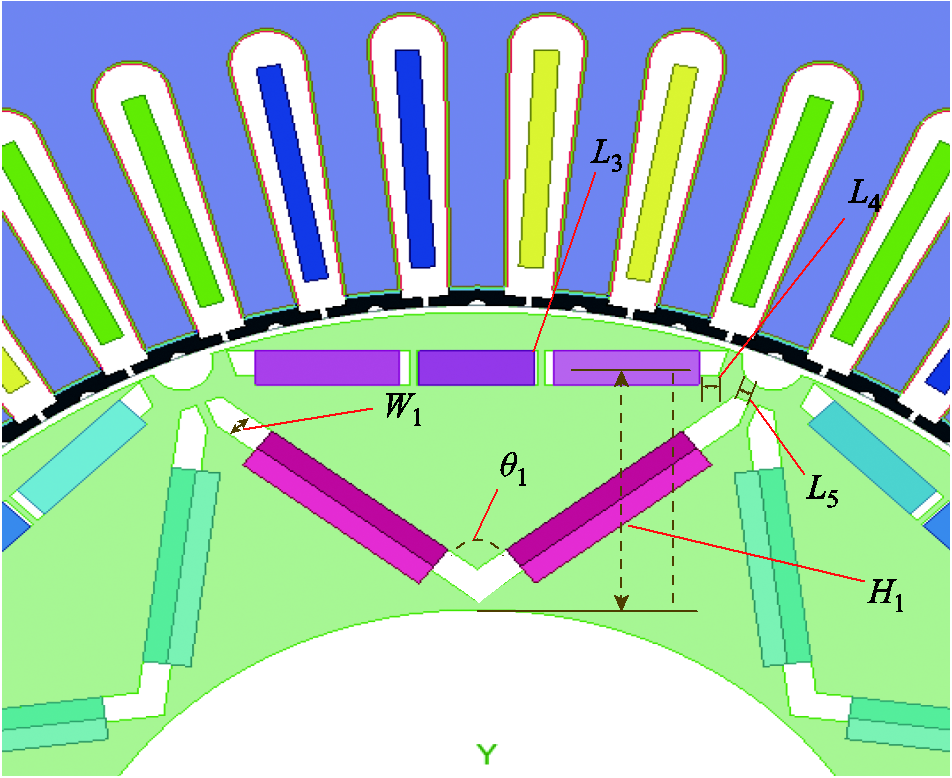
图4 第二层参数示意图
Fig.4 Second layer parameter diagram
通过参数敏感度的数值判断各参数之间的优先级，数值越大表示参数对优化目标的影响权重越大。根据式（11）中参数敏感度的计算方法，求解得到各参数的敏感度大小见表4，表中，Gs为综合敏感度。图5为各参数敏感度的示意图。
表4 优化参数的敏感度及综合敏感度
Tab.4 Optimize the sensitivity and comprehensive sensitivity of parameters
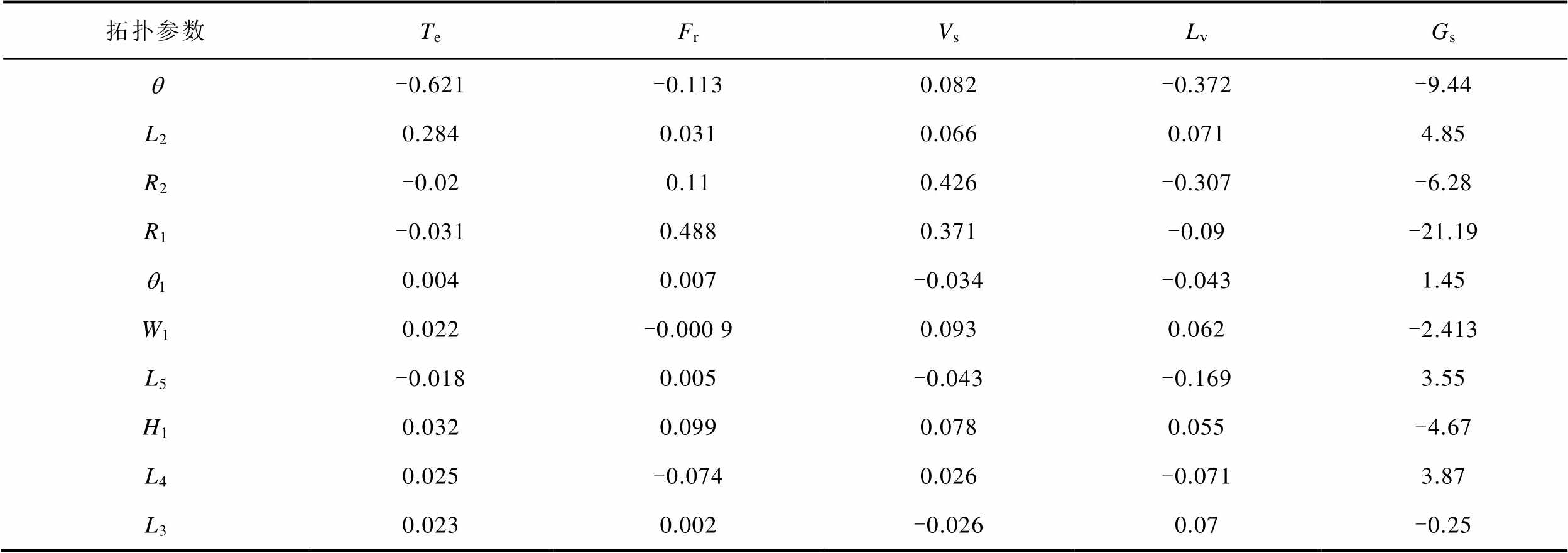
拓扑参数TeFrVsLvGs q-0.621-0.1130.082-0.372-9.44 L20.2840.0310.0660.0714.85 R2-0.020.110.426-0.307-6.28 R1-0.0310.4880.371-0.09-21.19 q10.0040.007-0.034-0.0431.45 W10.022-0.000 90.0930.062-2.413 L5-0.0180.005-0.043-0.1693.55 H10.0320.0990.0780.055-4.67 L40.025-0.0740.026-0.0713.87 L30.0230.002-0.0260.07-0.25
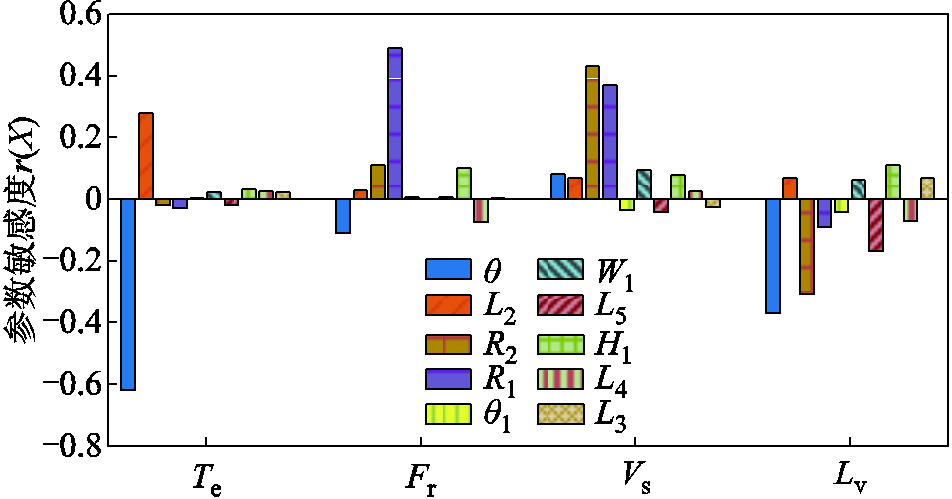
图5 参数敏感度分析
Fig.5 Parameter sensitivity analysis
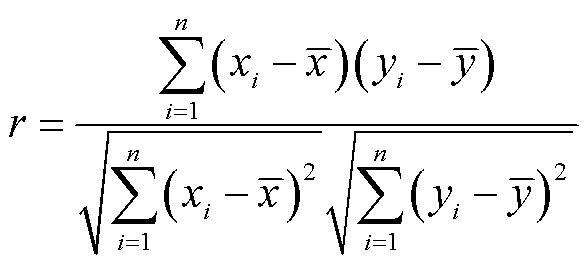（11）
式中，r为单个优化参数对应单个优化目标的敏感度值；xi为单个优化参数的第i个数值；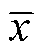
为单个优化参数的平均值；yi为单个优化参数第i个数值所对应单个优化目标值；
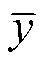为单个优化参数所对应单个优化目标的平均值。
由于每个参数针对4个优化目标有不同的敏感度，为判断参数的优先级，提出一种参数综合敏感度Gs(X)，计算方法如式（12）所示，给每个优化目标赋予敏感权重因子W(Yi)，Te、Fr、Vs、Lv分别为30、-30、-20、-20。若敏感度为正值代表参数对优化目标呈正相关；反之，呈负相关。由于电磁转矩的敏感度呈正相关，故其敏感权重因子为正值，径向电磁力等其他3个参数的敏感度呈负相关，令其敏感权重因子为负值，代表参数的综合敏感度皆与优化目标呈正相关，并且综合敏感度的绝对值越大表示参数对优化目标的权重越大。
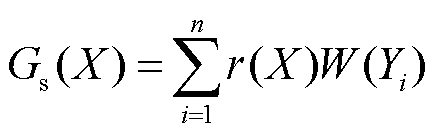（12）
每个参数的综合敏感度Gs见表4，其中R1、R2、L2、q 4个参数的综合敏感度绝对值较大，因此选择以上4个参数为第一层优化方案，参数优先级为R1、R2、L2、q；其余6个参数为第二层扫描法寻优。相较于传统方法，区分了参数之间的权重关系，利用不同的参数优先级将优化重心放在影响更大的参数上，降低了全局参数优化的误差。
对于第一层参数，提出一种电机拓扑协同优化方案如图6所示，具体优化方案分为以下四个步骤：
（1）根据敏感度大小对待优化参数进行分层，具体方法如图2所示；敏感度较大的4个参数采用拓扑协同优化方案，其余参数采用扫描法寻优。
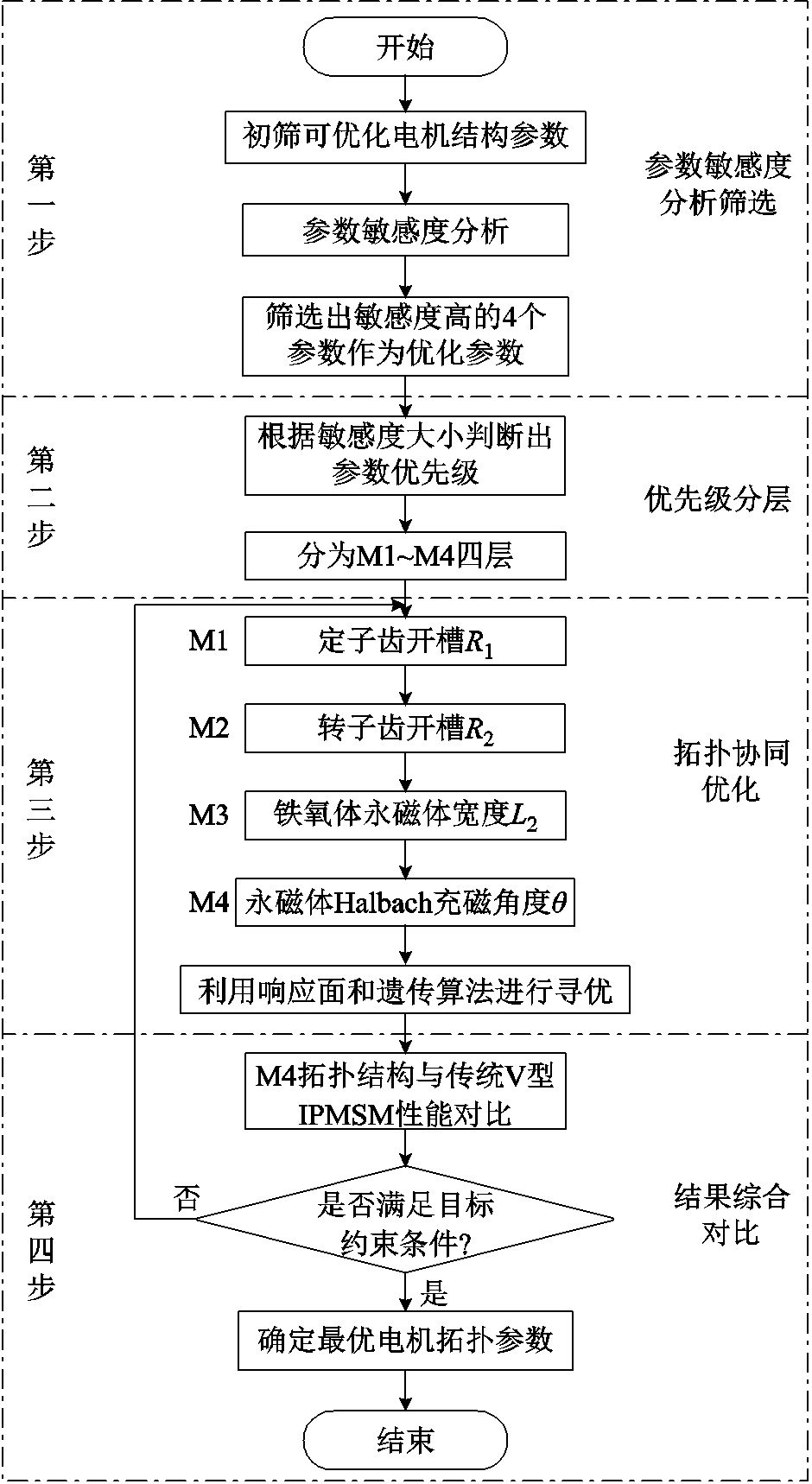
图6 电机拓扑协同优化方案
Fig.6 Cooperative optimization scheme of motor topology
（2）依据参数的敏感度优先级，将4个参数分级优化。
（3）将拓扑优化流程分为四个阶段，对4个参数按照综合敏感度的优先级进行分级拓扑协同优化。M代表原始电机拓扑，M1为优化第一优先级R1后的结构拓扑，M2、M3、M4依次代表拓扑协同优化R2、L2、q3个参数下的电机结构，在4个优化过程中结合响应面法和遗传算法提高优化效率和准确性。
（4）将经过优化的电机性能与传统的V型IPMSM进行比较，以确保优化结果具有高可靠性。
首先对定子齿部进行开半圆形辅助槽优化，R1为定子齿部的半圆形槽的半径，电磁转矩及其脉动曲线如图7所示。随着R1的增大，转矩脉动从6.4%下降到3%，下降率达53%，电机转矩损失在1%范围内，同时R1的取值对于径向电磁力的影响较小，最终选取R1=1.05 mm。
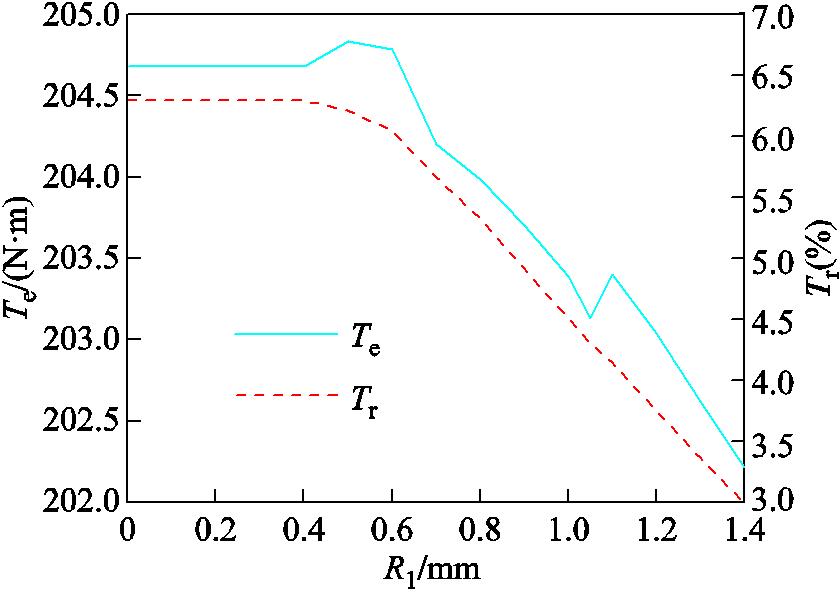
图7 电磁转矩及其脉动曲线
Fig.7 Electromagnetic torque and its pulsation curves
转子齿部开槽可以改变转子的磁力线分布路径，从而改善磁通密度过饱和现象。M2拓扑是在M1拓扑结构的基础上进行，选择R1=1.05 mm。从图8中可知，绿线为定子不开槽的情况，此时转子开槽对于径向电磁力的影响效果并不理想。当R1=1.05 mm时，随着转子开槽半径的增大，径向电磁力曲线出现了大幅度降低，下降率达21%，而两个参数未协同优化时下降率仅为5%。因此，在R1和R2两个参数协同作用下对优化目标的改善效果更好。
图9、图10所示为电磁转矩和转矩脉动两个优化目标进行响应面拟合的结果，当R1=1.05 mm时，随着R2的增大电磁转矩不断增大，最优值在3～ 4 mm的范围内。如图10所示，随着定转子开槽半径R1和R2的增大，转矩脉动大幅度下降，最终权衡得到R2=3.3 mm。
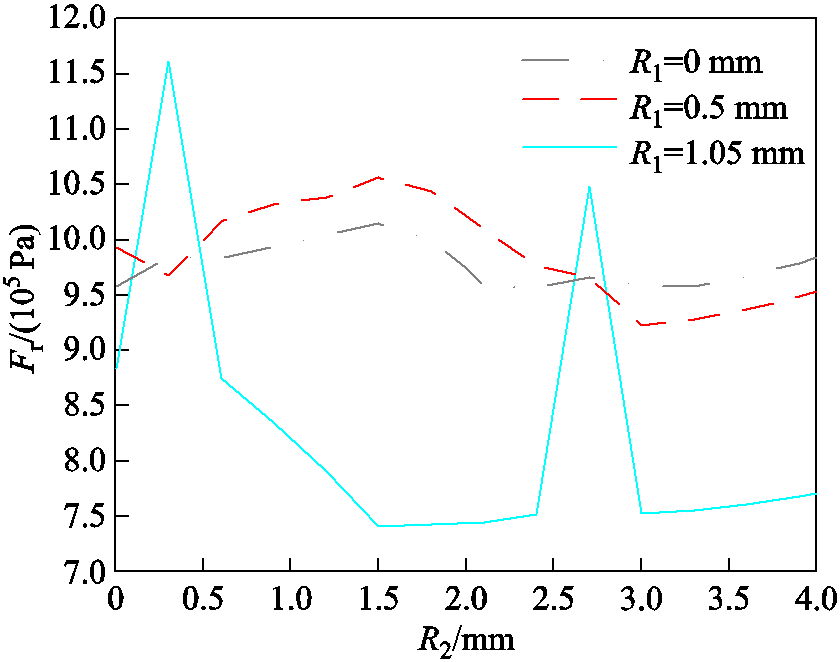
图8 径向电磁力变化曲线
Fig.8 Radial electromagnetic force variation curves
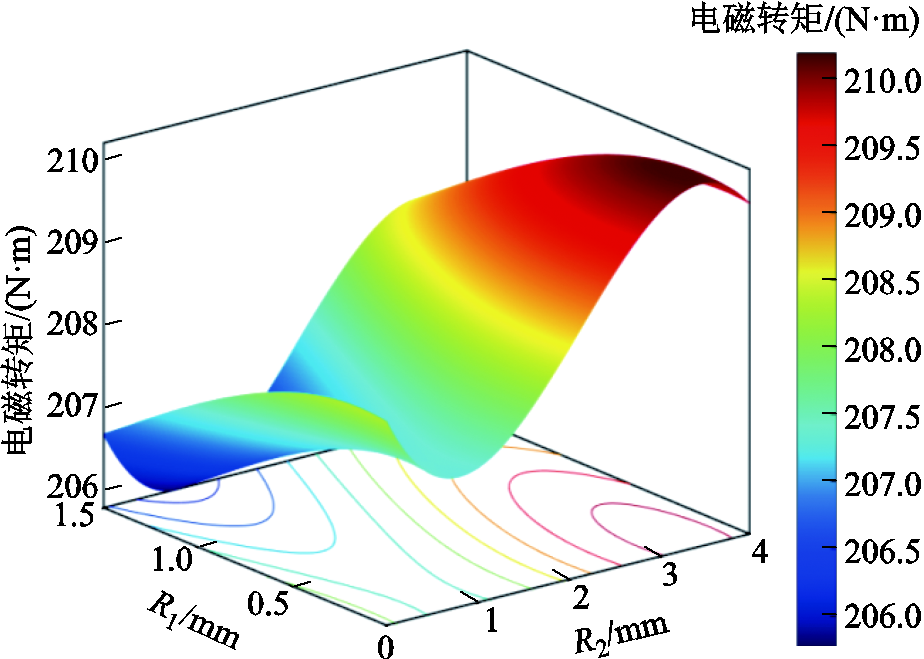
图9 电磁转矩响应面
Fig.9 Electromagnetic torque response surface
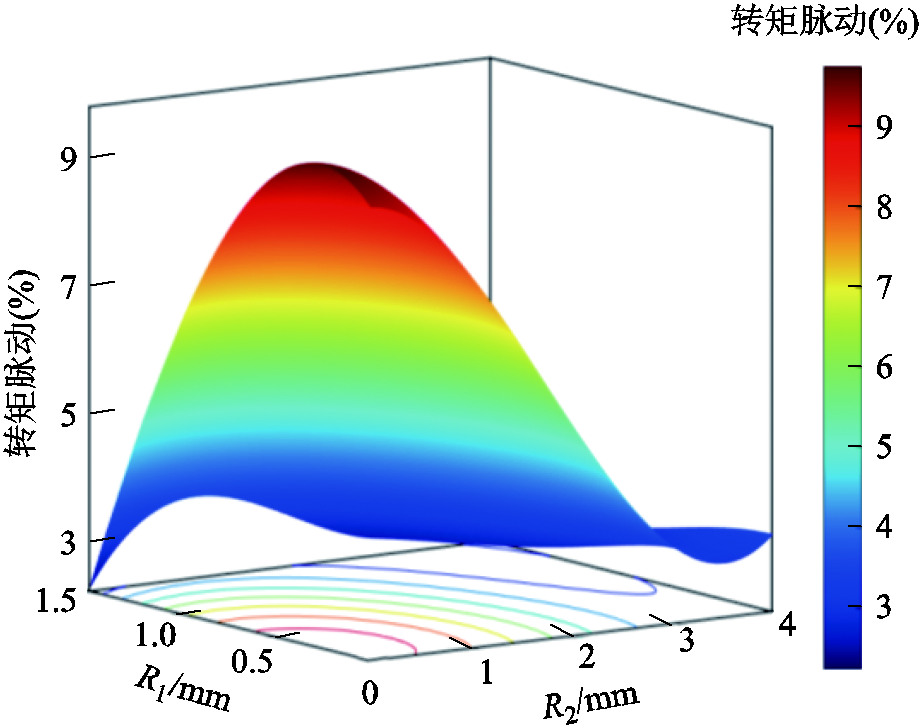
图10 转矩脉动响应面
Fig.10 Torque ripple response surface
NdFeB钕铁硼永磁体拥有出色的磁性能和高矫顽力等特点，但稀土永磁材料是一种不可再生的资源。IPMSM采用铁氧体和钕铁硼相结合的方法以期减少稀土资源的使用率，降低永磁体的使用成本，每kg可以降低500元左右，两种永磁体性能参数见表5。
表5 永磁体材料属性
Tab.5 Material properties of permanent magnet
属性钕铁硼铁氧体 最大磁积能/(J/m3)30～520.8～5.2 矫顽力/(kA/m)796～108 2176～270 价格/(元/kg)530～55633～47 M中含量占比（%）1000 M3中含量占比（%）5050
电磁转矩和径向电磁力变化曲线如图11所示，随着铁氧体宽度的增大，电机转矩均值和径向电磁力均呈下降趋势，转矩损失在5%范围内。相较于M0拓扑，M3协同优化下径向电磁力和转矩脉动得到了抑制，最终选择L2=2.5 mm。M3拓扑通过混合永磁体的方法，在保证电机性能的基础上降低了永磁体的使用成本，具有实际的应用生产借鉴价值。
径向电磁力和转矩脉动变化曲线如图12所示，展示了分段永磁体Halbach充磁角度q优化过程，随着q的增大，径向电磁力幅值Fr呈下降趋势，转矩脉动Tr 略有增大，故选择30°～65°作为优化范围，进一步根据遗传算法寻优得到最优取值为37°。
图11 电磁转矩和径向电磁力变化曲线
Fig.11 Curves of electromagnetic torque and radial electromagnetic force
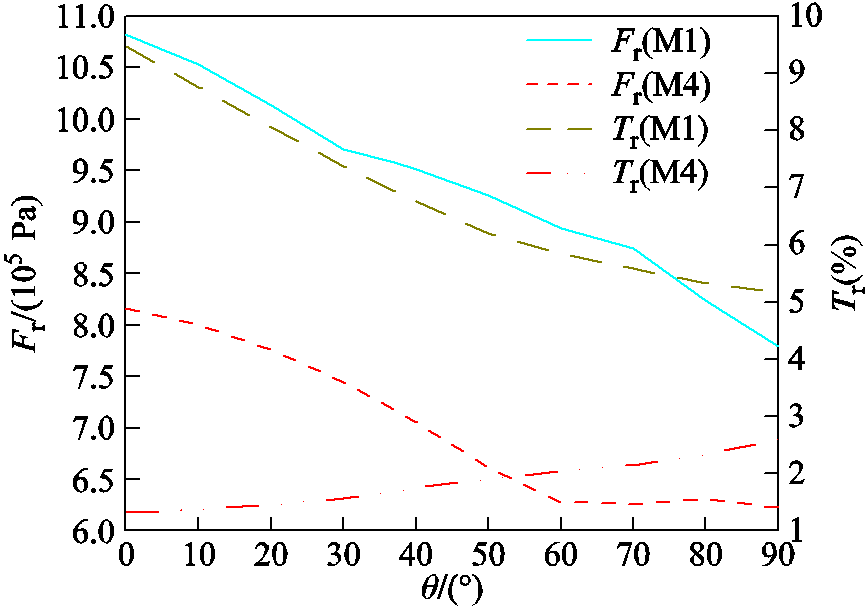
图12 径向电磁力和转矩脉动变化曲线
Fig.12 Curves of radial electromagnetic force And torque pulsation
经过以上4个阶段电机拓扑协同优化后，每个参数的最终取值见表6，后一阶段拓扑结构在前一阶段基础上依次进行新参数的优化，达到拓扑协同优化的效果。如图13所示为4个阶段的电机拓扑结构示意图，4个分区内依次为M1、M2、M3、M4的电机结构，M1阶段确定了定子辅助槽R1，M2阶段在M1的基础上增加了转子辅助槽R2，M3阶段在M2的基础上增加了铁氧体永磁体L2，M4阶段在M3的基础上增加了一型分段永磁体Halbach充磁角度q。通过以上电机拓扑协同优化，得到优化后最终拓扑结构M4。
表6 各阶段电机拓扑优化参数
Tab.6 Motor topological parameters at each stage
M0M1M2M3M4 R1/mm—1.051.051.051.05 R2/mm——3.33.33.3 L2/mm———2.52.5 q/(°)————37
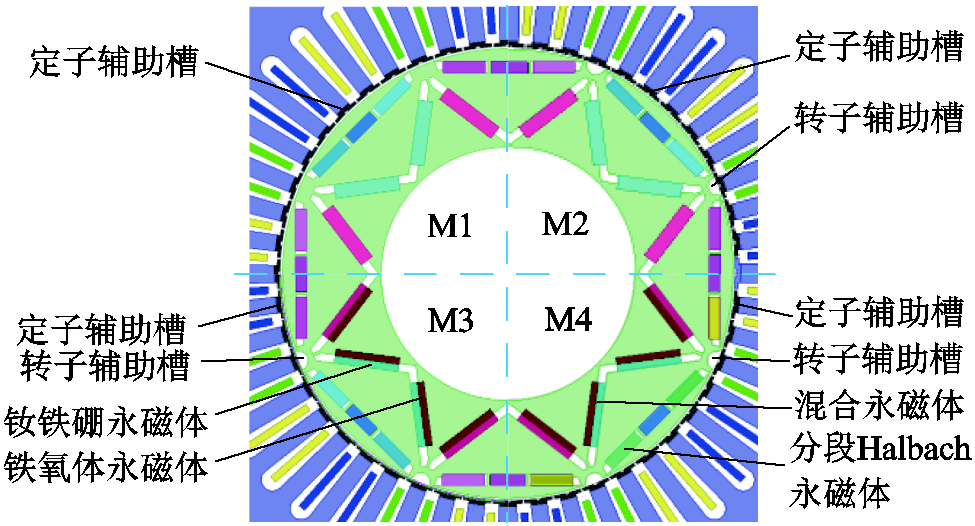
图13 4个阶段的电机拓扑结构
Fig.13 Four-stage motor topology
随着4个阶段的拓扑协同优化过程，M0～M4五种电机拓扑的径向电磁力波形对比曲线如图14所示，径向电磁力幅值及其均值得到了降低；表7为径向电磁力幅值和均值的数据对比，随着径向电磁力幅值的降低，电磁力均值也相应得到抑制，从而验证拓扑协同优化方案得到了较为优异的径向电磁力抑制效果。
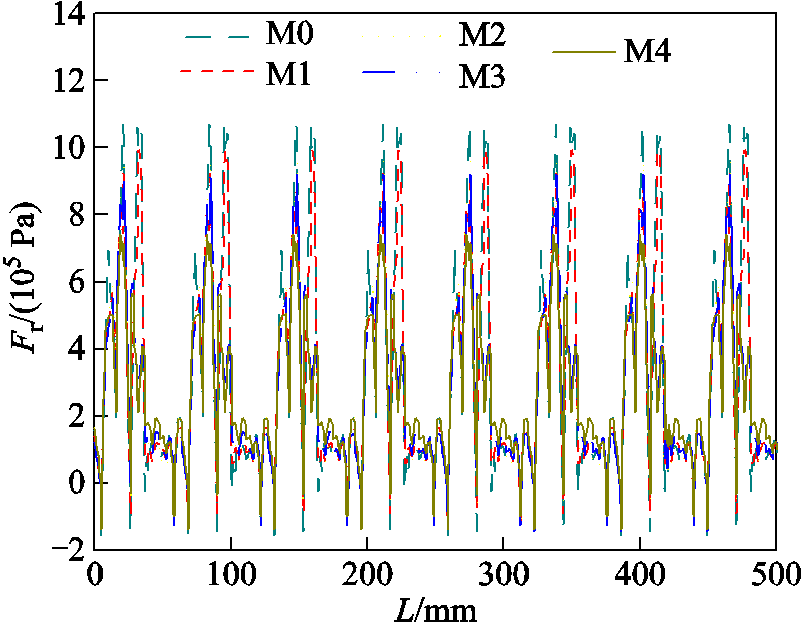
图14 五个阶段电机拓扑的径向电磁力
Fig.14 Radial electromagnetic force of five stage motor topology
表7 各阶段电机拓扑参数
Tab.7 Motor topological parameters at each stage （单位：MPa）
径向电磁力M0M1M2M3M4 幅值1.0680.9930.9650.9230.74 均值0.3180.3070.280.2790.272
4个阶段优化后电机性能见表8，转矩均值相较于优化前下降了3.2%，转矩脉动从9.7%下降到2.3%，齿槽转矩在采用永磁体Halbach充磁后优化效果显著，下降率达66%，径向电磁力下降到0.74 MPa，同时空载气隙的磁通密度和反电动势的幅度有略微的减少。
表8 电机拓扑协同优化结果
Tab.8 Results of cooperative optimization of motor topology
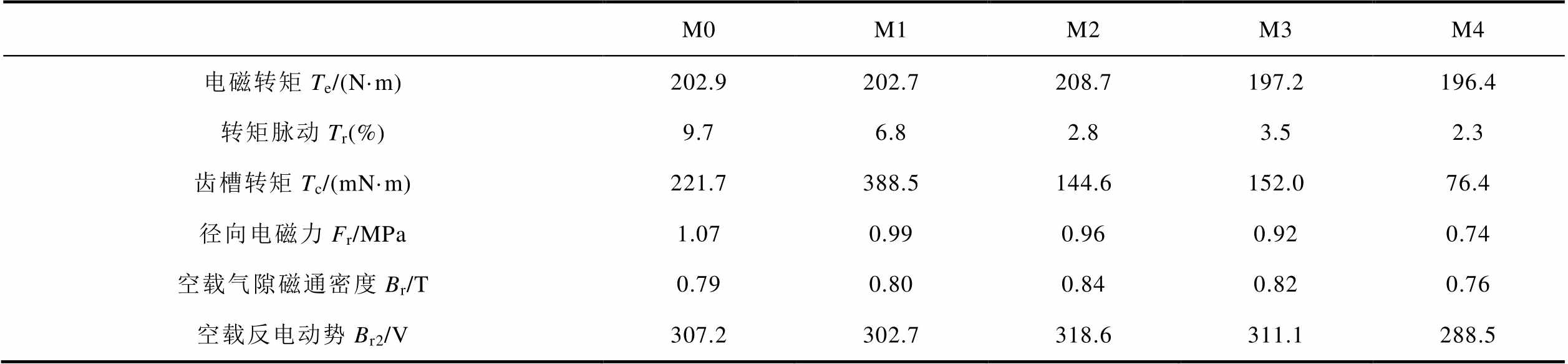
M0M1M2M3M4 电磁转矩Te/(N·m)202.9202.7208.7197.2196.4 转矩脉动Tr(%)9.76.82.83.52.3 齿槽转矩Tc/(mN·m)221.7388.5144.6152.076.4 径向电磁力Fr/MPa1.070.990.960.920.74 空载气隙磁通密度Br/T0.790.800.840.820.76 空载反电动势Br2/V307.2302.7318.6311.1288.5
为验证所优化电机拓扑结构的优越性，将M4拓扑与传统V型永磁体IPMSM结构相比较分析，两台电机定转子尺寸相同且永磁体体积一致，两者的拓扑结构对比如图15所示。如图16所示为电磁转矩对比曲线，M4拓扑的转矩脉动为2.3%，远小于V型结构的10.1%，M4电机相较于V型IPMSM电磁转矩下降率仅为1.4%。
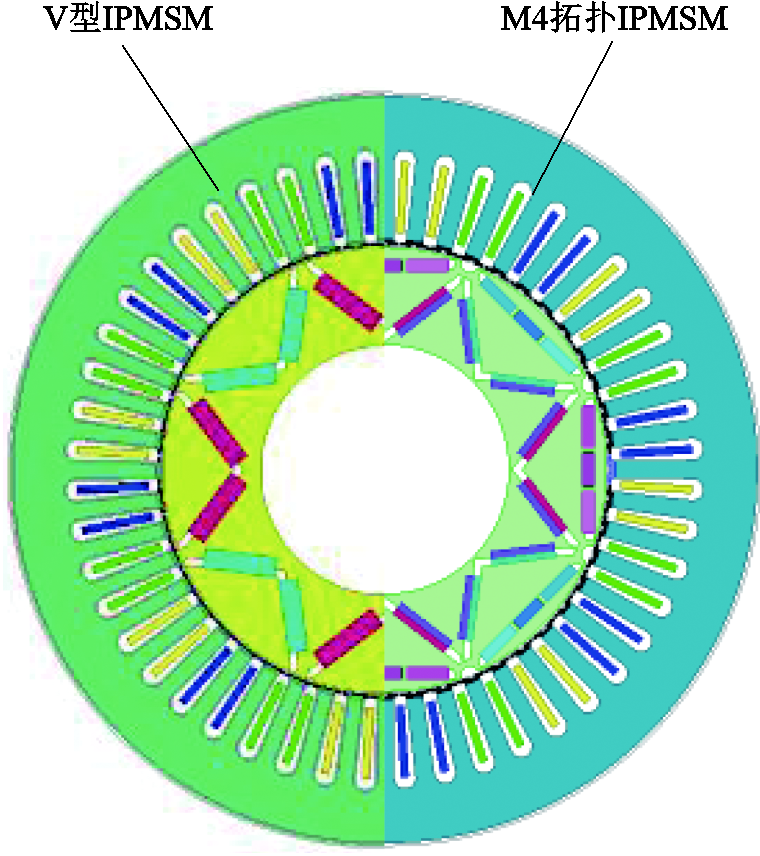
图15 V型、M4电机模型示意图
Fig.15 V-type, M4 motor model diagrams
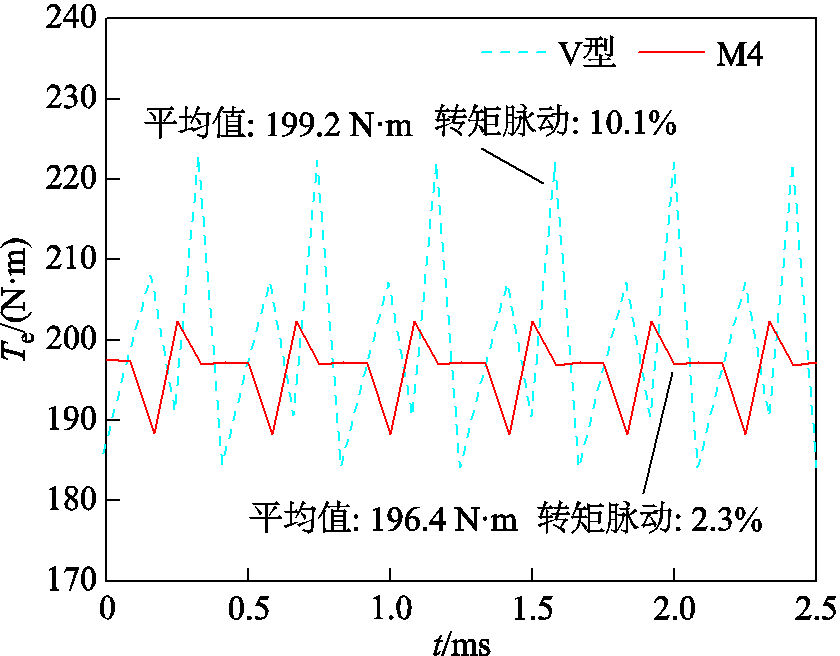
图16 电磁转矩对比曲线
Fig.16 Electromagnetic torque comparison curves
两台电机的径向电磁力对比如图17所示，M4拓扑的径向电磁力幅值明显下降，从源头上抑制了电机振动噪声的发生。
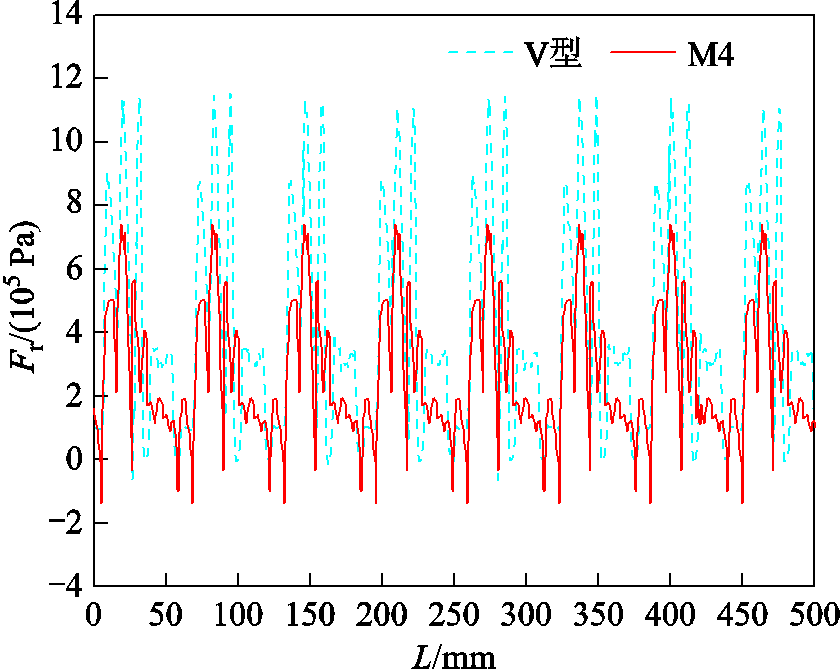
图17 径向电磁力
Fig.17 Radial electromagnetic force
齿槽转矩对比曲线如图18所示，所提结构电机齿槽转矩幅值大幅度降低，从203mN·m下降到 76.4mN·m，从而提高了电机运行的稳定性。综上所述，电机通过拓扑协同的优化方案[20]，在保证电磁转矩输出的基础上，径向电磁力、转矩脉动、齿槽转矩均得到一定程度的抑制。
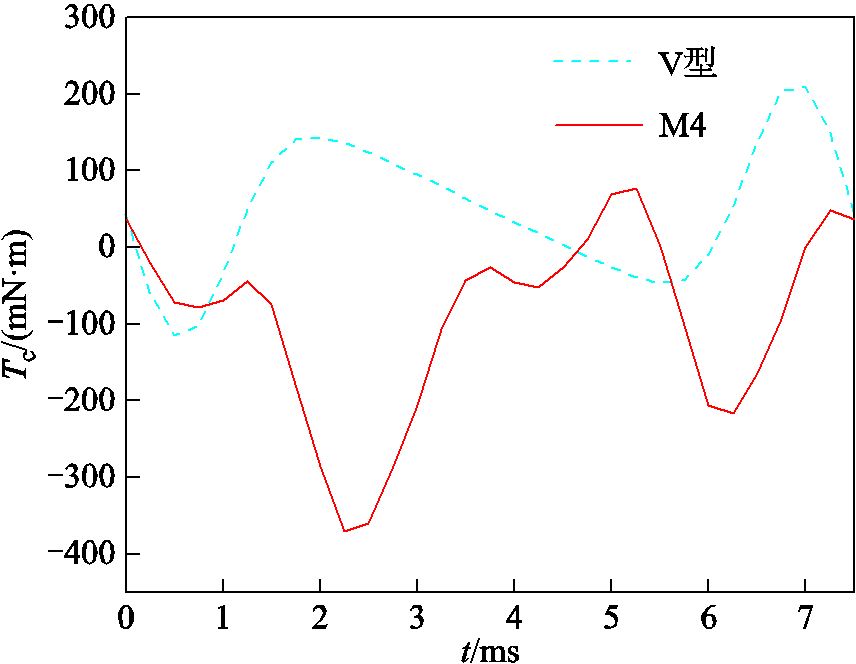
图18 齿槽转矩对比曲线
Fig.18 Cogging torque comparison curves
电机的振动和噪声分析涉及电磁场、机械场与声场的耦合联系，设计了一种多物理场仿真方案如图19所示。对电磁场中的径向电磁力进行空间和时间谐波下的傅里叶分解，并将力波信息作用到定子齿部，径向电磁力给定子齿部施加垂直作用力。将机械场中计算得到的定子振动速度导入到声场中进行分析，并通过反馈优化后，得到最优的电机振动噪声特性[21-24]。
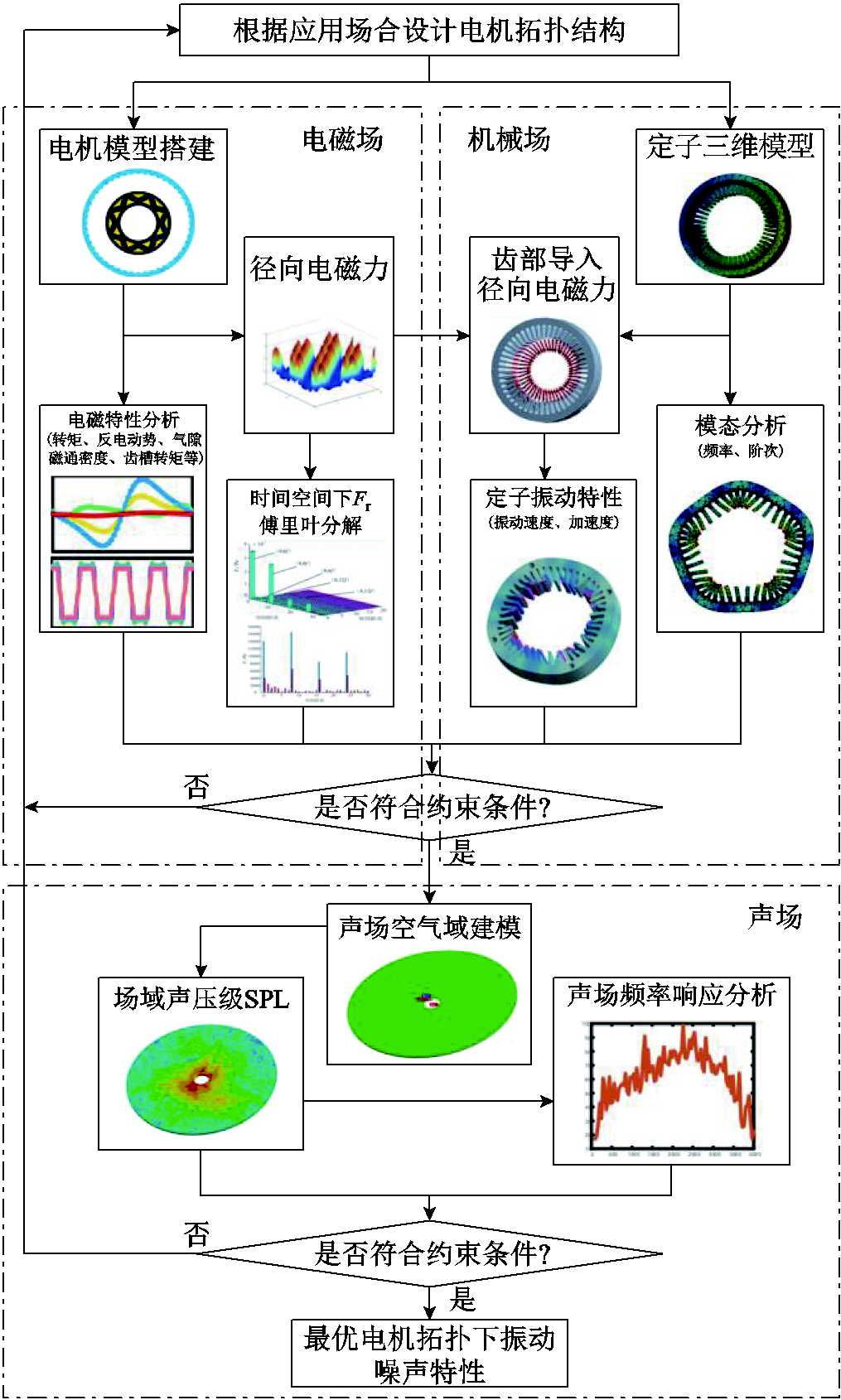
图19 多物理场优化方案
Fig.19 Multi-physical field optimization scheme
电机模态各阶次频率为电机的机械固有频率，电机模态分析结果见表9，在机械场中对电机定子采用无外加约束的方式求解各阶次模态。
表9 电机模态分析结果
Tab.9 Motor modal analysis results
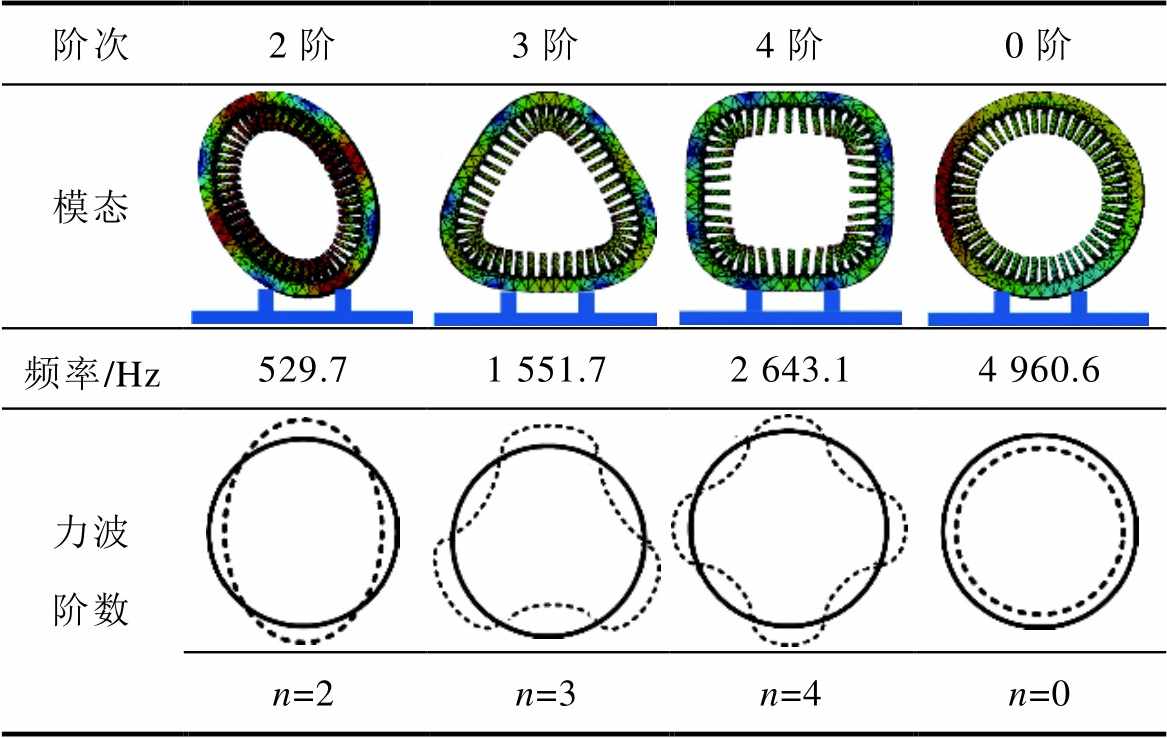
阶次2阶3阶4阶0阶 模态 频率/Hz529.71 551.72 643.14 960.6 力波阶数 n=2n=3n=4n=0
对径向电磁力进行傅里叶分解如图20所示，时间谐波0次下，电磁力幅值较大但由于频率为0 Hz不会对电机产生影响。空间0、8、16阶次和时间谐波6、12次为主要分析对象。由于电机振幅与阶次的4次方呈反比关系，故重点分析空间0阶次和时间6次谐波。
图20 径向电磁力傅里叶分解
Fig.20 Fourier decomposition of radial electromagnetic force
如图21所示为M0和M4拓扑电机在空间0阶下的傅里叶分解。从M4曲线可得，整体的各阶电磁力幅值大幅度降低，6阶的幅值为5 kPa，12阶的幅值下降率为91%。时间谐波6次下的傅里叶分解如图22所示。M4拓扑的空间8阶、16阶次的幅值均小于M0拓扑结构。
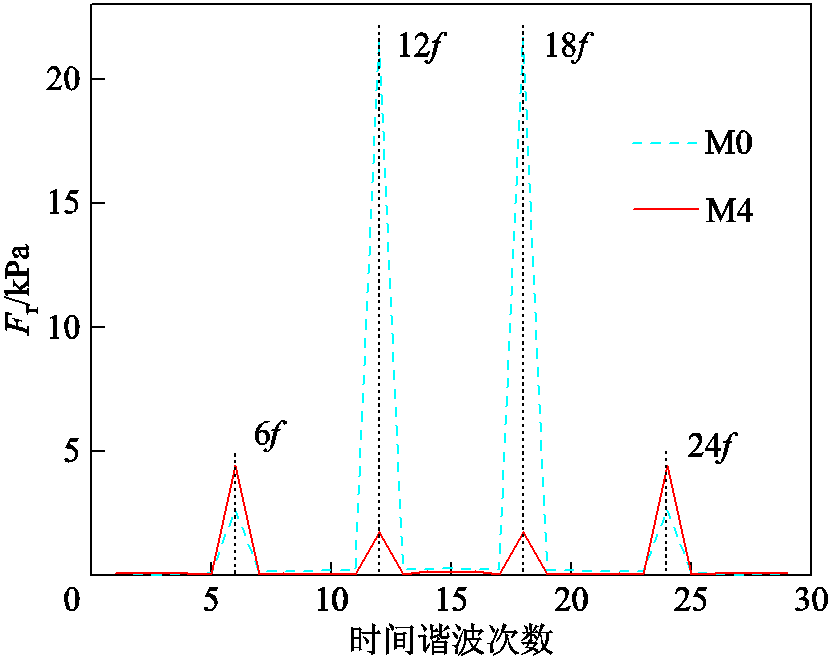
图21 空间0阶的径向电磁力
Fig.21 Radial electromagnetic force of order 0 in space
图22 时间6次谐波的径向电磁力对比
Fig.22 Radial electromagnetic force comparison of time 6th harmonics
如图23a、图23b所示为2 400 Hz频率下，M4和V型两台IPMSM的机械场定子齿部振幅表现，M4电机的最大振幅为76 nm，发生在齿部最前端，相较于V型电机的最大振幅121 nm，下降率为37.2%。电机径向电磁力经定子齿部传递给机壳，后者通过空气域向外界辐射噪声，在电机周围1 m的范围内搭建如图23c～图23f所示的声场空气域模型，M4电机的噪声声压级传递明显小于V型电机，2 400 Hz下两者的噪声平均值分别为80.7、68 dB， 4 800 Hz下两者的噪声平均值分别为110、85.5 dB。计算V型和M4型电机在基频400～4 800 Hz区间内的平均噪声值Lv分别为90.1、76.6 dB，见表10，噪声平均值的下降率为15%。表10中，Vs为2 400 Hz下定子齿部的振动幅值，Lv为400～4 800 Hz下噪声的平均值。
图23 振动幅值和声压级对比
Fig.23 Comparison of vibration amplitude and sound pressure level
表10 V型、M4电机对比分析结果
Tab.10 Comparative analysis results of V-type and M4 motors
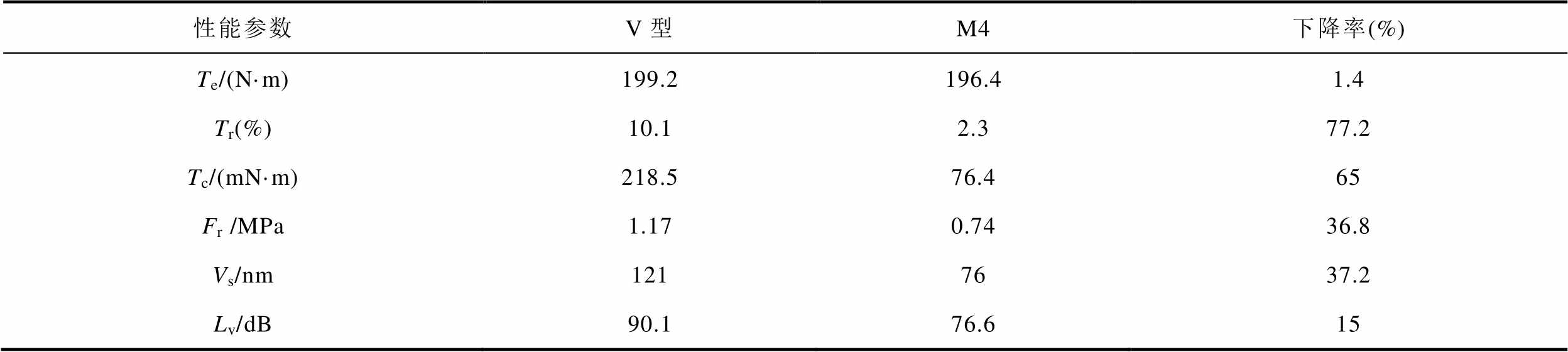
性能参数V型M4下降率(%) Te/(N·m)199.2196.41.4 Tr(%)10.12.377.2 Tc/(mN·m)218.576.465 Fr /MPa1.170.7436.8 Vs/nm1217637.2 Lv/dB90.176.615
对比普通V型内置式永磁同步电机和优化后“一+V”型M4电机的多物理场性能，由表10可知，后者在保证转矩输出的基础上，抑制了IPMSM的振动噪声特性，定子齿部振幅和噪声均值下降率分别为37.2%和15%。相较于传统的V型IPMSM拓扑结构，“一+V”型IPMSM具有更大的优化设计优势，通过永磁体之间的相互配合，“一”型永磁体采用分段式结构，“V”型永磁体采用Halbach充磁方式，同时使用钕铁硼和铁氧体的混合永磁体结构，使IPMSM的多物理场综合表现更加优异。
电机转子的机械强度稳定性对于电机设计至关重要，转子和永磁体材料属性见表11，对转子与永磁体进行机械结构的应力分析。转子永磁体所采用的装配方式为过盈方式，通过Workbench的偏移量offset设置为0.05 mm，正值代表过盈配合，负值代表间隙配合。在额定转速下，转子和永磁体所承受的等效应力如图24所示，其中转子承受的最大等效应力达到0.726 MPa，这一数值显著低于硅钢片的450 MPa屈服强度；钕铁硼与铁氧体永磁体所承受的等效应力的最大值分别为0.22、0.25 MPa，远小于永磁体的抗拉屈服强度。
表11 转子材料属性
Tab.11 rotor material properties
材料属性硅钢片钕铁硼铁氧体 密度/(kg/m3)7 6007 4004 600 泊松比0.310.30.33 屈服强度/MPa45080100
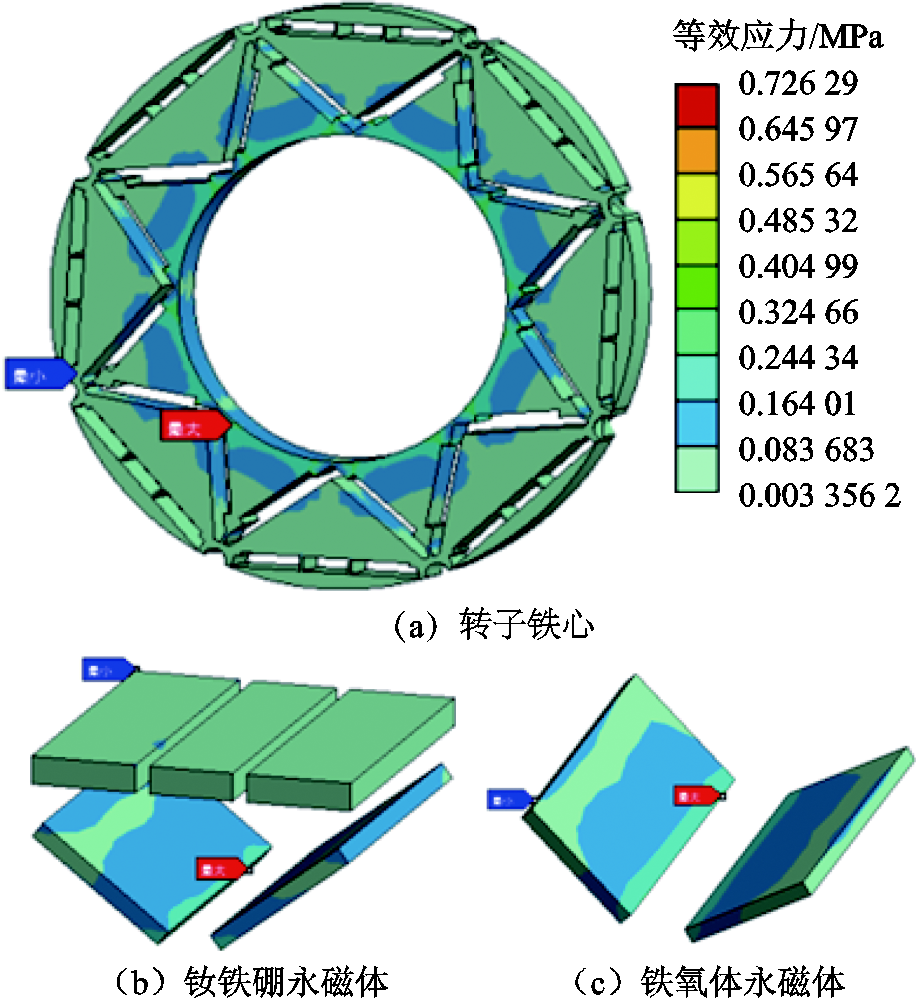
图24 转子等效应力
Fig.24 Rotor equivalent stresst
转子在运行过程中自身硅钢片结构和永磁体之间会产生力的作用，通过对整个转子结构的等效应力仿真可得转子存在两个危险截面如图25a所示，截面1为转子磁障面，截面2为V型永磁体底部与转子受力面。通过分别对两个危险截面进行等效应力仿真可得，截面1的最大等效应力为0.72 MPa，截面2的最大等效应力为0.69 MPa，且两个危险截面的应力分布较为均匀，等效应力分布符合屈服强度要求。
转子总变形如图26所示，转子在运行过程中受切向离心力与电磁力的共同作用，最大形变位置在转子的最外侧为0.016 μm，而永磁体内侧的形变量最大为0.011 μm；其中V型永磁体的形变量小于一型永磁体，因为V型永磁体更靠近转轴内侧，而最大形变发生在转子外侧切线方向[25-26]。
图25 转子危险截面
Fig.25 Rotor danger section
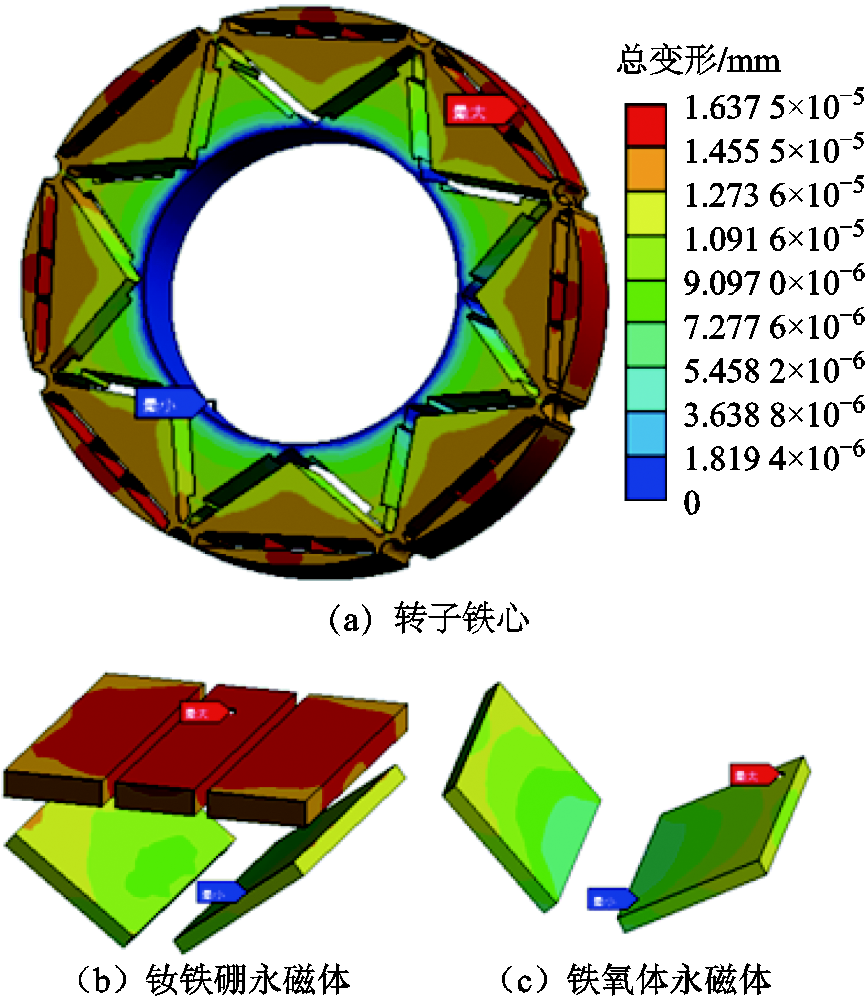
图26 转子总变形
Fig.26 Total rotor deformation
1）提出一种定转子开辅助槽、转子采用钕铁硼和铁氧体混合永磁体，同时“一”型永磁体分段Halbach充磁方式的“一+V”型内置式永磁同步电机拓扑结构，利用电机拓扑协同分层优化的方法，优化后电机电磁转矩降低了3.2%，转矩脉动下降率为76.3%，径向电磁力下降率为30.8%，齿槽转矩下降到76.4mN·m。
2）所提电机结构与普通V型IPMSM进行对比，各阶次径向电磁力大幅降低，定子最大振动幅值为76 nm，降低了37.2%，噪声声压级平均值下降到76.6 dB，下降率为15%。
3）通过铁氧体和钕铁硼永磁体相混合的方式，可以大幅降低电机成本，同时电磁转矩下降率保持在5%范围内。
4）在额定转速下，转子及永磁体所受等效应力远小于屈服强度，电机机械结构强度符合允许的范围值。
所提出的电机拓扑协同优化方案可以广泛应用于各类电机结构，提高电机优化的效率与精度。
参考文献
[1] 唐任远. 现代永磁电机: 理论与设计[M]. 北京: 机械工业出版社, 1997.
[2] 陈永校. 电机噪声的分析和控制[M]. 杭州: 浙江大学出版社, 1987.
[3] Deng Wenzhe, Zuo Shuguang, Chen Wei, et al. Comparison of eccentricity impact on electromagnetic forces in internal- and external-rotor permanent magnet synchronous motors[J]. IEEE Transactions on Transportation Electrification, 2022, 8(1): 1242-1254.
[4] Liang Wenyi, Wang Jianfeng, Luk P C K, et al. Analytical study of stator tooth modulation on electromagnetic radial force in permanent magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 11731-11739.
[5] Liang Jianbin, Callegaro A D, Bilgin B, et al. A novel three-dimensional analytical approach for acoustic noise modeling in switched reluctance machines[J]. IEEE Transactions on Energy Conversion, 2021, 36(3): 2099-2109.
[6] Yang S J. Low-noise electrical motors[M]. Oxford: Oxford Clarendon Press, 1981.
[7] 陈永校, 诸福磊, 应善成. 电机噪声的分析和控制[M]. 杭州: 浙江大学出版社, 1987.
[8] 张冉, 王秀和, 乔东伟, 等. 基于辅助槽的永磁电机激振力波削弱方法[J]. 中国电机工程学报, 2010, 30(18): 103-108.
Zhang Ran, Wang Xiuhe, Qiao Dongwei, et al. Reduction of exciting force wave for permanent magnet motors by teeth notching[J]. Proceedings of the CSEE, 2010, 30(18): 103-108.
[9] 谢颖, 李飞, 黎志伟, 等. 内置永磁同步电机减振设计与研究[J]. 中国电机工程学报, 2017, 37(18): 5437-5445, 5543.
Xie Ying, Li Fei, Li Zhiwei, et al. Optimized design and research of vibration reduction with an interior permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2017, 37(18): 5437-5445, 5543.
[10] 王晓远, 贺晓钰, 高鹏. 电动汽车用V型磁钢转子永磁电机的电磁振动噪声削弱方法研究[J]. 中国电机工程学报, 2019, 39(16): 4919-4926, 4994.
Wang Xiaoyuan, He Xiaoyu, Gao Peng. Research on electromagnetic vibration and noise reduction method of V type magnet rotor permanent magnet motor electric vehicles[J]. Proceedings of the CSEE, 2019, 39(16): 4919-4926, 4994.
[11] 李晓华, 赵容健, 田晓彤, 等. 逆变器供电对电动汽车内置式永磁同步电机振动噪声特性影响研究[J]. 电工技术学报, 2020, 35(21): 4455-4464.
Li Xiaohua, Zhao Rongjian, Tian Xiaotong, et al. Study on vibration and noise characteristics of interior permanent magnet synchronous machine for electric vehicles by inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4455-4464.
[12] 孔令星. 基于kriging算法的直线感应电机多目标优化设计研究[D]. 成都: 西南交通大学, 2018: 35-43.
Kong Lingxing. Research on multi-objective optimization design of linear induction motor based on kriging algorithm[D]. Chengdu: Southwest Jiaotong University, 2018: 35-43.
[13] 曹永娟, 冯亮亮, 毛瑞, 等. 轴向磁场永磁记忆电机多目标分层优化设计[J]. 中国电机工程学报, 2021, 41(6): 1983-1992.
Cao Yongjuan, Feng Liangliang, Mao Rui, et al. Multi-objective stratified optimization design of axial-flux permanent magnet memory motor[J]. Proceedings of the CSEE, 2021, 41(6): 1983-1992.
[14] 林玥兵, 郑晓钦, 陈春涛. 正弦削极修正模型的表贴式多相永磁电机模型-数据融合优化设计[J]. 中国电机工程学报, 2024, 44(增刊1): 296-305.
Lin Yuebin, Zhen Xiaoqin, Chen Chuntao. Model and data complementary optimization design of surface mounted multiphase permanent magnet motors based on sinusoidal poling modified model[J]. Proceedings of the CSEE, 2024, 44(S1): 296-305..
[15] 华逸舟, 刘奕辰, 潘伟, 等. 基于改进粒子群算法的无轴承永磁同步电机多目标优化设计[J]. 中国电机工程学报, 2023, 43(11): 4443-4452.
Hua Yizhou, Liu Yichen, Pan Wei, et al. Multi-objective optimization design of bearingless permanent magnet synchronous motor using improved particle swarm optimization algorithm[J]. Proceedings of the CSEE, 2023, 43(11): 4443-4452.
[16] Song Juncai, Dong Fei, Zhao Jiwen. An efficient multiobjective design optimization method for a PMSLM based on an extreme learning machine[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1001-1011.
[17] 赵耀, 徐笠, 李东东, 等. 五相混合励磁双凸极电机多目标分层分期优化设计[J]. 电工技术学报, 2024, 39(22): 7045-7058.
Zhao Yao, Xu Li, Li Dongdong, et al. Multi-objective layered and phased optimization design of five phase hybrid-excited double salient machine[J]. Transactions of China electrotechnical Society, 2024, 39(22): 7045-7058.
[18] Zhu Xiaoyong, Huang Juan, Quan Li, et al. Comprehensive sensitivity analysis and multiobjective optimization research of permanent magnet flux-intensifying motors[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2613-2627.
[19] Deng Wenzhe, Zuo Shuguang. Comparative study of sideband electromagnetic force in internal and external rotor PMSMs with SVPWM technique[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 956-966.
[20] 高锋阳, 高建宁, 李明明, 等. 内置式Halbach永磁同步电机的参数敏感度分层优化设计[J]. 西安交通大学学报, 2022, 56(5): 180-190.
Gao Fengyang, Gao Jianning, Li Mingming, et al. Optimization design of Halbach interior permanent magnet synchronous motor based on parameter sensitivity stratification[J]. Journal of Xi’an Jiaotong University, 2022, 56(5): 180-190.
[21] 李泽星, 夏加宽, 刘铁法, 等. 基于分段交错不等磁极的表贴式永磁电机极频振动的削弱[J]. 电工技术学报, 2023, 38(4): 945-956.
Li Zexing, Xia Jiakuan, Liu Tiefa, et al. Reduction of pole-frequency vibration of surface-mounted permanent magnet synchronous machines with piecewise stagger unequal poles[J]. Transactions of China Electro-technical Society, 2023, 38(4): 945-956.
[22] 鲍晓华, 明帅, 陈国玮, 等. 变频驱动下双斜槽转子感应电机径向电磁力特性分析[J]. 电工技术学报, 2023, 38(10): 2613-2624.
Bao Xiaohua, Ming Shuai, Chen Guowei, et al. Analysis of radial electromagnetic force characteristics of inverter drive double skewed rotor induction motor[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2613-2624.
[23] 刘壮, 韩雪岩, 高俊. 基于热固耦合的高速永磁电动机转子强度分析[J]. 电气技术, 2021, 22(5): 1-5, 101.
Liu Zhuang, Han Xueyan, Gao Jun. Strength analysis of high-speed permanent magnet motor rotor based on thermo-solid coupling[J]. Electrical Engineering, 2021, 22(5): 1-5, 101.
[24] 李玮, 汪泽润, 张凤阁. 基于FEM/Kriging近似模型结合进化算法的表贴式高速永磁电机转子强度优化[J]. 电工技术学报, 2023, 38(4): 936-944, 956.
Li Wei, Wang Zerun, Zhang Fengge. Rotor strength optimization of surface mount high speed permanent magnet motor based on FEM/Kriging approximate model and evolutionary algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 936-944, 956.
[25] 高建宁, 高锋阳, 姚普, 等. 基于敏感度分层优化的Halbach永磁电机电磁振动分析[J]. 哈尔滨工业大学学报, 2024, 56(7): 142-153.
Gao Jianning, Gao Fengyang, Yao Pu, et al. Electromagnetic vibration analysis of Halbach permanent magnet motor based on sensitivity stratification optimization[J]. Journal of Harbin Institute of Technology, 2024, 56(7): 142-153.
[26] 刘栋良, 詹成根, 屈峰, 等. 无人机17 kW电机振动噪声分析与巡航转速下尖端噪声优化[J]. 电工技术学报, 2024, 39(6): 1749-1763.
Liu Dongliang, Zhan Chenggen, Qu Feng, et al. Vibration noise analysis and tip noise optimization of unmanned aerial vehicle 17 kW motor at cruise speed[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1749-1763.
Topology Cooperative Optimization Design of Halbach Interior Permanent Magnet Synchronous Motor Considering Vibration and Noise Suppression
Abstract Addressing the problem of severe electromagnetic oscillations and disturbances in the synchronous motor of an internal permanent magnet, a kind of motor topology with auxiliary slots in fixed rotor is proposed. Composed of NdFeB and a ferrite mixed permanent magnet, the rotor functions in the Halbach magnetization setting of the permanent magnet section. Firstly, the resolution of the analytical depiction of motor vibration noise resulted in the development of a finite element motor model. Secondly, the suggestion is made for a joint optimization approach in motor topology, integrating parameter sensitivity analysis with the response surface technique. Taking into account the interplay among topological parameters, the optimization of topological structure parameters is conducted as per the suggested approach. Subsequently, the refined motor undergoes a multi-physical field coupling simulation, employing electromagnetic, mechanical, and acoustic fields to capture its vibration and noise characteristics. Comparisons are made between the outcomes of the stator's peak vibration amplitude and the level of noise sound pressure and those from the V-type internal permanent magnet motor. The results suggest that the proposed model can diminish the torque ripple, slot torque, and the intensity of the radial electromagnetic force, based on its ability to ensure the electromagnetic torque, thereby diminishing the motor's vibration intensity and noise pressure intensity. To confirm the motor structure's logic, the rotor's equivalent stress and total deformation in the mechanical field are computed.
Firstly, motor rotor topology parameters are intricate, and conventional single structure optimization frequently culminates in an optimization goal, challenging to assess the efficacy of several motors. The optimization of single topological structure parameters will change the specific motor performance objectives, and the coupling optimization of multiple structure parameters will have nonlinear effects on the motor performance owing to alterations in the magnetic field environment of the air gap. Therefore, it is particularly important to consider the synergistic coupling effect of multiple topological parameters on the optimization objective. Simulations of the stator surface's vibration speed and amplitude are conducted within the mechanical environment. Concurrently, the surface's vibrational speed is incorporated into the sound field model, and a model simulating the spread of sound pressure levels due to noise within the air domain, within a 1 m radius of the motor, is conducted. Finally, the data are compared and analyzed to obtain the optimal vibration and noise characteristics of the motor.
Aiming at the vibration and noise problem of IPMSM, a topology cooperative optimization scheme combining parameter sensitivity layering and response surface method is proposed in this paper. Initially, the study delves into the theoretical aspects of motor vibration and noise, leading to the construction of a finite element simulation model for motors. Then a hierarchical collaborative optimization method is adopted for multiple topology optimization parameters.Additionally, simulations and analyses of the optimized motor structure's vibration and noise are conducted in a multi-physics field, and juxtaposed with a V-type IPMSM motor. Ultimately, the steadiness of the motor's framework has been confirmed within the machine field.
Keywords：Interiorpermanent magnet synchronous motor, Halbach permanent magnet, radial electromagnetic force, vibration noise
中图分类号：TM301.4
DOI: 10.19595/j.cnki.1000-6753.tces.L11031
国家自然科学基金资助项目（52275009, 52207038）。
收稿日期 2024-07-12
改稿日期 2024-08-13
高建宁 男，1998年生，博士研究生，研究方向为永磁电机的多目标优化设计多物理场分析、电机控制算法。
E-mail：230238838@seu.edu.cn
徐 炜 男，1982年生，教授，博士生导师，研究方向为新能源汽车电驱系统的建模、设计及控制等。
E-mail：weixu@seu.edu.cn（通信作者）
（编辑 崔文静）