考虑屏蔽套失效的主泵电机建模及性能分析
刘能青1 向学位1 陈 智2 李 辉1 蒋 鹏1
(1.输变电装备技术全国重点实验室(重庆大学) 重庆 400044 2. 中国核动力研究设计院核反应堆系统设计技术重点实验室 成都 610213)
摘要 屏蔽套是主泵电机的关键部件,由于屏蔽套受到多种应力作用容易发生失效及难以加装相关传感器观测屏蔽套状态,因此研究屏蔽套失效对主泵电机性能的影响很重要。目前,缺乏相关屏蔽套失效模型和失效对主泵电机性能的影响分析,该文提出了考虑屏蔽套失效的主泵电机建模及性能影响分析方法。首先,考虑屏蔽套鼓包、磨损与破裂三种常见失效模式,分别建立有限元模型,分析不同失效模式和失效程度对主泵电机电磁转矩、定子绕组电流、气隙磁通密度、反电动势和屏蔽套涡流损耗等性能的影响规律;其次,针对失效对屏蔽套涡流损耗的影响,提出考虑不同失效模式的屏蔽套涡流损耗计算解析式;最后,对屏蔽套不同失效模式和失效程度的性能变化进行比较分析。结果表明,屏蔽套失效对主泵电机涡流损耗的影响较为明显,对主泵电机的其他性能影响不明显;考虑不同屏蔽套失效涡流损耗解析计算方法是有效的,屏蔽套上的涡流损耗与屏蔽套失效的程度呈线性关系。
关键词:屏蔽套 主泵电机 失效模拟 性能分析 涡流损耗
0 引言
主泵屏蔽套是主泵电机中一个至关重要的部件,主要由哈氏合金C-276材料制成,具有良好的耐腐蚀性和机械性能。其主要功能是隔离电机定子、转子与反应堆冷却剂介质,确保主泵电机在高温高压环境下的正常运行,是主泵电机的核心部件之一。由于屏蔽套在运行过程中会受到高温高压冷却剂、电磁力及工况变化的综合作用,容易发生膨胀变形、磨损和破裂等失效现象。屏蔽套工作在高温高压以及空间狭小的环境中,并且难以加装相关的传感器监测其运行状态。据不完全统计,屏蔽套失效的故障数量约占主泵总故障次数的35%。屏蔽套作为主泵屏蔽电机的关键组件,其失效不仅会直接影响电机的性能,还可能对主泵的整体安全运行构成重大威胁。屏蔽套失效可能导致主泵电机发生一系列问题,屏蔽套破裂和磨损可能导致冷却剂泄漏,影响电机的冷却效率,进而导致电机过热,甚至引发火灾或爆炸。屏蔽套鼓包失效可能引发转子与定子之间的机械摩擦,导致电机部件的机械磨损和损坏,进一步增加维修成本和停机时间。这些失效模式不仅会直接影响主泵电机的性能和寿命,还可能导致更严重的设备故障和安全隐患;屏蔽套失效可能导致主泵电机内部涡流损耗变化,进而影响主泵电机的效率和稳定性[1-2]。当前,屏蔽套失效对主泵电机性能的影响尚未得到充分研究。鉴于其在核电站等关键设施中的应用,亟需一套有效的模型和分析方法来评估屏蔽套故障对主泵电机性能的影响,从而为故障预测和预防提供理论依据。
目前,针对主泵电机的性能和涡流损耗研究,都是从设计的角度考虑的,没有考虑屏蔽失效导致的主泵电机性能变化。其中,针对主泵电机的涡流损耗的计算方法研究较多,主要分为解析法、有限元法、有限元与解析结合法。文献[3]首先提出了屏蔽套上的涡流损耗解析计算方法,并采用了经验系数修正计算结果。文献[4]提出了通过减小定子铁心内径和降低气隙磁通密度的方法降低屏蔽套涡流损耗。文献[5]研究了屏蔽套采用不同材料对损耗、磁化电流等性能的影响规律。文献[6]提出了一种永磁屏蔽电机屏蔽套效应的解析模型,分析了屏蔽套厚度和材料对屏蔽电机的性能和损耗的影响情况。文献[7]提出了一种基于有限元二维磁场数值分析和麦克斯韦方程组相结合的方法,对主泵电机的屏蔽套涡流损耗进行了分析和计算,这种方法提高了解析法的精度,减少了有限元法的时间。文献[8-9]提出了液浸电机的屏蔽套涡流损耗的理论分析与有限元解析计算方法,详细计算了液浸电机屏蔽套涡流损耗。以上关于屏蔽套涡流损耗的计算方法都是从设计方面考虑的,针对的主泵电机的屏蔽套都是正常的。文献[10-13]分别从屏蔽电动机的运行效率、涡流损耗、功率、运行性能等方面对电机进行了研究。文献[14]提出了用粒子群算法对核主泵电机进行多目标优化设计的方法,提高了主泵电机的优化速度。文献[15]基于AP1000的主泵电机相关参数,完成了主泵电机设计参数对性能的敏感性分析。文献[16-17]基于精确子域法,建立了一个考虑涡流反作用和各次时空谐波的高速永磁同步电机转子涡流损耗解析模型;研究了不同变频器开关频率及气隙长度下,转子屏蔽套上涡流损耗的变化规律。文献[18-20]研究了高速永磁电机的转子屏蔽套、永磁体、电机绕组涡流损耗计算模型,实现了对高速永磁电机涡流损耗的高效计算。文献[21-22]分别采用等效磁路法、解析法、有限元法对笼型实心转子屏蔽感应电机性能进行了分析,并对几种方法分析的结果进行了对比。文献[23]基于薄壁圆柱壳体稳定性理论和屈曲稳定性问题的有限元理论,研究了不同厚度的屏蔽套屈曲稳定性问题。文献[24]对AP1000笼型实心转子屏蔽感应电机的磁场和冷却流场分析,得到了屏蔽套上电磁力的分布情况和流场对定转子屏蔽套的压力。文献[25]对屏蔽式电动机的屏蔽套上的涡流损耗和热应力进行了研究,得到了一种安全可靠的新型移相屏蔽电动机结构。
综上所述,相关领域缺乏对屏蔽套失效后的主泵电机性能变化的系统研究和模型分析。本文正是在这一背景下,提出了对屏蔽套失效的主泵电机进行建模及性能影响分析的方法。首先,考虑屏蔽套鼓包、磨损与破裂三种常见失效模式,分别建立有限元模型,分析了不同失效模式对性能的影响规律;其次,针对屏蔽套失效对屏蔽套涡流损耗的影响,提出了考虑不同失效模式的屏蔽套涡流损耗计算解析式,并与有限元结果进行比较;最后,对屏蔽套不同失效模式和失效程度的影响进行了比较分析。
1 考虑屏蔽套失效的主泵电机有限元建模和分析
1.1 主泵电机有限元建模
为了准确计算主泵电机的性能和涡流损耗,首先通过理论计算初步确定了主泵电机的参数,并建立几何模型;然后分析了定转子及屏蔽套材料,确定了材料属性;最后对网格划分进行了设置,并确定了边界条件与激励设置,从而得到了初步的主泵电机Maxwell二维有限元模型。
通过与有限元结果相对比,设计和优化了主泵电机定子外径、定子内径、定转子槽尺寸和数量等参数,完成了主泵电机参数确定,主泵电机的主要参数见表1。
表1 主泵电机参数
Tab.1 Parameters for main pump canned motor
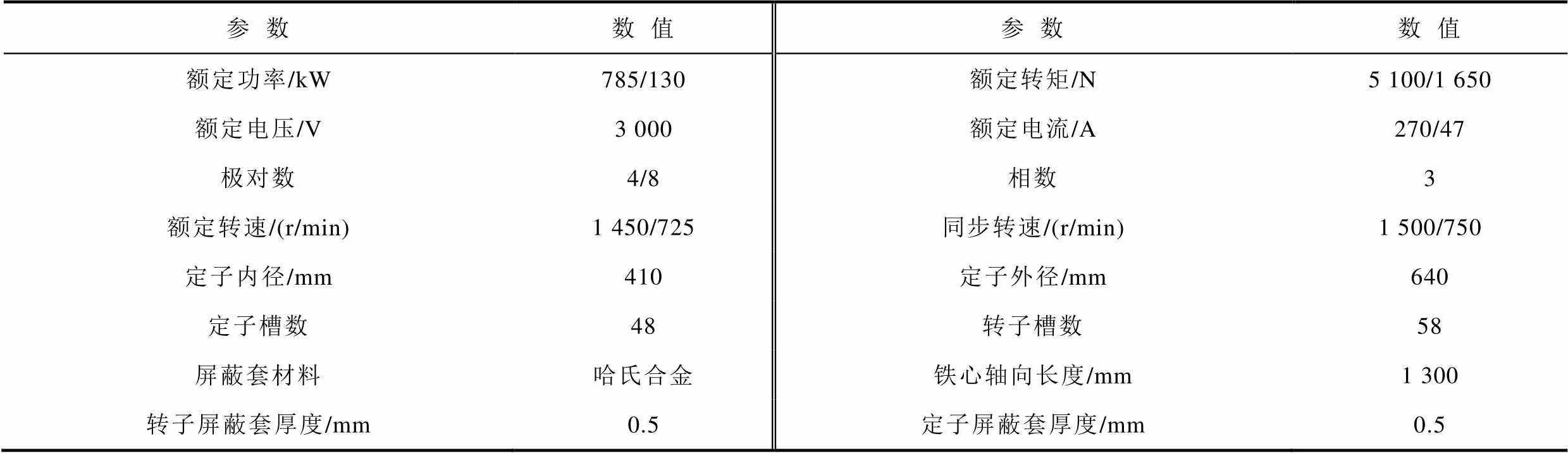
参数数值参数数值 额定功率/kW785/130额定转矩/N5 100/1 650 额定电压/V3 000额定电流/A270/47 极对数4/8相数3 额定转速/(r/min)1 450/725同步转速/(r/min)1 500/750 定子内径/mm410定子外径/mm640 定子槽数48转子槽数58 屏蔽套材料哈氏合金铁心轴向长度/mm1 300 转子屏蔽套厚度/mm0.5定子屏蔽套厚度/mm0.5
图1所示为最终的主泵电机Maxwell二维有限元模型,主泵电机主要包含定子绕组、转子导条、转子铁心、定子铁心、定子屏蔽套和转子屏蔽套。
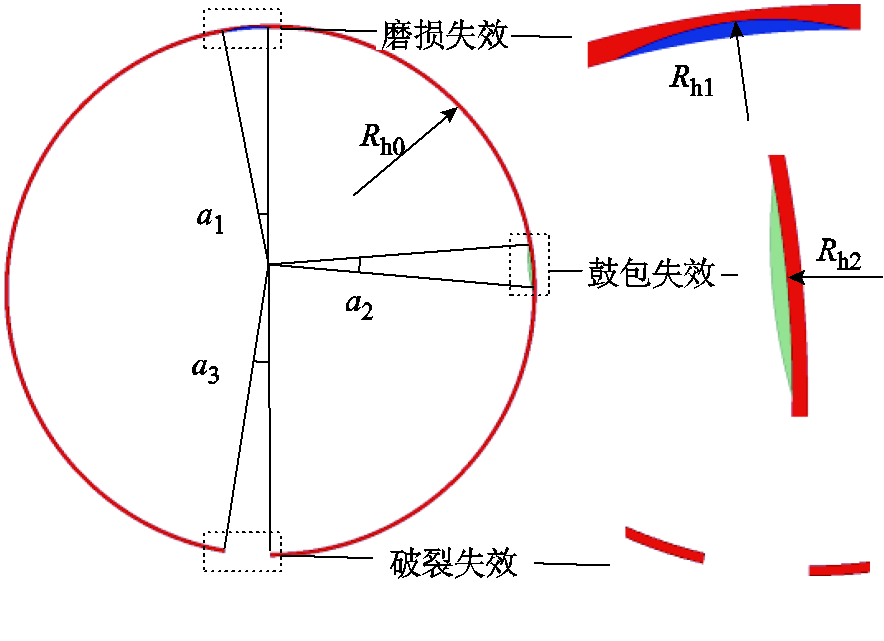
由于电机在实际运行中,定子屏蔽套的失效概率远大于转子屏蔽套失效的概率,因此本文着重针对定子屏蔽套的失效进行了仿真分析。主泵电机屏蔽套在实际运行中常见的失效模式主要有鼓包、磨损、破裂三种。因此,根据实际可能的情况,在Maxwell中利用参数化绘图,分别建立了鼓包、磨损、破裂的定子屏蔽套参数化模型。
定子屏蔽套失效参数化模型如图2所示。屏蔽套磨损失效模型考虑了磨损径向最大位移和磨损占圆周角度两个变量,径向最大位移(ΔR1<0)是指磨损处最大位移处相较于正常时的变化量,它可以表示为ΔR1=Rh1-Rh0,由于定子屏蔽套厚度为 0.5 mm,因此屏蔽套磨损厚度应该小于屏蔽套本身的厚度,故ΔR1的变化范围为0.05~0.45 mm,磨损占圆周角度范围在图中表示为a1变化范围,为1°~50°;屏蔽套鼓包失效模型考虑了鼓包径向最大位移和鼓包占圆周角度两个变量,径向最大位移(ΔR2>0)是指鼓包处最大位移处相较于正常时的变化量,它可以表示为ΔR2=Rh2-Rh0,由于气隙的长度为1.5 mm,因此在定子屏蔽套与转子屏蔽套不发生碰撞情况下,ΔR1的变化范围为0.1~1.4 mm,鼓包占圆周角度的范围表示为a2变化范围,为1°~50°;屏蔽套破裂失效模型则只考虑了破裂的角度一个变量,表示为a3变化范围,为1°~50°。
由于研究的重点是屏蔽套失效对电机性能的影响,因此在使用有限元进行计算时,应该着重关注屏蔽套的网格剖分和屏蔽套上的涡流损耗。为了更加准确地计算屏蔽套失效对主泵电机的影响,应该同时考虑定子和转子屏蔽套的涡流效应,同时为了涡流的计算更加准确,还应该考虑定转子屏蔽套上的趋肤效应并对屏蔽套的网格进行额外加细剖分。在主泵电机运行时,定子屏蔽套上电磁场频率为输入电源的频率f(额定频率),然而转子屏蔽套所处位置的电磁场频率为f1=sf,其中s为转差率。屏蔽套上的涡流趋肤深度[26]为
式中,D为趋肤深度;ω为屏蔽套上电磁场的角频率,ω=2πf;μ和σ分别为屏蔽套的磁导率、电导率。
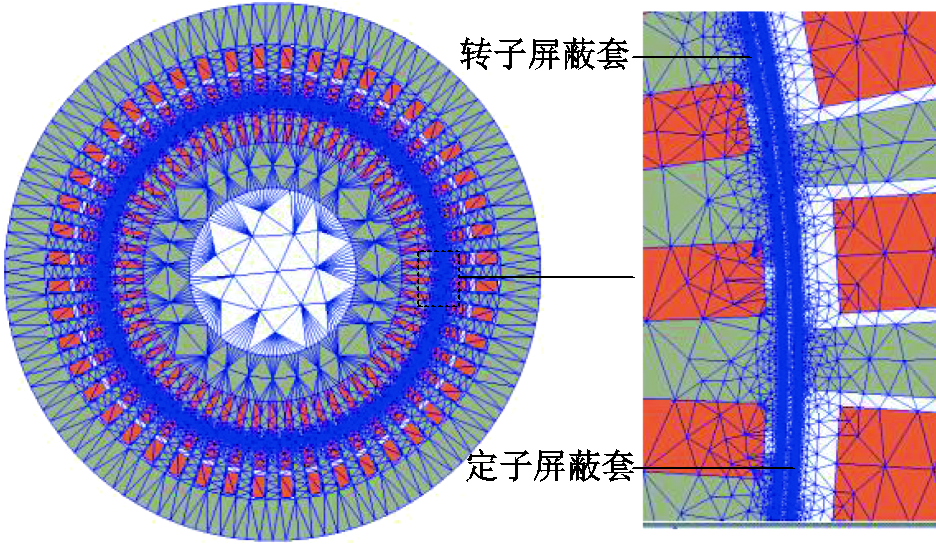
主泵电机二维有限元模型剖分结果如图3所示,对屏蔽套上的网格进行了分层剖分,其中定子屏蔽套被分为4层,转子屏蔽套被分为2层,增加了屏蔽套的网格数量,使计算结果更精确。
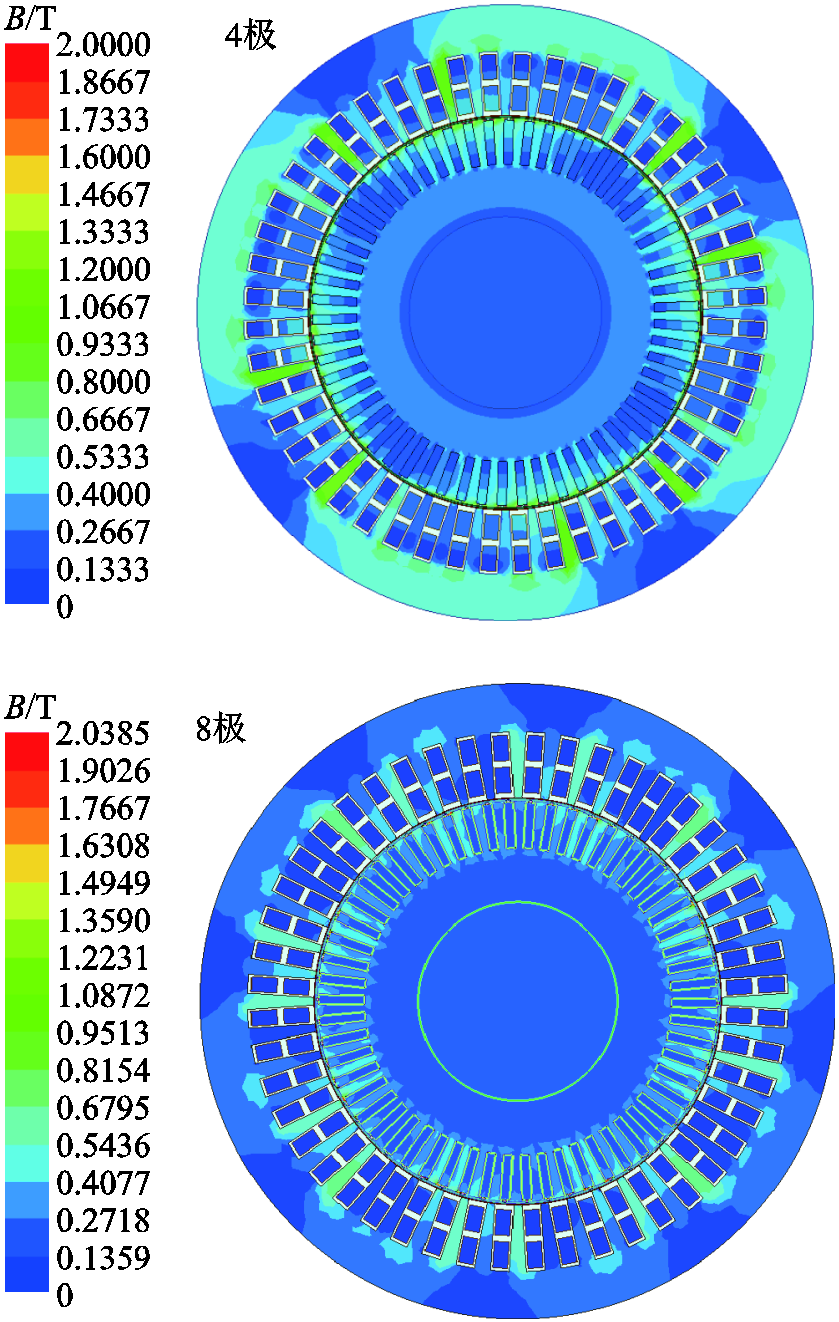
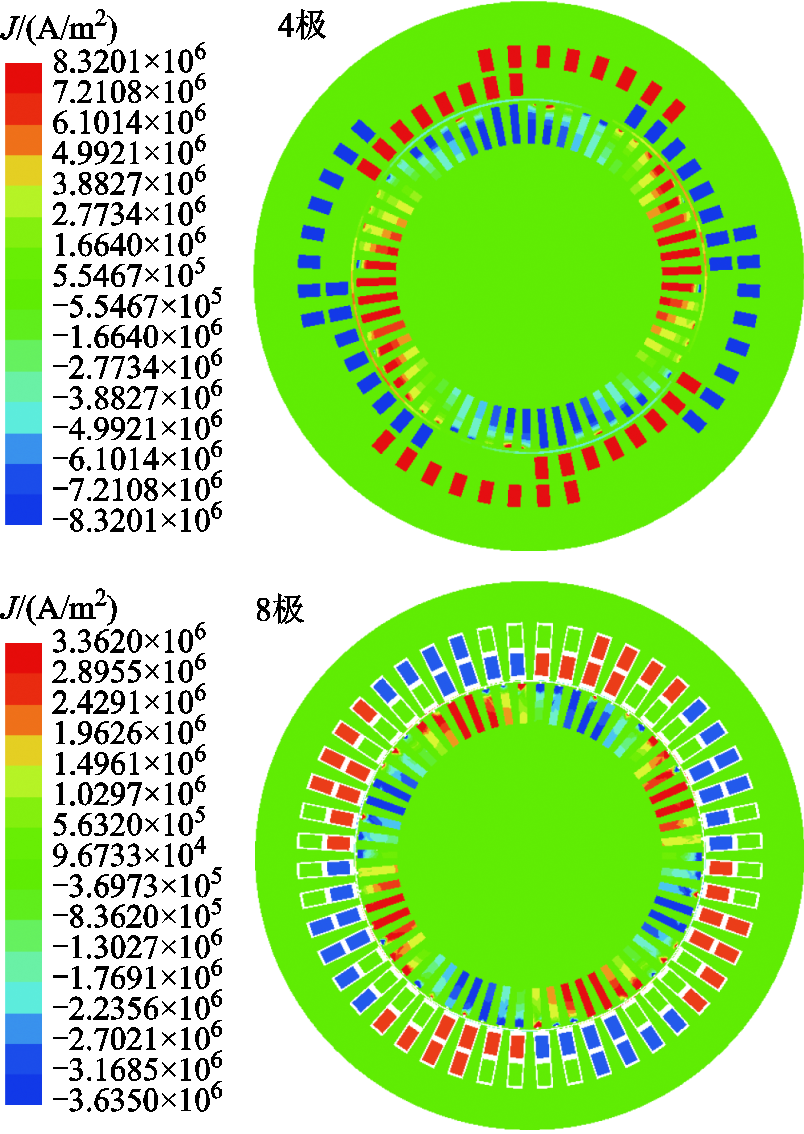
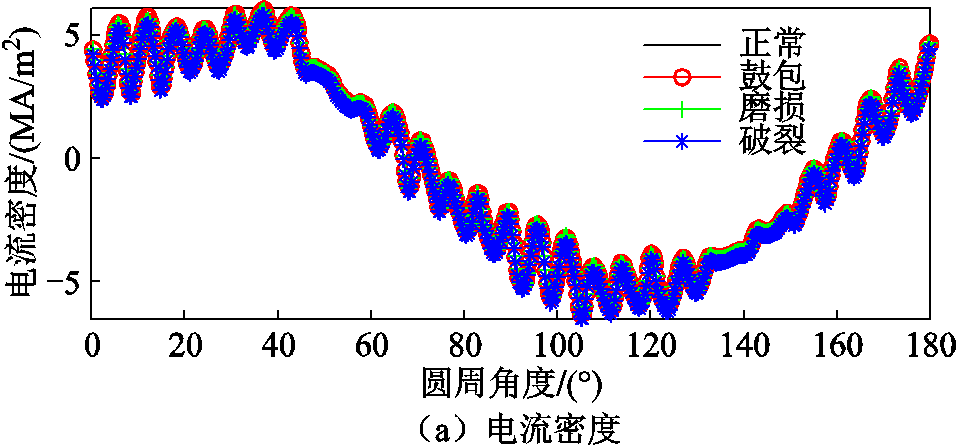
4/8极空载工况下电机磁通密度、电流密度分布云图如图4和图5所示。可以看出,由于此时主泵电机在4极工况下,磁通密度和电流密度的分布是1/2圆对称;在8极工况下,磁通密度和电流密度的分布是1/4圆对称。
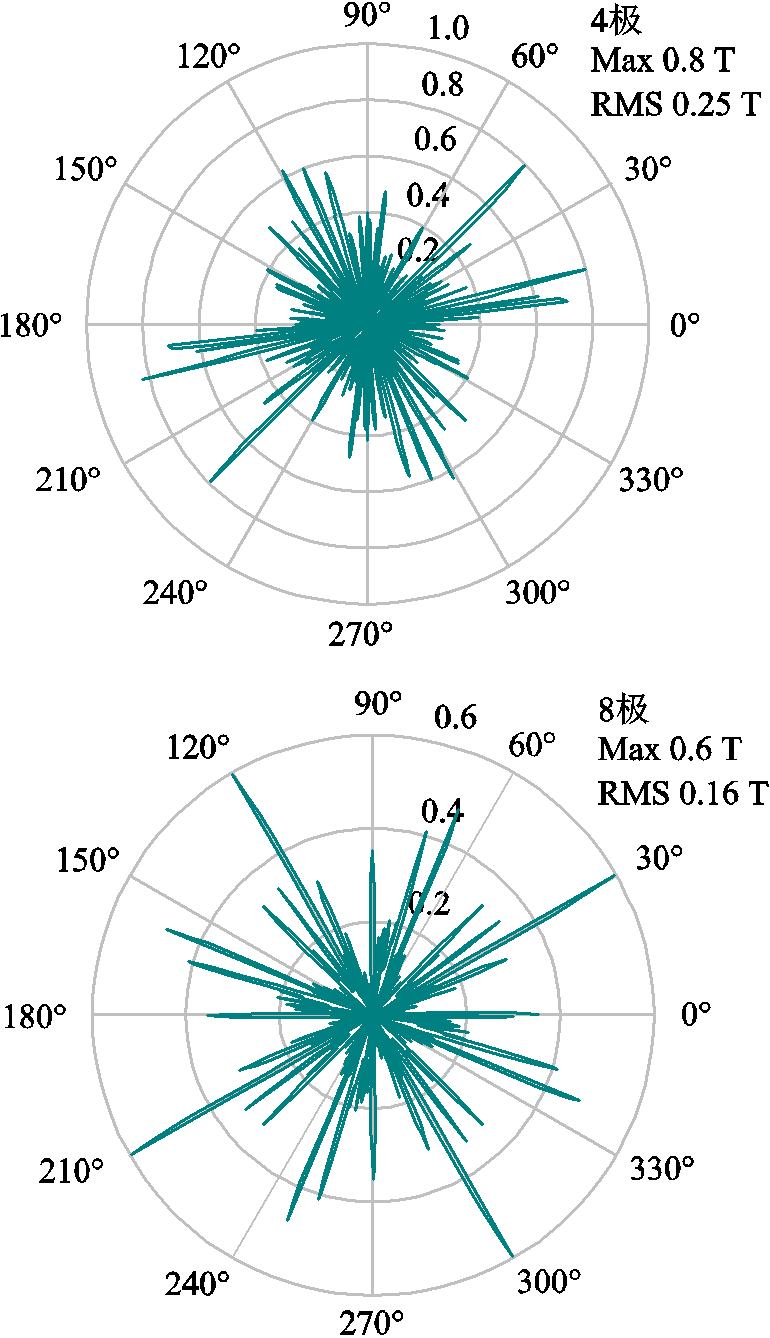
由图6气隙磁通密度计算结果可以看出,4/8极工况下,气隙磁通密度峰值为0.8 T/0.6 T,有效值为0.25 T/0.16 T,符合主泵电机运行的实际情况。从电流密度计算结果可以看出,在转子导条、定转子屏蔽套、定子绕组上都有较大的电流密度,符合实际情况。
1.2 不同失效模式对电机性能影响情况
在建立屏蔽套失效模型和设计完成主泵电机的各个参数以后,建立了定子屏蔽套失效的主泵电机Maxwell模型,计算了主泵电机在不同定子屏蔽套失效情况下的电磁转矩、定子绕组电流、气隙磁通密度、反电动势、涡流损耗和电流密度的变化情况。通过建立的考虑定子屏蔽套失效的主泵屏蔽套模型,分别对鼓包、磨损与破裂三种失效模式进行了有限元计算。
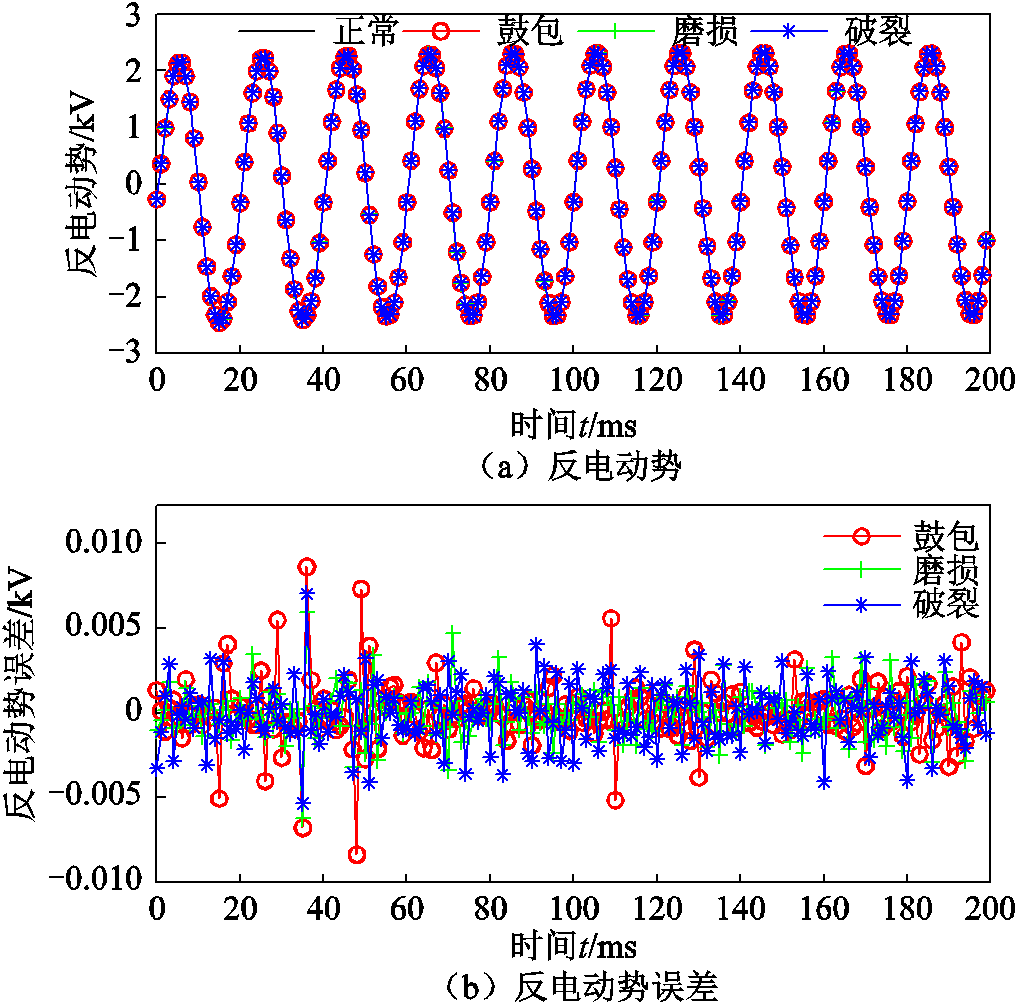
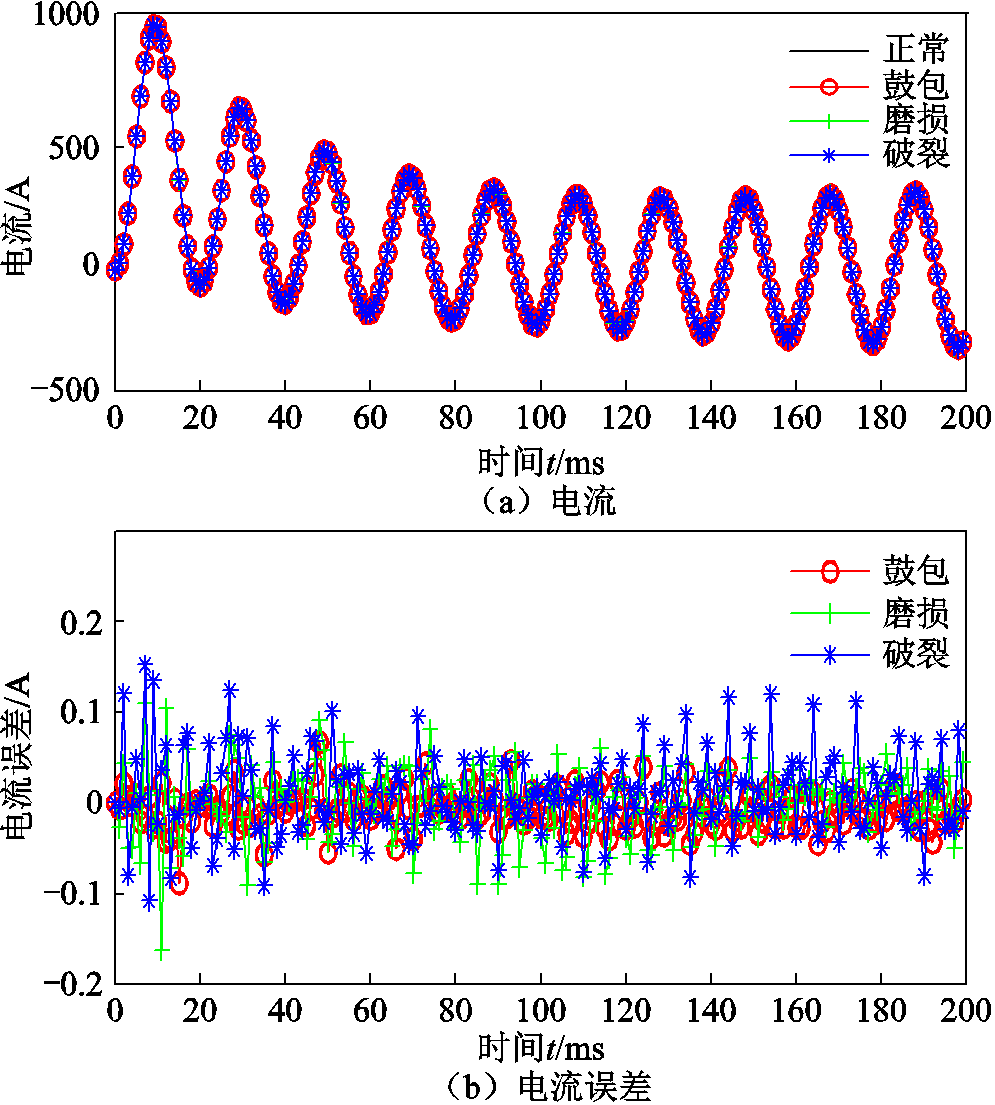
屏蔽套失效与正常时A相反电动势及误差对比、A相电流及误差对比如图7、图8所示。
考虑到三相定子绕组电流和三相反电动势的波形是类似的,这里只展示了A相的定子绕组电流和A相反电动势的误差曲线。从图7和图8可以看出,反电动势误差值集中在-0.005~0.005 kV,反电动势峰值为2.31 kV,定子绕组电流误差集中在-0.1~0.1 A,定子绕组电流峰值为1 000 A,因此说明在定子屏蔽套失效时,电流和反电动势的幅值变化较小;通过观察误差曲线,难以看出这两个性能变化规律。
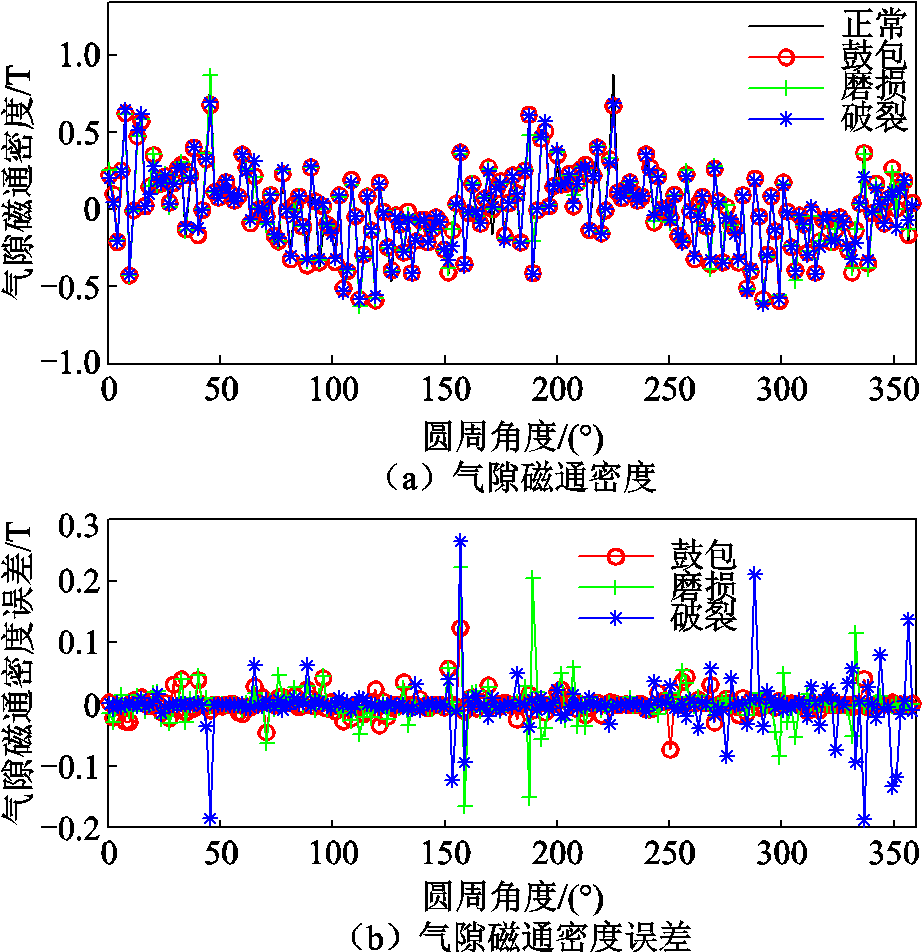
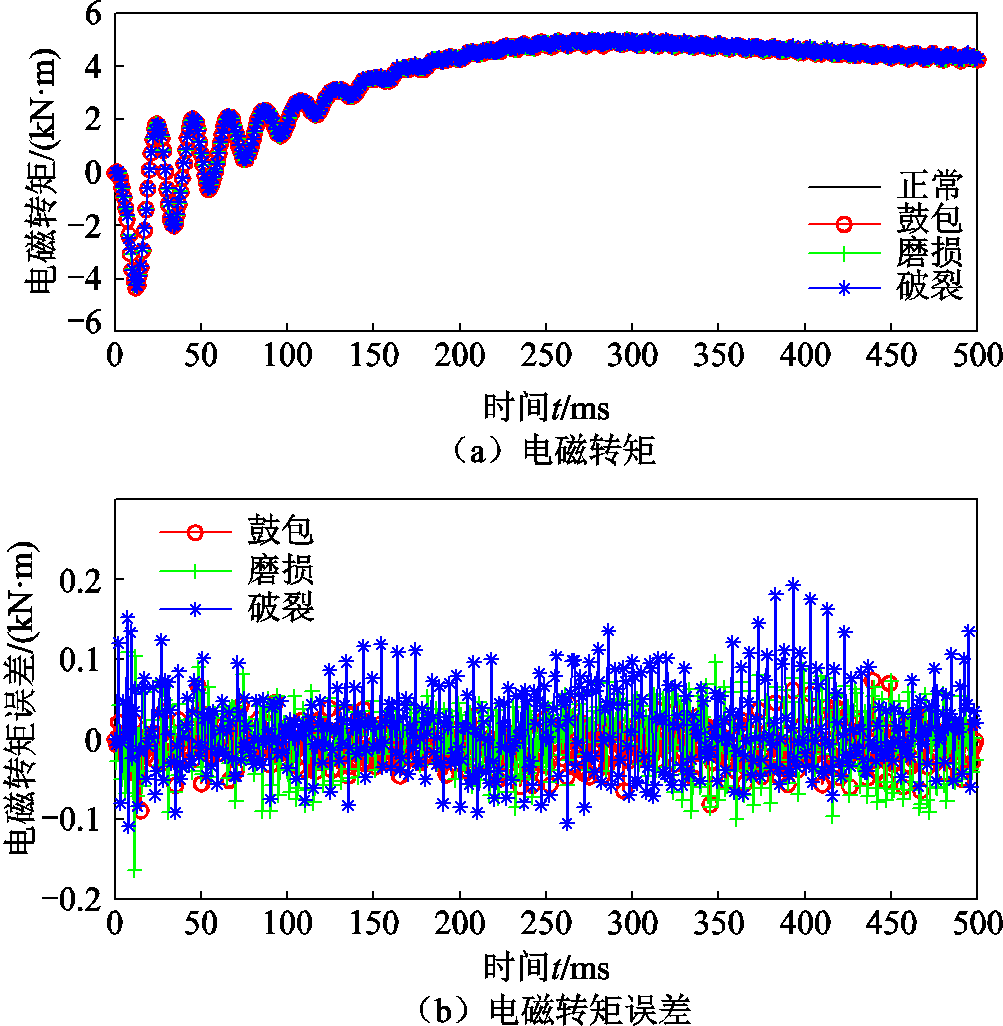
屏蔽套失效和正常时气隙磁通密度及误差对比、电磁转矩及误差对比如图9、图10所示。
从图9和图10可以看出,相较于失效时定子绕组和反电动势的误差曲线,电磁转矩和气隙磁通密度误差曲线变化较大一些;但是从气隙磁通密度误差值的结果来看,破裂和磨损有个别点的变化较大,但是大部分点还是集中在-0.05~0.05 T,电磁转矩大部分的值集中在-0.1~0.1 kN·m,故气隙磁通密度和电磁转矩的变化也较小,同时从误差曲线也难以得到相关规律。
由于屏蔽套失效之后的电磁转矩、气隙磁通密度、定子绕组电流及反电动势变化不明显,又进一步计算了定子屏蔽套上的涡流损耗和电流密度的变化情况。
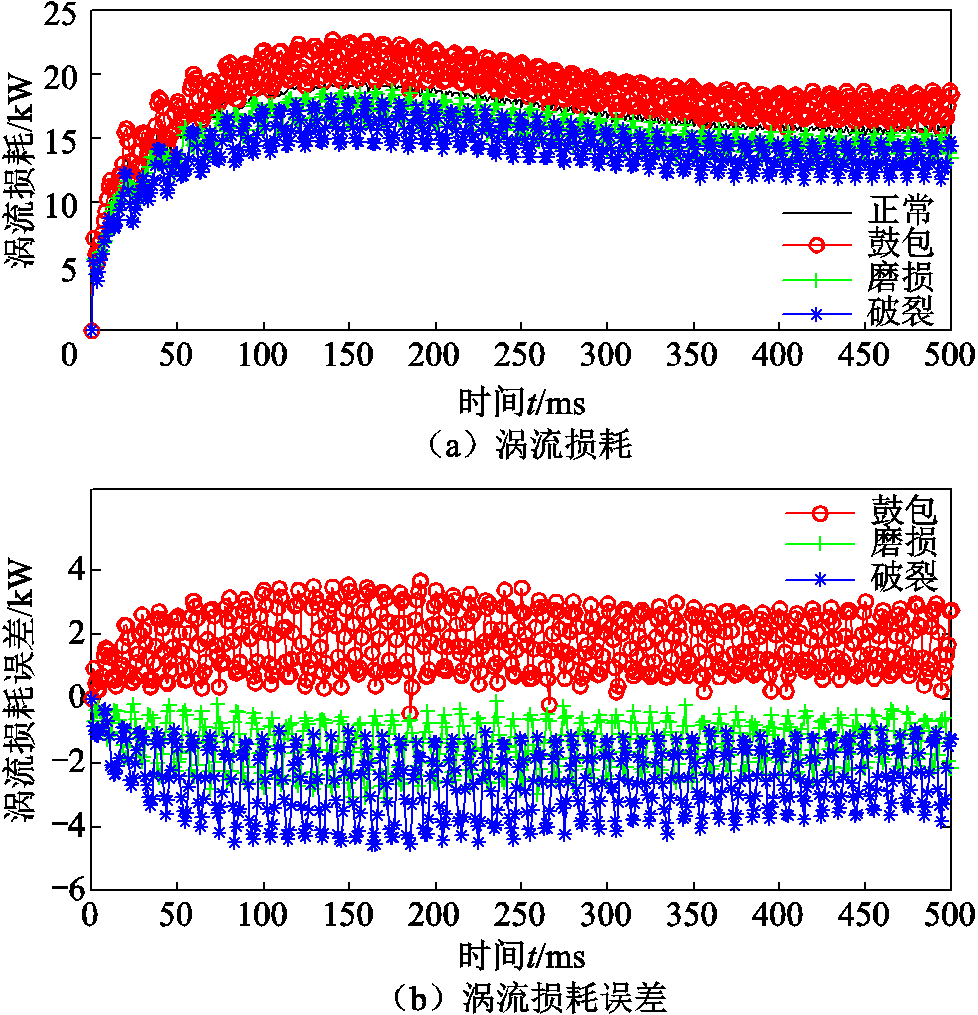
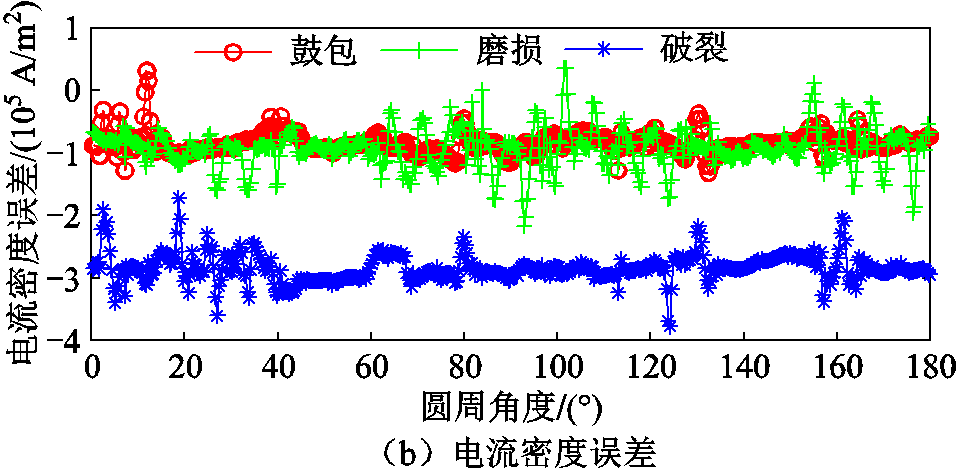
屏蔽套失效与正常时涡流损耗及误差对比、电流密度及误差对比如图11、图12所示。
从图11和图12可以看出,定子屏蔽套在不同失效模式下,屏蔽套上的涡流损耗和电流密度误差曲线有明显的规律;鼓包失效情况下,涡流损耗误差值在0~4 kW,电流密度误差值在-1×105 A/m2附近;磨损失效情况下,涡流损耗误差值在0~-2 kW,电流密度误差值在-1×105 A/m2附近;破裂失效情况下,涡流损耗误差值在-4~-1 kW,电流密度误差值在-3×105 A/m2附近;正常情况下屏蔽套涡流损耗为15 kW,电流密度的峰值为6 MA/m2;因此从计算的结果可以看出,失效对涡流损耗的影响较大,对电流密度的影响较小,不同失效的影响效果有明显区别。
1.3 不同失效程度对主泵电机性能影响分析
在分析了不同失效模式对主泵电机性能的影响之后,分别针对鼓包、磨损与破裂失效情况下的不同失效程度对电机性能影响的变化率进行了分析。
式中,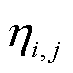 为主泵电机不同性能不同失效模式下的变化率;
为主泵电机不同性能不同失效模式下的变化率;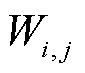 为主泵电机的各种性能在屏蔽套不同失效模式下的值;
为主泵电机的各种性能在屏蔽套不同失效模式下的值;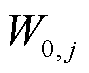 为主泵电机的各种性能在正常情况下的值;i为屏蔽套的状态,i=0, 1, 2, 3,分别代表正常、鼓包、磨损与破裂四种情况;j为不同性能,j=1, 2, 3, 4,分别表示主泵电机的转矩、电流、气隙磁通密度和反电动势。
为主泵电机的各种性能在正常情况下的值;i为屏蔽套的状态,i=0, 1, 2, 3,分别代表正常、鼓包、磨损与破裂四种情况;j为不同性能,j=1, 2, 3, 4,分别表示主泵电机的转矩、电流、气隙磁通密度和反电动势。
通过式(2)计算得到定子屏蔽套不同失效模式和失效程度下的主泵电机性能变化率,见表2。
表2 定子屏蔽套不同失效程度下主泵电机性能变化率
Tab.2 Rates of change in motor performance at different levels of stator can failure (%)
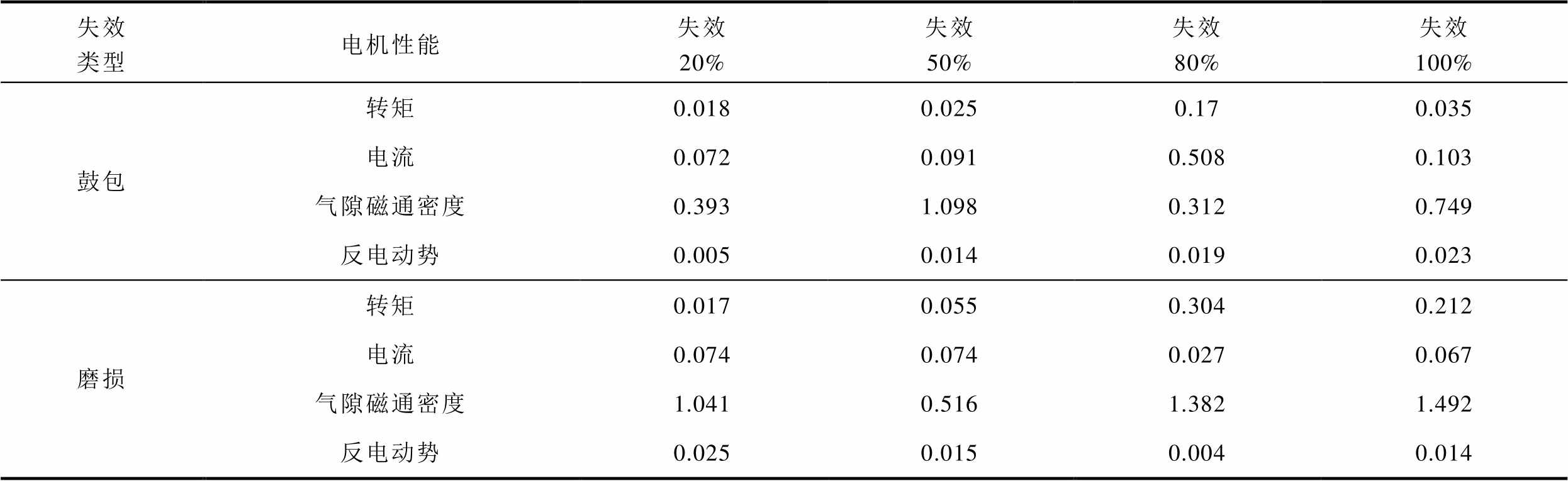
失效类型电机性能失效20%失效50%失效80%失效100% 鼓包转矩0.0180.0250.170.035 电流0.0720.0910.5080.103 气隙磁通密度0.3931.0980.3120.749 反电动势0.0050.0140.0190.023 磨损转矩0.0170.0550.3040.212 电流0.0740.0740.0270.067 气隙磁通密度1.0410.5161.3821.492 反电动势0.0250.0150.0040.014
(续)

失效类型电机性能失效20%失效50%失效80%失效100% 破裂转矩0.9251.6642.1080.945 电流0.0150.0280.0280.044 气隙磁通密度1.7480.1891.0370.722 反电动势0.0010.0010.0020.003
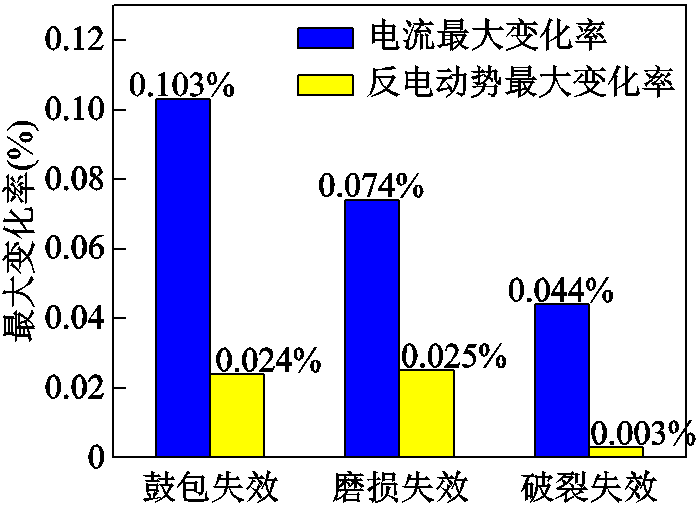
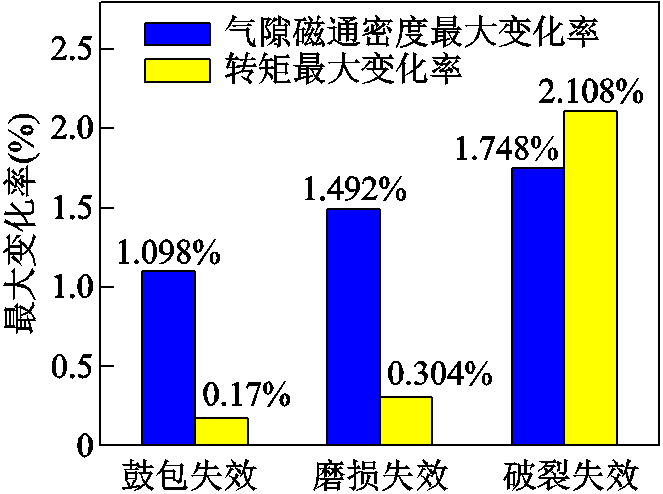
根据计算出的结果,进一步分析了不同失效模式下的主泵电机电流、反电动势、气隙磁通密度和转矩的最大变化率,如图13和图14所示。
从图13中可以看出,当定子屏蔽套失效时,A相电流的最大变化率为0.103%,反电动势的最大变化率为0.025%。从图14中可以看出,当定子屏蔽套失效时,电磁转矩的最大变化率为2.108%,气隙磁通密度最大变化率为1.748%。
综上所述,从仿真计算的结果来看,屏蔽套鼓包、磨损和破裂对主泵电机的定子绕组电流和反电动势基本没有影响,对主泵电机的转矩、气隙磁通密度及屏蔽套的电流密度影响较小,对屏蔽套的涡流损耗影响较大且具有一定的规律。
2 屏蔽套失效模式的涡流损耗计算方法
从上述研究发现,屏蔽套失效之后,主泵电机的各种性能变化不明显,仅有屏蔽套上的涡流损耗变化较大。因此,提出了考虑屏蔽套不同失效模式的屏蔽套涡流损耗计算方法,并将解析计算结果与有限元分析结果进行了比较。
2.1 不同失效模式的涡流损耗解析式
主泵电机与普通的笼式感应电机相比,只是多了定子和转子屏蔽套。因此,可以对普通结构的感应电机T型等效电路进行改进,从而得到主泵电机的等效电路。由于主泵电机屏蔽套上的漏感和互感较小,因此忽略了定子屏蔽套和定子绕组之间的互感、定子屏蔽套的自感、转子屏蔽套的自感、转子屏蔽套与笼条之间的互感。
主泵电机简化等效电路如图15所示,图中Rs和Rr分别为定子、转子屏蔽套的电阻。图15中所有的量都是折算到定子侧的量,R1和X1分别为定子绕组相电阻和每相定子漏抗,Xm为每相磁化电抗,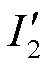 为折算后的转子每相电流,R2为折算前的每相转子电阻,
为折算后的转子每相电流,R2为折算前的每相转子电阻,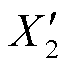 为折算后的转子漏抗。
为折算后的转子漏抗。
定子侧电压方程为
转子侧电压方程为
电动势方程为
式中,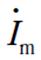 为励磁电流;
为励磁电流;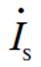 为定子屏蔽套电流;
为定子屏蔽套电流;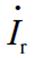 为转子屏蔽套电流。
为转子屏蔽套电流。
由图15和式(3)~式(5)计算可知,主泵电机的反电动势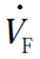 、定子绕组电流
、定子绕组电流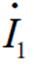 为
为
由于屏蔽套材料的磁导率与空气的一致,因此在计算主泵电机的气隙磁通密度时,可以将屏蔽套近似为空气进行计算。在二维电磁场中,感应电机定子和转子受到的切向电磁力密度为ft=BrBθ/μ0,其中,Br、Bθ分别为半径r处气隙磁通密度的径向、切向分量,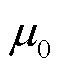 为真空磁导率。因此电磁转矩的表达式为
为真空磁导率。因此电磁转矩的表达式为
式中,L为定子铁心的轴向长度;r为气隙中的任意电机半径;θ为圆周上不同位置的角度。
通过主泵电机简化等效电路分析了转矩和定子绕组电流的情况,后续将通过对电磁场的分析,研究屏蔽套上涡流损耗的计算方法。
忽略转子和定子绕组的趋肤效应,以及铁心长度以外的屏蔽套损耗,设屏蔽套材料为各向同性,气隙磁场为正弦分布。在上述情况下,为了保证电机磁场更接近真实值,选取了整个电机作为求解域,因此二维涡流场混合边值问题表示[22]为
式中,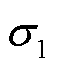 为电机内部导体的电导率;
为电机内部导体的电导率;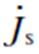 为外加电流源的电流密度;Az为矢量磁位在z方向上的分量;Ω1为电机定子外径处的边界;Ω2为电机转子内径处的边界;A0为Az在Ω1上的磁位;
为外加电流源的电流密度;Az为矢量磁位在z方向上的分量;Ω1为电机定子外径处的边界;Ω2为电机转子内径处的边界;A0为Az在Ω1上的磁位;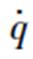 为Ω2边界上的电荷;n为法向单位向量。
为Ω2边界上的电荷;n为法向单位向量。
在电磁场中标量电位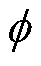 与磁位Az、电场强度E之间的关系为
与磁位Az、电场强度E之间的关系为
将屏蔽套视为一个导体,可以通过式(9)和式(10)解得流过电机定子屏蔽套上的电流密度为
式中,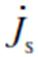 为定子屏蔽套上的电流密度;C1为电机磁场中屏蔽套失效前所占区域;ε为介电常数。
为定子屏蔽套上的电流密度;C1为电机磁场中屏蔽套失效前所占区域;ε为介电常数。
因此,可以通过Re函数取得复电流密度的实部,有
由于计算出的电流密度是空间中分布的矢量,因此计算通过屏蔽套上电流可以按照式(13)计算,式中的n可以将电流密度在空间中的分布投影到C1,通过对C1电流密度的二次方进行积分然后除以整个截面的面积Sa得到屏蔽套上电流密度的有效值J0。
通过计算的电流密度有效值和屏蔽套等效电阻可以得到屏蔽套上电流Is与损耗Ps分别为
式中,ρ1为哈式合金的电阻率;l为屏蔽套的轴向长度;Rs为定子屏蔽套失效前的等效电阻;Sa为定子屏蔽套失效前的横截面积。
主泵电机屏蔽套在实际运行中,定子屏蔽套有可能发生破裂、磨损及鼓包三种失效。为了在失效后能准确计算屏蔽套涡流损耗,使用定子屏蔽套的横截面积作为失效的变量,不同失效类型和失效程度的定子屏蔽套横截面积不同。定子屏蔽套在破裂和磨损时,其横截面积将会下降;定子屏蔽套在鼓包时,其横截面积将会增加。因此,屏蔽套失效后的等效电阻Rs1和电流密度有效值J1分别为
式中,Rs1为屏蔽套失效后的电阻;ΔS为屏蔽套失效后横截面积的变化值;C2为屏蔽套失效后的区域;J1为屏蔽套失效后的电流密度有效值。
根据式(14)和式(15),得到失效后屏蔽套涡流损耗计算公式为
2.2 有限元与解析式计算结果对比与分析
为了保证计算的准确性,通过理论计算定子屏蔽套正常时的涡流损耗及定子屏蔽套不同失效模式和不同失效程度时的涡流损耗变化率,并通过Maxwell仿真结果验证了解析计算结果的准确性,得到的结果见表3和表4。
表3 定子屏蔽套正常时的涡流损耗
Tab.3 Eddy current loss of stator can at normal state (单位:kW)

725 r/min1 450 r/min 理论计算2.67115.064 仿真分析2.57415.075
表4 定子屏蔽套失效时的涡流损耗最大变化率
Tab.4 Maximum rate of change of eddy current loss in case of stator can failure (%)

鼓包磨损破裂 理论计算5.165.2613.9 仿真分析4.84.914.2
表3结果表明,定子屏蔽套涡流损耗在 725 r/min和1 450 r/min两种工况下的理论计算与仿真分析基本一致。表4结果表明,理论计算和仿真分析的结果共同证明了当定子屏蔽套失效后,定子屏蔽套涡流损耗变化较大,其中鼓包和磨损情况下,涡流损耗的变化率接近5%,破裂情况下则达到14%。因此定子屏蔽套失效时,可以通过定子屏蔽套上的涡流损耗变化值来间接判断定子屏蔽套的失效类型及是否出现失效。
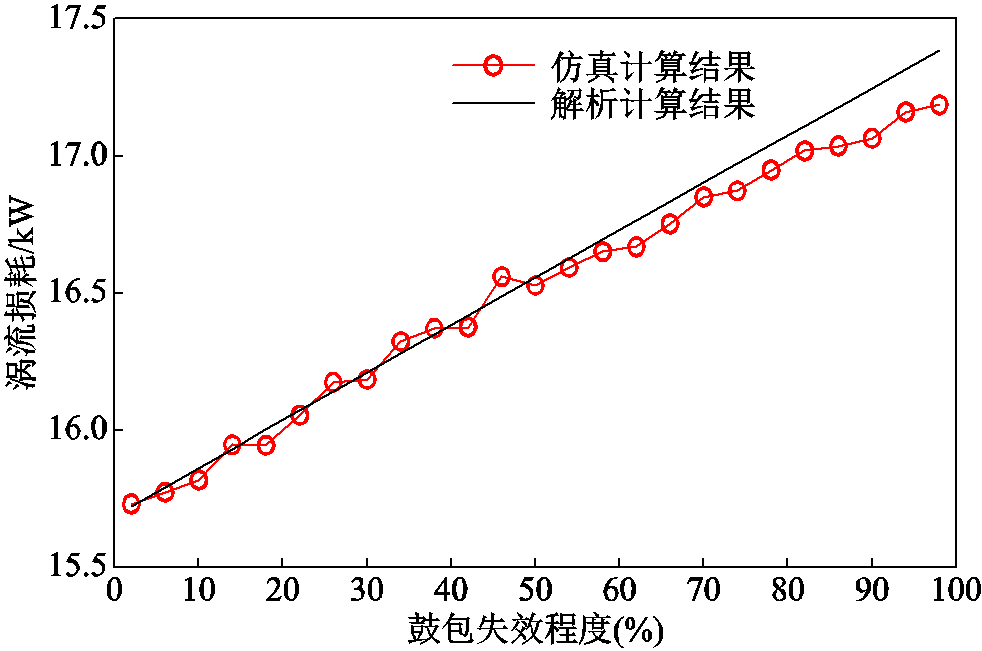
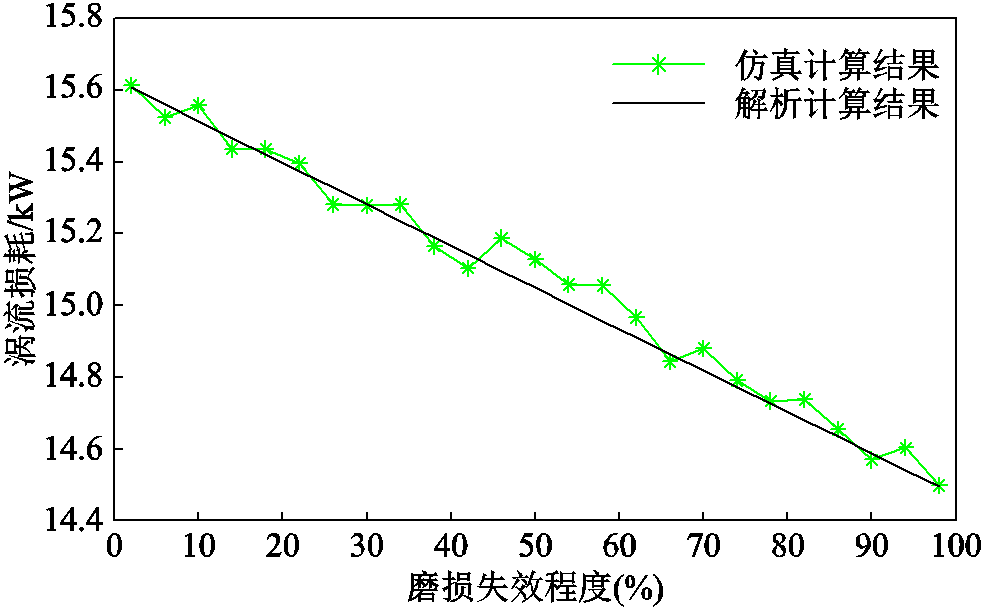
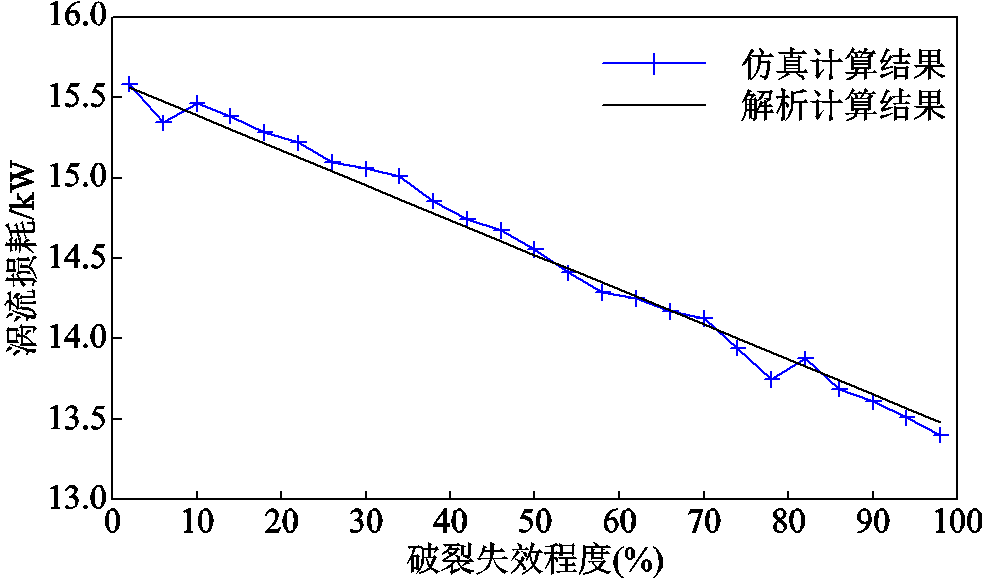
为了进一步验证解析表达式的正确性,对屏蔽套不同失效模式下的不同失效程度的涡流损耗变化率进行了对比,其中鼓包、磨损和破裂的失效程度都是采用其失效范围占圆周的范围来表示的,进而得到了涡流损耗的有限元结果和解析计算结果如图16~图18所示。
从图16~图18可以看出,当屏蔽套鼓包失效时,屏蔽套上的涡流损耗随着鼓包程度的增大而线性增大;当屏蔽套破裂和磨损失效时,屏蔽套上的涡流损耗随着破裂和磨损程度的增大而线性减小。
从解析计算结果和仿真计算曲线的结果对比可以看出,曲线的趋势一致,解析结果和仿真计算结果基本吻合。因此,针对不同失效模式建立的涡流损耗解析表达式是有效的,同时屏蔽套的失效程度与屏蔽套上的涡流损耗存在一定的线性关系。
3 结论
为了研究屏蔽套鼓包、磨损和破裂失效模式对主泵电机性能的影响,本文采用了有限元模型、解析计算模型对不同失效模式和失效程度对涡流损耗和性能的影响进行了综合比较分析,最后通过比较解析结果和有限元结果,验证了解析计算方法的有效性,并得到了这些失效模式对涡流损耗的影响规律。所得主要结论如下:
1)相比主泵电机其他性能,屏蔽套失效对屏蔽套上的涡流损耗的影响较大,这与理论分析基本一致。在屏蔽套鼓包和磨损情况下,涡流损耗的最大变化率接近5%,在破裂情况下,涡流损耗的最大变化率达到14.2%。
2)提出的考虑屏蔽套失效时鼓包、磨损及破裂面积的涡流损耗计算方法是有效的,通过解析计算与有限元计算结果比较的误差小于5%,进一步证明了计算方法的有效性。
3)屏蔽套上的涡流损耗与屏蔽套失效的程度呈线性关系:定子屏蔽套鼓包失效时,屏蔽套上的涡流损耗随着鼓包程度的增大而增大;屏蔽套磨损和破裂失效时,屏蔽套上的涡流损耗随着磨损程度和破裂程度的增大而减小。上述结论为屏蔽套失效状态监测奠定了基础。
参考文献
[1] 张明乾, 刘昱, 李承亮. 浅谈压水堆核电站AP1000屏蔽式电动主泵[J]. 水泵技术, 2008(4): 1-5.
Zhang Mingqian, Liu Yu, Li Chengliang. Discussion on AP1000 shielded electric main pump in PWR nuclear power plant[J]. Pump Technology, 2008(4): 1-5.
[2] 关锐, 高永军. AP1000反应堆主泵屏蔽套制造工艺浅析[J]. 中国核电, 2008, 1(1): 49-53.
Guan Rui, Gao Yongjun. Brief analysis on fabrication process of AP1000 reactor coolant pump can[J]. China Nuclear Power, 2008, 1(1): 49-53.
[3] Robinson R C, Rowe I, Donelan L E. The calculation of can losses in canned motors[J]. Transactions of the American Institute of Electrical Engineers Part III: Power Apparatus and Systems, 1957, 76(3): 312-315.
[4] 孙树林, 李觉民. 屏蔽式感应电动机屏蔽套损耗的计算及减少途径[J]. 大电机技术, 1987(6): 30-33.
Sun Shulin, Li Juemin. Calculation of electric loss on the shield for canned inductive motor and the ways of its reduction[J]. Large Electric Machine and Hydraulic Turbine, 1987(6): 30-33.
[5] Gao Lianlian, Wei Jingwei, Li Cangxue, et al. Analyses on performances of megawatt double-canned induction motors with different can materials[J]. IEEE Transactions on Energy Conversion, 2017, 32(2): 667-674.
[6] Yu Qiang, Wang Xuesong, Cheng Yuhu. Electromagnetic calculation and characteristic analysis of can effect of a canned permanent magnet motor[J]. IEEE Transactions on Magnetics, 2016, 52(12): 8108706.
[7] 梁艳萍, 张广超, 高莲莲, 等. 核主泵驱动电动机屏蔽套涡流损耗混合算法研究[J]. 电工技术学报, 2018, 33(5): 1015-1023.
Liang Yanping, Zhang Guangchao, Gao Lianlian, et al. Research on hybrid algorithm of can losses in double canned induction motor for nuclear pump[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1015-1023.
[8] 张晓晨, 李伟力, 曹君慈. 屏蔽电机屏蔽损耗与电机性能的计算与分析[J]. 哈尔滨工业大学学报, 2007, 39(9): 1422-1426.
Zhang Xiaochen, Li Weili, Cao Junci. Calculation and analysis for the can loss and performance of canned motors[J]. Journal of Harbin Institute of Technology, 2007, 39(9): 1422-1426.
[9] 何畅. 液浸电机屏蔽套能耗分析与优化[D]. 徐州: 中国矿业大学, 2020.
He Chang. Analysis and optimization of energy consumption of shielding sleeve of liquid immersed motor[D]. Xuzhou: China University of Mining and Technology, 2020.
[10] 纪繁祥, 吴庆广. 屏蔽电动机运行性能分析[J]. 防爆电机, 2015, 50(3): 22-24.
Ji Fanxiang, Wu Qingguang. Analyses on running performance of canned motor[J]. Explosion-Proof Electric Machine, 2015, 50(3): 22-24.
[11] 张亮. 无刷直流屏蔽电动机的涡流损耗与性能研究[J]. 微电机, 2016, 49(8): 16-18.
Zhang Liang. Research on eddy current losses and performance parameters of brushless DC canned motor[J]. Micromotors, 2016, 49(8): 16-18.
[12] 张建涛, 梁艳萍, 王鸿鹄, 等. 双屏蔽复合转子电动机性能分析[J]. 大电机技术, 2010(4): 22-26.
Zhang Jiantao, Liang Yanping, Wang Honghu, et al. The performance analysis of the double-cans composite-rotor motor[J]. Large Electric Machine and Hydraulic Turbine, 2010(4): 22-26.
[13] 金永星, 王爱元, 孙健, 等. 核屏蔽感应电机效率和功率因数综合优化设计[J]. 电机技术, 2019(2): 1-3, 8.
Jin Yongxing, Wang Aiyuan, Sun Jian, et al. Synthetic optimized design on efficiency and power factor of nuclear shielding induction motors[J]. Electrical Machinery Technology, 2019(2): 1-3, 8.
[14] 金永星, 王爱元, 王涛, 等. 基于粒子群算法的核屏蔽感应电机多目标优化设计[J]. 电机与控制应用, 2019, 46(9): 53-57.
Jin Yongxing, Wang Aiyuan, Wang Tao, et al. Multi-objective optimization design of nuclear canned induction motor based on particle swarm optimization[J]. Electric Machines & Control Application, 2019, 46(9): 53-57.
[15] 李贵敬, 阎昌琪, 王建军. 屏蔽电机设计性能的参数效应分析[J]. 原子能科学技术, 2013, 47(3): 442-448.
Li Guijing, Yan Changqi, Wang Jianjun. Effect analysis of parameters on canned motor’s design performance[J]. Atomic Energy Science and Technology, 2013, 47(3): 442-448.
[16] 佟文明, 侯明君, 孙鲁, 等. 基于精确子域模型的带护套转子高速永磁电机转子涡流损耗解析方法[J]. 电工技术学报, 2022, 37(16): 4047-4059.
Tong Wenming, Hou Mingjun, Sun Lu, et al. Analytical method of rotor eddy current loss for high-speed surface-mounted permanent magnet motor with rotor retaining sleeve[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4047-4059.
[17] 佟文明, 田野, 李晓健, 等. 双层复合护套高速永磁电机转子涡流损耗解析模型[J]. 电工技术学报, 2024, 39(14): 4328-4340.
Tong Wenming, Tian Ye, Li Xiaojian, et al. Analytical modeling for rotor eddy current loss of high-speed surface-mounted permanent magnet motor with double-layer compound retaining sleeve[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4328-4340.
[18] 刘细平, 朱治国, 陈栋, 等. 基于转子永磁分段优化的轴向磁通永磁电机涡流损耗分析与试验[J]. 电工技术学报, 2024, 39(12): 3616-3629.
Liu Xiping, Zhu Zhiguo, Chen Dong, et al. Analysis and experiment of eddy current loss of axial flux permanent magnet motor based on rotor segment optimization[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3616-3629.
[19] 曹龙飞, 范兴纲, 李大伟, 等. 基于快速有限元的永磁电机绕组涡流损耗半解析高效计算[J]. 电工技术学报, 2023, 38(1): 153-165.
Cao Longfei, Fan Xinggang, Li Dawei, et al. Semi analytical and efficient calculation method of eddy current loss in windings of permanent magnet machines based on fast finite element method[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 153-165.
[20] 陈浈斐, 邢宁, 马宏忠, 等. 分数槽永磁电机永磁体谐波涡流损耗建模与分析[J]. 电工技术学报, 2022, 37(14): 3514-3527.
Chen Zhenfei, Xing Ning, Ma Hongzhong, et al. Analytical modeling and analysis of magnet harmonic loss in fractional slot permanent-magnet machines[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3514-3527.
[21] 凌在汛, 周理兵, 张毅, 等. 笼型实心转子屏蔽感应电机电磁场及参数研究(一): 等效电路及其参数分析[J]. 电工技术学报, 2018, 33(15): 3518-3526.
Ling Zaixun, Zhou Libing, Zhang Yi, et al. Parameters determination and electromagnetic field analysis of canned solid-rotor induction motor(1): an overview of motor’s equivalent circuit and its parameter analysis method[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3518-3526.
[22] 凌在汛, 周理兵, 张毅, 等. 笼型实心转子屏蔽感应电机电磁场及参数研究(二): 二维多层电磁场模型及其解析计算[J]. 电工技术学报, 2018, 33(17): 4016-4028.
Ling Zaixun, Zhou Libing, Zhang Yi, et al. Parameters determination and electromagnetic field analysis of canned solid-rotor induction motor(2): 2D-multilayer electromagnetic model and its analytical calculation [J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4016-4028.
[23] 胡月. 屏蔽电机主泵定子屏蔽套屈曲稳定性研究[D]. 上海: 上海交通大学, 2013.
Hu Yue. Study on buckling stability of stator shield sleeve of main pump of shielded motor[D]. Shanghai: Shanghai Jiao Tong University, 2013.
[24] 冯颖慧. AP1000屏蔽电机主泵屏蔽套力学分析[D]. 上海: 上海交通大学, 2011.
Feng Yinghui. Mechanical analysis of main pump shielding sleeve of AP1000 shielded motor[D]. Shanghai: Shanghai Jiao Tong University, 2011.
[25] 张强. 新型移相式屏蔽电动机定子屏蔽套涡流与热应力研究[D]. 沈阳: 沈阳工业大学, 2015.
Zhang Qiang. Study on eddy current and thermal stress of stator shield sleeve of new phase-shifting shielded motor[D]. Shenyang: Shenyang University of Techno-logy, 2015.
[26] 汤蕴璆, 梁艳萍. 电机电磁场的分析与计算[M]. 北京: 机械工业出版社, 2010.
Modeling and Performance Impact Analysis of Main Pump Canned Motor Considering Can Failure
Liu Nengqing1 Xiang Xuewei1 Chen Zhi2 Li Hui1 Jiang Peng1
(1. State Key Laboratory of Power Transmission Equipment Technology Chongqing University Chongqing 40044 China 2. Key Laboratory of Nuclear Reactor System Design Technology Nuclear Power Institute of China Chengdu 610213 China)
Abstract The can is a critical component of the main pump canned motor, located within the air gap of the main pump. It endures various stresses such as electromagnetic force, coolant pressure, and thermal stress, making it prone to failure. Due to the limited installation space, it is challenging to install relevant sensors to monitor its condition, thus making the study of can faults and their impact on the performance of the main pump canned motor significantly important. Currently, there is a lack of models and analysis focusing on can faults and their effects on the performance of the main pump canned motor. This paper proposes a modeling method that considers can faults and analyzes their impact on the performance of canned motors for main pumps.
Firstly, to accurately calculate the performance of the main pump canned motor, a finite element model of the main pump canned motor was established. This model considers three common failure modes of the can: bulging, wear, and cracking. Maxwell finite element models of the main pump canned motor were developed for each type of can fault. Based on finite element calculation results, the impact of different can fault modes and varying degrees of severity on the performance of the main pump canned motor was analyzed. The study revealed that can failures have a significant effect on the eddy current loss within the can, but have minimal impact on back electromotive force and winding current, and relatively little effect on torque and air gap magnetic flux density. Finally, to address the impact of can failures on eddy current losses within the can, an analytical expression for eddy current loss calculation was proposed, considering the cross-sectional area variations of the can due to different fault modes. The changes in eddy current losses under different fault modes and severity levels were analyzed using this analytical expression and compared with simulation results.
The results indicate that: (1) When the main pump motor can fails, the maximum change rate of electromagnetic torque is 2.108%, the maximum change rate of air gap magnetic flux density is 1.748%, the maximum change rate of phase A current is 0.103%, and the maximum change rate of back electromotive force is 0.025%. Therefore, compared to other aspects of the main pump canned motor’s performance, can faults have a significant impact on the eddy current loss within the can, consistent with theoretical analysis. Under bulging and wear conditions, the maximum change rate of eddy current loss reached 5%, while under cracking conditions, it reached 14%. (2) The proposed eddy current loss calculation method considering bulging, wear, and cracking areas during can failure is effective, with the error between the analytical calculation and finite element calculation results being less than 5%, further proving the effectiveness of the calculation method. (3) Eddy current losses within the can exhibit a linear relationship with the degree of can failure. When a bulging fault occurs in the stator can, the eddy current loss within the can increases with the degree of bulging. In the cases of wear and cracking faults, the eddy current loss within the can decreases as the extent of wear or cracking increases.
Keywords:Can, main pump canned motor, failure simulation, performance analysis, eddy current
中图分类号:TM346
DOI: 10.19595/j.cnki.1000-6753.tces.L11046
国家自然科学基金资助项目(U2267206)。
收稿日期 2024-07-14
改稿日期 2024-07-31
作者简介
刘能青 男,2000年生,硕士研究生,研究方向为屏蔽电机失效故障诊断。
E-mail:1713286063@qq.com
向学位 男,1993年生,副研究员,硕士生导师,研究方向为新型电机的运行理论及控制。
E-mail:xueweixiang@cqu.edu.cn(通信作者)
(编辑 崔文静)


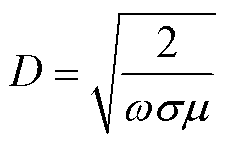 (1)
(1)
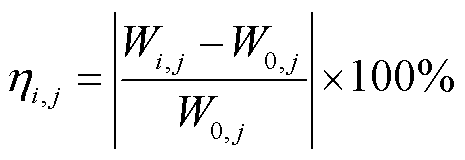 (2)
(2)
 为主泵电机不同性能不同失效模式下的变化率;
为主泵电机不同性能不同失效模式下的变化率;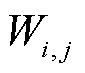 为主泵电机的各种性能在屏蔽套不同失效模式下的值;
为主泵电机的各种性能在屏蔽套不同失效模式下的值;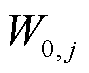 为主泵电机的各种性能在正常情况下的值;i为屏蔽套的状态,i=0, 1, 2, 3,分别代表正常、鼓包、磨损与破裂四种情况;j为不同性能,j=1, 2, 3, 4,分别表示主泵电机的转矩、电流、气隙磁通密度和反电动势。
为主泵电机的各种性能在正常情况下的值;i为屏蔽套的状态,i=0, 1, 2, 3,分别代表正常、鼓包、磨损与破裂四种情况;j为不同性能,j=1, 2, 3, 4,分别表示主泵电机的转矩、电流、气隙磁通密度和反电动势。

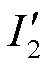 为折算后的转子每相电流,R
为折算后的转子每相电流,R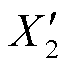 为折算后的转子漏抗。
为折算后的转子漏抗。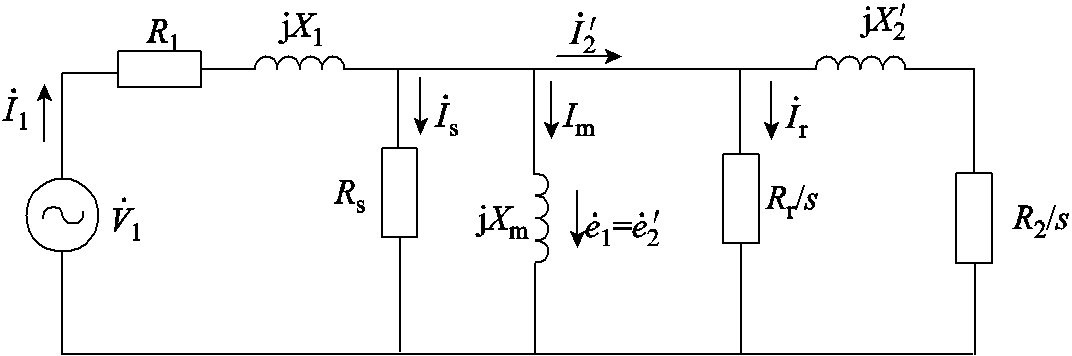
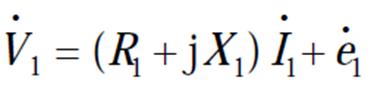 (3)
(3)
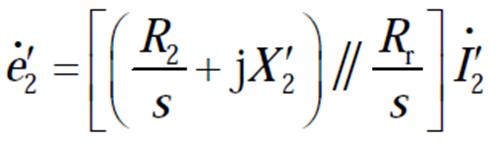 (4)
(4)
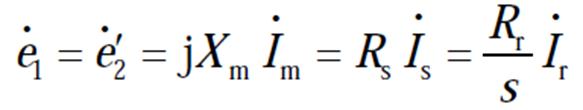 (5)
(5)
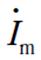 为励磁电流;
为励磁电流;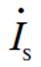 为定子屏蔽套电流;
为定子屏蔽套电流;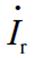 为转子屏蔽套电流。
为转子屏蔽套电流。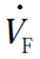 、定子绕组电流
、定子绕组电流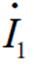 为
为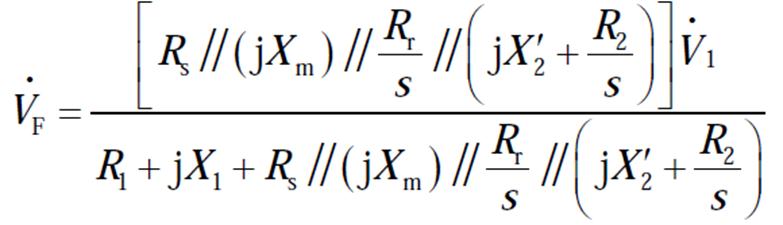 (6)
(6)
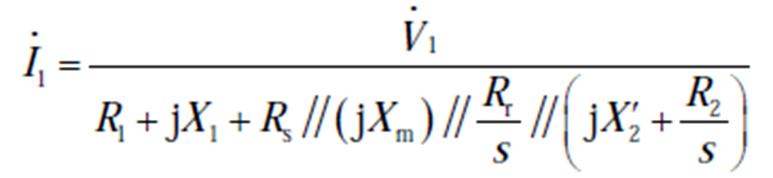 (7)
(7)
 为真空磁导率。因此电磁转矩的表达式为
为真空磁导率。因此电磁转矩的表达式为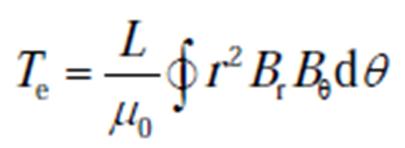 (8)
(8)
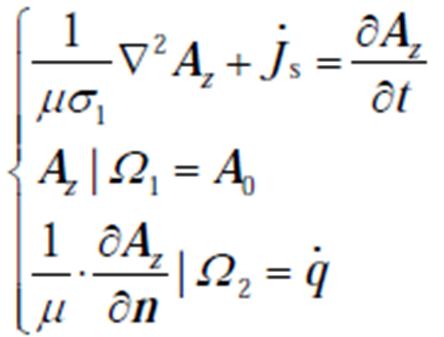 (9)
(9)
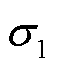 为电机内部导体的电导率;
为电机内部导体的电导率;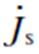 为外加电流源的电流密度;A
为外加电流源的电流密度;A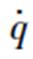 为Ω
为Ω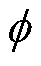 与磁位A
与磁位A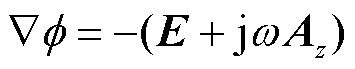 (10)
(10)
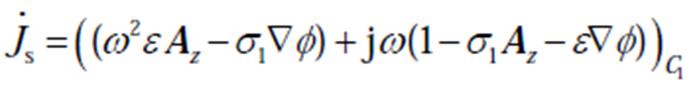 (11)
(11)
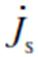 为定子屏蔽套上的电流密度;C
为定子屏蔽套上的电流密度;C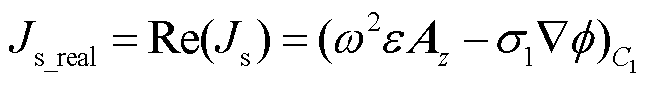 (12)
(12)
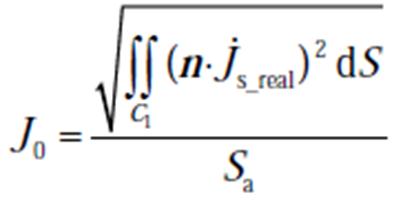 (13)
(13)
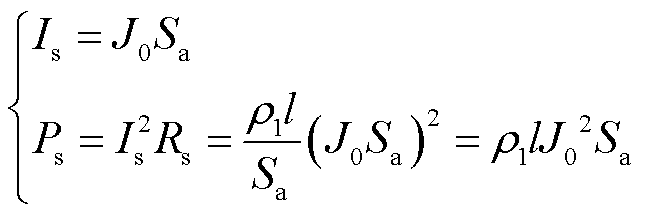 (14)
(14)
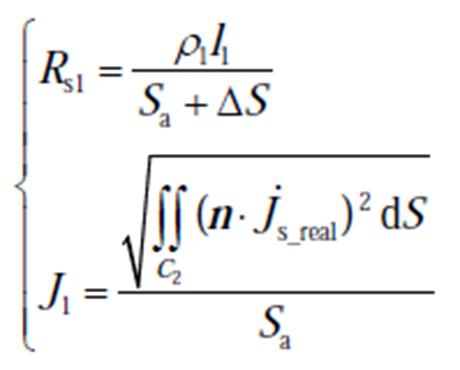 (15)
(15)
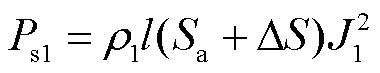 (16)
(16)