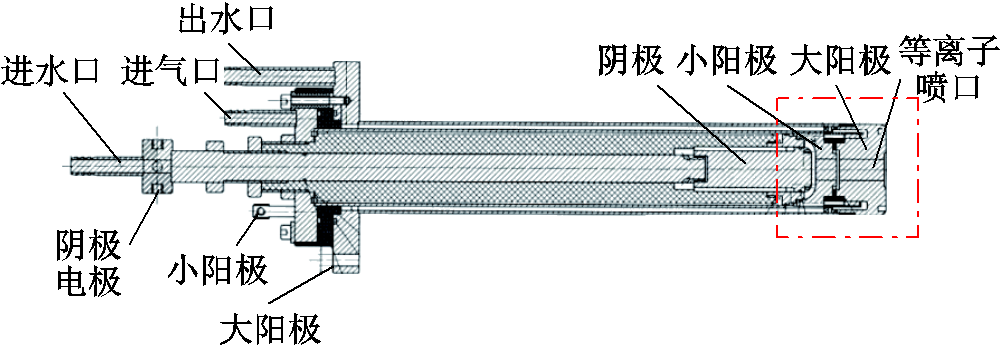
图1 等离子体炬结构
Fig.1 Structure of plasma torch
摘要 非转移直流电弧等离子体炬是放射性废物等离子体熔融处理系统中的核心设备,射流的物理场参数不仅是设计和优化等离子体炬的重要指标,也是提高系统能量利用率和玻璃体生成物质量的关键。该文针对一款级联阳极结构的等离子体炬,基于磁流体力学理论,采用有限元仿真软件COMSOL对氮气热等离子体射流流入冷氮气域现象进行三维稳态数值模拟,建立电-磁-流-热的多物理场耦合模型,计算射流物理场参数,将计算结果与相关实验数据进行对比,并分析固定电流强度工况下改变输入气流量对等离子体炬性能的影响。结果显示模型能够较好地预测实际情况,所得到的射流温度场、速度场数据以及电极表面的温度、电流密度分布数据可为等离子体炬的设计和优化提供参考。
关键词:非转移直流电弧等离子体炬 放射性废物处理 数值模拟 多物理场耦合
非转移直流电弧等离子体炬是一种利用电弧能量加热气体产生热等离子体射流的装置,因其能够提供玻璃固化所需的高温热源而被视为放射性废物等离子体熔融处理系统中的核心设备[1-3]。热等离子体射流的物理场参数不仅是设计和优化等离子体炬的重要指标,也是提高系统能量利用率和玻璃体生成物质量的关键,国内外学者对此展开了大量研究。研究方式主要分为实验和数值模拟两种。实验研究即直接用仪器测量的方式获取所需数据[4-6],但等离子体炬内部空间狭小,射流温度极高,对测量仪器的精度、可操作性和可靠性要求十分苛刻,遇到需要重复进行的实验不仅会消耗大量的人力、物力,还会因为电极损耗、设备老化等客观原因造成数据失真,增加安全风险。随着计算机性能的提升和相关软件的开发,数值模拟已经成为研究等离子体现象的重要工具[7-11],与实验研究相比,其在经济性、灵活性和安全性上均具有明显优势,不仅速度快而且能提供详细的可视化数据,故而被广泛使用。
等离子体炬内部物理过程十分复杂,是电场、磁场、流体和传热相互作用的多物理场耦合现象,如何建立合理的模型一直是研究的热点。王飞等[12]通过二维轴对称稳态模型,研究了射流的温度场与速度场分布;Tao Jing等[13]通过二维轴对称稳态模型,研究了不同气体组分对射流特性的影响;师浩阳等[14]通过三维稳态模型,研究了射流射出后的温度和速度变化,并进行了等离子体诊断;Liu Senhui等[15]通过三维稳态模型,研究了一款新型阳极通道结构的等离子体炬射流特性,并分析了通道结构对射流质量的影响,以及阳极弧根运动轨迹随工况条件发生的变化;R. Zhukovskii等[16]通过三维瞬态模型,对比分析了采用局部热力学平衡(Local Thermodynamic Equilibrium, LTE)假设和双温度(2-T)假设所预测的1 ms内电弧波动计算结果。
大量研究表明,二维轴对称稳态模型因为忽略了湍流等离子体的三维效应,在远离轴线的区域,温度和速度等重要参数计算上有明显的失真;而三维瞬态模型由于考虑了电弧的波动过程或两类粒子状态,计算时间区间小,计算量大且比较复杂,后续研究中如果采用该方法将等离子体炬与热等离子体反应器进行耦合计算则会导致计算成本显著增加,但实际上电弧波动对熔融区域温度的影响很小,几乎可以忽略;此外,传统计算流体动力(Computational Fluid Dynamics, CFD)学软件如Fluent、OpenFOAM、CFX等,需要在流体计算之外再对电场和磁场撰写自编程计算程序,随着研究的深入无疑会带来相当大的工作量,倘若为了简化计算大量采用一类边界条件,则会与实际发生偏离。
本文基于磁流体力学理论,采用有限元仿真软件COMSOL对氮气热等离子体射流流入冷氮气域现象进行三维稳态数值模拟。计算区域包括整个炬管和射流开放区域,其中对电极区域的边界条件作出如下针对性的设置:①将固体电极与流体接触的面设置为“平衡放电边界热源”,用于计算被忽略的鞘层中的能量传输;②将“接地”和“电流终端”边界设置在电极的背面,用于计算电极本体产生的焦耳热;③用“冷却水流动”区域模拟电极的冷却过程。前两项避免了设置一类边界条件对计算结果产生的误差影响,可以同步预测电极性能,第三项设置使模型可以直接与反应器进行耦合计算;提高了后续研究的便捷性。通过合理的网格划分方案和求解器配置保证计算结果精度和收敛性,用一组固定电流强度下改变气流量运行所得到的实验数据与计算结果进行对比分析,最后得出相关结论。
本文研究的等离子体炬结构如图1所示。功率等级为10~30 kW,载气为纯氮气,内部采用水冷保护。等离子体炬在工作时,电弧首先在阴极和小阳极之间形成,随后阳极弧根在气动力的作用下从小阳极转移至大阳极,最后稳定燃烧,运行过程中小阳极处于悬空电位。大小阳极之间是级联结构,用绝缘垫片分离。

图1 等离子体炬结构
Fig.1 Structure of plasma torch
简化后的二维结构如图2所示。图中,域①是阴极底座,材料为钨(固体);域②③是等离子体发生域;域④是小阳极炬管;域⑤是大阳极炬管,材料均为铜(固体);域⑥是冷气域,材料均为氮气(非固体);域⑦⑧是炬管保护套,材料为不锈钢(固体);域⑨是冷却水流动区域,材料为去离子水(非固体)。所有材料物性参数均取自于COMSOL材料库。
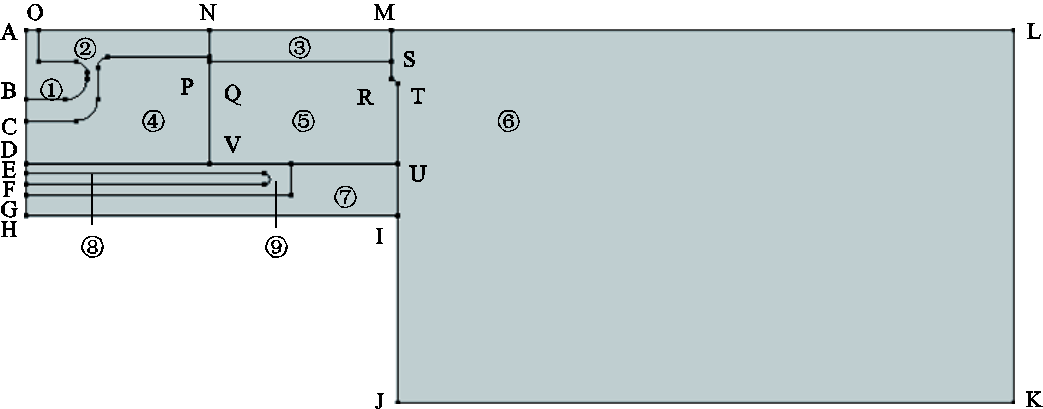
图2 二维结构
Fig.2 Two-dimensional structure
图2所示的简化二维结构中,BC段为载气入口(4 mm),SM段为射流出口(6 mm),IJKL段为自由射流边界,IJ段长35 mm,JK段长140 mm,LK段长70 mm;QV段为大小阳极之间的绝缘垫片,NP段为氮气流动域的虚拟分界线,PQ段为大小阳极之间的台阶(1 mm),CQ段为小阳极表面,QS段为大阳极表面,BO段为阴极表面,HI段为炬管,长70 mm;FG段为冷却水入口,DE段为冷却水出口;除轴线AONML段以外,其余线段均为壁。以AONML段为中心轴旋转一周得到三维结构,如图3所示。
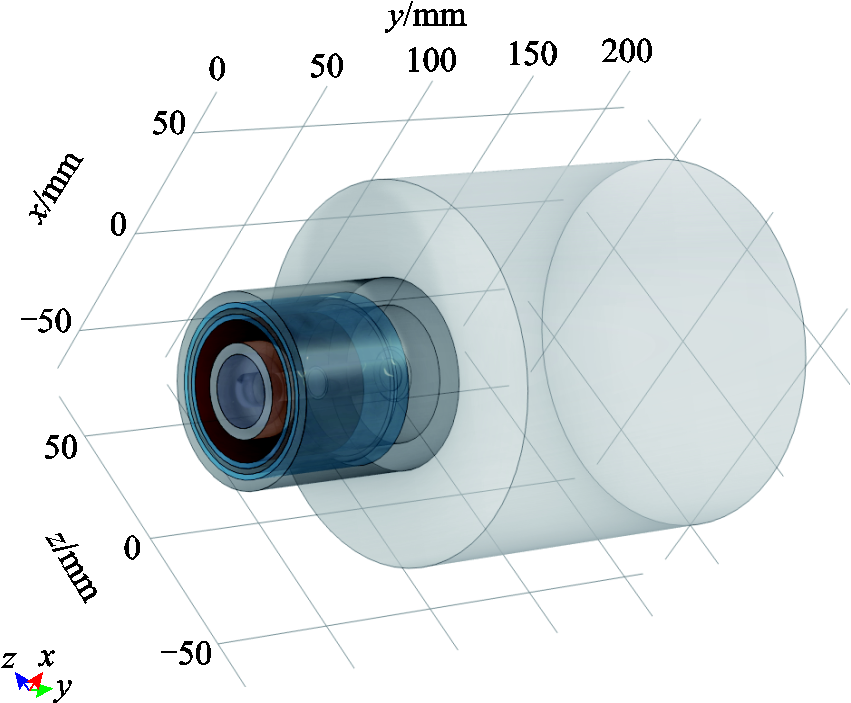
图3 三维结构
Fig.3 Three-dimensional structure
基于磁流体力学理论[17],作如下假设:①等离子体是完全电离的双组份(离子和电子)混合物;②等离子体处于局部热力学平衡状态(离子与电子温度近似相等),是局部电中性的牛顿流体;③等离子体射流是弱可压缩的准稳定湍流,采用标准k-ε模型计算[18];④等离子体是光学薄的,气体辐射传热采用总体积辐射系数计算;⑤等离子体的物性参数只是温度的函数;⑥炬在工作时小阳极完全绝缘,忽略电极鞘层以及烧蚀现象;⑦忽略重力影响以及流体中的压力做功;⑧冷却水流动是不可压缩的准稳定层流。
1)域①②③⑤中的电磁方程
电流连续性方程为
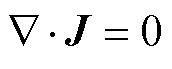 (1)
(1)
安培定律为
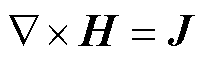 (2)
(2)
磁感应强度矢量B的定义为
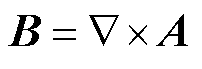 (3)
(3)
电场强度矢量E的定义为
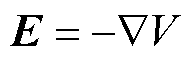 (4)
(4)
欧姆定律为
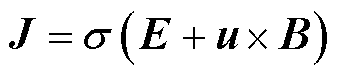 (5)
(5)
式中,J为总电流密度矢量;H为磁场强度矢量;B为磁感应强度矢量;A为磁矢势;V为标量电势;σ为电导率;u为流体速度矢量;u×B为感应电场。
2)域②③⑥中的标准k-ε湍流方程
动量守恒方程为
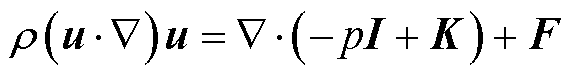 (6)
(6)
质量守恒方程为
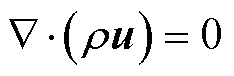 (7)
(7)
应力张量K的定义为
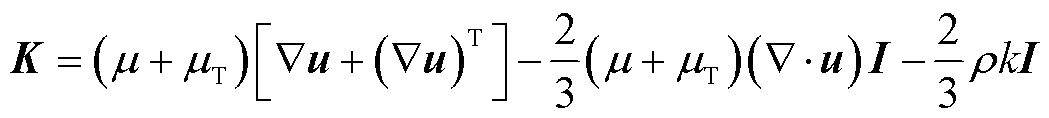 (8)
(8)
湍动能k输运方程为
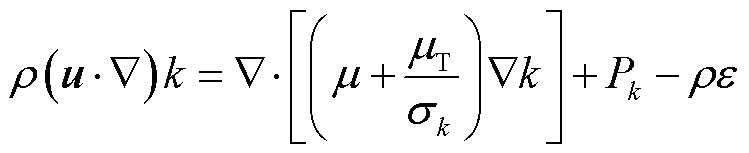 (9)
(9)
湍流耗散率ε输运方程为
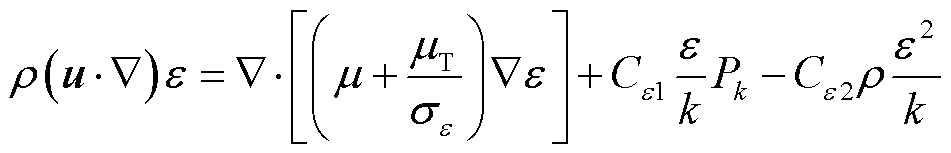 (10)
(10)
湍流黏性系数μT定义式为
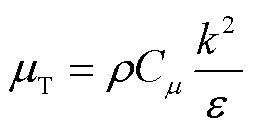 (11)
(11)
湍流动能项Pk定义式为
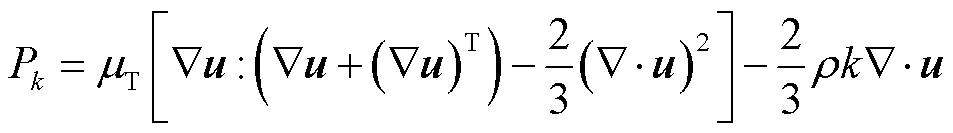 (12)
(12)
式中,p为压力;ρ为流体密度;I为单位张量;F为洛伦兹力,F=J×B;μ为流体动力黏度;σk、σε分别为与湍动能和湍流耗散率相关的普朗特数;Cε1、Cε2和Cμ均为经验常数;“:”表示双点积运算。
3)域⑨中的层流方程
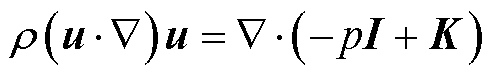 (13)
(13)
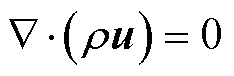 (14)
(14)
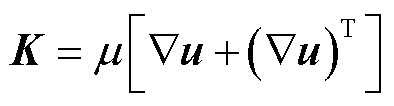 (15)
(15)
4)传热方程
(1)傅里叶热传导定律为
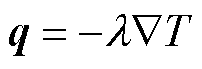 (16)
(16)
式中,T为温度;q为热通量矢量;λ为热导率。
(2)计算流体域②③⑥的能量守恒方程为
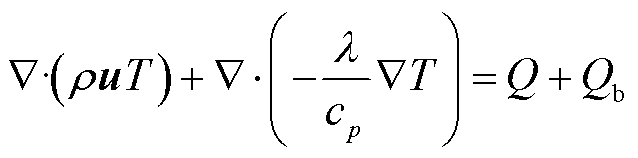 (17)
(17)
其中
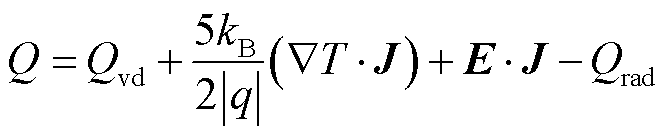
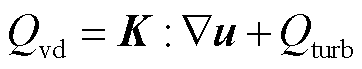
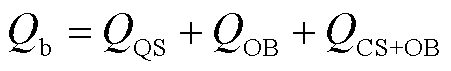
式中,cp为材料比定压热容;Q为体积热源项;Qb为边界热源项;kB为玻耳兹曼常数;q为电荷量;Qvd为黏性耗散项;Qrad为辐射热;Qturb为湍流引起的热量传递,本文选择的传热湍流模型为Kays-Crawford模型,热壁函数选择标准函数;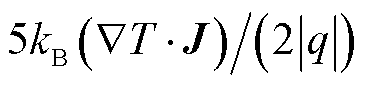 为焓传递;E·J为焦耳热;QQS、QOB和QCS+OB分别为大阳极边界QS段、阴极边界OB段和整个阳极边界CS段与阴极边界OB段上的辐射热源分项,具体表示为
为焓传递;E·J为焦耳热;QQS、QOB和QCS+OB分别为大阳极边界QS段、阴极边界OB段和整个阳极边界CS段与阴极边界OB段上的辐射热源分项,具体表示为
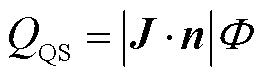 (18)
(18)
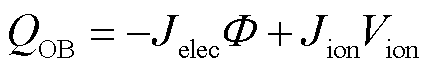 (19)
(19)
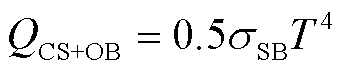 (20)
(20)
其中
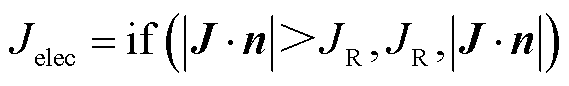 (21)
(21)
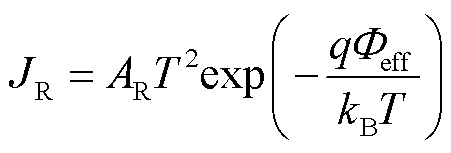 (22)
(22)
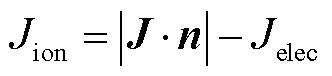 (23)
(23)
式中,Φ为表面功函数;n为指向流体域外的法向量;Jelec为电子电流密度;JR为发射电流密度;Jion为离子电流密度;Vion为等离子体电离势;AR为有效理查德森系数;Φeff为有效功函数;σSB为斯忒藩-玻耳兹曼常数。
对于大阳极边界QS段上的放电热源分项QQS,模型不考虑电极鞘层中的物理过程,将其看作边界热源简化计算[19-20]。阳极边界产生的热量主要来自接收电子所释放的能量,相关研究表明阳极附近电子数占到总量的99%以上,电弧中的阳离子主要来自介质的碰撞与电离,从阳极发射的阳离子数小于总量的1%,是极小量,可以忽略。
对于阴极边界OB段上的放电热源分项QOB,-JelecΦ表示电子发射时消耗的逸出功,JionVion表示接收离子所释放的能量。与阳极附近的粒子分布情况不同,阴极附近的电子数占总数的80%左右,阴极边界能量传递主要来自于离子的轰击和热电子发射,并且热电子发射的冷却作用十分明显。
(3)计算域流体域⑨的能量守恒方程为
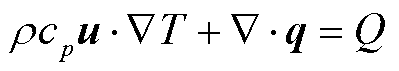 (24)
(24)
式中,Q为体积热源项,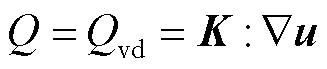 。
。
(4)计算固体域①⑤⑦⑧的能量守恒方程为
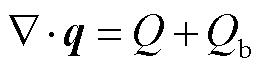 (25)
(25)
式中,对于域①⑤,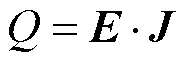 ,Qb=-QCS+OB;对于域⑦⑧,Q=Qb=0。
,Qb=-QCS+OB;对于域⑦⑧,Q=Qb=0。
详细的边界条件设置见表1。为了使计算结果更容易收敛,入口和出口的边界条件设置十分关键。模型在氮气入口指定速度条件,在出口指定压力条件,并且自由射流域取得足够大。假设边界IJKL为净流出边界,设置包括:①将IJ段设置为固定温度293.15 K,此边界流出气体极少,温度几乎不变,将JK、KL两段设置为热绝缘,以计算热量传递;②将KL段设置为“出口”,IJ、JK两段设置为“充分发展的流动出口”,二者的区别在于前者规定边界上切向速度不为零而后者为零,因为在法向速度较小的边界上通过忽略切向速度可以大幅度减少计算量。
表1 边界条件设置
Tab.1 Boundary condition setting
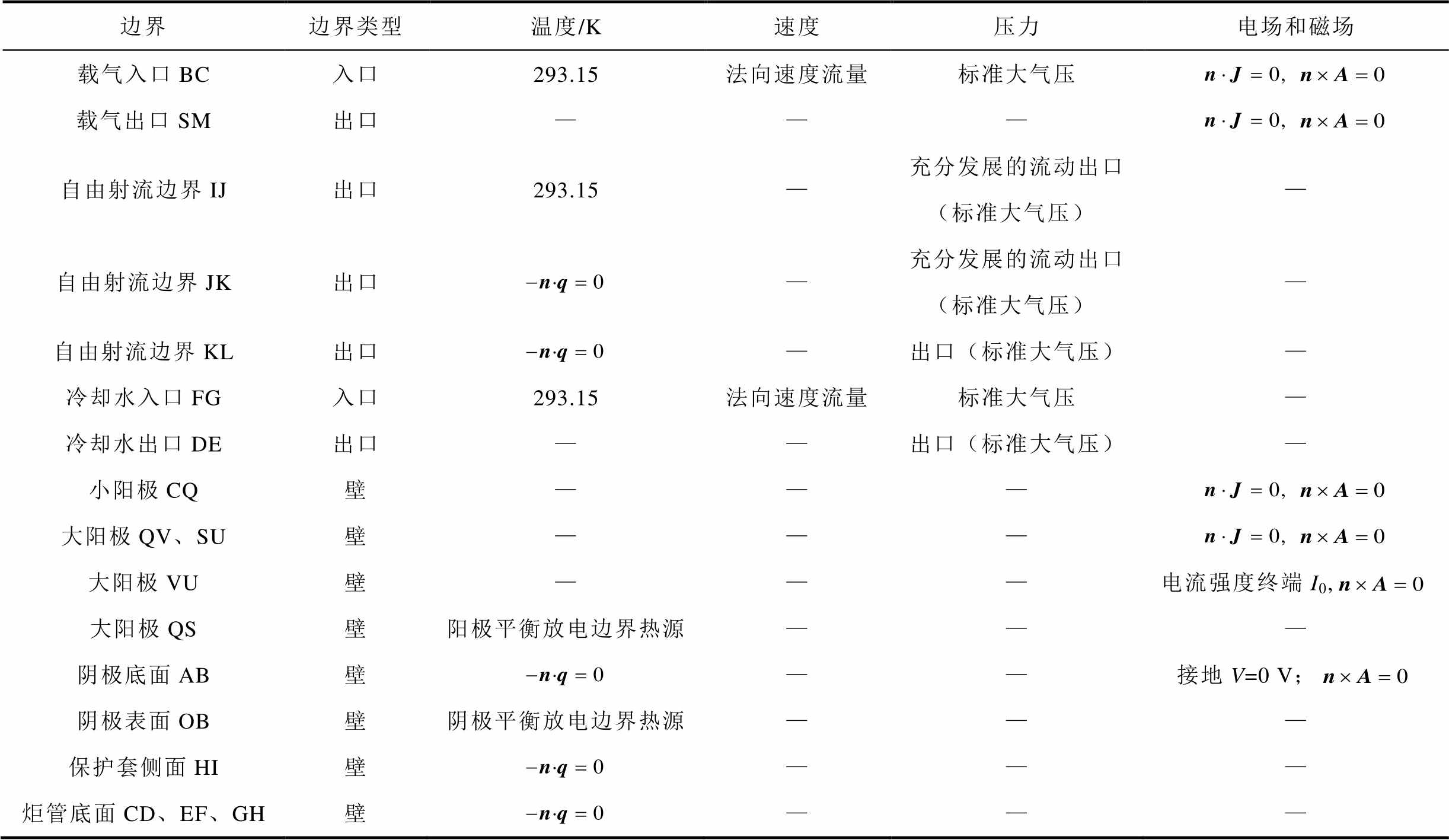
边界边界类型温度/K速度压力电场和磁场 载气入口BC入口293.15法向速度流量标准大气压 载气出口SM出口——— 自由射流边界IJ出口293.15—充分发展的流动出口(标准大气压)— 自由射流边界JK出口 —充分发展的流动出口(标准大气压)— 自由射流边界KL出口—出口(标准大气压)— 冷却水入口FG入口293.15法向速度流量标准大气压— 冷却水出口DE出口——出口(标准大气压)— 小阳极CQ壁——— 大阳极QV、SU壁——— 大阳极VU壁———电流强度终端I0, 大阳极QS壁阳极平衡放电边界热源——— 阴极底面AB壁——接地V=0 V; 阴极表面OB壁阴极平衡放电边界热源——— 保护套侧面HI壁——— 炬管底面CD、EF、GH壁———
模型基于LTE假设进行计算,但实验表明只有电弧柱区域的粒子分布近似满足这一特性,阴极附近等离子体与冷气流强相互作用的区域以及阳极表面等离子体被水冷壁强制冷却的区域是明显偏离的。这两个冷域中重粒子温度Th很低但电子温度Te却很高,宏观上是低温但又呈现较高的导电性,而在LTE假设下,温度小于8 000 K时等离子体电导率迅速下降,低于5 000 K基本不导电,直接计算会出现振荡现象,即冷域中的等离子体首先因为低电导率而产生高焦耳热,温度上升后电导率升高使焦耳热下降,与冷气流对流换热后又回到低温,循环往复使得稳态计算的结果不能收敛[21-25]。
为了避免这一问题,模型对等离子体在不同区域中的最小电导率σmin进行设置,包括:①在近阴极区设置域②中残余电导率σmin=180 S/m,近似对应Te=7 000 K、Th=1 000 K的2-T氮气等离子体的物理特性,目的是允许等离子体与阳极弧根接触之前通过焦耳热获得部分稳定的能量,保证计算收敛;②在近大阳极区QR上人为地定义一个厚度为0.1 mm、σmin=5 000 S/m的高电导率边界层,用于模拟电弧柱足够靠近大阳极壁时发生击穿。
网格划分是确保计算精度和结果收敛的重要环节,模型在常规流体计算网格划分方法的基础上,结合相关电磁场仿真经验,作出了一些针对性的设置[26-27]:①在阴极正前方1 mm处设置一个虚拟边界进行网格加密,用于捕捉等离子体运动最剧烈处的物理场细节;②将CQ段表面的边界层粗化处理,以减小此处计算时能量方程的刚性;③细化电极表面网格,提高“平衡放电边界热源”计算精度;④在域③中设置自适应网格加密,对脱离电弧后的等离子体射流区域进行网格细化;⑤在域⑥中设置各向异性网格,根据速度变化方向自动调整网格的形状和排列,以减少计算资源消耗。此外还做了必要的网格无关性验证,以轴线上的温度分布计算结果作为判据,分别对比了网格数量约为10万、35万、80万和150万的计算结果,发现差异很小,但网格数为10万的模型用于计算低电流强度工况时很容易报错,80万和150万网格的模型计算时间比较长,因此综合考虑选择网格数为35万的方案。模型中磁矢势、电势、流体均采用一阶离散,求解器选择PRADISO稳态求解器自动求解。
用于实验验证的熔融系统结构如图4所示,将等离子体炬与高温裂解炉分离后平放在定制支架上进行实验。固定电流强度为100 A,从最小气流量2.0 m3/h开始引弧点火,随后缓慢递增,直至气流量大于4.0 m3/h后火炬熄灭,每间隔0.5 m3/h记录一次数据,同时在射流正前方轴线上放置一排钨棒,间隔5 mm,每根钨棒直径为1 mm、长为100 mm,用于估算射流温度。记录如下数据:①电源柜上的平均电压读数,以及示波器测量的电弧电压波形;②冷却水流速以及入口与出口温度,用于计算冷却功率;③炬管表面最高温度;④钨棒熔断过程全程录像。
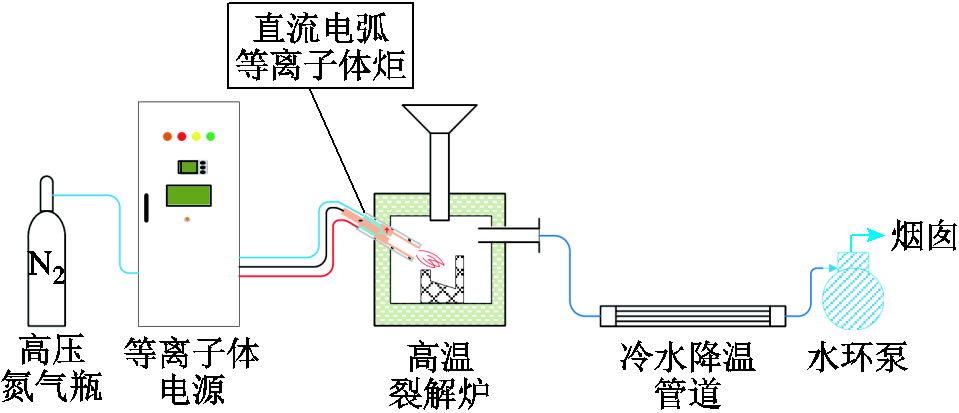
图4 熔融系统结构
Fig.4 Structure of plasma melting system
计算与实验电压数据对比见表2。固定电流强度下,气流量增大,电弧平均电压升高,但波动更加剧烈,这是大阳极弧根发生附着-击穿-再附着过程的直观反映,如果气流量过大,这一动平衡就会被打破,导致火炬熄灭。整体上看,计算电压略低于实验平均电压,与波动电压最小值十分贴近,这说明人工电导率的设置较为合理,误差主要来源于稳态假设条件。如果在本模型基础上借助高性能计算机和动网格技术,还可以对电压波动过程进行进一步预测,但计算成本会显著增加。
表2 电压数据对比
Tab.2 Voltage data comparison
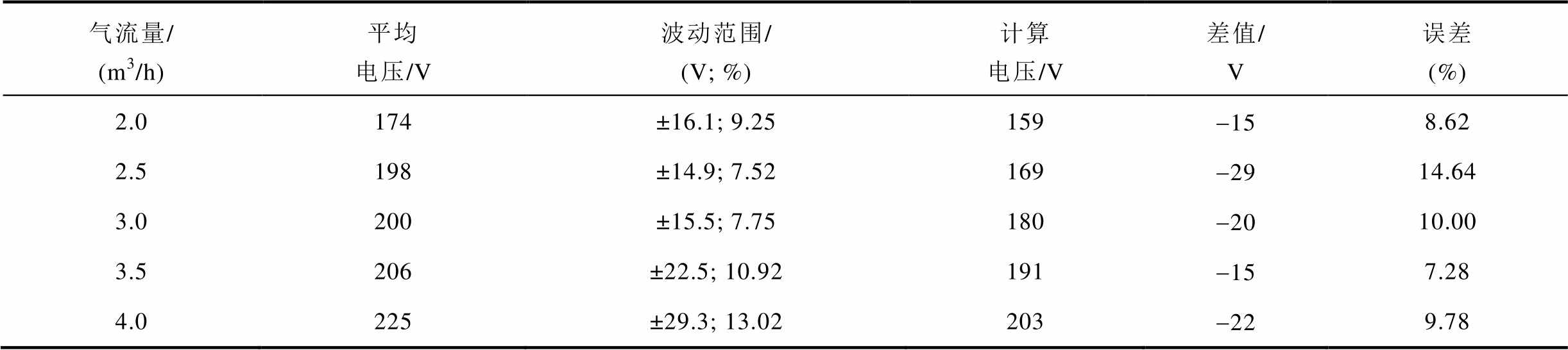
气流量/(m3/h)平均电压/V波动范围/(V; %)计算电压/V差值/V误差(%) 2.0174±16.1; 9.25159-158.62 2.5198±14.9; 7.52169-2914.64 3.0200±15.5; 7.75180-2010.00 3.5206±22.5; 10.92191-157.28 4.0225±29.3; 13.02203-229.78
电弧功率和热效率数据对比如图5所示。火炬在工作时,热效率等于电弧功率与冷却功率的差值除以电弧功率;计算的热效率定义为射流功率与电弧功率的比值;射流功率定义为射流出口SM段截面的总焓通量面积分。从图5可以看到,热效率随着电弧功率的增大而增大,实测最大值为66%、最小值为45%,计算最大值为58.27%、最小值为41.57%,数据表明此款火炬单独工作时能量转换率比较低。实验测量数据偏高是由于将SI段截面上金属和气体之间的热传导过程一并算入所导致的。
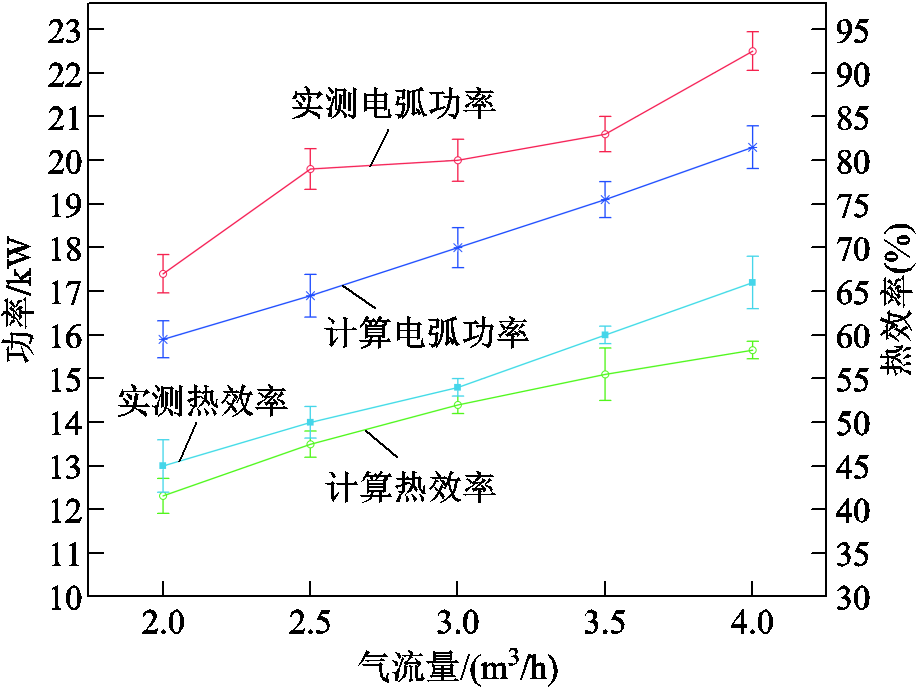
图5 电弧功率和热效率数据对比
Fig.5 Comparison of arc power and thermal efficiency datas
图6a和图6b分别为气流量为3.0 m3/h时炬管表面和切面的温度分布。表面温度在靠近射流出口一侧最高,朝进气口方向迅速衰减至室温。随气流量增大所计算的最高温度依次为80、78.9、78.4、78.6、79.4℃,用红外测温枪测量均在70℃左右,误差约13%。模型忽略了空气散热而将炬管表面设置为热绝缘,用冷却水流动模拟大、小阳极的外表面冷却,计算出内部最高温度248℃出现在阳极弧根附着区域,并且发现切面温度的变化十分明显。冷却水的加入避免了直接设置“对流热通量”一类边界条件时,“传热系数”和“外部温度”取值不准所带来的射流域计算误差。此外,如果将本模型与热等离子体反应器进行耦合计算,只需调整模型射流开放区域边界条件即可,无需对炬本体做修改,极大地提高了后续研究的便捷性。
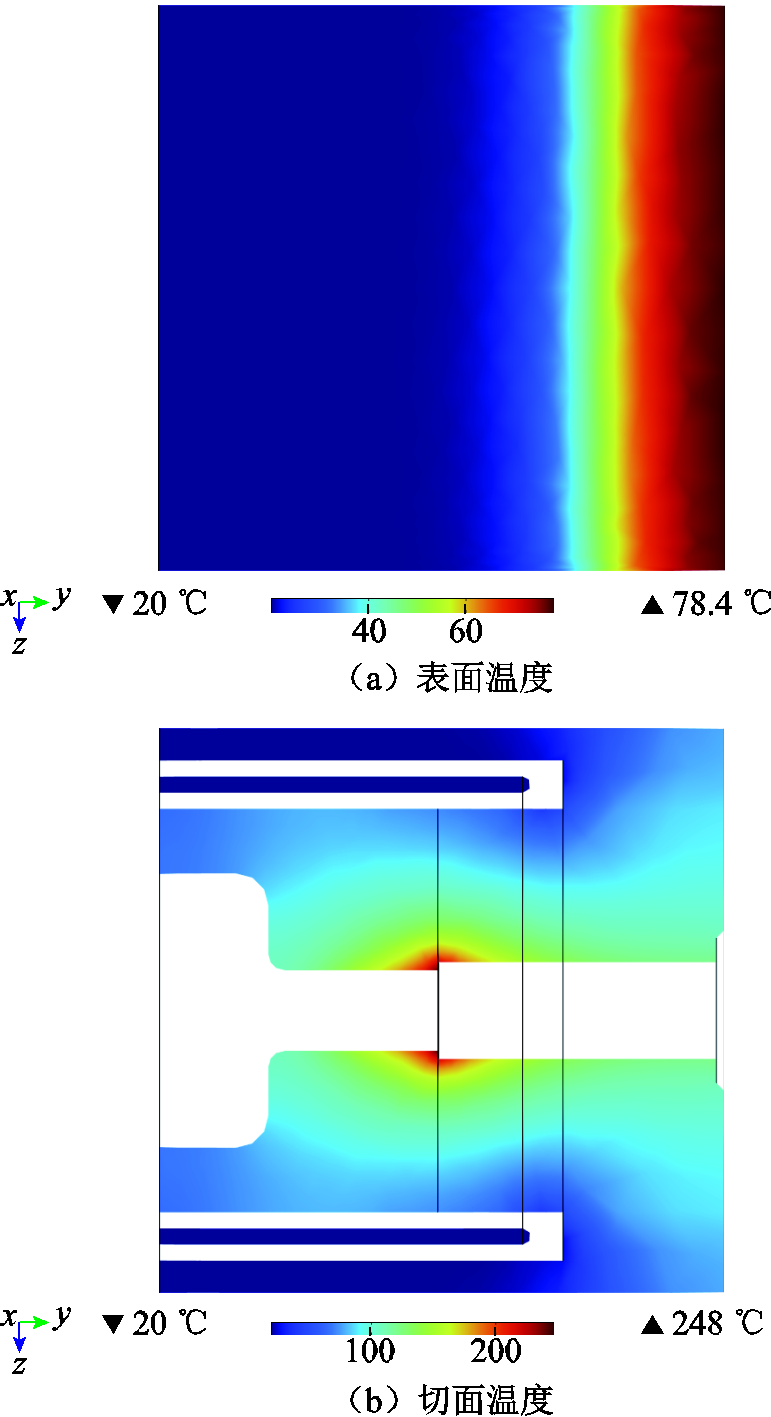
图6 炬管表面和切面温度分布
Fig.6 Temperature distribution of torch tube surface and section
射流温度是评价炬性能的重要参数,实验中用摄像机记录钨棒的熔断情况(避免中途停机),把最后一根熔断的和第一根未熔断的钨棒中间位置假设为基准点(平均温度为3 410℃),用基准点与出口的相对位置作为判据,对比分析实验结果、三维模型预测结果以及相同结构的二维轴对称稳态模型预测结果。气流量为4.0 m3/h时的钨棒烧蚀结果如图7所示,第一根熔断的钨棒距离出口30 mm,基准点距离出口62.5 mm。基准点位置分布如图8所示,实际测量的相对位置区间为52.5~62.5 mm(绿线),三维模型为63.5~70.5 mm(红线),二维模型为70.3~72.7 mm(蓝线)。结果表明,三维模型对温度的预测精度略高于二维,主要原因是二维计算所得到的阳极弧根一定是沿着圆周均匀分布,并被吹向下游呈发散趋势,三维计算则表现为强烈收缩且运动轨迹不规则的窄域。模型与实验之间的误差是因为忽略了冷空气与热等离子体之间的卷吸现象以及空气在高温下发生的相关化学反应。熔融系统工作前,需要向封闭的反应器内持续通入氮气,以尽可能地减少熔融时氮氧化合物的生成,模型为了贴近实际,将自由射流域设置为氮气,自由射流边界设置为足够大的净流出边界,结果显示误差在可接受范围之内。受测量仪器限制,本文未对射流速度进行分析。

图7 钨棒烧蚀结果
Fig.7 Tungsten rod ablation results
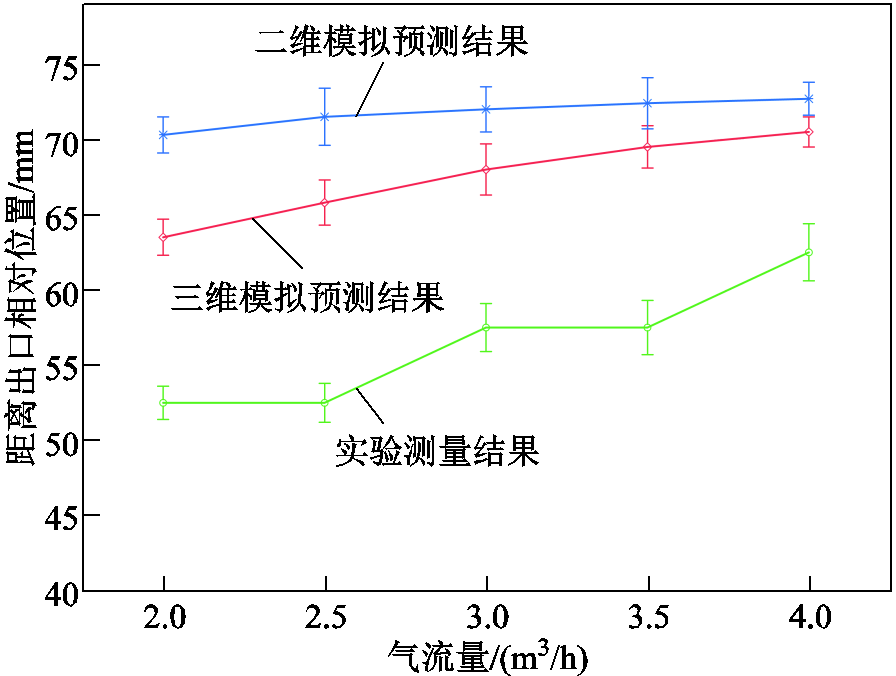
图8 基准点位置分布
Fig.8 Reference point position distribution
取工况条件为100 A、3.0 m3/h的算例进行分析,得到射流速度场和温度场分布分别如图9a和图9b所示。可以看到,冷气体与等离子体之间的压力梯度和径向洛伦兹力作用的结果十分明显,速度和温度在径向上都大幅衰减,最大值均出现在阳级弧根附着区域。
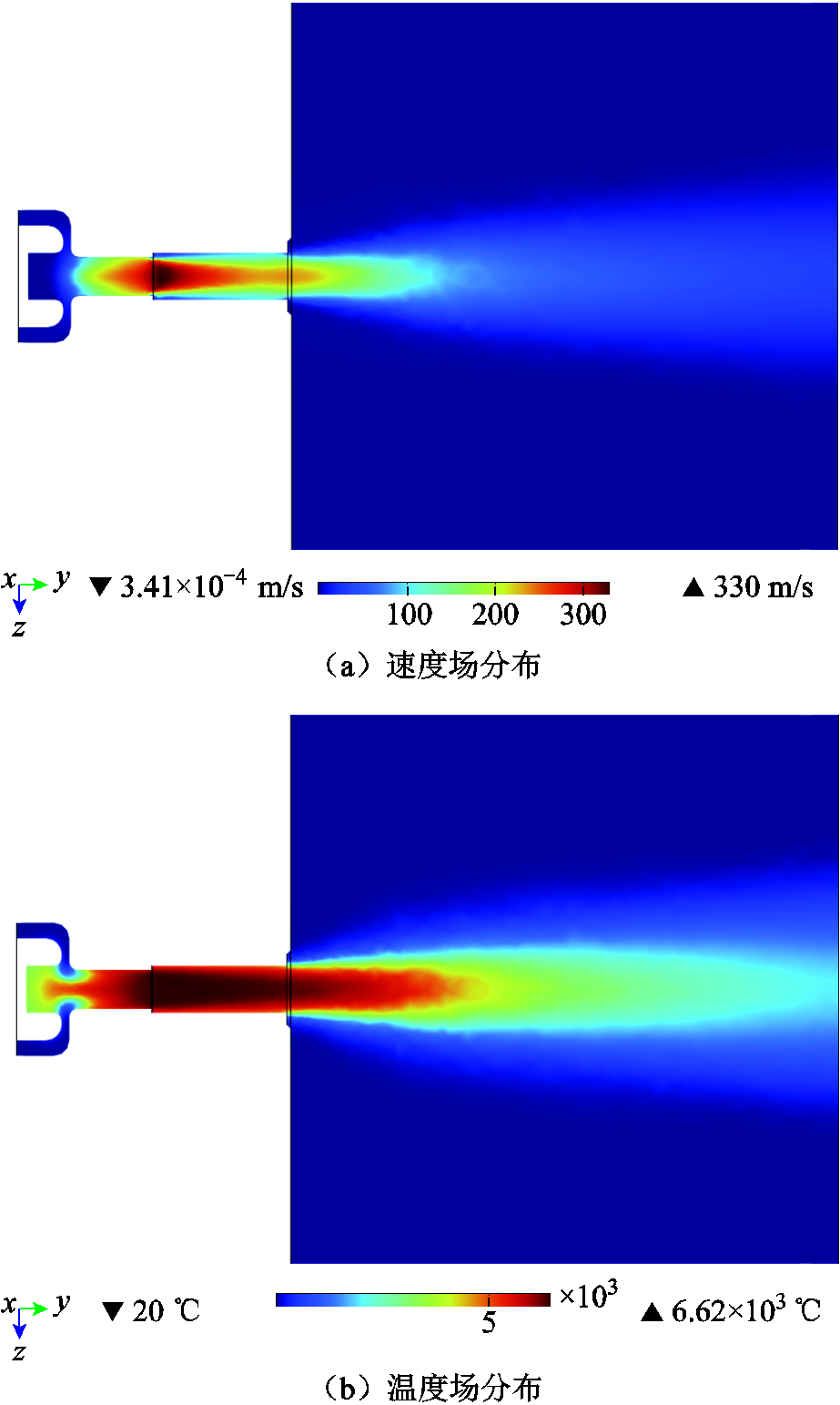
图9 速度场和温度场分布
Fig.9 Velocity and temperature field distribution
轴线速度分布曲线如图10所示,可见所有工况下速度均出现了两个极大值。第一个极大值出现在弧根附着区域(38 mm)附近,此处温度最高,等离子体动能最大,随后脱离电弧向下游运动;第二个极大值出现在出口(70 mm)附近,射流射出时受到出口周围金属壁面高温影响被轻微加速,随后开始迅速衰减。
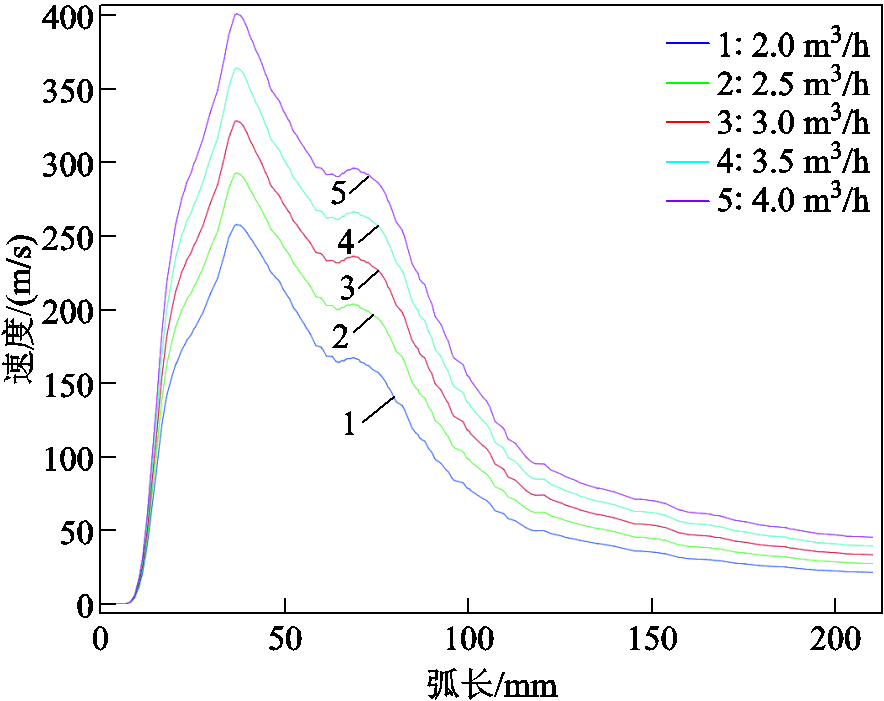
图10 轴线速度分布曲线
Fig.10 Axis velocity distribution curves
轴线温度曲线如图11所示。在炬管内,气流量越大则温度越低,大阳极弧根(38 mm)附近温度最高为6 850℃(2.0 m3/h)、最低为6 250℃(4.0 m3/h);出口(70 mm)温度最高为6 450℃(2.0 m3/h)、最低为6 200℃(4.0 m3/h);射流射出后温度迅速衰减,充分发展(210 mm)时最高温度为1 987℃(4.0 m3/h)、最低为1 967℃(2.0 m3/h),气流量越大则温度越高,但差异极小,这是因为射流域为开放的冷氮气域。结果表明,炬在工作时,高气流量有助于降低炬内最高温度,延长电极寿命,如果将射流末端温度作为火炬性能评判依据,还需要与反应器进行耦合研究分析二者之间的适配性,因为反应器的聚热作用也是确保射流到达熔融池时气体温度满足熔融条件的关键。
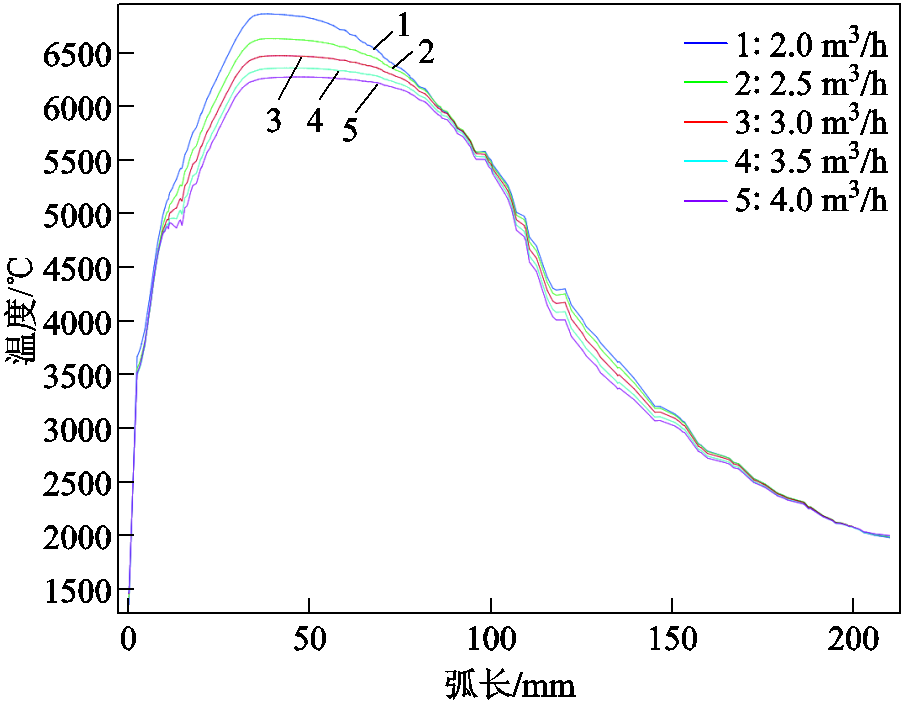
图11 轴线温度分布曲线
Fig.11 Axis temperature distribution curves
大阳极表面温度和电流密度分布分别如图12a和图12b所示。炬工作时,阳极弧根在气动力和洛伦兹力的作用下,沿着壁面快速旋转,对这一现象进行预测使域③中远离轴线的区域计算结果更贴近实际。最大电流密度达到了6.64×106 A/m2,沿轴向朝下游迅速衰减,高电流密度区域同时也是高温区域,大阳极表面最高温度2 930℃、最低温度1 880℃,均大于紫铜的熔点1 083℃。实验观测发现,一个新的阳极在点火1次、5次和多次后,光滑表面立刻出现烧蚀熔化的痕迹并且逐渐加深,其粗糙程度从出口向上游递增,尽管有冷却系统的存在,但只能在一定程度上减缓这种损耗,并且冷却系统也是射流热量损失的主要原因,随着工作时间的增加,光滑的电极表面变得非常粗糙后,就必须更换新的电极。
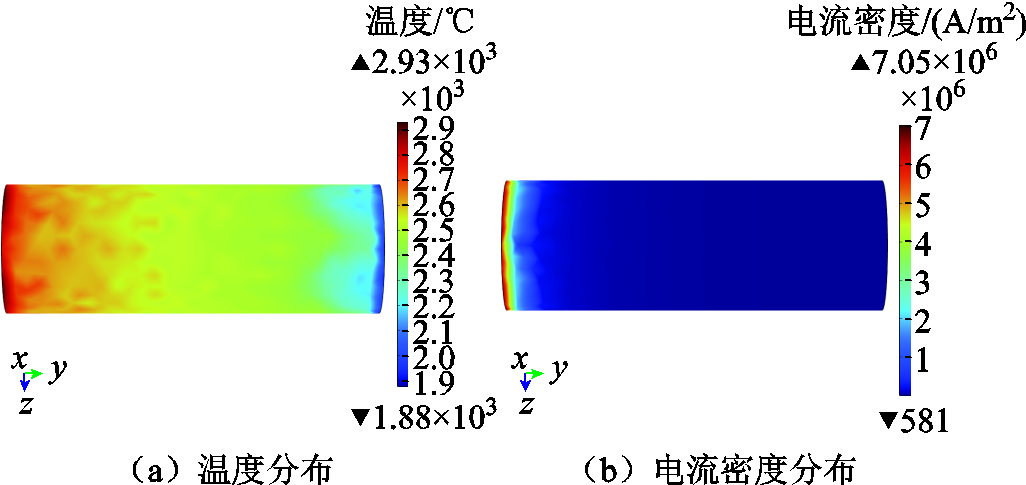
图12 大阳极表面温度和电流密度分布
Fig.12 Large anode surface temperature and current density distribution
阴极表面温度和电流密度分布分别如图13a和图13b所示。模型基于热电子发射定律,将接地条件设置在阴极背面,把阴极表面看作为平衡放电边界热源,与选择将阴极表面温度和电流密度的经验函数作为一类边界条件的简化方法相比,避免了阴极附近温度场计算不准进而影响下游计算结果,同时也考虑到了电极电阻产生的焦耳热。阴极表面温度从中心沿着径向衰减,最大温度为2 550℃,远离中心温度迅速降低,最低为687℃。对电极检测发现,计算温度分布与电极表面的黑色氧化层痕迹基本吻合。电流密度最大值5.6×105 A/m2出现在凹陷边缘,低于阳极一个数量级。电极表面物理场数据可以为电极寿命预测提供参考。
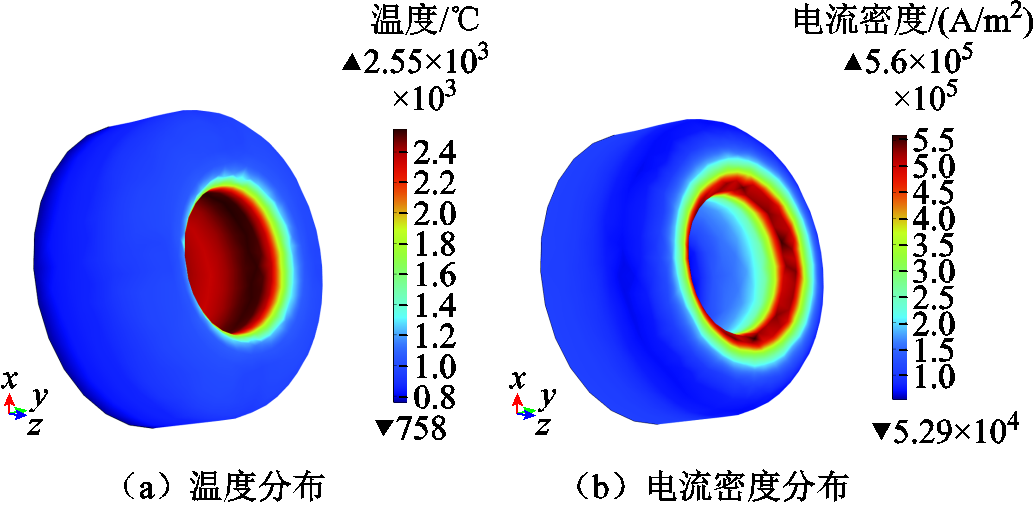
图13 阴极表面温度和电流密度分布
Fig.13 Cathode surface temperature and current density distribution
本文针对一款级联阳极结构的非转移直流电弧等离子体炬,基于磁流体力学理论,用有限元软件COMSOL对氮气热等离子体射流流入冷氮气域现象进行了三维稳态数值模拟,得出了以下结论:
1)建立的三维稳态数值模型能够较好地预测实际,相对于其他两类模拟方法,在计算速度和计算精度的平衡性上更适用于放射性废物等离子体熔融处理技术的研究,得到的稳态电压数据贴近平均电压,热效率计算可靠。
2)模型中冷却水散热环节的加入避免了阳极外侧一类边界条件取值不准带来的误差,提高了炬管整体的温度场计算精度,模型可以直接作为研究等离子体炬与热等离子体反应器适配性的标准输入源。
3)考虑到湍流等离子体三维运动效应的三维模型,计算所得到的基准点预测精度略高于二维轴对称模型。温度和速度场的计算结果表明,在炬管内速度越高、温度越低,射流充分发展后则相反。固定电流强度下,气流量增大,电弧功率和热效率都增大,但热效率比较低。
4)在电极表面设置平衡放电边界热源用于替换一类边界条件,预测得到大阳极表面的弧根运动轨迹是一个强烈收缩的不规则窄域,表面温度分布不均匀且均超过材料熔点;阴极表面最高温度出现在凹陷位置,外侧温度最低,电流密度小于阳极一个数量级。电极表面物理场数据可以用于预测电极寿命。
模型可为直流电弧等离子体炬设计和优化工作提供参考,后续研究将在此基础上陆续展开,主要集中于不同种类的工作气体、进气方式、电流强度与气流量的工况组合、不同形状的电极结构组合等不同变量对射流特性和热效率的影响分析。
参考文献
[1] 马中洋, 李淩豪, 孙红梅, 等. 大尺寸电弧等离子体的产生、控制及应用[J]. 力学学报, 2023, 55(12): 2876-2890.
Ma Zhongyang, Li Linghao, Sun Hongmei, et al. Generation of large volume arc plasma, control and its application[J]. Chinese Journal of Theoretical and Applied Mechanics, 2023, 55(12): 2876-2890.
[2] 陈思邈, 程昌明, 李平川, 等. 等离子体熔融技术在核电站放射性废物处理中的研究应用现状[J]. 真空科学与技术学报, 2022, 42(7): 483-490.
Chen Simiao, Cheng Changming, Li Pingchuan, et al. Application progress of plasma melting technology for disposal of radioactive waste in nuclear power plants[J]. Chinese Journal of Vacuum Science and Technology, 2022, 42(7): 483-490.
[3] Ma Yuheng, Chu Haoran, Zheng Bowen. Research progress of plasma melting technology in radioactive waste treatment of nuclear power plants[J]. Annals of Nuclear Energy, 2024, 198: 110307.
[4] 曹亚文, 韩先伟, 谭畅, 等. 双弧室磁控空气等离子体炬电弧特性的实验研究[J]. 高电压技术, 2021, 47(3): 832-839.
Cao Yawen, Han Xianwei, Tan Chang, et al. Characteristic researches on arc generated by magnetic double-chamber air plasma torch[J]. High Voltage Engineering, 2021, 47(3): 832-839.
[5] 赵明波, 曹修全, 郭文钰, 等. 氮氩直流电弧等离子体射流特性实验研究[J]. 高电压技术, 2023, 49(5): 2206-2215.
Zhao Mingbo, Cao Xiuquan, Guo Wenyu, et al. Experimental study on the characteristics of nitrogen-argon DC arc plasma jet[J]. High Voltage Engineering, 2023, 49(5): 2206-2215.
[6] Li Kuan, Zhu Cheng, Zhang Yunfei, et al. Experimental study of the discharge characteristics of a stepped-nozzle arc plasma torch[J]. Plasma Chemistry and Plasma Processing, 2024, 44(4): 1469-1492.
[7] 姚聪林, 朱红春, 姜周华, 等. 电弧炉内长电弧等离子体的数值模拟[J]. 工程科学学报, 2020, 42(增刊1): 60-67.
Yao Conglin, Zhu Hongchun, Jiang Zhouhua, et al. Numerical simulation of a long arc plasma in an electric arc furnace[J]. Chinese Journal of Engineering, 2020, 42(S1): 60-67.
[8] 徐云聪, 张逸, 林才华, 等. 基于电气特性-物理参数耦合的交流电弧炉模型[J]. 电工技术学报, 2024, 39(6): 1643-1655.
Xu Yuncong, Zhang Yi, Lin Caihua, et al. AC arc furnace model based on coupling of electrical and physical parameters[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1643-1655.
[9] 赵梦静, 王勇, 杨树峰, 等. 电弧等离子体多物理场分布特征[J]. 机械工程学报, 2022, 58(8): 153-159.
Zhao Mengjing, Wang Yong, Yang Shufeng, et al. Distribution characteristics of multi-physics fields in arc plasma[J]. Journal of Mechanical Engineering, 2022, 58(8): 153-159.
[10] 崔建, 孙帅, 张国钢, 等. 基于双温度磁流体电弧仿真改进Mayr电弧模型的特快速暂态过电压仿真方法[J]. 电工技术学报, 2024, 39(16): 5149-5161.
Cui Jian, Sun Shuai, Zhang Guogang, et al. The very fast transient overvoltage simulation method based on two-temperature MHD arc simulation to improve Mayr arc model[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5149-5161.
[11] 张在秦, 刘志远, 王闯, 等. 大电流真空电弧中阳极熔化过程的实验与仿真研究[J]. 电工技术学报, 2024, 39(7): 2143-2152, 2160.
Zhang Zaiqin, Liu Zhiyuan, Wang Chuang, et al. Experimental and numerical study on anode melting in high current vacuum arcs[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2143-2152, 2160.
[12] 王飞, 曹亚文, 林榕, 等. 一种小功率孔形阳极喷嘴等离子体炬的研究[J]. 推进技术, 2021, 42(11): 2600-2609.
Wang Fei, Cao Yawen, Lin Rong, et al. Low-power plasma torch with hole-mouthed anode[J]. Journal of Propulsion Technology, 2021, 42(11): 2600-2609.
[13] Tao Jing, Li Changpeng, Cao Xiuquan, et al. Modeling of the arc characteristics inside a thermal laminar plasma torch with different gas components[J]. Processes, 2024, 12(6): 1207.
[14] 师浩阳, 王平阳, 王淑. 直流电弧等离子体炬数值模拟与诊断[J]. 上海航天(中英文), 2024, 41(1): 122-129.
Shi Haoyang, Wang Pingyang, Wang Shu. Numerical simulation and diagnostic analysis on DC arc plasma torch[J]. Aerospace Shanghai (Chinese & English), 2024, 41(1): 122-129.
[15] Liu Senhui, Trelles J P, Murphy A B, et al. Numerical simulation of the flow characteristics inside a novel plasma spray torch[J]. Journal of Physics D: Applied Physics, 2019, 52(33): 335203.
[16] Zhukovskii R, Chazelas C, Rat V, et al. Predicted anode arc attachment by LTE (local thermodynamic equilibrium) and 2-T (two-temperature) arc models in a cascaded-anode DC plasma spray torch[J]. Journal of Thermal Spray Technology, 2022, 31(1): 28-45.
[17] Boulos M I, Fauchais P L, Pfender E. Thermodynamic Properties of Plasmas[M]//Handbook of Thermal Plasmas. Cham: Springer International Publishing, 2023: 211-256.
[18] Pan Zihan, Ye Lei, Qian Shulou, et al. Comparison of Reynolds average Navier-Stokes turbulence models in numerical simulations of the DC arc plasma torch[J]. Plasma Science and Technology, 2020, 22(2): 025401.
[19] Zhukovskii R, Chazelas C, Vardelle A, et al. Effect of electromagnetic boundary conditions on reliability of plasma torch models[J]. Journal of Thermal Spray Technology, 2020, 29(5): 894-907.
[20] Boulos M I, Fauchais P L, Pfender E. Electrode Phenomena in Plasma Sources[M]//Handbook of Thermal Plasmas. Cham: Springer International Publishing, 2023: 553-594.
[21] 孙强. 电弧等离子体全域数值模拟[D]. 合肥: 中国科学技术大学, 2019.
Sun Qiang. A global numerical simulation of arc plasmas[D]. Hefei: University of Science and Technology of China, 2019.
[22] 盛德杰, 王尧, 邢云琪, 等. 基于磁流体动力学仿真的低压交流串联故障电弧致火风险研究[J/OL]. 电工技术学报, 2024: 1-13[2024-10-11]. https://doi. org/10.19595/j.cnki.1000-6753.tces.240786.
Sheng Dejie, Wang Yao, Xing Yunqi, et al. Research on fire risk of low voltage AC series fault arc based on magnetohydrodynamics simulation[J/OL]. Transac-tions of China Electrotechnical Society, 2024: 1-13[2024-10-11]. https://doi.org/10.19595/j.cnki.1000-6753.tces.240786.
[23] 边晨曦, 何柏娜, 姜仁卓, 等. C4F7N二元混合气体电弧温度特性研究[J]. 高压电器, 2024, 60(9): 53-60.
Bian Chenxi, He Baina, Jiang Renzhuo, et al. Research on arc temperature characteristics of C4F7N binary gas mixture[J]. High Voltage Apparatus, 2024, 60(9): 53-60.
[24] 陈默, 陆宁懿, 翟国富. 基于电弧磁流体仿真的DC 1500 V两极塑壳断路器气道优化设计[J]. 电工技术学报, 2023, 38(8): 2222-2232.
Chen Mo, Lu Ningyi, Zhai Guofu. Arc chamber optimization of DC 1 500 V two-pole circuit breakers based on arc magneto hydro dynamics simulation[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2222-2232.
[25] 周旭. 热等离子体流动特性的数值研究[D]. 合肥: 中国科学技术大学, 2022.
Zhou Xu. Numerical study on flow characteristics of thermal plasma[D]. Hefei: University of Science and Technology of China, 2022.
[26] Stone J M, Tomida K, White C J, et al. The Athena++ adaptive mesh refinement framework: design and magnetohydrodynamic solvers[J]. The Astrophysical Journal Supplement Series, 2020, 249(1): 4.
[27] Wang J, Duan J M, Ma Z W, et al. An adaptive moving mesh finite difference scheme for tokamak magneto-hydrodynamic simulations[J]. Computer Physics Communications, 2024, 294: 108951.
Three-Dimensional Steady State Numerical Simulation of Non-Transferred DC Arc Plasma Torch
Abstract The non-transfered DC arc plasma torch is the core equipment in the radioactive waste plasma melting treatment system. The physical field parameters of the jet are not only an important index for the design and optimization of the plasma torch, but also the key to improve the system energy utilization rate and the quality of the vitreous products. Aiming at a plasma torch with cascade anode structure, based on the theory of magnetohydrodynamics, this paper uses the finite element software COMSOL to conduct three-dimensional steady-state numerical simulation of the phenomenon of nitrogen hot plasma jet flowing into the cold nitrogen domain, establishes a multi-physical field coupling model of electric-magnetic-flow-heat, calculates the physical field parameters of the jet, and compares the calculated results with relevant experimental data. The effect of changing the input gas flow rate on the performance of plasma torch under the condition of fixed current intensity is analyzed. The results show that the model can predict the actual situation well, and the obtained data of jet temperature field, velocity field, electrode surface temperature and current density distribution can provide reference for the design and optimization of plasma torch.
Firstly, the 3D structure diagram of the plasma torch is accurately drawn in COMSOL, and the materials are defined in different areas. Secondly, based on the theory of magnetohydrodynamics, relevant assumptions and mathematical equations are listed, which include electromagnetic field, fluid and heat transfer. Thirdly, the boundary conditions of the model and the artificial conductivity of nitrogen plasma in different regions are introduced in detail, and some specific Settings are explained. Finally, the experimental platform is built, and the data obtained by a series of continuous experiments are compared with the simulation results.
Comparing the experimental data with the simulation data, it is found that the calculated average voltage is very close to the actual measurement results but a little lower, and the error comes from the steady-state hypothesis. Thermal efficiency calculation is reliable; The temperature changes of the torch tube surface and section are very obvious, which indicates that the calculation accuracy can be improved by adding the "cooling water" calculation area to replace a class of boundary conditions in the model. The prediction accuracy of the datum point of jet temperature 3 410℃ is slightly higher than that of the two-dimensional model. By analyzing the simulation data, it is found that the pressure gradient and radial Lorentz force between the cold gas and the plasma are obvious. There are two maximum values of speed under all conditions. In the torch tube, the higher the gas flow rate, the lower the temperature, and the opposite is true outside the torch tube. The electrode boundary can be regarded as a "balanced discharge boundary heat source" to predict the electrode performance synchronously, and the temperature distribution data of the electrode is consistent with the ablation test results.
The model can provide a reference for the design and optimization of DC arc plasma torches, and subsequent studies will be carried out on this basis, mainly focusing on the analysis of the influence of different variables on jet characteristics and thermal efficiency, including different types of working gases, intake modes, the combination of current intensity and gas flow conditions, and the combination of electrode structures with different shapes.
Keywords:Non-transfered DC arc plasma torches, radioactive waste treatment, numerical simulation, multi-physics coupling
中图分类号:O53;V439.2
DOI: 10.19595/j.cnki.1000-6753.tces.L11026
收稿日期 2024-07-11
改稿日期 2024-09-29
程文博 男,2000年生,硕士研究生,研究方向为中低放射性废物等离子体熔融处理技术。
E-mail:624946939@qq.com
吴 楠 男,1989年生,讲师,研究方向为放电等离子体及其应用。
E-mail:245803598@qq.com(通信作者)
(编辑 陈 诚)