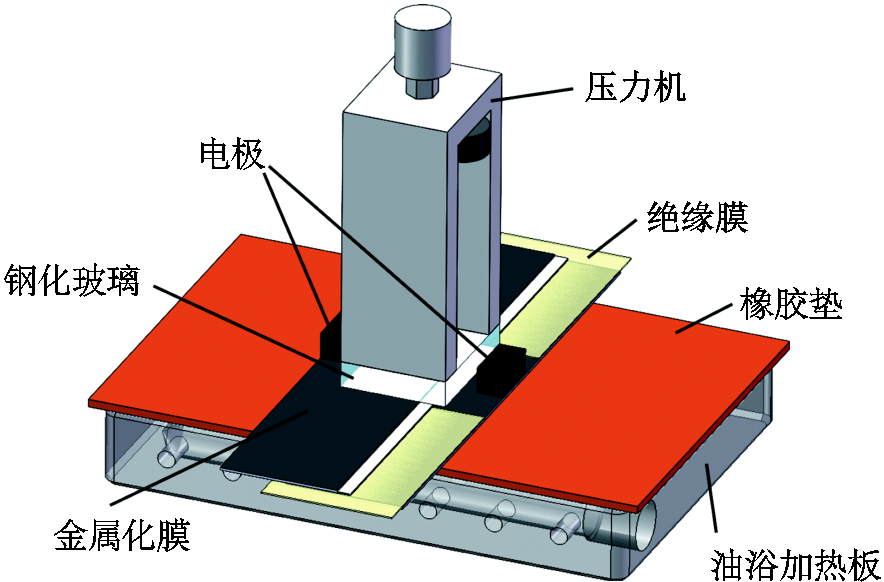
图1 金属化膜自愈试验平台
Fig.1 Self-healing test platform in metallized film
摘要 金属化膜电容器因具有稳定性高、容量大、自愈性能好等特点,在许多电力电子领域中被广泛采用。研究复杂应力下金属化膜自愈微观机理,有助于优化金属化膜电容器制造工艺,提高产品寿命和稳定性。该文搭建了多物理场下金属化膜自愈特性测试平台,展开不同电热力环境下金属化膜自愈试验,表征了自愈面积与自愈形貌,并搭建了多物理场下自愈模型。仿真和试验结果表明:气态与等离子环境下的放电通道形成时间仅为ns级,发展形式与电子崩相似,且放电通道完全贯穿所需的时间与电压和温度成反比,与压强成正比;金属层蒸发面积和等离子化区域大小与施加的电压等级和温度成正比,与压强成反比,在不同电压、温度与压强下等离子化区域均占蒸发面积的43%左右;自愈过程中电介质层的炭化量极少,炭化区域半径和深度与电压、温度成正比,与压强成反比,炭化区域半径约为自愈面积半径的1.6倍,炭化深度约为膜厚的7%,仿真计算结果与相同条件下的自愈试验结果吻合。
关键词:金属化膜电容器 双极性载流子-运输模型 自愈模型 放电通道 等离子体 炭化
与箔式电容器相比,干式金属化膜电容器(Metallized Film Capacitor, MFC)具有体积小、质量轻、噪声小、环境污染小、自愈(Self-Healing, SH)特性等优点[1],被广泛应用于电力系统中的高、低压交流无功补偿和电力电子滤波领域。与箔式电容器击穿后绝缘不可恢复不同,金属化膜电容器具有自愈特性。在电压作用下,金属化膜上存在的电弱点会被击穿,电弱点的来源包括:薄膜生产过程中引入的气泡、杂质和缺陷等由于介质老化产生的电弱点[2]。在承受高电压时,这些电弱点处的介质膜率先被击穿并形成放电通道流经大电流,电流产生的热效应导致局部金属层受热蒸发形成等离子体并向外扩散,电弧等离子体的作用将使部分介质分子分解成原子状态并产生气体,当该过程持续至能量低于临界值时,放电电弧难以维持并熄灭,膜间绝缘重新恢复[3]。
第一个关于自愈过程的复杂模型由J. Kammermaier等在1989年提出[4],该模型基于等离子体物理学和气体动力学,首次揭示了自愈过程中等离子体的存在与作用以及等离子体引起有机电介质的碳沉积现象,研究表明,自愈的动态过程是由聚合物表面侵蚀决定的。V. Belko等在仿真模型中考虑了金属化膜自愈过程中热量向电介质层的传递[5],在对分段门极电流破坏进行数值模拟中加入了聚合物层受热产生的影响。J. H. Tortai等介绍了一种用于分析金属化聚丙烯膜自愈过程中产生的等离子体的光谱学工具[6],通过仿真模拟铝等离子体的发射线的宽化效应,可以确定等离子体的物理特性,如温度、密度和等离子体区域的厚度等。V. O. Belko等用数值模型分析了金属化膜电容器在过载下的退化过程[7],分别用于评估MFC在自愈(SH)过程中的电热状态和过载模式下的热状态。通过分析SH事件对MFC参数的影响,文章还提出了MFC退化的诊断参数与方法并进行了加速寿命测试。国内华中科技大学的章妙建立了金属化膜自愈过程的热学等效模型[8],结果表明层间空气影响自愈过程中电弧等离子体的发展过程,造成自愈点形态和自愈面积的差异,层间空气将扩大电弧作用区域,使自愈点面积扩大,但基于热学等效模型计算的自愈面积与实测值存在较大差异。李化团队搭建了专业的自愈试验测试平台,探究了层间压强、方阻、电压、温度以及热处理工艺等对金属化膜自愈特性的影响规律[9-12]。
以上学者都从宏观层面系统、详细地分析了金属化膜自愈特性的宏观规律,但对于自愈的产生机制以及金属蒸发、介质炭化的动态变化过程缺少相应的研究,目前对金属化膜电容器的仿真研究没有涉及不同电热力环境对自愈过程中金属层等离子体产生与电介质层炭化的影响,对于不同环境在微观领域如何影响放电通道的形成与发展尚缺乏相应的建模与论证。现今金属化膜生产工艺的改进主要依赖经验主义,造成大量浪费,工业上亟须自愈特性的理论指导。
本文利用多物理场金属化膜自愈试验平台探究了不同电热力环境下金属化膜的自愈特性,表征了自愈面积与自愈形貌,使用COMSOL Multiphysics 6.2有限元仿真软件搭建了金属化聚丙烯薄膜自愈模型,首先通过双极性载流子运输模型研究了不同时间放电通道内空间电荷的分布,并以此结果作为初始值,利用气体放电模型探究不同电热力环境下等离子体形成放电通道的过程;然后研究了电热力耦合下金属化膜电容器自愈过程中金属层气化后受电场影响形成的等离子体以及电弧等离子高温对聚丙烯层的炭化作用;最后通过仿真与试验验证了模型的准确性。
金属化膜是先在有机薄膜表面蒸镀一层极薄的金属层,蒸镀的金属可以是金、银、锡、铝、铝锌复合等[13],再经过卷绕制成金属化膜电容器元件。为探究不同电热力环境下金属化膜电容器自愈的形貌与面积,使用南洋MDP 5.8 μm厚度聚丙烯金属化膜来进行自愈试验,金属层为铝。试验中取两片金属化膜交错铺设,两片重合部分即为自愈发生部位。
使用的金属化膜自愈试验平台如图1所示,该试验平台可模拟包含电、热、力多重物理环境,其电路如图2所示。其中信号发生器采用RIGOL DG5071型,输出频率为70 MHz,采样率为1 GS/s;功率放大器为Trek Model 675型,放大倍数为1 000倍;示波器为TELEDYNE HDO6054型,采样率为10 GS/s,用于监测样品两端电压;试验设置的电压等级分别为1.8、2.3、2.8、3.3、3.8 kV;加热设备采用国辉JW-0510型恒温油浴循环器,样品通过一层1 mm的硅胶片平铺在金属加热板上,确保样品在均匀受热的同时硅胶片起到绝缘的作用。参考GB/T 11024.1—2019《标称电压1 000 V以上交流电力系统用并联电容器第1部分:总则》中的试验环境温度15~35℃,且电容器在实际运行时的最大温升温度在6~11℃之间,取30℃为电容器运行温度的平均值;参考GB/T 11024.1中规定的环境温度年平均最高上限55℃以及实际测量得到的电容器内部温度,取70℃为电容器可长期连续工作的上限温度。综上所述,本试验设置的温度分别为30、40、50、60和70℃。压力装置采用量程为2 kN的东日仪器DR-502AS型拉力试验机,压力机通过一块3.5 cm× 5.5 cm的玻璃块与样品相接,玻璃块完全覆盖两金属化膜重合部分以确保压力均匀地施加在自愈发生位置。绕制薄膜电容器中的金属化膜受到径向压力,且越内层的金属化膜承受的压强越大,自愈现象主要发生在50%以下深度。综上所述,本试验设置的压强分别为1.8 MPa(考虑外包膜时最外层压强)、4.3 MPa(25%深度)、8 MPa(40%深度)、11 MPa(50%深度)和15 MPa(55%深度)。

图1 金属化膜自愈试验平台
Fig.1 Self-healing test platform in metallized film
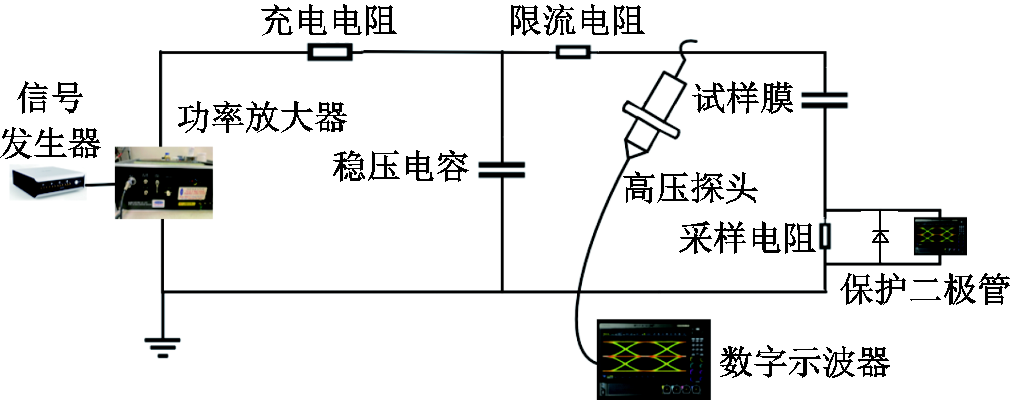
图2 试验电路
Fig.2 Test circuit
在电压设置为1.8、2.3、2.8、3.3和3.8 kV,压强为1.8 MPa的环境条件下分别记录金属化膜样品在30、40、50、60和70℃不同温度下的自愈形貌与面积;在电压设置为1.8、2.3、2.8、3.3和3.8 kV,温度为50℃的环境条件下分别记录金属化膜样品在1.8、4.3、8、11和15 MPa不同压强下的自愈形貌与面积。
典型自愈波形如图3所示。
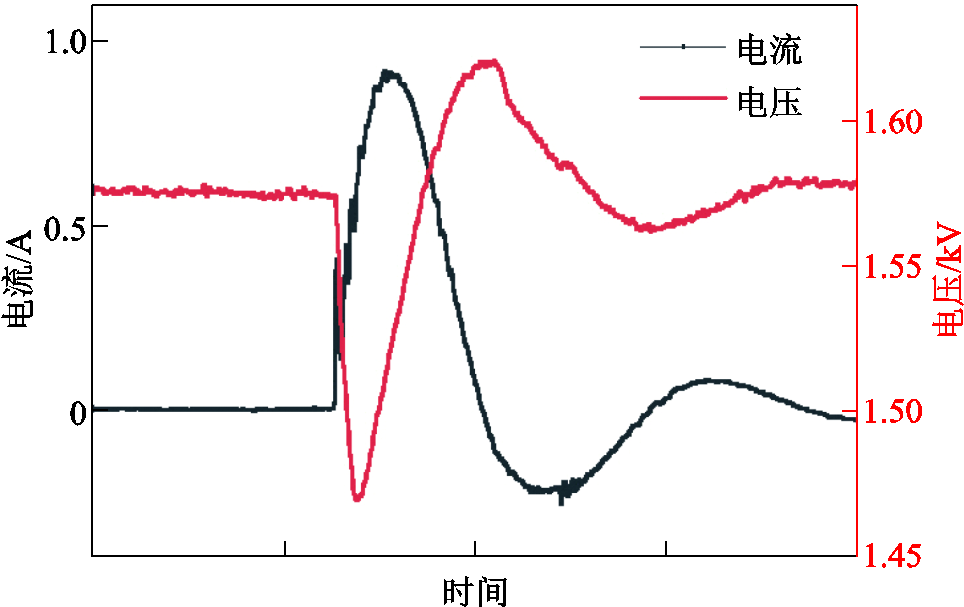
图3 典型自愈波形
Fig.3 Typical self-healing waveforms
使用SOPTOP-SZN71型光学显微镜对自愈后的试样进行形貌观测,利用长度为1 mm的标尺作为参考进行拍摄。图4给出了在2.8 kV、1.8 MPa环境中,不同温度下的试样自愈形貌和1.8 MPa、30℃环境中,不同电压等级下的试样自愈形貌。在相同电压等级与压强的环境中,随着温度的上升,相邻自愈面积之间的细丝状放电通道数量增加,通道变粗,且各自愈点开始大面积地通过细丝状放电连接在一起。随着电压等级的提升,自愈点数量增加且相邻各点自愈面积开始通过较为强烈的放电形成的细丝状放电通道连接在一起[14]。

图4 不同温度、电压下的自愈形貌
Fig.4 Self-healing morphology under different temperatures and voltages
自愈面积随温度与电压的变化如图5所示。由图5可看出,自愈面积与温度和电压呈正相关,在1.8 MPa下,50℃和70℃的自愈面积随电压变化的曲线较为相似。在30℃温度下,自愈面积的增长随电压变化的曲线较50℃和80℃时更为平缓。在实际工程应用中,较低的工作温度环境会使金属化膜电容器的自愈特性更加稳定,可预测性也会更高。从图5中可以看出,电压等级越大,温度对自愈面积的影响越大,电压超过2 kV时,在50℃和70℃更高的温度下,自愈面积开始大幅度地增加。
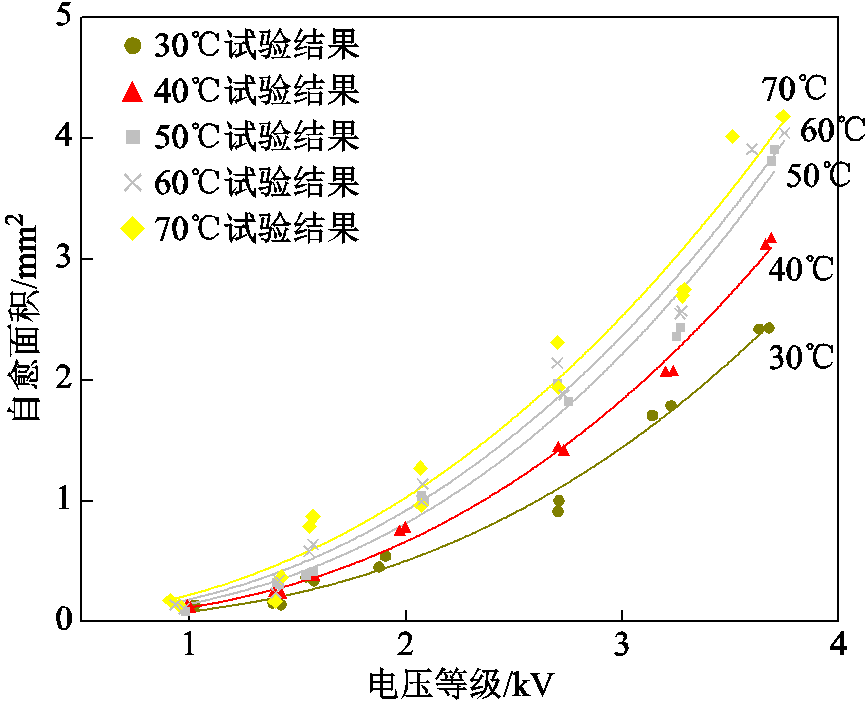
图5 不同温度下自愈面积与电压等级的关系
Fig.5 The relationship between self-healing area and voltage levels at different temperatures
图6给出了在1.8 kV、50℃环境中,不同压强下的试样自愈形貌和4.3 MPa、50℃环境中,不同电压等级下的试样自愈形貌。在较低电压等级下,自愈数量少,自愈面积小且自愈形貌的边缘较为规则和清晰,说明此时的自愈放电较为轻微与温和[15]。在相同电压与温度下,随着压强的上升,样品的自愈数量下降,自愈形貌也更加接近圆形。

图6 不同压强、电压下的自愈形貌
Fig.6 Self-healing morphology under different pressures and voltages
自愈面积随压强与电压的变化如图7所示,由图7可看出,自愈面积与压强呈现负相关。1.8 MPa压强下,随着电压等级的提高,自愈面积的增长程度较为剧烈。在15 MPa压强下,自愈面积大概只占1.8 MPa下自愈面积的11%,自愈面积与电压的关系也更为线性,高压强在一定程度上使电压升高对金属化膜自愈的正向激励作用得到抑制。
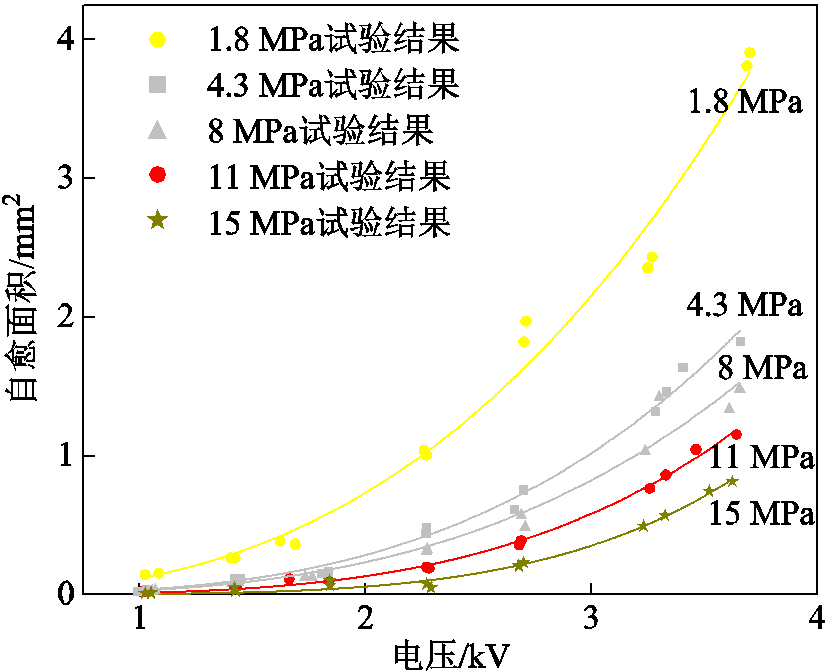
图7 不同压强下自愈面积与电压等级的关系
Fig.7 The relationship between self-healing area and voltage levels at different pressures
金属化膜电容器自愈过程如图8所示。在卷绕制薄膜电容器中,金属化膜承受着非常复杂的应力作用。由于薄膜制作工艺存在的不稳定性,介质中必然存在“绝缘弱点”,随着电容器作业过程中电压不断地作用,电弱点区域会率先发生电荷积聚,电荷的积聚会导致局部电场强度出现畸变,首先利用双极性载流子运输模型模拟电荷的积聚(阶段一)。随着电荷的积聚,电弱点区域内的等效电流逐渐增大,增大到一定值后金属化膜内的杂质率先被击穿使得区域内出现丝状放电[16],此时放电通道由固态转变为气态,仿真模型也由固体本征载流子运输模型改变为气体放电模型(阶段二),其中气态放电模型中的初始电荷分布由双极性载流子运输模型计算得出。丝状放电的出现会大大加速介质的劣化,最终导致“绝缘弱点”被击穿。当介质中的电弱点被击穿时,大量的电流涌向击穿点(阶段三),产生的焦耳热使金属层受热蒸发,其中一部分金属蒸气离子化,焦耳热也会使电介质层炭化(阶段四)。随着金属层的蒸发,“自愈面积”不断增大,金属层蒸发边缘与击穿点之间的等效电阻不断上升,“自愈电流”不断减小,最终电流减小为零,绝缘恢复,自愈完成。
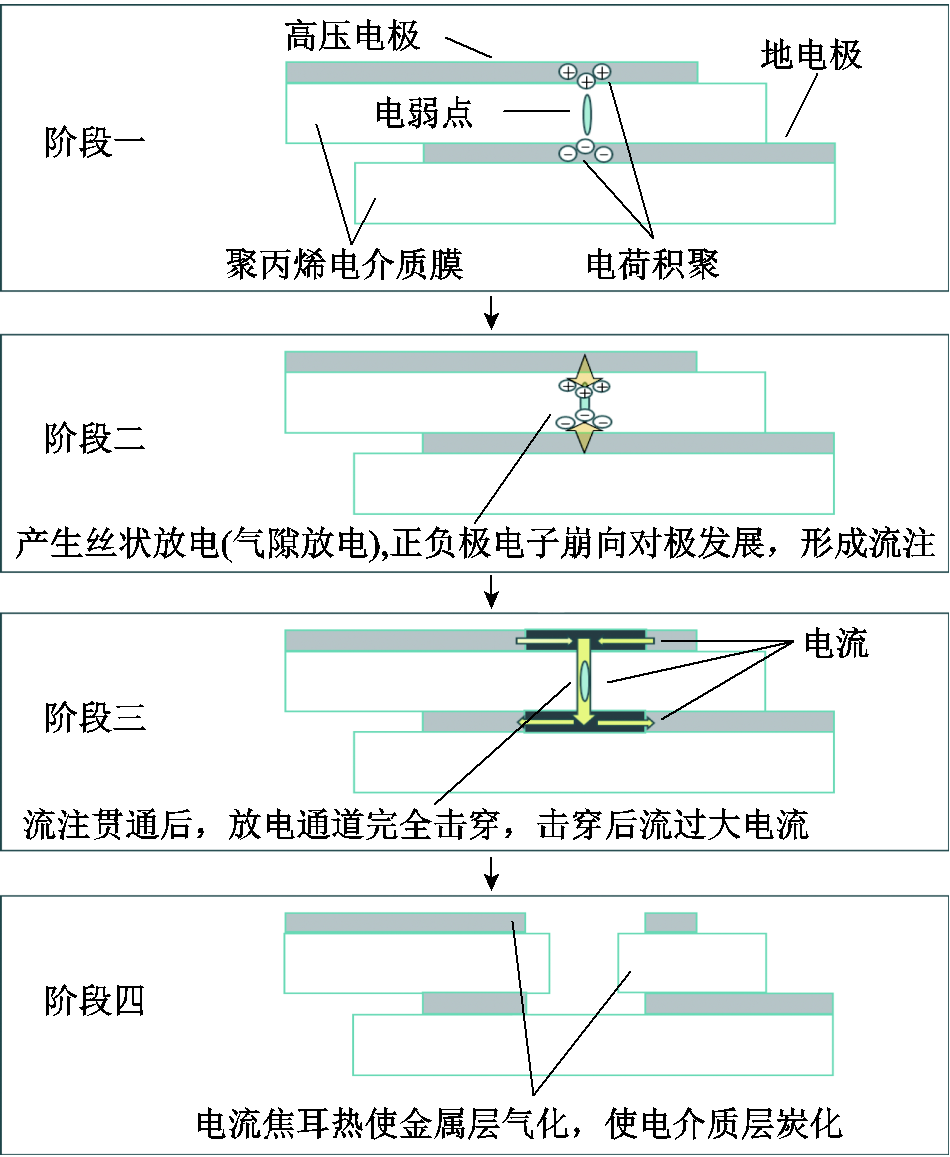
图8 金属化膜电容器自愈过程
Fig.8 Self-healing process of metallized film capacitors
首先利用双极性载流子运输模型计算电弱点区域内空间电荷的分布,作为之后放电通道模型的初始值。当施加电场时,在金属化膜电容器电介质层与金属层之间聚集起来的载流子将会向电介质层内部迁移,迁移过程中载流子会在电介质层中固有的空穴陷阱中入陷和脱陷。双极性载流子运输模型[17]可以用来表征上述的聚合物材料在极化状态下电荷的动态行为,具体模型如图9所示。
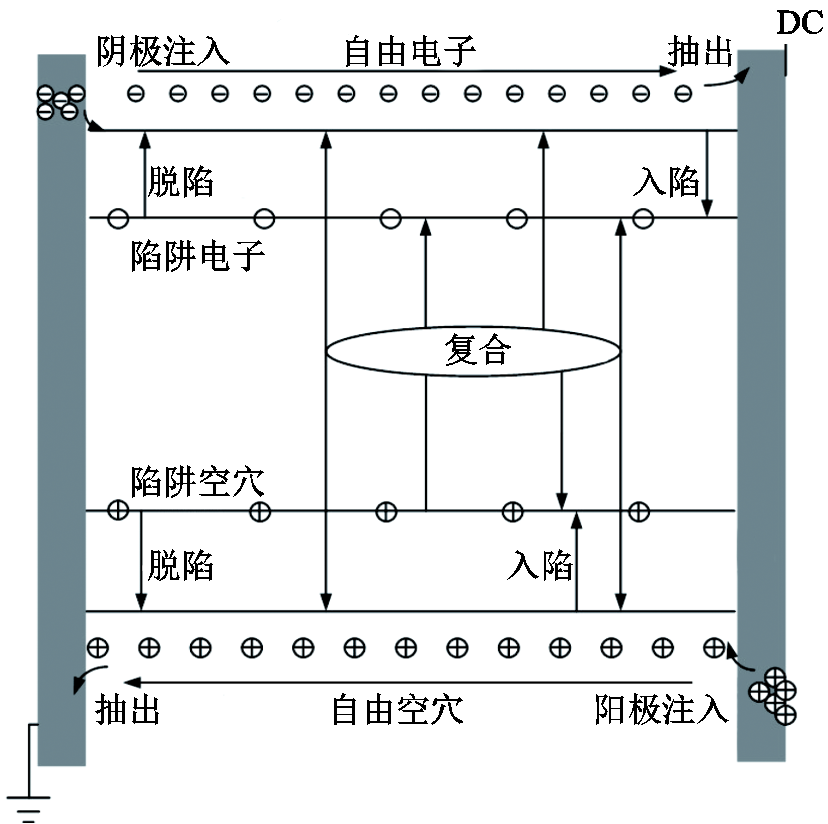
图9 双极性载流子运输模型
Fig.9 Bipolar carrier transport model
该模型考虑了从阴极注入的自由电子与从阳极注入的自由空穴,整个电荷迁移的过程中还涉及由于电介质内部物理和化学缺陷而产生的陷阱电子与陷阱空穴。在电荷迁移过程中,正、负电荷被陷阱捕获后分别形成陷阱空穴和陷阱电子,陷阱空穴和陷阱电子获得能量后有一定概率逃脱陷阱束缚,重新形成可自由移动的带电粒子。模型中电荷复合类型包括自由电子与自由空穴、自由电子与陷阱空穴、自由空穴与陷阱电子、陷阱电子与陷阱空穴的复合。陷阱电荷复合后,将空出陷阱位置,使其重新获得捕获自由电荷的能力[12]。式(1)为电流传导方程,描述载流子在通道内的流动;式(2)为电流连续性方程,体现空间电荷在介质内的分布;式(3)为泊松方程,计算介质内的电场变化。
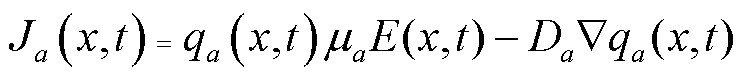 (1)
(1)
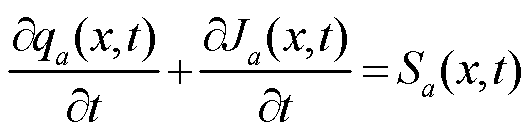
 (2)
(2)
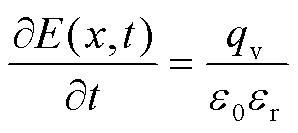 (3)
(3)
式中,Ja为单位体积内电流密度,下标a代表电荷种类,在本文中分别代表自由电子、自由空穴、入陷电子和入陷空穴,A/m2;q为单位体积内电荷量密度,C/m3;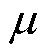 为磁导率;E(x,t)为聚丙烯薄膜内部x位置处于t时刻的电场强度,kV/mm;S为各类电荷粒子源项;
为磁导率;E(x,t)为聚丙烯薄膜内部x位置处于t时刻的电场强度,kV/mm;S为各类电荷粒子源项; 为聚丙烯薄膜内部的空间电荷密度,C/m3;
为聚丙烯薄膜内部的空间电荷密度,C/m3;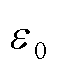 为真空介电常数;
为真空介电常数;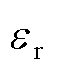 为相对介电常数;D为扩散系数。
为相对介电常数;D为扩散系数。
本文利用COMSOL Multiphysics 6.2仿真软件的等离子体模块建立了气体状态下的放电通道模型,以探究不同电热力环境下对放电通道形成与发展的影响。在实际试样中,聚丙烯薄膜厚度最大只有6 μm,放电通道半径与聚丙烯薄膜厚度的比值非常小,因此在研究聚丙烯薄膜厚度方向上的放电通道内空间电荷特性时,建立沿聚丙烯薄膜厚度方向的一维仿真模型[18],放电通道模型的初始值为先前通道内空间电荷分布的计算结果,仿真模型涉及的主要方程如下。
电子密度的连续性方程为
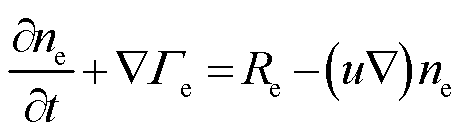 (4)
(4)
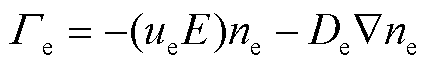 (5)
(5)
式中,ne为电子密度,C/m3;Re为电子速率,m-3·s-1;ue为电子迁移系数,m2/(V·s);E为电场强度,V/m;De为电子扩散系数,m2/s;u为中性流体速度,m/s。
电子能密度的能量守恒方程为
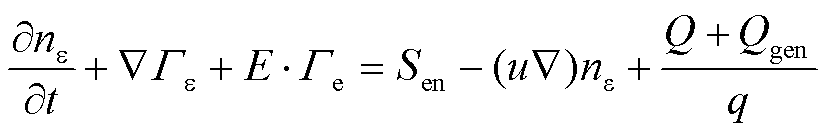 (6)
(6)
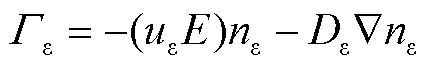 (7)
(7)
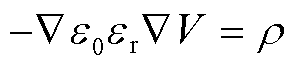 (8)
(8)
式中,ne为电子能量密度,V/m3;Sen为由于非弹性碰撞的能量得失,V/(m3·s);Q为外部热源,W/m3;ue为电子能量迁移率,m2/(V·s);Qgen为广义热源,W/m3;De为电子能量扩散系数,m2/s;q为电荷量,C;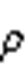 为空间电荷密度,C/m3;V为气体放电通道内电压,V。
为空间电荷密度,C/m3;V为气体放电通道内电压,V。
泊松方程为
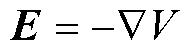 (9)
(9)
表1 放电通道模型参数
Tab.1 Discharge channel model parameters

参数数值 Re/(m3·s)-1(x表示路径) ue/[m2/(V·s)]4×1024 E/(V/m)4.82×108 De/(m2/s)1×1025 u/(m/s)1×10-4 Sen/(W/m3)10 Q/(W/m3)0 uε/[m2/(V·s)]6×1024 Dε/(m2/s)1×1025 q/C1.6×10-19
在金属化膜自愈发生时,电弱点处发展形成的放电通道内流经大电流产生的焦耳热不仅使电弱点附近的金属层气化、离子化,也会使附近的电介质层炭化。随着金属层电离化面积的扩大,击穿点和金属层边缘之间的等效电阻增大,导致自愈电流减小。自愈电流的减小一直持续到金属层与击穿点之间的距离足以恢复绝缘为止[19]。本文利用COMSOL仿真软件中的电磁热耦合模块来模拟这一过程,通过模型中温度的分布来体现金属化膜自愈过程中金属层蒸发面积及自愈面积、等离子化区域、介质层炭化区域与深度。模型为二维轴旋转结构,其3D图如图10所示。
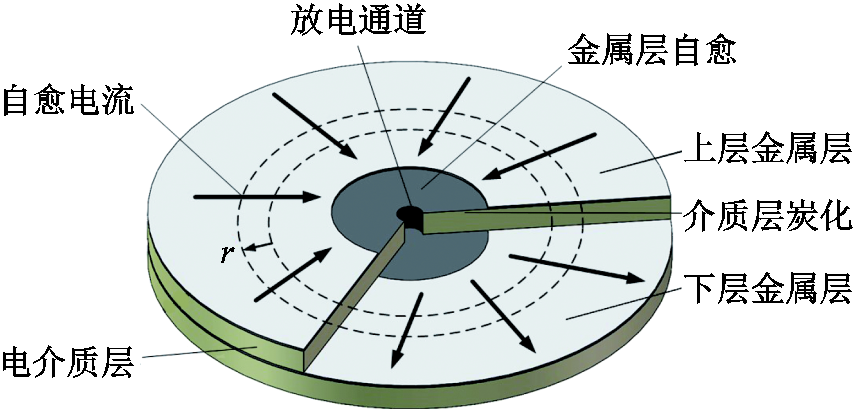
图10 金属化膜自愈模型
Fig.10 Model of self-healing in metallized films
模型涉及的主要方程为
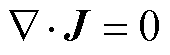 (10)
(10)
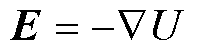 (11)
(11)
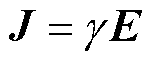 (12)
(12)
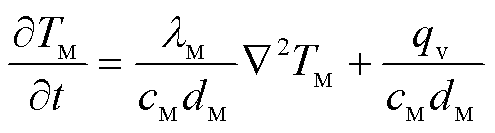 (13)
(13)
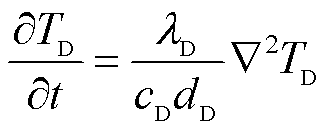 (14)
(14)
式中,U为金属层电压;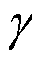 为电导率;
为电导率;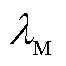 、
、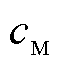 、
、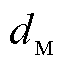 分别为金属层的热导率、比热容、密度;
分别为金属层的热导率、比热容、密度;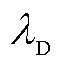 、
、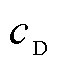 、
、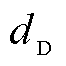 分别为电介质层的热导率、比热容、密度。边界条件和初始条件如下。
分别为电介质层的热导率、比热容、密度。边界条件和初始条件如下。
边界条件为
 (15)
(15)
初始条件
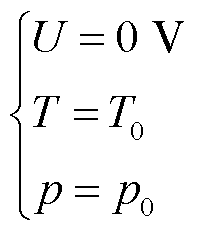 (16)
(16)
式中,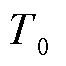 为初始温度;
为初始温度;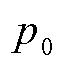 为初始压强。
为初始压强。
为了更真实地模拟金属层的蒸发与电介质层的炭化,模型在材料方面考虑了铝金属从固态转变为等离子体时电导率的剧烈变化以及电介质层炭化后电导率与热导率的变化,即
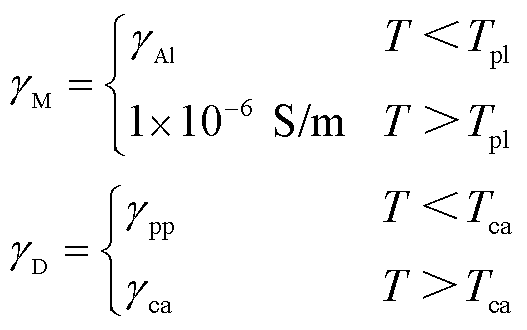
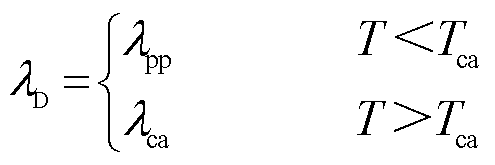 (17)
(17)
式中,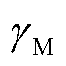 为金属层的电导率;
为金属层的电导率;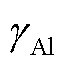 为铝金属电导率;Tpl为铝金属等离子化时的温度;
为铝金属电导率;Tpl为铝金属等离子化时的温度; 为电介质层的电导率;γpp为聚丙烯电导率;
为电介质层的电导率;γpp为聚丙烯电导率;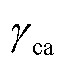 为碳电导率;Tca为聚丙烯炭化温度;λpp为聚丙烯热导率;λca为碳导热率。
为碳电导率;Tca为聚丙烯炭化温度;λpp为聚丙烯热导率;λca为碳导热率。
为了与试验相验证,自愈仿真模型将采用与试验相同的电热力环境,电压的初始条件U0分别设置为1.8、2.3、2.8、3.3和3.8 kV,温度的初始条件T0分别为303.15、313.15、323.15、333.15和343.15 K;压强的初始条件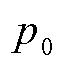 分别为1.8、4.3、8、11和15 MPa。
分别为1.8、4.3、8、11和15 MPa。
表2 自愈模型参数
Tab.2 Self-healing model parameters

参数数值 2 370 0.88×103 2.7×103 0.21 1.9×103 0.89×103
利用双极性载流子运输模型计算出的放电通道内的空间电荷分布如图11所示。
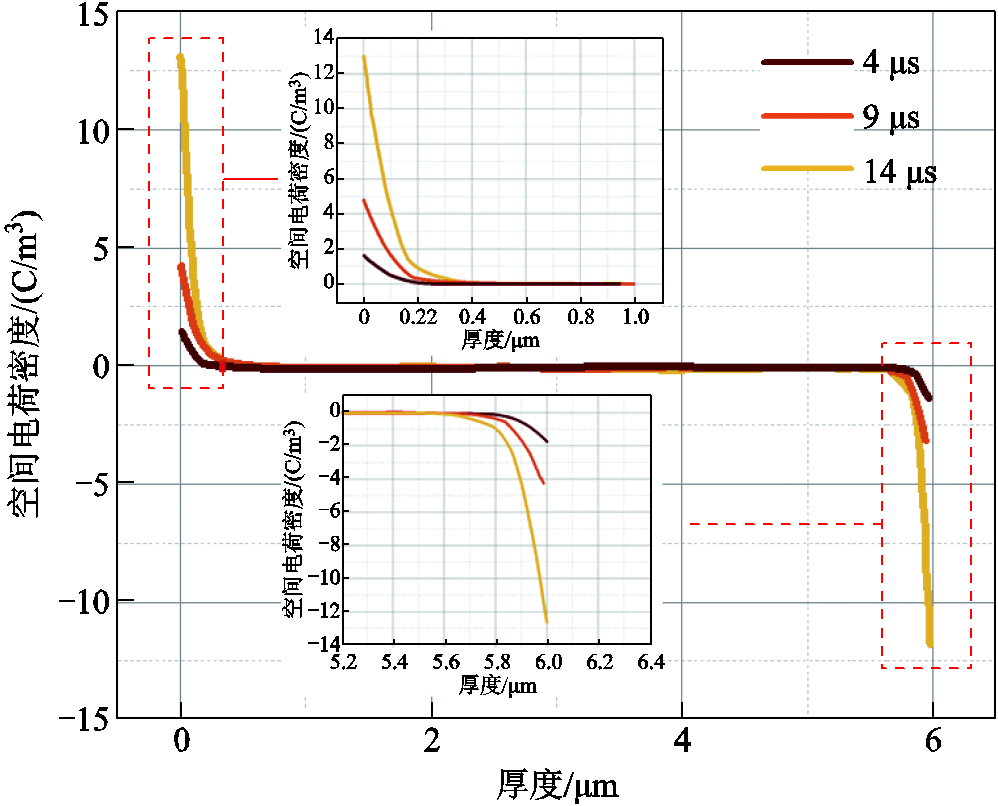
图11 不同发展时间下放电通道内空间电荷分布
Fig.11 Spatial charge distribution in the discharge channel at different stages of development
从图11可以看出,大量电荷在放电通道两极积聚,而中间电荷密度基本为零,这是因为随着电荷的迁移,通道中间部分陷阱数量减小,导致电荷入陷与脱陷行为减少,从而导致空间电荷积聚在通道两端的电极附近[20]。
随着载流子的流动,放电通道内的等效电流逐渐增大,当等效电流密度增大到3 mA/m2时,放电通道会从固体放电转化为气体的流注放电[21]。不同时间的等效电流密度如图12所示,放电通道内的电流密度大概在13 μs的时候达到该值。把图11中14 ms时放电通道内的最大、最小空间电荷密度仿真计算结果代入气体放电通道模型中,设置通道0 mm处为接地端,电压施加在6 mm处,以此来探究不同电热力环境对气体与等离子体混合状态下放电通道形成的影响。
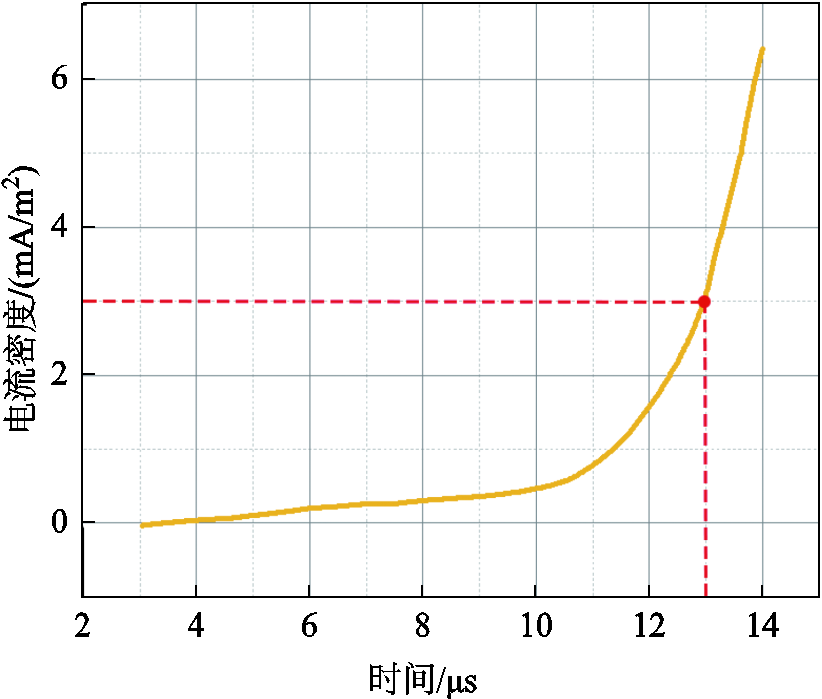
图12 不同时间的等效电流密度
Fig.12 Equivalent current density in different time
当温度为30℃、压强为1.8 MPa时,在2.5、3.0和3.5 kV电压等级下模型的计算结果如图13所示。1.8 MPa、30℃、2.5 kV下放电通道发展过程中,3个不同时间点时通道内迁移电子通量的变化如图14所示。
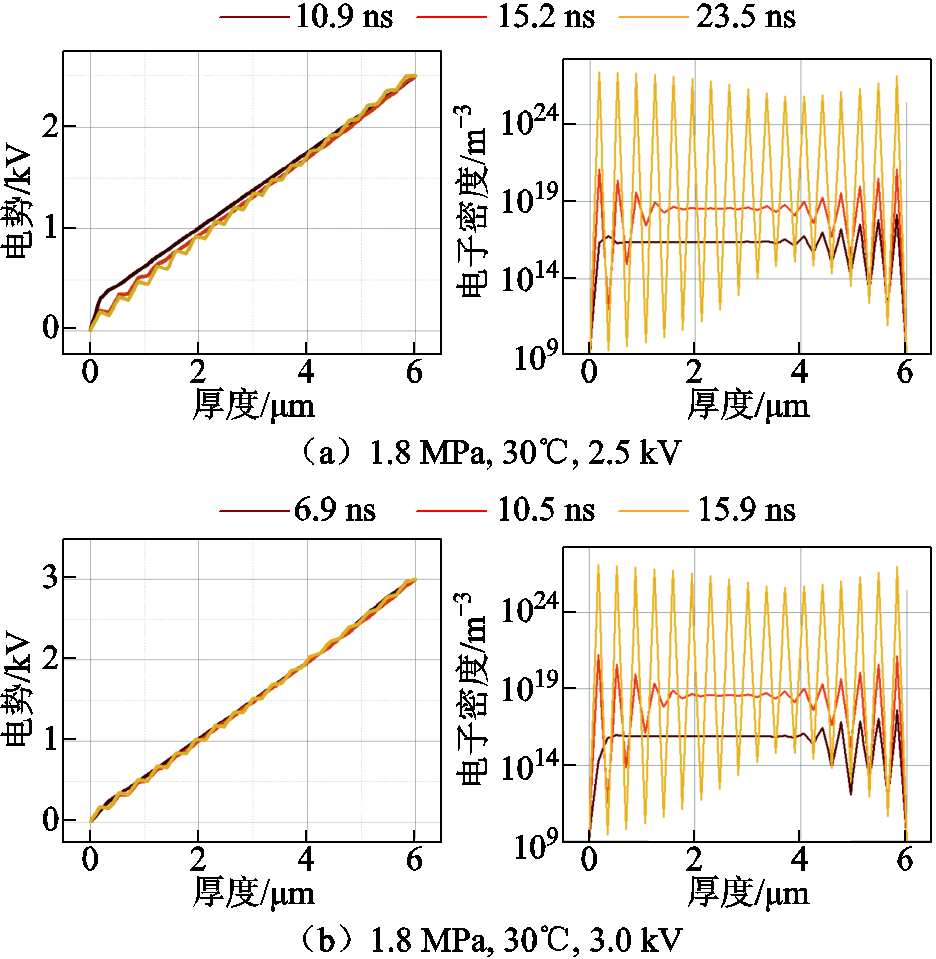
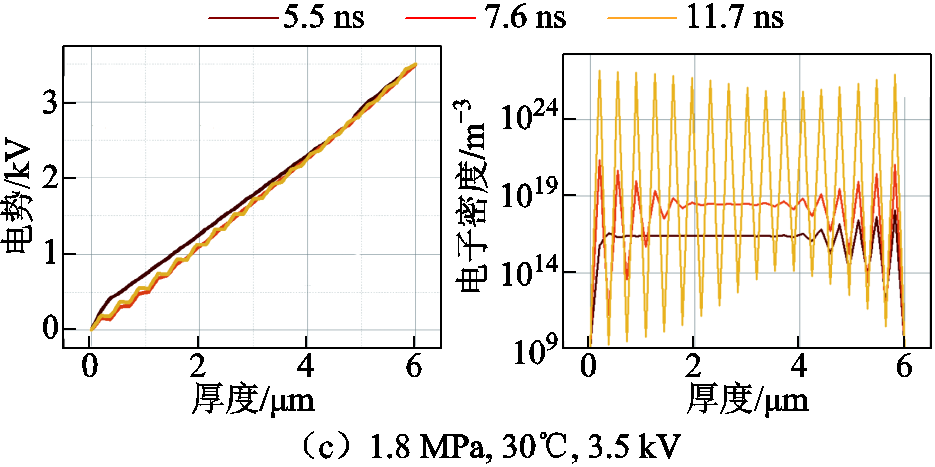
图13 不同电压下放电通道形成时的电势和电子密度变化
Fig.13 Changes in electric potential and electron density during the formation of discharge channels at different voltages
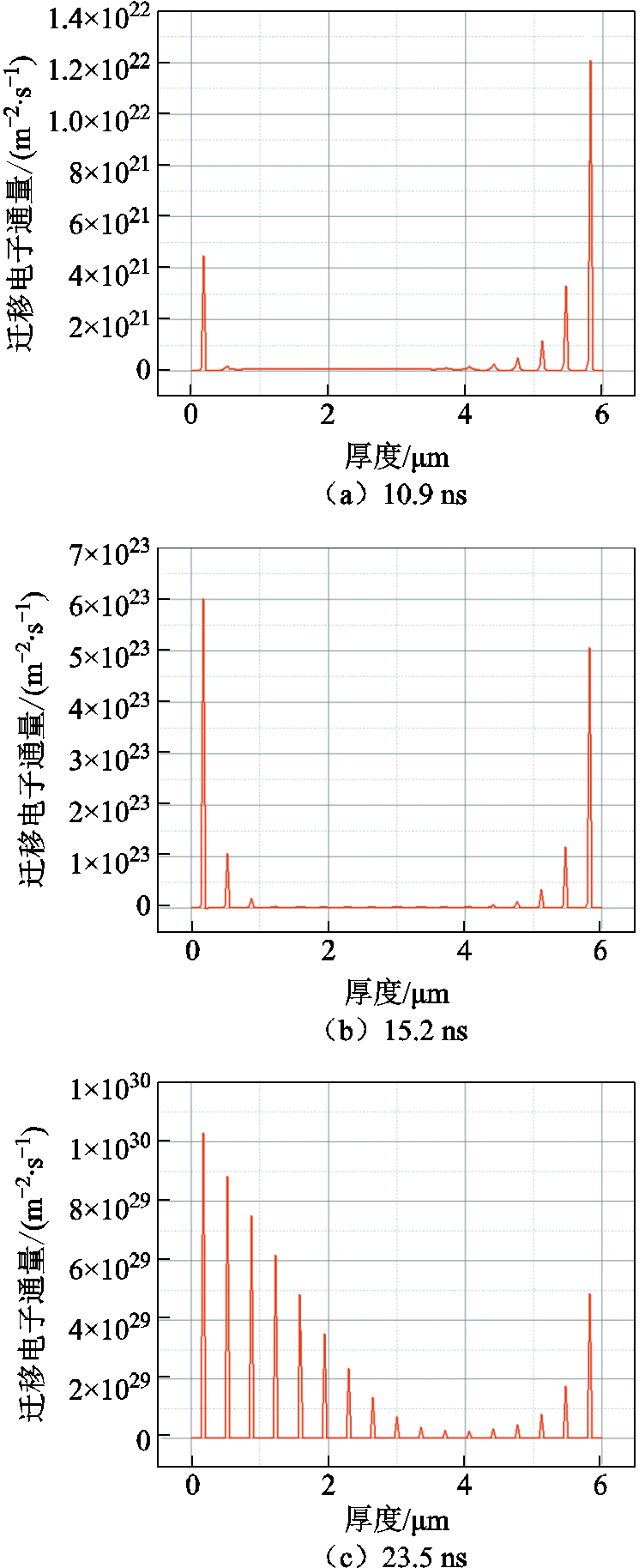
图14 1.8 MPa、30℃、2.5 kV下放电通道内迁移电子通量的变化
Fig.14 The variation of electron flux in the discharge channel at 1.8 MPa, 30℃, 2.5 kV
从图13左侧电势变化可以看出,放电通道内的电场畸变逐渐由接地端(0 mm)向对极(6 mm)发展,直至23.5 ns时贯穿整个通道。在此过程中放电通道内的迁移电子通量也在发生变化,迁移电子通量描述了电子在电场作用下的移动速率。随着放电通道的发展,接地端附近的电子迁移快速增加并朝着阳极发展,但在10.9 ns和15.2 ns时,放电通道中间部分的电子迁移速率仍为较低值,在23.5 ns时,两极的发展在中间汇合,并使放电通道中间部分的迁移电子通量加速到2.62×1028 m-2·s-1,至此可判断放电通道完全贯穿[22]。
在2.5、3和3.5 kV下,放电通道分别在23.5、15.9和11.7 ns完全贯穿,贯穿所用时间随电压的升高而缩短,当气压与温度相同时,施加的电场强度越大,电子在一个平均自由程内获得的能量越大,故流注形成与发展的速度越快[20]。由电子密度结果可以看出,阴极放电波头向对极的迁移直至贯通的过程。种子电子在电场加速作用下从阴极附近向阳极运动,与背景气体分子碰撞,形成初始电子崩,电子崩向阳极发展[20]。电子崩向阳极发展的过程中电子密度在几纳秒或十几纳秒内迅速由1×109 m-3倍增到1×1027 m-3。在放电通道未完全贯通之前,聚丙烯薄膜中间部分的电子数量也随着放电通道的发展而增多,从而使放电通道内等效电流密度逐渐增加。
设置电压为3.5 kV、压强为1.8 MPa,在20、30和40℃不同温度下模型的计算结果如图15所示。
在20、30和40℃下,放电通道完全贯穿所需要的时间分别为12.4、11.7和11.4 ns,可见温度的上升对放电通道的形成具有正向的激励作用。温度升高会增加气体分子的热运动,从而提高电子的平均能量,使得电子更容易通过碰撞来电离气体分子,这可以增加电子密度以及带电粒子的迁移速度和扩散速度,从而加速电子碰撞电离的过程,促进放电通道的发展[23]。
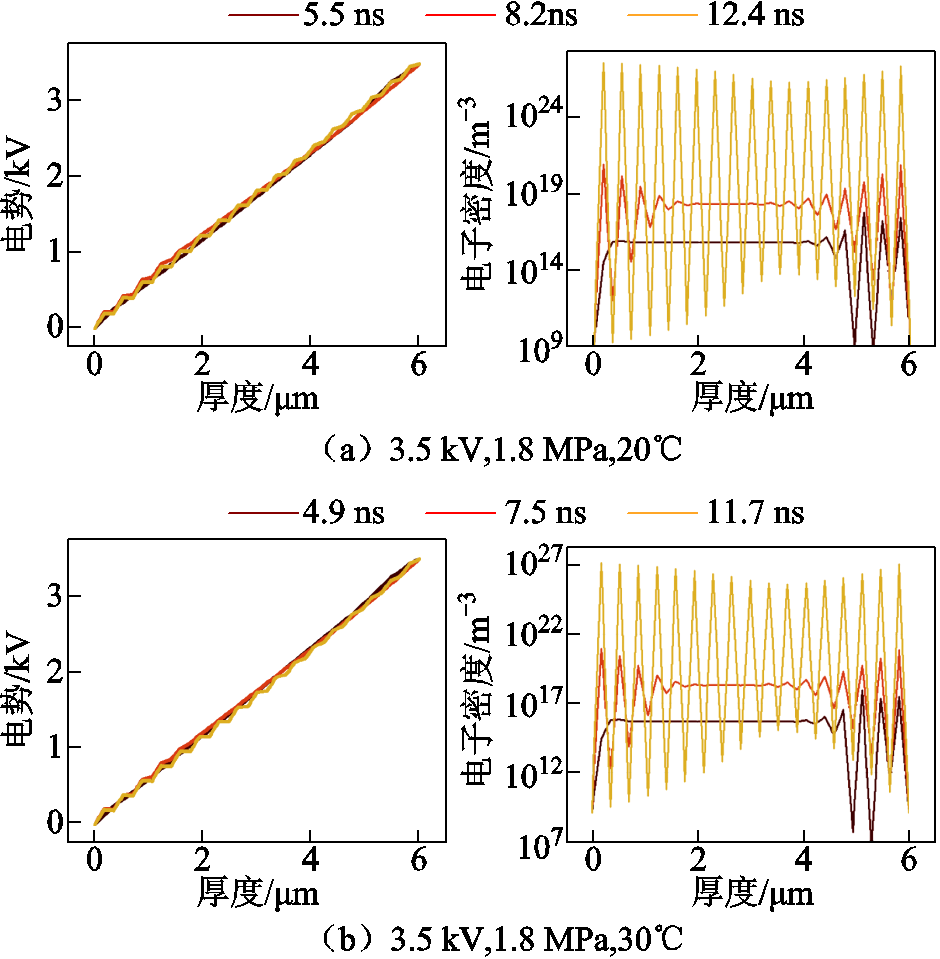
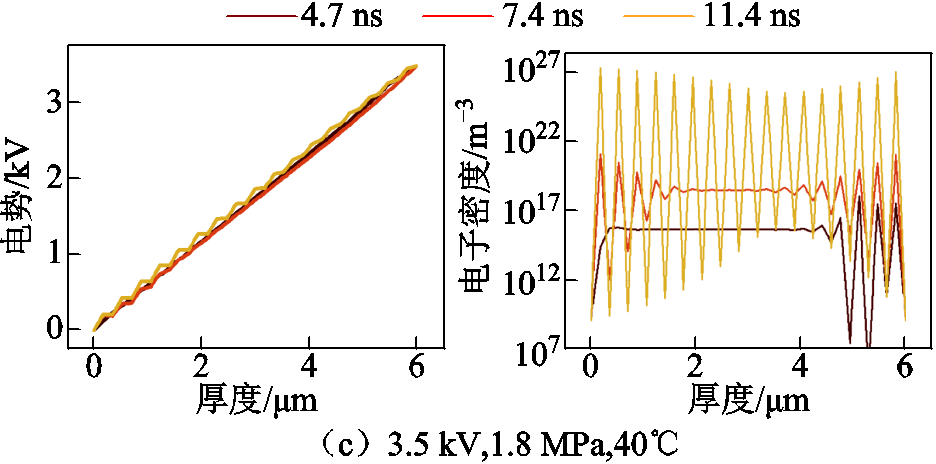
图15 不同温度下放电通道形成时的电势和电子密度变化
Fig.15 Changes in electric potential and electron density during the formation of discharge channels at different temperatures
设置电压为3.5 kV、温度为30℃,在1.2、1.8和2.4 MPa不同压强下模型的计算结果如图16所示。

图16 不同压强下放电通道形成时的电势和电子密度变化
Fig.16 Changes in electric potential and electron density during the formation of discharge channels at different pressures
在1.2、1.8和2.4 MPa不同压强下,放电通道分别在7.9、11.7和16.1 ns时贯通,随着压强的增大,放电通道形成所需要的时间逐渐变长,压强的增大对电子密度的发展也有抑制作用。当电场强度相同时,压强增大,电子平均自由程减小,电子在一个平均自由程内获得的能量减小,与中性分子碰撞概率增大,越频繁的碰撞越会降低流注发展速度[20]。
试验所采用的金属化薄膜的金属层部分材料为铝,电介质层材料为聚丙烯。铝金属气化温度为 2 600 K[24],而铝金属的等离子化温度并没有一个固定的值,这是因为等离子化是一个渐进的过程,而且受周围环境条件的影响。利用光谱线的相对强度推算出铝金属等离子体温度在5 500~10 000 K之间[25],仿真中取5 600 K。聚丙烯的炭化温度为600℃,即873 K[26]。仿真结果如图17和图18所示。
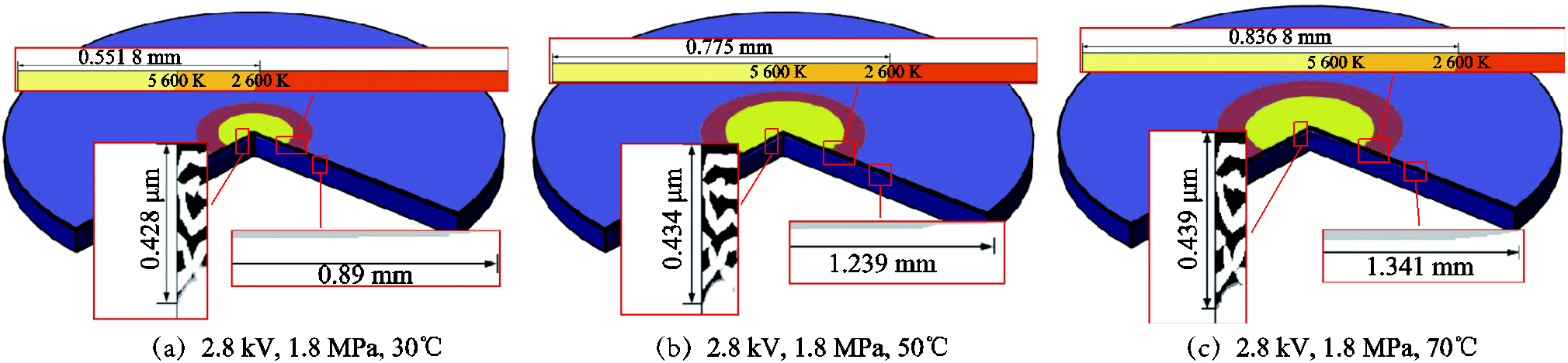
图17 不同温度下的自愈模型仿真结果
Fig.17 Simulation results of self-healing model at different temperatures

图18 不同压强下自愈模型仿真结果
Fig.18 Simulation results of self-healing model at different pressures
图17和图18分别是在1.8 MPa和2.8 kV下,30、50和70℃时的仿真结果,以及在50℃、2.8 kV下,1.8、4.3和15 MPa时的仿真结果。图中温度超过5 600 K及上层淡黄色部分为金属层等离子化部分,温度超过2 600 K及图中上层淡黄色与淡橙色部分为金属层蒸发部分,温度超过873 K及图中下层黑灰色部分为介质层炭化结果。图中炭化区域为黑白相间,说明炭化并不均匀,这里只关注炭化区域在不同电热力环境下可达到的最大炭化深度与平行于自愈面积的炭化区域扩散半径。由于使用实验室现有的设备观察不到金属层等离子化面积与介质层炭化面积,所以通过比较金属层的蒸发面积,即自愈面积来验证模型的准确性,验证结果如图19所示。
由图19可以看出,仿真结果与试验结果有较高的吻合度,验证了仿真的有效性和模型的可靠性。为更好地量化不同电热力环境对自愈过程中金属层等离子体的产生以及介质层炭化的影响,图20、图21、图22分别为不同电热力下自愈半径、等离子化半径、炭化半径以及炭化深度的变化曲线。
从图17可以看出,在30、50和70℃下,金属层温度大于2 600 K部分的半径,即蒸发面积半径分别为0.551 8、0.775和0.836 8 mm,对应的蒸发面积分别为0.956 6、1.886 9和2.2 mm2;而温度大于5 600 K部分的半径,即等离子化区域半径分别为0.364 2、0.512 4和0.553 1 mm,对应的等离子化区域为0.416 7、0.824 8和0.9611 mm2,分别占蒸发面积的43.56%、43.71%和43.69%,从图17可以看出,在1.8、4.3和15 MPa下,仿真的蒸发面积半径分别为0.775、0.437和0.264 6 mm,对应的蒸发面积为1.886 9、0.6和0.22 mm2,等离子区域半径为0.512 4、0.286 8和0.174 6 mm,对应的等离子化区域为0.824 8、0.258和0.095 8 mm2,分别占蒸发面积的43.71%、43.07%和43.55%。自愈发生时,电弱点处流经的大电流会使金属层局部受热,当加热的温度超过铝金属的沸点,铝金属层就会蒸发气化,随着温度的继续升高,铝金属会进一步等离子化。在自愈击穿的情况下,形成的等离子体会在电极之间形成一个短路桥[4]。
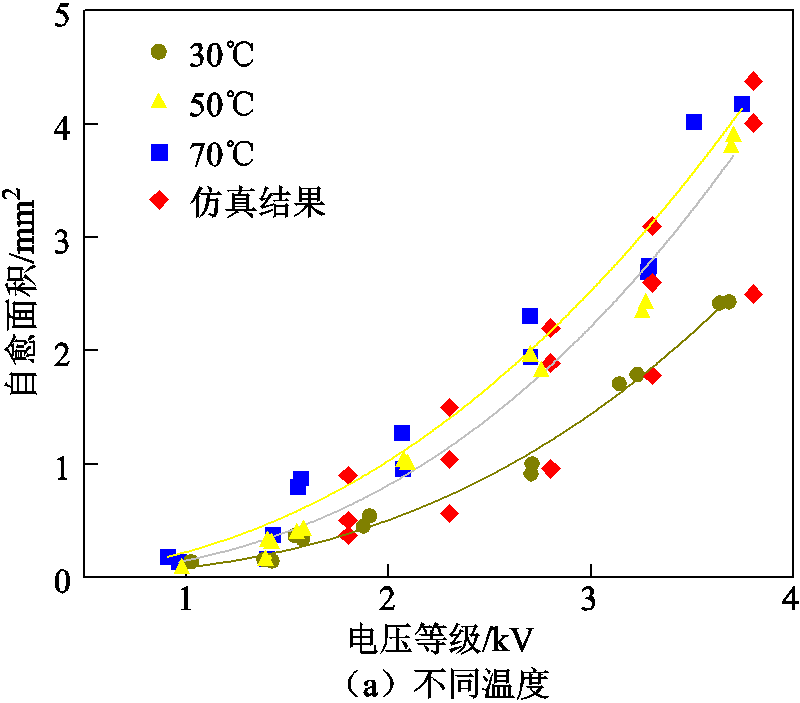
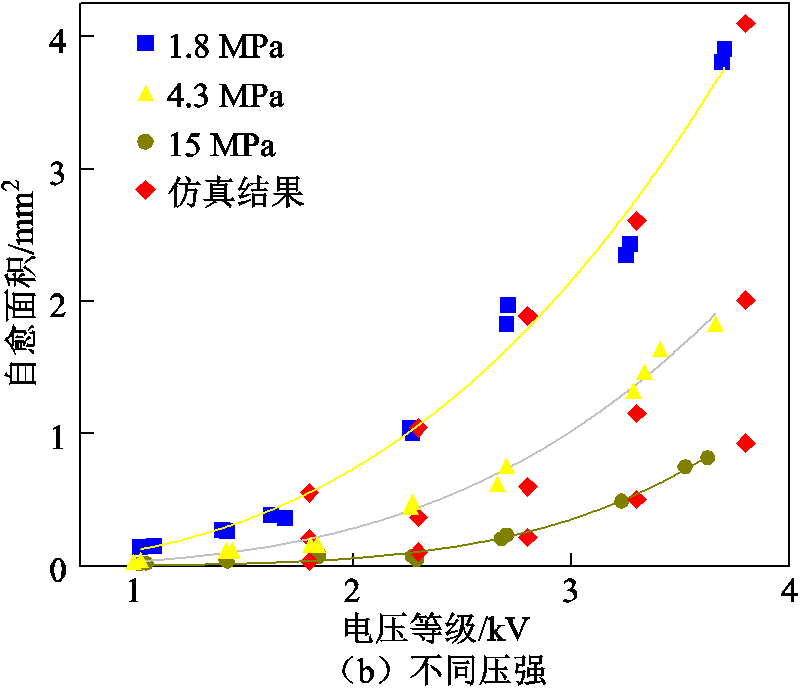
图19 不同温度和压强下金属化膜自愈面积与施加电压关系的试验与仿真结果
Fig.19 Self-healing area versus voltage applied on metallized films by experience and simulation at different temperatures and pressures
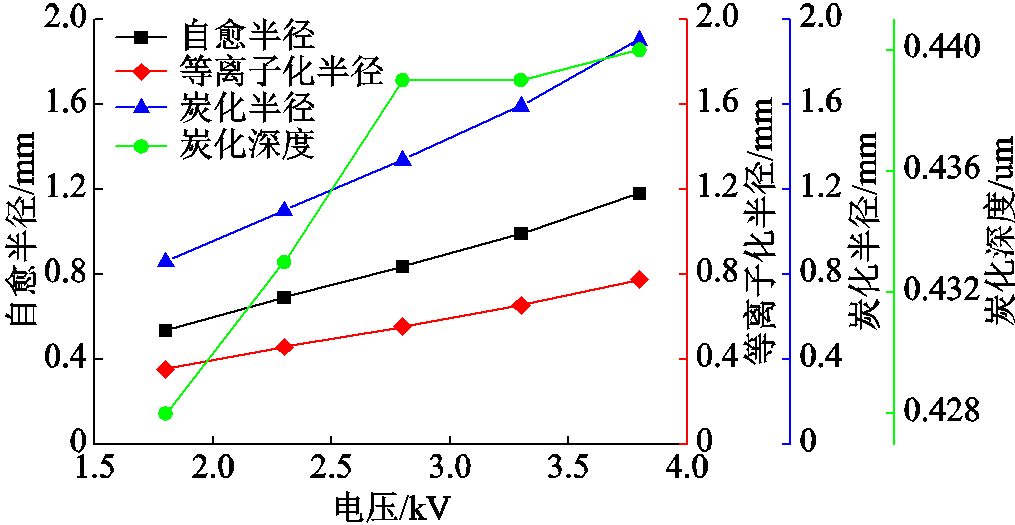
图20 70℃、1.8 MPa,不同电压时的仿真结果
Fig.20 Simulation results at 70℃, 1.8 MPa, different voltages
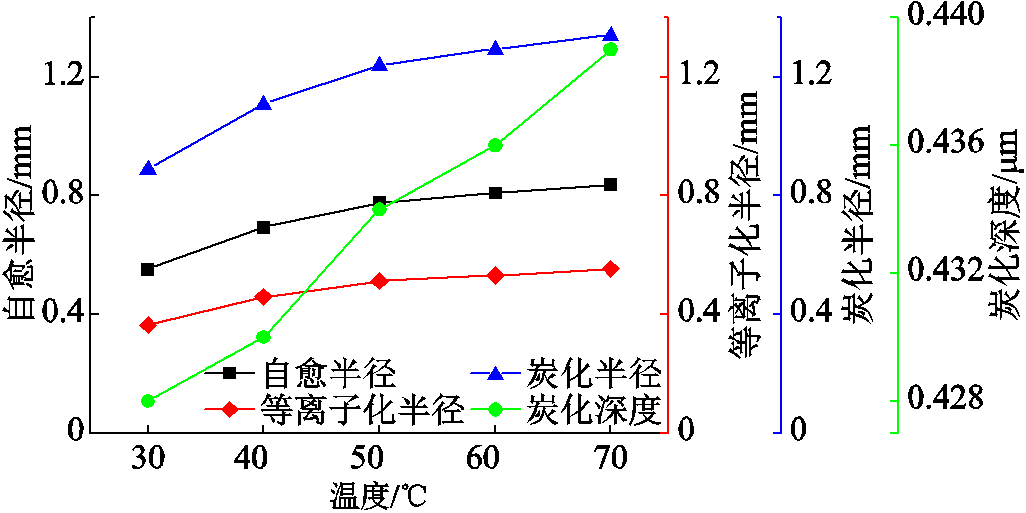
图21 2.8 kV、1.8 MPa,不同温度时的仿真结果
Fig.21 Simulation results at 2.8 kV, 1.8 MPa, different temperatures
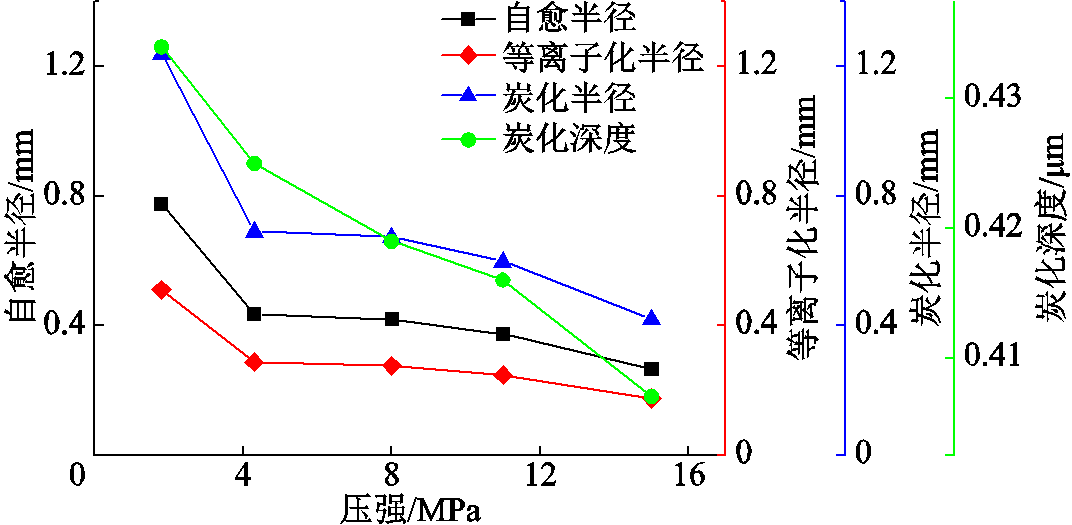
图22 2.8 kV、50℃,不同压强下的仿真结果
Fig.22 Simulation results at 2.8 kV, 50℃, different pressures
由图20~图22可以看出,金属层受超高温形成的等离子体区域半径同金属层蒸发面积半径一样,随施加电压和温度的升高而增加,随压强的升高而降低。金属层等离子体区域半径虽然会随着电热力环境的改变而改变,但其曲线的变化趋势与自愈面积半径曲线的变化趋势极为相似,说明这两者之间的比例关系保持在一恒定值附近,该值为0.66,即金属层等离子化区域占自愈面积的比例一直保持在43%左右。电压、温度与压强的变化对该比例造成的影响较小,可能是因为设置的五种环境温度只占5 600 K的5.41%、5.59%、5.77%、5.95%和6.12%,相比较而言,数值波动极小导致差异性也极小。而对压强而言,随着压强的变化,铝原子开始等离子化的温度或多或少也会发生改变,但等离子化温度通常在极端高压(如GPa级别,109Pa)下才会有显著的变化,因为这时原子间的相互作用和电子行为会发生重大变化,但由于缺少这方面的数据,故单一地把5600 K看作是离子化开始的温度。然而,在本文自愈过程的仿真中,不同压力环境下金属层的温度分布也较为稳定。从温度方面来看,自愈过程中放电电弧会使金属层达到极高的温度, 5 600 K已经接近太阳表面的温度,实际中,该温度的维持时间也是极短的,这也是金属化膜电容器自愈时间仅为μs级别的主要原因。自愈时间取决于自愈过程中产生的等离子体的维持时间[4],自愈发生时,施加在金属层的电压几乎保持恒定,但放电电弧仍会熄灭,主要原因就是等离子化区域需要得到持久的加热以保持较高的导电性[3]。
由图17和图18可以看出,在30、50和70℃不同温度下,电介质层炭化区域的辐射半径为 0.89、1.239和1.341 mm,分别是金属层蒸发面积半径的1.612倍、1.599倍和1.602倍;炭化深度为0.428、0.434和0.439 mm,分别占金属化膜膜厚的7.38%、7.48%和7.57%。在1.8、4.3和15 MPa不同压强下,电介质的炭化辐射半径为1.239、0.692和0.421 mm,分别是金属层蒸发面积半径的1.599倍、1.583倍和1.592倍;炭化深度分别为0.434、0.425和0.407 mm,分别占金属化膜膜厚的7.48%、7.33%和7.02%。
从仿真结果可以看出,自愈过程中电介质层受热产生的石墨量极少,因为在含氧环境下,除了H2和CH4之外的CmHn物质都会被氧化为CO和H2O,因此没有石墨沉积或只生成少量的石墨[4]。
由图20~图22可以看出,随着电压与温度的上升,自愈面积半径逐渐增大,炭化区域半径也随之增大;随着压强的增加,自愈面积逐渐减小,炭化区域也随之减小,但炭化区域与金属层蒸发面积的比值似乎在不同温度与压强环境下均保持在1.6附近,这是由于石墨沉积只与蒸发电极的厚度与面积有关[4]。从仿真结果中可以看出,自愈过程中电介质的炭化层厚度极薄,仅为0.4 mm左右。自愈过程中的清理电弧蒸发掉击穿点附近的金属,凝结而成的石墨(来自电介质层分解)和金属分布足够广泛(厚度足够薄),以避免在两个金属化电极之间导电[27]。本仿真中模拟了厚度为5.8 mm的金属化膜,电极层的厚度为十几纳米,在金属层完全蒸发掉的部分,蒸发电极厚度保持恒定,与前人的结论不同,环境温度与压强的改变对电介质层炭化深度也造成了影响,尽管这个影响较小。由图17和图18可以看出,随着温度的升高,炭化深度占金属化膜厚度的比值从7.38%增加到7.48%和7.57%,随着压强的增高,该比值从7.48%减小到7.33%和7.02%,电介质层的炭化深度与温度呈正相关,与压强呈负相关。自愈过程中形成的石墨层越厚,自愈越难成功[27],实际应用中,高效的散热与紧致的金属化膜电容器卷绕方式可以延长设备的使用寿命。
本文搭建了多物理场下的金属化膜电容器自愈特性试验平台,利用试验平台探究了铝金属化聚丙烯薄膜的自愈面积与形貌随不同电热力环境的变化,搭建了气态放电通道模型和金属化薄膜自愈仿真模型,利用气态放电通道模型探究了不同电热力环境对金属化膜电容器自愈过程中放电通道形成的影响,利用金属层自愈等离子体模型研究了不同热力条件下金属化膜电容器自愈过程中金属层的蒸发与离子化和电介质层的炭化结果,并利用试验进行了验证,最后得出以下结论:
1)放电通道的形成时间极短,仅为ns级别,通道内的电子密度在此期间极速增高,发展形式与电子崩类似。放电通道的形成时间受电压、温度与压强的影响,在温度与压强不变的情况下,施加的电压等级越高,通道贯通所用的时间越短;在电压与压强相同的情况下,放电通道完全贯穿所需的时间与温度成反比;在电压与温度相同的情况下,放电通过贯穿时间与压强成正比。
2)自愈过程中金属层的温度可超过5 600 K,该温度下铝金属蒸气开始等离子化,金属层的等离子化区域随电热力不同环境的变化趋势同金属层的蒸发面积(自愈面积)一致,均与电压和温度呈正相关,与压强呈负相关,但不同电热力环境对金属层等离子化区域占自愈面积的比例似乎没有特定的影响,该比值均在43%附近。
3)自愈过程中电介质层的炭化量极少,在与试验相同的电热力环境下,电介质层炭化区域比金属层自愈面积略大,但炭化深度只有0.4 mm左右,大概占膜厚的7%。炭化区域半径与施加的电压等级和温度成正比,与压强成反比,但其与自愈半径之间的比值在不同电热力环境下均保持在1.6附近。环境温度与压强的改变也会对电介质层的炭化深度造成影响,尽管该影响对炭化深度的改变极为微小,但也存在电介质层的炭化深度与温度呈正相关,与压强呈负相关的关系。
参考文献
[1] Tingström J, Swanström L, Karlsson R. Sustainability management in product development projects–the ABB experience[J]. Journal of Cleaner Production, 2006, 14(15/16): 1377-1385.
[2] MacDonald J R, Schneider M A, Ennis J B, et al. High energy density capacitors[C]//2009 IEEE Electrical Insulation Conference, Montreal, QC, Canada, 2009: 306-309.
[3] Tortai J H, Denat A, Bonifaci N. Self-healing of capacitors with metallized film technology: experi-mental observations and theoretical model[J]. Journal of Electrostatics, 2001, 53(2): 159-169.
[4] Kammermaier J, Rittmayer G, Birkle S. Modeling of plasma-induced self-healing in organic dielectrics[J]. 1989, 66(4): 1594-1609.
[5] Belko V, Emelyanov O, Ivanov I. The experimental investigation and numerical simulation of self-healing in metallized film capacitors[C]//2016 IEEE Inter-national Conference on Dielectrics (ICD), Montpellier, France, 2016: 613-616.
[6] Tortai J H, Bonifaci N, Denat A, et al. Diagnostic of the self-healing of metallized polypropylene film by modeling of the broadening emission lines of aluminum emitted by plasma discharge[J]. Journal of Applied Physics, 2005, 97(5): 053304.
[7] Belko V O, Emelyanov O A. Self-healing processes of metallized film capacitors in overload modes: Part II: theoretical and computer modeling[J]. IEEE Transactions on Plasma Science, 2021, 49(6): 1898-1905.
[8] 章妙. 金属化膜电容器自愈特性研究[D]. 武汉: 华中科技大学, 2012.
Zhang Miao. Study on self-healing characteristics of metallized film capacitor[D]. Wuhan: Huazhong University of Science and Technology, 2012.
[9] ChenYaohong, Li Hua, Lin Fuchang, et al. Effect of interlayer air on performance of dry-type metalized film capacitor in DC, AC and pulsed applications[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2011, 18(4): 1301-1306.
[10] Li Hua, Chen Yaohong, Lin Fuchang, et al. The capacitance loss mechanism of metallized film capacitor under pulsed discharge condition[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2011, 18(6): 2089-2094.
[11] Li Zhiwei, Li Hua, Lin Fuchang, et al. Lifetime improvement of metallized film capacitors by inner pressure strengthening[J]. IEEE Transactions on Plasma Science, 2013, 41(10): 3063-3068.
[12] 李化, 章妙, 林福昌, 等. 金属化膜电容器自愈理论及规律研究[J]. 电工技术学报, 2012, 27(9): 218-223, 230.
Li Hua, Zhang Miao, Lin Fuchang, et al. Study on theory and influence factors of self-healing in metallized film capacitors[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 218-223, 230.
[13] Reed C W, Cichanowskil S W. The fundamentals of aging in HV polymer-film capacitors[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1994, 1(5): 904-922.
[14] LiHaoyuan, Li Hua, Li Zhiwei, et al. T pattern fuse construction in segment metallized film capacitors based on self-healing characteristics[J]. Microelectronics Reliability, 2015, 55(6): 945-951.
[15] 孔中华, 林福昌, 戴玲, 等. 混合电极与全膜电容器的金属化膜自愈特性[J]. 高电压技术, 2008, 34(2), 385-388.
Kong Zhonghua, Lin Fuchang, Dai Ling, et al. Self-healing characteristics of metallized hy brid electrode and metallized capacitors[J]. High Voltage Engineering, 2008, 34(2): 385-388.
[16] 陈斗南. 薄介质膜击穿全过程的探讨[J]. 物理学报, 1987,36(7): 838-846.
Chen Dounan.A research for the entire breakdown procedure in thin dielectric films[J]. Acta Physica Sinica, 1987, 36(7): 838-846.
[17] Boufayed F, Teyssèdre G, Laurent C, et al. Models of bipolar charge transport in polyethylene[J]. 2006, 100(10): 104105.
[18] 宋柯, 王伟, 钱定冬, 等. 杂质浓度梯度下XLPE空间电荷与电场分布特性仿真研究[J]. 绝缘材料, 2023, 56(4): 40-47.
Song Ke, Wang Wei, Qian Dingdong, et al. Simulation research on space charge and electric field distribution characteristics of XLPE under impurity concentration gradient[J]. Insulating Materials, 2023, 56(4): 40-47.
[19] Walgenwitz B, Tortai J H, Bonifaci N, et al. Self-healing of metallized polymer films of different nature[C]//Proceedings of the 2004 IEEE International Conference on Solid Dielectrics, 2004. ICSD, Toulouse, France, 2004: 29-32.
[20] 李永东, 蒋铭, 曾博. 均匀场中负流注放电形成过程粒子模拟[J]. 高电压技术, 2014, 40(10): 2991-2996.
Li Yongdong, Jiang Ming, Zeng Bo. Particle-in-cell simulation of propagation process of negative streamer discharge in uniform field[J]. High Voltage Engineering, 2014, 40(10): 2991-2996.
[21] 李婉茹. 金属化薄膜电容器用聚丙烯高场电荷输运特性研究[D]. 北京: 北京交通大学, 2020.
Li Wanru. Study on high field charge transport characteristics of polypropylene for metallized thin filmcapacitors[D]. Beijing: Beijing Jiaotong University, 2020.
[22] Starikovskiy A, Bazelyan E, Aleksandrov N. Mechanisms controlling the electric field in the channel of a long streamer[C]//2022 IEEE International Conference on Plasma Science (ICOPS), Seattle, WA, USA, 2022: 1-2.
[23] Sun H Y, Lu B X, Wang M, et al. The role of photoionization in negative corona discharge: The influences of temperature, humidity, and air pressure ona corona[J]. Physics of Plasmas, 2017, 24(10): 103506.
[24] Lowell J. Absorption and conduction currents in polymers: a unified model[J]. Journal of Physics D Applied Physics, 1990, 23(2): 205-210.
[25] Lu Yongfeng, Tao Zibo, Hong Minhui. Characteristics of excimer laser induced plasma from an aluminum target by spectroscopic study[J]. Japanese Journal of Applied Physics, 1999, 38(5R): 2958.
[26] Ye J L, Cao Q, Zhao Y S. Co-pyrolysis of polypropylene and biomass[J]. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 2008, 30(18): 1689-1697.
[27] Heywang H. physical and chemical processes in self-curing plastic capacitors[J]. Colloid and Polymer Science, 1976, 254: 138-147.
Numerical Simulation of Self-Healing in Metallized Films under Electro-Thermo-Mechanical Coupling
Abstract Metalized film capacitors are widely used in many power electronics fields due to their high stability, large capacity, and good self-healing properties. Studying the self-healing micro mechanism of metalized film under complex stress can help optimize the manufacturing process of metalized film capacitors, improve product lifespan, and stability. This article constructs a self-healing characteristic test platform for metalized film under multiple physical fields, conducts self-healing experiments under different electro-thermal environments, characterizes the self-healing area and morphology, In the experiments, a Nanyang MDP5.8 micrometer-thick polypropylene metalized film with an aluminum metal layer was used. The applied voltages on the samples were 1.8 kV, 2.3 kV, 2.8 kV, 3.3 kV, and 3.8 kV. The temperatures were set at 30, 40, 50, 60, and 70°C, and the pressures were 1.8 MPa, 2.3 MPa, 8 MPa, 11 MPa, and 15 MPa. The self-healed samples were observed for morphology using an SOPTOP-SZN71 optical microscope.This article uses COMSOL MULTIPHYSICS 6.2 to build a self-healing model under multiple physical fields to explore the micro and macro characteristics of self-healing in metalized film.
The article first used a bipolar carrier transport model to simulate the phenomenon of charge concentration in weak spots under continuous voltage stress during capacitor operation, calculating the distribution of charges within the material at different times. As charges accumulate, the equivalent current in the weak spot region gradually increases. Once it reaches a certain value, impurities within the metalized film first break down, leading to filamentary discharge within the region. At this point, the discharge channel transitions from solid-state to gaseous, and the simulation model shifts from a solid intrinsic carrier transport model to a gas discharge model. This model is constructed using the plasma model in COMSOL to investigate the effects of different electro-thermal environments on the formation and development of discharge channels. Finally, the electromagnetic coupled thermal module is used to simulate the effects of Joule heating on vaporization and ionization of the metal layer, as well as carbonization of the dielectric layer during the self-healing process of the metalized film under various electro-thermal environments. The model's accuracy is validated by comparing it with previous experimental results.
From the experimental and simulation results, the following conclusions can be drawn: (1) The formation time of the discharge channel is on the order of nanoseconds, and its development is similar to electron avalanche. The time required for the discharge channel to fully penetrate is inversely proportional to the voltage and temperature, and directly proportional to the pressure. (2) During the self-healing process, the temperature of the metal layer can exceed 5 600 K. The ionized region of the metal layer is positively correlated with voltage and temperature, and negatively correlated with pressure. However, the proportion of the ionized region to the self-healing area remains around 43% under different electro-thermal environments. (3) The carbonization of the dielectric layer is minimal during the self-healing process. The carbonized region of the dielectric layer is slightly larger than the self-healing area of the metal layer, but the carbonization depth is only about 0.4 micrometers, roughly 7% of the film thickness. The radius and depth of carbonization are directly proportional to the applied voltage level and temperature, and inversely proportional to the pressure. However, the ratio between the carbonization radius and the self-healing radius remains around 1.6 under different electro-thermal environments.
Keywords:Metallized film capacitor, bipolar carrier, transportation model, self-healing model, discharge channel, plasma, carbonization
中图分类号:TM215
DOI: 10.19595/j.cnki.1000-6753.tces.L11008
国家重点研发计划资助项目(2021YFB2401503)。
收稿日期 2024-07-06
改稿日期 2024-10-20
王 泽 男,1999年生,硕士研究生,研究方向为高电压与绝缘技术。
E-mail:roym19990205@126.com
王 伟 男,1960年生,教授,博士生导师,研究方向为高电压与绝缘技术、先进电工材料等。
E-mail:roym19990205@126.com(通信作者)
(编辑 郭丽军)