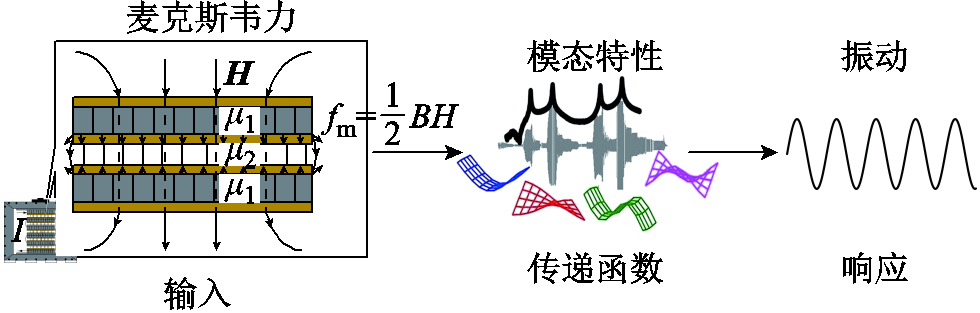
图1 非耦合模型
Fig.1 Non-coupling model
摘要 铁心振动模型是故障诊断和减振降噪的基础。传统研究认为铁心振动过程中麦克斯韦力仅是时间的正弦函数,对实际可能出现的多谐波频谱解释不全面。该文提出,麦克斯韦力与振动之间存在的耦合作用是导致铁心振动中包含多谐波分量的原因之一。借助拉格朗日力学基本原理,建立了电抗器铁心振动基本单元模型。利用摄动法分析了模型远离共振区的解的频域特征,并用林滋泰德-庞加莱摄动法分析了模型发生超谐共振和亚谐共振时解的频域特征。研究结果表明:根据模型计算结果,麦克斯韦力-振动耦合效应会使油浸式并联电抗器铁心振动包含2h(h=1,2,3,…)次谐波,且谐波幅值随频率升高而快速减小;若铁心柱发生超谐共振,产生2h(h=1,2,3,…)次谐波,且200 Hz振动分量显著增大;若铁心柱发生亚谐共振,产生h(h=1,2,3,…)次谐波,且50 Hz振动分量显著增大。铁心松动和环氧树脂垫块老化等因素可导致其固有频率发生偏移,此时发生超谐共振和亚谐共振的可能性增加。1 000 kV和500 kV变电站现场实测结果符合该文提出的理论预测,说明了所建立机理模型的合理性。研究结果为现场人员根据电抗器油箱表面的振动信号判断电抗器铁心柱的轴向松紧程度提供了新的视角和认识。
关键词:高压油浸式并联电抗器 振动 麦克斯韦力 耦合 频谱特征
高压油浸式并联电抗器是高压输电工程中重要的无功补偿设备,对线路和系统的安全运行有重要意义[1-3]。处于运行状态的高压油浸式并联电抗器在电磁力作用下发生振动,铁心和绕组的紧固件在振动过程中可能会松动,相应的绝缘部件在长期循环应力作用下会加速老化,这些因素可能给设备的健康运行带来隐患[4-7];此外,高压油浸式并联电抗器外壳的振动向空气辐射,产生可听噪声,对周围环境造成污染,降低居民生活质量。因此,高压油浸式并联电抗器的振动与噪声问题得到了广泛关注[8]。铁心是高压油浸式并联电抗器振动与噪声的主要来源[9],同时也是可能发生机械故障的部件,所以研究并联电抗器铁心振动问题具有重要意义。
高压油浸式并联电抗器的铁心柱存在气隙,其振动机理与变压器铁心振动机理有所不同。并联电抗器铁心在麦克斯韦力和磁致伸缩效应的共同作用下产生受迫振动。目前国内外广泛开展了并联电抗器铁心振动研究工作。栾涛计算了750 kV油浸式并联电抗器铁心固有频率和振型,并进行了试验模态验证[10]。Gao Yanhui等同时考虑磁致伸缩效应和麦克斯韦力,计算了1/4电抗器铁心振动位移[11]。张鹏宁等通过有限元计算和实验对比了麦克斯韦力和磁致伸缩效应对并联电抗器铁心振动的贡献[12]。祝丽花等提出了一种磁致伸缩-机械强耦合模型[13]。Yan Rongge等分析了不同谐波作用下电抗器铁心振动及其所受麦克斯韦力的特性[14]。Gao Yanhui等提出了一种优化气隙刚度减小电抗器振动的方法,反映了气隙填充物刚度对电抗器振动的影响[15]。黄中华等将正交实验优化方法应用于电抗器振动测试,提高了测试效率[16]。
由上述研究现状可以看出,目前国内外已经在电抗器铁心振动机理、振动测试方法和铁心减振降噪方法等方面取得了大量成果,但是在研究麦克斯韦力对电抗器铁心振动的影响时,对麦克斯韦力和振动间的关系进行简单的线性化假设,未考虑铁心振动位移对磁场力的影响,这种非耦合模型如图1所示。这种假设使铁心振动信号的理论分析结果和实测结果的频谱特征可能存在差异。另一方面,为满足1.5、1.4倍过电压线性度要求,实际运行的高压并联电抗器铁心在额定运行工况下处于低磁通密度的状态,磁致伸缩作用主要集中在100 Hz[17-18],对振动谐波的贡献比较小;且目前基于磁致伸缩的谐波理论不能很好地解释铁心结构力学特性的改变,即固有频率的偏移对振动谐波的影响。实际上,电抗器铁心振动不仅会对其周围部件的振动产生影响,也会对作用于自身的麦克斯韦力产生影响,具体体现为:铁心在麦克斯韦力作用下振动,麦克斯韦力会随着铁心饼间的相对运动发生改变,进而改变铁心振动,这种麦克斯韦力和振动响应间的耦合关系存在于电抗器铁心振动的整个过程中,如图2所示。麦克斯韦力和振动响应间存在的耦合关系也会使电抗器铁心振动呈现多倍频特征,且振动频域特征会随着铁心固有频率的偏移而发生改变,但目前对此尚缺乏深入的研究,因此对稳定运行状态下并联电抗器铁心振动信号中所含谐波分量的理解仍不够全面和深入。

图1 非耦合模型
Fig.1 Non-coupling model
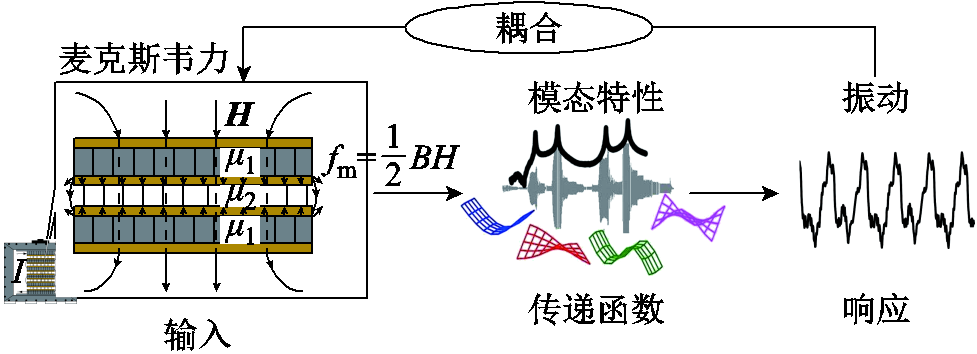
图2 耦合模型
Fig.2 Coupling model
为探讨电抗器铁心振动过程中麦克斯韦力与振动的耦合效应及其影响,本文借助拉格朗日力学原理建立麦克斯韦力作用下电抗器铁心饼轴向振动单元模型;进而利用摄动法分析处于正常运行状态的电抗器铁心饼轴向振动单元模型的解析解;对处于超谐或亚谐共振状态下的单元模型,借助林滋泰德-庞加莱法进行求解,并给出共振条件;最后通过对比分析高压并联电抗器箱体外壳振动实测结果和理论分析结果,验证所建立的模型。
高压油浸式并联电抗器由铁心、绕组和油箱等部件构成。高压油浸式并联电抗器振动传播并辐射噪声的过程可被划分为三个部分。①振源:通电绕组在漏磁场作用下振动和铁心在磁致伸缩效应及麦克斯韦力作用下振动;②传递:绕组和铁心的振动通过其部件及电抗器油传播至油箱表面,引发油箱振动;③辐射:油箱本体振动通过空气向外辐射产生可听噪声。已有研究表明,电抗器绕组振动比铁心振动小一个数量级[19],铁心是电抗器油箱振动的最主要源头。而对电抗器铁心而言,其主要振源为铁心柱,王起悟计算了工作状态下油浸式并联电抗器铁心的变形,发现铁心柱变形以轴向为主[20]。因此,探讨铁心电抗器铁心振动过程中的麦克斯韦力-振动耦合效应的关键是建立合理的麦克斯韦力作用下铁心柱轴向振动单元模型。
典型的高压油浸式并联电抗器铁心结构如图3所示。铁心由上下铁轭、左右旁轭、夹件、紧固装置和铁心柱等部件构成。铁心柱由铁心饼沿轴向堆叠而成,上下两端由上下铁轭固定,预紧力可通过上铁轭的压紧装置改变。铁心饼由硅钢片、环氧树脂垫片或大理石构成。为避免涡流损耗造成的局部过热,铁心饼上下两端垫有磁屏蔽板。铁心饼被划分为若干个扇区,各扇区采用辐射式叠片方式。
根据电抗器铁心结构,首先做出如下假设:
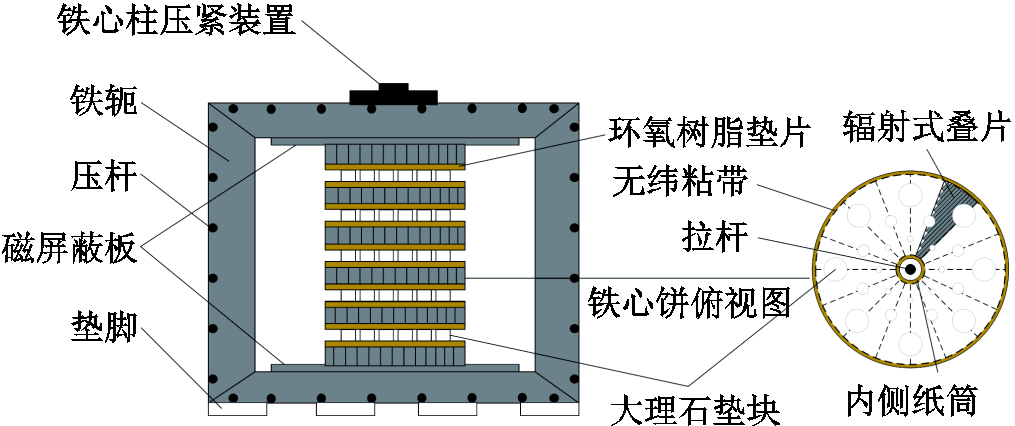
图3 高压油浸式并联电抗器铁心结构
Fig.3 Core structure of high voltage oil-immersed shunt reactor
1)假设铁心柱端部部件刚度无穷大,铁心柱振动不使其变形。尽管现有研究表明上铁轭会随铁心柱的轴向振动发生弯曲[20],但是上铁轭的弯曲可被等效为模型中顶端弹簧元件刚度系数和阻尼元件阻尼系数的改变。
2)假设电抗器油和环氧树脂垫片阻尼效应可等效为黏性阻尼。
3)假设辐射式硅钢叠片刚度无穷大,不发生变形,且大理石和环氧树脂垫片质量忽略不计,硅钢叠片视为质量块。硅钢叠片的杨氏模量远大于大理石和环氧树脂垫片的杨氏模量,可认为发生变形的主要是气隙填充物。
根据高压油浸式并联电抗器铁心结构和上述假设,建立描述麦克斯韦力作用下铁心柱轴向振动的质量-弹簧数学模型,如图4所示,该模型可体现铁心柱的主要机械特性。图中,Mi为第i层硅钢叠片的质量,用于表征铁心饼的惯性,Ki为第i层硅钢叠片的刚度系数,Ci为第i层硅钢叠片的阻尼系数,Fi为第i层硅钢叠片的铁心饼所受麦克斯韦力。
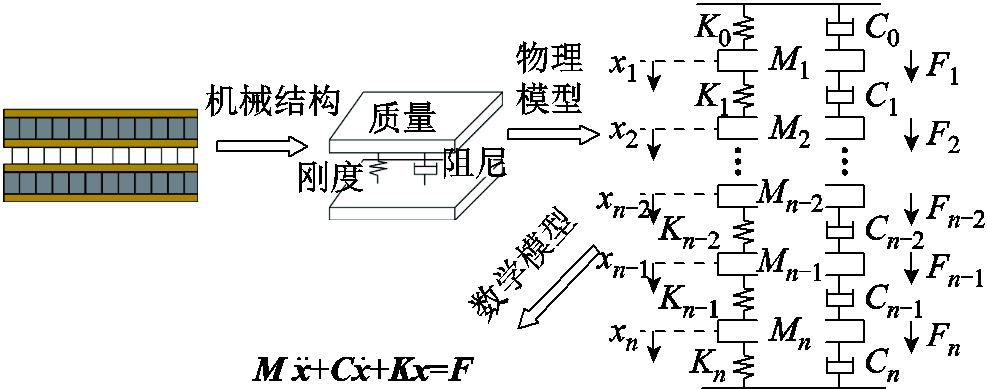
图4 铁心柱质量-弹簧模型
Fig.4 Mass-spring model of core column
基于图4模型,建立n自由度的二阶线性微分方程组描述铁心柱轴向的动力学行为,即
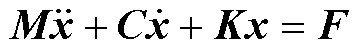 (1)
(1)
式中,M为铁心饼质量矩阵;C为阻尼系数矩阵;K为刚度系数矩阵;F为麦克斯韦力矩阵;x为铁心柱位移矩阵。
采用数值计算方法可方便求解方程组,但由于方程中的系数矩阵为非对角阵,方程组难以解耦,几乎不可能利用该模型的解析解分析麦克斯韦力作用下铁心柱的轴向振动。同时,方程组左端系数由系统的质量、刚度、阻尼决定,若不考虑振动瞬时位移对麦克斯韦力的影响,右端的麦克斯韦力矩阵仅是时间t的函数,对振动响应的分析仍停留在线性系统阶段。
铁心柱由铁心饼堆叠而成,每对相邻铁心饼具备铁心柱基本的机械要素和磁场要素,可视为铁心柱基本单元。因此,取一对铁心饼作为基本研究对象,建立铁心柱的麦克斯韦力-轴向振动耦合单元模型,如图5所示。图中,m1为上铁心饼的质量,m2为下铁心饼的质量,k为等效刚度系数,体现铁心饼间气隙填充物的弹性,c为等效阻尼系数,体现了电抗器油和气隙填充物的阻尼效应,O是坐标原点,同时也是系统质心,x1是描述上铁心饼运动的矢径,x2是描述下铁心饼运动的矢径。该模型既包含系统的机械特性,又包含系统的磁场特性,有别于之前的线性模型。
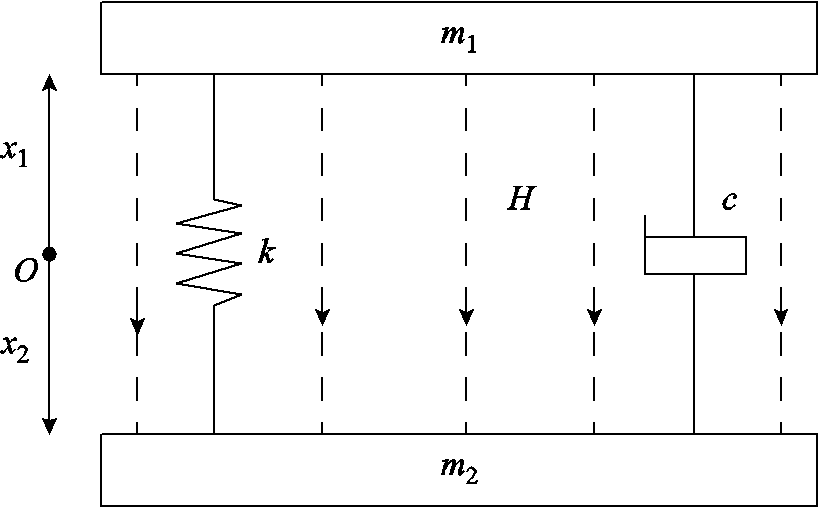
图5 麦克斯韦力-振动耦合基本单元模型
Fig.5 Maxwell force-vibration coupling basic model
以图5中物理模型为基础,进行动力学系统建模。分析动力学系统一般存在两种途径,分别是矢量动力学和分析动力学。矢量动力学要求具体分析系统内部的相对运动和受力情况,理论基础是牛顿运动定律;分析动力学则从系统整体能量出发,不考虑系统具体受力,提供了一种对复杂动力学系统建立动力学方程的简易方法,具有良好的系统可添加性,理论基础是拉格朗日第二类方程[21]。因此,本文选择分析动力学作为建模的基本途径。
对图5中模型,不考虑重力等外力作用,建立系统在交变机械量和磁场量作用下的稳态振动数学模型。则根据质心运动定理,坐标原点O位置不发生改变,满足关系m1x1+m2x2=0。因为仅考虑系统轴向运动,该运动为一维运动,所以矢径x1、x2可用标量x1、x2替代,这样可以简化动力学方程形式。则综合考虑单元模型动能、弹性势能和磁场能的拉格朗日函数为
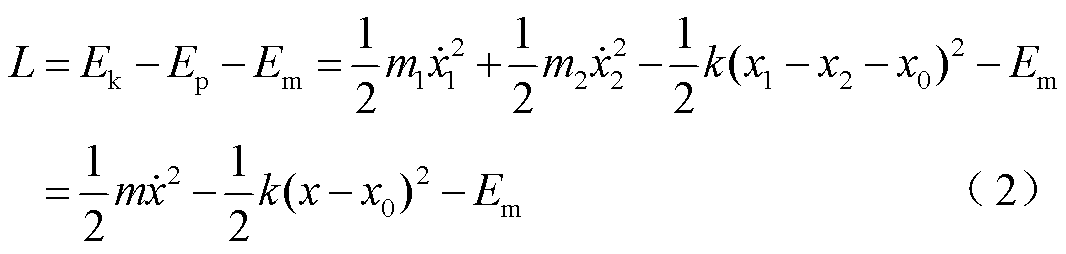
式中,Ek为铁心饼往复运动时的动能;Ep为系统存储的弹性势能;Em为系统包含的磁场能量;x为上下铁心饼间距,定义为x=x1-x2;x0为系统弹性势能为零时的距离;m为等效质量,定义为m=m1m2/( m1+ m2),它们共同构成系统的拉格朗日函数L。
系统的磁场能量可借助磁路理论进行近似分析。假设大理石、环氧树脂垫片、电抗器油磁导率相等,铁心柱各气隙轴向长度相等,认为气隙中磁场近似均匀分布,则电抗器铁心等效磁路模型如图6所示。
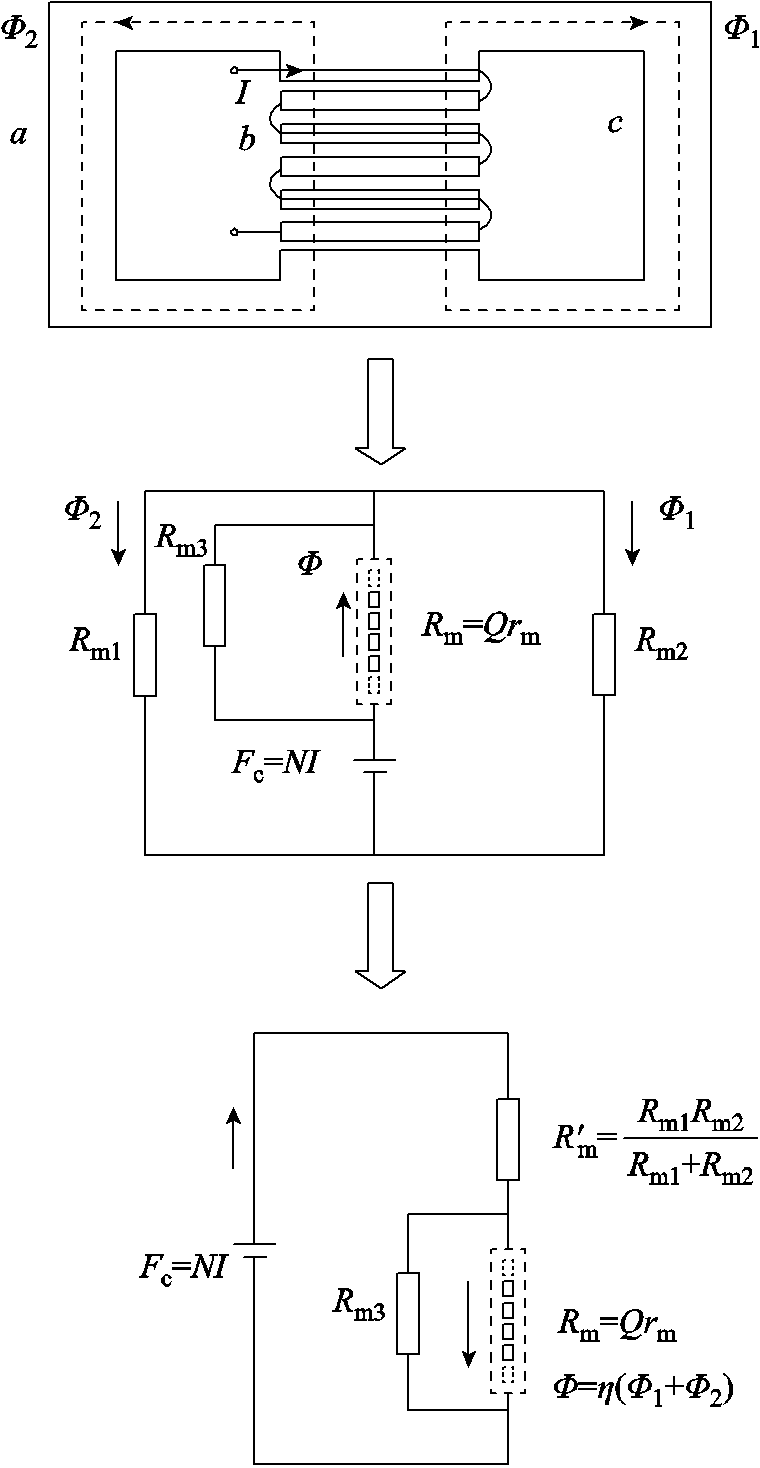
图6 高压油浸式并联电抗器铁心等效磁路
Fig.6 Equivalent magnetic circuit of high voltage oil-immersed shunt reactor core
图6中,I为流过电抗器的电流,Q为铁心柱中基本单元对的数量,N为线圈匝数,rm为单个气隙等效磁阻,Rm为气隙的等效总磁阻,Rm1为铁心左半边等效磁阻,Rm2为铁心右半边等效磁阻,Rm3为漏抗磁阻,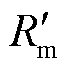 为铁心气隙以外部分的等效磁阻,Φ1为左铁轭磁通,Φ2为右铁轭磁通,Φ为铁心柱气隙磁通,η体现气隙外漏磁通的作用,Fc为磁动势。虽然总气隙长度小于铁心长度,但由于气隙的相对磁导率远远小于铁心,使得气隙的总磁阻远远大于铁心,可认为磁动势总体降落在气隙所在支路上。单个气隙承担的磁势Um计算公式为
为铁心气隙以外部分的等效磁阻,Φ1为左铁轭磁通,Φ2为右铁轭磁通,Φ为铁心柱气隙磁通,η体现气隙外漏磁通的作用,Fc为磁动势。虽然总气隙长度小于铁心长度,但由于气隙的相对磁导率远远小于铁心,使得气隙的总磁阻远远大于铁心,可认为磁动势总体降落在气隙所在支路上。单个气隙承担的磁势Um计算公式为
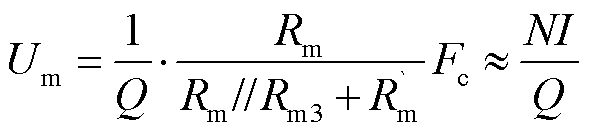 (3)
(3)
而
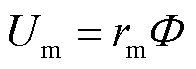 (4)
(4)
气隙磁通为
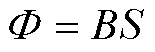 (5)
(5)
气隙磁阻为
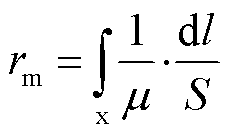 (6)
(6)
气隙中磁场能量密度为
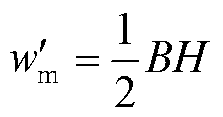 (7)
(7)
磁通密度B和磁场强度H的关系为
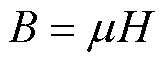 (8)
(8)
气隙体积为
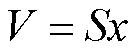 (9)
(9)
则气隙磁场能量为
 (10)
(10)
联立式(3)~式(10),得气隙磁场能量计算表达式为
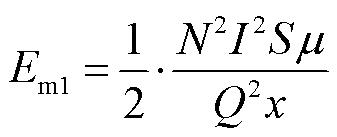 (11)
(11)
式中,μ为气隙磁导率;S为气隙横截面积。
系统磁场能量Em由气隙磁场能量Em1、铁心饼磁场能量Em2和气隙外漏磁场能量Em3三部分构成,气隙磁场能量和漏磁场能量远大于铁心磁场能量,因此单元模型磁场能量可以用气隙磁场能量和气隙外漏磁场能量近似代替为
 (12)
(12)
式中,h(η)体现了系统磁场能量与气隙磁场能量的比例关系。将系统磁场能量在x0处泰勒展开,取二阶近似,即
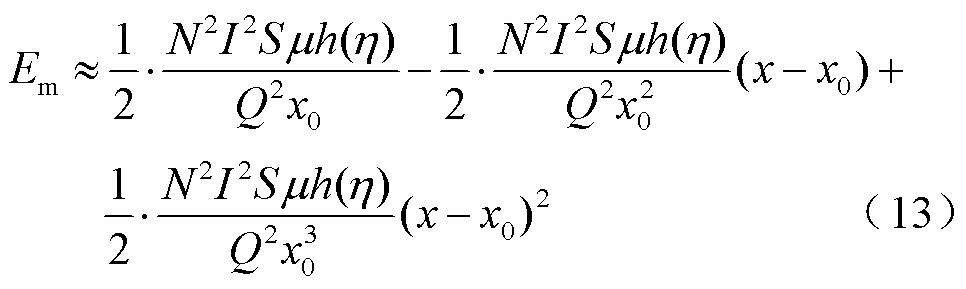
将式(13)代入式(2),得
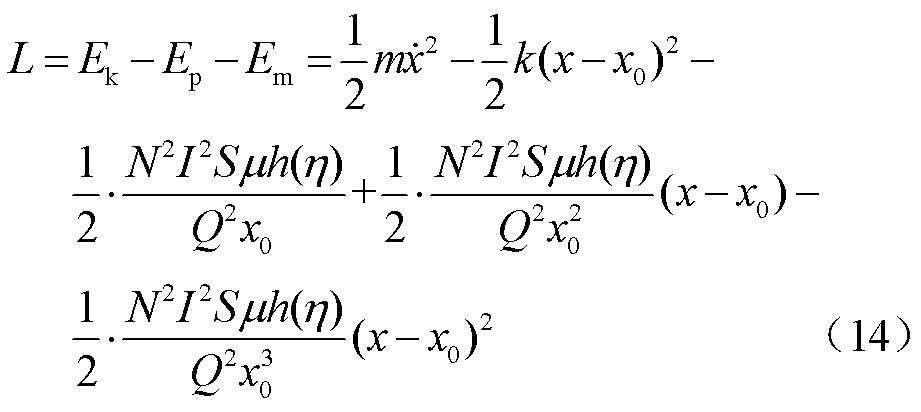
狭义拉格朗日第二方程为
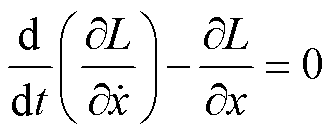 (15)
(15)
该方程仅适用于非耗散系统,然而本文的单元模型存在黏性阻尼,阻尼力是速度的函数,为耗散系统。对于耗散系统,引入耗散函数D,满足
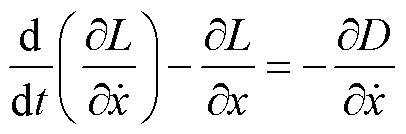 (16)
(16)
单元模型的耗散函数为
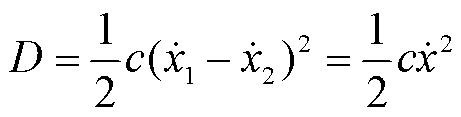 (17)
(17)
综合式(14)、式(16)、式(17),得系统运动方程为
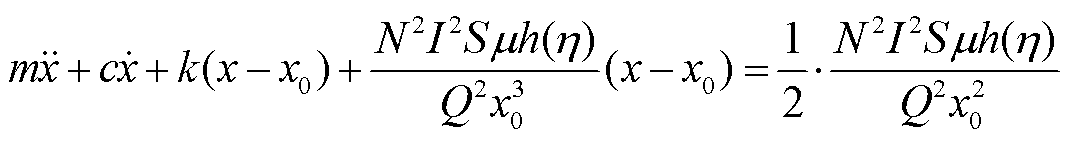 (18)
(18)
假设流过电抗器电流为
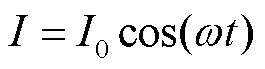 (19)
(19)
令r=x-x0,则系统运动方程为
 (20)
(20)
其中
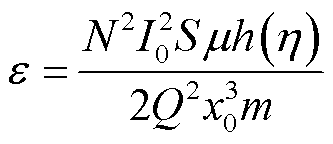
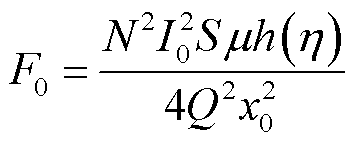
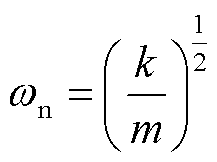
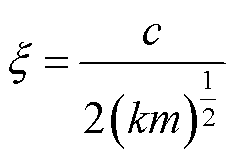
式(20)是变系数非齐次微分方程,方程等号右端项体现了麦克斯韦力的激励作用,激励力包含不随时间变化的恒定力和频率是电源频率2倍的随时间变化的正弦力;方程左端变系数项则体现了麦克斯韦力与振动的耦合作用,使得系统等效刚度不是常量,而是以2ω为周期的交变量,因此系统模型呈现非线性特征。
忽略麦克斯韦力与振动的耦合作用,方程退化为
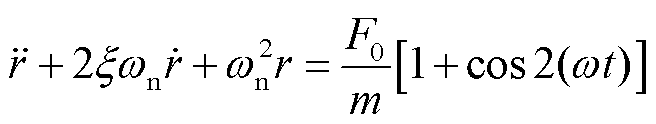 (21)
(21)
对于实际的物理系统,其阻尼一般都很小,假定系统处于欠阻尼状态,方程的解为
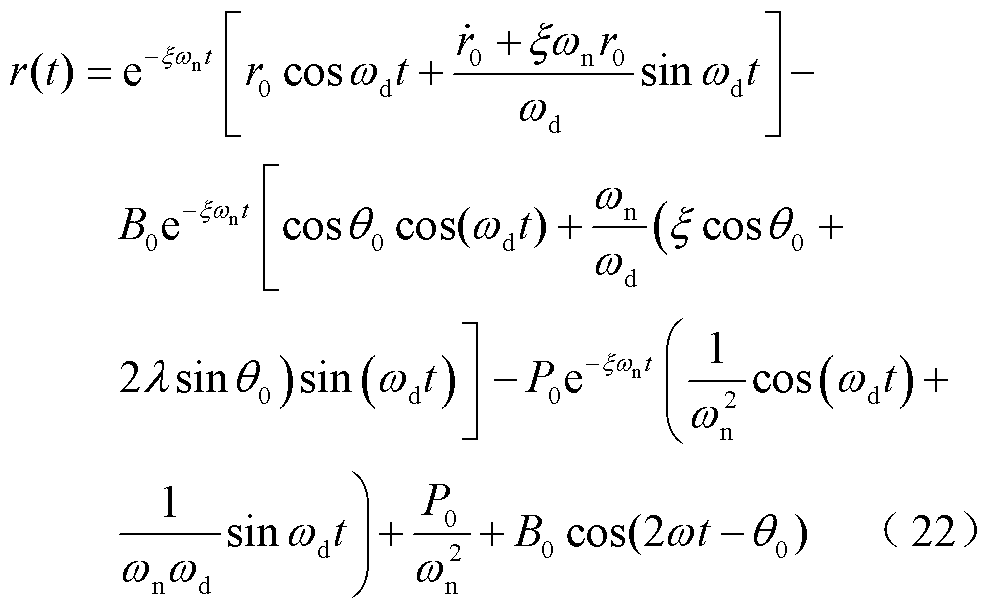
其中
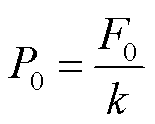
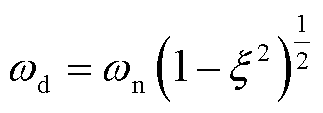
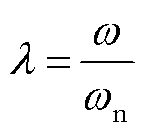
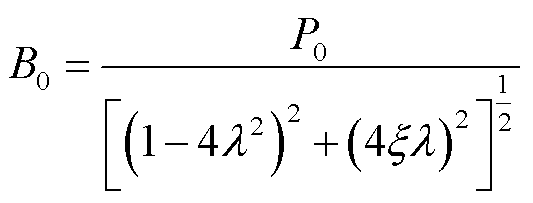
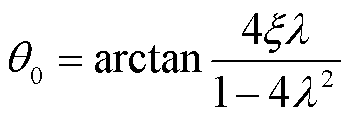
式中,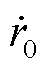 和r0为初始条件。
和r0为初始条件。
式(22)等号右端五项分别是:无激励时系统的自由振动、正弦力决定的自由伴随振动、恒定力决定的自由伴随振动、恒定力决定的受迫振动和正弦力决定的受迫振动。本文考虑单元模型的稳态运动,其振动主频是电源频率的2倍,即
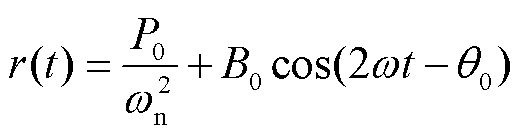 (23)
(23)
当系统远离共振区时,可借助摄动法,求取考虑麦克斯韦力与振动耦合作用的系统动力学方程解析解。令
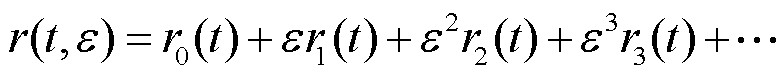 (24)
(24)
将式(24)代入式(20),令方程两端ε的同次幂系数相等,得微分方程组为
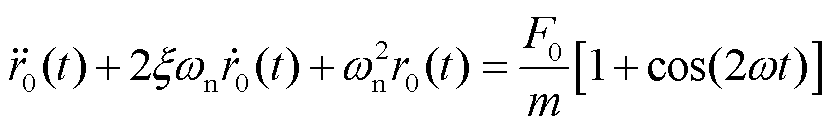 (25)
(25)
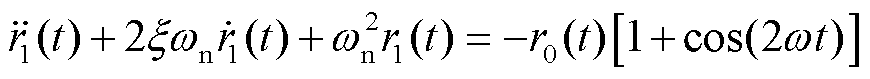 (26)
(26)
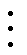
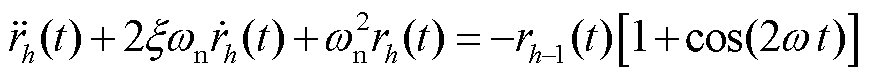 (27)
(27)
本文中铁心电抗器处于稳定运行状态,因此只分析单元模型的稳态解,方程式(20)零次近似稳态解为
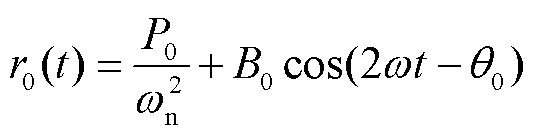 (28)
(28)
零次近似稳态解与式(23)具有相同的形式,说明系统是在不考虑麦克斯韦力-振动耦合效应的动力学系统基础上展开摄动的。一次近似稳态解为
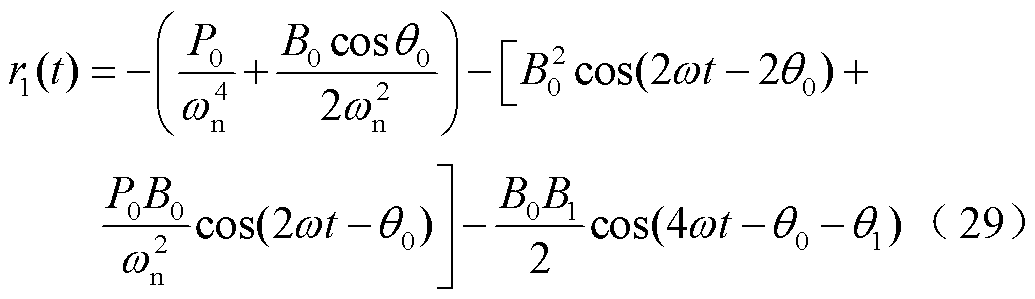
其中
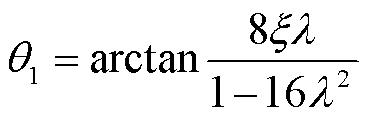
方程解析解为

由式(30)可知,由于零次近似稳态解中含有频率为2ω的分量,使得一次近似解中出现频率为4ω的分量,依次类推使得方程的近似解中出现2hω(h=2, 3, 4, ×××)等频率的高次谐波含量,这是基于麦克斯韦力-振动耦合动力学系统特有现象。由于
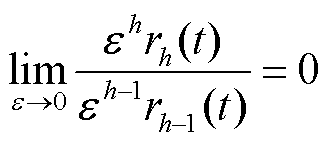 (31)
(31)
使得高次谐波是低次谐波的高阶无穷小量,即随着谐波次数的增加,振动幅值会快速减小。
随着高压并联电抗器运行年限的增加,铁心将不可避免地发生松动,铁心饼中的环氧树脂垫片在振动过程中因受到机械循环应力作用而逐渐变松软,系统固有频率发生偏移,环氧树脂垫片的阻尼作用变得极其微弱,可忽略不计。系统可能发生亚谐波共振或超谐波共振,振动的频谱特征发生改变。
此时麦克斯韦力-振动耦合动力学系统解析解中出现长期项,会使得解发散无界。为解决近似解中存在长期项的问题,采用林滋泰德-庞加莱摄动法求解近似解,这种方法在摄动法的基础上假设角频率也是振动幅值的函数,可展开为小量ε的幂级数,通过每一步近似保持周期性来消除长期项。忽略阻尼效应,令ωt=τ,动力学方程为
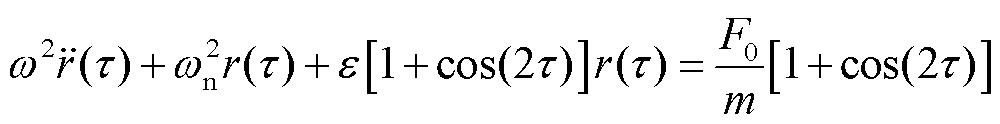 (32)
(32)
若系统处于亚谐共振区,令
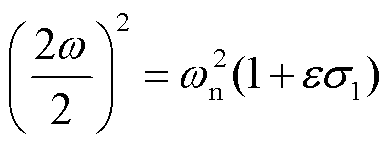 (33)
(33)
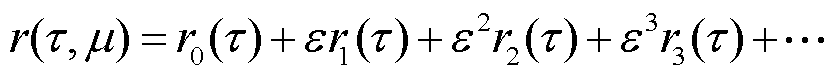 (34)
(34)
得
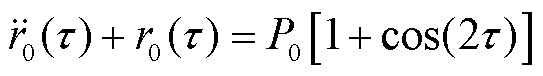 (35)
(35)
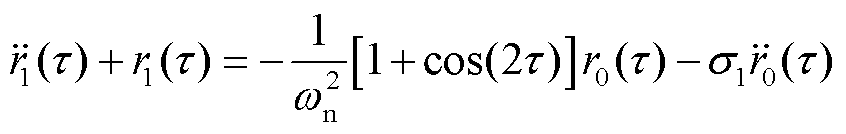 (36)
(36)
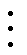
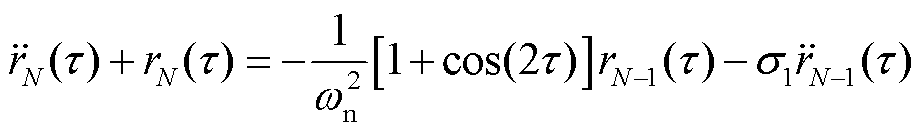 (37)
(37)
方程式(32)零次近似稳态解为
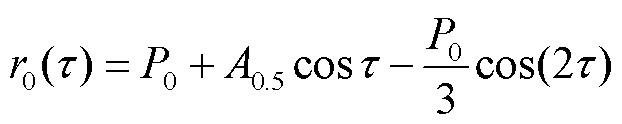 (38)
(38)
零次近似稳态解比式(23)多出A0.5cosτ,这一项频率由零阶受迫振动系统固有频率决定,幅值由初始条件决定,假定系统初始条件均为零,则A0.5= -2P0/3。将式(38)代入式(36),得
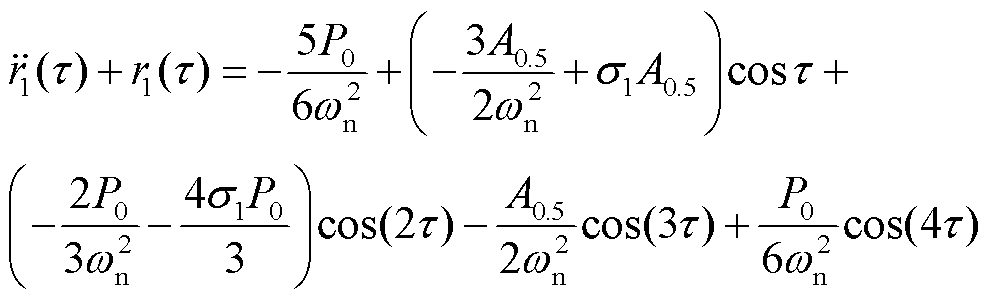 (39)
(39)
令-3A0.5/(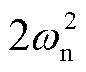 )+ σ1A0.5=0,可消除长期项τcosτ,此时σ1=3/(
)+ σ1A0.5=0,可消除长期项τcosτ,此时σ1=3/(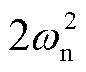 ),方程(39)化简为
),方程(39)化简为
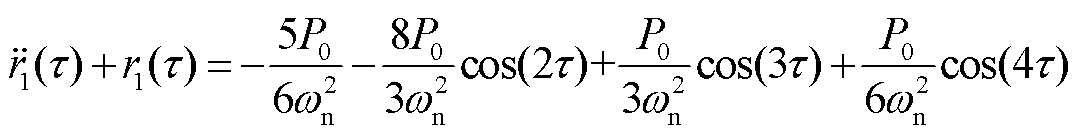 (40)
(40)
一次近似稳态为
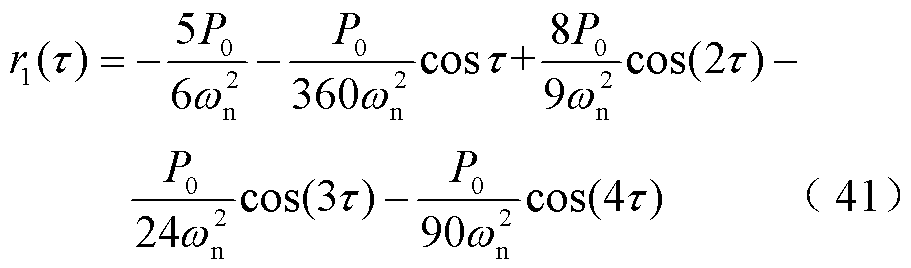
方程解析解为
 (42)
(42)
方程解具有hω(h=2, 3, 4, 5, ×××)的频率特征,振动不仅出现偶次谐波分量,还出现奇次谐波分量。cosτ项和cos(2τ)项是同阶量,即50 Hz振动和100 Hz振动幅值相近,其余高次谐波幅值随频率增加快速减小。
若系统处于超谐共振区,令
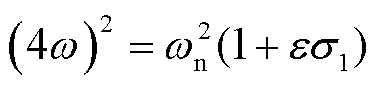 (43)
(43)
得
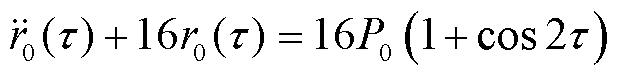 (44)
(44)
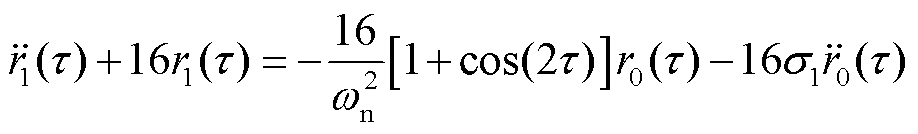 (45)
(45)
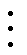
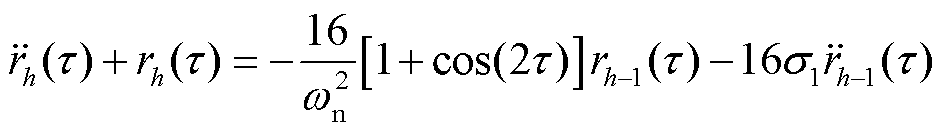 (46)
(46)
类似地,假定系统初始条件均为零,得方程解析解为
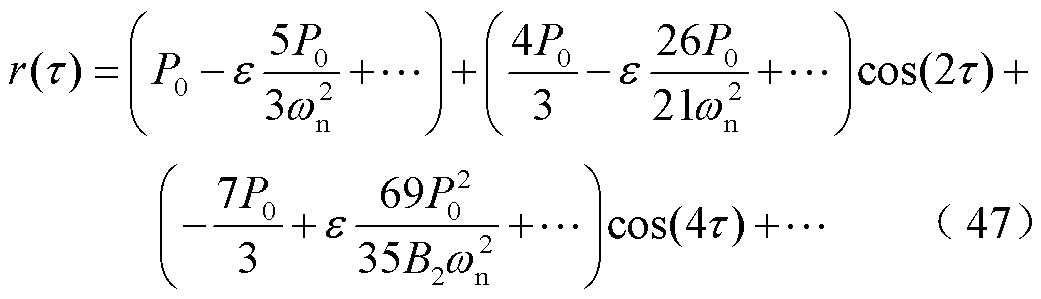
方程解具有2hω(h=2, 3, 4, 5, ···)频率特征,振动仅包含偶次谐波分量,cos(2τ)项不再是cos(4τ)项的小量,即200 Hz振动和100 Hz振动幅值相近,其余高次谐波随频率增加幅值快速减小。
根据文献[22]中的方法,得到系统发生亚谐共振和超谐共振的条件分别是4ω/(5g) ≤ω0≤4ω/(3g)、16ω/(5g)≤ω0≤16ω/(3g),式中q=F0/m, δ=k/m+ε, ω0=δ1/2,g=2q/δ。由此可以发现:系统更容易发生超谐共振,随着超谐共振阶次的提高,发生超谐共振的条件变得苛刻,实际系统一般不具备诱发条件。
麦克斯韦力-轴向振动耦合基本单元模型可体现电抗器铁心振动的基本特点,尤其是频谱特征。虽然油箱内部电抗器油对高次谐波具有一定的阻尼作用,且线圈振动的非线性也会引入高次谐波分量,但油的阻尼仅对高频振动幅值有影响,而线圈振动又远远小于铁心,因此电抗器油箱表面的振动主要由铁心振动决定,其振动频谱特征与单元模型分析结果具有相似性。
本文对河北省部分在运高压油浸式并联电抗器油箱表面振动进行了测量,采用如图7所示的振动-声学测量系统。
图8是某变电站1 000 kV特高压油浸式并联电抗器,投运于2016年,测点布置如图8a所示;所测得的油箱表面振动时域和频域信号如图8b所示。由此可见,电抗器油箱振动频谱集中在100、200、300、400 Hz,存在明显的多倍频振动现象,可认为该现象与铁心振动密切相关。同时由于电抗器投运年限短,铁心不易发生松动,内部部件也未发生严重老化,因此振动频谱呈随频率增加幅值快速减小的特征,这与式(31)推导结果相符合。
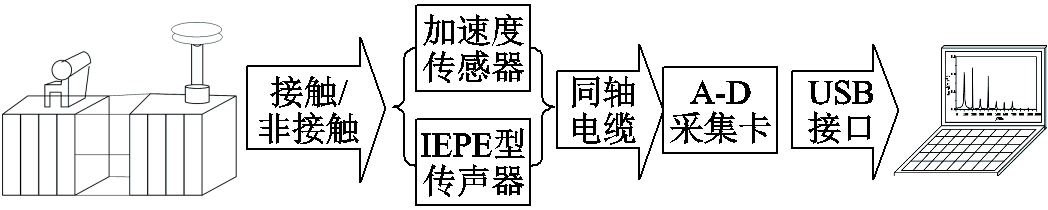
图7 振动-声学测量系统
Fig.7 Vibration-acoustic measurement system
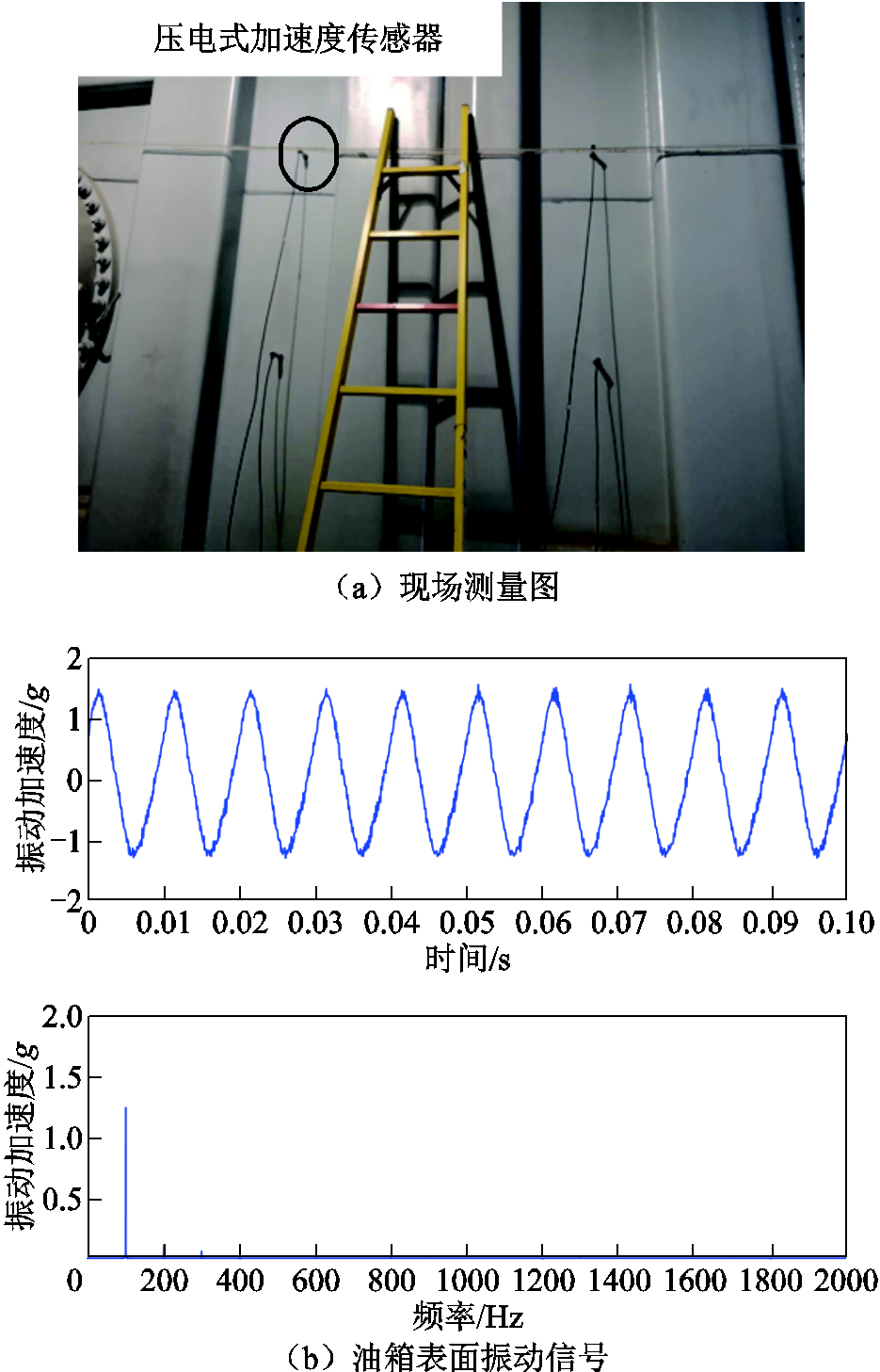
图8 1 000 kV变电站特高压油浸式并联电抗器
Fig.8 UHV oil-immersed shunt reactor in 1 000 kV substation
图9是某变电站500 kV高压油浸式并联电抗器,投运于1997年,测点布置如图9a所示;所测得的油箱表面振动时域和频域信号如图9b所示。从图9b中可以看出:电抗器油箱振动频谱不仅包含100、200、300、400 Hz分量,并且200 Hz振动分量大小同100 Hz振动分量接近,这与式(47)推导结果相符合。推测出现这种现象的原因是:被测电抗器运行年限久,铁心部分部件发生老化和松动,铁心高阶固有频率偏移使超谐共振频率区间偏移,导致铁心发生超谐共振。由式(1)和式(23)可知,麦克斯韦力作用下的并联电抗器铁心基频振动与流过电抗器电流或电压的二次方成正比,图9b中基频幅值小于图8b。
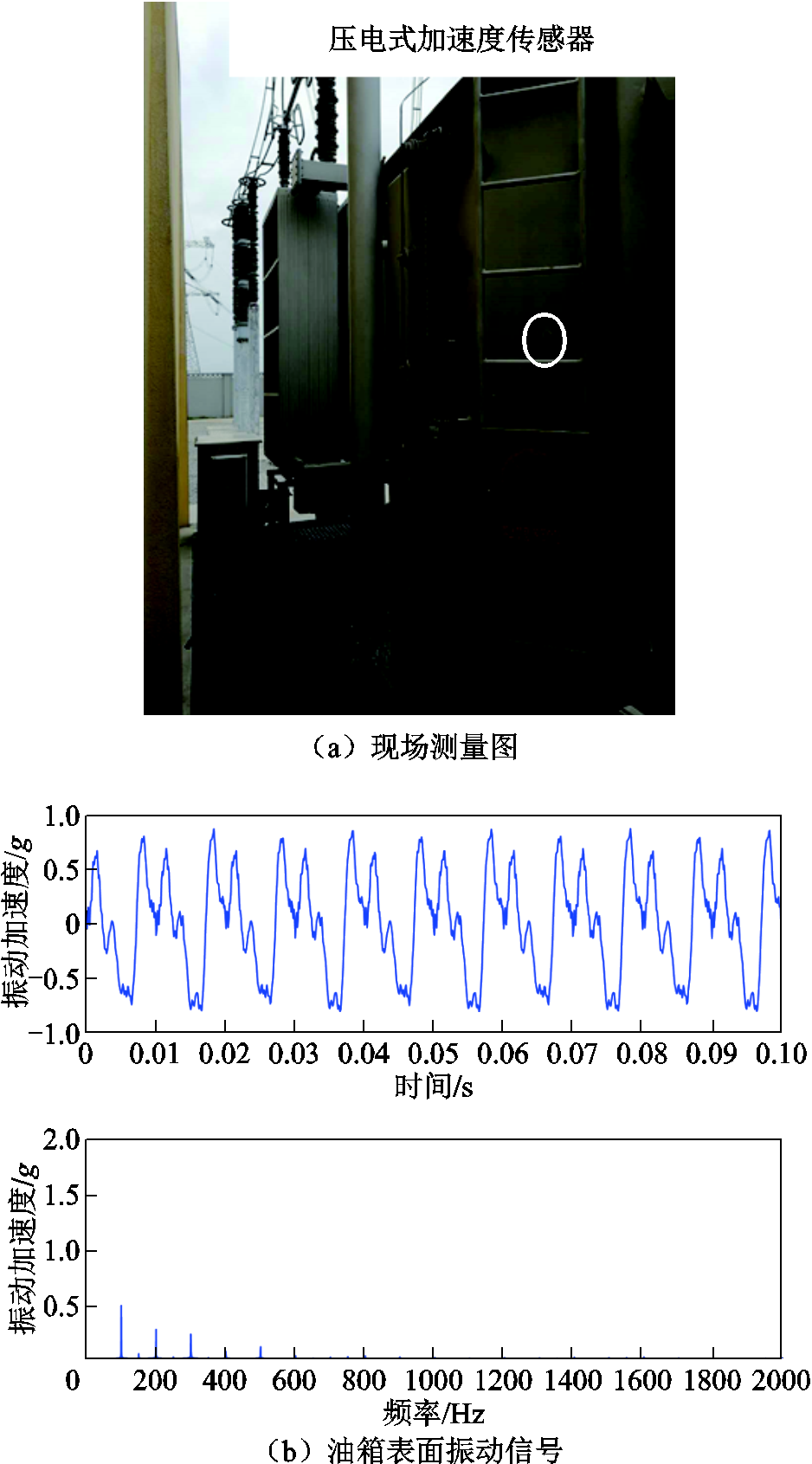
图9 500 kV变电站高压油浸式并联电抗器
Fig.9 High voltage oil immersed shunt reactor in 500 kV substation
可以根据模型推测,若铁心松动或老化更加严重,其低阶固有频率偏移,使亚谐共振频率区间偏移,导致铁心发生亚谐共振,油浸式并联电抗器箱体表面振动将出现奇次谐波,50 Hz将分量变得较为显著。对于文中测量的油浸式并联电抗器,箱体表面未检测出明显的50 Hz谐波,说明铁心松动和老化并不是十分严重。
本文围绕高压油浸式并联电抗器铁心的麦克斯韦力和振动耦合关系,建立了电抗器铁心柱麦克斯韦力-轴向振动耦合基本单元模型,给出了模型解析解,分析了不同条件下解析解的结构特点,并对现场在运高压油浸式并联电抗器油箱表面振动进行了测量分析。研究得到的主要结论包括:
1)电抗器铁心振动存在多谐波特点的重要原因是铁心饼振动过程中麦克斯韦力和振动的耦合作用,远离共振区的电抗器铁心振动以电源频率的偶数倍频为主,且随着频率增高,相应幅值大幅减小。
2)铁心发生亚谐共振和超谐共振时,振动频谱特征明显改变。当铁心低阶固有频率靠近系统工作频率(50 Hz)时,铁心将发生亚谐共振,振动频谱出现奇次谐波,且50 Hz振动和100 Hz振动幅值相近,高次谐波幅值快速减小;当铁心高阶固有频率靠近4倍系统工作频率(200 Hz)时,铁心将发生超谐共振,200 Hz振动不再是100 Hz振动小量,二者幅值相近,其余高次谐波幅值快速减小。
3)随着电抗器运行年限增加,铁心松动和环氧树脂垫块老化等因素将导致固有频率发生偏移,发生铁心超谐共振的可能性增加,实测200 Hz等偶数次谐波分量增大,与理论模型预测频谱特征吻合。
下一步将搭建实物实验平台,进一步验证模型的正确性。此外,还需更多的实验定量研究,从而建立基于麦克斯韦力-振动耦合模型的电抗器铁心柱轴向松紧度判据。
参考文献
[1] Liu Wenye, Luo Longfu, Dong Shuda, et al. Overview of power controllable reactor technology[J]. Energy Procedia, 2012, 17: 483-491.
[2] 王梦云. 2005年度110(66)kV及以上变压器事故与缺陷统计分析[J. 电力设备,2006, 7(11) 99-102.
Wang Mengyun. Statistic analysis of transformer's faults and defects at voltage 110(66)kV and above[J]. Electrical Equipment, 2006, 7(11) 99-102.
[3] 国家电力公司发输电运营部. 500(300)kV变压器及电抗器质量调查报告[R]. 北京: 国家电力公司, 2002.
[4] 张仲先. 500 kV高压并联电抗器故障实例[J]. 高电压技术, 2000, 26(4): 75-77.
Zhang Zhongxian. Fault example of 500 kV high voltage shunt reactor[J]. High Voltage Engineering, 2000, 26(4): 75-77.
[5] 刘金, 王贵山, 孙上元, 等. 一起500 kV并联电抗器故障分析[J]. 广西电力, 2015, 38(3): 33-35.
Liu Jin, Wang Guishan, Sun Shangyuan, et al. Analysis of a 500 kV shunt reactor fault[J]. Guangxi Electric Power, 2015, 38(3): 33-35.
[6] 尹立群, 顾南峰. 平果变电站天平二回500 kV并联电抗器的故障分析及处理[J]. 广西电力技术, 1999, 22(1): 15-18.
Yin Liqun, Gu Nanfeng. Accident analysis and repair of 500 kV shunt reactor on 2nd Tian-Ping transmission line in Pingguo substation[J]. Guangxi Electric Power, 1999, 22(1): 15-18.
[7] 包艳艳, 温定筠, 张广东, 等. 一起750 kV并联电抗器故障分析及修复方案[J]. 电力电容器与无功补偿, 2019, 40(2): 40-44.
Bao Yanyan, Wen Dinjun, Zhang Guangdong, et al. Fault analysis and repair proposal on 750 kV shunt reactor[J]. Power Capacitor & Reactive Power Compensation, 2019, 40(2): 40-44.
[8] 宋春艳. 城市变电所设计中的环境保护问题[J]. 供用电, 2002(2): 9-11.
Song Chunyan. Environmental protection problems of urban substation design[J]. Distribution & Utilization, 2002(2): 9-11.
[9] 郑涛, 赵彦杰. 超/特高压可控并联电抗器关键技术综述[J]. 电力系统自动化, 2014, 38(7): 127-135.
Zheng Tao, Zhao Yanjie. Overview of key techniques of EHV/UHV controllable shunt reactor[J]. Auto-mation of Electric Power Systems, 2014, 38(7): 127-135.
[10] 栾涛. 750 kV油浸式并联电抗器电磁与振动研究[D]. 大连: 大连理工大学, 2015.
Luan Tao. Study on electromagnetism and vibration of 750 kV oil-immersed shunt reactor[D]. Dalian: Dalian University of Technology, 2015.
[11] Gao Yanhui, Muramatsu K, Fujiwara K, et al. Vibration analysis of a reactor driven by an inverter power supply considering electromagnetism and magnetostriction[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4789-4792.
[12] Zhang Pengning, Li Lin, Cheng Zhiguang, et al. Study on vibration of iron core of transformer and reactor based on Maxwell stress and anisotropic magneto-striction[J]. IEEE Transactions on Magnetics, 2019, 55(2): 9400205.
[13] 祝丽花, 杨庆新, 闫荣格, 等. 考虑磁致伸缩效应电力变压器振动噪声的研究[J]. 电工技术学报, 2013, 28(4): 1-6, 19.
Zhu Lihua, Yang Qingxin, Yan Rongge, et al. Research on vibration and noise of power transformer cores including magnetostriction effects[J]. Transactionsof China Electrotechnical Society, 2013, 28(4): 1-6, 19.
[14] Yan Rongge, Gao Xu, Zhu Lihua, et al. Research on three-dimensional stress distribution of reactor core[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 0602004.
[15] Gao Yanhui, Nagata M, Muramatsu K, et al. Noise reduction of a three-phase reactor by optimization of gaps between cores considering electromagnetism and magnetostriction[J]. IEEE Transactions on Magnetics, 2011, 47(10): 2772-2775.
[16] 黄中华, 王勇劲, 赵文强, 等. 正交试验优化方法在电抗器振动测试上的应用[J]. 青海电力, 2014, 33(4): 16-18, 26.
Huang Zhonghua, Wang Yongjin, Zhao Wenqiang, et al. Application of orthogonal test optimization in reactor vibration test[J]. Qinghai Electric Power, 2014, 33(4): 16-18, 26.
[17] 张艳丽, 李强, 王洋洋, 等. 谐波磁场下硅钢片磁致伸缩特性分析[J]. 电工技术学报, 2015, 30(14): 545-550.
Zhang Yanli, Li Qiang, Wang Yangyang, et al. Analysis on magnetostrictive properties of silicon steel sheet under harmonic magnetic field[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 545-550.
[18] 张艳丽, 孙小光, 谢德馨, 等. 无取向电工钢片磁致伸缩特性测量与模拟[J]. 电工技术学报, 2013, 28(11): 176-181.
Zhang Yanli, Sun Xiaoguang, Xie Dexin, et al. Measurement and simulation of magnetostrictive properties for non-grain oriented electrical steel sheet[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 176-181.
[19] 张鹏宁, 李琳, 聂京凯, 等. 考虑铁心磁致伸缩与绕组受力的高压并联电抗器振动研究[J]. 电工技术学报, 2018, 33(13): 3130-3139.
Zhang Pengning, Li Lin, Nie Jingkai, et al. Study on the vibration of high voltage shunt reactor considering of magnetostriction and winding force[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3130-3139.
[20] 王起悟. 油浸式电抗器振动噪音研究[D]. 大连: 大连理工大学, 2013.
Wang Qiwu. Study on vibration and noise of oil-immersed reactor[D]. Dalian: Dalian University of Technology, 2013.
[21] 叶敏, 肖龙翔. 分析力学[M]. 天津: 天津大学出版社, 2001.
[22] Lifshitze M, Landaul D. Volume 1 of course theoretical physics[M]. Oxford: Pergamon Press, 2000.
Study on Multi-Harmonic Vibration Mechanism of High-Voltage Shunt Reactor Core Based On Coupling between Maxwell Force and Vibration
Abstract The vibration model of high-voltage shunt reactor core is the basis for its fault detection and noise reduction. Traditionally, it is believed that the Maxwell force on the core is only a sinusoidal function of time, which can not explain the multi-harmonic components of vibration signal on the tank measured in practice fully. This paper presents a theory that the coupling effect between Maxwell force and vibration is one of the reasons for the multi-harmonic phenomenon. The basic element vibration model of shunt reactor core was established using Lagrange mechanics. The frequency domain characteristics of the model's solution far away from the resonance region were analyzed using normal perturbation method, and the frequency domain characteristics were analyzed respectively at super-harmonic resonance and sub-harmonic resonance, using L-P method. The results show that the coupling between Maxwell force and vibration is one of the causes of 2hω (h=1,2,3,…, ω=50 Hz) harmonics and explain the phenomenon that the amplitude decreases rapidly with the increasing frequency. When super-harmonic resonance occurs in the core, 2hω (h=1, 2, 3,…, ω=50 Hz) harmonics appear, and the 200 Hz vibration component increases significantly. When subharmonic resonance occurs in the core, hω (h=1, 2, 3,…, ω=50 Hz) harmonics appear, and the 50 Hz vibration component increases significantly. The reactor tank vibration tests results of 1 000 kV and 500 kV shunt reactor are consistent with the theoretical prediction proposed in this paper, indicating the rationality of the model. The results provide a new perspective and understanding to judge the axial tightness of shunt reactor core based on the vibration of reactor tank.
Keywords:High-voltage oil-immersed shunt reactor, vibration, Maxwell force, coupling, spectral characteristics
中图分类号:TM472
DOI: 10.19595/j.cnki.1000-6753.tces.241475
国家自然科学基金(51877168)和国家电网有限公司总部科技项目(5200-201913054A-0-0-00)资助。
收稿日期 2024-08-20
改稿日期 2024-12-03
党永亮 男,1996年生,硕士研究生,研究方向为电力设备振动噪声特性研究及计算、电力设备的故障诊断。
E-mail:877759724@qq.com
祝令瑜 男,1988年生,副教授,研究方向为电力设备振动噪声特性及其机理、高压柔性直流输电。
E-mail:zhuly1026@xjtu.edu.cn(通信作者)
(编辑 郭丽军)