 (1)
(1)
摘要 作为容性投切的重要设备,真空断路器的可靠运行对于维持电网的稳定至关重要。在并联电容器组投入时,真空断路器会出现合闸预击穿燃弧,导致触头的烧损、熔焊和材料转移等问题,严重影响其开断性能。因此,对断路器关合时的预击穿燃弧时间进行准确分析,不仅可以对容性开断水平进行实时评估,还可以应用于高压大电流老炼中,实现容性投切能力的定量提升。基于此,该文提出一种基于经验小波变换(EWT)的真空断路器关合预击穿燃弧时间分析方法。首先,对断路器的合闸位移信号进行最小二乘预处理,降低信号采集时的干扰;其次,对处理后的位移特征曲线进行EWT分解,利用峭度准则选取能准确反映刚合点的特征量,结合预击穿涌流波形,得到关合预击穿燃弧时间;最后,通过模拟分析和现场试验,对不同影响因素下的关合预击穿燃弧时间开展分析。相较于传统方式,该分析方法可在现有传感器的测量基础上,大幅提高预击穿燃弧时间的检测准确度,为断路器容性开断能力的准确评估和定量提升提供可靠支撑。
关键词:真空断路器 预击穿燃弧时间 位移信号 最小二乘 经验小波变换 峭度
真空断路器作为配电网系统中无功补偿用电容器组投切的重要设备,其可靠性直接影响电力系统的稳定运行。随着新能源的接入比例呈指数级上升,电容器组的投切也变得更加频繁,据统计,电容器组投切用断路器平均一天需开合1~2次,而在沿海地区,平均开合次数高达4~5次[1-2]。投入电容器组过程中,在断路器出现合闸预击穿的瞬间,关合涌流同步出现,直至触头刚合前,涌流电流以燃弧的形式存在,称为预击穿燃弧[3-6]。预击穿燃弧会引起触头的烧损、熔焊和材料转移,降低断路器的容性开断能力,断路器断口容易出现重击穿,在切除电容器组时可能会引起电容器组击穿、爆炸等严重事故。
目前,大连理工大学联合中国电科院共同开展了高压大电流老炼试验,对提升电容器组投切用断路器的容性开断性能展开研究。对真空断路器关合时的预击穿燃弧时间进行准确分析,不仅可以实时评估断路器的容性投切水平[7-9],更可以将其应用于高压大电流老炼中,对其容性投切水平进行定量提升[10-11]。
目前已有部分学者对真空断路器容性投入时的预击穿燃弧时间分析方法进行了研究,主要是通过对刚合点处的信号进行检测,包括振动信号、压力信号、角传感器信号以及位移信号等,进而实现预击穿燃弧时间的计算分析。文献[12]提出基于零相位数字滤波的振动信号处理方法;文献[13]使用短时能量法对合闸振动信号进行分析;文献[14]通过Hilbert变换法提取压力信号包络;文献[15]采用角度传感器,实现机械特性的在线监测,但该方式对传感器位置要求高,过短的安装距离不利于信号的采集,使得断路器的紧凑化设计受到影响;文献[16]通过位移传感器测量断路器动触头的位移曲线,实现机械特性的在线监测;还有部分文献用小波分析[17]、Hilbert-Huang变换[18]、D-S证据理论[19]等对位移信号开展分析,但所采用方法均存在模态混叠、鲁棒性较差的问题。
当电容器组投入时,断路器触头间的关合涌流最大可达20 kA[20],所产生的电动斥力使得触头在刚合瞬间的末速度出现变化。另外,在开展高压大电流老炼时[21],需要进行上百次合闸操作,断路器机构自身的机械分散性也会影响刚合点的定位,降低预击穿燃弧时间的计算准确度。以上的信号检测方式均存在较大缺陷,无法满足实际应用需求。另外,现有研究多关注于合闸速度、位移、超程等机械特性的分析,对预击穿燃弧时间的分析讨论较少。
针对电容器组投切用真空断路器的工况,对位移信号进行分析,可直观地反映断路器触头刚合瞬间小幅值的高频信号阶跃,实现预击穿燃弧时间的准确分析,且位移传感器安装简单,受振动、电磁等环境噪声的影响相对较小。经验小波变换(Empirical Wavelet Transform, EWT)[22-23]克服了小波分析、Hilbert-Huang变换及经验模态分解(Empirical Mode Decomposition, EMD)等方式的缺陷[23],可较大程度地减少信号分割时引起的过分解等误差,高度还原断路器触头刚合瞬间位移信号出现的阶跃变化,实现预击穿燃弧时间的准确分析。
基于此,本文依据容性投切用真空断路器的机械特性,提出基于EWT的关合预击穿燃弧时间分析方法,并开展不同影响因素下的关合预击穿试验。相较于现有测量方式,基于EWT的预击穿燃弧时间分析方法可在不额外增加传感器的基础上,大幅提高容性投入时断路器燃弧时间的检测准确度,为断路器的开断水平评估和高压大电流老炼提供可靠的支撑。
位移传感器通常安装在断路器动触头下方,而在强磁场环境以及位移信号采集时的振动噪声干扰下,测量结果会失真、零漂,从而影响对燃弧时间的准确分析。
最小二乘法是A. M. Legendre提出的数学优化算法,是拟合曲线常用的方法,通过最小化求得数据和实际数据之差(即误差或残差)的平方和来求解未知参数[24-25],非常适用于位移曲线这种线性模型。因此,采用最小二乘法进行曲线拟合,可较大程度地保留位移信号中刚合点的信号变化。
对于给定的数据(xs, fs)(s=1, 2,…, m),在取定的假设空间H中,求解φ(x)∈H,使得残差rs=φ(xs)-fs的2-范数最小,即
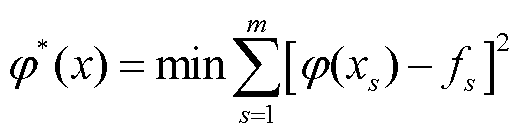 (1)
(1)
式中,φ*(x)即为最小二乘的解或拟合函数。
根据上述给定的m个点,对最小二乘法的解进行拟合求解时,并不要求这条曲线精准地经过每一个点,按照近似曲线与实际曲线的误差平方和最小原则,求曲线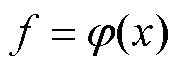 的近似曲线
的近似曲线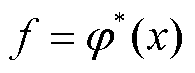 ,得到预处理后的位移曲线。
,得到预处理后的位移曲线。
经验小波变换(EWT)通过构建自适应小波以实现位移信号的分解[22],可有效地避免分解时出现的模态混叠现象。该方法实现步骤如下:
1)首先将信号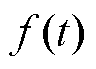 进行傅里叶变换得到
进行傅里叶变换得到
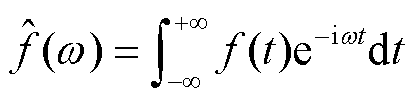 (2)
(2)
式中,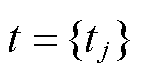 (j=1, 2,…, M),M为样本数量。求出傅里叶谱中tM的最大值。并计算出相应的频率。
(j=1, 2,…, M),M为样本数量。求出傅里叶谱中tM的最大值。并计算出相应的频率。
2)对傅里叶频谱进行N段分割,提取不同的频率分量。将分割的两个连续最大值的边界定义为Ωl,表示为
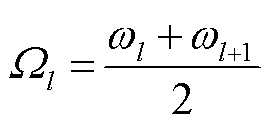 (3)
(3)
式中,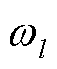 和
和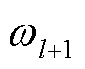 为分割的两个频率;边界Ω定义为
为分割的两个频率;边界Ω定义为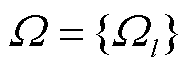 (l=1, 2,…, N-1)。
(l=1, 2,…, N-1)。
3)由一个低通滤波器和N-1个基于边界的带通滤波器组成N个小波滤波器组,对每个检测到的频率分段进行尺度变换和低通滤波。尺度变换函数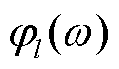 的傅里叶变换表达式和经验小波函数
的傅里叶变换表达式和经验小波函数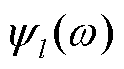 的表达式分别为
的表达式分别为
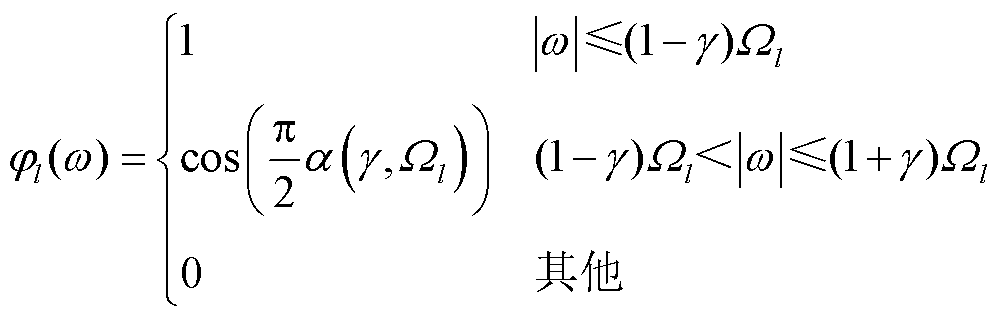 (4)
(4)
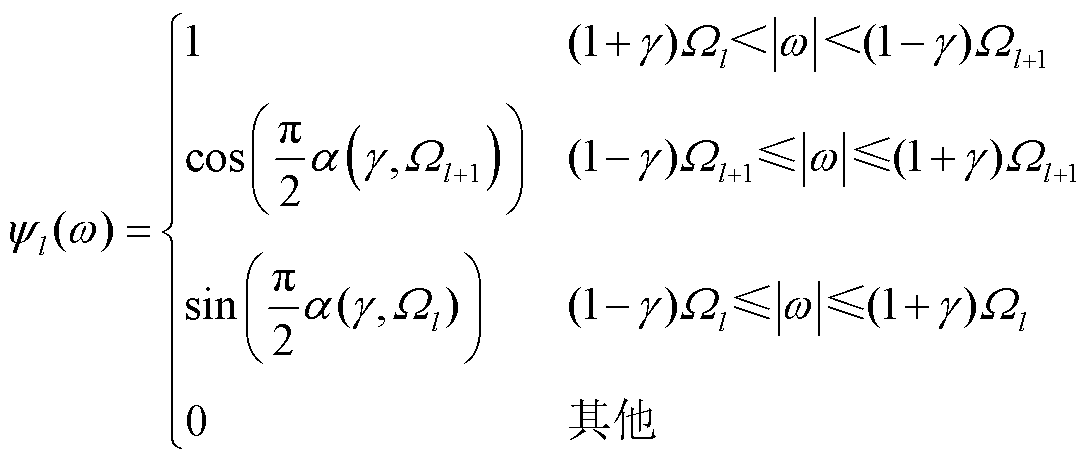 (5)
(5)
其中
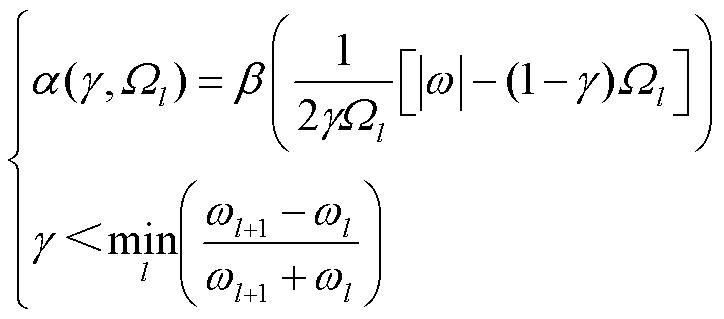 (6)
(6)
式中,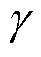 为参数,保证相邻连续的变换之间不重叠;β(·)为区间[0, 1]内的过渡函数,定义为
为参数,保证相邻连续的变换之间不重叠;β(·)为区间[0, 1]内的过渡函数,定义为
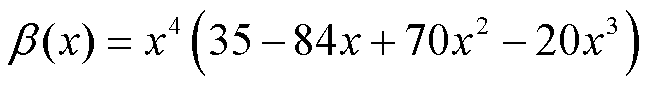 (7)
(7)
4)执行尺度变换和小波变换获得不同模式的分量,近似系数可用信号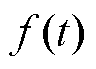 与尺度变换函数
与尺度变换函数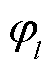 的内积表示为
的内积表示为
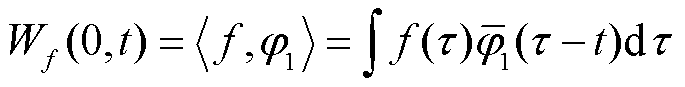 (8)
(8)
同样地,通过经验小波分析信号f的内积可以求出细节系数为
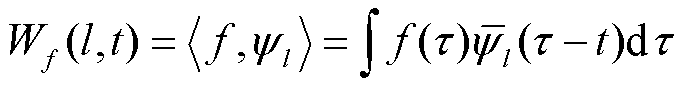 (9)
(9)
式中,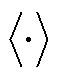 为内积运算;
为内积运算;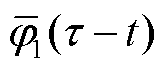 和
和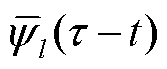 分别为
分别为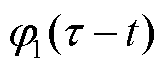 和
和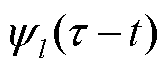 的复共轭。
的复共轭。
5)根据近似系数和细节系数,重构信号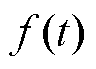 为
为
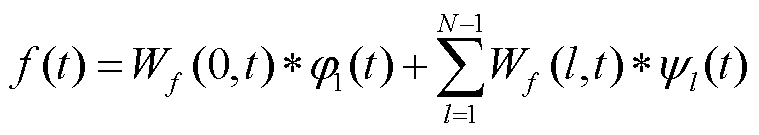 (10)
(10)
式中,“*”为卷积运算。则信号f(t)可分为N个经验小波函数(Empirical Wavelet Function, EWF),即
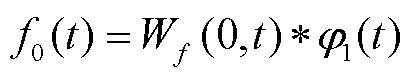 (11)
(11)
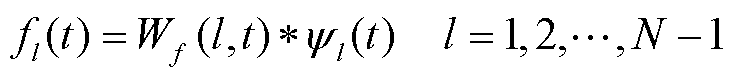 (12)
(12)
峭度(Kurtosis)是一种归一化4阶中心距,可用于表示信号的分布特性。峭度对信号的高频部分非常敏感,能够有效描述波形的突变[26-27],因此,将其应用于断路器合闸位移信号分析中,可实现触头刚合时刻高频阶跃信号的准确定位。
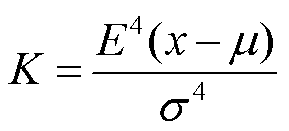 (13)
(13)
式中,K为峭度;µ为信号的均值;σ为信号的标准差;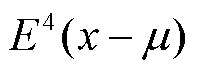 为4阶期望值。
为4阶期望值。
本文主要通过对断路器合闸时的机构位移曲线信号进行分析处理,得到关合预击穿燃弧时间。具体步骤如下:
1)求解断路器合闸位移信号的原始采样点,实现对位移信号的预处理,得到平滑的曲线信息。
2)对预处理后的位移信号进行EWT分解,得到包含动静触头刚合信息的分量组。
3)对分解得到的经验小波函数(EWF)分量进行峭度值计算,筛选出反映刚合点阶跃信号的EWF分量。
4)将筛选出的EWF分量与位移曲线进行时间轴对比,得到动静触头刚合点时刻。
5)根据关合涌流波形表征的预击穿燃弧起始时刻,得到预击穿燃弧时间。
综上所述,预击穿燃弧时间分析流程如图1所示。
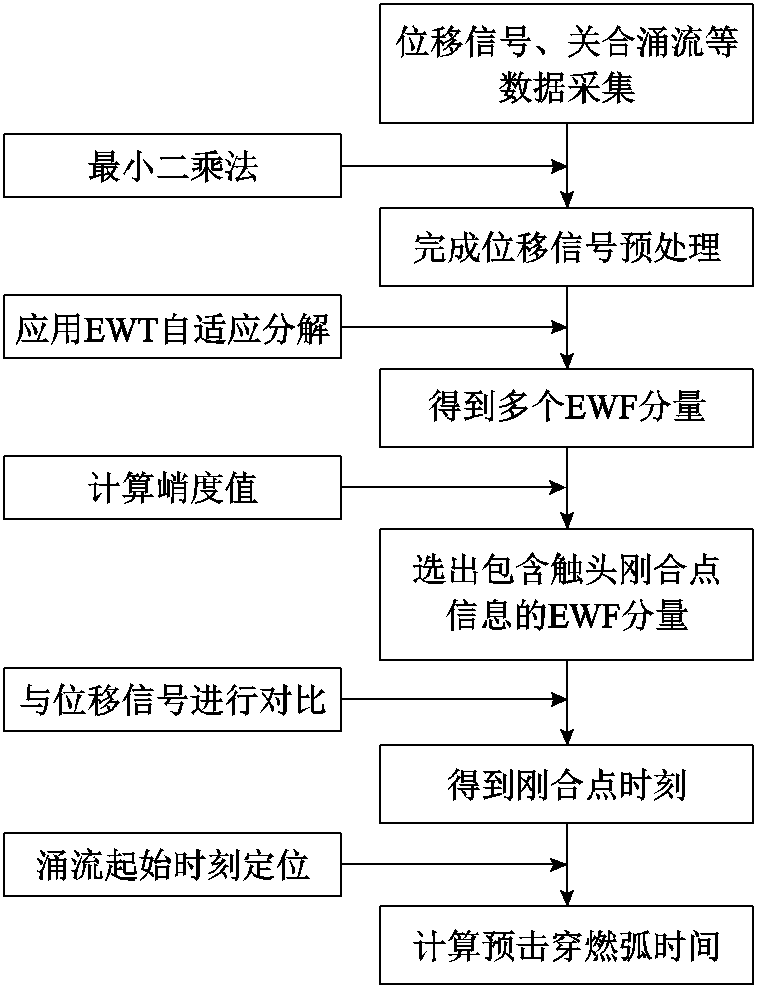
图1 预击穿燃弧时间分析流程
Fig.1 Pre-strike arcing time analysis flow chart
真空断路器预击穿燃弧时间分析采用12 kV电压等级VS1-12系列的真空断路器,机构合闸速度为0.85 m/s,试验所使用位移传感器分辨率为10 μm。
现场采集的断路器合闸位移曲线如图2a所示。在强磁和环境噪声干扰下,所采集到的位移信号中动静触头刚合瞬间的有效信息已经被掩盖,无法进行刚合点有效定位,进而影响后续预击穿燃弧时间分析。
为获取准确的关合预击穿燃弧时间,使用最小二乘法对采集到的合闸位移信号进行预处理,其结果如图2b所示。通过找到误差平方和最小的全局最优解,可有效地降低刚合点信号数据的过度拟合,处理后的拟合曲线十分接近离线测量时的位移曲线,完整地保留了刚合点的阶跃变化,为后续关合预击穿燃弧时间的准确计算提供了保障。
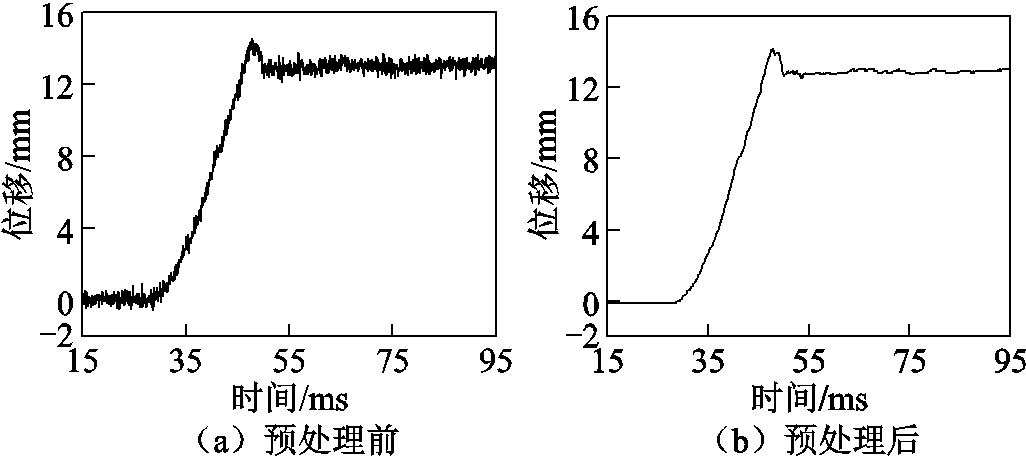
图2 预处理前后的位移曲线
Fig.2 Displacement curve before and after pretreatment
为验证本文预击穿燃弧时间分析方法的实际效果,首先开展模拟分析。
对图2b中预处理后的位移信号进行EWT分解,结果如图3a所示。可见,按所在频域不同,EWT将位移信号分解为6个EWF分量。为直观地展示该方法的分解效果,与图3b传统EMD和图3c集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)的分解结果进行对比,并对不同方法分解后的分量分别计算峭度值K,结果见表1。
针对位移曲线进行分析时,在EMD所分解的6个本征模态函数(Intrinsic Mode Function, IMF)分量中,由于模态混叠的影响,刚合点的高频分量并未被完整地分离出来,而是淹没在IMF3和IMF4中。由EEMD分解的IMF分量可知,EMD方法的模态混叠和端点效应得到了一定的改善,但IMF2~IMF4中高低频之间的界限仍不明显,刚合点的有效信息仍无法被准确判断。EMD和EEMD分解分量所计算的峭度值也未出现较大差异,说明使用这两种方法分解位移曲线时,未能将刚合瞬间的高频分量进行有效分离。
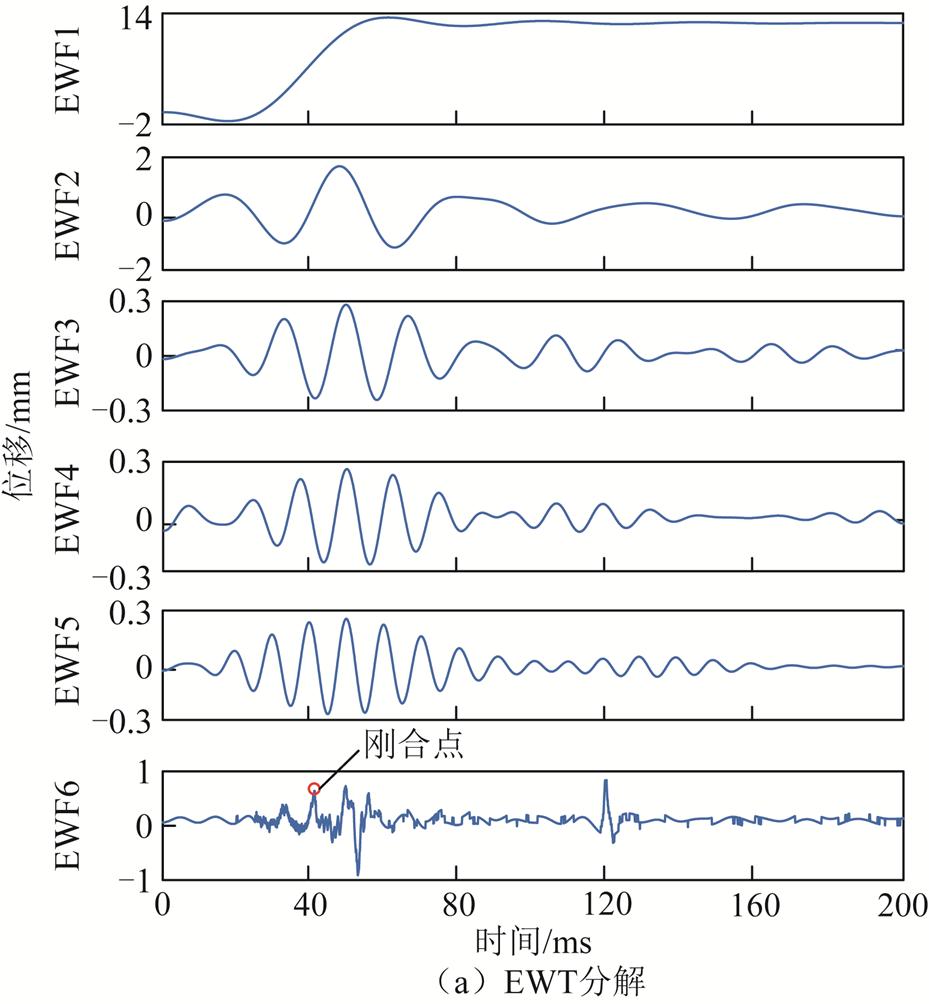
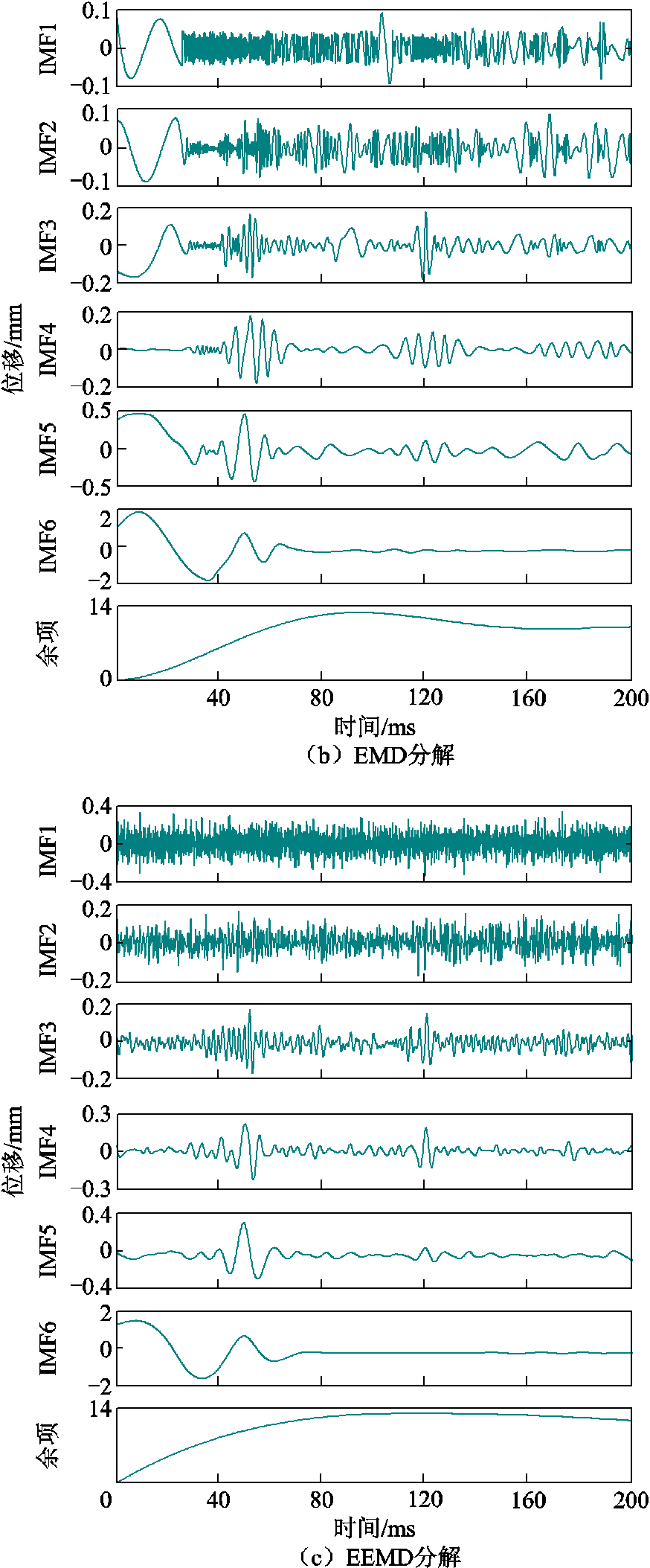
图3 不同方法的分解结果
Fig.3 Decomposition results of different methods
表1 不同分量的峭度值
Tab.1 Kurtosis value of different components
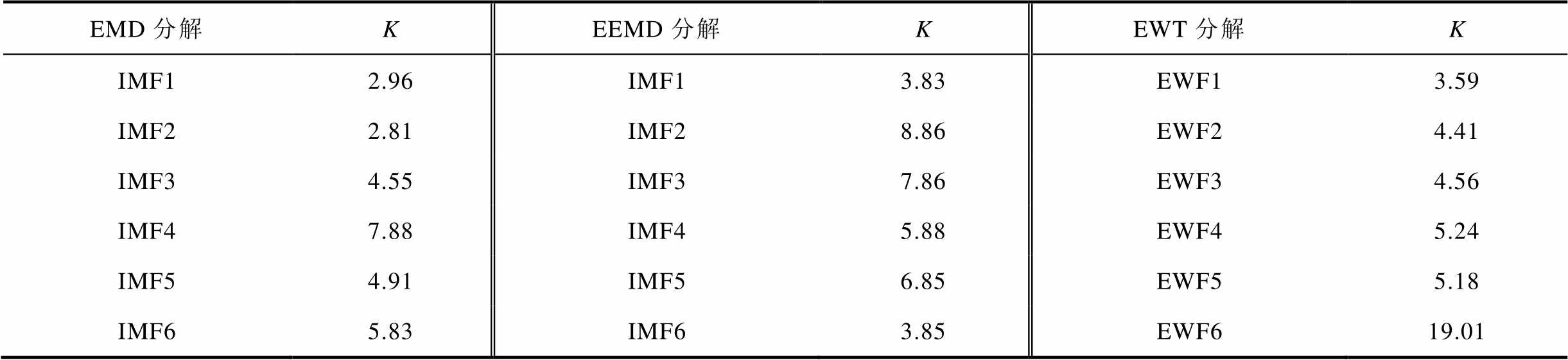
EMD分解KEEMD分解KEWT分解K IMF12.96IMF13.83EWF13.59 IMF22.81IMF28.86EWF24.41 IMF34.55IMF37.86EWF34.56 IMF47.88IMF45.88EWF45.24 IMF54.91IMF56.85EWF55.18 IMF65.83IMF63.85EWF619.01
相较于传统分解方法,EWT分解有效地抑制了模态混叠和端点效应,断路器在刚合点的高频分量得以完整保留。EWF6的K值明显区别于其余分量,且与其他频段区分明显,具有较高的分解适应性,为后续预击穿燃弧时间的准确分析提供了前提和保障。因此,选择EWF6分量进行重构。将所筛选的EWF分量与关合位移曲线进行时间轴对比,即可得到准确的动静触头刚合时刻。
刚合点离线测量方法如图4所示。采用传统离线法测量关合预击穿燃弧时间时,需要先将断路器离线,在断口两端接入12 V电源,断路器机构的分闸位上同样需要安装12 V电源供电的光电位置传感器,进行断路器合闸操作并测量光电信号和12 V电压信号的阶跃位置。由于12 V电压在真空中不会出现提前击穿,因此,断路器合闸时电压信号阶跃处即为断路器动静触头刚合点。断路器接入电力系统后,无法测量12 V电压信号,故而无法得到准确的刚合点位置,需要将断路器离线时测量到的光电信号阶跃位置与12 V电压信号阶跃位置作差,根据光电位置和时间差,推算触头合闸时的刚合点,再计算预击穿燃弧时间。
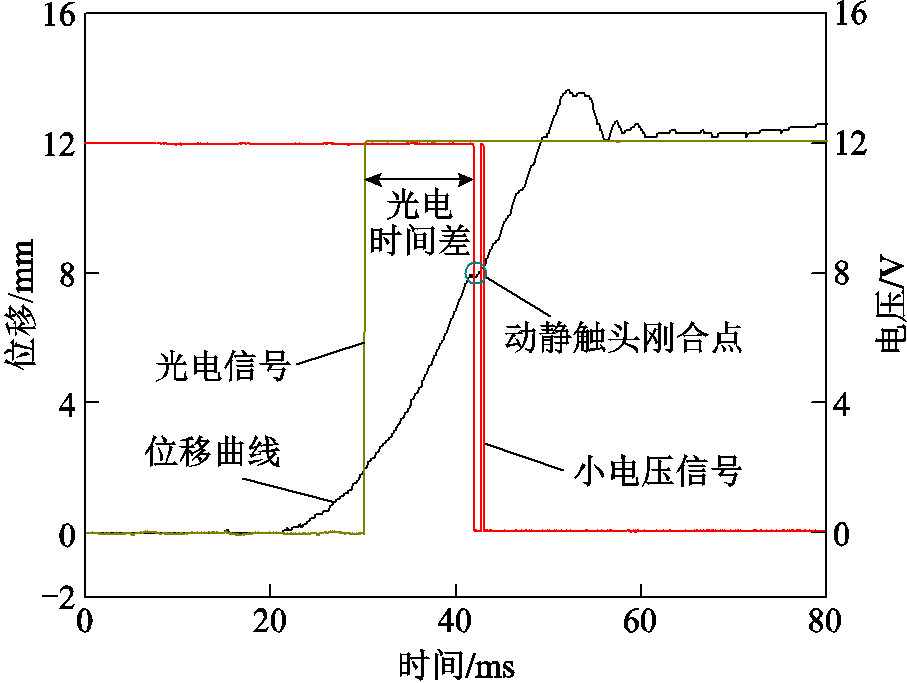
图4 刚合点离线测量方法
Fig.4 Off-line measurement method of instant closing point
真空断路器关合时的预击穿燃弧时间通常在0.5~3.5 ms范围内。在模拟分析时,由于断路器处于离线状态,没有关合涌流,通过对刚合点时刻进行定位,实现预击穿燃弧时间的模拟分析。以12 V电压信号测量到的刚合点为基准,模拟触头合闸前1.76 ms出现预击穿,并将EWF分量的幅值进行放大以清晰地表示与刚合点的对应关系。基于EWT的模拟预击穿燃弧时间测量结果如图5所示。
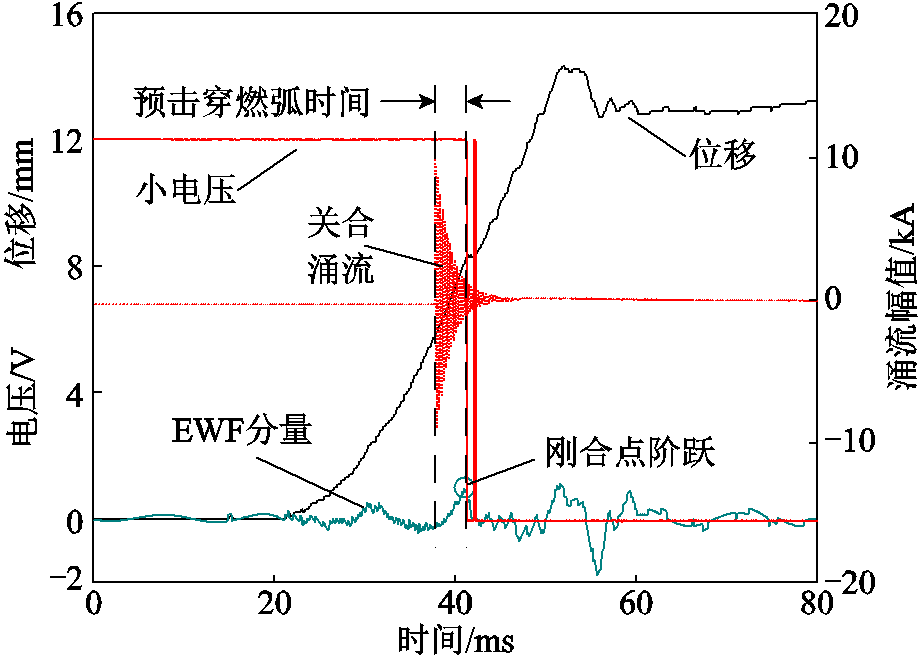
图5 模拟预击穿燃弧时间
Fig.5 Simulated pre-strike arcing time
由图5可知,经过EWT分解,位移信号中触头刚合点信号的阶跃变化被完整保留,其峰值位置与离线测量时的小电压信号阶跃位置基本重合。当断路器投入系统运行或开展高压大电流试验时,无需小电压信号,只依赖断路器关合时的位移信号即可对刚合点进行计算,实现预击穿燃弧时间的准确分析。
本文选取两种常用的参数来评价预击穿燃弧时间的分析效果:方均误差(Mean-Square Error, MSE)和绝对平均误差(Mean Absolute Error, MAE)[28-29]。MAE越小,燃弧时间的计算准确度越高;MSE值越小,误差的分散性越小,预击穿燃弧时间分析方法的适应性越好。MSE和MAE的定义式分别为
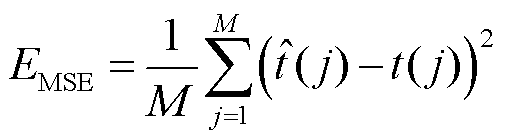 (14)
(14)
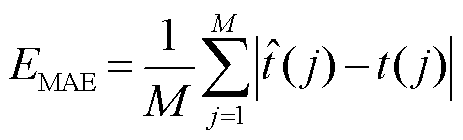 (15)
(15)
式中,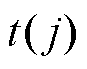 为燃弧时间的基准值(实际值);
为燃弧时间的基准值(实际值);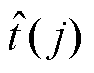 为位移信号分析后的燃弧时间。
为位移信号分析后的燃弧时间。
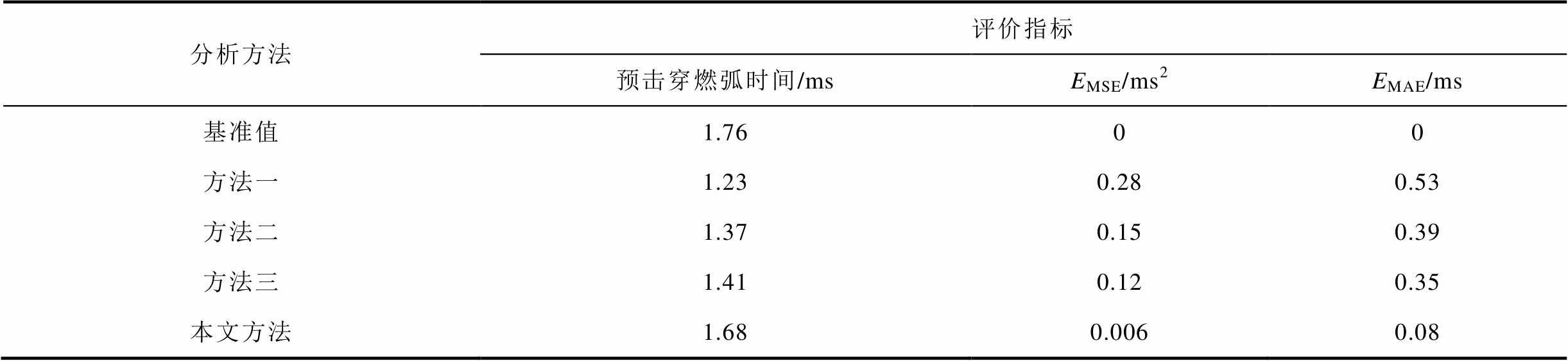
采用四种不同的预击穿燃弧时间分析方法进行对比:方法一为基于合闸振动信号的短时能量窗法;方法二为基于EMD的分析方法;方法三为基于EEMD的分析方法;方法四为本文所提方法。其中,方法二、方法三和本文所提方法均针对合闸位移信号展开分析。各方法的计算结果及评价指标见表2。
表2 预击穿燃弧时间分析结果评价
Tab.2 Evaluation of pre-strike arcing time analysis effect
分析方法评价指标 预击穿燃弧时间/msEMSE/ms2EMAE/ms 基准值1.7600 方法一1.230.280.53 方法二1.370.150.39 方法三1.410.120.35 本文方法1.680.0060.08
从表2可知,四种方法都可以对断路器关合时的预击穿燃弧时间进行计算,但本文所提方法的燃弧时间误差更小,更接近真实数值,刚合点的高频阶跃信号在直观上基本无波形畸变,且评价指标明显优于其他三种方法。
根据对断路器厂家及运行现场的调研,投入电容器组时,断路器合闸过程出现的高频涌流幅值最高可达20 kA。在国家标准GB 1984—2014《高压交流断路器》针对C2级断路器的要求中,关合背对背电容器组试验时,需满足涌流峰值20 kA的要求[7-8,12]。而在开展高压大电流老炼试验时,不仅需要考虑涌流幅值对预击穿燃弧时间的影响,也需要探究试验电压、机构速度等因素的影响。
基于此,在实验室搭建关合涌流试验平台,开展不同影响因素下的关合预击穿试验,验证本文所提真空断路器关合预击穿燃弧时间分析方法在容性关合工况和老炼试验研究中的适应性。现场试验平台如图6所示。
试验平台由充电回路和振荡放电回路组成。充电回路包括直流高压充电装置、限流电阻R、储能电容C、接触器K和阻容分压器。振荡放电回路包括电容C、电抗L、试验断路器、位移传感器、测量涌流电流的罗氏线圈、测量弧压的差分探头以及示波器等设备。试验使用额定短路开断电流为25 kA的VS1-12系列12 kV商用真空断路器。
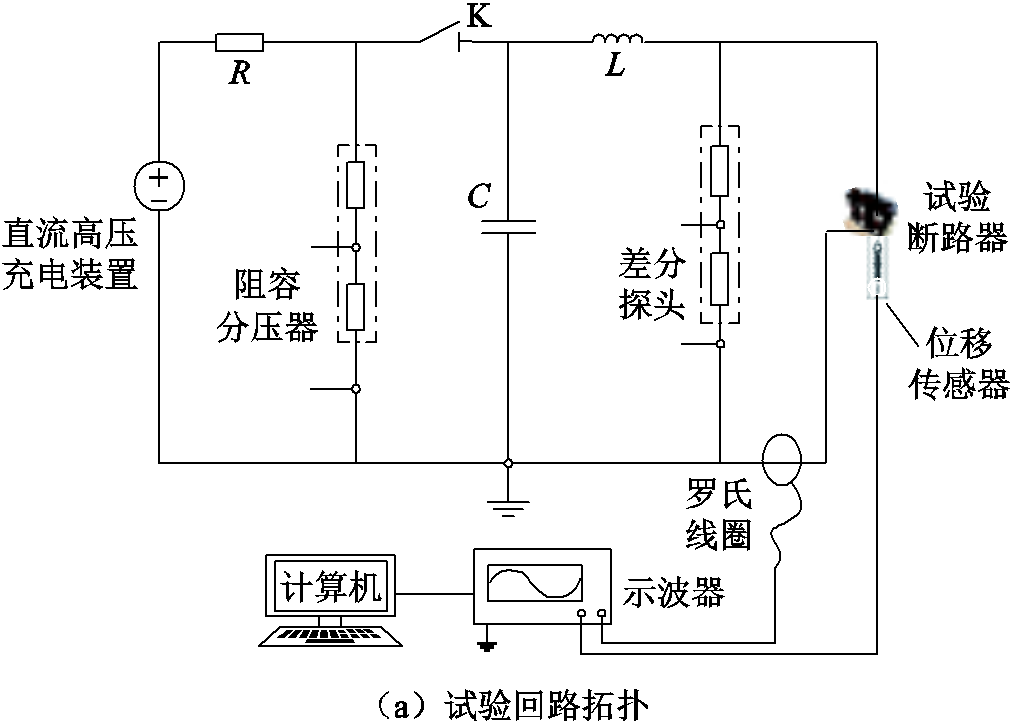

图6 现场试验平台
Fig.6 Field test platform
由于实际工况下断路器无法接入小电压信号,故在试验中引入差分探头以测量弧压,作为燃弧时间的基准值。
试验前,试验断路器处于分闸状态,将K合闸,使用直流高压充电装置,经限流电阻R为电容C充电,阻容分压器用于测量电容C的电压。达到所需试验电压后关闭直流高压充电装置,控制K分闸将充电回路与放电回路隔离。试验时,控制试验断路器合闸操作,断口出现预击穿时,L、C串联谐振放电即产生所需的关合涌流,示波器同步采集位移信号、电流信号和弧压信号。
根据真空击穿理论,在较低的关合电压条件下,随着关合电压的增加,关合预击穿燃弧时间会逐步增大。设计10、25、45 kV三个电压等级开展关合预击穿试验。由于实验室环境与断路器实际运行的强磁环境有一定的差异,参考断路器实际工作环境的噪声影响,向采集的位移信号加入6 dB的白噪声,以模拟现场采集时的干扰。
45 kV电压下现场试验测量到的关合涌流、合闸位移曲线以及电弧电压信号如图7所示。在断路器给出合闸控制信号后,22.7 ms时断路器动触头开始动作,在36.22 ms时出现预击穿,39.88 ms时动静触头接触,根据电弧电压的起始和终止位置,得到预击穿燃弧时间为3.66 ms。
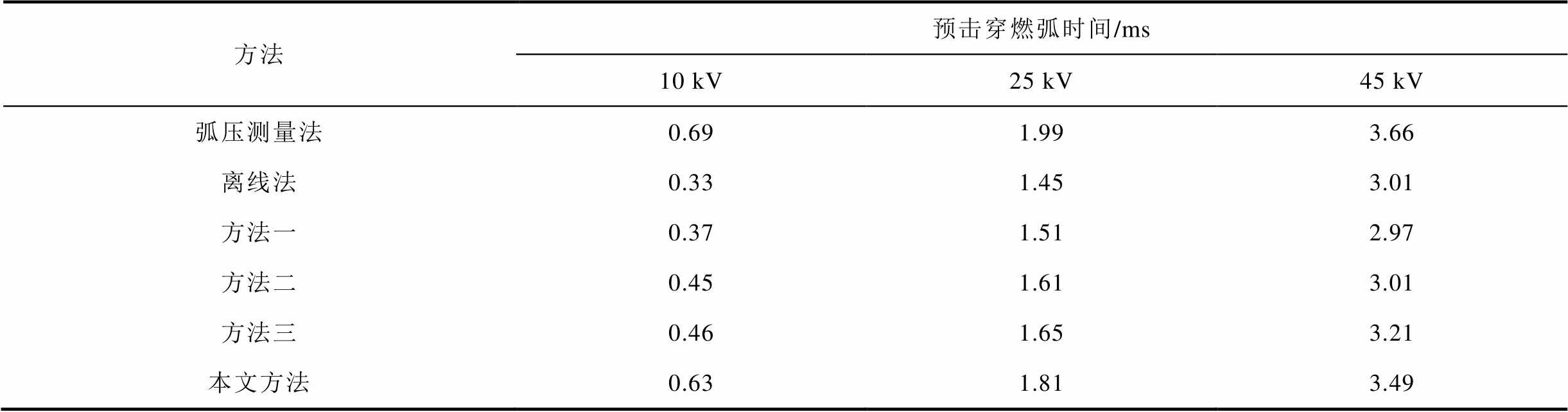
分别采用离线法、方法一、方法二、方法三以及本文所提方法进行预击穿燃弧时间计算,并与现场试验结果对比,得到不同电压下的试验结果见表3。
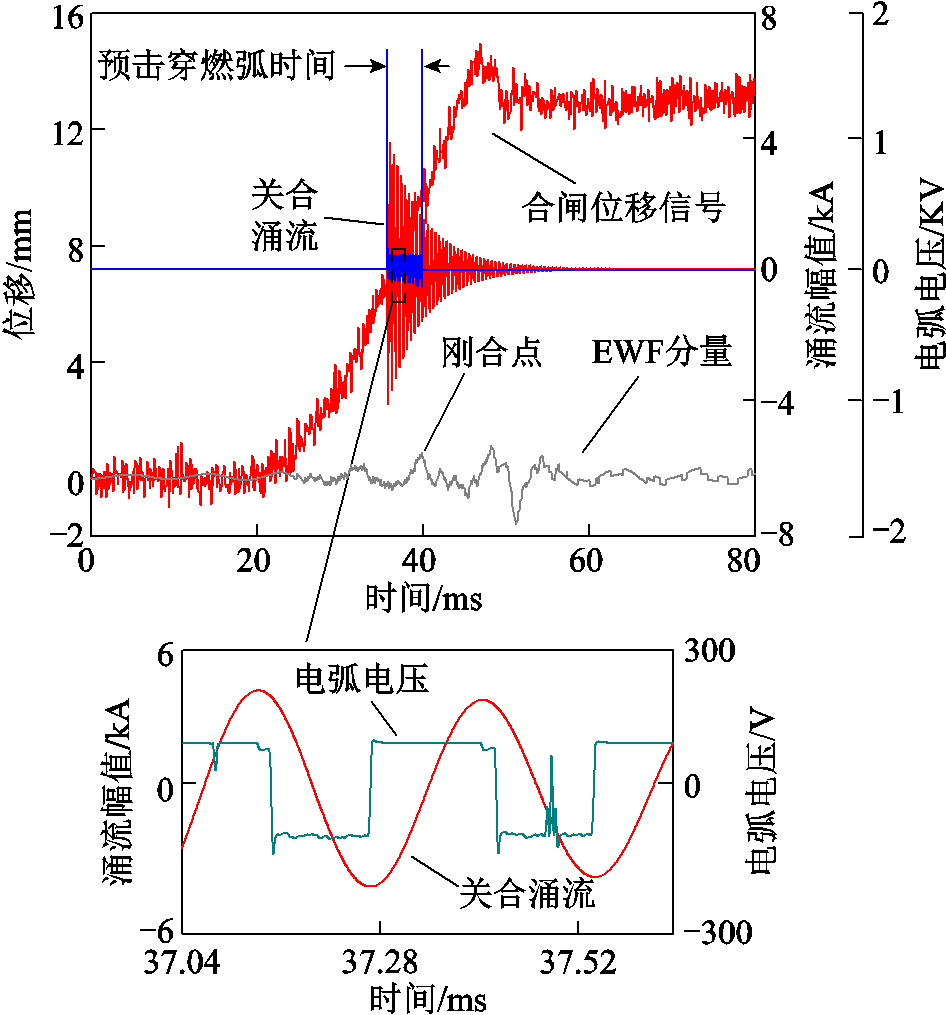
图7 现场试验预击穿燃弧波形
Fig.7 Field test pre-strike arcing waveforms
表3 不同电压下的试验结果
Tab.3 Test results under different voltage
方法预击穿燃弧时间/ms 10 kV25 kV45 kV 弧压测量法0.691.993.66 离线法0.331.453.01 方法一0.371.512.97 方法二0.451.613.01 方法三0.461.653.21 本文方法0.631.813.49
由表3可知,在关合电压较低的10 kV下,预击穿燃弧时间的误差整体较小,随着试验电压逐步升高,误差水平出现波动。离线法的测试结果受光电位置时间差的影响较大,需频繁地将断路器离线进行光电时间差测量,以提升预击穿燃弧时间的计算准确度。方法一采用振动信号进行处理,由于触头刚合瞬间的振动轻微,刚合点信息无法被有效捕捉,预击穿燃弧时间的误差较大。受分解精度的影响,方法二和方法三与本文所提方法的结果相比仍有较大误差。而本文基于EWT的预击穿燃弧时间分析方法在不同试验电压下,预击穿燃弧时间的误差始终保持稳定,误差保持在0.2 ms以内,准确度更高。
由于真空击穿存在一定的分散性,在不同试验电压下,分别重复5次关合试验。为直观地展示试验结果,先对相同试验电压下不同分析方法的重复试验结果计算出MSE和MAE,再计算不同电压下试验结果的MSE、MAE,如图8所示。
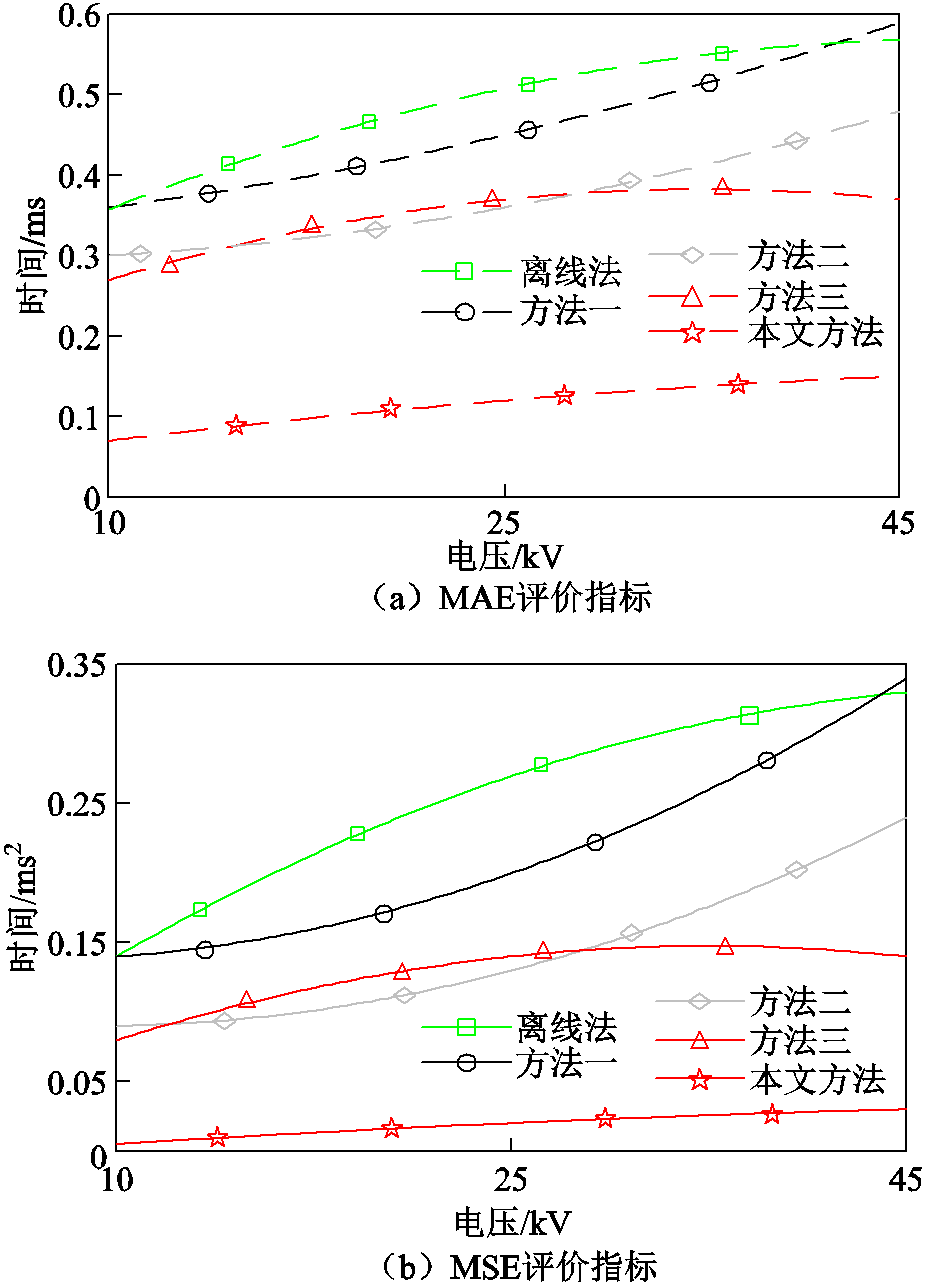
图8 不同电压的试验结果
Fig.8 Test results of different voltages
图8a所示的MAE评价指标主要表征计算准确度,相较于所对比的其他方法,基于EWT的预击穿燃弧时间分析方法与实际结果的误差的平均值始终小于0.2 ms,且在不同电压下的试验结果中始终处于最好的水平,具有较高的准确度。而图8b主要表征计算结果与实际数值之间差异的分散性,可见在不同试验电压下,其误差的分散性也远小于所对比的其他方法。
当电容器组投入系统时,若关合涌流较大,会导致触头表面产生与合闸方向相反的电动斥力,减缓机构刚合前的末速度,使预击穿燃弧时间受到影响。基于此,设计6、10、20 kA三种不同涌流幅值开展关合预击穿试验,同样加入白噪声模拟现场的干扰。
在不同关合涌流幅值下,重复5次试验,绘制MSE和MAE结果如图9所示。
随着关合涌流幅值的增大,在电动斥力作用下,所对比四种方法的预击穿燃弧时间的误差和分散性再次增加,试验结果的稳定性无法得到保证。而本文所提的分析方法,由于其EWT分解的优势,可最大程度地减小电动斥力对合闸预击穿燃弧时间计算造成的影响,使得计算结果的准确度和分散性均保持最佳。
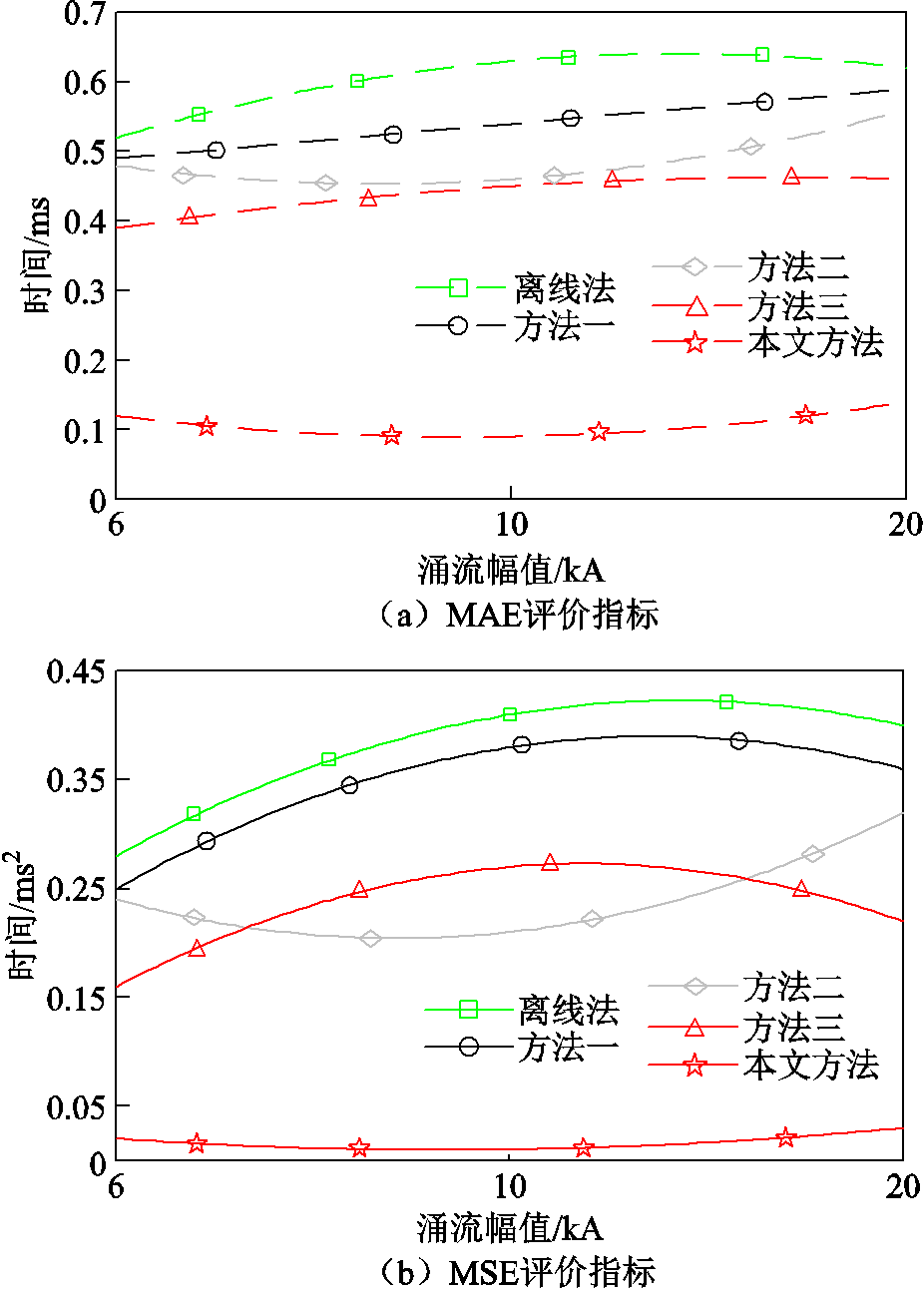
图9 不同关合涌流的试验结果
Fig.9 Test results of different closing inrush currents
为验证所提出预击穿燃弧时间分析方法的适应性,充分考虑容性投切工况,针对不同机构合闸速度下的预击穿燃弧时间开展试验分析。选择常规断路器和快速断路器两种类型进行对比,其关合速度分别为0.85 m/s和1.81 m/s,分别开展重复试验,得到不同机构速度的试验结果见表4。
表4 不同机构速度的试验结果
Tab.4 Test results under different closing velocity

机构类型MSE/ms2MAE/ms 常规机构0.030.18 快速机构0.010.12
当采用快速机构时,合闸速度大幅提高,相同试验条件下,其预击穿燃弧时间显著缩小。快速断路器的预击穿燃弧时间平均误差为0.12 ms,常规断路器的平均误差为0.18 ms,预击穿燃弧时间结果在计算准确度方面存在小幅差异。在不同机构速度下,计算结果误差的分散性仍保持一致,误差范围均小于0.2 ms,可满足不同设计、不同工况下的断路器容性开断能力评估以及高压大电流老炼对于预击穿燃弧时间准确计算的要求,具有显著的工程应用优势。
本文通过对断路器机构合闸时的位移曲线进行预处理,基于经验小波变换分解,引入峭度值筛选算法,实现刚合点定位,并结合关合涌流波形,进而实现真空断路器关合时的预击穿燃弧时间的准确分析。通过模拟分析以及现场试验验证,得到结论如下:
1)利用最小二乘法对位移信号这一关键参量进行预处理,可显著降低断路器工作环境对于信号采集和传输时的噪声影响。
2)通过对预处理后的位移信号进行EWT分解,利用其高鲁棒性的优点,可有效地保留触头刚合瞬间的高频分量。
3)通过峭度值K的筛选,提取刚合瞬间信号的阶跃位置,结合刚合点信息以及关合涌流波形,计算得到预击穿燃弧时间。
4)通过模拟分析和现场试验,并与多种方法进行对比分析,从多维度验证了本文所提关合预击穿燃弧时间分析方法具有较高的准确性和鲁棒性。
5)本文所提方法可在不依赖高精度差分探头的前提下实现预击穿燃弧时间的计算,并控制误差的平均值始终保持在0.2 ms以内,具有较高的工程应用价值。在此基础上,后续将对触头表面开展高压大电流老炼,定量提升断路器的容性开断能力。
参考文献
[1] 马喜平, 贾嵘, 梁琛, 等. 高比例新能源接入下电力系统降损研究综述[J]. 电网技术, 2022, 46(11): 4305-4315.
Ma Xiping, Jia Rong, Liang Chen, et al. Review of researches on loss reduction in context of high penetration of renewable power generation[J]. Power System Technology, 2022, 46(11): 4305-4315.
[2] Zhao Heng, Xiao Xianyong, Sun Qiuqin. Identifying electric shock in the human body via α dispersion[J]. IEEE Transactions on Power Delivery, 2018, 33(3): 1107-1114.
[3] 韩翔宇, 纽春萍, 何海龙, 等. 电磁式断路器状态监测与智能评估技术综述[J]. 电工技术学报, 2023, 38(8): 2191-2210.
Han Xiangyu, Niu Chunping, He Hailong, et al. Review of condition monitoring and intelligent assessment of electromagnetic circuit breaker[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2191-2210.
[4] 甘战, 冯田, 张鹏, 等. 基于录波数据的断路器关合时间整定计算方法研究[J]. 电力系统保护与控制, 2019, 47(18): 145-151.
Gan Zhan, Feng Tian, Zhang Peng, et al. Calculation method on circuit breaker closing time based on fault recording data[J]. Power System Protection and Control, 2019, 47(18): 145-151.
[5] Razi-Kazemi A A, Vakilian M, Niayesh K, et al. Priority assessment of online monitoring investment for power system circuit breakers: part I: qualitative-quantitative approach[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 928-938.
[6] 高崇, 邵在康, 康忠健, 等. 基于扩展卡尔曼滤波的水中放电阶段辨识方法[J]. 电工技术学报, 2024, 39(11): 3475-3485.
Gao Chong, Shao Zaikang, Kang Zhongjian, et al. Method for identifying stages of discharge in water based on extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3475-3485.
[7] 刘士利, 吕东建, 张飞. 断路器并联动态合闸电阻对滤波器合闸涌流的抑制效能研究[J]. 电网技术, 2024, 48(9): 3931-3937.
Liu Shili, Lü Dongjian, Zhang Fei. Study on the suppression efficacy of filter closing inrush currents by shunt dynamic closing resistor of circuit breaker[J]. Power System Technology, 2024, 48(9): 3931-3937.
[8] 吴燕, 余勇祥, 韩筛根, 等. 真空开关容性电流开断技术[J]. 高压电器, 2017, 53(3): 26-34.
Wu Yan, Yu Yongxiang, Han Shaigen, et al. Technique of capacitive switching for vacuum switches[J]. High Voltage Apparatus, 2017, 53(3): 26-34.
[9] 雷雨, 李光辉, 王伟胜, 等. 跟网型和构网型新能源并网控制阻抗对比与振荡机理分析[J]. 中国电机工程学报, 2025, 45(1): 150-163.
Lei Yu, Li Guanghui, Wang Weisheng. et al. Comparison of impedance characteristics and oscillation mechanism for grid following and grid forming renewable energy[J]. Proceedings of the CSEE, 2025, 45(1): 150-163.
[10] 田阳, 李志兵, 田宇, 等. 高比例新能源接入下快速真空断路器容性开合能力提升研究[J]. 电网技术, 2024, 48(6): 2670-2679.
Tian Yang, Li Zhibing, Tian Yu, et al. Research on the improvement of capacitive opening and closing ability of fast circuit breaker under high proportion of new energy access[J]. Power System Technology, 2024, 48(6): 2670-2679.
[11] 李世民, 徐勋晨, 张潮海. 基于深度学习的冲击电压老炼过程中真空击穿机制甄别优化方法[J]. 电工技术学报, 2024, 39(13): 4153-4163.
Li Shimin, Xu Xunchen, Zhang Chaohai. Optimization method for classifying breakdown mechanism during impulse voltage conditioning process based on deep learning[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4153-4163.
[12] 常广, 王毅, 王玮. 采用振动信号零相位滤波时频熵的高压断路器机械故障诊断[J]. 中国电机工程学报, 2013, 33(3): 155-162, 3.
Chang Guang, Wang Yi, Wang Wei. Mechanical fault diagnosis of high voltage circuit breakers utilizing zero-phase filter time-frequency entropy of vibration signal[J]. Proceedings of the CSEE, 2013, 33(3): 155-162, 3.
[13] 周进飞, 罗勇, 韩耀东. 12kV真空断路器刚合点在线监测方法研究[J]. 高压电器, 2023, 59(9): 219-225.
Zhou Jinfei, Luo Yong, Han Yaodong. Research on online monitoring method of the instant closing point of 12kV vacuum circuit breaker[J]. High Voltage Apparatus, 2023, 59(9): 219-225.
[14] 岳宇鑫. 投切10kV电容器用真空断路器寿命评估方法研究[D]. 北京: 华北电力大学, 2022.
Yue Yuxin. Research on key technologies of partial porousexternally pressurized gas bearing[D]. Beijing: North China Electric Power University, 2022.
[15] Razi-Kazemi A A, Niayesh K, Nilchi R. A probabilistic model-aided failure prediction approach for spring-type operating mechanism of high-voltage circuit breakers[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1280-1290.
[16] 胡博凯, 李奎, 牛峰, 等. 低压断路器机械特性状态监测方法研究[J]. 电工技术学报, 2022, 37(13): 3317-3330.
Hu Bokai, Li Kui, Niu Feng, et al. Research on condition monitoring method of mechanical characteristics of low-voltage circuit breaker[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3317-3330.
[17] Yang Qiuyu, Ruan Jiangjun, Zhuang Zhijian, et al. Chaotic analysis and feature extraction of vibration signals from power circuit breakers[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1124-1135.
[18] Albernaz Lacerda V, Monaro R M, Campos-Gaona D, et al. Distance protection algorithm for multiterminal HVDC systems using the Hilbert–Huang transform[J]. IET Generation, Transmission & Distribution, 2020, 14(15): 3022-3032.
[19] 林湘宁, 刘畅, 汪致洵, 等. 基于动态权重修正D-S证据理论的最后断路器多判据保护跳闸策略[J]. 中国电机工程学报, 2018, 38(9): 2609-2621, 2829.
Lin Xiangning, Liu Chang, Wang Zhixun, et al. Tripping strategy of multi criteria of last breaker protections based on dynamic weight correction D-S evidence theory[J]. Proceedings of the CSEE, 2018, 38(9): 2609-2621, 2829.
[20] 张志丰, 张凯, 董轩, 等. 基于电流有效值实时算法的限流器快速故障辨识方法[J]. 电气技术, 2022, 23(7): 81-88.
Zhang Zhifeng, Zhang Kai, Dong Xuan, et al. Fast fault identification method based on real-time algorithm of current root mean square value for fault current limiter[J]. Electrical Engineering, 2022, 23(7): 81-88.
[21] 何俊佳, 邹积岩, 张汉明, 等. 火花老炼对真空灭弧室绝缘强度的影响[J]. 电工技术学报, 1997, 12(3): 33-36.
He Junjia, Zou Jiyan, Zhang Hanming, et al. Effect of spark conditioning treatment on electrical strength of vacuum interrupters[J]. Transactions of China Electro-technical Society, 1997, 12(3): 33-36.
[22] Gilles J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010.
[23] Elouaham S, Dliou A, Nassiri B, et al. Combination method for denoising EMG signals using EWT and EMD techniques[C]//2023 IEEE International Con-ference on Advances in Data-Driven Analytics and Intelligent Systems (ADACIS), Marrakesh, Morocco, 2023: 1-6.
[24] Wei D, Ramamurthy K N, Katz-Rogozhnikov D A, et al. Multiplicative regression via constrained least squares[C]//2014 IEEE Workshop on Statistical Signal Processing (SSP), Gold Coast, Australia, 2014: 304-307.
[25] Zhao Hui, Wang Ruyan, Song Daiping, et al. Minimum norm least squares extrapolation estimate for discrete (a, b, c, d)-bandlimited signals[J]. IEEE Signal Processing Letters, 2012, 19(12): 853-856.
[26] 王晓卫, 王雪, 王毅钊, 等. 基于图像信息熵与多元变分模态分解的电缆局放信号去噪方法[J]. 电工技术学报, 2024, 39(13): 4100-4115, 4152.
Wang Xiaowei, Wang Xue, Wang Yizhao, et al. A denoising algorithm for cable partial discharge signals based on image information entropy and multivariate variational mode decomposition[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4100-4115, 4152.
[27] Khazaal A, Cabot F, Anterrieu E, et al. A kurtosis-based approach to detect RFI in SMOS image reconstruction data processor[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(11): 7038-7047.
[28] Hussein R, Shaban K B, El-Hag A H. Denoising different types of acoustic partial discharge signals using power spectral subtraction[J]. High Voltage, 2018, 3(1): 44-50.
[29] 刘萍, 李泽文, 蔡雨思, 等. 基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法[J]. 电工技术学报, 2024, 39(10): 3232-3243.
Liu Ping, Li Zewen, Cai Yusi, et al. Joint estimation method of SOC and SOH based on fusion of equivalent circuit model and data-driven model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3232-3243.
Analysis of Pre-Strike Arcing Time for Vacuum Circuit Breaker Closure Based on Empirical Wavelet Transform
Abstract As an important equipment for switching capacitor banks for reactive power compensation in distribution network system, the reliability of vacuum circuit breaker directly affects the stable operation of power system. In the process of putting into the capacitor bank, when the circuit breaker is pre-strike, the closing inrush current appears synchronously until the contact is just closed, and the inrush current exists in the form of arcing, which is called pre-strike arcing. It will cause contact burning, fusion welding and material transfer, reduce the capacitive breaking capacity of the circuit breaker. Therefore, the accurate analysis of the pre-strike arcing time when the vacuum circuit breaker is closing can be used to evaluate the capacitive breaking capacity of the circuit breaker in real time.
When the capacitor bank is put into the system, the inrush current between the contacts of the circuit breaker can reach up to 20 kA, and the generated electric repulsion makes the final speed of the contact change at the moment of closing. In addition, when carrying out high-voltage and high-current conditioning, hundreds of closing operations are required. The mechanical dispersion of the circuit breaker mechanism itself will also affect the accurate positioning of the instant closing point and reduce the calculation accuracy of the pre-strike arcing time. The displacement signal contains the accurate information of the instant closing point. Based on this, this paper proposes an analysis method of closing pre-strike arcing time based on empirical wavelet transform (EWT).
Firstly, the least squares method is used to preprocess the collected closing displacement signal. On the premise of completely retaining the step change at the instant closing point, the environmental noise interference during signal acquisition is eliminated, which provides a guarantee for the accurate calculation of the subsequent closing pre-strike arcing time. After that, the pre-processed displacement signal is decomposed by EWT, and it is divided into six empirical wavelet function (EWF) components according to different frequency bands, and the high-frequency components of the contact closing moment are completely separated. Next, the kurtosis criterion is used to filter out the EWF component containing the effective information of the rigid point, and the effective positioning of the rigid point is realized. Finally, the starting time of the closing inrush current waveform is positioned, and the time difference between the starting time of the closing inrush current and the closing point is measured, and the pre-strike arcing time is obtained.
Through carrying out simulation analysis and comparing with different methods, the error range of the pre-strike arcing time analysis method based on EWT is within 0.18 ms, which is higher than the 0.35~0.5 ms of the comparison methods, showing higher accuracy. On this basis, considering the influence of different test voltages, different inrush current amplitudes, and different mechanism speeds, field tests were carried out. The experimental results show that the mean error represented by the mean absolute error (MAE) evaluation index is always less than 0.2 ms, and the error dispersion represented by mean-square error (MSE) is always less than 0.03 ms2, which can meet the needs of accurate calculation of pre-strike arcing time without high-precision differential probes.
Subsequently, on this basis, the pre-strike arcing time analysis method can be further applied to high-voltage and high-current conditioning, and the quantitative improvement of capacitive breaking capacity can be realized by precise control of pre-strike arcing energy.
Keywords:Vacuum circuit breaker, pre-strike arcing time, displacement signal, least squares, empirical wavelet transform, kurtosis
中图分类号:TM561.2
DOI: 10.19595/j.cnki.1000-6753.tces.L11013
国家电网公司总部科技项目资助(5500-202255129A-1-1-ZN)。
收稿日期 2024-07-06
改稿日期 2024-08-31
张登奎 男,1993年生,博士研究生,研究方向真空断路器容性投切技术。
E-mail:zdkkk@mail.dlut.edu.cn
董恩源 男,1973年生,教授,博士生导师,研究方向为智能化高压电器等。
E-mail:dey@dlut.edu.cn(通信作者)
(编辑 李 冰)