
图1 高温超导磁浮工程化样车及轨道、悬浮器结构
Fig.1 High-temperature superconducting HTS maglev engineering prototype and test line track structure of HTS maglev train and inner structure of HTS superconducting levitator
摘要 因恶劣磁场环境激励下超导块材内部温升与悬浮力之间的关系目前仍未可知,所以超导块材内部温升实时监测手段还有待提高。该文搭建了针对超导块材热力学-动力学特性的测试装置,利用Halbach永磁轮产生交变磁场。研究发现,随着永磁轮交变磁场频率的增加,超导块材内部温升呈现逐渐增加的趋势。同时,该文提出了一种结合超导块材温-振特性和BP神经网络(BPNN)的非接触式新型温升测试方法。以逐级加速磁场下的温升-振动数据集为例,利用小波分解提取振动加速度特征,结合BPNN对温升进行识别,准确率可达到99.9%以上。进而研究了超导块材在对极型永磁轨道产生的0.06~0.15 T磁场不平顺激励下的动态特性与内部温升之间的内在关系,识别准确率同样超过99.5%。该文旨在为未来高温超导磁悬浮列车的智能监测和故障诊断提供参考。
关键词:超导悬浮器 磁悬浮列车 温升 振动 BP神经网络 智能监测
与传统轨道交通系统相比,磁悬浮轨道交通技术具有低能耗、无磨损、低污染、安全可靠等优点[1-5]。高温超导(High Temperature Superconductivity, HTS)钉扎磁悬浮技术基于电磁感应原理,利用高温超导块材的磁通钉扎特性与地面永磁轨道产生的外磁场之间相互作用,产生稳定的悬浮力和导向力[6]。除了在磁悬浮交通中的应用外,高温超导钉扎技术还可用于磁悬浮飞轮[7-8]、磁悬浮发射[9-10]、直线电机[11-12]和限流器[13]等。
2021年1月13日,设计速度为620 km/h的高温超导高速磁悬浮工程化样车试验线在四川省成都市启动,如图1a所示。这标志着高温超导钉扎磁悬浮列车工程化研究从无到有的突破[14]。高温超导钉扎磁悬浮列车主要由三个设备组成:超导悬浮器(包括车载高温超导块材和液氮)、地面永磁轨道及地面直线电机[1]。超导悬浮器相当于轮轨列车转向架下的一个“轮对”。超导块材是高温超导磁悬浮列车的核心,其热稳定性决定了列车能否安全运行。超导悬浮器(图1c)中的热力学过程为:超导悬浮器中的液氮通过冷却导板对超导块材阵列进行制冷,最终超导块材与液氮达到热平衡。

图1 高温超导磁浮工程化样车及轨道、悬浮器结构
Fig.1 High-temperature superconducting HTS maglev engineering prototype and test line track structure of HTS maglev train and inner structure of HTS superconducting levitator
高温超导磁悬浮列车的稳定运行根本上取决于超导块材的三个关键参数:临界温度Tc、临界磁场Hc和临界电流Jc。当任何一个参数超过临界值时,超导块材的状态将从超导状态变为正常状态,磁悬浮系统立即失效,这对于列车的高速运行极其危险。地面永磁轨道提供的磁场在地域环境温度变化中一般不会超过其临界值,然而,由交变磁场引起的超导块材内部温升已被人们发现会超过临界温度 Tc(92 K)[15-16]。此外,高温超导块材的电流密度J与其内部温度成反比,悬浮力与电流密度和外部磁场成正比,因此,如果电流密度降低,悬浮力将不可避免地发生下降。
因此,超导块材的温升是评估超导钉扎磁浮系统悬浮性能的重要参量。目前的研究主要集中在超导块材的悬浮性能[17-21]和振动特性[22-23]上,对其温升和悬浮力之间的耦合关系尚未清晰。综合分析来看,现有关于高温超导钉扎磁悬浮系统悬浮力-热耦合特性的研究大多采用仿真方法进行分析,尚未得到实验验证。尽管文献[15-16]实验得到了在交变磁场中超导块材内部温升的一些具体测量结果,但并未探明温升与动态悬浮力之间的内在耦合关系。随着高温超导磁悬浮工程化研究的不断推进,超导块材内部温升作为超导钉扎磁浮列车智能监测的第一步,探索超导块材内部温升和动态悬浮性能关联显得尤为重要。
精确灵敏的温升检测方法是开展超导块材温升和动态悬浮性能研究的前提条件,及时检测其温度并且避免磁浮列车高速运行中超导块材内部温度的大幅上升是需要重点关注的问题。目前,检测超导块材内部实时温度的最有效的方法是直接测试法[26-29]。但直接测量超导块材内部实时温度,会损坏超导块材的结构,而且温度传感器也容易脱落。此外,由于超导悬浮器内部的工作空间较窄且结构真空密封,在高温超导列车的超导悬浮器内安装温度传感器极具有挑战性。文献[30]模拟了超导块材在外部磁场激励下的温升与动态响应之间的耦合关系。文献[31]根据实际情况进行了动态测试实验,实验发现在动态激励下超导块材的温升与振动加速度基本呈线性关系。现有的超导块材温升直接测试法通常采用的是Cernox及Pt100温度传感器,相比于PT100的0.1 K测试精度,Cernox温度传感器的测试精度可达0.016 K,更适用于超导块材的微弱温升测试。与超导块材的内部温升检测相比,超导块材的振动加速度对超导块材的悬浮性能的变化更为敏感。因此,探索超导块材的振动加速度与内部温升之间的内在联系将成为一种全新且有效的检测方法。
特征提取与神经网络相结合的方法可以用来研究振动加速度与温升的内在联系。2024年,美国得克萨斯州农工大学的A. E. Kio等利用小波包分解结合深度学习方法实现了精确的风速预测[32]。2020年,土耳其大学的M. Kuncan结合一维局部二进制模式及灰色关联分析实现了最高100%的轴承故障诊断率[33]。
近年来,随着人工智能算法的发展,超导技术与人工智能技术的结合正成为一个全新的研究方向[34-35]。2022年,英国M. Yazdani-Asrami等使用数据驱动方法来预测在不同温度和磁通密度下高温超导带材的标准临界电流值和应力,同时,设计了一个自适应模糊神经网络,并进行了灵敏度分析,以准确预测和模拟扭曲高温超导带材的机电行为[36]。因此,超导技术与人工智能技术相结合展现出了其独特的优势。
针对超导悬浮器内部空间狭窄,难以放入大量温度传感器的问题,本文将超导块材的温-振特性与BP神经网络(Back Propagation Neural Network, BPNN)结合,为未来超导悬浮器在高速运行环境下提供一种新型超导块材内部温升检测方法。本文面向超导磁浮智能监测与预测理论和技术方向,利用自主研发的SCML-01实验装置[24]和温升测量设备构建了一种新型实验装置,探究了不同磁场频率波动下超导块材动态悬浮力和内部温升的耦合机制,使用小波分解提取振动加速度特征,并利用BPNN进行温升智能识别结果分析,验证了本文所提出的针对超导块材内部温升智能无接触识别方法的有效性。最后,通过理论分析和实验证明了针对高温超导块材的智能温升监测方法的有效性。
由于超导块材内部的强各向异性及磁轨空间磁场的非线性分布,造成块材不同位置的捕获磁通量和感应电流不同,对悬浮力的贡献也不同。因此,为了更清楚地研究超导块材内部温升特性,使用特制的陶瓷钻孔设备在超导块材内部钻出三个孔,如图2a所示。为了保证温度传感器检测到的是超导块材本身的温升,在液氮温度范围内,选择热导率与超导块材相似的花岗岩作为对照。在花岗岩相同位置钻取相同尺寸的孔,如图2b所示,并放入相同类型的温度传感器。

图2 超导块材和花岗岩
Fig.2 HTS bulk and granite
实验装置中的温升测试设备主要包括温度测量设备和永磁轮两部分。温度测量设备主要包括低温温度传感器(CX-1030-SD,Lakeshore)和温度监测器(224,Lakeshore),详细参数分别见表1和表2。温度测量设备用于测试和记录超导块材内部的实时温度,如图3所示。
表1 CX-1030-SD传感器详细参数
Tab.1 The detailed parameters of the CX-1030-SD sensor

名称数值 测温范围0.1~325 K 检测精度0.016 K 热响应时间77 K:0.25 s 推荐激励(T>1.2 K)小于或等于10 mV
表2 温度监视器详细参数
Tab.2 The detailed parameters of temperature monitor

名称参数 激励类型恒定激励电流 测量类型四线法 输入通道2个专用通道,10个扫描通道 A/D分辨率24位

图3 超导块材温度测量设备示意图
Fig.3 Schematic diagram of HTS bulk temperature measurement equipment
自制的永磁轮结构如图4所示,由16个NdFeB永磁体组成,这些永磁体按照Halbach结构阵列排列。Halbach 磁轮系统主要包括电子调速器、直流无刷电机、两个磁轮、温度传感器和直流电源。表3为环形Halbach 磁轮的设计参数。

图4 磁轮和磁化方向示意图
Fig.4 Schematic diagram of magnetic wheel and magnetic field direction
表3 Halbach磁轮设计参数
Tab.3 Design parameters of Halbach magnetic wheel

参数数值 永磁体牌号N35 外径/mm50.0 内径/mm32.5 宽度/mm35.0 剩磁/T1.19 磁极对数4
图5为距离磁轮表面2~20 mm的径向磁通密度,这里的距离代表超导块材底面与永磁轮标记点的垂直距离,磁场呈现正弦分布。永磁轮上方磁场的测试步骤为:将三维磁场扫描仪探头安装在永磁磁轮正上方,然后转动一圈永磁轮,最后记录探头采集的磁场数值。由于本文仅针对超导块材在8 mm处的温度特性进行研究,不对场冷高度的影响规律进行讨论,所以只采集了工作高度附近的磁场分布。研究发现,实际永磁轨道的磁场不规则性分布也呈现正弦波动[37],本研究中的磁轮磁场对研究超导块材在永磁轨道磁场不平顺激励下的悬浮特性具有一定的参考意义[25]。
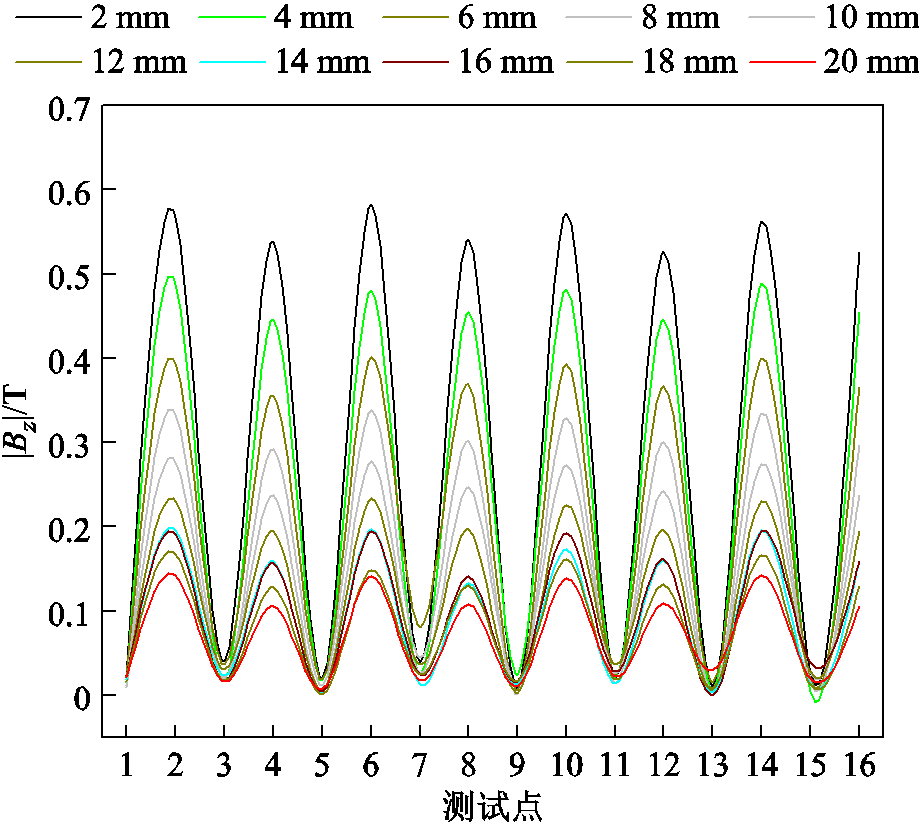
图5 不同高度处的磁通密度
Fig.5 Magnetic flux density at different heights
值得一提的是,由于永磁轮存在一定的曲率效应,其提供的磁场与直线型轨道磁场存在一定的区别,设R为超导块材底部与永磁轮表面的距离,超导块材底部相对永磁轮表面位置示意图如图6所示。通过勾股定理可得出超导块材边缘处与永磁轮的垂直距离相对超导块材中心处高出: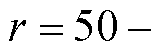
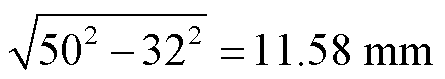 。
。
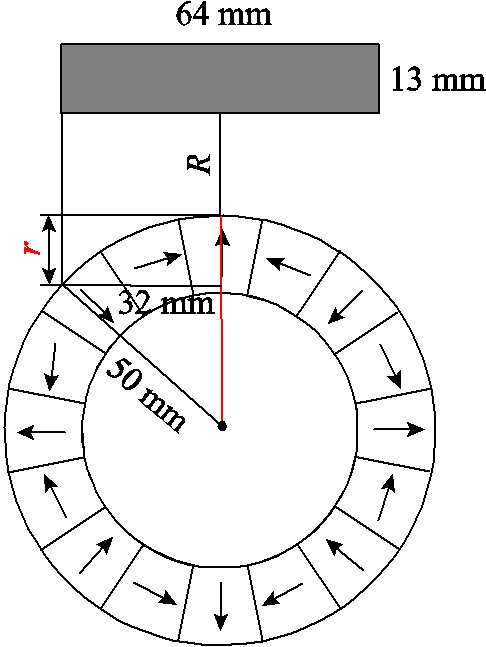
图6 超导块材底部相对永磁轮表面位置示意图
Fig. 6 The position of the HTS bulk bottom relative to the surface of the permanent magnet wheel
永磁轨道的集合不平顺实验测试表明[40],永磁轨道垂向高度差最大可达到10 mm左右,因此,永磁轮一方面可以模拟直线型永磁轨道的磁场不平顺,另一方面还可以模拟轨道的几何不平顺。
SCML-01装置最初被设计用于测量高温超导磁悬浮系统的悬浮力[24],因此,将温度测量设备和磁轮安装在SCML-01上,可以同时测量超导块材的动态悬浮力和温升,超导块材温升-动态悬浮力实验装置如图7所示。
实验包括超导块材内部温升以及磁轮与超导块材之间动态悬浮力的测量,实验测试过程如下:
(1)将温度传感器分别放入超导块材及花岗岩内部,其中,超导块材内部放入3个传感器,花岗岩内部放入1个传感器。利用高真空润滑脂和硅胶泥进行密封,如图7所示。然后,将对照组花岗岩和超导块材固定在一起放入夹具中,为了便于后续分析,传感器在超导块材和花岗岩内部的安装位置如图8中的A、B、C和D所示。
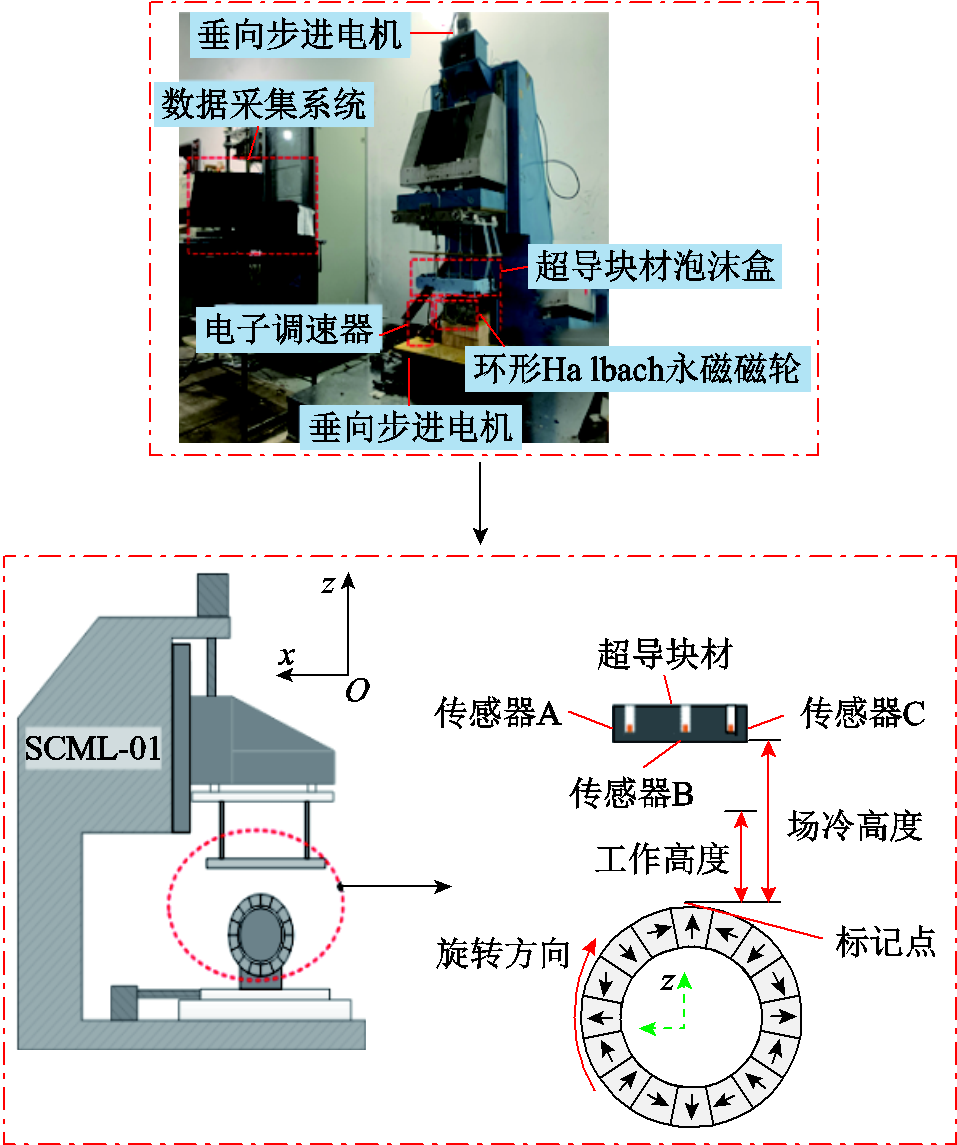
图7 超导块材温升-动态悬浮力实验装置
Fig.7 Experimental device for thermal-dynamic levitation forceof the HTS bulk

图8 温度传感器安装位置
Fig.8 Installation position of temperature sensors
(2)实验测试过程如图9所示,选择垂直磁化永磁体上方作为初始位置,在场冷高度处向夹具中加入液氮进行浴冷15 min后,降到工作高度。将场冷高度40 mm、工作高度8 mm作为实验工况。
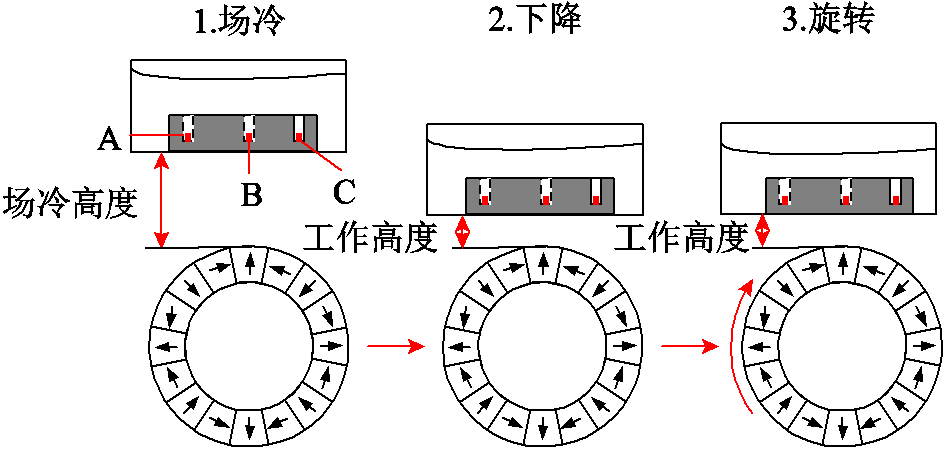
图9 实验测试过程
Fig.9 Experimental testing process
(3)同时打开悬浮力及温升检测装置,实验开始后记录点A、B、C、D的温度值及悬浮力的变化,并逐渐增加Halbach 磁轮转速,选择永磁轮转速从0一直加速到4 000 r/min,间隔为500 r/min,每种转速保持2 min,然后加速到下一转速,最后将永磁轮转速降至0,记录温升及悬浮力变化,实验结束。
实验选用花岗岩作为对照组,发现在磁轮磁场激励下花岗岩内部温升没有波动,因此,可以确认超导块材中的A点、B点和C点的温升是由于外部磁场激励引起的。由于在磁场激励下,超导块材内部的温升是由交流损耗和磁滞损耗两部分共同引起的,而本文重点研究永磁轮磁场激励下超导块材内部的温升变化,故在此不再对两者进行区分。
逐级加速下超导块材各点温升如图10所示。在每种转速下,超导块材温升都呈现先增加后稳定的趋势;随着转速的逐级增加,超导块材A、B、C三点的温度也逐渐升高,这是由于在不同转速时,超导块材经历的磁场频率波动加大,引起超导块材内部磁通运动,产生温升,打破了原有的热平衡状态。从图10中可以看出,相同磁场激励下,C点温升最大,B点温升最小,这是由于超导块材属于各向异性材料,在超导块材场冷并且降至工作高度的过程中,超导块材本身不同位置捕获的磁通大小存在差异,导致温升不同。通过温升测试结果确认,C点处捕获磁通量最大,B点处捕获磁通量最少。
图11为逐级加速下超导块材悬浮力测试结果,悬浮力随着转速增加呈现不断减小的趋势。当转速从0上升到500 r/min时,悬浮力的衰减最多,对比图10,也可以发现此时的温升幅值也最大;随着转速的持续增加,悬浮力呈现小幅度衰减,与温升变化趋势基本一致。通过分析可以发现,逐级加速过程中,若超导块材内部温升已经达到饱和,则悬浮力不再随着速度的增大而继续衰减,基本呈现稳定状态。从图11中也可以看出,当转速从0加速到500 r/min时,超导块材的悬浮力衰减最大,随着转速的增加,悬浮力的衰减幅度逐渐减小,当转速超过3 000 r/min后,悬浮力不会再发生衰减。但是,随着转速的增加,悬浮力的波动幅值不断增大,从温升结果中也可以看出,此时温度已经接近饱和,超导块材的悬浮力基本处于稳定。另外,随着磁场频率的不断增加,超导块材的穿透深度进一步增加,产生正的屏蔽电流;随着交变磁场幅值的减小,产生相反的屏蔽电流。随着磁场频率和幅值的不断变化,超导块材的悬浮力将产生振荡,且磁场变化频率越大,悬浮力波动越大。
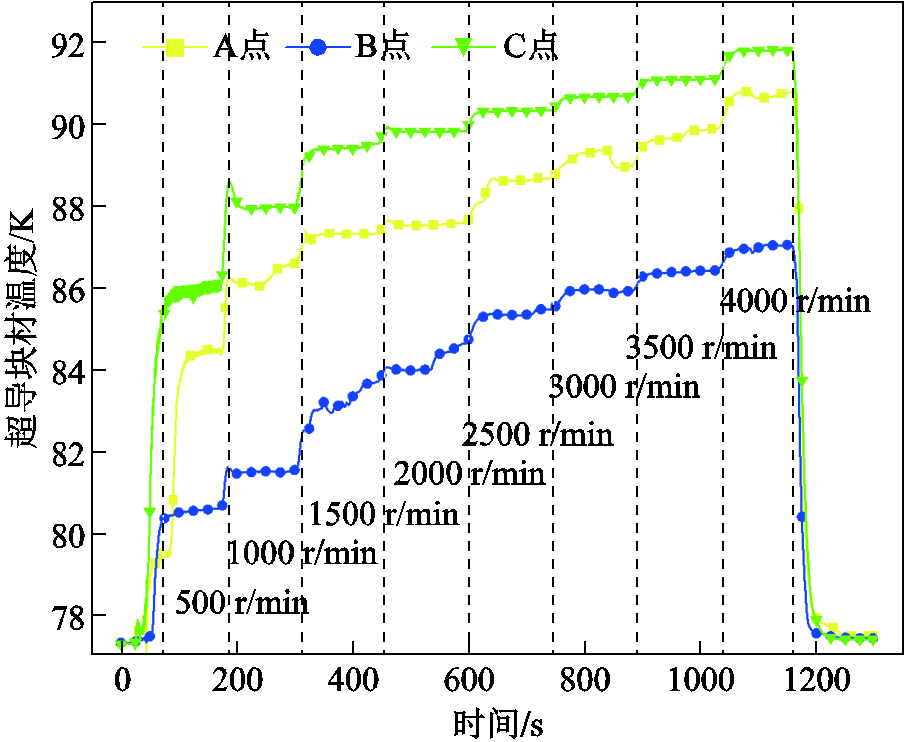
图10 逐级加速下超导块材各点温升
Fig.10 Temperature rise at each point of HTS bulk under stepwise acceleration
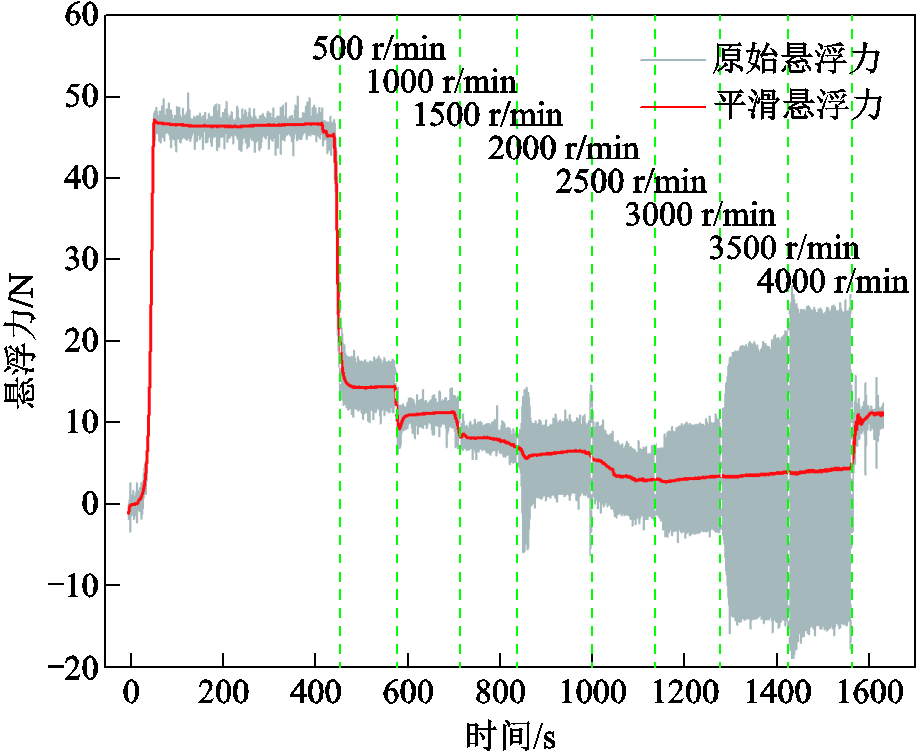
图11 逐级加速下超导块材悬浮力变化
Fig.11 Levitation force of HTS bulk under stepwise acceleration
从温升及悬浮力变化曲线中可以看出,超导块材温度的变化与悬浮力一致,内部温升和悬浮力之间存在强烈的耦合关系。临界状态模型中超导块材热损失的功率密度表示为
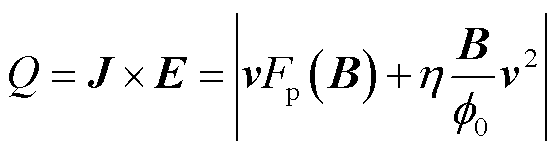 (1)
(1)
式中,J为超导块材内部的电流密度;E为超导块材内部的电场强度;B为磁通密度;Q为超导块材的焦耳热损失功率密度;v为磁通密度变化速率;Fp为钉扎力密度;h为黏着系数;f0为磁通量;Q为超导块材的焦耳热损失功率密度;v为磁通密度变化速率;Fp为钉扎力密度;h为黏着系数;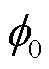 为磁通量。等式右侧的
为磁通量。等式右侧的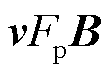 和
和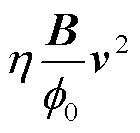 分别表示钉扎力和黏着力的损耗。通常,黏着力密度远小于磁通钉扎力的损失密度,并且经常被忽略。从式(1)中可以看出,超导块材的热损耗和悬浮力之间存在耦合关系。
分别表示钉扎力和黏着力的损耗。通常,黏着力密度远小于磁通钉扎力的损失密度,并且经常被忽略。从式(1)中可以看出,超导块材的热损耗和悬浮力之间存在耦合关系。
考虑到在超导块材内部打孔会破坏超导体结构,同时,超导悬浮器内部有限的空间也难以放入过多的温度传感器。因此,在上述实验结果的基础上,以超导块材的振动加速度与内部温升的内在关系为主,本文提出了小波分解与BPNN相结合的新型非接触式温升测试方法。由于本文中超导块材固定在SCML-01装置上,因此,采用等效振动加速度的方法进行分析,有
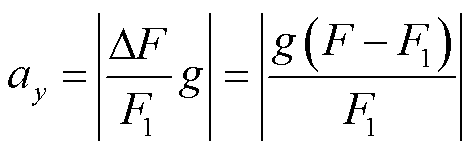 (2)
(2)
式中,ay为超导块材的垂直等效振动加速度;F为实时悬浮力;F1为永磁轮开始旋转前的悬浮力;g为重力加速度。
小波变换是一种用于分析时频域信号的方法,它根据所选的分解级别提供可变的时间-频率分辨率,对于信号的高频分量,时间分辨率越低,频率分辨率越高,低频分量则相反。小波分解是将频带按多个级别划分,对未经分析和细分的多分辨率高频分量进行进一步分解,以提高频率分辨率[38]。根据以往小波分解经验,选择了四层小波分解方法,因为这可以确保最大程度地提取信号的特征信息。经过小波分解后,可以得到小波分解的高频和低频系数。
小波分解后的小波系数序列为{S1,S2,S3,S4,S5}, n=1,2,×××,5。S1是低频信号的小波系数,S2~S5是高频小波系数。将分解后获得的五个频带的小波系数进行平方并求和,频带能量计算式为
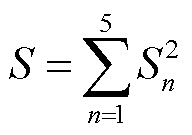 (3)
(3)
式中,S为频带总能量,归一化式为
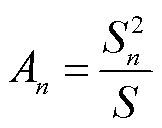 (4)
(4)
式中,A1, A2, A3, A4, A5分别表示S1, S2, S3, S4, S5归一化后系数。
以每种转速下动态悬浮力衰减并稳定后的温度-动态悬浮力结果为例,悬浮力的采样频率为100 Hz。在悬浮力衰减后的稳定阶段,每个速度下选择稳定27 s的采样时间作为测试数据,同时以9 s的数据为一个样本,则每种速度下有三个样本。因此,每个速度对应三组信号特征,每组900个点,八种速度下共7 200个点。式(2)用于将动态悬浮力转换为等效振动加速度。通过式(3)和式(4)可以得到等效振动加速度归一化的小波频带能量值,见表4。
表4 逐级加速下的四层小波分解和频带能量
Tab.4 Four layer wavelet decomposition and frequency band energy at stepwise acceleration

转速/(r/min)频带能量 温度/KA1A2A3A4A5 500-183.032 0.997 684 0.000 866 0.001 424 0.000 022 0.000 005 500-20.997 805 0.000 784 0.001 376 0.000 027 0.000 008 500-30.997 840 0.000 809 0.001 333 0.000 013 0.000 004 1000-185.2190.996 7820.001 6900.001 1720.000 2220.000 134 1000-20.996 7450.001 5740.001 4650.000 1550.000 061 1000-30.996 8560.001 5620.001 3750.000 1520.000 054 1500-186.7340.999 851 0.000 096 0.000 048 0.000 003 0.000 002 1500-20.999 838 0.000 100 0.000 056 0.000 005 0.000 001 1500-30.999 836 0.000 098 0.000 056 0.000 007 0.000 004 2000-187.1430.996 429 0.003 390 0.000 144 0.000 026 0.000 010 2000-20.996 339 0.003 425 0.000 179 0.000 038 0.000 019 2000-30.996 370 0.003 452 0.000 156 0.000 016 0.000 006 2500-188.12330.997 476 0.001 902 0.000 503 0.000 116 0.000 002 2500-20.997 370 0.002 064 0.000 460 0.000 100 0.000 005 2500-30.997 215 0.002 022 0.000 596 0.000 154 0.000 013 3000-188.6940.990 427 0.009 531 0.000 024 0.000 012 0.000 006 3000-20.990 346 0.009 581 0.000 025 0.000 029 0.000 020 3000-30.990 007 0.009 889 0.000 044 0.000 038 0.000 022 3500-189.1320.946 790 0.052 138 0.000 668 0.000 251 0.000 153 3500-20.947 175 0.051 785 0.000 766 0.000 165 0.000 109 3500-30.946 088 0.053 134 0.000 601 0.000 112 0.000 066 4000-190.2530.926 730 0.066 542 0.006 424 0.000 170 0.000 134 4000-20.928 498 0.064 215 0.006 703 0.000 347 0.000 237 4000-30.928 626 0.064 025 0.006 708 0.000 397 0.000 245
从表4中可以看出,不同的运行速度下,振动加速度的频带能量呈现非线性变化,BPNN等人工智能算法在处理非线性问题方面具有显著优势[39]。
3.2.1 BPNN原理
BPNN具有由输入层、隐藏层和输出层组成的单隐藏层神经网络的连接结构。在BPNN的训练中,将表4中特定速度下的五个小波频带能量值A1、A2、A3、A4、A5作为训练集进行网络输入x1、x2、x3、x4、x5,并将相应的温升作为输出。同时,另取稳定3 s的数据作为测试样本,测试BPNN的识别性能。表5展示了测试样本的频带能量值,用于BPNN识别准确性的验证,BPNN的详细参数见表6。
表5 小波频带能量值测试集
Tab.5 Wavelet band energy value test set
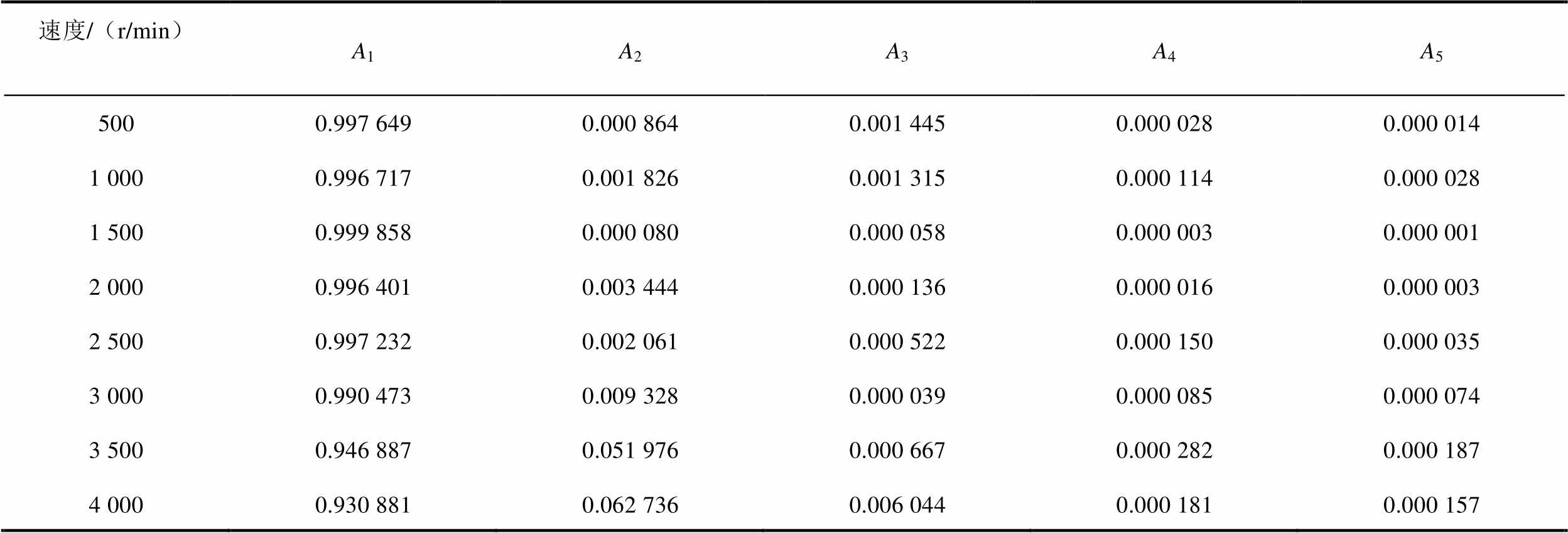
速度/(r/min)A1A2A3A4A5 5000.997 649 0.000 864 0.001 445 0.000 028 0.000 014 1 0000.996 7170.001 8260.001 3150.000 1140.000 028 1 5000.999 858 0.000 080 0.000 058 0.000 003 0.000 001 2 0000.996 401 0.003 444 0.000 136 0.000 016 0.000 003 2 5000.997 232 0.002 061 0.000 522 0.000 150 0.000 035 3 0000.990 473 0.009 328 0.000 039 0.000 085 0.000 074 3 5000.946 887 0.051 976 0.000 667 0.000 282 0.000 187 4 0000.930 881 0.062 736 0.006 044 0.000 181 0.000 157
表6 BPNN详细参数
Tab.6 Detailed parameters of BPNN

参数数值 隐藏层神经元个数5 输入层神经元数5 学习率系数0.001 训练频率1 000 训练目标的最小误差1´10-6
3.2.2 识别结果
在训练样本中,一组永磁轮转速对应一组超导块材温升,被视为一个组合。为了方便BPNN的训练和识别,可以使用二进制来描述,见表7。
表7 二进制表示
Tab.7 Binary representation

测试组速度/(r/min)对应的二进制 15001 0 0 0 0 0 0 0 21 0000 1 0 0 0 0 0 0 31 5000 0 1 0 0 0 0 0
(续)

测试组速度/(r/min)对应的二进制 42 0000 0 0 1 0 0 0 0 52 5000 0 0 0 1 0 0 0 63 0000 0 0 0 0 1 0 0 73 5000 0 0 0 0 0 1 0 84 0000 0 0 0 0 0 0 1
将测试样本输入训练好的BPNN中进行训练,得到的分类结果如图12所示,y1~y8表示在相应的测试组下识别结果的概率。例如,在测试组1中,y1下的识别结果为0.998 668,表示这个测试组属于y1的概率为99.866 8%。类似地,在测试组2中,y2下的识别结果为0.997 303 7,表示这个测试组属于y2的概率为99.730 37%,依此类推。根据所有的识别结果,可以明显看出,y3、y5、y6及y8组的识别准确率最高,为100%。这初步证明了BPNN在超导块材温升识别中的有效性。

图12 BPNN识别结果
Fig.12 The recognition results of BPNN
虽然在永磁轮交变磁场下验证了小波分解结合BPNN用于超导块材温升识别的有效性,但是永磁轮磁场与实际磁场之间存在差别,为了进一步验证小波分解结合BPNN应用于高温超导磁悬浮温度识别中的有效性,本节结合真实的永磁轨道磁场进行超导块材的温-振特性研究。以SCML-03[37]测试装置所采用的对极型永磁轨道为例,由于永磁体制作工艺的差异以及安装过程中不可避免会出现错位、缝隙等引起的误差,并且随着永磁轨道服役时间的增加,永磁体会出现微弱退磁,这些都会造成磁轨上方磁场不平顺[40]。
已经有大量研究对超导悬浮系统的电磁热力多物理场进行有限元建模计算,并取得了准确的计算结果[41-42]。由于实验条件的限制,需要借助仿真手段,进行超导块材动态特性的拓展研究。超导块材虽然处于超导状态下,但仍然属于电磁材料,所以可以使用Maxwell方程组进行超导体电-磁特性建模。
法拉第电磁感应定律为
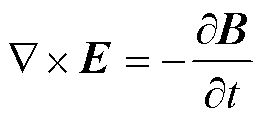 (5)
(5)
安培定律为
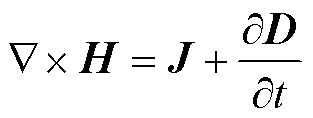 (6)
(6)
高斯定律为
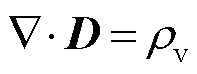 (7)
(7)
磁通守恒定律为
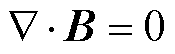 (8)
(8)
式中,E为电场强度(V/m);B为磁感应强度(T);H为磁场强度(A/m);J为电流密度(A/m2);D为电位移矢量(C/m2);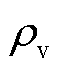 为电荷体密度(C/m3)。
为电荷体密度(C/m3)。
另外,进行电磁场仿真计算时,还需要补充电磁本构方程为
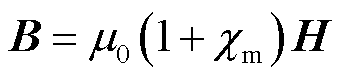 (9)
(9)
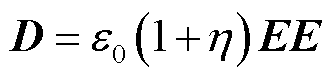 (10)
(10)
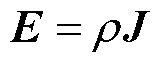 (11)
(11)
式中,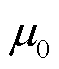 为真空磁导率;
为真空磁导率;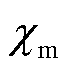 为磁化系数;ε0为真空中的介电常数,
为磁化系数;ε0为真空中的介电常数,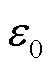 = 8.854×10-12 F/m;η为电极化率;ρ为电阻率(Ω·m);
= 8.854×10-12 F/m;η为电极化率;ρ为电阻率(Ω·m);
目前,描述超导体的E-J电磁本构关系的模型主要有三种:临界态模型、幂指数模型以及磁通流动与蠕动模型,其中,幂指数模型收敛性好,并且能够真实反映超导体的E-J关系,详细方程为
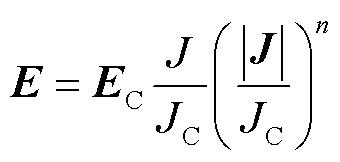 (12)
(12)
式中,EC为临界电场强度;n为幂指数模型参数。
超导体内的传热过程也符合传统的热传导模型,具体公式为
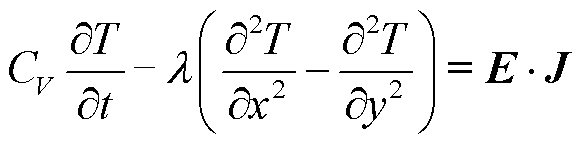 (13)
(13)
式中,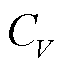 为超导体单位体积热容(J/(kg·K));λ为超导体导热系数(W/(m·K));E·J为超导体单位时间内的电磁损耗密度(W/m3)。
为超导体单位体积热容(J/(kg·K));λ为超导体导热系数(W/(m·K));E·J为超导体单位时间内的电磁损耗密度(W/m3)。
利用PDE模块自定义偏微分方程[28],通过设置狄利克雷边界条件给高温超导体添加时变外磁场,建立轨道空间磁场与永磁体磁化强度M0之间的关系,实现真实轨道磁场不平顺的模拟,公式为
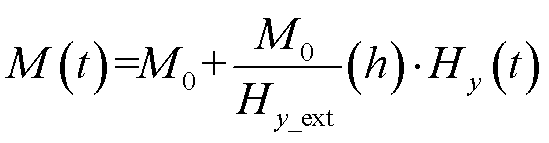 (14)
(14)
式中,M(t)为磁场不平顺;Hy(t)为垂直方向磁场波动;Hy_ext为空间外磁场波动。
利用PDE模块与固体传热接口相耦合实现高温超导钉扎磁浮系统动态磁-热-力多场耦合模型的建立与求解,具体的求解过程如图13所示。
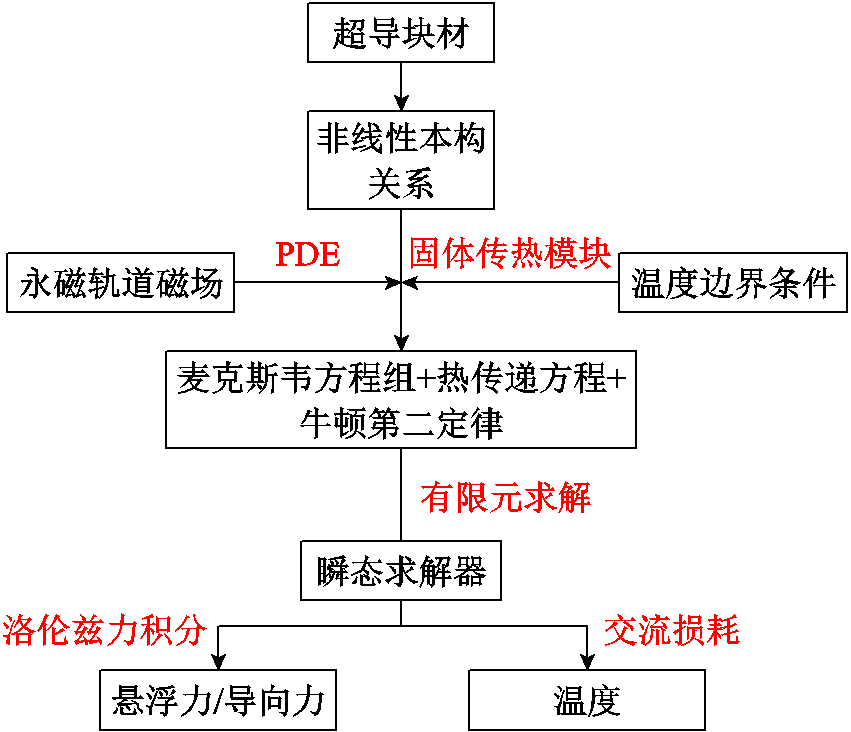
图13 有限元求解过程
Fig.13 Finite element solution process
详细的建模过程可以参考文献[28],本文仅对其进行描述。为了模拟磁场波动下超导块材的温升与悬浮力特性,在永磁轨道上方布置小磁体增加磁场波动。图14为在SCML-03装置的永磁轨道上方布置小磁体后的磁场分布。

图14 布置小磁体后永磁轨道上方磁场波动
Fig.14 Magnetic field fluctuation diagram above the PMG after arranging small magnets
图15为利用有限元仿真得到的磁场波动,可以看出,仿真计算值与实验测试值较为接近,变化趋势也基本相同,这在一定程度上证明了仿真方法的有效性。
本文选择的磁场波动频率为20 Hz、场冷高度为30 mm、工作高度为10 mm、磁场波动幅值为 0.06、0.08、0.10、0.11、0.12、0.13、0.14、0.15 T。仿真过程为:在0~20 s内,超导块材从场冷高度下降到工作高度,下降速度为1 mm/s,20~80 s内,超导块材进行磁豫,80~125 s内,磁场开始波动,模拟超导块材的实际运动,计算磁场波动过程中的动态悬浮力及超导块材的最大温升变化。
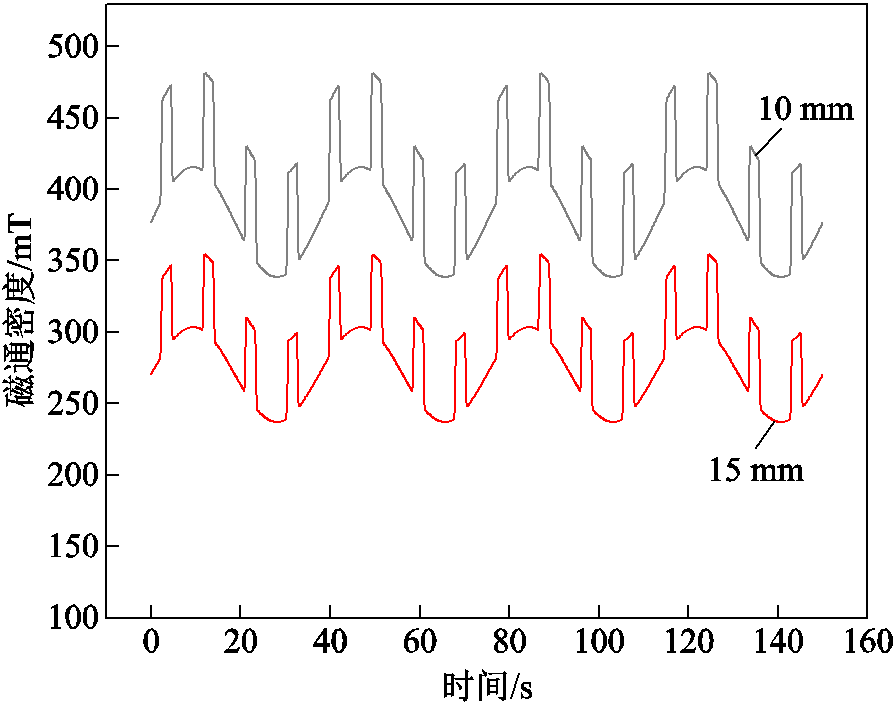
图15 利用有限元仿真得到的磁场波动
Fig.15 Magnetic field fluctuations obtained through finite element simulation
悬浮力计算结果如图16所示。从图中可以看出,随着磁场波动幅值的增加,超导块材的悬浮力波动幅值也在不断增加。超导块材内部最大温升如图17所示,与悬浮力变化趋势相同,随着磁感应强度幅值的增加,超导块材内部的温度不断增加。从超导块材的悬浮力及内部温升最大值可以得出,在0.06~0.15 T磁场波动范围内超导块材最大温升范围为0.1~4.0 K。在0.14 T时,超导块材的内部温升达到了3.5 K,已快要接近悬浮力衰减的拐点。
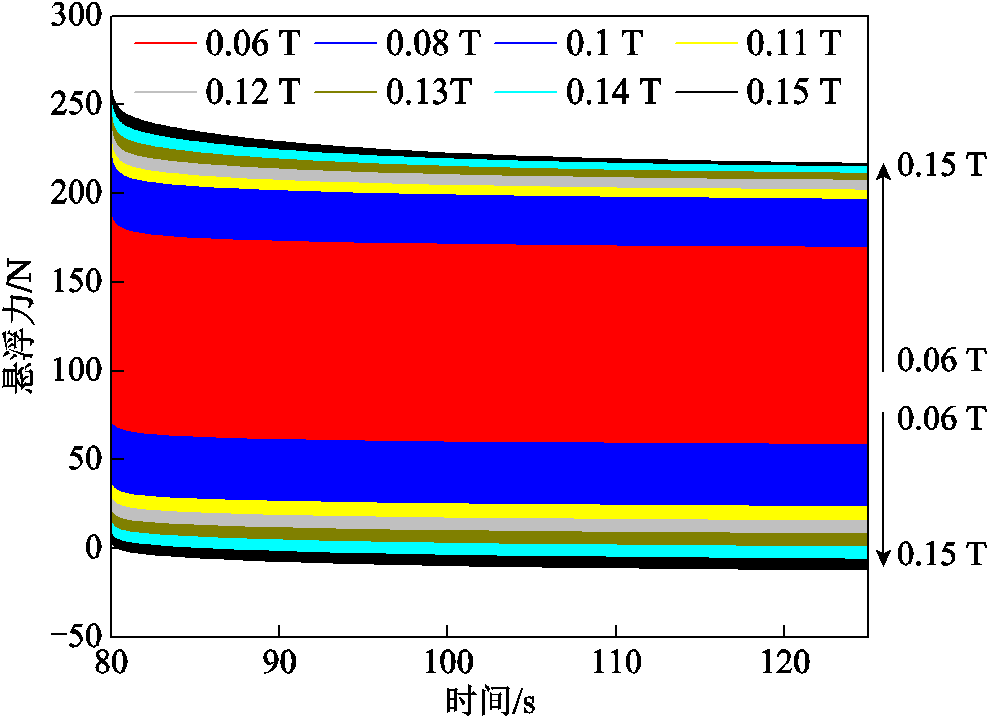
图16 悬浮力结果
Fig.16 The results of levitation force
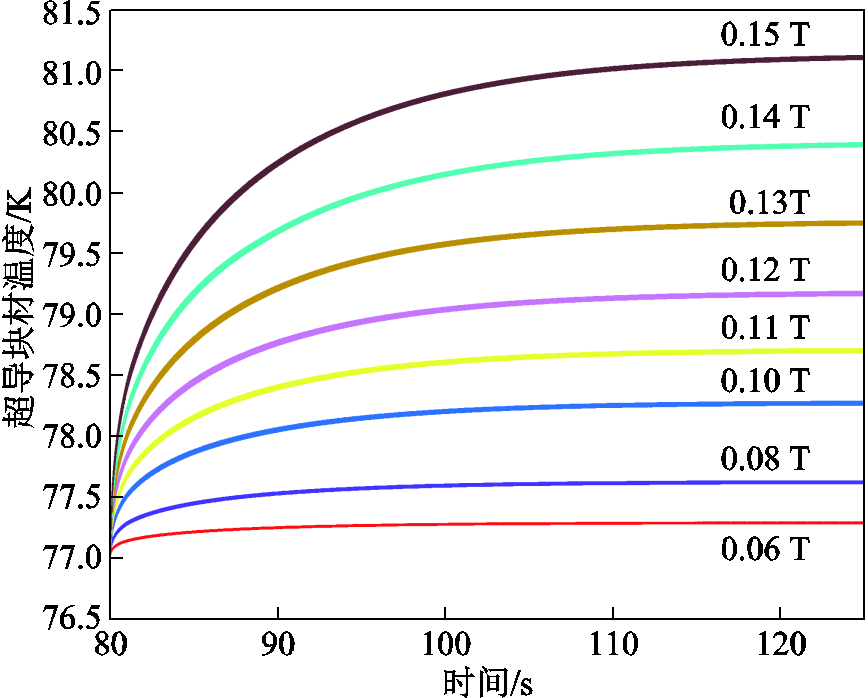
图17 超导块材内部最大温升
Fig.17 Internal maximum temperature rise of HTS bulk
从图17中可以看出,在110 s以后,超导块材内部的温升达到稳定,此时悬浮力的波动也达到稳定,可以利用小波分解与BPNN进行超导块材的温升识别分析。利用小波分解对超导块材的等效振动加速度进行特征分解,以110~125 s内的超导块材的数据作为样本进行测试,其中,110~120 s内的数据为训练样本,120~125 s为测试样本,以5 s作为一个样本进行分析,将提取的小波特征输入BPNN中,得到的识别结果如图18所示。
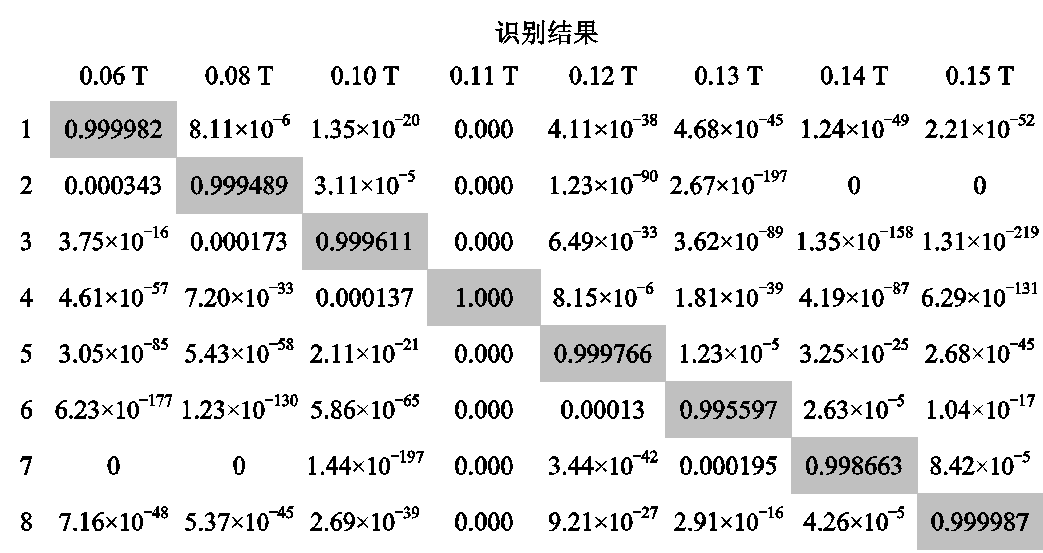
图18 超导块材温升识别结果
Fig.18 Temperature rise identification results of superconducting bulk material
针对超导块材温升每种状态下的识别结果可以看出,所提方法对于每种磁场波动下的温升识别结果准确率可以达到99.5%以上,针对0.11 T的准确率同样可以达到100%,这进一步验证了基于小波分解与BPNN结合进行超导悬浮系统温升识别的有效性。
在传统的轮轨交通中,振动加速度常常用来进行关键位置的故障诊断,并且能够实现车辆状态的提前预警。随着高温超导钉扎磁浮工程化的发展,本文探究的超导磁浮的温度-振动耦合映射关系及人工智能检测方法为车载超导悬浮器核心设备的智能在线监测奠定了基础。其中,基于小波变换和BPNN进行了高温超导磁悬浮系统的温度与振动的相关性分析。该方法提供了一种通过分析振动加速度来直接检测超导块材内部温升而不损坏超导体结构的方法。本文的具体结论如下:
1)在永磁轮提供的交变磁场条件下,磁场变化频率越高,超导块材内部温升越高,悬浮力衰减越大。此外,超导块材的温升与磁场频率之间非简单线性关系。
2)超导块材的小波能量值在交变磁场的不同波动频率下是不同的,并且与传统特征(如悬浮高度)也有区别,这些小波特征可以作为超导块材监测的主要参量。
3)在永磁轮提供的交变磁场条件下,使用BPNN进行超导块材内部温升识别分析,可实现99.9%以上的准确率,同时,在磁场不平顺激励下同样可以达到99.5%以上的识别准确率。这种方法可以作为监测超导悬浮器动态悬浮性能的有效手段。
本文的研究结果可以充分证明本文所提方法的有效性。这种无接触式的智能温升检测方法可以不占用超导悬浮器内部的使用空间,适用于磁浮车动态运行工况,降低超导块材温升测试的技术难度。在实际的超导钉扎磁浮车应用中,由于永磁轨道的磁场不平顺程度较小,超导块材内部的温升相对微弱,因此在后续的研究中,将关注在弱温升下的温-振耦合特性,有必要探索新的特征提取方法和智能状态识别模型,同时,在干扰条件下进行有效的信号提取也是未来高温超导磁悬浮车智能在线监测的重要研究方向。
参考文献
[1] Jin Jianxun, Sheng Guang, Bi Yanfang, et al. Applied superconductivity and electromagnetic devices- principles and current exploration highlights[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 7000529.
[2] 秦伟, 马育华, 张洁龙, 等. 不均匀气隙工况下轴向磁通永磁电动式磁悬浮电机的磁场与力特性分析[J]. 电工技术学报, 2023, 38(4): 889-902.
Qin Wei, Ma Yuhua, Zhang Jielong, et al. Characteristic and magnetic field analysis of an axial flux permanent magnets maglev motor with non-uniform air gap[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 889-902.
[3] 余嘉淇, 周凌云, 刘顺攀, 等. 基于集电线圈复用的电动磁浮列车感应式电能传输技术研究[J]. 电工技术学报, 2024, 39(4): 976-986.
Yu Jiaqi, Zhou Lingyun, Liu Shunpan, et al. Research on inductive power transfer method for electrodynamic suspension maglev train based on collector coil reuse[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 976-986.
[4] Wang Xiaonong, Huang Jingyu. Research on electromagnetic relationship and passive electro-magnetic damping characteristics of superconducting electrodynamic maglev train[J]. IEEE Transactions on Applied Superconductivity, 2022, 32(7): 3602618.
[5] Ohashi S, Ueda N. Influence of the damper coil system on the levitation characteristics in the superconducting magnetically levitated system in case of SC coil quenching[J]. IEEE Transactions on Magnetics, 2014, 50(11): 8300304.
[6] Wang Jiasu, Wang Suyu, Zeng Youwen, et al. The first man-loading high temperature superconducting Maglev test vehicle in the world[J]. Physica C: Superconductivity, 2002, 378: 809-814.
[7] Werfel F N, Floegel-Delor U, Rothfeld R, et al. Superconductor bearings, flywheels and transportation [J]. Superconductor Science and Technology, 2012, 25(1): 014007.
[8] Werfel F N, Floegel-Delor U, Riedel T, et al. Towards high-capacity HTS flywheel systems[J]. IEEE Transactions on Applied Superconductivity, 2010, 20(4): 2272-2275.
[9] 马伟明, 鲁军勇. 电磁发射技术的研究现状与挑战[J]. 电工技术学报, 2023, 38(15): 3944-3958.
Ma Weiming, Lu Junyong. Research progress and challenges of electromagnetic launch technology[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 3944-3958.
[10] Schultz J H, Radovinsky A, Thome R J, et al. Superconducting magnets for Maglifter launch assist sleds[J]. IEEE Transactions on Applied Superco-nductivity, 2001, 11(1): 1749-1752.
[11] 鲁军勇, 柳应全. 电磁发射用直线电机及其控制技术综述[J]. 电工技术学报, 2024, 39(19): 5899-5913.
Lu Junyong, Liu Yingquan. Review on linear motor for electromagnetic launch and its control technology[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5899-5913.
[12] 张明远, 史黎明, 范满义, 等. 长初级双边直线感应电动机分段推力协同控制和测速算法[J]. 电工技术学报, 2023, 38(3): 659-669.
Zhang Mingyuan, Shi Liming, Fan Manyi, et al. Thrust cooperative control and speed measurement algorithm of segmented long primary double-sided linear induction motor[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 659-669.
[13] 邓步青, 文云峰, 于琳琳, 等. 限流器配置与网架结构优化协同的受端电网短路电流抑制策略[J]. 电力系统自动化, 2024, 48(9): 151-161.
Deng Buqing, Wen Yunfeng, Yu Linlin, et al. Short-circuit current suppression strategy for receiving-end power grid based on coordination of current limiter configuration and network structure optimization[J]. Automation of Electric Power Systems, 2024, 48(9): 151-161.
[14] Lei Wuyang, Zheng Jun, Huang Zhichuan, et al. Study of long-time levitation performance of high temperature superconducting maglev under vertical vibration[J]. Physica C: Superconductivity and Its Applications, 2022, 600: 1354099.
[15] Pang Peng, Liu Wei, Ren Xiaochen, et al. Experimental analysis on temperature characteristics of a rectangular bulk YBCO exposed to alternating magnetic field[J]. SN Applied Sciences, 2019, 1(7): 749.
[16] Pang Peng, Liu Wei, Ren Xiaochen, et al. Temperature characteristics of bulk YBCO exposed to high frequency fluctuant magnetic field in high-TC superconducting maglev system[J]. Physica C: Superconductivity and Its Applications, 2020, 572: 1353616.
[17] Zhang Weifeng, Deng Zigang, Zhang Yong, et al. Magnetic levitation and guidance performance of Y–Ba–Cu–O and Gd–Ba–Cu–O bulk superconductors under low ambient pressure[J]. Journal of Physics D: Applied Physics, 2019, 52(36): 365001.
[18] Gou Xiaofan, Zheng Xiaojing, Zhou Youhe. Drift of levitated/suspended body in high-Tc superconducting levitation systems under vibration: Part II: drift velocity for gap varying with time[J]. IEEE Transactions on Applied Superconductivity, 2007, 17(3): 3803-3808.
[19] Yang Wenjiao, Ma Guangtong, Li Jing, et al. The effect of running speed and guideway irregularity on the levitation performance of a linear HTS maglev bearing[J]. IEEE Transactions on Applied Superco-nductivity, 2021, 31(5): 3601606.
[20] Si Shuaishuai, Zheng Jun, Zheng Botian, et al. Levitation performance of different bulk YBaCuO arrays above a permanent magnet guideway for HTS maglev systems[J]. Journal of Alloys and Compounds, 2017, 705: 301-308.
[21] Sotelo G G, Dias D H N, de Andrade R, et al. Experimental and theoretical levitation forces in a superconducting bearing for a real-scale maglev system[J]. IEEE Transactions on Applied Superconductivity, 2011, 21(5): 3532-3540.
[22] Zheng Jun, Deng Zigang, Wang Lulin, et al. Stability of the maglev vehicle model using bulk high Tc superconductors at low speed[J]. IEEE Transactions on Applied Superconductivity, 2007, 17(2): 2103-2106.
[23] Zheng Jun, Deng Zigang, Zhang Ya, et al. Performance improvement of high temperature superconducting maglev system by eddy current damper[J]. IEEE Transactions on Applied Superconductivity, 2009, 19(3): 2148-2151.
[24] Zeng Rong, Wang Suyu, Wang Jiasu, et al. An improved high-Tc superconducting maglev measurement system with multi-parameter test and movement functions[J]. IEEE Transactions on Applied Superconductivity, 2013, 23(3): 9000904.
[25] Sun Ruixue, Zheng Jun, Zheng Botian, et al. Study on the magnetic field inhomogeneity of a halbach permanent-magnet guideway due to different defects[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(1): 3600107.
[26] Laurent P, Vanderbemden P, Meslin S, et al. Measurements of thermal effects in a bulk YBCO single domain superconductor submitted to a variable magnetic field[J]. IEEE Transactions on Applied Superconductivity, 2007, 17(2): 3036-3039.
[27] 温鹏. 磁浮动态激扰下高温超导块材温升与悬浮特性研究[D]. 成都: 西南交通大学, 2021.
Wen Peng. Study on temperature rise and suspension characteristics of high temperature superconducting bulk under dynamic excitation of maglev[D]. Chengdu: Southwest Jiaotong University, 2021.
[28] 陈楠. 永磁轨道磁场波动下高温超导块材温升与悬浮行为研究[D]. 成都: 西南交通大学, 2021.
Chen Nan. Study on temperature rise and suspension behavior of high temperature superconducting bulk under fluctuation of permanent magnet track magnetic field[D]. Chengdu: Southwest Jiaotong University, 2021.
[29] Zheng Jun, Wei Minghui, Quan Siyi, et al. Review on thermal-related measurement methods for superco-nducting devices and prospect for high-speed maglev transportation application[J]. Superconductivity, 2022, 3: 100020.
[30] Huang Chenguang, Xu Bin, Zhou Youhe. Dynamic simulations of actual superconducting maglev systems considering thermal and rotational effects[J]. Superconductor Science Technology, 2019, 32(4): 045002.
[31] Mizuno K, Tanaka M, Ogata M. Monitoring and protection method of a REBCO magnet designed for electromagnetic vibration tests[J]. Quarterly Report of RTRI, 2020, 61(1): 60-65.
[32] Kio A E, Xu Jin, Gautam N, et al. Wavelet decomposition and neural networks: a potent combination for short term wind speed and power forecasting[J]. Frontiers in Energy Research, 2024, 12: 1277464.
[33] Kuncan M. An intelligent approach for bearing fault diagnosis: combination of 1D-LBP and GRA[J]. IEEE Access, 2020, 8: 137517-137529.
[34] Yazdani-Asrami M, Sadeghi A, Song Wenjuan, et al. Artificial intelligence methods for applied superconductivity: material, design, manufacturing, testing, operation, and condition monitoring[J]. Superconductor Science Technology, 2022, 35(12): 123001.
[35] Yazdani-Asrami M, Song Wenjuan, Morandi A, et al. Roadmap on artificial intelligence and big data techniques for superconductivity[J]. Superconductor Science and Technology, 2023, 36(4): 043501.
[36] Yazdani-Asrami M, Sadeghi A, Seyyedbarzegar S M, et al. Advanced experimental-based data-driven model for the electromechanical behavior of twisted YBCO tapes considering thermomagnetic constraints[J]. Superconductor Science and Technology, 2022, 35(5): 054004.
[37] 车通. 高温超导钉扎磁浮动态特性及改善方法研究[D]. 成都: 西南交通大学, 2016.
Che Tong. Study on dynamic characteristic and its improvement method of high temperature superconducting maglev[D]. Chengdu: Southwest Jiaotong University, 2016.
[38] 张玲玲, 肖静. 基于MATLAB的机械故障诊断技术案例教程[M]. 北京: 高等教育出版社, 2016.
[39] 一种基于深度学习的超导悬浮器内部温升检测方法及装置[P]. 中国: CN117537951B. 2024-04-01.
[40] Lei Wuyang, Deng Zigang, Zheng Jun. A non-contact measuring method for the joint size and geometry irregularity of Halbach permanent magnet guideway in the high-temperature superconducting maglev system[J]. Measurement, 2024, 227: 114306.
[41] Zheng Jun, Huang Huan, Zhang Shuai, et al. A general method to simulate the electromagnetic characteristics of HTS maglev systems by finite element software[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(5): 3600808.
[42] Lei Wuyang, Wang Zihan, Zheng Jun, et al. A 6 degrees of freedom electromagnetic-thermal-dynamic coupling model for high-temperature superconducting levitation system[J]. Journal of Applied Physics, 2023, 134(20): 203903.
Abstract On January 13, 2021, the first high-temperature superconducting (HTS) pinning high-speed maglev engineering vehicle was launched in Chengdu, China, marking that HTS maglev technology has entered the stage of engineering research. The temperature rise of the HTS bulk in the superconducting levitator and the relevant operation parameters directly determine the safe and stable operation of maglev train. It is urgent to carry out the research of intelligent state recognition theory and test platform to promote the technology development for safe operation of HTS maglev. The temperature rise of the HTS bulk in the superconducting levitator directly determines the levitation performance of the HTS maglev system. However, due to the limitation of the internal structure space inside the superconducting levitator, it is difficult to put in many temperature sensors. On the other hand, although the temperature sensor can directly measure the real-time temperature inside the HTS bulk, it may damage the structure of the HTS bulk. Therefore, a new non-contact temperature rise measurement method combining the thermal-vibration characteristics of the HTS bulk and BP neural network (BPNN) is proposed in this paper, which can achieve a high temperature rise recognition rate.
Firstly, a test device for thermal-vibration characteristics of the HTS bulk was built in this paper and an alternating magnetic field (MF) was generated by Halbach permanent magnet (PM) wheel. The temperature rise and dynamic force change of the HTS bulk at 0~4000 r/min were tested experimentally. It was found that the internal temperature rise of the HTS bulk increases progressively with the frequency of the alternating MF generated by the PM wheel. At the same time, based on the temperature rise and vibration data, the vibration acceleration features are extracted by wavelet decomposition, and the temperature rise is identified by BPNN with an accuracy of over 99.9%.
Then, to further verify the effectiveness of wavelet decomposition combined with BPNN in temperature identification of the HTS bulk under the excitation of a real permanent magnet guideway (PMG), the thermal-vibration characteristics of the HTS bulk were studied in combination with the real MF provided by opposite-pole PMG used in the testing equipment of SCML-03. The thermal-vibration characteristics of the HTS bulk under the abnormal excitation of the PMG were studied by finite element simulation. The intrinsic relationship between the dynamic characteristics of the HTS bulk and the internal temperature rise under the simulated excitation of the actual MF irregularity was studied, and the recognition accuracy was also over 99.5%.
The following conclusions can be drawn from the analysis: under the condition of alternating MF provided by PM wheel, the higher the MF change frequency, the higher the internal temperature rise of the HTS bulk, leading to a greater levitation force attenuation. The wavelet energy values of the HTS bulk are different under different fluctuating frequencies of alternating MF, and are different from traditional characteristics such as levitation height. These features can also be used as the main parameters for monitoring the HTS bulk. The non-contact intelligent temperature rise detection method in this paper does not occupy the space inside the superconducting levitator, and is suitable for the dynamic operating conditions of the HTS maglev vehicle, weakening the technical difficulty of the inside of the onboard levitators.
Keywords: Superconducting levitator, maglev train, temperature rise, vibration, BP neural network (BPNN), intelligent monitoring
中图分类号:U237
DOI: 10.19595/j.cnki.1000-6753.tces.L11047
郑 珺 女,1980年生,研究员,博士生导师,研究方向为超导磁悬浮技术、机电耦合理论与方法、智能监测与预测。
E-mail:jzheng@swjtu.edu.cn(通信作者)
庞 鹏 男,1993年生,博士研究生,研究方向为高温超导磁浮系统的有限元仿真及在线监测技术。
E-mail:pangp@my.swjtu.edu.cn
(编辑 郭丽军)