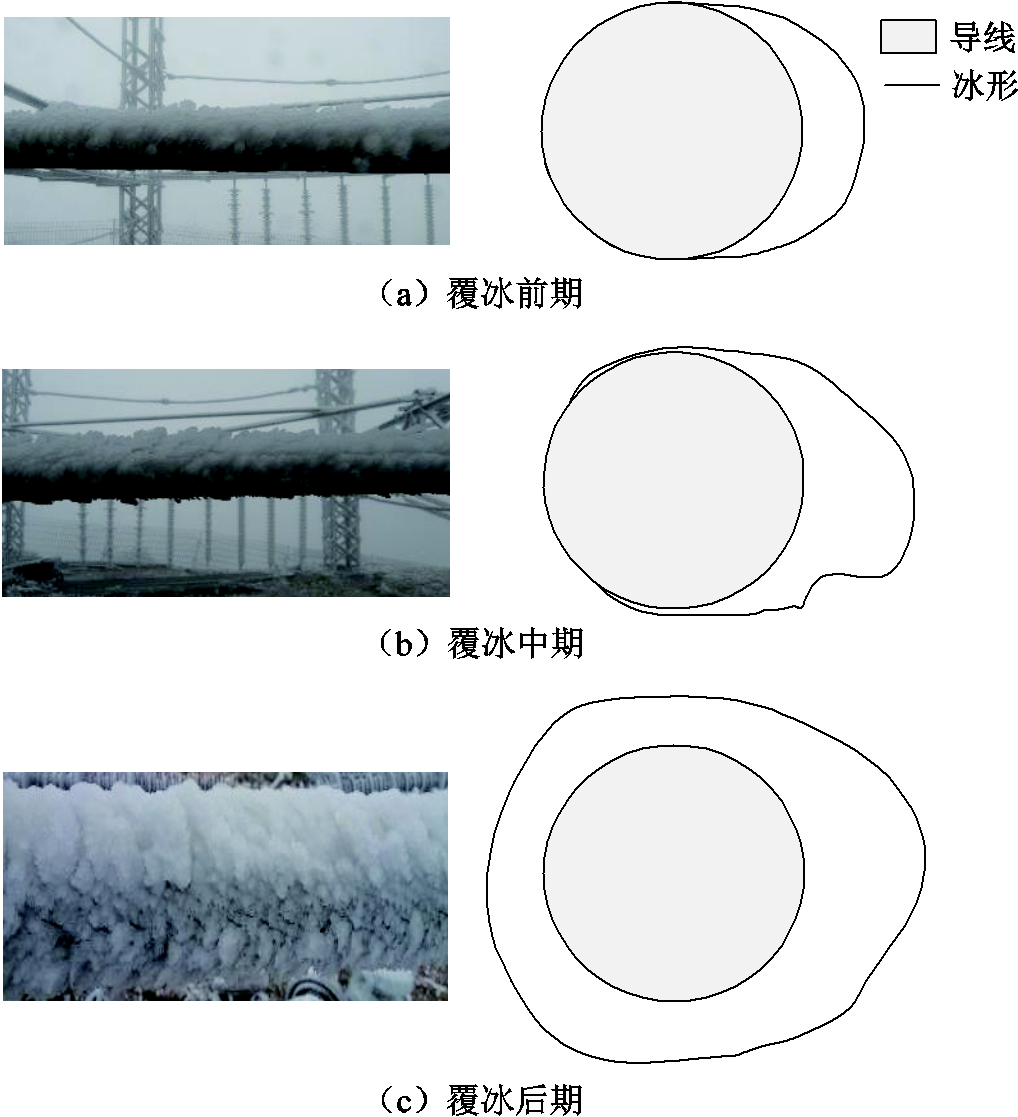
图1 输电线路单导线覆冰形状变化
Fig.1 Improvement of ice shape on conductor
摘要 直流大电流融冰是输电线路冰灾防御的有效手段。根据实际运行条件下输电线路单导线覆冰形状在导线各处不一的情况,计算分析单导线圆形覆冰和翼形覆冰的直流大电流融冰时间。计算结果表明,翼形冰融冰时间仅为圆形冰融冰时间的10%左右。在重庆大学雪峰山能源装备安全国家野外观测研究站对LGJ—300/50和LGJ—400/35两种型号单导线进行直流大电流融冰实验。实验结果表明:LGJ—300/50导线翼形冰融冰时间为圆形冰融冰时间的10.6%,LGJ—400/35导线翼形冰融冰时间为圆形冰融冰时间的8.3%。基于此,该文提出抑制导线形成圆形冰促使其生长为翼形冰可降低直流大电流融冰时间,减少融冰能量消耗。
关键词:输电线路 圆形冰 翼形冰 融冰时间 直流大电流
我国输电线路长期遭受冰灾威胁。在冬季,输电线路冰灾已经成为严重威胁我国电网安全的重要原因之一[1]。自2008年南方重大冰灾后,我国已在输电线路冰灾防御方面取得一定进展,有效防止了大面积、长时间的大电网冰灾发生[2-3]。随着我国电网建设的不断推进和特高压、超高压工程的大力发展,越来越多的输电线路不可避免地需要穿过低温高湿的易覆冰区。输电线路冰灾防御形势依旧严峻,相关研究仍需大力推进[4]。
除冰是输电线路覆冰后的最佳应对方式。经过国内外学者的持续努力,研究开发了数十种输电线路除冰方法。按照其工作原理可分为机械除冰法、热力融冰法和被动除冰法等。J. C. Pohlman最早提出了“AD HOC”的机械除冰方法,除冰时,工作人员通过各种途径敲击输电线路冰层使其脱落[5]。发展至今,机械除冰依然是研究人员关注的重点。A. Leblond开发了通过爆炸产生冲击力的机械除冰装置,T. Kalman等验证了100 m档距下冲击机械力除冰的效果[6-8]。胡琴等开展了电磁脉冲除冰系统用于地线除冰的试验研究[9]。热力融冰主要是通过加大导线电流,通过焦耳热效应使导线表面冰层脱落。文献[10]开展了电力设备热水除冰研究,提出利用无人机喷射高压热水的热力融冰方法。被动除冰法指的是在导线表面刷防冰涂料、加装防除冰设备、改变输电线路结构等非人工干预式防除冰方法[11-14]。尽管除冰方法众多,但实践证明,直流大电流融冰仍旧是最为广泛采用的除冰方式[15-16]。然而其缺点同样明显,每次融冰均需线路停电接入融冰设备,融冰时间长,能源消耗高[4,17]。输电线路覆冰情况与直流大电流融冰工作息息相关,既决定了融冰电流的大小,也决定了融冰时间的长短。掌握输电线路覆冰规律对于推动直流大电流融冰技术发展至关重要。
重庆大学蒋兴良等于1998年对三峡地区输电线路进行长期观测,对导线覆冰进行数值仿真分析,获取了输电线路与大气覆冰环境参数的关系[18]。庄文兵、桂重、胡京等指出输电线路覆冰具有典型的“微地形、小气候”特性,输电线路常因局部地形的改变引发气象因子变化,促进输电线路覆冰[19-22]。郝艳捧等[23]则进一步提出了考虑特殊地形的输电线路等值覆冰厚度计算模型。何青等[24]从导线覆冰的物理过程出发,优化了冻结系数的计算方法,提高了导线覆冰仿真分析的准确性。黄新波等[25]考虑了输电线路冰层表面粗糙度对冰层对流换热的影响,通过数值模拟研究输电线路结冰过程的热交换规律,提升了导线覆冰仿真分析效率。文献[26-27]采用有限元方法对输电线路覆冰过程进行动态模拟,实现了对输电线路覆冰情况的实时获取。文献[28]建立了输电线路扭转覆冰的数值仿真模型,实现了输电线路圆形冰的数值模拟。韩兴波等[29]分析了导线扭转和覆冰发展的相互影响机制,说明了扭转是输电线路覆冰的重要影响因素。
综上所述,直流大电流融冰技术仍旧是现阶段输电线路冰灾防御的首选方法。尽管研究人员对输电线路覆冰过程、机理的研究越发深入,但对直流大电流融冰技术而言,却只能更好地确定融冰电流和启动时间,优化融冰工作流程。并没有很好地解决直流融冰时间长、能源消耗高的问题。基于此,本文以输电线路单导线覆冰形状为研究主体,分析翼形冰和圆形冰融冰时间的差别,并开展野外自然融冰实验研究。由此提出改变输电线路覆冰形状来降低输电线路直流大电流融冰时间且减少融冰能耗的方法。本文的研究成果可为输电线路除冰工作及电网冰灾防御研究人员提供参考。
图1所示为野外自然环境下导线覆冰形状随覆冰发展的变化情况。输电线路覆冰由空气中过冷却水滴随气流运动遭遇导线后在导线表面冻结凝固而成。因此,覆冰首先在导线迎风侧发生,随着过冷却水滴冻结数量的增加,覆冰在导线表面逐渐累积为图1a所示的翼形冰。

图1 输电线路单导线覆冰形状变化
Fig.1 Improvement of ice shape on conductor
随着覆冰时间增加,导线覆冰质量逐步增长,导线在覆冰带动下绕其中心扭转一定角度。原本位于背风侧的导线在扭转后转向迎风侧;位于迎风侧的冰层也从翼形冰的前缘部分改变为翼形冰的上表面部分,覆冰继续在导线迎风侧增长,如图1b所示。此后,反复出现覆冰质量增加到一定程度后冰层带动导线扭转一定角度的情况,导线覆冰形状也由之前的翼形逐渐向圆形发展,最终呈现为圆形冰,如图1c所示。
由上述分析可知,导线在冰层带动下自由扭转是导线覆冰形状呈现圆形的根本原因。导线自身具备一定的抗扭转能力,用扭转刚度表征。扭转刚度越大,导线覆冰时越不容易发生扭转,越难形成圆形冰。对铝钢绞线,其扭转刚度为
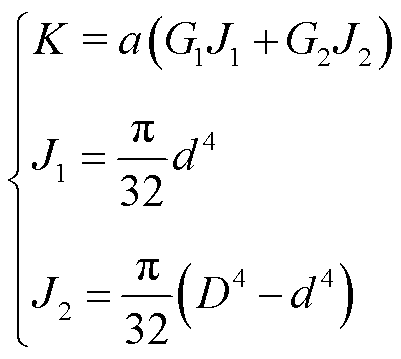 (1)
(1)
式中,K为导线的扭转刚度,N·m2/rad ;a为绕拧系数;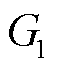 为钢芯的扭转弹性模量,Pa;
为钢芯的扭转弹性模量,Pa;![]() 为铝绞层的扭转弹性模量,Pa;
为铝绞层的扭转弹性模量,Pa;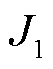 为钢芯层的扭转极惯性矩,m4;
为钢芯层的扭转极惯性矩,m4;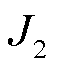 为铝绞线层的扭转极惯性矩,m4;D为导线直径,m;d为钢芯层直径,m。
为铝绞线层的扭转极惯性矩,m4;D为导线直径,m;d为钢芯层直径,m。
由式(1)可知,导线的扭转刚度为其固有属性。但对于两端固定的架空单导线,导线沿线的扭转刚度分布不均。长为L的导线上j处的扭转刚度可等效为长度为xj的导线与长度为L-xj的导线并联的等效扭转刚度K( j )[30],即
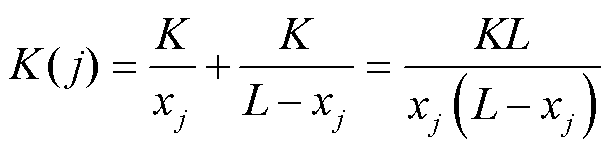 (2)
(2)
分析式(2)可知,长度一定的架空单导线,越靠近导线中心点,其等效扭转刚度越低;而越靠近导线两侧悬挂点,导线等效扭转刚度越高。因此,输电线路覆冰时,从导线的两端悬挂点出发,越靠近导线中心,导线覆冰形状越接近于圆形;而越靠近导线两端悬挂点,导线形状越接近于翼形。
单导线圆形冰融冰可分为三个阶段:首先是导线覆冰粘结力失效阶段。在大电流产生的焦耳热效应下,导线和冰层温度开始逐步升高。一定时间后,导线外表面与冰层内表面温度达到0℃,在导线与冰层之间形成水膜。此时,冰层与导线之间的粘结力失效,随即进入第二阶段,即冰层旋转阶段。冰层与导线粘结力失效后,在重力作用下发生旋转,覆冰较薄的一侧质量更轻,旋转之后位于导线上方。第一阶段形成的水膜从冰层的微孔当中流出[31],空气随之流入填充于导线与冰层之间形成气隙。最后是导线上方冰层融化阶段。位于导线正上方的冰层在电流作用下不断融化,冰层厚度逐渐降低,直至其全部融化后圆形冰从导线表面脱落,融冰结束。
根据前文分析,翼形冰由导线不扭转时过冷却水滴在导线迎风侧累积而成,因此其背风侧几乎不发生覆冰。因此,本文认为翼形冰融冰在导线覆冰粘结力失效后即刻结束,并做出如下规定:
(1)不考虑冰层表面粗糙度及冰棱的影响。
(2)导线大电流融冰过程中,忽略阳光辐射和导线脱冰跳跃等外部机械力的作用。
(3)导线外表面与翼形冰内表面之间因加热产生水膜后,翼形冰即刻脱离导线。
导线加电流融冰的关键参量为融冰电流与融冰时间。实际融冰时,覆冰环境保持不变,覆冰将继续发展,且单根导线中只能通过一个确定的电流,即不能针对导线各处覆冰形状不一而提供不同大小的电流。因此,本文主要分析覆冰环境一致且融冰电流相同的情况下,圆形冰和翼形冰融冰时间的差别。
图2所示为覆冰单导线圆形冰融冰过程的热平衡示意图。电流产生的焦耳热使导线外表面与冰层内表面产生水膜时,热量主要在钢芯(Φ1)、铝芯(Φ2)和冰层(Φ4)之间传递,其所需时间为[31]
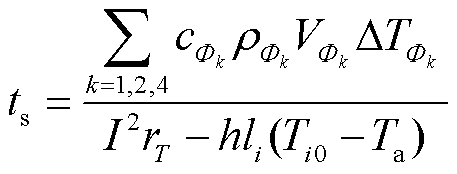 (3)
(3)
式中,ts为圆形冰内部形成水膜的时间,同时也为翼形冰的融冰时间,在后文中,未做特别说明时,ts均表示翼形冰的融冰时间,s;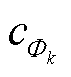 为
为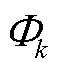 区域的比热容,J/(kg·℃);
区域的比热容,J/(kg·℃);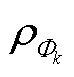 为Φk的密度,kg/m3;
为Φk的密度,kg/m3;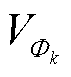 为区域
为区域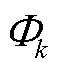 的体积,m3;
的体积,m3;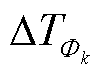 为Φk区域的温升,℃;I为融冰电流,A;
为Φk区域的温升,℃;I为融冰电流,A;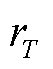 为温度为T时导线的电阻率,Ω/m;h为冰层外表面与环境对流传热和辐射换热的表面传热系数,W/(m2·K);
为温度为T时导线的电阻率,Ω/m;h为冰层外表面与环境对流传热和辐射换热的表面传热系数,W/(m2·K);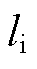 为覆冰外表面表面积,m2;
为覆冰外表面表面积,m2;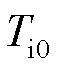 为冰层内部温度为0时,冰层外表面的温度,℃;
为冰层内部温度为0时,冰层外表面的温度,℃;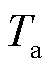 为环境温度,℃。
为环境温度,℃。
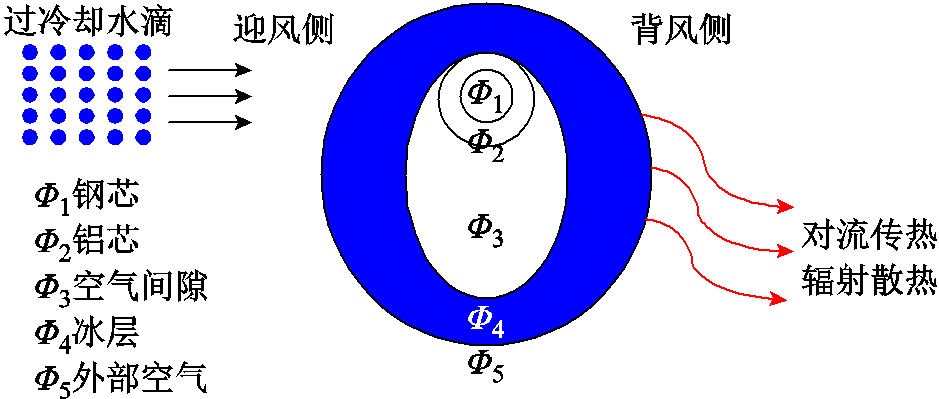
图2 单导线圆形冰融冰过程的热平衡示意图
Fig.2 Sketch of heat balance about circular ice on transmission lines
表面传热系数可由式(4)获取。
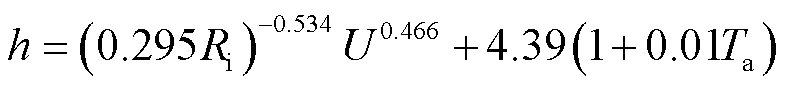 (4)
(4)
式中,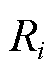 为导线覆冰后导线与冰层形成的圆柱体的半径,m;U为环境风速,m/s。
为导线覆冰后导线与冰层形成的圆柱体的半径,m;U为环境风速,m/s。
圆形冰的融化时间可由式(5)获取。
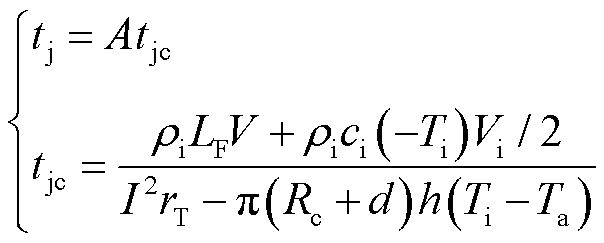 (5)
(5)
式中,tj为圆形冰的融冰时间,s;A为校正系数,本文根据长期的野外实验数据,取A为1.2;tjc为圆形冰融化时间的初步计算公式[30];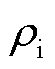 为冰层密度,kg/m³;
为冰层密度,kg/m³;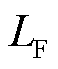 为冰的融化潜热,LF=335 kJ/kg;V为冰层融化部分的体积,m³;
为冰的融化潜热,LF=335 kJ/kg;V为冰层融化部分的体积,m³;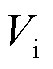 为初始状态下冰层体积,m³;
为初始状态下冰层体积,m³;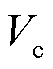 为导线体积,m³;
为导线体积,m³;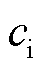 为冰的比热容,J/(kg·℃);
为冰的比热容,J/(kg·℃);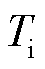 为初始时刻覆冰导体背风侧温度,℃;
为初始时刻覆冰导体背风侧温度,℃;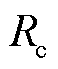 为未覆冰导线半径,m;d为冰层厚度,m。
为未覆冰导线半径,m;d为冰层厚度,m。
V可表示为
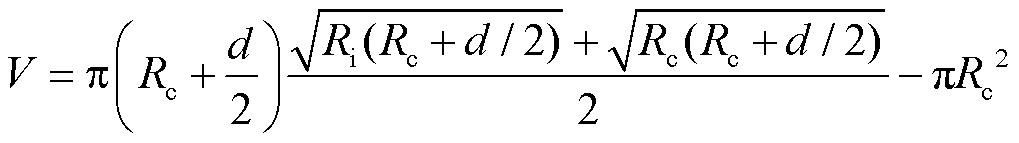 (6)
(6)
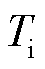 表达式为
表达式为
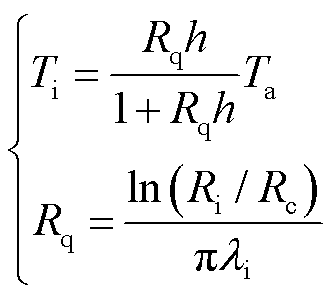 (7)
(7)
式中,Rq为冰层热阻;λi为冰层热导率,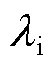 =2.22 W/(m·K)。
=2.22 W/(m·K)。
由式(3)~式(7)分别计算LGJ—240/30、LGJ—300/50、LGJ—400/35三种导线圆形冰与翼形冰的融冰时间,三种导线的基本参数见表1。
表1 导线基本技术参数
Tab.1 Basic technical parameters of wire

导线型号铝绞线钢芯外径/mm直流电阻/(Ω/km) 根数直径/mm根数直径/mm LGJ—240/30243.672.421.600.118 1 LGJ—300/50263.8372.9824.260.096 4 LGJ—400/35483.2272.526.820.073 89
计算时,覆冰厚度为10 mm,环境风速为3 m/s,环境温度为-5℃。由于不同型号导线的通流能力不同,融冰时由融冰电流密度确定电流大小。本文分别对三种型号的导线依次按照1.5 A/mm2、2 A/mm2和3 A/mm2的电流密度加载融冰电流,计算结果如表2、图3和图4所示。
表2 融冰时间计算
Tab.2 Melt-icing time of different conductors
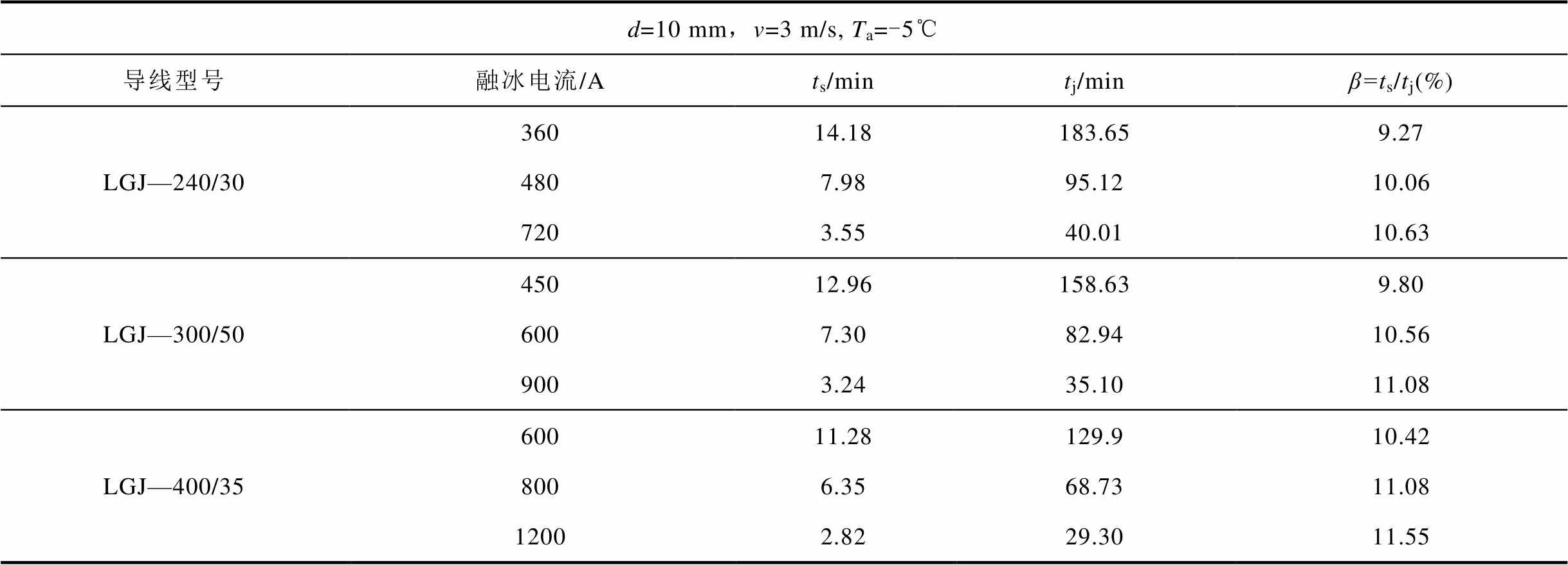
d=10 mm,v=3 m/s, Ta=-5℃ 导线型号融冰电流/Ats/mintj/minβ=ts/tj(%) LGJ—240/3036014.18183.659.27 4807.9895.1210.06 7203.5540.0110.63 LGJ—300/5045012.96158.639.80 6007.3082.9410.56 9003.2435.1011.08 LGJ—400/3560011.28129.910.42 8006.3568.7311.08 12002.8229.3011.55
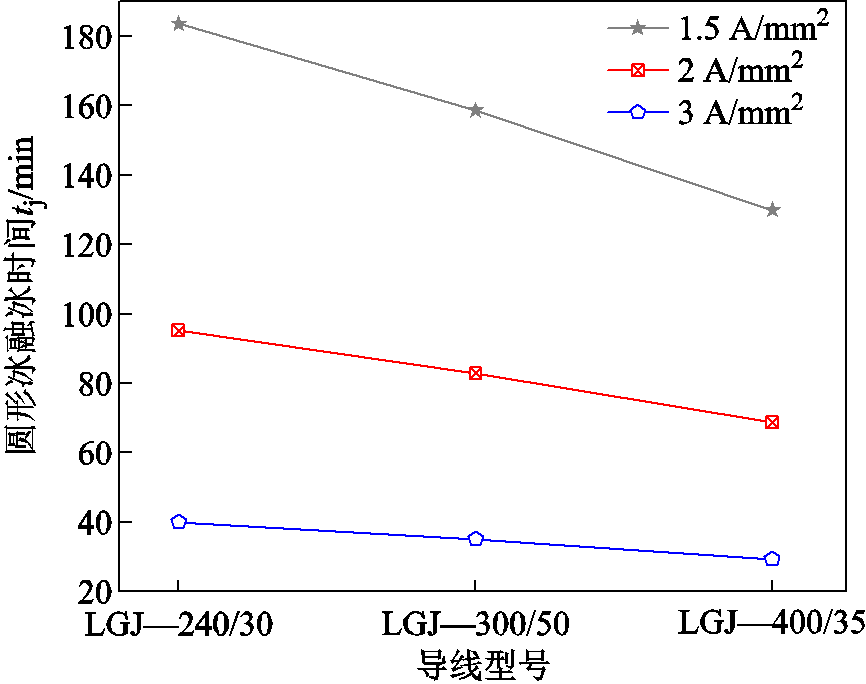
图3 各导线圆形冰融冰时间
Fig.3 Melt-icing time of circular ice on different conductors
从表2和图3可以看出,导线型号相同的情况下,融冰电流密度越大,圆形冰的融冰时间越短。当融冰电流密度从1.5 A/mm2提高到3 A/mm2后,三种导线的圆形冰融冰时间分别为原来的21.78%、22.13%和22.55%。在融冰电流密度相同的情况下,导线截面积越大,导线圆形冰融冰时间越短。当导线型号从LGJ—240/30变为LGJ—400/35后,后者在三种融冰电流密度下圆形冰融冰时间分别为前者的70.73%、72.26%和73.25%。可以看出,相同覆冰环境下,融冰电流密度比导线类型对圆形冰融冰时间的影响更大。
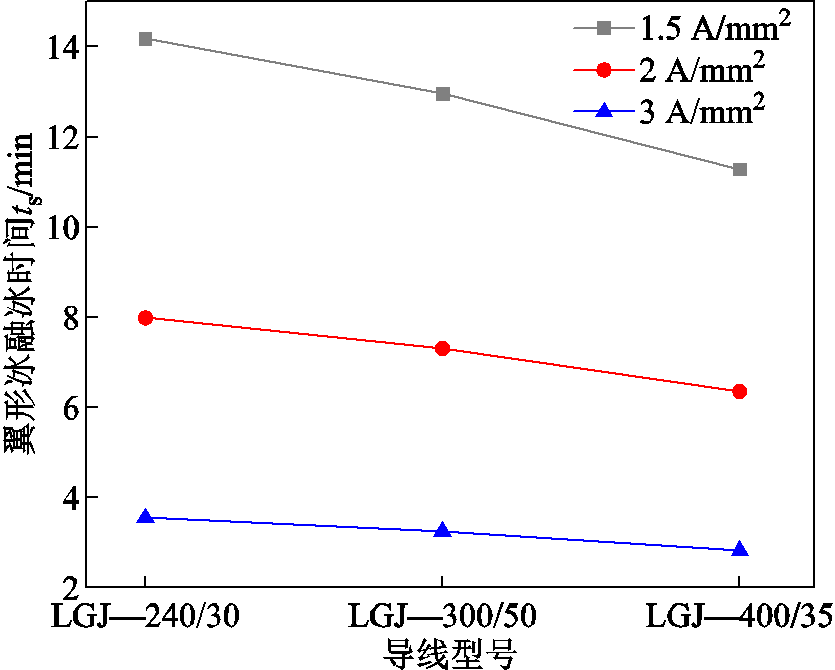
图4 各导线翼形冰融冰时间
Fig.4 Melt-icing time of wing ice on different conductors
由表2和图4可以看出,翼形冰的融冰时间随融冰电流密度和导线型号的变化规律与圆形冰一致。但在数值上,翼形冰的融冰时间远小于圆形冰。定义β为输电线路翼形冰融冰时间ts与圆形变融冰时间tj的比值。由表2可知,β的最大值为11.55%,最小值为9.27%,平均值为10.49%,即单导线翼形冰的融冰时间约为圆形冰的10%。在导线型号相同的情况下,β随融冰电流密度的增加而增加,以融冰电流密度1.5 A/mm2为基准,LGJ—240/30导线在融冰电流密度为2 A/mm2时β增长比例最大,为8.52%。在融冰电流密度相同的情况下,β随导线截面变大而变大,以LGJ—240/30导线为基准,LGJ—300/50导线在融冰电流为2 A/mm2时β增长比例最大,为12.41%。
本文在“雪峰山国家野外站”开展单导线野外自然环境大电流加热融冰实验。实验布置如图5所示,LGJ—300/50导线和LGJ—400/35导线架设在两座雨凇塔之间,长度均为100 m。在雨凇塔一侧用300 mm2的纱编织铜线连接两根导线,另一侧通过300 mm2的纱编织铜线分别连接于整流装置两端。实验所需电流由大电流发生器经过整流装置提供,其最大输出可达5 000 A,满足融冰要求。实验前通过游标卡尺测量输电线路圆形冰厚度,为降低误差,在导线上分别采集10个位置的圆形冰测量厚度,并取其平均值作为本次融冰实验的覆冰厚度值。环境温度及风速由如图6所示布置在站内的六要素气象传感器获得,其环境温度的测量范围为(-50±0.2)℃~(+100±0.2)℃,风速的测量范围为(0~60±0.3)m/s,满足本次实验需求。
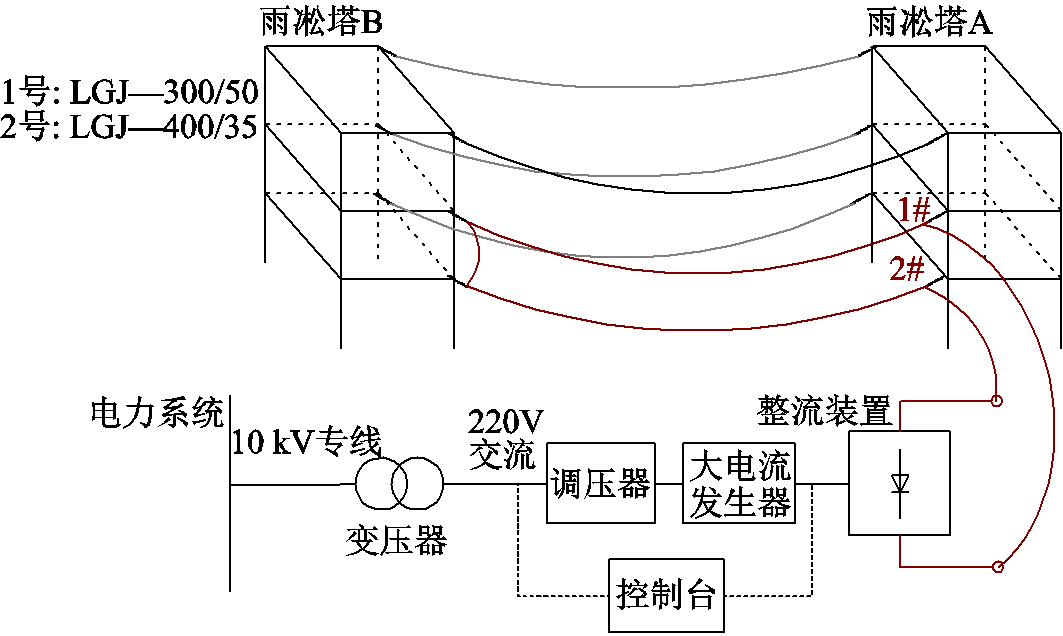
图5 野外自然融冰实验布置
Fig.5 Layout of melt-icing experiment on natural environment

图6 六要素气象传感器
Fig.6 Six elements meteorological sensor
实验前测量得到LGJ—300/50导线的覆冰厚度为15.5 mm,LGJ—400/35导线的覆冰厚度为9.3 mm。两种型号的导线在靠近雨凇塔一侧覆冰均呈翼形,测量两根导线表面呈翼形冰的长度,LGJ—400/35导线两侧呈翼形冰的线路长度合计为31.5 m,LGJ—300/50导线两侧呈翼形冰的线路长度合计为25.7 m。两根导线串联后将以不同的融冰电流密度通过相同大小的电流。实验时,实验回路加载900 A的直流电流,记录导线圆形冰与翼形冰的融冰时间,并实时记录实验期间的环境温度和风速。
实验结束后求得实验期间环境温度的平均值为-3.6℃,风速的平均值为2.8 m/s。将开始融冰实验时导线覆冰厚度、导线所加融冰电流、实验期间环境温度和风速的平均值代入式(3)~式(7)得到两种导线融冰时间的计算值,将其与实验结果进行比较分析。
本次实验的实验值与计算值见表3和表4,表中各变量含义和前文一致,下标中带“cal”字表明该值为计算所得,带“mea”字表明该值为实验所得。
表3 LGJ—300/50融冰时间的计算值与实验值
Tab.3 Melt-icing time by simulation and experiment of LGJ—300/50

d=15.5 mm,v=2.8 m/s, Ta=-3.6℃, I=900 A tscal/mintsmea/mintjcal/mintjmea/minΒcal(%)Βmea(%) 4.524.7548.2344.869.410.6
表4 LGJ—400/35融冰时间的计算值与实验值
Tab.4 Melt-icing time by simulation and experiment of LGJ—400/35

d=9.3 mm,v=2.8 m/s, Ta=-3.6℃, I=900 A tscal/mintsmea/mintjcal/mintjmea/minΒcal(%)Βmea(%) 3.733.4738.3342.059.78.3
根据式(8)得到各值的计算误差见表5。
 (8)
(8)
表5 计算值与实验值的计算误差
Tab.5 Errors of simulation and experiment (%)

导线型号ts计算误差tj计算误差β计算误差 LGJ—300/504.847.5111.32 LGJ—400/357.498.8416.87
由表3~表5可知:
LGJ—300/50导线翼形冰融冰时间远小于圆形冰融冰时间,实验时,翼形冰融冰时间占圆形冰融冰时间的10.6%。翼形冰融冰时间的实验值比计算值大;圆形冰融冰时间实验值比计算值小;翼形冰融冰时间占圆形冰融冰时间的比值上,实验结果比计算结果大。在计算误差上,导线圆形冰与翼形冰融冰时间的计算误差均小于10%,β值的计算误差最大,为11.32%,ts的计算误差最小,为4.84%。
LGJ—400/35导线翼形冰融冰时间远小于圆形冰融冰时间,实验时,翼形冰的融冰时间占圆形冰融冰时间的8.3%。翼形冰融冰时间实验值比计算值小;圆形冰融冰时间实验值比计算值大;翼形冰融冰时间占圆形冰融冰时间的比值上,实验结果比计算结果小。在计算误差上,导线圆形冰与翼形冰融冰时间的计算误差均小于10%,β值的计算误差最大,为16.87%,ts的计算误差最小,为7.49%。
两种型号导线计算误差均为β最大,ts最小的原因为:β为无量纲比值,比值项自身具备误差时,再度计算使其误差变大。按照本文对ts的定义,在实验中其为输电线路翼形冰发生第一次脱落时记录的值,因此其比较精准。
但事实上,导线所有翼形冰并不是同时脱离导线表面。原因在于越靠近导线中心点,翼形冰会跟随导线一起发生扭转,并非严格与导线截面保持水平状态,从而导致翼形冰的背侧会生成部分冰层。因此,到ts时间后翼形冰与导线粘结失效后并未直接脱离导线,而是和圆形冰一样发生旋转,直到其背部的冰层融化后才最终脱离导线表面。为进一步分析翼形冰实际脱落时间与圆形冰脱落时间的差异,从导线第一次翼形冰发生脱落起,分别记录两根导线翼形冰每次脱落发生的时间和长度,直到翼形冰全部脱落为止。
翼形冰单次脱落时间点及长度如图7所示。从图中可以看出,LGJ—300/50导线表面翼形冰脱落共发生4次,单次脱落的最大长度为9.7 m,最后一次脱落发生在融冰开始后的第15.2 min,翼形冰融冰时间占圆形冰融冰时间的33.88%。LGJ—400/35导线发生了5次翼形冰脱落。单次脱落的最大长度为12.2 m,并在融冰开始后的第14.3 min,导线表面的翼形冰全部脱落。翼形冰融冰时间占导线圆形冰融冰时间的34.01%。
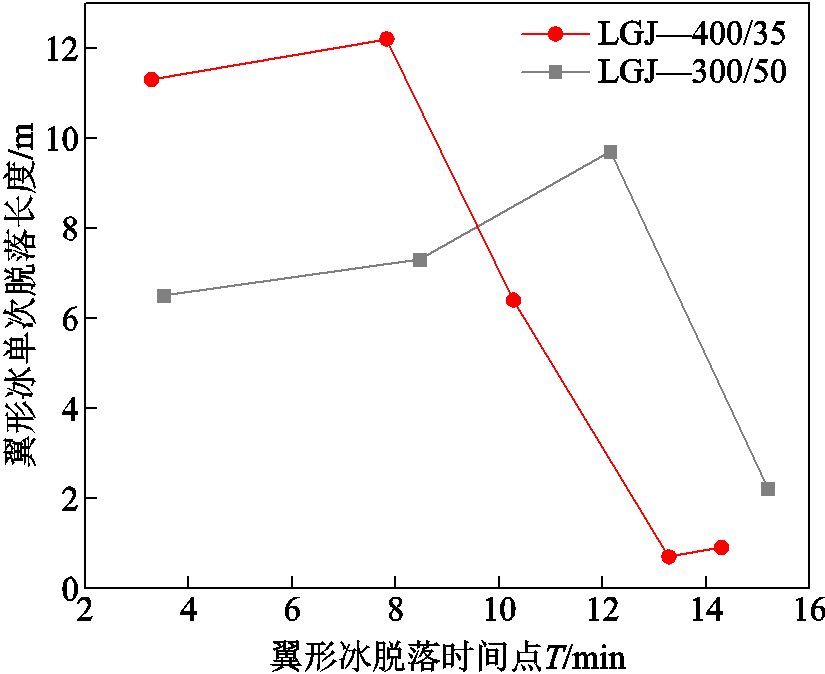
图7 翼形冰单次脱落时间点及长度
Fig.7 The length and time point when wing ice separate from conductor
1)野外自然环境下,输电线路单导线覆冰质量增加后,会带动导线绕其中心自由扭转,覆冰形状最终呈现为圆形。对于两端固定的架空输电线路,越靠近导线中心点,导线扭转刚度越低,覆冰越容易形成圆形,而越靠近导线两端悬挂点,导线覆冰形状越接近于翼形。
2)相较于圆形冰,翼形冰融冰过程更为简单,比圆形冰更快脱离导线。计算表明,单导线翼形冰的融冰时间仅为圆形冰的10%左右。
3)在雪峰山国家野外站开展单导线大电流直流融冰野外自然实验。单导线融冰时间的实验结果与计算结果的误差在10%以内,翼形冰融冰时间与圆形冰融冰时间的比值分别为10.6%和8.3%。
4)实验过程中发现,由于导线发生扭转,单导线两端有部分翼形冰在导线背风侧同样发生覆冰,从而增加了翼形冰融冰时间。以导线所有翼形冰全部脱离的时间节点为翼形冰的融冰时间,两种导线翼形冰实验时的融冰时间分别为圆形冰融冰时间的33.88%和34.01%。
5)根据本文的研究结果,若能促使单导线沿线不生成圆形冰而生成翼形冰,则直流大电流融冰时间将降低约70%~90%。其中尤以导线沿线全部形成严格的翼形冰(导线不发生扭转,背风侧无冰层累积)的效果为佳。
参考文献
[1] 蒋兴良, 易辉. 输电线路覆冰及防护[M]. 北京: 中国电力出版社, 2002.
[2] 张晓辉, 李阳, 钟嘉庆, 等. 基于安全因子及协同因子的源网多目标协调规划[J]. 电工技术学报, 2021, 36(9): 1842-1856. Zhang Xiaohui, Li Yang, Zhong Jiaqing, et al. Multi-objective coordinated planning of source network based on safety factor and coordination factor[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1842-1856.
[3] 卢志刚, 李丹, 吕雪姣, 等. 含分布式电源的冰灾下配电网多故障抢修策略[J]. 电工技术学报, 2018, 33(2): 423-432. Lu Zhigang, Li Dan, Lü Xuejiao, et al. Multiple faults repair strategy under ice storm for distribution network with distributed generators[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 423-432.
[4] 蒋兴良, 张志劲, 胡琴, 等. 再次面临电网冰雪灾害的反思与思考[J]. 高电压技术, 2018, 44(2): 463-469. Jiang Xingliang, Zhang Zhijin, Hu Qin, et al. Thinkings on the restrike of ice and snow disaster to the power grid[J]. High Voltage Engineering, 2018, 44(2): 463-469.
[5] Pohlman J C, Landers P. Present state-of-the-art of transmission line icing[J]. IEEE Transactions on Power Apparatus and Systems, 1982 (8): 2443-2450.
[6] Kálmán T, Farzaneh M, McClure G. Numerical analysis of the dynamic effects of shock-load-induced ice shedding on overhead ground wires[J]. Computers & Structures, 2007, 85(7/8): 375-384.
[7] Kalman T.Dynamic behavior of iced cables subjected to mechanical shocks[D].Chicoutimi: Université du Québec à Chicoutimi, 2007.
[8] Leblond A, Lamarche B, Bouchard D, et al.Development of a portable de-icing device for overhead ground wires[C]//Proceedings of the 11th International Workshop on Atmospheric Icing of Structures, Montreal, Canada, 2005: 399-404.
[9] 胡琴, 姜涛, 蒋兴良, 等. 地线电磁脉冲除冰系统的振动加速度试验研究[J]. 电网技术, 2022, 46(11): 4541-4548. Hu Qin, Jiang Tao, Jiang Xingliang, et al. Experimental study on vibration acceleration of ground electromagnetic pulse deicing system[J]. Power System Technology, 2022, 46(11): 4541-4548.
[10] 张志劲, 杨晟欢, 蒋兴良, 等. 电力设备热水除冰过程水射流特性[J]. 高电压技术, 2021, 47(3): 1012-1019. Zhang Zhijin, Yang Shenghuan, Jiang Xingliang, et al. Characteristics of water jet in hot water deicing process of power equipment[J]. High Voltage Engineering, 2021, 47(3): 1012-1019.
[11] 蒋兴良, 毕聪来, 王涵, 等. 倒T型布置对绝缘子串覆冰及其交流闪络特性的影响[J].电工技术学报, 2019, 34(17): 3713-3720. Jiang Xingliang, Bi Conglai, Wang Han, et al. Effect of inverted T arrangement on icing and AC flashover characteristics of insulator string[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3713-3720.
[12] 黄亚飞, 蒋兴良, 任晓东, 等. 采用涡流自热环防止输电线路冰雪灾害的方法研究[J].电工技术学报, 2021, 36(10): 2169-2177. Huang Yafei, Jiang Xingliang, Ren Xiaodong, et al. Research on prevention of snow and ice disaster of transmission lines by eddy current self-heating ring[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2169-2177.
[13] 毕聪来, 蒋兴良, 韩兴波, 等. 采用扩径导线替代分裂导线的防冰方法[J].电工技术学报, 2020, 35(11): 2469-2477. Bi Conglai, Jiang Xingliang, Han Xingbo, et al. Anti-icing method using expanded wire instead of split wire[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2469-2477.
[14] 韩兴波, 吴海涛, 郭思华, 等. 用于覆冰环境测量的旋转多导体直径选择方法研究[J].电工技术学报, 2022, 37(15): 3973-3980. Han Xingbo, Wu Haitao, Guo Sihua, et al. Research on Diameter selection method of rotating multi-conductor for Measurement of Icy Environment[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3973-3980.
[15] 夏正春. 特高压输电线的覆冰舞动及脱冰跳跃研究[D]. 武汉: 华中科技大学, 2008. Xia Zhengchun. Research on galloping and ice-shedding of ultra-high-voltage transmission conductors [D]. Wuhan: Huazhong University of Science and Technology, 2008.
[16] Meng X, Wang L, Hou L, et al. Dynamic characteristic of ice-shedding on UHV overhead transmission lines[J]. Cold Regions Science and Technology, 2011, 66(1): 44-52.
[17] 曾薇, 周羽生, 黄欣超, 等. 考虑冰层下移的输电线路高频融冰温升影响因素分析[J]. 高压电器, 2023, 59(4): 98-105. Zheng Wei,Zhou Yusheng,Huang Xinchao, et al. Influencing factors analysis of high frequency ice melting temperature rise for transmission lines considering ice moving down[J]. High Voltage Apparatus, 2023, 59(4): 98-105.
[18] 蒋兴良, 孙才新, 顾乐观, 等. 三峡地区导线覆冰的特性及雾凇覆冰模型[J]. 重庆大学学报(自然科学版), 1998, 21(2): 18-21. Jiang Xingliang, Sun Caixin, Gu Leguan, et al. Characteristics of traverse ice coating and Rime ice coating model in Three Gorges Area[J]. Journal of Chongqing University (Natural Science Edition), 1998, 21(02): 18-21.
[19] 庄文兵, 祁创, 熊小伏, 等. 计及气象因素时间累积效应的输电线路覆冰预测[J]. 电力系统保护与控制, 2019, 47(17): 6-13. Zhuang Wenbing, Qi Chuang, Xiong Xiaofu, et al. Icing prediction of transmission lines considering the time cumulative effect of meteorological factors[J]. Power System Protection and Control, 2019, 47(17): 6-13
[20] 庄文兵, 祁创, 王建, 等. 基于微气象监测的输电线路覆冰动态过程估计模型[J]. 电力系统保护与控制, 2019, 47(14): 87-94. Zhuang Wenbing, Qi Chuang, Wang Jian, et al. Based on meteorological monitoring transmission lines ice dynamic process estimation model[J]. Power System Protection and Control, 2019, 47 (14) : 87-94.
[21] 桂重. 基于输电线路临域微地形因子的覆冰厚度预测模型研究[J].电工技术, 2022(15): 140-142. Gui Zhong. Research on ice cover thickness prediction model based on microtopographic factor in adjacent region of transmission lines[J]. China Electrical Engineering, 2022(15):140-142.
[22] 胡京, 邓颖, 蒋兴良, 等. 输电线路覆冰垭口微地形的特征提取与识别方法[J]. 中国电力, 2022, 55(8): 135-142. Hu Jing, Deng Ying, Jiang Xingliang, et al. Feature extraction and recognition method of microterrain in transmission line ice pass[J]. Electric Power of China,2022,55(08):135-142.
[23] 郝艳捧, 魏发生, 王斌, 等. 特殊地形下输电线路等值覆冰厚度计算模型有效性分析和改进研究[J].电网技术, 2022, 46(7): 2786-2793. Hao Yanbao, Wei Fa-Fei, Wang Bin, et al. Effectiveness analysis and improvement of equivalent ice thickness calculation model for transmission lines under special terrain[J]. Power System Technology, 202, 46(7):2786-2793.
[24] 何青, 李军辉, 邓梦妍, 等. 架空输电导线覆冰冻结系数计算及其影响因素分析[J]. 电工技术学报, 2019, 34(19): 4162-4169. He Qing, Li Junhui, Deng Mengyan, et al. Calculation of Freezing Coefficient of Overhead Transmission Wire and Its Influencing Factors[J]. Transactions of China Electrotechnical Society,2019,34(19):4162-4169.
[25] 黄新波, 高华, 朱永灿, 等. 输电导线粗糙覆冰表面对流换热特性[J]. 高电压技术, 2018, 44(11): 3509-3516. Huang Xinbo, Gao Hua, Zhu Yongcan, et al. Characteristics of convective heat transfer on rough ice-covered surface of transmission wire[J]. High Voltage Engineering, 2018, 44(11): 3509-3516.
[26] 蒋兴良, 姜方义, 汪泉霖. 基于最优时间步长模型的输电导线雾凇覆冰预测[J]. 电工技术学报, 2018, 33(18): 4409-4418. Jiang Xingliang, Jiang Fangyi, Wang Quanlin, et al. Prediction of rime accretion on transmission line based on optimal time step model[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4408-4418.
[27] Zhang Jian, Makkonen L, He Qing. A 2D numerical study on the effect of conductor shape on icing collision efficiency[J]. Cold Regions Science and Technology, 2017, 143: 52-58.
[28] 蒋兴良, 侯乐东, 韩兴波, 等. 输电线路导线覆冰扭转特性的数值模拟[J].电工技术学报, 2020, 35(8): 1818-1826. Jiang Xingliang, Hou Ledong, Han Xingbo, et al. Numerical simulation of ice torsional characteristics of transmission line conductors[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1818-1826.
[29] 韩兴波, 吴海涛, 郭思华, 等. 输电线路单导线覆冰和扭转的相互影响机制分析[J].电工技术学报, 2022, 37(17): 4508-4516. Han Xingbo, Wu Haitao, Guo Sihua, et al. Analysis on the Interaction Mechanism of single conductor Icing and Torsion in Transmission Line[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4508-4516.
[30] 郭应龙, 李国兴, 尤传永. 输电线路舞动[M]. 北京: 中国电力出版社, 2003.
[31] 蒋兴良, 范松海, 胡建林, 等. 输电线路直流短路融冰的临界电流分析[J]. 中国电机工程学报, 2010, 30(1): 111-116. Jiang Xingliang, Fan Songhai, Hu Jianlin, et al. Critical current analysis of DC short-circuit ice melting in transmission lines[J]. Proceedings of the CSEE, 2010, 30(1): 111-116.
Abstract In winter, the icing of transmission lines has emerged as a significant threat to power grid safety. Scholars have diligently researched and developed numerous de-icing methods, categorizing them based on their working principles into mechanical, thermal melt-icing, passive, and other methods. Despite these alternatives, DC high current melt-icing technology remains the preferred choice for transmission line de-icing. This study focuses on the actual operating conditions of single wire icing shapes on transmission lines, using three wire types (LGJ-240/30, LGJ-300/50, and LGJ-400/35) to calculate and analyze the DC high current melt-icing time for both circular and wing-shaped ice.
Under the same wire type, an increase in melt-icing current density leads to a shorter melt-icing time for circular ice. For instance, when the current density increased from 1.5 A/mm² to 3 A/mm², the melt-icing time for circular ice decreased by 21.78%, 22.13%, and 22.55% for the three wire types. Similarly, with the same melt-icing current density, a larger wire cross-section results in a shorter circular ice melt-icing time. Comparing wire types from LGJ-240/30 to LGJ-400/35, the latter's melt-icing time was 70.73%, 72.26%, and 73.25% of the former across the three current densities.
The impact of melt-icing current density on circular ice melt-icing time is more significant than the wire type under the same ice-covered environment. The pattern of melt-icing time variation with current density and wire type for wing-shaped ice mirrors that of circular ice, but numerically, the melt-icing time for wing-shaped ice is notably smaller. The ratio β, representing the wing-shaped ice melt-icing time to circular ice melt-icing time, ranges from 9.27% to 11.55%, with an average of 10.49%. In natural DC high-current melt-icing, LGJ-300/50 wire's wing-shaped ice melt-icing time was 10.6% of the circular ice melt-icing time, and for LGJ-400/35 wire, it was 8.3%. Consequently, the paper suggests inhibiting circular ice formation to promote wing-shaped ice growth as a means to reduce DC high current melt-icing time and decrease energy consumption.
keywords:Powertransmission lines, circular ice, wing-shaped ice, ice-melting time, DC high current
DOI: 10.19595/j.cnki.1000-6753.tces.230088
中图分类号:TM85
中央高校基本科研业务费(2023CDJYXTD-005)和国家自然科学基金(52077018)资助项目。
收稿日期 2023-01-18
改稿日期 2023-03-16
杨国林 男,1994年生,博士研究生,研究方向为电网高压绝缘与冰灾防护。E-mail:GL_Yang@cqu.edu.cn(通信作者)
蒋兴良 男,1961年生,教授,博士生导师,研究方向为高电压与绝缘技术、能源装备安全与灾害防御。E-mail:xljiang@cqu.edu.cn
(编辑 郭丽军)