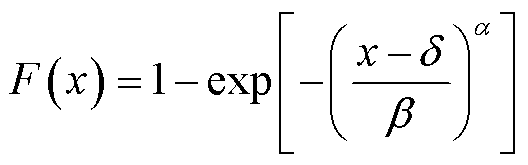 (1)
(1)
摘要 特高压直流(UHVDC)输电线路下方的离子流场是电磁环境的重要评估指标之一。风速作为常见也是影响较大的因素之一,有着明显的地域特点。为了避免资源浪费,在对地高度设计时,应考虑到不同地区的风速分布差异,而不是用过大裕度换取安全度。为此,该文提出一种基于风速概率分布与风切变指数的输电线路离子流场数值模拟方法。该方法通过待计算地区的风速数据构建Weibull风速概率分布函数模型,选择风速数据在95%以内的最大临界风速作为参考值,考虑风速传感器的安装高度,根据风切变指数计算场域不同高度处的风速分布,作为离子流场计算中不同高度节点的风速输入量。结果表明,引入风切变指数后的离子流密度与合成电场强度误差分别下降了16.2百分点和3.8百分点,明显优于传统固定风速模型。并以昆明地区某 ±800 kV直流输电线路为例,采用该方法进行了计算。该方法能够有针对性地考虑输电线路所处区域的风速影响,特别是在高海拔高风速地区,可为输电线路在合成电场安全限值下的对地高度设计提供参考依据。
关键词:特高压直流 离子流场 Weibull分布 风切变指数 数值模拟
大力建设特高压直流输电工程符合我国构建新型电力系统、实现“双碳”目标和节能减排的要求[1]。随着线路电压等级和输送功率的不断提高,输电线路周围的电磁环境问题日益突出,其中离子流场的计算分析对输电线路设计、运行和管理均有着重要的指导意义[2-4]。
在影响离子流场空间分布的环境因素中,风速是最常见也是影响最大的因素之一[5-8]。由于我国幅员辽阔,输电线路横跨范围大,不同区域的环境特点相差很大,尤其体现在风速差别上。目前学者们常采用恒定风速代替自然风速,这容易产生以下两个问题:一是造成资源浪费,虽然计算时采用的当地风速越大,离子流场计算得到的裕度就越大,但线路架设高度每提高1 m就会使工程总造价提升很多,因此不同地区应当采用不同的风速进行校核;二是与实际情况不符,由于风速与高度有关,在近地侧呈现梯度关系,因此应当考虑风速在垂直方向上的变化对离子流场的影响。
风受环境的影响很大,具有高度的随机性,需要利用概率模型来描述其统计特征。文献[9]通过对比近三十年中国各地区近地面风速的测量数据,得到了风速遵循的渐进分布,发现Weibull风速概率分布函数模型的拟合度最好;文献[10-12]也得到了相同的结论。在电力行业,Weibull风速分布的研究多用在风电场的风能评估上,文献[13]较早地使用该分布模型得到了风电统计特性;文献[14]运用该模型研究了某风电场的日平均风速、平均风能密度及风能可利用时数;文献[15]在对海上风能资源进行评估与利用时认为,为提高风速概率模型的适应性,采用该分布模型描述风的统计特性是必要的;文献[16]在研究风机系统中功率器件的可靠性时,建立了计入风电场中风速概率分布的功率器件寿命的概率评估模型。可以看到,当前以Weibull概率分布函数为代表的风速概率分布模型多用在与风电场相关的研究中,还未曾应用在输电线路的离子流场计算中,因此当前的离子流场计算研究中引入的风速模型还暂未体现地域性的风速差别。
风速除了具有地域性差异外,在近地侧,风速随高度的变化也有着显著的不同。风切变指数能够很好地描述风速在竖直方向上的变化,基于此,文献[17]引入风速与坐标节点高度的计算关系,通过仿真研究了不同风速对±800 kV输电线路离子流场分布规律的影响;文献[18]提出了考虑风梯度的自然风模型,虽然在仿真之外还进行了试验验证,但缺少与传统模型的对比分析。
鉴于此,本文提出一种基于Weibull风速概率分布与风切变指数的直流输电线路离子流场数值模拟方法。该方法通过待计算地区的风速数据构建Weibull风速概率分布函数模型,选择风速数据在95%以内的临界风速作为参考值,考虑风速传感器的安装高度,根据风切变指数计算导线下方不同高度处的风速分布,作为离子流场计算中不同高度节点的风速输入量。试验表明,引入风切变指数后的模型计算结果与试验数据相比,离子流密度与合成电场强度误差分别下降了16.3百分点和3.8百分点,明显优于传统固定风速模型。最后本文以昆明地区某±800 kV直流输电线路为例,采用本方法进行了计算,还给出了不同对地高度下的计算值作为对比。结果表明,本文提出的改进输电线路离子流场计算方法能够考虑输电线路所处地域的风速差异与近地侧的风速梯度关系,为线路在合成电场安全限值下的对地高度设计提供参考依据,判断离子流场的限值是否是影响该线路段对地高度设计的决定性因素,有助于在保证电磁环境安全的前提下,降低我国特高压直流输电工程的总造价,具备一定的指导意义和潜在的经济性效益。
风是自然界中的常见现象,会改变输电线路下方电荷的迁移方向与速度,导致地面离子流场分布受风速影响较大。因此在进行离子流场计算前,需要先分析待计算地区的风速分布特征,给出一个合理的风速校验值作为后续计算的关键输入。
风受地理因素和气候因素影响,具有波动性与随机性,需要利用概率模型描述其统计特征。常用的分布概率模型有Gumble分布、Frechet分布和Weibull分布三种[19],其中Weibull分布普遍被认为与实测风速分布具有较好的拟合度,在各个行业中得到了广泛应用。三参数的Weibull分布是一种单峰函数簇,其分布函数和概率密度分布函数分别为
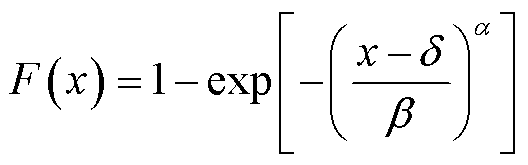 (1)
(1)
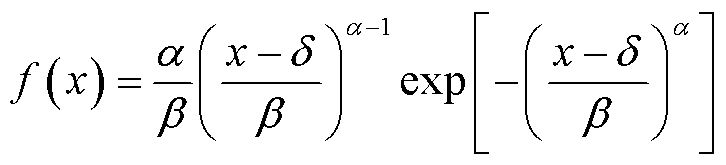 (2)
(2)
式中,x为随机变量;a为形状参数,a>0;b为尺度参数,b>0;d为位置参数,d小于随机变量中的最小值xmin。
当d=0时,公式退化为双参数Weibull分布。通过统计当地的风速数据,采用极大似然估计法可以得到Weibull分布函数的各个参数。
由于水平压力梯度力和摩擦力的作用,产生了风梯度。因此,风速随着距离地面高度的增加而增加。同时,自然风速与地形、天气有关。在地面附近时,越靠近地面阻力越大。因此当高度增加时,空气流动受到的阻力将会越小,此时风速越大,在地面处的风速接近零。垂直切面上风速随高度的变化按照以地面粗糙度为系数的指数函数规律分布,近地侧风切变指数示意图如图1所示。
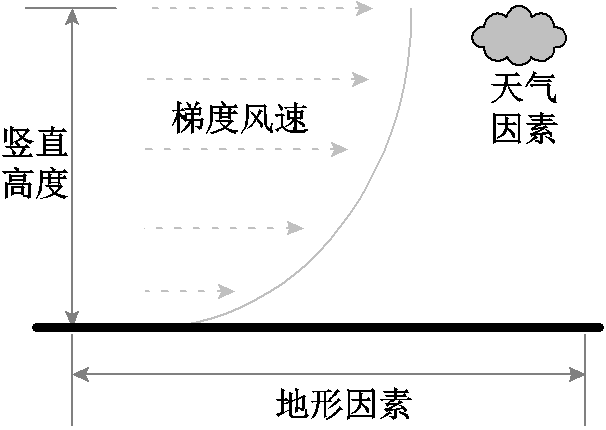
图1 近地侧风切变指数示意图
Fig.1 Schematic diagram of near-ground wind shear exponent
针对特高压直流输电线路,引入了简化的基于近地侧风切变指数的自然风速模型,该模型可表示为
![]() (3)
(3)
式中,h为某已知高度(即实测点的高度),m;Wh为该高度处的风速(即在该实测点处测得的风速),m/s;hi为某待计算节点i的高度,m;Wi为该待计算节点i的风速,m/s;τ为地形和天气系数,在晴天且平滑地形下一般取0.3。
根据气象站或实测点的实际海拔位置与测得的风速值,根据式(3),即可得出输电线路下方风速梯度的分布。
双极性输电线路的离子流场控制方程可以简化为
![]() (5)
(5)
![]() (6)
(6)
![]() (8)
(8)
![]() (9)
(9)
式中,j为电位,V;r+、r-分别为正、负空间电荷密度,C/m3;E为电场强度,V/m;k+、k-分别为正、负离子迁移率,m2/(V×s);j+、j-分别为正、负离子流密度,A/m2;W为水平方向风速,m/s;Rion为离子的复合系数;ε0为真空介电常数,ε0=8.85´10-12 F/m;e为电子电荷量,e= 1.6´10-19 C。
求解时需要的边界条件为:导线表面电位为运行电压Un;人工边界与地面为0电位;导线表面的电场强度维持在起晕场强E0,即满足Kaptzov假设。
考虑到风会对输电线路下方的离子流场分布造成很大影响,导致线路下方的电荷顺着风的方向偏移并积累,下风区的合成电场强度和离子流密度容易超过电磁环境规定的标准限值。一般情况下(风速在8 m/s以内),该状况会随着风速的增加变得更为严重[7,17],即离子流场与风速的对应关系是一个单调递增函数。因此结合之前的分析可得,大跨越的输电线路在不同地区应当采用不同的风速进行校核,且由于风速与高度有关,在近地侧呈现梯度关系,求解时也应当考虑风速在垂直方向上的变化对离子流场的影响。
按照国家标准GB 39220—2020《直流输电工程合成电场限值及其监测方法》[20]中的规定,用累计百分合成电场值En来表示电场强度的限值,如E95、E80分别表示95%、80%的测量时间内测量数据绝对值小于或等于E95、E80。为控制合成电场所致公众曝露,直流架空输电线路下方的合成电场强度E95的限值为30 kV/m,且应给出警示和防护指示标志。考虑到风速与离子流场的对应关系,将一个时间段内的风速测量数据绝对值从小到大排序,则第95%个风速数据对应的合成电场强度值即为E95,只要风速不超标,则E95的值同样不会超标。结合式(1)与式(2)可知,由于风速按照概率密度分布,在拟合出风速的Weibull分布函数后就可以很方便地从中截取前95%的区域,用其中的最大临界风速作为该区域的风速校核值。再结合测速点的高度,通过式(3)就可以得到最终离子流场计算中不同高度节点上应当采用的风速。
以正离子为例,将式(1)与式(3)代入式(6),可得
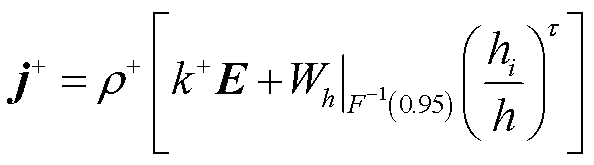 (10)
(10)
式中,![]() 为风速分布函数F中前95%对应的临界最大风速。
为风速分布函数F中前95%对应的临界最大风速。
在有限元求解中,节点i处的电荷密度满足方程
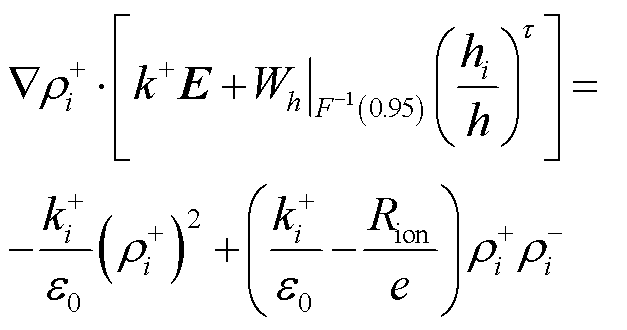 (11)
(11)
综上所述,本文提出的基于风速概率分布与风切变指数的输电线路离子流场数值模拟方法计算流程如图2所示。
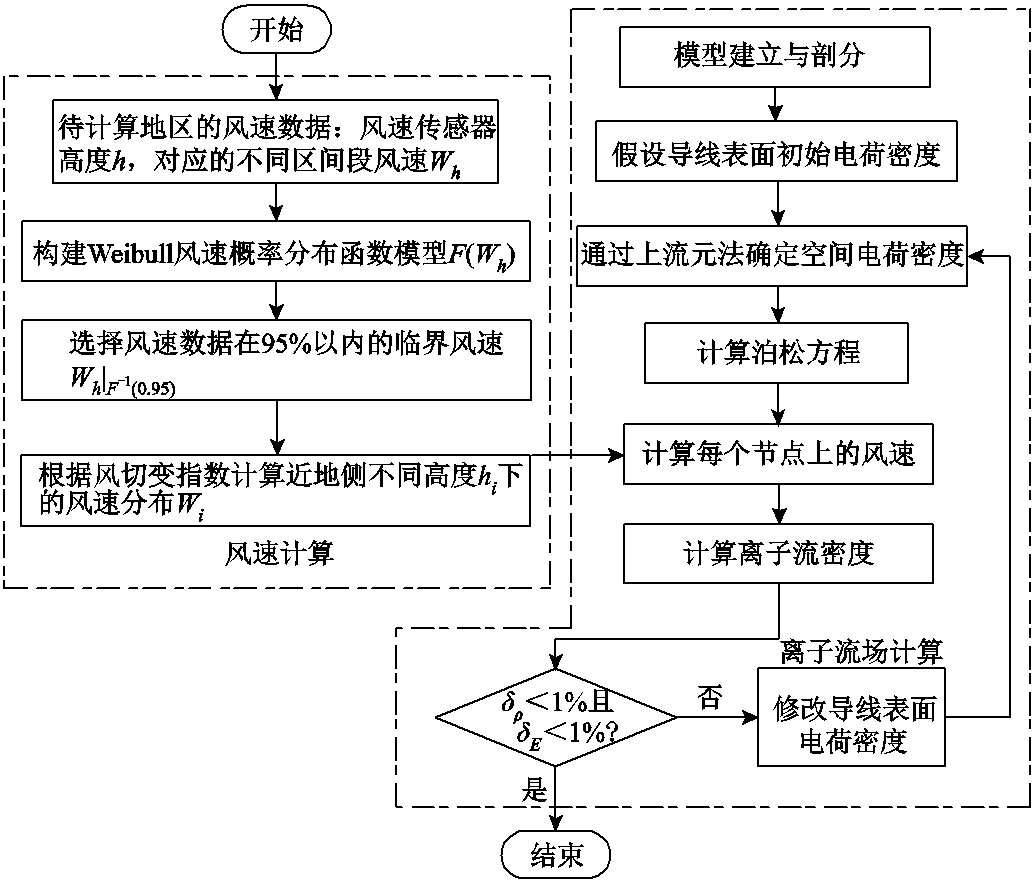
图2 计算流程
Fig.2 Calculation flow chart
计算方法分为风速计算与离子流场计算两部分。在风速计算部分中,根据待计算地区的风速数据构建Weibull风速概率分布函数模型,选择风速数据在95%以内的临界最大风速作为参考值,考虑风速传感器的安装高度,根据风切变指数计算导线下方不同高度处的风速分布,作为离子流场计算中不同高度节点的风速输入。
在离子流场计算中,认为导线起晕后表面电场强度保持不变,即Kaptzov假设,采用迭代方法进行求解,先假定空间各节点电荷密度初值,由泊松方程计算得到各节点电位及电场强度,根据空间各节点电场强度,采用上流元电荷密度更新方法计算各点电荷密度[21],再根据新的空间电荷密度分布计算得到新的电位及电场强度,通过对比导线表面电场强度与起晕电场强度的差异更新导线表面电荷密度,再重新迭代计算,直到满足导线表面电场强度与起晕电场强度的误差![]() <1%,以及求解场域内各节点电荷密度前后两次迭代步之间误差
<1%,以及求解场域内各节点电荷密度前后两次迭代步之间误差![]() <1%,认为计算达到稳态。
<1%,认为计算达到稳态。
本文提出的方法通过风速概率分布函数考虑了风速的地域性差别,通过风切变指数考虑了风速在近地侧的高度差别,因此有着很强的工程实用性。
首先对引入风切变指数后的计算模型的准确性进行验证。试验地点为昆明地区某户外试验场,线路电压等级为±800 kV,导线为6分裂,子导线半径为1.68 cm,子导线横截面积为630 mm2,导线对地高度为16.5 m,极间距为22 m,海拔约为2 000 m,晴朗天气。试验测量的风速方向为从负极性导线(上风区)指向正极性导线(下风区),风速测量点距地面1 m,风速保持在0.5~1 m/s之间。离子流场的测量点布置如图3所示,试验现场如图4所示。
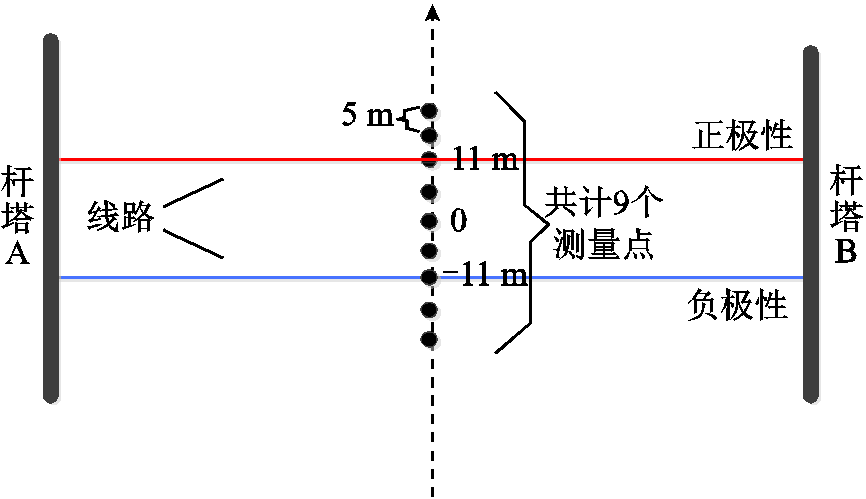
图3 测量点布置
Fig.3 Layout of measuring points
由于风速一直在小范围内波动,因此试验时每个测量点的结果取三次测量得到的平均值,仿真时按照风速范围的平均值0.75 m/s进行校核。同时高海拔地区要对子导线起晕电场强度、离子迁移率、复合系数等参数进行修正[18,22],其中子导线起晕电场强度的变化对结果影响最大。将海拔影响转换为相对空气密度的影响,再代入Peek公式中求得正、负极性的子导线起晕电场强度修正值分别为14.57 kV/cm与14.07 kV/cm。进一步,为简化整个计算过程,根据电晕程度等效方法[23],可以将分裂子导线的起晕电场强度转换为等效单根的起晕电场强度。

图4 试验现场
Fig.4 Photo of test
考虑风切变指数和传统固定风速方法的计算结果与自然风情况下实际测量结果的对比如图5所示。
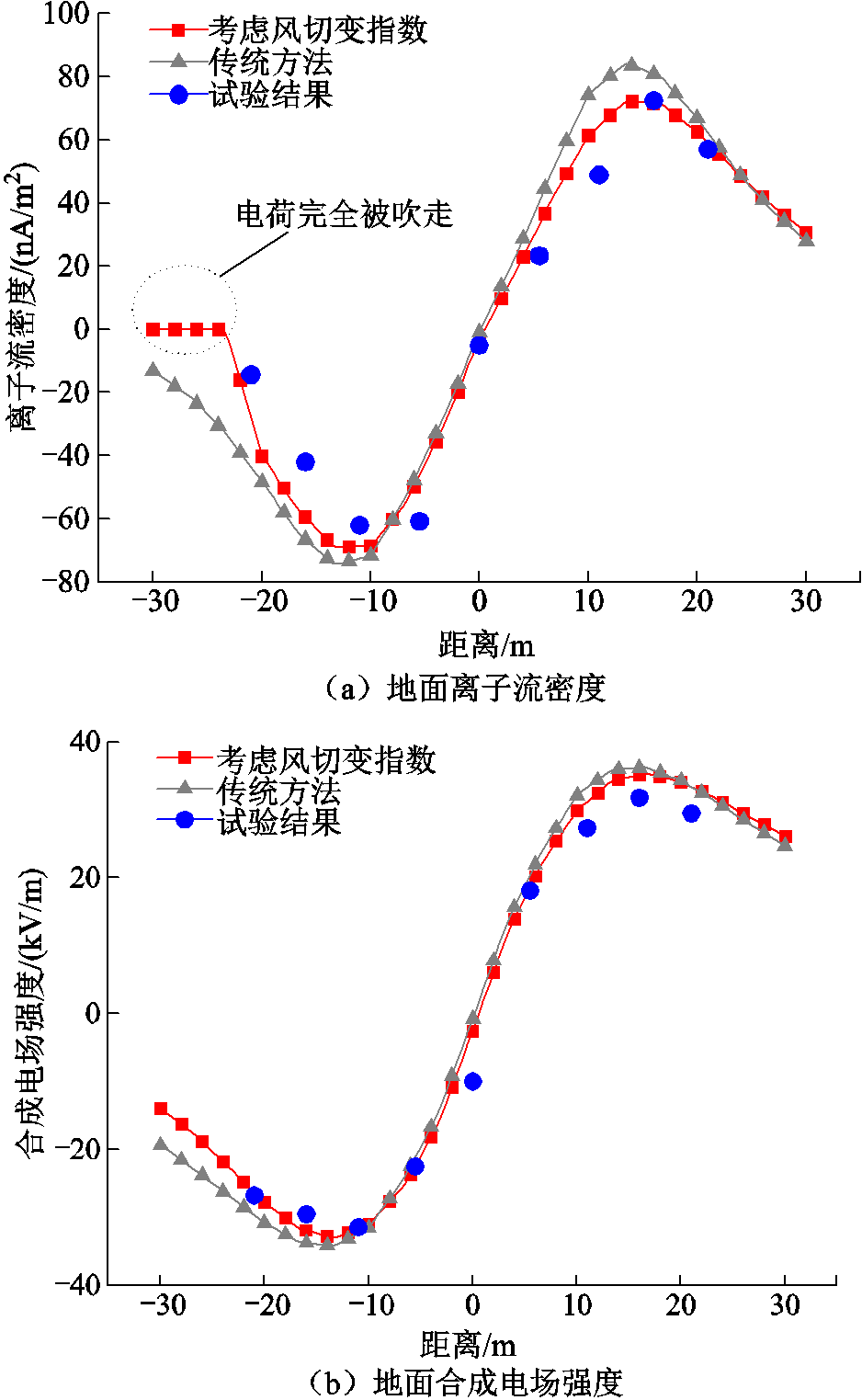
图5 仿真与试验结果对比
Fig.5 Comparison between simulation results and tests
由图5可得,考虑风切变指数后的离子流密度和合成电场强度分布与试验结果拟合度更好。体现在离子流密度上,九个测量点在传统方法下与试验结果的平均误差达到了37.3%,而考虑风切变指数后的平均误差下降到了21.1%。导致离子流场仿真与试验结果误差较大的原因有很多,其中一个重要因素是离子流的数量级为nA/m2,测量时对仪器精度要求很高,且测量场地位于户外,环境因素复杂,仿真中的参数很难与真实情况完全相符。然而,由于两个方法除了在风速输入上有所不同外,其他参数和后续离子流场求解程序完全相同,因此考虑风切变指数后,误差与传统方法相比降低了16.2百分点,准确性显著提升。
事实上,高空的风速相较地面会变得很大,此时会有更多的空间电荷从负极性侧被吹往正极性侧,进而导致负极性侧远端的电荷被完全吹走,离子流密度为0。可以看到,考虑风切变指数后的仿真结果很好地体现了这一现象。
体现在合成电场强度上,九个测量点在传统方法下与试验结果的平均误差为11.1%,而考虑风切变指数后变为7.3%,下降了3.8百分点,同样有较大的提升。合成电场强度由于其本身数量级较大,测量仪器受环境影响较小,因此整体误差相较离子流场要小得多。
综上所述,在引入风切变指数后,离子流场的计算结果与真实情况更加相符,误差与传统的固定风速方法相比明显下降。
以昆明地区实际运行的±800 kV特高压直流输电线路为例,采用本方法进行了计算。昆明地区的风速数据采用昆明国家基准气候站(风速传感器离地高度10.5 m)测得的近10年数据[24]。在除去发生频率极低的大风日(风速大于5 m/s)后,昆明地区各等级风速分布见表1。分析案例采用的±800 kV特高压直流输电线路参数为:线路导线为6分裂,子导线半径为1.68 cm,子导线横截面积为630 mm2,导线最低处对地高度为27.5 m,极间距为22 m,线路段平均海拔高度约为1 960 m,晴朗天气。假定风速方向为从负极性导线(上风区)指向正极性导线(下风区)方向。
表1 昆明地区各等级风速分布
Tab.1 Frequency distribution table of wind speed at various levels in Kunming area

风速等级/(m/s)12345 次数2211 3031 6771 000581
按照本文提出的计算方法,首先进行风速计算。根据表1的数据可拟合得到昆明地区Weibull概率密度分布函数各个参数为:a=3.5、b=3.172,由于风速没有负值,d=0,表明此时的三参数Weibull分布退化为二参数分布。
绘制出昆明地区风速的Weibull分布如图6所示。计算得到概率分布曲线的95%风速范围以内的临界最大风速为4.36 m/s,考虑到风速传感器离地高度为10.5 m,按照式(3)计算出每个节点上的风速值,作为离子流场计算的输入。
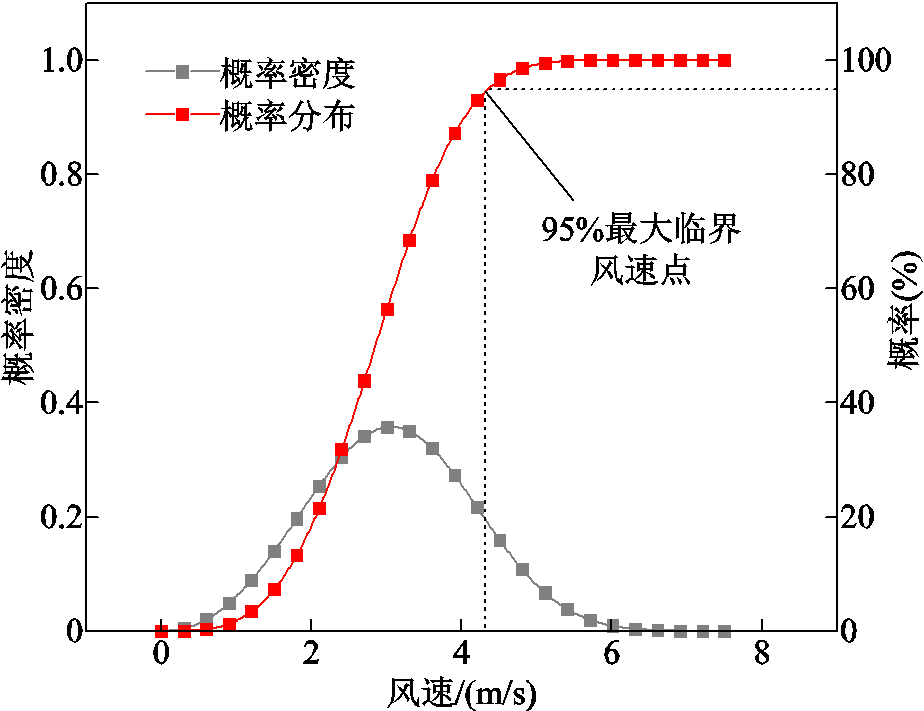
图6 昆明地区风速的Weibull分布
Fig.6 Weibull distribution of wind speed in Kunming area
最终得到的实际±800 kV线路的仿真结果如图7所示,不同导线对地高度的离子流场结果峰值见表2,同时图7中还给出了不同对地高度下的计算值作为对比。
可以看到,在离子流密度方面,由于该实际运行的±800 kV特高压直流输电线路对地高度高达27.5 m,且处在较大风速下,因此绝大部分电荷都被吹走,进而无法在地面形成电流通路。实测该地在无风情况下的离子流密度最大不超过6 nA/m2,计算得到的有风情况下导线下方离子流密度最大值不超过2 nA/m2,其分布近似为一条水平直线。图7中曲线整体趋势为:随着导线高度的降低,离子流密度逐渐增大,同时曲线的过零点也向负极性侧偏移。这一方面是因为导线距离地面更近,另一方面是因为导线附近风速随着导线高度的降低而同步减小。
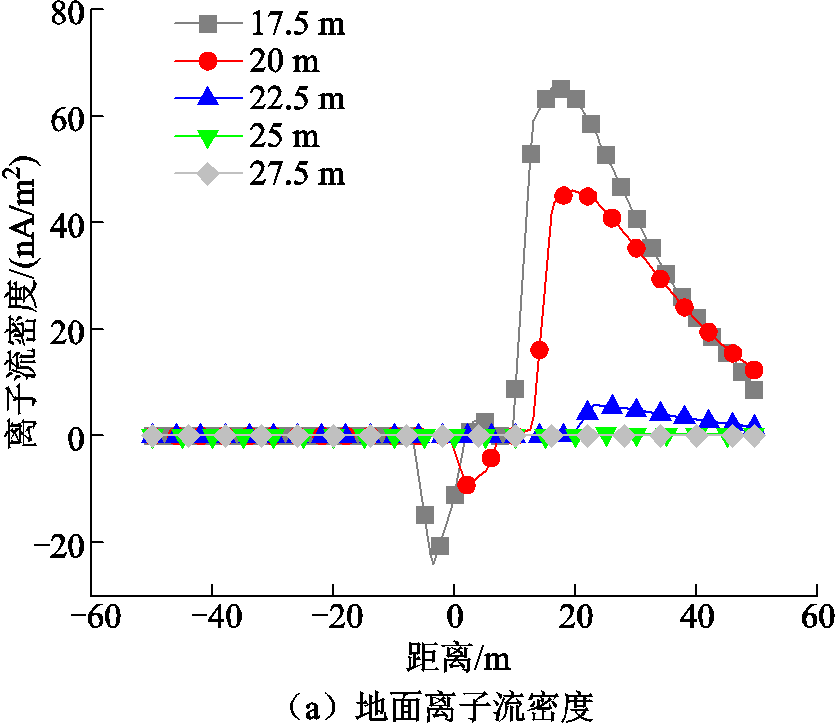
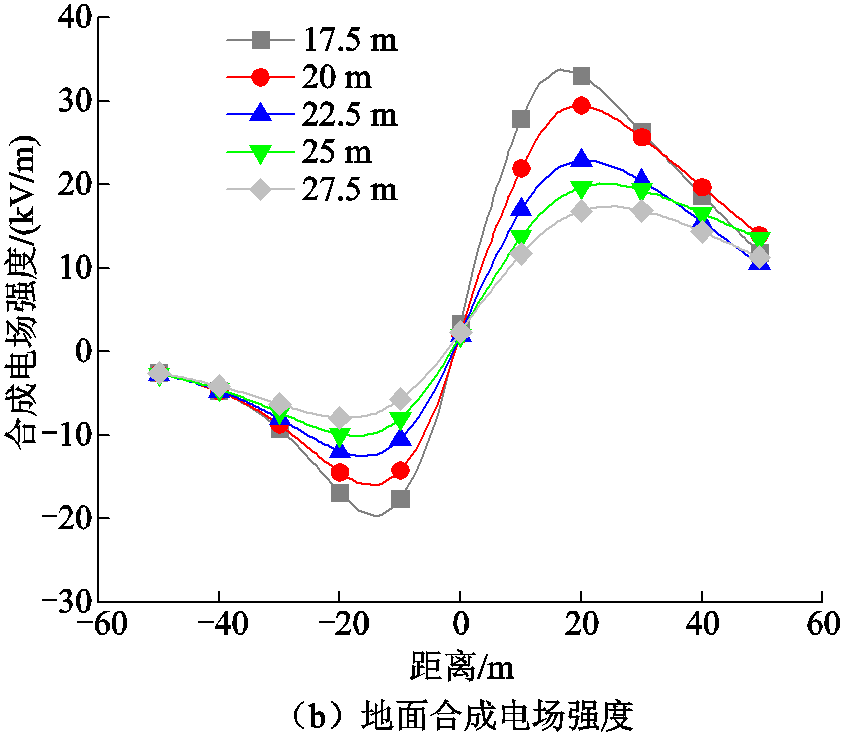
图7 不同导线对地高度的离子流场仿真结果
Fig.7 Simulation results of ion flow field at different conductor heights to ground
表2 不同导线对地高度的离子流场结果峰值
Tab.2 Peak value table of ion flow field results for different conductor heights to ground

对地高度/m离子流密度/(nA/m2)合成电场强度/(kV/m) 17.565.533.7 2046.229.5 22.55.7622.9 252.0120.1 27.51.7317.3
在合成电场强度方面,电场强度随着导线高度的降低而升高。在对地高度为20 m时,其峰值电场强度为29.5 kV/m,与±800 kV直流输电线路的限制电场强度基本一致。事实上,在导线对地高度的设计上,需要考虑的因素有很多,包括导线本身的力学性能、线路段载流量特性、当地气候温度等,但在本算例的高海拔地区,离子流场的限值是导致该线路段对地高度较高的主要因素,按照本文分析,导线对地高度最低可为20 m,这与该线路段实际采用的对地高度27.5 m之间还有较大的裕度差。
风速作为影响输电线路离子流场分布的最常见也是较大因素之一,有着明显的地域特点。为了避免资源浪费,在设计输电线路对地高度时,应当考虑不同地区的风速分布差异,而不是简单地用大裕度换取安全度。为此,本文通过研究得到结论如下:
1)提出一种基于风速概率分布与风切变指数的输电线路离子流场数值模拟方法。该方法通过待计算地区的风速数据构建Weibull风速概率分布函数模型,选择风速数据在95%以内的最大临界风速作为参考值,考虑风速传感器的安装高度,根据风切变指数计算场域不同高度处的风速分布,作为离子流场计算中不同高度节点的风速输入。
2)通过户外试验对引入风切变指数后的计算模型的准确性进行验证。与试验数据相比,引入风切变指数后,离子流密度与合成电场强度误差分别下降了16.2百分点和3.8百分点,明显优于传统固定风速模型。
3)以实际运行的±800 kV特高压直流输电线路为例,采用本方法进行了计算。结果表明,在考虑合成电场强度满足标准的条件下,导线对地高度最低可为20 m,这与该线路段实际采用的对地高度27.5 m之间还有较大的裕度差。
本文提出的改进离子流场计算方法能够考虑输电线路所处区域的风速差异,针对性地给出在保证合成电场安全限值下的线路对地高度设计参考依据,既具备一定的指导意义,又具有潜在的经济性效益。
参考文献
[1] 刘其辉, 逄思敏, 吴林林, 等. 大规模风电汇集系统电压不平衡机理、因素及影响规律[J] 电工技术学报, 2022, 37(21): 5435-5450. Liu Qihui, Pang Simin, Wu Linlin, et al. The mechanism, factors and influence rules of voltage imbalance in wind power integration areas[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5435-5450.
[2] 张海兵, 吴海涛, 胡琴, 等. 架空输电线路可听噪声问题综述[J]. 高压电器, 2022, 58(5): 1-6. Zhang Haibing, Wu Haitao, Hu Qin, et al. Review of audible noise of overhead transmission lines[J]. High Voltage Apparatus, 2022, 58(5): 1-6.
[3] 申南轩, 苏子寒, 张远航, 等. 湿度对悬浮液滴荷电特性及离子流场特性的影响[J]. 电工技术学报, 2022, 37(13): 3422-3430, 3452. Shen Nanxuan, Su Zihan, Zhang Yuanhang, et al. Influence of humidity on the charge characteristics of suspension droplets and the characteristics of ion flow field[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3422-3430, 3452.
[4] 程启问, 万保权, 张建功, 等. 基于误差传递方程的离子流场迎风有限元高精度计算方法[J]. 电工技术学报, 2020, 35(21): 4432-4438. Cheng Qiwen, Wan Baoquan, Zhang Jiangong, et al. A highly accurate upwind finite element method for ion-flow field based on the error transport equation[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4432-4438.
[5] 汪沨, 范竞敏, 李敏, 等. 高精度上流有限元法在特高压直流输电线路离子流场计算中的应用[J]. 高电压技术, 2016, 42(4): 1061-1067. Wang Feng, Fan Jingmin, Li Min, et al. Application of the high precision upstream FEM to calculation of the ionized field of HVDC transmission line[J]. High Voltage Engineering, 2016, 42(4): 1061-1067.
[6] 修连成, 杜志叶, 岳国华, 等. 特高压直流输电线路离子流场快速稳定计算方法[J]. 南方电网技术, 2021, 15(10): 80-86. Xiu Liancheng, Du Zhiye, Yue Guohua, et al. Fast and stable calculation method for ion flow field of UHVDC power transmission lines[J]. Southern Power System Technology, 2021, 15(10): 80-86.
[7] 乔骥, 路遥, 刘增训, 等. 横向风对特高压交直流混合线路地面电场与离子流场分布特性的影响[J]. 电网技术, 2018, 42(4): 1234-1240. Qiao Ji, Lu Yao, Liu Zengxun, et al. Influence of transverse wind on ground-level electric field and ion flow profiles of hybrid HVAC/HVDC transmission lines[J]. Power System Technology, 2018, 42(4): 1234-1240.
[8] 张建功, 万保权, 程启问, 等. 一种高效鲁棒的低阶迭代通量线方法求解高压直流输电线路离子流场[J]. 电工技术学报, 2021, 36(8): 1718-1725. Zhang Jiangong, Wan Baoquan, Cheng Qiwen, et al. An efficient and robust low-order iterative flux tracing method for calculating ion flow field of HVDC transmission lines[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1718-1725.
[9] 曲延禄, 阎书源, 张程道. 我国地面气温极值和地面风速极值的渐近分布[J]. 气象学报, 1988, 46(2): 187-193. Qu Yanlu, Yan Shuyuan, Zhang Chengdao. On asymptotic distributions for extremes of surface temperature and surface wind over China[J]. Acta Meteorologica Sinica, 1988, 46(2): 187-193.
[10] Carta J A, Ramírez P. Analysis of two-component mixture Weibull statistics for estimation of wind speed distributions[J]. Renewable Energy, 2007, 32(3): 518-531.
[11] 温华洋, 朱华亮, 刘壮, 等. 基于三参数Weibull分布的安徽省年最大风速均一性检验[J]. 气象与环境学报, 2021, 37(2): 77-83. Wen Huayang, Zhu Hualiang, Liu Zhuang, et al. A homogeneity test for annual maximum wind speed based on three-parameter Weibull distribution[J]. Journal of Meteorology and Environment, 2021, 37(2): 77-83.
[12] 王文新, 陈可欣, 白杨, 等. 基于实测数据的呼和浩特近郊风速分布模型对比研究[J]. 太阳能学报, 2021, 42(9): 370-376. Wang Wenxin, Chen Kexin, Bai Yang, et al. Comparative study on wind speed distribution models of Hohhot suburb based on measured data[J]. Acta Energiae Solaris Sinica, 2021, 42(9): 370-376.
[13] 丁明, 吴义纯, 张立军. 风电场风速概率分布参数计算方法的研究[J]. 中国电机工程学报, 2005, 25(10): 107-110. Ding Ming, Wu Yichun, Zhang Lijun. Study on the algorithm to the probabilistic distribution parameters of wind speed in wind farms[J]. Proceedings of the CSEE, 2005, 25(10): 107-110.
[14] 陈练, 李栋梁, 吴洪宝. 中国风速概率分布及在风能评估中的应用[J]. 太阳能学报, 2010, 31(9): 1209-1214. Chen Lian, Li Dongliang, Wu Hongbao. The probability distribution of wind speed and its application in estimation of wind energy in China[J]. Acta Energiae Solaris Sinica, 2010, 31(9): 1209-1214.
[15] 潘晓春. 风速概率分布参数估计的低阶概率权重矩法[J]. 中国电机工程学报, 2012, 32(5): 131-136. Pan Xiaochun. Low-order probability-weighted moments method for wind speed probability distribution parameter estimation[J]. Proceedings of the CSEE, 2012, 32(5): 131-136.
[16] 杜雄, 李高显, 刘洪纪, 等. 风速概率分布对风电变流器中功率器件寿命的影响[J]. 电工技术学报, 2015, 30(15): 109-117. Du Xiong, Li Gaoxian, Liu Hongji, et al. Effect of wind speed probability distribution on lifetime of power semiconductors in the wind power converters[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 109-117.
[17] 汪沨, 李敏, 吕建红, 等. 风速对特高压直流输电线路离子流场分布的影响[J]. 高电压技术, 2016, 42(9): 2897-2901. Wang Feng, Li Min, Lü Jianhong, et al. Effect of wind speed on ion flow field under UHVDC transmission lines[J]. High Voltage Engineering, 2016, 42(9): 2897-2901.
[18] Du Zhiye, Xiu Liancheng, He Jingxuan, et al. Computation of total electric field considering natural wind under high-altitude UHVDC transmission lines[J]. IEEE Transactions on Magnetics, 2022, 58(9): 1-4.
[19] 黄洁亭. 不同气象地形条件下风速概率分布模型研究[D]. 北京: 华北电力大学, 2014. Huang Jieting. Research on wind speed probability distribution models under different weather and terrain conditions[D]. Beijing: North China Electric Power University, 2014.
[20] 中华人民共和国生态环境部, 国家市场监督管理总局. 直流输电工程合成电场限值及其监测方法: GB 39220—2020[S]. 北京: 中国环境科学出版社, 2020.
[21] 黄国栋, 阮江军, 杜志叶, 等. 改进三维上流元法计算特高压直流线路离子流场(英文)[J]. 中国电机工程学报, 2013, 33(33): 19, 152-159. Huang Guodong, Ruan Jiangjun, Du Zhiye, et al. Improved 3-D upwind FEM for solving ionized field of HVDC transmission lines[J]. Proceedings of the CSEE, 2013, 33(33): 19, 152-159.
[22] 卢铁兵, 申南轩, 苏子寒, 等. 计及海拔、湿度和颗粒物影响的高压直流输电线路离子流场特性研究综述[J]. 南方电网技术, 2021, 15(10): 46-58. Lu Tiebing, Shen Nanxuan, Su Zihan, et al. Review of researches on ion flow field characteristics of HVDC transmission lines considering altitude, humidity and particulate matter[J]. Southern Power System Technology, 2021, 15(10): 46-58.
[23] 余峰. 高压直流输电线下合成场强及离子流密度的计算[D]. 北京: 中国电力科学研究院, 1998. Yu Feng. Calculation of total field strength and ion density under HVDC transmission lines[D]. Beijing: China Electric Power Research Institute, 1998.
[24] 杨燕妮, 吕静. 昆明风场特征与风能资源分析评估[J]. 城市建设理论研究(电子版), 2020(4): 26.
Abstract The ion flow field under ultra high voltage direct current (UHVDC) transmission lines is one of the important evaluation indicators for electromagnetic environment. Wind speed, as one of the most common and influential factors, has obvious regional characteristics. At present, scholars often use constant wind speed to replace natural wind speed, which can easily lead to the following two problems. One is the waste of resources, as the local wind speed used in the calculation is not necessarily as high as possible. Every 1 m increase in the height of the line installation will significantly increase the total project cost. Secondly, it is inconsistent with the actual situation. Due to the relationship between wind speed and height, there is a gradient relationship on the near ground side. Therefore, the impact of wind speed changes in the vertical direction on the ion flow field should be considered.
In view of this, this paper proposes a numerical simulation method of transmission line ion flow field based on wind speed probability distribution and wind shear exponent. The calculation method is divided into two parts: wind speed calculation and ion flow field calculation. This method builds a Weibull wind speed probability distribution function model based on the wind speed data of the region to be calculated, and selects the critical wind speed with the max wind speed data within 95% as the reference value. It considers the installation height of the wind speed sensor, and calculates the wind speed distribution at different heights according to the wind shear exponent, as the wind speed input at different height nodes in the calculation of the ion flow field.
The accuracy of the calculation model after the introduction of wind shear exponent is verified through outdoor tests. The voltage level is ±800 kV, the conductor is 6-split, the radius of the sub conductor is 1.68 cm, the cross-sectional area of the sub conductor is 630 mm2, the height of the conductor to the ground is 16.5 m, the pole spacing is 22 m, the altitude is about 2 000 m, and the weather is sunny. The wind speed measurement point is 1m above the ground, and the wind speed is maintained between 0.5~1 m/s. A total of 9 measurement points are arranged below the line. Due to the high altitude region, this article also corrected the parameters such as the corona field strength, ion mobility, and recombination coefficient. Compared with the traditional wind speed model, after the introduction of the wind shear exponent, the errors between the ion current density and the total electric field strength decreased by 16.2% and 3.8%, respectively. The results show that the method is more consistent with the actual distribution.
Taking the actual operating ±800 kV UHVDC transmission line in Kunming area as an example, this method was used for calculation. First, to calculate the wind speed. The parameters of Weibull probability density distribution function in Kunming area obtained by fitting are:a=3.5, b=3.172, d=0. The critical maximum wind speed within the 95% wind speed range of the probability distribution curve is calculated to be 4.36 m/s. Combined with the height above the ground of the wind speed sensor, the wind shear exponent is used to calculate the wind speed at each node in the solution field as the input of the ion flow field calculation. At the same time, this paper also provides calculated values for different heights as a comparison. The results show that, under the condition that the total electric field strength meets the standard, the minimum height of the conductor could be 20 m, which has a significant margin difference from the actual height of 27.5 m used in the actual line section.
In summary, the method proposed in this paper can specifically consider the impact of wind speed in the area where the line is located, provide a reference basis for the design of the line to ground height under the safety limit of the total electric field, especially in areas with high sea level and high wind speed.
keywords:Ultra high voltage direct current (UHVDC), ion flow field, Weibull distribution, wind shear exponent, numerical simulation
DOI: 10.19595/j.cnki.1000-6753.tces.230332
中图分类号:TM723
国家自然科学基金资助项目(51977152)。
收稿日期 2023-03-20
改稿日期 2023-05-04
岳国华 男,1997年生,博士研究生,研究方向为高压直流输电线路的电磁环境。E-mail:yueguohua@whu.edu.cn
杜志叶 男,1974年生,教授,博士生导师,研究方向为高压直流输电线路电磁环境、智能电气设备、电磁多物理场耦合计算技术等。E-mail:Duzhiye@126.com(通信作者)
(编辑 李 冰)