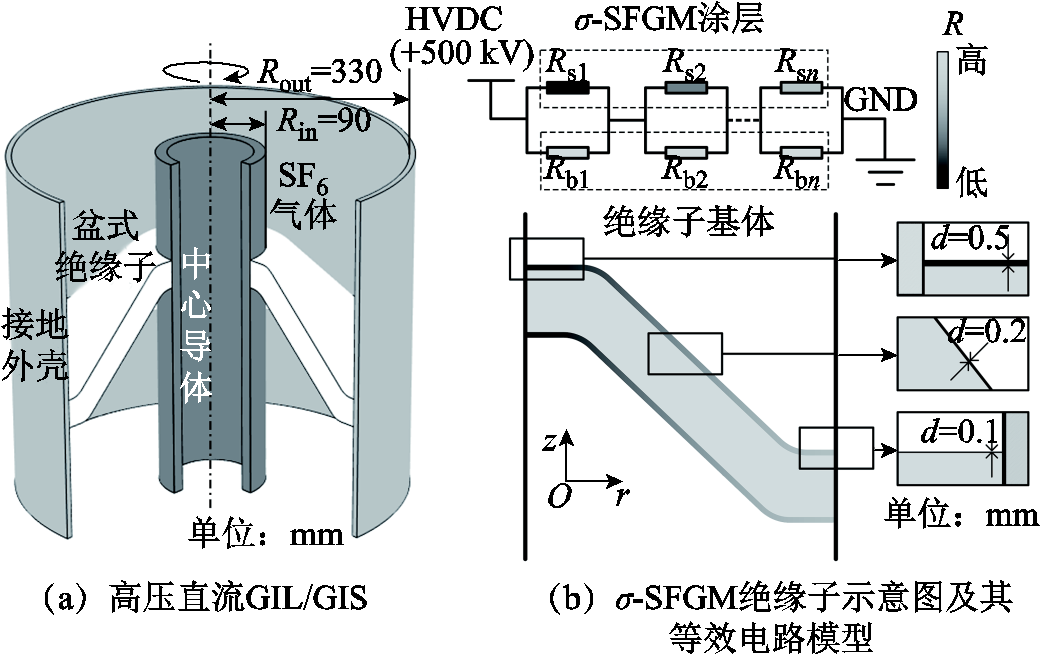
图1 高压直流GIL/GIS仿真模型与σ-SFGM绝缘子示意图
Fig.1 HVDC GIL/GIS simulation model and schematic diagram of the σ-SFGM spacer
摘要 为了优化时变温差工况下直流GIL/GIS盆式绝缘子的沿面电场分布,基于表层电导梯度材料(σ-SFGM)设计了以室温(RT)电场均化为目标的RT-SFGM绝缘子与兼顾不同温度梯度(GT)条件的GT-SFGM绝缘子。迭代优化后,RT-SFGM 绝缘子的涂层厚度从导体到外壳梯度减小,而GT-SFGM绝缘子的凸面涂层厚度则呈现U型梯度分布。室温条件下,均匀绝缘子的凹面高压三结合点处电场畸变严重,相同位置处的RT-SFGM绝缘子与GT-SFGM绝缘子电场强度分别下降了53.3%和49.5%。随着高压导体温度的上升,绝缘子最大电场位置逐渐向接地外壳附近转移。在40℃温差条件下,GT-SFGM绝缘子的电场畸变抑制效果明显优于RT-SFGM绝缘子,最大电场强度下降59.2%。在负荷加载与负荷波动工况下,GT-SFGM绝缘子的电场变化率分别仅为7%与13.1%,可实现时变温差工况下绝缘子直流电场分布的稳定控制。
关键词:直流 GIL/GIS绝缘子 表面电导梯度材料 时变温差 电场均化
随着高压直流(High Voltage Direct Current, HVDC)输电技术的快速发展,我国能源资源与用电负荷分布不平衡的状况得到了有效的改善。相较于电缆与架空线路,以SF6气体作为绝缘介质的气体绝缘输电管道(Gas Insulated transmission Line, GIL)与气体绝缘金属封闭开关(Gas Insulated Switchgear, GIS)凭借其占地面积小、可靠性高、环境适应性强等优势,在高压直流输电工程建设中得到了广泛的应用[1-3]。盆式绝缘子作为直流GIL/GIS的关键绝缘部件,同时还发挥着机械支撑与气室隔离等重要作用。但近年来,我国气体绝缘设备在运行过程中频繁发生沿面闪络与绝缘失效故障,日益突出的电气绝缘问题造成了巨大的经济损失,严重威胁电力系统的安全稳定运行。
一般认为,由气固界面介电参数不匹配导致的电场畸变,是引发绝缘子沿面放电与闪络事故的根本原因[4-6]。采用功能梯度材料(Functional Gradient Materials, FGM)使绝缘子的介电参数(介电常数、电导率)呈现梯度变化,可以达到均匀电场分布的目的[7-11]。由经典电磁场理论可知,绝缘子直流电场分布主要由绝缘材料的电导分布决定[12]。通过在绝缘子表面构建具有电导梯度分布的涂层来调控绝缘子沿面电场,是一种简单有效的直流电场畸变抑制方法。采用表层分子结构改性处理环氧绝缘子,在其表面形成电导梯度层,绝缘子的直流稳态切向电场强度最大值降低33.6%,在直流电场下绝缘子沿面闪络电压提升约21%[13-14]。
在实际运行过程中,直流GIL/GIS母线通流产生焦耳热导致温度升高,在绝缘子上形成从导体到外壳递减的温度梯度分布。绝缘子通常由环氧树脂浇注固化成型,其电导率随温度变化较大,当母线温升达到65℃时,电场畸变程度增加18%,沿面闪络电压降低16%[15]。此外,由于风机发电量与电网负荷功率实时变化,输电线路中的负荷电流及GIL/GIS导体温升随时间波动[16],导致绝缘子沿面电场畸变动态变化,为时变温差工况下电场调控带来极大难度。
本文建立±500 kV直流GIL/GIS盆式绝缘子电-热耦合场仿真模型,考虑室温(Room Temperature, RT)与温度梯度(Gradient Temperature, GT)工况,设计具有表面电导梯度涂层(Surface Functionally Conductivity Graded Materials, σ-SFGM)的RT-SFGM绝缘子与GT-SFGM绝缘子,研究不同绝缘子在稳态温差下的直流电场分布特性与时变温差工况下的动态电场畸变抑制效果。研究结果有望为极端环境下直流GIL/GIS盆式绝缘子的优化设计提供参考依据。
±500 kV直流GIL/GIS的简化几何模型如图1a所示,其基本结构主要包括高压导体、接地外壳与盆式绝缘子。导体呈同轴圆柱结构,连接+500 kV直流电压,其外半径为90 mm,厚度为20 mm。接地外壳内半径为330 mm。盆式绝缘子位于导体与外壳之间,厚度为50 mm。管道内部其余部分填充气压为0.5 MPa的SF6气体,流体属性设置为湍流,模型考虑气体流动情况下各部分之间的传热。

图1 高压直流GIL/GIS仿真模型与σ-SFGM绝缘子示意图
Fig.1 HVDC GIL/GIS simulation model and schematic diagram of the σ-SFGM spacer
图1b所示为表面电导梯度(σ-SFGM)绝缘子示意图及其等效电路模型。直流电压下盆式绝缘子的电场分布遵循欧姆定律,绝缘子基体与高电导涂层可以由两个相互并联的串联电阻电路(∑Rb//∑Rs)表示,每个涂层单元的等效电阻(Rsi,i=1, 2,…, n)由该位置处的电导率与厚度共同决定。因此,通过对σ-SFGM绝缘子涂层的电导率或厚度参数进行梯度设计,均可以调控绝缘子沿面直流电场分布。
1)热场理论
导体产生的热量主要来自负荷电流产生的焦耳热,其在直流GIL/GIS中的主要传递方式有三种[17]:相互接触固体介质之间的热传导;固体介质与气体、接地外壳与外部环境之间的热对流;固体表面以及气体区域的热辐射。
2)电场理论
当温度变化时,由于其对材料电导率的影响,电场分布也发生变化,基于电流连续性方程的控制方程为
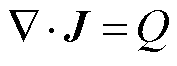 (1)
(1)
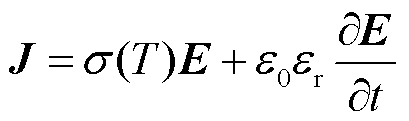 (2)
(2)
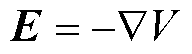 (3)
(3)
式中,J为电流密度;Q为空间电荷量;σ为电介质的电导率;E为电场强度;T为温度;ε0与εr分别为真空介电常数与材料的相对介电常数;t为时间;V为电势。
直流GIL/GIS仿真模型中主要包括环氧树脂/ Al2O3复合绝缘子、SF6绝缘气体、铝合金导体与外壳等材料,其关键电热参数见表1。SF6气体热导率k(T)、密度ρ(T)、比热容c(T)等受温度影响较大的参数均被设置为关于温度T的函数[18],分别表示为
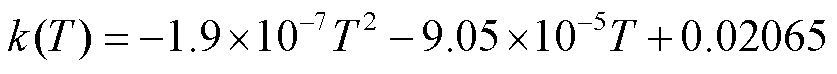 (4)
(4)
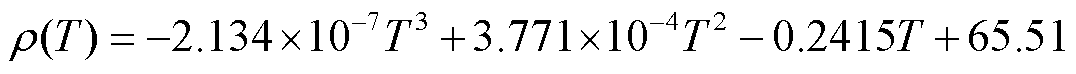 (5)
(5)
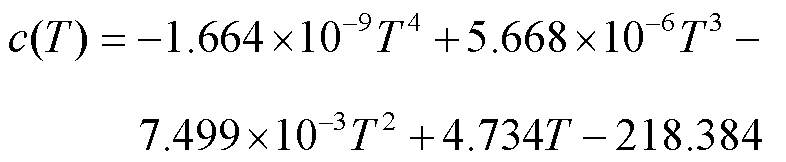 (6)
(6)
表1 材料参数
Tab.1 Materials parameters

材料相对介电常数电导率/(S/m)热导率/[W/(m·K)]密度/(kg/m3)比热容/[J/(kg·K)] 基体/涂层5σb(T)/σs(T)0.351 1171 800 铝合金2382 700900 SF6110-20k(T)ρ(T)c(T)
绝缘子基体选择环氧树脂/Al2O3复合材料,Al2O3质量分数为76.7%;高电导涂层选择环氧树脂/导电炭黑复合材料,导电炭黑质量分数为8%。图2所示为绝缘子基体与涂层材料的电导率-温度关系,两种材料的电导率都与温度呈正相关关系。当温度提高60℃时,绝缘子基体电导率具有较强的温度依赖性,其增长超过100倍,而涂层电导率随温度的变化较小。在有限元仿真中,环氧树脂绝缘子基体电导率σb与涂层材料电导率σs均被拟合成与温度T(单位为K)有关的函数,分别表示为
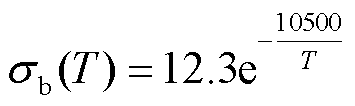 (7)
(7)
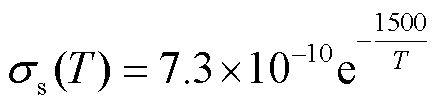 (8)
(8)
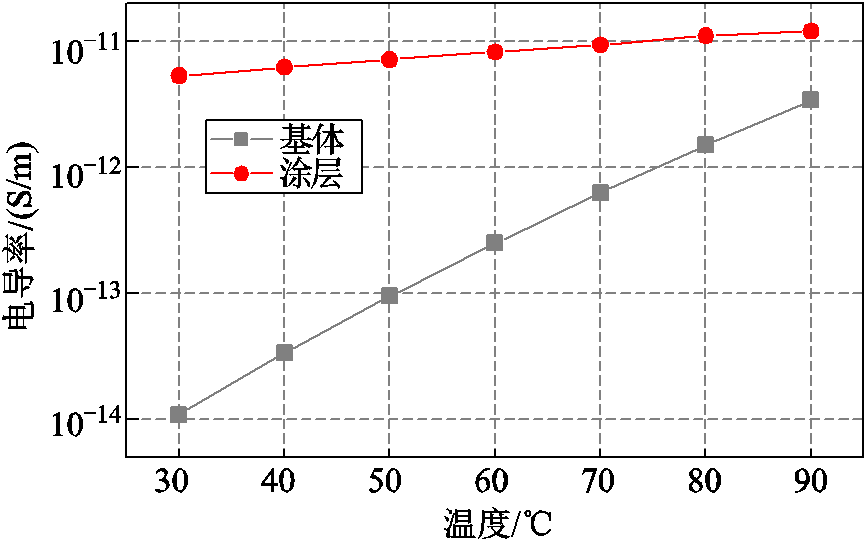
图2 环氧树脂复合材料电导率-温度关系
Fig.2 Relation between the temperature and the conductivity of the epoxy resin composites
本节采用迭代方法对盆式绝缘子的表面涂层参数进行梯度优化[19]。迭代变量为σ-SFGM涂层的厚度d,优化目标为均匀绝缘子的电场分布。涂层厚度的迭代公式为
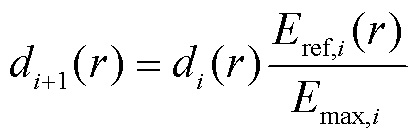 (9)
(9)
式中,di(r)与di+1(r)分别为第i次与第i+1次迭代中坐标r位置的涂层厚度;Eref,i(r)为第i次迭代中坐标r位置的参考电场强度;Emax,i为第i次迭代中最大参考电场强度。每次迭代后计算绝缘子电场分布,当相邻两次迭代计算结果差距小于1%时停止循环,输出涂层厚度分布结果。根据文献[20],涂层厚度上限需满足式(10)中的设计准则才能达到电场优化效果。
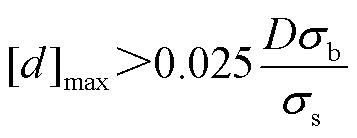 (10)
(10)
式中,D为绝缘子厚度。根据电力行业标准DL/T 664规定,GIL/GIS导体发热部分的最高允许温度为90℃,将此温度下绝缘子和涂层的电导率代入式(10),计算可得[d]max>0.14 mm。考虑涂层制备工艺等实际情况,本文规定涂层迭代优化的上限和下限分别为0.5 mm和0.1 mm。
以室温条件下沿面电场均匀化为目标,将恒温条件下的沿面切向电场设置为参考电场,优化设计了RT-SFGM绝缘子。图3与图4为迭代过程中RT- SFGM绝缘子涂层厚度与沿面电场分布的变化。优化结果显示,RT-SFGM绝缘子凹面与凸面的涂层厚度均沿径向减小,优化后的RT-SFGM绝缘子沿面最大电场强度下降,整体电场分布变得更加均匀,最大电场强度位于凹面高压三结合点处。
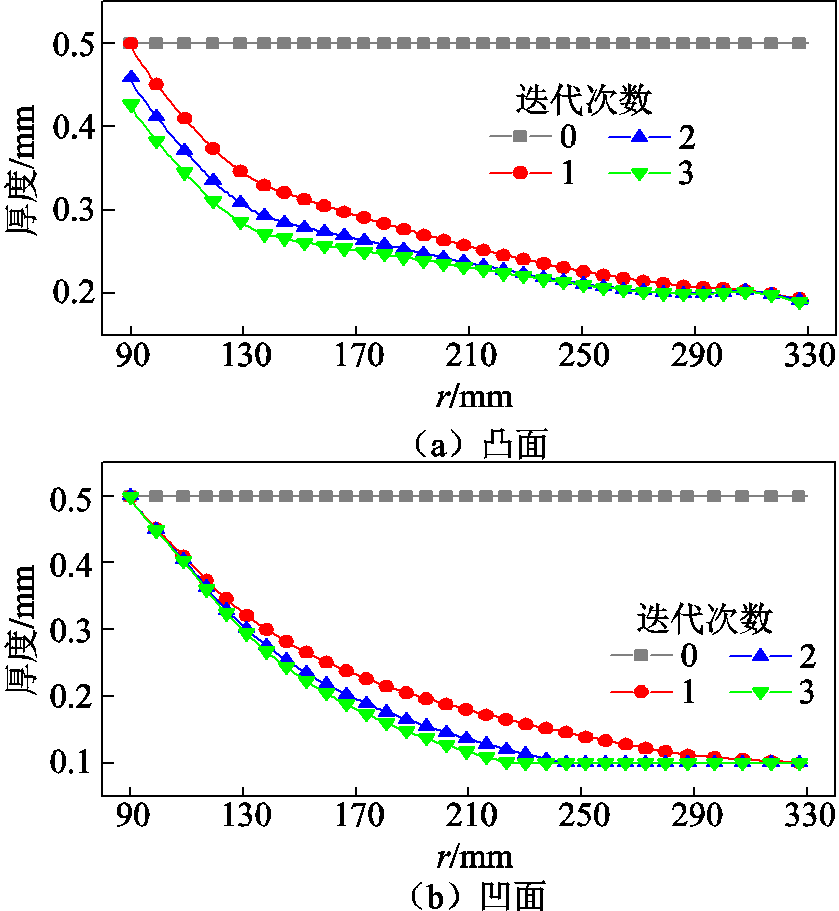
图3 优化过程中RT-SFGM绝缘子涂层厚度变化
Fig.3 Coating layer thickness variations of the RT-SFGM spacer during optimization
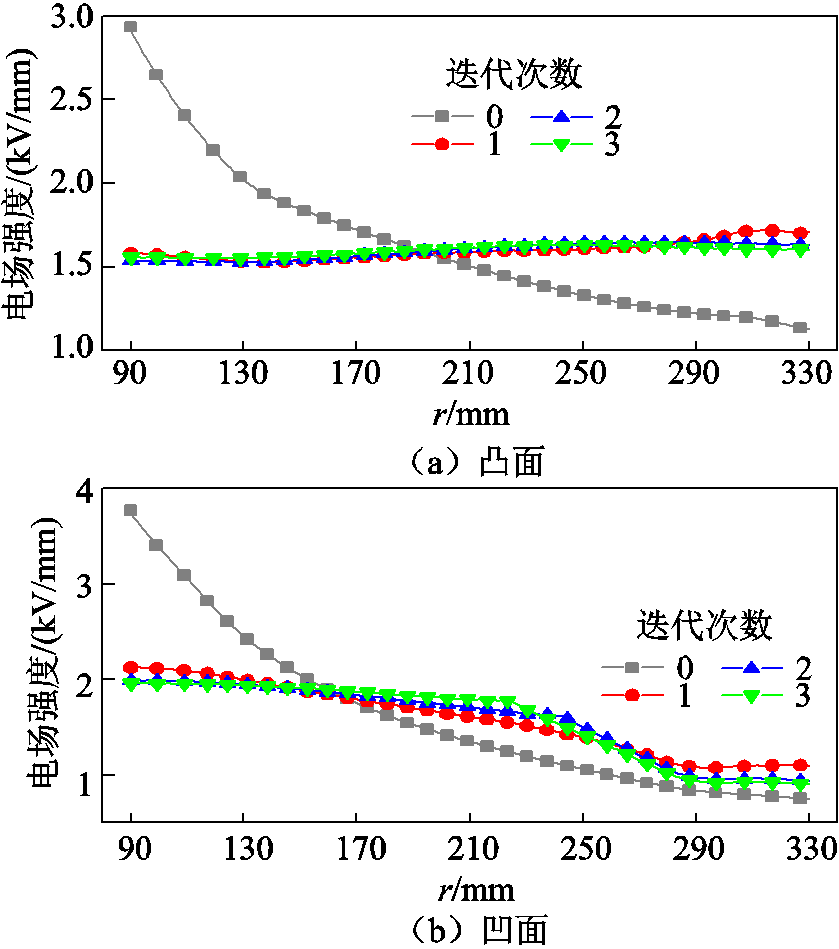
图4 优化过程中RT-SFGM绝缘子电场强度变化
Fig.4 Electric field variations of the RT-SFGM spacer during optimization
直流GIL/GIS内部温度分布与气体流动方向如图5a所示,可见由于导体负荷电流热效应的影响,高压导体附近的温度较高,额定工况下绝缘子两端承受温差可达40℃。图5b所示为40℃温差下均匀绝缘子的电场分布。由式(7)可知,绝缘子材料的电导率受温度影响较大,由导体到外壳的温度梯度改变了绝缘子的直流电场分布,此时接地外壳附近的最大电场强度达到5.15 kV/mm,电场分布不均匀度较高。
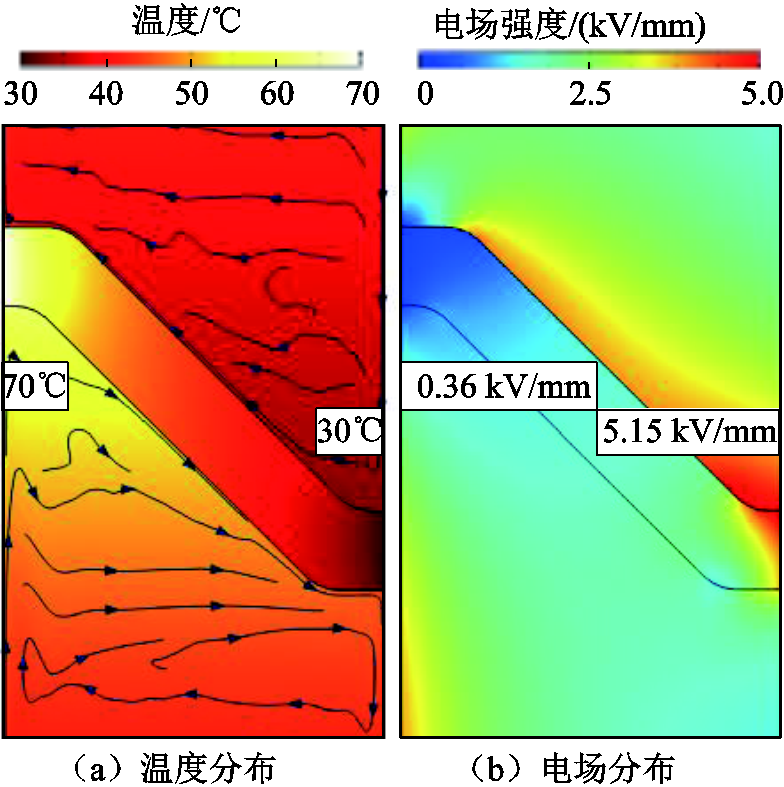
图5 40℃温差下均匀绝缘子温度和电场分布
Fig.5 Temperature and electric field distributions of the uniform spacer under temperature gradient of 40℃
基于2.1节的迭代优化方法,兼顾室温及不同温差条件下沿面电场分布优化的目标,设计了GT-SFGM绝缘子。分别计算绝缘子在恒定室温与40℃温差(导体70℃、外壳30℃)条件下的沿面切向电场分布,取各位置处的电场较大值组成GT-SFGM绝缘子的参考电场,如图6所示。图7与图8所示为迭代过程中GT-SFGM绝缘子涂层厚度与参考电场分布的变化。优化后的GT-SFGM绝缘子的凹面涂层厚度沿径向梯度减小,其凸面涂层厚度则呈现U型梯度分布。随着迭代次数的增加,GT-SFGM绝缘子参考电场分布更加均匀。
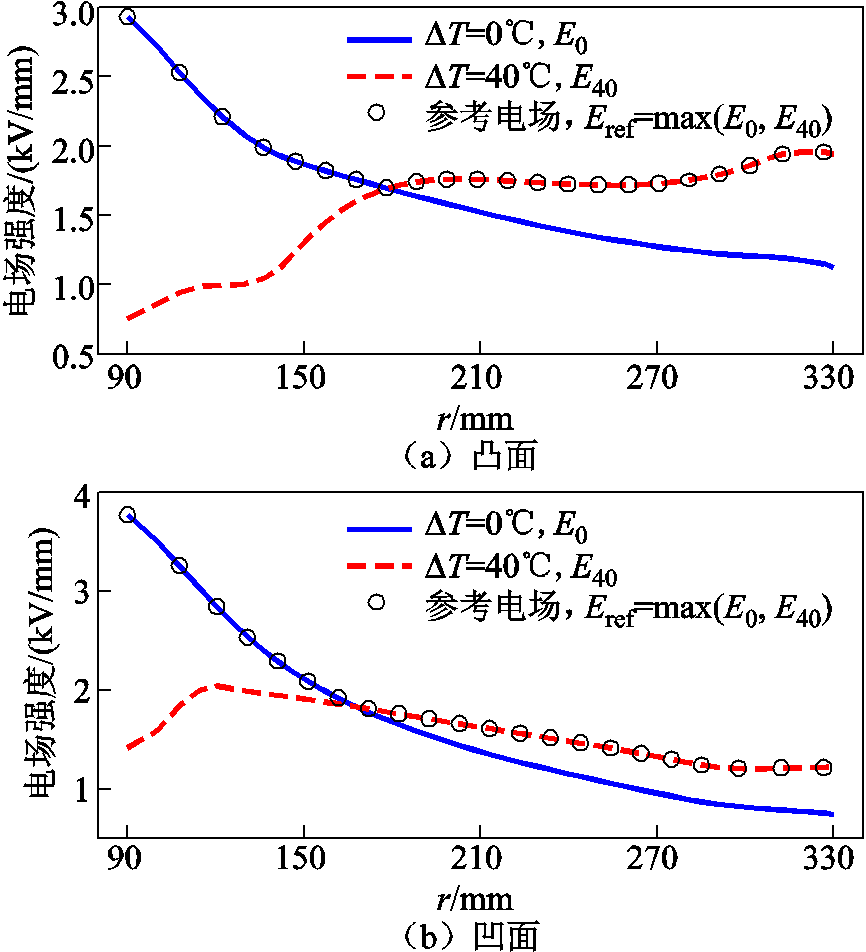
图6 GT-SFGM绝缘子参考电场分布
Fig.6 Reference electric field distributions of the GT-SFGM spacer
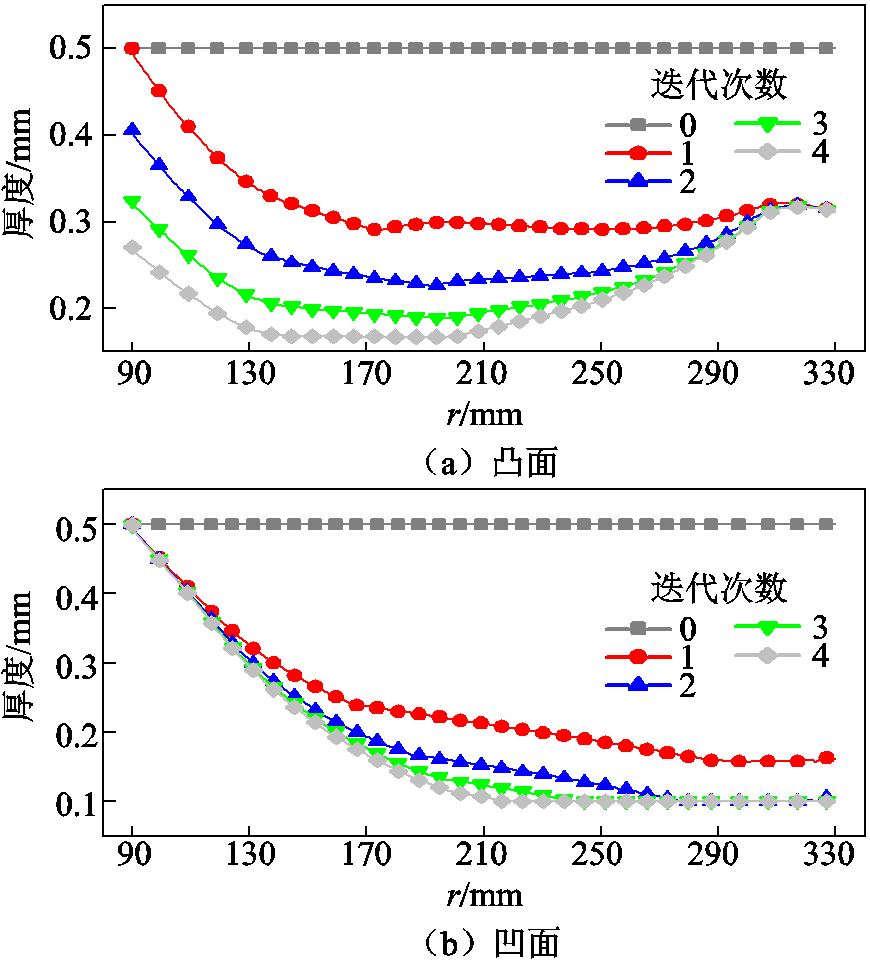
图7 优化过程中GT-SFGM绝缘子涂层厚度变化
Fig.7 Coating layer thickness variations of the GT-SFGM spacer during optimization
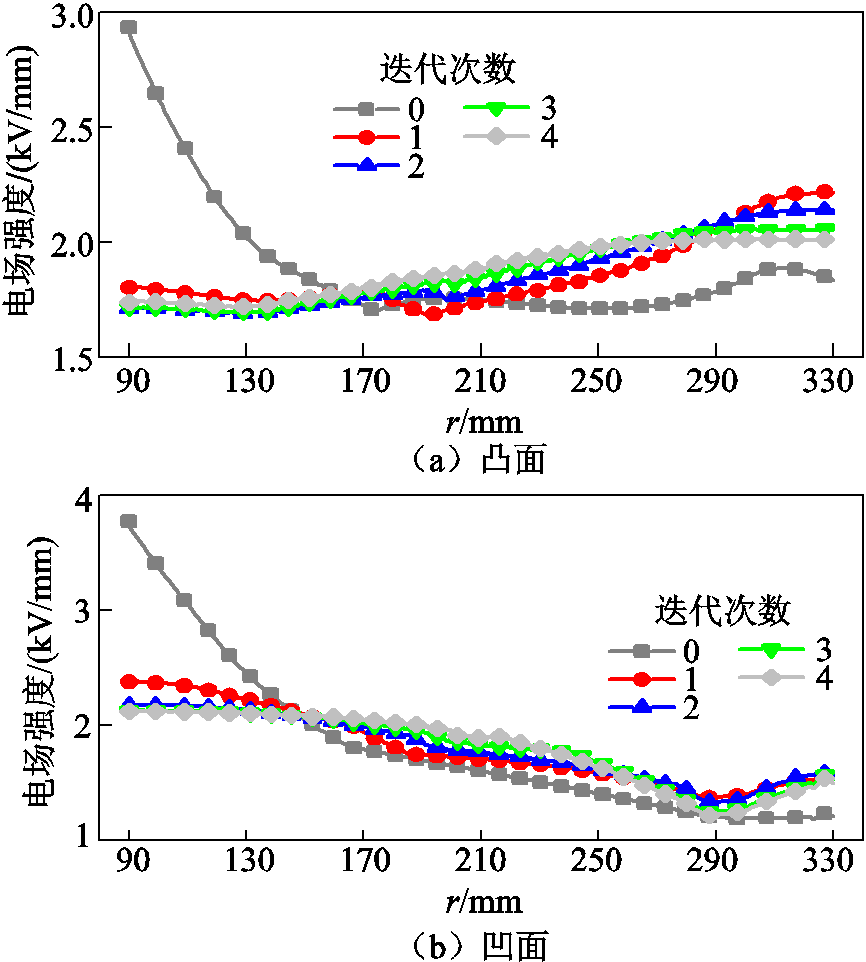
图8 优化过程中GT-SFGM绝缘子参考电场变化
Fig.8 Reference electric field variations of the GT-SFGM spacer during optimization
均匀绝缘子、RT-SFGM绝缘子和GT-SFGM绝缘子在不同温差下的沿面切向电场分布如图9所示。恒温条件下均匀绝缘子的最大电场强度出现在凹面高压三结合点处,电场强度为4.2 kV/mm。随着绝缘子两端温差逐渐增加,均匀绝缘子的畸变电场位置逐渐从高压导体转移到接地外壳附近,其电场强度上升至5.15 kV/mm。恒温条件下,RT-SFGM绝缘子沿面电场分布均匀度较高,电场畸变得到了有效的抑制,最大电场强度下降了53.3%。但随着导体温度的升高,绝缘子两端温差增加,RT-SFGM绝缘子接地外壳附近电场提升,电场不均匀度逐渐提高。在恒温与40℃温差条件下,相比于均匀绝缘子,GT-SFGM绝缘子最大电场强度分别下降至2.12 kV/mm与2.1 kV/mm,下降幅度分别达到49.5%和59.2%。40℃温差条件下,GT-SFGM绝缘子的直流电场分布均匀程度最高,其在大温度梯度下的电场畸变抑制效果明显优于RT-SFGM绝缘子。
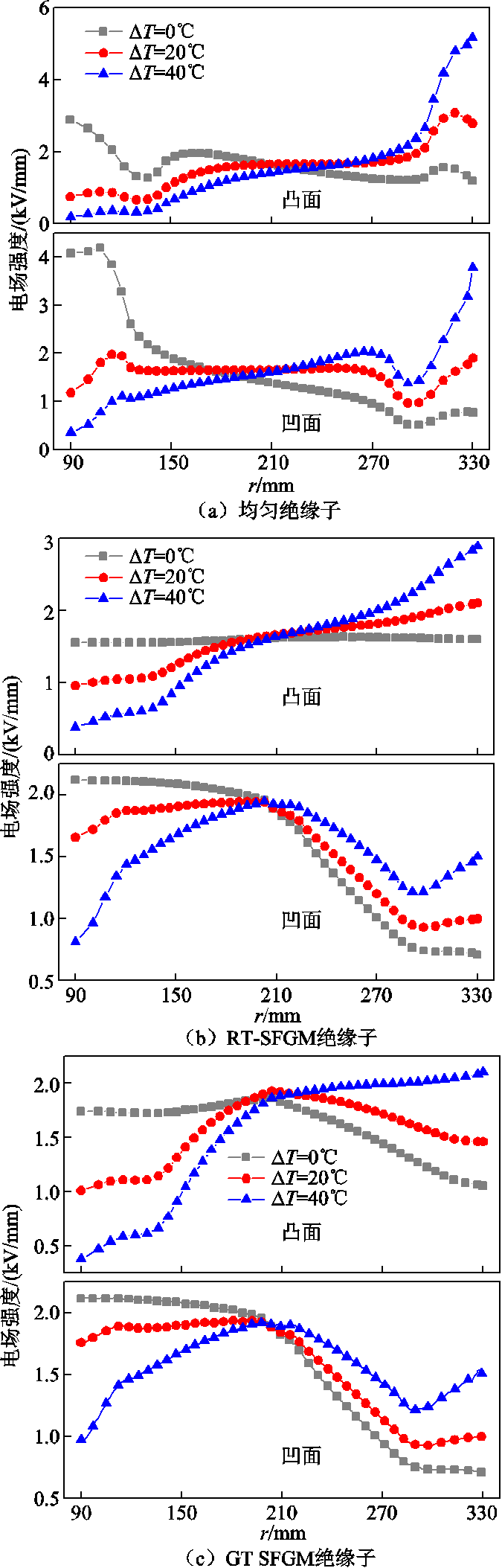
图9 不同温差下不同绝缘子的沿面电场分布
Fig.9 Surface electric field distributions of different spacers under different temperature gradients
均匀绝缘子、RT-SFGM绝缘子与GT-SFGM绝缘子的表面电荷分布如图10所示。恒温条件下,均匀绝缘子凹面上积聚的负电荷与正极性导体相互作用,在绝缘子表面和导体之间产生局部高电场区域。由于局部表面电导的增加,RT-SFGM与GT-SFGM绝缘子凹面积聚与导体极性相同的电荷,削弱了导体周围的电场强度。40℃温差下,均匀绝缘子凸面积聚正极性电荷,与外壳相互作用在接地三结合点处产生电场畸变。在σ-SFGM绝缘子的调节作用下,绝缘子凸面靠近外壳区域积聚电荷极性与外壳相同,抑制了该区域的电场畸变。
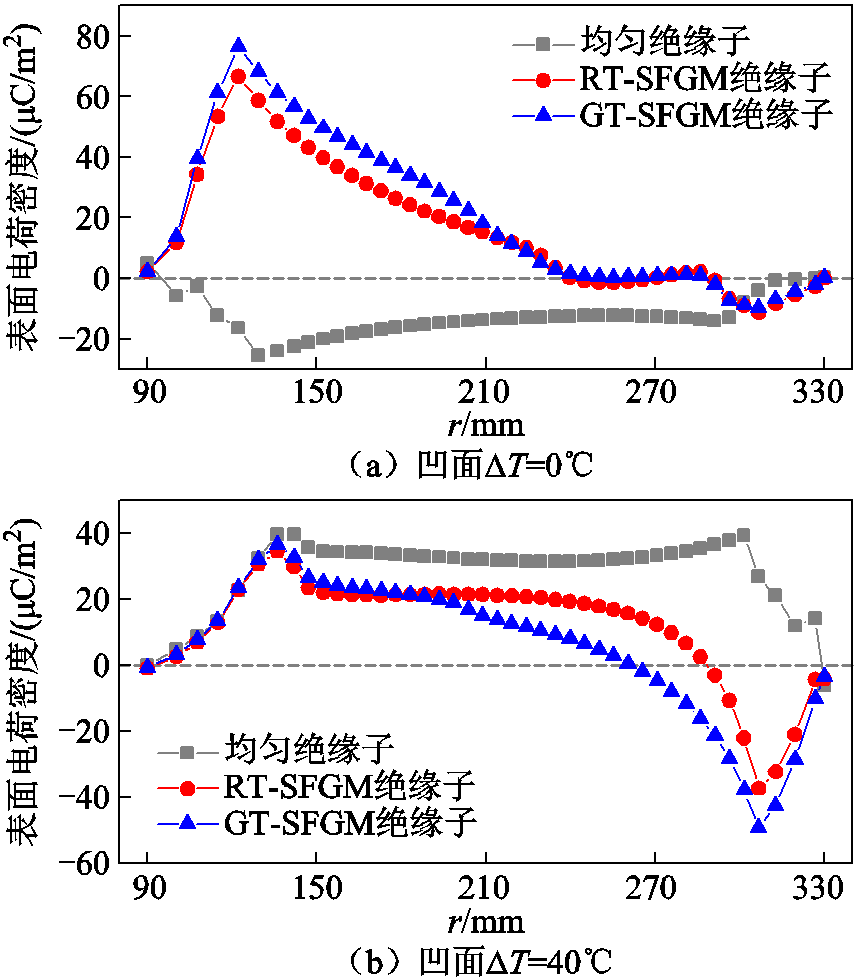
图10 不同绝缘子的表面电荷分布
Fig.10 Surface charge distributions of different spacers
本节设置负荷加载和负荷波动两种典型工况,考核两种σ-SFGM绝缘子在时变温差工况下的电场畸变抑制效果。
3.2.1 负荷加载工况
图11a所示为在倒闸开关操作过程中的负荷加载工况的电流时域变化。在t=0时刻向导体内通入4 kA的负荷电流,利用有限元方法计算20 h内绝缘子的温度与电场变化。图11b所示为负荷加载条件下高压导体与接地外壳的温度时域变化。为了探究导体与外壳在升温过程中的温度变化规律,定义升温稳定时间t90为
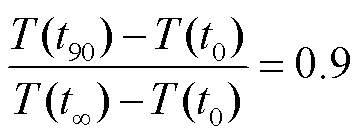 (11)
(11)
式中,T(t∞)和T(t0)分别为稳态和初始的温度。在负荷电流的热效应下,导体温度逐渐升高,升温速率逐渐减小,在9 h左右基本达到稳定。随着时间的增加,导体产生的热量逐渐向外扩散。相比于导体,外壳温度的提升幅度较小,变化也较为平缓。外壳温度在14 h左右达到稳定,滞后于导体的温度变化。稳态条件下导体与外壳的温度分别为73.7℃和34.4℃,绝缘子两端温差达到39.3℃。为了探究绝缘子最大电场强度随时间的变化,定义电场变化率k为
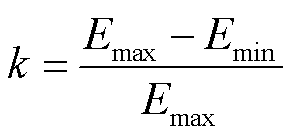 (12)
(12)
式中,Emax与Emin分别为一段时间范围内绝缘子畸变电场强度的最大值与最小值。
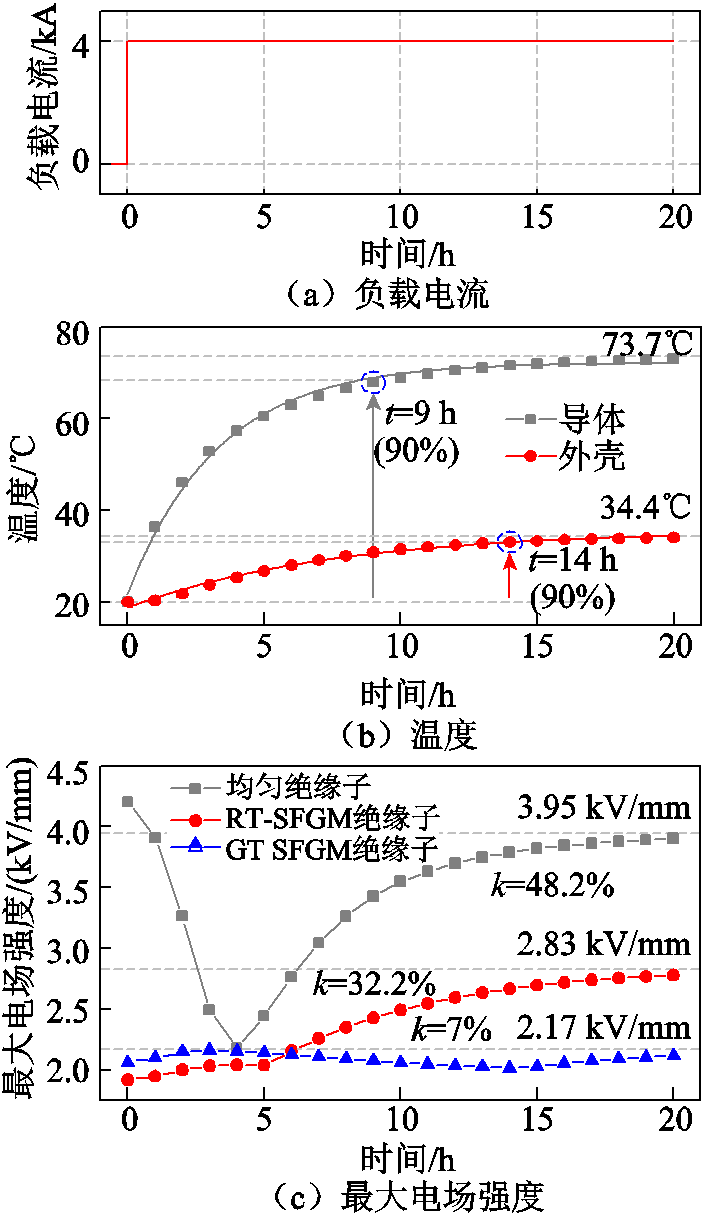
图11 负荷加载工况下负载电流、温度与最大电场强度的时域变化
Fig.11 Time domain variations of the load current, the temperature and the maxium electric field strength under current-loading condition
图11c所示为绝缘子的电场强度最大值的时域变化。随着负荷电流的加载,均匀绝缘子最大电场强度先快速减小,4 h后逐渐增大,最后缓慢接近稳态。由1.2节可知,随着温差的增加,均匀绝缘子畸变电场位置发生转移,其电场强度也出现了剧烈的波动,电场变化率达到48.2%。在t=0恒温时刻,RT-SFGM绝缘子的畸变电场强度最低,但随着时间的增加,其最大电场强度逐渐提高,20 h内的电场变化率达到32.2%。GT-SFGM绝缘子的稳态畸变电场强度最小,且在整个负荷加载的过程中其电场强度最大值仅在小范围内波动,电场变化率为7%。
3.2.2 负荷波动工况
图12a模拟了负荷波动工况下直流GIL/GIS导体内电流的时域变化,48 h内负荷电流在0~4 kA之间呈周期性变化。图12b所示为导体与外壳的温度时域变化。t=0时刻导体与外壳均为常温20℃;在0~6 h时间段,随着负荷电流的线性增加,导体温度快速提高,升温速率也逐渐加快;在6~18 h时间段,负荷电流保持不变,导体温度增长速度逐渐放缓,温度分布趋于稳定;在18~24 h时间段,随着负荷电流的减小,导体温度也明显降低。同时,随着导体温度的变化,外壳温度也出现了小幅度波动,其温度变化略滞后于导体;在24~48 h时间段内,负荷电流重复0~24 h时段变化,导体与外壳的温度变化趋势也基本与0~24 h时段相同。绝缘子两端最大温差出现在t=41 h时刻,约为38.7℃。
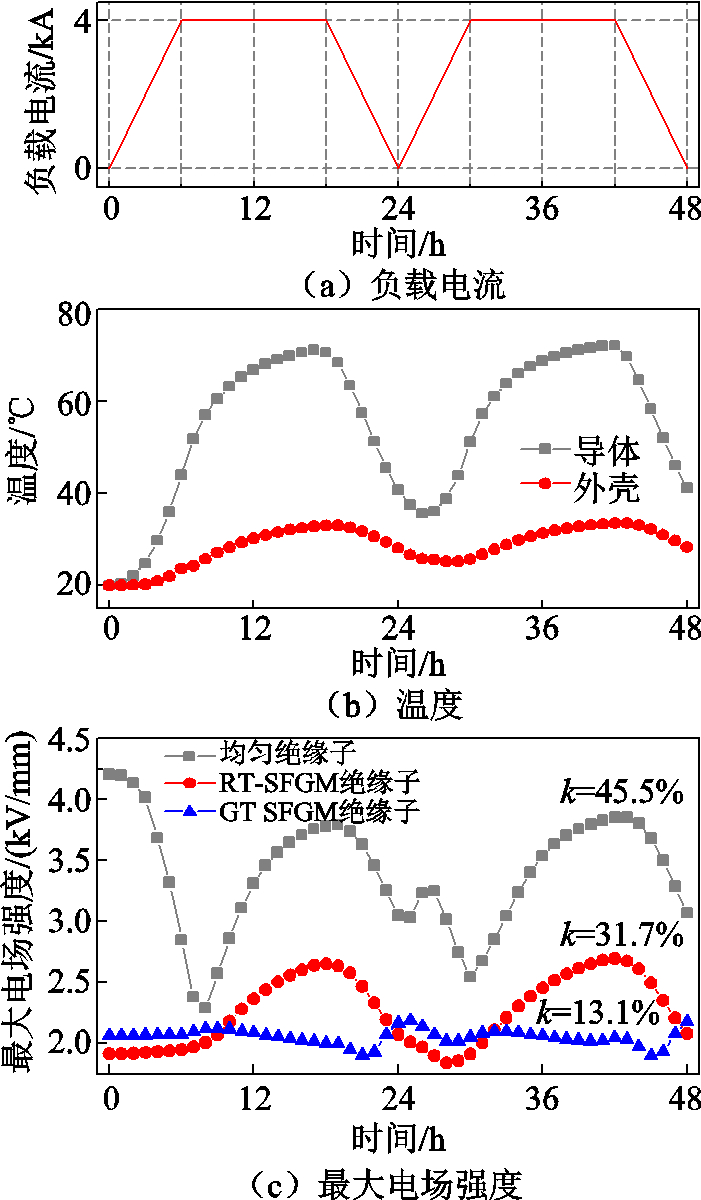
图12 负荷波动工况下负载电流、温度与最大电场强度的时域变化
Fig.12 Time domain variations of the load current, the temperature and the maxium electric field strength under load-fluctuating condition
图12c所示为负荷波动工况下均匀绝缘子、RT- SFGM绝缘子和GT-SFGM绝缘子的电场强度最大值的时域变化。均匀绝缘子的电场强度随着负载电流的变化波动剧烈,同时其最大电场强度位置也随着温度变化在高压导体与接地外壳之间移动,48 h内的电场变化率约为45.5%。RT-SFGM绝缘子电场变化趋势基本与均匀绝缘子一致,但波动幅度减小,电场变化率下降至31.7%。GT-SFGM绝缘子的电场较为稳定,其电场强度最大值随着负荷的波动没有发生明显变化,电场变化率仅有13.1%。
本文建立了±500 kV直流GIL/GIS盆式绝缘子电-热场耦合仿真模型,设计了具有表面电导梯度涂层的RT-SFGM绝缘子与GT-SFGM绝缘子,研究了时变温差工况下绝缘子的温度与电场分布特性。主要结论如下:
1)迭代优化后RT-SFGM绝缘子的涂层厚度从导体到外壳梯度减小,GT-SFGM绝缘子的凸面涂层厚度呈现U型梯度分布。恒温条件下,均匀绝缘子最大电场位于凹面高压三结合点处,RT-SFGM绝缘子与GT-SFGM绝缘子的最大电场强度分别下降了53.3%和49.5%。
2)随着导体温度的上升,绝缘子最大电场位置转移至外壳附近。在40℃温差条件下,均匀绝缘子的畸变电场强度上升至5.15 kV/mm,GT-SFGM绝缘子的电场畸变抑制效果明显优于RT-SFGM绝缘子,最大电场强度下降59.2%。
3)在负荷加载及波动的时变温差工况下,均匀绝缘子与RT-SFGM绝缘子的温度与电场随时间变化剧烈,均匀绝缘子在两种工况下的电场畸变率分别为48.2%与45.5%;RT-SFGM绝缘子的电场畸变率分别为32.2%和31.7%;而GT-SFGM绝缘子的电场变化率分别下降至7%和13.1%。GT-SFGM绝缘子可有效抑制时变温差工况下动态电场畸变与波动,实现绝缘子直流电场分布的稳定控制。
参考文献
[1] 李进, 王泽华, 陈允, 等. 高压气体绝缘输电设备用功能梯度材料研究进展[J]. 高电压技术, 2020, 46(7): 2471-2477. Li Jin, Wang Zehua, Chen Yun, et al. Research progress on functionally graded materials for high voltage gas insulated transmission apparatus[J]. High Voltage Engineering, 2020, 46(7): 2471-2477.
[2] 李文栋, 王超, 陈泰然, 等. 550kV GIS盆式绝缘子小型化设计(二): 介电分布优化[J]. 电工技术学报, 2022, 37(11): 2743-2752. Li Wendong, Wang Chao, Chen Tairan, et al. Compact design of 550kV basin-type spacer in gas insulated switchgear (partⅡ)—dielectric distribution optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2743-2752.
[3] 张博雅, 张贵新. 直流GIL中固-气界面电荷特性研究综述Ⅰ: 测量技术及积聚机理[J]. 电工技术学报, 2018, 33(20): 4649-4662. Zhang Boya, Zhang Guixin. Review of charge accumulation characteristics at gas-solid interface in DC GIL, part Ⅰ: measurement and mechanisms[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4649-4662.
[4] Li Chuanyang, Deng Baojia, Zhang Zi, et al. Full life property of surface charge accumulation on HVDC spacers considering transient and steady states[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2019, 26(5): 1686-1692.
[5] Nakane R, Hayakawa N, Okubo H. Time and space transition of DC electric field distribution based on emerging field by accumulated charge in gas-solid composite insulation structure[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2021, 28(2): 440-447.
[6] Liang Hucheng, Du Boxue, Li Jin. Electric field regulation and parameter optimization of surface nonlinear conductivity spacer for 500 kV DC-GIL[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(4): 1330-1338.
[7] Kurimoto M, Kato K, Hanai M, et al. Application of functionally graded material for reducing electric field on electrode and spacer interface[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(1): 256-263.
[8] 李文栋, 刘哲, 有晓宇, 等. 叠层式介电功能梯度绝缘子的介电常数分布优化[J]. 西安交通大学学报, 2016, 50(10): 19-26. Li Wendong, Liu Zhe, You Xiaoyu, et al. Permittivity distribution optimization for multi-layer dielectric FGM insulator[J]. Journal of Xi’an Jiaotong University, 2016, 50(10): 19-26.
[9] 梁虎成, 杜伯学, 陈允, 等. 基于迭代算法的功能梯度绝缘子介电常数分布优化[J]. 电工技术学报, 2020, 35(17): 3758-3764. Liang Hucheng, Du Boxue, Chen Yun, et al. Permittivity distribution optimization of functionally graded insulator based on iterative method[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3758-3764.
[10] 孙秋芹, 郭晓和, 张永涛, 等. 基于介电功能梯度材料的盆式绝缘子电场分布优化[J]. 湖南大学学报(自然科学版), 2018, 45(8): 99-106. Sun Qiuqin, Guo Xiaohe, Zhang Yongtao, et al. Optimization of electric field distribution for spacer based on dielectric functionally graded material[J]. Journal of Hunan University (Natural Sciences), 2018, 45(8): 99-106.
[11] 尹昊阳, 李文栋, 王超, 等. 介电功能梯度绝缘子设计中的电场优化方法对比[J]. 高压电器, 2021, 57(4): 105-111, 119. Yin Haoyang, Li Wendong, Wang Chao, et al. Comparison of electric field optimization method in the design of dielectric functional gradient insulator[J]. High Voltage Apparatus, 2021, 57(4): 105-111, 119.
[12] Winter A, Kindersberger J. Stationary resistive field distribution along epoxy resin insulators in air under DC voltage[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2012, 19(5): 1732-1739.
[13] Du Boxue, Ran Zhaoyu, Li Jin, et al. Novel insulator with interfacial σ-FGM for DC compact gaseous insulated pipeline[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2019, 26(3): 818-825.
[14] Du Boxue, Ran Zhaoyu, Li Jin, et al. Fluorinated epoxy insulator with interfacial conductivity graded material for HVDC gaseous insulated pipeline[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(4): 1305-1312.
[15] 何顺, 郑易谷, 林川杰, 等. 温度梯度下电荷行为与直流沿面闪络的关联性[J]. 高电压技术, 2020, 46(10): 3597-3604. He Shun, Zheng Yigu, Lin Chuanjie, et al. Relation between charge behavior and DC surface flashover under temperature gradient[J]. High Voltage Engineering, 2020, 46(10): 3597-3604.
[16] Hering M, Speck J, Großmann S, et al. Influence of gas temperature on the breakdown voltage in gas-insulated systems[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(1): 401-408.
[17] 王增彬, 刘姝嫔, 周宏扬, 等. GIS盆式绝缘子温度多物理场仿真方法[J]. 高电压技术, 2019, 45(12): 3820-3826. Wang Zengbin, Liu Shupin, Zhou Hongyang, et al. Multiphysics simulation method for GIS epoxy spacer temperature[J]. High Voltage Engineering, 2019, 45(12): 3820-3826.
[18] 张震, 林莘, 余伟成, 等. C4F7N/CO2和C4F7N/N2混合气体热力学物性参数计算[J]. 高电压技术, 2020, 46(1): 250-256. Zhang Zhen, Lin Xin, Yu Weicheng, et al. Thermodynamic calculation of physical properties of C4F7N/CO2 and C4F7N/N2[J]. High Voltage Engineering, 2020, 46(1): 250-256.
[19] Du Boxue, Yao Hang, Liang Hucheng, et al. Multidimensional functionally graded materials (ε/σ-MFGM) for HVDC GIL/GIS spacers[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, 29(5): 1966-1973.
[20] Yao Hang, Du Boxue, Liang Hucheng, et al. Electric field relaxation of HVDC GIL spacer with surface conductivity gradient material (σ-SFGM) using electrospinning technology[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, 29(3): 1167-1174.
Abstract In real applications of the DC gas insulated transmission line (GIL) and gas insulated switchgear (GIS), there are large temperature gradients between the HV conductor and the grounding shell of the spacer, which leads to a completely different electric field distribution compared to that at room temperature. The DC electric field distribution is mainly related to the conductivity parameter of the insulating materials. By applying the coating with conductivity gradient, the surface functionally graded material (SFGM) spacer is considered to be an effective way to uniform the electric field distribution in DC-GIL/GIS. Meanwhile, due to the change of power generation and load, the temperature of the HV conductor also fluctuates with time, which brings difficulties to the optimal design of SFGM spacers under complex working conditions. To optimize the surface electric field distribution of the DC-GIL/GIS basin spacer under variable temperature gradient, based on the surface conductivity graded materials (σ-SFGM), the RT-SFGM spacer with the goal of regulating the surface electric field distribution at room temperature (RT) and the GT-SFGM spacer with consideration of different gradients of temperature (GT) are designed in this paper.
Firstly, an electric-heat coupling model of a ±500 kV DC GIL/GIS basin-type spacer is modelled to calculate the electric field distributions under temperature gradients. Considering the gas flow inside the DC-GIL/GIS, the temperature distribution of the spacer is simulated. Experimental results show that the conductivity of the epoxy composites has a strong temperature dependence. As the temperature increases from 30°C to 90°C, the conductivity of the spacer bulk increases by more than 100 times. Compared to the spacer bulk, the conductivity of the coating has a smaller variation with the temperature. Different reference electric fields are selected as optimization goals for the RT-SFGM spacer and the GT-SFGM spacer. Based on the iterative optimization method, the thickness of the RT-SFGM spacer and the GT-SFGM spacer are designed. After iterative optimization, the coating layer thickness of the optimized RT-SFGM spacer decreases from the conductor to the shell, while the coating thickness on the convex surface of the GT-SFGM spacer presents a U-shaped distribution.
Simulation results show that, at room temperature, the electric field at the high-voltage triple junction of the uniform spacer is seriously distorted, and the electric field strength of the RT-SFGM spacer and the GT-SFGM spacer at the same position decreases by 53.3% and 49.5%, respectively. With the increasing temperature of the high voltage conductor, the maximum electric field of the uniform spacer gradually transfers to the grounding shell. Under the temperature gradient of 40℃, the GT-SFGM spacer has a better electric field relaxation effect than the RT-SFGM spacer, and the maximum electric field strength decreases by 59.2%. Under current loading and fluctuation conditions, the electric field distribution of the uniform spacer presents a wide range of fluctuation with the current, and the maximum electric field position transfers between the conductor and the shell. The electric field of the GT-SFGM spacer does not change drastically with the current changing, and the electric field change rate is only 7% and 13.1% under current loading and fluctuation conditions, which achieves the stable control of electric field under the variable temperature gradient condition.
keywords:DC, GIL/GIS spacer, surface conductivity graded materials (σ-SFGM), variable temperature gradient, electric field relaxation
DOI: 10.19595/j.cnki.1000-6753.tces.230213
中图分类号:TM216
国家自然科学基金(52220105002)和博士后创新人才支持计划(BX2021210)资助项目。
收稿日期 2023-02-23
改稿日期 2023-04-24
杜伯学 男,1961年生,教授,博士生导师,研究方向为聚合物绝缘材料的介电失效机理。E-mail:duboxue@tju.edu.cn
梁虎成 男,1992年生,博士后,研究方向为直流气体绝缘输电管道电场调控。E-mail:hcliang@tju.edu.cn(通信作者)
(编辑 李 冰)