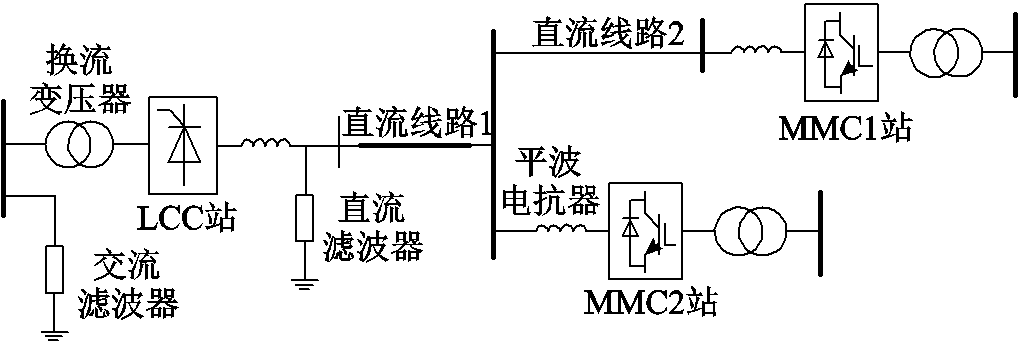
图1 三端混合直流输电系统拓扑
Fig.1 Topology of three-terminal hybrid DC transmission system
摘要 多端混合直流输电系统故障发展迅速、短路电流水平超标问题严重,换流站高度非线性特征使现有短路电流求解忽略了控制系统的响应过程且多依赖建模仿真结果,无法得到短路电流的具体解析式,实现故障特性的定量分析计算。为此,该文提出三种兼顾准确性与计算复杂程度的系统模型简化措施,并在此基础上提出计及控制系统作用的短路电流复频域近似求解方法,利用Pade逼近以及分段线性化法对模型进行降阶处理,通过拉普拉斯逆变换求得短路电流的时域解析式。最后,基于PSCAD/EMTDC对不同故障距离、过渡电阻以及故障类型进行了仿真分析。结果表明,该方法能在故障的暂态阶段(10 ms内)对短路电流有较为准确的刻画,能为直流保护定值整定、断路器额定容量选取、直流输电控制策略切换以及系统规划设计等提供重要依据。
关键词:短路电流计算 控制系统 网络等值 多端混合直流输电 线路故障
我国能源负荷整体呈逆向分布,特高压直流输电凭借更高的输电能力和输电效率承担着电力区域间调动的重要职能,在能源资源优化配置领域备受青睐。直流输电按换流技术可分为常规高压直流输电(Line Commutated Converter-High Voltage Direct Current, LCC-HVDC)、柔性高压直流输电(Modular Multilevel Converter-High Voltage Direct Current, MMC-HVDC)和混合直流输电三类。其中,混合直流输电技术结合LCC与MMC的优点[1],充分发挥二者在经济、技术方面的优势,为大规模风力发电、光伏等新能源接入电网提供了新思路,是我国直流电网建设中的重要组成部分。2015年12月,乌东德、白鹤滩、溪洛渡、向家坝等大型水电站全面施工,2020年12月,特高压“昆柳龙”多端混合直流示范工程正式启动投产送电,标志着大容量、远距离的多端混合直流输电技术已成功应用至工程实际中,有效地拓宽了传统直流输电的应用范围。
对于混合直流输电系统,其输电线路较长、工作环境复杂,故障概率较大;直流线路一旦发生短路故障,会在10 ms内产生数倍于额定电流的故障电流,使整个系统面临严重的过电流风险,威胁系统的稳定运行。因此,剖析直流线路故障后的暂态阶段,定量计算线路故障电流,不仅能为多端混合直流系统规划设计与控制保护策略的优化提供理论基础,对寻求降低故障电流水平的方法亦具有重要的理论和工程应用价值。目前,国内外在直流侧故障电流分析计算方面开展了较多研究。文献[2]基于状态空间理论分析得出LCC输电系统短路电流的时域表达式;文献[3]对柔性直流电网极间故障特性展开了分析;文献[4]提出将环形直流网络简化为两端网络,但对于不同多端拓扑的简化缺乏一定的普适性;文献[5]提出一种基于伴随网络的直流电网短路电流计算方法,但需要额外增加模型离散化处理过程;文献[6]基于基尔霍夫定律对直流系统列写状态空间微分方程,但未给出具体的故障电流解析式,因此无法全面研究系统参数对故障电流的影响;为此,文献[7]对不同主电路参数对直流短路故障电流的影响程度展开了分析。
此外,上述计算过程均未考虑到触发延迟角的非线性变化、换流站控制模式等响应过程对故障电流的影响,默认在直流故障暂态阶段控制系统尚未发挥作用,因此增加了短路电流计算的误差。为此,文献[8]在计及MMC直流电压控制的条件下,提出一种基于微分方程的故障电流改进算法,但只对极间故障进行了等值处理,并不适用于混合输电网络;文献[9]对逆变侧交流故障展开分析,将传递函数输入量近似取为系统稳态运行点的值,最终在复频域中求得直流电流的近似解,但该方法仅适用于双端的LCC拓扑;文献[10]提出了MMC零直流电压控制策略;文献[11]基于该控制策略通过对子模块电容电压进行修正,从而更准确地计算双端系统短路电流,但并未明确给出零压控制启动时刻;文献[12]考虑了MMC控制系统作用对故障电流的影响,但忽略直流侧功率变化对故障电流的影响。
本文综合考虑MMC与LCC换流站控制特性,根据故障类型以及电网运行特点对多端网络进行合理简化,兼顾计算精度与计算效率对触发延迟角进行修正,利用Pade逼近等数学算法对控制模型降阶,最终求得各节点短路电流近似表达式。通过计算10 ms内短路电流的极值,可在系统规划设计时确定直流电网中的关键节点以加强监测,同时可利用暂态阶段短路电流的突变量对行波保护等定值进行分析优化,为多端混合输电系统控保协同配合的研究提供理论支撑。
三端混合直流输电系统拓扑如图1所示,系统采用真双极形式连接,在正负极均配置有高、低两个串联阀组以增大传输容量[13]。送端采用LCC输电方式,在交流侧配置交流滤波器和无功补偿设备等,直流侧配置直流滤波器和平波电抗器;受端经平波电抗器通过MMC输电技术馈入负荷中心,可以避免换相失败的发生并实现对直流系统进行迅速调节。

图1 三端混合直流输电系统拓扑
Fig.1 Topology of three-terminal hybrid DC transmission system
LCC换流站等效电路如图2所示,LCC换流站对外可视为换流器与线路出口及中性线电抗器串联后经直流滤波器并联而成。
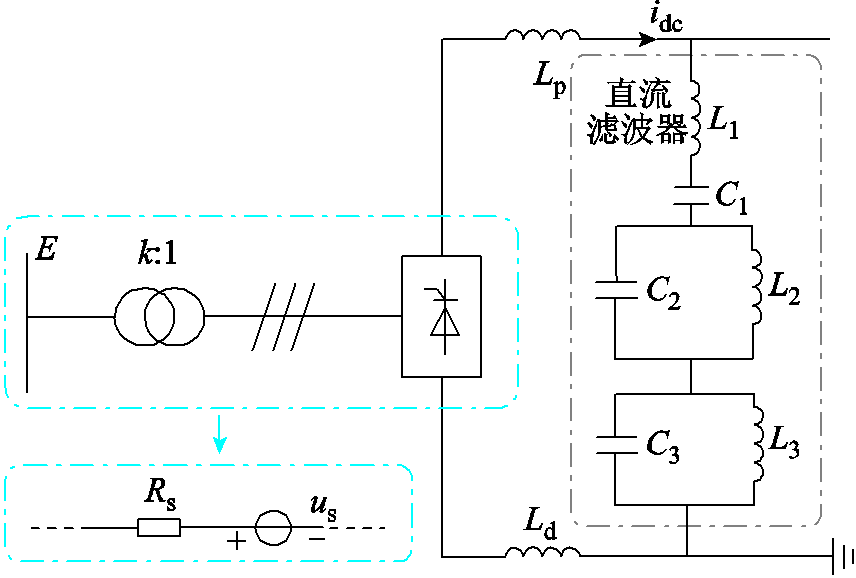
图2 LCC换流站等效电路
Fig.2 Equivalent circuit of LCC converter station
图2中,![]() 为平波电抗器,
为平波电抗器,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 为双调谐直流滤波器相关参数,
为双调谐直流滤波器相关参数,![]() 为中性线电感,
为中性线电感,![]() 为换流变压器匝比,
为换流变压器匝比,![]() 为LCC换流站交流母线线电压的有效值,
为LCC换流站交流母线线电压的有效值,![]() 为系统等值阻抗,
为系统等值阻抗,![]() 为整流侧直流电流,
为整流侧直流电流,![]() 为换流站等值电压源。各变量之间的关系为
为换流站等值电压源。各变量之间的关系为
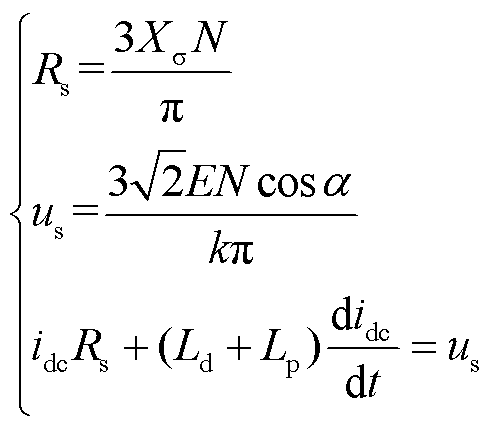 (1)
(1)
式中,![]() 为换流变压器漏抗;N为换流站每极6脉动换流桥个数;α为换流阀触发延迟角。
为换流变压器漏抗;N为换流站每极6脉动换流桥个数;α为换流阀触发延迟角。
换流站的复频域等值阻抗可列写为
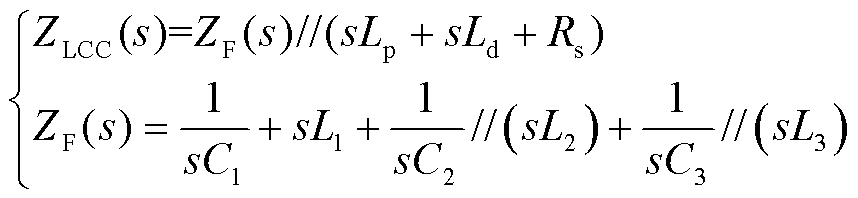 (2)
(2)
式中,![]() 与
与![]() 分别为LCC换流站与直流滤波器的复频域阻抗值。
分别为LCC换流站与直流滤波器的复频域阻抗值。
MMC桥臂拓扑电路结构如图3所示。为了提高直流输电系统的故障穿越能力,混合直流工程逆变侧MMC采用半桥型子模块与全桥型子模块组合的拓扑结构;此外,MMC换流器在直流侧出口处串联平波电抗器![]() ,其与桥臂电抗器
,其与桥臂电抗器![]() 配合,可有效地降低直流侧发生短路时故障电流的上升率,使绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)在较低的过电流情况下关断[14]。
配合,可有效地降低直流侧发生短路时故障电流的上升率,使绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)在较低的过电流情况下关断[14]。
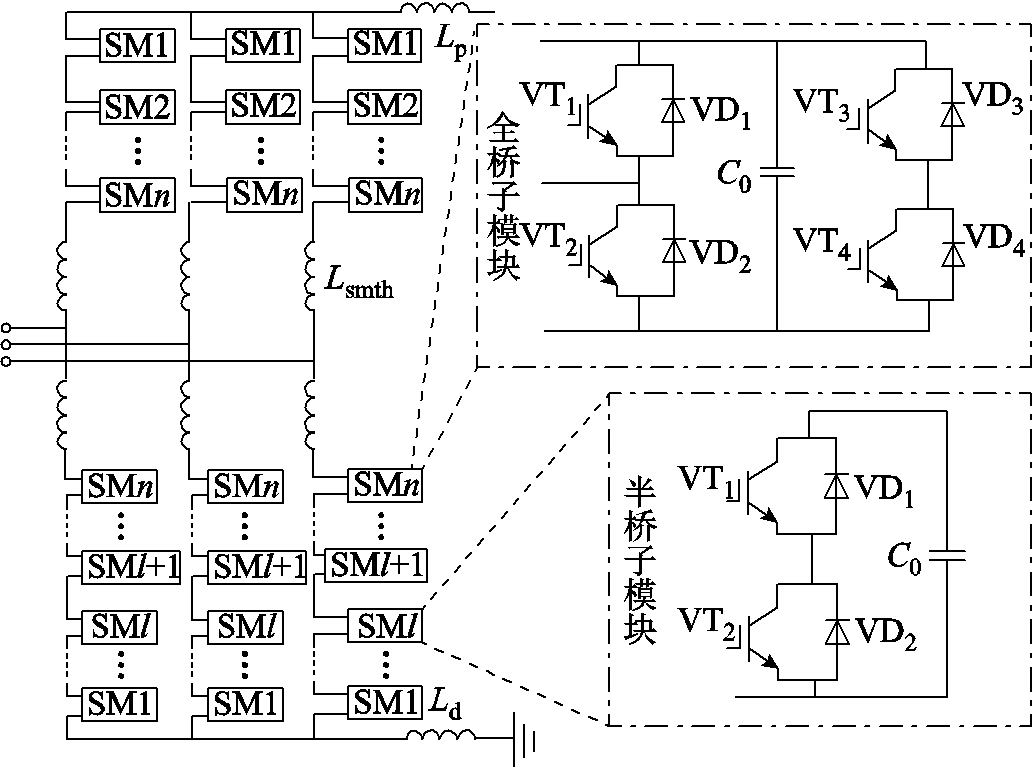
图3 MMC桥臂拓扑电路结构
Fig.3 Topology of MMC bridge arm
在直流故障后的5~10 ms内,MMC换流站提供的短路电流主要由子模块电容器的放电提供。当桥臂全桥型子模块工作于正投入、负投入与切除状态时,在故障初期为维持电压稳定,上、下桥臂投入子模块数量恒定。此时桥臂电阻和电抗的参数与半桥型MMC拓扑方式一致[15]。通过忽略交流馈入电流,混合型MMC的详细模型最终可等效为RLC串联电路,如图4所示。其中,![]() 、
、![]() 、
、![]() 为换流站RLC等值参数。
为换流站RLC等值参数。
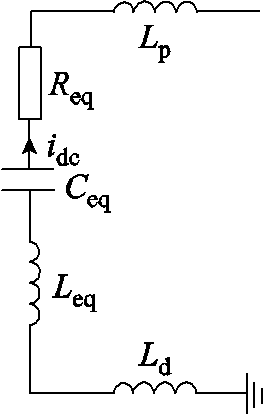
图4 混合型MMC换流站等效电路
Fig.4 Equivalent circuit of hybrid MMC converter station
当直流侧发生短路故障时,在电容均压控制策略下子模块电压保持均衡。根据能量守恒原则,单相桥臂等效电容可表示为
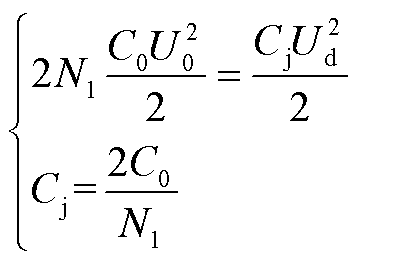 (3)
(3)
式中,![]() 为子模块电容值;
为子模块电容值;![]() 为单相桥臂等值电容;
为单相桥臂等值电容;![]() 为单相桥臂子模块级联数量;
为单相桥臂子模块级联数量;![]() 与
与![]() 分别为故障发生后子模块电容电压和直流侧电压,二者在故障进入稳态阶段之前近似相等。
分别为故障发生后子模块电容电压和直流侧电压,二者在故障进入稳态阶段之前近似相等。
由于MMC换流站的等值是单相上下桥臂各自等值电阻、电容和电感串联后经三相并联得到的混联电路[16],因此,MMC等值参数的计算式为
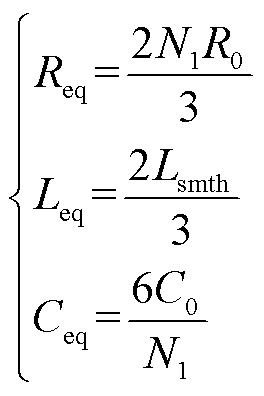 (4)
(4)
式中,![]() 为子模块的导通电阻。则换流站的复频域等值阻抗可写为
为子模块的导通电阻。则换流站的复频域等值阻抗可写为
高压直流电网大多数采用架空线路进行功率传输。受线路参数频变特性的影响,不同频率的暂态电气量沿着输电线路的传播具有不同的传播速度和衰减系数,因此增加了利用数学模型求解短路电流的难度。为求得直流故障电流的解析解,本文在计算中采用简化后的RL集中参数代替依频模型以减少拉普拉斯逆变换的计算阶数。这种算法虽然无法反映行波发生折反射的具体细节,但能描述短路电流的整体变化规律[17],且能确保误差在合理的范围内,满足故障电流分析计算的精度要求。
LCC换流站采用带最小触发延迟角限制的定直流电流控制模式[18]。若系统发生扰动或故障使直流电流超过额定值时,触发延迟角![]() 会在各控制器的配合下迅速增大,但不会超过最大触发延迟角。在此过程中直流电压输出值快速下降,从而限制暂态电流值以保护换流站核心元件。其控制逻辑如图5所示。其中,
会在各控制器的配合下迅速增大,但不会超过最大触发延迟角。在此过程中直流电压输出值快速下降,从而限制暂态电流值以保护换流站核心元件。其控制逻辑如图5所示。其中,![]() 为直流电流参考值,若不配备低压限流环节其值取为1;
为直流电流参考值,若不配备低压限流环节其值取为1;![]() 、
、![]() 为增益系数;
为增益系数;![]() 、
、![]() 为延时系数。
为延时系数。

图5 整流侧定电流控制
Fig.5 Rectifier-side current control
若故障尚未进入稳态阶段且保护尚未发出移相命令,输出![]() 不会抵达上限与下限,因此输入量
不会抵达上限与下限,因此输入量![]() 与输出量
与输出量![]() 函数的关系为
函数的关系为
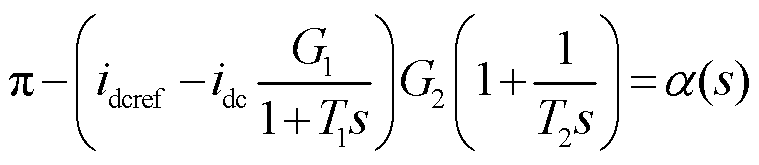 (6)
(6)
MMC基于矢量控制方式的双环结构框图如图6所示。外环控制器可以根据不同的控制指令计算内环电流控制的输入,内环控制器可以使直流电流d轴与q轴分量(![]() 、
、![]() )跟踪参考值[19]。图6中,
)跟踪参考值[19]。图6中,![]() 、
、![]() 、
、![]() 、
、![]() 为MMC控制系统参数,
为MMC控制系统参数,![]() 、
、![]() 分别为d轴与q轴电流参考值。
分别为d轴与q轴电流参考值。
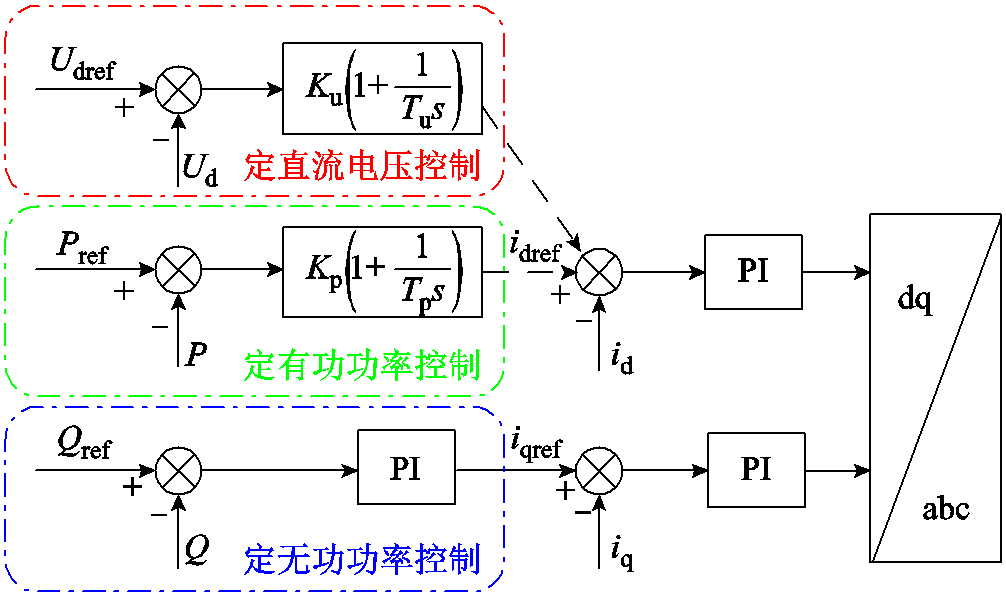
图6 MMC双环控制框图
Fig.6 Dual-loop control diagram of MMC
在多端直流输电系统中,每一端换流站均需具备有功类控制指令和无功类控制指令进行控制。对于两端及多端柔性直流输电系统而言,正常运行时必须有一侧的换流站采用定直流电压控制,并配有定无功功率控制;其余换流站一般采用定有功功率控制和定无功功率控制。此外,MMC控制系统还包含子模块均压控制、环流抑制控制等环节,但上述控制特性并不会对故障电流的计算产生影响[20],此处不再赘述。
2.2.1 定有功功率控制
当MMC站采用定有功功率指令控制时,有功功率与额定值做差值后经过PI环节输出![]() ,因此在故障初期,控制系统等值电流源
,因此在故障初期,控制系统等值电流源![]() 可写为
可写为
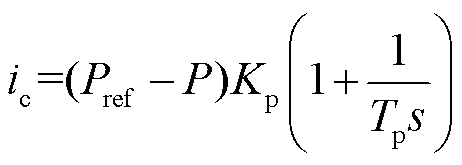 (7)
(7)
2.2.2 定直流电压控制
如图6所示,当MMC站采用定直流电压指令控制时,直流电压与其参考值做差后经过PI 控制器生成![]() 。此时控制系统等值电流源
。此时控制系统等值电流源![]() 近似等于外环电流控制器输出电流[12],可列写为
近似等于外环电流控制器输出电流[12],可列写为
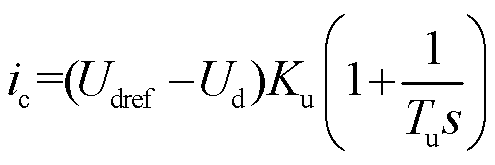 (8)
(8)
直流输电线路双极间存在一定程度的电磁耦合,首先利用式(9)所示的相模变换,完成直流双极输电系统两极电气量的解耦,得到独立的线模量和地模分量,最后再进行逆变换![]() 得到正、负极电压和电流值。
得到正、负极电压和电流值。
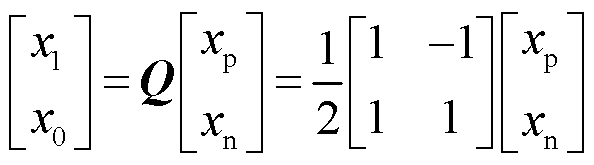 (9)
(9)
式中,![]() 、
、![]() 分别为直流电压、电流的线模和地模分量;
分别为直流电压、电流的线模和地模分量;![]() 、
、![]() 分别为正极分量和负极分量。
分别为正极分量和负极分量。
以直流线路1发生单极接地故障为例,健全极电流变化量将远小于故障极电流变化量,可以继续正常运行,因此本文仅对故障极线路短路电流进行分析。此时,线模网络与地模网络在故障支路端口处呈现串联的关系[21],如图7所示。其中,上角标(0)与(1)分别代表元件的地模和线模参数,![]() 为过渡电阻,
为过渡电阻,![]() 为故障点稳态电压分量。
为故障点稳态电压分量。
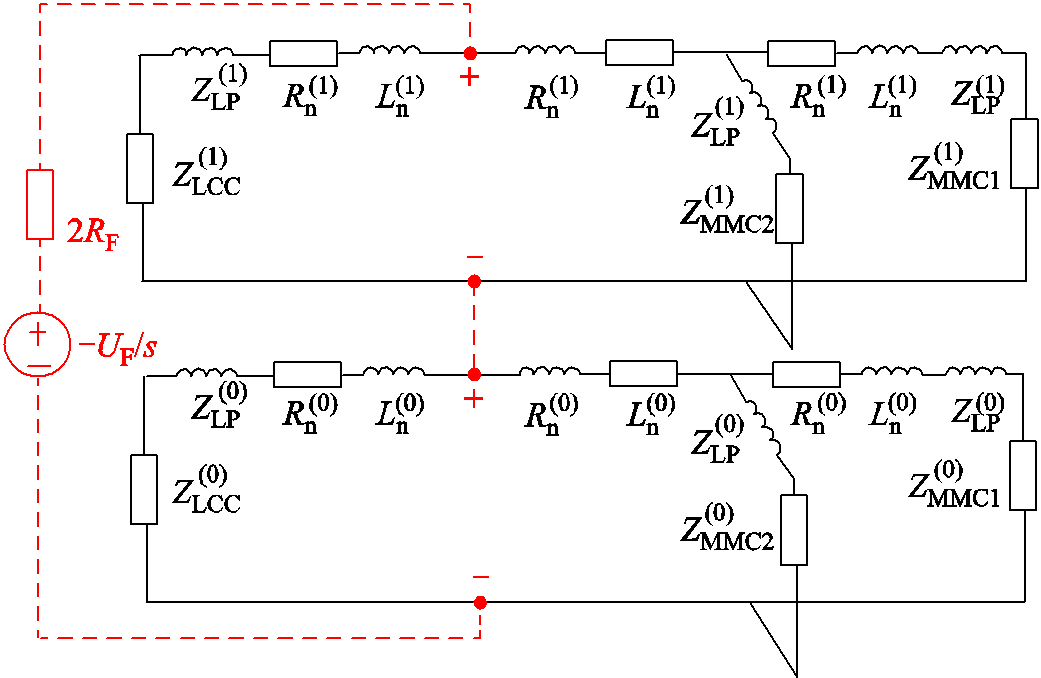
图7 直流系统发生单极接地故障后的暂态等值电路图
Fig.7 Transient equivalent circuit of DC system after single-pole grounding fault
对于故障极短路电流的近似计算而言,为了降低算法的数据处理量,线路电感、电阻参数可通过式(10)进行简化求取[22]。
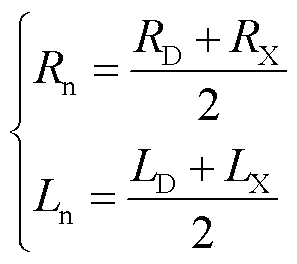 (10)
(10)
式中,![]() 、
、![]() 分别为线路单位长度地模和线模电阻值;
分别为线路单位长度地模和线模电阻值;![]() 、
、![]() 分别为线路单位长度地模和线模电感值;
分别为线路单位长度地模和线模电感值;![]() 、
、![]() 分别为在直流系统发生单极故障时线路的等值电阻和电感。
分别为在直流系统发生单极故障时线路的等值电阻和电感。
双极短路与单极接地故障过程相似,但两极线路均发生故障反应。由于直流系统正负极间完全对称,因此极间短路故障等值中仅存在线模分量,并不会产生地模分量。
1)端口处理:多端直流输电系统常采用二端口网络进行等效,此时线路电流故障分量将仅由故障线路相邻换流站电源提供[4],但这种方法在故障后5~10 ms的误差会由于子模块电容储能数量较原有网络减少而进一步增大,因此本文在线路故障后保留全部换流站,远端换流站系统对于故障暂态电流将起到分流的作用。
2)非故障极放电回路处理:非故障极换流器的放电回路必须流经其他非故障极换流器,由割集矩阵KCL推导可知,非故障极仅会对故障极产生数值较小的扰动电流[23],因此本文通过对非故障极开路处理进而忽略其对故障点的放电过程。
3)交流系统处理:当直流侧发生故障时,在 10 ms以内换流站交流侧系统仍是三相对称的,交流电流只流经每个桥臂,并不会馈入直流侧[24],因此本文在近似计算中将换流站与交流侧进行断开处理。
综上所述,三端混合直流输电系统在发生单极接地故障后的等效电路如图8所示。对于极间故障而言,只需将故障支路中的过渡电阻![]() 修改为
修改为![]() 即可。其中,f为故障点;
即可。其中,f为故障点;![]() 、
、![]() 与
与![]() 为线路复频域阻抗值。
为线路复频域阻抗值。
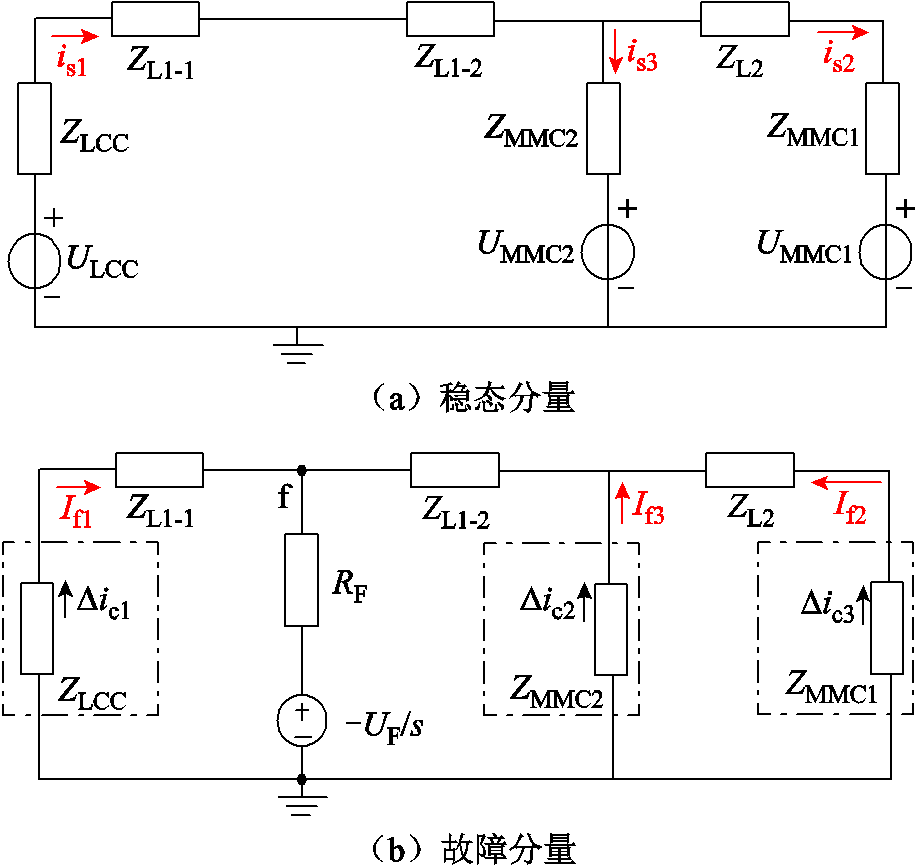
图8 系统在f点发生故障时的等效电路
Fig.8 System equivalent circuit during fault at f
在线路发生故障时,可将直流系统分解为正常状态和故障附加状态的叠加,并最终得到故障电流的变化特征。然而,这种计算方式忽略了换流站控制特性对直流电流的贡献作用。对于LCC端,在采用定直流电流控制时,触发延迟角![]() 会随直流电压的降低以及直流电流的激增而不断变化,而非系统处于稳定时的恒定值;对于MMC端,换流器不同的控制特性使得其对短路电流的贡献能力有所差异[25]。
会随直流电压的降低以及直流电流的激增而不断变化,而非系统处于稳定时的恒定值;对于MMC端,换流器不同的控制特性使得其对短路电流的贡献能力有所差异[25]。
因此,本文在原有正常负荷分量和故障分量的基础上,叠加控制系统对短路电流的修正量。由于换流站是高度非线性系统,因此通过在故障后的一段时间(10 ms)内将控制系统修正电流近似线性化处理,从而有效降低问题的复杂程度,最终得到短路电流为
式中,![]() 为短路电流;
为短路电流;![]() 为稳态运行电流;
为稳态运行电流;![]() 为故障附加电源提供的电流;
为故障附加电源提供的电流;![]() 为计及控制系统影响下的修正电流;m=1, 2, 3,分别代表LCC、MMC1与MMC2换流站。
为计及控制系统影响下的修正电流;m=1, 2, 3,分别代表LCC、MMC1与MMC2换流站。
由于直流电网中包含多个储能元件,其参数与频率有关,通过时域法求解短路电流解析式存在一定困难。因此本文从复频域内展开分析,首先通过故障网络的等值求解短路电流的复频域表达式,再通过拉普拉斯逆变换将复频域结果转换为对应的时域暂态形式,即
式中,![]() 为可变的正常数。
为可变的正常数。
下面以直流线路1发生单极接地故障为例进行展开分析。
此时,根据基尔霍夫电流及欧姆定律,![]() 可表示为
可表示为
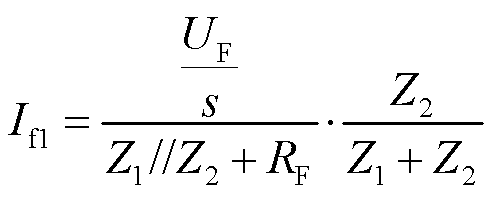 (13)
(13)
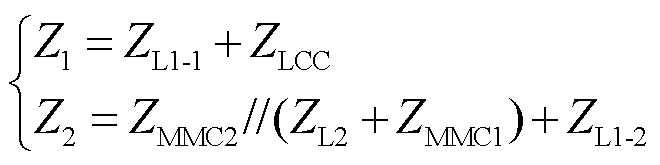 (14)
(14)
同理,![]() 、
、![]() 可分别通过式(15)、式(16)进行求取。
可分别通过式(15)、式(16)进行求取。
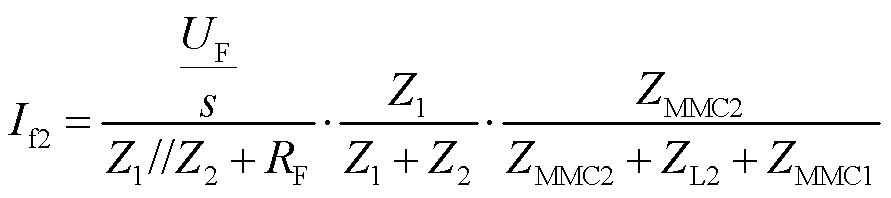 (15)
(15)
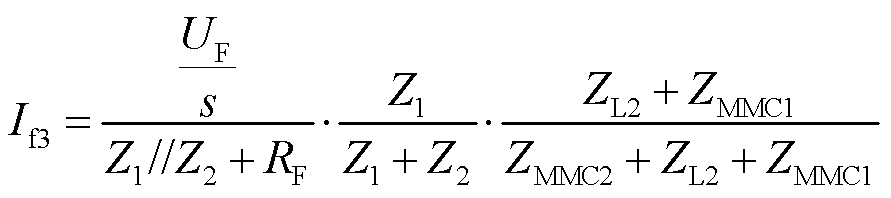 (16)
(16)
基于控制系统修正电流与换流站控制模式密切相关,以三端混合直流输电系统典型控制模式为例进行分析。
1)LCC站计及控制系统影响下的修正电流![]() 与系统各时刻运行状态下的触发延迟角
与系统各时刻运行状态下的触发延迟角![]() 以及直流电压
以及直流电压![]() 呈迭代关系,因此为简化计算,通过式(6)利用不计及LCC控制时的直流电流求取触发延迟角
呈迭代关系,因此为简化计算,通过式(6)利用不计及LCC控制时的直流电流求取触发延迟角![]() 的近似表达式,得到
的近似表达式,得到![]() 为
为
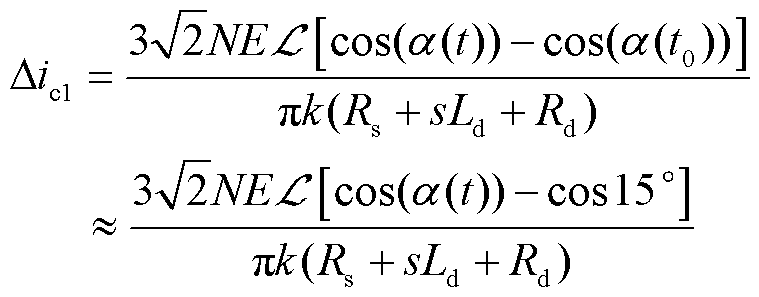 (17)
(17)
式中,![]() 为拉普拉斯变换运算符号;
为拉普拉斯变换运算符号;![]() 为前一时刻的触发延迟角,当系统处于稳态运行时触发延迟角一般可取15°~17°之间。为了降低复频域计算控制系统的阶数,对于
为前一时刻的触发延迟角,当系统处于稳态运行时触发延迟角一般可取15°~17°之间。为了降低复频域计算控制系统的阶数,对于![]() 的时变函数常利用分段函数进行线性拟合。
的时变函数常利用分段函数进行线性拟合。
某接地故障情况下触发延迟角计算及拟合图像如图9所示,曲线1为某接地故障情况下通过式(6)计算得到的触发延迟角变化特性曲线,曲线2与曲线3分别为对曲线1采用分段的线性函数拟合结果。实验结果表明,当拟合结果越逼近于![]() 的计算结果时,求取
的计算结果时,求取![]() 时的误差越小,一般以三段式拟合为宜。
时的误差越小,一般以三段式拟合为宜。
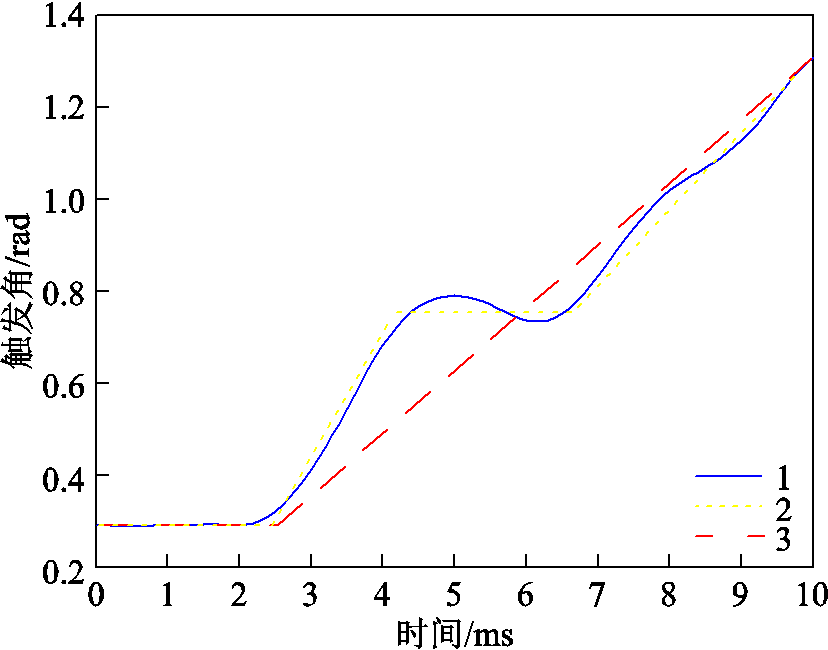
图9 某接地故障情况下触发延迟角计算及拟合图像
Fig.9 Triggering angle calculation and fitting image under a grounding fault
设某一段![]() 图像列写为式(18)的形式,则
图像列写为式(18)的形式,则![]() 可改写为式(19)的形式。
可改写为式(19)的形式。
![]() (18)
(18)
2)MMC1站计及控制系统影响下的修正电流![]() 求解:根据式(8),当MMC采用定直流电压控制时
求解:根据式(8),当MMC采用定直流电压控制时![]() 可改写为
可改写为
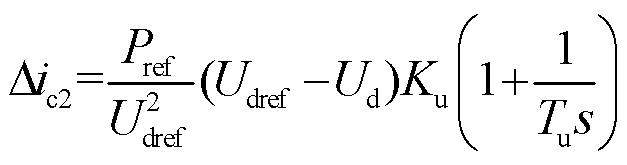 (20)
(20)
式中,实际值![]() 为
为
式(20)最终改写为
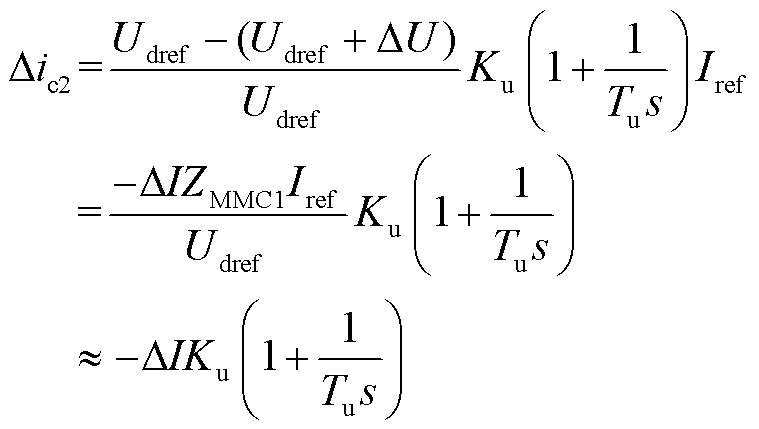 (22)
(22)
式中,![]() 、
、![]() 、
、![]() 分别为直流功率、直流电压及直流电流的参考值;
分别为直流功率、直流电压及直流电流的参考值;![]() 为暂态电压增量。
为暂态电压增量。
3)MMC2站计及控制系统影响下的修正电流![]() 求解:计及直流侧功率变化对故障电流的影响,根据图6,
求解:计及直流侧功率变化对故障电流的影响,根据图6,![]() 可写作
可写作
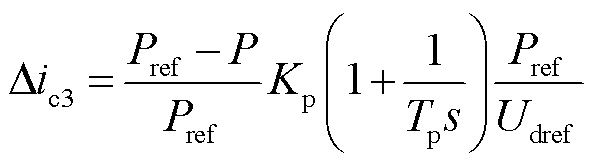 (23)
(23)
进一步改写为
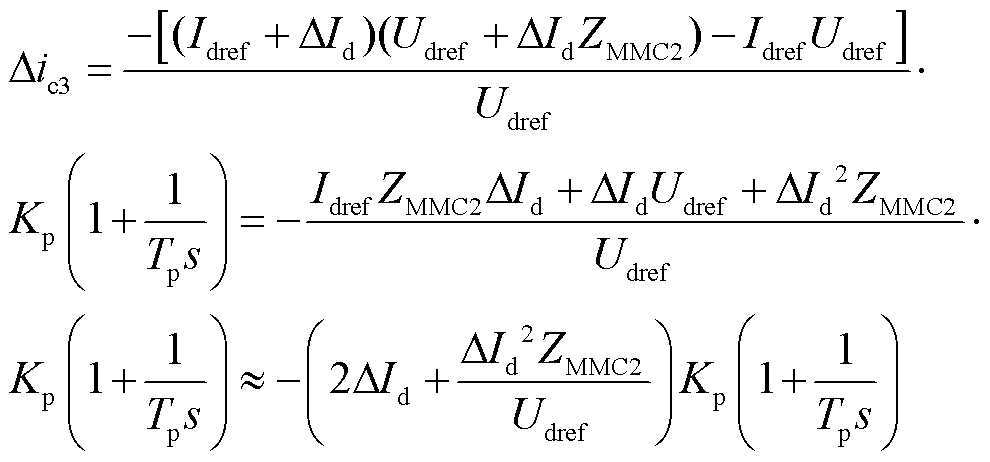 (24)
(24)
式中,![]() 为直流功率实际值;
为直流功率实际值;![]() 为暂态电流增量,计算时对前一时刻电流进行修正。
为暂态电流增量,计算时对前一时刻电流进行修正。
综上所述,计及控制作用的电流修正量均为不计控制下短路电流暂态增量的函数,在求取计及控制系统影响下的修正电流![]() 表达式时,为了将高阶传递函数尽可能降到较低的阶数,工程中可采用Pade逼近法、时间矩拟合等方法实现。其中,基于Routh稳定判据的Pade逼近法可以有效地以低阶次的有理函数逼近如式(25)所示的高阶传递函数。其逼近的原理部分在此不展开赘述。
表达式时,为了将高阶传递函数尽可能降到较低的阶数,工程中可采用Pade逼近法、时间矩拟合等方法实现。其中,基于Routh稳定判据的Pade逼近法可以有效地以低阶次的有理函数逼近如式(25)所示的高阶传递函数。其逼近的原理部分在此不展开赘述。
将![]() 展开为连分式的形式如式(26)所示,通过Routh稳定判据阵列求得低阶传递函数,进而在暂态阶段对故障电流进行拉普拉斯逆变换求得时域解。然而,Pade逼近的截断误差会随着时间推移而逐渐增大[26],因此若采用Pade逼近对结果进行降阶不宜将时间尺度设置过长。
展开为连分式的形式如式(26)所示,通过Routh稳定判据阵列求得低阶传递函数,进而在暂态阶段对故障电流进行拉普拉斯逆变换求得时域解。然而,Pade逼近的截断误差会随着时间推移而逐渐增大[26],因此若采用Pade逼近对结果进行降阶不宜将时间尺度设置过长。
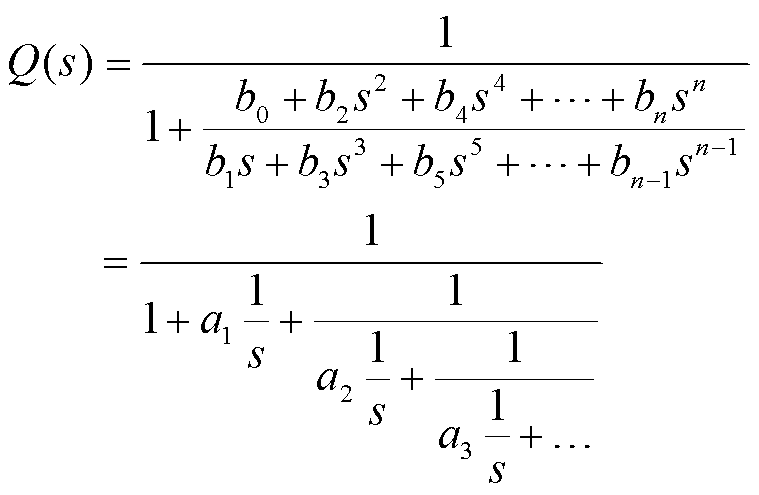 (26)
(26)
对于短路点距离首端较远时,在故障初始时刻首行波尚未抵达,因此会有行波传输时间![]() 的延时,其大小可通过式(27)求取,为减小计算误差在数据处理时需考虑这一延时过程。
的延时,其大小可通过式(27)求取,为减小计算误差在数据处理时需考虑这一延时过程。
![]() (27)
(27)
式中,![]() 为故障距离;
为故障距离;![]() 为行波波速,其随频率增高而增大,近似计算可取
为行波波速,其随频率增高而增大,近似计算可取![]() 。
。
整体上,本文短路电流计算流程如图10所示。
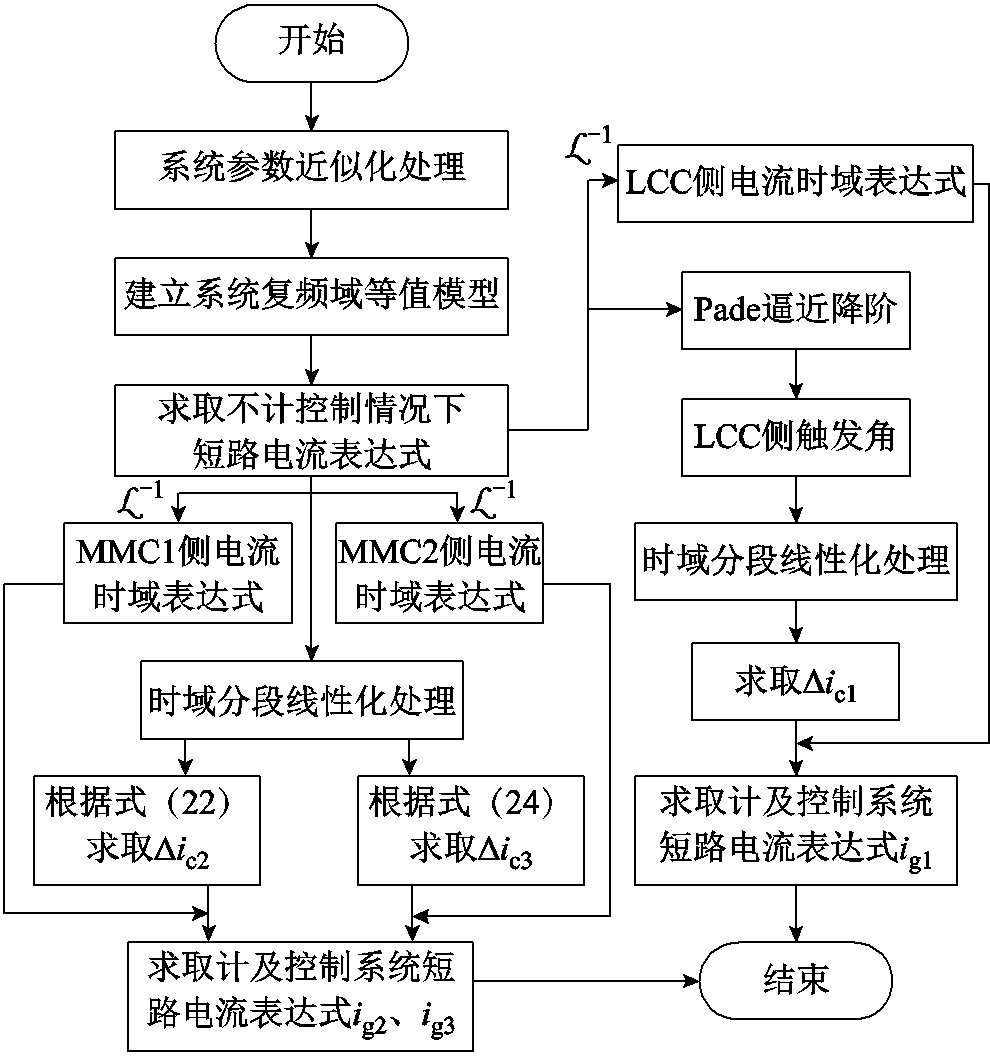
图10 短路电流计算流程
Fig.10 Short circuit current calculation flow chart
为了验证所提计算方法的正确性,利用电磁暂态仿真平台PSCAD/EMTDC搭建三端混合直流输电系统作为算例,传输线路采用Bergeron模型表示,LCC站采取定直流电流控制,MMC1站采取定直流电压控制,MMC2站采取定有功功率控制,各换流站及线路的具体参数分别见表1、表2。在对称双极系统中,不同直流线路发生故障后具有相似的故障特性,因此,本文以线路1故障为例进行仿真验证。
表1 各换流站具体参数
Tab.1 Parameters of converter stations
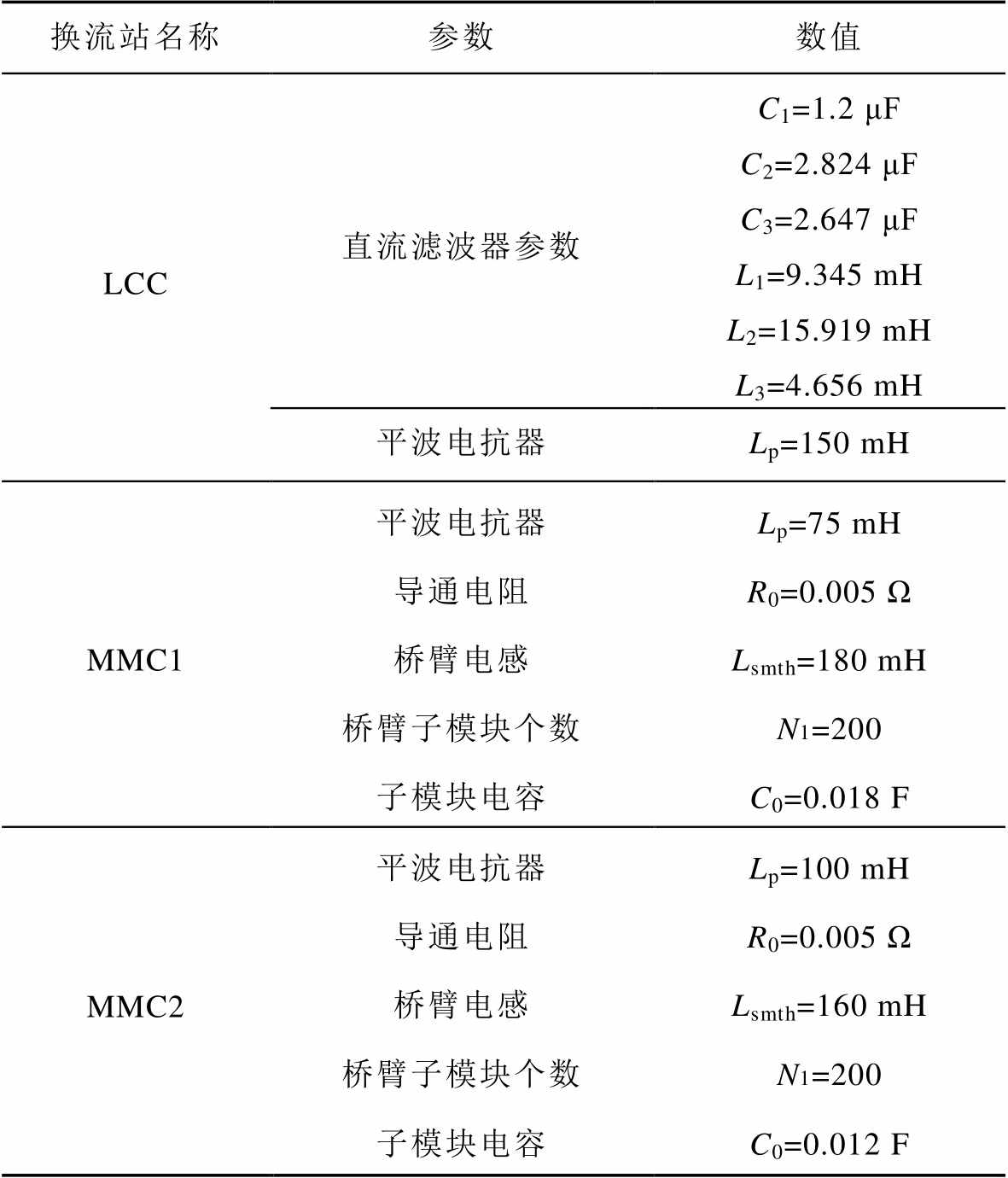
换流站名称参数数值 LCC直流滤波器参数C1=1.2 μF C2=2.824 μFC3=2.647 μF L1=9.345 mHL2=15.919 mHL3=4.656 mH 平波电抗器Lp=150 mH MMC1平波电抗器Lp=75 mH 导通电阻R0=0.005 Ω 桥臂电感Lsmth=180 mH 桥臂子模块个数N1=200 子模块电容C0=0.018 F MMC2平波电抗器Lp=100 mH 导通电阻R0=0.005 Ω 桥臂电感Lsmth=160 mH 桥臂子模块个数N1=200 子模块电容C0=0.012 F
表2 直流线路具体参数
Tab.2 Parameters of DC transmission line

模量电感/(mH/km)电阻/(Ω/km) 线模0.860.030 4 地模1.780.209
图11~图13给出了直流线路1在正极线路中点发生接地故障后,三个换流站出口短路电流示意图,过渡电阻分别为20、50和![]() 。图14为当线路不同位置经
。图14为当线路不同位置经![]() 过渡电阻接地时,LCC站的出口短路电流示意图。其中曲线1为短路电流的仿真结果,曲线2与曲线3分别为计及控制与不计控制作用下短路电流的计算结果。
过渡电阻接地时,LCC站的出口短路电流示意图。其中曲线1为短路电流的仿真结果,曲线2与曲线3分别为计及控制与不计控制作用下短路电流的计算结果。
如图11a所示,直流线路故障后,故障行波向两侧换流站传播,若其尚未抵达各换流站出口侧,各测点电流值仍维持为故障前稳态电流大小。当故障初始行波抵达换流站出口(图中j点),直流电流呈阶梯状增加;随后故障行波在换流站端口与故障端口间不断地折反射,最终短路电流的实际值表现为所有折射与反射波的叠加。
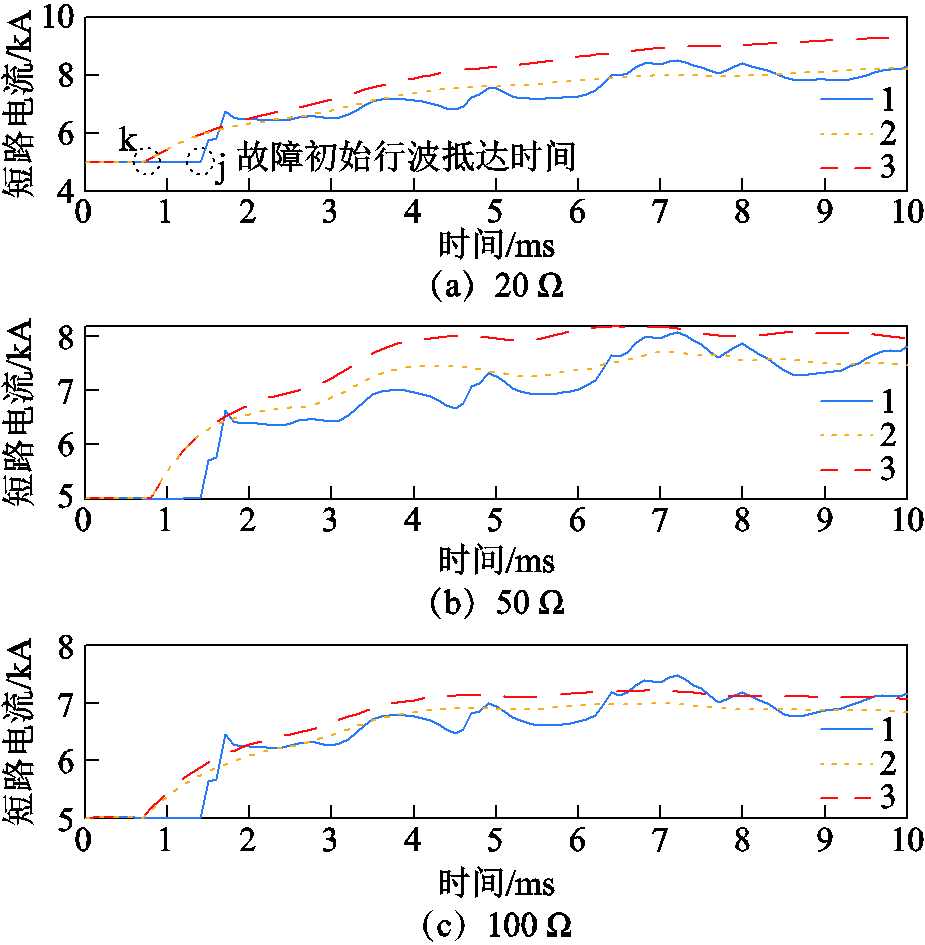
图11 不同过渡电阻下的单极接地故障(LCC测点)
Fig.11 Single-pole grounding fault under different fault resistances (LCC measuring point)
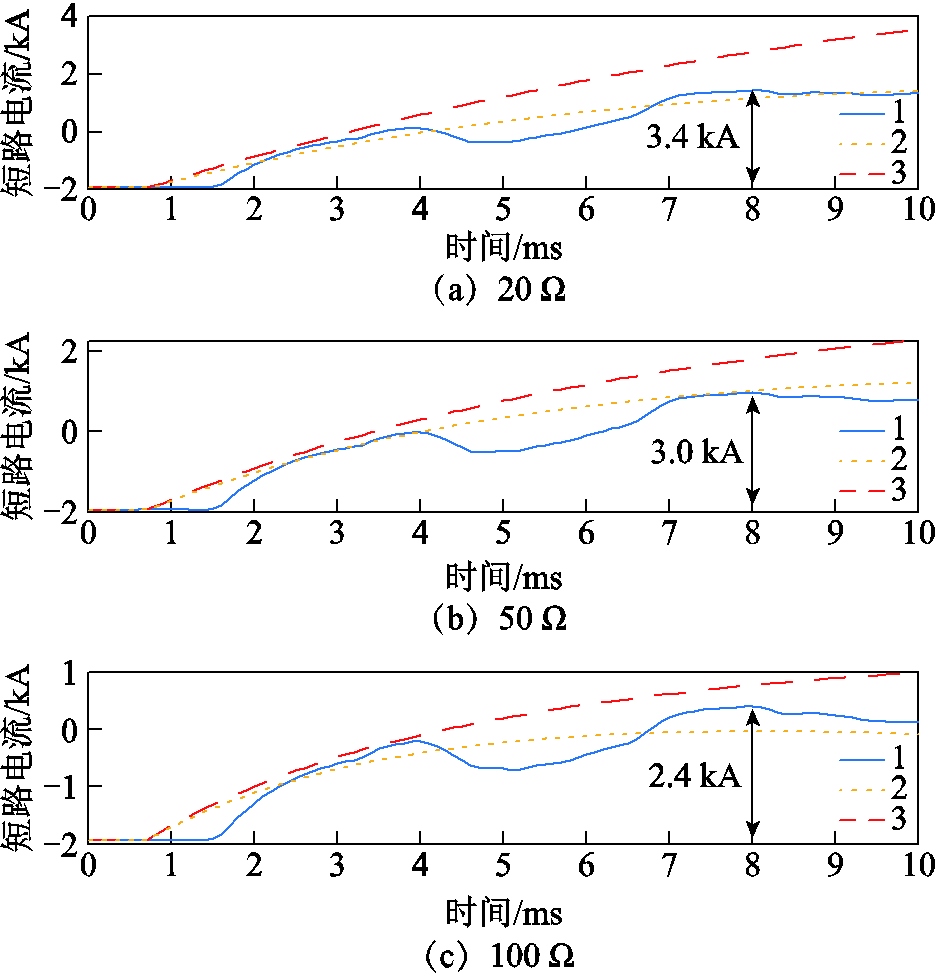
图12 不同过渡电阻下的单极接地故障(MMC2测点)
Fig.12 Single-pole grounding fault under different fault resistances (MMC2 measuring point)
随着故障距离的增加,行波色散现象越来越显著[27],地模波波速发生畸变,初始故障行波抵达LCC换流站所需时间会与理论计算所得![]()
![]() (图中k点)存在一定误差。如图12所示,随着过渡电阻的增加,线模分量与地模分量的幅值进一步减小,直流电流暂态增量下降,但初始行波抵达换流站的时间与短路电流整体变化趋势基本相同。
(图中k点)存在一定误差。如图12所示,随着过渡电阻的增加,线模分量与地模分量的幅值进一步减小,直流电流暂态增量下降,但初始行波抵达换流站的时间与短路电流整体变化趋势基本相同。
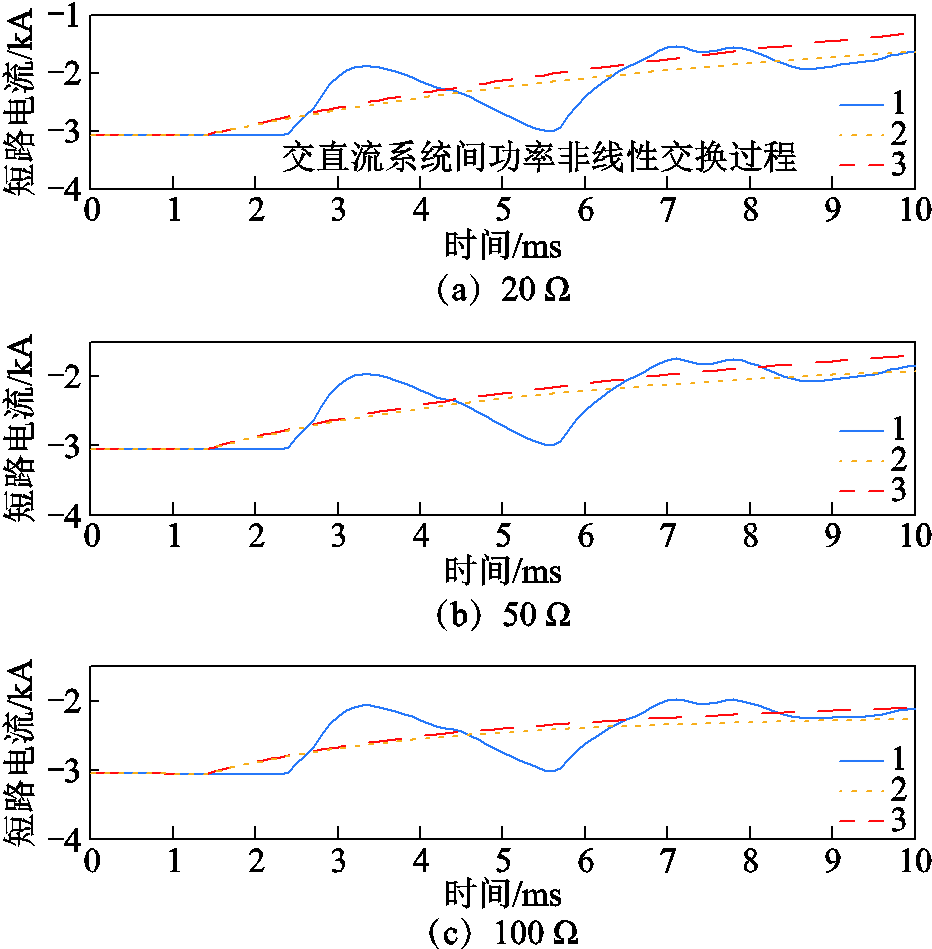
图13 不同过渡电阻下的单极接地故障(MMC1测点)
Fig.13 Single-pole grounding fault under different fault resistances (MMC1 measuring point)
此外,当输电线路采用Bergeron模型时计及了行波的传播特性,线路等值阻抗会在高频范围出现谐振点,如图14所示,短路电流因此发生高频振荡现象,但其振幅较小,对故障电流整体变化趋势不会产生影响。对于MMC侧的故障电流而言,在换流站发生闭锁前,交流侧与直流侧能量的非线性交换过程较为复杂,通过解析计算仅能得到故障电流的变化趋势,精确求解较为困难。如图13所示,在2~6 ms期间本文算法虽然对于MMC定直流电压换流站短路电流计算存在一定误差,但在10 ms内短路电流的最大暂态增量的计算值与仿真结果相近,计算结果在6 ms后能对短路电流实现较好的跟踪。
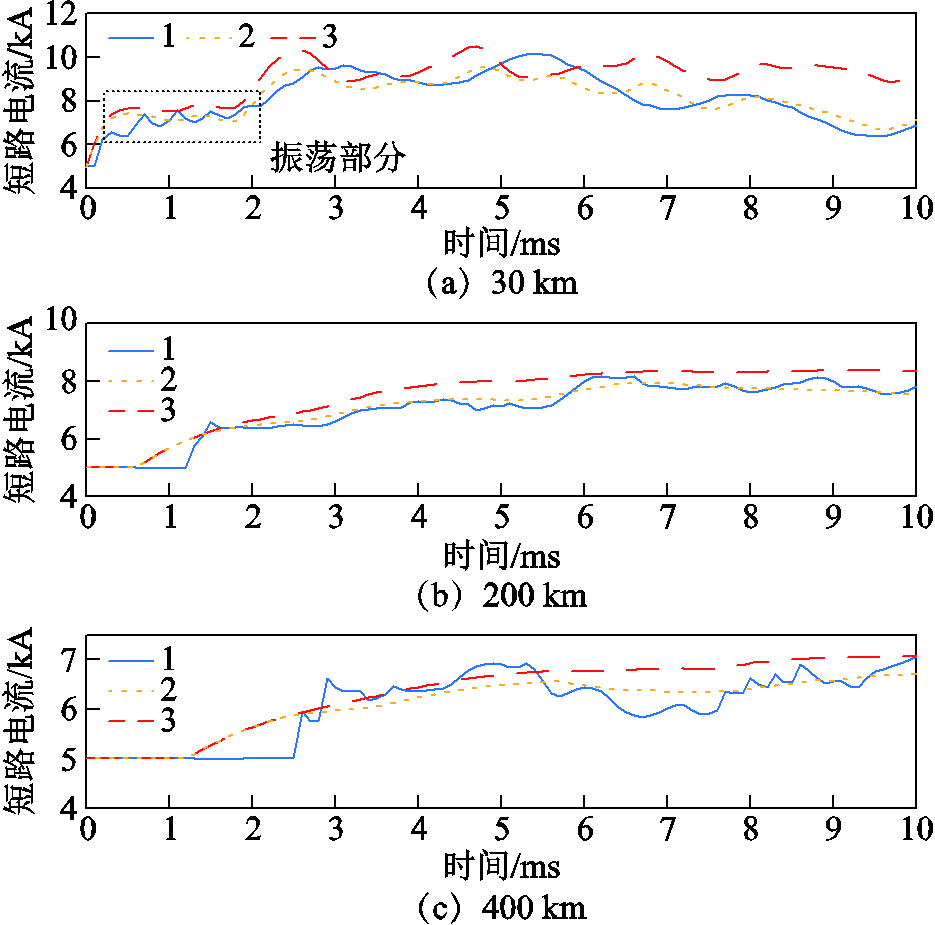
图14 不同距离下的单极接地故障(LCC测点)
Fig.14 Single-pole grounding fault at different distances (LCC measuring point)
如若考虑行波传播过程的折反射细节,对于10 ms内的n次折反射需要计算![]() 的电流行波进行叠加才能求得精确的故障电流解析式。因此本文算法综合考虑计算精度与复杂程度,通过系统RLC合理等值,在误差允许范围内大大降低了短路电流的求解难度。
的电流行波进行叠加才能求得精确的故障电流解析式。因此本文算法综合考虑计算精度与复杂程度,通过系统RLC合理等值,在误差允许范围内大大降低了短路电流的求解难度。
图15~图17给出了直流线路1线路中点发生极间故障的仿真结果,过渡电阻分别为20、50和![]() 。图18为当线路不同位置经
。图18为当线路不同位置经![]() 过渡电阻极间短路时,LCC站出口短路电流示意图。
过渡电阻极间短路时,LCC站出口短路电流示意图。
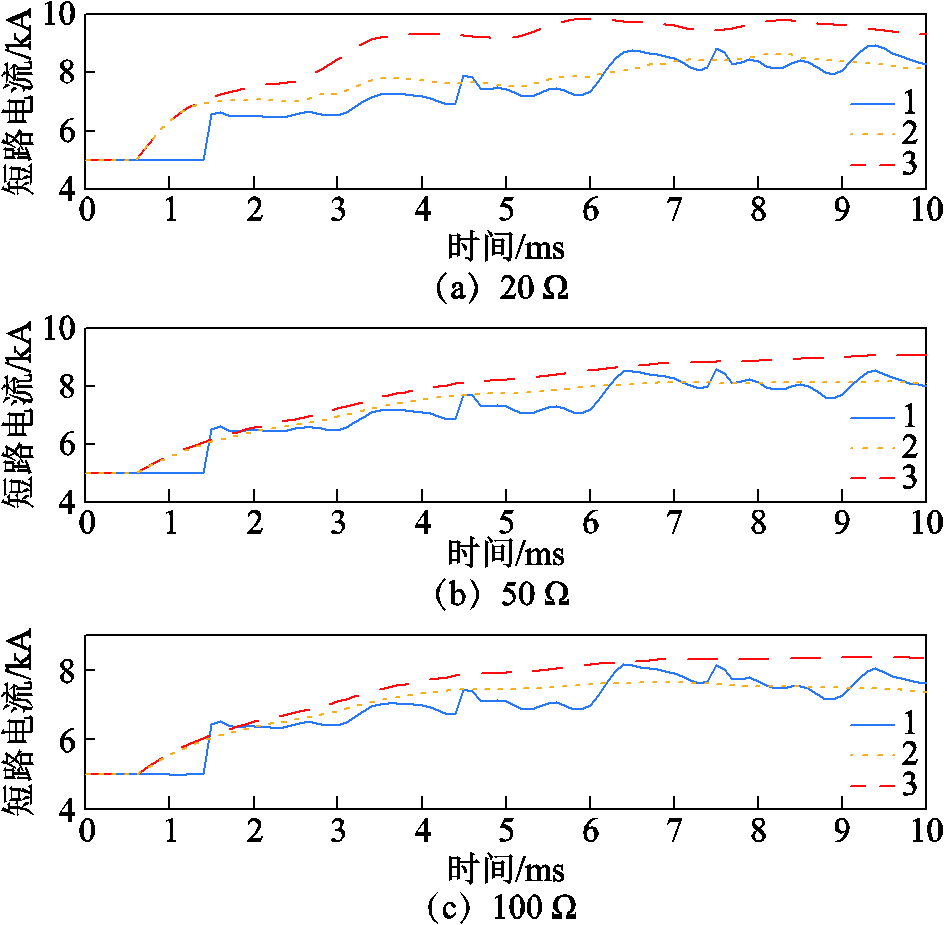
图15 不同过渡电阻下的极间故障(LCC测点)
Fig.15 Pole-to-pole faults under different transition resistances (LCC measuring point)
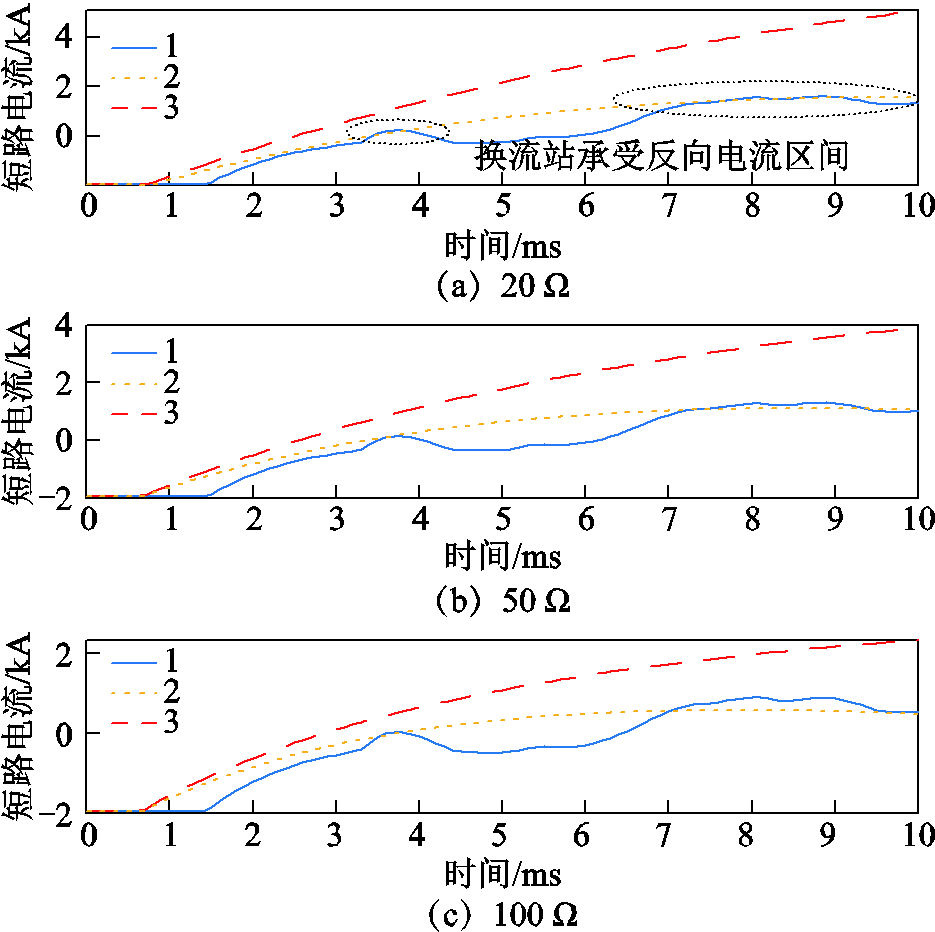
图16 不同过渡电阻下的极间故障(MMC2测点)
Fig.16 Pole-to-pole faults under different fault resistances (MMC2 measuring point)
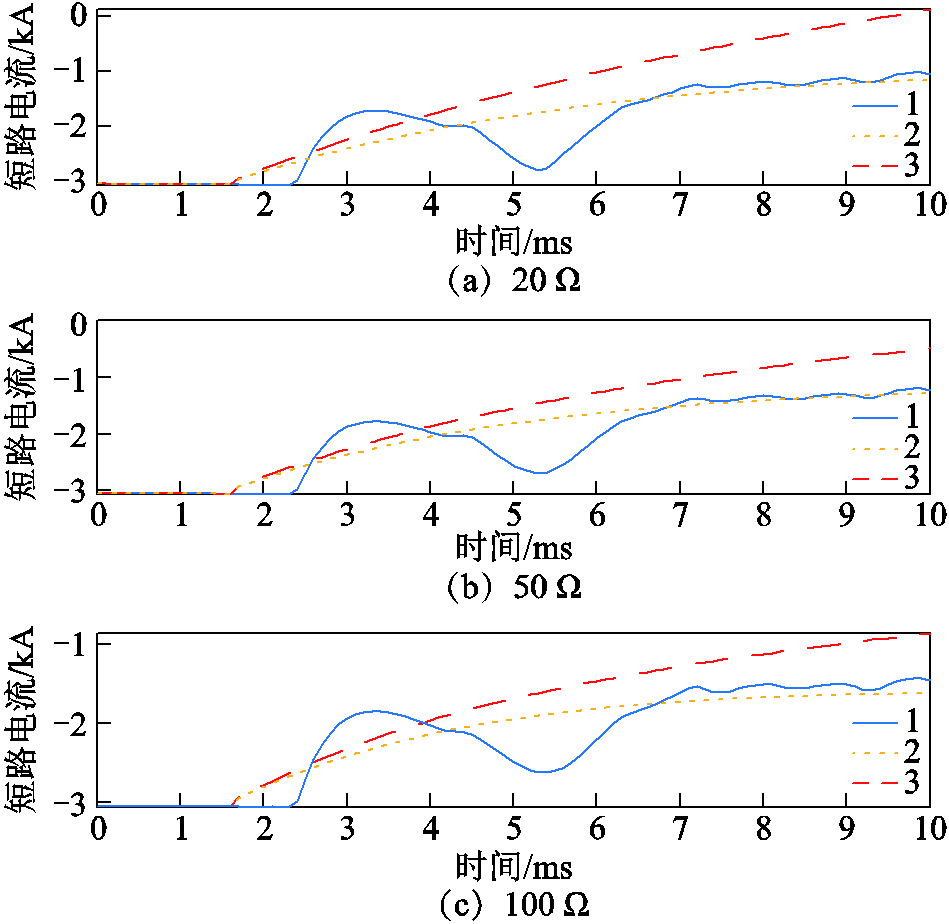
图17 不同过渡电阻下的极间故障(MMC1测点)
Fig.17 Pole-to-pole faults under different fault resistances (MMC1 measuring point)
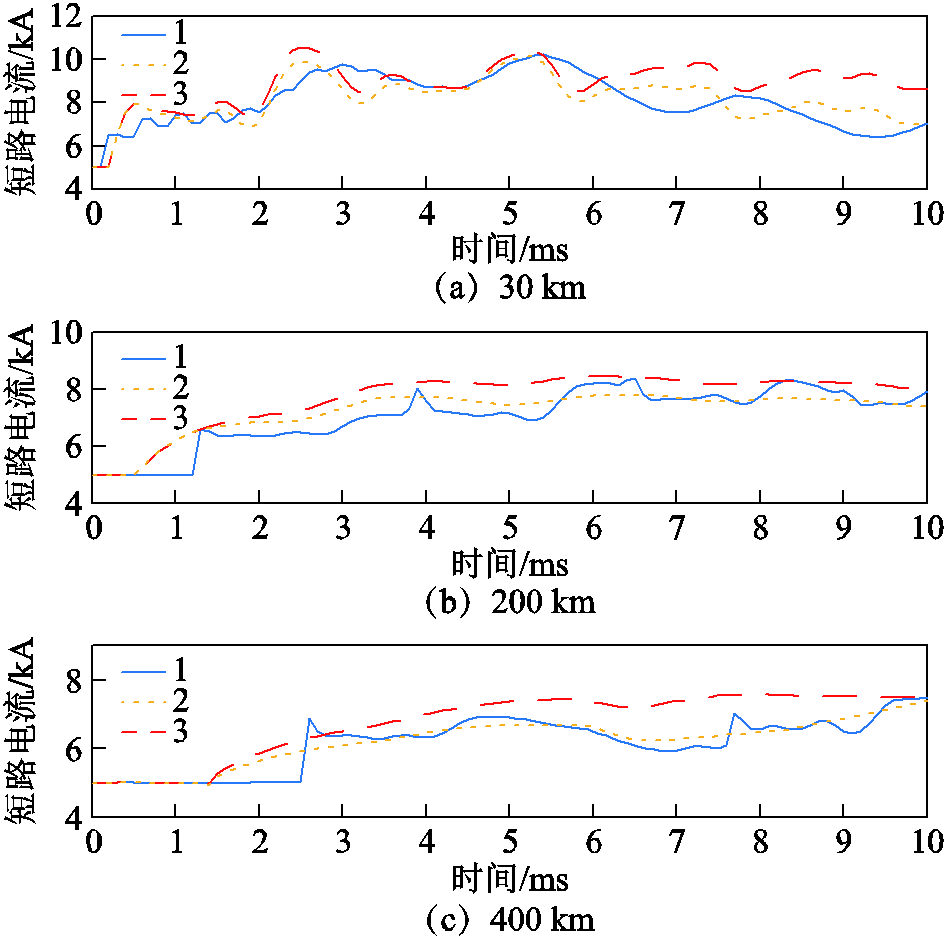
图18 不同距离下的极间故障(LCC测点)
Fig.18 Pole-to-pole faults at different distances (LCC measuring point)
直流输电线路的极间故障是直流侧最严重的故障,短路电流分析过程与单极接地故障类似,如图15所示,对于LCC换流站而言,短路电流峰值会上升至额定电流的2倍而后逐渐下降;如图16a所示,对于逆变MMC换流站而言,暂态电流分量由子模块电容放电提供,MMC换流站由于短路产生较大的暂态分量而在换流站闭锁前出现反向电流流通,传输功率迅速中断。
计及控制响应误差对比见表3。在计及控制系统影响下会减小暂态电流变化量,使计算结果更趋近于实际仿真结果,进一步降低通过复频域算法计算短路电流的误差。实验结果表明:本文算法可以实现不同故障类型、故障距离、过渡电阻下短路电流的定量计算,其对于LCC侧短路电流拟合效果较好,10 ms内短路电流计算的平均误差在5%以内、最大误差在10%以内;对于MMC侧短路电流,在忽略高频分量振荡的情况下能描述其总体的变化规律,并能较为准确地求得10 ms内最大的暂态电流变化量。此外,为更直观地体现短路电流的整体变化,附录中给出了某典型故障情况下短路电流近似计算的解析解。
表3 计及控制响应误差对比
Tab.3 Comparison of control response errors
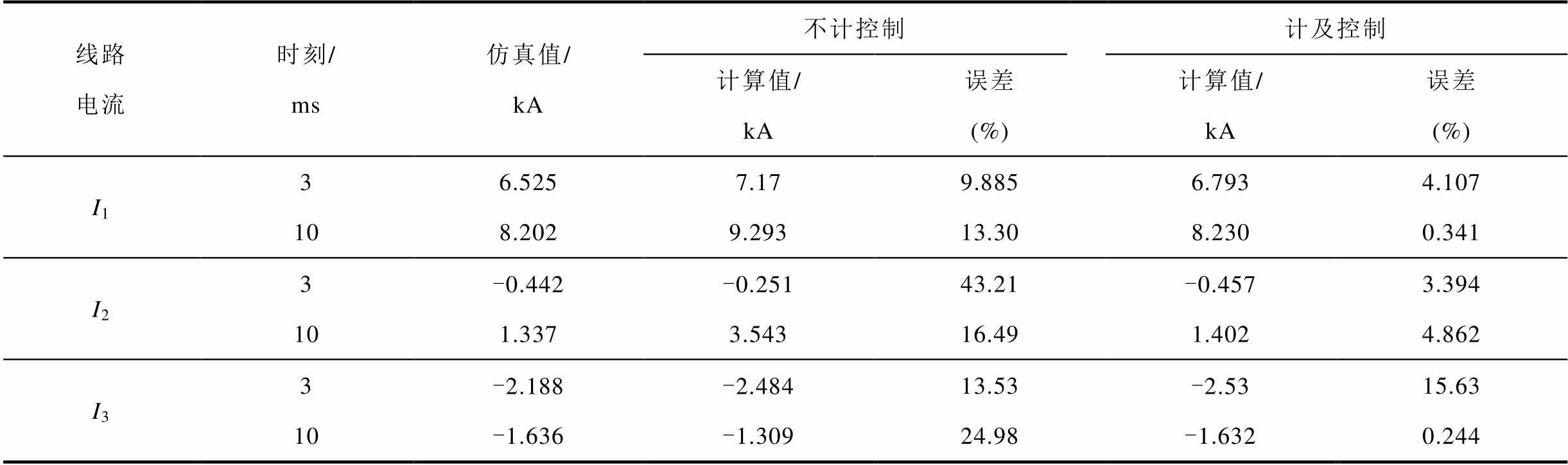
线路电流时刻/ms仿真值/kA不计控制计及控制 计算值/kA误差(%)计算值/kA误差(%) I136.5257.179.8856.7934.107 108.2029.29313.308.2300.341 I23-0.442-0.25143.21-0.4573.394 101.3373.54316.491.4024.862 I33-2.188-2.48413.53-2.5315.63 10-1.636-1.30924.98-1.6320.244
利用本文算法在不计控制系统作用下求得的短路电流幅值较仿真值大,可用于暂态特征快速分析研判。计及控制系统作用下的短路电流计算结果更接近于实际仿真结果,可用于规划设计阶段定量分析寻找系统关键节点、直流断路器选型等;也可用于分析和优化基于暂态阶段保护(如电流变化率保护)、构建控保协同的自适应保护原理等。
为进一步证明方法的适应性,附录中给出了其他拓扑结构下的验证结果。
所提短路电流近似计算时绝对误差的大小主要与计算过程中忽略或简化的因素有关,包括:模型近似等值处理、波形近似拟合过程以及中间变量求取时保留的精度等。由于式(13)计算代入的![]() 为系统额定电压值而非故障点故障前电压稳态值,不同故障点位置、线路损耗过程、系统运行方式等会使二者存在一定的数值差异,并导致计算误差有所增加,但不会超过5%;此外故障点位置除影响
为系统额定电压值而非故障点故障前电压稳态值,不同故障点位置、线路损耗过程、系统运行方式等会使二者存在一定的数值差异,并导致计算误差有所增加,但不会超过5%;此外故障点位置除影响![]() 外(故障点越靠近定电压站故障前稳态电压越接近于系统额定电压),还与式(13)中
外(故障点越靠近定电压站故障前稳态电压越接近于系统额定电压),还与式(13)中![]() 、
、![]() 的大小有关,由于近似计算忽略了行波的传播过程,故障点距两端换流站越近,折反射过程越剧烈,控制系统非线性响应过程越显著,整体而言计算误差与故障点位置大致呈U型函数关系(见附表1);对于控制系统参数取值,短路电流的计算结果由于控制电流的修正作用能较好地跟踪实际波形,在合理调整系统控制参数,使系统不会出现振荡、失稳等情况下,计算的相对误差基本不变。
的大小有关,由于近似计算忽略了行波的传播过程,故障点距两端换流站越近,折反射过程越剧烈,控制系统非线性响应过程越显著,整体而言计算误差与故障点位置大致呈U型函数关系(见附表1);对于控制系统参数取值,短路电流的计算结果由于控制电流的修正作用能较好地跟踪实际波形,在合理调整系统控制参数,使系统不会出现振荡、失稳等情况下,计算的相对误差基本不变。
在计算效率方面,计算机配置为Intel Core i7-10750 H,利用PSCAD/EMTDC对故障后10 ms的特征量进行仿真,所用总时长为1.267 5 s;在不计控制响应下故障电流计算总耗时为0.140 7 s;在不采取降阶时计及控制响应下故障电流计算总耗时为3.525 1 s,利用分段线性拟合结果对故障电流进行计算能有效降低控制电流的拉氏反变换所需时间,最终总耗时为0.788 2 s。综上所述,采用本文所提方法对传递函数进行合理降阶虽在一定程度上降低了计算精度,但能避免计算量过大的问题,有效地提高计算效率。此外,若需更加精确地分析系统故障暂态过程,则应利用控制响应特性补偿各次行波的折反射过程[28]。
针对目前多端混合直流输电系统短路电流难以定量分析的问题,以昆柳龙三端混合直流输电模型为例,完成了各换流站的等值建模,提出计及控制响应的故障电流简化计算方法,并得到以下结论:
1)仿真数据表明,所提方法能对MMC站闭锁前(10 ms内)各换流站出口故障电流的暂态特征与变化趋势进行准确刻画,并得到故障电流的解析表达式,有利于分析不同电气参数对故障电流时域特性的影响,为电网规划及设备参数选择、保护定值整定等提供了故障电流定量计算方法。
2)计及换流站控制特性后的暂态电流增量要小于不计换流站控制特性的增量;故障点距离换流站越近,短路电流增量越大,控制系统响应特性也越明显,所提方法能有效降低LCC近端故障时的计算误差。
3)本方法虽以三端混合直流输电系统为例进行分析,但模型简化等值处理以及短路电流近似计算方法同样适用于两端及多端等其他网络拓扑。
附 录
1. 短路电流计算结果及误差分析
附表1 单极故障下LCC侧短路电流最大计算误差
App.Tab.1 Maximum calculation error of LCC side short circuit current under unipolar fault

时间/ms计算误差(%) 0%l20%l40%l50%l60%l80%l100%l 38.1166.1064.9124.1074.6425.8667.782 1011.6288.7217.2086.3407.0148.20610.166
以直流线路1距首端300 km经50 W过渡电阻接地故障为例,短路电流的计算解析解如式(A1)~式(A6)所示,其中未降阶下控制修正电流的计算结果因篇幅原因不再列出。
LCC侧不计控制短路电流表达式为
 (A1)
(A1)
式中,![]() ,
,![]() 为故障初始行波传输至换流站的时间。
为故障初始行波传输至换流站的时间。
修正电流近似表达式为
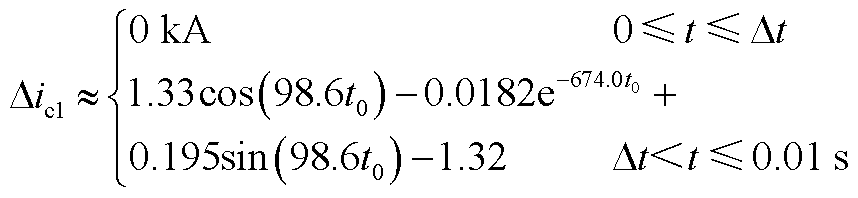 (A2)
(A2)
MMC1侧不计控制短路电流表达式为
 (A3)
(A3)
修正电流近似表达式为
MMC2侧不计控制短路电流表达式为
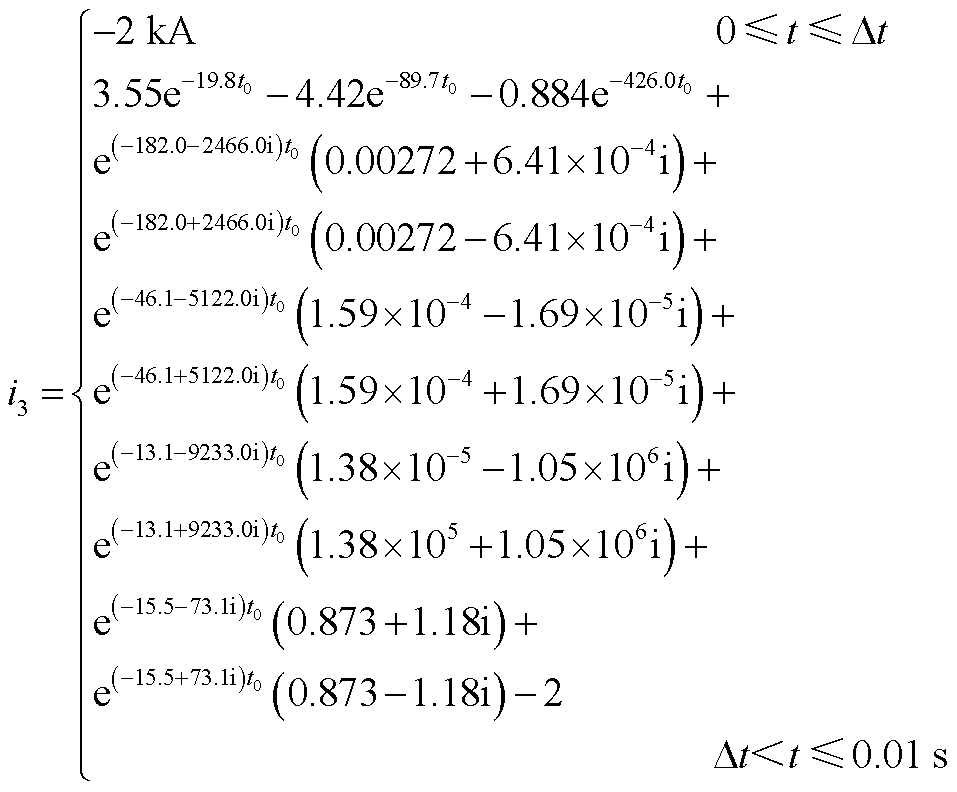 (A5)
(A5)
修正电流近似表达式为
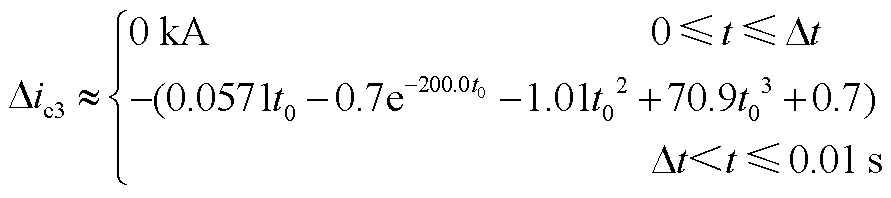 (A6)
(A6)
附图1为计算结果与仿真结果对比,曲线1为利用PSCAD/EMTDC得到的短路电流仿真结果;曲线2为不计控制下短路电流的近似计算结果;曲线3为计及控制作用下无降阶处理时短路电流的近似计算结果;曲线4为计及控制作用下传递函数经降阶处理后短路电流的近似计算结果。
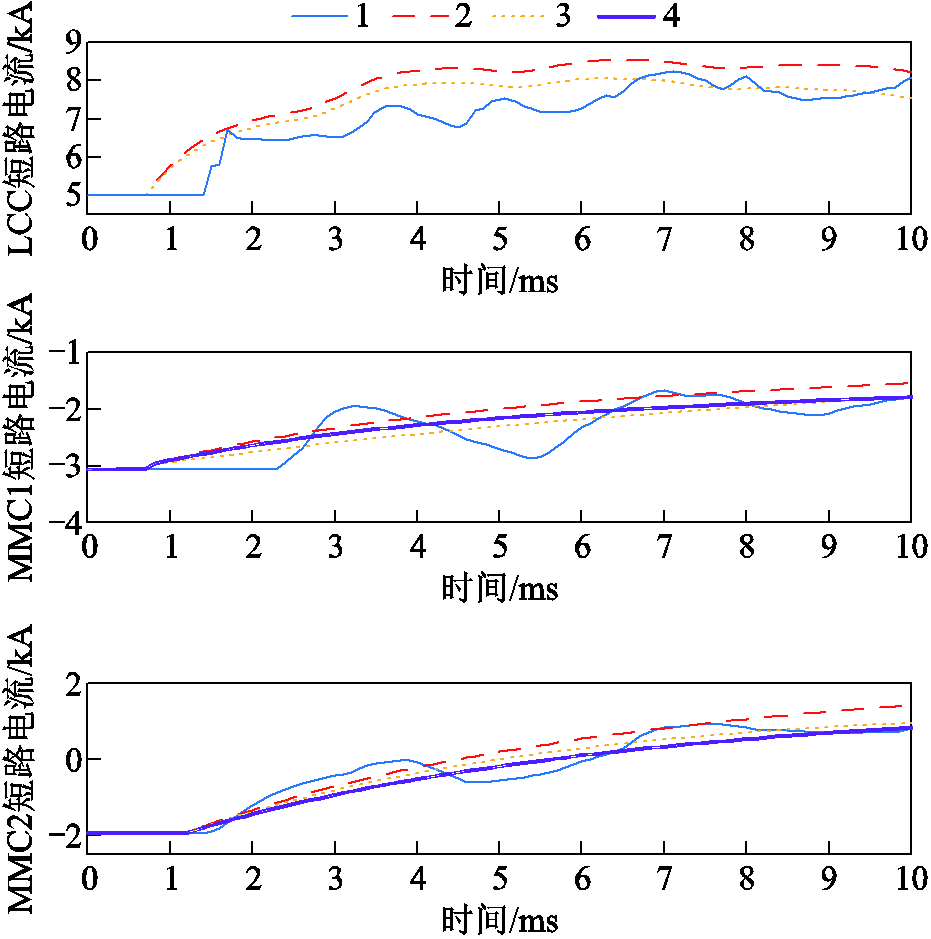
附图1 电流计算值与仿真值对比
App.Fig.1 Current calculation value and simulation value comparison
2. 算法适应性验证
为验证方法的普适性,本文在原有混合三端拓扑的基础上构造送端LCC,受端MMC的四端拓扑结构如附图2所示。LCC送端输送电流为5 kA,电压为600 kV,当系统进入稳态后,在直流线路1中点位置设置单极经20 W过渡电阻的接地故障,故障复频域等效电路如附图3所示,此时不计控制系统作用下故障电流的复频域表达式为
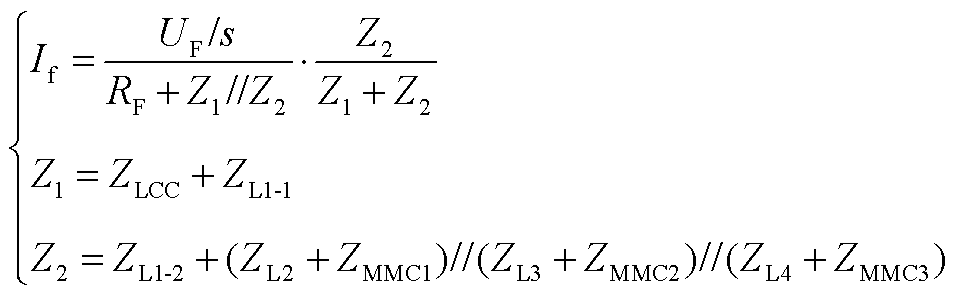 (A7)
(A7)
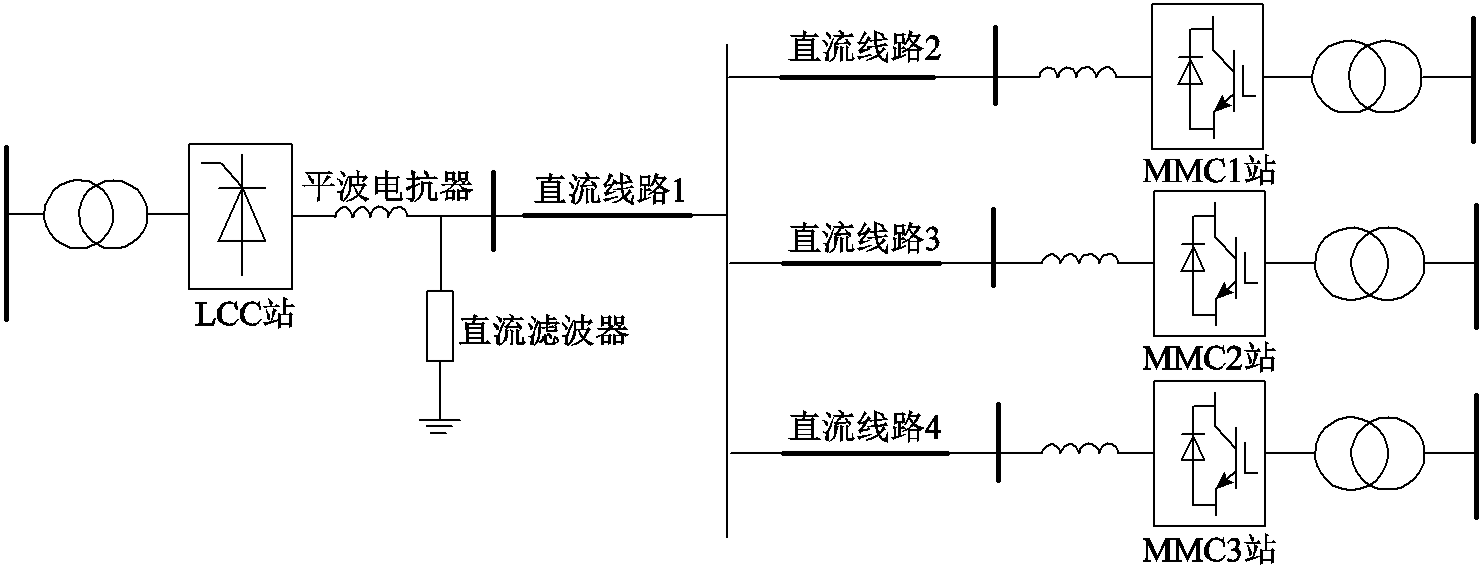
附图2 混合四端拓扑结构
App.Fig.2 Hybrid four-terminal topology
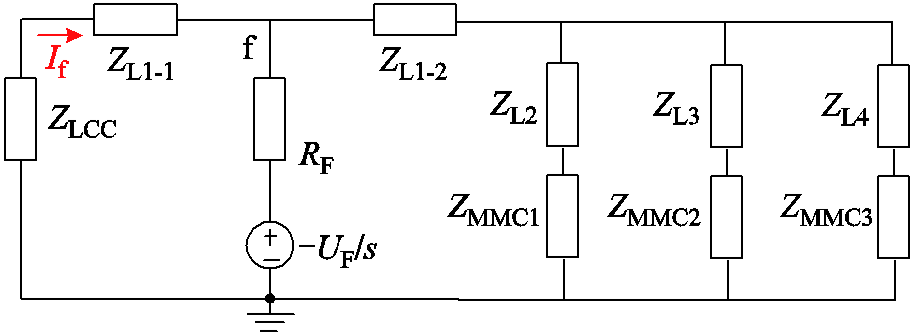
附图3 故障复频域等效电路
App.Fig.3 Fault complex frequency domain equivalent circuit
附图4为LCC侧短路电流的仿真结果及计算结果对比,其中曲线1为仿真结果;曲线2与3分别为本文所提方法在不计、计及控制系统作用下故障电流的计算结果。结果表明计算结果可以较好地描述故障电流的变化趋势,最大误差在10%以内,平均误差在7%以内,满足短路电流近似计算的精度要求。
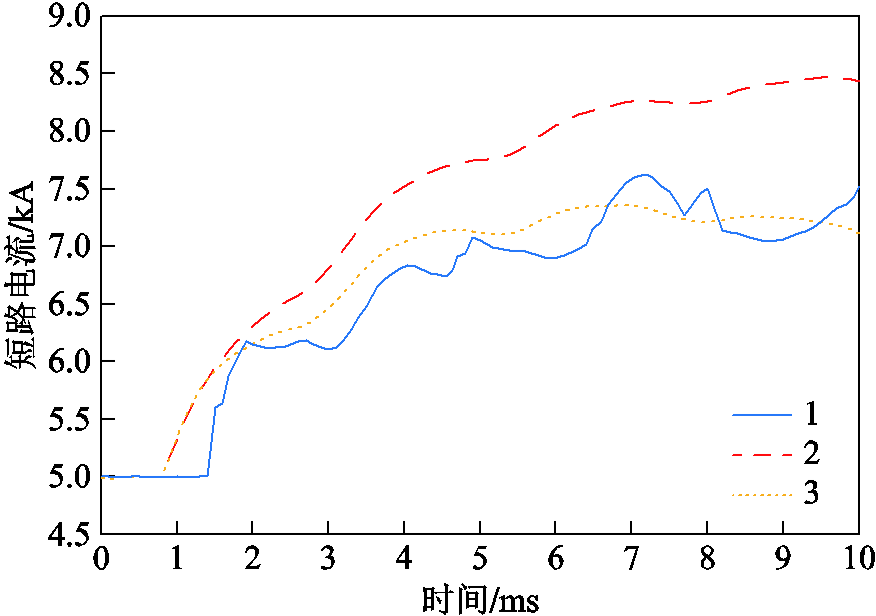
附图4 LCC侧短路电流
App.Fig.4 LCC side short circuit current
参考文献
[1] 贺永杰, 向往, 周家培, 等. LCC-MMC串联型混合直流输电系统小信号建模[J]. 电工技术学报, 2021, 36(7): 1492-1506. He Yongjie, Xiang Wang, Zhou Jiapei, et al. Small-signal modelling of LCC-MMC series hybrid HVDC transmission system[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1492-1506.
[2] Dai Zhihui, Liu Ningning, Zhang Cheng, et al. State-space analysis based pole-to-ground line fault isolation strategy for LCC-HVDC systems[J]. IET Generation, Transmission & Distribution, 2019, 13(10): 1933-1941.
[3] 苏见燊, 郭敬东, 金涛. 柔性直流电网中直流故障特性分析及线路故障重启策略[J]. 电工技术学报, 2019, 34(增刊1): 352-359. Su Jianshen, Guo Jingdong, Jin Tao. DC fault characteristics and line fault recovery strategy in flexible DC power network[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 352-359.
[4] 郝亮亮, 李伟杰, 王卓雅, 等. MMC-HVDC电网输电线路双极短路故障电流的实用计算[J]. 电力系统自动化, 2020, 44(5): 68-76. Hao Liangliang, Li Weijie, Wang Zhuoya, et al. Practical calculation for bipolar short-circuit fault current of transmission line in MMC-HVDC grid[J]. Automation of Electric Power Systems, 2020, 44(5): 68-76.
[5] 王子文, 张英敏, 刘天琪, 等. 基于伴随网络的直流电网短路电流计算方法[J]. 中国电力, 2021, 54(10): 2-10, 27. Wang Ziwen, Zhang Yingmin, Liu Tianqi, et al. A short-circuit current calculation method based on adjoint network for DC grid[J]. Electric Power, 2021, 54(10): 2-10, 27.
[6] 彭宇锋, 张英敏, 李俊松, 等. 考虑线路电容的MMC-HVDC系统直流接地故障电流计算方法[J]. 电力系统保护与控制, 2020, 48(23): 57-63. Peng Yufeng, Zhang Yingmin, Li Junsong, et al. Ground fault current calculation method for an MMC-HVDC system considering line capacitance[J]. Power System Protection and Control, 2020, 48(23): 57-63.
[7] 袁敏, 茆美琴, 程德健, 等. 主电路参数对MMC-HVDC电网直流短路故障电流综合影响分析[J]. 中国电力, 2021, 54(10): 11-19. Yuan Min, Mao Meiqin, Cheng Dejian, et al. Analysis of comprehensive influence of main circuit parameters on DC short circuit fault current of MMC-HVDC grid[J]. Electric Power, 2021, 54(10): 11-19.
[8] Langwasser M, De Carne G, Liserre M, et al. Improved fault current calculation method for pole-to-pole faults in MMC multi-terminal HVDC grids considering control dynamics[C]//2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 2018: 5529-5535.
[9] 王彤, 孙奕, 裴林, 等. 考虑控制系统的LCC-HVDC直流电流暂态特性分析与交流短路电流近似解析方法[J]. 中国电机工程学报, 2022, 42(23): 8509-8523. Wang Tong, Sun Yi, Pei Lin, et al. Analysis of DC current transient characteristics of LCC-HVDC considering control system and approximate analytical method of AC short-circuit current[J]. Proceedings of the CSEE, 2022, 42(23): 8509-8523.
[10] 尹太元, 王跃, 段国朝, 等. 基于零直流电压控制的混合型MMC-HVDC直流短路故障穿越策略[J]. 电工技术学报, 2019, 34(增刊1): 343-351. Yin Taiyuan, Wang Yue, Duan Guozhao, et al. Zero DC voltage control based DC fault ride-through strategy for hybrid modular multilevel converter in HVDC[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 343-351.
[11] 辛业春, 刘熠, 江守其, 等. 计及零直流电压控制的混合型MMC-HVDC输电系统短路电流计算方法[J]. 电网技术, 2023, 47(7): 2820-2828. Xin Yechun, Liu Yi, Jiang Shouqi, et al. Short-circuit current calculation method for FHMMC-HVDC transmission systems with zero DC voltage control[J]. Power System Technology, 2023, 47(7): 2820-2828.
[12] 李海锋, 许灿雄, 梁远升, 等. 计及换流站控制特性的多端混合直流输电系统故障暂态计算方法[J]. 中国电机工程学报, 2023, 43(4): 1426-1438. Li Haifeng, Xu Canxiong, Liang Yuansheng, et al. Fault transient calculation method for multi-terminal hybrid HVDC systems considering control characteristics of converter station[J]. Proceedings of the CSEE, 2023, 43(4): 1426-1438.
[13] Rao Hong, Zhou Yuebin, Xu Shukai, et al. Key technologies of ultra-high voltage hybrid LCC-VSC MTDC systems[J]. CSEE Journal of Power and Energy Systems, 2019, 5(3): 365-373.
[14] 耿学锋, 何赟泽, 王广鑫, 等. IGBT关断时刻的应力波测量优化及影响因素分析[J]. 电工技术学报, 2022, 37(21): 5503-5512. Geng Xuefeng, He Yunze, Wang Guangxin, et al. Measurement optimization and analysis of influencing factors of IGBT’s turn-off stress wave[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5503-5512.
[15] Beddard A, Sheridan C E, Barnes M, et al. Improved accuracy average value models of modular multilevel converters[J]. IEEE Transactions on Power Delivery, 2016, 31(5): 2260-2269.
[16] 樊强, 俞永杰, 夏嘉航, 等. 低容值半桥型模块化多电平变换器直流故障辅助清除策略[J]. 电工技术学报, 2022, 37(14): 3713-3722. Fan Qiang, Yu Yongjie, Xia Jiahang, et al. Auxiliary strategy for DC fault clearing of low capacitance half-bridge modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3713-3722.
[17] 辛业春, 罗鑫, 王拓, 等. 计及过渡电阻影响的直流电网不同拓扑结构故障电流简化计算方法[J]. 电网技术, 2023, 47(2): 804-817. Xin Yechun, Luo Xin, Wang Tuo, et al. Simplified calculation method of fault current in different topological structures of DC grid considering the influence of transition resistance[J]. Power System Technology, 2023, 47(2): 804-817.
[18] 高本锋, 王刚, 刘毅, 等. LCC-HVDC送端电网等值方案研究[J]. 电工技术学报, 2021, 36(15): 3250-3263, 3271. Gao Benfeng, Wang Gang, Liu Yi, et al. Study on equivalence method of AC system in sending-end of LCC-HVDC[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3250-3263, 3271.
[19] 姚骏, 谭义, 裴金鑫, 等. 模块化多电平变流器高压直流输电系统直流故障改进控制策略[J]. 电工技术学报, 2018, 33(14): 3306-3318. Yao Jun, Tan Yi, Pei Jinxin, et al. Improved control strategy for DC fault in modular multi-level converter-HVDC system[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3306-3318.
[20] Langwasser M, De Carne G, Liserre M, et al. Fault Current estimation in multi-terminal HVDC grids considering MMC control[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2179-2189.
[21] 余修勇, 顾菊平, 张新松, 等. 多端柔性直流电网线路故障暂态等值电路及暂态特征分析[J]. 中国电机工程学报, 2023, 43(24): 9546-9557. Yu Xiuyong, Gu Juping, Zhang Xinsong, et al. Study on the transient equivalent circuits and the transient characteristics of multi-terminal flexible DC grids after line faults[J]. Proceedings of the CSEE, 2023, 43(24): 9546-9557.
[22] 汤兰西, 董新洲. MMC直流输电网线路短路故障电流的近似计算方法[J]. 中国电机工程学报, 2019, 39(2): 490-498, 646. Tang Lanxi, Dong Xinzhou. An approximate method for the calculation of transmission line fault current in MMC-HVDC grid[J]. Proceedings of the CSEE, 2019, 39(2): 490-498, 646.
[23] 邓文军, 刘麒麟, 张英敏, 等. 张北柔直电网单极接地故障短路电流计算方法及接地策略[J]. 高电压技术, 2022, 48(10): 4050-4059. Deng Wenjun, Liu Qilin, Zhang Yingmin, et al. Short circuit current calculation method and grounding strategy of pole-to-ground fault in Zhangbei flexible DC power grid[J]. High Voltage Engineering, 2022, 48(10): 4050-4059.
[24] Li Chengyu, Zhao Chengyong, Xu Jianzhong, et al. A pole-to-pole short-circuit fault current calculation method for DC grids[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4943-4953.
[25] 高飘, 郑晓冬, 晁晨栩, 等. 基于控制特征量响应的多端柔性直流输电线路保护[J]. 电力系统自动化, 2022, 46(5): 122-131. Gao Piao, Zheng Xiaodong, Chao Chenxu, et al. Protection for multi-terminal flexible DC transmission lines based on response of control characteristics[J]. Automation of Electric Power Systems, 2022, 46(5): 122-131.
[26] 吴通华, 戴魏, 李新东, 等. 基于数值拉普拉斯逆变换的MMC-HVDC故障电流计算[J]. 电力工程技术, 2022, 41(5): 40-49. Wu Tonghua, Dai Wei, Li Xindong, et al. Calculation of fault current in MMC-HVDC based on numerical inverse Laplace transform[J]. Jiangsu Electrical Engineering, 2022, 41(5): 40-49.
[27] 陈玉林, 张杰, 黄涛, 等. 高压直流输电线路行波色散及行波测距研究[J]. 电气技术, 2021, 22(12): 8-13. Chen Yulin, Zhang Jie, Huang Tao, et al. Research on traveling wave dispersion and fault location for high voltage direct current transmission lines[J]. Electrical Engineering, 2021, 22(12): 8-13.
[28] Xie Zhongrun, Li Bin, He Jiawei, et al. Hybrid HVDC system fault transient analysis considering traveling wave propagation and converter control response[J]. International Journal of Electrical Power & Energy Systems, 2023, 147: 108794.
Abstract The hybrid DC transmission system, which gives full play to the advantages of conventional DC and flexible DC, has become a research hotspot in the fields of long-distance transmission and renewable-energy grid connection. However, HVDC transmission lines are long and the working environment is complex, resulting in high fault probability. Once a short-circuit fault occurs on the DC line, it will generate fault current several times the rated current within 10ms, exposing the whole system to a serious overcurrent risk and threatening the sTab.operation of the system. In addition, the highly nonlinear characteristics of the converter station make the existing short-circuit current solutions ignore the response process of the control system and rely on the modeling and simulation results. It is impossible to obtain the specific analytical formula of the short-circuit current to realize the quantitative analysis and calculation of the fault characteristics, which brings difficulties to the protection and design of DC control systems and restricts the development of hybrid DC transmission technologies. Therefore, considering control response, an approximate calculation method for short-circuit current of multi-terminal hybrid DC transmission systems is proposed.
First, three system model simplification measures are proposed, which take into account both accuracy and computational complexity, including port processing, non-fault-pole discharging-loop processing and AC system processing. Second, the system topology model and control model are modeled. Based on the fault-component network, the short-circuit current is obtained regardless of the action of the control system, and then the corrected current under the control action is obtained by using this calculation result. The two are superimposed to obtain the final complex frequency domain analytical formula for the short-circuit current, and the inverse Laplace transform is used to obtain the time-domain solution for the short-circuit current. The proposed method corrects the trigger angle of the LCC side, using Pade approximation and piecewise linearization method to reasonably reduce the order of short-circuit current model, which takes into account the calculation accuracy and efficiency, to effectively avoid the problem that the inverse Laplace transform cannot be solved due to the high order of complex frequency domain expression. Finally, based on PSCAD/EMTDC, the simulation analysis on different fault distances, transition resistance and fault types is carried out.
It can be concluded that, the proposed method can accurately describe the transient characteristics and trend of the fault current at the outlet of each converter station before the blocking of the MMC station, obtaining the analytical expression of the fault current which provides a quantitative calculation method of fault current for power grid planning, equipment parameter selection and protection setting. In addition, the transient current increment considering the control characteristics of the converter station is less than that without considering the control characteristics. Therefore, the fault transient characteristics can be quickly analyzed and judged by using the fault current calculation results without considering the control. Finally, it can be concluded that, in terms of calculation efficiency, the proposed method does not have the problem of excessive computational complexity due to the order reduction. The calculation error is mainly related to the factors neglected or simplified in the calculation process, including the approximate equivalent processing of the model, the approximate fitting process of the waveform and the accuracy reserved when the intermediate variables are obtained, but the overall relative error is still controlled within 10% to meet the accuracy requirements of fault current calculation.
Keywords:Short-circuit current calculation, control system, network equivalence, multi-terminal hybrid HVDC transmission, line fault
DOI: 10.19595/j.cnki.1000-6753.tces.230281
中图分类号:TM713
国家自然科学基金资助项目(51877084)。
收稿日期 2023-03-12
改稿日期 2023-05-24
李杭泽 男,1999年生,硕士研究生,研究方向为直流输电系统保护与控制。E-mail:925449790@qq.com
戴志辉 男,1980年生,教授,博士生导师,研究方向为电力系统保护与控制。E-mail:daihuadian@163.com(通信作者)
(编辑 赫 蕾)