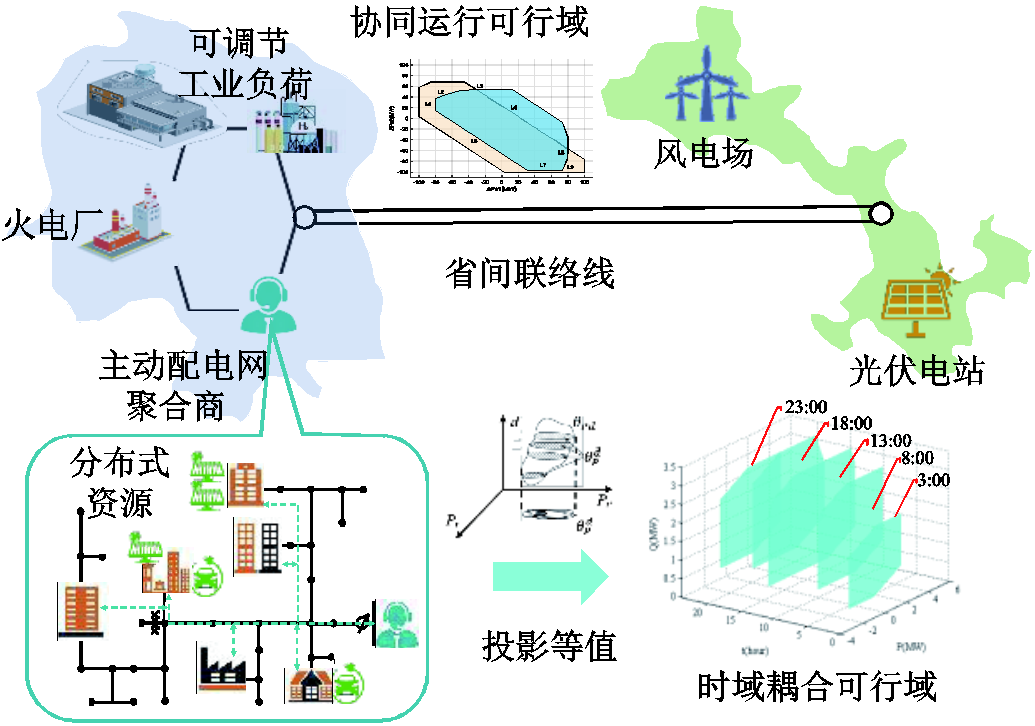
图1 基于可行域投影的新能源电力系统运行模式
Fig.1 Renewable energy power system operation model based on feasible region projection theory
摘要 随着新能源逐步成为电力系统的主体,传统电网体系的深层缺陷也日益显露。跨省区资源优化配置困难和分布式能源利用率低等能源协同体系的不足成为制约新型电力系统建设的瓶颈。为此,该文通过基于外割法的可行域投影等值算法刻画区域系统可行域,并通过并行伞约束辨识法剔除模型冗余约束,进而提出一种基于投影等值理论的新能源电力系统协同运行模式,通过可行域的交互实现各级调度体系间的高效协同,并提出了三种应用场景:配电网/虚拟电厂可行域聚合、省间多通道安全域计算和多时段输配电网协同运行。算例结果表明,所提算法和模式能够有效地降低区域电网规模,从而降低区域电网与调度中心的信息交互量,提升新能源电力系统运行优化效率。
关键词:新能源电力系统 可行域 投影等值 协同调度
大力发展以最大化消纳新能源为主要任务的新型电力系统,构建清洁低碳、安全高效的能源体系,是我国达成“3060碳达峰、碳中和”目标的必由之路[1]。预计到2025年,我国风电、光伏装机容量约占总装机容量的1/3,煤电装机比重降至约40%[2-3]。随着新能源渗透率的提高,现有电力系统的运营体系和发展范式将发生革命性改变[4-5]。国家发展改革委员会和国家能源局于2022年1月联合印发的《关于完善能源绿色低碳转型体制机制和政策措施的意见》中明确提出,要完善适应可再生能源广域规模输送和局域深度利用的电网体系,完善可再生能源电力输送和消纳协同机制,发展高比例分布式能源渗透的智能配电网[6]。
近年来,我国传统能源体系的深层缺陷逐步显露[7]。一方面,跨省间大规模电能传输受限。我国能源资源呈逆向分布,可再生能源需要通过特高压输电通道跨省跨区输送。然而,省间的协调交易受省内平衡、输电通道传输能力和新能源消纳等约束限制,难以制定考虑发用电两侧出力特性的交易计划以满足市场进行大规模资源优化配置与清洁能源消纳的需要[8]。为此,我国提出构建各省/区域市场联合运行的全国统一电力市场体系,为省间协同提供了制度基础[9]。然而,随着电网内部结构日益复杂、跨省间输电通道数目增加,传统不精细化建模的可用输电容量(Available Transfer Capability, ATC)计算方法难以满足提高输电通道利用效率和降低阻塞风险的需求[10]。因此,如何精准地刻画跨省间输电通道的传输能力,提出省间电力系统的高效协同模式和方法,是实现可再生能源广域规模输送的关键。
另一方面,分布式资源灵活调节能力难以高效利用。如屋顶光伏、电动汽车等具有天然随机性与波动性的分布式能源大规模并网,给电力系统安全运行带来了前所未有的压力。由于配电网内的分布式能源种类繁多且参数各异,上级输电网调度难以精细观测并控制每一个分布式能源的运行状态[11]。为了提高分布式能源的可控性和可观性,可以将配电网聚合为一个独立可控的整体参与输电网调度和市场出清。然而,如何聚合配电网海量分布式能源、形成与输电网高效互补的协同模式和方法,是实现新能源局域深度利用的关键难题[12]。综上所述,新能源电力系统的发展亟待打破传统运营体系的壁垒,实现跨区域、跨等级的高效协同,在更大的范围内进行资源优化配置。
现有的电力系统协同方法主要可以分为两类:分解协调法和等值法。分解协调法的基本思路是将一个难以处理的全局优化问题分解为多个易求解的局部子问题,通过协调优化子问题的解从而求得全局问题的解。然而,诸如Lagrange松弛[13-14]、Benders分解[15]等分解协调方法都是基于迭代寻优的,实现高效的协同就会牺牲计算精度,甚至会出现收敛振荡的问题[16]。等值法是一种非迭代的协调算法,其通过刻画子问题的等值模型以便于实现集中优化,具有流程清晰、计算高效的优势[17]。近年来,等值理论受到学界的广泛关注。
在电力系统中,等值理论可应用于区域系统的外特性等值。目前已有诸多文献将等值理论应用于电力系统的协同优化中[18-19]。文献[20]将等值理论应用于跨区域互联电网可用输电能力研究中,仅交换少量节点信息即可实现对跨区互联系统可用传输容量的精准评估。文献[21]利用伞约束辨识法剔除模型中的冗余约束,从而减少了跨区最优潮流计算中的信息传递,但该算法会使模型规模增大,不适用于单次优化问题。文献[22]通过多端口戴维南等值方法,实现了对换相高压直流输电系统的简化。基于投影的等值问题,本质上是刻画模型约束条件所形成的可行空间向特定方向的投影。文献[23]提出了基于Minkowski法的可行域刻画方法,用于研究可控负荷参与辅助服务的可调节空间。文献[24]通过枚举法估算了配电网与输电网交互节点的有功和无功功率灵活可调区间。文献[25]中提出了一种基于多参数规划(Multi-Parametric Programming, MPP)的联络线传输功率关键域刻画方法。上述可行域刻画方法的核心思路均是从可行域内部向外遍历其顶点,但随着模型约束条件数目和维数的增加,会造成维数灾使问题难以被求解。
为实现电力系统跨区域、跨等级的高效协同运行,本文提出一种基于外割法的可行域投影等值算法,通过伞约束辨识法剔除模型冗余约束,并提出算法在新能源电力系统协同中的三种应用场景:①配电网/虚拟电厂可行域聚合,以实现高比例分布式资源渗透的配电网/虚拟电厂与传统电力调度模式的高效兼容;②省间多联络线安全域刻画,考虑省内安全约束对多联络线传输功率的影响,为省间市场出清提供精确的安全边界;③多时段输配电网协同运行,旨在聚合配电网中大量时间耦合、空间交错时变资源,便于更精准合理地制定考虑时域耦合约束的输配协同调度计划。应用场景的研究思路遵从逐步深入、问题导向型的研究逻辑。在空间上,从区域电网到配电网再到输配协同的下沉、细化研究;在技术路线上,初步研究区域电网单时段可行空间,随着配电网内时域耦合约束被考虑进来,逐步从单时段问题研究到多时段耦合问题。
在以新能源为主体的新型电力系统中,传统电力系统垂直一体化的调度运行模式难以为继。一方面,海量特性各异且约束条件复杂的新能源主体带来信息交互量剧增的问题,使集中式优化调度模型的规模和维数过高;另一方面,传统调度模式下各级系统间的协同能力不足,大规模具有随机性、波动性的新能源并网威胁电力系统安全稳定运行,电力系统调度对灵活性资源的需求增加。因此,新能源电力系统对区域间高效协同运行的需求日益增长,构建子系统简洁、可观的等值模型是一种有效手段。
为此,本文提出一种基于可行域投影理论的新型电力系统协同运行模式,旨在刻画子系统简洁、可观的等值可行域,从而在保证安全稳定的前提下有效地减少各级调度体系之间的信息交互量,实现新能源电力系统的高效协同运行。基于可行域投影的新能源电力系统运行模式如图1所示,基本思路如下:首先,各子系统聚合内部运行约束条件形成高维可行空间,并根据投影等值理论向公共连接点投影,形成其等值可行域;进而,上级系统根据子系统可行域进行全网电力平衡调度,实现各级调度体系间的高效协同,例如,由海量分布式电源、可控负荷、储能等聚合而成的主动配电网经投影等值刻画其可行域并递交区域电网。区域电网将主动配电网可行域作为约束条件同传统火力发电厂、风电场、联络线传输功率等进行区域电力调度,并下达调度指令。对于区域系统之间通过刻画区域联络线安全域递交总调度中心,总调度中心依据区域联络线安全域制定区域间协同调度计划。

图1 基于可行域投影的新能源电力系统运行模式
Fig.1 Renewable energy power system operation model based on feasible region projection theory
区域电力系统运行模型主要包括以下几类约束:①线路潮流约束,如潮流方程、线路最大传输容量约束等;②发电出力约束,如火电机组的最大/最小技术出力、风/光机组的实时出力上限等;③时域耦合约束,主要有机组爬坡约束和负荷需求响应约束。
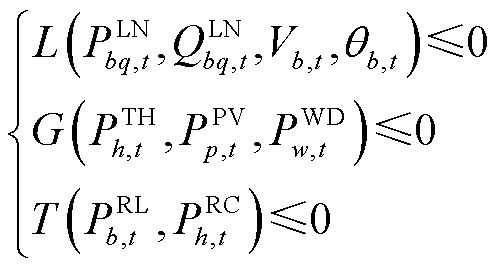 (1)
(1)
式中,L(·)、G(·)和T(·)分别代表线路潮流、发电出力和时域耦合约束,约束中的常数项均移至公式左侧,等式约束可写作如0≤L(·)≤0的形式;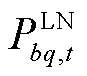 和
和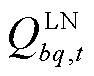 分别为节点b与q之间线路在t时刻的有功和无功功率;
分别为节点b与q之间线路在t时刻的有功和无功功率;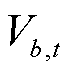 和
和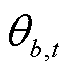 分别为节点b在t时刻的电压幅值和相角;
分别为节点b在t时刻的电压幅值和相角;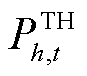 、
、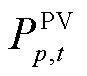 和
和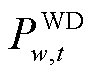 分别为火电机组h、光伏电站p和风电机组w在t时刻的有功功率;
分别为火电机组h、光伏电站p和风电机组w在t时刻的有功功率;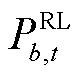 为节点b在t时刻的需求响应有功功率;
为节点b在t时刻的需求响应有功功率;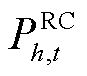 为火电机组h在t时刻的爬坡速率。
为火电机组h在t时刻的爬坡速率。
基于投影等值理论的新能源电力系统协同运行模式有以下优点:①协同高效,基于等值法的协调优化可有效减少交互信息,使计算高效且无迭代振荡问题;②路径依赖,无需颠覆现有电网分级分区管理与市场体系,且能够实现对新兴电力主体公平公正的接纳;③隐私保护,以提交等值模型代替全部约束条件参与电力市场优化出清,能够有效保护市场主体的信息隐私。
可行域的几何含义是指由不违背原问题任意约束的可行解组成的最大空间。在新型电力系统中,可行域是指一个区域电网内部包括新能源出力、线路、负荷等全部约束集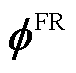 形成的凸多胞体向功率交互节点的投影。电网约束集可以简化为
形成的凸多胞体向功率交互节点的投影。电网约束集可以简化为
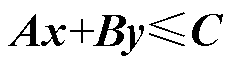 (2)
(2)
式中,x为投影变量,即表征投影后可行域的物理量,在电力系统中通常为交互节点的传输功率;y为调节变量,可以改变可行解在可行域中的位置,如机组出力、可控负荷等;A和B分别为变量x和y的系数矩阵;C表征系统中的常数向量。
结合电网简化模型,从物理角度解释,区域电网的可行域即为:在空间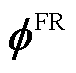 中,对于任意交互功率x指令,总存在至少一个相应的调节方案y使其可以被执行。通过数学语言表述的定义如下。
中,对于任意交互功率x指令,总存在至少一个相应的调节方案y使其可以被执行。通过数学语言表述的定义如下。
定义1:可行域是一组集合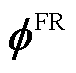 满足
满足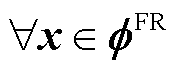 ,
,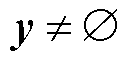 ;且
;且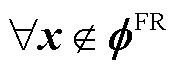 ,
,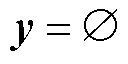 。
。
根据可行域的定义,可行域是由变量x和y组成的高维多胞体向变量x方向上的投影,即
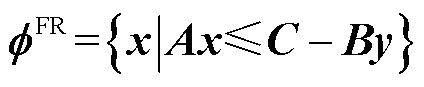 (3)
(3)
由于投影的过程是一个线性映射,一个高维凸多胞体的投影仍为凸多胞体。因此,可行域可以通过一组线性不等式的形式描述为
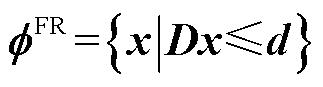 (4)
(4)
式中,D和d为边界参数,蕴含着可行域凸多胞体的边界信息。可行域刻画的本质即为求解投影后的边界参数D和d。
为刻画可行域的边界,可以由点入手。对于一个投影面上的点x0,设计以下优化问题判断该点是否在可行域内。
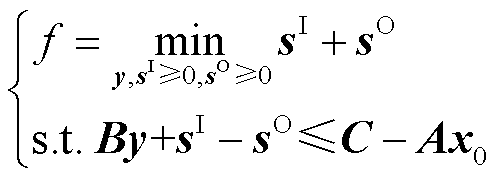 (5)
(5)
式中,sI和sO分别为内、外松弛变量,在几何学上等效于对可行域边界的内、外位移量。在优化问题式(5)中求取满足约束条件下两个松弛变量的最小加和值。如果优化结果f >0,则证明sI和sO至少有一个为正,这说明点x0无法满足约束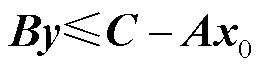 ,即该点在可行域外;如优化结果f =0则证明点x0在可行域内。因此,可以得出结论:f =0是x0在可行域内的充要条件。
,即该点在可行域外;如优化结果f =0则证明点x0在可行域内。因此,可以得出结论:f =0是x0在可行域内的充要条件。
由点及面,当点x为当前空间RC中任意点时,借鉴鲁棒优化的思想可以设计如下最大-最小化双层优化问题来判断RC是否在可行域内部。
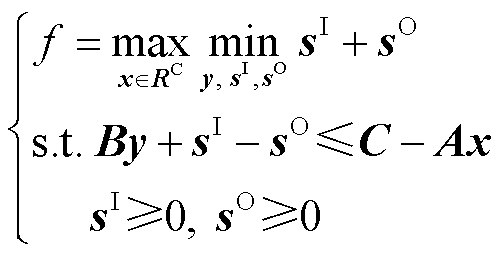 (6)
(6)
优化问题式(6)可以被理解为判断当前空间中的最外点是否在可行域内部,如果RC中的最外点都在可行域内部,那么证明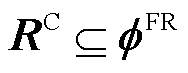 。但是,目前大部分求解器无法直接处理最大-最小化问题。为了解决这个问题,引入对偶变换法将问题式(6)中内层的最小化问题替换为其对偶问题。
。但是,目前大部分求解器无法直接处理最大-最小化问题。为了解决这个问题,引入对偶变换法将问题式(6)中内层的最小化问题替换为其对偶问题。
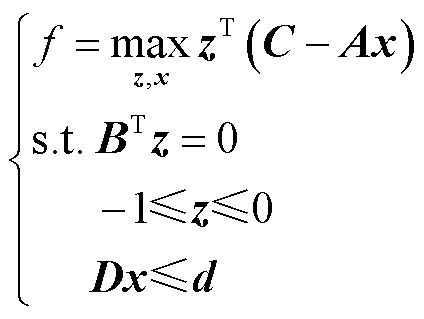 (7)
(7)
式中,z为对偶变量。根据弱对偶性质,对偶问题式(7)的最大值小于原问题式(6)的最小值。因此,当f =0时,有
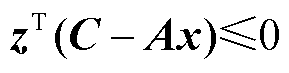 (8)
(8)
当x在RC中变化时,问题式(7)的最优解z也在对偶空间中取极值,即空间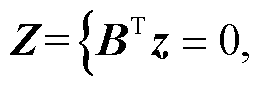
 中的顶点。经推导,可行域的多胞体形式为
中的顶点。经推导,可行域的多胞体形式为
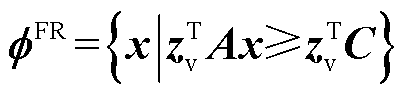 (9)
(9)
式中,zv为对偶空间z的顶点。至此,搜索原问题对偶空间的顶点成为可行域的刻画问题的关键,具体算法将在下文阐述。
根据可行域的多胞体形式可知,为刻画可行域需要找到对偶空间的所有顶点。然而,电力系统中的冗余约束条件使得对偶问题的变量数过多,即使结构简单的区域电网也难以通过遍历的方式检索高维数空间中的所有顶点。为避免传统从内部向外搜索的可行域刻画方法中边界重复生成、遗漏顶点的问题,本节提出了基于外割法的可行域刻画方法。为了加速可行域边界辨识效率,提出了一种基于并行伞约束辨识的模型降维加速算法,筛选可行域判断模型的起作用约束,滤除模型冗余约束,显著提升可行域刻画算法计算效率。
问题式(7)的目标函数并非线性,难以被直接求解。而变量z与x的约束条件解耦,因此问题式(7)可以被分解为两部分,表示为
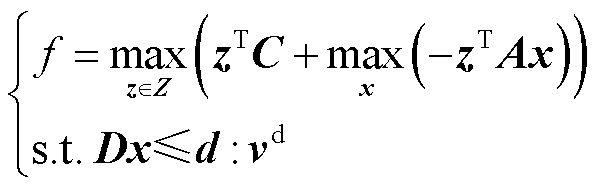 (10)
(10)
式中,vd为可行域约束的对偶变量。内部最大化问题取最优解时的KKT条件为
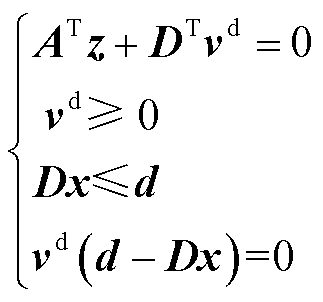 (11)
(11)
根据强对偶性,问题式(10)的内部最大化问题可以被其对偶问题替换,以实现对问题式(7)目标函数的线性化。至此,问题式(7)可以被转换为一个混合整数线性规划问题,即
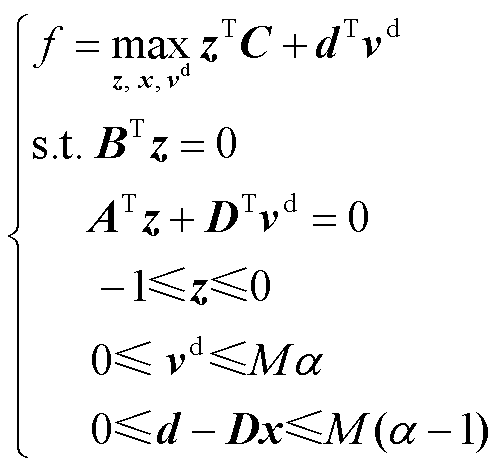 (12)
(12)
式中,M为一个足够大的常数;α为0-1变量,用于解耦式(11)中的vd与x。
求解问题式(12)能够找到对偶空间的顶点,根据定义式(9),每一个顶点可以生成可行域的一条边界。据此设计了一种逐次分割可行空间的可行域刻画算法,以二维可行域为例,流程如图2所示。
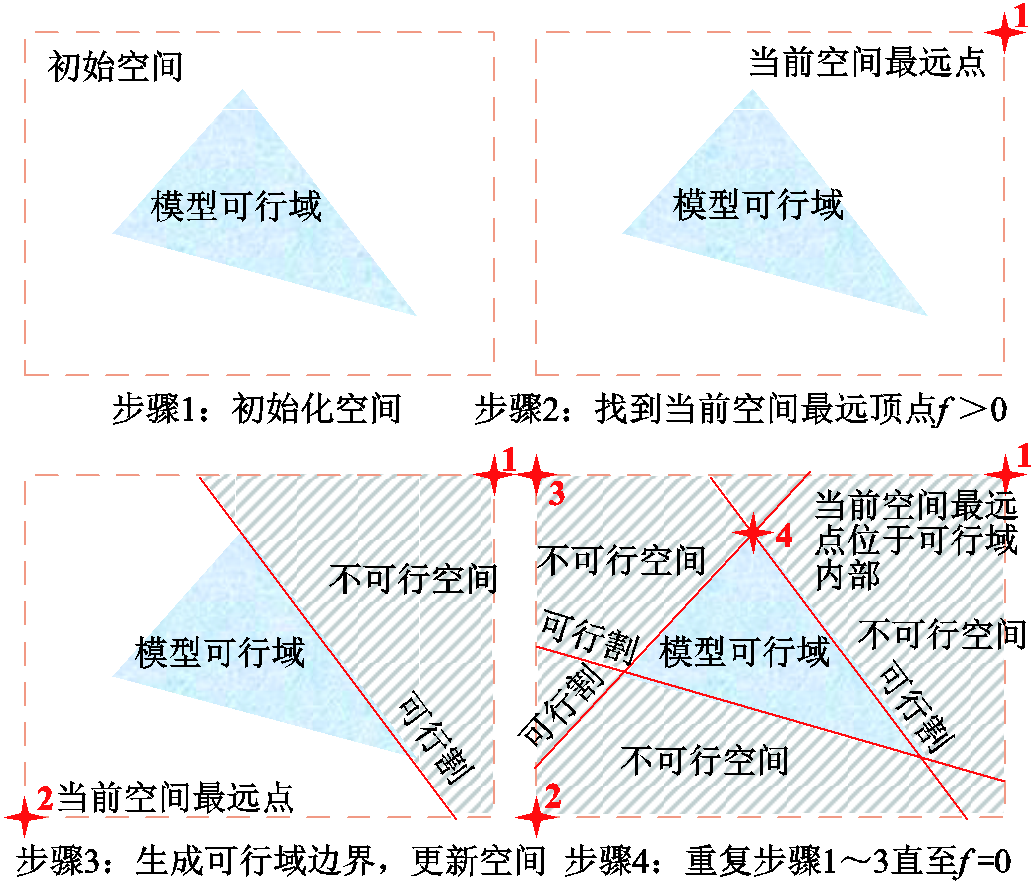
图2 可行域刻画流程
Fig.2 Feasible region characterization flow chart
其基本思路是初始化一个足够大的可行空间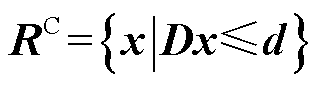 ;在该空间下求解问题式(12)来找到一个对偶空间的顶点zv;通过该顶点生成一条可行域边界
;在该空间下求解问题式(12)来找到一个对偶空间的顶点zv;通过该顶点生成一条可行域边界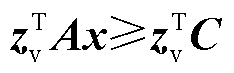 ;将该边界更新至当前空间中;重复以上步骤直至f =0。
;将该边界更新至当前空间中;重复以上步骤直至f =0。
电力系统中存在大量电源、复杂线路和安全约束,在实际运行中许多不会生效的冗余约束也被考虑进区域系统模型中,这会使可行域刻画中对偶空间的维数过高而引起组合爆炸的问题。因此,需要辨识出优化运行中真正生效的约束条件,即伞约束。设Ej、wj和ej分别为数学模型中第j条约束条件的系数向量、变量和常数项,则伞约束的定义如下。
定义2:对于第j条约束条件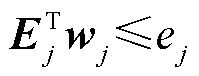 ,当
,当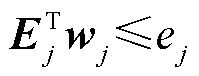 上存在一点满足其他所有约束条件时,第j条约束为伞约束。
上存在一点满足其他所有约束条件时,第j条约束为伞约束。
根据定义2可以设计一个优化问题来辨识伞约束,即
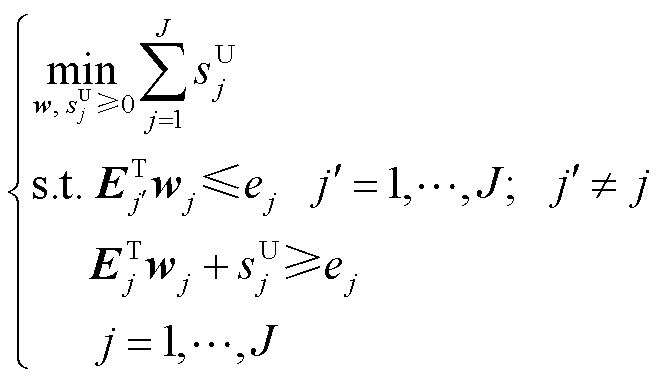 (13)
(13)
式中,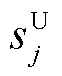 为伞约束松弛变量。在几何学中,可以将
为伞约束松弛变量。在几何学中,可以将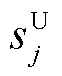 理解为约束j与可行域之间的最短欧氏距离。当
理解为约束j与可行域之间的最短欧氏距离。当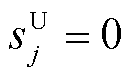 时,约束与可行域“搭界”,说明存在一个解wj可以使
时,约束与可行域“搭界”,说明存在一个解wj可以使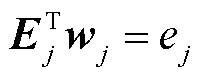 成立的同时满足其他所有约束条件,即约束j为起作用的伞约束。优化问题式(13)的最优解中取零值的松弛变量为伞约束,其他为非伞约束。以图3为例,C1~C4为数学模型的4条约束条件,无论向任何方向取极值,可行解永远位于C1~C3形成的可行域中,即约束C1~C3上总有点位于可行域内部。而C4上距离可行域的最短距离
成立的同时满足其他所有约束条件,即约束j为起作用的伞约束。优化问题式(13)的最优解中取零值的松弛变量为伞约束,其他为非伞约束。以图3为例,C1~C4为数学模型的4条约束条件,无论向任何方向取极值,可行解永远位于C1~C3形成的可行域中,即约束C1~C3上总有点位于可行域内部。而C4上距离可行域的最短距离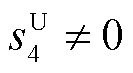 ,该约束不会对优化结果产生任何影响,即为非伞约束。将原问题的数学模型代入优化问题
,该约束不会对优化结果产生任何影响,即为非伞约束。将原问题的数学模型代入优化问题
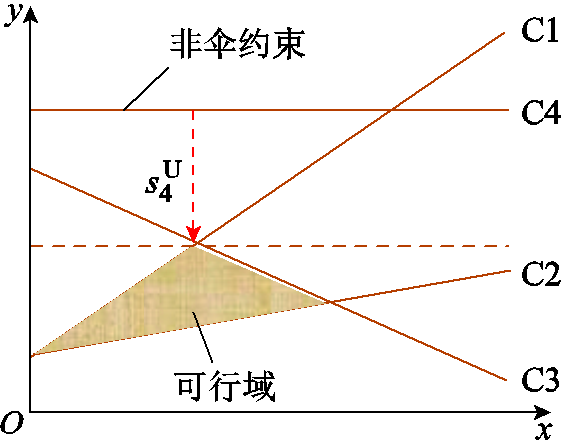
图3 伞约束辨识方法
Fig.3 Umbrella constraints identification
式(13),可以将模型中实际永远不会生效的非伞约束剔除,适用于电力系统这类大规模且安全约束冗余的数学模型。
对于一个有I个优化变量和J条约束的优化问题,采用问题式(13)所示的伞约束方法需要优化J(I+1)个变量和J(J+1)条约束,即使一个小型电力系统模型也将产生庞大的优化问题,从而难以被求解器处理。为了解决这个问题,并行计算的思想被引入,将问题式(13)分解为多个易求解的子问题。
经过上文的推导可以发现,伞约束辨识算法中各条约束的辨识问题之间是相互解耦的,即可以采用并行循环的方式单独执行各条约束的辨识问题,即
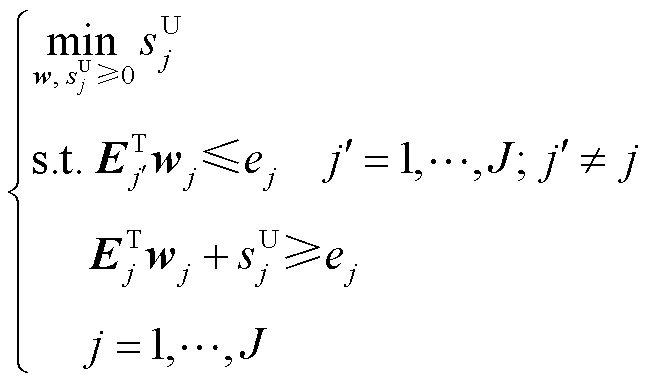 (14)
(14)
并行伞约束辨识法将问题式(13)分解为J个子问题,根据计算机的并行能力将J个子问题分为多组进行并行循环运算,每个子问题仅有I+1个变量和J+1条约束,与原问题规模相似。因此并行伞约束方法可以减少优化计算规模并提高辨识效率。
前文介绍了基于外割法的可行域刻画算法的求解思路,结合并行伞约束辨识法,设计了一套高效求解区域电力系统可行域的总体算法流程,如图4所示。图中,τ为容许偏差;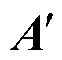 、
、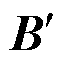 和
和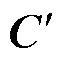 为伞约束辨识后精简模型的系数矩阵。
为伞约束辨识后精简模型的系数矩阵。
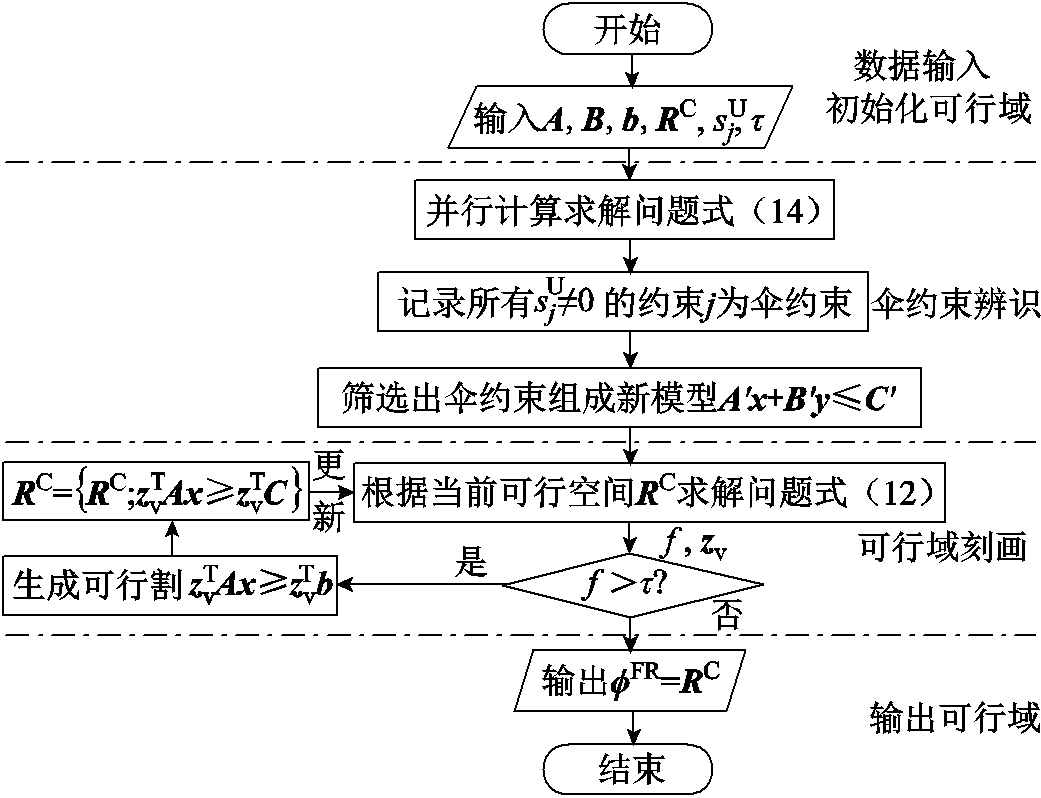
图4 总体算法流程
Fig.4 Overall algorithm flow chart
算法流程分为以下4个步骤。
1)输入初始化:输入区域电网数学模型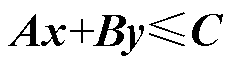 ,初始化一个足够大的可行空间RC。
,初始化一个足够大的可行空间RC。
2)求解问题式(14)辨识出模型中的伞约束,剔除非伞约束,形成精简模型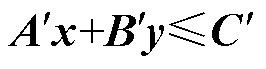 。
。
3)根据精简模型和当前可行空间求解问题式(14),若目标函数值大于容许偏差,根据顶点zv生成可行割并改变当前空间,重复步骤3)直至满足冗余偏差。
4)输出可行域:输出当前空间即为可行域。
本文结合并行伞约束辨识方法和基于外割法的可行域刻画算法,能够有效处理电力系统协同运行所需的大规模、高维数可行域刻画难题,为新型电力系统中输-配电网协同、省间电网协同等问题提供有效的解决方案和技术支撑。
配电网中分布式能源的高比例渗透是新型电力系统的典型特征,然而海量分布式光伏、电动汽车等随机性资源的并网接入已经向大电网的安全与经济运行提出严峻挑战,调度中心难以处理如此大规模精细化的优化问题。传统被动响应的调度模式逐渐难以适用,因此迫切需要解决需求侧资源如何主动参与上级电网协同调度的难题。
为降低分布式能源的随机性并提升其可控性,将分布式电源、负荷、储能、变流器及监控保护等装置有机结合,聚合形成一个类似发电厂的独立可控系统,即“虚拟电厂”。应用可行域投影理论,虚拟电厂可以聚合海量分布式能源并刻画其与输电网交互功率的可行域。通过向上级电网申报虚拟电厂的等值可行域,调度中心将虚拟电厂视为独立主体与其他传统发电主体进行集中优化调度,而不必处理配电网中的大规模、高维数约束。基于可行域投影理论,实现了高比例分布式资源渗透的配电网与传统电力调度模式的对称兼容,配电网能够高效主动地参与上级电网协同运行,同时避免内部隐私信息的泄露。以改进的IEEE 33节点配电网为例,验证可行域投影等值理论应用于配电网中的有效性,配电网数学模型及算例数据详见附录1。
图5刻画了不同分布式能源渗透率下的虚拟电厂公共连接点的传输功率可行域,该可行域为x轴和z轴组成的二维空间,每一个切片图表示在特定分布式能源渗透率下虚拟电厂能够与外界交互的有功、无功功率可行空间。分布式能源渗透率Rp指的是配电网中分布式能源装机容量与负荷的比值。
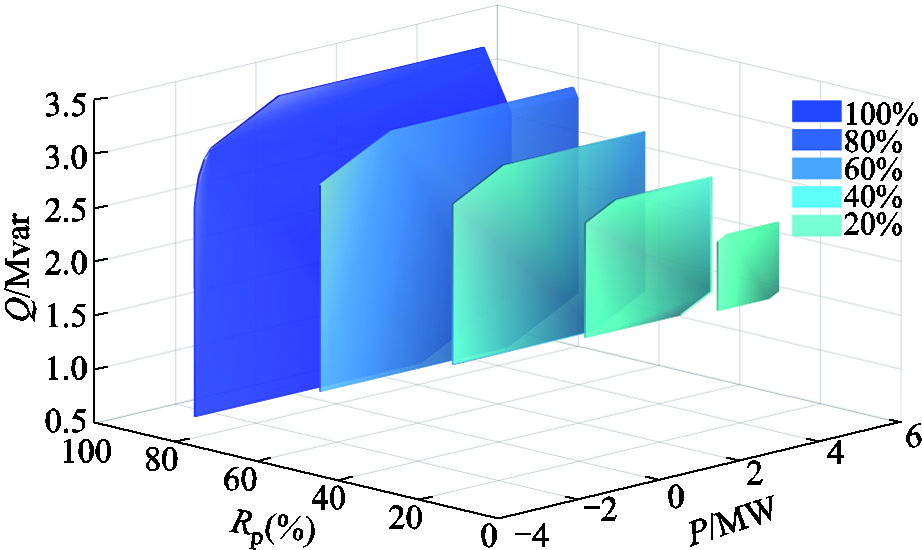
图5 不同分布式能源渗透率下虚拟电厂的可行域
Fig.5 Feasible regions of virtual power plants under different distributed energy resources penetration
从图4可知,在渗透率较低时,可行域的形状近似长方形,说明有功功率与无功功率几乎解耦,公共节点的输出功率受线路约束较小,可再生能源全部就地消纳。随着分布式能源渗透率的增加,虚拟电厂的可行域范围逐渐扩大,形状也越发不规则。这说明随着交互功率范围的扩大,更多的约束条件生效并投影至可行域上。
本文所提伞约束辨识方法和投影等值法在配电网中削减约束的效果如图6所示。随着分布式能源机组并网数目的增加,原问题模型中的约束条件明显增加。
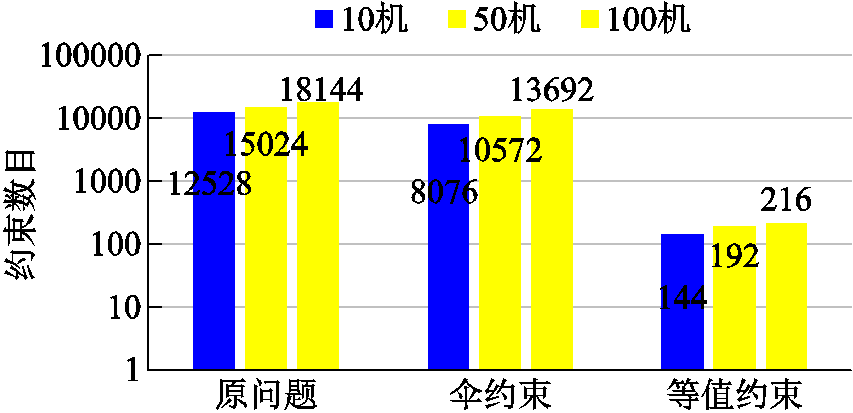
图6 可行域约束数目的精简效果
Fig.6 The reduction of constraints number
表1分析了枚举法、多参数规划法和本文算法的性能对比。枚举法的计算精度受搜索方向影响,搜索方向数目较小时,计算时间较短,但可行域刻画误差较大,为使精度达到要求会牺牲大量搜索时间;多参数规划法计算时间远大于其他算法,且受约束条件数目的影响较大,难以适应大规模问题的可行域刻画;采用本文所提外割法,等值可行域的约束条件大幅减小,相比其他算法的计算时间也有明显优势。经伞约束辨识后,原问题中冗余的非伞约束被剔除,模型冗余约束约占总约束的24.5%~35.6%,计算时间进一步缩短。经过本文所提的投影等值方法,大幅降低了虚拟电厂与调度中心的信息交互量,提升了电力系统协同运行优化效率。
表1 各类可行域刻画算法的性能对比
Tab.1 Performance comparison of various feasible region characterization algorithms
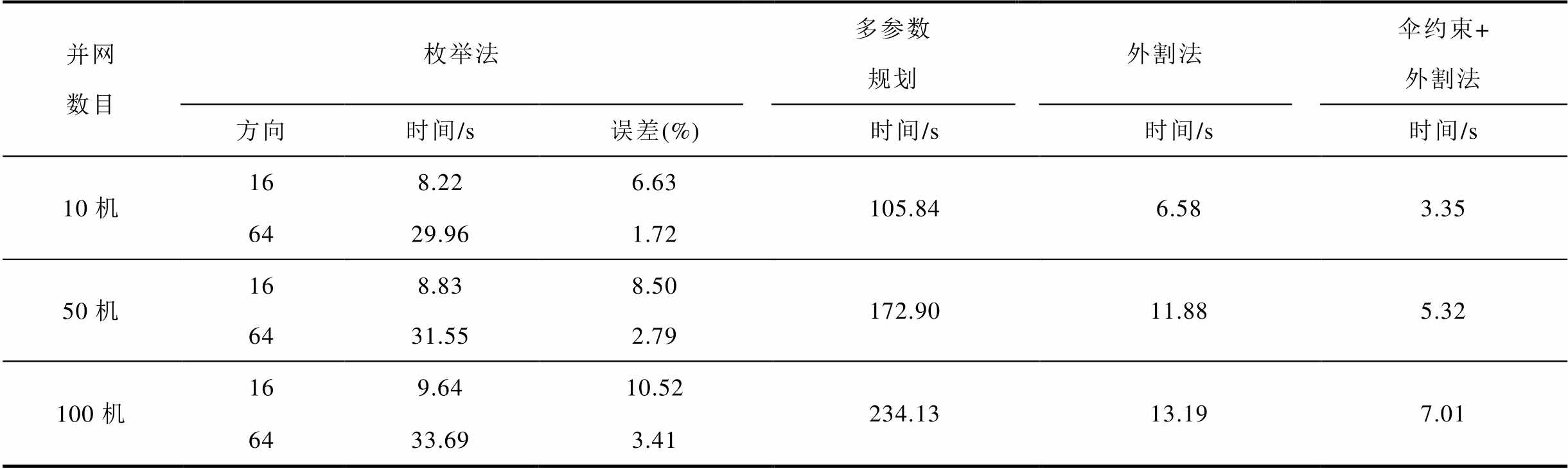
并网数目枚举法多参数规划外割法伞约束+外割法 方向时间/s误差(%)时间/s时间/s时间/s 10机168.226.63105.846.583.35 6429.961.72 50机168.838.50172.9011.885.32 6431.552.79 100机169.6410.52234.1313.197.01 6433.693.41
我国新能源的发展趋势与分布特性决定了跨省跨区输电的规模将日益增大,省间的互联耦合越发紧密。传统省间通道可用传输容量的计算仅考虑联络线本身的功率传输极限,无法反映送/受端的实际物理约束。随着省间通道数目的增加,各通道的传输功率受省内安全约束影响而耦合,因此可以通过可行域投影方法来刻画多通道联络线功率可行域,为省间市场出清提供精确的安全边界。本节考虑受端电网省内安全约束,将省内安全约束向省间联络线投影,提出省间联络线可传输功率安全域的概念,刻画联络线之间传输功率的耦合关系。以省级电力市场优化送、受端电力资源配置,有效应对我国电力资源在区域间分配不均的主要矛盾,实现我国能源资源的跨区域优化配置。
为验证投影等值理论在省间多通道安全域计算上的有效性与实用性,基于IEEE 39节点和IEEE 118节点的互联系统进行算例验证,数学模型及算例数据详见附录2。图7分别展示了IEEE 39节点送端电网与IEEE 118节点受端电网内部约束向3条联络线传输功率投影等值的可行域。由可行域的不规则形状可知3条输电通道传输功率之间存在耦合关系,这是省内安全约束的限制作用。
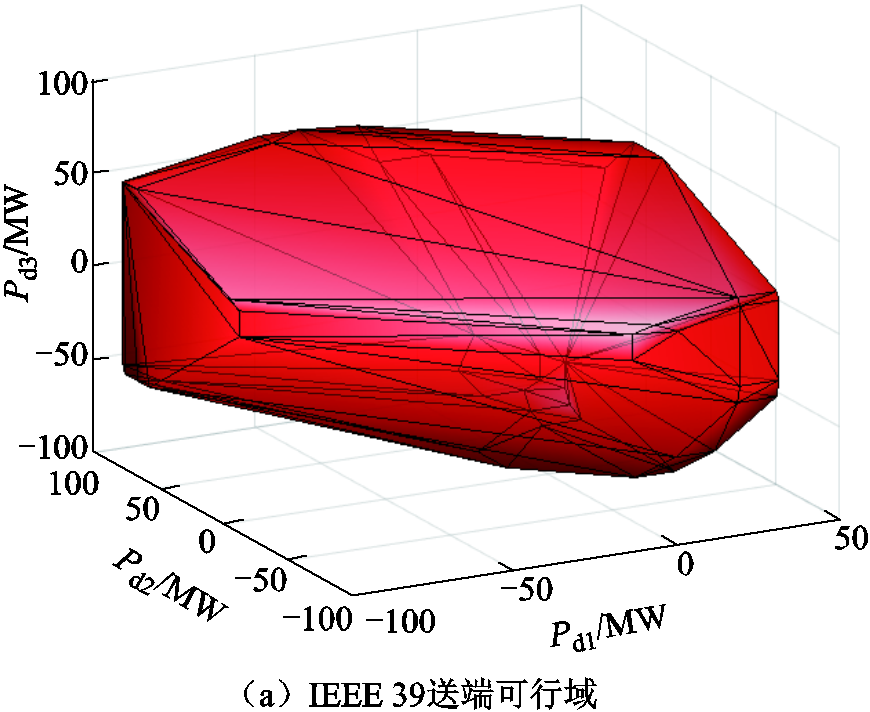
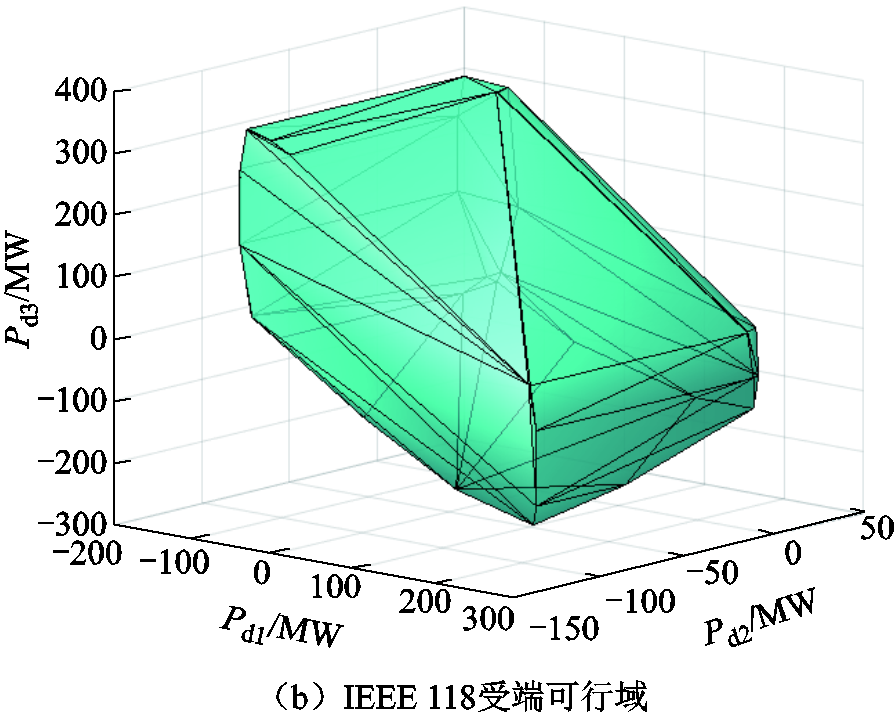
图7 IEEE 39送端可行域和IEEE 118受端可行域
Fig.7 Feasible region of IEEE 39 sending power grid and feasible region of IEEE 118 receiving power grid
将图7a与图7b置于同尺度空间内,其重合部分即为满足送受两端省内安全约束的3通道联络线可行空间,如图8所示。该空间可用于全国统一电力市场的优化调度和市场出清,只要出清结果位于重合可行域内部,那么必然满足送受端电网的省内安全约束。在该模式下,省间市场的优化出清问题简洁清晰、无须颠覆现有电力市场机制体制,符合电力系统发展的路径依赖理论。
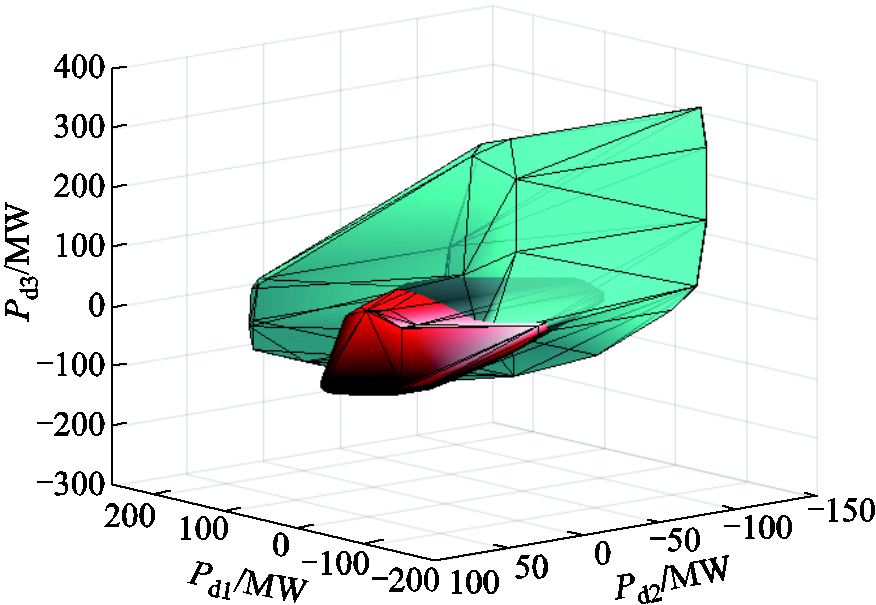
图8 省间多联络线安全域
Fig.8 Inter-provincial multiline security region
在传统输电网调度运行中,约束繁杂且调节能力弱的配电网通常被当作固定负荷处理,输电网根据配电网负荷曲线制定机组出力计划。在新型电力系统中,具有随机性和波动性的新能源渗透率的提高使得输电网对灵活性资源的需求增加,配电网中各类可调节资源的并网能够与输电网形成互补。然而,配电网中蕴含了大量时间耦合、空间交错的分布式能源、需求响应、储能等时变资源,其运行可行域随需求侧资源的运行状态而动态改变。因此传统电力系统调度难以掌握配电网的动态可行域和内部时域耦合约束。基于3.1节提出的配电网可行域聚合方法,本文提出了“动态可行域”的概念,使输配电网的高效协同调度运行成为可能。该模式下,实现了更大的范围内的资源优化配置,在提高配电网分布式资源利用率的同时增强了输电网的灵活性。
以改进的IEEE 33节点配电网和IEEE 30节点输电网为例,验证考虑时域耦合的配电网聚合参与考虑安全约束的机组组合中的有效性,IEEE 33节点配电网算例与3.1节相同,考虑安全约束的机组组合(Security-Constrained Unit Commitment, SCUC)数学模型与IEEE 30节点输电网算例详见附录3。图9展示了配电网3个连续时段有功功率的可行域。不规则的多面体证明了3个时段有功功率之间存在耦合关系,这样的耦合关系是受燃气轮机爬坡速度、负荷需求响应约束造成的。
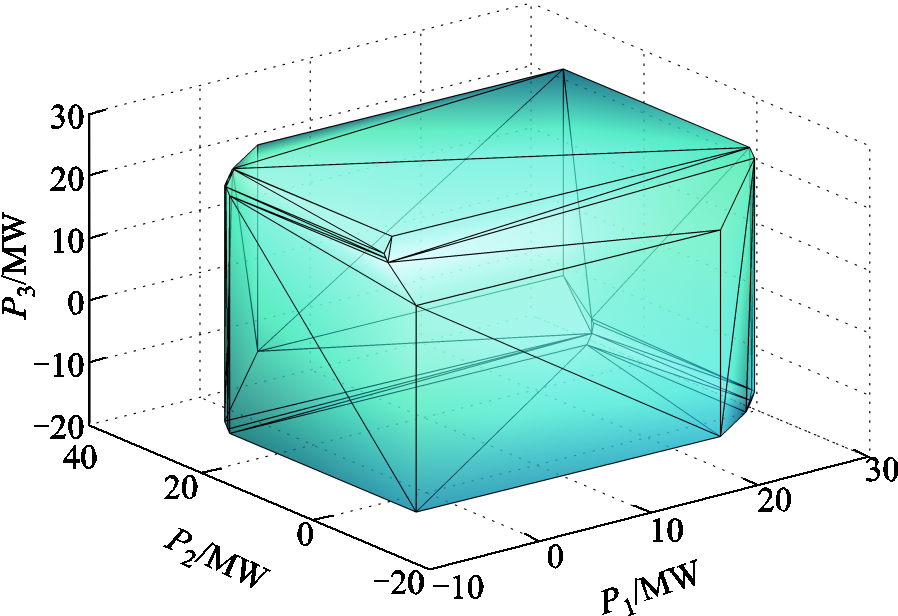
图9 配电网时域耦合可行域
Fig.9 Temporal-coupled feasible region of distribution network
配电网聚合为独立主体参与机组组合的调度结果如图10所示。图中,DN1和DN2为主动配电网;G1~G6为火电机组;W为风电机组。在夜间1:00时刻为风电高发时,配电网吸收输电网中过剩风电;在5:00—13:00时,负荷升高,配电网向输电网输送电能以满足系统调峰需求;17:00时,负荷骤降,配电网维持内部功率平衡以减少火电机组的停机。特别需要指出的是,13:00时,负荷较9:00时增加,配电网内部分布式能源可输出功率较高,实际却减少了对输电网的电能输送,这是为了应对17:00的负荷骤降。说明机组组合计算中配电网的时域耦合约束生效,相比于传统输配协同调度中仅考虑配电网单时段可行域,时域耦合可行域是投影等值算法的主要应用之一。
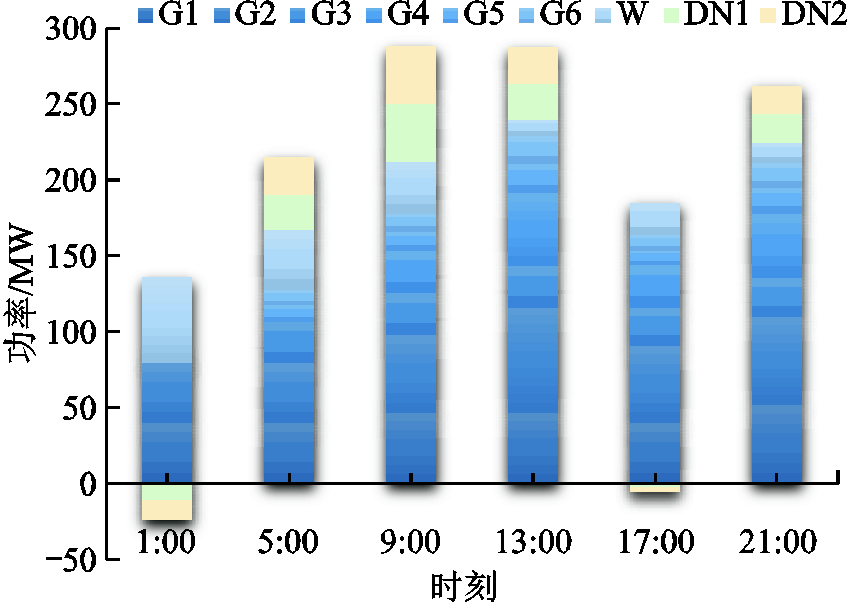
图10 配电网参与的机组组合
Fig.10 Unit combination with distribution network participation
表2中展示了本文所提算法在可行域刻画时间和协调时间上相比于其他协调方法的优越性。分解协调法为分布式算法,无需刻画可行域,单在面对多个配电网协调问题时需多次迭代,因此计算时间明显大于集中式的协调方法。实际的配电网与输电网协同运行是一个多时段高维数问题,枚举法和多参数规划方法难以高效刻画配电网的可行域。综上所述,本文所提算法相比于其他协调模式在可行域刻画效率和协调速度上有明显优势。
表2 各类协调方法的对比
Tab.2 Performance comparison of various feasible region characterization algorithms

算法模式可行域刻画时间/s协调时间/s 分解协调法分布式1 008.22 枚举法集中式1 464.6715.66 多参数规划集中式720.213.17 伞约束+外割法集中式21.382.72
针对新型电力系统的形态特征和发展方向,本文提出了一种基于外割法的可行域投影等值算法,通过伞约束辨识法剔除模型冗余约束,提出了基于可行域投影理论的新能源电力系统协同运行模式,并提出了三种应用场景:配电网/虚拟电厂可行域聚合、省间多通道安全域计算和多时段输配电网协同运行。得到如下结论:
1)基于投影等值理论的区域协调模式简洁清晰、无须颠覆现有电力市场机制体制,符合电力系统发展的路径依赖理论。
2)本文提出的并行伞约束辨识法和可行域投影等值法能够有效降低区域电网模型的变量和约束数目,从而降低区域电网与调度中心的信息交互量,提升电力系统运行优化效率。
3)本文提出的动态可行域能够表征配电网内部的时域耦合约束,从而能够更精准合理地制定输配协同调度计划。
需要说明的是,本文的研究重点为提出面向新型电力系统协同运行的可行域高效刻画方法,其本质是电力系统模型的高维可行域向所研究物理量上的投影等值。针对不同的问题,电力系统模型中考虑的约束条件可以改变,投影方向也可根据研究内容决定,只要在模型中考虑了电压、频率等研究所需的约束条件,无论向任何方向投影后的可行域必然满足其内部的安全约束。因此本文提出的可行域刻画方法可以应用于其他需要降低模型维数的场景。未来研究中,将着重探索基于可行域投影的综合能源系统协调运行方法,以及基于多参数规划的配电网参与电力市场报价函数研究。
期待本文工作对我国新型电力系统协同运行模式建设有重要参考价值。
附 录
1. 配电网数学模型及算例设置
1)配电网数学模型
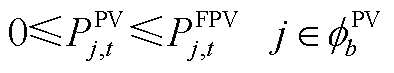 (A1)
(A1)
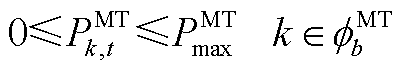 (A2)
(A2)
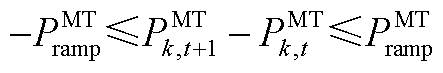 (A3)
(A3)
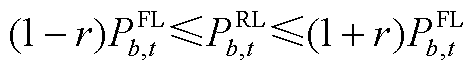 (A4)
(A4)
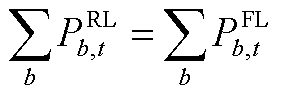 (A5)
(A5)
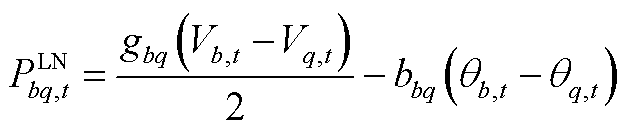 (A6)
(A6)
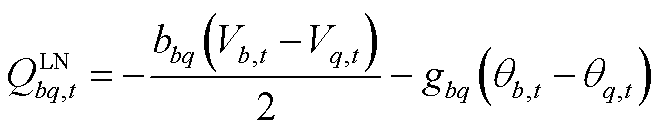 (A7)
(A7)
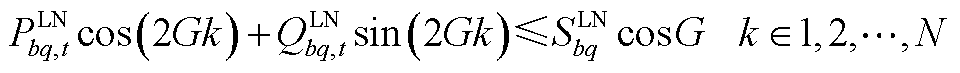 (A8)
(A8)
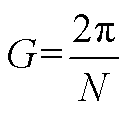 (A9)
(A9)
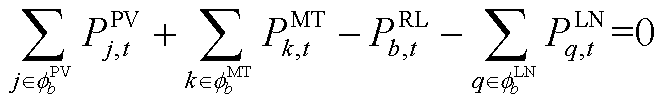 (A10)
(A10)
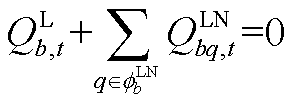 (A11)
(A11)
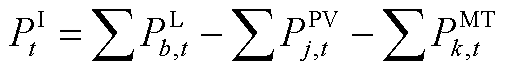 (A12)
(A12)
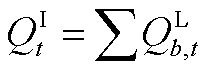 (A13)
(A13)
式中,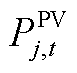 和
和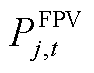 分别为风机j在t时刻的实际和预测出力;
分别为风机j在t时刻的实际和预测出力;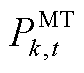 、
、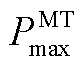 和
和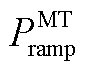 分别为微型燃气轮机的实际出力、最大出力和爬坡速率;
分别为微型燃气轮机的实际出力、最大出力和爬坡速率;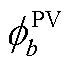 和
和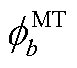 分别为光伏和燃气轮机的编号集合;
分别为光伏和燃气轮机的编号集合;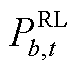 、
、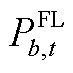 和r分别为可控负荷的实际负荷、预测负荷和调节率;
和r分别为可控负荷的实际负荷、预测负荷和调节率;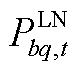 、
、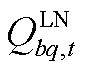 、
、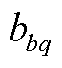 、
、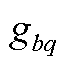 分别为节点b和q之间线路的有功、无功功率、电纳和电导值;
分别为节点b和q之间线路的有功、无功功率、电纳和电导值;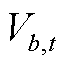 、
、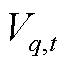 和
和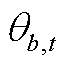 、
、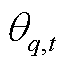 分别为节点b和q的电压和相角;N、k和G分别为分段数目、索引和角度;
分别为节点b和q的电压和相角;N、k和G分别为分段数目、索引和角度;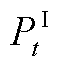 和
和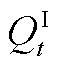 分别为配电网与输电网公共节点的有功、无功功率。
分别为配电网与输电网公共节点的有功、无功功率。
式(A1)表示光伏的出力约束;式(A2)和式(A3)为微型燃气轮机的功率约束;负荷的需求响应通过式(A4)和式(A5)表示;式(A6)~式(A9)通过分段线性化的方式近似配电网潮流约束[26];式(A10)~式(A13)为节点功率平衡约束。值得注意的是,配电网模型中的燃气轮机爬坡约束(A3)和可控负荷的需求响应约束(A5)为时域耦合约束。
2)配电网算例设置
为验证投影等值理论在配电网/虚拟电厂中的应用效果,3.1节中采用了改进的IEEE 33节点配电网进行算例验证,其电气接线图如附图1所示,基础算例中配电网接入了6台0.2 MW的光伏设备、5台1MW的微型燃气轮机,负荷需求响应能力占总负荷的20%。
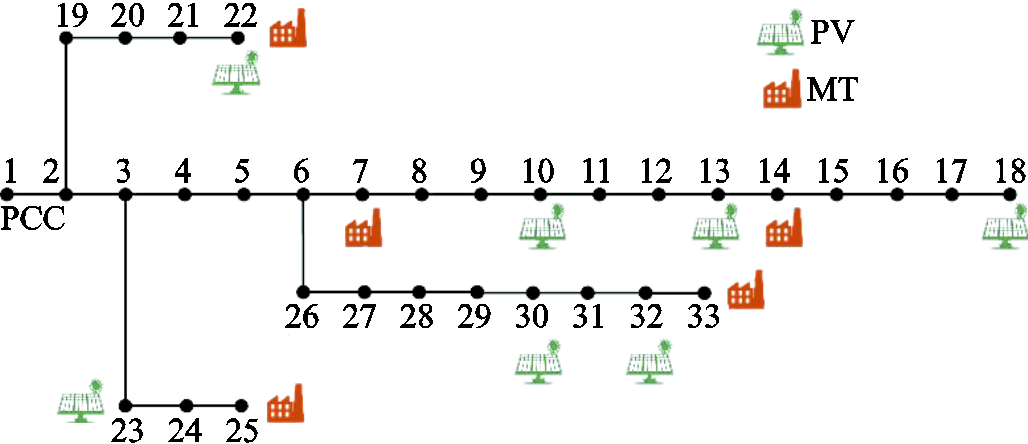
附图1 改进IEEE 33节点配电网
App.Fig.1 Modified IEEE 33 bus feeder system
2. 考虑安全约束的省间多联络线模型及算例设置
1)省间多通道数学模型
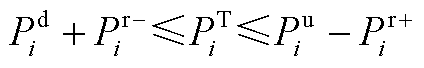 (A14)
(A14)
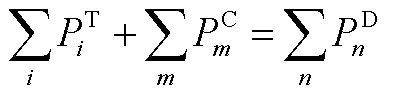 (A15)
(A15)
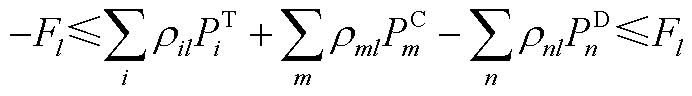 (A16)
(A16)
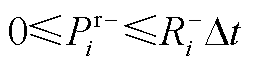 (A17)
(A17)
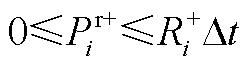 (A18)
(A18)
式中,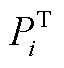 、
、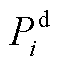 、
、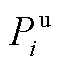 、
、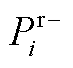 和
和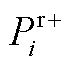 分别为省内机组的出力、最小/大技术出力、下/上备用容量;
分别为省内机组的出力、最小/大技术出力、下/上备用容量;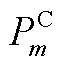 为省间联络线向省内传输的有功功率;
为省间联络线向省内传输的有功功率;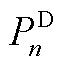 为省内负荷;
为省内负荷;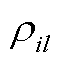 、
、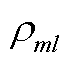 和
和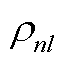 分别为省内机组、省间联络线和负荷对线路的潮流转移分布因子;
分别为省内机组、省间联络线和负荷对线路的潮流转移分布因子;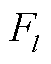 为省间联络线功率传输极限;
为省间联络线功率传输极限;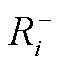 和
和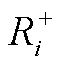 为省内机组的下/上爬坡速率。
为省内机组的下/上爬坡速率。
式(A14)表示省内发电机组出力约束;式(A15)表示考虑省间联络线传输功率的省内功率平衡约束;式(A16)为线路潮流约束;式(A17)和式(A18)表示省内机组备用容量约束。
2)省间互联算例设置
为验证投影等值理论在省间多通道安全域计算中的应用有效性,3.2节中采用IEEE 39节点和IEEE 118节点的互联系统进行验证。IEEE 39节点系统为新能源送出省,IEEE 118节点系统为新能源受端,两省间系统通过3条联络线互联,系统接线图如附图2所示。
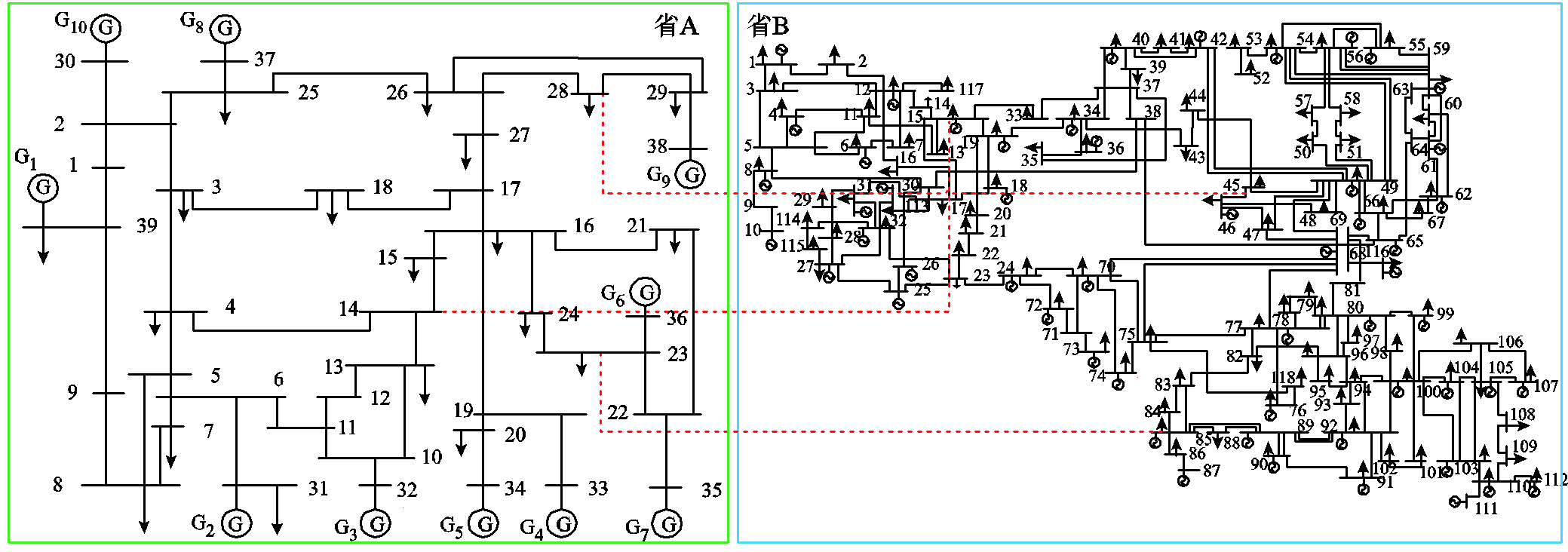
附图2 IEEE 39节点和IEEE 118节点互联电力系统
App.Fig.2 IEEE 39 node and IEEE 118 node power system
3. 输配电网协同运行模型及算例设置
1)考虑安全约束的机组组合模型
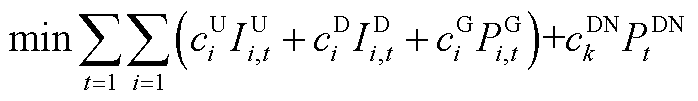 (A19)
(A19)
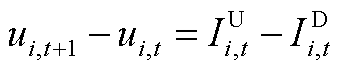 (A20)
(A20)
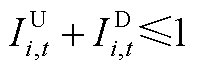 (A21)
(A21)
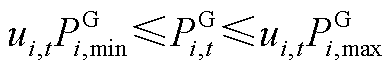 (A22)
(A22)
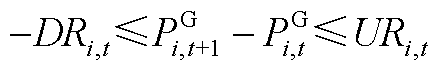 (A23)
(A23)
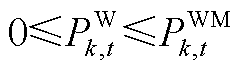 (A24)
(A24)
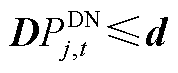 (A25)
(A25)
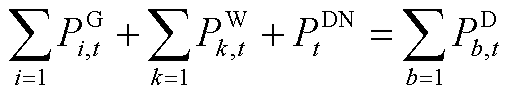 (A26)
(A26)
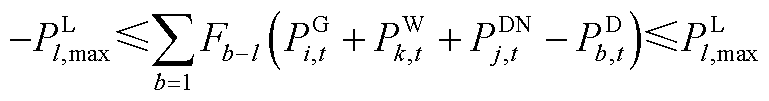 (A27)
(A27)
式中,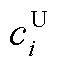 、
、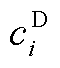 、
、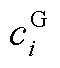 和
和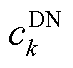 分别为火电机组起、停、发电成本和配电网函数;
分别为火电机组起、停、发电成本和配电网函数;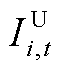 和
和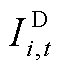 为整数变量,分别表示机组起、停状态;
为整数变量,分别表示机组起、停状态;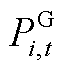 、
、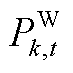 和
和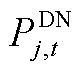 分别为火电、风电机组和配电网向输电网输送的功率;
分别为火电、风电机组和配电网向输电网输送的功率;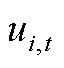 为火电机组起停状态;
为火电机组起停状态;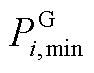 分别和
分别和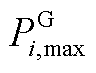 为火电机组最小/最大技术出力;
为火电机组最小/最大技术出力;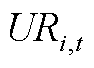 和
和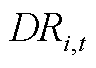 分别为上/下爬坡速率;
分别为上/下爬坡速率;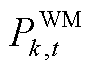 为风电机组出力上限;
为风电机组出力上限;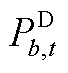 为各节点b上的负荷;
为各节点b上的负荷;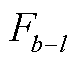 为节点b向线路l的潮流转移分布因子;
为节点b向线路l的潮流转移分布因子;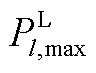 为输电网线路的最大传输功率。
为输电网线路的最大传输功率。
式(A19)为机组组合问题的目标函数,目的是降低系统运行成本以实现社会福利最大化;式(A20)和式(A21)限制了机组的起停;式(A22)和式(A23)为火电机组功率和爬坡约束;式(A24)为风电机组功率约束;式(A25)为配电网可行域约束;式(A26)和式(A27)分别为系统功率平衡与线路潮流约束。
2)输配协同算例设置
为验证投影等值理论在输配协同中的应用有效性,3.3节中采用改进IEEE 33节点配电网和IEEE 30节点输电网的输配协同系统进行验证。IEEE 30节点输电网有6台共计335 MW的火电机组和60 MW的风电站,改进IEEE 33节点配电网与附图1一致,配电网接入输电网8节点,如附图3所示。
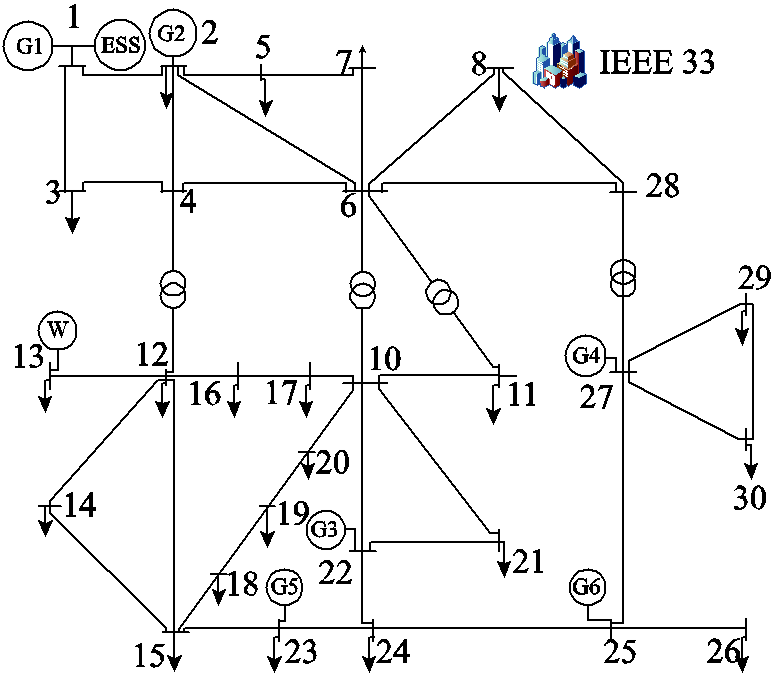
附图3 IEEE 33配电网与IEEE 30输电网协同
App.Fig.3 Coordination between IEEE 33 distribution network and IEEE 30 transmission network
参考文献
[1] Chen Xinyu, Liu Yaxing, Wang Qin, et al. Pathway toward carbon-neutral electrical systems in China by mid-century with negative CO2 abatement costs informed by high-resolution modeling[J]. Joule, 2021, 5(10): 2715-2741.
[2] Wang Jianxiao, Zhong Haiwang, Yang Zhifang, et al. Exploring the trade-offs between electric heating policy and carbon mitigation in China[J]. Nature Communications, 2020, 11: 6054.
[3] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677. Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[4] 王剑晓, 夏清, 李庚银, 等. 基于多市场均衡的综合能源市场机制设计[J]. 中国电机工程学报, 2021, 41(17): 5789-5803. Wang Jianxiao, Xia Qing, Li Gengyin, et al. Mechanism design for integrated energy markets based on multi-market equilibrium[J]. Proceedings of the CSEE, 2021, 41(17): 5789-5803.
[5] Pan Ersheng, Liu Siwei, Liu Jianqin, et al. The state grid corporation of China’s practice and outlook for promoting new energy development[J]. Energy Conversion and Economics, 2020, 1(2): 71-80.
[6] 国家发展改革委, 国家能源局. 关于完善能源绿色低碳转型体制机制和政策措施的意见[EB/OL] (2022-01-30). https://www.ndrc.gov.cn/xxgk/zcfb/tz/ 202202/t20220210_1314511.html.
[7] 魏泓屹, 卓振宇, 张宁, 等. 中国电力系统碳达峰·碳中和转型路径优化与影响因素分析[J]. 电力系统自动化, 2022, 46(19): 1-12. Wei Hongyi, Zhuo Zhenyu, Zhang Ning, et al. Transition path optimization and influencing factor analysis of carbon emission peak and carbon neutrality for power system of China[J]. Automation of Electric Power Systems, 2022, 46(19): 1-12.
[8] 李军徽, 安晨宇, 李翠萍, 等. 计及调峰市场交易的储能-新能源-火电多目标优化调度[J]. 电工技术学报, 2023, 38(23): 6391-6406. Li Junhui, An Chenyu, Li Cuiping, et al. Multi-objective optimization scheduling method considering peak regulating market transactions for energy storage-new energy-thermal power[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6391-6406.
[9] 张衡, 张沈习, 程浩忠, 等. Stackelberg博弈在电力市场中的应用研究综述[J]. 电工技术学报, 2022, 37(13): 3250-3262. Zhang Heng, Zhang Shenxi, Cheng Haozhong, et al. A state-of-the-art review on Stackelberg game and its applications in power market[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3250-3262.
[10] 杨浩, 苏文栋, 谷毅, 等. 面向耦合系统的交替方向滚动时域电压分层协同优化控制[J]. 电工技术学报, 2023, 38(21): 5846-5861. Yang Hao, Su Wendong, Gu Yi, et al. Voltage hierarchical cooperative control of coupled system using model predictive control and alternating direction method of multipliers[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5846-5861.
[11] Yu Mingkai, Wang Jianxiao, Yan Jie, et al. Pricing information in smart grids: a quality-based data valuation paradigm[J]. IEEE Transactions on Smart Grid, 2022, 13(5): 3735-3747.
[12] Qu Ming, Ding Tao, Wei Wei, et al. An analytical method for generation unit aggregation in virtual power plants[J]. IEEE Transactions on Smart Grid, 2020, 11(6): 5466-5469.
[13] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049. Yang Jun, Hou Junhao, Liu Yawei, et al. Distributed cooperative control method and application in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4035-4049.
[14] Bragin M A, Dvorkin Y. TSO-DSO operational planning coordination through “l1-Proximal” surrogate Lagrangian relaxation[J]. IEEE Transactions on Power Systems, 2022, 37(2): 1274-1285.
[15] Li Zhigang, Wu Wenchuan, Zhang Boming, et al. Decentralized multi-area dynamic economic dispatch using modified generalized benders decomposition[J]. IEEE Transactions on Power Systems, 2016, 31(1): 526-538.
[16] Molzahn D K, Dörfler F, Sandberg H, et al. A survey of distributed optimization and control algorithms for electric power systems[J]. IEEE Transactions on Smart Grid, 2017, 8(6): 2941-2962.
[17] Tan Zhenfei, Zhong Haiwang, Xia Qing, et al. Non-iterative multi-area coordinated dispatch via condensed system representation[J]. IEEE Transactions on Power Systems, 2021, 36(2): 1594-1604.
[18] Wei Wei, Liu Feng, Mei Shengwei. Real-time dispatchability of bulk power systems with volatile renewable generations[J]. IEEE Transactions on Sustainable Energy, 2015, 6(3): 738-747.
[19] Tan Zhenfei, Zhong Haiwang, Xia Qing, et al. Estimating the robust P-Q capability of a technical virtual power plant under uncertainties[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4285-4296.
[20] 姜涛, 贾宏杰, 姜懿郎, 等. 跨区互联电网热稳定安全域边界近似方法[J]. 电工技术学报, 2016, 31(8): 134-146. Jiang Tao, Jia Hongjie, Jiang Yilang, et al. Approximating method of wide area thermal security region boundary in bulk power system[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 134-146.
[21] Ardakani A J, Bouffard F. Identification of umbrella constraints in DC-based security-constrained optimal power flow[J]. IEEE Transactions on Power Systems, 2013, 28(4): 3924-3934.
[22] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938. Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessmentmethod for renewables VSC-HVDC delivery system[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[23] Zhao Lin, Zhang Wei, Hao He, et al. A geometric approach to aggregate flexibility modeling of thermostatically controlled loads[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4721-4731.
[24] Silva J, Sumaili J, Bessa R J, et al. Estimating the active and reactive power flexibility area at the TSO-DSO interface[J]. IEEE Transactions on Power Systems, 2018, 33(5): 4741-4750.
[25] Lin Wei, Yang Zhifang, Yu Juan, et al. Tie-line power transmission region in a hybrid grid: fast characterization and expansion strategy[J]. IEEE Transactions on Power Systems, 2020, 35(3): 2222-2231.
[26] Yang Zhifang, Zhong Haiwang, Bose A, et al. A linearized OPF model with reactive power and voltage magnitude: a pathway to improve the MW-only DC OPF[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1734-1745.
Abstract Vigorously developing the new-type power system dominated by renewable energy to build a clean, low-carbon, safe and efficient energy system is the path for China to achieve the "3060 carbon dioxide emission and carbon neutrality target". With the gradual increase of the penetration of renewable energy, the deep defects of the traditional energy system have gradually emerged. The imperfect energy coordination system, such as difficulty in optimal allocation of resources across provinces and low utilization of distributed energy, has become a bottleneck restricting the construction of new-type power systems. Therefore, the development of the new power system urgently needs to break the barriers of the traditional operation system, realize the efficient cooperation across regions and levels, and optimize the allocation of resources in a larger scope.
Firstly, a new cooperative operation mode of power system based on feasible region projection theory is proposed. Each subsystem in the power system forms a high-dimensional feasible space by aggregating the internal operation constraints and projecting to the common connection points to form its equivalent feasible region. The superior system implements the power balance dispatching of the whole network according to the feasible region of the subsystem to realize the efficient cooperation among all levels of the dispatching system.
Subsequently, the definition of feasible region and its mathematical expression of polyhedron are proposed. It is necessary to find all vertices of the dual space to describe the feasible region. However, the redundancy constraint in power system leads to numerous variables in the dual problem. Even all vertices in the high-dimensional space of regional power grid with simple structure are difficult to be retrieved by traversal. Therefore, combined with umbrella constraint identification method, a feasible region characterization method based on external approximation method is proposed in this paper. The redundant constraints of the original problem are eliminated by umbrella constraint identification, and the feasible region is quickly segmented by external approximation algorithm.
Three application scenarios are proposed: (1) Feasible regions aggregation of distribution network/virtual power plants. (2) Inter-provincial multiline available transmission capacity calculation. (3) Multi-period transmission and distribution network coordinated operation. Case studies show that the algorithm and model proposed in this paper can effectively reduce the scale of the regional power grid, thereby reducing the information interaction between the regional power grid and the system operator, and improving the operation optimization efficiency of the renewable energy power system.
keywords:Renewable energy power system, feasible region, equivalent projection, coordination scheduling
DOI: 10.19595/j.cnki.1000-6753.tces.230196
中图分类号:TM732
国家自然科学基金资助项目(52277092)。
收稿日期 2023-02-17
改稿日期 2023-06-02
张天策 男,1995年生,博士研究生,研究方向为新能源电力系统分析与控制、电力市场等。E-mail:ncepu_ztc@ncepu.edu.cn
李庚银 男,1964年生,教授,博士生导师,研究方向为新能源电力系统分析与控制、电力市场、新型输配电技术等。E-mail:ligy@ncepu.edu.cn(通信作者)
(编辑 李 冰)