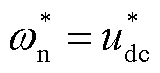 。因此,匹配控制能够通过直流电压自主感知电网频率,并根据电网频率波动快速调节新能源场站的有功出力,实现对电网的主动支撑功能。
。因此,匹配控制能够通过直流电压自主感知电网频率,并根据电网频率波动快速调节新能源场站的有功出力,实现对电网的主动支撑功能。摘要 近年来,具有低时延和惯量同步等优势的匹配控制成为主流构网型控制方案之一,但基于匹配控制的构网型直驱风电场的次同步振荡机理及特性尚不明确。因此,该文建立构网型直驱风电场并网系统的小信号模型,通过特征值法分析了系统的振荡模态及参与因子,并借鉴同步机中阻尼转矩法分析构网型直驱风电场的次同步振荡机理。结果表明,构网型直驱风电场中匹配控制主导的振荡模态在强电网下呈现负阻尼特性,系统存在次同步振荡的风险,但匹配控制振荡模态相较于跟网型控制的锁相环振荡模态具有更好的弱电网适应能力;匹配控制振荡模态存在类似于同步机转子运动方程的动态特性,使得构网型直驱风电场可能发生弱阻尼振荡;减小交流电网强度或无功控制器积分系数,增大构网型直驱风机台数或无功控制器比例系数,能够增大匹配控制振荡模态的阻尼,降低系统次同步振荡风险。
关键词:匹配控制 构网型直驱风电场 次同步振荡 特征值法
以风电、光伏为主的新能源通过电力电子变流器大规模接入电网时,电力系统容易形成弱电网并网环境[1],这给基于锁相环(Phase-Locked Loop, PLL)同步并网的传统跟网型新能源机组的稳定运行带来严峻挑战[2-3]。因此,具有较好弱电网适应能力的构网型新能源机组成为近年来国内外研究的前沿和热点[4]。德国、日本等一些国家已经开始对构网型新能源发电机组的工程应用进行规划[5-6];我国国网和金风科技也在多地开展了构网型新能源机组并网测试[7]。随着构网型控制技术的推广和应用,研究构网型新能源机组并网系统稳定性具有重要的现实意义和工程应用价值。
目前,国内外学者已经提出了多种构网型控制策略,如下垂控制、虚拟同步发电机(Virtual Synchronous Generator, VSG)控制及匹配控制等[8-9]。其中,匹配控制是近几年专家提出的一种构网型控制策略,其主要利用变流器直流母线电容能量来模拟同步机转子能量,进而实现电压源型构网控制。相较于其他构网型控制策略,匹配控制仅需测量直流电容电压即可实现自主同步功能,具有较快的响应速度[10]。并且,直流电容积分环节直接提供了系统的等效惯性,无需再额外模拟惯性[11]。因此,近年来基于匹配控制的构网型控制策略在新能源机组尤其是直驱风电机组中得到了广泛的应用。
目前,基于匹配控制的构网型新能源机组的相关研究主要集中在其电网支撑和惯量响应特性的分析中。在直驱风电场网侧换流器(Grid-Side Converter, GSC)采用匹配控制的前提下,文献[12]分析了机侧惯量传递对直驱风电机组弱电网运行稳定性的影响,并在网侧、机侧换流器设计致稳控制策略,提高直驱风电机组的惯量响应能力;文献[13]提出了一种以直驱风电机组为主电源的孤岛微电网的黑启动控制策略,实现了风速波动条件下孤岛微电网的稳定运行;文献[14]研究得到,基于匹配控制的双馈风电机组同样能够自主参与电网惯量响应,并具有较强的弱电网稳定运行与电网频率暂态支持能力。上述文献虽然对基于匹配控制的构网型新能源机组并网时的稳定性有一定的分析,但其具体的次同步振荡(Subsynchronous Oscillation, SSO)机理特性尚不清楚,缺乏更深入的研究。
现阶段常用的SSO分析方法[15-16]主要有阻抗分析法和特征值分析法。阻抗分析法主要基于序阻抗[17]或dq阻抗[18]模型,采用伯德图或奈奎斯特图等方法判断系统稳定性,但阻抗分析法难以准确地对系统初始状态进行数值分析,只适用于单输入单输出系统的SSO机理研究。相较于阻抗分析法,基于状态空间模型的特征值分析法能够准确地分析多输入多输出系统的稳定性,且具有更好的可观测性和可控性。特征值分析法主要采用数值方法分析系统的不稳定振荡模态及其参与因子,被广泛应用于构网型新能源机组的SSO阻尼特性和影响因素研究中[19-20]。另外,近年来有专家提出将同步机中的阻尼转矩法推广到跟网型新能源机组的SSO分析[21-22],通过类比同步发电机的二阶转子运动方程,从同步机阻尼角度分析新能源机组主导振荡模式的振荡机理,并通过阻尼系数量化评估系统的等效阻尼。
然而,尚无文献应用同步发电机中的阻尼转矩法研究构网型新能源机组的机理特性,并且目前构网型新能源机组的SSO分析主要聚焦于VSG控制的构网型变流器[17-20],基于匹配控制的构网型新能源机组的SSO机理特性鲜有文献展开研究。考虑到VSG控制和匹配控制两类构网型控制策略的拓扑结构存在较大差异[8],现有VSG控制的SSO研究结论对基于匹配控制的构网型直驱风电场的参考价值有限。因此,本文针对基于匹配控制的构网型直驱风电场SSO机理特性展开研究,通过特征值法详细分析其不同振荡模态的阻尼特性及参与因子,并在匹配控制动态中引入阻尼转矩法,从同步机阻尼角度揭示构网型直驱风电场的振荡机理。
本文主要工作如下:首先,采用模块化建模方法建立构网型直驱风电场并入交流电网的小信号模型;其次,通过特征值法分析构网型直驱风电场的主要振荡模态及参与因子,并分析其相较于传统跟网型直驱风电场在弱电网工况下的稳定性;然后,借鉴阻尼转矩法分析基于匹配控制的构网型直驱风电场的振荡机理;最后,通过特征值根轨迹研究交流电网强度、构网型直驱风机台数和无功控制器PI参数对系统SSO模态阻尼特性的影响。
近年来,基于GSC和同步发电机在结构和动态上的相似性[12-14],专家学者提出一种“匹配控制”的电压源型构网方案。基于匹配控制的新能源机组通过建立GSC直流电容电压udc与输出电压角频率ωn之间的匹配关系,依赖直流电容的惯量实现对电网的自主同步功能。图1给出了“匹配控制”型功率同步变换器的结构,直驱风机GSC直流电压udc的测量值经过增益为ωn/udc0的积分后,输出GSC调制电压的相位θdc,实现直流电压与输出电压角频率之间的实时联动,即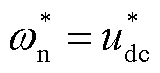 。因此,匹配控制能够通过直流电压自主感知电网频率,并根据电网频率波动快速调节新能源场站的有功出力,实现对电网的主动支撑功能。
。因此,匹配控制能够通过直流电压自主感知电网频率,并根据电网频率波动快速调节新能源场站的有功出力,实现对电网的主动支撑功能。
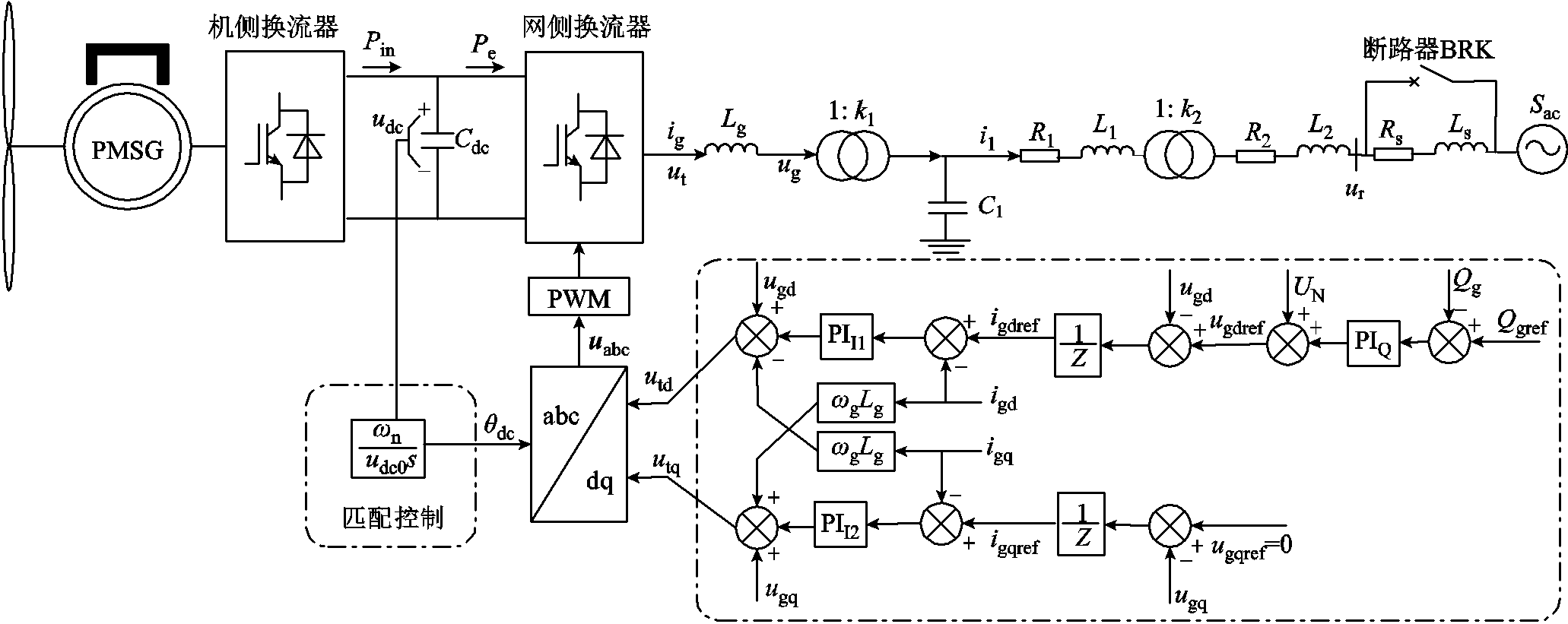
图1 构网型直驱风电场并网系统结构
Fig.1 Schematic diagram of the grid-forming direct-drive wind farm integrated to AC grid system
然而,目前基于匹配控制的构网型新能源机组的相关研究主要聚焦于电网支撑能力和惯量响应特性,其在不同电网强度下的SSO小信号稳定性尚不清晰。文献[14]指出匹配控制的核心思想是基于新能源机组GSC直流电容电压动态方程与同步发电机转子动态方程的相似性,通过类比控制使新能源机组对电网呈现出同步机“电压源”外特性。此时,基于匹配控制的GSC与同步发电机转子具有类似的数学形式和动态特性,两者之间的振荡失稳机理也有一定的相似之处,基于匹配控制的构网型直驱风电场可能存在类似于同步发电机转子的振荡风险。因此,本文将基于GSC与同步发电机的类比关系,从同步发电机阻尼的角度分析基于匹配控制的构网型直驱风电场SSO机理特性。
构网型直驱风电场并网系统的结构如图1所示。图中,Pin、Pe分别为机侧换流器输出有功功率、GSC输入有功功率;ut、ug分别为GSC输出电压、一级升压变压器低压侧电压;ig、il分别为GSC输出电流、输电线路电流。由图1可知,直驱风电场输出电能通过一级升压变压器和汇集线路接入35 kV场站,并入35 kV的电能经过二级升压变压器和输电线路送入110 kV电网。其中,本文采用聚合等值模型分析构网型直驱风电场整体并入交流电网时系统的SSO特性[23-24],构网型直驱风电场由70台直驱永磁风电机组通过受控源聚合等值得到,每台机组额定容量为5 MW。系统主要参数见附表1。
本文构网型直驱风电机组的机侧换流器采用基于转子磁链定向的空间矢量控制策略,以及定发电机转速外环和定电流内环的双闭环解耦控制。不同于传统跟网型GSC基于电网电压定向的空间矢量控制策略,构网型直驱风电机组GSC通过“匹配控制”策略来产生输出电压的相位[12],并通过无功功率控制外环、电流控制内环的双环控制策略来产生输出电压的幅值基准。此时,直驱风电机组GSC具备构网运行的能力。另外,构网型GSC在双环控制中加入虚拟阻抗控制来增加GSC的输出阻抗,提高系统稳定性。构网型GSC的具体控制结构如图1所示,本文所研构网型直驱风机GSC的控制参数见附表2。
本文引入系统短路比(Short Circuit Ratio, SCR)的概念来描述交流电网强度,表示为
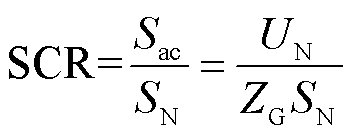 (1)
(1)
式中,Sac和SN分别为交流系统短路容量和风电场额定输出功率;UN为电网额定电压;ZG为交流系统等值阻抗,ZG=Z2+Zs,Z2和Zs分别为110 kV线路阻抗和电网等效阻抗。
本文通过控制图1中断路器BRK的运行状态来改变输电线路阻抗,得到不同SCR的系统运行工况。通过计算可得,断路器BRK断开与闭合时,系统SCR分别为2和40,可模拟构网型直驱风电场并入弱或强交流电网两种工况。
针对传统小信号建模方法计算量大、灵活性较差等问题,本文采用模块化小信号建模方法搭建系统的小信号模型[25]。采用模块化建模方法的关键在于推导建立系统各部分的动态数学模型及其相应的状态空间模型子模块。然后,只需按照系统内各模块之间的电气连接关系,连接各个状态空间模型子模块的输入输出端口,便能够得到全系统的小信号模型。
因此,当系统中部分子模块的数学模型发生变化时,模块化建模方法能够快速调整相应的状态空间模型,得到新系统的小信号模型。
本节数学模型的变量与图1中变量意义相同,下标d、q和x、y分别表示变量在相应坐标系下的分量,下标ref表示变量的基准值。
已有大量文献对跟网型直驱风电机组各模块的数学模型进行了详细的介绍,并通过模块化建模得到了跟网型直驱风电机组的小信号模型[26]。本节基于文献[26]中跟网型直驱风电场小信号模型,采用模块化建模方法建立构网型直驱风电场并网系统的小信号模型。
由第1节可知,相较于文献[26]中跟网型直驱风电机组,本文所研究的系统主要调整了跟网型控制中GSC和PLL的控制策略,其余模块的结构或控制策略基本一致。构网型直驱风电机组GSC和匹配控制的数学模型分别如式(2)和式(3)所示。限于篇幅,系统其余各模块的数学模型在附录中给出。
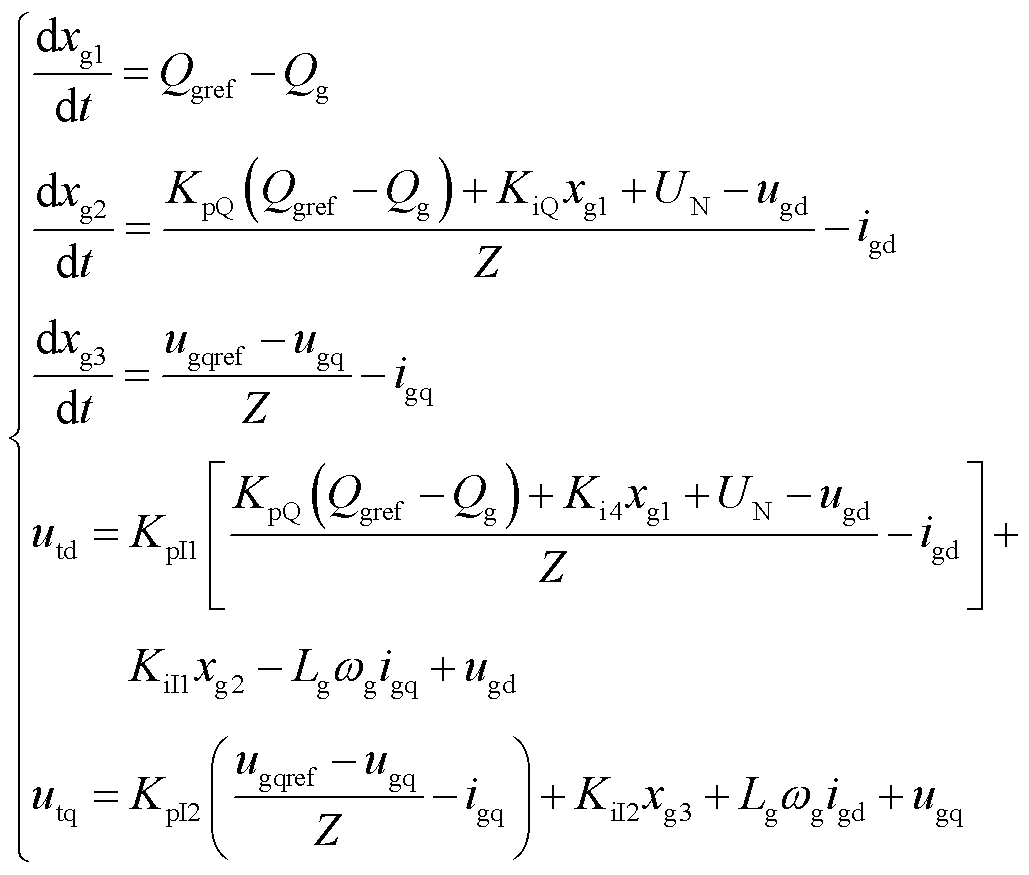 (2)
(2)
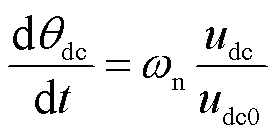 (3)
(3)
式中,xg1、xg2和xg3为GSC的中间状态变量;Qg和Qgref分别为并网点无功功率的实际值与基准值;Z为GSC虚拟阻抗;Lg为滤波电感;ωg和ωn分别为GSC的电角速度实际值和指令值;KpQ、KiQ分别为GSC无功控制外环的PI参数;KpI、KiI分别为GSC电流控制内环的PI参数;udc0为直流电容电压基准值;θdc为匹配控制输出相位。
综合式(2)和式(3)所示的GSC和匹配控制动态方程,以及附录中轴系、同步发电机、机侧换流器、直流电容、滤波电感、并联电容和输电线路的动态方程,得到本文构网型直驱风电场并网系统各模块的动态数学模型。
基于附表1和附表2的系统参数进行潮流计算,求取各状态变量的稳态值,并将系统各模块数学模型的非线性微分方程在稳定运行点附近线性化。然后,根据式(4),可推导得到构网型直驱风电场并网系统各模块的状态空间模型。
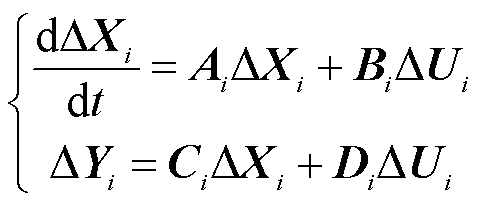 (4)
(4)
式中,Xi、Ui和Yi分别为模块i的状态变量矩阵、输入变量矩阵和输出变量矩阵;Ai、Bi、Ci、Di为模块i的相关系数矩阵。以构网型直驱风电机组GSC和匹配控制模块为例,附录中给出了它们状态空间模型的具体表达式。
另外,本文构网型直驱风电场各部分模块建立在dq坐标系,而输电线路模块建立在xy坐标系。因此,需要在子系统连接处引入坐标变换,以实现系统状态空间模型的闭环连接。图2给出了dq坐标与xy坐标的映射关系,得到任意变量在dq坐标系和xy坐标系间的转换关系为
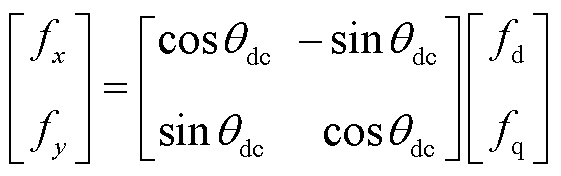 (5)
(5)
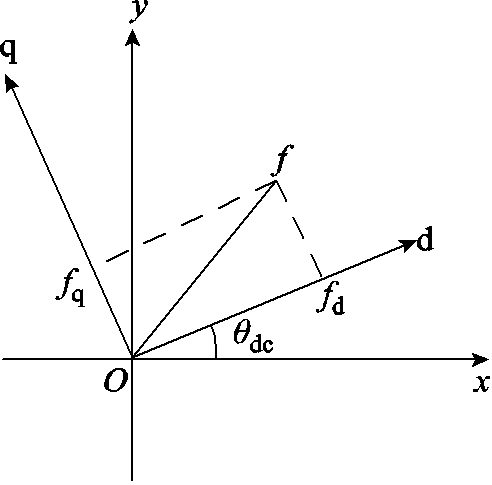
图2 dq坐标系和xy坐标系的映射关系
Fig.2 Relationship between dq and xy reference frames
根据构网型直驱风电场并网系统各模块间的对应关系,图3给出了系统内部各个状态空间模型子模块间的接口关系(图中深绿色部分为构网型风机匹配控制子模块及其状态空间模型表达式)。通过依次连接各个状态空间模型子模块的输入、输出变量,得到构网型直驱风电场并网系统的全阶数学模型。
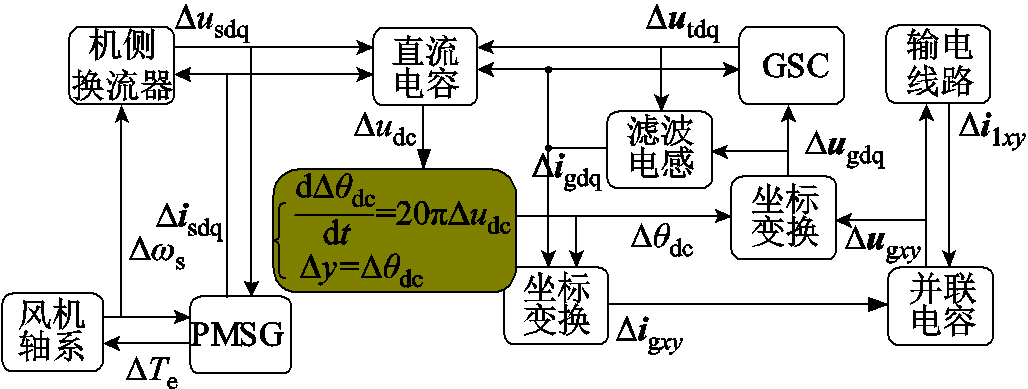
图3 构网型直驱风电场并网系统接口关系
Fig.3 The interface diagram of grid-forming direct-drive wind farm integrated to AC grid system
最后,利用Matlab中的“linmod”函数,可得到构网型直驱风电场并网系统的小信号模型为
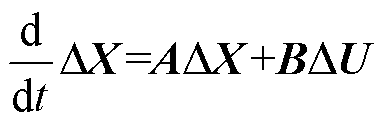 (6)
(6)
式中,X和U分别为系统的状态变量矩阵和输入变量矩阵;A和B分别为系统的状态系数矩阵和输入系数矩阵。其中,A矩阵为20阶;X共包含20个状态变量,即X= [igd igq ugx ugy θdc txy/dq xQ xg1 xg2 xg3 tdq/xy ilx ily udc isd isq ωs xs1 xs2 xs3]T,按照图3中的子模块划分,本文将X中的状态变量分成11个组,见表1;U共包含5个变量,即U=[ωsref isdref Qgref ugqref UN]T。
表1 构网型直驱风电场并网系统的状态变量
Tab.1 State variables of the grid-forming direct-drive wind farm integrated to AC grid system

模块状态变量编号 滤波电感igd, igq1, 2 并联电容ugx, ugy3, 4 匹配控制θdc5 xy/dq坐标变换txy/dq6 GSCxQ, xg1, xg2, xg37~10 dq/xy坐标变换tdq/xy11 输电线路ilx, ily12, 13 直流电容udc14 风机isd, isq15, 16 轴系ωs17 机侧换流器xs1, xs2, xs318~20
基于上述小信号模型,本节首先进行特征值分析以确定构网型直驱风电场的主要振荡模态;然后,比较分析构网型和跟网型两类直驱风电场分别并入弱电网时的系统SSO稳定性;最后,基于PSCAD/ EMTDC的电磁暂态模型仿真验证了特征值分析结果的准确性。
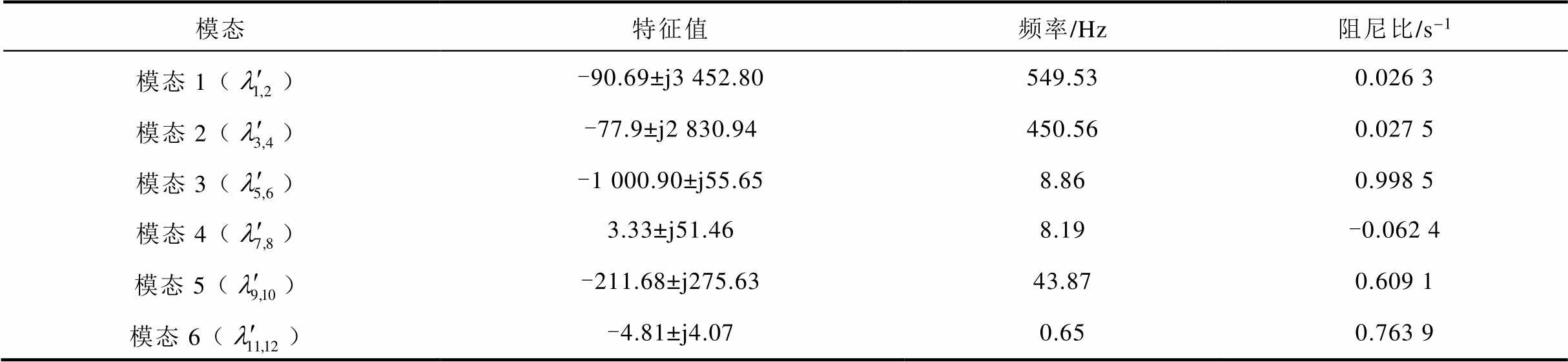
本节采用附表2中的典型控制参数,通过特征值法计算得到构网型直驱风电场并入强电网(SCR=40)时系统的振荡模式。表2列出了系统主要振荡模式的特征值、振荡频率及阻尼比。
表2 构网型直驱风电场并网系统振荡模式
Tab.2 Oscillation mode of grid-forming direct-drive wind farm integrated to AC grid system
模态特征值频率/Hz阻尼比/s-1 模态1()-90.69±j3 452.80549.530.026 3 模态2()-77.9±j2 830.94450.560.027 5 模态3()-1 000.90±j55.658.860.998 5 模态4()3.33±j51.468.19-0.062 4 模态5()-211.68±j275.6343.870.609 1 模态6()-4.81±j4.070.650.763 9
由表2可知,系统主要存在六种振荡模式,分别为两种中高频振荡模式(模态1和2)、三种SSO模式(模态3~5)和一种低频振荡模式(模态6)。由于模态1和2振荡频率较高,模态3对系统呈现较强阻尼,对系统稳定性影响较小。因此,本节将针对模态4~6展开相关研究,分析构网型直驱风电场的SSO特性。其中,模态5和模态6呈现正阻尼特性,模态4呈现负阻尼特性,构网型直驱风电场并入强电网时存在SSO的风险,可能影响电力系统的稳定运行。图4给出了模态4~6的归一化参与因子分析结果,图中各个状态变量编号的定义及所属模块与表1所示一致。
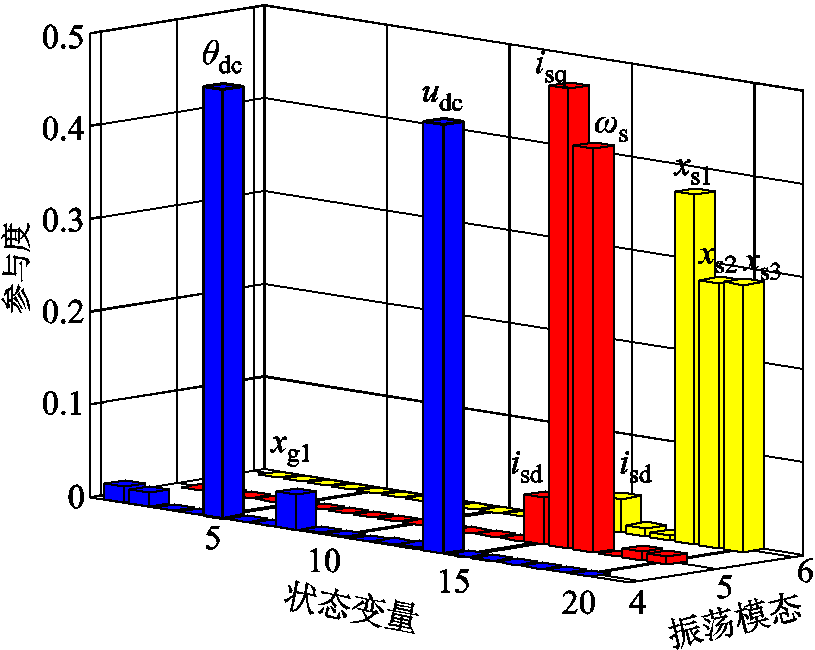
图4 模态4~6的参与因子分析结果
Fig.4 Results of participation factors analysis of modes 4~6
由图4可知,模态4的强相关状态变量为θdc、xg1和udc,其中θdc和udc主要与匹配控制和直流电容模块相关,因此,将模态4称作匹配控制振荡模态;模态5的强相关状态变量为isd、isq和ωs,其中isd和isq主要与风力发电机模块相关,ωs主要与风机轴系模块相关,因此,将模态5称作轴系-发电机振荡模态;模态6的强相关状态变量为xs1、xs2、xs3和isd,其中xs1、xs2、xs3主要与机侧换流器模块相关,因此,将模态6称作机侧换流器振荡模态。
为进一步研究交流电网强度对系统主要振荡模态的影响,本节分析了不同SCR时系统模态4~6的参与因子变化情况,其强相关状态变量参与度随SCR的变化曲线如图5所示。
由图5可得,随着SCR的增加,系统匹配控制振荡模态(模态4)强相关变量udc和θdc的参与度略微减小,强相关变量xg1的参与度略微增大;系统轴系-发电机振荡模态(模态5)和机侧换流器振荡模态(模态6)的强相关变量的参与度几乎没有变化。因此,基于匹配控制的构网型直驱风电场并入强交流电网时,其主要振荡模态的强相关变量基本不随SCR的增加而发生变化,能够根据图4中振荡模态强相关变量分析不同SCR对系统不稳定振荡模态阻尼特性的影响。
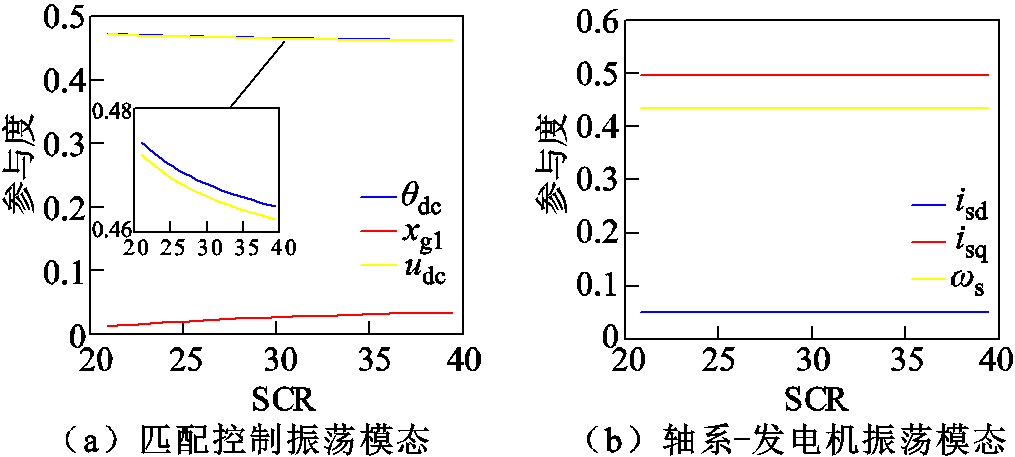
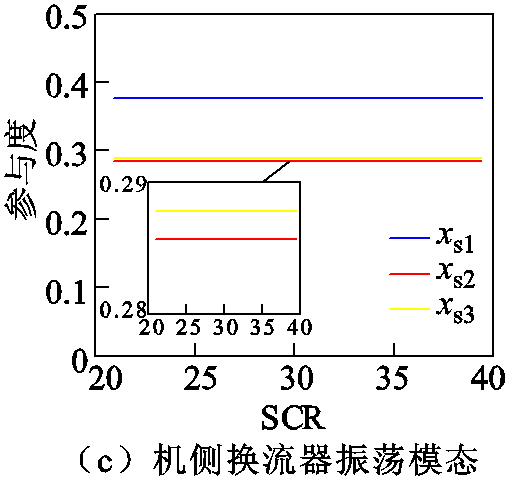
图5 强相关状态变量变化曲线(SCR变化)
Fig.5 Change curve of Strongly correlated state variable (SCR change)
综上所述,构网型直驱风电场并网系统稳定性主要受到匹配控制振荡模态阻尼特性的影响,且匹配控制振荡模态强相关变量基本不随SCR的增加而发生变化。并且,不同于传统跟网型直驱风电场,基于匹配控制的构网型直驱风电场并入强电网时,其匹配控制振荡模态呈现负阻尼特性,系统存在SSO的风险。
本节通过比较构网型和跟网型两类直驱风电场的振荡模态,分析了基于匹配控制的构网型直驱风电场并入弱电网时的SSO稳定性。
基于第2节的构网型和跟网型两类直驱风电场并网系统小信号模型,在相同拓扑结构下分别对两类直驱风电场并入弱电网系统(SCR=2)进行特征值分析。此时,其主要振荡模态见表3。
表3 直驱风电场并入弱交流电网特征值分析
Tab.3 Eigenvalue analysis of the direct-drive wind farm integrated to weakly AC grid system

风机类型模态特征值频率/Hz 构网型直驱风电场模态4()-34.28±j23.803.79 模态5()-211.68±j275.6343.87 模态6()-4.81±j4.070.65 跟网型直驱风电场模态1()4.60±j71.0411.34 模态2()-14.79±j48.807.77 模态3()-209.86±j277.0244.09 模态4()-4.82±j4.060.65
表3中,构网型直驱风电场各个振荡模态的定义与图4参与因子分析结果一致。限于篇幅,跟网型直驱风电场并网系统特征值的参与因子分析结果在附图2中给出。根据参与因子分析的结果,跟网型直驱风电场模态1~4分别被称为PLL振荡模态、直流电容振荡模态、轴系-发电机振荡模态和机侧换流器振荡模态。
由表3可知,构网型与跟网型直驱风电场都存在轴系-发电机振荡模态和机侧换流器振荡模态。并且它们的阻尼特性和振荡频率十分接近,均呈现正阻尼特性。然而,两类直驱风电场网侧相关振荡模态的阻尼特性存在较大差异。在弱电网工况下,虽然直流电容振荡模态呈现正阻尼特性,但由于PLL振荡模态呈现负阻尼特性,跟网型直驱风电场存在SSO风险;而构网型直驱风电场中相应的匹配控制振荡模态则呈现正阻尼特性,构网型直驱风电场并入弱电网系统不存在振荡失稳的问题。
综上所述,构网型直驱风电场主要改变了传统跟网型控制在弱电网工况下不稳定的直流电容和PLL振荡模态,其相应的匹配控制振荡模态具有更好的弱电网适应能力。相较于传统跟网型直驱风电场,具有“电压源”外特性的构网型直驱风电场能够在弱电网下稳定运行。
为进一步分析基于匹配控制的构网型直驱风电场并入弱交流电网时的稳定性,本节计算分析了不同风速(低于额定风速)时构网型直驱风电场的特征值。表4分别给出了风速为6、7和8 m/s时系统主要振荡模态的特征值。
表4 不同风速下系统的特征值分析结果
Tab.4 Eigenvalue analysis results of the system under different wind speeds

风速v/(m/s)模态4()模态5()模态6() 6-34.29±j23.79-113.69±j318.05-6.38±j2.98 7-34.28±j23.80-156.17±j306.48-5.56±j3.70 8-34.28±j23.80-211.68±j275.63-4.81±j4.07
由表4可得,随着风速的增加,构网型直驱风电场并入弱交流电网的匹配控制振荡模态(模态4)的特征值几乎无变化;轴系-发电机振荡模态(模态5)的特征值实部随着风速的增加而减小,机侧换流器振荡模态(模态6)则正好相反。并且,系统的主要振荡模态在不同风速下的特征值实部始终为负值,基于匹配控制的构网型直驱风电场并入弱交流电网系统在低于额定风速时能够稳定运行。
为验证上述理论分析结果,本文基于PSCAD/ EMTDC搭建构网型直驱风电场并网系统的电磁暂态仿真模型,并通过与匹配控制振荡模态强相关的直流电容电压udc波形来判断系统的阻尼特性。本节假设构网型直驱风电场初始风速为6 m/s,4 s时风速切换为7 m/s,6 s时切换为额定风速8 m/s,模拟不同工况对系统弱电网稳定性的影响。并且,在8 s时,改变输电线路阻抗(断路器BRK由关断切换为闭合状态),使系统SCR从2变为40,模拟构网型直驱风电场并入强交流电网。此时,构网型直驱风电场直流电容电压udc的波形及系统SSO频谱分析结果如图6所示。
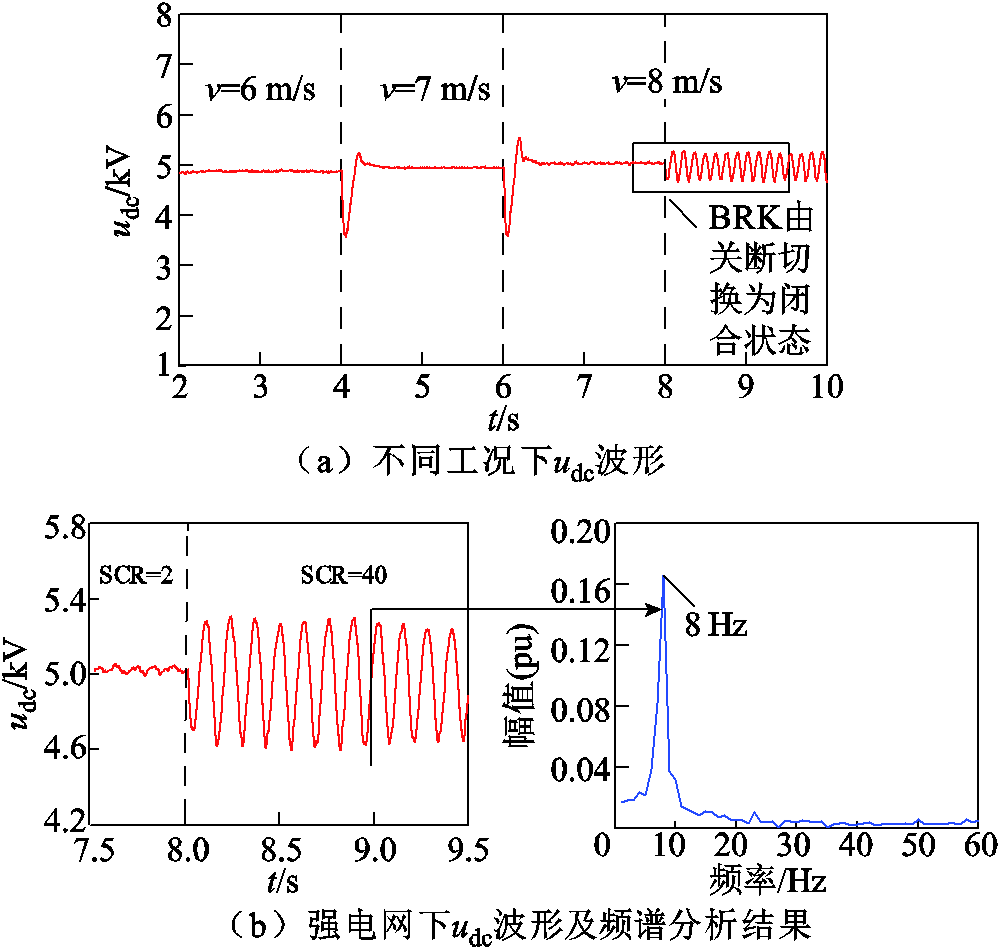
图6 直流电容电压udc波形及频谱分析结果
Fig.6 Waveforms and FFT analysis results of DC capacitor voltage udc
由图6可知,在低于额定风速时,构网型直驱风电场并入弱交流电网系统仍然能够稳定运行,与3.2节构网型直驱风电场弱电网稳定性分析结果一致。然而,当构网型直驱风电场并入强交流电网时,udc发生了振荡,与3.1节的特征值分析结果一致。并且,udc的振荡频率为8 Hz,与表2中匹配控制振荡模态的振荡频率(8.19 Hz)接近。因此,时域仿真结果验证了基于构网型直驱风电场并网系统小信号模型的特征值分析结果的准确性。
由第3节特征值分析得到,匹配控制振荡模态是构网型直驱风电场并网系统SSO的主导因素,但现有文献对基于匹配控制的构网型直驱风电场振荡机理的相关研究较少。
文献[12-13]指出直驱风电场GSC采用匹配控制时,直驱风电场对电网呈现出类似于同步发电机的“电压源”外特性。因此,本节将同步发电机中的阻尼转矩法推广到匹配控制振荡模态,借鉴同步发电机的振荡特性揭示构网型直驱风电场的振荡机理。
阻尼转矩法中同步机转子的线性化动态方程可表示为
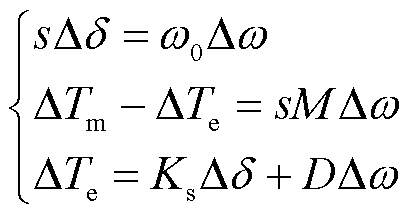 (7)
(7)
式中,Δδ和Δω分别为功角增量和角速度增量;M为转子惯性系数;ΔTm和ΔTe分别为机械转矩增量和电磁转矩增量;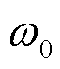 为同步角速度;Ks和D分别为同步系数和阻尼系数。其中,阻尼系数D反映系统振荡模态阻尼的大小,同步系数Ks则主要反映系统振荡频率。
为同步角速度;Ks和D分别为同步系数和阻尼系数。其中,阻尼系数D反映系统振荡模态阻尼的大小,同步系数Ks则主要反映系统振荡频率。
文献[21]在借鉴阻尼转矩法分析跟网型风机直流电容振荡模态时,将Δudc/s定义为假设的变量Δx,得到了类似于式(7)的同步机转子运动方程,揭示了直流电容振荡模态的阻尼成因。而本文构网型变流器的匹配控制策略将直流侧电容电压类比为同步发电机转速,即Δudc=Δω,满足Δudc/s=Δθdc。因此,参考文献[21]中直流电容振荡模态的动态方程,构网型直驱风电场匹配控制振荡模态同样存在类似于同步机转子运动方程的动态特性,表示为
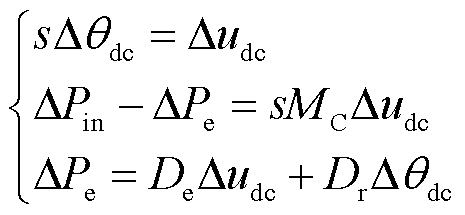 (8)
(8)
式中,MC为电容等效惯性系数,MC=Cdcudc0;De和Dr分别为匹配控制振荡模态相应的阻尼系数和同步系数。根据Δudc和Δθdc的相量关系,电磁功率ΔPe分解为阻尼分量ΔPd和同步分量ΔPr,得到相应的阻尼系数De和同步系数Dr,如图7所示。
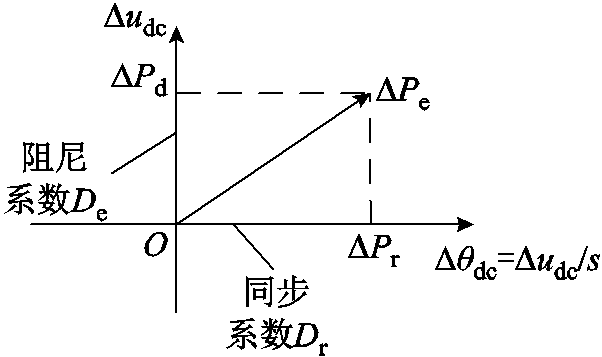
图7 阻尼系数和同步系数的相量图
Fig.7 Phasor diagram of damping coefficient and synchronization coefficient
根据式(7)和式(8),图8分别给出了同步机转子和构网型直驱风电场的动态方程框图。对比式(7)和式(8)可以看出,式(8)中匹配控制的动态变量udc、θdc、Pin和Pe可分别类比为式(7)中同步发电机的ω、δ、Tm和Te,式(8)中的电容惯性时间常数MC可类比为式(7)中转子惯性时间常数M,与文献[12]中匹配控制与同步发电机的“类比关系”分析结论基本一致。此时,基于匹配控制的构网型直驱风电场具有和同步机转子运动方程类似的表达式。因此,构网型直驱风电场在对电网呈现出同步发电机“电压源”外特性的同时,直流电容和匹配控制动态将导致系统存在类似于同步机转子的轴系振荡模态,即表2中特征值法分析得到的“匹配控制振荡模态”。并且,由图8b可得,匹配控制振荡模态主要是由直流电容和匹配控制共同作用导致的,与图4中匹配控制振荡模态的参与因子分析结果一致。
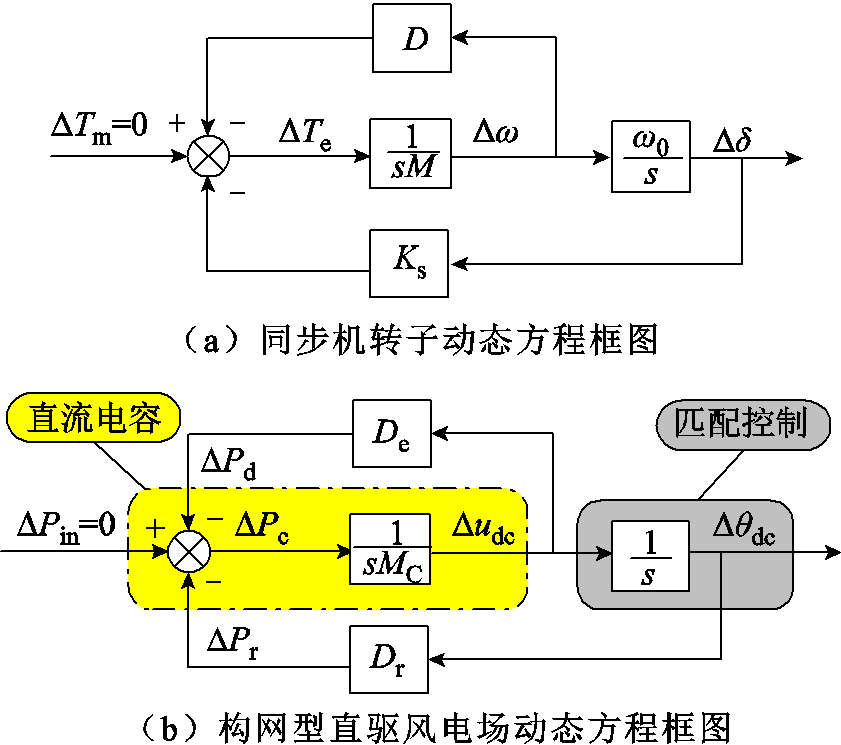
图8 阻尼转矩法动态特性分析及应用
Fig.8 Analysis and application of DTA dynamic characteristics
针对构网型直驱风电场中的匹配控制振荡模态,由式(8)可得,当直驱风电场有功功率ΔPin和ΔPe不平衡时,系统直流电容电压Δudc和输出相位Δθdc将偏离稳定工作点,并进一步影响有功功率ΔPe的动态,最终可能引起系统振荡。此时,参考传统阻尼转矩法中阻尼系数的物理意义,构网型直驱风电场并网系统由于阻尼系数De的作用,其匹配控制振荡模态将围绕直流电容和匹配控制形成正阻尼,抑制系统振荡[21]。然而,当阻尼系数De为负时,匹配控制振荡模态可能由于阻尼不足而呈现负阻尼特性,系统存在振荡失稳的风险。
依据上述机理分析结果,阻尼系数De能够作为构网型直驱风电场匹配控制振荡模态阻尼的量化评估指标,并通过相应振荡频率下的阻尼系数判断系统稳定性。图9给出了在不同SCR接入条件下,构网型直驱风电场并网系统阻尼系数De的频率特性曲线。
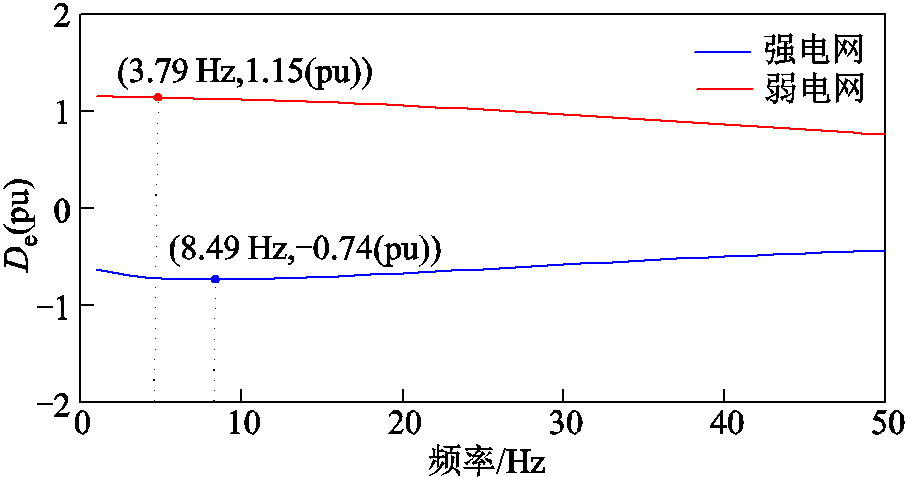
图9 阻尼系数De的频率特性曲线
Fig.9 Frequency characteristic curves of De
由图9可得,构网型直驱风电场并入强电网时,系统阻尼系数De在振荡频率8.49 Hz附近为负值(-0.74(pu)),系统存在SSO的风险;而构网型直驱风电场并入弱电网时,阻尼系数De在振荡频率3.79 Hz附近为正值(1.15(pu)),系统能够稳定运行。系统阻尼的量化评估结果与第3节基于特征值的匹配控制振荡模态阻尼特性分析结论一致,验证了本节构网型直驱风电场振荡机理分析的有效性。
针对不同影响因素对系统SSO特性的影响,本节根据第3节中的特征值分析结果,重点分析了交流电网强度、构网型直驱风机台数及其GSC无功控制外环对系统匹配控制振荡模态阻尼特性的影响。其中,发电机-轴系振荡模态与机侧换流器振荡模态对网侧参数变化不敏感,不是分析重点。
本节通过改变构网型直驱风电场并入强交流电网系统的输电线路阻抗,模拟不同交流电网强度的影响。当SCR以1为步长由20增加到40,系统其他参数与附录1保持一致时,系统匹配控制振荡模态的根轨迹如图10所示。箭头表示特征值随控制参数增加而变化的方向。
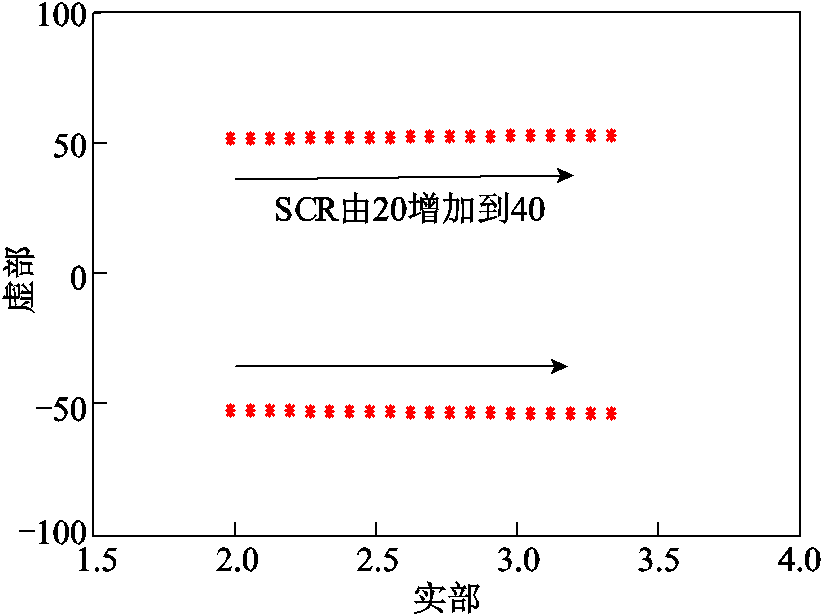
图10 SCR的影响(强交流电网)
Fig.10 Impact of SCR (strong AC grid)
由图10可知,在强电网工况下,随着SCR的增加,系统匹配控制振荡模态阻尼减小。此时,匹配控制振荡模态主导的构网型直驱风电场并网系统SSO风险将增加。
对上述分析进行时域仿真验证,在3.0 s时电网强度切换为不同SCR的强交流电网。图11给出了SCR分别为20、30和40时,构网型直驱风电场直流电容电压udc的时域仿真波形。
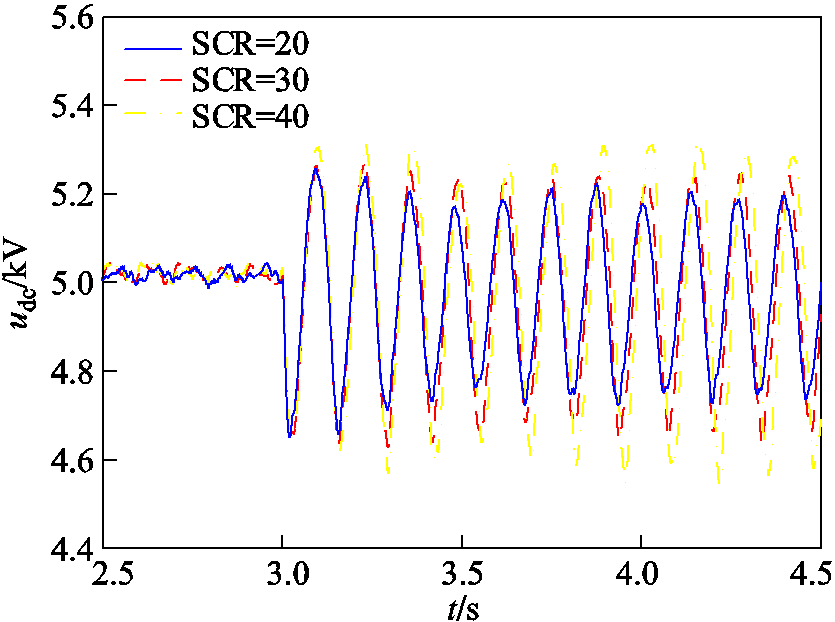
图11 直流电容电压udc波形(SCR变化)
Fig.11 Waveforms of udc (SCR changes)
由图11可得,在强电网工况下,随着SCR的增加,udc振幅逐渐增大,对应系统匹配控制振荡模态阻尼逐渐减小。时域仿真验证了理论分析结果的正确性。
当构网型直驱风机台数n以4为步长由1增加到81台,系统其他参数与附录1保持一致时,系统匹配控制振荡模态的根轨迹如图12所示。
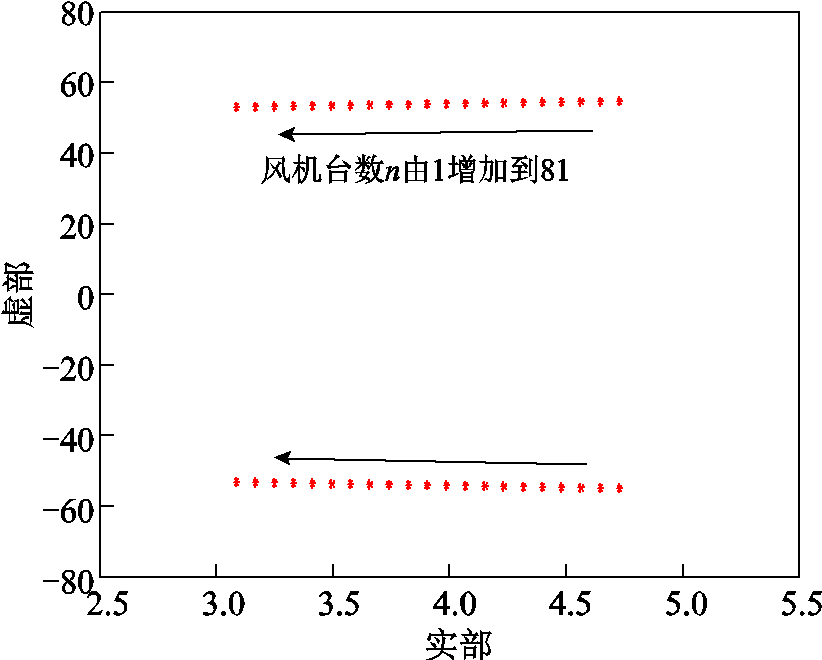
图12 风机台数的影响
Fig.12 Impact of number n of wind farm
由图12可知,在强电网工况下,随着构网型直驱风机台数的增加,系统匹配控制振荡模态阻尼增大。此时,匹配控制振荡模态主导的构网型直驱风电场并网系统SSO风险将降低。
对上述分析进行时域仿真验证,在3.0 s时电网强度切换为强交流电网,并改变构网型直驱风机台数n。图13给出了构网型直驱风机台数n分别为10、40和70时,构网型直驱风电场直流电容电压udc的时域仿真波形。
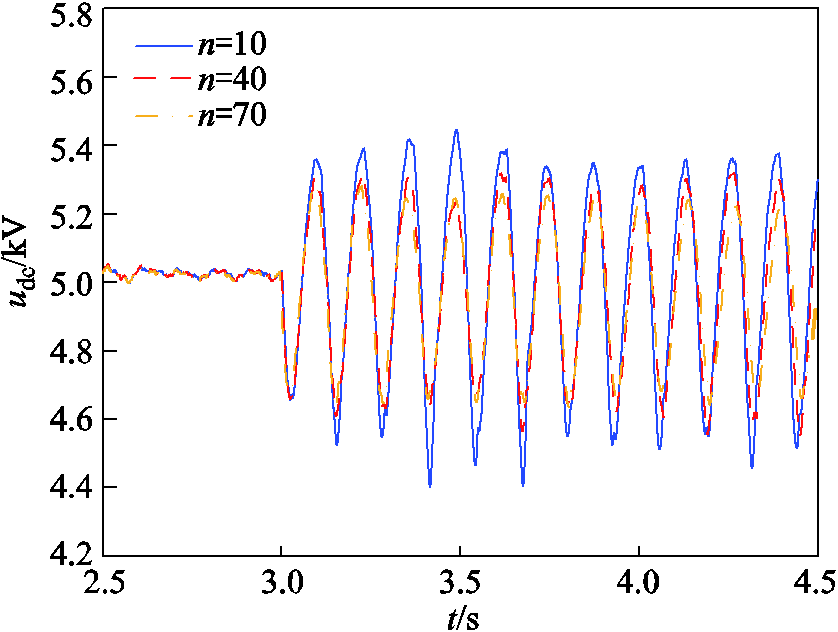
图13 直流电容电压udc波形(风电场台数n变化)
Fig.13 Waveforms of udc (number n of wind farm changes)
由图13可得,在强电网工况下,随着构网型直驱风机台数的增加,udc振幅逐渐减小,对应系统匹配控制振荡模态阻尼逐渐增大。值得注意的是,在构网型直驱风机台数较少时,系统在强电网下存在SSO的风险。时域仿真验证了理论分析结果的正确性,增加构网型直驱风电场中风机台数,能够降低构网型直驱风电场并入强电网时的SSO风险。
5.3.1 无功控制比例系数
当GSC的无功控制比例系数KpQ以0.02为步长由0.2增加到0.6,系统其他参数与附录1保持一致时,系统匹配控制振荡模态的根轨迹如图14所示。
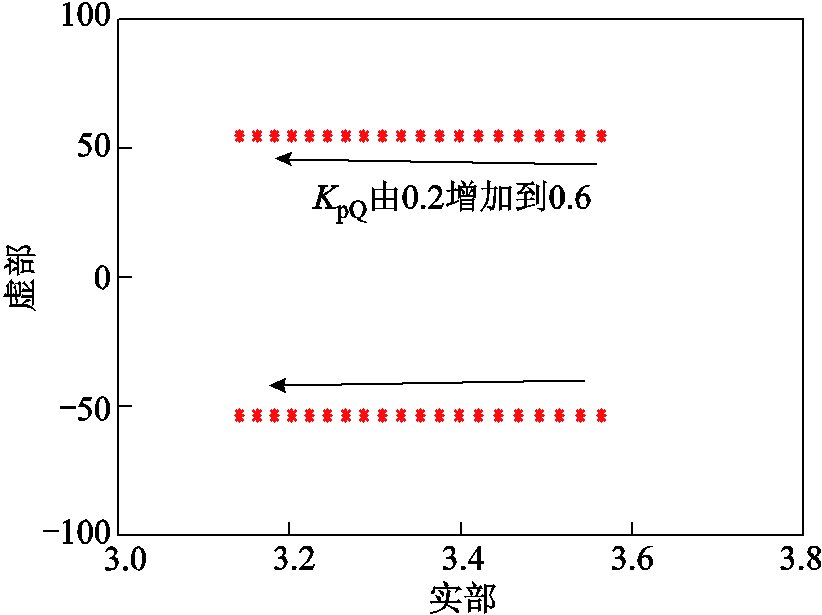
图14 无功控制比例系数KpQ的影响
Fig.14 Impact of proportional factor of reactive power control KpQ
由图14可知,随着无功控制比例系数KpQ的增加,系统匹配控制振荡模态阻尼增大。此时,匹配控制振荡模态主导的构网型直驱风电场并网系统SSO风险将降低。
对上述分析进行时域仿真验证,在3.0 s时电网强度切换为强交流电网,并改变无功控制比例系数KpQ。图15给出了无功控制比例系数KpQ分别为0.2、0.4和0.6时,构网型直驱风电场直流电容电压udc的时域仿真波形。
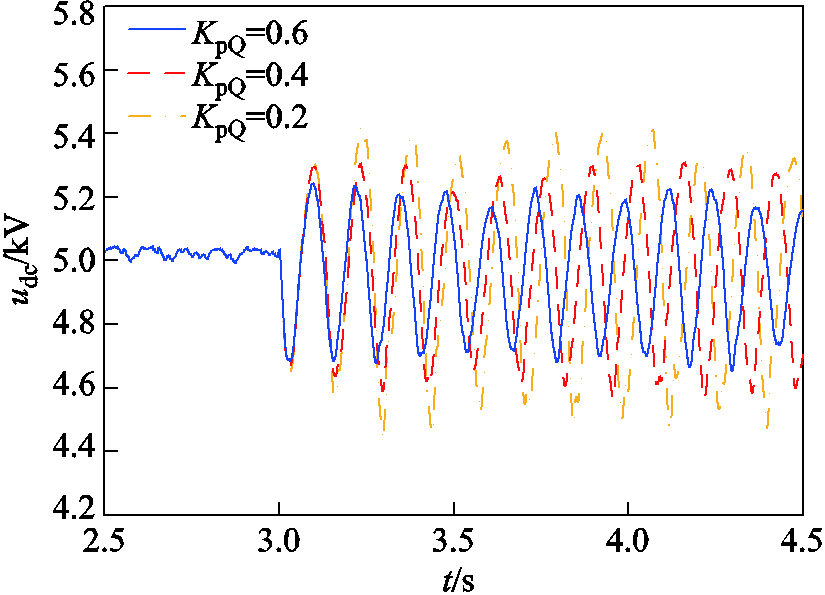
图15 直流电容电压udc波形(KpQ变化)
Fig.15 Waveforms of udc (KpQ changes)
由图15可得,随着无功控制比例系数KpQ的增加,udc振幅逐渐减小,对应系统匹配控制振荡模态阻尼逐渐增大。因此,时域仿真验证了理论分析结果的正确性,增加无功控制比例系数KpQ,能够降低构网型直驱风电场并入强电网时的SSO风险。
5.3.2 无功控制外环积分系数
当GSC的无功控制外环积分系数KiQ以2为步长由80增加到120,系统其他参数与附录1保持一致时,系统匹配控制振荡模态的根轨迹如图16所示。
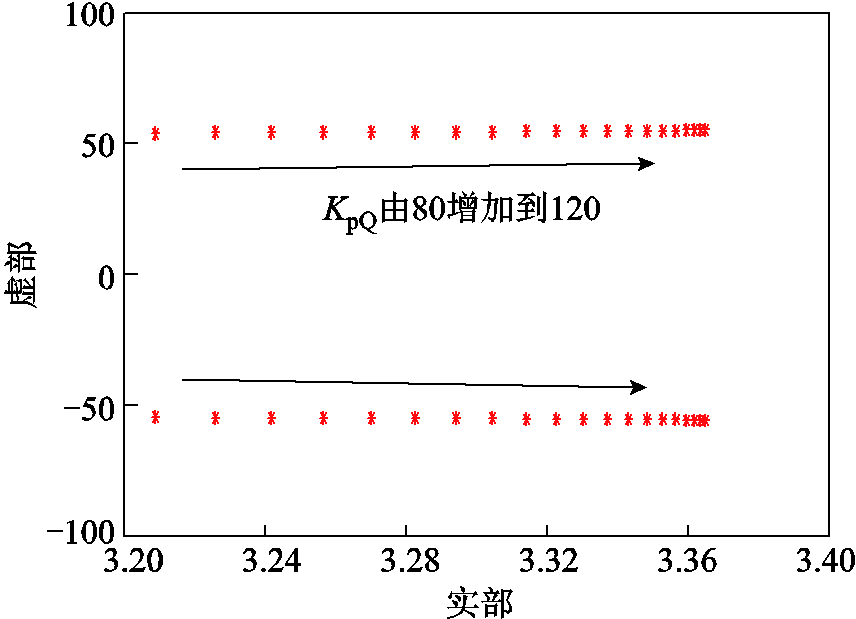
图16 无功控制积分系数KiQ的影响
Fig.16 Impact of integral factor of reactive power control KiQ
由图16可知,随着无功控制积分系数KiQ的增加,系统匹配控制振荡模态阻尼减小。此时,匹配控制振荡模态主导的构网型直驱风电场并网系统SSO风险将增加。
对上述分析进行时域仿真验证,在3.0 s时电网强度切换为强交流电网,并改变无功控制外环积分系数KiQ。图17给出了无功控制外环积分系数KiQ分别为80、100和120时,构网型直驱风电场直流电容电压udc的时域仿真波形。
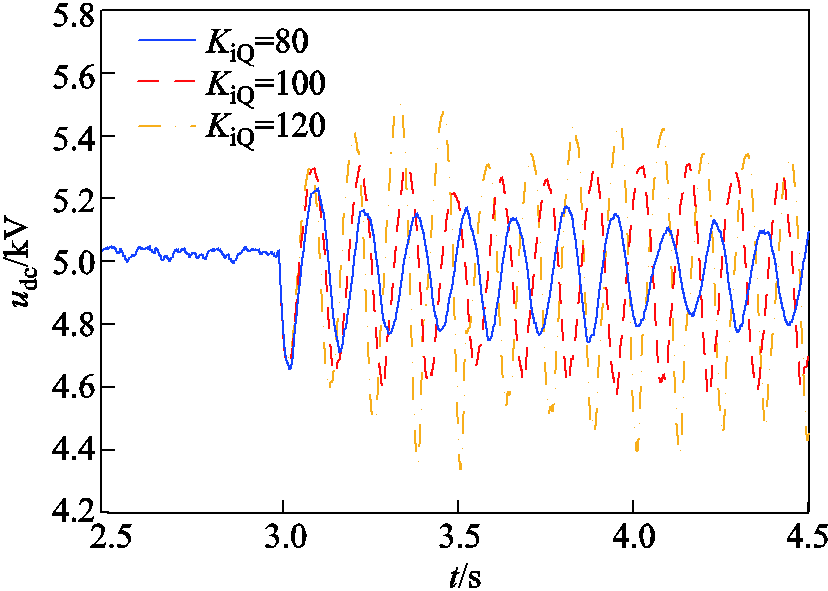
图17 直流电容电压udc波形(KiQ变化)
Fig.17 Waveforms of udc (KiQ changes)
由图17可得,随着无功控制积分系数KiQ的增加,udc振幅逐渐增大,对应系统匹配控制振荡模态的阻尼逐渐减小。因此,时域仿真验证了理论分析结果的正确性,减小无功控制积分系数KiQ,能够降低构网型直驱风电场并入强电网时的SSO风险。
本文采用模块化建模方法建立了构网型直驱风电场并网系统的小信号模型,通过特征值分析法研究了系统SSO特性,并借鉴阻尼转矩法分析了构网型直驱风电场的振荡机理。主要研究结论如下:
1)构网型直驱风电场并网系统的SSO稳定性主要受到匹配控制振荡模态阻尼的影响。在强电网工况下,匹配控制振荡模态呈现负阻尼特性,系统存在SSO的风险。
2)相较于跟网型直驱风电场中直流电容和PLL振荡模态,构网型直驱风电场并网系统中相应的匹配控制振荡模态具有更好的弱电网适应能力,系统能够在弱电网工况下稳定运行。
3)构网型直驱风电场直流电容和匹配控制共同作用时,其匹配控制振荡模态存在类似于同步机转子运动方程的动态特性,使得构网型直驱风电场并网系统可能由于阻尼不足而发生振荡失稳。
4)在一定范围内,通过减小交流电网强度或GSC的无功控制积分系数、增大构网型直驱风机台数或GSC的无功控制比例系数,可以增加匹配控制振荡模态的阻尼,提高构网型直驱风电场并网系统的SSO稳定性。
本文针对基于匹配控制的构网型直驱风电场SSO机理特性的研究结论,对于后续分析构网型新能源机组占比、提升电网惯量阻尼特性等相关研究有一定的参考价值。并且,为了使理论分析更接近工程实际,大型风电场内不同类型的构网型机组间交互作用对系统SSO阻尼特性的影响分析将是下一步的研究工作。
附 录
1. 系统参数
附表1 构网型直驱风电场并网系统的主要参数
App.Tab.1 Main parameters of grid-forming direct-drive wind farm integrated to AC grid system
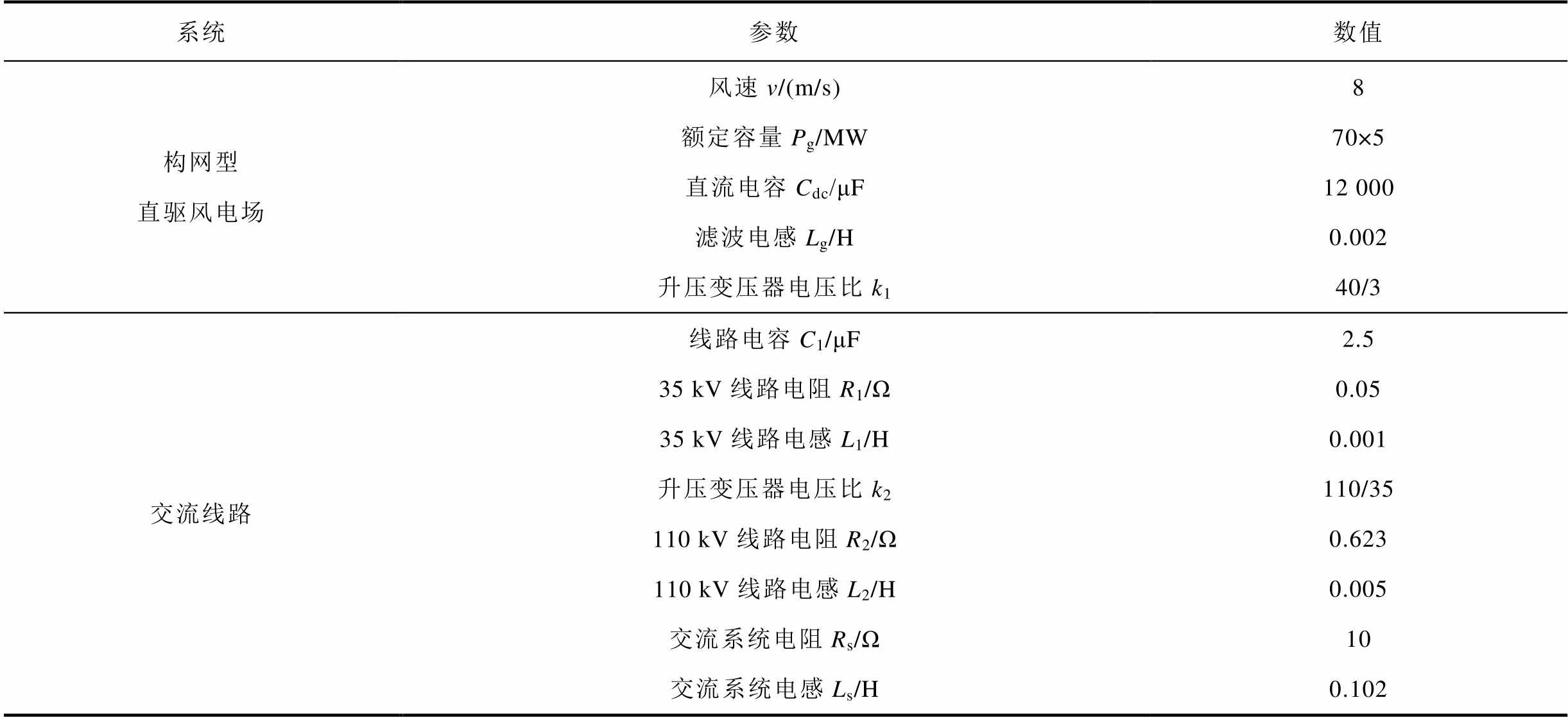
系统参数数值 构网型直驱风电场风速v/(m/s)8 额定容量Pg/MW70×5 直流电容Cdc/μF12 000 滤波电感Lg/H0.002 升压变压器电压比k140/3 交流线路线路电容C1/μF2.5 35 kV线路电阻R1/Ω0.05 35 kV线路电感L1/H0.001 升压变压器电压比k2110/35 110 kV线路电阻R2/Ω0.623 110 kV线路电感L2/H0.005 交流系统电阻Rs/Ω10 交流系统电感Ls/H0.102
附表2 控制器参数
App.Tab.2 Controller parameters

系统参数数值 构网型换流器无功外环比例系数KpQ0.4 无功外环积分系数KiQ10 电流内环比例系数KpI2 电流内环积分系数KiI6.67 虚拟阻抗Z/Ω3 直流电压udc/kV5 电网角速度ωn/(rad/s)100π 跟网型换流器直流电压外环比例系数Kpdc4 直流电压外环积分系数Kidc10 电流内环比例系数KpI2 电流内环积分系数KiI6.67 锁相环比例系数Kppll50 锁相环积分系数Kipll9 000
2. 构网型直驱风电场模块化建模
1)构网型直驱风电场并网系统数学模型
(1)轴系模型
直驱永磁同步发电机采用单质量块模型的轴系模型,其动态方程为

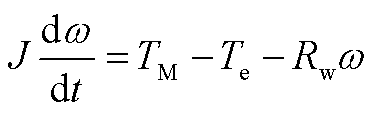 (A1)
(A1)
式中,J和Rw分别为系统的等效转动惯量和旋转阻力系数;ω为发电机转子角速度;TM、Te分别为机械转矩、电磁转矩。
(2)同步发电机模型
假设气隙磁场呈正弦均匀分布,且忽略涡流损耗和磁滞损耗,在dq坐标系下,发电机动态方程为
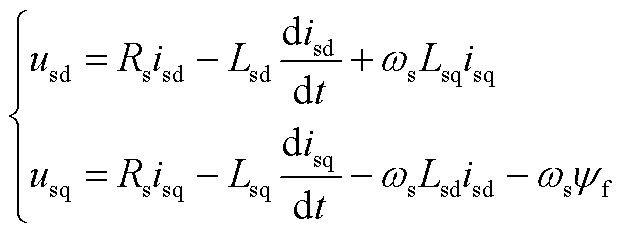 (A2)
(A2)
式中,ωs为电角速度;Rs为定子绕组电阻;Lsd、Lsq为定子d、q轴电感;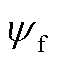 为定子磁链。
为定子磁链。
(3)机侧换流器模型
机侧换流器控制框图如附图1所示,其动态方程为
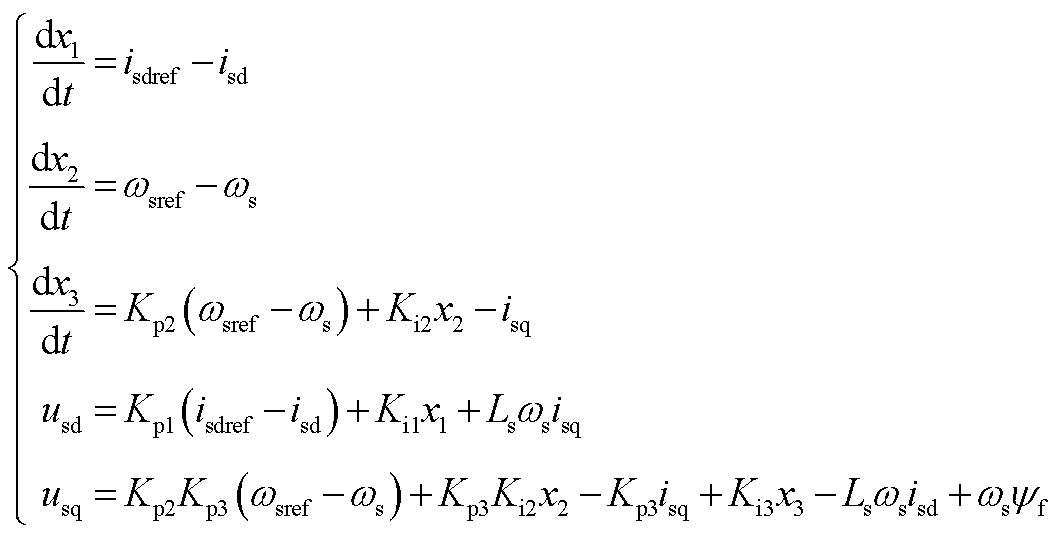
 (A3)
(A3)
式中,x1、x2和x3分别为机侧换流器的状态变量;is为发电机定子电流;Kp1、Ki1分别为机侧换流器d轴电流环控制器的PI参数;Kp2、Ki2分别为机侧换流器q轴转速外环控制器的PI参数;Kp3、Ki3分别为机侧换流器q轴电流内环控制器的PI参数。
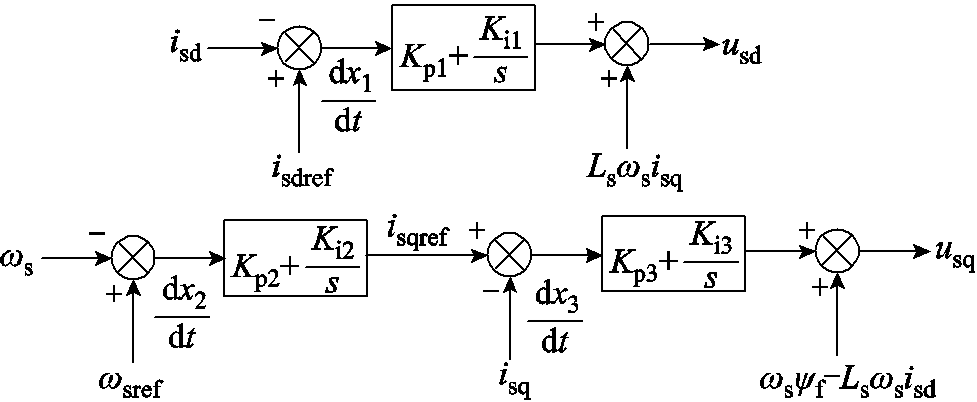
附图1 机侧换流器控制框图
App.Fig.1 Control block diagram of machine side converter
(4)直流电容模型
根据功率平衡方程,可得到直流电容的动态方程为
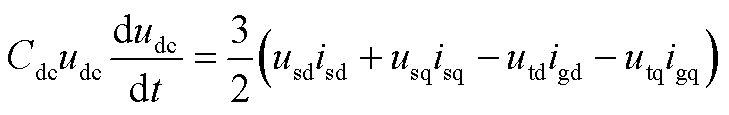 (A4)
(A4)
(5)构网型直驱风电场GSC和匹配控制的动态方程分别如式(2)和式(3)所示。
(6)输电线路
构网型直驱风电场输出电能依次通过滤波电感、并联电容和输电线路,其动态方程分别为
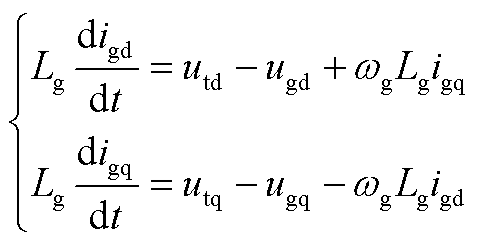 (A5)
(A5)
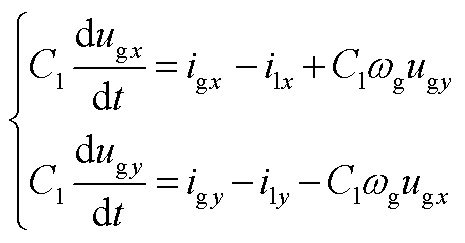 (A6)
(A6)
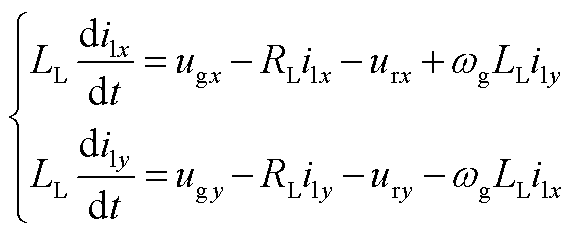 (A7)
(A7)
式中,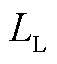 和
和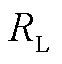 分别为交流输电线路等值电感和等值电阻。变量在dq坐标系和xy坐标系间的转换关系如式(5)所示。
分别为交流输电线路等值电感和等值电阻。变量在dq坐标系和xy坐标系间的转换关系如式(5)所示。
2)系统状态空间模型
由式(2)推导得到构网型直驱风电场GSC的状态空间模型,其相关系数矩阵为
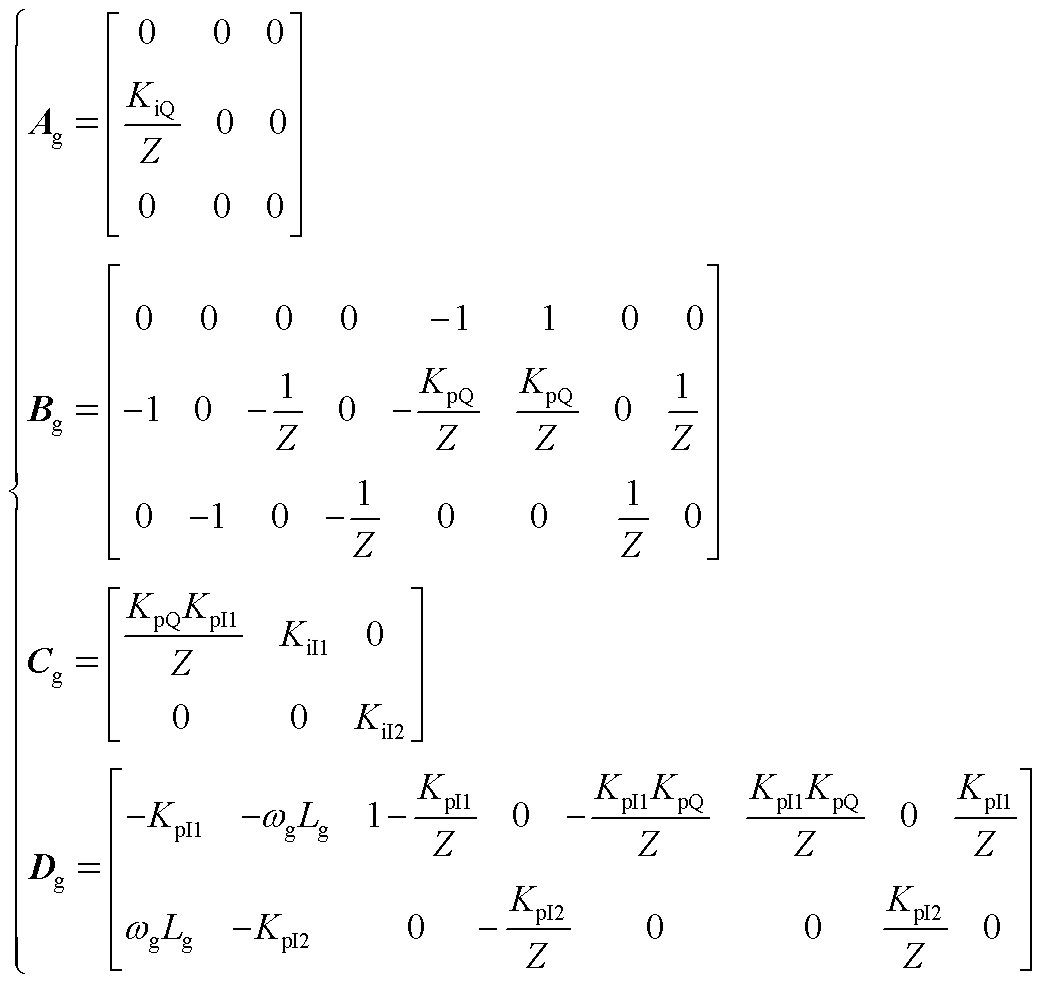 (A8)
(A8)
并且,GSC的状态变量矩阵为Xg=[xg1 xg2 xg3]T;输入变量矩阵为Ug=[igd igq ugd ugq Qg Qgref ugqref UN]T;输出变量矩阵为Yg=[utd utq]T。
由式(3)推导得到匹配控制模块的状态空间模型,其相关系数矩阵分别为App=[0]、Bpp=[20π]、Cpp=[1]、Dpp=[0]。并且,匹配控制模块的状态变量为Xpp=[θdc];输入变量为Upp=[udc];输出变量为Ypp=[θdc]。
3. 跟网型直驱风电场并网系统
跟网型直驱风电场的GSC参数见附表2。附图2给出了跟网型直驱风电场并入弱电网时系统主要振荡模式的参与因子分析结果。其中,系统状态变量及标号见附表3。
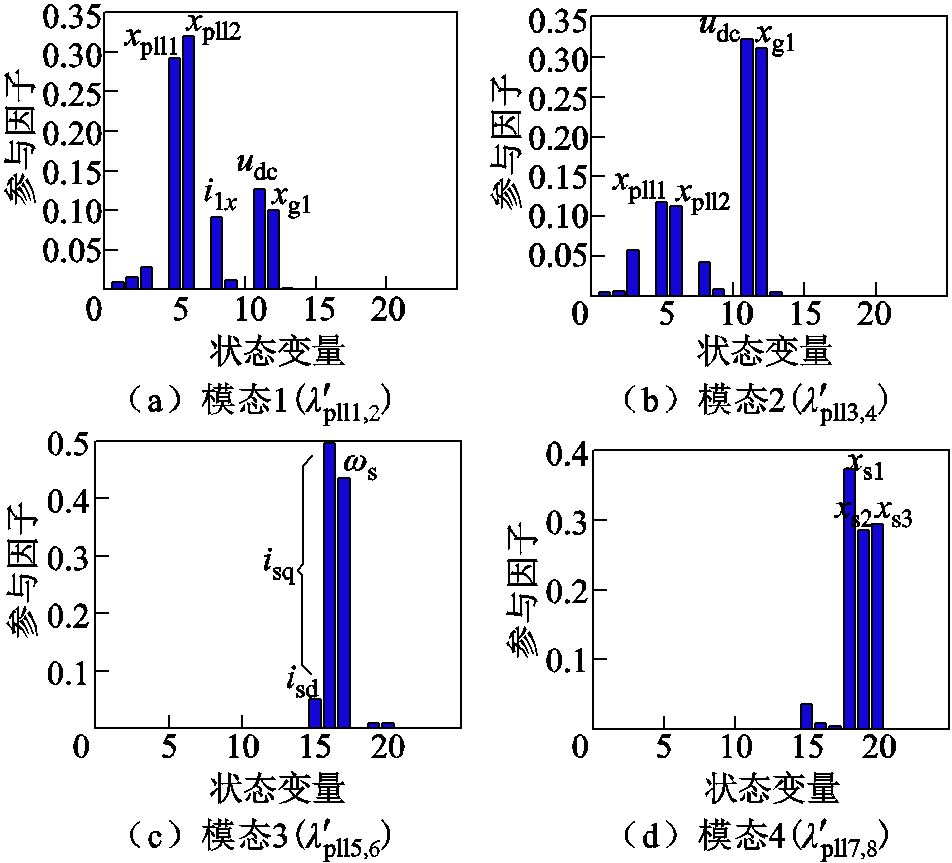
附图2 参与因子分析结果
App.Fig.2 Results of participation factors analysis
附表3 跟网型直驱风电场的状态变量
App.Tab.3 State variables of the grid-following direct-drive wind farm

模块状态变量编号 并联电容ugx, ugy1, 2 滤波电感igd, igq3, 4 PLLxpll1, xpll25, 6 xy/dq坐标变换txy/dq7 输电线路ilx, ily8, 9 dq/xy坐标变换tdq/xy10 直流电容udc11 GSCxg1, xg2, xg312~14 风机isd, isq15, 16 轴系ωs17 机侧换流器xs1, xs2, xs318~20
参考文献
[1] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191. Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[2] 杨明, 杨倬, 李玉龙, 等. 高渗透率下基于并网逆变器阻抗重塑的锁相环设计方法[J]. 电工技术学报, 2024, 39(2): 554-566. Yang Ming, Yang Zhuo, Li Yulong, et al. High permeability based on grid inverter phase-locked loop design method of impedance remodeling[J]. Transactions of China Electrotechnical Society, 2024, 33(2): 554-566.
[3] 董文凯, 杜文娟, 王海风. 弱连接条件下锁相环动态主导的并网直驱风电场小干扰稳定性研究[J]. 电工技术学报, 2021, 36(3): 609-622. Dong Wenkai, Du Wenjuan, Wang Haifeng. Small-signal stability of a grid-connected PMSG wind farm dominated by dynamics of PLLs under weak grid connection[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 609-622.
[4] Rosso R, Wang Xiongfei, Liserre M, et al. Grid-forming converters: control approaches, grid-synchronization, and future trends—a review[J]. IEEE Open Journal of Industry Applications, 2021, 2: 93-109.
[5] Popella H, Hennig T, Kaiser M, et al. Necessary development of inverter-based generation with grid forming capabilities in Germany[C]//20th International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Power Plants (WIW 2021), Hybrid Conference, Germany, 2021: 125-129.
[6] Roscoe A, Knueppel T, Da Silva R, et al. Response of a grid forming wind farm to system events, and the impact of external and internal damping[J]. IET Renewable Power Generation, 2020, 14(19): 3908-3917.
[7] 秦世耀, 齐琛, 李少林, 等. 电压源型构网风电机组研究现状及展望[J]. 中国电机工程学报, 2023, 43(4): 1314-1334. Qin Shiyao, Qi Chen, Li Shaolin, et al. Review of the voltage-source grid forming wind turbine[J]. Proceedings of the CSEE, 2023, 43(4): 1314-1334.
[8] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339-2359. Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2359.
[9] 薛翼程, 张哲任, 徐政, 等. 构网型变流器对交流系统低频振荡的影响分析与阻尼控制[J]. 电力系统自动化, 2023, 47(16): 103-113. Xue Yicheng, Zhang Zheren, Xu Zheng, et al. Impact analysis and damping control of grid-forming converter for low-frequency oscillation of AC system[J]. Automation of Electric Power Systems, 2023, 47(16): 103-113.
[10] 许诘翊, 刘威, 刘树, 等. 电力系统变流器构网控制技术的现状与发展趋势[J]. 电网技术, 2022, 46(9): 3586-3595. Xu Jieyi, Liu Wei, Liu Shu, et al. Current state and development trends of power system converter grid-forming control technology[J]. Power System Technology, 2022, 46(9): 3586-3595.
[11] Arghir C, Dörfler F. The electronic realization of synchronous machines: model matching, angle tracking, and energy shaping techniques[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4398-4410.
[12] 桑顺, 张琛, 蔡旭, 等. 全功率变换风电机组的电压源控制(一):控制架构与弱电网运行稳定性分析[J]. 中国电机工程学报, 2021, 41(16): 5604-5616. Sang Shun, Zhang Chen, Cai Xu, et al. Voltage source control of wind turbines with full-scale converters (part Ⅰ): control architecture and stability analysis under weak grid conditions[J]. Proceedings of the CSEE, 2021, 41(16): 5604-5616.
[13] 桑顺, 齐琛, 张新松, 等. 永磁直驱风电机组的构网型控制与黑启动[J]. 电网技术, 2022, 46(8): 3168-3180. Sang Shun, Qi Chen, Zhang Xinsong, et al. Grid-forming control and black start of PMSG-based direct-driven wind turbine[J]. Power System Technology, 2022, 46(8): 3168-3180.
[14] 张琛, 蔡旭, 李征. 具有自主电网同步与弱网稳定运行能力的双馈风电机组控制方法[J]. 中国电机工程学报, 2017, 37(2): 476-486. Zhang Chen, Cai Xu, Li Zheng. Control of DFIG-based wind turbines with the capability of automatic grid-synchronization and stable operation under weak grid condition[J]. Proceedings of the CSEE, 2017, 37(2): 476-486.
[15] 薛安成, 付潇宇, 乔登科, 等. 风电参与的电力系统次同步振荡机理研究综述和展望[J]. 电力自动化设备, 2020, 40(9): 118-128. Xue Ancheng, Fu Xiaoyu, Qiao Dengke, et al. Review and prospect of research on sub-synchronous oscillation mechanism for power system with wind power participation[J]. Electric Power Automation Equipment, 2020, 40(9): 118-128.
[16] 张天翼, 王海风. 风电并入弱交流系统引发次同步振荡的研究方法综述[J]. 电力系统保护与控制, 2021, 49(16): 177-187. Zhang Tianyi, Wang Haifeng. Research methods for subsynchronous oscillation induced by wind power under weak AC system: a review[J]. Power System Protection and Control, 2021, 49(16): 177-187.
[17] 刘其辉, 高瑜, 郭天飞, 等. 风电并网系统阻抗稳定性分析及次同步振荡因素研究[J]. 太阳能学报, 2022, 43(1): 89-100. Liu Qihui, Gao Yu, Guo Tianfei, et al. Research on impedance stability analysis and subsynchronous oscillation factors of wind power grid-connected system[J]. Acta Energiae Solaris Sinica, 2022, 43(1): 89-100.
[18] Li Gaoxiang, Chen Yandong, Luo An, et al. Analysis and mitigation of subsynchronous resonance in series-compensated grid-connected system controlled by a virtual synchronous generator[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 11096-11107.
[19] 韩应生, 孙海顺, 秦世耀, 等. 电压源型双馈风电并网系统小扰动低频稳定性分析[J]. 电工技术学报, 2023, 38(5): 1312-1324, 1374. Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low-frequency stability analysis of voltage-sourced doubly-fed wind power grid-connected system under small disturbance[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1312-1324, 1374.
[20] 刘志坚, 骆军, 梁宁, 等. 虚拟同步控制对风电并网系统次同步振荡阻尼影响分析[J]. 电力系统自动化, 2023, 47(1): 135-142. Liu Zhijian, Luo Jun, Liang Ning, et al. Analysis of influence of virtual synchronous control on subsynchronous oscillation damping for grid-connected wind power system[J]. Automation of Electric Power Systems, 2023, 47(1): 135-142.
[21] 高本锋, 刘毅, 李蕴红, 等. 直驱风电场与LCC-HVDC次同步交互作用的扰动传递路径及阻尼特性分析[J]. 中国电机工程学报, 2021, 41(5): 1713-1729. Gao Benfeng, Liu Yi, Li Yunhong, et al. Analysis on disturbance transfer path and damping characteristics of sub-synchronous interaction between D-PMSG-based wind farm and LCC-HVDC[J]. Proceedings of the CSEE, 2021, 41(5): 1713-1729.
[22] 高本锋, 王义, 曾四鸣, 等. 直驱风电场并入弱交流电网的次同步分量通路及阻尼特性分析[J]. 中国电机工程学报, 2022, 42(14): 5089-5103. Gao Benfeng, Wang Yi, Zeng Siming, et al. Analysis of sub-synchronous component path and damping characteristics of D-PMSG-based wind farm incorporated into weak AC grid[J]. Proceedings of the CSEE, 2022, 42(14): 5089-5103.
[23] 李龙源, 付瑞清, 吕晓琴, 等. 接入弱电网的同型机直驱风电场单机等值建模[J]. 电工技术学报, 2023, 38(3): 712-725. Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 712-725.
[24] 董文凯, 任必兴, 王海风, 等. 适用于系统次同步振荡分析的风电场等值建模方法综述[J]. 电力工程技术, 2022, 41(4): 33-43. Dong Wenkai, Ren Bixing, Wang Haifeng, et al. Small-signal equivalent modeling methods of the wind farm and its application in sub-synchronous oscillations analysis of gird-connected wind power systems[J]. Electric Power Engineering Technology, 2022, 41(4): 33-43.
[25] 赵书强, 李忍, 高本锋, 等. 适用于多源系统次同步振荡分析的图形化建模方法[J]. 电工技术学报, 2017, 32(14): 184-193, 228. Zhao Shuqiang, Li Ren, Gao Benfeng, et al. A graphical modeling method applied for multi-sources system subsynchronous oscillation analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 184-193, 228.
[26] 高本锋, 崔意婵, 邵冰冰, 等. 直驱风电机组全运行区域的次同步振荡特性分析[J]. 电力建设, 2020, 41(2): 85-93. Gao Benfeng, Cui Yichan, Shao Bingbing, et al. Sub-synchronous oscillation characteristics of direct-drive PMSG under all operation regions when wind farms connected to weak AC system[J]. Electric Power Construction, 2020, 41(2): 85-93.
Abstract When new energy, mainly wind power and photovoltaic, is connected to the AC grid through power electronic converters on a large scale, the power system is prone to form a weak AC grid environment, which brings severe challenges to the stable operation of traditional grid-following new energy units. Therefore, grid-forming new energy units with better adaptability to weak AC grid have become the forefront and hot spot of research at home and abroad in recent years, and a variety of grid-forming control strategies have been proposed, such as sagging control, virtual synchronous generator control and matching control. Compared with other grid-forming control strategies, matching control only needs to measure the DC voltage to realize the autonomous synchronization function and has a faster response speed, which has been widely used in new energy units, especially direct-driven wind turbines. However, at present, relevant studies of grid-forming new energy units based on matching control mainly focus on the supporting capacity and inertia response characteristics of AC grid, and its subsynchronous oscillation (SSO) stability under different AC grid strength is not clear.
In order to solve the above problems, this paper firstly establishes the small signal model of grid-forming direct drive wind farm (DDWF) integrated to AC grid system based on the modular modeling method. Secondly, the eigenvalue analysis method is used to analyze the main oscillation modes and participating factors of the grid-forming DDWF, and to analyze its stability in the weak AC grid compared with the traditional grid-following DDWF. Then, the damping torque method in synchronous generator is used to analyze the oscillation mechanism of the grid-forming DDWF based on matching control. Finally, the influence of AC grid strength, the number of direct drive fans and reactive power controller PI parameter on SSO mode damping characteristics of the grid-forming DDWF integrated to AC grid system is studied by eigenvalue root locus.
Based on the eigenvalue analysis, it is concluded that the SSO stability of the grid-forming DDWF integrated to AC grid system is mainly affected by the oscillation mode dominated by matching control. Under strong AC grid condition, the oscillation mode dominated by matching control presents negative damping characteristic, and the system has SSO risk. However, compared with the DC capacitance and phase-locked loop (PLL) oscillation modes in the grid-following DDWF, the oscillation mode dominated by matching control in the grid-forming DDWF have better adaptability to the weak AC grid. In addition, when the DC capacitance and the matching control act together, the oscillation mode dominated by matching control has a dynamic characteristic similar to the rotor motion equation of the synchronous machine, which makes the grid-forming DDWF may be unstable due to insufficient damping.
The following conclusions can be drawn from the simulation and experiment analysis: (1) The oscillation mode dominated by matching control in the grid-forming DDWF presents negative damping characteristics under the strong AC grid, and the risk of SSO exists in the grid-forming DDWF integrated to AC grid system. However, the oscillation mode dominated by matching control has better adaptability to weak AC grid, and the grid-forming DDWF can run stably under the weak AC grid. (2) The oscillation mode dominated by matching control has a dynamic characteristic similar to the rotor motion equation of synchronous machine, which makes the grid-forming DDWF may have weakly damping oscillation. (3) Reducing the AC grid strength or the integral coefficient of reactive power controller, increasing the number of direct drive fans or the proportional coefficient of reactive power controller, can increase the damping of the oscillation mode dominated by matching control and reduce the SSO risk of the grid-forming DDWF.
keywords:Matching control, grid-forming direct drive wind farm, subsynchronous oscillation, eigenvalue analysis
DOI: 10.19595/j.cnki.1000-6753.tces.230329
中图分类号:TM712
国家重点研发计划资助项目(2021YFB2400800)。
收稿日期 2023-03-21
改稿日期 2023-05-22
高本锋 男,1981年生,副教授,研究方向为高压直流输电和电力系统次同步振荡。E-mail:gaobenfeng@126.com
邓鹏程 男,1998年生,硕士研究生,研究方向为新能源并网系统次同步振荡分析。E-mail:1533202670@qq.com(通信作者)
(编辑 李 冰)