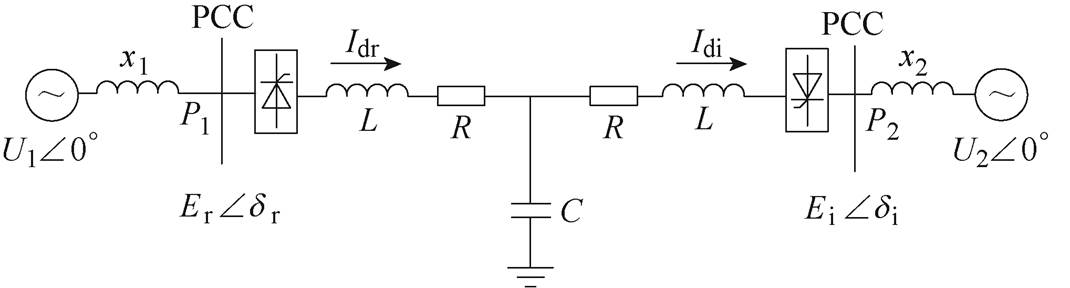
图1 双端直流输电系统单线图
Fig.1 Single line diagram of double end DC transmission system
摘要 高压直流输电系统送、受端存在电气耦合及两端的控制配合,因此,送端振荡可通过系统控制逻辑、电气量及控制量变化等影响受端系统的运行状态,增加了受端换相失败的风险。现有工作主要研究了送端大扰动引发受端换相失败的现象与机理,通过对标准直流系统进行小信号分析,发现直流系统中存在低频频段的固有振荡频率,一旦交流系统发生相近频段的振荡,将可能诱发直流系统共振。在此基础上,首先分析共振引起系统电气量以及控制量的波动对换相失败的影响,通过HVDC的准稳态方程分析共振后直流电流上升导致关断角下降,进而引发首次换相失败的机理;然后从两端的控制系统出发,研究逆变侧控制切换引发后续换相失败的机理;最后对CIGRE直流输电标准测试系统进行验证,并结合换相失败发生机理对换相失败的抑制策略进行了初步讨论。
关键词:高压直流输电 送端振荡 受端换相失败 机理分析
高压直流输电(High Voltage Direct Current, HVDC)因其输电距离远、输送容量大、输电损耗小等优点已被广泛运用于远距离输电及非同步联网领域[1-5]。换相失败(Commutation Failure, CF)是直流输电系统最常见的故障之一,发生换相失败会导致直流电流骤增、直流电压骤降,严重时甚至会造成直流闭锁,对电网的安全稳定运行造成严重冲击[6-8]。一般认为,换相失败是由受端(逆变侧)交流系统故障引发的瞬时电压降、过零点偏移或电压失真导致的,对受端交流故障引起换相失败机理的研究已相对成熟[9-13]。
由于直流送、受端存在电气及控制耦合,送端(整流侧)系统遭受扰动后有可能导致受端电气量响应变化以及控制切换,进而引发换相失败,近年来逐渐引起了研究者的关注。文献[14]考虑了送端交流系统故障对换相失败的影响,研究了送端交流系统故障后恢复过程中受端发生换相失败的现象和产生原因,结果表明,故障恢复过程中逆变器电流偏差控制的不良激活是产生换相失败的直接原因,但未能阐明故障恢复过程中逆变侧控制响应过程及电流偏差控制启动的原因,无法指导换相失败控制策略的制定。文献[15]在文献[14]的基础上进一步研究了严重程度不同的送端故障对换相失败的影响特性,将送端故障分为轻微故障(三相非金属性故障)和严重故障(三相金属性故障),指出轻微故障下换相失败是由于故障清除后直流脉冲电流和整流侧采用最小触发角控制策略;严重故障下,恢复过程中逆变侧控制的切换亦增大了换相失败的风险,因而控制器的交互作用是换相失败的主要原因。文献[16]曾指出,逆变侧系统的控制交互不当是影响换相失败的主要因素之一。文献[17]由此分析整流侧交流系统发生严重故障与轻微故障时系统受故障影响的动态行为传递至逆变侧的过程及其与逆变侧控制交互的影响规律,发现严重故障时受端的控制切换以及受端换流器无功消耗过多,导致其换流母线电压跌落是造成换相失败的主要原因。并进一步在送端交流系统无功不平衡状态下,详细剖析了送端交流系统故障对换相失败风险大小的影响,分析指出送端交流系统无功补偿不足会减小换相失败概率,而无功补偿过剩将增加换相失败概率。
文献[18]从受端大扰动下电压不同跌落程度的角度来展开研究。针对送端换流母线电压恢复导致逆变器关断角减小的问题,分析了整流侧换流母线电压跌落程度不同时整流器及逆变器所采用的控制方式,推导了电压跌落程度不同时的关断角表达式。基于表达式分析得出整流侧换流母线电压跌落越大,则电压恢复瞬间关断角越小,严重时会发生换相失败的结论。在文献[18]的基础上,文献[19]分析了电压恢复期间逆变侧控制系统的控制特性,发现由定电流控制切换为定关断角控制瞬间及之后一段时间内,直流电流较大且增速过快引起电流偏差控制输出较小且快速降低是诱发换相失败的原因。综上所述,现有研究主要分析了送端交流系统大扰动对受端电气量和控制系统的影响特性,对送端系统故障引发受端换相失败机理有了初步认识。
近年来随着“双碳”目标的提出,沙漠、戈壁、荒漠地区建设大型风电、光伏发电基地是落实“双碳”目标的重要举措,大型新能源基地经HVDC系统送出是其规模化开发的主要模式。然而,新能源送端系统附近无常规机组支撑,新能源电源主导下设备间多时间尺度耦合作用增强,易引发新能源送端系统的振荡问题。研究中发现,振荡不仅会增加送端系统的运行风险,振荡传递到受端也会引发受端换相失败,现有研究无法解释此类换相失败发生的原因。因此,本文首次提出并研究了HVDC送端系统振荡导致受端换相失败的现象,为沙戈荒地区大型新能源基地与送出HVDC系统的设计和运行提供参考。
本文首先通过仿真算例介绍了送端振荡引发受端换相失败的实例和具体发展过程;然后对直流系统进行小信号分析,研究直流系统的固有频率及主导动态;在此基础上,结合直流系统准稳态模型,分阶段分析送端振荡传递至逆变侧的过程及其与逆变侧控制的交互影响规律,结果表明,送端振荡与控制系统共振导致电气量和控制量异常与控制切换是受端系统换相失败发生的根本原因;最后通过PSCAD/EMTDC全电磁暂态仿真验证了送端振荡导致受端换相失败现象与机理分析的正确性,并依据换相失败产生的原因提出换相失败的预防控制策略。本文的主要贡献总结如下:
1)基于HVDC的准稳态模型,推导了直流电流和送端直流电压关于送端换相电压的关系、受端直流电压关于送端直流电压的关系,分析了受端电气量及控制量与送端振荡耦合后的动态行为。
2)研究了送端振荡与受端控制的交互影响规律,分析了直流系统控制策略及参数对换相失败的影响特性,揭示了送端振荡与控制系统共振进而引发受端换相失败的机理。
为了说明送端振荡对受端换相失败的影响,本文通过图1所示的CIGRE HVDC标准测试模型进行演示,由送端交流电源、受端交流电源、整流器、逆变器及直流输电线路构成。CIGRE HVDC标准测试模型采用的控制器属于极控级[15]。其整流侧通常有定电流控制与定最小触发角控制,逆变侧通常有定电流(Constant Current, CC)控制、定关断角(Constant Extinction Angle, CEA)控制、低压限流环节(Voltage Dependent Current Order Limiter, VDCOL)、电流偏差控制(Current Error Controller, CEC),其中CEC可实现CEA与CC的平滑切换。

图1 双端直流输电系统单线图
Fig.1 Single line diagram of double end DC transmission system
通过在送端交流母线加入不同频率、幅值较低的三相电压源模拟送端系统发生振荡扰动。结果发现注入1.2 Hz左右的振荡源时,系统电气量及控制量变化较为明显,且伴随受端换相失败的出现,其仿真结果如图2所示。
从图2中的仿真波形可以看到,向系统注入1.2 Hz的振荡后,系统电气量和控制量的变化大致可以分为四个阶段:
(1)阶段1,系统仍处于稳定状态,电压、电流等电气量以及触发角、关断角等控制量几乎保持不变。
(2)阶段2,大约0.2 s以后系统开始振荡,电气量及控制量开始产生细微变化。
(3)阶段3,电气量及控制量的变化幅度显著增大,具体表现为直流电流开始上升,逆变侧换流母线电压逐渐降低,有功功率也进入大幅度振荡状态。同时,整流侧触发角有下降到最小触发角的趋势,CEA控制输出值上升,CC控制输出值不变,最终随着直流电流上升到较大值的时候,系统发生第一次换相失败。首次换相失败后,CEA控制输出值开始下降,CC控制输出值上升,逆变侧控制开始发生切换。
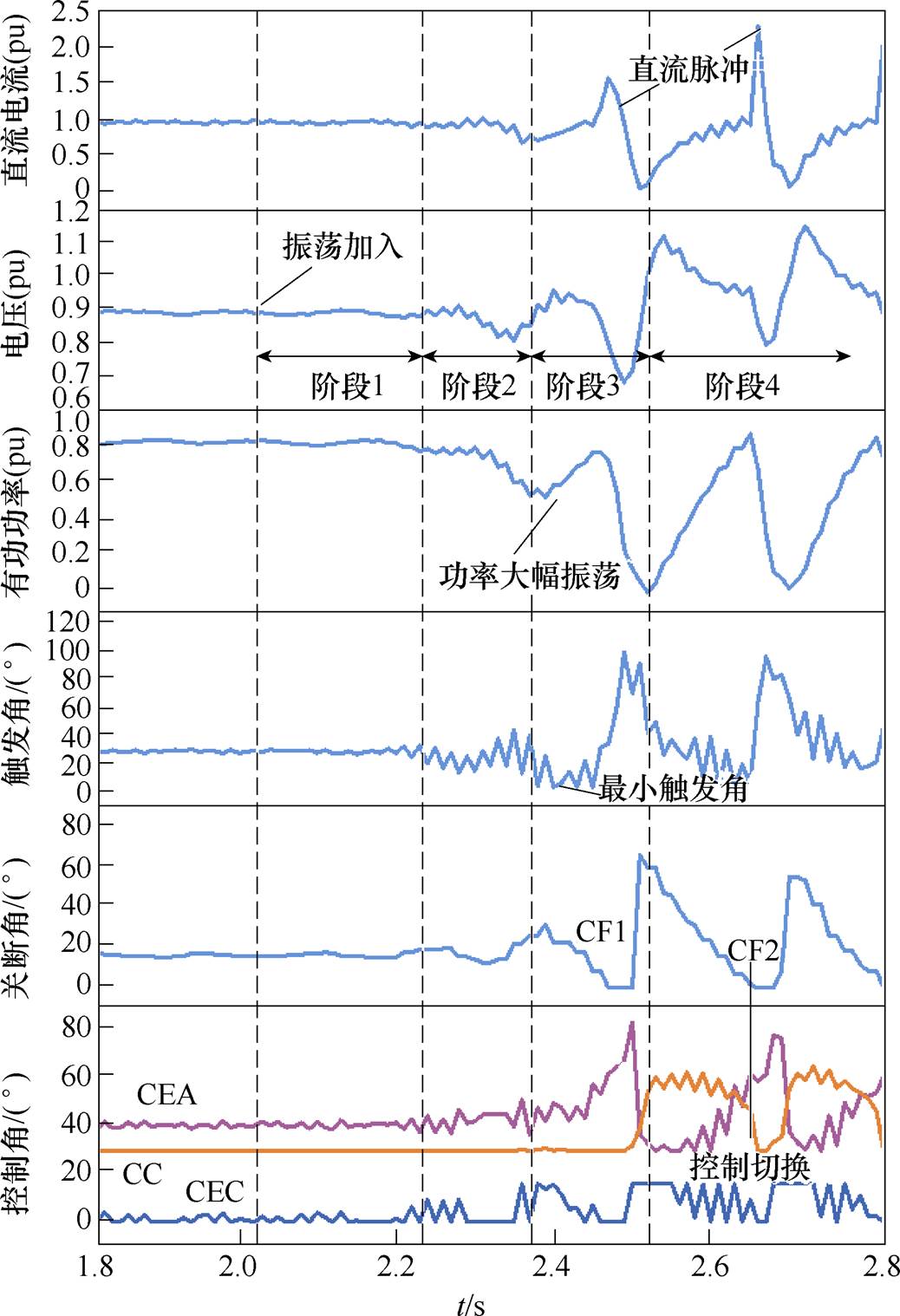
图2 换相失败发展波形
Fig.2 Waveforms of commutation failure
(4)阶段4,系统各量持续保持振荡状态,重复阶段3的过程,在CEA控制与CC控制的下一次切换时,发生后续换相失败。
仿真中展示的换相失败现象表明,当送端系统发生振荡时,送、受端电气量的耦合会对受端控制量产生影响,从而导致系统电气量及控制量出现大幅度振荡,最终引发受端系统的换相失败。换相失败将会危害直流输电系统和受端交流系统的稳定性,因此有必要对其进行深入分析。
图1中,r和i分别代表整流侧和逆变侧,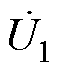 及
及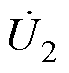 分别为送端和受端的交流电源,
分别为送端和受端的交流电源,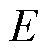 、
、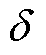 分别为换相线电压和相位,
分别为换相线电压和相位,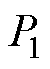 及
及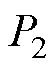 分别为整流侧和逆变侧的有功功率,
分别为整流侧和逆变侧的有功功率,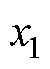 、
、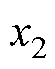 分别为送端和受端的交流线路电抗,
分别为送端和受端的交流线路电抗,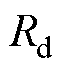 、
、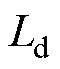 分别为直流线路两端电阻、电抗,
分别为直流线路两端电阻、电抗,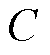 为直流线路中端电容,
为直流线路中端电容,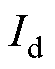 为直流电流。为便于解析分析,忽略直流线路的分布电容及电感的影响,
为直流电流。为便于解析分析,忽略直流线路的分布电容及电感的影响,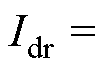
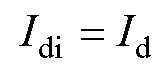 ,则HVDC准稳态模型的方程为
,则HVDC准稳态模型的方程为
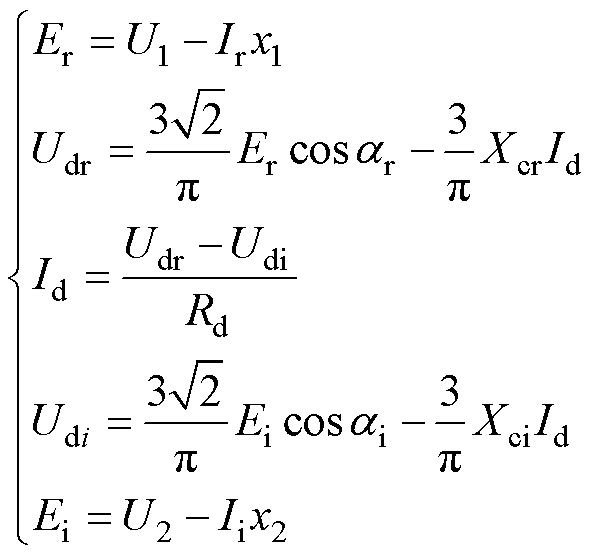 (1)
(1)
式中, 、
、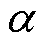 、
、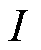 分别为直流电压、触发角、交流电流;
分别为直流电压、触发角、交流电流;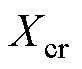 、
、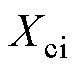 分别为整流器和逆变器的换相电抗。
分别为整流器和逆变器的换相电抗。
CIGRE HVDC标准测试模型的控制系统中,逆变侧的定电流控制指令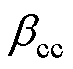 的计算式为
的计算式为
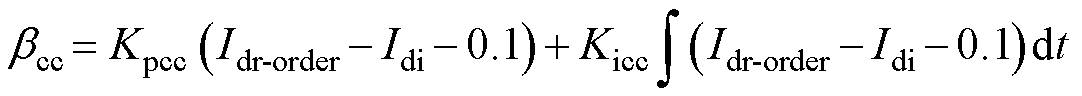 (2)
(2)
式中,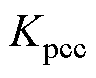 、
、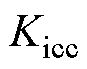 分别为PI控制器在CC控制中的比例增益和积分增益;
分别为PI控制器在CC控制中的比例增益和积分增益;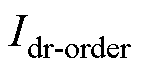 为逆变侧传输至整流侧的直流电流指令值;
为逆变侧传输至整流侧的直流电流指令值;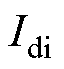 为逆变侧直流电流测量值。
为逆变侧直流电流测量值。
定关断角控制的超前触发角指令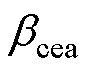 计算公式为
计算公式为
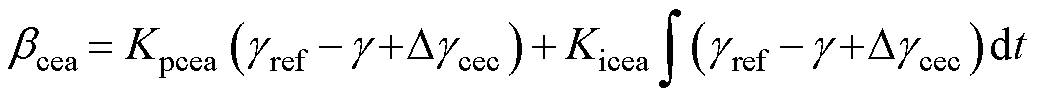 (3)
(3)
式中,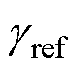 为CEA控制模式的关断角参考值;
为CEA控制模式的关断角参考值;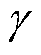 为逆变侧关断角测量值;
为逆变侧关断角测量值;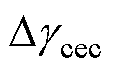 为逆变侧电流偏差控制CEC输出值,
为逆变侧电流偏差控制CEC输出值,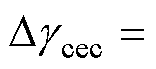
 ,
,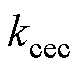 为CEC控制的最大极限与斜率;
为CEC控制的最大极限与斜率;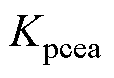 、
、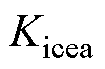 分别为PI控制器在CEA控制中的比例增益和积分增益。
分别为PI控制器在CEA控制中的比例增益和积分增益。
依据文献[20]建立的HVDC小信号模型进行分析,基于图1的HVDC系统结构,忽略线路阻抗和交流滤波器的影响,仅考虑两端控制部分、线路中断电容以及与关断角有关的电气量,选取系统的状态变量为
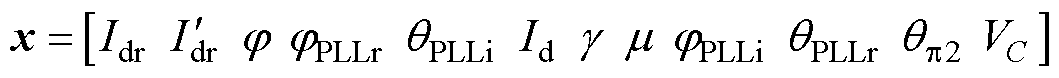 (4)
(4)
式中,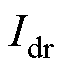 为整流侧直流线路电流;
为整流侧直流线路电流;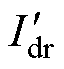 为经一阶测量环节滤波后的直流电流;
为经一阶测量环节滤波后的直流电流;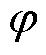 为送端定电流控制中PI控制器积分环节的输出量;
为送端定电流控制中PI控制器积分环节的输出量;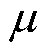 为受端定关断角控制中PI控制器中积分环节的输出量;
为受端定关断角控制中PI控制器中积分环节的输出量;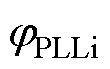 、
、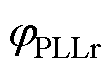 分别为整流侧和逆变侧锁相环PI器中积分环节的输出;
分别为整流侧和逆变侧锁相环PI器中积分环节的输出;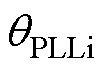 、
、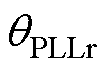 分别为整流侧和逆变侧锁相环输出相位;
分别为整流侧和逆变侧锁相环输出相位;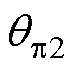 为考虑电压动态过程的电压相角变化;
为考虑电压动态过程的电压相角变化;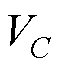 为直流线路中端电容电压。计算HVDC系统特征值、振荡频率以及最大参与因子相关的状态变量,结果见表1。
为直流线路中端电容电压。计算HVDC系统特征值、振荡频率以及最大参与因子相关的状态变量,结果见表1。
表1 LCC-HVDC模型模态结果
Tab.1 Modal results of LCC-HVDC model

特征值振荡频率/Hz阻尼比最大参与因子变量 -0.880 7±j0.417 466.423 80.930 7 1.001 8±j—1— -0.539 7±j0—1— 0.077 5±j0.048 37.680 8-0.848 8 -0.024 2±j0.007 61.215 50.953 6 -0.005 2±j0.005 20.822 20.706 2 -0.004 4±j0.004 00.640 60.738 3
由模态分析结果可知,HVDC系统中存在频率为五种固有振荡模式,其中,频率为1.215 5 Hz的固有振荡模式与引发受端换相失败的送端振荡频率最为接近,易与送端振荡形成共振。该振荡模式的参与因子分布结果如图3所示,最大参与因子变量为送端定电流控制中PI控制器积分环节的输出量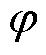 ,其他影响较高的变量有受端定关断角控制中PI控制器积分环节的输出量
,其他影响较高的变量有受端定关断角控制中PI控制器积分环节的输出量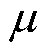 以及锁相环输出
以及锁相环输出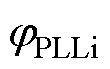 ,说明该振荡模式受直流控制系统的影响较大。
,说明该振荡模式受直流控制系统的影响较大。
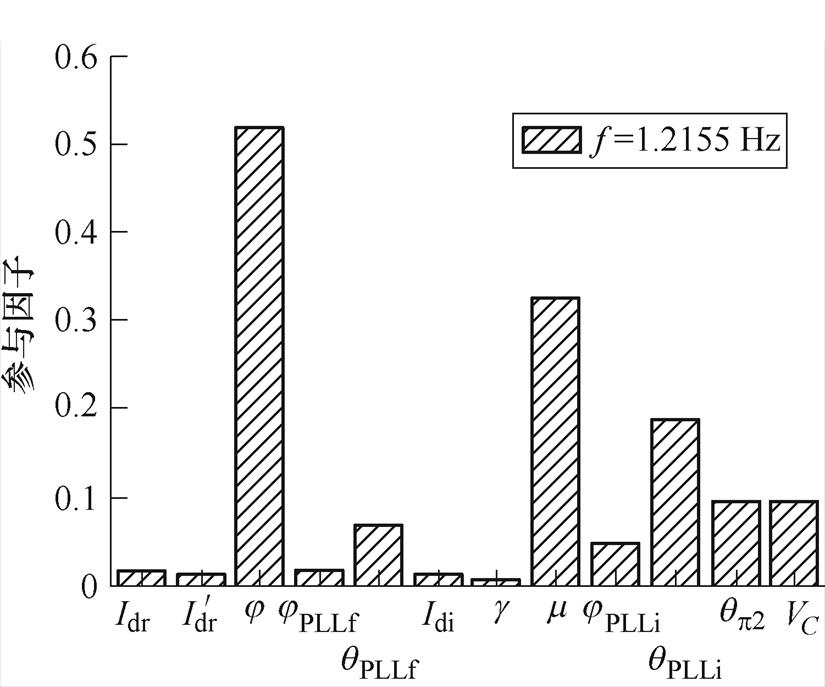
图3 参与因子
Fig.3 Diagram of participatory factor
观察图2的仿真曲线可知,送端振荡发生之后,初期不会对系统产生明显的影响,但后期随着振荡的持续累积,会引起系统的电气量和控制量发生变化。鉴于关断角主要与直流电流、逆变侧换相电压有关,当这两个量发生变化,可能会导致关断角减小,引发换相失败。同时,从控制系统的角度分析,逆变侧在稳态时处于定关断角控制,将关断角调节在正常范围内;若系统在扰动后控制量发生变化则可能导致控制切换,进而使关断角失去控制,发生换相失败。下文将分阶段对换相失败过程及产生机理进行分析。
2.3.1 振荡初始阶段
当送端系统出现与直流控制系统主导的固有频率接近的振荡时将会产生共振,导致触发角等控制量、电压电流等电气量起伏变化。系统中的这些量不会即刻响应变化,而是在PI积分控制器的累积作用下,一段时间后才开始呈现明显的波形起伏。因此,振荡刚发生时系统维持正常运行状态,各电气量均保持稳定,整流侧处于CC控制模式,逆变侧CEA控制超前触发角输出值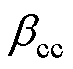 大于CC控制超前触发角输出值
大于CC控制超前触发角输出值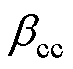 ,触发角由CEA闭环调节。
,触发角由CEA闭环调节。
2.3.2 振荡持续阶段
随着HVDC系统共振持续,系统电气量及控制量开始振荡,受端换相失败持续发生,亦可分为两个阶段来详细探讨。
1)首次换相失败
共振后系统电气量和控制量开始小幅度波动,直流电流开始下降,整流侧先处于CC控制以维持电流,由于准稳态模型中直流电流的表达式亦可用式(5)表示,可看出为抬升直流电流需减小整流侧触发角,但整流侧有最小触发角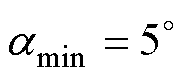 限制。最终随着直流电流的不断减小,导致CC控制失去对Id的控制,切换为最小触发角控制。
限制。最终随着直流电流的不断减小,导致CC控制失去对Id的控制,切换为最小触发角控制。
 (5)
(5)
式中,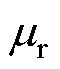 为整流侧换相角。
为整流侧换相角。
之后,直流电流开始上升,系统电气量和控制量开始剧烈波动,因此整流侧触发角在一定范围内振荡,由于整流侧存在最小触发角控制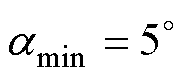 ,同时考虑到关断角最小为7°、换相角一般为20°及安全裕量角取10°,由以上因素可推算出触发角最大可为143°。因此,在系统共振期间,触发角的变化范围为
,同时考虑到关断角最小为7°、换相角一般为20°及安全裕量角取10°,由以上因素可推算出触发角最大可为143°。因此,在系统共振期间,触发角的变化范围为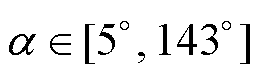 。送端直流电压公式为
。送端直流电压公式为
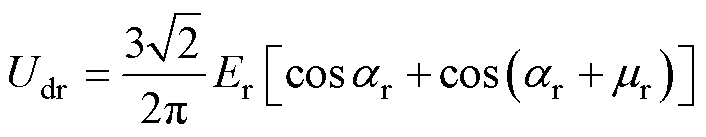 (6)
(6)
不考虑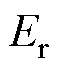 的变化影响,将其视为额定值,则当触发角在变化范围内逐渐上升时,送端直流电压Udr随触发角
的变化影响,将其视为额定值,则当触发角在变化范围内逐渐上升时,送端直流电压Udr随触发角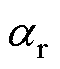 变化的波形如图4所示,可以看出,Udr随着
变化的波形如图4所示,可以看出,Udr随着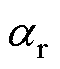 的增大而减小。
的增大而减小。
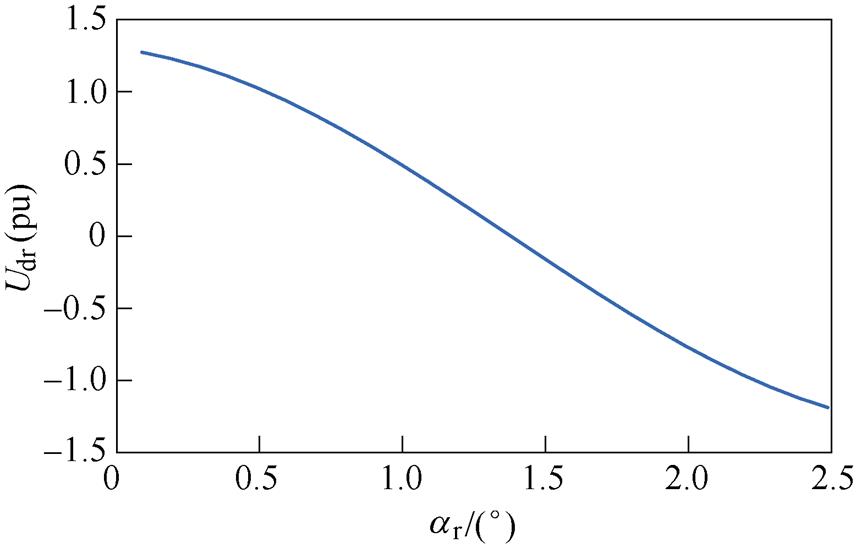
图4 送端直流电压随触发角的变化
Fig.4 Diagram of DC voltage change with trigger angle
通过前述的HVDC直流系统准稳态方程可解得直流电流、送端以及受端直流电压在准稳态模式下的表达式为
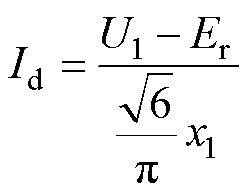 (7)
(7)
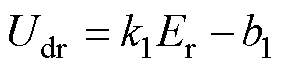 (8)
(8)
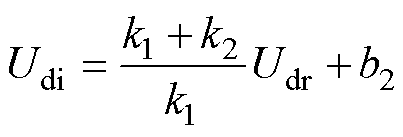 (9)
(9)
其中
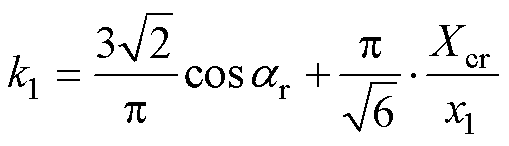
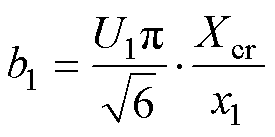
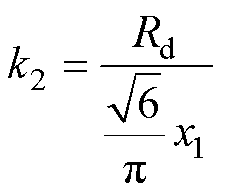
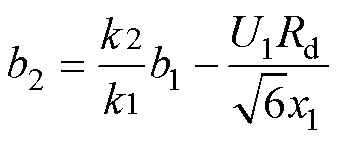
从式(9)可以看出,受端直流电压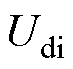 与送端直流电压
与送端直流电压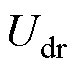 变化趋势相同,但
变化趋势相同,但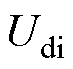 的波形斜率比
的波形斜率比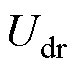 更大,故
更大,故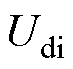 的下降速度更快。同时,由受端直流电流表达式
的下降速度更快。同时,由受端直流电流表达式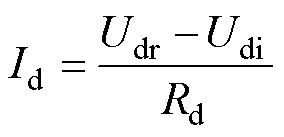 可知,直流线路电阻较小,则一定的直流电压差即可产生较大的直流电流。
可知,直流线路电阻较小,则一定的直流电压差即可产生较大的直流电流。
综上所述,在送端振荡持续一段时间后,电气量和控制量开始小幅度波动,此时整流侧先切为最小触发角控制,逆变侧控制不变。之后系统开始剧烈振荡,换流母线电压下降,两端直流电压随触发角增大而下降,直流电流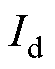 随直流电压的降低而增大,逆变侧关断角随
随直流电压的降低而增大,逆变侧关断角随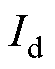 的增大而降低,首次换相失败由此发生。于此同时,整流侧触发角上升,再次CC控制直流电流,逆变侧
的增大而降低,首次换相失败由此发生。于此同时,整流侧触发角上升,再次CC控制直流电流,逆变侧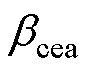 增大,保持CEA控制。因此,在送端振荡下受端首次换相失败发生的直接原因是直流电流在振荡后增大,整个过程的具体演化机理以及交互影响如图5所示,其中虚线箭头表示电气量与控制量之间的交互影响。在首次换相失败之后,
增大,保持CEA控制。因此,在送端振荡下受端首次换相失败发生的直接原因是直流电流在振荡后增大,整个过程的具体演化机理以及交互影响如图5所示,其中虚线箭头表示电气量与控制量之间的交互影响。在首次换相失败之后,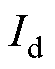 下降,导致
下降,导致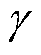 上升,
上升,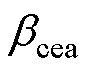 减小,
减小,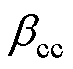 增大,CEA控制切换为CC控制。
增大,CEA控制切换为CC控制。
2)后续换相失败
首次换相失败发生之后,受端交流母线电压上升,恢复至指令值附近,直流电流开始下降,关断角上升,由逆变侧定电流控制和定关断角控制的式(2)、式(3)可知,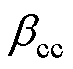 增大,
增大,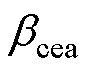 减小,逆变侧由CEA控制切换到CC控制。同时整流侧也处于CC控制,直流电流振荡于两侧CC指令值之间,即
减小,逆变侧由CEA控制切换到CC控制。同时整流侧也处于CC控制,直流电流振荡于两侧CC指令值之间,即
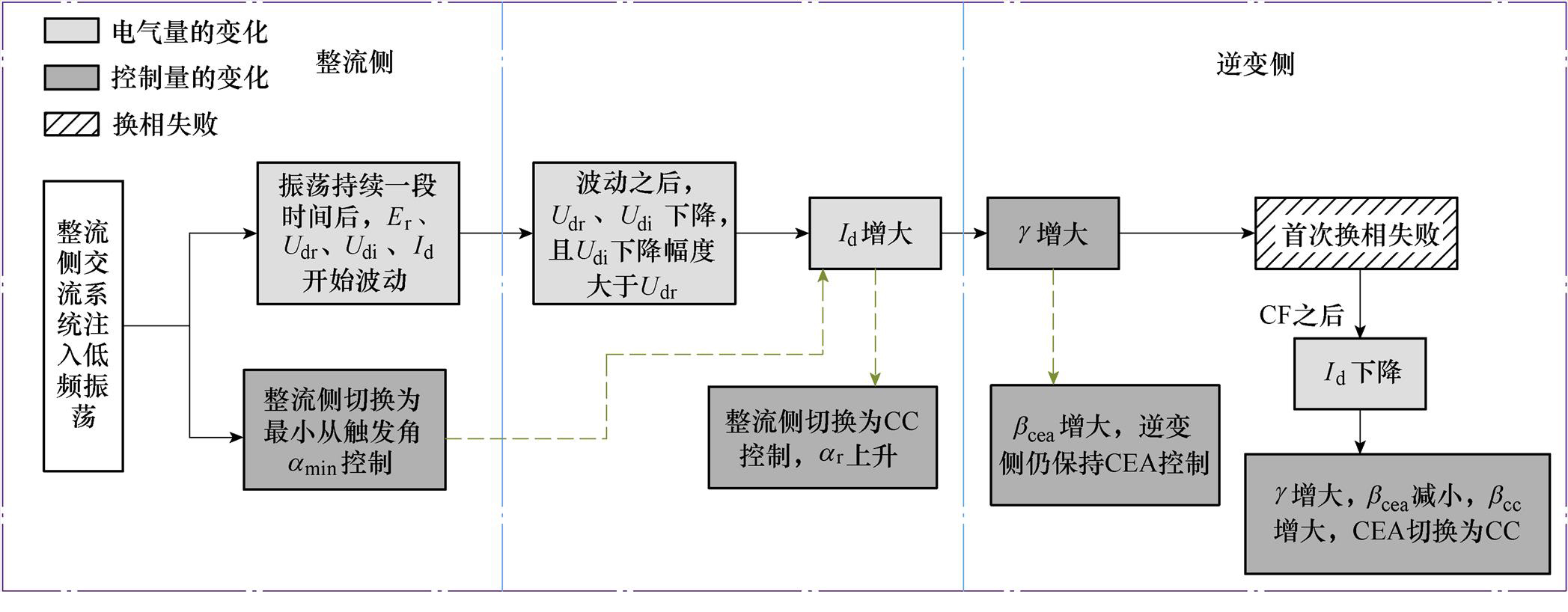
图5 首次换相失败的演化机理
Fig.5 Evolution mechanism of the first commutation failure
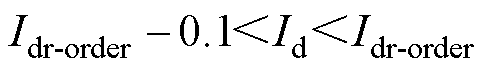 (10)
(10)
式中,0.1是两端电流指令值之间的阈值。
由式(10)可知,电流偏差控制CEC的输出指令值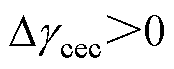 ,逆变侧CEC触发,在直流电流第二次上升,且导致关断角下降时,
,逆变侧CEC触发,在直流电流第二次上升,且导致关断角下降时,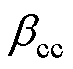 减小,
减小,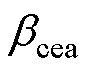 增大,CC控制向CEA控制切换。切换过程中,关断角处于不受控状态,换相失败发生。因此,后续换相失败发生的直接原因是逆变侧控制的切换。
增大,CC控制向CEA控制切换。切换过程中,关断角处于不受控状态,换相失败发生。因此,后续换相失败发生的直接原因是逆变侧控制的切换。
进一步地,在逆变侧从CC控制切换到CEA控制过程中,逆变侧的超前触发角 增大以抬升关断角
增大以抬升关断角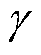 ,导致触发角
,导致触发角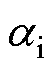 (
(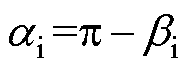 )减小,而逆变侧功率因数表达式为
)减小,而逆变侧功率因数表达式为
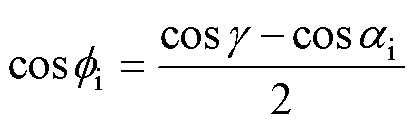 (11)
(11)
式中,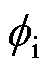 为逆变侧功率因数角。由式(11)可知,逆变侧功率因数会因为
为逆变侧功率因数角。由式(11)可知,逆变侧功率因数会因为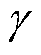 的增大和
的增大和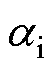 的减小而减小,继而导致换流器消耗的无功增大,最终使受端交流母线电压跌落,进一步增加受端换相失败的风险。
的减小而减小,继而导致换流器消耗的无功增大,最终使受端交流母线电压跌落,进一步增加受端换相失败的风险。
故由上述分析过程,总结后续换相失败过程的具体演化机理及电气量与控制量之间的交互影响(图中虚线箭头所示)如图6所示。图中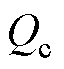 为逆变侧换流器消耗的无功功率,
为逆变侧换流器消耗的无功功率,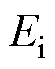 为逆变侧换流母线电压。
为逆变侧换流母线电压。
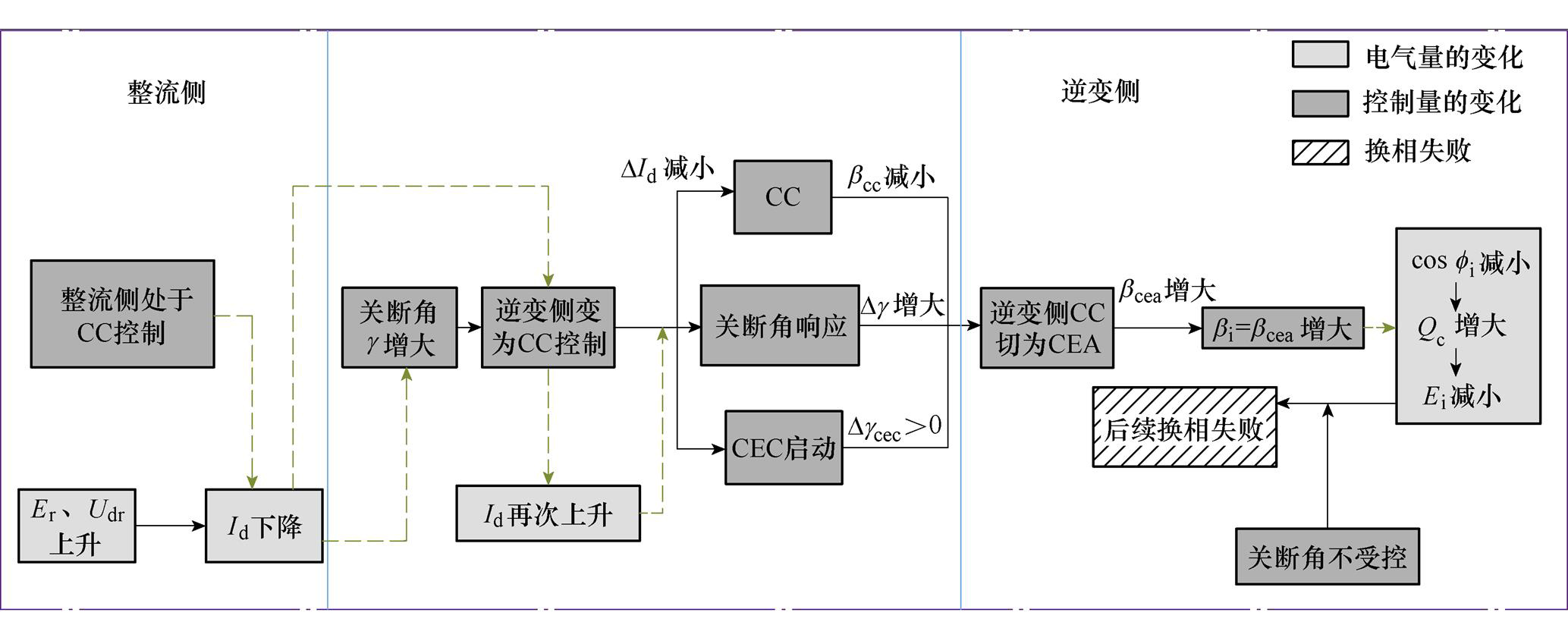
图6 后续换相失败的演化机理
Fig.6 Evolution mechanism of subsequent commutation failure
本文采用PSCAD/EMTDC 电磁暂态仿真软件,利用CIGRE HVDC标准测试模型仿真验证。在系统的整流侧交流母线处设置振荡源(电压幅值为3 kV,约0.009(pu)),调整振荡源频率,观察电气量和控制量的变化,以判断受端是否发生换相失败现象。该系统整流侧及交流侧的SCR分别为2.5和2.0,两侧无功补偿平衡。
设置振荡源频率为1.2 Hz来验证该固有频率能够引发系统共振,并进一步具体分析逆变侧控制切换的全过程;分别设置振荡源频率为7.6 Hz和66 Hz来验证该固有频率不会导致受端换相失败;分别设置振荡源频率为0.6 Hz和0.8 Hz来验证该固有频率,由于处在低频段范围内与1.2 Hz非常接近,也可导致受端换相失败。
最后为分析低频频段内不同振荡频率对受端换相失败的影响,分别设置振荡源为0.1 Hz、1.2 Hz和0.8 Hz,观察系统电气量和控制量的变化,分析送端不同振荡频率下的受端换相失败响应区别。
将振荡源的频率设为1.2 Hz,得到系统的电气量与控制量的变化情况如图7所示,同时图8展示了控制切换导致后续换相失败的系统响应过程,其中控制切换区域如图8所示。由图7可知,在1.2 Hz振荡加入0.2 s后,各量开始变化,其中整流侧触发角逐渐降低为最小触发角控制。0.4 s后振荡开始剧烈呈现,触发角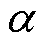 开始上升,
开始上升,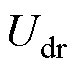 和
和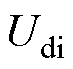 开始下降,由图中可以看出,代表送端直流电压的曲线斜率稍低于受端直流电压的曲线斜率。因此直流电流
开始下降,由图中可以看出,代表送端直流电压的曲线斜率稍低于受端直流电压的曲线斜率。因此直流电流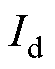 上升,在t=2.44 s时达到峰值,从而导致关断角降低,首次换相失败发生,同时,逆变侧CEA指令下降,CC指令上升,在2.5 s时CEA控制切换为CC控制。之后从图8的区域B可见,直流电流的实测值
上升,在t=2.44 s时达到峰值,从而导致关断角降低,首次换相失败发生,同时,逆变侧CEA指令下降,CC指令上升,在2.5 s时CEA控制切换为CC控制。之后从图8的区域B可见,直流电流的实测值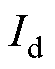 小于整流侧指令值
小于整流侧指令值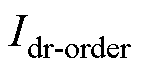 且大于逆变侧指令值
且大于逆变侧指令值 ,导致两侧对直流电流的调节方向相反为:整流侧触发角减小以抬升
,导致两侧对直流电流的调节方向相反为:整流侧触发角减小以抬升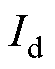 至
至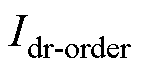 ,而逆变侧增大触发角以降低
,而逆变侧增大触发角以降低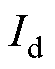 至
至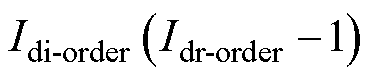 。此时
。此时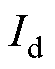 的控制目标不明确,使得直流电流波动。
的控制目标不明确,使得直流电流波动。
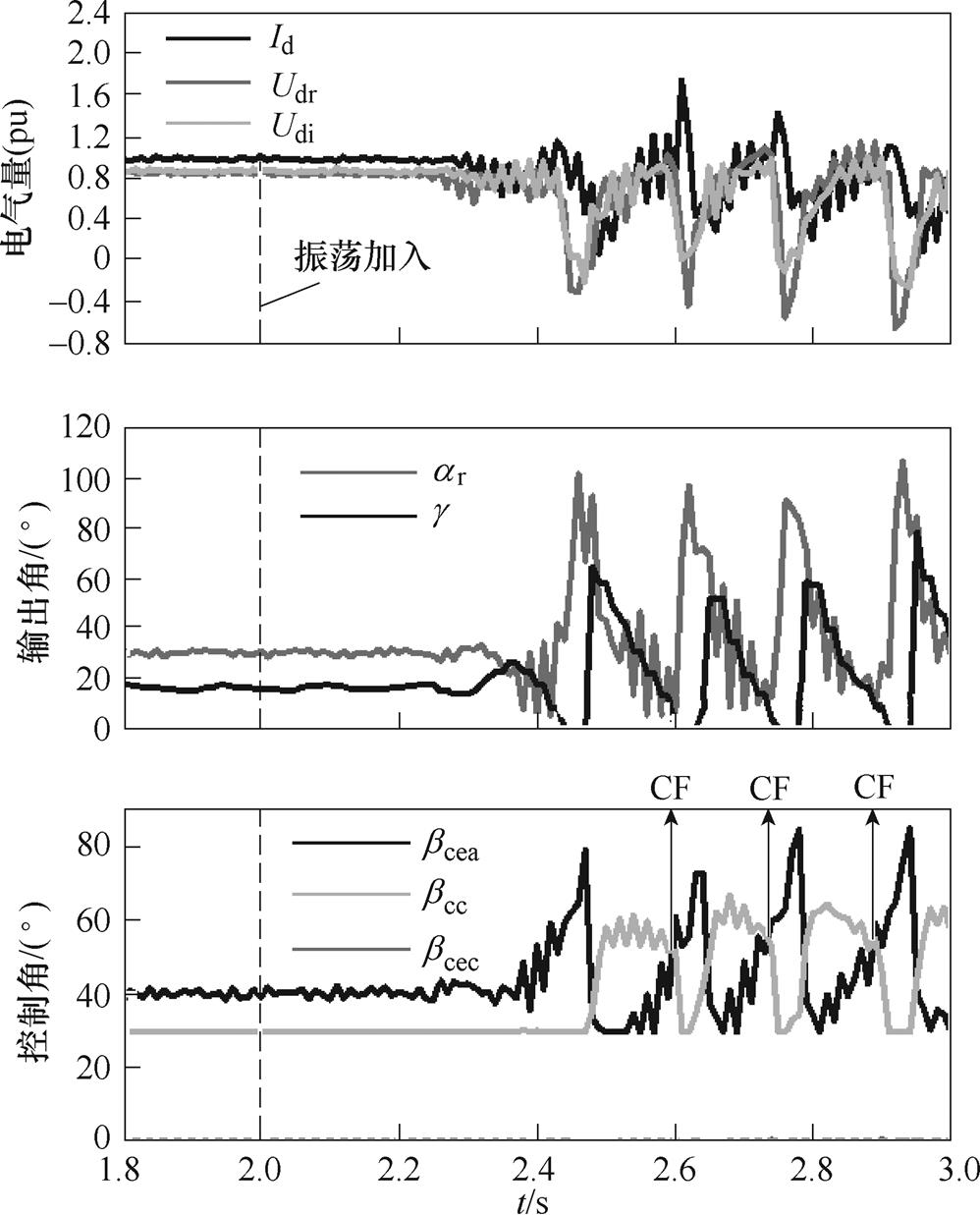
图7 1.2 Hz振荡对系统电气量及控制量的影响
Fig.7 The effect of 1.2 Hz oscillation on system electric quantity and control quantity
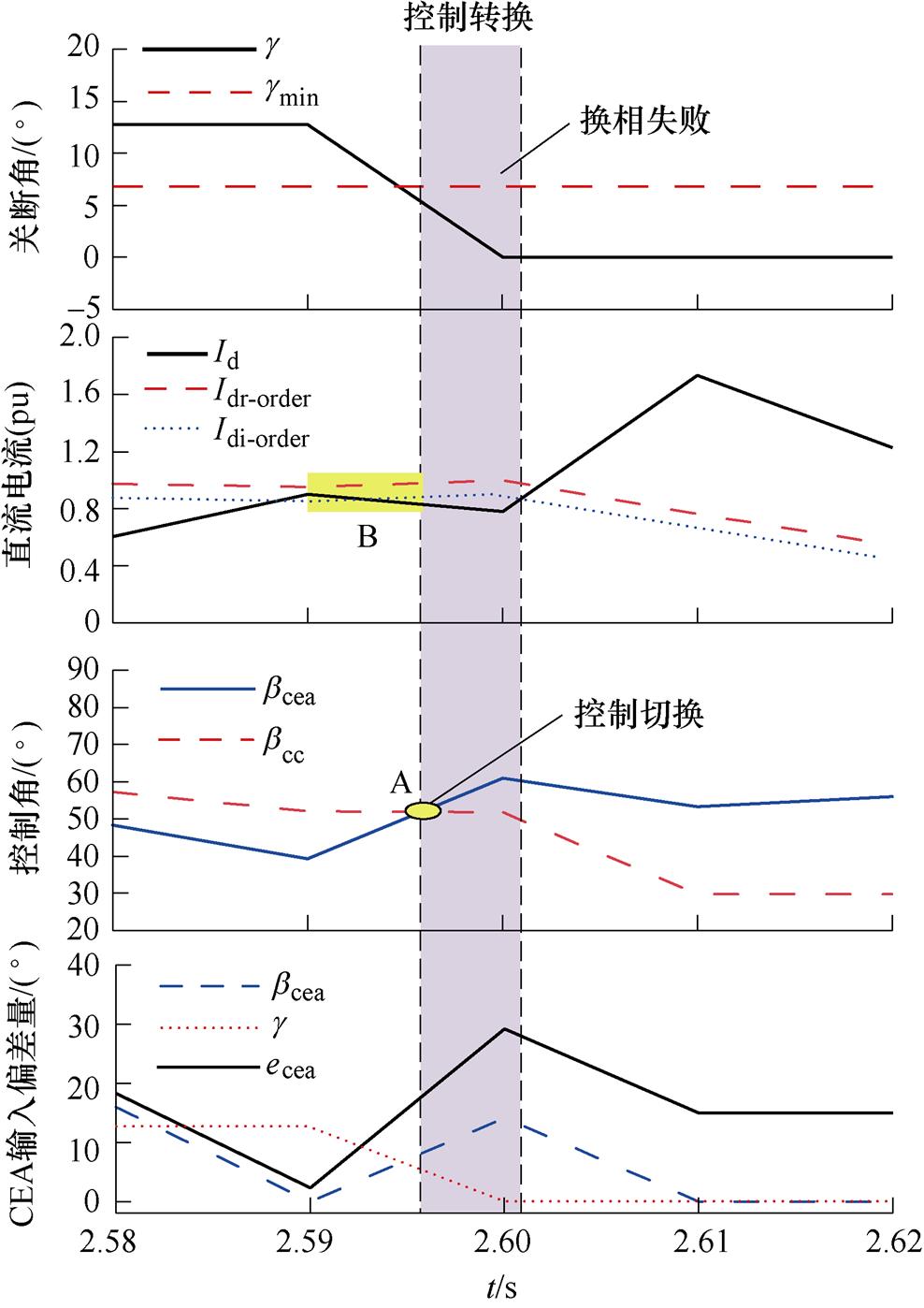
图8 控制切换时系统的响应过程
Fig.8 The response process of system during the control switching
由图8可知,在直流电流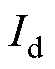 上升的作用下,关断角开始减小,之后随着
上升的作用下,关断角开始减小,之后随着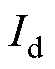 在两侧指令值之间波动轻微下降时,
在两侧指令值之间波动轻微下降时,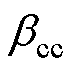 减小,
减小,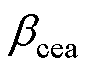 增大,当两者波形相交,即图8中的A点t=2.595 s时,CC控制切换为CEA控制。此时,整流侧获得直流电流控制权,在t=2.6 s时,逐渐增大
增大,当两者波形相交,即图8中的A点t=2.595 s时,CC控制切换为CEA控制。此时,整流侧获得直流电流控制权,在t=2.6 s时,逐渐增大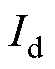 ,导致CEC的输出
,导致CEC的输出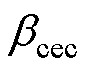 减小,并快速降为0,同时关断角随之进一步降为0,致使CEA的输入偏差
减小,并快速降为0,同时关断角随之进一步降为0,致使CEA的输入偏差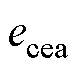
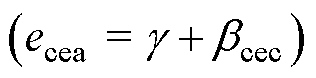 降低。故在CEC的输出快速降低的过程中,CEA控制的输出随
降低。故在CEC的输出快速降低的过程中,CEA控制的输出随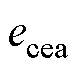 的降低而下降,因此,即使关断角大幅度下降,CEA控制也难以及时快速地调节触发角指令,从而在短时间内失效,导致关断角进一步降为0,引发后续换相失败。
的降低而下降,因此,即使关断角大幅度下降,CEA控制也难以及时快速地调节触发角指令,从而在短时间内失效,导致关断角进一步降为0,引发后续换相失败。
此后,若未加入抑制措施,则不断发生后续换相失败,均为首次换相失败后控制量的波动引起逆变侧控制不断切换导致的。
将振荡源的频率分别设为7.6 Hz和66 Hz,得到系统的电气量与控制量的变化情况如图9所示。
由表1可知,7.6 Hz为直流线路中端电容电压主导的系统固有振荡模态,66 Hz为整流侧直流线路电流主导的系统固有振荡模态。由图9可以看出,虽然7.6 Hz和66 Hz都是系统的固有振荡模态,但由于其主导动态与直流控制系统无关,所以不会引起系统控制量失控和受端换相失败。
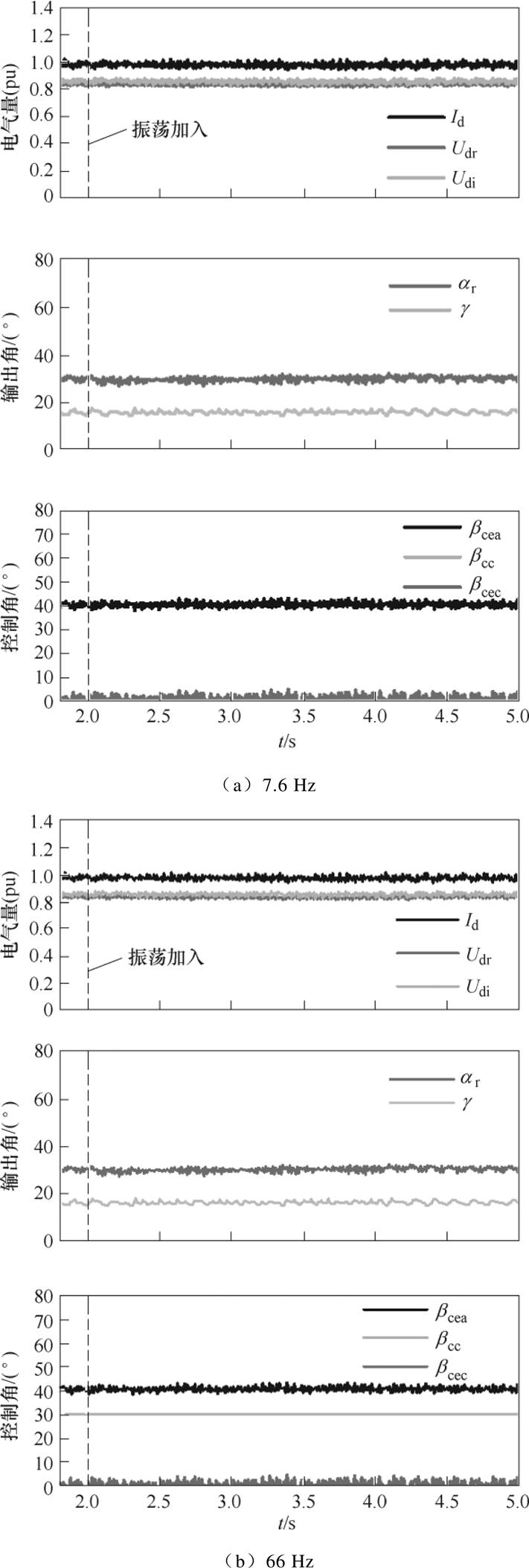
图9 7.6 Hz和66 Hz振荡对系统电气量及控制量的影响
Fig.9 The effect of 7.6 Hz and 66 Hz oscillation on system electric quantity and control quantity
测试直流系统剩下的两个固有频率,将振荡源的频率分别设为0.6 Hz和0.8 Hz,得到系统的电气量与控制量的变化情况如图10所示。
可以看出,0.6 Hz和0.8 Hz的振荡不仅固有振荡模态主要与受端锁相环PLL相关,而且这两个频率与1.2 Hz非常接近。因此,送端注入0.6 Hz或0.8 Hz的振荡扰动时,也能激发1.2 Hz的固有振荡模态发生共振,从而引发受端发生换相失败。
由以上仿真现象可证明当送端交流系统受到低频频段的振荡扰动后,随着HVDC控制系统与送端振荡的持续交互,可引起系统发生共振,从而导致系统电气量与控制量的波动,并在电气量与控制量的交互影响过程中,受端系统由于直流电流上升触发首次换相失败,在后续的控制不断交换过程中引发后续换相失败。
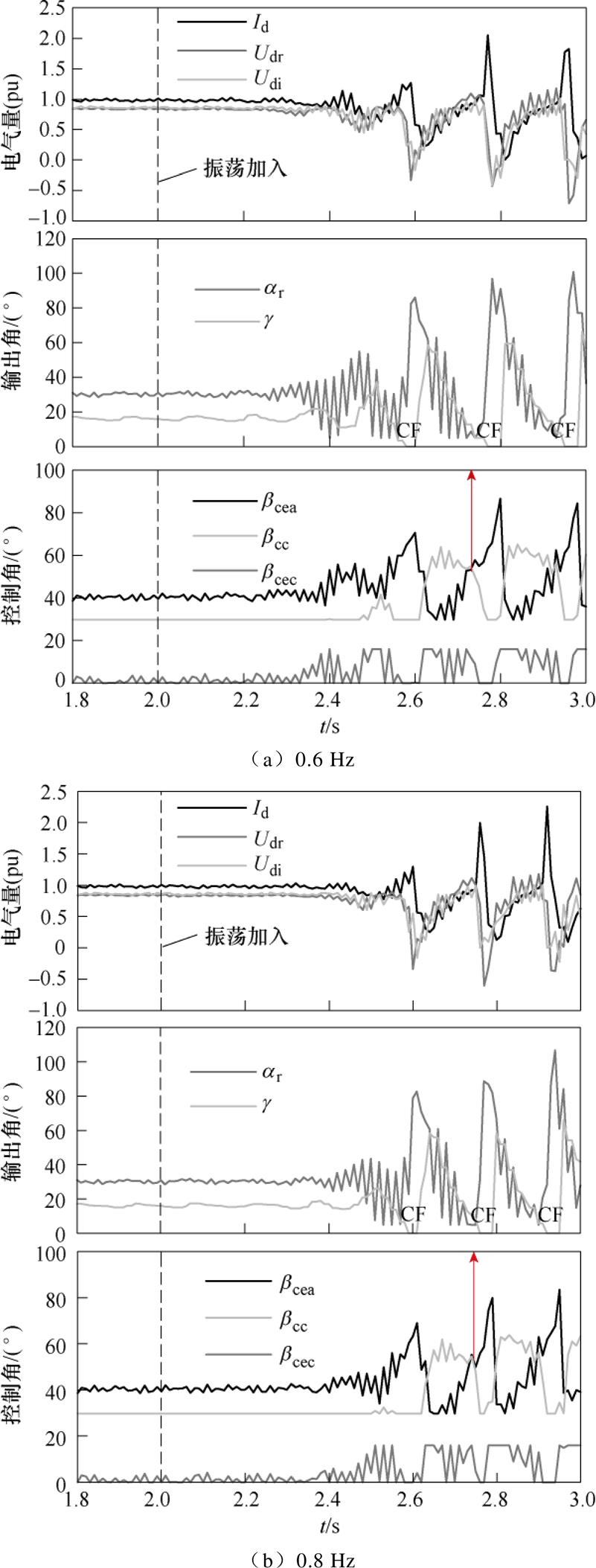
图10 0.6 Hz和0.8 Hz振荡对系统电气及控制量的影响
Fig.10 The effect of 0.6 Hz and 0.8 Hz oscillation on system electric quantity and control quantity
为了验证这个现象,通过试验进一步发现,当送端振荡频率处于0.1~2.5 Hz之间时均会引发受端发生换相失败,在这个频段之外则不会。同时,还可观测到,能够引发受端换相失败的送端频率中,越靠近1.2 Hz换相失败发生的就越快。下文将结合具体的仿真曲线进行说明。
将振荡源的频率分别设为0.1 Hz和2.5 Hz,系统的电气量与控制量的变化情况如图11所示。
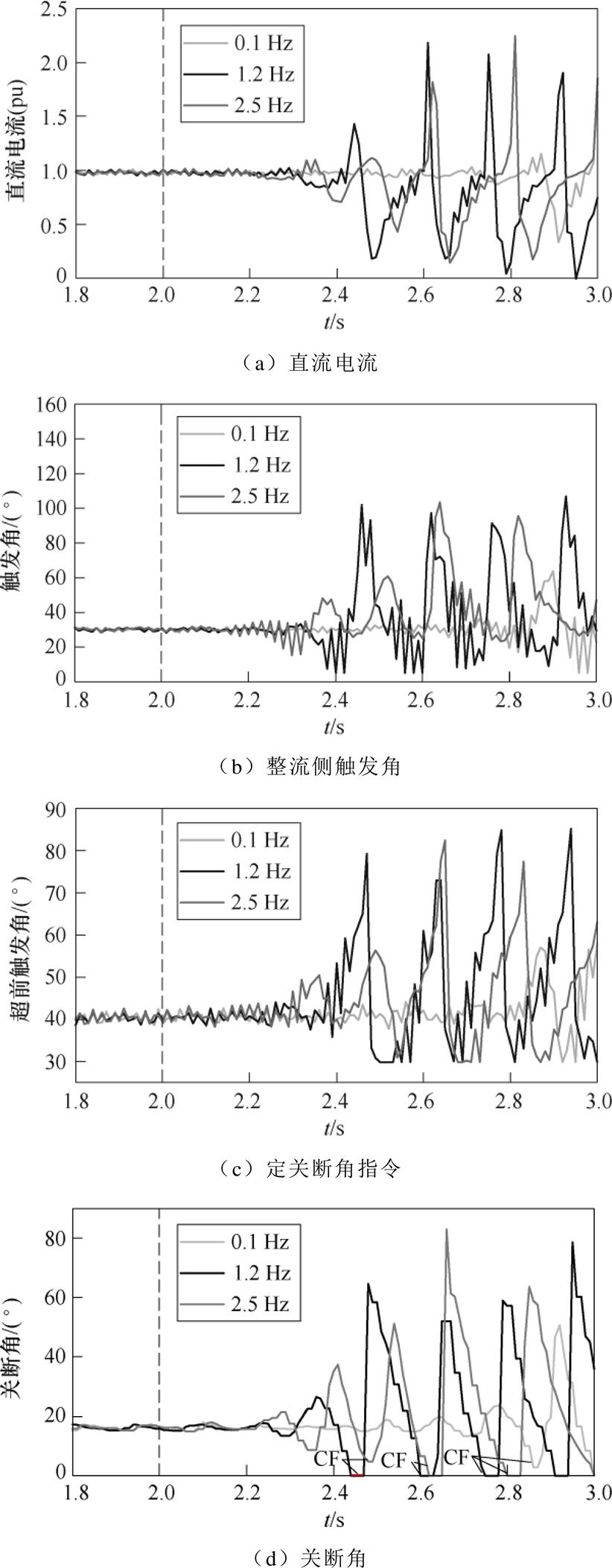
图11 系统电气量及控制量在不同频率下的变化
Fig.11 Changes of system electrical quantity and control quantity at different frequency
图11a~图11d分别为系统的直流电流、整流侧触发角、逆变侧定关断角(CEA)控制的输出以及关断角的变化曲线。从图11a可知,1.2 Hz的振荡最先导致直流电流上升至峰值,其次是2.5 Hz、0.1 Hz的变化最慢。其中在0.1 Hz振荡注入后的0.5 s直流电流开始小幅度振荡,随着时间的累积到2.8 s后才开始大幅度振荡,同样地,图11b中,1.2 Hz振荡下触发角最先进入最小触发角控制,0.1 Hz振荡在2.9 s后开始进入最小触发角控制模式。图11c中,1.2 Hz振荡下逆变侧定关断角(CEA)控制最先开始下降,切换为定电流(CC)控制。最后,在关断角曲线图11d中,可以看见1.2 Hz振荡下,由于引起系统的共振,导致换相失败发生最快,次之是2.5 Hz,0.1 Hz的换相失败发生的最慢。
因此,虽然0.1 Hz和2.5 Hz的振荡不是HVDC系统的固有振荡模态,但是因为离1.2 Hz较近,同样会引发直流控制系统共振导致换相失败,但是受端换相失败的出现速度较慢。
表2总结了送端系统不同振荡频率下受端换相失败出现的情况。
表2 送端系统振荡与受端换相失败情况汇总
Tab.2 The CF outcome with different oscillation frequency
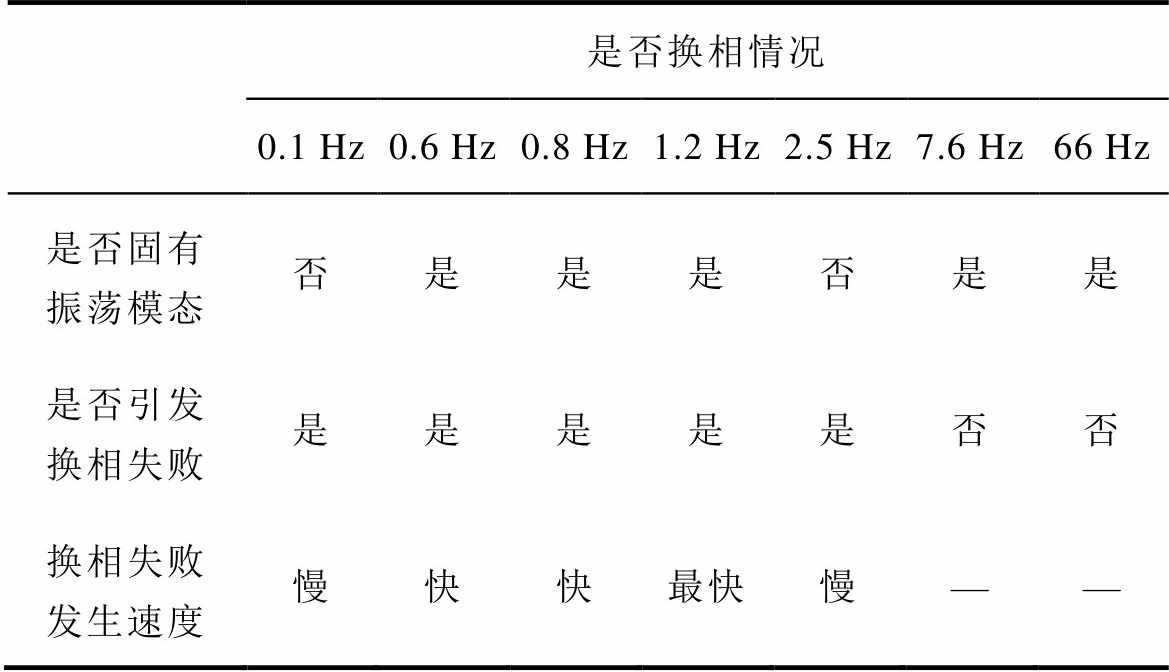
是否换相情况 0.1 Hz0.6 Hz0.8 Hz1.2 Hz2.5 Hz7.6 Hz66 Hz 是否固有振荡模态否是是是否是是 是否引发换相失败是是是是是否否 换相失败发生速度慢快快最快慢——
通过以上分析可知,若送端系统振荡频率与直流控制系统主导的固有振荡模态频率接近时,易导致受端系统发生换相失败。此外,由表1可知,1.2 Hz固有振荡模态对应的阻尼比较小,无法有效抑制共振。由此,可提出以下两点预防换相失败的控制策略。
(1)调整定电流控制PI控制器的参数或增加附加控制回路,使HVDC系统固有振荡频率避开送端系统常见的振荡频段,甚至使该固有振荡频率消失,从而抑制换相失败。
(2)针对阻尼比较小,可通过附加控制,以提高系统阻尼比,达到抑制共振的效果,进而抑制换相失败。
本文首次分析了送端系统振荡引发受端换相失败的现象,揭示了换相失败的演化机理,并通过仿真进行验证。得出以下结论:
1)现象:阶段1,送端系统初现低频振荡时,直流系统处于稳定;阶段2,系统开始出现轻微幅度的振荡,电气量和控制量在稳定范围内波动;阶段3,振荡积累一段时间后,系统电气量剧烈变化,继而直流电流上升,受端关断角下降,首次换相失败发生;阶段4,控制器的输出量变化幅度增大,受端CC控制与CEA控制不断切换,在CC控制切换为CEA控制时,换相失败再次发生。
2)机理:送端系统振荡频率与直流控制系统主导的固有振荡模态频率接近,共振会引发电气量与控制量的大范围振荡,导致的直流电流增大是首次换相失败的直接原因;引发的受端控制切换,导致后续换相失败,关断角的不受控成为后续换相失败的主要原因,并在CC切换到CEA控制时换相失败发生。此外,送端系统振荡频率与直流控制系统主导的固有振荡模态频率越接近,换相失败发生得越快。
3)最后,通过PSCAD/EMTDC全电磁暂态仿真,验证了理论分析得到的送端振荡引发受端换相失败机理。同时,依据换相失败发生的机理,提出了初步的抑制策略。
参考文献
[1] 郭春义, 赵剑, 刘炜, 等. 抑制高压直流输电系统换相失败方法综述[J]. 中国电机工程学报, 2018, 38(增刊1): 1-10.
Guo Chunyi, Zhao Jian, Liu Wei, et al. A review of methods to mitigate the commutation failure for LCC-HVDC[J]. Proceedings of the CSEE, 2018, 38(S1): 1-10.
[2] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822.
Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electrote- chnical Society, 2022, 37(19): 4808-4822.
[3] 贺永杰, 向往, 周家培, 等. LCC-MMC串联型混合直流输电系统小信号建模[J]. 电工技术学报, 2021, 36(7):1492-1506.
He Yongjie, Xiang Wang, Zhou Jiapei, et al. Small- signal modelling of LCC-MMC series hybrid HVDC transmission system[J]. Transactions of China Elec- trotechnical Society, 2021, 36(7): 1492-1506.
[4] 武传健, 张大海. 受端混联型LCC-VSC直流输电线路快速后备保护[J]. 电工技术学报, 2021, 36(增刊2): 541-553.
Wu Chuanjian, Zhang Dahai. Fast back-up protection scheme of receiving-end hybrid LCC-VSC DC trans- mission lines[J]. Transactions of China Electro- technical Society, 2021, 36(S2): 541-553.
[5] 周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904.
Zhou Xiaoxin, Chen Shuyong, Lu Zongxiang, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904.
[6] 曾亮, 李永丽, 张云柯, 等. 逆变侧交流系统不对称故障引发HVDC系统连续换相失败的机理及抑制策略研究[J]. 中国电机工程学报, 2019, 39(11): 3159-3167.
Zeng Liang, Li Yongli, Zhang Yunke, et al. Research on mechanism and control strategy of continuous commutation failures in HVDC system caused by asymmetrical fault in inverter-side AC system[J]. Proceedings of the CSEE, 2019, 39(11): 3159-3167.
[7] 汤奕, 郑晨一. 高压直流输电系统换相失败影响因素研究综述[J]. 中国电机工程学报, 2019, 39(2): 499-513.
Tang Yi, Zheng Chenyi. Review on influencing factors of commutation failure in HVDC systems[J]. Proceedings of the CSEE, 2019, 39(2): 499-513.
[8] Wang Qi, Zhang Chaoming, Wu Xingquan, et al. Commutation failure prediction method considering commutation voltage distortion and DC current variation[J]. IEEE Access, 2019, 7: 96531-96539.
[9] 景柳铭, 王宾, 董新洲, 等. 高压直流输电系统连续换相失败研究综述[J]. 电力自动化设备, 2019, 39(9): 116-123
Jing Liuming, Wang Bin, Dong Xinzhou, et al. Review of consecutive commutation failure research for HVDC transmission system[J]. Electric Power Automation Equipment, 2019, 39(9): 116-123.
[10] 宋金钊, 李永丽, 曾亮, 等. 高压直流输电系统换相失败研究综述[J]. 电力系统自动化, 2020, 44(22): 2-13.
Song Jinzhao, Li Yongli, Zeng Liang, et al. Review on commutation failure of HVDC transmission system[J]. Automation of Electric Power Systems, 2020, 44(22): 2-13.
[11] 王增平, 刘席洋, 郑博文, 等. 基于电压波形拟合的换相失败快速预测与抑制措施[J]. 电工技术学报, 2020, 35(7): 1454-1463.
Wang Zengping, Liu Xiyang, Zheng Bowen, et al. The research on fast prediction and suppression measures of commutation failure based on voltage waveform fitting[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1454-1463.
[12] 李培平, 周泓宇, 姚伟, 等. 多馈入结构背景下的高压直流输电系统换相失败研究综述[J]. 电网技术, 2022, 46(3): 834-850.
Li Peiping, Zhou Hongyu, Yao Wei, et al. Review of commutation failure on HVDC transmission system under background of multi-infeed structure[J]. Power System Technology, 2022, 46(3): 834-850.
[13] 许汉平, 杨炜晨, 张东寅, 等. 考虑换相失败相互影响的多馈入高压直流系统换相失败判断方法[J]. 电工技术学报, 2020, 35(8): 1776-1786.
Xu Hanping, Yang Weichen, Zhang Dongyin, et al. Commutation failure judgment method for multi- infeed HVDC systems considering the interaction of commutation failures[J]. Transactions of China Elec- trotechnical Society, 2020, 35(8): 1776-1786.
[14] Xiao Hao, Li Yinhong, Lan Tongkun. Sending end AC faults can cause commutation failure in LCC- HVDC inverters[J]. IEEE Transactions on Power Delivery, 2020, 35(5): 2554-2557.
[15] Hong Lerong, Zhou Xiaoping, Xia Haitao, et al. Mechanism and prevention of commutation failure in LCC-HVDC caused by sending end AC faults[J]. IEEE Transactions on Power Delivery, 2021, 36(1): 473-476.
[16] 刘磊, 林圣, 刘健, 等. 控制器交互不当引发后续换相失败的机理分析[J]. 电网技术, 2019, 43(10): 3562-3568.
Liu Lei, Lin Sheng, Liu Jian, et al. Mechanism analysis of subsequent commutation failures caused by improper interaction of controllers[J]. Power System Technology, 2019, 43(10): 3562-3568.
[17] 林圣, 雷雨晴, 刘健, 等. HVDC送端系统故障引发受端换相失败分析[J]. 中国电机工程学报, 2022, 42(5): 1669-1679.
Lin Sheng, Lei Yuqing, Liu Jian, et al. Analysis of receiving-side commutation failure mechanism caused by HVDC sending-side system fault[J]. Proceedings of the CSEE, 2022, 42(5): 1669-1679.
[18] 马星, 李凤婷, 尹纯亚. 整流侧换流母线电压恢复对逆变器换相的影响[J]. 电网技术, 2020, 44(8): 2950-2956.
Ma Xing, Li Fengting, Yin Chunya. Impact of voltage restoration of commutation bus on rectifier side on commutation of inverters[J]. Power System Tech- nology, 2020, 44(8): 2950-2956.
[19] 马星, 李凤婷, 尹纯亚, 等. 整流侧换流母线电压恢复导致逆变器换相失败的机理分析[J]. 电力工程技术, 2021, 40(4): 83-88.
Ma Xing, Li Fengting, Yin Chunya, et al. Mechanism analysis of inverter commutation failure caused by voltage recovery of commutation bus at rectifier side[J]. Jiangsu Electrical Engineering, 2021, 40(4): 83-88.
[20] 李至峪. 考虑电压动态过程的交直流混合系统小信号建模方法研究与应用[D]. 北京: 华北电力大学, 2021.
Li Zhiyu. Research and application of small signal modeling method for AC/DC hybrid system considering voltage variation[D]. Beijing: North China Electric Power University, 2021.
Abstract Strong electrical and control coupling exists between the sending and receiving ends of a high voltage direct current (HVDC) transmission system. Therefore, disturbances on the sending end can affect the operation state of the receiving end system through changes in control logic, electrical, or control quantities, increasing the risk of commutation failure (CF) on the receiving end. The phenomenon and mechanism of CF at the receiving end caused by large disturbances at the sending end have been studied in existing literature. This paper identifies the existence of inherent oscillation modes with frequencies situated in the low-frequency range in the system. When oscillations of similar frequencies manifest in the sending AC system, resonance in the DC system becomes alikely outcome, causing CF in the receiving end. Without timely control of this resonance, it triggers switching of constant current control and constant extinction angle control at the inverter side. An uncontrolled extinction angle during control switching will likely cause subsequent CFs, even DC blocking. Therefore, discovering the mechanism of such CF is important to contribute to the operational safety and stability of HVDC transmission systems.
Firstly, the whole process of the CF caused by the sending end oscillation is analyzed using simulation curves from the CIGRE benchmark HVDC system. According to the simulation results, four different stages have been identified after the first detection of the sending end oscillation.
Secondly, the eigen values of the CIGRE benchmark HVDC system are calculated using a small-signal stability model, and the inherent oscillation modes of the system are determined. A special mode, in which the sending end current controller plays a pivotal role, is identified based on participation factor values. The frequency of the special mode of the CIGRE benchmark system is 1.2 Hz, located in the low-frequency range. When the sending system encounters oscillations of nearby frequencies, resonance is easily induced, causing corruption in the sending end controller. The quasi-steady-state equations are used to derive the DC current equation to analyze the rise of DC current after resonance, resulting in a fall in the extinction angle and triggering the first CF. Then, the control equations are used to analyze the switching process of the system controller and elucidate the mechanism through which control switching leads to subsequent CFs.
Finally, the theoretical analysis is validated by simulations in PSCAD/EMTDC. A series of oscillations with different frequencies are tested, i.e., 0.1 Hz, 0.6 Hz, 0.8 Hz, 1.2 Hz, 2.5 Hz, 7.6 Hz, and 66 Hz. The results show that oscillations in the low-frequency band of 0.1~2.5 Hz can trigger resonance in the system, leading to CF at the receiving end. Moreover, the first CF is observed around 0.5 s after injecting the 1.2 Hz oscillation into the sending end system, faster than other oscillations from 0.1 Hz to 2.5 Hz, given that 1.2 Hz is the inherent oscillation frequency. Additionally, oscillations of 7.6 Hz and 66 Hz donot cause CFs, although they are also inherent oscillation frequencies. Their participation factors indicate that these two inherent oscillations are unrelated to the system controller.
The following conclusions can be drawn from the paper: (1) Four stages exist after the sending end oscillation occurs, and CFs will happen if the frequency is in a specific range. (2) The root cause of CFs arising from sending end oscillations is the resonance between these oscillations and the inherent oscillation modes of the HVDC system, inducing fluctuations in electrical and control quantities. The rise of DC current induces the first CF, and the control switching leads to subsequent CFs. (3) The key to preventing CFs caused by sending end oscillations is to tune the system parameters so that the inherent oscillation mode has a strong damping ratio in the common frequency band.
keywords:High voltage direct current, sending end oscillation, commutation failure, mechanism analysis
DOI: 10.19595/j.cnki.1000-6753.tces.222381
中图分类号:TM614
国家重点研发计划“储能与智能电网技术”重点专项2022年度项目“无常规电源支撑的大规模新能源发电基地稳定运行及直流送出关键技术”(2022YFB2402700)资助项目。
收稿日期 2023-01-03
改稿日期 2023-05-10
郑 乐 男,1989年生,讲师,研究方向为人工智能及其在电力系统稳定与控制的应用。E-mail: zhengl20@ncepu.edu.cn
刘崇茹 女,1977年生,教授,博士生导师,研究方向为交直流混合系统分析与仿真、运行与控制。E-mail: chongru.liu@ncepu.edu.cn(通信作者)
(编辑 郭丽军)