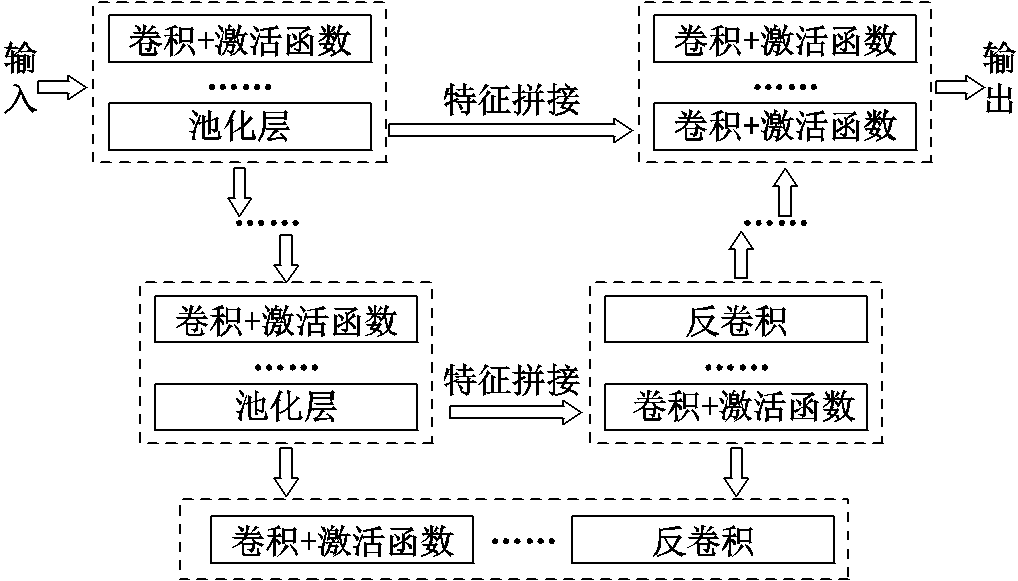
图1 U-net CNN基本结构
Fig.1 Architecture of U-net CNN
摘要 有限元法（FEM）是物理场分析常用的方法，但庞大的求解自由度导致FEM计算成本很大。针对FEM计算时间长的问题，构建一种基于U-net卷积神经网络的物理场快速计算方法，将样本数据通过栅格化或点云化处理后作为神经网络的输入和标签数据，通过网络训练实现物理场的快速计算并研究该方法在电磁场计算中的应用。结果表明，该方法能准确有效地预测电势、电场强度、磁感应强度等物理量的分布，且预测时间较FEM仿真计算时间大幅缩短。同时，通过合理选择数据集大小，即使在小数据集下也能有较高的预测精度。
关键词：电磁场 卷积神经网络 快速计算 有限元法
在工程案例设计环节，为了求解研究对象的物理场，需要利用有限元法（Finite Element Method, FEM）建模分析，庞大的求解自由度导致FEM的计算时间较长[1-4]，尤其是在求解多物理场耦合的三维问题中。文献[5]针对快速真空断路器的FEM仿真时，整体计算区域的网格剖分数量达到4 776万个，文献[6]在分析特高压直流换流阀厅时，网格单元数更是达到了9 100万个，求解时间也长达22.5 h。而随着模型复杂度的增加，当对象参数发生变化时，即使是细微变化，通常也会重新建模分析[7-8]。当设备投入使用后发生故障时，为及时找出故障的位置及故障发生原因，仍需使用FEM对设备工作状态进行仿真分析，并结合采集到的设备状态信息反演进行故障诊断[9]。此外，在设计类问题中，例如，电机参数优化设计[10]，通常需要数千次迭代计算才能寻找到最优解，若采用有限元方法则需要数月才能完成，严重影响项目进度。而在电机数字孪生建模[11]、风电场尾流实时计算[12]、变压器热点温度实时计算[13]等方向，需要根据传感器数据对设备状态进行评估，若采用计算时间较长的有限元方法，则故障可能会因无法被及时排除而引发更大的危害。各界学者也提出了诸如Kriging模型[10]、降阶模型[11,13]的方法尝试解决，但是这些方法往往需要大量的数据或是复杂的数学推导。
近年来，深度学习方法由于能处理复杂映射关系而在计算机工程领域迅速发展，将深度学习方法同物理场数值模拟结合以实现快速仿真计算已经成为一种可能[14-16]。目前已有国内外学者在某些领域进行了一些研究，如在弹塑性力学[16]、流体力学[17]、超弹性材料[18]、温度场分析[19]、声学仿真[20]等。其中文献[16]使用卷积神经网络（Convolutional Neural Network, CNN）完成了对von-Mise应力场的高效预测；文献[17]使用U-net网络对翼型流动雷诺平均方程的解进行了快速模拟；文献[18]以肝脏为例对神经网络在超弹性材料仿真中的应用进行了研究；文献[19]利用编码器-解码器结构网络实现了对建筑结构温度场的快速预测；文献[20]使用深度卷积神经网络对介孔材料的吸声性能实现了高效计算。通过使用上述方法，对于有限元计算中耗时长的问题，也可以有效解决。
“编码器-解码器”（Encoder-Decoder）结构[21]最早用于机器翻译领域，目前应用最为广泛的是全卷积神经网络[22]（Fully Convolution Networks, FCNs）和在FCNs结构的基础上加入跳跃连接结构的U-net卷积神经网络（U-net CNN）。本文选择U-net CNN作为快速计算的底层结构，并与FCNs-16进行比较。
本文将FEM和U-net卷积神经网络结合，构建了一种基于深度学习的物理场快速计算方法，研究其在电磁场中应用的有效性。首先根据实际物理模型使用有限元法对研究对象进行建模仿真计算；其次将获取到的仿真结果导出，按模型几何参数、边界条件及物理场求解结果等进行划分、栅格化和点云化处理，并保存为数据集；之后使用U-net CNN进行网络参数训练，通过训练好的模型实现对研究对象物理场的快速计算。通过该方法的预测准确率以及同仿真软件仿真时长的对比，说明在保证准确率的前提下，可以实现对电磁场的快速计算，同时通过合理选择数据集大小，即使在小的数据集下也能有较高的预测精度。
CNN作为一种深度学习模型，其卷积操作能够有效地提取数据中的高维非线性特征[14]。已有学者将其应用在加速求解有限元单元刚度矩阵问题中，使用有限元计算结果作为训练样本进行网络参数训练，实现实时计算单元刚度矩阵[15]。因为卷积神经网络完成训练后，网络参数已经固定，再次对新的输入进行预测计算时即可实现实时输出。
作为卷积神经网络中的一种经典模型，U-net CNN以其独特的结构和高效的性能被广泛用于图像处理领域，近年来在计算工程领域也被用于加快计算速度[17,19]。图1为U-net CNN的基本结构，主要包括卷积层、激活函数层、池化层和反卷积层等。
图1 U-net CNN基本结构
Fig.1 Architecture of U-net CNN
U-net CNN是一种典型的“编码器-解码器”结构，其通过“编码器”对输入不断进行下采样以提取特征，通过“解码器”上采样而得到与输入尺寸相同的输出结果。此外，U-net CNN使用特征拼接操作将下采样提取到的浅层特征与上采样提取到的深层特征进行融合，使得各个层级的信息得以保留，确保网络能够更好地提取数据所包含的特征信息。而相较于目前部分卷积神经网络，U-net CNN层数适中，网络参数量较少，进而在训练及预测时能够有较快的运行速度[23]。
一种基于U-net CNN的物理场快速计算方法，是基于FEM求解结果构建出数据集，将数据放入U-net CNN进行训练，通过网络参数训练得到数据中所包含的深层非线性关系，同时这种关系会以U-net CNN权重参数的形式储存，再次给定输入即可快速预测物理场计算结果。该方法的结构如图2所示，对于任意研究对象，该方法均包括模型仿真、数据生成、网络训练和预测结果四个部分。
图2 基于U-net CNN的物理场快速计算
Fig.2 Principle of fast calculation of physical field based on U-net CNN
1）模型仿真：为获得有限元仿真计算的结果，需要根据研究对象建立近似的二维或三维等效几何模型，定义几何模型内各几何区域的材料参数，根据所研究物理场确定控制方程、边界条件以及为模型施加载荷。控制有限元网格剖分求解域，求解网格剖分后联立得到的有限元方程组，即得到物理场问题的数值解。
2）数据生成：将FEM仿真计算的结果导出为数据集，每一个样本数据均包含输入和输出两部分。输入部分为易于获得或测量的参数，如模型的几何参数、加载的边界条件和载荷等；输出则为对应的有限元法物理场求解结果。最后，将导出的数据集按8:2的比例划分为训练集和测试集。
考虑到计算成本和计算精度，可以按需求选择模型的部分区域，仅导出该区域的输入和输出，并按栅格形式导出为数据集。在导出时，每个栅格点的值对应模型中该栅格点位置的参数值。
二维栅格数据生成如图3所示。在导出模型几何参数时，对模型中每个几何区域编号，处于第i号区域的栅格点数据用数值“i”表示。数据导出时根据选区大小、精度要求、硬件能力等合理选择栅格密度，因栅格密度越大，单个样本数据所占内存空间也越大，计算成本也会相应地增加。
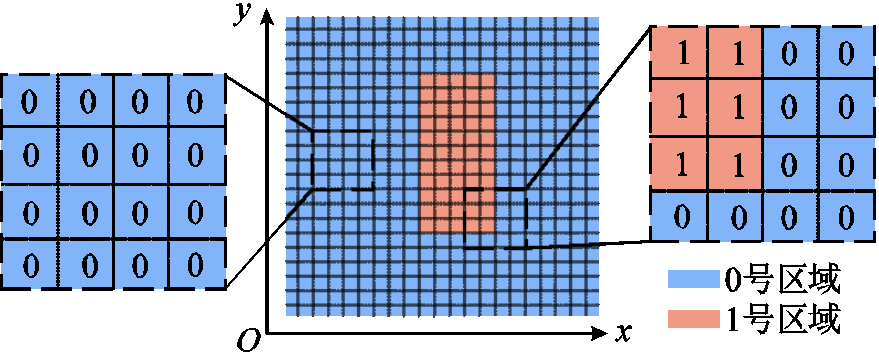
图3 二维栅格数据生成
Fig.3 Generation of 2-D raster data
对于三维模型，导出的栅格数据又称体素（Volumetric）数据，这是三维数据的一种表述形式[24]，显然，三维栅格数据会比二维栅格数据占用更多空间。点云数据即三维空间中能够代表物体表面特性或其他特征的点的集合，这也是三维数据的一种表述形式[24]。点云数据生成的方法如图4所示，其用海量的点去表现出物体的外轮廓，同时每个点的值包含了该点的三维坐标信息以及其他能够表征物体特征的量，如点A1的值就包含了其坐标(x1, y1, z1)以及特征量(v1, v2,…)。为了更方便地展示本方法与有限元方法在精度上的对比，本文只导出物体的表面数据。需要补充的是，点云数据保证了采样点均位于模型内部，所获得的数据均为有效数据。
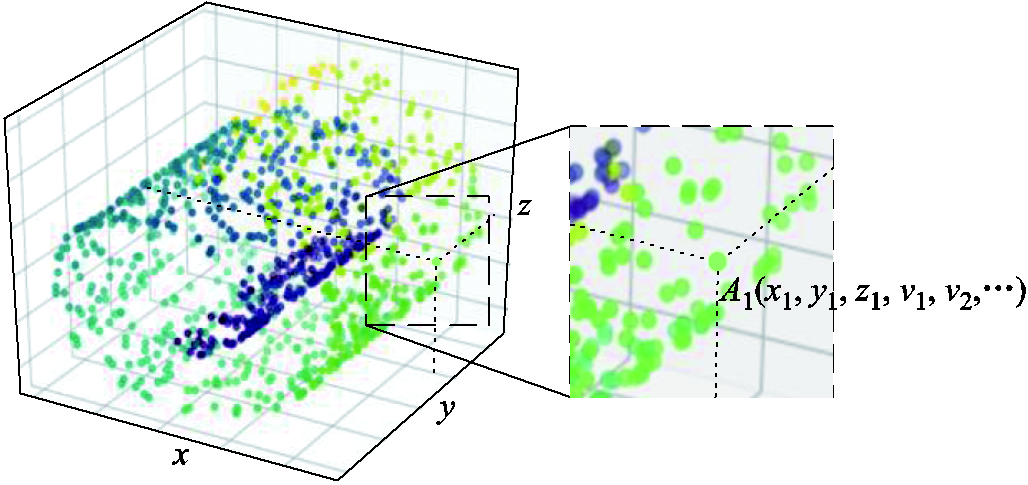
图4 点云数据生成
Fig.4 Generation of point cloud data
3）网络训练：根据建立的FEM仿真模型维度，构建二维或三维U-net CNN，设置训练时的学习率、学习率衰减、批量大小、迭代周期、损失函数等超参数。网络配置好后，使用训练集对网络进行训练，训练集中80%用于训练，20%用于训练时验证。
所构建的U-net CNN采用空洞卷积核，在卷积操作时可以获得更大的感受野，有利于提取更大范围内的特征信息；在“解码器”部分应用上采样加卷积的方式替代原本的反卷积操作，避免反卷积后“棋盘现象”的出现[17]；并且在每两层之间使用Batch Normalization和LeakyReLU激活函数，防止训练过程中梯度消失，同时加快网络的收敛速度。
网络训练过程中所用的损失函数为Huber损失函数，该损失函数通过超参数δ被分成两种情况：当训练误差小于δ时，Huber损失函数更接近于L2损失函数；反之，更接近于L1损失函数。通过这种分段的方式，Huber损失函数结合了L1和L2两种损失函数的优点，在误差较大时不至于梯度过大，误差较小时也处处可导，能够加快收敛速度[25]。
L1、L2损失函数定义为
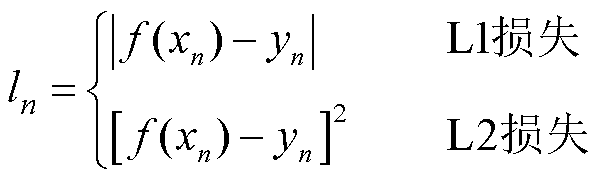（1）
Huber损失函数的定义为
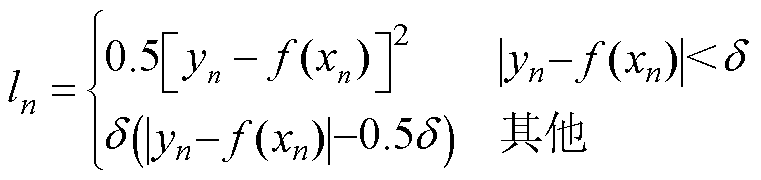（2）
式中，ln为每个批量中第n个数据的损失值；xn、yn与f(xn)分别为第n个数据的输入值、真实值与对应输入的网络预测值；δ为超参数。
4）预测结果：使用测试集对训练好的网络进行测试，输出测试集中样本的物理场预测结果，并比较网络预测结果与FEM计算真实结果，对模型性能进行评估分析，实现对物理场的快速计算。通过预测准确率PACC对模型性能进行评估。PACC的计算公式为
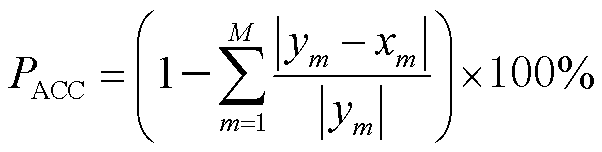（3）
式中，m为数据编号；M为数据总数。
使用U-net CNN进行快速计算的流程如图5所示。
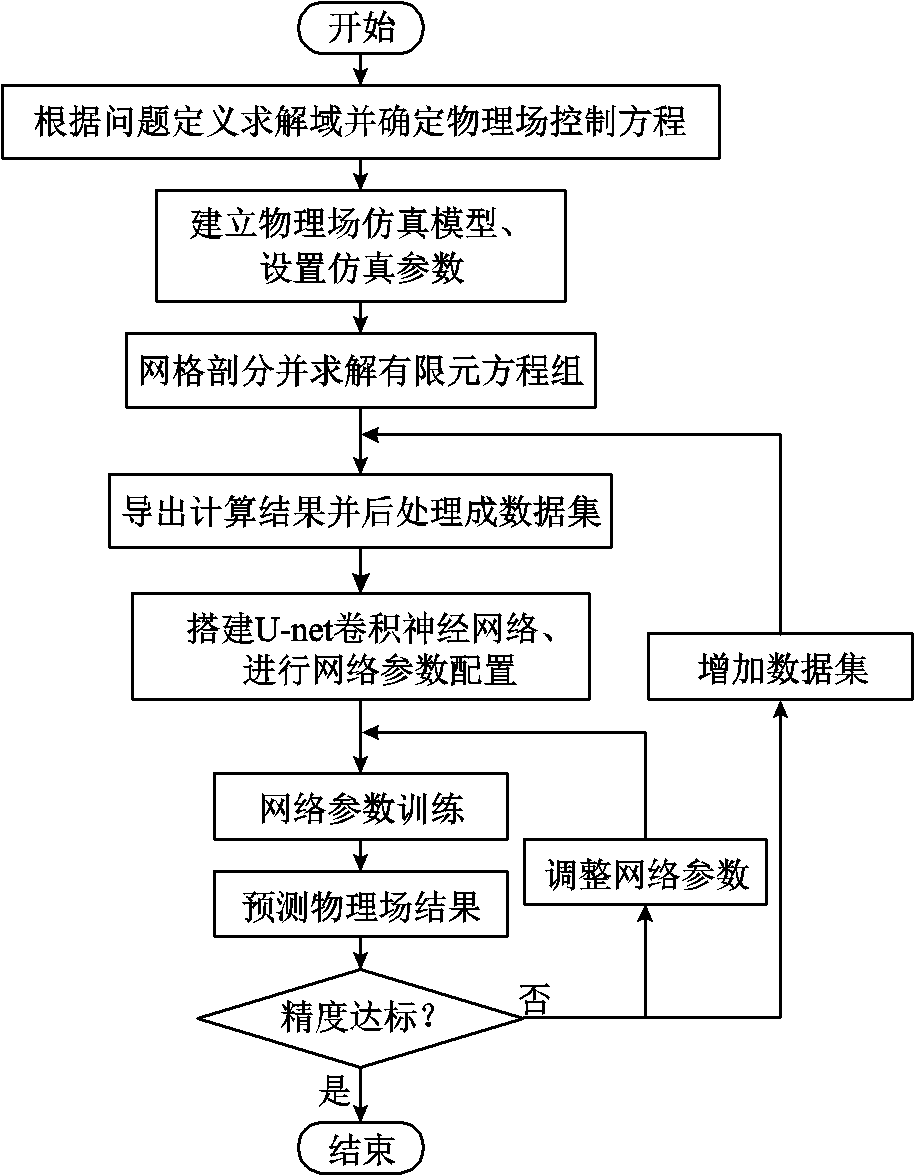
图5 U-net CNN算法流程
Fig.5 Algorithm flow chart of U-net CNN
首先，确定求解域下的控制方程；其次根据所研究对象建立二维或三维仿真模型，对模型设置材料参数、边界条件、载荷等；然后对模型进行网格剖分，控制网格剖分精细程度，求解剖分后得到的有限元方程组而获得FEM计算结果；之后将计算结果，如几何参数、加载电压、电势分布、电场强度等导出为数据集；再将数据投入设计好的U-net CNN进行训练，不断优化网络参数完成训练；最后使用测试集对网络进行测试，如若测试精度未达到要求，则重复上述步骤，调整参数配置或增加数据集再次训练，直至精度符合要求。
工程中为了简化计算，会尽可能地将三维模型转换为二维轴对称模型，例如，绝缘子串[26]、套管[27]、电抗器[28]等。复合绝缘子是电网建设中用于维系电力传输安全绝缘性能的极其重要的部件之一，而均压环作为另一个与绝缘子共同配合以提高绝缘子绝缘性能的重要部件，可以提升输电线路的安全可靠性，但是其模型较为复杂。基于此，本文选择复合绝缘子均压环作为二维轴对称模型的代表，对其静电场进行分析。
采用1 100 kV特高压直流输电线路所使用的复合绝缘子及均压环，大均压环的型号为FJ-1000HSZ-600。分析时可以将绝缘子串和均压环整体等效为二维轴对称模型，如图6所示，其中小均压环的大、小半径与大均压环类似，这里未予展示。绝缘子串模型总长度为9.75 m，低压端金具和均压环与外空气包外表面接地，高压端金具和均压环施加898.15 kV（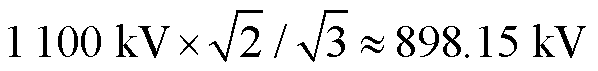
）电压。为了模拟绝缘子实际在线路中运行状态，设置其离地高度为46 m。改变高压端大、小均压环的尺寸及摆放位置，并以高压端均压环附近电势及电场强度分布情况作为后续研究对象。
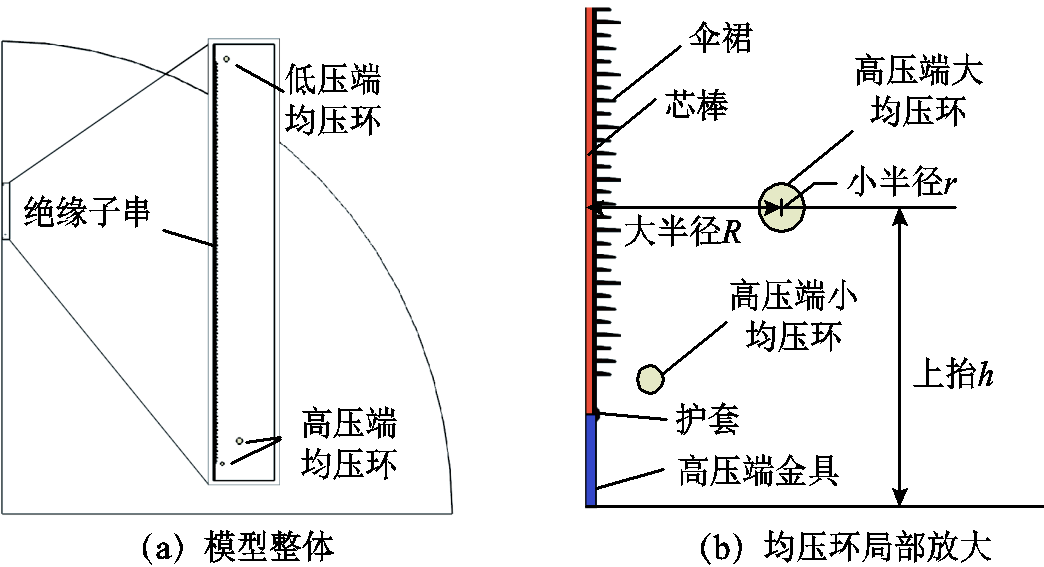
图6 绝缘子均压环二维仿真模型
Fig.6 2D simulation model of the insulator and shield
采用有限元分析软件COMSOL Multiphysics 5.6进行网格剖分和物理场计算。为了兼顾计算成本和准确度，采用分区域剖分的网格剖分方式，绝缘子串内部和贴近绝缘子串的部分采用“超细化”网络剖分大小，其余部分采用“细化”网格剖分大小。共剖分57 593个单元。
由于工程实际中更加关注高压端物理场的分布，因此选择高压端均压环附近的127 cm×127 cm范围内的电势和电场强度分布作为研究的内容。为了能够更好地反映整体空间的分布，在COMSOL中采用密度为128×128的栅格进行导出。改变均压环结构参数并在COMSOL中多次仿真，生成数据集。一共导出9个参数，分别为几何模型参数；大均压环大半径R、小半径r、上抬h；小均压环大半径R、小半径r、上抬h；电势和电场强度分布。其中R、r、h的变化范围见表1。几何模型参数是按照模型的不同材料参数进行分类，分成0～3四部分：空气的相对介电常数er=1；金属为大、小均压环，e r=1010；硅橡胶包括伞裙、护套部分，er=3.5；环氧芯棒即芯棒，e r=4.95。
表1 均压环结构参数变化范围
Tab.1 Variation range of the shieldstructure parameters
参数变化范围 大均压环R/m[0.55, 0.70] r/m[0.06, 0.08] h/m[0.50, 0.80] 小均压环R/m[0.20, 0.30] r/m[0.02, 0.03] h/m[0.08, 0.12]
数据集大小方面，大均压环中，等距选取4组R（0.55 m, 0.6 m, 0.65 m, 0.7 m）、3组r、4组h；小均压环中，等距选取3组R，3组r、5组h，仿真计算4×3×4×3×3×5=2 160组数据。
取数据集中的第一组数据，不同输入通道输入输出的栅格图像如图7所示。需要说明的是，改变R、r、h参数都可以在几何模型参数中显示，例如，大均压环r从0.06 m变为0.08 m，则图7点画线框中大均压环（金属）的圆形面积会变大。所以本文考虑两种输入通道，单通道输入仅考虑几何模型参数，尺寸为1×128×128；多通道除几何模型参数外，还包括大小均压环R、r、h参数。这里的通道指n×128×128的第一个参数，若n=1则为单通道，n＞1为多通道。显然一组数据中R、r、h参数值为常数，但卷积神经网络的输入要求尺寸的统一，所以将大、小均压环R、r、h展开为6个128×128的栅格数据，每个128×128栅格均为固定常数值，如图7下半部分所示。多通道总的输入尺寸为7×128×128。单通道和多通道的输出均为电势和电场强度。
图7 绝缘子均压环神经网络输入输出
Fig.7 Neural network input and output of the insulator and shield
为了缩小样本所占的内存空间以便于加速训练过程，将大、小均压环的结构参数利用高斯分布融合在一起。高斯分布的计算公式为
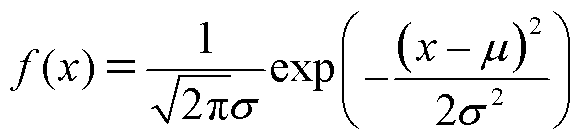（4）
首先由式（4）生成一个均值为0，标准差为h的高斯分布序列x～N(0, h)，序列长度为128。其次调整序列的幅值，使分布序列的最大值fmax为rR。再将获得的一维序列扩展成二维矩阵分布，如图8所示。中心处为高斯分布最大值rR，由内向外呈高斯分布递减。需要强调的是，R、r、h是均压环的参数，融合后的图像参考图8右侧的正方形区域。
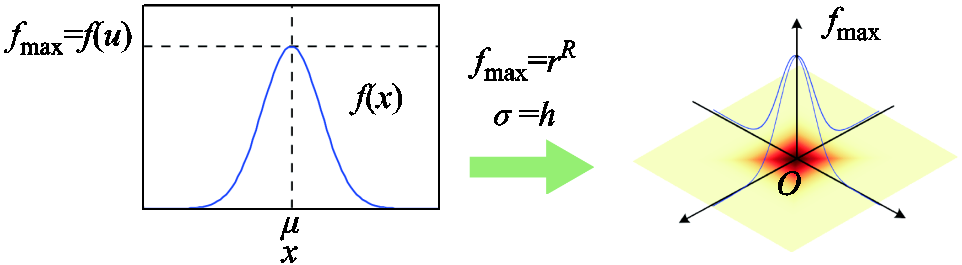
图8 均压环特征信息高斯分布融合过程
Fig.8 Gaussian distribution fusion process of characteristic information of shield
按照该方法对大均压环的R、r、h参数和小均压环的R、r、h参数分别进行融合。大均压环数据由原来的3×128×128变为1×128×128，小均压环同理，由此减少了内存空间。融合完成后，多通道的输入尺寸为3×128×128。
考虑单输入和多输入通道下的网络训练情况，其中单输入为模型几何区域参数，多输入为模型几何区域参数、高斯分布后大均压环特征信息和高斯分布后小均压环特征信息。
选取学习率为0.001，批大小为4，迭代周期为100的超参数，选用Huber损失函数，随机从所有数据集中选择100组样本为测试集，剩余2 060组为训练集。并采用Huber函数作为损失函数，在Python编程语言下的PyTorch框架下进行训练并使用GPU进行加速，开发环境为PyCharm 2020。所使用的计算机硬件见表2。单输入通道验证集的预测准确率随迭代周期的变化曲线如图9a所示，共耗时1 h 44 min；多输入通道如图9b所示，共耗时2 h 8 min。
随着迭代周期的提升，单通道和多通道的预测准确率均先逐渐提升，最后趋于平稳。最终单通道在验证集上的电势和电场强度预测准确率分别为99.53%和97.99%，多通道的分别为99.65%和98.82%。结果表明在相同的迭代周期下，单通道训练时间更短，多通道精度更高，且在训练初期即可达到较高的精度。
表2 硬件参数
Tab.2 Hardware parameters
名称参数 CPUIntel Xeon(R)E5-2637 v2 3.5 GHz 内存64 GB DDR3 1333 MHz GPUNVIDIA RTX2070(8 GB)
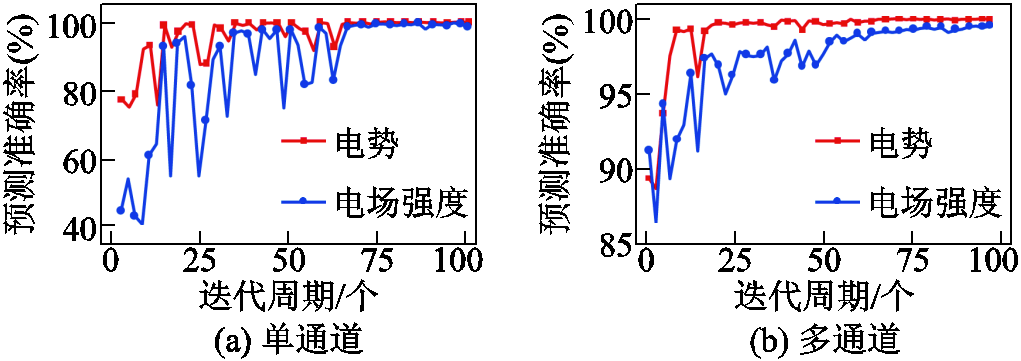
图9 绝缘子均压环精度曲线
Fig.9 Accuracy curves of the insulator and shield
首先选取学习率为0.001，批大小为4，迭代周期为100，损失函数为Huber。随机选择两阻测试集中的数据，单通道和多通道预测结果如图10所示。
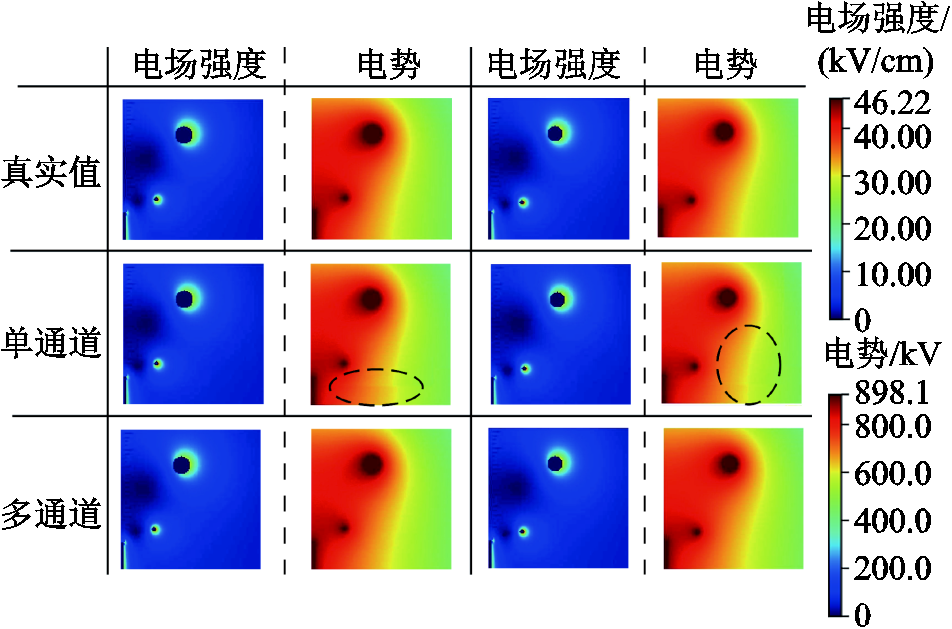
图10 绝缘子均压环不同通道预测结果
Fig.10 Prediction results of the insulator and shield under different input channels
结果表明，在电势的预测中，单通道下网络预测的结果存在物理场过渡不平滑、畸变及断层的现象，如图10中虚线框所示。多通道预测结果相对更好，分布较为均匀。电场强度预测中两种通道相差很小。
采用相同的网络结构，单通道U-net CNN系列网络和FCNs-16网络的预测准确率随迭代周期的变化如图11所示。其中，FCNs-16网络是将最后一次卷积的结果2倍上采样后与倒数第二次池化后的结果进行结合，再进行16倍上采样恢复至输入尺寸大小。结果表明，在电势和电场强度的计算中，U-net CNN的表现均好于FCNs-16。U-net CNN在使用Huber损失函数时电势准确率达到最高为99.88%，在使用L1损失函数时电场强度准确率达到最高为99.52%；FCNs-16在使用L2损失函数时电势准确率达到最高为99.15%；在使用Huber函数时电场强度准确率达到最高为98.33%。
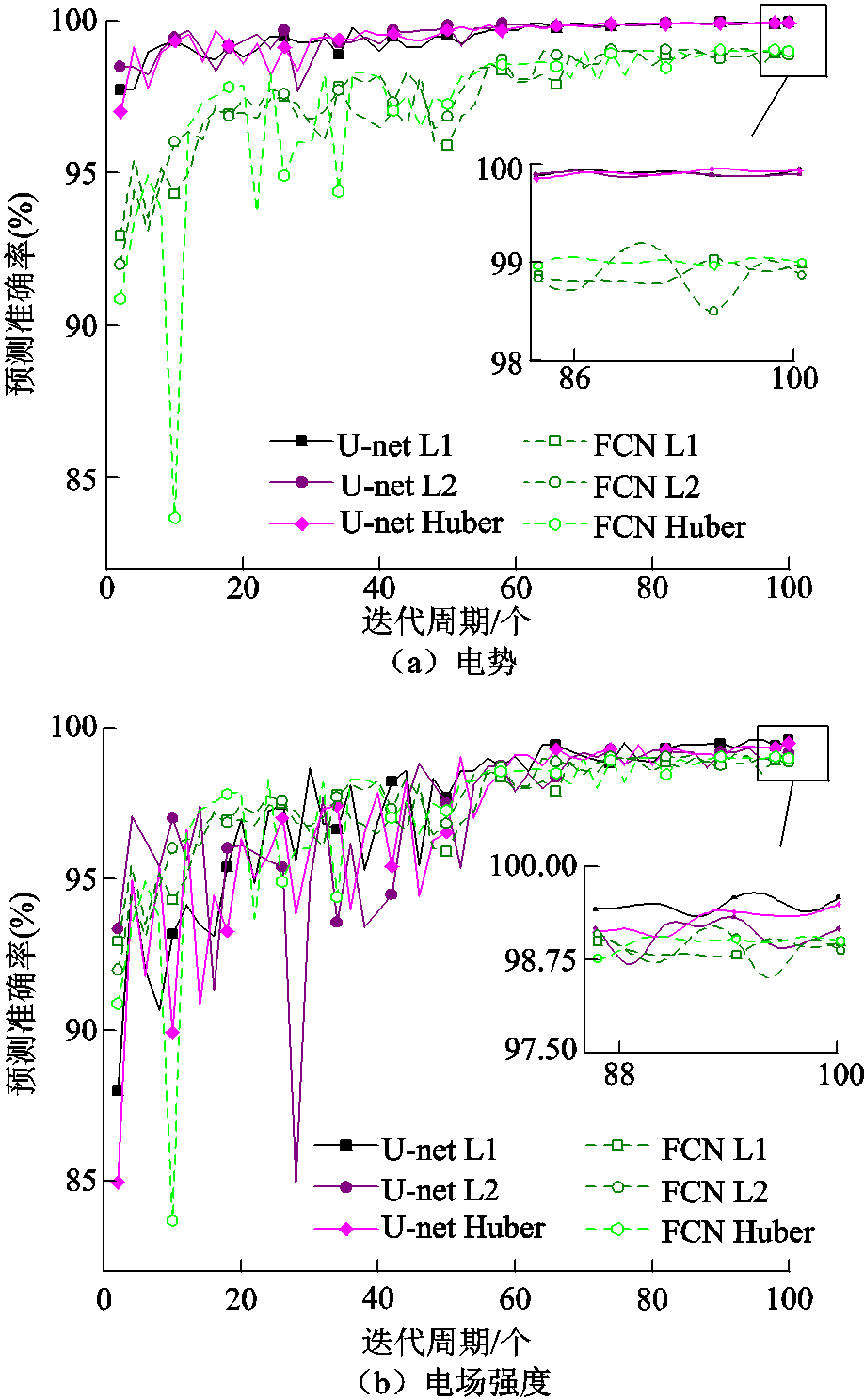
图11 不同网络下绝缘子均压环单通道精度曲线
Fig.11 Accuracy curves of the insulator and shield with single-channel under different networks
多通道U-net CNN系列网络和FCNs-16网络的预测准确率随迭代周期的变化如图12所示。结果表明FCNs-16的准确率有较大幅度的上升但仍不如U-net CNN。其中U-net CNN在使用L1损失函数时电势和电场强度的准确率均达到最高，分别为99.93%和99.52%。FCNs-16在使用L2损失函数时电势准确率达到最高为99.80%；在使用L1损失函数时电场强度准确率达到最高为99.24%。
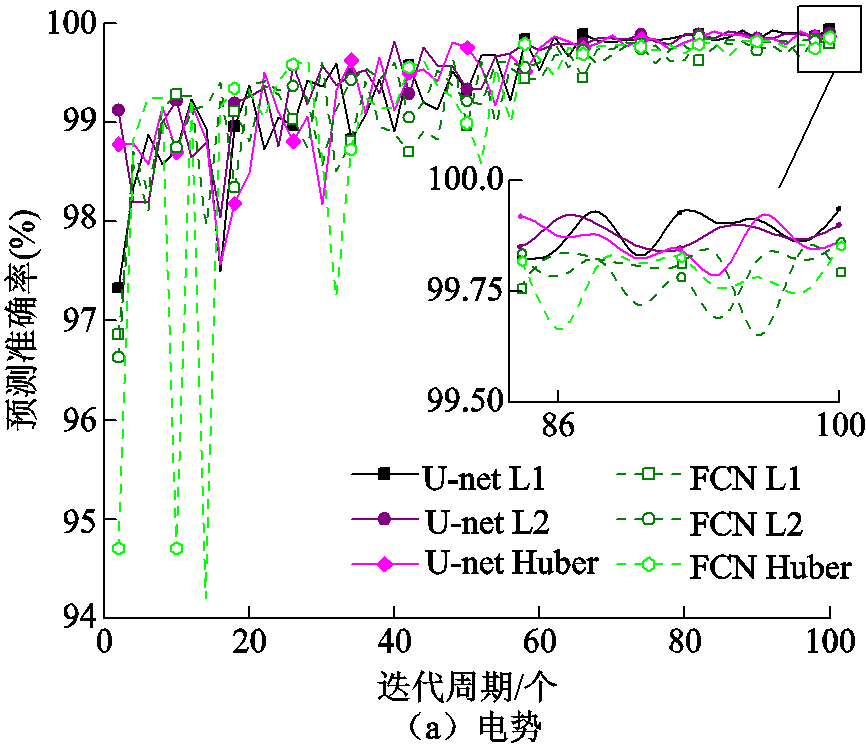
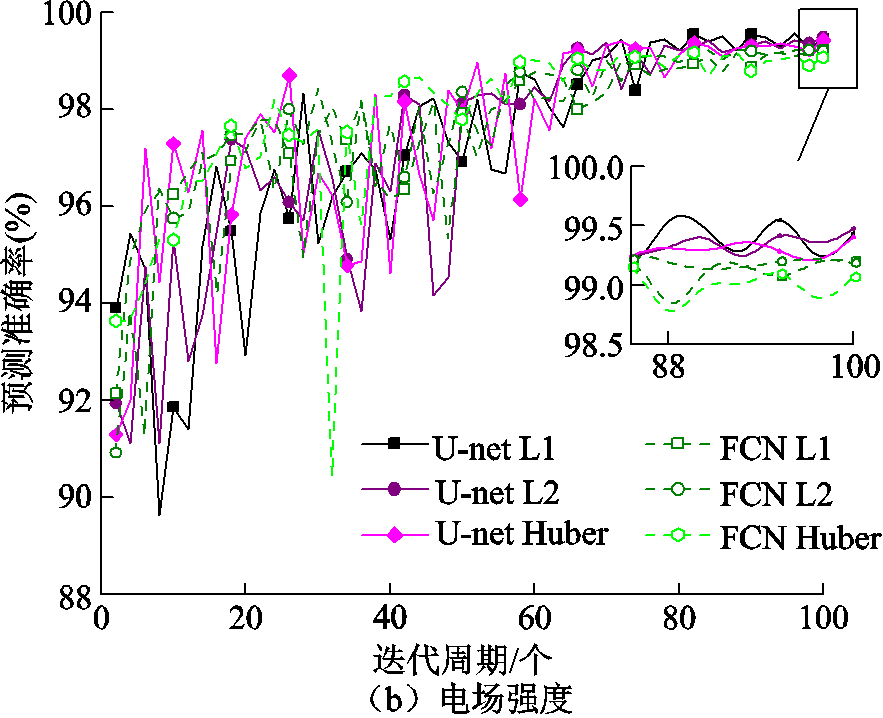
图12 不同网络下绝缘子均压环多通道精度曲线
Fig.12 Accuracy curves of the insulator and shield with multi-channel under different networks
为了保持与有限元计算所用硬件的一致性，神经网络在预测时均采用CPU进行运算，预测时间包括将神经网络模型（.pth文件）加载到Python中和将输入数据送入神经网络进行计算并输出结果的时间。U-net CNN单通道计算时间为0.017 s，多通道为0.016 s；FCNs-16单通道为0.039 s，多通道为0.042 s，均远远小于有限元计算。
最后，研究训练集样本数和预测准确率之间的关系。如图13所示，多通道下的模型拟合效果相比单通道更好，当数据集为306组时仍有90%以上的预测准确率，即使数据集仅有203组，网络的预测准确率也有85%以上。说明该模型在多输入通道下即使在数据集较少时也能有很好的训练效果，通过合理调整数据集大小能够取得较高的预测准确率。
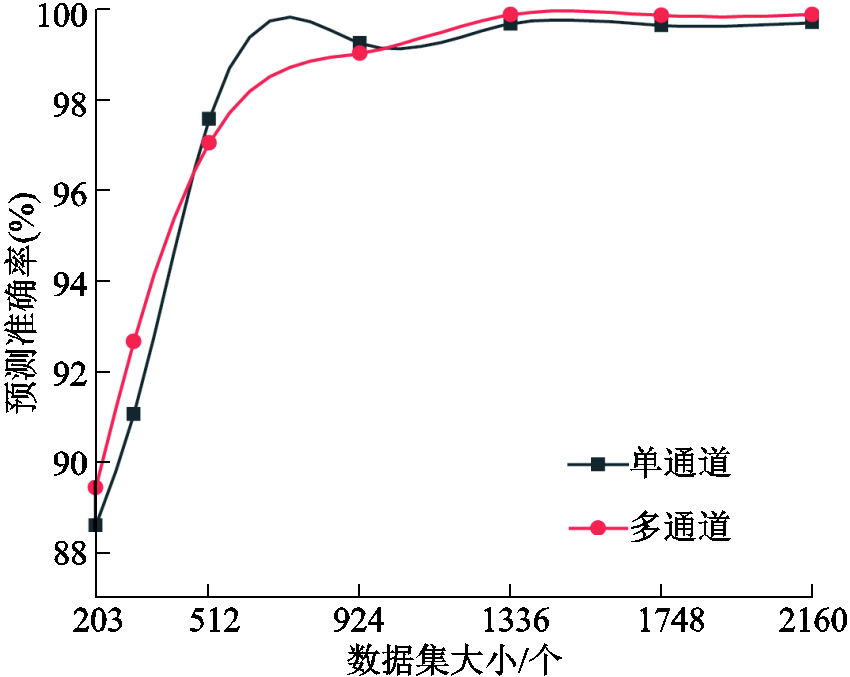
图13 绝缘子均压环不同数据集大小下的训练效果
Fig.13 Training performance of the insulator and shield under different dataset sizes
部分电力设备在特定工况下可以简化为二维轴对称模型，但大部分电力设备无法简单等效成二维问题，变压器场路耦合问题[29]便是其中之一。本文以单相变压器为算例，结合场路耦合原理，对变压器时变电磁场进行分析。
采用单相E磁心变压器，其三维模型如图14所示。采用场路耦合的方式将模型和外部模拟电路连接，其中一次绕组电阻值为100 Ω，匝数为30匝，二次绕组的电阻值为10 kΩ，匝数为3 000匝，铁心的材料为软铁。采用瞬态分析的方式仿真变压器在输入电压为Va、频率为50 Hz时的磁场，并以在不同输入电压下t =0.05 s时刻的磁场分布情况作为后续研究对象。
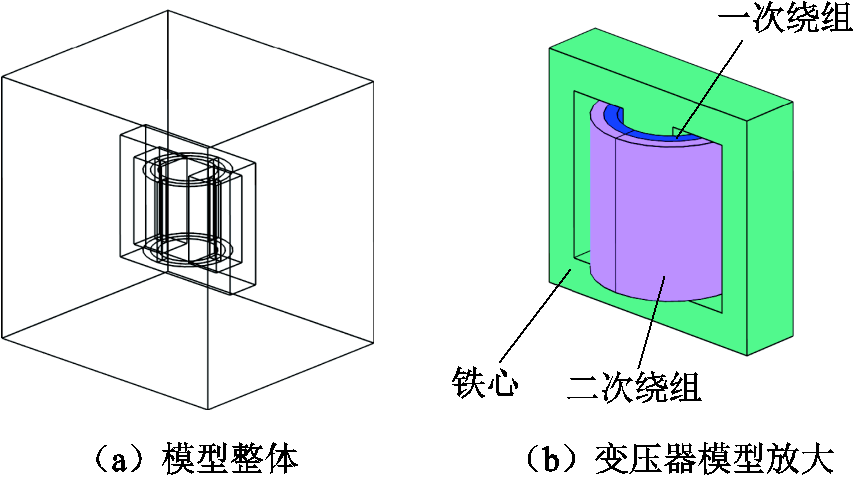
图14 变压器三维仿真模型
Fig.14 3D simulation model of the transformer
使用COMSOL进行网格剖分和物理场计算。采用分区域剖分的网格剖分方式，变压器部分网格大小设置为“超细化”，并设置最大和最小单元格大小分别为6 mm和4 mm；外部空气域网格大小设置为“较粗”，共剖分57 649个网格。
考虑到变压器为三维模型，结构较为复杂，因此考虑点云数据格式进行存储。通过仿真软件将采集到的变压器仿真结果的点云数据点导出，每个点云数据点包含点的空间坐标(x, y, z)、输入电压Va的大小以及点的磁感应强度的大小。通过合理设置数据点显示透明度α，可以看清更多细节处的点云数据情况。不同透明度下变压器磁场局部放大如图15所示，当α为0.5时，可以看到大部分的数据点。因此本文选择α=0.5作为后续数据的生成和展示。
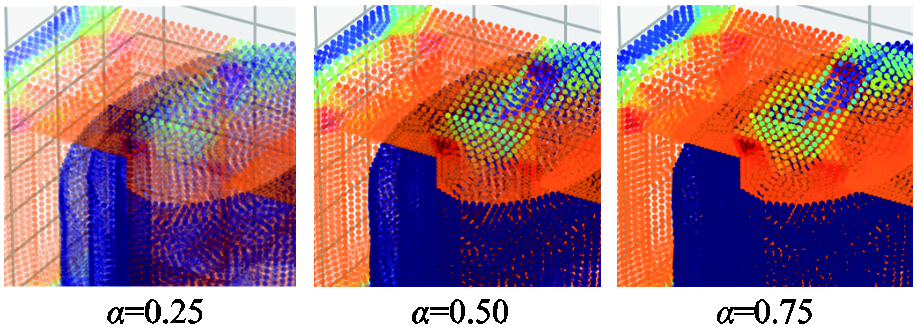
图15 不同透明度下变压器磁场局部放大
Fig.15 Zoom in transformer magnetic field under different transparencies
输入电压的Va变化范围为[200 V, 500 V]，每隔1 V记录一次数据，由此一共生成301组数据，每组数据包含32 561个数据点。
考虑到研究对象是三维模型，需要将所获得的一维数据点再塑形成三维数据。在进行卷积操作时，为了方便卷积核进行“扫描”操作，会将输入数据保持为正方形或正方体，且输入的尺寸一般为2的指数幂，例如32、128和256等。如图16所示，由于32 561个数据点接近32 678=32×32×32，所以选择再塑形后的数据尺寸为32×32×32。这就需要在原有数据上填充207个数据。这些点均为原有数据第0个数据点的值。需要说明的是，这种填充预处理的操作不会影响神经网络的训练效果[30]。
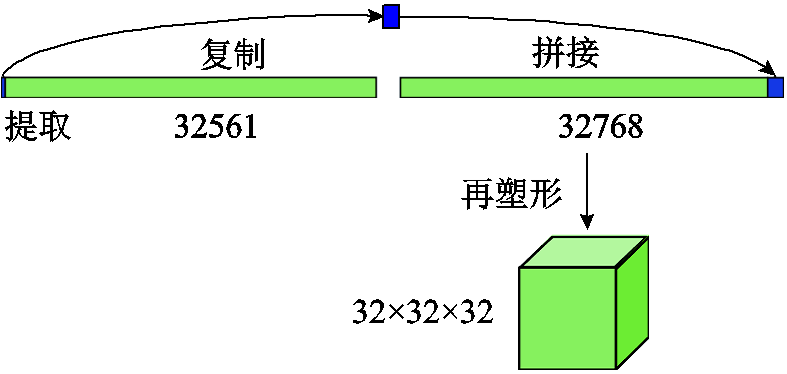
图16 点云数据再塑形操作过程
Fig.16 Reshaping operation process of point cloud data
再塑形完成后，U-net CNN的输入尺寸为4×32×32×32。其中4为通道数，包括了坐标x、坐标y、坐标z、输入电压Va四部分。与绝缘子均压环一致，电压Va在每个32×32×32的区域中为固定常数值。值得注意的是，这并未改变变压器的结构，添加坐标信息是为了让神经网络学习到模型的位置信息。二维栅格数据是将整个模型区域均匀地划分成一个个小正方形，即128×128的栅格中包含了模型的位置信息。点云数据是由一个个点组成的，点的位置由坐标表示，将其再塑形是为了将输入变为正方体的形式，使得卷积神经网络具有更大的感受视野，加快计算速度。
首先选择学习率为0.001、批大小为4、迭代周期为200的超参数，将301组数据按照9:1的比例划分训练集和测试集，即271组用于训练，30组用于测试。使用L1损失函数，损失值和验证集的预测准确率随迭代周期的变化曲线如图17所示。
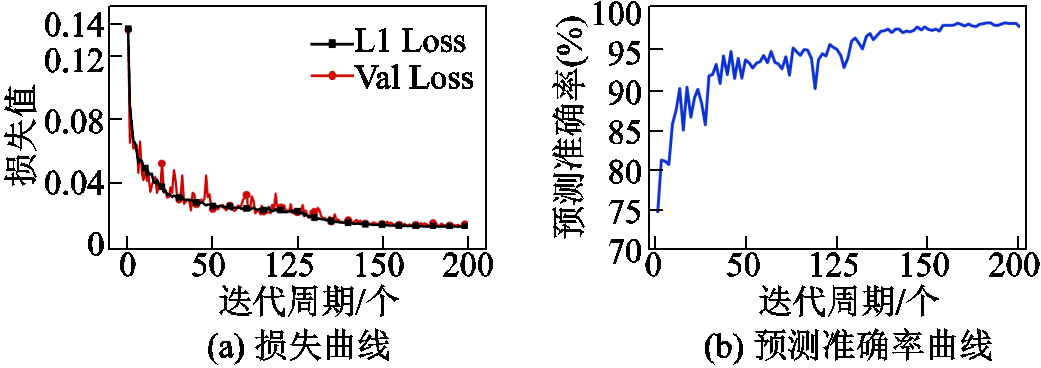
图17 变压器结果曲线
Fig.17 Result curves of transformer
从损失曲线可以看出模型的收敛速度很快，在训练到最后一个周期时，训练集损失为0.004 388，验证集损失为0.005 171，均已下降到一个较小的值，且没有出现欠拟合现象。从验证集中随机选取3组数据，其预测结果如图18所示。
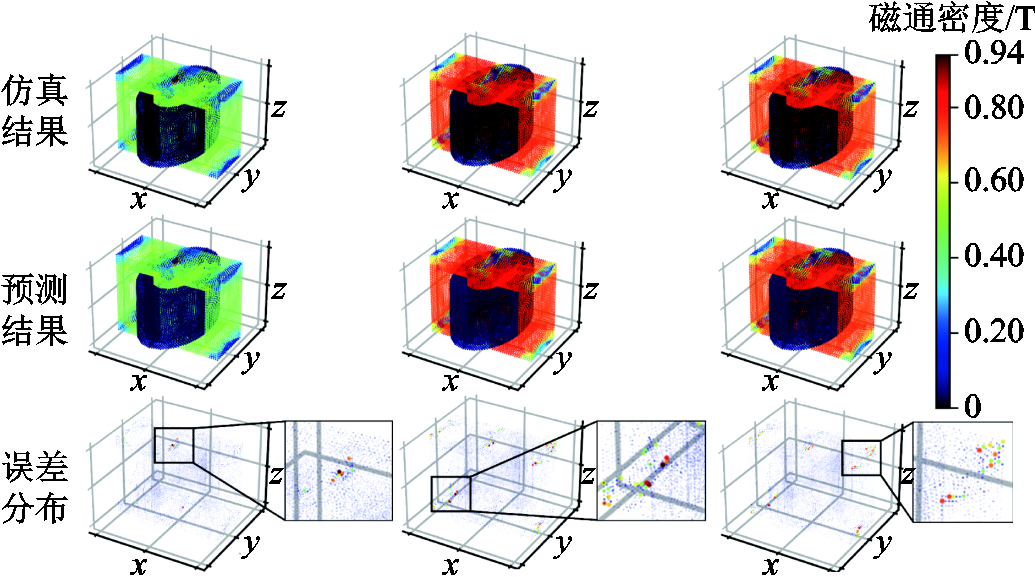
图18 变压器预测结果
Fig.18 Prediction results of the transformer
为了说明U-net CNN网络的普适性以及寻找到一个较好的训练模型，本文采用控制变量法，分别改变损失函数、学习率和训练集样本数量。
图19是在固定学习率为0.001的情况下，U-net CNN网络和FCNs-16网络在L1、L2和Huber损失函数下预测准确率随迭代周期的变化。
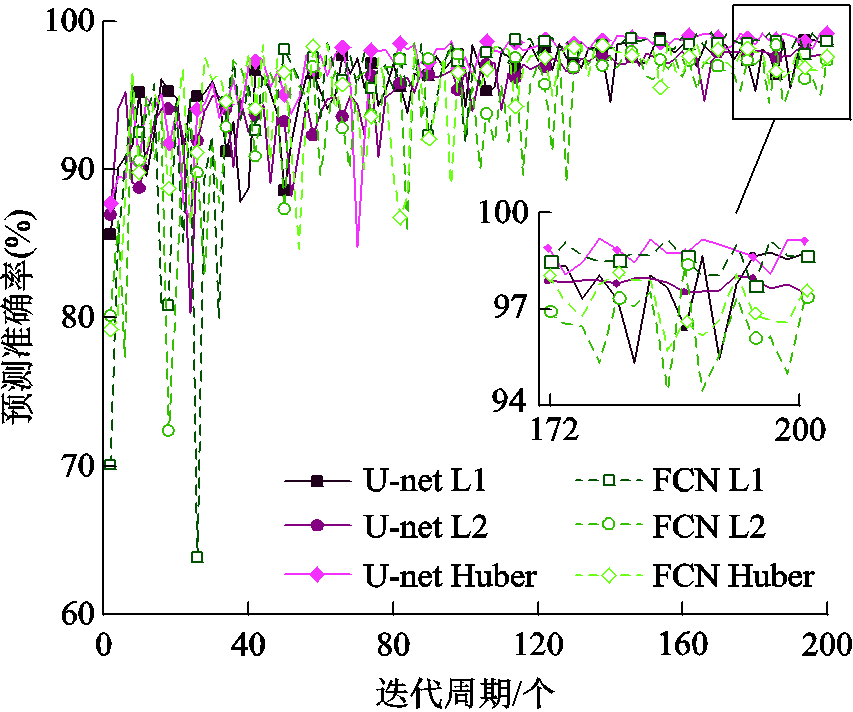
图19 变压器不同网络下的训练效果
Fig.19 Training performance of the transformer under different networks
结果显示，U-net CNN在使用Huber函数时的效果最好，预测准确率达到了99.26%。FCNs-16在使用L1函数时效果最好，预测准确率达到了98.91%。此外，模型在训练完成之后，单次预测的时间也不相同，U-net CNN预测用时为0.094 s，FCNs-16为0.121 s，而有限元计算一次的时间为 294 s，U-net CNN方法单次预测时间约为FEM计算时间的10-4倍。可见U-net CNN可以大幅度提高计算速度。
图20是U-net CNN在固定迭代周期为200的情况下，不同学习率和损失函数下的预测准确率，其中横坐标为对数坐标。
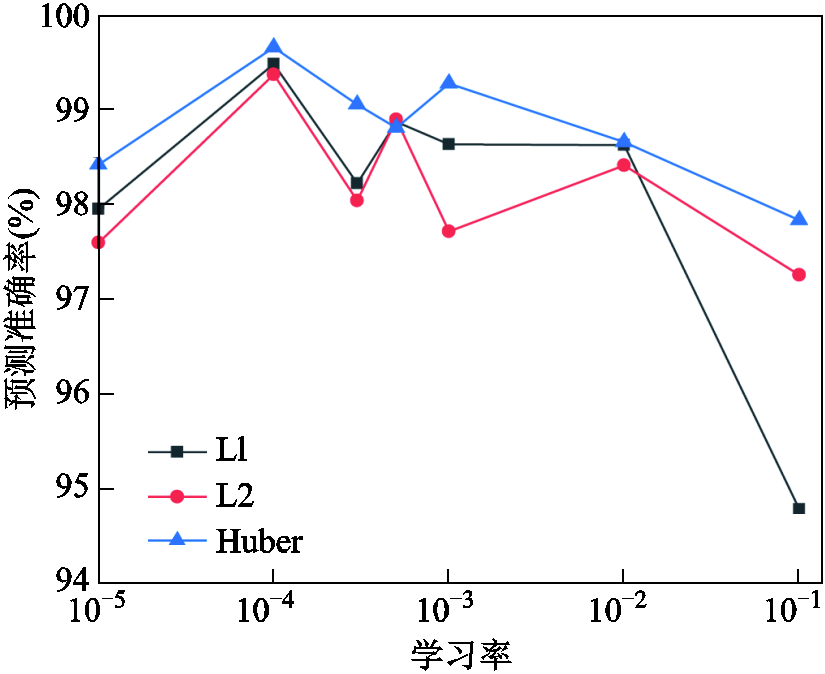
图20 变压器不同损失函数和学习率下的训练效果
Fig.20 Training performance of the transformer under different loss functions and learning rates
结果显示，当学习率为0.000 1时，三种损失函数的准确率均达到最高，其中Huber函数达到了99.64%。
图21是在固定学习率为0.000 1，迭代周期为200的情况下，训练集样本数和预测准确率之间的关系。其中验证集保持30组不变，设置训练集为原始数据集的20%、40%、60%、80%和100%，即53、108、163、217和271组，则可以将数据集大小分别为83、138、193、247和301组。
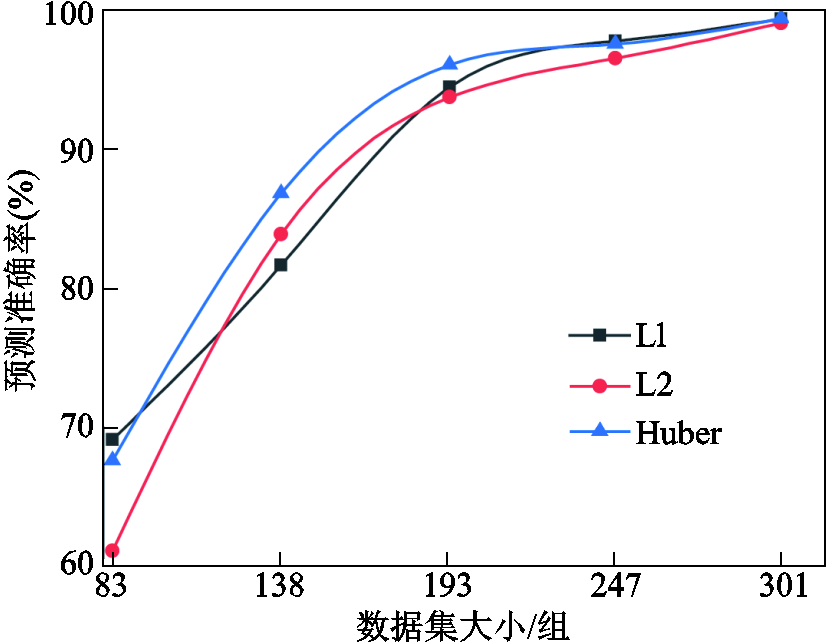
图21 变压器不同数据集大小下的训练效果
Fig.21 Training performance of transformer under different dataset sizes
结果显示，模型数据在193组的时候仍然能够保证较高的预测精度，即通过选择合适大小的数据集，既能避免生成大量数据、加快训练速度，也可以获得较好的模型。
针对FEM计算时间较长的问题，介绍了一种基于U-net CNN的物理场快速计算方法，并研究了其在电磁场计算中的应用，最后以绝缘子均压环和变压器为案例，得到了以下结论：
1）使用该方法，能实现对绝缘子均压环和变压器的电势、电场强度和磁感应强度的准确预测，准确率最高分别为99.93%、99.52%和99.64%，相较于FCNs-16具有更高的准确率，且单次预测时间约为FEM计算时间的10-4倍，说明该方法能够对仿真计算结果实现快速、准确的预测。
2）使用高斯分布在减少数据量的同时融合了绝缘子均压环的特征信息；分别针对单输入通道和多输入通道进行训练预测，并比较不同超参数下的模型性能。结果显示，在电势的预测中，多输入通道比单输入通道下的网络预测效果更好，而在电场强度的预测中二者无明显差别。
3）比较不同大小数据集下训练模型的性能，绝缘子均压环在数据集大于1 136组时，对电势和电场强度的预测准确率基本保持稳定，在数据集仅有203组的情况下准确率也可以达到85%以上；变压器在数据集大于193组时也能达到90%的准确率，说明该方法在小数据集下仍具有可靠性。
此外，本文方法并非为了代替传统FEM仿真计算，而是以传统FEM为基础，探索的一种将FEM与深度学习进行结合的方法，为其他物理场FEM计算提供了一种研究思路，具有一定借鉴意义。在未来，通过优化神经网络架构，可以更快、更准确地预测多物理场，进一步解决有限元在设备状态评估实时计算和需要多次迭代的设计环节中计算时间过长的问题。通过结合物理信息和迁移学习，对于同一类场的不同对象，可以直接使用源域的权重参数以加快训练速度，甚至无需额外训练。
参考文献
[1] 赵升, 舒亮, 吴自然, 等. 电磁-永磁复合型接触器数值仿真与控制方法[J]. 电工技术学报, 2020, 35(5): 1083-1092. Zhao Sheng, Shu Liang, Wu Ziran, et al. Numerical simulation and control method of electromagnetic- permanent composite contactor[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1083-1092.
[2] 阮江军, 张宇, 张宇娇, 等. 电气设备电磁多物理场数值仿真研究与应用[J]. 高电压技术, 2020, 46(03): 739-756. RuanJiangjun, Zhang Yu, Zhang Yujiao, et al. Numerical simulation research and applications of electromagnetic multiphysical field for electrical equipment[J]. High Voltage Engineering, 2020, 46(3): 739-756.
[3] Liu C, Hu S, Han K, et al. electric-field distribution and insulation status of ±800 kV UHVDC converter valve after implanting full-view micro-sensor detector[J]. IEEE Access, 2019, 201(7): 86534-86544.
[4] 曹龙飞, 范兴纲, 李大伟, 等. 基于快速有限元的永磁电机绕组涡流损耗半解析高效计算[J]. 电工技术学报, 2023, 38(1): 153-165. Cao Longfei, Fan Xinggang, Li Dawei, et al. Semi analytical and efficient calculation method of eddy current loss in windings of permanent magnet machines based on fast finite element method[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 153-165.
[5] 黄永宁, 余晓, 樊益平, 等. 363 kV多断口快速真空断路器电场仿真分析[J]. 高压电器, 2019, 55(10): 19-24, 32. Huang Yongning, Yu Xiao, Fan Yiping, et al. Electric Field simulation of the 363 kV multi-break fast vacuum circuit breaker[J]. High Voltage Apparatus, 2019, 55(10): 19-24, 32.
[6] 杜志叶, 田雨, 金硕, 等. 大规模复杂模型电场计算的快速精细化有限元数值建模[J]. 中国电机工程学报, 2018, 38(24): 7166-7173, 7443. Du Zhiye, Tian Yu, Jin Shuo, et al. A fast finite element numerical modeling method for the calculation of electric field in large scale complex model[J]. Proceedings of the CSEE, 2018, 38(24): 7166-7173, 7443.
[7] 狄冲, 鲍晓华, 潘晋, 等. 基于Elmer开源有限元平台的铁氧体辅助同步磁阻电机的建模和分析[J].电工技术学报, 2022, 37(5): 1136-1144. Di Chong, Bao Xiaohua, Pan Jin, et al. modelling and analysis of a ferrite assisted synchronous reluctance machine based on the open-source platform Elmer[J]. Transactions of China Electrotechnical Society, 2022, 2022, 37(5): 1136-1144.
[8] 赵玉顺, 戴义贤, 庄加才, 等. 基于热固耦合的中频变压器绝缘材料性能参数优化配合方法[J]. 电工技术学报, 2023, 38(4): 1051-1063. Zhao Yushun, Dai Yixian, Zhuang Jiacai, et al. optimization of insulation material performance parameters for medium frequency transformers based on thermosolid coupling[J]. Transactions of China Electrotechnical Society, 2023, 38(04): 1051-1063.
[9] 刘素贞, 王淑娟, 张闯, 等. 钢板电磁超声表面波的仿真分析及缺陷定量检测[J]. 电工技术学报, 2020, 35(1): 97-105. Liu Suzhen, Wang Shujuan, Zhang Chuang, et al. Simulation analysis of electromagnetic acoustic surface wave of steel plate and quantitative defect detection[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 97-105.
[10] 于丰源, 陈昊, 闫文举, 等. 宽窄定子极轴向磁通开关磁阻电机的设计与分析[J]. 电工技术学报, 2023, 38(5): 1261-1274. Yu Fengyuan, Chen Hao, Yan Wenju, et al. Design and characteristic analysis of a wide-narrow stator poles axial flux switched reluctance machine[J]. Transactions of China Electrotechnical Society, 2023, 38(05): 1261-1274.
[11] 刘利强, 尹彦博, 齐咏生, 等. 一种多模型融合的风电系统永磁同步发电机数字孪生建模方法[J].电机与控制学报, 2023, 27, 17(11): 149-162. LiuLiqiang, Yin Yanbo, Qi Yongsheng, et al. A digital twin modeling method of wind power system permanent magnet synchronous generator based on multi model fusion[J]. Electric Machines and Control, 2023, 27, 17(11): 149-162.
[12] Li Ning, Liu Yongqian, Li Li, et al. Numerical simulation of wind turbine wake based on extended k-epsilon turbulence model coupling with actuator disc considering nacelle and tower[J]. IET Renewable Power Generation, 2020, 14(1): 3834-3842.
[13] 胡万君, 刘刚, 朱章宸, 等. 油浸式电力变压器绕组稳态温升降阶计算方法研究[J].中国电机工程学报, 2023, 43(16): 6505-6517. Hu Wanjun, Liu Gang, Zhu Zhangchen. Reduced order calculation method of steady temperature rise of oil immersed power transformer[J]. Proceedings of the CSEE, 2023, 43(16): 6505-6517.
[14] 张翼, 朱永利. 图信号与图卷积网络相结合的局部放电模式识别方法[J]. 中国电机工程学报, 2021, 41(18): 6472-6481. Zhang Yi, Zhu Yongli. A partial discharge pattern recognition method combining graph signal and graph convolutional network[J]. Proceedings of the CSEE, 2021, 41(18): 6472-6481.
[15] 贾光辉, 于云瑞, 王丹. 卷积神经网络求解有限元单元刚度矩阵[J]. 北京航空航天大学学报, 2020, 46(3): 481-487. Jia Guanghui, Yu Yunrui, Wang Dan. Solving finite element stiffness matrix based on convolutional neural network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(3): 481-487.
[16] Bhaduri A, Gupta A, Graham-Brady L. Stress field prediction in fiber-reinforced composite materials using a deep learning approach[J/OL]. ArXiv, 2021: 2111.05271. https://arxiv.org/abs/2111.05271v1.
[17] Thuerey N, Weissenow K, Prantl L, et al. Deep learning methods for Reynolds-averaged Navier-Stokes simulations of airfoil flows[J]. AIAA Journal, 2020, 58(1): 25-36.
[18] Mendizabal A, Márquez-Neila P, Cotin S. Simulation of hyperelastic materials in real-time using deep learning[J]. Medical Image Analysis, 2020, 59: 101569(1-11).
[19] Kim D J, Kim S I, Kim H S. Thermal simulation trained deep neural networks for fast and accurate prediction of thermal distribution and heat losses of building structures[J]. Applied Thermal Engineering, 2022, 202: 117908(1-11).
[20] Zhang H, Wang Y, Lu K, et al. SAP-Net: deep learning to predict sound absorption performance of metaporous materials[J]. Materials & Design, 2021, 212: 110156(1-7).
[21] 黄巨挺, 高宏力, 戴志坤. 基于编码解码结构的移动端电力线语义分割方法[J]. 计算机应用, 2021, 41(10): 2952-2958. Huang Junting, Gao Hongli, Dai Zhikun. Semantic segmentation method of power line on mobile terminals based on encoder-decoder structure[J]. Journal of Computer Applications, 2021, 41(10): 2952-2958.
[22] 裴少通, 杨家骏, 马子儒, 等. 基于深度学习的输变电设备紫外放电光斑分割方法[J]. 科学技术与工程, 2022, 22(33): 14759-14766.Pei Shaotong, Yang Jiajun, Ma Ziru, et al. transmission and distribution equipment ultraviolet discharge spot segmentation method based on deep learning[J]. Science Technology and Engineering, 2022, 22(33): 14759-14766.
[23] Siddique N, Paheding S, Elkin C P, et al. U-Net and its variants for medical image segmentation: a review of theory and applications[J]. IEEE Access, 2021, 9: 82031-82057.
[24] Charles R Q, Su H, Kaichun M, et al. PointNet: deep learning on point sets for 3D classification and segmentation[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 2017: 77-85.
[25] Balasundaram S, Prasad S C. Robust twin support vector regression based on Huber loss function[J]. Neural Computing and Applications, 2020, 32(15): 11285-11309.
[26] 王思华, 王军军, 赵磊, 等. 污秽成分对复合绝缘子表面电场的影响[J]. 中国电力, 2021, 54(7): 149-157. Wang Sihua, Wang Junjun, Zhao Lei, et al. influence of pollution components on surface electric field of composite insulators[J]. Electric Power, 2021, 54(7): 149-157.
[27] 赵建利, 姚顺, 岳永刚, 等. 500 kV SF6瓷质套管多工况仿真与故障分析[J]. 电工技术学报, 2021, 36(增刊2): 736-745. Zhao Jianli, Yao Shun, Yue Yonggang, et al. Simulation and failure analysis of 500 kV SF6porcelain bushing under complicated working conditions[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 736-745.
[28] 鲁尧, 咸日常, 王立权, 等. 干式空心串联电抗器绕组匝间短路电磁特性研究[J]. 高压电器, 2021, 57(11): 116-123. Lu Yao, Xian Richang, Wang Liquan, et al. Study on electromagnetic characteristics of winding inter-turn short circuit of dry-type air-core series reactor[J]. High Voltage Apparatus, 2021, 57(11): 116-123.
[29] 潘超, 米俭, 王格万, 等. 基于场路耦合的变压器绕组匝间短路电磁谐响应分析方法[J]. 电工技术学报, 2019, 34(4): 673-682. Pan Chao, Mi Jian, Wang Gewan, Cai Guowei, et al. electromagnetic harmonic response analysis method of inter-turn short circuit in transformer winding based on field circuit coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 673-682.
[30] Park Y R, Seol Y J, Kim Y J, et al. Comparison on the deep learning performance of a field of view variable color images of uterine cervix[C]//International Forum on Medical Imaging in Asia, Taipei, 2021: 99-102.
Abstract During the engineering case design session, Finite Element Method (FEM) analysis is essential to address the physical fields of the study object. However, the significant number of degrees of freedom often results in lengthy computation times for FEM, particularly when solving 3D problems involving coupled multi-physical fields. In design-oriented problems like battery structure optimization, finding the optimal solution typically requires thousands of iterations. If the FEM method is employed, this process could take months to complete, significantly delaying project schedules. Furthermore, it is crucial to assess equipment status based on sensor data such as motor digital twin modeling and transformer hot spot temperature real-time calculation. Utilizing the time-consuming finite element method in these scenarios may lead to delayed identification and resolution of failures, potentially causing further harm.
A deep learning-based fast computation method for physical fields is proposed by combining FEM with the U-net convolutional neural network (U-net CNN), studying the effectiveness of this approach in electromagnetic fields. Firstly, we employ the finite element method to model and simulate the research object based on the actual physical model. Secondly, we export the obtained simulation results and transform the model by dividing, rasterizing, and converting it into a point cloud. These modifications are based on the geometric parameters, boundary conditions, and physical field solution results. Thirdly, we train the U-net CNN by optimizing its network parameters and utilize the trained model for swift physical field calculations of the research object. The trained model allows for rapid computation of the physical field.
To assess the practicality of our method, we select a two-dimensional insulator uniform pressure ring model and a three-dimensional transformer model to calculate the electrostatic and magnetic fields. In the two-dimensional model, we employ both single-channel and multi-channel inputs. The single-channel input solely consists of the geometric model parameters, while the multi-channel input includes additional data including the radius and uplift of the size equalizing ring. To minimize memory space, we merge the multi-channel inputs using a Gaussian distribution. The results demonstrate that the single-channel U-net CNN achieves the accuracy of 99.88% for potential and 99.52% for electric field strength. Meanwhile, the FCNs-16 model achieves a potential accuracy of 99.15% and an electric field strength of 98.33%. The potential accuracy attained with the multi-channel input is 99.93%, with an electric field strength of 99.52%. The potential accuracy achieved with the FCNs-16 model is 99.80%, along with an electric field strength of 99.24%. Additionally, the computation time for the U-net CNN is 0.017 s for the single-channel input and 0.016 s for the multi-channel input both significantly faster than the finite element method. Finally, by reducing the size of the dataset, the network's prediction accuracy remains above 90% with 306 groups of data, and even with just 203 groups, it maintains an accuracy of over 85%. In the three-dimensional model, we address the magnetic field of the transformer at t=0.05 s through field-path coupling. The inputs for this model consist of Sampling pointcoordinates and voltage. The results reveal that the U-net CNN achieves the highest accuracy for magnetic induction intensity at 99.26%, while the FCNs-16 model achieves an accuracy of 98.91%. By reducing the dataset size, the model can still maintain a high prediction accuracy, even with only 193 groups of data.
The method possesses the capability to be employed in real-time calculations for equipment condition assessment, as well as in design sessions necessitating multiple iterations.
keywords：Electromagnetic fields, convolutional neural network (CNN), fast calculation, finite element method (FEM)
DOI: 10.19595/j.cnki.1000-6753.tces.230650
中图分类号：TM15
国家自然科学基金资助项目（52377005）。
收稿日期 2023-05-06
改稿日期 2023-06-12
张宇娇 女，1978年生，教授，博士生导师，研究方向为电气设备多物理场建模与仿真、电磁多物理场快速计算方法、基于数字孪生技术的电气设备故障诊断与健康寿命管理。E-mail：zhangyujiao@hfut.edu.cn
黄雄峰 男，1980年生，副教授，硕士生导师，研究方向为检测技术与自动化装置、人工智能新技术及应用。E-mail：hfut_huangxf@hfut.edu.cn（通信作者）
（编辑 郭丽军）