摘要 随着可再生能源在电网中的占比不断提高,电网逐渐呈现出弱电网特性,即电网阻抗不可忽略且频繁波动。电网阻抗的存在会改变逆变器控制环路的增益,导致控制环路的稳定裕度减小,因而引发稳定性问题,同时,控制环路的截止频率也因电网阻抗的存在而减小,环路带宽也随之减小,使得逆变器动态性能变差。针对弱电网下电网阻抗变化引发的相关问题,现有的控制策略往往侧重于提升逆变器的并网稳定性,而对其动态性能下降的问题缺乏关注。鉴于此,为同时解决以上问题,该文提出一种基于环路增益测量的自适应控制策略以保障逆变器优越且恒定的控制性能,首先通过环路增益的在线测量实现对逆变器控制性能的实时监测;然后依据实时监测的控制性能指标参数自适应地调整控制器的参数,以提升逆变器对弱电网的适应性;最后以单相并网逆变器为例进行实验验证,实验结果证明了所提方案的有效性。
关键词:稳定性 自适应控制 弱电网 并网逆变器
随着分布式发电系统的不断发展,风电、光伏等新能源在电网中的占比不断提高。由于新能源发电具有随机性、间歇性、出力波动大、资源分布偏远等特点,电网逐渐呈现出弱电网特性,即电网阻抗不可忽略且频繁波动[1-6]。并网逆变器作为新能源接入电网的关键接口装置,其控制性能及稳定性受到弱电网场景的巨大挑战,电网阻抗的频繁波动会导致逆变器并网环路的环路增益发生改变,使得逆变器稳定性受到影响,通常表现为稳定裕度下降。同时,控制环路的动态性能也因电网阻抗的存在而变差,导致环路响应速度下降,通常表现为控制环路的截止频率下降。
针对电网阻抗波动导致的稳定性问题,基于不同的角度分析,目前已有众多方案被提出,比如,基于虚拟阻抗分析,可以实现对逆变器输出阻抗的校正以提升逆变器的鲁棒性和抗扰性能[6-8];从锁相环设计角度分析,文献[9-11]改进了锁相环的结构和参数设计,提升逆变器对弱电网的适应能力;从延时补偿的角度分析,文献[12]提出了电容电流即时反馈的有源阻尼方法,提升了逆变器对电网阻抗波动的适应性和鲁棒性;从无源性设计的角度分析,文献[13]通过阻抗重塑消除逆变器输出阻抗的负电阻成分,以提升逆变器的稳定性。
上述策略从不同的角度分析,提升了逆变器的稳定性与鲁棒性,但忽略了电网阻抗变化对逆变器动态性能的影响,并且为了适应弱电网场景,其控制参数往往依据电网阻抗大幅波动时的极端情况设定,这导致在电网阻抗频繁变化时,逆变器无法发挥出最佳性能。因此基于电网阻抗在线测量的自适应控制策略得到关注与发展,其基本思路是依据在线测量的电网阻抗值,实时改变逆变器的控制参数,比如:调节器参数、有源阻尼系数等,以提升逆变器的控制性能和稳定性,提升其适应电网阻抗变化的能力。文献[14]中提出了基于电网阻抗在线测量实现锁相环参数和前馈系数自适应调节的方案;文献[15-17]针对电网电压前馈带来的稳定裕度降低问题,通过直接或间接的电网阻抗测量,实现对前馈补偿电压和电流调节器的自适应调整;文献[18-19]提出基于电网阻抗估测实现自适应调节有源阻尼系数的方案;文献[20]基于在线测量的电网阻抗,自适应地改变调节器参数,以提高逆变器在不同电网阻抗下的鲁棒性。上述基于电网阻抗测量的自适应方案提高了逆变器对电网阻抗的适应性,但在监测到电网阻抗后,逆变器相关参数的整定依然要依据逆变器的理论模型实现,因此这类方案无法解决理论模型与实际装置的参数失配问题,如在大电流工况下,滤波电感的感值可能会大幅下降,导致在自适应调整控制参数后,逆变器依然无法达到期望的性能。
因此,基于环路增益在线测量的自适应控制方案逐渐得到关注与发展。此类方案的基本思路是:在线测量控制环路的环路增益,并以环路增益为依据实现控制参数的自适应整定。文献[21-22]基于环路增益测量实现对Buck变换器的自适应控制,保证了在断续导通模式(Discontinuous Conduction Mode, DCM)与连续导通模式(Continuous Conduction Mode, CCM)切换过程中控制性能的平稳性;文献[23-24]改进了环路增益的测量方案,并实现了对PI调节器参数的自适应整定。然而上述基于环路增益测量的自适应方案多应用于Buck电路等DC-DC场景,其在并网逆变的多背景谐波交流场景下的适用性有待进一步研究,并且其自适应策略仅针对比例积分(Proportional Integral, PI)调节器实现,并未推广到并网逆变器中应用非常广泛的比例谐振(Proportional Resonant, PR)调节器。
鉴于此,针对并网逆变场景,本文提出一种基于环路增益在线测量的自适应控制方案,以提高逆变器在弱电网下的稳定性和动态性能,并将该方案推广至PR调节器中。在线测量的环路增益中兼具逆变器和电网阻抗的信息,真实地反映出逆变器在弱电网下的控制性能,因此依据环路增益在线测量实现的自适应控制,可以保证逆变器的稳定性和动态性能精准地达到期望效果。本文方案的优势可总结如下:①保证逆变器的稳定性并同时提升其动态性能;②监测逆变器的真实控制性能,解决理论模型与实际装置失配的问题;③通用性强,可适用于PI、PR等多种调节器;④可适用于低/零电压穿越等故障工况。结构上,本文首先以单相并网逆变器为例分析了电网阻抗对其稳定性和动态性能的影响;然后介绍了所提自适应方案的基本原理,以及其设计与实现方法,并进一步给出了相关的参数设计;最后在一台单相并网逆变器样机上验证了所提方案的有效性。
图1为单相并网逆变器结构及控制框图,Vin为直流输入电压,Cin为直流侧滤波电容,直流源经全桥逆变输出后接LCL滤波器,L1为逆变器侧电感,L2为网侧电感,C为滤波电容,ZG=RG+sLG为等效电网阻抗,VG为电网电压,![]() 为并网电流,
为并网电流,![]() 为并网电流指令。控制策略采用电感电流-电容电压-并网电流(内环-外环)三环控制[25],最外环为并网电流环,其环路增益表达式为
为并网电流指令。控制策略采用电感电流-电容电压-并网电流(内环-外环)三环控制[25],最外环为并网电流环,其环路增益表达式为
式中,![]() 为电压内环的闭环传递函数;
为电压内环的闭环传递函数;![]() 为逆变器输出阻抗;
为逆变器输出阻抗;![]() 为网侧电感及其寄生电阻的阻抗[25];
为网侧电感及其寄生电阻的阻抗[25];![]() 为并网电流调节器。相比于PI调节器,PR调节器具有稳态误差小、不需要坐标变换等优势[26-27],因此以PR调节器为例进行分析,其表达式为
为并网电流调节器。相比于PI调节器,PR调节器具有稳态误差小、不需要坐标变换等优势[26-27],因此以PR调节器为例进行分析,其表达式为
![]() (2)
(2)
式中,Kp为比例系数;Kr为谐振系数;wo为基波角频率;wi为-3dB要求的谐振项带宽,wi的引入可以增强PR调节器对电网频率的适应性,通常考虑电网频率波动为±0.5 Hz,则wi=2p×0.5=prad/s[12]。
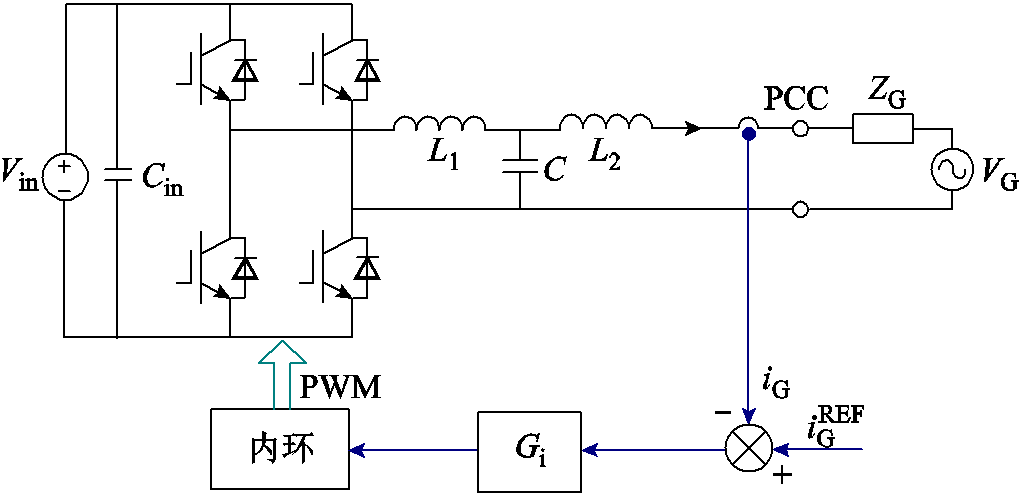
图1 单相LCL型并网逆变器拓扑及其控制结构
Fig.1 Topology and control scheme of LCL-type single-phase grid-connected inverter
由式(1)可知,环路增益与电网阻抗直接相关,图2给出了电网阻抗改变时环路增益曲线的变化。图2a中,当电网阻抗的阻性成分RG增加时,幅频曲线中截止频率以下的低频段出现明显下降,相频曲线中低频段则被明显提高。图2b中,当电网阻抗的感性成分LG增加时,幅频曲线全频段下滑,而相频曲线几乎不变。
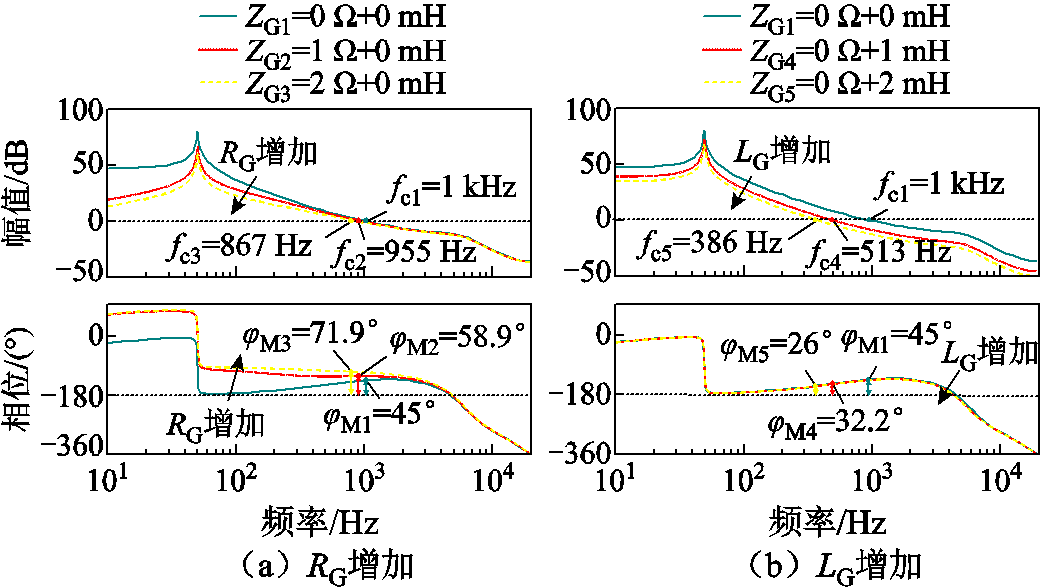
图2 电网阻抗改变时的环路增益曲线
Fig.2 Loop gian diagram under grid impedance variations
在环路增益受到电网阻抗影响时,环路增益曲线上表征控制性能的关键指标也随之发生变化,其中有,表征环路动态性能的截止频率fc及表征环路稳定性的相位裕度jM[28]。这里的截止频率fc指控制系统开环传递函数幅频曲线穿越0 dB时的频率,而带宽指控制系统闭环传递函数中,幅值相对于零频率处幅值下降3 dB的频率,系统闭环带宽通常以设定系统开环截止频率的方式来选择,二者近似相等,因此针对带宽的分析和设计可以借助对截止频率的分析与设计实现[29]。为描述方便,将截止频率fc与相位裕度jM统一称为控制性能指标。
图3对电网阻抗ZG与控制性能指标的关系进行了定量分析。图3a中,fc随ZG的增加而明显降低,当LG增加到2.0 mH时,fc由初始设计值1 000 Hz下降到386 Hz。图3b展示了![]() 与ZG的关系,当LG增加到2.0 mH时,
与ZG的关系,当LG增加到2.0 mH时,![]() 由45°下降到26°,而电网阻抗中的阻性成分RG则因其阻尼效果会对jM带来一定补偿。综上所述,随电网阻抗的增加,fc和jM都大幅降低,并且和RG相比,LG对逆变器的稳定性和动态性能影响更加严重。
由45°下降到26°,而电网阻抗中的阻性成分RG则因其阻尼效果会对jM带来一定补偿。综上所述,随电网阻抗的增加,fc和jM都大幅降低,并且和RG相比,LG对逆变器的稳定性和动态性能影响更加严重。
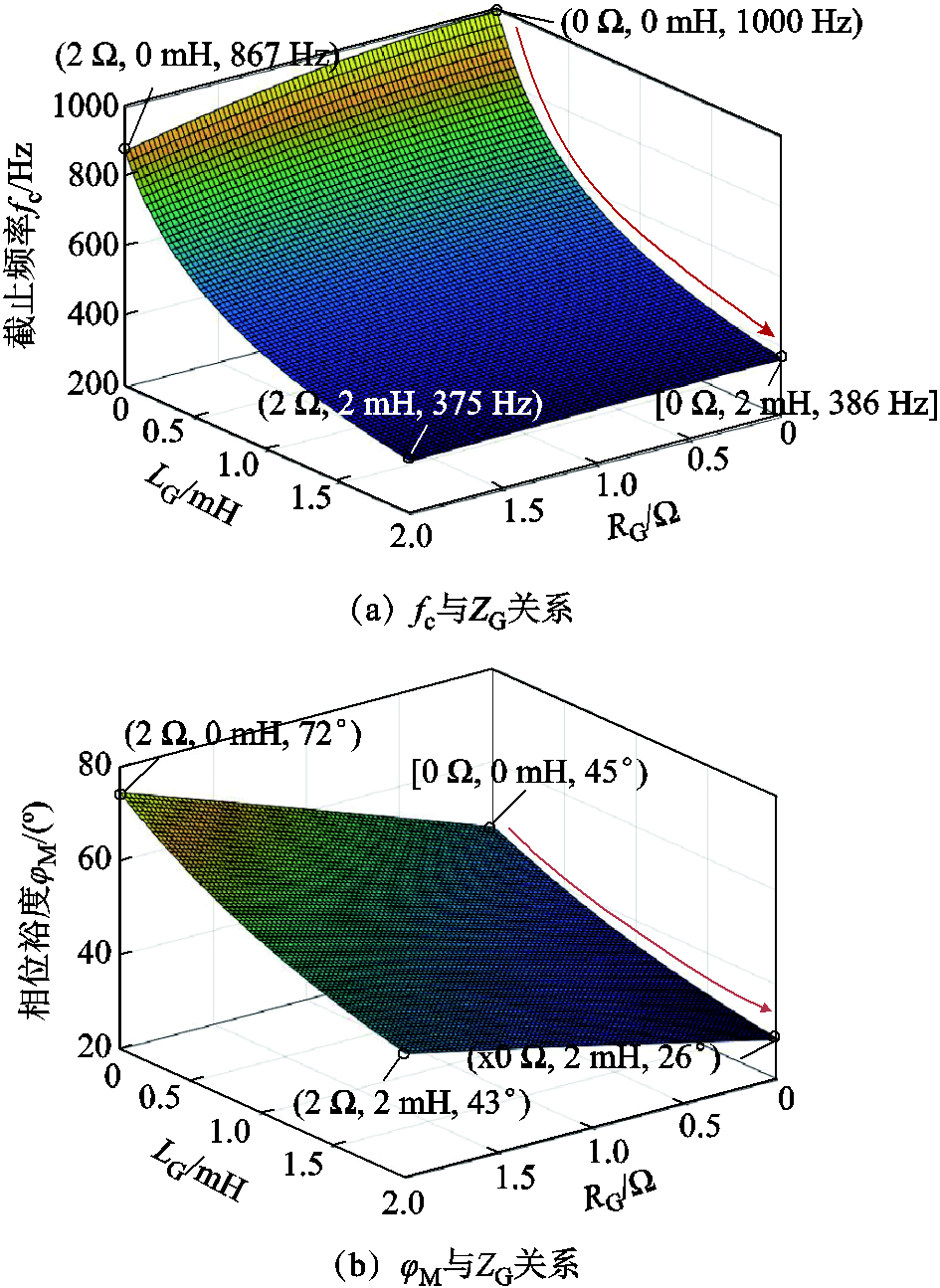
图3 控制性能指标(fc, jM)与电网阻抗ZG关系
Fig.3 Relationalships between control performance indexes (fc, jM) and the grid impedance ZG
图4给出了电网阻抗变化时控制环路的阶跃响应曲线变化。可以看到,随着电网阻抗的增加,阶跃响应的上升时间、调节时间、超调量等指标皆出现明显增加,环路动态性能全面下滑,导致环路动态响应速度下降,环路跟随性能变差。
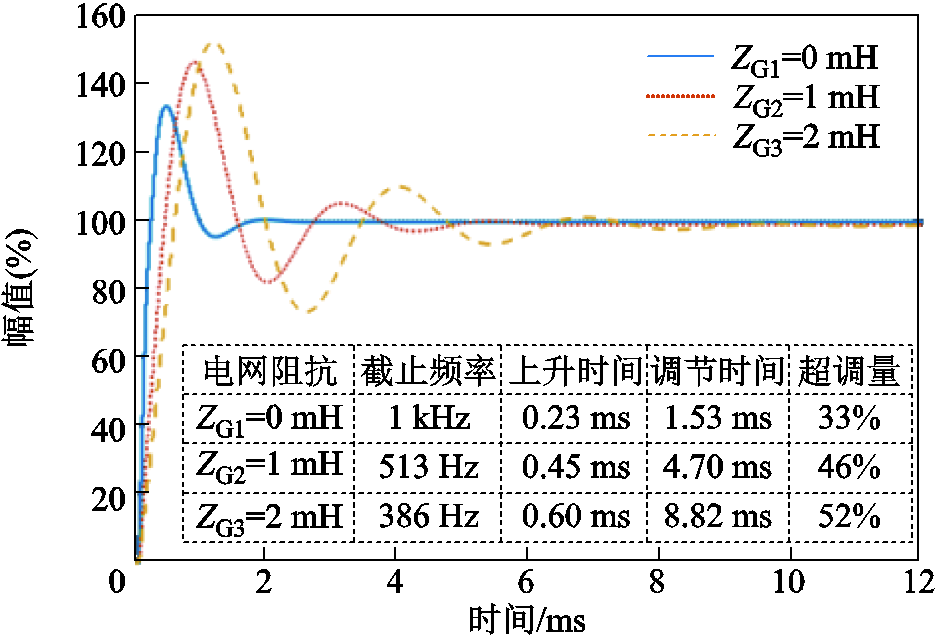
图4 电网阻抗变化时控制环路阶跃响应
Fig.4 Step respose of the control loop under grid impedance variations
因此在电网阻抗变化时,若能实时地调整逆变器控制参数,对逆变器的环路增益进行在线校正,保证环路具有充足的相位裕度和理想的截止频率,就可以提高逆变器的稳定性和动态性能,以及其对弱电网的适应能力。
图5为所提自适应控制方案的原理,其中主电路与底层控制部分与图1系统相同,控制性能监测器和自适应整定器则用来实现对逆变器控制参数的自适应调节。本文所提自适应方案的实现包括两个关键环节:①基于环路增益测量原理实现对相位裕度和截止频率的在线监测,此环节由控制性能监测器实现;②根据监测的相位裕度和截止频率,依据设计的自适应规律自动调节控制器参数,使环路具有充足的相位裕度以保证稳定性,并提高环路截止频率以保证良好的动态性能,此环节由自适应整定器实现。本文方案可以对PI、PR等多种调节器的参数进行自适应整定,这里以PR调节器为例进行介绍。
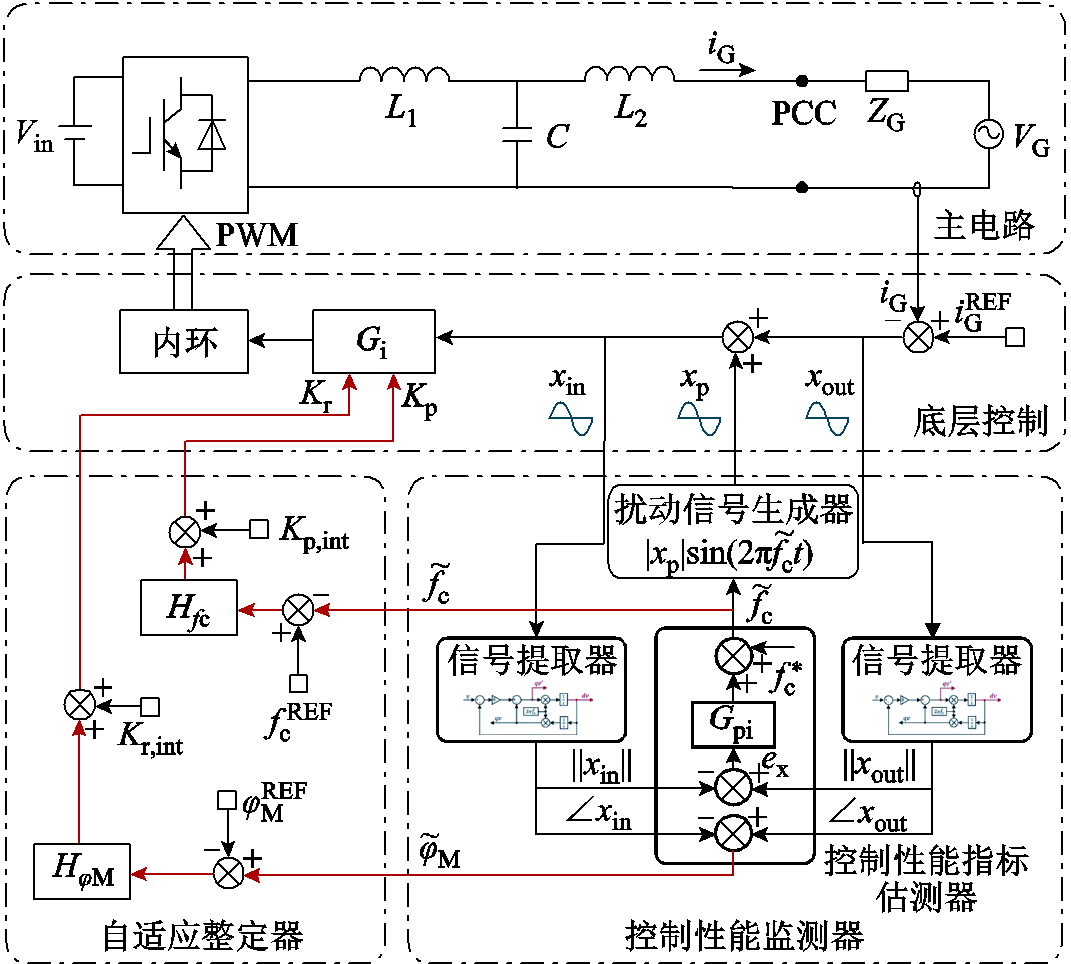
图5 自适应控制原理
Fig.5 Principle diagram of the adaptive control strategy
本文的自适应方案基于环路增益测量实现[30],图6展示了环路增益测量的原理,![]() 为待测的并网电流环的环路增益,控制性能监测器向控制环路中注入一个频率可控的正弦小扰动信号xp作为激励信号,并在注入点前后分别提取相应频率的响应信号xin和xout,经推导可以得到两个响应信号与激励信号的关系为
为待测的并网电流环的环路增益,控制性能监测器向控制环路中注入一个频率可控的正弦小扰动信号xp作为激励信号,并在注入点前后分别提取相应频率的响应信号xin和xout,经推导可以得到两个响应信号与激励信号的关系为
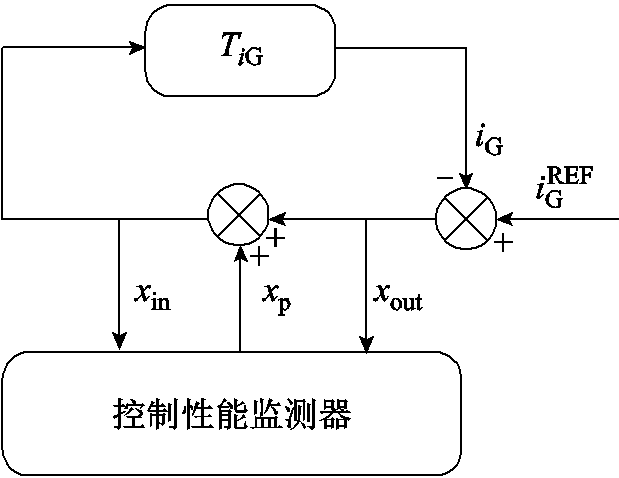
图6 环路增益测量原理
Fig.6 Principle of loop gian measurement
将式(3)代入式(4)中,消去扰动信号xp后,可以得到两个响应信号与环路增益的关系为
![]() (5)
(5)
如果不断改变所注入小信号的频率,使其在所需频段内扫频,就可以依据式(5)得到完整的环路增益曲线。然而以扫频方式完整测量环路增益,意味着需要依次注入足够多个频率的扰动小信号,这往往需要较长的时间。如前所述,截止频率和相位裕度可以表征环路的动态性能和稳定性,因此可以将环路增益测量的关键聚焦到对这两个关键指标的监测上。
图7为动态寻频实现截止频率与相位裕度监测的原理,设扰动小信号的频率为![]() ,环路增益可以表达为
,环路增益可以表达为
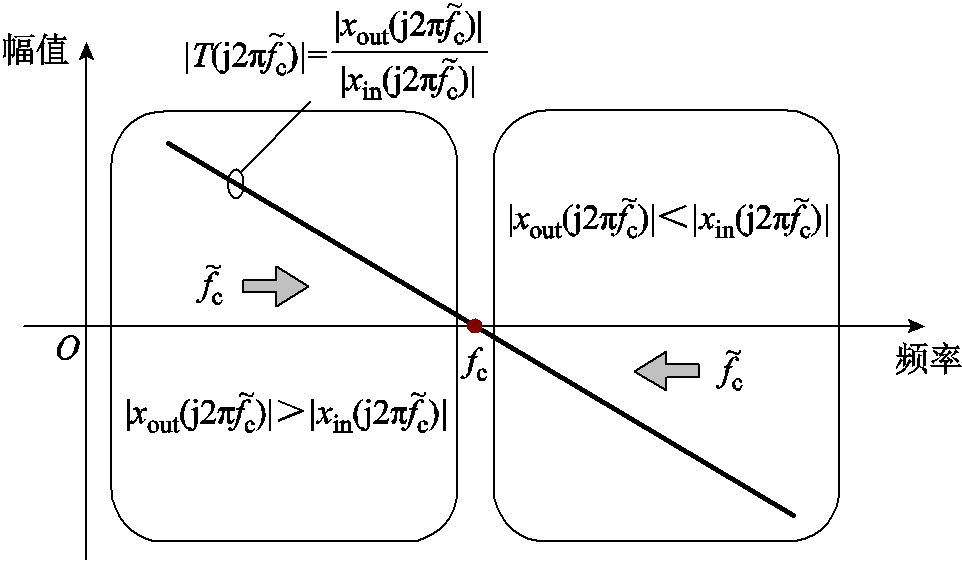
图7 动态寻频原理
Fig.7 Automatic locating principle of the crossover frequency
当扰动小信号频率与环路实际截止频率一致(![]() =
=![]() )时,满足
)时,满足
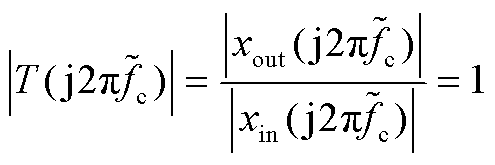 (7)
(7)
此时环路增益幅值为1,即![]() =
=![]() 。当
。当![]() >
>![]() 时,有
时,有![]() <
<![]() ,此时需要减小扰动小信号的注入频率;当
,此时需要减小扰动小信号的注入频率;当![]() <
<![]() 时,有
时,有![]() >
>![]() ,此时需要增加扰动小信号的注入频率。因此,依据
,此时需要增加扰动小信号的注入频率。因此,依据![]() 与
与![]() 的幅值关系,动态调整扰动小信号的注入频率,直到满足式(7),即可监测到环路实际截止频率。
的幅值关系,动态调整扰动小信号的注入频率,直到满足式(7),即可监测到环路实际截止频率。
准确监测到环路截止频率后,![]() 与
与![]() 的相位差即为相位裕度,有
的相位差即为相位裕度,有
依据动态寻频原理,控制性能监测器可以实现对控制性能指标的实时监测,并网逆变器的稳定性和动态性能得以在线表征。
控制性能指标(fc, jM)在被准确监测到后,可以用来指导逆变器控制参数的调整。依据在线监测的控制性能指标实时地调节并网电流环调节器的参数是实现自适应控制的关键,因此需要设计一定的自适应规律以建立二者之间的调节关系。
为设计合理的自适应规律,需要分析调节器参数对控制性能指标的影响。图8所示为PR调节器参数改变时,截止频率fc、相位裕度jM的变化规律,图8a中,Kp增加至理论值的2倍和3倍,Kr保持不变,随着Kp的增加,幅频曲线在100 Hz以上的频段被明显提升,使得fc大幅提高;相频曲线也因Kp的增加,在100 Hz~5 kHz的频段被提升,而jM同时受到fc变化和相频曲线变化的影响,则呈现先增加后减小趋势。图8b中,Kp保持不变,Kr变为理论值的2倍和3倍,可以看到随着Kr的增加,幅频曲线在2 kHz以下的频段出现小幅提升,使得fc小幅增加,而相频曲线则随Kr的增加明显降低,使得![]() 出现大幅下降。
出现大幅下降。
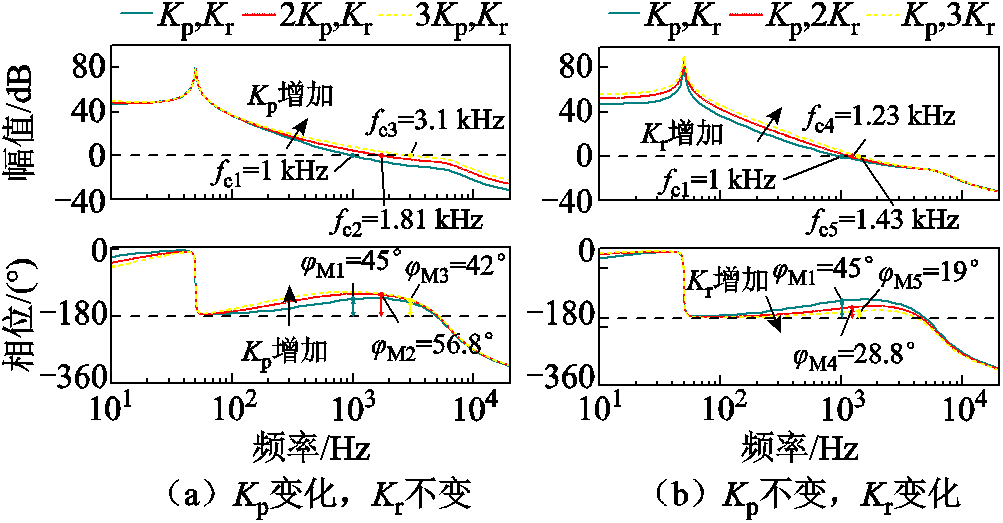
图8 控制性能指标(fc, jM)与调节器参数(Kp, Kr)关系
Fig.8 Relationship between control performance indexes (fc, jM) and regulator parameters (Kp, Kr)
由2.3节分析可知,若要提高截止频率fc,需要增加Kp与Kr,若要提高相位裕度jM,则需要在一定范围内增加Kp、减小Kr。依据此调节关系可以设计自适应整定器实现对调节器参数的调整,但显然该自适应整定器是一个耦合的多输入多输出系统,其设计与实现相对复杂,因此,本文采用了灵敏度分析的方式对控制性能指标与调节器参数的关系进行解耦设计,将一个双输入双输出的系统转换为两个单输入单输出的系统,使得自适应整定器的设计更简洁、实用。
图9给出了控制性能指标与调节器参数之间的灵敏度分析。图9a展示了截止频率与调节器参数的灵敏度关系,由于本方案截止频率期望值设定为1 kHz,因此所考虑频率范围选择为500~1 500 Hz。以截止频率对调节器参数偏微分的比值来表征灵敏度,由图9a中可知,偏微分比值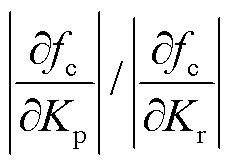 始终大于1,说明截止频率fc对Kp的灵敏度始终大于对Kr的灵敏度。图9b展示了相位裕度与调节器参数的灵敏度关系,采用同样的思路,得到与相位裕度相关的偏微分比值
始终大于1,说明截止频率fc对Kp的灵敏度始终大于对Kr的灵敏度。图9b展示了相位裕度与调节器参数的灵敏度关系,采用同样的思路,得到与相位裕度相关的偏微分比值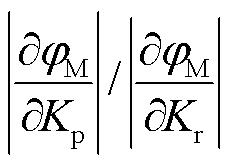 ,该比值始终小于1,说明相位裕度jM对Kr的灵敏度始终大于对Kp的灵敏度。
,该比值始终小于1,说明相位裕度jM对Kr的灵敏度始终大于对Kp的灵敏度。
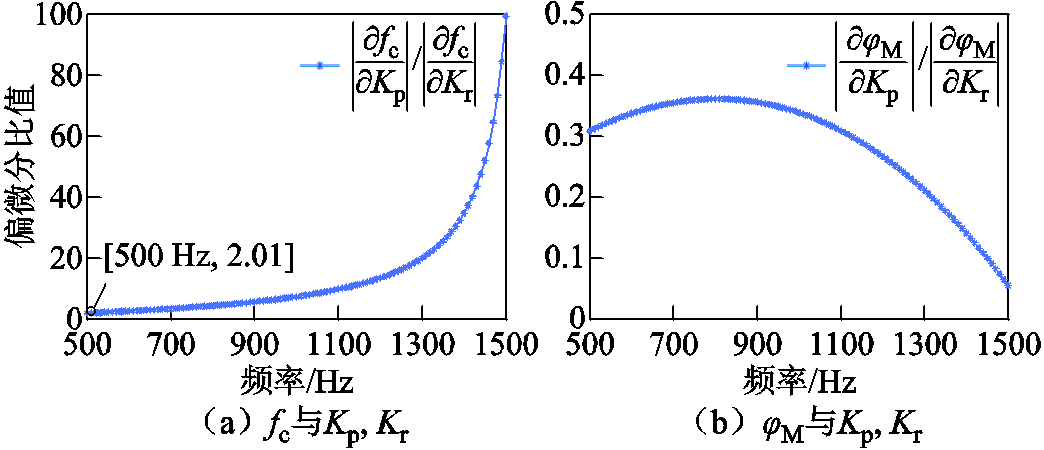
图9 控制性能指标(fc,jM)与调节器参数(Kp, Kr)之间灵敏度分析
Fig.9 Sensitivity analysis between control performance indexes (fc,jM) and regulator parameters (Kp, Kr)
由灵敏度分析可知,截止频率fc与Kp相关度更高,相位裕度jM与Kr相关度更高,因此可以将控制性能指标与调节器参数之间的关系进行解耦,设定自适应规律如下:依据截止频率fc调节比例系数Kp,当实测截止频率![]() 低于期望值时,增加Kp以提高截止频率。同时,依据相位裕度jM调节谐振系数Kr,当实测相位裕度
低于期望值时,增加Kp以提高截止频率。同时,依据相位裕度jM调节谐振系数Kr,当实测相位裕度![]() 低于期望值时,降低Kr以提高相位裕度。相似地,针对PI调节器也可以采用相同的灵敏度分析方法进行自适应规律的设计,实现基于PI调节器的自适应调参,这里不再赘述。
低于期望值时,降低Kr以提高相位裕度。相似地,针对PI调节器也可以采用相同的灵敏度分析方法进行自适应规律的设计,实现基于PI调节器的自适应调参,这里不再赘述。
控制性能监测器的设计会影响在线监测的速度及精准度,影响稳定性和动态性能在线表征的效果及后续自适应调参的效果。为提升监测精准度和监测速度,设计控制性能监测器如图5所示,主要由三个部分构成:扰动信号生成器、信号提取器、控制性能指标估测器。
3.1.1 扰动信号生成器
扰动信号生成器用来生成正弦小信号xp,有
式中,![]() 为频率,由控制性能指标估测器决定;
为频率,由控制性能指标估测器决定;![]() 为小扰动信号的幅值。
为小扰动信号的幅值。
3.1.2 信号提取器
控制环路中含有多种频率的周期信号,信号提取器用来滤波以提取与扰动小信号同频的响应信号(xin, xout),并计算响应信号的幅值和相位。这里采用二阶广义积分器(Second-Order Generalized Integrator, SOGI)实现滤波并生成一对正交信号以便进行幅值与相位的计算,图10给出了SOGI的结构,其中v为输入信号,dv和qv¢为一对正交的输出信号,相应传递函数为
![]() (11)
(11)
式中,![]() ;k为SOGI结构中决定带通滤波带宽的系数。
;k为SOGI结构中决定带通滤波带宽的系数。
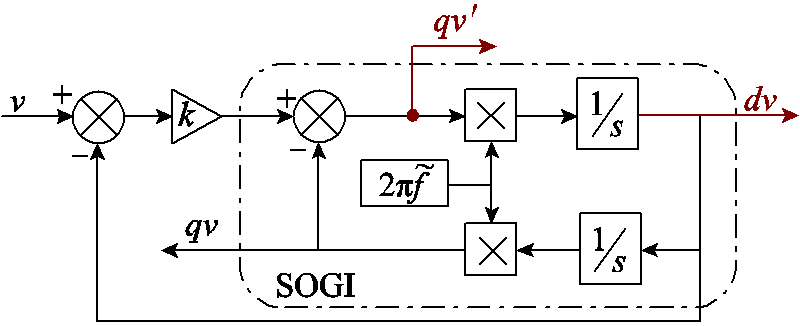
图10 SOGI结构
Fig.10 Basic structure of SOGI
经过SOGI滤波,仅频率为![]() 的周期信号被保留,其他频率的周期信号被滤除。因此,这里仅考虑频率为
的周期信号被保留,其他频率的周期信号被滤除。因此,这里仅考虑频率为![]() 的响应信号(xin, xout)作为SOGI的输入信号v,以计算xin和xout的幅值和相位。首先以xin为例分析,可以假定其表达式为
的响应信号(xin, xout)作为SOGI的输入信号v,以计算xin和xout的幅值和相位。首先以xin为例分析,可以假定其表达式为
经过SOGI后生成的一对正交信号可以表示为dv(t)和qv¢(t),即
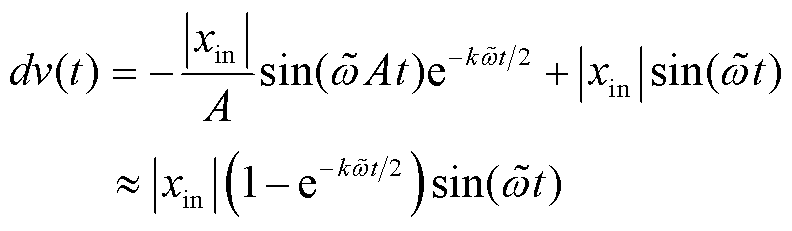 (13)
(13)
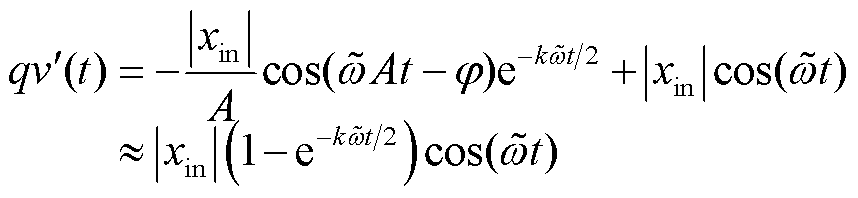 (14)
(14)
式中,![]() ;
;![]() 。当满足
。当满足![]()
![]() 及
及![]() 时,式(13)、式(14)中的近似成立。
时,式(13)、式(14)中的近似成立。
在生成正交信号后,![]() 的幅值估测值
的幅值估测值![]() 可以由式(15)计算,相位
可以由式(15)计算,相位![]() 可以由式(16)计算。
可以由式(16)计算。
![]() (16)
(16)
式中,![]() 为xin的真实幅值;
为xin的真实幅值;![]() 为经由信号提取器得到的xin的幅值估测值。xout的幅值估测值
为经由信号提取器得到的xin的幅值估测值。xout的幅值估测值![]() 和相位
和相位![]() 也可以用同样的方法计算得到。幅值估测值
也可以用同样的方法计算得到。幅值估测值![]() 与真实幅值
与真实幅值![]() 之间的传递函数可以统一表示为
之间的传递函数可以统一表示为
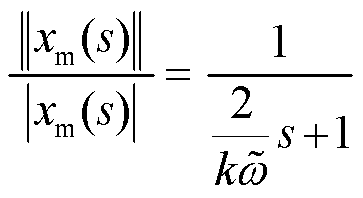 (17)
(17)
式(17)可以认为是一个转折频率为![]() 的一阶低通滤波器,这意味着
的一阶低通滤波器,这意味着![]() 可以以优良的动态性能精准地模拟真实幅值
可以以优良的动态性能精准地模拟真实幅值![]() 。
。
信号提取器的滤波效果是影响在线监测精准度的关键,其算法复杂程度则会影响在线监测的速度。不同于传统SOGI以dv和qv作为输出信号,这里的SOGI结构采用dv和qv¢作为一对正交输出信号。由式(11)可知,用qv¢作为输出时,![]() 是一个近似的高通滤波器,而传统SOGI采用qv时,是一个低通滤波器,但控制环路中低频信号含量较高,因此若采用传统形式的SOGI,需要额外增加一级滤波以滤除qv中无法滤除的低频谐波,这样不仅增加了计算的复杂度,还影响了控制性能监测器的动态性能,降低在线监测的速度。而若采用新型SOGI结构,即采用qv¢作为输出时,作为一个高通滤波器,可以很好地滤除环路中的低频谐波,因此有效滤波和正交信号生成这两个功能采用一个简洁的新型SOGI结构即可实现。在增强滤波效果、提高在线监测精准度的同时,也提升了在线监测的速度[31]。
是一个近似的高通滤波器,而传统SOGI采用qv时,是一个低通滤波器,但控制环路中低频信号含量较高,因此若采用传统形式的SOGI,需要额外增加一级滤波以滤除qv中无法滤除的低频谐波,这样不仅增加了计算的复杂度,还影响了控制性能监测器的动态性能,降低在线监测的速度。而若采用新型SOGI结构,即采用qv¢作为输出时,作为一个高通滤波器,可以很好地滤除环路中的低频谐波,因此有效滤波和正交信号生成这两个功能采用一个简洁的新型SOGI结构即可实现。在增强滤波效果、提高在线监测精准度的同时,也提升了在线监测的速度[31]。
3.1.3 控制性能指标估测器
控制性能指标估测器用来估测截止频率和相位裕度,由2.2节中动态寻频的原理可知,当![]() 时,可以准确监测到实际截止频率,因此将
时,可以准确监测到实际截止频率,因此将![]() 作为控制目标,将幅值差控制为0即可实现动态寻频。这里采用一个PI调节器实现对幅值差的控制,有
作为控制目标,将幅值差控制为0即可实现动态寻频。这里采用一个PI调节器实现对幅值差的控制,有
式中,Gpi为所采用的PI调节器;![]() 为理论设计的截止频率,作为动态寻频的基准值,并以信号提取器得到的幅值估测值(
为理论设计的截止频率,作为动态寻频的基准值,并以信号提取器得到的幅值估测值(![]() ,
, ![]() )替代无法获取的真实幅值(
)替代无法获取的真实幅值(![]() ,
, ![]() )。
)。
当动态寻频准确地锁定实际截止频率后,此频率下的响应信号的相位差即为实际相位裕度,有
由2.3节和2.4节分析可知,可以依据截止频率![]() 调节Kp,依据相位裕度
调节Kp,依据相位裕度![]() 调节Kr,如图5中自适应整定器部分,以截止频率
调节Kr,如图5中自适应整定器部分,以截止频率![]() 与其期望值
与其期望值![]() 的误差值调节Kp,使得截止频率维持在
的误差值调节Kp,使得截止频率维持在![]() 附近,保证环路优良的动态性能。以相位裕度
附近,保证环路优良的动态性能。以相位裕度![]() 与其期望值
与其期望值![]() 的误差值调节Kr,使得相位裕度维持在
的误差值调节Kr,使得相位裕度维持在![]() 附近,以保证环路的稳定性。调节过程可以表达为
附近,以保证环路的稳定性。调节过程可以表达为
![]() (21)
(21)
式中,Hfc和HjM为实现调节过程采用的调节器;Kp,int和Kr,int为在强电网情况(ZG=0)下的PR参数的理论设计值。
Hfc和HjM可以采用PI调节器或I调节器实现,自适应整定环路的带宽需远小于控制性能监测环路带宽,当对自适应调参的速度不做过高要求时,采用纯积分形式的I调节器即可完成调参过程,有
![]() (22)
(22)
![]() (23)
(23)
式中,![]() 和
和![]() 为调节器的控制参数。
为调节器的控制参数。
注入小信号幅值的选取需要考虑两个方面的因素。
1)为减少对并网电流的谐波污染,注入幅值不能过大,注入小信号xp对并网电流iG的干扰可以由二者之间的传递函数分析。
2)为保证控制性能指标监测的准确性,注入幅值不能过小,通常以信噪比(Signal-to-Noise Ratio, SNR)作为衡量准确性的指标,SNR越高,指标监测越准确[32]。
综合以上考虑,本方案注入小信号幅值![]() 选择为并网逆变器额定电流值的2.5%。
选择为并网逆变器额定电流值的2.5%。
SOGI中系数k的选取需要考虑以下几个因素:
1)为满足式(13)、式(14)中的近似条件,要求![]() ,
,![]() ,当k≤0.2时,可以满足上述近似条件。
,当k≤0.2时,可以满足上述近似条件。
2)k的选取需要兼顾SOGI结构的滤波效果和动态性能,k过大会使滤波效果变差,k过小则会影响动态性能[33]。
综上所述,k的合理取值范围为0.1~0.2,本文方案的理论分析和实验中k皆选取为0.2。
图5中控制性能监测器部分的调节器Gpi功能是依据监测到的响应信号幅值差![]() 调节小信号注入频率
调节小信号注入频率![]() ,因此为设计调节器Gpi,需推导
,因此为设计调节器Gpi,需推导![]() 与
与![]() 之间的传递函数
之间的传递函数![]() 。
。
根据式(3)、式(4)、式(17),![]() 可以表示为
可以表示为
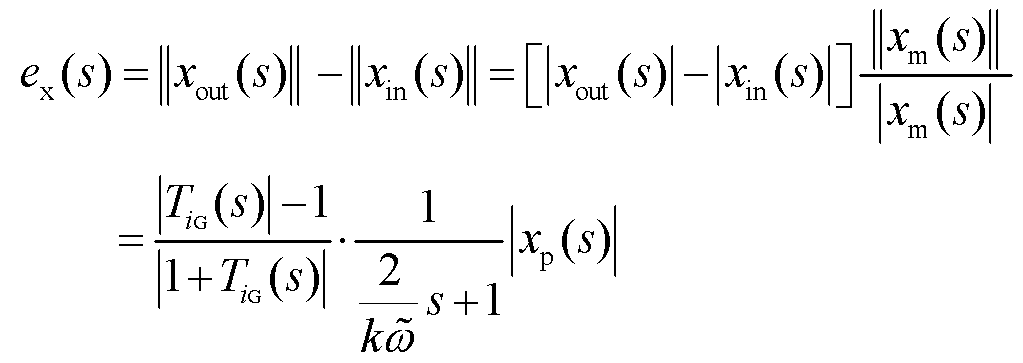 (25)
(25)
由于自适应整定器的动态性能远低于控制性能监测器的动态性能,因此在设计控制性能监测器时可以假定电流调节器参数是不变的,即环路增益是不变的。以小信号扰动分析推导传递函数![]() ,假定
,假定![]() 上产生一个小扰动变化,经过多层传递转变为
上产生一个小扰动变化,经过多层传递转变为![]() 的小扰动变化。该小扰动信号传递过程可以分为两个环节:①
的小扰动变化。该小扰动信号传递过程可以分为两个环节:①![]() 的小扰动传递至
的小扰动传递至![]() 和
和![]() 的小扰动;②
的小扰动;②![]() 和
和![]() 的小扰动传递至
的小扰动传递至![]() 和
和![]() 的小扰动,即
的小扰动,即![]() 的小扰动。环节①的动态性能大幅优于环节②,即环节②主导了控制性能监测环路的动态性能,相比之下,环节①可以认为是瞬时变化。因此环节①中
的小扰动。环节①的动态性能大幅优于环节②,即环节②主导了控制性能监测环路的动态性能,相比之下,环节①可以认为是瞬时变化。因此环节①中![]() 与
与![]() 的关系可以由式(25)的稳态值在
的关系可以由式(25)的稳态值在![]() 处的偏微分近似取代,环节②由式(17)决定[24]。
处的偏微分近似取代,环节②由式(17)决定[24]。
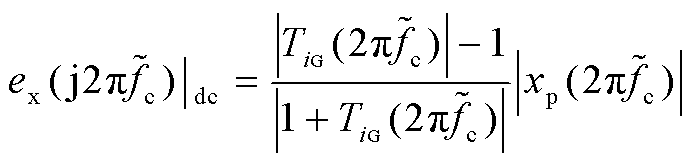 (26)
(26)
结合环节①和②,![]() 可以近似表示为
可以近似表示为
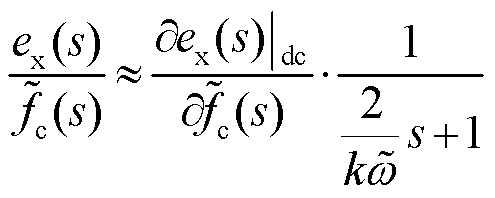 (27)
(27)
调节器![]() 可以依据式(27)进行规范设计。
可以依据式(27)进行规范设计。
为设计调节器Hfc,需要推导![]() 与Kp之间的传递函数
与Kp之间的传递函数![]() /Kp。由于控制性能监测器的动态性能远高于自适应整定器,因此在设计Hfc时,控制性能监测环路的动态性能可以被忽略。Kp的小扰动变化可以瞬时反映在
/Kp。由于控制性能监测器的动态性能远高于自适应整定器,因此在设计Hfc时,控制性能监测环路的动态性能可以被忽略。Kp的小扰动变化可以瞬时反映在![]() 中,所以
中,所以![]() /Kp可以由其稳态值的偏微分近似取代,即
/Kp可以由其稳态值的偏微分近似取代,即
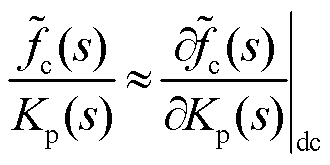 (28)
(28)
Hfc可以依据式(28)进行规范设计。
为设计调节器HjM,需要推导![]() 与Kr之间的传递函数
与Kr之间的传递函数![]() /Kr,同样做近似分析,认为Kr的小扰动变化可以瞬时反映在
/Kr,同样做近似分析,认为Kr的小扰动变化可以瞬时反映在![]() 中,因此
中,因此![]() /Kr可以由其稳态值的偏微分近似取代,即
/Kr可以由其稳态值的偏微分近似取代,即
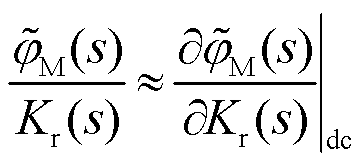 (29)
(29)
HjM可以依据式(29)进行规范设计。
本文在一台1.5 kV·A的单相并网逆变器样机上进行实验验证。图11为实验装置,逆变器相关参数见表1。控制策略采用三环控制[25],控制器采用内嵌高性能FPGA的NI cRIO-9057平台。期望的控制性能指标设计为![]() =1 kHz,
=1 kHz,![]() =45°。
=45°。
表1 1.5kV·A单相并网逆变器参数
Tab.1 Parameters of 1.5 kV·A grid-connected inverter

参数数值 直流侧电压 Vin/V400 开关频率fSW/kHz20 逆变器侧电感L1/mH1.5 滤波器电容C/mF15 网侧电感L2/mH0.55 额定功率SO/(kV·A)1.5

图11 实验装置
Fig.11 Experimental setup
为验证控制性能指标在线监测方案的有效性、监测精准度及监测速度,对电网阻抗跳变前后控制性能指标理论值与实测值进行对比验证。
图12给出了电网阻抗跳变前后控制性能指标的波形,电网阻抗跳变前(ZG=0 W+0 mH),控制性能指标理论值为:fc_theo=1 kHz、jM_theo=45°,控制性能指标实测值经过校正后也调整为:![]() =1 kHz、
=1 kHz、![]() =45°。电网阻抗跳变后(ZG=1 W+0.4 mH),控制性能指标理论值应改变为:fc_theo=927 Hz、jM_theo=34.3°,控制性能指标实测值则变化为:
=45°。电网阻抗跳变后(ZG=1 W+0.4 mH),控制性能指标理论值应改变为:fc_theo=927 Hz、jM_theo=34.3°,控制性能指标实测值则变化为:![]() = 912 Hz、
= 912 Hz、![]() =35.7°。从图12中可以看到,电网阻抗跳变后,实测截止频率
=35.7°。从图12中可以看到,电网阻抗跳变后,实测截止频率![]() 经过了52 ms,从1 kHz下降为912 Hz,测量误差
经过了52 ms,从1 kHz下降为912 Hz,测量误差![]() 小于1.5%,相位裕度
小于1.5%,相位裕度![]() 经过了59 ms,从45°下降为35.7°,测量误差
经过了59 ms,从45°下降为35.7°,测量误差![]() 小于4%。
小于4%。
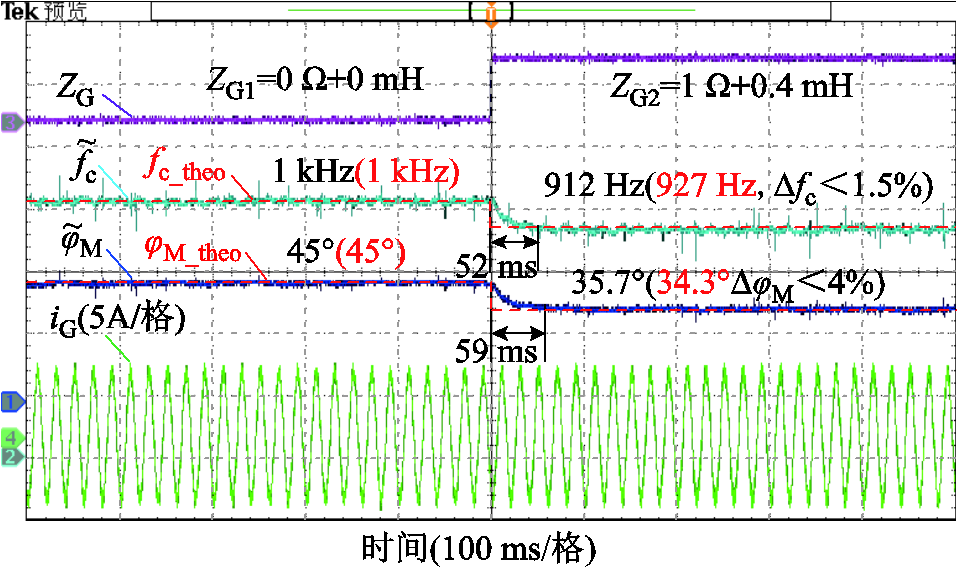
图12 电网阻抗改变时控制性能指标(fc, jM)波形
Fig.12 The experimental waveforms of control performance indexes (fc, jM) under grid impedance variation
因此,在线监测方案的有效性得以验证,监测精准度可达到96%以上,监测速度在50 ms左右,可满足后续自适应调参的需求。若要求更高的监测精准度和更快的监测速度,可通过优化设计相关的参数来实现。
为验证自适应控制策略的有效性,设计了自适应控制开启前后的对比实验,图13a是自适应控制开启前控制性能指标及响应信号的稳态波形,此时的PR参数为强电网下的理论设计值:Kp=3.28、Kr=2 071。由于理论模型与实验装置存在一定程度的失配,实测的截止频率为966 Hz,实测的相位裕度为41.82°,与期望值均存在一定偏差。图13b为自适应控制开启过程中的暂态波形,自适应整定器自动调节参数,直到达到期望的控制性能指标。图13c为自适应控制开启后的稳态波形,此时Kp增加到了3.59,Kr减小为1 866,使得截止频率提升到1 kHz,相位裕度提升到45°。
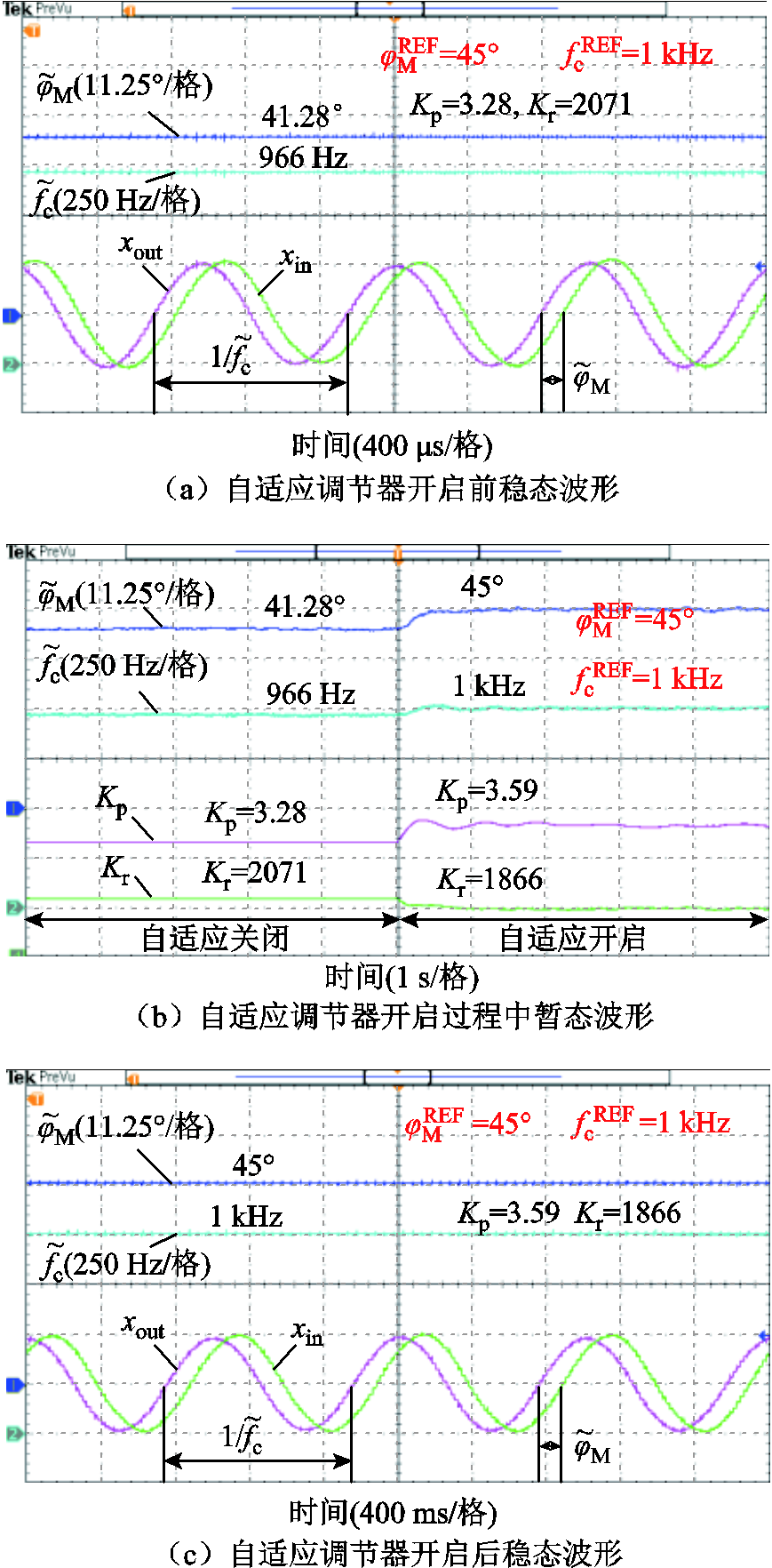
图13 自适应过程中控制性能指标(fc, jM)波形及响应信号(xout, xin)波形
Fig.13 The experimental waveforms of control performance indexes (fc, jM) and the measured response signals (xout, xin)
为验证自适应控制在电网阻抗波动下的有效性,需设计不同的电网阻抗值并使其频繁切换,电网阻抗(ZG=RG+jwLG)通常被等效为电阻与电感串联的模型,阻性成分可以在一定程度上补偿相位裕度,因此这里仅以电感模拟电网阻抗,分析相对恶劣的弱电网环境。
图14a是电网阻抗增加过程中控制性能指标(fc, jM)及控制器参数(Kp, Kr)波形,随着LG不断增加,自适应整定器不断校正PR调节器参数,Kp不断增加,Kr不断减小,使得截止频率始终保持为 1 kHz,相位裕度保持为45°。图14c为图14a中蓝色阴影部分的细节放大图,可以看到自适应整定的调节时间为316 ms。图14b是电网阻抗减小过程中控制性能指标(fc, jM)及控制器参数(Kp, Kr)波形,随LG逐渐减小,自适应整定器同样不断校正PR调节器参数,Kp不断减小,Kr不断增加,使得截止频率和相位裕度始终保持在期望值。由实验结果可知:无论电网阻抗增加还是减小,相位裕度始终保持在45°,保证了逆变器的稳定性;截止频率始终保持在1 kHz,保证了逆变器的动态性能。
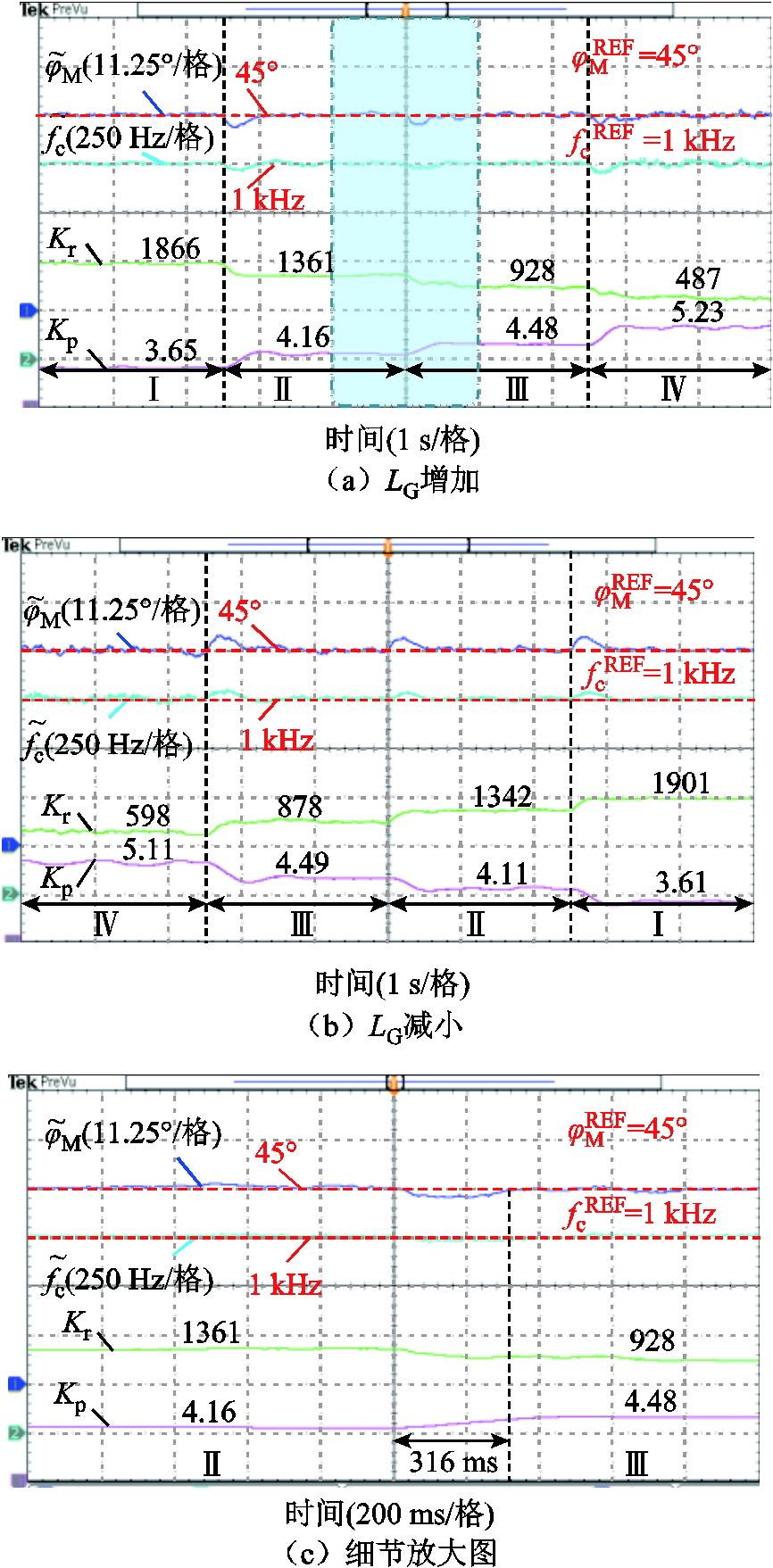
图14 电网阻抗变化时的实验波形(Ⅰ:LG=0 mH, Ⅱ: LG=0.2 mH, Ⅲ: LG=0.4 mH, Ⅳ: LG=0.6 mH)
Fig.14 The experimental waveforms under grid impedance variations(Ⅰ: LG=0 mH, Ⅱ: LG=0.2 mH, Ⅲ: LG=0.4 mH, Ⅳ: LG=0.6 mH)
为验证自适应方案对电网电压的谐波抑制能力,采用可编程交流源(Chroma 61830)模拟富含背景谐波的电网电压,注入3、5、7、9次谐波,注入幅值相对于基波幅值分别为10%、5%、3%、3%,相位分别为0°、210°、0°、0°,并选定电网阻抗为RG=1.5 W和LG=0.4 mH。图15a为自适应控制未开启时的并网点电压uPCC及并网电流iG波形,此情况下并网电流总谐波畸变率(Total Harmonic Distortion, THD)为5.68%,图15b为自适应控制开启后的波形,此时并网电流THD降低为4.13%,符合并网标准。

图15 电网含背景谐波及低电压穿越情况下的实验波形(ZG=1.5 W+0.4 mH)
Fig.15 The experimental waveforms with grid background harmonics and under the low-voltage ride through condition(ZG=1.5 W+0.4 mH)
图15c给出了在低电压穿越情况下自适应控制的相关波形,此时电网阻抗选定为:RG=1.5 W、LG=0.4 mH,可以看到当并网点电压uPCC跌落为0时,逆变器依然稳定运行,自适应控制策略依然有效,截止频率和相位裕度依然保持在期望值。
针对并网逆变器在弱电网阻抗变化情况下稳定性降低和动态性能下降的问题,本文提出了一种基于环路增益测量的自适应控制方法以保持逆变器优越的控制性能,得到如下结论:
1)弱电网下电网阻抗的波动,不仅导致逆变器稳定性下降,还影响其动态性能,本文方案基于环路增益测量原理实现对截止频率和相位裕度的在线监测,逆变器的稳定性和动态性能得以在线表征。
2)本方案采用灵敏度分析的方法设计自适应规律,实现自适应整定器的解耦设计,调节器参数可以实时自适应整定,在保证逆变器稳定性的同时,提升其动态性能,并且本方案可适用于PI、PR等多种调节器。
3)论文给出了控制性能监测器和自适应整定器的实现方案,并给出了相应的参数选取和调节器设计方法。
4)实验表明,本文方案可以解决理论模型与实际装置的失配问题,在电网阻抗波动时,可以保证逆变器的稳定性和动态性能,同时具备一定的谐波抑制能力以及在低电压穿越等故障工况下持续运行的能力。
参考文献
[1] Blaabjerg F, Teodorescu R, Liserre M, et al. Overview of control and grid synchronization for distributed power generation systems[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1398-1409.
[2] 沈姝衡, 方天治, 章益凡. 高带宽数字控制LCL型并网逆变器及其提高并网系统鲁棒性的谐振抑制技术研究[J]. 电工技术学报, 2022, 37(21): 5548-5561. Shen Shuheng, Fang Tianzhi, Zhang Yifan. A high-bandwidth digital-control LCL-type grid-tied inverter and resonance-suppressing technique for improving therobustness of grid-connected system[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5548-5561.
[3] 涂春鸣, 邹凯星, 高家元, 等. 基于不对称正负反馈效应的PQ功率控制并网逆变器稳定性分析[J]. 电工技术学报, 2023, 38(2): 496-509. Tu Chunming, Zou Kaixing, Gao Jiayuan, et al. Stability analysis of grid-connected inverter under PQ power control based on asymmetric positive-negative-feedback effects[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 496-509.
[4] 洪芦诚, 徐佳裕, 唐润悦, 等. 三相LCL型逆变器序阻抗简化建模方法及并网稳定性分析[J]. 电力系统自动化, 2023, 47(7): 150-157. Hong Lucheng, Xu Jiayu, Tang Runyue, et al. Simplified modeling method of sequence impedance and grid-connected stability analysis for three-phase LCL inverter[J]. Automation of Electric Power Systems, 2023, 47(7): 150-157.
[5] 高本锋, 邓鹏程, 梁纪峰, 等. 光伏电站与弱交流电网间次同步交互作用路径及阻尼特性分析[J]. 电工技术学报, 2023, 38(24): 6679-6694. Gao Benfeng, Deng Pengcheng, Liang Jifeng, et al. Analysis of path and damping characteristics of subsynchronous interaction between photovoltaic plant and weak AC grid[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6679-6694.
[6] Yang Dongsheng, Ruan Xinbo, Wu Heng. Impedance shaping of the grid-connected inverter with LCL filter to improve its adaptability to the weak grid condition[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 5795-5805.
[7] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146. Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impedance[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[8] 涂春鸣, 高家元, 赵晋斌, 等. 弱电网下具有定稳定裕度的并网逆变器阻抗重塑分析与设计[J]. 电工技术学报, 2020, 35(6): 1327-1335. Tu Chunming, Gao Jiayuan, Zhao Jinbin, et al. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1327-1335.
[9] 曾君, 岑德海, 陈润, 等. 针对直流偏移和谐波干扰的单相锁相环[J]. 电工技术学报, 2021, 36(16): 3504-3515. Zeng Jun, Cen Dehai, Chen Run, et al. Single-phase phase-locked loop for DC offset and harmonic interference[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3504-3515.
[10] 闫培雷, 葛兴来, 王惠民, 等. 弱电网下新能源并网逆变器锁相环参数优化设计方法[J]. 电网技术, 2022, 46(6): 2210-2221. Yan Peilei, Ge Xinglai, Wang Huimin, et al. PLL parameter optimization design for renewable energy grid-connected inverters in weak grid[J]. Power System Technology, 2022, 46(6): 2210-2221.
[11] 姜云龙, 司鑫尧, 史鸿飞, 等. 弱电网下计及锁相环影响的并网逆变器稳定性提升方法[J]. 电力系统自动化, 2022, 46(24): 113-120. Jiang Yunlong, Si Xinyao, Shi Hongfei, et al. Stability improvement method of grid-connected inverter considering phase-locked loop effect in weak grid[J]. Automation of Electric Power Systems, 2022, 46(24): 113-120.
[12] Pan Donghua, Ruan Xinbo, Bao Chenlei, et al. Capacitor-current-feedback active damping with reduced computation delay for improving robustness of LCL-type grid-connected inverter[J]. IEEE Trans-actions on Power Electronics, 2014, 29(7): 3414-3427.
[13] Wang Cheng, Wang Xuehua, He Yuying, et al. Passivity-oriented impedance shaping for LCL-filtered grid-connected inverters[J]. IEEE Transactions on Industrial Electronics, 2023, 70(9): 9078-9090.
[14] Cespedes M, Sun Jian. Adaptive control of grid-connected inverters based on online grid impedance measurements[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 516-523.
[15] 许津铭, 谢少军, 唐婷. 弱电网下LCL滤波并网逆变器自适应电流控制[J]. 中国电机工程学报, 2014, 34(24): 4031-4039. Xu Jinming, Xie Shaojun, Tang Ting. An adaptive current control for grid-connected LCL-filtered inverters in weak grid case[J]. Proceedings of the CSEE, 2014, 34(24): 4031-4039.
[16] Xu Jinming, Xie Shaojun, Tang Ting. Improved control strategy with grid-voltage feedforward for LCL-filter-based inverter connected to weak grid[J]. IET Power Electronics, 2014, 7(10): 2660-2671.
[17] Xu Jinming, Xie Shaojun, Qian Qiang, et al. Adaptive feedforward algorithm without grid impedance estimation for inverters to suppress grid current instabilities and harmonics due to grid impedance and grid voltage distortion[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7574-7586.
[18] Zhou Xiaohu, Fan Jiwei, Huang A Q. High-frequency resonance mitigation for plug-in hybrid electric vehicles’ integration with a wide range of grid conditions[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4459-4471.
[19] Li Hong, Ding Xin, Xue Ruinan, et al. Active damping adaptive controller for grid-connected inverter under weak grid[J]. IEEE Access, 2021, 9: 132442-132454.
[20] 陈新, 王赟程, 华淼杰, 等. 采用混合阻尼自适应调整的并网逆变器控制方法[J]. 中国电机工程学报, 2016, 36(3): 765-774. Chen Xin, Wang Yuncheng, Hua Miaojie, et al. Grid-connected inverters control schemes based on hybrid damping adaptive control[J]. Proceedings of the CSEE, 2016, 36(3): 765-774.
[21] Morroni J, Corradini L, Zane R, et al. Adaptive tuning of switched-mode power supplies operating in discontinuous and continuous conduction modes[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2603-2611.
[22] Morroni J, Zane R, Maksimovic D. Design and implementation of an adaptive tuning system based on desired phase margin for digitally controlled DC-DC converters[J]. IEEE Transactions on Power Electronics, 2009, 24(2): 559-564.
[23] Khodamoradi A, Liu Guangyuan, Mattavelli P. Online controller tuning for DC microgrid power converters with the ability to track maximum allowable bandwidth[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1888-1897.
[24] Liu Qing, Caldognetto T, Buso S. Stability analysis and auto-tuning of interlinking converters connected to weak grids[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 9435-9446.
[25] Buso S, Caldognetto T, Liu Qing. Analysis and experimental characterization of a large-bandwidth triple-loop controller for grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1936-1949.
[26] Teodorescu R, Blaabjerg F, Borup U, et al. A new control structure for grid-connected LCL PV inverters with zero steady-state error and selective harmonic compensation[C]//Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 2004: 580-586.
[27] 游小杰, 杨才伟, 王剑, 等. 一种适用于机车PWM整流器的比例积分-谐振电流控制器设计[J]. 电工技术学报, 2021, 36(23): 4926-4936. You Xiaojie, Yang Caiwei, Wang Jian, et al. A tuning method for proportional integral-resonant current controller in locomotive PWM rectifiers[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4926-4936.
[28] 鲍陈磊, 阮新波, 王学华, 等. 基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计[J]. 中国电机工程学报, 2012, 32(25): 19, 133-142. Bao Chenlei, Ruan Xinbo, Wang Xuehua, et al. Design of grid-connected inverters with LCL filter based on PI regulator and capacitor current feedback active damping[J]. Proceedings of the CSEE, 2012, 32(25): 19, 133-142.
[29] Basso C P. Designing Control Loops For Linear and Switching Power Supplies: A Tutorial Guide[M]. Norwood: Artech House, 2012.
[30] Middlebrook R D. Measurement of loop gain in feedback systems[J]. International Journal of Electronics, 1975, 38(4): 485-512.
[31] Wang Jiachen, Liu Qing, Zeng Xiangchen, et al. Control performance characterization and monitoring scheme for power converters in weak grids[J]. IEEE Open Journal of Power Electronics, 2023, 4: 791-800.
[32] Nian Heng, Li Meng, Hu Bin, et al. Design method of multisine signal for broadband impedance measurement [J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(3): 2737-2747.
[33] Rodríguez P, Luna A, Muñoz-Aguilar R S, et al. A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions[J]. IEEE Transactions on Power Electronics, 2012, 27(1): 99-112.
Abstract Driven by the large-scale adoption of electronic power converters for widespread renewable generation, power grids gradually present weak grid characteristics, i.e., the grid impedance can’t be ignored and fluctuates frequently. The grid impedance directly affects the control loop gain of inverters, which can decrease the stability margin and lead to poor dynamic performance. To solve these issues jointly, an adaptive control strategy based on loop gain measurement technique is proposed in this work to improve the adaptability of inverters to pre-unknown weak grid conditions.
The proposed adaptive control strategy includes two important steps: (1) The monitoring of control performance indexes and (2) Auto-tuning of controller parameters. Firstly, a control performance monitor is proposed for online monitoring of control performance indexes (crossover frequency fc, phase margin jM) of inverter systems. These indexes can be used to characterize, in real time, the dynamic performance and stability, respectively. The proposed control performance monitor is designed based on Middlebrook’s loop gain measurement technique with small signal injection. The corresponding signal extraction structure is realized by a high-pass second order generalized integrator (HPSOGI), which can enhance the attenuation ability of low-frequency harmonics. With the measured performance indexes (fc, jM), an auto-tuner is then designed to adjust controller parameters of inverters accordingly. The sensitivity analysis method is adopted to decouple the controller parameters (Kp, Kr) and control performance indexes (fc, jM). A general adaptive law is therefore designed as following: the crossover frequency fc is designed to adjust the proportional gain Kp until the desired crossover frequency ![]() is achieved; the phase margin jM is designed to adjust the resonance gain Kr until the desired phase margin
is achieved; the phase margin jM is designed to adjust the resonance gain Kr until the desired phase margin ![]() is achieved. In this way, high dynamic performance and sufficient stability margin can be guaranteed simultaneously by the proposed auto-tuner. Additionally, the relevant parameters selection and design of regulators are discussed.
is achieved. In this way, high dynamic performance and sufficient stability margin can be guaranteed simultaneously by the proposed auto-tuner. Additionally, the relevant parameters selection and design of regulators are discussed.
The experimental results show that the monitoring process can be completed within 60ms with an accuracy of 96%, which is sufficient for the subsequent auto-tuning process. Both the measurement time and the accuracy can be further improved by refining the auto-tuner coefficients. With the proposed adaptive control strategy, the crossover frequency and phase margin can be maintained at expected value (fc=1 kHz, jM=45°) under grid impedance variations and low-voltage ride through conditions. With the increased loop gain, total harmonic distortion (THD) of the injected grid current is also decreased.
The following conclusions are drawn from this paper: (1) The HPSOGI structure adopted in control performance monitor can improve accuracy and speed of the monitoring process. (2) Sensitivity analysis method can be used to design adaptive law to improve the adaptability of adaptive control strategy to various regulators such as PI and PR regulator. (3) The proposed adaptive control strategy can maintain high dynamic performance and sufficient stability margin of inverter system under grid impedance variation and fault conditions such as low-voltage ride through.
keywords:Stability, adaptive control, weak grids, grid-connected inverters
DOI: 10.19595/j.cnki.1000-6753.tces.231765
中图分类号:TM464
国家自然科学基金青年项目(62003126)、河北省自然科学基金绿色通道项目(E2021202157)和河北省留学人员资助项目(C20220318)资助。
收稿日期 2023-10-24
改稿日期 2024-01-11
曾祥辰 男,1999年生,硕士研究生,研究方向为并网逆变器控制及稳定性分析。E-mail:202121401093@stu.hebut.edu.cn
刘 青 女,1990年生,副教授,研究方向为电力电子系统建模、控制与稳定性分析。E-mail:qing.liu@hebut.edu.cn(通信作者)
(编辑 赫 蕾)