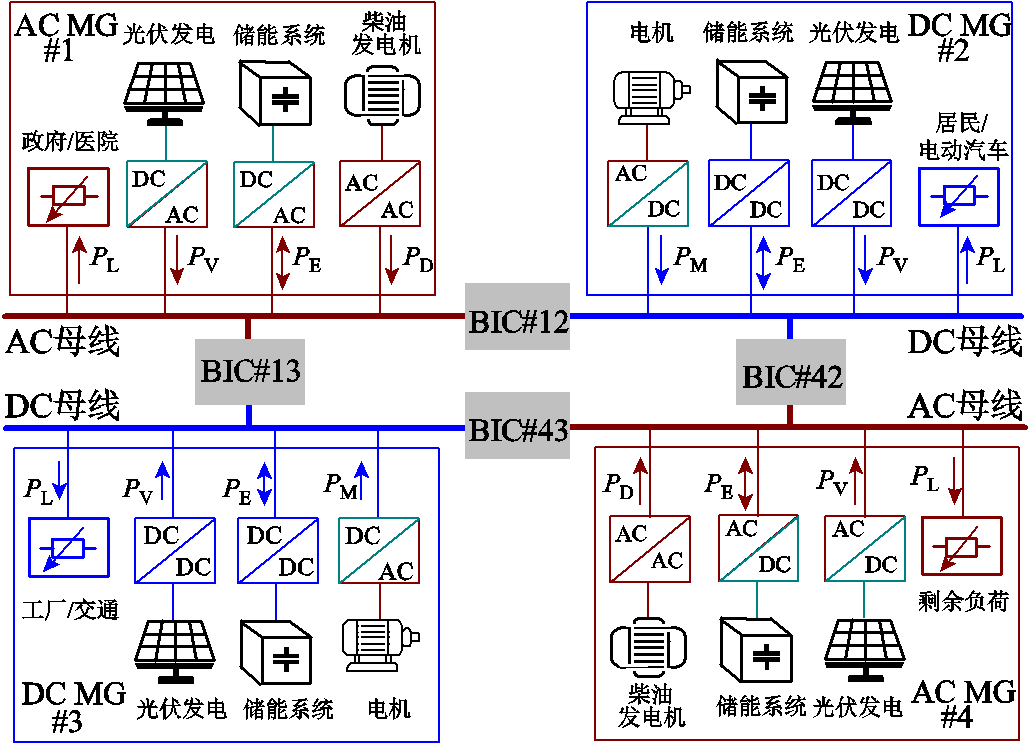
图1 HMG-Cluster配置方案
Fig.1 HMG-Cluster configuration schemes
摘要 随着可再生能源渗透率的不断提高,交直流混合微电网集群逐渐成为新型电力系统的弹性解决方案。考虑到实际运行中各子电网优先级和电能质量需求存在差异,该文提出一种基于子网优先级驱动的交直流混合微网集群双向互联变流器分散式控制策略,以实现系统的弹性功率交互。首先,通过将归一化的交流频率和直流电压值作为子电网的状态偏差因子,以最小化全局总偏差因子为目标构建了用于交直流混合微电网集群的最优电力交换模型,该模型充分考虑了子电网的优先级指数和供电容量;其次,基于最优电力交换目标,提出用于双向互联变流器的准下垂控制策略,由于该策略中双向互联变流器仅需检测本地交流频率/直流电压的状态偏差因子,因此可以实现对交直流混合微电网集群整体偏差因子最小化的分散式最优功率自主协同控制;最后,构造了两个仿真实例,并利用半实物仿真系统验证了所提策略的有效性。
关键词:交直流混合微电网集群 双向互联变流器 状态偏差 优先级驱动 分散式控制
随着以可再生能源为代表的直流系统渗透水平不断提高,以及交通系统以电动汽车为代表的直流负载迅速部署,交流负载在配电系统的主导地位逐渐被直流负载所取代[1]。然而,发达的交流网络和从交流到直流的转换损耗限制了直流电网的充分利用。对此,为提高电力利用效率并更好地促进能源管理,交直流混合微电网(Hybrid AC-DC Microgrid, HMG)的拓扑范式因具有转换成本低、系统效率高、灵活控制能力强的优势被广泛部署[2]。
作为互联和协同AC和DC微电网的关键组件,双向互联变流器(Bidirectional Interlinking Converter, BIC)能够实现HMG系统高效的电源管理和故障穿越[3]。然而由于单个HMG通常受限于接入容量固定、供电范围小等限制,很难满足系统负荷对高比例可再生能源的功率需求。对此,基于BIC设备将多个HMG互联并构建HMG集群(HMG-Cluster)不仅能够避免可再生能源发电的间歇性和负载的不确定性,而且可以协同多HMG之间的功率交互并缓解功率过载情况[4]。尽管当前已有诸多研究者证明了基于BIC的控制策略显著影响系统的最佳电力交换[5]、电能质量[6]、系统稳定性[7]等,然而当其处理具有多个不同容量微电网功率协同时仍因存在限制而影响协同效果。因此,在实现多个BIC间自主协同的基础上,如何控制和设计用于HMG-Cluster系统基于多个BIC的功率协同仍然是一项根本性的挑战。
根据BIC对通信设备的依赖程度,其控制策略可被分为集中式、分布式和分散式三类[8]。其中,集中式控制是指以中央处理器为中心,并利用信息流和能量流的耦合实现微电网的能量管理,以及对所有信息的一致性分配,然而该策略严重依赖中央控制器,一旦该组件出现故障则会导致系统级瘫痪,严重影响系统的安全可靠运行[9]。分布式控制是基于各变换器单元之间的邻域通信替代中央控制器实现所有微电网之间的信息传递,尽管该策略能够避免单点故障对可靠性的影响,但其底层通信通常会消耗大量时间,不利于对紧急情况的处理。此外,由于分布式控制策略依赖相邻控制器间的信息交互,因此任意控制器的失效或故障都有可能导致交互信息误差甚至相邻控制器故障[10-11]。
相较于分布式控制,分散式控制策略是通过监测本地微电网的频率、电压或操作约束等信息,并通过比例积分(Proportional Integral, PI)控制器将测量值和标称值之间的操作误差反馈至下垂控制单元而实现的微电网功率补偿,因此分散式控制策略可以在不依赖任何通信设备的情况下实现功率交互,这不仅能够降低控制策略的复杂性,而且可以提升系统的响应速度。此外,由于分散式控制策略下各变换器的控制功能分散,因此任一控制器故障既不会对剩余控制器造成影响也不会引起全局瘫痪,此外还可以将其功能分担给剩余可用控制器,进而有效提高系统的可靠性和可拓展性[12-13]。综上所述,分散式控制因具有扩展性好、响应及时、可靠性较高等优点,能够为管理没有通信的复杂微电网提供一种替代解决方案。
当前,针对BIC的功率控制策略已经得到了越来越多研究者的关注。在分布式控制策略方面,文献[14]针对HMG系统基于多并行BIC互联的场景提出一种分布式的统一控制策略,该策略中多并行BIC之间的协调依赖低带宽邻域通信,通过规划通信以实现准确的功率共享。文献[15]针对HMG系统基于多并行BIC互联的场景提出一种分布式电源管理策略,该策略为每个BIC设计了本地化的分布式控制器,以允许所有BIC在分布式通信网中交换信息,并根据不同的额定功率以完全分布式的方式按比例分配给每个BIC。然而,当其被扩展至HMG-Cluster系统时,由于任意AC或DC微电网都会被通过两个非并行BIC连接至具有不同功率容量的DC或AC微电网,尽管此时基于低带宽通信可以协调所有的BIC,但由于通信故障所导致的不稳定性,以及任意非并行BIC功率交互参考值的不确定性,都使得用于HMG-Cluster的非并行BIC控制相较于两个微电网间的多并行BIC控制更为复杂。
在分散式控制策略方面,文献[16]针对DC微电网提出一种自适应反步控制策略,该策略基于对变流器的动态模型设计能够使系统在初始参数有限的情况下实现分散自主控制。文献[17]提出一种基于电压分层控制的DC微电网及其储能扩容单元功率协同控制策略,该策略能够实现电压分层下多储能单元的分散协调控制。然而,由于该策略仅面向DC微电网的储能设备,并不能实现多子电网之间的功率分散式自适应协同控制。此外,文献[18]提出一种针对HMG的分散式双向电压支持控制方案,并在双向下垂控制方程中加入了权重系数,然而该策略仅适用于HMG系统基于单个BIC互联场景下的功率交互。
基于已有研究的不足,本文提出一种基于优先级驱动的BIC分散式控制策略,以保证以HMG-Cluster不同优先级和容量需求子电网之间的最优功率交换。首先,本文构建了多个子电网经多BIC互联的HMG-Cluster配置方案,并在归一化处理方案基础上提出将AC频率和DC电压的归一化值作为子电网的状态偏差因子;其次,本文构建了以HMG-Cluster总偏差因子最小的功率交互目标函数,实现了在HMG-Cluster功率盈余和故障状态下基于子电网优先级指数和容量需求的自主协同;再次,本文构建了基于BIC的分散式准下垂控制策略,由于BIC仅监测本地的AC频率和DC电压值,因此可以在无需任何通信链路情况下实现系统整体偏差因子最小的分散式自优化潮流控制;最后,本文基于硬件在环(Hardware in the Loop, HIL)仿真系统,验证了所提控制策略相较现有“全局功率平等/ 比例共享”控制策略在子电网负载突变和突发故障两种案例下的控制效果。
为了提高微电网中各电源的利用效率,并避免AC和DC子电网之间的多次反向交互,系统内所有可再生能源和负载根据其AC或DC特性分别被接入AC或DC主母线,并通过部署分布式能源以补偿可再生能源的间歇性。
包含四个子电网的HMG-Cluster配置方案如图1所示。所提HMG-Cluster由AC子电网、DC子电网和BIC三部分组成。任意子电网由不可调度的可再生能源(包括但不限于光伏组件),可调度的分布式电源(包括但不限于储能、柴油发电机、电动机)及各类负载组成。任意两个子电网之间通过BIC实现互联。需要说明的是,这里的BIC可以根据主母线类型相应设计为AC-AC、DC-DC或AC-DC型变流器,其中AC和DC子电网的稳定运行在很大程度上依赖于AC-AC和DC-DC变流器的设计,以确保系统具有足够的稳定裕度和快速的动态响应,然而这些控制器在现有文献中已经得到了成熟的研究[19-20]。进一步,由于本文的重点是HMG-Cluster中BIC的控制,且计划利用子电网的归一化值,因此本文关注于AC-DC型BIC。

图1 HMG-Cluster配置方案
Fig.1 HMG-Cluster configuration schemes
1.2.1 不可调度源的控制
为最大限度地获得HMG-Cluster系统内可再生能源的可用电量,除分布式电源处于满电或放电等极端条件下,其余时刻可再生能源发电的功率控制模式被设定在最大功率点跟踪(Maximum Power Point Tracking, MPPT)模式下运行。当前基于可再生能源的最大功率点控制策略已被大量研究与应用,本文不再赘述。
1.2.2 可调度源的控制
为建立AC和DC母线电压并支持可再生能源系统在MPPT控制策略下稳定运行,分布式发电机和储能通常工作在电压调节模式。下垂控制作为一种分散控制策略能够实现基于下垂方程设计的不同功率共享目标,且通信网络的独立性可以提高微电网的稳定与灵活运行。对此,本文采用下垂控制实现子电网内所有可调度源的功率共享。
对于AC子电网,使用fac-Pac及Vac-Qac下垂控制调节子电网内的功率协同[21],有
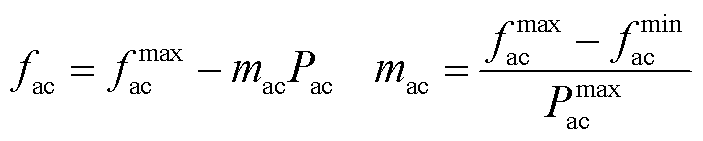 (1)
(1)
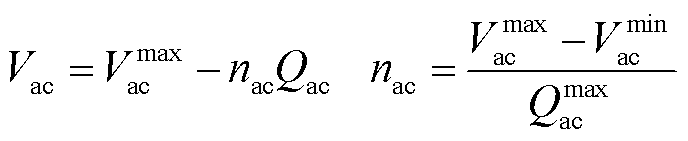 (2)
(2)
式中,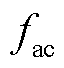 和
和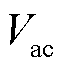 分别为AC子电网的频率和输出电压幅值;mac和nac分别为fac-Pac及Vac-Qac下垂系数;Pac和Qac分别为AC子电网中可调度电源输出的有功和无功功率;上标max和min分别表示该变量的最大和最小值。
分别为AC子电网的频率和输出电压幅值;mac和nac分别为fac-Pac及Vac-Qac下垂系数;Pac和Qac分别为AC子电网中可调度电源输出的有功和无功功率;上标max和min分别表示该变量的最大和最小值。
对于DC子电网,使用Vdc-Pdc下垂控制调节子电网内的功率协同,有
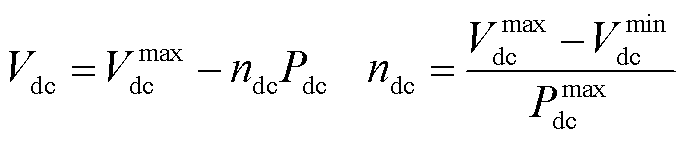 (3)
(3)
式中,Vdc为DC子电网的输出电压幅值;ndc为Vdc-Pdc下垂系数;Pdc为DC子电网中可调度电源输出的有功功率。
根据下垂控制特性可知,任意AC或DC子电网内负载需求的增加会导致AC子电网频率或DC子电网电压的下降,因此基于AC频率和DC电压相对于额定值的相对偏差可以用于指示该子电网的实时运行状态偏差[22-23]。利用该特性,在HMG系统中基于对AC频率和DC电压的归一化处理即可在不使用通信设备的前提下实现AC与DC子电网间的功率自主交互,其归一化方程为
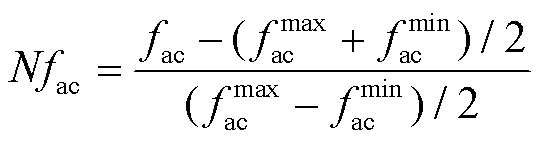 (4)
(4)
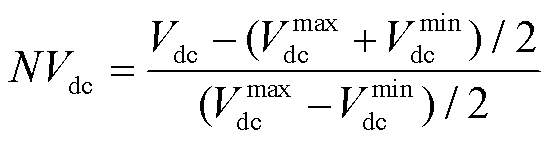 (5)
(5)
式中,Nfac和NVdc分别为归一化后的AC频率值和DC电压值,归一化区间均为[-1,1]。如图2给出了HMG-Cluster子电网的归一化处理。
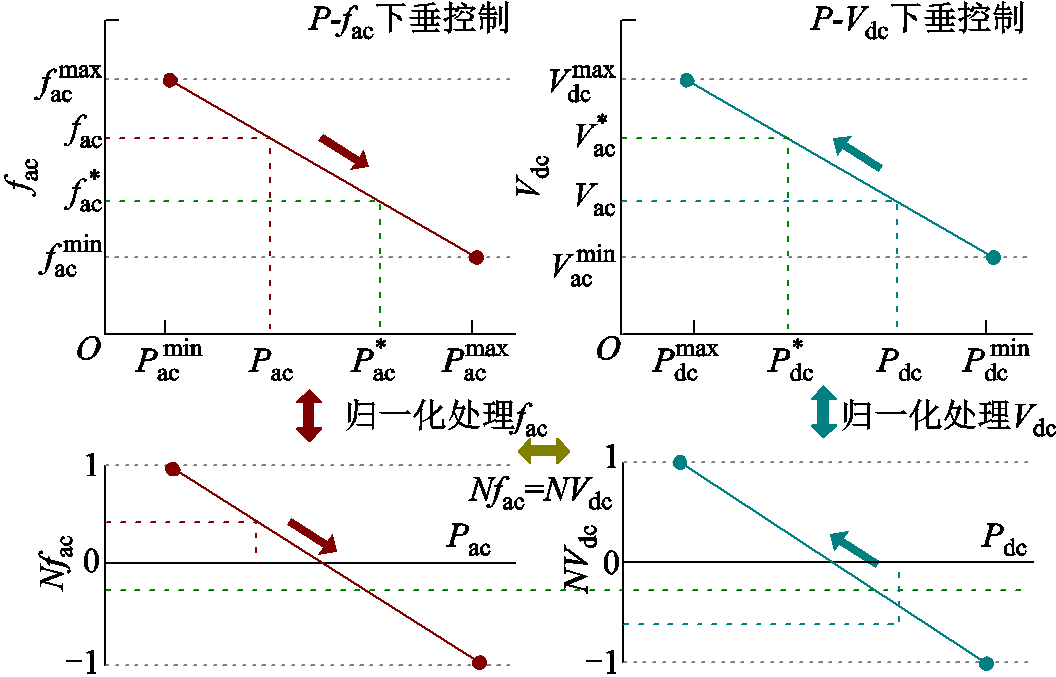
图2 HMG-Cluster子电网的归一化处理
Fig.2 Normalization processing of HMG-Cluster subgrid
本文提出使用统一的状态偏差因子Nηi代表任一AC或DC子电网因负载需求增加而导致的功率供给空缺状态。当AC型子电网的功率供给空缺,Nηi=Nfac.i;当DC型子电网的功率供给空缺,Nηi=NVdc.i,即
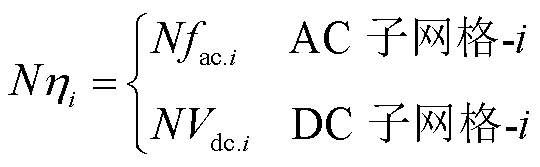 (6)
(6)
根据式(4)和式(5),Nηi=1表示该子电网在功率供给充足状态,Nηi=-1表示该子电网在功率供给不足状态,Nηi=0表示该子电网在标称状态。
与现有研究成果[14-15]所解决“全局功率平等/比例共享”概念不同,在实际HMG-Cluster控制中,具备不同类型负荷的子电网在运行中可能存在优先级差异。为保证故障状态下,HMG-Cluster能够保证对重要负荷的优先持续供电,本文计划根据子电网的馈线负载特征将其优先等级分为三类:将包含负载断开将会造成人身伤亡或政治经济重大损失的子电网定义为A类子电网;将包含负载断开将造成严重停工停产或交通阻塞的子电网定义为B类子电网;并将剩余子电网定义为C类子电网。在此基础上,本文分别定义了不同等级子电网的允许电压偏差值见表1。表1中,ferror为子电网的频率偏差因子。
表1 子电网的优先级和电压偏差值
Tab.1 Priority and voltage deviation values of sub-grid

子电网类型负荷类型优先级允许电压偏差值(%) A类医院/银行/政府高|V/ferror|<0.5 B类工厂/交通中|V/ferror|<1 C类其他低|V/ferror|<3
本节首先描述了基于子网优先级驱动的BIC最优功率交换模型,实现了面向全局最优的BIC初级准下垂控制策略。其次构建了基于BIC的分散式功率控制方案,并给出各子电网的功率交换参考值。其中主控制器通过双电压电流闭环来实现精确的功率跟踪。
基于子电网优先级驱动的BIC最优功率交换目标是使HMG-Cluster系统在不使用任何通信或中央处理器的情况下,BIC通过识别各子网的功率容量需求确定两个相邻子电网之间的功率交换值。
根据式(1)~式(3)的下垂控制原理可知,每个子电网内负载需求的增加或降低将导致AC子电网频率或DC子电网电压的降低,因此该值可被作为子电网的功率需求信号值。进一步,为防止过量功率交换所导致的偏差因子变化,本文以“最小化HMG-Cluster系统总偏差因子”为目标,提出基于子电网优先级和供电容量的功率交换策略以实现基于BIC设备的最优功率交换,该优化问题为
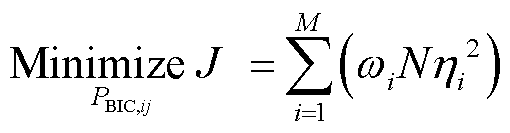 (7)
(7)
式中,PBIC,ij为子电网i与子电网j之间经BIC所交换的功率值;ωi为子电网i的优先级权重系数;M为HMG-Cluster中子电网的总数。
为使上述问题遵循“最小化HMG-Cluster总偏差因子”,则如式(7)所示的优化目标需要满足
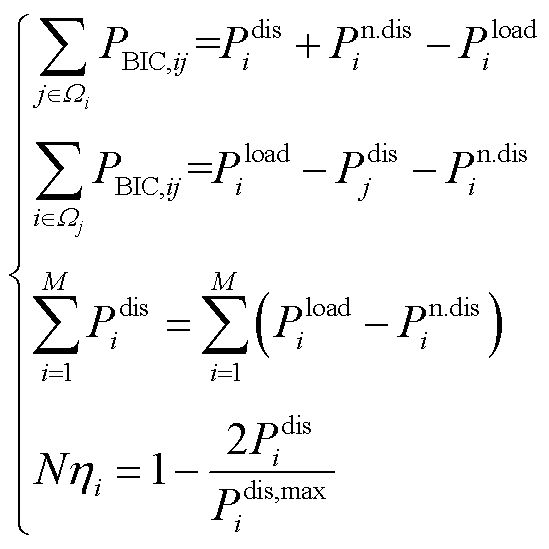 (8)
(8)
式中,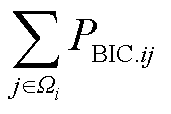 等式和
等式和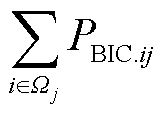 等式分别为第i个子电网和第j个子电网的供需功率平衡目标;Ωi、Ωj分别为与第i个和第j个子电网物理相连的子电网集合;PBIC,ij为从第i个子电网经BIC传输到第j个子电网的有功功率值;Pdis i、Pn.dis i分别为第i个子电网内可调度源、不可调度源的输出功率;Pdis,max i为第i个子电网的可调度源最大输出功率;Pload i为第i个子电网的负荷功率需求;
等式分别为第i个子电网和第j个子电网的供需功率平衡目标;Ωi、Ωj分别为与第i个和第j个子电网物理相连的子电网集合;PBIC,ij为从第i个子电网经BIC传输到第j个子电网的有功功率值;Pdis i、Pn.dis i分别为第i个子电网内可调度源、不可调度源的输出功率;Pdis,max i为第i个子电网的可调度源最大输出功率;Pload i为第i个子电网的负荷功率需求;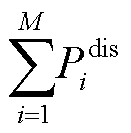 等式为具有M个子电网HMG-Cluster的供需功率平衡目标;Nηi等式描述了各子电网的归一化特征。
等式为具有M个子电网HMG-Cluster的供需功率平衡目标;Nηi等式描述了各子电网的归一化特征。
因此,本文所提最优化功率交换方案问题的数学描述为
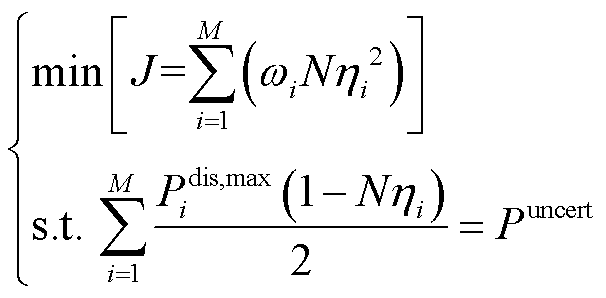 (9)
(9)
式中,Puncert为由分布式能源和负载不确定性而产生的等效负载需求。
由式(8)和式(9)可知,本文所提优化目标J是变量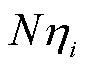 的二次函数,且其二阶导数的Hessian矩阵
的二次函数,且其二阶导数的Hessian矩阵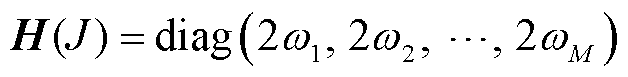 是正定矩阵,因此目标函数J是凸函数。进一步,由于如式(9)所示的优化约束是变量
是正定矩阵,因此目标函数J是凸函数。进一步,由于如式(9)所示的优化约束是变量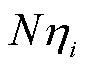 的一阶函数,可知其可行域是凸集。因此所提优化问题为凸优化,存在极小值。值得注意的是,由于该优化问题侧重于确定由任一子电网到相邻子电网经BIC所交换的功率,因此可以忽略线路阻抗的功率损耗和各子电网的节点功率方程。
的一阶函数,可知其可行域是凸集。因此所提优化问题为凸优化,存在极小值。值得注意的是,由于该优化问题侧重于确定由任一子电网到相邻子电网经BIC所交换的功率,因此可以忽略线路阻抗的功率损耗和各子电网的节点功率方程。
进一步,通过构建并求解所提优化问题的拉格朗日函数,即可获得所提优化问题的最优解。对此,基于文献[24]所构建的拉格朗日函数为
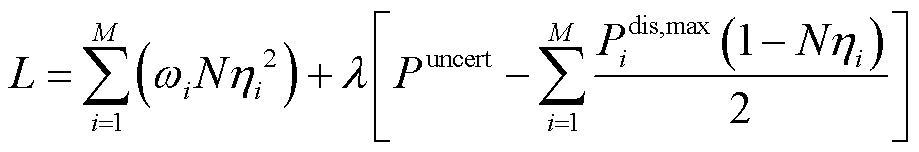 (10)
(10)
式中,λ为拉格朗日乘子。
通过求解式(10)所示方程即可获得所提优化问题的最优解,即
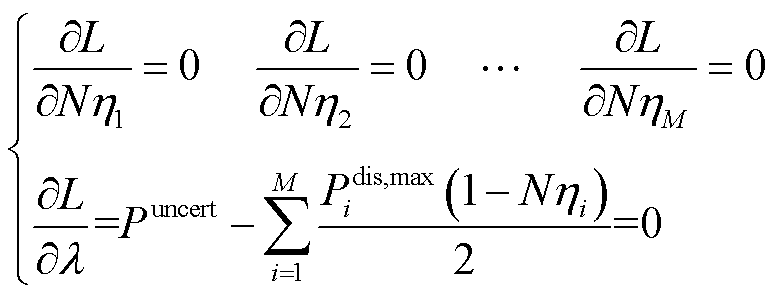 (11)
(11)
简化式(11)可得到最优性的必要条件为
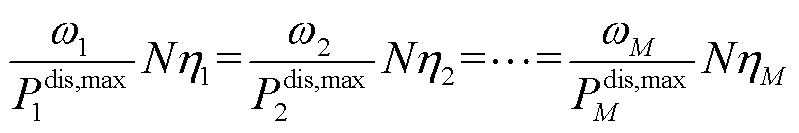 (12)
(12)
根据式(12)可知,尽管由于分布式能源和负载的不确定性使子电网所交互的功率值PBIC,ij很难被直接求解,但是当其满足如式(12)所示的必要条件时,可以很容易得到如式(8)所示的最小值。由于HMG-Cluster是由所有BIC物理相连而构成,因此可以通过分散控制每一个BIC即可满足式(12)所示的必要条件。此外,由于稳定运行偏差指数Nηi是一个常数值,因此各BIC所需的功率交换目标值可以通过稳态零误差的PI控制器设计,即
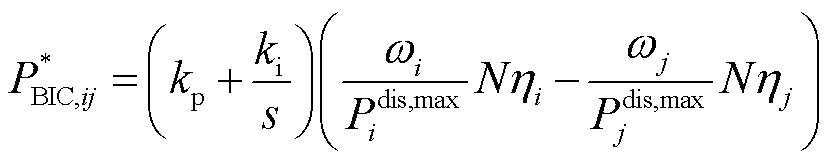 (13)
(13)
式中,P* BIC.ij为从任意第i个子电网传输到第j个子电网的功率交换目标值;kp和ki分别为PI控制的比例因子和积分因子。
由式(12)和式(13)可知,由于第i个子电网优先级权重系数及最大可调度功率容量值可以由子电网优先级及可用容量离线计算,因此所提出的潮流计算值是灵活可靠的,并且可以根据HMG-Cluster的应用场景灵活设计。
实际上,当基于子电网优先级权重的概念来评估每个子电网的负载重要性时,可以将其定义为某个子电网中重要负载需求在总负载需求中的占比。而所得优先级权重系数通常是根据各子电网对电压偏差的要求来设计的。这里,假设任意三个重要级别分别不同的子电网具有相同的功率容量,根据式(12)所得到的最优解,首先需要保证稳态方程,即ω1Nη1= ω2Nη2= ω3Nη3;其次根据各子电网的供电优先级要求来设置该网格所允许的电压偏差值,即|V/ferror.1|<3%,|V/ferror.2|<1%,|V/ferror.3|<0.5%。因此,参考如图2所示的BIC下垂控制曲线,可得到各子电网的优先等级比如图3所示。
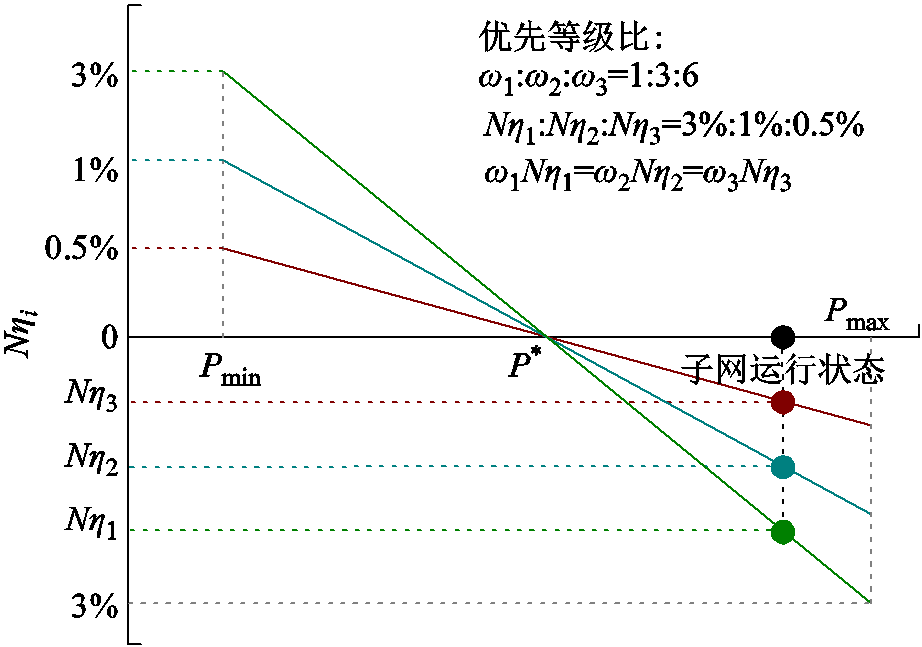
图3 不同优先等级比关系
Fig.3 Relationship between different priority weights
由图3可知,具有更高权重系数的子电网在功率交换过程中有更高的电力交换优先级和更高的电能质量保证。特别是在极端灾害所导致的HMG-Cluster电力短缺情况下,为了保证具有更高优先级子电网的不间断供电,可以选择牺牲较低供电优先级子电网的电力需求或电能质量来实现。具体做法是,对供电优先级较低的子电网实施局部自主频率或电压偏差等来实现负荷减少或转移。此时,如何将HMG-Cluster总线上剩余的可用电量在考虑供电优先级和电力需求情况下实现功率的精准分配将是另一个需要被解决的问题。
为了实现式(12)和式(13)所确定的功率分配方案,本文提出了针对BIC的分散式准下垂控制策略,有
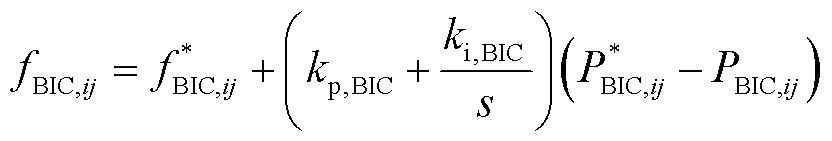 (14)
(14)
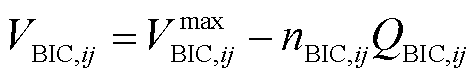 (15)
(15)
式中,kp,BIC和ki,BIC分别为对BIC实施P-f准下垂控制的比例因子和积分因子;PBIC,ij为任意AC与DC子电网传输的有功功率交换值,设定功率从AC侧到DC侧流动的方向为正,因此当其大于零时工作在整流器模式,当其小于零时工作在逆变器模式;VBIC,ij为连接AC与DC子电网的BIC电压幅值;nBIC,ij为对BIC实施Q-V准下垂控制中的下垂系数;QBIC,ij为AC与DC子电网传输的无功功率交换值。
根据AC与DC子电网的实时数据信息,式(14)用于生成BIC的频率参考值。式(15)采用QBIC,ij-VBIC,ij准下垂控制对AC子电网进行电压控制和无功功率补偿。式(14)和式(15)用于指示双电压电流闭环的内部电压参考,而电压和电流参考值通过比例谐振控制器进行跟踪。需要说明的是,BIC可以作为电压和电流控制源进行操作,其控制模式可以根据电流动态响应、电能质量和系统稳定性的实际要求来选择。其控制策略如图4所示。
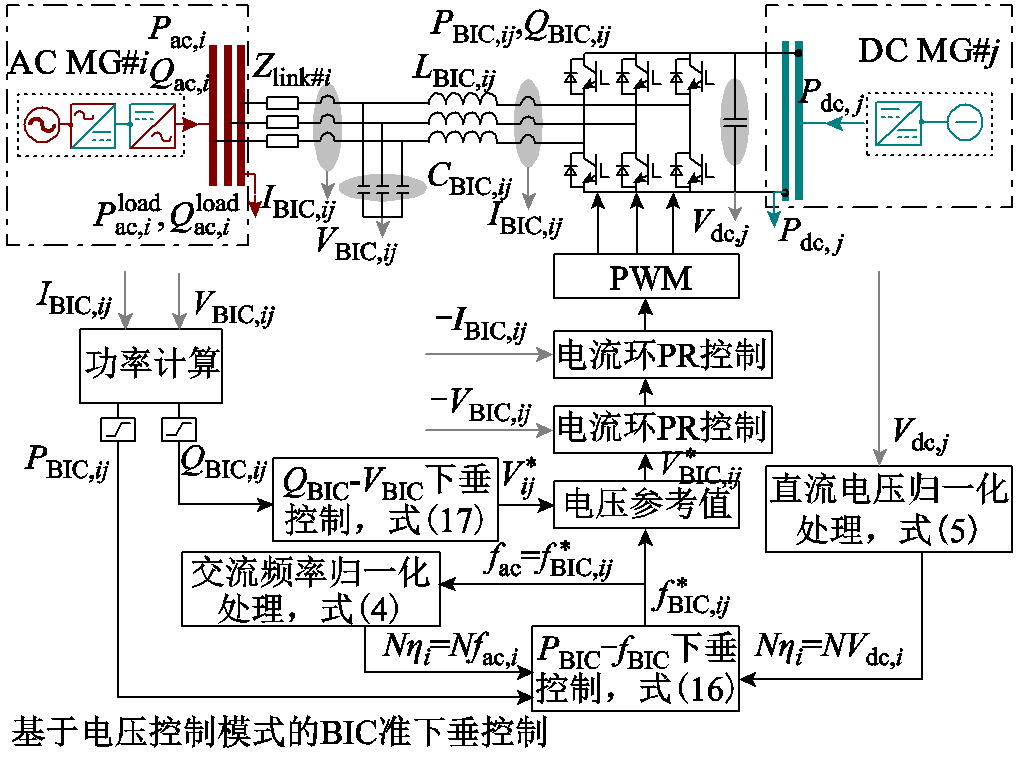
图4 基于BIC的分散式准下垂控制
Fig.4 Distributed quasi droop control based on the BIC
基于BIC的稳定性分析和控制器设计对于系统正常稳定运行至关重要,因此本文对BIC进行了小信号稳定性分析。在此之前,由于本文所关注的时间尺度是电力交换控制动力学(通常为2~15 Hz),因此本文的控制策略忽略了双电压电流闭环控制回路(数百赫兹)的动力学。电力线路的电阻分量和电磁瞬态被忽略。由于频率控制和电压控制的动力学之间有着显著的时间尺度差异,BIC的电压幅度可被认为是常数。此外,假设BIC的AC和DC总线动力学符合下垂控制特性,并能够为恒定功率负载提供电力。
BIC的功率传输模型为
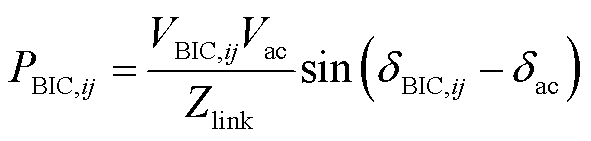 (16)
(16)
式中,VBIC,ij和δBIC,ij分别为流经BIC的电压幅值与相位;Vac和δac分别为 AC总线的电压幅值与相位;Zlink为BIC与AC总线之间的线路阻抗。
围绕着稳态运行点线性化,本文所应用的子电网下垂控制方程和归一化处理方程,即式(1)、式(3)~式(5),BIC的功率参考值方程及准下垂控制策略方程,即式(14)、式(15),以及基于BIC的功率传输方程,即式(16),可分别得到
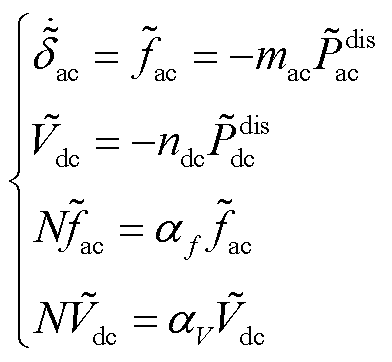 (17)
(17)
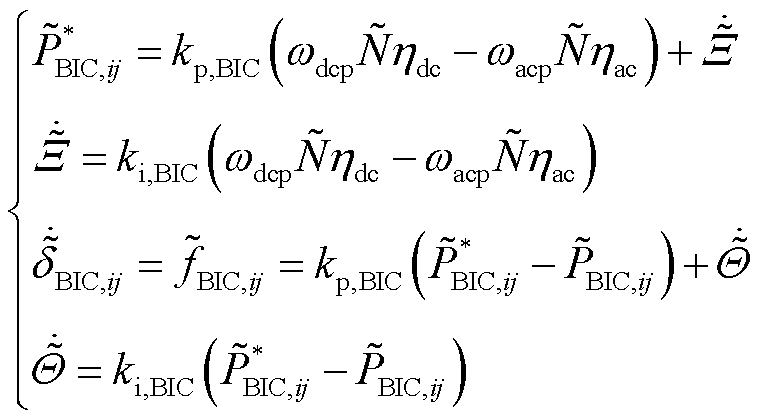 (18)
(18)
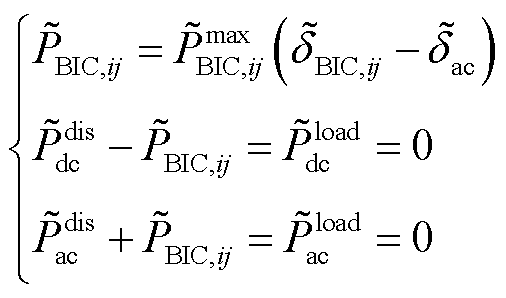 (19)
(19)
式中,“~”表示平衡点周围的小扰动;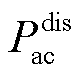 及
及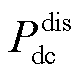 分别为AC及DC子电网内可调度源的输出功率;
分别为AC及DC子电网内可调度源的输出功率;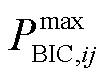 为从子电网i经BIC传递至将子电网j的可调度源最大输出功率;
为从子电网i经BIC传递至将子电网j的可调度源最大输出功率;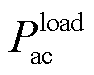 、
、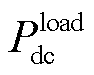 分别为AC与DC子电网的负荷功率需求。此外,af、aV、ωacp、ωdcp及Pmax BIC,ij的取值分别为:
分别为AC与DC子电网的负荷功率需求。此外,af、aV、ωacp、ωdcp及Pmax BIC,ij的取值分别为: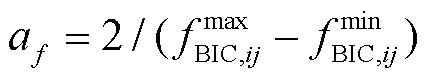 ,
,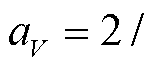
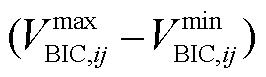 ,且
,且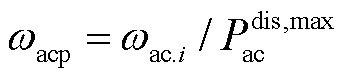 ,
,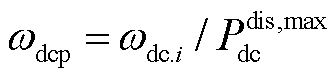 ,
,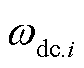 、
、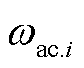 分别为DC及AC子电网i的优先级权重系数,
分别为DC及AC子电网i的优先级权重系数,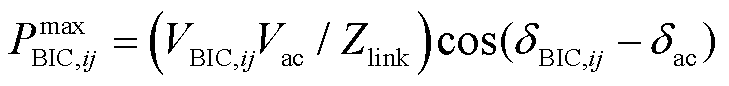 。
。
以矩阵方程形式改写式(17)~式(19),即可得到用于BIC功率控制稳定性的状态空间方程式为
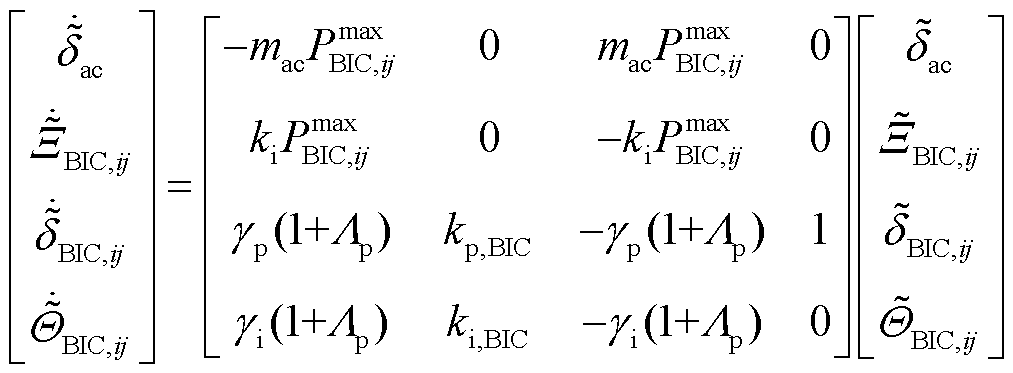 (20)
(20)
式中,γp=kp,BICPmax BIC,ij;Λp=kp(ωdcpαVndc+ωacpαf mac);γi=ki,BICPmax BIC,ij。
通过计算如式(20)的特征值即可用于研究BIC在平衡状态附近的稳定性。对于在第4节中所进行的HIL测试系统,当同时改变BIC#12的比例增益参数kp,BIC和积分增益参数ki,BIC时可得到如图5所示的根轨迹。
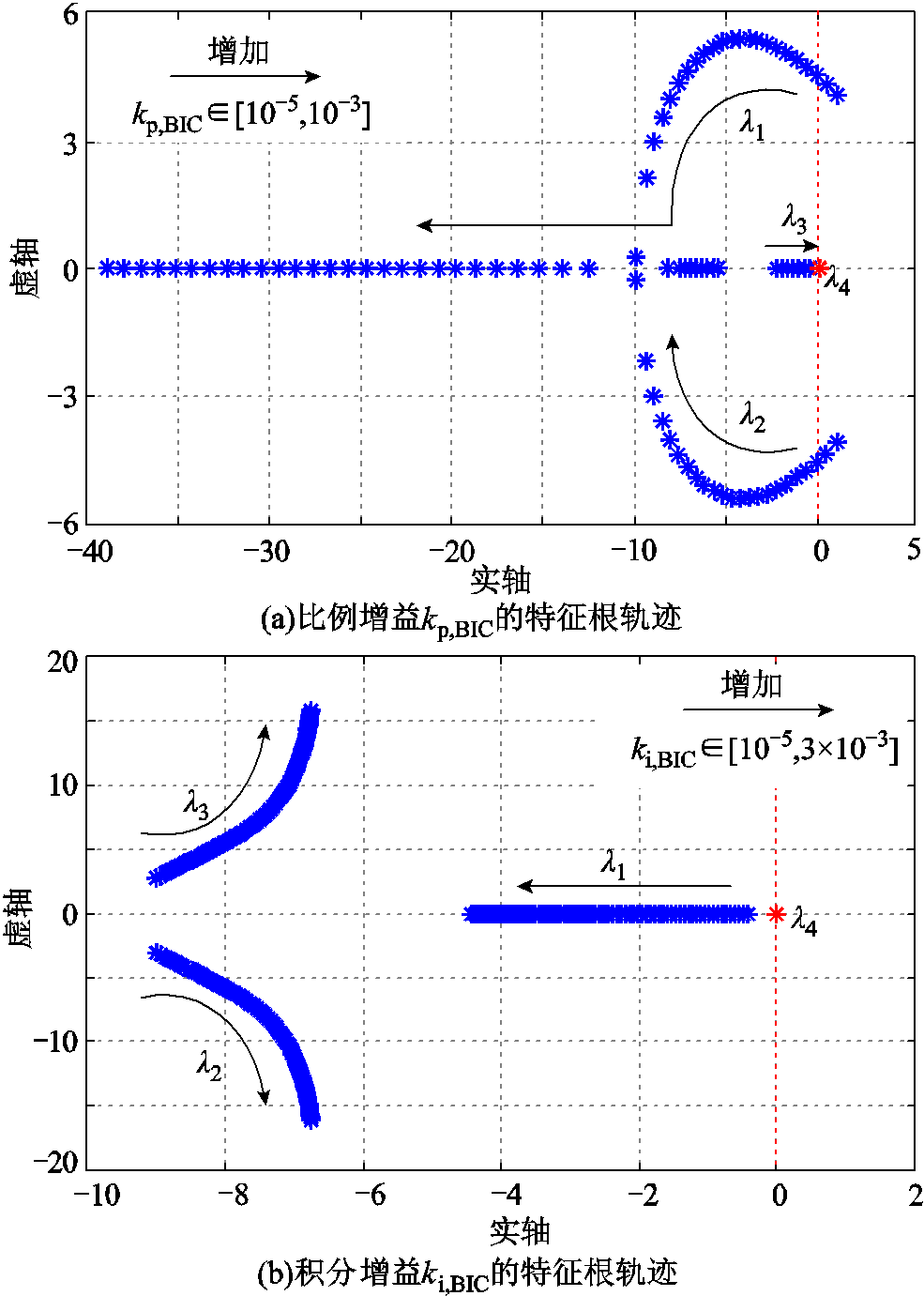
图5 基于BIC的特征值轨迹分析
Fig.5 Engenvalue trajectory analysis based on the BIC
如图5a显示了比例增益kp,BIC从10-5增加到10-3时的特征根轨迹。其中,在零点处存在一个简单的特征值,对应于旋转对称性,这在文献[25]中已经得到证明。由图5a可知,当比例增益kp,BIC>3×10-5时,系统的所有特征根全部位于左半平面,这代表比例增益kp,BIC无论在区间(3×10-5, 10-3)内如何取值,系统都是稳定的。如图5b显示了积分增益ki,BIC从10-5增加到3×10-3时的特征根轨迹。其中,在零点处也存在一个简单的特征值。由图5b可知,当比例增益ki,BIC>10-5时,系统的所有特征根全部位于左半平面,这代表比例增益ki,BIC无论在区间(10-5, 3×10-3)内如何取值,系统都是稳定的。
本文通过HIL测试了所提基于子电网优先级驱动的分散式控制策略对HMG-Cluster弹性控制的有效性。该HIL由Opal-RT OP5700数字仿真器和NI-PXIe-1071算法控制器组成,如图6所示。其中,所提策略的物理主电路在实时模拟器完成,时间步长为20 μs,可以准确有效地模拟电力电子元件的动态特性。所提控制策略和功率交互方案则是在算法控制器中完成的。其采样频率为20 kHz。由于转换器为开关器件模型,且AC和DC子电网之间仅有功率转移发生,因此仿真中AC和DC负载均被设置为纯电阻负载。基于上述基础,本文测试了两种案例,并展示了示波器所得仿真结果。

图6 HIL平台的物理设置
Fig.6 Physical setup of the HIL platform.
本文所研究HMG-Cluster系统模型及主要结构如图7所示。其中,MG#1和MG#4为AC型MG,MG#2和MG#3为DC型MG。图7中所有MG基于双向BIC互联四个子电网,这些BIC的控制策略基于第2节给出的分散式准下垂控制策略完成。假设有功功率流正值的参考方向是从AC侧到DC侧,以BIC#12的功率交换是从AC MG#1到DC MG#2,则当功率值大于零时,BIC#12工作在整流器模式;当功率值小于零时,BIC#12工作在逆变器模式。
HIL系统的物理和控制参数见表2。本文设置MG#1、MG#2、MG#3、MG#4的优先级权重分别为3、0.5、0.5和1;额定功率分别为3、3、4、4 kW;最大可调度功率分别为5、5、8、8 kW;额定有功功率负载和无功功率负载分别为4、6、6、4 kW和0、2、2、0 kvar。根据式(12)中的最优解,分散式优先级控制策略下仿真测试中各子电网偏差值遵循条件Nη1: Nη2: Nη3: Nη4=1: 6: 6: 3,以最小化式(7)中的目标函数。
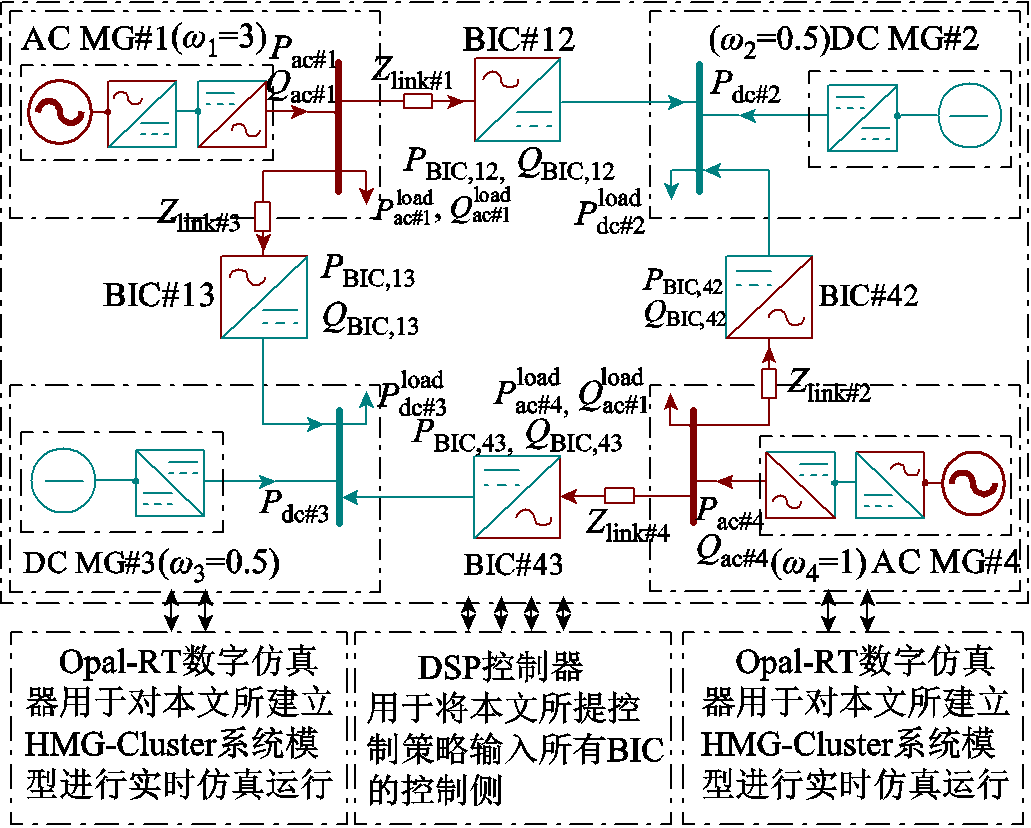
图7 HMG-Cluster仿真系统模型
Fig.7 Model of HMG-Cluster simulation system
表2 HIL系统的物理和控制参数
Tab.2 Physical and control parameter of HIL system

参数数值 系统物理参数DC子电网电压()/V685, 700, 715 AC子电网频率()/Hz50.5, 50, 49.5 AC子电网电压()/V321, 311, 301 子网优先级(ω1, ω2, ω3, ω4)/V3, 0.5, 0.5, 1 可调度额定功率()/kW4, 6, 6, 4 可调度最大功率()/kW8, 12, 12, 8 负载所需有功功率()/kW4, 6, 6, 4 负载所需无功功率()/kvar0, 2, 2, 0 系统控制参数参考电压321 频率50 P-f下垂控制参数(kp.BIC, ki.BIC)2×10-4, 10-4 Q-V下垂控制参数nBIC3×10-3 功率控制参数(kp,BIC, ki,BIC)5×104, 104
为了验证本文所提基于子电网优先级驱动的HMG-Cluster分散式控制策略有效性,构建了两种仿真案例,其行动顺序及系统数据见表3。
案例一,为验证本文所提基于分散式优先级控制策略的有效性,案例对比了其与全局比例共享控制在某一时刻任一子电网可用出力发生突变工况下的仿真结果[14-15]。即在0~5 s时,HMG-Cluster系统的可调度总有功功率为20 kW,负载总需求为16 kW。在5 s时,DC MG#3的负荷需求从2 kW突增到10 kW,其他子电网的负荷均不变。因此,在5~10 s时,HMG-Cluster系统的可调度有功功率仍为20 kW,但负载总需求为24 kW。
表3 两种案例的行动顺序
Tab.3 Action sequence for two cases

时间/s案例一案例二 0~5=20 kW, =16 kW=20 kW, =20 kW 5: 16 kW→24 kW: 20 kW→16 kW 5~10=20 kW, =24 kW=16 kW, =20 kW
案例二,为验证本文所提分散式自优化功率控制策略的有效性,案例对比了其与基于“全局功率平等/比例共享”控制策略在任一子电网故障造成可调度出力受限工况下的仿真结果。即在0~5 s时,HMG-Cluster系统的可调度总有功功率为20 kW,负载总需求为20 kW。在5 s时,DC MG#1发生故障,可调度的有功功率从20 kW缩减到16 kW,其他子电网的负荷均不变。因此,在5~10 s时,HMG-Cluster系统的可调度有功功率为16 kW,但负载总需求仍为20 kW。
4.2.1 案例一:负载突变工况下的仿真结果对比
图8和图9分别给出了基于本文所提分散式优先级控制和基于分布式全局比例共享控制在案例一工况下的仿真结果。
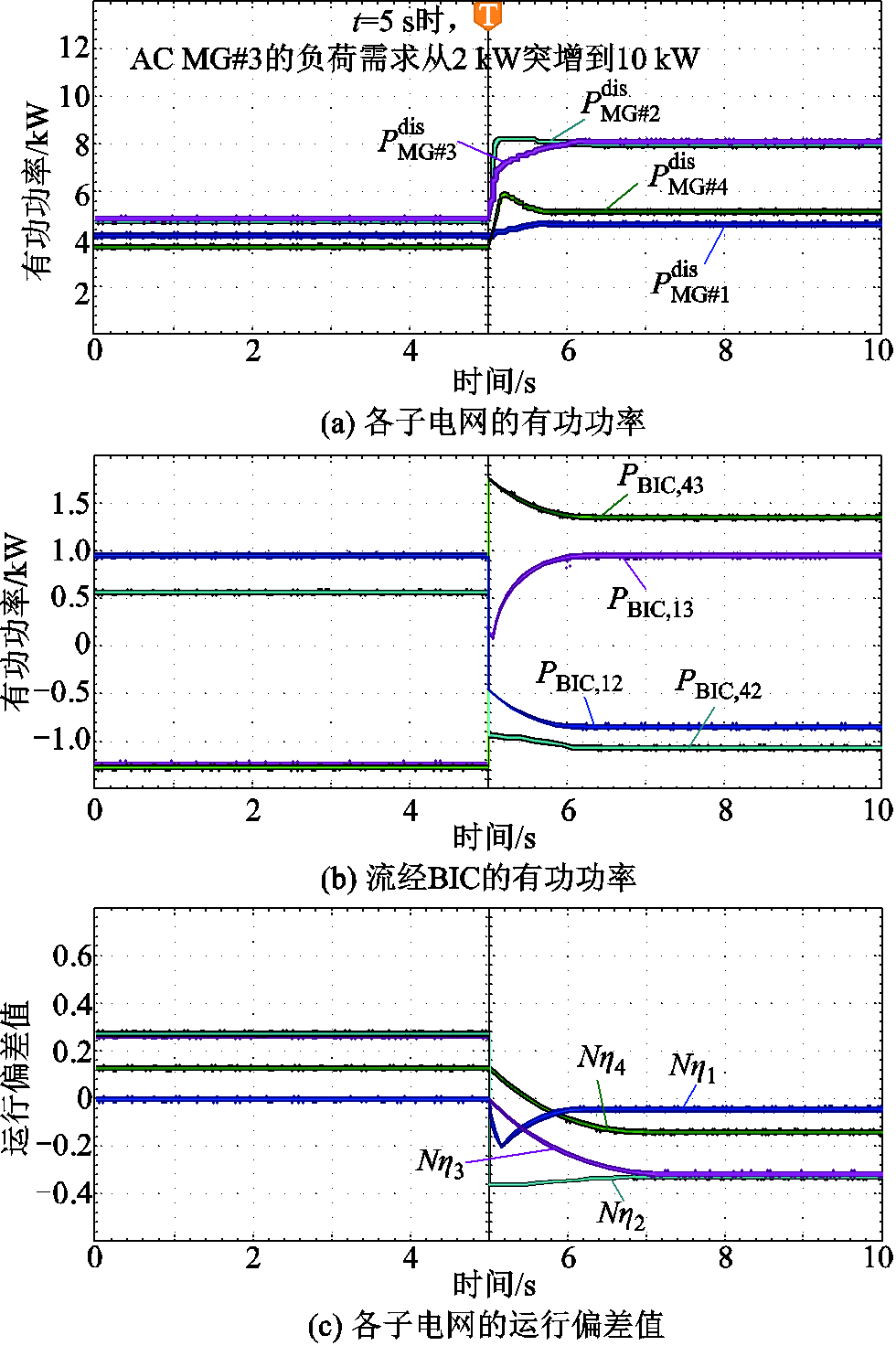
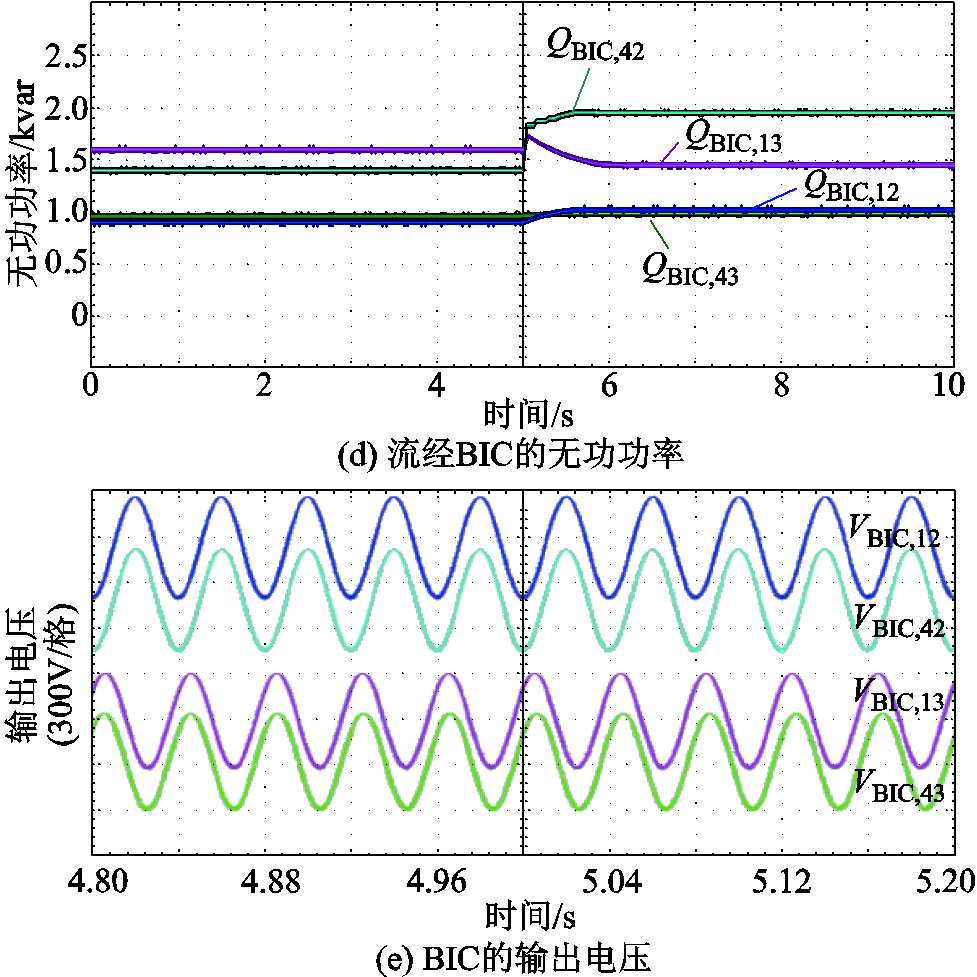
图8 案例一工况分散式优先级控制的仿真结果
Fig.8 Simulation results of decentralized priority control for Case I
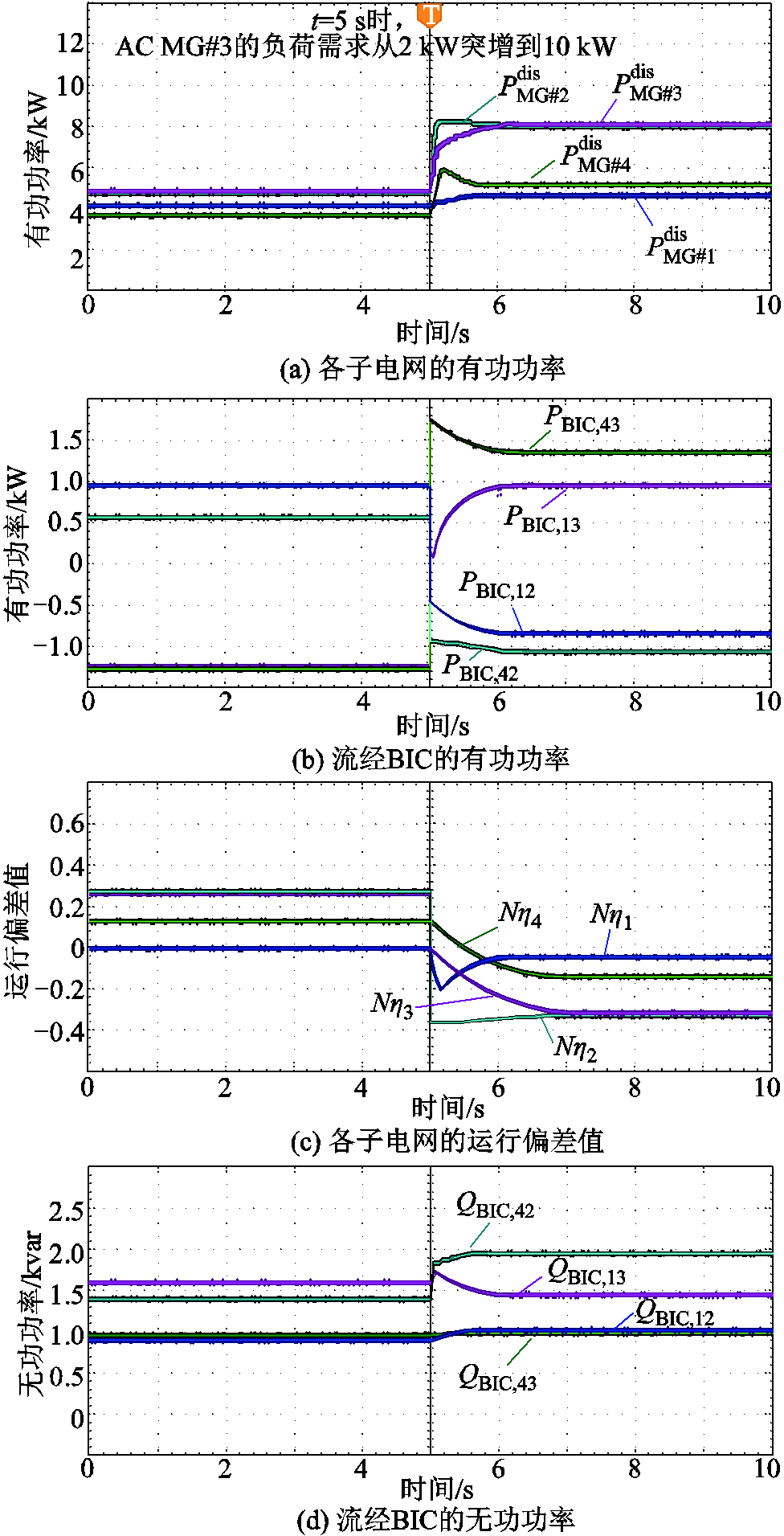
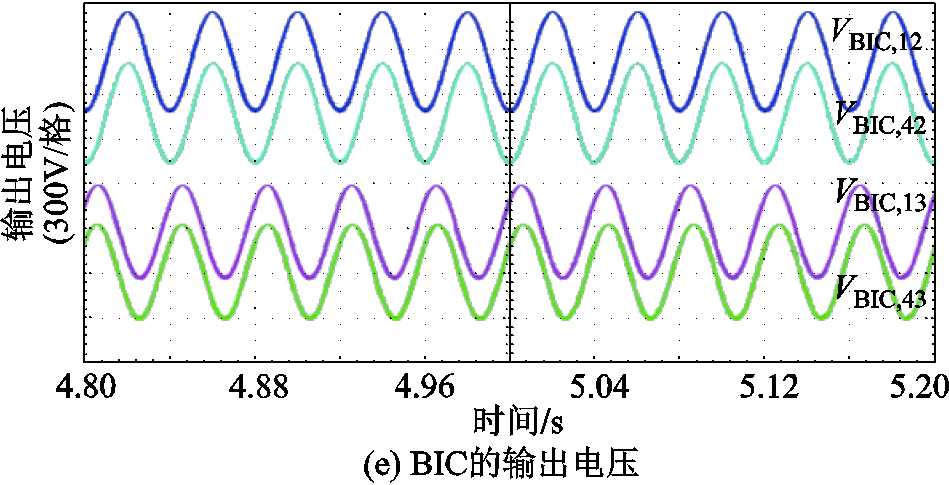
图9 案例一工况分布式全局比例共享控制的仿真结果
Fig.9 Simulation results of distributed global proportional shared control for Case I
如图8a~图8c和图9a~图9c分别为两种控制策略下各子电网的可调度有功功率、经BIC交互的有功功率、各子电网的运行偏差值。由此可知,系统各子电网可调度有功功率能够经BIC实现共享,并确保系统总功率的平衡。在0~5 s时,HMG-Cluster系统工作在总有功功率盈余状态,根据全局功率平衡原则,子电网MG#3的剩余可用有功功率能够经BIC转移至其他子电网,因此两种控制策略下子电网运行状态偏差值均为正值。其中,基于本文所提控制策略下MG#1、MG#2、MG#3、MG#4的运行状态偏差值分别为0.05、0.3、0.3和0.15,基于“全局功率平等/比例共享”控制的运行状态偏差值分别为0.2、0.2、0.2和0.2。在5 s时,系统负荷功率需求从2 kW突增到10 kW。在5~10 s时,HMG-Cluster系统工作在总有功功率短缺状态,因此两种控制策略下的运行状态偏差值均为负值。其中,基于本文所提控制下MG#1、MG#2、MG#3、MG#4的运行状态偏差值分别为-0.05、-0.3、-0.3和-0.15,基于分布式全局比例共享控制的运行状态偏差值分别为-0.2、-0.2、-0.2和-0.2。
图8d、图8e和图9d、图9e分别为两种控制策略下各子电网的无功功率和电压波形。由此可知,基于本文所提根据BIC的准下垂控制不仅能够实现各子电网之间灵活的自优化功率共享,而且能够有效支撑系统的无功功率补偿和电压支撑。
对比两种控制策略在案例一工况下的状态偏差指数和优化目标值可知,各子电网的状态偏差值满足本文所预设的子电网偏差值要求,即分散式优先级控制的各子电网偏差值为1:6:6:3,而分布式全局比例共享控制的各子电网偏差值为1:1:1:1。此外,基于分散式优先级控制策略的优化目标值仅为0.101 1,这远小于基于分布式全局比例共享控制策略的优化目标值0.2。
进一步,各子电网及流经BIC的在案例一工况下的详细运行结果对比见表4。
表4 负载突变工况下的结果对比
Tab.4 Simulation comparison under sudden load changes

参数所提控制策略现有控制策略 t∈[0, 5]st∈(5, 10]st∈[0, 5]st∈(5, 10]s ACMG#13.84.23.24.8 4.0 PBIC,12/kW1.0-0.80.6-0.6 DC MG#24.47.64.87.2 6.0 PBIC,42/kW0.6-0.80.6-0.6 AC MG#34.47.64.87.2 2.010.02.010.0 PBIC,13/kW-1.21.0-1.41.4 DC MG#43.44.64.34.8 4.0 PBIC,43/kW-1.21.4-1.41.4 子电网运行偏差值Nη10.05-0.050.2-0.2 Nη20.3-0.30.2-0.2 Nη30.3-0.30.2-0.2 Nη40.15-0.150.2-0.2 优化目标J0.101 10.20
4.2.2 案例二:任一子电网故障工况下的仿真结果
图10和图11分别给出了基于本文所提分散式优先级控制和基于分布式全局比例共享控制在案例二工况下的仿真结果。
图10a~图10c和图11a~图11c分别为两种控制策略下各子电网的可调度有功功率、经BIC交互的有功功率、各子电网的运行偏差值。由此而知,在0~5 s时,HMG-Cluster系统处于自洽状态,系统总功率平衡且各子电网无偏差;在t=5 s时,MG#3故障,该网格可被调度的有功功率从6 kW变为0,这时MG#3的状态偏差值降到-1;在5~10 s时,HMG-Cluster系统工作在总有功功率短缺状态,因此两种控制策略下MG#1、MG#2、MG#3、MG#4的运行状态偏差值均为负值。其中,基于本文所提控制策略,MG#1、MG#2、MG#3、MG#4的运行状态偏差值分别为-0.062 5、-0.416 7、-0.416 7和-0.187 5,而基于“全局功率平等/比例共享”控制的运行状态偏差值分别为-0.3、-0.3、-0.3和-0.3。
图10d、图10e和图11d、图11e分别为两种控制策略下各子电网的无功功率和电压波形。由此可知,基于本文所提根据BIC的准下垂控制不仅能够实现各子电网之间灵活的自优化功率共享,而且能够有效支撑系统的无功功率补偿和电压支撑。
对比两种控制策略在案例二工况下的状态偏差指数和优化目标值可知,无论仿真工况如何变化,各子电网的状态偏差值始终能够在满足本文所预设的子电网偏差值要求下运行。此外,相较“全局功率平等/比例共享”控制策略的优化目标值0.45,本文所提基于优先级驱动控制策略可将系统的优化目标值为0.220 5。
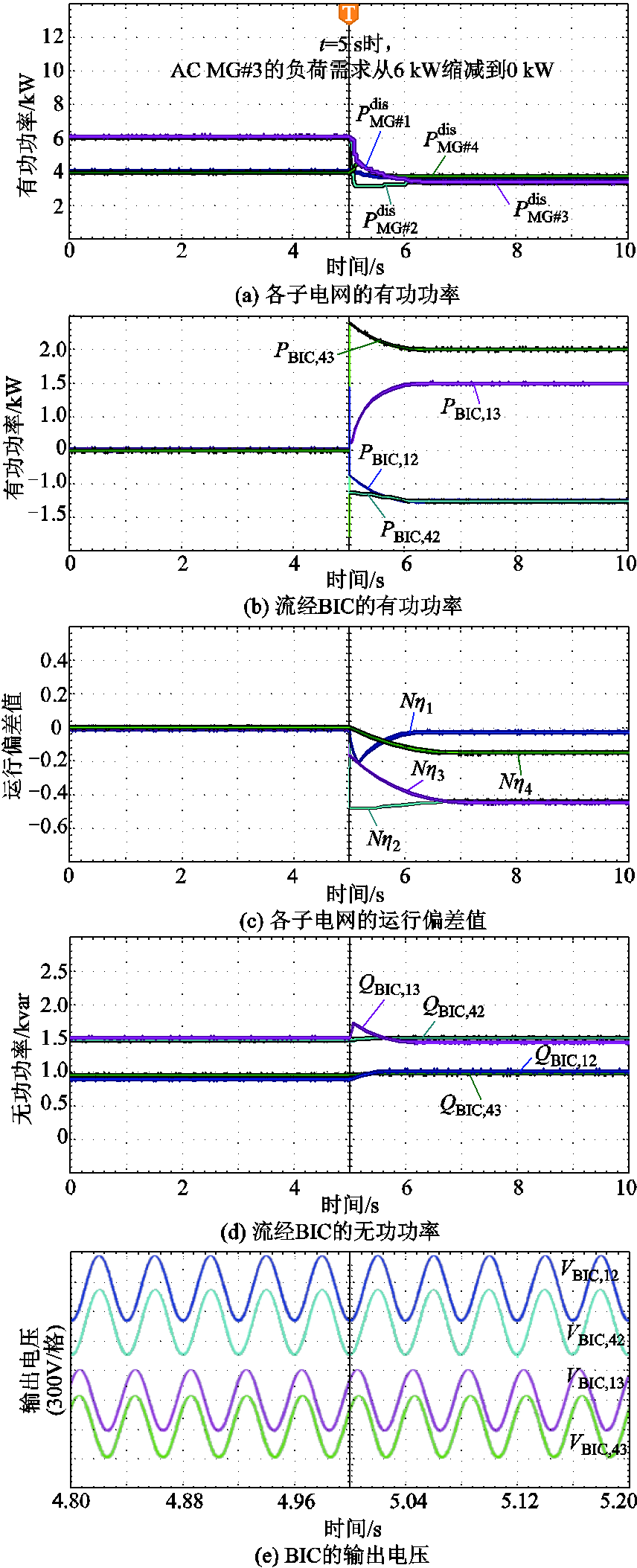
图10 案例二工况分散式优先级控制的仿真结果
Fig.10 Simulation results of decentralized priority control for Case II
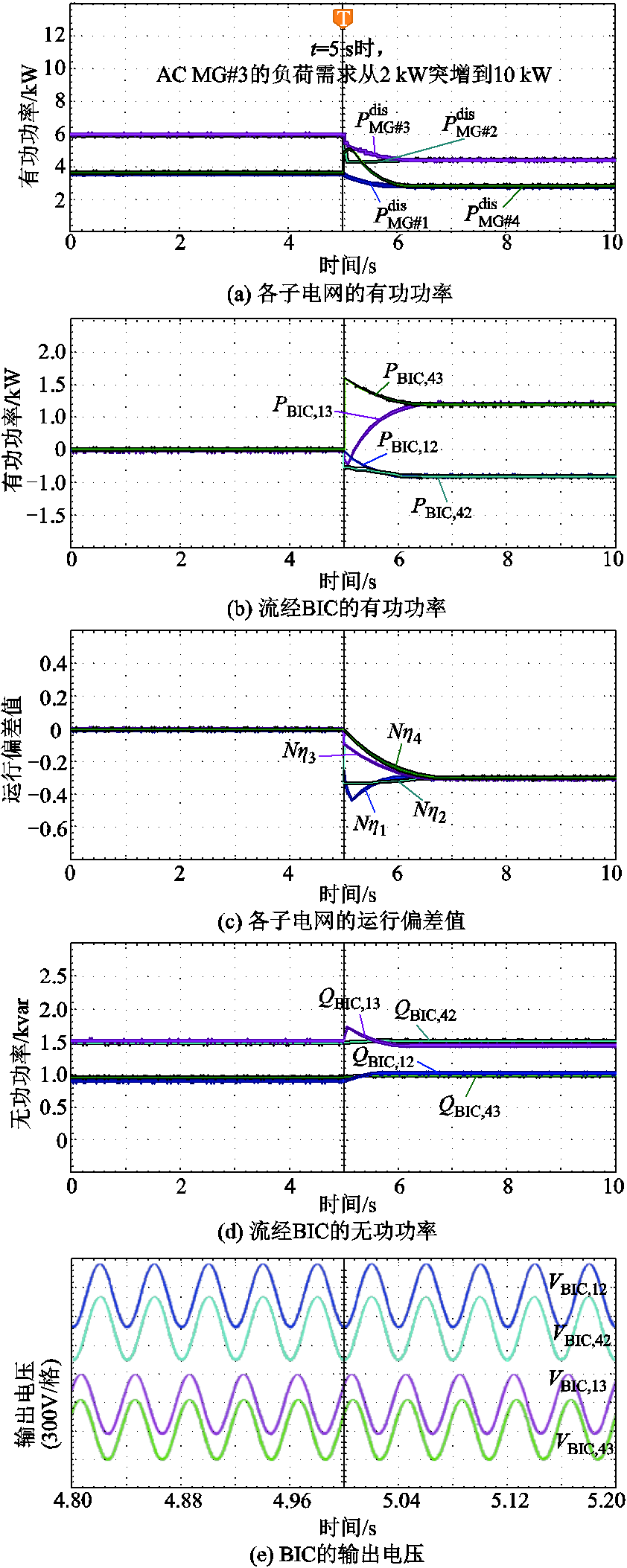
图11 案例二工况分布式全局比例共享控制的仿真结果
Fig.11 Simulation results of distributed global proportional shared control for Case II
进一步,各子电网及流经BIC的在案例一工况下的详细运行结果对比见表5。
表5 子电网故障工况下的仿真对比
Tab.5 Simulation comparison under sub-grid fault states
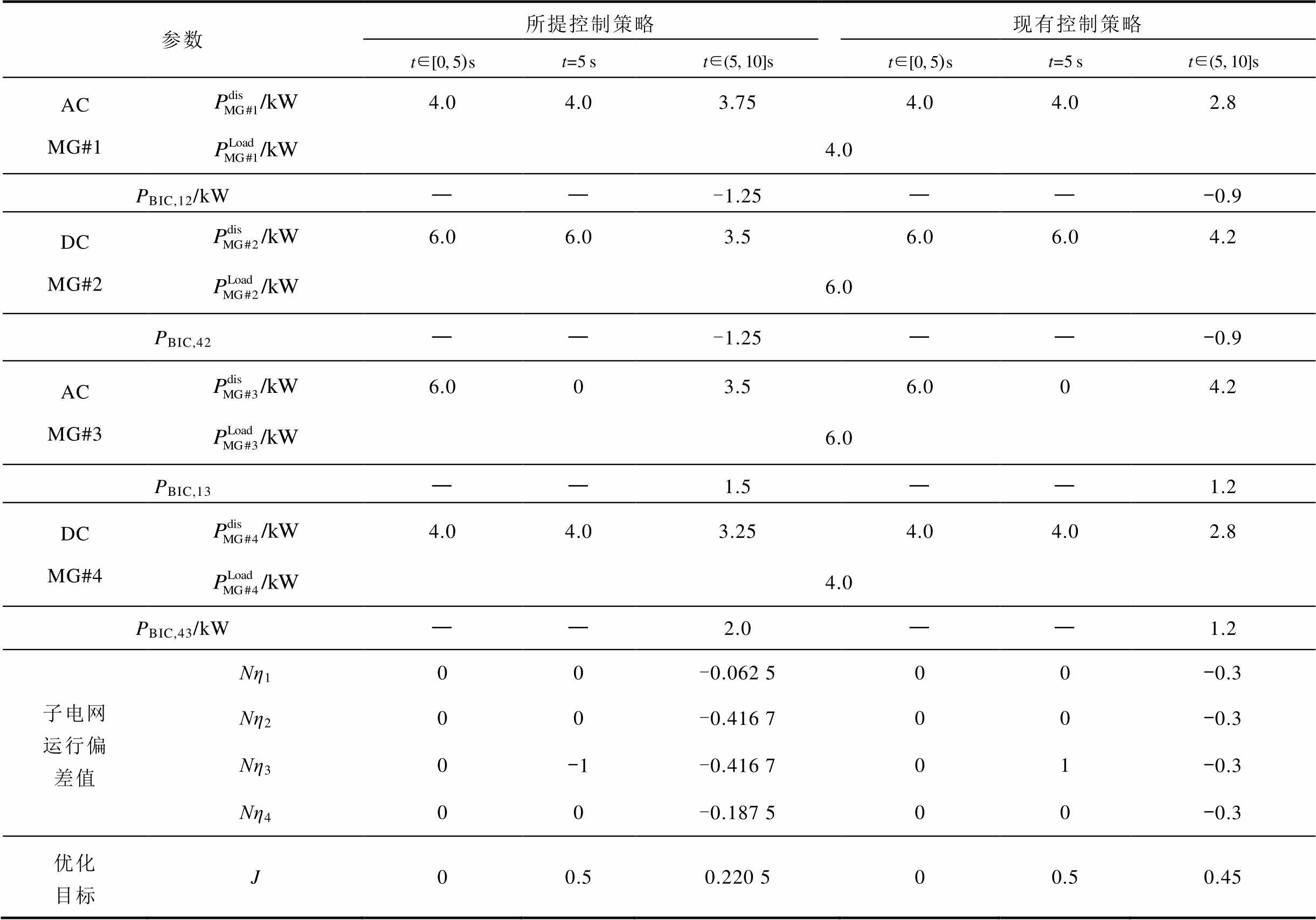
参数所提控制策略现有控制策略 t∈[0, 5)st=5 st∈(5, 10]st∈[0, 5)st=5 st∈(5, 10]s AC MG#14.04.03.754.04.02.8 4.0 PBIC,12/kW——-1.25——-0.9 DC MG#26.06.03.56.06.04.2 6.0 PBIC,42——-1.25——-0.9 AC MG#36.003.56.004.2 6.0 PBIC,13——1.5——1.2 DC MG#44.04.03.254.04.02.8 4.0 PBIC,43/kW——2.0——1.2 子电网运行偏差值Nη100-0.062 500-0.3 Nη200-0.416 700-0.3 Nη30-1-0.416 701-0.3 Nη400-0.187 500-0.3 优化目标J00.50.220 500.50.45
综上所述,基于表4和表5所示两种控制策略的电力交互情况可以发现,在案例一工况下的0~5 s时,MG#3处于电力充足状态,因此其可调度有功功率可经相邻BIC转移到其他子电网,此时BIC#12和BIC#42处于整流工作状态,BIC#13和BIC#43处于逆变工作状态。在5~10 s时,MG#3处于功率不足状态,因此剩余子电网的可调度有功功率将通过BIC转移至该子电网,此时BIC#12和BIC#42处于逆变工作状态,BIC#13和BIC#43处于整流工作状态。在案例二工况下的0~5 s时,各子电网均处于自洽模式,HMG-Cluster系统内无功率流动。在5~10 s时,MG#3由于故障脱网而使其可调度有功功率为零,剩余子电网的可调度有功功率将通过BIC转移至该子电网,此时,BIC#12和BIC#42处于逆变工作状态,BIC#13和BIC#43处于整流工作状态。由此可知,系统总可调度功率能够通过跟踪子电网运行状态而其各子电网有功功率在HMG-Cluster系统内基于优先级要求实现功率自主交互。
HMG-Cluster系统的功率交互示意图如图12所示。
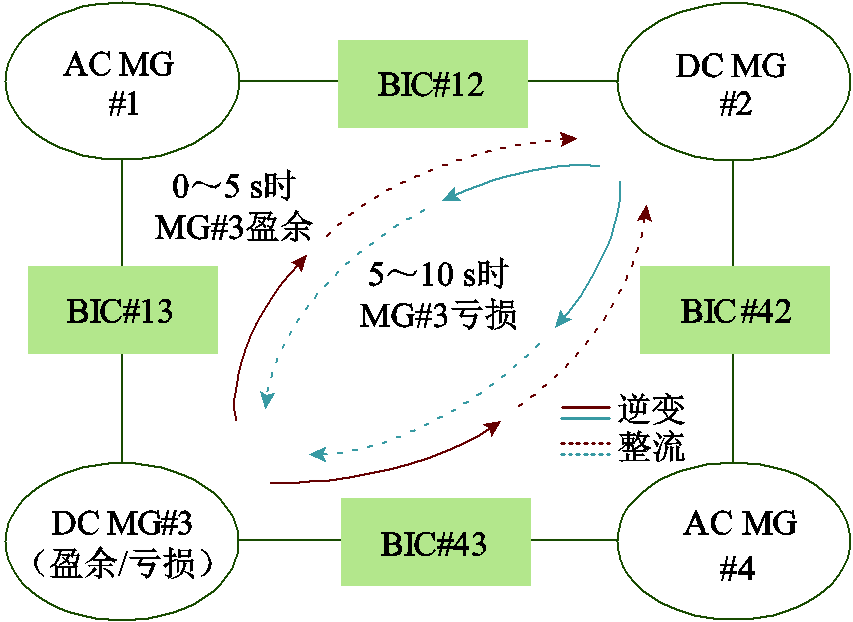
图12 HMG-Cluster系统的功率交互示意图
Fig.12 Power interaction diagram of HMG-Cluster system
根据表4和表5可知,HMG-Cluster系统内各子电网及BIC设备的交互始终满足如式(21)所示的功率平衡关系,这遵循式(8)所示的功率流动约束。
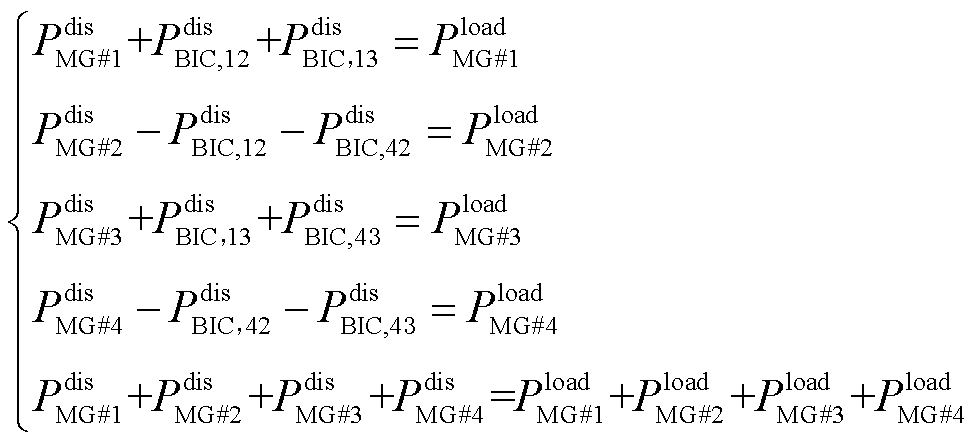 (21)
(21)
综上所述,无论系统处于功率盈余还是故障工况下,所提控制策略始终能够在子电网优先级驱动下运行,且其状态偏差因子比始终一致。与“全局功率平等/比例共享”控制策略相比,具有更高优先级的子电网具有更高的电压值和更高的优先级指数。进一步地,在系统中可调度电力严重短缺的情况下,较低优先级的子电网将通过自动甩负荷和增加偏差因子来确保较高优先级负荷的优先恢复。由此可知,与“全局功率平等/比例共享”控制策略相比,本文所提控制策略具有较小的优化目标值。
本文提出了一种基于HMG-Cluster子电网优先级驱动的BIC分散式控制策略,与基于“全局功率平等/比例共享”控制策略相比,所提策略不仅能够实现全局子电网的功率自主协调,而且能够保证系统优化目标值最小。具体成果如下:
1)本文以最小化全局总偏差因子为目标构建了用于HMG-Cluster的最优电力交换模型。该模型以AC子电网频率和DC子电网电压的归一化偏差值作为偏差因子,并通过对各子电网的优先级排序保证了系统在可调度功率严重不足的情况下能够通过牺牲低优先级子电网的偏差因子来保证高优先级子电网的优先恢复。HIL结果表明,无论子电网负载条件如何,各子电网的状态偏差因子比始终一致。这不仅实现了功率在各子电网之间的最优交换,而且保证了较高关键子电网在电能质量要求下运行。
2)基于最优电力交换目标,本文提出了用于BIC的准下垂控制策略。由于该策略中所有BIC设备仅需检测本地交流频率/直流电压的状态偏差因子,因此可以实现对交直流混合微电网集群整体偏差因子最小化的分散式最优功率自主协同控制。HIL结果表明,相较于现有“全局功率平等/比例共享”控制策略,所提控制策略在案例一和案例二工况下将最优目标值分别降低0.098 9和0.229 5。这不仅避免了对通信设备的成本投入,而且避免了通信设备故障对系统可靠性造成的威胁,有效地提高了系统的成本效益和可靠效益。
3)本文所提基于优先级驱动的HMG-Cluster系统分散式控制策略作为一项基础研究,可以实现与任何高级控制算法的兼容,并在未来的研究工作中实现更高级别的控制目标。此外,所提分散式控制策略可以在任何通信瘫痪或故障等极端事件下实现系统在自优化控制下的弹性运行。
参考文献
[1] 张昊, 李昱, 尹亚飞, 等. 直流微电网集成式高品质协同控制策略[J]. 电工技术学报, 2023, 38(23): 6345-6358. Zhang Hao, Li Yu, Yin Yafei, et al. An integrated high-quality cooperative control strategy of DC microgrids[J]. Transactions of China Electrotechnical society, 2023, 38(23): 6345-6358.
[2] 张璐, 唐巍, 卢莹, 等. 面向新型源荷接入的交直流混合配电网关键技术研究综述[J]. 供用电, 2020, 37(10): 3-9, 21. Zhang Lu, Tang Wei, Lu Ying, et al. Overview of hybrid AC-DC distribution network key technologies facing novel source and load integration[J]. Distribution & Utilization, 2020, 37(10): 3-9, 21.
[3] 杜燕, 言明明, 王鑫, 等. 交直流子网双边惯量约束下互联变流器动态功率控制策略[J]. 电力系统自动化, 2023, 47(4): 172-179. Du Yan, Yan Mingming, Wang Xin, et al. Dynamic power control strategy for interlinking converter under bilateral inertia constraints in AC-DC subgrid[J]. Automation of Electric Power Systems, 2023, 47(4): 172-179.
[4] 丁明, 潘浩, 张晶晶. 分布式电源接入交直流混合微电网群优化规划研究[J]. 太阳能学报, 2021, 42(6): 54-62. Ding Ming, Pan Hao, Zhang Jingjing. Research on optimal planning of AC-DC hybrid microgrid cluster with distributed generation access[J]. Acta Energiae Solaris Sinica, 2021, 42(6): 54-62.
[5] 楼冠男, 秦琦, 顾伟, 等. 考虑移动式储能均衡的微电网群分布式动态协同控制策略[J]. 电力系统自动化, 2023, 47(19): 74-85. Lou Guannan, Qin Qi, Gu Wei, et al. Distributed dynamic cooperative control strategy for microgrid clusters considering equalization of mobile energy storage[J]. Automation of Electric Power Systems, 2023, 47(19): 74-85.
[6] Sun Kai, Wang Xiaosheng, Li Yun wei, et al. Parallel operation of bidirectional interfacing converters in a hybrid AC-DC microgrid under unbalanced grid voltage conditions[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 1872-1884.
[7] 张国荣, 丁晓通, 彭勃, 等. 交直流混合微电网互联变流器改进控制策略[J]. 电力系统保护与控制, 2020, 48(14): 50-58. Zhang Guorong, Ding Xiaotong, Peng Bo, et al. Improved control strategy for an AC-DC hybrid microgrid interlinking converter[J]. Power System Protection and Control, 2020, 48(14): 50-58.
[8] 郑重, 苗世洪, 李超, 等. 面向微型能源互联网接入的交直流配电网协同优化调度策略[J]. 电工技术学报, 2022, 37(1): 192-207. Zheng Zhong, Miao Shihong, Li Chao, et al. Coordinated optimal dispatching strategy of AC-DC distribution network for the integration of micro energy Internet[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 192-207.
[9] 杨义, 杨苹. 面向集中式控制的微电网信息物理系统分层建模方法[J]. 中国电机工程学报, 2022, 42(19): 7088-7102. Yang Yi, Yang Ping. The hierarchical modeling approach for centralized control microgrid cyber physical system[J]. Proceedings of the CSEE, 2022, 42(19): 7088-7102.
[10] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049. Yang Jun, Hou Junhao, Liu Yawei, et al. Distributed cooperative control method and application in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4035-4049.
[11] Zuo Kunyu, Wu Lei. A review of decentralized and distributed control approaches for islanded microgrids: novel designs, current trends, and emerging challenges[J]. The Electricity Journal, 2022, 35(5): 107138.
[12] 王干, 汤茂东, 曲小慧, 等. 一种含高比例分布式电源的直流电网组网的无差分散式协调控制[J]. 电网技术, 2023, 47(5): 2089-2098. Wang Gan, Tang Maodong, Qu Xiaohui, et al. A non-deviation distributed coordinated control in DC power grid with high proportional renewable sources[J]. Power System Technology, 2023, 47(5): 2089-2098.
[13] Yu Hang, Niu Songyan, Shao Ziyun, et al. A scalable and reconfigurable hybrid AC-DC microgrid clustering architecture with decentralized control for coordinated operation[J]. International Journal of Electrical Power & Energy Systems, 2022, 135: 107476.
[14] Wang Junjun, Dong Chaoyu, Jin Chi, et al. Distributed uniform control for parallel bidirectional interlinking converters for resilient operation of hybrid AC-DC microgrid[J]. IEEE Transactions on Sustainable Energy, 2022, 13(1): 3-13.
[15] Lin Pengfeng, Wang Peng, Jin Chi, et al. A distributed power management strategy for multi-paralleled bidirectional interlinking converters in hybrid AC-DC microgrids[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 5696-5711.
[16] 张泽华, 宋桂英, 张晓璐, 等. 考虑恒功率负载的直流微电网稳定性与鲁棒性控制策略[J]. 电工技术学报, 2023, 38(16): 4391-4405. Zhang Zehua, Song Guiying, Zhang Xiaolu, et al. Stability and robustness control strategy of DC microgrid considering constant power load[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4391-4405.
[17] 郭慧, 汪飞, 顾永文, 等. 基于电压分层控制的直流微电网及其储能扩容单元功率协调控制策略[J]. 电工技术学报, 2022, 37(12): 3117-3131. Guo Hui, Wang Fei, Gu Yongwen, et al. Coordinated power control strategy for DC microgrid and storage expansion unit based on voltage hierarchical control[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3117-3131.
[18] 田浩, 黄文焘, 余墨多, 等. 交直流混合独立微网互联变换器自适应双向下垂控制策略[J]. 中国电机工程学报, 2022, 42(19): 7063-7074. Tian Hao, Huang Wentao, Yu Moduo, et al. Adaptive bidirectional droop control strategy for the interlinking converter in the islanding hybrid AC-DC microgrids[J]. Proceedings of the CSEE, 2022, 42(19): 7063-7074.
[19] 郭强, 向文凯, 李山. 交直流混合微电网并联双向互联变换器环流抑制与功率控制[J]. 电气工程学报, 2022, 17(1): 31-40. Guo Qiang, Xiang Wenkai, Li Shan. Circulating Current suppression and power control of paralleled bidirectional interlinking converters in hybrid AC-DC microgrid[J]. Journal of Electrical Engineering, 2022, 17(1): 31-40.
[20] Yang Pengcheng, Yu Miao, Wu Qiuwei, et al. Decentralized bidirectional voltage supporting control for multi-mode hybrid AC-DC microgrid[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2615-2626.
[21] Eajal A A, Yazdavar A H, El-Saadany E F, et al. Optimizing the droop characteristics of AC-DC hybrid microgrids for precise power sharing[J]. IEEE Systems Journal, 2020, 15(1): 560-569.
[22] Chang J W, Moon S I, Lee G S, et al. A new local control method of interlinking converters to improve global power sharing in an islanded hybrid AC-DC microgrid[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 1014-1025.
[23] Loh P C, Li Ding, Chai Yi kang, et al. Autonomous operation of hybrid microgrid with AC and DC subgrids[J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2214-2223.
[24] Yuan Wenbin, Wang Yanbo, Liu Dong, et al. Efficiency-prioritized droop control strategy of AC microgrid[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 9(3): 2936-2950.
[25] Cao Wenyuan, Han Minxiao, Zhang Xiahui, et al. A novel power sharing scheme of controlling parallel-operated inverters in islanded microgrids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(5): 5732-5746.
Abstract With the increasing penetration of renewable energy, hybrid AC-DC microgrid clusters (HMG-Cluster) are gradually becoming resilient solutions for new power systems. As a key component for interconnecting and synergizing AC and DC microgrids, bidirectional interlinking converter (BIC) enables efficient power management and fault ride-through in HMG systems. However, how to control and optimize the power allocation scheme of BIC remains a fundamental challenge. To fill the gap in the existing research, a priority-driven BIC decentralized control strategy is proposed to ensure the optimization of the power exchange of the HMG-Cluster according to the different priorities and capacity requirements of the sub-grids in the system.
First, the optimal power exchange model for HMG-Cluster is realized by taking the normalized AC frequency and DC voltage values as the state deviation factors of the sub-grids, and proposing a power exchange strategy with the objective of minimizing the total global deviation factor and considering the sub-grid priority and power supply capacity. Further, the optimal solution of the proposed optimization problem can be obtained by transforming the proposed power exchange model into a solvable mathematical problem and by constructing and solving the Lagrange function of the proposed optimization problem. Second, according to the optimal power exchange objective, A decentralized quasi-sag control strategy based on BICs is proposed. Since the BIC in this strategy only needs to detect the state deviation factor of the local AC frequency or DC voltage, the decentralized optimal power autonomous cooperative control can be achieved. In addition, since the main controller therein achieves accurate power tracking through dual voltage-current closed-loop, which in turn enables the HMG-Cluster energy to operate in the state of minimizing the overall deviation factor. Finally, the effectiveness of the proposed strategy is verified based on two simulation cases on a hardware-in-the-loop (HIL) system.
Based on the simulation results under the two cases, the results show the control strategy proposed can be operated under sub-grid priority-driven, i.e., the state deviation coefficient ratios of the sub-grids are always consistent regardless of the system load surge or fault conditions, and the sub-grids with higher priority have higher voltage index and priority index compared to the global shared control strategy. In addition, in the case of insufficient system dispatchable power, the low-priority sub-grids will ensure that the loads with high priority are restored first by automatically dumping loads and increasing the deviation factor. Therefore, the optimization objective value of the control strategy proposed is smaller compared with the global shared control strategy.
In summary, the following conclusions can be drawn: (1) The optimal power exchange model for HMG-Cluster with the objective of minimizing the global total deviation factor is constructed. The model is able to realize autonomous power interaction among sub-grids of the HMG-Cluster system based on the self-optimizing cooperative control of the BIC state deviation factor. (2) A decentralized quasi-sag control strategy for a BIC is proposed. Since the BIC in this strategy only needs to detect the local AC frequency and DC voltage signals, a decentralized quasi-sag control strategy based on BIC is proposed and used to realize power autonomous synergy in HMG-Cluster. (3) The decentralized control strategy based on priority driven HMG-Cluster system proposed in this article is a fundamental research that can achieve compatibility with any advanced control algorithm and achieve higher level control objectives in future research work.
keywords:Hybrid AC-DC microgrid cluster, bidirectional interconnect converter, state deviation, priority driven, decentralized control
DOI: 10.19595/j.cnki.1000-6753.tces.231379
中图分类号:TM46
国家重点研发计划资助项目(2021YFB1600202)。
收稿日期 2023-08-25
改稿日期 2023-10-19
孔惠文 女,1994年生,博士研究生,研究方向为新能源电力系统的分析、稳定与控制,综合交通与能源系统等。E-mail:hwkong@ncepu.edu.cn
马 静 男,1981年生,教授,博士生导师,研究方向为电力系统分析、稳定与控制等。E-mail:hdmajing@163.com(通信作者)
(编辑 赫 蕾)