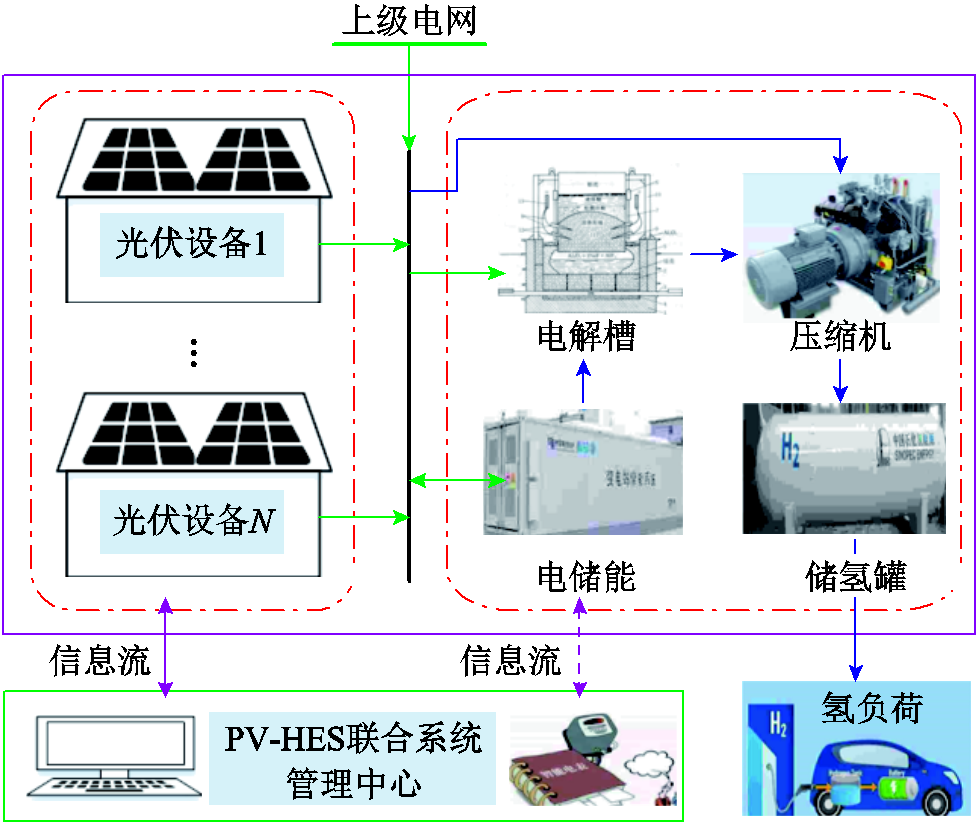
图1 PV-HES联合运行系统
Fig.1 PV-HES joint operation system
摘要 将光伏(PV)主体与氢储能(HES)主体结合,形成PV-HES联合系统,是促进可再生能源就地消纳,实现能源低碳转型的有效措施。针对光伏出力随机干扰及主体互异等问题,提出PV-HES的分散协同调度模型。首先,基于Nash-Harsanyi讨价还价理论建立PV-HES的多主体合作运行模型,并将其等效转换为电能交易量确定子问题和电能交易成本确定子问题;然后,为了保护各主体隐私,运用改进的交替方向乘子法对上述两个子问题进行分布式求解;最后,在一个典型的PV-HES联合系统中进行算例仿真,以验证所提分散协同调度模型以及分布式求解算法的有效性。仿真结果表明,氢储能主体的运营成本分别降低了11.67%和10.48%,光伏运营商的收益提高了15.72%。此外,通过对交替方向乘子法的改进也提高了系统的求解效率。
关键词:光伏系统 氢储能 PV-HES联合系统 Nash-Harsanyi讨价还价 改进交替方向乘子法 分散协同调度
为贯彻“双碳”目标和满足新型电力系统建设要求,各地相继出台能源发展规划,旨在进一步发展可再生能源,促进清洁低碳、安全高效的能源体系构建[1-2]。以北京为例,截至2022年2月,各类可再生能源发电装机占全市总装机容量的28%,其中分布式光伏占比为57.7%。分布式光伏的规模化接入,加重了电网在稳定运行、可再生能源消纳等方面的压力[3]。有效提升就地利用水平是分布式光伏可持续发展需解决的主要问题。
氢储能是利用电制氢、氢存储等环节高效实现以氢储电的一项新兴储能技术[4]。由于氢能具有能量密度大、无污染和零碳排放等特点[5],已逐渐成为促进波动性可再生能源消纳的重要手段之一。显然,光伏(Photovoltaic, PV)系统与氢储能(Hydrogen Energy Storage, HES)系统有机结合(形成PV-HES联合系统),可将部分光伏出力用于制氢、存储与利用。从而有效提升光伏的就地利用水平,缓解电网消纳压力;显著降低氢能生产成本,促进氢能的利用及推广。此外,PV-HES联合系统主要由太阳能和氢能驱动,这使其在促进能源清洁低碳转型等方面具有重要的现实意义。
氢储能优势实现的前提是对PV-HES联合系统运行的科学优化为前提。然而,一方面,系统内部光伏出力与负荷具有强随机性,影响系统的稳定运行;另一方面,PV和HES通常隶属于不同的利益主体,各自仅掌握自身的信息,且均理性追逐自身利益的最大化,这些均对PV-HES联合系统的高效运行产生制约。因此,如何在计及光伏出力、负荷等多重不确定性以及能量交易的前提下协调PV-HES联合系统内部各主体关系,从而保障PV-HES联合系统稳定运行是亟须解决的问题。
目前,国内外学者针对PV-HES联合运行系统运行问题的研究中,多将其视为一个整体,寻求系统整体收益的最大化。如文献[6]构建了含可再生能源-氢能的园区综合能源系统的集中优化模型,结果表明其有效提高了系统经济性。文献[7-8]分别从中长期和短期的角度出发,考虑了含氢能和可再生能源的系统优化运行问题,由结果可知氢能的引入有利于可再生能源消纳。文献[9]针对高速公路服务区中的多能负荷需求,提出了由可再生能源供能的“无废”多能微电网运行模式。文献[10]将氢储能与新的灵活技术相结合,通过促进可再生能源调度和将峰值负荷需求转移到非高峰时间,可以降低总运营成本。此外,针对系统中的光伏出力和负荷等不确定性因素,通常使用随机优化[11-12]、鲁棒优化[13]和信息间歇理论[14]等方法处理。然而上述研究场景中多以园区微能源网为例,且将可再生能源和氢储能考虑为同一主体而进行集中调度。
考虑到PV和HES之间的利益相关性以及各自信息的隐私性,所以在实际中PV和HES通常隶属于不同的主体。而博弈论为其提供了一个重要的解决手段,包括非合作博弈和合作博弈[15-16]。文献[17-18]立足于可再生能源、储能等不同主体,建立了基于非合作博弈的运行优化模型。文献[19-20]分别考虑负荷聚合商和供需资源模型,构建了电力公司与用户之间的非合作博弈模型。然而,使用非合作博弈虽然可以得到各主体间的纳什均衡解,但过于强调个体理性,可能会导致局部最优[15,21]。
合作博弈则可以兼顾个体与整体的统一,从而实现整体最优[22-23]。讨价还价博弈是典型的合作博弈方法,且在电力系统中得到广泛应用。文献[24]基于纳什讨价还价博弈理论,提出了一种风氢供热多智能体能源系统的合作规划和运行模型。文献[25]提出了基于讨价还价理论的配电公司和微电网合作投资社区储能扩展计划,以实现公平的合作。文献[26]提出了多个园区综合能源系统之间的合作运行模型,并引入讨价还价模型进行能量交易。
虽然现有研究中已利用讨价还价博弈模型对能源系统中多主体之间的合作关系进行分析,但是这些研究中较少考虑各个主体在合作过程中的贡献,即各主体的议价能力。而部分研究也只是以边际贡献率为依据量化主体的议价能力,无法全面体现各主体在合作中的实际贡献。除此之外,讨价还价博弈模型进行求解时常使用交替方向乘子算法,然而该算法在对拉格朗日乘子进行更新时,步长固定不变,从而可能导致其性能在迭代后期逐渐恶化。
基于此,本文首先提出了基于Nash-Harsanyi讨价还价博弈(N-H讨价还价博弈)的PV-HES合作运行框架。N-H讨价还价博弈将纳什讨价还价博弈改进为非对称博弈模型,从而可以反映参与者的议价能力及合作中的贡献,以确保合理的收益分配。其次,考虑源荷双侧的多重不确定性,构建PV和HES系统的随机优化运行模型,以最小化合作运行成本。最后,为了保护各主体的隐私并提高收敛效率,采用改进的交替方向乘子算法(Alternating Direction Method of Multipliers, ADMM)对其进行分布式求解,并在一个典型的PV-HES系统中对所提模型进行了算例仿真,以验证本文模型降低合作运行成本、提高求解效率以及促进可再生能源消纳等方面的优势。
本文所研究的PV-HES联合系统结构如图1所示。光伏运营商可以通过电网线路与氢储能主体进行能量交互,并向上级电网支付过网费。

图1 PV-HES联合运行系统
Fig.1 PV-HES joint operation system
从图1中可以看出,光伏运营商可以与上级电网和氢储能系统进行交易;氢储能系统内部包含电解槽、压缩机、储氢罐、电储能及氢负荷等。通常情况下,光伏运营商和氢储能系统分别隶属于不同的利益主体。在非合作模式下,光伏运营商将所生产的电能按照上网电价销售给电网,氢储能系统以市场电价从电力市场中购买电能以满足系统内部的需求。而在合作模式下,光伏运营商可以通过与氢储能主体签订合作协议,经过谈判和协商确定多主体之间交易的电量及相应的价格。
以图1所示的联合系统结构为基础,系统内各主体之间的合作运行主要可以分为两个子问题,具体如下。
子问题1:电能交易量确定。联合系统内部各个主体均以运行成本最小为目标,而为了保护各主体的隐私,将采用分布式求解方法。各个主体只需要向其他主体发送电能交易量的期望值,借助改进ADMM算法求得运行成本最小下各主体的最优电能交易量。
子问题2:电能交易成本确定。当第一步获取最优电能交易量后,需要进一步计算主体之间的电能交易价格,从而可以确定各主体的收益值。同时,也将借助改进ADMM算法,进行分布式求解,即各主体仅需要向其他主体发送电能交易价格的期望值,从而可以满足各个主体的利益需求。
在能源系统中,光伏出力和氢负荷具有不确定性,且难以准确预测,因此光伏运营商和氢储能主体在制定运行方案时需要将由于光伏随机出力和氢负荷波动所导致的不确定性考虑在内。基于此,本节将通过概率场景对不确定性进行建模,进而构建基于随机优化的运行模型。
2.1.1 目标函数
以光伏运营商主体运营成本 的最低运行成本为目标,即
的最低运行成本为目标,即
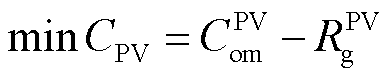 (1)
(1)
式中,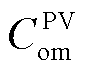 为光伏的维护成本;
为光伏的维护成本;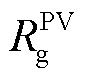 为向电网售电的收益。
为向电网售电的收益。
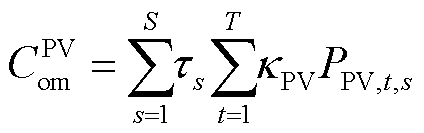 (2)
(2)
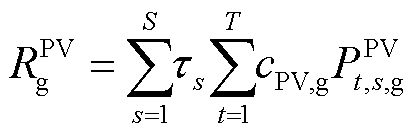 (3)
(3)
式中,s为光伏出力的场景,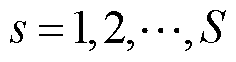 ;
;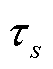 为场景发生的概率;t
为场景发生的概率;t![]()
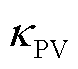 为光伏的单位发电量维护成本系数;
为光伏的单位发电量维护成本系数;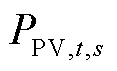 为场景s下光伏的发电量;
为场景s下光伏的发电量;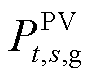 为场景s下光伏运营商向电网出售的电能;
为场景s下光伏运营商向电网出售的电能;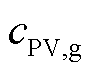 为相应的上网电价。
为相应的上网电价。
2.1.2 约束条件
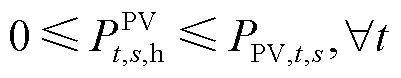 (4)
(4)
式中,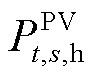 为场景s下光伏运营商可以向氢储能主体出售的电能。式(4)表示的是光伏运营商向电网出售的电能不能超过光伏的发电量。
为场景s下光伏运营商可以向氢储能主体出售的电能。式(4)表示的是光伏运营商向电网出售的电能不能超过光伏的发电量。
当光伏运行商与氢储能主体合作时,还需要满足额外考虑与氢储能主体之间进行直接交易时的过网费成本以及相应的约束条件。
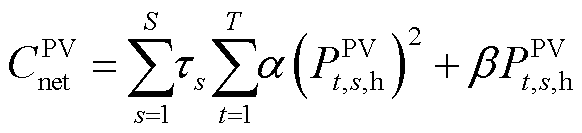 (5)
(5)
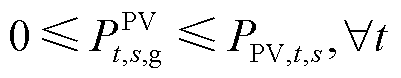 (6)
(6)
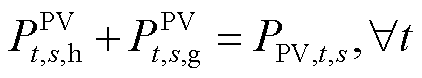 (7)
(7)
式中, 为与氢储能主体进行电能交易产生的过网费成本;α和β为过网费的折算系数。式(6)、式(7)表示光伏运营商向氢储能主体出售的电能不能超过光伏的发电量,且向电网出售电能和向氢储能主体出售电能之和等于光伏发电量。
为与氢储能主体进行电能交易产生的过网费成本;α和β为过网费的折算系数。式(6)、式(7)表示光伏运营商向氢储能主体出售的电能不能超过光伏的发电量,且向电网出售电能和向氢储能主体出售电能之和等于光伏发电量。
氢储能主体以最小化运行成本为目标,优化生产计划,从而确定从上级电网和光伏运营商中的购电量,满足次日氢储能主体的电能需求。
2.2.1 目标函数
以氢储能主体运营成本 的最低期望值为目标,即
的最低期望值为目标,即
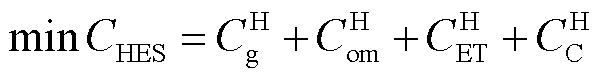 (8)
(8)
式中,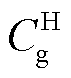 为从电网的购电成本;
为从电网的购电成本;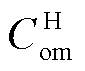 为氢储能内部机组的运行维护成本;
为氢储能内部机组的运行维护成本;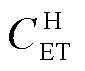 为氢储能系统中电储能的运行损耗成本;
为氢储能系统中电储能的运行损耗成本;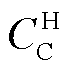 为从电网购电的碳成本。
为从电网购电的碳成本。
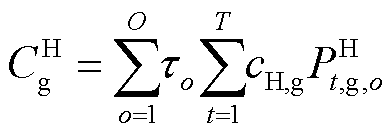 (9)
(9)
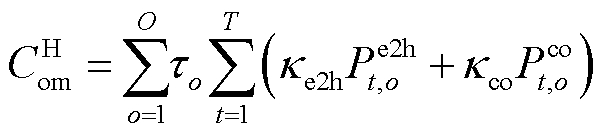 (10)
(10)
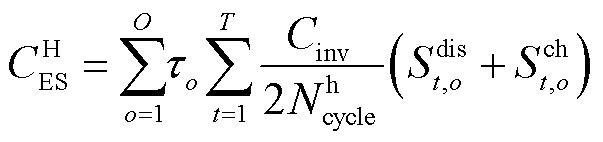 (11)
(11)
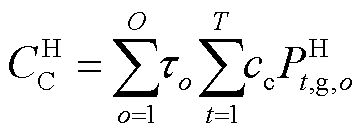 (12)
(12)
式中,o为氢负荷的场景,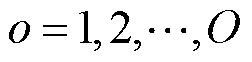 ;
;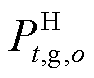 为场景o下从电网中购买的电能;
为场景o下从电网中购买的电能;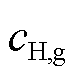 为相应的价格;
为相应的价格;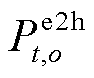 和
和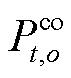 分别为场景
分别为场景![]() 下电解槽和压缩机消耗的电能;
下电解槽和压缩机消耗的电能;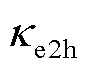 和
和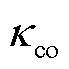 分别为电解槽和压缩机的单位电量维护成本系数;
分别为电解槽和压缩机的单位电量维护成本系数;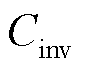 和
和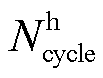 分别为电储能的投资成本和循环次数;
分别为电储能的投资成本和循环次数;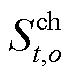 和
和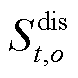 分别为场景o下电储能的充电量和放电量;
分别为场景o下电储能的充电量和放电量;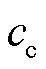 为碳成本系数。
为碳成本系数。
2.2.2 约束条件
1)电解槽
电解水制氢通过将直流电注入电解槽中产生氢气和氧气,化学反应过程为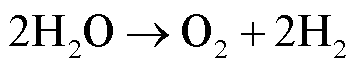 。场景
。场景![]() 下氢气产量
下氢气产量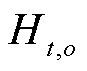 的计算公式为
的计算公式为
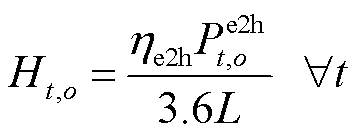 (13)
(13)
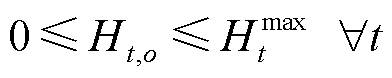 (14)
(14)
式中,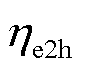 为电解水制氢的效率;L为氢气的低热值,L=119.64 MJ/kg;
为电解水制氢的效率;L为氢气的低热值,L=119.64 MJ/kg;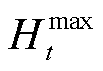 为产氢量的最大值。
为产氢量的最大值。
2)氢气压缩机
为了便于氢气的储存,需要将电解槽制取的氢气进行压缩。氢气压缩机的运行公式为
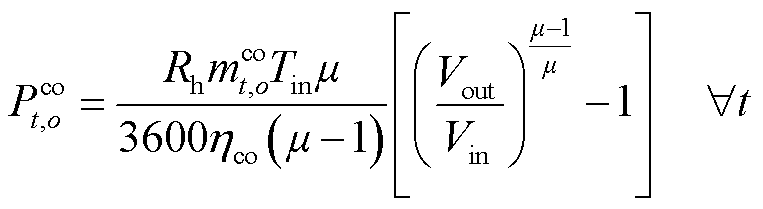 (15)
(15)
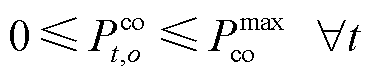 (16)
(16)
式中,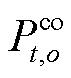 为场景o下压缩机消耗的电能;
为场景o下压缩机消耗的电能;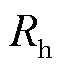 为氢气比热容;
为氢气比热容;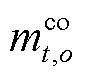 为场景o下压缩的氢气流量;
为场景o下压缩的氢气流量;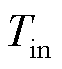 为输入氢气的温度;
为输入氢气的温度;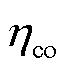 为氢气压缩效率值;
为氢气压缩效率值;![]() 为氢气等熵指数;
为氢气等熵指数;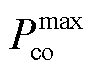 为氢气压缩机的最大功率;
为氢气压缩机的最大功率;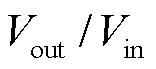 为氢气压缩机的压缩比。
为氢气压缩机的压缩比。
3)储氢罐
经压缩后的氢气可以储存在储氢罐中备用。储氢罐中的储氢量一般使用内部气压表示,其运行公式为
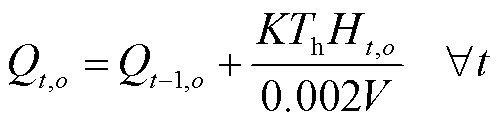 (17)
(17)
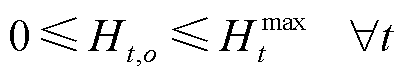 (18)
(18)
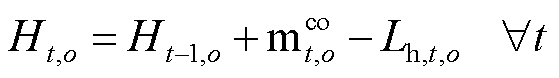 (19)
(19)
式中,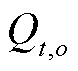 为场景
为场景![]() 下储氢罐内的压强;K为通用气体常数;Th为储氢罐内的温度;V为储氢罐的容积;Ht,o为场景o下储氢量;
下储氢罐内的压强;K为通用气体常数;Th为储氢罐内的温度;V为储氢罐的容积;Ht,o为场景o下储氢量;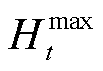 为储氢罐的最大容量;Lh,t,o为场景o下氢气消耗量,即氢负荷。式(19)为储氢量平衡约束。
为储氢罐的最大容量;Lh,t,o为场景o下氢气消耗量,即氢负荷。式(19)为储氢量平衡约束。
4)电储能
当电网的市场电价较低时,氢储能系统可以多购买一定量的电能,并使用电储能机组进行存储,从而在市场电价较高时,优先使用储能内电量,并减少从电网的购买量,以优化用能成本。
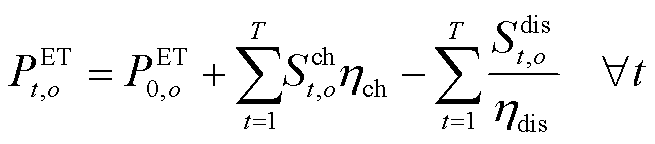 (20)
(20)
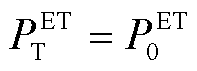 (21)
(21)
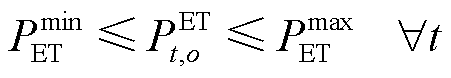 (22)
(22)
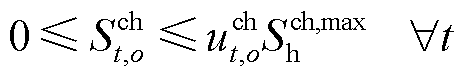 (23)
(23)
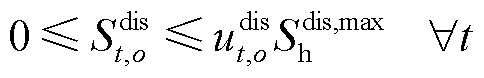 (24)
(24)
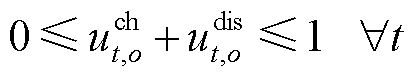 (25)
(25)
式中,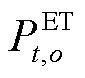 为场景o下电储能的存储的能量;
为场景o下电储能的存储的能量;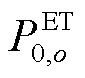 为场景o下初始时刻的能量;
为场景o下初始时刻的能量;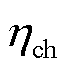 和
和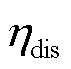 分别为电储能的充电和放电效率;
分别为电储能的充电和放电效率;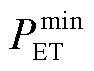 和
和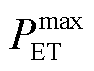 分别为电储能的最小和最大储存能量;
分别为电储能的最小和最大储存能量;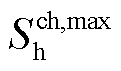 和
和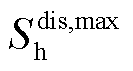 分别为电储能的最大充、放电功率;
分别为电储能的最大充、放电功率;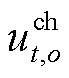 和
和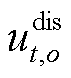 分别为场景o下充、放电的状态,是0-1变量。
分别为场景o下充、放电的状态,是0-1变量。
5)市场交互
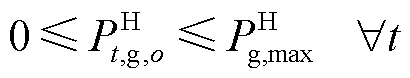 (26)
(26)
式中,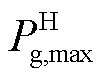 为从电网中购买的最大购电量。
为从电网中购买的最大购电量。
6)功率平衡
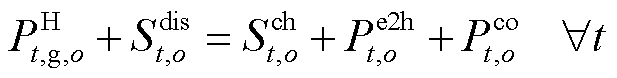 (27)
(27)
在独立运行模式中,光伏运营商和氢储能系统均是独立和理性的个体,并追逐自身利益的最大化。然而,这些系统在更大范围内的优化运行可以为所有实体带来更好的收益,从而激励光伏运营商和氢储能系统等主体展开合作,进行电能交易。考虑到合作,一个关键的问题是光伏运营商和氢储能系统之间如何达成谈判协议,从而在公平的前提下,保障各个主体收益均得到提升。Nash-Harsanyi讨价还价博弈(Nash-Harsanyi Bargaining Game, NHBG)作为博弈论的重要分支,可以兼顾个体和集体的利益,适用于求解此类问题。
对于一般的讨价还价问题,Nash在四条公理(个体理性、Pareto强有效性、尺度协变性、无关选择的独立性)设定下证明了使得式(28)最大化的解即为讨价还价问题的均衡解,同时均衡解可使得合作联盟的参与者成本最小或获得收益最大[27]。
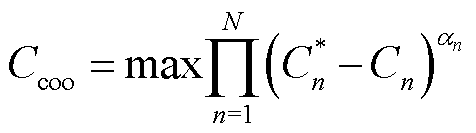 (28)
(28)
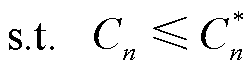 (29)
(29)
式中,N为参与博弈主体的总数;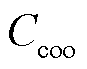 为合作联盟的总收益;
为合作联盟的总收益;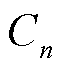 为博弈主体n的运行成本;
为博弈主体n的运行成本;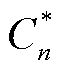 为谈判破裂点,即独立运行时的成本;
为谈判破裂点,即独立运行时的成本;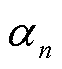 为各个参与者的谈判力,满足
为各个参与者的谈判力,满足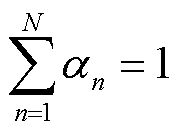 。
。
基于此,本文构建了PV-HES多主体合作运行NHBG策略与合作效益之间的关系模型。
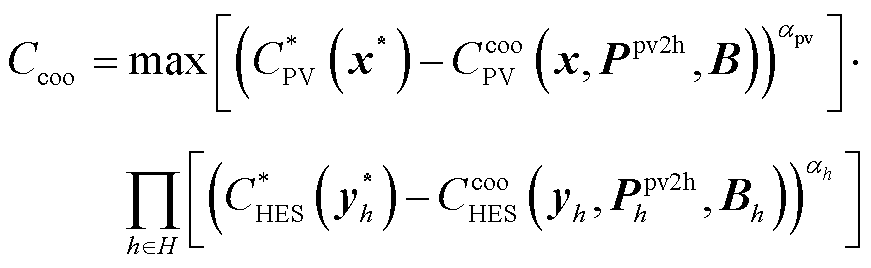 (30)
(30)
式中,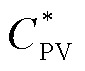 和
和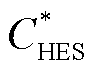 为各主体独立运行时的成本值,是常数;h为氢储能主体的个数,
为各主体独立运行时的成本值,是常数;h为氢储能主体的个数,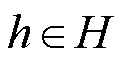 ,H为氢储能系统集合;x和
,H为氢储能系统集合;x和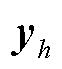 分别为主体的独立运行时的决策变量;
分别为主体的独立运行时的决策变量;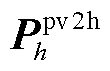 为PV和HES主体合作协商后确定的购买电量;
为PV和HES主体合作协商后确定的购买电量;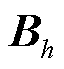 为相应的购买成本;
为相应的购买成本;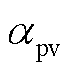 和
和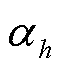 为两个主体的谈判力,即议价能力,求解方法见附录。并需要满足约束条件式(1)~式(7)、式(8)~式(27)以及式(31)、式(32)。
为两个主体的谈判力,即议价能力,求解方法见附录。并需要满足约束条件式(1)~式(7)、式(8)~式(27)以及式(31)、式(32)。
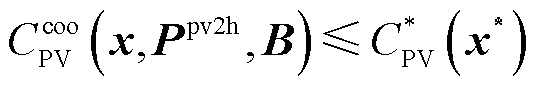 (31)
(31)
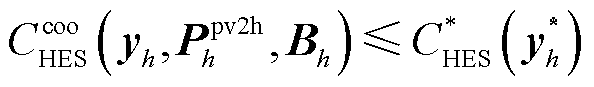 (32)
(32)
上述构建的合作模型为非凸非线性问题,直接求解较为困难。此外,在多主体合作中,需要注重对自身信息隐私的保护。所以本文首先将NHBG模型进行等效转换为易求解的子问题并分别使用改进的ADMM分布式算法进行求解,以保护主体隐私。
3.2.1 NHBG模型的等效转换
在文献[28]中,证明了能源交易问题的解也是运营成本的最优解。基于文献[28]可以将原PV-HES多主体NHBG模型分解为两个子问题。其中
SP1:电能交易量确定
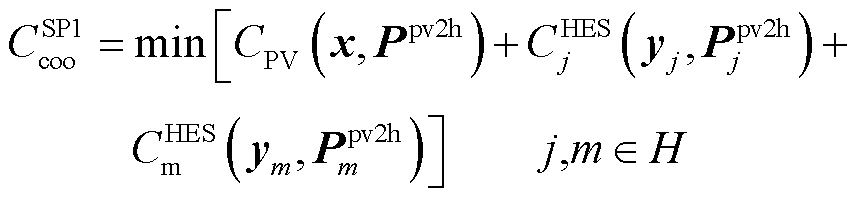 (33)
(33)
s.t.式(2)~式(7)、式(9)~式(27)(34)
SP2:电能交易成本确定
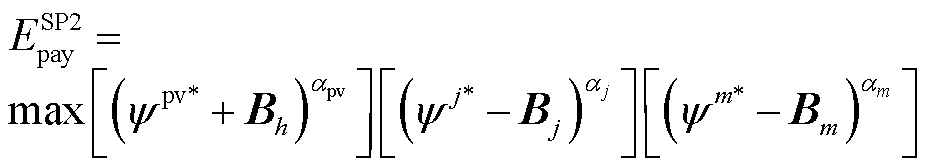
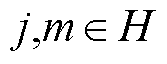 (35)
(35)
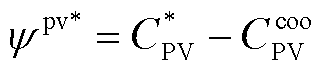 (36)
(36)
 (37)
(37)
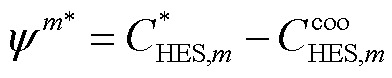 (38)
(38)
s.t.
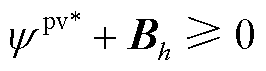 (39)
(39)
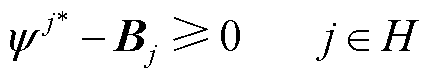 (40)
(40)
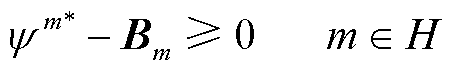 (41)
(41)
式中,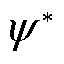 为各主体合作运行时相对于独立运行时节约的成本;
为各主体合作运行时相对于独立运行时节约的成本;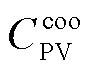 和
和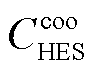 分别为通过求解SP1问题所获得的各个主体的运行成本值。
分别为通过求解SP1问题所获得的各个主体的运行成本值。
在SP1中,目标函数为最小化能源中各主体的运行成本之和。各个主体只有在获得额外收益的情况下才会积极参加多方合作。具体而言,参与合作后的多个主体可以通过出售多余能源获得相应的收益,以减少自身运行成本。因此,可以通过利益分配优化这些主体的运行成本,从而提高PV-HES联合系统总的额外收益,即分解后的子问题SP2。SP2通过支付协议将利益公平分配给每个交易主体。
在对SP1求解后,可以获得总的合作超额收益(独立运行成本减去合作运行成本)以及主体谈判力![]() 。然后,每个参与主体的最终收益由主体内部交易收益和合作收益分配(
。然后,每个参与主体的最终收益由主体内部交易收益和合作收益分配(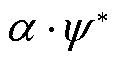 )两部分构成。具体证明见附录。
)两部分构成。具体证明见附录。
3.2.2 改进ADMM算法介绍
为了保护联合系统内部各主体的隐私,保障联合系统的正常运行,本节将采用分布式算法——改进的交替方向乘子法(ADMM)对上述NHBG问题进行求解。由于ADMM算法具有收敛性好、形式简单、鲁棒性强等优点,常被用于求解具有可分离变量的优化问题,详细求解思路参见文献[29]。ADMM算法的收敛速度主要受拉格朗日乘子和步长的影响,而原始ADMM算法中仅对拉格朗日乘子进行更新,而步长通常固定不变。因此,该算法的性能可能在迭代后期逐渐恶化。针对该问题,本文采用两阶段动态步长修正方法来改进原始ADMM算法。
1)如式(42)所示,在每次迭代期间计算原始残差和对偶残差的变化值。如果原始残差和对偶残差的最小值变化大于设定值Δ(如0.15),则步长保持不变,因为当前步长朝向原始残差和对偶残差的减小;否则,当前步长可能会恶化算法的收敛性。在这种情况下,根据阶段2)更新步长。
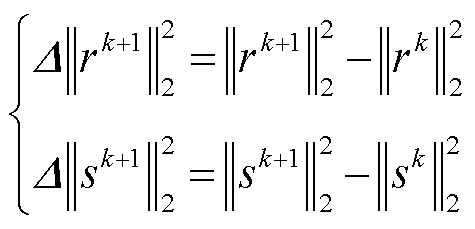 (42)
(42)
2)根据原始残差和对偶残差的当前值更新步长,如式(43)所示。如果原始残差远大于对偶残差,则步长将增大,从而导致违反原始可行性的严重惩罚;如果对偶残差远大于原始残差,则由于对偶可行性收敛,步长减小。在这种情况下,原始可行度和对偶可行度的收敛可以交替平衡。
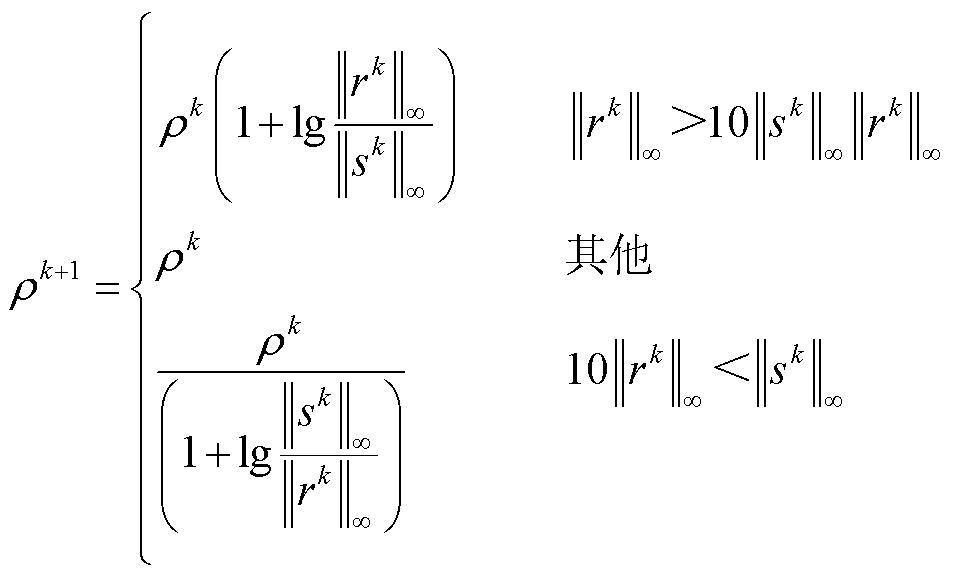 (43)
(43)
3.2.3 基于改进ADMM算法的模型分布式求解
对于子问题SP1,首先令
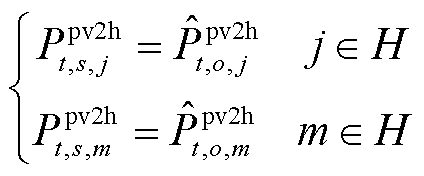 (44)
(44)
式中,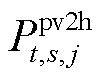 和
和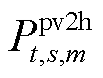 分别为场景s下光伏运营商主体向氢储能j和氢储能m主体期望出售的电能;
分别为场景s下光伏运营商主体向氢储能j和氢储能m主体期望出售的电能;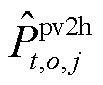 和
和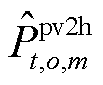 分别为场景
分别为场景![]() 下氢储能j和氢储能m主体期望从光伏运营商中购买的电能。
下氢储能j和氢储能m主体期望从光伏运营商中购买的电能。
当式(44)成立时,表明光伏运营商主体与氢储能j和氢储能m主体达成合作协议。进一步引入拉格朗日乘子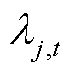 和
和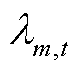 以及迭代步长
以及迭代步长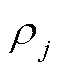 和
和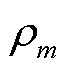 ,可得SP1问题目标函数的增广拉格朗日函数为
,可得SP1问题目标函数的增广拉格朗日函数为
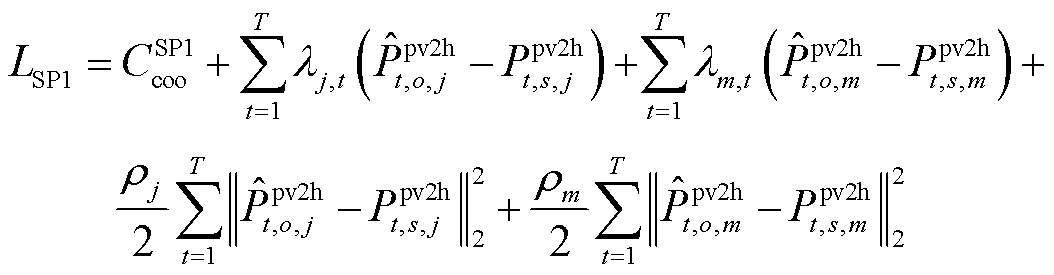 (45)
(45)
根据ADMM算法原理,对式(45)进行分解,分别可以得到光伏运营商和氢储能的分布式优化运行模型。
1)光伏运营商
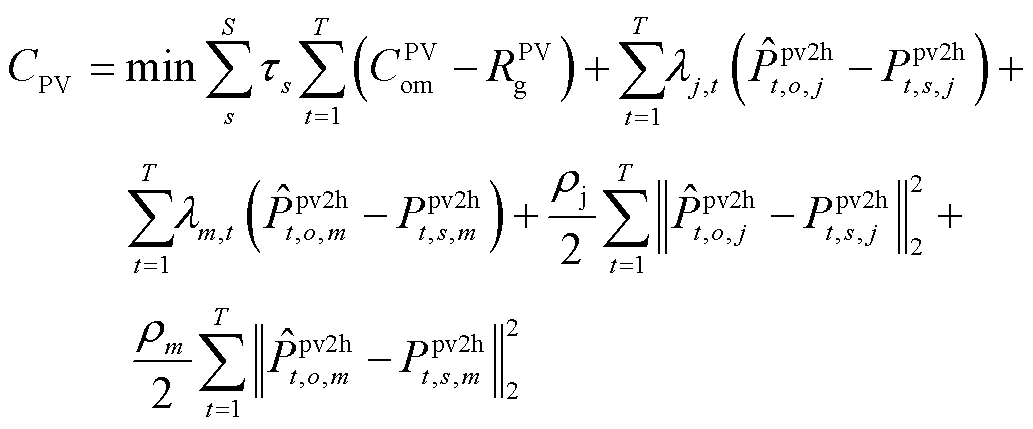 (46)
(46)
s.t. 式(2)~式(7) (47)
其中,式(2)~式(7)表示光伏运营商运行时的约束条件。
2)氢储能j主体( )
)
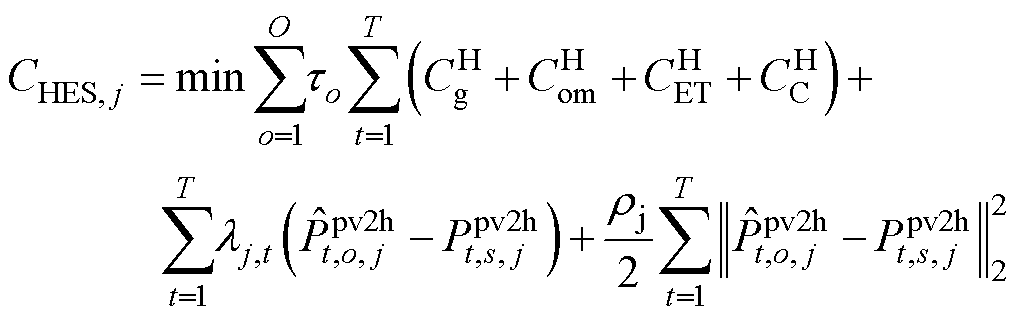 (48)
(48)
s.t. 式(9)~式(27) (49)
其中,式(9)~式(27)表示氢储能j主体在运行时需要满足的约束条件。
3)氢储能m主体(HESm)
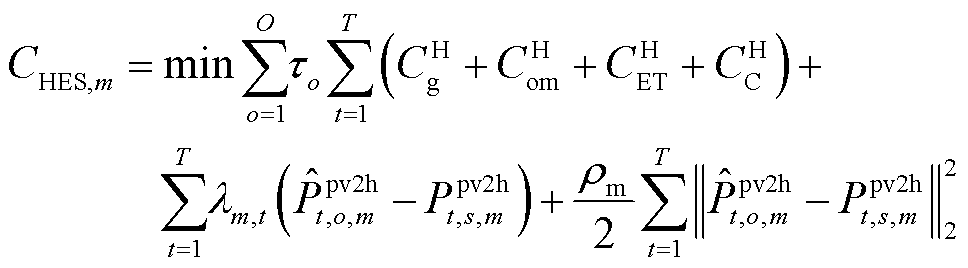 (50)
(50)
s.t. 式(9)~式(27) (51)
其中,式(9)~式(27)表示氢储能m主体在运行时需要满足的约束条件。
根据改进ADMM算法,对SP1问题进行分布式求解,步骤如下:
(1)设置收敛精度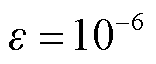 ,迭代步长
,迭代步长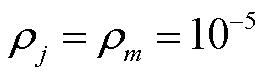 ;初始化迭代次数k=0,初始化光伏运营商的售电量
;初始化迭代次数k=0,初始化光伏运营商的售电量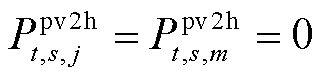 ,拉格朗日乘子
,拉格朗日乘子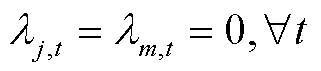 。
。
(2)对于氢储能j主体,从光伏运营商处接收期望售电量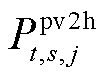 ,求解模型式(48),得出氢储能j的期望购电量
,求解模型式(48),得出氢储能j的期望购电量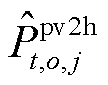 。
。
(3)对于氢储能m主体,从光伏运营商处接收期望售电量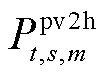 ,求解模型式(50),得出氢储能m主体的期望购电量
,求解模型式(50),得出氢储能m主体的期望购电量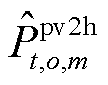 。
。
(4)对于光伏运营商,从氢储能j和氢储能m处接收期望购电量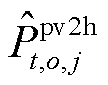 和
和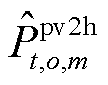 ,求解模型式(46),得出光伏运营商的期望售电量
,求解模型式(46),得出光伏运营商的期望售电量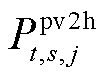 和
和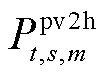 。
。
(5)根据式(52)计算第k次迭代的原始残差和对偶残差。检验各主体计算结果是否满足收敛判据,若收敛则迭代结束,输出调度结果;否则进入步骤(6)。
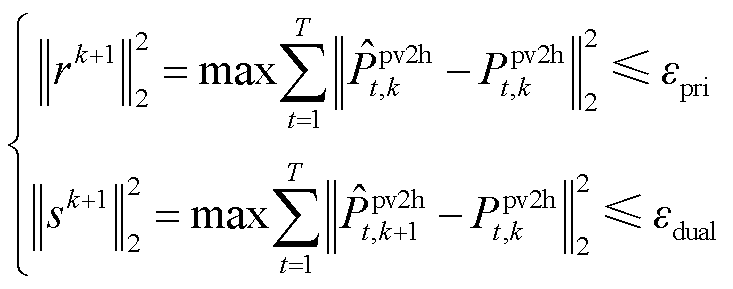 (52)
(52)
(6)根据式(53)更新拉格朗日乘子,根据式(42)、式(43)更新步长,置迭代次数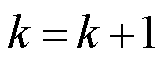 ,返回步骤(2)。
,返回步骤(2)。
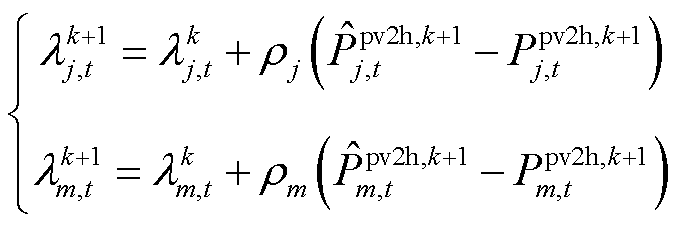 (53)
(53)
与SP1类似,SP2问题也可以通过引入辅助变量进行分解并计算。由于篇幅原因,不再赘述。算法流程如附图1所示。
由上述流程可知,各子区的模型求解、迭代算子计算及残差求取均在本主体内部进行,仅在进行联络线变量参考值提取和残差收敛判断时与其他主体进行交互,交互信息少,通信需求低,保护了各主体的信息隐私。由此可见,本文所提出的调度模型无需中枢机构协调,仅通过各主体间的迭代交互即可实现全系统调度策略的分布式收敛,实现了主体自治、分散协调的分布式优化。
4.1.1 系统相关参数设置
在一个典型的PV-HES联合系统中,对本文所提出的随机-N-H讨价还价博弈模型进行验证。该仿真系统主要包括三个主体,分别是一个光伏运营商以及两个氢储能主体。各个主体内部机组的相关参数设置见附表1、附表2;光伏运营商向电网出售电能的价格为上网电价,采用分时电价的形式;从电网购电的价格为电力市场实时价格,如附图2所示[30]。在仿真分析中,本文采用Matlab软件中Yalmip工具包调用Gurobi对其进行求解,计算机参数为Intel(R) Core(TM)i5 1.4 GHz,8 GB内存。
4.1.2 不确定性场景设置
如前述模型所述,PV-HES联合系统在制定机组调度计划时,所面临的不确定性主要来自于光伏出力和氢负荷。
受客观条件和相关技术的限制,氢负荷值通常与预测值存在偏差,本文假定其偏差服从正态分布。基于氢负荷的预测值和偏差值的随机抽样结果,分别等概率地生成500个氢负荷场景。对于光伏出力而言,其出力值主要受太阳光照辐射强度影响,服从β分布的概率密度函数。对其进行随机抽样,并生成500个太阳光照发电的场景。为了既保障场景的代表性,又可以降低求解难度,将使用拉丁超立方抽样、Wasserstein距离和0-1场景降维方法对随机场景进行降维[31]。最终生成包含氢负荷和光照发电的场景各三个,如图2所示。
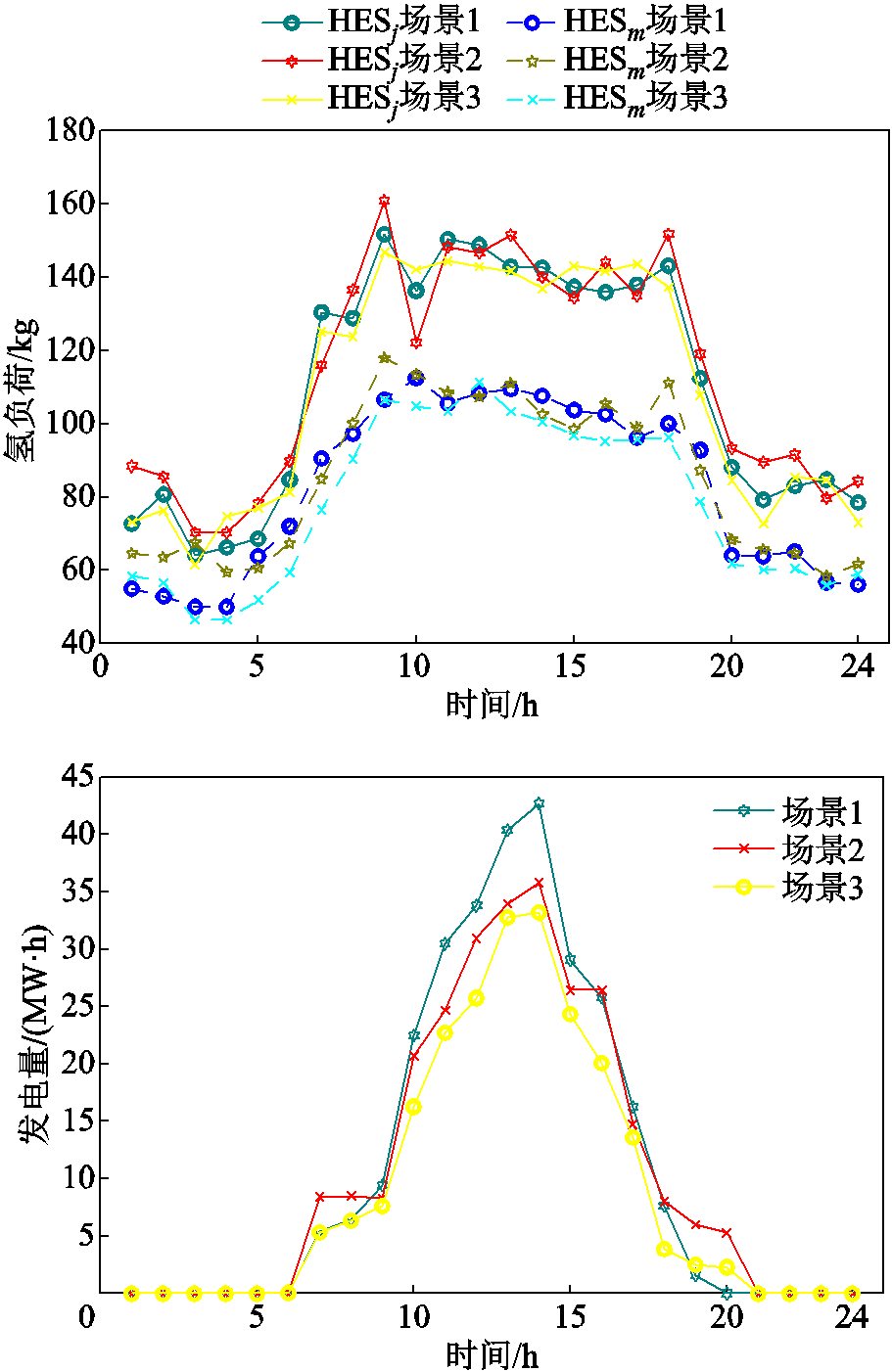
图2 氢负荷和光伏发电场景
Fig.2 Hydrogen load and PV scenario
4.2.1 多主体合作运行交易量分析
当PV-HESs联合运行时,氢储能可以从电网和光伏运营商处购买电能,以满足自身的电负荷需求。图3a和图3b分别为在PV-HESs联合运行情况下,氢储能j主体和氢储能m主体的电能交易策略。
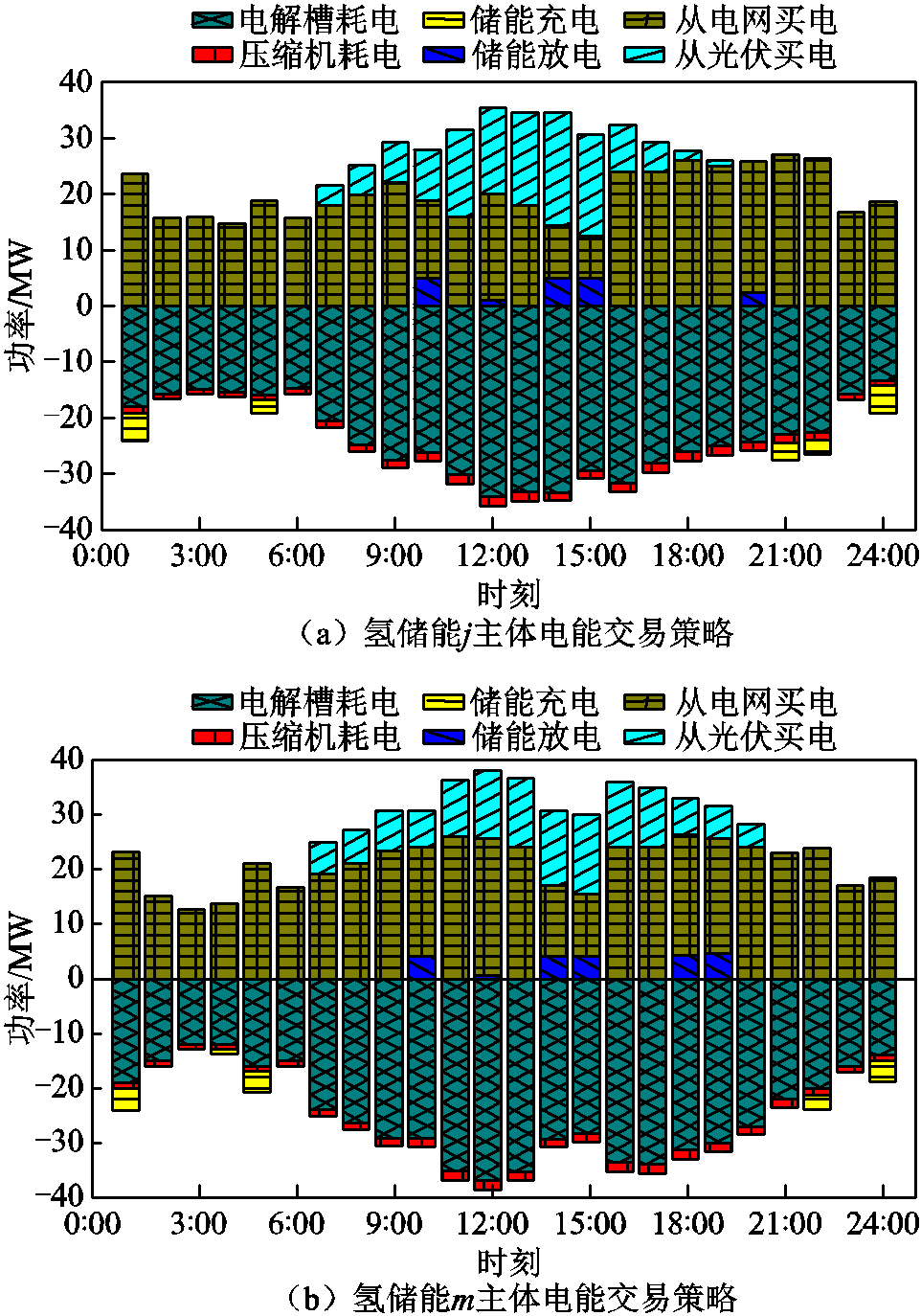
图3 氢储能主体的电能交易策略
Fig.3 Electric energy trading strategy of HES
从图3中可以看出,两个氢储能主体在电网电价低谷时刻1:00—5:00,会优先从电网购买电能,而在电价较高的时段,氢储能主体主要从光伏运营商处购电,以满足自身电制氢用电需求。尤其是在14:00和15:00,氢储能主体所需要的电能50%以上都是由光伏运营商主体提供的,主要原因在于,此时光伏运营商中光伏出力较大,光伏运营商在向电网售电的同时,有余量可以满足氢储能主体的用能需求。在17:00以后,由于光伏运营商内部的光伏出力减少,此时氢储能主体从电网购买部分电能。通过这种方式安排购电计划,可以最大程度地降低用能成本。此外,氢储能j主体与氢储能m主体相比,由于自身氢负荷较大,所以从光伏运营商和电网处购买的电能也高于氢储能m主体。
光伏运营商的电能交易策略如图4所示。从图4中可以看出,光伏运营商的交易结果分为三种。前期为全部上网;中期为既向电网售电,又向氢储能主体售电;后期则全部出售给氢储能主体。其主要原因在于,前期上网电价高于电网向氢储能售电的市场电价,因此光伏运营商选择全额上网。中、后期随着市场电价的升高,氢储能开始从光伏运营商中购电。
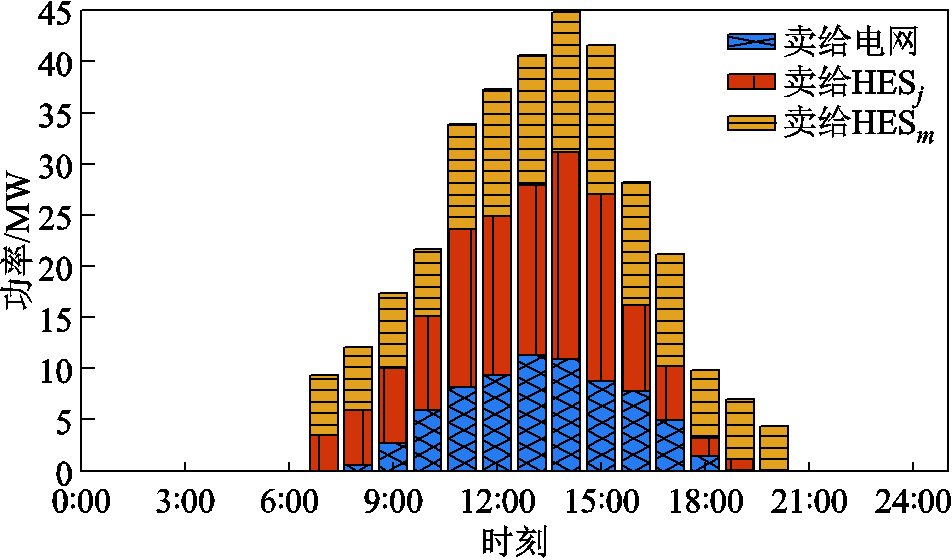
图4 光伏运营商电能交易策略
Fig.4 Electric energy trading of PV aggregator
4.2.2 多主体合作运行交易成本分析
在解决SP1中的PV-HESs系统优化运行问题后,可以计算每个主体的议价能力,见表1。
表1 各主体议价能力
Tab.1 Bargaining power of each entity

光伏运营商氢储能主体j氢储能主体m 0.3150.4020.283
与平均分配不同,本文所提出的NHBG模型可以利用议价能力确定参与者的贡献。氢储能主体的相关交易成本如图5所示。交易成本是通过氢储能主体与光伏运营商之间的讨价还价确定的。
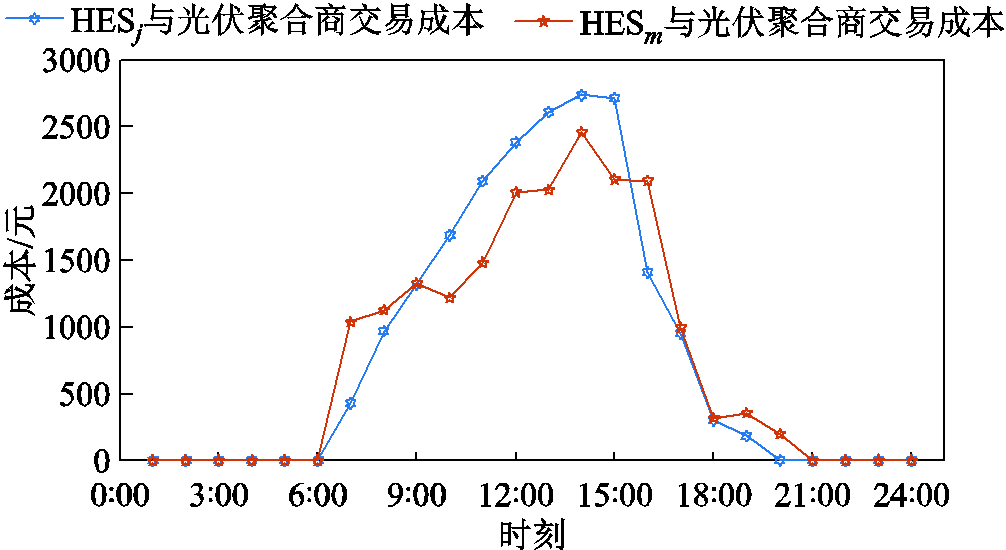
图5 氢储能主体交易成本
Fig.5 Transaction costs of hydrogen energy storage entities
多主体之间电力交易价格可以进一步根据交易电量和交易成本来确定,如图6所示。
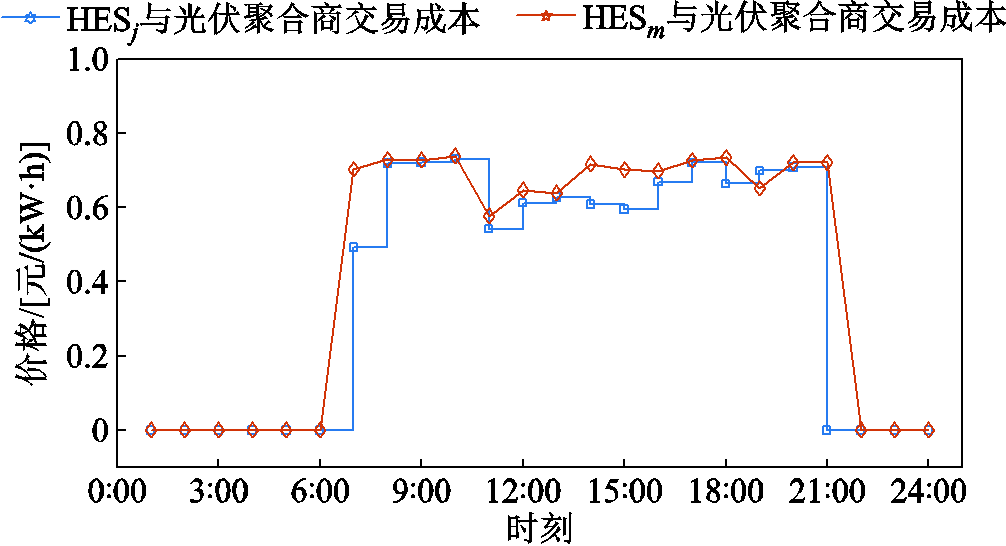
图6 主体之间交易价格
Fig.6 Transaction price between entities
从图6可以看出,当光伏运营商和氢储能主体之间不进行电力交易时,交易价格为0。在电力交易时,光伏运营商和氢储能主体的交易价格高于上网电价,低于电力市场价格。这促进了光伏运营商和氢储能之间的交易,也保护了多个主体的利益。
4.2.3 算法收敛性分析
本文采用改进的ADMM算法实现了PV-HESs联合系统交易量子问题和交易成本子问题的分布式求解。两个子问题的收敛过程如图7和图8所示。
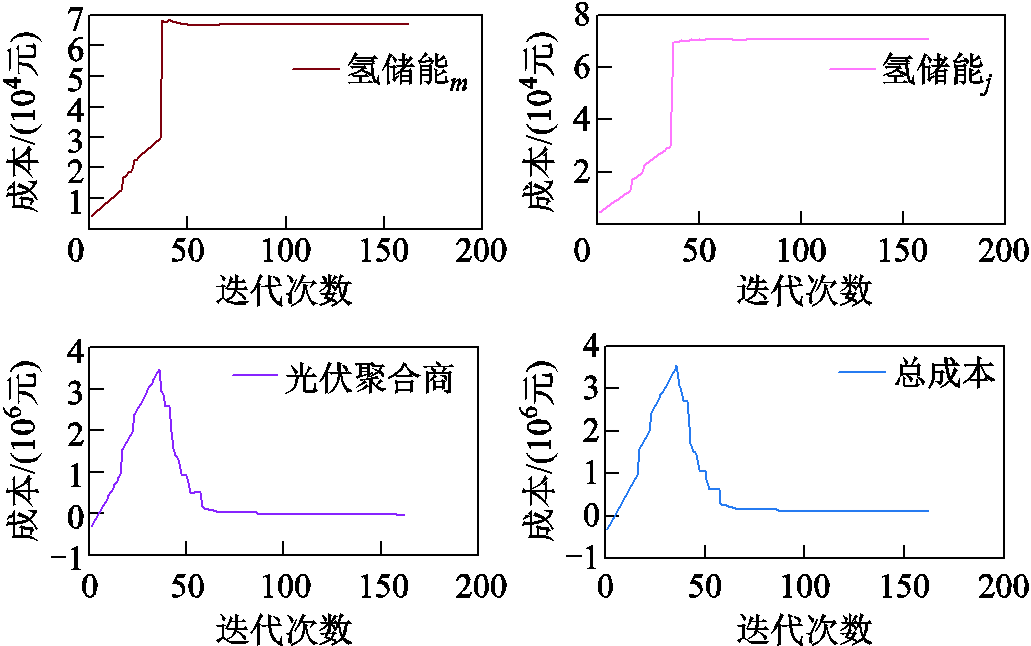
图7 交易量子问题收敛过程
Fig.7 Convergence process of transaction subproblem
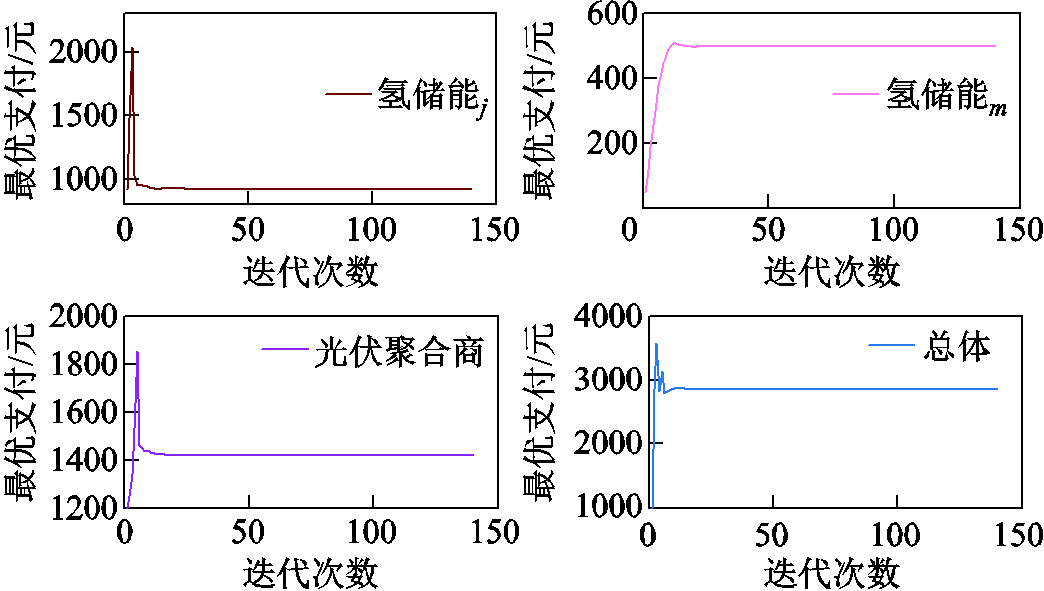
图8 交易成本子问题收敛过程
Fig.8 Convergence process of transaction cost subproblem
图7显示了PV-HESs联合系统交易量子问题中每个参与者成本和联合系统总成本的收敛结果。从图7中可以看出,使用所提出的改进ADMM算法在55次迭代后实现了收敛。图8显示出了交易成本子问题中PV-HESj交易价格和PV-HESm交易价格的收敛性。可以看出,使用所提出的改进ADMM算法在30次迭代后实现了收敛。这表明本文提出的改进ADMM算法在求解这两个子问题时具有良好的收敛性。在保护每个主体的隐私信息的同时,可以实现对两个子问题的分布式高效求解。
4.3.1 运行成本分析
当多个参与者通过协商达成合作协议时,参与者将通过降低运营成本获得超额利润。光伏运营商和氢储能主体在独立和合作模式下的运营收益和成本见表2和表3。
表2 光伏运营商运营收益
Tab.2 Operating benefit of rural PV aggregator

项目独立模式/元合作模式/元成本降低率(%) 光伏维护成本414.4413.50.21 向电网售电收益58 741.630 144.048.68 向HESs售电收益—37 767.9— 收益值58 327.267 498.5-15.72
表3 氢储能主体运营成本
Tab.3 Operating cost of hydrogen energy storage (单位:元)
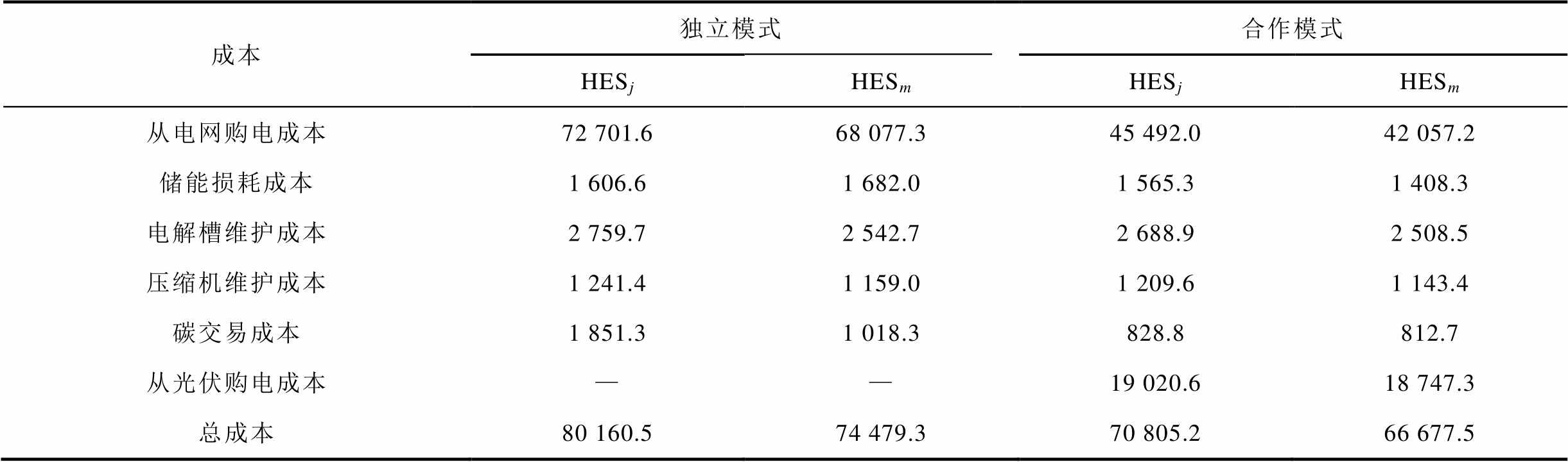
成本独立模式合作模式 HESjHESmHESjHESm 从电网购电成本72 701.668 077.345 492.042 057.2 储能损耗成本1 606.61 682.01 565.31 408.3 电解槽维护成本2 759.72 542.72 688.92 508.5 压缩机维护成本1 241.41 159.01 209.61 143.4 碳交易成本1 851.31 018.3828.8812.7 从光伏购电成本——19 020.618 747.3 总成本80 160.574 479.370 805.266 677.5
由表2可知,在合作运营后,光伏运营商运行收益提高了9 171.3元,占15.72%。这表明多个参与者的合作后,光伏运营商运行收益得到提高。从表3可以看出,合作后氢储能主体的成本分别降低了9 355.3元和7 801.7元,分别占总成本的11.67%和10.48%。氢储能j成本降幅更大的原因在于其氢负荷大于氢储能m,其在光伏出力高峰购买较多的低价电能,所以成本降幅更大。
4.3.2 改进ADMM算法优势分析
为了说明该方法的有效性,本节主要比较了目标级联算法、传统的ADMM算法、改进的ADMM算法、分布式内点法以及集中式优化算法,不同分布式求解算法对比见表4。
表4 不同分布式求解算法对比
Tab.4 Comparison of different distributed solution algorithms

方法总运行成本/元计算时间/s迭代次数 目标级联法158 951.41 634.1387 传统ADMM法159 312.01 839.2401 改进ADMM法137 482.7393.5163 分布式内点法[32]154 372.0878.2254 集中式优化140 328.412.51
表4首先比较了使用目标级联算法和ADMM分布式算法求解子问题SP1的计算效率。结果表明,ADMM算法比目标级联算法更快,且两种方法均具有保护参与主体隐私的优势。传统ADMM算法与改进的ADMM算法的比较表明,传统的ADMM方法在第401次收敛,改进的ADMM方法在第163次收敛。同时,该方法的计算时间为393.5 s,大大少于其他方法。分布式内点法的求解结果与本文使用方法相比,求解时间和迭代次数均较长。通过分布式求解方法的对比中可以看出,改进后的ADMM算法在进行分布式求解时具有较大优势。此外,对比改进ADMM和集中式求解可知,两者得出的总运行成本的误差仅为2.03%,确保了求解精度。虽然分布式求解比集中优化求解用时更长,却可以保证各个主体的隐私信息安全,实现区域自治,并获得最优的运行方案。显然,本文的方法有助于提高算法的收敛性能。
4.3.3 不同运行模式对比分析
上文的分析中并未考虑网络约束的影响,而在光伏-氢储能主体联合实际运行中双方能量的交互也将受到网络约束的限制。基于此,本节进一步在伊利诺伊理工大学的6节点的系统中进行分析[33],并对部分数据进行了改编,具体参数如附图3所示。此外,在上述模型中引入直流潮流约束进行计算[34]。考虑网络约束的场景1与不考虑网络约束场景2的运行结果见表5(以14点为例)。
表5 不同场景的运行结果对比
Tab.5 Comparison of operating results in different scenarios

运行结果数值变化率 场景1场景2 光伏向HESj出售电量/MW20.218.7-8.0% 光伏向HESm出售电量/MW13.714.23.5% 光伏与HESj交易价格/[元/(kW∙h)]0.6080.68711.4% 光伏与HESm交易价格/[元/(kW∙h)]0.7170.7291.6%
从表5中可以看出,当考虑网络约束后光伏聚合商与氢储能主体的交易电量,以及相应的交易价格均有所变化。其主要原因在于当考虑网络约束后可能存在线路阻塞情况,从而对交易电量和交易价格产生影响。但是从总体上看,当考虑网络运行约束后依然可以制定合理的交易策略,如达成的交易价格略低于电力市场价格,保证了各主体的收益。
在清洁能源建设工程,并积极探索建设多能互补的分布式低碳能源系统的背景下,本文提出基于随机-N-H讨价还价博弈的光伏运营商与氢储能系统分散协同调度机制,将其等价转换为电能交易量子问题和电能交易成本子问题,并使用改进的ADMM分布式求解算法对其依次求解。主要结论如下:
1)本文提出的PV-HESs合作运营模型可以兼顾个人理性和联盟理性。通过协同运行,氢储能j和氢储能m的运行成本分别比独立运行降低了11.67%、10.48%。光伏运营商的收益提高了15.72%。与传统的合作运营不同,该模型充分考虑了能源交易、主体议价能力、信息隐私和源荷多种不确定性。
2)通过使用改进ADMM分布式求解算法对电能交易量子问题和电能交易成本子问题进行求解,具有良好的收敛特性。与传统的ADMM算法相比,求解时间降低了70%。因此,在保护每个玩家的私有信息的同时,改进的ADMM算法可以有效解决PV-HESs多主体合作运行问题。
需要指出的是,本文在处理系统源荷双侧的不确定性因素影响时采用的是随机优化方法,但是随着随机场景的增多,会导致计算的维数灾,因此可以进一步引入鲁棒优化或分布鲁棒优化对不确定性因素进行处理。此外,我国正逐步降低对光伏的补贴,推行平价上网,为保障系统的收益,有必要在未来进一步探究光伏上网电价对系统收益的影响。
附 录
1. 议价能力
在不对称条件下,如果一个参与者的议价能力增强,在利益分配时该参与者将获得更多的利润。本文将从边际贡献率和主要设备利用率来量化谈判能力。
边际贡献率(MC):每个参与者在合作运行中的贡献。每个参与者的贡献可以通过比较加入前后的成本变化(SP1中的成本)来反映。边际贡献率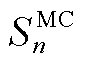 的计算式为
的计算式为
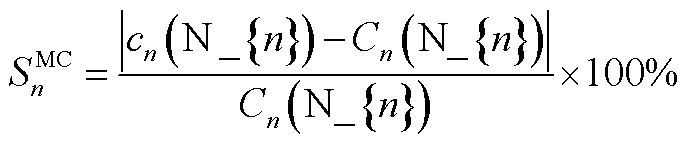 (A1)
(A1)
式中,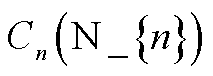 为合作运行时每个参与者n的成本,即SP1;
为合作运行时每个参与者n的成本,即SP1;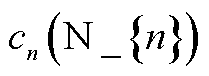 为在独立运行时每个参与者的收入。
为在独立运行时每个参与者的收入。
设备使用率(UR):每个参与者的设备使用效率。使用率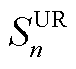 的计算式为
的计算式为
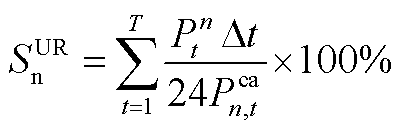 (A2)
(A2)
式中,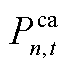 为各参与者的设备装机容量;
为各参与者的设备装机容量;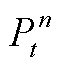 为各个参与者设备的实际出力。
为各个参与者设备的实际出力。
基于以上两个因素,可以得到每个参与者的总分为
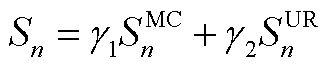 (A3)
(A3)
式中,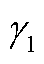 和
和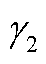 分别为MC和UR在体现议价能力时的权重,并且满足
分别为MC和UR在体现议价能力时的权重,并且满足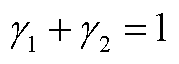 。通过对上述公式进行归一化,可以获得每个参与者的议价能力
。通过对上述公式进行归一化,可以获得每个参与者的议价能力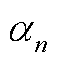 ,即
,即
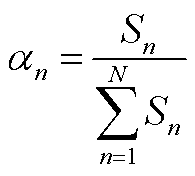 (A4)
(A4)
2. 利润分配证明
通过对子问题SP2的目标函数进行对数变换,可以将其变换为
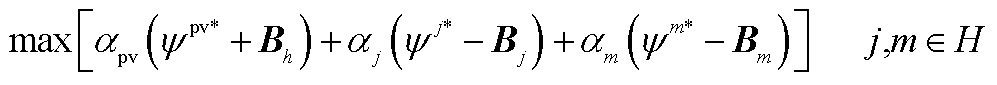 (A5)
(A5)
由于买方的总成本等于卖方的总收入,因此约束被描述为
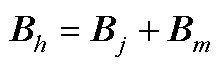 (A6)
(A6)
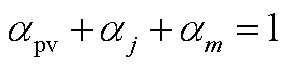 (A7)
(A7)
通过将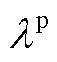 作为拉格朗日乘子,上述模型的拉格朗日日函数为
作为拉格朗日乘子,上述模型的拉格朗日日函数为
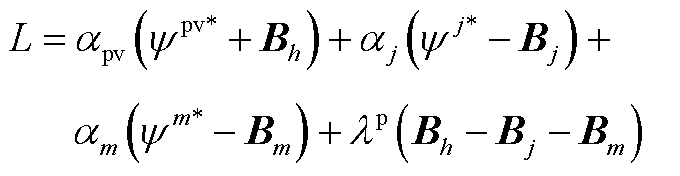 (A8)
(A8)
对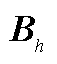 、
、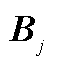 和
和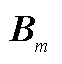 求偏导,可得
求偏导,可得
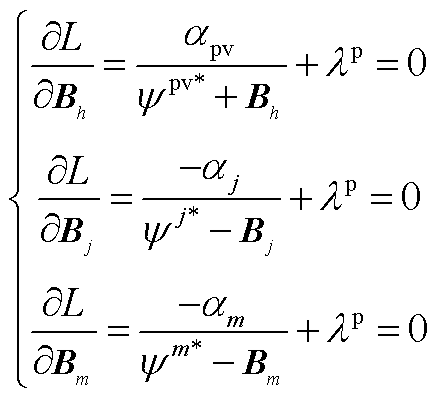 (A9)
(A9)
可以得到
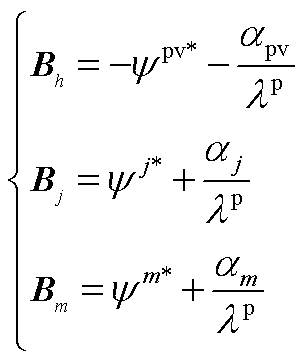 (A10)
(A10)
根据式(A6)和式(A7),式(A10)可以进一步变换,如式(A11)~式(A13)所示。
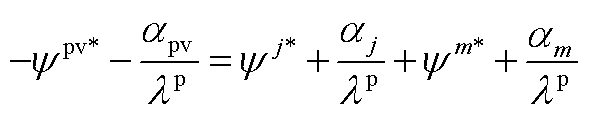 (A11)
(A11)
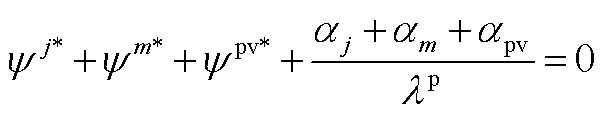 (A12)
(A12)
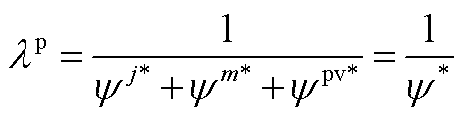 (A13)
(A13)
式中,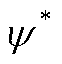 为合作利润总额。
为合作利润总额。
然后,节省成本可以表示为
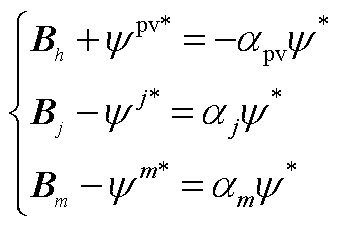 (A14)
(A14)
根据式(A14)可知,每个参与主体可以根据其议价能力获得利润,以确保公平的利润分配。
3. 改进APMM算法求解流程
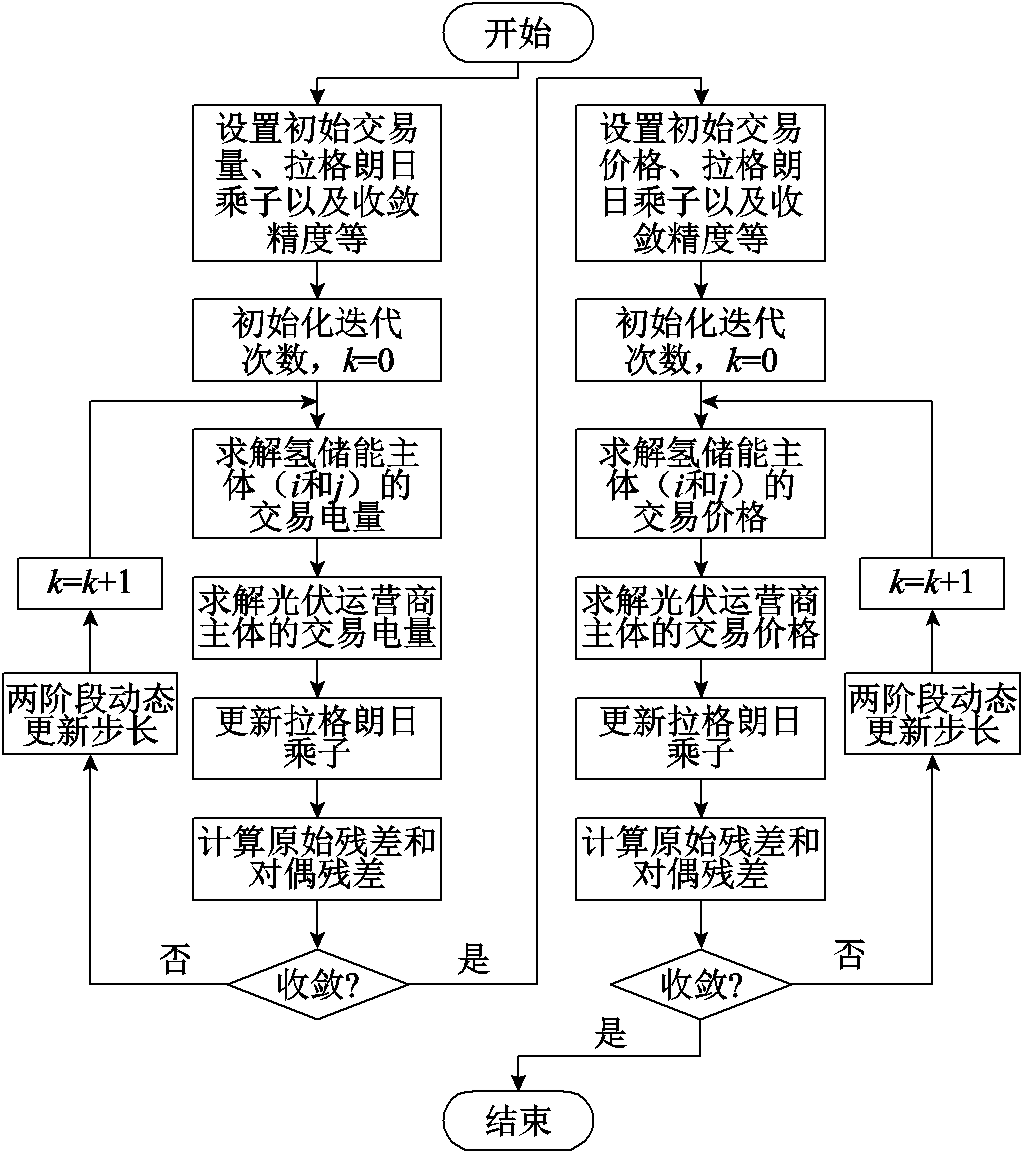
附图1 改进ADMM算法求解流程
App.Fig.1 Improved ADMM algorithm solving flow chart
附表1 光伏系统参数设置
App.Tab.1 PV system parameter setting

参数数值 0.009 5 α0.000 03 β0.01
附表2 氢储能参数设置
App.Tab.2 HES system parameter setting

参数数值参数数值 0.0180.018 0.020.02 0.06[kJ/(kg×K)]14.304 0.750.70
(续)
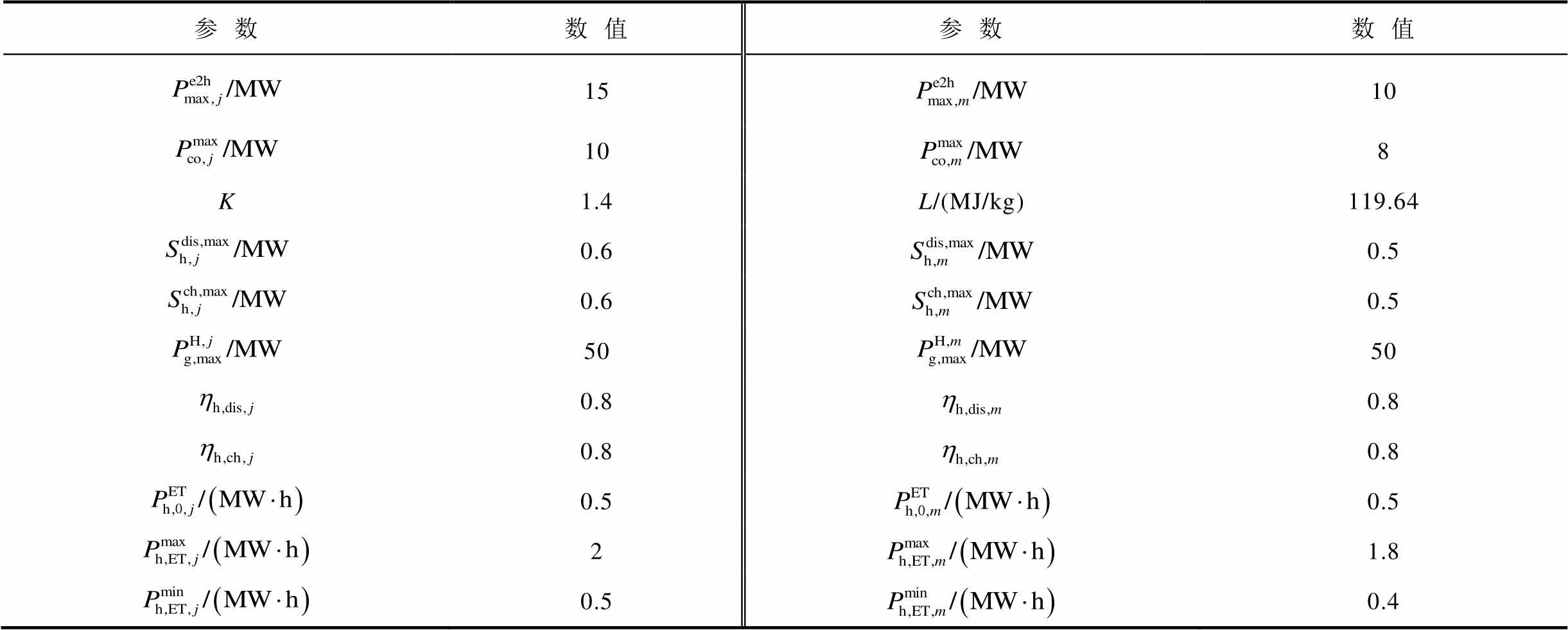
参数数值参数数值 15 10 10 8 K1.4L/(MJ/kg)119.64 0.6 0.5 0.6 0.5 5050 0.80.8 0.8 0.8 0.5 0.5 21.8 0.50.4
4. 算例相关参数设置
附表3 分时电价
App.Tab.3 Time of use tariff

分类时间段电价/[元/(kW·h)] 峰时8:00—11:00; 17:00—22:000.659 1 平时6:00—8:00; 11:00—17:000.505 2 谷时0:00—6:00; 22:00—24:000.393 8
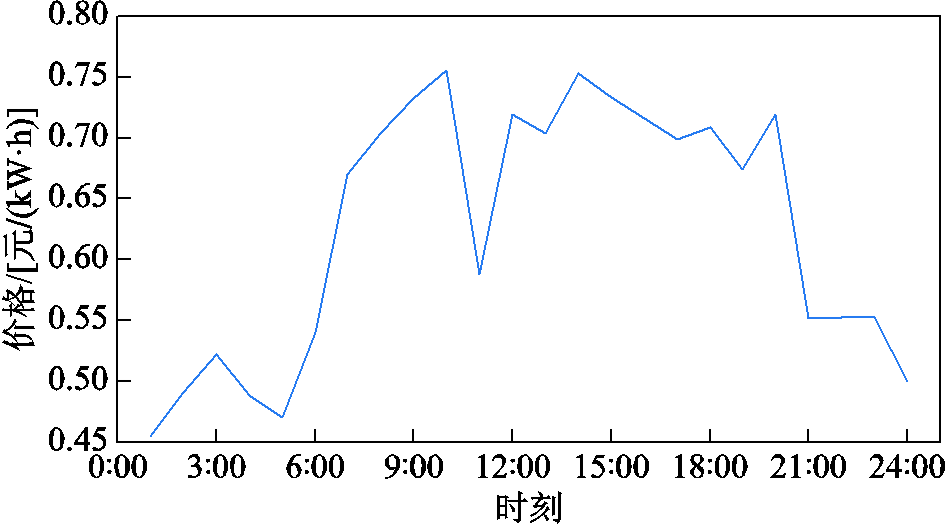
附图2 电力市场实时价格
App.Fig.2 Real time price of electricity market
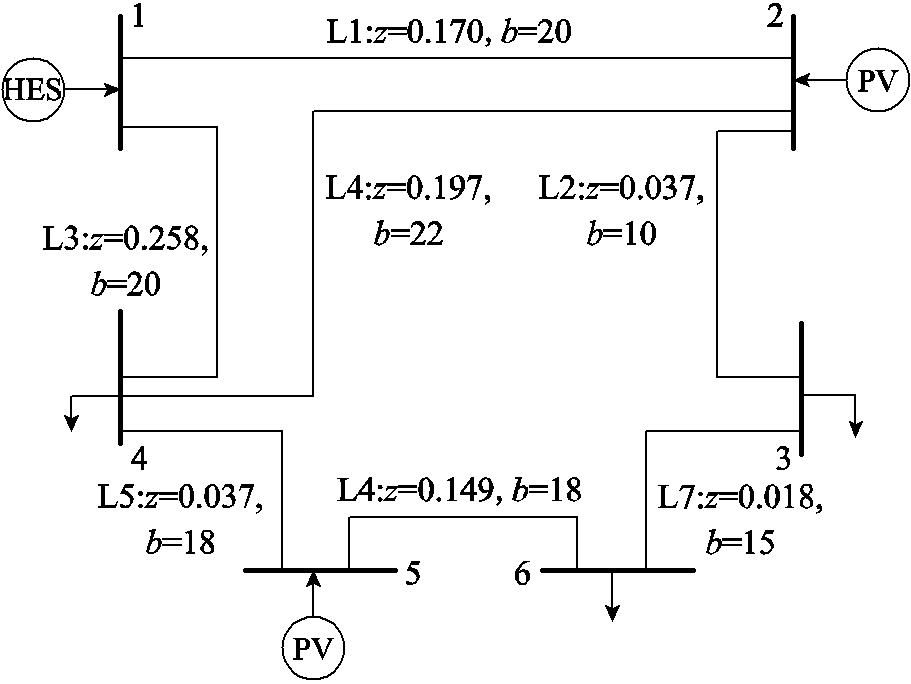
附图3 IIT-6节点系统
App.Fig.3 IIT-6 bus system
参考文献
[1] Zhao Xin, Ma Xiaowei, Chen Boyang, et al. Challenges toward carbon neutrality in China: strategies and countermeasures[J]. Resources, Conservation and Recycling, 2022, 176: 105959.
[2] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822. Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4808-4822.
[3] 孟广雨, 于洁潇, 杨挺. 基于随机网络演算的分布式能源调控系统时延上界计算[J]. 电工技术学报, 2020, 35(11): 2360-2371. Meng Guangyu, Yu Jiexiao, Yang Ting. Upper bound calculation of delay of distributed energy resource coordinated-control system based on stochastic network calculus[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2360-2371..
[4] 刘语忱, 闫群民, 郭阳, 等. 基于完备局部均值分解和相关分析的光伏发电侧电-氢混合储能优化配置[J]. 电气技术, 2022, 23(11): 21-29. Liu Yuchen, Yan Qunmin, Guo Yang, et al. Optimal configuration of electricity-hydrogen hybrid energy storage on photovoltaic generation side based on ensemble local mean decomposition and correlation analysis[J]. Electrical Engineering, 2022, 23(11): 21-29.
[5] Zhang Hongjie, Yu Wenfei, Hua Wei. Design and key technology of oil-free centrifugal air compressor for hydrogen fuel cell[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 11-19.
[6] 粟世玮, 郝翊彤, 宋玉娇, 等. 含风电-氢能-电转气的园区综合能源系统优化调度[J]. 广西师范大学学报(自然科学版), 2023, 41(1): 48-57. Su Shiwei, Hao Yitong, Song Yujiao, et al. Optimal dispatch of park integrated energy system including wind power-hydrogen energy-P2G[J]. Journal of Guangxi Normal University (Natural Science Edition), 2023, 41(1): 48-57.
[7] 任洲洋, 罗潇, 覃惠玲, 等. 考虑储氢物理特性的含氢区域综合能源系统中长期优化运行[J]. 电网技术, 2022, 46(9): 3324-3333. Ren Zhouyang, Luo Xiao, Qin Huiling, et al. Mid/long-term optimal operation of regional integrated energy systems considering hydrogen physical characteristics[J]. Power System Technology, 2022, 46(9): 3324-3333.
[8] 顾玖, 王晨磊, 解大. 电力市场环境下的电-氢一体化站优化运行[J]. 电力科学与技术学报, 2022, 37(1): 130-139. Gu Jiu, Wang Chenlei, Xie Da. Research on optimal operation of electricity-hydrogen integrated station in electricity market environment[J]. Journal of Electric Power Science and Technology, 2022, 37(1): 130-139.
[9] 滕云, 闫佳佳, 回茜, 等. “无废”电-氢充能服务区多源微网优化运行模型[J]. 中国电机工程学报, 2021, 41(6): 2074-2088. Teng Yun, Yan Jiajia, Hui Qian, et al. Optimization operation model of “zero-waste” electricity-hydrogen charging service area multi-energy microgrid[J]. Proceedings of the CSEE, 2021, 41(6): 2074-2088.
[10] Ibrahim A, Ali A, Ali E. Stochastic day-ahead unit commitment scheduling of integrated electricity and gas networks with hydrogen energy storage (HES), plug-in electric vehicles (PEVs) and renewable energies[J]. Sustainable Cities and Society, 2021, 67: 102736.
[11] Shao Chengcheng, Feng Chenjia, Shahidehpour M, et al. Optimal stochastic operation of integrated electric power and renewable energy with vehicle-based hydrogen energy system[J]. IEEE Transactions on Power Systems, 2021, 36(5): 4310-4321.
[12] 王雨晴, 王文诗, 徐心竹, 等. 面向低碳交通的含新能源汽车共享站电-氢微能源网区间-随机混合规划方法[J]. 电工技术学报, 2023, 38(23): 6373-6390. Wang Yuqing, Wang Wenshi, Xu Xinzhu, et al. Hybrid interval/stochastic planning method for new energy vehicle sharing station-based electro-hydrogen micro-energy system for low-carbon transportation[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6373-6390.
[13] Lei Gang, Wang Tianshi, Zhu Jianguo, et al. Robust multiobjective and multidisciplinary design optimization of electrical drive systems[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(4): 409-416.
[14] Kafaei M, Sedighizadeh D, Sedighizadeh M, et al. An IGDT/Scenario based stochastic model for an energy hub considering hydrogen energy and electric vehicles: a case study of Qeshm Island, Iran[J]. International Journal of Electrical Power & Energy Systems, 2022, 135: 107477.
[15] 王再闯, 陈来军, 李笑竹, 等. 基于合作博弈的产销者社区分布式光伏与共享储能容量优化[J]. 电工技术学报, 2022, 37(23): 5922-5932. Wang Zaichuang, Chen Laijun, Li Xiaozhu, et al. Capacity optimization of distributed PV and shared energy storage of prosumer community based on cooperative game[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5922-5932.
[16] 任洲洋, 程欢, 周桂平, 等. 考虑外部博弈和内部协同的耦合系统时序随机生产模拟[J]. 电工技术学报, 2023, 38(22): 6204-6217. Ren Zhouyang, Cheng Huan, Zhou Guiping, et al. A sequential probabilistic production simulation method for coupled systems considering external game and internal coordination[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6204-6217.
[17] 希望·阿不都瓦依提, 吕海鹏, 晁勤. 基于非合作博弈的风-光-氢微电网容量优化配置[J]. 电力工程技术, 2022, 41(2): 110-118. Xiwang Abuduwayiti, Lü Haipeng, Chao Qin. Optimal capacity configuration of wind-photovoltaic-hydrogen microgrid based on non-cooperative game theory[J]. Electric Power Engineering Technology, 2022, 41(2): 110-118.
[18] 郭旭升, 文汀, 林湘宁, 等. 面向多利益主体的清洁能源化大型离网海岛源储一体化优化定容[J]. 中国电机工程学报, 2019, 39(增刊1): 1-14. Guo Xusheng, Wen Ting, Lin Xiangning, et al. Integration capacity optimization of multi-stakeholder generation-storage on large-scale off-grid island[J]. Proceedings of the CSEE, 2019, 39(S1): 1-14.
[19] Wang Haiyang, Zhang Chenghui, Li Ke, et al. Distributed coordinative transaction of a community integrated energy system based on a tri-level game model[J]. Applied Energy, 2021, 295: 116972.
[20] Guo Ningxuan, Wang Yinan, Yan Gangfeng. A double-sided non-cooperative game in electricity market with demand response and parameterization of supply functions[J]. International Journal of Electrical Power & Energy Systems, 2021, 126: 106565.
[21] 刘晓峰, 高丙团, 李扬. 博弈论在电力需求侧的应用研究综述[J]. 电网技术, 2018, 42(8): 2704-2711. Liu Xiaofeng, Gao Bingtuan, Li Yang. Review on application of game theory in power demand side[J]. Power System Technology, 2018, 42(8): 2704-2711.
[22] 晏鸣宇, 王玲玲, 滕飞, 等. 面向分布式能源的可交易能源市场研究综述与展望[J]. 电力系统自动化, 2023, 47(18): 33-48. Yan Mingyu, Wang Lingling, Teng Fei, et al. Review and prospect on transactive energy market for accommodating distributed energy resources[J]. Automation of Electric Power System, 2023, 47(18): 33-48.
[23] 赵会茹, 王学杰, 李兵抗, 等. 考虑能量共享的多社区光储系统分布鲁棒优化调度[J]. 电力系统自动化, 2022, 46(9): 21-31. Zhao Huiru, Wang Xuejie, Li Bingkang, et al. Distributionally robust optimal dispatch for multi-community photovoltaic and energy storage system considering energy sharing[J]. Automation of Electric Power Systems, 2022, 46(9): 21-31.
[24] Ma Tengfei, Pei Wei, Deng Wei, et al. A Nash bargaining-based cooperative planning and operation method for wind-hydrogen-heat multi-agent energy system[J]. Energy, 2022, 239: 122435.
[25] Nazari A, Keypour R, Amjady N. Joint investment of community energy storage systems in distribution networks using modified Nash bargaining theory[J]. Applied Energy, 2021, 301: 117475.
[26] 黄海涛, 陈曦, 查俊吉. 多园区综合能源系统分区自治式能量合作社区及联合优化调度[J]. 电网技术, 2022, 46(8): 2955-2965. Huang Haitao, Chen Xi, Zha Junji. Partition autonomous energy cooperation community and its joint optimal scheduling for multi-park integrated energy system[J]. Power System Technology, 2022, 46(8): 2955-2965.
[27] Du Yan, Wang Zhiwei, Liu Guangyi, et al. A cooperative game approach for coordinating multi-microgrid operation within distribution systems[J]. Applied Energy, 2018, 222: 383-395.
[28] Kim H, Lee J, Bahrami S, et al. Direct energy trading of microgrids in distribution energy market[J]. IEEE Transactions on Power Systems, 2020, 35(1): 639-651.
[29] Ghadimi E, Teixeira A, Shames I, et al. Optimal parameter selection for the alternating direction method of multipliers (ADMM): quadratic problems[J]. IEEE Transactions on Automatic Control, 2015, 60(3): 644-658.
[30] Nord Pool. Day-ahead prices[DB/OL]. [2023-12-12]. http://data.nordpoolgroup.com/auction/day-ahead/prices? deliveryDate=latest¤cy=EUR&aggregation=Hourly&deliveryAreas=AT.
[31] Yan Rujing, Lu Zherui, Wang Jiangjiang, et al. Stochastic multi-scenario optimization for a hybrid combined cooling, heating and power system considering multi-criteria[J]. Energy Conversion and Management, 2021, 233: 113911.
[32] 林敏洪, 侯祖锋, 王超, 等. 基于分布式内点法的输配协同优化调度[J]. 可再生能源, 2020, 38(9): 1226-1232. Lin Minhong, Hou Zufeng, Wang Chao, et al. Optimal dispatch for transmission distribution coordination system based on distributed interior point method[J]. Renewable Energy Resources, 2020, 38(9): 1226-1232.
[33] 吴辰晔, 孙健. 凸包定价模式下的电力市场潜在市场力分析方法[J]. 电力系统自动化, 2021, 45(6): 101-108. Wu Chenye, Sun Jian. Analysis method for potential market power of electricity market in convex hull pricing mode[J]. Automation of Electric Power Systems, 2021, 45(6): 101-108.
[34] Li Hongze, Wang Xuejie, Li Fengyun, et al. A robust day-ahead electricity market clearing model considering wind power penetration[J]. Energies, 2018, 11(7): 1772.
Abstract Integrating photovoltaic (PV) and hydrogen energy storage (HES) into a PV-HES joint system proves to be an effective strategy in boosting local consumption of renewable energy and facilitating the low-carbon transformation of energy. The system's internal photovoltaic output and load exhibit considerable randomness, influencing the system's stable operation. Additionally, PV and HES, being typically associated with different stakeholders, each prioritize maximizing their own interests, which limits the effective operation of the PV-HES joint system. Current research often overlooks the bargaining power of diverse entities within the system, failing to fully portray each entity's actual contributions in cooperative efforts amidst uncertainties. In response to these problems, the relationships between entities in the PV-HES combined system should be coordinated and multiple uncertainties should be considered to ensure the stable operation of the PV-HES combined system.
Initially, utilizing Nash-Harsanyi bargaining game theory, the study formulates a multi-agent cooperative operational model for PV-HES. This model equivalently addresses the determination of power transaction volume and power transaction cost as distinct subproblems. The Nash-Harsanyi bargaining game extends the Nash bargaining game into an asymmetric game model. This model accounts for participants' bargaining power and their contributions in cooperative efforts, ensuring a fair distribution of benefits. Secondly, stochastic optimal operating models for PV and HES systems were created using probabilistic scenarios, considering uncertainties in both energy supply and load aspects. These models aim to minimize cooperative operational costs. Thirdly, to safeguard the privacy of each participant, the improvement of alternating direction multiplier method (ADMM) is employed to address the aforementioned two subproblems. This method utilizes a two-stage dynamic step size correction approach.
To validate the efficacy of the proposed decentralized collaborative scheduling model and distributed solving algorithm, simulations were performed on a standard PV-HES joint system. "The simulation results indicate a reduction in operating costs for HES entities by 11.67% and 10.48% respectively, alongside a 15.72% increase in profit for PV aggregators. Furthermore, the improvement of ADMM method significantly boosts system efficiency, reducing solving time by 70% compared to the traditional ADMM algorithm. The calculation outcomes validate the model's advantages in reducing cooperative operating costs, enhancing solving efficiency, and fostering the utilization of renewable energy.
The simulation analysis yields the following conclusions: (1) The proposed multi-agent cooperative operation model of PV-HES strikes a balance between individual rationality and alliance rationality. Unlike traditional cooperative approaches, this model comprehensively accounts for various uncertainties, including energy trading, entities' bargaining power, information privacy, and source load. (2) Employing the enhanced alternating direction multiplier method (ADMM) to resolve the electricity trading quantum problem and its associated cost exhibits favorable convergence characteristics. While safeguarding the confidentiality of individual data, this improved ADMM algorithm effectively addresses the multi-agent collaborative operation problem within PV-HES.
Keywords:PV system, Hydrogen energy storage, PV-HES joint system, Nash-Harsanyi bargaining game, improved alternating direction multiplier method, decentralized cooperative dispatching model
DOI: 10.19595/j.cnki.1000-6753.tces.231369
中图分类号:TM732
国家自然科学基金(72101089)和中央高校基金(2022MS026)资助项目。
收稿日期 2023-08-22
改稿日期 2023-12-12
王学杰 男,1993年生,博士,研究方向为电力市场应用技术。E-mail:wangxuejie155@163.com(通信作者)
赵会茹 女,1963年生,教授,博士生导师,研究方向为电力市场理论及应用技术等。E-mail:zhaohuiru@ncepu.edu.cn
(编辑 赫 蕾)