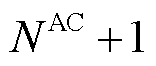 个交流节点,
个交流节点,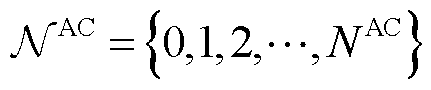 表示交流节点集合,其中,变电站节点编号为0;
表示交流节点集合,其中,变电站节点编号为0;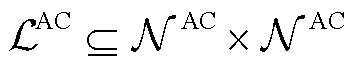 表示交流线路集合。引入
表示交流线路集合。引入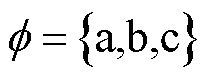 来表征各相的集合,由此,对于节点
来表征各相的集合,由此,对于节点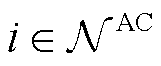 ,其三相电压列向量为
,其三相电压列向量为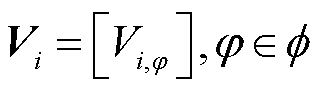 ,例如
,例如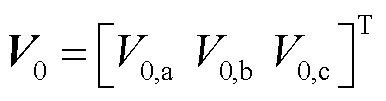 ,其负荷三相功率向量为
,其负荷三相功率向量为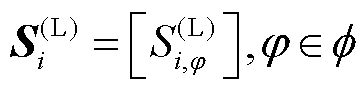 。对于线路
。对于线路 ,线路上流过的三相电流向量为
,线路上流过的三相电流向量为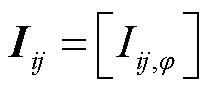 ,
,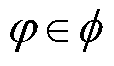 ;线路上的三相阻抗矩阵为
;线路上的三相阻抗矩阵为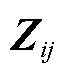 ,由线路ij的三相自阻抗与互阻抗组成。
,由线路ij的三相自阻抗与互阻抗组成。摘要 交直流主动配电网作为未来配电网的主要发展形态,实现其有功无功资源的协同优化控制具有重要的研究意义。然而配电网负荷单相接入和分布式发电三相功率不一致,将导致配电网三相不平衡现象越发严重。为了应对交直流主动配电网的三相不平衡问题,提出考虑相间耦合与三相不平衡度限制的三相有功无功联合优化方法。首先,建立考虑相间耦合的原始三相潮流模型并对其进行升维映射;其次,采用半正定松弛方法,推导了交直流主动配电网各子系统的完整三相潮流模型以及序分量形式下的三相电压不平衡度约束;再次,提出以总运行成本最小化为目标函数的交直流主动配电网三相有功无功联合优化模型;最后,采用改进IEEE 33节点、69节点、141节点和1056节点交直流配电网算例分析,验证了该文所提方法的有效性。
关键词:交直流主动配电网 三相不平衡 有功无功联合优化 半正定松弛 分布式电源
随着全球范围内可再生能源的普及与能源的绿色低碳化转型,电能的生产利用方式正在发生深刻的改变[1]。直流分布式电源(Distributed Generator, DG)的广泛安装以及电动汽车、直流电机等直流负载使用需求的不断增加,使得交流主动配电网的线路拓扑与节点类型的配置变得更加复杂[2-4]。为更好地容纳各种直流设备,提高直流电源的利用率,将传统交流配电网中的部分线路用直流线路替代是一种可行的解决方案[5-6]。同时,随着电压源型换流器(Voltage Source Converter, VSC)的发展日益成熟,直流配电技术已被广泛应用到交流配电网中[7-10]。因此,交直流主动配电网将成为未来配电网的发展形态。
在主动配电网中,DG的发电功率有着较强的随机性和间断性,并会使网络中产生双向潮流,导致电压频繁波动甚至产生过电压现象。针对此问题,文献[11-14]考虑主动配电网中多种可调无功设备的无功特性,对无功优化进行了大量研究,实现对配电网电压的优化控制。同时,针对DG的有功出力特性,文献[15-16]研究了DG的优化配置及有功功率优化调度问题,实现配电网对分布式能源消纳能力的最大化。然而在这些研究中,有功功率和无功功率的优化都是分开的,这样的优化结果不仅难以提供全局最优的配电网调度方案,也增加了DG等设备调控的复杂度。因此,文献[17-20]提出了配电网有功无功联合优化的方法,综合无功优化网损成本最小和有功优化购电成本最小的目标函数,通过对有功无功的协调控制,降低配电网的总运行成本。但是这些研究只考虑了单相形式下的配电网潮流模型。实际上,随着各种分布式设备种类的多元化,负荷的单相接入和DG三相功率不一致都会使配电网中的三相不平衡现象越发严重[21-22]。三相不平衡不仅会降低变压器等设备的使用寿命,也会导致线路损耗进一步增加,同时还会降低电能质量,影响配电网安全稳定运行[23-24]。因此,在配电网优化模型中,亟须研究三相形式下完整精确的交直流潮流模型。
针对主动配电网的三相潮流模型,国内外学者已经开展了一些研究,在技术路线上主要分为“近似处理法”[25-27]与“凸松弛方法”[28-31]两种。文献[25]对配电网的三相进行了解耦处理,未考虑相间互阻抗,这种忽略相间电磁耦合的近似处理方法显然是不精确的。文献[26]建立了完整的三相潮流模型,通过假设电压三相平衡与假设部分变量为恒定值的方法,对线路三相潮流约束进行了线性化处理,但这些假设在三相不平衡时是不成立的。文献[27]将三相潮流约束中与相间相角相关的非线性部分表达式进行了二阶展开,并采用展开后的线性表达式来代替。显然,这些近似处理方法的优化结果会与全局最优解存在误差。凸松弛方法则将原问题松弛为一个凸优化问题,文献[28]建立了基于节点注入平衡的三相潮流模型,文献[29]在其基础上运用升维映射的方法,将原有潮流模型映射到高维空间,建立了基于支路潮流平衡的三相潮流模型,通过秩1松弛得到半正定优化(Semidefinite Programming, SDP)模型进行求解,并被证明有更好的求解稳定性。文献[30-31]沿用文献[29]中的潮流模型,采用二阶锥(Second-Order Cone Programming, SOCP)松弛方法对SDP模型中的秩1约束进行进一步松弛,但是SOC松弛在实际系统中的松弛精确性无法得到保证[32]。
值得注意的是,上述有关三相潮流的相关研究都是针对交流系统的,且都没有考虑如何通过有功无功优化调度限制配电系统的三相不平衡度。综上所述,目前亟须研究一种既能够考虑交直流主动配电网完整三相潮流模型,又能限制三相不平衡度的有功无功联合优化方法。
本文以交直流主动配电网为研究对象,从三相有功无功联合优化角度出发,首先建立了交流子系统考虑三相相间耦合的SDP松弛潮流模型和直流子系统的SDP松弛潮流模型;然后推导了序分量形式下的电压三相不平衡度约束,给出了完整的三相有功无功联合优化数学模型;最后在算例分析中,对比分析了本文所提方法在计算精度与计算效率上的表现,论证了本文所提方法在大规模配电测试系统中的计算性能。
本文中,假设三相交流网中包含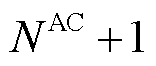 个交流节点,
个交流节点,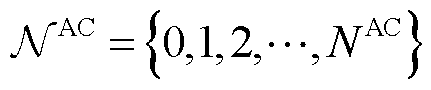 表示交流节点集合,其中,变电站节点编号为0;
表示交流节点集合,其中,变电站节点编号为0;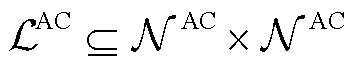 表示交流线路集合。引入
表示交流线路集合。引入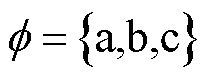 来表征各相的集合,由此,对于节点
来表征各相的集合,由此,对于节点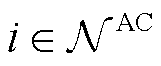 ,其三相电压列向量为
,其三相电压列向量为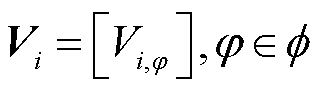 ,例如
,例如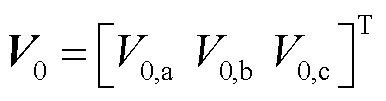 ,其负荷三相功率向量为
,其负荷三相功率向量为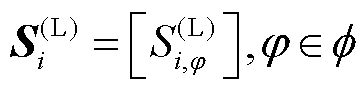 。对于线路
。对于线路 ,线路上流过的三相电流向量为
,线路上流过的三相电流向量为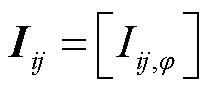 ,
,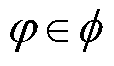 ;线路上的三相阻抗矩阵为
;线路上的三相阻抗矩阵为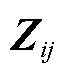 ,由线路ij的三相自阻抗与互阻抗组成。
,由线路ij的三相自阻抗与互阻抗组成。
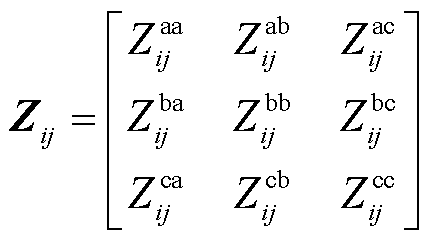 (1)
(1)
本文在交流网中设置DG接入节点。其中,交流DG节点集合为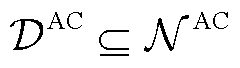 ,其三相功率向量为
,其三相功率向量为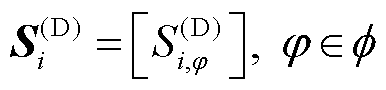 ;其实际运行约束可以表述为
;其实际运行约束可以表述为
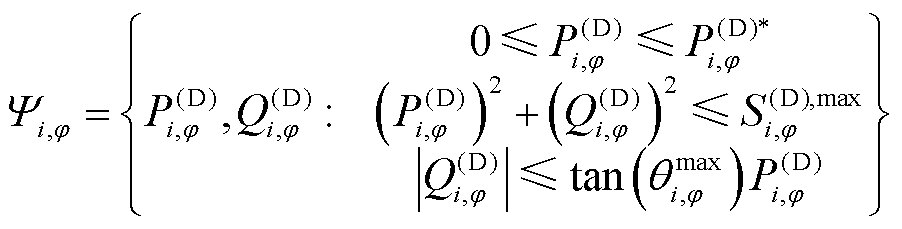 (2)
(2)
式中,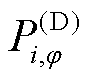 和
和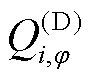 分别为i节点的DG在
分别为i节点的DG在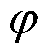 相的有功功率和无功功率;
相的有功功率和无功功率;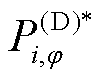 为i节点的DG在
为i节点的DG在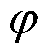 相的有功功率预测值;
相的有功功率预测值;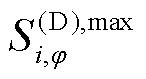 和
和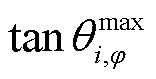 分别为i节点的DG在
分别为i节点的DG在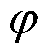 相的视在功率最大值和功率因数最大值。
相的视在功率最大值和功率因数最大值。
式(2)中分别对DG并网的有功功率、视在功率以及功率因数进行了限制。在本文中,对DG采用对其有功功率及功率因数进行约束的运行模式。
交流配电网中潮流模型多以支路功率平衡的形式出现,模型由节点电压、支路电流和支路功率等变量组成。
因此在交流三相潮流模型中,对于线路 ,其线路潮流约束为
,其线路潮流约束为
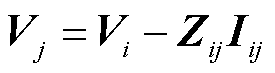 (3)
(3)
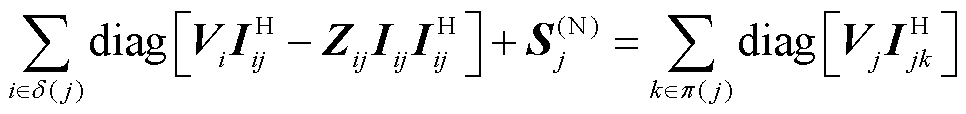 (4)
(4)
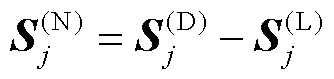 (5)
(5)
式中,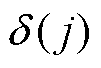 为以节点j为子节点的母节点集合;
为以节点j为子节点的母节点集合;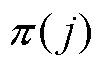 为以节点j为母节点的子节点集合;
为以节点j为母节点的子节点集合;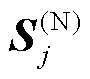 为节点j的注入功率向量;diag(·)表示取矩阵的全部对角元素组成的列向量;(·)H表示共轭转置。
为节点j的注入功率向量;diag(·)表示取矩阵的全部对角元素组成的列向量;(·)H表示共轭转置。
同时在潮流模型中考虑变电站节点电压约束、线路热稳定极限约束、其他节点电压约束。
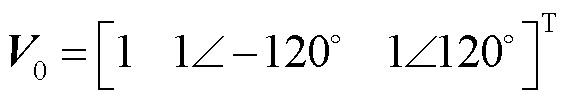 (6)
(6)
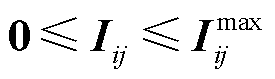 (7)
(7)
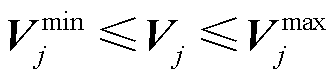 (8)
(8)
式中,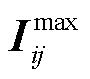 为线路ij各相电流的热稳定限值;
为线路ij各相电流的热稳定限值;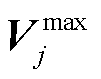 和
和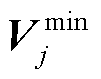 分别为节点j各相电压的最大允许值和最小允许值。
分别为节点j各相电压的最大允许值和最小允许值。
可以看到在潮流模型式(3)~式(8)中,约束式(4)是非凸的,因此需要对其进行凸松弛。为此,对于约束式(4)中非凸的电压电流乘积部分,本文采用lift-and-project的松弛方式。它通过“升维映射”将原有的待求变量V和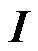 转换为新的待求变量
转换为新的待求变量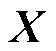 ,从而将原有的非凸形式转换为更易松弛的非凸形式,最后再通过“逆映射”将求得的最优解恢复为原问题的最优解[29]。
,从而将原有的非凸形式转换为更易松弛的非凸形式,最后再通过“逆映射”将求得的最优解恢复为原问题的最优解[29]。
下面介绍本文采用的升维映射形式,按照式(9)定义Hermitian矩阵变量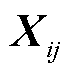 ,将原有的待求变量
,将原有的待求变量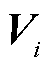 和
和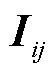 转换为新定义的二次型变量
转换为新定义的二次型变量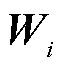 、
、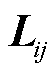 和
和 。
。
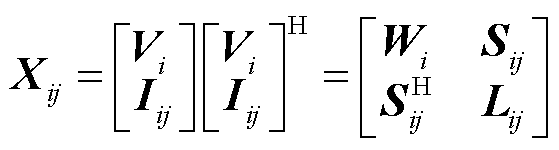 (9)
(9)
式中,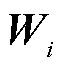 、
、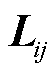 和
和 均为二次型变量,且
均为二次型变量,且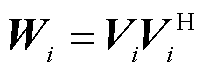 ,
,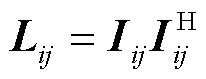 ,
,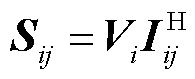 。
。
在上述定义下,采用新定义的二次型变量替换原有的电压电流向量,则原始潮流方程式(3)~式(8)可以重构为如下的等价形式。
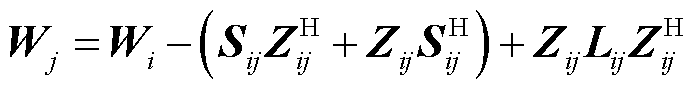 (10)
(10)
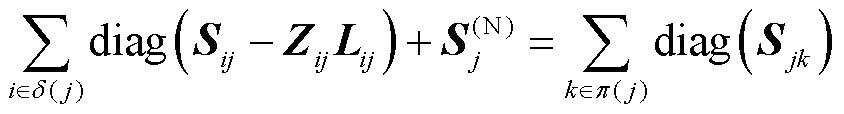 (11)
(11)
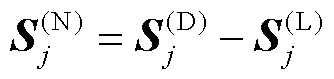 (12)
(12)
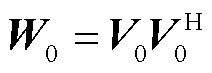 (13)
(13)
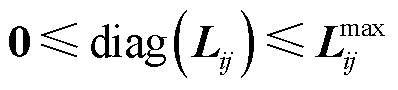 (14)
(14)
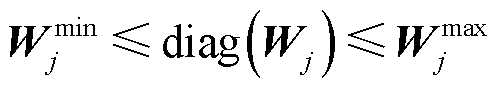 (15)
(15)
式中,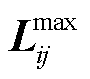 为线路ij热稳定限值二次方向量;
为线路ij热稳定限值二次方向量;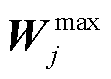 和
和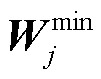 分别为节点j电压的最大允许值二次方向量和最小允许值二次方向量。
分别为节点j电压的最大允许值二次方向量和最小允许值二次方向量。
同时,二次型变量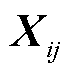 的定义方程式(9)可等价为
的定义方程式(9)可等价为
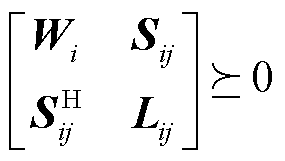 (16)
(16)
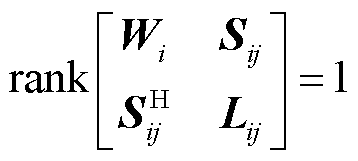 (17)
(17)
式中,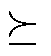 为矩阵半正定符号;
为矩阵半正定符号;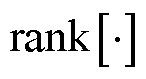 表示求矩阵的秩。其中,式(16)为凸约束,式(17)为秩1约束是非凸约束。至此,原有的非凸优化模型式(3)~式(8)转换为含秩1约束的SDP优化模型式(10)~式(17)。基于凸松弛思想,对非凸的秩1约束式(17)进行松弛,优化模型的剩余部分式(10)~式(16)均为凸约束,可以运用成熟的商业求解器对上述SDP模型进行直接求解,求得原模型的SDP松弛解。最后再将SDP松弛解代入秩1约束式(17),检验其是否满足秩1约束。若SDP松弛解满足秩1约束,说明SDP松弛解是精确的,则该解为松弛前原模型的最优解;反之则说明该解不可行。
表示求矩阵的秩。其中,式(16)为凸约束,式(17)为秩1约束是非凸约束。至此,原有的非凸优化模型式(3)~式(8)转换为含秩1约束的SDP优化模型式(10)~式(17)。基于凸松弛思想,对非凸的秩1约束式(17)进行松弛,优化模型的剩余部分式(10)~式(16)均为凸约束,可以运用成熟的商业求解器对上述SDP模型进行直接求解,求得原模型的SDP松弛解。最后再将SDP松弛解代入秩1约束式(17),检验其是否满足秩1约束。若SDP松弛解满足秩1约束,说明SDP松弛解是精确的,则该解为松弛前原模型的最优解;反之则说明该解不可行。
对比本文所提方法,传统的基于SOCP的三相潮流模型[33]并未考虑三相相间耦合的影响,而仅将单相潮流模型在三相线路上独立使用三次。在考虑三相潮流尤其是三相负载与线路不平衡时,这样的相间解耦处理方式将产生较大误差,从而对优化结果产生较大影响。本文所提方法考虑了三相相间耦合的影响,建立了完整的三相潮流模型,能够更好地应对各种三相不平衡状态。
在基于支路功率平衡(Branch Flow)的三相潮流模型中,采用升维映射的松弛方法将原有非凸潮流模型转换为SDP松弛潮流模型,其理论上的精确性以及在IEEE测试系统数值实验上的精确性已经被证实[29,31]。而本文所采用的交流序分量三相SDP松弛潮流模型,在数值稳定性和计算精确性方面的优越性也已被证实[34-35]。
根据对称分量法,节点i的三序电压向量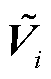 为
为
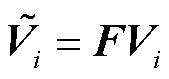 (18)
(18)
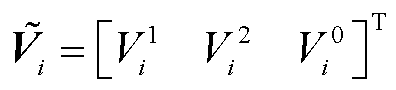 (19)
(19)
其中
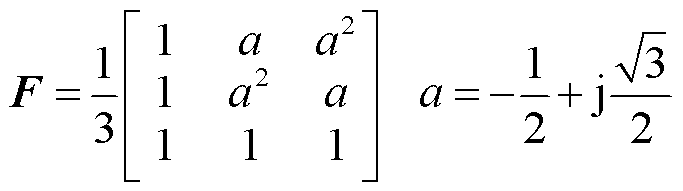 (20)
(20)
式中,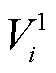 、
、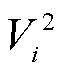 和
和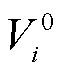 分别为节点i的正序、负序和零序电压分量。
分别为节点i的正序、负序和零序电压分量。
由此,原潮流模型中的二次型变量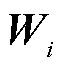 可以等价变换为序分量形式的二次型变量
可以等价变换为序分量形式的二次型变量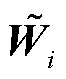 。
。
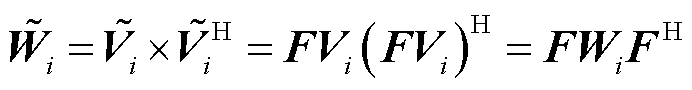 (21)
(21)
以此类推,相分量形式下SDP潮流模型的其他二次型变量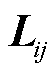 、
、 以及三相阻抗矩阵
以及三相阻抗矩阵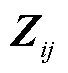 均可等价变换到序分量形式,有
均可等价变换到序分量形式,有
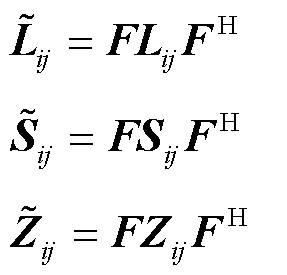 (22)
(22)
因此,相分量形式下的潮流模型式(10)~式(17)可以重构为等价的序分量形式,即
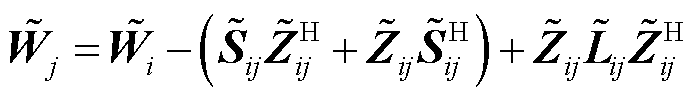 (23)
(23)
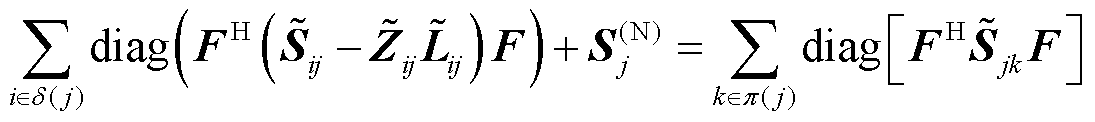 (24)
(24)
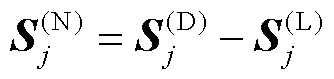 (25)
(25)
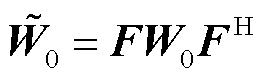 (26)
(26)
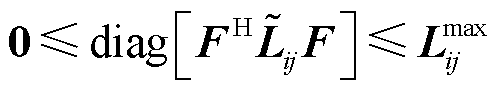 (27)
(27)
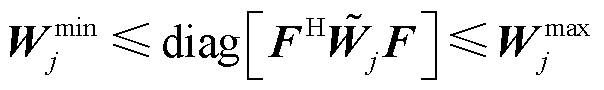 (28)
(28)
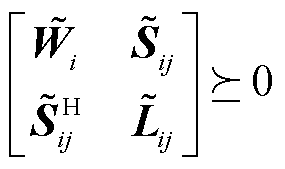 (29)
(29)
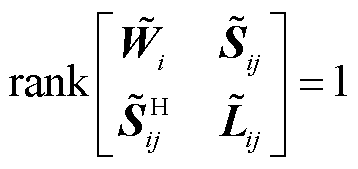 (30)
(30)
同样的,将秩1约束式(30)松弛后,序分量形式下的三相交流SDP潮流模型可以直接进行求解,再验证松弛解是否满足秩1约束。
在直流部分中,假设直流网包含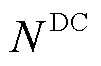 个直流节点,
个直流节点,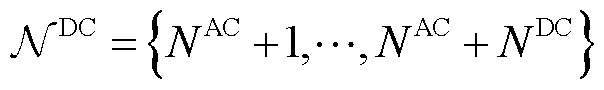 表示直流节点集合;
表示直流节点集合;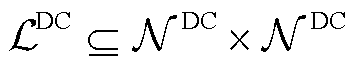 表示直流线路集合。因此,对于节点
表示直流线路集合。因此,对于节点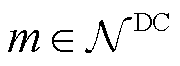 ,其节点电压为
,其节点电压为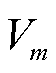 ;对于线路
;对于线路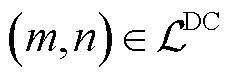 ,线路上流过的电流为
,线路上流过的电流为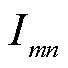 ,线路上的电阻为
,线路上的电阻为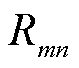 。
。
同时,在直流网中也设置直流DG接入节点,直流DG节点集合为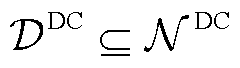 。对于连接有DG的节点
。对于连接有DG的节点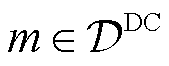 ,其有功功率为
,其有功功率为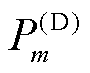 ,有功功率预测值为
,有功功率预测值为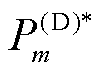 ;节点m的有功负荷为
;节点m的有功负荷为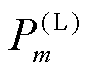 。
。
在直流部分,同样采用支路功率平衡形式的潮流模型。类似地,对于线路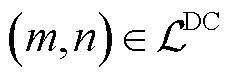 ,其潮流模型为
,其潮流模型为
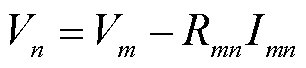 (31)
(31)
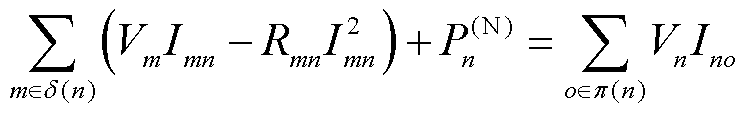 (32)
(32)
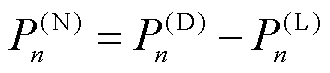 (33)
(33)
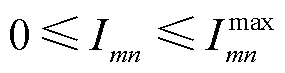 (34)
(34)
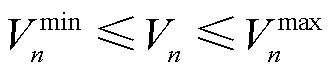 (35)
(35)
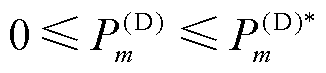 (36)
(36)
式中,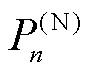 为节点n的注入功率;
为节点n的注入功率;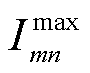 为线路mn热稳定限值;
为线路mn热稳定限值;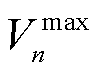 和
和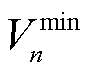 分别为节点n的最大、最小电压允许值。
分别为节点n的最大、最小电压允许值。
与交流潮流模型类似,由于存在电压与电流的乘积项,直流潮流模型式(31)~式(36)同样是非凸的,因此仍采用三相潮流模型中相同的升维映射和秩1松弛方法对直流潮流模型进行凸松弛。
定义Hermitian矩阵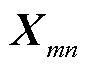 为
为
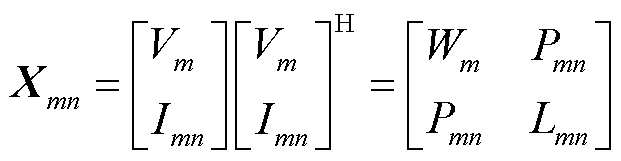 (37)
(37)
式中,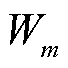 、
、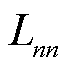 和
和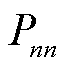 均为二次项变量,且
均为二次项变量,且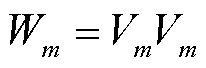 ,
,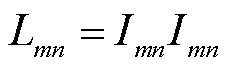 ,
,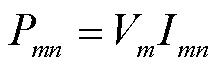 。
。
按照以上定义,直流部分约束可写为
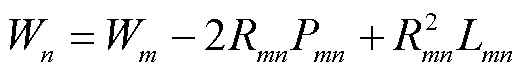 (38)
(38)
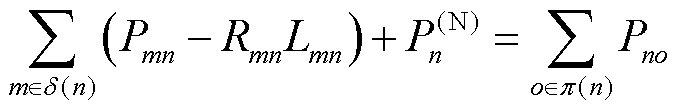 (39)
(39)
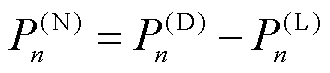 (40)
(40)
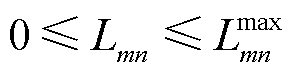 (41)
(41)
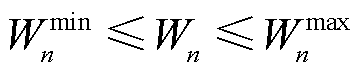 (42)
(42)
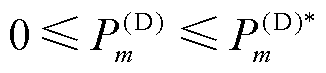 (43)
(43)
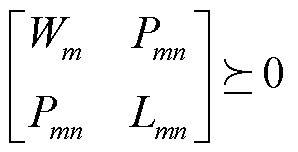 (44)
(44)
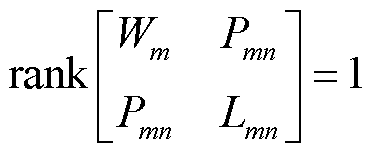 (45)
(45)
式中,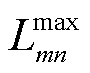 为线路mn热稳定限值的二次方;
为线路mn热稳定限值的二次方;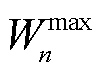 和
和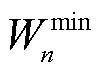 分别为节点m最大允许电压的二次方和最小允许电压的二次方。
分别为节点m最大允许电压的二次方和最小允许电压的二次方。
同样地,将秩1约束式(45)松弛后,SDP直流潮流模型也可以直接进行求解,再验证松弛解是否满足秩1约束。
图1为三相换流器模型。为简化处理,本文将VSC划分为等效阻抗部分与理想换流部分[36]。如图1所示,等效后将在交流侧引入新的节点x,内部阻抗等效为支路ix的三相阻抗。
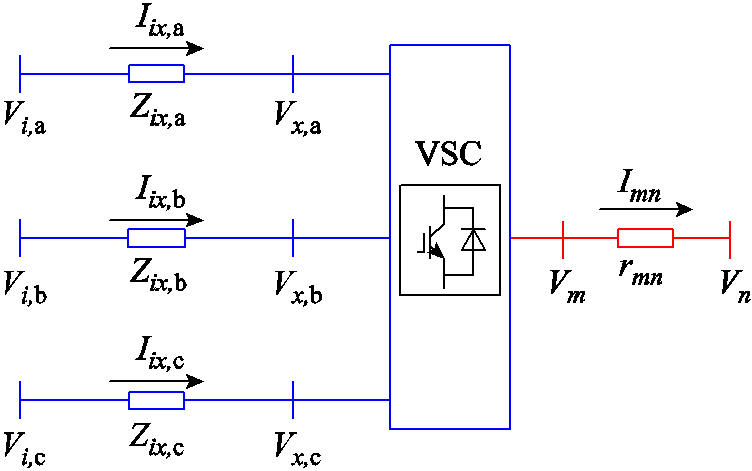
图1 交直流配电网三相VSC换流器模型
Fig.1 Three-phase VSC circuit diagram in AC-DC hybrid distribution network
按照图1所示,VSC损耗可以由内部等效阻抗所产生的网损来表示,因此VSC损耗成本将包含在线路网损成本中。于是VSC换流器的理想换流部分交直流两侧满足功率平衡约束,也就是交流侧注入VSC的有功功率与经VSC流入直流侧的有功功率相等,即
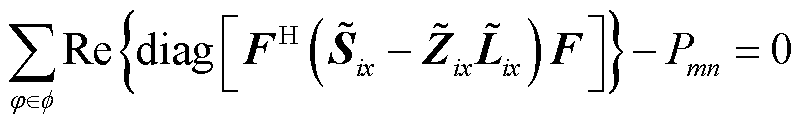 (46)
(46)
式中,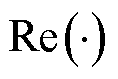 表示取复数列向量的实部;
表示取复数列向量的实部;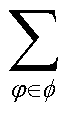 表示将三相的值进行求和。
表示将三相的值进行求和。
交直流主动配电网三相有功无功联合优化的目的是通过调节网络中各设备的有功出力、无功出力,在降低配电网调度成本的同时减少各节点的三相不平衡度。因此,本文以最小化配电网的总运行成本为目标函数,即
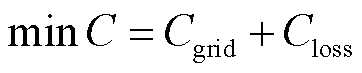 (47)
(47)
式中,C为总运行成本;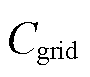 为向上级电网购电成本;
为向上级电网购电成本;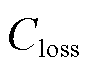 为线路网损成本。
为线路网损成本。
1)上级电网购电成本
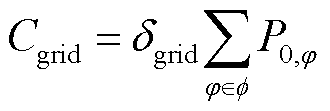 (48)
(48)
式中, 为向上级电网单位购电成本;
为向上级电网单位购电成本;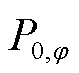 为变电站节点φ相注入的单相有功功率。
为变电站节点φ相注入的单相有功功率。
2)线路网损成本
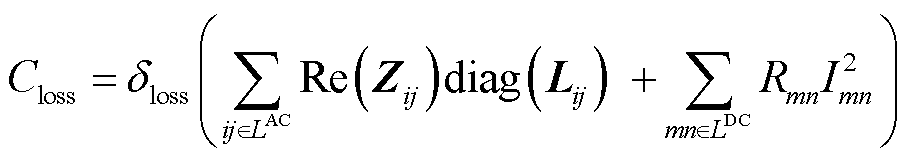 (49)
(49)
式中,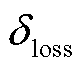 为单位网损成本。
为单位网损成本。
电压不平衡度是反映电能质量高低的一个重要指标。文献[37]给出了不同行业协会制定的三相不平衡度指标定义与计算方法。由于本文在交流部分采用序分量形式的三相潮流模型,因此更符合IEC关于三相不平衡度指标的定义。本文将三相电压的不平衡度定义为电压负序分量二次方与正序分量二次方的百分比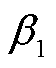 ,以及电压零序分量二次方与正序分量二次方的百分比
,以及电压零序分量二次方与正序分量二次方的百分比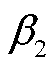 ,有
,有
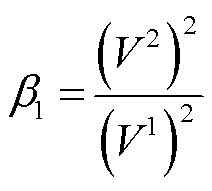 (50)
(50)
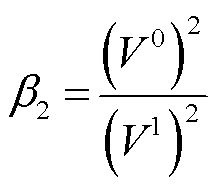 (51)
(51)
为了降低实际运行中的三相不平衡度,要求三相电压的不平衡度低于某一设定值。
对于节点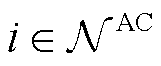 ,根据式(21)可知
,根据式(21)可知
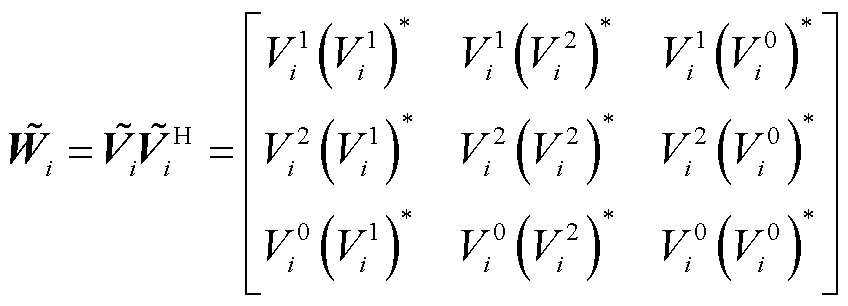 (52)
(52)
式中,(·)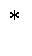 表示共轭。
表示共轭。
由式(52)可以看到,矩阵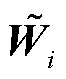 中对角线元素分别为电压正序分量、负序分量和零序分量的二次方。因此,定义
中对角线元素分别为电压正序分量、负序分量和零序分量的二次方。因此,定义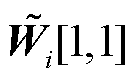 为矩阵
为矩阵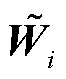 中第1行第1列的元素,则节点i三相电压不平衡约束可写为
中第1行第1列的元素,则节点i三相电压不平衡约束可写为
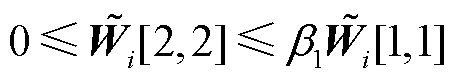 (53)
(53)
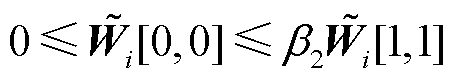 (54)
(54)
除了上述电压不平衡约束式(53)、式(54)以外,三相有功无功联合优化模型的约束条件还包括前面介绍的DG运行约束、SDP交流潮流约束、SDP直流潮流约束和换流器约束。综上所述,交直流主动配电网三相有功无功联合优化问题为
 (55)
(55)
上述优化模型为SDP优化模型,可以使用商业求解器对其进行直接求解。
为了验证所提三相有功无功联合优化算法的精确性与适用性,本文在改进IEEE 33节点交直流配电系统算例中,在设置不同的三相不平衡度情况下,首先对所提方法的松弛精确性进行测试验证;其次,将本文所提方法与基于相分量的三相SDP优化调度方法进行对比,验证所提方法的计算精确性;再次,对比分析了不同方法和不同情形下的调度成本与节点电压,验证了考虑相间互阻抗的必要性与考虑电压三相不平衡度的必要性;最后,将本文所提算法应用在改进IEEE 69、141和1056节点交直流配电系统中,测试了所提方法的求解性能和可扩展性。
本节使用改进IEEE 33节点交直流配电系统进行测试,其系统拓扑如图2所示。该测试系统功率基准值为100 MV·A,电压基准值为12.66 kV;节点电压幅值允许范围为[0.9, 1.1] (pu)(本文中电压均采用标幺值)。
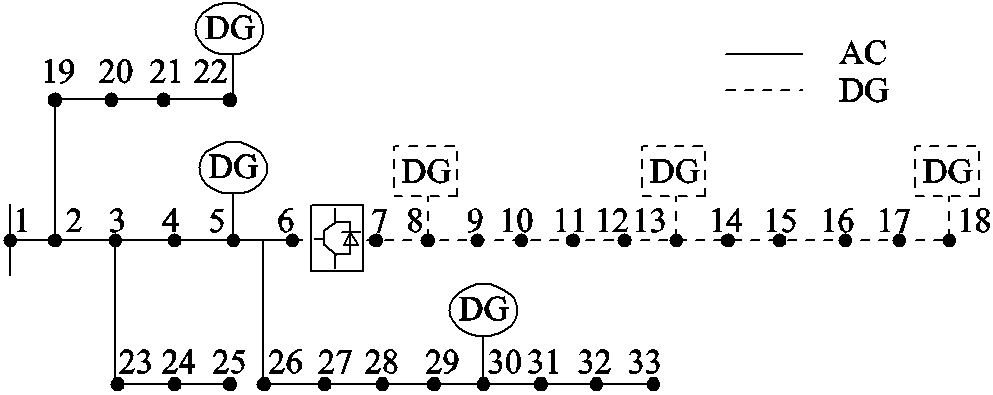
图2 改进IEEE 33节点交直流配电系统拓扑
Fig.2 Diagram of the modified IEEE 33 bus AC-DC distribution system
在配电系统中安装DG,其中,交流DG安装节点集合为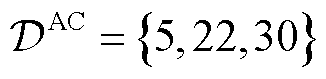 ,每台DG的单相输出有功范围为[0, 20] kW,各相最大功率因数均为0.95,且三相输出的有功无功均独立可调;直流DG安装节点集合为
,每台DG的单相输出有功范围为[0, 20] kW,各相最大功率因数均为0.95,且三相输出的有功无功均独立可调;直流DG安装节点集合为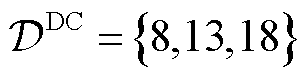 ,每台DG的输出有功范围同样为[0, 20] kW。
,每台DG的输出有功范围同样为[0, 20] kW。
本部分算例通过分别改变负载三相不平衡度与线路三相参数不平衡度来刻画配电网中所出现的不平衡严重程度。为描述负载三相不平衡,在a相负载保持不变的同时,将b相负载分别增加10%和20%,将c相负载分别减少10%和20%;为描述三相线路参数不平衡,线路a相自阻抗保持不变,将线路b相自阻抗分别增加10%和20%,c相线路自阻抗分别减少10%和20%。然后在不同的三相不平衡程度下,对所提算法的精确性与适应性分别进行验证。
4.1.1 松弛精确性
根据1.3节与2.2节,本文所提方法中SDP松弛的精确性,需要通过检验SDP松弛解是否满足秩1约束式(30)和式(45)来进行验证。然而,由于求解器的数值精度是有限的,所以对于满足SDP松弛精确性的数值解,其组成的二次型变量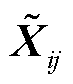 也只是近似满足秩1约束。利用特征根信息来检验SDP数值解是否满足秩1约束,是基于SDP的三相潮流模型研究中衡量SDP松弛精确性的常用方法之一[29,38-39]。为衡量二次型变量
也只是近似满足秩1约束。利用特征根信息来检验SDP数值解是否满足秩1约束,是基于SDP的三相潮流模型研究中衡量SDP松弛精确性的常用方法之一[29,38-39]。为衡量二次型变量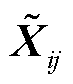 是否满足秩1约束,通过计算
是否满足秩1约束,通过计算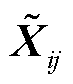 的两个最大特征根
的两个最大特征根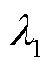 和
和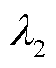 来衡量
来衡量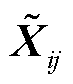 对秩1的接近程度,其比值
对秩1的接近程度,其比值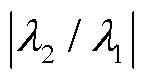 越小,说明
越小,说明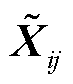 越接近秩1。因此,定义最大松弛偏差为
越接近秩1。因此,定义最大松弛偏差为
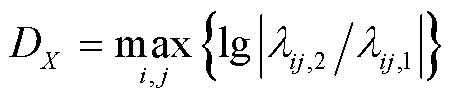 (56)
(56)
式中,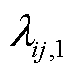 和
和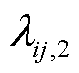 分别为二次型变量
分别为二次型变量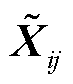 的两个最大特征根。
的两个最大特征根。
不同三相不平衡度程度下所提方法的最大松弛偏差DX结果见表1。从表1中可以看到,在三相平衡时,SDP模型的最大松弛偏差达到最小值-18.914 3。然而随着负载不平衡度的增加以及线路参数不平衡度的增加,SDP模型的最大松弛偏差在不断增大,且在线路参数20%不平衡度的情况下达到最大值-7.154 2。同时,在不同的三相不平衡度程度下,SDP模型的最大松弛偏差均在-7以下,表明SDP松弛解两个最大特征根的比值不超过10-7,即可说明SDP松弛解是满足秩1约束的。因此,在本算例中,本文所提方法得到SDP松弛解是精确的。
表1 不同三相不平衡度下的松弛误差计算结果
Tab.1 Calculation results of relaxation mismatch under different three-phase unbalanced circumstances

三相不平衡度DXDYDZ 三相平衡-18.914 3-13.162 4-13.638 3 负载10%不平衡-16.858 2-11.527 2-12.378 8 负载20%不平衡-14.803 2-10.498 9-10.233 6 线路参数10%不平衡-7.931 2-7.559 1-6.889 4 线路参数20%不平衡-7.154 2-6.363 5-5.484 1
松弛误差是由对非凸约束进行凸松弛所产生的,因此将松弛解代入原非凸约束并衡量原非凸约束的满足程度可以从物理层面衡量松弛误差。在本文潮流模型中,松弛误差体现在线路潮流约束与线路压降约束中。为了更直观地评估松弛误差,定义最大对数松弛误差为
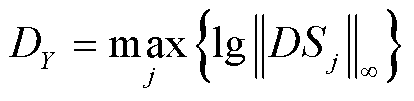 (57)
(57)
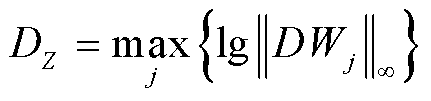 (58)
(58)
式中,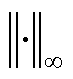 表示取无穷范数;DSj和DWj分别为节点j的潮流不平衡量和压降不平衡量,有
表示取无穷范数;DSj和DWj分别为节点j的潮流不平衡量和压降不平衡量,有
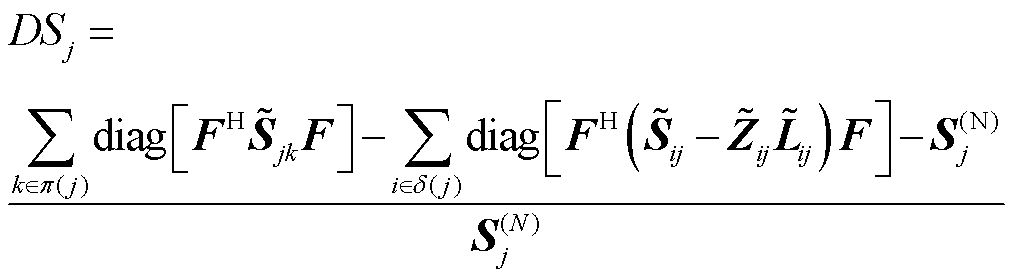 (59)
(59)
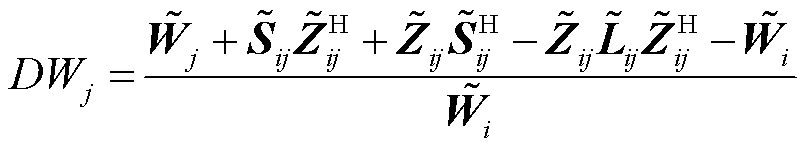 (60)
(60)
其中,式(59)按注入功率向量进行了归一化,式(60)按二次电压矩阵进行了归一化。需要注意的是,式(59)和式(60)的除法均是按元素进行计算,即将向量或矩阵相同位置上元素相除。
当松弛解为全局最优解时,DSj和DWj应等于0,而DY与DZ应等于负无穷。因此当DY与DZ数值越负时,松弛解越精确。由表1第二列和第三列数据可以看出,在三相平衡时,SDP模型的最大对数松弛误差DY与DZ仅为-13.162 4和-13.638 3。尽管随着负载不平衡度的增加以及线路参数不平衡度的增加,SDP模型的松弛误差在不断增大,并在线路参数20%不平衡度情况下达到最大值,分别为-6.363 5和-5.484 1。但是在不同的三相不平衡度下,SDP模型的最大松弛误差仍可保持在10-5以下,这进一步说明在本算例中,本文所提方法得到的SDP松弛解是精确的。
同时在测试系统中进行了数值实验,得到了DX与DY和DZ的大致对应关系如图3所示。灰色虚线代表最大误差允许值,为10-4,其对应的DX数值约为-5.5。因此可以认为,当DX<-5.5时,松弛结果都是精确的。表1中结果均满足DX<-5.5的条件,由此也可以说明在本算例中,本文所提方法得到SDP松弛解是精确的。
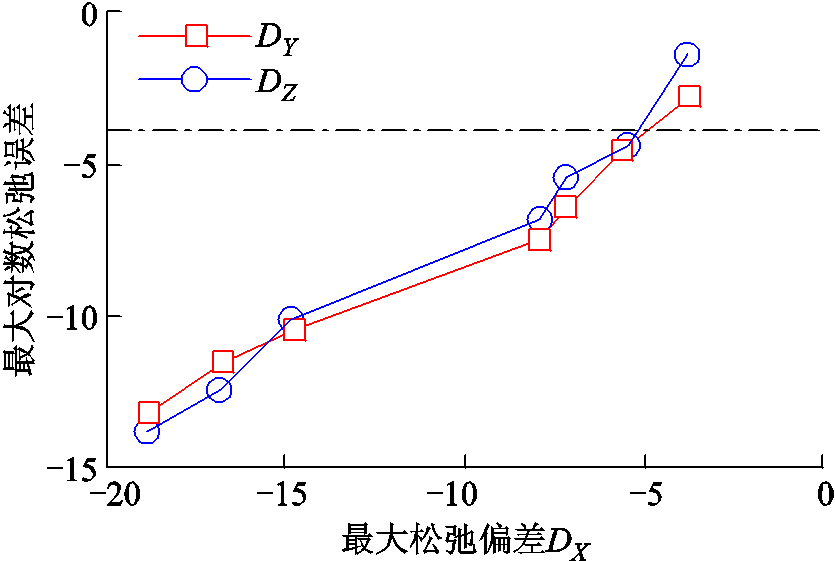
图3 最大对数松弛误差DY和DZ与最大松弛偏差DX的对应关系
Fig.3 Correspondence between the maximum logarithmic relaxation mismatch DY and DZ and the maximum relaxation deviation
4.1.2 计算精确性
为了验证本文所提方法的计算精确性,本节将对比基于序分量的三相SDP优化结果(即本文所提方法)和基于相分量的三相SDP优化结果。首先将DG有功、无功功率设为固定值,在这种情况下,求解优化调度问题等同于求解配电网络的潮流计算结果。同时,本节在负载10%不平衡度情形下,分别获取了两种方法下的优化调度结果,并与潮流计算结果进行比较。
定义节点i单相电压偏差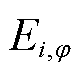 为
为
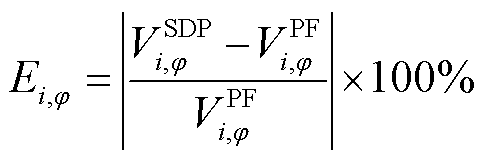 (61)
(61)
式中,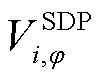 和
和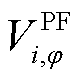 分别为三相SDP优化调度和潮流计算得到的节点i的
分别为三相SDP优化调度和潮流计算得到的节点i的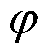 相电压。
相电压。
两种方法下各交流节点单相电压偏差及直流节点电压偏差结果如图4所示。由图4中可以看到,两种方法下的所有交流节点(节点1~6和节点19~33)各相电压偏差均小于2.0%,所有直流节点(节点7~18)各相电压偏差均小于2.5%。在各节点处,序分量三相SDP模型的电压偏差均小于相分量三相SDP模型。特别是在直流节点(节点7~18)处,序分量三相SDP模型的电压偏差明显更低。因此可以看出,相较于相分量三相SDP模型,本文所提的序分量三相SDP模型更适用于交直流配电系统,该方法拥有更好的计算精确性。
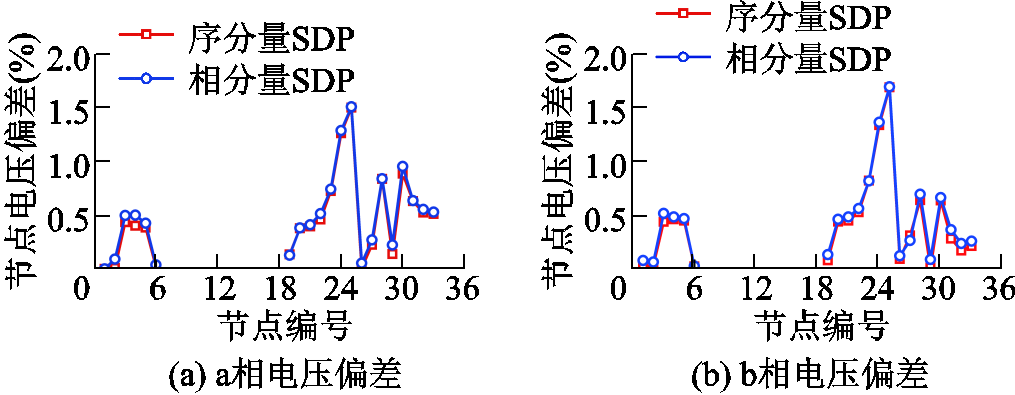
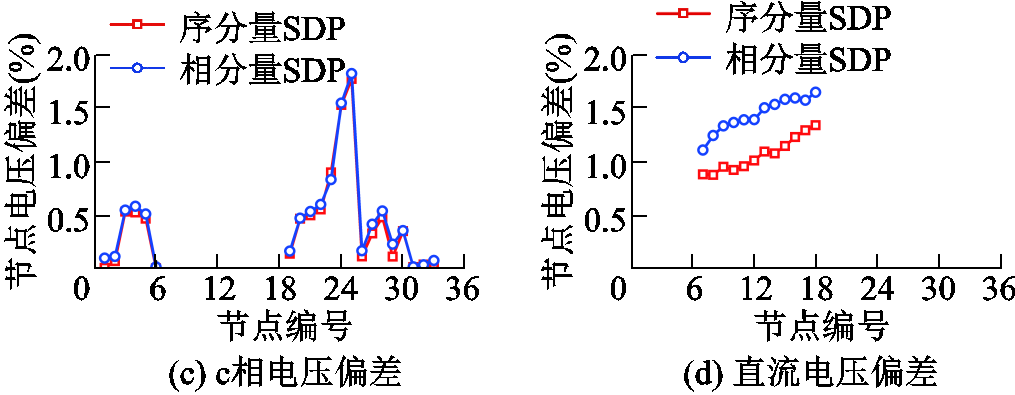
图4 负载10%不平衡度下两种方法的节点单相电压偏差百分比结果
Fig.4 Results of voltage deviation percentage of the two methods in 10% three-phase unbalanced situation
4.1.3 优化结果比较
在配电网优化调度问题中,当考虑三相潮流时,传统方法通常忽略三相的相间互阻抗,从而对三相线路进行解耦处理。而随着配电网中设备数量与种类的增多,负载与线路的不平衡日趋严重。因此在考虑三相潮流时,仅采用三相解耦后的潮流模型会对配电网有功无功优化结果产生较大的影响。因此,本节首先对比了本文所提方法(方法1,即考虑三相耦合)与三相解耦算法(方法2)在不同三相不平衡度下的优化调度结果,验证了所提方法考虑三相耦合的必要性与合理性。
设定互阻抗与自阻抗的比值为0.1,分别选取三相平衡时与负载10%不平衡时,比较方法1和方法2得出的各节点电压幅值,如图5所示,图中展示的是三相电压的平均值。从图5a中可以看出,相较于方法2,方法1求得的交流侧各节点电压幅值整体更高。由于方法1考虑了相间耦合,而相间互阻抗的存在会抬高电压幅值。因此相较于方法2,方法1所获得的交流侧电压计算结果更接近真实电压。而方法2没有考虑相间耦合,其求得的交流侧电压偏低,无法准确描述配电网运行时真实的三相电压。因此方法1的三相电压计算结果更准确,从而能够满足配电网实际运行状态中的电压约束。而在直流侧,在满足换流器功率平衡的条件下,方法1得到的各直流节点电压幅值整体更低。总的来说,与方法2相比,方法1所得到的各节点间电压幅值差距更小。由于线路网损主要取决于线路两端节点的电压幅值差,因此在方法1中,各节点间线路上的网损更低,故方法1所得到的电压结果与目标函数式(47)中最小化线路网损式(49)的出发点是一致的。同样的结论在图5b中也可以得出,因此可以说明方法1在考虑三相潮流时的优化结果更为合理。
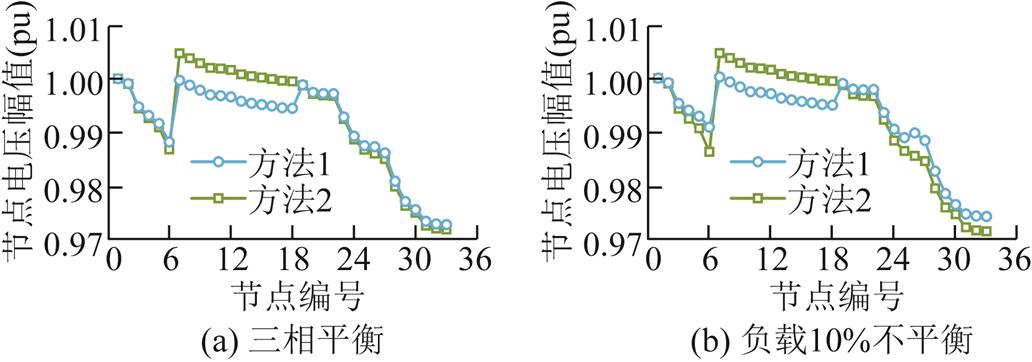
图5 三相平衡和负载10%不平衡度下两种方法的三相节点电压平均值
Fig.5 Three-phase average voltage of the two methods in three-phase balanced situation and 10% three-phase unbalanced situation
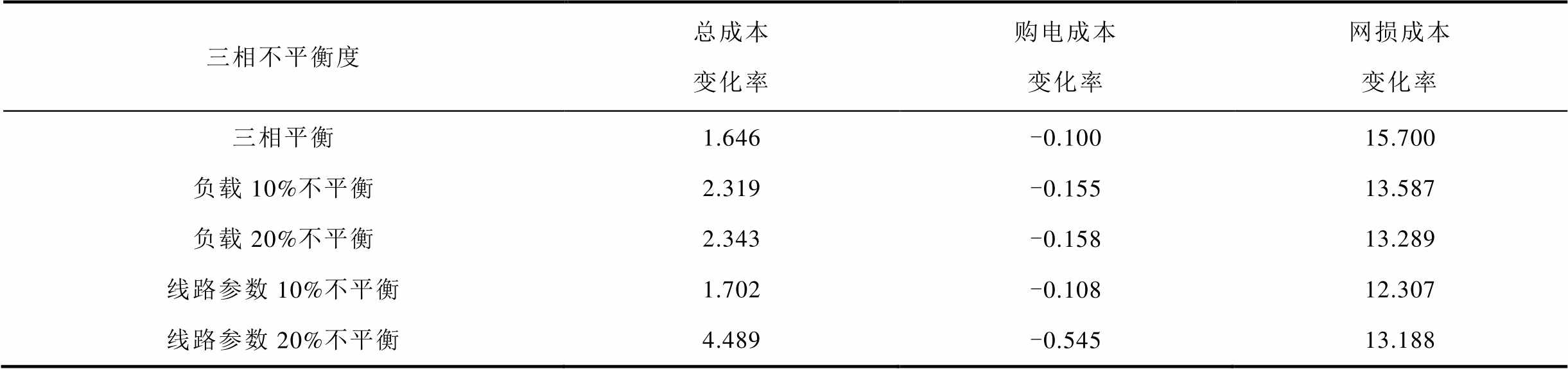
为进一步展示两种方法在不同三相不平衡度下的优化结果的差异,表2给出了在不同三相不平衡度下方法2相对方法1的目标函数百分比差值。在不同三相不平衡度下,两种方法的各交流DG与直流DG有功功率均达到最大值。在成本方面,方法1的网损成本相比方法2显著降低,在三相平衡时降低程度最大,达到了15.7%。而方法2的购电成本相比方法1略微降低,并且在线路参数20%不平衡时,其节约的购电成本为0.545%。然而,方法2在购电成本上的降低程度远小于方法1在网损成本上的降低程度,最终体现在总成本上,在任意三相不平衡度下,方法1总能获得更低的总成本。并且在线路参数20%不平衡时,方法1的总成本相比方法2降低程度最大,达到了4.489%。因此,方法1能够获得更好的有功无功联合优化结果,说明考虑相间互阻抗(即三相耦合)是非常必要的。
表2 不同三相不平衡度下方法2相对方法1的目标函数百分比差值
Tab.2 Percentage difference of objective function between Method 2 & Method 1 in case 1 under different three-phase unbalanced circumstances (%)
三相不平衡度总成本变化率购电成本变化率网损成本变化率 三相平衡1.646-0.10015.700 负载10%不平衡2.319-0.15513.587 负载20%不平衡2.343-0.15813.289 线路参数10%不平衡1.702-0.10812.307 线路参数20%不平衡4.489-0.54513.188
与此同时,配电网中不平衡负载的接入或者网络线路参数不平衡会导致交流侧产生负序分量与零序分量,导致交流侧三相电压不平衡度增加,降低了电能质量。因此,在优化调度中对三相电压不平衡度加以限制是必要的。为了验证本文所提方法中三相电压不平衡约束式(53)、式(54)对限制电压不平衡度的有效性,本算例在不同三相不平衡度下,分别对“有约束(情形1)”和“无约束(情形2)”两种情况下的电压三相不平衡度结果进行了分析。
定义节点i单相电压不平衡度 为
为
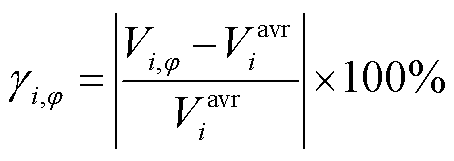 (62)
(62)
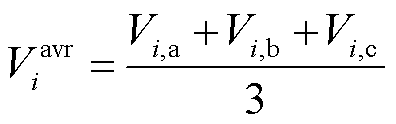 (63)
(63)
设置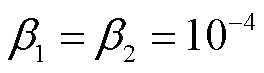 ,两种情形下的各相电压不平衡度平均值计算结果见表3。
,两种情形下的各相电压不平衡度平均值计算结果见表3。
表3 不同三相不平衡度下的三相电压不平衡度平均值计算结果(情形1和情形2)
Tab.3 Results of three-phase voltage unbalance factor under different three-phase unbalanced circumstances (case1 & case2) (%)

三相不平衡度情形1情形2 a相b相c相a相b相c相 负载10%不平衡0.0010.1960.2080.0130.3810.381 负载20%不平衡0.0410.1590.1930.1900.4030.331 线路参数10%不平衡0.0910.0150.0760.3670.1580.209 线路参数20%不平衡0.1990.1040.0950.4720.1910.281
从表2中可以看到,相较于不对三相电压不平衡度进行约束的情况,引入三相电压不平衡约束式(53)、式(54)可以有效降低系统各相电压的不平衡度。而随着负载不平衡度或线路参数不平衡度的增加,这种限制效果更加显著,因此可以说明本文所提方法对三相电压不平衡度加以限制是必要且有效的。
为进一步探究不平衡度设定值对优化结果的影响,在负载三相不平衡度20%情况下,选取不同的不平衡度设定值,并对不同设定值下的优化结果进行对比分析,结果见表4。
表4 不同三相不平衡度设定值下的优化结果
Tab.4 Optimization results under different three-phase unbalanced values

三相不平衡度设定值电压不平衡度平均值(%)总成本/元 a相b相c相 0.0410.1590.1931 124 0.6130.4110.5491 208 1.0653.0402.0681 060
由表4中数据可以看出,随着设定值的增加,三相不平衡度随之增加,并且在设定值为10-2情况下不平衡度已经超出了2%的限制,尽管此时总成本最低,但其调度结果已不能满足配电网实际运行要求。因此为了保证调度结果的有效性,需要根据配电网运行要求选取合适的不平衡度设定值。
为了检验本文所提方法在大规模配电系统的计算性能,本节分别在改进IEEE 69、141、1056节点交直流配电系统进行测试。其中,改进IEEE 1056节点系统由改进IEEE 33节点系统逐级级联而成。
首先,对本文所提的基于序分量三相SDP模型和基于相分量三相SDP模型在求解性能上进行对比,算例分析结果见表5。
表5 不同算例类型下两种方法的求解性能对比
Tab.5 Comparison of calculation performances of the two methods under different cases

算例类型序分量SDP相分量SDP 松弛偏差平均误差(%)求解时间/s松弛偏差平均误差(%)求解时间/s 69节点-13.73210.310.45-11.91450.990.39 141节点-8.59810.710.84-6.67791.660.71 1056节点-5.48111.147.01-3.76232.536.33
表5中的“松弛偏差”即第4.1.1节定义的最大松弛偏差DX,由于其为负数,因此其值越小越表明松弛精确性越高。从表5可以看到,随着配电网络规模的增加,两种方法的松弛偏差和平均误差都在增加。但是本文所提方法产生的松弛偏差和平均误差均小于基于相分量的三相SDP方法,这说明基于序分量的三相SDP方法可以提供更准确的调度结果。此外,在各节点测试算例中,两种方法的求解时间差距较小,因此本文所提方法在大规模测试系统中也能够胜任。
同时,对比了本文所提的基于序分量三相SDP模型和线性化模型[29]在优化结果与求解性能上的差异,所选取的线性化模型忽略了线路网损部分,并且假设三相近似平衡,因此在三相平衡的情况下对上述两种方法进行算例对比分析,优化结果与求解性能对比见表6。
从表6中数据可以看到,相较于序分量SDP模型,线性化模型由于忽略了非凸的线路网损部分,其总能获得较低的运行成本,并且线性化模型在求解速度方面有着显著的优势。但是由于线性化模型牺牲了一定程度的建模精确性,导致其优化结果存在明显的误差,并且随着配电系统规模的增加,这种误差也不断增加。除此之外,其三相近似平衡的假设会导致线性化模型在三相不平衡状态时失效。因此线性化模型无法满足配电网的实际运行状况。
表6 不同算例类型下两种方法的优化结果与求解性能对比
Tab.6 Comparison of optimization results and calculation performances of the two methods under different cases
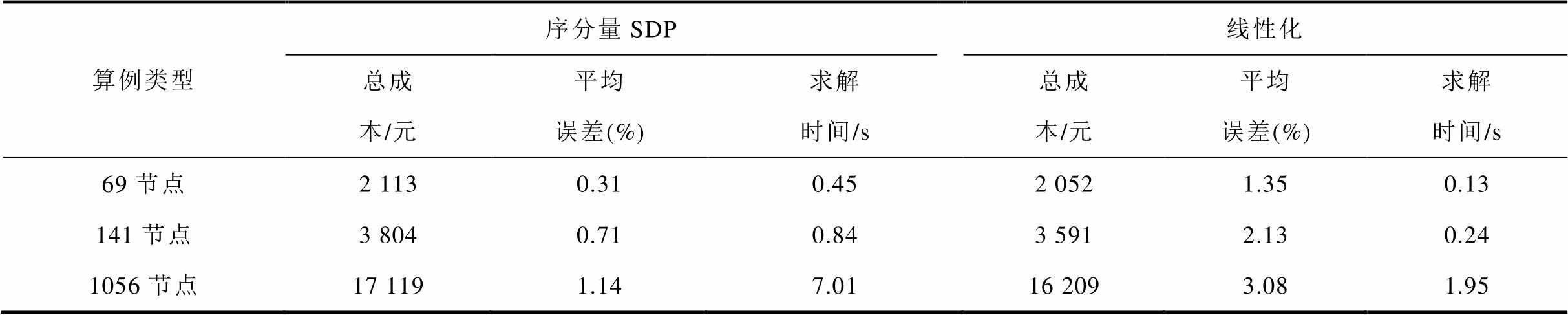
算例类型序分量SDP线性化 总成本/元平均误差(%)求解时间/s总成本/元平均误差(%)求解时间/s 69节点2 1130.310.452 0521.350.13 141节点3 8040.710.843 5912.130.24 1056节点17 1191.147.0116 2093.081.95
本文提出了适应三相不平衡交直流主动配电网的三相有功无功联合优化方法。本文所提方法综合考虑了三相相间耦合关系与三相不平衡度限制,通过升维映射方法和半正定松弛方法建立了完整的三相有功无功联合优化模型。通过算例分析可知,一方面,在不同三相不平衡度情况下,本文所提方法均可以保证算法松弛精确性与模型计算精确性。另一方面,相较于传统优化方法,本文所提方法可以获得更小的配电网总运行成本,并同时实现对系统电压三相不平衡度进行有效限制。此外,在大规模配电测试系统中,本文所提方法在计算精度方面表现优越,在计算性能方面无明显劣势。
参考文献
[1] 赵冬梅, 王浩翔, 陶然. 计及风电-负荷不确定性的风-火-核-碳捕集多源协调优化调度[J]. 电工技术学报, 2022, 37(3): 707-718. Zhao Dongmei, Wang Haoxiang, Tao Ran. A multi-source coordinated optimal scheduling model considering wind-load uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 707-718.
[2] 朱晓荣, 司羽. 考虑物理—信息—交通网耦合的配电网多时段动态供电恢复策略[J]. 电工技术学报, 2023, 38(12): 3306-3320. Zhu Xiaorong, Si Yu. Multi-period dynamic power supply restoration strategy considering physical-cyber-traffic network coupling[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3306-3320.
[3] 黄伟, 熊伟鹏, 华亮亮, 等. 基于动态调度优先级的主动配电网多目标优化调度[J]. 电工技术学报, 2018, 33(15): 3486-3498. Huang Wei, Xiong Weipeng, Hua Liangliang, et al. Multi-objective optimization dispatch of active distribution network based on dynamic schedule priority[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3486-3498.
[4] 虎智峰, 陈静, 张婧菲, 等. 考虑新能源不确定性边界的主动配电网优化调度[J]. 智慧电力, 2022, 50(11): 48-55. Hu Zhifeng, Chen Jing, Zhang Jingfei, et al. Optimal dispatch of active distribution network considering uncertainty boundary of renewable power generation[J]. Smart Power, 2022, 50(11): 48-55.
[5] Ahmed H M A, Eltantawy A B, Salama M M A. A planning approach for the network configuration of AC-DC hybrid distribution systems[J]. IEEE Transactions on Smart Grid, 2018, 9(3): 2203-2213.
[6] Zhang Lu, Liang Jun, Tang Wei, et al. Converting AC distribution lines to DC to increase transfer capacities and DG penetration[J]. IEEE Transactions on Smart Grid, 2018, 10(2): 1477-1487.
[7] 张涛, 穆云飞, 贾宏杰, 等. 含电力电子变压器的交直流配电网随机运行优化[J]. 电网技术, 2022, 46(3): 860-869. Zhang Tao, Mu Yunfei, Jia Hongjie, et al. Stochastic operation optimization for AC/DC distribution network with power electronic transformer[J]. Power System Technology, 2022, 46(3): 860-869.
[8] 姜涛, 李雪, 李国庆, 等. 含多端柔性直流的交直流电力系统静态电压稳定域构建方法[J]. 电工技术学报, 2022, 37(7): 1746-1759. Jiang Tao, Li Xue, Li Guoqing, et al. A predictor-corrector algorithm for forming voltage stability region of hybrid AC/DC power grid with inclusion of VSC-MTDC[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1746-1759.
[9] 孙旭, 邱晓燕, 张志荣, 等. 基于数据驱动的交直流配电网分布鲁棒优化调度[J]. 电网技术, 2021, 45(12): 4768-4778. Sun Xu, Qiu Xiaoyan, Zhang Zhirong, et al. Distributed robust optimal dispatching of AC/DC distribution network based on data driven mode[J]. Power System Technology, 2021, 45(12): 4768-4778.
[10] 郑重, 苗世洪, 李超, 等. 面向微型能源互联网接入的交直流配电网协同优化调度策略[J]. 电工技术学报, 2022, 37(1): 192-207. Zheng Zhong, Miao Shihong, Li Chao, et al. Coordinated optimal dispatching strategy of AC/DC distribution network for the integration of micro energy Internet[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 192-207.
[11] 张晓英, 张艺, 王琨, 等. 基于改进NSGA-Ⅱ算法的含分布式电源配电网无功优化[J]. 电力系统保护与控制, 2020, 48(1): 55-64. Zhang Xiaoying, Zhang Yi, Wang Kun, et al. Reactive power optimization of distribution network with distributed generations based on improved NSGA-Ⅱ algorithm[J]. Power System Protection and Control, 2020, 48(1): 55-64.
[12] 乐健, 周谦, 王曹, 等. 基于分布式协同的配电网电压和功率优化控制方法研究[J]. 中国电机工程学报, 2020, 40(4): 1249-1257, 1415. Le Jian, Zhou Qian, Wang Cao, et al. Research on voltage and power optimal control strategy of distribution network based on distributed collaborative principle[J]. Proceedings of the CSEE, 2020, 40(4): 1249-1257, 1415.
[13] Zarrilli D, Giannitrapani A, Paoletti S, et al. Energy storage operation for voltage control in distribution networks: a receding horizon approach[J]. IEEE Transactions on Control Systems Technology, 2018, 26(2): 599-609.
[14] 胡丹尔, 彭勇刚, 韦巍, 等. 多时间尺度的配电网深度强化学习无功优化策略[J]. 中国电机工程学报, 2022, 42(14): 3, 5034-5044. Hu Daner, Peng Yonggang, Wei Wei, et al. Multi-timescale deep reinforcement learning for reactive power optimization of distribution network[J]. Proceedings of the CSEE, 2022, 42(14): 3, 5034-5044.
[15] 姜涛, 张东辉, 李雪, 等. 含分布式光伏的主动配电网电压分布式优化控制[J]. 电力自动化设备, 2021, 41(9): 102-109, 125. Jiang Tao, Zhang Donghui, Li Xue, et al. Distributed optimal control of voltage in active distribution network with distributed photovoltaic[J]. Electric Power Automation Equipment, 2021, 41(9): 102-109, 125.
[16] 张沈习, 李珂, 程浩忠, 等. 间歇性分布式电源在主动配电网中的优化配置[J]. 电力自动化设备, 2015, 35(11): 45-51. Zhang Shenxi, Li Ke, Cheng Haozhong, et al. Optimal allocation of intermittent distributed generator in active distribution network[J]. Electric Power Automation Equipment, 2015, 35(11): 45-51.
[17] 刘一兵, 吴文传, 张伯明, 等. 基于有功-无功协调优化的主动配电网过电压预防控制方法[J]. 电力系统自动化, 2014, 38(9): 184-191. Liu Yibing, Wu Wenchuan, Zhang Boming, et al. Overvoltage preventive control method based on active and reactive power coordinated optimization in active distribution network[J]. Automation of Electric Power Systems, 2014, 38(9): 184-191.
[18] Gao Hongjun, Liu Junyong, Wang Lingfeng. Robust coordinated optimization of active and reactive power in active distribution systems[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 4436-4447.
[19] 刘洪, 徐正阳, 葛少云, 等. 考虑储能调节的主动配电网有功—无功协调运行与电压控制[J]. 电力系统自动化, 2019, 43(11): 51-58. Liu Hong, Xu Zhengyang, Ge Shaoyun, et al. Coordinated operation of active-reactive power and voltage control for active distribution network considering regulation of energy storage[J]. Automation of Electric Power Systems, 2019, 43(11): 51-58.
[20] 寇凌峰, 吴鸣, 李洋, 等. 主动配电网分布式有功无功优化调控方法[J]. 中国电机工程学报, 2020, 40(6): 1856-1865. Kou Lingfeng, Wu Ming, Li Yang, et al. Optimization and control method of distributed active and reactive power in active distribution network[J]. Proceedings of the CSEE, 2020, 40(6): 1856-1865.
[21] 赵晋泉, 刘绪, 林昌年, 等. 单相光伏大量接入的三相不平衡配电网无功优化[J]. 电力系统自动化, 2016, 40(13): 13-18, 70. Zhao Jinquan, Liu Xu, Lin Changnian, et al. Three-phase unbalanced reactive power optimization for distribution systems with a large number of single phase solar generators[J]. Automation of Electric Power Systems, 2016, 40(13): 13-18, 70.
[22] 唐冬来, 郝建维, 刘荣刚, 等. 基于动态规划的配电台区三相负荷不平衡治理方法[J]. 电力系统保护与控制, 2020, 48(21): 58-66. Tang Donglai, Hao Jianwei, Liu Ronggang, et al. Control method of three phase load imbalance in a distribution station area based on dynamic programming[J]. Power System Protection and Control, 2020, 48(21): 58-66.
[23] Liu Shengyuan, Jin Renyun, Qiu Haifeng, et al. Practical method for mitigating three-phase unbalance based on data-driven user phase identification[J]. IEEE Transactions on Power Systems, 2020, 35(2): 1653-1656.
[24] 程湘, 田昊, 周群, 等. 考虑相位不平衡的智能换相开关控制策略[J]. 电力系统保护与控制, 2021, 49(6): 48-55. Cheng Xiang, Tian Hao, Zhou Qun, et al. Control strategy of intelligent commutation switch considering phase imbalance[J]. Power System Protection and Control, 2021, 49(6): 48-55.
[25] 伍鸿兵, 罗勇, 王嵩, 等. 计及分布式电源接入的三相不平衡配电网无功优化研究[J]. 计算技术与自动化, 2020, 39(3): 17-21, 36. Wu Hongbing, Luo Yong, Wang Song, et al. Research on reactive power optimization of three-phase unbalanced distribution network with access of distributed power supply[J]. Computing Technology and Automation, 2020, 39(3): 17-21, 36.
[26] Robbins B A, Dominguez-Garcia A D. Optimal reactive power dispatch for voltage regulation in unbalanced distribution systems[J]. IEEE Transactions on Power Systems, 2016, 31(4): 2903-2913.
[27] Chowdhury M M U T, Biswas B D, Kamalasadan S. Second-order cone programming (SOCP) model for three phase optimal power flow (OPF) in active distribution networks[J]. IEEE Transactions on Smart Grid, 2023, 14(5): 3732-3743.
[28] Dall'Anese E, Zhu Hao, Giannakis G B. Distributed optimal power flow for smart microgrids[J]. IEEE Transactions on Smart Grid, 2013, 4(3): 1464-1475.
[29] Gan Lingwen, Low S H. Convex relaxations and linear approximation for optimal power flow in multiphase radial networks[C]//2014 Power Systems Computation Conference, Wrocław, Poland, 2014: 1-9.
[30] 徐添锐, 丁涛, 李立, 等. 适应三相不平衡主动配电网无功优化的二阶锥松弛模型[J]. 电力系统自动化, 2021, 45(24): 81-88. Xu Tianrui, Ding Tao, Li Li, et al. Second-order cone relaxation model adapting to reactive power optimization for three-phase unbalanced active distribution network[J]. Automation of Electric Power Systems, 2021, 45(24): 81-88.
[31] 巨云涛, 黄炎, 张若思. 基于二阶锥规划凸松弛的三相交直流混合主动配电网最优潮流[J]. 电工技术学报, 2021, 36(9): 1866-1875. Ju Yuntao, Huang Yan, Zhang Ruosi. Optimal power flow of three-phase hybrid AC-DC in active distribution network based on second order cone programming[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1866-1875.
[32] Rahul R, Adedoyin I, Biswajit D, et al. Distribution grid optimal power flow (D-OPF): Modeling, analysis, and benchmarking[J]. IEEE Transactions on Power Systems. 2023, 38(4): 3654-3668.
[33] Chen Xin, Wu Wenchuan, Zhang Boming. Robust capacity assessment of distributed generation in unbalanced distribution networks incorporating ANM techniques[J]. IEEE Transactions on Sustainable Energy, 2018, 9(2): 651-663.
[34] Wang Zeyu, Kirschen D S, Zhang Baosen. Accurate semidefinite programming models for optimal power flow in distribution systems[EB/OL]. arXiv, 2017 1711.07853. https://arxiv.org/abs/1711.07853.pdf.
[35] Wang Zeyu, Wang Jianhui, Chen Chen. A three-phase microgrid restoration model considering unbalanced operation of distributed generation[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3594-3604.
[36] Opathella C, Venkatesh B. Three-phase unbalanced power flow using a π model of controllable AC-DC converters[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4286-4296.
[37] Girigoudar K, Roald L A. On the impact of different voltage unbalance metrics in distribution system optimization[J]. Electric Power Systems Research, 2020, 189: 106656.
[38] Wang Wei, Yu Nanpeng. Chordal conversion based convex iteration algorithm for three-phase optimal power flow problems[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1603-1613.
[39] Alsaleh I, Fan Lingling, Bazrafshan M. Extended radial distribution ACOPF model: retrieving exactness via convex iteration[J]. IEEE Transactions on Power Systems, 2021, 36(6): 4967-4978.
Abstract As the main outlook of the future distribution network, it is of great research value to jointly allocate active-reactive power resources of AC-DC active distribution network. However, the access of single-phase load and the three-phase power inconsistency of distributed generation will lead to more severe three-phase unbalance situation in the distribution network. To deal with the three-phase unbalance problem in AC-DC active distribution network, a joint three-phase active and reactive power optimization method is proposed, which takes the phase-to-phase coupling relationship and the three-phase unbalance factor limitation into account.
Firstly, the original three-phase power flow model considering the phase-to-phase coupling relationship is established and the model is mapped to a high-dimensional space then. Secondly, the complete symmetrical three-phase power flow model of each subsystem of AC-DC active distribution network and the symmetrical three-phase voltage unbalance factor constraints are derived using the semidefinite programming. Then, a joint three-phase active-reactive power optimization model of AC-DC active distribution network with the objective of minimizing the total network operation cost is proposed.
To verify the accuracy and effectiveness of the proposed method, the maximum relaxation deviation and maximum logarithmic relaxation mismatch results are firstly demonstrated via case studies on the modified IEEE 33-bus AC-DC distribution system. Under different unbalanced circumstances, the maximum relaxation deviations of the proposed method are always lower than 10-7 with the corresponding relaxation mismatch under 10-5. Besides, the results of voltage deviation percentage of the proposed method are lower than the results of the standard three-phase SDP method. Moreover, in contrast to the traditional three-phase decoupled model, the proposed method is able to obtain a smaller operation cost results, e.g., 4.489% and 13.188% reduction on operation cost and transmission loss cost under 20%-line impedance unbalance circumstance, and more real voltage results. And it can effectively limit the three-phase unbalance of the system voltage with the voltage unbalance factor model always under the pre-set 2% threshold at the same time. To further verify the calculation performances on large scale systems, case studies are carried out on the modified IEEE 69-,141- and 1056-bus AC-DC distribution systems. Compared with the standard three-phase SDP method, the proposed method can provide more accurate optimization results while the computing time do not increase too much. Meanwhile, compared with the linearized model, the average mismatches are always smaller, which indicates the infeasibility of the linearized model.
The following conclusions can be drawn from the simulation analysis: (1) Under different three-phase unbalance circumstances, the proposed method can guarantee the relaxation accuracy of the algorithm and gain better performances on accuracies compared with the standard three-phase SDP method. (2) The proposed method can obtain a smaller operation cost and more real bus voltages compared with the traditional three-phase decoupled model, which indicates its’ applicability in the actual operation states of the AC-DC distribution network. (3) The effectiveness of the three-phase voltage unbalance limitation constraint is verified which consequently proves that the proposed model satisfies the actual operation requirements of the AC-DC distribution network. (4) In large-scale AC-DC distribution test systems, the proposed method is superior on calculation accuracy, but has no evident disadvantages on calculation speed performance.
Keywords:AC-DC active distribution network, three-phase unbalance, joint active-reactive power optimization, semidefinite programming, distributed generator
DOI: 10.19595/j.cnki.1000-6753.tces.231652
中图分类号:TM715
国家自然科学基金(51907151)和陕西省自然科学基础研究计划(2023-JC-QN-0391)资助项目。
收稿日期 2023-10-10
改稿日期 2023-11-22
孙乾皓 男,1997年生,博士研究生,研究方向为交直流主动配电网潮流计算、优化运行。E-mail:qianhaosun@stu.xjtu.edu.cn
张 耀 男,1988年生,副教授,博士生导师,研究方向为可再生能源预测与并网消纳、电力大数据与人工智能等。E-mail:yaozhang_ee@xjtu.edu.cn(通信作者)
(编辑 赫 蕾)