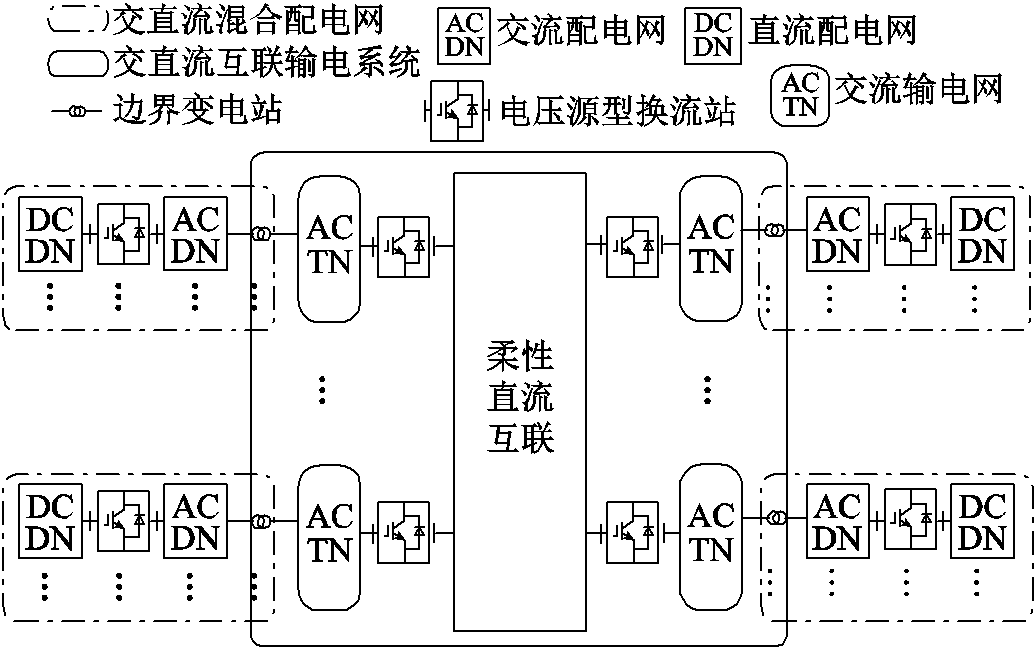
图1 输配协同的交直流混合电网结构
Fig.1 Integrated transmission and distribution grids structure with multi-terminal VSC flexible interconnected
摘要 多端柔性互联输配一体化电网内部的运行方式复杂、网损特性差异显著，导致传统一刀切的网损补偿方法难以准确刻画网损的实际情况，影响了输（配）电交直流有损潮流模型的应用潜力和输配边界潮流的一致性。为此，该文提出一种基于双层定点迭代的精细化有损潮流模型。针对网损补偿方法不准确的问题，综合考虑网络类型、数据属性和物理特征等因素，为输、配电网及交、直流电网的精准有损潮流分析建立了差异化的网损补偿模型。针对输配边界潮流的不一致问题，将输配一体化有损潮流建模为一个双层定点迭代问题，并采用主从分裂法实现协同求解。在多个算例中分析了不同有损潮流模型的性能差异及其原因，讨论了所提模型在求解精度、收敛速度和计算效率等方面的优势，验证了所提模型在不同控制方式和优化目标下的鲁棒性和通用性。
关键词：柔性互联 输配一体化 潮流分析 网损补偿 定点迭代
现阶段我国能源结构面临着巨大的变革，需要大力推进柔性直流输电技术的发展以及输配协同管理体系的建设[1-3]。目前，我国已有若干个柔性直流输电工程和输配一体化调控管理的成功案例[4-6]。然而，大多数研究依然将二者视为独立的课题，缺乏统一的建模理论。为进一步加快电力系统转型，有必要充分发挥二者的技术优势，研究多端柔性互联的输配一体化电网的全贯通建模和分析方法，为实现电网的多区域交直流灵活互联和输-配电多层级协同调控提供理论和技术支撑。
随着可再生能源的规模化和电网结构的复杂化，网络传输损耗对电力系统运行的影响日益突出。常规线性潮流模型因忽略网损导致误差较大，进而限制了模型在优化调度等电网高级应用中的适用性和有效性。与之相反，有损潮流[7-8]将忽略网损的线性潮流扩展为以节点潮流信息为定点的迭代问题，利用已知的节点电压将网损补偿到相应节点重新求解线性潮流，能够更好地逼近系统的实际运行状态，因而在精度方面具有明显的优势[9-11]。此类模型同样易于嵌入含不确定性[12-15]和线性规划[16-21]的优化问题，能在保证较低计算复杂度的同时避免收敛困难，逐渐成为电力系统分析的主流方法之一[22]。
针对交流输电网，文献[23-24]依靠主观经验给定系数的方式确定损耗，模型稳定性较差。文献[25]提出了有损直流潮流模型。然而，损耗计算过程仅考虑了电压相位而忽略了电压幅值。为此，文献[26]提出一种新的线路解耦等值模型，并充分考虑了有功和无功损耗，但是误差修正的稳定性仍然受系统状态和运行条件的影响较大。文献[27-28]提出两种根据当前潮流信息估计损耗的方法，在一定程度上减少了由于主观猜测参数而引起的误差。然而，上述方法的迭代过程较为繁琐，随着系统规模的扩大可能增加额外的计算负担。
针对交流配电网，文献[29]提出一种有损DistFlow模型，利用若干配电馈线训练网损的线性解析表达，提高了常规线性DistFlow模型的计算精度。然而，该模型的参数上下界依赖一套可自动生成配电网拓扑的算法软件[30]，因此该方法在实际配电网中的适用性有待进一步探讨。
针对高压直流电网，文献[31]为交直流混联电力系统的高压直流部分提出一种有损潮流算法，可根据当前的直流电压幅值直接更新节点注入功率，提升了直流电网有损潮流的求解精度。然而，此方法被简述为一个仅有两次迭代的流程而没有建模为一个严格的定点迭代问题，换句话说，只讨论了一种性能趋势而未形成一套完整的数学表达。
综上所述，目前关于有损潮流的精细化建模存在不足，仅面向单区域、单层级及单类型的电网，且主要集中于交流输电网。对于柔性互联输配一体化电网，如果直接采用上述模型，会放大输-配系统内部和边界的潮流误差，同时也将削弱模型在不同控制策略和优化目标下的应用价值。原因是传统一刀切式的网损补偿方法无法兼顾由系统内部运行方式的复杂性而引起的显著网损特性差异，进而难以准确量化不同层级和不同类型电网的损耗对潮流误差的影响。
综上所述，本文针对多端柔性互联的输配一体化电网提出了一种基于双层定点迭代的精细化有损潮流模型。首先，为解决网损补偿方法不准确的问题，本文充分考虑了网络结构、数据属性和物理特征等方面的特点，为输、配电以及交、直流电网的有损潮流分析建立了差异化的网损补偿模型；其次，为解决输配边界潮流的不一致问题，本文将有损潮流建模为一个双层定点迭代问题，其中外层以网络边界节点为迭代变量，内层以网络内部节点为迭代变量，并采用主从分裂法进行协同求解；最后，通过仿真算例的分析和讨论，验证了所提模型的性能优势和应用潜力，为柔性互联输配一体化有损潮流的精细化建模提供了思路。
具有输配协同结构的柔性多端互联系统的结构如图1所示，主要由三部分组成：交直流输电网、交直流配电网和边界变电站（或边界节点）。
图1 输配协同的交直流混合电网结构
Fig.1 Integrated transmission and distribution grids structure with multi-terminal VSC flexible interconnected
柔性互联的输配一体化潮流模型的数学表达式为
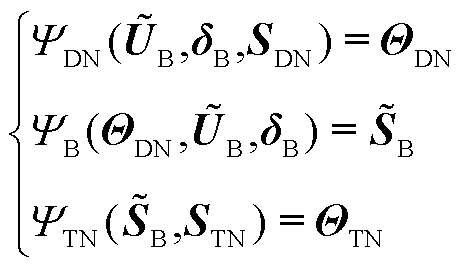（1）
式中，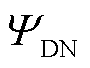
为交直流配电网的潮流方程；
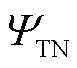为交直流输电网的潮流方程；
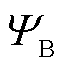为边界节点变量的求解模型；
、
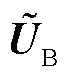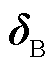和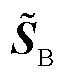
分别为边界节点的电压幅值、相位和注入功率；下标DN表示配电网，TN表示输电网。将式（1）抽象为定点迭代问题，则第x次迭代的输配一体化潮流模型的紧凑形式为
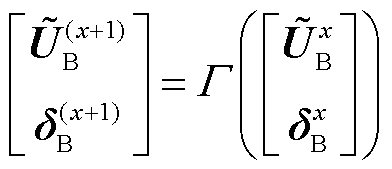（2）
根据图1可知，含柔性设备的输电网和配电网均由纯交流电网、纯直流电网和电压源换流器（Voltage Source Converter, VSC）换流站三大模块集成。对于直流电网，线性潮流模型的向量表达为[31]
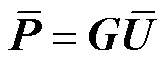（3）
式中，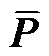
为直流有功注入；G为导纳矩阵的实部；
为直流电压幅值。
对于交流电网，解耦线性潮流模型的向量表达可描述为[32]
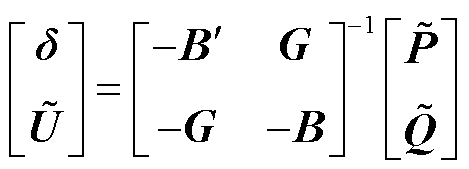（4）
式中，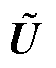
为交流电压幅值；
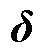为电压相位；
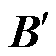为忽略线路对地并联导纳的虚部；
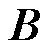为导纳矩阵的虚部；
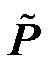为交流有功注入；
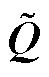为交流有功注入。
对于VSC换流站，其潮流的传递与交互通过交流侧和直流侧之间的有功功率平衡方程实现[33]，即
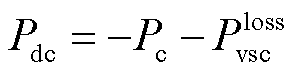（5）
式中，Pdc为从VSC换流站流入直流电网的有功功率；Pc为流过VSC换流站的有功功率；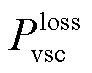
为换流站的有功损耗。
第1节建立的线性潮流模型默认所有支路的发送功率和接收功率的绝对值相等，意味着系统中的损耗被忽略，导致节点的注入功率存在一定的不平衡量。这些不平衡量最终全部被平衡节点承担，增大了注入功率误差，进而影响到整体的潮流分布。
为此，根据网损等值负荷理论提出有损潮流模型[23]，将线路损耗视为阻抗为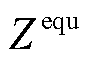
（直流系统为
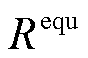）的等值虚拟负荷处理，其消耗的功率在数值上等于与该负荷所在节点相连的所有支路损耗之和的1/2。利用网损近似值修正节点注入功率，然后重新计算式（3）和式（4）的线性潮流模型直到收敛。以交流电网为例，网损等值负荷模型如图2所示。
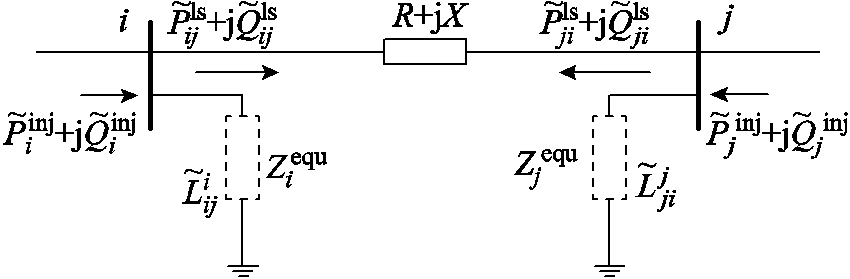
图2 交流系统的网损等值负荷模型
Fig.2 Equivalent load model of network losses for AC grid
在交流电网中，支路损耗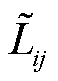
可解耦为有功损耗和无功损耗，即
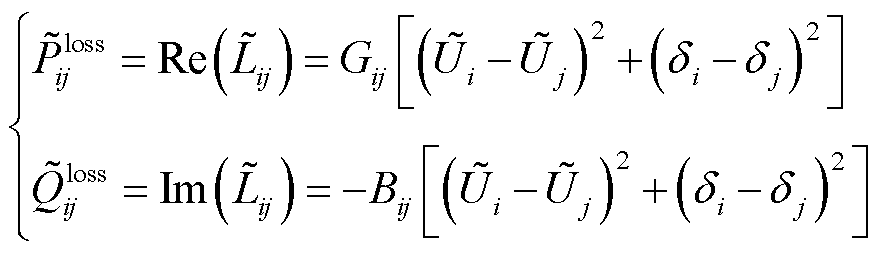（6）
式中，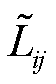
为交流支路ij的损耗；
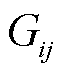为支路导纳的实部；
、
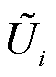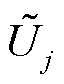分别为交流节点i、j的电压幅值；
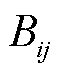为支路导纳的虚部；
、
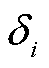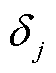分别为节点i、j的电压相位。
为了修正线性化引起的支路潮流误差，应分别为支路的首末节点分配相应的损耗，有
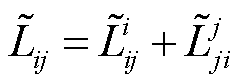（7）
式中，
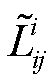和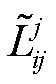
分别为按平均分配给支路首节点i和末节点j的损耗，由此可得
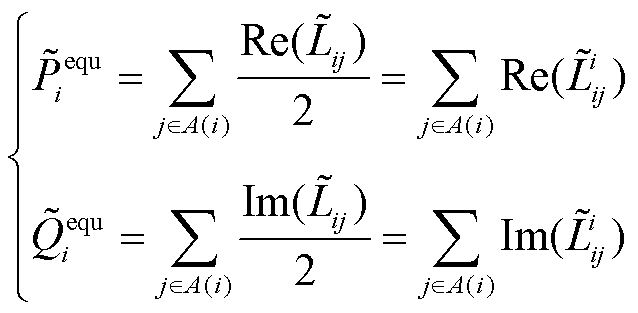（8）
式中，
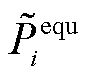和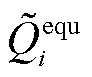
分别为阻抗为Zequ的等值负荷所消耗的有功和无功功率，在数值上等于与节点i相连的所有支路损耗的1/2；A(i)为所有与节点i相连的节点集合。由此，节点i的注入功率不仅取决于自身的发电量和负荷量，还与网损等值负荷有关。因此，考虑损耗补偿的节点注入功率满足如下迭代关系：
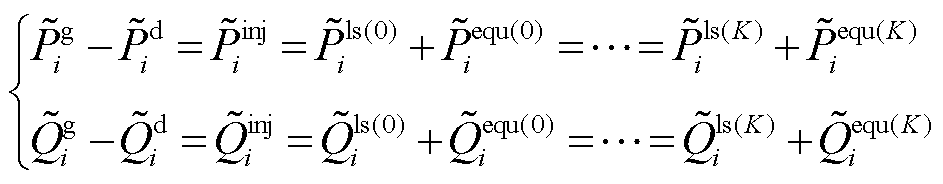（9）
式中，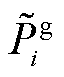
为节点发电有功；
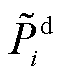为节点负荷有功；
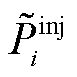和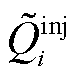
分别为所有PQ和PV节点实际注入的有功和无功功率；
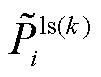和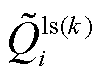
分别为有损潮流在第k次迭代节点注入的有功和无功功率；
、
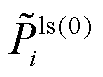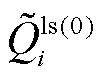分别为不考虑损耗的节点有功、无功功率注入；
、
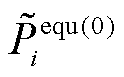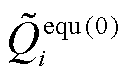分别为不考虑损耗的网损等值有功、无功负荷值，取值为0。上述理论可自然地迁移至直流电网，则交直流定点的不平衡方程组为
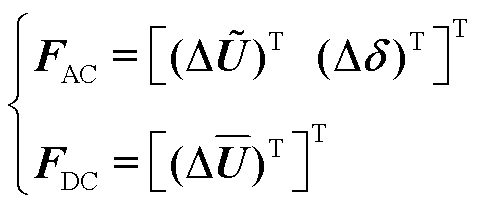（10）
式中，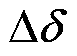
为交流电压相位的偏差量；
、
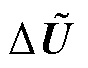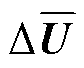分别为交、直流电压幅值的偏差量。
针对配电网和直流输电网，本文提出了一种基于直接推导的网损补偿方法。以交流配电网为例，其等效电路模型如图3所示。假设下一次迭代的潮流信息已知，利用网损等值负荷理论推导出迭代前后节点注入之间的近似关系，相当于提前为下一迭代的节点注入补偿了相应的损耗，具有“先知先觉”的特点，因而能够有预见性地修正误差。
图3 基于直接推导法的等效电路模型
Fig.3 Equivalent model based on direct derivation method
根据节点与支路之间的关系，利用解耦线性化的假设条件可得支路潮流的线性方程为[32]
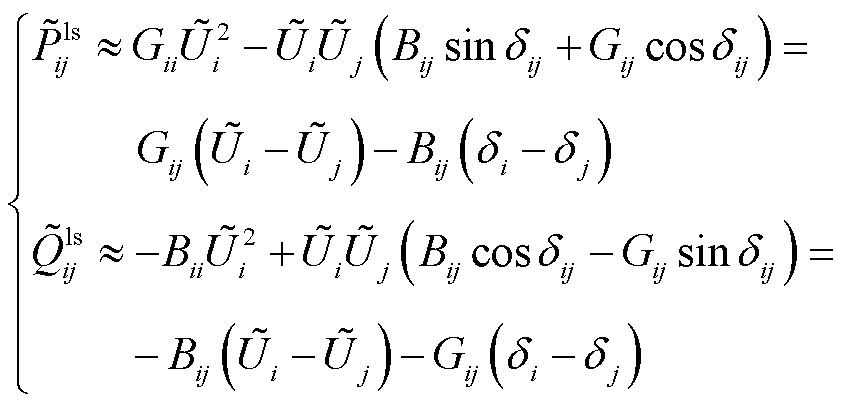（11）
对于第k次迭代，可解得X(k)，同时假设待更新的解X(k+1)也已知，则第k+1次迭代的支路线性潮流和近似损耗分别如式（12）和式（13）所示。
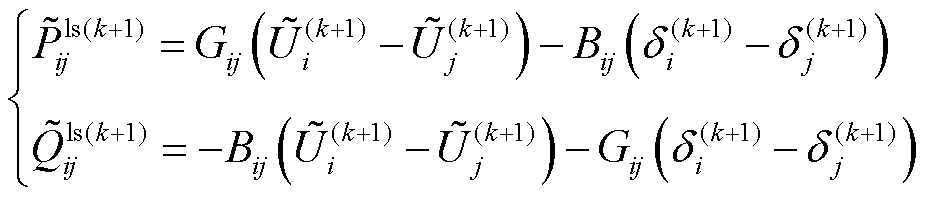（12）
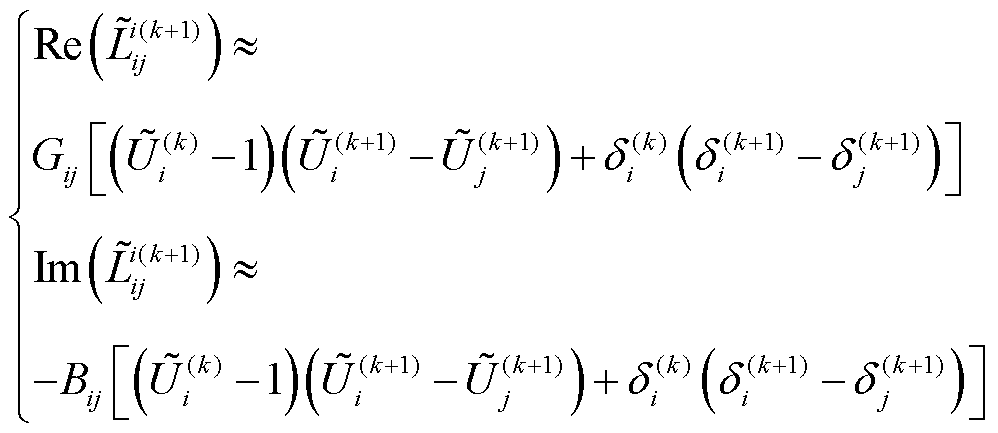（13）
在实际配电网中相位差的绝对值大多数在10°以内[32]。因此，当忽略相位对损耗的影响时，式（13）可被进一步化简为
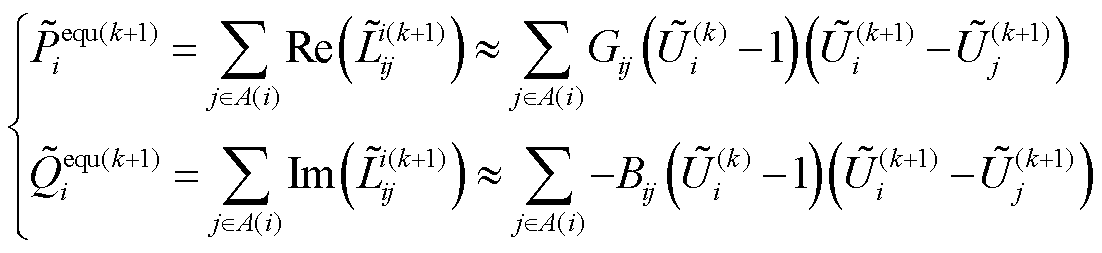（14）
将式（12）和式（14）代入式（9）中可得
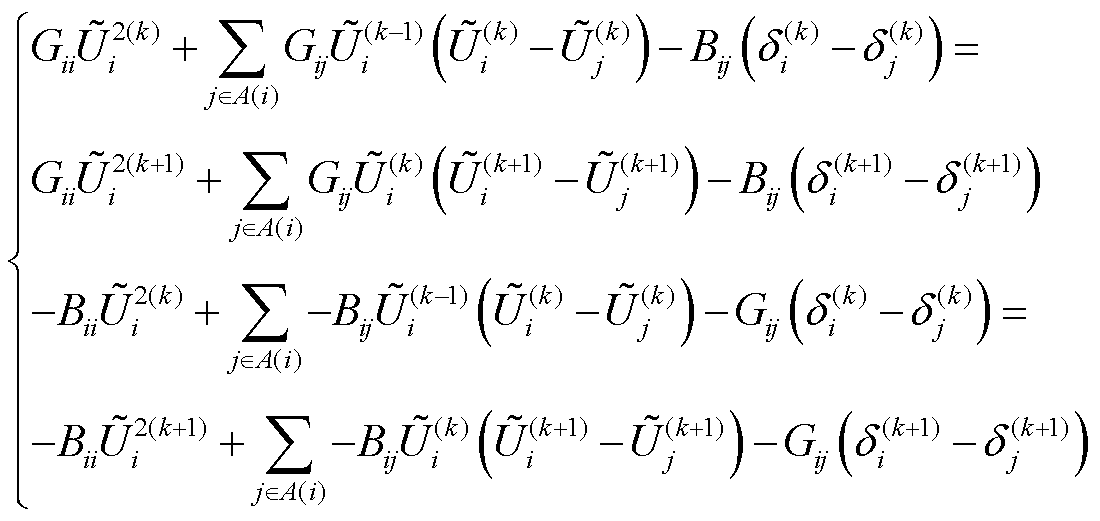（15）
假设式（15）左右两侧的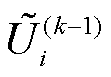
和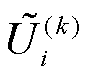
项近似为1(pu)，则可进一步整理得到
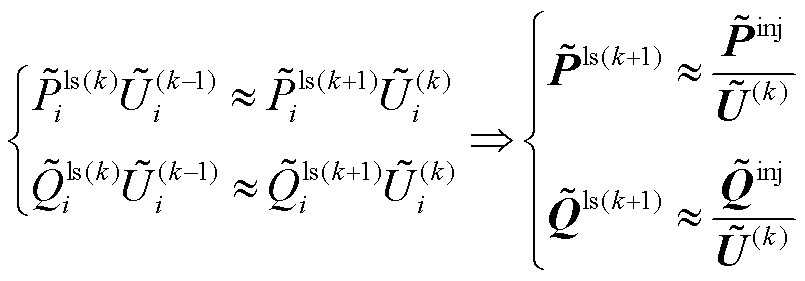（16）
结合式（4）和式（16），则基于直接推导法的交流配电网有损潮流的定点迭代方程为
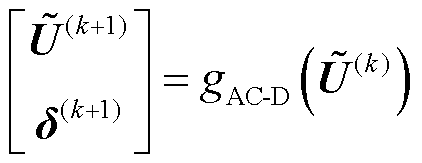（17）
由于直流电网不存在相位，损耗仅保留式（6）中有功损耗的电压幅值部分，因此可简化为
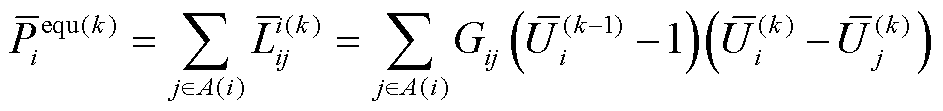（18）
因此根据式（3）和式（18），对应当前迭代和下一次迭代分别为
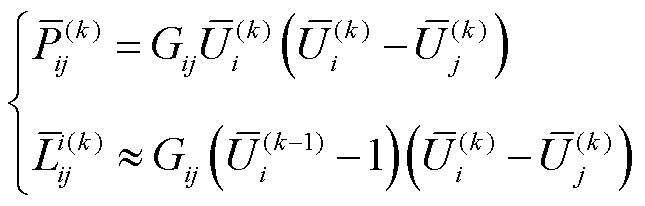（19）
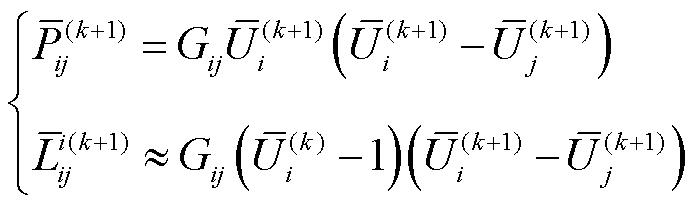（20）
将式（19）和式（20）代入式（9）中可得
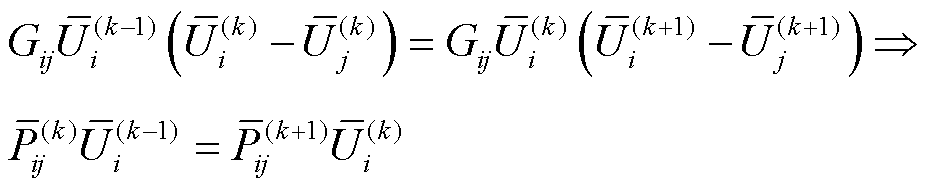（21）
结合直流节点和支路之间的关系[31]，可推导出直流电网的节点注入功率修正方程为
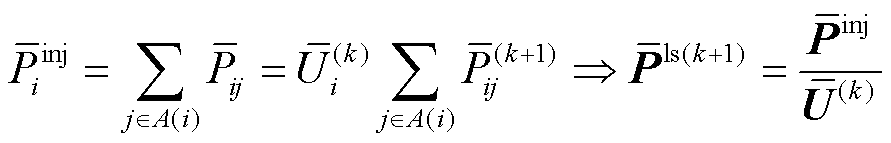（22）
则基于直接推导法的直流输（配）电网有损潮流的定点迭代方程为
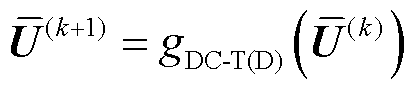（23）
显然，式（23）属于式（17）的一种特殊形式。直接推导法以忽略相位为前提条件，因此，该方法应用于交流（直流）配电网和直流输电网时具有天然的性能优势。
对于交流输电网，本文提出了另一种网损补偿方法，即将直接推导法与现有的近似估计法结合得到联合补偿法。近似估计法的交流等效电路模型如图4所示，其计算过程如下：在第k次迭代中，利用式（6）直接估算支路损耗L(k)并近似为第k+1次迭代的损耗。
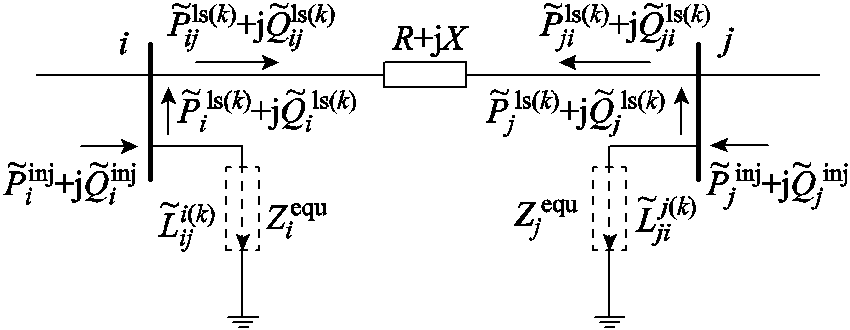
图4 基于近似估计法的等效电路模型
Fig.4 Equivalent circuit model based on approximate estimation method
根据式（6）～式（8），在第k次迭代时，节点i的交流网损等值负荷的表达式为
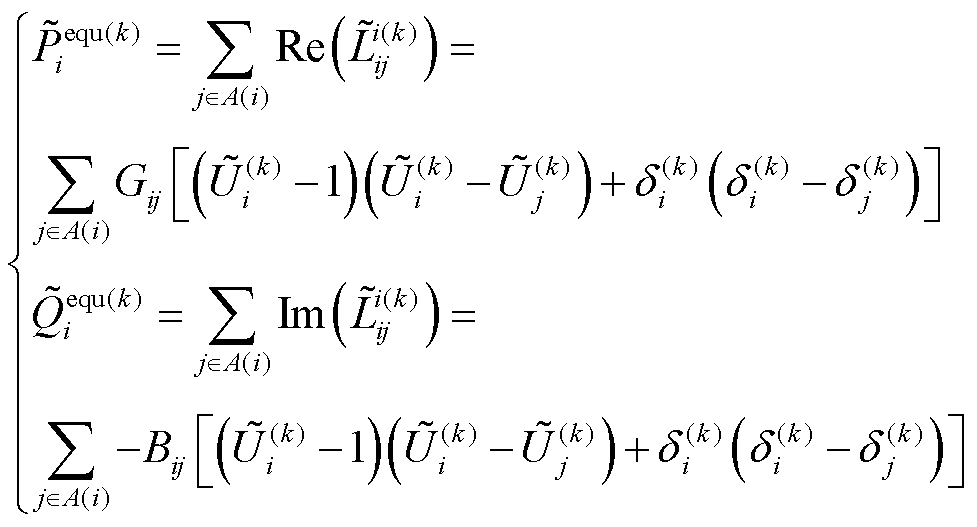（24）
将式（24）代入式（9），则更新后的交流节点注入功率的矩阵形式为
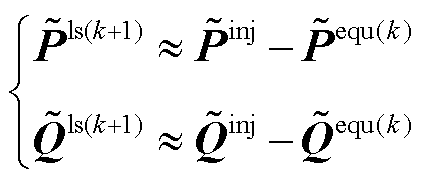（25）
根据式（4）和式（25），可进一步简化得到基于近似估计法的交流有损潮流的定点迭代方程为
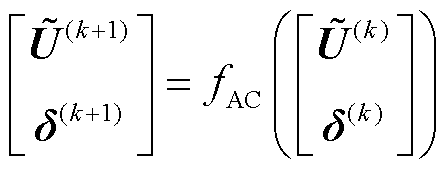（26）
同理，对于直流电网，修正后的直流节点注入功率的向量形式为
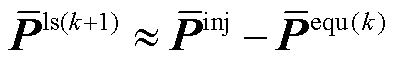（27）
根据式（3）和式（27），可得基于近似估计法的直流有损潮流的定点迭代方程为
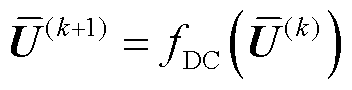（28）
然而，近似估计法仅根据当前已知的潮流估算损耗进而修正节点注入量，具有“后知后觉”的特点，因而误差修正效果相对保守。为此，考虑到有功、无功的损耗差异提出了两种联合补偿模型：①使用直接推导法补偿有功损耗，同时使用近似估计法补偿无功损耗；②使用近似估计法补偿有功损耗，同时使用直接推导法补偿无功损耗。两种联合补偿法的紧凑形式可分别描述为
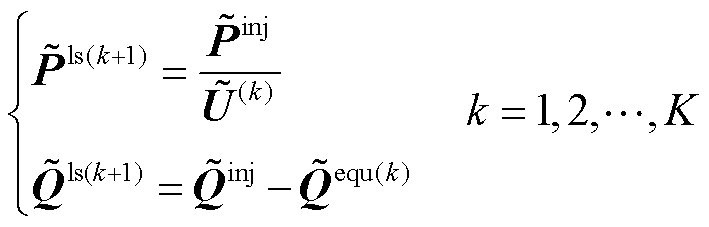（29）
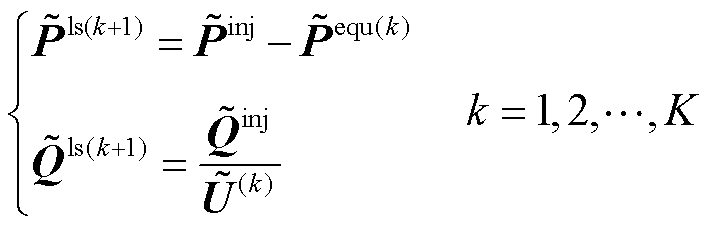（30）
基于交流定点迭代方程式（29）或式（30），结合式（4）可构建不同的交流有损潮流模型。最终，基于联合补偿法的交流输电网有损潮流的定点形式为
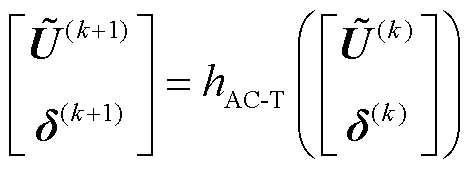（31）
本文提出的有损潮流模型被构建为一个双层定点迭代问题。外层模型解决输-配边界潮流的不一致问题，并采用主从分裂法协同求解。求解输电网潮流时，将配电网等效为负荷，得到边界节点的电压信息；求解配电网潮流时，则将输电网等效为电源，利用已知的边界节点电压作为配电系统平衡节点的运行条件，得到边界节点的注入功率。内层模型解决基于差异化网损补偿的交直流有损潮流问题，如式（17）、式（23）和式（31）所示。综上所述，本文算法的整体流程如图5所示。
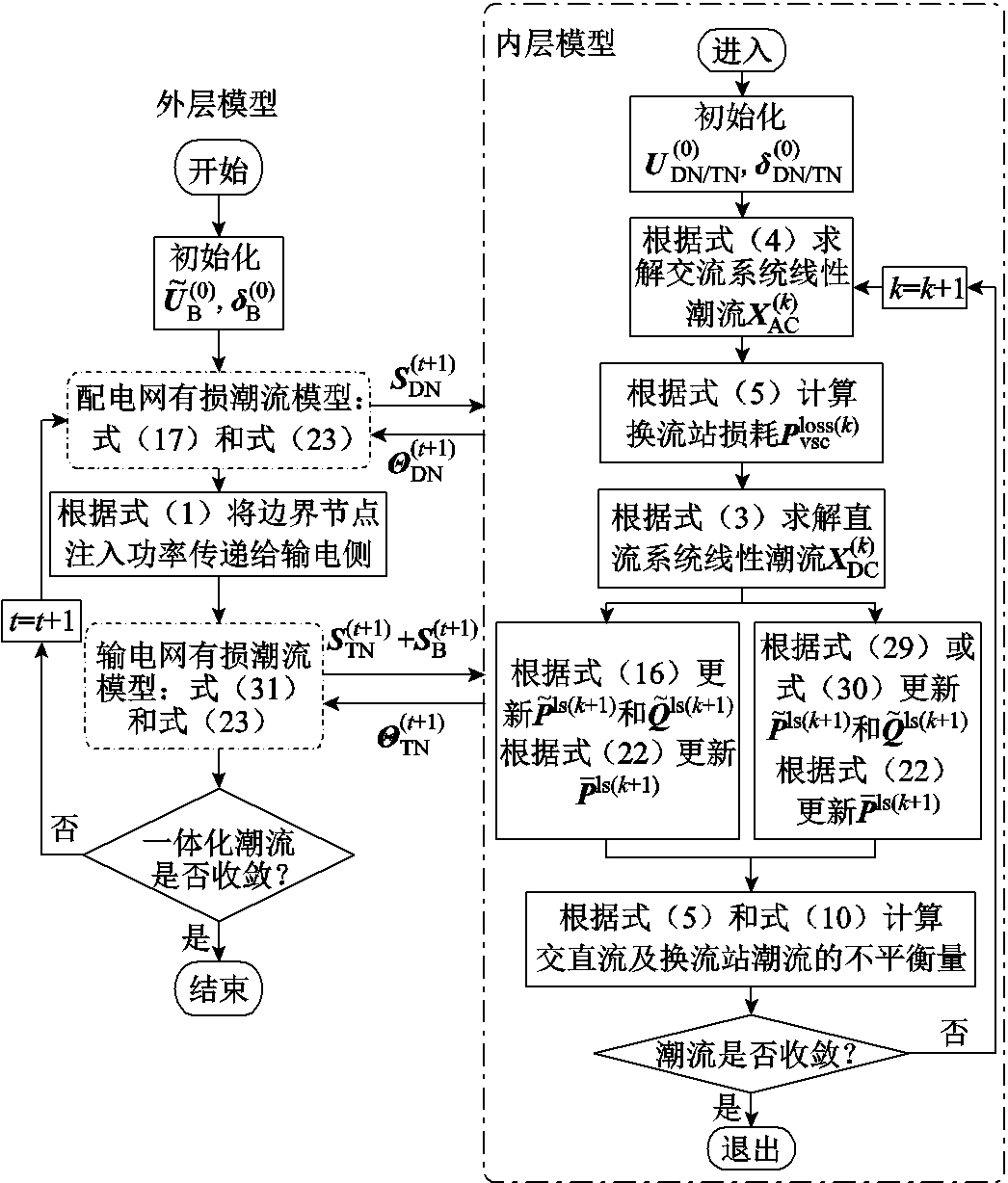
图5 基于双层定点迭代的有损潮流求解框架
Fig.5 Lossy power flow framework based on two-layer fixed-point iteration
具体步骤如下：
1）初始化交直流输配系统的基准值、收敛精度以及边界节点的电压向量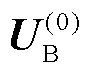
和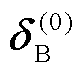
。
2）求解交直流混合配电网的有损潮流。
（1）初始化并使用式（4）求解交流配电网线性潮流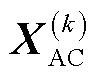
，并利用式（5）计算换流器的损耗
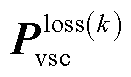，代入式（3）求解直流配电网线性潮流
。
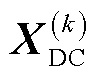（2）利用提出的差异化网损补偿方法分别更新内层交流节点和直流节点的注入功率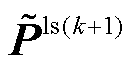
、
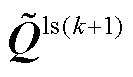和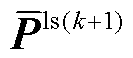
。
（3）更新VSC的潮流信息，即主从控制的主换流站或下垂控制换流站的有功功率注入。
（4）利用式（10）求解交直流配电网在第k次内层迭代的定点不平衡量，同时，利用式（5）求解VSC换流站潮流的不平衡量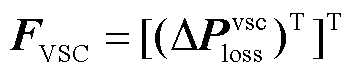
，若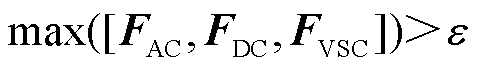
，则将步骤（2）和步骤（3）的新值返回给步骤（1）执行下一次迭代；反之转到步骤3）。
3）将配电网平衡节点的注入功率传递给边界节点，更新交直流输电网的节点输入信息。
4）求解交直流输电网的有损潮流，并计算第k次内层迭代的定点不平衡量，其计算过程与步骤（1）～步骤（4）相同，直到满足收敛条件后转入步骤5）。
5）计算第t次外层迭代的定点不平衡量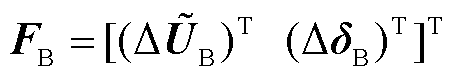
并判断其收敛性，若
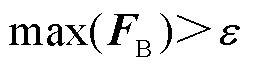则重新执行步骤2）；反之算法结束，输出结果。
本节首先分析了不同模型的性能差异，从计算精度、收敛速度、求解效率三个维度对所提模型的优越性进行了充分的论证；其次讨论了所提模型在不同规模和电网类型中的适用性和稳健性；最后验证了所提模型在不同控制策略和优化目标下的应用价值和潜力。实验所需的程序在Matlab 2020b环境中编译，使用的计算机处理器为AMD4800H CPU @3.2 GHz，内存RAM为16 GB。为方便表述，本文将两种基于近似估计法的有损潮流模型记为CEM[27]和VEM[28]，其中CEM利用电流信息计算损耗，VEM利用电压信息计算损耗。将提出的基于直接推导法的有损潮流模型记为IM，将提出的基于联合补偿法的有损潮流模型记为PM1和PM2，分别对应式（29）和式（30）。本文根据已有的标准测试系统和实际电网案例修改得到一系列不同规模的柔性互联输配一体化电网，用T&D-1到T&D-10进行编号，网络参数信息见附表1和附表2。算法收敛系数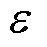
=10-8。
将一体化电网分为交流输电网、直流输电网、交流配电网和直流配电网四种类型，分别验证所提模型在各子系统中的精度优势。为保证模型对比不受其他网络类型的干扰，实验过程中需要遵循控制变量的原则，比如分析交流输电网时，直流输电网以及交直流混合配电网均使用传统牛拉法作为基准。为此，选取附表2中的五个不同规模的柔性互联输配一体化电网作为此节的研究案例，包括T&D-2、T&D-4、T&D-7、T&D-8和T&D-10。
对于交流电网本文采用五种模型，包括CEM、VEM、IM、PM1和PM2。对于直流电网采用两种模型，包括VEM和IM。图6和图7分别展示了不同网络所有潮流信息的误差均值，包括节点电压幅值、节点电压相角和支路有功、无功功率。为全面衡量不同模型的整体精度表现，使用不同类型的误差指标进行评价，包括平均绝对误差（Mean Absolute Error, MAE）、平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）、均方误差（Mean Square Error, MSE）和方均根误差（Root Mean Square Error, RMSE），相应的计算公式为
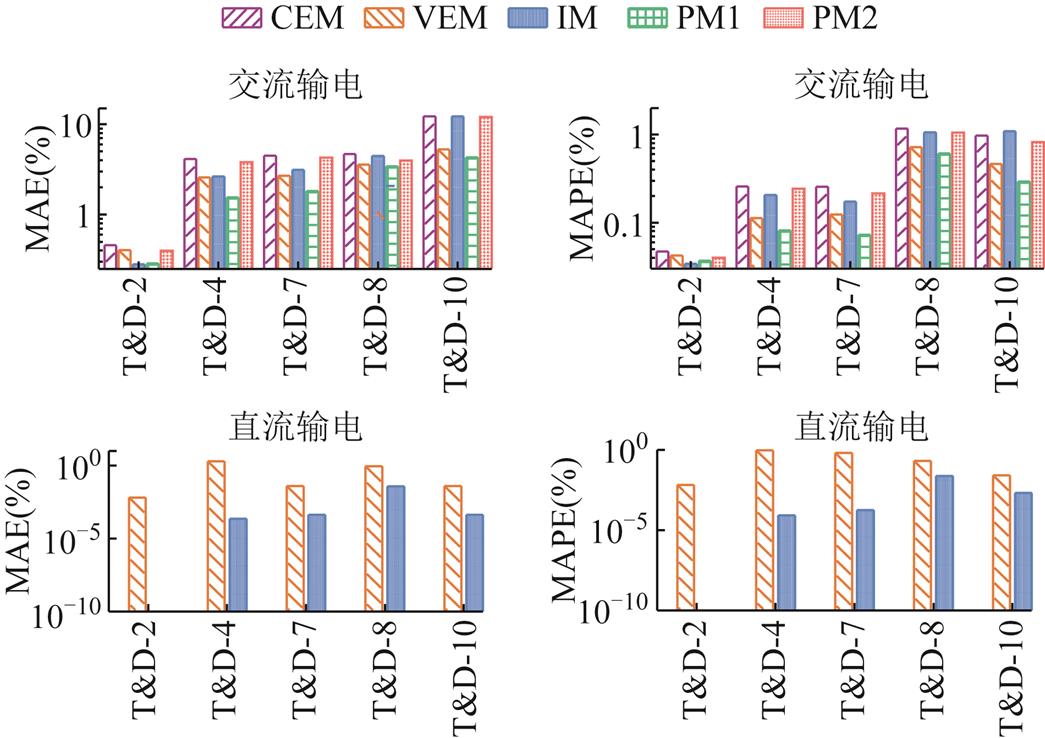
图6 交（直）流输电网的潮流误差对比
Fig.6 Comparison of power flow errors for hybrid AC(DC) transmission power grids
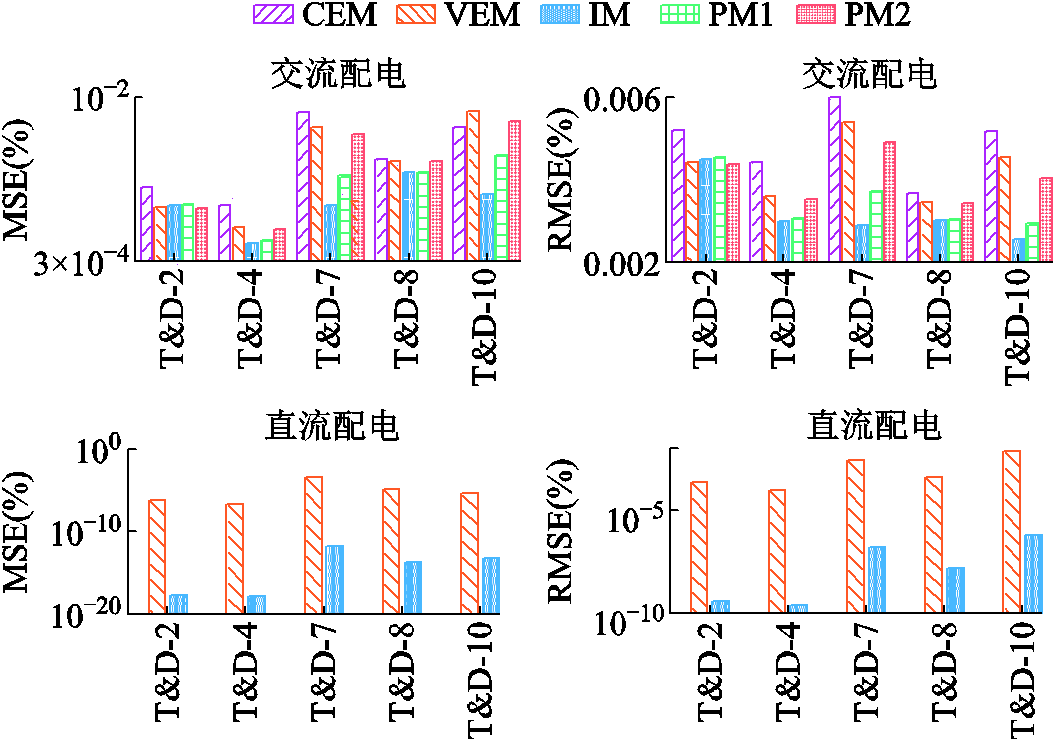
图7 交（直）流配电网的潮流误差对比
Fig.7 Comparison of power flow errors for hybrid AC(DC) distribution networks
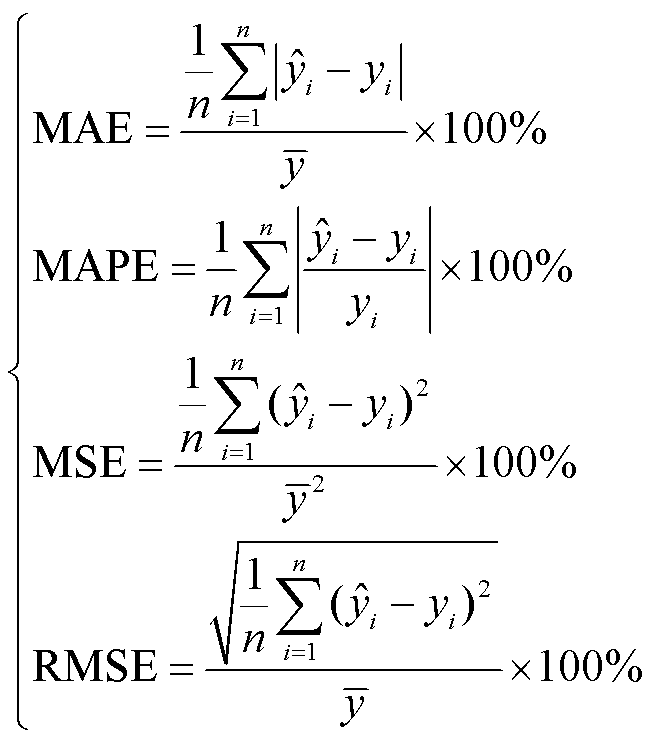（32）
式中，n为样本数量；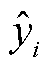
为估计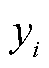值；
为真实值；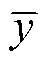
为样本平均值。
对于交流电网，以图6的T&D-2为例，PM1模型与IM模型在小规模输电网中都表现出较高的精度，但随着电网规模扩大和互联程度加深，PM1模型的误差表现优于IM模型及其他对比模型。同理，从图7可以看出，对于T&D-2和T&D-4的小型交流配电网，PM1模型和IM模型的性能差异不大，但随着配电网规模扩大和数量增多，比如T&D-7和T&D-10，PM1模型的性能明显降低，而IM模型始终能保持更小的误差。对于直流电网，结合图6和图7可看出，不论是输电网还是配电网，也不论系统规模的复杂程度，IM模型的误差始终小于VEM模型。
由于系统规模、网络类型和线路电气特性的差异，导致模型之间存在一定的性能偏差。由式（6）可知，交流网损取决于节点电压和支路阻抗，直流网损取决于节点电压和支路电阻。对于直流输电网、配电网和小规模交流输电网而言，它们的共同特点是网损较小，且支路不存在电抗或电抗较小，此时与电压相位有关的网损分量远小于电压幅值。因此，仅考虑电压幅值而忽略相位的直接推导法对潮流误差的影响较小，因此IM模型在这三类网络中的误差表现优于VEM和PM1法。
然而，复杂大规模交流输电网满足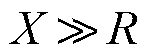
，此时与电压幅值有关的网损分量明显大于与电压相位有关的，导致IM模型的精度变差。与之相反，本文提出的PM1模型可以对解耦的有功、无功网损进行差异化补偿，从而进一步提升有损潮流的精度。一方面，根据损耗公式（6），不同于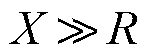，Uij与dij在数值上更为接近，因此交流输电网的无功损耗一般大于有功损耗。此时与电压相位有关的有功网损分量小于无功网损分量，因此可以采用IM模型计算有功网损。另一方面，无功网损会显著影响有功功率的分布并进一步增大有功损耗。因此，可以使用VEM模型计算无功损耗，有效降低其对有功功率误差的不确定性。
综上所述，本文所提的网损差异化补偿体现在两方面：①对交流输电网的有功、无功损耗进行差异化补偿；②对输、配电网损耗进行差异化补偿。其中，交流输电网使用提出的PM1模型，直流输电网、交流配电网和直流配电网使用提出的IM模型，该组合构成了柔性互联输配一体化电网的精细化有损潮流模型。
为验证所提模型可以获得比任何单一模型更好的精度，将柔性互联输配一体化电网视为一个整体，选取两种对比模型来比较一体化电网的边界和全局潮流的求解精度：①对比模型1：所有电网均使用提出的IM模型；②对比模型2：所有电网均使用文献[28]中的VEM模型。
不同模型的输-配边界节点的潮流误差对比见表1。可以看出，由于PM1模型解得的边界节点电压比VEM和IM模型更准确，同时IM模型求解的边界节点功率比VEM更准确，验证了所提差异化模型在求解边界潮流方面的精度优势。不同模型的全局潮流误差对比见表2。结合4.2节中的讨论，从表2可以看出所提方法的全局潮流精度和稳定性始终优于对比模型。与之相反，由于单一的补偿方法无法兼顾输、配电网的网损特性，导致对比模型的求解精度较低且难以保持稳定。以T&D-8为例，对比模型1使用IM模型，不仅不能发挥其在配电网中的优势，反而放大了其在输电网中的劣势，误差甚至超过了对比模型2。而在T&D-9中却相反，对比模型2的误差大于对比模型1，这说明使用单一的VEM模型也会出现类似的问题。综上所述，对于柔性互联的输配一体化电网，本文提出的差异化模型比一刀切的模型表现出更好的精度优势。
表1 不同模型的边界潮流误差对比
Tab.1 Comparison of boundary power flow errors of different models （%）
模型符号T&D-3T&D-7T&D-8T&D-9T&D-10 本文UB1.18×10-56.12×10-33.39×10-31.52×10-31.79×10-3 dB5.78×10-33.05×10-21.57×10-26.16×10-21.84×10-1 PB5.78×10-31.69×10-31.68×10-28.80×10-42.04×10-2 QB2.60×10-35.12×10-31.71×10-22.20×10-32.32×10-2 MAPEB2.23×10-31.08×10-21.32×10-21.66×10-25.73×10-2 对比模型1UB1.21×10-57.39×10-35.62×10-31.14×10-34.72×10-3 dB5.94×10-33.44×10-22.60×10-22.46×10-14.27×10-1 PB5.24×10-41.68×10-34.40×10-21.22×10-22.15×10-2 QB2.60×10-35.06×10-31.17×10-21.48×10-22.50×10-2 MAPEB2.27×10-31.21×10-22.19×10-26.86×10-21.19×10-1 对比模型2UB3.56×10-55.71×10-37.85×10-31.23×10-21.67×10-3 dB1.86×10-25.83×10-21.54×10-24.22×10-17.14×10-1 PB6.91×10-42.63×10-21.54×10-21.38×10-35.24×10-2 QB2.53×10-33.34×10-21.58×10-23.04×10-39.86×10-3 MAPEB5.47×10-33.09×10-21.36×10-21.10×10-11.94×10-1
表2 不同模型的全局潮流误差对比
Tab.2 Comparison of global power flow errors of different models （%）
模型符号T&D-3T&D-7T&D-8T&D-9T&D-10 本文UG1.44×10-52.46×10-30.0321.87×10-31.05×10-3 dG0.9180.6850.3250.7450.624 PLG1.02×10-30.0170.3240.0160.021 QLG1.8204.3828.8214.3138.519 MAPEG0.6841.2722.3751.2692.291 对比模型1UG1.58×10-53.25×10-30.0510.0133.13×10-3 dG0.9180.7030.3500.8490.643 PLG1.02×10-30.0190.7860.0540.023 QLG1.8204.3998.9958.9958.543 MAPEG0.6851.2812.5451.3232.303 对比模型2UG2.32×10-55.39×10-30.0351.87×10-36.59×10-3 dG0.9190.6930.3280.7850.670 PLG3.95×10-30.1080.6380.0300.118 QLG1.8516.1428.6725.4028.770 MAPEG0.6931.7372.4181.5552.391
选取三个不同规模的算例论证所提模型在收敛性能和计算效率方面的优势，结果见表3和表4。对于交直流混合输（配）电网，本文使用统一迭代法，因此交、直流的迭代保持同步，属于内层迭代，而输-配协同求解属于外层迭代。
从表3可以看出，对于输电网的内层迭代过程，所提模型会出现迭代次数大于对比模型2的情况。对于外层迭代过程，所提模型的迭代次数始终小于两个对比模型。结合表3和表4，尽管所提模型在内层的收敛速度与对比模型2相比不具有明显优势，但所提模型的计算复杂度较低，因此整体的求解时间依然低于对比模型2。此外，虽然对比模型1的计算复杂度最低，但在输电网的内层迭代次数最多，导致求解时间略长于所提模型。综合来看，本文提出的模型在收敛性能方面整体优于现有模型。
表3 不同模型的收敛速度
Tab.3 Convergence speed for different models
测试系统网络类型内层迭代次数外层迭代次数 本文对比模型1对比模型2本文对比模型1对比模型2 T&D-5输电454333 配电444 T&D-8输电101410556 配电777 T&D-10输电12149445 配电888
表4 不同模型的计算时间
Tab.4 Computational time for different models
测试系统求解时间/ms 本文对比模型1对比模型2 T&D-562.763.975.2 T&D-8245.3254.5264.5 T&D-10267.8280.9340.3
4.2节、4.3节已经验证了所提模型在确定性条件下的精度优势。除此之外，有必要分析所提模型在面对不确定性或扰动的情况下，是否能够保持其预期的功能和性能。为验证所提出模型在不同参数下的鲁棒性，本节探讨了三种不确定性阻塞场景，包括线路阻抗的变化、随机N-1故障、源-荷的双重波动。其中，前两者改变了线路的物理特性和拓扑结构，后者则改变了电力系统的运行条件，从不同角度描述了电力系统运行状态的动态随机特性。为了分析不同模型在不同阻抗参数下的误差敏感程度，本节引入误差灵敏度指标（Error Sensitivity Index, ESI），其表达式为
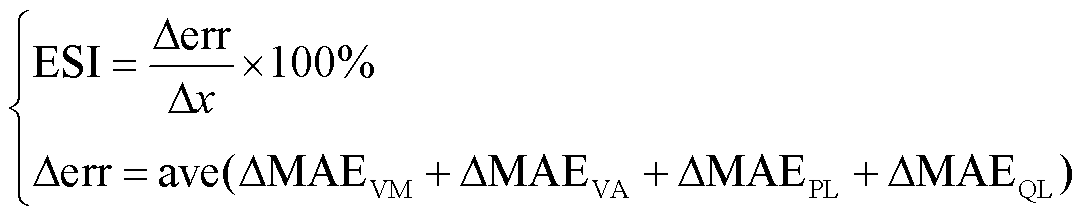（33）
式中，ESI为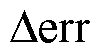
随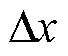
的单位变化量，它是一种趋势类指标，可以表征不同模型的潮流误差对系统运行条件变化的敏感程度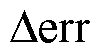；为误差变化量的均值，它涵盖了所有的潮流误差信息，即输（配）电网的节点电压幅值（VM）、节点电压相位（VA）、支路有功功率（PL）和无功功率（QL）的MAE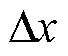；为参数的单位变化量。显然，模型对参数的误差灵敏度指标越小意味着该模型的抗干扰能力越强。为此，设置了T&D-7和T&D-9作为研究案例，通过改变交流线路和直流线路的电阻和电抗构建不同的场景，具体信息见表5。其中，直流线路与交流线路的电阻变化范围一致。括号中的数值代表参数的变化范围和步长。
表5 线路阻抗变化范围
Tab.5 Variation range of branch impedance
测试系统网络类型电阻变化(pu)电抗变化(pu) 案例1: T&D-7输电网[0.6,0.05,1.1][0.8,0.05,1.3] 配电网[0.5,0.15,2][0.5,0.2,2.5] 案例2: T&D-9输电网[0.8,0.04,1.2][0.9,0.02,1.1] 配电网[0.5,0.2,2.5][0.5,0.3,3.5]
交流电网和直流电网的潮流误差及相应的灵敏度指标随支路参数的变化情况如图8和图9所示。对于交流电网，横向对比图8a～图8d可看出，随着支路参数的变化，本文所提模型在输（配）电网的潮流误差均明显小于对比模型。横向对比图8e～图8h可以看出，所提模型比对比模型的误差灵敏度更低，表明其对支路阻抗的变化有更强的抗干扰能力。同理，对于直流电网，从图9中可以看到本文所提模型的潮流误差和对支路电阻的灵敏度都显著低于对比模型。此外，对于案例1中的交流电网，如图8a、图8b所示，对比模型2的潮流误差始终低于对比模型1，然而直流电网的结果却相反，对比模型1的潮流误差低于对比模型2，如图9a、图9b所示。这一现象进一步证明了传统一刀切的方法无法同时兼顾输配一体化电网内部复杂的运行特性，因此难以准确量化不同电网的损耗，导致求解精度较低。
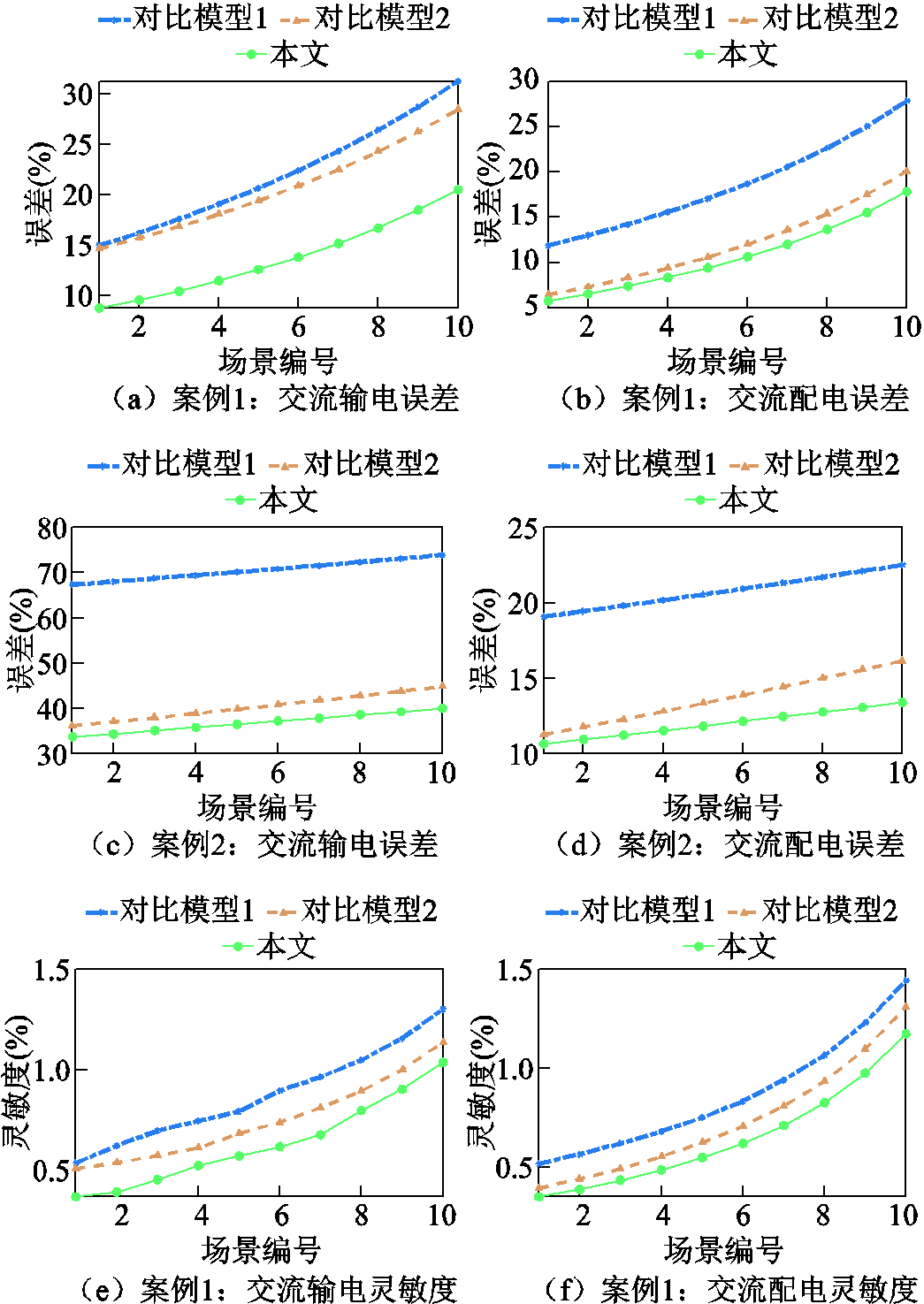
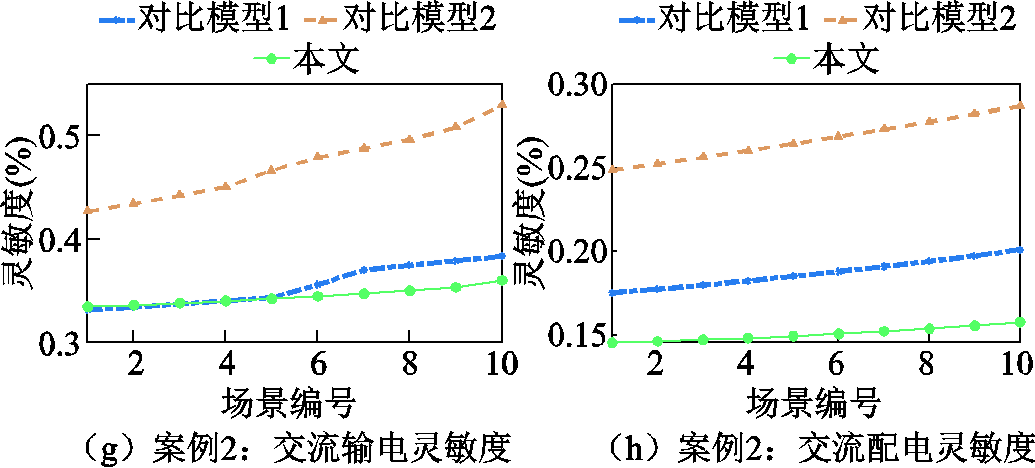
图8 阻抗变化下的交流输（配）电网潮流误差趋势及灵敏度曲线
Fig.8 Trends and sensitivity curves of AC transmission-distribution power flow errors under impedance variation
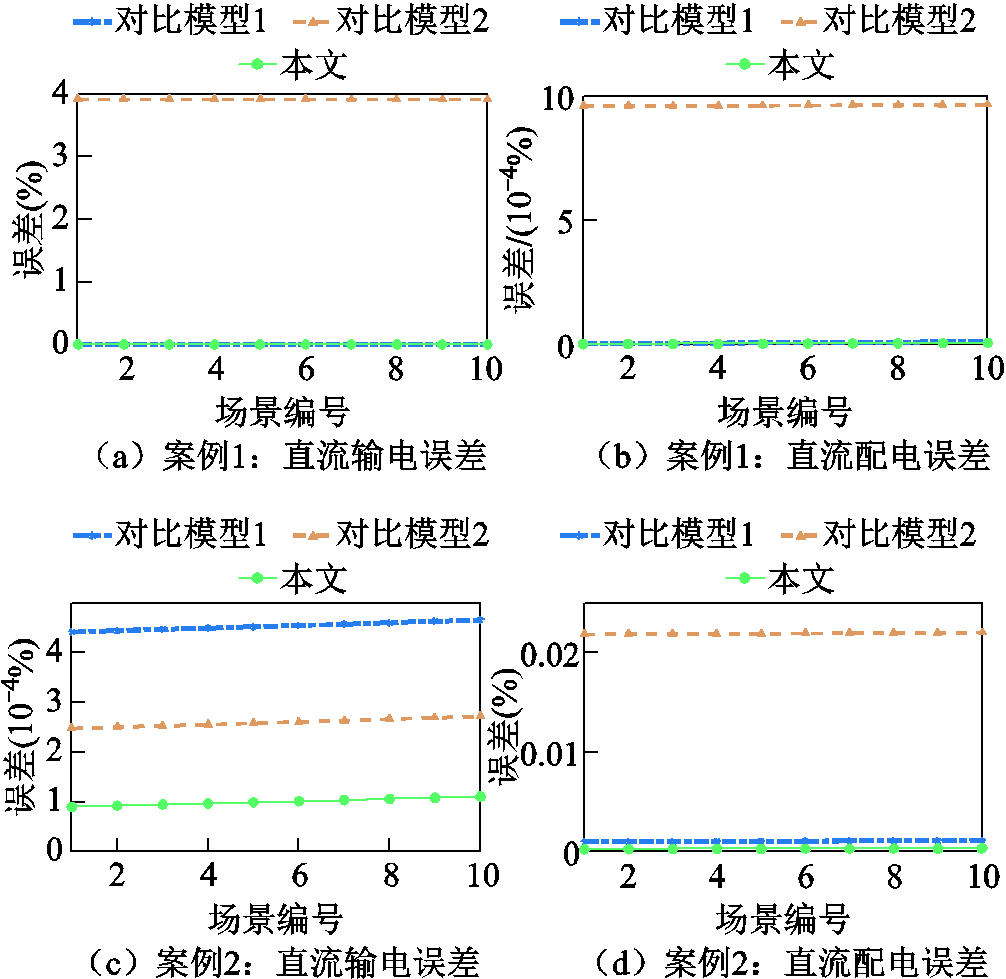
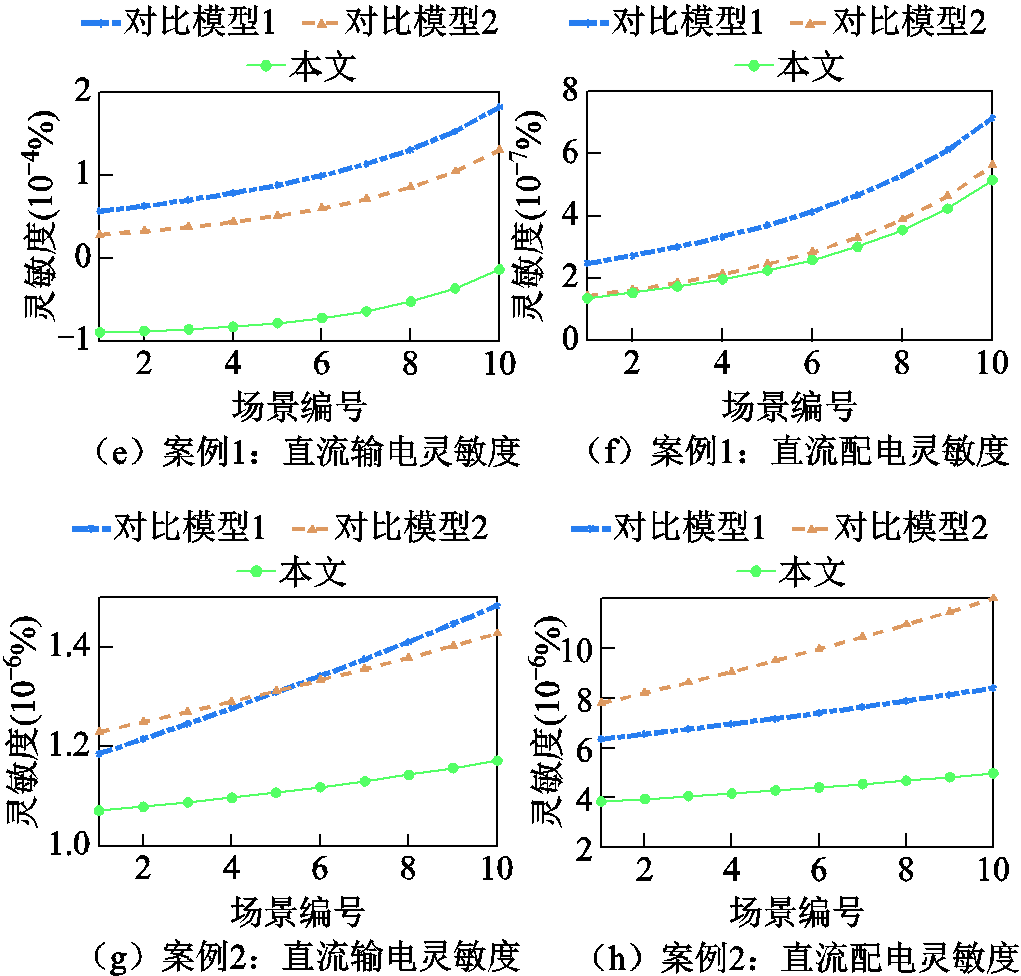
图9 电阻变化下的直流输（配）电网潮流误差趋势及灵敏度曲线
Fig.9 Trends and sensitivity curves of DC transmission-distribution power flow errors under resistance variation
除了考虑线路电气参数的变化外，源-荷的双重不确定性和电网的停电事件也会影响电网的运行状态。因此，有必要检验提出的模型在上述随机场景下的稳定性。选取T&D-6和T&D-10系统作为测试案例，使用均匀分布生成1 000组随机N-1故障场景，使用拉丁超立方抽样法在预定范围内生成1 000组随机源-荷场景。不同网络类型在随机N-1故障场景和随机源-荷场景下的全局潮流误差结果见表6。
表6 不确定性场景下的全局潮流误差结果
Tab.6 Global errors for uncertainty scenarios （%）
测试系统网络类型随机N-1故障场景 本文对比模型1对比模型2 T&D-6交流输电9.8210.2810.99 交流配电3.778.873.83 直流输电2.54×10-33.75×10-30.88 直流配电6.65×10-106.65×10-42.18×10-4 T&D-10交流输电22.1325.9123.63 交流配电0.332.681.37 直流输电4.87×10-62.57×10-51.71×10-2 直流配电7.48×10-53.51×10-57.39×10-3 测试系统网络类型随机源-荷场景 本文对比模型1对比模型2 T&D-6交流输电9.7810.2010.97 交流配电3.197.973.28 直流输电1.08×10-32.62×10-30.85 直流配电4.99×10-104.99×10-101.63×10-4 T&D-10交流输电20.1224.1422.90 交流配电0.502.681.29 直流输电3.35×10-62.30×10-31.71×10-3 直流配电2.79×10-46.55×10-41.10×10-2
可以看出，不论是交流电网还是直流电网，所提模型的求解精度始终高于两个对比模型。同时，所提模型在不同规模的案例中都有较好的表现，证明了其在随机源-荷条件下的适用性和稳健性。
设计四个算例验证所提模型在不同控制策略和优化目标下的应用价值和潜力。针对交流电网侧换流站考虑了主从控制策略和下垂控制策略，针对输电网和配电网的业务需求构建了两类优化运行问题，具体描述如下。
1）算例1：T&D-1
控制策略：输电网侧换流站采用主从控制，配电网侧换流站采用主从控制。优化目标：输电网以发电成本最小为目标，配电网以网损最小为目标。
2）算例2：T&D-4
控制策略：输电网侧换流站采用下垂控制，配电网侧换流站采用主从控制。优化目标：输电网以网损最小为目标，配电网以发电成本最小为目标。
3）算例3：T&D-5
控制策略：输电网侧换流站采用下垂控制，配电网侧换流站采用主从+下垂控制。优化目标：输电网以发电成本最小为目标，配电网以网损最小为目标。
4）算例4：T&D-9
控制策略：输电网侧换流站采用主从控制，配电网侧换流站采用主从+下垂控制。优化目标：输电网以网损最小为目标，配电网以发电成本最小为目标。
不同算例的相对误差结果见表7。可以看出，面对不同的控制策略和不同的优化目标，所提模型的优化结果误差均小于对比模型，这意味着所提模型可以为决策者提供更合理的经济调度方案。
表7 使用不同模型的优化结果的相对误差
Tab.7 Relative error of optimization results using different models （%）
测试系统网络类型本文对比模型1对比模型2 T&D-1输电网1.65×10-34.59×10-39.89×10-3 配电网2.49×10-23.17×10-22.69×10-2 T&D-4输电网0.1640.1880.203 配电网0.1240.1250.131 T&D-5输电网1.10×10-21.63×10-21.58×10-2 配电网0.1140.1340.115 T&D-9输电网1.12×10-24.10×10-22.96×10-2 配电网3.45×10-28.21×10-28.79×10-2
本文面向多端柔性互联的输配一体化电网提出了一种精细化的有损潮流模型，充分考虑了系统内部复杂的运行方式，实现了输-配电网和交、直流电网损耗补偿的差异化建模。与传统的基于一刀切网损补偿的有损潮流模型相比，所提的差异化建模方法能够兼顾不同电网层级和网络类型的特点。一系列仿真结果表明所提模型在计算精度、收敛速度和稳健性方面拥有出色的性能，在面对不同的控制模式和优化目标下表现出良好的适用性和有效性。
未来的研究可以考虑将提出的模型集成到柔性互联输配一体化电网的不确定性分析及其协同优化等领域。
附 录
附表1 交直流输电/配电测试系统参数
App.Tab.1 Parameters of AC/DC transmission/distribution test systems
测试系统交流系统直流系统主从控制VSC编号下垂控制VSC编号普通VSC编号 网络数量基准容量基准电压/kV网络数量基准容量基准电压/kV IEEE 5PtP- Master11003451100±3452—1 MTDC-Master11003451100±3452—1,3 MTDC-Droop11003451100±34521,3— IEEE RTS791100138/2302100±345—3,61,2,4,5 IEEE 3011001351100±1355—1,2,3,4 IEEE RTS963100138/2302100±150/±3001,4—2,3,7,8,9 IEEE [57+118+162]3100138/230/3452100±3456,223,12,18,26,301,2,4,5,7-11,13-17,19-21,23-25,27-29,31-33 New England Test System21003451100±3453—1,2,4,5,6,7,8,9,10 Nordic Test System31004001100±400246,9,14,20,23,261,2,3,4,5,7,8,10,11,12,13,15,16,17,18,19,21,22,24,25,27,28 IEEE 33PtP110012.661100±101—2 MTDC110012.661100±1012,3— IEEE [33+69]210012.663100±102,4,7—1,3,5,6,8 IEEE 12321004.163100±31,4,63,72,5,8
注：PtP表示两终端互联方式；MTDC表示多终端互联方式。Master表示主从控制模式；Droop表示下垂控制模式。IEEE [57+118+162]由IEEE 57、IEEE 118和IEEE 162三个标准输电系统互联组成。IEEE [33+69]由IEEE 33和IEEE 69两个标准配电系统互联组成。
附表2 柔性互联的输配一体化测试系统信息
App.Tab.2 Information for integrated transmission and distribution grids with multi-terminal flexible interconnected
案例名称输电系统名称配电系统名称配电系统数量边界节点编号 T&D-1IEEE 5 PtP- MasterIEEE 33 PtP1(3) T&D-2IEEE 5 MTDC-MasterIEEE 33 MTDC1(3) T&D-3IEEE 5 MTDC-DroopIEEE 1231(2,3) T&D-4IEEE RTS79IEEE 33 PtP2(9)，(11)，(12) T&D-5IEEE RTS79IEEE 33 MTDC4(3)，(6)，(8)，(10)，(12)，(15) T&D-6IEEE30IEEE [33+69] MTDC4(5,6)，(9,10)，(14,15)，(26,27) T&D-7IEEE RTS96IEEE 33 MTDC3(2)，(5)，(8) IEEE [33+69]6(11,12)，(17,21)，(22,23)，(35,36)，(45,46)，(48,49) T&D-8IEEE [57+118+162]IEEE [33+69]5(4,7)，(21,22)，(36,37)，(45,46)，(120,121) IEEE 1235 (24,26)，(39,40)，(82,83)，(125,126)，(144,146) T&D-9New England Test SystemIEEE 1235(5,6)，(10,11)，(13,14)，(17,18)，(34,35) T&D-10Nordic Test SystemIEEE [33+69]4(6)，(20)，(26)，(35) IEEE 1235(44,45)，(54,55)，(60,61)，(64,65)，(71,72)
注：(X)和(X,Y)分别表示与输电网相连的配电网为辐射状和环状。
参考文献
[1] 姚良忠, 吴婧, 王志冰, 等. 未来高压直流电网发展形态分析[J]. 中国电机工程学报, 2014, 34(34): 6007-6020.Yao Liangzhong, Wu Jing, Wang Zhibing, et al. Pattern analysis of future HVDC grid development[J]. Proceedings of the CSEE, 2014, 34(34): 6007-6020.
[2] 束洪春, 邵宗学, 赵伟, 等. 含柔性直流的交直流混联电力系统紧急频率控制研究[J]. 电工技术学报, 2023, 38(20): 5590-5604.Shu Hongchun, Shao Zongxue, Zhao Wei, et al. Research on emergency power control of AC-DC hybrid power system with flexible DC[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5590-5604.
[3] 陈一丰, 唐坤杰, 董树锋, 等. 输配一体化潮流计算收敛性分析及提升方法[J]. 中国电机工程学报, 2022, 42(20): 7524-7535.Chen Yifeng, Tang Kunjie, Dong Shufeng, et al. Convergence analysis and promotion method of power flow calculation of integrated transmission and distribution networks[J]. Proceedings of the CSEE, 2022, 42(20): 7524-7535.
[4] 辛保安, 郭铭群, 王绍武, 等. 适应大规模新能源友好送出的直流输电技术与工程实践[J]. 电力系统自动化, 2021, 45(22): 1-8.Xin Baoan, Guo Mingqun, Wang Shaowu, et al. Friendly HVDC transmission technologies for large-scale renewable energy and their engineering practice[J]. Automation of Electric Power Systems, 2021, 45(22): 1-8.
[5] 唐巍, 张起铭, 张璐, 等. 新型配电系统多层级交直流互联理念、关键技术与发展方向[J]. 电力系统自动化, 2023, 47(6): 2-17.Tang Wei, Zhang Qiming, Zhang Lu, et al. Concept, key technologies and development direction of multilevel AC/DC interconnection in new distribution system[J]. Automation of Electric Power Systems, 2023, 47(6): 2-17.
[6] 郑宗强, 韩冰, 闪鑫, 等. 输配电网高级应用协同运行关键技术分析[J]. 电力系统自动化, 2017, 41(6): 122-128.Zheng Zongqiang, Han Bing, Shan Xin, et al. Analysis on key technologies for coordinated operation of advanced application software in transmission and distribution network[J]. Automation of Electric Power Systems, 2017, 41(6): 122-128.
[7] Simpson-Porco J W. Lossy DC power flow[J]. IEEE Transactions on Power Systems, 2018, 33(3): 2477-2485.
[8] Neumann F, Hagenmeyer V, Brown T. Assessments of linear power flow and transmission loss approximations in coordinated capacity expansion problems[J]. Applied Energy, 2022, 314: 118859.
[9] Sood P, Tylavsky D J, Qi Y. Improved dc network model for contingency analysis[C]//2014 North American Power Symposium (NAPS), Pullman, WA, USA, 2014: 1-6.
[10] Fatemi S M, Abedi S, Gharehpetian G B, et al. Introducing a novel DC power flow method with reactive power considerations[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3012-3023.
[11] Qi Yingying, Shi Di, Tylavsky D. Impact of assumptions on DC power flow model accuracy[C]// 2012 North American Power Symposium (NAPS), Champaign, IL, USA, 2012: 1-6.
[12] 马钰, 韦钢, 李扬, 等. 考虑孤岛源-荷不确定性的直流配电网可靠性评估[J]. 电工技术学报, 2021, 36(22): 4726-4738.Ma Yu, Wei Gang, Li Yang, et al. Reliability evaluation of DC distribution network considering islanding source-load uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4726-4738.
[13] Guo Libang, Ding Yi, Bao Minglei, et al. Nodal reliability evaluation for a VSC-MTDC-based hybrid AC/DC power system[J]. IEEE Transactions on Power Systems, 2020, 35(3): 2300-2312.
[14] Tang Kunjie, Dong Shufeng, Zhu Chengzhi, et al. Affine arithmetic-based coordinated interval power flow of integrated transmission and distribution networks[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 4116-4132.
[15] 房宇轩, 胡俊杰, 马文帅. 计及用户意愿的电动汽车聚合商主从博弈优化调度策略[J/OL]. 电工技术学报, 2023: 1-13. https://doi.org/10.19595/j.cnki. 1000-6753.tces.230923.Fang Yuxuan, Hu Junjie, Ma Wenshuai. Optimal dispatch strategy for electric vehicle aggregators based on stackelberg game theory considering user intention[J/OL]. Transactions of China Electrotechnical Society, 2023: 1-13. https://doi.org/10.19595/j.cnki. 1000-6753.tces.230923
[16] 李振坤, 钱晋, 符杨, 等. 基于负荷聚合商优选分级的配电网多重阻塞管理[J]. 电力系统自动化, 2021, 45(19): 109-116.Li Zhenkun, Qian Jin, Fu Yang, et al. Multiple congestion management for distribution network based on optimization classification of load aggregators[J]. Automation of Electric Power Systems, 2021, 45(19): 109-116.
[17] 李勇, 凌锋, 乔学博, 等. 基于网侧资源协调的自储能柔性互联配电系统日前-日内优化[J]. 电工技术学报, 2024, 39(3): 758-773.Li Yong, Ling Feng, Qiao Boxue. Day-ahead and intra-day optimization of flexible interconnected distribution system with self-energy storage based on the grid-side resource coordination[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 758-773.
[18] 胡珺如, 窦晓波, 李晨, 等. 面向中低压配电网的分布式协同无功优化策略[J]. 电力系统自动化, 2021, 45(22): 47-54.Hu Junru, Dou Xiaobo, Li Chen, et al. Distributed cooperative reactive power optimization strategy for medium-and low-voltage distribution network[J]. Automation of Electric Power Systems, 2021, 45(22): 47-54.
[19] Lin Chenhui, Wu Wenchuan, Zhang Boming, et al. Decentralized reactive power optimization method for transmission and distribution networks accommodating large-scale DG integration[J]. IEEE Transactions on Sustainable Energy, 2017, 8(1): 363-373.
[20] 蔡瑶, 卢志刚, 潘尧, 等. 计及多重差异的交直流混合多能微网多时间尺度优化调度[J/OL]. 电工技术学报, 2023: 1-19. https://doi.org/10.19595/j. cnki.1000-6753.tces.230645.Cai Yao, Lu Zhigang, Pan Yao. Multi-time-scale optimal scheduling of AC-DC hybrid multi-energy microgrid considering multiple differences[J/OL]. Transactions of China Electrotechnical Society, 2023: 1-19. https://doi.org/10.19595/j.cnki.1000-6753.tces. 230645.
[21] Zhong Haiwang, Zhang Guanglun, Tan Zhenfei, et al. Hierarchical collaborative expansion planning for transmission and distribution networks considering transmission cost allocation[J]. Applied Energy, 2022, 307: 118147.
[22] Stott B, Jardim J, Alsac O. DC power flow revisited[J]. IEEE Transactions on Power Systems, 2009, 24(3): 1290-1300.
[23] 王虹富, 王毅, 高崇, 等. 基于网损等值负荷模型的直流潮流迭代算法[J]. 电力系统自动化, 2015, 39(1): 99-103.Wang Hongfu, Wang Yi, Gao Chong, et al. Iterative algorithm of DC power flow based on network loss equivalent load model[J]. Automation of Electric Power Systems, 2015, 39(1): 99-103.
[24] 何天雨, 卫志农, 孙国强, 等. 基于网损等值负荷模型的改进直流最优潮流算法[J]. 电力系统自动化, 2016, 40(6): 58-64.He Tianyu, Wei Zhinong, Sun Guoqiang, et al. Modified direct current optimal power flow algorithm based on net loss equivalent load model[J]. Automation of Electric Power Systems, 2016, 40(6): 58-64.
[25] 卫志农, 朱梓荣, 赵静波, 等. 电力系统半线性与全线性最优潮流模型[J]. 电力系统自动化, 2018, 42(14): 107-114.Wei Zhinong, Zhu Zirong, Zhao Jingbo, et al. Semi-linearized model and full-linearized model of optimal power flow in power system[J]. Automation of Electric Power Systems, 2018, 42(14): 107-114.
[26] 卫志农, 张清松, 赵静波, 等. 电力系统线性化模型研究综述与改进[J]. 电网技术, 2017, 41(9): 2919-2927.Wei Zhinong, Zhang Qingsong, Zhao Jingbo, et al. Review and improvement of power system linearization models[J]. Power System Technology, 2017, 41(9): 2919-2927.
[27] 赵静波, 卫志农, 刘建坤, 等. 电力系统线性化动态最优潮流模型[J]. 电力系统自动化, 2018, 42(20): 86-92.Zhao Jingbo, Wei Zhinong, Liu Jiankun, et al. Linearized dynamic optimal power flow model for power system[J]. Automation of Electric Power Systems, 2018, 42(20): 86-92.
[28] 李少岩, 张友好, 顾雪平. 基于梯级流水法与裕度线性化交流潮流的目标骨干网架优化方法[J]. 电网技术, 2023, 47(7): 2788-2799.Li Shaoyan, Zhang Youhao, Gu Xueping. Skeleton network optimization method based on cascade flow method and margin linearization AC power flow model[J]. Power System Technology, 2023, 47(7): 2788-2799.
[29] Schweitzer E, Saha S, Scaglione A, et al. Lossy DistFlow formulation for single and multiphase radial feeders[J]. IEEE Transactions on Power Systems, 2020, 35(3): 1758-1768.
[30] Schweitzer E, Scaglione A, Monti A, et al. Automated generation algorithm for synthetic medium voltage radial distribution systems[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2017, 7(2): 271-284.
[31] Fernández-Pérez J C, Echavarren Cerezo F M, Rouco Rodríguez L. Linear power flow algorithm with losses for multi-terminal VSC AC/DC power systems[J]. IEEE Transactions on Power Systems, 2022, 37(3): 1739-1749.
[32] Yang Jingwei, Zhang Ning, Kang Chongqing, et al. A state-independent linear power flow model with accurate estimation of voltage magnitude[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3607-3617.
[33] Beerten J, Cole S, Belmans R. A sequential AC/DC power flow algorithm for networks containing Multi-terminal VSC HVDC systems[C]//IEEE PES General Meeting, Minneapolis, MN, USA, 2010: 1-7.
Abstract Lossy power flow model is an extension of the lossless linear power flow (LPF) model and has become one of the mainstream methods for approximation calculation and analysis in power systems. Mathematically, it is defined as a fixed-point iterative problem formulated jointly by the lossless LPF model and the network losses compensation model. Currently, existing network losses compensation models are only oriented to single-region, single-voltage level, and single-type of power grids, and mainly focuses on AC transmission grids. However, the operation modes of the integrated transmission and distribution grid with multi-terminal flexible interconnected are complex, and the network losses characteristics vary significantly. Obviously, existing models would weaken the applicability and effectiveness of the lossy power flow in the integrated transmission and distribution grids, also lead to further deterioration of the mismatch of the transmission and distribution boundary power flow. The reason is that conventional network losses compensation models cannot consider the significant differences of losses characteristics caused by the complexity of grids, which makes it difficult to accurately quantify the impact of the losses on power flow errors at different levels and types of grids. For this reason, a precise lossy power flow model based on two-layer fixed-point iteration is proposed in this paper.
For the problem of inaccurate network losses compensation, this paper fully considers the characteristics of network structure, data attributes and physical features, and proposes precise lossy power flow models for transmission, distribution, AC and DC grids. First, the lossless LPF model is formulated for AC and DC grids. Second, differentiated network losses compensation models are proposed to modify the node power injection according to the characteristics of AC, DC, transmission, and distribution grids. Finally, the modified node power injections are re-substituted into the lossless LPF model and solved iteratively until convergence.
For the mismatch problem of transmission-distribution boundary power flow, the integrated transmission and distribution lossy power flow is formulated as a two-layer fixed-point iterative problem. Among them, the outer fixed-point is the transmission-distribution boundary node, which is used to solve the mismatch problem of power flow between transmission and distribution grids, and the master-slave splitting method is used to solve the problem collaboratively. For the transmission grid power flow calculation, the distribution network is equated to the load, and the boundary node voltage information is solved. For the distribution network power flow calculation, the transmission grid is equated to the source, and the voltage information of the boundary node is utilized as the operating point for the slack node of the distribution network to solve the boundary node power injection. The inner fixed-point is node voltage information in the network to solve the AC/DC lossy power flow based on the proposed network losses compensation model.
The errors and reasons for different lossy power flow models are analyzed in several test cases, and compared in terms of solution accuracy, convergence speed and computational efficiency. The results show that the proposed precise lossy power flow model achieves higher computational accuracy under both deterministic and uncertainty scenarios. In addition, the proposed model is overall better than the existing model in terms of convergence performance and has lower computational complexity. Finally, for different control strategies and optimization objectives, the optimization errors of the proposed model are smaller than those of the conventional models, implying that the proposed model can provide operators with more reasonable economic scheduling decisions.
keywords：Flexible interconnection, transmission and distribution integration, power flow analysis, network losses compensation, fixed-point iteration
DOI: 10.19595/j.cnki.1000-6753.tces.231811
中图分类号：TM744
国家自然科学基金资助项目（52022016）。
收稿日期 2023-10-31
改稿日期 2024-01-21
王 淏 男，1996年生，博士研究生，研究方向柔性互联输配一体化电网的建模和协调运行优化、大数据和人工智能在电力系统中的应用。E-mail：20211101053@cqu.edu.cn
谢开贵 男，1972年生，教授，博士生导师，研究方向为电力和能源系统可靠性、电力和能源系统的规划、电力和能源系统的优化运行等。E-mail：kaiguixie@vip.163.com（通信作者）
（编辑 赫 蕾）