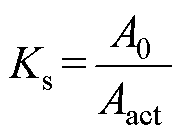 (1)
(1)
摘要 多次短路会逐渐积累绕组机械损伤,最终导致电力变压器损坏。然而,目前缺乏一种量化评估方法来评估此类损伤,这对电网的安全运行构成了威胁。因此,该文提出一种考虑绕组的非线性特点和累积过程的电力变压器绕组短路累积机械损伤评价方法,为评估绕组短路对电力变压器的影响提供了新的途径。该方法采用阻尼比和可靠性损失系数作为特征量,通过指数型曲线来模拟绕组机械弱化过程。同时考虑变压器的初始承受短路的能力、短路电流幅值和故障次数等影响因素,量化了短路损伤与绕组动态机械寿命之间的关系。此外,通过对一台110 kV电力变压器进行多次短路破坏性试验,验证了该评价方法的正确性。最后,阐述了提出的评价方法适用于不同的校核控制方法,并强调了控制阻尼比在减少累积损伤方面的积极作用。
关键词:电力变压器 短路 累积损伤 可靠性 评价
电力变压器出口短路产生的电磁力超过绕组的承受能力时,可能引起变压器损坏、变电站起火,甚至导致电网停电,从而危及电力系统和人身安全。因此,变压器的抗短路能力倍受关注[1]。短路故障引起变压器绕组的机械损伤,其起始原因可能是一次机械破坏,更常见的原因是多次冲击造成的机械变形或绝缘破损[2-3]。通过计算绕组承受单次短路冲击的能力,可以指导变压器的设计制造;而研究绕组的短路累积机械损伤,实现对绕组动态机械性能的评价,并保障其可靠运行同样具有重要意义[4-5]。
然而,由于变压器短路涉及多种物理场,如磁场、机械和热场,精确计算较为困难。同时,短路故障具有较大的破坏性,进行短路试验成本较高,很难通过故障案例或试验得到临界载荷能力[6-7]。因此,研究变压器承受短路能力的方法包括材料和模型试验[8-9]、状态检测与反演[10-12]和仿真研究[13-14]。鉴于制造工艺的特殊性,国家标准、国际电工委员会(International Electrotechnical Commission, IEC)标准和美国电子电机工程师学会(Institute of Electrical and Electronic Engineers, IEEE)标准主要侧重于试验验证的方法[15-17]。尽管高校、研究院和制造厂已完成了较多的研究,但目前行业尚未统一短路强度的标准算法。同时,由于实际变压器的临界承受能力难以准确获得,每次短路故障电流占承受能力的比例也无法确定,作用力的影响难以量化,导致多次短路的累积损伤评价成为行业亟须研究和解决的难题。
变压器短路累积效应的研究主要包括三个方向:长时运行引起绝缘热老化[18]、故障电流下绝缘机械损伤[19]和瞬时冲击绕组变形或稳定性丧失[20]。其中,长时绝缘老化会发展为机械强度和绝缘强度降低,这种累积随变压器使用年限的增长而增加。研究人员通过加速老化研究了不同支撑刚度引起的辐向屈曲临界载荷的变化[19]。还有研究表明,多次足够大的短路电流冲击会在绕组上产生塑性变形并保持不可恢复状态,累积变形量随着冲击次数的增加而稳定[21]。然而,目前这些累积效应的分析方法尚无法指导设计或运行维护工作。
绕组短路累积效应主要体现在材料非线性特征引起的残余变形。针对不同的短路工况和破坏形式,绕组短路累积损伤也存在一定的差异,需要区分判断状态特征量[22-24]。例如,对于内绕组辐向失稳的累积效应,需要重点关注导线和支撑材料的非线性特征,可以通过阻抗变化来判断。而对于绕组轴向倒伏的累积效应,重点关注绝缘材料的非线性和端部支撑压紧作用力的降低,可以通过整体振动反馈来判断。虽然已有相关文献研究了局部特征量、机理和测量方法,但目前尚未形成宏观评估算法。要想总结出一种考虑多次累积冲击损伤的评价方法,需要从整体出发,充分考虑绕组出厂原始承受短路能力和各次冲击的影响,以提出特定的特征量和判断方法。然而,目前关于累积冲击损伤的量化评价研究和报道还非常有限。
为了解决短路累积损伤难以量化的问题,本文提出了一种电力变压器短路累积机械损伤评价算法。该算法基于自定义的可靠性损失系数,以变压器出厂的承受短路的能力、短路电流幅值和故障次数作为研究的输入条件,计算累积短路对绕组机械性能的影响。通过量化某次短路引起的绕组机械性能降低程度,并计算承受某一电流冲击的次数,从而评估短路累积机械损伤的情况。
在评估变压器短路冲击绕组的累积机械损伤时,需要考虑绕组参数和制造控制对其抗短路能力的影响。出厂时的安全系数应被视为研究短路累积损伤的基准。评估某次冲击对绕组机械寿命的影响时,应考虑该次冲击电流占基准承受能力的比例。虽然变压器的运行会导致绝缘老化和结构件振动引起的机械性能降低,但这些降低的机理与故障时的大电流冲击是完全不同的。因此,本文暂不考虑老化和疲劳引起的性能降低,而是重点分析每次大电流冲击引起性能的下降过程,并提出了变压器短路绕组累积机械损伤的评价方法。为了准确描述这种评价方法,本文首先定义了所使用的特征概念和方法。
1.1.1 短路机械强度安全系数
本文使用的安全系数是指绕组承受短路的机械强度安全系数,它被定义为允许值与实际载荷之比,有
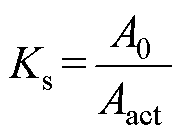 (1)
(1)
式中,Ks为安全系数;A0为考虑一定裕度的允许载荷集合,随短路次数的增加而降低;Aact为实际载荷集合。上述特征量集合包括用于评估强度、刚度和稳定性机械性能的作用力、位移、振动和应力等。
根据国家标准GB 1094.5-2008《电力变压器 第五部分:承受短路的能力》,变压器标准短路试验为每相3次,考虑电流与电磁力关系,提出安全系数控制阈值:假设安全系数的控制值为Kcr,Kcr>1.0,则应满足最大承受电流Imax连续短路3次后,安全系数由Kcr降低至1.00的临界值。由于校核时使用的理论体系可能存在差异,不同算法对应的Kcr绝对值可能会有所差异。然而根据定义,当经历3次冲击后,安全系数将降至1.00,这意味着如果再次发生相同水平的冲击,绕组将面临机械损坏的风险。
变压器绕组承受短路的安全性受到设计参数、制造工艺、短路工况、短路电流幅值和持续时间等多种因素的影响。由于短路试验具有较大的破坏性,无法通过一次试验得到临界值。因此,在进行累积损伤分析时,需要预先确定最大承受电流值IMT,以此值为基准,按一定比例递增电流进行多次短路试验。在完成多次试验后,再进行复算,以获得绕组承受短路的能力。为考虑预判值的偏差,一般会选择70%~120%的比例范围来递增电流进行试验,可以更全面地评估绕组的承受短路的能力,并提供可靠的数据支持。
1.1.2 可靠性损失系数
变压器承受短路冲击后,绕组的机械强度安全系数可能会下降并积累,这主要是由于结构和材料的非线性特性影响所致。其中,结构非线性与绕组的边界条件相关,本文暂不展开讨论。图1展示了绕组中典型的非线性铜导线材料的应力-应变曲线。在初始阶段,应力与应变之间呈线性关系,但随着应变的增加,材料的应力响应逐渐变得非线性。这种非线性特性可能导致绕组在受到冲击后产生变形和应力集中,进而影响其机械强度和稳定性。
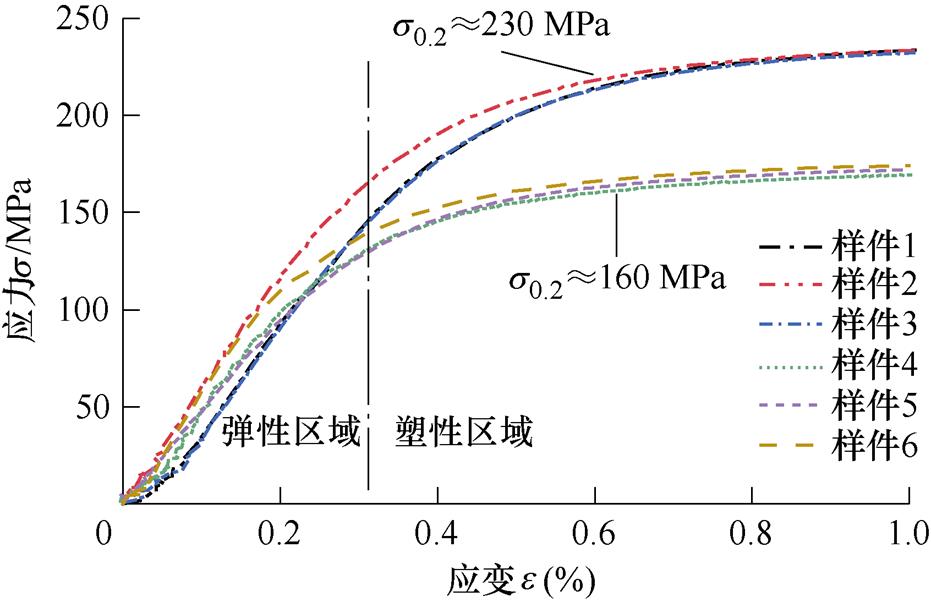
图1 铜导线应力-应变曲线
Fig.1 Stress-strain curves of copper
铜导线在受力过程中的累积效应主要体现在图1中的塑性应变和残余变形上,这与导线的屈服强度和实际受力情况相关。其中,塑性应变是指材料在超过其弹性限度后发生的不可逆应变,而残余变形是指材料在受力后无法完全恢复原状的不可逆变形。在评估绕组的安全性时,需要比较A0与Aact之间的关系,以掌握导线受力的累积效应。
图2展示了垫块多次冲击压缩的变形曲线,这是另一种典型的非线性材料。试验中使用了六组样品,其中三组为常规干燥,另外三组进行了恒压干燥。每组样品的总厚度都是6 mm,每次冲击力为20 MPa。
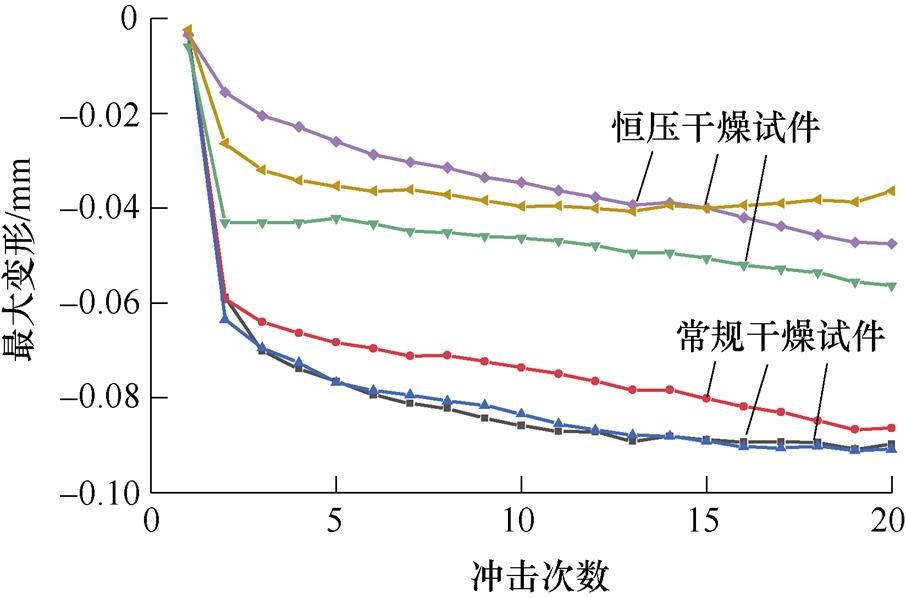
图2 垫块多次冲击压缩变形曲线
Fig.2 Deformation curves of insulation spacer
从图2中可以清晰地看出,随着冲击次数的增加,垫块的累积变形明显增大,但增加的幅度逐渐变缓。垫块的累积变形可能会导致绕组轴向压力降低,从而增加动态振动。同时,制造和控制过程也会对短路累积效应产生影响,因此工艺加工对垫块性能的影响不可忽视。
本文重点研究每次冲击相对于冲击前强度安全系数的损失,以量化变压器短路累积损伤的影响。之前的研究已经报道了与绕组材料、结构和工艺控制相关的内容,但缺乏定量的评价方法。因此,本文关注累积冲击引起的特征量变化,如短路阻抗和振动信号的变化,工程上认为这些变化反映了材料性能和结构参数的变化。以商积计算,第n次短路引起的损失可以表示为
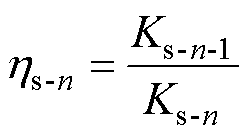 (2)
(2)
式中,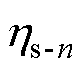 定义为第n次短路引起的可靠性损失系数;
定义为第n次短路引起的可靠性损失系数;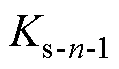 和
和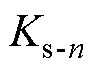 分别为第n次短路前后的安全系数。根据变压器短路物理特性,
分别为第n次短路前后的安全系数。根据变压器短路物理特性,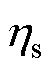 ≥1。
≥1。
1.1.3 冲击载荷比例
根据电磁学原理,冲击电流决定了作用力大小及累积损伤程度,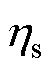 =1.00表示此次冲击电流对绕组的累积损伤没有贡献。在变压器出口发生短路时,由于大电流产生的磁通大部分通过绕组附近的空气区域闭合,与正常运行时铁心闭合磁路存在差异。因此,故障时绕组上的电磁力或应力与短路电流的二次方成正比。为了表示这种冲击的比例关系,引入变压器承受的短路电流比例
=1.00表示此次冲击电流对绕组的累积损伤没有贡献。在变压器出口发生短路时,由于大电流产生的磁通大部分通过绕组附近的空气区域闭合,与正常运行时铁心闭合磁路存在差异。因此,故障时绕组上的电磁力或应力与短路电流的二次方成正比。为了表示这种冲击的比例关系,引入变压器承受的短路电流比例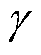 和冲击载荷比例
和冲击载荷比例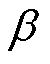 ,表示为
,表示为
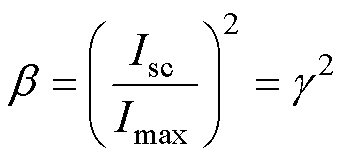 (3)
(3)
式中,Isc为短路冲击电流;Imax为最大承受电流。
冲击载荷比例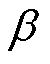 决定作用在绕组上的冲击力水平,是产生绕组可靠性损失的关键参数,在本文中,将作为本文提出评价方法的变量。
决定作用在绕组上的冲击力水平,是产生绕组可靠性损失的关键参数,在本文中,将作为本文提出评价方法的变量。
最大承受电流Imax随着短路次数的增加而逐渐减小,并且在研究初期尚未确定。在进行累积短路试验研究时,暂时忽略Imax的变化,假设已经通过仿真计算或对比验证得到了初始值。某次短路的冲击载荷比例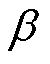 可以表示为
可以表示为
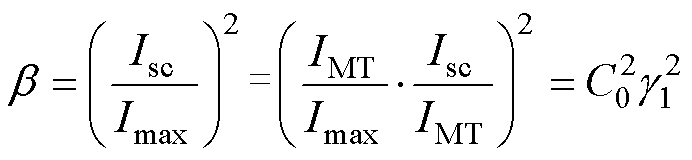 (4)
(4)
式中,C0为考虑预判电流IMT与实际最大承受电流Imax偏差的增益系数;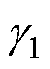 为基于预判承受短路IMT的电流比例。
为基于预判承受短路IMT的电流比例。
1.1.4 可靠性损失阻尼曲线
在短路过程中,绕组在受力后的变形恢复会受到一定的阻碍。当载荷超过一定限制时,绕组将发生不可逆的塑性变形,从而导致累积损伤。其中一种典型的累积过程是由绝缘材料的收缩引起的支撑弱化。课题组提出了改进的辐向屈曲分析方法和等效刚度的径向失稳计算方法,并结合仿真和数值拟合建立了绕组辐向屈曲与内支撑刚度之间的函数关系[25-26]。通过研究发现,用于表征短路累积冲击的等效支撑刚度在降低到一定程度后,表征机械性能的临界载荷因子将会快速下降,并呈指数下降的趋势。同时,在分析短路轴向受力累积损伤时,通过考虑绝缘支撑材料等效杨氏模量的变化趋势,建立了线饼振动和线饼相对位移与轴向动态稳定性之间的指数型函数的关联性[27]。
由于上述辐向与轴向两种损伤是变压器绕组损坏最典型和常见破坏形式,具有较高的代表性与参考意义。为分析上述短路引起的绕组可靠性损失,定量计算变压器经受短路的累积损伤,本文提出如图3所示的可靠性损失系数分析方法。
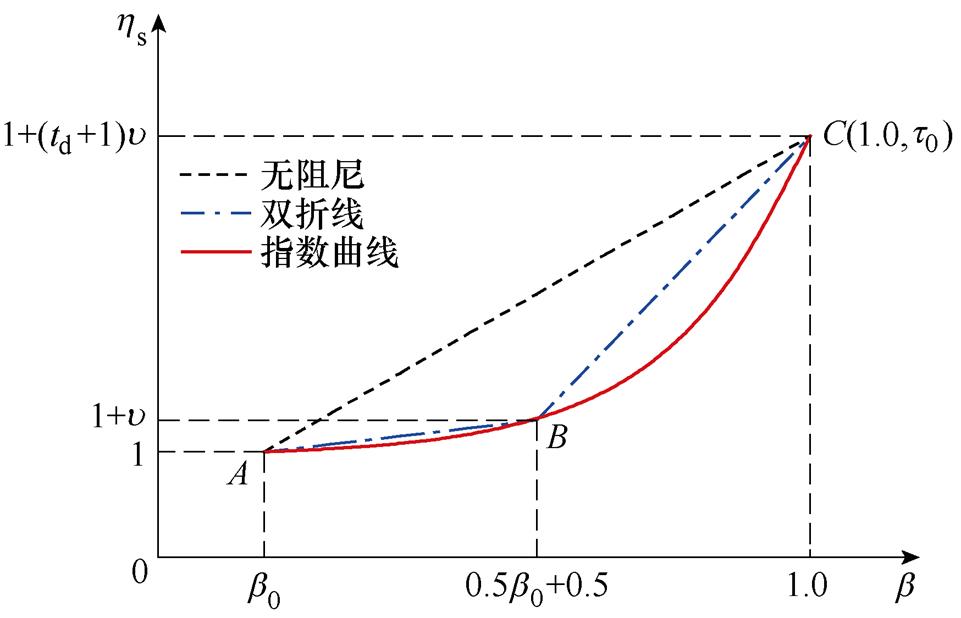
图3 可靠性损失系数示意图
Fig.3 Schematic diagram of reliability loss coefficient
图3中,横坐标为冲击载荷比例,纵坐标为可靠性损失系数。A(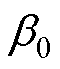 , 1) 点为累积计入起始点,C(1.0,
, 1) 点为累积计入起始点,C(1.0, 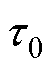 ) 点为计次结束点,B点为提取的特征累积横坐标中点,目的是将阻尼区域划分为前后两部分,以更准确地表征累积损伤与冲击载荷比例的关系。
) 点为计次结束点,B点为提取的特征累积横坐标中点,目的是将阻尼区域划分为前后两部分,以更准确地表征累积损伤与冲击载荷比例的关系。
本文定义:
(1)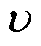 为阻尼系数,1+
为阻尼系数,1+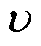 表示累积中点的可靠性损失系数,
表示累积中点的可靠性损失系数,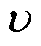 >0。绕组累积损伤阻尼来源包括材料非性线、几何非线性、摩擦力和压紧力等边界 差异。
>0。绕组累积损伤阻尼来源包括材料非性线、几何非线性、摩擦力和压紧力等边界 差异。
(2)td为阻尼比,表征累积结束点与中点的增加值td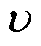 除以中点损失与起始点的增加值
除以中点损失与起始点的增加值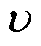 ,td>1,td值越小,说明起始累积的作用越明显。
,td>1,td值越小,说明起始累积的作用越明显。
(3)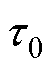 =1+(td+1)
=1+(td+1)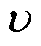 表示100%最大承受电流冲击下的可靠性损失系数。
表示100%最大承受电流冲击下的可靠性损失系数。
基于上述定义的短路物理特征,图3中,由A、B和C点组成的红色或蓝色区域表征阻碍累积效应的能力。在本文提出的方法中,这个区域被定义为阻尼区域,其面积表示对短路累积损伤的限制作用,区域越大,累积作用越明显。当图3中B点在线段AC上,区域面积为零,可认为无阻尼作用。螺旋绕组扭转变形可恢复性较差,其累积效应可近似为此种无阻尼模型。不同的短路累积损伤对应的阻尼特性差异,将在以后的工作中详细研究。载荷达到计次点A后,累积效应与受力呈线性正相关。当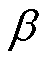 <
<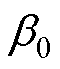 时,定义为无短路累积贡献区域,当
时,定义为无短路累积贡献区域,当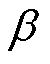 >1.00时,即Isc>Imax,视为破坏性冲击区域。
>1.00时,即Isc>Imax,视为破坏性冲击区域。
根据研究需要,曲线ABC可以增加更多的特征点,并通过数据定义相应的拟合曲线。本文以多段线和指数型曲线为例模拟说明。
1.1.5 多段线模拟曲线
如图3所示红色实线,以双折线为例说明多段线模拟方法,以A、B和C点为数据源,当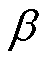 在区间[
在区间[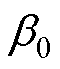 , 0.5+0.5
, 0.5+0.5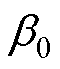 ]时,可靠性损伤系数为
]时,可靠性损伤系数为
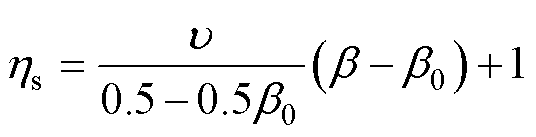 (5)
(5)
当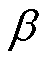 在区间(0.5+
在区间(0.5+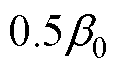 , 1.0
, 1.0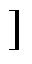 时,可靠性损伤系数可表示为
时,可靠性损伤系数可表示为
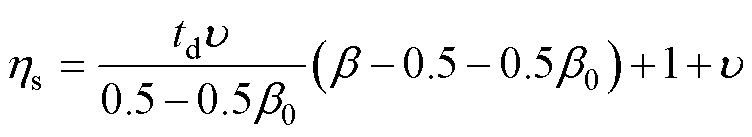 (6)
(6)
式中,td=1为特殊情况,此时双折线变为直线AC,呈现无阻尼关系,损失系数与载荷系数呈正线性关系,满足
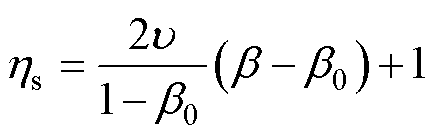 (7)
(7)
双折线计算累积损伤时,关键是确定特征参数td、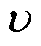 和
和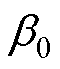 。多段线模拟方法可在双折线的基础上增加更多的特征点。
。多段线模拟方法可在双折线的基础上增加更多的特征点。
1.1.6 指数型模拟曲线
多段折线模拟方式更适合计算编程后应用。工程中可使用一种近似的曲线模拟。根据物理特性,结合图3所示方法,选择指数型模拟曲线近似表示可靠性损失系数,有
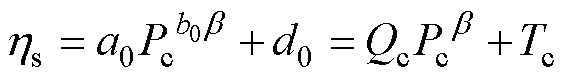 (8)
(8)
式中,a0、b0、d0和Pc为描述此指数曲线的待定常数,折算后以Qc、Pc和Tc三个常数代替。借助图3,代入A、B和C三点数据,便可求解待求参数Qc、Pc和Tc。
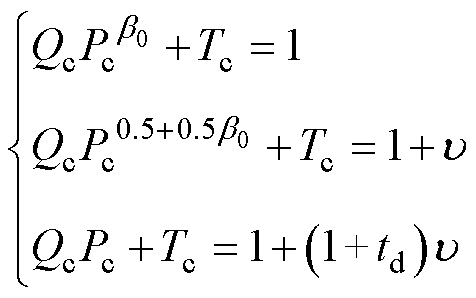 (9)
(9)
通过式(9)变换,当td≠1时,可求得未知参数的具体值为
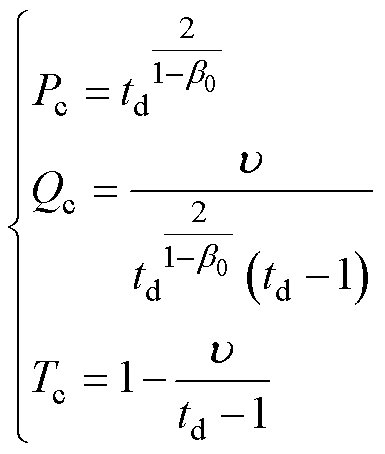 (10)
(10)
得到指数型曲线模拟可靠性损失系数的表达式为
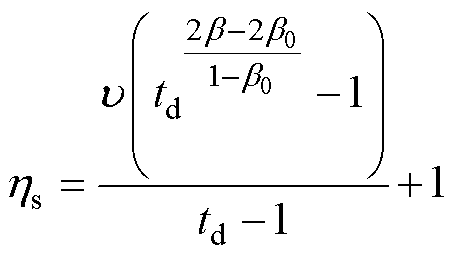 (11)
(11)
如前所述,td=1时,损失曲线为直线。
同理,表达式中需要确定关键参数td、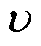 和
和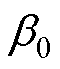 。以行业惯例,假设取
。以行业惯例,假设取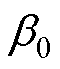 =0.5为起始累积计次点,简化式(11)为
=0.5为起始累积计次点,简化式(11)为
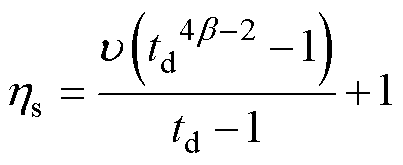 (12)
(12)
式(11)和式(12)描述了一次短路引起的绕组机械可靠性损失,每次冲击损失系数均应基于冲击前的安全系数。若需要计算变压器多次冲击后的安全系数,应迭代至出厂承受短路能力。不难知道,经n次冲击后的总损失系数为
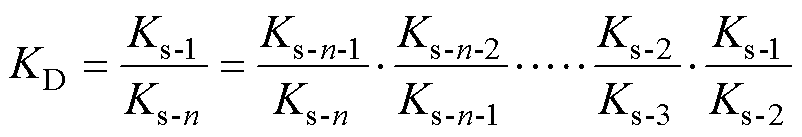 (13)
(13)
代入式(2)的变形型式可得经过N次冲击后的绕组机械强度可靠性损失系数为
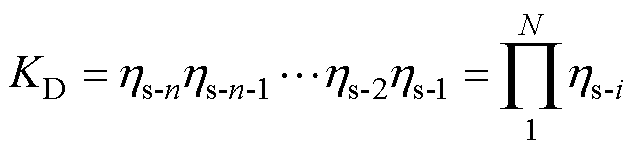 (14)
(14)
式中,KD为考虑短路累积效应的总可靠性损失系数;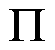 表示求乘积函数。
表示求乘积函数。
根据变压器短路特点及1.1节定义的关系,一次Imax电流冲击产生的可靠性损失系数为
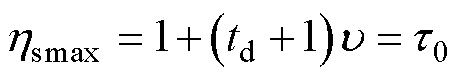 (15)
(15)
在此试验研究中,若忽略3次冲击过程中Imax的损失,假设3次冲击造成的损伤相同,以简化计算。经过3次冲击后,总损失系数的临界值为
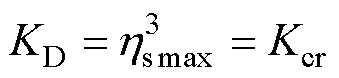 (16)
(16)
可靠性损失系数累积阈值为KD≤Kcr。应用时,若KD>Kcr,则判断变压器绕组抗短路能力超过临界条件,存在累积损坏风险。
第1节以双折线和指数型曲线为例描述本文提出的模拟变压器短路绕组累积作用的研究方法,得到了一种评价变压器承受短路后累积损伤的定量算法。本节将进一步说明上述特征量的确定方法,并介绍此评价方法的应用。
基于可靠性损失系数的定义,承受短路累积冲击能力的评价方法关键是确定本文提出的三种特征量td、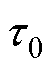 (或
(或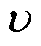 )和
)和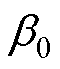 。如图3所示,点(1.0,
。如图3所示,点(1.0, 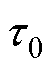 )表示在此电流下可承受3次短路冲击的安全系数,根据安全系数的定义,满足
)表示在此电流下可承受3次短路冲击的安全系数,根据安全系数的定义,满足
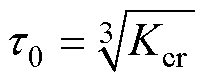 (17)
(17)
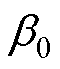 表示开始计次的累积效应起点,考虑变压器短路试验中调波电流为70%标准试验电流,
表示开始计次的累积效应起点,考虑变压器短路试验中调波电流为70%标准试验电流,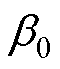 经验取值0.5(0.5≈0.72)。具体数据可使用某一预设试验电流完成10次以上短路冲击,若没有特征量的变化,则可设定为起始点。如前所述,阻尼比td表征了变压器制造工艺加强措施与边界约束效果,其值越小,累积效应越明显。
经验取值0.5(0.5≈0.72)。具体数据可使用某一预设试验电流完成10次以上短路冲击,若没有特征量的变化,则可设定为起始点。如前所述,阻尼比td表征了变压器制造工艺加强措施与边界约束效果,其值越小,累积效应越明显。
在实际工程中,确定关键特征参数td、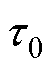 (或
(或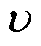 )和
)和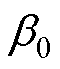 时,可采用理论方法或试验方法,包括直接电气参数或间接特征量。例如,短路试验的阻抗变化、绕组变形和振动差异。然而,由于空间和材料的非线性、制造分散性、选择物理判断量的差异、校核体系以及状态反馈函数等一系列因素的影响,不同方法得到的结果可能存在差异。因此,在确定这些特征参数时,需要综合考虑不同方法的结果,并进行合理的校核和比较。
时,可采用理论方法或试验方法,包括直接电气参数或间接特征量。例如,短路试验的阻抗变化、绕组变形和振动差异。然而,由于空间和材料的非线性、制造分散性、选择物理判断量的差异、校核体系以及状态反馈函数等一系列因素的影响,不同方法得到的结果可能存在差异。因此,在确定这些特征参数时,需要综合考虑不同方法的结果,并进行合理的校核和比较。
绕组的不同机械性能导致累积作用的机理和研究方法存在差异。例如,对于内部绕组的辐向失稳,需要重点关注导线和支撑材料的非线性问题,可以通过阻抗变化的反馈来进行宏观观察。对于绕组的轴向倒伏累积效应,需要关注绝缘材料的非线性问题以及支撑压紧结构的非线性特征,可以通过绕组或油箱的振动反演来进行宏观观察。而对于螺旋绕组的扭曲累积作用,与压紧作用力和升层角度相关,宏观检测比较困难。上述问题的具体研究工作应通过试验的方法持续研究,不断完善。
量化短路对变压器绕组机械寿命的累积损伤时,应统计同类短路工况。评价方法的应用主要包括如下三类。
2.2.1 绕组机械性能降低的分析
根据短路电流大小,归算到变压器承受电流比值g和冲击载荷比例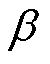 ,获得每次短路的可靠性损失系数。在确定了累积效应关键参数td、
,获得每次短路的可靠性损失系数。在确定了累积效应关键参数td、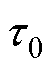 (或
(或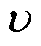 )和
)和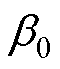 以及变压器承受短路电流Imax后,可计算出第i次短路的可靠性损失系数为
以及变压器承受短路电流Imax后,可计算出第i次短路的可靠性损失系数为
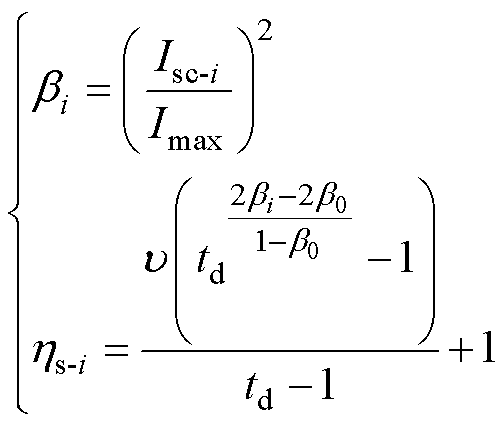 (18)
(18)
式中,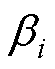 为每次冲击的载荷比例系数;
为每次冲击的载荷比例系数;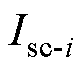 为第i次短路冲击电流;
为第i次短路冲击电流;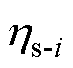 为第i次短路引起的可靠性损失系数。
为第i次短路引起的可靠性损失系数。
若需要计及历史短路影响,总损失系数即为累积的降低程度,此时有
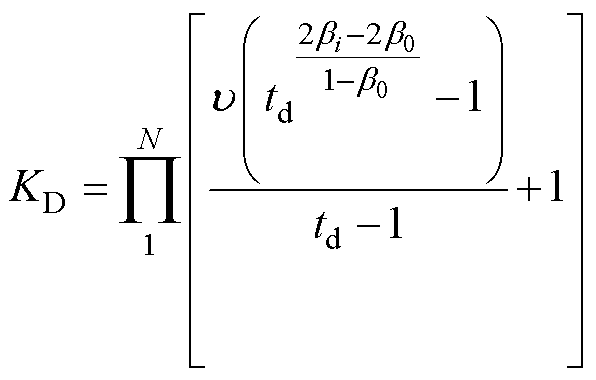 (19)
(19)
预测剩余机械寿命G为
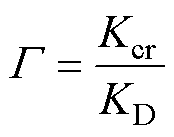 (20)
(20)
可靠性损失系数累积临界控制条件为
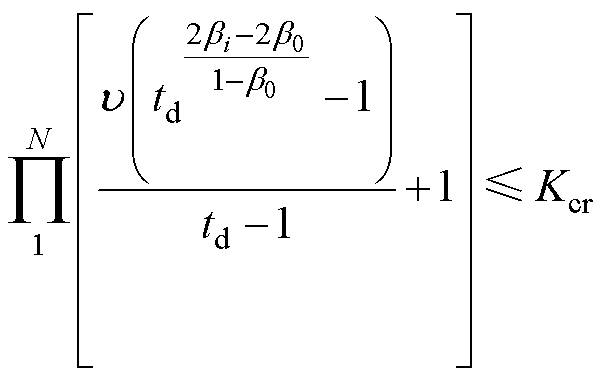 (21)
(21)
2.2.2 可承受某一电流冲击的次数
根据可靠性损失系数定义,某一短路电流连续多次冲击造成绕组机械强度降低系数应满足式(21)的判断方法。
忽略Imax在冲击过程中的变化时,可求得能承受此短路电流的冲击次数为
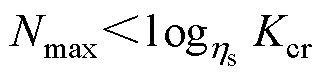 (22)
(22)
试验或短路故障均为计次方式,故某一特定短路工况下可承受短路次数为上述表达式取整。
2.2.3 获取变压器初始承受短路的能力
由于短路试验的特殊性,变压器承受短路的实际能力难以通过单次冲击试验获得。传统的方法校核在变压器承受短路能力时,通常基于理论或仿真计算得到变压器的承受短路电流的能力,即第1节提到的预判短路IMT。实际承受电流与此值的比值已定义为C0,它表征了仿真计算的准确性与偏差范围,需要进行分析和求解。由本文所述的累积损伤损失系数,可以通过试验方法准确地获得变压器承受短路能力的临界值,从而解决技术上的难题。具体方法如下:
短路试验研究时,首次试验电流应小于预判临界电流的70%,以逐渐增大电流的试验方式实施短路试验。假设完成了N次试验,最大试验电流为ITsc,取ITsc替换基准电流Imax,折算出第i次冲击的载荷比例系数为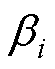 ,
,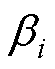 >
>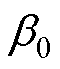 计算累积作用,可求得总累积损失系数为
计算累积作用,可求得总累积损失系数为
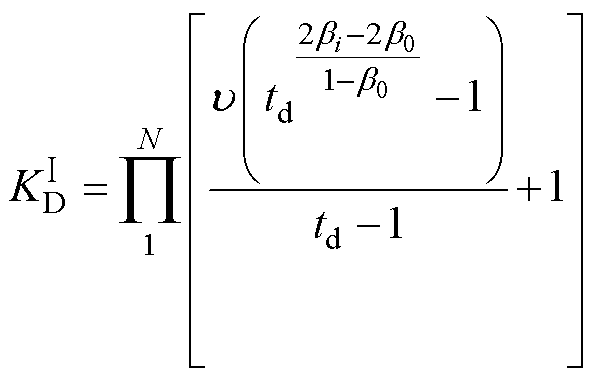 (23)
(23)
式中,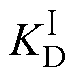 为未进行累积损伤归算的累积效应总可靠性损失系数,“Ⅰ”表示未归算的数据。
为未进行累积损伤归算的累积效应总可靠性损失系数,“Ⅰ”表示未归算的数据。
累积损伤为单调递增函数,必然存在唯一确定的增益系数C0满足
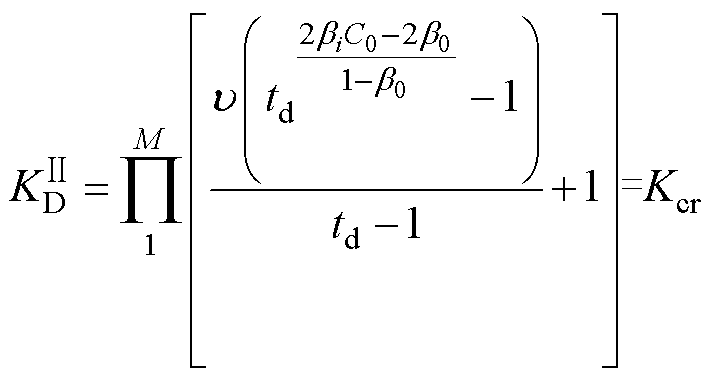 (24)
(24)
式中,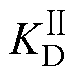 为归算后的累积效应总可靠性损失系数,“Ⅱ”表示基于式(24)归算后的数据;M为归算后的有效短路冲击次数。
为归算后的累积效应总可靠性损失系数,“Ⅱ”表示基于式(24)归算后的数据;M为归算后的有效短路冲击次数。
需要注意,由于基准电流发生变化,累积计次数量可能发生变化,即当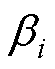 <
<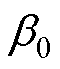 时,累积损伤无贡献,应忽略。归算后有效累积次数M与冲击次数N不一定相等。
时,累积损伤无贡献,应忽略。归算后有效累积次数M与冲击次数N不一定相等。
假设预判短路IMT下,绕组可承受的临界作用力与应力的仿真计算值分别为Fcr0和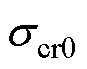 ,则可推算出变压器对应的最大承受短路的能力分别为
,则可推算出变压器对应的最大承受短路的能力分别为
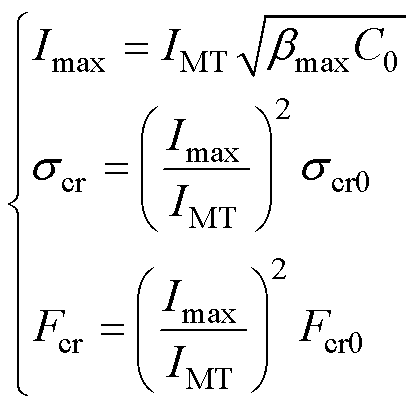 (25)
(25)
式中,Fcr和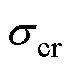 分别为绕组实际可承受的临界作用力和应力;
分别为绕组实际可承受的临界作用力和应力;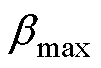 为最大冲击载荷比例。
为最大冲击载荷比例。
电力变压器的短路试验是一种破坏性试验,通常采用仿真计算或设计验证对比的方法进行可靠性论证[4, 15]。实物试验研究多数基于缩比模型。然而,变压器短路引起的机械损伤主要是由本文提出的阻尼条件引起,缩比模型很难准确反映其累积效应。因此,本文设计并制造了一台容量为50 MV·A、电压为110 kV的变压器,以实际的累积短路试验为例,阐述了本文提出的累积机械损伤评价方法。
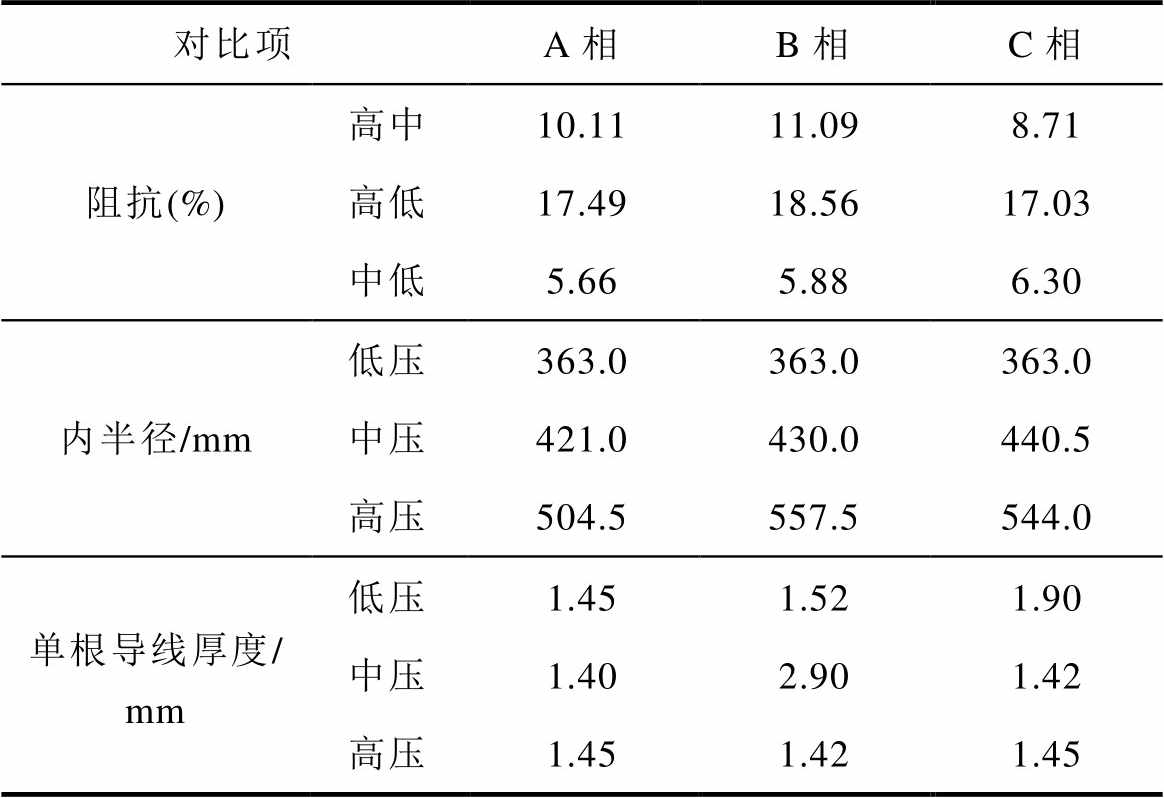
考虑到不同短路破坏形式的累积效应差异,此试验变压器被设计为三相不同结构。各相进行了高中和高低试验的纵向比较,并设置了A、B和C相之间的横向比较。表1列出了该变压器绕组的基本参数统计信息。
表1 绕组参数
Tab.1 Winding parameters
对比项A相B相C相 阻抗(%)高中10.1111.098.71 高低17.4918.5617.03 中低5.665.886.30 内半径/mm低压363.0363.0363.0 中压421.0430.0440.5 高压504.5557.5544.0 单根导线厚度/ mm低压1.451.521.90 中压1.402.901.42 高压1.451.421.45
为了确保试验的安全性,在拆解变压器后可以观察到试验机械的变形情况,实现研究临界值和累积变化过程,生产制造过程中采取了增加硬绝缘筒、绕组绑扎等加强措施。
短路试验采用高压供电、中压或低压短路的方式。在某种短路工况下,薄弱点应以安全系数较小的绕组为准。例如,高低试验时低压绕组设计为薄弱点,完成后执行高中试验,薄弱点设置在中压或高压绕组。
为了指导短路试验与后续分析,表2统计了短路试验时低压与中压承受的电流峰值,此数据将作为试验研究的基准电流,即式(4)中的预判短路IMT。
表2 短路试验基准电流
Tab.2 Reference currents of short-circuit tests (单位: A)

短路工况A相B相C相 高压-低压3 860.23 564.33 924.7 高压-中压6 219.36 302.78 107.7
图4为基于累积短路试验法获取变压器承受短路冲击的能力及可靠性评价的流程。
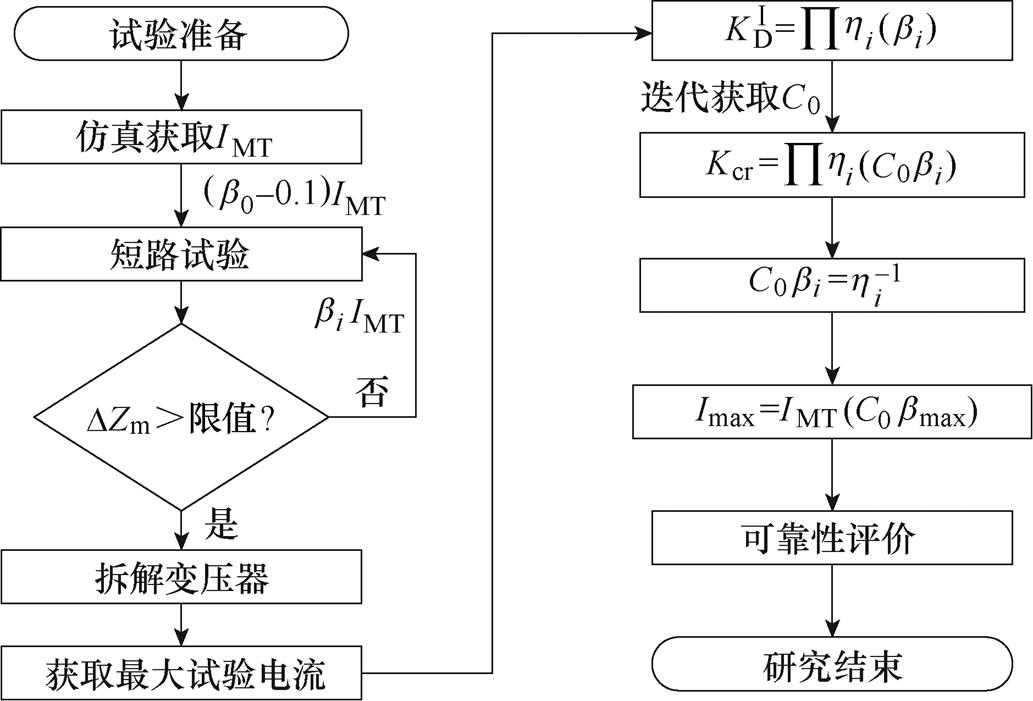
图4 累积短路试验研究流程
Fig.4 Flow chart of cumulative short-circuit test
首先,通过仿真获得试验的基准电流IMT;其次,逐渐增加电流直到阻抗超过限值,结束试验并获得最大的试验电流;再次,计算初始可靠性损失系数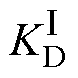 ,并比较Kcr和
,并比较Kcr和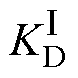 之间的关系;最后,通过迭代获取增益系数C0,计算绕组实际承受短路的能力,评价机械性能的可靠性。
之间的关系;最后,通过迭代获取增益系数C0,计算绕组实际承受短路的能力,评价机械性能的可靠性。
变压器各类状态量检测和分析包括试验过程中的振动、噪声、油流和油压信号,每次试验完成后测量短路阻抗。其中,阻抗变化是主要的判断依据,用于确定是否结束该相试验。而变压器的振动和噪声等测量则作为辅助判断数据[10],通过对比每次冲击的瞬时波形和幅值变化,来支撑阻抗判断结果。
图5为本次试验研究中的状态量测试情况。试验过程中采集了编号为①~⑤的信号,分别表示顶部油流速、油箱振动a套、油箱振动b套、箱壁油压和绕组振动。

图5 短路试验现场特征量测试
Fig.5 Characteristic quantity measurement
为了确保变压器试验过程的安全,参考国家标准对阻抗的控制规范,本文不仅使用阻抗绝对变化率的标准判断方法,还提出并应用了改进的累积短路试验方法和结束判断条件,即阻抗相对变化率的判断方法。这种改进方法能够更全面地评估变压器的试验状态,并提供更准确的结束判断依据。此种判断方法的表达式为
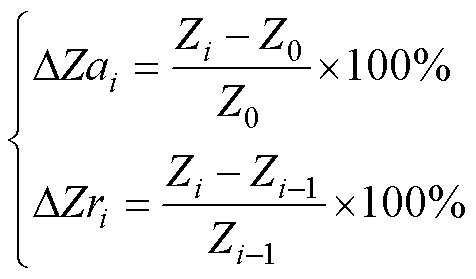 (26)
(26)
式中,DZai和DZri分别为第i次短路阻抗绝对变化率与相对变化率;Zi为第i次短路试验后的短路阻抗;Z0为短路试验前测量的短路阻抗。DZai接近1.0%或DZri接近0.3%为试验结束的判断阈值。
本次三相六组短路试验总共进行了122次,其中一组试验最少8次,最多33次,表3及图6为典型的B相高压-低压(High Voltage-Low Voltage, HV-LV)短路试验为例,对本文提出的评价方法应用进行说明。
表3 短路试验数据分析
Tab.3 Data analysis of short circuit tests

试验次数Isc/ADZai (%)DZri (%)GNmax 12 593-0.22-0.2264.201.000 001.000 01.150 0无数次 22 778-0.200.0268.701.000 001.000 01.150 0无数次 32 988-0.190.0173.954.671.000 701.000 01.150 0无数次 42 983-0.170.0273.854.491.000 701.000 01.150 0无数次 53 123-0.20-0.0377.359.731.001 751.941.000 31.149 7531 63 128-0.20077.459.921.001 852.101.000 31.149 4486 73 153-0.29-0.0978.060.881.002 052.941.000 41.148 9338 83 323-0.37-0.0882.267.621.004 258.801.001 51.147 292 93 323-0.37082.267.621.004 258.801.001 51.145 492 103 303-0.39-0.0281.766.811.003 958.101.001 41.143 9103 113 498-0.39086.674.931.007 965.161.003 31.140 142 123 493-0.39086.474.721.007 864.971.003 21.136 543 133 493-0.360.0386.474.721.007 864.971.003 21.132 843 143 688-0.37-0.0191.383.291.014 972.431.006 41.125 621 153 693-0.37091.483.521.015 272.621.006 51.118 321 163 678-0.360.0191.082.841.014 572.041.006 21.111 422 173 678-0.36091.082.841.014 572.041.006 21.104 522 183 683-0.340.0291.183.071.014 772.231.006 31.097 622 193 908-0.36-0.0296.793.531.030 781.331.012 91.083 610 203 903-0.330.0396.693.291.030 281.121.012 71.070 011 213 903-0.33096.693.291.030 281.121.012 71.056 511 223 888-0.300.0396.292.571.028 880.501.012 21.043 811 233 898-0.30096.593.051.029 880.911.012 51.030 911 244 04100.30100.0100.01.047 786.961.019 51.011 27 253 8630.220.2295.691.381.026 579.461.011 21.000 012
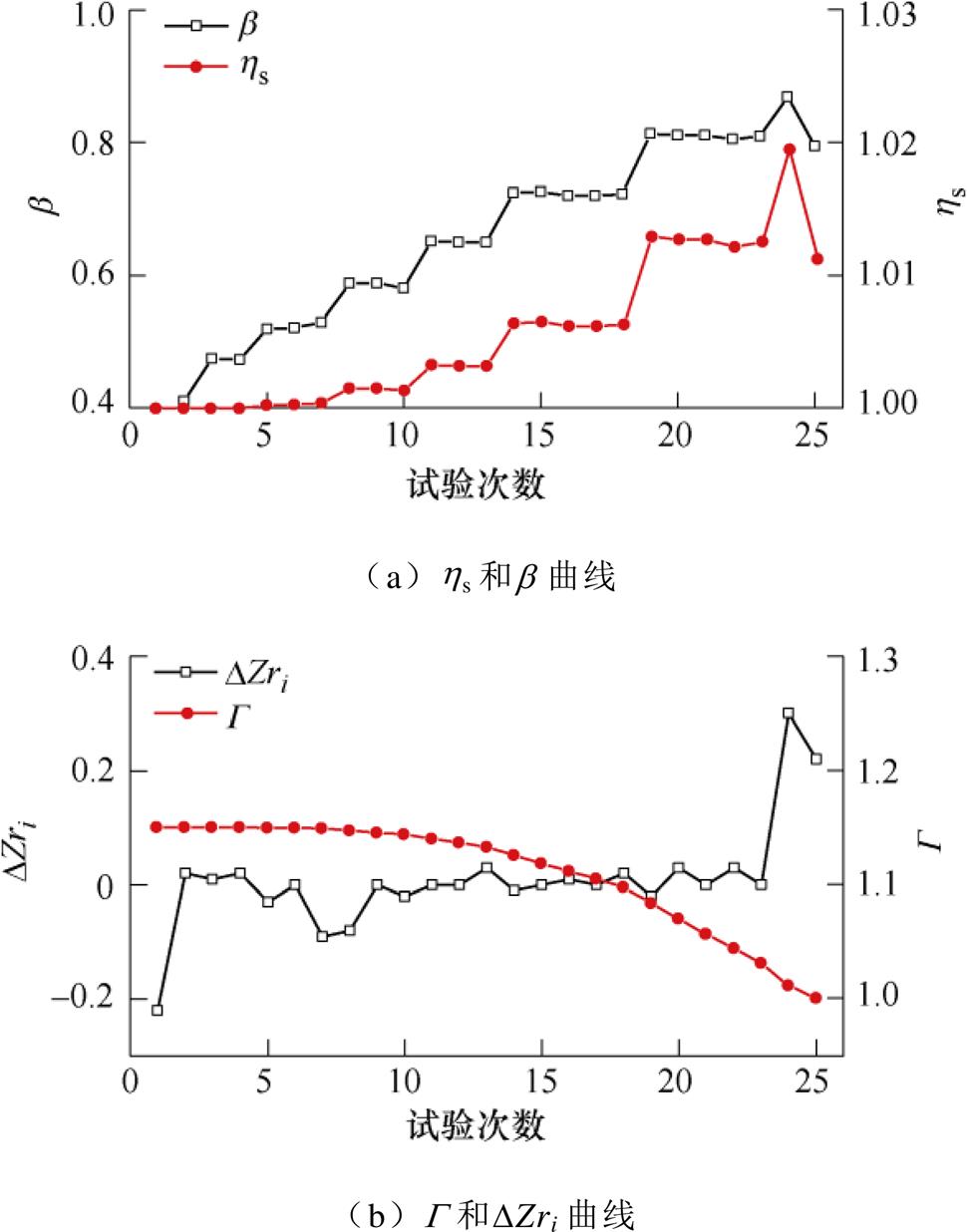
图6 B相HV-LV短路试验
Fig.6 B phase HV-LV short circuit test
根据表2统计信息,预判承受电流为3 564 A,对应的低压径向压缩应力为36.4 MPa。以第24次试验电流4 041 A为分析基准电流IMT,得到一组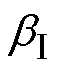 。取b0=0.5,假设C0=1.15时,可求得u =0.007 84,td=5.008。最终确定变压器承受短路的最大电流为4 333.4 A,临界压缩应力为50.8 MPa。
。取b0=0.5,假设C0=1.15时,可求得u =0.007 84,td=5.008。最终确定变压器承受短路的最大电流为4 333.4 A,临界压缩应力为50.8 MPa。
观察试验数据可知:
(1)随着载荷比例系数b 增大,可靠性损失系数hs也会增加。
(2)随着试验次数及试验电流增大,短路阻抗相对变化率DZr会增加,同时,预测剩余机械寿命G 会逐渐减少,直到达到临界条件1.0。
根据试验结果,相对于仿真预判电流,适当的工艺加强对绕组的短路能力是必要且实用的。如果不考虑短路的累积效应,变压器承受短路的最大电流应为表3中的4 041 A,这相当于考虑了累积损伤结果的96.96%。同时,当考虑累积损伤评价方法时,耐受电流冲击能力可以单独承受4 041 A的冲击7次,而不考虑累积损伤的情况下,只能承受3次冲击。这进一步证明了考虑累积损伤的重要性。
试验后,解体各绕组,不同绕组在安全系数薄弱的位置发生累积损坏。图7展示了部分解体绕组的照片,左图为中压内绕组辐向屈曲变形,右图为高压外绕组轴向倒伏照片。

图7 绕组解体照片
Fig.7 Disassembly photo of windings
通过使用本研究提出的基于相对变化率判断的短路试验方法,观察到了明显的变形现象,同时未出现由于机械损伤引起的次生绝缘击穿或内部短路现象。这表明基于相对变化率判断方法研究短路累积损伤是非常有效的。
本文提出的短路累积机械损伤评价算法基于自定义的可靠性损失系数,在工程应用时可采用指数型曲线进行等效模拟。该算法需要研究td、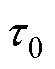 (或
(或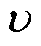 )和
)和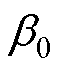 ,其中
,其中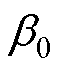 应根据试验进行论证,本文取调波电流为起始点。
应根据试验进行论证,本文取调波电流为起始点。
表4列举了不同的td和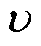 (或
(或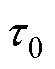 )对上述短路试验研究结果的影响。
)对上述短路试验研究结果的影响。
表4 计及累积效应的临界承受电流
Tab.4 Critical current considering cumulative effect
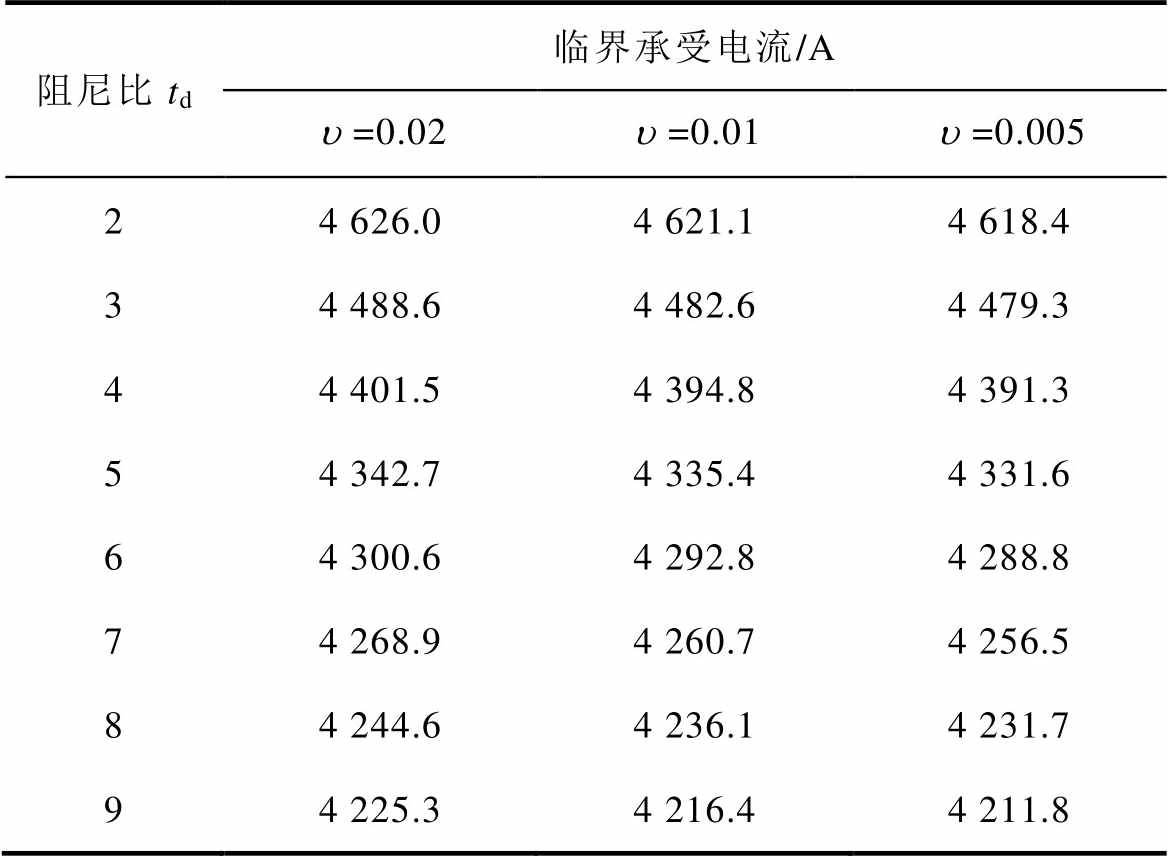
阻尼比td临界承受电流/A =0.02=0.01=0.005 24 626.04 621.14 618.4 34 488.64 482.64 479.3 44 401.54 394.84 391.3 54 342.74 335.44 331.6 64 300.64 292.84 288.8 74 268.94 260.74 256.5 84 244.64 236.14 231.7 94 225.34 216.44 211.8
表4中,不同td对临界承受电流的影响较大。td=9时,偏差为4.56%,计算式为
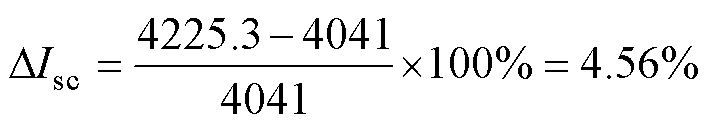
td=2时,偏差将增大至14.48%,计算式为
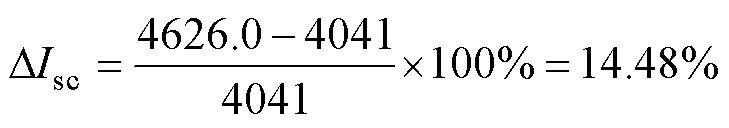
分析产生上述偏差的原因:阻尼比td定义为后半段损失系数与前半段损失系数的比值,表征了系统的阻尼特性。阻尼比越小,则越早产生累积效应越明显,这意味着每次短路的贡献越大,绕组实际承受短路的能力与最大试验电流偏差会更大。
基于上述分析结果,增加阻尼可以限制小电流冲击的累积损伤,提高绕组机械可靠性。除了提高铜导线屈服强度和绝缘垫块的材料机械性能、增加压紧力及绕组绑扎等工程方法外,定期检测也是非常重要的。通过定期检测,可以及时发现和修复绕组中的潜在缺陷,避免损伤进一步扩大。
相同td值时,选择不同的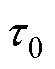 值,Imax最大偏差仅为0.32%,表明
值,Imax最大偏差仅为0.32%,表明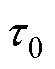 对于累积效应计算结果的影响可忽略,累积损失系数受校核方法的控制阈值
对于累积效应计算结果的影响可忽略,累积损失系数受校核方法的控制阈值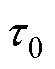 影响较小。
影响较小。
因此,本文提出的短路累积机械损伤评价方法可适用于不同理论校核体系。为确保评价的准确性,控制本文中提出的阻尼比td非常重要。课题组后期将加强对材料和结构的非线性特性产生的阻尼作用的研究,通过更多的仿真或试验分析来获取更准确的td值。
基于自定义可靠性损失系数,本文提出了一种电力变压器短路累积机械损伤评价方法。该方法使用指数型曲线模拟,通过考虑变压器出厂时承受短路的能力、短路电流幅值和短路次数对绕组累积损伤的影响,可以对绕组累积损伤问题进行准确的计算和分析。
该方法通过一台新制造的容量为50 MV·A、电压为110 kV的变压器的破坏性累积短路试验完成了应用验证。通过该方法,可以对变压器的短路累积损伤问题进行量化计算,分析某次短路对绕组机械性能降低的影响,计算出能够承受某一电流冲击的次数,并预测剩余机械寿命系数。
总之,此种变压器短路累积机械损伤评价方法为行业提供了一种量化计算手段,能够更好地了解和评估变压器短路引起的绕组机械损伤情况,对于变压器的设计、运行和维护具有重要的指导意义。
参考文献
[1] 国家电网公司. 变压器抗短路校核工作总结[R]. 北京: 中国电力科学研究院, 2012: 1-9.
[2] Shipp D D, Dionise T J, Lorch V, et al. Transformer failure due to circuit-breaker-induced switching tran- sients[J]. IEEE Transactions on Industry Applications, 2011, 47(2): 707-718.
[3] Venkateswarlu G, Agarwal Y, Takkher M S, et al. Significance of tank current measurement during short circuit testing of power transformer[C]//2019 International Conference on High Voltage Engin- eering and Technology (ICHVET), Hyderabad, India, 2019: 1-5.
[4] 国家质量监督检验检疫总局. 电力变压器 第5部分: 承受短路的能力: GB 1094.5-2003[S]. 北京: 中国标准出版社, 2004.
[5] 张博, 李岩. 多次冲击条件下的大型变压器绕组辐向失稳[J]. 电工技术学报, 2017, 32(增刊2): 71-76.
Zhang Bo, Li Yan. Radial stability of large trans- former windings under multiple inrush conditions[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 71-76.
[6] 欧强, 罗隆福, 李小蓉, 等. 电力变压器承受短路能力国家标准的几点理解和研究[J]. 变压器, 2021, 58(2): 11-18.
Ou Qiang, Luo Longfu, Li Xiaorong, et al. Interpreting and research on national standard of ability to withstand short-circuit on power trans- former[J]. Transformer, 2021, 58(2): 11-18.
[7] 张俊杰, 刘兰荣, 刘东升, 等. 用场路耦合模拟变压器线圈部分短路故障电流的方法[J]. 电工技术学报, 2015, 30(20): 65-70.
Zhang Junjie, Liu Lanrong, Liu Dongsheng, et al. A method of simulating the fault current using field- circuit coupling for partially short-circuited trans- former winding[J]. Transactions of China Electro- technical Society, 2015, 30(20): 65-70.
[8] 汪佐宪, 张书琦, 徐征宇, 等. 多因素条件下变压器自粘换位导线抗弯能力试验及评估[J]. 高电压技术, 2022, 48(9): 3660-3669.
Wang Zuoxian, Zhang Shuqi, Xu Zhengyu, et al. Research and evaluation of bending resistance of epoxy continuously transposed conductors in trans- formers under multi-factor conditions[J]. High Voltage Engineering, 2022, 48(9): 3660-3669.
[9] Geibler D, Leibfried T. Short-circuit strength of power transformer windings-verification of tests by a finite element analysis-based model[J]. IEEE Transa- ctions on Power Delivery, 2017, 32(4): 1705-1712.
[10] 杜厚贤, 刘昊, 雷龙武, 等. 基于振动信号多特征值的电力变压器故障检测研究[J]. 电工技术学报, 2023, 38(1): 83-94.
Du Houxian, Liu Hao, Lei Longwu, et al. Power transformer fault detection based on multi- eigenvalues of vibration signal[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 83-94.
[11] 沈明, 尹毅, 吴建东, 等. 变压器绕组变形在线监测实验研究[J]. 电工技术学报, 2014, 29(11): 184- 190.
Shen Ming, Yin Yi, Wu Jiandong, et al. Experimental investigating on on-line monitoring of winding deformation of power transformers[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 184- 190.
[12] Shi Yuhang, Ji Shengchang, Zhang Fan, et al. Multi- frequency acoustic signal under short-circuit transient and its application on the condition monitoring of transformer winding[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1666-1673.
[13] 闫晨光, 张芃, 徐雅, 等. 换流变压器有载分接开关级间短路故障差动保护动作特性[J]. 电工技术学报, 2023, 38(21): 5878-5888.
Yan Chenguang, Zhang Peng, Xu Ya, et al. Differential protection performance for converter transformer intertap short-circuit faults in on-load tap changers[J]. Transactions of China Electro- technical Society, 2023, 38(21): 5878-5888.
[14] 马奎, 王曙鸿, 姚晓飞. 110kV变阻抗变压器短路电流首峰值限制方法[J]. 电工技术学报, 2021, 36(增刊2): 723-729, 745.
Ma Kui, Wang Shuhong, Yao Xiaofei. Limiting method of first peak of short-circuit current of 110kV variable impedance transformer[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 723- 729, 745.
[15] Power transformer part 5: ability to withstand short circuit: IEC 60076-5-2006[S]. 2006.
[16] IEEE draft standard for general requirements for liquid-immersed distribution, power, and regulating transformers: IEEE PC57.12.00/D1.2[S]. 2015.
[17] IEEE guide for establishing short-circuit withstand capabilities of liquid-filled power transformers, regulators, and reactors: IEEE C57.164-2021[S]. Institute of Electrical and Electronics Engineers, 2021.
[18] 李长云, 王铮. 机-热效应对换流变绝缘纸机械性能劣化影响的实验研究[J]. 中国电机工程学报, 2019, 39(2): 612-620, 658.
Li Changyun, Wang Zheng. Experiments research on the deterioration of inverter transformer insulation paper mechanical properties with mechanical-thermal synergy[J]. Proceedings of the CSEE, 2019, 39(2): 612-620, 658.
[19] 张凡, 李秀广, 朱筱瑜, 等. 计及热老化程度的变压器绕组内线圈短路承受能力评估方法[J]. 中国电机工程学报, 2022, 42(10): 3836-3846.
Zhang Fan, Li Xiuguang, Zhu Xiaoyu, et al. Assessment of the withstand ability to short circuit of inner windings in power transformers considering the degree of thermal aging[J]. Proceedings of the CSEE, 2022, 42(10): 3836-3846.
[20] Wang Shuhong, Zhang Haijun, Wang Song, et al. Cumulative deformation analysis for transformer winding under short-circuit fault using magnetic- structural coupling model[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): -5.
[21] Yao Shaoyong, Hao Zhiguo, Si Jianan, et al. Dynamic deformation analysis of power transformer windings under multiple short-circuit impacts[C]//2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), Xi’an, China, 2020: 1394-1397.
[22] 李典阳, 张育杰, 冯健, 等. 变压器故障样本多维诊断及结果可信度分析[J]. 电工技术学报, 2022, 37(3): 667-675.
Li Dianyang, Zhang Yujie, Feng Jian, et al. Multi- dimensional diagnosis of transformer fault sample and credibility analysis[J]. Transactions of China Electro- technical Society, 2022, 37(3): 667-675.
[23] 律方成, 汪鑫宇, 王平, 等. 基于振动偏离及加权熵的多次短路冲击下变压器绕组机械形变辨识[J]. 电工技术学报, 2023, 38(11): 3022-3032.
Lü Fangcheng, Wang Xinyu, Wang Ping, et al. Mechanical deformation identification of transformer winding under multiple short-circuit impacts based on vibration deviation and weighted entropy[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(11): 3022-3032.
[24] 曹辰, 徐博文, 李辉. 基于振动与电抗信息的变压器绕组形变状态综合监测方法[J]. 高电压技术, 2022, 48(4): 1518-1530.
Cao Chen, Xu Bowen, Li Hui. Composite monitoring method for the state of transformer winding defor- mation based on vibration and reactance infor- mation[J]. High Voltage Engineering, 2022, 48(4): 1518-1530.
[25] Ou Qiang, Luo Longfu, Li Yong, et al. An improved radial buckling analysis method and test investigation for power transformer under short circuit impact[J]. IEEE Transactions on Power Delivery, 2023, 38(4): 2854-2863.
[26] Ou Qiang, Luo Longfu, Li Yong, et al. Buckling strength investigation for power transformer winding under short circuit impact considering manufacture and operation[J]. IEEE Access, 2023, 11: 7850- 7859.
[27] Ou Qiang, Luo Longfu, Li Yong, et al. A dynamic relative displacement evaluation method for extra- high voltage transformer withstanding short-circuit impact[J]. IET Generation, Transmission & Dis- tribution, 2023, 17(6): 1310-1320.
Abstract Multiple short circuits can gradually accumulate mechanical damage to the windings, leading to the failure of power transformers. However, a quantitative assessment method is lacking to evaluate such damage, and grasping the mechanical state of the transformer winding after a short-circuit impact is challenging. The cumulative damage of windings caused by multiple short circuits is still an urgent problem in the industry, which poses a threat to the secure operation of power grids. Therefore, this paper proposes an evaluation method for assessing the accumulated mechanical damage caused by short circuits in power transformer windings, considering the nonlinear characteristics of windings and the cumulative process.
Firstly, the method utilizes the damping ratio and reliability loss coefficient as features. Exponential curves are used to simulate the mechanical weakening process of windings. Additionally, the initial short-circuit withstanding capability, short-circuit current magnitude, and the number of faults are considered. The influence of a short circuit on the mechanical performance of the winding is theoretically analyzed, the number of times that it can withstand a current impact is calculated, and the residual mechanical life coefficient is predicted.
The correctness of this evaluation method is validated through destructive short-circuit tests on a 50 MVA/110 kV power transformer. This three-phase, three-winding, differential-designed transformer provides six sets of short-circuit test data. The end of the test is determined by gradually increasing the loading current and the relative change rate of the impedance. 122 short circuit tests are implemented, ranging from 8 times to a maximum of 33 times. All the windings are disassembled after short-circuit tests. Several significant deformations are observed, consistent with predicted failure forms. Moreover, no secondary insulation breakdown or internal short circuit faults caused by mechanical damage are reported. Taking multiple short circuit tests as an example, the dynamic curve of winding mechanical life is obtained, and the dynamic ability of transformer winding to withstand short circuits in operation is characterized.
By analyzing critical parameters of the evaluation method, it is found that the influence deviation of different checking systems on cumulative effect evaluation results is less than 1%, and the influence of the damping ratio on the cumulative effect is more than 10%. Therefore, this method is suitable for different checking algorithms. Process control and auxiliary strengthening measures can enhance the withstanding ability for short circuits and reduce cumulative damage or winding destruction.
In a word, the method provides a quantitative calculation method for evaluating short-circuit cumulative mechanical damage. Moreover, this method can better describe the winding mechanical state after short circuits, which can provide a reference to transformer design, operation, and maintenance.
keywords:Power transformer, short circuit, cumulative damage, reliability, evaluation
DOI: 10.19595/j.cnki.1000-6753.tces.230120
中图分类号:TM411
国家自然科学基金项目(52061130217)和中国南方电网有限责任公司研究开发项目(036100KK52200045)资助。
收稿日期 2023-02-06
改稿日期 2023-07-28
欧 强 男,1983年生,博士,高级工程师,研究方向为高压电磁设备的设计和性能优化,电力变压器电磁场和短路强度领域的理论研究和应用。E-mail: 361885843@qq.com
罗隆福 男,1962年生,男,教授,博士生导师,研究方向为电能变换系统与装备理论、HVDC 系统的关键技术与装备研制等。E-mail: llf@hnu.edu.cn(通信作者)
(编辑 崔文静)