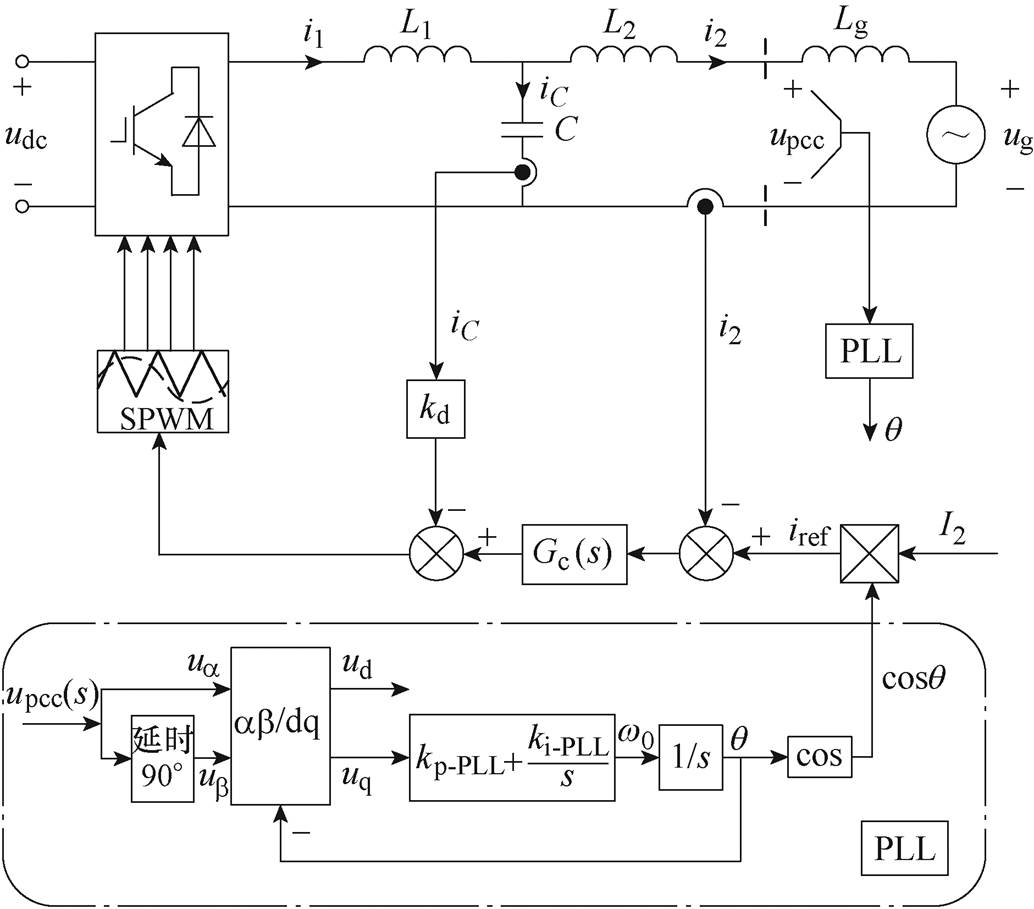
图1 单相并网逆变器的拓扑结构
Fig.1 Topology of single-phase grid-connected inverter
摘要 弱电网下,锁相环在基波以上频段引入的负阻特性,会降低系统输出阻抗的相位,严重影响系统稳定性。鉴于此,该文通过系统控制框图等效变换,推导得到可以消除锁相环负阻特性的电网电压前馈函数,进而提出一种基于电网电压前馈控制的并网逆变器阻抗重塑控制策略。同时,为了提高该策略的普适性,该文利用函数近似和多目标约束为电网电压前馈函数的优化提供两种设计方法,并从系统基波电流跟踪性能、并网功率因数等方面进行误差分析,从而证明其函数优化设计方法的可行性。理论分析表明,优化后的电网电压前馈控制策略,可以有效地对系统输出阻抗相位特性进行重塑,很大程度上拓宽了系统对电网阻抗的适应范围。最后,通过仿真与实验验证所提控制策略的有效性。
关键词:弱电网 并网逆变器 阻抗重塑 锁相环 稳定性
为了解决传统化石能源带来的环境污染问题,新能源发电技术得到了快速发展与广泛应用,高渗透率新能源发电已成为必然趋势,然而高渗透率往往导致并网公共耦合点(Point of Common Coupling, PCC)的等效电网阻抗出现大幅波动,使得电网呈现出弱电网甚至极弱电网特性[1-3]。并网逆变器作为新能源与电网之间接口,锁相环(Phase-Locked Loop, PLL)作为并网逆变器与电网之间同步单元,两者与电网阻抗相互耦合,给系统的稳定运行带来严峻挑战[4-6]。因此,弱电网下PLL对并网逆变器稳定性影响的分析与研究是十分必要的。
近年来,国内外学者主要从两方面对弱电网下考虑锁相环影响的并网逆变器稳定性问题进行研究。一方面,基于逆变器输出阻抗模型,研究考虑锁相环影响时弱电网对逆变器系统稳定性的影响。例如,文献[7-9]通过串联二阶低通滤波器、自适应谐振积分滤波器、复数滤波器对锁相环进行改进设计,但上述所提方案与结构较为复杂,并且需要额外的相位补偿环节。另一方面,基于电网阻抗对锁相环系统阻尼的影响,研究弱电网下逆变器系统鲁棒性降低问题。例如,文献[10-11]针对电网阻抗引起的锁相环系统阻尼比下降问题,给出了两种不同的锁相环参数设计方法。文献[12]通过零点分析,得出电网阻抗幅值增大会导致锁相环系统阻尼减小的结论,进而提出了一种自适应锁相环控制方案,但上述三种方案均无法适应电网阻抗宽范围变化。综上所述,寻求一种简单有效的控制策略,用以降低弱电网下锁相环对并网逆变器系统稳定性的影响,仍是目前亟须解决的问题。
电网电压前馈控制因其简单有效、便于实现等优势在并网逆变器控制方面获得了广泛关注,其中,在并网逆变器阻抗重塑方面的研究更是得到了广泛应用。例如,文献[13]提出了一种基于电网电压与并网电流前馈的虚拟阻抗方法,兼顾了弱电网下计及数字延时的并网系统鲁棒性与抗扰性。文献[14]通过分析常见的电压前馈环节与电网阻抗耦合关系,提出一种基于非理想广义积分器的改进型电网电压前馈控制,有效地降低了电网阻抗对系统稳定性的影响。文献[15]提出了一种加权电网电压前馈控制策略,通过调整电网电压前馈通道串联的比例系数,显著提高了逆变器输出阻抗的相位。同样地,文献[16-17]采用电网电压比例前馈控制策略,有效地提高了系统稳定裕度,避免低频振荡的发生。文献[18]提出了一种基于谐振控制器的改进型电网电压前馈控制策略,实现了对输出阻抗相频特性的重塑,同时降低了控制过程中的高次谐波对系统的影响。综上所述,虽然基于电网电压前馈控制的阻抗重塑策略多种多样,但通过采用电网电压前馈来解决锁相环导致的系统稳定问题,仍未被充分研究。
基于上述研究现状,本文以弱电网下单相LCL并网逆变器为研究对象,通过系统控制框图等效变换,推导得到可以完全消除锁相环对系统输出阻抗影响的电网电压前馈函数,进而提出了一种基于电网电压前馈的并网逆变器阻抗重塑控制策略。同时,利用函数近似法和多目标约束法对前馈函数进行设计,使所提控制策略更加具有可行性与普适性。理论分析和实验结果表明,该控制策略无需额外的相位补偿环节,且不影响系统基波电流跟踪性能,可以有效解决弱电网下考虑锁相环时系统鲁棒性下降或失稳问题。
图1为采用并网电流反馈和电容电流有源阻尼策略的单相并网逆变器拓扑结构。

图1 单相并网逆变器的拓扑结构
Fig.1 Topology of single-phase grid-connected inverter
图1中,逆变侧电感L1、滤波电容C和网侧电感L2构成LCL滤波器;电网等效为电压源与电网阻抗串联的等效模型,ug为电网电压;Lg为电网阻抗(由于电网阻抗的阻性分量,有利于系统稳定[19],因此,本文考虑最恶劣情况,即电网阻抗为纯电感);udc、upcc分别为直流母线电压、PCC处电压;i1、i2、iC分别为逆变器机侧电流、并网电流、滤波电容电流;iref、I2分别为并网电流基准值、并网电流给定幅值;q 为PLL输出相位(PCC处相位);kp-PLL、ki-PLL分别为PLL控制器的比例系数、积分系数;kd为电容电流有源阻尼系数;kPWM为脉宽调制系数;Gc(s)为电流控制器。本文采用准比例谐振(Quasi Pro- portional Resonant, QPR)控制器对电流进行控制[20]。
 (1)
(1)
式中,kp、kr、w0、wc分别为QPR控制器的比例系数、谐振系数、谐振角频率和控制带宽。
此外,传统PLL环节的传递函数表达式[20]为
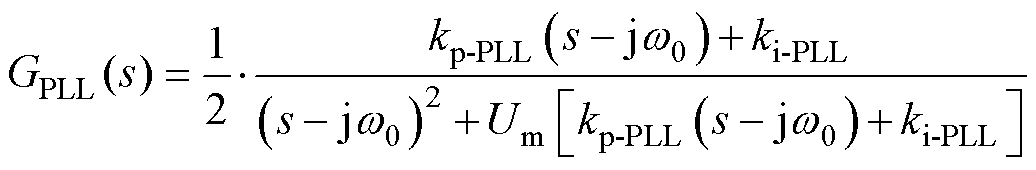 (2)
(2)
式中,Um为并网点电压upcc的幅值。
LCL并网逆变器的控制框图如图2a所示,通过控制框图的等效变换,可进一步简化为如图2b所示,图2b中
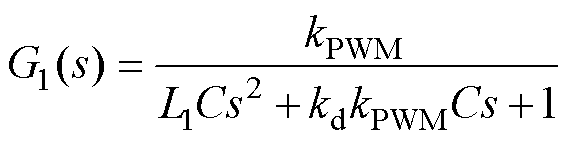 (3)
(3)
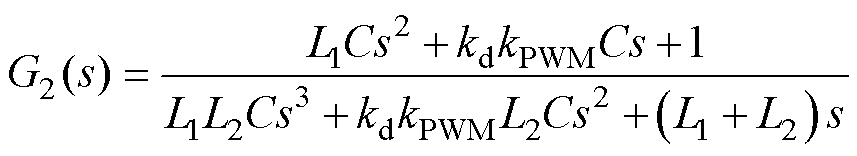 (4)
(4)
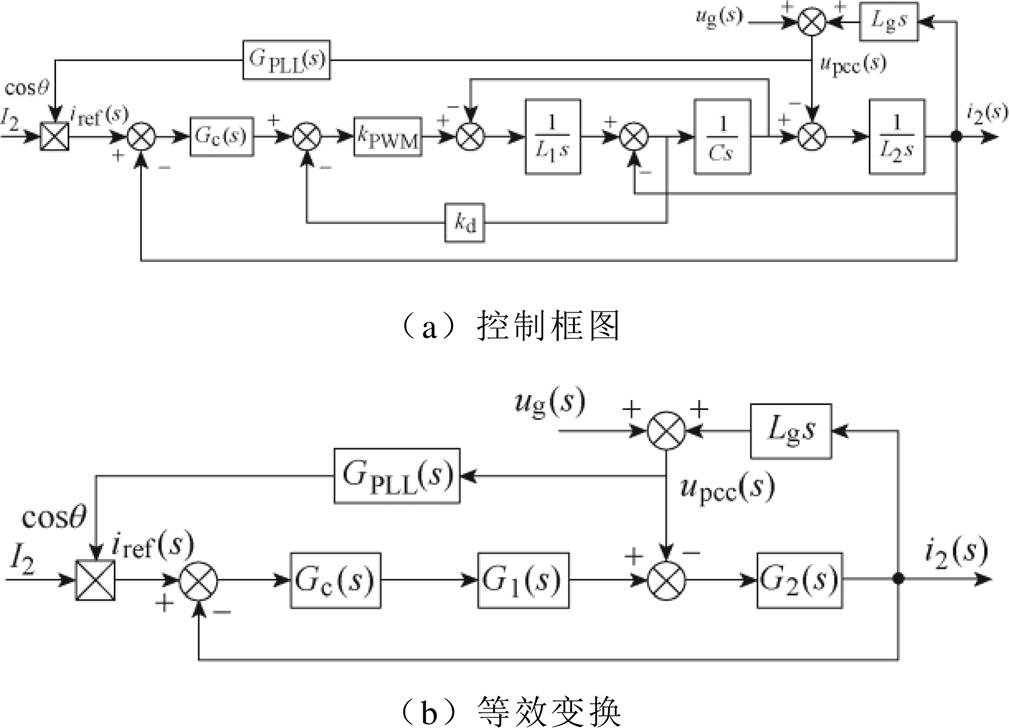
图2 LCL型并网逆变器控制框图及其等效变换
Fig.2 Control block diagram of LCL grid-connected inverter and its equivalent transformation
目前,针对弱电网下考虑锁相环时,并网逆变器系统稳定性问题的研究已有大量文献进行讨 论[7-10],并且已论述的十分清晰,因此,为了推导电网电压前馈函数,本文只做一些简单论述分析。
由图2b所示系统等效控制框图可以推导出并网电流i2(s)表达式为
 (5)
(5)
不考虑PLL时,GPLL(s)=0,即参考电流iref(s)=0,将其代入式(5)化简可得
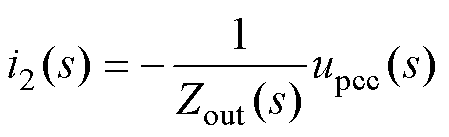 (6)
(6)
式中,Zout为不考虑PLL时的系统输出阻抗。
考虑PLL因素时,根据图2a可知参考电流iref(s)=I2GPLL(s)upcc(s),将其代入式(5)化简可得
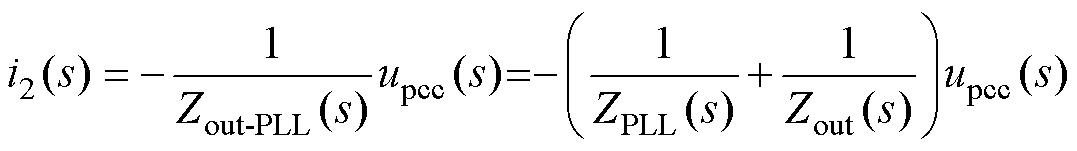 (7)
(7)
式中,Zout-PLL(s)为考虑PLL时系统输出阻抗;ZPLL(s)为考虑PLL时所引入的负阻抗[10]。
根据式(7)可得考虑PLL时的并网逆变器等效电路如图3所示。
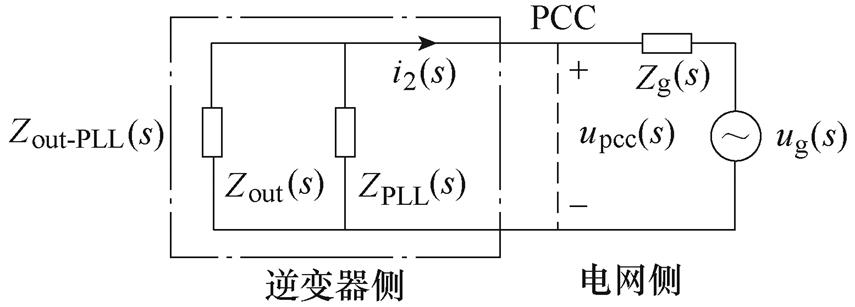
图3 考虑PLL时的并网逆变器等效电路
Fig.3 Consider the equivalent circuit of grid-connected inverter in PLL
图3中,Zg(s)为电网阻抗,Zout(s)、Zout-PLL(s)、ZPLL(s)和Zg(s)的表达式分别为
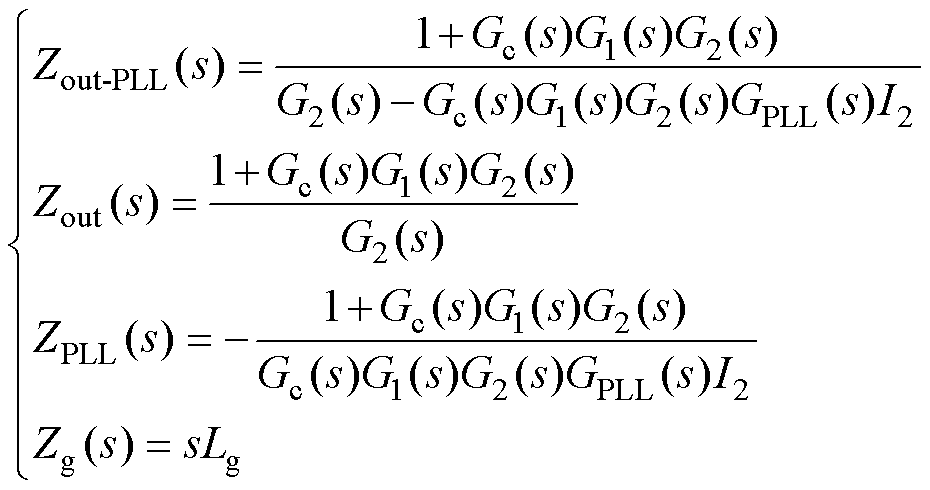 (8)
(8)
为了便于下文对比分析,首先给出并网逆变器的相关参数见表1。尽管降低PLL带宽可以降低PLL负阻特性对系统稳定性的影响,但为了保证PLL具有较好的动态响应能力,本文以PLL带宽fBW= 250 Hz为例进行设计[10]。
表1 并网逆变器相关参数
Tab.1 Relevant parameters of grid-connected inverter

参 数数 值 额定功率Pout/kW1 直流母线电压udc/V250 滤波器参数L1/mH3 L2/mH0.5 C/mF10 有源阻尼系数kd0.15 脉宽调制系数kPWM250 锁相环kp-PLL6.1 电网电压ugrms/V100 电网频率f0/Hz50 控制器参数kp0.09 kr4.4 wc/(rad/s)π 开关频率fsw/kHz10 采样频率fs/kHz20 锁相环ki-PLL2 636.3
根据式(8)并结合表1所示参数,可绘制Zout(s)、Zout-PLL(s)、Zg(s)的伯德图如图4所示。
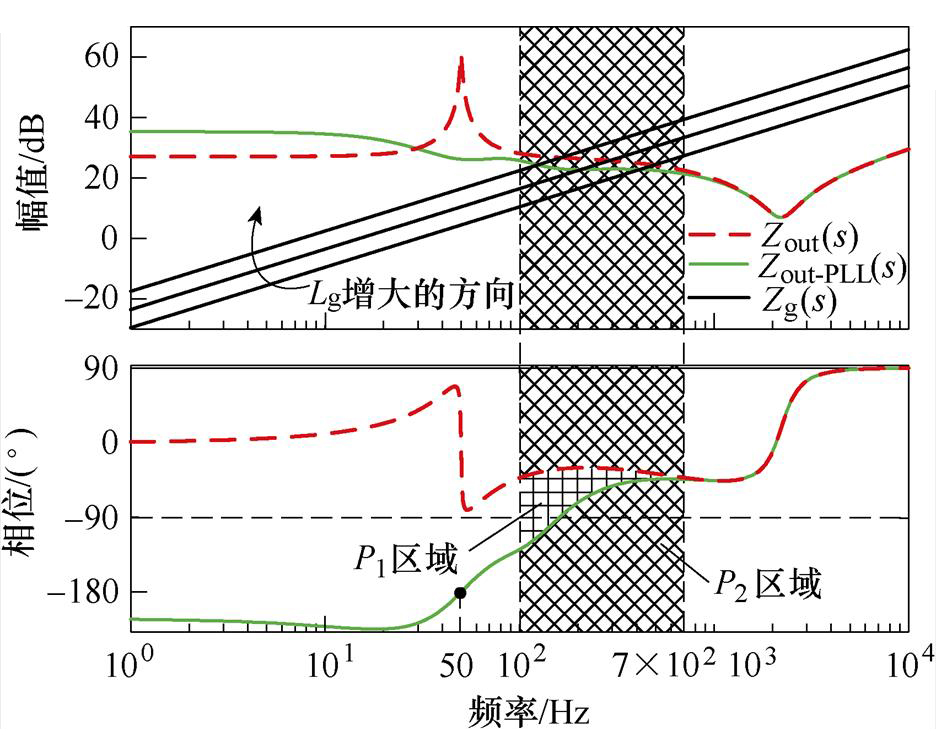
图4 系统输出阻抗伯德图
Fig.4 Bode diagram of system output impedance
根据文献[21],并网逆变器系统稳定的条件为系统相位裕度PM>0°,即系统输出阻抗在交截频率处的相位须大于-90°。结合表1参数与图4可知,系统交截频率通常位于100~700 Hz频率范围内,即图4所示P2区域内。
分析P2区域,处于相同电网阻抗时,阻抗Zout-PLL(s)的幅值与相位均小于阻抗Zout(s)的幅值与相位,导致考虑锁相环时系统输出阻抗的交截频率有所下降,同时,相位裕度也会出现大幅下降,如P1区域所示[10]。因此,弱电网下考虑锁相环时,可能会造成系统稳定裕度不足甚至系统失稳的情况。
对比式(6)与式(7)并结合上述分析可知,考虑锁相环时,系统所引入的负阻抗ZPLL(s)对系统输出阻抗的幅值和相位均产生不同程度的负面影响,进而影响系统稳定性。鉴于此,本文提出一种基于电网电压前馈的并网逆变器阻抗重塑控制策略,以降低甚至消除负阻抗ZPLL(s)对系统输出阻抗的影响。
通过分析式(7)与图3可知,考虑锁相环时,逆变器输出阻抗可以通过并联阻抗Zpal(s)进行重塑,阻抗重塑时并网逆变器等效电路如图5所示。合理地设计并联阻抗Zpal(s)即可实现对负阻抗ZPLL(s)的抑制,进而达到提升并网逆变器系统稳定性的目的。
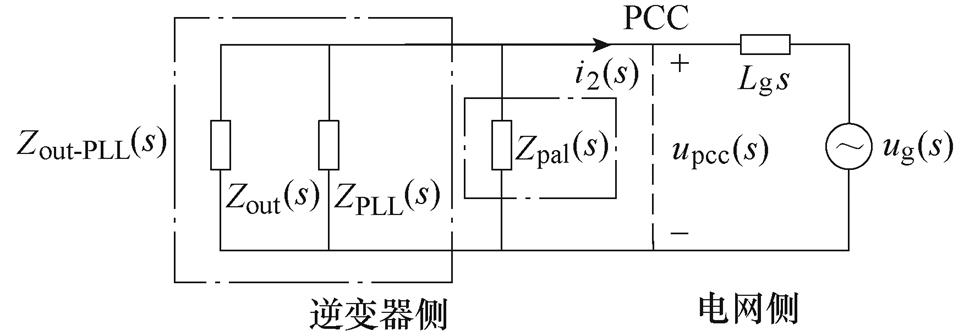
图5 阻抗重塑时并网逆变器等效电路
Fig.5 Impedance remodelling when grid-connected inverter equivalent circuit
考虑阻抗重塑时系统控制框图及其等效变换如图6所示。图6a给出了并联阻抗Zpal(s)的实现方法,即在图2b基础上,从并网点电压upcc到并网电流i2之间引入一条传递函数为-1/Zpal(s)的支路。
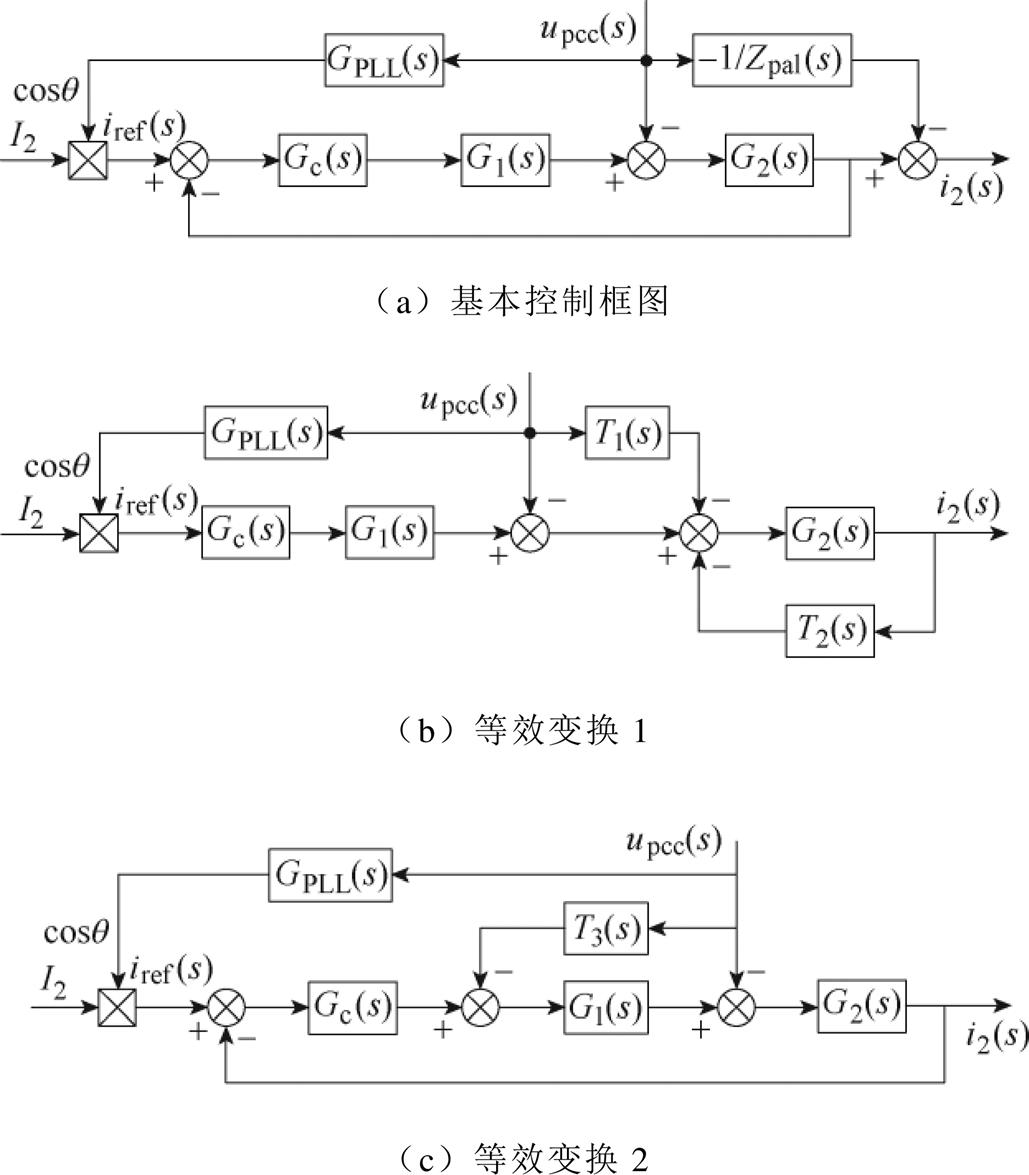
图6 考虑阻抗重塑时系统控制框图及其等效变换
Fig.6 The system control block diagram and its equivalent transformation are considered in impedance remodeling
在图6a系统控制框图基础上,将i2的前馈点从Gc(s)的输入端移至G2(s)的输入端,并调整i2的前馈函数为T2(s);将upcc的前馈点从G2(s)的输出端移至G2(s)的输入端,并调整upcc的前馈函数为T1(s),如图6b所示。图6b中,T1(s)、T2(s)的表达式分别为
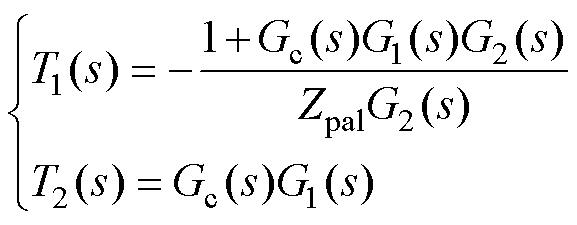 (9)
(9)
进一步地,在图6b基础上,将upcc的前馈点从G2(s)的输入端移至G1(s)的输入端,并调整upcc的前馈函数为T3(s),将i2前馈点还原至图6a初始状态,如图6c所示。图6c中前馈函数T3(s)为
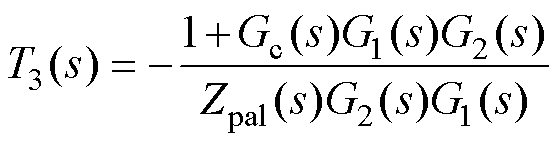 (10)
(10)
为了完全消除锁相环对并网逆变器输出阻抗及其稳定性的影响,令图5中Zpal(s)=-ZPLL(s)。同时,将式(8)代入到式(10)中,则图6c中函数前馈函数T3(s)可进一步化简为
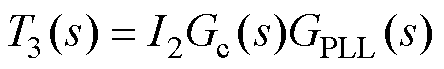 (11)
(11)
由于图6c是通过图6a进行控制框图等效变换得到的,因此,按图6c所示的电网电压前馈的方法,即可实现图5所示系统阻抗重塑,进而消除锁相环对系统稳定性的影响。
根据以上分析即可得出如图7所示的基于电网电压前馈控制的并网逆变器系统拓扑结构及控制 框图。
并网逆变器系统鲁棒性可通过推导其输出阻抗并借助稳定阻抗判据进行分析,鉴于此,本节首先给出了考虑PLL时,基于电网电压前馈控制的系统输出阻抗,然后通过设计示例从理论层面说明本文所提控制策略的有效性。
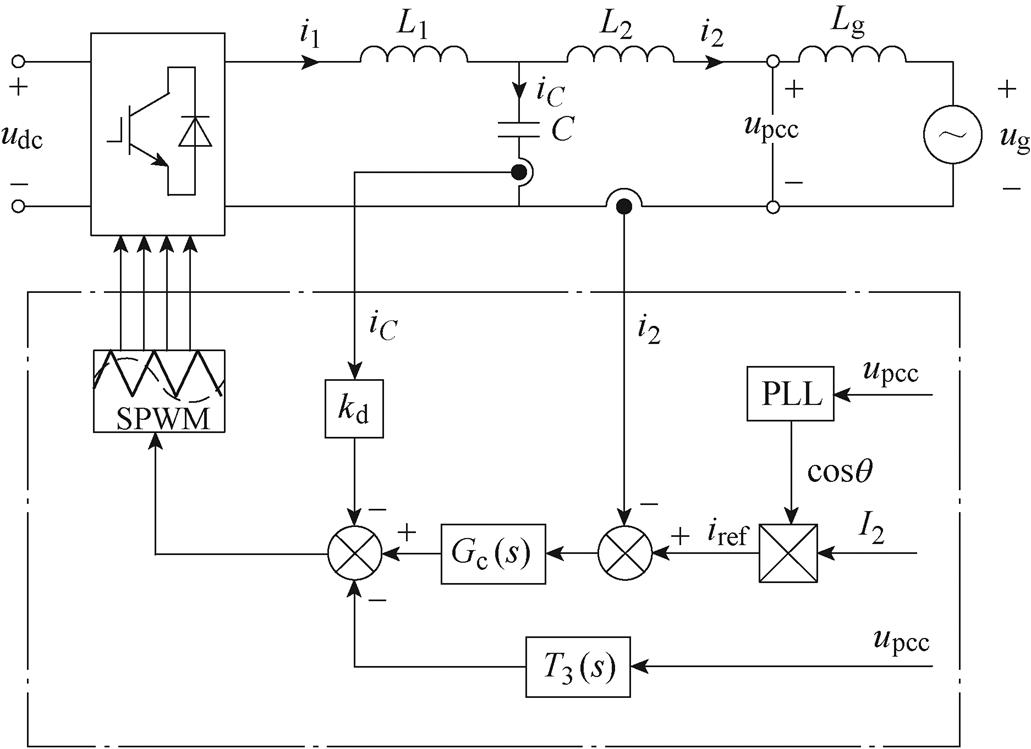
图7 基于电网电压前馈控制的并网逆变器系统拓扑结构及控制框图
Fig.7 Topology structure and control block diagram of grid-connected inverter system based on power grid voltage feedforward control
根据图6c所示系统控制框图并结合式(7)、式(8)与式(11),可以推导出考虑PLL与电网电压前馈时系统输出阻抗Zout-ZPLL(s)为
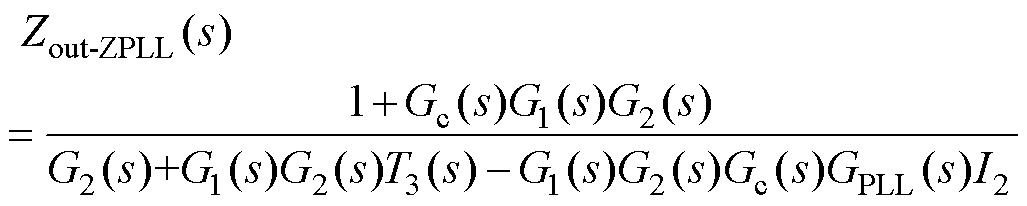
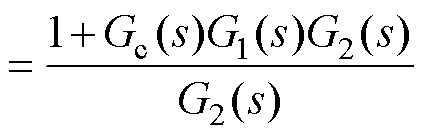 (12)
(12)
根据式(8)、式(12)与表1参数,绘制出如图8所示的不同短路比(Short Circuit Ratio, SCR)时,阻抗Zout-PLL(s)与阻抗Zout-ZPLL(s)的伯德图。
从图8中可以看出,当系统采用电网电压前馈控制策略时,系统稳定裕度得到了显著提升。当电网阻抗Lg=5.3 mH(SCR=6)、Lg=10.6 mH(SCR=3)时,相位裕度分别达到了53°、58.9°,分别提升了8.6°、38.4°,系统鲁棒性得到了保证。极弱电网下,当电网阻抗Lg=15.9 mH(SCR=2)时,系统相位裕度达到59.9°,提升了67.7°,系统依旧具有极高鲁棒性,证明了基于电网电压前馈阻抗重塑策略的有效性。
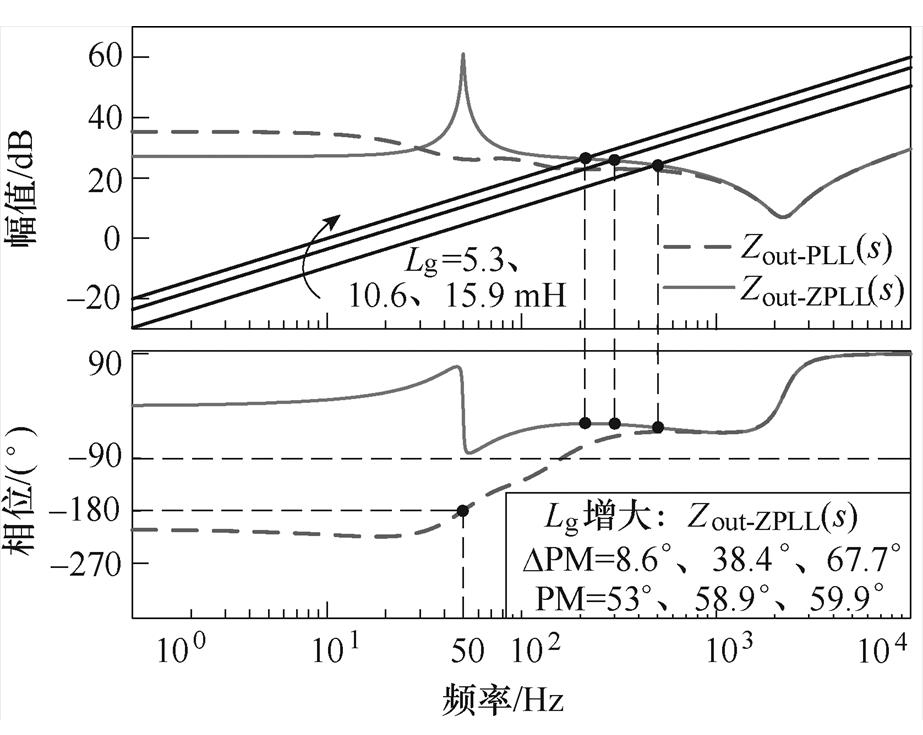
图8 Zout-PLL(s)与Zout-ZPLL(s)阻抗伯德图
Fig.8 Bode diagram of impedance of Zout-PLL(s) versus Zout-ZPLL(s)
此外,分析式(1)、式(2)与式(11),由于PLL传递函数GPLL(s)中所含s-jw0项在实际工程中难以实现,并且函数T3(s)涉及s4项过于复杂,所以在不影响电流跟踪性能和保证电网电压前馈效果的前提下,对前馈函数T3(s)进行优化设计,提升基于电网电压前馈阻抗重塑策略的可行性。
对式(11)进行“拆分”与近似等效,第一项I2为并网电流给定幅值,因此无需化简;第二项Gc(s)为电流控制器函数,根据其幅相特性利用函数Gc-eq(s)=kp进行近似等效;第三项GPLL(s)为锁相环函数,将函数中所含s-jw0项近似等效为s,则可得近似等效锁相环函数GPLL-eq(s)为
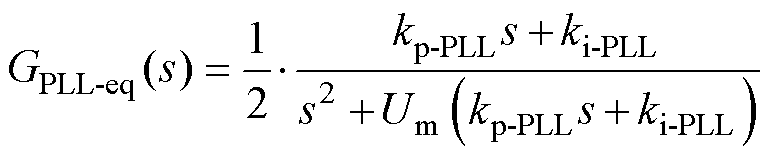 (13)
(13)
此时,前馈函数近似等效为Ta(s)=I2Gc-eq(s)·GPLL-eq(s),根据式(12)与式(13),可以推导出基于函数近似的电网电压前馈控制时,系统的输出阻抗Zout-ZPLL-eq(s)为
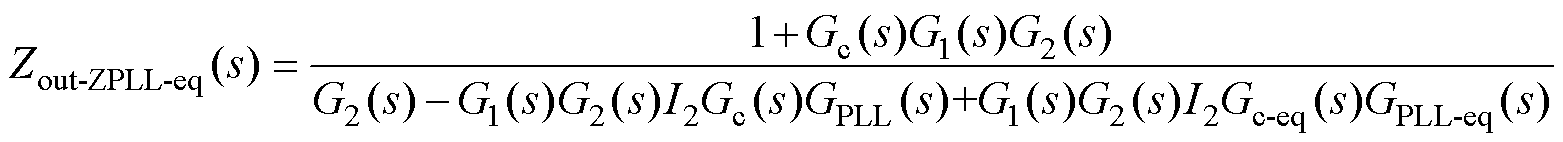 (14)
(14)
同时,并联阻抗Zpal(s)近似等效为阻抗Zpal-eq(s),结合式(8),Zpal-eq(s)表达式为
 (15)
(15)
根据式(1)、式(2)、式(13)与表1参数绘制Gc(s)、Gc-eq(s)、GPLL(s)、GPLL-eq(s)伯德图,如图9所示。
通过1.2节分析可知,基于电网电压前馈的阻抗重塑控制策略,其目的是消除锁相环在100~700 Hz频率范围内对系统稳定性造成的影响。首先,分析图9中100~700 Hz频率范围内,即P1所示区域。P1区域内,Gc(s)与Gc-eq(s)幅值一致,根据式(1)可知,幅值为定值-20lgkp,但相位存在一定误差,如图P2所示区域;GPLL(s)与GPLL-eq(s)幅值几乎一致,相位存在一定误差,如P3所示区域。此外,分析图9中50 Hz基频处,Gc(s)与Gc-eq(s)的相位一致,幅值存在误差;GPLL(s)与GPLL-eq(s)的相位与幅值均存在误差。
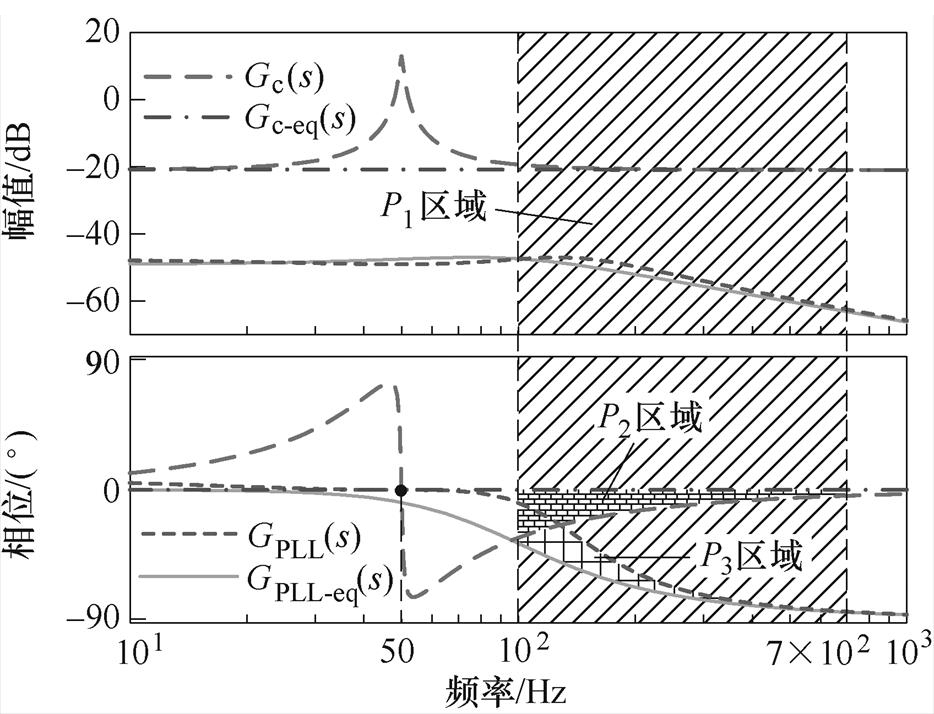
图9 Gc(s)、Gc-eq(s)、GPLL(s)、GPLL-eq(s)函数伯德图
Fig.9 Bode graphs of Gc(s), Gc-eq(s), GPLL(s), GPLL-eq(s)
根据上述分析可知,在前馈函数进行近似等效时会对50 Hz基频处幅值与相位造成不同程度的误差,可能会对系统基波电流跟踪性能产生影响,因此需要对基于阻抗Zpal-eq(s)实现阻抗重塑的并网逆变器系统及其输出阻抗基波幅值、相位进行进一步分析。
1)基波幅值分析
为了便于进行基波幅值分析,对式(14)进行如下化简
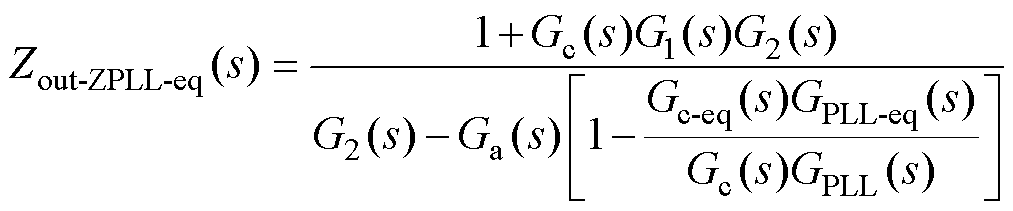 (16)
(16)
其中
Ga(s)=G1(s)G2(s)Gc(s)GPLL(s)I2
对比分析式(8)与式(16),误差项为[Gc-eq(s)GPLL-eq(s)]/[Gc(s)GPLL(s)],结合表1参数,误差项在基波处幅值为
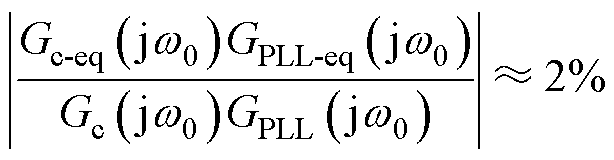 (17)
(17)
通过式(17)可知,此时误差项幅值极小,符合并网标准[22],因此Gc-eq(s)、GPLL-eq(s)对基波幅值增益的影响可以忽略。
2)基波相位分析
根据式(8)与式(14)并结合表1参数,阻抗重塑前后系统输出阻抗的基波相位误差|Dq1|为
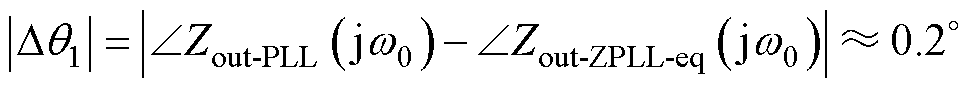 (18)
(18)
基波相位误差|Dq1|即为功率因数误差角,所以阻抗重塑前后的系统功率因数误差仅为4×10-6,因此Gc-eq(s)、GPLL-eq(s)对系统基波相位的影响可以忽略,系统仍可视为单位功率因数并网。
根据上述分析,采用函数近似优化后的电网电压前馈控制对系统基波电流跟踪性能的影响可忽略不计。但是,采用函数近似等效时,会存在如图9中P2、P3所示区域的相位误差,因此,相较于未采用函数近似时的电网电压前馈控制而言,系统阻抗重塑效果可能会受到一定程度的影响,因此还需要对系统鲁棒性作进一步进行分析。
为了对采用函数近似优化后的电网电压前馈控制,其输出阻抗重塑效果作进一步分析。根据式(12)、式(14)与表1参数,绘制出如图10所示阻抗Zout-ZPLL(s)与阻抗Zout-ZPLL-eq(s)的伯德图。
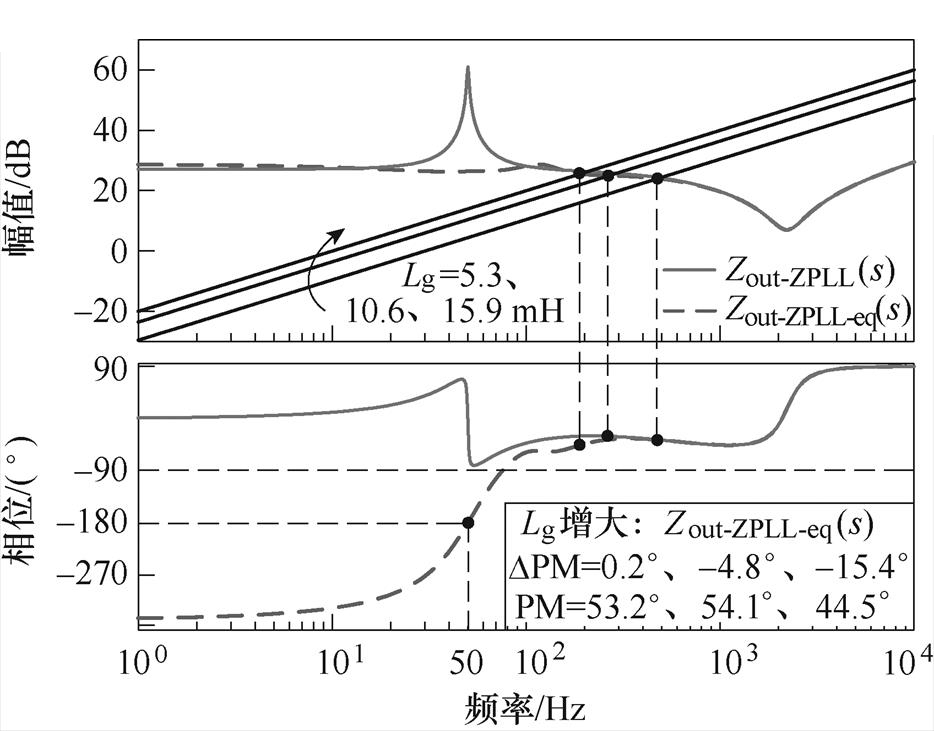
图10 Zout-ZPLL(s)、Zout-ZPLL-eq(s)阻抗伯德图
Fig.10 Bode graphs of Zout-ZPLL(s), Zout-ZPLL-eq(s)
根据3.1节分析,函数近似等效时,在100~700 Hz会出现相位误差,因此分析图10所示伯德图,与未采用函数近似优化时相比,基于优化后的电网电压前馈控制时,系统稳定裕度会产生一定程度下降,但依旧能够保持稳定。当电网阻抗Lg= 5.3 mH(SCR=6)时,系统相位裕度为53.2°,提升了0.2°,系统鲁棒性得到保证;当电网阻抗Lg= 10.6 mH(SCR=3)、Lg=15.9 mH(SCR=2)时,系统相位裕度分别为54.1°、44.5°,虽然分别下降了4.8°、15.4°,但相位裕度依旧大于30°,系统仍具有一定的鲁棒性。
根据上述分析可知,基于函数近似的电网电压前馈环节的优化设计,在不影响系统基波电流跟踪性能的前提下,可以有效地对系统输出阻抗相位特性进行重塑,在一定程度上降低了PLL对系统输出阻抗的影响,扩宽了逆变器对电网阻抗的适应范围,并且控制参数易于获取,在实际工程当中更易实现。此外,将图7中的前馈函数T3(s)替换为Ta(s)即可得到采用函数近似法时,基于电网电压前馈控制的并网逆变器系统拓扑结构及控制框图。
基于函数近似的电网电压前馈环节优化设计,虽然在很大程度上简化了前馈函数的参数计算,极大地提高了电网电压前馈控制策略的可行性,但是其对系统输出阻抗相位特性的重塑效果有所下降。当系统处于极弱电网下时,可能会造成系统稳定裕度不足,影响系统稳定运行。为了使电网电压前馈控制策略更加具有普适性,本文给出第二种方法,利用多目标约束对电网电压前馈环节进行优化设计[23]。
采用多目标约束对电网电压前馈函数进行优化设计时,为了简化计算,使用系数kp替代函数Gc(s),由于本节会对基波性能、系统相位裕度进行约束,因此暂不考虑此替代方案可能引起的相位与幅值误差,此时,式(11)化简可得Tb(s)为
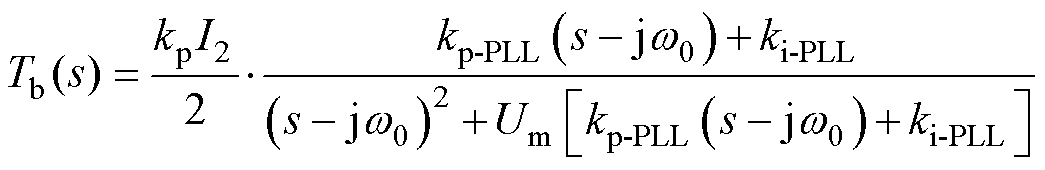 (19)
(19)
根据式(19),给出多目标约束下电网电压前馈函数的零极点一般式Tb-uc(s)为
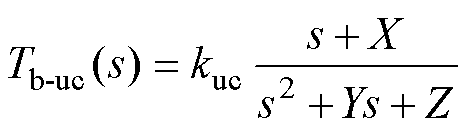 (20)
(20)
式中,kuc=kpI2kp-PLL/2;X、Y、Z为待求参数,结合表1参数与式(19)的零极点分布,X、Y、Z的值均大于零。
此时,根据式(11)、式(12)与式(20),可以推导出基于多目标约束的电网电压前馈控制时,系统的输出阻抗Zout-ZPLL-uc(s)为
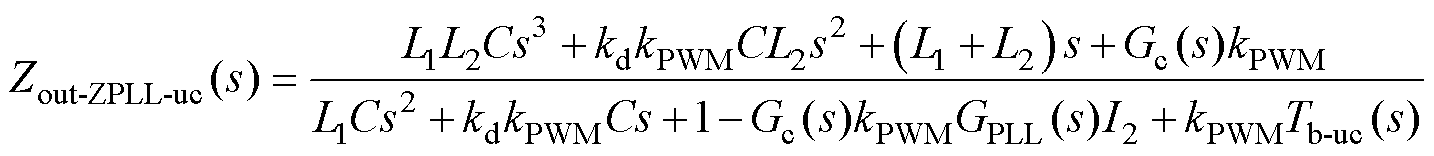 (21)
(21)
同时,多目标约束下的并联阻抗Zpal(s)简化为阻抗Zpal-uc(s),即
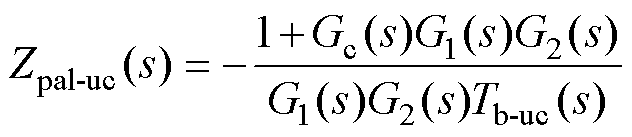 (22)
(22)
为了保证系统稳定性,本节以系统基波电流跟踪性能、稳定裕度与低频幅值为约束条件,对电网电压前馈函数Tb-uc(s)中的参数进行优化设计。由于以下分析均在低频与中频下进行,因此忽略滤波电容C,此外Gc(s)kPWM项中准PR控制器Gc(s)在基波处增益近乎无穷大,(L1+L2)s项可被进一步忽略,阻抗Zout-ZPLL-uc(s)可进一步化简为Zout-ZPLL-ucr(s),即
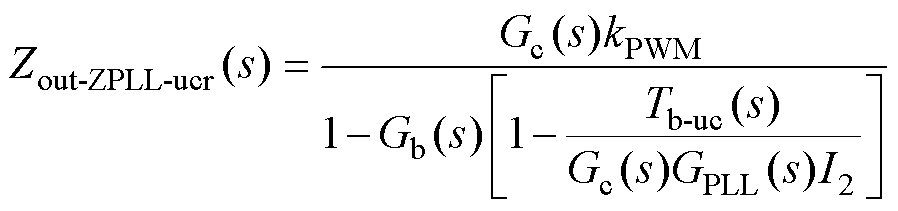 (23)
(23)
其中
Gb(s)=Gc(s)GPLL(s)kPWMI2
1)基波电流跟踪性能
为确保采用多目标约束法时,基于电网电压前馈控制的系统依旧具有良好的基波电流跟踪性能,从系统输出阻抗基波幅值与相位两方面对多目标约束下电网电压前馈函数Tb-uc(s)进行约束。基波幅值约束条件为
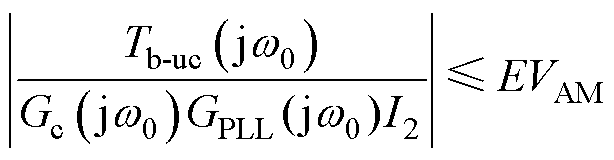 (24)
(24)
式中,EVAM为基波幅值比,当EVAM极小时,可认为|Tb-uc(jw0)| |[Gc(jw0) GPLL(jw0) I2]|,此时Tb-uc(s)对输出阻抗Zout-ZPLL-ucr(s)基波幅值影响极小可以忽略。本文设定EVAM取5%。
|[Gc(jw0) GPLL(jw0) I2]|,此时Tb-uc(s)对输出阻抗Zout-ZPLL-ucr(s)基波幅值影响极小可以忽略。本文设定EVAM取5%。
基波相位约束条件为
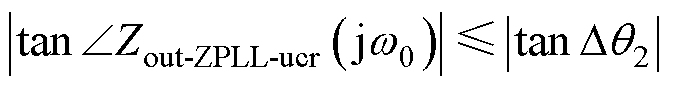 (25)
(25)
式中,Dq2为多目标约束时系统功率因数误差角,当|tanDq2|极小时,可认为功率因数误差EVPF近似为0,此时,逆变器单位功率因数并网,即Tb-uc(s)对输出阻抗Zout-ZPLL-ucr(s)基波相位影响极小可以忽略。本文设定EVPF取0.01%,对应Dq2=0.81°。
2)系统稳定裕度
为确保采用多目标约束法时,基于电网电压前馈控制的系统在弱电网包括极弱电网下依旧具有较高稳定裕度,以SCR=2为基准进行系统稳定裕度约束。在实际工程中,PM1=30°即可认为系统达到稳定,考虑到式(23)化简前后可能会存在一定的相位误差,为进一步确保系统具有足够的稳定裕度,本文设定以PM2=45°进行系统稳定裕度约束。
SCR=2时,由于阻抗Zout-ZPLL-ucr(s)与阻抗Zg(s)的交截频率未知,因此使用阻抗Zout-PLL(s)与阻抗Zg(s)的交截频率wg=209 Hz进行替代,为确保此替代方案的有效性,首先对阻抗Zout-ZPLL-ucr(s)与阻抗Zg(s)的交截频率进行约束,保证其交截频率在wg附近或大于wg。
系统输出阻抗交截频率约束条件为
 (26)
(26)
式中,EVCF为交截频率处幅值误差,当EVCF极小时,可认为SCR=2时,Zout-ZPLL-ucr(s)与阻抗Zg(s)的交截频率为wg或者大于wg。本文设定EVAM取10%。
根据上述分析可得,系统稳定裕度约束条件为
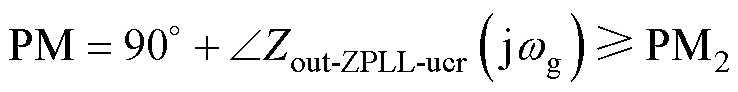 (27)
(27)
3)低频幅值
若输出阻抗Zout-ZPLL-ucr(s)与阻抗Zg(s)在低频范围内出现多个交点,则会对系统稳定运行产生不利影响。为确保基频以下逆变器输出阻抗Zout-ZPLL-ucr(s)与阻抗Zg(s)无交点,只需保证零至基频范围内|Zout-ZPLL-ucr(s)|的最小值大于|Zg(s)|的最大值即可,其中|Zg(s)|的最大值在基频处取得,|Zout-ZPLL-ucr(s)|最小值对应频率可通过数学求导等方式获取。
根据以上分析可得,低频幅值约束条件为
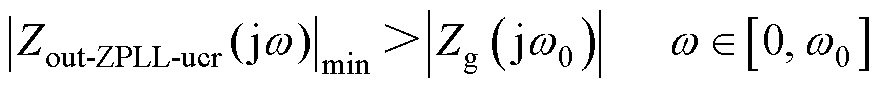 (28)
(28)
分析图5可知,阻抗Zout-ZPLL-ucr(s)由阻抗Zout(s)、负阻抗ZPLL(s)、阻抗Zpal-uc(s)三者并联所得,在低频范围内,Zout(s)的模值远大于ZPLL(s)与Zpal-uc(s)并联后阻抗模值,忽略滤波电容C与s(L1+L2)项。可得到简化后的低频幅值约束条件为
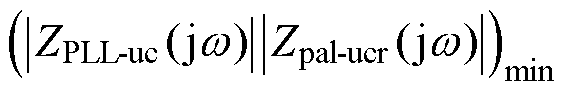
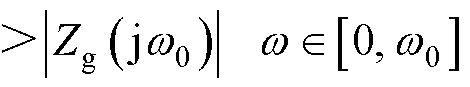 (29)
(29)
其中
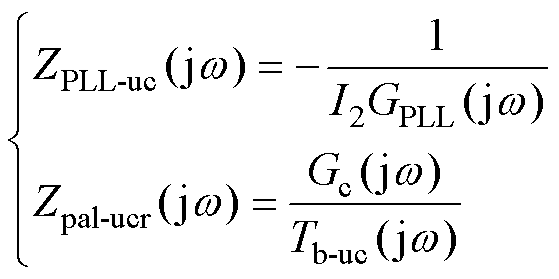 (30)
(30)
通过对约束式(24)~式(27)、式(29)进行化简与参数代入,可以得到多目标约束下电网电压前馈函数Tb-uc(s)中未知量X、Y、Z的取值范围,在此取值范围内随机取值,即可得到前馈函数,进而实现电网电压前馈控制策略。
为了对采用多目标约束优化后的电网电压进行前馈控制,对其输出阻抗重塑效果作进一步分析。根据上述约束条件所得到的X、Y、Z取值范围,并结合表1参数,本文以X=1 492,Y=1 260,Z= 1 100 000取值为例。
此时,对于约束条件而言,基波幅值比为2.45%,小于EVAM=5%,满足基波幅值约束条件;基波相位正切值为1.13×10-3,小于tanDq2=1.41×10-2,满足基波相位约束条件;交截频率处幅值比为93.3%,大于1-EVCF=90%,满足交截频率约束条件;在交截频率wg=209 Hz处系统稳定裕度为63.3°,大于PM2= 45°,满足系统稳定裕度约束条件;零至基频范围内系统输出阻抗最小值为19.275,大于|Zg(jw0)|=5.012,满足低频幅值约束条件。证明了X、Y、Z选值的正确性。
根据式(12)、式(20)与表1参数,绘制出如图11所示阻抗Zout-ZPLL(s)与阻抗Zout-ZPLL-uc(s)伯德图。
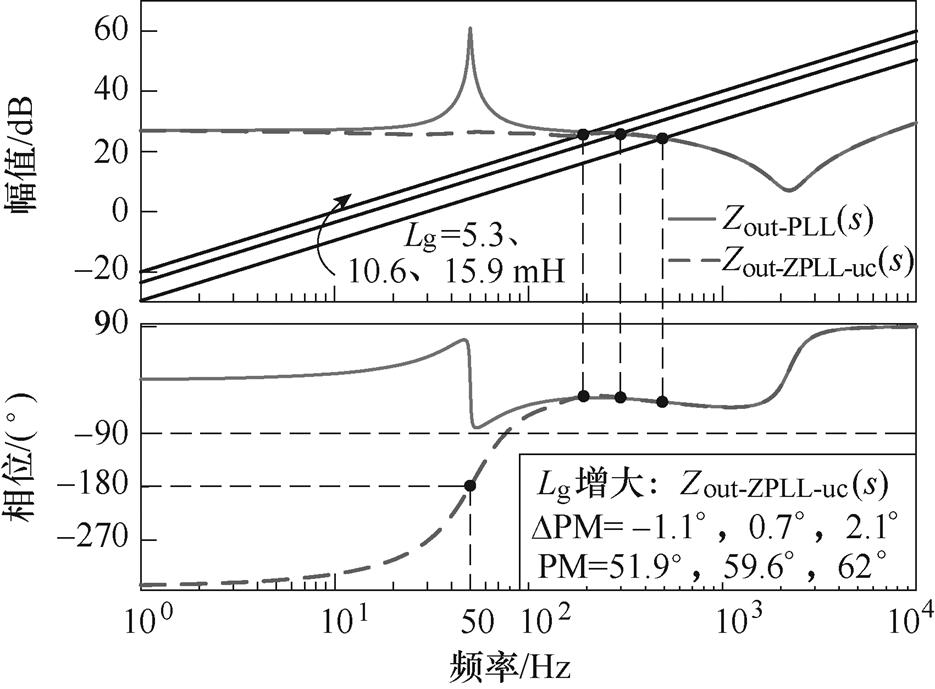
图11 Zout-ZPLL(s)、Zout-ZPLL-uc(s)阻抗伯德图
Fig.11 Bode graphs of Zout-ZPLL(s)、Zout-ZPLL-uc(s)
从图11中可以看出,与未采用多目标约束时相比,当采用多目标约束法时,基于电网电压前馈控制的系统稳定裕度基本保持不变。弱电网下,当电网阻抗Lg=5.3 mH(SCR=6)时,系统相位裕度为51.9°,降低了1.1°,系统具有极高的鲁棒性;当电网阻抗Lg=10.6 mH(SCR=3)、Lg=15.9 mH(SCR=2)时,系统相位裕度分别达到59.6°、62°,分别提升了0.7°、2.1°,系统同样具有极高的鲁棒性。
根据上述分析可知,基于多目标约束的电网电压前馈环节优化设计,在不影响系统基波电流跟踪性能的前提下,可以有效地对系统输出阻抗相位特性进行重塑,极大程度上降低了PLL对系统输出阻抗的影响,扩宽了逆变器对电网阻抗的适应范围。相较于第3节函数近似法而言,此方法具有更强的普适性,可以根据实际工程中的不同标准与要求,对约束条件进行调整与补充,实现对前馈函数的自由设计,不足之处是计算量偏大,此缺陷可通过编程等其他方法解决。
此外,将图7中的前馈函数T3(s)替换为Tb-uc(s)即可得到采用多目标约束法时,基于电网电压前馈控制的并网逆变器系统拓扑结构及控制框图。
为验证所提基于电网电压前馈的并网逆变器阻抗重塑策略的有效性,在Matlab/Simulink中搭建了如表1参数所示的单相LCL型并网逆变器仿真模型。
图12为有无采用电网电压前馈控制时的并网电流仿真波形。未采用电网电压前馈控制时,如图12a所示,当电网阻抗Lg=5 mH时,并网电流波形保持稳定;当Lg=9.5 mH时,并网电流波形畸变较为严重,其总谐波畸变率(Total Harmonic Distortion, THD)为11.4%,已无法满足并网要求;当Lg=14 mH时,并网电流发生严重振荡,系统已处于失稳状态。采用电网电压前馈控制时,如图12b和图12c所示,无论是弱电网还是极弱电网情况下,并网电流质量均得到明显改善,并且电流THD均小于2%,满足并网要求;进一步对比分析图12b与图12c可知,多目标约束下,基于电网电压前馈控制的系统并网THD更小,系统稳定性更高。
图13为采用电网电压前馈控制时的系统并网点电流、电压仿真波形,分析图13a与图13b可知,无论采用函数近似法还是多目标约束法,基于电网电压前馈控制的系统,均可以保证并网点单位功率因数并网,并网点电压、电流不存在相位偏差。
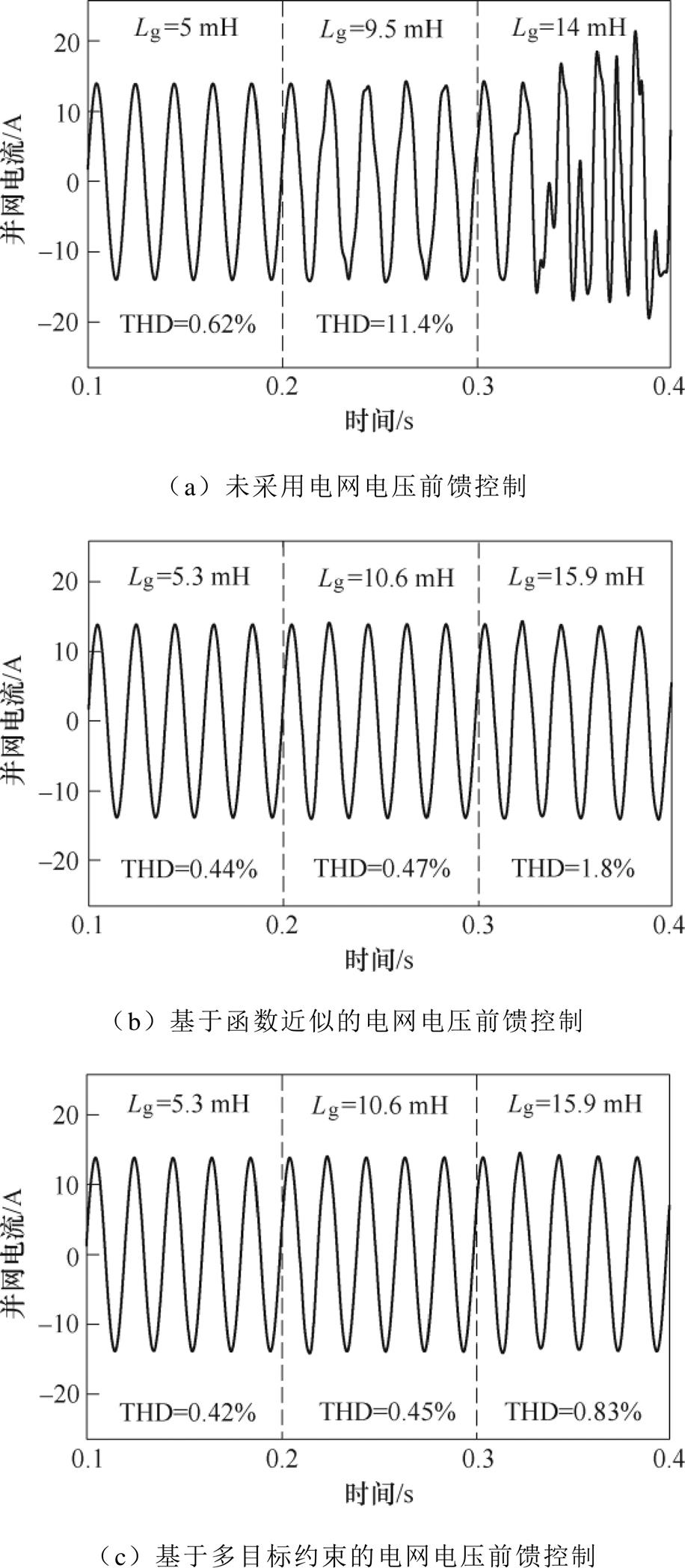
图12 有无采用电网电压前馈控制时的并网电流仿真波形
Fig.12 Simulation waveforms of grid-connected current when using feedforward control of grid voltage
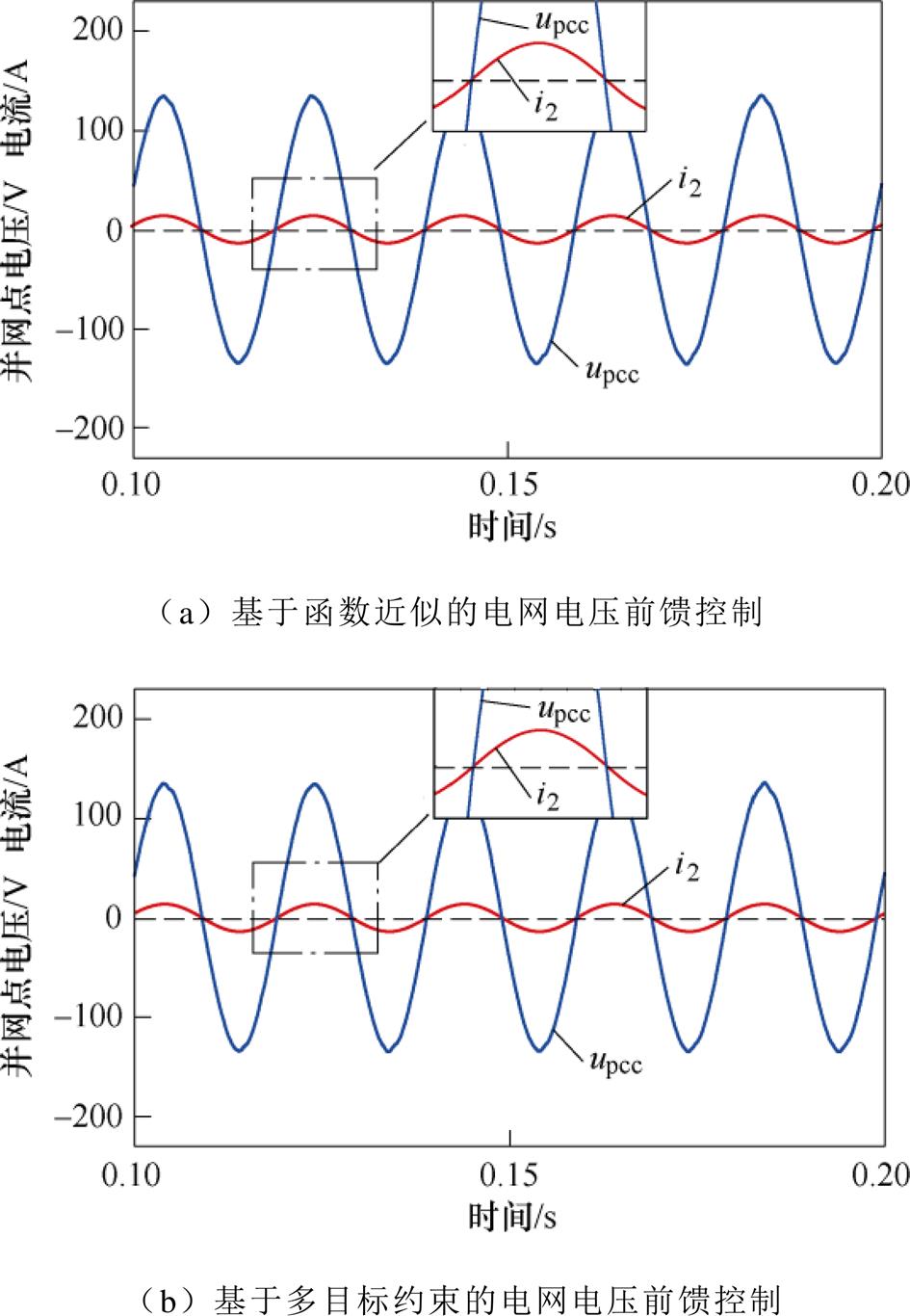
图13 电网电压前馈控制时并网点电流、电压仿真波形
Fig.13 Simulation waveforms of current and voltage of grid connection point in feedforward control of grid voltage
为进一步验证本文所提基于电网电压前馈的并网逆变器阻抗重塑策略的有效性,采用实时数字控制器RTU-BOX204控制平台,搭建了如图14所示的1 kW单相LCL型并网逆变器实验平台,具体参数与表1一致。

图14 实验平台示意图
Fig.14 Schematic diagram of experimental platform
图15为未采用电网电压前馈控制时的并网点电压、电流实验波形。如图15所示,当电网阻抗Lg=9.5 mH时,并网电流畸变严重,已无法满足并网要求,当Lg继续增大时,并网电流发生严重振荡,实验样机自动保护,系统断开。
图16为采用电网电压前馈控制时的并网点电压、电流实验波形。如图16a和图16b所示,当电网阻抗Lg=15 mH时,无论采用函数近似法还是在多目标约束下,基于电网电压前馈控制时的并网电流稳定运行,系统鲁棒性得到增强,并且并网点电压与并网点电流同时过零点,无相位偏差。
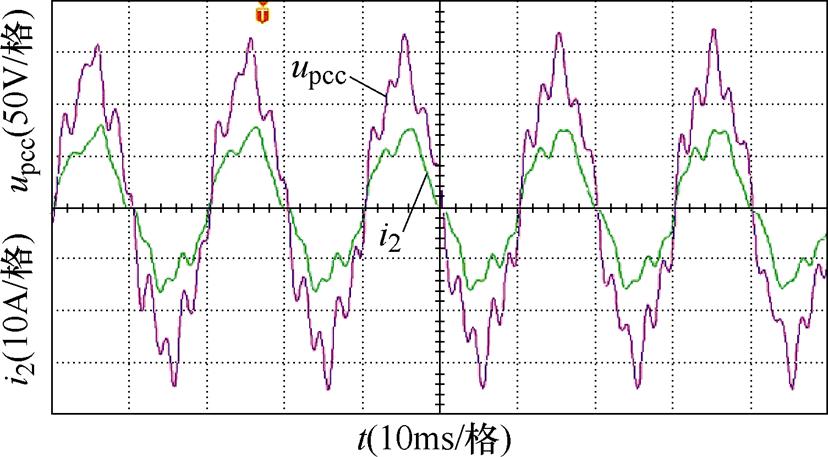
图15 未采用电网电压前馈控制时并网电压、电流实验波形
Fig.15 Experimental waveforms of grid-connected voltage and current without feedforward control of grid voltage
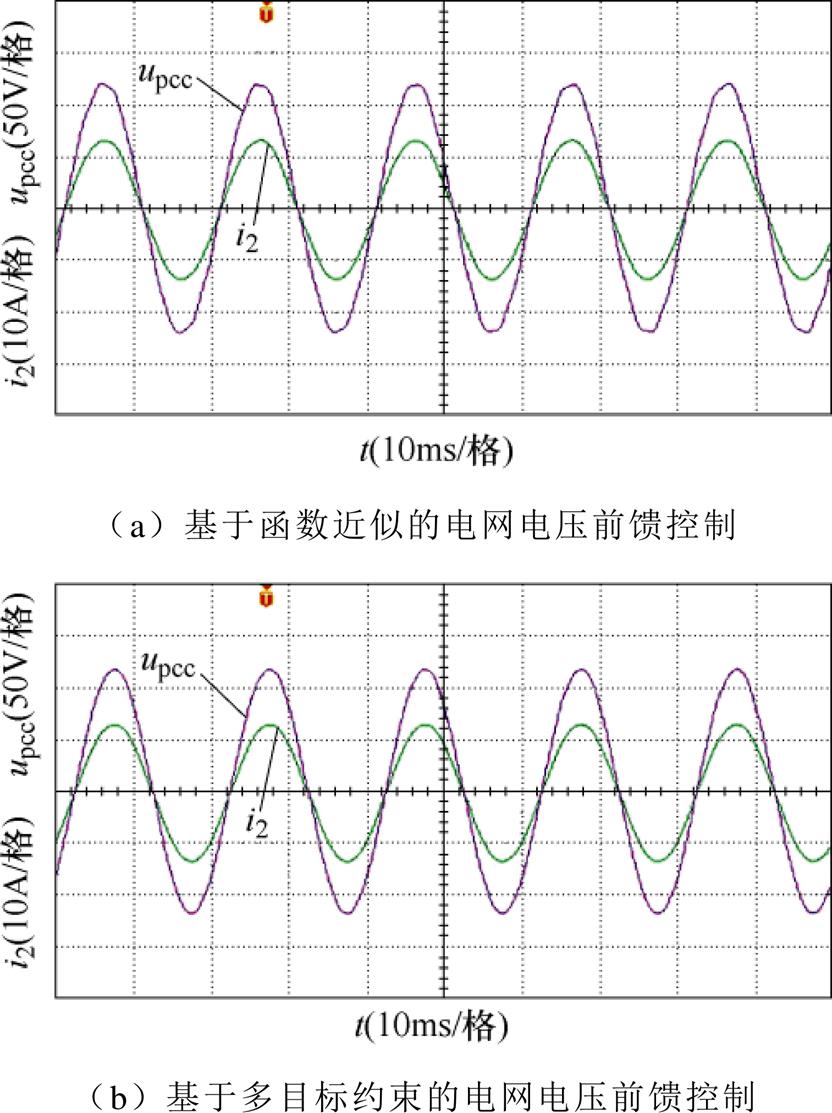
图16 电网电压前馈控制时并网点电流、电压实验波形
Fig.16 Experimental waveforms of current and voltage of grid connection points during feedforward control of grid voltage
图17给出了采用电网电压前馈控制时,并网电流跳变时的动态实验波形,为使动态实验波形更加清晰直观,此实验选择在电网阻抗Lg=5.3 mH的情况下进行,此时并网点电压、电流畸变率均较小。如图17a和图17b所示,当实验设置参考电流由满载到半载跳变时,无论采用函数近似法还是在多目标约束下,并网电流在跳变瞬间均会出现短暂的调节过程,并在半个周期内进入稳态,说明系统具有良好的动态性能。
基于上述仿真与实验验证表明,本文所提基于电网电压前馈的并网逆变器阻抗重塑控制策略可以有效解决弱电网下系统鲁棒性下降甚至失稳问题,拓宽了弱电网甚至极弱电网下系统对电网阻抗宽范围变化的适应能力。
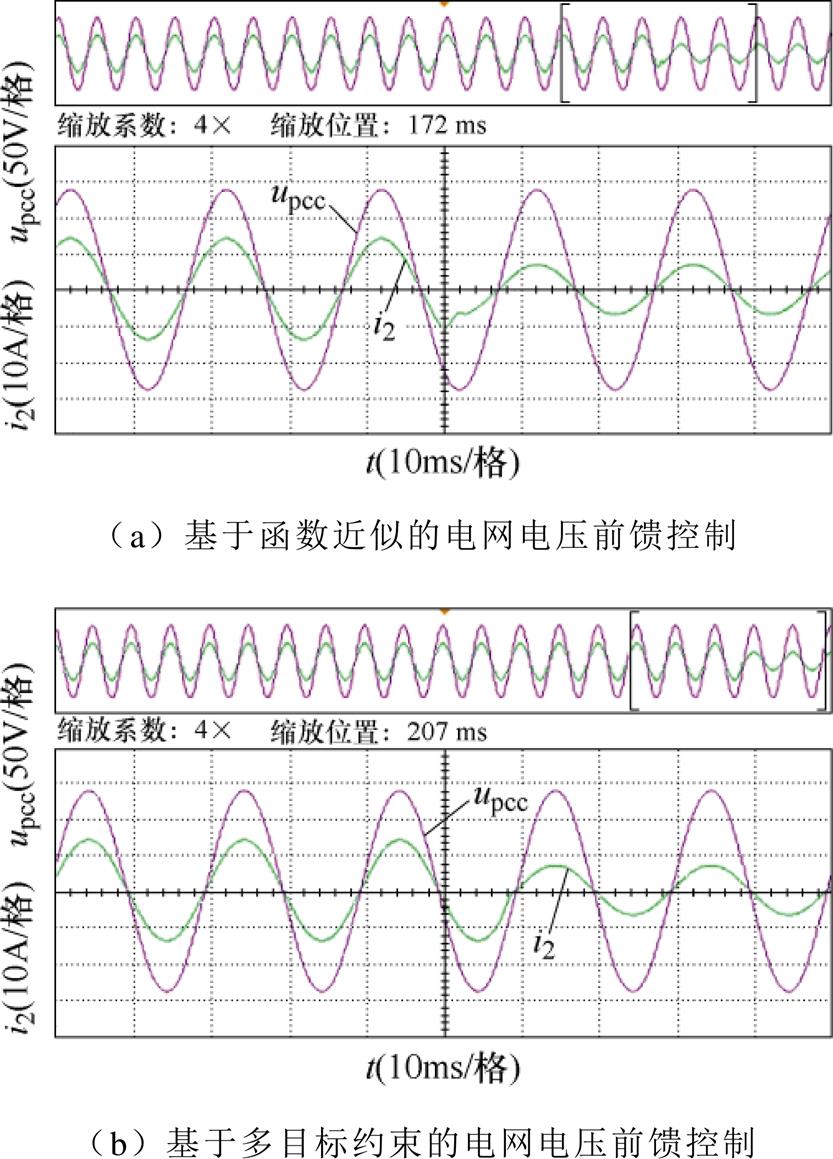
图17 电网电压前馈控制时并网电流、电压动态实验波形
Fig.17 Dynamic experimental waveforms of current and voltage at connection points under feedforward control of grid voltage
本文以单相LCL滤波并网逆变器为例,提出了一种基于电网电压前馈的并网逆变器阻抗重塑控制策略,所提控制策略可以有效地解决PLL在基波以上频段引入的负阻特性对系统稳定性的影响,并得到以下几点结论:
1)弱电网下,PLL所引入的负阻抗从幅值与相位两方面影响系统输出阻抗,导致系统输出阻抗交截频率降低、交截频率处相位减小,严重影响逆变器系统稳定裕度。
2)本文通过系统控制框图等效变换,推导得到的电网电压前馈函数,通过理论分析,证明了此前馈函数可以完全消除PLL负阻特性对系统输出阻抗的影响。同时,本文给出了两种前馈函数设计方法,在不影响逆变器系统性能的前提下,均有良好的电网电压前馈控制效果。
3)当并网系统标准较低、参数对系统基波电流跟踪性能影响极小时,基于函数近似的电网电压前馈控制具有极高的可行性与有效性;当并网系统要求较为严苛时,基于多目标约束的电网电压前馈控制可根据实际情况进行调整,以满足实际工程要求。
参考文献
[1] Wang Xiongfei, Blaabjerg F, Loh P C. Grid-current- feedback active damping for LCL resonance in grid- connected voltage-source converters[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(1): 213-223.
[2] 沈姝衡, 方天治, 章益凡. 高带宽数字控制LCL型并网逆变器及其提高并网系统鲁棒性的谐振抑制技术研究[J]. 电工技术学报, 2022, 37(21): 5548- 5561.
Shen Shuheng, Fang Tianzhi, Zhang Yifan. A high- bandwidth digital-control LCL-type grid-tied inverter and resonance-suppressing technique for improving the robustness of grid-connected system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(21): 5548-5561.
[3] 涂春鸣, 邹凯星, 高家元, 等. 基于不对称正负反馈效应的PQ功率控制并网逆变器稳定性分析[J]. 电工技术学报, 2023, 38(2): 496-509.
Tu Chunming, Zou Kaixing, Gao Jiayuan, et al. Stability analysis of grid-connected inverter under PQ power control based on asymmetric positive-negative- feedback effects[J]. Transactions of China Electro- technical Society, 2023, 38(2): 496-509.
[4] 郭小强, 朱铁影. 新型非隔离型三相三电平光伏并网逆变器及其漏电流抑制研究[J]. 电工技术学报, 2018, 33(1): 26-37.
Guo Xiaoqiang, Zhu Tieying. Research on leakage current suppression of novel three-phase three-level non-isolated PV inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 26-37.
[5] 许水清, 黄文展, 何怡刚, 等. 基于自适应滑模观测器的中点钳位型三电平并网逆变器开路故障诊断[J]. 电工技术学报, 2023, 38(4): 1010-1022.
Xu Shuiqing, Huang Wenzhan, He Yigang, et al. Open-circuit fault diagnosis method of neutral point clamped three-level grid-connected inverter based on adaptive sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 1010- 1022.
[6] 于彦雪, 马慧敏, 陈晓光, 等. 弱电网下基于准静态模型的混合控制微电网逆变器同步稳定性研究[J]. 电工技术学报, 2022, 37(1): 152-164.
Yu Yanxue, Ma Huimin, Chen Xiaoguang, et al. Synchronous stability research of inverters in hybrid microgrid based on the quasi-static models under weak grid[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 152-164.
[7] 许津铭, 卞申一阳, 钱浩, 等. 弱电网下单相并网逆器延时锁相环的鲁棒控制及优化方法[J]. 中国电机工程学报, 2020, 40(7): 2062-2070, 2386.
Xu Jinming, Bian Shenyiyang, Qian Hao, et al. Robust control and optimization of delay-based phase-locked loop of single-phase grid-connected inverters under weak grid conditions[J]. Proceedings of the CSEE, 2020, 40(7): 2062-2070, 2386.
[8] 高家元, 肖凡, 姜飞, 等. 弱电网下具有新型PLL结构的并网逆变器阻抗相位重塑控制[J]. 中国电机工程学报, 2020, 40(20): 6682-6694.
Gao Jiayuan, Xiao Fan, Jiang Fei, et al. Grid- connected inverter impedance phase reshaping control with novel PLL structure in weak grid[J]. Proceedings of the CSEE, 2020, 40(20): 6682-6694.
[9] 涂春鸣, 高家元, 李庆, 等. 复数滤波器结构锁相环的并网逆变器对弱电网的适应性研究[J]. 电工技术学报, 2020, 35(12): 2632-2642.
Tu Chunming, Gao Jiayuan, Li Qing, et al. Research on adaptability of grid-connected inverter with complex coefficient-filter structure phase locked loop to weak grid[J]. Transactions of China Electro- technical Society, 2020, 35(12): 2632-2642.
[10] 吴恒, 阮新波, 杨东升. 弱电网条件下锁相环对LCL型并网逆变器稳定性的影响研究及锁相环参数设计[J]. 中国电机工程学报, 2014, 34(30): 5259- 5268.
Wu Heng, Ruan Xinbo, Yang Dongsheng. Research on the stability caused by phase-locked loop for LCL-type grid-connected inverter in weak grid condition[J]. Proceedings of the CSEE, 2014, 34(30): 5259-5268.
[11] Zhao Jiantao, Huang Meng, Zha Xiaoming. Nonlinear analysis of PLL damping characteristics in weak- grid-tied inverters[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2020, 67(11): 2752-2756.
[12] 张云飞, 赵晋斌, 周鸣倢, 等. 弱电网下自适应同步旋转坐标系锁相环鲁棒性分析及研究[J]. 中国电机工程学报, 2020, 40(7): 2234-2243, 2402.
Zhang Yunfei, Zhao Jinbin, Zhou Mingjie, et al. Robustness analysis and research of adaptive synchronous-reference-frame phase-locked loop under weak grid[J]. Proceedings of the CSEE, 2020, 40(7): 2234-2243, 2402.
[13] 杨东升, 阮新波, 吴恒. 提高LCL型并网逆变器对弱电网适应能力的虚拟阻抗方法[J]. 中国电机工程学报, 2014, 34(15): 2327-2335.
Yang Dongsheng, Ruan Xinbo, Wu Heng. A virtual impedance method to improve the performance of LCL-type grid-connected inverters under weak grid conditions[J]. Proceedings of the CSEE, 2014, 34(15): 2327-2335.
[14] 杨兴武, 王涛, 徐依明, 等. 基于虚拟电感的LCL型并网逆变器电网电压前馈控制策略[J]. 太阳能学报, 2020, 41(11): 56-63.
Yang Xingwu, Wang Tao, Xu Yiming, et al. Voltage feedforward control of LCL grid-connected inverter based on virtual inductor[J]. Acta Energiae Solaris Sinica, 2020, 41(11): 56-63.
[15] Li Ming, Zhang Xing, Zhang Haizheng, et al. An Improved grid voltage feedforward compensation scheme of grid-connected inverter in weak grid[C]// IEEE International Power Electronics and Application Conference and Exposition, Shenzhen, China, 2018: 1-6.
[16] Qian Qiang, Xie Shaojun, Huang Liuliu, et al. Harmonic suppression and stability enhancement for parallel multiple grid-connected inverters based on passive inverter output impedance[J]. IEEE Transa- ctions on Industrial Electronics, 2017, 64(9): 7587- 7598.
[17] Wang Guoning, Du Xiong, Shi Ying, et al. Effects on oscillation mechanism and design of grid-voltage feedforward in grid-tied converter under weak grid[J]. IET Power Electronics, 2019, 12(5): 1094-1101.
[18] 王翰文, 曾成碧, 苗虹. 基于多谐振电网电压前馈的并网逆变器相位补偿算法研究[J]. 电力系统保护与控制, 2021, 49(18): 81-89.
Wang Hanwen, Zeng Chengbi, Miao Hong. A phase compensation algorithm of a grid-connected inverter based on a feedforward multi-resonant grid voltage[J]. Power System Protection and Control, 2021, 49(18): 81-89.
[19] 解宝. 电网阻抗影响下大型光伏并网系统稳定性分析及控制策略研究[D]. 重庆: 重庆大学, 2020.
[20] 杨明, 赵月圆, 杨杰, 等. 高渗透率下一种提高LCL滤波并网逆变器鲁棒性的新型锁相环设计方法[J]. 中国电机工程学报, 2023, 43(10): 3938-3949.
Yang Ming, Zhao Yueyuan, Yang Jie, et al. A new phase-locked loop design scheme to improve the robustness of LCL filtered grid-connected inverters under high permeability[J]. Proceedings of the CSEE, 2023, 43(10): 3938-3949.
[21] 洪芦诚, 徐佳裕, 唐润悦, 等. 三相LCL型逆变器序阻抗简化建模方法及并网稳定性分析[J]. 电力系统自动化, 2023, 47(7): 150-157.
Hong Lucheng, Xu Jiayu, Tang Runyue, et al. Simplified modeling method of sequence impedance and grid-connected stability analysis for three-phase LCL inverter[J]. Automation of Electric Power Systems, 2023, 47(7): 150-157.
[22] 国家电网公司. 光伏电站接入电网技术规定: Q/GDW 617-2015[S]. 北京: 中国电力出版社, 2011.
[23] 杜燕, 言明明, 杨向真, 等. 多目标约束下逆变器阻抗的电流矫正方法[J]. 控制理论与应用, 2022, 39(4): 701-710.
Du Yan, Yan Mingming, Yang Xiangzhen, et al. Current correction method for grid-connected inverter impedance under multi-objective constraints[J]. Con- trol Theory & Applications, 2022, 39(4): 701-710.
Abstract Under weak grid conditions, the negative impedance characteristics introduced by the phase- locked loop (PLL) in the frequency range above the fundamental frequency can reduce the phase of the output impedance of grid-tied inverter systems, thereby severely affecting the stability of the system. Additionally, grid voltage feedforward control has gained widespread attention in grid-tied inverter control due to its simplicity, effectiveness, and ease of implementation. Among them, research on grid-tied inverter impedance reshaping has been widely applied.
In order to seek a simple and effective control strategy to improve the stability of the system, this paper focuses on single-phase LCL-filtered grid-tied inverters under weak grid conditions. By performing system control diagram equivalence transformation, the grid voltage feedforward function that eliminates the impact of the PLL on the system's output impedance is derived. Subsequently, a grid voltage feedforward control-based grid-tied inverter impedance reshaping control strategy is proposed. Furthermore, the optimization design of the grid voltage feedforward function is achieved using function approximation and multi-objective constraint methods, making the proposed control strategy more feasible and universally applicable.
The analysis of the robustness of grid-tied inverter systems based on grid voltage feedforward control shows that whether using function approximation or multi-objective constraint methods, this control strategy can reshape the inverter output impedance, improve the phase angle at the crossover frequency, and ensure that the system has a phase margin greater than 30° under weak or fragile grid conditions. It guarantees the robustness of the system without additional phase compensation stages, and has negligible impact on the fundamental current tracking performance of the system.
Simulation and experimental verification demonstrate that, regardless of whether function approximation or multi-objective constraint methods are used, the grid current quality of the system based on grid voltage feedforward control has been significantly improved. The grid-tied point voltage and current exhibit no phase deviation, satisfying the requirement of the unity power factor grid connection. Additionally, the system exhibits excellent dynamic performance, effectively expanding the adaptability range of grid-tied inverter systems considering the PLL under weak grid conditions.
The optimization design method of the feedforward function based on function approximation facilitates the acquisition of control parameters, greatly improving the feasibility of the grid voltage feedforward control strategy. However, its effect on reshaping the phase characteristics of the system's output impedance is reduced. On the other hand, the method based on multi-objective constraints can adjust and supplement the constraint conditions according to different engineering standards and specifications, enabling the free design of the feedforward function and enhancing the universality of this control strategy. Its drawback lies in high computational complexity and feedforward function parameter acquisition. In practical engineering, the method selection can be made according to actual circumstances.
keywords:Weak grid, grid-connected inverter, impedance remodeling, phase-locked loop, stability
国家自然科学基金资助项目(U1804143)。
收稿日期 2023-03-01
DOI: 10.19595/j.cnki.1000-6753.tces.230236
中图分类号:TM464
杨 明 男,1982年生,博士,副教授,研究方向为新能源并网发电技术、电能质量控制、虚拟同步发电机等。E-mail: yangming0391@163.com
杨 倬 男,1999年生,硕士研究生,研究方向为并网逆变器控制及稳定性分析。E-mail: 1135229637@qq.com(通信作者)
改稿日期 2023-05-24
(编辑 陈 诚)