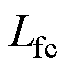 为桥臂侧电感,
为桥臂侧电感,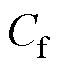 为滤波电容,
为滤波电容,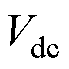 为直流侧电容电压,
为直流侧电容电压,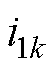 、
、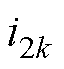 、
、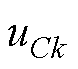 分别为桥臂侧三相电流、网侧三相电流、电容三相电压(
分别为桥臂侧三相电流、网侧三相电流、电容三相电压(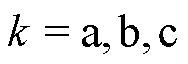 ),变流器通过升压变压器接入电网ug。为便于分析,将变压器匝数比设置为1,变压器漏感
),变流器通过升压变压器接入电网ug。为便于分析,将变压器匝数比设置为1,变压器漏感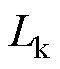 作为网侧电感,
作为网侧电感,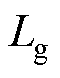 为电网阻抗(只考虑纯电感代表的最恶劣情况)。因此,等效网侧总电感
为电网阻抗(只考虑纯电感代表的最恶劣情况)。因此,等效网侧总电感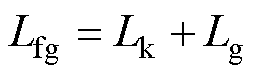 。
。摘要 兆瓦级大功率并网变流器的开关频率较低,延迟和离散化误差对控制性能影响较大,导致动态响应慢、电网背景谐波影响大等问题。因此,直接离散域控制系统设计成为必要。该文针对LCL滤波并网变流器建立离散域数学模型,并基于此提出桥臂侧电流和网侧电流融合的离散域电流控制器。同时,为了在不额外增加电流传感器和检测电路的情况下获取并网电流信息,设计电容电压微分器,实现网侧电流的估算,降低硬件复杂性和控制成本。研究表明,该文设计的离散域电流控制器,具有较好的动态性能和电网背景谐波抑制能力。最后,通过硬件在环半实物仿真系统对所提设计进行了实验验证。
关键词:LCL型并网变流器 低开关频率 离散域控制 背景谐波
相比于单电感L滤波器,高阶LCL滤波器具有较好的谐波衰减特性,尤其在大功率并网变流器场合得到广泛应用。然而,LCL滤波器欠阻尼特性影响了控制系统运行稳定性,增加了电网背景谐波敏感性。串联电阻的无源阻尼方案[1]能够增加阻尼,抑制谐振,但损耗较大,在大功率场合难以应用。为此,基于控制算法的有源阻尼方案受到关注[2-4]。但在数字控制系统中,尤其在大功率应用场合,开关频率较低,采样和控制延迟较大,对有源阻尼甚至系统的实际控制性能的影响随着功率等级的增加而凸显。因此,如何实现大功率LCL型并网变流器的高性能控制是当前研究热点。
文献[5-6]分析了延迟对有源阻尼控制的影响并引入了延迟补偿,提升了系统的阻尼特性,但系统的动态性能仍不足。文献[7-8]分别分析了数字控制延迟对电流环解耦的影响以及对控制带宽的限制。带宽的降低,导致电流动态响应不足,谐波电流增加。文献[9]利用状态观测器对电流进行一拍超前预测,以补偿数字控制延迟影响。参数鲁棒性和系统稳定性影响了状态观测器的效果。文献[10]采用过采样方法、文献[11-12]采用即时采样法减小延迟,但采样易受开关噪声影响,且加载时刻的变化可能会产生多次比较现象。文献[13]通过对反馈电流的延迟补偿,提高了系统的阻尼特性和控制带宽。文献[14]在状态空间控制零极点配置的基础上,引入了相位超前补偿环节,提高了系统的稳定性和动态性能。文献[15-16]进一步直接在离散域中进行零极点配置和延迟补偿,克服了离散化误差影响,使系统动态性能得到进一步提升。实际上,在开关频率较低时,直接针对离散化模型进行控制系统设计,可以将延迟作为控制对象的一部分,从而在控制器设计时作为广义对象加以考虑,有助于控制性能的提升。同时,直接离散域设计也避免了连续域控制器数字化实现时的离散化误差问题。直接基于离散化模型的设计以进一步提升动态性能,仍有较好的研究空间。
当前电网由于大量非线性装置的接入,电网电压中包含有较为丰富的谐波成分[17-18],从而产生并网电流谐波,因此如何提升并网变流器对电网背景谐波扰动的抑制能力也受到关注。文献[19-20]采用多矢量比例积分(Vector Proportional Integral, VPI)控制器,增大谐波频率处控制增益,实现谐波抑制。文献[21]分析了桥臂侧电感电流反馈的间接电流控制技术在谐波抑制方面的不足,提出在多谐振控制器输入端引入电容电流附加补偿回路,从而增强谐波抑制能力。文献[22]在前文基础上进一步利用多二阶广义积分器(Multi-Second-Order Generalized Integrator, MSOGI)提取指定的谐波电流,并引入到控制器输入端,从而既具有桥臂侧电流反馈(Converter Current Feedback, CCF)控制方案优越的稳定性又具有并网电流反馈(Grid Current Feedback, GCF)控制方案优良的谐波抑制能力。多个谐波控制器的并联应用不仅实现复杂,而且稳定性不足。文献[23]采用双环控制,针对桥臂侧电流利用比例积分控制器实现基波无静差跟踪,同时利用比例谐振控制器对并网电流谐波进行抑制,实现基波跟随和谐波抑制。文献[24-25]采用电网电压前馈控制策略,以抑制电网背景谐波对并网电流的影响,但间接离散化设计降低了谐波抑制效果。文献[26]针对工程中常用的利用变压器漏感作为网侧电感的方案难以直接测量电网电压的问题,进一步提出了电容电压全反馈方案。实际上,电网背景谐波对控制系统而言是一种扰动,若能够通过控制器设计提升系统抗扰动能力,则将有助于抑制电网背景谐波对电流的影响。
针对上述大功率LCL型并网变流器电流控制性能依然不足问题,本文提出一种具有高动态性能和强电网背景谐波抑制能力的融合离散状态空间控制方案。相对于文献[15, 23]中的方案而言,本文方案对电流状态反馈进行整体设计,增强了设计的灵活性,有利于控制性能的提升。同时,为节省并网电流传感器和检测电路,简化硬件设计和控制成本,引入了微分器,实现并网电流的估算。
图1为LCL型并网变流器的主电路拓扑结构,图中,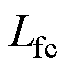 为桥臂侧电感,
为桥臂侧电感,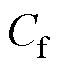 为滤波电容,
为滤波电容,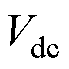 为直流侧电容电压,
为直流侧电容电压,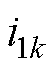 、
、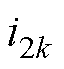 、
、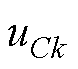 分别为桥臂侧三相电流、网侧三相电流、电容三相电压(
分别为桥臂侧三相电流、网侧三相电流、电容三相电压(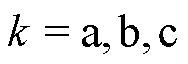 ),变流器通过升压变压器接入电网ug。为便于分析,将变压器匝数比设置为1,变压器漏感
),变流器通过升压变压器接入电网ug。为便于分析,将变压器匝数比设置为1,变压器漏感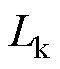 作为网侧电感,
作为网侧电感,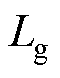 为电网阻抗(只考虑纯电感代表的最恶劣情况)。因此,等效网侧总电感
为电网阻抗(只考虑纯电感代表的最恶劣情况)。因此,等效网侧总电感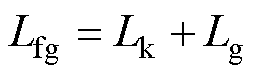 。
。
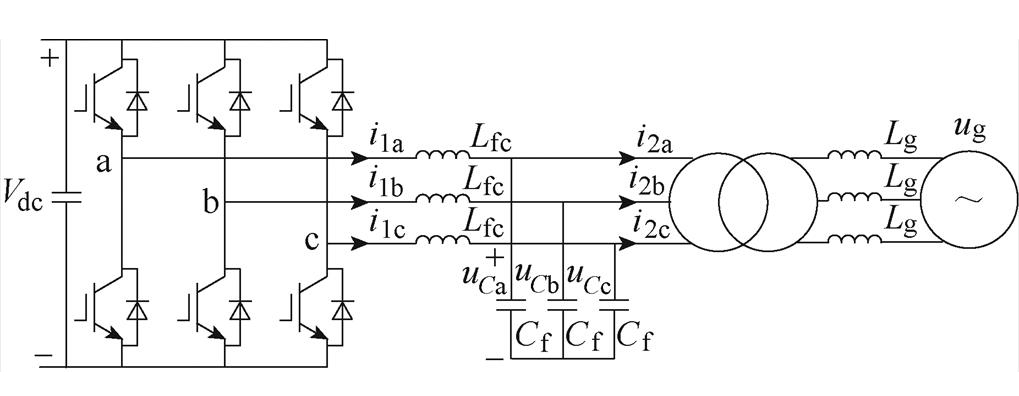
图1 LCL型并网变流器拓扑
Fig.1 Topology of LCL-type grid-connected converter
采用复矢量表述方式(如桥臂侧电流复矢量可表述为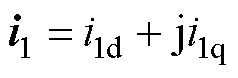 ,下标d和q分别表示坐标系的d和q轴分量),在同步旋转坐标系下对LCL型并网变流器进行建模[15]。
,下标d和q分别表示坐标系的d和q轴分量),在同步旋转坐标系下对LCL型并网变流器进行建模[15]。
状态向量选为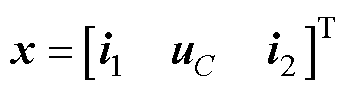 ,其中
,其中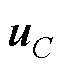 为滤波电容电压,
为滤波电容电压,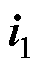 和
和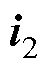 分别为桥臂侧和网侧电流。在电网同步旋转坐标系下,变流器的状态空间模型可表示为
分别为桥臂侧和网侧电流。在电网同步旋转坐标系下,变流器的状态空间模型可表示为
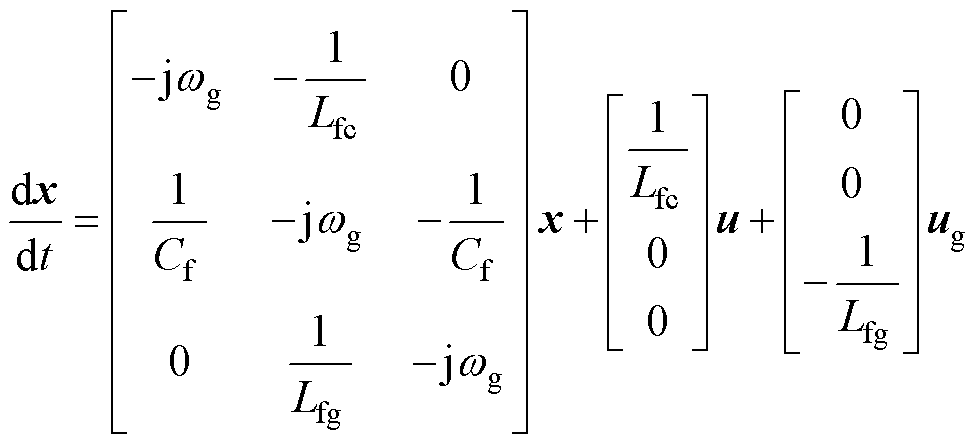 (1)
(1)
式中,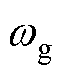 为电网角频率;u为输入电压;ug为电网电压。
为电网角频率;u为输入电压;ug为电网电压。
令
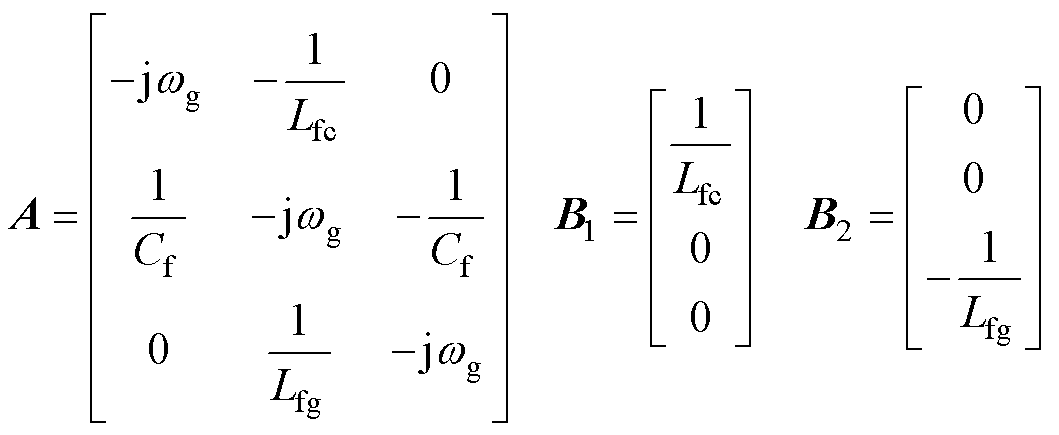
则式(1)状态方程可简化为
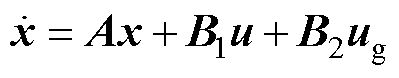 (2)
(2)
依据PWM的零阶保持原理,静止坐标系下变流器输出电压 在一个开关周期
在一个开关周期 内,即
内,即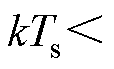
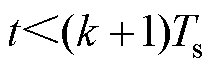 (
(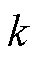 为离散时间指数)期间是恒定的,而电网电压
为离散时间指数)期间是恒定的,而电网电压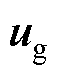 可被视为在同步坐标下一个开关周期内保持恒定。式(2)的离散域模型可表示为
可被视为在同步坐标下一个开关周期内保持恒定。式(2)的离散域模型可表示为
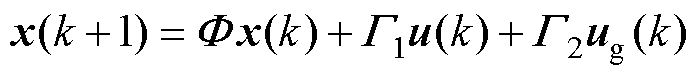 (3)
(3)
其中
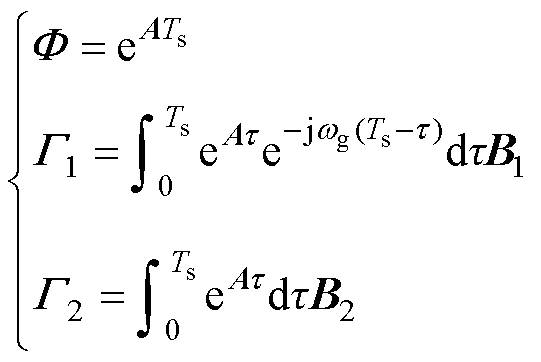 (4)
(4)
具体表达式如附录第1节所示。
考虑到坐标旋转,一个采样周期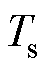 的延迟可以表示为
的延迟可以表示为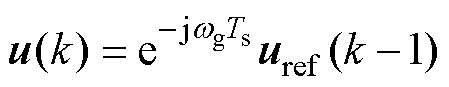 。其中,
。其中,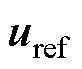 为控制输出电压,
为控制输出电压,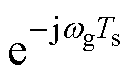 为同步坐标下延迟造成的相位偏差,可以通过坐标变换进行补偿。因此,为简洁起见,在后文数学分析中不再包含相位偏差
为同步坐标下延迟造成的相位偏差,可以通过坐标变换进行补偿。因此,为简洁起见,在后文数学分析中不再包含相位偏差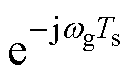 。考虑到一拍延迟,结合式(3)可得各状态的z域表达式为
。考虑到一拍延迟,结合式(3)可得各状态的z域表达式为
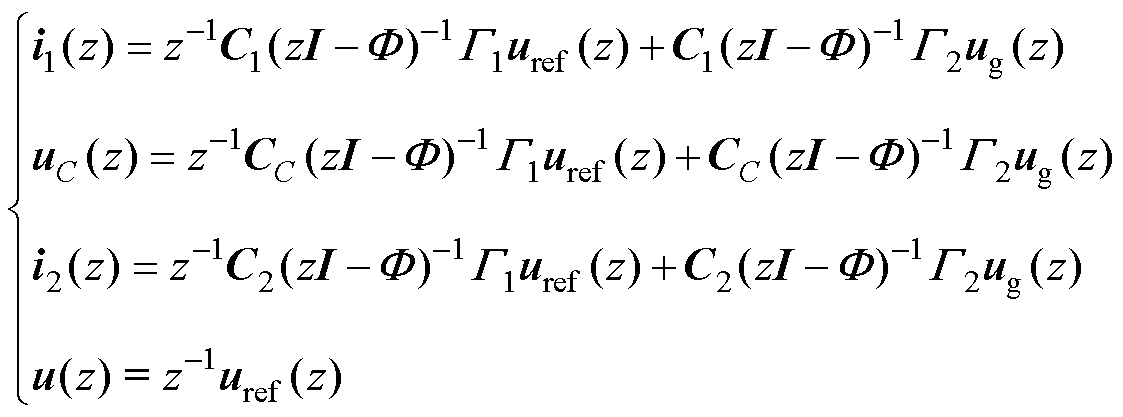 (5)
(5)
其中
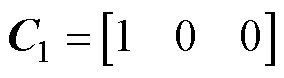
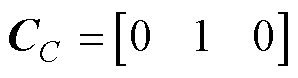
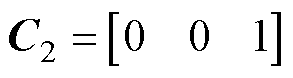
令
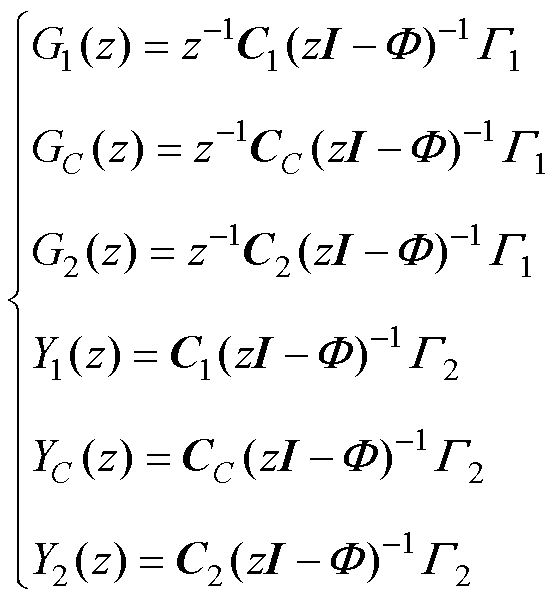 (6)
(6)
则各状态表达式可简记为
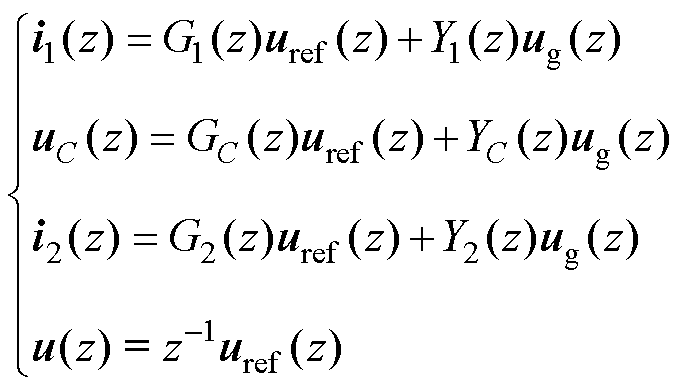 (7)
(7)
如图2所示为典型电流控制框图[15]。由图2计算可得,电流指令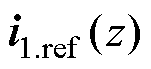 到桥臂电流
到桥臂电流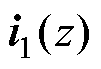 的传递函数,即跟随传递函数[15]为
的传递函数,即跟随传递函数[15]为
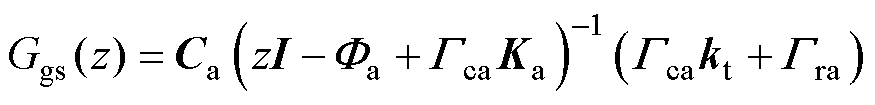 (8)
(8)
式中,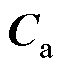 、
、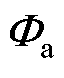 、
、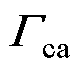 、
、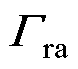 与变流器参数有关,具体表达式见附录第1节;控制参数矩阵
与变流器参数有关,具体表达式见附录第1节;控制参数矩阵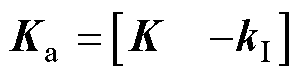 分别由反馈系数向量
分别由反馈系数向量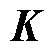 和误差控制增益
和误差控制增益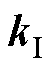 构成,且
构成,且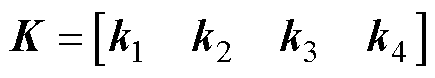 。式(8)反映了桥臂电流对指令电流的跟随性能。对LCL滤波并网变流器而言,由于电容支路的存在,桥臂电流与并网电流不相等。图3给出了桥臂电流
。式(8)反映了桥臂电流对指令电流的跟随性能。对LCL滤波并网变流器而言,由于电容支路的存在,桥臂电流与并网电流不相等。图3给出了桥臂电流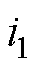 与并网电流
与并网电流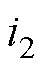 关系示意图。流过电容支路的电流主要为谐波电流,包括变流器输出电压形成的谐波电流
关系示意图。流过电容支路的电流主要为谐波电流,包括变流器输出电压形成的谐波电流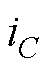 和电网谐波电压引起的谐波电流
和电网谐波电压引起的谐波电流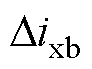 。对于前者而言,电容起到滤波作用,能够改善并网电流质量;对于后者而言,电容支路电流会造成并网电流谐波增加,需要加以抑制。LCL滤波器电流回路如图3所示。
。对于前者而言,电容起到滤波作用,能够改善并网电流质量;对于后者而言,电容支路电流会造成并网电流谐波增加,需要加以抑制。LCL滤波器电流回路如图3所示。
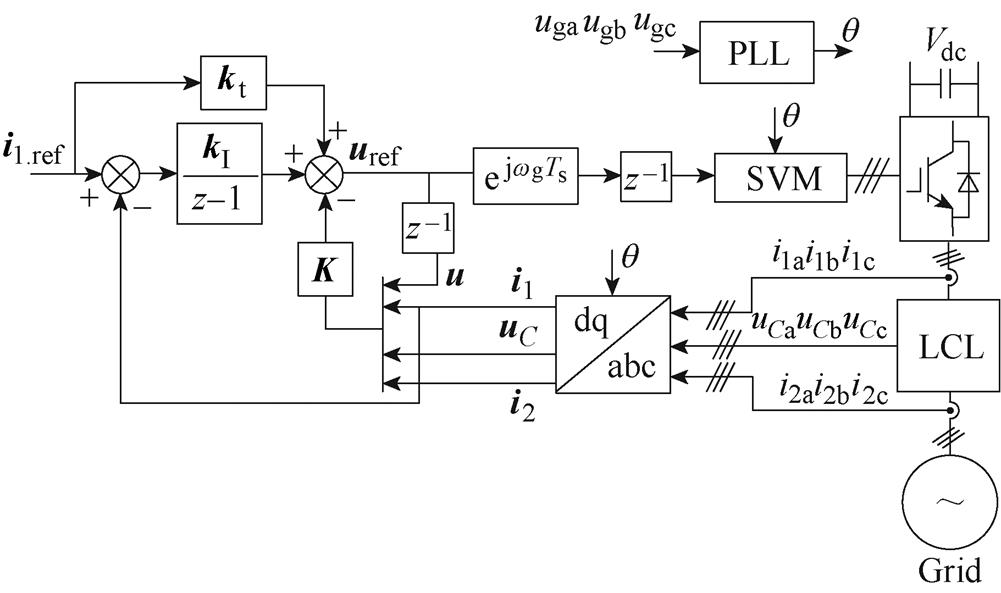
图2 典型电流控制框图
Fig.2 Block diagram of the typical current control
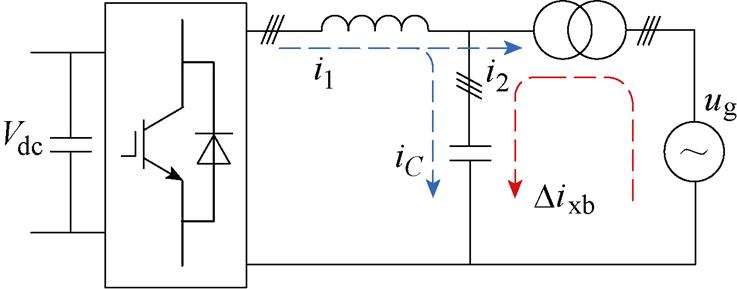
图3 LCL滤波器电流回路
Fig.3 Current loops in the LCL filter
电网谐波电压对并网电流的影响,可以通过电网电压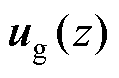 到并网电流
到并网电流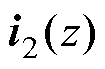 的传递函数,即变流器输出导纳进行分析。由控制结构框图2可以计算出导纳表达式[15]为
的传递函数,即变流器输出导纳进行分析。由控制结构框图2可以计算出导纳表达式[15]为
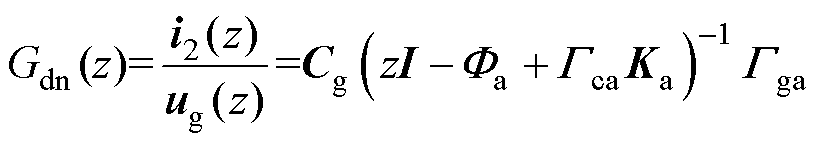 (9)
(9)
式中,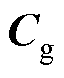 、
、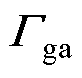 与变流器参数直接相关,具体表达式见附录第1节。为了使表述更加明确,后文所说的抗扰特性均指代变流器对电网电压影响的抑制特性。
与变流器参数直接相关,具体表达式见附录第1节。为了使表述更加明确,后文所说的抗扰特性均指代变流器对电网电压影响的抑制特性。
闭环系统特征多项式为
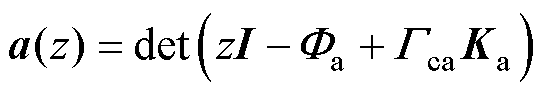 (10)
(10)
多项式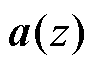 为5阶矩阵,且控制参数矩阵
为5阶矩阵,且控制参数矩阵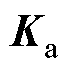 包含5个可设计参数
包含5个可设计参数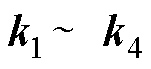 、
、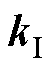 ,理论上可以实现闭环系统极点的任意配置。但对比式(8)和式(9)不难发现,极点的配置不仅影响跟随性能,而且会影响到变流器输出导纳特性。按照主导极点理论,直接决定系统带宽的为主导极点,带宽限制了
,理论上可以实现闭环系统极点的任意配置。但对比式(8)和式(9)不难发现,极点的配置不仅影响跟随性能,而且会影响到变流器输出导纳特性。按照主导极点理论,直接决定系统带宽的为主导极点,带宽限制了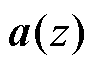 的配置。图4分别给出了带宽增加时跟随传递函数和输出导纳的幅频响应特性。
的配置。图4分别给出了带宽增加时跟随传递函数和输出导纳的幅频响应特性。
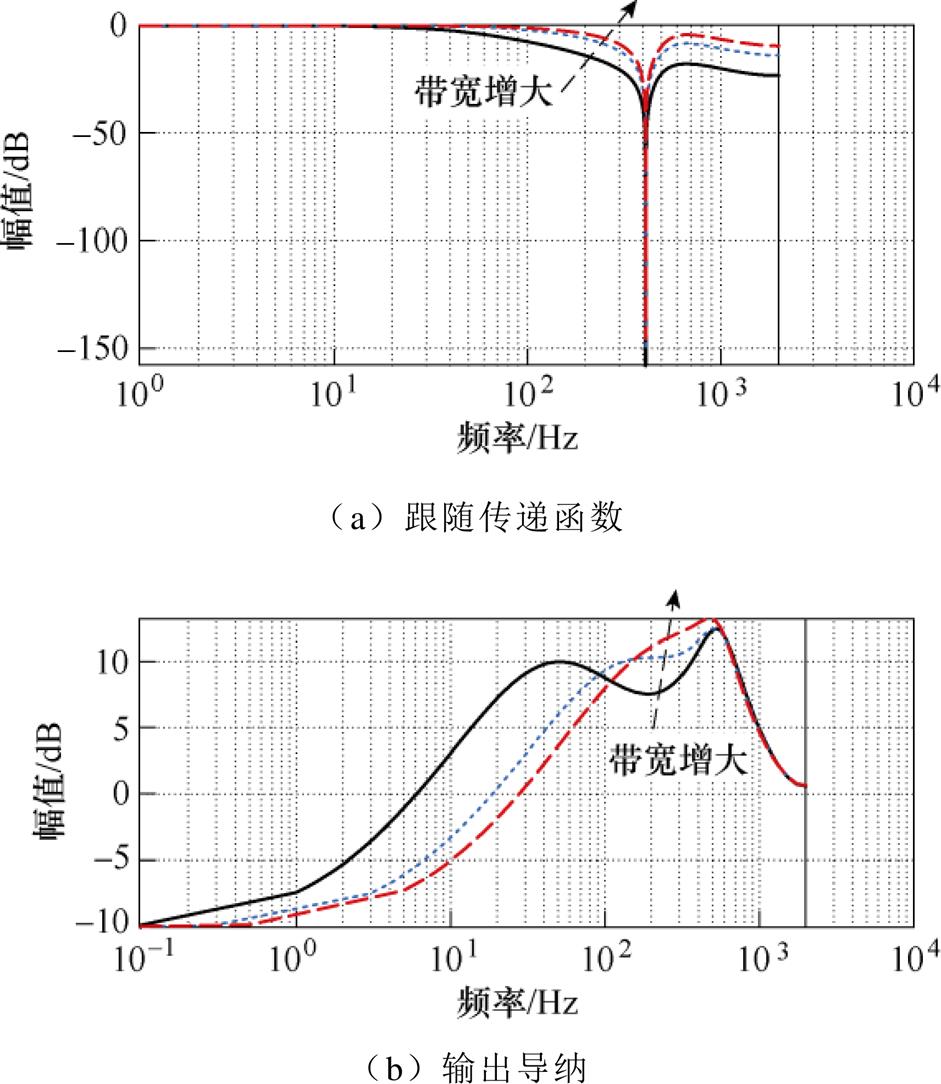
图4 不同带宽下跟随传递函数和输出导纳特性
Fig.4 Characteristics of the tracking transfer function and the output admittance under different bandwidths
由图4可以发现,通过极点的配置能够增加系统控制带宽,提升桥臂电流的跟随性能,但同时增加了变流器输出导纳在100~1 000 Hz频段区间的幅值,增加了该频段电压谐波对并网电流的影响。实际电网中主要谐波为5、7、9和11次谐波,对应频率刚好位于该频段。因此,通过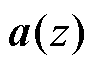 对应极点配置难以兼顾跟随性能和抗扰性能。实际上,即便降低跟随特性,在该频段输出导纳幅值依然较高,仍然难以满足抑制电网背景谐波影响的需求。
对应极点配置难以兼顾跟随性能和抗扰性能。实际上,即便降低跟随特性,在该频段输出导纳幅值依然较高,仍然难以满足抑制电网背景谐波影响的需求。
如何提升变流器对电网背景谐波干扰的抑制能力成为进一步提高并网变流器性能的关键。文献[15]中的桥臂电流控制方案直接在离散域中进行零极点配置和延迟补偿,使系统动态性能得到大幅提升,但是由于电容支路的存在,难以通过极点配置消除背景谐波对并网电流的影响。文献[23]通过引入并网电流谐波控制环路,能够起到对并网电流谐波的直接控制作用,提升并网电流质量。但是该设计方案缺少控制器的正向一体化设计,整体性能优化受到限制。鉴于此,本文提出了一种融合电流控制方案,能够在系统获得较好动态性能的同时显著提升背景谐波抑制能力。
为提升对电网背景谐波扰动的抑制能力,理论上需要能够在控制环路中反映出并网电流谐波。如文献[23]直接引入谐波控制回路,形成双回路并行控制结构。本文直接引入桥臂和并网电流双状态反馈,进行状态空间融合设计,电流控制框图如图5所示。图中,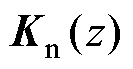 为状态融合反馈函数矩阵,
为状态融合反馈函数矩阵,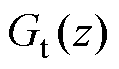 为前馈补偿环节。
为前馈补偿环节。
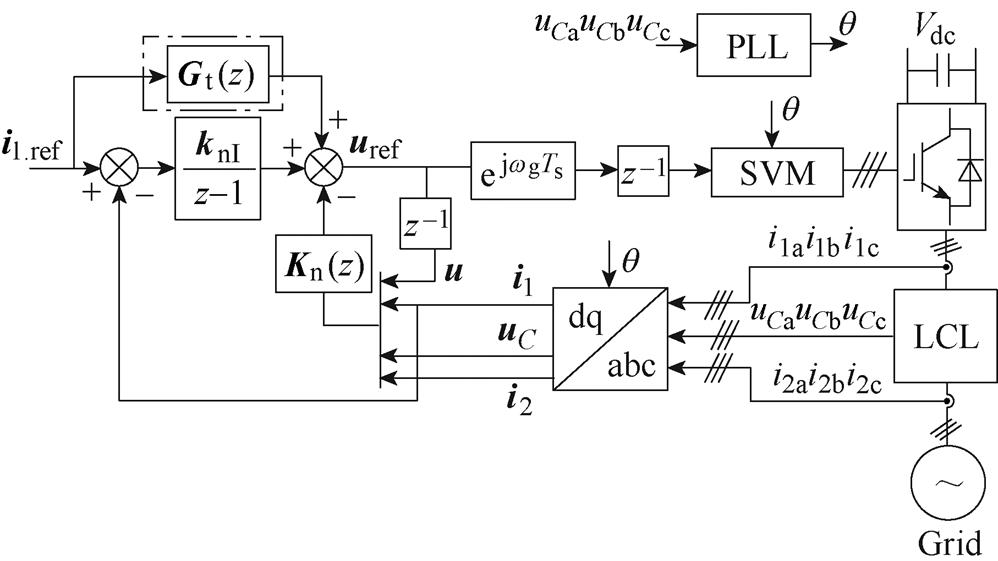
图5 电流控制框图
Fig.5 Block diagram of current control
设计反馈函数矩阵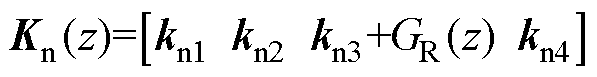 ,其中
,其中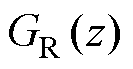 为谐波控制环节,用于并网电流谐波提取。在离散域中
为谐波控制环节,用于并网电流谐波提取。在离散域中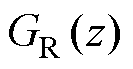 可表示为
可表示为
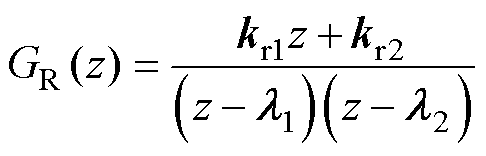 (11)
(11)
式中,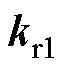 、
、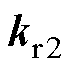 、
、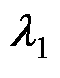 、
、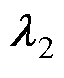 为设计参数,其值将通过整体设计获得。
为设计参数,其值将通过整体设计获得。
在典型电流控制方案中,通常设计参考电流前馈补偿环节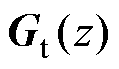 为
为
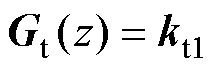 (12)
(12)
于是,可将控制输出描述为
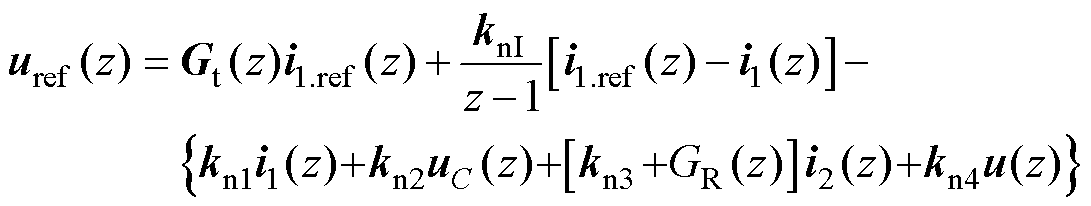 (13)
(13)
式中,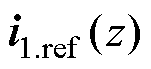 为电流指令;
为电流指令;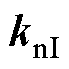 为积分增益;
为积分增益;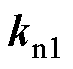 、
、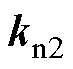 、
、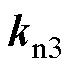 、
、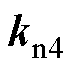 分别为桥臂电流
分别为桥臂电流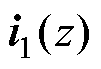 、电容电压
、电容电压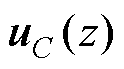 、并网电流
、并网电流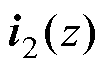 以及延迟控制输出
以及延迟控制输出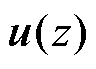 的反馈增益。
的反馈增益。
将式(12)和式(13)代入式(7)可得图5所示控制方案桥臂电流的跟随传递函数为
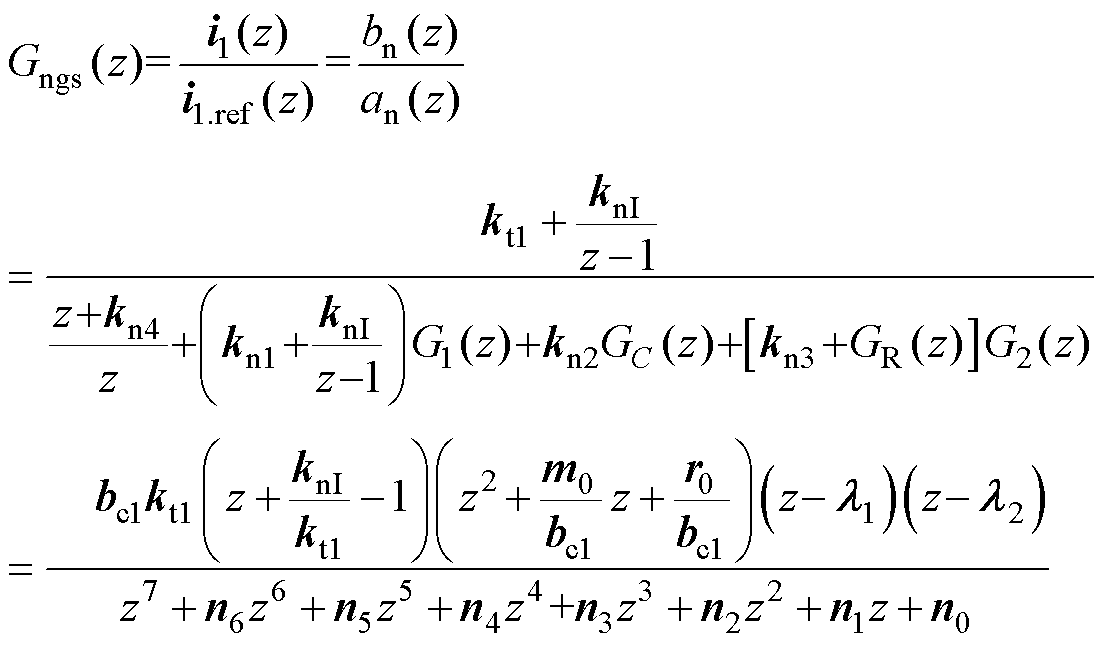 (14)
(14)
式中, 、
、 与变流器参数有关;
与变流器参数有关; 与控制参数有关,具体表达式见附录第2节。
与控制参数有关,具体表达式见附录第2节。
此时对应的并网电流的输出导纳为
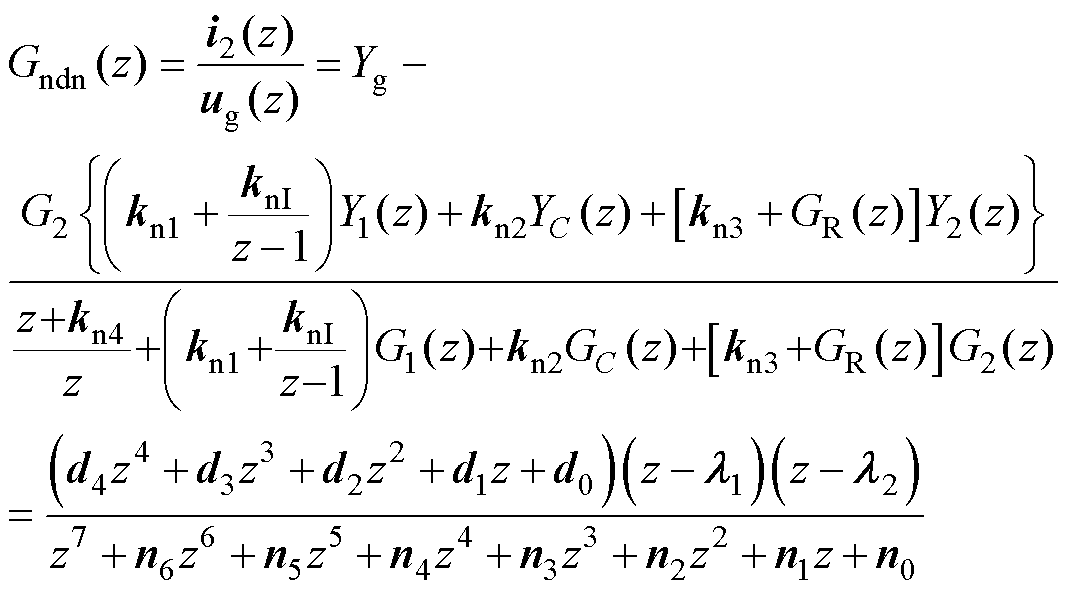 (15)
(15)
式中,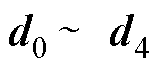 与控制参数相关,表达式见附录第3节。
与控制参数相关,表达式见附录第3节。
对比式(9)和式(15)不难发现,尽管通过并网电流状态的融合反馈设计输出导纳和跟随传递函数仍具有相同的分母,但与式(9)所示的输出导纳不同,式(15)中导纳表达式存在零点因式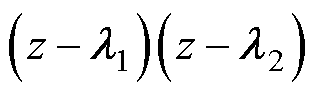 。这是由式(11)中谐振环节引入的,在谐振频率处因式模值为零,即式(15)所示的输出导纳在设计的谐振频率处幅值为0,理论上能够完全抑制谐振频率处电网背景谐波的影响。以下对参数设计进行讨论。
。这是由式(11)中谐振环节引入的,在谐振频率处因式模值为零,即式(15)所示的输出导纳在设计的谐振频率处幅值为0,理论上能够完全抑制谐振频率处电网背景谐波的影响。以下对参数设计进行讨论。
1)参数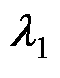 、
、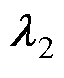 选择
选择
参数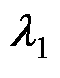 、
、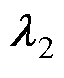 是由谐振环节式(11)引入,其值对应于所选择的谐振频率。典型地,考虑5、7次电网背景谐波,则
是由谐振环节式(11)引入,其值对应于所选择的谐振频率。典型地,考虑5、7次电网背景谐波,则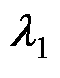 和
和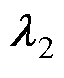 可设计为
可设计为
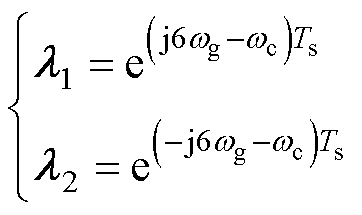 (16)
(16)
式中,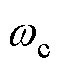 为谐振环节的带宽,适当取值以保证谐波抑制能力和稳定性。
为谐振环节的带宽,适当取值以保证谐波抑制能力和稳定性。
2)跟随传递函数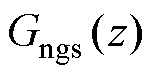 的极点配置
的极点配置
图6为LCL滤波并网变流器由控制电压到桥臂电流的开环传递函数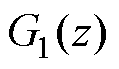 (见式(6))的零极点分布,其中极点
(见式(6))的零极点分布,其中极点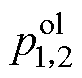 和
和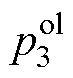 分别为LCL滤波器的谐振和低频极点,而极点
分别为LCL滤波器的谐振和低频极点,而极点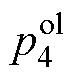 是由控制延迟引入。
是由控制延迟引入。
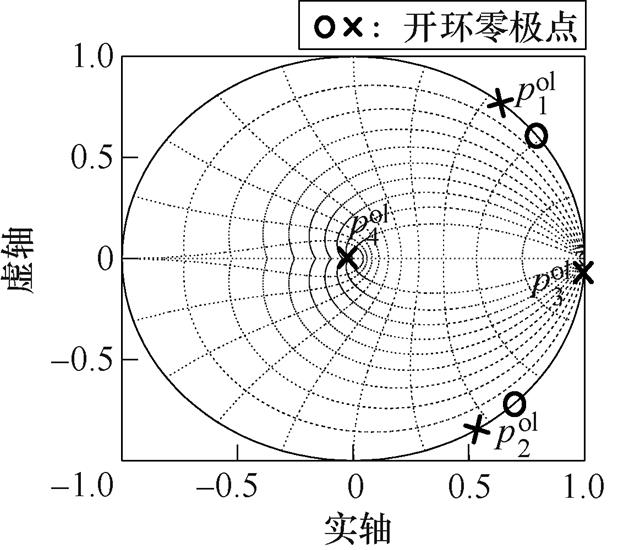
图6 开环传递函数零极点分布
Fig.6 Zero-pole plot of open-loop transfer function
由跟随传递函数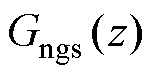 的表达式(14)可得闭环系统的特征多项式为
的表达式(14)可得闭环系统的特征多项式为
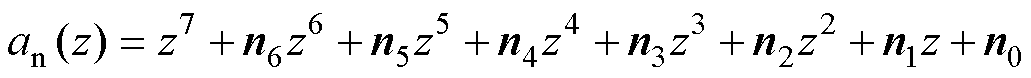 (17)
(17)
显然,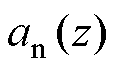 为7阶多项式,且各项系数
为7阶多项式,且各项系数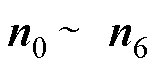 中共包含了
中共包含了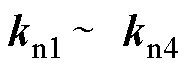 、
、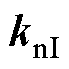 、
、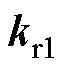 和
和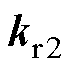 7个未知参数。因此,可以根据期望的闭环极点利用数值工具求解出控制系统中各待设计参数。
7个未知参数。因此,可以根据期望的闭环极点利用数值工具求解出控制系统中各待设计参数。
令期望的闭环系统特征多项式为
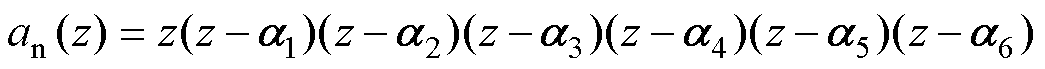 (18)
(18)
式中,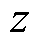 表示延迟;
表示延迟;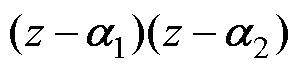 表示跟随性能;
表示跟随性能;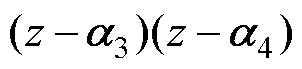 表示谐振性能;
表示谐振性能;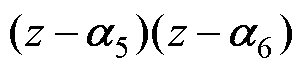 表示谐波性能。极点
表示谐波性能。极点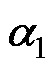 、
、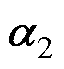 为主导极点,其取值决定跟随性能,极点
为主导极点,其取值决定跟随性能,极点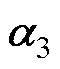 、
、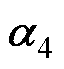 决定系统的谐振性能,而
决定系统的谐振性能,而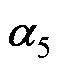 、
、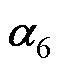 与2.2节设计参数
与2.2节设计参数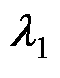 、
、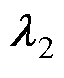 一起决定系统的谐波性能。因此,式(18)可分为四部分,其中源于计算延迟的极点z已经处于最优位置0处。以下对其余6个闭环极点进行配置。
一起决定系统的谐波性能。因此,式(18)可分为四部分,其中源于计算延迟的极点z已经处于最优位置0处。以下对其余6个闭环极点进行配置。
(1)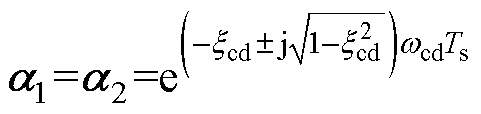 。
。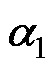 、
、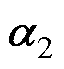 设计为主导极点,
设计为主导极点,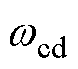 决定系统的带宽。为避免超调,选择
决定系统的带宽。为避免超调,选择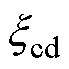 =1[15]。
=1[15]。
(2)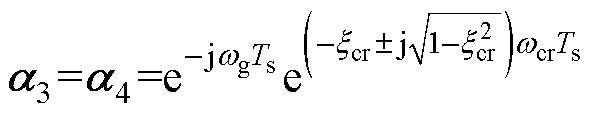 。
。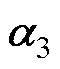 、
、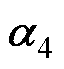 来源于受控对象的谐振极点
来源于受控对象的谐振极点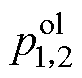 ,因此本文采用径向投影技术[15, 27]即保持在原有开环极点附近并进行阻尼设计以最小化控制量。通常
,因此本文采用径向投影技术[15, 27]即保持在原有开环极点附近并进行阻尼设计以最小化控制量。通常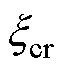 取为0.1~0.4,并且
取为0.1~0.4,并且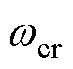 位于
位于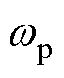 附近。本文选择
附近。本文选择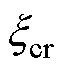 =0.3[15],
=0.3[15],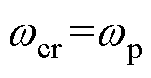 。
。
(3)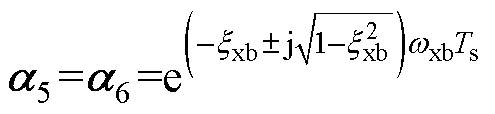 。
。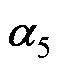 、
、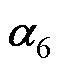 影响系统的谐波抑制能力。为了在提升5、7次频率谐波抑制能力的同时,避免放大周围频段谐波,通常
影响系统的谐波抑制能力。为了在提升5、7次频率谐波抑制能力的同时,避免放大周围频段谐波,通常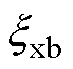 取为0.2~0.4,并且
取为0.2~0.4,并且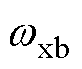 位于
位于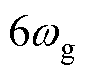 附近[28]。下面对该极点的影响做进一步详细分析。
附近[28]。下面对该极点的影响做进一步详细分析。
由式(15)可得:并网电流输出导纳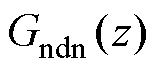 的分子因式由
的分子因式由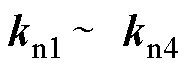 、
、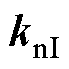 、
、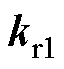 、
、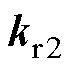 7个参数以及
7个参数以及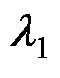 、
、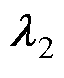 参数决定,即在跟随传递函数
参数决定,即在跟随传递函数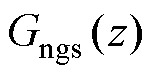 的极点确定后,输出导纳
的极点确定后,输出导纳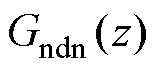 中分子因式
中分子因式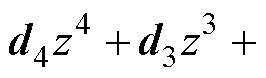
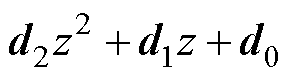 也唯一确定,而因式
也唯一确定,而因式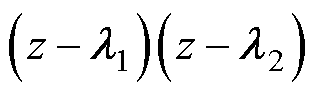 已由选定的谐振频率确定。输出导纳
已由选定的谐振频率确定。输出导纳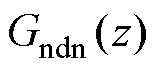 的分母多项式与跟随传递函数
的分母多项式与跟随传递函数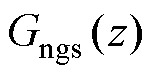 的分母多项式完全相同,也随着闭环极点的确定而唯一确定。因此,在极点确定后,导纳也随之确定。图7中给出了极点
的分母多项式完全相同,也随着闭环极点的确定而唯一确定。因此,在极点确定后,导纳也随之确定。图7中给出了极点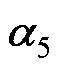 、
、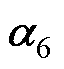 的阻尼系数
的阻尼系数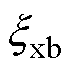 不同取值时输出导纳
不同取值时输出导纳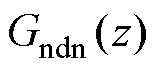 的Bode图。不难发现,当系统闭环极点
的Bode图。不难发现,当系统闭环极点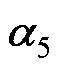 、
、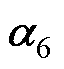 的阻尼系数
的阻尼系数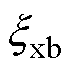 配置为0且
配置为0且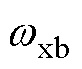 =
=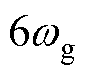 时,本文融合方案的幅频曲线与文献[15]中状态空间方案的曲线重合。这是由于
时,本文融合方案的幅频曲线与文献[15]中状态空间方案的曲线重合。这是由于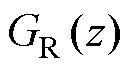 引入的零点
引入的零点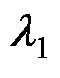 、
、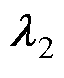 与配置的极点
与配置的极点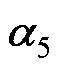 、
、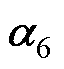 相互对消造成的。此时,方案退化为文献[15]中方案,也就是说文献[15]所设计的状态空间电流控制方案可以看作本文状态空间融合控制方案的特例。因此,不当的极点配置将影响到谐振环节对背景谐波影响的抑制作用。进一步可以发现,随着阻尼系数
相互对消造成的。此时,方案退化为文献[15]中方案,也就是说文献[15]所设计的状态空间电流控制方案可以看作本文状态空间融合控制方案的特例。因此,不当的极点配置将影响到谐振环节对背景谐波影响的抑制作用。进一步可以发现,随着阻尼系数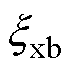 的增大,5、7次谐波即图中
的增大,5、7次谐波即图中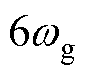 处幅值降低,谐波抑制能力增强,但也造成了选定谐波频率附近频段内导纳幅值增加。因此,要根据谐波抑制能力和其他频段抗扰需求进行折中设计,本文选择
处幅值降低,谐波抑制能力增强,但也造成了选定谐波频率附近频段内导纳幅值增加。因此,要根据谐波抑制能力和其他频段抗扰需求进行折中设计,本文选择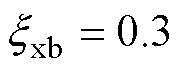 、
、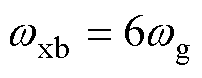 。
。
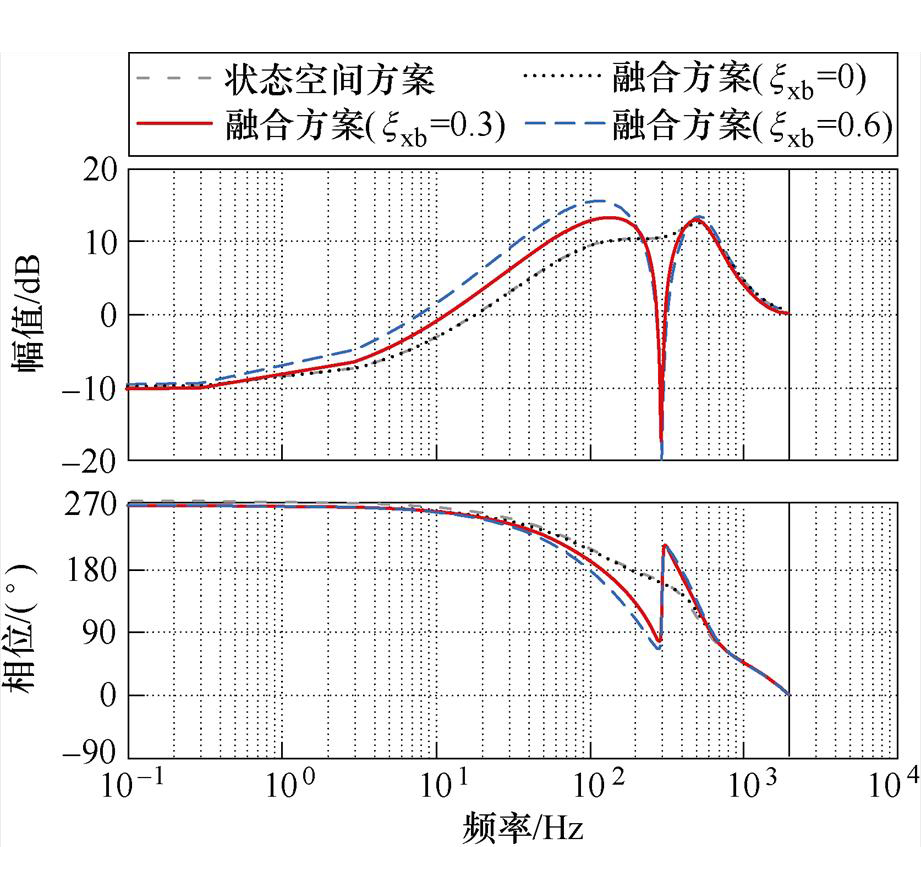
图7 输出导纳伯德图
Fig.7 Bode diagram of output conduction
3)跟随传递函数 零点配置
零点配置
在上述极点配置的情况下,式(14)可化简为
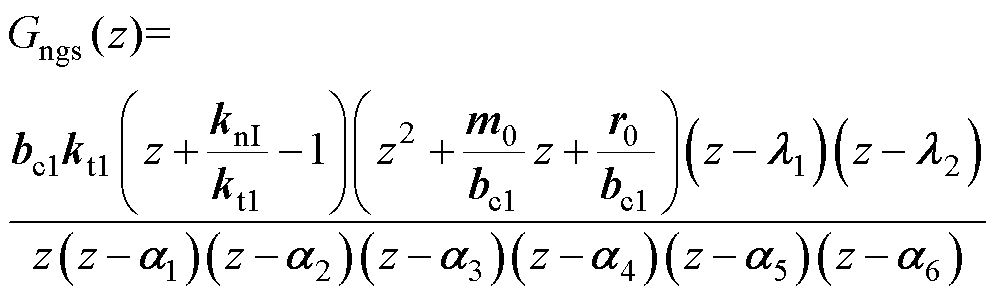 (19)
(19)
由式(19)可以发现:因式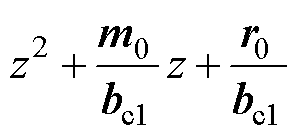 中参数均为对象固有参数,包含的解为系统的固有零点,如图6所示。零点
中参数均为对象固有参数,包含的解为系统的固有零点,如图6所示。零点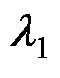 、
、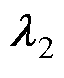 由谐振环节引入。因式
由谐振环节引入。因式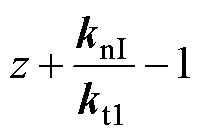 包含了可调参数
包含了可调参数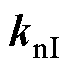 、
、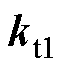 ,可以对该零点进行配置,实现对消主导极点
,可以对该零点进行配置,实现对消主导极点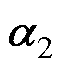 ,提升系统的跟随性能[15]。但式(19)中仍然存在慢衰减零点
,提升系统的跟随性能[15]。但式(19)中仍然存在慢衰减零点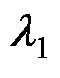 、
、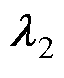 和极点
和极点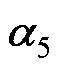 、
、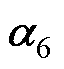 ,系统的跟随性能仍有待提高。因此仅参考电流的比例前馈无法实现所有慢衰减零极点的对消,需进一步优化前馈补偿环节。
,系统的跟随性能仍有待提高。因此仅参考电流的比例前馈无法实现所有慢衰减零极点的对消,需进一步优化前馈补偿环节。
为此,本文将传统的比例前馈环节修改为
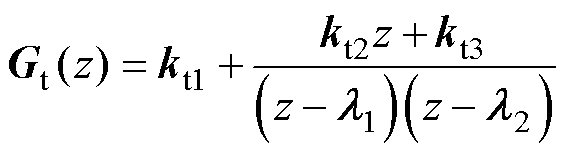 (20)
(20)
相比于比例前馈,式(20)额外引入了因式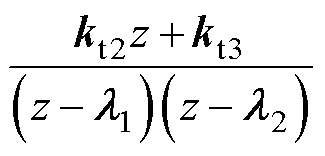 ,可用于对消多余的慢衰减零极点,从而加快系统的动态跟随特性。
,可用于对消多余的慢衰减零极点,从而加快系统的动态跟随特性。
将式(13)与式(20)代入式(7)中可得
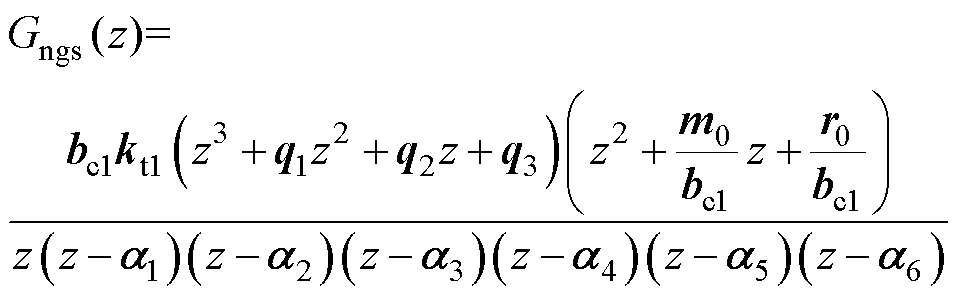 (21)
(21)
其中
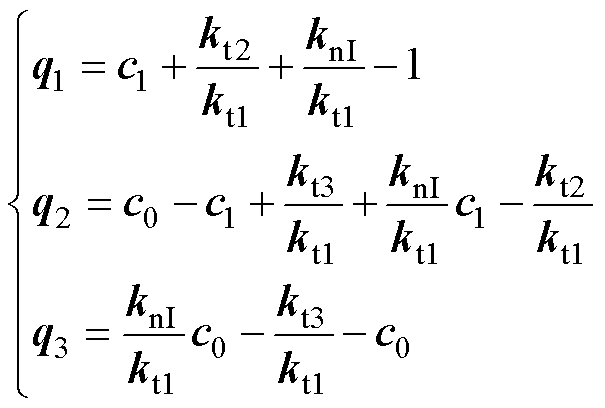 (22)
(22)
对比式(19)与式(21)可以发现:两式中都包含系统的固有零点,但式(21)中慢衰减零点 已被对消,且分子多项式中引入了未知因式
已被对消,且分子多项式中引入了未知因式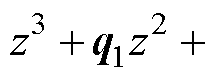
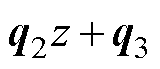 ,由于该因式为3阶多项式,且式中包含了3个可调参数
,由于该因式为3阶多项式,且式中包含了3个可调参数 、
、 、
、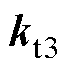 ,因此可以实现该因式零点的任意配置,从而进一步消除慢衰减极点
,因此可以实现该因式零点的任意配置,从而进一步消除慢衰减极点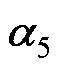 、
、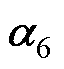 以及主导极点
以及主导极点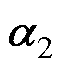 的影响,实现所有慢衰减零极点的对消。
的影响,实现所有慢衰减零极点的对消。
令
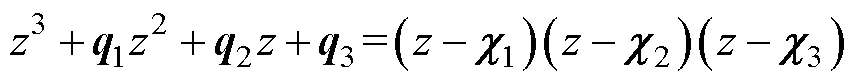 (23)
(23)
式中,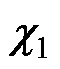 、
、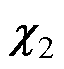 、
、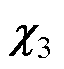 为期望零点,设计如下:
为期望零点,设计如下:
(1)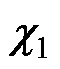 、
、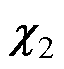 选择在闭环极点
选择在闭环极点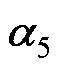 、
、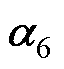 处,用来对消
处,用来对消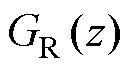 引入的慢极点,抵消其对系统跟随性能的不利影响。
引入的慢极点,抵消其对系统跟随性能的不利影响。
(2)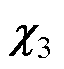 选择在
选择在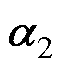 处,用于对消主导极点
处,用于对消主导极点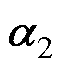 ,进一步提升系统的跟随性能[15]。
,进一步提升系统的跟随性能[15]。
则最终本文方案的跟随传递函数为
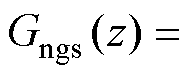
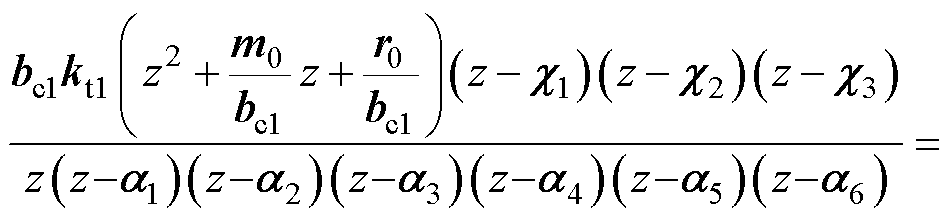
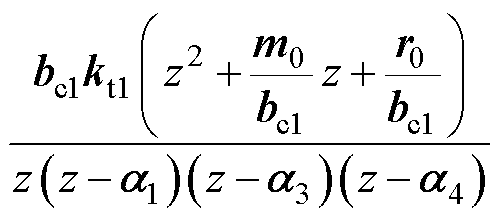 (24)
(24)
综上所述,由式(15)和式(24)可以发现:上述改进的前馈补偿环节可以较好地提升系统的跟随性能,但不影响系统的输出导纳特性。
为便于叙述和对比分析,将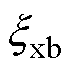 =0和
=0和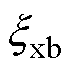 =0.3的两种情况分别称为方案1和方案3,且仅包含比例前馈环节的方案称为方案2。2.2节中分析表明,方案1对应文献[15]的方案。方案1和3的跟随传递函数零极点分布见图8a。由于极点
=0.3的两种情况分别称为方案1和方案3,且仅包含比例前馈环节的方案称为方案2。2.2节中分析表明,方案1对应文献[15]的方案。方案1和3的跟随传递函数零极点分布见图8a。由于极点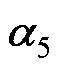 、
、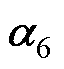 以及极点
以及极点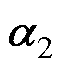 都被对消,方案3的有效零极点和方案1保持一致,即本文所设计的方案3在显著提升变流器对电网谐波抑制能力的同时,保留了文献[15]方案即方案1响应的快速性。图8b中绘出了各方案跟随特性的幅频响应。显然,方案1和方案3有着相同的快跟随特性,而方案2跟随性能相对较差。
都被对消,方案3的有效零极点和方案1保持一致,即本文所设计的方案3在显著提升变流器对电网谐波抑制能力的同时,保留了文献[15]方案即方案1响应的快速性。图8b中绘出了各方案跟随特性的幅频响应。显然,方案1和方案3有着相同的快跟随特性,而方案2跟随性能相对较差。
由于实际系统采集电容电压进行锁相的特殊结构,因此考虑利用微分器,根据电容电压对并网电流进行估计,降低硬件复杂性和控制成本。
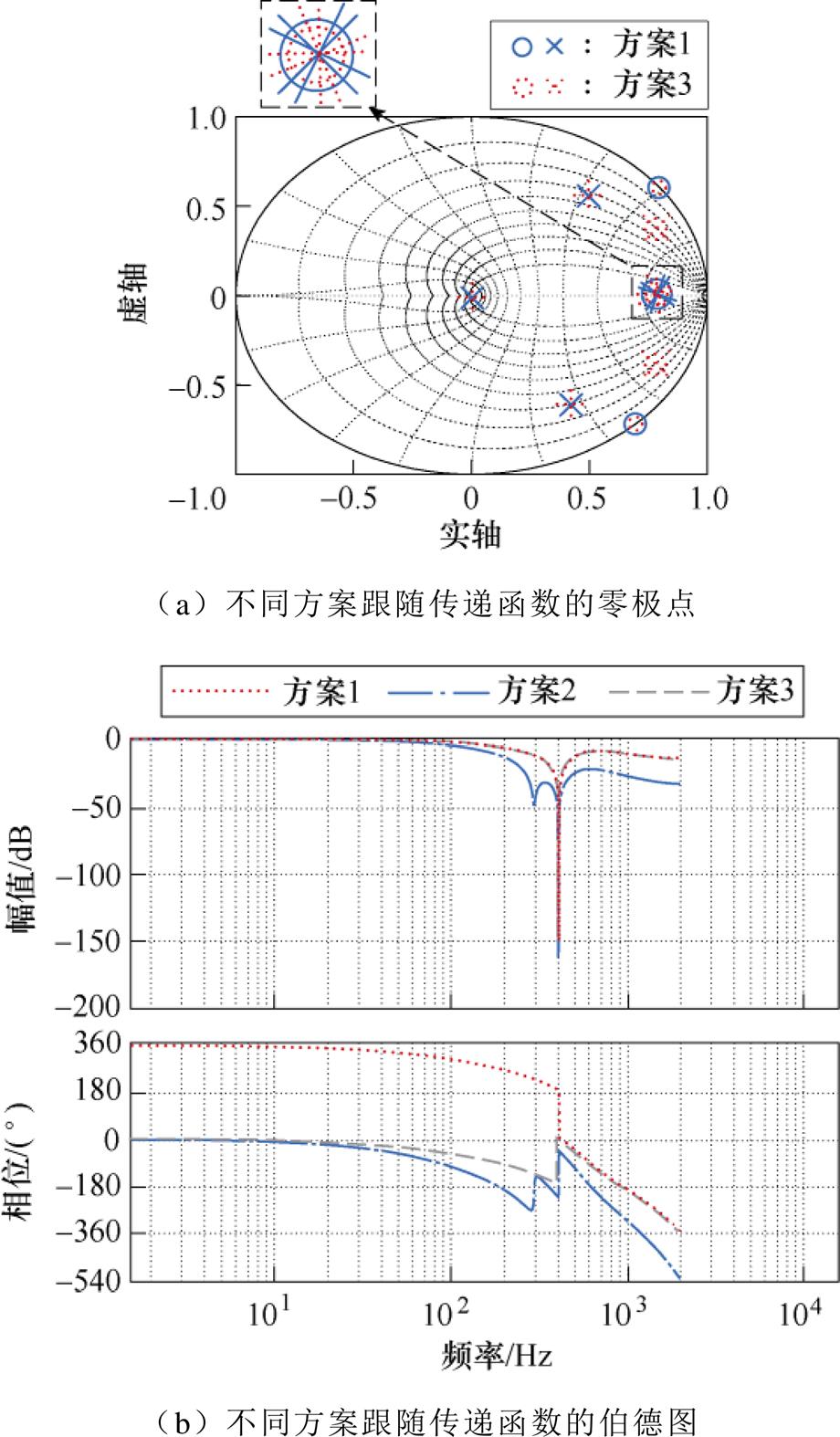
图8 不同方案的跟随传递函数的零极点和伯德图
Fig.8 Zero-pole and Bode diagrams of transfer function under different schemes
文献[3-4]较为完整地介绍了目前微分器设计的方法,因此本文直接在离散域中设计微分器。
针对理想微分“s”采用后向欧拉法对其离散化,得到表达式为
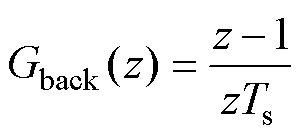 (25)
(25)
如图9所示为理想微分“s”与后向欧拉离散化后的微分器 的伯德图。由图9中可以看出:微分器
的伯德图。由图9中可以看出:微分器 有着良好的幅频响应,但是在高频处存在严重的相位滞后,从而使其失去导数效果。因此本文考虑直接在离散域中对其相位滞后进行补偿,设计一阶超前补偿环节为
有着良好的幅频响应,但是在高频处存在严重的相位滞后,从而使其失去导数效果。因此本文考虑直接在离散域中对其相位滞后进行补偿,设计一阶超前补偿环节为
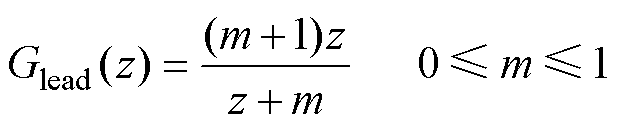 (26)
(26)
将式(25)与式(26)相乘,构造出基于后向欧拉和一阶超前补偿的微分器,其表达式为
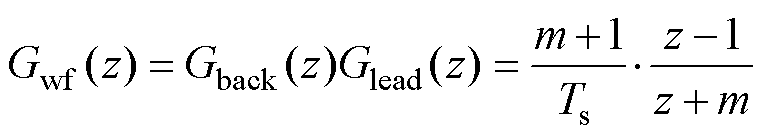 (27)
(27)
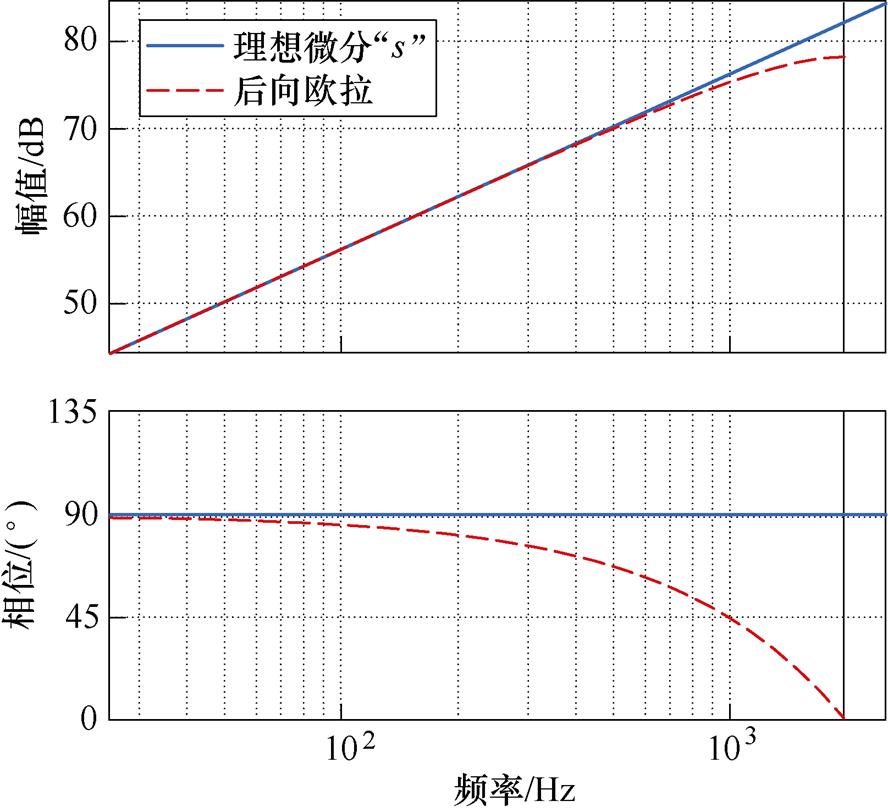
图9 理想微分与后向欧拉后微分器的伯德图
Fig.9 Bode diagrams of ideal and backward Euler differentiators
如图10所示为不同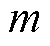 取值下的微分器
取值下的微分器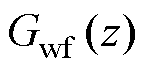 的频率响应曲线。
的频率响应曲线。
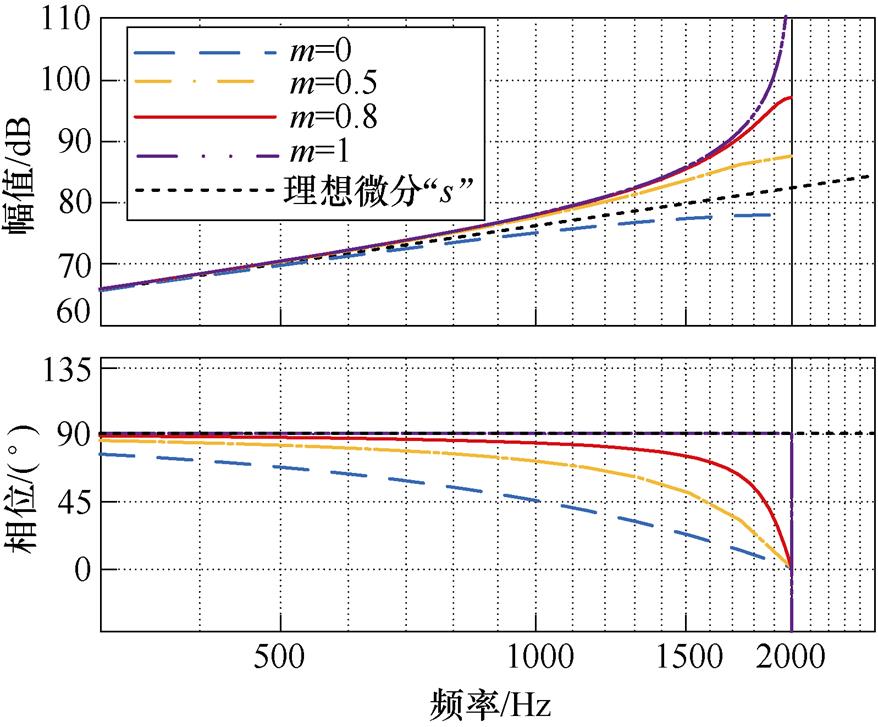
图10 微分器的伯德图
Fig.10 Bode diagrams of differentiators
由图10可以看出: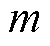 越大,对相位的补偿效果越好,但是对高频幅值的放大倍数也越高,因此综合考虑,最终选择
越大,对相位的补偿效果越好,但是对高频幅值的放大倍数也越高,因此综合考虑,最终选择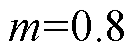 ,则微分器的表达式为
,则微分器的表达式为
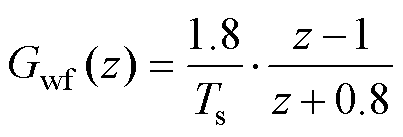 (28)
(28)
因此估算并网电流表达式为
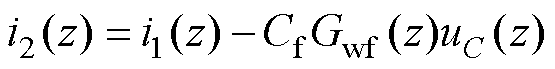 (29)
(29)
为了分析电流估算对控制方案性能的影响,这里将基于电流估算的方案命名为方案4。图11为方案4对应的控制框图。
图12中给出了不同方案的跟随传递函数和输出导纳伯德图。由图12可以看出,微分环节的使用几乎不影响系统的跟随响应曲线,仍具有较快的跟随性能。且不难发现:相对于采集并网电流而言,采用估算并网电流,输出导纳有所增大,对背景谐波抑制能力有所降低,但仍然较强。
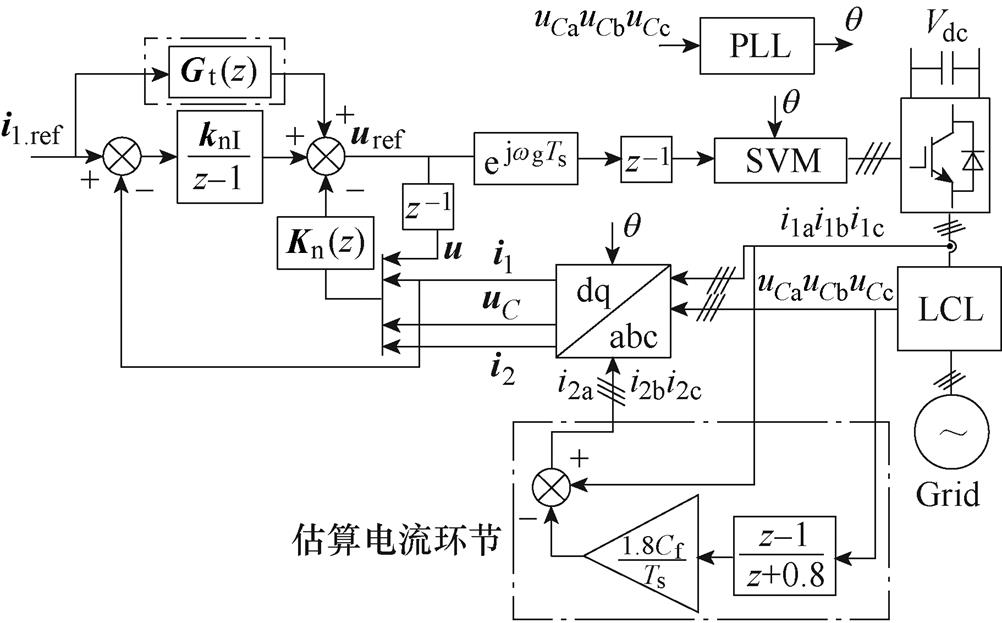
图11 方案4控制框图
Fig.11 Control block diagram of scheme 4
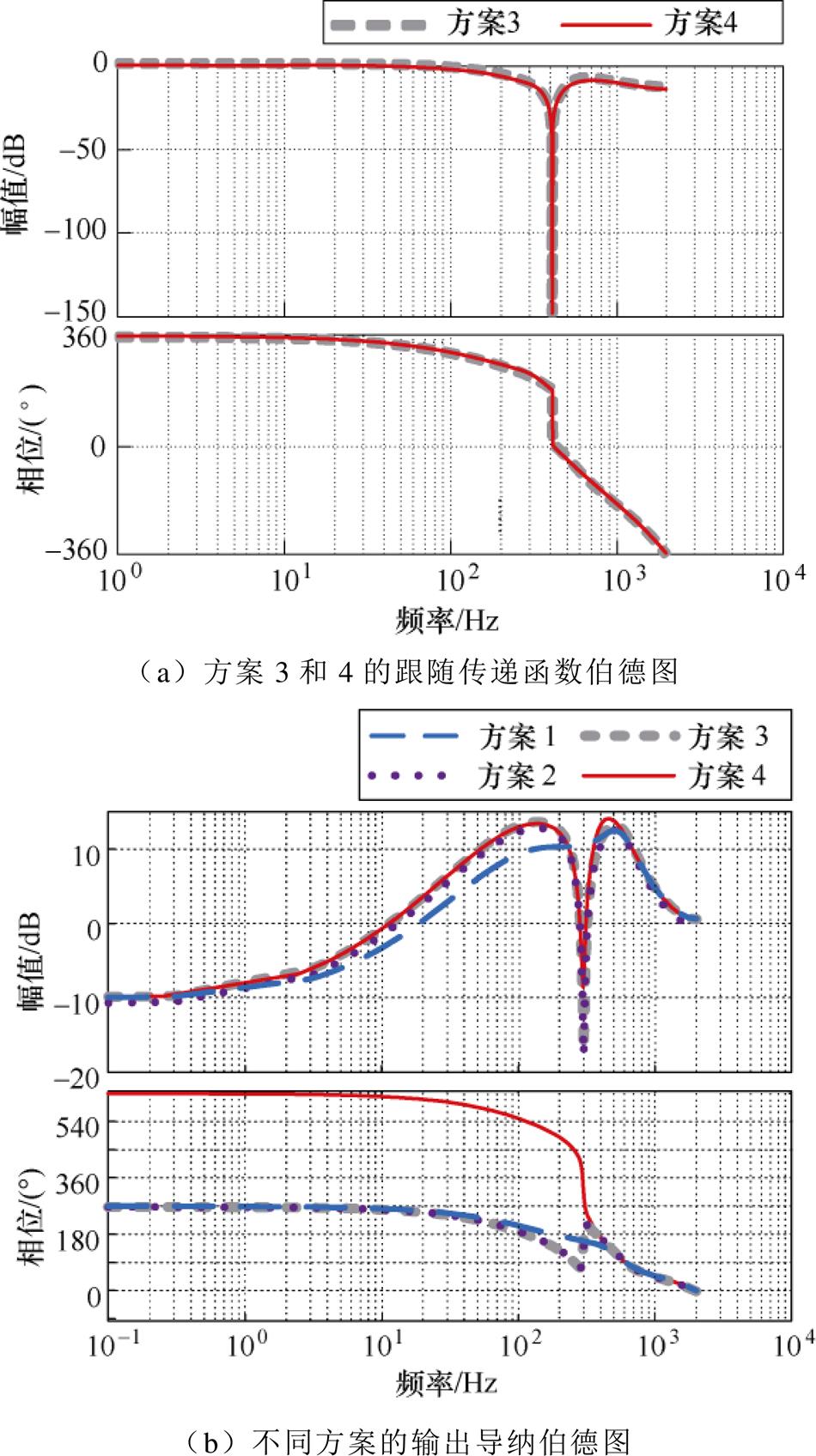
图12 不同方案的伯德图
Fig.12 Bode diagrams of different schemes
为了对上述融合离散状态空间控制方案进行验证和对比,本文搭建了Matlab/Simulink仿真模型,仿真参数见表1。为了反映工程实际情况,本文系统参数选用某型号MW级并网变流器参数。
表1 MW级并网变流器参数
Tab.1 MW-class grid-side converter parameters
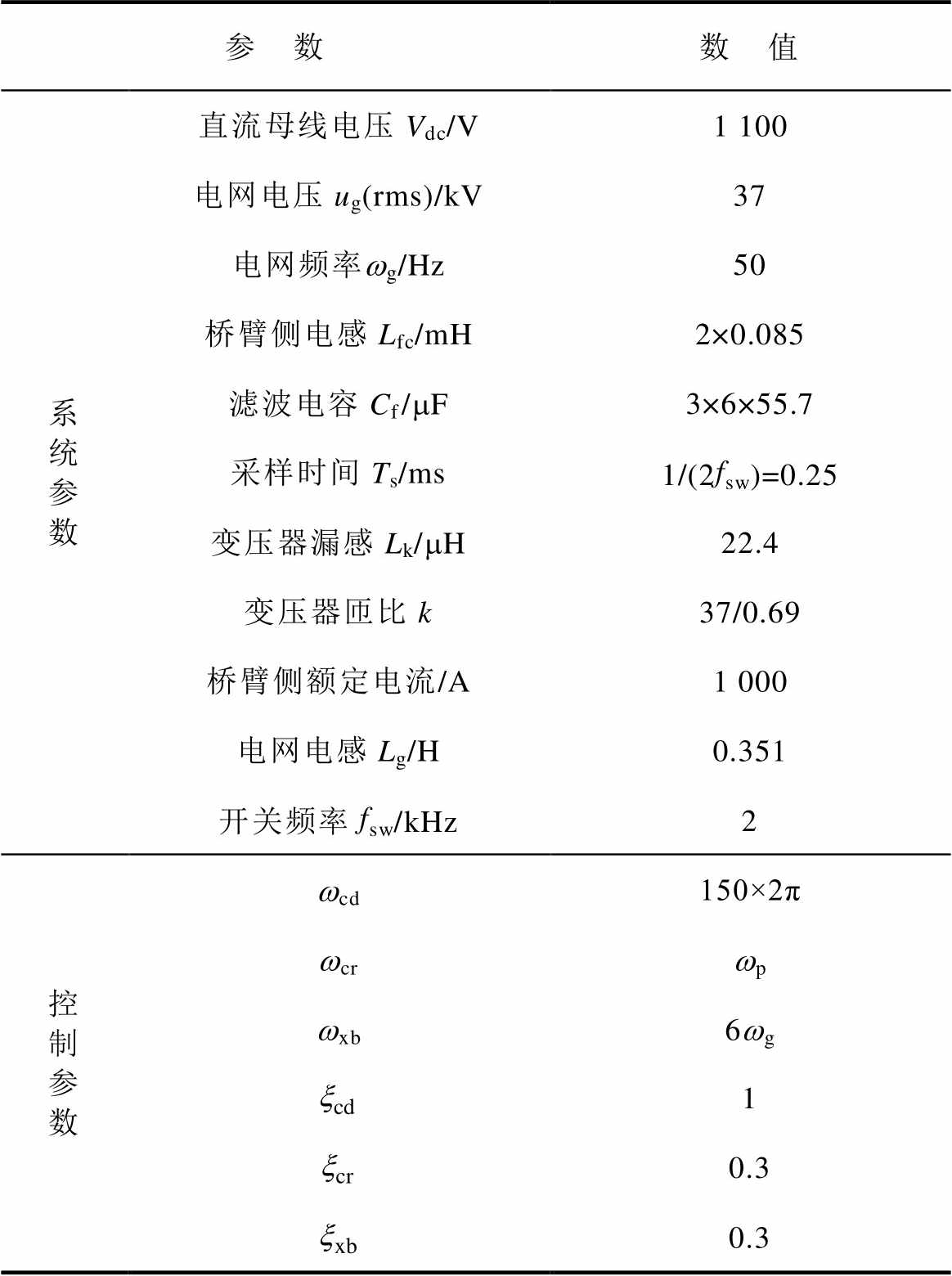
参 数数 值 系统参数直流母线电压Vdc/V1 100 电网电压ug(rms)/kV37 电网频率wg/Hz50 桥臂侧电感Lfc/mH2×0.085 滤波电容Cf/mF3×6×55.7 采样时间Ts/ms1/(2fsw)=0.25 变压器漏感Lk/mH22.4 变压器匝比k37/0.69 桥臂侧额定电流/A1 000 电网电感Lg/H0.351 开关频率fsw/kHz2 控制参数wcd150×2π wcrwp wxb6wg 1 0.3 0.3
由于方案4利用微分器对并网电流进行估计,因此需对估算电流的精度进行分析。图13为估算和采集的并网电流的波形,可以看出:估算的并网电流较为准确地跟踪采集并网电流,且存在高频放大现象,这是由于图10中设计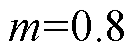 的微分器
的微分器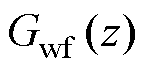 (见式(28))对高频信号的幅值存在一定的放大,但相对于采集的并网电流而言,误差较小,精度较高,因此可用估算并网电流代替采集的并网电流。
(见式(28))对高频信号的幅值存在一定的放大,但相对于采集的并网电流而言,误差较小,精度较高,因此可用估算并网电流代替采集的并网电流。
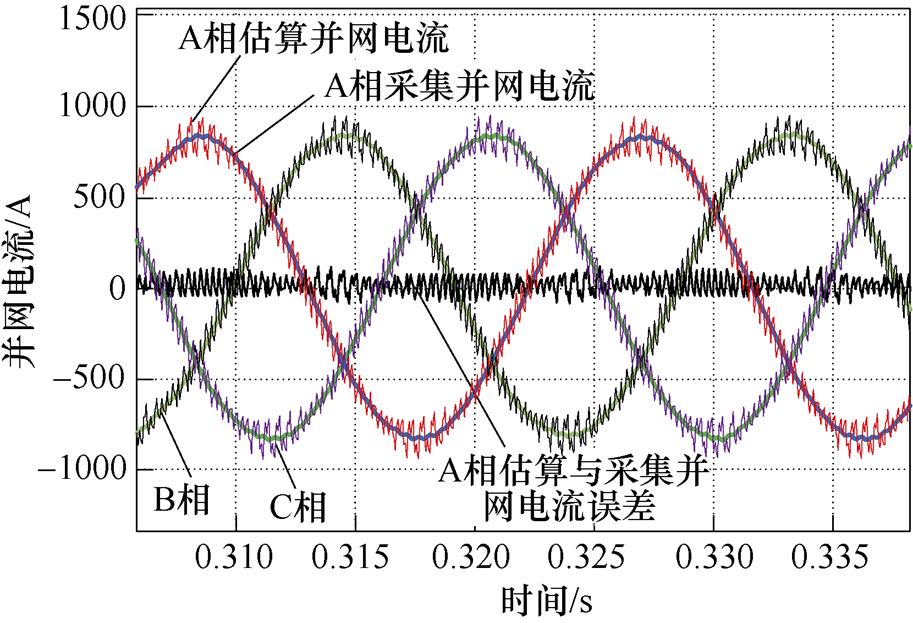
图13 估算和采集并网电流的波形
Fig.13 Waveforms of estimating and sampling currents
图14为电流指令发生阶跃变化时不同方案对应的桥臂侧dq轴电流仿真波形。由图14c可以看出,方案4的电流上升时间约为4.5 ms,且几乎没有超调,与图14a中方案1的跟随波形几乎一致,而图14b中方案2的电流上升时间约为7.5 ms。正如2.2节分析一样,方案4通过改进前馈补偿环节,保持了方案1近似一阶系统的跟随性能,虽然微分环节的使用造成期望零极点的偏移,但最终跟随响应曲线几乎保持一致,具有较好的动态跟随性能。
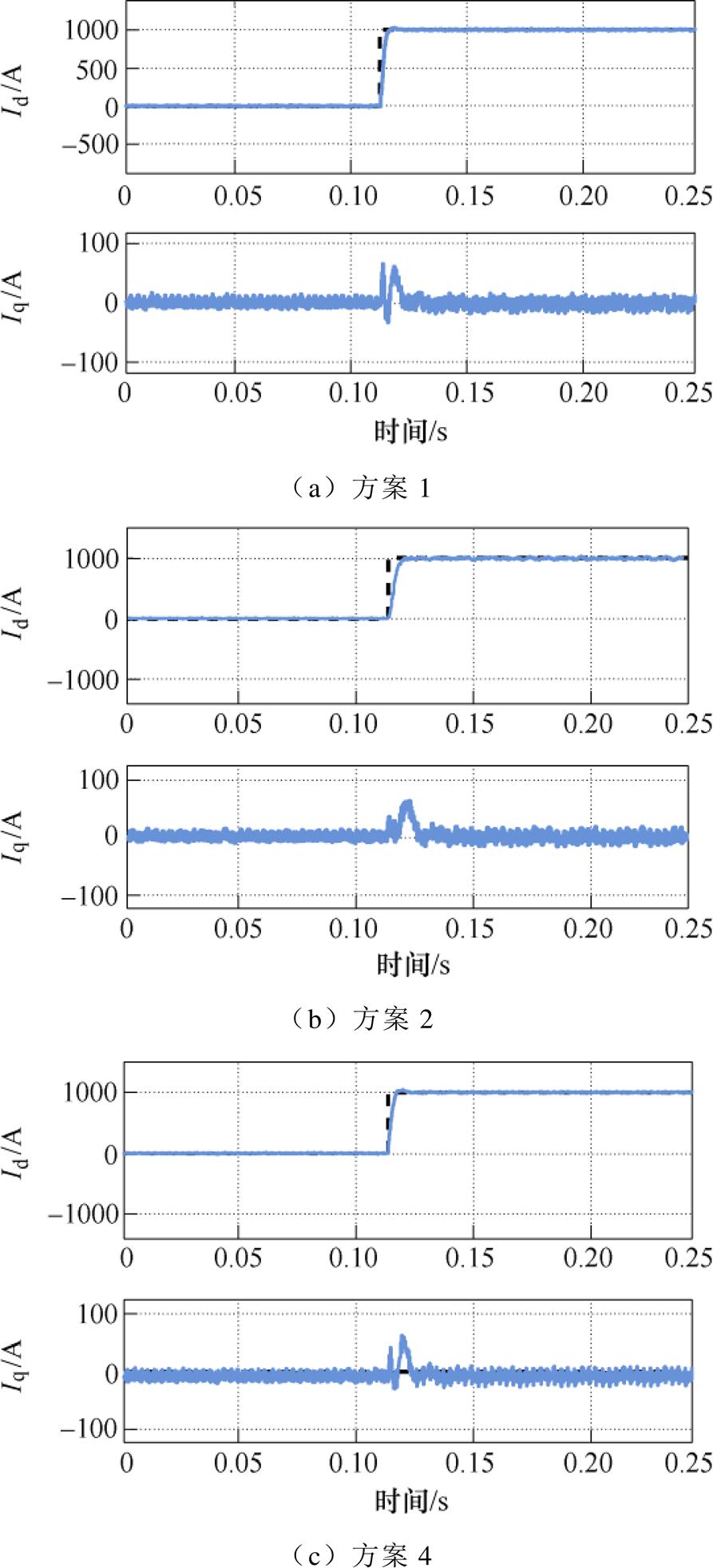
图14 阶跃变化时不同方案的电流仿真波形
Fig.14 Current simulation waveforms of different schemes during step change
3.2.1 电网电压骤降
图15为0.11 s发生40 %电网电压骤降时不同方案对应的dq轴电流波形。不难发现方案2、4与方案1具有近乎相同的抗电网电压阶跃变化能力,由图15b和图15c可以看出,方案2和4对于阶跃性干扰可以在10 ms内恢复,与图15a中方案1的恢复时间相比,几乎一致,这一点也可以由图12b中0 Hz处幅频特性看出,使2.3节理论分析得到验证。
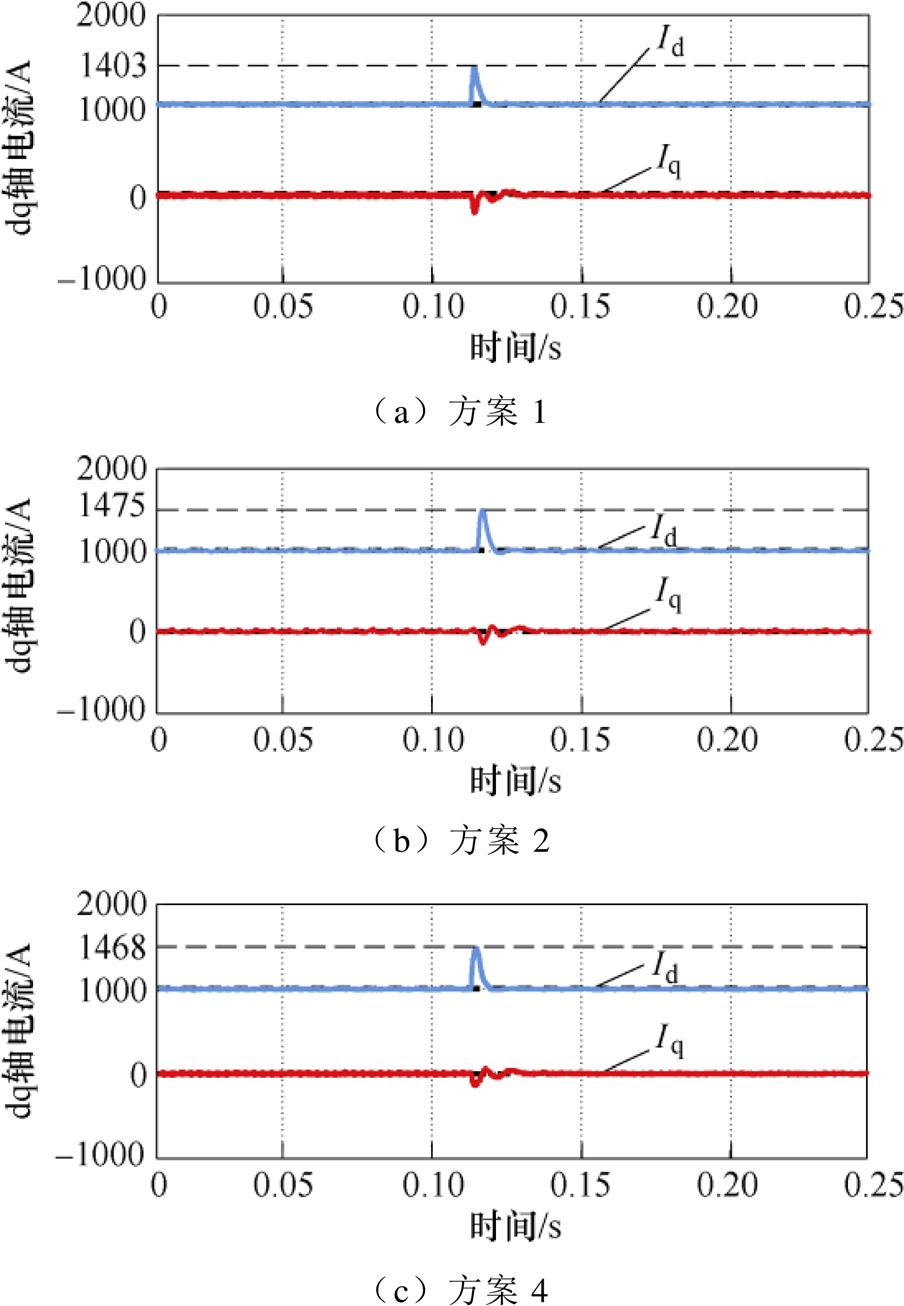
图15 电网电压骤降时不同方案的电流仿真波形
Fig.15 Current simulation waveforms of different schemes during grid voltage dip
3.2.2 电网电压背景谐波影响
图16为0.3 s后电网电压注入6 %的5、7次谐波前后对应的并网电流波形。由图16a可以看出,并网电流发生畸变,此时对应的总谐波畸变率(Total Harmonic Distortion, THD)为15.91 %,已远远超过并网标准的5 %。表明方案1对于电网电压背景谐波的抑制能力不足,这一点与图12幅频特性分析一致。而图16b所示的方案2与图16c所示的方案3和图16d所示的方案4所获得的电流波形没有明显畸变,对应的电流THD分别为1.33 %、1.35 %和1.68 %,这也与图12中的幅频响应结果一致。表明本文设计的融合电流控制方案,在保留快速电流动态响应能力的同时,有效地提升了电网背景谐波的抑制能力。
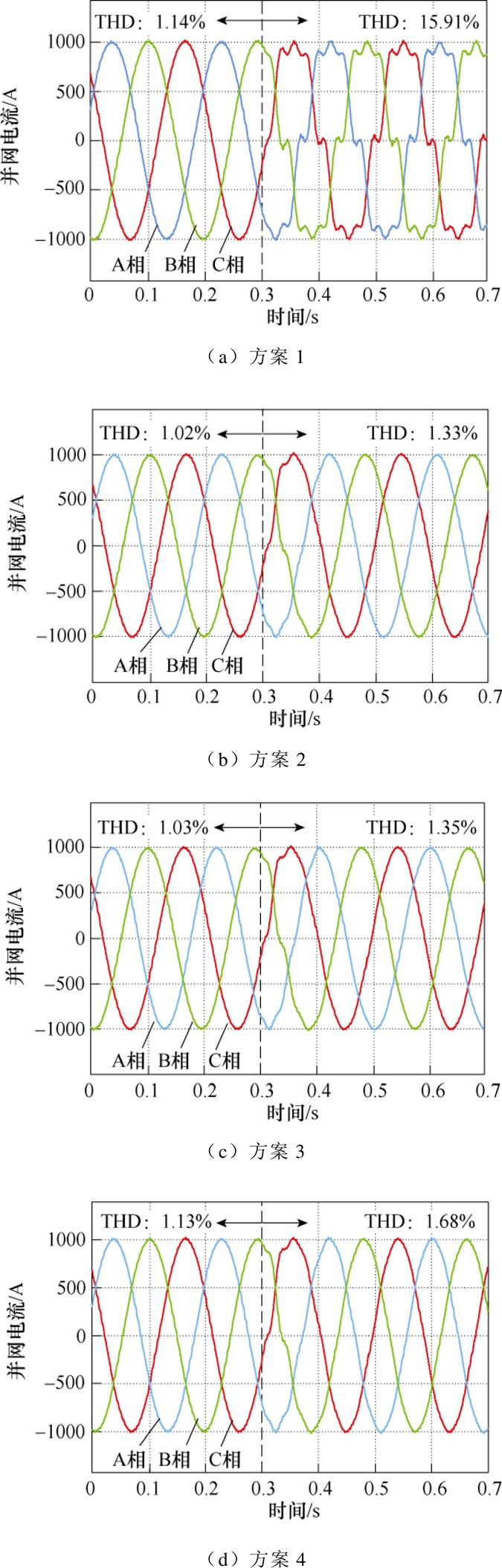
图16 电网电压畸变时不同方案的电流仿真波形
Fig.16 Current simulation waveforms of different schemes during grid voltage distortion
在电流环设计中反馈增益的计算都是基于滤波器标称参数设计,而实际系统参数由于温度等因素可能会发生变化。图17所示为实际滤波器参数发生偏差时方案4对应的稳定区域。本文方案中 =
= 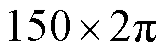 ,由图17可以看出,所容许的参数变化范围:桥臂侧电感
,由图17可以看出,所容许的参数变化范围:桥臂侧电感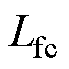 为
为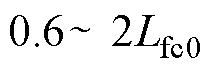 ,滤波电容
,滤波电容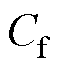 为
为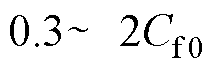 ,网侧电感
,网侧电感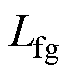 为
为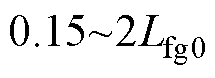 ,其中
,其中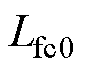 、
、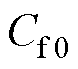 、
、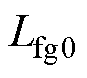 为系统的标称参数。不难发现,本文融合方案能在较大的参数偏差范围内稳定运行,有着强参数鲁棒性。
为系统的标称参数。不难发现,本文融合方案能在较大的参数偏差范围内稳定运行,有着强参数鲁棒性。
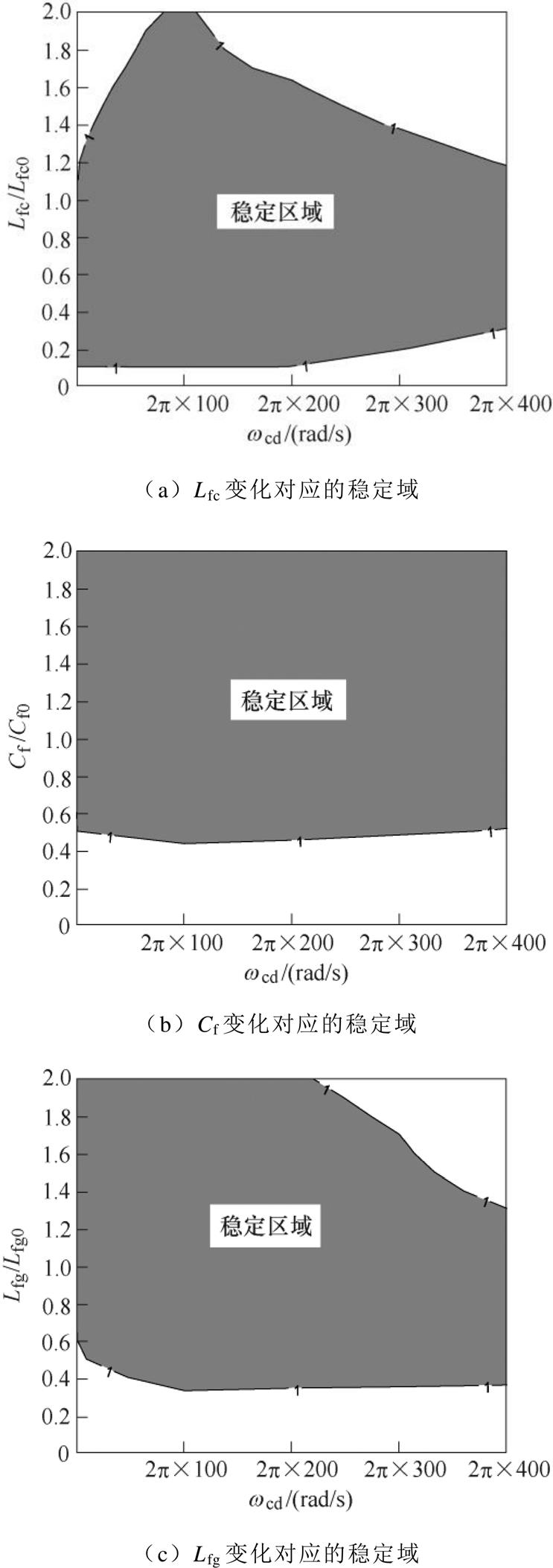
图17 参数变化的稳定
Fig.17 Stability maps of various parameters
为了进一步验证本文融合离散状态空间控制方案的有效性以及反馈增益设计的合理性,根据表1中实际系统参数,利用半实物仿真箱RT-Lab以及硬件箱搭建了硬件在环仿真实验平台,如图18所示,其对应的原理框图如图19所示。硬件箱采用DSP TMS320F28335为核心控制器,芯片AD7606进行电流和电压采样。开关死区设计为4.8  。实验电流波形为示波器真实捕获的波形。
。实验电流波形为示波器真实捕获的波形。
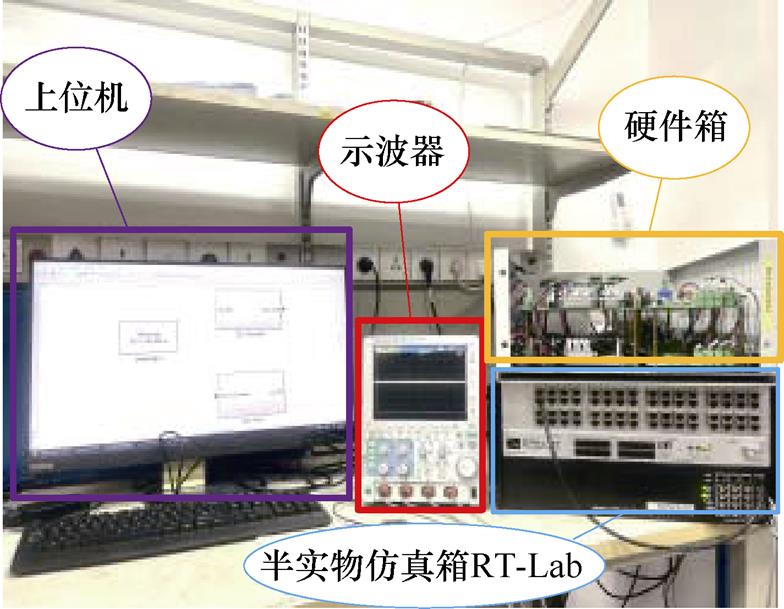
图18 半实物实验框图
Fig.18 Hardware-in-the-loop block diagram
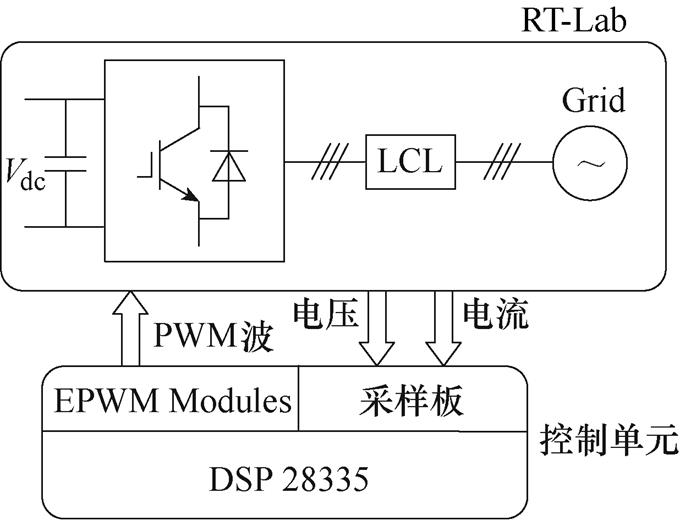
图19 半实物实验平台
Fig.19 Hardware-in-the-loop experimental platform
图20记录了在电流参考值发生1 000 A的阶跃变化时桥臂侧电流的动态响应过程。可以看出:方案4与方案1的电流响应波形几乎保持一致,具有较快的动态性能,且明显快于方案2。
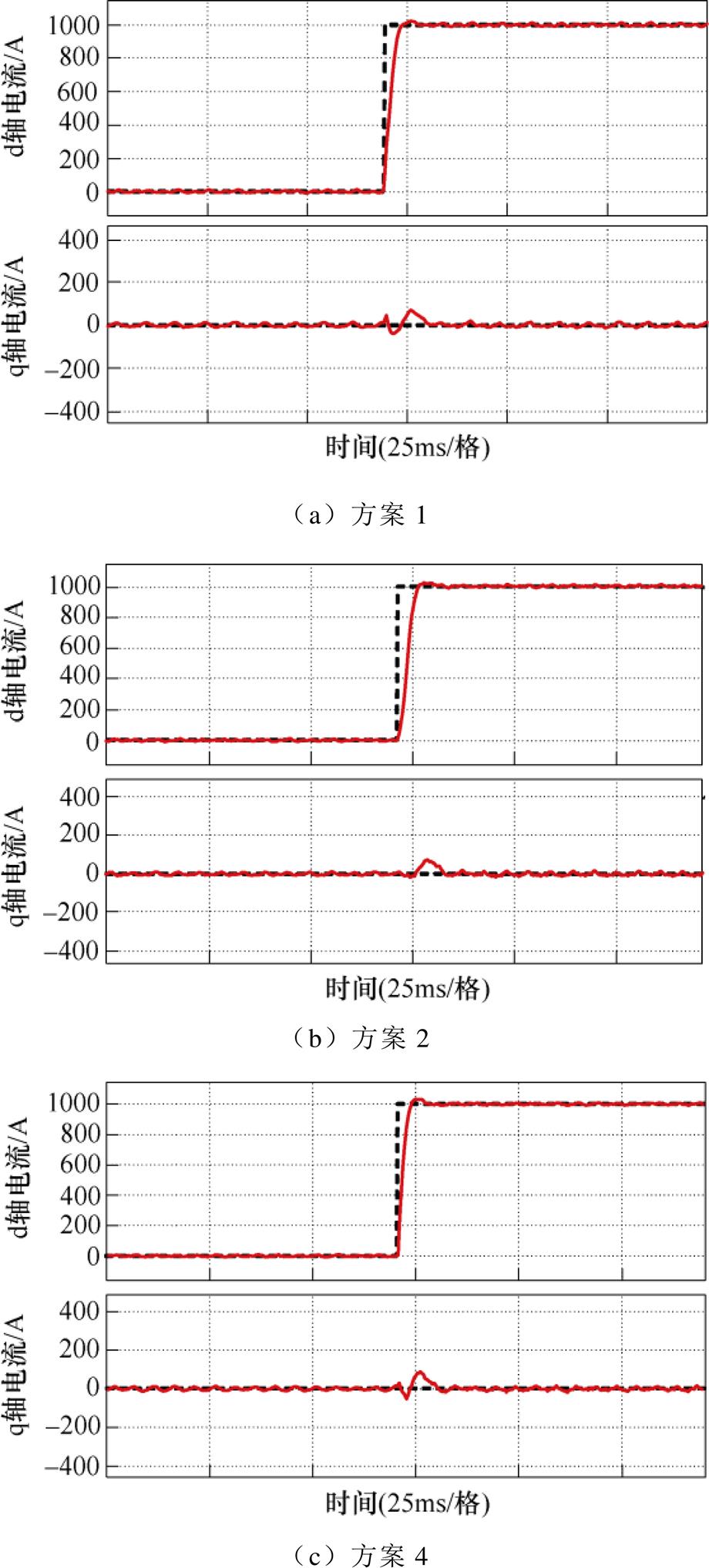
图20 阶跃变化时不同方案的电流实验波形
Fig.20 Current experimental waveforms of different schemes during step change
实验评估了本文方案在电网电压骤降和畸变时的抗扰性能。
4.2.1 电网电压骤降
图21为电网电压发生0.4(pu)骤降时的电流响应。与理论分析和仿真一致,方案2的动态性能不足,但和方案4一样都具有较好的抗阶跃扰动抑制能力。
4.2.2 电网电压谐波
图22为电网中加入6 %的5和7次谐波前后的并网电流波形。不难看出在理想电网下,各方案的电流THD相似,均能满足并网电流谐波要求。但是当电网电压含有背景谐波时,方案1的并网电流已经发生畸变,THD=15.56 %;而方案2、3和4仍然保持较好的正弦度,THD分别为2.14 %、2.07 %和2.28 %,依然能够较好地满足并网要求。且由图22d可以发现,增大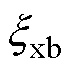 能够进一步提升特定次电网谐波影响的抑制能力,这与图7的幅频特性分析一致。
能够进一步提升特定次电网谐波影响的抑制能力,这与图7的幅频特性分析一致。
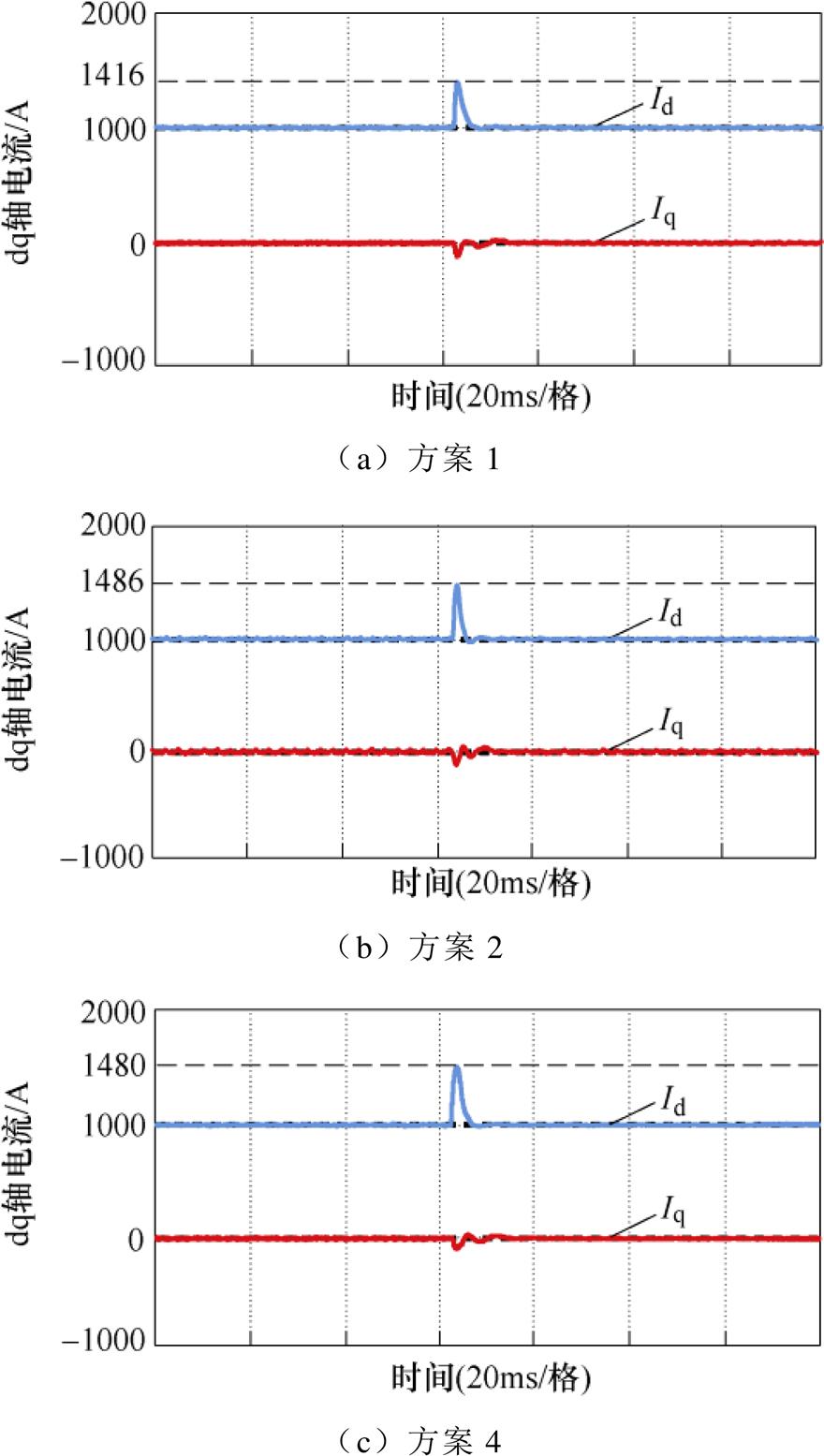
图21 电网电压骤降时不同方案的电流实验波形
Fig.21 Current experimental waveforms of different schemes during grid voltage dips
图23中记录了实际滤波器参数发生变化时方案4的运行性能。由图可以看出,当实际桥臂侧电感参数、滤波电容参数以及网侧电感参数发生一定范围的变化时,系统仍稳定运行。这与图17中关于稳定性的分析一致。
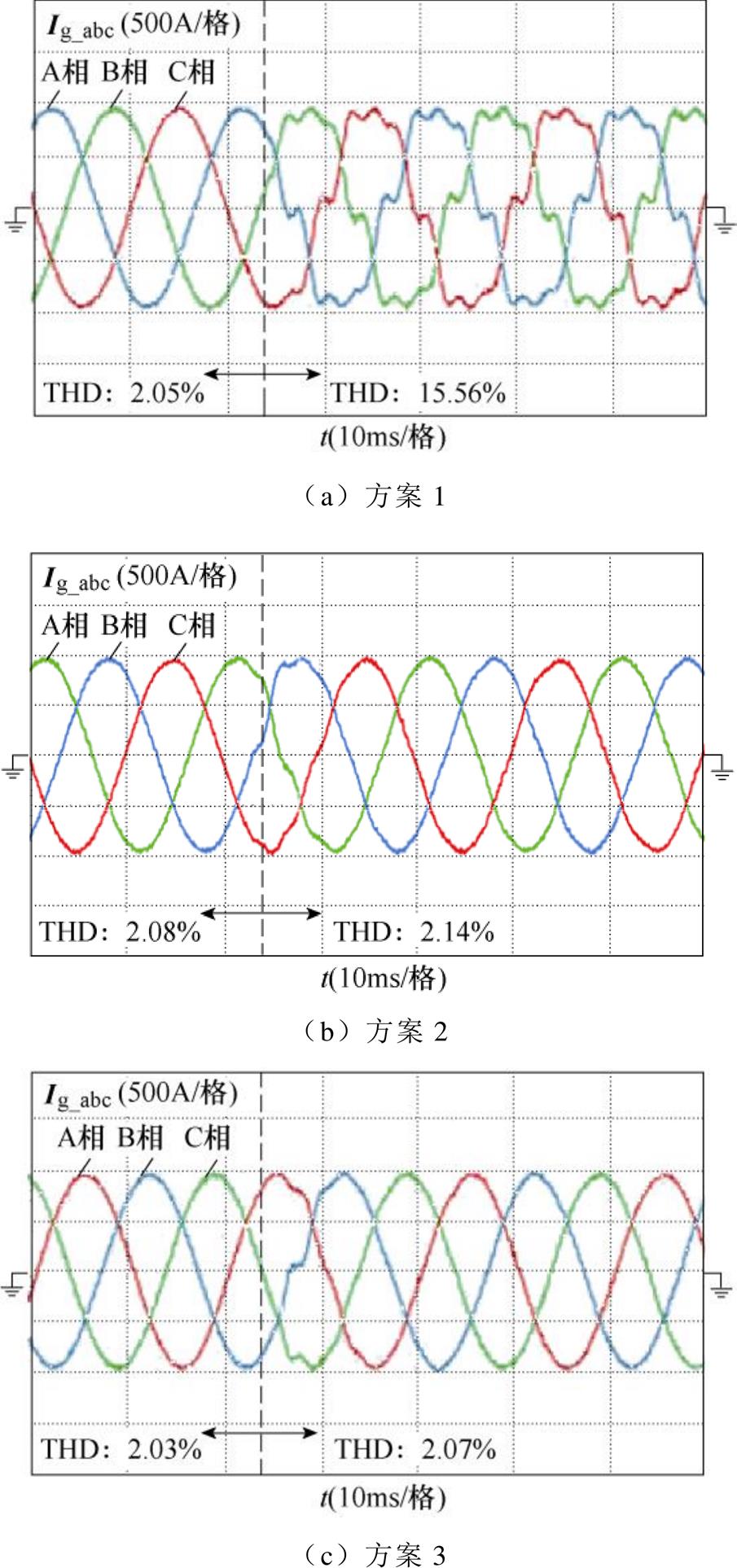
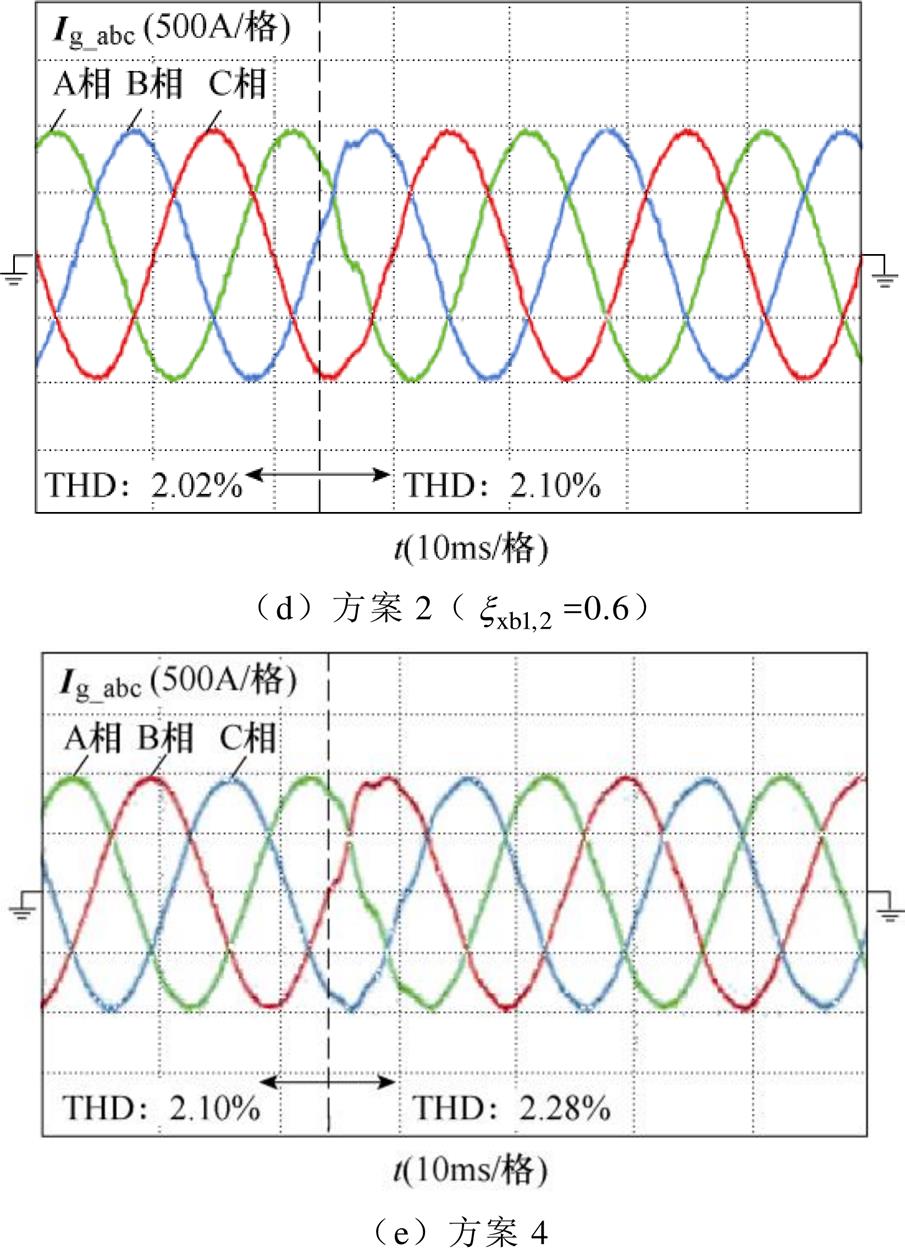
图22 电网电压畸变时不同方案的电流实验波形
Fig.22 Current experimental waveforms of different schemes during grid voltage distortion
本文提出一种融合离散状态空间控制方案,用于大功率LCL并网变流器的电流控制。基波和谐波回路的融合设计简化了设计复杂性,提升了设计优化自由度。同时,微分器的使用节省了并网电流的检测,降低了硬件的复杂性和控制成本。本文分析了零极点影响,并基于零极点配置实现了控制器参数的优化设计。对比分析了微分器引入前后的控制性能,讨论了参数鲁棒性。最后,通过仿真和硬件在环实验对其分析和设计进行了验证。研究表明,本文所设计的控制方案,在保留较好的动态响应性能的同时,能够明显提升对电网背景谐波扰动的抑制能力,提升了并网电流质量。
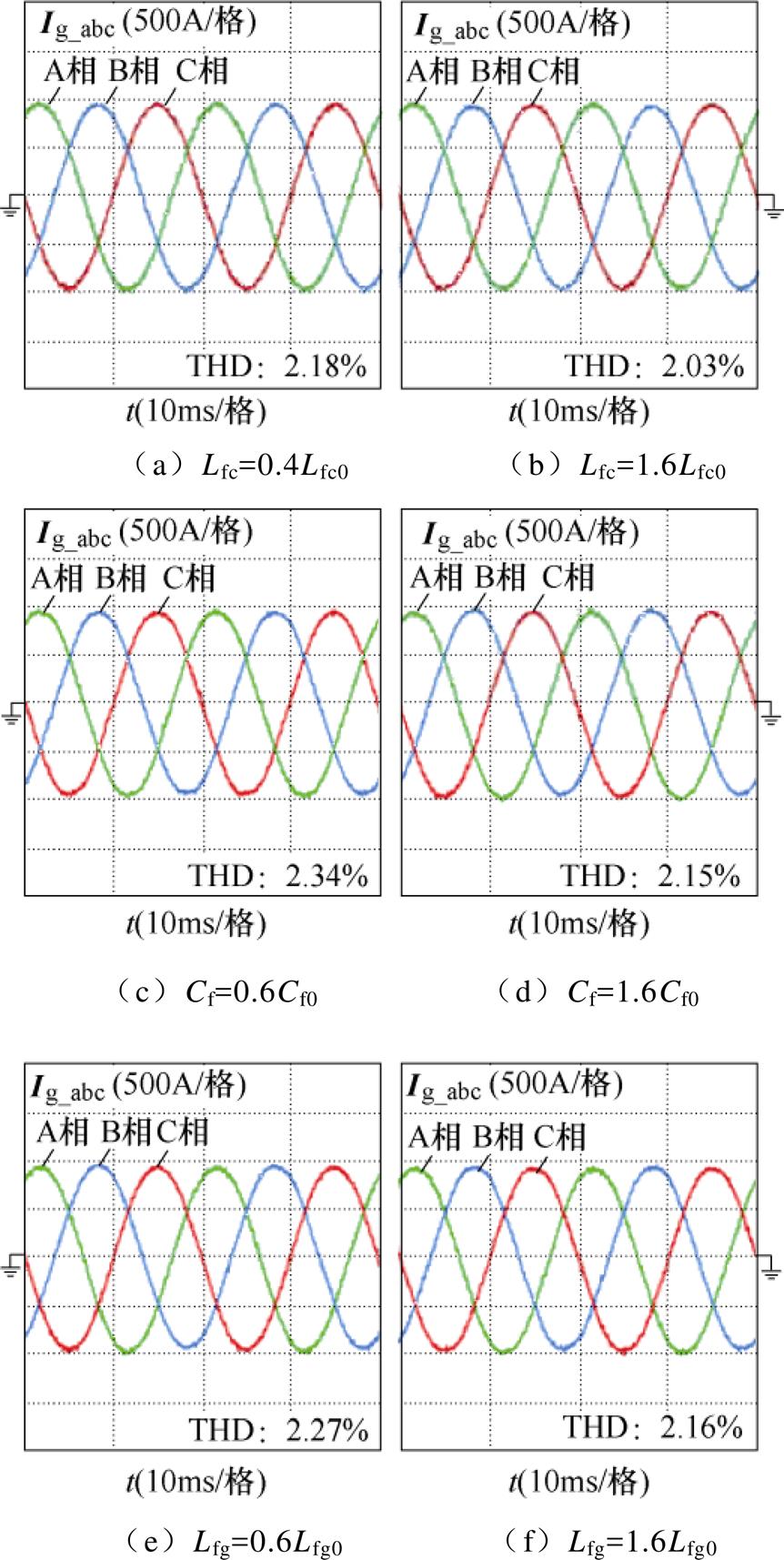
图23 参数变化时方案4的并网电流波形
Fig.23 Current experimental waveforms of scheme 4 under various parameters
附 录
1. 零阶保持离散化模型如下:
式(4)中的状态转移矩阵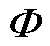 可以利用线性变换的方法进行求解。令A的相似对角阵为
可以利用线性变换的方法进行求解。令A的相似对角阵为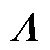 ,则
,则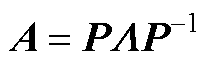 ,其中P为线性变换矩阵,相应的表达式为
,其中P为线性变换矩阵,相应的表达式为
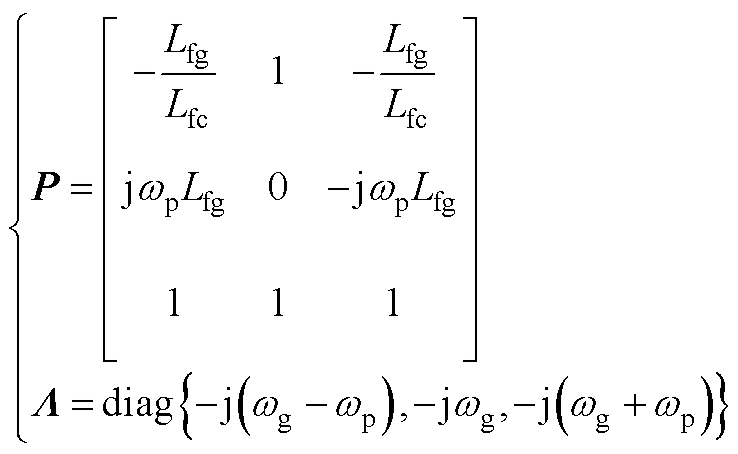 (A1)
(A1)
其中
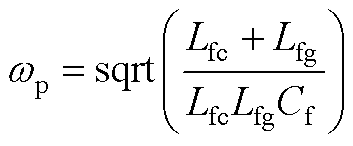
因此
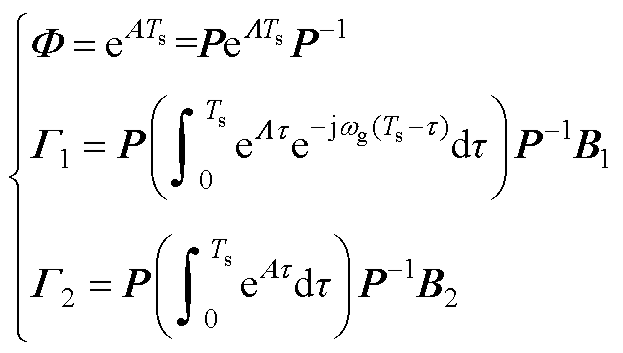 (A2)
(A2)
具体表达式为
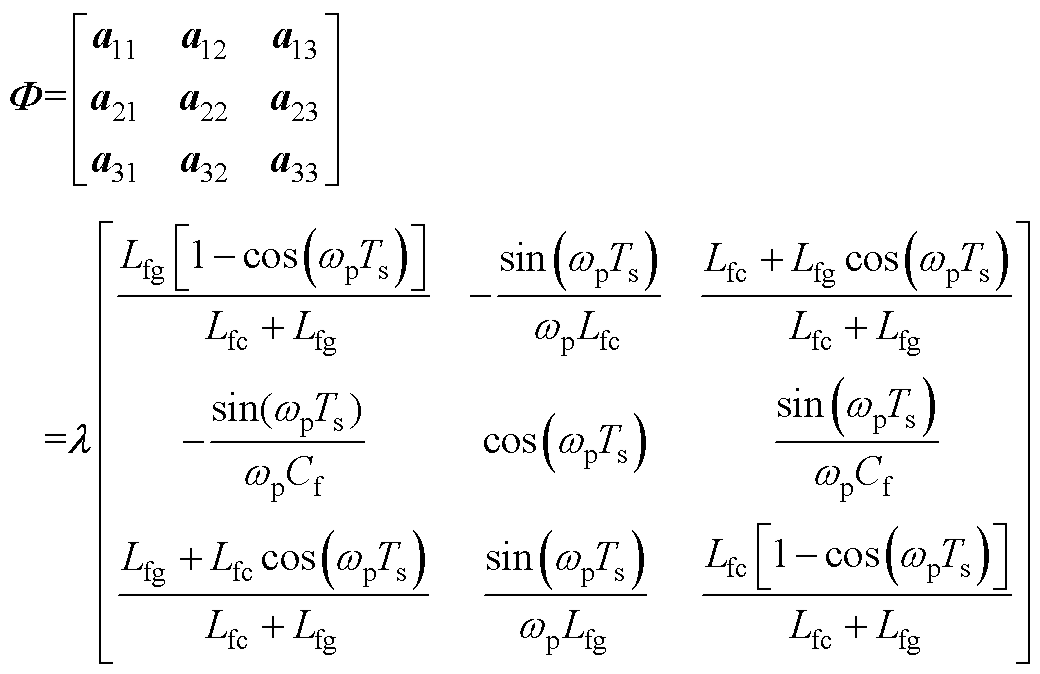
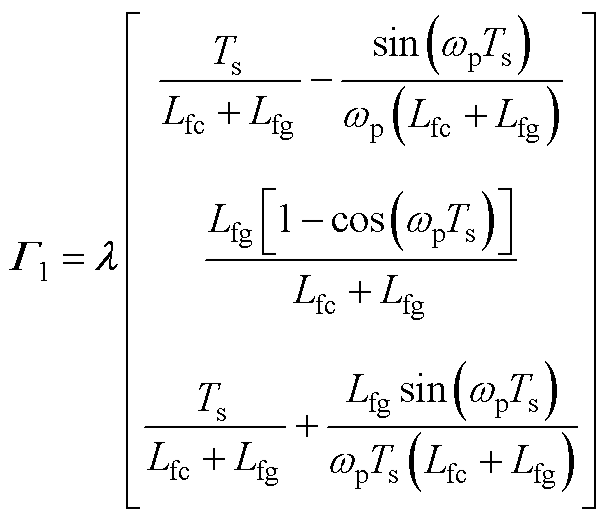
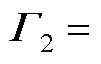
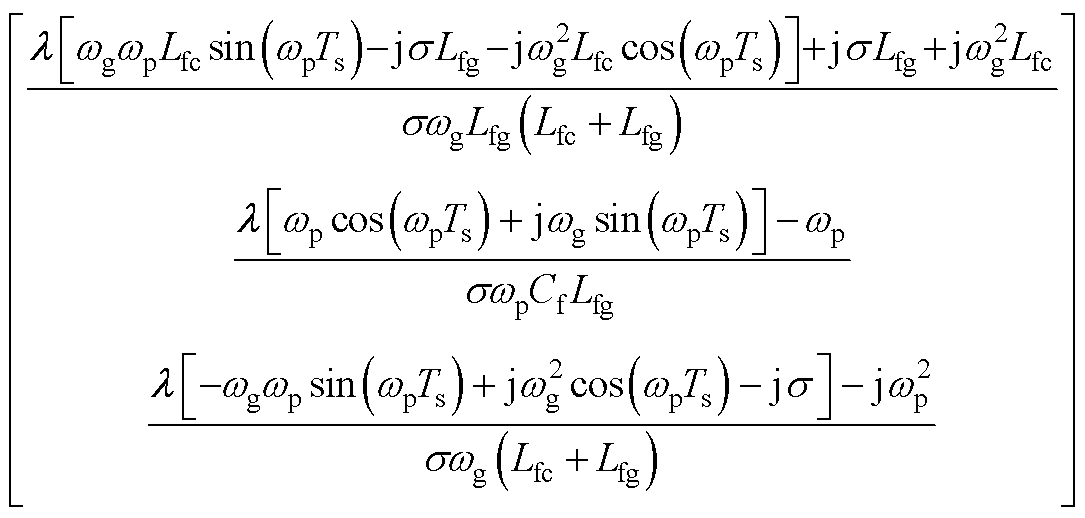
式中,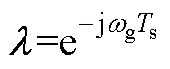 ;
;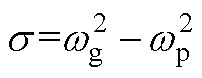 。
。
进一步可得
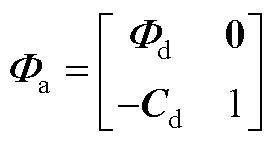
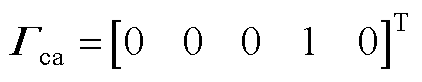
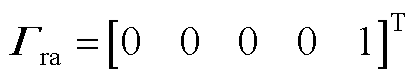
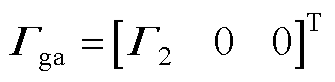
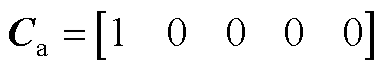
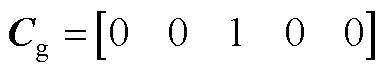
其中
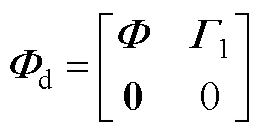
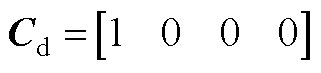
2. 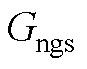 中相关系数
中相关系数
为了方便表述,设计辅助参数如下
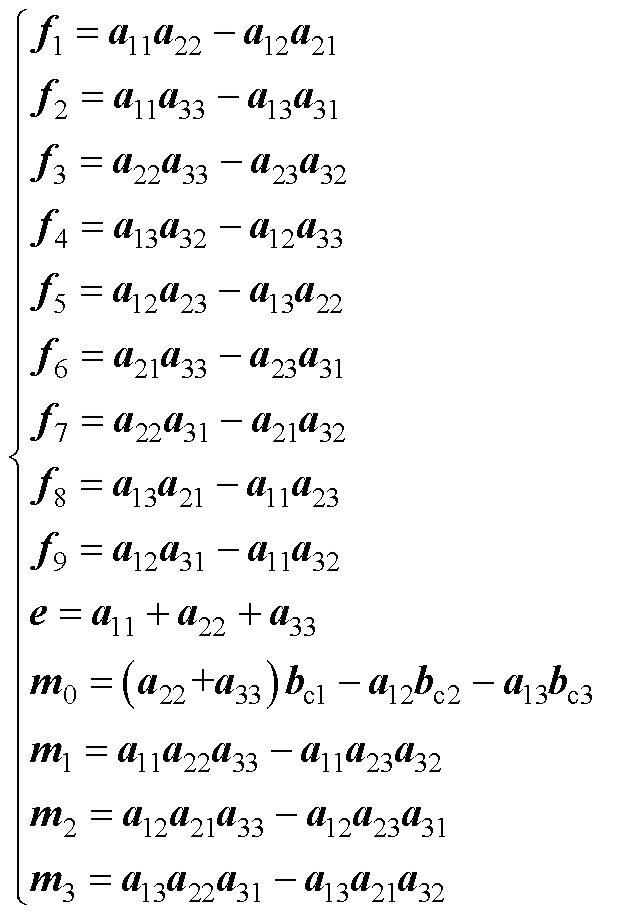 (A3)
(A3)
进一步设计辅助参数如下
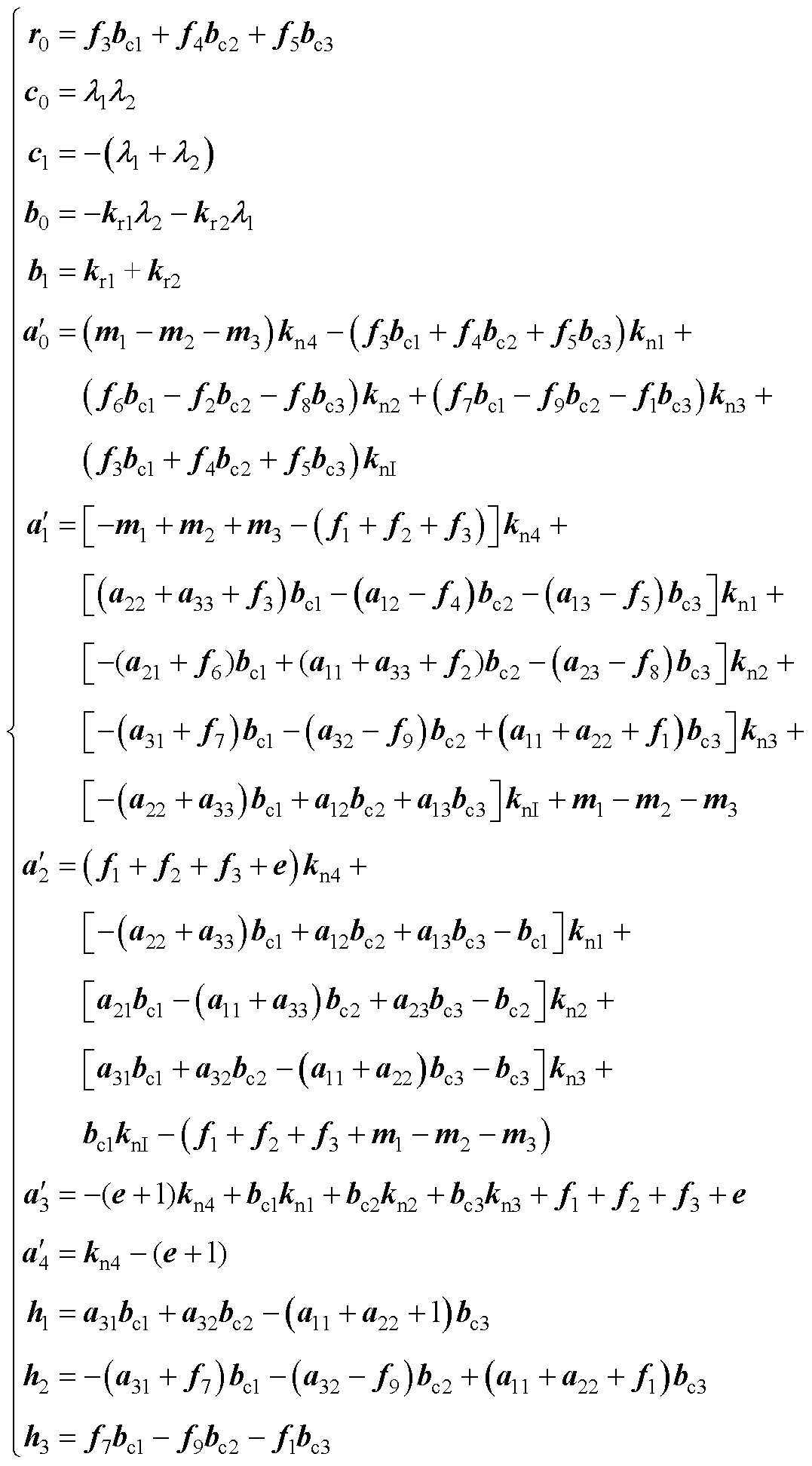 (A4)
(A4)
因此
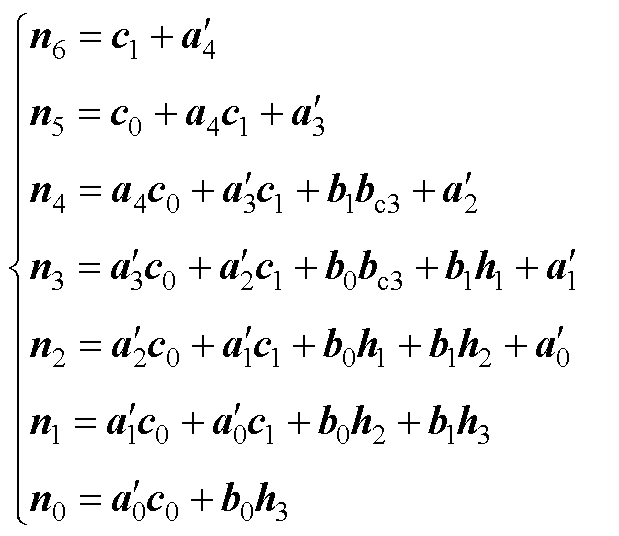 (A5)
(A5)
3. 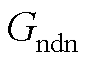 中相关系数
中相关系数
为了方便表述,设计辅助参数如下
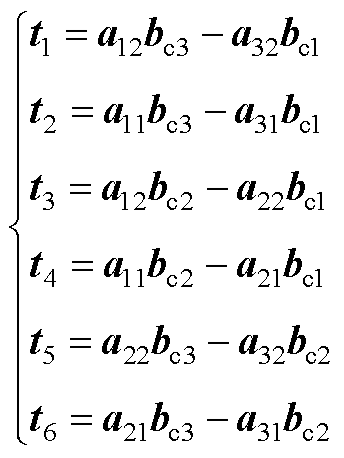 (A6)
(A6)
因此
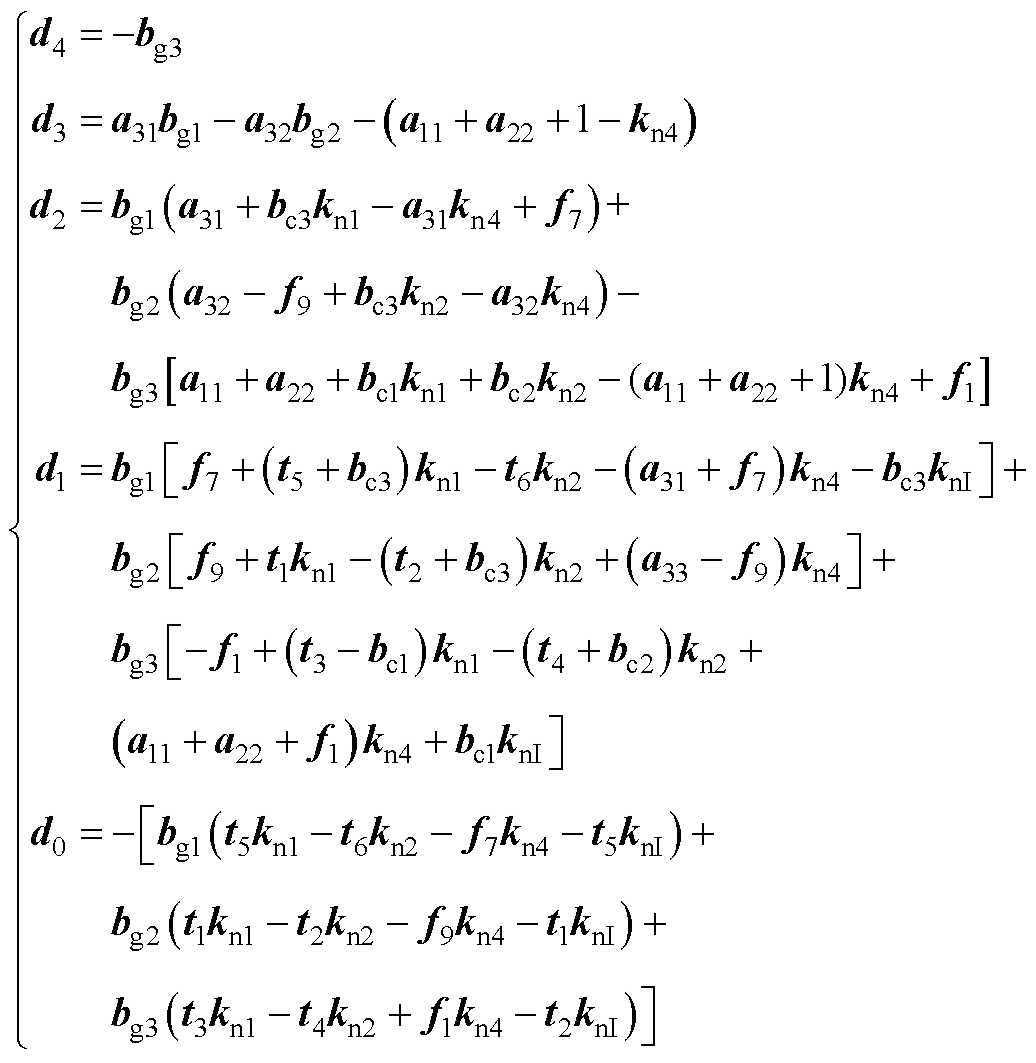 (A7)
(A7)
参考文献
[1] Sharma H R, Suryawanshi H M, Chaturvedi P, et al. Implementation of passive damping technique in LCL filter for three-phase grid connected inverter[C]//2022 IEEE 2nd International Conference on Sustainable Energy and Future Electric Transportation (SeFeT), Hyderabad, India, 2022: 1-6.
[2] Li Xiaoqiang, Wu Xiaojie, Geng Yiwen, et al. Wide damping region for LCL-type grid-connected inverter with an improved capacitor-current-feedback method[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 5247-5259.
[3] Xin Zhen, Loh P C, Wang Xiongfei, et al. Highly accurate derivatives for LCL-filtered grid converter with capacitor voltage active damping[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3612-3625.
[4] Pan Donghua, Ruan Xinbo, Wang Xuehua. Direct realization of digital differentiators in discrete domain for active damping of LCL-type grid-connected inver- ter[J]. IEEE Transactions on Power Electronic, 2018, 33(10): 8461-8473.
[5] Chen Chen, Xiong Jian, Wan Zhiqiang, et al. A time delay compensation method based on area equiva- lence for active damping of an LCL-type converter[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 762-772.
[6] 方天治, 黄淳, 陈乃铭, 等. 一种提高弱电网下LCL型并网逆变器鲁棒性的相位超前补偿策略[J]. 电工技术学报, 2018, 33(20): 4813-4822.
Fang Tianzhi, Huang Chun, Chen Naiming, et al. A phase-lead compensation strategy on enhancing robustness of LCL-type grid-tied inverters under weak grid conditions[J]. Transactions of China Elec- trotechnical Society, 2018, 33(20): 4813-4822.
[7] 张森, 赵剑锋, 刘康礼, 等. 数字控制延时对电流环解耦有效性的影响[J]. 电工技术学报, 2020, 35(增刊2): 484-493.
Zhang Sen, Zhao Jianfeng, Liu Kangli, et al. Research on the impacts of digital control delay on the effectiveness of current loop decoupling[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(S2): 484-493.
[8] Dannehl J, Liserre M, Fuchs F W. Filter-based active damping of voltage source converters with LCL filter[J]. IEEE Transactions on Industrial Electronics, 2011, 58(8): 3623-3633.
[9] Nussbaumer T, Heldwein M L, Gong Guanghai, et al. Comparison of prediction techniques to compensate time delays caused by digital control of a three-phase Buck-type PWM rectifier system[J]. IEEE Transa- ctions on Industrial Electronics, 2008, 55(2): 791- 799.
[10] Corradini L, Stefanutti W, Mattavelli P. Analysis of multi-sampled current control for active filters[C]// 2007 IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 2007: 1608-1615.
[11] 潘冬华, 阮新波, 王学华, 等. 提高LCL型并网逆变器鲁棒性的电容电流即时反馈有源阻尼方法[J]. 中国电机工程学报, 2013, 33(18): 1-10, 21.
Pan Donghua, Ruan Xinbo, Wang Xuehua, et al. A capacitor-current real-time feedback active damping method for improving robustness of the LCL-type grid-connected inverter[J]. Proceedings of the CSEE, 2013, 33(18): 1-10, 21.
[12] Pan Donghua, Ruan Xinbo, Bao Chenlei, et al. Capacitor-current-feedback active damping with reduced computation delay for improving robustness of LCL-type grid-connected inverter[J]. IEEE Transa- ctions on Power Electronics, 2013, 29(7): 3414-3427.
[13] 王林, 孙鹏菊, 薛统宇, 等. 一种提高LCL型并网逆变器电流控制性能的延时补偿方法[J]. 中国电机工程学报, 2020, 40(19): 6320-6330.
Wang Lin, Sun Pengju, Xue Tongyu, et al. A delay compensation method to improve the current control performance of the LCL-type grid-connected inver- ter[J]. Proceedings of the CSEE, 2020, 40(19): 6320- 6330.
[14] Kukkola J, Hinkkanen M. Observer-based state-space current control for a three-phase grid-connected converter equipped with an LCL filter[J]. IEEE Transactions on Industry Applications, 2014, 50(4): 2700-2709.
[15] Kukkola J, Hinkkanen M, Zenger K. Observer-based state-space current controller for a grid converter equipped with an LCL filter: analytical method for direct discrete-time design[J]. IEEE Transactions on Industry Applications, 2015, 51(5): 4079-4090.
[16] Pérez-Estévez D, Doval-Gandoy J, Yepes A G, et al. Positive- and negative-sequence current controller with direct discrete-time pole placement for grid-tied converters with LCL filter[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 7207-7221.
[17] 陈杰, 章新颖, 闫震宇, 等. 基于虚拟阻抗的逆变器死区补偿及谐波电流抑制分析[J]. 电工技术学报, 2021, 36(8): 1671-1680.
Chen Jie, Zhang Xinying, Yan Zhenyu, et al. Dead- time effect and background grid-voltage harmonic suppression methods for inverters with virtual impedance control[J]. Transactions of China Elec- trotechnical Society, 2021, 36(8): 1671-1680.
[18] 林丽娟, 贾清泉, 田书娅, 等. 基于一致性算法的配电网谐波分布式治理策略[J]. 电力系统自动化, 2022, 46(2): 109-117.
Lin Lijuan, Jia Qingquan, Tian Shuya, et al. Distributed harmonic mitigation strategy of dis- tribution network based on consensus algorithm[J]. Automation of Electric Power Systems, 2022, 46(2): 109-117.
[19] 游小杰, 杨才伟, 王剑, 等. 一种适用于机车PWM整流器的比例积分-谐振电流控制器设计[J]. 电工技术学报, 2021, 36(23): 4926-4936.
You Xiaojie, Yang Caiwei, Wang Jian, et al. A tuning method for proportional integral-resonant current controller in locomotive PWM rectifiers[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(23): 4926-4936.
[20] 黄仁志, 全相军, 吴在军, 等. 基于多重谐振控制器的参考值前馈自适应控制[J]. 电工技术学报, 2022, 37(16): 4212-4224.
Huang Renzhi, Quan Xiangjun, Wu Zaijun, et al. A multiple resonant based on reference feedforward adaptive voltage control of three-phase inverter[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4212-4224.
[21] Xin Zhen, Mattavelli P, Yao Wenli, et al. Mitigation of grid-current distortion for LCL-filtered voltage- source inverter with inverter-current feedback con- trol[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 6248-6261.
[22] Zhao Rende, Li Qian, Xu Hailiang, et al. Harmonic current suppression strategy for grid-connected PWM converters with LCL filters[J]. IEEE Access, 2019, 7: 16264-16273.
[23] 谢震, 汪兴, 张兴, 等. 基于谐振阻尼的三相LCL型并网逆变器谐波抑制优化策略[J]. 电力系统自动化, 2015, 39(24): 96-103.
Xie Zhen, Wang Xing, Zhang Xing, et al. Optimized harmonic suppression strategy of grid-connected inverter with an LCL-type filter based on resonance damping[J]. Automation of Electric Power Systems, 2015, 39(24): 96-103.
[24] 徐健, 曹鑫, 郝振洋, 等. 基于电网谐波电压前馈的虚拟同步整流器电流谐波抑制方法[J]. 电工技术学报, 2022, 37(8): 2018-2029.
Xu Jian, Cao Xin, Hao Zhenyang, et al. A harmonic- current suppression method for virtual synchronous rectifier based on feedforward of grid harmonic voltage[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2018-2029.
[25] Li Weiwei, Ruan Xinbo, Pan Donghua et al. Full- feedforward schemes of grid voltages for a three- phase LCL-type grid-connected inverter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2237-2250.
[26] Zhang Hao, Ruan Xinbo, Lin Zhiheng, et al. Capacitor voltage full feedback scheme for LCL-type grid-connected inverter to suppress current distortion due to grid voltage harmonics[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 2996-3006.
[27] Franklin G F, Powell J D, Workman M L. Digital control of dynamic systems[M]. Menlo Park, CA, USA: Addison-Wesley, 1997.
[28] Hu Mingjin, Hua Wei, Ma Guangtong, et al. Improved current dynamics of proportional-integral-resonant controller for a dual three-phase FSPM machine[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 11719-11730.
Abstract For high-power grid-connected converters, the switching frequency usually is low. Consequently, the adverse effects enforced by the control delay and discretizing errors are heavy. However, traditional current control strategies generally ignore these effects, reducing the performance of the designed controller. Recently, some strategies were presented to compensate for the control delay and the discretizing errors. However, most suffer from low dynamic response and high sensitivity to the power grid harmonics. Therefore, a current control strategy combining the bridge arm-side and the grid-side currents is designed directly in the discrete-time domain, and pole-zero placement is used in synchronous coordinates. Meanwhile, a differentiator to the capacitor voltageis introduced to estimate the grid-side currents.Consequently,hardware complexity and the corresponding control cost are reduced.
The discrete-time model of the converter with LCL is built in synchronous coordinates as the output filter, including the computational delay, firstly. The corresponding structure of the combined state-space control scheme is as follows: the harmonic control loop of the grid-side currents is constructed and combined with the fundamental current control loop on the bridge arm-side using the full state-feedback control. And then, the integral controller is introduced for improved disturbance rejection, and the reference-feedforward controller is designed to increase the reference-tracking dynamic performance. Consequently, the closed-loop transfer function of the system is obtained based on the discrete-time model and the control scheme. Then the state feedback function matrix and the feedforward module are optimized based on the pole-zero placement. Finally, a differentiator is introduced to estimate the grid-side currents, reducing the hardware cost.
Experiment results based on a hardware-in-loop simulator show that the response time of the bridge arm-side currents to a 1 000 A step-up change is about 4.5 ms; the recovery time of the bridge arm-side currents facing a grid-voltage dip of 0.4(pu) is about 10ms; and the total harmonic distortion of the grid-side currents is 2.28 %, below the 5 % limit given in standards, in the circumstances of 6 % fifth and seventh harmonic components appearing in the grid voltage. Finally, to verify the robustness of the proposed strategy to the parameter deviations, the actual system parameters are deviated artificially from their nominal values. The results show that the proposed strategy can operate satisfactorily in the range of ±40 % parameter deviations, and the influence of the parameter deviations is low.
The following conclusions can be drawn from the experiment results: (1) Compared with the typical discrete-time state-space control strategy, the proposed strategy keeps the same dynamic performance while improving the capability of rejecting the grid harmonic disturbance. (2) The proposed control strategy simplifies the design complexity based on the direct pole-zero placement and increases freedom degrees by combining the design of fundamental current and harmonic control loops. (3) The differentiator to the capacitor voltage is designed to acquire grid-side currents without additional current sensors and the corresponding sampling circuit, reducing the hardware complexity and the cost.
keywords:Grid-connected converter with LCL, low switching frequency, discrete-time control, grid harmonics
安徽省科技重大专项资助项目(202003a05020029)。
收稿日期 2022-12-13
改稿日期 2023-01-13
DOI: 10.19595/j.cnki.1000-6753.tces.222309
中图分类号:TM464
王 旭 男,1998年生,硕士研究生,研究方向为大功率风电变流器电流控制。E-mail: wx1998_wangxu@163.com
杨淑英 男,1980年生,教授,博士生导师,研究方向为风力发电系统和电驱动系统。E-mail: yangsyhfah@163.com(通信作者)
(编辑 陈 诚)