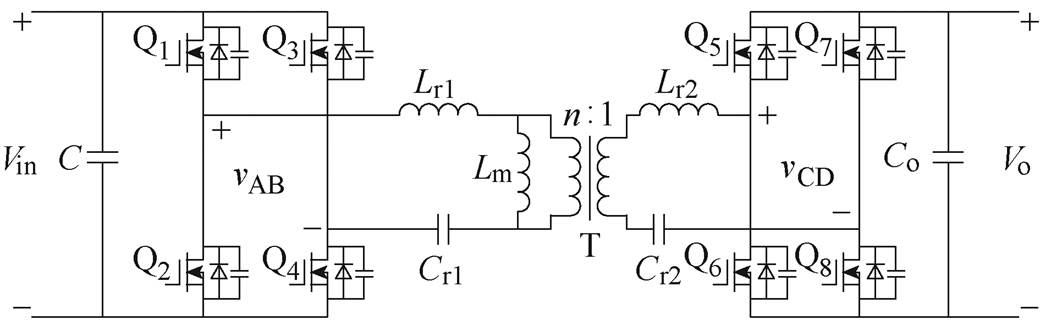
图1 CLLLC变换器拓扑结构
Fig.1 Topology of CLLLC converter
摘要 在输入电压宽范围变化时,变频调制CLLLC变换器存在开关频率变化范围宽的问题,而移相调制CLLLC变换器难以实现宽范围零电压导通(ZVS)。为了实现宽输入电压CLLLC变换器的高效率,该文提出一种变频双移相调制方法。通过同时调节开关频率、一次侧全桥和二次侧全桥之间的移相角,拓宽CLLLC变换器的增益并提高其效率。采用时域分析法求解变频双移相调制CLLLC变换器的电压增益与谐振电感电流有效值,并分析频率以及移相角对电压增益和谐振电感电流有效值的影响。最后,通过搭建一台100~300 V输入、48 V/400 W输出的实验样机,验证了理论分析的正确性。
关键词:变频双移相调制 宽输入电压 CLLLC变换器 时域分析 零电压导通
大功率隔离型双向DC-DC变换器可实现直流电能的变换,具有高效率、高功率密度等优点,广泛应用于电动汽车、可再生能源发电等领域[1-2]。如双有源桥(Dual Active Bridge, DAB)变换器,功率密度高且易于实现软开关,故受到越来越多的关 注[3-4]。但DAB变换器在输入输出电压不匹配时存在回流功率大的问题[5-6]。此外,轻载情况下难以实现软开关也成了DAB变换器的另一大弊端[7]。文献[8-9]对CLLLC变换器的工作原理进行分析,其谐振槽在正向、反向运行时完全对称。因此,无论正向工作还是反向工作时,CLLLC变换器都具备LLC变换器的软开关特性。
当CLLLC变换器采用变频调制时,可以实现一次侧开关管的零电压导通(Zero Voltage Switching,ZVS)和二次侧开关管的零电流关断(Zero Current Switching, ZCS)[10-12],具有效率高的优势。但是,这种调制方式存在电压调节能力有限的缺点。当电压增益大于1时,CLLLC变换器可在较窄的开关频率范围内实现较高升压。而当电压增益小于1时,CLLLC变换器需要在较大的开关频率范围内变化,才能实现降压,且降压范围有限,同时给参数设计带来了困难[13-14]。当CLLLC变换器采用单移相调制时,开关频率是恒定的,这有助于优化电路参 数[15-17]。然而,这种调制方法只能使其工作于降压模式[18]。相关研究学者提出了一种变频调制与单移相调制相结合的新型调制策略,即在电压增益大于1时采用变频调制,电压增益小于1时采用单移相调制的混合调制方法,可有效拓宽电压增益范围[19-22]。然而,分段混合调制的调制切换增加了调制电路设计与实现的复杂度。文献[23]提出负载发生变化时调整变换器的移相角和开关频率,在宽负载范围内实现开关管ZVS,但控制算法较为复杂。文献[24]提出一种脉冲宽度-脉冲频率混合调制方法,在变换器一次侧全桥内引入移相角,调节频率的同时调节移相角,可实现输出电压的宽范围调节,但其效率较低。文献[25]提出一种双移相调制方法,即分别在CLLLC变换器一次侧全桥内及一次侧、二次侧全桥间引入移相角,可实现输出电压的宽范围调节,但其没有考虑整体效率的优化。文献[26]根据两个移相角之间的关系对双移相调制进行优化,但仅对轻载效率进行了优化。
为此,本文提出一种变频双移相(Variable- Frequency Dual-Phase-Shift, VF-DPS)调制方法,同时改变开关频率与移相角,以拓宽CLLLC变换器的电压增益范围,同时提高其效率。
本文首先描述CLLLC变换器的拓扑结构,分析该拓扑在变频双移相调制下的工作原理;然后通过对变频双移相调制CLLLC变换器的时域分析,分析变换器电压增益特性、谐振电感电流的有效值和开关管的ZVS范围;最后通过一台100~300 V输入、48 V/400 W输出的实验样机验证理论分析的正确性。
CLLLC变换器拓扑结构如图1所示,其中开关管Q1~Q4组成一次侧逆变电路,开关管Q5~Q8组成二次侧整流电路,Lm为变压器的励磁电感,Lr1、Lr2分别为一次侧、二次侧谐振电感,Cr1、Cr2分别为一次侧、二次侧谐振电容,n为变压器的电压比。当输入电压高于额定输入电压时,变换器通过改变一次侧全桥和一、二次侧全桥之间的移相角,使增益G<1,记为Buck模式;当输入电压低于额定输入电压时,变换器通过改变二次侧全桥和一、二次侧全桥之间的移相角,使增益G>1,记为Boost模式;其关键波形分别如图2a和图2b所示。

图1 CLLLC变换器拓扑结构
Fig.1 Topology of CLLLC converter
图2中,iLm和iLr1分别为励磁电感电流、一次侧谐振电感电流;vAB和vCD分别为全桥逆变输出电压和全桥整流输入电压;vgs1~vgs8为开关管Q1~Q8的驱动信号。在Buck模式下,开关管Q1和Q4之间增加内移相角D1Ts,使Q4滞后于开关管Q1。同理,开关管Q1和开关管Q5、Q8之间增加外移相角D2Ts,使Q5、Q8滞后于开关管Q1。在Boost模式下,开关管Q5和Q8之间增加内移相角D1Ts,使Q8滞后于开关管Q5;开关管Q5和开关管Q1、Q4之间增加外移相角D2Ts,使Q1、Q4滞后于开关管Q5。
半个开关周期内,变频双移相调制CLLLC变换器可分为三种运行模态,其持续时间有如下关系
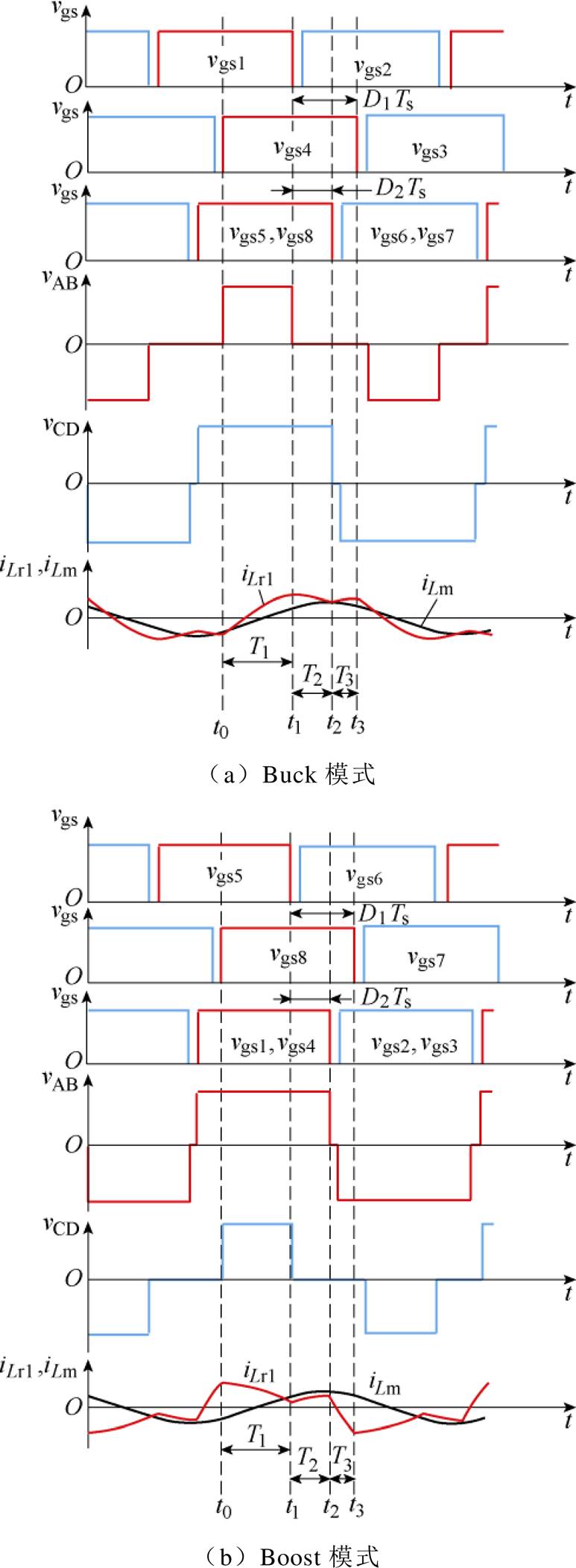
图2 变频双移相调制CLLLC变换器的关键波形
Fig.2 The key waveforms of CLLLC converter with VF-DPS modulation
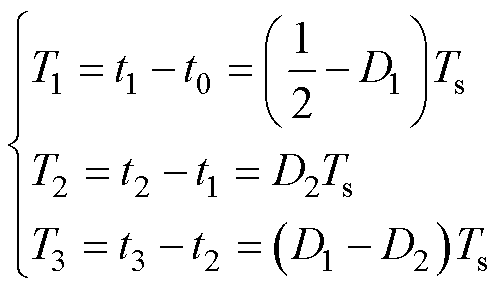 (1)
(1)
式中,D1、D2、Ts分别为内移相占空比、外移相占空比和开关周期。
CLLLC变换器正向工作与反向工作的原理相同,此处只分析其正向工作原理。Buck模式CLLLC变换器的模态电路如图3所示。
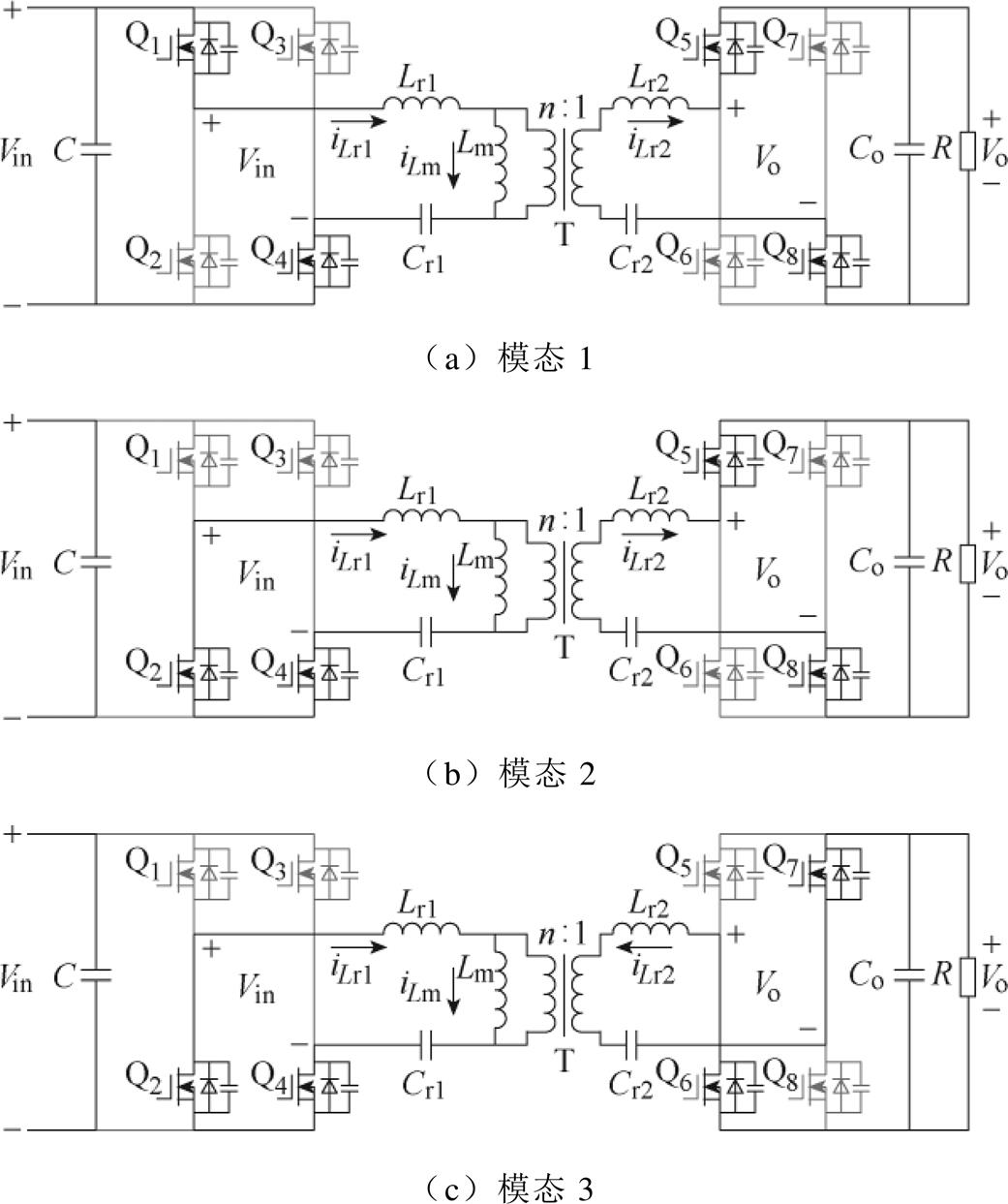
图3 Buck模式下的模态电路
Fig.3 The modal circuits in Buck mode
Buck模式CLLLC变换器存在三种模态,相应的工作过程描述如下:
模态1 [t0, t1 :t0时刻,-iLr1使得开关管Q4反并联二极管导通,实现开关管Q4的ZVS,vAB=Vin,vCD=Vo,谐振电感Lr1和谐振电容Cr1发生谐振,一次侧谐振电感电压vLr1和一次侧谐振电容电压vCr1之和接近于(Vin-nVo)/2,励磁电感两端电压为(Vin+nVo)/2。该模态下iLr1、iLm和vLr1表达式分别为
:t0时刻,-iLr1使得开关管Q4反并联二极管导通,实现开关管Q4的ZVS,vAB=Vin,vCD=Vo,谐振电感Lr1和谐振电容Cr1发生谐振,一次侧谐振电感电压vLr1和一次侧谐振电容电压vCr1之和接近于(Vin-nVo)/2,励磁电感两端电压为(Vin+nVo)/2。该模态下iLr1、iLm和vLr1表达式分别为
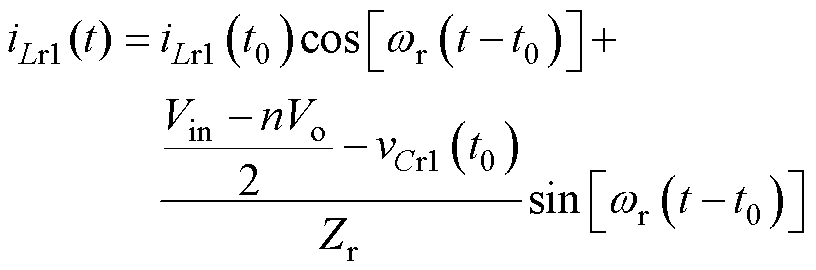 (2)
(2)
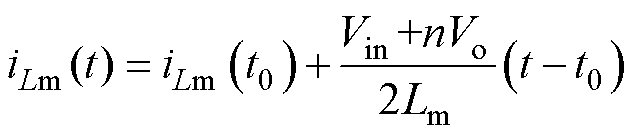 (3)
(3)
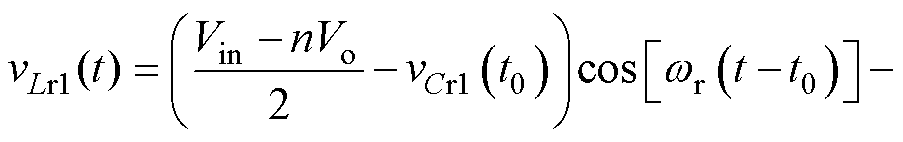
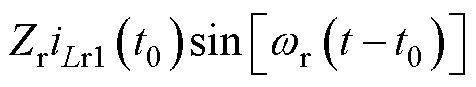 (4)
(4)
式中,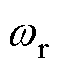 为谐振角频率;
为谐振角频率;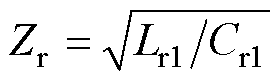 为特征阻抗。
为特征阻抗。
模态2 [t1, t2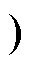 :在t1时刻,iLr1为正,使得开关管Q2反并联二极管导通,实现开关管Q2的ZVS,vAB=0,vCD=Vo,vLr1与vCr1之和接近于-nVo/2,励磁电感两端电压为nVo/2。该模态下iLr1和iLm的表达式分别为
:在t1时刻,iLr1为正,使得开关管Q2反并联二极管导通,实现开关管Q2的ZVS,vAB=0,vCD=Vo,vLr1与vCr1之和接近于-nVo/2,励磁电感两端电压为nVo/2。该模态下iLr1和iLm的表达式分别为
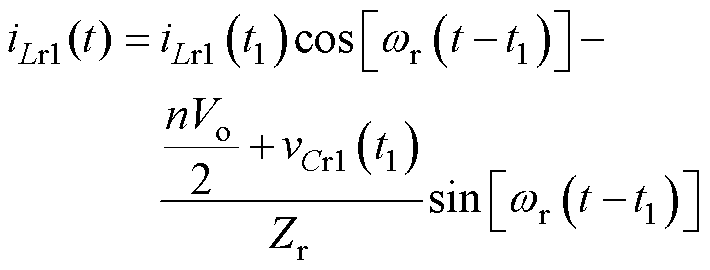 (5)
(5)
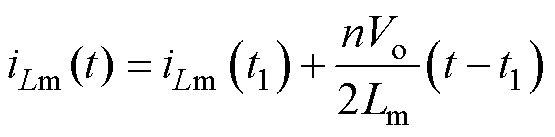 (6)
(6)
模态3 [t2, t3]:在t2时刻,开关管Q5、Q8关断,vAB=0,vCD=-Vo,vLr1与vCr1之和接近于nVo/2,励磁电感两端电压为-nVo/2。该模态下iLr1和iLm的表达式分别为
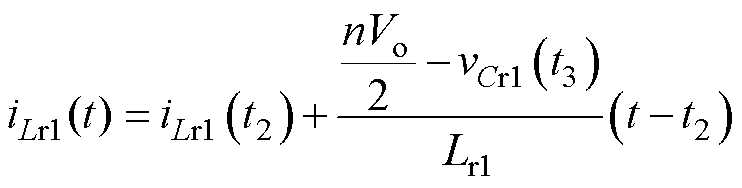 (7)
(7)
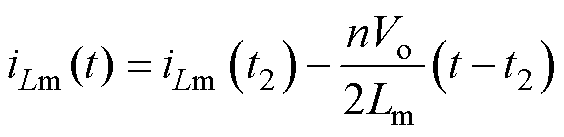 (8)
(8)
Boost模式下的模态电路分析与Buck模式类似,故不再赘述。
以Buck模式为例,分析正向工作时的增益特性。一次侧谐振电容电压vCr1在t0和t0+Ts/2的值相反,联立平均输出电流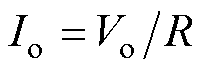 可得
可得
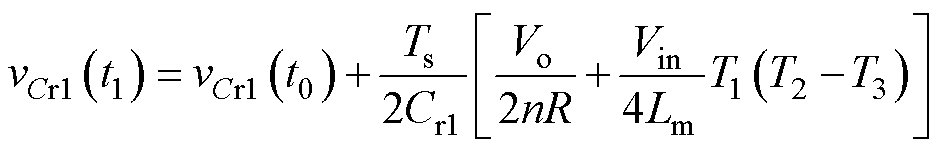 (9)
(9)
在模态1时,vLr1与vCr1之和接近于(Vin-nVo)/2,故t1时刻vCr1的表达式为
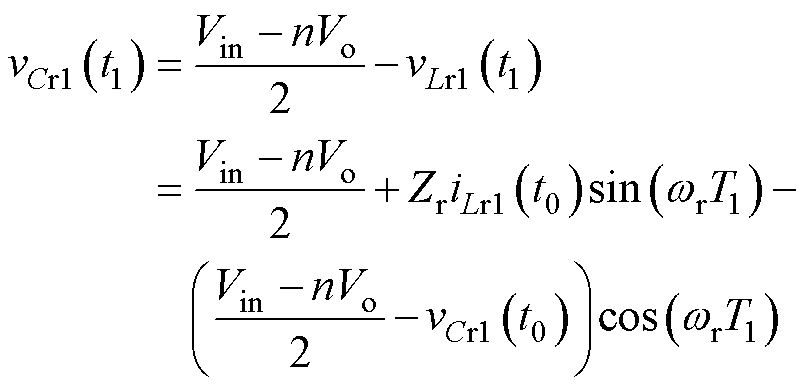 (10)
(10)
一次侧谐振电感电流iLr1在t0和t3=t0+Ts/2时刻的值相反,其表达式为
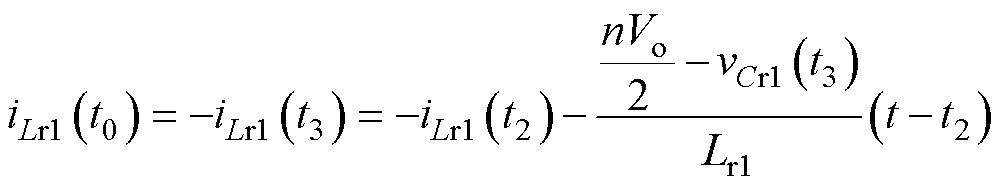 (11)
(11)
将开关管Q5关断的时刻设为tx,在tx时刻,有iLr1(tx)=iLm(tx)。联立式(9)~式(11)进行化简可得
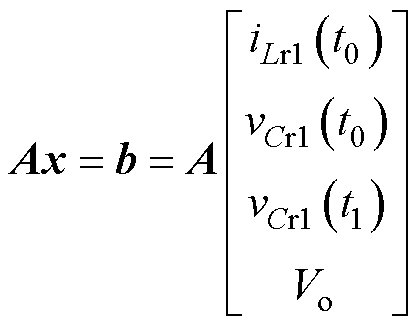 (12)
(12)
式中,A的表达式如附录式(A1)所示,且
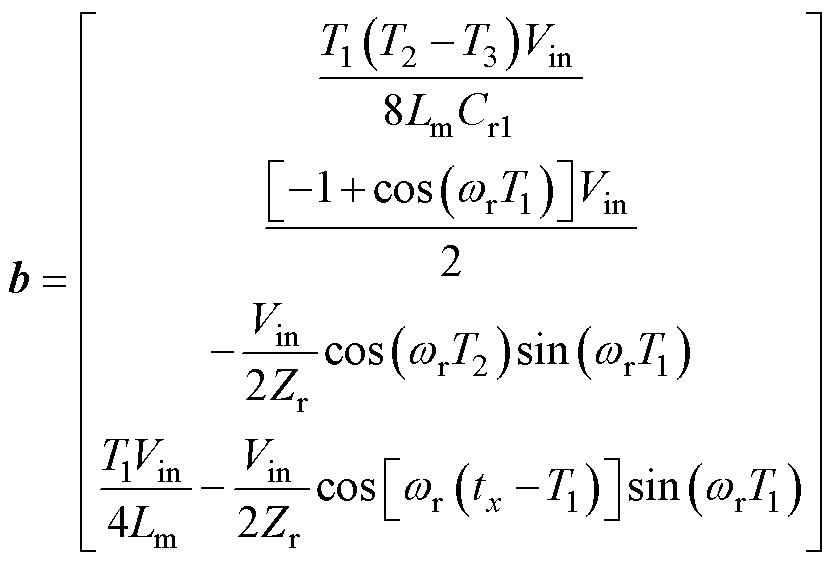 (13)
(13)
因此,上述矩阵方程的解x=A-1b。求解后可以得到4个变量iLr1(t0)、vCr1(t0)、vCr1(t1)和Vo。电压增益可以计算为
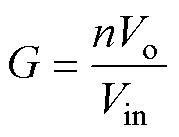 (14)
(14)
通过式(2)~式(8),计算一次、二次侧谐振电感电流有效值ILr1_rms和ILr2_rms分别为
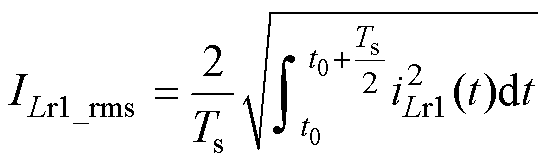 (15)
(15)
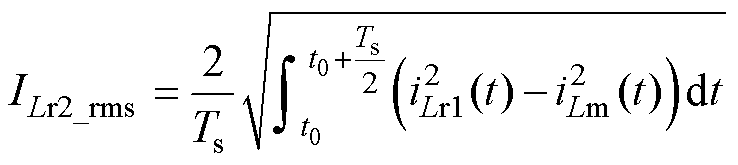 (16)
(16)
同理,在Boost模式下也可得到一个方程为
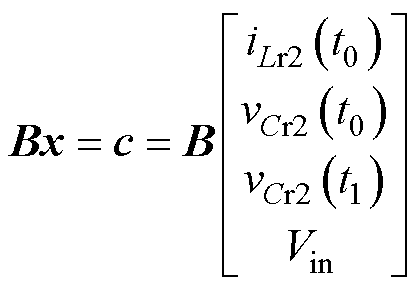 (17)
(17)
式中,B如附录式(A2)所示,且
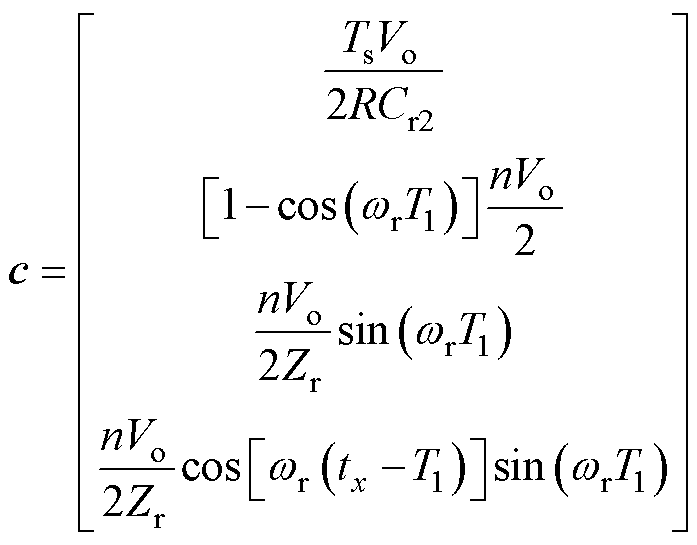 (18)
(18)
为了研究占空比D1、D2和开关频率fs ( fs=1/Ts)对电压增益和谐振电感电流的影响,将不同的D1、D2和fs代入式(12)、式(A1)、式(13)和式(17)、式(A2)、式(18),求解G、ILr1_rms和ILr2_rms。通过Matlab查找ILr1_rms和ILr2_rms的最小值,拟合得到不同谐振状态下D1和D2的关系。
变换器存在三种不同的谐振状态,当开关频率fs等于谐振频率fr时,变换器工作在准谐振状态;当fs<fr时,变换器工作在欠谐振状态;当fs>fr时,变换器工作在过谐振状态。图4为在Buck模式下准谐振时ILr1_rms、ILr2_rms与占空比D1、D2之间的关系。从图4中可以看出,对于确定的D1,ILr1_rms和ILr2_rms总是在D2=0.5D1时得到最小值。在准谐振状态下,为了实现效率最高,应取D2=0.5D1。

图4 准谐振时ILr1_rms、ILr2_rms与占空比之间的关系
Fig.4 Relationship among ILr1_rms, ILr2_rms and duty cyclesin the case of quasi-resonance
图5显示了Buck模式下欠谐振时ILr1_rms、ILr2_rms与D1、D2之间的关系。从图5可以看出,对于确定的D1,ILr2_rms在D2=0.5D1-0.05时得到最小值。故在欠谐振状态下,为了实现效率最高,应取D2= 0.5D1-0.05。

图5 欠谐振时ILr1_rms、ILr2_rms与占空比之间的关系
Fig.5 Relationship among ILr1_rms, ILr2_rms and duty cycles in the case of under-resonance
图6显示了Buck模式下过谐振时ILr1_rms、ILr2_rms与D1、D2之间的关系。从图6可以看出,对于确定的D1,ILr2_rms在D2=0.5D1+0.025时得到最小值。ILr1_rms在D2>0.5D1+0.025时得到最小值。在过谐振状态下,为了实现效率最高,应取D2=0.5D1+0.025。
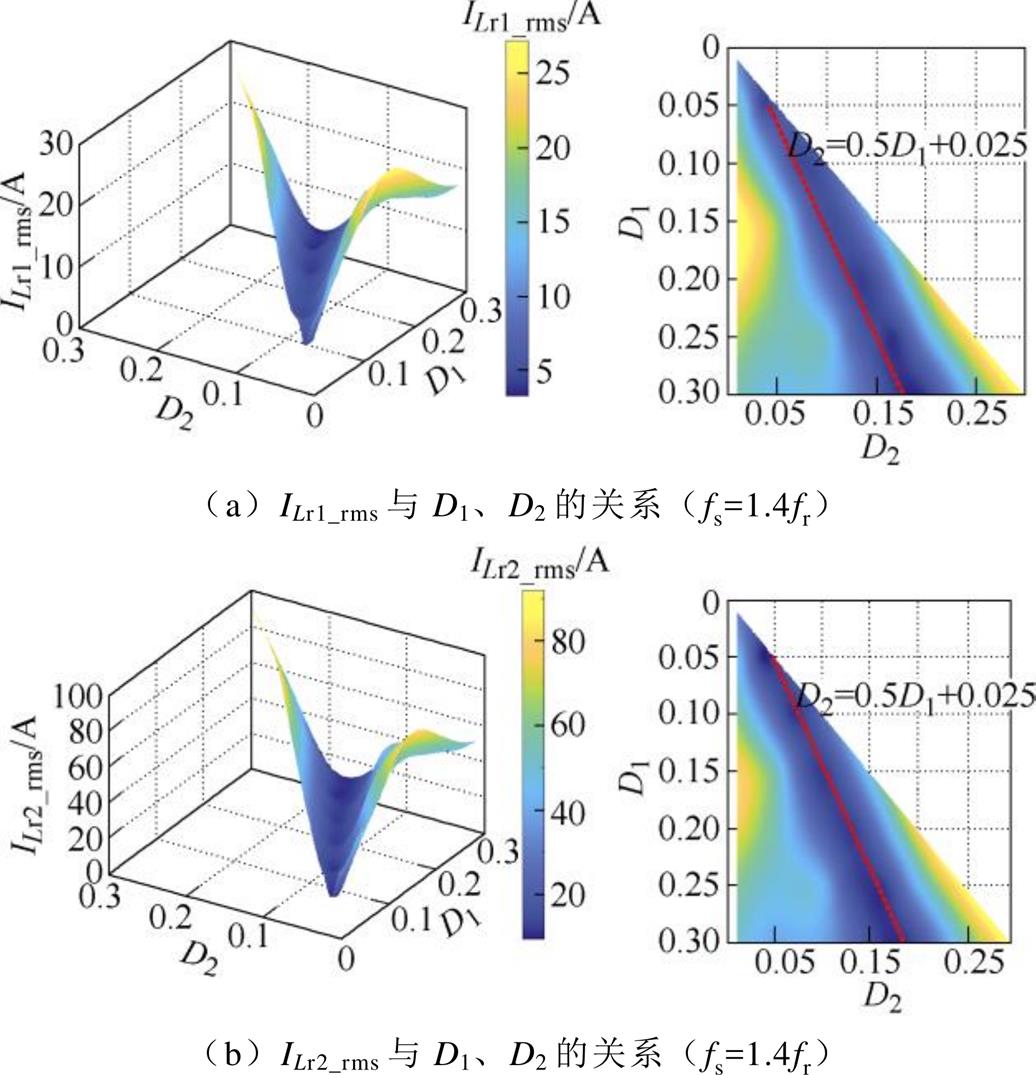
图6 过谐振时ILr1_rms、ILr2_rms与占空比之间的关系
Fig.6 Relationship among ILr1_rms, ILr2_rms and duty cycles in the case of over-resonance
CLLLC变换器在不同频率下的电压增益如图7所示。欠谐振情况下,增益随着D1增加而增加;对于确定的D1,当D2增大时,电压增益G减小,可实现效率最高的电压增益范围为0.7~0.91。准谐振情况下,G随着D1增加而减小;对于确定的D1,当D2增大时,G先增大后减小,可实现效率最高的电压增益范围为0.58~1。过谐振情况下,增益随着D1增加而减小;对于确定的D1,当D2增大时,G增大,可实现效率最高的电压增益范围为0.46~0.87。
变频双移相调制CLLLC变换器是通过闭环控制内移相角来实现目标电压,而外移相角对CLLLC变换器的ZVS性能和效率有很大影响。在Buck模式下,G和D1、fs之间的关系如图8所示。对于确定的D1,当fs增大时,电压增益先增大后减小。
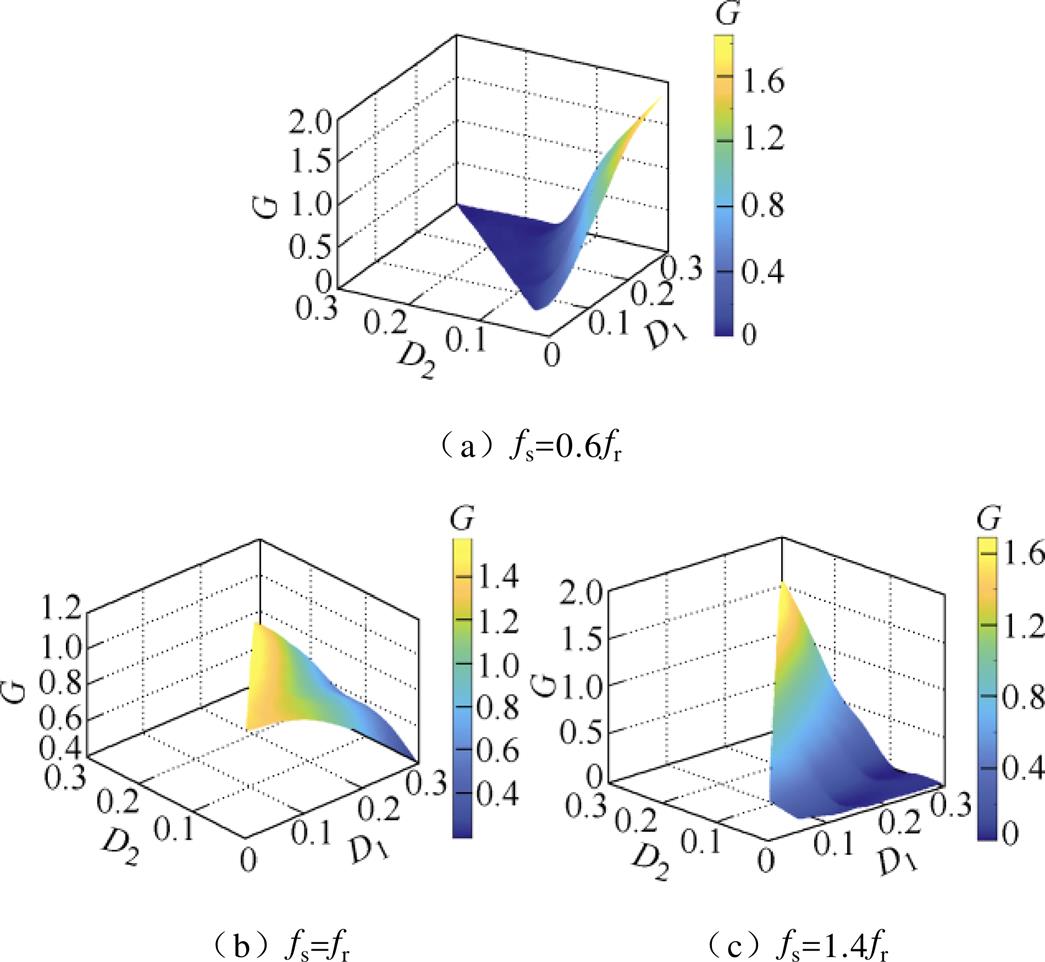
图7 不同频率下电压增益与占空比的关系
Fig.7 Relationship among voltage gain and duty cycles with different frequencies
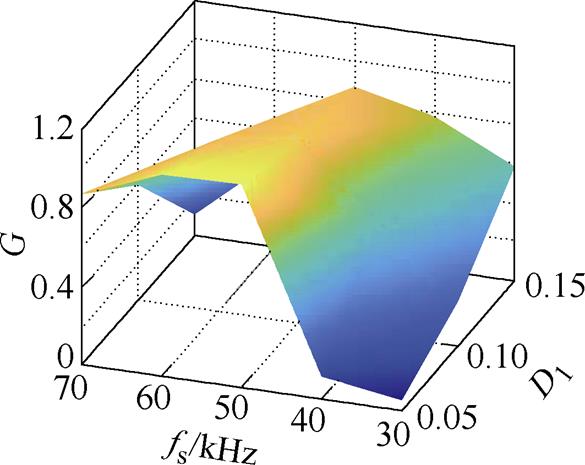
图8 G与D1、fs的关系
Fig.8 Relationship among G, D1 and fs
为了实现效率最高,在不同的谐振状态下拟合得到ILr1_rms和ILr2_rms为最小值时D1、D2之间的关系式,且在该关系式下,电压增益范围为0.46~1,可实现较宽范围的降压;相比于欠谐振和准谐振情况,过谐振状态下ILr2_rms的最小值更小,变换器效率更高。故在Buck模式下,为实现更高效率和更低增益,应使变换器工作在过谐振状态。
在Boost模式下,表1给出了不同谐振状态下效率最高时的占空比关系式和电压增益范围。欠谐振状态下,增益随着D1增加而减小;对于确定的D1,当D2增大时,电压增益增大,可实现效率最高的电压增益范围为1.25~1.4。准谐振状态下,增益随着D1增加而减小;对于确定的D1,当D2增大时,电压增益先增大后减小,电压增益范围为1~1.6。过谐振状态下,电压增益随着D1增加而增大;对于确定的D1,当D2增大时,电压增益减小,可实现效率最高的电压增益范围为1~1.2。
表1 Boost模式下占空比关系式以及电压增益范围
Tab.1 Phase shift angle relation and voltage gain range for Boost mode

谐振状态占空比关系式电压增益范围 欠谐振D2=0.5D1+0.0751.25~1.4 准谐振D2=0.5D11~1.6 过谐振D2=0.5D1-0.0451~1.2
为了实现最高效率,在不同的谐振状态下拟合得到ILr1_rms和ILr2_rms为最小值时两个占空比之间的关系式,且在该关系式下,电压增益范围为1~1.6,可实现较宽范围的升压;相比于欠谐振和过谐振状态,准谐振状态下的电压增益范围最大,最大可达到1.6。故在Boost模式下,为实现更高效率和更高的增益,应使变换器工作在准谐振状态。
为了实现Buck模式下所有开关的软开关,首先要保证谐振电流的正负要求,iLr1需要在t0~t0+Td死区期间为负,使Q1和Q4的输出电容放电,在t1~t1+Td期间为正,实现Q2和Q3的ZVS;iLr2需要在t2~t2+Td期间为负,实现Q5~Q8的ZVS,故可以通过判断在死区时间的开始和结束时刻的谐振电流值来判断ZVS区域。因此,实现ZVS的条件可以总结如式(19)。由于Boost模式的软开关条件与Buck模式类似,故不在此详述。
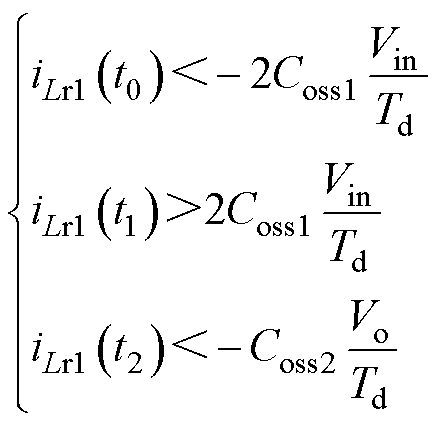 (19)
(19)
式中,Coss1、Coss2分别为一、二次侧开关管的输出电容。
图9为根据式(19)绘制出的不同频率下的ZVS区域,其中图9a~图9c的左图为Buck模式、右图为Boost模式。从图9a~9c的左图可以看出,Buck模式下,准谐振时ZVS区域分布在D2=0.5D1附近。以D2=0.5D1为分界线;欠谐振时,频率越小,ZVS区域越向下移动;过谐振时,频率越大,ZVS区域越向上移动。从图9a~9c的右图可以看出,Boost模式下,ZVS区域分布与Buck模式类似,不再详述。ZVS范围总是分布在取得谐振电流最小值的占空比关系式附近,故变频双移相调制可以实现全频率范围软开关,同时获得较高效率。
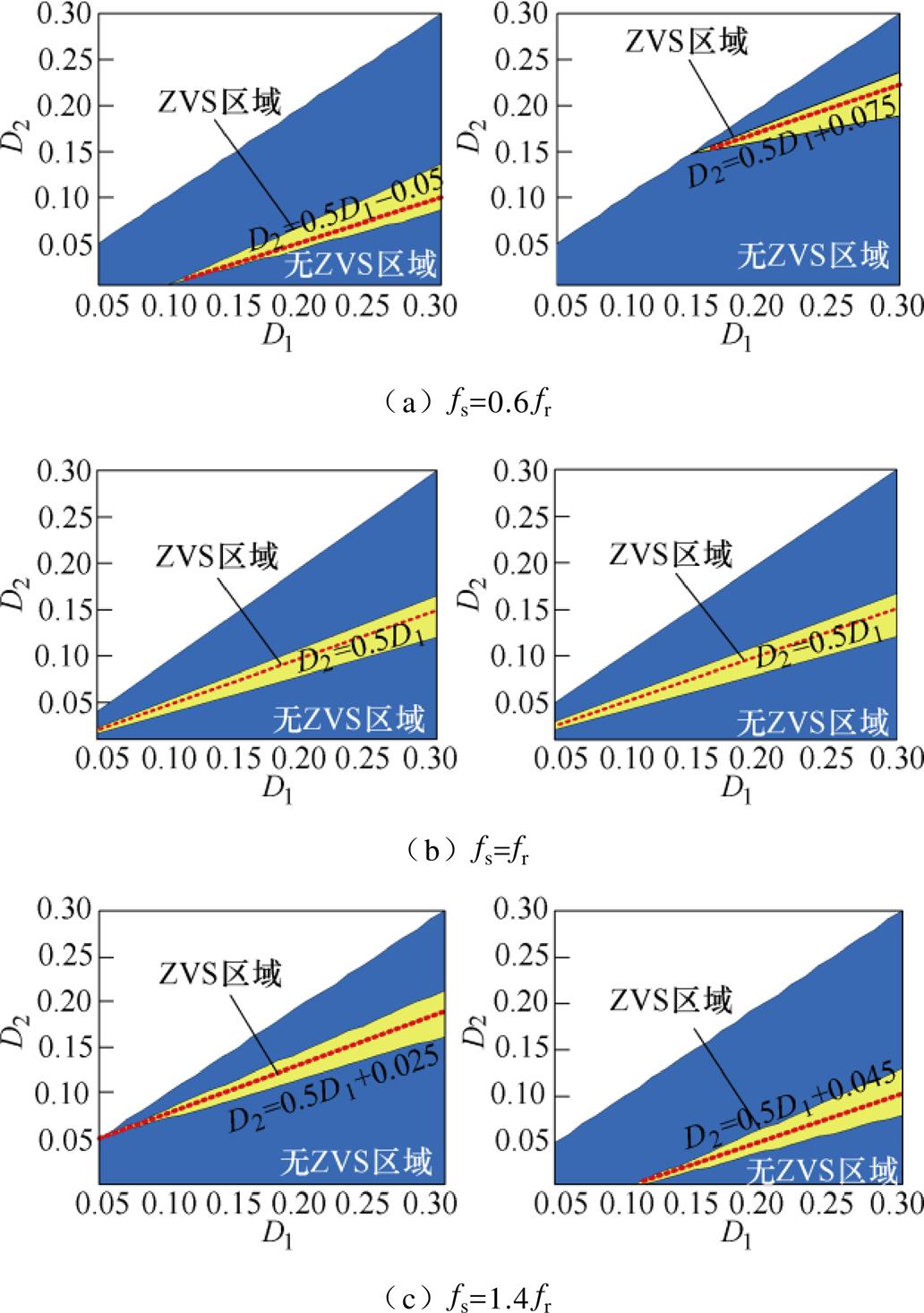
图9 不同频率下的软开关区域
Fig.9 ZVS region for different frequency
变频双移相调制CLLLC变换器的损耗主要分为开关管损耗、磁性元件损耗和输出电容损耗。
1)开关管损耗。开关管一、二次侧均实现ZVS,故不存在开通损耗,因此,开关管的主要损耗为导通损耗和关断损耗。一次侧开关管的型号为C3M0065090D,二次侧开关管的型号为IRFB4332,开关管导通损耗可表示为
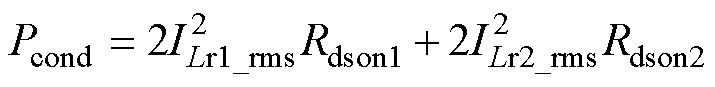 (20)
(20)
式中,Rdson1、Rdson2分别为一、二次侧开关管的导通电阻。开关管的关断损耗表达式为
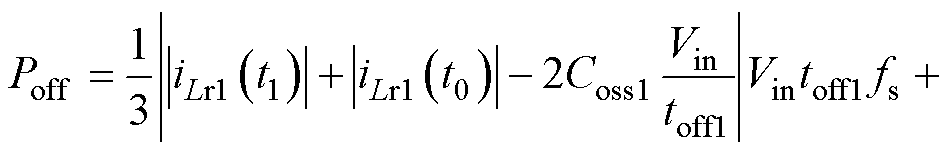
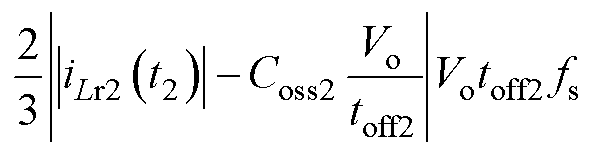 (21)
(21)
式中,toff1、toff2分别为一、二次侧开关管的关断时间。
2)磁性元件损耗。CLLLC变换器中的磁性元件包含变压器和谐振电感,磁性元件的损耗主要包含绕组损耗和磁心损耗。磁性元件绕组损耗为
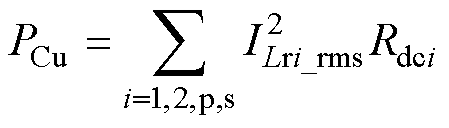 (22)
(22)
式中,Rdc1、Rdc2、Rdcp、Rdcs分别为一、二次侧谐振电感和变压器一、二次侧的直流电阻;ILrp_rms、ILrs_rms分别为变压器的一、二次电流有效值。通过Steinmetz公式计算电感的磁心损耗为
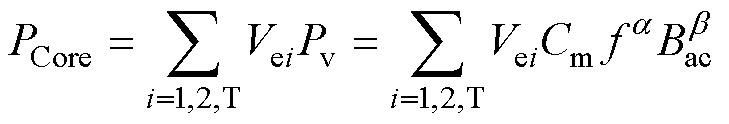 (23)
(23)
式中,Ve1、Ve2、VeT分别为一、二次侧谐振电感和变压器磁心的有效体积;Pv为单位体积的磁心损耗;Cm为磁损系数;f为工作频率;Bac为磁通变化量;a、b 为磁心材料参数。
3)输出电容损耗。输出电容型号为EGD2GM151M35OT。电容损耗主要取决于其串联等效电阻,其表达式为
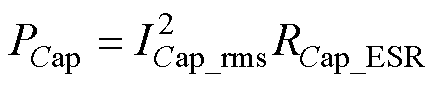 (24)
(24)
式中,ICap_rms为输出电容电流有效值;RCap_ESR为输出电容的串联等效电阻。
综上所述,当CLLLC变换器的输入电压为300 V、输出功率为400 W时,CLLLC变换器的效率为
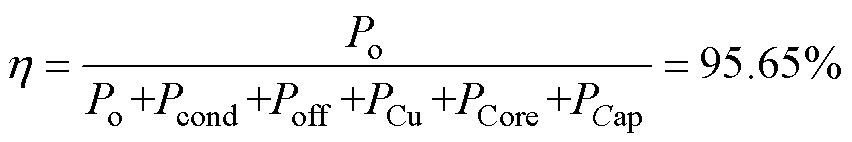 (25)
(25)
式中,Po为输出功率。
不同负载情况下,CLLLC变换器的理论效率及损耗占比如图10所示,由于输出电容的损耗占比远远小于1%,故在图中没有标注。

图10 CLLLC变换器的理论效率和损耗占比
Fig.10 The theoretical efficiency and loss ratio of CLLLC converter
图11a、图11b分别为变频双移相混合调制策略关键波形及框图。由图11可知,当输入电压或者负载变化时,PI调节器的输出vfs发生变化;运算电路通过vfs计算得到内移相函数vd =-kvfs+b和外移相函数vq =-kvfs+c,其中,k、b、c均为常数;锯齿波发生电路根据vfs输出指定频率的锯齿波vsaw;在vsaw的每一个周期起始时刻,锯齿波电路输出触发信号vc1;vd 和vq 通过比较器得到控制信号vc2和vc3;控制信号vc2和vc3与触发信号vc1通过驱动电路生成开关管驱动信号vgs1~vgs8,实现CLLLC变换器稳定输出。通过程序中添加条件语句,即可实现当输入电压变化、变换器在Buck与Boost模式之间切换时,实现宽输入电压范围内所提控制策略的自适应控制。
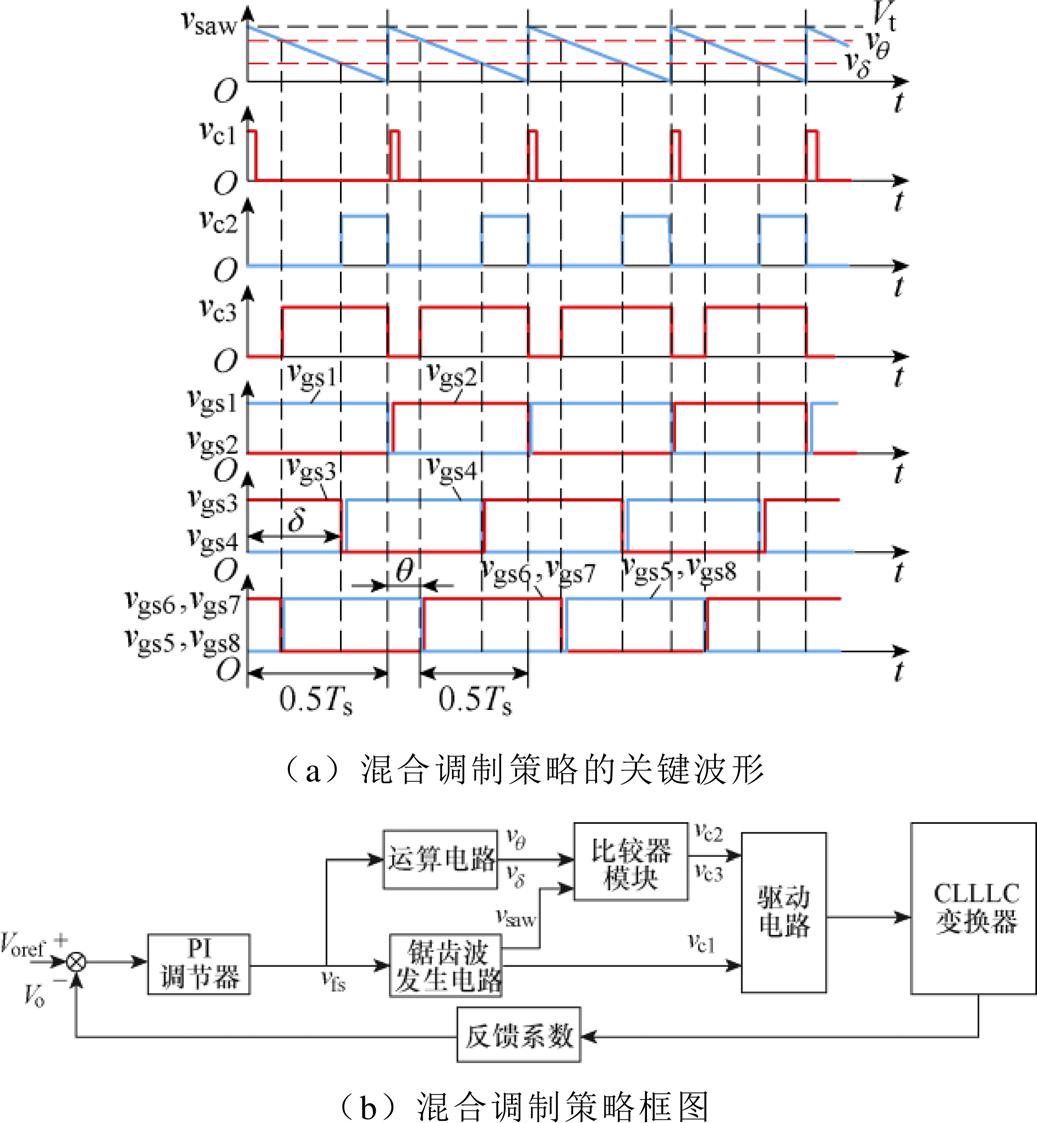
图11 混合调制策略关键波形及框图
Fig.11 The key waveforms and block diagram of hybrid modulation
为了验证本文所提方法的可行性,采用表2所示的主要电路参数研制了相应的实验样机,并进行正向运行、反向运行实验分析。变频双移相调制CLLLC变换器的控制器选用TMS320F280049,当输入电压为300 V时,通过改变一次侧开关管的移相寄存器可实现一次侧全桥内部移相;当输入电压为100 V时通过改变二次侧开关管的移相寄存器值可实现二次侧全桥内部移相。
表2 CLLLC变换器参数
Tab.2 CLLLC converter parameters

参 数数 值 正向输入电压Vin/V100~300 正向输出电压Vo/V48 反向输入电压Vin/V28~84 反向输出电压Vo/V150 功率Po/W400 变压器电压比n3.1 谐振电感Lr1/mH28.3 Lr2/mH2.83 谐振电容Cr1/mF0.33 Cr2/mF3.33
图12分别给出了一次侧谐振电感电流iLr1、Q1的驱动信号vgs1和两端电压vds1、Q4的驱动信号vgs4和两端电压vds4、Q5的驱动信号vgs5和两端电压vds5以及Q8的驱动信号vgs8和两端电压vds8。从图12可以看出,所有开关管均实现ZVS。输入电压为100~300 V,电路仍能保持ZVS,实现了宽输入电压范围软开关,与理论分析一致。
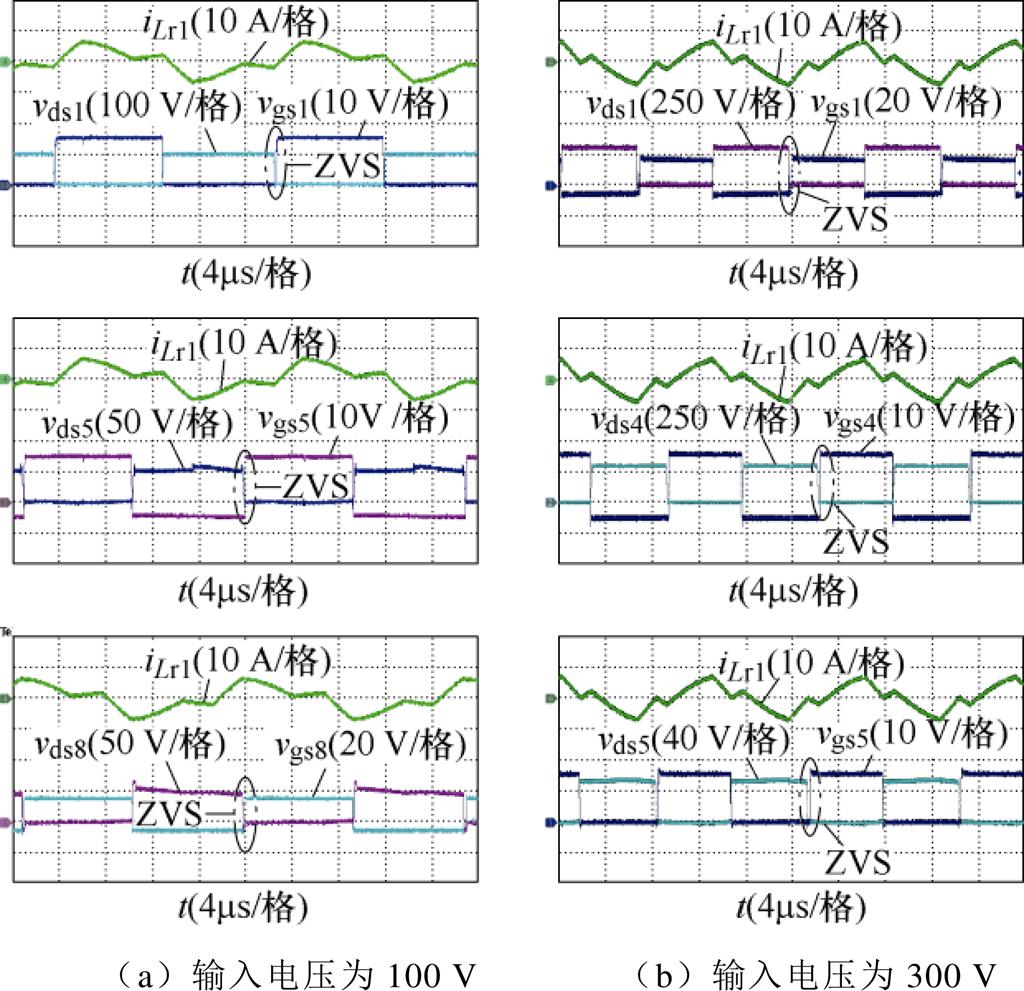
图12 正向工作时变换器的稳态实验波形
Fig.12 Steady-state experimental waveforms of converter in forward operation
图13给出了变换器输入电压分别为100 V、300 V的效率曲线。从图13可以看出,输出相同功率,输入电压为300 V时的效率比100 V时的效率更高,且在输出功率为250 W时,变换器有最高的功率。相比于输入电压为100 V时,输入电压为300 V时的谐振电感电流应力较小,开关管导通损耗以及磁性元件的绕组损耗较小,故效率较高,峰值效率为95.1%。
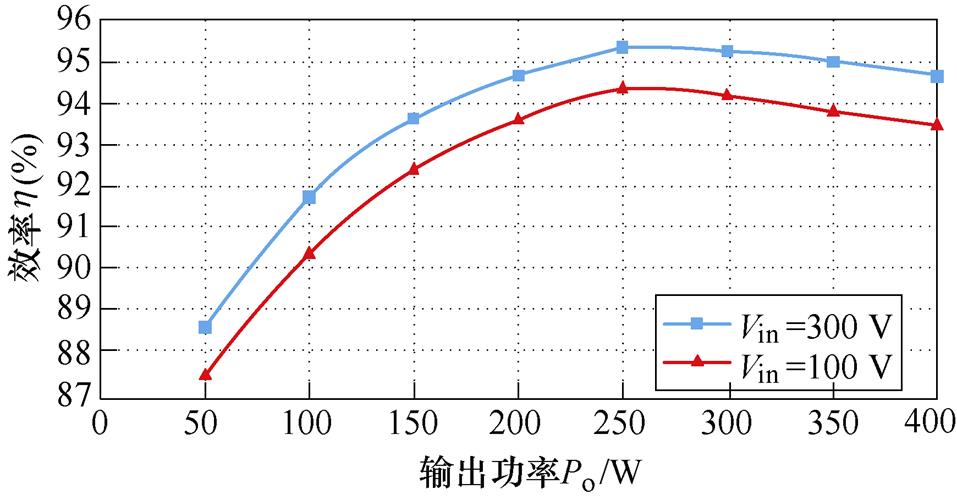
图13 不同负载下的效率曲线
Fig.13 Efficient curves under different loads
反向运行时输入电压为28~84 V,输出电压为150 V。图14a、图14b分别为输入电压为28 V、84 V时变换器反向工作的稳态实验波形。图14分别给出了iLr1,Q1、Q4的驱动信号vgs1、vgs4和两端电压vds1、vds4以及Q5、Q8的驱动信号vgs5、vgs8和两端电压vds5、vds8。输入电压为28~84 V时,电路仍能保持ZVS,实现了宽输入电压范围软开关,与理论分析一致。
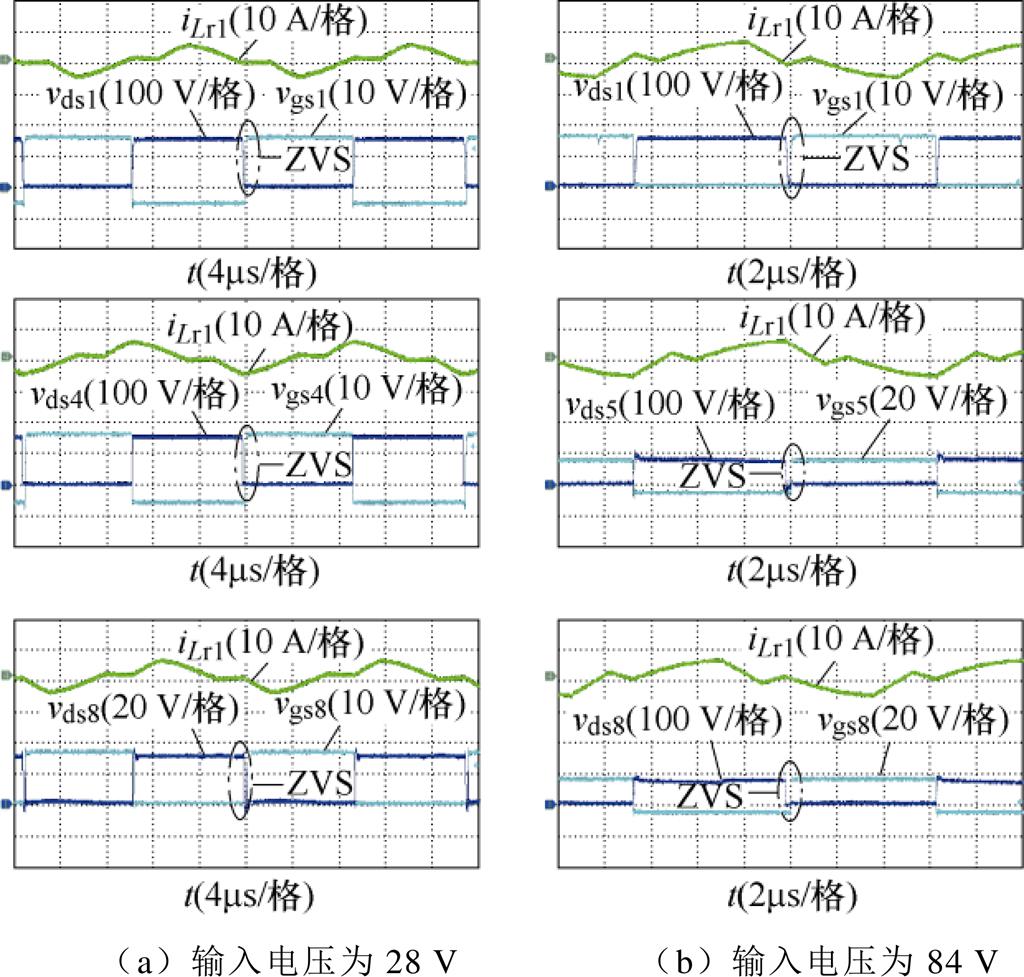
图14 反向工作时变换器的稳态实验波形
Fig.14 Steady-state experimental waveforms in reverse operation
图15a、图15b分别为满载-半载跳变暂态实验波形、半载-满载跳变暂态实验波形。图15分别给出了iLr1、输出电压交流量VoAC和输出电流Io波形。从图15a可以看出,满载跳变到半载时,VoAC上冲量为2.1 V,经过6.7 ms重回稳态;从图15b可以看出,半载跳变到满载时,VoAC下冲量为3.2 V,经过8 ms重回稳态。
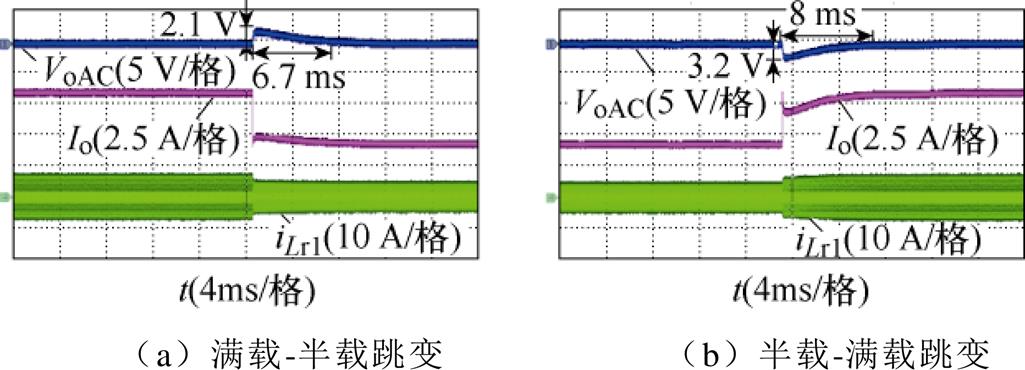
图15 变换器的暂态实验波形
Fig.15 Transient experimental waveforms of converter
变频单移相调制策略在增益大于1时采用变频调制,增益小于1时采用移相调制。采用相同的实验参数,输入电压为100~200 V、输出电压为48 V的CLLLC变换器实验波形如图16a和图16b所示。为了进行效率对比,采用相同的增益进行实验,变频双移相调制CLLLC变换器的实验波形如图16c和图16d所示。图16a和图16c均为输入电压100 V,可以看出,电感电流iLr1峰值分别为10 A和7 A左右。由图16b和图16d可以看出,电感电流iLr1峰值分别为10 A和6 A左右。
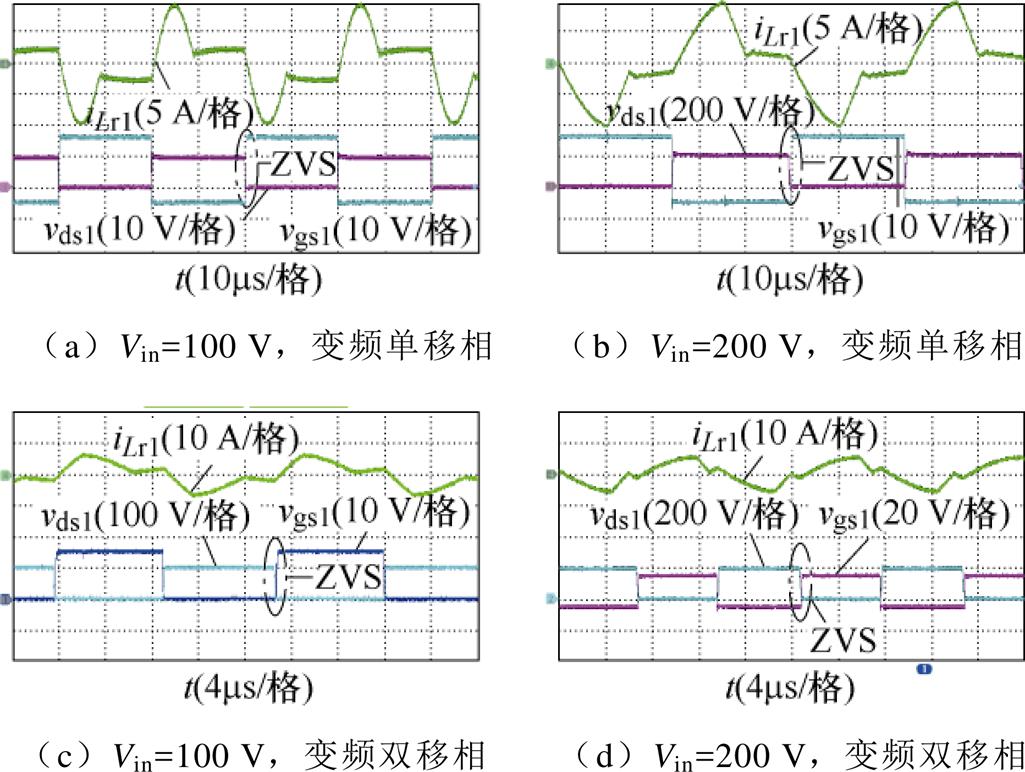
图16 相同电压增益下采用不同调制策略的实验波形
Fig.16 Experimental waveforms of different modulation strategies with same voltage gain
不同负载条件下的实验效率曲线如图17所示。从图17可以看出,在相同增益范围和负载条件下,变频双移相调制的效率比变频单移相调制的效率更高。相比于变频单移相调制,变频双移相调制CLLLC变换器的谐振电感电流值变小,故绕组损耗、导通损耗均变小,但降压时开关频率会增加,断态损耗变化不定。但由图10可知,断态损耗占比较小,故影响较小。综上所述,相比于变频单移相调制,变频双移相调制的电压增益范围更宽且效率更高。
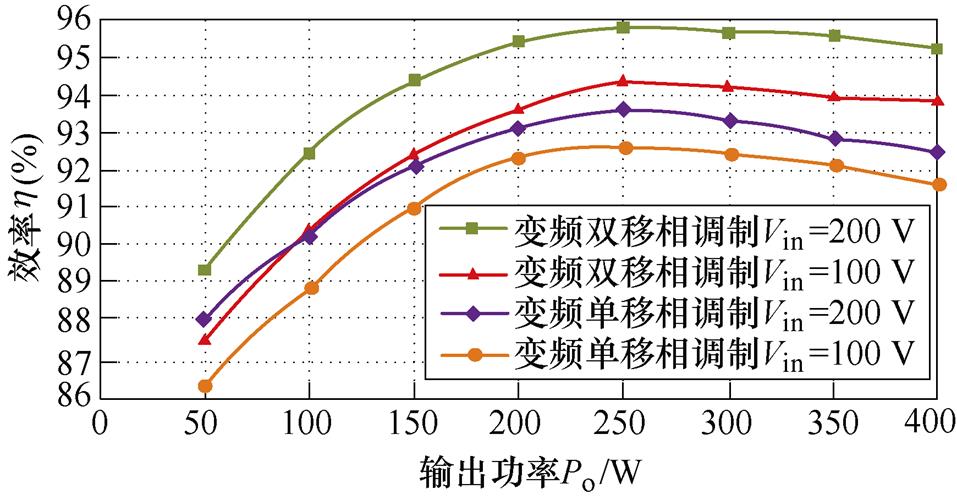
图17 不同负载和调制策略下的效率曲线
Fig.17 Efficiency curves under different loads and modulation strategies
本文针对CLLLC变换器的变频调制增益范围有限、移相调制效率较低的问题,提出了一种变频双移相调制方法,该方法可以在宽输入电压范围内实现软开关。采用时域分析法,求解了电压增益和谐振电流有效值,分析了不同移相角和开关频率对电压增益和谐振电流大小的影响。当输入电压较高时,变换器工作在Buck模式,过谐振情况下能实现更高效率和更低增益;当输入电压较低时,变换器工作在Boost模式,准谐振情况下能实现更高效率和更高增益。采用变频双移相调制,变换器获得3倍的电压增益范围且具有较高的效率,峰值效率为95.1%。
附 录
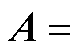
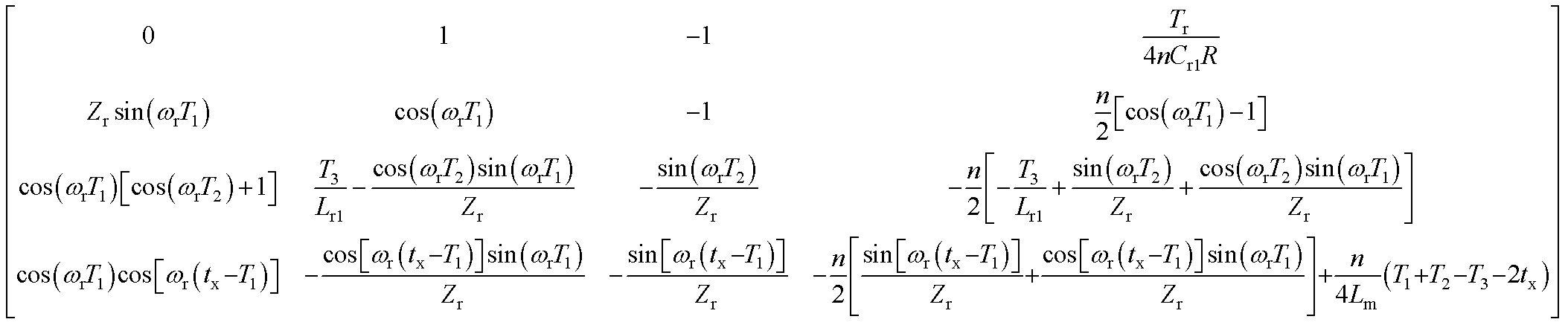 (A1)
(A1)
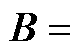
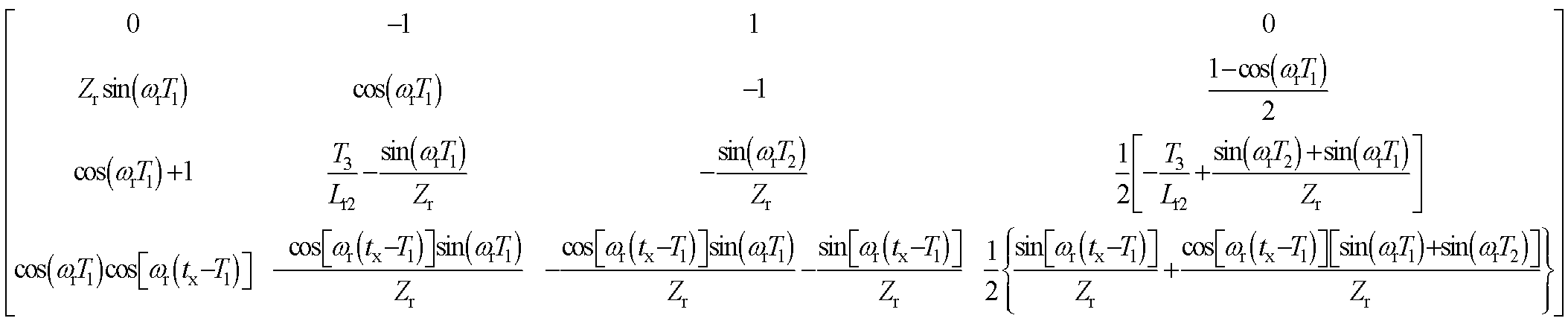 (A2)
(A2)
参考文献
[1] Azizi I, Radjeai H. A bidirectional DC-DC converter fed DC motor for electric vehicle application[C]// 2015 4th International Conference on Electrical Engineering (ICEE), Boumerdes, Algeria, 2016: 1-5.
[2] 王攀攀, 徐泽涵, 王莉, 等. 基于三重移相的双有源桥DC-DC变换器效率与动态性能混合优化控制策略[J]. 电工技术学报, 2022, 37(18): 4720-4731.
Wang Panpan, Xu Zehan, Wang Li, et al. A hybrid optimization control strategy of efficiency and dynamic performance of dual-active-bridge DC-DC converter based on triple-phase-shift[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4720-4731.
[3] Hu Yan, Zhang Yu, Chen Qing, et al. Efficiency evaluation for DAB converter with reactive power minimization strategy and full ZVS operation[C]// 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 2019: 4274-4280.
[4] Tong Anping, Hang Lijun, Li Guojie, et al. Modeling and analysis of a dual-active-bridge-isolated bidire- ctional DC/DC converter to minimize RMS current with whole operating range[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5302-5316.
[5] 杨向真, 王锦秀, 孔令浩, 等. 电压不匹配运行条件下双有源桥变换器的效率优化方法[J]. 电工技术学报, 2022, 37(24): 6239-6251.
Yang Xiangzhen, Wang Jinxiu, Kong Linghao, et al. Efficiency optimization method of DAB converters under wide-voltage operating conditions[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(24): 6239-6251.
[6] 高宇, 李若愚, 李林柘, 等. 三重移相调制模式下双有源变换器的直接功率控制[J]. 电工技术学报, 2022, 37(18): 4707-4719.
Gao Yu, Li Ruoyu, Li Linzhe, et al. Triple phase shift modulation-based direct power control strategy for a dual active bridge converter[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4707-4719.
[7] Chen Xiaoying, Xu Guo, Han Hua, et al. Light-load efficiency enhancement of high-frequency dual- active-bridge converter under SPS control[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 12941-12946.
[8] Jung J H, Kim H S, Ryu M H, et al. Design metho- dology of bidirectional CLLC resonant converter for high-frequency isolation of DC distribution systems[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1741-1755.
[9] Zahid Z U, Dalala Z, Lai J S J. Design and control of bidirectional resonant converter for vehicle-to-grid (V2G) applications[C]//IECON 2014-40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 2015: 1370-1376.
[10] Chen Wei, Rong Ping, Lu Zhengyu. Snubberless bidirectional DC-DC converter with new CLLC resonant tank featuring minimized switching loss[J]. IEEE Transactions on Industrial Electronics, 2010, 57(9): 3075-3086.
[11] Liu Chaohui, Wang Jiabin, Colombage K, et al. A CLLC resonant converter based bidirectional EV charger with maximum efficiency tracking[C]//8th IET International Conference on Power Electronics, Machines and Drives (PEMD 2016), Glasgow, UK, 2016: 1-6.
[12] 赵子先, 康龙云, 于玮, 等. 基于简化时域模型的CLLC直流变换器参数设计[J]. 电工技术学报, 2022, 37(5): 1262-1274.
Zhao Zixian, Kang Longyun, Yu Wei, et al. Parameter design method of CLLC DC-DC converter based on simplified time domain model[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1262-1274.
[13] 文伟仲, 舒杰, 王浩, 等. 高效宽电压增益CLLC谐振变换器分段控制研究[J]. 电源技术, 2021, 45(11): 1500-1504.
Wen Weizhong, Shu Jie, Wang Hao, et al. Study of piecewise-control of high efficiency and wide voltage gain CLLC resonant converter[J]. Chinese Journal of Power Sources, 2021, 45(11): 1500-1504.
[14] 曲璐, 王昕, 许家誉, 等. 用于车载充电的双向CLLC变换器设计[J]. 哈尔滨工业大学学报, 2021, 53(9): 144-155.
Qu Lu, Wang Xin, Xu Jiayu, et al. Design method of bidirectional CLLC resonant converter for on-board charger applications[J]. Journal of Harbin Institute of Technology, 2021, 53(9): 144-155.
[15] Twiname R P, Thrimawithana D J, Madawala U K, et al. A dual-active bridge topology with a tuned CLC network[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 6543-6550.
[16] Malan W L, Vilathgamuwa D M, Walker G R. Modeling and control of a resonant dual active bridge with a tuned CLLC network[J]. IEEE Transactions on Power Electronics, 2016, 31(10): 7297-7310.
[17] Kim J H, Kim C E, Kim J K, et al. Analysis on load-adaptive phase-shift control for high efficiency full-bridge LLC resonant converter under light-load conditions[J]. IEEE Transactions on Power Elec- tronics, 2016, 31(7): 4942-4955.
[18] Lo Y K, Lin C Y, Hsieh M T, et al. Phase-shifted full-bridge series-resonant DC-DC converters for wide load variations[J]. IEEE Transactions on Indu- strial Electronics, 2011, 58(6): 2572-2575.
[19] Li Kai, Wang Yue, Xu Jinghui, et al. Modeling and hybrid controller design of CLLLC[C]//2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 2019: 168-172.
[20] 陶文栋, 王玉斌, 张丰一, 等. 双向LLC谐振变换器的变频-移相控制方法[J]. 电工技术学报, 2018, 33(24): 5856-5863.
Tao Wendong, Wang Yubin, Zhang Fengyi, et al. Pulse frequency modulation and phase shift combined control method for bidirectional LLC resonant converter[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5856-5863.
[21] 李小双, 田钦元, 王正仕. 双向CLLLC谐振变换器的混合控制策略[J]. 电力电子技术, 2022, 56(6): 111-114, 140.
Li Xiaoshuang, Tian Qinyuan, Wang Zhengshi. Hybrid control strategy of bidirectional CLLLC resonant converter[J]. Power Electronics, 2022, 56(6): 111-114, 140.
[22] 吕正, 颜湘武, 孙磊. 基于变频-移相混合控制的L-LLC谐振双向DC-DC变换器[J]. 电工技术学报, 2017, 32(4): 12-24.
Lü Zheng, Yan Xiangwu, Sun Lei. A L-LLC resonant bidirectional DC-DC converter based on hybrid control of variable frequency and phase shift[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 12-24.
[23] Ryu S H, Kim D H, Kim M J, et al. Adjustable frequency-duty-cycle hybrid control strategy for full-bridge series resonant converters in electric vehicle chargers[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5354-5362.
[24] 曹靖, 许建平, 陈一鸣, 等. PWM-PFM混合控制LCC谐振变换器研究[J]. 中国电机工程学报, 2018, 38(12): 3629-3637, 23.
Cao Jing, Xu Jianping, Chen Yiming, et al. Study of PWM-PFM hybrid controlled LCC resonant con- verter[J]. Proceedings of the CSEE, 2018, 38(12): 3629-3637, 23.
[25] Hua Wenmin, Wu Hongfei, Yu Zhiyuan, et al. A phase-shift modulation strategy for a bidirectional CLLC resonant converter[C]//2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019-ECCE Asia), Busan, Korea (South), 2019: 1-6.
[26] Zhu Tianhua, Zhuo Fang, Zhao Fangzhou, et al. Optimization of extended phase-shift control for full-bridge CLLC resonant converter with improved light-load efficiency[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 11129-11142.
Abstract In the DC microgrid, a bidirectional isolated DC-DC converter with a wide range of input voltage is required to ensure the safety and efficiency of power conversion. The CLLLC converter was selected by discussing the advantages and disadvantages of various DC-DC converters. Aiming at the problem of large secondary switch loss and limited step-down range of variable-frequency phase-shift modulated CLLLC converter, this paper proposes a variable-frequency dual-phase-shift (VF-DPS) modulation strategy. The proposed VF-DPS modulation strategy can enhance the voltage gain and efficiency of the CLLLC converter by simultaneously adjusting the switching frequency, phase-shift angle in the primary side full bridge, and phase-shift angle between the primary and secondary sides.
The proposed strategy operates in two modes: the buck mode and the boost mode. In the buck mode, when the input voltage exceeds the rated input voltage, adjustments in the phase-shift angle in the primary side full bridge achieve a voltage gain of less than 1. In the boost mode, when the input voltage is below the rated input voltage, adjustments in the phase-shift angle in the secondary side full bridge result in a voltage gain greater than 1. According to these two modes, VF-DPS modulation is adopted for the CLLLC converter. The waveform shapes of the resonant inductor current and excitation inductor current are changed by VF-DPS modulation, achieving zero voltage switching (ZVS) for all switches. The modal analysis of the VF-DPS modulated CLLLC converter is conducted. Time domain analysis method is used to solve the voltage gain and resonant inductor current. Furthermore, the influence of different frequencies and phase-shift angles on the voltage gain and root mean square of the resonant inductor current is analyzed.
An experimental prototype was designed with an input voltage of 100~300 V and an output of 400 W/ 48V. The experiments tested the wide input range, working mode, soft switching, and efficiency of the CLLLC converter. The peak efficiency is 95.1% in the buck mode and 94.4% in the boost mode, confirming soft switching in both operating modes. The VF-DPS modulated CLLLC converter has a wider gain range and higher efficiency than the variable-frequency phase-shift modulation.
The proposed VF-DPS modulated CLLLC converter addresses challenges of wide switching frequency variations and ZVS losses in the wide input voltage of the variable-frequency modulated CLLLC converter and the phase-shift modulated CLLLC converter, respectively. The VF-DPS modulated CLLLC converter realizes the soft switching of all switches. Moreover, the converter achieves a voltage gain range of 3 times and a peak efficiency of 95.1%. Future research will focus on integrated magnetic design to further enhance efficiency and reduce the volume of the converter.
keywords:Variable-frequency dual-phase-shift modulation, wide input voltage, CLLLC converter, time domain analysis, zero voltage switching
国家自然科学基金资助项目(62271417)。
收稿日期 2023-02-09
改稿日期 2023-06-30
DOI: 10.19595/j.cnki.1000-6753.tces.230147
中图分类号:TM46
周国华 男,1983年生,教授,博士生导师,研究方向为开关变换器调制与控制技术、数字控制技术、建模与稳定性分析,电力电子技术在新能源发电系统中的应用等。E-mail: ghzhou-swjtu@163.com(通信作者)
王 淇 女,1998年生,硕士研究生,主要研究方向为双向谐振型变换器。E-mail: wq_pece@163.com
(编辑 陈 诚)