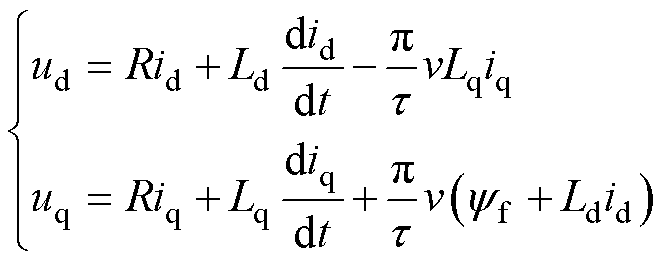（1）
摘要 针对永磁同步直线伺服电机（PMSLM）传统位移控制算法中控制器系数固定带来的控制精度不足等问题，提出一种基于复合神经网络重构对象的PMSLM变参数型位移速度并行控制策略。首先，利用动子位移、线速度的误差信息设计变参数并行控制器；其次，建立含有控制对象多维信息的复合径向基神经网络观测动子位移，并得到控制对象的偏导信息；再次，基于闭环稳定条件，以周期检索的误差与控制目标的比较结果为基础，构建完整的位移速度并行控制器参数更新策略；最后，实验结果表明，该文所提控制策略能实现不同给定位移的高精度控制，且具有控制不同对象参数的泛用性。
关键词：永磁同步直线电机 并行控制 复合径向基神经网络 变参数 更新机制
永磁同步直线电机具有高推力密度、高效率、快速控制响应等特点，广泛应用于轨道交通、数控机床、高速物流等领域[1]。然而，在各类应用场合中，由于存在永磁同步直线电机（Permanent Magnet Synchronous Linear Motor, PMSLM）电气或机械参数的变化、非线性摩擦力的干扰等因素，会影响动子位移的高精度响应，从而降低伺服系统的控制性能[2]。因此，稳定、高效的位移控制算法对于提高系统性能具有重要的工程应用价值[3]。
按照位移、速度环相对位置的不同，伺服控制系统可以分为串行系统和并行系统。串行系统作为经典的控制策略已有大量研究，如比例积分微分（Proportion Integration Differentiation, PID）控制[4]、滑模算法[5]等；而并行系统作为新兴的研究方向，近年来也有不少学者提出了相关控制策略。文献[6]利用曲线规划替代自抗扰控制的跟踪微分器，构造了一种位移速度一体化的控制结构，提高了系统的抗扰能力。文献[7]将位移环与速度环进行并联设计，构建二阶自抗扰控制系统，提高了位移控制的抗扰性能及跟踪性能。文献[8]提出了基于动态滑模控制的位移速度控制方法，同时对电机的位移和速度进行控制，有效减少了滑模抖振。除此之外，并行控制在工业上也有应用，如高创伺服驱动器采用一种基于误差信号反馈的并行控制策略，有效提高了伺服系统的控制性能。
然而，不论是串行控制还是并行控制，多数控制器参数需要提前整定，并且一般情况下固定不变，无法对实际的控制效果做出调整[9]。对此，模糊算法[10]、最小二乘算法[11]、神经网络[12-13]等被应用到PMSLM的控制中去，此类方法可以对控制器参数在线更新，保证算法更高效的控制。其中，径向基神经网络（Radial Basis Function-Neural Network, RBF-NN）由于具有良好的非线性逼近能力与自修正机制[14]，常常与各类控制算法相结合应用，现有的研究主要针对网络观测和参数更新两个环节进行改进。在网络观测环节，文献[15]将改进粒子群算法与RBF-NN相结合，通过改善网络的观测效果来提高系统响应速度。文献[16]用混沌遗传算法来优化RBF-NN参数，增强网络对不确定因素的适应性，但引入更复杂的寻优过程使得处理器的运算压力显著增加。在系数更新环节，文献[17]在PID的基础上引入RBF-NN，利用梯度下降法进行控制器参数的在线调整，有效提高了伺服系统的动态性能。文献[18]在文献[17]的基础上提出基于事件触发的控制器更新机制，降低执行器损耗，但该方法在给定信号变化的情况下无法完成工作。
根据以上分析，本文提出了一种基于复合神经网络重构对象的PMSLM变参数型位移速度并行控制（Variable Parameter-Parallel Control, VP-PC）策略，利用神经网络的映射特性观测动子位移，结合参数更新机制，可以实时调整并行控制器的参数，实现高精度的动子位移控制。
在PMSLM动子磁场定向的两相旋转dq坐标系中，动子绕组电压平衡方程式为
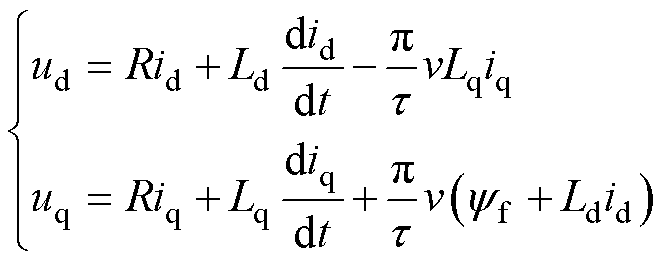（1）
式中，ud、uq分别为d、q轴电压；id、iq分别为d、q轴电流；R为动子相绕组电阻；Ld、Lq分别为d、q轴电感；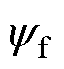
为永磁体磁链；
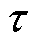为电机极距；v为动子线速度。
控制PMSLM动子运动的电磁推力可表示为
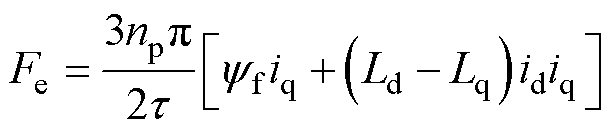（2）
式中，Fe为动子电磁推力；np为电机极对数。
PMSLM动子运动过程中，定义位移误差ep和线速度误差ev如下
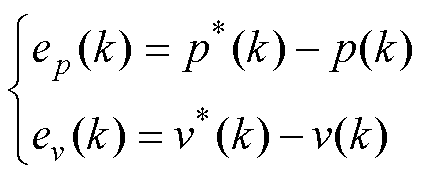（3）
式中，p*、v*分别为位移和线速度的给定。
利用式（3）所示的误差信号设计并行控制器（Parallel Controller, PC），其中位移环采用比例-积分控制器，保证位移控制精度；速度环采用比例-微分控制器，改善速度控制动态性能，进而提升位移控制效果，控制律为
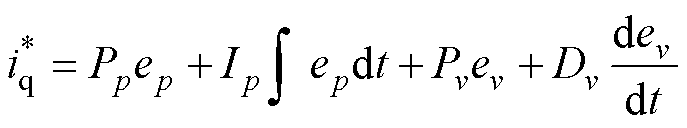（4）
式中，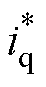
为q轴电流给定信号；Pp、Ip分别为并行位移环的比例、积分系数；Pv、Dv分别为并行速度环的比例、微分系数。
位移速度并行控制双环系统结构如图1所示。图中，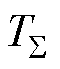
为电流环近似时间常数；Kf为推力力矩系数；Ff为负载阻力；M为动子质量。
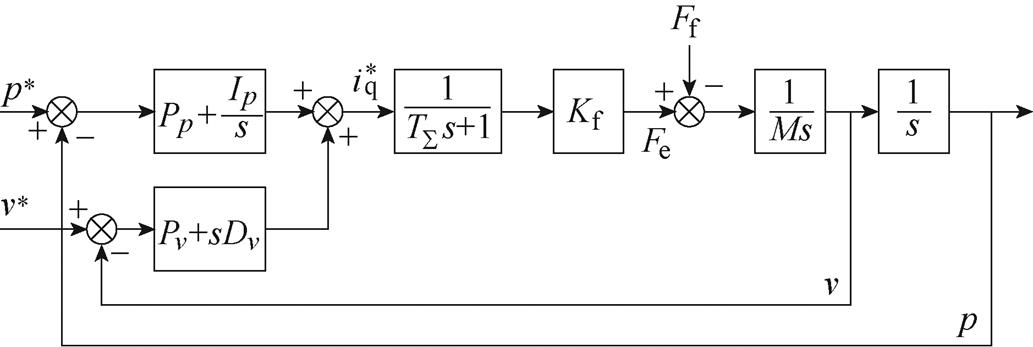
图1 位移速度并行控制结构
Fig.1 Parallel control structure of displacement velocity
图1的并行控制系统位移传递函数推导为
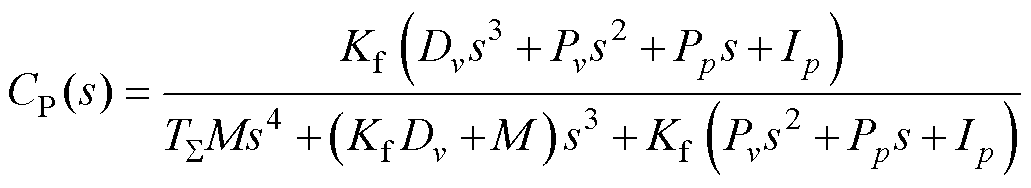（5）
根据劳斯判据可得上述系统稳定的充要条件为
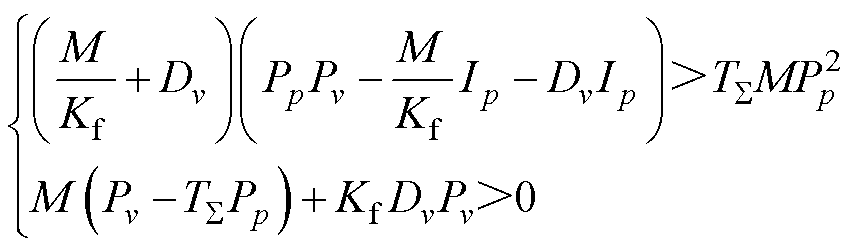（6）
图2为控制器各参数对系统带宽的影响，可见Pv、Dv对并行系统的带宽有较为显著的影响。
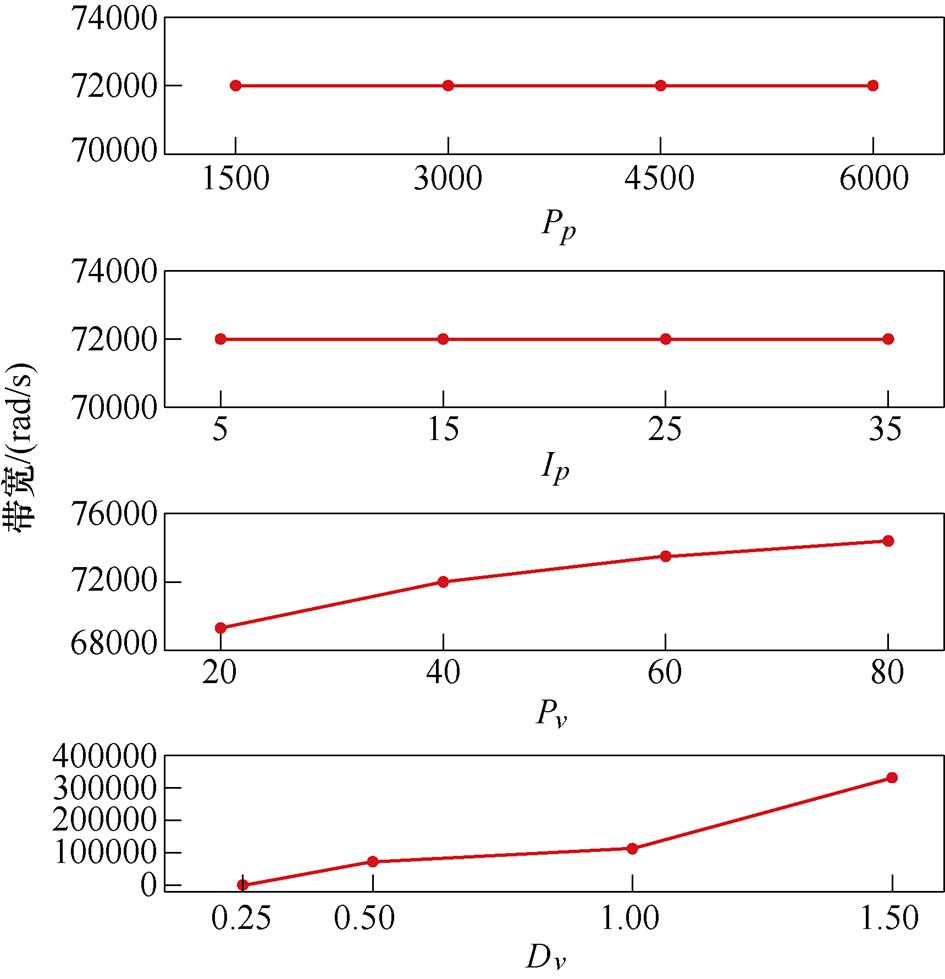
图2 控制器各参数对系统带宽的影响
Fig.2 Influence of controller parameters on system bandwidth
为了进一步提高1.2节并行控制性能，适应动子各种运动状态下，快速减小位移控制误差需要，本文进一步提出变参数型位移速度并行控制策略结构，框图如图3所示。复合神经网络通过映射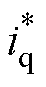、p、v得到观测位移pobs，结合ep、ev、观测位移以及控制输入的偏导项
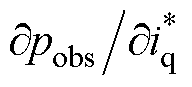驱动更新机制，实现对1.2节中并行控制器Pp、Ip、Pv、Dv 4个参数实时调节。
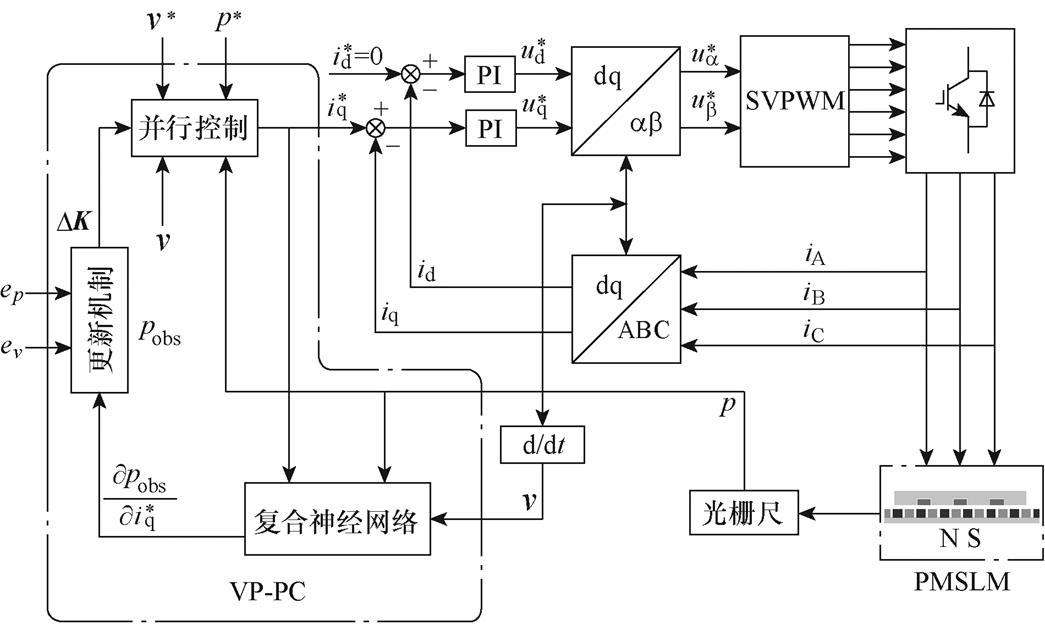
图3 PMSLM变参数型位移速度并行控制策略框图
Fig.3 Block diagram of PMSLM displacement velocity parallel control strategy with variable parameters
图3中，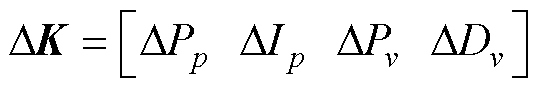
为更新机制输出的控制器参数更新集；上标“*”表示变量的给定控制；
、
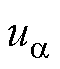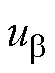分别为两相静止坐标系下的
、
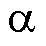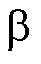轴电压；iA、iB、iC分别为A、B、C相电流。
定义位移控制误差函数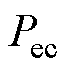
如下
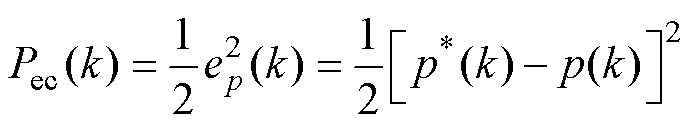（7）
式中，“k”为变量第k时刻的值。
为了实现位移控制误差函数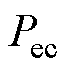快速收敛的目的，提出如下增益自适应变化的梯度下降并行控制器参数更新策略。各参数调整策略为
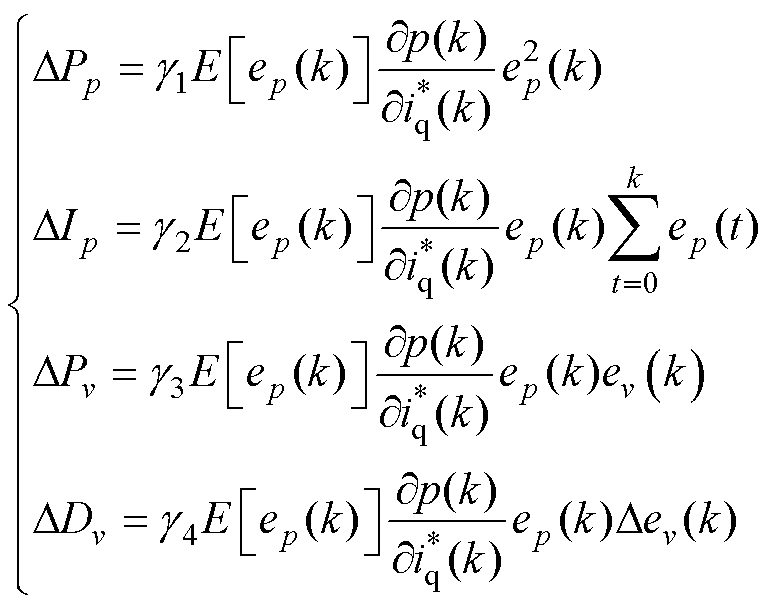（8）
式中，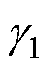
、
、
、
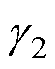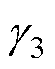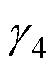为Pp、Ip、Pv、Dv对应的更新增益；
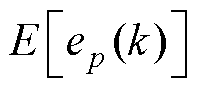为更新增益的自适应函数，定义为
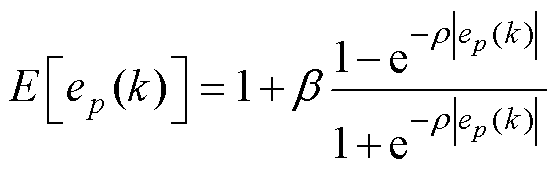（9）
式中，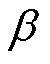
为自适应系数；
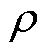为饱和系数。
由式（9）可知，当位移误差ep较大时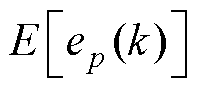，也随之增大，此时更新增益在自适应函数的影响下变大，使得并行控制器的各参数更新加快；另一方面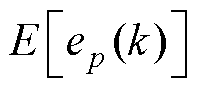，具有饱和特性，使得更新过程中参数不会产生过大的调整量而对控制产生不利影响。当位移误差ep较小时，更新增益也减小，避免参数调整出现不必要的振荡。
1.4.1 复合神经网络结构
在1.3节式（8）的更新算法中，由于PMSLM实际模型对象较为复杂，动子位移p对控制输入的偏导项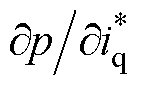
难以求取，而若采用符号函数近似替代的方法只能得到±1的结果，精度较低。为此，本文提出复合神经网络重构控制对象算法，利用重构对象观测动子位移，进而求得偏导项。
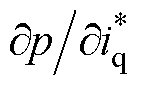由图1和图3可见，影响动子位移的不仅有q轴电流产生的电磁推力，还有外在的负载阻力，但负载阻力无法准确获知，为此，本文提出以动子位移、速度为输入层，观测位移为输出层的复合径向基神经网络（Composite Radial Basis Function- Neural Network, CRBF-NN），具体讲解如下。
CRBF-NN主要由双输入层、双映射层、组合层、输出层四个部分组成：
（1）根据图1所示的并行结构特点，位移、速度信息经过并行控制器后产生控制信号，进一步得到电磁推力、负载阻力的合力驱动动子运动产生位移。因此，输入层中除了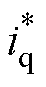，还利用位移、速度信息替代负载阻力进行映射。双输入层包含位移输入层和速度输入层，分别含有i和j个输入节点。
（2）双映射层包含位移映射层和速度映射层，分别由m和n个神经元组成。
（3）组合层由m×n个节点构成，由位移和速度映射神经元输出加权求和产生。
（4）输出层对各组合节点的加权结果进行相加得到最终的观测位移。对应网络的具体结构如图4所示。
图4中，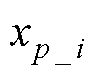
、
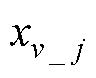分别为位移、速度输入层的输入量，本文选取
、
；
、
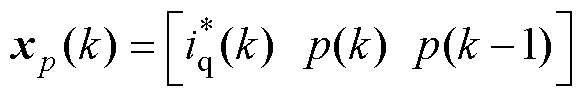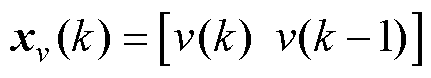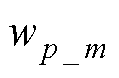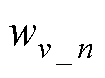分别为位移、速度映射层的输出加权因子；“ws”表示加权求和；
、
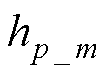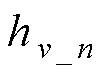分别为位移、速度映射层的映射函数，均采用高斯径向基函数的形式，具体表达式为
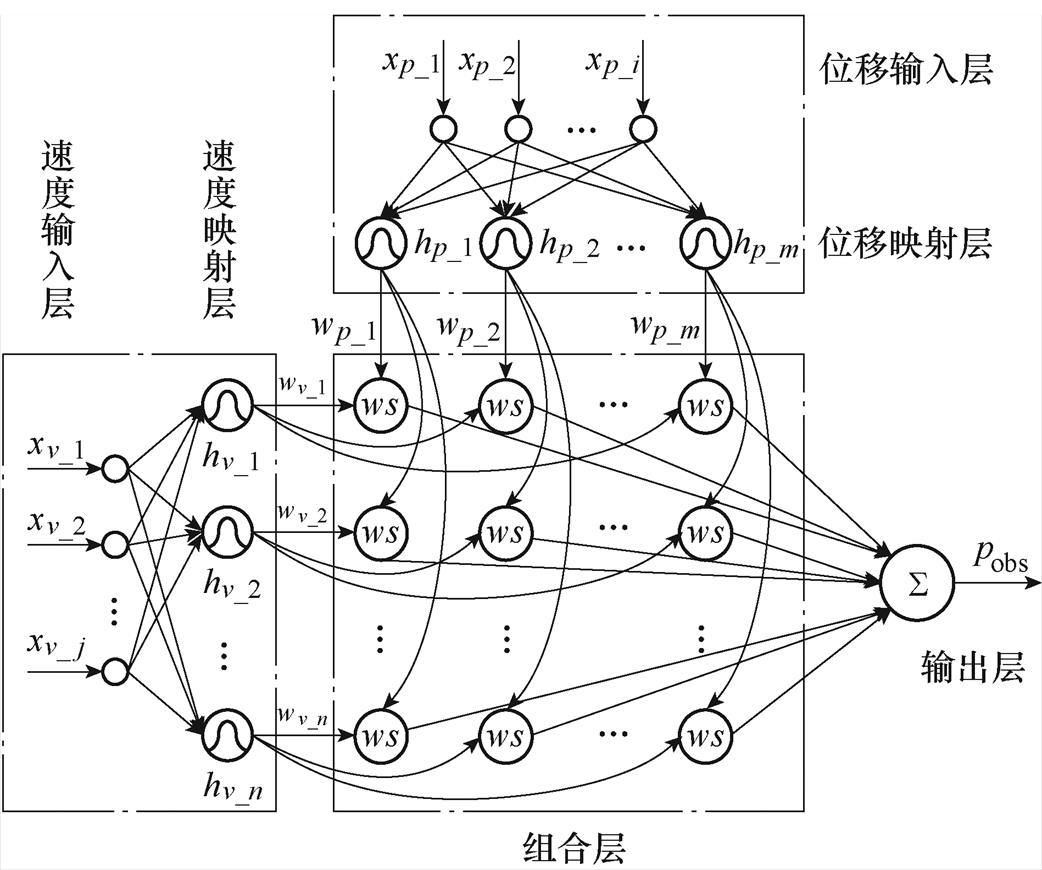
图4 CRBF-NN结构
Fig.4 Structure of CRBF-NN
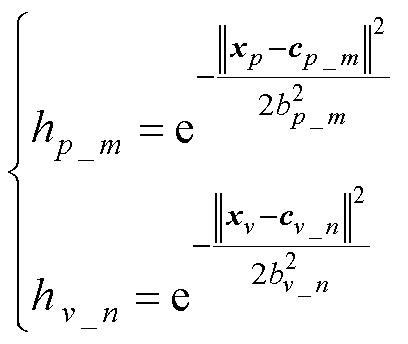（10）
式中，
、
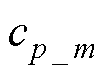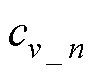分别为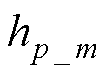、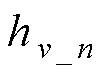的中心向量集，每个位移、速度径向基函数对应的向量集分别含有i、j个元素；
、
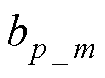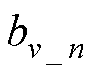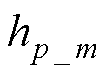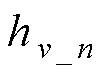分别为、的宽度。
相较于传统的RBF-NN，CRBF-NN额外引入了速度子网络，利用控制对象更多的输出信息，能够有效提升观测性能。
1.4.2 复合神经网络双映射层设计
双映射层的神经元数量影响整个网络的性能，过多的神经元会增加处理器的运算压力，同时给网络修正造成一定的困难；神经元数量较少则对输入信息的映射能力不足，造成观测性能下降。本文采用K均值聚类算法[19]分别对位移映射层和速度映射层进行分析，借助最佳聚类结果选择映射层神经元数量。以位移映射层为例，算法具体步骤如下：
（1）初始化聚类数范围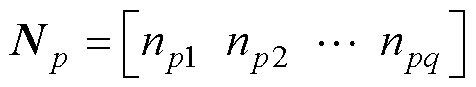
。
（2）获取输入层信息xp，分别以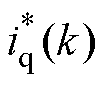
、
、
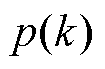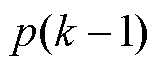作为样本的三维信息，得到位移样本点sp，同时选择本次迭代聚类数npt（t =1, 2,…,q）。
（3）在样本中随机选择npt个点构成位移类心集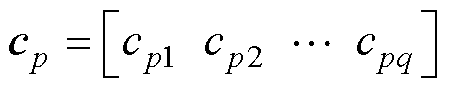
，计算每个位移样本到各类心的欧式距离do为
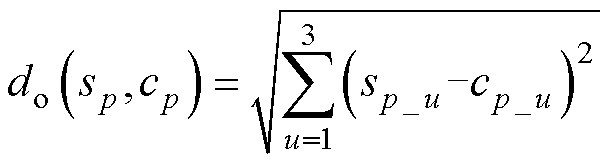（11）
（4）对于每个样本点，将其归类到最小欧式距离所对应的位移类中，得到分类结果。
（5）计算各位移类内的样本均值，作为该类的新类心，并重复步骤（3）～步骤（5）直到各类心不再发生变化。
（6）选择下一个聚类数np(t+1)，重复步骤（3）～步骤（6）。
（7）所有聚类数情况迭代完毕，根据式（12）计算各聚类数对应的截维斯-博尔丁（Davies- Bouldin, DB）和卡林斯基-哈拉巴斯（Calinski- Harabaz, CH）指标。
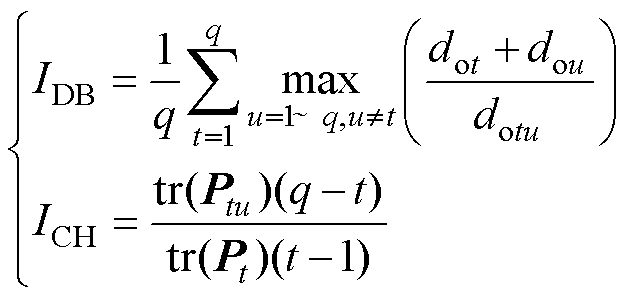（12）
式中，dot、dou分别为第t位移类内样本点散度、第u位移类与第t位移类间样本点散度；dotu为t、u两个位移类心的距离；Ptu、Pt分别为位移类间、类内协方差矩阵。算法具体流程如图5所示。
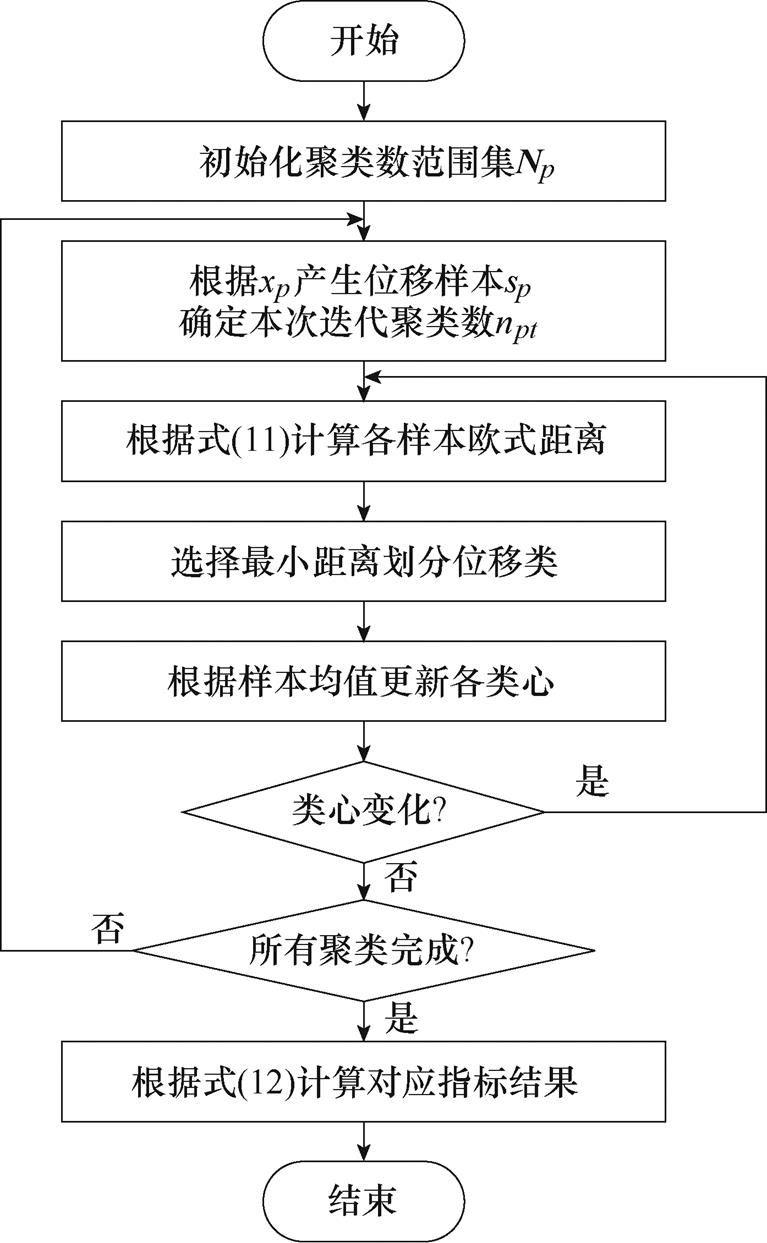
图5 聚类算法流程
Fig.5 Flow chart of clustering algorithm
1.4.3 复合神经网络双映射层设计
定义CRBF-NN各权值修正过程为
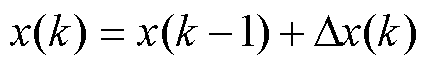（13）
式中，x为CRBF-NN各项权值；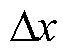
为各项权值对应的修正量。
定义CRBF-NN观测误差函数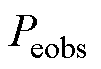
为
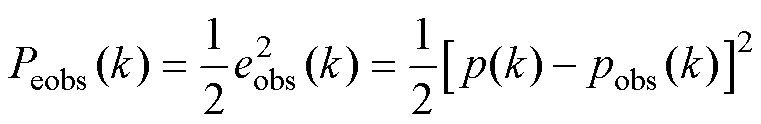（14）
在式（14）的基础上，采用梯度下降法求得式（15）～式（17）对应的各权值修正量。
1）加权权值
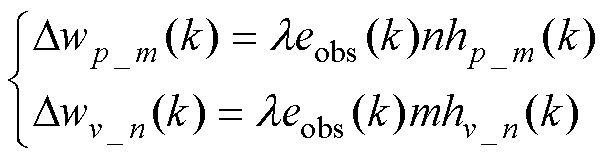（15）
式中，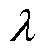
为学习因子。
2）映射函数宽度
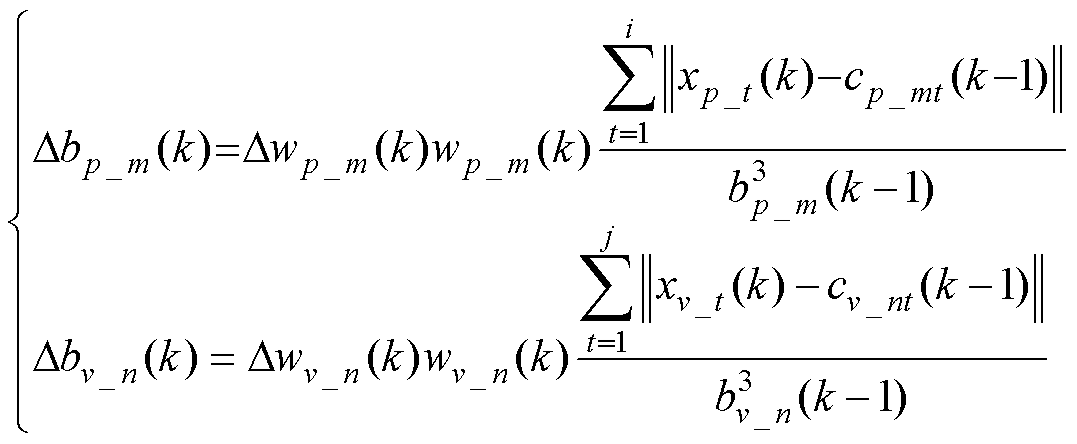（16）
3）映射函数中心
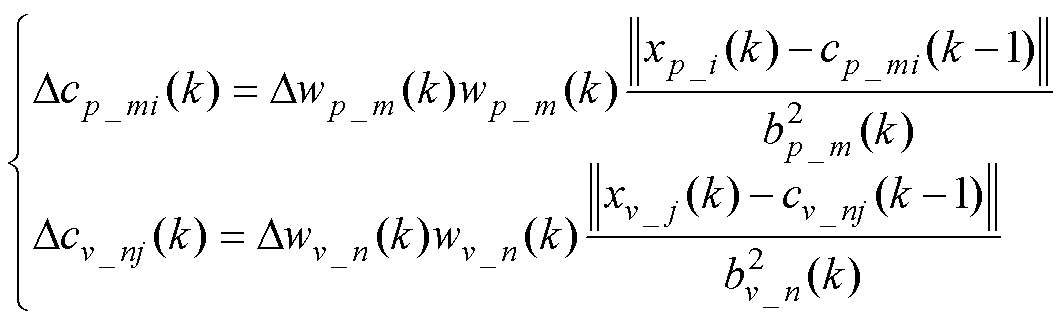（17）
在网络自修正的过程中，可求得式（8）中偏导项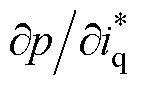
如下
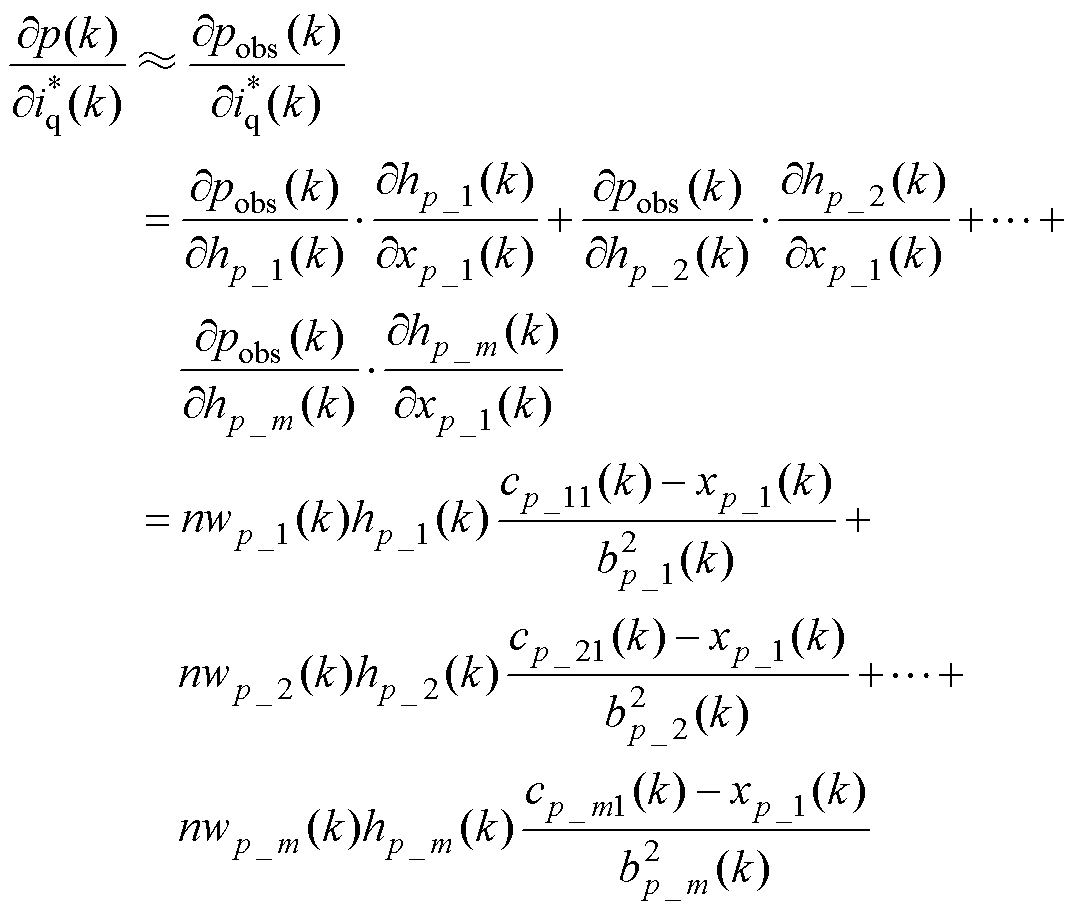
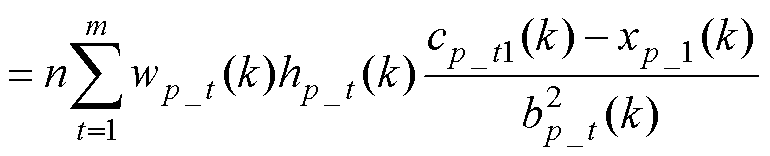（18）
由上述分析可知，CRBF-NN采用实际控制对象的一些输入来映射动子位移输出，从而用清晰、简单的网络结构模拟重构复杂的PMSLM对象，这样能够用网络的内部信息更容易地计算偏导项。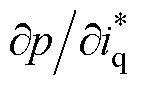
根据式（8）可知，PMSLM控制过程中若存在位移误差ep，则系数更新过程会频繁进行。但工程应用中，除了控制算法自身的滞后特性，各种软硬件层面上的因素，都会使得动子实际位移无法完全跟随给定，即使系统稳定之后，ep也不恒为0。对此本文提出一种基于闭环稳定和误差检索的并行控制器参数更新策略，能够在满足控制性能目标的同时有效减少PC参数更新次数，从而降低运算器资源占用。算法具体步骤如下：
（1）等待观测误差绝对值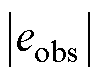
收敛至
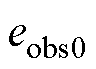以内。
（2）在本检索周期Ts内检索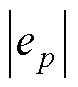
最大值eM。
（3）若周期检索完成，则执行步骤（4）；否则，返回执行步骤（2）。
（4）将eM与误差阈值eT相比较，若eM＞eT，则执行步骤（5）；否则，执行步骤（7）。
（5）判断PC各项系数是否满足式（6）的闭环稳定条件，若满足，则执行步骤（6）；否则，执行步骤（7）。
（6）根据式（8）进行PC各系数的在线更新。
（7）最大误差绝对值小于阈值，或PC各系数更新过程中达到闭环稳定条件边界，停止系数更新。
完整的位移速度并行控制器参数更新策略具体流程如图6所示。
为验证本文所提的变参数型位移速度并行控制策略的性能，利用Matlab/Simulink软件对图3所示的并行控制系统进行仿真建模。为了便于算法验证，采用式（19）和式（20）所示误差方均根、误差最大绝对值两项指标进行分析。
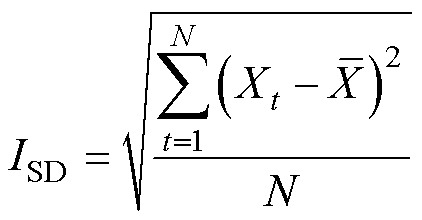（19）
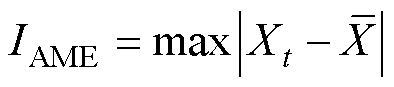（20）
式中，Xt为数据样本点；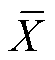
为数据样本平均值；N为样本数量。
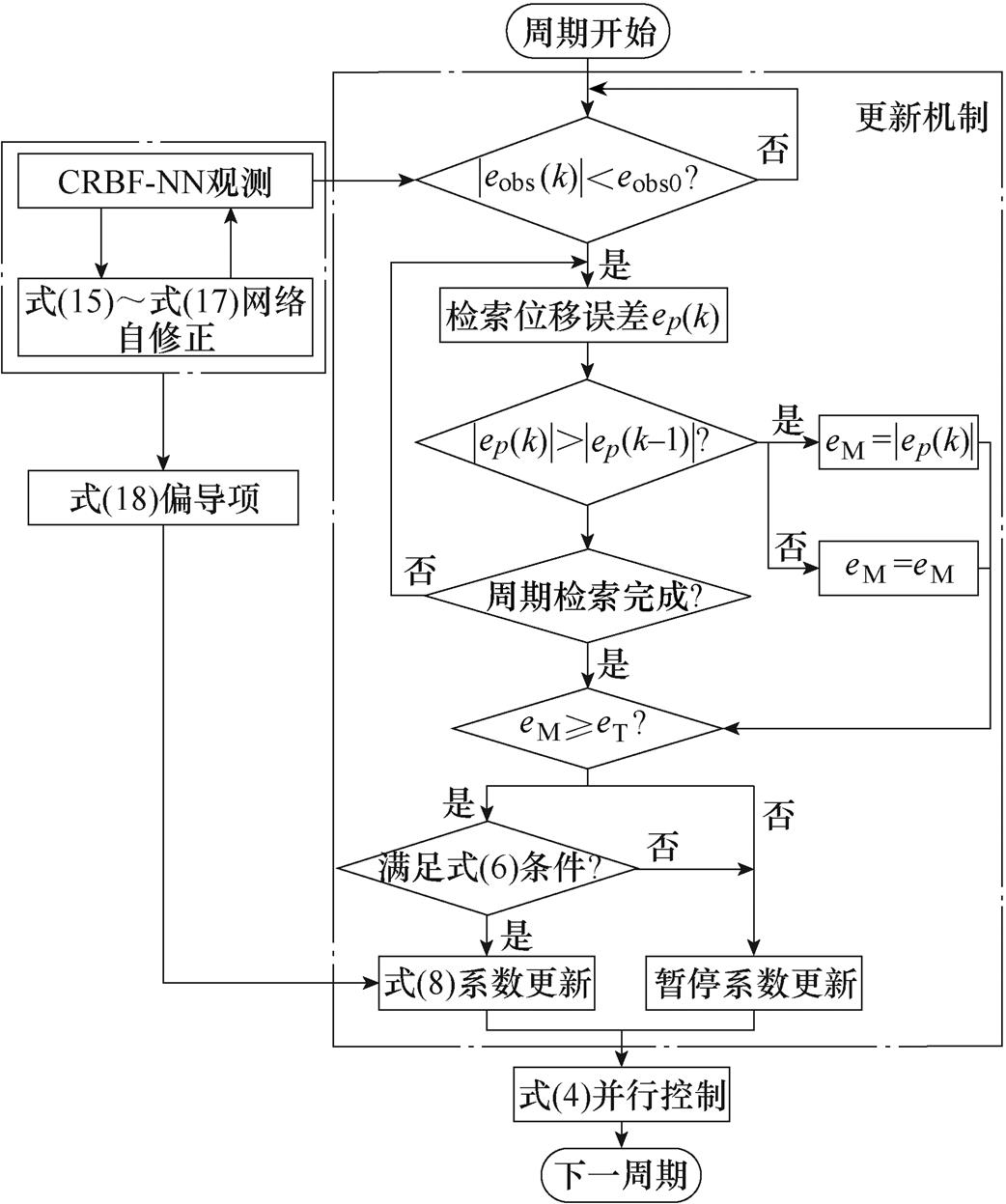
图6 并行控制器参数更新流程
Fig.6 Parallel controller parameter update flow chart
仿真中对比PID（方法A）、PC（方法B）、VP-PC （方法C）三者的控制效果。正弦位移实仿真如图7所示。图7a为动子运动给定的正弦位置信号以及三种方法的误差波形。设定验证的控制目标为0.10 mm，从图7b～图7g可见。
（1）图7b中，上图为误差尖峰处波形，下图为常态误差波形。可见三种方法中，采用VP-PC算法的控制系统，位置控制误差明显小于其他两种方法，且满足设定要求。
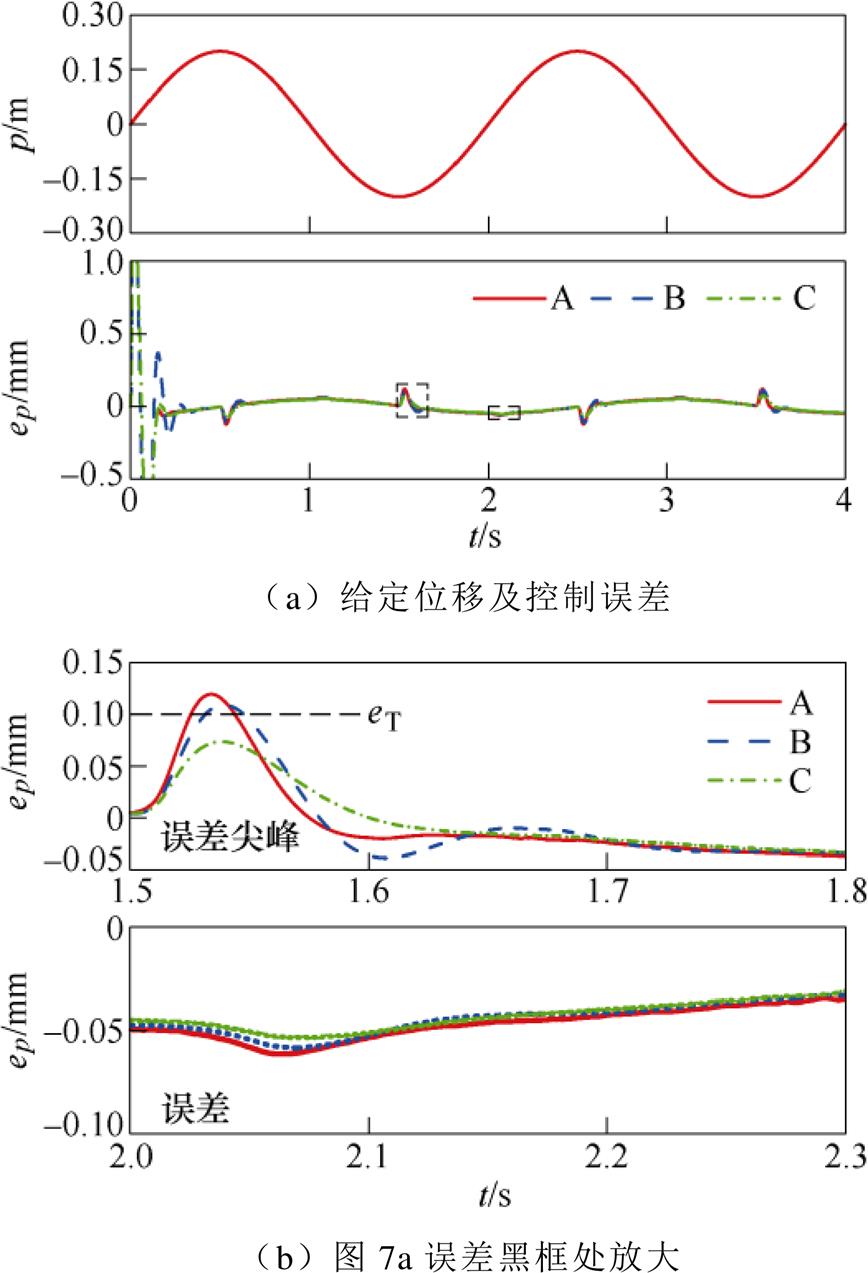
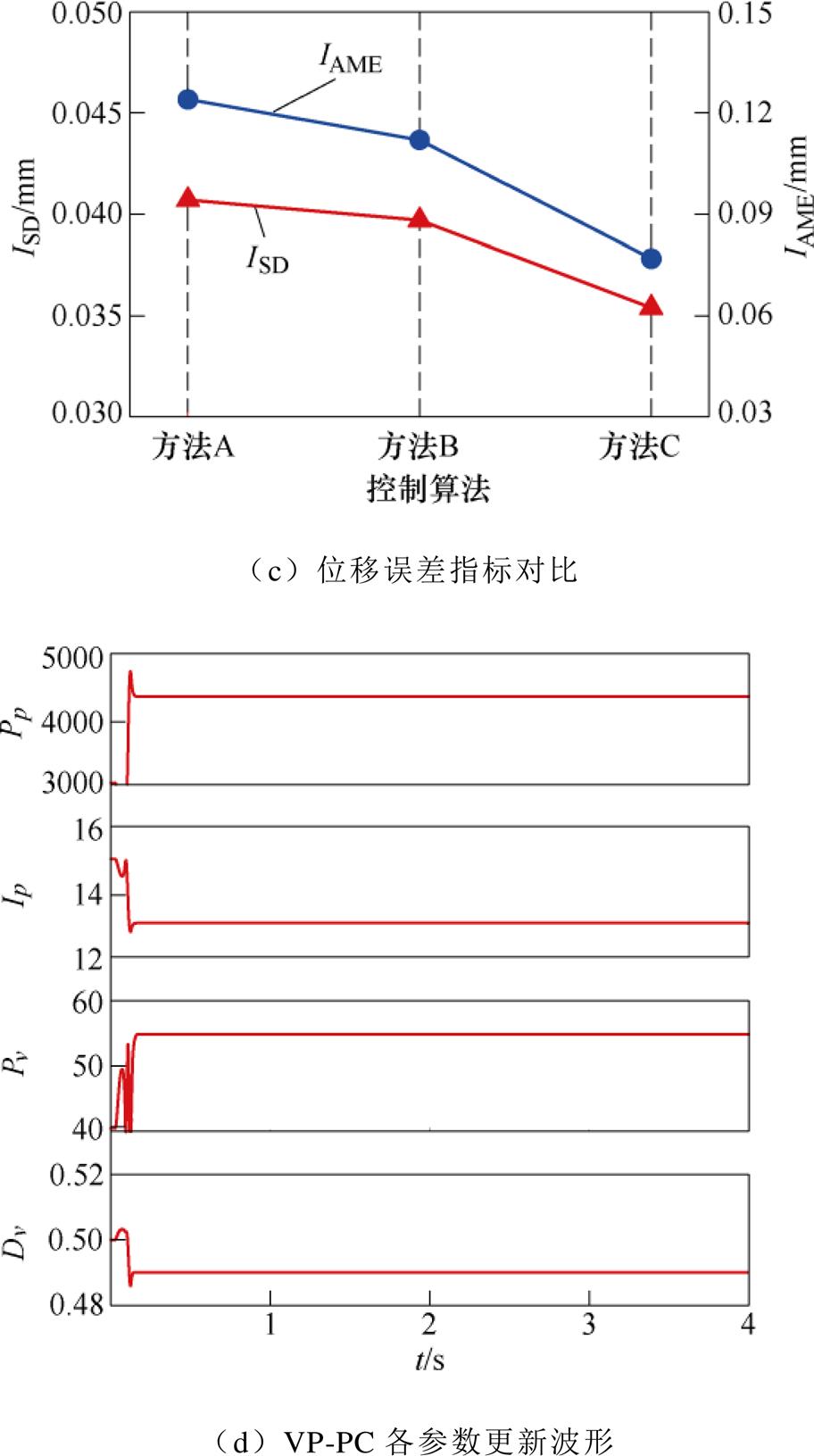
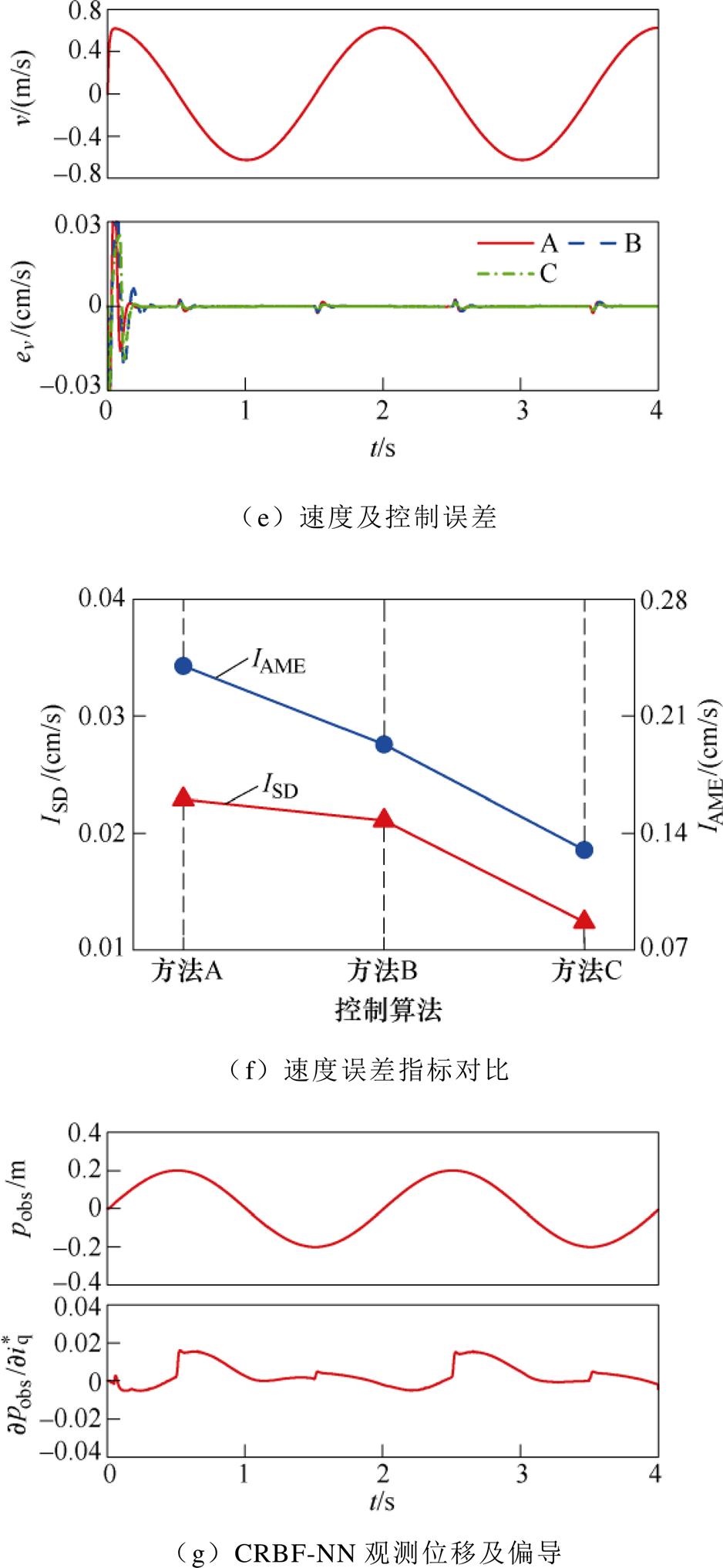
图7 正弦位移实仿真
Fig.7 Simulated diagram of sinusoidal displacement
（2）图7c中，PID的ISD、IAME分别为0.041 mm、0.124 mm，而PC的ISD、IAME分别为0.039 mm、0.112 mm，较前者有所改善。在此基础上加入CRBF- NN之后，两项指标均进一步减小，分别为0.035 mm、0.077 mm。
（3）图7d为VP-PC参数更新的波形。可见各参数均在t=0.2 s左右更新完毕，即此时系统的控制误差已满足控制目标要求。
（4）图7e～图7f展示的是三种方法的速度控制对比，可见采用VP-PC算法控制系统的速度误差指标ISD、IAME明显小于其他两种方法。
（5）图7g为CRBF-NN的位移观测和偏导输出，可见控制过程中网络具有快速、高精度的观测性能。
为分析本文所提算法的有效性，采用以TMS320F28388D为核心的实验平台进行研究，实验中所用电机和硬件平台如图8所示，其中PMLSM标称参数见表1，系统控制周期为125 ms。
图8 实验平台实物
Fig. 8 Photo of experimental platform
表1 PMSLM标称参数
Tab.1 PMSLM nominal parameters
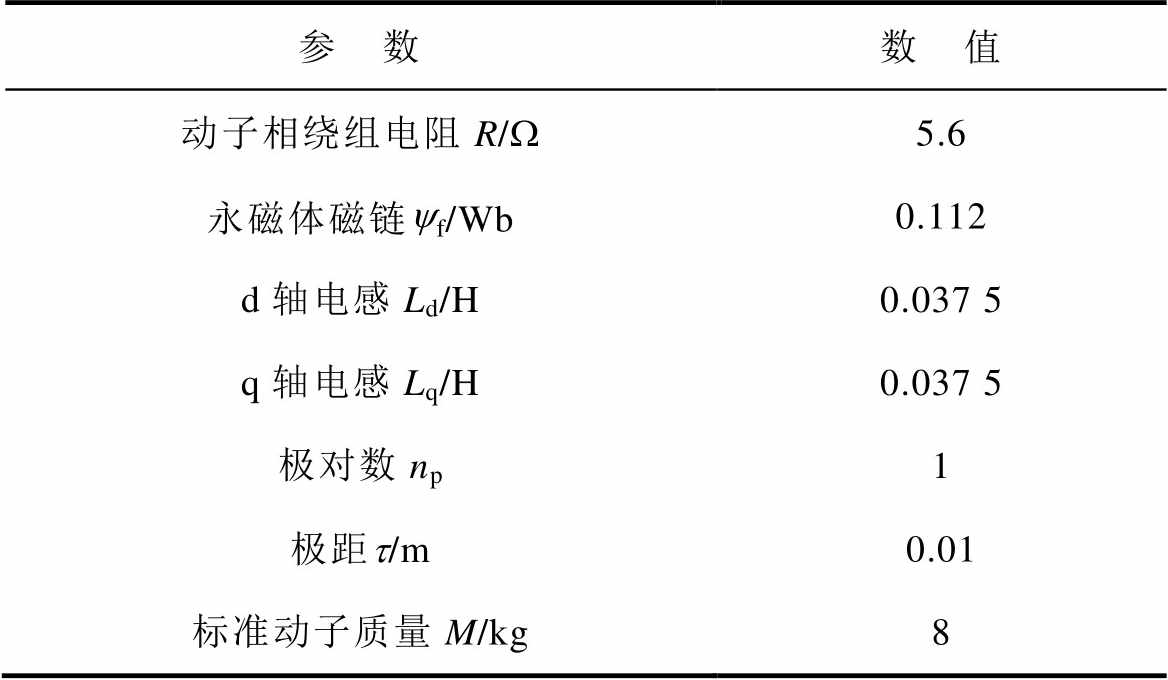
参 数数 值 动子相绕组电阻R/W5.6 永磁体磁链yf/Wb0.112 d轴电感Ld/H0.037 5 q轴电感Lq/H0.037 5 极对数np1 极距t/m0.01 标准动子质量M/kg8
图9为位移和速度映射的聚类指标结果。
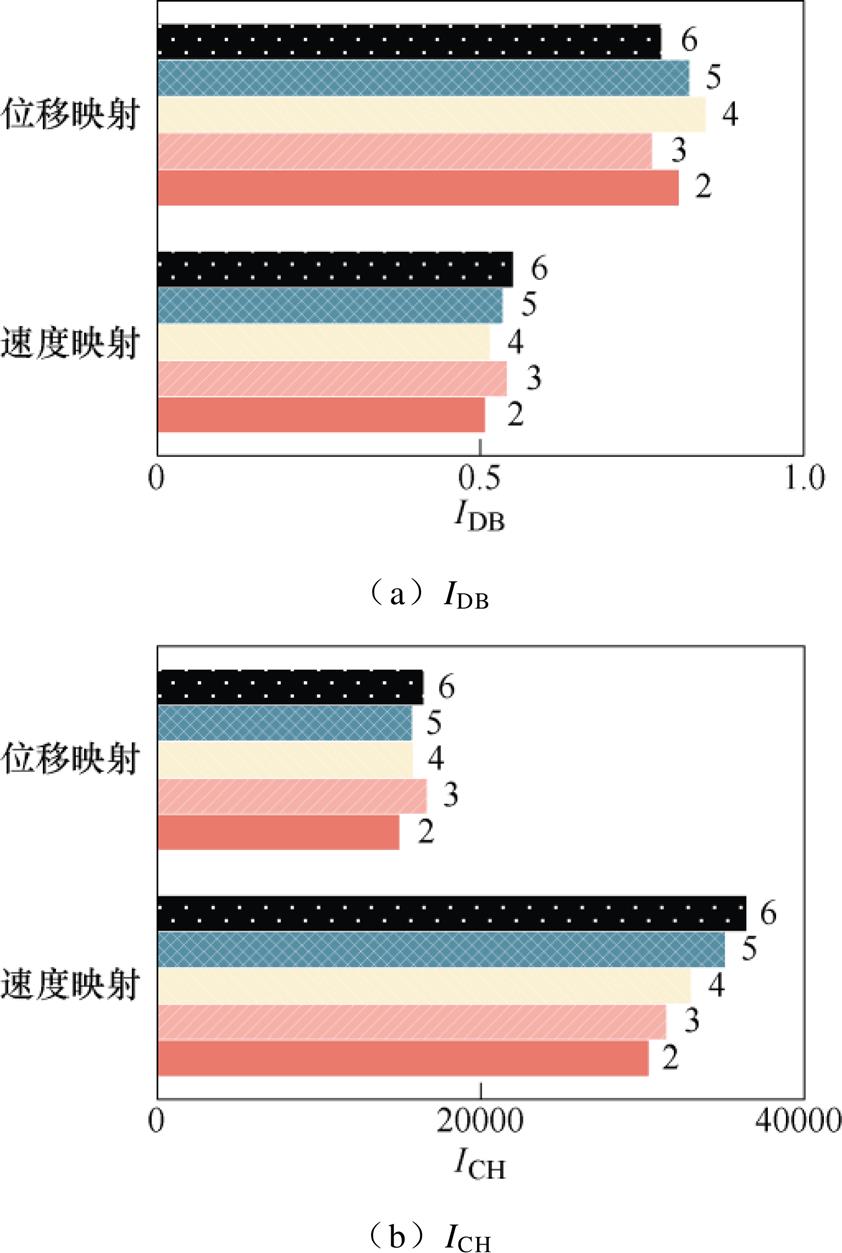
图9 不同聚类数指标对比
Fig.9 Comparison of different cluster number indexes
从图9中可以看出：
（1）位移映射实验中，当聚类数为3时IDB最小，为0.765 7；同时此聚类数对应的ICH最大，为16 691。
（2）速度映射实验中，当聚类数为2时IDB最小，为0.507 4；当聚类数为6时ICH最大，为36 453。
综合考虑双指标性能和网络结构的复杂程度，最终选择位移映射层神经元数量为3，速度映射层神经元数量为2。
相较于CRBF-NN，传统的RBF-NN只利用控制对象的单一输出构建输入层，对系统的信息利用不足。此外，对RBF-NN观测效果的改进主要通过增加映射层神经元数量或在自修正的过程中引入动量因子[20-21]。实验中，同样采用式（19）、式（20）所示的两项指标分别对RBF-NN（只有CRBF-NN位移输入层部分，无组合层，输入、映射、输出的节点数量分别为3、3、1）、RBF-NN（增加2个映射神经元）、RBF-NN（引入动量因子）、CRBF-NN的位移观测性能进行比对。
图10为四种观测网络的性能指标对比，图11为四种网络观测时间对比。实验中各观测网络除结构有所差异，其余参数均保持一致，从图中可以看出：
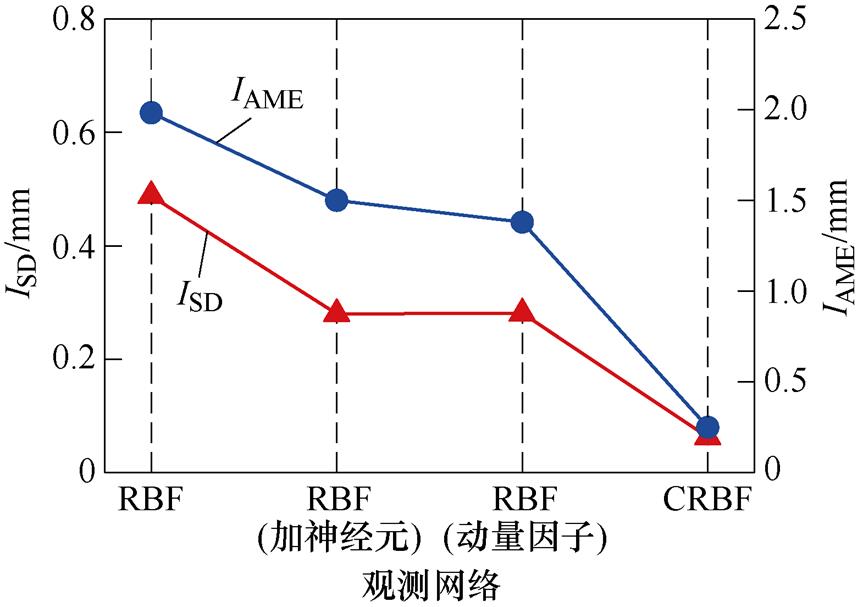
图10 网络观测性能指标
Fig.10 Network observation performance index chart
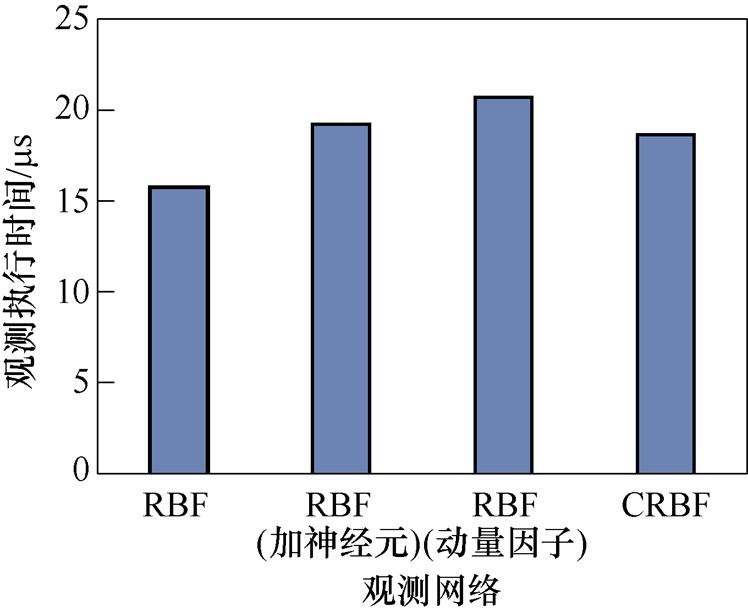
图11 网络观测时间对比
Fig.11 Comparison chart of network observation time
（1）RBF观测所需时间最短为15.75 ms，但观测效果最差，ISD=0.488 mm，IAME=1.983 mm。
（2）RBF经过增加映射层神经元数量或引入动量因子后，网络观测效果有所改善，ISD各减少至0.280 mm、0.281 mm，IAME分别减少至1.502 mm、1.381 mm，但二者观测时间分别增至19.22 ms、20.72 ms。
（3）CRBF-NN复合结构有效改善网络观测性能，ISD=0.063 mm，IAME=0.25 mm，观测时间为18.63 ms。
实验结果验证了本文所提CRBF-NN结构比RBF-NN结构具有更优的观测效果；并且对比传统RBF-NN结构的改进方法，也能更高效地观测动子位移，同时带给处理器额外的运算压力也更小。
实验中给予动子不同形式的位移信号，并采用式（19）、式（20）指标进行分析。各方法系数见表2。
表2 三种控制方法参数
Tab.2 The coefficients of three control methods
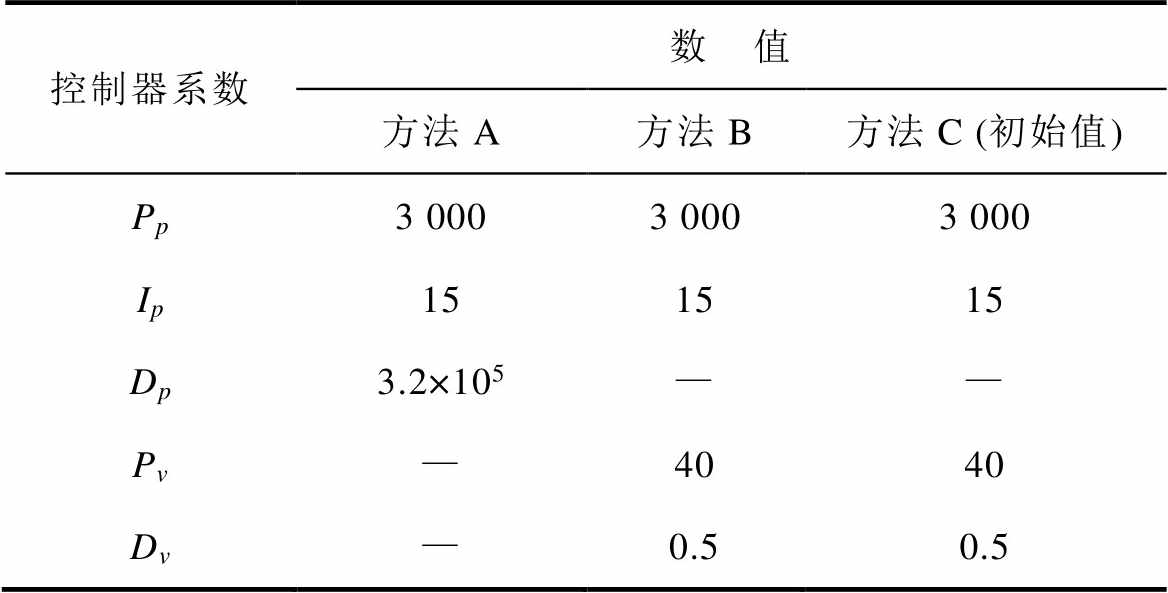
控制器系数数 值 方法A方法B方法C (初始值) Pp3 0003 0003 000 Ip151515 Dp3.2×105—— Pv—4040 Dv—0.50.5
注：Dp为位移环PID的微分系数，已进行换算。
3.3.1 正弦位移实验分析
正弦位移实验如图12所示。图12a为动子运动给定的正弦位移信号以及三种方法的控制误差波形。正弦位移下设定验证控制目标为eT=0.06 mm。从图12b～图12g可以看出：
（1）图12b中，上图为误差尖峰处波形，下图为常态误差波形。可见三种方法中，采用VP-PC算法的控制系统，位移控制误差明显小于其他两种方法，且满足设定要求eM≤eT。
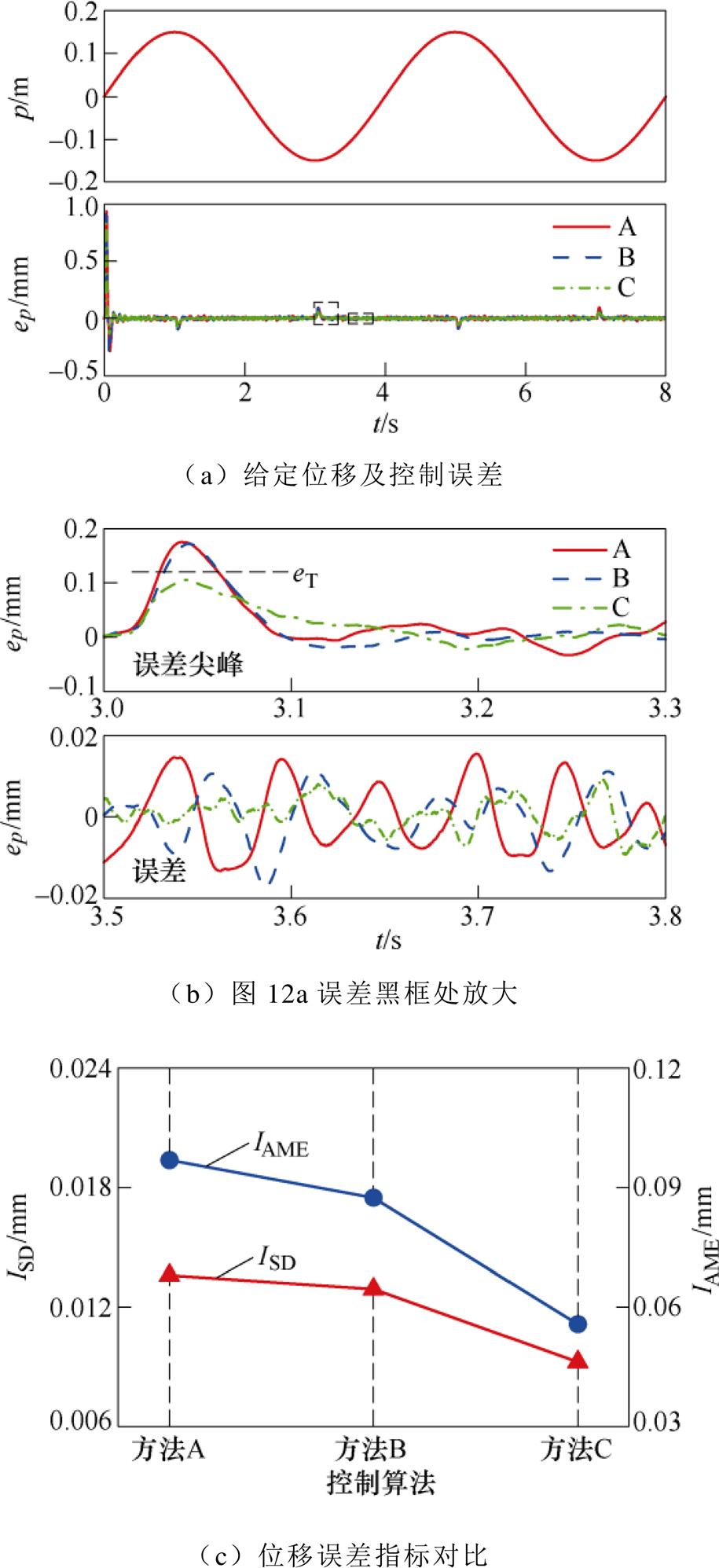
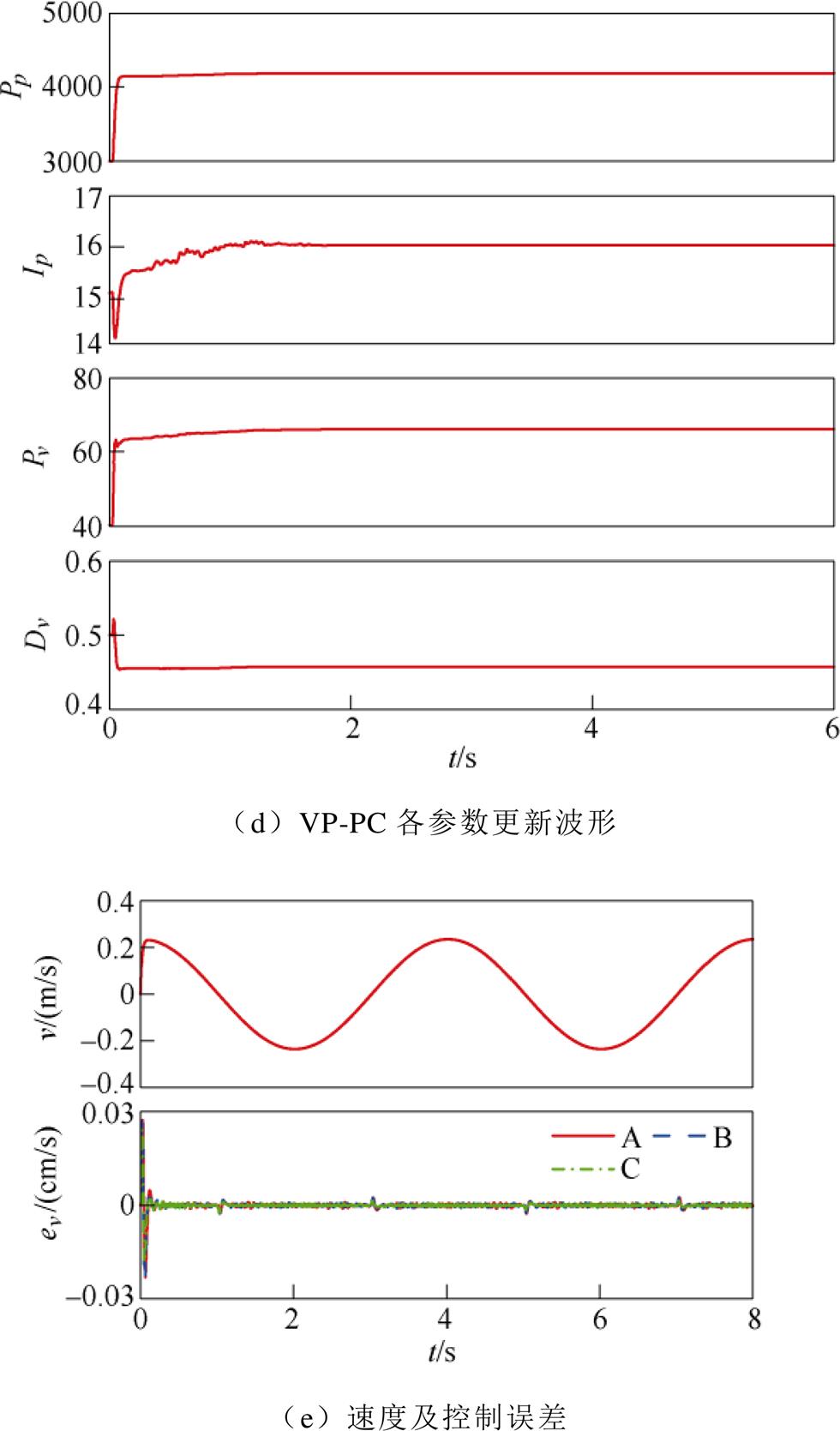
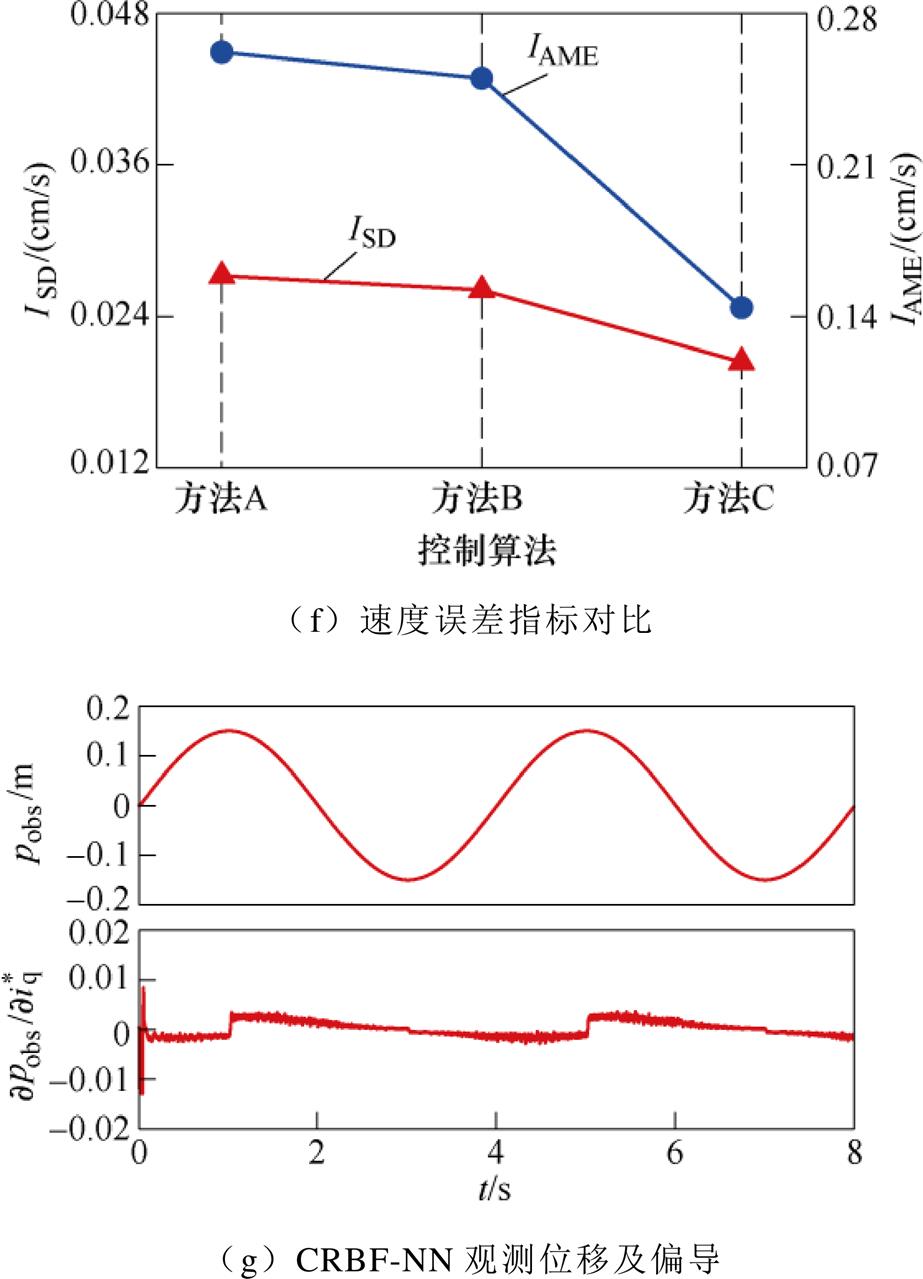
图12 正弦位移实验
Fig.12 Experimental diagram of sinusoidal displacement
（2）图12c中，PID的ISD、IAME分别为0.014 mm、0.097 mm，而PC的ISD、IAME分别为0.013 mm、0.087 mm，较前者有所改善。在此基础上加入CRBF-NN之后，两项指标均进一步减小，分别为0.009 mm、0.056 mm。
（3）图12d为VP-PC参数更新的波形。可见控制器各参数在t =1.8 s左右更新完毕，即此时系统的控制误差已满足控制目标要求。
（4）图12e、图12f展示的是三种方法的速度控制对比，可见采用VP-PC算法控制系统的速度误差指标ISD、IAME明显小于其他两种方法。
（5）图12g为CRBF-NN的位移观测和偏导输出，可见控制过程中网络具有快速、高精度的观测性能。
3.3.2 梯形位移实验分析
梯形位移实验如图13所示。图13a为动子运动给定的梯形位移信号以及三种方法的控制误差波形。该位移下设定的控制目标eT=0.2 mm。从图13b～图13g可以看出：
（1）图13b中，上图为误差尖峰处波形，下图为常态误差波形。可见三种方法中，采用VP-PC算法的控制系统，位移控制误差明显小于其他两种方法，且满足设定要求eM≤eT。
（2）图13c中，PID的ISD、IAME分别为0.067 mm、0.410 mm，而PC的ISD、IAME分别为0.063 mm、0.391 mm，较前者有所改善。而VP-PC算法的两项指标均进一步减小，分别为0.030 mm、0.194 mm。
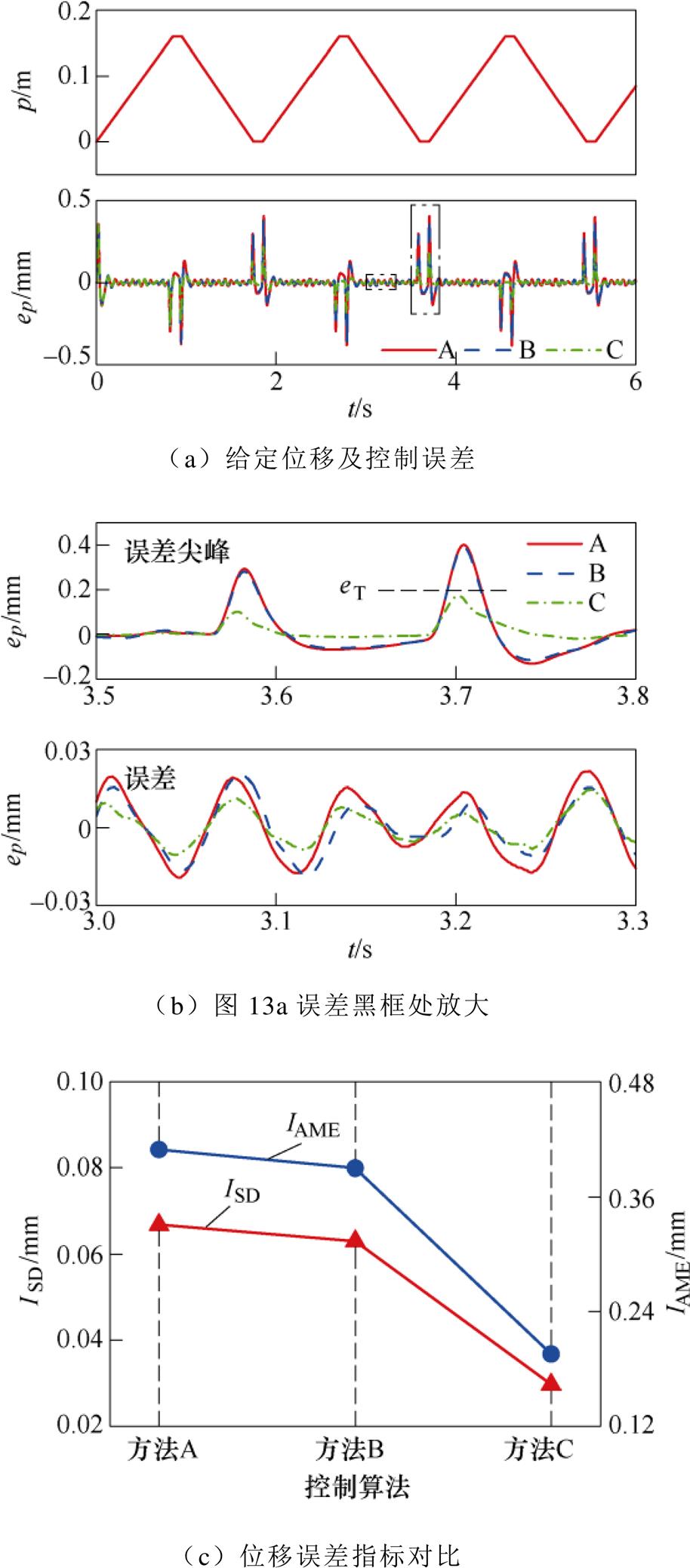
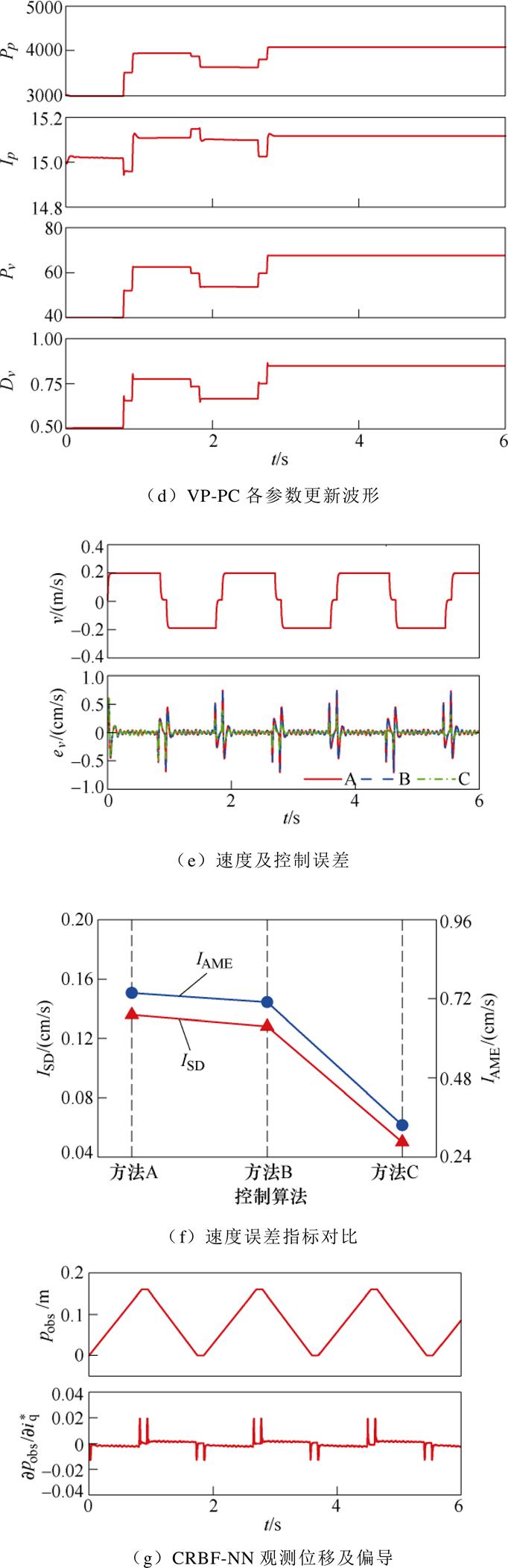
图13 梯形位移实验
Fig.13 Experimental diagram of trapezoidal displacement
（3）图13d为VP-PC的参数更新波形。可见控制器各参数在t =2.4 s左右更新完毕，即此时系统的控制误差已满足控制目标要求。
（4）图13e、图13f展示的是三种方法的速度控制对比，可见采用VP-PC算法的控制系统，速度误差指标ISD、IAME明显小于其他两种方法。
（5）图13g为CRBF-NN的位移观测和偏导输出，可见控制过程中网络具有快速、高精度的观测性能。
3.3.3 变位移实验分析
变位移实验如图14所示。图14a为动子给定的变位移信号以及三种方法控制误差波形，验证伺服控制中位置突变时不同算法的控制性能。从图14b～图14g可以看出：
（1）图14b中，VP-PC控制下的误差较PID和PC更小，且满足设定要求eM≤eT。
（2）图14c中，PID的ISD、IAME分别为0.014 mm、0.091 mm，而PC的ISD、IAME分别为0.014 mm、0.087 mm。而VP-PC算法的两项指标均进一步减小，分别为0.011 mm、0.059 mm。
（3）图14d为VP-PC的参数更新波形。在前段位移阶段，控制器各项参数在t =1 s左右更新完毕；而在圈1处，由于更新机制检测到周期内的某个时刻误差尖峰振荡略微超过eT，故控制器参数继续进行小幅度更新。在后段位移阶段，圈2处由于位移给定发生突变，相应产生的误差尖峰明显超过eT，故控制器参数继续进行较大幅度更新，约0.5 s完成。
（4）图14e、图14f展示的是三种方法的速度控制对比，可见采用VP-PC算法控制系统的速度误差指标ISD、IAME明显小于其他两种方法。
（5）图14g为CRBF-NN的位移观测和偏导输出，可见控制过程中网络具有快速、高精度的观测性能。
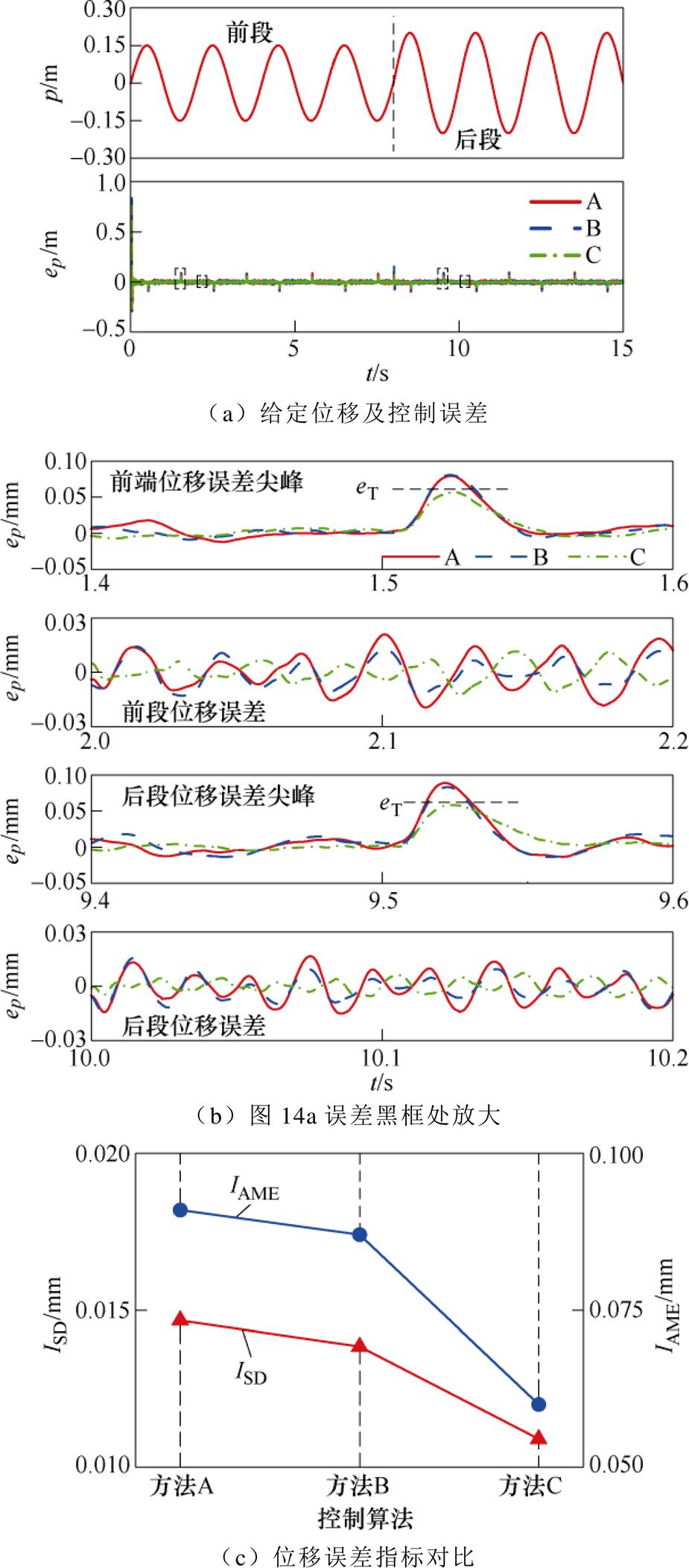
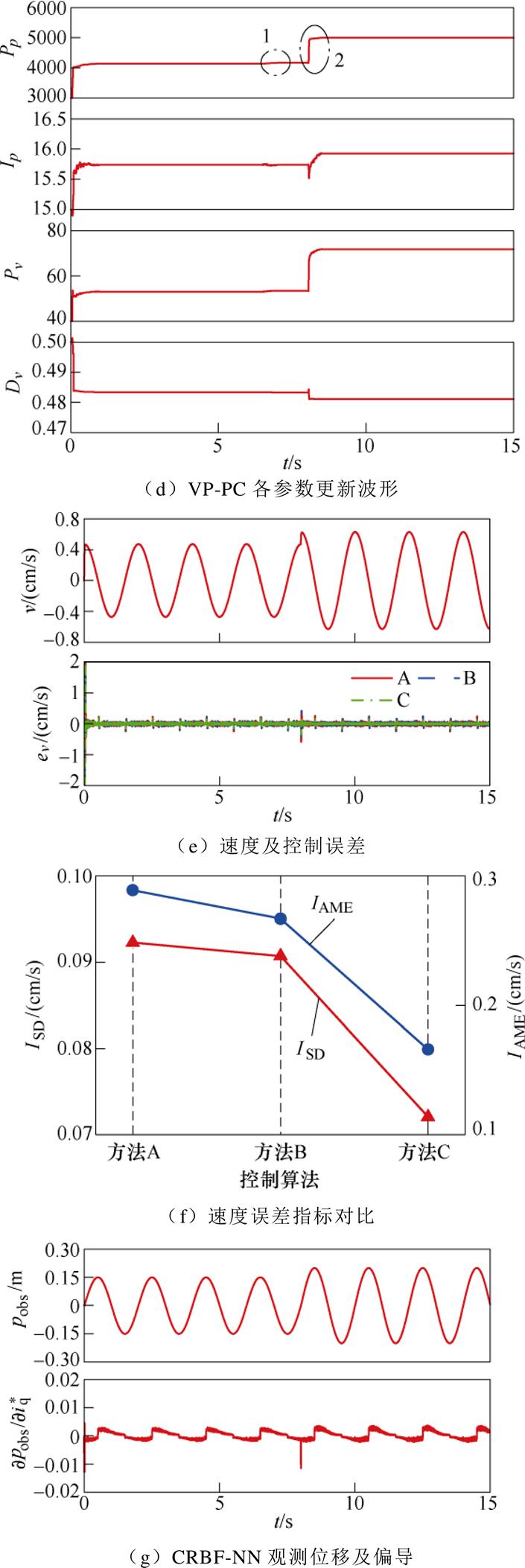
图14 变位移实验
Fig.14 Experimental diagram of variable displacement
实验中，通过改变动子质量参数（3、8、13 kg）来验证VP-PC控制不同对象时的算法有效性。
位移信号给定与图12a一致，图15a～图15f所示的是不同质量动子的位移控制实验波形。从图中可以看出：
（1）图15a中，在三种不同质量动子的位移控制实验中，均能满足设定要求eM≤eT=0.06 mm。
（2）图15b中，不同对象参数的ISD分别为0.010、0.012、0.015 mm；IAME分别为0.057、0.059、0.060 mm，可见三种对象参数的两项指标之间相差不大，算法稳定。
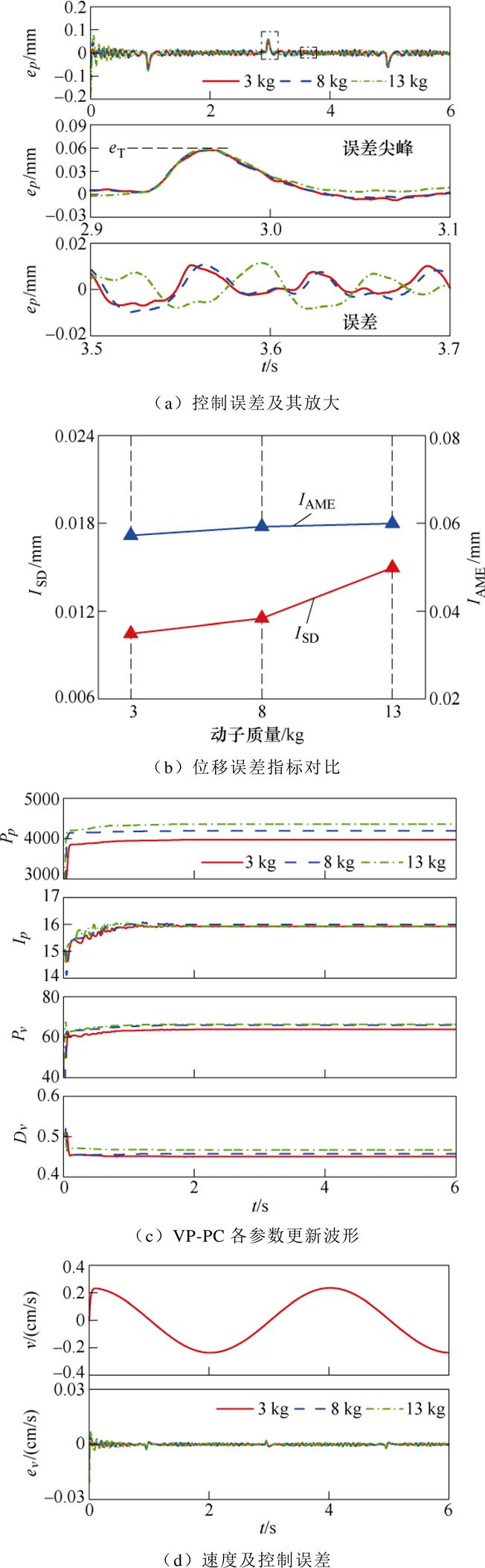
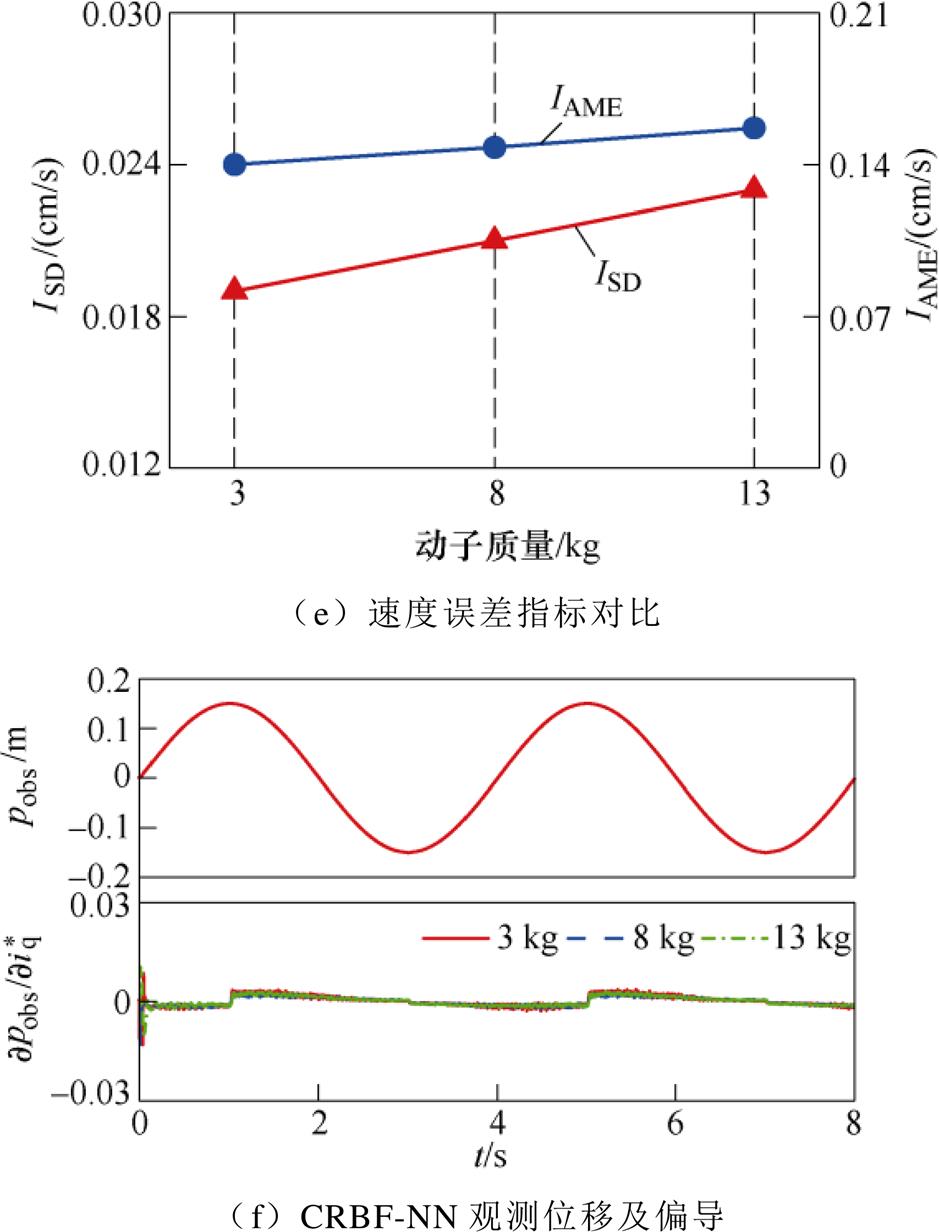
图15 不同质量对象位移控制实验
Fig.15 Experimental diagram of displacement control with different masses
（3）图15c为VP-PC的参数更新波形，均在2 s左右调整完毕，可见算法具有一定泛用性。
（4）图15d、图15e展示的是三种不同动子质量的速度控制误差对比，可见VP-PC算法在速度控制上具有良好的稳定性。
（5）图15f为CRBF-NN的位移观测和偏导输出，可见控制过程中网络具有快速、高精度的观测性能。
本文提出一种基于复合神经网络重构对象的永磁同步直线伺服电机变参数型位移速度并行控制策略，理论分析和实验结果表明：
1）本文提出的CRBF-NN结构相较于传统的RBF-NN具有更好的观测性能；相较于传统的改进方法，在带给处理器更小的运算压力前提下，也能有更好的改善效果。
2）本文所构建的VP-PC策略相比于定系数算法如PID，能有效改善动子位移的控制性能。
3）本文所提的VP-PC策略在不同位移给定、控制不同对象参数的情况下均能够保证高精度的控制效果，具有一定的泛用性。
参考文献
[1] 武志涛, 李帅, 程万胜. 基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J]. 电工技术学报, 2022, 37(10): 2503-2512.
Wu Zhitao, Li Shuai, Cheng Wansheng. Fixed- structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2503-2512.
[2] Birbilen U, Lazoglu I. Design and analysis of a novel miniature tubular linear actuator[J]. IEEE Transa- ctions on Magnetics, 2018, 54(4): 1-6.
[3] Wang Ze, Hu Chuxiong, Zhu Yu, et al. Newton-ILC contouring error estimation and coordinated motion control for precision multiaxis systems with com- parative experiments[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1470-1480.
[4] Liu Yachao, Gao Jian, Zhong Yongbin, et al. Extended state observer-based IMC-PID tracking control of PMLSM servo systems[J]. IEEE Access, 2021, 9: 49036-49046.
[5] 付培华, 陈振, 丛炳龙, 等. 基于反步自适应滑模控制的永磁同步电机位置伺服系统[J]. 电工技术学报, 2013, 28(9): 288-293, 301.
Fu Peihua, Chen Zhen, Cong Binglong, et al. A position servo system of permanent magnet syn- chronous motor based on back-stepping adaptive sliding mode control[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 288-293, 301.
[6] 邵佳威, 蒋全, 倪燕青, 等. 基于改进自抗扰控制的永磁同步电机位置控制策略[J]. 控制工程, 2022, 29(8): 1487-1496.
Shao Jiawei, Jiang Quan, Ni Yanqing, et al. Position control strategy of permanent magnet synchronous motor based on improved active disturbance rejection control[J]. Control Engineering of China, 2022, 29(8): 1487-1496.
[7] 董顶峰, 黄文新, 卜飞飞, 等. 圆筒型反向式横向磁通直线电机定位力补偿二阶自抗扰控制器位置控制[J]. 电工技术学报, 2021, 36(11): 2365-2373.
Dong Dingfeng, Huang Wenxin, Bu Feifei, et al. Second-order ADRC position control with detent force compensation for tubular reversal transverse flux linear machine[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2365-2373.
[8] 许叙遥, 林辉. 基于动态滑模控制的永磁同步电机位置速度一体化设计[J]. 电工技术学报, 2014, 29(5): 77-83.
Xu Xuyao, Lin Hui. Integrated design for permanent magnet synchronous motor servo systems based on dynamic sliding mode control[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 77-83.
[9] Zhang Jianhua, Zhou Shuqing, Ren Mifeng, et al. Adaptive neural network cascade control system with entropy-based design[J]. IET Control Theory & Applications, 2016, 10(10): 1151-1160.
[10] 孙强, 张为堂. 磁通切换永磁电机模糊自适应PI控制策略[J]. 中国电机工程学报, 2017, 37(22): 6611- 6618, 6773.
Sun Qiang, Zhang Weitang. An adaptive-fuzzy PI control strategy for flux-switching permanent magnet motors[J]. Proceedings of the CSEE, 2017, 37(22): 6611-6618, 6773.
[11] 黄依婷, 沈建新, 王云冲, 等. 基于递推最小二乘法观测器的永磁同步伺服电机变参数滑模控制[J]. 中国电机工程学报, 2022, 42(18): 6835-6846.
Huang Yiting, Shen Jianxin, Wang Yunchong, et al. Variable parameter sliding mode control of permanent magnet synchronous servo motor based on recursive least square observer[J]. Proceedings of the CSEE, 2022, 42(18): 6835-6846.
[12] 许德智, 黄泊珉, 杨玮林. 神经网络自适应的永磁直线同步电机超扭曲终端滑模控制[J]. 电力系统保护与控制, 2021, 49(13): 64-71.
Xu Dezhi, Huang Bomin, Yang Weilin. Neural network adaptive super twist terminal sliding mode control for a permanent magnet linear synchronous motor[J]. Power System Protection and Control, 2021, 49(13): 64-71.
[13] Wang Ze, Hu Chuxiong, Zhu Yu, et al. Neural network learning adaptive robust control of an industrial linear motor-driven stage with disturbance rejection ability[J]. IEEE Transactions on Industrial Informatics, 2017, 13(5): 2172-2183.
[14] Yang Hongjun, Liu Jinkun. An adaptive RBF neural network control method for a class of nonlinear systems[J]. IEEE/CAA Journal of Automatica Sinica, 2018, 5(2): 457-462.
[15] 唐志勇, 马福源, 裴忠才. 四旋翼的改进PSO-RBF神经网络自适应滑模控制[J/OL]. 北京航空航天大学学报: 1-14[2022-11-10]. DOI: 10.13700/j.bh. 1001-5965.2021.0477.
Tang Zhiyong, Ma Fuyuan, Pei Zhongcai. Improved PSO-RBF neural network adaptive sliding mode control for quadrotor system[J/OL]. Journal of Beijing University of Aeronautics and Astronautics: 1-14[2022-11-10]. DOI: 10.13700/j.bh.1001-5965.2021. 0477.
[16] 王爽心, 杨辉, 张秀霞. 基于混沌遗传算法的主汽温系统RBF-PID控制[J]. 中国电机工程学报, 2008, 28(23): 87-92.
Wang Shuangxin, Yang Hui, Zhang Xiuxia. A novel RBF-PID control strategy for fresh steam temperature based on chaotic genetic algorithm[J]. Proceedings of the CSEE, 2008, 28(23): 87-92.
[17] 李明, 封航, 张延顺. 基于UMAC的RBF神经网络PID控制[J]. 北京航空航天大学学报, 2018, 44(10): 2063-2070.
Li Ming, Feng Hang, Zhang Yanshun. RBF neural network tuning PID control based on UMAC[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(10): 2063-2070.
[18] 何海军, 蒙西, 汤健, 等. 基于ET-RBF-PID的城市固废焚烧过程炉膛温度控制方法[J]. 控制理论与应用, 2022, 39(12): 2262-2273.
He Haijun, Meng Xi, Tang Jian, et al. ET-RBF-PID- based control method for furnace temperature of municipal waste incineration process[J]. Control Theory & Applications, 2022, 39(12): 2262-2273.
[19] 王卓, 王玉静, 王庆岩, 等. 基于协同深度学习的二阶段绝缘子故障检测方法[J]. 电工技术学报, 2021, 36(17): 3594-3604.
Wang Zhuo, Wang Yujing, Wang Qingyan, et al. Two stage insulator fault detection method based on collaborative deep learning[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3594-3604.
[20] 杨旭红, 陈阳, 贾巍, 等. 基于RBF神经网络的电压外环滑模控制的Vienna整流器[J]. 电力系统保护与控制, 2022, 50(18): 103-115.
Yang Xuhong, Chen Yang, Jia Wei, et al. Vienna rectifier with voltage outer loop sliding mode control based on RBF neural network[J]. Power System Protection and Control, 2022, 50(18): 103-115.
[21] 杜晓闯, 涂红兵, 黎岢, 等. 基于径向基神经网络仿真γ能谱模板库的核素识别方法[J]. 清华大学学报(自然科学版), 2021, 61(11): 1308-1315.
Du Xiaochuang, Tu Hongbin, Li Ke, et al. Radionu- clide identification method based on a gamma-spectra template library simulated by radial basis function neural networks[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(11): 1308-1315.
Abstract Apermanent magnet synchronous linear servo motor has the characteristics of high thrust density, high efficiency, and fast control response. It is widely used in rail transit, intelligent manufacturing, and aerospace fields. The electrical or mechanical parameters of the motor and nonlinear resistance interference will affect the high precision control of the linear servo. Therefore, the stable and efficient displacement control algorithm has important engineering application value to improve the system performance. Servo control can be divided into serial and parallel systems according to the relative position of displacement and velocity loop. However, whether serial or parallel control, most controller parameters need to be set in advance and are generally fixed, and adjusting the actual control effect is impossible. This paper proposes a parallel control strategy of variable parameter displacement velocity of permanent magnet synchronous linear motor based on composite neural network reconstruction object, which realizes the high-performance control of linear servo motor.
Firstly, a parallel controller with variable parameters is designed using the error information of the moving displacement and linear velocity. Then, the displacement output of the permanent magnet synchronous linear motor is reconstructed by a composite radial basis neural network containing multi-dimensional information of the control object, and the partial derivative of the displacement to the control signal is obtained. Finally, based on the closed-loop stability condition of the system, a complete parameter update strategy of parallel controller with displacement velocity is provided according to the comparison between periodic retrieval errors and control targets.
In the experiment, a permanent magnet synchronous linear servo system is designed, and different network observations, position controls, and object parameter controls are compared. The network comparison shows that the composite radial-based neural network has fast observation speed and high observation accuracy, and the observation time and root mean square error are 18.63 ms and 0.063 mm, respectively. The position control comparison shows that the variable parameter parallel algorithm has higher control precision than the fixed parameter algorithm, such as PID control, with a 30%～50% improvement effect in the displacement and velocity control error indexes. The parameter control comparison shows that in the variable parameter parallel control strategy, when the moving mass changes, the root mean square of displacement error is less than 0.015 mm, and the absolute maximum error is less than 0.060 mm, which means that the algorithm has stability and universality.
The following conclusions can be drawn: (1) The composite RBF neural network structure has better observation performance than the traditional RBF neural network. Compared with the traditional improvement method, it has a better effect with less computing pressure on the processor. (2) Compared with the fixed coefficient algorithm, such as PID, the proposed variable parameter parallel control strategy can effectively improve the control performance of the actuator displacement. (3) The variable parameter parallel control strategy can guarantee the high precision control effect under different displacement settings and object parameters.
keywords：Permanent magnet synchronous linear motor, parallel control, composite radial basis function neural network, variable parameters, update mechanism
福建省自然科学基金资助项目（2021J02023）。
收稿日期 2023-01-04
改稿日期 2023-05-18
DOI: 10.19595/j.cnki.1000-6753.tces.230104
中图分类号：TM359.4
鲍明堃 男，1998年生，硕士研究生，研究方向为现代调速系统。E-mail: 879527923@qq.com
周扬忠 男，1971年生，博士，教授，博士生导师，研究方向为现代调速系统、新能源发电系统等。E-mail: zhty_75313@sina.com（通信作者）
（编辑 陈 诚）