基于主动式阻尼的混合式步进电机转速振荡抑制控制
施 雨1 武志涛1 苏晓英1 佟文明2
(1. 辽宁科技大学电子与信息工程学院 鞍山 114051 2. 沈阳工业大学特种电机与高压电器教育部重点实验室 沈阳 110870)
摘要 混合式步进电机因其特殊的机械结构导致自身阻尼极小,在实际运行过程中会发生振荡过大,甚至失步的问题。为提高混合式步进电机的控制品质,提出一种基于主动式阻尼的步进电机转速振荡抑制方法。首先,将电机模型转化至同步旋转dq坐标系,将电流id控制恒为额定电流,利用位置误差和速度误差调节电流iq生成瞬时转矩,抑制电机运行时存在的振荡现象。其次,为实现电机闭环反馈控制,提出一种将同步频率提取滤波器(SFF)与三阶锁相环(PLL3rd)相结合的无传感器控制方法。SFF可以滤除反电动势信号中的高次谐波,PLL3rd能消除转速变化过程中的稳态误差。实验证明,该方法有效抑制了步进电机运行过程中的振荡现象,提升了电机的运行品质。
关键词:混合式步进电机 双闭环控制 主动式阻尼控制 锁相环 同步频率提取滤波器
0 引言
步进电机广泛应用于医疗、办公和工业自动化等领域。在各种类型的步进电机中,混合式步进电机(Hybrid Stepper Motor, HSM)因其拥有更高的工作效率和输出转矩,应用最为普遍[1-2]。混合式步进电机一般采用开环运行,但因其特殊的机械结构,导致电机的黏滞阻尼系数很小,在实际运行过程中易产生抖振、失步等问题,严重限制了混合式步进电机的应用场景。
为了解决上述问题,必须以外加或控制的方式增加电机的阻尼。外加阻尼的方法分为机械式和电子式,例如,文献[3]在电机轴与端盖之间放置一个阻尼胶圈,利用胶圈与转轴间的摩擦来增加阻尼。但是,机械阻尼存在安装空间,以及阻尼使用过久令造成阻尼参数改变的问题。电子式阻尼通常利用无源元件如电阻或电容改善步进电机的阻尼系数过小的问题,但此方法会减小电机的输出转矩。利用微步进(micro-stepping)控制[4]亦可有效减少由于阻尼过小所造成的振荡,但此方法仅降低振荡的幅度,并未改变其阻尼。除上述的方法之外,以闭回路的控制方式改变电机阻尼参数,也可以大幅提高步进电机的性能[5]。文献[6]在电机闭环控制过程中,根据实际值与估测值间的误差调节生成补偿电流以解决电机振荡问题,但此方法计算需基于电机参数且通过光学编码器实现闭环控制。文献[7]提出了一种基于人工神经网络的阻尼控制器,用以改善电机共振现象,但此控制器只适用于电机低速运行,且相关电机转子信息通过编码器进行反馈。外加编码器会导致系统成本增加,并且当温度变化或是处于恶劣环境时,编码器会降低电机控制系统的可靠性,而无传感器控制方式则可以避免出现上述问题。
电机无传感器控制方法一般可以分为两类,分别为低速状态下的高频信号注入法和中高速状态下的反电动势观测法。文献[8]采用脉振高频信号注入法,对估计的dq轴注入直流信号,通过功率计算跟踪最大转矩电流比工作点,提高电机的转矩输出。高频信号注入法虽然不受电机参数变化的影响,但缺点是需外加信号且信号处理过程较复杂,电机动稳态特性不理想同时会影响控制系统带宽。目前,主流方法为反电动势观测法,即通过对反电动势观测并处理获取电机转子信息。目前,主要的反电动势观测法包括模型参考自适应法、滑模观测器法、状态观测器法等。文献[9]提出基于滑模观测器的无传感器速度控制,并通过李雅普诺夫函数分析确定观测器的增益。滑模观测器法不依赖于精确的电机数学模型,且对外部扰动具有较强鲁棒性,一定程度上解决了系统参数变化及扰动带来的影响。但传统滑模观测器容易导致系统发生抖振现象[10],并且外加低通滤波器会引起相位滞后,降低了滑模观测器的观测精度。文献[11]提出了一种基于李雅普诺夫稳定理论的自适应神经网络无速度传感器控制方法,但此方法存在设计参数多及计算量大等问题。此外,该方法在高速域的观测精度也有待提高。文献[12]针对步进电机中高速运行阶段,通过龙伯格观测器获得反电动势信息,利用锁相环对反电动势进行处理得到转子位置。传统锁相环虽然可以避免微分运算引起的噪声影响,但当电机转速发生变化时其动态性能较差。
综上所述,为有效抑制步进电机实际运行过程中的振荡问题,本文提出了一种基于主动式阻尼的混合式步进电机转速振荡抑制方法。首先,该方法基于同步旋转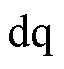 坐标系下的电机模型,将电流
坐标系下的电机模型,将电流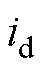 控制恒为电流额定值,利用位置与速度误差产生调节电流iq主动增加电机阻尼,以达到抑制振荡、减少稳定时间的目的。其次,主动式阻尼控制需要获取转速和位置信息,提出一种将同步频率提取滤波器(Synchronous Frequency-extract Filter, SFF)与三阶锁相环(third-order Phase Locked Loop, PLL3rd)相结合的无传感器控制方法。SFF可以滤除反电动势信号中的谐波分量,PLL3rd能消除转速变化过程中的稳态误差。最后,通过实验证明了本文设计方法的有效性。
控制恒为电流额定值,利用位置与速度误差产生调节电流iq主动增加电机阻尼,以达到抑制振荡、减少稳定时间的目的。其次,主动式阻尼控制需要获取转速和位置信息,提出一种将同步频率提取滤波器(Synchronous Frequency-extract Filter, SFF)与三阶锁相环(third-order Phase Locked Loop, PLL3rd)相结合的无传感器控制方法。SFF可以滤除反电动势信号中的谐波分量,PLL3rd能消除转速变化过程中的稳态误差。最后,通过实验证明了本文设计方法的有效性。
1 混合式步进电机数学模型
在固定坐标系中,两相混合式步进电机的数学模型[13]表示为
式中,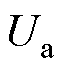 和
和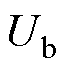 分别为
分别为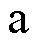 、
、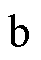 轴电压;
轴电压;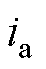 、
、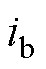 分别为
分别为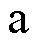 、
、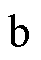 轴电流;p为微分算子,
轴电流;p为微分算子,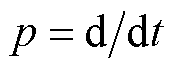 ;
;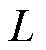 和
和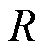 分别为定子绕组电感和电阻;
分别为定子绕组电感和电阻;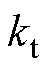 为转矩系数;
为转矩系数;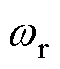 为转子电角速度;
为转子电角速度;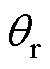 为转子电角度。
为转子电角度。
本文采用同步坐标电流控制,利用 变换将固定坐标系转化为与定子电流保持同步旋转的dq坐标系,两坐标系之间的矢量图如图1所示。
变换将固定坐标系转化为与定子电流保持同步旋转的dq坐标系,两坐标系之间的矢量图如图1所示。
转换至同步dq坐标系的电机数学模型表示为
式中,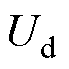 和Uq分别为
和Uq分别为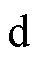 、
、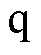 轴电压;
轴电压;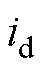 、iq分别为
、iq分别为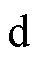 、
、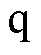 轴电流;
轴电流;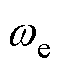 为定子电流电角速度;
为定子电流电角速度;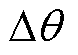 为电机负载角,
为电机负载角,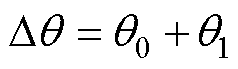 ,
,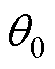 为稳态分量,
为稳态分量,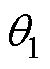 为暂态 分量。
为暂态 分量。
同步dq坐标系下的电机输出转矩方程为
步进电机的机械运动方程[14]为
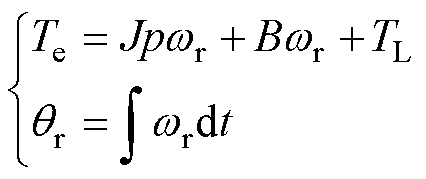 (4)
(4)
式中,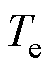 为输出转矩;
为输出转矩;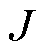 为转动惯量;
为转动惯量;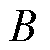 为黏滞系数;
为黏滞系数;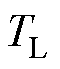 为负载转矩。
为负载转矩。
2 步进电机主动式阻尼双闭环控制
为有效抑制混合式步进电机运行过程中的振荡现象,需对电机阻尼进行控制。相比于文献[15]仅采用位置闭环对电机进行阻尼控制的方式,本文提出了一种基于位置和速度误差的主动式阻尼双闭环控制方案,结构框图如图2所示,设计两个比例阻尼增益,即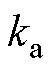 、
、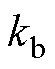 ,分别用于调节指令
,分别用于调节指令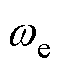 、
、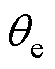 与估计的电机速度
与估计的电机速度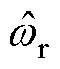 和位置
和位置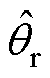 之间的误差,本文采用常规PI电流控制器。
之间的误差,本文采用常规PI电流控制器。
本文提出的主动式阻尼双闭环控制方法,将电流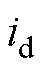 控制恒为电流额定值,利用位置与速度误差产生调节电流iq主动增加电机阻尼,以达到抑制振荡、减少稳定时间的目的。当步进电机稳态运行时,输出转矩仅由电流
控制恒为电流额定值,利用位置与速度误差产生调节电流iq主动增加电机阻尼,以达到抑制振荡、减少稳定时间的目的。当步进电机稳态运行时,输出转矩仅由电流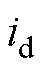 产生,当负载不超过
产生,当负载不超过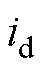 单独所能产生的最大保持转矩时,电机电流矢量和转子保持同步旋转。当电机发生振荡时,转子位置会超前或滞后于电流矢量,此时根据定子电流矢量转速
单独所能产生的最大保持转矩时,电机电流矢量和转子保持同步旋转。当电机发生振荡时,转子位置会超前或滞后于电流矢量,此时根据定子电流矢量转速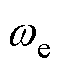 与转子观测转速
与转子观测转速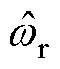 间的误差
间的误差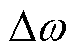 及电流矢量角度
及电流矢量角度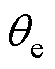 与转子观测电角度
与转子观测电角度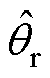 之间的误差
之间的误差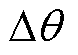 调节生成电流iq,以抑制振荡。
调节生成电流iq,以抑制振荡。
由图2可得
式中,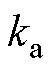 、
、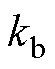 为阻尼增益;
为阻尼增益;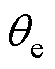 为定子电流矢量角度;
为定子电流矢量角度;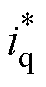 为命令电流,将式(5)代入式(3)和式(4)联立可得
为命令电流,将式(5)代入式(3)和式(4)联立可得
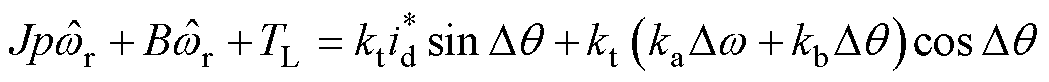 (6)
(6)
式中,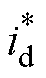 为命令电流。
为命令电流。
由于
式(6)求导后,将式(7)代入可推出
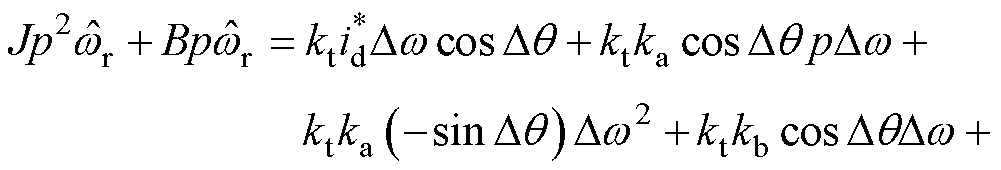
电机稳态运行时定子电流矢量转速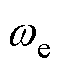 与观测转速
与观测转速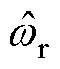 基本保持同步,因此
基本保持同步,因此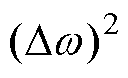 及
及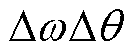 值很小可以忽略,又因为电流
值很小可以忽略,又因为电流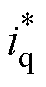 为极小的暂态值,即电流
为极小的暂态值,即电流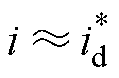 ,根据
,根据 可得暂态分量
可得暂态分量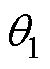 角度很小,即
角度很小,即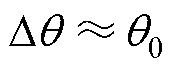 。因此,由式(8)可得传递函数为
。因此,由式(8)可得传递函数为
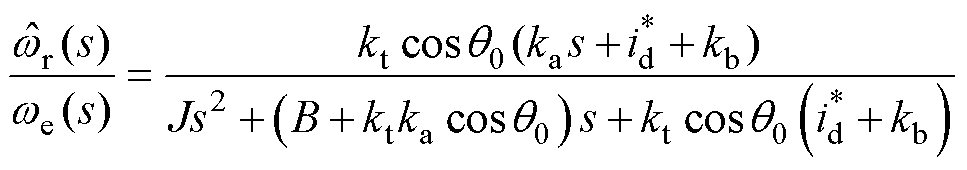 (9)
(9)
标准二阶系统传递函数表示为
将式(9)与式(10)相对照可得自然频率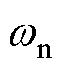 和阻尼比
和阻尼比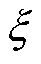 可以分别表示为
可以分别表示为
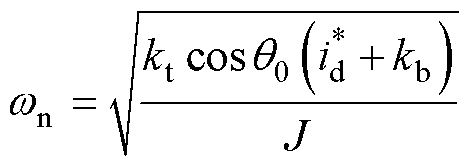 (11)
(11)
根据式(12)可知,阻尼增益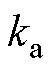 、
、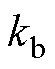 的改变可以有效调节系统阻尼比。同时,式(9)表明,此时控制系统的根轨迹亦是
的改变可以有效调节系统阻尼比。同时,式(9)表明,此时控制系统的根轨迹亦是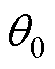 的函数,为了解析其对控制系统的影响,进行根轨迹分析。
的函数,为了解析其对控制系统的影响,进行根轨迹分析。
图3a给出了当阻尼比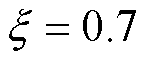 时(通过调节
时(通过调节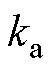 、
、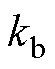 值),
值),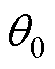 从0°~90°的根轨迹,由图可知,当电机以远小于90°的负载角运行时,控制系统是稳定的。图3b给出了
从0°~90°的根轨迹,由图可知,当电机以远小于90°的负载角运行时,控制系统是稳定的。图3b给出了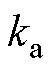 与
与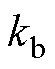 均为零即无阻尼控制时的根轨迹,由图可以看出,无阻尼控制时,步进电机的系统响应是振荡的,因为其根轨迹非常靠近虚轴。
均为零即无阻尼控制时的根轨迹,由图可以看出,无阻尼控制时,步进电机的系统响应是振荡的,因为其根轨迹非常靠近虚轴。
基于上述根轨迹分析,可知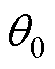 对主动式阻尼控制系统存在较大影响,为防止传递函数的极点随着
对主动式阻尼控制系统存在较大影响,为防止传递函数的极点随着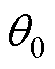 变化,阻尼增益
变化,阻尼增益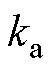 、
、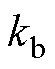 的计算公式为
的计算公式为
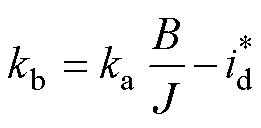 (14)
(14)
式中,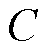 为常数。
为常数。
将式(13)、式(14)代入式(9)中,可得
此时,系统传递函数与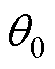 无关。
无关。
3 SFF-PLL3rd速度观测器
3.1 基于三阶锁相环(PLL3rd)的速度观测器
获取电机转子位置和速度信息是实现电机主动式阻尼双闭环控制的重要环节,本文设计了一种基于三阶锁相环(PLL3rd)的速度观测器。
根据式(1)可得电机的反电动势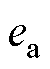 、
、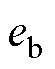 表示为
表示为
由式(16)可得反电动势中包含了电机转子信息,通过反正切运算后即可获得转子位置。
 (17)
(17)
再对转子位置信息进行微分就可以得到转子速度,但微分运算将放大高频噪声,会降低速度观测器的观测精度。反电动势信号输出后利用锁相环对其进行处理,能避免微分运算引起的噪声影响[16]。
基于文献[17]中设计的传统锁相环(Phase Locked Loop, PLL),通过对其分析可得电机转速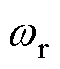 与观测转速
与观测转速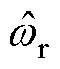 间的传递函数为
间的传递函数为
式中,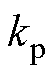 、
、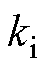 分别为锁相环的比例和积分增益。PLL实际转速
分别为锁相环的比例和积分增益。PLL实际转速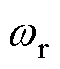 与观测转速
与观测转速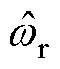 之间的误差
之间的误差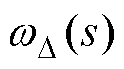 表示为
表示为
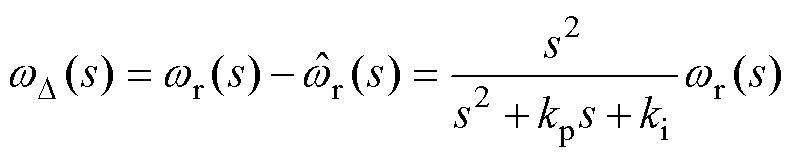 (19)
(19)
利用终值定理分析电机在恒定速度(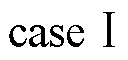 )以及加减速状态(
)以及加减速状态(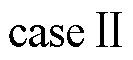 )下的稳态误差
)下的稳态误差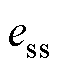 为
为
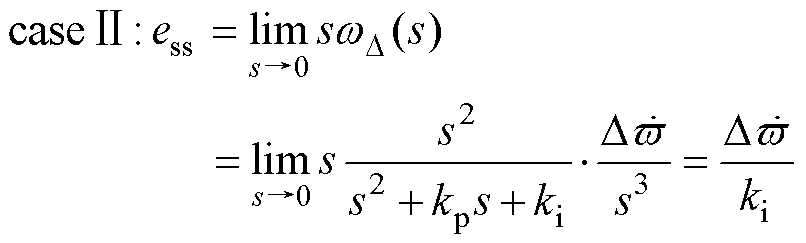 (21)
(21)
式中,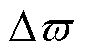 为电机加减速状态下的速度变化率。由式(21)可得,基于传统锁相环(PLL)的步进电机在加速或减速运行时存在稳态误差
为电机加减速状态下的速度变化率。由式(21)可得,基于传统锁相环(PLL)的步进电机在加速或减速运行时存在稳态误差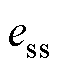 。针对此问题,本文设计了一种三阶锁相环(PLL3rd)以消除稳态误差。三阶锁相环结构框图如图4所示。
。针对此问题,本文设计了一种三阶锁相环(PLL3rd)以消除稳态误差。三阶锁相环结构框图如图4所示。
由图4可知
其中
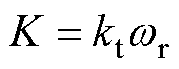
当角度跟踪误差较小时可得
根据图4和式(23)可得PLL3rd闭环传递函数表示为
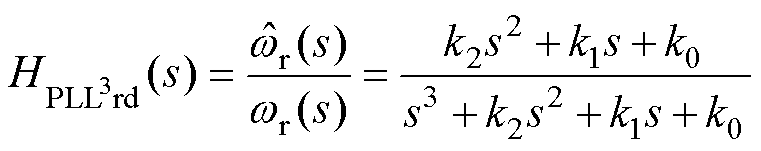 (24)
(24)
式中,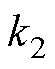 、
、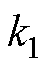 和
和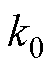 为三阶锁相环增益。PLL3rd中的误差
为三阶锁相环增益。PLL3rd中的误差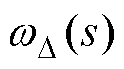 表示为
表示为
此时,电机在恒定速度(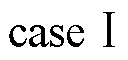 )以及加减速(
)以及加减速(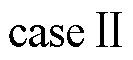 )状态下的稳态误差为
)状态下的稳态误差为
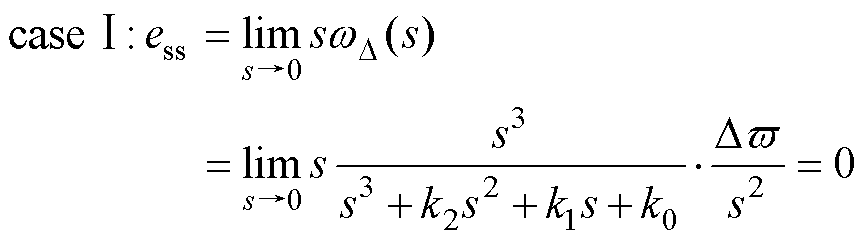 (26)
(26)
将式(27)和式(21)对比分析可得,PLL3rd可以有效消除电机的稳态误差,在加减速状态下将稳态误差降为零。
3.2 同步频率提取滤波器(SFF)
由式(16)得到的反电动势信号中常含有大量谐波分量[18],表示为
式中,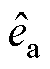 、
、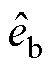 为反电动势观测值;
为反电动势观测值;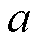 为基波分量的幅值;
为基波分量的幅值;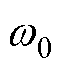 为基波频率;
为基波频率;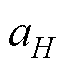 为谐波分量的幅值;
为谐波分量的幅值;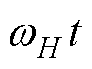 为
为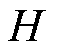 次谐波分量的频率。
次谐波分量的频率。
锁相环虽然可以对反电动势信号进行处理得到转子信息,但无法抑制谐波分量对观测器精度的影响,为了提高速度观察器的观测精度,本文先利用同步频率提取滤波器(SFF)对反电动势的基波分量进行提取,再将处理后的信号送入PLL3rd获取转子信息,SFF结构框图如图5所示。
通过式(28)和图5的结构框图,可得
式中,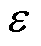 为滤波器增益;
为滤波器增益;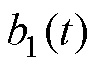 、
、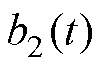 为滤波器中间过程量;
为滤波器中间过程量;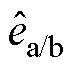 表示滤波器输入信号为
表示滤波器输入信号为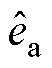 或
或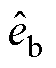 ;
;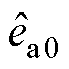 、
、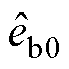 为同步频率提取滤波器的输出结果。对式(29)进行拉氏变换可得
为同步频率提取滤波器的输出结果。对式(29)进行拉氏变换可得
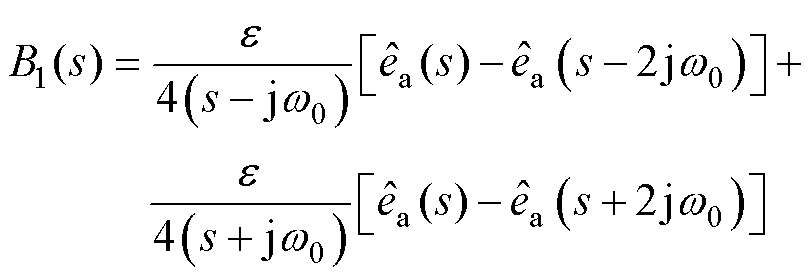 (30)
(30)
因此,同步频率提取滤波器的传递函数表示为
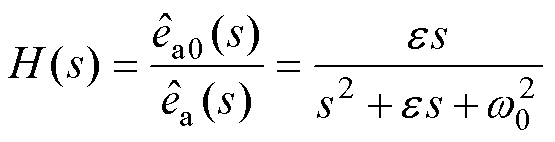 (32)
(32)
由式(32)可得其幅频特性为
根据式(33)可得若频率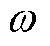 =
=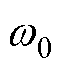 ,则SFF的幅值等于1,反电动势信号的基波分量可以无衰减地通过SFF。若输入频率
,则SFF的幅值等于1,反电动势信号的基波分量可以无衰减地通过SFF。若输入频率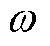 大于或小于
大于或小于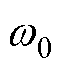 ,SFF的幅值将会大幅衰减。因此,SFF可以有效提取频率为
,SFF的幅值将会大幅衰减。因此,SFF可以有效提取频率为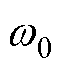 的信号,并滤除其他频率的干扰。
的信号,并滤除其他频率的干扰。
4 实验与分析
为验证本文提出的主动式阻尼双闭环控制方法的有效性,本实验所用混合式步进电机的参数见表1。基于STM32F407开发板的电机控制实验装置如图6所示,带负载转矩为额定值1.2 N×m,同时采用N38-06-N型600线增量型旋转编码器(未参与控制,仅用于对比观测值)测量电机真实速度,以对比验证速度观测器的有效性。
表1 混合式步进电机参数
Tab.1 Parameters of HSM
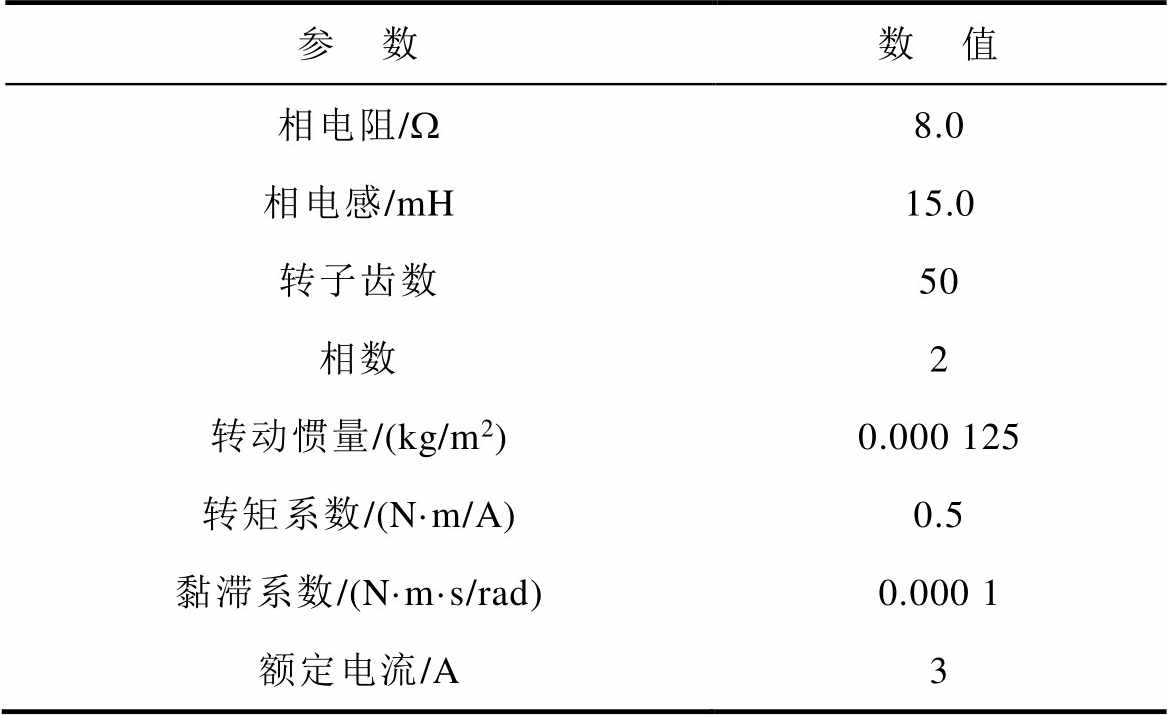
参 数数 值 相电阻/W8.0 相电感/mH15.0 转子齿数50 相数2 转动惯量/(kg/m2)0.000 125 转矩系数/(N·m/A)0.5 黏滞系数/(N·m·s/rad)0.000 1 额定电流/A3
4.1 HSM反电动势信号分析实验
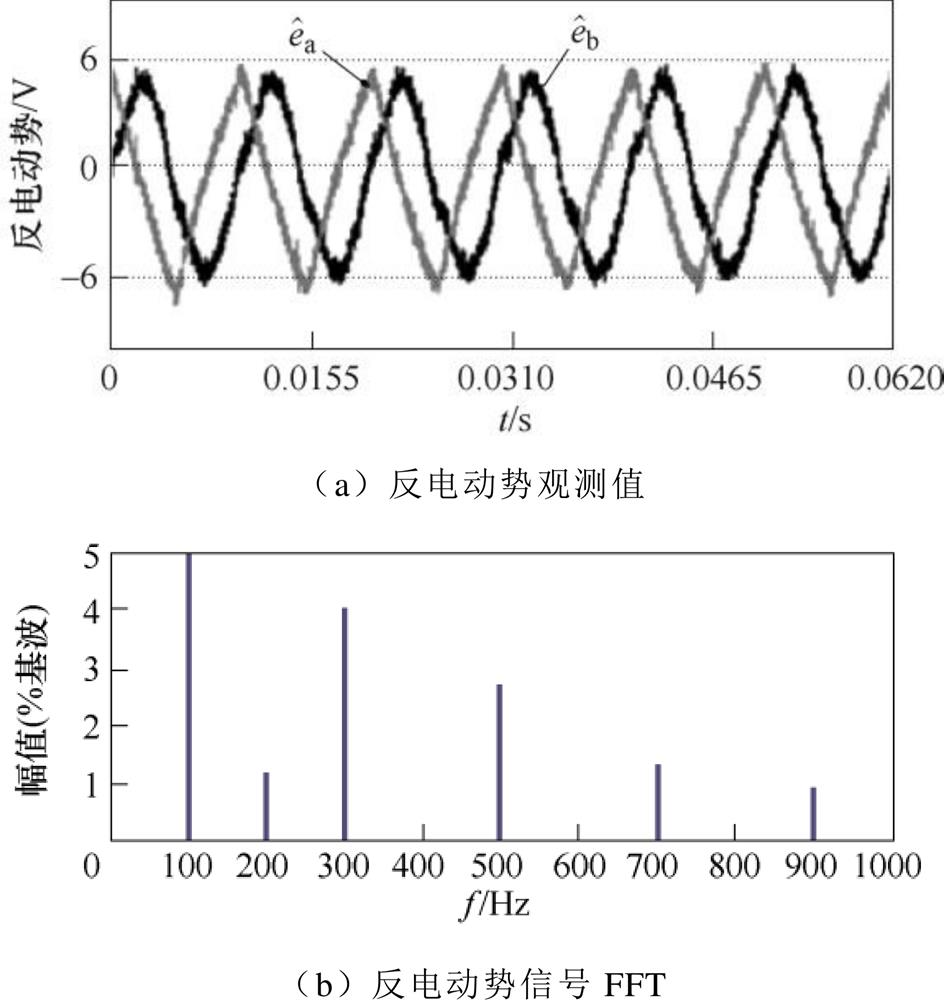
分别采用传统PLL及SFF-PLL3rd观测器运行,反电动势信号及傅里叶分析实验结果如图7、图8所示。
图7为在额定负载下,转速恒为100 Hz时采用传统PLL方法获得的实验结果。图7a中反电动势信号发生明显畸变,信号中含有谐波分量。利用傅里叶变换(Fast Fourier Transform, FFT)分析反电动势信号中的谐波成分,其中谐波分量的主要成分为3、5、7次谐波,如图7b所示。
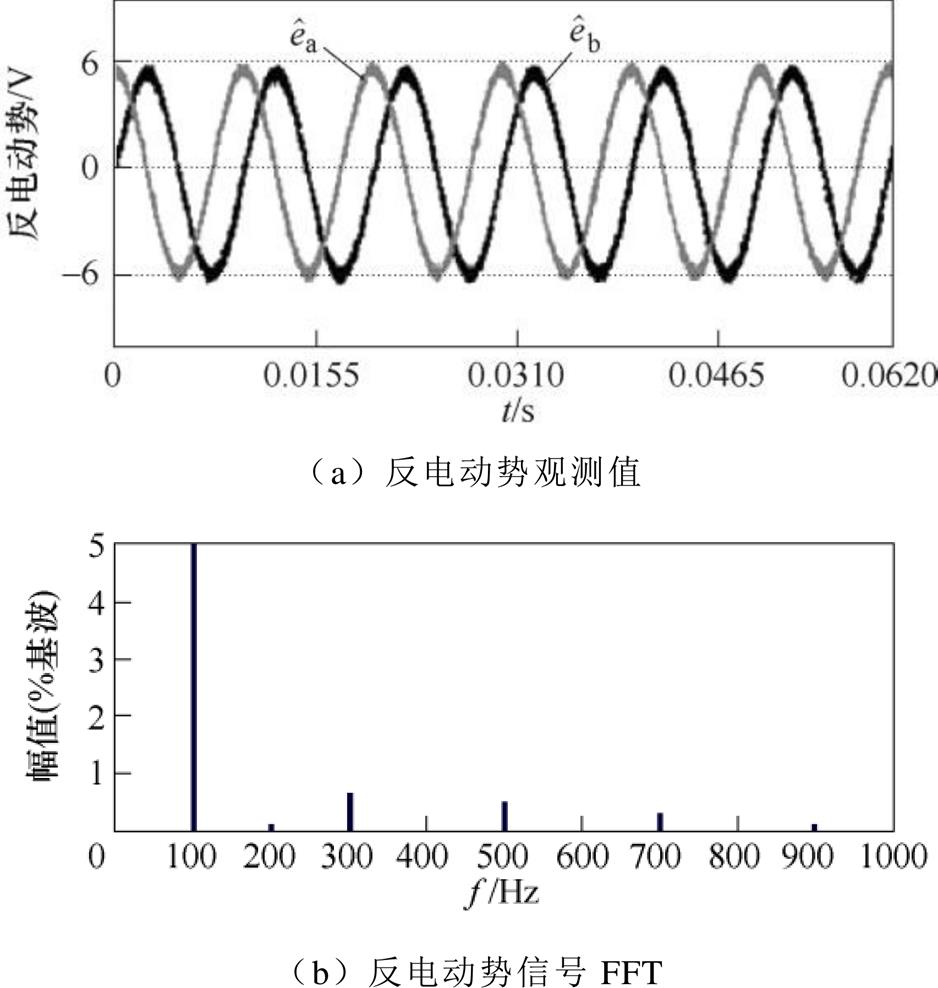
图8为转速恒为100 Hz时,电机在额定负载下通过SFF-PLL3rd方法获得的实验结果。图8a与图7a对比可得,反电动势波形更加平滑。图8b与图7b对比可知,2、3、5、7次谐波分量幅值明显减小,证明SFF能有效滤除其他频率的干扰。由上述实验可得,本文提出的SFF-PLL3rd的信号处理方法有效滤除反电动势中的谐波分量,提高信息观测精度。
4.2 混合式步进电机转速振荡抑制实验
本文提出的阻尼控制的设计原则是在电机低速运行时,阻尼控制可以对转速振荡现象起到一定抑制效果(可用性原则),而在中高速时,阻尼控制能有效抑制转速振荡(有效性原则)。因此,在不同转速下,验证基于主动式阻尼的双闭环控制方法对混合式步进电机转速振荡的抑制效果。
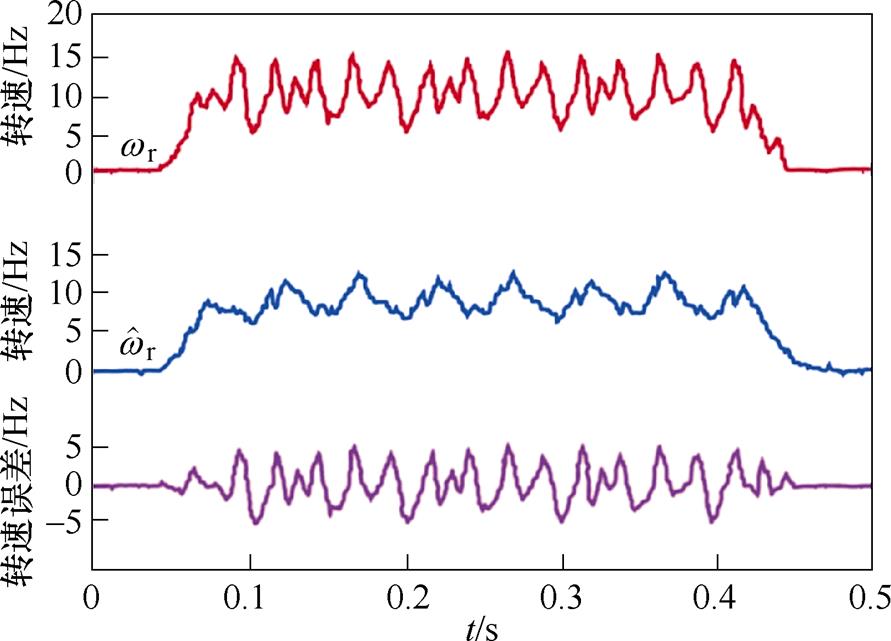
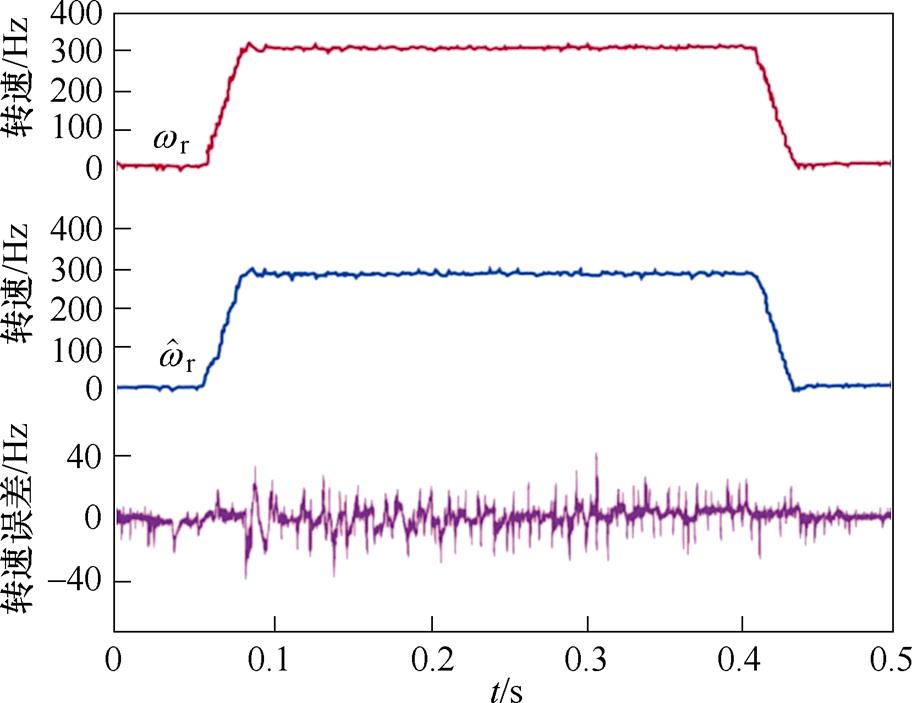
图9、图10分别为步进电机在无/有主动式阻尼控制下,电机转速从0 Hz加速至10 Hz最后减速至静止状态的转速响应曲线,图中自上而下依次为实际转速、估测转速以及实际转速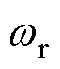 与估测转速
与估测转速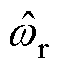 间的误差曲线。由图9可见,当无阻尼控制时,转速曲线存在明显振荡现象,这是由于实际转速与估测转速间存在较大误差,实际转速
间的误差曲线。由图9可见,当无阻尼控制时,转速曲线存在明显振荡现象,这是由于实际转速与估测转速间存在较大误差,实际转速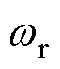 与估测转速
与估测转速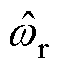 间最大转速误差约为6 Hz。对比图9和图10可见,阻尼控制使转速曲线的振荡幅度相较无阻尼时减小,电机实际转速
间最大转速误差约为6 Hz。对比图9和图10可见,阻尼控制使转速曲线的振荡幅度相较无阻尼时减小,电机实际转速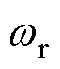 与估测转速
与估测转速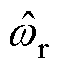 间误差减小至4 Hz。由上述结果可知,本文提出的主动式阻尼双闭环控制在电机低速运行状态下能抑制电机运行过程中的振荡现象。
间误差减小至4 Hz。由上述结果可知,本文提出的主动式阻尼双闭环控制在电机低速运行状态下能抑制电机运行过程中的振荡现象。
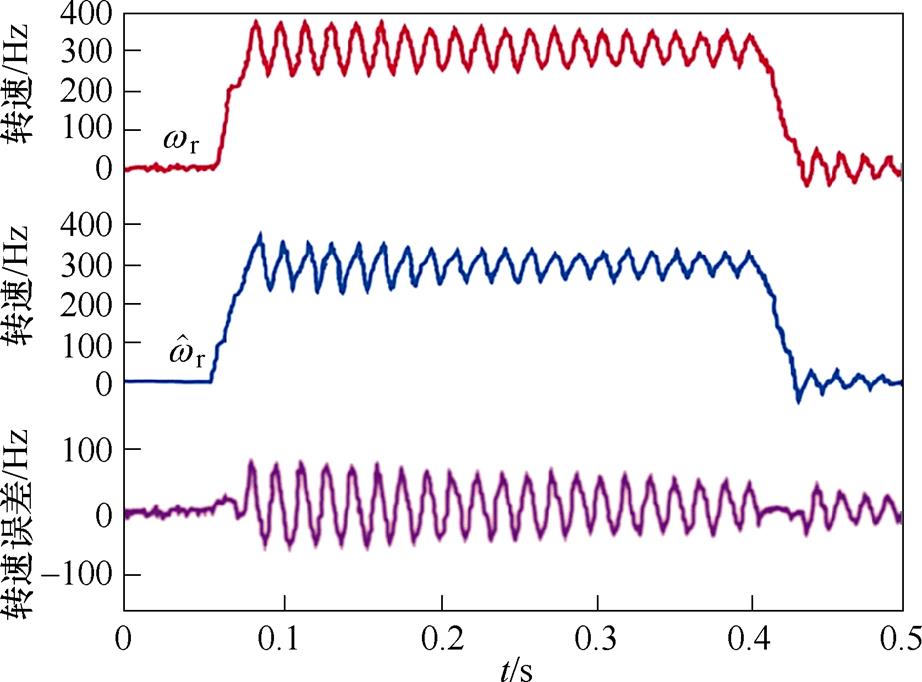
图11、图12为电机从0 Hz加速至300 Hz最后减速至静止状态的实验结果。由图11可见,无阻尼控制时,电机转速存在明显振荡,振荡持续时间较长,这是由于混合式步进电机阻尼较小导致的,实际转速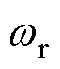 与估测转速
与估测转速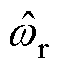 间的最大转速误差约为90 Hz。图11与图12对比可见,阻尼控制使电机的转速振荡得到有效抑制,转速变化过程平稳,实际转速
间的最大转速误差约为90 Hz。图11与图12对比可见,阻尼控制使电机的转速振荡得到有效抑制,转速变化过程平稳,实际转速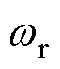 与估测转速
与估测转速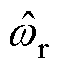 误差减小至36 Hz左右。观测器输出的估测转速
误差减小至36 Hz左右。观测器输出的估测转速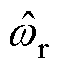 曲线也更为平稳,与实际转速曲线相近。此外,将图10和图12对比可见,本文提出的主动式阻尼双闭环控制方法在电机转速较大时抑制振荡的效果更好。
曲线也更为平稳,与实际转速曲线相近。此外,将图10和图12对比可见,本文提出的主动式阻尼双闭环控制方法在电机转速较大时抑制振荡的效果更好。
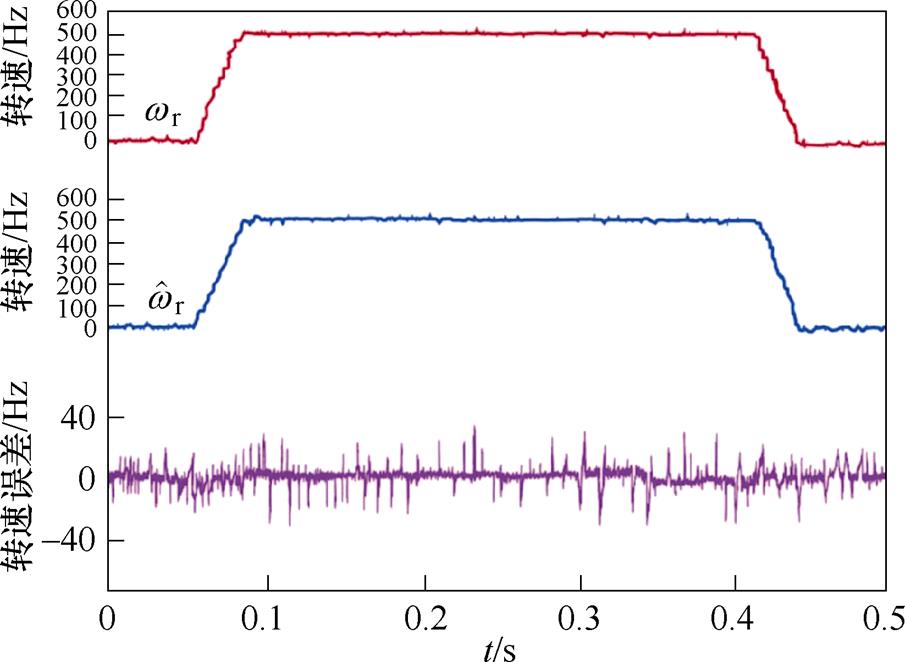
图13、图14为电机转速由0 Hz加速至500 Hz后减速至0 Hz的实验结果。图13与图11结果相似,由于电机阻尼较小导致电机加速到稳态时仍然存在振荡现象,持续时间较长,实际转速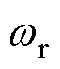 与估测转速
与估测转速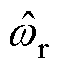 间的误差约为70 Hz。由图14可以看出,阻尼控制对电机转速振荡的抑制效果明显,实际转速和估测转速间误差明显减小约为35 Hz,步进电机呈现稳态运行,观测器输出的电机转速
间的误差约为70 Hz。由图14可以看出,阻尼控制对电机转速振荡的抑制效果明显,实际转速和估测转速间误差明显减小约为35 Hz,步进电机呈现稳态运行,观测器输出的电机转速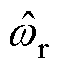 与实际转速曲线相近。由此可得,在高速状态下主动式阻尼双闭环控制能有效抑制电机实际运行中的振荡现象。此外,将图14与图10、图12对比可见,随着转速的增大,主动式阻尼控制对抑制电机振荡的效果也更为明显。
与实际转速曲线相近。由此可得,在高速状态下主动式阻尼双闭环控制能有效抑制电机实际运行中的振荡现象。此外,将图14与图10、图12对比可见,随着转速的增大,主动式阻尼控制对抑制电机振荡的效果也更为明显。
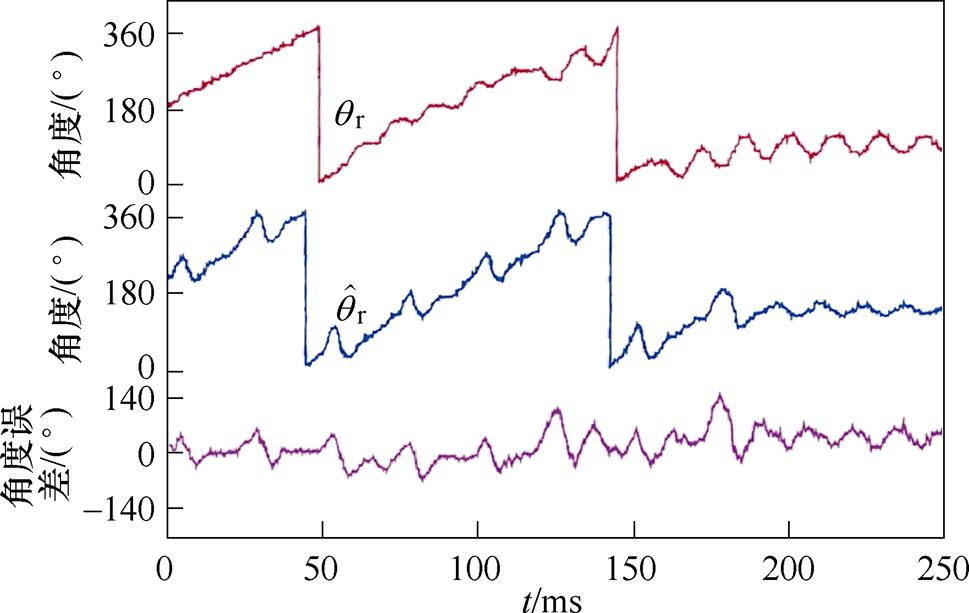
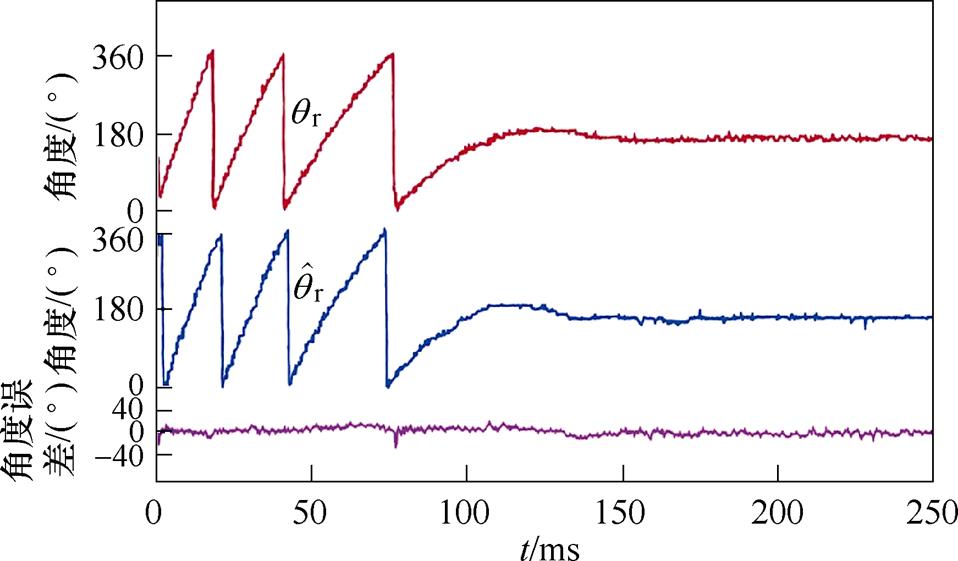
图15、图16分别为步进电机在无/有主动式阻尼控制下,电机转速由10 Hz减速至0 Hz时的转子位置响应曲线,图中自上而下依次为实际转子电角度、估测转子电角度及误差曲线。由图15可见,转子角度曲线存在明显振荡,因为实际转子电角度和估测转子电角度间误差较大,实际转子电角度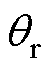 和估测角度间的最大误差约为135°。由图16可见,阻尼控制使转子电角度曲线振荡幅度减小,实际转子电角度
和估测角度间的最大误差约为135°。由图16可见,阻尼控制使转子电角度曲线振荡幅度减小,实际转子电角度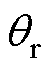 和观测电角度之间的误差减小为112°,并且电机减速至0 Hz后,转子快速趋于稳定静止状态。
和观测电角度之间的误差减小为112°,并且电机减速至0 Hz后,转子快速趋于稳定静止状态。
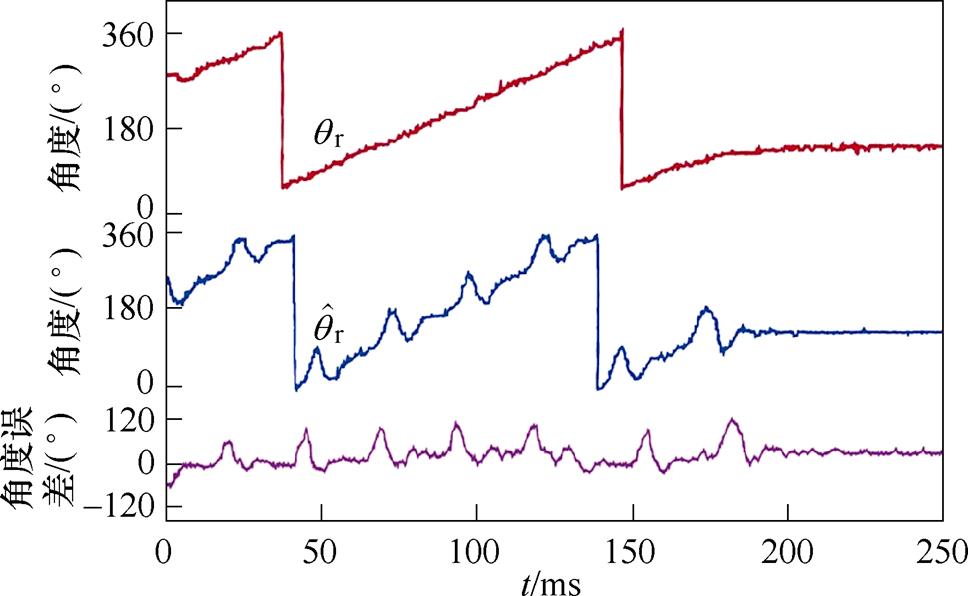
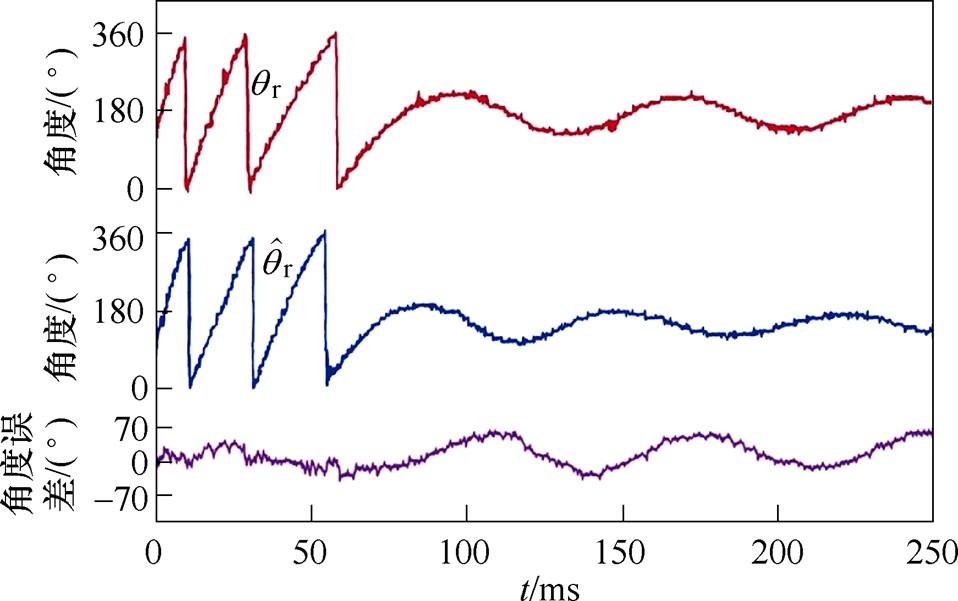
图17、图18分别为电机在无/有阻尼控制下,电机转速由300 Hz减速至0 Hz时的实验结果。由图17可见,由于混合式步进电机阻尼较小导致转子电角度曲线存在明显振荡,实际转子电角度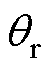 和估测转子电角度之间误差约为90°。由图18可见,阻尼控制使电机减速至静止的过程无明显振荡,实际转子电角度
和估测转子电角度之间误差约为90°。由图18可见,阻尼控制使电机减速至静止的过程无明显振荡,实际转子电角度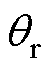 和估测电角度的最大误差减小至约为40°,估测转子电角度曲线也更为平稳,与实际转子电角度曲线结果相近似。
和估测电角度的最大误差减小至约为40°,估测转子电角度曲线也更为平稳,与实际转子电角度曲线结果相近似。
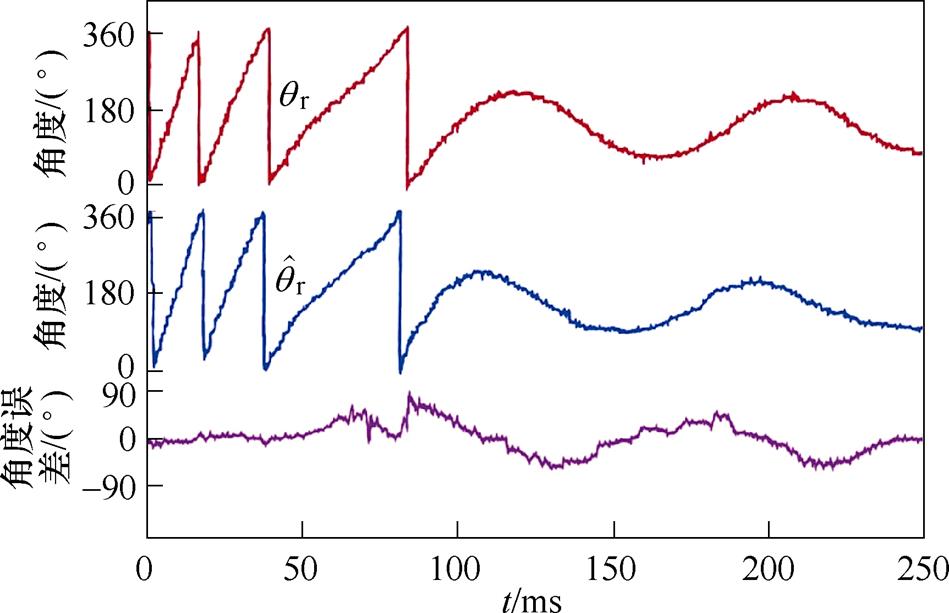
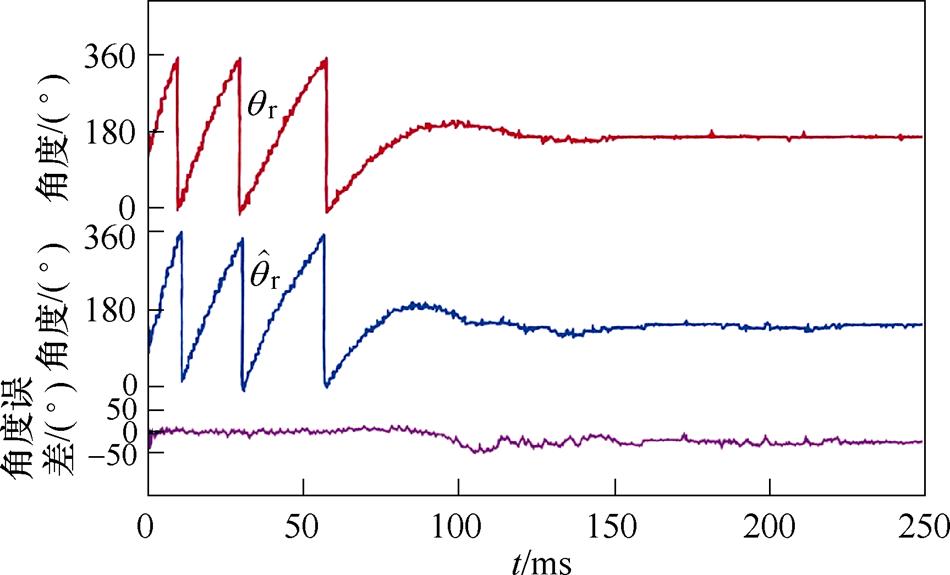
图19、图20分别为电机在无/有阻尼控制下,电机转速由500 Hz减速至0 Hz时的实验结果。由图19可以看出,电机阻尼较小导致转子曲线存在振荡现象,实际转子电角度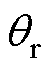 和估测角度间的最大误差约为65°。由图20可见,阻尼控制使电机减速至静止的过程无振荡现象,两角度间的误差减少约为45°,观测器输出的估测转子电角度与实际转子电角度曲线基本一致。由此可得,基于主动式阻尼的混合式步进电机转速振荡抑制方法可以有效地改善步进电机阻尼过小的缺点,使电机减速至静止的过程无振荡现象。
和估测角度间的最大误差约为65°。由图20可见,阻尼控制使电机减速至静止的过程无振荡现象,两角度间的误差减少约为45°,观测器输出的估测转子电角度与实际转子电角度曲线基本一致。由此可得,基于主动式阻尼的混合式步进电机转速振荡抑制方法可以有效地改善步进电机阻尼过小的缺点,使电机减速至静止的过程无振荡现象。
5 结论
本文提出了一种基于主动式阻尼的步进电机转速振荡抑制方法。该方法通过将电流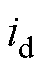 控制恒为电流额定值,利用位置与速度误差产生调节电流主动式增加电机阻尼,可以达到抑制振荡、减少稳定时间的目的。此外,为实现闭环控制,设计SFF-PLL3rd速度观测器获取电机转子位置和速度信息,SFF可以滤除信号中的谐波分量,同时PLL3rd能有效消除电机加减速运行过程中的稳态误差。实验结果证明,本文提出的控制方案可以有效改善步进电机阻尼过小的缺点,并抑制实际运行过程中的振荡现象,使电机平稳运行。
控制恒为电流额定值,利用位置与速度误差产生调节电流主动式增加电机阻尼,可以达到抑制振荡、减少稳定时间的目的。此外,为实现闭环控制,设计SFF-PLL3rd速度观测器获取电机转子位置和速度信息,SFF可以滤除信号中的谐波分量,同时PLL3rd能有效消除电机加减速运行过程中的稳态误差。实验结果证明,本文提出的控制方案可以有效改善步进电机阻尼过小的缺点,并抑制实际运行过程中的振荡现象,使电机平稳运行。
参考文献
[1] Normanyo E, Agyare O R, Rashid R A. Matlab implementation of position control of a hybrid stepper motor using fuzzy logic controller[C]//2019 IEEE AFRICON, Accra, Ghana, 2020: 1-8.
[2] Kim S K, Ahn C K. Variable-performance positioning law for hybrid-type stepper motors via active damping injection and disturbance observer[J]. IEEE Transa- ctions on Circuits and Systems II: Express Briefs, 2021, 68(4): 1308-1312.
[3] Kenjō T. Stepping motors and their microprocessor controls[M]. Oxford: Clarendon Press, 1984.
[4] 陈学军. 步进电机细分驱动控制系统的研究与实现[J]. 电机与控制应用, 2006, 33(6): 48-50.
Chen Xuejun. Research and realization of subdivided driving system of stepping motor[J]. Electric Machines & Control Application, 2006, 33(6): 48-50.
[5] Sun Hongbo, Jiang Dong, Yang Jichang. Synchronous vibration suppression of magnetic bearing systems without angular sensors[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 70-77.
[6] Le K M, Van Hoang H, Jeon J W. An advanced closed-loop control to improve the performance of hybrid stepper motors[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 7244-7255.
[7] Le Q N, Jeon J W. Neural-network-based low-speed- damping controller for stepper motor with an FPGA[J]. IEEE Transactions on Industrial Electronics, 2010, 57(9): 3167-3180.
[8] 赵文祥, 刘桓, 陶涛, 等. 基于虚拟信号和高频脉振信号注入的无位置传感器内置式永磁同步电机MTPA控制[J]. 电工技术学报, 2021, 36(24): 5092- 5100.
Zhao Wengxiang, Liu Huan, Tao Tao, et al. MTPA control of sensorless IPMSM based on virtual signal and high-frequency pulsating signal injection[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5092-5100.
[9] Saadaoui O, Khlaief A, Abassi M, et al. A sliding- mode observer for high-performance sensorless control of PMSM with initial rotor position dete- ction[J]. International Journal of Control, 2017, 90(2): 377-392.
[10] 梅三冠, 卢闻州, 樊启高, 等. 基于滑模观测器误差补偿的永磁同步电机无位置传感器控制策略[J]. 电工技术学报, 2023, 38(2): 398-408.
Mei Sanguan, Lu Wenzhou, Fan Qigao, et al. Sensorless control strategy of permanent magnet synchronous motor based on error compensation estimated by sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 398- 408.
[11] Zhang Guoqiang, Wang Gaolin, Xu Dianguo, et al. ADALINE-network-based PLL for position sensorless interior permanent magnet synchronous motor drives[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1450-1460.
[12] Du Bochao, Wu Shaopeng, Han Shouliang, et al. Application of linear active disturbance rejection controller for sensorless control of internal permanent- magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3019-3027.
[13] Wang Chunlei, Cao Dongxing. New sensorless speed control of a hybrid stepper motor based on fuzzy sliding mode observer[J]. Energies, 2020, 13(18): 4939.
[14] 战家治, 崔皆凡. 基于神经网络的两相混合式步进电机反步控制[J]. 电机与控制应用, 2022, 49(1): 28-33, 55.
Zhan Jiazhi, Cui Jiefan. Backstepping control of two-phase hybrid stepping motor based on neural network[J]. Electric Machines & Control Application, 2022, 49(1): 28-33, 55.
[15] Yang Shengming, Su P D. Active damping control of hybrid stepping motor[C]//4th IEEE International Conference on Power Electronics and Drive Systems, Denpasar, Indonesia, 2002: 749-754.
[16] 王晓琳, 刘思豪, 顾聪. 基于自适应基准锁相环的高速永磁电机转子位置误差全补偿方法[J]. 电工技术学报, 2021, 36(20): 4308-4317.
Wang Xiaolin, Liu Sihao, Gu Cong. A rotor position error compensation algorithm for high-speed per- manent magnet motor based on phase-locked loop with adaptive reference[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4308-4317.
[17] 王菁, 颜建虎, 季国东, 等. 一种基于双位置观测器的永磁同步电机低速无位置传感器控制方法[J]. 电工技术学报, 2023, 38(2): 375-386.
Wang Jing, Yan Jianhu, Ji Guodong, et al. A sensorless control method for permanent magnet synchronous machine based on dual position obser- vers at low speed[J]. Transactions of China Elec- trotechnical Society, 2023, 38(2): 375-386.
[18] 李垣江, 苗奎星, 魏海峰, 等. 基于带通频率跟踪滤波器的永磁同步电机转子位置与速度估算[J]. 电工技术学报, 2022, 37(21): 5402-5413.
Li Yuanjiang, Miao Kuixing, Wei Haifeng, et al. Permanent magnet synchronous motor rotor position and speed estimation methodology based on band- pass frequency tracking filter[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5402- 5413.
Hybrid Stepper Motor Speed Oscillation Suppression Control Based on Active Damping
Shi Yu1 Wu Zhitao1 Su Xiaoying1 Tong Wenming2
(1. School of Electronic and Information Engineering University of Science and Technology Liaoning Anshan 114051 China 2. Key Laboratory of Special Machine and High Voltage Apparatus Ministry of Education Shenyang University of Technology Shenyang 110870 China)
Abstract Hybrid stepper motors are widely used in medical and industrial automation due to their high efficiency and output torque. The stepper motor generally uses open-loop operation. However, its special mechanical structure can lead to a small viscous damping coefficient of the motor, which is sensitive to jitter vibration and prone to step loss during actual operation. This paper proposes an active damping-based method for suppressing speed oscillations in hybrid stepper motors.
A motor model is established in the synchronous rotating coordinate system, and the current id is controlled as a constant current rating. The motor damping is increased by position and speed errors to generate the regulation current iq, which produces instantaneous torque to suppress oscillation. Damping control requires speed and position information. Thus, a sensorless control method with a synchronous frequency-extract filter (SFF) and third-order phase-locked loop (PLL3rd) is proposed. SFF can filter harmonic components in the back EMF, and PLL3rd can eliminate steady-state errors during speed variation.
The motor speed is set constant at 100 Hz to compare conventional PLL and the SFF-PLL3rd methods under rated loads. The conventional PLL observes a distorted back EMF signal containing harmonic components. The SFF-PLL3rd method achieves a smoother back EMF waveform with reduced 2nd, 3rd, 5th, and 7th harmonic components, indicating improved rotor information observation accuracy.
Subsequently, speed curves between undamped and damping control are compared at different speeds. The motor speed is accelerated from 0 Hz to 10 Hz and decelerated to a standstill, with a maximum speed difference of approximately 6 Hz between the actual and estimated speed. With damping control, the speed oscillation is reduced, and the difference between the actual and estimated speed is reduced to 4 Hz. When the motor accelerates from 0 Hz to 300 Hz and then decelerates to a standstill, the speed oscillation is obvious without damping control, and the maximum speed error is about 90 Hz. Damping control effectively suppresses speed oscillation by reducing the difference to about 36 Hz. When the motor speed is accelerated from 0 Hz to 500 Hz and then decelerated to 0 Hz, the difference is about 70 Hz without damping control. In contrast, damping control suppresses speed oscillation with a difference of about 35 Hz. The stepper motor shows steady-state operation.
The experimental results indicate that the proposed control can suppress oscillation during motor operation at low speeds. As the speed increases, the effect of damping control on motor oscillation suppression becomes more apparent. The overall control scheme effectively improves insufficient damping of the stepper motor and suppresses oscillation during the actual operation, resulting in smooth motor operation.
keywords:Hybrid stepper motor, dual closed-loop control, active damping control, phase locked loop, synchronous frequency-extract filter
辽宁省自然科学基金计划项目(2022-KF-14-03)和特种电机与高压电器教育部重点实验室开放课题项目(KFKT202104)资助。
收稿日期 2023-03-01
DOI: 10.19595/j.cnki.1000-6753.tces.230235
中图分类号:TM383.6
作者简介
施 雨 女,1997年生,硕士研究生,研究方向为混合式步进电机的控制。E-mail: sshhiyu@163.com
武志涛 男,1981年生,博士,副教授,研究方向为直线电机伺服驱动技术。E-mail: aswzt@163.com(通信作者)
改稿日期 2023-04-04
(编辑 崔文静)
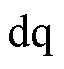 坐标系下的电机模型,将电流
坐标系下的电机模型,将电流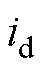 控制恒为电流额定值,利用位置与速度误差产生调节电流iq主动增加电机阻尼,以达到抑制振荡、减少稳定时间的目的。其次,主动式阻尼控制需要获取转速和位置信息,提出一种将同步频率提取滤波器(Synchronous Frequency-extract Filter, SFF)与三阶锁相环(third-order Phase Locked Loop, PLL3rd)相结合的无传感器控制方法。SFF可以滤除反电动势信号中的谐波分量,PLL3rd能消除转速变化过程中的稳态误差。最后,通过实验证明了本文设计方法的有效性。
控制恒为电流额定值,利用位置与速度误差产生调节电流iq主动增加电机阻尼,以达到抑制振荡、减少稳定时间的目的。其次,主动式阻尼控制需要获取转速和位置信息,提出一种将同步频率提取滤波器(Synchronous Frequency-extract Filter, SFF)与三阶锁相环(third-order Phase Locked Loop, PLL3rd)相结合的无传感器控制方法。SFF可以滤除反电动势信号中的谐波分量,PLL3rd能消除转速变化过程中的稳态误差。最后,通过实验证明了本文设计方法的有效性。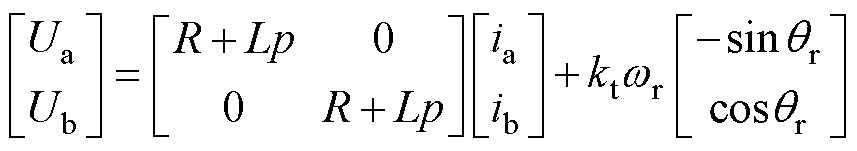 (1)
(1)
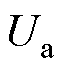 和
和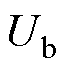 分别为
分别为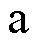 、
、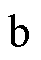 轴电压;
轴电压;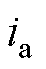 、
、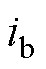 分别为
分别为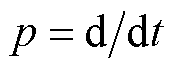 ;
;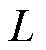 和
和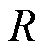 分别为定子绕组电感和电阻;
分别为定子绕组电感和电阻;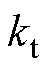 为转矩系数;
为转矩系数;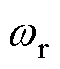 为转子电角速度;
为转子电角速度;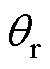 为转子电角度。
为转子电角度。 变换将固定坐标系转化为与定子电流保持同步旋转的dq坐标系,两坐标系之间的矢量图如图1所示。
变换将固定坐标系转化为与定子电流保持同步旋转的dq坐标系,两坐标系之间的矢量图如图1所示。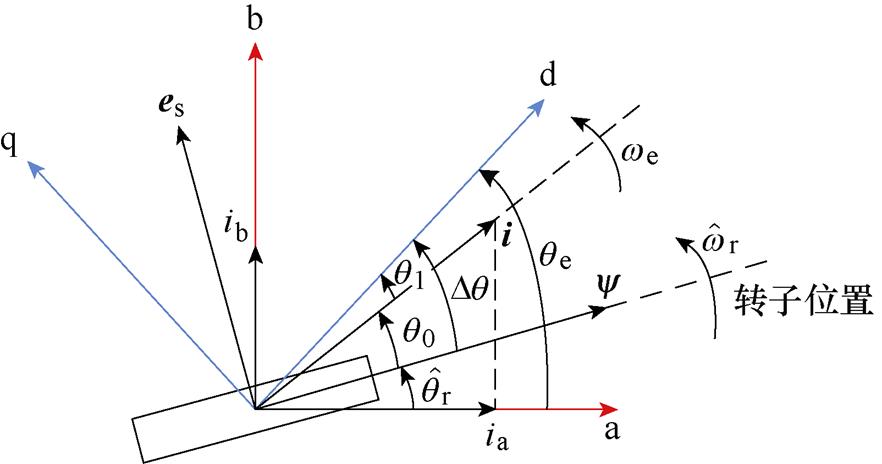
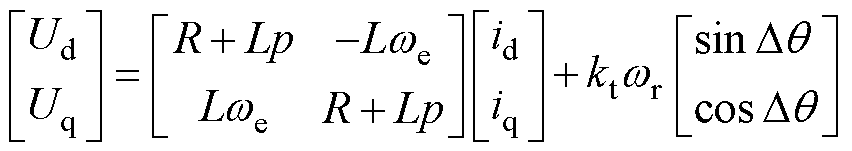 (2)
(2)
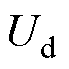 和U
和U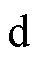 、
、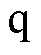 轴电压;
轴电压;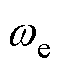 为定子电流电角速度;
为定子电流电角速度;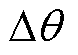 为电机负载角,
为电机负载角,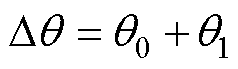 ,
,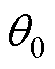 为稳态分量,
为稳态分量,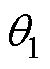 为暂态 分量。
为暂态 分量。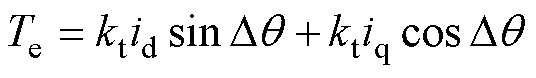 (3)
(3)
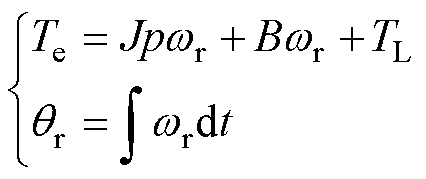 (4)
(4)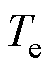 为输出转矩;
为输出转矩;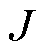 为转动惯量;
为转动惯量;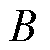 为黏滞系数;
为黏滞系数;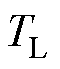 为负载转矩。
为负载转矩。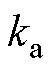 、
、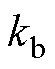 ,分别用于调节指令
,分别用于调节指令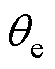 与估计的电机速度
与估计的电机速度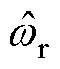 和位置
和位置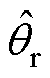 之间的误差,本文采用常规PI电流控制器。
之间的误差,本文采用常规PI电流控制器。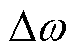 及电流矢量角度
及电流矢量角度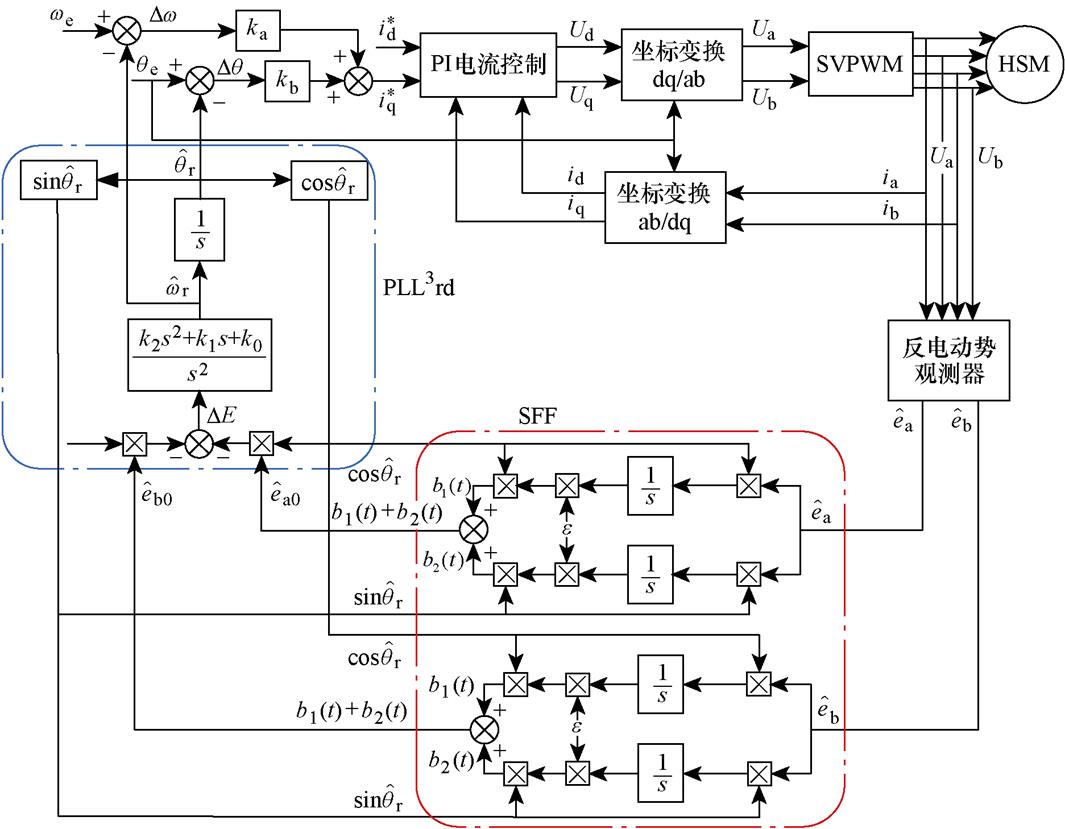
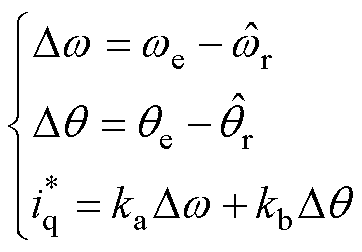 (5)
(5)
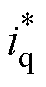 为命令电流,将式(5)代入式(3)和式(4)联立可得
为命令电流,将式(5)代入式(3)和式(4)联立可得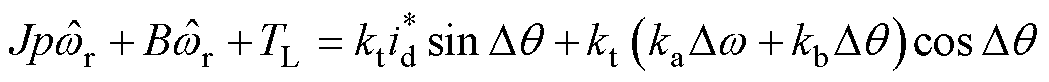 (6)
(6) 为命令电流。
为命令电流。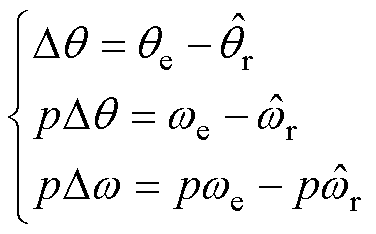 (7)
(7)
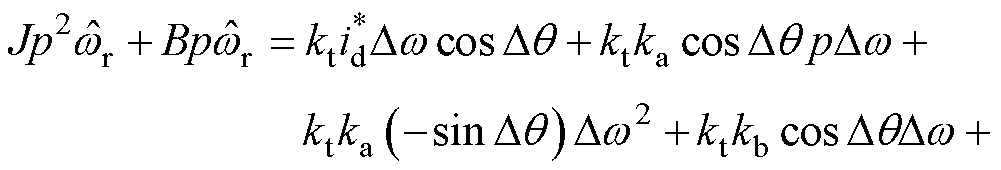
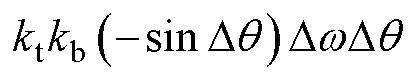 (8)
(8)
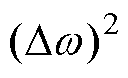 及
及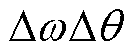 值很小可以忽略,又因为电流
值很小可以忽略,又因为电流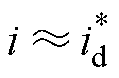 ,根据
,根据 可得暂态分量
可得暂态分量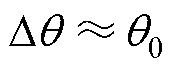 。因此,由式(8)可得传递函数为
。因此,由式(8)可得传递函数为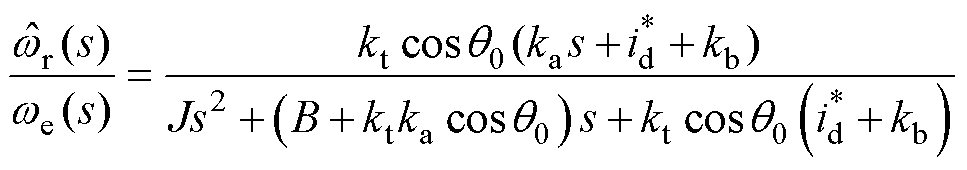 (9)
(9)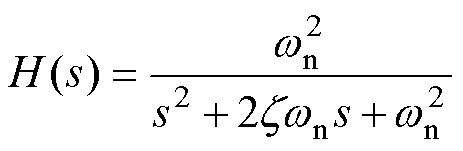 (10)
(10)
 和阻尼比
和阻尼比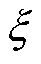 可以分别表示为
可以分别表示为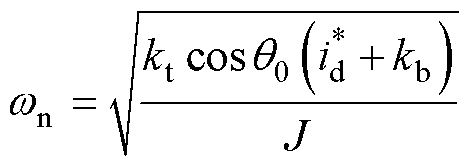 (11)
(11)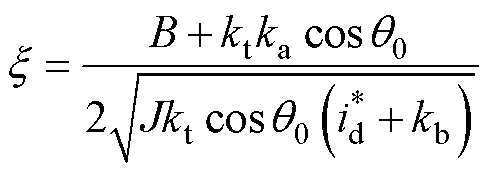 (12)
(12)
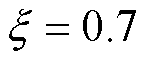 时(通过调节
时(通过调节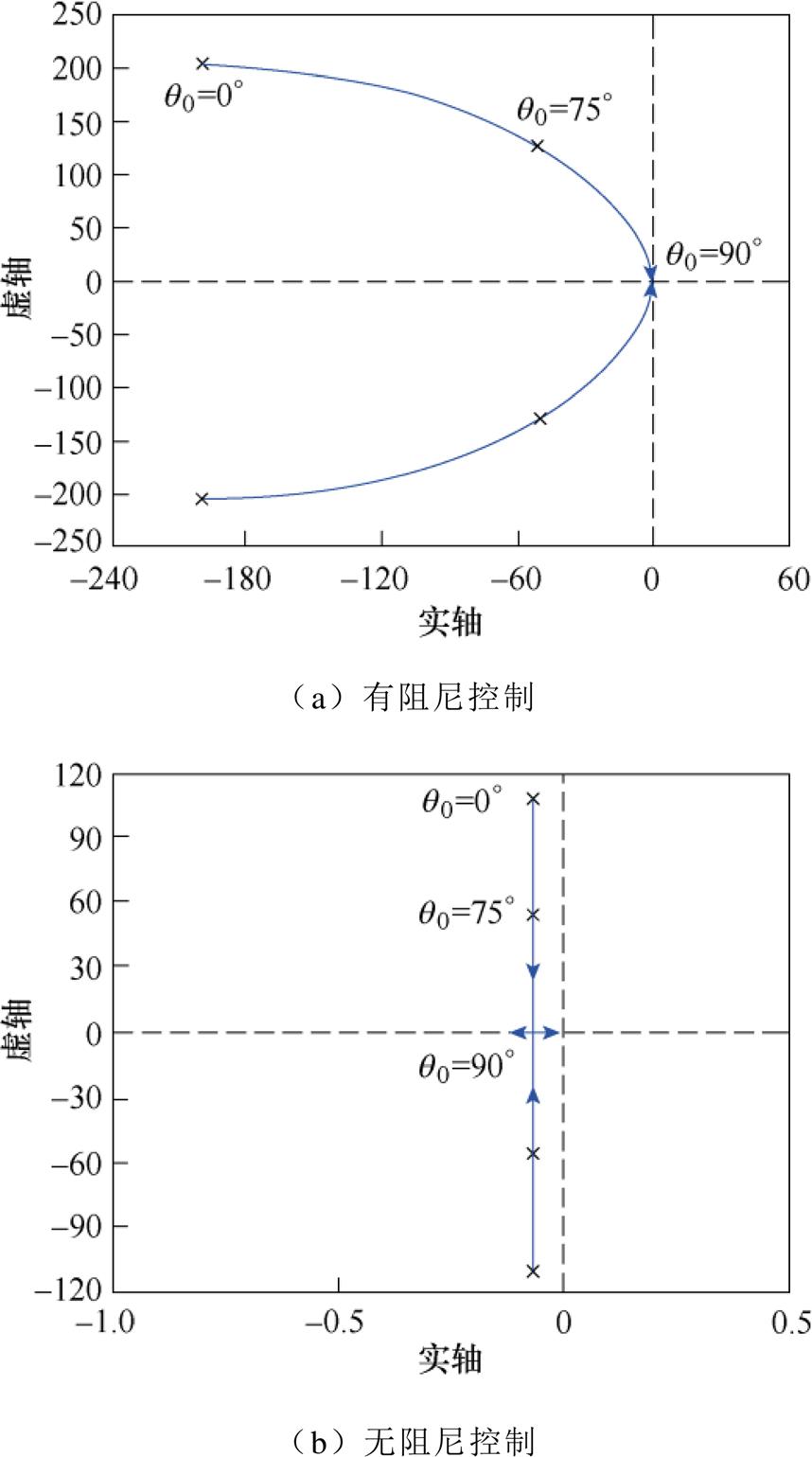
 变化时系统根轨迹图
变化时系统根轨迹图 (13)
(13)
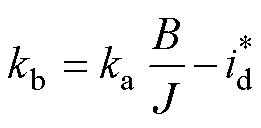 (14)
(14)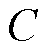 为常数。
为常数。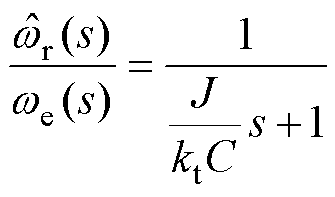 (15)
(15)
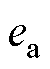 、
、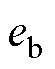 表示为
表示为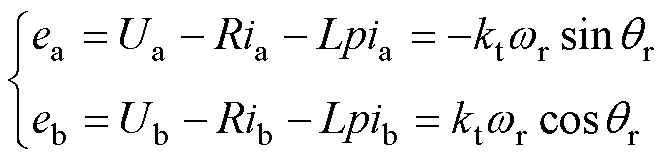 (16)
(16)
 (17)
(17)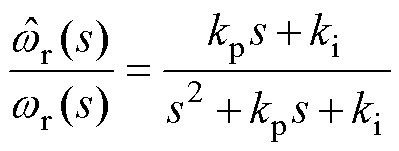 (18)
(18)
 、
、 分别为锁相环的比例和积分增益。PLL实际转速
分别为锁相环的比例和积分增益。PLL实际转速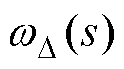 表示为
表示为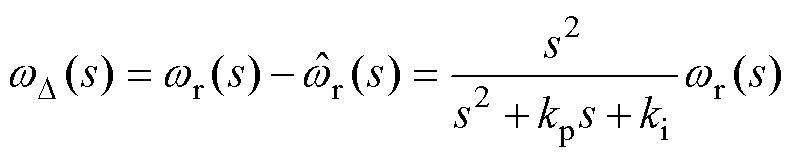 (19)
(19) )以及加减速状态(
)以及加减速状态( )下的稳态误差
)下的稳态误差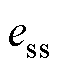 为
为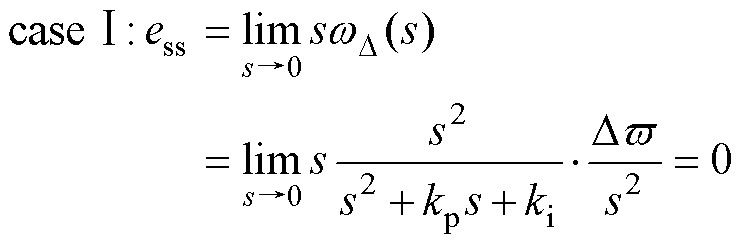 (20)
(20)
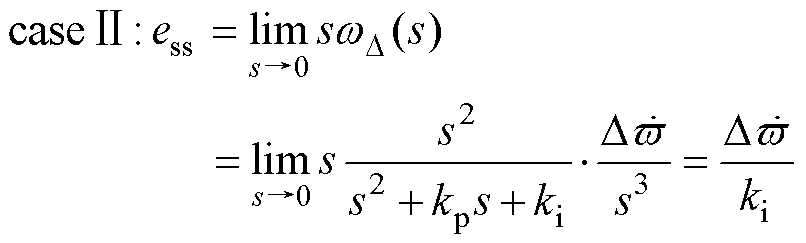 (21)
(21)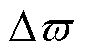 为电机加减速状态下的速度变化率。由式(21)可得,基于传统锁相环(PLL)的步进电机在加速或减速运行时存在稳态误差
为电机加减速状态下的速度变化率。由式(21)可得,基于传统锁相环(PLL)的步进电机在加速或减速运行时存在稳态误差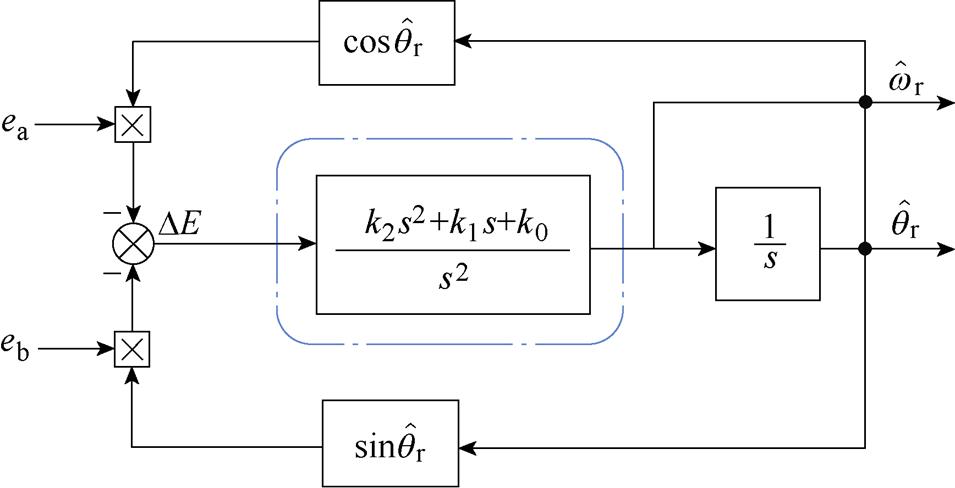
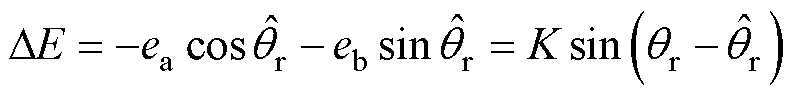 (22)
(22)
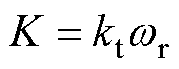
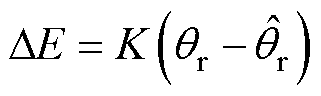 (23)
(23)
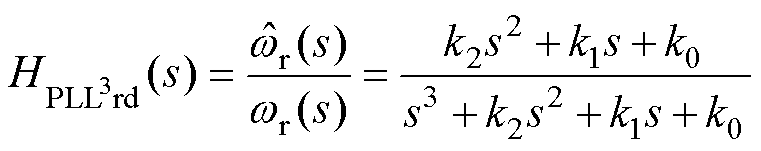 (24)
(24)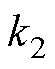 、
、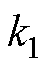 和
和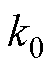 为三阶锁相环增益。PLL
为三阶锁相环增益。PLL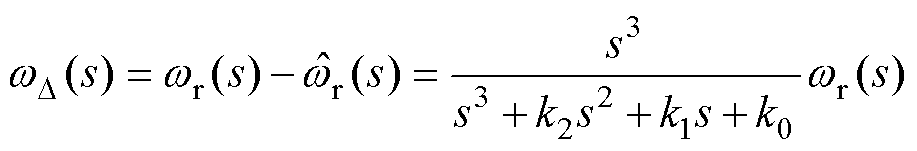 (25)
(25)
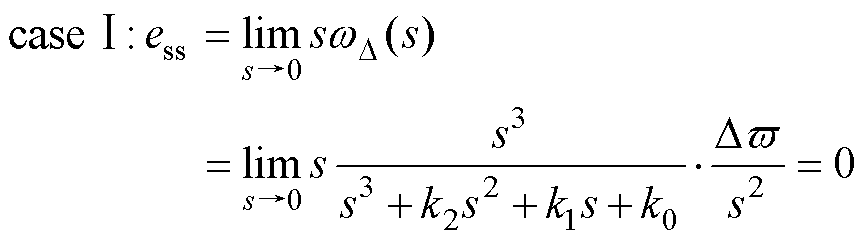 (26)
(26)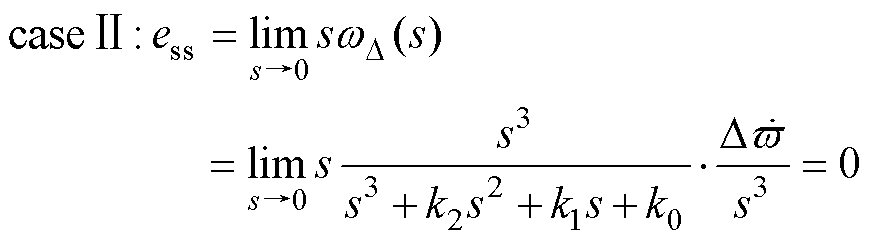 (27)
(27)
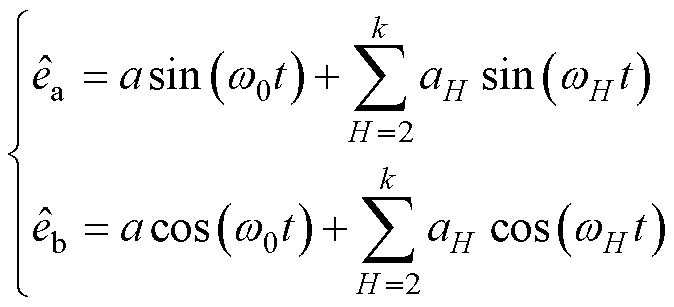 (28)
(28)
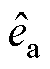 、
、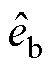 为反电动势观测值;
为反电动势观测值;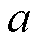 为基波分量的幅值;
为基波分量的幅值;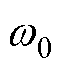 为基波频率;
为基波频率;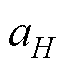 为谐波分量的幅值;
为谐波分量的幅值;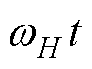 为
为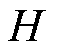 次谐波分量的频率。
次谐波分量的频率。
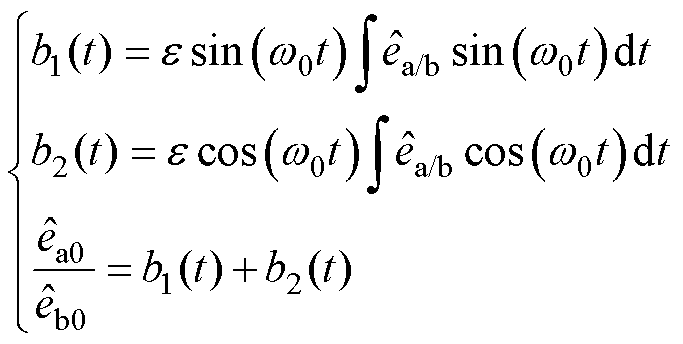 (29)
(29)
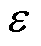 为滤波器增益;
为滤波器增益;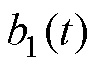 、
、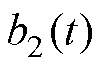 为滤波器中间过程量;
为滤波器中间过程量;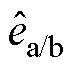 表示滤波器输入信号为
表示滤波器输入信号为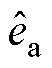 或
或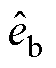 ;
;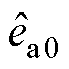 、
、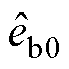 为同步频率提取滤波器的输出结果。对式(29)进行拉氏变换可得
为同步频率提取滤波器的输出结果。对式(29)进行拉氏变换可得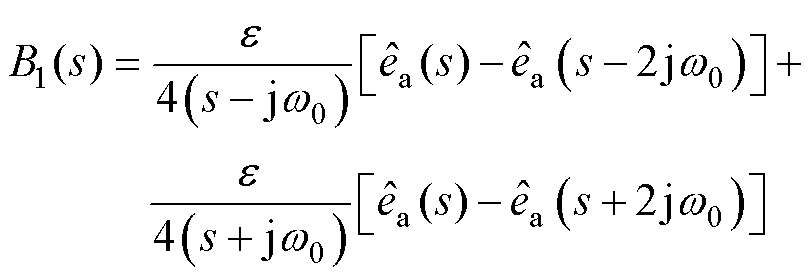 (30)
(30)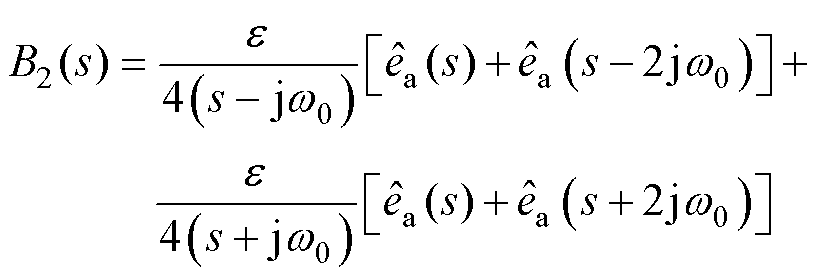 (31)
(31)
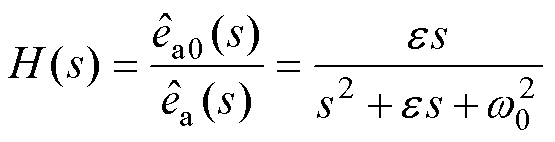 (32)
(32)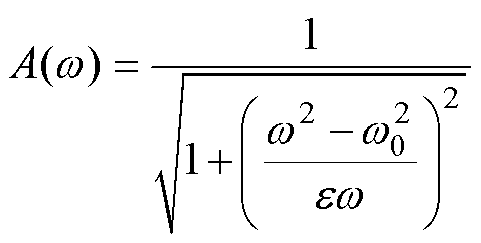 (33)
(33)
 =
=

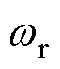 与估测转速
与估测转速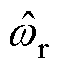 间的误差曲线。由图9可见,当无阻尼控制时,转速曲线存在明显振荡现象,这是由于实际转速与估测转速间存在较大误差,实际转速
间的误差曲线。由图9可见,当无阻尼控制时,转速曲线存在明显振荡现象,这是由于实际转速与估测转速间存在较大误差,实际转速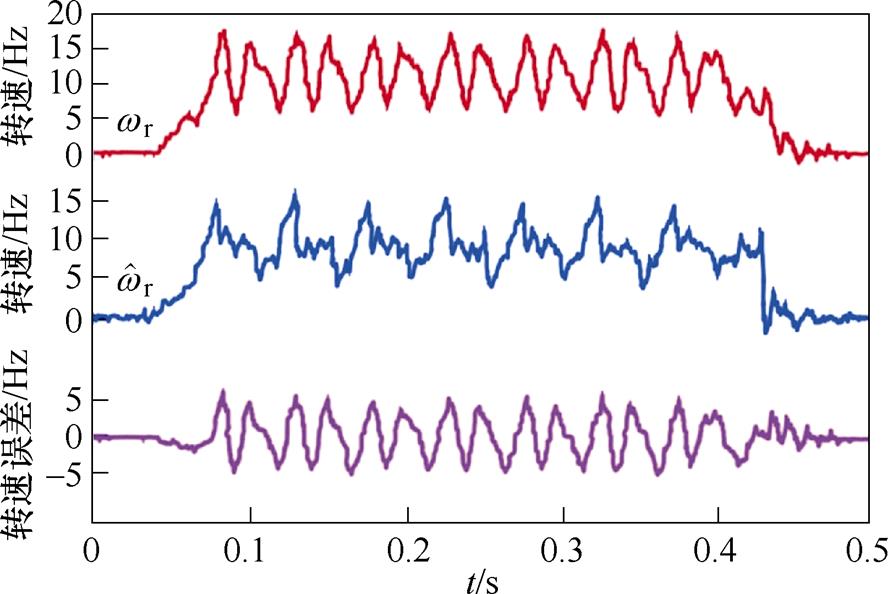
 和估测角度间的最大误差约为135°。由图16可见,阻尼控制使转子电角度曲线振荡幅度减小,实际转子电角度
和估测角度间的最大误差约为135°。由图16可见,阻尼控制使转子电角度曲线振荡幅度减小,实际转子电角度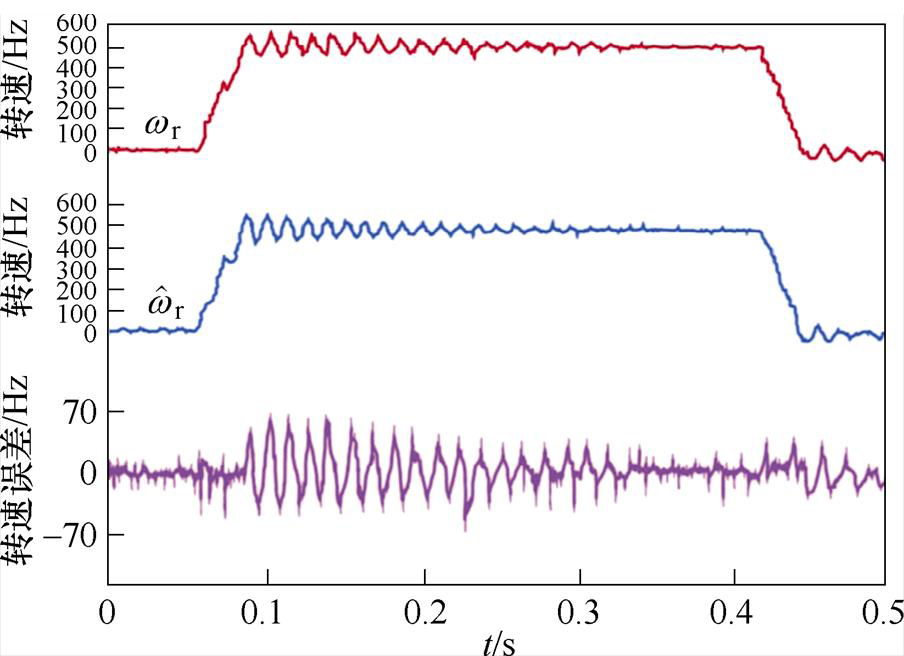
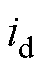 控制恒为电流额定值,利用位置与速度误差产生调节电流主动式增加电机阻尼,可以达到抑制振荡、减少稳定时间的目的。此外,为实现闭环控制,设计SFF-PLL
控制恒为电流额定值,利用位置与速度误差产生调节电流主动式增加电机阻尼,可以达到抑制振荡、减少稳定时间的目的。此外,为实现闭环控制,设计SFF-PLL