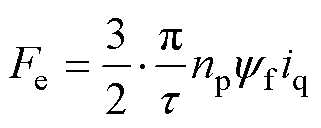（1）
摘要 定位力是永磁同步直线电机（PMLSM）产生推力波动的主要原因，导致振动和噪声，恶化驱动系统运行性能。针对这一问题，该文提出一种基于比例谐振内模扩张状态观测器（PR-IMESO）的PMLSM推力波动抑制策略以提高系统控制精度和运行性能。首先，对PMLSM推力波动进行建模与分析，针对推力波动中占比较大的定位力分量，根据内模原理研究考虑定位力模型的内模扩张状态观测器（IMESO），并在观测器中引入谐振项以加强对二次脉动定位力的抑制。所提出抑制策略对PMLSM定位力具有良好的观测及补偿能力，还可对其余未建模的复杂动子推力波动进行抑制，具有较好的推力波动整体抑制效果。最后，在一台750 W的PMLSM实验平台上验证所提出抑制策略的有效性。
关键词：永磁同步直线电机 定位力 比例谐振内模扩张状态观测器 推力波动抑制
永磁同步直线电机（Permanent Magnet Linear Synchronous Motor, PMLSM）无需任何中间传动装置可直接产生直线运动，具有机械结构简单、响应速度快、推力大等优点[1-3]，在自动控制系统、自动化精密机床、工业机器人等场合获得了广泛的应用，如要求高精度、高动态性能的光刻机、数控加工机床等[4-5]。
虽然，PMLSM在控制精度和响应速度上有较大优势，但由于缺乏中间传递环节的缓冲和阻尼作用，PMLSM驱动系统更容易受到推力波动、外界扰动和参数变化等影响[6]。PMLSM初级铁心的开断和绕组边端排列的不连续导致其存在端部效应力，且初级铁心采用的开槽硅钢叠片聚合磁路导致其存在齿槽效应力。通常将端部效应力和齿槽效应力的合力称为定位力，其为PMLSM输出推力波动的主要原因，会导致电机输出速度产生复杂的谐波脉动，对PMLSM驱动系统低速运行时的控制精度影响较大[1, 7-8]。为进一步提高PMLSM驱动系统的控制精度及运行性能，需对其推力波动进行抑制。
目前，PMLSM推力波动抑制策略的研究主要包括改进电机本体结构设计和优化电机控制算法两类[9]。电机本体结构设计改进层面，可以通过阶梯式双辅助极[10]、凹型端齿[11]、Halbach永磁阵列[12]等方法削弱PMLSM推力波动。但该类方法会增加电机设计成本与难度，且对复杂推力波动的抑制效果有限，具有一定的局限性。因此，很多学者在优化控制算法层面展开研究来抑制PMLSM推力波动，提出了多种实用有效的方法，如自抗扰控制[13-14]、自适应控制[15]、滑模控制[16]、预测控制[17]、迭代学习控制[18]等抑制策略。文献[14]在PMLSM控制系统速度环中设计二阶自抗扰控制器，通过仿真验证了其在永磁磁通变化和受到外界扰动时具有较好的鲁棒性。文献[16]提出一种定结构滑模控制器与扩展滑模扰动观测器相结合的复合式滑模位置控制方法来抑制推力波动。文献[19]针对多扰动永磁同步电机，将扰动模型适当嵌入扰动观测器的设计中，提出一种基于复合扰动观测器的控制方法，给PMLSM推力波动抑制带来启发。相对于电机本体结构设计优化的方法，优化电机控制算法的抑制策略具有成本低、实用性强、应用更加灵活等优点。自抗扰控制不依赖于PMLSM具体数学模型，将作用于直线电机的未知扰动都归结为“总扰动”，利用电机的输入输出信息对其进行估计并给予补偿，具有较好的控制性能。传统的自抗扰抑制策略，如基于扩张状态观测器（Extended State Observer, ESO）的控制只能抑制渐进常数或缓慢变化的扰动，而PMLSM在实际工作中总是受到多种且复杂的扰动，尤其是周期性扰动，其不能起到有效的推力波动抑制作用。
针对PMLSM动子推力波动问题，本文提出一种基于比例谐振内模扩张状态观测器（Proportional Resonant Internal Model ESO, PR-IMESO）的PMLSM驱动系统推力波动抑制策略。首先，对PMLSM推力波动进行数学建模与分析，针对推力波动中占比较大的定位力分量，将内模原理与扩张状态观测器相结合，研究并设计考虑定位力模型的改进扩张状态观测器，即内模扩张状态观测器。其次，在观测器中引入谐振项以加强对二次脉动定位力的抑制。所提出的PR-IMESO不仅可以对已建模的推力波动主要分量——定位力进行抑制，而且对包括负载扰动、电流畸变、摩擦力在内的其余未建模复杂动子推力波动也具有良好的抑制效果。最后，通过750 W PMLSM实验平台验证了所提出的基于PR-IMESO的推力波动抑制策略的有效性。
在dq坐标系下建立理想的PMLSM动力学模型。推力方程为
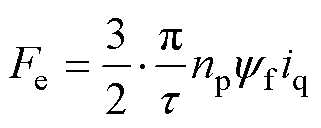（1）
式中，Fe为电磁推力；t 为电机极距；np为电机极对数；yf为永磁体磁链；iq为q轴电流。
运动方程为
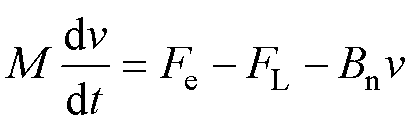（2）
式中，M为动子质量；v为动子速度；FL为负载拉力；Bn为黏滞摩擦系数。
PMLSM动子与平台刚性连接，缺乏中间机械传动环节的缓冲作用，因此更容易受到推力波动、外界扰动、参数变化等影响。这些扰动都会在一定程度上导致PMLSM产生输出推力波动，使得电机输出速度产生复杂的谐波脉动，从而影响PMLSM驱动系统的运行性能。
与旋转电机相同，PMLSM的初级铁心同样采用开槽硅钢叠片聚合磁路，使得直线电机初级槽里的气隙磁阻远大于初级齿的磁阻，从而导致齿槽效应。齿槽效应力是一个周期函数，其与动子位置有关，调整永磁体的位置后，整个电机动子的齿槽力Fcog可用傅里叶级数表示[20]为
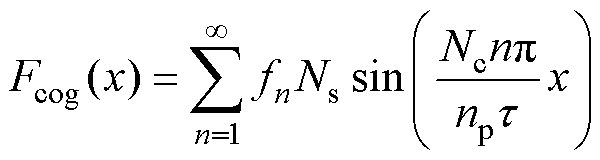（3）
式中，fn为傅里叶级数各项系数；x为动子位移；Nc为电机极数
与槽数Ns的最小公倍数。由式（3）可知，齿槽力是以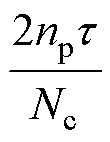
为周期与动子位置相关的函数，同时也是以电机极距t 为周期的函数。
端部效应是由电机初级铁心的开断和初级绕组边端排列的不连续产生一个与齿槽力类似的周期性的推力波动。端部效应力Fend的傅里叶级数表示[21]为
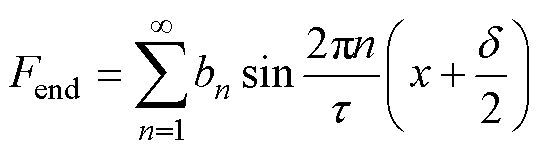（4）
其中
d =kt-Ls
式中，bn为傅里叶级数各项系数；Ls为动子长度；k为整数。
端部效应力和齿槽效应力的合力称为定位力，是PMLSM产生推力波动的主要原因。根据式（3）和式（4），定位力Fdet可表示为
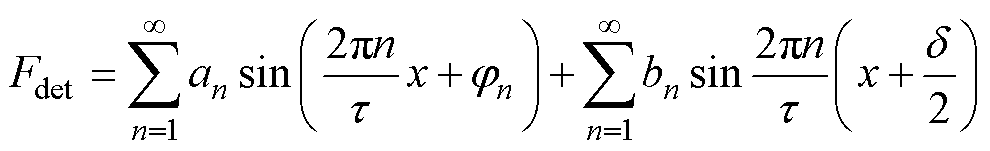（5）
式中，an为傅里叶级数各项系数；jn为各级数相位。
由数学模型式（5）可知，定位力是以电机极距t 为周期的关于电机动子位置的函数。根据PMLSM动子速度表达式v=2t f（f为电机运行频率）可得出，定位力的频率为初级绕组相电流频率的2倍。定位力对PMLSM驱动系统的控制精度影响较大，在PMLSM低速运行时影响尤为明显。因此，抑制PMLSM定位力，从而降低电机推力波动以提高PMLSM驱动系统控制精度与运行性能具有重要意义。
PMLSM推力波动是一个成分复杂的谐波脉动，与动子位置相关的频率为初级绕组相电流频率2倍的定位力是推力波动的主要成分。
针对PMLSM的复杂推力波动，本文提出一种基于比例谐振内模扩张状态观测器的PMLSM推力波动抑制策略，其框图如图1所示。PR-IMESO的输入为q轴电流给定值iqref和速度反馈值v，通过PR-IMESO对PMLSM受到的扰动进行观测估计，输出扰动补偿信号d(t)对推力电流指令iqref进行前馈补偿修正。该抑制策略既可以对推力波动主要分量——定位力进行有效抑制，还可以对未建模的其余动子推力波动进行观测及补偿，实现主动抗扰的功能，从而达到较好的PMLSM推力波动抑制效果。
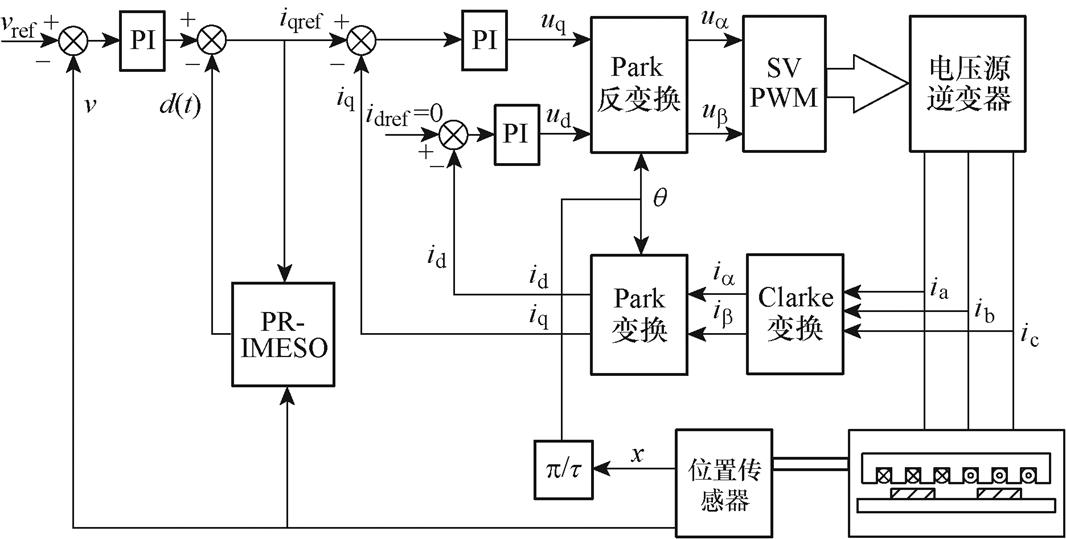
图1 基于PR-IMESO的推力波动抑制策略框图
Fig.1 Thrust ripple suppression strategy based on PR-IMESO
PR-IMESO结构框图如图2所示。其中，IMESO为一个考虑定位力模型的四阶观测器，其偏差信号的前馈比例项与谐振控制器R(s)构成比例谐振控制器，得到PR-IMESO。
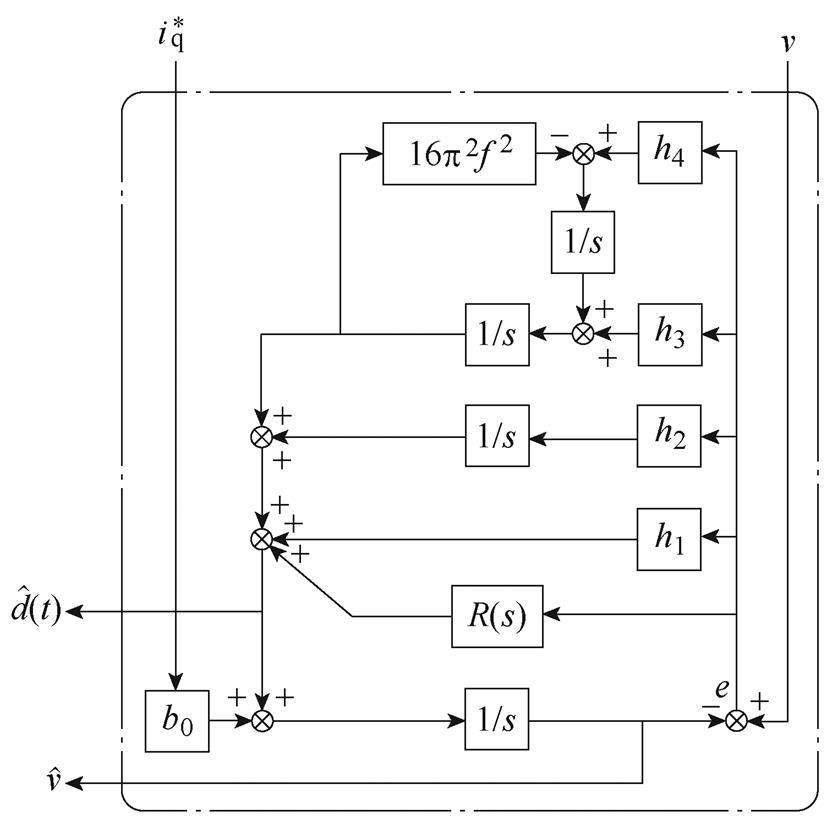
图2 PR-IMESO结构框图
Fig.2 Block diagram of PR-IMESO
考虑PMLSM的各项推力扰动时，其运动方程可表示为
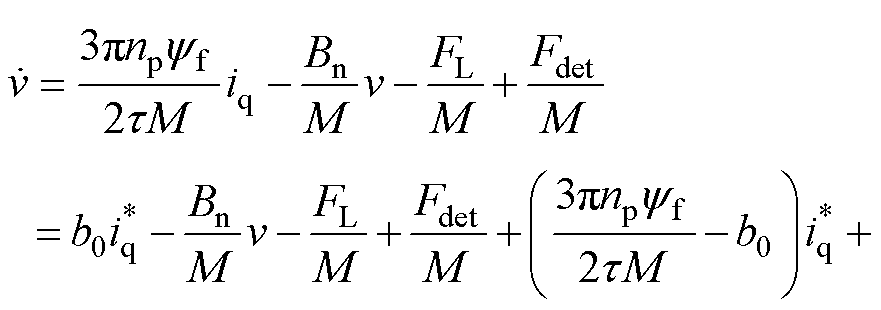
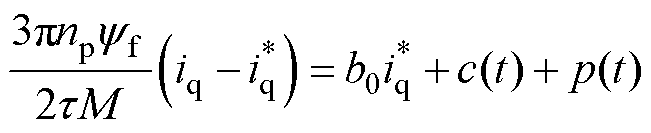（6）
其中
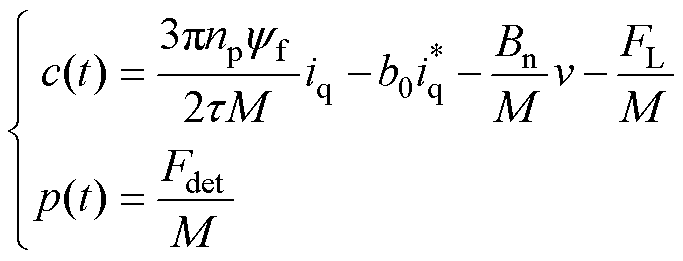（7）
式中，b0为控制增益；Fdet为电机定位力；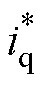
为q轴电流给定值；c(t)为集中扰动，即包括负载扰动、参数变化、电流畸变在内的其余未建模扰动；p(t)为定位力扰动，可表示为
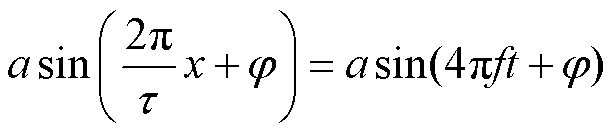，其中，a为未知幅值，j 为未知相位。
定义各状态变量为
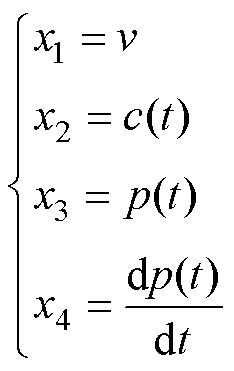
设计内模扩张状态观测器为
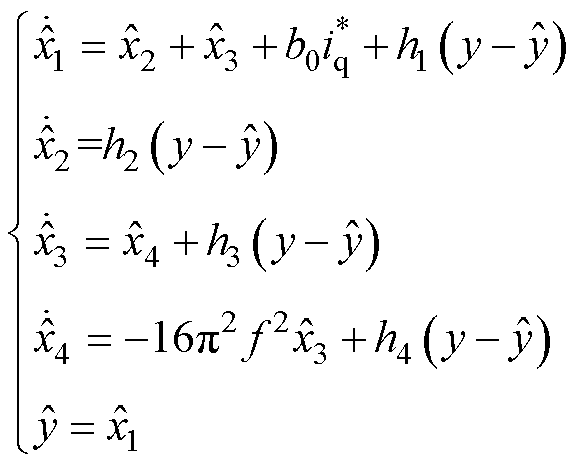（8）
式中，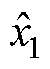
、
、
、
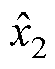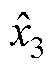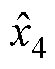为状态变量v、c(t)、p(t)、
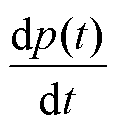的估计值；h1、h2、h3、h4为IMESO的4个增益；
、
、
、
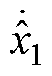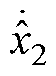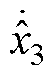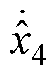为状态变量估计值的微分；y、
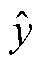分别为速度的实际值和估计值。
IMESO可对定位力进行补偿抑制，并对其余未建模推力波动进行实时估计及补偿，但其不能完全消除定位力的负面效应，故仍需提高观测器对固定频率定位力波动的补偿能力。
将s域下的理想积分器用一阶低通滤波器代替，得到准PR控制器传递函数为
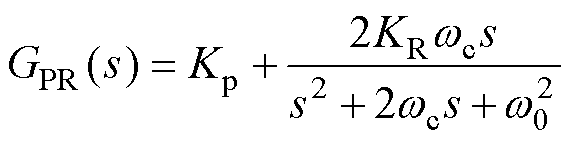（9）
式中，KP为比例系数；KR为谐振系数；wc为谐振带宽；w0为谐振角频率。
准PR控制器在谐振频率点附近有较大的幅值，有优良的跟随性能和动态性能，对固定频率交流信号有较好的跟随作用，可以用来加强系统对固定频率定位力的抑制效果。本文采用PR-IMESO，其扰动补偿信号由偏差信号的PR输出与PMLSM定位力扰动观测值构成。
根据式（6）可知，观测器的控制增益b0为
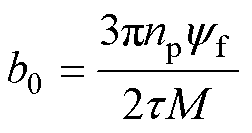（10）
根据dq轴下PMLSM推力式（1）可得永磁体的磁链yf为
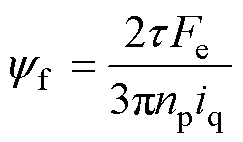（11）
将式（11）代入式（10），根据PMLSM推力常数Fe/iq可得到控制增益b0的数值。
通过观测器带宽对4个参数进行整定，将其整定为极点全部重合的四阶系统。目标系统特征多项式形式为
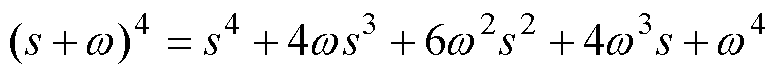（12）
根据式（8）可得IMESO的特征多项式c(s)为
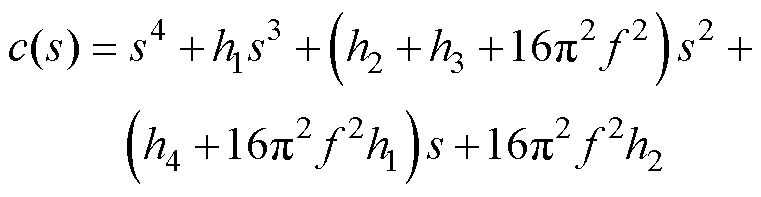（13）
将式（12）和式（13）系数进行对应，可得观测器4个参数表达式分别为
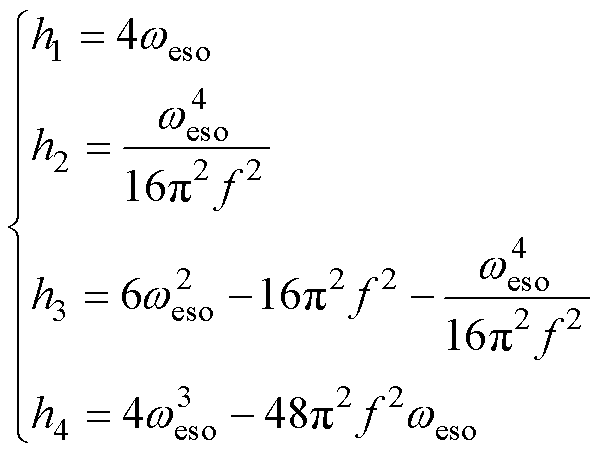（14）
式中，weso为观测器带宽。
PR控制器在电机控制和并网逆变器电流控制技术中取得广泛应用，其稳定性不再详细分析。本节主要对IMESO的稳定性及参数特性进行分析。
根据式（8）可得IMESO拉普拉斯变换后的表达式为
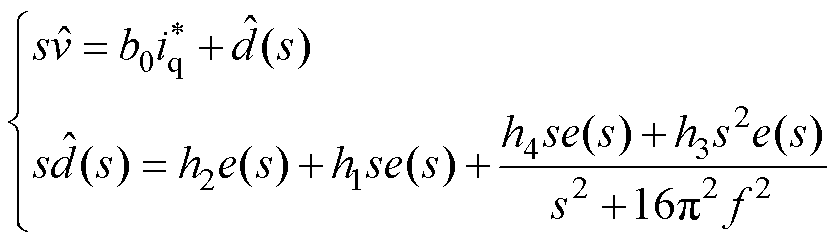（15）
根据式（15）可得IMESO输出扰动补偿量的表达式为
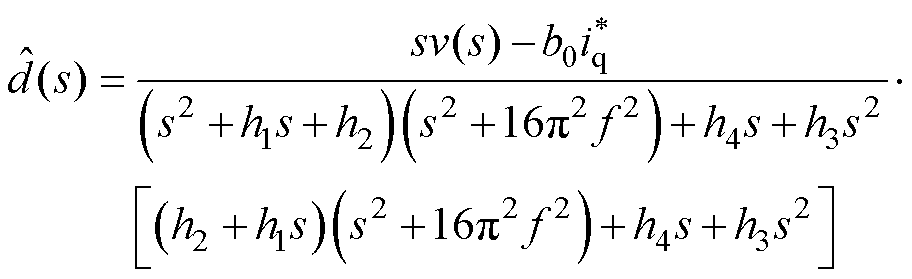（16）
系统“总扰动”可以表示为
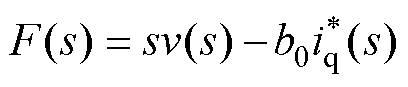（17）
此处考察内模扩张观测器的补偿量与系统的“总扰动”间的传递函数，取观测器输入iq=0，可得到内模扩张状态观测器的传递函数为
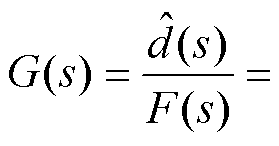
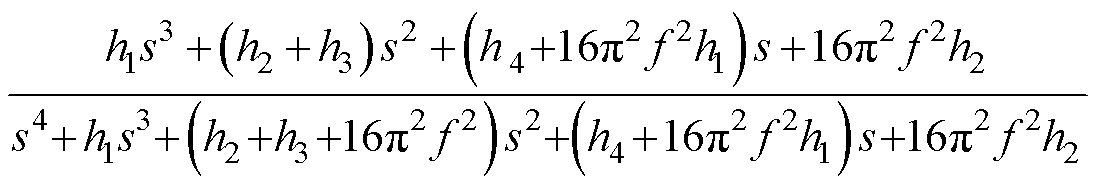（18）
由于该观测器的传递函数与电机运行速度有关，根据式（18）可得到直线电机不同运行频率下的观测器Nyquist图。考虑到定位力带来的负面效应在电机低速运行时尤为凸显，严重影响电机低速工作时的控制精度与工作性能。因此，主要分析永磁同步直线电机低速运行时IMESO的稳定性和参数特性。
取电机运行频率f=2 Hz，IMESO带宽weso分别取为15、20、30、100 rad/s，其Nyquist图如图3所示。可知，IMESO带宽weso从-∞变化到+∞时，观测器的Nyquist曲线均不包围（-1, j0）点，根据Nyquist稳定判据，可以得出所研究的IMESO是稳定的。
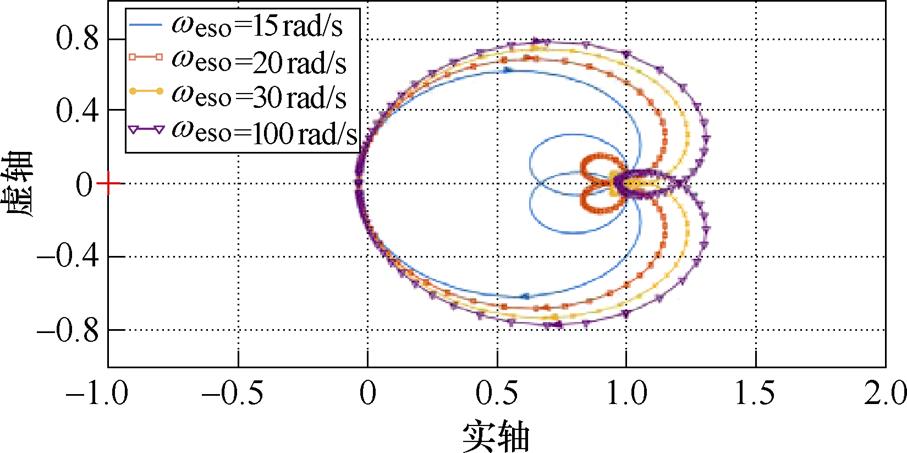
图3 f=2 Hz时内模扩张状态观测器的Nyquist图
Fig.3 Nyquist diagram of IMESO when f=2 Hz
根据IMESO传递函数式（18）可得到其在不同带宽下的Bode图，如图4所示。可见，随着weso增大，观测器扰动估计的带宽增大，观测器的增益也更加稳定，扰动估计性能更加优良。
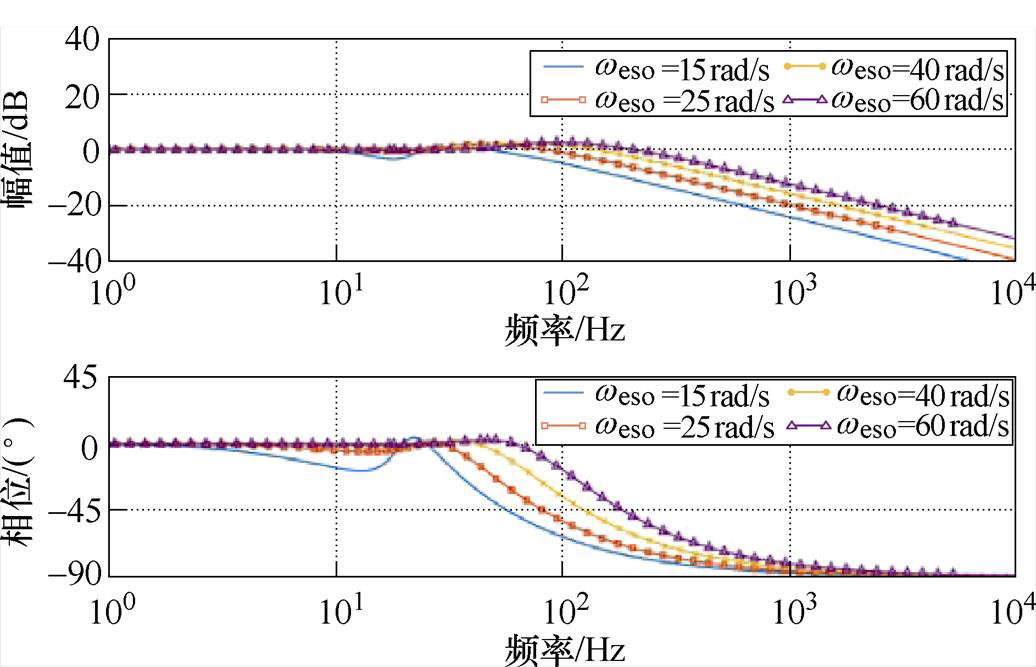
图4 f=2 Hz时内模扩张状态观测器的Bode图
Fig.4 Bode diagrams of IMESO when f=2 Hz
由于观测器传递函数极点与观测器带宽有关，weso过大或过小，都可能会改变极点的符号，从而影响系统整体的稳定性和收敛性。且观测器的极点也与直线电机运行速度有关，带宽应与运行速度相匹配。因此，在实际应用时需根据系统的实际情况，综合考虑确定最佳的IMESO带宽，从而完成观测器4个参数的选择。
为从理论上验证所提出抑制策略的正确性，先进行仿真验证。根据PMLSM考虑各项推力扰动时的运动方程在电机机械仿真结构部分加入波动幅值为2 N的定位力扰动。设置电机运行速度0.06 m/s，负载拉力为10 N。系统在0.6 s时刻切入PR-IMESO，1.2 s时突加负载，可得到加入PR-IMESO抑制策略后直线电机动子实际速度波形如图5所示。由仿真结果可知，加入PR-IMESO抑制策略后速度波动的幅值衰减为未加策略时速度波动幅值的3.4%，抑制率为96.6%，突加负载后，系统回到稳态后速度波动抑制率可达96.7%，所提出的PR-IMESO推力波动抑制策略对频率为2次波动的定位力有很好的抑制效果。
为验证所提出抑制策略的有效性，在一台如图6所示的750 W PMLSM（深圳克洛诺斯公司商用电机，型号为LK140-1000-103-289-1N03-C10A-101）实验平台上进行实验验证。主控芯片采用STM32F103，逆变器的PWM开关频率为6 kHz，所用PMLSM具体参数见表1。
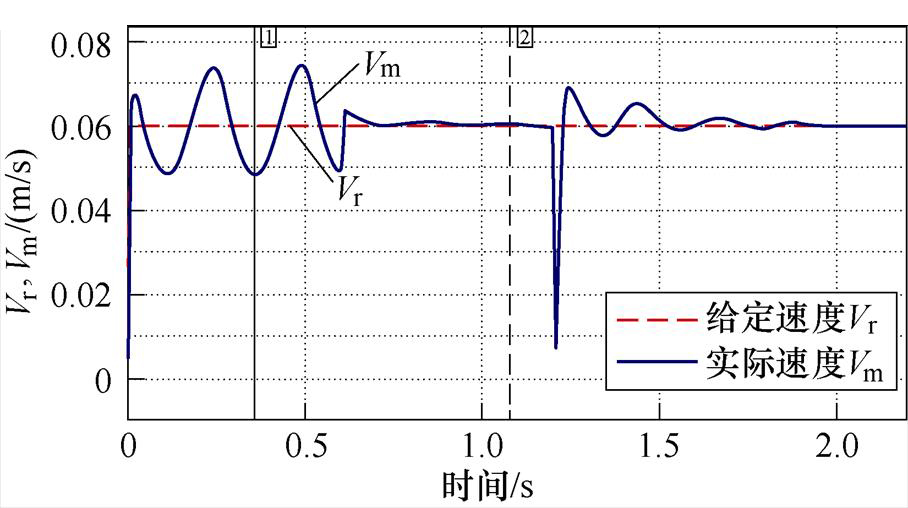
图5 突加负载时加入PR-IMESO动子速度仿真波形
Fig.5 The simulation waveforms of mover speed with PR-IMESO under sudden load
图6 750 W PMLSM实验平台
Fig.6 750 W PMLSM experimental platform
表1 PMLSM参数
Tab.1 Parameters of PMLSM
参 数数 值 连续推力/N103 连续电流/A2.1 推力常数/(N/A)48.6 线间电阻/W8.4 线间电感/mH37.1 极对距/mm30 磁栅尺脉冲数/ppr7 500 动子质量/kg0.7
将电机动子初始定位后，在实验平台上进行不同负载、不同速度条件下的PMLSM推力波动抑制策略实验。由于实验无法直接测得动子推力，故通过测量动子速度偏差来对推力波动抑制效果进行评估。本文主要研究对推力波动中定位力分量的抑制效果，而定位力产生的负面效应在电机低速运行时尤为凸显，所以实验在电机低速运行时进行。在电机运行速度0.03、0.06 m/s，空载、负载2、3、4 kg的工况下对基于ESO、IMESO、PR-IMESO的直线电机推力波动抑制策略进行系统的实验验证。
电机负载4 kg，运行速度0.03 m/s时，不同抑制策略下电机的动子速度偏差、q轴电流、a相绕组电流波形如图7所示。可见，不加任何抑制策略时，动子速度存在着较大的复杂波动，波动幅值为2.1 cm/s；加入ESO抑制策略，动子速度波动幅值降为1.4 cm/s，抑制率为33.3%；加入IMESO抑制策略，速度波动幅值大大降低，动子速度波动幅值降为0.72 cm/s，抑制率为65.7%；加入本文所提出的抑制策略，动子速度波动幅值降为0.63 cm/s，抑制率达70.0%。
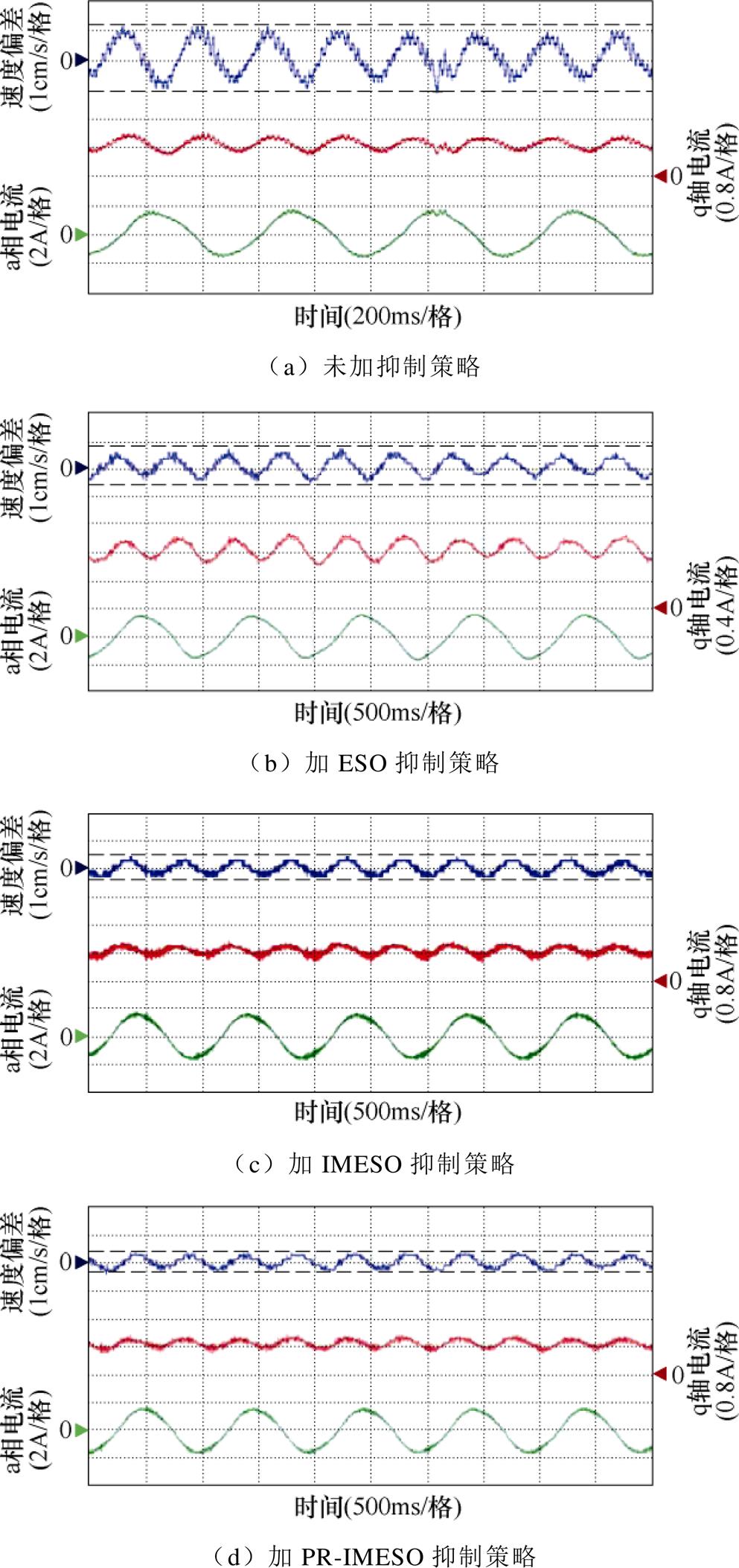
图7 运行速度0.03 m/s时各抑制策略实验结果
Fig.7 Experimental results of each supression strategy at the speed of 0.03 m/s
电机负载4 kg，运行速度0.06 m/s时，不同抑制策略下电机的动子速度偏差、q轴电流、a相电流波形如图8所示。可知，不加任何抑制策略时，电机动子速度波动幅值为2 cm/s；加入ESO抑制策略，动子速度波动幅值降为1.65 m/s，抑制率为17.5%；加入IMESO抑制策略，电机动子速度波动幅值降为0.62 cm/s，抑制率为69.0%；加入本文提出的抑制策略时，电机动子速度波动幅值降为0.54 cm/s，抑制率为73.0%。
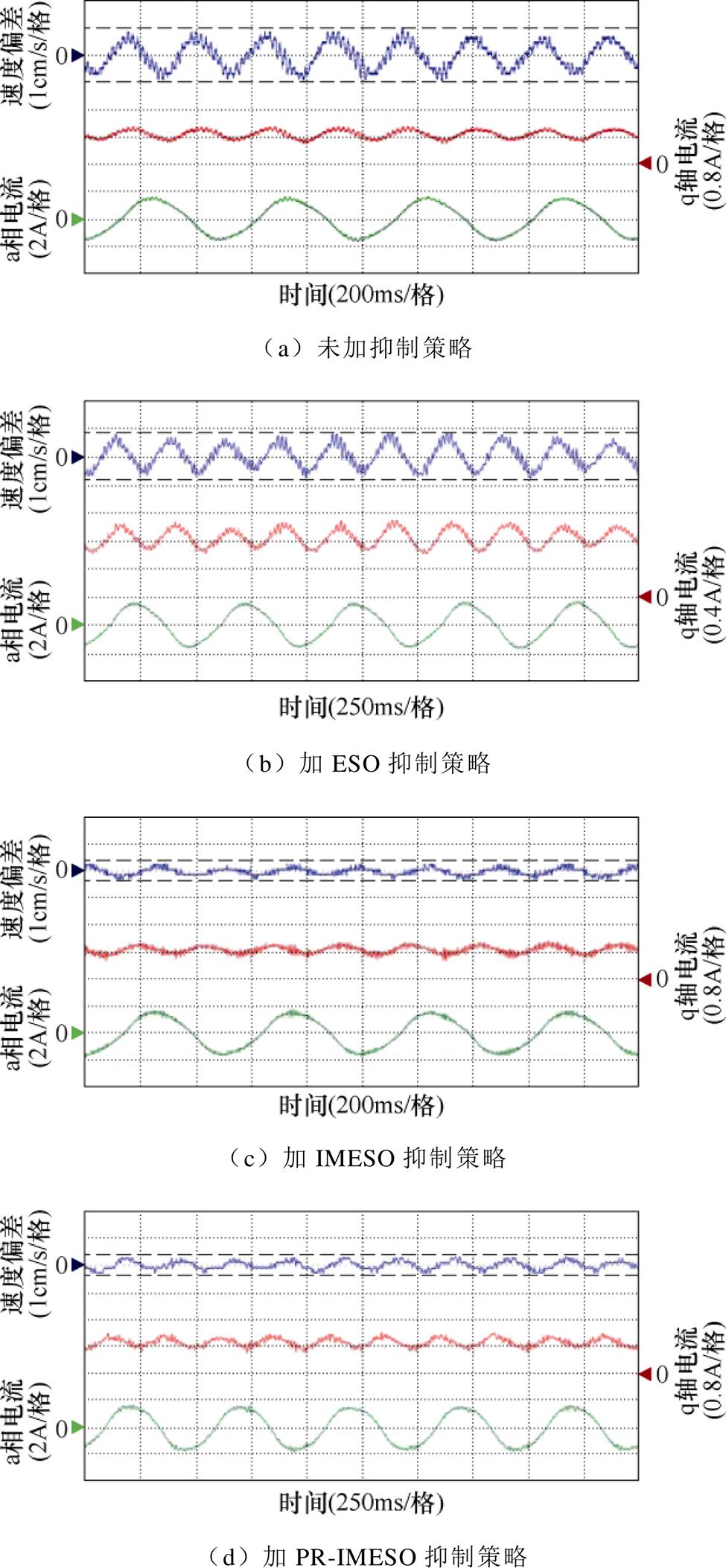
图8 运行速度0.06 m/s时各抑制策略实验结果
Fig.8 Experimental results of each supression strategy at the speed of 0.06 m/s
以突加4 kg负载工况为例，通过实验说明PR- IMESO推力波动抑制策略动态性能。突加4 kg负载，电机运行速度0.03 m/s，电机的动子速度偏差、q轴电流、a相绕组电流波形如图9所示。可知，当不采取任何抑制策略时，突加负载前后，动子速度存在着很大的波动，加入PR-IMESO抑制策略后，整个运行过程的动子速度波动明显减小。突加负载过程中，速度偏差及q轴电流过渡平滑，且迅速稳定，动态性能良好。
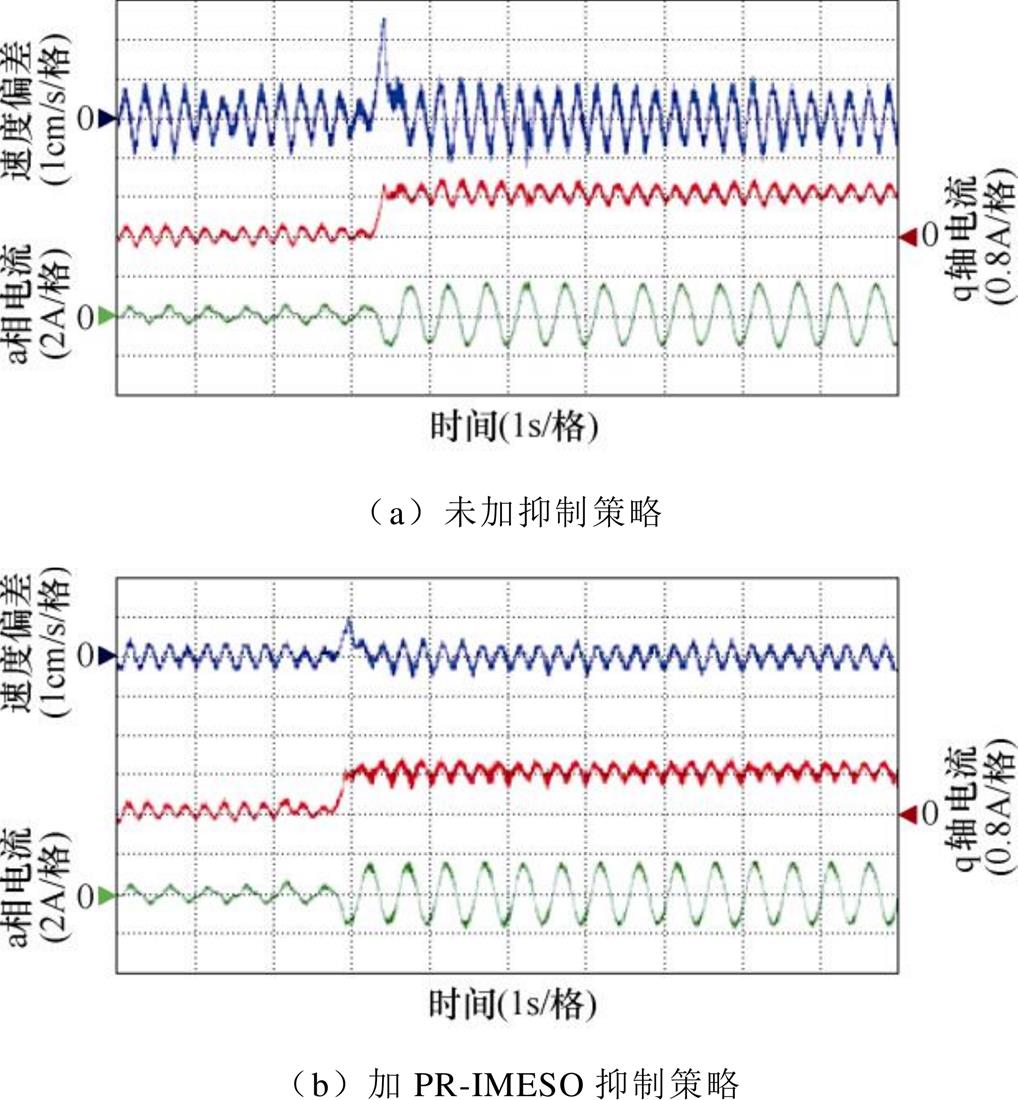
图9 突加负载动态过程实验结果
Fig.9 Experimental results of dynamic process of sudden load loading
将前述基于ESO、IMESO、PR-IMESO直线电机推力波动抑制策略不同工况下实验结果进行汇总对比，运行速度0.03 m/s时的实验结果汇总如图10所示，运行速度0.06 m/s时实验结果汇总如图11所示。由实验结果可知，采用PR-IMESO抑制策略后，各种工况下的速度波动均明显下降，抑制率最高可达73.5%，波动幅值由2 cm/s降为0.53 cm/s。可知，本文所研究的抑制策略在不同速度、不同负载条件下对PMLSM的推力波动都能起到很好的抑制效果。除定位力外，PMLSM在实际运行中还受到多种复杂的扰动，仿真的还原程度有限，所以仿真结果的抑制率比实验结果的要高，但都证明了所提出PR-IMESO抑制策略的正确性和有效性。
本文提出了一种基于PR-IMESO的PMLSM推力波动抑制策略。针对推力波动中占比较大的定位力分量，根据内模原理研究并设计了考虑定位力模型的内模扩张状态观测器，在观测器引入谐振项以加强对2次脉动定位力的抑制。从理论上对该抑制策略的稳定性及参数特性进行详细分析。本文所研究的PR-IMESO抑制策略不仅对推力波动中占比较大的定位力具有较强的抑制效果，对未建模的其余动子推力波动也能起到较好的观测及补偿效果。通过仿真与实验验证了所提出抑制策略的可行性和有效性，与理论分析一致，动子速度波动的平均抑制率可达68.7%。
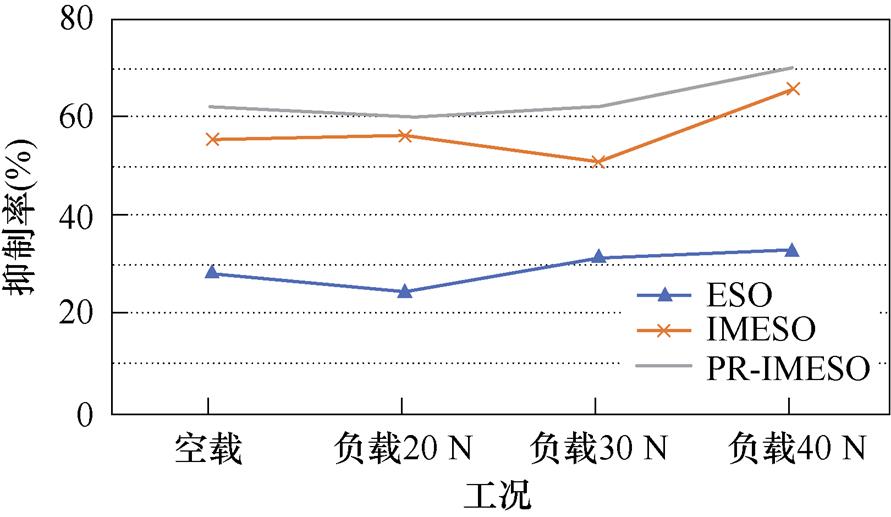
图10 运行速度0.03 m/s实验结果汇总
Fig.10 Experimental results at the speed of 0.03 m/s
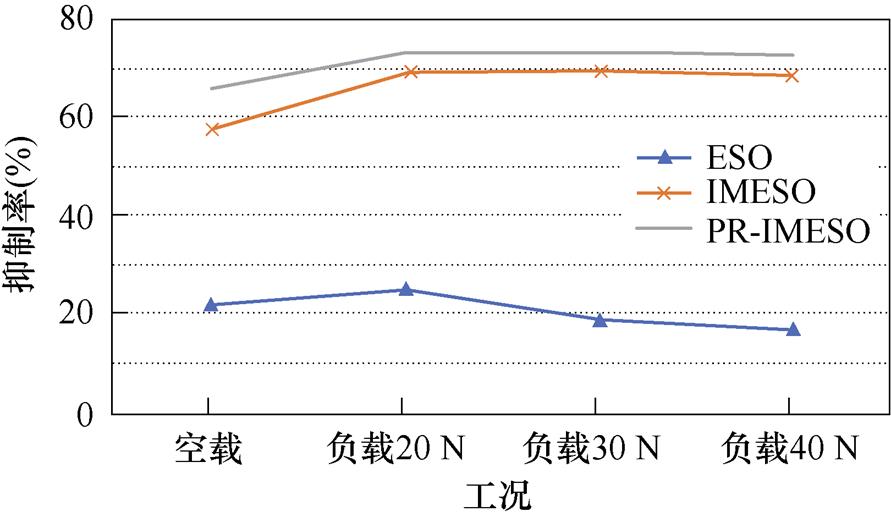
图11 运行速度0.06 m/s实验结果汇总
Fig.11 Experimental results at the speed of 0.06 m/s
参考文献
[1] Yang Rui, Wang Mingyi, Li Liyi, et al. Robust predictive current control of PMLSM with extended state modeling based Kalman filter: for time-varying disturbance rejection[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 2208-2221.
[2] 李雄松, 崔鹤松, 胡纯福, 等. 平板型永磁直线同步电机推力特性的优化设计[J]. 电工技术学报, 2021, 36(5): 916-923.
Li Xiongsong, Cui Hesong, Hu Chunfu, et al. Optimal design of thrust characteristics of flat-type permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 916- 923.
[3] 王明杰, 贾宛英, 张志艳, 等. 永磁直线同步电机空载反电动势和推力的解析计算[J]. 电工技术学报, 2021, 36(5): 954-963.
Wang Mingjie, Jia Wanying, Zhang Zhiyan, et al. Analytical calculation of no-load eletromotive force and thrust in permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 954-963.
[4] Chung S U, Kim J M. Double-sided iron-core PMLSM mover teeth arrangement design for reduction of detent force and speed ripple[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3000-3008.
[5] 方馨, 王丽梅, 张康. 基于扰动观测器的永磁直线电机高阶非奇异快速终端滑模控制[J]. 电工技术学报, 2023, 38(2): 409-421.
Fang Xin, Wang Limei, Zhang Kang. High order nonsingular fast terminal sliding mode control of permanent magnet linear motor based on disturbance observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 409-421.
[6] Cui H, Teng Qingfang, Xu Ruiqi. Adaptive super- twisting speed control for PMLSM system using generalized proportional integral observer[C]//2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 2021: 1-6.
[7] Chen S Y, Chiang H H, Liu T S, et al. Precision motion control of permanent magnet linear syn- chronous motors using adaptive fuzzy fractional-order sliding-mode control[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(2): 741-752.
[8] 魏惠芳, 王丽梅. 永磁直线同步电机自适应模糊神经网络时变滑模控制[J]. 电工技术学报, 2022, 37(4): 861-869.
Wei Huifang, Wang Limei. Adaptive fuzzy neural network time-varying sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 861-869.
[9] Chen Lifang, Lan Zhiyong, Xie Bin, et al. Develop- ment of the method of suppressing thrust fluctuation in permanent magnet linear synchronous motor[C]// 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 2021: 1-6.
[10] Zhang Chao, Zhang Liwei, Huang Xianjin, et al. Research on the method of suppressing the end detent force of permanent magnet linear synchronous motor based on stepped double auxiliary pole[J]. IEEE Access, 2020, 8: 112539-112552.
[11] 彭兵, 刘铁法, 张囡, 等. 凹型端齿削弱永磁直线电机端部力波动方法[J]. 电工技术学报, 2015, 30(7): 119-124.
Peng Bing, Liu Tiefa, Zhang Nan, et al. A method for reducing the end effect force fluctuation by the concave profile end-tooth in permanent magnet linear motors[J]. Transactions of China Electrotechnical Society, 2015, 30(7): 119-124.
[12] 许孝卓, 孙震, 汪旭东, 等. Halbach交替极永磁同步直线电机特性分析[J]. 电工技术学报, 2019, 34(9): 1825-1833.
Xu Xiaozhuo, Sun Zhen, Wang Xudong, et al. Characteristic of a novel permanent magnet linear synchronous motor with Halbach array consequent- pole[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1825-1833.
[13] 董家臣, 高钦和, 陈志翔, 等. 考虑电流环动态响应的永磁直线同步电机新型线性自抗扰控制[J]. 中国电机工程学报, 2019, 39(8): 2436-2448, 26.
Dong Jiachen, Gao Qinhe, Chen Zhixiang, et al. New LADRC design for permanent magnet linear syn- chronous motor considering dynamic response of current loop[J]. Proceedings of the CSEE, 2019, 39(8): 2436-2448, 26.
[14] Zhao Jiwen, Wang Lijun, Dong Fei, et al. Robust high bandwidth current regulation for permanent magnet synchronous linear motor drivers by using two- degree-of-freedom controller and thrust ripple observer[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(3): 1804-1812.
[15] 赵鑫宇, 王丽梅. 永磁直线同步电机自适应分数阶终端滑模控制[J]. 电工技术学报, 2023, 38(20): 5434-5443.
Zhao Xinyu, Wang Limei. Adaptive fractional-order terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5434-5443.
[16] 武志涛, 李帅, 程万胜. 基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J]. 电工技术学报, 2022, 37(10): 2503-2512.
Wu Zhitao, Li Shuai, Cheng Wansheng. Fixed structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2503-2512.
[17] Yang Rui, Li Liyi, Wang Mingyi, et al. Force ripple compensation and robust predictive current control of PMLSM using augmented generalized proportional- integral observer[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 302-315.
[18] 王丽梅, 孙璐, 初升. 基于经验模态分解算法的永磁直线同步电机迭代学习控制[J]. 电工技术学报, 2017, 32(6): 164-171.
Wang Limei, Sun Lu, Chu Sheng. Iterative learning control of permanent magnet linear synchronous motor based on empirical mode decomposition algorithm[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 164-171.
[19] Yan Yunda, Sun Zhiyuan, Li Shihua. Disturbance rejection control method based on composite dis- turbance observer for permanent magnet synchronous motor[C]//IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 2016: 3137-3142.
[20] Zhu Z Q, Ruangsinchaiwanich S, Chen Y, et al. Evaluation of superposition technique for calculating cogging torque in permanent-magnet brushless machines[J]. IEEE Transactions on Magnetics, 2006, 42(5): 1597-1603.
[21] Huang Xu zhen, Yu Han chuan, Zhou Bo, et al. Detent-force minimization of double-sided permanent magnet linear synchronous motor by shifting one of the primary components[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 180-191.
Abstract Permanent magnet synchronous linear motor (PMLSM) has excellent control accuracy and response speed. It is widely applied in automatic control systems, automatic precision machine tools, and other occasions. However, due to its structure, PMLSM has thrust ripples, which can cause vibration and noise, greatly affecting the control accuracy of the motor drive at low speeds. The detent force is the main cause of thrust ripples, containing end and cogging forces. This paper proposes a thrust ripple suppression strategy based on the proportional resonant internal model extended state observer (PR-IMESO) to improve system performance and control accuracy.
Firstly, thrust ripples are modeled and analyzed, and cogging force and end force models are established. Then, the detent force model, a function of mover position with motor pole distance t as the period, is obtained. Its frequency is twice the frequency of the primary winding phase current. Aiming at the large detent force in thrust ripples, the internal model expanded state observer is studied, considering the detent force model to compensate for the detent force and other unmodeled thrust ripples in real-time. In addition, a resonant term is introduced into the observer to enhance the compensation ability of the fixed frequency detent force. The observer is designed according to the motion equation of PMLSM considering various thrust disturbances, and parameters are adjusted by the observer bandwidth.
Finally, simulation and experiment are carried out. Set the motor running speed to 0.06 m/s and load tension to 10 N. According to the simulation results, the amplitude of velocity fluctuation with the PR-IMESO suppression strategy attenuates to 3.4% of the amplitude of velocity fluctuation, and the suppression rate is 96.6%. It is theoretically verified that the proposed strategy has a significant suppression effect on the detent force with a secondary fluctuation frequency. Further, the experiment is carried out with a 750 W PMLSM experimental platform. The PMLSM thrust ripple suppression strategies based on ESO, IMESO, and PR-IMESO are verified under the motor speed of 0.03 m/s, 0.0 6m/s, no-load, load 2 kg, 3 kg, and 4 kg. The velocity fluctuation significantly decreases with the proposed strategy. The suppression rate can reach up to 73.5%, and the average suppression rate is 68.7%. In addition, the dynamic performance of the PR-IMESO thrust ripple suppression strategy is demonstrated in the sudden loading of 4 kg. Great fluctuations of the mover velocity before and after the sudden loading exist without a suppression strategy. After adding the proposed strategy, the fluctuation of the mover velocity is significantly reduced during the whole motion process. In the process of sudden loading, the transition of the velocity error and Q-axis current is smooth and rapid. The average suppression rate of the mover velocity fluctuation is 68.7%.
keywords：Permanent magnet linear synchronous motor, detent force, proportional resonant internal model extended state observer, thrust ripple suppression
DOI: 10.19595/j.cnki.1000-6753.tces.L10072
中图分类号：TM341
收稿日期 2023-01-13
改稿日期 2023-04-25
张国强 男，1987年生，博士，教授，研究方向为交流电机控制理论与应用技术。E-mail: ZhGQ@hit.edu.cn（通信作者）
赵新茹 女，2000年生，硕士研究生，研究方向为永磁同步直线电机驱动控制技术。E-mail: 19845178600@163.com
（编辑 崔文静）