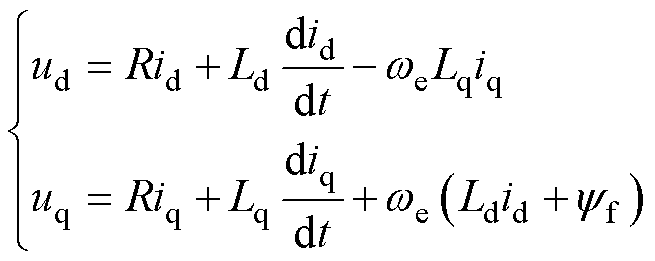 (1)
(1)
摘要 模型预测控制方法已经被广泛应用于内置式永磁同步电机(IPMSM)的控制之中,传统模型预测控制方法由于候选电压矢量数量有限,在电机运行过程中会产生较大的电流和转矩谐波。为了增加候选电压矢量数量,提出了构建虚拟电压矢量的方法。但是在应用虚拟矢量调制方法时,系统计算的负担会随虚拟矢量数量的增加而增加,因此控制效果会受到系统计算能力的限制。针对此问题,该文提出了一种新型的虚拟电压矢量调制方法,首先将电压扇区进行细分来增加虚拟电压矢量的数量,然后通过对指令电压矢量坐标进行标幺化处理的方法求得其角度,最后从基础和虚拟电压矢量之中由角度搜索选出最优电压矢量。在该方法中,系统的计算量大小与虚拟电压矢量的数量无关,因此可以在不增加系统计算负担的情况下提升系统的控制性能。实验结果表明,与虚拟矢量数量受到限制的虚拟矢量预测控制方法相比,该方法有效减少了三相电流谐波含量,并且减少了控制算法的执行时间。
关键词:永磁同步电机 模型预测电流控制 虚拟电压矢量 占空比调制
永磁同步电机具有动态性能强、功率密度高等优点,被广泛应用于电动汽车、伺服系统、风力发电等领域[1-5]。而在永磁同步电机的控制方法之中,模型预测控制方法由于简单易于实施、动态性能好等特点,成为传统PI控制方法一个很好的替换选择[6]。模型预测控制方法可以分为有限集预测控制方法[7-8]和连续集预测控制方法[9]。其中有限集预测控制方法通过对不同开关状态下的输出量进行预测选出最优的开关状态,省去了空间脉宽调制阶段,相较于连续集预测控制方法更为简易。此外,有限集预测控制方法还可以在预设的成本函数加入限制条件实现对于指定目标的约束[10-11]。
然而,传统有限集预测电流控制(Finite Control Set Model Predictive Current Control, FCS-MPCC)方法只从基础的6个非零电压矢量和零电压矢量之中进行寻优选择,寻优的候选电压数量有限且在一个周期内逆变器的开关状态维持不变。这会造成一个周期内电流变化较大,从而产生较大的电流脉动和转矩脉动[12-14]。因此,为提升传统有限集预测控制方法的运行性能,只能提高系统控制频率,然而这对硬件性能要求较高,不具备通用性[15]。
为了在不提升系统控制频率的基础上提高有限集预测控制方法的控制性能,目前许多文献提出了通过基础电压矢量合成更多虚拟电压矢量,从而增加候选电压矢量数量的方法。文献[16]构建了虚拟电压矢量并对不同虚拟电压矢量数量下的控制性能进行了对比。文献[17]将7个基础电压矢量两两组合,在排除掉不合适的电压矢量组合之后对剩下的25种电压矢量组合进行遍历寻优。然而,合成电压矢量在增加候选电压矢量数量的同时,也增加了成本函数的计算次数,越多的电压矢量选择会带来越大的计算量。针对这个问题,一些文献提出了在寻优前先对候选电压矢量进行筛选的方法。文献[18]在增加了6个虚拟电压矢量之后,根据每个电压矢量对于电流的增减作用初步筛选出5个候选电压矢量,并通过每个候选电压矢量令电流预测值达到参考值的时间来求解出其中的最优电压矢量。文献[19]首先通过成本函数的计算得到6个基础非零电压矢量之中的最佳和次最佳电压矢量,再通过将这两个电压矢量之间的虚拟电压矢量全部代入成本函数得到最优的虚拟电压矢量。然而,上述方法只是通过筛选减少了需要计算的候选电压矢量数量,并没有改变传统FCS-MPCC使用穷举法寻优的本质,所构建的虚拟电压矢量数量会受到硬件计算能力的限制。
为了进一步缩小候选电压矢量的寻优范围,文献[20]将每个扇区分为许多三角区域,通过电压指令矢量与边界的距离计算得到电压指令矢量所在三角区域。此时,候选电压矢量范围缩小到了此三角区域的3个角,最后再通过成本函数计算求出3个候选电压矢量之中最优的电压矢量。但是这种方法在虚拟矢量数量不同时,所使用的三角区域判断标准需要修改,且计算量同样会随着虚拟矢量数量的增加而增加。文献[21]提出的多电压矢量合成预测电流控制(Multiple Voltage Vector synthesis Model Predictive Current Control, MVV-MPCC)方法,在文献[20]的基础上,进行坐标变换,将所构建的电压虚拟矢量标幺化,并通过坐标变换后的指令电压矢量坐标判断电压矢量指令值所处的三角区域,选出3个候选的电压虚拟矢量代入成本函数求出最优虚拟矢量。文献[21]中的三角区域判断方法相较于文献[20]更为简单,但是在得到候选电压矢量之后仍需要进行寻优操作。
针对上述问题,本文提出了一种基于新型虚拟矢量调制方法的模型预测电流控制方法。首先,通过坐标变换对指令电压矢量进行坐标标幺化处理,将任意扇区的指令电压矢量统一到第Ⅰ扇区进行计算。然后,通过将每个扇区细分的方法构建虚拟电压矢量来扩充候选电压矢量,并通过角度判断得到与电压指令矢量最接近的候选电压矢量,使计算量大小不受虚拟矢量数量的影响。最后,构建新的成本函数获得占空比大小,将从候选电压矢量中选出的最优电压矢量还原到原本扇区,计算每周期各相开关开通时间。与目前所提出的虚拟矢量调制方法相比,本文提出方法所构建的虚拟电压矢量数量不会受到计算能力的限制,且构建不同数量的虚拟电压矢量时可以采用统一的调制方法。因此,在本文方法中,所构建的虚拟矢量数量可以任意指定,在系统计算负担较小的情况下获得更好的控制效果。此外,占空比计算的引入也保证了开关频率的恒定。实验结果也证明了该方法的有效性和准确性。
在不考虑涡流损耗、磁滞损耗和电机定转子铁心磁阻的情况下,dq轴中的内置式永磁同步电动机(Interior Permanent Magnet Synchronous Motor, IPMSM)电压方程可以表示为
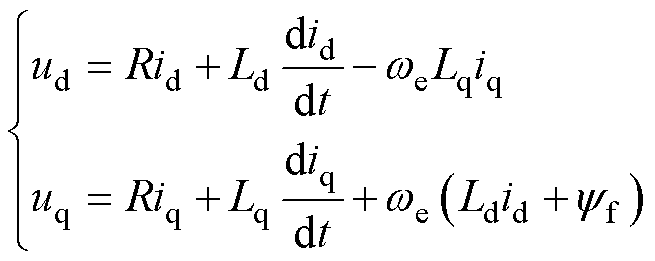 (1)
(1)
式中,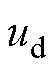 和
和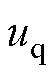 分别为定子绕组d轴和q轴电压分量;
分别为定子绕组d轴和q轴电压分量;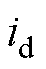 和
和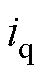 分别为定子绕组d轴和q轴电流分量;
分别为定子绕组d轴和q轴电流分量;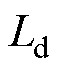 和
和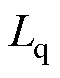 分别d轴电感和q轴电感;
分别d轴电感和q轴电感;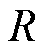 为定子电阻;
为定子电阻;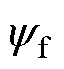 为永磁体磁链;
为永磁体磁链;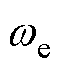 为电角速度。
为电角速度。
对于电压方程式(1)进行离散化处理得到电流下一周期的预测值为
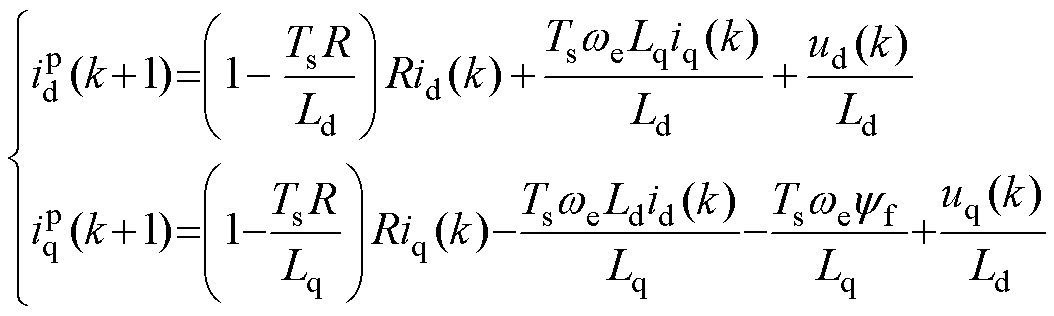 (2)
(2)
式中,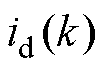 和
和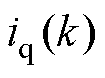 为k时刻的d轴和q轴电流测量值;
为k时刻的d轴和q轴电流测量值;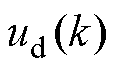 和
和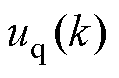 为k~k+1时刻之间的d轴和q轴电压给定值;
为k~k+1时刻之间的d轴和q轴电压给定值;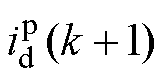 和
和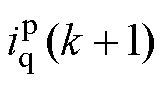 分别为经过预测计算得到的k+1时刻的d轴和q轴电流预测值;Ts为控制系统控制周期。
分别为经过预测计算得到的k+1时刻的d轴和q轴电流预测值;Ts为控制系统控制周期。
在预测控制方法之中,选取不同的电压矢量可以计算出不同的电流预测值。为了选出能使实际电流最接近指令电流的电压矢量,在得到式(2)中的下一周期电流预测值之后,构建成本函数[22]为
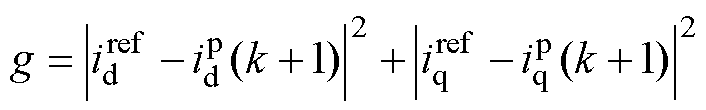 (3)
(3)
式中,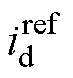 和
和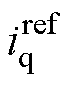 分别为k时刻的d轴和q轴电流指令值。
分别为k时刻的d轴和q轴电流指令值。
传统模型预测控制中,候选电压矢量为基础的6个非零电压矢量和1个零电压矢量。通过成本函数计算,选出让成本函数最小的电压矢量。
传统模型预测控制中,候选电压矢量全部为基础电压矢量,有限的候选电压矢量数量会造成较大的电流脉动。因此,为了增加候选电压矢量数量,本文在有限集预测控制方法的基础上,提出了一种新型的虚拟矢量调制方法,整个系统的控制框图如图1所示。
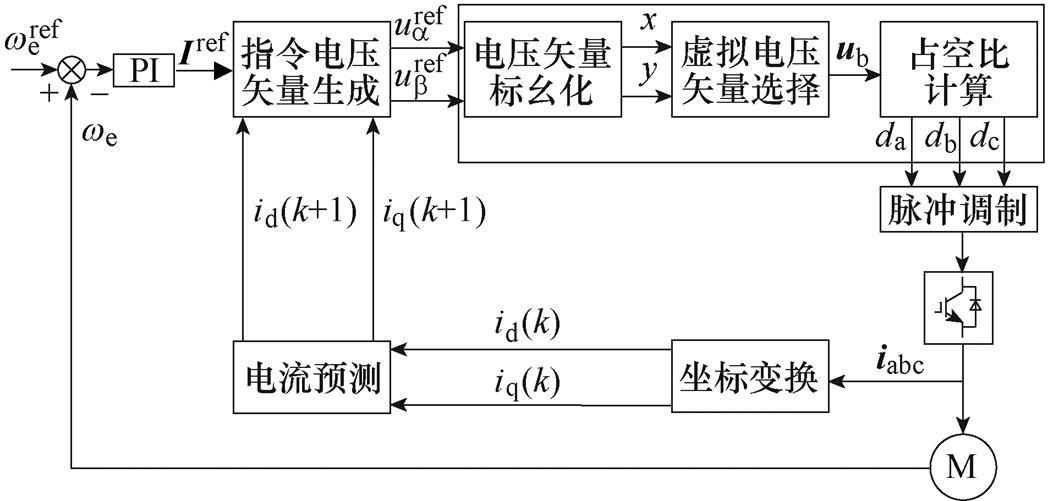
图1 所提出控制方法框图
Fig.1 Flow chart of the proposed control method
为了便于扇区的判断,首先结合离散化之后的式(1)和式(2)得到消除了一步延时效应影响之后的指令电压为
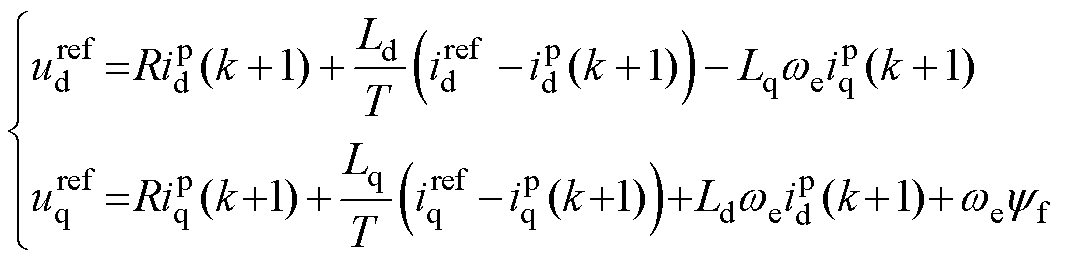 (4)
(4)
式中,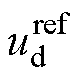 、
、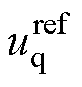 分别为定子绕组d轴和q轴电压指定值。
分别为定子绕组d轴和q轴电压指定值。
为了计算方便,将指令电压矢量由dq旋转坐标系变换到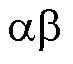 固定坐标系,有
固定坐标系,有
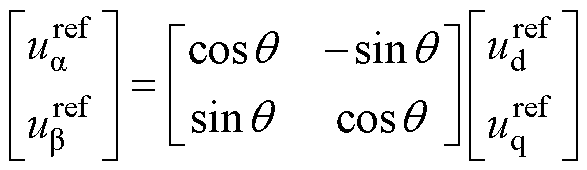 (5)
(5)
式中,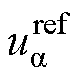 、
、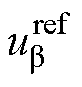 分别为定子绕组a 轴和b 轴电压指定值;
分别为定子绕组a 轴和b 轴电压指定值;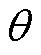 为电机电角度。
为电机电角度。
为了便于电压扇区的判断以及后续调制方法的进行,本文选择将电压矢量进行标幺化处理。将电压矢量再次进行坐标变换由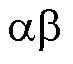 固定坐标系变换到gh坐标系,变换后的基础电压矢量坐标如图2所示,
固定坐标系变换到gh坐标系,变换后的基础电压矢量坐标如图2所示,
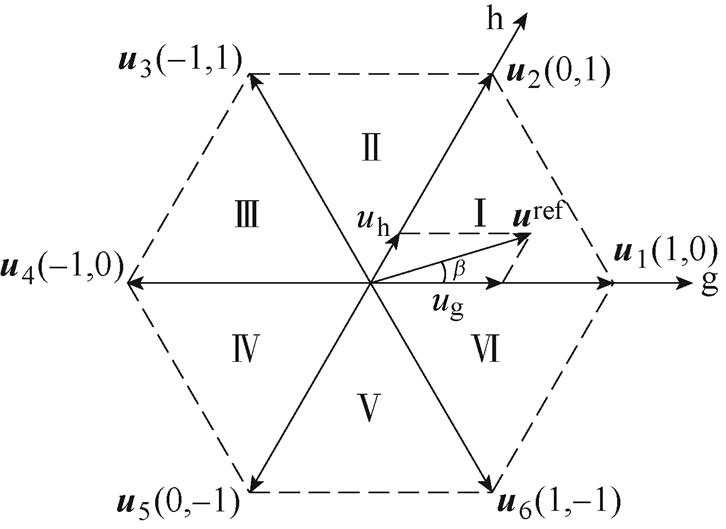
图2 gh坐标系
Fig.2 gh coordinate system
式(4)中的指令电压矢量变换过程为
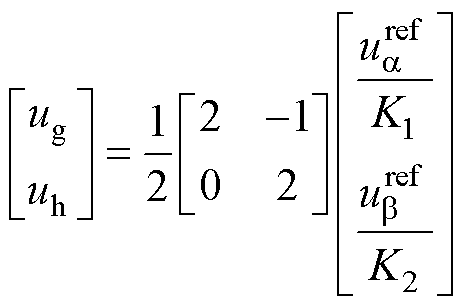 (6)
(6)
其中
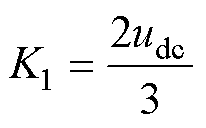 (7)
(7)
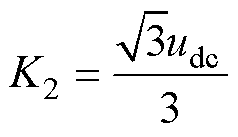 (8)
(8)
式中,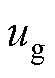 和
和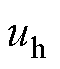 分别为变换到g、h坐标系的指令电压矢量坐标;K1、K2为坐标变换中的参数;
分别为变换到g、h坐标系的指令电压矢量坐标;K1、K2为坐标变换中的参数;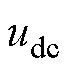 为直流母线电压。
为直流母线电压。
对于基础电压矢量同样进行式(6)中的坐标变换,坐标变换后的基础电压矢量坐标以及gh坐标系如图2所示。
在坐标变换以后,基础电压矢量已经经过标幺化处理,因此由坐标变换后的指令电压矢量坐标可以直接判断指令电压矢量的扇区。并且,通过指令电压矢量的坐标,可以直接得到指令电压矢量与相邻两非零矢量之间的合成关系如图2所示。扇区判断和矢量合成见表1。表中,x表示所在扇区顺时针方向上的相邻基础非零电压矢量所占比例,y表示所在扇区逆时针方向上的相邻基础非零电压矢量所占比例。
表1 扇区判断与矢量合成
Tab.1 Sector judgment and vector synthesis

扇区扇区判断矢量合成 1ug≥0 && uh≥0x=ug,y=uh 2ug<0 && uh≥0 && (ug+uh)≥0x=uh+ug, y=-ug 3ug<0 && uh≥0 && (ug+uh)<0x=uh, y=-ug-uh 4ug<0 && uh<0x=-ug, y=-uh 5ug≥0 && uh<0 && (ug+uh)<0x=-ug-uh, y=ug 6ug≥0 && uh<0 && (ug+uh)≥0x=-uh, y=ug+uh
在得到表1中的电压指令矢量与相邻两矢量的合成关系之后,电压指令矢量与所在扇区顺时针方向上的相邻基础非零电压矢量之间的角度为
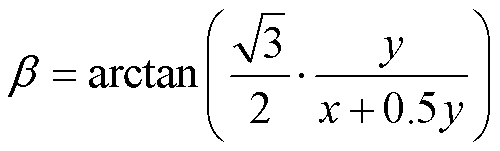 (9)
(9)
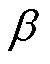 的范围为0°~60°,通过
的范围为0°~60°,通过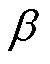 角的计算,不同扇区的电压指令矢量等效到一个扇区进行处理。
角的计算,不同扇区的电压指令矢量等效到一个扇区进行处理。
传统有限集预测控制方法的候选矢量有限,因此为了增加候选矢量的数量,本文将每个扇区分为N个小区域,每个小区域上的虚拟电压矢量由此扇区边界的两个非零电压矢量合成得到。由于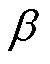 角的等效作用,将所有扇区统一等效到Ⅰ扇区进行处理。
角的等效作用,将所有扇区统一等效到Ⅰ扇区进行处理。
当Ⅰ扇区被分为N个区域以后,其中存在N+1个电压矢量,包括两个非零基础电压矢量以及N-1个虚拟电压矢量。对全部电压矢量进行编号,顺时针方向基础电压矢量编号为1,逆时针方向基础电压矢量编号为N+1,两非零电压矢量之间的虚拟电压矢量编号依次从2~N。虚拟电压矢量两个非零基础电压矢量之间均匀排布,所有电压矢量在gh轴坐标系中的坐标为
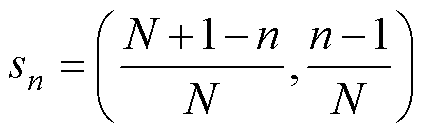 (10)
(10)
式中,n为电压矢量编号,当n为1~N+1时代表基础电压矢量,当n为2~N时代表合成的虚拟电压矢量。
为了从候选电压矢量中搜寻到最优电压矢量,近似认为每个小区域所占角度为60/N。近似认为每个小区域所占角度相同会造成一定的误差,如图3中划分为4个区域后的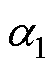 和
和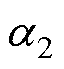 大小并不会完全相同。但是,随着N的增大这种误差会逐渐减小,因此不会对控制效果造成影响。
大小并不会完全相同。但是,随着N的增大这种误差会逐渐减小,因此不会对控制效果造成影响。
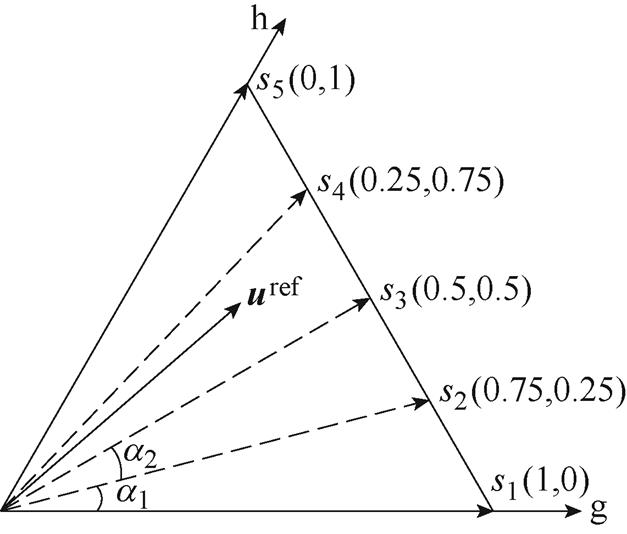
图3 划分4个区域后的虚拟矢量
Fig.3 Virtual vectors after sector division into four regions
当指令电压矢量等效到Ⅰ扇区后,此时角度与指令电压矢量角度最接近的候选电压矢量即为最优电压矢量。
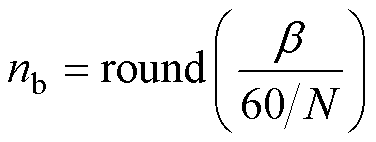 (11)
(11)
式中,round为近似取整函数,将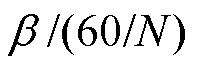 所得到的结果进行四舍五入;
所得到的结果进行四舍五入;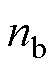 为角度与指令电压矢量角度最接近的电压矢量编号。
为角度与指令电压矢量角度最接近的电压矢量编号。
在通过round函数计算得到等效到Ⅰ扇区的最优电压矢量编号之后,通过下述变换得到还原后的最优电压矢量,有
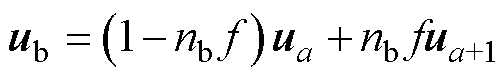 (12)
(12)
其中
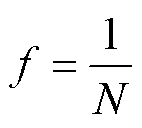
式中,a为选取的最优电压矢量所在的扇区号,大小为1~6;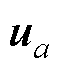 和
和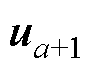 分别为编号为a和a+1的基础电压矢量,当最优电压矢量处于扇区Ⅵ时,
分别为编号为a和a+1的基础电压矢量,当最优电压矢量处于扇区Ⅵ时,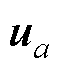 和
和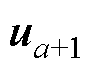 分别为
分别为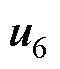 和
和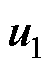 。
。
式(12)中的基础电压矢量可以表示为
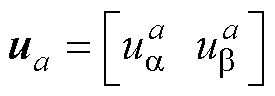 (13)
(13)
其中
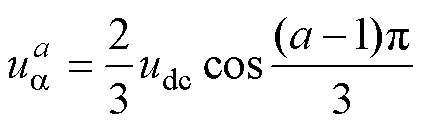 (14)
(14)
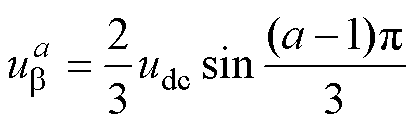 (15)
(15)
上述构造方法中的N可以任意设置,且调制方法不受N取值大小的影响,只需改变式(10)~式(12)中的N值大小,即可实现虚拟电压矢量数量的改变。因此,扩充虚拟电压矢量的数量并不会增加系统的计算量。
在得到最优电压矢量之后,为了进一步提高控制效果,需要对其进行占空比调制。因此,构建新的成本函数,为
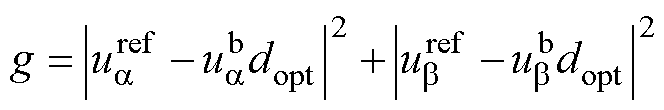 (16)
(16)
式中,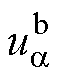 和
和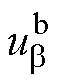 分别为最优电压矢量
分别为最优电压矢量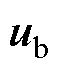 在
在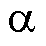 轴和
轴和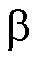 轴的电压分量;
轴的电压分量;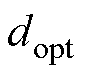 为占空比大小。
为占空比大小。
为了使成本函数最小,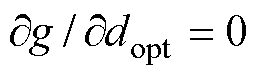 ,计算得到最优占空比大小为
,计算得到最优占空比大小为
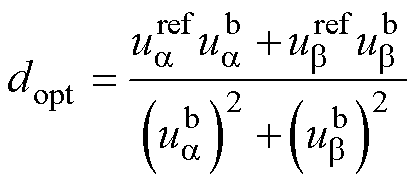 (17)
(17)
当转速或者速度突变时,系统可能会出现过调制现象,计算出的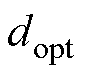 >1,此时对占空比进行调 整,有
>1,此时对占空比进行调 整,有
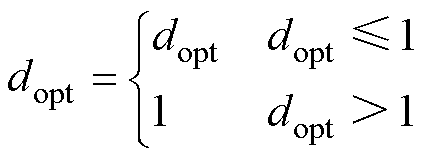 (18)
(18)
当最优电压矢量处于Ⅰ扇区时,在计算得到最优电压矢量编号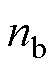 以及占空比以后,基础电压矢量
以及占空比以后,基础电压矢量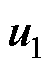 在一个周期作用时间应为
在一个周期作用时间应为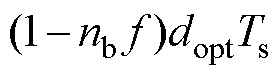 ,基础电压矢量
,基础电压矢量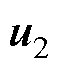 作用时间应为
作用时间应为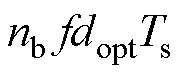 ,零电压矢量作用时间应为
,零电压矢量作用时间应为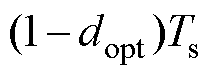 。为了减少电流谐波大小,将零电压矢量作用时间的1/4分配给一个周期的开始和结尾阶段,1/2分配给中间阶段。最优电压矢量处于Ⅰ扇区时的ABC相开关状态如图4所示,图中,SA、SB和SC分别为A、B、C三相开关状态,0表示关断,1表示开通,
。为了减少电流谐波大小,将零电压矢量作用时间的1/4分配给一个周期的开始和结尾阶段,1/2分配给中间阶段。最优电压矢量处于Ⅰ扇区时的ABC相开关状态如图4所示,图中,SA、SB和SC分别为A、B、C三相开关状态,0表示关断,1表示开通,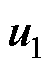 、
、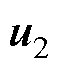 和
和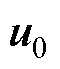 分别为在该时段内作用的电压矢量是基础电压矢量
分别为在该时段内作用的电压矢量是基础电压矢量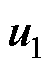 、
、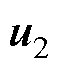 和零电压矢量
和零电压矢量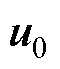 。则一个周期中开关的开通时间计算为
。则一个周期中开关的开通时间计算为
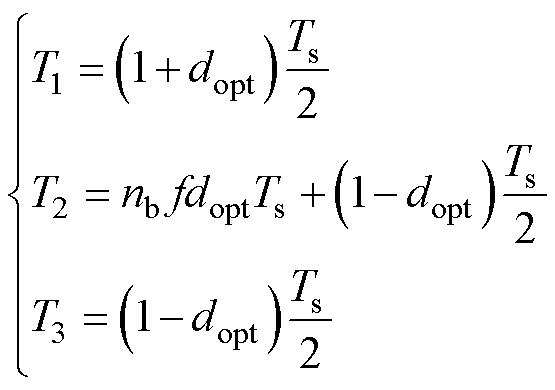 (19)
(19)
式中,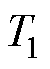 、
、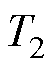 、
、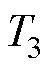 分别为当最优电压矢量处于Ⅰ扇区时A相、B相、C相开关在一个周期的开通时间。当最优电压矢量处于其他扇区时,各相开通时间与
分别为当最优电压矢量处于Ⅰ扇区时A相、B相、C相开关在一个周期的开通时间。当最优电压矢量处于其他扇区时,各相开通时间与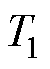 、
、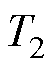 、
、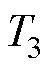 的对应关系见表2。
的对应关系见表2。
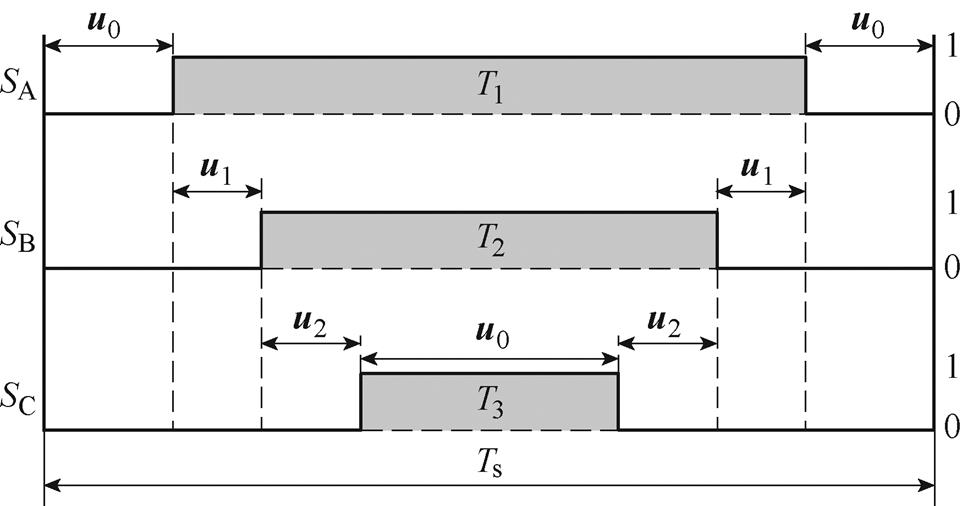
图4 扇区Ⅰ各相开关状态
Fig.4 Switching status of each phase of sector Ⅰ
表2 三相开关开通时间
Tab.2 Three-phase switch-on time

扇区A相B相C相 1T1T2T3 2T2T1T3 3T3T1T2 4T3T2T1 5T2T3T1 6T1T3T2
本文基于新型虚拟矢量调制方法的IPMSM预测电流控制方法的具体实施步骤如下:
(1)利用式(6)对指令电压矢量进行坐标变换以达到标幺化的目的,再通过坐标变换后的坐标进行扇区判断及获得指令电压矢量与相邻两基础电压矢量之间的合成关系,具体的扇区判断方法和合成关系获得方法见表1。
(2)首先将计算全部等效到第Ⅰ扇区,利用式(10)对基础电压矢量及虚拟矢量编号之后,通过式(11)由角度得到最优电压矢量编号,最后由式(12)获得还原到原来扇区的最优电压矢量。
(3)通过式(16)中成本函数的构建获得最优占空比大小,在一个周期内对各电压矢量进行时间分配,最后根据式(17)、式(18)和表2由已获得的最优电压矢量编号和最优占空比大小计算得到三相开关各相的开通时间。
为了验证上述提出方法的有效性和可靠性,本文在一台额定功率为1.5 kW的IPMSM上进行了实验。实验平台如图5所示,其中使用磁粉制动器作为负载转矩,IPMSM由数字信号处理器(Digital Singnal Processor, DSP)进行驱动控制,系统采样频率为10 kHz,IPMSM参数见表3。

图5 实验平台
Fig.5 Experimental platform
为了比较所提出方法与现有方法的控制性能,实验对文献[23]中提出的在一个控制周期内采用一个基础电压矢量和一个零矢量组合的占空比FCS- MPCC方法、文献[21]中所提出的多电压矢量合成电流预测控制(MVV-MPCC)方法和本文所提出的基于新型虚拟矢量的模型电流预测控制(Novel Virtual Vector Model Predictive Current Control, NVV-MPCC)方法进行了对比。本文提出的NVV- MPCC方法每个扇区划分区域数N选为12。
表3 IPMSM参数
Tab.3 Design parameters of IPMSM
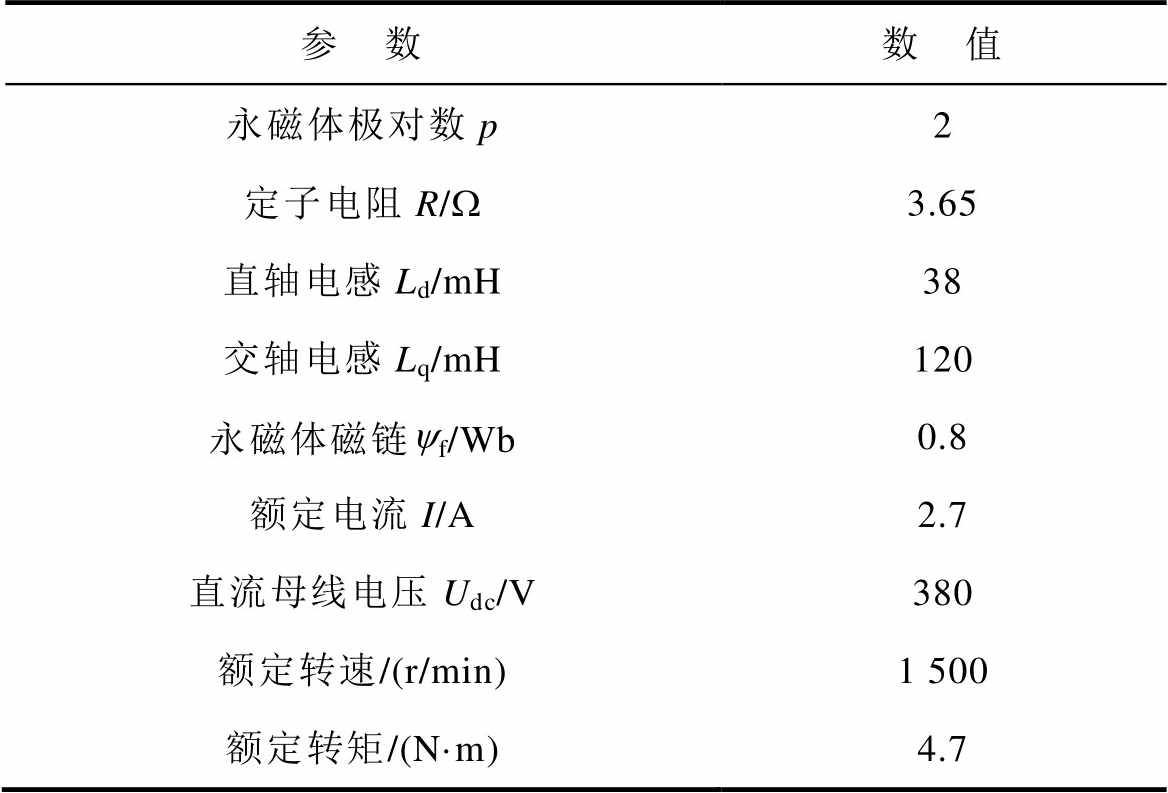
参 数数 值 永磁体极对数p2 定子电阻R/W3.65 直轴电感Ld/mH38 交轴电感Lq/mH120 永磁体磁链yf/Wb0.8 额定电流I/A2.7 直流母线电压Udc/V380 额定转速/(r/min)1 500 额定转矩/(N·m)4.7
对三种方法的稳态控制性能进行对比分析,图6为三种方法在转速为400 r/min、负载转矩为额定转矩的75%即3.5 N·m时的三相电流控制性能,并对A相的电流进行了快速傅里叶变换分析。其中,占空比FCS-MPCC方法的A相电流总谐波畸变率(Total Harmonic Distortion, THD)为4.11%,MVV- MPCC方法的A相电流THD=2.56%,本文所提出的NVV-MPCC方法的A相电流THD=1.58%。
图7为图6运行条件下的指令电压矢量扇区,通过扇区判断得到了每周期电压矢量所在扇区,由图可知,占空比FCS-MPCC方法和MVV-MPCC方法存在指令电压矢量在相邻扇区来回振荡的现象,而本文提出的NVV-MPCC方法不存在这种现象。结合图6和图7分析可知,由于占空比FCS-MPCC方法和MVV-MPCC方法的电压候选矢量的数量有限,所选出的电压矢量与实际电压指令矢量之间存在一定误差,这种误差使得实际电流不能完全跟随指令电流,电机运动产生小幅振荡,并最终产生了额外的电流谐波。相较于占空比FCS-MPCC方法,本文所提出的NVV-MPCC方法可以增加候选电压矢量的数量。而且NVV-MPCC方法中的候选电压矢量数量不受硬件计算能力的限制,因此可以无限制地增加候选电压矢量数量。从而最终消除了指令电压矢量在相邻扇区振荡的现象,大幅提升了系统的控制性能。
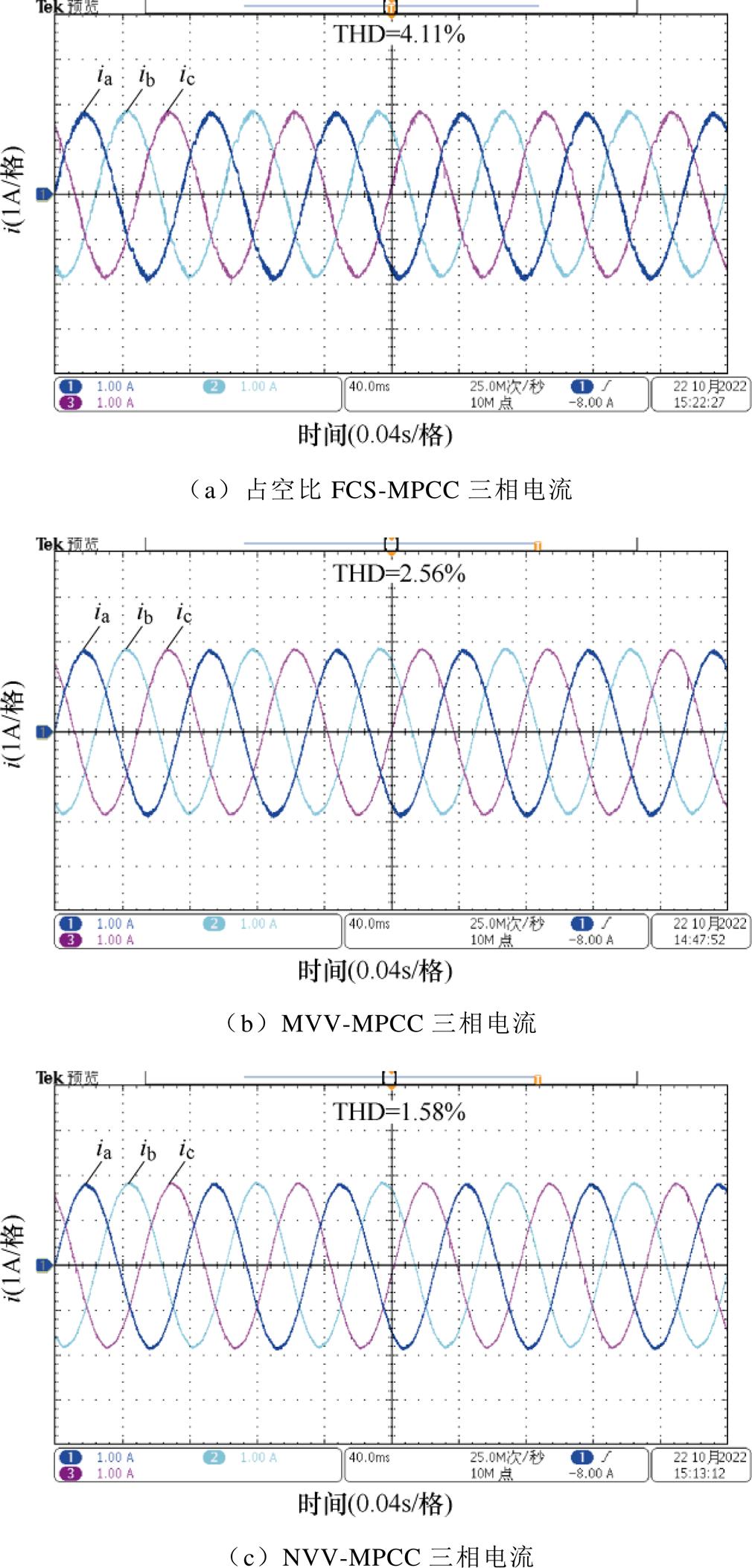
图6 转速400 r/min稳态电流控制性能
Fig.6 Current control performance at 400 r/min
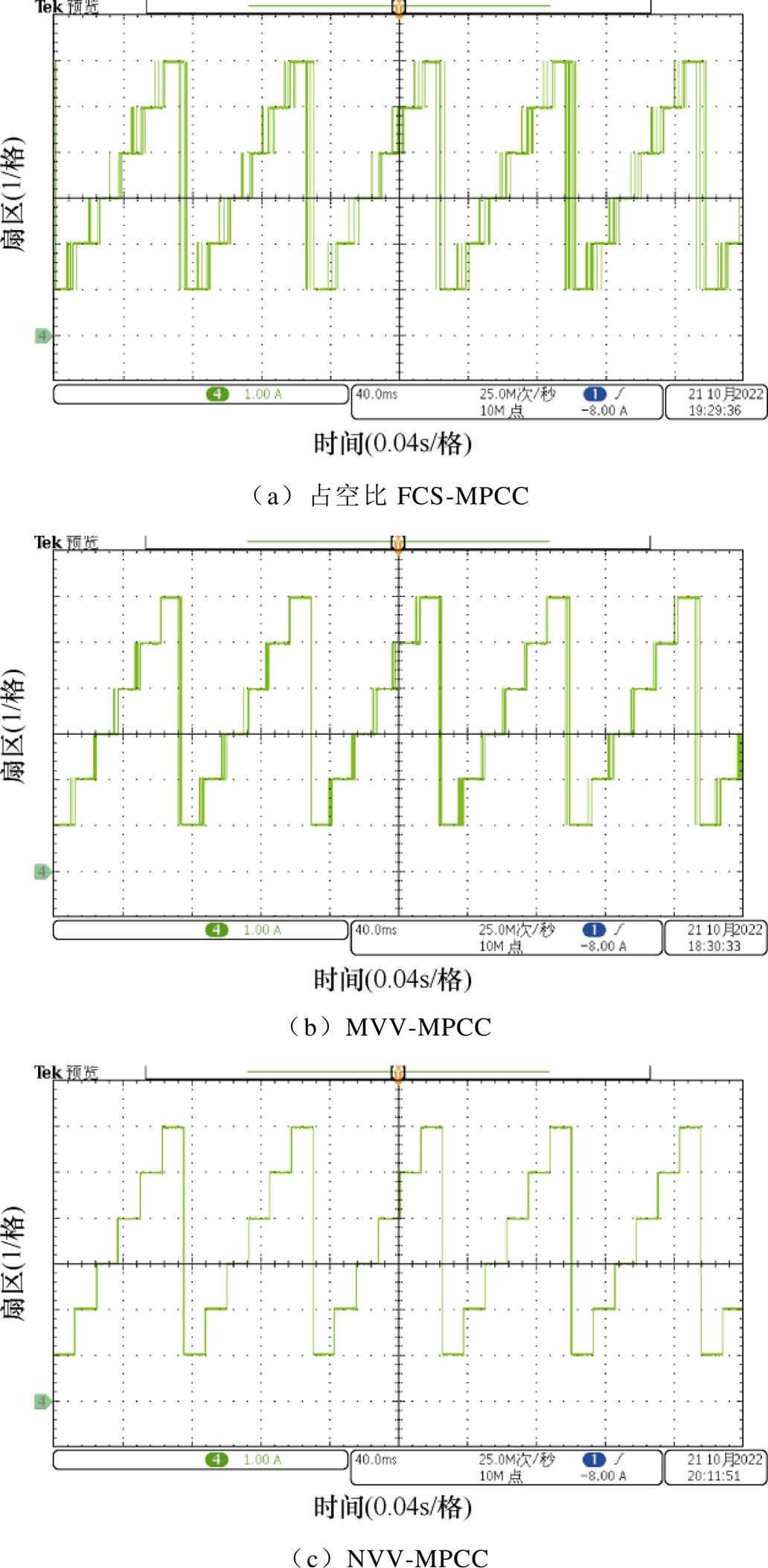
图7 转速400 r/min指令电压矢量扇区
Fig.7 Command voltage vector sector at 400 r/min
图8和图9展示了三种方法在转速为150 r/min、负载为3.5 N·m时的控制性能,图8中,占空比FCS- MPCC方法A相电流THD=5.42%,MVV-MPCC方法A相电流THD=3.18%,本文所提出的NVV-MPCC方法A相电流THD=2.04%。相较于图7,在如图9所示的低速情况下,占空比FCS-MPCC方法和MVV-MPCC方法的电压指令矢量的振荡现象更加明显,但是本文所提出的NVV-MPCC方法依然可以消除这种振荡现象。
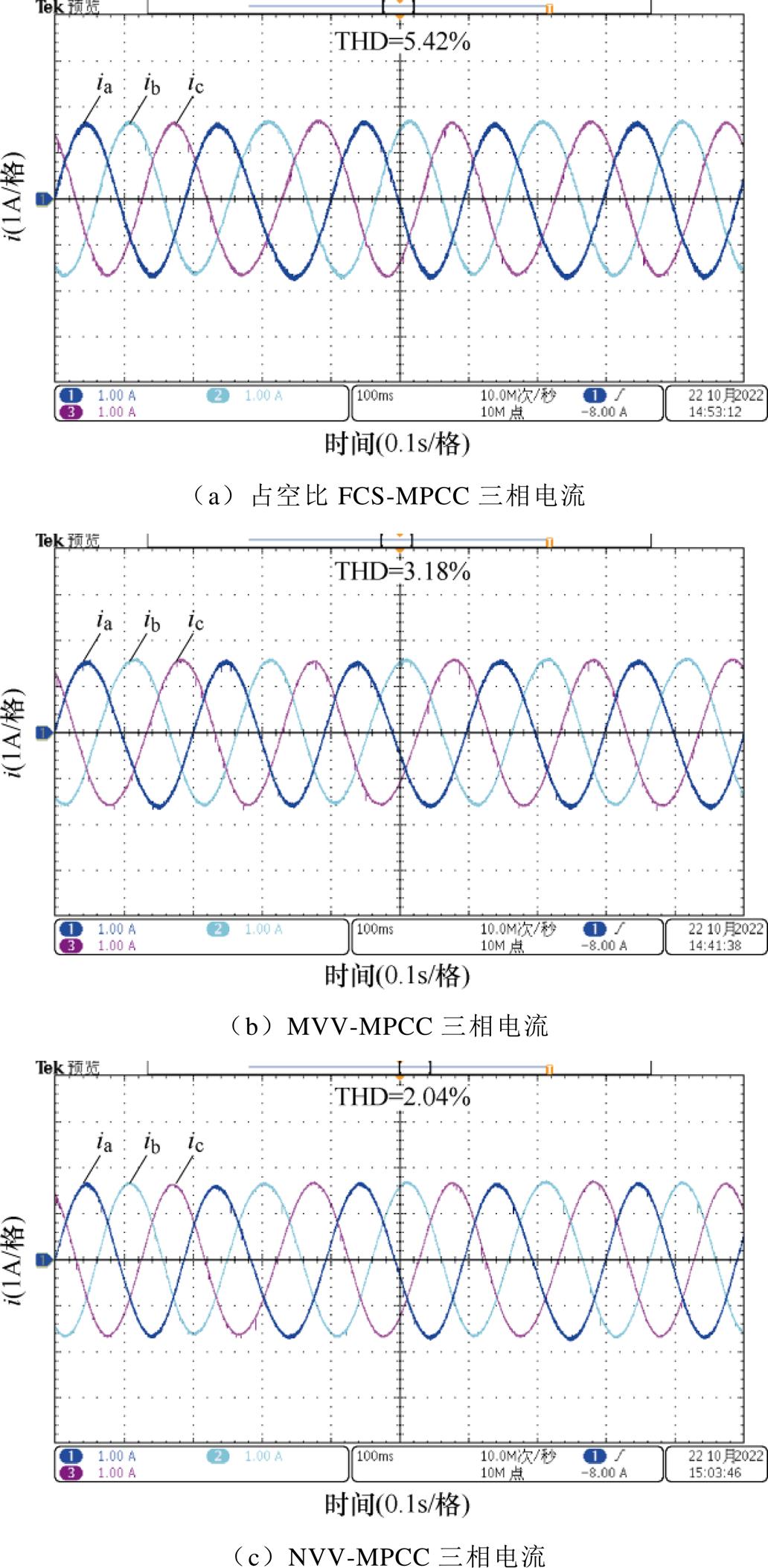
图8 转速150 r/min稳态电流控制性能
Fig.8 Current control performance at 150 r/min
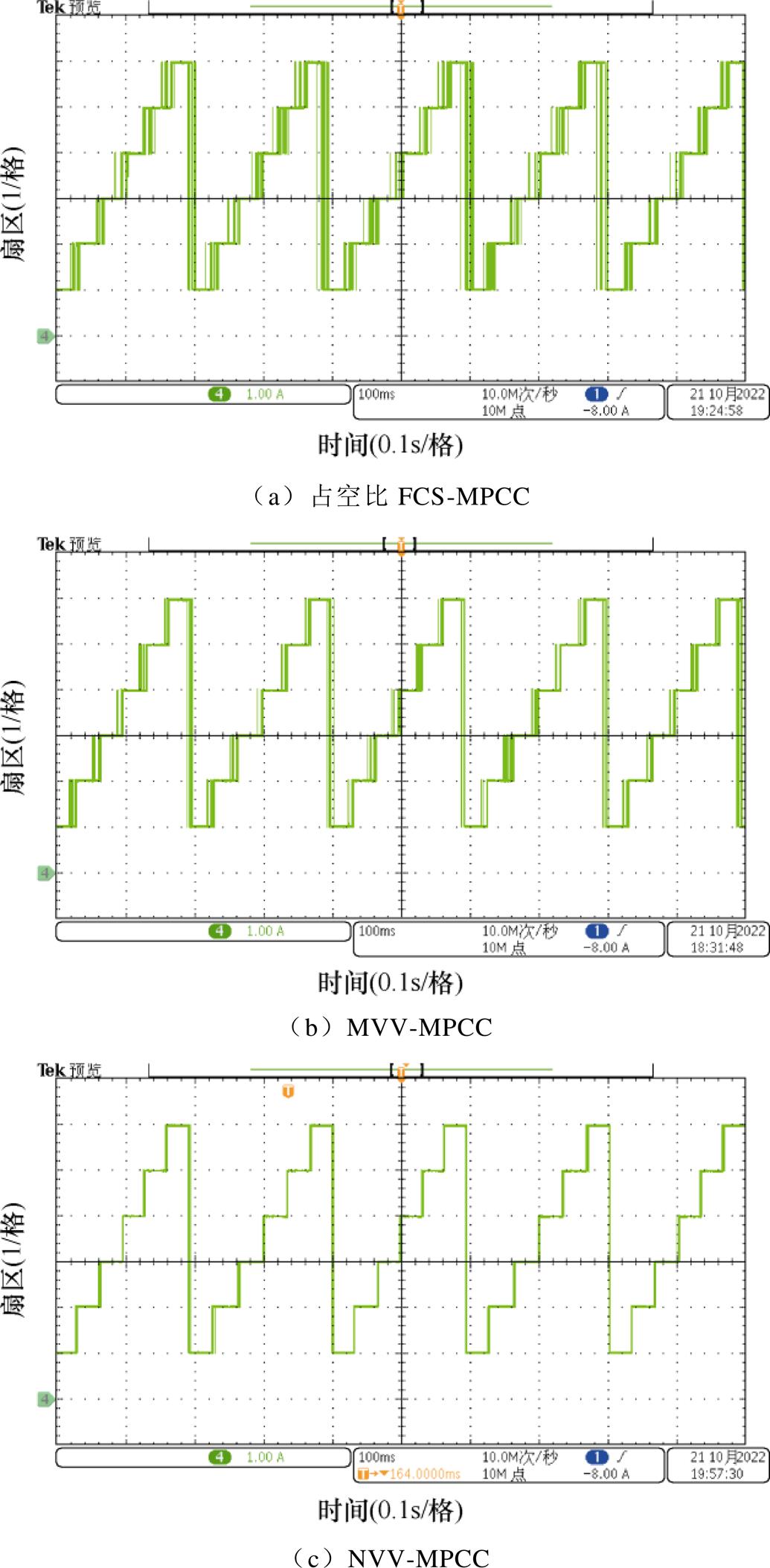
图9 转速150 r/min指令电压矢量扇区
Fig.9 Command voltage vector sector at 150 r/min
图10给出了占空比FCS-MPCC方法、本文提出的NVV-MPCC方法以及采用空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)的无差拍预测控制方法在不同转速下的A相电流THD对比。其中,为了对比本文所提出的NVV- MPCC方法中不同N值对于控制性能的影响,增加了N值设置为4与原有的N值为12的情况进行对比实验。如图10所示,在实验的5个不同转速中,所有方法的三相电流THD值都是在转速为额定转速的27%即400 r/min时最小。当电机运行转速为额定转速的10%即150 r/min时,在相对低速的情况下,N值为4的NVV-MPCC方法的三相电流谐波相较于转速为400 r/min时有较大的增加,而N值为12的NVV-MPCC方法的电流谐波基本不变。在NVV- MPCC方法中,当转速从400 r/min逐渐增加时,N值由4~12的增加带来的A相电流THD的下降会随着转速增加越来越明显。因此,本文所提出的NVV-MPCC方法中N值在一定范围内的增加可以有效提升系统在宽调速范围下的控制性能。此外,在NVV-MPCC方法中的N值增加到12以后,A相电流的THD大小与采用SVPWM的无差拍预测控制方法接近。这说明在N值足够大的情况下,本文所提出方法可以在省去SVPWM的情况下获得与使用SVPWM的无差拍预测控制方法相同的控制性能。
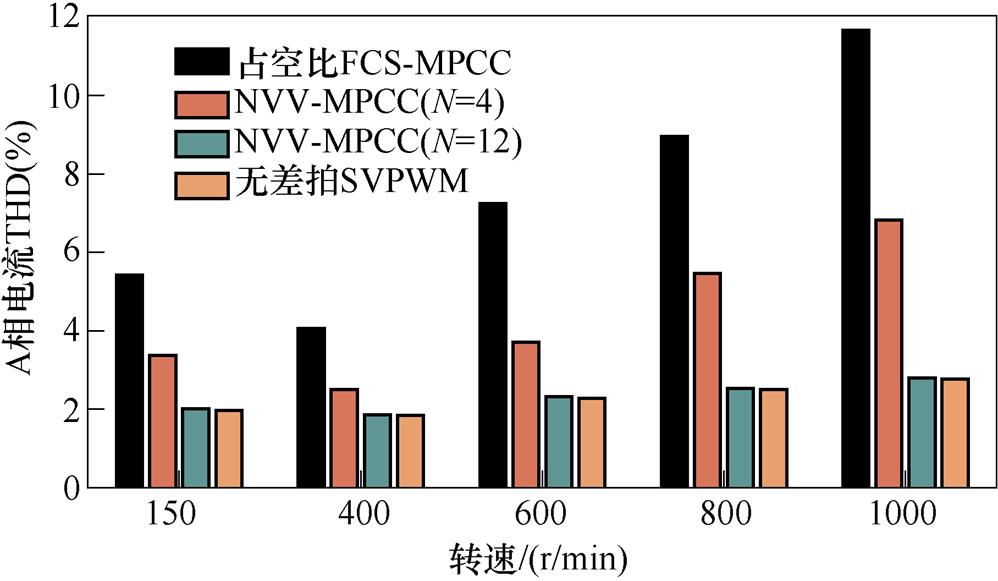
图10 不同转速下性能对比结果
Fig.10 Performance comparison at different speeds
图11为三种方法在由空载突加转矩为额定转矩75%即3.5 N·m负载之后的动态响应,由图11可见,本文所提出的NVV-MPCC方法的dq轴电流脉动相较于占空比FCS- MPCC方法和MVV-MPCC方法有明显的减小。同时,相较于其他两种方法,本文所提出的NVV-MPCC方法的dq轴电流可以更迅速地增加,从而拖动负载转矩。图12则为三种方法在转速由200 r/min突变到300 r/min之后的动态响应,可见,相较于另外两种方法,NVV-MPCC方法的动态响应时间更短,具有更好的动态响应能力和转速跟踪能力,且在转速突变后产生的电流振荡相对较小。由图11和图12可知,本文所提出的NVV- MPCC方法在提升候选电压矢量数量时,并没有影响系统的动态响应能力。
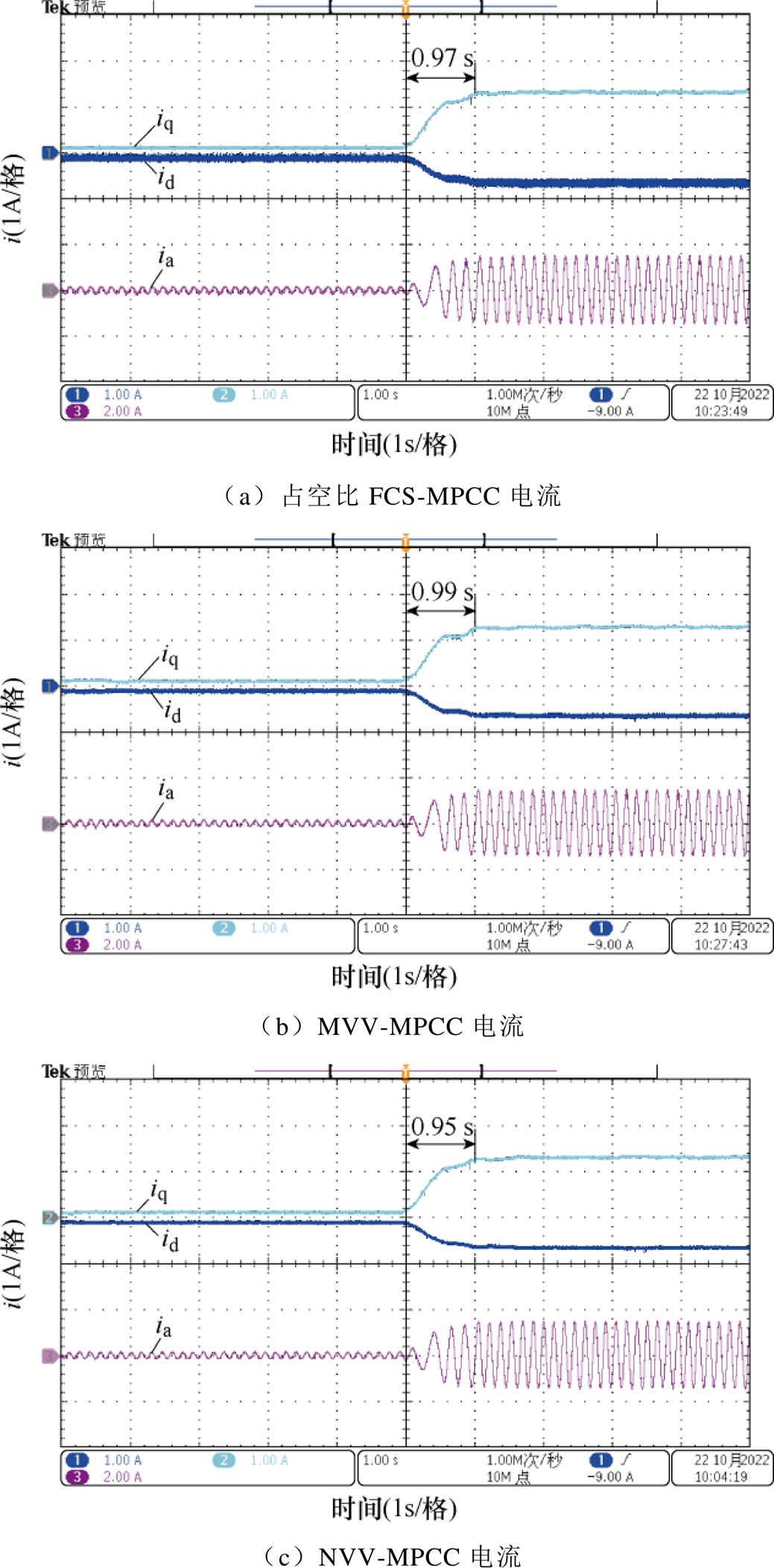
图11 突加转矩时的动态响应
Fig.11 Dynamic response during sudden torque increase
表4中展示了不同方法的执行时间对比,本文所提出的NVV-MPCC方法由于减少了电压矢量的搜索范围,省略了遍历寻优的过程,因此相较于其他两种方法具有更短的执行时间。此外,如表4所示,虚拟矢量的增加也不会影响本文提出方法的执行时间。
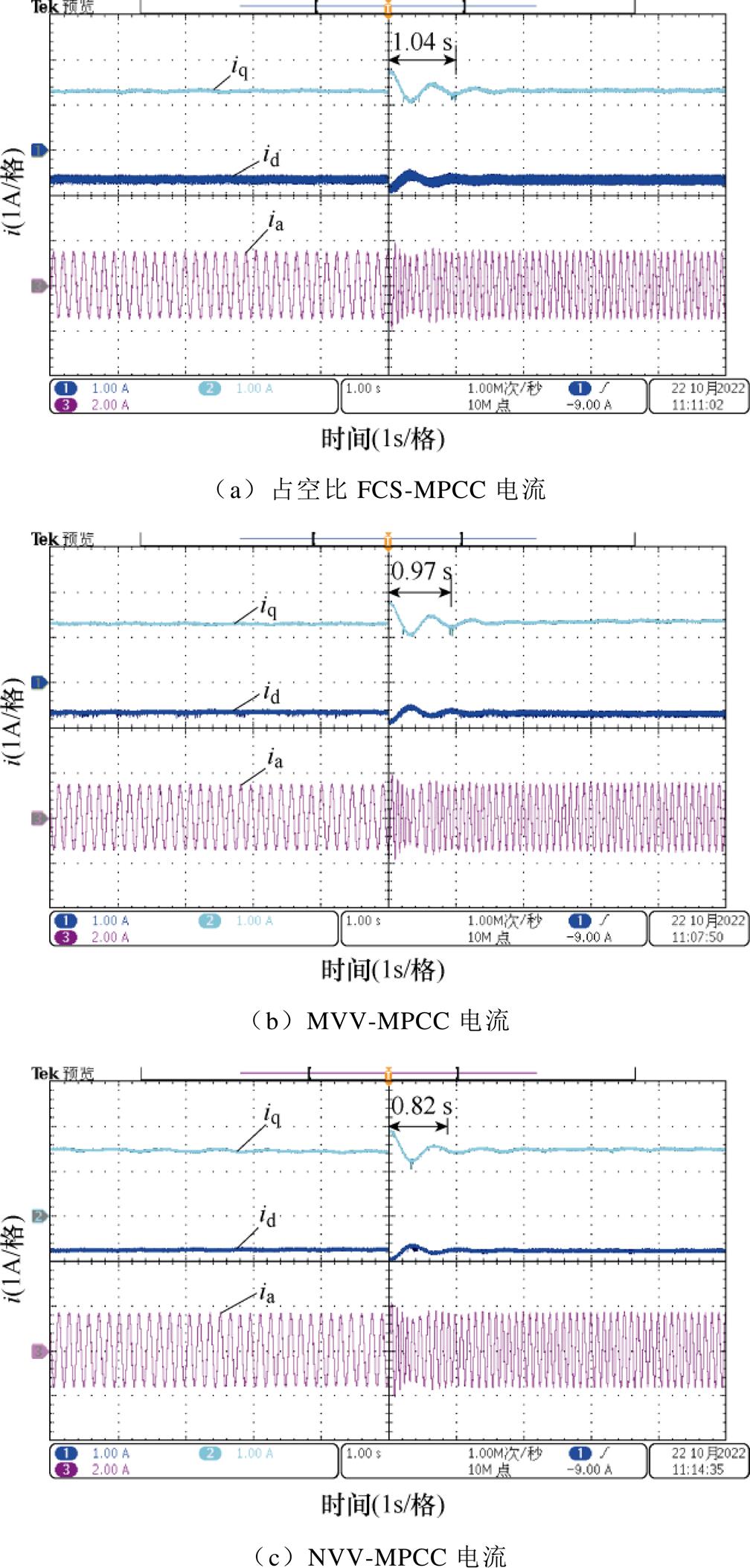
图12 转速突变时的动态响应
Fig.12 Dynamic response during sudden speed changes
表4 执行时间
Tab.4 Execution time

方 法执行时间/ms FCS-MPCC48.1 MVV-MPCC45.6 NVV-MPCC (N=4)42.3 NVV-MPCC (N=12)42.3
针对永磁同步电机传统模型电流预测控制方法存在的电流控制效果受到基础电压矢量数量限制的问题,本文提出了一种基于新型虚拟矢量调制方法的模型预测电流控制方法。所提出方法将计算过程统一到一个扇区,将编号后的虚拟电压矢量与基础电压矢量一起构成电压候选矢量,简化了电压候选矢量的寻优过程。此外,本文提出的方法去除了遍历寻优过程,虚拟电压矢量数量的增加不会增加系统的计算量。因此,实现了所构建的虚拟电压矢量数量可以任意选择的目的,控制效果再不会受到硬件计算能力的限制。实验结果表明,所提出方法在不影响系统动态响应能力的基础上,减小了电流的谐波大小,提升了系统的稳态控制性能。并且由于寻优方式的简化,所提出方法具有更短的执行时间,提高了系统的控制效率。
参考文献
[1] 梅三冠, 卢闻州, 樊启高, 等. 基于滑模观测器误差补偿的永磁同步电机无位置传感器控制策略[J]. 电工技术学报, 2023, 38(2): 398-408.
Mei Sanguan, Lu Wenzhou, Fan Qigao, et al. Sensorless control strategy of permanent magnet synchronous motor based on error compensation estimated by sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 398- 408.
[2] 章回炫, 范涛, 边元均, 等. 永磁同步电机高性能电流预测控制[J]. 电工技术学报, 2022, 37(17): 4335-4345.
Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.
[3] 李思毅, 苏健勇, 杨贵杰. 基于自抗扰控制的永磁同步电机弱磁控制策略[J]. 电工技术学报, 2022, 37(23): 6135-6144.
Li Siyi, Su Jianyong, Yang Guijie. Flux weakening control strategy of permanent magnet synchronous motor based on active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6135-6144.
[4] 谷鑫, 鲁金月, 王志强, 等. 基于无差拍电流预测控制的永磁同步电机谐波电流抑制策略[J]. 电工技术学报, 2022, 37(24): 6345-6356.
Gu Xin, Lu Jinyue, Wang Zhiqiang, et al. Harmonic Current suppression strategy for permanent magnet synchronous motor based on deadbeat current predi- ction control[J]. Transactions of China Electro- technical Society, 2022, 37(24): 6345-6356.
[5] 李祥林, 薛志伟, 阎学雨, 等. 基于电压矢量快速筛选的永磁同步电机三矢量模型预测转矩控制[J]. 电工技术学报, 2022, 37(7): 1666-1678.
Li Xianglin, Xue Zhiwei, Yan Xueyu, et al. Voltage vector rapid screening-based three-vector model predictive torque control for permanent magnet synchronous motor[J]. Transactions of China Electro- technical Society, 2022, 37(7): 1666-1678.
[6] Li Xinyue, Tian Wei, Gao Xiaonan, et al. A generalized observer-based robust predictive current control strategy for PMSM drive system[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1322-1332.
[7] Karamanakos P, Geyer T. Guidelines for the design of finite control set model predictive controllers[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 7434-7450.
[8] 姚绪梁, 麻宸伟, 王景芳, 等. 基于预测误差补偿的鲁棒型永磁同步电机模型预测电流控制[J]. 中国电机工程学报, 2021, 41(17): 6071-6081.
Yao Xuliang, Ma Chenwei, Wang Jingfang, et al. Robust model predictive current control for PMSM based on prediction error compensation[J]. Pro- ceedings of the CSEE, 2021, 41(17): 6071-6081.
[9] Zhang Xiaoguang, Hou Benshuai, Mei Yang. Deadbeat predictive current control of permanent- magnet synchronous motors with stator current and disturbance observer[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3818-3834.
[10] Vafaie M H, Dehkordi B M, Moallem P, et al. Improving the steady-state and transient-state per- formances of PMSM through an advanced deadbeat direct torque and flux control system[J]. IEEE Transactions on Power Electronics, 2017, 32(4): 2964-2975.
[11] 颜宁, 曹鑫, 张蕾, 等. 基于直接转矩控制的开关磁阻电机模型预测控制方法[J]. 中国电机工程学报, 2017, 37(18): 5446-5453, 5544.
Yan Ning, Cao Xin, Zhang Lei, et al. Direct torque control-based model predictive control of switched reluctance motors[J]. Proceedings of the CSEE, 2017, 37(18): 5446-5453, 5544.
[12] Zhang Yongchang, Bai Yuning, Yang Haitao. A universal multiple-vector-based model predictive control of induction motor drives[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(8): 6957-6969.
[13] Yan Liming, Dou Manfeng, Hua Zhiguang, et al. Optimal duty cycle model predictive current control of high-altitude ventilator induction motor with extended minimum stator current operation[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 7240-7251.
[14] 刘佳敏, 葛召炎, 吴轩, 等. 基于占空比调制的永磁同步电机预测电流控制[J]. 中国电机工程学报, 2020, 40(10): 3319-3328.
Liu Jiamin, Ge Zhaoyan, Wu Xuan, et al. Predictive current control of permanent magnet synchronous motor based on duty-cycle modulation[J]. Pro- ceedings of the CSEE, 2020, 40(10): 3319-3328.
[15] 夏长亮, 仇旭东, 王志强, 等. 基于矢量作用时间的新型预测转矩控制[J]. 中国电机工程学报, 2016, 36(11): 3045-3053.
Xia Changliang, Qiu Xudong, Wang Zhiqiang, et al. Predictive torque control based on optimal operating time of vector[J]. Proceedings of the CSEE, 2016, 36(11): 3045-3053.
[16] Vazquez S, Leon J I, Franquelo L G, et al. Model predictive control with constant switching frequency using a discrete space vector modulation with virtual state vectors[C]//2009 IEEE International Conference on Industrial Technology, Churchill, VIC, Australia, 2009: 1-6.
[17] 徐艳平, 张保程, 周钦. 永磁同步电机双矢量模型预测电流控制[J]. 电工技术学报, 2017, 32(20): 222-230.
Xu Yanping, Zhang Baocheng, Zhou Qin. Two-vector based model predictive current control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 222-230.
[18] 史婷娜, 张维, 肖萌, 等. 基于矢量作用时间的永磁同步电机预测电流控制[J]. 电工技术学报, 2017, 32(19): 1-10.
Shi Tingna, Zhang Wei, Xiao Meng, et al. Predictive Current control for permanent magnet synchronous motor based on operating time of vector[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(19): 1-10.
[19] Zhou Zhanqing, Xia Changliang, Yan Yan, et al. Torque ripple minimization of predictive torque control for PMSM with extended control set[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 6930-6939.
[20] Wang Yuanlin, Wang Xiaocan, Xie Wei, et al. Deadbeat model-predictive torque control with dis- crete space-vector modulation for PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 3537-3547.
[21] Agoro S, Husain I. Robust deadbeat finite-set predi- ctive current control with torque oscillation and noise reduction for PMSM drives[J]. IEEE Transactions on Industry Applications, 2022, 58(1): 365-374.
[22] Zhang Xiaoguang, Wang Ziwei. Simple robust model predictive current control for PMSM drives without flux-linkage parameter[J]. IEEE Transactions on Industrial Electronics, 2022, 70(4): 3515-3524.
[23] Morel F, Lin-Shi X, Retif J M, et al. A comparative study of predictive current control schemes for a permanent-magnet synchronous machine drive[J]. IEEE Transactions on Industrial Electronics, 2009, 56(7): 2715-2728.
Abstract The model predictive control method has been widely applied to control internal permanent magnet synchronous motors (IPMSM). Conventional model predictive control methods only select voltage vectors from the basic voltage vector, resulting in a restricted number of candidate voltage vectors, which can generate large current and torque harmonics during motor operation. To increase the number of candidate voltage vectors, some studies have proposed methods for constructing virtual voltage vectors. However, the computational burden of the system will increase with the increase in the virtual vectors number, posing constraints on control performance. Therefore, this paper proposes a novel virtual voltage vector modulation method, which reduces the system computational burden by calculating the angle of the voltage vector.
The specific steps of the proposed method are as follows. First, coordinate transformation is performed on the command voltage vector, and the command voltage vector is normalized by incorporating the magnitude of the DC bus voltage. Then, the sector in which the command voltage vector is located is determined by the coordinate values. The composite relationship between the command voltage vector and the adjacent two basic voltage vectors is obtained. Accordingly, the angle of the command voltage vector in the sector is obtained, and the voltage vector processing is equivalent to the first voltage sector. Subsequently, each voltage sector is evenly divided into N parts to construct virtual voltage vectors, and the virtual voltage vectors in the first voltage sector are numbered. The virtual voltage vector with the closest angle to the command voltage vector is selected through the rounding function. Finally, the optimal duty cycle is obtained through the cost function. The opening time of each phase of the three-phase switch is calculated based on the obtained optimal voltage vector number and duty cycle.
Experiments on an IPMSM are conducted with a rated power of 1.5 kW to verify the proposed method. The experimental results show that under steady-state conditions, compared to the predictive control method using a limited number of voltage vectors, this method reduces the harmonic content of the three-phase current by up to 3.4%. Moreover, when the number of sector partitions N is large enough, the proposed method approaches the current control performance of the deadbeat predictive current control using SVPWM modulation at different speeds. In dynamic situations, the proposed method demonstrates faster dynamic response and smaller current harmonics during sudden changes in torque and speed. In addition, as the traversal optimization process is omitted, the proposed method effectively reduces the system execution time, and the execution time of the system is the same for different N values.
In conclusion, the proposed method simplifies the modulation process of the model predictive control method and avoids complex calculations caused by traversal optimization, enabling an unrestricted increase in virtual voltage vectors.
keywords:Permanent magnet synchronous motor, model predictive current control, virtual voltage vector, duty cycle modulation
国家自然科学基金资助项目(52277047)。
收稿日期 2023-02-01
改稿日期 2023-03-20
DOI: 10.19595/j.cnki.1000-6753.tces.230105
中图分类号:TM351
汪逸哲 男,1994年生,博士研究生,研究方向为永磁同步电机设计与控制技术等。E-mail: wangyizhe927@hnu.edn.cn
黄 晟 男,1988年生,博士,教授,研究方向为风电机组群协调优化控制技术等。E-mail: huangsheng319@hnu.edu.cn(通信作者)
(编辑 崔文静)