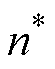 和n分别为转速给定值和实际值,
和n分别为转速给定值和实际值,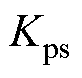 和
和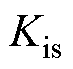 分别为转速调节器的比例和积分参数,
分别为转速调节器的比例和积分参数,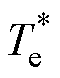 和
和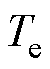 分别为电磁转矩给定值和实际值,
分别为电磁转矩给定值和实际值,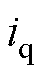 为q轴电流,
为q轴电流,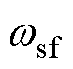 为转速低通滤波带宽,
为转速低通滤波带宽,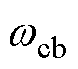 为电流环带宽,K为永磁电机转矩系数,TL为负载转矩,J为伺服系统转动惯量。
为电流环带宽,K为永磁电机转矩系数,TL为负载转矩,J为伺服系统转动惯量。摘要 在永磁伺服控制系统中,传统的转速控制策略在低频段存在幅值与相位偏差问题,降低了转速跟踪控制精度。为解决该问题,该文提出了一种高精度的转速跟踪控制策略与数据驱动的参数设计方法。主要思路是在转速控制环节串联一个滞后-超前补偿器,用以校正低频段的幅值与相位;以低频段补偿后的幅值及相位误差最小为优化目标,同时约束补偿器在全频带范围内的最大幅值增益和相移,设计了一种数据驱动的补偿器参数优化方法,并对补偿后控制系统的性能进行了分析评估。实验结果表明,基于实验数据所设计的补偿器在转速指令频率小于1 rad/s的低频段区间内,转速跟踪误差小于2 r/min,相较于传统方法控制精度显著提升;在跟踪转速阶跃指令时,该文方法和传统方法的控制效果相当,这说明该文方法在改善低频段跟踪性能的同时,保持了控制系统在中高频段原有的幅频和相频特性。
关键词:永磁伺服系统 转速控制 滞后-超前补偿器 数据驱动 参数优化
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因其结构简单、转矩密度大、功率因数和运行效率高等优点[1-3],目前已被应用于生产生活中的诸多场合,尤其在航空航天、工业驱动和高速伺服系统等对控制精度需求较高的领域得到广泛推广[4-6]。但PMSM本身是一个多变量、强耦合、非线性的控制对象[7],电机参数随着环境改变及运行工况的不同会发生明显的变化,给伺服系统转速控制带来困难。尤其是伺服系统在低频工况运行时,采用传统的转速控制策略,实际转速与目标值的幅值和相位通常都存在偏差,影响伺服系统的控制效果,因而实现永磁伺服系统的高精度转速跟踪控制仍有难点亟待解决,有必要开展学术研究。目前,针对永磁伺服系统转速跟踪控制策略的研究主要集中在PI参数整定[8-9]、转速采样及滤波器设计[10]、鲁棒自适应控制[11]、滑模控制[12-13]、基于迭代学习的控制方法[14]以及其他智能算法[15-17]等方面。
PI参数整定方法可以分为基于模型的PI参数整定和基于规则的PI参数整定,前者是基于伺服系统的精确数学模型,按照传统控制理论对PI参数值进行设计;后者是以伺服系统实际的控制效果为依据,采用相应的评价函数和优化准则来获取PI参数的最优值。文献[8]根据PMSM调速系统的频域模型,推导PI控制器参数的解析计算式,由期望的电流环和速度环开环截止频率和相位裕度,从而解析得到具体的PI控制器参数。文献[9]提出通过基于当前控制效果不断迭代学习调整PI参数,从而进一步改善伺服系统的控制效果,对于抑制转速脉动起到了一定改善。该类方法原理简单,便于实现,使用也较为普遍,但是由于PI调节器固有特性,即使设定最佳的PI参数也不能保证控制性能达到理论上的最优效果。
提高转速采样的精度和信噪比,以及设计合适的转速滤波器也可提高转速控制精度,但需要折中考虑成本以及滤波时间常数对系统动态与稳态性能的影响。鲁棒自适应控制可以提高系统对参数摄动的鲁棒性,滑模控制在一定程度上提升了系统的响应速度,但通常也降低了对扰动的抑制能力。基于迭代学习的控制方法只适用于跟踪固定轨迹的场合,通用性较差,而诸如神经网络、机器学习的控制算法还基本停留在仿真和实验室阶段。部分学者针对以上方法的问题进行了探索,文献[18]基于电感和转矩系数不变的假设,提出了一种基于离散转速跟踪微分器的转动惯量辨识方法,利用辨识得到的转动惯量自动调整控制器参数,提高了系统对转动惯量的自适应性,但是对于不同伺服系统的普适性还有待提高。文献[19]提出了一种基于新型趋近律的滑模变结构控制方法,解决原有趋近律的抖振问题和在远离滑模面时趋近速度慢的问题,但是参数整定复杂,难以直接应用。文献[20]基于直驱永磁同步电机的物理结构模型,提出了一种虚拟齿槽转矩控制方法,用于降低直驱永磁同步电机伺服系统在低速条件下的速度脉动,取得了一定效果,但是也存在动态响应性能较差的问题。文献[21]将滞后-超前补偿器应用于伺服系统,虽然能够弥补低转速工况的转速跟踪精度,但由于补偿器基于低速大扭矩设计,对于动态性能的改善有限,并且只停留在基于精简指令集处理器(Advanced RISC Machine, ARM)芯片上运行控制算法,模型参数相对理想,实际应用效果未得到验证。文献[22-23]对比了几种常见的滞后-超前补偿器,提高了模型设计的自由度,对于系统稳定性、快速性及稳态精度方面都有一定改善,但是对于各类补偿器的理论边界和适用范围没有展开详细分析,普适性还有待提高。虽然滞后-超前补偿器在工程实践中已有所应用,但在系统参数不匹配时仍然难以避免性能下降的问题,因而有必要对补偿器的参数进行优化设计。
为了减小伺服系统转速跟踪时的幅值与相位偏差,改善传统控制策略在低频段的转速跟踪控制精度,并保持较好的动态响应性能,本文提出了一种基于串联滞后-超前补偿的永磁伺服系统高精度转速跟踪控制策略。由于永磁伺服系统传统转速控制策略在低频段存在明显的幅值与相位偏移,首先,设计一个滞后-超前补偿器串联在转速控制环节,以修正低频段的幅值和相位,提升转速跟踪控制精度;然后,采用数据驱动的参数优化设计方法,依据仿真或实验数据对滞后-超前补偿器的参数进行优化设计;最后,通过实际系统采用不同控制策略的效果对比,验证了本文所提方法的可行性和有效性。
图1给出了永磁伺服系统传统转速控制传递函数框图[24-25]。图中,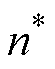 和n分别为转速给定值和实际值,
和n分别为转速给定值和实际值,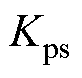 和
和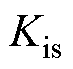 分别为转速调节器的比例和积分参数,
分别为转速调节器的比例和积分参数,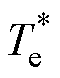 和
和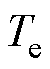 分别为电磁转矩给定值和实际值,
分别为电磁转矩给定值和实际值,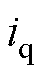 为q轴电流,
为q轴电流,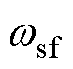 为转速低通滤波带宽,
为转速低通滤波带宽,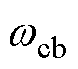 为电流环带宽,K为永磁电机转矩系数,TL为负载转矩,J为伺服系统转动惯量。
为电流环带宽,K为永磁电机转矩系数,TL为负载转矩,J为伺服系统转动惯量。
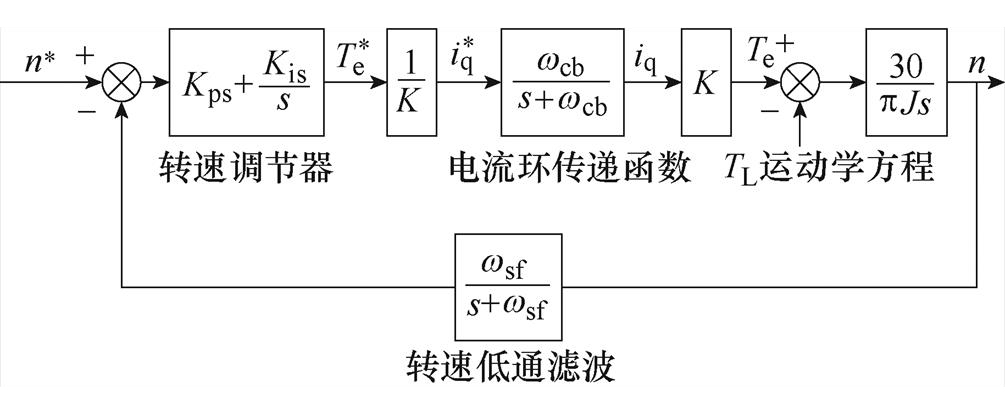
图1 永磁伺服系统传统转速控制传递函数框图
Fig.1 Transfer function block diagram of traditional speed control for permanent magnet servo systems
该转速环开环传递函数为
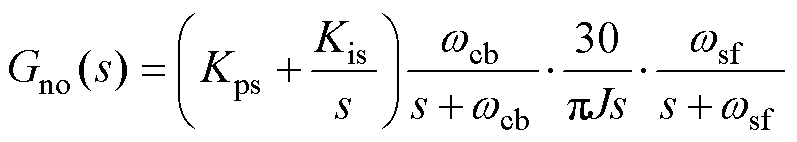 (1)
(1)
设转速环开环截止频率和相位裕度分别为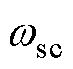 和
和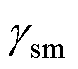 ,则转速环开环传递函数应满足如下的幅频和相频关系。
,则转速环开环传递函数应满足如下的幅频和相频关系。
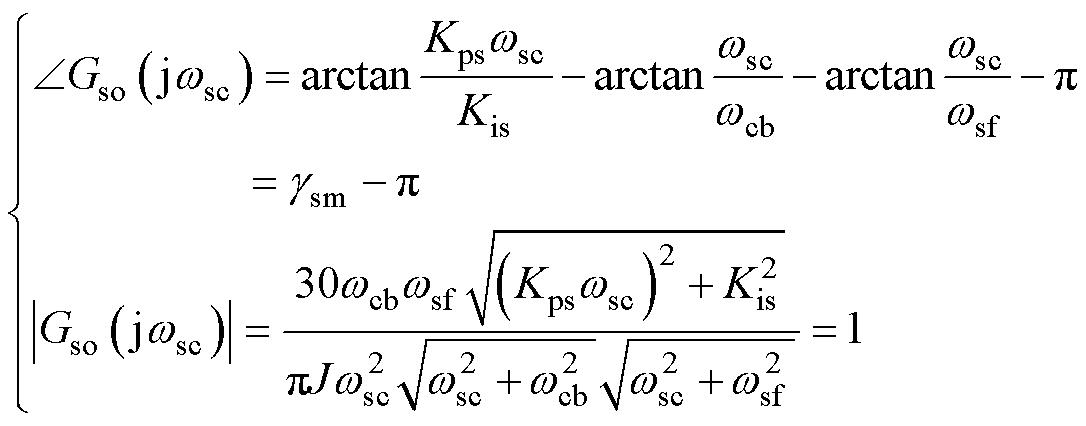 (2)
(2)
通过式(1)可以解出满足设定开环截止频率和相位裕度的转速环比例和积分参数,有
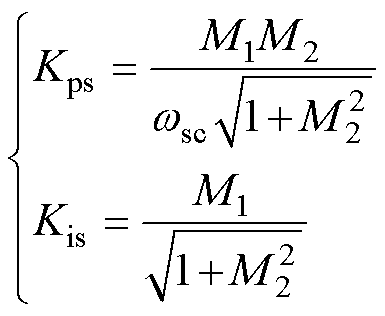 (3)
(3)
其中
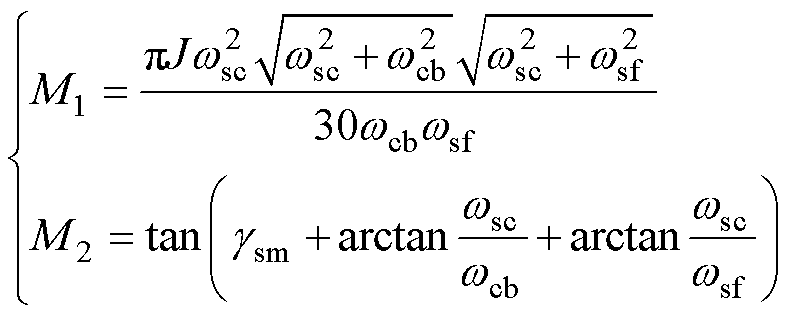 (4)
(4)
由于转速环的闭环带宽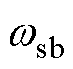 要远小于电流环的带宽
要远小于电流环的带宽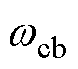 ,因此令
,因此令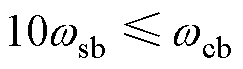 。此外,工程上常近似取闭环带宽为开环截止频率的1.1~1.6倍,在这里选择
。此外,工程上常近似取闭环带宽为开环截止频率的1.1~1.6倍,在这里选择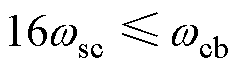 。考虑到开环截止频率过小会使得动态响应变差,令
。考虑到开环截止频率过小会使得动态响应变差,令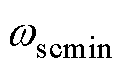 为满足响应要求的最小截止频率,则速度环的开环截止频率应满足
为满足响应要求的最小截止频率,则速度环的开环截止频率应满足
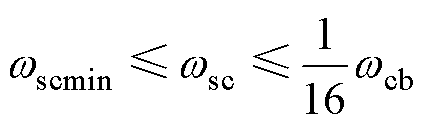 (5)
(5)
工程上通常取相位裕度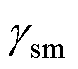 满足
满足
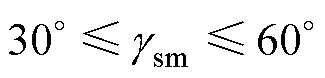 (6)
(6)
当开环截止频率和相位裕度根据式(5)、式(6)确定之后,通过式(3)可以计算出速度环PI调节器的参数。
图2给出了传统转速跟踪控制方法在不同开环截止频率和相位裕度下的低频段(0.2~1 rad/s)闭环幅频特性。当幅值增益为0 dB、相位偏移为0°时,可以实现转速的无差跟踪,但从图2可见,传统方法在不同开环截止频率和相位裕度条件下,幅值和相位均有不同程度的偏差,并且随着频率的提高偏差变大,这是传统方法在低频段转速跟踪控制性能不佳的直接原因。
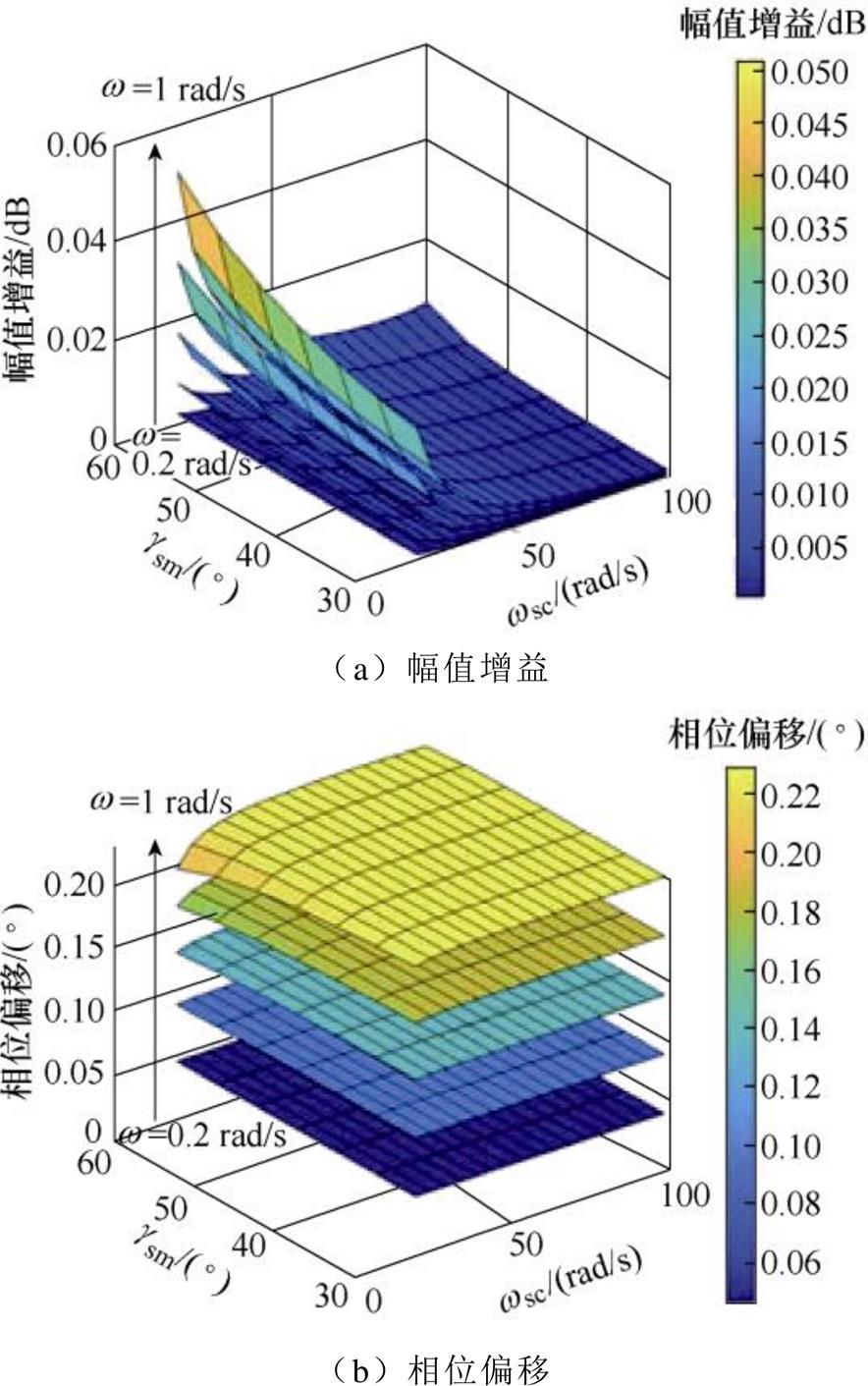
图2 传统转速跟踪控制方法在低频段的闭环幅频特性
Fig.2 Closed-loop amplitude-frequency characteristics of traditional speed control method in low frequency region
若转速环在某频段的幅值增益和相移均为零,则相应的转速跟踪误差也为零,达到无误差跟踪控制的目的。因此,如果在如图1所示传统策略的输入端串联一个滞后-超前补偿器对低频段的幅值和相位进行修正,则有望使得修正后的幅值增益和相移均趋于零,从而提高转速跟踪精度,如图3所示,图中,参数a、b、T1和T2为均为正值且a>1、0<b<1。
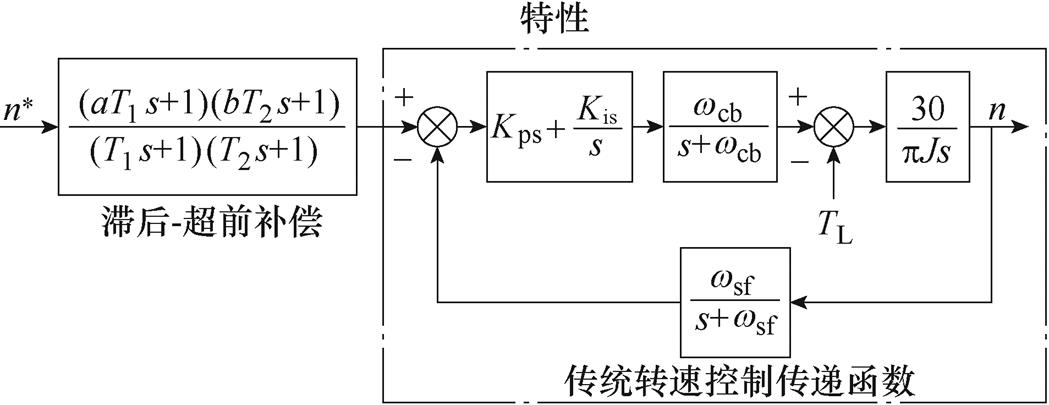
图3 采用串联滞后-超前补偿的转速控制传递函数框图
Fig.3 Block diagram of speed control transfer function with series lag-lead compensation
用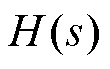 表示该滞后-超前补偿器的传递函数,即
表示该滞后-超前补偿器的传递函数,即
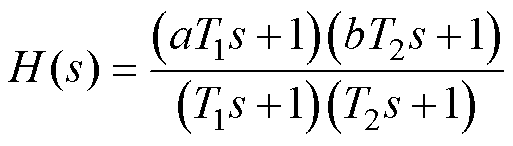 (7)
(7)
则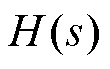 的幅值和相位分别为
的幅值和相位分别为
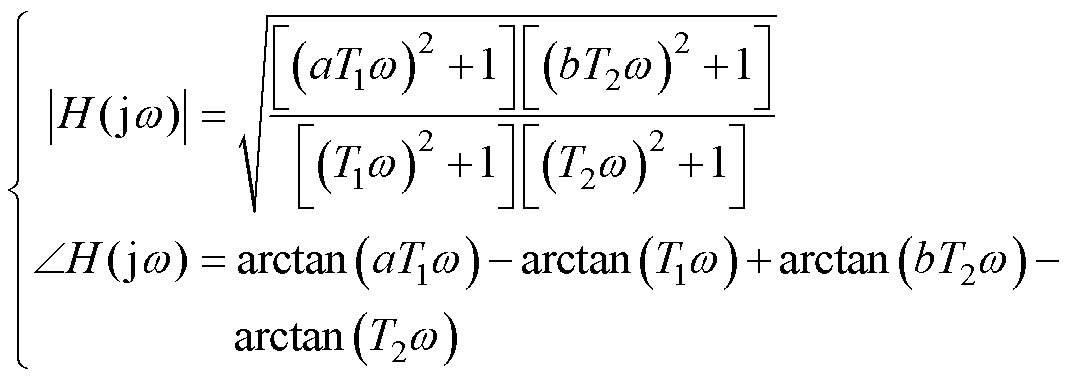 (8)
(8)
传递函数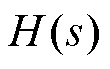 的设计既要保证补偿后低频段的幅值和相位精度,又要尽量不影响中高频段的原有特性[26],属于多目标的优化设计问题,难以采用经典控制理论进行参数设计。
的设计既要保证补偿后低频段的幅值和相位精度,又要尽量不影响中高频段的原有特性[26],属于多目标的优化设计问题,难以采用经典控制理论进行参数设计。
根据上述的设计要求,本文采用数据驱动的参数优化设计方法。这里的数据可以是仿真数据,也可以是实验数据。前者实现简单,但建模误差会降低实际的控制性能;后者实现相对复杂,但可以较好地应对实际系统中转动惯量不匹配等不确定因素带来的负面影响。
该数据驱动的参数优化设计方法的基本思想是根据仿真或实验数据得到系统在低频段的实际幅值增益和相移[27],然后采用优化算法对滞后-超前补偿器的参数进行优化设计,使得补偿后的幅值增益和相移具有最小的均方误差。具体的实现方法如下所述。
1)获取实际的幅值增益和相移
设定需要优化的N个频点为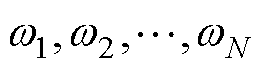 ,若采用仿真数据,则根据如图1所示的闭环传递函数可直接计算出相应的幅值增益
,若采用仿真数据,则根据如图1所示的闭环传递函数可直接计算出相应的幅值增益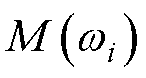 和相移
和相移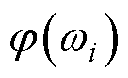 ,其中,
,其中, 。
。
若采用实验数据,令转速指令为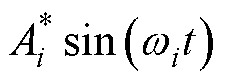 ,其中,
,其中,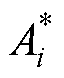 为转速指令幅值,
为转速指令幅值,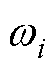 为转速指令的频率,则在不串联滞后补偿器的情况下,通过实验得到相应的实际转速
为转速指令的频率,则在不串联滞后补偿器的情况下,通过实验得到相应的实际转速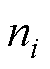 并进行曲线拟合,可得
并进行曲线拟合,可得
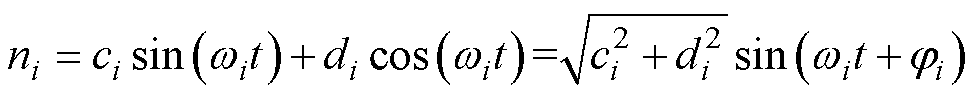 (9)
(9)
其中
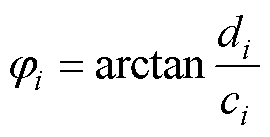
式中,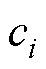 和
和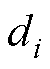 为参数,可以通过最小二乘法来计算获得。
为参数,可以通过最小二乘法来计算获得。
因此,在频点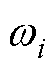 处的幅值增益
处的幅值增益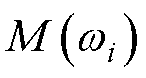 和相移
和相移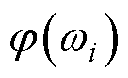 分别为
分别为
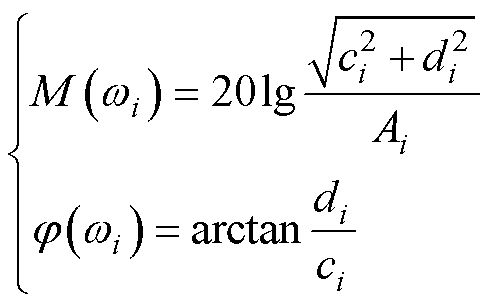 (10)
(10)
2)参数优化设计的目标函数
若要将频率为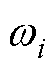 处的幅值和相位修正至0 dB和0°,则对于所有的
处的幅值和相位修正至0 dB和0°,则对于所有的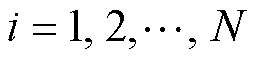 ,式(7)中
,式(7)中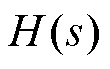 的参数a、b、T1和T2应满足
的参数a、b、T1和T2应满足
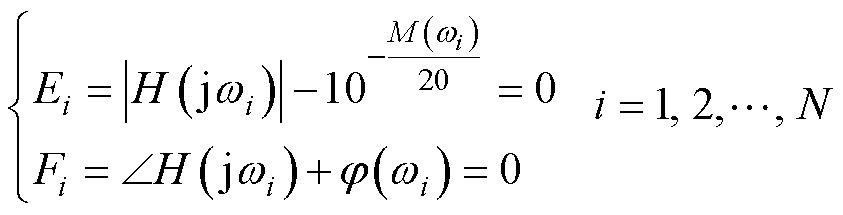 (11)
(11)
式中,Ei为幅值误差;Fi为相位误差。
事实上,当N>2时,上述方程组通常是无解的,但可以通过全局寻优的方法来确定参数a、b、T1和T2,使得幅值增益和相移具有最小的均方误差。
令优化的目标函数为
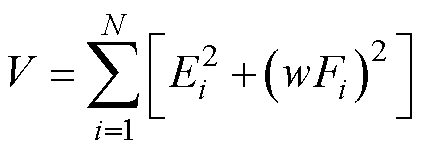 (12)
(12)
式中,w为相位补偿误差的权值系数,下面介绍如何确定该值。
当幅值误差为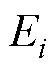 并且相位误差为
并且相位误差为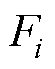 时,在跟踪单位正弦转速指令
时,在跟踪单位正弦转速指令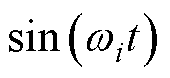 时的最大跟踪误差为
时的最大跟踪误差为
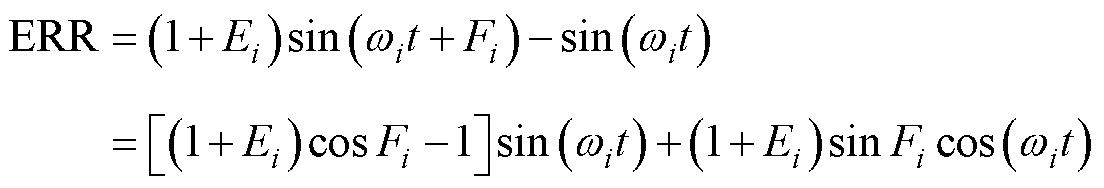
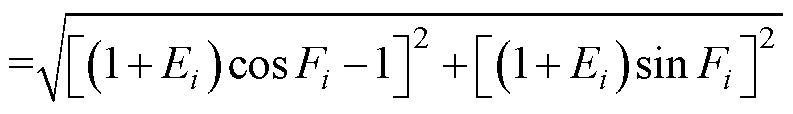 (13)
(13)
当幅值误差为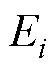 并且相位误差
并且相位误差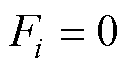 时,最大跟踪误差为
时,最大跟踪误差为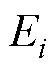 ;当相位误差为
;当相位误差为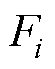 并且幅值误差
并且幅值误差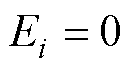 时,最大跟踪误差化简后为
时,最大跟踪误差化简后为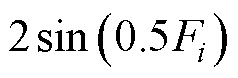 。由于
。由于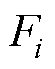 本身非常小,有
本身非常小,有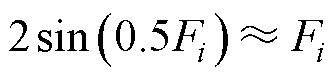 。可见,相同的幅值误差和相位误差对最大跟踪误差的影响程度基本是一致的,因此相位补偿误差的权值系数w=1,则优化目标函数为
。可见,相同的幅值误差和相位误差对最大跟踪误差的影响程度基本是一致的,因此相位补偿误差的权值系数w=1,则优化目标函数为
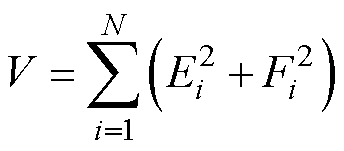 (14)
(14)
3)参数优化设计的约束条件
为了最大限度地降低在串联滞后-超前补偿器后对中高频幅频和相频特性的影响,应对滞后-超前补偿器在全频带范围内自身的最大幅值增益和相移进行约束,因此优化后的参数应使滞后-超前补偿器在全频带范围满足如下约束条件。
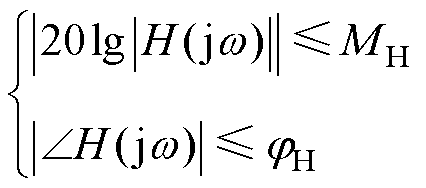 (15)
(15)
式中,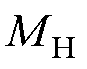 、
、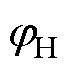 分别为幅值增益和相移的限制值。
分别为幅值增益和相移的限制值。
在确定好优化的目标函数式(14)和约束条件式(15)后,即可采用合适的优化算法对参数a、b、T1和T2进行优化设计。本文采用遗传算法进行参数的优化设计,由于遗传算法在理论和应用方面都已经比较成熟,因此不作为本文的研究重点,具体可通过Matlab里面的遗传算法工具箱实现[28]。为便于工程实现,图4给出了基于数据驱动与遗传算法的参数优化设计过程。
采用表1中的参数设置,结合如图1所示的闭环传递函数,选定频率以0.1 rad/s为起始,步长为0.1 rad/s,最大为1 rad/s共计N=10个频点,对滞后-超前补偿器的参数进行优化设计。
图5给出了基于仿真数据的参数优化曲线,可见在经过500次迭代后,目标函数收敛并得到了寻优后的参数a、b、T1和T2,其收敛值为

图4 基于数据驱动与遗传算法的参数优化设计
Fig.4 Parameter optimization design based on data-driven and genetic algorithm
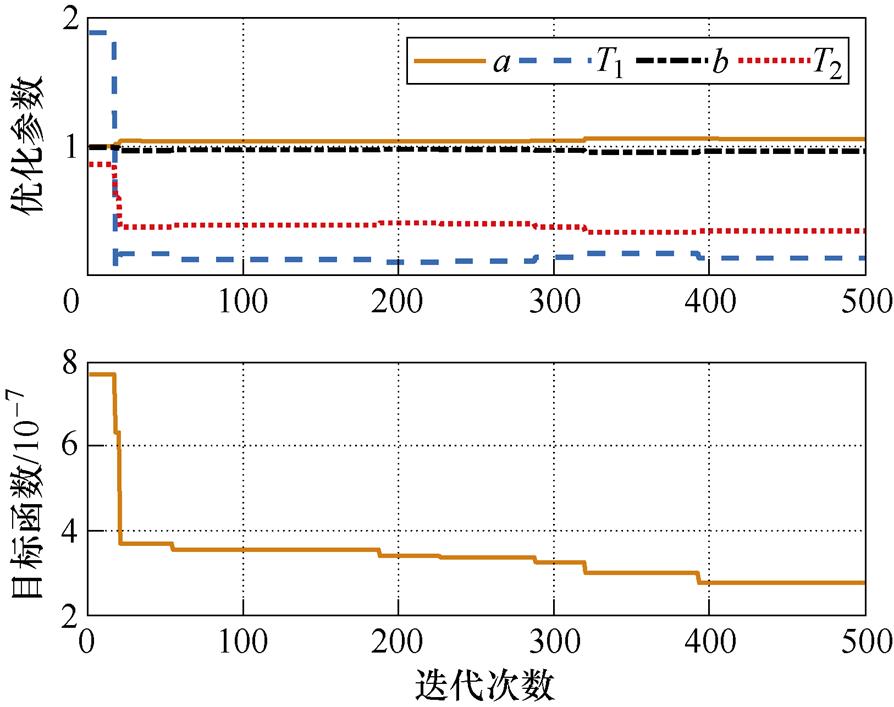
图5 基于仿真数据的参数优化结果
Fig.5 Parameter optimization results based on simulation data
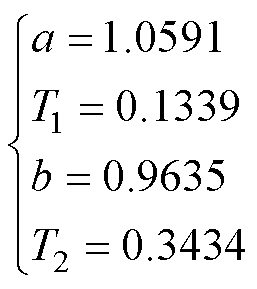 (16)
(16)
图6对比了补偿前后的闭环控制系统幅频和相频特性,易见在补偿后低频段的幅频和相频特性得到显著改善,而中高频段幅频和相频特性与原先基本保持一致,即闭环带宽、谐振峰值等关键指标没有因为串联滞后-超前补偿器而发生明显改变,达到了优化设计的目的。
永磁伺服系统的实验硬件主要由PC端上位机、驱动器、伺服电机、减速箱和惯量盘组成,现场依据功能分配搭建了如图7所示的实验平台。其中伺服驱动器包括控制板、传感器以及IGBT等模块,控制板负责控制算法的实现,其核心芯片为Cyclone Ⅳ E系列FPGA和TI公司的TMS320F28335 DSP;传感器用于外部信号的采集;IGBT模块按照指令开通关断实现直流电源到交流电源的变换,从而驱动永磁伺服电机带动惯量负载运行。永磁伺服驱动器控制系统的主要参数见表1。
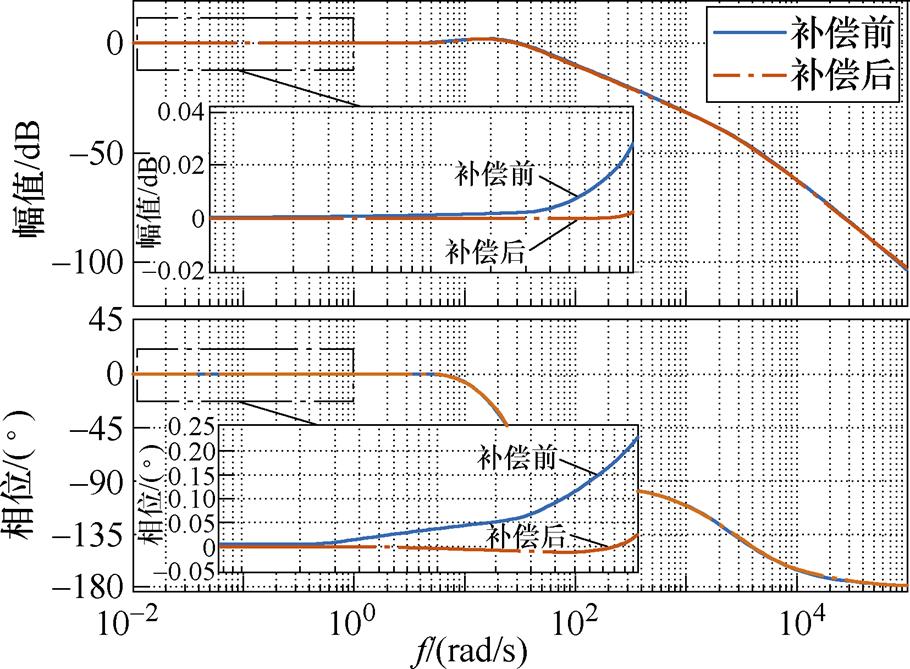
图6 闭环控制系统伯德图
Fig.6 Bode diagram of closed-loop control system
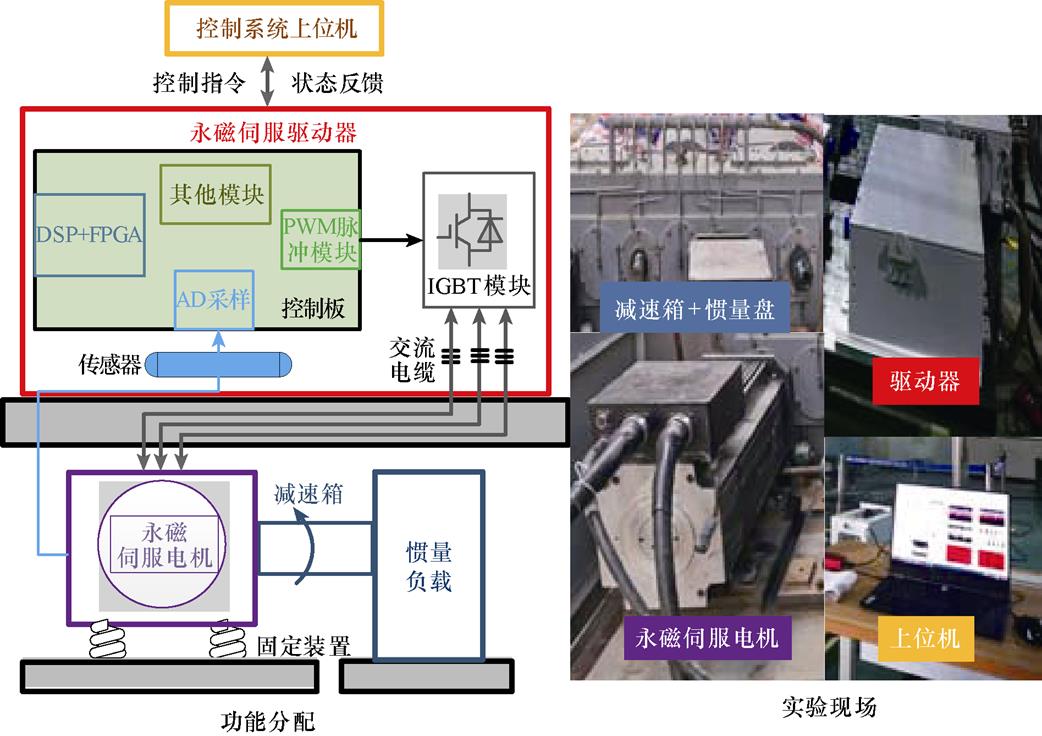
图7 永磁伺服系统实验平台
Fig.7 Experimental platform for permanent magnet servo system
首先采用传统方法进行实验,一方面是为了评估传统方法的控制性能;另一方面也是为了获取实验数据进行参数优化设计。根据该伺服系统的设计要求,需要实现转速幅值3 000 r/min、频率1 rad/s以内的高精度转速跟踪控制。因此,选取与2.2节相同的10个频点,采用传统方法获取相关实验数据,并根据2.1节基于实验数据的参数设计方法对滞后-超前补偿器的参数进行优化设计,主要结果如图8所示。其中补偿前的幅值增益和相移是基于实验数据计算得到,可见其偏差随着频率的提升而增大,势必降低该频段的转速跟踪精度;补偿后的幅值增益和相移在该频段十分接近0 dB和0°,这显然会提升该频段的转速跟踪能力。参数a、b、T1和T2的收敛值为
表1 控制系统主要参数
Tab.1 Main parameters of the control system
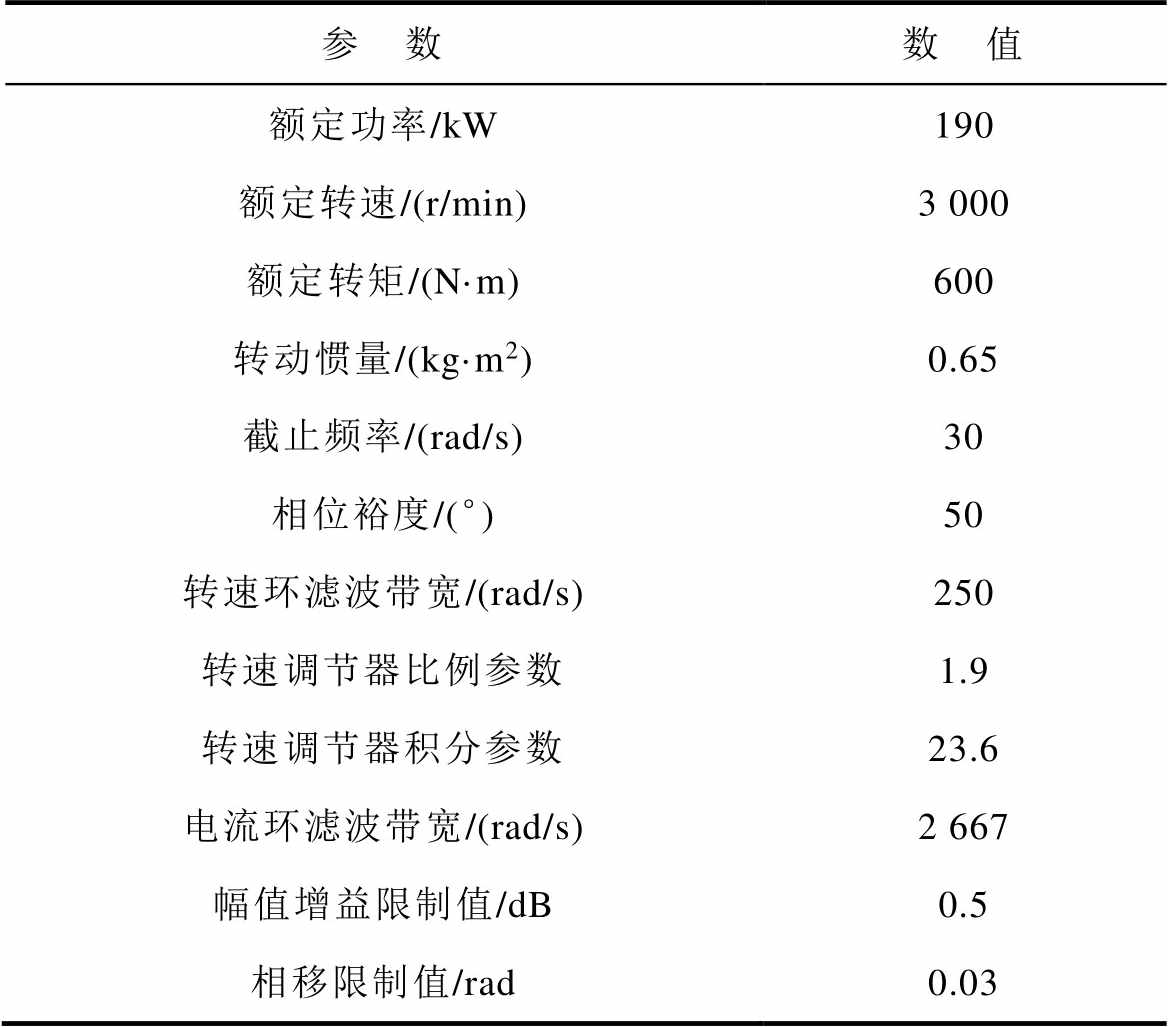
参 数数 值 额定功率/kW190 额定转速/(r/min)3 000 额定转矩/(N·m)600 转动惯量/(kg·m2)0.65 截止频率/(rad/s)30 相位裕度/(°)50 转速环滤波带宽/(rad/s)250 转速调节器比例参数1.9 转速调节器积分参数23.6 电流环滤波带宽/(rad/s)2 667 幅值增益限制值/dB0.5 相移限制值/rad0.03
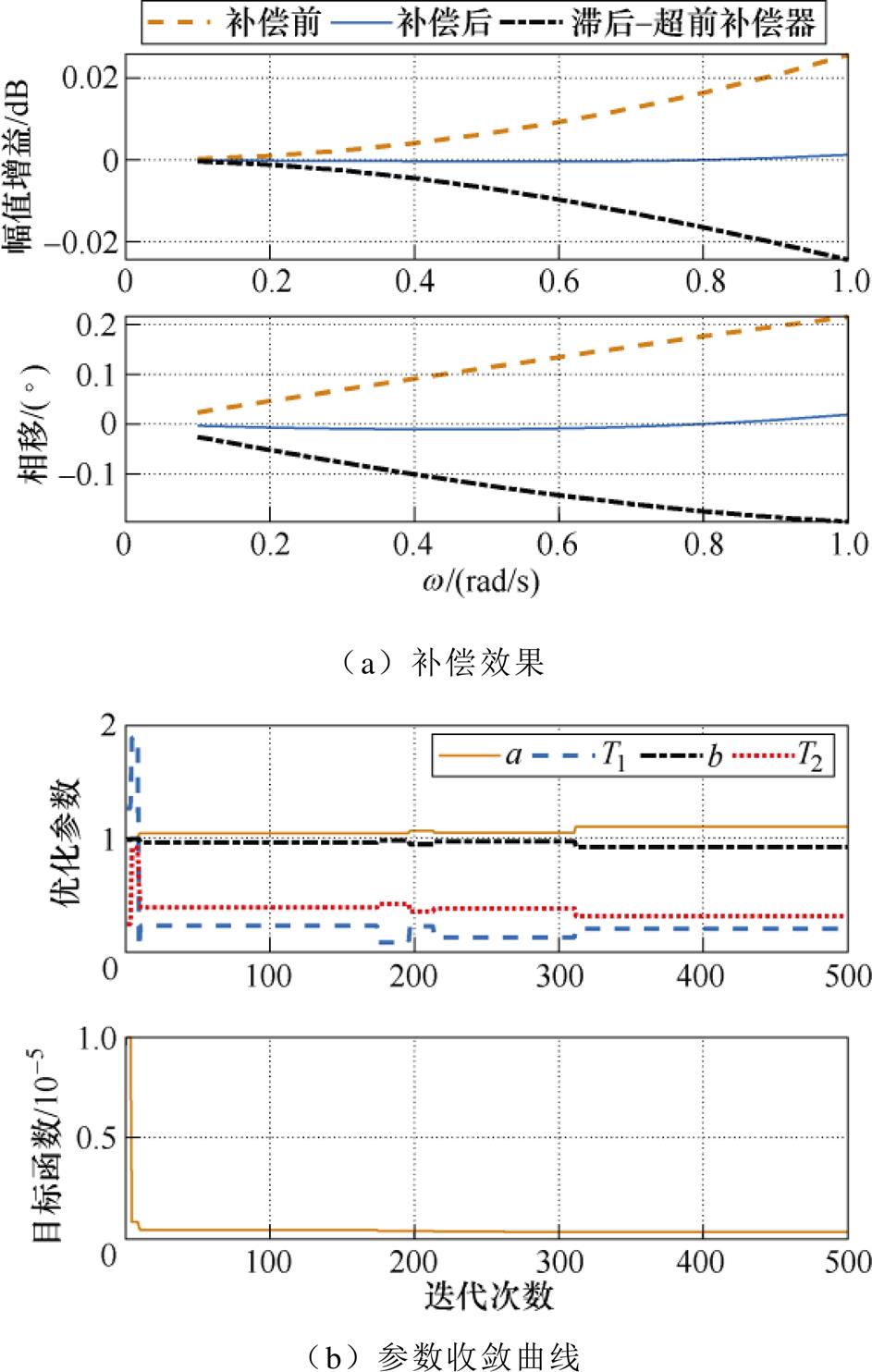
图8 基于实验数据的参数优化结果
Fig.8 Parameter optimization results based on experimental data
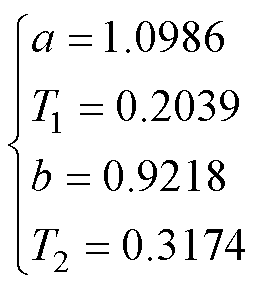 (17)
(17)
可见,式(16)和式(17)的参数优化结果有所差别,这主要是由仿真模型与实际系统不匹配造成的,如转动惯量、摩擦力矩、系统非线性及其他未知不确定因素等。
图9给出了四种典型正弦频率指令下的转速跟踪效果对比。在采用传统的转速控制策略时,转速跟踪误差总是最大的;在采用串联滞后-超前补偿器后,转速跟踪误差显著降低,其中仿真参数指的是如式(16)所示的基于仿真模型设计的参数,实验参数指的是如式(17)所示的基于实验数据所设计的参数,可见采用实验参数可以进一步提升转速跟踪精度。
图10给出了以0.1 rad/s为步长、0.1~1 rad/s区间的低频段转速跟踪误差对比结果,其中每个频点的转速误差指的是在对该频点误差数据进行曲线拟合后取的最大值。可见,在该频段补偿后的跟踪性能显著提升,特别是采用实验参数对补偿器参数进行优化设计后,最大跟踪误差小于1 r/min。
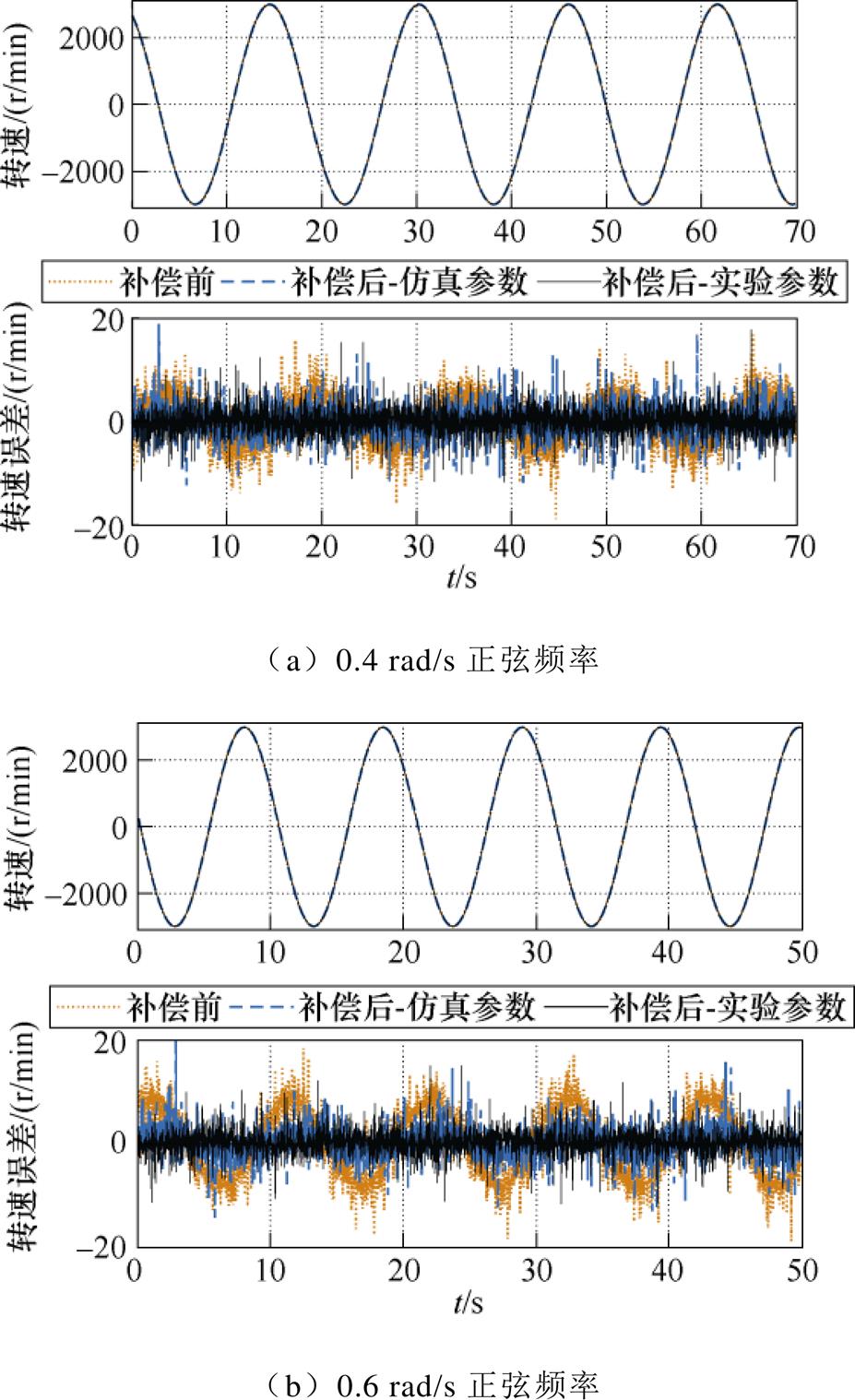
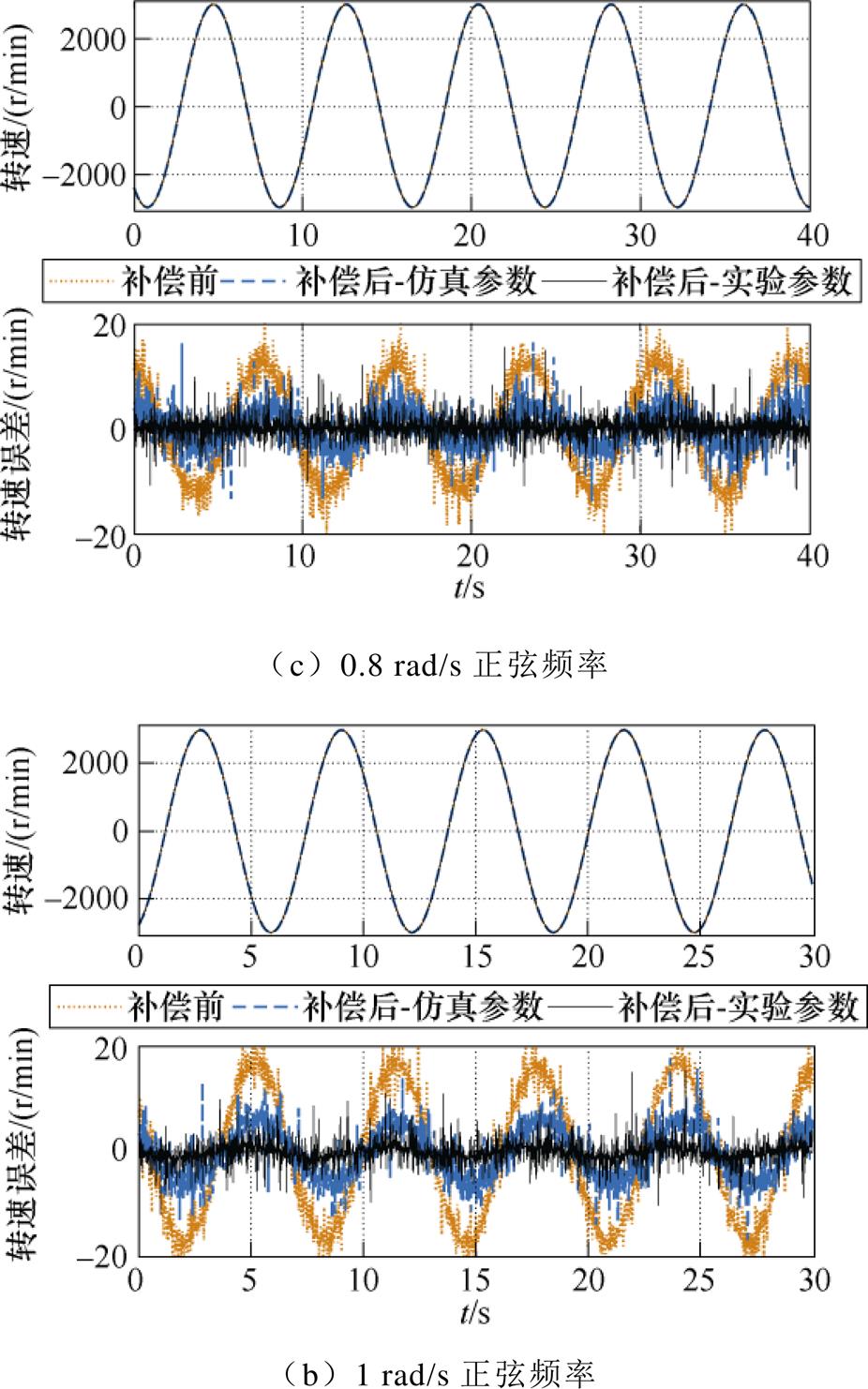
图9 四种典型正弦频率指令下转速跟踪性能对比
Fig.9 Speed tracking performance comparison under four typical sinusoidal frequency commands
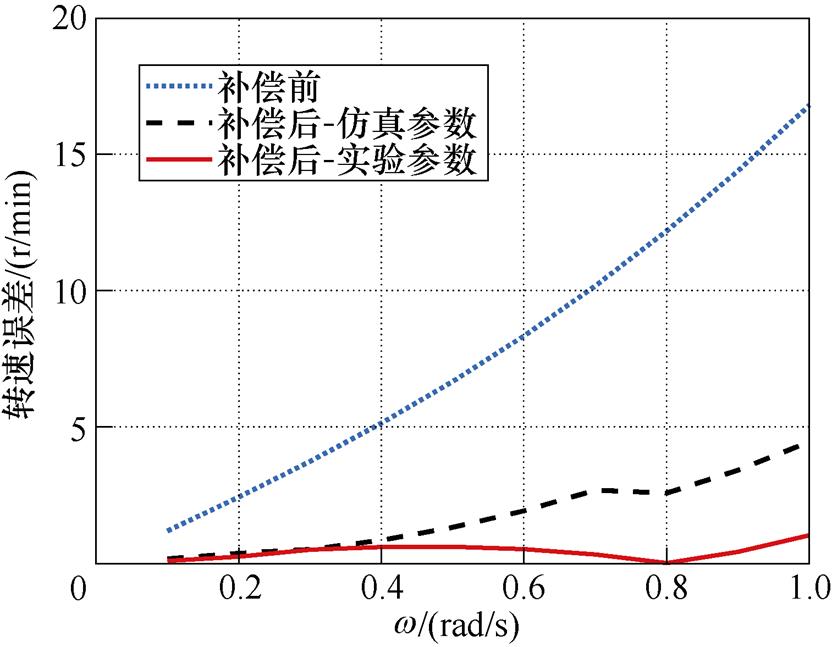
图10 低频段转速跟踪误差
Fig.10 Speed tracking errors in low frequency region
图11给出了在转速阶跃指令下的调速性能对比结果。可见,传统方法和采用实验参数补偿后的效果基本相当,而采用仿真参数的超调量略微增加,但整体看来,三者在跟踪转速阶跃指令时的控制性能差别较小。这说明本文提出的方法在提升低频段转速跟踪能力的同时,并未对系统的高动态性能产生明显影响,这与本文方法的设计初衷保持一致。
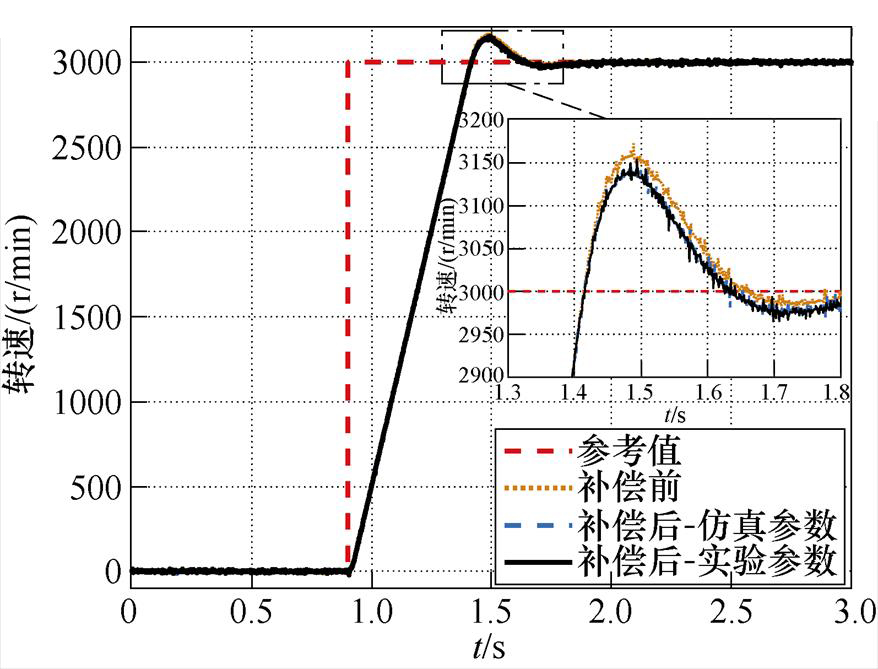
图11 转速阶跃指令下的调速性能
Fig.11 Speed control performance under speed step command
为提高永磁伺服系统转速跟踪控制精度,本文提出了一种基于滞后-超前补偿的高精度转速跟踪控制策略。由于传统转速控制策略在低频段存在明显的幅值与相位偏移,因此在转速控制环节串联一个滞后-超前补偿器,用以校正低频段的幅值与相位,并采用数据驱动的参数优化设计方法对补偿器的参数进行设计。实验结果表明,本文方法显著提升了低频段的转速跟踪精度,特别是基于实验数据所设计的补偿器在转速指令频率小于1 rad/s的低频段区间,转速跟踪误差小于2 r/min,并且基本保持了控制系统在中高频段的原有幅频和相频特性。
参考文献
[1] 高宇. 航天用永磁同步电机直驱伺服系统低速运行控制技术研究[D]. 南京: 南京航空航天大学, 2019.
[2] 韩镇锚. 永磁同步电机直驱式位置伺服系统控制成策略研究[D]. 南京: 南京航空航天大学, 2017.
[3] Li Guangjin, Ren Bin, Zhu Z Q, et al. Cogging torque mitigation of modular permanent magnet machines[J]. IEEE Transactions on Magnetics, 2016, 52(1): 1-10.
[4] 耿强, 王亮, 周湛清, 等. 五桥臂逆变器双永磁电机三矢量预测控制[J]. 电工技术学报, 2021, 36(1): 87-95.
Geng Qiang, Wang Liang, Zhou Zhanqing, et al. Three-vector-based predictive control for dual per- manent magnet synchronous motors fed by the five-leg inverter[J]. Transactions of China Electro- technical Society, 2021, 36(1): 87-95.
[5] 贾成禹, 王旭东, 周凯. 基于线性变参数模型预测控制的内置式永磁同步电机转速控制器设计[J]. 电工技术学报, 2020, 35(22): 4666-4677.
Jia Chengyu, Wang Xudong, Zhou Kai. Design of interior permanent magnet synchronous motor speed controller based on linear parameter-varying model predictive control[J]. Transactions of China Electro- technical Society, 2020, 35(22): 4666-4677.
[6] 张康, 王丽梅. 基于反馈线性化的永磁直线同步电机自适应动态滑模控制[J]. 电工技术学报, 2021, 36(19): 4016-4024.
Zhang Kang, Wang Limei. Adaptive dynamic sliding mode control of permanent magnet linear syn- chronous motor based on feedback linearization[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4016-4024.
[7] Yan Yunda, Yang Jun, Sun Zhenxing, et al. Robust speed regulation for PMSM servo system with multiple sources of disturbances via an augmented disturbance observer[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(2): 769-780.
[8] 王莉娜, 朱鸿悦, 杨宗军. 永磁同步电动机调速系统PI控制器参数整定方法[J]. 电工技术学报, 2014, 29(5): 104-117.
Wang Lina, Zhu Hongyue, Yang Zongjun. Tuning method for PI controllers of PMSM driving system[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 104-117.
[9] 李文善. 基于PI型迭代学习控制的永磁同步电机转矩脉动抑制策略[D]. 天津: 天津大学, 2012.
[10] 闫宏亮, 李家鹏, 李雷明. 永磁同步电机伺服系统自抗扰控制器设计[J]. 太赫兹科学与电子信息学报, 2021, 19(1): 138-144.
Yan Hongliang, Li Jiapeng, Li Leiming. Active disturbance rejection controller design for PMSM servo system[J]. Journal of Terahertz Science and Electronic Information Technology, 2021, 19(1): 138- 144.
[11] 王永, 窦晓华, 方浩, 等. 永磁同步电机非线性黄金分割自适应转速控制[J]. 电机与控制学报, 2017, 21(10): 23-29.
Wang Yong, Dou Xiaohua, Fang Hao, et al. Nonlinear golden-section adaptive speed control of permanent magnet synchronous motor[J]. Electric Machines and Control, 2017, 21(10): 23-29.
[12] 王旻. 引入负载扰动补偿的永磁同步电机新型非奇异终端滑模转速控制研究[D]. 西安: 西安理工大学, 2021.
[13] 武志涛, 李帅, 程万胜. 基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J]. 电工技术学报, 2022, 37(10): 2503-2512.
Wu Zhitao, Li Shuai, Cheng Wansheng. Fixed structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2503-2512.
[14] 黄宣睿, 宋宇洋, 李秋生, 等. 一种基于内模控制的工业机器人关节伺服系统振动抑制算法[J]. 电工技术学报, 2019, 34(3): 497-505.
Huang Xuanrui, Song Yuyang, Li Qiusheng, et al. A vibration suppression algorithm for industrial robot joint servo system based on internal model control[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 497-505.
[15] Chang Y C, Chen C H, Zhu Zhongchuan, et al. Speed control of the surface-mounted permanent-magnet synchronous motor based on takagi-sugeno fuzzy models[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6504-6510.
[16] 张康, 王丽梅. 基于反馈线性化的永磁直线同步电机自适应动态滑模控制[J]. 电工技术学报, 2021, 36(19): 4016-4024.
Zhang Kang, Wang Limei. Adaptive dynamic sliding mode control of permanent magnet linear syn- chronous motor based on feedback linearization[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4016-4024.
[17] 卜飞飞, 郭子韬, 顾毅君, 等. 基于改进型降阶观测器的永磁直驱伺服电动机转矩扰动抑制策略[J]. 电工技术学报, 2022, 37(16): 4104-4115.
Bu Feifei, Guo Zitao, Gu Yijun, et al. Torque disturbance suppression strategy of permanent magnet direct drive servo motor based on improved reduced order observer[J]. Transactions of China Electro- technical Society, 2022, 37(16): 4104-4115.
[18] 左月飞. 永磁同步电机伺服系统的转速控制策略研究[D]. 南京: 南京航空航天大学, 2016.
[19] 朱笋, 洪荣晶, 李盛寅. 基于新型滑模算法的永磁同步电机转速控制研究[J]. 电机与控制应用, 2019, 46(5): 58-63.
Zhu Sun, Hong Rongjing, Li Shengyin. Research on speed control of permanent magnet synchronous motor based on new sliding mode algorithm[J]. Electric Machines & Control Application, 2019, 46(5): 58-63.
[20] Bu Feifei, Yang Zhida, Gao Yu, et al. Speed ripple reduction of direct-drive PMSM servo system at low-speed operation using virtual cogging torque control method[J]. IEEE Transactions on Industrial Electronics, 2021, 68(1): 160-174.
[21] 张政. 基于超前滞后补偿算法的光电雷达伺服控制系统设计[D]. 沈阳: 沈阳理工大学, 2018.
[22] 李军, 刘哲, 周永言. 一种新型高性能控制器的研究与应用[J]. 自动化学报, 2020, 46(12): 2558-2571.
Li Jun, Liu Zhe, Zhou Yongyan. Research and application of a new higher performance controller[J]. Acta Automatica Sinica, 2020, 46(12): 2558-2571.
[23] 王美健. 几种新型滞后—超前补偿器的设计与应用[D]. 青岛: 中国海洋大学, 2010.
[24] 黄依婷. 基于模糊逻辑控制和滑模控制算法的永磁同步电机伺服控制系统研究[D]. 杭州: 浙江大学, 2022.
[25] 刘宁, 夏长亮, 周湛清, 等. 基于比例增益补偿的永磁同步电机转速平滑控制[J]. 电工技术学报, 2018, 33(17): 4007-4015.
Liu Ning, Xia Changliang, Zhou Zhanqing, et al. Smooth speed control for permanent magnet synchronous motor using proportional gain com- pensation[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4007-4015.
[26] Yuan Lei, Jiang Yunhao, Xiong Lu, et al. Sliding mode control approach with integrated disturbance observer for PMSM speed system[J]. CES Transa- ctions on Electrical Machines and Systems, 2023, 7(1): 118-127.
[27] 李耀华, 赵承辉, 周逸凡, 等. 基于数据驱动的永磁同步电机深度神经网络控制[J]. 电机与控制学报, 2022, 26(1): 115-125.
Li Yaohua, Zhao Chenghui, Zhou Yifan, et al. Deep neural network control for PMSM based on data drive[J]. Electric Machines and Control, 2022, 26(1): 115-125.
[28] 赵希梅, 陈广国, 金鸿雁. 基于改进灰狼优化算法的PMSM滑模自抗扰控制[J]. 电机与控制学报, 2022, 26(11): 132-140.
Zhao Ximei, Chen Guangguo, Jin Hongyan. Sliding mode active disturbance rejection control for PMSM based on improved grey wolf optimization algo- rithm[J]. Electric Machines and Control, 2022, 26(11): 132-140.
Abstract The servo system is also called a follow-up system, a feedback control system to follow or reproduce a process accurately. The position, orientation, state, and other controlled output variables of the object can follow the arbitrary changes of the input target (or given value). Because the servo system can achieve precise speed and position control in a wide range, it is generally used in applications requiring high system performance, such as industrial production and military defense security. With the improvement in manufacturing technology of permanent magnet materials, the permanent magnet servo system has been developed rapidly, and the control performance has been improved. However, traditional speed control strategies in the servo system have amplitude and phase deviation problems in the low-frequency band, which reduces the precision of speed tracking control.
A high-precision speed-tracking control strategy and a data-driven parameter design method are proposed to improve the speed-tracking accuracy of the servo system in the entire speed range. Firstly, a lag-lead compensator is connected in series in the speed control link to correct the amplitude and phase of the low-frequency band. Speed tracking accuracy is improved by making the corrected amplitude and phase shift tend to zero. Secondly, a data-driven parameter optimization design method is proposed to minimize amplitude and phase errors after low-frequency compensation and constrain the maximum value gain and phase shift of the compensator in the full-frequency band. Thirdly, according to simulation or experimental data, the actual amplitude gain and phase shift of the system in the low-frequency band are obtained, enhancing the adaptability of parameters. The parameters of the lag-lead compensator are continuously optimized based on the feedback junction. Thus, the compensated amplitude gain and phase shift have the minimum mean square error. Compared with traditional methods, the designed lag-lead compensator and parameter optimization method match the actual system, avoiding adverse effects caused by uncertain factors like the mismatch of the moment of inertia.
The experimental results show that the compensator designed based on experimental data has a speed tracking error of less than 2 r/min in the low-frequency range with a speed instruction frequency of less than 1 rad/s, significantly improving the speed control accuracy. Moreover, the control effect is equivalent to that of the traditional method when tracking the speed step command, which does not affect the dynamic characteristics of the servo system.
The proposed method improves tracking performance in the low-frequency band while maintaining the original amplitude-frequency and phase-frequency characteristics of the control system in the middle and high-frequency bands. It is conducive to improving the speed tracking accuracy of the servo system in the entire speed range, promoting the engineering application of permanent magnet servo systems.
keywords:Permanent magnet servo system, speed control, lag-lead compensator, data-driven, parameter optimization
国家自然科学基金(51807200, 52177202)和国家重点基础研究发展计划(973)(2015CB251004)资助项目。
收稿日期 2023-02-14
改稿日期 2023-03-07
DOI: 10.19595/j.cnki.1000-6753.tces.230163
中图分类号:TM351
连传强 男,1986年生,博士,副研究员,研究方向为电机系统及其控制、人工智能。E-mail: wzdslcq@163.com
张伟伟 男,1989年生,博士,助理研究员,研究方向为永磁同步电机驱动控制技术等。E-mail: zw7589@163.com(通信作者)
(编辑 崔文静)