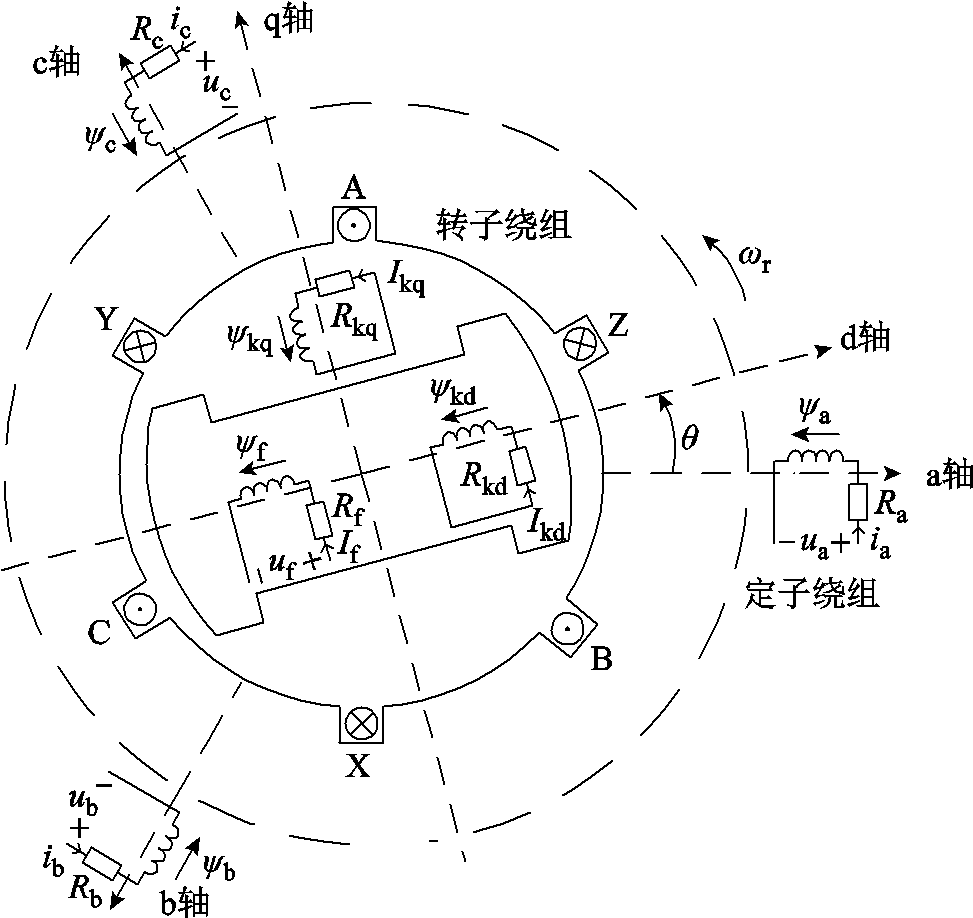
图1 同步电机示意图
Fig.1 Schematic of synchronous motor
摘要 海上风电的建模与仿真是构建新能源为主体的新型电力系统的关键支撑技术。永磁同步发电机(PMSG)作为直驱或半直驱机型的核心元件,现有模型存在一定的局限性:商业软件提供的灰箱模型无法得知建模原理,开放程度不够,限制了风电机组应用高效电磁暂态建模算法与并行加速算法;目前常用的PMSG建模方法无法生成接口与外电路连接;PMSG是同步发电机的一种,而同步发电机有不同阶数的数学模型,现有模型不便更改。针对上述问题,该文提出阶数可选的PMSG电磁暂态等效建模方法。首先对发电机电压、磁链方程进行离散化;然后通过单步长延时消除代数环,重构PMSG模型,推导得到其诺顿等效电路并构建模型整体仿真框架;最后,在RTDS仿真平台中进行仿真分析。结果表明四阶、二阶模型在场站级仿真具有适用性,而六阶模型实现了对基准模型的多工况高度拟合,平均相对误差小于4%,能够同时满足场站级与机组内部各仿真需求。
关键词:海上风电直驱或半直驱机型 永磁同步发电机 等效建模 阶数可选模型
随着国家“碳达峰,碳中和”目标的提出,风电的规划和建设速度持续加快。海上风电具有风速大、不占用陆地资源的优势,是构建新能源为主体的新型电力系统的战略支撑,针对海上风电的建模与仿真是其中的关键支撑技术[1-2]。
直驱和半直驱机型是海上风电发展的主流方向,永磁同步发电机(Permanent Magnet Synchronous Generator, PMSG)是其重要元件[3]。目前,主流电磁暂态仿真软件如Matlab/Simulink、PSCAD/ EMTDC和RTDS等都提供了PMSG模型。但商业软件的灰箱模型仅给出了参数输入窗口和最原始的数学模型,具体建模原理无法得知,总体开放程度不够。各个软件模型依据的方程略有差异、需要输入的参数个数与物理意义也不相同,使得相关领域的研究者对PMSG模型进行机理分析时不便于明确所使用仿真软件的模型信息。并且,海上风电仿真计算复杂度高,面临仿真效率低下的问题。使用仿真软件的灰箱模型限制了整体机组应用一些高效电磁暂态建模的处理方法,例如,已在模块化多电平换流器(Modular Multilevel Converter, MMC)、电力电子变压器(Power Electronic Transformer, PET)中有应用的嵌套同时快速求解(Nested Fast and Simultaneous Solution, NFSS)算法[4-5],以及一些细颗粒度的并行加速算法[6-7]。
近年来,针对海上风电故障特性、机组内部动态响应等问题的研究,对直驱型风电机组建模要求逐渐提高[8-14]。除部分情况直接应用商业软件提供的PMSG模型外,国内外学者对风电机组建模时通常需要考虑对PMSG进行建模。文献[15-16]基于状态空间法搭建了直驱和双馈机型的相量模型。相量模型多用于稳定性分析,而电磁暂态模型可以接入任意非线性网络反映电磁暂态过程,是基于电路的模型。文献[17-18]基于Matlab/Simulink搭建了PMSG模型。文献[19-20]基于PSCAD/EMTDC搭建了PMSG模型,上述文献所建立的模型功能上实现了发电机的输入输出关系,但其均是dq坐标系下的模型,输出的电压电流均是数字信号而非电气信号,需要依靠变换与受控源与外部网络形成连接,依然无法直接作为元件连入abc相的外电路。文献[21-22]将基于Hilbert变换的移频电磁暂态方法应用于PMSG建模,该方法适用于大步长仿真,并且主要针对含窄带信号的交流系统,在含宽频、多频段信号的仿真中有局限性[23]。现有PMSG建模方法在适用场景上有一定限制,需要研究一种有直接接口的电磁暂态建模方法。
PMSG是一种以永磁体励磁的特殊同步发电机,而同步发电机根据考虑的绕组数会有不同阶数的数学模型。文献[24]表明各阶模型应用场景不同,需要精确分析系统动态过程时采用高阶模型,电力系统规划常采用经典二阶模型。应用于风电机组时,针对不同的仿真研究对象,如高低电压穿越、宽频振荡、内部故障溯源等,以及考虑不同的精度要求时,采用的模型阶数也有所差异。
为解决上述问题,本文提出一种面向海上风电的阶数可选的永磁同步发电机电磁暂态等效建模方法。首先介绍了不同阶数的同步发电机模型基本方程以及分类依据;然后详细介绍PMSG的模型重构与推导过程,并进行适用性分析;其次构建整体仿真框架;最后对仿真精度进行多工况验证。
图1为同步电机的示意图。转子励磁绕组中心轴为d轴,并设q轴沿转子旋转方向领先d轴90°电角度。定子上有a、b、c三相绕组,转子在d轴上有励磁绕组f及等值阻尼绕组D,在q轴上有等值阻尼绕组Q。对于实心转子汽轮机,q轴有时需要考虑转子g绕组,本文面向海上风电研究直驱机型,故对于g绕组不予考虑。

图1 同步电机示意图
Fig.1 Schematic of synchronous motor
同步发电机的基本方程由电压方程、磁链方程和转子运动方程组成,为便于分析计算,通常在dq0旋转坐标系下求解常系数微分方程。同步发电机dq0坐标系下的上述三组方程(电动机惯例)分别为
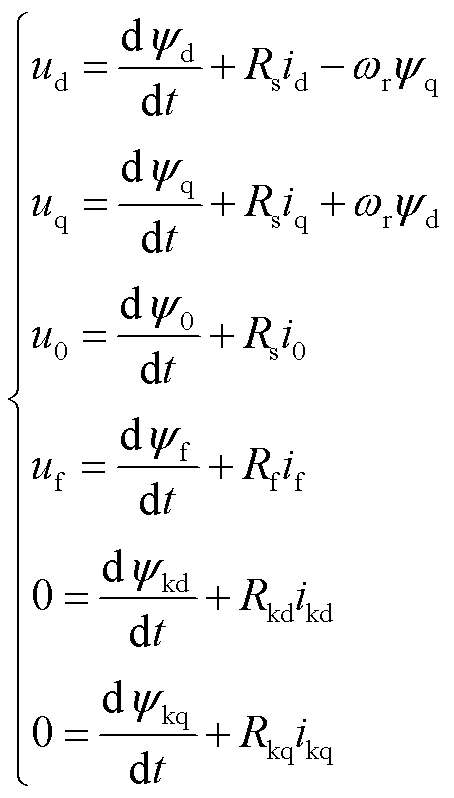 (1)
(1)
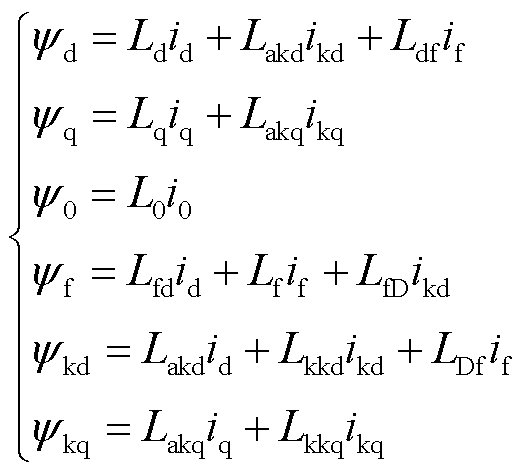 (2)
(2)
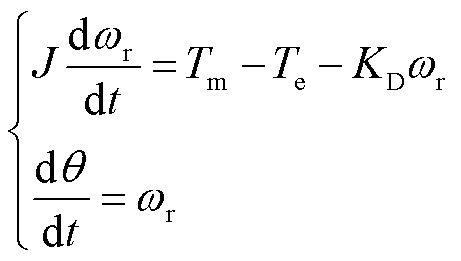 (3)
(3)
式中,ud、uq、u0为dq0轴定子绕组电压;id、iq、i0、ikd、ikq分别为dq0轴定子绕组电流与DQ阻尼绕组电流;Ldf为定子绕组和励磁绕组的互感;LDf、LfD为阻尼绕组和励磁绕阻的互感,LDf=LfD;Lf为励磁绕组的自感;if为励磁绕组的电流;KD为阻尼系数;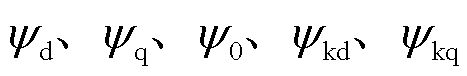 分别为dq0轴定子绕组磁链与DQ阻尼绕组磁链;
分别为dq0轴定子绕组磁链与DQ阻尼绕组磁链;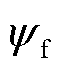 为永磁体励磁;Rs、Rkd、Rkq分别为定子绕组电阻、D轴阻尼绕组电阻、Q轴阻尼绕组电阻;Ld、Lq、Lkkd和L0、Lkkq分别为dq0轴定子绕组电感与DQ阻尼绕组电感;Lakd、Lakq分别为定子d轴与阻尼D轴的互感、定子q轴与阻尼Q轴的互感;wr为转子转速;Tm为原动机施加于电机轴的机械力矩;Te为发电机电磁力矩;q为转子机械角位移;J为转子的转动惯量。
为永磁体励磁;Rs、Rkd、Rkq分别为定子绕组电阻、D轴阻尼绕组电阻、Q轴阻尼绕组电阻;Ld、Lq、Lkkd和L0、Lkkq分别为dq0轴定子绕组电感与DQ阻尼绕组电感;Lakd、Lakq分别为定子d轴与阻尼D轴的互感、定子q轴与阻尼Q轴的互感;wr为转子转速;Tm为原动机施加于电机轴的机械力矩;Te为发电机电磁力矩;q为转子机械角位移;J为转子的转动惯量。
文献[25]介绍了不同阶数的同步发电机数学模型。对于dq0坐标下的同步发电机方程,如果单独考虑与定子d绕组、q绕组相独立的零轴绕组,则在计及d、q、f、D、Q五个绕组的电磁过渡过程以及转子机械过渡过程时,电机为七阶模型。针对不同的实际问题及分析工具,常对同步发电机的数学模型作不同程度的简化。当假定忽略定子绕组暂态,即令式(1)中定子电压微分方程的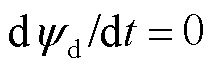 、
、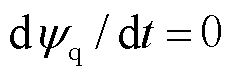 ,则简化为五阶模型。在五阶模型基础上,忽略阻尼绕组作用,即移除式(1)、式(2)中的后两行,则简化为三阶模型。在三阶模型基础上,忽略励磁绕组暂态,近似计及励磁绕组的作用,即移除式(1)中的第四行并令Ldfif=LDfif为常数,则简化为二阶模型。计及g绕组时,三阶、五阶模型则分别化为四阶、六阶模型。
,则简化为五阶模型。在五阶模型基础上,忽略阻尼绕组作用,即移除式(1)、式(2)中的后两行,则简化为三阶模型。在三阶模型基础上,忽略励磁绕组暂态,近似计及励磁绕组的作用,即移除式(1)中的第四行并令Ldfif=LDfif为常数,则简化为二阶模型。计及g绕组时,三阶、五阶模型则分别化为四阶、六阶模型。
由于本文面向海上风电研究PMSG模型,不再考虑计及g绕组的四阶、六阶同步发电机模型。永磁机型本身以永磁体励磁替代励磁绕组励磁,忽略励磁绕组暂态,所以对应于同步发电机的五阶、七阶模型,PMSG需分别降一阶,成为四阶、六阶模型。
因此,本文将以PMSG的六阶、四阶、二阶模型为例,推导建模过程。
此外,为了统一在定子侧进行分析和度量,简化的发电机实用模型通常建模时会引入一些折合到定子侧的实用变量以取代转子变量。引入实用变量使得简化的发电机实用模型的状态变量不再是式(1)中的磁链变量,而是如q轴超瞬变电动势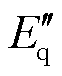 、d轴超瞬变电动势
、d轴超瞬变电动势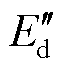 等电动势变量,具体推导过程较为繁复,在文献[25]中有详细推导过程,本文不再赘述。引入实用变量电动势使得方程的物理意义更为明确,但不同阶数发电机模型使用不同的状态变量会导致建模方法不完全统一。本文不引入实用变量,由式(1)、式(2)统一推导各阶模型,并形成一个阶数可选的PMSG模型。后文公式中实线框内表示PMSG四阶模型需要置0的部分,虚线以下部分为在实线框部分置0基础上二阶模型还需要置0的部分。
等电动势变量,具体推导过程较为繁复,在文献[25]中有详细推导过程,本文不再赘述。引入实用变量电动势使得方程的物理意义更为明确,但不同阶数发电机模型使用不同的状态变量会导致建模方法不完全统一。本文不引入实用变量,由式(1)、式(2)统一推导各阶模型,并形成一个阶数可选的PMSG模型。后文公式中实线框内表示PMSG四阶模型需要置0的部分,虚线以下部分为在实线框部分置0基础上二阶模型还需要置0的部分。
本节将根据上述不同阶数的PMSG基本方程进行推导,给出PMSG等效模型建立方法。
从式(1)、式(2)出发,选取电流作为状态变量,将磁链方程代入电压方程,并写成矩阵形式,得到
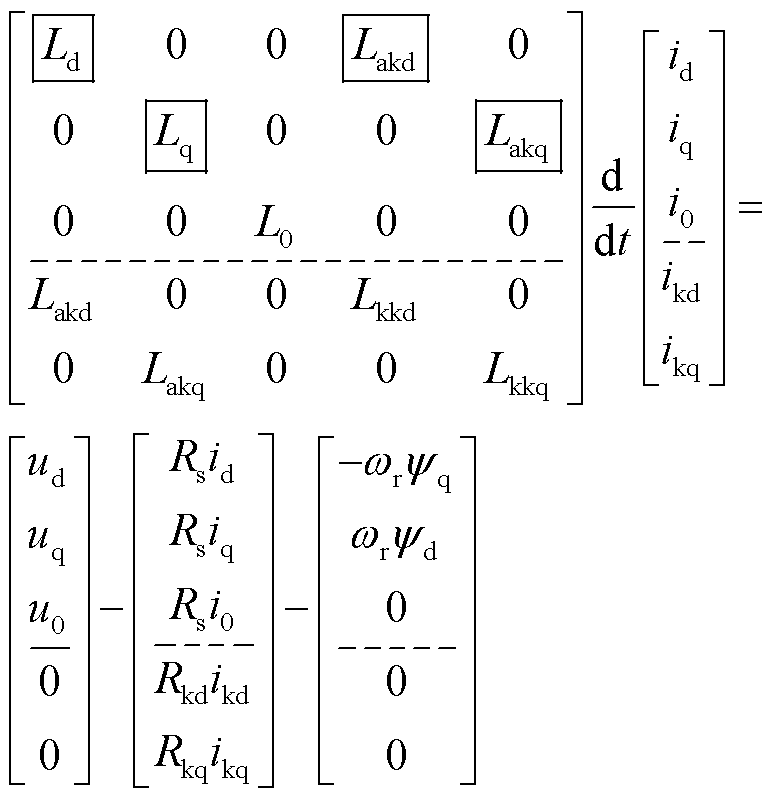 (4)
(4)
将式(4)前两行展开,得到
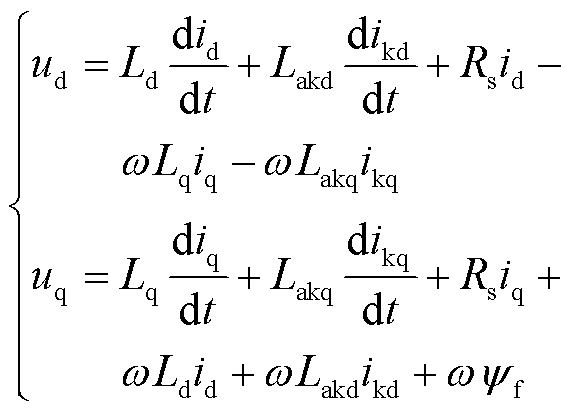 (5)
(5)
式中,-wLqiq-wLakqikq与wLdid+wLakdikd+w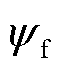 无法用常规的R、L、C表示,在电路中表现为受控电压源形式。根据式(5),可得到如图2所示的dq轴等效电路。
无法用常规的R、L、C表示,在电路中表现为受控电压源形式。根据式(5),可得到如图2所示的dq轴等效电路。
图2 dq轴等效电路
Fig.2 dq axis equivalent circuit
基于Matlab/Simulink的同步电机仿真会存在代数环问题[26],在等效电路中体现为:求解d轴电路需要给受控源输入iq,求解q轴电路需要给受控源输入id,即输入取决于输出,输出也取决于输入的“死锁”关系。Matlab/Simulink中常用的消除代数环的方法有利用变换法消除代数环和在直通模块前插入存储器模块[27]。而发电机模型非常复杂,变换法难以应用。建模中可以借鉴存储器的思路,对d、q轴耦合部分进行一个步长的延时。
首先采用隐式欧拉法对式(4)进行离散化可得式(6),然后将PMSG方程中d、q轴耦合部分wr (t)y(t)近似为wr (t-Δt)y(t-Δt),并进行整理,这样得到重构PMSG模型方程见式(7)。
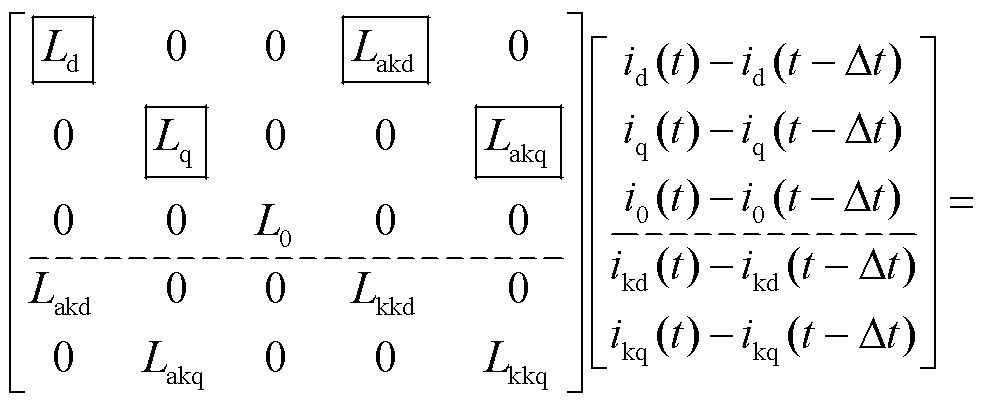
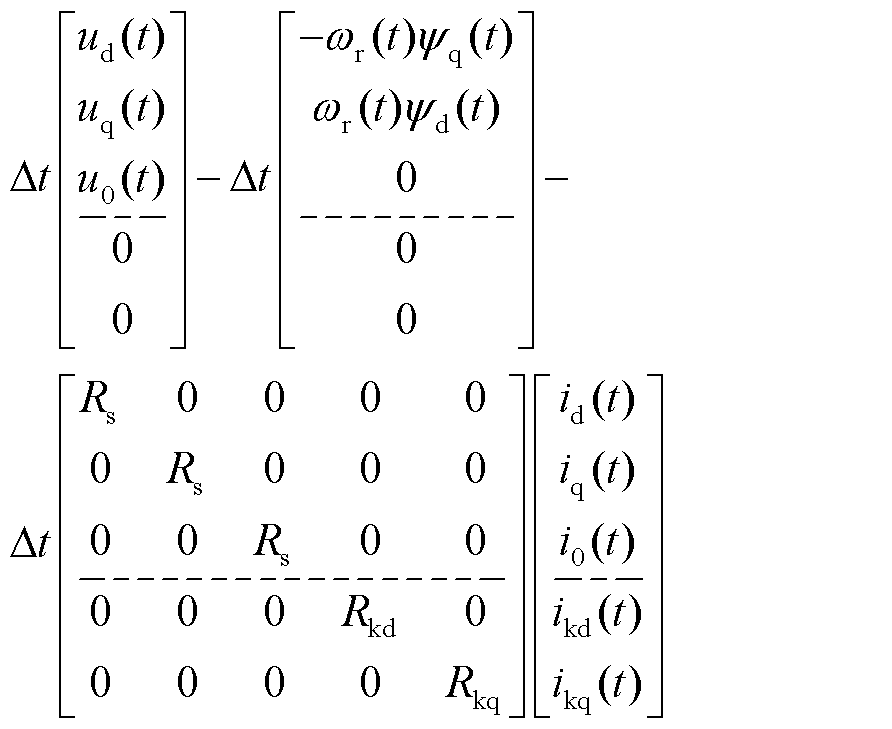 (6)
(6)
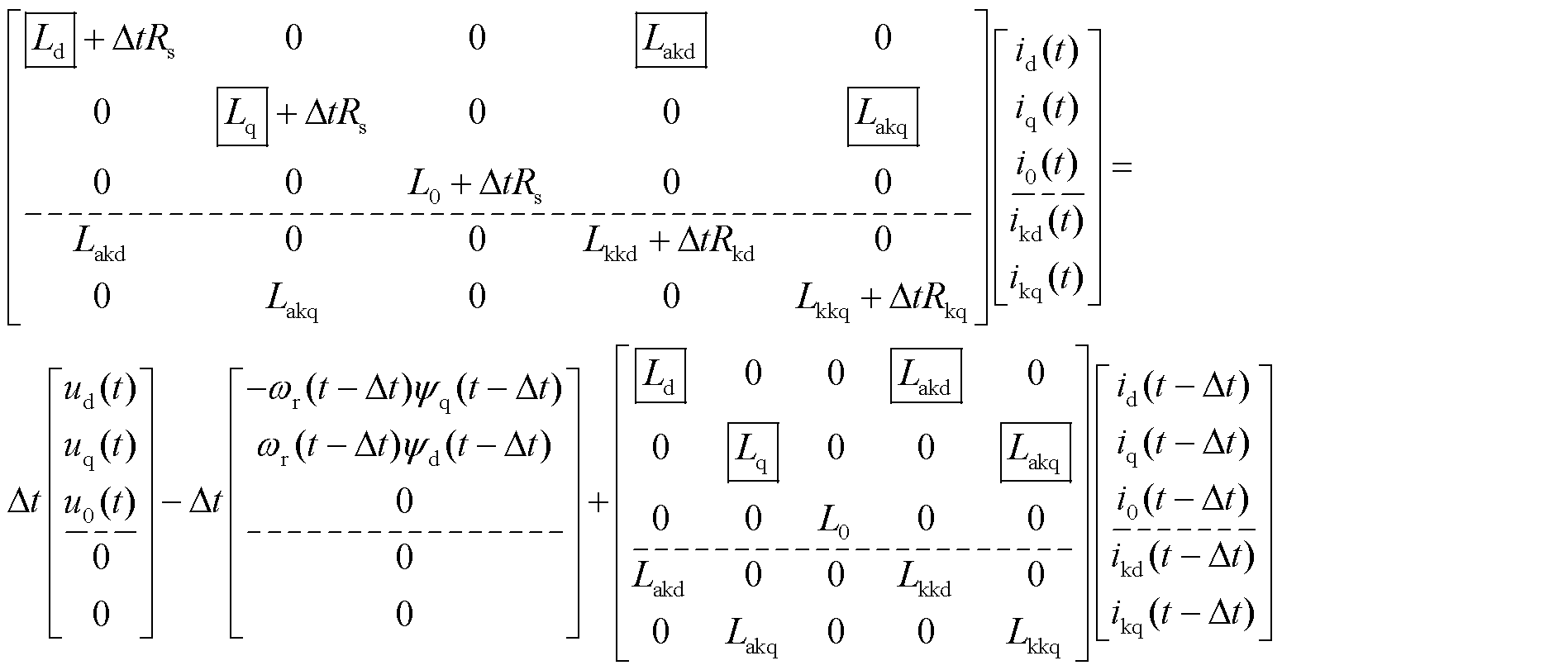 (7)
(7)
本节基于2.1节重构的PMSG方程继续推导得到诺顿等效模型。由于所建模型需与外电路连接,且需要变换到abc坐标系下,故引入派克变换,然后将方程化为I=YU+J形式,并将abc三相方程与DQ阻尼方程分开,得到式(8)、式(9)。具体推导过程见附录。PMSG由定子向外输出电压、电流,转子不接入电路。因此,可由式(8)得到发电机诺顿等效电路,与外电路连接。而式(9)表示的DQ阻尼绕组电流,在推导中也需要更新,但提供下一步时式(8)中的ikdq(t-Δt),不生成诺顿电路对外连接。
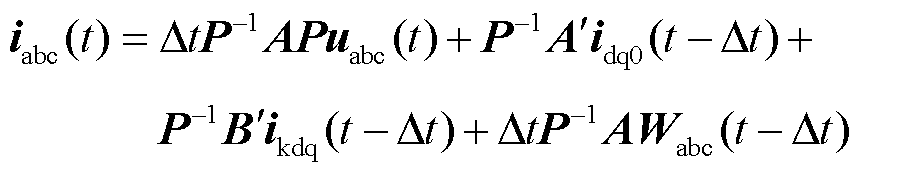 (8)
(8)
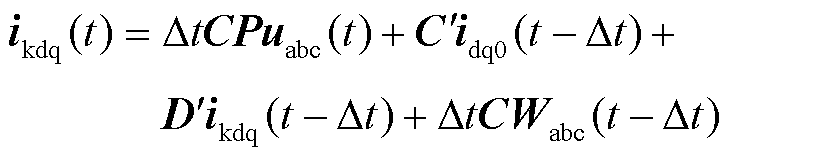 (9)
(9)
对转子运动方程式(3)同样用隐式欧拉法进行离散化处理得到式(10)。角位移用于更新派克变换矩阵,即用于式(8)和式(9)中的P矩阵更新。
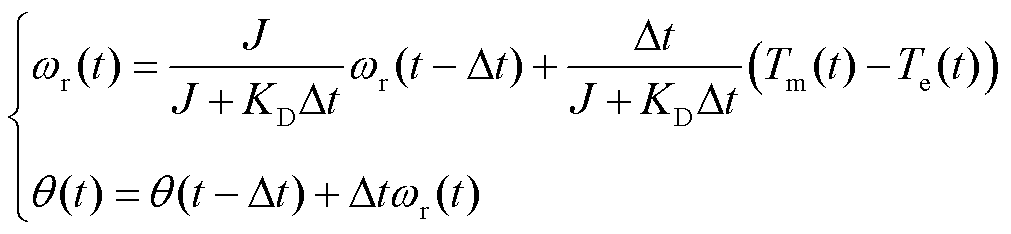 (10)
(10)
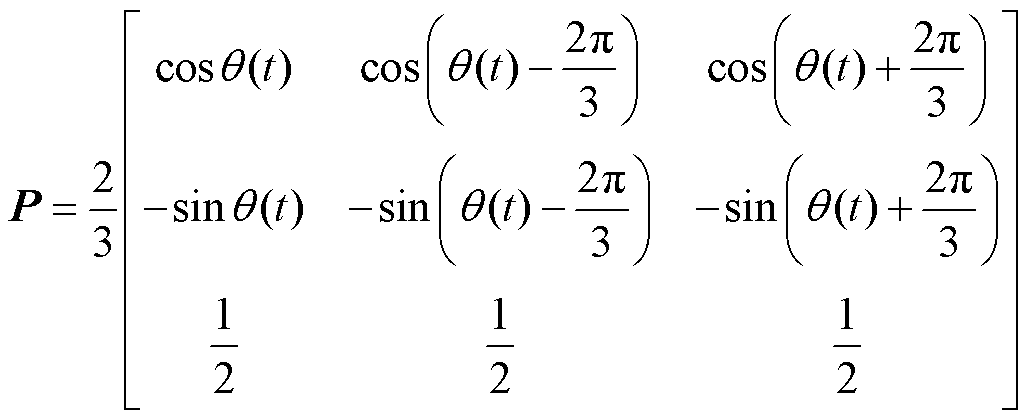 (11)
(11)
由于2.1节对PMSG方程进行了近似处理,式中A矩阵为对角矩阵,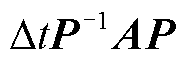 为对称矩阵,在RTDS自定义元件中可编写程序,通过电导与电流源形式形成四节点六支路的诺顿等效电路,参考节点G接地,该模型与外电路连接后可通过全电磁仿真平台求解,按步更新。各电导与电流源由式(8)展开得到,结果为
为对称矩阵,在RTDS自定义元件中可编写程序,通过电导与电流源形式形成四节点六支路的诺顿等效电路,参考节点G接地,该模型与外电路连接后可通过全电磁仿真平台求解,按步更新。各电导与电流源由式(8)展开得到,结果为
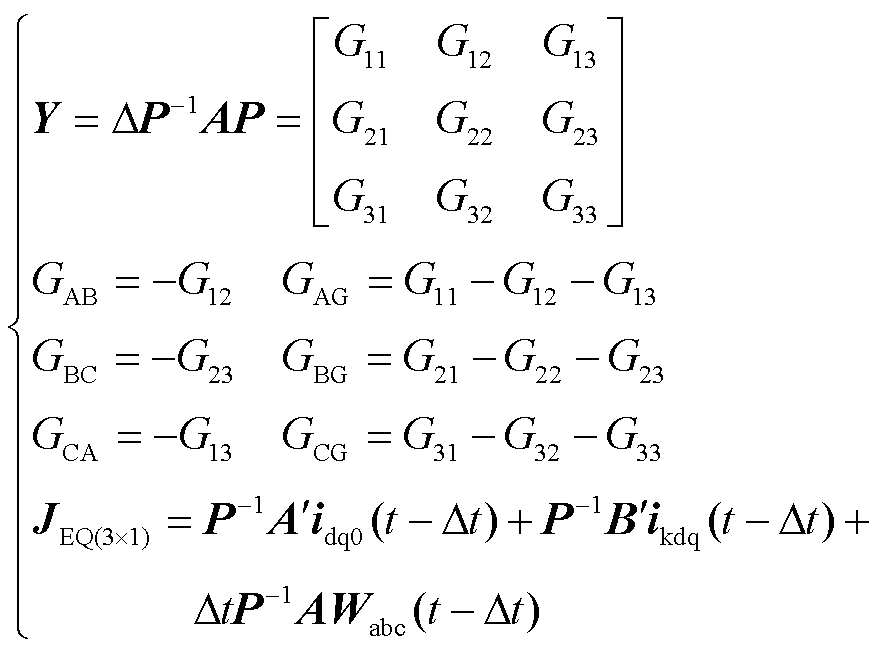 (12)
(12)
最终得到PMSG等效电路如图3所示。
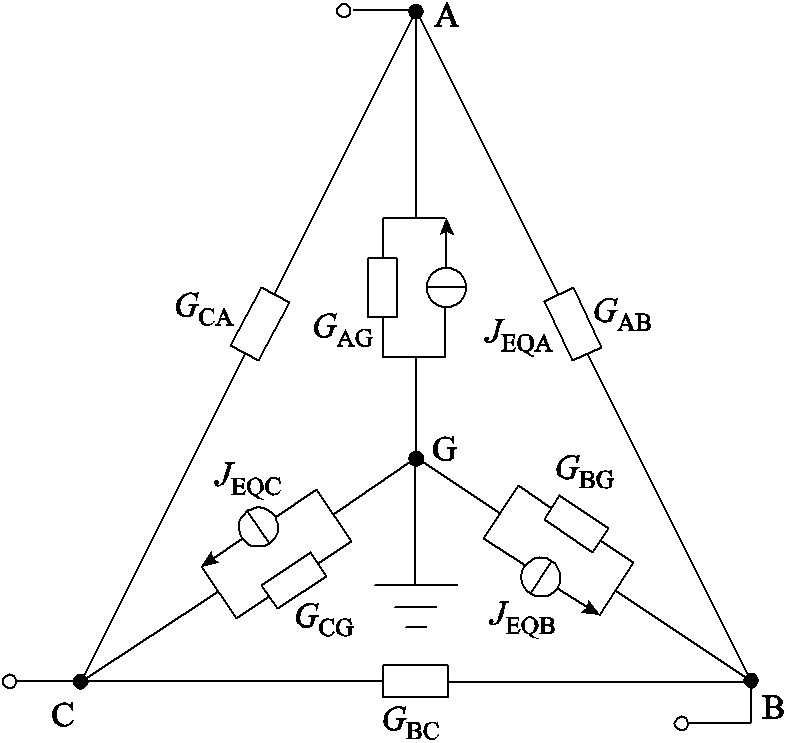
图3 永磁同步发电机等效电路
Fig.3 Equivalent circuit of PMSG
综上所述,PMSG等效模型构建完成。该方法借鉴了消除代数环的存储器思路,在式(8)、式(9)中,A, B, C, D,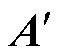 ,
,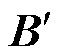 ,
,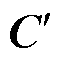 ,
, 为常数矩阵,可以预存处理,一定程度上简化了模型的解算和各系数矩阵的运算,规避了未重构模型时大量时变矩阵的乘法和求逆过程。
为常数矩阵,可以预存处理,一定程度上简化了模型的解算和各系数矩阵的运算,规避了未重构模型时大量时变矩阵的乘法和求逆过程。
本文所提的等效建模方法适用于不同阶数的同步发电机的电磁暂态仿真。基于PMSG的六阶、四阶、二阶模型的具体推导已在上文中说明,其余阶数同步电机模型可参考该过程,增添、减少一些方程或改变方程中的某些系数。例如,考虑g绕组时只需多加入两个方程式(13)和式(14),之后的推导仅使得式(9)变为行数为3的矩阵计算,不改变式(8)的行数与PMSG的等效电路。
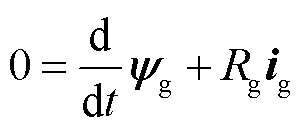 (13)
(13)
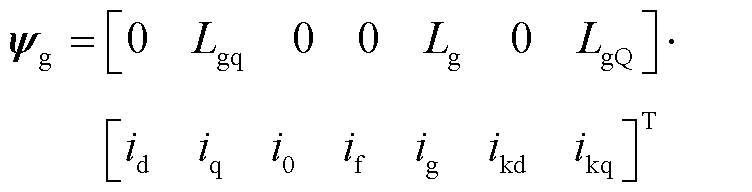 (14)
(14)
当短路发生在离电源较远处时,可近似认为电源电压恒定,即忽略了同步电机的电抗。应用于海上风电,结合目前风场模型仿真效率低的问题,以及单机、多机模型和分群指标,可在距离故障近的风机采用详细的六阶PMSG模型,在距离故障远处的风机采用低阶模型,节省仿真资源。
常用的积分离散方法有梯形积分法和隐式欧拉法。上文展示了隐式欧拉法的推导过程,对于梯形积分法,该方法同样适用,相比隐式欧拉法的结果,历史电流源部分多了一项,提升了精度,小幅地降低了计算效率。
PMSG等效模型的仿真框架如图4所示。本节将根据前述2.2节所提出的建模方法以及RTDS仿真平台自定义元件工具Cbuilder的各代码段使用方法,构建模型整体仿真框架。
代码部分分为三部分:
(1)预计算存储。RAM代码段负责完成电压、电流、阻抗基准值的计算,以及式(8)、式(9)中各常数系数矩阵A, B, C, D,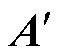 ,
,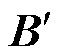 ,
,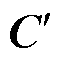 ,
, 的计算,计算结果存入寄存器中,在Begin_T0、T0_T2中使用。RAM代码段只在仿真开始后第1个步长执行。
的计算,计算结果存入寄存器中,在Begin_T0、T0_T2中使用。RAM代码段只在仿真开始后第1个步长执行。
(2)等效电路生成。Begin_T0代码段负责根据计算导纳矩阵与注入电流源。根据RAM段提供的系数矩阵与T0_T2段提供的各电压、电流历史值,可代入式(8)、式(9)计算得到图3电路中各导纳与注入电流源的值,通过代码生成等效电路。
(3)内部电气信息反解。T0_T2代码段负责进行内部电气信息反解。搭建仿真模型,将等效模型与外电路连接解算后,T0_T2段中可测量等效模型各端子的电气量,由各端子电气量解出各支路的电气量,作为下一个步长Begin_T0段所用的电压、电流历史值。同时,需要更新PMSG所关注的转速、角位移、电磁转矩,并进行输出。
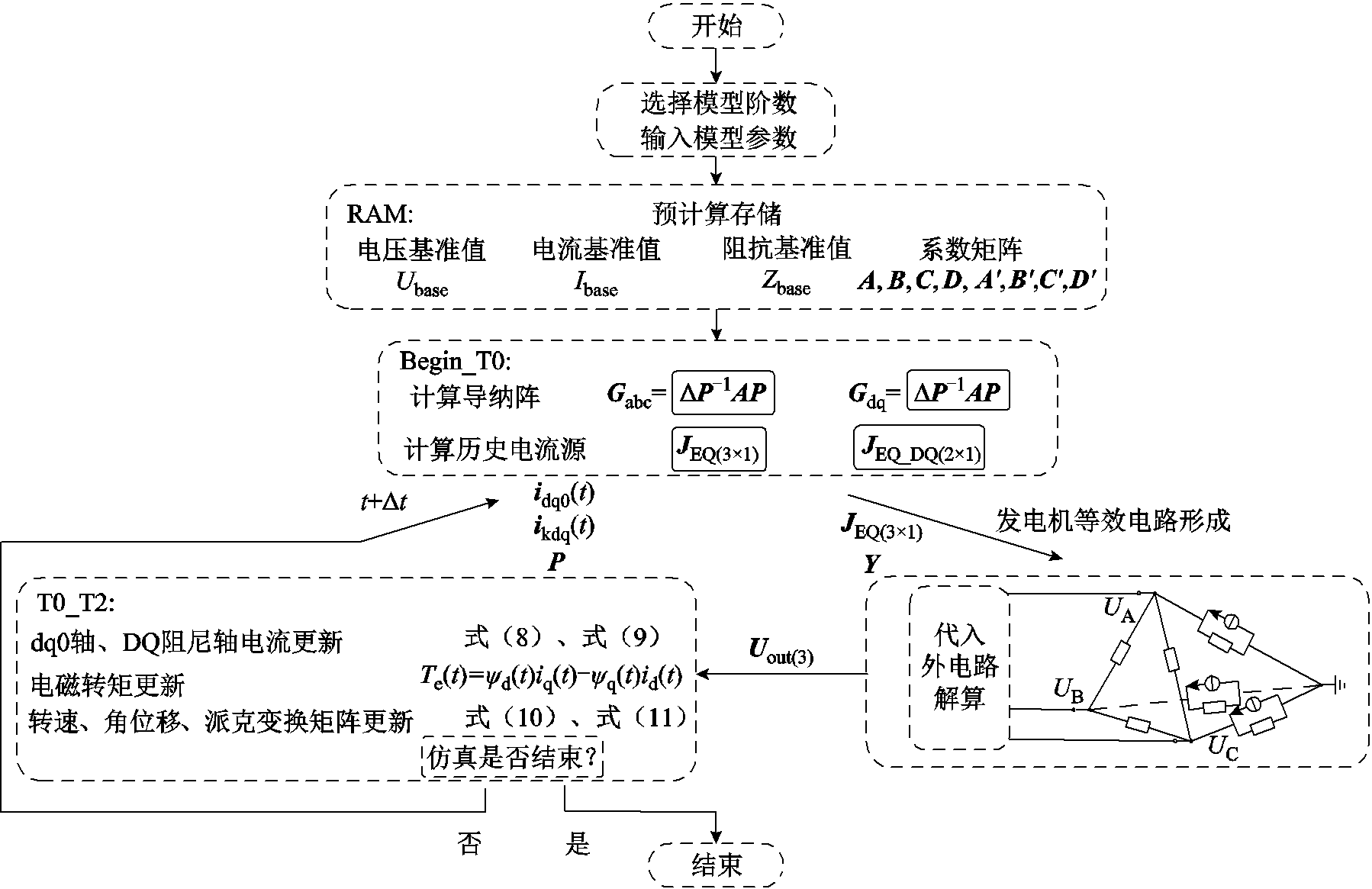
图4 整体仿真框架
Fig.4 Integral simulation framework
本节在RTDS实时仿真平台中搭建了直驱型风电机组仿真测试模型,测试所建立PMSG模型的多工况仿真精度与适用场景。测试系统采用典型的单机倍乘风场模型,模型拓扑示意图如图5所示。共四个模型进行测试对比,分别是使用本文所提的六阶、四阶、二阶PMSG等效模型的测试模型与RTDS提供的基准模型。波形中BM(Benchmark Model)表示基准模型,EM 6(Equivalent Model)、EM 4、 EM 2分别表示使用六阶、四阶、二阶PMSG等效模型的测试模型。
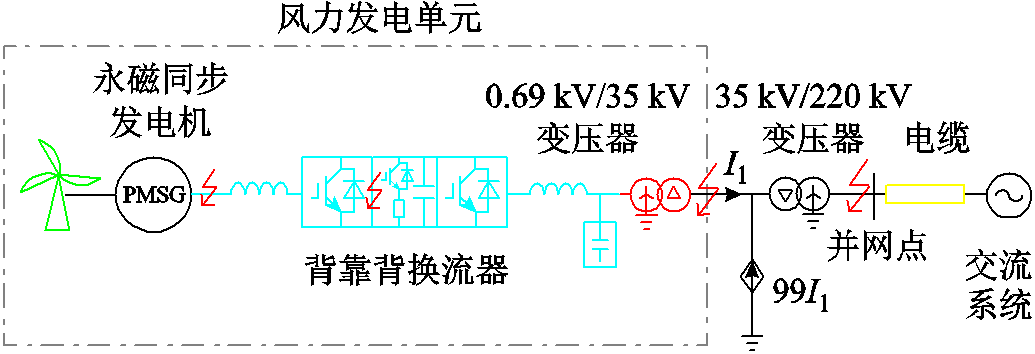
图5 测试系统示意图
Fig.5 Schematic of the test system
换流器采取典型的电压外环、电流内环的双环矢量控制策略。网侧换流器控制为定直流电压与定交流电压控制,机侧换流器控制发电机电磁转矩与无功功率。表1为仿真模型主要参数。
表1 仿真模型主要参数
Tab.1 Main parameters of the simulation model
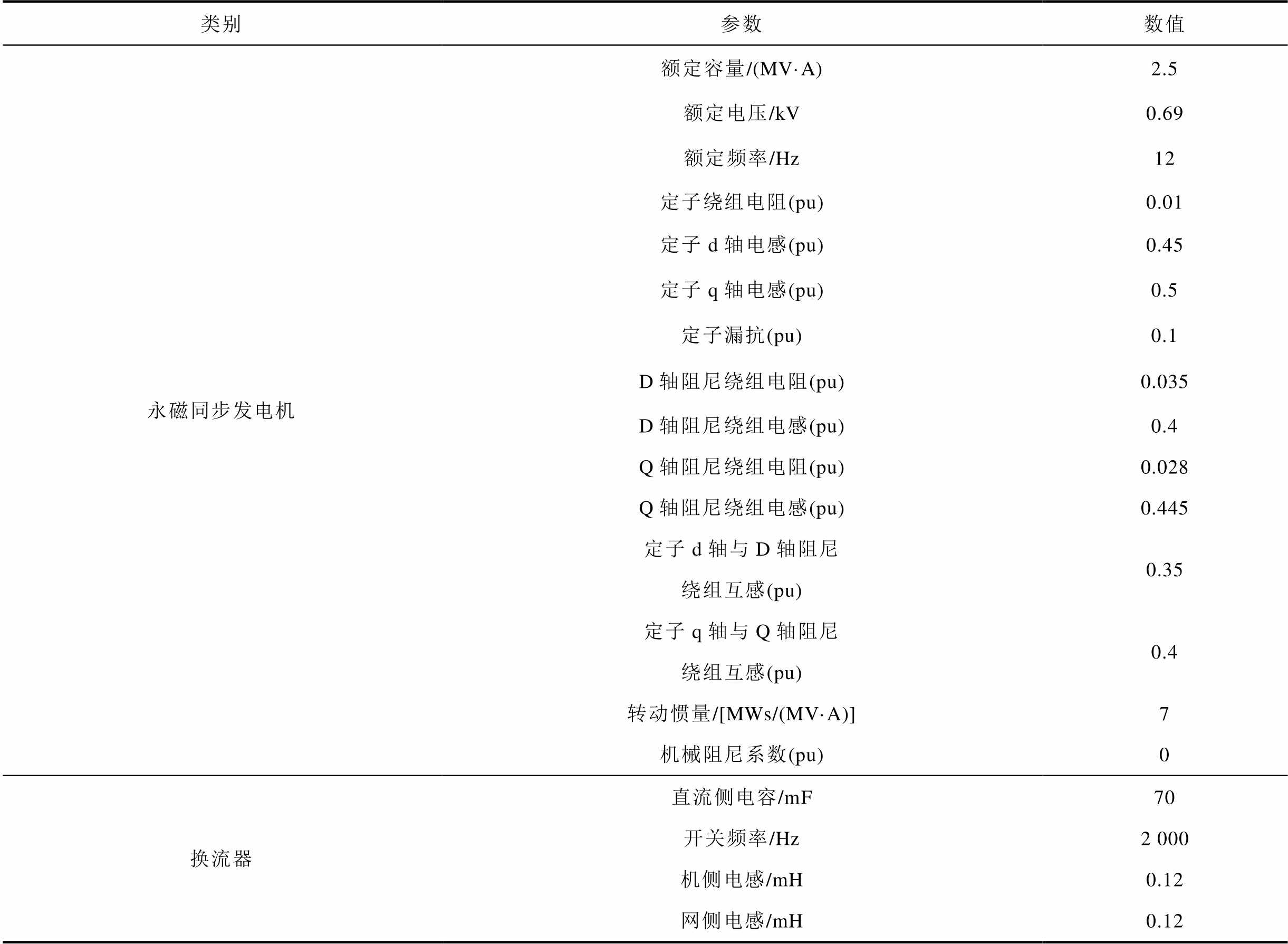
类别参数数值 永磁同步发电机额定容量/(MV·A)2.5 额定电压/kV0.69 额定频率/Hz12 定子绕组电阻(pu)0.01 定子d轴电感(pu)0.45 定子q轴电感(pu)0.5 定子漏抗(pu)0.1 D轴阻尼绕组电阻(pu)0.035 D轴阻尼绕组电感(pu)0.4 Q轴阻尼绕组电阻(pu)0.028 Q轴阻尼绕组电感(pu)0.445 定子d轴与D轴阻尼绕组互感(pu)0.35 定子q轴与Q轴阻尼绕组互感(pu)0.4 转动惯量/[MWs/(MV·A)]7 机械阻尼系数(pu)0 换流器直流侧电容/mF70 开关频率/Hz2 000 机侧电感/mH0.12 网侧电感/mH0.12
(续)
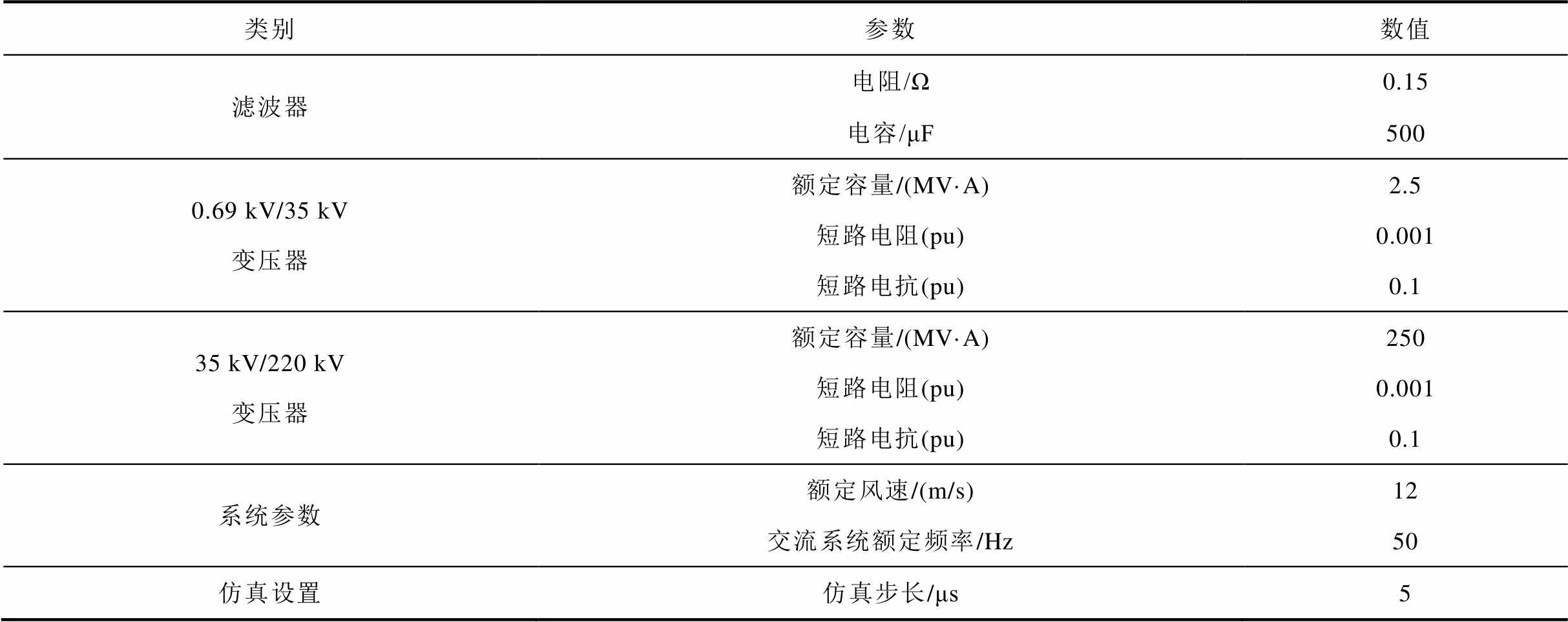
类别参数数值 滤波器电阻/Ω0.15 电容/μF500 0.69 kV/35 kV变压器额定容量/(MV·A)2.5 短路电阻(pu)0.001 短路电抗(pu)0.1 35 kV/220 kV变压器额定容量/(MV·A)250 短路电阻(pu)0.001 短路电抗(pu)0.1 系统参数额定风速/(m/s)12 交流系统额定频率/Hz50 仿真设置仿真步长/μs5
本节设置四个故障点,进行短路故障仿真,验证所建等效模型大扰动下的仿真精度,并验证2.3节故障较远处可使用低阶模型的分析结果是否正确。如图5所示,四个故障从电网至PMSG依次为并网点三相短路接地故障、0.69 kV/35 kV变压器出口三相短路接地故障、直流双极短路故障、发电机出口三相短路接地故障。故障发生时间为0.4 s,故障持续时间为0.1 s。
1)并网点故障与0.69 kV/35 kV变压器出口故障波形如图6所示。
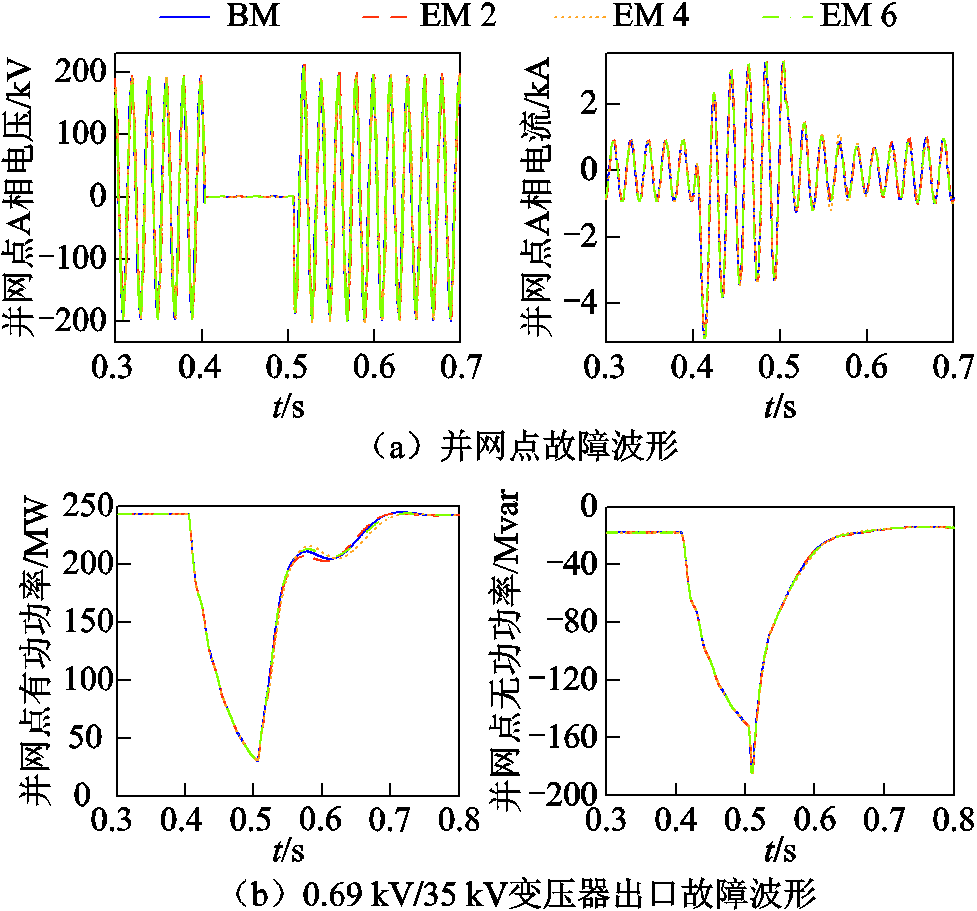
图6 故障工况波形
Fig.6 Waveforms of fault conditions
由于故障点距离发电机较远且风电机组的背靠背换流器具有故障隔离的特性,六阶、四阶、二阶测试模型在网侧换流器与电网之间的短路故障测试波形差异不大。经测算,并网点处的电压、电流平均相对误差小于3%,有功功率、无功功率平均相对误差小于1.5%。图6波形表明,场站级的仿真时,发电机模型对于风电场站对外输出特性影响较小,通常仿真精度在5%以内时,认为模型较为准确,六阶、四阶、二阶均满足仿真精度要求。
2)发电机出口故障与直流双极短路故障波形如图7、图8所示。
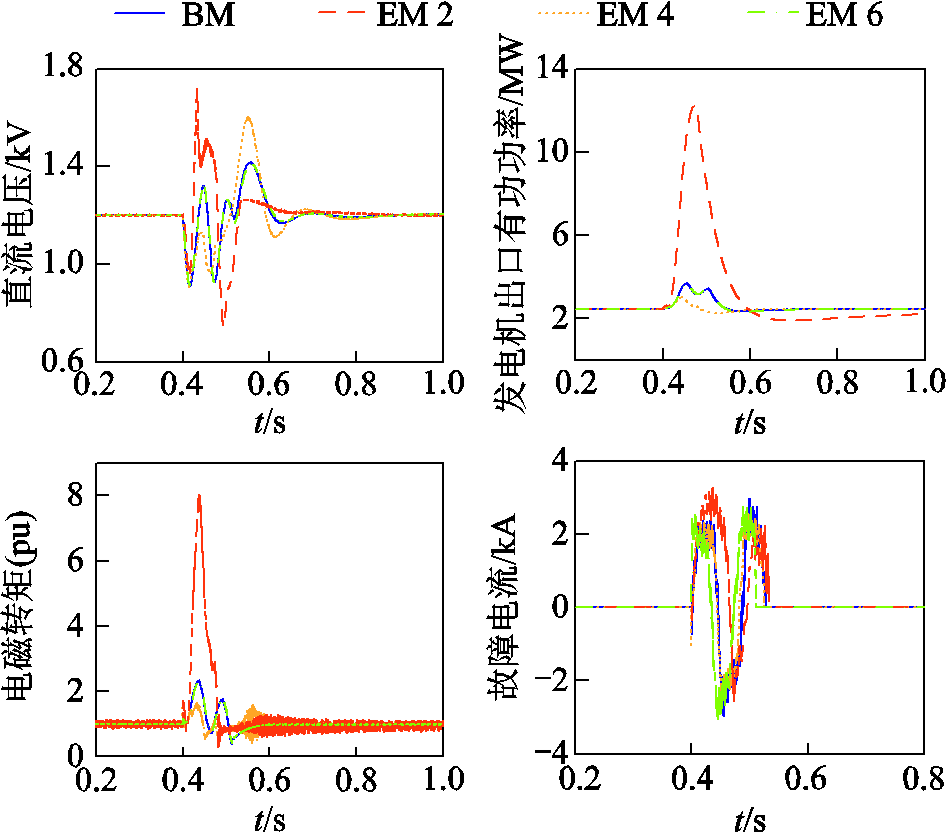
图7 发电机出口故障波形
Fig.7 Waveforms of generator outlet fault
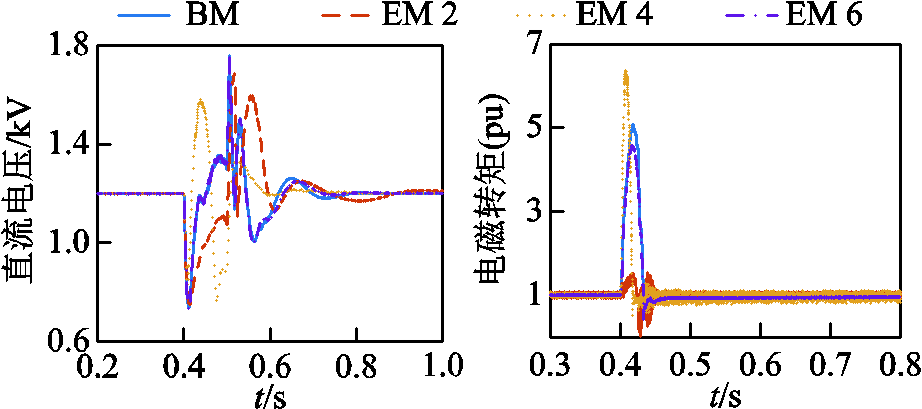
图8 直流双极短路故障波形
Fig.8 Waveforms of DC bipolar short circuit fault
图7和图8波形显示,六阶模型在直流故障与发电机出口故障依然精度较高,而四阶、二阶模型波形由于不同程度上忽略了暂态过程,尤其是二阶模型,忽略了阻尼绕组,缺少了对定子绕组电流变化的抑制作用,趋势已与基准模型差别较大。经测算,发电机出口故障时六阶、四阶、二阶模型的电磁转矩波形平均相对误差分别为1.45%、12.95%、18.77%,直流故障时六阶、四阶、二阶模型的直流电压波形最大相对误差分别为3.62%、77.29%、36.42%,结果表明,四阶、二阶模型误差较高,已不适合发电机至直流母线之间的故障测试场景。
本节通过调节机侧换流器控制参数激发振荡,验证所建各阶模型与机侧换流器之间小扰动工况的耦合特性是否正确。
机侧换流器电压外环d轴PI控制器的Kp参数由2变为100的仿真波形如图9所示。
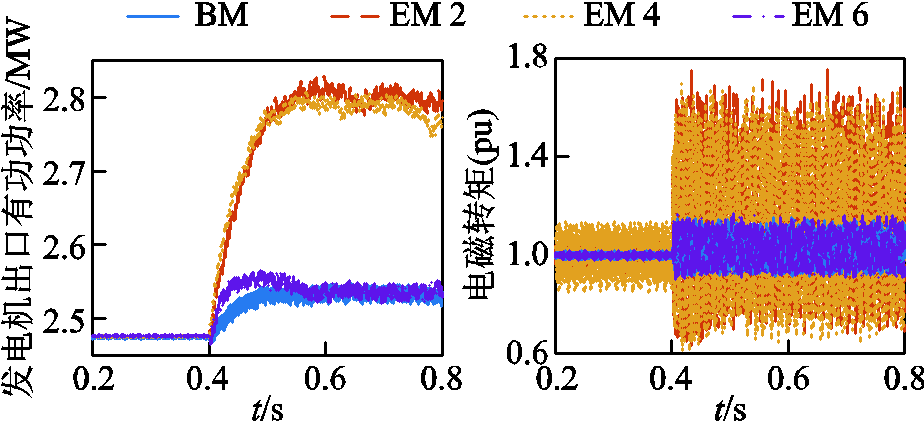
图9 小扰动工况波形
Fig.9 Waveforms of small disturbance condition
0.4 s时各电气量出现次同步振荡,其中电磁转矩波形较为明显。经测算,六阶模型波形的平均相对误差小于4%,而四阶、二阶模型发电机出口有功功率波形平均相对误差已大于10%,且发电机电磁转矩波形振幅明显大于基准模型,无法正确模拟小扰动工况。
除了电路之间的直接联系,PMSG还与风力机有信息的交互,风力机为PMSG提供机械转矩的输入,而PMSG将发电机转速信息返回至风力机。风力机的扰动工况主要体现在风速的变化。本节设置风速由12 m/s降为6 m/s与风速由6 m/s升为20 m/s两个场景,发电机出口有功功率和发电机转速波形如图10所示。
由于风力机本身有桨距角控制,风速变化并不会造成风力机输出的机械转矩突变。在风速降低工况下,各阶模型与基准模型拟合得都较好,而在风速升高工况下,仅六阶模型依然有较高的精度,四阶、二阶模型在电磁转矩上有较严重的振荡。
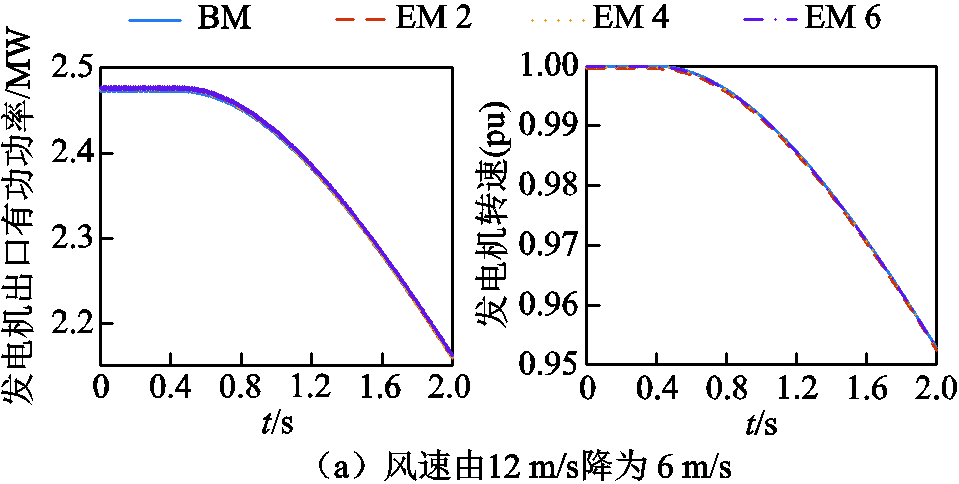
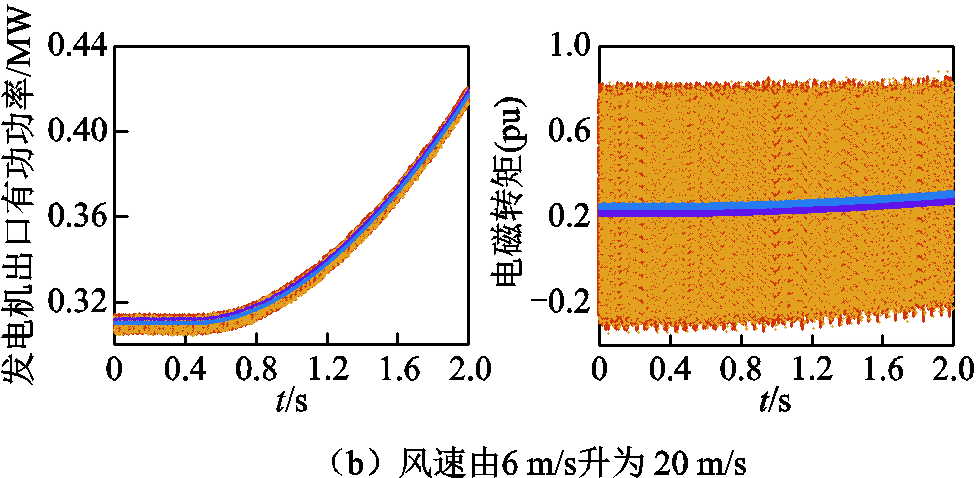
图10 风速变化工况波形
Fig.10 Waveform of wind speed variation conditions
根据4.2节~4.4节的仿真测试结果,本文所建六阶等效模型在多工况下都有较高的仿真精度,同时适用于机组内部与场站级的仿真。四阶、二阶模型在场站级仿真中有一定适用性,而无法反映PMSG、机侧换流器、风力机之间的耦合特性,不适用于风电机组内部的仿真场景。
本文提出了一种面向海上风电的永磁同步发电机电磁暂态建模方法,详细介绍了PMSG模型的重构及推导过程。该方法通过延时操作消除了模型中的代数环问题,基于软件自定义元件功能建立了四节点六支路的等效模型,可以直接与外电路接口进行仿真。
本文所建立的等效模型具有阶数可选的优势,可面向海上风电不同仿真需求灵活选择。现有PMSG等效建模方法在不同程度上做了简化,而本文所建六阶等效模型保留了PMSG的全阶方程,在不同故障点、小扰动、风速变化等工况下实现与基准模型的高度拟合,能够应用于机组内部仿真与场站级仿真。四阶、二阶模型在离PMSG较远处的故障仿真依然有较好的精度与稳定性,在场站级的仿真中已经可以满足仿真需求。所提模型为海上风电仿真应用高效电磁暂态建模方法以及并行加速算法提供了机理透明且便于程序实现的PMSG模型基础。
附 录
由式(7)引入派克变换可得
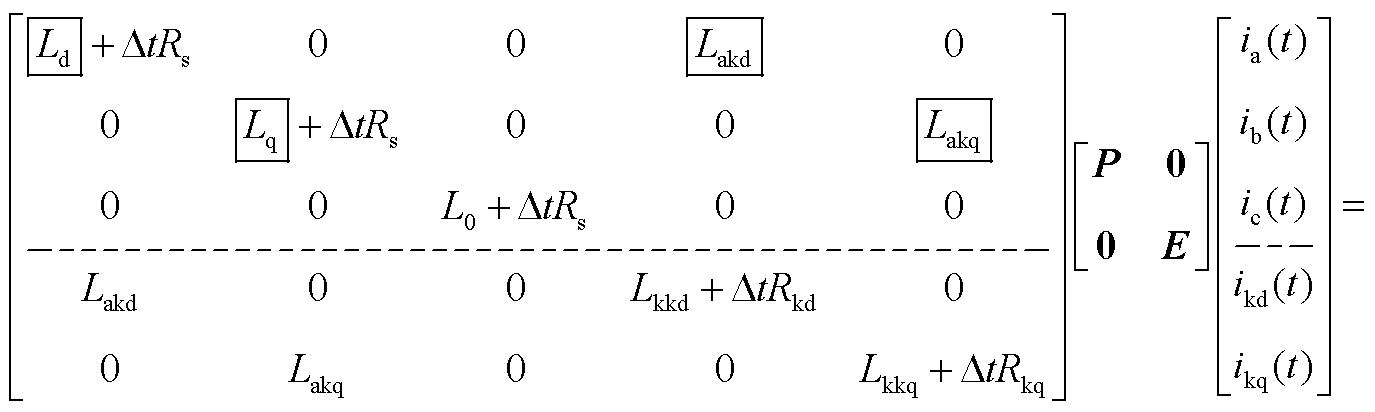
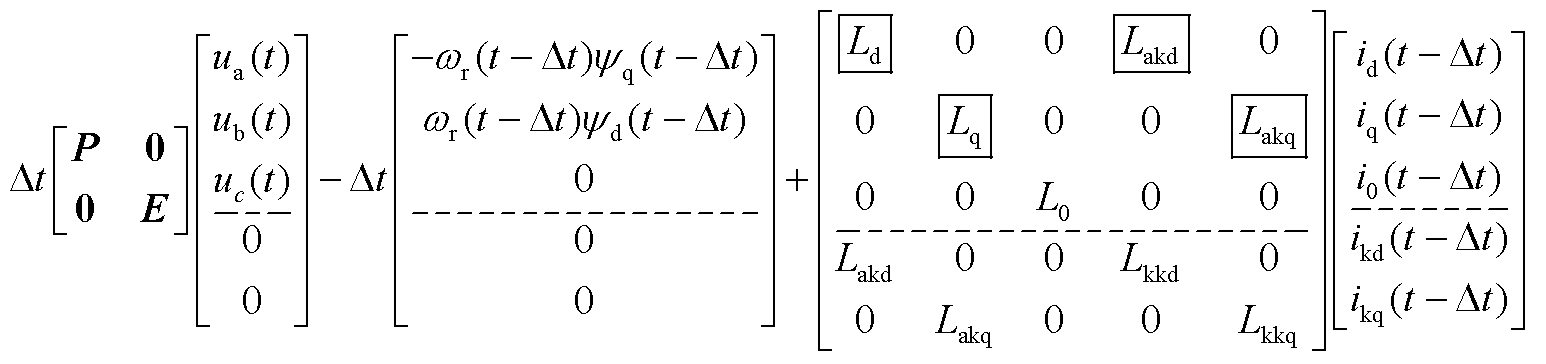 (A2)
(A2)
式中,P为派克变换矩阵;E为单位矩阵;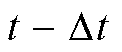 时刻的电流作为历史电流源的一部分,不需要变换到abc坐标系下。
时刻的电流作为历史电流源的一部分,不需要变换到abc坐标系下。
通过矩阵分块将abc三相公式与DQ阻尼绕组公式分别计算,分块过程如式(A2)~式(A4)所示。
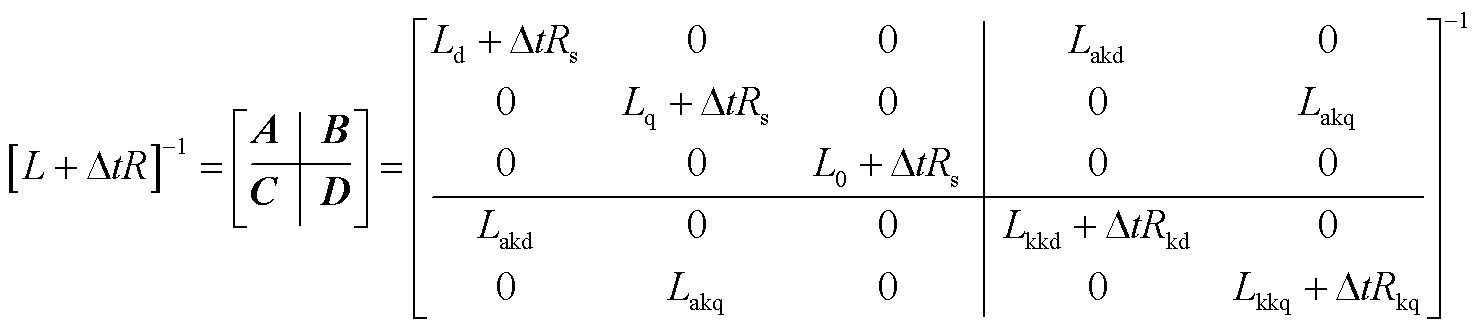 (A2)
(A2)
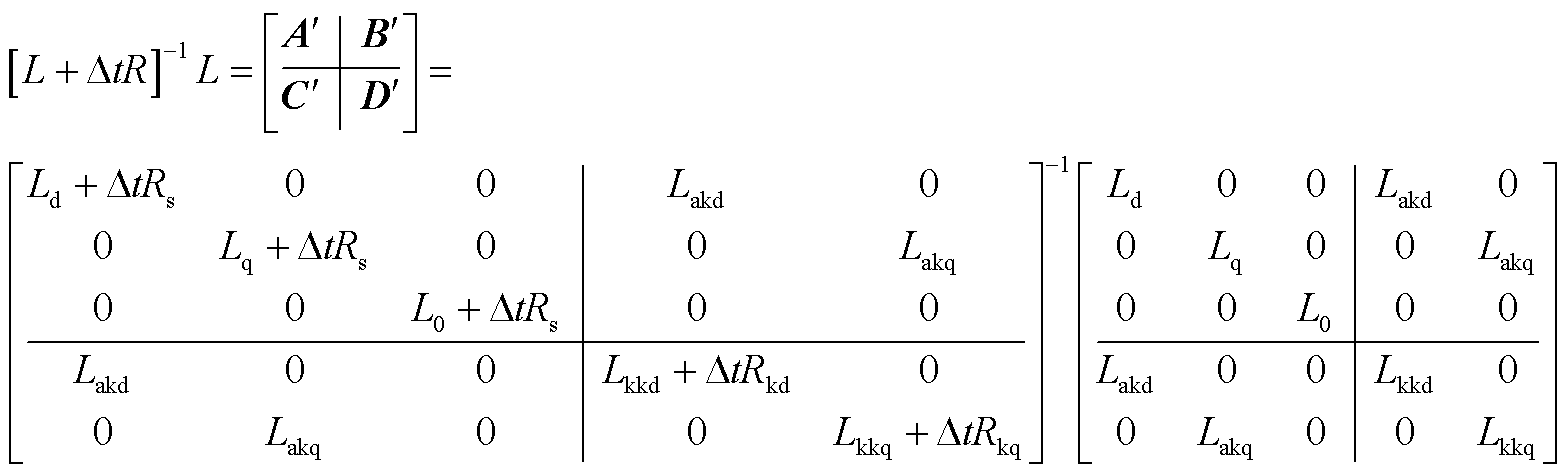 (A3)
(A3)
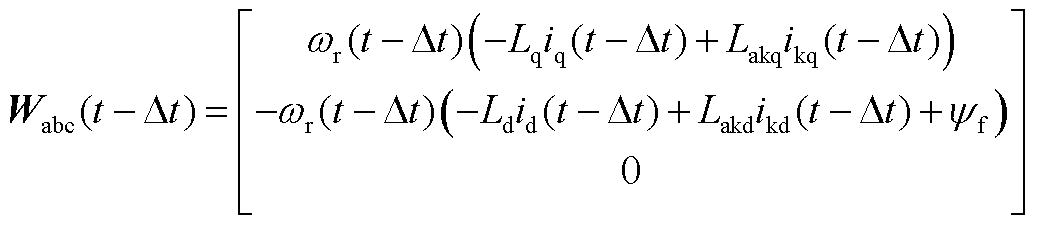 (A4)
(A4)
式(A1)等式两边同乘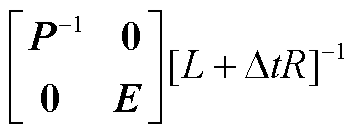 ,化为I=YU+J形式,化简整理得到
,化为I=YU+J形式,化简整理得到
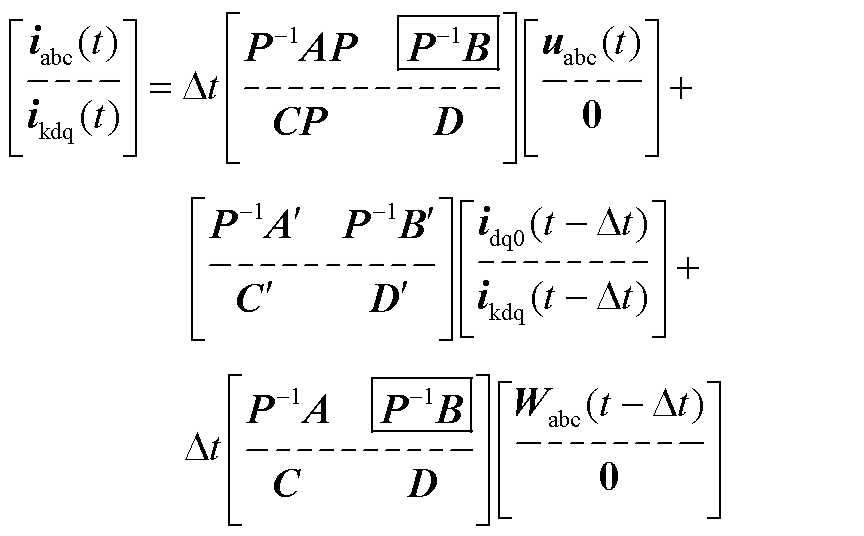 (A5)
(A5)
将式(A5)展开,并将abc三相方程与DQ阻尼绕组方程分开,得到式(8)和式(9)。
参考文献
[1] 崔鹤松, 李雪萍, 黄晟, 等. 模块化多相永磁风力发电机串并联直流海上风电场电压协调控制[J]. 电工技术学报, 2023, 38(4): 925-935. Cui Hesong, Li Xueping, Huang Sheng, et al. Voltage coordinated control strategy for modular multi-phase pmsg-based series-parallel DC connected offshore wind farm[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 925-935.
[2] 迟永宁, 梁伟, 张占奎, 等. 大规模海上风电输电与并网关键技术研究综述[J]. 中国电机工程学报, 2016, 36(14): 3758-3770. Chi Yongning, Liang Wei, Zhang Zhankui, et al. An overview on key technologies regarding power transmission and grid integration of large scaleoffshore wind power[J]. Proceedings of the CSEE, 2016, 36(14): 3758-3770.
[3] 杨培文, 李洪涛, 杨锡运, 等. 风电机组技术现状分析及未来发展趋势预测[J]. 电力电子技术, 2020, 54(3): 79-82. Yang Peiwen, Li Hongtao, Yang Xiyun, et al. Analysis of the present situation of wind turbine technology and forecast of future development trend[J]. Power Elctronics, 2020, 54(3): 79-82.
[4] Gnanarathna U N, Gole A M, Jayasinghe R P. Efficient modeling of modular multilevel HVDC converters (MMC) on electromagnetic transient simulation programs[J]. IEEE Transactions on Power Delivery, 2011, 26(1): 316-324.
[5] 高晨祥, 丁江萍, 许建中, 等. 输入串联输出并联型双有源桥变换器等效建模方法[J]. 中国电机工程学报, 2020, 40(15): 4955-4965. Gao Chenxiang, Ding Jiangping, Xu Jianzhong, et al. Equivalent modeling method of input series output parallel type dual active bridge converter[J]. Proceedings of the CSEE, 2020, 40(15): 4955-4965.
[6] 郭琦, 卢远宏. 新型电力系统的建模仿真关键技术及展望[J]. 电力系统自动化, 2022, 46(10): 18-32. Guo Qi, Lu Yuanhong. Key technologies and prospects of modeling and simulation of new power system[J]. Automation of Electric Power Systems, 2022, 46(10): 18-32.
[7] 何绍民, 张喆, 卢倚平, 等. 基于计算前沿面的实时仿真数值积分并行构造及其数值模型解耦加速方法[J]. 电工技术学报, 2023, 38(16): 4246-4262. He Shaomin, Zhang Zhe, Lu Yiping, et al. Numerical model decoupling acceleration method with numerical integration parallelism construction based on computation front in real-time simuation[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4246-4262.
[8] 邵冰冰, 赵峥, 肖琪, 等. 多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J]. 电工技术学报, 2023, 38(3): 754-769. Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillation modes’ participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
[9] U. Karaagac, Mahseredjian J, Gagnon R, et al. A generic EMT-Type model for wind parks with permanent magnet synchronous generator full size converter wind turbines[J]. IEEE Power and Energy Technology Systems Journal, 2019, 6(3): 131-141.
[10] Ugalde-Loo C E, Ekanayake J B, Jenkins N. State-space modeling of wind turbine generators for power system studies[J]. IEEE Transactions on Industry Applications, 2013, 49(1): 223-232.
[11] Trudnowski D J, Gentile A, Khan J M, et al. Fixed-speed wind-generator and wind-park modeling for transient stability studies[J]. IEEE Transactions on Power Systems, 2004, 19(4): 1911-1917.
[12] Ali M, Ilie I S, Milanovic J V, et al. Wind farm model aggregation using probabilistic clustering[J]. IEEE Transactions on Power Systems, 2013, 28(1): 309-316.
[13] 刘其辉, 逄思敏, 吴林林, 等. 大规模风电汇集系统电压不平衡机理、因素及影响规律[J]. 电工技术学报, 2022, 37(21): 5435-5450. Liu Qihui, Pang Simin, Wu Linlin, et al. Themechanism, factors and influence rules of voltageimbalance in wind power integration areas[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5435-5450.
[14] 李龙源, 付瑞清, 吕晓琴, 等. 接入弱电网的同型机直驱风电场单机等值建模[J]. 电工技术学报, 2023, 38(3): 712-725. Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Singlemachine equivalent modeling of weak grid connectedwind farm with same type PMSGs[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 712-725.
[15] Sanchez-Gasca J J. Generic wind turbine generator models for WECC-a second status report[C]//IEEE Power & Energy Society General Meeting, Denver, CO, USA 2015: 1-5.
[16] 毕天姝, 王清, 薛安成,等.基于状态矩阵和摄动理论的双馈风力发电机与同步机小扰动互作用机理[J].电工技术学报,2016,31(7):126-135. BiTianshu, Wang Qing, Xue Ancheng,et al. The mechanism of small signal dynamic interaction Between DFIG and synchronous generator based on state matrix and perturbation theories[J]. Transactions ofChina Electrotechnical Society, 2016, 31(7): 126-135.
[17] 尹明, 李庚银, 张建成, 等. 直驱式永磁同步风力发电机组建模及其控制策略[J]. 电网技术, 2007(15): 61-65. Yin Ming, Li Gengyin, Zhang Jiancheng, et al. Modeling and control strategies of directly driven wind turbine with permanent magnet syn-chronous generator[J]. Power System Technology, 2007 , 31(15) : 61-65.
[18] 马威. 基于永磁同步发电机的直驱式风电系统建模与仿真[D]. 兰州:兰州理工大学, 2010. Ma Wei. Modeling and simulation for direct-drive permanent magnet wind power system[D]. Lanzhou: Lanzhou University of Technology, 2010.
[19] 王林富, 许丹枫, 赵湖珊, 等. 直驱永磁风力发电系统建模与仿真方法研究[J]. 电子测量技术, 2019, 42(20): 44-50. Wang Linfu, Xu Danfeng, Zhao Hushan, et al. Modeling and simulation of direct-drive permanent magnet wind power generation system based on PSCAD/EMTDC[J]. Electronic Measure ment Technology, 2019, 42(20): 44-50.
[20] 严干贵, 魏治成, 穆钢, 等. 直驱永磁同步风电机组的动态建模与运行控制[J]. 电力系统及其自动化学报, 2009, 21(6): 34-39. Yan Gangui, Wei Zhicheng, Mu Gang,et al. Dynamic modeling and control of directly-driven permanent magnet synchronous generator wind turbine[J]. Proceedings of the CSU-EPSA, 2009, 21(6): 34-39.
[21] Huang Y, Chapariha M, Therrien F, et al. A constant-parameter voltage-behind-reactance synchronous machine model based on shifted-frequency analysis[J]. IEEE Transactions on Energy Conversion, 2015, 30(2): 761-771.
[22] Zhang P, Marti J R, Dommel H W. Synchronous machine modeling based on shifted frequency analysis[J]. IEEE Transactions on Power Systems, 2007, 22(3): 1139-1147.
[23] 高仕林, 宋炎侃, 陈颖, 等. 电力系统移频电磁暂态仿真原理及应用综述[J]. 电力系统自动化, 2021, 45(14): 173-183. Gao Shilin, SongYankan, Chen Ying, et al. Overview on principle and application of shifted frequency based electromagnetic transient simulation for power system[J]. Automation of Electric Power Systems, 2021, 45(14): 173-183.
[24] 申健, 金钧. 电力系统仿真分析中几种同步发电机数学模型的比选[J]. 电气技术, 2007,8(9): 48-51. Shen Jian, Jin Jun. Compare several mathematical models of synchronous machine in power system simulation analysis[J]. Electrical Engineering, 2007(9): 53-56.
[25] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[26] 王爽, 高朝晖, 陈思宇, 等. 基于Simulink的同步发电机仿真代数环问题研究[J]. 系统仿真学报, 2022, 34(3): 482-489. Wang Shuang, Gao Zhaohui, Chen Siyu, et al. Research on algebraic loop of synchronous generator simulation based on simulink[J]. Journal of System Simulation, 2022, 34(3): 482-489.
[27] 马晓虹. Matlab中的代数环问题及其消除方法[J]. 科技广场, 2010(7): 159-161. Ma Xiaohong. Algebraic rings in Matlab and their elimination methods[J]. Science and Technology Square, 2010(7): 159-161.
Abstract Modeling and simulation of offshore wind power is the key supporting technology for building a new power system with new energy as the main body. As the core component of direct drive or semi-direct drive models, the existing models of permanent magnet synchronous generator (PMSG) have certain limitations: the grey box model provided by commercial software cannot be known about the modeling principle and are manifested in insufficient openness, which limits the application of efficient electromagnetic transient modeling algorithms and parallel acceleration algorithms for wind turbine units; The commonly used PMSG modeling method cannot generate interface and external circuit connections; PMSG is a kind of synchronous generator which has different order mathematical models, and the existing models are inconvenient to change.
In order to solve the above problems, this paper proposes a permanent magnet synchronous generator equivalent model which has several advantages compared to existing models and can be applied to different scenarios. On the premise of meeting the accuracy, the model considers the adjustable order of the model, and is an integrated model that can directly connect external circuits.
Firstly, starting from the synchronous motor equation, the voltage and flux equations of the generator are discretized, then analyze the algebraic loop problem in generator simulation. Secondly, reconstruct the PMSG model by applying a single step delay to the coupling variables to eliminate the algebraic loop. Thirdly, introduce Park transformation and use matrix block calculation methods to derive its Norton equivalent circuit, completing the construction of the model, and conduct applicability analysis of the method. Finally, based on the modeling method proposed and the usage methods of various code segments of the component tool Cbuilder on the RTDS simulation platform, construct an overall simulation framework for the model.
The benchmark model of all components in RTDS and the test model of PMSG model with three orders are built. Then the test of multiple working conditions is carried out, including short circuit fault conditions at four different fault points, small disturbance condition and wind speed variation conditions. The results show that the fourth and second order models were found to be applicable for station level simulation, but they cannot accurately reflect the coupling characteristics between the generator and the machine side converter, as well as between the generator and the wind turbine. The sixth order model achieved high fitting of the benchmark model under multiple operating conditions, with an average relative error of less than 4%, which can simultaneously meet the simulation needs of both station level and internal units.
In summary, this paper attempts to solve the limitations of existing PMSG models from the aspect of simulation modeling. For the simulation of offshore wind power, the equivalent model proposed in this paper can be flexibly adjusted and used according to different simulation objectives. The proposed method provides a PMSG model which istransparent and easy to program in simulation platformfor the application of efficient electromagnetic transient modeling methods in overall wind turbine modeling and parallel acceleration algorithms in offshore wind power simulation.
keywords:Offshore wind power, direct drive or semi-direct drive wind power system, permanent magnet synchronous generator (PMSG), equivalent modeling, model with adjustable order
国家自然科学基金资助项目(52277094)。
收稿日期 2023-02-02
DOI:10.19595/j.cnki.1000-6753.tces.230128
中图分类号:TM 313; TM341
刘逸凡 男,1999年生,硕士研究生,研究方向为直驱风机建模。E-mail:lyf373781@163.com
许建中 男,1987年生,博士,教授,研究方向为新型电力系统电磁暂态建模和仿真。E-mail:xujianzhong@ncepu.edu.cn(通信作者)
改稿日期 2023-08-11
(编辑 郭丽军)